Механические колебания – материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания – это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания – это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия – это положение маятника при отсутствии отклонения.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела – это величина его наибольшего отклонения от положения равновесия.
Период колебаний – это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний – это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т.
Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .
Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер.
Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
.
График гармонических колебаний в этом случае представлен на рис. 2.
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:
.
График колебаний представлен на рис. 3.
Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их.
Две константы определяются из начальных условий – по начальным значениям координаты и скорости.
Пружинный маятник.
Пружинный маятник – это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины.
Второй закон Ньютона для груза в проекции на ось имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
Математический маятник.
Математический маятник – это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис.
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):
,
или
.
Это – уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы.
Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
| Рис. 6. Затухающие колебания |
Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний.
Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс – явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .
Механические колебания | Физика
Колебания являются очень распространенным видом движения.
Это покачивание веток деревьев на ветру, вибрация струн у музыкальных инструментов, движение поршня в цилиндре двигателя автомобиля, качания маятника в настенных часах и даже биения нашего сердца.
Рассмотрим колебательное движение на примере двух маятников — нитяного и пружинного.
Нитяной маятник изображен на рисунке 30. Он представляет собой шарик, прикрепленный к тонкой, легкой нити. Если этот шарик сместить в сторону от положения равновесия и отпустить, то он начнет колебаться, т. е. совершать повторяющиеся движения, периодически проходя через положение равновесия.
На рисунке 31 изображен пружинный маятник. Он представляет собой груз, способный колебаться под действием силы упругости пружины.
Колебательное движение характеризуют амплитудой, периодом и частотой колебаний:
A — амплитуда; T — период; ν — частота.
Амплитуда колебаний — это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д.
Период колебаний — это время, за которое совершается одно колебание. Период колебаний измеряется в единицах времени — секундах, минутах и т. д.
Частота колебаний — это число колебаний, совершаемых за 1 с. Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857—1894). Если частота колебаний равна 1 Гц, то это означает, что за каждую секунду совершается одно колебание. Если же, например, частота ν = 50 Гц, то это означает, что за каждую секунду совершается 50 колебаний.
Для периода T и частоты ν колебаний справедливы те же формулы, что и для периода и частоты обращения, которые рассматривались при изучении равномерного движения по окружности (см. § 6).
1. Чтобы найти период колебаний, надо время t, за которое совершено несколько колебаний, разделить на число n этих колебаний:
2. Чтобы найти частоту колебаний, надо число колебаний разделить на время, в течение которого они произошли:
При подсчете числа колебаний на практике следует четко понимать, что представляет собой одно (полное) колебание.
Если, например, маятник начинает двигаться из положения 1 (см. рис. 30), то одним колебанием является такое его движение, когда он, пройдя положение равновесия 0, а затем крайнее положение 2, возвращается через положение равновесия 0 снова в положение 1.
Сравнивая формулы (17.1) и (17.2), мы видим, что период и частота колебаний — величины взаимно обратные, т. е.
В процессе колебаний положение тела непрерывно меняется. График зависимости координаты колеблющегося тела от времени называют графиком колебаний. По горизонтальной оси на этом графике откладывают время t, по вертикальной — координату x. Модуль этой координаты показывает, на каком расстоянии от положения равновесия находится колеблющееся тело (материальная точка) в данный момент времени. При переходе тела через положение равновесия знак координаты меняется на противоположный, указывая тем самым, что тело оказалось по другую сторону от среднего положения.
О форме графика колебаний можно судить на основе следующих опытов.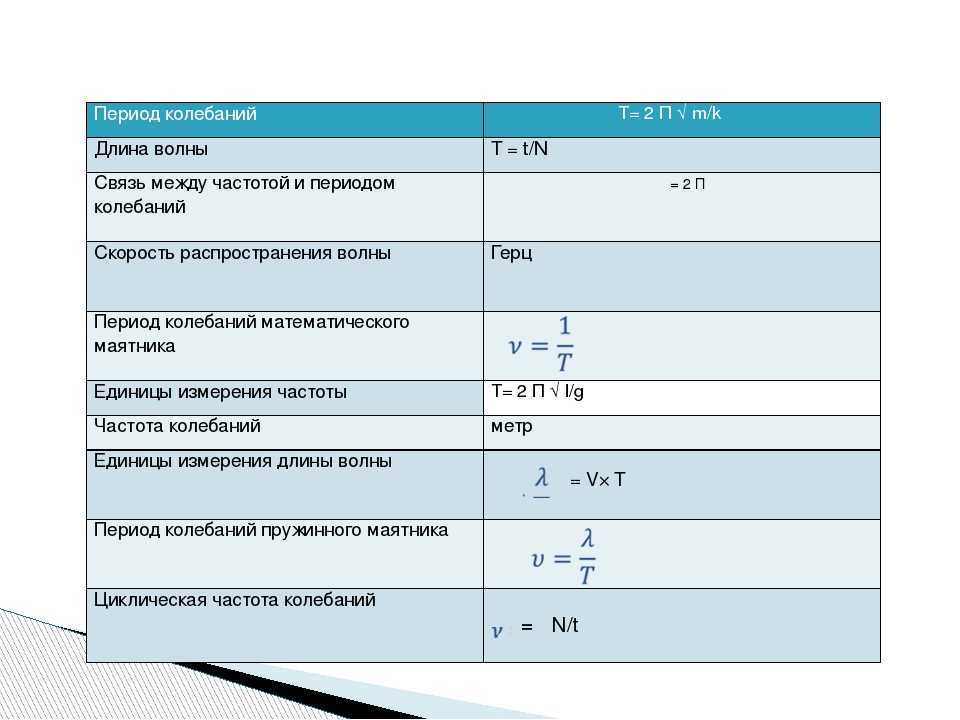
Соединим пружинный маятник с пишущим устройством (например, кисточкой) и начнем перед колеблющимся телом равномерно перемещать бумажную ленту (рис. 32). Кисточка нарисует на ленте линию, которая по форме будет совпадать с графиком колебаний.
Для записи колебаний нитяного маятника можно воспользоваться установкой, изображенной на рисунке 33. Маятником здесь служит воронка с песком. Если под колеблющейся воронкой перемещать бумажную ленту (или деревянную доску), высыпающийся из воронки песок оставит на ней характерный след.
При достаточно малом трении и на протяжении небольших интервалов времени графиком колебаний каждого из маятников является синусоидальная кривая, или кратко синусоида.
По графику колебаний можно определить все характеристики колебательного движения. Так, например, график, изображенный на рисунке 34, описывает колебания с амплитудой A=5 см, периодом F=4 с и частотой ν = 1/T = 0,25 Гц.
1. Приведите примеры колебаний.
2. Что называют амплитудой колебаний? 3. Что такое период колебаний? 4. Что называют частотой колебаний? 5. Как называется единица частоты колебаний? 6. Чем отличается пружинный маятник от нитяного? 7. Какая сила заставляет опускаться нитяной маятник после того, как он был выведен из положения равновесия? Почему он не останавливается в положении равновесия? 8. Под действием какой силы происходят колебания пружинного маятника?
16.2 Период и частота колебаний – Физика колледжа 2e
Цели обучения
К концу этого раздела вы сможете:
- Наблюдайте за колебаниями гитарной струны.
- Определить частоту колебаний.
Рисунок 16,8 Струны этой гитары вибрируют через равные промежутки времени. (Фото: JAR)
Когда вы дергаете гитарную струну, звук получается устойчивым и длится долго. Каждое последующее колебание струны занимает такое же время, как и предыдущее. Мы определяем периодическое движение как движение, которое повторяется через равные промежутки времени, например гитарная струна или объект на пружине, движущийся вверх и вниз.
Время совершения одного колебания остается постоянным и называется периодом ТТ. Его единицами обычно являются секунды, но может быть любая удобная единица времени. Слово «период» относится ко времени какого-либо события, повторяющегося или нет; но нас прежде всего будет интересовать периодическое движение, которое по определению является повторяющимся. Понятие, тесно связанное с периодом, — это частота события. Например, если вы получаете зарплату два раза в месяц, частота выплат — две в месяц, а период между проверками — полмесяца. Частота ff определяется как количество событий в единицу времени. Для периодического движения частота – это число колебаний в единицу времени. Отношение между частотой и периодом равно
f=1T.f=1T.
16,8
Единицей частоты в СИ является цикл в секунду , который определяется как герц (Гц):
1 Гц знак равно 1 цикл с или 1 Гц знак равно 1 с 1 Гц знак равно 1 цикл с или 1 Гц знак равно 1 с
16,9
Цикл – это одно полное колебание.
Обратите внимание, что вибрация может быть одиночным или множественным событием, тогда как колебания обычно повторяются в течение значительного числа циклов.
Пример 16,3
Определение частоты двух колебаний: медицинский ультразвук и период среднего C
Мы можем использовать формулы, представленные в этом модуле, для определения как частоты на основе известных колебаний, так и колебаний на основе известной частоты. Давайте попробуем по одному примеру каждого. (a) Медицинское устройство визуализации производит ультразвук путем колебаний с периодом 0,400 мкс. Какова частота этих колебаний? (b) Частота среднего C на типичном музыкальном инструменте составляет 264 Гц. За какое время совершается одно полное колебание?
Стратегия
На оба вопроса (a) и (b) можно ответить, используя соотношение между периодом и частотой. В вопросе (а) дан период TT и нас просят найти частоту ff.
В вопросе (b) дана частота ff, и нас просят найти период TT .
Раствор a
- Заменитель
0
.
400
мю
с
0
.
400
мю
s для TT в f=1Tf=1T:
f=1T=10,400×10-6 с. f=1T=10,400×10-6 с.
16,10
Найдите
f=2,50× 106 Гц.f=2,50× 106 Гц.
16.11
Обсуждение a
Частота звука в (а) намного выше, чем самая высокая частота, которую может слышать человек, и поэтому называется ультразвуком. Соответствующие колебания на этой частоте генерируют ультразвук, используемый для неинвазивной медицинской диагностики, например, для наблюдения за плодом в утробе матери.
Раствор б
- Определите известные значения:
Время одного полного колебания равно периоду TT :
f=1T.
f=1T.16.12
- Решите для TT :
Т=1ф.Т=1ф.
16.13
- Подставить заданное значение частоты в полученное выражение:
T=1f=1264 Гц=1264 цикла/с=3,79×10-3с=3,79 мс. T=1f=1264 Гц=1264 цикла/с=3,79×10-3с=3,79 мс.
16.14
f=1T.Обсуждение b
Период, найденный в (b), представляет собой время за цикл, но это значение часто указывается просто как время в удобных единицах (в данном случае мс или миллисекунды).
Проверьте свое понимание
Назовите событие в вашей жизни (например, получение зарплаты), которое происходит регулярно. Определите как период, так и частоту этого события.
Решение
Каждое второе воскресенье я прихожу к родителям на ужин. Частота моих посещений составляет 26 за календарный год.
Срок – две недели.
Период времени, простой маятник и формула
Период означает время, необходимое для совершения одного колебания. Периодом колебаний волны называется время, необходимое любому элементу струны для совершения одного такого колебания. Например, если маятник качается, то время, затраченное на максимальное перемещение назад, затем движение вперед и, наконец, возвращение в среднее положение, считается периодом времени. Период времени обозначается буквой «Т», тогда как секунда (с) является единицей периода времени в системе СИ. Простой маятник — это идеальный маятник, состоящий из точки массы (m), подвешенной на невесомой, нерастяжимой, мягкой нити и способной колебаться без трения.
Что такое период?
Термин «период» относится к продолжительности времени, необходимому для выполнения чего-либо. Когда событие происходит одновременно, оно является периодическим и относится ко времени повторения события как к периоду. Период времени T представляет собой время, за которое полный цикл колебаний проходит заданную точку.
Период времени измеряется такими единицами, как секунды, часы, дни или годы. Период обращения Земли вокруг Солнца составляет примерно 365 дней; Земля завершает цикл за 365 дней. Минутной стрелке часов требуется 3600 секунд, чтобы совершить один оборот вокруг часов (60 минут).
Между Периодом и Частотой существует взаимосвязь, которая может быть выражена математически следующим образом: Период = Общее время / Циклы. Период волны уменьшается, а частота волн увеличивается. Частица среды совершает одно колебание за период времени волны.
Каждое полное колебание называется периодом и является постоянным. Формула для определения периода маятника: T = 2π √L/g, где L — длина маятника, а g — ускорение свободного падения. Последовательные циклы называются периодами. Период маятника — это время, за которое маятник совершает одно полное колебание вперед и назад.
Что такое период времени?
Период времени, в течение которого что-то происходит или ожидается. Время, необходимое для одного полного колебания плотности среды, называется периодом волны.
В качестве альтернативы, это может относиться ко времени, которое требуется двум последовательным сжатиям или разрежениям для пересечения фиксированной точки. Время, за которое маятник совершает одно колебание, называется периодом времени. Время измеряется в секундах.
Период времени вещи — это количество времени, необходимое для того, чтобы она совершила одно колебание. Угловая частота – это угловое смещение любого элемента волн в единицу времени. Формула для времени: – T = 1/f, где T – период, а f – частота. λ= c / f, где c — скорость волны (м/с), а f — частота (Гц). Единица герц (Гц) известна как число циклов в секунду. Звуковые волны и электромагнитные волны следуют приведенному ниже уравнению. Например, когда волна с периодом времени 2 секунды имеет частоту. т. е. 1/2 = 0,5 Гц.
ПРОСТОЙ МАЯТНИК
Простой маятник можно определить как устройство, в котором его точечная масса прикреплена к легкой нерастяжимой струне и подвешена к неподвижной опоре. Положение равновесия подвергается возвращающей силе, когда маятник смещается в сторону от положения покоя из-за силы тяжести, которая ускоряет его обратно к положению равновесия.
Простой маятник состоит из небольшого металлического шарика (называемого бобом), подвешенного на длинной нити к жесткой опоре с помощью невесомой и нерастяжимой нити, так что грузик может свободно раскачиваться вперед и назад. Когда груз из его среднего положения перетаскивают в одну сторону, а затем отпускают, маятник приходит в движение, и груз движется в противоположных направлениях по обе стороны от своего среднего положения. А при смещении маятникового груза он колеблется в плоскости относительно вертикальной линии, проходящей через опору. Частота простого маятника зависит от его длины и ускорения свободного падения. Уравнение: f=1/2π√g/L. Период (T) простого маятника равен T=2π√L/g.
Простой маятник состоит из массы (m), подвешенной на веревке длиной (L) и закрепленной в точке вращения (P). Когда его смещают на начальный угол, а затем отпускают, маятник будет периодически качаться вперед и назад.
ЗАКЛЮЧЕНИЕ
Следовательно, период (T) — это время, за которое полный цикл волн проходит точку.