Первое начало термодинамики формула и формулировка: Первое начало термодинамики формулировки - Справочник химика 21 - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Первое начало термодинамики формулировки – Справочник химика 21

Это уравнение является математическим выражением первого начала термодинамики, которое в данном случае имеет следующую формулировку подведенное к системе тепло Q идет на увеличение внутренней энергии системы и на совершение внешней работы [c.52]

С учетом уравнения (3.1) формулировку первого начала термодинамики представим в виде [c.47]

Общая формулировка первого начала термодинамики дана Гельмгольцем, который ввел в рассмотрение все виды работ, а не только механическую работу. Согласно Гельмгольцу, [c.16]

Согласно закону Гесса тепловой эффект реакции не зависит от промежуточных стадий, а определяется лишь начальным и конечным состоянием системы при условии, что давление или объем в течение всего процесса остаются неизменными. Математическая формулировка закона Гесса является непосредственным следствием первого начала термодинамики и выражается уравнениями [c. 24]

Уравнение (II, 1) представляет собой математическую формулировку первого начала термодинамики. Величины Аи, и Л в урав- [c.86]

Одним из следствий первого начала термодинамики является открытый в 18 6 г. русским химиком Г. И. Гессом закон, который часто называют законом постоянства сумм теплот. Установленный еще до окончательной формулировки первого начала, он является основой всех термохимических расчетов с учетом того, что тепловые [c.25]

Отсюда следует, во-первых, что не существует никаких функций состояния или IV и, во-вторых, что в отдельности ни 8Q, ни б не обладают математическими свойствами дифференциала. Однако из формулы (1.4.26) следует, что алгебраическая сумма (б — бИ ), равная сШ, есть полный дифференциал функции состояния и. В этом заключается математическое содержание формулы (1.4.26), которая представляет собой математическую формулировку первого начала термодинамики для закрытых систем.

[c. 16]

Второе начало (закон) термодинамики является одним из важнейших законов природы. Он охватывает широкий круг явлений природы, поэтому его смысл выражают в различных формулировках. Закон сохранения энергии (первое начало термодинамики) не содержит указаний о направлении процессов в изолированной системе. Второе начало (закон) термодинамики позволяет предвидеть направление химических процессов в изолированной системе.

[c.41]

Закон Гесса (см, раздел 7,2) является следствием более общего Первого начала термодинамики, В самом деле, если внести в его формулировку слова при постоянном давлении в отсутствие всех других видов работы, кроме работы расширения , то в соответствии с уравнением (106) выяснится, что речь идет о функции состояния энтальпии, изменение которой в процессе не зависит от пути, а зависит только от конечного и начального состояний. [c.343]

Выражение (1.11) является математической формулировкой первого начала термодинамики. [c.6]

Первая ясная формулировка первого начала термодинамики приписывается обычно Ю. Майеру, который вычислил механический эквивалент теплоты результаты этой работы были опубликованы в 1842 г. Примерно в это же время независимо от Ю. Майера к тем же выводам пришел Дж. Джоуль. Он опубликовал (1843) точные измерения механического эквивалента теплоты. Любопытно, что первое начало термодинамики было установлено намного позднее второго. [c.60]

Закон Гесса точен при условии, что все процессы протекают или при постоянном объеме, или при постоянном давлении. Закон Гесса является частной формулировкой первого начала термодинамики в применении к химическим процессам. Если бы количество теплоты при одинаковых начальных и конечных состояниях на различных путях было неодинаково, то, направляя реакцию по одному пути, а затем в обратном направлении — по-друго-Д1у, можно было бы получить энергию из ничего, т.

е. осуществить вечный двигатель I рода . [c.85]

Первое начало термодинамики и реально осуществимые процессы. Варианты формулировки второго начала термодинамики

[c.87]

Формулировка Клаузиуса включает и первое начало термодинамики энергия мира постоянна, энтропия мира стремится к максимуму. [c.91]

Таким образом, для того, чтобы функция А являлась функцией состояния системы в данный момент времени и не зависела от характера происходящих в системе изменений, необходимо и достаточно, чтобы соблюдались равенства (VII.30), (VII.31). Необходимые и достаточные условия существования функции состояния А можно представить также в другой формулировке. Используя уравнение первого начала термодинамики (11.25) и соотношение (VII. 17), для произвольного бесконечно малого изменения в закрытой системе получаем

[c.171]

Этот постулат не вытекает из первого начала термодинамики и является самостоятельным законом природы, который находится в полном соответствии со всем опытом человечества. Однако формулировка постулата, данная Клаузиусом, допускала неоднозначное толкование этого закона. Поэтому в дальнейшем развитии учения о втором начале термодинамики были высказаны другие формулировки постулата второго начала, более строгие. Планку принадлежит, вероятно, наиболее удачная [c.25]

Мы не будем касаться истоков общей термодинамики, возникшей при решении теплотехнических проблем в первой половине XIX в. [4, с. 167], и только напомним, что формулировка первого начала термодинамики и его экспериментальное подтверждение относятся к 40-м годам XIX в. (Майер, Джоуль), а формулировка второго начала термодинамики и его математическое выражение — к 50-м годам (Клаузиус, В. Томсон). Важнейшее понятие химической термодинамики — понятие энтропии — было введено Клаузиусом в 1865 г.

[c.120]

Вечный двигатель первого рода (15) — циклически действующая машина, способная совершать работу без затраты теплоты. Постулат о невозможности подобного устройства является формулировкой первого начала термодинамики [c.

308]

Первое начало термодинамики может быть сформулировано иначе следующим образом внутренняя энергия V является функцией состояния. Изменение внутренней энергии АС/ системы, переходящей из состояния 1 в состояние 2,— алгебраическая сумма всех энергий, обменивающихся с внешней средой. Эта формулировка включает утверждение, что внутренняя энергия 7 системы зависит только от состояния системы. Отсюда следует, что изменение энергии А [/ системы при переходе из состояния 1 в состояние 2 всегда одинаково вне зависимости от того, какой путь выбран для этого перехода это изменение равно разности величин V внутренней энергии системы в состояниях 2 и 1 соответственно

[c.165]

Это еще одна формулировка первого начала термодинамики. [c.61]

Формулировки первого начала термодинамики [c.68]

Приведите формулировки и математическое выражение первого начала термодинамики. [c.109]

Основываясь на этой формуле можно дать следующую формулировку первого начала термодинамики [c. 6]

Положения [5-В] и [5-В ] выражают первое начало термодинамики в случаях, когда система совершает цикл. Эти положения приводят к формулировкам первого начала, справедливым для любых (конечных и элементарных) процессов.

[c.69]

Все сказанное приводит к следующей формулировке первого начала термодинамики, справедливой для всех — обратимых, необратимых, элементарных, конечных — процессов [c.71]

Имея в виду химическую термодинамику, воспользуемся следующей математической формулировкой первого начала термодинамики [c.15]

Формулировки первого начала термодинамики. Первое начало термодинамики является законом сохранения и превращения энергии в применении к термодинамическим системам. Оно было установлено в результате опытных и теоретических исследований в области физики и химии. Завершающим этапом этих исследований явилось открытие принципа эквивалентности работы и теплоты. Для всякого кругового процесса, протекающего в любой термодинамической системе, отношение суммы всех работ к сумме всех теплот есть величина постоянная, равная единице

[c. 58]

Из первого начала термодинамики вытекает, как одно из его следствий, открытый еще в 1836 г. русским термохимиком Г. И. Гессом закон, который часто называют законом постоянства сумм тепла. Установленный еще до окончательной формулировки первого начала, он является основой для всех термохимических расчетов. [c.30]

Первое начало термодинамики может быть выражено в различных формулировках, которые в сущности равноценны, так как из каждой из них могут быть выведены все остальные. Одной из таких формулировок является указанное утверждение о невозможности построения вечного двигателя (первого рода). [c.93]

Таким образом, мы приходим к выводу, что теплота является формой энергии и можем расширить нашу прежнюю формулировку и сказать, что в изолированной системе сумма механической энергии и тепловой энергии остается постоянной. В этой формулировке выражена основная идея первого начала термодинамики.

Поскольку мы теперь рассматриваем теплоту как одну из форм энергии, желательно и измерять ее в тех же единицах, как и другие формы энергии, а именно в джоулях. По историческим причинам, однако, до сих пор теплоту измеряют в калориях. За последнее время, впрочем, было несколько попыток прекратить такую практику, и в настоящей книге мы часто будем давать тепловые величины, выраженные и в калориях и в джоулях. [c.41]

Приведенная формулировка представляет собой выражение первого начала термодинамики, а формула (9-4) — его аналитическое (математическое) выражение. [c.164]

Уравнение (1,21) в термодинамике было получено довольно сложным путем. Поскольку (1,21) нельзя вывести на основе первого начала термодинамики и известных законов физики, то первоначальная задача заключалась в том, чтобы доказать существование функции состояния 5 на основе какого-либо предположения (оно и принималось за формулировку второго начала термодинамики), которое вместе с тем можно было бы считать обобщением результатов опыта. В середине прошлого века такие данные содержались в теории тепловых машин, и поэтому до сих пор в общей и химической термодинамике большое место занимает теория циклических процессов и анализ пере.-ходов теплоты в работу. Необходимое и достаточное условие существования функции состояния 5 можно записать в виде условия [c.22]

Рассматривая деятельность Гесса, нельзя не придти к выводу, что наиболее важным для науки достижением было открытие им закона постоянства сумм тепла, в котором он настолько близко подошел к полной и строгой формулировке первого начала термодинамики, что участие его в этом творческом акте, вообще говоря принадлежащем не одному исследователю, а целой группе ученых, заслуживает особого обсуждения. В этом обсуждении следует тщательно взвесить как положительные, так и слабые стороны труда Гесса. [c.170]

Сопоставляя уже приведенную нами выше (стр. 169) формулировку закона Гесса с результатами экспериментального исследования, мы видим, что Гесс в ясной и убедительной форме установил независимость энергетических изменений от пути процесса, т. е. именно то, что представляет собою одну из фундаментальных формулировок первого начала термодинамики. [c.171]

Для таких процессов есть изменение какой-то функции состояния, и поэтому 6(3 = ( (3. В рамках первого начала термодинамики вид и смысл ОТОЙ функции состояния не мог быть определен. Математическая формулировка второго начала термодинамики позволила строго утверждать, что для обратимых процессов отношение йЯ1Т (это отношение называют приведенной теплотой) равно дифференциалу функции состояния, называемой энтропией [c.47]

В предыдущем параграфе мы рассмотрели различие между обратимым процессом и полностью необратимым процессом. Однако системы, взятые в качестве примеров, обладали довольно сильно различающимися харак-теристиками. Для завершения рассуждений, ведущих к формулировке первого начала термодинамики, познакомимся еще с двумя устройствами, изображенными на рис. 73. Эти устройства почти тождественны, но в одном из них можно проводить необратимые процессы. [c.217]

Некоторые формулировки, сделанные при изложении первого начала термодинамики, не вполне строги и могут создать представление о запасе теплоты и работы. Уравнение (3.4) записано в полных дифференциалах работы (йА) и теплоты ( С ), тогда как в общем случае изменения работы и теплоты зависят от пути процесса. Более подробно и глубоко ознакомиться с этими вопросами можно, например, по книге И. Р. Кричевскнй. Понятия и основы термодинамики . Госхимиздат, 1962. Прим. ред. [c.49]

В ЭТИХ сообщениях Томсоном и Клаузиусом было сформулировано первое начало термодинамики (принцин эквивалентности теплоты и работы). Далее Клаузиус на основе анализа цикла Карно показал, что вывод Карно представляет собой выражение некоторого общего закона Тепло не может переходить само собой от более холодного тела к более теплому без соответствующей компенсации. Это — одна из формулировок второго начала термодинамики. У. Томсон также дал формулировку второго начала. Он распространил действие этого закона на всю Вселенную и пришел к известному выводу о неизбежности тепловой смерти Вселенной, что вызвало справедливые возражения ученых. [c.411]

В настоящее время, как известно, первое начало термодинамики имеет шесть различных формулировок [18]. Остановимся на одной из них, по своей значимости вполне эквивалентной остальным. В этой формулировке говорится о том, что сумма тепла и работы не зависит от пути процесса. В ней сразу видно близкое соответствие данного положения закону Гесса, гласящему, что тепловой эффект процесса не зависит от пути процесса. Действительно, согласно общеизвестному определению, тепловой эффект как раз и представляет собою 1) или теплоту, выделенную системой при постоянном объеме ((2,), когда работа равна нулю, 2) или теплоту, выделенную системой при постоянцом давлении, когда тецлдвой эффект состоит из топ-йоты, выделенной при постоянном объеме плюс работа системы, то, что ныне обозначается, как QJ или ЛЛ. [c.170]

Первое начало термодинамики – Лекция

Лекция №14

Первое начало термодинамики

План

Основные термодинамические понятия: внутренняя энергия, работа, теплота. Уравнение первого начала термодинамики.
Применение первого начала термодинамики к изопроцессам идеального газа. Зависимость теплоёмкости идеального газа от вида процесса. Формула Майера.
Работа, совершаемая газом при изопроцессах.
Адиабатический процесс. Политропические процессы.

Основные термодинамические понятия

Термодинамика в отличие от молекулярно-кинетической теории не вдаётся в рассмотрение микроскопической картины явлений (оперирует с макропараметрами). Термодинамика рассматривает явления, опираясь на основные законы (начала), которые являются обобщением огромного количества опытных данных.

Внутренняя энергия – энергия физической системы, зависящая от её внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т.д.) и энергию взаимодействия этих частиц. Кинетическая энергия движения системы как целого и её потенциальная энергия во внешних силовых полях во внутреннюю энергию не входит. В термодинамике и её приложениях представляет интерес не само значение внутренней энергии, а её изменение при изменении состояния системы. Внутренняя энергия – функция состояния системы.

Работа термодинамической системы над внешними телами заключается в изменении состояния этих тел и определяется количеством энергии, передаваемой системой внешним телам при изменении объема.

Работа в термодинамике не является полным дифференциалом (не является функцией состояния, а зависит от пути) и обозначается .

Для того чтобы изменить объём, занимаемый газом, надо совершить работу. Представим себе газ, заключённый в цилиндрический объём с поршнем, движением которого изменяется объём газа (рис. 14.1).

Рис. 14.1

Сила, создаваемая давлением газа на поршень площади равна . Работа, совершаемая при перемещении поршня , равна , где изменение объёма газа (рис. 14.1), то есть

Теплота (количество теплоты) – количество энергии, получаемой или отдаваемой системой при теплообмене. Элементарное количество теплоты не является в общем случае дифференциалом какой-либо функции параметров состояния. Передаваемое системе количество теплоты, как и работа, зависит от того, каким способом система переходит из начального состояния в конечное. (В отличие от внутренней энергии, для которой , но , нельзя сказать, сколько работы содержит тело, “это функция” процесса – динамическая характеристика).

1-ый закон (начало) термодинамики: количество теплоты, сообщённое системе, идёт на приращение внутренней энергии системы и на совершение системой работы над внешними телами.

где количество сообщённой телу теплоты;

и начальное и конечное значения внутренней энергии;

работа, совершённая системой над внешними телами.

В дифференциальной форме 1-ое начало:

сообщённое телу элементарное количество теплоты;

изменение внутренней энергии;

совершённая телом работа (например, работа, совершённая при расширении газа).

Применение 1-го начала термодинамики к изопроцессам идеального газа

(Изопроцессы от (греч.) – равный). Процессы, происходящие при каком-то постоянном параметре (изотермический; изобарический; изохорический).

Теплоёмкостью тела называется величина, равная отношению сообщённого телу количества теплоты к соответствующему приращению температуры .

Размерность теплоёмкости тела .

Аналогичные определения вводятся для 1 моля (молярная теплоёмкость

), и для единицы массы вещества .

Рассмотрим нагревание газа при постоянном объёме. По первому закону термодинамики:

, т.к. , то .

по определению, а для процесса с :

, где

теплоёмкость газа при постоянном объёме.

Тогда и

Теплоёмкость газа при постоянном давлении:

Для идеального газа для 1 моля (из уравнения Менделеева-Клапейрона).

Продифференцируем это выражения по температуре Т, получим:

, получим для 1 моля

Но выражение называется уравнением Майера. Оно показывает, что всегда больше на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении по сравнению с процессом при постоянном объёме, требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т. к. постоянство давления обеспечивается увеличением объёма газа.

При адиабатическом процессе (процесс протекающий без теплообмена с внешней средой).

, , т.е. теплоёмкость в адиабатическом процессе равна нулю.

При изотермическом процессе , , и, следовательно, теплоёмкость .

Существуют процессы, при которых газ, расширяясь, совершает работу большую, чем полученная теплота, тогда его температура понижается, несмотря на приток теплоты. Теплоёмкость в этом случае отрицательна. В общем случае .

3. Работа, совершаемая газом при изопроцессах

Изобарный .

И определяется площадью заштрихованного прямоугольника на рис. 14.2.

Изохорный процесс (). Диаграмма этого процесса

Изотермический процесс является идеальным процессом, т. к. расширение газа при постоянной температуре может происходить только бесконечно медленно. При конечной скорости расширения возникнут градиенты температуры.

4. Адиабатический (адиабатный) процесс

Это процесс, происходящий без теплообмена с окружающими телами. Рассмотрим, при каких условиях можно реально осуществить адиабатический процесс, или приблизиться к нему.

1. Необходима адиабатическая оболочка, теплопроводность которой равна нулю. Приближением к такой оболочке может служить сосуд Дьюара.

2. 2-ой случай – процессы, протекающие очень быстро. Теплота не успевает распространиться и в течение некоторого времени можно полагать .

3. Процессы, протекающие в очень больших объёмах газа, например, в атмосфере (области циклонов, антициклонов). Для выравнивания температуры передача теплоты должна происходить из соседних, более нагретых слоёв воздуха, на это часто требуется значительное время.

Для адиабатического процесса первый закон термодинамики:

или .

В случае расширения газа , , (температура понизится). Если произошло сжатие газа , то (температура повышается). Выведем уравнение, связывающее параметры газа при адиабатическом процессе. Учтём, что для идеального газа , тогда

Разделим обе части уравнения на :

Из уравнения Майера , тогда

Обозначим .

Проинтегрируем это уравнение:

Отсюда

Получили уравнение Пуассона (для адиабаты) (1 – ая форма). Заменим :

т. к. для данной массы газа величина постоянная, то

2 – ая форма уравнения Пуассона. На рис. 14.5 представлены сравнительные графики изотермы и адиабаты.

Рис. 14.5

Так как , то график адиабаты более крутой по сравнению с изотермой. Вычислим работу при адиабатическом процессе:

т.е

Политропические процессы.

Так называют процессы, уравнение которых в переменных имеет вид

где n-произвольное число, как положительное, так и отрицательное, а также равное нулю. Соответствующую кривую называют политропой. Политропическими являются, в частности, процессы адиабатический, изотермический, изобарический, изохорический.

Вопросы для самоконтроля

Чем термодинамический метод исследования свойств систем отличается от молекулярно-кинетического?
Какую часть энергии системы называют внутренней?
Как определяется работа в термодинамике?
Что называется количеством теплоты?
Какая из величин А, Q,U является функцией состояния термодинамической системы? Почему?
Сформулируйте первое начало термодинамики.
Запишите первое начало термодинамики для всех известных вам изопроцессов идеального газа.
Что такое теплоемкость тела? Чем отличаются удельная и молярная теплоемкости?
Чему равна теплоемкость для каждого изопроцесса? Почему теплоемкость ?
Получите выражение для работы в каждом процессе. При каком изо- процессе не совершается работа?
Какой процесс называется адиабатным? Как можно осуществить процесс, близкий к адиабатному?
Проделайте вывод уравнения Пуассона для адиабатного процесса.

Лекция №15

Второе начало термодинамики

План

Обратимые и необратимые процессы. Круговой процесс (цикл). Равновесные состояния и процессы.
Цикл Карно и его КПД для идеального газа. Максимальный КПД теплового движения.
Тепловые двигатели и холодильные машины.
Энтропия. Закон возрастания энтропии.
Статистический вес (термодинамическая вероятность). Второе начало термодинамики и его статистическое толкование.

1. Обратимые и необратимые процессы

Пусть в результате некоторого процесса в изолированной системе тело переходит из состояния А в состояние В и затем возвращается в начальное состояние А. Процесс называется обратимым, если возможно осуществить обратный переход из В в А через те же промежуточные состояния, что и в прямом процессе, чтобы не осталось никаких изменений и в самом теле и в окружающих телах. Если же обратный процесс невозможен, или по окончании процесса в окружающих телах и в самом теле остались какие-либо изменения, то процесс является необратимым.

Примеры необратимых процессов. Любой процесс сопровождаемый трением является необратимым (теплота, выделяющаяся при трении не может без затраты работы другого тела собраться и вновь превратиться в работу). Все процессы, сопровождаемые теплопередачей от нагретого тела к менее нагретому, является необратимыми (например, теплопроводность). К необратимым процессам также относятся диффузия, вязкое течение. Все необратимые процессы являются неравновесными.

Равновесные – это такие процессы, которые представляют из себя последовательность равновесных состояний. Равновесное состояние – это такое состояние, в котором без внешних воздействий тело может находиться сколь угодно долго. (Строго говоря, равновесный процесс может быть только бесконечно медленным. Любые реальные процессы в природе протекают с конечной скоростью и сопровождаются рассеянием энергии. Обратимые процессы – идеализация, когда необратимыми процессами можно пренебречь).

Круговой процесс (цикл). Если тело из состояния А в состояние В переходит через одни промежуточные состояния, а возвращается в начальное состояние А через другие промежуточные состояния, то совершается круговой процесс, или цикл.

Круговой процесс является обратимым, если все его части обратимы. Если какая-либо часть цикла необратима, то и весь процесс необратим.

Различают прямой цикл, или цикл тепловой машины и обратный цикл, или цикл холодильной машины (о нём в вопросе № 3).

Совершенная за цикл работа равна разности между количеством теплоты, полученной телом при расширении и количество теплоты, отданным при сжатии. Работа в координатах равна площади цикла (рис. 15.1):

Рис. 15.1

2. Цикл Карно и его КПД для идеального газа

(Сади Карно (1796 – 1832) – французский физик).

Рис. 15.2

Цикл Карно заключается в следующем. Сначала система, имея температуру , приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, её заставляют расширяться по изотерме 1-2. При этом она получает тепло от нагревателя и производит работу против внешнего давления.

Рабочий цикл состоит из двух равновесных изотерм и двух равновесных адиабат (рис. 15.2). В машине, как допускают, отсутствуют потери на трение, теплопроводность и т.д. С машиной связаны два резервуара теплоты. Один, имеющий температуру , называется нагревателем, другой имеющий более низкую температуру – холодильником (или теплоприёмником). Резервуары настолько велики, что отдача или получение теплоты не изменяет их температуру.

После этого систему адиабатически изолируют и заставляют расширяться по адиабате 2 – 3, пока её температура не достигает температуры холодильника . При адиабатическом расширении система также совершает некоторую работу против внешнего давления. В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывным увеличением давления изотермически сжимают её до некоторого состояния 4. При этом над системой производится работа (т.е. сама система совершает отрицательную работу ), и она отдаёт холодильнику некоторое количество тепла . Состояние 4 выбирается так, чтобы можно было сжатием по адиабате 4 – 1 вернуть систему в исходное состояние. Для этого над системой надо совершить работу (система должна произвести отрицательную работу ). В результате кругового процесса Карно внутренняя энергия системы не изменяется, поэтому произведённая работа

Рассчитаем коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно. Эта величина равна отношению количества теплоты, превращённого в работу, к количеству теплоты, полученному от нагревателя.

Полезная работа за цикл равна сумме всех работ отдельных частей цикла:

Работа изотермического расширения:

адиабатического расширения:

изотермического сжатия:

адиабатического сжатия:

Адиабатические участки цикла не влияют на общий результат, т.к. работы на них равны и противоположны по знаку, следовательно .

. (1)

Так как состояния газа, описываемые точками 2 и 3 лежат на одной адиабате, то параметры газа связаны уравнением Пуассона:

Аналогично для точек 4 и 1:

Разделив почленно эти уравнения, получим:

, тогда из (1) получается

То есть КПД цикла Карно определяется только температурами нагревателя и холодильника.

Теорема Карно (без доказательства): КПД всех обратимых машин, работающих при одних и тех же температурах нагревателя и холодильника одинаков и определяется только температурами нагревателя и холодильника.

Замечание: КПД реальной тепловой машины всегда ниже, чем КПД идеальной тепловой машины (в реальной машине существуют потери тепла, которые не учитываются при рассмотрении идеальной машины).

3. Принцип действия теплового двигателя и холодильной машины

Любой тепловой двигатель состоит из 3-х основных частей: рабочего тела, нагревателя и холодильника.

Рабочее тело получает некоторое количество теплоты , от нагревателя. При сжатии газ передаёт некоторое количество теплоты холодильнику. Полученная работа, совершаемая двигателем за цикл:

(неравенство – характеризует реальные машины, равенство для идеальных машин).

(Замечание: реальные тепловые двигатели обычно работают по так называемому разомкнутому циклу, когда газ после расширения выбрасывается, и сжимается новая порция. Однако это существенно не влияет на термодинамику процесса. В замкнутом цикле расширяется и сжимается одна и та же порция. ).

Холодильная машина. Цикл Карно обратим, следовательно, его можно провести в обратном направлении. (4-3-2-1-4 (рис.15.3)) От холодильной камеры поглощается тепло .

Нагревателю рабочее тело передаёт некоторое количество теплоты . Внешние силы совершают работу , тогда

В результате цикла некоторое количество теплоты переходит от холодного тела к телу с более высокой температурой.

Реально рабочим телом в холодильной установке обычно служат пары легкокипящих жидкостей – аммиак, фреон и т. п. К машине подводится энергия от

Рис. 15.3

электрической сети. За счёт этой энергии и совершается процесс “передачи теплоты” от холодильной камеры к более нагретым телам (к окружающей среде).

Эффективность холодильной установки оценивается по холодильному коэффициенту:

Тепловой насос. Это непрерывно действующая машина, которая за счёт затрат работы (электроэнергии) отбирает тепло от источника с низкой температурой (чаще всего близкой к температуре окружающей среды) и передаёт источнику тепла с более высокой температурой количество теплоты , равна сумме тепла, отобранного от низкотемпературного источника и затраченной работы: .

“Отопительный” коэффициент

всегда больше единицы (максимально возможный ).

Для сравнения: если отапливать помещение с помощью обычных электронагревателей, то количество теплоты, выделенное в нагревательных элементах, в точности равно расходу электроэнергии.

4. Энтропия. Закон возрастания энтропии

В термодинамике понятие “энтропия” было введено немецким физиком Р. Клаузиусом (1865 г.).

Из статической физики: отношение количества теплоты , сообщаемого системе, к температуре (системы) есть приращение некоторой функции состояния (энтропий).

полный дифференциал функции состояния , названной энтропией. (греч. поворот, превращение)

Каждое состояние тела характеризуется определённым значением энтропии . Если обозначить энтропию в состояниях 1 и 2 как и , то по определению для обратимых процессов:

Значение произвольной постоянной, с которой определена энтропия, не играет роли. Физический смысл имеет не сама энтропия, а разность энтропий.

Закон возрастания энтропии.

Допустим, что изолированная система переходит из равновесного

состояния 1 в равновесное состояние 2, но процесс перехода 1 – 2 является необратимым – на рисунке 15.4 обозначен пунктиром. Обратный переход обратимый. Воспользуемся неравенством Клаузиуса (без вывода).
	Рис. 15.4

(для обратного процесса знак “=” , для необратимого “<”).

Для нашего перехода 1 – 2 – 1 :

Так как процесс 2 – 1 обратимый, то будет равенство

, отсюда

Под температурой понимается температура системы, при которой она отдаёт или принимает тепло .

Если система адиабатически изолирована, то и

Таким образом, энтропия адиабатически изолированной системы не может убывать, она либо возрастает, либо остаётся постоянной. (Закон возрастания энтропии).

5. Статистический вес (термодинамическая вероятность).

Под термодинамической вероятностью понимается число микросостояний (микрораспределений, например, распределений молекул по пространству или энергии) которыми может определяться рассматриваемое макрораспределение.

Пример. Имеется сосуд, состоящий из двух частей, в котором может находится 4 молекулы. Сколькими способами можно распределить эти молекулы, чтобы в левой части была одна молекула, а в правой– три молекулы? Могут быть следующие варианты: в левой части 1-ая молекула, а 2-я,

Рис. 15.5

3-я и 4-я – в первой и т. д. ( рис. 15.5).

Число распределений можно подсчитать следующим образом:

где общее число молекул, число молекул в 1 – ой части сосуда, во второй. Термодинамическая вероятность в рассматриваемом примере.

Аналогично для распределения :

Для .

Заметим, что наибольшая термодинамическая вероятность у равномерного распределения, оно может осуществляться наибольшим числом способов.

Связь энтропии с вероятностью была установлена Больцманом, постулировавшим, что энтропия пропорциональна логарифму вероятности состояния

(энтропия определяется с точностью до константы

const),
где константа Больцмана, термодинамическая вероятность.

Второе начало термодинамики и его статистическое толкование

Формулировка Больцмана:

Все процессы в природе протекают в направлении, приводящим к увеличению вероятности состояния.

Формулировка Клаузиуса:

Невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела менее нагретого, к телу более нагретому.

С точки зрения формулировки Больцмана переход от холодного тела к нагретому принципиально возможен, но маловероятен.

Пример. Пользуясь формулой Больцмана, вычислим по изменению энтропии 2-х тел, находящихся при температурах 301 К и 300 К соответственно, отношение вероятности пребывания тел в этих состояниях , если от одного тела к другому передаётся количество теплоты в . Обозначим вероятность пребывания при температуре 300 К, 301 К.

, отсюда

Ввиду малости передаваемой энергии разность можно оценить используя соотношение:.

, тогда

Это означает, что на каждый случаев переходов от тела с температурой 301 К к телу с температурой 300 К может произойти один случай перехода того же количества теплоты от тела с температурой 300 К к телу с температурой 301 К. (Заметим, что для совсем малого количества теплоты вероятности становится сравнимыми и для таких случаев второе начало применить уже нельзя.).

Вообще же, говоря если в системе имеется многовариантность путей, процессов, то, рассчитав энтропию конечных состояний, можно теоретически определить вероятность того или иного пути, процесса, не производя их реально и в этом важное практическое применение формулы, связывающей термодинамическую вероятность с энтропией.

Вопросы для самоконтроля

Чем отличается обратимый процесс от необратимого? От обратного?
Охарактеризуйте равновесное состояние. Можно ли реализовать равновесный процесс?
Что такое цикл?
При каких условиях должна работать идеальная машина Карно?
Из каких процессов состоит цикл Карно?
Почему в выражении для работы за цикл идеальной машины Карно не входит работа, совершенная при адиабатных процессах?
Чему равен КПД идеальной машины Карно? Что характеризуют температуры в формуле для идеальной машины Карно?
Как работают холодильная машины и тепловой насос?
Что такое энтропия?
Чему равно приращение энтропии при протекании обратимого процесса?
Как изменяется энтропия при протекании необратимого процесса в адиабатически изолированной системе?
Что такое термодинамическая вероятность?
Как связана энтропия с термодинамической вероятностью?
Сформулируйте 2-ое начало термодинамики.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Иродов И.Е. Физика макросистем. – М. – С. – Пб.: Физматлит,

2001. – 197с.

2. Савельев И.В. Курс общей физики: В 3 т. – М.: Наука, 1977. Т.1. – 432с.

3.Матвеев А.Н. Молекулярная физика. – М.: Высш. Шк., 1987.

360с.

4.Сивухин Д.В. Общий курс физики: В 5т. – М.: Наука, 1975. т.2.

552с.

5.Телеснин Р.В. Молекулярная физика. – М.: Высш. шк., 1973. –

360с.

6.Зисман Г.А., Тодес О.М. Курс общей физики: В 3т. – М.:

Наука., 1969. Т 1. – 340с.

7.Трофимова Т.И. Курс физики. – М. : Высш. шк., 1990. – 478с.

8. Кунин В.Н. Конспект лекций по трудным разделам физики

Владим. политехн. ин-т. – Владимир, 1982/ – 52с.

9.Физика. Программа, методические указания и задачи для

студентов – заочников ( с примерами решения) / Сост.: А.Ф. Гал-

кин, А.А. Кулиш, В.Н. Кунин и др.; Под ред. А.А. Кулиша; Вла-

дим. гос. ун-т. – Владимир, 2002. – 128с.

10.Методические указания для самостоятельной работы по фи

зике / Сост.: Е.В. Орлик, Э.Д. Корж, В.Г. Прокошев; Владим.

гос. ун-т. – Владимир, 1988. – 48с.

Оглавление

Введение…………………………………………………………………………………3

МОЛЕКУЛЯРНАЯ ФИЗИКА…………………………………………………………4

Лекция № 7. молекулярно-кинетическая теория

идеального газа………………………………………………….4

Лекция № 8. элементы классической статистики

(статистической физике)……………………………………12

Лекция № 9. реальные газы……………………………………………………..25

Лекция № 10. свойства жидкостей………………………………………….32

Лекция № 11. свойства твердых тел………………………………………….40

Лекция № 12. фазовые равновесия и фазовые переходы………….47

Лекция № 13. элементы физической кинетики…………………………50

ТЕРМОДИНАМИКА………………………………………………………………….58

Лекция № 14. первое начало термодинамики……………………………58

Лекция № 15. второе начало термодинамики………………………….66

Библиографический список…………………………………………………………..76

Первое начало термодинамики, теория и примеры

Основные понятия первого начала термодинамики

В качестве основной задачи термодинамики ставят изучение свойств тел, характеризуя их состояния при помощи макроскопических параметров, при этом за основу берут общие законы, которые называют началами термодинамики.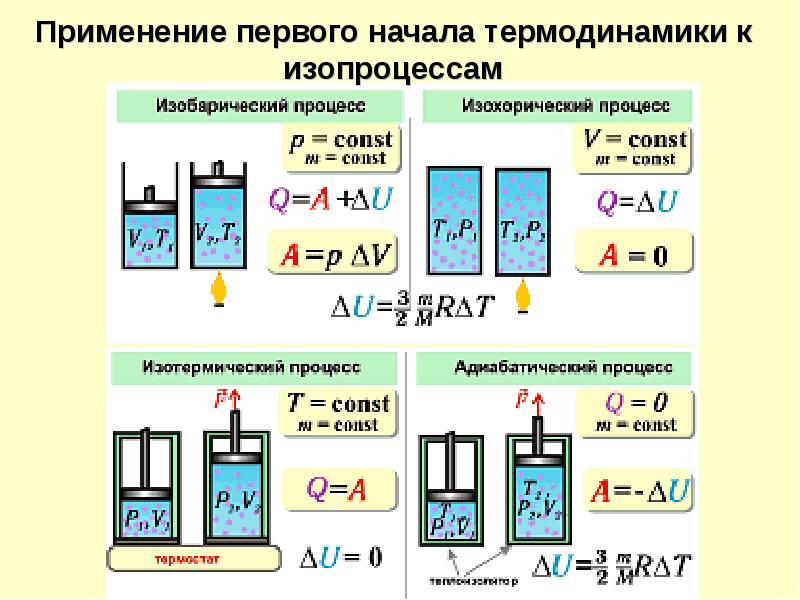 В термодинамике не пытаются выяснить микроскопические механизмы исследуемых явлений. В основе термодинамики лежат три основных закона (три начала). Первое начала термодинамики – это применение закона сохранения энергии для процессов, рассматриваемых в термодинамике. Закон сохранения энергии для теплоты (как одной из форм энергии) (), внутренней энергии () и работы (A), совершаемой термодинамической системой можно интегральном виде записать как:

что означает: Количество теплоты, подводимое к термодинамической системе, идет на совершение данной системой работы и изменение ее внутренней энергии. Условлено считать, что если теплота к системе подводится, то она больше нуля () и если работу выполняет сама термодинамическая система, то она положительна ().

Первое начало термодинамики в дифференциальном виде

Часто первое начало термодинамики используют в дифференциальном виде:

где – бесконечно малое количество теплоты, подводимое к системе; – элементарная работа системы; – малое изменение внутренней энергии системы. При рассмотрении в качестве термодинамической системы идеального газа, работу, выполняемую им, связывают с изменением объема (), поэтому выражение первого начала термодинамики представляют как:

Как и в механике, закон сохранения энергии не указывает на направление процесса, происходящего в термодинамической системе. Первое начало показывает только как, изменяются параметры, если процесс в системе происходит. В механике движение описывают при помощи уравнений движения. В термодинамике направление, в котором развивается процесс, определяют при помощи второго начала.

И так, первое начало термодинамики – это выражение закона сохранения энергии для процессов, в которых участвует теплота. Работа — это передача энергии связанная с изменением макропараметров системы. Передача теплоты реализуется при помощи перехода энергии движения молекул. Изменение при этом макропараметров – это следствие изменения энергетических условий на молекулярном уровне.

Запишем первое начало термодинамики в дифференциальном виде для изопроцессов, в качестве термодинамической системы рассматривая идеальный газ. Для изобарного процесса первое начало термодинамики не изменяет своего вида (3). Для изотермического процесса первое начало примет вид:

В изотермическом процессе все тело. которое получает система идет на совершение данной системой работы.

Для изохорного процесса мы получим:

Все тепло, которое получает газ идет на изменение его внутренней энергии.

Адиабатный процесс происходит без обмена в окружающей средой теплом, следовательно:

В адиабатном процессе система совершает работу за счет уменьшения внутренней энергии.

Примеры решения задач

Первое начало термодинамики (№2) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Первое начало термодинамики — это закон сохранения энергии для термодинамической системы.

Зная, что такое работа, теплота и энергия в термодинамике, мы сможем дать точную формулировку первого начала термодинамики. Фактически, исходя из него, можно прийти к определению теплоты (но само определение не зависит от закона сохранения энергии!).

Изменение внутренней энергии закрытой системы ΔU происходит за счет того, что система поглощает теплоту Q и совершает работу A:

ΔU = Q — A.

А как быть, если система открыта, т. е. по крайней мере, часть стенок воображаемая? Это означает, что количество частиц N в системе непостоянно — допустимы потоки вещества сквозь стенки. В этом случае внутренняя энергия может изменяться и без совершения работы или получения теплоты, а только за счет изменения числа частиц N.

Введем новую термодинамическую величину μ — химический потенциал, равный, по определению:

μ = dU / dN. [dA = 0; dQ = 0]

Термин «химический» возник исторически — в химических реакциях число частиц обычно не сохраняется.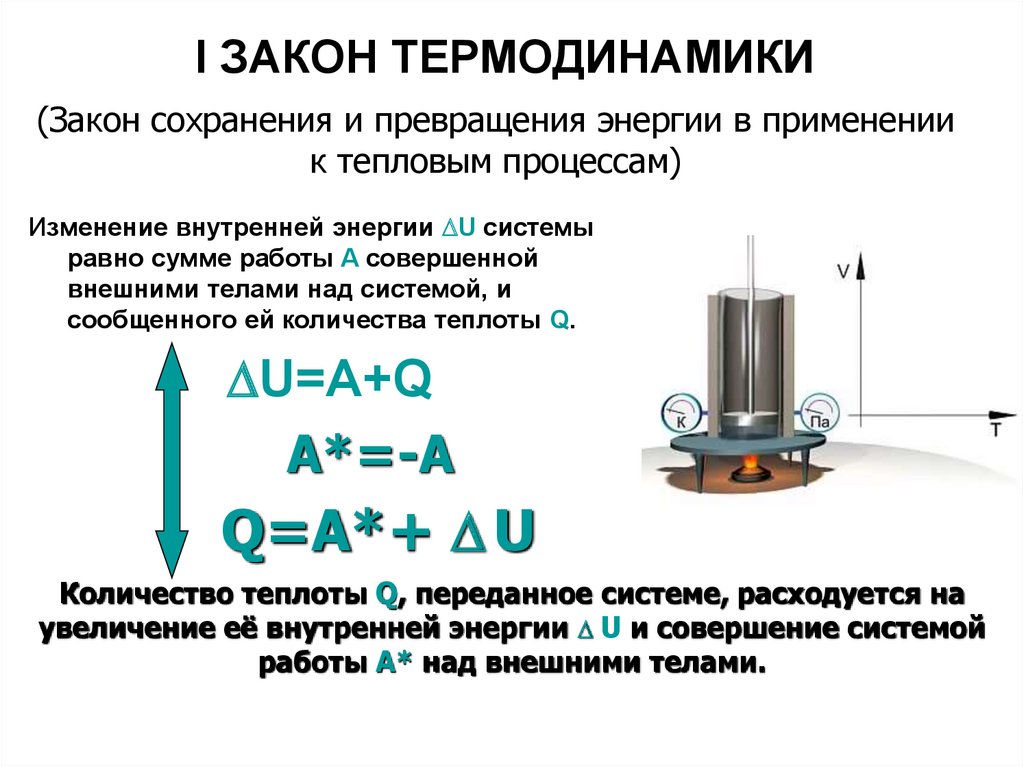 Первые открытые термодинамические системы рассматривались в термохимии.

Смысл этой величины понятен: это изменение внутренней энергии системы U при удалении из нее одной частицы. Удалять (или добавлять) частицу надо так, чтобы система не совершала работы (dA = 0) и не получала теплоты (dQ = 0). С использованием химического потенциала можно сформулировать первое начало термодинамики для открытых систем:

изменение внутренней энергии открытой системы ΔU происходит за счет того, что система поглощает теплоту Q, совершает работу A и теряет N частиц:

ΔU = Q — A — μN.

Применимо к финансовым аналогам, можно сказать, что химический потенциал — это нарицательная стоимость ценных бумаг — частиц, хранящихся в системе, которые некие «химики» (без всяких затрат!) извлекают сквозь воображаемые стенки системы. Материал с сайта http://worldofschool.ru

Вечный двигатель, сконструированный в XX в., так же как и двигатель, сделанный в 1834 г., не работает

На этой странице материал по темам:

Первое начало термодинамики формула кратко

3. Первое начало термодинамики . Неорганическая химия

Первое начало термодинамики относится к числу фун–даментальных законов природы, которые не могут быть выведены из каких-то других законов. Его справедливость доказывают многочисленные эксперименты, в частности неудачные попытки построить вечный двигатель первого рода, т. е. такую машину, которая смогла бы как угодно долго совершать работу без подвода энергии извне.

В зависимости от условий протекания процесса в сис–теме используют различные функции состояния, которые выводят из первого начала термодинамики. При этом вместо сложных биологических систем для получения выводов о превращениях массы и энергии используют упрощенные модели. Давление в системе при этом под–держивается постоянным, оно равно внешнему давле–нию. Такие процессы, протекающие при р = const, назы–ваются изобарными. Работа расширения, совершае-мая при изобарном процессе, как известно, равна:

W = –??V,

где ?V – приращение объема системы, равное раз–ности объемов в состояниях 2 и 1.

Подставляя работу расширения в математическое выражение первого начала и проведя несложные пре–образования, получаем:

Q_? = ?E + p?V = (E₂ + ?V₂) – (E₁ + ??V₁)

где Q? – теплота изобарного процесса;

1, 2 – индексы, относящиеся к началу и концу процесса.

Величина (E+ pV) – функция состояния системы, обоз–начаемая через Н и называемая энтальпией:

H = E + ?V.

Соответственно, выражение можно записать в виде:

Q_p = Н₂ – Н₁ = ?H.

Из данного выражения следует, что энтальпия – функция состояния, приращение которой равно теп–лоте, полученной системой в изобарном процессе.

Измерение приращения энтальпии в некотором про–цессе может быть осуществлено при проведении это–го процесса в калориметре при постоянном давлении. Именно так проводили свои эксперименты А. М. Ла–вуазье и П. С. Лаплас, изучая энергетику метаболиз–ма в живом организме.

В тех случаях, когда изменение состояния системы происходит при постоянном объеме, процесс называ–ется изохорным. Изменение объема AV при этом рав–но нулю, и в соответствии с формулой работа расшире–ния W = 0. Тогда из математического выражения первого начала термодинамики следует:

Q_v = ?E.

Из вышеуказанного соотношения вытекает термо–динамическое определение: внутренняя энергия – функция состояния, приращение которой равно теп–лоте QV , полученной системой в изохорном процессе. Следовательно, изменение внутренней энергии в не–котором процессе может быть измерено при проведе–нии этого процесса в калориметре при постоянном объеме. Следует, что при ? = const приращения внут–ренней энергии и энтальпии связаны соотношением:

?H = ?E + ??V.

Первое начало термодинамики и его применение

Первое начало термодинамики и его применение
PPTX / 1.05 Мб
Первое начало термодинамики и его применение
DOCX / 468 Кб
ФИО: Новоселова Юлия Михайловна

Место работы: КОПОБУ «НТМСХ» г Нолинск Кировской области

Курс: первый; Предмет: физика

Дидактическая цель урока: создать условия для осознания и осмысления блока новой учебной информации, контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений посредством использования ИКТ

Образовательная цель: ввести первое начало термодинамики как закон сохранения и превращения энергии термодинамической системы; ввести понятие об адиабатном процессе; раскрыть физическое содержание первого начала термодинамики при рассмотрении конкретных процессов; продолжить формирование умений описывать тепловые процессы физическими величинами и законами; продолжить развитие теоретического мышления обучающихся при решении задач; выражать в устной и письменной речи этапы решения задач, обосновывать свои практические и умственные действия.

Развивающая цель: продолжить формирование навыков исследовательской работы; умения анализировать, делать выводы на основе полученных результатов; умения принимать решения; развитие коммуникативных умений докладывать о результатах своего исследования, участвовать в дискуссии; активизация познавательной и творческой деятельность обучающихся.

Воспитательная цель: способствовать формированию сотрудничества и взаимовыручки в учебном коллективе; воспитывать интерес к предмету изучения, любознательность; развитие объективной самооценки.

Тип урока: комбинированный урок с использованием ИКТ.

Планируемые результаты.

Предметные: умение проводить наблюдения, анализировать, представлять результаты измерений с помощью таблиц, графиков и формул, обнаруживать зависимости между физическими величинами, объяснять результаты и делать выводы.

Метапредметные:

-познавательные: умение структурировать знания, осуществлять постановку и формулировку проблемы и поиск путей ее решения;

-регулятивные: целеполагание как постановка учебной задачи, планирование, прогнозирование;

– коммуникативные: умение работать в коллективе, осознанно и произвольно строить речевые высказывания на основе полученных знаний.

Личностные: сформированность познавательных интересов на основе развития интеллектуальных и творческих способностей обучающихся;

самостоятельность в приобретении новых знаний и практических умений;

Методы обучения: репродуктивный, частично-поисковый, проблемного изложения.

Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.

Средства обучения: проектор, ПК, толстостенный сосуд, насос, учебник физики, сборник задач по физике.

Список литературы

Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 216-224.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2009.- С.81-89.

Сауров Ю. А. Физика в 10 классе: Модели уроков: Кн.для учителя. – М.: «Просвещение», 2005

Интерактивный курс Физика 7-11 класс «Ваш Репетитор» (TeachPro)

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА (2 часа)

Этапы урока

Деятельность преподавателя

Деятельность обучающихся

1 Организационный момент

Слайд 1

Приветствует студентов. Создает позитивный настрой на познавательную деятельность, определяет готовность студентов к занятию

Настраиваются на работу, проверяют готовность своего рабочего места

2 Целеполагание, мотивация

Слайд 2

Создает проблемную ситуацию, которая подтолкнет обучающихся к формулированию цели урока.

Организует тестирование студентов (ссылка: https://onlinetestpad.com/ho2dy6lp4amq2)

Определяет место урока в курсе изучения раздела. Помогает сформулировать цель занятия

Отвечают на вопросы теста, осмысливают результаты тестирования. Вместе с преподавателем определяют для себя цели на предстоящем занятии.

3 Актуализация

Задает вопросы:

Как теоретически доказать, что работа газа при изотермическом и изобарном процессе неодинакова?

Как определяется полная механическая энергия любой системы?

Как формулируется закон сохранения полной механической энергии?

Когда происходит изменение кинетической (потенциальной) энергии тела? Приведите примеры превращения одного вида энергии в другой

Взаимодействуют с учителем во время беседы, осуществляемой во фронтальном режиме.

Слушают собеседника, строят понятные для собеседника высказывания, формулируют

собственное мнение и позицию

Принимают решения и осуществляют самостоятельный

Учатся планировать свою деятельность в соответствии с целевой установкой

4 Первичное усвоение знаний

Слайд 3

Организует работу студентов на познание нового

Предлагает выполнить задание (Слайд 4): Определите процессы, в которых участвует термодинамическая система идеальный газ, и прочитайте уравнение первого начала термодинамики для каждого случая. (приложение 1)

Проводит взаимоконтроль

Подводит итоги

Задает вопросы:

Какие изопроцессы вам известны?

Какой физической системой они происходят?

Можно ли изопроцессы назвать термодинамическими процессами?

Организует работу студентов по заполнению таблицы Применение первого закона термодинамики к различным процессам

Вопросы при заполнении таблицы:

Назовите формулы для определения внутренней энергии идеального газа, работы газа при изобарном процессе.

Почему при изотермическом процессе не изменяется внутренняя энергия?

Что происходит с газом при его сжатии?

Совершается ли работа при изохорном процессе? За счет чего изменятся внутренняя энергия газа?

Изменяется ли температура газа при изобарном процессе? За счет чего?

Какие экспериментальные факты доказывают, что при изобарном процессе газ совершает работу?

(приложение 2)

Демонстрирует опыт с толстостенным сосудом:

В толстостенный сосуд с пробкой, содержащий влажный воздух, накачиваем насосом воздух. Через некоторое время пробка вылетает и над сосудом образуется туман. Объясните наблюдаемое явление? За счет чего вылетает пробка? Почему над сосудом образуется туман?

(Слайд 5,6)

Изучение нового материала продолжается с использованием интерактивного курса Физика 7-11 класс «Ваш Репетитор» (TeachPro) Первый закон тнрмодинамики

Организует просмотр, прослушивание и обсуждение учебного материала

Слушают преподавателя. Ведут записи в тетради. Пытаются самостоятельно по определению первого закона термодинамики записать его формулу,

корректируют запись формулы, отвечают на вопросы

преподавателя.

Запись в тетради

Первый закон (первое начало) термодинамики – закон сохранения и превращения энергии, распространенный на тепловые явления:

Количество теплоты, сообщённое системе, равно сумме работы газа против внешних сил и изменения внутренней энергии системы:

Q = A + ΔU

Работа (A) и количество теплоты (Q) – характеристики процесса изменения внутренней энергии

Составляют план и последовательность действий. Определяют последовательность промежуточных целей с учетом конечного результата. Самостоятельно добывают «новые знания» по плану действий.

Отвечают на поставленные вопросы, осуществляют взаимоконтроль. Заполняют таблицу. Контролируют способ действия и его результат

Корректируют ошибки, восполняют пробелы.

Учатся ориентироваться в социальных ролях и межличностных отношениях

Наблюдают опыт и анализируют его результат. Отвечают на вопросы преподавателя

Записывают в тетрадь

Адиабатный процесс – это процесс, протекающий в системе без теплообмена с окружающими телами (Q=0). Адиабатными можно считать и быстро протекающие процессы, например, взрыв горючей смеси при работе двигателя внутреннего сгорания

Дополняют таблицу

Слушают, анализируют, проверяют записи в тетради.

5 Первичная проверка понимания

Предлагает выполнить задание (Слайд 7):

Как изменяется внутренняя энергия газа, если с ним происходят указанные процессы? (приложение 3)

Проводит взаимоконтроль

Отвечают на поставленные вопросы, осуществляют взаимоконтроль

6 Первичное закрепление

Организует решение задач (приложение 4) (Слайд 8-10) и самостоятельную работу по решению качественных задач (приложение 5)

Проверяет работу обучающихся

Выполняют задания, записывают ответ

Через организацию самостоятельной

делают выводы, получают результаты Самостоятельно активизируют мыслительные процессы, осуществляют контроль правильности сопоставления информации

7 Информация о домашнем задании, инструктаж по его выполнению

Объясняет домашнее задание

Определяют область применения полученных знаний. Обсуждают, задают вопросы. Самостоятельно определяют степень сложности выполнения задания и

необходимой помощи. Готовность к самостоятельным действиям по воспроизведению и применению

полученных знаний

8 Рефлексия

Организует и проводит рефлексию учебной деятельности, обсуждение результатов занятия

(Слайд 11)

Анализируют результаты собственной деятельности; определяют существующие

пробелы в полученных знаниях

Формулируют выводы о достижении цели урока

Оценивают личностною значимость полученной на уроке информации с

практической точки зрения, умения

обобщать, формулировать вывод

ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

I начало термодинамики Открытию I начала термодинамики предшествовало: – многочисленные экспериментальные и теоретические исследования в области физики, химии, развития тепловых двигателей, принцип исключения построения вечного двигателя первого рода (1775 год – решение французской академии наук) (невозможно производить работу без получения энергии извне) – закон Гесса (1840 год) – закон о независимости теплового эффекта химической реакции от промежуточных стадий; – принцип эквивалентности тепла и работы (опыт Джоуля) (1850 год). l

I начало термодинамики l Пример выражения закона Гесса

Опыт Джоуля (Q=AL)

Опыт Джоуля (Q=AL) l Превращение теплоты в работу и работы в теплоту осуществляется всегда в одном и том же строго постоянном количественном соотношении Q=AL А = 1 Дж/Дж – коэффициент пропорциональности, величина всегда постоянная, не зависит от способа получения теплоты и работы, не зависит от температуры.

I начало термодинамики Суть первого начала термодинамики – работа совершается только за счет теплоты или какой-либо другой формы энергии l Первое начало устанавливает, что внутренняя энергия системы является функцией ее состояния и изменяется только под влиянием внешних воздействий l Все энергетические взаимодействия сводятся к передаче теплоты и работы l

I начало термодинамики Математическое определение первого начала термодинамики: изменение внутренней энергии тела или системы (ΔU=U 2 -U 1) равно алгебраической сумме подведенных из вне количества теплоты (Q*12) и работы (-L*12 ): или d. U – изменение внутренней энергии в элементарном процессе; δQ* – количество теплоты, подведенное в элементарном процессе (если δQ* >0 – теплота подводится к системе (телу), если δQ*0 – система сама совершает работу, если δL*

I начало термодинамики Уравнения не учитывают потери работы на необратимости, которые существуют в реальных процессах. l Полная термодинамическая работа с учетом необратимых потерь определяется как l δL= δL* +δL**, где δL** – работа необратимых потерь, превращается в теплоту внутреннего теплообмена δQ**, где δL** = δQ** > 0.

I начало термодинамики l Выражения первое начало термодинамики по балансу рабочего тела в дифференциальной и интегральной форме: δQ = δQ* + δQ** = d. U + δL, Q 12 = Q*12 + Q**12 = U 2 – U 1 + L 12. Данные уравнения используются для анализа реальных процессов. l В условиях обратимого процесса δQ**= 0. l

I начало термодинамики для простых тел l Простое тело – тело, состояние которого определяется двумя независимыми параметрами (р, v), (р, t) или (v, t) (пары, газы, жидкости, твердые изотропные тела) l Термодинамическая работа для простых тел определяется формулой

I начало термодинамики для простых тел l Потенциальная работа: l l – энтальпия или теплосодержание. Теплосодержание (энтальпия) определяется суммой внутренней энергии и потенциальной функцией (pv), не имеет определенного физического смысла, но является удобной расчетной величиной, является функцией состояния.

I начало термодинамики для простых тел l. I начало термодинамики для простых тел по балансу рабочего тела:

I начало термодинамики для идеальных газов l Количество теплоты можно определить через теплоемкость: – Для изобарного процесса р=idem, – Для изохорного процесса

I начало термодинамики для идеальных газов l I начало термодинамики в аналитической форме: l Из закона Джоуля для идеальных газов – в изохорном процессе: – в изобарном процессе:

I начало термодинамики для идеальных газов l Первое начало термодинамики для идеальных газов

I начало термодинамики для идеальных газов Из первого начала термодинамики для идеальных газов следует закон Майера.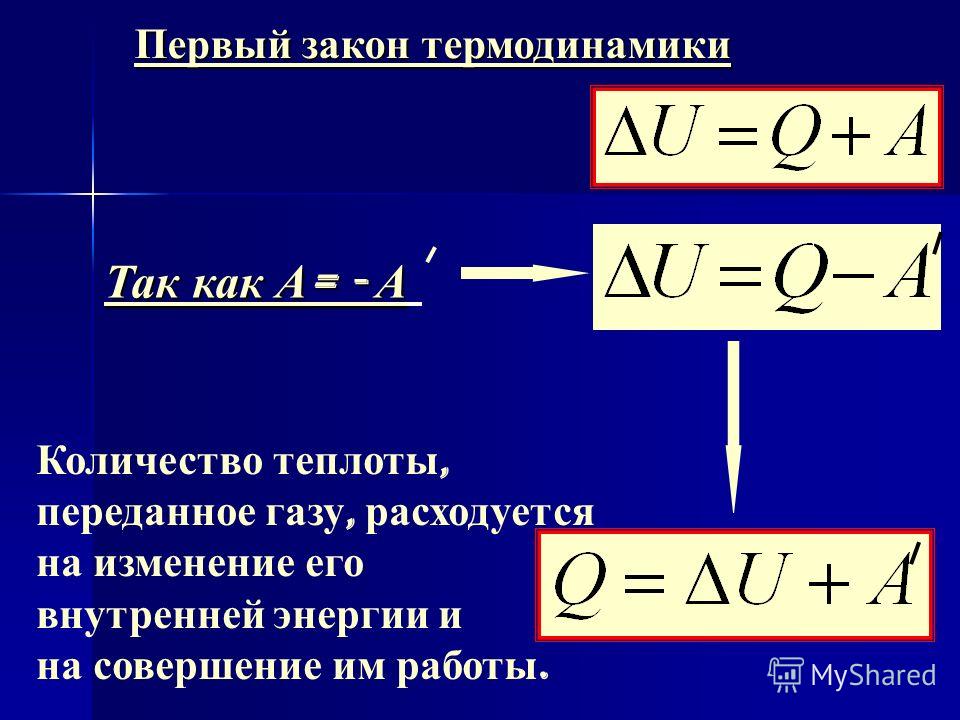 l Закон Майера устанавливает равенство между разностью изобарной и изохорной теплоемкостями и удельной газовой постоянной. l Для мольных теплоемкостей: изобарная изохорная l

Энтропия идеального газа l Согласно понятию энтропия при использовании уравнения I начала термодинамики для идеального газа

Энтропия идеального газа l Согласно l. В уравнению Клапейрона интегральной форме:

I начало термодинамики для потока l Для потока справедливо уравнение первого начала термодинамики где (u 2 -u 1) определяется как Δ l u=cv(t 2 -t 1) Для определения Q 1 -2 рассмотрим канал

I начало термодинамики для потока К определению первого начала термодинамики для потока

I начало термодинамики для потока G – массовый расход 1) т. к. давление и объем в сечениях различны, учитываем работу проталкивания: l 2) т. к. скорости потока в сечениях различны С 1 ≠ С 2 , находим изменение кинетической энергии:

I начало термодинамики для потока 3) т. к. канал расположен под углом к горизонту, т. е. высоты сечений по отношению к горизонту не равны х1 ≠ х2 , учитываем изменение потенциальной работы 4) в канале может быть установлено какое-либо устройство, производящее техническую работу, тогда техническая работа равна Lтех; 5) в канале существуют силы трения потока вещества о стенки канала, поэтому учитывается работа трения Lтр.

I начало термодинамики для потока l Подставляя полученные выражения в формулу первого начала термодинамики, получим: l Перейдем к удельным единицам, поделив обе части уравнения G:

I начало термодинамики для потока Т. к. l Первое начало термодинамики для потока в интегральной форме l в дифференциальной форме

(PDF) О правильной формулировке первого закона термодинамики

[16] Т.З. Каланов, “К проблеме познания Вселенной”, Вестник амер. физ.

Соц. (Апрельское собрание), Vol. 48, № 2 (2003), стр. 154-155.

[17] Т.З. Каланов, “Теория относительности: Ошибка преобразования координат”,

Бюллетень амер. физ. соц. (Апрельское собрание), т. 48, № 2 (2003), с. 155.

[18] Т.З. Каланов, “О логических ошибках, лежащих в основе специальной теории относительности”, Журнал

Теоретика. Том. 6-1, 2004 г. (http://www.journaloftheoretics.com).

[19] Т.З. Каланов, “Правильный теоретический анализ оснований квантовой механики”,

Журнал ультра ученых физических наук (Международный журнал физических наук, Индия),

Т. 16, № 2 (2004), стр. 191 -198.

[20] Т.З. Каланов, “О правильном теоретическом анализе основ квантовой механики”,

Вестник амер.физ. соц. (Апрельское собрание), т. 50, № 2 (2005), с. 65.

[21] Т.З. Каланов, “О новой теории физического вакуума”, Вестник амер. физ. соц. (Апрель

Собрание), Vol. 50, № 2 (2005).

[22] Т.З. Каланов, “О новом подходе к решению проблемы квантования энергии”,

Бюллетень амер. физ. соц. (Апрельское собрание), т. 51, № 2 (2006), с. 62.

[23] Т.З. Каланов, “О новой теории черной дыры”, Бюллетень амер.физ. соц. (Апрель

Собрание), Vol. 51, № 2 (2006), с. 62.

[24] Т.З. Каланов, “Проблема SETI: методологическая ошибка в космологии и

астрофизике”, Вестник амер. физ. соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 60-61.

[25] Т.З. Каланов, “О гипотезе “системного блока” Вселенной”, Бюллетень амер. физ.

Соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 61.

[26] Т.З. Каланов, “О правильной формулировке первого закона термодинамики”, Бюллетень

амер. физ. соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 60.

[27] Т.З. Каланов, “Второй закон термодинамики: математическая ошибка”, Вестник амер.

Физ. соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 60.

[28] Т.З. Каланов, “Метод Бозе: логическая ошибка”, Вестник амер. физ. соц. (Апрель

Собрание), Vol.51, № 2 (2006), с. 61.

[29] Т.З. Каланов, “Теория физического вакуума Дирака: продолжение логических ошибок Бозе”,

Вестник амер. физ. соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 61.

[30] Т.З. Каланов, “Статистика Бозе-Эйнштейна и статистика Ферми-Дирака: логическая ошибка”, Бюллетень

амер. физ. соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 61.

[31] Т.З. Каланов, “О правильном анализе распределения Максвелла”, Бюллетень амер.физ.

Соц. (Апрельское собрание), Vol. 51, № 2 (2006), с. 61-62.

[32] Т.З. Каланов, “О правильном анализе основ специальной теории

относительности”, Бюллетень амер. физ. соц. (Апрельское собрание), Vol. 52, № 2 (2007), с. 120.

Законы термодинамики – обзор

25.4.3 Понимание Второго закона посредством эксергии

Второй закон термодинамики (СТТ) часто вызывает страх у студентов, изучающих термодинамику.Введение понятия энтропии обычно только усиливает их трепет. Даже студенты, которые проходят курсы по термодинамике и в конечном итоге заканчивают обучение, часто сохраняют страхи перед SLT и энтропией и чувствуют, что они на самом деле не понимают эти темы. Арендтс (1980), например, начинает одну из своих статей об эксергетических методах словами: «Термодинамика не очень популярная наука, потому что концепции термодинамики не соответствуют простому человеческому опыту». Сосредоточившись на SLT, он продолжает: «Традиционные формулировки Второго закона препятствуют простому пониманию преобразований энергии, потому что применение концепции энтропии к этим процессам часто рассматривается как чудо.”

Другие также согласились с этими опасениями и разработали различные подходы к обучению SLT. Одним из примеров является текст по термодинамике Диксона (1975), в предисловии к которому говорится, что «энтропия является [не] наиболее важным или полезным аспектом Второго закона» и «Второй закон имеет отношение к концепции деградации энергии; то есть с потерей полезного трудового потенциала». Диксон вводит SLT через концепцию деградации энергии, утверждая, что «деградация… потому что это рабочий термин, это легко понять».Сосредоточив внимание на деградации энергии, а не на абстрактном свойстве энтропии, Диксон считает, что его книга приводит к «более ясному физическому смыслу энтропии».

Этот подход, хотя и поучителен для некоторых, все же несколько абстрактен и расплывчат. Этот подход близок к обучению SLT с помощью эксергии, и, вероятно, был бы понятнее, если бы это было так. Эксергия обеспечивает перспективу SLT и энтропии, которая намного более интуитивно понятна студентам. Определение эксергии, в котором говорится, что эксергия — это максимальная работа, которую можно получить от системы или потока в эталонной среде, обычно намного проще, чем определение энтропии.Кроме того, характеристики эксергии, такие как несохраняющаяся величина, обычно легче понять учащимся, чем концепции, связанные с энтропией и ее характеристиками.

Таким образом, мы считаем, что эксергия должна составлять центральный компонент курсов термодинамики. В частности, эксергия должна играть важную роль в обучении SLT. Такой подход, вероятно, сделал бы SLT более понятным и практичным и менее внушающим опасения. Некоторые читатели правильно укажут, что существуют некоторые дополнительные сложности при работе с эксергией, а не с энтропией (например, с энтропией). g., эталонная среда должна быть введена и определена). Тем не менее, мы считаем, что общие преимущества приближения к SLT с помощью эксергии перевешивают трудности.

Первый закон термодинамики (химия): примеры, ограничения

Первый закон термодинамики: Сначала мы должны понять взаимосвязь между теплом и работой, а также понятие внутренней энергии, прежде чем переходить к первому закону термодинамики. Как и масса, энергия всегда сохраняется, т.е.е. его нельзя создать или разрушить, но можно преобразовать в различные формы. Внутренняя энергия — это термодинамическое свойство системы, которое относится к энергии, связанной с молекулами системы, включая кинетическую и потенциальную энергию.

Очень важно, чтобы учащиеся сначала поняли основную концепцию, лежащую в основе этой теории, а затем внимательно прочитали ее для лучшего понимания. Всякий раз, когда система претерпевает изменения в результате взаимодействия теплоты, работы и внутренней энергии, происходит множество переносов и преобразований энергии.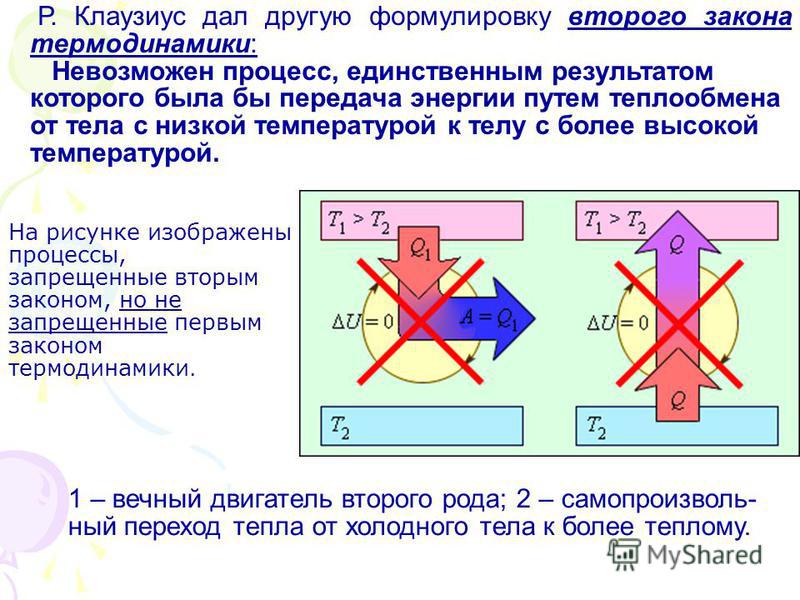 Однако в ходе этих обменов нет чистого изменения полной энергии. В этой статье вы узнаете об определении и ограничениях первого закона термодинамики.

Государственный первый закон термодинамики

Первый закон термодинамики — это просто закон сохранения энергии, который гласит, что энергия не может быть ни создана, ни уничтожена, хотя она может быть преобразована из одной формы в другую.

Изучение концепций экзамена на Embibe

Закон также может быть сформулирован следующим образом.

Полная энергия изолированной системы остается постоянной, хотя и может переходить из одной формы в другую.
Всякий раз, когда некоторое количество какой-либо формы энергии исчезает, должно производиться точно эквивалентное количество какой-либо другой формы энергии.
Невозможно построить вечный двигатель, который непрерывно производил бы работу, не потребляя энергии (Гельмгольц, \(1847\)).
Для системы, находящейся в контакте с окружающей средой, сумма энергий системы и окружающей среды в определенный момент времени остается постоянной. Однако, по-разному, он может быть разделен между ними двумя.
Эквивалентность теплоты и механической работы, установленная Джоулем, также следует как конференция первого начала термодинамики. Предположим, что нет эквивалентности между теплотой и работой. Теперь предположим, что \({\rm{Q}}\) калорий тепла преобразуются в механическую работу, и такое же количество проделанной работы преобразуется обратно в определенное количество тепла, скажем, \({\rm{Q}}’\ ). Если \({\rm{Q}} \ne {\rm{Q}}’\), то \({\rm{Q}} > {\rm{Q}}’\) или \({\rm{ Q}} < {\rm{Q}}'.2}\)

Где Е — энергия, полученная при разрушении массы m, а с — скорость света. Это не противоречит первому началу термодинамики, поскольку массу в ее обобщенном виде можно рассматривать как своего рода потенциальную энергию. Закон сохранения массы и закон сохранения энергии в совокупности дают закон сохранения массы и энергии. Измененный закон можно сформулировать следующим образом.

‘Общая масса и энергия изолированной системы остаются постоянными в химической термодинамике.

Однако в обычных химических реакциях, сопровождающихся выделением тепла, изменение массы настолько мало, что почти не обнаруживается ни при каких химических весах. Следовательно, приведенное выше соотношение не имеет значения в химической термодинамике.

Практические экзаменационные вопросы

Математическая формулировка первого закона термодинамики

Внутреннюю энергию системы можно увеличить двумя способами:

Подавая тепло в систему,
Выполняя работу в системе.

Предположим, что начальная внутренняя энергия системы \( = {{\rm{E}}_1}\)

Если он поглотит тепло \({\rm{q}}\), его внутренняя энергия станет \( = {{\rm{E}}_1} + {\rm{q}}\)

Если над системой будет совершена дальнейшая работа \({\rm{w}}\), внутренняя энергия еще больше увеличится и станет \( = {{\rm{E}}_1} + {\rm{q}} + {\rm{w}}\). Назовем эту конечную внутреннюю энергию как \({{\rm{E}}_2}\). Тогда \({{\rm{E}}_2} = {{\rm{E}}_1} + {\rm{q}} + {\rm{w}}\) или \({{\rm{ E}}_2} – {{\rm{E}}_1} = {\rm{q}} + {\rm{w}}\)

Или \(\Delta {\rm{E}} = {\rm{q}} + {\rm{w}} \ldots \ldots \ldots (1)\)

Это уравнение является математической формулировкой первого закона термодинамики.

Если выполненная работа является работой расширения, то \({\rm{w}} = \,- {\rm{P\Delta V}}\), где \({\rm{\Delta V}} \) – изменение объема, а \({\rm{P}}\) – внешнее давление. Уравнение \({\rm{(i)}}\) тогда можно записать как

\({\rm{\Delta E}} = {\rm{q}} – {\rm{P\Delta V}}\) или \({\rm{q}} = {\rm{q}} = {\rm{q}} E}} + {\rm{P\Delta V}}………….{\rm{(2)}}\)

Два интересных результата следуют из математической формулировки первого закона термодинамики, например,

Ни \({\rm{q}}\), ни w не являются функциями состояния, однако величина \({\rm{q}} + {\rm{w}}( = {\rm{\Delta E }})\) является функцией состояния (поскольку \({\rm{\Delta E}}\) является функцией состояния).
Внутренняя энергия \({\rm{(E)}}\) идеального газа является функцией температуры. Следовательно, для идеального газа, подвергающегося изотермическому превращению, \({\rm{\Delta E}} = 0.\) Следовательно, \({\rm{q}} =\, – {\rm{w}}\ ), т. е. теплота, поглощаемая системой, равна работе, совершаемой системой.

Во время адиабатического изменения \({\rm{q}} = 0\), так что \({\rm{\Delta E}} = {{\rm{w}}_{{\rm{адиабатический }}}}\)

Некоторые специальные формы первого закона термодинамики

При особых условиях уравнение \(\left( 1 \right)\) для первого начала термодинамики изменяется, как показано ниже.

Для циклического процесса, приводящего к исходному состоянию, т. е. для процесса изотермического расширения идеального газа,
\({\rm{\Delta E}} = 0\)
\(\следовательно \,{ \rm{q}} = {\rm{w}}\)
т. е. работа, совершаемая газом, в точности равна поглощенному теплу.
Для процесса, в котором объем остается постоянным, работа расширения не совершается, т. е. \({\rm{W}} = 0.\) Отсюда уравнение \(\left( 1 \right)\) для первый закон термодинамики принимает вид
\({\rm{\Delta E}} = {{\rm{Q}}_{\rm{v}}}\) (\({\rm{v}}\) постоянный объем)
Поскольку \({\rm{\Delta E}}\) является функцией состояния, \({{\rm{Q}}_{\rm{v}}}\) также должна быть функцией состояния .
Таким образом, при постоянном объеме увеличение внутренней энергии газа (на что указывает повышение его температуры) равно поглощенному теплу.
Для адиабатического процесса расширения, т. е. когда тепло не передается и не теряется в окружающую среду, что возможно, когда система хорошо изолирована,
\({\rm{dQ}} = 0\)
\(\следовательно \ ,{\rm{\Delta E}} = – {{\rm{W}}_{\rm{q}}}\) (\({\rm{q}}\) указывает на постоянное тепло)

Таким образом, в таких случаях уменьшение внутренней энергии точно равно произведенной работе.Знак минус показывает, что система совершает работу над окружающей средой.

Попытка пробных тестов

Внутренняя энергия является функцией состояния

Внутренняя энергия является функцией состояния, то есть когда происходит процесс, изменение ее значения зависит только от ее значений в начальном и конечном состояниях и не зависит от пути, по которому происходит изменение.

Рассмотрим систему, имеющую определенное давление, объем и температуру, представленную точкой \({\rm{A}}\) (начальное состояние) на рисунке. Предположим, что давление, объем и температура изменены так, что система приводится в точку \({\rm{B}}\) (конечное состояние) по пути \({\rm{I}}\). Пусть изменение внутренней энергии системы при превращении \({\rm{A}}\) в \({\rm{B}}\) равно \({\rm{\Delta E}}\)

Далее, предположим, что \({\rm{B}}\) преобразуется обратно в \({\rm{A}}\), но через другой путь, путь \({\rm{II}}\), изменение во внутренней энергии во время этого процесса (скажем, \({\rm{\Delta E}}\)) должна быть равна по величине той, что участвует в пути \({\rm{I}}\).{\rm{Путь II}}} {\rm{A}}\)

Система вернется в исходное состояние, чтобы создать определенное количество энергии, равное \({\rm{\Delta E – \Delta E’}}\). При многократном повторении одного и того же цикла энергия будет генерироваться непрерывно, и вечный двигатель станет возможным, вопреки первому закону термодинамики. Отсюда \({\rm{\Delta E = \Delta E’}}\).

Таким образом, мы можем сказать, что изменение энергии, сопровождающее процесс, зависит от начального и конечного состояний системы и не зависит от пути, по которому эти изменения произошли.

Следует отметить два важных момента, касающихся внутренней энергии:

Внутренняя энергия зависит от количества вещества, присутствующего в системе. Следовательно, это обширное свойство.
Внутренняя энергия идеальных газов зависит только от температуры. Следовательно, в изотермических процессах (процессах, протекающих при постоянной температуре) внутренняя энергия не изменяется, т. е. \({\rm{\Delta E = }}0\)

Работа и Теплота являются функциями пути

Пусть система переходит из состояния \({\rm{A}}\) в состояние \({\rm{B}}\).Это можно сделать, следуя различным путям, как показано на следующих рисунках.

Ограничимся только работой расширения. Мы знаем, что работа, совершаемая при небольшом изменении объема \({\rm{dV}}\), равна \({\rm{P\, dV}}\), где \({\rm{P}}\) это внешнее давление. Таким образом, полная проделанная работа представляет собой сумму \({\rm{P\, dV}}\) слагаемых, что эквивалентно площади под кривой в \({\rm{P}} – {\rm{ V}}\) диаграмма.

Поскольку площади (или члены \({\rm{P\, dV}}\)) под кривыми на трех приведенных выше рисунках различны, работа, выполненная на трех путях, будет разной.Следовательно, мы можем сказать, что работа есть функция пути, т. е. ее значение не зависит от начального и конечного состояний системы, а зависит от пути, по которому осуществляется это изменение.

Тепло также является функцией пути, а не функцией состояния. Это может быть непосредственно реализовано из математической формулировки первого закона термодинамики, а именно.

\({\rm{\Delta E}} = {\rm{Q}} – {\rm{W}}\)

\({\rm{\Delta E}}\) является определенной величиной. если \({\rm{W}}\) не является определенной величиной, \({\rm{Q}}\) не может быть определенной величиной.Интересно отметить, что ни \({\rm{Q}}\), ни \({\rm{W}}\) не являются функциями состояния, однако величина \({\rm{Q}} – {\ rm{W}}\) (т. е. \({\rm{\Delta E}}\)) – это функция состояния.

Ограничения первого закона термодинамики

Основным ограничением первого начала термодинамики является то, что он просто указывает на точную эквивалентность между различными формами энергии, вовлеченными в любой процесс. Тем не менее, он не дает никакой информации о спонтанности или осуществимости процесса, т.е.д., возможен этот процесс или нет.

Например, первый закон не указывает, может ли теплота течь от холодного конца к горячему или нет. Это говорит нам о том, что если бы этот процесс происходил, то тепловая энергия, полученная одним концом, была бы в точности равна энергии, потерянной другим концом. Точно так же первый закон не говорит, может ли газ диффундировать из низкого давления в высокое давление, может ли вода сама течь вверх или нет и т. д.

Резюме

Термодинамику можно понять с помощью определенных законов.Самым простым из них является первый закон. Согласно первому закону термодинамики энергия в процессе может переходить из одной формы в другую, но не создается и не уничтожается. Первый закон термодинамики известен как закон сохранения энергии.
В этой статье вы узнаете об определении первого закона термодинамики, математической формулировке первого закона термодинамики и его ограничениях.

Часто задаваемые вопросы

В.1. Что говорит первый закон термодинамики?
Ответ: Первый закон термодинамики — это просто закон сохранения энергии, который гласит, что энергия не может быть ни создана, ни уничтожена. Однако он может быть преобразован из одной формы в другую.

Q.2. Что такое 1-й, 2-й и 3-й законы термодинамики?
Ответ: Первый закон термодинамики утверждает, что полная энергия Вселенной (т. е. системы и окружающей среды) остается постоянной.Однако он может претерпевать трансформацию из одной формы в другую.
Второй закон термодинамики утверждает, что энтропия любой изолированной системы всегда увеличивается.
Энтропия идеально кристаллического твердого тела стремится к нулю, когда температура приближается к абсолютному нулю.

В.3. Кто дал первый закон термодинамики?
Ответ: Первый закон термодинамики был дан Робертом Майером и Гельмгольцем.

Q.4. Каково применение первого закона термодинамики?
Ans: В изотермическом процессе температура идеального газа остается постоянной.Это означает, что тепло, подаваемое в систему, используется для совершения работы с окружающей средой. При плавлении твердого тела в жидкость его внутренняя энергия увеличивается.

В.5. Кто является отцом термодинамики?
Ответ: Николя Леонара Сади Карно часто называют «отцом термодинамики».

В.6. Кто написал закон термодинамики?
Ответ: К \(1860,\), формализованному в работах таких ученых, как Рудольф Клаузиус и Уильям Томсон, были установлены то, что сейчас известно как первый и второй законы .Позже теорема Нернста (или постулат Нернста), которая сейчас известна как третий закон, была сформулирована Вальтером Нернстом за \(1906 – 12.\)

Мы надеемся, что эта статья «Первый закон термодинамики» помогла вам. Если у вас есть какие-либо вопросы, оставьте комментарий ниже, и мы свяжемся с вами.

55 просмотров

Энтропия газа

Термодинамика — раздел физики который имеет дело с энергией и работой системы. В аэродинамике, нас больше всего интересует термодинамика при изучении движения системы и понимание высокой скорости течет.Первый закон термодинамики указывает на то, что полная энергия системы сохраняется. Общая энергия включает в себя потенциальную и кинетическую энергию, Работа осуществляется системой, и передача нагревать через систему. То второй закон термодинамики показывает что, хотя многие физические процессы, удовлетворяющие первому закону, возможно, в природе происходят только те процессы, для которых энтропия системы либо остается постоянной, либо увеличивается.

Энтропия, как и температура давление, может быть объяснено как на макромасштаб и микромасштаб.Поскольку термодинамика имеет дело только с макромасштабом, изменение энтропии дельта S определяется здесь теплопередача дельта Q в систему, разделенную на температура T :

дельта S = дельта Q / T

При термодинамическом процессе температура T объекта изменяется при подаче или отводе тепла Q . Более правильное определение энтропия S является дифференциальной формой, которая объясняет это вариация.

dS = dQ/T

Тогда изменение энтропии обратно температуры, интегрированной по изменению теплоотдачи. За газы, есть два возможных способа оценить изменение энтропии. Начнем с использования первого закона термодинамики:

dE = dQ – dW

где E — внутренняя энергия, а Вт — работа, совершенная система. Замена определения работы для газа.

dQ = dE + p dV

где p – это давление а В это объем газа.Если мы используем определение энтальпия H газа:

Н = Е + р * В

Потом:

dH = dE + p dV + V dp

Подставляем в уравнение первого закона:

dQ = dH – V dp – p dV + p dV

dQ = dH – V dp

альтернативный способ представить первый закон термодинамики. Для идеального газа уравнение состояния записывается:

р * В = Р * Т

где R — газовая постоянная. Теплопередача газа равна произведению теплоемкости на изменение температура; в дифференциальной форме:

dQ = C * dT

Если у нас есть процесс постоянного объема, формулировка первого закона дает:

dE = dQ = C (постоянный объем) * dT

Аналогично, для процесса с постоянным давлением формулировка первого закона дает:

dH = dQ = C (постоянное давление) * dT

Если предположить, что теплоемкость не зависит от температуры, мы можем использовать эти два уравнения, чтобы определить изменение энтальпии и внутренней энергии.Если мы подставим значение вместо p из уравнения состояния, а определение dE в первом уравнении энергии получаем:

dQ = C (постоянный объем) * dT + R * T dV / V

Аналогичным образом подставив значение В на из уравнения состояние, и определение dH мы получаем альтернативную форму:

dQ = C (постоянное давление) * dT – R * T dp/p

Подставив эти формы вместо dQ в дифференциальную форму уравнения энтропии дает:

dS = C (постоянный объем) * dT / T + R * dV / V

dS = C (постоянное давление) * dT / T – R * dp / p

Эти уравнения можно проинтегрировать от условия «1» до условие “2”, чтобы дать:

S2 – S1 = Cv * ln (T2 / T1) + R * ln (V2 / V1)

S2 – S1 = Cp * ln ( T2 / T1) – R * ln ( p2 / p1)

где Cv – теплоемкость при постоянном объеме, Cp – теплоемкость при постоянном давлении, и в является символом для логарифмическая функция.

Если разделить оба уравнения на массу газа, то можно получить внутренний, или “конкретный” формы обоих уравнений:

s2 – s1 = cv * ln ( T2 / T1) + R * ln ( v2 / v1)

s2 – s1 = cp * ln ( T2 / T1) – R * ln ( p2 / p1)

где cp и cv — удельные теплоемкости. В зависимости от типа процесса, с которым мы сталкиваемся, мы теперь можем определить изменение энтропии газа.

Эти уравнения могут немного сбивать с толку, потому что мы используем удельную теплоемкость при постоянный объем, когда у нас есть процесс, изменяющий объем, и конкретный тепло при постоянном давлении, когда процесс меняет давление. Чтобы прояснить ситуацию, давайте посмотрим на первое уравнение:

s2 – s1 = cv * ln ( T2 / T1) + R * ln ( v2 / v1)

Если у нас есть процесс постоянного объема, второй член в уравнении равен к нулю, так как v2/v1 = 1. Тогда мы можем определить значение удельной теплоемкости для процесса постоянного объема. Но если у нас есть процесс, который изменяет громкость, второй член уравнения не равен нулю. Мы можем думать о первом члене уравнения как вклад для процесса постоянного объема, а второй член как дополнительный изменение, вызванное изменением объема. Подобный тип аргумента может быть сделан для уравнения, используемого для изменения давления.

Деятельность:

Экскурсии с гидом

Навигация ..

Домашняя страница руководства для начинающих

Первый закон термодинамики – Universe Today

[/подпись]

Вы когда-нибудь задумывались, как на самом деле работает тепло? Что ж, не так давно ученые, стремящиеся сделать свои паровые двигатели более эффективными, стремились сделать именно это.Их попытки понять взаимосвязь между преобразованием энергии, теплотой и механической работой (и, следовательно, более крупными переменными, такими как температура, объем и давление) стали известны как термодинамика, происходящая от греческих слов «термо» (что означает «тепло») и « dynamis» (имеется в виду сила). Как и большинство областей научных исследований, термодинамика подчиняется ряду законов, которые были реализованы благодаря постоянным наблюдениям и экспериментам. Первый закон термодинамики, возможно, самый важный, является выражением принципа сохранения энергии.

В соответствии с этим принципом первый закон гласит, что энергия может быть преобразована (т. е. преобразована из одной формы в другую), но не может быть создана или уничтожена. Обычно его формулируют, утверждая, что изменение внутренней энергии (т. е. полной энергии), содержащейся в системе, равно количеству тепла, подведенного к этой системе, за вычетом количества работы, выполненной системой в ее окружении. Работа и теплота возникают в результате процессов, которые добавляют или вычитают энергию, в то время как внутренняя энергия является особой формой энергии, связанной с системой, свойством системы, в то время как выполненная работа и подведенное тепло не являются таковыми.Важным результатом этого различия является то, что данное изменение внутренней энергии может быть достигнуто многими комбинациями тепла и работы.

Этот закон был впервые сформулирован Рудольфом Клаузиусом в 1850 году, когда он сказал: «Существует функция состояния Е, называемая «энергией», дифференциал которой равен работе, обмениваемой с окружающей средой во время адиабатического процесса». Тем не менее, именно Гермен Гесс (через закон Гесса), а затем Юлиус Роберт фон Майер первым сформулировал закон, хотя и неформально. Его можно выразить с помощью простого уравнения E2 – E1 = Q – W, где E представляет собой изменение внутренней энергии, Q представляет собой теплопередачу, а W – выполненную работу.Другое распространенное выражение этого закона, встречающееся в учебниках по естествознанию, — ?U=Q+W, где ? представляет изменение и U, тепло.

Важным понятием в термодинамике является «термодинамическая система», точно определенная область изучаемой Вселенной. Все во вселенной, кроме системы, известно как окружение и отделено от системы границей, которая может быть воображаемой или реальной, но по соглашению ограничивает конечный объем. Через эту границу происходит обмен работой, теплом или веществом между системой и окружающей средой.Термодинамика имеет дело только с крупномасштабной реакцией системы, которую мы можем наблюдать и измерять в экспериментах (например, паровые двигатели, для которых исследование было впервые разработано).

Мы написали много статей о Первом Законе Термодинамики для Вселенной Сегодня. Вот статья об энтропии, а вот статья о законе Гука.

Если вам нужна дополнительная информация о Первом законе термодинамики, загляните в Исследовательский центр Гленна НАСА, а вот ссылка на Гиперфизику.

Мы также записали серию Astronomy Cast о планете Земля. Послушайте, Эпизод 51: Земля.

Источники:
http://en.wikipedia.org/wiki/First_law_of_thermodynamics
http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
http://en.wikipedia.org/ wiki/Internal_energy
http://www.grc.nasa.gov/WWW/K-12/airplane/thermo1.html
http://en.wikipedia.org/wiki/Thermodynamics
http://en. wikipedia. org/wiki/Законы_термодинамики

Нравится:

Нравится Загрузка…

Исторические заметки из книги Стивена Вольфрама «Новый вид науки»

От: Стивен Вольфрам, Новый вид науки
Примечания к главе 9: Фундаментальная физика
Раздел: Необратимость и второй закон термодинамики
Страница 1019

История термодинамики. Основные физические представления о тепле и температуре были установлены в 1600-х годах, и ученые того времени, по-видимому, правильно полагали, что тепло связано с движением микроскопических составляющих материи.Но в 1700-х годах стало широко распространено мнение, что тепло — это отдельная текучая субстанция. Эксперименты Джеймса Джоуля и других в 1840-х годах поставили это под сомнение, и, наконец, в 1850-х годах было признано, что тепло на самом деле является формой энергии. Связь между теплом и энергией была важна для разработки паровых двигателей, и в 1824 году Сади Карно уловил некоторые идеи термодинамики в своем обсуждении эффективности идеализированного двигателя. Примерно в 1850 году Рудольф Клаузиус и Уильям Томсон (Кельвин) сформулировали как первый закон (о том, что полная энергия сохраняется), так и второй закон термодинамики.Второй закон первоначально был сформулирован в терминах того факта, что теплота не переходит самопроизвольно от более холодного тела к более горячему. Другие формулировки последовали быстро, и Кельвин, в частности, понял некоторые общие последствия закона. Идея о том, что газы состоят из движущихся молекул, довольно подробно обсуждалась Даниэлем Бернулли в 1738 г., но потеряла популярность и была возрождена Клаузиусом в 1857 г. После этого Джеймс Клерк Максвелл в 1860 г. вывел из механики отдельных молекулярные столкновения ожидаемое распределение молекулярных скоростей в газе.В течение следующих нескольких лет кинетическая теория газов быстро развивалась, и были вычислены многие макроскопические свойства газов, находящихся в равновесии. В 1872 году Людвиг Больцман построил уравнение, которое, по его мнению, могло подробно описать развитие газа во времени, независимо от того, находится он в равновесии или нет. В 1860-х годах Клаузиус ввел энтропию как отношение теплоты к температуре и сформулировал второй закон в терминах увеличения этой величины. Затем Больцман показал, что из его уравнения следует так называемая H-теорема, которая утверждает, что величина, равная энтропии в состоянии равновесия, всегда должна возрастать со временем.Сначала казалось, что Больцман успешно доказал второй закон. Но затем было замечено, что, поскольку молекулярные столкновения считались обратимыми, его вывод можно было провести в обратном порядке, и тогда он подразумевал бы обратное второму закону. Гораздо позже стало понятно, что исходное уравнение Больцмана неявно предполагало, что молекулы не коррелированы перед каждым столкновением, но не после него, тем самым вводя фундаментальную асимметрию во времени. В начале 1870-х Максвелл и Кельвин, по-видимому, уже поняли, что второй закон формально не может быть выведен из микроскопической физики, а должен каким-то образом быть следствием неспособности человека отслеживать большое количество молекул.Отвечая на возражения относительно обратимости, Больцман около 1876 г. понял, что в газе гораздо больше состояний, которые кажутся случайными, чем упорядоченными. Это осознание привело его к утверждению, что энтропия должна быть пропорциональна логарифму числа возможных состояний системы, и к формулировке идей об эргодичности. Статистическая механика систем частиц была помещена в более общий контекст Уиллардом Гиббсом, начиная примерно с 1900 года. Гиббс ввел понятие ансамбля – набора многих возможных состояний системы, каждому из которых присвоена определенная вероятность.Он утверждал, что если эволюция во времени одного состояния должна была посетить все другие состояния в ансамбле — так называемая эргодическая гипотеза — то усредненное за достаточно долгое время одно состояние будет вести себя так, как это типично для ансамбля. Гиббс также привел качественные аргументы в пользу того, что энтропия увеличилась бы, если бы ее измеряли «крупнозернистым» способом, при котором соседние состояния не различались. В начале 1900-х годов развитие термодинамики было в значительной степени омрачено квантовой теорией, и над ней было сделано мало фундаментальных работ.Тем не менее к 1930-м годам Второй закон каким-то образом стал широко рассматриваться как принцип физики, основы которого следует подвергать сомнению только из любопытства. Однако, несмотря на пренебрежение в физике, эргодическая теория стала активной областью чистой математики, и с 1920-х по 1960-е годы свойства, связанные с эргодичностью, были установлены для многих видов простых систем. Когда в 1950-х годах стали доступны электронные компьютеры, Энрико Ферми и другие начали исследовать эргодические свойства нелинейных систем пружин.Но в итоге они сосредоточились на повторяющихся явлениях, связанных с солитонами, и не рассматривали общие вопросы, связанные со Вторым законом. Во многом то же самое произошло в 1960-х годах, когда первые модели газов твердых сфер сосредоточились на конкретном явлении длинных хвостов. И к 1970-м годам компьютерные эксперименты в основном были ориентированы на обыкновенные дифференциальные уравнения и странные аттракторы, а не на системы с большим количеством компонентов, к которым мог бы применяться второй закон.Начиная с 1950-х годов было признано, что энтропия — это просто отрицательное значение количества информации, введенного в 1940-х годах Клодом Шенноном. Следуя утверждениям Джона фон Неймана, считалось, что любой вычислительный процесс обязательно должен увеличивать энтропию, но к началу 1970-х годов, особенно благодаря работам Чарльза Беннета, было признано, что это не так (см. стр. 1023), что заложило некоторые ранние основы. для связи вычислительных и термодинамических идей.

Первый закон термодинамики Примеры Вывод формулы и задачи

Формулировка первого закона термодинамики

Первый закон термодинамики, также известный как «Закон сохранения энергии».

«Энергия не может быть ни создана, ни уничтожена, а только преобразована из одной формы в другую».

Или

«Полная энергия системы и ее окружения остается постоянной».

Математическая форма и вывод

Рассмотрим систему, исходной системой которой является «E ₁». Пусть количество тепла «q» поглощается системой из окружающей среды и совершает некоторую работу «W» над окружающей средой, в то время как внутренняя энергия изменить на

‘E ₂‘.

Тогда изменение внутренней энергии определяется как

ΔE = E ₁ – E ₂

Согласно первому закону термодинамики

ΔE = q – W

Значение теряет энергию и положительный, когда система получает энергию.

Давление-объем Работа

Рассмотрим газ, заключенный в цилиндр, снабженный поршнем, не имеющим трения и невесомым. Пусть площадь поршня равна «А» внешнему давлению, действующему на поршень «Р», силе, действующей со стороны газа на поршень «F».

Теперь, если система расширяется, и поршень движется против окружающей среды, проходя расстояние «ΔI». Тогда

Работа = Сила x Перемещение

Вт = F x ΔI ———– 1

Поскольку,

P = F/A

Следовательно,

F = P x A ———— 2

Поместите значение ‘f’ в уравнение № 1, мы получим

W = P x A x ΔI ———— 3

Так как,

A x ΔL = ΔV

Итак, уравнение № 3 мы можем записать как

W = P x ΔV

Или

W = P ΔV

По первому закону термодинамики В уравнении № 4 мы получаем

ΔE = Q – P ΔV

или

q = δ e + p δ v

Применение первого закона термодинамики

Процесс при постоянном Объем

Согласно первому закону термодинамики

ΔE = q – P Δ V

ΔE = qv – P Δ V ————– 1

Вт здесь qv = теплота, поглощаемая при постоянном объеме, когда объем системы не меняется

Δ V = 0

При этом условии работа не совершается становится

Δ E = qv ————- 2

Это уравнение показывает, что при постоянном объеме выделяемая теплота равна изменению внутренней энергии, и работа не совершается.

Процесс при постоянном давлении

При подводе теплоты к системе при постоянном давлении внутренняя энергия системы увеличивается, в результате чего система совершает работу над окружающей средой:

Таким образом,

qp = Δe + pδv —- 1

, где QP – это тепло, поглощенное на постоянном давлении

, мы знаем, что

ΔE = E ₁ – E ₂

ΔV = V ₁ – V ₂

Тогда уравнение № 1 можно записать как:

= (E ₂ – E ₁ – E ₁) + P (V ₂ – V ₁)

QP = (E ₂ + PV ₂ ) – (E ₁ + PV ₁ ) ———- 2

энтальпия «H» математически определяется как:

H = 9 E + PV 3

H ₁ = E ₁ + PV ₁

В конечном состоянии

H ₂ = E ₂ + PV ₂ + PV ₂

Подставляя значение в уравнении № 2 Мы получаем

QP = H ₂ – H ₁ = Δ H

QP = ΔH – —– 3

Уравнение №1 можно записать в виде:

ΔH = Δe + PΔV ———- 4

Уравнение №3 показывает, что теплота, поглощаемая или выделяемая системой при постоянном давлении, равна изменению энтальпии система.

Первое начало термодинамики формула и формулировка: Первое начало термодинамики формулировки – Справочник химика 21