Первообразная примеры: Вычисление первообразной функции — что это такое? - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Вычисление первообразной функции — что это такое?

Поможем понять и полюбить математику

Начать учиться

Какие ассоциации вызывает у вас понятие «первообразная»? Пожалуй, таким званием можно наградить супергероиню из популярного сериала: эта характеристика внушает трепет и уважение. Только представьте: «Первообразная, Королева дифференциалов из Дома Интегрированных, Властительница Констант и Производных». 👑

Поговорим мы сегодня именно об этой прекрасной даме: узнаем, что такое первообразная, как она связана с интегралами и производными, и что самое важное, как её рассчитать без особого труда.

Дифференцирование и интегрирование

Если проанализировать все математические действия, то большинству из них будет соответствовать какое-то обратное:

сложение обратно вычитанию,
умножение — делению,
возведение в степень — извлечению арифметического корня.

С производной то же самое: мы можем продифференцировать функцию, а можем произвести обратный процесс — интегрирование.

Дифференциация — операция взятия полной или частной производной функции.

Интегрирование — процесс поиска интеграла; восстановление функции по её производной.

Нахождение производной от функции обозначается знаком ′. Так, если исходная функция —

y, то её производная будет обозначаться y′.

Чтобы взять производную от функции, мы воспользуемся таблицей производных и правилами дифференцирования.

Функция f (x)	Производная f’ (х)
С (т. е. константа, любое число)	0
х	1
xⁿ	nx^n-1
√x	1/(2√x)
sin x	cos x
cos x	-sin x
tg x	1/cos²(х)
ctg x	-1/sin²x
e^x	e^x
a^x	a^x * ln a
ln x	1/x
log_ax	1/(x * ln a)

Правила дифференцирования

(c ⋅ f)′ = c ⋅ f′

(u + v)′ = u′ + v′

(u – v)′ = u′ – v′

(u ⋅ v)′ = u′v + v′u

(u/v)’ = (u’v – v’u)/v²

u, v, f — это функции, а c — константа (любое число).

У интегрирования тоже есть своё обозначение — ∫. То есть если мы хотим взять интеграл от функции f(x), мы запишем это так: ∫f(x) dx.

Внимательные заметили в записи интегрирования непривычное для нас «dx». Что это такое? Зачем добавлять эти буквы в выражение для интеграла? Сейчас во всём разберёмся!

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Дифференциал

Разберём буквы dx по отдельности:

d — это дифференциал,
х — функция, по которой будет произведено дифференцирование.

Так, если мы дифференцируем функции y, f, m, то их дифференциалы запишем соответственно как dy, df, dm.

Дифференциал в математике (от лат. differentia — разность, различие) — линейная часть приращения функции.

То есть это понятие родственно производной — но для чего его записывать рядом с интегралом?

Для понимания важности дифференциала в записи рассмотрим рисунок:

Геометрический смысл интеграла — это площадь фигуры под кривой функции. Если поместить график в декартову систему координат OХY, то эту площадь можно рассчитать относительно и оси ОХ, и оси ОУ, и именно дифференциал вносит ясность в выбор.

Понятие дифференциала в математике очень важное, глубокое, имеет множество нюансов использования, но сейчас нам важно понимать две вещи:

дифференциал показывает, какую конкретно функцию мы будем интегрировать;
его обязательно нужно записывать рядом с интегралом!

Что такое первообразная?

Пришло время познакомиться с её величеством первообразной! Начнём с определения.

Первообразная для функции f(x) — это такая функция F(x), производная которой равна f(x). То есть выполняется равенство F'(x) = f(x).

Пример 1: мы знаем, что ускорение является производной от скорости. Тогда по нему можно найти скорость, восстановив функцию и найдя его первообразную.

Пример 2: производная функции –sin(x). Посмотрим внимательно в таблицу производных: cos'(x) = –sin(x). Тогда первообразная функции sin(x) будет равна –cos(x) + С с учётом постоянной величины.

Константа

Зачем добавлять константу к первообразной?

Представьте, что нам необходимо найти производную функций:

−cos(x) + 3,
−cos(x) + 5,
−cos(x) − 6.

Тогда производная будет равна sin(x) для всех трёх вариантов, так как производная любого числа равна нулю:

(−cos(x) + 3)’ = sin (x),
(−cos(x) + 5)’ = sin (x),
(−cos(x) − 6)’ = sin (x).

Выходит, что получить исходную функцию в первозданном виде невозможно, но учесть дополнительное слагаемое в виде числа нам нужно. Именно поэтому в первообразной добавляют константу «+ С». Выражение, которое имеет общий вид F(x) + С, называется множеством первообразных функции.

Отсюда вытекает свойство первообразной: любые две первообразные одной и той же функции отличаются друг от друга не более чем на постоянную величину C.

Правила нахождения первообразной

Нахождение первообразной функции технически связано с поиском неопределённого интеграла функции.

Неопределённый интеграл — это интеграл, для которого не задан промежуток интегрирования.

Важный момент: если продифференцировать можно любую функцию, то найти первообразную функции можно не всегда.

Об этом говорит достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.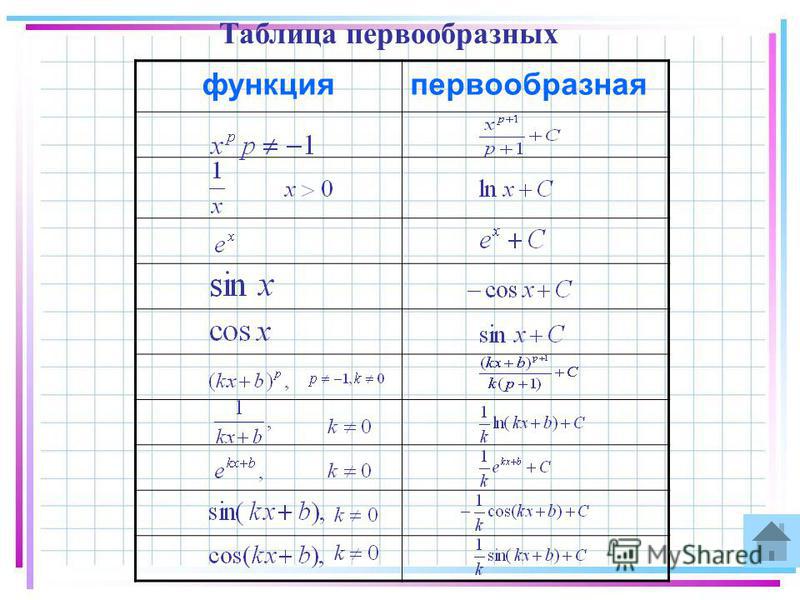

Каким образом можно найти первообразную функцию? Всё просто! Как и в случае с производной, мы можем воспользоваться готовой таблицей первообразных и свойствами неопределённого интеграла!

«Высокий» логарифм:
«Длинный» логарифм:

Свойства неопределённого интеграла

Свойства неопределённого интеграла можно назвать правилами интегрирования — основываясь на них, мы сможем находить первообразную сложных функций, сводя их к лёгким.

Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:
Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
Константу можно вынести из-под знака интеграла: то есть, если , то .
Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:

Примеры решения заданий

Задание 1

Найди первообразную функции

Записываем неопределённый интеграл:
Применяем свойство неопределённого интеграла об алгебраической сумме функций:
Выносим константы за знак интеграла:
Проводим интегрирование согласно таблице первообразных:

Задание 2

Вычисли неопределенный интеграл

Раскрываем скобку по формуле квадрата суммы и вносим х в скобку:
Воспользуемся свойством неопределенного интеграла об алгебраической сумме функций, выносим константы за знак интеграла и находим первообразную:

Интегрирование и нахождение первообразной — одна из самых сложных, но одновременно интересных тем алгебры.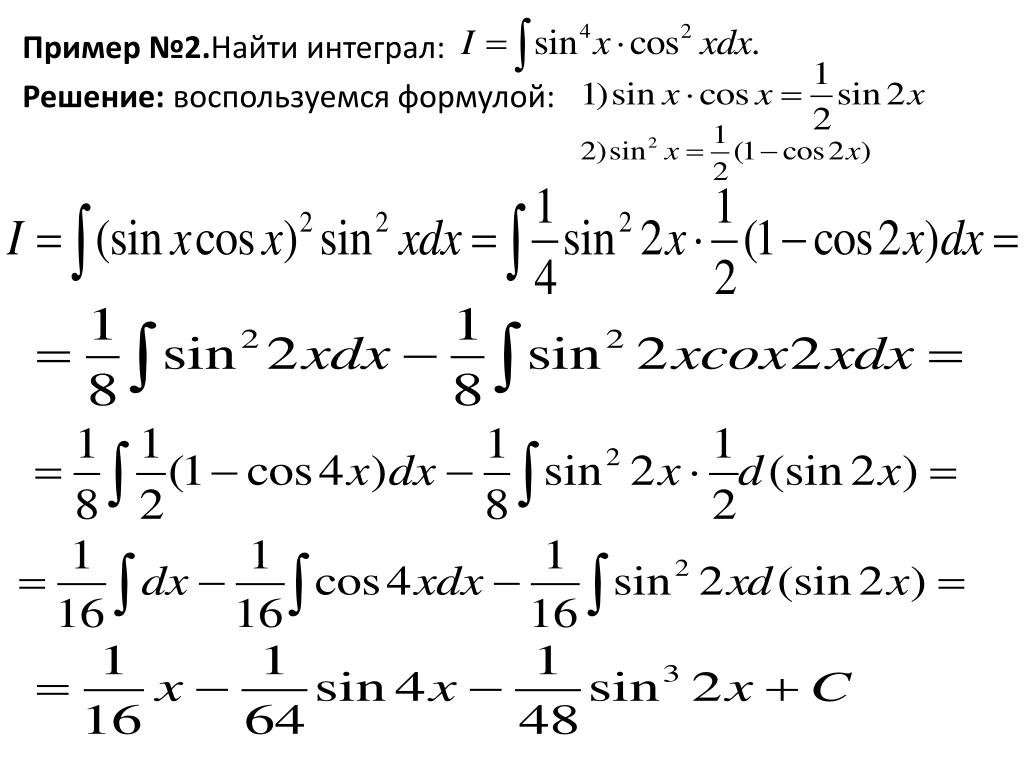 Иногда задания похожи на головоломку: необходимо выбрать верный способ решения, учесть все нюансы, выполнить верные вычисления. Научиться выполнять такие задания можно на уроках онлайн-курса математики в школе Skysmart: там вы не только подготовитесь к экзаменам, но и научитесь находить нестандартные решения, мыслить логически и строить самые неопровержимые доказательства.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Нахождение наибольшего и наименьшего значения функции

К следующей статье

Как подготовиться к ЕГЭ по математике

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

определение, неопределенный интеграл и его свойства, таблица, примеры

Понятие первообразной

Основное свойство первообразной.

2\) является первообразной для $f(x)=2x$, т.к. для любого $x$ производная $F'(x)=f(x)$.
2) Функция $F(x)=cos⁡x$ является первообразной для $f(x)=sin⁡x$, т.к. для любого $x$ производная $F'(x)=f(x)$.

Поиск производной данной функции называют дифференцированием.
Поиск первообразной данной функции называют интегрированием.
Дифференцирование и интегрирование являются взаимно обратными операциями.

п.2. Основное свойство первообразной. Неопределенный интеграл

Каждая первообразная для функции $f(x)$ имеет вид $F(x)+C$, где $F(x)$ – одна из этих первообразных, $C$ – произвольная постоянная.

Действительно, по правилу нахождения производной суммы: $$ (F(x)+C)’=F'(x)+C’=f(x)+0=f(x) $$ Т.е. первообразная определена с точностью до константы.

Например:

Для $f(x)=sin⁡x$
Первообразными будут \begin{gather*} F(x)=cos⁡x,\ F(x)=cos⁡x+1, \\ F(x)=cos⁡x-2,\ F(x)=cos⁡x+0,100500 \end{gather*} и т.д.

Множество всех первообразных функции $f(x)$ называют неопределенным интегралом этой функции: $$ \int f(x)dx=F(x)+C $$

Например: $$ \int x^2 dx=\frac{x^3}{3}+C,\ \ \int \frac{dx}{\sqrt{x}}=2\sqrt{x}+C $$

п.

6}{3}-cosx+C\)

Постоянный множитель функции является постоянным множителем первообразной.
Если $F(x)$ является первообразной для $f(x)$,
то $kF(x)$ – первообразная для $kf(x)$.

Действительно $$ \left(kF(x)\right)’=kF'(x)=kf(x) $$
Например:
Найдем первообразную функции $y=5sinx+2=5\cdot sinx+2\cdot 1$
Первообразная для синуса $F_1(x)=-cosx$, первообразная для единицы $F_2(x)=⁡x$
Общая первообразная
$F(x)=-5cosx+2x$

Линейное преобразование аргумента функции.
Если $F(x)$ является первообразной для $f(x)$,
то для функции с аргументом $f(kx+b)$ – первообразной будет $\frac1k F(kx+b)$.

Действительно
Для $x$ получаем цепочку отображений: $x\rightarrow kx+b\rightarrow F(kx+b)$
По правилу дифференцирования сложной функции (см. §45 данного справочника) \begin{gather*} \left(\frac1k F(kx+b)\right)’=\frac1k\cdot F'(kx+b)\cdot (kx+b)’=\frac1k\cdot F'(kx+b)\cdot k=F'(kx+b)=\\ =f(kx+b) \end{gather*}
Например:
Найдем первообразную функции $y=sin(5x+2) $
Нам известно, что первообразная для $f(x)=sin⁡x,\ F=-cos⁡x$
При преобразовании аргумента $x\rightarrow 5x+2$ у новой первообразной будет новый аргумент и множитель $\frac1k=\frac15$. 4-4x+4\frac14 $$

Правила первообразных – список, формулы, примеры

Правила первообразных в исчислении являются основными правилами, которые используются для нахождения первообразных различных комбинаций функций. Как следует из названия, антидифференцировка — это процесс, обратный дифференцировке. Эти первообразные правила помогают нам найти первообразную суммы или разности функций, произведение и частное функций, скалярное кратное функции и постоянной функции, а также композицию функций. Правила первообразных помогают нам сделать процесс нахождения первообразных проще и проще.

Далее в этой статье мы приступим к подробному изучению первообразных правил. Мы также рассмотрим первообразные правила некоторых важных и конкретных функций вместе с некоторыми решенными примерами для лучшего понимания концепции.

1.	Что такое первообразные правила?
2.	Список антипроизводных правил
3.	Основные антипроизводные правила
4.	Первообразные правила для конкретных функций
5.	Часто задаваемые вопросы об антипроизводных правилах

Что такое первообразные правила?

Правила первообразных являются одними из важных правил для нахождения первообразных различных форм комбинаций функций. Мы можем использовать эти правила первообразных, чтобы найти первообразные произведения, частного, суммы, разности, скалярного кратного и композиции функций. Эти правила можно использовать для антидифференцирования алгебраических функций, экспоненциальной функции, тригонометрических функций, гиперболических функций, логарифмической функции и постоянной функции. Давайте рассмотрим важные правила первообразных в разделах ниже.

Список первообразных правил

Список наиболее часто используемых первообразных правил для произведения, частного, суммы, разности и композиции функций выглядит следующим образом:

Степенное первообразное правило
Антипроизводное цепное правило
Антипроизводное правило произведения
Правило первообразных частных
Правило первообразной для скалярного кратного функции
Правило первообразной суммы и разности функций

Основные антипроизводные правила

В этом разделе мы подробно рассмотрим формулы для различных правил первообразных, рассмотренных выше. Мы обсудим правила антидифференцирования алгебраических функций со степенью и различные комбинации функций. Правила первообразных являются общими для типов функций, таких как тригонометрические, экспоненциальные, логарифмические и алгебраические функции.

Правило первообразной степени

Теперь правило первообразной степени x определяется как ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C, где n ≠ -1. Это правило широко известно как правило первообразной мощности. Давайте рассмотрим некоторые примеры этого первообразного правила, чтобы лучше понять это правило.

∫x ² dx = x ²⁺¹ /(2+1) + C = x ³ /3 + C
∫x ^-4 dx = x ^-4+1 /(-4+1) + C = x ^-3 /(-3) + С = -х ^-3 /3 + С

Используя правило степени первообразной, мы можем заключить, что для n = 0 имеем ∫x ⁰ dx = ∫1 dx = ∫dx = x ⁰⁺¹ /(0+1) + C = x + C. Пожалуйста, не путайте это правило степенной первообразной ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C, где n ≠ -1, со степенным правилом производной d(x ⁿ )/dx = nx ^n-1 .

Правило первообразной цепи

Мы знаем, что антидифференцировка — это процесс, обратный дифференцированию, поэтому правила производных приводят к некоторым первообразным правилам. Цепное правило производных дает нам цепное правило первообразных, также известное как метод антидифференцирования u-подстановки. Цепное правило первообразных используется, если интеграл имеет вид ∫u'(x) f(u(x)) dx. Давайте посмотрим на пример и решим интеграл, используя это правило первообразной.

Пример: Решить ∫2x cos (x ² ) dx

Решение: Предположим, что x ² = u ⇒ 2x dx = du. Подставим это в интеграл, получим

∫2x cos (x ² ) dx = ∫cos u du

= sin u + C

= sin (x ² ) + C 9077 Правило 9 Антипроизводная

Правило первообразного произведения также обычно называют методом интегрирования по частям. Это одно из важных правил антипроизводных, которое используется, когда необходимо определить антидифференцирование произведения функций. Формула правила первообразного произведения: ∫f(x).g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) [ ∫g(x) dx)]dx + C , Выбор первой функции осуществляется на основе приведенной ниже последовательности. Этот метод также широко известен как метод интегрирования ILATE или LIATE, сокращенно:

I – Обратная тригонометрическая функция
L – Логарифмическая функция
А – Алгебраическая функция
T – Тригонометрическая функция
E – Экспоненциальная функция

Например, нам нужно найти первообразную x ln x. Тогда, в соответствии с приведенной выше последовательностью, первая функция — это ln x, а вторая функция — это x. Следовательно, имеем

∫x ln x dx = ln x ∫x dx – ∫[(ln x)’ ∫x dx] dx

= (x ² /2) ln x – ∫(1/x)(x ² /2) dx

= (x ² /2) ln x – ∫(x/2) dx

= (x ² /2) ln x – x ² /4 + C

Правило первообразных частных

Правило первообразных частных используется, когда функция представлена в виде числителя и знаменателя. Если в состав функции входят алгебраические функции, то можно использовать интегрирование дробями методом антидифференцирования. Другой способ определить первообразную отношения функций — рассмотреть функцию вида f(x)/g(x). Теперь, дифференцируя это, мы имеем,

d(f(x)/g(x))/dx = [f'(x)g(x) – g'(x)f(x)]/[g(x)] ²

Теперь, интегрируя обе части приведенного выше уравнения, мы имеем

f(x)/g(x) = ∫{[f'(x)g(x) – g'(x)f(x)]/[g (x)] ² } dx

= ∫[f'(x)/g(x)] dx – ∫[f(x)g'(x)/[g(x)] ² ] dx

⇒ ∫[f'(x)/g(x)] dx = f(x)/g(x) + ∫[f(x)g'(x)/[g(x)] ² ] dx

Если f(x) = u и g(x) = v, то мы имеем правило антидеривативных частных как:

∫du/v = u/v + ∫[u/v ² ] dv

Правило первообразной для скалярного кратного функции

Чтобы найти первообразную скалярного кратного функции f(x), мы можем найти ее, используя формулу, заданную ∫kf(x) dx = k ∫ f(x)dx. Это означает, что антидифференциация kf(x) равна k, умноженной на антидифференциацию f(x), где k — скаляр. Пример использования этого правила первообразной:

∫4x dx = 4 ∫xdx

= 4 × x ² /2 + C

= 2x ² + C

Правило первообразной суммы и разности

Это правило является одним из самых простых первообразных правил. Когда необходимо определить антидифференцирование суммы и разности функций, то это можно сделать, используя следующие формулы:

∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x)dx
∫[f(x) – g(x)] dx = ∫f(x) dx – ∫g(x) dx

Вот некоторые примеры правила первообразной суммы и разности функций:

∫[4 + x ² ] dx = ∫4 dx + ∫x ² dx = 4x + x ³ /3 + C
∫(sin x – log x) dx = ∫sin x dx – ∫ log x dx = -cos x – x log x + x + C

Первообразные правила для конкретных функций

Чтобы использовать правила первообразных, мы должны знать первообразные некоторых определенных функций, таких как экспоненциальная функция, тригонометрические функции, логарифмические функции, гиперболические функции и обратные тригонометрические функции. Пройдемся по правилам первообразных для этих функций:

Правила первообразных для тригонометрических функций

У нас есть шесть основных тригонометрических функций, а именно синус, косинус, тангенс, котангенс, секанс и косеканс. Теперь мы исследуем их первообразные правила этих тригонометрических функций следующим образом:

∫sin x dx = -cos x + C
∫cos x dx = sin x + C
∫tan x dx = ln |sec x| + С
∫cot x dx = ln |sin x| + С
∫sec x dx = ln |sec x + tan x| + С
∫csc x dx = ln |cosec x – кроватка x| + С

Правила первообразных для обратных тригонометрических функций

У нас есть шесть основных обратных тригонометрических функций, а именно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс и арккосеканс. Теперь мы исследуем их первообразные правила этих тригонометрических функций следующим образом:

∫sin ^-1 x dx = x sin ^-1 x + √(1 – x ² ) + C
∫cos ^-1 x dx = x cos ^-1 x – √(1 – x ² ) + C
∫tan ^-1 x dx = x tan ^-1 x – (1/2) ln(1 + x ² ) + C
∫cot ^-1 x dx = x cot ^-1 x + (1/2) ln(1 + x ² ) + C
∫сек ^-1 x dx = x сек ^-1 x – ln |x + √(x ² – 1)| + С
∫csc ^-1 x dx = x csc ^-1 x + ln |x + √(x ² – 1)| + С

Правила первообразных для показательных функций

Показательная функция имеет вид f(x) = a ^x , где a — основание (действительное число), а x — переменная. Когда a равно числу Эйлера e, тогда мы имеем f(x) = e ^x, где e — константа, значение которой приблизительно равно 2,718. Теперь первообразные правила для этих двух форм показательных функций таковы:

∫a ^x dx = a ^х /лн а + С
∫e ^x dx = e ^x + C [Поскольку ln e = 1]

Правила первообразных для логарифмических функций

Логарифмическая функция обычно имеет вид f(x) = log _a x, где a — основание, а x — переменная. Если основание a равно числу Эйлера e, то она называется функцией натурального логарифма и записывается как f(x) = ln x. Правила первообразной для логарифмической функции:

∫log _a x dx = x log _a x – x/ln a + C
∫ln x dx = x ln x – x + C

Правила первообразия для гиперболических функций

Теперь гиперболические функции аналогичны тригонометрическим функциям, но они выводятся с использованием гиперболы, а не единичного круга, как в случае тригонометрических функций. Шесть основных гиперболических функций — это sinh x, ch x, tanh x, coth x, sech x и csch x. Правила первообразных гиперболических функций:

∫sin x dx = ch x + C
∫кош х дх = ш х + С
∫tanh x dx = ln (ch x) + C
∫coth x dx = ln (sinx x) + C
∫sech x dx = arctan(sinx) + C
∫csch x dx = ln(tanh (x/2)) + C

Важные замечания по правилам первообразных

Правила первообразных используются для нахождения первообразных различных комбинаций алгебраических, тригонометрических, логарифмических, экспоненциальных, обратных тригонометрических и гиперболических функций.
Большинство правил дифференцирования имеют соответствующие первообразные правила для антидифференцирования.
Правило первообразной для постоянной функции f(x) = k имеет вид ∫k dx = kx + C.

☛ Статьи по теме:

Первообразная формула
Первообразная Ln x
Интегральное исчисление

Часто задаваемые вопросы об антипроизводных правилах

Что такое первообразные правила в исчислении?

Правила первообразных — это некоторые из важных правил исчисления, которые используются для нахождения первообразных различных форм комбинаций функций. Эти первообразные правила помогают нам найти первообразную суммы или разности функций, произведение и частное функций, скалярное кратное функции и постоянной функции, а также композицию функций.

Как использовать цепное правило первообразной производной?

Цепное правило первообразных используется, если интеграл имеет вид ∫u'(x) f(u(x)) dx. Он широко известен как метод антидифференцировки с u-замещением. Обычно мы заменяем функцию u(x), предполагая, что это другая переменная.

Каковы обычно используемые первообразные правила?

Наиболее часто используемые первообразные правила для произведения, частного, суммы, разности и композиции функций следующие:

Правило первообразной степени
Антипроизводное цепное правило
Антипроизводное правило произведения
Правило первообразных частных
Правило первообразной для скалярного кратного функции
Правило первообразной суммы и разности функций

Каковы первообразные правила для триггерных функций?

Правила первообразия шести тригонометрических функций следующие:

∫sin x dx = -cos x + C
∫cos x dx = sin x + C
∫tan x dx = ln |sec x| + С
∫cot x dx = ln |sin x| + С
∫sec x dx = ln |sec x + tan x| + С
∫csc x dx = ln |cosec x – кроватка x| + С

Как использовать первообразные правила для экспоненциальных функций?

Правила первообразия для двух форм показательных функций:

∫a ^x dx = a ^x /ln a + C
∫e ^x dx = e ^x + C

Что такое правило первообразного произведения?

Формула правила первообразного произведения: ∫f(x). g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) [ ∫g(x) dx)]dx + C где нам нужно найти первообразную произведения двух или более функций.

4.10 Первообразные | Исчисление, том 1

Цели обучения

Найти общую первообразную заданной функции.
Объясните термины и обозначения неопределенного интеграла.
Сформулируйте правило степени для интегралов.
Используйте антидифференцирование для решения простых задач с начальными значениями.

К этому моменту мы увидели, как вычислять производные многих функций, и познакомились с различными их приложениями. Теперь мы задаем вопрос, который переворачивает этот процесс: если задана функция [latex]f[/latex], как нам найти функцию с производной [latex]f[/latex] и почему нам может быть интересна такая функция ?

Мы отвечаем на первую часть этого вопроса, определяя первообразные. Первопроизводная функции [latex]f[/latex] — это функция с производной [latex]f[/latex]. {\prime}(t)[/latex], определение функции положения требует, чтобы мы нашли первообразную функции скорости. Прямолинейное движение — это только один случай, когда возникает необходимость в первообразных. В оставшейся части текста мы увидим еще много примеров. А пока давайте рассмотрим терминологию и обозначения первообразных и определим первообразные для нескольких типов функций. Мы рассматриваем различные методы нахождения первообразных более сложных функций во втором томе этого текста (Введение в методы интегрирования).

На данный момент мы знаем, как находить производные различных функций. Теперь мы задаем противоположный вопрос. Учитывая функцию [latex]f[/latex], как мы можем найти функцию с производной [latex]f[/latex]? Если мы можем найти функцию [latex]F[/latex] с производной [latex]f[/latex], мы называем [latex]F[/latex] первообразной функции [latex]f[/latex].

Определение

Функция [латекс]F[/латекс] является первообразной функции [латекс]f[/латекс], если

[латекс]F^{\prime}(x)=f(x )[/латекс] 9{\prime}(x)[/latex], тогда [latex]F(x)-G(x)=C[/latex] для некоторой константы [latex]C[/latex]. Этот факт приводит к следующей важной теореме.

Общая форма первообразной

Пусть [latex]F[/latex] будет первообразной [latex]f[/latex] на интервале [latex]I[/latex]. Затем,

для каждой константы [latex]C[/latex], функция [latex]F(x)+C[/latex] также является первообразной [latex]f[/latex] над [latex]I [/латекс];
, если [latex]G[/latex] является первообразом [latex]f[/latex] над [latex]I[/latex], существует константа [latex]C[/latex], для которой [latex]G (x)=F(x)+C[/latex] над [latex]I[/latex]. 9{\prime}(x)[/latex] или [latex]\frac{df}{dx}[/latex] для обозначения производной от [latex]f[/latex]. Здесь мы вводим обозначения для первообразных. Если [латекс]F[/латекс] является производной от [латекс]f[/латекс], мы говорим, что [латекс]F(x)+C[/латекс] является наиболее общей производной от [латекс]f[/ латекс] и напишите
[латекс]\int f(x) dx=F(x)+C[/латекс].
Символ [латекс]\int [/латекс] называется знаком интеграла , а [латекс]\int f(x) dx[/латекс] называется неопределенным интегралом из [латекс]ф[/латекс]. 2+С [/latex], пишем 9{\prime}(x)[/latex]
для любого действительного числа [latex]k[/latex], мы заключаем, что
[latex]\int kf(x) dx=kF(x)+C[/ латекс].
Эти свойства приведены ниже.
Свойства неопределенных интегралов
Пусть [латекс]F[/латекс] и [латекс]G[/латекс] являются первообразными [латекс]f[/латекс] и [латекс]g[/латекс] соответственно, и пусть [latex]k[/latex] будет любым вещественным числом.
Суммы и разности
[латекс]\int (f(x) \pm g(x)) dx=F(x) \pm G(x)+C[/latex]
Постоянные кратные
[латекс]\int kf(x) dx=kF(x)+C[/латекс]
С помощью этой теоремы мы можем вычислить любой интеграл, включающий сумму, разность или постоянное кратное функций с первообразные, которые известны. Вычисление интегралов, включающих произведения, частные или композиции, является более сложным (см. (Рисунок)b. пример, включающий первообразную произведения.) Мы рассматриваем интегралы, включающие эти более сложные функции, во Введении в интегрирование. В следующем примере мы исследуем, как использовать эту теорему для вычисления неопределенных интегралов нескольких функций. 92+x-7) dx[/латекс].
Показать решение
Ниже в тексте мы рассмотрим методы интеграции большого количества функций, включающих произведения, частные и композиции. Здесь мы обратимся к одному распространенному использованию первообразных, которое часто встречается во многих приложениях: решение дифференциальных уравнений.
Дифференциальное уравнение — это уравнение, связывающее неизвестную функцию и одну или несколько ее производных. Уравнение
[латекс]\frac{dy}{dx}=f(x)[/latex] 93+C[/латекс].
Иногда нас интересует, проходит ли конкретная кривая решения через определенную точку [latex](x_0,y_0)[/latex], то есть [latex]y(x_0)=y_0[/latex]. Задача нахождения функции [latex]y[/latex], удовлетворяющей дифференциальному уравнению
[latex]\frac{dy}{dx}=f(x)[/latex]
с дополнительным условием
[ латекс]y(x_0)=y_0[/latex]
является примером задачи с начальным значением . Условие [latex]y(x_0)=y_0[/latex] известно как 9{-2}, \, y(1)=2[/латекс].
Показать решение
Проблемы с начальными значениями возникают во многих приложениях. Далее рассмотрим задачу, в которой водитель нажимает на тормоз автомобиля. Нас интересует, через какое время автомобиль остановится. Напомним, что функция скорости [latex]v(t)[/latex] является производной функции положения [latex]s(t)[/latex], а ускорение [latex]a(t)[/latex] равно производная функции скорости. В более ранних примерах в тексте мы могли рассчитать скорость по положению, а затем вычислить ускорение по скорости. В следующем примере мы работаем наоборот. Учитывая функцию ускорения, мы вычисляем функцию скорости. Затем мы используем функцию скорости для определения функции положения.
Замедление автомобиля
Автомобиль движется со скоростью 88 футов/сек (60 миль/ч) при включенных тормозах. Автомобиль начинает замедляться с постоянной скоростью 15 футов/сек ² .
1. Сколько секунд проходит до остановки автомобиля?
2. Какое расстояние проедет автомобиль за это время?
Показать решение
Предположим, что автомобиль движется со скоростью 44 фута/сек. Через какое время машина остановится? Какое расстояние проедет машина?
Показать ответ

Ключевые понятия
- Если [латекс]F[/латекс] является производной [латекс]f[/латекс], то каждая производная [латекс]f[/латекс] имеет вид [латекс] F(x)+C[/latex] для некоторой константы [latex]C[/latex].
- Решение задачи с начальным значением
  [латекс]\frac{dy}{dx}=f(x),y(x_0)=y_0[/латекс]
  требует, чтобы мы сначала нашли набор первообразных [латекс]f[/латекс], а затем искали конкретную первообразную, которая также удовлетворяет начальному условию. 9{-2x}- \sin x[/latex]
  45. Автомобиль движется со скоростью 40 миль в час при включенных тормозах. Автомобиль замедляется с постоянной скоростью 10 футов/сек ² . Через какое время машина остановится?
  Показать решение
  46. В предыдущей задаче подсчитайте, какое расстояние проедет автомобиль за время, необходимое для остановки.
  47. Вы выезжаете на шоссе, ускоряясь с постоянной скоростью 12 футов/сек ² . Сколько времени вам потребуется, чтобы достичь скорости слияния 60 миль в час?
  Показать решение
  48. Основываясь на предыдущей задаче, какое расстояние проедет автомобиль, чтобы достичь скорости слияния?
  49. Автомобильная компания хочет, чтобы ее новейшая модель могла останавливаться за 8 секунд при движении со скоростью 75 миль в час. Если мы предполагаем постоянное замедление, найдите значение замедления, обеспечивающее это.
  Показать решение
  50.