Первообразная с решением онлайн: Калькулятор Первообразной Функции – Symbolab

Первообразная – презентация онлайн

Похожие презентации:

Первообразная

Первообразная и интеграл

Первообразная

Первообразная. Геометрический смысл первообразной

Первообразная. Интеграл

Первообразная функции. Неопределенный интеграл

Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл

Первообразная. Интеграл

Дифференциальное и интегральное исчисление

Первообразная функция. Неопределенный интеграл

1. Первообразная

Определение производной функции?
Производной функции в данной точке называется
предел отношения приращения функции в этой точке к
приращению аргумента, когда приращение аргумента ,
стремиться к нулю.
Устная работа
1
сosх
sinх+12
Устная работа
Используя определение производной функции,
решают ряд задач в алгебре, физике, химии.
Рассмотрим физический смысл производной.
материальная
точка
s(t) закон
движения
Задача:
Точка движется прямолинейно по закону
s(t) = t3+ 2t ( где s(t) – измеряется в м).
Найдите скорость точки в момент времени t=2с.
Решение:
v(t) = 3t2 + 2
v(2) =
Ответ: 14 м/с.
Что мы сделали за часть урока?
Повторили определение производной функции и
формулы дифференцирования.
Решили задачу на применение производной:
зная закон движения, нашли скорость при
заданном времени.
В математике часто приходиться решать
обратную задачу:
зная скорость найти закон движения.
Задача: По прямой движется материальная точка,
скорость которой в момент времени t задается
формулой v(t) = 3t2. Найдите закон движения.
Решение: Пусть s(t) – закон движения

надо найти функцию,
производная которой
равна 3t2 .
Эта задача решена верно, но не полно.
Эта задача имеет бесконечное множество решений.
3t2
3t2
3t2
3t2
можно сделать вывод, что
любая функция вида
s(t)=t3+C является
решением данной задачи,
где C любое число.
При решении задачи, мы, зная производную
функции, восстановили ее первичный образ.
Эта операция восстановления – операция
интегрирования.
Востановленная функция – первообразная
( первичный образ функции)
Операция
дифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
Определение первообразной
y = F(x) называют
первообразной для y = f(x) на
промежутке X, если при x ∈ X
F'(x) = f(x)
Операция
дифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
В математике много операций которые
являются обратными
32 = 9
?
?
Сегодня мы познакомились с новой операцией
интегрирование
? дифференцирование
Запомните: Первообразная – это родитель
производной:
f(x)
1
F(x)
Задача:
Найдите все первообразные
для функций:
f(х)=3
f(х)= х2
f(х)=cosx
f(х)=12
f(х)=х5
Три правила нахождения первообразных
Если функции у=f(x) и у=g(x) имеют на
промежутке
первообразные соответственно у=F(x) и у=G(x), то
Функция
Первообразная
у = f(x) + g(x)
у = F(x) + G(x)
Первообразная суммы равна сумме первообразных
у =k f(x)
у =k F(x)
Постоянный множитель можно выносить за знак первообразной
Найти первообразные для функции
f ( x) 5 x e
3
f(x)
2 x 7
F(x)
4
4 cos x
Решение:
Используя правила
нахождения
первообразных и
таблицу получим
x 1 2 x 7
F ( x) 5 e
4 sin x C
4 2
Для функции y=f(x) найдите хотя бы одну первообразную:

English     Русский Правила

Алгебра Первообразная

Материалы к уроку

Конспект урока

Первообразная

На прошлых занятиях вы познакомились с правилами нахождения производной функции, узнали о применении производной для исследования функции на монотонность и экстремум; научились находить касательную к графику функции. Вспомним правила вычисления производных: Производная любого числа равна нулю. Производная икса равна единице. Производная ка икс плюс эм равна ка. Производная единицы, делённой на икс, равна минус единице, делённой на икс в квадрате. Производная корень из икс равна единице, делённой на два корень из икс. Производная синуса икс равна косинус икс. Производная косинуса икс равна минус синус икс. Производная икс в степени эн равна эн, умноженное на икс в степени эн минус один.	Формулы дифференцирования:
Иногда приходится решать и обратные задачи, к примеру, восстановить закон движения по известной скорости. В математике принято взаимно обратным операциям присваивать специальные названия. Например, операция, обратная умножению, — это деление. Операция извлечения квадратного корня обратна возведению в квадрат. Процесс нахождения производной заданной функции называется дифференцированием, а операция, обратная ей, — интегрированием (процесс  нахождения функции по данной производной).	Взаимно обратные операции: Сложение-вычитание; Умножение-деление; Извлечение квадратного корня–возведение в квадрат;   Дифференцирование–интегрирование (нахождение функции по данной производной).
То есть функцию, выступающую как бы родоначальником для производной данной функции, принято называть первообразной. Определение: функцию игрек равное эф большое от икс называют первообразной для функции игрек равное эф малое от икс на заданном промежутке икс большое, если для любого икс, принадлежащего данному промежутку, выполнено равенство Промежуток, которому принадлежит  икс, обычно не указывают, но подразумевают.
Рассмотрим примеры. 1.Функция игрек, равное икс в квадрате, является первообразной для функции игрек, равное два икс, так как для любого икс справедливо равенство: производная икс в квадрате равна два икс. 2. Функция игрек, равное икс в кубе, является первообразной для функции игрек, равное три икс в квадрате,  так как для любого икс справедливо равенство: производная икс в кубе равна три икс в квадрате. 3.Функция игрек, равное синус икс, является первообразной для функции игрек, равное косинус икс, так как для любого икс выполняется равенство: производная синуса икс равна косинус икс. 4.Функция игрек, равное корень из икс, является первообразной для функции игрек, равное один, делённое на два корень из икс, на промежутке от нуля до бесконечности, так как для любого икс больше нуля выполняется равенство: производная корень из икс равна единице, делённой на два корень из икс.
Зная формулы для нахождения производных, не сложно составить таблицу первообразных: 1. Первообразная нуля равна константе. 2.Первообразная единицы равна икс. 3.Первообразная для икс равна икс в квадрате, делённое на два. 4. Первообразная для функции икс в степени эн, эн принадлежит множеству натуральных чисел, равна икс в степени эн плюс один, делённое на эн плюс один. 5.Первообразная для функции один, делённое на икс в квадрате, равна минус один, делённое на икс. 6.Первообразная для функции один, делённое на корень из икс равна два корень из икс, причём икс больше нуля. 7. Первообразная для функции синус икс равна минус косинус икс. 8. Первообразная для функции косинус икс равна синус икс. 9. Первообразная для функции один, делённое на синус в квадрате икс, равна минус котангенс икс. 10. Первообразная для функции один, делённое на косинус в квадрате икс, равна тангенс икс.
Рассмотрим примеры на нахождение первообразной различных функций. Задание 1 Доказать, что функция является первообразной для функции , если первообразная функции равна икс в шестой степени, сама функция равна шесть икс в пятой степени. Решение: 1. По определению первообразной, функцию игрек, равное эф большое от икс, называют первообразной для функции игрек, равное эф малое от икс, на заданном промежутке икс большое, если для любого икс, принадлежащего данному промежутку, выполнено равенство 2. Найдём производную эф большое по формуле нахождения производной степенной функции , она равна шесть икс в пятой степени. Мы получили равенство двух выражений, значит, по определению первообразной, функция эф большое, равная икс в шестой степени, является первообразной для функции эф малая, равной шесть икс в пятой степени.	Пример 1.
Задание 2 Для функции (игрек, равное эф от икс малое) найти первообразную, если  (эф от икс равно минус один, делённое на икс в кубе). Решение: 1.По определению степени с целым отрицательным показателем представим выражение минус один, делённое на икс в кубе, в виде: минус икс в минус третьей степени.   2. По формуле нахождения первообразной степенной функции, найдём первообразную для функции эф от икс, равное минус икс в минус третьей степени. Получим, минус икс в степени минус три плюс один, делённое на минус три плюс один. Упрощая выражение, имеем минус икс в степени минус два, делённое на минус два, сократив минусы, получаем: икс в степени минус два, делённое на два. По определению степени с целым отрицательным показателем представим выражение в виде: один, делённое на два икс в квадрате. Таким образом, первообразной для функции эф от икс малое, равной минус один, делённое на икс в кубе, является функция эф большое, равная один, делённое на два икс в квадрате.	Пример 2.

 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Калькулятор первообразных с шагами – Калькулятор интегралов

Содержание

---

Калькулятор первообразных с шагами

Калькулятор первообразных находит первообразную функции шаг за шагом по переменной, т. е. з . Этот онлайн-калькулятор интеграции также поддерживает верхнюю границу и нижнюю границу , если вы работаете с минимальным или максимальным значением интервалов.

С помощью этого интегрального калькулятора вы можете получить пошаговые вычисления:

• Определенный интеграл
• Неопределенный интеграл

Он может найти интегралы логарифмических, а также тригонометрических функций. Этот инструмент оценивает входную функцию и использует интегральные правила для вычисления интегралов площади, объема и т. д.

Как работает калькулятор первообразной производной?

 Вы можете найти первообразную (интеграл) любой функции, выполнив следующие действия.

• Выберите вариант определенный или неопределенный .
• Введите функцию в данное поле ввода.
• Нажмите кнопку Загрузить пример , если вы хотите использовать образец примера.
• Укажите переменную. По умолчанию установлено значение x .
• Введите верхнюю границу и нижнюю границу , если выше был выбран определенный интеграл .
• Нажмите Вычислить   кнопка. Вы получите результат с пошаговыми расчетами.

Вы можете скачать решение, нажав на иконку.

Что такое интеграл?

Интеграл может быть определен как

«Интеграл присваивает числа функциям таким образом, который описывает объем, площадь, перемещение и другие идеи, возникающие при объединении бесконечно малых данных”.

Процесс нахождения интегралов называется интегрированием. Интеграл также называют первообразной, потому что это обратная операция вывода.

Наряду с дифференцированием интегрирование является важной операцией исчисления и служит инструментом для решения задач в математике и физике, связанных с длиной кривой, объемом твердого тела и площадью произвольной формы среди других.

Интеграл функции F ( x ) относительно реальной переменной x На интервале [A, B] написан как: [A, B] .2+C\)

Часто задаваемые вопросы

Каков интеграл от 1/x?

Интеграл от 1/x является абсолютным значением: ln ( |x |) + C. 90 Это стандартное значение интегрирования.

В чем разница между определенным и неопределенным интегралом?

Определенный интеграл обозначает число, верхняя и нижняя границы которого являются постоянными. С другой стороны, неопределенный интеграл — это семейство функций, производные которых равны 92

Ссылки

1. Что такое первообразная? с правилами, формулами и примерами из Study.com
2. Интегральное определение Openstax.org

Исчисление I — константа интегрирования

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. 4} – 9{- 1}} + с\]

Мы также склонны играть быстро и свободно с константами интегрирования в некоторых задачах правил подстановки. Рассмотрим следующую задачу:

\[\int{{\cos\left({1 + 2x} \right) + \sin\left({1 + 2x} \right)\,dx}} = \frac{1}{2}\int{ {\ cos u + \ sin u \, du}} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} u = 1 + 2x \]

Технически при интеграции мы должны получить

\[\int{{\cos\left({1 + 2x} \right) + \sin\left({1 + 2x} \right)\,dx}} = \frac{1}{2}\left( {\ грех ты – \ соз и + с} \ справа) \]

Поскольку весь интеграл умножается на \(\frac{1}{2}\), весь ответ, включая постоянную интегрирования, следует умножить на \(\frac{1}{2}\). Умножив \(\frac{1}{2}\) на ответ, мы получим

\[\int{{\cos\left({1 + 2x} \right) + \sin \left({1 + 2x} \right)\,dx}} = \frac{1}{2}\sin u – \frac{1}{2}\cos u + \frac{c}{2}\]

Однако, поскольку константа интегрирования является неизвестной константой, деление ее на 2 не изменит этого факта, поэтому мы склонны просто записывать дробь как \(c\).

\[\int{{\cos\left({1 + 2x} \right) + \sin \left({1 + 2x} \right)\,dx}} = \frac{1}{2}\sin u – \frac{1}{2}\cos u + c\]

В общем, нам не нужно беспокоиться о том, как быстро и лузово мы сыграли с константой интегрирования в любом из двух приведенных выше примеров.

Настоящая проблема, однако, заключается в том, что из-за того, что мы играем быстро и свободно с этими константами интегрирования, большинство студентов на самом деле плохо их понимают и не понимают, что бывают моменты, когда константы интегрирования важны и что мы нужно быть осторожным с ними.

Чтобы увидеть, как непонимание константы интегрирования может вызвать проблемы, рассмотрим следующий интеграл.

\[\int{{\frac{1}{{2x}}\,dx}}\]

Это очень простой интеграл. Однако есть два способа (оба простые) интегрировать его, и именно здесь возникает проблема.

Первый метод интегрирования состоит в том, чтобы просто разбить дробь и вычислить интеграл.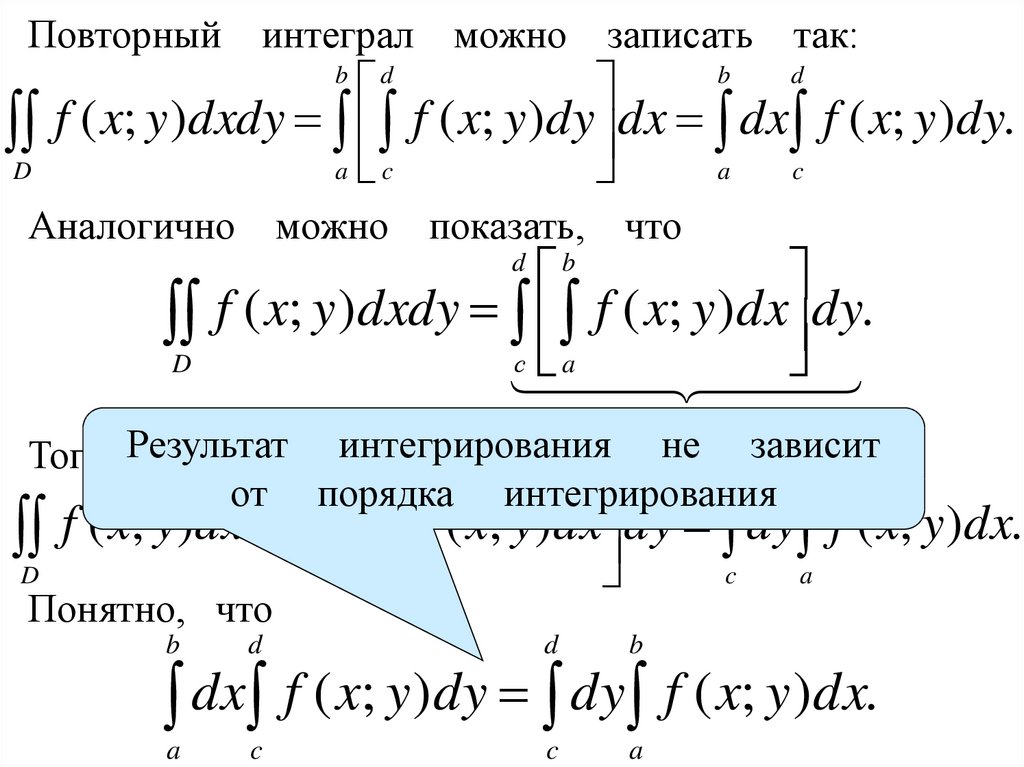

\[\int{{\frac{1}{{2x}}\,dx}} = \int{{\frac{1}{2}\frac{1}{x}\,dx}} = \frac {1}{2}\ln \left| х \ справа | + с\]

Второй способ заключается в использовании следующей замены.

\[u = 2x\hspace{0,25 дюйма}\hspace{0,25 дюйма}du = 2dx\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}\,\,dx = \frac{1}{2}du\ ] \[\int{{\frac{1}{{2x}}\,dx}} = \frac{1}{2}\int{{\frac{1}{u}\,du}} = \frac {1}{2}\ln \left| ты \право| + c = \frac{1}{2}\ln \left| {2x} \справа| + с\]

Вы видите проблему? Мы интегрировали одну и ту же функцию и получили очень разные ответы. Это не имеет никакого смысла. Интеграция той же функции должна дать нам тот же ответ. Мы использовали только разные методы для вычисления интеграла, и оба метода являются вполне допустимыми. Итак, как использование разных методов может привести к разным ответам?

Первое, что мы должны заметить, это то, что, поскольку мы использовали разные методы для каждого из них, нет оснований полагать, что константа интегрирования на самом деле будет одним и тем же числом, и поэтому мы действительно должны использовать разные буквы для каждого из них.

Более подходящими ответами были бы

\[\int{{\frac{1}{{2x}}\,dx}} = \frac{1}{2}\ln \left| х \ справа | + c \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ int {{\ frac {1} {{2x}} \, dx}} = \ frac {1 {2}\ln \влево| {2x} \справа| + к\]

Теперь давайте еще раз посмотрим на второй ответ. Используя свойство логарифмов, мы можем записать ответ на второй интеграл следующим образом:

\[\begin{align*}\int{{\frac{1}{{2x}}\,dx}} & = \frac{1}{2}\ln \left| {2x} \справа| + k\\ & = \frac{1}{2}\left( {\ln 2 + \ln \left| x \right|} \right) + k\\ & = \frac{1}{2}\ пер \ влево | х \ справа | + \frac{1}{2}\ln 2 + k\end{align*}\]

Сделав это, мы увидим, что ответы на самом деле не так уж и отличаются. На самом деле они отличаются только на константу, и мы даже можем найти связь между \(c\) и \(k\). Похоже,

\[c = \frac{1}{2}\ln 2 + k\]

Таким образом, без надлежащего понимания константы интегрирования, в частности, использование различных методов интегрирования для одного и того же интеграла, вероятно, даст другую константу интегрирования, мы никогда не сможем понять, почему мы получили «разные» ответы для интеграла.

Также обратите внимание, что получение ответов, отличающихся на константу, не нарушает никаких принципов исчисления. На самом деле, мы действительно видели факт, который предполагал, что это может произойти. Мы видели факт в разделе теоремы о среднем значении, который гласил, что если \(f’\left( x \right) = g’\left( x \right)\), то \(f\left( x \right) = g \влево( х \вправо) + с\). Другими словами, если две функции имеют одинаковую производную, то они могут отличаться не более чем на константу.

Это именно то, что у нас есть. Две функции,

\[f\left( x \right) = \frac{1}{2}\ln \left| x \right|\hspace{0,25 дюйма}\hspace{0,25 дюйма}\hspace{0,25 дюйма}\hspace{0,25 дюйма}\hspace{0,25 дюйма}g\left( x \right) = \frac{1}{2 }\ln\влево| {2x} \справа|\]

имеют точно такую ​​же производную,

\[\frac{1}{{2x}}\]

, и, как мы показали, на самом деле они отличаются только на константу.

Существует еще один интеграл, который также демонстрирует такое поведение. Считай,

\[\ int{{\sin\left(x\right)\cos\left(x\right)\,dx}}\]

На самом деле есть три разных метода вычисления этого интеграла.

Метод 1 :
В этом методе используется тригонометрическая формула

. \[\sin\left({2x}\right) = 2\sin\left(x\right)\cos\left(x\right)\]

Используя эту формулу (и быструю замену), интеграл становится равным

\[\int{{\sin\left(x\right)\cos\left(x\right)\,dx}} = \frac{1}{2}\int{{\sin\left({2x}) \right)\,dx}} = – \frac{1}{4}\cos \left( {2x} \right) + {c_1}\] 92}\left( x \right) + \frac{1}{4} + {c_1}\end{align*}\]

Это ответ, который мы получили от второго метода с немного другой константой. Другими словами,

\[{c_2} = \frac{1}{4} + {c_1}\]

Аналогичную манипуляцию мы можем проделать, чтобы получить ответ из третьего метода.