Конспект “Закон Архимеда” – УчительPRO
«Закон Архимеда. Плавание тел»
Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.
Закон Архимеда. На погружённое в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).
FА = pж • g • Vж = mж • g = Pж
где: FА — Архимедова сила, pж — плотность жидкости, g — ускорение свободного падения, Vж — объем жидкости, mж — масса жидкости, Pж — вес жидкости.
Плавание — это способность тела удерживаться на поверхности жидкости или на определённом уровне внутри жидкости. На любое тело, находящееся в жидкости, действуют две силы, направленные в противоположные стороны: сила тяжести и архимедова сила. Сила тяжести равна весу тела и направлена вниз, архимедова же сила зависит от плотности жидкости и направлена вверх.
Тело тонет, если рт > рж ; тело всплывает, если рт < рж .
Условие плавания тела на поверхности жидкости: для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой: Fв = М • g
Условие плавания тела на поверхности жидкости можно представить в виде рт • Vт = рж • Vж .

Конспект урока «Архимедова сила».
Следующая тема: «Сообщающиеся сосуды. Шлюзы».
Закон Архимеда
4.8 (96%) 5 vote[s]Закон Архимеда. Условие плавания тел | LAMPA
Выталкивающую силу называют силой Архимеда, а её формулу, которую мы только что вывели, – законом Архимеда:
FАрхимеда=ρжидкостиgVтелаF_{Архимеда} = \rho_{жидкости} gV_{тела}FАрхимеда=ρжидкостиgVтела
Обратите внимание на то, от каких величин зависит сила Архимеда.
1. От плотности жидкости. Чем плотнее жидкость, тем сильнее она будет выталкивать тело. Поэтому, например, в солёной морской воде плавать легче, чем в пресной речной.
2. От ускорения свободного падения. Фактически – от того, насколько сильно Земля притягивает. Можно сделать вывод, что на других планетах сила Архимеда будет другой – потому что там у ускорения свободного падения другие значения.
3. От объёма тела. Чем больше объём тела, тем сильнее его выталкивает жидкость. Вспомните, как легко удержать под водой маленький мячик (например, мячик для игры в настольный теннис) и как сложно сделать то же самое с большим надувным мячом для игр на пляже.
Закон Архимеда справедлив для тела любой формы – не только кубика. И в формуле будет использоваться объем погруженного тела.
В формуле фигурирует не объём всего тела, а только той его части, что погружена в воду.
То есть, если какая-то часть тела “выглядывает” из воды – она в формуле закона Архимеда не участвует.
lampa.io
Закон Архимеда • Джеймс Трефил, энциклопедия «Двести законов мироздания»
«Эврика!» («Нашел!») — именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда — то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, — и корабль плывет.
elementy.ru
Закон Архимеда ≪ ∀ x, y, z
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу вытесненной им жидкости.«Эврика!» («Нашел!») — именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
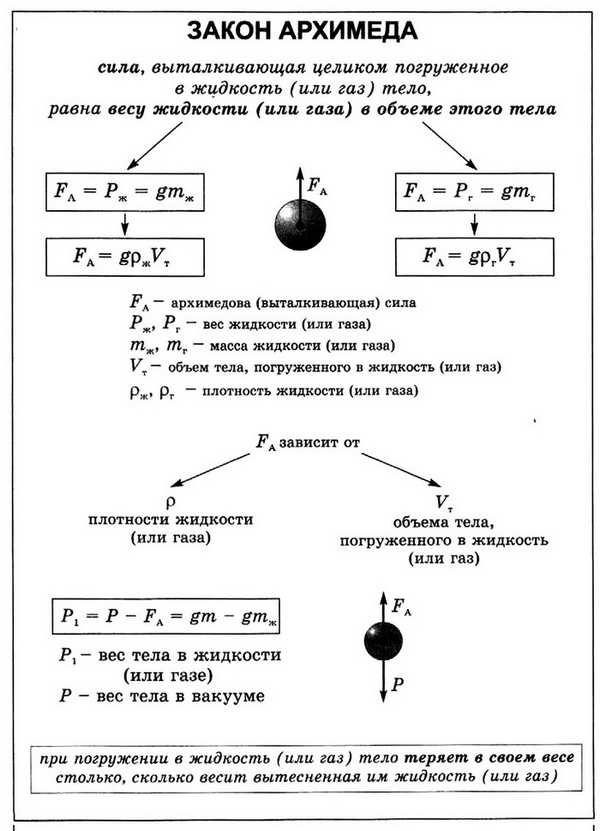
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими — например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни — такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит — вне водной среды животное не может передвигаться — его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос — почему тело плавает (а другое — тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые — тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
 Рис. 1. |
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине — очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью — это закон Паскаля.
Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены — они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть — глубина погружения верхней грани, — плотность жидкости, — ускорение силы тяжести; тогда давление на верхнюю грань равно
а на нижнюю.
Сила давления равна давлению, умноженному на площадь, т.е.,
,
где — ребро кубика, причем сила направлена вниз, а сила — вверх. Таким образом, действие жидкости на кубик сводится к двум силам — и и определяется их разностью, которая и является выталкивающей силой:
Сила — выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина равна объему тела (кубика) , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.
 Рис. 2. |
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема — тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема . Так как вес жидкости в объеме тела равен и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме , т.е. .
Сделав мысленно обратную замену — поместив в объеме данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема , можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.
Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» , т.е. веса единицы объема вещества: ; если принять, что для воды , то сплошное тело из вещества, у которого утонет, а при будет плавать на поверхности; при тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, — и корабль плывет.
Архимед из Сиракуз / Archimedes of Siracuse, ок. 287–212 г. до н. э.
Древнегреческий математик, изобретатель и натурфилософ. О его жизни известно мало. Доказал ряд основополагающих математических теорем, прославился благодаря изобретению различных механизмов, до сих пор находящих широкое применение как в быту, так и в оборонной промышленности. Легенда гласит, что Архимед умер насильственной смертью, пав от руки римского воина во время осады Сиракуз, не пожелав укрыться в доме, поскольку был всецело поглощен геометрической задачей, начертанной им на прибрежном песке.
forany.xyz
Архимед. Закон Архимеда – Блог Юрия Ретромана
 Архимед (287 до н.э. — 212 до н.э.) родился в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца.
Архимед (287 до н.э. — 212 до н.э.) родился в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца.
В теоретическом отношении труд этого великого ученого был блистателен. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. В сочинении «Параболы квадратуры» Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления.
В труде «Об измерении круга» Архимед впервые вычислил число «пи» — отношение длины окружности к диаметру — и доказал, что оно одинаково для любого круга. Мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел.
Любопытен отзыв Цицерона, великого оратора древности, увидевшего «архимедову сферу» — модель, показывающую движение небесных светил вокруг Земли: «Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть».
Архимед проверяет и создает теорию пяти механизмов, известных в его время и именуемых «простые механизмы». Это — рычаг («Дайте мне точку опоры, — говорил Архимед, — и я сдвину Землю»), клин, блок, бесконечный винт и лебедка.
Но Архимед знал также, что предметы имеют не только форму и измерение: они движутся, или могут двигаться, или остаются неподвижными под действием определенных сил, которые двигают предметы вперед или приводят в равновесие.
Великий сиракузец изучал эти силы и изобретал новую отрасль математики, в которой материальные тела, приведенные к их геометрической форме, сохраняют в то же время свою тяжесть. Эта геометрия веса и есть рациональная механика, статика, а также гидростатика.
Учение о гидростатике Архимед развивает в труде «О плавающих телах». «Предположим, — говорит ученый, — что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными и что каждая из ее частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком-нибудь сосуде и не сдавливается еще чем-нибудь другим». Полагаясь на это положение, Архимед математически доказывает, что следующие ниже «следствия» полностью объясняются с помощью приведенной гипотезы:
«1) Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости, и не будут двигаться вниз.
2) Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости.
3) Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной [части тела], имел вес, равный весу всего тела.
4) Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела.
5) Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».
Пункт 5 содержит фактически общеизвестный закон Архимеда, открытие которого позволило ему, согласно преданию, осуществить проверку состава короны сиракузского царя Гиерона. Знаменитый рассказ о первом практическом применении Закона Архимеда приведен у древнеримского автора Витрувия в его труде «Об архитектуре»:
«…Исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, — один из золота, другой из серебра. Сделав это, он наполнил водой сосуд до самых краев и опустил в него серебряный слиток, и вот, какой объем слитка был погружен в сосуд, соответственное ему количество вытекло воды. Вынув слиток, он долил в сосуд такое количество воды, на какое количество стало там ее меньше, отмеряя вливаемую воду секстарием, чтобы, как и прежде, сосуд был наполнен водой до самых краев. Так отсюда он нашел, какой вес серебра соответствует какому определенному количеству воды.
Произведя такое исследование, он после этого таким же образом опустил золотой слиток в полный сосуд. Потом, вынув его и добавив той же мерой вылившееся количество воды, нашел на основании меньшего количества секстариев воды, насколько меньший объем занимает слиток золота по сравнению с одинаково с ним весящим слитком серебра. После этого, наполнив сосуд и опустив в ту же воду корону, нашел, что при погружении короны вытекло больше воды, чем при погружении золотой массы одинакового с ней веса; и таким образом на основании того заключения, что короной вытеснялось большее количество воды, чем золотым слитком, он вскрыл примесь в золоте серебра и обнаружил явное воровство поставщика».
«В этом рассказе, — отмечает Я.Г. Дорфман, — убедительно лишь заключение Архимеда о том, что корона состоит из сплава, а не из чистого золота. Но ниоткуда не следует, что второй компонентой было обязательно серебро. Во всяком случае, следует отметить, что это выдающееся открытие Архимеда знаменует собой первое в истории применение физического измерительного метода к контролю и анализу химического состава без нарушения целостности изделия. Огромное практическое значение этого открытия в эпоху, когда еще никаких других методов подобного рода не было, естественно, привлекло к себе всеобщее внимание и стало предметом дальнейших исследований и практических использований на протяжении многих последующих веков.
По-видимому, и сам Архимед не ограничился описанным полукачественным экспериментом, а перешел к более точному количественному измерению. Автор арабского сочинения XII века «Книга о весах мудрости» ал-Хазини, цитируя «слово в слово» не дошедший до нас трактат грека Менелая, жившего во времена римского императора Домициана (81—96 гг. до н.э.), сообщает, что Архимед «изобрел механическое приспособление, которое благодаря своему тонкому устройству позволило ему определить, сколько золота и сколько серебра содержится в короне, не нарушая ее формы». Ал-Хазини приводит также схему устройства «весов Архимеда» с подвижным грузом.
Сравнивая на этом приборе веса упомянутых слитков в воде, Архимед мог с помощью подвижного груза определять численное отношение удельных весов золота и серебра, а, сопоставляя таким же способом веса короны и одного из этих слитков, мог установить относительное количество золота и серебра в короне (если в состав короны входили только эти два металла)».
Синезий из Кирэны в IV веке, ученик знаменитой александрийской ученой Ипатии, основываясь на принципах Архимеда, изобрел «гидроскоп» — ареометр для определения удельного веса жидкостей. Прибор, изготовленный из бронзы, имел насечки. По-видимому, этот прибор использовался для составления таблиц удельных весов различных жидкостей. К сожалению, подобные таблицы до нас не дошли.
По материалам книги “100 Великих Открытий”
Документальное видео о жизни Архимеда из проекта Энциклопедия
httpv://www.youtube.com/watch?v=Fz4lkEo3R7Y
retroman.ru
Kvant. Закон Архимеда — PhysBook
Чивилев В.И. Закон Архимеда //Квант. — 1987. — № 1. — С. 29-30.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
«…Удар сжатого воздуха хлопнул в трубах, вода в цистерне зажурчала, и глубомер пополз вверх. Лодка всплыла на ровном киле, и глубомер показал, что рубка уже вышла из воды»,— так описывается всплытие подводной лодки в книге Л. Соболева «Морская душа».
Причина всплытия — сила Архимеда, называемая еще выталкивающей силой, которая после продувки цистерн с водой сжатым воздухом превысила по модулю силу тяжести лодки. Когда же и в каком случае возникает сила Архимеда? Со стороны чего она действует? Куда приложена, как направлена и чему равна?
Выталкивающая сила — это сумма всех сил давления, действующих со стороны жидкости или газа на поверхность погруженного в нее тела (рис. 1). Истинная причина появления выталкивающей силы — наличие различного гидростатического давления на разных уровнях жидкости.
Рис. 1
Для нахождения силы Архимеда мысленно заменим погруженное тело жидкостью в объеме этого тела (рис. 2).
Рис. 2
На нее со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость (вытесненная жидкость) будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это — вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета (необязательно инерциальной), называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m(g + a). Это значит, что вес ящика равен Р = m(g + a), в то время как сила тяжести, действующая на ящик, равна mg. Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m(g – a).
Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями.
При доказательстве закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис. 3).
Рис. 3
Приведенная формулировка закона Архимеда остается справедливой и в случае, когда тело лишь частично опущено в жидкость, но не соприкасается со стенками сосуда. (Доказательство аналогично случаю полностью погруженного в жидкость тела.)
Нам осталось научиться находить вес вытесненной жидкости и линию действия выталкивающей силы. В общем случае (например, когда тело погружено в жидкость, вращающуюся вместе с сосудом) это не так легко сделать.
Рассмотрим наиболее простой и часто встречающийся на практике случай. Пусть сосуд с жидкостью неподвижен в некоторой инерциальной системе отсчета. Тогда, как известно, вес любого неподвижного тела равен силе тяжести, действующей на тело. Поэтому и выталкивающая сила равна по модулю силе тяжести, действующей на вытесненную жидкость, и противоположно ей направлена. Линия действия выталкивающей силы будет проходить через центр тяжести вытесненного объема жидкости. Покажем это.
На вытесненный объем жидкости массой m (рис. 4) действуют две силы — сила тяжести \(~m \vec g\), приложенная в центре тяжести этого объема, и выталкивающая сила \(~\vec F_B\). Так как жидкость находится в равновесии, то по правилу рычага (см. § 62 «Физики 6-7» или § 47 «Физики 8») действующие на нее силы обратно пропорциональны плечам этих сил. Плечо силы тяжести относительно оси, проходящей через центр тяжести, равно нулю. Значит, и плечо выталкивающей силы тоже равно нулю, т. е. линия действия выталкивающей силы проходит через центр тяжести «вытесненного» объема жидкости.
Рис. 4
Поскольку точку приложения силы можно переносить вдоль линии ее действия, обычно выталкивающую силу помещают в центр тяжести вытесненной жидкости и называют эту точку также центром давлений.
www.physbook.ru
Миф имени Архимеда (полный закон Архимеда)
Полный закон Архимеда
Мы живём в мире, где век географических открытий в мире может смениться веком открытий в самом себе. Для новых открытий в окружающем нас мире не нужно готовить экспедиции в неизведанные страны. Самая неизведанная страна это сам человек. Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Физика это одна из основных наук, изучающих природу. По своему определению это точная наука. Но законы физики пишут люди, и иногда им проще не описывать физический смысл законов, а старательно уходить от этого. Естественно, при изучении законов, составленных таким образом, возможно только механическое запоминание теоретического материала вместе с ошибками. Иногда процесс клонирования ошибок в основных законах физики длится тысячи лет. Подключение логики для усвоения таких знаний совершенно бесполезно. Может быть, поэтому некоторым ученикам, вполне успешным в изучении других предметов, с таким трудом даётся физика?
Для примера рассмотрим формулировку одного из основных законов физики – закон Архимеда. Закон Архимеда это первый закон физики, и он за 23 века своего существования должен был быть изучен до идеального состояния, однако этого не произошло. Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является основным законом раздела физики аэрогидростатики. Однако закон Архимеда не только не доведён до идеального состояния, но даже ещё не сформулирован. В этом законе отсутствует как формулировка, так и основное уравнение, без чего физических законов не бывает.
Всем известная формулировка: «на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной жидкости» является формулировкой правила Архимеда для определения выталкивающей силы. По описанию закона Архимеда в учебниках физики можно произвести расчёт Архимедовой силы для жидкостей и газов, но что потом с этой силой делать? Для решения практических задач знание только Архимедовой силы бесполезно.
Если нам нужно решить задачу по закону Архимеда, и узнать, что произойдёт с телом, погруженным в жидкость, нужен алгоритм решения задач. Более того, в описании закона Архимеда не хватает данных. Для того, чтобы узнать, что произойдёт с телом, нужно ещё знать объём тела и его вес.
Алгоритм решения задач по закону Архимеда не изложен в учебниках при описании самого закона, его предлагается усвоить решением большого количества примеров, где показывается буквально на пальцах, что делать с Архимедовой силой в одном случае, а что в другом. Этот подход значительно усложняет как преподавание закона Архимеда, так и его усвоение. Не проще ли один раз вывести формулу закона Архимеда, и решать все задачи одним способом, по одному алгоритму.
Для вывода формулы полного закона Архимеда рассмотрим общий случай тела, погруженного в выталкивающую среду.
На это тело действуют три силы:
Первая сила в формуле – архимедова сила , равная весу вытесненной среды.
Вторая сила – вес тела .
Но есть ещё третья сила, не очень известная в теории. Это архимедова сила, не задействованная для плавания тел – запас плавучести . В судостроении эта величина называется грузоподъёмностью.
Если к телу, не полностью погруженному в выталкивающую среду, добавить вес, по величине равный , тело полностью погрузится.
В этом случае тело будет уравновешенно в выталкивающей среде, и мы можем написать основное уравнение закона Архимеда.
,
Где – максимально возможная архимедова сила (в судостроении называется водоизмещением),
– архимедова сила, используемая для плавания (равна весу судна Р).
– запас плавучести (в судостроении называется грузоподъёмностью).
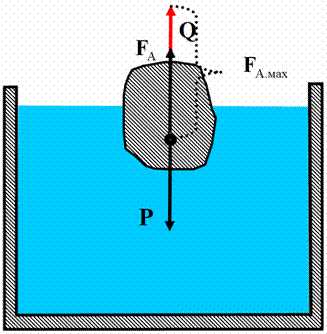
У не полностью погруженного тела запас плавучести .
Основное уравнение (формулу) закона Архимеда можно также составить относительно веса погруженного тела , равного и противоположного архимедовой силе , но смысла это не меняет.
Физическое определение полного закона Архимеда можно вывести из его основного уравнения: максимально возможная архимедова сила погруженного тела равна сумме архимедовой силы и запаса плавучести. Она также равна весу жидкости во всём объёме тела и противоположно ему направлена.
Без учёта запаса плавучести невозможно узнать конечный результат погружения тела в выталкивающую среду. Именно её величина определяет поведение погруженного тела в выталкивающей среде:
1) При погруженное тело висит неподвижно, или сохраняет направление своего движения (при отсутствии других сил).
2) При , погруженное тело всплывает (при отсутствии других сил).
3) При , погруженное тело тонет (при отсутствии других сил).
Строители кораблей на практике давно поняли, что закон Архимеда для плавания тел не полный. Они ввели в закон Архимеда для плавания судов понятие водоизмещения, имеющего смысл максимально возможной выталкивающей силы , грузоподъёмности , и собственного веса корабля , равного архимедовой силе и противоположно ей направленного.
Это показывает, что в судостроении давно пользуются формулой полного закона Архимеда. Однако эту формулу выводят каждый раз, исходя из здравого смысла. Это же самое делают и в школе. Не проще ли один раз вывести формулу закона Архимеда и потом ей пользоваться? Если при чтении возникают проблемы с открытием формулы закона Архимеда, полный закон Архимеда можно прочитать на http://sciteclibrary.ru/rus/catalog/pages/9433.html
drjukow.narod.ru
