| 1. |
Действие каких сил компенсируется?
Сложность: лёгкое |
1 |
| 2. |
Как движется вагон?
Сложность: лёгкое |
1 |
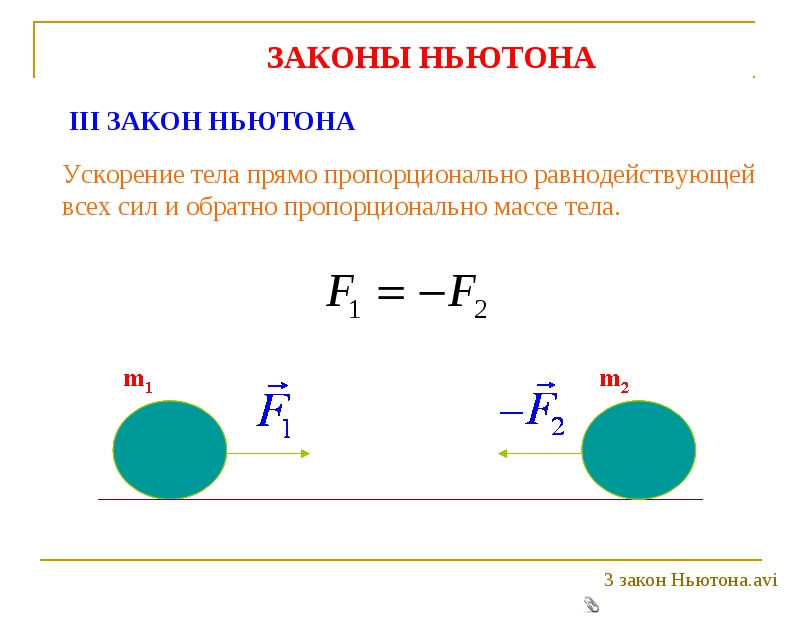
3.
|
Инерциальная система отсчёта
Сложность: лёгкое |
1 |
| 4. |
Вид движения
Сложность: среднее |
2 |
5.
|
Сила тяги двигателя лифта
Сложность: среднее |
2 |
| 6. |
Бусинка на нити
Сложность: среднее |
2 |
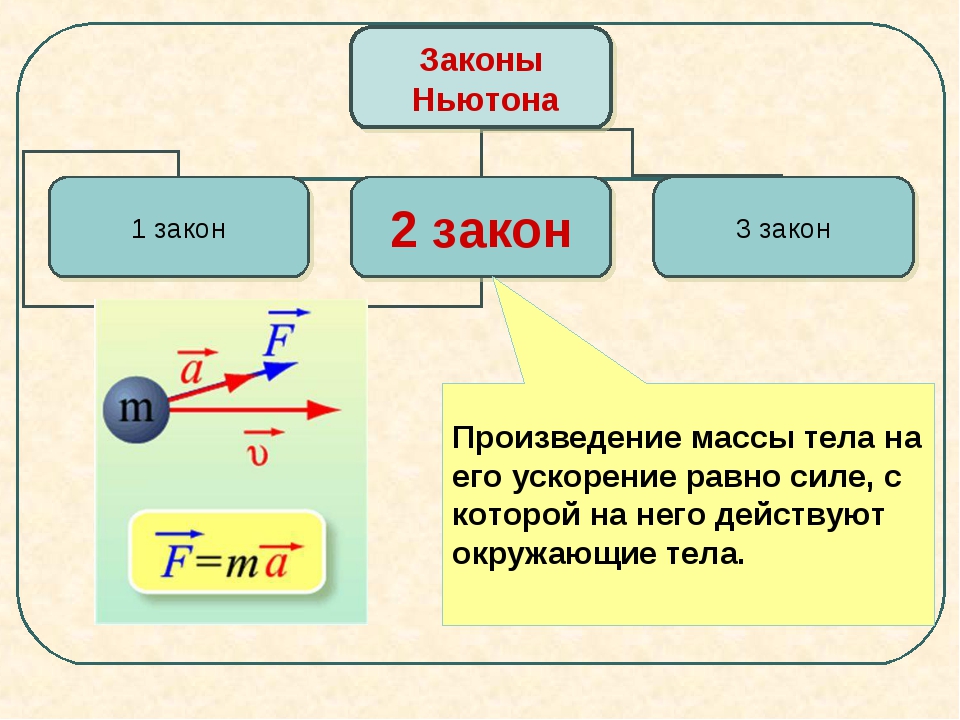
7.
|
Брусок и пружина
Сложность: сложное |
3 |
| 8. |
Шарик в жидкости
Сложность: сложное | 3 |
9.
|
Подъём груза на верёвке
Сложность: сложное |
3 |
Первый закон Ньютона | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Раздел: Законы классической механики
В основе механики лежат три постулата, сформулированные Ньютоном, впоследствии названные законами Ньютона. Все остальные утверждения ньютоновской механики являются математическими следствиями этих законов.
Очень важно, что эти законы касаются поведения тел в инерциальных системах отсчета. Соответственно все их следствия относятся также к поведению тел в инерциальных системах отсчета.
Первый закон Ньютона. Свободная частица (частица, на которую не действует сила) движется с постоянной скоростью или покоится.
Первый закон Ньютона предоставляет критерий инерциальности системы отсчета:
система отсчета, в которой свободная частица движется с постоянной скоростью, является инерциальной
Первый закон Ньютона является следствием второго. Фактически первый закон есть утверждение о существовании инерциальных систем отсчета.
Речь в первом законе Ньютона идет о частице, а не о протяженном теле потому, что скорости всех точек достаточно малой частицы можно считать одинаковыми. Это придает смысл понятию «скорость частицы». Материал с сайта http://worldofschool.ru
Это придает смысл понятию «скорость частицы». Материал с сайта http://worldofschool.ru
С античных времен до Галилея господствовало мнение, подкрепленное авторитетом Аристотеля, что естественным состоянием тела является состояние покоя и чтобы заставить тело двигаться, необходимо приложить силу. На этом фоне первый закон Ньютона выглядел очень сильным и далеко не очевидным утверждением. Хотя главная заслуга в осознании того, что свободная частица движется сама по себе с постоянной скоростью, принадлежит Галилею.
Первый закон ньютона. .шпора
Краткие лекции по теме законы ньютона
Механика ньютона кратко
Краткое доклад законы ньютона
Первый закон механики (первый закон Ньютона)
Первый закон Ньютона опровергнул традиционное схоластическое представление, основанное на физике Аристотеля, о том, что естественным состоянием материи является состояние покоя (с взглядами Аристотеля связано представление о так называемой косности материи).
Согласно первому закону Ньютона тело в инерциальной системе отсчета не может само по себе изменить своего состояния покоя или равномерного прямолинейного движения, это состояние оно изменяет только под действием других реальных тел. Следовательно, первый закон Ньютона отражает в рамках механики инерциальных систем причинную связь явлений. Опыт показывает, что ни одно явление природы не может возникнуть само по себе оно появляется лишь как следствие другого явления. Признание объективной причиной связи в природе является одним из основных положений диалектического материализма — основы нашего мировоззрения.
Как видно из предыдущего, в основу первого закона Ньютона положены представления о пространстве и времени, характерные для классической механики ( 30, 31). В частности, понятие о прямолинейности движения точки основывается на предварительном предположении, что физическое пространство является пространством Евклида. [c.218]
Как будет показано дальше ( 25), первый закон Ньютона не является самостоятельным законом, а представляет собой лишь частный случай второго закона Ньютона. Ньютон все же счел необходимым выделить этот частный случай и сформулировал его отдельно как первый закон механики , по-видимому, потому, что сама возможность движения тела в отсутствие сил, которые бы это движение поддерживали , до Ньютона вызывала сомнения. Чтобы подчеркнуть возможность движения тел в отсутствие действия сил и определить тот единственный тип движения, который в этих случаях возможен (равномерное и прямолинейное движение), Ньютон и сформулировал первый закон движения. Движение в отсутствие сил, о котором идет речь в этом законе, называют движением по инерции, и поэтому первый закон Ньютона часто называют законом инерции .
[c.72]
Движение в отсутствие сил, о котором идет речь в этом законе, называют движением по инерции, и поэтому первый закон Ньютона часто называют законом инерции .
[c.72]
Основными понятиями классической механики являются понятия о пространстве и времени, о силе и массе, об инерциальной системе отсчета. Основными законами являются закон инерции Галилея — Ньютона (первый закон Ньютона), уравнение движения относительно инерциальной системы отсчета (второй закон Ньютона), закон равенства действия и противодействия (третий закон Ньютона). Эти понятия и законы были сформулированы И. Ньютоном в его гениальном трактате Математические начала натуральной философии (1687). [c.7]
Это следствие так называемого второго из тех трех законов, которые положены Ньютоном в основу всей механики. Первый — закон инерции третий — закон противодействия. [c.24]
Замкнутые системы представляют собой абстрактные модели, родственные изолированной точке, к которой относится первый закон Ньютона.
 Примеры замкнутых систем можно найти в небесной механике и в физике.
[c.122]
Примеры замкнутых систем можно найти в небесной механике и в физике.
[c.122]Галилей первый (1638 г.) обнародовал закон инерциального движения тел. Этот закон Галилея Ньютон (1686 г.) сформулировал в более общей форме, приведенной нами в 3 и 36, и назвал первым законом механики. [c.256]
Основной принцип первый и второй законы Ньютона и классическом механики [c.53]
Утверждение, что инерциальные системы отсчета существуют, составляет содержание первого закона механики — закона инерции Галилея — Ньютона. [c.35]
Работами Ньютона (1643—1727) заканчивается по словам Ф. Энгельса первый период нового естествознания. Ньютон объединил, обобщил и обосновал современные ему достижения механики в своем выдающемся труде Математические начала натуральной философии (1687). В этой книге указаны основные положения классической механики. Огромным достижением Ньютона было установление закона всемирного тяготения. [c.21]
[c.21]
Многочисленные наблюдения над механическими движениями, анализ свойств этих движений и обобщающие выводы из этого анализа привели к установлению первого основного закона механики — закона инерции, или первого закона Ньютона ), который формулируется так [c.216]
Первый и второй законы механики Ньютона инвариантны относительно преобразований координат, обусловливающих переход от неподвижной системы координат к подвижной, движущейся поступательно, равномерно и прямолинейно относительно условно неподвижной. [c.230]
Определение массы, опирающееся на третий закон Ньютона, приводит к иной последовательности при изложении основных положений механики, отличающейся от изложенной выше. Эта последовательность в общих чертах такова за первым законом Ньютона рассматривается третий закон и определение массы и лишь после этого — второй закон Ньютона. [c.232]
Первой и важнейшей аксиомой этой группы надо полагать третий закон Ньютона ( 130), устанавливающий необходимость существования реакций связей. Мы рассмотрели содержание этого закона механики достаточно подробно и возвращаться здесь к нему не будем. Рассмотрим другие аксиомы о связях.
[c.239]
Мы рассмотрели содержание этого закона механики достаточно подробно и возвращаться здесь к нему не будем. Рассмотрим другие аксиомы о связях.
[c.239]
Законы Ньютона и законы сохранения. При выводе уравнений движения или покоя среды возможны два подхода. Первый — метод материальной частицы — заключается в составлении на основе второго закона Ньютона дифференциального уравнения движения (покоя) с последующим его интегрированием такой подход применяется главным образом в гидроаэромеханике. Второй — метод контрольных объемов — использует общие законы механики и физики (законы сохранения) для составления суммарных (интегральных) характеристик движения он характерен для гидравлики. [c.7]
Механика опирается на небольшое число основных законов, которые невозможно вывести непосредственно и к которым пришли длинным путем индукций. Полученные из них следствия подтверждаются наблюдениями. Первая идея этих законов принадлежит Галилею, который при исследовании законов падения тел (наклонная плоскость, маятник, параболическое движение) ввел понятия инерции, ускорения, сложения движений. Гюйгенс был продолжателем Галилея в теории движения точки. Он же первый изучал движение материальной системы. Наконец, Ньютон расширил область механики открытием закона всемирного тяготения.
[c.86]
Гюйгенс был продолжателем Галилея в теории движения точки. Он же первый изучал движение материальной системы. Наконец, Ньютон расширил область механики открытием закона всемирного тяготения.
[c.86]
Механика точки как наука была основана Галилеем в начале семнадцатого столетия и после его смерти развивалась Гюйгенсом. Основные принципы были установлены и сформулированы Ньютоном, чье великое сочинение Математические начала натуральной философии [1] появилось в 1687 г. В 1743 г. Даламбер [2] распространил законы Ньютона на задачи механики твердого тела. Основания аналитической механики были заложены Эйлером уже в 1736 г. [3], но выдающимся событием в ранней истории этой науки стал выход в свет Аналитической механики Лагранжа в 1788 г. [4]. Развитие аналитической механики со времен Лагранжа связано с именами многих прославленных математиков. Среди тех, кому принадлежат наиболее фундаментальные открытия в этой области, в первую очередь следует назвать Лапласа, Гамильтона, Якоби, Гаусса и Пуанкаре. [c.11]
[c.11]
Одной из трудностей, которые должна была преодолеть механика Ньютона, была проблема фигуры Земли. Не меньшие трудности возникали при изучении движения тел Солнечной системы и прежде всего Луны. Основанные на законе тяготения расчеты Клеро (1713—1765) и Даламбера, произведенные в 1745 г., дали для апогея лунной орбиты период обращения в 18 лет, величину, вдвое превосходившую данные наблюдений. Многие ученые полагали, что закон тяготения Ньютона нуждается в поправке так думали, в частности, Клеро и Эйлер. Некоторое время спустя, однако, Клеро пришел к заключению, что причиной расхождения теории с наблюдениями является не ошибочность закона Ньютона, а недостаточная точность применявшегося метода вычислений, при которых ограничивались первым приближением. Второе приближение уже давало результаты, согласные с наблюденными. В 1749 г. Клеро сообщил об этом Эйлеру. Для окончательного решения вопроса Эйлер, в то время живший в Берлине, рекомендовал Петербургской академии паук объявить конкурс на тему Согласуются или же нет все неравенства, наблюдаемые в движении Луны, с теорией Ньютона Предложение Эйлера было принято, и он вошел в состав жюри.
 В 1751 г. премия, на основании отзыва Эйлера, вполне убежденного вычислениями Клеро, была присуждена этому французскому ученому. Его Теория Луны, выведенная из одного только принципа притяжения, обратно пропорционального квадратам расстояний была издана на французском языке Петербургской академией наук (1752).
[c.189]
В 1751 г. премия, на основании отзыва Эйлера, вполне убежденного вычислениями Клеро, была присуждена этому французскому ученому. Его Теория Луны, выведенная из одного только принципа притяжения, обратно пропорционального квадратам расстояний была издана на французском языке Петербургской академией наук (1752).
[c.189]Архимеда, т. е. до времени Стевина (1548—1620), который в 1586 г. впервые занялся механикой наклонной плоскости, и Галилея (1564 — 1642), который сделал первое важное открытие в области кинематики. Таким образом механические принципы, относящиеся к движению тел, не были известны почти до нового времени. Основной ошибкой в рассуждениях большинства исследователей было их предположение о необходимости непрерывно действующей силы для поддержания движения тела. Они думали, что для тела более свойственно состояние покоя, чем движения, что противоречит закону инерции (первый закон Ньютона). Этот закон был открыт Галилеем совершенно случайно при изучении движения тел, скатывающихся по наклонной плоскости на горизонтальную поверхность.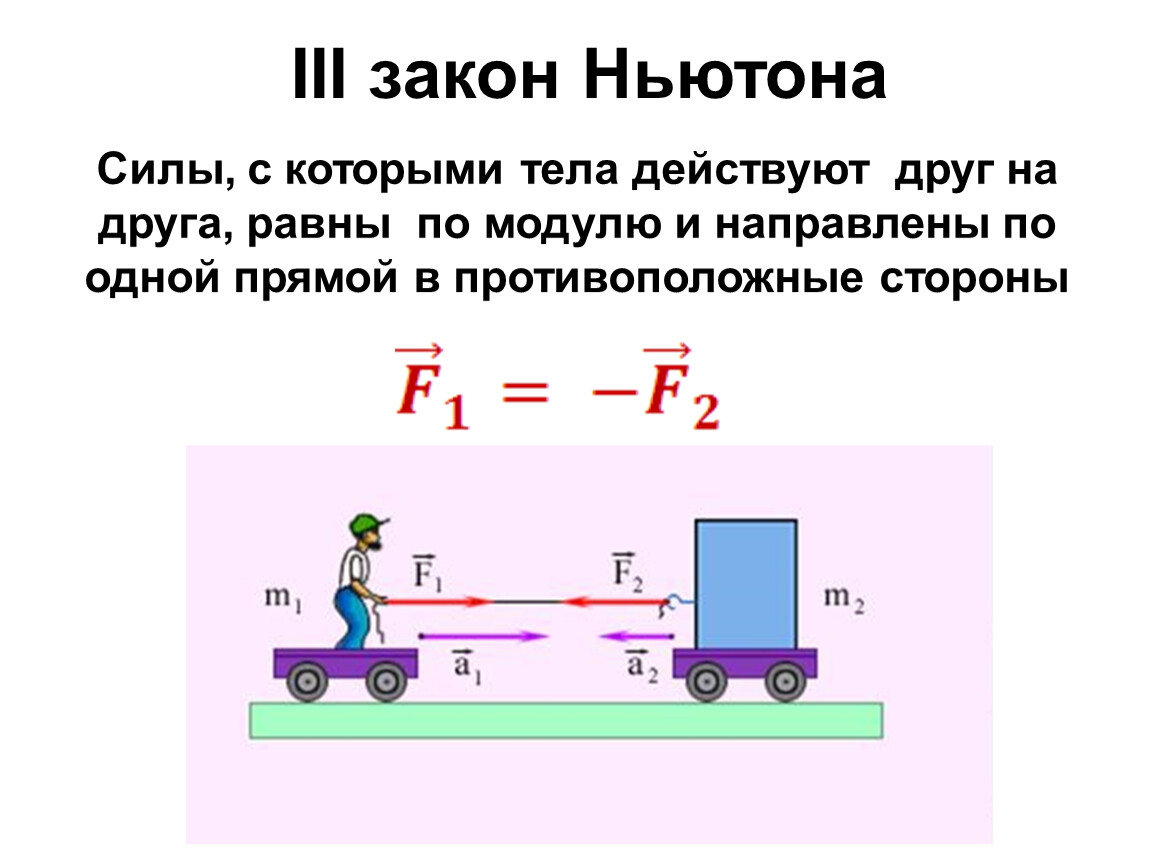 Галилей принял следующее основное положение изменение скорости или ускорение определяется силами, которые действуют на тело. Это положение содержит почти целиком два первые положения Ньютона. Галилей применил свои принципы с полным успехом при открытии законов падающих тел и законов движения снарядов. Благодаря своим открытиям он справедливо считается основателем динамики. Он первый применил маятник для измерения времени.
[c.43]
Галилей принял следующее основное положение изменение скорости или ускорение определяется силами, которые действуют на тело. Это положение содержит почти целиком два первые положения Ньютона. Галилей применил свои принципы с полным успехом при открытии законов падающих тел и законов движения снарядов. Благодаря своим открытиям он справедливо считается основателем динамики. Он первый применил маятник для измерения времени.
[c.43]
В механике Ньютона естественным движением в том смысле, как его понимал Аристотель, является прямолинейное равномерное движение материальной точки. В формулировке первого закона Ньютона устанавливаются условия, при которых это естественное движение (инерциальное) осуществляется. Он позволяет выбрать такую систему координат, в которой такие естественные движения существуют. Вторым законом Ньютона устанавливается, что сила об словливает не скорость материальной точки, а ее ускоре- [c.12]
Там же, с. 37. Одна и нанбопее совершенных о современной точки зрения формулировок первого закона Ньютона приведена в учебнике теоретической механики профессора С. М. Тарга Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя пли равпомерпото прямолинейного движения до тех нор, нот а приложенные силы но заставят ее изменить это состояние Тарг С. М. Краткий курс теоретической механики. М. Наука, 1970, с. 244). Тут же автор добавляет, что движение, совершаемое точкой при отсутствии сил, называется движением по инерции ,
[c.22]
М. Тарга Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя пли равпомерпото прямолинейного движения до тех нор, нот а приложенные силы но заставят ее изменить это состояние Тарг С. М. Краткий курс теоретической механики. М. Наука, 1970, с. 244). Тут же автор добавляет, что движение, совершаемое точкой при отсутствии сил, называется движением по инерции ,
[c.22]
ИНЕРЦИИ ЗАКОН (первый закон Ньютона) — см. Ньютона ваконы механики. [c.108]
В формулировке первого закона Ньютона устанавливаются условия, при которых это естественное движение (инерциальное) ос)шдествляется. Он дает возможность выбрать такую систему координат, в которой такие естественные движения существуют. Вторым законом Ньютона устанавливается, что сила обусловливает не скорость материальной точки, а ее ускорение, причем не вообще ускорение, а ускорение в той системе координат, в которой при отсутствии силы скорость тела была бы постоянной, т. е. движение было бы естественным . Как и в механике Аристотеля, сила учитывает влияние внешних условий на движение тела. Источниками силы являются материальные тела и, следовательно, сила является количественной мерой взаимодействия материальных тел. Третий закон Ньютона устанавливает, что сила, с которой одно из взаимодействующих тел действует на др тое, равна по абсолютной величине, но направлена противоположно силе, с которой это другое тело действует на первое.
[c.345]
е. движение было бы естественным . Как и в механике Аристотеля, сила учитывает влияние внешних условий на движение тела. Источниками силы являются материальные тела и, следовательно, сила является количественной мерой взаимодействия материальных тел. Третий закон Ньютона устанавливает, что сила, с которой одно из взаимодействующих тел действует на др тое, равна по абсолютной величине, но направлена противоположно силе, с которой это другое тело действует на первое.
[c.345]
Новый основной принцип прямейшего пути Герц сформулировал как эмпирический основной закон каждое естественное движение самостоятельной материальной системы состоит в том, что система движется с постоянной скоростью по одному из своих прямейших путей. Это положение объединяет обычный закон энергии и принцип наименьшего принуждения Гаусса в одно утверждение… Если бы связи были разрушены (на один момент), то массы рассеялись бы в прямолинейном и равномерном движении… Это первый и последний основной принцип механики. Из него и допущенной гипотезы скрытых масс дедуктивно выводится содержание механики [27]. В предложенном законе Герц усматривает также объединение первого закона Ньютона и принципа наименьшего принуждения Гаусса, а в числе преимуществ отмечает, что метод бросает яркий свет на разработанный Гамильто-
[c.85]
Из него и допущенной гипотезы скрытых масс дедуктивно выводится содержание механики [27]. В предложенном законе Герц усматривает также объединение первого закона Ньютона и принципа наименьшего принуждения Гаусса, а в числе преимуществ отмечает, что метод бросает яркий свет на разработанный Гамильто-
[c.85]
Почти во всех учебниках встречается утверждение, что первый закон Ньютона — закон инерций — был высказан уже Галилеем. Однако вни-дмательное чтение произведений Галилея этого не подтверждает более того, даже неизвестно, каким образом могло возникнуть такое представление. Так как Галилея, как механика, поднял на щит знаменитый Мах, то автор этих строк долгое время думал, что это представление принадлежит Маху однако последний в своей книге Механика в своем развитии (гл. II, 1, 8 стр. 140 немецкого издания 1901 г.) цитирует работу Вольвиля (1884 г.), показавшего, что предшественники Галилея и даже сам Галилей, лишь очень постепенно освобождаясь от аристотелевых представлений, дошли до понимания закона инерции .
 В своем пути Галилей остановился на стадии введенного Коперником принципа космической инерции, иными словами равномерного кругового движения тел, находящихся на поверхности Земли в своем естественном месте. Широко известна написанная Галилеем художественная картина поведения брошенных шаров, текущей воды, летающих бабочек и т. д. в каюте равномерно движущегося по спокойному морю корабля, но мало кто обращает внимание на то, что этот корабль в действительности движется по дуге большого круга Земли. Решающим местом в этом отношении является следующее. В начале четвертого дня Бесед и математических доказательств относительно двух новых наук Галилей утверждает (стр. 417 русского издания 1934 г.) Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления движению, то. движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца. Если же плоскость конечна…, то тело, имеющее вес, достигнув конца плоскости, продолжает двигаться далее таким образом, что к его первоначальному равномерному беспрепятственному движению присоединяется другое, вызываемое силой тяжести, благодаря чему возникает сложное движение, слагающееся из равномерного горизонтального и естественно ускоренного движений его я называю движением бросаемых тел .
В своем пути Галилей остановился на стадии введенного Коперником принципа космической инерции, иными словами равномерного кругового движения тел, находящихся на поверхности Земли в своем естественном месте. Широко известна написанная Галилеем художественная картина поведения брошенных шаров, текущей воды, летающих бабочек и т. д. в каюте равномерно движущегося по спокойному морю корабля, но мало кто обращает внимание на то, что этот корабль в действительности движется по дуге большого круга Земли. Решающим местом в этом отношении является следующее. В начале четвертого дня Бесед и математических доказательств относительно двух новых наук Галилей утверждает (стр. 417 русского издания 1934 г.) Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления движению, то. движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца. Если же плоскость конечна…, то тело, имеющее вес, достигнув конца плоскости, продолжает двигаться далее таким образом, что к его первоначальному равномерному беспрепятственному движению присоединяется другое, вызываемое силой тяжести, благодаря чему возникает сложное движение, слагающееся из равномерного горизонтального и естественно ускоренного движений его я называю движением бросаемых тел .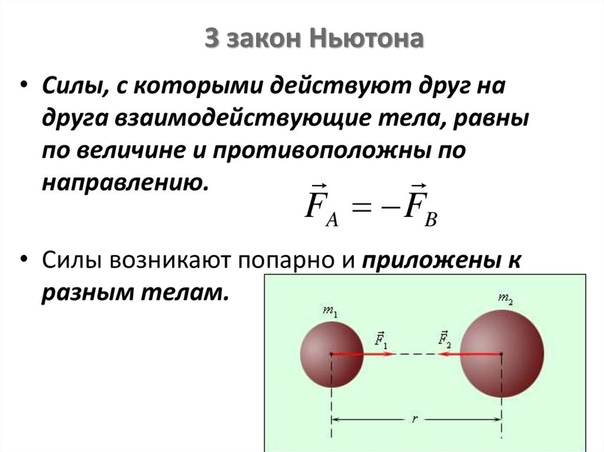 [c.84]
[c.84]Упомянутые выше критические выступления в печати по-видимому связаны с тем, что их авторы ошибочно отнесли понятие о коэффициенте восстановления к числу общих законов механики. Кроме того, они неверно представляют область явлений, подчиненных законам классической механики. Об этом свидетельствует выдержка из монографии Е. В. Александрова и В. Б. Соколинского Одни авторы, а их большинство, базируются на принципах классической механики Ньютона. Другие— исходят из основных положений теории упругости и опираются на теорию Сен-Венана. Первые считают, что тела абсолютно твердые… >. [c.20]
Иначе обстоит дело в релятивистской механике, обсуждаемой в следующей главе. Прерогатива в формировании критерия инерциальности системы отсчета в релятивистской механике переходит от уравнений Ньютона к уравнениям электродинамики Максвелла. В этом случае первый закон Ньютона превращается в самостоятельное и независимое необходимое условие инерциальности. Поэтому представляет большой интерес выяснение вопроса о том, как же связаны друг с другом те системы отсчета, которые удовлетворяют этому необходимому условию инерциальности.
[c.265]
Поэтому представляет большой интерес выяснение вопроса о том, как же связаны друг с другом те системы отсчета, которые удовлетворяют этому необходимому условию инерциальности.
[c.265]
Исходя нз представления об изменении количества движения окру- жающей тело жидкости, Ньютон получает квадратичный закон зависимости первой составляющей сопротивления от скорости. Что касается второй составляюш,еп сопротивления, зависящей от трения, то для ее определения Ньютон дал.ставшую классической формулу пропорциональности касательного напряжения трения в вязкой жидкости производной скорости по нормали к направлению потока. Формула эта обобщена на случай любого движения как несжимаемой жидкости, так и сжимаемого газа и служит основой современной механики вязкой жидкости. Сопротивление трения, но Ньютону, оказывается пропорциональным первой степени скорости, остальные составляющие сопротивления (упругость газа, силы сцепления в нем) Ньютон оценивает некоторой постоянной величшюй, вследствие чего для полного сопротивления получает трехчленную формулу, состоящую нз квадратичного члена, линейного члена и постоянного слагаемого. В настоящее время эта формула yлie не представляет интереса, но свою историческую роль она сыграла. Следует отметить, что Ньютои определял коэффициенты этой трехчленной формулы на основании ряда тщательно проведенных опытов.
[c.19]
В настоящее время эта формула yлie не представляет интереса, но свою историческую роль она сыграла. Следует отметить, что Ньютои определял коэффициенты этой трехчленной формулы на основании ряда тщательно проведенных опытов.
[c.19]
В этой главе будет рассмотрен ряд основных положений динамики, дающих возможность находить первые интегралы дифференциальных уравнений двилгения материальной точки. Эти положения динамики будем называть теоремами, так как они являются непосредственными следствиями из основных законов и аксиом механики. Заметим, что иногда эти теоремы называют также законами, но, конечно, при этом их надо четко отличать от основных законов механики — законов Ньютона. Основные теоремы динамики — это выводы в первую очередь из второго закона Ньютона, который поэтому называется основным законом механики. [c.359]
Наиболее простыми примерами, иллюстрирующими инвариантность законов механики, являются задачи, в которых применяется не сам второй закон Ньютона, а вытекающие из него законы сохранения импульса и энергии, применяемые для решения задачи об ударе. Это и понятно, так как в задачах об ударе мы не рассматриваем сил и ускорений и пользуемся только лишь формулами преобразования скоростей, связь между которыми устанавливается на рсновании законов сохранения. Первым таким примером может служить задача об абсолютно неупругом ударе, рассмотренная в 59. Действительно, из закона сохранения импульса при этом рассмотрении была получена формула преобразования скоростей (9.14), которая представляет собой частный случай общей формулы (9.48), вытекающей из преобразований Лорентца — Эйнштейна. Следовательно, если бы мы шли по обратному пути, т. е. применили бы формулу (9.48) к преобразованию скорости при переходе от системы /закон сохранения импульса соблюдается в системе К.
[c.294]
Это и понятно, так как в задачах об ударе мы не рассматриваем сил и ускорений и пользуемся только лишь формулами преобразования скоростей, связь между которыми устанавливается на рсновании законов сохранения. Первым таким примером может служить задача об абсолютно неупругом ударе, рассмотренная в 59. Действительно, из закона сохранения импульса при этом рассмотрении была получена формула преобразования скоростей (9.14), которая представляет собой частный случай общей формулы (9.48), вытекающей из преобразований Лорентца — Эйнштейна. Следовательно, если бы мы шли по обратному пути, т. е. применили бы формулу (9.48) к преобразованию скорости при переходе от системы /закон сохранения импульса соблюдается в системе К.
[c.294]
Мы оказались перед альтернативой. Либо мы должны предположить, что второй закон Ньютона справедлив не всегда, т. е. что в некоторых случаях ускорения вызываются не силами, а какими-либо другими причинами либо нужно предположить, что не всегда мы в состоянии указать то тело, со стороны которого действует данная сила.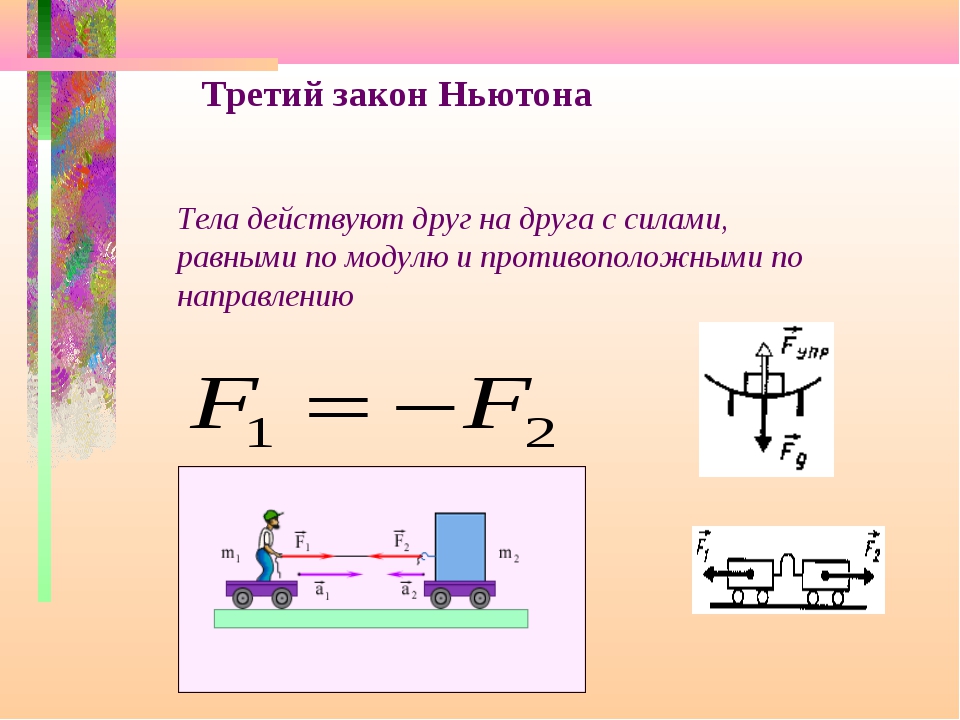 Но закон есть закон и должен соблюдаться всегда, в противном случае он перестает быть законом. Поэтому, если мы выберем первый пз альтернативных ответов, то второй закон Ньютона рухнет, а вместе с ним и вся механика Ньютона. Между тем второй альтернативный ответ, допускающий, что существуют такие силы, для которых мы не можем указать то конкретьюе тело, со стороны которого данная сила действует, хотя и требует существенного пересмотра некоторых положений механики Ньютона, но отнюдь не грознт ньютоновой механике катастрофой.
[c.335]
Но закон есть закон и должен соблюдаться всегда, в противном случае он перестает быть законом. Поэтому, если мы выберем первый пз альтернативных ответов, то второй закон Ньютона рухнет, а вместе с ним и вся механика Ньютона. Между тем второй альтернативный ответ, допускающий, что существуют такие силы, для которых мы не можем указать то конкретьюе тело, со стороны которого данная сила действует, хотя и требует существенного пересмотра некоторых положений механики Ньютона, но отнюдь не грознт ньютоновой механике катастрофой.
[c.335]
Через несколько лет Эдмунд Г аллей на основе третьего закона Кеплера пришел к выводу, что сила притяжения Солниа тоже должна уменьшаться обратно пропорционально квадрату расстояния планет от него, и пытался определить их пути. Не сумев этого сделать и не получив помощи от Гука и Рена, он поехал к Ньютону, у которого с удивлением обнаружил не только уже гото вое решение, но и еще немало важных материалов. Галлей предложил немедленно опубликовать их, но Ньютон, боясь новых споров и скандалов, только в 1686 г.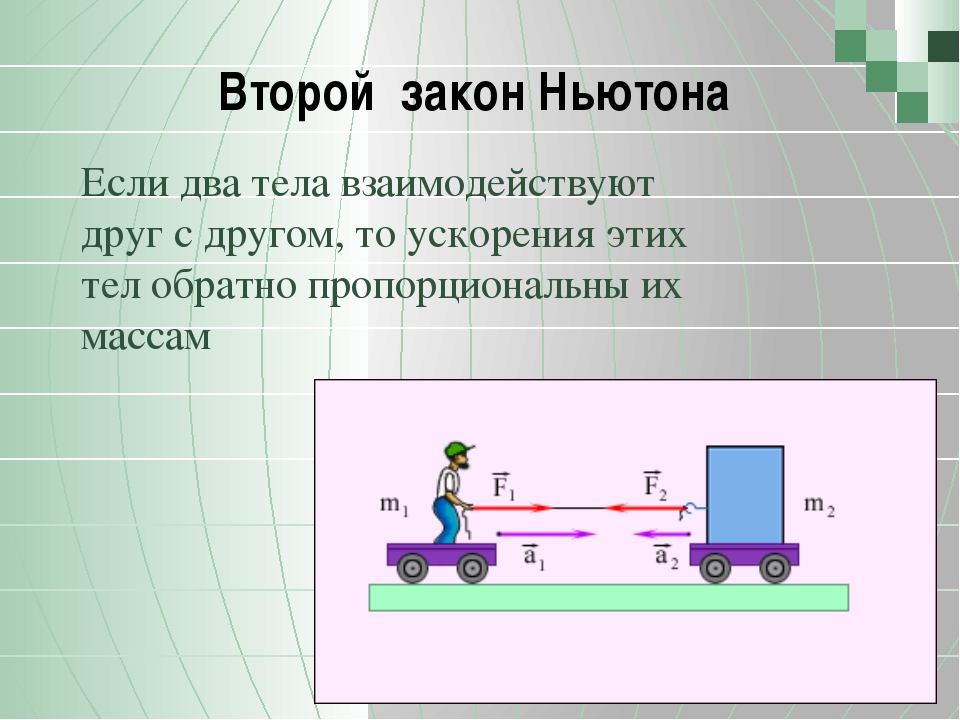 представил их в Королевское общество. Гук немедленно заявил, что Ньютон использовал его результаты. Ньютон ответил резким письмом Галлею, указав, что Гук сам черпает свои данные у Борелли, а возможно, и у него, поскольку еще в 1673 г. он писал о законе обратных квадратов Гюйгенсу через Королевское общество, секретарем которого был Гук. Наконец конфликт уладили, и в 1687 г. труд Ньютона в трех книгах вышел в свет под названием Математические начала натуральной философии . В нем упоминались имена Гука, Рена и Галлея. Первые две книги посвящены классической механике, в третьей законы механики применяются для описания системы мира — это небесная механика, неизбежно затрагивающая интересы официальной христианской идеологии. Ньютон долга не соглашался на издание третьей книги. 22 мая 1686 г. он писал Третью книгу я намерен теперь устранить, философия — это такая наглая и сутяжная дама, что иметь с ней дело — это все равно, что быть вовлеченным в судебную тяжбу .
[c.85]
представил их в Королевское общество. Гук немедленно заявил, что Ньютон использовал его результаты. Ньютон ответил резким письмом Галлею, указав, что Гук сам черпает свои данные у Борелли, а возможно, и у него, поскольку еще в 1673 г. он писал о законе обратных квадратов Гюйгенсу через Королевское общество, секретарем которого был Гук. Наконец конфликт уладили, и в 1687 г. труд Ньютона в трех книгах вышел в свет под названием Математические начала натуральной философии . В нем упоминались имена Гука, Рена и Галлея. Первые две книги посвящены классической механике, в третьей законы механики применяются для описания системы мира — это небесная механика, неизбежно затрагивающая интересы официальной христианской идеологии. Ньютон долга не соглашался на издание третьей книги. 22 мая 1686 г. он писал Третью книгу я намерен теперь устранить, философия — это такая наглая и сутяжная дама, что иметь с ней дело — это все равно, что быть вовлеченным в судебную тяжбу .
[c.85]
Во-первых, изменено название книги , вместо Основы аналитической механики дано название Теоретическая механика , что с точки зрения современной терминологии более отвечает содержанию книги.
 Затем, в изложение введены символы и операции векторного исчисления. В сбязи с этим вводная глава о векторах дополнена элементами векторной алгебры и анализа. Переход на векторное изложение- вызвал некоторые изменения в изложении кинематики, общих теорем динамики, динамики твёрдого тела и теории связей. Там, где это оказалось возможным сделать без нарушения стиля автора, терминология и обозначения приведены в соответствие с ныне употребляемыми. Уточнены некоторые доказательства и устранены встречающиеся иногда редакционные недосмотры и шероховатости текста. Переработано приложение Третий закон Ньютона имеющиеся здесь положения частично включены в гл. XIV Основные законы механики . Кроме того, исправлены ошибки в вычислениях, встречающиеся в некоторых примерах, а также несколько увеличено число чертежей (вместо 12й дано 155).
[c.659]
Затем, в изложение введены символы и операции векторного исчисления. В сбязи с этим вводная глава о векторах дополнена элементами векторной алгебры и анализа. Переход на векторное изложение- вызвал некоторые изменения в изложении кинематики, общих теорем динамики, динамики твёрдого тела и теории связей. Там, где это оказалось возможным сделать без нарушения стиля автора, терминология и обозначения приведены в соответствие с ныне употребляемыми. Уточнены некоторые доказательства и устранены встречающиеся иногда редакционные недосмотры и шероховатости текста. Переработано приложение Третий закон Ньютона имеющиеся здесь положения частично включены в гл. XIV Основные законы механики . Кроме того, исправлены ошибки в вычислениях, встречающиеся в некоторых примерах, а также несколько увеличено число чертежей (вместо 12й дано 155).
[c.659]Если первое положение представляет собой непосредственное математическое следствие основных законов механики, миллионы раз проверенных на практике и неизменно оказывавшихся правильными, то второе с этими законами ничем не связано и является допущением Ньютона. Он экспериментировал с шерстяными клубками, стеклянными и стальными шарами и находил для них значения коэффициентов восстановления скорости, совершенно необоснованно пренебрегая размерами и формой соударяющихся тел. Полагаясь на непогрешимость Ньютона, несколько поколений ученых и инженеров уточняли эти значения для различных материалов. В любом учебнике для вуза или техникума, в любом техническом справочнике, а иногда и на обратной стороне логарифмической линейки вы найдете аккуратненькие таблицы коэффициентов для стали и дерева, слоновой кости, стекла и пластмассы. Но самое странное заключается в том, что численные значения коэффициентов в разных книгах для одних и тех же материалов не имеют ничего общего. Так, для стали они колеблются от 0,55 до 1. Какие же цифры правильны Никакие. К такому выводу пришел Евгений Всеволодович после тщательных и исчерпывающих экспериментов. Измерять значения коэффициентов восстановления скорости так же бессмысленно, как находить точную продолжительность поездки из Ленинграда в Москву, независимо от того, идешь ли ты пешком или летишь на самолете.
Он экспериментировал с шерстяными клубками, стеклянными и стальными шарами и находил для них значения коэффициентов восстановления скорости, совершенно необоснованно пренебрегая размерами и формой соударяющихся тел. Полагаясь на непогрешимость Ньютона, несколько поколений ученых и инженеров уточняли эти значения для различных материалов. В любом учебнике для вуза или техникума, в любом техническом справочнике, а иногда и на обратной стороне логарифмической линейки вы найдете аккуратненькие таблицы коэффициентов для стали и дерева, слоновой кости, стекла и пластмассы. Но самое странное заключается в том, что численные значения коэффициентов в разных книгах для одних и тех же материалов не имеют ничего общего. Так, для стали они колеблются от 0,55 до 1. Какие же цифры правильны Никакие. К такому выводу пришел Евгений Всеволодович после тщательных и исчерпывающих экспериментов. Измерять значения коэффициентов восстановления скорости так же бессмысленно, как находить точную продолжительность поездки из Ленинграда в Москву, независимо от того, идешь ли ты пешком или летишь на самолете. Оказалось, что для любого материала — будь это сталь, стекло, плексиглас, эбонит — коэффициент восстановления можно заставить принимать любые значения от О до 1, хотя во всех этих случаях удар остается упругим и необратимых пластических деформаций не возникает. Надо лишь определенным образом менять формы и массы соударяю-
[c.222]
Оказалось, что для любого материала — будь это сталь, стекло, плексиглас, эбонит — коэффициент восстановления можно заставить принимать любые значения от О до 1, хотя во всех этих случаях удар остается упругим и необратимых пластических деформаций не возникает. Надо лишь определенным образом менять формы и массы соударяю-
[c.222]
Уравнение (4-6) представляет собой общий вид уравнения Бернулли для установившегося notoKa К Оно является следствием законов механики, открытых Ньютоном за 150 лет до провозглашения первого закона термодинамики или, иначе, закона сохранения энергии. [c.26]
ИНЁРЦИИ ЗАКОН — закон механики, согласно к-рому тело при взаимном уравновешивании всех действующих на него сил сохраняет состояние покоя или равномерного прямолинейного движения, пока приложенные силы не заставляют его изменить это состояние. Открыт Г. Галилеем в 1632, сформулирован И. Ньютоном в 1С87 как первый из Ньютона законов механики. И, 3,— частный случай закона сохранения кол-ва движения системы. [c.146]
[c.146]
Таким образом и здесь, по существу, используется некая модель истинного движения, в которой эйлеровы, т. е. переносные п кориолисовы, силы инерции становятся как бы реальными физическими силами. Однако это — всего лишь модель. При торможении железнодорожной платформы плохо укрепленный предмет начинает движение по отношению к ней не потому, что на него начинает действовать сила инерции переносного движения. С точки зрения классической механики он просто стремится продолжать то же движение, что и до торможения, удерживаемый в какой-то степени силами, развиваемыми креплением к платформе. Однако первая трактовка нагляднее. Надо лишь точно оговорить, что платформа принимается условно за неподвижную, и вследствие этого надлежит ввести как бы физические ( квазиньютоновы , ибо они не имеют никакого отношения к третьему закону Ньютона), силы, равные переносным силам инерции. И тогда все становится ясным и верным. [c.7]
Что такое инерция? Определение, формула
Понятие инерция в формулировках Галилея и Ньютона
Галилео Галилей и Исаак Ньютон внесли свой вклад в развитие такого раздела физики, как механика. Неудивительно, что каждый из них предложил свою формулировку.
Неудивительно, что каждый из них предложил свою формулировку.
Галилео Галилей | Исаак Ньютон | |
Формулировка закона инерции | Когда тело движется по горизонтальной поверхности, не встречая никакого сопротивления движению, то его движение — равномерно, и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца. | Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние. |
Определение инерции | Инерция — это физическое явление, при котором тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела. | Инерция – это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано. |
Варианты формулировки не противоречат друг другу и говорят по сути об одном и том же, просто разными словами — выбирайте ту, что вам нравится больше.
Сила: первый закон Ньютона
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — сила.
Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Она измеряется в Ньютонах (в честь Исаака Ньютона, разумеется). Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат. |
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
В данном случае результат выражается в направлении движения.
Теперь зная, что такое сила, мы можем вернуться к ньютоновской формулировке закона инерции — он же, Его Величество, первый закон Ньютона:
Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость постоянной, в том числе равной нулю, если действие на него других сил отсутствует или скомпенсировано.
Первый закон Ньютона R — результирующая сила, сумма всех сил, действующих на тело [Н] v — скорость [м/с] const — постоянная величина |
В этом законе встречается такое словосочетание, как «система отсчета». Оно изучается в самом начале курса физики, но там это понятие читают в контексте «такие системы отсчета». Напрашивается вопрос: какие такие системы отсчета?
Напрашивается вопрос: какие такие системы отсчета?
Системы отсчета: инерциальные и неинерциальные
Чтобы описать движение нам нужны три штуки:
- тело отсчета, относительно которого определяем местоположение других тел;
- система координат: в школьном курсе мы используем прямоугольную декартову систему координат;
- часы, чтобы измерять время.
В совокупности эти три опции образуют систему отсчета:
Инерциальная система отсчета — система отсчёта, в которой все тела движутся прямолинейно и равномерно, либо покоятся.
Неинерциальная система отсчета — система отсчёта, движущаяся с ускорением.
Рассмотрим разницу между этими системами отсчета на примере задачи.
Аэростат — летательный аппарат на картиночке ниже — движется равномерно и прямолинейно параллельно горизонтальной дороге, по которой равноускоренно движется автомобиль.
Выберите правильное утверждение:
- Система отсчёта, связанная с аэростатом, является инерциальной, а система отсчёта, связанная с автомобилем, инерциальной не является.
- Система отсчёта, связанная с автомобилем, является инерциальной, а система отсчёта, связанная с аэростатом, инерциальной не является.
- Система отсчёта, связанная с любым из этих тел, является инерциальной.
- Система отсчёта, связанная с любым из этих тел, не является инерциальной.
Решение:
Система отсчёта, связанная с землёй, инерциальна. Да, планета движется и вращается, но для всех процессов вблизи планеты этим можно пренебречь. Во всех задачах систему отсчета, связанную с землей можно считать инерциальной.
Поскольку система отсчёта, связанная с землёй инерциальна, любая другая система, которая движется относительно земли равномерно и прямолинейно или покоится — по первому закону Ньютона тоже инерциальна.
Движение аэростата удовлетворяет этому условию, так как оно равномерное и прямолинейное, а равноускоренное движение автомобиля — нет. Аэростат — инерциальная система отсчёта, а автомобиль — неинерциальная.
Ответ: 1.
Инерция покоя
На столе лежит лист бумаги. На него поставили стакан и резко выдернули лист бумаги из-под него. Стакан почти не двинулся.
То, что стакан остался в состоянии покоя, можно объяснить законом инерции, так как «скорость остается постоянной, в том числе равной нулю». В данном случае инерция покоя — это способность тела сохранять состояние полного механического покоя и «сопротивляться» любым внешним воздействиям. То есть та часть закона инерции, в котором скорость равна нулю.
Так, например, если выбивать пыль из ковра, то в ковер-самолет ваш любимый предмет интерьера не превратится — вместе с пылью не улетит.
Инерция движения
В случае с движением мы берем ту часть первого закона Ньютона, в которой скорость постоянна, но не равна нулю.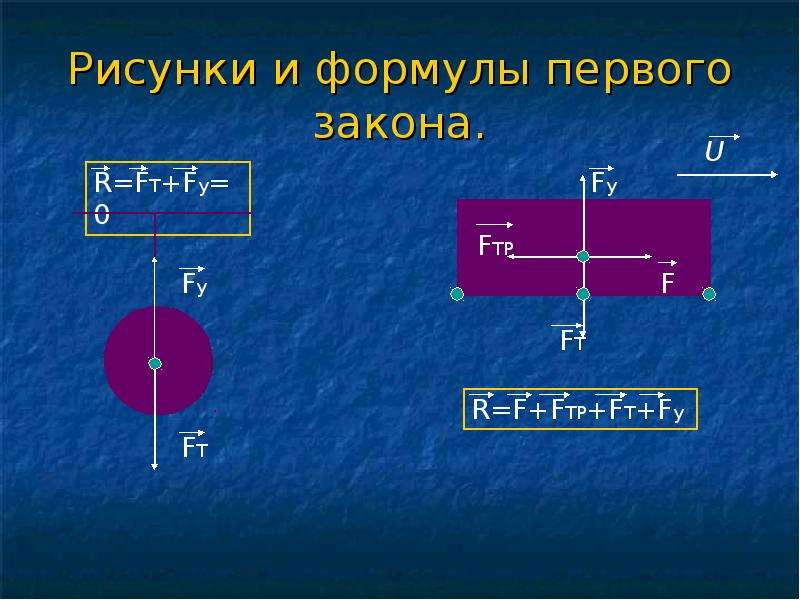 Здесь мы откроем способность тела к движению, которое было вызвано силой, прекратившей своё действие на тело.
Здесь мы откроем способность тела к движению, которое было вызвано силой, прекратившей своё действие на тело.
Вернемся к самому началу:
Велосипедист наезжает на камень и падает с велосипеда. Благодаря инерции скорость велосипедиста сохраняется, несмотря на то, что сам велосипед не едет дальше. Наездник слетает с лошади, если та остановилась. Это тоже происходит из-за инерции — скорость наездника остается постоянной, при этом сама лошадь останавливается. |
Мир не идеален
К сожалению, а может быть и к счастью, мы не живем в мире, в котором все тела движутся прямолинейно и равномерно. Из-за этого инерция в реальной жизни невозможна, потому что всегда есть трение, сопротивление воздуха и прочие, препятствующие движению, факторы.
Пуля, вылетевшая из ружья, продолжала бы двигаться, сохраняя свою скорость, если бы на неё не действовало другое тело — воздух. Поэтому скорость пули уменьшается.
Поэтому скорость пули уменьшается.
Велосипедист, перестав работать педалями, смог бы сохранить скорость своего движения, если бы на велосипед не действовало трение. Поэтому, если педали не крутить — скорость велосипедиста уменьшается, и он останавливается.
Физика
Программа
вступительных испытаний по физике на направления подготовки высшего образованияI. МЕХАНИКА
Кинематика
- Механическое движение. Материальная точка. Абсолютно твердое тело. Основная задача кинематики. Система отсчета. Радиус-вектор. Траектория. Путь и перемещение. Законы движения.
- Классификация механических движений. Скорость.
- Относительность механического движения. Сложения скоростей.
- Ускорение. Нормальная и тангенциальная составляющие ускорения.
- Прямолинейное равномерное и равнопеременное движение.

- Аналитическое и графическое представление движения: зависимости проекций скорости, ускорения, перемещения, а также координаты и пути от времени. Свободное падение тел. Ускорение свободно падающего тела.
- Криволинейное движение. Равномерное движение по окружности. Линейная и угловая скорости, связь между ними. Период обращения, частота. Ускорение при движении тела по окружности. Принцип независимости движений. Движение тела, брошенного горизонтально и под углом к горизонту. Дальность полета. Высота полета.
- Поступательное и вращательное движение тела.
2. Динамика
- Основная задача динамики. Взаимодействие тел.
- Первый закон Ньютона. Понятие об инерциальных и неинерциальных системах отсчета.
- Инертность тел. Масса. Плотность. Сила. Второй закон Ньютона. Принцип независимости действия сил.
- Третий закон Ньютона.
- Фундаментальные взаимодействия. Классификация сил в механике.

- Закон всемирного тяготения. Гравитационное поле. Сила тяжести. Ускорение свободного падения Зависимость ускорения свободного падения от высоты. Вес тела. Невесомость. Перегрузки.
- Силы упругости. Закон Гука.
- Силы трения. Сухое трение. Сила трения покоя. Сила трения скольжения. Коэффициент трения.
- Применение законов Ньютона к поступательному движению тел.
- Применение законов Ньютона к движению материальной точки по окружности. Движение планет и искусственных спутников. Первая и вторая космические скорости.
3. Закон сохранения в механике
- Импульс тела. Импульс силы. Связь между приращением импульса тела и импульсом силы. Импульс системы тел. Понятие замкнутой системы тел. Закон сохранения импульса.
- Реактивное движение.
- Механическая работа. Мощность. Мгновенная мощность.
- Энергия. Механическая энергия: кинетическая и потенциальная.
- Кинетическая энергия.
 Связь между приращением кинетической энергии тела и работой приложенных к телу сил.
Связь между приращением кинетической энергии тела и работой приложенных к телу сил. - Потенциальная энергия. Потенциальная энергия тел при гравитационном взаимодействии. Потенциальная энергия упруго деформированного тела. Связь между изменением потенциальной энергии и работой.
- Закон сохранения энергии в механике. Условия, необходимые для его выполнения. Коэффициент полезного действия.
- Применение законов сохранения к абсолютно упругим и абсолютно неупругим столкновениям.
- Границы применимости механики Ньютона.
4. Механика жидкостей и газов
- Давление. Закон Лапласа. Гидравлический пресс. Гидростатическое давление. Давление жидкости на дно и стенки сосуда. Сообщающиеся сосуды.
- Атмосферное давление. Опыт Торричелли. Нормальное и атмосферное давление. Внесистемная единица давления-миллиматр ртутного столба. Ртутный и металлический барометры.
- Закон Архимеда для жидкостей и газов.
 Условие плавания тел.
Условие плавания тел.
II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
1. Основы молекулярно-кинетической теории строения вещества. Идеальный газ
- Основные положение молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Диффузия в газах, жидкостях, твердых телах. Масса и размеры молекул. Моль вещества. Число Авогадро. Взаимодействие атомов и молекул вещества.
- Понятие о статистическом и термодинамическом методах в молекулярной физике. Тепловое равновесие. Шкала температур Цельсия.
- Модель идеального газа. Основное уравнение молекулярно-кинетической теории идеального газа. Средняя кинетическая энергия молекул и температура. Постоянная Больцмана. Абсолютная температурная шкала.
- Законы Бойля-Мариотта, Гей-Люссака, Шарля. Объединенный газовый закон. Уравнение Менделеева-Клапейрона.
2. Элементы термодинамики
- Первый закон термодинамики.
 Внутренняя энергия термодинамической системы. Количество теплоты и работа как меры изменения внутренней энергии. Применение первого закона термодинамики к изопроцессам.
Внутренняя энергия термодинамической системы. Количество теплоты и работа как меры изменения внутренней энергии. Применение первого закона термодинамики к изопроцессам. - Теплоемкость тела. Уравнение теплового баланса.
- Физические основы работы тепловых двигателей. КПД теплового двигателя.
3. Изменения агрегатного состояния вещества
- Парообразование, испарение и кипение. Удельная теплота парообразования. Насыщенный и ненасыщенный пар. Зависимость давления и плотности насыщенного пара от температуры. Зависимость температуры кипения от давления.
- Абсолютная и относительная влажность. Точка росы. Кристаллическое и аморфное состояние вещества. Плавление. Удельная теплота плавления.
III. ЭЛЕКТРОДИНАМИКА
1. Электростатика
- Электрические заряды. Элементарный электрический заряд.
 Точечный заряд. Способы электризации. Проводники и диэлектрики. Закон сохранения электрического заряда. Взаимодействие электрических зарядов. Закон Кулона. Диэлектрическая проницаемость вещества.
Точечный заряд. Способы электризации. Проводники и диэлектрики. Закон сохранения электрического заряда. Взаимодействие электрических зарядов. Закон Кулона. Диэлектрическая проницаемость вещества. - Электрическое поле. Напряженность электрического поля. Однородное электрическое поле. Напряженность электростатического поля точечного заряда. Силовые линии электрического поля. Принцип суперпозиции полей.
- Работа сил электростатического поля по перемещению заряда. Потенциал и разность потенциалов электростатического поля. Потенциал поля точечного заряда. Принцип суперпозиции. Связь разности потенциалов с напряженностью электростатического поля. Эквипотенциальные поверхности.
- Проводники и диэлектрики в электростатическом поле.
- Электроемкость. Конденсаторы. Электроемкость простейших конденсаторов. Соединение конденсаторов.
- Энергия электрического поля.
2. Постоянный ток
- Электрический ток.
 Сила и плотность тока. Условия существования тока в цепи. Электродвижущая сила. Напряжение. Закон Ома для участка цепи, не содержащей ЭДС. Омическое сопротивление проводника. Удельное сопротивление. Зависимость удельного сопротивления от температуры. Последовательное и параллельное соединения проводников.
Сила и плотность тока. Условия существования тока в цепи. Электродвижущая сила. Напряжение. Закон Ома для участка цепи, не содержащей ЭДС. Омическое сопротивление проводника. Удельное сопротивление. Зависимость удельного сопротивления от температуры. Последовательное и параллельное соединения проводников. - Закон Ома для замкнутой цепи. Источники тока, их соединение. Измерение тока и напряжения в цепи амперметром и вольтметром.
- Работа и мощность тока. Энергия электрического тока и ее преобразование в другие виды энергии. Закон Джоуля-Ленца. КПД источника тока.
- Электрический ток в электролитах. Законы Фарадея для электролиза. Применение электролиза.
- Электрический ток в вакууме. Термоэлектронная эмиссия. Электронные лампы: диод и триод. Электронно-лучевая трубка.
3. Магнетизм
- Магнитное поле. Действия магнитного поля на рамку с током. Индукция магнитного поля. Линии индукции магнитного поля. Магнитное поле прямого тока, соленоида, тороида (без вывода).
- Сила, действующая на проводник с током в магнитном поле. Взаимодействие параллельных токов. Единица силы тока – ампер. Электроизмерительные приборы магнитоэлектрической системы.
- Сила Лоренца. Принцип действия циклотрона.
- Магнетизм. Магнитная проницаемость вещества.
4. Электромагнитная индукция
- Магнитный поток. Опыты Фарадея. Явление электромагнитной индукции. ЭДС индукции. Вихревое электрическое поле. Закон электромагнитной индукции. Индукционный ток. Правило Ленца.
- Явление самоиндукции. Индуктивность соленоида (без вывода). ЭДС самоиндукции.
- Энергия магнитного поля.
IV. КОЛЕБАНИЯ И ВОЛНЫ
1. Механические колебания
- Понятие о колебательном движении. Условия возникновения свободных колебаний. Пружинный маятник. Математический маятник. Уравнения движения. Гармонические колебания. Смещение. Амплитуда, фаза, период, частота. Скорость и ускорение при гармонических колебаниях. Превращение энергии при колебательных движениях. Графическое описание колебательных движений.
- Затухающие колебания. Вынужденные колебания. Механический резонанс. Резонанс в технике.
2. Электромагнитные колебания
- Колебательный контур. Превращение энергии в колебательному контуре. Формула Томсона. Затухающие электромагнитные колебания.
- Переменный электрический ток. Действующие значения силы тока и напряжения.
- Трансформатор. Передача и распределение электрической энергии.
3. Волны
- Понятие о волновых процессах. Продольные и поперечные волны. Длина волны, скорость распространения волн. Интерференция волн. Стоячие волны. Дифракция волн.
- Звуковые волны. Громкость и высота звука. Ультразвук.
- Электромагнитные волны, их свойства, излучение и прием электромагнитных волн. Изобретение радио А.С.Поповым.
V. ОПТИКА
1. Геометрическая оптика
- Развитие взглядов на природу света. Закон прямолинейного распространения света. Понятие луча.
- Законы отражения света. Плоское зеркало. Сферические зеркала. Построение изображений в зеркалах.
- Законы преломления света. Абсолютный и относительный показатели преломления. Ход лучей в плоскопараллельной пластика. Ход лучей в призме. Явление полного отражения. Предельный угол полного отражения.
- Тонкие линзы. Оптическая сила линзы. Зависимость оптической силы линзы от показателя преломления и радиусов кривизны линзы. Построение изображения в собирающих и рассеивающих линзах. Формула линзы. Увеличение, даваемое линзами.
- Оптические приборы: лупа, фотоаппарат, проекционный аппарат, микроскоп. Ход лучей в этих приборах. Глаз.
2. Элементы физической оптики
- Волновые свойства света. Электромагнитная природа света.
- Скорость света в однородной среде. Опыт Майкельсона. Дисперсия света. Спектроскоп. Шкала электромагнитных волн. Инфракрасная и ультрафиолетовая части спектра.
- Интерференция света. Когерентные источники и способы их получения. Условия образования максимумов и минимумов в интерференционной картине.
- Дифракция света. Дифракционная решетка. Дифракционный спектр.
- Корпускулярные свойства света. Фотоэлектрический эффект. Работы А. Г. Столетова, законы фотоэффекта. Уравнение Эйнштейна. Фотоэлементы и их применение.
VI. АТОМЫ И АТОМНОЕ ЯДРО
- Явления, подтверждающие сложное строение атома. Опыт Резерфорда по рассеянию a-частиц. Строение атома: электронная оболочка и ядро. Постулаты Бора. Виды спектров: сплошной, линейчатый, полосатый. Спектры испускания и поглощения. Излучение и поглощение энергии атомами.
- Экспериментальные методы регистрации заряженных частиц: камера Вильсона, счетчик Гейгера, фотоэмульсионный метод.
- Составные части ядра атома – протоны и нейтроны. Энергия связи атомных ядер. Цепная реакция. Выделение энергии при делении тяжелых ядер.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1) Касьянов В.А. Учебник по физике 10 класс. М.: Дрофа, 2013. 288 с.
2) Касьянов В.А. Учебник по физике 11 класс. М.: Дрофа, 2012. 288 с.
3) Тихомирова С.А., Яворский Б.М. Учебник по физике 10 класс. М.: Мнемозина, 2013. 272 с.
4) Тихомирова С.А., Яворский Б.М. Учебник по физике 11 класс. М.: Мнемозина, 2012. 271 с.
5) Рымкевич А.П. Физика. Задачник. 10-11 классы. М.: Дрофа, 2013. 192 с.
Интернет-ресурсы:
Электронный учебник физики: http://www.physbook.ru/
Электронное пособие по подготовке к ЕГЭ: http://www.college.ru/fizika/
СИСТЕМА И КРИТЕРИИ
оценки знаний поступающих на вступительных испытаниях
на программы высшего образования бакалавриата
Выполненное экзаменационное задание по всем предметам оценивается по стобалльной системе.
Одно правильно выполненное задание частей экзаменационного теста оценивается:
| Предмет | Номера/части заданий | Количество баллов, выставляемых за одно правильно выполненное задание | Количество баллов за все правильно выполненные задания данной части | Минимальное количество баллов, подтверждающее успешное прохождение вступительного испытания |
| Физика | часть 1 | 3 | 36 | 36 |
| часть 2 | 4 | 28 | ||
| часть 3 | 6 | 36 |
За неправильные ответы баллы не начисляются.
В целом за экзаменационную работу выставляется итоговый балл как сумма баллов за отдельные задания.
Минимальное количество баллов успешного прохождения вступительного испытания составляет 50 (пятьдесят) баллов.
Программа одобрена на Ученом совете университета протокол № 7 от 28 сентября 2017 г.
Первый закон Ньютона (Закон инерции)
Давайте переформулируем первый закон Ньютона в повседневных терминах:
Покоящийся объект будет оставаться в покое навсегда, пока ничто его не толкает и не тянет. Движущийся объект будет оставаться в движении, путешествуя по прямой, вечно, пока что-то не толкнет или не потянет его.
Часть «навсегда» иногда трудно проглотить. Но представьте, что у вас есть три пандуса, как показано ниже. Также представьте, что пандусы бесконечно длинные и бесконечно плавные.Вы позволяете мрамору скатиться с первой рампы, которая находится под небольшим наклоном. Спускаясь по рампе, шарик ускоряется. Теперь вы слегка толкаете мрамор, идущий в гору по второй рампе. Он замедляется по мере роста. Наконец, вы толкаете шарик по пандусу, который представляет собой среднее состояние между первыми двумя – другими словами, пандус, который является идеально горизонтальным. В этом случае шарик не будет ни замедляться, ни ускоряться. Фактически, он должен продолжать катиться. Навсегда.
Физики используют термин инерция , чтобы описать эту тенденцию объекта сопротивляться изменению его движения.Латинский корень «инерция» является тем же корнем, что и «инертный», что означает отсутствие способности двигаться. Итак, вы можете видеть, как ученые придумали это слово. Что еще более удивительно, так это то, что они придумали эту концепцию. Инерция не является очевидным физическим свойством, например длиной или объемом. Однако это связано с массой объекта. Чтобы понять, как это происходит, рассмотрим борца сумо и мальчика, показанных ниже.
Допустим, у борца слева масса 136 килограммов, а у мальчика справа – 30 килограммов (ученые измеряют массу в килограммах).Помните, что цель борьбы сумо – сместить противника с его позиции. Кого из людей в нашем примере было бы легче переехать? Здравый смысл подсказывает, что мальчику будет легче двигаться или он будет менее устойчив к инерции.
Вы все время чувствуете инерцию движущегося автомобиля. Фактически, ремни безопасности существуют в автомобилях специально для противодействия эффекту инерции. Представьте на мгновение, что машина на испытательном треке движется со скоростью 55 миль в час. А теперь представьте, что манекен для краш-теста находится внутри этой машины на переднем сиденье.Если машина врезается в стену, манекен летит вперед в приборную панель. Почему? Потому что, согласно первому закону Ньютона, движущийся объект будет оставаться в движении до тех пор, пока на него не подействует внешняя сила. Когда автомобиль ударяется о стену, манекен продолжает двигаться по прямой с постоянной скоростью, пока приборная панель не приложит силу. Ремни безопасности удерживают манекенов (и пассажиров), защищая их от собственной инерции.
Интересно, что Ньютон не был первым ученым, придумавшим закон инерции.Эта честь принадлежит Галилею и Рене Декарту. Фактически, описанный ранее мысленный эксперимент с мраморным пандусом приписывают Галилею. Ньютон многим обязан событиям и людям, которые ему предшествовали. Прежде чем мы продолжим рассмотрение двух других его законов, давайте рассмотрим некоторые важные истории, которые повлияли на них.
Законы движения Ньютона
силаПроще говоря, сила – это толкающая или тянущая сила. В физике у этого есть более конкретное определение. Сила – это мера взаимодействия между объектами.сила – это векторная величина, поэтому она имеет как величину, так и направление. Единица силы определяется в единицах массы и ускорения. В единицах СИ единицей силы является Ньютон (Н), который определяется как
Многие силы возникают в результате прямого контакта, например, когда человек толкает камень или тянет за веревку, прикрепленную к ней. объект. Существуют также дальнодействующие силы, действующие на разделенные объекты. Примерами сил, действующих на расстоянии, являются гравитация и электромагнетизм.
Когда на объект действует несколько сил, общее воздействие на объект равно векторной сумме сил. Если на объект действуют силы и т. Д., То общая сила (чистая сила) на объект равна
Это означает, что влияние на движение объекта такое же, как если бы одна сила действует на это. Это называется суперпозицией сил.
Первый закон Ньютона
Сэр Исаак Ньютон (1643–1727) написал набор законов движения, которые описывают, как на объекты действуют силы.Первый из этих законов относится к суперпозиции сил. Чистая сила, действующая на объект, представляет собой сумму сил, действующих на него (как написано выше),
Это также можно записать в виде суммирования,
В этом обозначении греческая заглавная буква Σ (” сигма ») используется для обозначения« суммы »всех сил, а i – это индекс для идентификации каждой силы в сумме.
Чистая сила, действующая на объект, равна нулю, если все эти силы уравновешены, и поэтому сумма сил равна нулю,
Если чистая сила равна нулю, то первый закон Ньютона утверждает, что объект находится в равновесии.Это означает, что объект не ускоряется или не замедляется, хотя это не означает, что объект не может двигаться. Если результирующая сила, действующая на объект, равна нулю, он может двигаться с постоянной скоростью. Если объект изначально находится в состоянии покоя, то он останется в покое. Если он изначально находится в движении, он продолжит двигаться с той же скоростью.
Первый закон Ньютона гласит, что когда векторная сумма всех сил, действующих на объект (результирующая сила), равна нулю, объект находится в равновесии. Если объект изначально находится в состоянии покоя, он остается неподвижным.Если он изначально находится в движении, он продолжает двигаться с постоянной скоростью.
Второй закон Ньютона
Второй закон Ньютона определяет, как сила связана с массой объекта. Если результирующая сила, действующая на объект, не равна нулю, то существует постоянная сила, которая вызывает ускорение объекта. Связь между чистой силой и ускорением – это масса. Чистая сила равна массе объекта, умноженной на ускорение объекта. Чистая сила и ускорение являются векторами, а масса – скалярным значением, которое их связывает:
Единицей массы является килограмм (кг), а единицей ускорения является м / с 2 .Этот закон часто записывают в терминах величин силы и ускорения,
F = ma
Второй закон Ньютона гласит, что векторная сумма всех сил, действующих на объект, равна массе объекта, умноженной на его ускорение. (F = ma).
Третий закон Ньютона
Третий закон Ньютона можно кратко сформулировать как «действие равно противодействию». Любая сила, действующая на объект, является результатом взаимодействия с другим объектом, и каждый объект оказывает силу на другой.Силы, действующие на эти объекты, имеют равные величины и противоположные направления. Например, если человек бьет по мячу, ступня человека воздействует на мяч с силой, но сила равной величины действует на ступню человека в противоположном направлении. Это верно независимо от того, являются ли силы результатом прямого контакта или они являются силами дальнего действия.
Третий закон можно сформулировать следующим образом. Если есть два объекта, называемые A и B, и есть сила, которая применяется объектом A к объекту B, то есть также сила, которая применяется объектом B к объекту A.Эти силы равны по величине и противоположны по направлению,
Другой способ сформулировать третий закон Ньютона состоит в том, что «для каждой силы воздействия существует равная и противоположная сила реакции». Таким образом, все силы между объектами образуют пары действие-противодействие. Важно отметить, что каждая сила в паре действие-противодействие действует только на один из двух объектов. Силы действия и противодействия никогда не действуют на один и тот же объект.
Законы Ньютона, сводка
1) Объект находится в равновесии, если результирующая сила, действующая на него, равна нулю.Если объект в равновесии изначально находится в состоянии покоя, он останется в покое. Если изначально он движется с постоянной скоростью, он останется с этой скоростью.
2) Чистая сила, действующая на объект, равна массе объекта, умноженной на его ускорение (F = ma).
3) Когда два объекта взаимодействуют, они оказывают друг на друга силы, равные по величине и противоположные по направлению.
Диаграммы свободного тела
Диаграммы свободного тела очень полезны для решения физических задач, связанных с законами Ньютона.Диаграмма свободного тела показывает все силы, действующие на один объект. Это утверждение важно, особенно в отношении пар сил действия и противодействия, связанных с третьим законом Ньютона.
Возьмем, например, силы, действующие на лифт, когда он находится на определенном этаже здания. В этом случае есть сила тяжести, направленная вниз, и сила натяжения троса, который удерживает его. Сумма этих двух сил должна быть равна нулю, если лифт находится в состоянии покоя, согласно первому закону Ньютона.Схема свободного тела для лифта ниже.
При рисовании диаграммы свободного тела важно определить направления главных осей. Включен небольшой рисунок, показывающий, какие направления положительны по осям x и y.
Чтобы лифт начал движение, должно быть ускорение. Чтобы лифт двигался вверх, двигатель должен увеличивать силу натяжения троса, поддерживающего лифт. В этом случае сумма сил равна массе, умноженной на ускорение лифта, согласно второму закону Ньютона.
Важно отметить, что правая часть уравнения не отображается на диаграмме свободного тела как сила. Это сумма всех показанных сил. Иногда может быть полезно нарисовать направление результирующего ускорения, но это должно быть показано как отдельный вектор, как показано на рисунке выше.
4.2 Первый закон движения Ньютона: инерция
Первый закон Ньютона и трение
Первый закон движения Ньютона гласит:
- Тело в состоянии покоя имеет тенденцию оставаться в покое.
- Движущееся тело стремится оставаться в движении с постоянной скоростью, если на него не действует чистая внешняя сила. (Напомним, что с постоянной скоростью означает, что тело движется по прямой линии с постоянной скоростью.)
На первый взгляд этот закон может показаться противоречащим повседневному опыту. Вы, вероятно, заметили, что движущийся объект обычно замедляется и останавливается, если не прилагать каких-либо усилий, чтобы удержать его в движении. Ключ к пониманию того, почему, например, скользящий ящик замедляется (по-видимому, сам по себе), состоит в том, чтобы сначала понять, что чистая внешняя сила действует на коробку, заставляя коробку замедляться.Без этой чистой внешней силы ящик продолжал бы скользить с постоянной скоростью (как указано в первом законе движения Ньютона). Какая сила действует на коробку, чтобы замедлить ее? Эта сила называется трением. Трение – это внешняя сила, действующая противоположно направлению движения (см. Рисунок 4.3). Думайте о трении как о сопротивлении движению, которое замедляет работу.
Рассмотрим стол для аэрохоккея. Когда подача воздуха отключена, шайба скользит лишь на небольшое расстояние, прежде чем трение замедляет ее до полной остановки.Однако, когда подается воздух, он слегка приподнимает шайбу, поэтому при движении по поверхности шайба испытывает очень небольшое трение. Когда трение почти исключено, шайба скользит с очень небольшим изменением скорости. На поверхности без трения шайба не будет испытывать чистой внешней силы (без учета сопротивления воздуха, которое также является формой трения). Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, насколько быстро объекты будут замедляться.
А теперь давайте подумаем о другом примере.Человек толкает коробку по полу с постоянной скоростью, прилагая силу
+50 Н. (Положительный знак означает, что по соглашению направление движения направо). Какая сила трения противодействует движение? Сила трения должна быть −50 Н. Почему? Согласно первому закону движения Ньютона, любой объект, движущийся с постоянной скоростью, не имеет чистой внешней силы, действующей на него, а это означает, что сумма сил, действующих на объект, должна быть равна нулю. Математический способ сказать, что никакая чистая внешняя сила не действует на объект: Fnet = 0 Fnet = 0 или ΣF = 0.ΣF = 0. Таким образом, если человек применяет силу +50 Н, тогда сила трения должна составлять -50 Н, чтобы две силы в сумме равнялись нулю (то есть, чтобы две силы, составляющие , компенсировали друг друга). Каждый раз, когда вы встречаете фразу при постоянной скорости , первый закон Ньютона говорит вам, что чистая внешняя сила равна нулю.Рис. 4.3. Для коробки, скользящей по полу, трение действует в направлении, противоположном скорости.
Сила трения зависит от двух факторов: коэффициента трения и нормальной силы.Для любых двух поверхностей, которые контактируют друг с другом, коэффициент трения является константой, которая зависит от характера поверхностей. Нормальная сила – это сила, действующая со стороны поверхности, которая толкает объект в ответ на гравитацию, притягивающую объект вниз. В форме уравнения сила трения равна
., где μ – коэффициент трения, а N – нормальная сила. (Коэффициент трения обсуждается более подробно в другой главе, а нормальная сила обсуждается более подробно в разделе Третий закон движения Ньютона .)
Вспомните из раздела о Силе, что чистая внешняя сила действует извне на интересующий объект. Более точное определение состоит в том, что он действует на интересующую систему. Система – это один или несколько объектов, которые вы выбираете для изучения. Важно определить систему в начале проблемы, чтобы выяснить, какие силы являются внешними и должны быть учтены, а какие – внутренними, и их можно игнорировать.
Например, на рис. 4.4 (а) двое детей толкают третьего ребенка в повозке с постоянной скоростью.Интересующая нас система – это повозка плюс маленький ребенок, как показано в части (b) рисунка. Двое детей позади вагона оказывают на эту систему внешние силы ( F 1, F 2). Трение f , действующее на оси колес и на поверхность, где колеса касаются земли, две другие внешние силы, действующие на систему. На систему действуют еще две внешние силы: вес W системы, тянущий вниз, и нормальная сила N , толкающая землю вверх.Обратите внимание, что повозка не ускоряется вертикально, поэтому первый закон Ньютона говорит нам, что нормальная сила уравновешивает вес. Поскольку повозка движется вперед с постоянной скоростью, сила трения должна иметь ту же силу, что и сумма сил, приложенных двумя детьми.
Рис. 4.4 (a) Повозка и всадник образуют систему , на которую действуют внешние силы. (b) Двое детей, толкающих повозку, и ребенок создают две внешние силы. Трение, действующее на оси колес и на поверхность шин, где они касаются земли, создает внешнюю силу, действующую против направления движения.Вес W и нормальная сила N от земли – это еще две внешние силы, действующие на систему. Все внешние силы изображены на рисунке стрелками. Все внешние силы, действующие на систему, складываются, но поскольку вагон движется с постоянной скоростью, все силы должны в сумме равняться нулю.
Законы движения Ньютона – 3 закона, формулы, примеры и часто задаваемые вопросы
Законы движения Ньютона
Законы движения Ньютона устанавливают научную взаимосвязь между силами, действующими на тело, и изменениями, которые происходят из-за этой силы.Сэр Исаак Ньютон сформулировал законы движения в 1686 году в своей книге «Principia Mathematica Philosophiae Naturalis»
Каковы три закона движения?
Три закона движения:
Первый закон Ньютона – первый закон движения Ньютона гласит, что если тело находится в состоянии покоя или движется с постоянной скоростью по прямой линии, то тело будет оставаться в состоянии покоя или продолжать движение по прямой, пока на него не воздействует внешняя сила.
Второй закон Ньютона – 2-й закон движения Ньютона гласит, что скорость изменения количества движения тела прямо пропорциональна силе, приложенной к нему, и импульс возникает в направлении общей приложенной силы.
Третий закон Ньютона – Согласно третьему закону движения Ньютона, на каждое действие всегда есть равная и противоположная реакция
Первый закон движения
Это свойство тела, неспособного изменить свое состояние, называется Инерция.Галилео Галилей первым сформулировал закон инерции для горизонтального движения планеты Земля. Позже он был обобщен на Рене Декарта. До Галилея считалось, что для движения тела требуется сила. Галилей пришел к выводу, что тело не может изменить свое состояние, если на него не действует сила (например, трение).
Состояние движения или покоя нельзя изменить без приложения силы. Если тело движется в определенном направлении, оно будет продолжать движение в этом направлении до тех пор, пока не будет приложена внешняя сила, чтобы остановить его.
Второй закон движения
Второй закон Ньютона дает количественное описание силы. Импульс тела эквивалентен произведению его массы и скорости. Иными словами, импульс – это векторная величина, имеющая как скорость, так и величину. Когда к телу прикладывается сила, оно может либо изменить свой импульс, либо скорость, либо и то, и другое. Второй закон движения Ньютона – один из важнейших законов классической физики.
Для тела постоянной массы m формула закона Ньютона имеет вид,
F = ma,
Где F – приложенная сила, a – создаваемое ускорение, а m – масса объекта.
Если результирующая сила, действующая на тело, положительна, тело ускоряется.И наоборот, если чистая сила равна 0, тело не ускоряется.
Согласно второму закону движения, если сила приложена к двум разным объектам разной массы, возникают разные ускорения (изменение движения). Тело с меньшей массой ускоряется больше.
Влияние силы силой около 15 Ньютон на футбол будет гораздо более значительным по сравнению с воздействием той же силы, применяемой при движении автомобиля. Это различие, по сути, связано с разницей масс двух объектов.
Третий закон движения
Согласно третьему закону движения Ньютона, на каждое действие всегда есть равная и противоположная реакция. Кроме того, действие и противодействие происходят в двух разных телах. Когда два тела взаимодействуют друг с другом, они обмениваются силой, равной по величине, но действующей в противоположных направлениях. Этот закон имеет огромное применение в статическом равновесии, где силы уравновешены, а также для объектов, которые подвергаются равномерному ускоренному движению.
Например, переносной компьютер, находящийся на столе, оказывает направленное вниз усилие, равное его весу на столе, и, следовательно, стол оказывает на переносной компьютер равную и противоположную силу.Эта сила вступает в игру, потому что вес ноутбука немного деформирует стол, и, в свою очередь, стол толкает ноутбук назад.
Некоторые примеры законов Ньютона приведены ниже.
1. Вы применяете силу, когда хотите переместить учебный стол из одной стороны комнаты в другую.
2. Грузовой поезд движется по рельсам со скоростью 60 километров в час.
3. Плавание в воде с почти постоянной скоростью.
Исаак Ньютон был ученым из Англии.Он был немного душным, с неприятными волосами, но был гениальным человеком. Ньютон является основателем дифференциального исчисления и посвятил свою жизнь миру физики. Одна из его значительных работ – законы классической физики. Его идеи и концепции проверялись экспериментально на протяжении многих лет. Они называются законами движения Ньютона.
Первый закон Ньютона второй закон третий закон движения инерция F = ma расчеты, включающие ускорение силы массы практические вопросы решение проблем igcse / gcse 9-1 Physics revision notes
3.Первый закон движения Ньютона, второй закон движения Ньютона, закон Ньютона Третий закон движения, инерция и F = ma на основе вычислений
Эта страница поможет вам узнать ответы на такие вопросы, как … Каков первый закон движения Ньютона? Что такое второй закон движения Ньютона? Как мы выполняем второй закон Ньютона расчеты? Как использовать уравнение F = ma в решение проблем? Что такое третий закон движения Ньютона? а что такое инерция?
Первый закон Ньютона гласит, что результирующая сила необходима для изменения движения любого объекта .
Если тело, такое как дорожное транспортное средство или самолет, движение с постоянной скоростью (постоянная скорость без изменения направления) движущая сила от двигателя и силы сопротивления трения (движущиеся части, сопротивление воздуха и т. д.) должны быть уравновешены т.е. равнодействующая сила равно нулю.
Слева – диаграмма силы свободного тела велосипедиста , на которой показаны все силы, действующие на тело.Если велосипедист движется с постоянной скоростью, то мы имеем дело с равномерным или постоянная скорость и без изменения направления. Нет равнодействующей силы, т.е. F1 = F3 и F2 = F4, поэтому велосипедист продолжает движение в том же направлении с той же скоростью .
Обратите внимание на относительный размер и направление стрелок и подумайте о Первом Ньютоне. Закон движения.
F1 – сопротивление воздуха из-за трение между поверхностью велосипеда и велосипедиста и воздухом, также трение между колесами и дорогой и трение в движущихся частях велосипед.Все три вместе противостоят прямому движению велосипеда и гонщика.
F2 – вес велосипеда + комбинация велосипедистов из-за силы тяжести, веса объекта, действующего на дорогу при нормальном контакте сила
F3 – толчок или толчок велосипед от энергии, производимой велосипедистом.
F4 – нормальное контактное усилие атомы дорожного покрытия отталкивают мотоцикл.
Если велосипедист применяет больше мощности (диаграмма левого свободного тела), силы F1 и F2 уменьшаются. неуравновешенный, что дает результирующую силу больше нуля справа налево.
Следовательно, велосипедист будет ускоряться и увеличение скорости. Это действие не влияет на силы F2 и F4, которые остаются сбалансированный. Результирующая сила вызывает ускорение .
Если велосипедист задействует тормоза (слева диаграмма свободного тела), в при этом он перестанет крутить педали, уменьшив силу F3 И увеличив трение. от тормозных колодок действуя на обод колеса, будет увеличиваться усилие F1 (левое диаграмму). И снова стрелки для сил F1 и F3 должны быть показаны неравными.Силы теперь неуравновешены, и велосипед и всадник замедляется (замедление , ). Ни одно из этих двух действий не влияет на силы F2 и F4, которые остаются сбалансированными. результирующая сила вызывает замедление .
Если появится другая сила, например, внезапный порыв бокового ветра (F5), тогда велосипедист и велосипед поменяют направление в направлении ветер, т.е. вынужденный направо, поскольку диаграмма указывает на порыв ветра с левый.Велосипедист затем применяет корректирующую «балансирующую» силу путем поворот руля для регулировки дополнительной силы F5, чтобы попытаться сохранить ту же скорость и направление цикла.
Это интересный случай, потому что он включает в себя ускорение, замедление и две конечные скорости!
1. 2. 3.
Три возможных «силовых» ситуации как парашютист спускается после выпрыгивания из самолета.
Обратите внимание на относительный размер и направление стрелки и подумайте о Первом законе движения Ньютона.
1. Когда сила сопротивления F1 меньше, чем сила веса F2, парашютист разгоняется.
2. Когда сила сопротивления F1 равна массе усилие F2, парашютист спускается с постоянной скоростью – терминал скорость.
3. Когда сила сопротивления F1 больше, чем сила веса F2, парашютист замедлится (на другой терминал скорость).
(б) Второй закон движения Ньютона F = ma
Второй закон движения Ньютона можно выразить как ускорение тела прямо пропорционально приложенной к нему силе. кузов . Помните, что ускорение – это изменение скорости на заданном временной период.
(i) Чем больше равнодействующая сила, действующая на тело, тем больше ускорение этого тела .
На самом деле вы можете из уравнения 2-го закона Ньютона видно, что ускорение испытываемый объектом, прямо пропорционален силе, действующей на Это. F А
(ii) Ускорение тела также обратно пропорционально пропорционально его массе : a 1 / м
Эти два утверждения могут быть выражены в общем формула:
равнодействующая сила (ньютон) = масса (килограммы) x ускорение (метров в секунду в квадрате),
это уравнение является математическим выражение 2-го закона Ньютона
F (N) = m (кг) x a (м / с 2 )
перестановка (я) F = ma дает (ii) а = F м и (iii) m = F a
чем больше сила, действующая на объект, тем больше объект ускоренный.
Ускорение обратно пропорционально массе.
Если одинаковая сила применяется к объектам разной массы, наименьшей массы будет ускорен больше всего.
Следствием утверждения (i) является то, что чем быстрее вы хотите ускорить (ускорить) объект, тем больше сила требуется (опустите ногу на акселератор автомобиля, чтобы увеличить сила). И наоборот, чем быстрее вы хотите, чтобы объект замедлялся (замедлить), тем большую силу сопротивления вы должны приложить (нажатие педаль тормоза авто сильнее).
Одним из следствий утверждения (ii) является то, что конкретная приложенная равнодействующая сила ускоряет тело меньшей массы больше чем тело большей массы. Или, чтобы выразить это по-другому, вам нужно применить большая сила для ускорения большего тела в той же степени, что и меньшее тело.
Примеры расчеты на основе 2-го закона Ньютона
(некоторые вопросы тоже нужны формула разгона а = ∆v / ∆t )
2 кв.1 Что результирующая сила должна быть приложена велосипедистом (массой 70,0 кг) к педалям велосипеда (8,50 кг), чтобы дать ускорение 0,15 м / с 2 ?
F (N) = м (кг) x a (м / с 2 )
F = (70 + 8,5) x 0,15
требуемое усилие = 11.8 с.ш.
Q2.2 The Двигатель автомобиля массой 1000 кг вырабатывает движущую силу 4200 Н.
Если автомобиль скорость 60 миль в час и общая сила сопротивления (трение в двигателе, дороге контакт и сопротивление воздуха) составляет 3800 Н каково ускорение автомобиля при этом точка?
F (N) = м (кг) x a (м / с 2 )
Результирующая поступательная сила = 4200 – 3800 = 400 Н
F = ma, поэтому a = F / m = 400/1000 = 0.40 м / с 2
Q2.3 Если тело испытывает результирующую силу 500 Н и ускоряется со скоростью 2,0 м / с 2 , какова масса тела?
F = ma, поэтому m = F / a = 500/2 = 250 кг
Q2.4 A автобус массой 2800 кг равномерно ускоряется от 0 до 15 м / с за 20 секунд.
(a) Рассчитайте ускорение автобуса.
ускорение (м / с 2 ) = изменение скорости (м / с) / затраченное время (s)
a = ∆v / ∆t = 15 / 20 = 0,75 м / с 2
(b) Рассчитайте результирующую силу, действующую на шину.
F = ma, замена дает равнодействующую силу = 2800 x 0,75 = 2100 N
2 кв.5 Двигатель фургона массой 2000 кг создает движущую силу 6000 Н.
Если он испытывает силу сопротивления из-за воздуха сопротивление 500 Н, рассчитайте его ускорение.
F = ma, a = F / m = 6000/2000 = 3 м / с 2
2,6 кв. Какая сила требуется для вертикального ускорения ракеты массой 8000 кг со скоростью 3 м / с 2 ? (g = 9,8 м / с 2 )
F1 = вес ракеты = вниз сила = 8000 х 9.8 = 78 400 Н
F2 = восходящая сила ракеты к преодолевать силу тяжести и ускоряться вертикально со скоростью 3 м / с 2
F = ma, F = чистая вертикальная сила = F2 – F1, m = масса ракеты, a = ускорение 3 м / с 2
F2 – F1 = ма, F2 = F1 + ма
F2 = F1 + ma = 78 400 + (8000 x 3) = 102 400 Н
Q2.7 Если сила, действующая на объект, увеличивается в четыре раза, а масса вдвое, что происходит с ускорением?
F = ma, a = F / m (назовем его 1)
a = 4f / 2m = 2 F / m, поэтому ускорение вдвое .
2,8 кв. Высокоскоростная фотография может использоваться для анализа движения спортивного инвентаря.
В крикете быстрый боулер посылает мяч для крикета падает со скоростью 36 м / с (~ 80 миль / ч, ~ 130 км / ч) в сторону игрока с битой.
Мяч для крикета имеет массу 160 г и немного потертый и слегка мягкий.
Бэтсмен все еще держит биту и блокирует мяч, который отскакивает прямо к боулеру со скоростью 30 м / с.
(a) Если время контакта оказалось равным 0,002 секунды, какую силу испытывал мяч для крикета и в каком направление?
(i) Сначала необходимо рассчитать ускорение – скорость изменения скорости, и следите за знаками, вы имея дело с векторными величинами!
а = ∆v / ∆t = (v – u) / ∆t , a = ускорение (м / с 2 ), v u = конечная и начальная скорости, ∆t = затраченное время.
u = +36 м / с, v = -30 м / с, а ∆t = 0,002 с, знак плюс означает направление на игрока с битой.
а = (-30) – (+36) / 0,002 = -33 000 м / с 2
(ii) Теперь вы можете вычислите силу из уравнения 2-го закона Ньютона.
F = ma, Сила F в Н, m = масса в кг, a = ускорение в м / с 2
F = (160/1000) х 33 000 = – 5280 Н
Мяч для крикета испытывает силу 5280 Н. котелок.
(b) Новый мяч тверже, чем использованный мяч, и время контакта может составлять всего 0,001 секунды.
Какой эффект это сказывается на силе, испытываемой новым мячом для крикета по сравнению с изношенный мяч в (а)?
Это означает, что ∆t уменьшается вдвое, ускорение увеличивается вдвое, так же как и удар сила удваивается, поэтому мяч для крикета испытывает силу 2 x 5280 = 10 560 Н дюйм направление обратно к котелку.
(c) Почему время удара изношенного мяча больше по сравнению с новым мячом?
Изношенный мяч немного мягче, и изменение скорости занимает немного больше времени – мягкость обладает амортизирующим эффектом, уменьшающим силу удара.
https://www.physics.usyd.edu.au/~cross/cricket.html это интересная страница по физике крикета, и этот вопрос берет упрощенный взгляд на «кинетическую» ситуацию!
Q2.9
ВЕРХ СТРАНИЦЫ и субиндекс страницы
(c) Эксперименты по исследовать 2-й закон движения Ньютона (F = ma)
Эксперименты, описанные ниже, могут быть использованы для исследования , как сила и масса влияют на ускорение .
В этих экспериментах используются световые ворота для измерять скорость – так им нужно объяснять !
Световые ворота направляют луч света от с одной стороны к детектору с другой стороны (детали не показаны, только этикетки!).
Когда световой луч перерезается что-то проходящее через световые ворота (например, карточка на тележке) световой затвор измеряет время, в течение которого световой луч не обнаруживается .
Для измерения ускорения движущийся объект должен дважды прервать световой луч, и есть два способа при этом – эксперименты версии 1 и 2 описаны ниже. Ю нужно две скорости и разница между ними для расчета ускорения.
Световой затвор подключен к компьютер , а остальное поясняется на схеме ниже.
В версии 1 с одним световым затвором вы используйте карту в форме перевернутой Π (прямоугольник с вырезанной средней частью).
Длина вертикальных секций, которые разрезают луч света – это d1 и d2 (которые можно сделать одинаковыми).
Когда тележка и карта проходят через световые ворота, первая секция карты длиной d1, отсекает световой луч на время t1 (для скорости 1).
Когда вторая часть карты длины d2 проходит через световые ворота, луч отсекается на время t2 (для скорости 2).
Здесь также комбинированные световые ворота записывает разницу во времени t3 между двумя измерениями скорости (для ускорение а). Так что для скорости s …
s1 = d1 / t1, s2 = d2 / t2, ускорение = изменение в скорости / затраченном времени = a = (s2 – s1) / t3
Однако все, что вам нужно сделать, это ввести d1 (= d2) в компьютер и программное обеспечение сделают расчет ускорения за вас!
Очевидно, компьютерная программная система должна быть настроены в соответствии с тем, как вы настроили эксперимент.
В версии 2 , с двумя световыми воротами, вы используете карту прямоугольной формы [] длины d.
Вы установили два световых врата подходящих расстояние друг от друга.
Когда тележка и карта проходят через первые световые ворота, луч обрезается на t1.
Пройдя через 2-е световые ворота, время t2 записывается.
Здесь также комбинированные световые ворота запишите разницу во времени t3 между двумя измерениями скорости.
Теперь ситуация с данными аналогична версии 1 эксперимента, так что для скорости s ….
s1 = d / t1, s2 = d / t2, ускорение = изменение в скорости / затраченном времени = a = (s2 – s1) / t3
Опять же, компьютерная программная система должна быть настроить в соответствии с тем, как вы настроили эксперимент, и расчет ускорения для вас.
Пример расчета для версии эксперимента 2
Предположим, что длина тележки 10 см (0.10 м) и прерывает 1-й световой шлюз на 0,25 с.
Скорость у первых световых ворот равна 0,10 / 0,25 = 0,40 м / с .
Тележка прерывает 2-е световые ворота в течение 0,10 с.
Скорость у 2-х световых ворот равна 0,10 / 0,10 = 1,0 м / с .
Время, затраченное на поездку тележки между световыми воротами было 0,80 с.
Следовательно, ускорение = (v – u) / ∆t = (1.0 – 0,40) / 0,80 = 0,75 м / с 2
ВЕРХ СТРАНИЦЫ и субиндекс страницы
Версия расследования 1 с использованием одного фонаря ворота
Исправление ошибок НЕ показано на схеме выше
Строго говоря, вы должны экспериментируйте на слегка наклоненной подножке, а не на горизонтальной лабораторный стенд, показанный на схемах выше.
Вы наклоняете рампу подножки вниз, чтобы вправо, пока тележка (без крюка) не начнет двигаться свой собственный.
Затем вы подпираете левый конец такой же высоты, а затем проведите эксперименты, как описано.
После этого вес тележка вниз по склону компенсирует трение, действующее между колеса тележки и аппарель подножки .
Также можно сделать эти исследования с горизонтальной воздушной трассой, на которой парит «тележка» струи воздуха – это альтернативный план исследования для минимизировать эффекты трения в экспериментах.
Эксперимент проводится на гладкой скамье, на которой установлена тележка. может свободно бегать.
Необходимо отметить на стартовой линии, чтобы вещи последовательны.
Общая масса тележки и доп. вес ( м ) измеряется и может быть изменен путем добавления лишние веса.
На тележке закреплен «прямоугольник» Џ фигурная карта, две руки которой дважды блокируют световой луч, когда тележка проходит через световые ворота, когда измеряет затраченное время дважды.
Тележка соединена проводом или тросом с грузы через колесо шкива, которые при падении создают опускающую силу для разогнать тележку по «взлетно-посадочной полосе»
Время, измеренное системой световых ворот, составляет записываются в электронном виде и передаются на подключенный регистратор данных или компьютер.
Поскольку Џ карта проходит сквозь свет световой луч дважды отсекается, поэтому измеряются две скорости и временной интервал между ними.
Принципы работы F = ma расчеты для версии 1.
Ускоряющая сила F определяется выражением падающий вес: масса в кг x 9,8 Н / кг
Ускоряемая масса = общая масса тележка с грузами ( м )
Ускорение задается световым затвором скорости, разделенные на интервал времени между ними: а = v 2 – v 1 / Δt
Вы можете провести серию экспериментов с постоянная масса тележки m и изменение ускоряющей силы F путем изменения падающих грузов на конце крючка.
Теоретически, график зависимости силы F от разгон у должен быть линейный – или как-то так выглядеть!
Градиент задается масса тележки м (постоянная) .
Вы обязательно сможете показать что при увеличении приложенной силы создается большее ускорение, в идеале ваши результаты представляют собой линейный график.
Уравнение 2-го закона Ньютона: F = ma, F a , а постоянный уклон должен соответствовать общей массе тележки.
Продление расследования
Затем вы можете исследовать эффект изменения веса тележки, изменения ее массы и , применяя постоянная сила ускорения с использованием того же падающего груза.
Вы измеряете ускорение в так же, как описано.
Вы должны показать чем больше общая масса тележки м (чем больше ее инерционность), тем меньше ускорение создается постоянной ускоряющей силой ( F ).
График зависимости массы от ускорения должна быть нисходящей кривой.
F = ma , так как m получает больше, становится меньше для постоянного F .
м = F / a и а = Ф / м
Вы можете провести анализ линейного графика ваши результаты e.грамм.
График м по сравнению с 1 / год должен быть линейный с уклоном F.
График ускорения а относительно 1 / м должна быть линейной с градиентом F.
Источники ошибки
Трение в осях колес и трение между колесами и подножкой будет иметь небольшой тормозящий эффект. Это немного снизит ускорение.
Один из способов компенсировать это – слегка наклоните подножку, пока тележка не начнет двигаться, но не переусердствуйте, иначе вы запишете большее ускорение, чем следовало бы.
Вы можете проводить более точные эксперименты с использованием воздушной трассы , на которой “тележка” вынуждена зависать струи воздуха.
Использование световых ворот и компьютера точнее, чем пытаться проводить прямые наблюдения с помощью секундомера.
–
ВЕРХ СТРАНИЦЫ и субиндекс страницы
Версия расследования 2 с использованием двух источников света ворота
Исправление ошибок НЕ показано на схеме выше
Строго говоря, вы должны экспериментируйте на слегка наклоненной подножке, а не на горизонтальной лабораторный стенд, показанный на схемах выше.
Вы наклоняете рампу подножки вниз, чтобы вправо, пока тележка (без крюка) не начнет двигаться свой собственный.
Затем вы подпираете левый конец такой же высоты, а затем проведите эксперименты, как описано.
После этого вес тележка вниз по склону компенсирует трение, действующее между колеса тележки и аппарель подножки .
Также можно сделать эти исследования с горизонтальной воздушной трассой, на которой парит «тележка» струи воздуха – это альтернативный план исследования для минимизировать эффекты трения в экспериментах.
Как [] Карта проходит мимо световых ворот, два интервалы времени для блокировки света дают вам начальную и конечную скорость, и временной интервал между этими двумя событиями можно использовать для расчета ускорение тележки.
Исследования, расчеты и графики можно сделать, как описано выше в способе 1.
Версия 3 из ускоренные эксперименты.
Вы можете запустить тележку по наклонной рампе на уровень. подножку, а затем мимо двух световых ворот (2 и 3), чтобы измерить финальный скорость.
Вы можете установить первые световые ворота (1) рядом с линией старта наклонная рампа – начальная скорость должна быть близка к нулю.
Угол ската можно варьировать – угол круче должен дать большее ускорение.
Вы можете изменить длину наклонного пандуса, чтобы проверить, более длинный спуск на спуске увеличивает ускорение.
Вы можете изменить общую массу тележки, если она никакого влияния на ускорение.
ВЕРХ СТРАНИЦЫ и субиндекс страницы
d) понятие инерции – сравнение я нерциальный масса и гравитационная масса
Инерцию можно определить как тенденцию движение объекта должно оставаться неизменным.
Если мы начнем с размышлений о подтексте Первый Закон движения Ньютона …
… а результирующая сила необходима для изменения движения любого объекта .
Другими словами, если результирующая сила, все неподвижное остается в покое (нулевая скорость), все что угодно moving продолжает двигаться с той же скоростью (той же скоростью и направлением).
Итак, мы можем сказать тенденция объект, который движется с той же скоростью, называется инерцией .
инерционный Масса измеряет сопротивление объекта ускорению силой (F = ма)
Мы можем измерить, насколько сложно изменить скорость объекта путем вычисления его инерционной массы.
Инерционная масса объекта – это мера того, насколько сложно изменить его скорость.
Мы можем сделать это, используя уравнение из Второй закон движения Ньютона (сила = масса x ускорение).
F = ma, по перестановке это дает: m = F / a , и это выражение определяет инерционную массу
т. инерционная масса (кг) = приложенная сила (Н) / ускорение (м / с 2 )
Еще один способ взглянуть на уравнение – это рассмотрите влияние силы на ускорение.
a = F / m , некоторые последствия …
, как уже говорилось, для данной массы на ускорение объекта пропорционально приложенной силе, но …
, если к приложена та же сила F две разные массы, меньшая масса с меньшей инерцией будет испытывать большую разгон ,
и, если два объекта имеют одинаковую массу, то приложение одинаковой силы к каждому объекту приведет к одинаковому ускорению.
Инерционные и движущиеся объекты
А также смотреть на инерцию с точки Из соображений ускорения подумайте о замедлении движущихся объектов.
Если два объекта разной массы двигаясь с той же скоростью, объекту большей массы потребуется больший сила, чтобы замедлить его (замедлить) из-за второго закона Ньютона.
Представьте, что две машины движутся одновременно скорости, и оба водителя убирают ногу с педали газа.Если две машины испытывают такое же сопротивление воздуха и силы трения колеса о дорогу, автомобиль большей массы продвинется дальше, прежде чем остановиться. Больший инертной массы, тем больше сила потребуется, чтобы привести ее к остановиться на том же тормозном пути, что и автомобиль меньшей массы. F = ma, сила пропорциональна массе.
Крупные объекты, такие как грузовые суда или остановка скоростных поездов может занять несколько километров.
В чем разница между i nertial масса и гравитационная масса
Инерционная масса измеряет объектную устойчивость к ускорению.
Инерционная масса = сила / ускорение ( м = F / a , от F = ma)
Гравитационная масса определяет гравитационная сила притяжения, которую он оказывает на другой объект
масса = вес / гравитационный постоянная поля ( м = Вт / г , от W = мг).
Инертная масса и гравитация массы числовые идентичны.
ВЕРХ СТРАНИЦЫ и субиндекс страницы
(е) Третий закон движения Ньютона
Третий закон движения Ньютона гласит, что когда два объекта взаимодействуют, силы, которые они оказывают друг на друга, равны по числовые значения, действуют в противоположных направлениях и относятся к одному типу.
Это сначала говорит о том, что ни один объект можете двигаться куда угодно, но у вас есть два объекта и два результата!
В общем, что можно сказать по силы в паре взаимодействующих объектов?
Они одинакового размера.
Они действуют в противоположных направлениях.
Действуют на разные предметы.
Они однотипные по силе.
Эти четыре пункта будут проиллюстрированы в следующих примерах.
(я) Стационарный пример 3-го числа Ньютона. Закон
Немного беспорядочно анализировать!
Считать колбу жидкостью стоя неподвижно на лабораторном столе.
Показаны два набора сил, действующих. стрелками противоположного направления, но одинаковой длины – одинаковой величины сила.
Оба набора сил являются примерами 3-го закона Ньютона, но не смешивайте два вверх!
(i) Нормальное контактное усилие из-за вес объекта, воздействующего (толкающего) на поверхность скамейки (F1), составляет уравновешивается скамейкой при мельчайшем сжатии атомов, выталкиваясь обратно до равного и противоположной стороны на колбу (F2).
Аналогичный аргумент применим, когда вы толкать неподвижный объект. Сила вашего толчка уравновешивается сжатыми атомами объекта. отталкиваясь!
(ii) Одновременно и колба, и Земля (включая скамейку) взаимно притягивают друг друга (F3 и F4) к равному и противоположная степень из-за бесконтактной силы силы тяжести.
Земля притягивает колбу и колба притягивает к себе Землю.
Это не делает разница, соприкасаются ли предметы или нет, здесь действует гравитация во всем!).
В описанных до сих пор случаях нет результирующая сила , все уравновешено.
Если силы не были уравновешены и было около чистой равнодействующей силы , объект сдвинется или изменится – что-то бы изменилось!
Для стационарных объектов, если результат сила, действующая на объект ноль объект находится в равновесие (фактически означает состояние баланса).
Позаботьтесь о ситуациях равновесия которые могут выглядеть как примеры третьего закона движения Ньютона
например предположим, что часы висят на конец золотой цепочки в ситуации стационарного равновесия.
Соответствует ли это Третьему Ньютону? Закон.
Ответ – нет, потому что силы не одного типа, и оба они действуют на часы.
Вес часов действует вниз из-за силы тяжести .
Натяжение цепи действует вверх от часов – натяжение связано с натягиванием атомов друг с другом.
(ii) Примеры движения третьего закона Ньютона и последствия движения
, иллюстрирующий все четыре точки перечисленные выше
Ситуация 1. Фигуристы на каток.
Предположим, что два фигуриста одинаковой массы, стоят рядом друг с другом, а затем один из них толкает другой с силой 80 Н, что будет дальше?
Оба фигуриста испытывают одинаковые ощущения нормальное контактное усилие 80 Н, но в противоположных направлениях.
Оба фигуриста разгонятся друг от друга в противоположных направлениях.
Однако они будут только разгоняются друг от друга с одинаковым ускорением, если они такой же массы.
Поскольку F = ma и a = F / m ,
, если у одного из фигуристов меньшая масса, чем другой, фигурист с меньшей массой будет двигаться в в противоположном направлении с большим ускорением (F – постоянная и а 1 / м ).
Ситуация 2. Космонавт с ракетой. рюкзак
В «космическом пространстве» в условиях невесомости ситуации, космонавт мог маневрировать с помощью небольшого реактивного ранца прикреплен к спине скафандра.
При выстреле газы ускоряются в одну сторону, и равная и противоположная сила действует на космонавта, который ускоряется в обратном направлении – надеюсь, обратно в космос станция или космический корабль!
Ситуация 3.Лоб в лоб столкновение двух объектов
Предположим, что два шара m1 и m2 масс m 1 и m 2 сталкиваются лицом к лицу с определенным нормальным контактным усилием .
Предположим, что масса m 1 меньше массы m 2 .
Допустим, до удара они движутся с одинаковой скоростью навстречу друг другу .
При ударе они оба летят назад в в противоположном направлении, чем до удара.
Согласно 3-му закону Ньютона, оба шары испытывают точно такую же силу, но действуют в противоположных направлениях .
Однако потому что у них разных инертные массы , следовательно, как следствие a = F / m (2-й закон Ньютона) ..
меньшая инерционная масса, шар m1, будет разогнаться больше и улететь с большей скоростью, чем мяч m2,
, большая инерционная масса, шар m2, будет меньше разгоняться и лететь с меньшей скоростью, чем мяч m1,
(iii) Лобовое столкновение между двумя дорогами транспортные средства
В примере (ii) мячи отскочили от друг друга, но каковы последствия столкновения двух объектов лицом к лицу и «хрустеть» вместе.
Итак, представьте, что едет машина весом 1000 кг. врезаться в автомобиль весом 500 кг, движущийся в противоположном направлении.
(а) Что вы можете сказать о воздействии сила, которую испытывает каждая машина?
Согласно 3-му закону Ньютона движения, обе машины испытывают одинаковую силу удара, но противоположную направления.
(б) Что можно сказать о родственнике замедление каждой машины и их относительные инерционные массы?
2-й закон движения Ньютона может быть указано как F = ma ,
F = сила удара, м = инерционная масса и a = замедление (отрицательное ускорение).
Поскольку сила удара одинакова, ma g для зеленой машины массой 1000 кг = ma b для синей машины массой 500 кг.
Это означает, что замедление (отрицательный a) для зеленой машины большей массы должно быть меньше, чем для синяя машина меньшей массы.
Фактически, мы можем сказать математически, для той же силы удара F
1000 x a зеленая машина = 500 x a синий автомобиль
Это означает, что родственник замедление синих / зеленых машин 1000/500 = 2.
Итак, «зажигалка» синяя машина замедляется вдвое быстрее, чем «более тяжелая» зеленая машина.
У зеленой машины намного больше инертная масса , и замедлить ее труднее, чем синюю машину с гораздо меньшей инерционной массой при той же силе удара.
(c) Каковы последствия для каждого драйвер из ваших ответов на (б)?
Последствия для водителя синий автомобиль потенциально гораздо серьезнее, чем последствия для водитель зеленой машины.
Водитель синей машины будет ускоряется вперёд вдвое быстрее, чем водитель зелёного автомобиля, с потенциально более серьезные травмы от удара – хотя все должны быть одеты ремни безопасности, все еще существует вероятность получения хлыстовых травм.
Вы также можете предположить, что в случае любого водителя, чем меньше масса водителя, тем больше ускоряться вперед.
(d) Если карты путешествовали в та же скорость до удара, и комбинация кранча продолжала двигаться как один объект, в каком направлении будет двигаться «обломок» и почему?
(i) “Комбинированное крушение” могло бы продолжайте движение вправо.
В конце концов остановка из-за трения о дорогу.
(ii) «Комбинированное крушение» продолжайте движение вправо из-за более тяжелой массы грина автомобиль.
У зеленой машины вдвое больше импульс (масса x скорость) синей машины.
Подробнее о (d) см. Q2.7 по импульс расчеты и 2-й закон движения Ньютона
(iv) Кот прыгает с земли, чтобы поймать бабочка!
Силовые последовательности (без учета воздуха сопротивление)
В начале пара равна действуют бесконтактные гравитационные силы – Земля привлекает кошку а кошка притягивает к себе Землю.
Совпадают нормальный контакт действующие силы – вес кошки давит на землю через кошачьи лапы и сжатая земля отталкиваются от , равного сила противоположного действия.
При прыжке кошачьи мышцы прикладывать повышенную нормальную контактную силу к земле через спину ноги и, опять же, земля толкается вверх с увеличенным равным противоположная нормальная контактная сила.
Нормальные контактные силы нет более длительная работа и сила, действующая вверх, создаваемая кошачьей мышцы должны изначально превышать вес кошки из-за силы тяжести – ускорение кота должно превышать силу притяжения Земли на него – иначе он не сможет оторваться от земли.
Накопитель кинетической энергии кошки (КЕ) уменьшается, а его запас гравитационной потенциальной энергии (GPE) увеличивается максимально на максимальной высоте кошка поднимается в воздух – KE равен нулю только на мгновение, а затем, когда он падает, GPE кошки преобразуется назад к KE.
Кот манит Землю и Земля в равной степени привлекает кошку, которая теперь падает на землю.
Нормальное контактное усилие кошачьей удары по земле равняются ударам атомов земли. резервное копирование.
См. также Эластичный и неупругие столкновения, расчет количества движения и 2-й закон движения Ньютона
ВЕРХ СТРАНИЦЫ и субиндекс страницы
Движение и связанные силы отмечает индекс (включая законы Ньютона Движение)
1.Скорость и скорость – взаимосвязь между расстояние и время, графики расстояние-время gcse Physics
2. Ускорение, интерпретация и расчеты графика скорость-время. решение проблем Примечания к редакции физики gcse
3. Ускорение, трение, эффекты сопротивления и эксперименты с конечной скоростью Примечания к редакции физики gcse
4. Первый, второй и третий законы Ньютона. Расчет движения, инерции и F = ma Примечания к редакции физики gcse
5.Время реакции тормозной путь и пример расчеты Примечания к редакции физики gcse
6. Упругие и неупругие столкновения, импульс. вычислений и 2-го закона Ньютона движение заметки gcse по физике
Версия IGCSE примечания законы движения инерции Ньютона F = ma вычисления KS4 физика Научные заметки на Законы инерции движения Ньютона F = ma вычисления руководство по физике GCSE заметки по законам Ньютона инерция движения F = ma расчеты для школ, колледжей, академий, учебных курсов, репетиторов изображений рисунки диаграммы для законов движения Ньютона инерция F = ma примечания к пересмотру науки расчетов на Законы инерции движения Ньютона F = ma расчеты для пересмотра модулей физики примечания по темам физики, чтобы помочь в понимании Законы движения Ньютона инерция F = ma вычисления университетские курсы физики карьера в науке, физике вакансии в машиностроении технический лаборант стажировка инженер стажировка по физике США 8 класс 9 класс 10 AQA Заметки о пересмотре физики GCSE 9-1 по законам Ньютона инерция движения F = ma вычисления GCSE примечания к законам движения инерции Ньютона F = ma вычисления Edexcel GCSE 9-1 физика наука исправление примечания к Законы инерции движения Ньютона F = ma расчеты для OCR GCSE 9-1 21 век физика, научные заметки о законах движения Ньютона, инерция F = ma расчеты OCR GCSE 9-1 Шлюз физики примечания к пересмотру законов движения Ньютона инерция F = ma расчеты WJEC gcse science CCEA / CEA gcse science
ВЕРХ СТРАНИЦЫ и субиндекс страницы
Проект простой физики на Первом законе Ньютона | Education
Первый закон движения Ньютона гласит, что «объект в движении, остается в движении.”Обратное, что неподвижный объект остается в покое, также верно. Оба предполагают, что постоянная скорость поддерживается только при наличии нулевой силы. Известный просто как закон инерции, Первый закон Ньютона имеет важные приложения в повседневной жизни. и множество простых экспериментов демонстрируют эту концепцию.
Пенни в чашке
Инерцию можно проиллюстрировать с помощью трех предметов домашнего обихода: пенни, пластиковой чашки и учётной карточки. Первый закон Ньютона гласит, что объект находится в состоянии покоя, при условии отсутствия силовых действий на нем, постараюсь оставаться в покое.Продемонстрируйте это, поместив учетную карточку на пластиковый стаканчик. Положив пенни на учетную карточку, быстро извлеките учетную карточку по горизонтали. Пенни должен упасть прямо на дно чашки. Студенты могут наблюдать, как сила тяжести воздействовала на монету, возвращая ее в состояние покоя.
Четверть улова
Используя четверть и локоть ученика, ученики могут записать мгновенную инерцию. Студенты должны начать с того, что закроют уши одной рукой так, чтобы их предплечья были примерно горизонтально относительно земли.Затем они должны сложить и уравновесить четыре четверти на своих руках и попытаться использовать руки на этих руках, чтобы поймать четверти. Большинству учеников будет сложно поймать четверть с первых же попыток. Однако они должны постепенно замечать, что, если они немного дернут локтями вверх, чтобы подбросить четвертаки вверх, монеты будет легче поймать. Это потому, что инерция заставляет четверти оставаться в подвешенном состоянии в воздухе, но лишь на короткое время, прежде чем сила тяжести преодолеет силу, приложенную, чтобы подтолкнуть их вверх.
Движущаяся тележка
Учащиеся могут смоделировать столкновение с автомобилем, когда инерция без ремня безопасности вызывает серьезные травмы. Используя простую тележку – подойдет кусок дерева с двумя осями колес – массу любого сорта и картонную коробку, ученики могут поместить массу на тележку и врезать ее в картон. Это можно сделать, приклеив картонную коробку к полу, а также отметив начальную точку скотчем на расстоянии около 5 футов. Затем ученики могут врезаться тележкой в картон с разной скоростью и видеть, насколько масса перемещается по тележке с разным расстоянием и скоростью.Это потому, что масса была приведена в движение и остается в этом положении по инерции, несмотря на то, что картон ее резко остановил. Студенты должны записать и обсудить последствия своих наблюдений, а также могут попробовать прикрепить массу к тележке, чтобы имитировать ремень безопасности.
Чаша и мрамор
Важной частью изучения Первого закона Ньютона является определение сил, даже если они кажутся невидимыми. Студенты могут попробовать катать шарик по стенке миски и смотреть, как он катится взад и вперед, пока не остановится на дне.В мире без силы начальная сила толкания шарика вниз по стенке чаши должна поддерживать шарик в движении навсегда, потому что движущийся объект остается в движении в отсутствие дополнительной силы. На этом этапе ученики должны понять, что присутствуют силы – трение и гравитация – которые замедляют шарик до тех пор, пока он не перестанет двигаться.
Ссылки
Биография писателя
Кевин Вандрей много писал о высшем образовании. Его работа была опубликована в «Каплан, Учебники.com и Shmoop, Inc., среди прочих. В настоящее время он получает степень магистра государственного управления в Корнельском университете.
Ньютоновский госпиталист | Госпиталист
Силы нашей вселенной описываются и измеряются серией законов и уравнений, известных под общим названием физика. Хотя мы, кажется, далеки от тех безмятежных (или Halcion) дней университетской физики, мы существуем во вселенной, все еще управляемой ими. В данном случае наш мир – это больница.
Странные векторы силы и трудные для понимания принципы кружатся, вызывая неожиданные изменения в нашей среде.Используя законы физики, мы можем попытаться понять эти силы.
ПЕРВЫЙ ЗАКОН НЬЮТОНА: Первый закон Ньютона – это утверждение об инерции. Покоящийся объект остается неподвижным; объект в движении остается в движении, если его не заставляют изменить свое состояние под действием внешней силы. Византийская бюрократия сохраняет значительную инерцию. Выражение «вот как мы всегда это делали здесь» лучше всего отражает эту философию.
ВТОРОЙ ЗАКОН НЬЮТОНА: Второй закон Ньютона исследует силу, необходимую для ускорения объекта по отношению к его массе (F = MA).Умеренная сила, приложенная к мячу для гольфа, может отбросить этот объект на 250 ярдов – крюк вправо, но та же сила, приложенная к самосвалу, не вызывает значительного движения.
В больнице мы часто видим большие затраты энергии, в результате чего мало движения. Это вообще административное явление.
ТРЕТИЙ ЗАКОН НЬЮТОНА: На каждое действие есть равная и противоположная реакция. Это важный закон в больнице. Самый свежий пример – изменение рабочего времени жителей.Казалось бы, простая проблема: жители, работающие слишком много часов, приводят к законодательным актам и обязательным часам. Это конкретное изменение имело непредвиденные последствия и повлияло на многие другие системы. В случае часов работы резидентом потенциальные преимущества в количестве отработанных часов привели к потенциально неблагоприятному воздействию на такие вещи, как непрерывность и обучение, а также к увеличению спроса на госпиталистов.
Никакие системные изменения не могут произойти без последствий, и все дело в том, чтобы идентифицировать эти изменения до того, как они произойдут.К счастью, большинство систем обладают значительной инерцией, и только самые большие силы вызывают серьезные изменения. Требуются огромные затраты энергии (например, государственное регулирование или местные наблюдательные комиссии), чтобы запросить силы, достаточные для преодоления скорости убегания и изменения.
Некоторые силы могут вызывать изменения не просто своим уровнем энергии, а своим стратегическим расположением. Небольшой сильный удар может расколоть алмаз. Звонок супруги жителя может привести к срыву программы. Откровенный комментарий коллеги может привести к катастрофическому урегулированию злоупотребления служебным положением.
ЦЕНТРОБЕЖНАЯ ПСЕВДОСИЛА: Псевдосила возникает, когда человек движется равномерно по кругу. Большинство из нас наблюдали это явление. Когда вы бегаете кругами, как пресловутая обезглавленная птица, мало что можно сделать, несмотря на ощущение затраченной энергии.
Связанный принцип – броуновское движение: частицы в газе или жидкости сталкиваются друг с другом и стенками контейнера, вызывая случайное движение. Временами день госпиталиста может казаться таким: активное движение, но по большей части ненаправленное.
КОПЕРНИКАНСКИЙ ПРИНЦИП: Идея, предложенная Коперником, заключалась в том, что Солнце, а не Земля, является центром этой вселенной. Это важный момент, о котором должны помнить госпиталисты. Мы тратим часы на изучение наших пациентов. Мы всегда должны помнить, что врач не является центром вселенной для госпитализированного пациента. Как следует из названия, когда мы «округляемся», мы являемся спутником.
ПРИНЦИП ПРИЧИНЫ: Причина должна следовать за следствием. Это опасная теория, иллюстрируемая классическим post-hoc, суфлером: потому что я что-то сделал, что-то произошло.
Применительно к пациентам принцип причинности может ввести в заблуждение. Когда начали принимать антибиотик, температура спала. Совпадение или причинно-следственная связь? Мы наняли госпитальера, и продолжительность нашего пребывания сократилась. Совпадение или причинно-следственная связь?
ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ: Знаменитое уравнение Эйнштейна E = mc2 представляет его теорию относительности. Это уравнение представляет собой соотношение между массой объекта и его энергией. Масса представлена формулой M = DV, где D – плотность, а V = объем.
В условиях больницы мы видим, что эта формула используется как следствие формулы Эйнштейна, называемое теорией родственников. Входя в палату пациента, человек часто сталкивается с большим количеством родственников, супругов, братьев и сестер, а также отчужденных детей, которых боятся. Эти ситуации почти всегда требуют повышенных затрат энергии на общение, достижение консенсуса и времени.
По мере увеличения абсолютного числа (или объема) членов семьи, одновременно с увеличением плотности отдельных членов, расход энергии резко возрастает.Это точно следует уравнению масс. В ситуациях, когда плотность отдельного члена семьи превышает измеримые уровни, можно использовать сценарий «черной дыры» (см. Иллюстрацию).
ЧЕРНЫЕ ДЫРЫ: Черная дыра – это область пространства-времени, из которой ничто не может вырваться, даже свет.
Черная дыра – это область такой экстремальной плотности, что вся энергия засасывается в ее гравитационное поле. Попав в ситуацию с черной дырой, наблюдатель может заметить ожидаемые явления, включая отсутствие света, потерю энергии, крайнюю усталость и недомогание, а также ощущение безнадежности.Этот эффект можно увидеть в комнатах комитетов или на палатах.
Единственное известное средство от этого состояния – предотвращение или прекращение обслуживания.
УРАВНЕНИЕ СВОБОДНОЙ ЭНЕРГИИ Гиббса: Уравнение свободной энергии Гиббса, G = H- (TS), является термодинамической формулой и мерой сохранения энергии. Проще говоря, энергия системы связана с энтальпией (H) или положительным вкладом творческой энергии за вычетом произведения времени и энтропии, естественной тенденции систем к распаду.
Этот эффект можно увидеть в создании госпиталистических программ.
Программа госпитализма иногда создается энергичным предпринимателем, реагирующим на вакуум или потенциальное пространство. Отличный дизайн ведет к функциональной программе (G). Госпиталист (H) должен постоянно вкладывать энергию в поддержание системы, иначе со временем (T) энтропия (S) возьмет верх, и система ухудшится. Госпиталистическая программа не может полагаться на свой первоначальный успешный дизайн, чтобы выжить.
ДУАЛЬНОСТЬ ЧАСТИЦ-ВОЛН: Кванты – это сгустки энергии. Мы видим эти базовые единицы в больнице на несубатомном уровне.
Кажется, что наши признания идут волнообразно. Кажется, что наша ежедневная рабочая нагрузка тоже волнообразна. Но главное в больничной медицине – это пациент. RVU может быть 1,33, LOS 3,2 дня и FTE 0,8, но я еще не видел полутора пациентов в комнате.
КРИТИЧЕСКАЯ МАССА: Критическая масса – это наименьшее количество расщепляющегося материала, необходимого для поддержания цепной ядерной реакции на постоянном уровне. Этот термин также используется для обозначения количества или уровня, необходимого для достижения определенного результата или нового действия.К счастью, госпиталистическое движение в Америке достигло этой самоподдерживающейся критической массы.
ЗАКЛЮЧЕНИЕ. Сидя под деревом из пословиц и наблюдая, как спелая бабушка Смит упала на его башку, сэр Исаак Ньютон не знал, насколько сильно он повлияет на мир больничной медицины. Что идет вверх, должно прийти вниз. Поступивший пациент должен быть выписан. И начатая редакционная статья должна в конце концов закончиться. TH
Джейми Ньюман, доктор медицины, FACP, врач-редактор журнала The Hopitalist и старший младший консультант отделения внутренней медицины больницы и доцент кафедры внутренней медицины и истории болезни Медицинского колледжа клиники Майо при Клиническом колледже Майо медицины, Рочестер, Миннесота.




 Связь между приращением кинетической энергии тела и работой приложенных к телу сил.
Связь между приращением кинетической энергии тела и работой приложенных к телу сил. Условие плавания тел.
Условие плавания тел. Внутренняя энергия термодинамической системы. Количество теплоты и работа как меры изменения внутренней энергии. Применение первого закона термодинамики к изопроцессам.
Внутренняя энергия термодинамической системы. Количество теплоты и работа как меры изменения внутренней энергии. Применение первого закона термодинамики к изопроцессам. Точечный заряд. Способы электризации. Проводники и диэлектрики. Закон сохранения электрического заряда. Взаимодействие электрических зарядов. Закон Кулона. Диэлектрическая проницаемость вещества.
Точечный заряд. Способы электризации. Проводники и диэлектрики. Закон сохранения электрического заряда. Взаимодействие электрических зарядов. Закон Кулона. Диэлектрическая проницаемость вещества.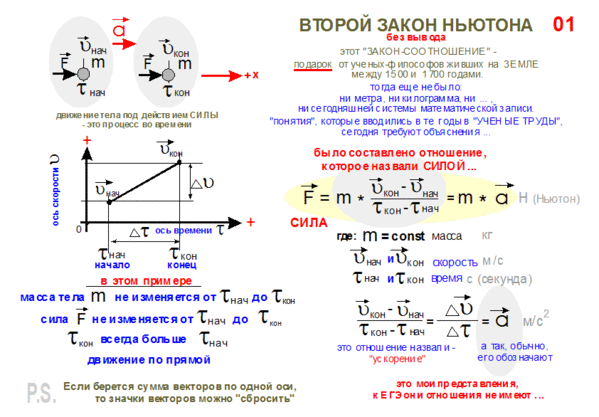 Сила и плотность тока. Условия существования тока в цепи. Электродвижущая сила. Напряжение. Закон Ома для участка цепи, не содержащей ЭДС. Омическое сопротивление проводника. Удельное сопротивление. Зависимость удельного сопротивления от температуры. Последовательное и параллельное соединения проводников.
Сила и плотность тока. Условия существования тока в цепи. Электродвижущая сила. Напряжение. Закон Ома для участка цепи, не содержащей ЭДС. Омическое сопротивление проводника. Удельное сопротивление. Зависимость удельного сопротивления от температуры. Последовательное и параллельное соединения проводников.