| 1. | Действие каких сил компенсируется? | 1 вид – рецептивный | лёгкое | 1 Б. | Отработка навыка определения сил, под действием которых тело покоится или движется равномерно и прямолинейно. |
| 2. | Как движется вагон? | 1 вид – рецептивный | лёгкое |
1 Б.
|
Отработка навыка определения характера движения системы отсчёта по характеру движения предмета в данной системе отсчёта. |
| 3. | Инерциальная система отсчёта | 1 вид – рецептивный | лёгкое | 1 Б. | Отработка навыка определения инерциальной системы отсчёта среди нескольких предложенных. |
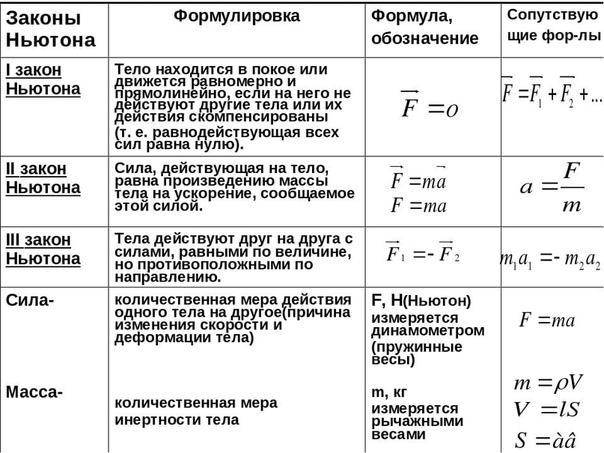
4.
|
Вид движения | 2 вид – интерпретация | среднее | 2 Б. | Отработка навыка определения вида движения тела по соотношению силы тяги и силы сопротивления. |
| 5. | Сила тяги двигателя лифта | 2 вид – интерпретация | среднее |
2 Б.
| Отработка навыка определения силы тяги двигателя лифта, поднимающегося равномерно вертикально вверх. |
| 6. | Бусинка на нити | 2 вид – интерпретация | среднее | 2 Б. | Отработка навыка определения минимальной силы трения, при которой бусинка заданной массы не соскальзывает с вертикально расположенной нити. |
7.
|
Брусок и пружина | 3 вид – анализ | сложное | 3 Б. | Отработка навыка определения жёсткости пружины, при помощи которой равномерно и прямолинейно тянут брусок по доске. |
| 8. | Шарик в жидкости | 3 вид – анализ | сложное |
3 Б.
|
Отработка навыка определения объёма воздушной полости в шарике, равномерно и прямолинейно всплывающего со дна стакана, наполненного жидкостью. |
| 9. | 3 вид – анализ | сложное | 3 Б. |
Отработка навыка определения силы тяги, которую необходимо приложить, чтобы начать подъём груза на верёвке, перекинутой через бревно.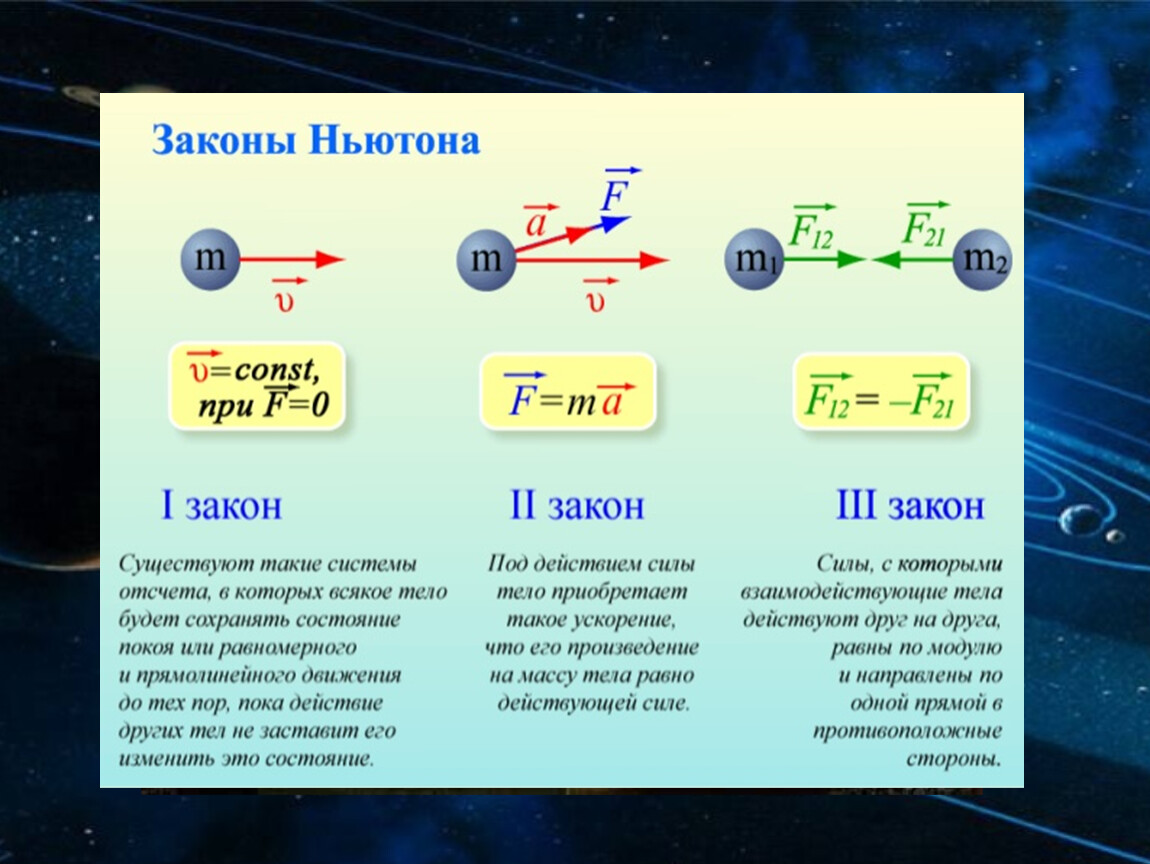
|
§4. Закон инерции (первый закон Ньютона).
Ньютон дал следующую формулировку закона инерции [6, с.232]: “Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние”.
Историю закона инерции следует начать с Галилея, так как до него понятия движения тел по инерции не было. Аристотель, например, утверждал, что для поддержания движения свободного тела к нему необходимо постоянно прикладывать силу. Галилей в своей работе “Диалоги о двух важнейших системах мира, птолемеевой и коперниковой” утверждал [6, с.161]: “Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления, то… движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца”.
 368-369]: “Первый закон природы: всякая вещь пребывает в том состоянии, в каком она находится, пока ее что-либо не изменит”.
368-369]: “Первый закон природы: всякая вещь пребывает в том состоянии, в каком она находится, пока ее что-либо не изменит”.“Второй закон природы: всякое движущееся тело стремится продолжать свое движение по прямой”.
И еще [7, с.200]: “…каждая частица материи в отдельности продолжает находиться в одном и том же состоянии до тех пор, пока столкновение с другими частицами не вынуждает ее изменить это состояние…раз уже она начала двигаться, то будет продолжать это движение постоянно с равной силой до тех пор, пока другие ее не остановят или не замедлят ее движение”.
В одной из современных формулировок закон инерции выглядит так [8, с.70]: “Если на материальную точку не действуют силы, то она сохраняет состояние покоя или равномерного и прямолинейного движения”.

Данная формулировка закона инерции очень похожа на формулировку И.Ньютона, но с одной только разницей: у Ньютона речь идет о теле, а здесь – о материальной точке. И это, на первый взгляд, не существенное различие, на самом деле является принципиальным.
Во-первых, понятие материальной точки является условным, поскольку в природе таких материальных объектов нет. Поэтому создателям механики и в голову не могло прийти сравнивать реальные тела с математической точкой, то есть с фикцией. Другое дело, что движение тел во многих случаях можно было описать как движение одной его точки, за которую принимался центр масс тела. Однако, некритическое отношение к этому вопросу привело в дальнейшем уже к принципиальному убеждению, что законы механики относятся только к материальной точке или к системе материальных точек, а не к реальным телам. Хотя ясно, что точка остается точкой, если ее даже и назвать материальной. И этим самым развитию механики был поставлен труднопреодолимый барьер.
 Ниже этот вопрос будет обсуждаться подробнее.
Ниже этот вопрос будет обсуждаться подробнее.Во-вторых, отнесение закона инерции к движению только материальной точки приводит к тому, что сам этот закон также становится фикцией, так как движутся все-таки реальные тела, состоящие из атомов, а в атомах имеются ядра и электроны, которые вращаются вокруг своих осей, а электроны еще и вокруг ядер, причем в целом довольно хаотично. И если средневековые ученые могли еще думать, что все частицы любого тела могут двигаться с одинаковыми скоростями, поскольку они не знали, что все тела состоят из атомов, то современные ученые должны этот факт учитывать.
Таким образом, к закону движения по инерции может быть два варианта отношения: или считать его условным, фиктивным, или учесть реальность и относить его к реальным телам, а не к точкам. При этом необходимо учесть и тот факт, что движения материальных объектов без силового воздействия на них в природе практически не существует.
Такая постановка вопроса приводит к необходимости осмысления новой сущности закона инерции и изменения его формулировки.
 В §4 первой главы мы уже говорили о необходимости представить этот закон в дифференциальной форме, то есть считать его справедливым, для любого момента движения материальных объектов, независимо от характера этого движения. Сейчас мы сделаем некоторые уточнения для предложенной там формулировки. Это связано, во-первых, с тем, что любое материальное тело представляет собой совокупность частиц, которые в одно и то же время могут иметь разные скорости и ускорения, как, например, во вращательном движении. И, во-вторых, необходимо иметь в виду, что силовое воздействие на тело и его частицы обусловлено подводом энергии
В §4 первой главы мы уже говорили о необходимости представить этот закон в дифференциальной форме, то есть считать его справедливым, для любого момента движения материальных объектов, независимо от характера этого движения. Сейчас мы сделаем некоторые уточнения для предложенной там формулировки. Это связано, во-первых, с тем, что любое материальное тело представляет собой совокупность частиц, которые в одно и то же время могут иметь разные скорости и ускорения, как, например, во вращательном движении. И, во-вторых, необходимо иметь в виду, что силовое воздействие на тело и его частицы обусловлено подводом энергии Тогда закон инерции можно сформулировать следующим образом:
– Инерция – это стремление тела, как единого целого сохранить состояние покоя или скорость (энергию) своего движения в любой момент этого движения как при действии на него сил, так и при отсутствии такого воздействия; при прекращении силового воздействия тело будет двигаться в соответствии с имеющейся у него на данный момент скоростью в любой выбранной системе отсчета.

Можно дать и другую формулировку закона инерции:
– В любой момент своего движения материальный объект стремится двигаться с имеющейся у него на данный момент скоростью (энергией) независимо от выбранной системы отсчета, и только внешние воздействия препятствуют такому движению.
Ярким подтверждением справедливости дифференциальной трактовки закона инерции является движение тел по окружности, не связанных жестко с центром вращения, как, например, при движении планет вокруг Солнца (в главе III будет показано, что движение планет вокруг Солнца можно считать вращательным движением). В популярной литературе это движение часто объясняется так: за счет притяжения Солнца планеты падают на него, но наличие у них скорости в касательном направлении смещает планету в сторону, в результате чего и получается движение по окружности (приближенно). С точки же зрения закона инерции круговой характер движения планет следует объяснять таким образом: в любой момент своего движения планета стремится двигаться по направлению имеющейся у нее на данный момент скорости, но под действием притяжения Солнца в каждый момент движения происходит изменение этой скорости (при круговом вращательном движении меняется только направление скорости), в результате чего траектория движения искривляется и становится окружностью при постоянной действующей силе.
 Здесь следует подчеркнуть, что основное движение планет это движение по инерции, а сила притяжения со стороны Солнца только искривляет траекторию этого движения.
Здесь следует подчеркнуть, что основное движение планет это движение по инерции, а сила притяжения со стороны Солнца только искривляет траекторию этого движения.Таким образом, если бы не было инерции у тел, то их движение всегда происходило бы только по направлению действующих на них сил.
Трактовка закона инерции в дифференциальной форме ставит также вопрос и о причинах его существования, то есть о его физической сущности. То, что тела при отсутствии на них силового воздействия должны двигаться с постоянной скоростью, нам понятно, так как при наличии сил появляется ускорение. Но движение по инерции пусть и мгновенное при постоянном силовом воздействии требует осмысления. Здесь, очевидно, следует сравнивать кинетические энергии, связанные с инерционным движением и силовым воздействием. Поскольку любое тело при движении имеет какую-то скорость, то оно имеет и определенную кинетическую энергию. Силовое воздействие тоже связано с затратами энергии. Из опыта нам известно, что чем больше будет сила, приложенная к движущемуся телу, тем сильнее изменится характер его движения.
 Это значит, что чем больше будет подведенная к телу энергия по сравнению с энергией его движения, тем больше будет ее влияние на характер движения тела. Поэтому можно утверждать, что инерция движущегося тела определяется его кинетической энергией. Именно соотношение кинетической энергии тела и энергии силового воздействия определяет закон движения тела.
Это значит, что чем больше будет подведенная к телу энергия по сравнению с энергией его движения, тем больше будет ее влияние на характер движения тела. Поэтому можно утверждать, что инерция движущегося тела определяется его кинетической энергией. Именно соотношение кинетической энергии тела и энергии силового воздействия определяет закон движения тела.Найдем затраты энергии на искривление траектории при вращательном движении тел. К телу, движущемуся по окружности (рис.1), подводится энергия в радиальном направлении, в результате чего изменяется направление его скорости, но не ее величина. Можно ли в этом случае сказать, что происходит изменение кинетической энергии тела? Если иметь в виду только ее величину, то нет. Если же учитывать направленность кинетической энергии, то да. Этот пример является еще одним подтверждением направленности кинетической энергии, ее векторной сущности при движении тел и их взаимодействии, потому что для изменения направления движения необходимо приложить силу, то есть подвести добавочную энергию в определенном направлении.
 Величина радиальной (центростремительной) силы определяется величиной изменения кинетической энергии тела , отнесенной к величине его радиального перемещения при угле поворота . Изменение кинетической энергии тела будет равно подведенной к нему энергии :
Величина радиальной (центростремительной) силы определяется величиной изменения кинетической энергии тела , отнесенной к величине его радиального перемещения при угле поворота . Изменение кинетической энергии тела будет равно подведенной к нему энергии :, (1)
где m – масса тела, – изменение окружной скорости тела при угле поворота от начального положения.
В соответствии с рис.1,б имеем:
, (2)
где V – окружная скорость тела.
Центростремительная сила определяется отношением при , где в соответствии с рис.1,а будет равно:
(3)
Тогда:
(4)
Затраты кинетической энергии определим, представив выражение (1) с учетом выражения (2) в виде:
(5)
Последовательно увеличивая значение угла в 2, 3,…n раз, придем к формуле:
, (6)
где за один полный оборот число шагов n будет равно:
(7)
В соответствии с формулой (6) затраты кинетической энергии при вращательном движении графически представлены на рис. 2. Поскольку энергия все время потребляется, то максимальное значение энергии , соответствующее половине оборота, следует удвоить, чтобы найти затраты энергии за полный оборот.
2. Поскольку энергия все время потребляется, то максимальное значение энергии , соответствующее половине оборота, следует удвоить, чтобы найти затраты энергии за полный оборот.
Тогда, имея в виду, что для половины оборота , получим:
(8)
Таким образом, чтобы заставить тело двигаться по окружности, к нему надо подвести энергию в 8 раз большую, чем его собственная энергия движения.
Интересно также отметить следующий результат, вытекающий из полученного нами соотношения. Поскольку затраты энергии можно определить через работу центростремительной силы:
, (9)
где S – перемещение точки приложения силы, соответствующее направлению ее действия.
Используя выражения (8) и (4), получим:
(10)
Отсюда следует, что перемещение S представляет собой два диаметра окружности радиуса r, а работа центростремительной силы будет определяться кратчайшим расстоянием между наиболее удаленными точками окружности при движении тела сперва в одну (удаление), а затем другую (приближение) стороны от его начального положения.
Таким образом, инерцию тела можно определить как его стремление сохранить свою кинетическую энергию при внешнем воздействии. Характер движения тела будет зависеть от соотношения его собственной кинетической энергии и энергии, к нему подведенной. При этом характер движения будет зависеть не только от величины подведенной энергии, но и от направления ее подведения.
Если к телу не подводится никакой энергии, то его энергия не изменяется и оно движется с постоянной по величине и направлению скоростью. Однако, здесь следует иметь в виду, что так можно говорить, если рассматривать тело как единое целое. Если же иметь в виду и частички, из которых состоит тело (электроны и ядра), то для них такое утверждение будет неверно, так как они движутся с переменными скоростями и ускорениями. Очевидно, о постоянстве скорости можно говорить только для центра масс тела. А в целом о теле можно сказать только, что оно движется с постоянной энергией, так как энергия его частичек тоже не меняется. При таком определении инерции не исключается возможность и вращательного движения тела по инерции с постоянной угловой скоростью, или даже сочетание его прямолинейного движения с постоянной скоростью и вращения вокруг центра масс с постоянной угловой скоростью.
При таком определении инерции не исключается возможность и вращательного движения тела по инерции с постоянной угловой скоростью, или даже сочетание его прямолинейного движения с постоянной скоростью и вращения вокруг центра масс с постоянной угловой скоростью.
Что касается затрат энергии на вращение частичек тела, то противоположно расположенные частички взаимно воздействуют друг на друга (без внешнего воздействия), в связи с чем затрат энергии не происходит.
В свете всего сказанного выше закон инерции Ньютона можно считать интегральным законом, справедливым для конечных промежутков времени. Этот закон можно обобщить и на случай вращательного движения, сформулировав его следующим образом:
– Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного или равномерного вращательного движения пока в результате взаимодействий не изменится его кинетическая энергия.
Таким образом, мы расширили существующее понятие интегрального закона инерции, обобщив его и на равномерное вращательное движение и связав его с постоянством кинетической энергии тела. Причем сделали мы это в классической традиции, связав его с постоянством скорости движения тел. Скорость движения будет постоянной как при отсутствии действия на тело каких-либо сил, так и при действии на него уравновешенной системы сил. Это обстоятельство учитывается в ряде современных формулировок закона инерции. Приведем наиболее развернутую характеристику закона инерции, данную в физической энциклопедии [9, с.144]: “Инертность (инерция) (от лат. iners, род. падеж inertis – бездеятельный) в механике – свойство материальных тел, проявляющееся в том, что тело сохраняет неизменным состояние своего движения или покоя по отношению к т. н. Инерциальной системе отсчета, когда внешние воздействия на тело (силы) отсутствуют или взаимно уравновешиваются. Если же на тело действует неуравновешенная система сил, то свойство инертности сказывается в том, что изменение состояния покоя или движения тела, то есть изменение скоростей его точек, происходит постепенно, а не мгновенно; при этом движение изменяется тем медленнее, чем больше инертность тела.
Причем сделали мы это в классической традиции, связав его с постоянством скорости движения тел. Скорость движения будет постоянной как при отсутствии действия на тело каких-либо сил, так и при действии на него уравновешенной системы сил. Это обстоятельство учитывается в ряде современных формулировок закона инерции. Приведем наиболее развернутую характеристику закона инерции, данную в физической энциклопедии [9, с.144]: “Инертность (инерция) (от лат. iners, род. падеж inertis – бездеятельный) в механике – свойство материальных тел, проявляющееся в том, что тело сохраняет неизменным состояние своего движения или покоя по отношению к т. н. Инерциальной системе отсчета, когда внешние воздействия на тело (силы) отсутствуют или взаимно уравновешиваются. Если же на тело действует неуравновешенная система сил, то свойство инертности сказывается в том, что изменение состояния покоя или движения тела, то есть изменение скоростей его точек, происходит постепенно, а не мгновенно; при этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела является его масса”.
Мерой инертности тела является его масса”.
Не будем подробно анализировать эту формулировку, обратим внимание только на утверждение о соответствии закону инерции движения тела под действием уравновешенной системы сил. Такое утверждение вызывает сомнения. Действительно, можно ли назвать движением по инерции движение автомобиля с работающим двигателем, хотя он и движется с постоянной скоростью? Ведь при таком движении происходят затраты энергии, внешней по отношению к автомобилю. Это обстоятельство заставляет задуматься при рассмотрении закона инерции с энергетических позиций. Сомнительно, чтобы движение по инерции было связано с затратами внешней энергии. Рассмотрим с этой точки зрения еще несколько примеров. Вернемся снова к движению планет по их орбитам. Предположим для упрощения, что орбиты будут круговыми. Тогда на планеты силы тяготения будут действовать только в радиальном направлении, в касательном же направлении никаких сил не будет и, значит, не будет затрат энергии. В этом случае возникает желание назвать движение в касательном направлении движением по инерции. Но тогда получается, что движение одного и того же тела (планеты) будет одновременно и по инерции в касательном направлении, при котором величина скорости будет постоянной и не инерционным в радиальном направлении, так как при этом будет изменяться направление скорости и будет затрачиваться внешняя энергия (энергия Солнца). Очевидно, что два указанных направления должны быть взаимно перпендикулярными, так как только тогда взаимодействия в этих направлениях не будут влиять друг на друга.
В этом случае возникает желание назвать движение в касательном направлении движением по инерции. Но тогда получается, что движение одного и того же тела (планеты) будет одновременно и по инерции в касательном направлении, при котором величина скорости будет постоянной и не инерционным в радиальном направлении, так как при этом будет изменяться направление скорости и будет затрачиваться внешняя энергия (энергия Солнца). Очевидно, что два указанных направления должны быть взаимно перпендикулярными, так как только тогда взаимодействия в этих направлениях не будут влиять друг на друга.
Рассмотрим теперь движение автомобиля с отключенным двигателем, то есть движение накатом, когда на машину действует только сила сопротивления. Машина при этом тормозится, а скорость ее уменьшается. Движение машины в этом случае происходит за счет ее собственной кинетической энергии без использования внешней энергии. Возникает вопрос: можно ли такое движение назвать движением по инерции? Если исходить из классической формулировки закона инерции, то нет. Если же попытаться понять сущность такого движения, то кроме собственной инерции у тела ничего нет, что заставляло бы его двигаться. Значит, именно инерция тела, связанная с его запасом кинетической энергии, заставляет тело продолжать движение до тех пор, пока не будет исчерпан весь ее запас. Если же это так, то такое движение тоже следует считать движением по инерции.
Если же попытаться понять сущность такого движения, то кроме собственной инерции у тела ничего нет, что заставляло бы его двигаться. Значит, именно инерция тела, связанная с его запасом кинетической энергии, заставляет тело продолжать движение до тех пор, пока не будет исчерпан весь ее запас. Если же это так, то такое движение тоже следует считать движением по инерции.
В связи со всем изложенным закон инерции в интегральной форме можно сформулировать следующим образом:
– Если в каком-либо направлении движение тела происходит без затрат внешней энергии или за счет собственной кинетической энергии, такое движение будет движением по инерции.
Под данное определение будут подходить прямолинейное и вращательное движения, совместное вращательное и прямолинейное движения без затрат внешней энергии и при торможении, вращение планет вокруг Солнца и т. п.
Автор выносит на обсуждение такое понимание сущности закона инерции.
И, наконец, следует подчеркнуть важное следствие, имеющее место при использовании закона инерции в дифференциальной форме: в случае реальности сил инерции все системы отсчета – инерциальные и неинерциальные – можно считать равноправными, так как в любой из них будут выполняться все законы механики.
Первый закон Ньютона. Инерциальные системы отсчёта. Взаимодействие тел. Сила. Масса. Второй закон Ньютона. Третий закон Ньютона
1. Первый закон Ньютона. Инерциальные системы отсчёта. Взаимодействие тел. Сила. Масса. Второй закон Ньютона. Третий закон
Санкт-Петербургское бюджетное профессиональное образовательное учреждение«Пожарно-спасательный колледж «Санкт-Петербургский центр подготовки
спасателей»
ПЕРВЫЙ ЗАКОН НЬЮТОНА. ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ
ОТСЧЁТА. ВЗАИМОДЕЙСТВИЕ ТЕЛ. СИЛА. МАССА. ВТОРОЙ
ЗАКОН НЬЮТОНА. ТРЕТИЙ ЗАКОН НЬЮТОНА.
НАД ПРЕЗЕНТАЦИЕЙ РАБОТАЛА:
АНИКИНА СОФИЯ АЛЕКСЕЕВНА
СТУДЕНТКА ГРУППЫ №671
ПРЕПОДАВАТЕЛЬ: ЗАХАРОВА О. А.
ОЦЕНКА:
2. Содержание
СОДЕРЖАНИЕ• Исаак Ньютон
• Первый закон Ньютона
• Инерциальные системы отсчёта
• Взаимодействие тел
• Сила
• Масса
• Второй закон Ньютона
• Третий закон Ньютона
3. ИсаÁк НьютÓн (04.01.1643– 31.03.1727)
ИСАÁК НЬЮТÓН(04.
 01.1643– 31.03.1727)
01.1643– 31.03.1727)Английский физик, математик, механик и
астроном, один из создателей классической
физики. Автор фундаментального труда
«Математические начала натуральной
философии», в котором он изложил закон
всемирного тяготения и три закона механики,
ставшие основой классической механики.
Разработал дифференциальное и интегральное
исчисления, теорию цвета, заложил основы
современной физической оптики, создал многие
другие математические и физические теории.
4. Первый Закон Ньютона
ПЕРВЫЙ ЗАКОН НЬЮТОНАТакже известен как закон инерции.
Инерция (инертность) — свойство тела
сохранять скорость своего движения
неизменной по величине и направлению,
когда не действуют никакие силы, а также
свойство тела сопротивляться изменению
его скорости.
5. формулировка
ФОРМУЛИРОВКА• Существуют такие инерциальные системы
отсчёта, относительно которых
материальные точки, когда на них не
действуют никакие силы, находятся в
состоянии покоя или равномерного
прямолинейного движения.

6. Инерциальные системы отсчёта
ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЁТА• Это системы отсчёта, в которой все свободные тела
движутся прямолинейно и равномерно, либо
покоятся.
• Термин «инерциальная система» был предложен в
1885 году Людвигом Ланге и означал систему
координат, в которой справедливы законы
Ньютона.
7. Взаимодействие тел
ВЗАИМОДЕЙСТВИЕ ТЕЛ• Это воздействие тел или частиц друг на друга, приводящее к изменению их движения.
• Если прикрепить к тележке упругую пластину, изогнуть, связать ниткой и перерезать
нить, то пластинка выпрямится, но тележка останется на своем месте.
• Если же вплотную к согнутой пластинке поставить такую же тележку и снова перерезать
нитку, пластинка выпрямится, в результате чего обе тележки придут в движение
относительно стола.
• Из опыта ясно – скорость тела меняется только в результате воздействия на него
другого тела. Тележки взаимодействуют. Следовательно, действие одного тела на
другое не одностороннее, оба тела взаимодействуют.

8. сила
СИЛА• Си́ла — физическая величина, являющаяся
мерой воздействия на данное тело со стороны
других тел. Приложение силы обусловливает
изменение скорости тела или появление
деформаций и механических напряжений.
Деформация может возникать как в самом
теле, так и в фиксирующих его объектах —
например, пружинах.
9. масса
МАССА• Масса – физическая величина, одна из
основных характеристик материи,
определяющая её инерционные и
гравитационные свойства.
Соответственно различают Массу
инертную и Массу гравитационную.
• Ρ – плотность
V – обьём
10. Второй закон Ньютона
ВТОРОЙ ЗАКОН НЬЮТОНА• Дифференциальный закон движения,
описывающий взаимосвязь между приложенной к
материальной точке силой и получающимся от
этого ускорением этой точки.
11. Формулировка
ФОРМУЛИРОВКА• В инерциальной системе отсчёта
ускорение, которое получает
материальная точка с постоянной
массой, прямо пропорционально
равнодействующей всех приложенных к
ней сил и обратно пропорционально её
массе.

• a — ускорение материальной точки;
F — равнодействующая всех сил,
приложенных к материальной точке;
m — масса материальной точки.
12. Третий закон Ньютона Формулировка
ТРЕТИЙ ЗАКОН НЬЮТОНА• Этот закон описывает, как
взаимодействуют две
материальные точки.
ФОРМУЛИРОВКА
• Материальные точки
взаимодействуют друг с другом
силами, имеющими одинаковую
природу, направленными вдоль
прямой, соединяющей эти точки,
равными по модулю и
противоположными по
направлению
13. Источники
ИСТОЧНИКИ1. https://ru.wikipedia.org/wiki
2. https://www.calc.ru/Vzaimodeystviye-V-Fizike.html
3. https://dic.academic.ru/dic.nsf/bse
4. http://www.its-physics.org/pervyy-zakon-nyutona-massa-sila
14. Спасибо за внимание!
СПАСИБО ЗА ВНИМАНИЕ!Первый закон Ньютона: текст, переводы, интерпретации и физическое образование
AAAS ¶ Американская ассоциация развития науки: 1990, «Наука для всех американцев», проект 2021 , Oxford University Press, NY, p. 53.
53.
Google Scholar
Эймс, Дж.С. & Murngham, FD: 1958/1937, Теоретическая механика. Введение в математическую физику , Довер, Нью-Йорк, с. 104.
Google Scholar
Аронс А.B.: 1990, A Guide to Introductive Physics Teaching , Wiley, NY, p. 52.
Google Scholar
Болл, WWR: 1972/1893, Эссе о принципах Ньютона , Джонсон, Нью-Йорк.
Google Scholar
Брунер, М.: 1960, Процесс образования , Vintage Books, NY, стр. 52–54.
Google Scholar
Чайкин С.Э.: 1963, Физические основы механики , Государственное Изд-во Физико-Математической Литературы, Москва.
Google Scholar
Clagett, M.: 1959, Механика в средние века , University of Wisconsin Press, Мэдисон, стр.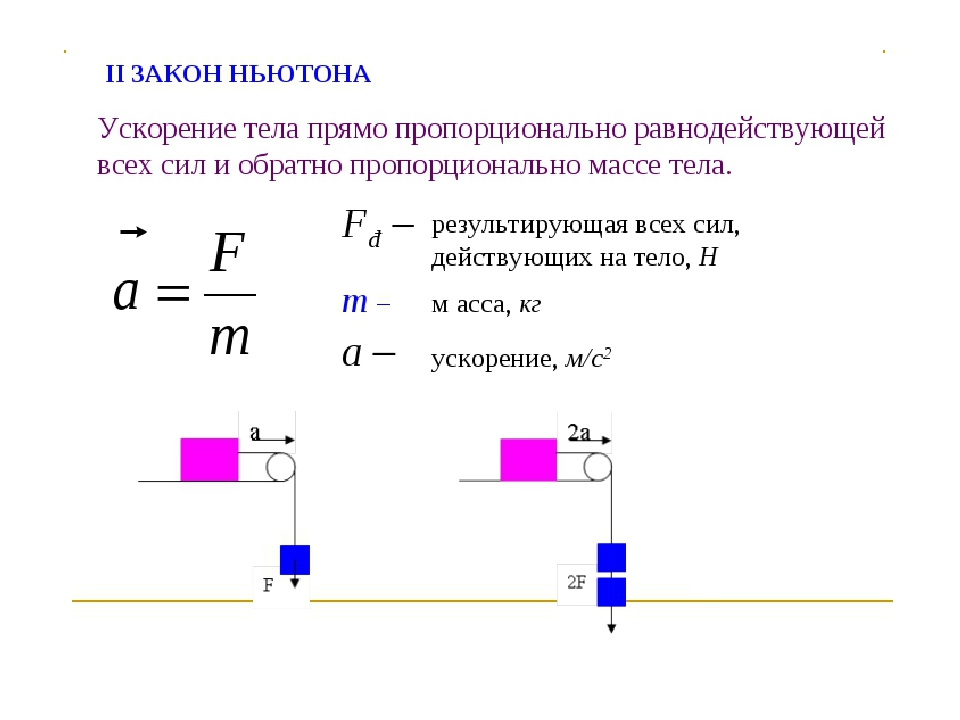 421–433.
421–433.
Google Scholar
Коэн, Б.: 1971, Введение в «Принципы» Ньютона University Press, Cambridge, стр.XVI, 28.
Google Scholar
Коэн, Б.: 1999, «Введение в « Principia » Ньютона», в I. Newton, Mathematical Principles of Natural Philosophy , University of California Press, Беркли, Калифорния, с. 110.
Google Scholar
Cooley, LRC: 1881, Natural Philosophy for Common and High Schools , Charles Scribner’s Sons, NY, p.58.
Google Scholar
Des-Cartes, Renati: 1656, Principia Philosophiae , Apud Johannem Jansonium Juniorem, Amstelodami.
Google Scholar
Декарт, Р.: 1984/1647, Принципы философии , Рейдель, Дордрехт, Часть II.
Google Scholar
Дейкстерхус, Э. J.: 1986, Механизация мира Picture , издательство Принстонского университета, Принстон, штат Нью-Джерси, с. 29.
J.: 1986, Механизация мира Picture , издательство Принстонского университета, Принстон, штат Нью-Джерси, с. 29.
Google Scholar
Дрейк, С.: 1978, Галилей за работой. Его научная биография , Довер, Нью-Йорк, с. 294.
Google Scholar
Duhem, P.: 1991/1905, Цель и структура физической теории , Princeston University Press, Принстон, Нью-Джерси.
Google Scholar
Эйнштейн, А. и Инфельд, Л.: 1938, Эволюция физики , University Press, Cambridge, p. 9.
Google Scholar
Encyclopedie Scientifique: 1930, De Mecanique Appliquee , Guston Doin, Paris, p. 18.
Frank, P.: 1957, Philosophy of Science , Prentice Hall, Englewood Cliffs, NJ., стр. 104–107.
Google Scholar
Galiley, G. : 1612/1995, «Второе письмо о солнечных пятнах», в S. Drake, Galileo at Work , Dover, NY, p. 186.
: 1612/1995, «Второе письмо о солнечных пятнах», в S. Drake, Galileo at Work , Dover, NY, p. 186.
Google Scholar
Galiley, G.: 1632/1953, Диалог о двух главных мировых системах , University of California Press, Беркли, Калифорния.
Google Scholar
Гарбер Д.: 1992, Метафизическая физика Декарта , University of Chicago Press, Чикаго, стр. 211–230.
Google Scholar
Джанколи, округ Колумбия: 1988, Физика для ученых и инженеров , Prentice Hall, Englewood Cliffs, NJ, стр. 69–72.
Google Scholar
Hartog, J.P.: 1961/1948, Mechanics , Dover, NY, p. 175.
Google Scholar
Хехт, Э.: 1996, Physics , Brooks & Cole, Pacific Grove, CA, p. 117.
Google Scholar
Герц, Х.: 1956/1900, Принципы механики (представлены в новой форме) , Довер, Нью-Йорк, с. 144.
Google Scholar
Хьюитт, П.: 1998, Концептуальная физика , Аддисон-Уэсли, Рединг, Массачусетс, с. 59.
Google Scholar
Джаммер, М.: 1957, Concepts of Force , Harper, NY, стр. 56, 81-92.
Google Scholar
Джаммер, М.: 1961, Concepts of Mass , Harper, NY.
Google Scholar
Джинс, JH: 1907, Элементарный трактат по теоретической механике , Ginn & Co., Бостон, с. 26.
Google Scholar
Джинсы, J.H.: 1947, The Growth of Physical Science , The University Press, Cambridge, p. 191.
191.
Google Scholar
Kittel, C., Knight, W.D. & Ruderman, MD: 1973, Mechanics, Berkeley Physics Course , McGraw Hill, NY, p. 58.
Google Scholar
Koyré, A.: 1968, Newtonian Studies , The University of Chicago Press, Chicago, p.66.
Google Scholar
Ландау Л.Д., Ахизер А.И. и Лифшиц Е.М.: 1969, Курс общей физики , Наука, Москва, с. 10.
Google Scholar
Лемон, Х. и Ференс, М.: 1943, Аналитическая экспериментальная физика , The University of Chicago Press, Чикаго, с. 33.
Google Scholar
Мах, Э.: 1960/1893, Наука о механике: критический и исторический отчет о ее развитии , Open Court, La Salle, p. 301.
Google Scholar
Maxwell, J. C.: 1956, Mater and Motion , Dover, NY, p. 28.
C.: 1956, Mater and Motion , Dover, NY, p. 28.
Google Scholar
Милликен Р.А., Роллер Д. и Уотсон Э.К.: 1965/1937, Механика, молекулярная физика, тепло и звук , The MIT Press, Cambridge, MA, p.35.
Google Scholar
Newtono Isaaco: 1687, Philosophiae Naturalis Principia Methematica , Dawson & Sons, Лондон, 1-е изд., с. 12.
Google Scholar
Newtono Isaaco: 1713/1723, Philosophiae Naturalis Principia Methematica , Sumptibus Societatis, Amstaelodami, 2nd ed., p. 12.
Google Scholar
Ньютоно Исаако: 1726/1779, Philosophiae Naturalis Principia Methematica , Dawson & Sons, Лондон, 3-е изд., п. 13.
Google Scholar
Ньютон, И.: 1729/1964, Математические основы натуральной философии , Бенджамин Мотте, Мидл-Темпл-Гейт на Флитстрит, Лондон, перевод А. Мотта; или Руны, Д.Д. и Кирнан, Т. (редакторы), Классическая научная библиотека , Философская библиотека, Нью-Йорк, с. 23.
Мотта; или Руны, Д.Д. и Кирнан, Т. (редакторы), Классическая научная библиотека , Философская библиотека, Нью-Йорк, с. 23.
Google Scholar
Ньютон, И.: 1759, Принципы математики естественной философии , Desaint & Saillant, Paris, Par feue Madame la Marquise du Chastelle.
Google Scholar
Newton, I.: 1776/1969, Mathematical Principles of Natural Philosophy , Dawson of Pall Mall, Лондон, перевод Р. Торпа, с. 22.
Google Scholar
Newton, I.: 1872, Mathematische Principien der Naturlehre , Verlag von Robert Oppenheim, Berlin, Herausgegeben von Prof. Dr. J. Ph. Wolfers, p. 32.
Google Scholar
Ньютон И.: 1934, Mathematical Principles of Natural Philosophy , University of California Press, Berkeley, CA, исправленное издание перевода Мотта, сделанное Ф. Каджори, с. 13.
Каджори, с. 13.
Google Scholar
Ньютон, И.: 1936/1989, Математические начала натуральной философии , Наука, Москва, перевод на русский язык А.Н. Крылов.
Google Scholar
Ньютон И.: 1978, Математические принципы натуральной философии , Britannica Great Books, Чикаго, с. 270.
Google Scholar
Ньютон, И.: 1999, Математические принципы натуральной философии , University of California Press, Беркли, Калифорния, новый перевод Б. Коэна и А. Уитмена.
Google Scholar
Osgood, W.F.: 1937, Mechanics , Macmillan, NY, p.50.
Google Scholar
Painlevé, P.: 1895, «Leçons sur l’Integration des Equations Differentielles de la Mechanique et Applications », Hermann, Paris.
Google Scholar
Peierls, RE: 1956, The Laws of Nature , Charles Scribner’s Sons, NY, p. 20.
Google Scholar
Пиппард, А.Б.: 1972, Forces and Particles , Wiley, NY, p. 20.
Google Scholar
Platrier, C.: 1954, Mechanique rationnelle , Дюно, Париж.
Google Scholar
Полак Л.С.: 1989, «Введение», в кн.: Ньютон, И., Математические начала натуральной философии , Наука, Москва, стр. 11–12.
Google Scholar
Помрой, Дж.H.: 1989, Science , Holt, Rinehart and Winston, NY, p. 150.
Google Scholar
Reichert, J.F.: 1991, A Modern Introduction to Mechanics , Prentice Hall, Engelwood Cliffs, NJ, p.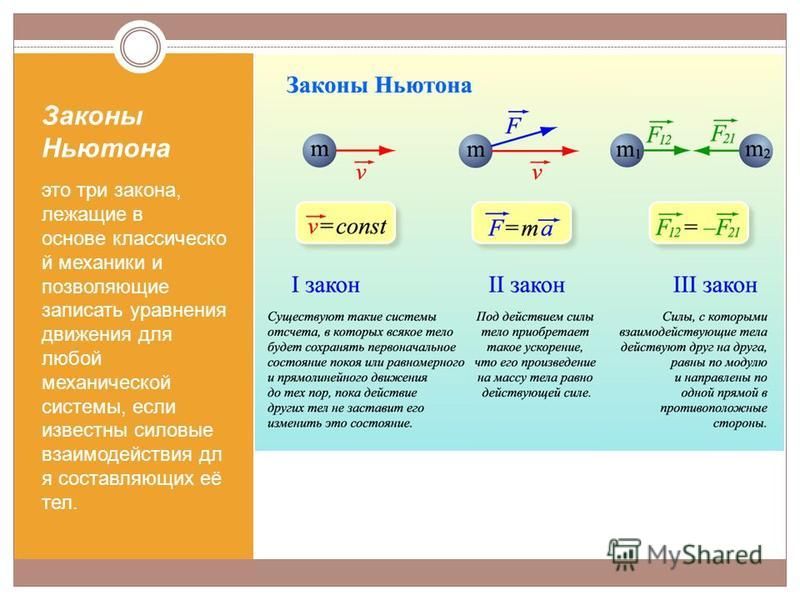 185.
185.
Google Scholar
Reif, F.: 1995, Understanding Basic Mechanics , Wiley, NY, p. 95.
Google Scholar
Резник Р., Halliday, D. & Krane, K.: 1992, Physics , Wiley, NY, Vol. 1, с. 79.
Google Scholar
Russell, B.: 1959, Wisdom of the West , Crescent Books, London, p. 190.
Google Scholar
Савельев И.В.: 1998, Курс общей физики , Наука, Москва, с. 55.
Google Scholar
Стиннер, А.: 1994, «История силы: от Аристотеля до Эйнштейна», Физическое образование 29 (2), 77–86.
Google Scholar
Taylor, LW: 1959/1941, Physics , Dover, NY, стр. 130–131.
Google Scholar
Тугер, Дж. : 1991, «Когда слова подводят нас», Учитель физики 29 (2), 90–95.
: 1991, «Когда слова подводят нас», Учитель физики 29 (2), 90–95.
Google Scholar
Вьенно, Л.: 1979, «Спонтанное мышление в элементарной динамике», European Journal of Science Education . 1 (2), 205–221.
Google Scholar
Выготский, Л.: 1986, Мысль и язык , MIT Press, Кембридж, Массачусетс.
Google Scholar
Westfall, RS: 1971, Force in Newton’s Physics , Macdonald, London.
Google Scholar
Вестфолл, Р.S.: 1977, The Construction of Modern Science , Cambridge University Press, Cambridge, p. 144.
Google Scholar
Уайт, Дж.Т. & Oxon, DD: 1948, The White Latin Dictionary , Follet Publishing Company, Чикаго.
Google Scholar
Уитроу, Г. : 1971, «Законы движения», Британский журнал истории науки 5 (19), 217–234.
: 1971, «Законы движения», Британский журнал истории науки 5 (19), 217–234.
Google Scholar
Whitside, DT (ed.): 1978, The Mathematical Papers of Isaac Newton , University Press, Cambridge, Vol. 6, с. 33.
Google Scholar
Whitside, DT (ed.): 1967-1981, The Mathematical Papers of Isaac Newton , University Press, Cambridge, 8 vols.
Google Scholar
Вольф, А.: 1952, История науки, техники и философии в 18 веке , Harper, NY, Vol. 1.
Google Scholar
Обратный словарь
Как вы, наверное, заметили, слова для термина перечислены выше. Надеюсь, сгенерированный список слов для «термина» выше удовлетворит ваши потребности. Если нет, вы можете проверить «Связанные слова» — еще один мой проект, в котором используется другая техника (несмотря на то, что она лучше всего работает с отдельными словами, а не с фразами).
Об обратном словаре
Обратный словарь работает очень просто. Он просто просматривает тонны словарных определений и выбирает те, которые наиболее точно соответствуют вашему поисковому запросу. Например, если вы наберете что-то вроде «тоска по прошлому», то движок вернет «ностальгия». На данный момент движок проиндексировал несколько миллионов определений, и на данном этапе он начинает давать неизменно хорошие результаты (хотя иногда он может возвращать странные результаты).Он во многом похож на тезаурус, за исключением того, что позволяет выполнять поиск по определению, а не по одному слову. Так что в некотором смысле этот инструмент является «поисковиком слов» или конвертером предложений в слова.
Я сделал этот инструмент после работы над «Связанными словами», который очень похож на инструмент, за исключением того, что он использует кучу алгоритмов и несколько баз данных для поиска слов, похожих на поисковый запрос. Этот проект ближе к тезаурусу в том смысле, что он возвращает синонимы для запроса слова (или короткой фразы), но он также возвращает много широко связанных слов, не включенных в тезаурус. Таким образом, этот проект, Reverse Dictionary, должен идти рука об руку с Related Words, чтобы действовать как набор инструментов для поиска слов и мозгового штурма. Для тех, кто заинтересован, я также разработал «Описывающие слова», которые помогут вам найти прилагательные и интересные описания для вещей (например, волн, закатов, деревьев и т. д.).
Таким образом, этот проект, Reverse Dictionary, должен идти рука об руку с Related Words, чтобы действовать как набор инструментов для поиска слов и мозгового штурма. Для тех, кто заинтересован, я также разработал «Описывающие слова», которые помогут вам найти прилагательные и интересные описания для вещей (например, волн, закатов, деревьев и т. д.).
Если вы не заметили, вы можете щелкнуть по словам в результатах поиска, и вам будет представлено определение этого слова (если оно доступно). Определения взяты из известной базы данных WordNet с открытым исходным кодом, поэтому огромное спасибо многим участникам за создание такого замечательного бесплатного ресурса.
Особая благодарность авторам открытого исходного кода, использованного в этом проекте: Elastic Search, @HubSpot, WordNet и @mongodb.
Обратите внимание, что Reverse Dictionary использует сторонние скрипты (такие как Google Analytics и рекламные объявления), которые используют файлы cookie. Чтобы узнать больше, ознакомьтесь с политикой конфиденциальности.
Чтобы узнать больше, ознакомьтесь с политикой конфиденциальности.
Inertia (глава из учебника Open Stax) – x-A-Learn PressBooks с законами Ньютона для C&BA
Это часть главы из Open Stax College Physics.Это бесплатно, и я могу импортировать его и адаптировать для своего курса. Мои вопросы и др.
Цели обучения
По окончании этого раздела студент сможет
- определение массы и инерции
- определяют первый закон движения Ньютона
Опыт подсказывает, что покоящийся объект останется в покое, если оставить его в покое, и что движущийся объект имеет тенденцию замедляться и останавливаться, если не предпринимать никаких усилий для поддержания его движения.Однако первый закон движения Ньютона утверждает следующее:
ПЕРВЫЙ ЗАКОН ДВИЖЕНИЯ НЬЮТОНА
Тело, находящееся в состоянии покоя, остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила.
Обратите внимание на повторное использование глагола «остается». Мы можем думать об этом законе как о сохранении статус-кво движения.
Вместо того, чтобы противоречить нашему опыту, Первый закон движения Ньютона утверждает, что должна быть причина (которая является чистой внешней силой) для любого изменения скорости (либо изменения величины, либо направления) .Мы определим чистую внешнюю силу в следующем разделе. Объект, скользящий по столу или полу, замедляется из-за суммарной силы трения, действующей на объект. Если трение исчезнет, будет ли объект по-прежнему замедляться?
Представление о причине и следствии имеет решающее значение для точного описания того, что происходит в различных ситуациях. Например, рассмотрим, что происходит с объектом, скользящим по шероховатой горизонтальной поверхности. Объект быстро останавливается. Если мы посыпаем поверхность тальком, чтобы сделать поверхность более гладкой, объект будет скользить дальше. Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше. Экстраполируя на поверхность без трения, мы можем представить объект, бесконечно скользящий по прямой линии. Таким образом, трение является причиной замедления (в соответствии с первым законом Ньютона). Объект вообще не замедлился бы, если бы трение было полностью устранено. Рассмотрим стол для аэрохоккея. Когда воздух отключен, шайба скользит только на короткое расстояние, прежде чем трение замедляет ее до остановки.Однако, когда воздух включен, создается поверхность, практически лишенная трения, и шайба скользит на большие расстояния, не замедляясь. Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, как быстро объект замедлится. Трение — это внешняя сила.
Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше. Экстраполируя на поверхность без трения, мы можем представить объект, бесконечно скользящий по прямой линии. Таким образом, трение является причиной замедления (в соответствии с первым законом Ньютона). Объект вообще не замедлился бы, если бы трение было полностью устранено. Рассмотрим стол для аэрохоккея. Когда воздух отключен, шайба скользит только на короткое расстояние, прежде чем трение замедляет ее до остановки.Однако, когда воздух включен, создается поверхность, практически лишенная трения, и шайба скользит на большие расстояния, не замедляясь. Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, как быстро объект замедлится. Трение — это внешняя сила.
Ключевые выводы
Первый закон Ньютона является полностью общим и может быть применен ко всему: от предмета, скользящего по столу, до спутника на орбите и до крови, перекачиваемой из сердца.
Эксперименты полностью подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой.Идея общеприменимых или универсальных законов важна не только здесь — это основная черта всех законов физики. Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности. Гениальность Галилея, впервые разработавшего идею первого закона, и Ньютона, уточнившего его, заключалась в том, чтобы задать основной вопрос…»
В чем причина?» Мышление в терминах причины и следствия — это мировоззрение, в корне отличное от типичного древнегреческого подхода, когда такие вопросы, как «Почему у тигра полосы?» ответили бы в аристотелевской манере: «Такова природа зверя.Возможно, правда, но не полезная информация.
Свойство тела оставаться в покое или оставаться в движении с постоянной скоростью называется инерцией . Первый закон Ньютона часто называют законом инерции .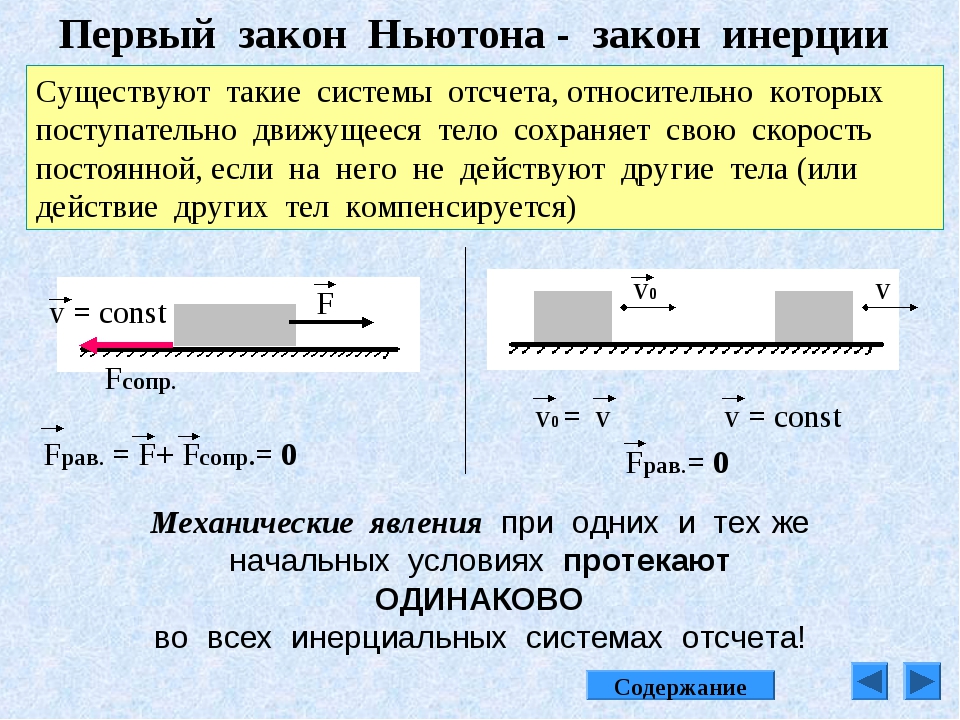 Как мы знаем из опыта, одни объекты обладают большей инерцией, чем другие. Очевидно, что изменить движение большого валуна сложнее, чем, например, баскетбольного мяча. Инерция объекта измеряется его массой . Грубо говоря, масса — это мера количества «вещества» (или материи) в чем-либо.Количество или количество материи в объекте определяется количеством содержащихся в нем атомов и молекул различных типов. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. На практике очень трудно сосчитать и идентифицировать все атомы и молекулы в объекте, поэтому массы не часто определяются таким образом. Оперативно массы предметов определяются путем сравнения с эталонным килограммом.
Как мы знаем из опыта, одни объекты обладают большей инерцией, чем другие. Очевидно, что изменить движение большого валуна сложнее, чем, например, баскетбольного мяча. Инерция объекта измеряется его массой . Грубо говоря, масса — это мера количества «вещества» (или материи) в чем-либо.Количество или количество материи в объекте определяется количеством содержащихся в нем атомов и молекул различных типов. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. На практике очень трудно сосчитать и идентифицировать все атомы и молекулы в объекте, поэтому массы не часто определяются таким образом. Оперативно массы предметов определяются путем сравнения с эталонным килограммом.
Проверьте свое понимание
1: Что имеет большую массу: килограмм ватных шариков или килограмм золота?
Исаак Ньютон писал в письме Роберту Гуку: «Если я и видел дальше, то потому, что стоял на плечах гигантов».
- Первый закон движения Ньютона гласит, что тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила. Это также известно как закон инерции .
- Инерция — это тенденция объекта оставаться в покое или оставаться в движении. Инерция связана с массой объекта.
- Масса – количество вещества в веществе.
Концептуальные вопросы
1: Как связаны инерция и масса?
2: Какая связь между весом и массой? Что является неотъемлемым и неизменным свойством тела?
Введите здесь собственные упражнения.Вот те из Open Stax College Physics
- Уборщик толкает тележку для белья массой 4,00 кг так, что результирующая внешняя сила, действующая на нее, равна 8,00 Н. Вычислите величину ее ускорения.

Поскольку астронавты на орбите, по-видимому, невесомы, необходим умный метод измерения их массы, чтобы контролировать их прирост или потерю массы для корректировки диеты. Один из способов сделать это — приложить к космонавту известную силу и измерить вызванное им ускорение. Предположим, что чистая внешняя сила равна 50.0 Н, и измеренное ускорение космонавта равно 0,893 м/с 2 . а) Вычислите ее массу. (b) Воздействуя на космонавта силой, транспортное средство, в котором они вращаются, испытывает равную и противоположную силу. Обсудите, как это повлияет на измерение ускорения космонавта. Предложите способ предотвращения отдачи автомобиля.
На Рисунке 4.7, показанном здесь: чистая внешняя сила, действующая на 24-килограммовую косилку, равна 51 Н. Если сила трения, противодействующая движению, равна 24 Н, какую силу F (в ньютонах) представляет человек, воздействующий на косилка? Предположим, косилка движется со скоростью 1.
Человек, толкающий газонокосилку. Изображение предоставлено: OpenStax College Physics, CC0. 5 м/с при снятии силы F . Какое расстояние пройдет косилка до остановки?
5 м/с при снятии силы F . Какое расстояние пройдет косилка до остановки?
Решения
Проверьте свое понимание
1: Они равны. Килограмм одного вещества равен по массе килограмму другого вещества. Величины, которые могут различаться между ними, – это объем и плотность.
Концептуальные вопросы
1: Как связаны инерция и масса? Они одинаковые.Масса является мерой инерции. Чем больше масса, тем больше инерция.
2: Какая связь между весом и массой? Что является неотъемлемым и неизменным свойством тела? Масса – это внутреннее неизменное свойство. Вес — это сила, и она зависит от силы гравитации. На Луне вы весите 1/6, но у вас такая же инерция.
Задачи и упражнения
- а = 2,00 м/с 2
- 56,0 кг
- а) 75 Н б) (заметки Дженнифер.
 Мне часто не нравится формулировка, используемая OpenStax. Я бы добавил больше деталей к этому вопросу. А именно, какова результирующая сила, действующая на косилку, когда человек перестает толкать, затем каково ускорение, затем каково расстояние, пройденное до ее остановки.) Это было бы 24 Н влево, поэтому ускорение равно замедлению 1,00 м/с 2 влево или -1,00 м/с 2 . водоизмещение = 1,1 м.
Мне часто не нравится формулировка, используемая OpenStax. Я бы добавил больше деталей к этому вопросу. А именно, какова результирующая сила, действующая на косилку, когда человек перестает толкать, затем каково ускорение, затем каково расстояние, пройденное до ее остановки.) Это было бы 24 Н влево, поэтому ускорение равно замедлению 1,00 м/с 2 влево или -1,00 м/с 2 . водоизмещение = 1,1 м.
Научные журналы – 404 СТРАНИЦА НЕ НАЙДЕНА
Вся правда проходит три стадии.Во-первых, это высмеивается. Во-вторых, яростно противится. В-третьих, это принимается как само собой разумеющееся: Артур Шопенгауэр. – В вопросах науки авторитет тысячи не стоит смиренных рассуждений одного человека. Галилео Галилей. зарабатывать этим на жизнь: Альберт Эйнштейн — Когда вы устраните невозможное, все, что когда-либо останется, каким бы невероятным оно ни было, должно быть правдой: Сэр Артур Конан Дойл — Мы все согласны с тем, что ваша теория безумна, но достаточно ли она безумна? Нильс Бор – Всякий раз, когда появляется истинная теория, она будет ее собственным доказательством. Его проверка состоит в том, что он объяснит все явления: Ральф Уолдо Эмерсон — С тех пор как математики вторглись в теорию относительности, я и сам ее больше не понимаю: Альберт Эйнштейн — Я бы сказал, что эфир — это среда, изобретенная человеком для распространения его заблуждения из одного места в другое: WFG Суонн: — Большинство фундаментальных идей науки по существу просты и, как правило, могут быть выражены на языке, понятном каждому: Альберт Эйнштейн — Физика является математической не потому, что мы так много знаем о физическом мире, а потому что мы так мало знаем: Бертран Рассел — Если бы я мог объяснить это обычному человеку, я не был бы достоин Нобелевской премии: Р.П. Фейнман. Я не чувствую себя обязанным верить, что тот же самый Бог, наделивший нас чувствами, разумом и интеллектом, предназначил нам отказаться от их использования: Галилео Галилей. Как мы смеем говорить о законах случая? Разве случайность не является антитезой всему закону?: Бертран Рассел — Только две вещи бесконечны, вселенная и человеческая глупость, и я не уверен в первом: Альберт Эйнштейн — Слава математики в том, что вы не должен сказать, о чем вы говорите: Ричард Фейнман — Все возможно, если вы не знаете, о чем говорите: Автор неизвестен — В жизни все относительно — кроме теории Эйнштейна: Леонид С.
Его проверка состоит в том, что он объяснит все явления: Ральф Уолдо Эмерсон — С тех пор как математики вторглись в теорию относительности, я и сам ее больше не понимаю: Альберт Эйнштейн — Я бы сказал, что эфир — это среда, изобретенная человеком для распространения его заблуждения из одного места в другое: WFG Суонн: — Большинство фундаментальных идей науки по существу просты и, как правило, могут быть выражены на языке, понятном каждому: Альберт Эйнштейн — Физика является математической не потому, что мы так много знаем о физическом мире, а потому что мы так мало знаем: Бертран Рассел — Если бы я мог объяснить это обычному человеку, я не был бы достоин Нобелевской премии: Р.П. Фейнман. Я не чувствую себя обязанным верить, что тот же самый Бог, наделивший нас чувствами, разумом и интеллектом, предназначил нам отказаться от их использования: Галилео Галилей. Как мы смеем говорить о законах случая? Разве случайность не является антитезой всему закону?: Бертран Рассел — Только две вещи бесконечны, вселенная и человеческая глупость, и я не уверен в первом: Альберт Эйнштейн — Слава математики в том, что вы не должен сказать, о чем вы говорите: Ричард Фейнман — Все возможно, если вы не знаете, о чем говорите: Автор неизвестен — В жизни все относительно — кроме теории Эйнштейна: Леонид С. Сухоруков: Не беспокойтесь о том, что люди могут украсть ваши идеи. Если ваши идеи хоть сколько-нибудь хороши, вам придется вбивать их людям в глотки: Говард Эйкен. Несомненно, придет день, когда эфир будет отброшен как бесполезный: А. Пуанкаре. Сначала они скажут вам, что вы неправильно, и они могут это доказать; тогда они говорят вам, что вы правы, но это не важно; тогда они говорят вам, что это важно, но они всегда это знали: Чарльз Кеттеринг — Не раз и не два, а бесчисленное количество раз одни и те же идеи появляются в мире: Аристотель — Противоположностью истинному утверждению является ложное утверждение.Противоположностью глубокой истине вполне может быть другая глубокая истина: Нильс Бор – Новая научная истина побеждает не потому, что убеждает своих противников и заставляет их увидеть свет, а скорее потому, что ее противники в конце концов умирают, и новое поколение вырастает, знаком с ним: Макс Планк — Евклид научил меня, что без допущений нет доказательств. Поэтому в любом споре исследуйте предположения: Эрик Темпл Белл — Половина этой игры на девяносто процентов ментальна: Йоги Берра
Сухоруков: Не беспокойтесь о том, что люди могут украсть ваши идеи. Если ваши идеи хоть сколько-нибудь хороши, вам придется вбивать их людям в глотки: Говард Эйкен. Несомненно, придет день, когда эфир будет отброшен как бесполезный: А. Пуанкаре. Сначала они скажут вам, что вы неправильно, и они могут это доказать; тогда они говорят вам, что вы правы, но это не важно; тогда они говорят вам, что это важно, но они всегда это знали: Чарльз Кеттеринг — Не раз и не два, а бесчисленное количество раз одни и те же идеи появляются в мире: Аристотель — Противоположностью истинному утверждению является ложное утверждение.Противоположностью глубокой истине вполне может быть другая глубокая истина: Нильс Бор – Новая научная истина побеждает не потому, что убеждает своих противников и заставляет их увидеть свет, а скорее потому, что ее противники в конце концов умирают, и новое поколение вырастает, знаком с ним: Макс Планк — Евклид научил меня, что без допущений нет доказательств. Поэтому в любом споре исследуйте предположения: Эрик Темпл Белл — Половина этой игры на девяносто процентов ментальна: Йоги Берра
Похоже, мы не можем найти эту страницу. Если вы использовали закладку или прямую ссылку, возможно, содержимое было перемещено.
Если вы использовали закладку или прямую ссылку, возможно, содержимое было перемещено.
Первый закон движения Ньютона
Ньютон Первый закон движения: В своем первом законе движения Ньютон заявил, что все объекты сохраняют свое состояние движения. Другими словами, если объект находится в состоянии покоя, он продолжает находиться в состоянии покоя, а если он движется, он продолжает двигаться, если к нему не приложена ненулевая сила. Что мы подразумеваем под словом «ненулевая сила»? Посмотрите на данную картинку, чтобы понять, что мы имеем в виду.
Мы также назвали ненулевую силу «чистой силой». Как видно из рисунка, если силы, действующие на объект, направлены в одну сторону, то они суммируются. Если же они противоположны, одну из них берем в отрицательное направление, проводим расчеты с учетом их знаков и находим вектор равнодействующей силы. В первой ситуации приложенные силы имеют противоположное направление, и, поскольку их величины одинаковы, результирующая сила становится равной нулю. Во втором случае силы имеют одинаковое направление и одинаковы по величине, поэтому результирующий вектор представляет собой их сумму.И в конечной ситуации силы имеют противоположное направление, однако их величины различны, поэтому результирующий вектор или результирующая сила имеет направление силы, имеющей большую величину.
Во втором случае силы имеют одинаковое направление и одинаковы по величине, поэтому результирующий вектор представляет собой их сумму.И в конечной ситуации силы имеют противоположное направление, однако их величины различны, поэтому результирующий вектор или результирующая сила имеет направление силы, имеющей большую величину.
После этих объяснений я думаю, что концепция чистой силы у вас ясна. Теперь обратимся к нашей основной теме «Первый закон движения Ньютона», другими словами «закон инерции». Мы сказали, что объекты хотят продолжать свое состояние движения независимо от того, находятся они в покое или в движении.Если на покоящийся объект нет результирующей силы, то он продолжает оставаться в покое, если нет результирующей силы на движущийся объект, он продолжает двигаться с постоянной скоростью. Посмотрите на приведенную ниже картинку. Как видите, пассажиры двигаются вперед, когда водитель тормозит автобус. Пассажиры перед торможением имеют одинаковую скорость с автобусом.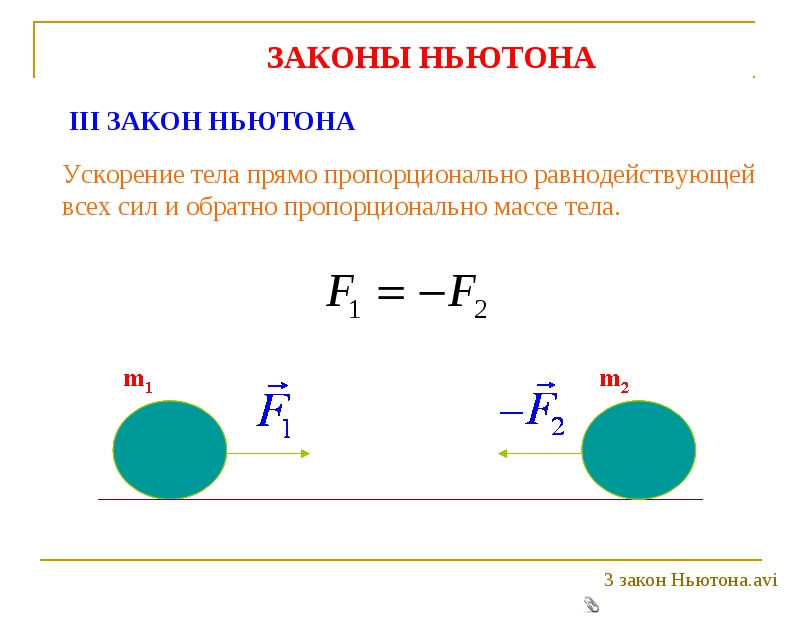 {#1}\!/_{\!#2}}
\ newcommand {\ convert} [2] {\ times \ left (\ frac {# 1} {# 2} \ right)} \newcommand{\deq}{\displaystyle} \newcommand{\ihat}{\шляпа я}
\ новая команда {\ jhat} {\ шляпа j}
\newcommand{\хат}{\шляпа к}
\newcommand{\vect}[3]{#1 \ihat #2 \jhat #3 \khat} \newcommand{\KE}{\mbox{KE}}
\newcommand{\PE}{\mbox{PE}}
\newcommand{\E}{\mbox{E}}
\newtheorem[S]{предложение}[теорема]{Соединение}
\newtheorem[S]{понимание}[теорема]{понимание}
\newtheorem[S]{предупреждение}[теорема]{предупреждение}
\newtheorem[S]{наблюдение}[теорема]{наблюдение}
\newtheorem[S]{примечание}[теорема]{интерпретация}
\newtheorem[M]{замечание}[теорема]{пояснение}
\newtheorem[M]{конвенция}[теорема]{конвенция}
\newtheorem[L]{пример}[теорема]{пример}
\newtheorem[L]{упражнение}[теорема]{упражнение}
\newtheorem[L]{эвристика}[теорема]{перевод}
\newtheorem[L]{исследование}[теорема]{исследование}
\newtheorem[L]{исследование}[теорема]{исследование}
\newtheorem[L]{деятельность}[теорема]{деятельность} \ newcommand {\ magdir} [7] {\ begin {массив} {lccl}
\text{Величина:} \amp \displaystyle #3 = \amp \displaystyle \sqrt{\left(#1\right)^2+\left(#2\right)^2} \amp = \displaystyle #4 \ \[6pt]
\text{Направление:} \amp \displaystyle #5 = \amp \displaystyle \tan^{-1}\left( \frac{#2}{#1} \right) \amp = \displaystyle #6 \mbox{ #7}
\конец{массив}} \newcounter{piclen}
\newcounter{picwid}
\newcounter{boxlen}
\newcounter{boxwid}
\newcounter{FBDlen}
\newcounter{FBDwid}
\newcounter{centx}
\newcounter{цент}
\ новый счетчик {lblx}
\newcounter{lbly}
\ новая команда {\ drawbox} [4] {
\setcounter{boxlen}{#1}\addtocounter{boxlen}{#3}
\setcounter{boxwid}{#2}\addtocounter{boxwid}{#4}
\ положить (# 1, # 2) {\ строка (1,0) {# 3}}
\ положить (# 1, # 2) {\ строка (0,1) {# 4}}
\ поставить (\ theboxlen, \ theboxwid) {\ строка (-1,0) {# 3}}
\ поставить (\ theboxlen, \ theboxwid) {\ строка (0,-1) {# 4}}} \newenvironment{FBD}[5]
{\ setcounter {centx} {# 3} \ addtocounter {centx} {# 1}
\setcounter{centy}{#4}\addtocounter{centy}{#2}
\setcounter{piclen}{\thecentx}\addtocounter{piclen}{\thecentx}
\setcounter{picwid}{\thecenty}\addtocounter{picwid}{\thecenty}
\setcounter{FBDlen}{#1}\addtocounter{FBDlen}{#1}
\setcounter{FBDwid}{#2}\addtocounter{FBDwid}{#2}
\setcounter{lbly}{#4}\addtocounter{lbly}{#2}\addtocounter{lbly}{#2}\addtocounter{lbly}{5}
\begin{центр}\begin{картинка}(\thepiclen,\thepicwid)
\put(#3,\thelbly){\setvlabel{$\scriptsize #5$}}
\drawbox{#3}{#4}{\theFBDlen}{\theFBDwid}}
{\конец{картинка}\конец{центр}}
\ новая команда {\ oneup} [3] {
\addtocounter{центы}{2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#1}\addtocounter{lbly}{-5}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-2}}
\ новая команда {\ onedo} [3] {
\addtocounter{центы}{-2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#1}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,-1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{2}}
\newcommand{\oneri}[3]{
\addtocounter{centx}{2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{-2}}
\newcommand{\onele}[3]{
\addtocounter{centx}{-2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (-1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{2}} \newcommand{\twoup}[6]{
\addtocounter{центы}{2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{centx}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-10}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#1}\addtocounter{lbly}{-5}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{5}
\addtocounter{centx}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#4}\addtocounter{lbly}{-5}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (0,1) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-5}
\addtocounter{центы}{-2}}
\newcommand{\twodo}[6]{
\addtocounter{центы}{-2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{centx}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-10}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#1}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,-1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{5}
\addtocounter{centx}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#4}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (0,-1) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-5}
\addtocounter{центы}{2}}
\ новая команда {\ twori} [6] {
\addtocounter{centx}{2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{центы}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-5}
\addtocounter{центы}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-10}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (1,0) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{центы}{5}
\addtocounter{centx}{-2}}
\ новая команда {\ twole} [6] {
\addtocounter{centx}{-2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{центы}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (-1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-5}
\addtocounter{центы}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-10}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (-1,0) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{центы}{5}
\addtocounter{centx}{2}}
\newcommand{\oneur}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#2}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\oneul}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#2}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\ новая команда {\ onedl} [6] {
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#2}\addtocounter{lbly}{#4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\onedr}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#2}\addtocounter{lbly}{#4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}} \newcommand{\studentA}{Абдул} \newcommand{\massA}{\mbox{$85.
{#1}\!/_{\!#2}}
\ newcommand {\ convert} [2] {\ times \ left (\ frac {# 1} {# 2} \ right)} \newcommand{\deq}{\displaystyle} \newcommand{\ihat}{\шляпа я}
\ новая команда {\ jhat} {\ шляпа j}
\newcommand{\хат}{\шляпа к}
\newcommand{\vect}[3]{#1 \ihat #2 \jhat #3 \khat} \newcommand{\KE}{\mbox{KE}}
\newcommand{\PE}{\mbox{PE}}
\newcommand{\E}{\mbox{E}}
\newtheorem[S]{предложение}[теорема]{Соединение}
\newtheorem[S]{понимание}[теорема]{понимание}
\newtheorem[S]{предупреждение}[теорема]{предупреждение}
\newtheorem[S]{наблюдение}[теорема]{наблюдение}
\newtheorem[S]{примечание}[теорема]{интерпретация}
\newtheorem[M]{замечание}[теорема]{пояснение}
\newtheorem[M]{конвенция}[теорема]{конвенция}
\newtheorem[L]{пример}[теорема]{пример}
\newtheorem[L]{упражнение}[теорема]{упражнение}
\newtheorem[L]{эвристика}[теорема]{перевод}
\newtheorem[L]{исследование}[теорема]{исследование}
\newtheorem[L]{исследование}[теорема]{исследование}
\newtheorem[L]{деятельность}[теорема]{деятельность} \ newcommand {\ magdir} [7] {\ begin {массив} {lccl}
\text{Величина:} \amp \displaystyle #3 = \amp \displaystyle \sqrt{\left(#1\right)^2+\left(#2\right)^2} \amp = \displaystyle #4 \ \[6pt]
\text{Направление:} \amp \displaystyle #5 = \amp \displaystyle \tan^{-1}\left( \frac{#2}{#1} \right) \amp = \displaystyle #6 \mbox{ #7}
\конец{массив}} \newcounter{piclen}
\newcounter{picwid}
\newcounter{boxlen}
\newcounter{boxwid}
\newcounter{FBDlen}
\newcounter{FBDwid}
\newcounter{centx}
\newcounter{цент}
\ новый счетчик {lblx}
\newcounter{lbly}
\ новая команда {\ drawbox} [4] {
\setcounter{boxlen}{#1}\addtocounter{boxlen}{#3}
\setcounter{boxwid}{#2}\addtocounter{boxwid}{#4}
\ положить (# 1, # 2) {\ строка (1,0) {# 3}}
\ положить (# 1, # 2) {\ строка (0,1) {# 4}}
\ поставить (\ theboxlen, \ theboxwid) {\ строка (-1,0) {# 3}}
\ поставить (\ theboxlen, \ theboxwid) {\ строка (0,-1) {# 4}}} \newenvironment{FBD}[5]
{\ setcounter {centx} {# 3} \ addtocounter {centx} {# 1}
\setcounter{centy}{#4}\addtocounter{centy}{#2}
\setcounter{piclen}{\thecentx}\addtocounter{piclen}{\thecentx}
\setcounter{picwid}{\thecenty}\addtocounter{picwid}{\thecenty}
\setcounter{FBDlen}{#1}\addtocounter{FBDlen}{#1}
\setcounter{FBDwid}{#2}\addtocounter{FBDwid}{#2}
\setcounter{lbly}{#4}\addtocounter{lbly}{#2}\addtocounter{lbly}{#2}\addtocounter{lbly}{5}
\begin{центр}\begin{картинка}(\thepiclen,\thepicwid)
\put(#3,\thelbly){\setvlabel{$\scriptsize #5$}}
\drawbox{#3}{#4}{\theFBDlen}{\theFBDwid}}
{\конец{картинка}\конец{центр}}
\ новая команда {\ oneup} [3] {
\addtocounter{центы}{2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#1}\addtocounter{lbly}{-5}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-2}}
\ новая команда {\ onedo} [3] {
\addtocounter{центы}{-2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#1}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,-1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{2}}
\newcommand{\oneri}[3]{
\addtocounter{centx}{2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{-2}}
\newcommand{\onele}[3]{
\addtocounter{centx}{-2}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (-1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{2}} \newcommand{\twoup}[6]{
\addtocounter{центы}{2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{centx}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-10}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#1}\addtocounter{lbly}{-5}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{5}
\addtocounter{centx}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#4}\addtocounter{lbly}{-5}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (0,1) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-5}
\addtocounter{центы}{-2}}
\newcommand{\twodo}[6]{
\addtocounter{центы}{-2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{centx}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-10}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#1}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (0,-1) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{centx}{5}
\addtocounter{centx}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#4}\addtocounter{lbly}{3}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (0,-1) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-5}
\addtocounter{центы}{2}}
\ новая команда {\ twori} [6] {
\addtocounter{centx}{2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{центы}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-5}
\addtocounter{центы}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}\addtocounter{lblx}{-5}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-10}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (1,0) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{центы}{5}
\addtocounter{centx}{-2}}
\ новая команда {\ twole} [6] {
\addtocounter{centx}{-2}
\ поставить (\ thecentx, \ thecenty) {\ круг * {1}}
\addtocounter{центы}{5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 3} \ вектор (-1,0) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 3} \ крошечный # 2}
\addtocounter{центы}{-5}
\addtocounter{центы}{-5}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}\addtocounter{lblx}{3}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-10}
\ поставить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (-1,0) {# 4}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{центы}{5}
\addtocounter{centx}{2}}
\newcommand{\oneur}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#2}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\oneul}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{#2}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\ новая команда {\ onedl} [6] {
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{-#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#2}\addtocounter{lbly}{#4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}}
\newcommand{\onedr}[6]{
\addtocounter{centx}{#3}
\addtocounter{центы}{#4}
\setcounter{lblx}{\thecentx}\addtocounter{lblx}{#1}
\setcounter{lbly}{\thecenty}\addtocounter{lbly}{-#2}\addtocounter{lbly}{#4}
\ положить (\ thecentx, \ thecenty) {\ цвет {# 6} \ вектор (# 3, # 4) {# 1}}
\ поставить (\ thelblx, \ thelbly) {\ цвет {# 6} \ крошечный # 5}
\addtocounter{centx}{-#3}
\addtocounter{центы}{-#4}} \newcommand{\studentA}{Абдул} \newcommand{\massA}{\mbox{$85. 0\единица{кг}$}}
\newcommand{\studentB}{Бет} \newcommand{\massB}{\mbox{75,0$\единица{кг}$}}
\newcommand{\studentC}{Карл} \newcommand{\massC}{\mbox{90,0$\единица{кг}$}}
\newcommand{\studentD}{Диана} \newcommand{\massD}{\mbox{80,0$\единица{кг}$}}
\newcommand{\studentE}{Эрик} \newcommand{\massE}{\mbox{95,0$\единица{кг}$}}
\newcommand{\studentF}{Фрэнсис} \newcommand{\massF}{\mbox{85,0$\единица{кг}$}}
\newcommand{\studentX}{Ксеркс} \newcommand{\massX}{\mbox{62,5$\единица{кг}$}}
\newcommand{\studentZ}{Замберт} \newcommand{\massZ}{\mbox{95 долларов.0\единица{кг}$}} \newcommand{\heA}{он}\newcommand{\himA}{его}\newcommand{\hisA}{его} \newcommand{\himselfA}{сам}
\newcommand{\HeA}{He}\newcommand{\HimA}{Him}\newcommand{\HisA}{His}
\newcommand{\heC}{он}\newcommand{\himC}{его}\newcommand{\hisC}{его} \newcommand{\himselfC}{сам}
\newcommand{\HeC}{He}\newcommand{\HimC}{Him}\newcommand{\HisC}{His}
\newcommand{\heE}{он}\newcommand{\himE}{его}\newcommand{\hisE}{его} \newcommand{\himselfE}{сам}
\newcommand{\HeE}{He}\newcommand{\HimE}{Him}\newcommand{\HisE}{His}
\newcommand{\heZ}{он}\newcommand{\himZ}{его}\newcommand{\hisZ}{его} \newcommand{\himselfZ}{сам}
\newcommand{\HeZ}{He}\newcommand{\HimZ}{Him}\newcommand{\HisZ}{His} \ newcommand {\ heB} {она} \ newcommand {\ himB} {ее} \ newcommand {\ hisB} {ее} \ newcommand {\ himselfB} {она}
\newcommand{\HeB}{She}\newcommand{\HimB}{Her}\newcommand{\HisB}{Her}
\newcommand{\heD}{она}\newcommand{\himD}{ее} \newcommand{\hisD}{ее} \ newcommand{\himselfD}{ее себя}
\newcommand{\HeD}{She}\newcommand{\HimD}{Her}\newcommand{\HisD}{Her}
\ newcommand {\ heF} {она} \ newcommand {\ himF} {ее} \ newcommand {\ hisF} {ее} \ newcommand {\ himselfF} {herself}
\newcommand{\HeF}{She}\newcommand{\HimF}{Her}\newcommand{\HisF}{Her} \newcommand{\heX}{\studentX}\newcommand{\himX}{\studentX}\newcommand{\hisX}{\studentX’s}\newcommand{\himselfX}{лицо \studentX}
\newcommand{\HeX}{\studentX}\newcommand{\HimX}{\studentX}\newcommand{\HisX}{\studentX’s}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
0\единица{кг}$}}
\newcommand{\studentB}{Бет} \newcommand{\massB}{\mbox{75,0$\единица{кг}$}}
\newcommand{\studentC}{Карл} \newcommand{\massC}{\mbox{90,0$\единица{кг}$}}
\newcommand{\studentD}{Диана} \newcommand{\massD}{\mbox{80,0$\единица{кг}$}}
\newcommand{\studentE}{Эрик} \newcommand{\massE}{\mbox{95,0$\единица{кг}$}}
\newcommand{\studentF}{Фрэнсис} \newcommand{\massF}{\mbox{85,0$\единица{кг}$}}
\newcommand{\studentX}{Ксеркс} \newcommand{\massX}{\mbox{62,5$\единица{кг}$}}
\newcommand{\studentZ}{Замберт} \newcommand{\massZ}{\mbox{95 долларов.0\единица{кг}$}} \newcommand{\heA}{он}\newcommand{\himA}{его}\newcommand{\hisA}{его} \newcommand{\himselfA}{сам}
\newcommand{\HeA}{He}\newcommand{\HimA}{Him}\newcommand{\HisA}{His}
\newcommand{\heC}{он}\newcommand{\himC}{его}\newcommand{\hisC}{его} \newcommand{\himselfC}{сам}
\newcommand{\HeC}{He}\newcommand{\HimC}{Him}\newcommand{\HisC}{His}
\newcommand{\heE}{он}\newcommand{\himE}{его}\newcommand{\hisE}{его} \newcommand{\himselfE}{сам}
\newcommand{\HeE}{He}\newcommand{\HimE}{Him}\newcommand{\HisE}{His}
\newcommand{\heZ}{он}\newcommand{\himZ}{его}\newcommand{\hisZ}{его} \newcommand{\himselfZ}{сам}
\newcommand{\HeZ}{He}\newcommand{\HimZ}{Him}\newcommand{\HisZ}{His} \ newcommand {\ heB} {она} \ newcommand {\ himB} {ее} \ newcommand {\ hisB} {ее} \ newcommand {\ himselfB} {она}
\newcommand{\HeB}{She}\newcommand{\HimB}{Her}\newcommand{\HisB}{Her}
\newcommand{\heD}{она}\newcommand{\himD}{ее} \newcommand{\hisD}{ее} \ newcommand{\himselfD}{ее себя}
\newcommand{\HeD}{She}\newcommand{\HimD}{Her}\newcommand{\HisD}{Her}
\ newcommand {\ heF} {она} \ newcommand {\ himF} {ее} \ newcommand {\ hisF} {ее} \ newcommand {\ himselfF} {herself}
\newcommand{\HeF}{She}\newcommand{\HimF}{Her}\newcommand{\HisF}{Her} \newcommand{\heX}{\studentX}\newcommand{\himX}{\studentX}\newcommand{\hisX}{\studentX’s}\newcommand{\himselfX}{лицо \studentX}
\newcommand{\HeX}{\studentX}\newcommand{\HimX}{\studentX}\newcommand{\HisX}{\studentX’s}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Результаты учащихсяПеревод первого закона Ньютона: Закон инерции
После успешного изучения данного подраздела учащиеся должны уметь …
Напишите первый закон Ньютона своими словами
Приведите примеры объектов без результирующей силы, сохраняющих свою скорость (статическую и динамическую)
Для примеров, в которых объекты имеют ускорение, определите действующую силу
Познакомьтесь с результатами учащихся по подразделам II.3.2.1.1 и II.3.2.1.2.
Подраздел, на который ссылается
Обсуждение способов описания сил
Первый закон Ньютона
Если смотреть из инерциальной системы отсчета, объект без действующих на него сил сохранит свою скорость, которая может быть равна нулю.
Пробный камень (инерциальные рамки)
Вы также можете вспомнить обсуждение в подразделе II. 1.6.1.
1.6.1.
Давайте разберем этот язык и соединим его с вашим повседневным опытом.
Как указано в Пояснении II.3.2.1, обычно безопасно предположить, что вы находитесь в инерциальной системе отсчета для своего повседневного опыта. Итак, на данный момент мы не будем беспокоиться о словах перед запятой.
Остальная часть этого утверждения часто записывается немного по-другому (и менее лаконично): «объект в состоянии покоя остается в покое, если на него не действует внешняя сила, а объект в движении остается в движении, если на него не действует внешняя сила». Поскольку «покоиться» — это утверждение о скорости\((\vec v=0)\), а «находиться в движении» — это также утверждение о скорости, каждое из этих утверждений можно понимать как утверждение, что
Другими словами, первый закон Ньютона гласит, что без силы скорость не изменится.
ConnectionII.3.2.5Заглядывая вперед
При обсуждении равновесия (подраздел II.3.2.2.4) мы отметим, что это часто расширяется, чтобы сказать, что без результирующей силы (в отличие от «без силы», как объясняется в подразделе II. 3.2.2.2) скорость не изменится, но это частный случай второго закона Ньютона (подраздел II.3.2.2).
3.2.2.2) скорость не изменится, но это частный случай второго закона Ньютона (подраздел II.3.2.2).
Параграф, на который ссылается
Раздел II.4.4
Построение интуиции
Теперь, когда мы разобрали язык, давайте подключим его к нашему повседневному опыту.Наша интуиция кричит нам, что если объект покоится, то нам не нужно ничего делать, чтобы он не двигался: объекты просто не двигаются спонтанно. Это кажется приемлемым для большинства студентов-физиков. Интересная часть первого закона заключается в том, что он говорит, что это верно и для движущихся объектов. Кажется, это противоречит здравому смыслу многих людей. Большинство объектов, которые мы приводим в движение, не поддерживают это движение, а вместо этого замедляются. Ключ к интересной физике — подумать о том, когда объекты замедляются, а когда ускоряются без вашей помощи.Для того, чтобы связать первый закон со своей интуицией, нужно внимательно наблюдать за тем, что происходит на самом деле.
Что нужно сделать: s-Ff. html плохо ссылается на этот раздел. Предложение с форума состояло в том, чтобы сделать предыдущую «p» «прелюдией», а последующую «p» – «постлюдией»; но в настоящее время пре-/пост-люди не появляются в упомянутом знании, которое было The Point. На самом деле я хочу только пре/пост и меня меньше беспокоит фактическое расследование в s-Ff.
html плохо ссылается на этот раздел. Предложение с форума состояло в том, чтобы сделать предыдущую «p» «прелюдией», а последующую «p» – «постлюдией»; но в настоящее время пре-/пост-люди не появляются в упомянутом знании, которое было The Point. На самом деле я хочу только пре/пост и меня меньше беспокоит фактическое расследование в s-Ff.ИсследованиеII.3.2.1Найти закономерность
(а)
Составьте список ситуаций, в которых движущийся объект замедляется без вашего вмешательства в его движение.Укажите, взаимодействует ли он с чем-либо еще.
Задача, на которую ссылается
Задача II.4.4.1.a
(b)
Составьте список ситуаций, в которых движущийся объект ускоряется без вашего вмешательства в его движение. Укажите, взаимодействует ли он с чем-либо еще.
(в)
Составьте список ситуаций, в которых движущийся объект сохраняет свое движение без вашего вмешательства в его движение. Укажите, взаимодействует ли он с чем-либо еще.
(г)
Есть шаблон?
Если вы сдвинете кирпич по ледяному пруду и сравните это с скольжением того же кирпича по ровной парковке, с скольжением того же кирпича по покрытой гравием подъездной дорожке, с скольжением того же кирпича по травянистой лужайке, вы быстро увидите, что кирпич ведет себя не так.Кирпич взаимодействует с поверхностью и движется. Это говорит нам (Понимание 2), что на кирпич действует сила, которая меняет способ его движения. Первый закон Ньютона неприменим к ситуации, когда на объект действуют силы. Когда действуют силы, нам нужно учитывать второй закон Ньютона, что мы и сделаем в подразделе II.3.2.2.
Подраздел II.3.2.1.1 Инерция
¶Результаты студентовИнерция
После успешного изучения этого подраздела учащиеся должны уметь …
Этот закон часто называют «законом инерции».Понятие инерции можно описать как тенденцию объекта сохранять свою скорость . Это описывает, как ведет себя объект, когда вы ничего с ним не делаете. Инерция не является величиной, которую вычисляют физики, но физики относятся к объектам как к объектам с большой инерцией, обычно для того, чтобы показать, что для изменения движения объекта потребуется большая сила, или как к объектам с небольшой инерцией, обычно для того, чтобы изменить движение объекта. указывают на то, что должно быть относительно легко изменить движение объекта.Однако инерция на самом деле не относится к необходимой силе. Вместо этого инерция чаще всего относится к «инерционной массе» объекта, которая проявляется во втором законе.
Это описывает, как ведет себя объект, когда вы ничего с ним не делаете. Инерция не является величиной, которую вычисляют физики, но физики относятся к объектам как к объектам с большой инерцией, обычно для того, чтобы показать, что для изменения движения объекта потребуется большая сила, или как к объектам с небольшой инерцией, обычно для того, чтобы изменить движение объекта. указывают на то, что должно быть относительно легко изменить движение объекта.Однако инерция на самом деле не относится к необходимой силе. Вместо этого инерция чаще всего относится к «инерционной массе» объекта, которая проявляется во втором законе.
Иногда, когда физики не следят за своим языком, кажется, что они используют слово «инерция» как синонимы термина «импульс», который мы обсудим более подробно в подразделе III.1.1.1.
Подподраздел II.3.2.1.2 Как законы работают вместе
¶Результаты учащихсяКак законы работают вместе
После успешного изучения этого подраздела учащиеся должны уметь …
Вы должны заметить, что первый закон Ньютона касается того, что происходит, когда вы не толкаете объект, то есть склонность объекта поддерживать собственное движение без действующей на него силы; это инерция объекта. С другой стороны, второй закон Ньютона касается того, что происходит с объектом , когда вы нажимаете на него . Это мы и рассмотрим далее. После этого третий закон Ньютона будет описывать, что происходит 90 631 с предметом, толкающим 90 632, а не только с предметом, которого толкают. В подразделе 5 подраздела II.3.2.2 эти идеи будут рассмотрены более подробно.
С другой стороны, второй закон Ньютона касается того, что происходит с объектом , когда вы нажимаете на него . Это мы и рассмотрим далее. После этого третий закон Ньютона будет описывать, что происходит 90 631 с предметом, толкающим 90 632, а не только с предметом, которого толкают. В подразделе 5 подраздела II.3.2.2 эти идеи будут рассмотрены более подробно.
Теперь мы готовы сделать более мощное переформулирование принцип инерции.
Другими словами, предполагается, что объект, первоначально находившийся в состоянии покоя, останется
в состоянии покоя, если суммарная сила, действующая на него, равна нулю, а тело в движении остается
при движении с той же скоростью в том же направлении. В будущем курсе физики или в другом учебнике вы можете встретить термин «чистая сила», который является просто синонимом общей сила. Что произойдет, если общая сила, действующая на объект, не равна нулю? Это ускоряется. Численное предсказание результирующего ускорения тема второго закона Ньютона, которую мы обсудим в следующем раздел. Это первый из трех законов движения Ньютона. Нет
важно запомнить, какие из трех законов Ньютона являются числами
один, два и три.Если вас о чем-то спрашивает будущий учитель физики
вроде “О каком из законов Ньютона вы имеете в виду?”
ответ: «О постоянной скорости, когда есть
нулевой суммарной силы». Понятия важнее, чем какие-либо конкретные
формулировка их. Ньютон писал на латыни, а я нет.
знает любой современный учебник, в котором используется дословный перевод
его формулировка законов движения.
Более общие комбинации сил Слишком накладно ограничивать наше внимание случаями, когда
все силы лежат вдоль линии движения центра масс. За
одно, мы не можем анализировать ни один случай горизонтального движения, так как
любой объект на земле будет подвергаться вертикальной гравитационной силе!
Например, когда вы едете на машине по прямой дороге,
существуют как горизонтальные силы, так и вертикальные силы.Тем не менее
вертикальные силы не влияют на движение центра масс, т.к.
восходящая сила дороги просто противодействует земной нисходящей
гравитационная сила и удерживает автомобиль от погружения в землю. Далее в книге мы рассмотрим наиболее общий случай из многих сил, действующих на объект под любыми углами, с помощью математических метод сложения векторов, но следующее небольшое обобщение первого закона Ньютона позволяет нам анализировать очень много случаев интерес: Предположим, что на объект действуют две группы сил, одна установить вдоль линии начального движения объекта, а другую установить перпендикулярно к первому набору.Если оба набора сил компенсируются, то центр масс объекта продолжает двигаться в том же состоянии.
Вопросы для обсуждения
|


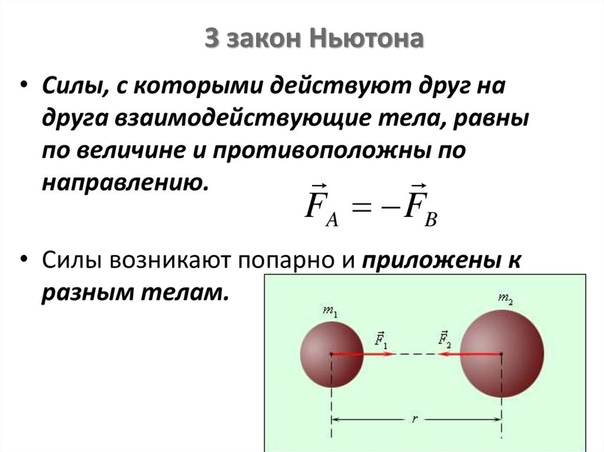 5 м/с при снятии силы F . Какое расстояние пройдет косилка до остановки?
5 м/с при снятии силы F . Какое расстояние пройдет косилка до остановки? Мне часто не нравится формулировка, используемая OpenStax. Я бы добавил больше деталей к этому вопросу. А именно, какова результирующая сила, действующая на косилку, когда человек перестает толкать, затем каково ускорение, затем каково расстояние, пройденное до ее остановки.) Это было бы 24 Н влево, поэтому ускорение равно замедлению 1,00 м/с 2 влево или -1,00 м/с 2 . водоизмещение = 1,1 м.
Мне часто не нравится формулировка, используемая OpenStax. Я бы добавил больше деталей к этому вопросу. А именно, какова результирующая сила, действующая на косилку, когда человек перестает толкать, затем каково ускорение, затем каково расстояние, пройденное до ее остановки.) Это было бы 24 Н влево, поэтому ускорение равно замедлению 1,00 м/с 2 влево или -1,00 м/с 2 . водоизмещение = 1,1 м. Обратное
Первый закон Ньютона также верен: если мы наблюдаем, как объект движется
с постоянной скоростью вдоль прямой линии, то полная сила на
он должен быть равен нулю.
Обратное
Первый закон Ньютона также верен: если мы наблюдаем, как объект движется
с постоянной скоростью вдоль прямой линии, то полная сила на
он должен быть равен нулю. Четкое письмо было не в моде
во времена Ньютона, и он сформулировал свои три закона в терминах концепции
теперь называется импульсом, лишь позднее связав его с понятием
сила.Почти все современные тексты, включая этот, начинаются с силы.
и сделать импульс позже.
Четкое письмо было не в моде
во времена Ньютона, и он сформулировал свои три закона в терминах концепции
теперь называется импульсом, лишь позднее связав его с понятием
сила.Почти все современные тексты, включая этот, начинаются с силы.
и сделать импульс позже.
