По какой формуле вычисляют быстроту изменения скорости: 404 - Страница не найдена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Найти ускорение без скорости. Формулы прямолинейного равноускоренного движения

Как изменяются показания спидометра в начале движения и при торможении автомобиля?
Какая физическая величина характеризует изменение скорости?

При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо жеодновременно как по модулю, так и по направлению.

Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает. Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис 1.26). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.

Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении).

Физическая величина, характеризующая быстроту изменения скорости, называется ускорением .

Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае её скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени t точка занимает положение М и имеет скорость (рис. 1.27). Спустя промежуток времени Δt точка займёт положение М 1 и будет иметь скорость 1 . Изменение скорости за время Δt 1 равно Δ 1 = 1 – . Вычитание вектора можно произвести путём прибавления к вектору 1 вектора (-):

Δ 1 = 1 – = 1 + (-).

Согласно правилу сложения векторов вектор изменения скорости Δ 1 направлен из начала вектора 1 в конец вектора (-), как это показано на рисунке 1.28.

Поделив вектор Δ 1 на промежуток времени Δt 1 получим вектор, направленный так же, как и вектор изменения скорости Δ 1 . Этот вектор называют средним ускорением точки за промежуток времени Δt 1 . Обозначив его через cр1 , запишем:

По аналогии с определением мгновенной скорости определим мгновенное ускорение . Для этого найдём теперь средние ускорения точки за всё меньшие и меньшие промежутки времени:

При уменьшении промежутка времени Δt вектор Δ уменьшается по модулю и меняется по направлению (рис. 1.29). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени Δt к нулю отношение изменения скорости к изменению времени стремится к определённому вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени или просто ускорением и обозначают .

Ускорение точки – это предел отношения изменения скорости Δ к промежутку времени Δt, в течение которого это изменение произошло, при стремлении Δt к нулю.

Ускорение направлено так, как направлен вектор изменения скорости Δ при стремлении промежутка времени Δt к нулю. В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения точки при прямолинейном и криволинейном движениях.

В общем случае ускорение направлено под углом к вектору скорости (рис. 1.30). Полное ускорение характеризует изменение скорости и по модулю, и по направлению. Часто полное ускорение считается равным векторной сумме двух ускорений – касательного ( к) и центростремительного ( цс). Касательное ускорение к характеризует изменение скорости по модулю и направлено по касательной к траектории движения. Центростремительное ускорение цс характеризует изменение скорости по направлению и перпендикулярно касательной, т. е. направлено к центру кривизны траектории в данной точке. В дальнейшем мы рассмотрим два частных случая: точка движется по прямой и скорость изменяется только по модулю; точка движется равномерно по окружности и скорость изменяется только по направлению.

Единица ускорения.

Движение точки может происходить как с переменным, так и с постоянным ускорением. Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени.

Поэтому обозначив через Δt некоторый произвольный промежуток времени, а через Δ – изменение скорости за этот промежуток, можно записать:

Так как промежуток времени Δt – величина положительная, то из этой формулы следует, что если ускорение точки с течением времени не изменяется, то оно направлено так же, как и вектор изменения скорости. Таким образом, если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени. Это позволяет установить единицы модуля ускорения и его проекций.

Запишем выражение для модуля ускорения:

Отсюда следует, что:
модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости изменяется на единицу.

Если время измерено в секундах, а скорость – в метрах в секунду, то единица ускорения – м/с 2 (метр на секунду в квадрате).

И зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи. 2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится.

Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, – это векторная величина).

> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

где – вектор ускорения .

Направление вектора ускорения совпадает с направлением изменения скорости Δ = – 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t1 (см. рис 1.8) тело имеет скорость 0 . В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – 0 . Тогда определить ускорение можно так:

Рис. 1.8. Среднее ускорение.

В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями а Х, a Y , a Z).

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

Если скорость тела по модулю уменьшается, то есть

V 2 то направление вектора ускорения противоположно направлению вектора скорости 2 . Иначе говоря, в данном случае происходит замедление движения , при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n . Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

= τ + n

Содержимое:

Ускорение характеризует быстроту изменения скорости движущегося тела. Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. Ускорение измеряется в метрах в секунду за секунду (м/с 2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.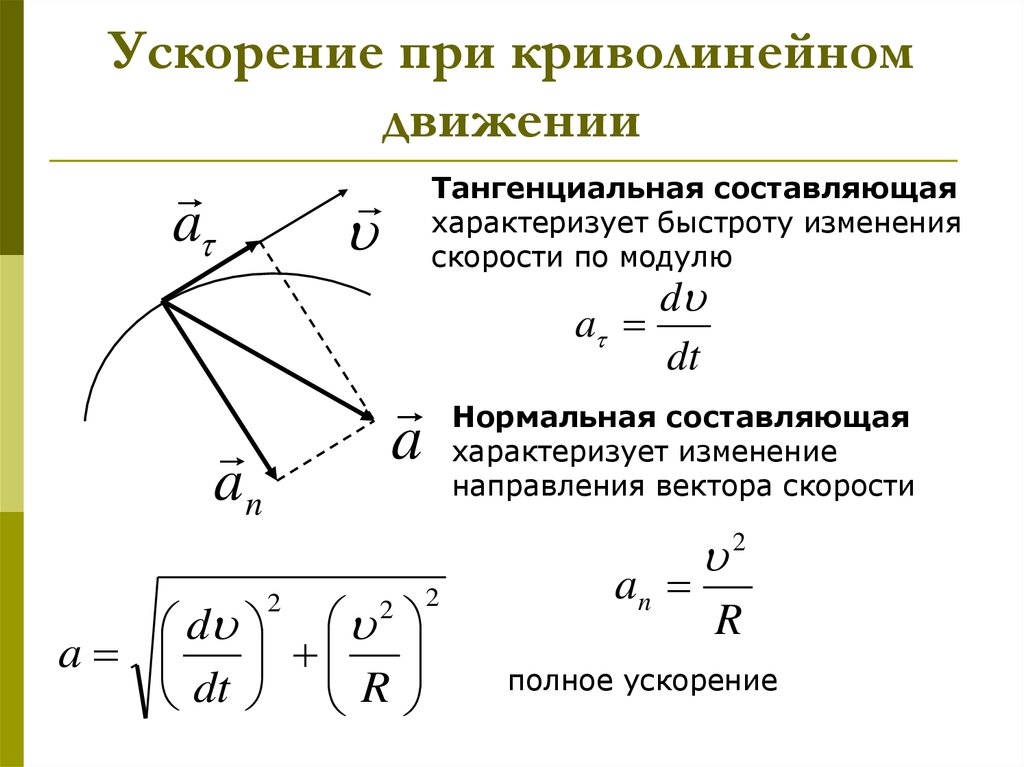

Шаги

1 Вычисление среднего ускорения по двум скоростям

1 Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt , где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с 2 .
- Ускорение является векторной величиной, то есть задается как значением, так и направлением. Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
2 Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v к – v н и Δt = t к – t н , где v к – конечная скорость, v н – начальная скорость, t к – конечное время, t н – начальное время.
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что t н = 0.
3 Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: . Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
Напишите переменные: v к = 46,1 м/с, v н = 18,5 м/с, t к = 2,47 с, t н = 0 с.
Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с 2 .
Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
Напишите переменные: v к = 0 м/с, v н = 22,4 м/с, t к = 2,55 с, t н = 0 с.
Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с 2 .

2 Вычисление ускорения по силе

1 Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело. Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
Второй закон Ньютона описывается формулой: F рез = m x a , где F рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с 2).
2 Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
3 Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы. Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
Помните, что 1 Н = 1 кг∙м/с 2 .
4 Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
5 Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
a = F/m = 10/2 = 5 м/с 2

3 Проверка ваших знаний

1 Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
2 Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с 2 . Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с 2 .
3 Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 – 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с 2 .

Шаги

Вычисление среднего ускорения по двум скоростям

Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt , где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.

Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v к – v н и Δt = t к – t н , где v к – конечная скорость, v н – начальная скорость, t к – конечное время, t н – начальное время.

Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
Если в задаче начальное время не дано, то подразумевается, что t н = 0.

Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: . Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.

Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
Напишите переменные: v к = 46,1 м/с, v н = 18,5 м/с, t к = 2,47 с, t н = 0 с.
Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с 2 .
Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
Напишите переменные: v к = 0 м/с, v н = 22,4 м/с, t к = 2,55 с, t н = 0 с.
Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с 2 .

Вычисление ускорения по силе

Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело. Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F рез = m x a , где F рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с 2).
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы. Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с 2

Проверка ваших знаний

Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с 2 . Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с 2 .

Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):

Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 – 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с 2 .

Тангенциальное ускорение определяется по формуле

Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.

Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.

Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.

В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением . Тангенциальное ускорение описывает степень изменения скорости по модулю:

Нормальное ускорение – это составляющая ускорения, которая направлена к центру кривизны траектории, то есть она является нормалью (направлена перпендикулярно) к скорости. Нормальное ускорение описывает степень изменения скорости по направлению:

Здесь R – это радиус кривизны траектории в заданной точке.

Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Нормальное, тангенциальное и полное ускорение

Ускорение при криволинейном движении

В случае движения материальной точки по криволинейной траектории различают нормальное и тангенциальное ускорения.

Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Оно направлено к центру кривизны траектории.

Модуль нормального ускорения определяют по формуле , где R – радиус кривизны траектории

Тангенциальное (касательное) ускорение характеризует изменение скорости по величине. Оно направлено по касательной к траектории.

Модуль тангенциального ускорения определяют по формуле .

Модуль полного ускорения .

Тело, деформациями которого в данных условиях движения, можно пренебречь называют абсолютно твердым телом.

При вращательном движении радиус-вектор каждой точки поворачивается за одно и то время на один и тот же угол .

называют углом поворота тела.

Угловой скоростью тела называют величину

– аксиальный вектор (направлен вдоль оси вращения в сторону, определяемую правилом правого винта).

Равномерное вращение характеризуется периодом обращения Т.

Периодом обращения называют промежуток времени, за которое тело делает один полный оборот (поворачивается на угол 2π).

Модуль угловой скорости равномерного движения

Частотой обращения называют число оборотов точки за единицу времени .

Таким образом,

Угловое ускорение характеризует быстроту изменения угловой скорости (в случае неравномерного вращения)

Линейная скорость тела связана с угловой соотношением .

Модуль нормального ускорения

Модуль тангенциального ускорения .

Дата добавления: 2014-11-18 ; Просмотров: 889 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.

В физике

Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:

Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.

Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:

Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.

Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).

Траектория движения и компоненты полного ускорения

Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?

Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:

Здесь u_t¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.

Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:

Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.

Ускорение тангенциальное

Запишем еще раз формулу для этой компоненты полного ускорения:

Это выражение позволяет описать свойства величины a_t¯:

Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор u_t¯.
Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.

Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.

Ускорение нормальное

Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:

Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:

Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:

То есть величина a_n¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор a_n¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.

Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.

Ускорение полное, нормальное и тангенциальное

Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:

Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и a_n¯ вычисляется так:

Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.

Решение задачи

Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:

Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.

Для тангенциального имеем:

Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:

Теперь можно воспользоваться формулой для a_n:

Таким образом, мы определили все величины, которые требовалось найти для решения задачи.

Ускорение тела вычисляется по формуле. Что такое ускорение? Движение по окружности равномерное и ускорение

Ускорение – знакомое слово. Не инженеру оно чаще всего попадается в новостных статьях и выпусках. Ускорение развития, сотрудничества, других общественных процессов. Исконное же значение этого слова связано с физическими явлениями. Как найти ускорение движущегося тела, или ускорение, как показатель мощности автомобиля? А может ли оно иметь иные значения?

Что происходит между 0 и 100 (определение термина)

Показателем мощности автомобиля принято считать время его разгона от нуля до сотни. А что же происходит в промежутке? Рассмотрим нашу “Ладу Веста” с ее заявленными 11 секундами.

Одна из формул как найти ускорение записывается так:

a = (V 2 – V 1) / t

В нашем случае:

a – ускорение, м/с∙с

V1 – начальная скорость, м/с;

V2 – конечная скорость, м/с;

Приведем данные в систему СИ, а именно км/ч пересчитаем в м/с:

100 км/ч = 100000 м / 3600 с = 27,28 м/с.

Теперь можно найти ускорение движения “Калины”:

a = (27,28 – 0) / 11 = 2,53 м/с∙с

Что обозначают эти цифры? Ускорение 2,53 метров в секунду за секунду говорит о том, что за каждую секунду скорость «болида» увеличивается на 2,53 м/с.

При старте с места (с нуля):

за первую секунду автомобиль разгонится до скорости 2,53 м/с;
за вторую – до 5,06 м/с;
к концу третьей секунды скорость составит 7,59 м/с и т. д.

Таким образом, можно подытожить: ускорение – рост скорости точки за единицу времени.

Второй закон Ньютона, это несложно

Итак, величина ускорения вычислена. Самое время задаться вопросом, откуда же это ускорение берется, что является его первоисточником. Ответ один – сила. Именно сила, с которой колеса толкают автомобиль вперед, и вызывает его ускорение. И как найти ускорение, если величина этой силы известна? Зависимость между этими двумя величинами и массой материальной точки была установлена Исааком Ньютоном (это произошло не в тот день, когда ему на голову упало яблоко, тогда он открыл другой физический закон).

А записывается этот закон так:

F = m ∙ a, где

F – сила, Н;

m – масса, кг;

a – ускорение, м/с∙с.

Применительно к изделию российского автопрома, можно подсчитать силу, с которой колеса толкают машину вперед.

F = m ∙ a = 1585 кг ∙ 2,53 м/с∙с = 4010 Н

или 4010 / 9,8 = 409 кг∙с

Это означает, что если не отпускать педаль газа, то машина будет набирать скорость до достижения скорости звука? Конечно же, нет. Уже при достижении ею скорости 70 км/ч (19,44 м/с) лобовое сопротивление воздуха достигает 2000 Н.

Как найти ускорение в момент времени, когда Лада «летит» с такой скоростью?

a = F / m = (F колес – F сопр.) / m = (4010 – 2000) / 1585 = 1,27 м/с∙с

Как видим, формула позволяет находить как ускорение, зная силу с которой на механизм воздействуют двигатели (другие силы: ветра, потока воды, вес и т. д.), так и наоборот.

Для чего необходимо знать ускорение

В первую очередь для того, чтобы вычислить скорость какого-либо материального тела в интересующий момент времени, а так же его местоположение.

Предположим, что наша “Лада Веста” разгоняется на Луне, где нет лобового сопротивления воздуха по причине отсутствия такового, тогда ускорение ее на каком-то этапе будет стабильным. В этом случае определим скорость машины через 5 секунд после старта.

V = V 0 + a ∙ t = 0 + 2,53 ∙ 5 = 12,65 м/с

или 12,62 ∙ 3600 / 1000 = 45,54 км/ч

V 0 – начальная скорость точки.

А на каком расстоянии от старта окажется в этот момент наш лунный автомобиль? Для этого проще всего воспользоваться универсальной формулой определения координаты:

x = x 0 + V 0 t + (at 2) / 2

х = 0 + 0 ∙ 5 + (2,53 ∙ 5 2) / 2 = 31,63 м

x 0 – начальная координата точки.

Именно на такое расстояние успеет за 5 секунд удалиться “Веста” от линии старта.

Но на деле, для того, чтобы найти скорость и ускорение точки в заданный момент времени, в реальности необходимо учитывать и просчитывать множество других факторов. На Луну, понятное дело, “Лада Веста” если и попадет, то нескоро, на ее ускорение, кроме мощности нового инжекторного движка, влияет не только сопротивление воздуха.

На разных оборотах мотора, он выдает разное усилие, это еще не беря в расчет номер включенной передачи, коэффициент сцепления колес с дорогой, уклон этой самой дороги, скорость ветра и многое другое.

Какие еще бывают ускорения

Сила умеет не только заставлять тело двигаться вперед по прямой. Например, сила притяжения Земли заставляет Луну постоянно искривлять траекторию своего полета таким образом, что она всегда кружится вокруг нас. На Луну в данном случае воздействует сила? Да, это та самая сила, которая и была открыта Ньютоном с помощью яблока – сила притяжения.

И ускорение, которое она придает нашему естественному спутнику, называется центростремительным. Как найти ускорение Луны при ее движении по орбите?

a ц = V 2 / R = 4π 2 R / T 2 , где

a ц – центростремительное ускорение, м/с∙с;

V – скорость движения Луны по орбите, м/с;

R – радиус орбиты, м;

T- период обращения Луны вокруг Земли, с.

a ц = 4 π 2 384 399 000 / 2360591 2 = 0,002723331 м/с∙с

Страница 6 из 12

§ 5. Ускорение.
Равноускоренное прямолинейное движение

1. При неравномерном движении скорость тела с течением времени изменяется. Рассмотрим самый простой случай неравномерного движения.

Движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение, называют равноускоренным.

Например, если за каждые 2 с скорость тела изменялась на4 м/с, то движение тела является равноускоренным. Модуль скорости при таком движении может как увеличиваться, так и уменьшаться.

2. Пусть в начальный момент времени t 0 = 0 скорость тела равна v 0 . В некоторый момент времени t она стала равной v . Тогда изменение скорости за промежуток времени t – t 0 = t равно v – v 0 , а за единицу времени – . Это отношение называется ускорением . Ускорение характеризует быстроту изменения скорости.

Ускорением тела при равноускоренном движении называют векторную физическую величину, равную отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

Единица ускорения в СИ – метр на секунду в квадрате (1 ):

[a ] === 1 .

За единицу ускорения принимают ускорение такого равноускоренного движения, при котором скорость тела за 1 с изменяется на 1 м/с.

3. Поскольку ускорение – величина векторная, необходимо выяснить, как оно направлено.

Пусть автомобиль движется прямолинейно, имея начальную скорость v 0 (скорость в момент времени t = 0) и скорость v в некоторый момент времени t . Модуль скорости автомобиля возрастает. На рисунке 22, а изображены вектор скорости автомобиля. Из определения ускорения, следует, что вектор ускорения направлен в ту же сторону, что и разность векторов v – v 0 . Следовательно в данном случае направление вектора ускорения совпадает с направлением движения тела (с направлением вектора скорости).

Пусть теперь модуль скорости автомобиля уменьшается (рис. 22б ). В этом случае направление вектора ускорения противоположно направлению движения тела (направлению вектора скорости).

4. Преобразовав формулу ускорения при равноускоренном прямолинейном движении, можно получить формулу для нахождения скорости тела в любой момент времени:

Если начальная скорость тела равна нулю, т. е. в начальный момент времени оно покоилось, то эта формула приобретает вид:

v = at .

5. При вычислении скорости или ускорения пользуются формулами, в которые входят не векторы, а проекции этих величин на координатную ось. Поскольку проекция суммы векторов равна сумме их проекций, то формула для проекции скорости на ось X имеет вид:

v x = v 0x + a x t ,

где v x – проекция скорости в момент времени t , v 0x – проекция начальной скорости, a x – проекция ускорения.

При решении задач необходимо учитывать знаки проекций. Так, в случае, изображенном на рисунке 22, а , проекции скоростей и ускорения на ось X положительны; модуль скоростис течением времени возрастает. В случае, изображенном на рисунке 22, б , проекции на ось X скоростей положительны, а проекция ускорения – отрицательна; модуль скорости с течением времени уменьшается.

6. Пример решения задачи

Скорость автомобиля при торможении уменьшилась от 23 до 15 м/с. Каково ускорение тела, если торможение длилось 5 с?

Дано :

Решение

v 0 = 23 м/с

v = 15 м/с

t = 5 с

Автомобиль движется равноускоренно и прямолинейно; модуль его скорости уменьшается.

Систему отсчета свяжем с Землей, ось X направим в сторону движения автомобиля (рис. 23), за начало отсчета времени примем начало торможения.

a ?

Запишем формулу для нахождения скорости при равноускоренном прямолинейном движении:

v = v 0 + at .

В проекциях на ось X получим

v x = v 0x + a x t .

Учитывая, что проекция ускорения тела на ось X отрицательна, а проекции скоростей на эту ось положительны, запишем: v = v 0 – at .

Откуда:

a = ;

a == 1,6 м/с 2 .

Ответ: a = 1,6 м/с 2 .

Вопросы для самопроверки

1. Какое движение называют равноускоренным?

2. Что называют ускорением равноускоренного движения?

3. По какой формуле вычисляется ускорение при равноускоренном движении?

4. Какова единица ускорения в СИ?

5. По какой формуле вычисляется скорость тела при равноускоренном прямолинейном движении?

6. Каков знак проекции ускорения на ось X по отношению к проекции скорости тела на эту же ось, если модуль его скорости увеличивается; уменьшается?

Задание 5

1. Чему равно ускорение автомобиля, если через 2 мин после начала движения из состояния покоя он приобрел скорость 72 км/ч?

2. Поезд, начальная скорость которого равна 36 км/ч, разгоняется с ускорением 0,5 м/ с 2 . Какую скорость приобретет поезд через 20 с?

3. Автомобиль, движущийся со скоростью 54 км/ч, останавливается у светофора в течение 15 с. Чему равно ускорение автомобиля?

4. Какую скорость приобретет велосипедист через 5 с после начала торможения, если его начальная скорость равна 10 м/с, а ускорение при торможении составляет 1,2 м/с 2 ?

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2.2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Рис. 1.8. Среднее ускорение. В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

V 2 > v 1

а направление вектора ускорения совпадает с вектором скорости

Если скорость тела по модулю уменьшается, то есть

V 2

то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения , при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Шаги

Вычисление среднего ускорения по двум скоростям

Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
Если в задаче начальное время не дано, то подразумевается, что t н = 0.

Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
Напишите переменные: v к = 46,1 м/с, v н = 18,5 м/с, t к = 2,47 с, t н = 0 с.
Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с 2 .
Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
Напишите формулу: a = Δv / Δt = (v к – v н)/(t к – t н)
Напишите переменные: v к = 0 м/с, v н = 22,4 м/с, t к = 2,55 с, t н = 0 с.
Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с 2 .

Вычисление ускорения по силе

Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело. Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F рез = m x a , где F рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с 2).
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы. Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с 2

Проверка ваших знаний

Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с 2 . Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с 2 .

Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 – 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с 2 .

Что значит модуль ускорения

Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Чему равен максимальный модуль ускорения? Ответ выразите в м/с 2 .

На всех рассматриваемых интервалах времени скорость автомобиля меняется равномерно, следовательно, ускорение на каждом интервале постоянно. Рассчитаем ускорения:

в интервале от 0 до 10 с:

в интервале от 10 до 20 с:

в интервале от 20 до 30 с:

в интервале от 30 до 40 с:

Максимальный модуль ускорения равен 2 м/с 2 .

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Что такое ускорение?

Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

Где v₂ и v₁ — скорости в моменты времени t₂ и t₁ соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с 2 ). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с 2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Здесь v_{— некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:}

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с 2 ).

Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным a_t и нормальным a_n ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина a_t может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента a_t линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с 2 ).

Нормальная компонента вычисляется так:

a_n = v 2 /r = 1/r*(2 + 3*t 2 + 2*t 3 ) 2 = 1/0,2*(2+27+54) 2 = 34445 м/c 2 .

Теперь можно рассчитать полное ускорение. Оно будет равно:

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Что такое ускорение?

Вам будет интересно: Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления

a = (v2 — v1)/(t2 — t1).

Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).

Нормальная компонента вычисляется так:

an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = at/r = 76/0,2 = 380 рад/с2.

Типы скорости | Sciencing

Физический термин, скорость описывает движение объектов. Скорость измеряет движение объектов в зависимости от их скорости и направления. Скорость объекта измеряет расстояние, которое он преодолевает за определенный период времени. Скорость – это скалярное измерение, поскольку оно определяет только величину скорости движения объекта. Скорость – это векторная величина, поскольку она описывает как скорость, так и направление.

Постоянная скорость

Объект с постоянной скоростью не изменяется ни по скорости, ни по направлению.Единственные объекты, которые квалифицируются как движущиеся с постоянной скоростью, – это те, которые движутся по прямой с постоянной скоростью. Объект за пределами Солнечной системы, в межзвездном пространстве, не находящийся под влиянием внешних сил, можно описать как объект, движущийся с постоянной скоростью.

Изменение скорости

Объекты с изменяющейся скоростью демонстрируют изменение скорости или направления с течением времени. Изменения скорости объектов измеряются как ускорение.Объекты с постоянной скоростью и изменяющимся направлением также ускоряются. Кометы и астероиды в Солнечной системе являются примерами объектов с изменяющейся скоростью, поскольку на их скорость или направление влияет сила тяжести.

Математика ускорения

Ускорение измеряет изменение скорости в результате изменений направления или скорости. Математически ускорение равно изменению скорости, деленному на определенное количество времени. Автомобиль, который увеличивает свою скорость на 10 миль в час каждые две секунды, ускоряется со скоростью 5 миль в час каждую секунду.Изменения направления объекта также составляют ускорение и обычно отображаются в виде графика.

Мгновенная скорость

Мгновенная скорость – это метод определения того, насколько быстро объект меняет свою скорость или направление в заданный момент времени. Мгновенная скорость определяется сокращением периода времени, используемого для измерения ускорения, до такой малой величины, что объект не ускоряется в течение заданного периода времени. Этот метод измерения скорости полезен для построения графиков, измеряющих серию изменений скорости.

Конечная скорость

Конечная скорость – это термин, используемый для описания движения объекта, свободно падающего в атмосфере. Предметы, падающие на землю в вакууме, будут постоянно ускоряться, пока не достигнут земли. Однако объект, падающий через атмосферу, в конечном итоге перестанет ускоряться из-за увеличения сопротивления воздуха. Точка, в которой сопротивление воздуха равно ускорению, вызванному силой тяжести или любой другой силой, действующей на объект, называется конечной скоростью.

Калькулятор скорости

Этот калькулятор скорости – это инструмент, который помогает вам определять среднюю скорость движущегося объекта на основе пройденного расстояния за определенное время. Если вы тестируете свой новый автомобиль, или просто собираетесь совершить пробежку или велосипед, этот калькулятор вам пригодится, если вы хотите узнать, как определить среднюю скорость.

В статье ниже вы можете найти много ценной информации, например, какова формула средней скорости.Мы также дадим вам несколько любопытных фактов о скорости (например, о скорости звука). Проверьте этот калькулятор скорости и расстояния и, наконец, найдите ответ на вопрос , как быстро я еду?

Скорость, расстояние, время

Все мы слышали о speed , но насколько вы уверены в своем понимании этой концепции? Скорость, по определению, связана с физикой. Однако, когда вы думаете об этом, вы не видите векторов и формул из учебника, а вместо этого видите велосипедиста, летающий самолет или стрелку спидометра.Мы больше ассоциируем скорость с движущимися объектами, чем с научными уравнениями. Более того, у нас есть чувство, которое говорит нам, насколько быстро мы путешествуем, то есть мы можем определить, быстро ли мы движемся или нет. Например, когда вы едете на машине со скоростью 50 км / ч, это не слишком быстро по сравнению с максимальной скоростью автомобиля, но когда вы едете на велосипеде с той же скоростью, она сильно падает. Итак, мы можем сказать, что человеческое восприятие скорости относительно.

Автомобили и поезда измеряют скорость в километрах в час (км / ч) или в милях в час (миль / ч), а на самолетах и кораблях мы обычно используем узлы (узлы).С другой стороны, физики чаще всего используют базовые единицы СИ – метры в секунду (м / с). За этими единицами скрывается определение скорости, и мы можем познакомиться с ним, изучив их. Скорость зависит от расстояния и времени. Единицы скорости определяются как единицы пройденного расстояния, разделенные на единицы времени, и это общее представление о скорости. Проще говоря – скорость – это расстояние, пройденное за единицу времени .

Как быстро я еду? – виды скорости

Скорость – неточный термин – есть несколько более точных значений, и их не следует путать друг с другом.Давайте рассмотрим разницу между мгновенной скоростью , средней скоростью и скоростью вращения . Для целей двух первых мы попытаемся визуализировать это на примере вождения автомобиля.

Вы едете по длинной открытой трассе. Вы смотрите на спидометр своей машины; он читает 100 километров в час. Отсюда вы узнаете, как далеко вы проедете, если будете поддерживать постоянную скорость. Мы знаем, что на практике поддерживать постоянную скорость практически невозможно (хотя на шоссе с круиз-контролем это почти возможно), и наша скорость все время более или менее колеблется.Фактическое расстояние, которое вы преодолеете за час, – это среднее значение всех этих скоростей. Вывод – средняя скорость – это общее расстояние, пройденное за единицу времени (например, за час).

Итак, что на самом деле означает цифра, которую показывает ваш спидометр? Это ваша мгновенная скорость; ваша скорость именно в этот момент. Согласно определению из учебника, , мгновенная скорость – это изменение положения объекта, x, между двумя моментами времени, t₁ и t₂ (где этот временной интервал приближается к нулю, т.е.е., t₂ – t₁ -> 0).

Скорость вращения – это немного другой термин, относящийся скорее к вращающимся объектам, чем к объектам, которые меняют свое положение в пространстве. Соответственно, частота вращения , , – это количество полных оборотов, которые объект делает за единицу времени . Он выражается в радианах в секунду (рад / с) или в оборотах в минуту (об / мин). Мы не будем больше останавливаться на этой теме, потому что это не является целью данного калькулятора скорости и расстояния. Если вы хотите узнать больше об угловой скорости, воспользуйтесь нашим калькулятором углового ускорения или калькулятором рациональной кинетической энергии.

Формула средней скорости

Поскольку основное назначение этого калькулятора – вычисление средней скорости, давайте более подробно рассмотрим эту тему. Средняя скорость измеряется в единицах расстояния за время, а формула средней скорости выглядит так:

средняя скорость = общее расстояние / общее время

Типичными единицами измерения являются километры в час (км / ч), мили в час (миль / ч), метры в секунду (м / с) и футы в секунду (фут / с). В нашем калькуляторе миль / ч единицей измерения по умолчанию является миль / час (км / ч для стран с метрическими единицами), но вы можете переключаться между любыми обычными единицами измерения.

Калькулятор скорости – как найти свою среднюю скорость?

Использовать этот скоростной калькулятор расстояния очень просто, и вы сразу же получите результат. Ознакомьтесь с пунктами ниже, чтобы узнать, как правильно пользоваться этим калькулятором:

Сначала нужно определить расстояние . Это может быть, например, расстояние, которое вы проехали от дома до другого города. Введите это в соответствующее поле.
Теперь необходимо определить время , которое потребовалось, чтобы преодолеть определенное расстояние.Введите это в калькулятор.
И вот она, вы получаете средней скорости .

Вы также можете нажать кнопку расширенного режима , вы получите доступ к дополнительным функциям этого калькулятора средней скорости. Здесь вы можете сравнить, какой будет разница во времени, если объект двигался с другой средней скоростью (положительное значение , если объект перемещается в течение более длительного времени, и отрицательное значение , если объект перемещается более короткое время. время).

Средняя скорость относительно средней скорости

Скорость и скорость могут показаться одним и тем же, но это не так. Скорость – это скалярная величина, она определяется только величиной. Проще говоря, он сообщает вам, насколько быстро движется объект. С другой стороны, скорость – это вектор – она определяется не только величиной, но и направлением. Он сообщает вам скорость, с которой объект меняет свое положение.

Представьте, что вы ведете машину на 100 метров вперед, а затем на 100 метров назад. Вы бы двигались с определенной средней скоростью в каждом направлении, но у вас была бы нулевая средняя скорость, поскольку скорость измеряется как скорость, с которой изменяется положение автомобиля, и, в целом, автомобиль не менял своего положения.Таким образом, достаточно сказать, что средняя скорость автомобиля составляла 50 миль в час, но при вычислении скорости нам нужно будет добавить направление, скажем, 50 миль в час на восток.

И если вы хотите знать, насколько быстро меняется ваша скорость или скорость, вам нужно рассчитать ускорение.

У вас есть потребность … жажда скорости? Взгляните на некоторые интересные факты и поразительные цифры в случае скорости различных предметов и животных!

Ничто не может двигаться быстрее скорости света, даже если принять во внимание, что скорость является относительной мерой.Свет движется со скоростью 299 792 458 метров в секунду, что примерно дает 300 000 километров в час или 186 000 миль в секунду. Время, необходимое для того, чтобы свет от Солнца достиг Земли, составляет около 8 минут.

Звук движется по воздуху со скоростью около 343 метров в секунду, что составляет 1234,8 км / ч или 767 миль в час (при 20 ° C / 68 ° F). Это означает, что звуковой волне в воздухе требуется около 2,9 секунды, чтобы пройти один километр, или 4,7 секунды, чтобы пройти милю – эти данные могут быть полезны охотникам за штормами для определения расстояния до освещения.В 2012 году австриец Феликс Баумгартнер преодолел звуковой барьер (своим телом!) Во время свободного падения с 228 000 футов. Он достиг скорости 833,9 миль в час. Чтобы поместить это в контекст, типичный пассажир реактивного самолета летит на высоте 33 000 – 35 000 футов со скоростью около 500 миль в час (в зависимости от типа самолета и скорости ветра).

Вы, наверное, слышали, что самое быстрое животное на земле – гепард, и это правда. Его максимальная скорость действительно невероятна, и, согласно последним исследованиям, он может развивать скорость до 58 миль в час! Еще один удивительный пример – соколы-сапсаны.Они могут развивать скорость, превышающую … 200 миль в час в воздухе! В воде самое быстрое животное – атлантический парусник – 68 миль в час в воде.

А как насчет людей? Спринтер Усэйн Болт – самый быстрый человек в истории, его скорость составляет 27,44 миль в час. Что интересно, ученые обнаружили, что человек, живший 20 000 лет назад в Австралии (по имени Т8), бежал со скоростью 23 мили в час. Обратите внимание, он делал это босиком по грязи, в то время как Болт использует современные кроссовки и специальную дорожку.

FAQ

Скорость такая же, как и скорость?

Скорость и скорость почти одинаковы. – фактически единственное различие между ними состоит в том, что скорость – это скорость с направлением .Скорость – это так называемая скалярная величина, то есть ее можно описать одним числом (насколько быстро вы движетесь). Это также величина скорости. Скорость, качество вектора, должна иметь как величину, так и направление, например путешествие на 90 миль в час на юго-восток.

Какая скорость движения самая экономичная?

В то время как самая экономичная скорость движения меняется с каждым автомобилем , общее мнение таково, что составляет около 50 миль в час (80 км / ч) .Однако есть еще несколько вещей, которые вы можете сделать для максимальной эффективности. Во-первых, попытайтесь поддерживать постоянную скорость , это заставит ваш двигатель работать максимально эффективно – используйте круиз-контроль на квартирах, если он у вас есть. Во-вторых, двигайтесь на максимально возможной передаче в пределах скорости , это снова помогает вашему двигателю работать с максимальной экономичностью. Другие советы включают в себя отключение переменного тока и уменьшение веса в автомобиле, насколько это возможно для .

Могут ли Карты Google сказать мне мою скорость?

Карты Google могут сказать вам вашу скорость, в них есть встроенный спидометр , который в настоящее время доступен только для пользователей Android.Он включен по умолчанию, но чтобы убедиться, что он включен, перейдите в настройки → настройки навигации , и в меню параметров вождения будет ползунок для него. Это полезно, так как , он изменит цвет, если вы превысите лимит , поэтому вам не нужно отрывать глаза от дороги. Вы также можете сообщить о камерах контроля скорости и ловушках , но только если вы находитесь в режиме навигации.

Как рассчитать миль / ч в секундах?

Измерьте текущую скорость в км / ч или миль / ч.
Разделите его на 60, чтобы получить километры в минуту или мили в минуту.
Снова разделите на 60, получив километры в секунду или мили в секунду.
Или разделите его на 3600 для прямого преобразования.

Какие бывают скорости?

Speed имеет много разных типов и терминов для ее описания:

Скорость – насколько быстро движется объект.
Скорость – насколько быстро объект движется в определенном направлении.
Acceleration – насколько быстро объект достигает определенной скорости.
Постоянная скорость – объект движется с одинаковой скоростью.
Переменная скорость – объект, движущийся с изменяющейся скоростью.
Средняя скорость – пройденное расстояние, разделенное на время прохождения.
Мгновенная скорость – скорость на конкретном экземпляре.

Какая единица измерения скорости?

Единица измерения скорости – это расстояние во времени , поскольку она определяется как количество времени, которое требуется объекту, чтобы преодолеть определенное расстояние.Базовая единица измерения или СИ – метры в секунду , но это не очень практично в повседневной жизни. Вы, вероятно, больше знакомы с такими единицами измерения, как километров в час, мили в час и узлы . Любое расстояние во времени – это единица измерения скорости, поэтому другие единицы скорости включают нанометры за две недели, Boeing 787 за солнечный год или бананы по Фридману.

Как вы переводите между миль / ч и км / ч?

в преобразовать из миль в час в километры в час :

Оцените скорость.
Умножьте значение на 1,6.

В конвертировать километры в час в мили в час :

Оцените скорость.
Умножьте значение на 0,62.

Если у вас нет калькулятора под рукой (например, вы за рулем), удобно использовать последовательность Фибоначчи (1, 1, 2, 3, 5, 8…). Возьмите число, следующим в последовательности будут километры, если предыдущее было в милях (например, 50 миль в час – это примерно 80 км / ч).

Как определить конечную скорость?

Если у вас средняя и начальная скорость :

Умножьте среднюю скорость на 2.
Вычтите начальную скорость.
Осталась конечная скорость .

Если у вас есть начальная скорость, ускорение и время :

Умножьте время и ускорение.
Добавьте к этому числу начальную скорость.
Попробуй свой расчет .

По какой формуле рассчитывается средняя скорость?

Самая распространенная формула для средней скорости – это расстояние, которое пройдено, разделенное на затраченное время .Другая формула: если у вас начальная и конечная скорость , сложите их вместе и разделите на 2.

Какие бывают виды разгона?

Существует двух типов ускорения: среднее и мгновенное . Среднее ускорение – это изменение скорости , деленное на изменение времени , и это то, как движение объекта изменяется со временем в среднем. Мгновенное ускорение – это производная скорости по времени или предел среднего ускорения за бесконечно малый период времени.Он используется для определения точного ускорения объекта в определенный момент времени.

3.4 Производные как скорость изменения – Объем расчетов 1

Цели обучения

3.4.1 Определите новое значение количества из старого значения и суммы изменения.
3.4.2 Рассчитайте среднюю скорость изменения и объясните, чем она отличается от мгновенной скорости изменения.
3.4.3 Применяйте скорость изменения к смещению, скорости и ускорению объекта, движущегося по прямой линии.
3.4.4 Спрогнозируйте численность населения в будущем, исходя из текущей стоимости и темпов роста населения.
3,4,5 Используйте производные инструменты для расчета предельных затрат и доходов в деловой ситуации.

В этом разделе мы рассмотрим некоторые применения производной, сосредоточив внимание на интерпретации производной как скорости изменения функции. Эти приложения включают ускорение и скорость в физике, темпы роста населения в биологии и маргинальные функции в экономике.

Формула суммы изменения

Одним из приложений для производных является оценка неизвестного значения функции в точке, используя известное значение функции в некоторой данной точке вместе со скоростью ее изменения в данной точке. Если f (x) f (x) – функция, определенная на интервале [a, a + h], [a, a + h], то величина изменения f (x) f (x) на интервале равна изменение значений yy функции на этом интервале и определяется как

f (a + h) −f (a) .f (a + h) −f (a).
Средняя скорость изменения функции ff за тот же интервал – это отношение величины изменения за этот интервал к соответствующему изменению в значениях xx.Выдается
f (a + h) −f (a) h.f (a + h) −f (a) h.
Как мы уже знаем, мгновенная скорость изменения f (x) f (x) в точке aa является ее производной
f ′ (a) = limh → 0f (a + h) −f (a) h.f ′ (a) = limh → 0f (a + h) −f (a) h.
Для достаточно малых значений h, f ′ (a) ≈f (a + h) −f (a) h.h, f ′ (a) ≈f (a + h) −f (a) h. Затем мы можем решить для f (a + h) f (a + h), чтобы получить формулу суммы изменения:
f (a + h) ≈f (a) + f ′ (a) h.f (a + h) ≈f (a) + f ′ (a) h.
(3.10)
Мы можем использовать эту формулу, если мы знаем только f (a) f (a) и f ′ (a) f ′ (a) и хотим оценить значение f (a + h).е (а + ч). Например, мы можем использовать текущее население города и скорость его роста, чтобы оценить его население в ближайшем будущем. Как видно на рисунке 3.22, мы аппроксимируем f (a + h) f (a + h) координатой yy в точке a + ha + h на прямой, касательной к f (x) f (x) в точке x = ax. = а. Обратите внимание, что точность этой оценки зависит от значения hh, а также от значения f ′ (a) .f ′ (a).
Фигура 3,22 Новое значение измененной величины равно исходному значению плюс скорость изменения, умноженная на интервал изменения: f (a + h) ≈f (a) + f ′ (a) h.f (a + h) ≈f (a) + f ′ (a) h.
Пример 3,33
Оценка значения функции
Если f (3) = 2f (3) = 2 и f ′ (3) = 5, f ′ (3) = 5, оценим f (3.2) .f (3.2).
Решение
Начните с поиска h.h. Имеем h = 3,2−3 = 0,2. H = 3,2−3 = 0,2. Таким образом,
f (3.2) = f (3 + 0.2) ≈f (3) + (0.2) f ′ (3) = 2 + 0.2 (5) = 3. f (3.2) = f (3 + 0.2) ≈f (3 ) + (0,2) f ′ (3) = 2 + 0,2 (5) = 3.
Контрольно-пропускной пункт 3,21
Учитывая f (10) = – 5f (10) = – 5 и f ′ (10) = 6, f ′ (10) = 6, оцените f (10.1) .f (10.1).
Движение по прямой
Другое использование производной – анализ движения вдоль линии. Мы описали скорость как скорость изменения положения. Если мы возьмем производную скорости, мы сможем найти ускорение или скорость изменения скорости. Также важно ввести понятие скорости, то есть ее величину. Таким образом, мы можем сформулировать следующие математические определения.
Определение
Пусть s (t) s (t) будет функцией, дающей положение объекта в момент времени t.т.
Скорость объекта в момент времени tt определяется выражением v (t) = s ′ (t) .v (t) = s ′ (t).
Скорость объекта в момент времени tt определяется как | v (t) |. | V (t) |.
Ускорение объекта в момент tt определяется как a (t) = v ′ (t) = s ″ (t) .a (t) = v ′ (t) = s ″ (t).
Пример 3,34
Сравнение мгновенной скорости и средней скорости
Мяч падает с высоты 64 фута. Его высота над землей (в футах) через tt секунд определяется выражением s (t) = – 16t2 + 64.s (t) = – 16t2 + 64.
Какова мгновенная скорость мяча, когда он падает на землю?
Какая средняя скорость при его падении?
Решение
Первое, что нужно сделать, это определить, сколько времени требуется мячу, чтобы коснуться земли. Для этого положим s (t) = 0. s (t) = 0. Решая −16t2 + 64 = 0, −16t2 + 64 = 0, мы получаем t = 2, t = 2, поэтому мячу требуется 2 секунды, чтобы достичь земли.
Мгновенная скорость мяча при ударе о землю равна v (2).v (2). Поскольку v (t) = s ′ (t) = – 32t, v (t) = s ′ (t) = – 32t, получаем v (t) = – 64ft / s.v (t) = – 64ft / s.
Средняя скорость мяча при падении
vave = s (2) −s (0) 2−0 = 0−642 = −32ft / s. vave = s (2) −s (0) 2−0 = 0−642 = −32ft / s.
Пример 3,35
Интерпретация взаимосвязи между v (t) v (t) и a (t) a (t)
Частица движется вдоль координатной оси в положительном направлении вправо. Его положение в момент времени tt определяется выражением s (t) = t3−4t + 2.s (t) = t3−4t + 2. Найдите v (1) v (1) и a (1) a (1) и используйте эти значения, чтобы ответить на следующие вопросы.
Движется ли частица слева направо или справа налево в момент времени t = 1? T = 1?
Частица ускоряется или замедляется в момент времени t = 1? T = 1?
Решение
Начните с поиска v (t) v (t) и a (t) .a (t).
v (t) = s ′ (t) = 3t2-4v (t) = s ′ (t) = 3t2-4 и a (t) = v ′ (t) = s ″ (t) = 6t. a (t) = v ′ (t) = s ″ (t) = 6t.
Вычисляя эти функции при t = 1, t = 1, получаем v (1) = – 1v (1) = – 1 и a (1) = 6.a (1) = 6.
Поскольку v (1) <0, v (1) <0, частица движется справа налево.
Поскольку v (1) <0v (1) <0 и a (1)> 0, a (1)> 0, скорость и ускорение действуют в противоположных направлениях. Другими словами, частица ускоряется в направлении, противоположном направлению, в котором она движется, в результате чего | v (t) || v (t) | чтобы уменьшить. Частица замедляется.
Пример 3,36
Положение и скорость
Положение частицы, движущейся вдоль координатной оси, определяется выражением s (t) = t3−9t2 + 24t + 4, t≥0.s (t) = t3−9t2 + 24t + 4, t≥0.
Найдите v (t) .v (t).
В какое время (а) частица покоится?
На каких временных интервалах частица движется слева направо? Справа налево?
Используйте полученную информацию, чтобы нарисовать путь частицы вдоль координатной оси.
Решение
Скорость является производной функции положения:
v (t) = s ′ (t) = 3t2−18t + 24. v (t) = s ′ (t) = 3t2−18t + 24.
Частица покоится, когда v (t) = 0, v (t) = 0, поэтому установите 3t2−18t + 24 = 0.3t2−18t + 24 = 0. Разложение левой части уравнения на множители дает 3 (t − 2) (t − 4) = 0,3 (t − 2) (t − 4) = 0. Решая, находим, что частица покоится при t = 2t = 2 и t = 4.t = 4.
Частица движется слева направо, когда v (t)> 0 v (t)> 0, и справа налево, когда v (t) <0. v (t) <0. Анализ знака v (t) v (t) для t≥0, t≥0, но он не представляет ось, вдоль которой движется частица.
Фигура 3,23 Знак v (t) определяет направление частицы.

Поскольку 3t2−18t + 24> 03t2−18t + 24> 0 на [0,2) ∪ (4, + ∞), [0,2) ∪ (4, + ∞), частица движется слева направо на эти интервалы.
Поскольку 3t2−18t + 24 <03t2−18t + 24 <0 на (2,4), (2,4), частица движется справа налево на этом интервале.
Прежде чем мы сможем нарисовать график частицы, нам нужно знать ее положение в момент начала движения (t = 0) (t = 0) и в моменты изменения направления (t = 2,4). ( t = 2,4). Имеем s (0) = 4, s (2) = 24, s (0) = 4, s (2) = 24 и s (4) = 20.s (4) = 20. Это означает, что частица начинается на координатной оси в точке 4 и меняет направление в точках 0 и 20 на координатной оси. Путь частицы показан на координатной оси на рис. 3.24.
Фигура 3,24 Путь частицы можно определить, анализируя v (t).
Контрольно-пропускной пункт 3,22
Частица движется по координатной оси. Его положение в момент времени tt определяется выражением s (t) = t2−5t + 1.s (t) = t2−5t + 1. Движется ли частица справа налево или слева направо в момент времени t = 3? T = 3?
Изменение численности населения
Помимо анализа скорости, скорости, ускорения и положения, мы можем использовать производные для анализа различных типов популяций, в том числе таких разнообразных, как колонии бактерий и города.Мы можем использовать текущую популяцию вместе со скоростью роста, чтобы оценить размер популяции в будущем. Скорость прироста населения – это скорость изменения численности населения и, следовательно, может быть представлена производной от численности населения.
Определение
Если P (t) P (t) – это количество сущностей, присутствующих в популяции, то скорость роста популяции P (t) P (t) определяется как P ′ (t) .P ′ (t).
Пример 3,37
Оценка населения
Население города увеличивается в три раза каждые 5 лет.Если его нынешнее население составляет 10 000 человек, какое будет его примерное население через 2 года?
Решение
Пусть P (t) P (t) будет численностью населения (в тысячах) через tt лет. Таким образом, мы знаем, что P (0) = 10P (0) = 10, и на основе информации мы ожидаем, что P (5) = 30.P (5) = 30. Теперь оцените P ′ (0), P ′ (0), текущий темп роста, используя
P ′ (0) ≈P (5) −P (0) 5−0 = 30−105 = 4. P ′ (0) ≈P (5) −P (0) 5−0 = 30−105 = 4.
Применяя уравнение 3.10 к P (t), P (t), мы можем оценить численность населения через 2 года, написав
P (2) ≈P (0) + (2) P ′ (0) ≈10 + 2 (4) = 18; P (2) ≈P (0) + (2) P ′ (0) ≈10 + 2 (4) = 18;
, таким образом, через 2 года население составит 18000 человек.
Контрольно-пропускной пункт 3,23
Известно, что в настоящее время в колонии комаров проживает 3000 человек; то есть P (0) = 3000. P (0) = 3000. Если P ′ (0) = 100, P ′ (0) = 100, оцените размер популяции через 3 дня, где tt измеряется в днях.
Изменения в стоимости и выручке
В дополнение к анализу движения вдоль линии и роста населения, производные инструменты полезны при анализе изменений в стоимости, доходе и прибыли. Концепция маржинальной функции распространена в сфере бизнеса и экономики и подразумевает использование производных финансовых инструментов.Предельные затраты – это производная от функции затрат. Предельный доход – это производная от функции дохода. Предельная прибыль – это производная от функции прибыли, которая основана на функции затрат и функции дохода.
Определение
Если C (x) C (x) – затраты на производство x единиц, то предельные затраты MC (x) MC (x) равны MC (x) = C ′ (x) .MC (x) = C ‘(Икс).
Если R (x) R (x) – это доход, полученный от продажи xx предметов, то предельный доход MR (x) MR (x) равен MR (x) = R ′ (x).MR (x) = R ′ (x).
Если P (x) = R (x) −C (x) P (x) = R (x) −C (x) – прибыль, полученная от продажи товаров x , то предельная прибыль MP (x) MP (x) определяется как MP (x) = P ′ (x) = MR (x) −MC (x) = R ′ (x) −C ′ (x). MP (x) = P ′ (x) = MR (x) −MC (x) = R ′ (x) −C ′ (x).
Мы можем приблизительно оценить
MC (x) = C ′ (x) = limh → 0C (x + h) −C (x) hMC (x) = C ′ (x) = limh → 0C (x + h) −C (x) h
, выбрав соответствующее значение для h.h. Поскольку x представляет объекты, разумным и малым значением для hh является 1. Таким образом, подставляя h = 1, h = 1, мы получаем приближение MC (x) = C ′ (x) ≈C (x + 1) −C (х).MC (x) = C ′ (x) ≈C (x + 1) −C (x). Следовательно, C ′ (x) C ′ (x) для данного значения xx можно рассматривать как изменение стоимости, связанное с производством одного дополнительного элемента. Аналогичным образом MR (x) = R ′ (x) MR (x) = R ′ (x) аппроксимирует доход, полученный от продажи одного дополнительного товара, а MP (x) = P ′ (x) MP (x) = P ′ (x) приблизительно соответствует прибыли, полученной от производства и продажи одного дополнительного товара.
Пример 3,38
Применение предельного дохода
Предположим, что количество обедов-барбекю, которые могут быть проданы, x, x, можно связать с взимаемой ценой p, p уравнением p (x) = 9−0.03x, 0≤x≤300.p (x) = 9−0,03x, 0≤x≤300.
В этом случае доход в долларах, полученный от продажи xx ужинов барбекю, равен
R (x) = xp (x) = x (9−0,03x) = – 0,03×2 + 9xfor0≤x≤300.R (x) = xp (x) = x (9−0,03x) = – 0,03×2 + 9xfor0≤x≤300.
Используйте функцию предельного дохода, чтобы оценить доход, полученный от продажи 101-го барбекю-ужина. Сравните это с фактическим доходом, полученным от продажи этого обеда.
Решение
Сначала найдите функцию предельного дохода: MR (x) = R ′ (x) = – 0.06x + 9.MR (x) = R ′ (x) = – 0,06x + 9.
Затем используйте R ‘(100) R’ (100), чтобы приблизительно определить R (101) -R (100), R (101) -R (100), доход, полученный от продажи 101-го обеда. Поскольку R ′ (100) = 3, R ′ (100) = 3, доход, полученный от продажи 101-го обеда, составляет приблизительно 3 доллара.
Фактическая выручка от продажи 101-го обеда составляет
. R (101) -R (100) = 602,97-600 = 2,97, или 2,97 доллара. R (101) -R (100) = 602,97-600 = 2,97, или 2,97 доллара.
В данном случае предельный доход является довольно хорошей оценкой, и его преимущество состоит в том, что его легко вычислить.
Контрольно-пропускной пункт 3,24
Предположим, что прибыль, полученная от продажи xx обедов из жареной рыбы, равна P (x) = – 0,03×2 + 8x − 50.P (x) = – 0,03×2 + 8x − 50. Используйте функцию маржинальной прибыли, чтобы оценить прибыль от продажи 101-го обеда из жареной рыбы.
Раздел 3.4 Упражнения
Для следующих упражнений данные функции представляют положение частицы, движущейся вдоль горизонтальной линии.
Найдите функции скорости и ускорения.
Определите временные интервалы, когда объект замедляется или ускоряется.
150 .
s (t) = 2t3−3t2−12t + 8s (t) = 2t3−3t2−12t + 8
151 .
s (t) = 2t3−15t2 + 36t − 10s (t) = 2t3−15t2 + 36t − 10
153 .
Ракета запускается вертикально вверх от земли. Расстояние ss в футах, которое ракета преодолевает от земли через tt секунд, определяется выражением s (t) = – 16t2 + 560t.s (t) = – 16t2 + 560t.
Найдите скорость ракеты через 3 секунды после выстрела.
Определите ускорение ракеты через 3 секунды после выстрела.
154 .
Мяч бросается вниз со скоростью 8 футов / с с вершины здания высотой 64 фута. После t секунд его высота над землей определяется как s (t) = – 16t2−8t + 64.s (t) = – 16t2−8t + 64.
Определите, сколько времени требуется мячу, чтобы коснуться земли.
Определите скорость мяча, когда он ударяется о землю.
155 .
Функция положения s (t) = t2−3t − 4s (t) = t2−3t − 4 представляет положение задней части автомобиля, выезжающего с проезжей части, а затем движущегося по прямой линии, где ss – в футах. и tt в секундах.В этом случае s (t) = 0 s (t) = 0 представляет время, когда задняя часть автомобиля находится у ворот гаража, поэтому s (0) = – 4s (0) = – 4 – начальная позиция машина, 4 фута в гараже.
Определите скорость автомобиля, когда s (t) = 0. s (t) = 0.
Определите скорость автомобиля, когда s (t) = 14. s (t) = 14.
156 .
Положение колибри, летящего по прямой линии за tt секунд, определяется как s (t) = 3t3−7ts (t) = 3t3−7t метров.
Определите скорость птицы при t = 1t = 1 сек.
Определите ускорение птицы при t = 1t = 1 сек.
Определите ускорение птицы, когда скорость равна 0.
157 .
Картофель запускается вертикально вверх с начальной скоростью 100 футов / с из картофельного ружья на вершине здания высотой 85 футов. Расстояние в футах, на которое картофель отрывается от земли через tt секунд, определяется выражением s (t) = – 16t2 + 100t + 85.s (t) = – 16t2 + 100t + 85.
Найдите скорость картофеля после 0.5s0.5s и 5.75s.5.75s.
Найдите скорость картофеля за 0,5 с и 5,75 с.
Определите, когда картофель достигнет максимальной высоты.
Найдите ускорение картофеля за 0,5 с 1,5 с.
Определите, как долго картофель находится в воздухе.
Определите скорость картофеля при ударе о землю.
158 .
Функция положения s (t) = t3−8ts (t) = t3−8t дает положение грузового поезда в милях, где восток – положительное направление, а tt измеряется в часах.
Определите направление, в котором движется поезд, когда s (t) = 0. s (t) = 0.
Определите направление, в котором движется поезд, когда a (t) = 0. a (t) = 0.
Определите временные интервалы, когда поезд замедляется или набирает скорость.
159 .
На следующем графике показано положение y = s (t) y = s (t) объекта, движущегося по прямой линии.
Используйте график функции положения, чтобы определить временные интервалы, когда скорость положительная, отрицательная или нулевая.
Нарисуйте график функции скорости.
Используйте график функции скорости, чтобы определить временные интервалы, когда ускорение является положительным, отрицательным или нулевым.
Определите временные интервалы, когда объект ускоряется или замедляется.
160 .
Функция затрат в долларах компании, производящей кухонные комбайны, определяется выражением C (x) = 200 + 7x + x27, C (x) = 200 + 7x + x27, где xx – количество произведенных кухонных комбайнов.
Найдите функцию предельных затрат.
Используйте функцию предельных затрат, чтобы оценить стоимость производства тринадцатого кухонного комбайна.
Найдите фактическую стоимость производства тринадцатого кухонного комбайна.
161 .
Цена pp (в долларах) и спрос xx на определенные цифровые радиочасы задаются функцией цена – спрос p = 10−0.001x.p = 10−0.001x.
Найдите функцию дохода R (x) .R (x).
Найдите функцию предельного дохода.
Найдите предельный доход при x = 2000x = 2000 и 5000.5000.
162 .
[T] Прибыль получается, когда выручка превышает затраты. Предположим, что функция прибыли производителя скейтбордов равна P (x) = 30x − 0,3×2−250, P (x) = 30x − 0,3×2−250, где xx – количество проданных скейтбордов.
Найдите точную прибыль от продажи тридцатого скейтборда.
Найдите функцию предельной прибыли и используйте ее для оценки прибыли от продажи тридцатого скейтборда.
163 .
[T] В общем, функция прибыли – это разница между функциями дохода и затрат: P (x) = R (x) −C (x).Р (х) = R (х) -С (х).
Предположим, что функции цена-спрос и затраты на производство аккумуляторных дрелей заданы соответственно как p = 143−0,03xp = 143−0,03x и C (x) = 75000 + 65x, C (x) = 75000 + 65x, где xx – это количество аккумуляторных дрелей, которые продаются по цене pp-долларов за дрель, а C (x) C (x) – стоимость производства xx аккумуляторных дрелей.
Найдите функцию предельных затрат.
Найдите функции дохода и предельного дохода.
Найдите R ′ (1000) R ′ (1000) и R ′ (4000).R ′ (4000). Интерпретируйте результаты.
Найдите функции прибыли и предельной прибыли.
Найдите P ′ (1000) P ′ (1000) и P ′ (4000) .P ′ (4000). Интерпретируйте результаты.
164 .
Небольшой городок в Огайо поручил актуарной фирме провести исследование, которое смоделировало скорость изменения численности населения города. Исследование показало, что численность населения города (в тысячах человек) может быть смоделирована функцией P (t) = – 13t3 + 64t + 3000, P (t) = – 13t3 + 64t + 3000, где tt измеряется в годах. .
Найдите функцию скорости изменения P ′ (t) P ′ (t) функции населения.
Найдите P ′ (1), P ′ (2), P ′ (3), P ′ (1), P ′ (2), P ′ (3) и P ′ (4) .P ′ (4) . Объясните, что результаты означают для города.
Найдите P ″ (1), P ″ (2), P ″ (3), P ″ (1), P ″ (2), P ″ (3) и P ″ (4) .P ″ (4) . Объясните, что результаты означают для населения города.
165 .
[T] Число культур бактерий растет в соответствии с функцией N (t) = 3000 (1 + 4tt2 + 100), N (t) = 3000 (1 + 4tt2 + 100), где tt измеряется в часы.
Найдите скорость изменения количества бактерий.
Найдите N ′ (0), N ′ (10), N ′ (20), N ′ (0), N ′ (10), N ′ (20) и N ′ (30). N ′ (30) .
Интерпретируйте результаты в (b).
Найдите N ″ (0), N ″ (10), N ″ (20), N ″ (0), N ″ (10), N ″ (20) и N ″ (30) .N ″ (30) . Объясните, что ответы говорят о росте популяции бактерий.
166 .
Центростремительная сила объекта массой мм определяется выражением F (r) = mv2r, F (r) = mv2r, где vv – скорость вращения, а rr – расстояние от центра вращения.
Найдите скорость изменения центростремительной силы по отношению к расстоянию от центра вращения.
Найдите скорость изменения центростремительной силы объекта массой 1000 кг, скоростью 13,89 м / с и расстоянием от центра вращения 200 метров.
Следующие вопросы касаются населения (в миллионах) Лондона по десятилетиям XIX века, которые перечислены в следующей таблице.
Годы с 1800 года Население (в миллионах)
1 0.8795
11 1,040
21 1,264
31 1,516
41 1,661
51 2.000
61 2,634
71 3,272
81 3,911
91 4,422
Стол 3.4 Население Лондона Источник: http://en.wikipedia.org/wiki/Demographics_of_London.
167 .
[Т]
Используя калькулятор или компьютерную программу, найдите наиболее подходящую линейную функцию для измерения численности населения.
Найдите производную уравнения в a. и объясните его физический смысл.
Найдите вторую производную уравнения и объясните ее физический смысл.
168 .
[Т]
Используя калькулятор или компьютерную программу, найдите наиболее подходящую квадратичную кривую по данным.
Найдите производную уравнения и объясните ее физический смысл.
Найдите вторую производную уравнения и объясните ее физический смысл.
Для следующих упражнений рассмотрим космонавта на большой планете в другой галактике. Чтобы узнать больше о составе этой планеты, космонавт бросает электронный датчик в глубокую траншею. Датчик каждую секунду передает свое вертикальное положение относительно положения космонавта. Сводка данных датчика падения отображается в следующей таблице.
Время после сброса (с) Позиция (м)
0 0
1 -1
2 −2
3 −5
4 −7
5 −14
169 .
[Т]
С помощью калькулятора или компьютерной программы найдите квадратичную кривую, которая наилучшим образом соответствует данным.
Найдите производную функции положения и объясните ее физический смысл.
Найдите вторую производную функции положения и объясните ее физический смысл.
170 .
[Т]
С помощью калькулятора или компьютерной программы найдите кубическую кривую, которая наилучшим образом соответствует данным.
Найдите производную функции положения и объясните ее физический смысл.
Найдите вторую производную функции положения и объясните ее физический смысл.
Используя результат c. объясните, почему кубическая функция не подходит для этой задачи.
Следующие задачи относятся к уравнениям Холлинга типа I, II и III. Эти уравнения описывают экологическое событие роста популяции хищников с учетом количества добычи, доступной для потребления.
171 .
[T] Уравнение Холлинга типа I описывается формулами f (x) = ax, f (x) = ax, где xx – количество доступной добычи, а a> 0a> 0 – скорость, с которой хищник встречает добыча для потребления.
Изобразите уравнение Холлинга типа I для a = 0,5.a = 0,5.
Определите первую производную уравнения Холлинга типа I и физически объясните, что подразумевает производная.
Определите вторую производную уравнения Холлинга типа I и физически объясните, что подразумевает эта производная.
Используя интерпретацию из б. и c. объясните, почему уравнение Холлинга типа I может быть нереалистичным.
172 .
[T] Уравнение Холлинга типа II описывается формулой f (x) = axn + x, f (x) = axn + x, где xx – количество доступной добычи, а a> 0a> 0 – максимальное потребление. скорость хищника.
Изобразите уравнение Холлинга типа II для a = 0,5a = 0,5 и n = 5.n = 5. В чем разница между уравнениями Холлинга I и II типа?
Возьмите первую производную уравнения Холлинга типа II и объясните физический смысл производной.
Покажите, что f (n) = 12af (n) = 12a, и интерпретируйте значение параметра n.n.
Найдите и интерпретируйте значение второй производной. Что делает функцию Холлинга II более реалистичной, чем функцию Холлинга I типа?
173 .
[T] Уравнение Холлинга типа III описывается формулой f (x) = ax2n2 + x2, f (x) = ax2n2 + x2, где xx – количество доступной добычи, а a> 0a> 0 – максимальное потребление. скорость хищника.
Изобразите уравнение Холлинга типа III для a = 0,5a = 0,5 и n = 5.n = 5. В чем разница между уравнениями Холлинга типа II и III?
Возьмите первую производную уравнения Холлинга типа III и объясните физический смысл производной.
Найдите и интерпретируйте значение второй производной (это может помочь построить график второй производной).
Какие дополнительные экологические явления описывает функция Холлинга типа III по сравнению с функцией Холлинга типа II?
174 .
[T] Популяции зайца-снегоступа (в тысячах) и рыси (в сотнях), собранные за 7 лет с 1937 по 1943 год, показаны в следующей таблице. Заяц-снегоступы – основная добыча рыси.
Численность зайца-снегоступа (тыс.) Численность рыси (сотни)
20 10
55 15
65 55
95 60
Стол 3.5 Популяции зайцев-снегоступов и рысей Источник: http://www.biotopics.co.uk/newgcse/predatorprey.html.
Изобразите точки данных и определите, какая функция типа Холлинга лучше всего соответствует данным.
Используя значения параметров aa и n, n, определите значения для этих параметров, исследуя график данных. Напомним, что nn измеряет, какая ценность жертвы дает половинную максимальную ценность хищника.
Постройте результирующие функции Холлинга I, II и III поверх данных.Был результат из части а. верный?
Является ли ускорение скоростью изменения скорости?
Это часть серии статей, посвященных распространенным заблуждениям.
Это правда или ложь?
Ускорение – это скорость изменения скорости.
Почему некоторые говорят, что это правда: Подумайте об ускорении в машине: когда вы нажимаете на педаль газа, вы ускоряетесь, а когда вы нажимаете на тормоз, вы замедляетесь. Ускорение обычно связано с изменением скорости.
Почему некоторые говорят, что это неправда: В физике направление имеет значение. Если направление движения меняется, это тоже можно рассматривать как ускорение, даже если скорость остается постоянной.
Выявите правильный ответ \ color {# 20A900} {\ text {Выявите правильный ответ}} Выявите правильный ответ
Утверждение ложно \ color {# D61F06} {\ textbf {false}} ложно.
Пояснение:
Ускорение определяется как скорость изменения скорости.Скорость – это вектор , что означает, что он содержит величину (числовое значение) и направление. Таким образом, скорость можно изменить либо путем изменения скорости, либо путем изменения направления движения (или и того, и другого). Следовательно, возможно, что скорость постоянна, но скорость меняется из-за изменения направления. В этом случае ускорение будет ненулевым и равным скорости изменения скорости.
Это общее заблуждение, что скорость изменения скорости равна величине скорости изменения скорости.Однако это верно не во всех случаях. Рассмотрим равномерное круговое движение: в случае равномерного кругового движения частица движется по круговой траектории с постоянной скоростью. Скорость остается постоянной, но направление движения постоянно меняется. Из-за изменения направления движения ускорение ненулевое. Это ускорение направлено к центру круга и известно как центростремительное ускорение.
В общем, ускорение можно разделить на две составляющие. Один компонент, который параллелен скорости, известен как тангенциальное ускорение.Этот компонент изменяет скорость частицы и равен скорости изменения скорости. Другой компонент ускорения, перпендикулярный скорости, известен как нормальное ускорение. Этот компонент отвечает за изменение направления скорости.
Скорость – это скорость изменения смещения, а скорость – это скорость изменения расстояния. Другими словами, скорость – это скорость изменения кратчайшего расстояния, пройденного телом от конечного положения до начального, а скорость – это скорость изменения общей длины пути, пройденного определенным телом.
См. Дальнейшие обсуждения \ color {# 3D99F6} {\ text {См. Дальнейшие обсуждения}} См. Дальнейшие обсуждения
Запрос : Что можно сказать об ускорении частицы, движущейся по зигзагообразной траектории с постоянной скоростью?
Ответ : Ускорение частицы должно быть ненулевым, поскольку частица меняет свое направление. Однако тангенциальная составляющая ускорения равна нулю, поскольку скорость остается постоянной.
Запрос : Если изменяется и скорость, и направление, то возможно ли получить нулевое ускорение?
Ответ : Нет.Если скорость изменяется, то тангенциальное ускорение не равно нулю. Если направление движения меняется, то нормальное ускорение не равно нулю. Результат этих двух ускорений никогда не может быть нулевым, поскольку они перпендикулярны друг другу.
Только (a) и (b) верны Только (a), (b) и (c) верны Только (c) и (d) верны Все варианты верны
Частица движется по круговой дорожке с постоянной ненулевой скоростью.\ circ 90∘.
См. Также
Скорость изменения (ROC)
Что такое скорость изменения (ROC)
Скорость изменения (ROC) – это скорость, с которой переменная изменяется в течение определенного периода времени. ROC часто используется, говоря об импульсе, и обычно может быть выражен как отношение между изменением одной переменной по отношению к соответствующему изменению в другой; графически скорость изменения представлена наклоном линии.ROC часто обозначается греческой буквой дельта.
Понимание скорости изменения (ROC)
Скорость изменения используется для математического описания процентного изменения значения за определенный период времени и представляет собой импульс переменной. Расчет ROC прост в том, что он берет текущую стоимость акции или индекса и делит ее на значение за более ранний период. Вычтите единицу и умножьте полученное число на 100, чтобы получить процентное представление.
р О C знак равно ( текущая стоимость предыдущее значение – 1 ) * 1 0 0 ROC = (\ frac {\ text {текущее значение}} {\ text {предыдущее значение}} – 1) * 100 ROC = (предыдущее значение, текущее значение -1) * 100
Важность измерения скорости изменений
Скорость изменения – чрезвычайно важная финансовая концепция, поскольку она позволяет инвесторам определять динамику безопасности и другие тенденции. Например, ценная бумага с высокой динамикой или положительная ROC обычно в краткосрочной перспективе превосходит рынок.И наоборот, ценная бумага с ROC, ниже ее скользящей средней, или с низкой или отрицательной ROC, скорее всего, снизится в цене и может рассматриваться как сигнал к продаже для инвесторов.
Скорость изменения также является хорошим индикатором рыночных пузырей. Даже несмотря на то, что импульс хороший и трейдеры ищут ценные бумаги с положительной ROC, если у широкого рынка ETF, индекса или паевого инвестиционного фонда наблюдается резкое увеличение ROC в краткосрочной перспективе, это может быть признаком неустойчивости рынка. Если ROC индекса или другой ценной бумаги широкого рынка превышает 50%, инвесторы должны опасаться пузыря.
Скорость изменения и ее связь с ценой
Скорость изменения чаще всего используется для измерения изменения цены ценной бумаги с течением времени. Это также известно как скорость изменения цен (ROC). Скорость изменения цены можно получить, взяв цену ценной бумаги в момент B за вычетом цены той же ценной бумаги в момент A и разделив полученный результат на цену в момент A.
Цена ROC знак равно B – А А × 1 0 0 куда: B знак равно цена на текущий момент А знак равно цена в предыдущий раз \ begin {align} & \ text {Price ROC} = \ frac {B – A} {A} \ times 100 \\ & \ textbf {где:} \\ & B = \ text {цена в текущее время} \\ & A = \ text {цена в предыдущий раз} \\ \ end {выровнена} Цена ROC = AB − A × 100, где: B = цена в текущий момент A = цена в предыдущий момент
Это важно, потому что многие трейдеры обращают пристальное внимание на скорость, с которой одна цена изменяется относительно другой.Например, трейдеры опционов изучают взаимосвязь между скоростью изменения цены опциона и небольшим изменением цены базового актива, известное как дельта опционов.
Формула скорости изменения – Что такое формула скорости изменения? Примеры
Функция скорости изменения определяется как скорость, с которой одно количество изменяется по отношению к другому количеству. Проще говоря, в скорости изменения количество изменений в одном элементе делится на соответствующее количество изменений в другом.Давайте узнаем о формуле скорости изменения на нескольких примерах в конце.
Формула скорости изменения дает соотношение, описывающее, как одна величина изменяется по отношению к изменению другой величины. Скорость изменения координат y в координаты x можно определить как Δy / Δx = (y ₂ – y ₁) / (x ₂ – x ₁). Для линейной функции скорость изменения m представлена в форме пересечения наклона для линии: y = mx + b, тогда как скорость изменения функций иначе определяется как, (f (b) -f (a)) / ba
Скорость изменения говорит нам, как что-то меняется с течением времени.
Давайте посмотрим на несколько решенных примеров, чтобы лучше понять формулу скорости изменения.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Примеры использования формулы скорости изменения
Пример 1: Используя формулу скорости изменения, вычислите скорость изменения для следующей информации в таблице:
Время вождения (в часах) Пройденное расстояние (в милях)
2 40
4 180
Решение:
Найти: Скорость изменения
Используя формулу скорости изменения,
Скорость изменения = (Изменение количества 1) / (Изменение количества 2)
Скорость изменения = (Изменение расстояния) / (Изменение во времени)
Скорость изменения = (180-40) / (4-2)
Скорость изменения = (140) / (2)
Скорость изменения = 70
Ответ: Скорость изменения составляет 70 или скорость изменения расстояния со временем составляет 70 миль в час.
Пример 2: Рассчитайте скорость изменения для следующей информации в таблице:
Время (в днях) Высота дерева (в дюймах)
50 4
140 7
Решение:
Найти: Скорость изменения.
Использование формулы скорости изменения,
Скорость изменения = (Изменение количества 1) / (Изменение количества 2)
Скорость изменения = (Изменение высоты дерева) / (Изменение в днях)
Скорость изменения = (7-4) / (140-50)
Скорость изменения = (3) / (90)
Скорость изменения = 1/30 = 0,033 ..
Ответ: Скорость изменения 0,033 или скорость изменения высоты дерева со временем в днях 0,033 дюйма в день.
Пример 3: Найдите скорость изменения ситуации: Рон выполнил 3 задания по математике за один час, а Дюк выполнил 6 заданий за два часа.
Решение:
Найти: Скорость изменения.
Использование формулы скорости изменения,
Скорость изменения = (Изменение количества 1) / (Изменение количества 2)
Скорость изменения = (Изменение выполненных заданий) / (Изменение в часах)
Скорость изменения = (6-3) / (2-1)
Скорость изменения = (3) / (1)
Скорость изменения = 3/1 = 3 задания / час
Ответ: Скорость изменения 3.0 или скорость изменения выполняемых заданий со временем в часах составляет 3 задания в час.
Часто задаваемые вопросы по формуле скорости изменений
Какова формула скорости изменения математики?
Формула скорости изменения используется для расчета скорости, которая описывает, как одно количество изменяется по отношению к изменению в другом количестве. Таким образом, формула скорости изменения: ROC = (Изменение количества 1) / (Изменение количества 2)
.
Какова формула средней скорости изменения?
Средняя скорость – это общее изменение, деленное на время, необходимое для того, чтобы это изменение произошло.Способ ее расчета аналогичен расчету средней скорости объекта. Например, средняя скорость изменения численности населения области может быть рассчитана только с учетом времени и численности населения в начале и в конце периода.
Как использовать формулу скорости изменения для графиков?
Скорость изменения может быть изображена и рассчитана по формуле скорости изменения, то есть \ (\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} \), обычно известная как формула наклона.
Что такое формула мгновенной скорости изменения?
Мгновенная скорость изменения определяется как изменение скорости в определенный момент.Это можно рассматривать как изменение значения производной в определенной точке. Для графика мгновенная скорость изменения в определенной точке совпадает с наклоном касательной линии.
Скорость, дистанция, время, калькулятор
Использование калькулятора
Рассчитайте скорость, расстояние или время по формуле d = st, расстояние равно скорости, умноженной на время. Калькулятор скорости, расстояния и времени может решить неизвестные sdt значение для двух известных значений.
Время можно ввести или рассчитать в секундах (с), минутах (мин), часах (час) или часах и минутах и секундах (чч: мм: сс). Видеть ярлыки для форматов времени ниже.
Чтобы найти расстояние, используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время.
расстояние = скорость x время
Скорость и скорость аналогичны, поскольку они оба представляют собой некоторое расстояние в единицу времени, например мили в час или километры в час.Если ставка r совпадает со скоростью с , r = s = d / t. Вы можете использовать эквивалентную формулу d = rt, что означает, что расстояние равно скорости, умноженной на время.
расстояние = скорость x время
Чтобы найти скорость или коэффициент, используйте формулу для скорости s = d / t, что означает, что скорость равна расстоянию, разделенному на время.
скорость = расстояние / время
Чтобы найти время, используйте формулу для времени, t = d / s, что означает, что время равно расстоянию, разделенному на скорость.
время = расстояние / скорость
Форматы ввода времени чч: мм: сс
В качестве разделителей можно использовать тире (-), точку (.) Или двоеточие (:), при этом всегда необходимо использовать 2 разделителя. Например, 15-06-22, 15.06.22 и 15:06:22 интерпретируются как 15 часов 6 минут 22 секунды или 15:06:22.
Разрешенные ограничения на вход:
часы 0 до 999
минут 0 до 59
секунд от 0 до 59
Ярлыки формата времени
Х..
5 ..
5 часов: 0 минут: 0 секунд
05:00:00
X.Y.
5.22.
5 часов: 22 минут: 0 секунд
05:22:00
X.Y.Z
5.22.10
5.01.15
5.3.6
5 часов: 22 минут: 10 секунд
5 часов: 1 минута: 15 секунд
5 часов: 3 минут: 6 секунд
05:22:10
05:01:15
05:03:06
.Y.
.22.
22 минуты
00:22:00
.Y.Z
. 22,15
22 минуты: 15 секунд
00:22:15
..Z
..5
5 секунд
00:00:05
X..Z
5..05
5 часов: 0 минут: 5 секунд
05:00:05
Связанные калькуляторы
Для физических расчетов со скоростью, смещением и скоростью используйте наш Калькулятор смещения для решения смещения с , средняя скорость v или время t .
.

Годы с 1800 года	Население (в миллионах)
1	0.8795
11	1,040
21	1,264
31	1,516
41	1,661
51	2.000
61	2,634
71	3,272
81	3,911
91	4,422