Матрицы и операции над ними
Далее будем рассматривать квадратные матрицы и (квадратные таблицы чисел с двумя строками и тремя столбцами и тремя строками и тремя столбцами). Все, что будет говориться, справедливо и для квадратных матриц порядка .
Определение. Две матрицы называются равными, если у них совпадают элементы, стоящие на одинаковых местах.
Определим сумму двух матриц. Пусть
Тогда суммой матриц и называется матрица
произведением матрицы на вещественное число — матрица
произведением строки на столбец — число
произведением матриц и — матрица
Здесь — -я строка матрицы , — -ый столбец матрицы .
Свойства операций над матрицами
1. .
2. .
3. Матрица , состоящая из нулей, играет роль нуля: для любой .
4. Противоположная матрица для матрицы — матрица : .
5. .
6. .
7. .
8. .
Умножение матриц не коммутативно!
Свойства умножения матриц
1. .
2. .
3. .
4. .
Определение. Единичной матрицей называется матрица, у которой элементы главной диагонали равны 1, а все остальные элементы — нули:
Очевидно, что .
Задачи.
1. Перемножьте матрицы
3. Докажите, что ранг произведения нескольких матриц не более ранга каждой из перемножаемых матриц.
4. Докажите, что если и — квадратные матрицы одного и того же порядка, причем , то
1) ;
2) .
Математика.
 Матрицы – презентация онлайн
Матрицы – презентация онлайн1. Математика
Матрицы.2. Виды матриц.
Матрицей называется упорядоченнаятаблица чисел, состоящая из m строк и n
столбцов.
Число строк и столбцов (m n) называется
размером матрицы.
аij называется элементом матрицы, где iномер строки, j-номер столбца матрицы.
3. Матрицы. Виды матриц.
4. Матрицы. Виды матриц.
Матрица называется квадратной, если вней число строк равно числу столбцов.
числу столбцов, то такая матрица называется
прямоугольной.
5. Матрицы. Виды матриц.
Матрица, элементы которой составляютстроку, называется матрица строка.
Матрица, элементы которой составляют
столбец, называется матрица столбец.
6. Матрицы. Виды матриц.
Главная диагональ квадратной матрицы- этодиагональ, которая начинается с элемента а11.
Квадратная матрица, у которой на главной
диагонали единицы, а все остальные элементы
равны нулю, называется единичной матрицей.

Матрица, у которой все элементы равны нулю,
7. Матрицы. Виды матриц.
Матрица, в которой строки и столбцызаменены местами, называется
транспонированной матрицей Ат.
8. Действия над матрицами
1. Равенство матриц.Две матрицы называются равными, если
они одного размера и равны их
соответствующие элементы.
9. Действия над матрицами
2. Сложение матриц.При сложении матриц (одного размера)
складываются их соответствующие
элементы.
10. Умножение матрицы на число.
При умножение матрицы на число, каждыйэлемент матрицы умножается на это число.
11. Умножение матриц.
1) Квадратные матрицы (одного размера)12. Умножение матриц.
2) Прямоугольные матрицы.Прямоугольные матрицы можно
перемножать тогда, когда число столбцов
первой матрицы равно числу строк
новая матрица, в которой столько строк,
сколько строк в первой и столько столбцов,
сколько столбцов во второй.

gaz.wiki – gaz.wiki
- Main page
Languages
- Deutsch
- Français
- Nederlands
- Русский
- Italiano
- Polski
- Português
- Norsk
- Suomen kieli
- Magyar
- Čeština
- Türkçe
- Dansk
- Română
- Svenska
| Главная > Учебные материалы > Математика: Матрицы | ||||
 Матрицы. Матрицы.2.Виды матриц. 3.Операции над матрицами.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1. Матрицы.Раздел математики, занимающийся изучением матриц, называется матричной алгеброй. Так как многие экономические явления и процессы можно записать в простой табличной форме, то данный раздел математики имеет важное значение в экономике. |
||||
Матрица представляет собой прямоугольную таблицу чисел размера m x n , содержащую m строк и n столбцов. Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. aij =bij для любых i = 1,2,3, …, m, j = 1,2,3, … n. |
||||
2.Виды матриц.Матрица, состоящая из одной строки, называется матрицей строкой. Матрица, состоящая из одного столбца – матрицей столбцом. Если число строк матрицы равно числу столбцов и равно n, то такая матрица называется квадратной n –го порядка, Элементы матрицы aij, у которой номер столбца равен номеру строки (i=j) , называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Матрица, у которой все элементы равны нулю, называется нулевой. |
||||
3.Операции над матрицами.Над матрицами можно производить следующие операции. |
||||
1.Умножение матрицы на число. Произведением матрицы А на число ƛ называется матрица В = ƛА, элементы которой bij = ƛ aij для i= 1,2,3, … m; j = 1,2,3, … n. 2.Сложение матриц. Если матрицы А и В имеют одинаковый размер m x n, то суммой двух матриц называется матрица С = А + В, элементы которой сij = aij + bij для i= 1,2,3, … m; j = 1,2,3, … n. 3.Вычитание матриц. Разность двух матриц одинакового размера определяется через сложение матриц: А-В = А+ (-1)*В. 4.Умножение матриц. Произведение матрицы А на матрицу В существует, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц А и В называется такая матрица С, каждый элемент которой cij равен сумме произведений элементов i – й строки матрицы А на соответствующие элементы j – го столбца матрицы В: |
||||
| Примеры: |
||||
| 1 2 3 4 5 6 7 8 9 | ||||
Математика для глубокого обучения: матрицы, сложение матриц и умножение матриц | Мишель Рекша | Phi Skills
Как вы можете видеть на изображении выше, есть один столбец для каждого игрока и строка для каждого хода.
Матрица заполняется значениями, представляющими счет конкретного игрока в конкретный ход. Например, на третьем повороте у Даниэля было 4 очка.
Согласно Википедии:
«Матрица представляет собой прямоугольный массив чисел или других математических объектов, для которых определены такие операции, как сложение и умножение».
Это определение матрицы тяготеет к трем концепциям:
- Измерение : фиксированное количество столбцов и фиксированное количество строк.
- Значения : значения, содержащиеся в матрице, должны быть согласованными. Если одни записи содержат информацию об апельсинах, а другие – о никотине, ваша матрица бесполезна.
- Операции: набор инструментов для математических операций, таких как сложение и умножение.
Как и все в Mathematics , , матрица – это идея, переведенная в определение и представленная в нотации .
Последнее очень просто, мы просто заключаем числа в квадратные скобки или круглые скобки:
Если вы не привыкли к Mathematics обозначениям , изображение выше может показаться устрашающим для Первый взгляд. Давайте разберемся вместе.
Символы с зеленым и красным подчеркиванием представляют элементы матрицы:
Значение, найденное в первой строке и втором столбцеЭто обозначение очень удобно, когда мы манипулируем огромными матрицами или когда мы хотим остаться общими и выразить что-то для каждой матрицы с m строк и n столбцов.В этом случае мы бы сказали, что матрица имеет размерность (m, n).
Следующая матрица представляет табло, которое мы видели в предыдущем разделе:
Матричное представление табло выше Если бы к игре присоединился другой игрок, нам пришлось бы добавить столбец для этого игрока на табло. То же самое произойдет с матрицей : нам потребуется 5 столбцов для представления всей игры.
То же самое произойдет с матрицей : нам потребуется 5 столбцов для представления всей игры.
Сложение матриц
Чтобы сложить две матрицы вместе, вам необходимо выполнить обычное добавление ввода за вводом, как показано на изображении ниже.
Вы могли заметить, что мы добавляем две матрицы с одинаковыми размерами. Это очень важно для матриц. В Mathematics добавление (или любая другая операция) определяется добавляемыми вами значениями. Вы можете думать об этом как о слове «медведь». В Finance , когда кто-то говорит «медведь», это обычно относится к падению фондового рынка, тогда как в лесу это обычно означает, что кто-то заметил медведя, и вам лучше убираться оттуда как можно быстрее.Здесь нам нужно помнить, что значение математической операции зависит от ее контекста .
Давайте посмотрим на простой пример, чтобы убедиться, что все мы находимся на одной странице.
Предположим, что мы хотим определить сложение для смайликов. Совершенно очевидно, что вы не можете использовать добавление , которое вы изучаете в школе, но вы всегда можете создать для него правило.
Например, мы могли бы сказать следующее:
😃 + 🙁 = 😐
Здесь наше сложение представляет собой среднюю эмоцию.Т.е. счастливое лицо с грустным лицом дает нейтральное лицо. Но вместо этого мы могли бы быть заинтересованы в подсчете количества лиц.
😃 + 🙁 = 2
Здесь добавление двух граней эквивалентно подсчету количества граней. Как видите, это совсем другое дело.
Если вам это интересно, я приглашаю вас проверить работы Джузеппе Пеано по аксиоматизации.
В итоге, сложение матриц представляет собой двухэтапный процесс:
- Убедитесь, что размеры соответствуют i.е. что обе матрицы имеют размерность (m, n)
- Просуммируйте все элементы в соответствии с их положением в матрице
Что происходит при умножении?
Умножение матриц
Умножение матриц – более сложная операция. Вы могли ожидать, что это работает как дополнение, но это не так.
Вы могли ожидать, что это работает как дополнение, но это не так.
Если вы когда-либо учились в средней школе Математика , вы, возможно, помните, как раньше решали уравнения с более чем одной переменной, например:
Чтобы решить эту проблему, вы можете сначала изолировать переменную, а затем заменить ее другой. уравнения, а затем повторите процесс.
Оказывается, математики очень умны, и они поняли, что мы можем определить Матричное умножение таким образом, чтобы автоматизировать метод решения вышеуказанной системы уравнений.
Умножение матриц Правила гарантируют, что следующее уравнение эквивалентно системе уравнений выше:
Как вы можете заметить, мы умножаем матрицу на вектор неизвестных переменных x , y и z . Матрицы можно рассматривать как словари , которые позволяют переводить один язык на другой. В нашем примере это означает, что мы переводим неизвестные переменные, чтобы получить правую часть уравнения. Столбцы матрицы представляют язык для перевода, а строки представляют язык, на который нужно перевести.
В нашем примере это означает, что мы переводим неизвестные переменные, чтобы получить правую часть уравнения. Столбцы матрицы представляют язык для перевода, а строки представляют язык, на который нужно перевести.
Следовательно, матрица умножение не является коммутативным : вы не можете изменить порядок множителей и ожидать в конечном итоге того же результата.Это означает, что обычно не может сказать, что a * b = b * a. Вы не можете этого сделать, потому что слева вы переводите с английского на китайский, а справа – с китайского на английский. Я почти уверен, что английский и китайский – это не одно и то же.
Теперь, когда у вас есть интуиция, я дам вам рецепт умножения матриц. Предположим, что A и B – это две матрицы с размерами соответственно (ma, na) и (mb, nb) и что вы вычисляете A * B.
- Вы можете выполнить матричное умножение на тогда и только тогда, когда na = mb . Другими словами, вы можете выполнять только в том случае, если количество столбцов левой матрицы равно количеству строк правой матрицы.
- Результатом умножения является матрица с размерами (ma, nb) .
- Каждая запись новой матрицы будет суммой произведения соответствующей строки в столбце A и столбца в B.
Эти соображения могут показаться вам непонятными, но после небольшого примера все станет яснее.
Допустим, мы перемножаем следующие матрицы:
Матрица слева имеет размерность (3, 2) : три строки и два столбца.
Матрица справа имеет размерность (2,1) : две строки и один столбец.
Следовательно, количество столбцов первой матрицы равно количеству строк, и мы можем выполнить умножение.
Теперь самый простой способ вычислить умножение – это следующий (используйте ручку и бумагу):
Зеленые и коричневые пунктирные линии показывают вам, какое число вам нужно умножить на каждом этапе процесса. Затем вы повторяете это для каждой строки в левой матрице:
Наконец, мы получаем желаемый результат:
Этот пример был очень простым, но что происходит, когда правая матрица имеет более одного столбца?
Как видите, мы повторяем один и тот же процесс для каждой строки левой матрицы и каждого столбца правой.
В итоге мы получаем следующее:
Заключение
В этой статье мы дали неформальное введение в матрицы и их две наиболее важные операции. Я изо всех сил старался написать статью, не предполагающую никаких математических знаний.
За несколько минут вы узнали:
- Что такое матрица
- Выполните сложение матриц
- Выполните умножение матрицы
Всего несколько минут, чтобы выучить самую важную математическую концепцию чтобы понять, как работают нейронные сети .
Матрицы могут использоваться для распараллеливания вычислений. Помните умножение матриц выше. Вычисляемые нами шаги независимы, что означает, что результаты могут вычислять разные люди или компьютеры одновременно. Если матрица мала, как та, которую мы видели, преимущества невелики, но в нейронной сети вы можете обнаружить, что обрабатываете матрицы с миллионами строк. Предположим, что каждое вычисление занимает одну секунду. Последовательное вычисление миллиона вычислений заняло бы один миллион секунд, что составляет около 260 часов или 11 дней.Вместо этого, если бы мы вычисляли их параллельно, это все равно заняло бы 1 секунду. Бьюсь об заклад, каждый выберет второе.
Линейная алгебра – это удивительная область изучения, которую можно найти практически в любой отрасли. Вы можете использовать их, чтобы связать рейтинги фильмов с пользователями, если вы работаете в Netflix, или вы можете использовать их в Physics и Finance . Любой компьютерный ученый видел их в какой-то момент своей жизни. Вы даже можете использовать их как табло, играя в карты с друзьями!
Любой компьютерный ученый видел их в какой-то момент своей жизни. Вы даже можете использовать их как табло, играя в карты с друзьями!
Всем, кто хочет узнать больше, я настоятельно рекомендую книгу Робера Мессера « Linear Algebra: Gateway to Mathematics ».
Ciao,
Michele
Матричная теория | Математика
Информация о промежуточных / заключительных экзаменах:
Дневное занятие
мая 11: 8-10 утра
Утренний урок
мая 13: 10:30 – 12: 30
Обзор
Образец финала
Описание курса
Основные свойства матриц, определителей, векторных пространств, линейные преобразования, собственные значения, собственные векторы и нормальные формы Жордана.Введение в написание доказательств.
Предварительные требования
Программа обучения
Учебник
Линейная алгебра с приложениями (7-е издание) Стивена Дж. Леона
Леона
Покрытые секции
- 1.1: Системы линейных уравнений
- 1.2: Форма эшелона строк
- 1.3: Матричная алгебра
- 1.4: Элементарные матрицы
- 1.5: многораздельные матрицы (необязательно)
- 2.1. Определитель матрицы
- 2.2: Свойства детерминантов
- 2.3: Правило Крамера
- 3.1: Определение и примеры
- 3.2: Подпространства
- 3.3: Линейная независимость
- 3.4: Основание и размер
- 3.5: Изменение базы
- 3.6: пространство строк и столбцов
- 4.1: Определение и примеры
- 4.2: Матричные представления линейных преобразований
- 4.3: Сходство
- 5.1: Скалярное произведение в Rn
- 5.2: Ортогональные подпространства
- 5.3: Задачи наименьших квадратов (необязательно)
- 5.4: Внутренние пространства продукта
- 5.5: ортонормальные наборы
- 5.6: Процесс ортогонализации по Граму-Шмидту
- 6.
 1: Собственные значения и собственные векторы
1: Собственные значения и собственные векторы - 6.4: Эрмитовы матрицы
Примечания к главе
Примечания к главам III и IV
Примечания к главе V
Примечания к главе VI
Предлагаемые задачи и задания
Сроки переуступки
| Домашнее задание | Срок оплаты |
| 1 | 01.01.15 |
| 2 | 01.01.15 |
| 3 | 01.01.15 |
| 4 | 01.01.15 |
| 5 | 01.01.15 |
| 6 | 01.01.15 |
| 7 | 01.01.15 |
Матрица | Math Wiki | Fandom
Матрица – это таблица (или массив) объектов, таких как количества, упорядоченная по строкам и столбцам.
Можно представить запись в матрице как то, где субиндекс проходит по строкам и ходит по колоннам. Например, запись в строке 3 и столбце 4.
Вот пример матрицы (матрицы с целыми элементами):
Матрицы могут быть сформированы с другими типами объектов.
Вот пример использования полиномов для записей.
Это -матрица, использующая многочлены одной переменной.
Матрицы также могут использоваться для моделирования переводов из.
Содержание
- 1 Формальное определение
- 2 Матричные операции
- 2.1 Сложение и вычитание матрицы
- 2.2 Умножение обыкновенных матриц
- 2.3 Умножение скалярных матриц
- 2.3.1 Разное
Формальное определение
- Пусть.
- Позвольте быть набор.
- Тогда матрица является отображением.
Операции с матрицами
Сложение и вычитание матриц
Сложение и вычитание матриц можно выполнять только для матриц одинаковой размерности. Соответствующие записи добавляются (или вычитаются).
Соответствующие записи добавляются (или вычитаются).
Умножение обыкновенных матриц
Обычное матричное произведение – наиболее часто используемый и самый важный способ умножения матриц. Он определяется между двумя матрицами, только если ширина первой матрицы равна высоте второй матрицы, и интерпретируется как применение преобразования первой матрицы ко второй.Умножение матрицы на матрицу приводит к матрице. Обычное матричное произведение ассоциативно, но не коммутативно.
Каждая запись в матрице произведения является скалярным произведением в связанной строке первой матрицы и связанном столбце второй матрицы.
Умножение скалярных матриц
Скалярное матричное произведение является результатом умножения матрицы на скаляр. Это влечет за собой не что иное, как умножение каждой записи в матрице на значение скаляра.Например, если быть скаляром и матрицей,
Разное
Чтобы удалить последнюю строку матрицы, умножьте ее на единичную матрицу, дополненную матрицей 0.
Если, то
[PDF] Матричная математика: теория, факты и формулы в применении к теории линейных систем
Матричная алгебра с использованием MINimal MATlab
Сила этого учебника заключается в тщательном изложении математического мышления, основных теоретико-множественных понятий и доказательств методы в сочетании с современными численными методами используются повсюду… Развернуть
- Посмотреть 3 выдержки, справочная информация
Теория матриц: основные результаты и методы
Предисловие ко второму изданию.- Предисловие. – Часто используемые обозначения и термины. – Часто используемые термины. – 1 Обзор элементарной линейной алгебры. – 2 разделенные матрицы, ранги и собственные значения. – 3… развернуть
Матричные алгоритмы, Том II: собственные системы
Эта книга второй том в прогнозируемом пятитомном обзоре числовой линейной алгебры и матричных алгоритмов. В этом томе рассматривается численное решение плотных и крупномасштабных собственных значений… Развернуть
- Просмотреть 1 отрывок, справочная информация
Неравенство трассировки для унитарных матриц
1. Б. Бозами, Введение в банаховы пространства и их геометрию, Северная Голландия, 1985. 2. С. Чанг, К. К. Ли, Некоторые изометрии на Rt, Линейная алгебра и ее приложения, 165 (1992) 251-265. 3.… Expand
Б. Бозами, Введение в банаховы пространства и их геометрию, Северная Голландия, 1985. 2. С. Чанг, К. К. Ли, Некоторые изометрии на Rt, Линейная алгебра и ее приложения, 165 (1992) 251-265. 3.… Expand
Матрицы: теория и приложения
Предисловие ко второму изданию. – Предисловие к первому изданию. – Список символов. – 1 Элементарная линейная и полилинейная алгебра. – 2 Что такое матрицы. – 3 квадратные матрицы. – 4 Тензор и внешний вид… Развернуть
Алгебраические уравнения Риккати
1.Предварительные сведения из теории матриц 2. Неопределенные скалярные произведения 3. Кососимметричные скалярные произведения 4. Теория матриц и управление 5. Линейные матричные уравнения 6. Рациональные матричные функции 7.… Развернуть
- Посмотреть 2 выдержки, ссылки, методы и справочную информацию
Прикладная линейная алгебра
1. Матричная алгебра. 2. Некоторые простые приложения и вопросы. 3. Решение уравнений и поиск обратных: методы. 4. Решение уравнений и поиск обратных: Теория. 5. Векторы и векторные пространства.6.… Expand
5. Векторы и векторные пространства.6.… Expand
Frontiers | Разложения CUR, матрицы подобия и кластеризация подпространств
1. Введение
Мы представляем здесь две сказки: одну о так называемой декомпозиции CUR (или иногда каркасной декомпозиции), а другую о проблеме кластеризации подпространств. Оказывается, существует сильная связь между этими двумя предметами в том, что разложение CUR обеспечивает общую основу для методов матрицы сходства, используемых для решения проблемы кластеризации подпространств, а также дает естественную связь между этими методами и другими проблемами минимизации, связанными с подпространственная кластеризация.
Разложение CUR примечательно своей простотой и красотой: заданную матрицу A можно разложить на произведение трех матриц, A = CU † R , где C – подмножество столбцов A , R – это подмножество строк A , а U – их пересечение (точное утверждение см. в теореме 1). На сегодняшний день разложение CUR в основном используется в области научных вычислений.В частности, он использовался в качестве метода аппроксимации низкого ранга, который более точен для структуры данных, чем другие факторизации [1, 2], приближения к разложению по сингулярным значениям [3–5], а также предоставил эффективные алгоритмы для вычисления и хранения массивных матриц в памяти. В дальнейшем будет показано, что это разложение является источником некоторых хорошо известных методов для решения проблемы кластеризации подпространств, а также добавляет построение множества матриц подобия на основе данных.
в теореме 1). На сегодняшний день разложение CUR в основном используется в области научных вычислений.В частности, он использовался в качестве метода аппроксимации низкого ранга, который более точен для структуры данных, чем другие факторизации [1, 2], приближения к разложению по сингулярным значениям [3–5], а также предоставил эффективные алгоритмы для вычисления и хранения массивных матриц в памяти. В дальнейшем будет показано, что это разложение является источником некоторых хорошо известных методов для решения проблемы кластеризации подпространств, а также добавляет построение множества матриц подобия на основе данных.
Проблема кластеризации подпространств может быть сформулирована следующим образом: предположим, что некоторые собранные векторы данных в 𝕂 m (при m больших, а 𝕂 либо, либо ℂ) происходят из объединения линейных подпространств (обычно низкоразмерный) 𝕂 м , который будет обозначен как U = ⋃Mi = 1Si. Однако никто не знает априори , что такое подпространства и даже сколько их существует. Следовательно, кто-то желает определить количество подпространств, представленных данными, размерность каждого подпространства, основу для каждого подпространства и, наконец, сгруппировать данные: данные {wj} j = 1n⊂U не упорядочены ни в каком конкретном Таким образом, кластеризация данных означает определение того, какие данные принадлежат одному и тому же подпространству.
Однако никто не знает априори , что такое подпространства и даже сколько их существует. Следовательно, кто-то желает определить количество подпространств, представленных данными, размерность каждого подпространства, основу для каждого подпространства и, наконец, сгруппировать данные: данные {wj} j = 1n⊂U не упорядочены ни в каком конкретном Таким образом, кластеризация данных означает определение того, какие данные принадлежат одному и тому же подпространству.
Действительно, существуют физические системы, которые вписываются в только что описанную модель. Два конкретных примера – отслеживание движения и распознавание лиц. Например, база данных лиц Йельского университета B [6] содержит изображения лиц, каждое из которых получено с 64 различными схемами освещения. Для конкретного объекта i имеется 64 изображения его лица, освещенных по-разному, и каждое изображение представляет собой вектор, лежащий приблизительно в линейном подпространстве низкой размерности, S i пространства более высокой размерности ℝ 307, 200 (в зависимости от размера изображений в градациях серого). Экспериментально показано, что изображения данного предмета приблизительно лежат в подпространстве S i размерности 9 [7]. Следовательно, матрица данных, полученная из изображений лиц при разном освещении, имеет столбцы, которые лежат в объединении низкоразмерных подпространств, и может потребоваться алгоритм, который может сортировать или кластеризовать данные, таким образом распознавая, какие лица являются одинаковыми.
Экспериментально показано, что изображения данного предмета приблизительно лежат в подпространстве S i размерности 9 [7]. Следовательно, матрица данных, полученная из изображений лиц при разном освещении, имеет столбцы, которые лежат в объединении низкоразмерных подпространств, и может потребоваться алгоритм, который может сортировать или кластеризовать данные, таким образом распознавая, какие лица являются одинаковыми.
Существует множество способов атаки на проблему кластеризации подпространств, включая итерационные и статистические методы [8–15], алгебраические методы [16–18], методы разреженности [19–22], методы задачи минимизации, вдохновленные сжатым зондированием [22, 23] и методы, основанные на спектральной кластеризации [20, 21, 24–29].Для получения подробного, хотя и неполного обзора проблемы спектральной кластеризации читателю предлагается обратиться к [30].
Некоторые из упомянутых выше методов начинаются с нахождения матрицы сходства для данного набора данных, то есть квадратной матрицы, элементы которой отличны от нуля именно тогда, когда соответствующие векторы данных лежат в одном подпространстве, S i , оператора U (точное определение см. в определении 3). Настоящая статья посвящена определенному методу факторизации матриц – разложению CUR – который обеспечивает довольно общую основу для поиска матрицы подобия для данных, которая соответствует модели подпространства, описанной выше.Будет продемонстрировано, что разложение CUR действительно создает множество матриц подобия для данных подпространства. Более того, это разложение обеспечивает мост между методами матричной факторизации и методами задачи минимизации, такими как представление низкого ранга [22, 23].
в определении 3). Настоящая статья посвящена определенному методу факторизации матриц – разложению CUR – который обеспечивает довольно общую основу для поиска матрицы подобия для данных, которая соответствует модели подпространства, описанной выше.Будет продемонстрировано, что разложение CUR действительно создает множество матриц подобия для данных подпространства. Более того, это разложение обеспечивает мост между методами матричной факторизации и методами задачи минимизации, такими как представление низкого ранга [22, 23].
1.1. Бумажные вклады
• В этой работе мы показываем, что разложение CUR приводит к появлению матриц подобия для кластеризации данных, которые поступают из объединения независимых подпространств. В частности, учитывая матрицу данных W = [w1 ⋯ wn] ⊂𝕂m, полученную из объединения U = ⋃i = 1MSi независимых подпространств {Si} i = 1M размеров {di} i = 1M, любое разложение CUR W = CU † R можно использовать для построения матрицы сходства для W . В частности, если Y = U † R и Q является поэлементной двоичной или абсолютной версией Y * Y , то ΞW = Qdmax является матрицей подобия для W ; т.е. Ξ W ( i, j ) ≠ 0, если столбцы w i и w j из W происходят из того же подпространства, и Ξ W ( i, j ) = 0, если столбцы w i и w j из W происходят из разных подпространств.
В частности, если Y = U † R и Q является поэлементной двоичной или абсолютной версией Y * Y , то ΞW = Qdmax является матрицей подобия для W ; т.е. Ξ W ( i, j ) ≠ 0, если столбцы w i и w j из W происходят из того же подпространства, и Ξ W ( i, j ) = 0, если столбцы w i и w j из W происходят из разных подпространств.
• Эта статья расширяет нашу предыдущую структуру для поиска матриц подобия для кластеризации данных, которые поступают из объединения независимых подпространств. В Aldroubi et al. [31], мы показали, что любая факторизация W = BP , где столбцы B происходят из U и образуют основу для пространства столбцов W , может быть использована для создания матрицы подобия Ξ Вт . Эта работа показывает, что нам не нужно ограничивать факторизацию W базами, но можно расширить ее до фреймов, что обеспечит большую гибкость.
Эта работа показывает, что нам не нужно ограничивать факторизацию W базами, но можно расширить ее до фреймов, что обеспечит большую гибкость.
• Начиная с структуры декомпозиции CUR, мы демонстрируем, что некоторые хорошо известные методы, используемые в кластеризации подпространств, следуют как частные случаи или напрямую связаны с декомпозицией CUR; Эти методы включают в себя матрицу взаимодействия форм [32, 33] и представление низкого ранга [22, 23].
• Представлен прототип алгоритма, который изменяет конструкцию матрицы подобия, упомянутую выше, чтобы обеспечить кластеризацию зашумленных данных подпространства. Затем проводятся эксперименты на синтетических и реальных данных (в частности, на наборе данных движения Hopkins155) для обоснования предложенной теоретической основы.Показано, что использование среднего из нескольких разложений CUR для нахождения матриц сходства для матрицы данных W превосходит многие известные методы в литературе, будучи при этом быстрыми в вычислениях.
• Алгоритм кластеризации, основанный на методологии матрицы взаимодействия робастных форм Ji et al. [33] также рассматривается, и использование нашей структуры разложения CUR вместе с их алгоритмом дает лучшую производительность на сегодняшний день для кластеризации набора данных движения Hopkins155.
1.2. Планировка
Остальная часть статьи развивается следующим образом: за кратким разделом, посвященным предварительным сведениям, следует формулировка и обсуждение наиболее общего точного разложения CUR. Раздел 4 содержит формулировки основных результатов статьи, а раздел 5 содержит отношение к общей структуре, которую CUR дает для решения проблемы кластеризации подпространств. Доказательства основных теорем перечислены в разделе 6, а наш алгоритм и численные эксперименты – в разделе 7, после чего статья завершается обсуждением будущих работ.
2. Предварительные условия
2.1. Определения и основные факты
В дальнейшем 𝕂 будет относиться либо к действительному, либо к комплексному полю (ℝ или ℂ соответственно). Для A ∈ 𝕂 m × n его псевдообратная матрица Мура – Пенроуза является уникальной матрицей A † ∈ 𝕂 n 906 следующие условия:
Для A ∈ 𝕂 m × n его псевдообратная матрица Мура – Пенроуза является уникальной матрицей A † ∈ 𝕂 n 906 следующие условия:
1) AA † A = A ,
2) A † AA † = A † ,
3) ( A A † ) * = AA † и
4) ( A † A ) * = A † A .
Кроме того, если A = UΣV * является разложением по сингулярным значениям для A , то A † = VΣ † U *, где псевдообратное значение × м. n матрица Σ = diag (σ 1 ,…, σ r , 0,…, 0) – матрица n × m Σ † = diag (1 / σ1,…, 1 / σr, 0…, 0). По поводу этих и связанных с ними понятий см. Раздел 5 Голуба и Ван Лоана [34].
Раздел 5 Голуба и Ван Лоана [34].
Также полезно для нашего анализа то, что матрица ранга r имеет так называемый тонкий SVD формы A = UrΣrVr *, где U r содержит первые r левых сингулярных векторов. of A , V r содержит первые r правых сингулярных векторов, и Σr = diag (σ1,…, σr) ∈Kr × r.Обратите внимание, что в случае, когда ранг ( A )> – , тощий SVD – это просто приближение низкого ранга к A .
Определение 1 (Независимые подпространства). Нетривиальные подпространства {Si⊂Km} i = 1M называются независимыми, если их размерности удовлетворяют следующему соотношению:
dim (S1 + ⋯ + SM) = dim (S1) + ⋯ + dim (SM) ≤m. Приведенное выше определение эквивалентно свойству, что любой набор ненулевых векторов { w 1 , ⋯, w M } так, что w i ∈ S i , i = 1,…, M линейно независим.
Определение 2 (Общие данные). Пусть S будет линейным подпространством 𝕂 м с размером d . Набор данных W , полученный из S, называется общим, если (i) | W | > d, и (ii) каждые d векторов из W образуют основу для S .
Обратите внимание, что это определение эквивалентно теоретико-фреймовому описанию, согласно которому столбцы W являются фреймом для S с искрой d +1 (см. [35, 36]).Также иногда говорят, что данные W находятся в общей позиции .
Определение 3 (матрица подобия). Предположим, что W = [w1 ⋯ wn] ⊂Km имеет столбцы, взятые из объединения подпространств U = ⋃i = 1MSi. Мы говорим: Ξ W – это матрица подобия для W тогда и только тогда, когда (i) Ξ W симметрично, и (ii) Ξ
59 W (i, j) ≠ 0 тогда и только тогда, когда w i и w j происходят из одного и того же подпространства.
Наконец, если A ∈ 𝕂 m × n , мы определяем его версию абсолютного значения через abs ( A ) ( i, j ) = | A ( i, j ) | и его двоичная версия через bin ( A ) ( i, j ) = 1, если A ( i, j ) ≠ 0 и bin ( A ) ( i, j ) = 0, если A ( i, j ) = 0.
2.2. Предположения
Далее мы будем предполагать, что U = ⋃i = 1MSi – нелинейное множество, состоящее из объединения нетривиальных независимых линейных подпространств {Si} i = 1M из 𝕂 m , с соответствующие размеры {di} i = 1M, при dmax: = max1≤i≤Mdi.Мы будем предполагать, что матрица данных W = [w1 ⋯ wn] ∈𝕂m × n имеет векторы-столбцы, взятые из U, и что данные, взятые из каждого подпространства S i , являются общими для этого подпространства.
3. Разложение CUR
Наша первая история – это замечательное разложение матрицы CUR, также известное как разложение скелета [37, 38], доказательство которого может быть получено с помощью базовой линейной алгебры.
Теорема 1 . Предположим, что A ∈ 𝕂 m × n имеет ранг r.Пусть I⊂ {1,…, m}, J⊂ {1,…, n} с | I | = s и | J | = k, и пусть C – матрица размера m × k, столбцы которой являются столбцами матрицы A, проиндексированной J. Пусть R – матрица размера s × n, строки которой являются строками матрицы A, индексированной I. -матрица матрицы A, элементы которой индексируются I × J. Если ранг (U) = r, то A = д.е. † р.
. Доказательство . Поскольку U имеет ранг r , ранг ( C ) = r . Таким образом, столбцы C образуют фрейм для пространства столбцов A , и у нас есть A = CX для некоторой (не обязательно уникальной) k × n матрицы X .Пусть P I будет матрицей выбора строк s × m , так что R = P I A ; тогда у нас есть R = P I A = P I CX . Также обратите внимание, что U = P I C , так что последнее уравнение может быть записано как R = UX .Поскольку ранг ( R ) = r , любое решение для R = UX также является решением для A = CX . Таким образом, вывод теоремы следует из наблюдения, что Y = U † R является решением для R = UX . Действительно, тот же аргумент, что и выше, подразумевает, что U † R является решением для R = UX тогда и только тогда, когда это решение для RP J = U = UXP J , где P J – это матрица выбора столбцов n × k , которая выбирает столбцы в соответствии с набором индексов J .Таким образом, если отметить, что UU † RPJ = UU † U = U завершает доказательство, откуда A = CY = CU † R .
Также обратите внимание, что U = P I C , так что последнее уравнение может быть записано как R = UX .Поскольку ранг ( R ) = r , любое решение для R = UX также является решением для A = CX . Таким образом, вывод теоремы следует из наблюдения, что Y = U † R является решением для R = UX . Действительно, тот же аргумент, что и выше, подразумевает, что U † R является решением для R = UX тогда и только тогда, когда это решение для RP J = U = UXP J , где P J – это матрица выбора столбцов n × k , которая выбирает столбцы в соответствии с набором индексов J .Таким образом, если отметить, что UU † RPJ = UU † U = U завершает доказательство, откуда A = CY = CU † R . □
□
Обратите внимание, что предположение о ранге U подразумевает, что k, s ≥ r в приведенной выше теореме. Хотя эта теорема носит довольно общий характер, следует отметить, что в некоторых частных случаях она сводится к гораздо более простому разложению, что зафиксировано в следующих следствиях. Доказательство каждого следствия следует из того факта, что псевдообратная формула U † принимает эти конкретные формы всякий раз, когда столбцы или строки линейно независимы ([34, с.257], например).
Следствие 1 . Пусть A, C, U и R такие, как в теореме 1, с C ∈ K m × r ; в частности, столбцы C линейно независимы. Тогда A = C (U * U) −1 U * R .
Следствие 2 . Пусть A, C, U и R такие же, как в теореме 1, с R ∈ K r × n ; в частности, строки R линейно независимы. Тогда A = CU * (UU *) −1 R .
Следствие 3 . Пусть A, C, U и R такие же, как в теореме 1, с U ∈ K r × r ; в частности, U обратима.Тогда A = д.е. -1 R .
Пусть A, C, U и R такие же, как в теореме 1, с U ∈ K r × r ; в частности, U обратима.Тогда A = д.е. -1 R .
В большинстве источников разложение следствия 3 – это то, что называется скелетным или CUR-разложением [39], хотя случай, когда k = s > r , рассматривался в Caiafa и Cichocki [40]. Утверждение теоремы 1 является наиболее общим вариантом точного разложения CUR.
Точную историю разложения CUR довольно трудно различить. Многие статьи цитируют Гантмахера [41], хотя авторам не удалось найти в нем термин «разложение скелета».Однако разложение действительно появляется неявно (и без доказательства) в статье Пенроуза 1955 г. [42]. Однако, возможно, современной отправной точкой в этом разложении является работа Горейнова и др. [37, 39]. Они начинают с разложения CUR, как в следствии 3, и изучают ошибку || A-CU-1R || 2 в случае, когда A имеет ранг больше, чем r , в результате чего разложение CU −1 R является приблизительным. Кроме того, они обеспечивают большую гибкость в выборе U , поскольку вычисление обратного значения напрямую может быть трудным в вычислительном отношении (см. Также [43–45]).
Кроме того, они обеспечивают большую гибкость в выборе U , поскольку вычисление обратного значения напрямую может быть трудным в вычислительном отношении (см. Также [43–45]).
В последнее время возобновился интерес к этой декомпозиции. В частности, Drineas et al. [5] предоставляют два рандомизированных алгоритма, которые вычисляют приблизительную факторизацию CUR данной матрицы A . Кроме того, они обеспечивают границы ошибок на основе вероятностного метода выбора C и R из A . Следует также отметить, что их средняя матрица U не является U † , как в теореме 1. Более того, Махони и Дринес [1] дают другой алгоритм CUR, основанный на способе выбора столбцов, который обеспечивает почти оптимальные границы ошибок. для || A – CUR || F (в том смысле, что оптимальное приближение ранга r к любой матрице A в норме Фробениуса является его тощим SVD ранга r , и они получают границы ошибки в форме || A-CUR || F≤ (2 + ε) || A-UrΣrVrT || F). Они также отмечают, что разложение CUR должно быть предпочтительным при анализе реальных данных, которые имеют низкую размерность, потому что матрицы C и R поддерживают структуру данных, а разложение CUR фактически допускает жизнеспособную интерпретацию данных в отличие от попытка интерпретации сингулярных векторов матрицы данных, которые обычно представляют собой линейные комбинации данных (см. также [46]).
Они также отмечают, что разложение CUR должно быть предпочтительным при анализе реальных данных, которые имеют низкую размерность, потому что матрицы C и R поддерживают структуру данных, а разложение CUR фактически допускает жизнеспособную интерпретацию данных в отличие от попытка интерпретации сингулярных векторов матрицы данных, которые обычно представляют собой линейные комбинации данных (см. также [46]).
Впоследствии другие рассмотрели алгоритмы для вычисления разложений CUR, которые все еще обеспечивают приблизительно оптимальные границы ошибок в описанном выше смысле (см., Например, [2, 38, 47–49]).Для применения разложения CUR в различных аспектах анализа данных в научных дисциплинах обратитесь к [50–53]. Наконец, совсем недавно в статье обсуждается выпуклая релаксация декомпозиции CUR и ее связь с проблемой совместного обучения [54].
Следует отметить, что разложение CUR является одним из длинного ряда методов матричной факторизации, многие из которых имеют похожую форму. Основная идея состоит в том, чтобы записать A = BX для некоторых менее сложных или более структурированных матриц B и X .В случае, когда B состоит из столбцов A , это называется интерполяционным разложением , особым случаем которого является CUR. Альтернативные методы включают классические подозреваемые, такие как LU , QR и разложения по сингулярным числам. Для более подробного рассмотрения таких вопросов читателю предлагается ознакомиться с превосходным обзором [55]. В общем, факторизация матриц с низким рангом находит применение в широком спектре приложений, включая защиту авторских прав [56, 57], отображение [58] и завершение матриц [59], и это лишь некоторые из них.
Основная идея состоит в том, чтобы записать A = BX для некоторых менее сложных или более структурированных матриц B и X .В случае, когда B состоит из столбцов A , это называется интерполяционным разложением , особым случаем которого является CUR. Альтернативные методы включают классические подозреваемые, такие как LU , QR и разложения по сингулярным числам. Для более подробного рассмотрения таких вопросов читателю предлагается ознакомиться с превосходным обзором [55]. В общем, факторизация матриц с низким рангом находит применение в широком спектре приложений, включая защиту авторских прав [56, 57], отображение [58] и завершение матриц [59], и это лишь некоторые из них.
4. Кластеризация подпространств с помощью декомпозиции CUR
Наша вторая история – это одна из полезностей разложения CUR в структуре матрицы подобия для решения проблемы сегментации подпространства, описанной выше. Предыдущие работы, как правило, были сосредоточены на CUR как методе аппроксимации матриц низкого ранга, который имеет низкую стоимость и также остается более верным исходным данным, чем разложение по сингулярным значениям. Эта перспектива весьма полезна, но здесь мы демонстрируем то, что кажется первым приложением, в котором CUR отвечает за всеобъемлющую структуру, а именно за кластеризацию подпространств.
Эта перспектива весьма полезна, но здесь мы демонстрируем то, что кажется первым приложением, в котором CUR отвечает за всеобъемлющую структуру, а именно за кластеризацию подпространств.
Как упоминалось во введении, один из подходов к кластеризации данных подпространства состоит в том, чтобы найти матрицу подобия, из которой можно просто считывать кластеры, по крайней мере, когда данные точно соответствуют модели и считаются не имеющими шума. Следующая теорема предоставляет способ найти множество матриц подобия для данной матрицы данных W , все из которых происходят из различных разложений CUR (напомним, что матрица имеет очень много разложений CUR в зависимости от того, какие столбцы и строки выбраны).
Теорема 2 . Пусть W = [w1 ⋯ wn] ∈Km × n – матрица ранга r, столбцы которой взяты из U , которая удовлетворяет предположениям в разделе 2.2. Пусть W разложено на множители как W = CU † R, где C ∈ m × k , R ∈ 𝕂 s × n и U ∈ 𝕂 s × k имеют вид в теореме 1, и пусть Y = U † R и Q будет либо двоичной, либо абсолютной версией Y * Y. Тогда , ΞW = Qdmax – матрица подобия для W .
Тогда , ΞW = Qdmax – матрица подобия для W .
Ключевым ингредиентом доказательства теоремы 2 является тот факт, что матрица Y = U † R , которая генерирует матрицу подобия, имеет блочно-диагональную структуру из-за независимой структуры подпространства U; этот факт зафиксирован в следующей теореме.
Теорема 3 . Пусть W , C, U и R такие же, как в теореме 2. Если Y = U † R, то существует матрица перестановок P такая, что
YP = [Y10 ⋯ 00Y2 ⋯ 0 ⋮⋮ ⋱ ⋮ 0 ⋯ 0YM], , где каждый Y i представляет собой матрицу размера k i × n i , где n i – количество столбцов в W из подпространства S i и k i – это количество столбцов в C от S до .Более того, , W P имеет вид [ W 1 … W M ], где столбцы W i происходят из подпространства S i .
Доказательства вышеуказанных фактов будут приведены в следующем разделе.
Роль d max в теореме 2 заключается в том, что Q является почти матрицей подобия, но каждый кластер не может быть полностью связан.Повышая Q до степени d max , мы гарантируем, что каждый кластер полностью подключен.
В следующем разделе будет показано, что некоторые хорошо известные решения проблемы кластеризации подпространств являются следствием разложения CUR. А пока давайте сформулируем некоторые потенциальные преимущества, которые естественным образом вытекают из утверждения теоремы 2. Одно из преимуществ разложения CUR состоит в том, что можно построить множество матриц подобия для матрицы данных W , выбирая различные репрезентативные строки и столбцы. ; я.е. выбор разных матриц C или R даст разные, но действительные матрицы подобия. Возможное преимущество этого заключается в том, что для больших матриц можно уменьшить вычислительную нагрузку, выбрав сравнительно небольшое количество строк и столбцов. Часто при получении реальных данных многие записи могут отсутствовать или сильно повреждены. Например, при отслеживании движения некоторые функции могут быть скрыты из поля зрения на несколько кадров. Следовательно, может потребоваться некоторая форма завершения матрицы.С другой стороны, взгляд на разложение CUR показывает, что целые строки матрицы данных могут отсутствовать, если мы все еще можем выбрать достаточно строк, чтобы результирующая матрица R имела тот же ранг, что и W . В реальных ситуациях, когда матрица данных зашумлена, тогда нет точного разложения CUR для W ; однако, если ранг чистых данных W хорошо оценен, то можно вычислить несколько приближений CUR для W , т.е.е. если чистые данные должны иметь ранг r , то приблизительно W ≈ CU † R , где C и R содержат не менее r столбцов и строк соответственно.
Часто при получении реальных данных многие записи могут отсутствовать или сильно повреждены. Например, при отслеживании движения некоторые функции могут быть скрыты из поля зрения на несколько кадров. Следовательно, может потребоваться некоторая форма завершения матрицы.С другой стороны, взгляд на разложение CUR показывает, что целые строки матрицы данных могут отсутствовать, если мы все еще можем выбрать достаточно строк, чтобы результирующая матрица R имела тот же ранг, что и W . В реальных ситуациях, когда матрица данных зашумлена, тогда нет точного разложения CUR для W ; однако, если ранг чистых данных W хорошо оценен, то можно вычислить несколько приближений CUR для W , т.е.е. если чистые данные должны иметь ранг r , то приблизительно W ≈ CU † R , где C и R содержат не менее r столбцов и строк соответственно. Из каждого из этих приближений может быть вычислено приблизительное подобие, как в теореме 2, и может быть выполнена некоторая процедура усреднения, чтобы получить лучшую приблизительную матрицу подобия для зашумленных данных. Эта идея более подробно рассматривается в разделе 7.
Из каждого из этих приближений может быть вычислено приблизительное подобие, как в теореме 2, и может быть выполнена некоторая процедура усреднения, чтобы получить лучшую приблизительную матрицу подобия для зашумленных данных. Эта идея более подробно рассматривается в разделе 7.
5. Особые случаи
5.1. Матрица взаимодействия форм
В своей новаторской работе над методами факторизации для отслеживания движения [32] Костейра и Канаде представили Shape Interaction Matrix , или SIM. Для матрицы данных W , тонкая SVD которой равна UrΣrVr *, SIM ( W ) определяется как VrVr *. После их работы это нашло широкое применение в теории и на практике. Их наблюдение заключалось в том, что SIM часто предоставляет матрицу подобия для данных, поступающих из независимых подпространств.Следует отметить, что в Aldroubi et al. [31] было показано, что примеры матриц данных W могут быть найдены такими, что VrVr * не является матрицей подобия для W ; однако там было отмечено, что SIM ( W ) почти наверняка является матрицей подобия (в некотором смысле, уточненном в ней).
Возможно, наиболее важным следствием теоремы 2 является то, что матрица взаимодействия форм является частным случаем общей структуры разложения CUR. Этот факт показан в следующих двух следствиях теоремы 2, доказательства которых можно найти в разделе 6.4.
Следствие 4 . Пусть W = [w1 ⋯ wn] ∈Km × n – матрица ранга r, столбцы которой взяты из U. Пусть W разложено на множители как W = WW † W , и пусть Q будет двоичной или абсолютной версией W † W . Тогда ΞW = Qdmax – это матрица подобия для W . Более того, если разложение по тонким сингулярным числам W составляет W = UrΣrVr *, тогда W † W = VrVr *.
Следствие 5 . Пусть W = [w1 ⋯ wn] ∈Km × n будет матрицей ранга r, столбцы которой взяты из U. Выберите C = W , и R, чтобы быть ограничением строки r любого ранга W . Тогда W = W R † R по теореме 1. Кроме того, , R † R = W † W = VrVr *, , где V r такое же, как в следствии 4 .
Из двух предыдущих следствий следует, что в идеале (т.е. случай без шума), матрица взаимодействия форм Костейры и Канаде является частным случаем более общего разложения CUR. Однако обратите внимание, что Qdmax не обязательно должен быть SIM, VrVr *, в более общем случае, когда C W .
5.2. Алгоритм представления низкого ранга
Другой класс методов решения проблемы кластеризации подпространств возникает из решения некоторого вида задачи минимизации. Было отмечено, что во многих случаях такие методы тесно связаны с некоторыми методами матричной факторизации [30, 60].
Одним из конкретных примеров алгоритма, основанного на минимизации, является алгоритм Low Rank Presentation (LRR) Лю и др. [22, 23]. В качестве отправной точки авторы рассматривают следующую задачу минимизации ранга:
minZrank (Z) s.t. W = AZ, (1), где A – это словарь, линейно охватывающий W .
Обратите внимание, что здесь действительно есть что минимизировать, поскольку если A = W , Z = I n × n удовлетворяет ограничению и, очевидно, rank ( Z ) = n ; однако, если rank ( W ) = r , то Z = W † W является решением W = W Z , и легко показать, что ранг ( W † W ) = r .Обратите внимание, что любой Z , удовлетворяющий W = W Z , должен иметь ранг не менее r , и поэтому мы имеем следующее.
Предложение 1 . Пусть W будет матрицей данных ранга r, столбцы которой взяты из U, , затем W † W – решение задачи минимизации
minZrank (Z) s.t. W = WZ.Отметим, что в общем случае решение этой задачи минимизации (1) является NP-трудным (частный случай результатов [61]; см. Также [62]).Обратите внимание, что эта проблема эквивалентна минимизации || σ ( Z ) || 0 где σ ( Z ) – вектор сингулярных значений Z , а || · || 0 – количество ненулевых элементов вектора. Кроме того, решение уравнения (1) обычно не является уникальным, поэтому обычно функция ранга заменяется некоторой нормой, чтобы создать задачу выпуклой оптимизации. Основываясь на интуиции из сжатой литературы по зондированию, естественно рассмотреть вопрос о замене || σ ( Z ) || 0 по || σ ( Z ) || 1 , что является определением ядерной нормы, обозначаемой || Z || * (также называемая нормой следа, нормой Ки – Фана или нормой Шаттена 1).В частности, в Liu et al. [22], считалось:
minZ || Z || * s.t. W = AZ. (2)Решение этой задачи минимизации применительно к кластеризации подпространств названо авторами в Liu et al. [22].
Давайте теперь специализируем эти проблемы на случае, когда словарь выбран как вся матрица данных, и в этом случае у нас есть
minZ || Z || * s.t. W = WZ. (3)Это было показано в Liu et al. [23] и Вэй и Линь [60], что SIM определена в разделе 5.1, является единственным решением задачи (3):
Теорема 4 ([60], теорема 3.1) . Пусть W ∈ 𝕂 m × n будет матрицей ранга r, столбцы которой взяты из U, , и пусть W = UrΣrVr * будет ее тонким SVD. Тогда VrVr * – единственное решение для (3) .
Для ясности и полноты изложения мы приводим здесь более простое доказательство теоремы 4, чем приведено в Wei и Lin [60].
Доказательство .Предположим, что W = UΣV * – это полное SVD W . Тогда, поскольку W имеет ранг r , мы можем написать
W = UΣV * = [UrŨr] [Σr000] [Vr * Ṽr *],, где UrΣrVr * – тонкий СВД W . Тогда, если W = W Z , мы имеем, что I – Z находится в нулевом пространстве W . Следовательно, I – Z = Ṽ r X для некоторых X .Таким образом, получаем, что
Z = I + ṼrX = VV * + ṼrX = VrVr * + ṼrṼr * + ṼrX = VrVr * + Ṽr (Ṽr * + X) =: A + B.Напомним, что ядерная норма не изменяется при умножении слева или справа на унитарные матрицы, в результате чего мы видим, что || Z || * = || V * Z || * = || V * A + V * B || *. Однако
V * A + V * B = [Vr * 0] + [0Ṽr * + X].Из-за вышеупомянутой структуры мы имеем || V * A + V * B || * ≥ || V * A || *, с равенством тогда и только тогда, когда V * B = 0 (например, , с помощью того же доказательства, что и [63, лемма 1], или также леммы 7.2 из [23]).
Отсюда следует, что
|| Z || *> || A || * = || VrVr * || *,для любого B ≠ 0. Следовательно, Z = VrVr * – единственный минимизатор задачи (3). □
Следствие 6 . Пусть W будет таким же, как в теореме 4, и пусть W = W R † R будет факторизацией W как в теореме 1. Тогда R † R = W † W = VrVr * – единственное решение задачи минимизации (3) .
Доказательство . Объедините следствие 5 и теорему 4. □
Отметим, что уникальный минимизатор задачи (2) известен для общих словарей, как демонстрирует следующий результат Лю, Линь, Янь, Сунь, Ю и Ма.
Теорема 5 ([23], теорема 4.1). Предположим, что A – это словарь, который линейно охватывает W . Тогда единственный минимизатор задачи (2) равен
Следующее следствие, таким образом, непосредственно из разложения CUR.
Следствие 7 . Если W имеет разложение CUR W = CC † W (, где R = W , , следовательно, U = C в теореме 1), тогда C † W – уникальное решение для
minZ || Z || * s.t. W = CZ.Приведенные выше теоремы и следствия обеспечивают теоретический мост между матрицей взаимодействия форм, разложением CUR и представлением низкого ранга.В частности, в работе Wei and Lin [60] авторы отмечают, что первостепенный интерес представляет то, что, хотя LRR проистекает из соображений разреженности а-ля сжатое зондирование, его решение в случае отсутствия шума фактически исходит из матричной факторизации, что весьма интересно.
5.3. Базовая структура Aldroubi et al. [31]
В заключение, предлагаемая здесь структура CUR дает более широкие возможности для получения матриц сходства, чем у Aldroubi et al. [31]. Рассмотрим следующий основной результат:
Теорема 6 ([31], теорема 2). Пусть W ∈ 𝕂 m × n будет матрицей ранга r, столбцы которой взяты из U. Предположим W = BP, где столбцы B образуют основу для пространства столбцов W и столбцы B лежат в U (, но не обязательно столбцы W ). Если Q = abs (P * P) или Q = bin (P * P), то ΞW = Qdmax – это матрица подобия для W .
На первый взгляд, теорема 6, с одной стороны, более конкретна, чем теорема 2, поскольку столбцы B должны быть основой для диапазона W , тогда как C может иметь некоторую избыточность (т. Е. Столбцы образуют рамка). С другой стороны, теорема 6 кажется более общей, поскольку столбцы B должны исходить только из U, но не обязательно должны быть столбцами W , как столбцы C . Однако нужно только заметить, что если W = BP , как в теореме выше, то определение W ~ = [WB] приводит к разложению CUR W ~ = BB † W ~.Но кластеризация столбцов W ~ с помощью теоремы 2 автоматически дает кластеры W .
6. Доказательства
Здесь мы перечисляем доказательства результатов раздела 4, начиная с некоторых лемм.
6.1. Некоторые полезные лемматы
Первая лемма непосредственно следует из определения независимых подпространств.
Лемма 1 . Предположим, U = [U 1 … U M ], где каждый U i является подматрицей, столбцы которой происходят из независимых подпространств 𝕂 m .Тогда мы можем написать
U = [B1… BM] [V10… 00V2… 0 ⋮⋮ ⋱ ⋮ 0… 0VM]., где столбцы B i образуют основу для пространства столбцов U i .
Следующая лемма является частным случаем [31, лемма 1].
Лемма 2 . Предположим, что U ∈ m × n имеет столбцы, которые являются общими для подпространства S m , из которого они взяты. Предположим, что P ∈ 𝕂 r × m – матрица выбора строк такая, что rank (PU) = rank (U).Тогда столбцы PU являются общими .
Лемма 3 . Предположим, что U = [U 1 … U M ], и что каждая U i является подматрицей, столбцы которой происходят из независимых подпространств S i , i = 1,…, M из K m , и что столбцы U i являются общими для S i . Предположим, что P ∈ K r × m с r≥rank (U) – матрица выбора строк такая, что rank (PU) = rank (U). Тогда подпространства P (S i ), i = 1,…, M независимы .
Доказательство . Пусть S = S 1 + ⋯ + S M . Пусть d i = dim ( S i ) и d = dim ( S ). Исходя из гипотезы, мы получаем, что ранг ( PU i ) = d i , а ранг (PU) = d = ∑i = 1Mdi. Следовательно, есть d линейно независимых векторов для P ( S ) в столбцах PU .Более того, поскольку PU = [ PU 1 ,…, PU M ], существуют d i линейно независимых векторов из столбцов PU i для P ( S i ). Таким образом, dimP (S) = d = ∑idi = ∑idimP (Si), и следует заключение леммы. □
Следующие несколько фактов, которые нам понадобятся, исходят из базовой теории графов. Предположим, что G = ( V, E ) – конечный неориентированный взвешенный граф с вершинами в наборе V = { v 1 ,…, v k } и ребрами E .Геодезическое расстояние между двумя вершинами v i , v j ∈ V – это длина (то есть количество ребер) кратчайшего пути, соединяющего v i и v j , а диаметр графа G является максимальным из попарных геодезических расстояний вершин. С каждым взвешенным графом связана матрица смежности, A , так что A ( i, j ) не равно нулю, если есть ребро между вершинами v i и v j , и 0, если нет.Мы называем график положительно взвешенным , если A ( i, j ) ≥ 0 для всех i и j . Из этих фактов вытекает следующая лемма.
Лемма 4 . Пусть G – конечный неориентированный положительно взвешенный граф с диаметром r такой, что каждая вершина имеет петлю, и пусть A – его матрица смежности. Тогда A r (i, j)> 0 для всех i, j. В частности, A r – это матрица смежности полносвязного графа .
Доказательство . См. [31, следствие 1].
Следующая лемма связывает теоретико-графические соображения с моделью подпространств, описанной в вводной части. □
Лемма 5 . Пусть V = {p 1 ,…, p N } будет набором общих векторов, которые представляют данные из подпространства S размерности r и N> r ≥ 1. Пусть Q такое же, как в теореме 2 для случая U = S. Наконец, пусть G – граф, вершины которого равны p i , а ребра – те p i p j , такие что Q (i, j)> 0.Тогда группа G связна и имеет диаметр не больше r. Более того, Q r является матрицей смежности полносвязного графа .
Доказательство . Доказательство по существу содержится в [31, леммы 2 и 3], но для полноты приведено здесь.
Во-первых, чтобы увидеть, что G подключен, сначала рассмотрим базовый случай, когда N = r + 1, и пусть C будет непустым набором вершин связного компонента G .Предположим от противного, что C C содержит 1 ≤ k ≤ r вершин. Тогда, поскольку N = r +1, мы имеем | C C | ≤ r , и, следовательно, векторы {pj} j∈CC линейно независимы в соответствии с общим предположением о данных. С другой стороны, | C | ≤ r , поэтому векторы { p i } i ∈ C также линейно независимы.Но по построению 〈 p, q 〉 = 0 для любых p ∈ C и q ∈ C C , следовательно, множество {pi} i∈C∪CC является линейно независимым набор векторов r +1 в S , что противоречит предположению, что S имеет размерность r . Следовательно, C C пуст, т.е. подключен G .
Для общего N > r предположим, что p ≠ q – произвольные элементы V .Достаточно показать, что существует путь, соединяющий p с q . Поскольку N > r и V является общим, существует набор V 0 ⊂ V \ { p, q } мощности r −1, такой что { p, q } ∪ V 0 – это набор линейно независимых векторов в S . Это подграф r +1 вершин графа G , который удовлетворяет условиям базового случая, когда N = r +1, и поэтому этот подграф связан.Следовательно, существует путь, соединяющий p и q , и, поскольку они были произвольными, мы можем сделать вывод, что G соединен.
Наконец, обратите внимание, что в доказательстве предыдущего шага для общего N > r мы фактически получаем, что существует путь длиной не более r , соединяющий любые две произвольные вершины p, q ∈ V . Таким образом, диаметр G не больше r . При этом утверждение непосредственно следует из леммы 4, и на этом доказательство завершено.□
6.2. Доказательство теоремы 3
Без ограничения общности, мы предполагаем, что W таково, что W = [ W 1 … W M ], где W i – это м м. × n i матрица для каждого i = 1,…, M и ∑ Mini = n, а векторные столбцы W i происходят из подпространства S и .В этом предположении мы покажем, что Y является блочно-диагональной матрицей.
Пусть P будет матрицей выбора строки, так что P W = R ; в частности, обратите внимание, что P отображает ℝ m на ℝ s , и что из-за структуры W мы можем написать R = [ R 1 … R M ], где столбцы R i принадлежат подпространству S ~ i: = P (Si).Отметим также, что столбцы каждого R i являются общими для подпространства S ~ i в силу леммы 2, и что подпространства S ~ i независимы по лемме 3. Кроме того, поскольку U состоит из определенные столбцы R и ранг ( U ) = ранг ( R ) = ранг ( W ) по предположению, мы имеем, что U = [ U 1 … U M ], где столбцы U i находятся в S ~ i.
Затем вспомните из доказательства разложения CUR, что Y = U † R является решением для R = UX ; Таким образом, R = UY . Предположим, что r является столбцом R 1 , и пусть y = [y1y2… yM] * будет соответствующим столбцом Y , так что r = Uy . Тогда имеем r = ∑j = 1MUjyj, и, в частности, поскольку r находится в R 1 ,
(U1y1-r) + U2y2 + ⋯ + UMyM = 0,, откуда независимость подпространств S ~ i означает, что U 1 y 1 = r и U i y i для каждого = i = 2,…, M .С другой стороны, обратите внимание, что ỹ = [y10… 0] * – другое решение; то есть r = Uỹ . Вспоминая, что U † y является решением задачи с минимальной нормой r = Uy , мы должны иметь это
|| y || 22 = ∑i = 1M || yi || 22≤ || ỹ || 22 = || y1 || 22.Следовательно, y = ỹ, и отсюда следует, что Y является диагональным блоком, если применить тот же аргумент для столбцов R i , i = 2,…, M .
6.3. Доказательство теоремы 2
Без ограничения общности, на основании теоремы 3, мы можем предположить, что Y является блочно-диагональным, как указано выше. Затем мы сначала демонстрируем, что каждый блок Y i имеет ранг d i = dim ( S i ) и имеет общие столбцы. Поскольку R i = U i Y i , and rank ( R i ) = rank ( 906 ) = d i , у нас есть ранг ( Y i ) ≥ d i , поскольку ранг продукта не превышает минимального из рангов.С другой стороны, поскольку Yi = U † Ri, ранг ( Y i ) ≤ ранг ( R i ) = d i , откуда ранг ( Y i ) = d i . Чтобы увидеть, что столбцы каждого Y i являются общими, пусть y 1 ,…, y d i be d i 9 столбцы в Y i и предположим, что существуют константы c 1 ,…, c d i такие, что ∑j = 1dicjyj = 0.Из блочно-диагональной структуры Y следует, что
0 = Ui (∑j = 1dicjyj) = ∑j = 1dicjUiyj = ∑j = 1dicjrj,, где r j , j = 1,…, d i – столбцы R i . Поскольку столбцы R i являются общими по лемме 2, следует, что c i = 0 для всех i , откуда столбцы Y i общий.
Теперь Q = Y * Y – это блочная диагональная матрица n × n , блоки которой задаются формулой Qi = Yi * Yi, i = 1,…, M , и мы может рассматривать каждый блок как матрицу смежности графа, как предписано в лемме 4. Таким образом, из приведенного там заключения каждый блок дает связный граф с диаметром d i , и поэтому Qdmax приведет к графу с M отдельные полностью связанные компоненты, где график, возникающий из Q i , соответствует данным в W , взятым из S i .Таким образом, Qdmax действительно является матрицей подобия для W .
6.4. Доказательства следствий
Доказательство. [Доказательство следствия 4] То, что Ξ W является матрицей подобия, следует непосредственно из теоремы 2. Чтобы увидеть дополнительное утверждение, напомним, что W † = VrΣr † Ur *, откуда W † W = VrΣr † UrUr * ΣrVr * = VrΣr † ΣrVr * = VrVr *. □
Доказательство. [Доказательство следствия 5] По лемме 1 мы можем записать W = BZ , где Z – диагональ блока, а B = [ B 1 … B M ] с колоннами B i , являющимися основой для S i .Пусть P будет матрицей выбора строк, которая дает R , то есть R = P W . Тогда R = PBZ . Столбцы B линейно независимы (как и столбцы PB по лемме 3), откуда W † = Z † B † и R † = Z † ( PB ) † . Кроме того, линейная независимость столбцов также подразумевает, что B † B и ( PB ) † PB являются идентичными матрицами подходящего размера, при этом
R † R = Z † (PB) † PBZ = Z † Z = Z † B † BZ = W † W,, что завершает доказательство (заметим, что окончательное тождество W † W = VrVr * сразу следует из следствия 4).□
7. Экспериментальные результаты
7.1. Прото-алгоритм для зашумленных данных подпространства
До этого момента мы рассматривали только случай отсутствия шума, когда W содержит неповрежденные столбцы данных, лежащие в объединении подпространств, удовлетворяющих предположениям в разделе 2.2. Теперь мы отойдем от этого и рассмотрим более интересный случай, когда данные зашумлены, что типично для приложений. В частности, мы предполагаем, что матрица данных W представляет собой небольшое возмущение идеальной матрицы данных, так что столбцы W приблизительно прибывают из объединения подпространств; то есть w i = u i + η i , где ui∈U и η i – вектор малых шумов.Для наших экспериментов мы ограничимся случаем данных о движении.
Сегментация движения начинается с видео и некоего алгоритма, который извлекает элементы из движущихся объектов и отслеживает их положение во времени. В конце видео получается матрица данных размером 2 F × N , где F – количество кадров в видео, а N – количество отслеживаемых функций. Каждый вектор соответствует траектории фиксированного объекта, т.е.е., имеет вид (x1, y1,…, xF, yF) T, где ( x i , y i ) – положение элемента в кадре 1 ≤ i ≤ F . Несмотря на то, что эти траектории являются векторами в многомерном окружающем пространстве ℝ 2 F , известно, что траектории всех характеристик, принадлежащих одному и тому же твердому телу, лежат в подпространстве размерности 4 [64]. Следовательно, сегментация движения представляет собой подходящую практическую проблему, которую нужно решить, чтобы проверить правильность предлагаемого подхода.
Прото-алгоритм: . Кластеризация подпространств CUR
Должно быть очевидно, что причина использования термина «прото-алгоритм» состоит в том, что некоторые шаги допускают некоторую неоднозначность в своей реализации. Например, в строке 2, как выбрать приближение CUR к W ? Было исследовано множество различных способов выбора столбцов и строк, например Drineas et al. [5], которые выбирают строки и столбцы случайным образом в соответствии с распределением вероятностей, отдавая предпочтение большим столбцам или строкам соответственно.С другой стороны, Деманет и Чиу [38] показывают, что единообразный выбор столбцов и строк также может работать достаточно хорошо. В наших последующих экспериментах мы выбрали случайный выбор строк и столбцов.
На этом шаге есть еще большая двусмысленность, поскольку он имеет гибкость для выбора разного количества столбцов и строк (при условии, что каждое число имеет ранг не менее W ). Наш выбор количества строк и столбцов будет обсуждаться в следующих подразделах.
В-третьих, некоторого внимания заслуживает этап определения порога в строке 4 прото-алгоритма. В ходе экспериментов мы попробовали несколько пороговых значений, многие из которых были основаны на сингулярных значениях матрицы данных W . Однако порог, который лучше всего работал для данных движения, был объемным на основе формы Y i , гарантированной теоремой 3. Действительно, если есть M подпространств, каждое из которых имеет одинаковое измерение, то Y i должно иметь ровно 1-1M часть его общего количества записей, равную 0.Таким образом, наша функция определения пороговых значений упорядочивает записи в порядке убывания и сохраняет верхние (1-1M) × (общее количество записей), а для остальных устанавливает значение 0.
Строка 7 – это просто способ использовать любую известную информацию о данных, чтобы помочь в окончательной кластеризации. Обычно не предполагается никакой априорной информации, кроме того факта, что мы, очевидно, знаем, что w i находится в том же подпространстве, что и он сам. Следовательно, здесь мы принудительно устанавливаем диагональные записи Ξ i равными 1, чтобы подчеркнуть, что это соединение гарантировано.
Причина появления шага усреднения в строке 8 заключается в том, что, хотя матрица подобия, сформированная из единственной аппроксимации CUR матрицы данных, может содержать много ошибок, это поведение должно усредняться для получения правильных кластеров. Медиана по входам семейства {ΞW (i)} i = 1k используется вместо среднего, чтобы обеспечить большую устойчивость к выбросам. Обратите внимание, что аналогичный метод усреднения приближений CUR был оценен для шумоподавляющих матриц в Sekmen et al. [65]; дополнительные методы матричной факторизации в шумоподавлении матрицы (или изображения) можно найти в Muhammad et al.[66], например.
Отметим также, что мы не берем степени матрицы Yi * Yi, как это предлагается в теореме 2. Причина этого в том, что когда шум добавляется к матрице подобия, умножение матричного произведения мультипликативно увеличивает шум и значительно ухудшает производительность алгоритм кластеризации. Есть убедительные доказательства того, что поэлементное произведение зашумленной матрицы подобия может улучшить производительность [26, 33]. Это действительно другая методология, чем взятие степеней матрицы, поэтому мы оставим это обсуждение на потом.
Наконец, этап кластеризации в строке 10 присутствует, потому что в этот момент у нас есть неидеальная матрица сходства Ξ W , что означает, что кластеры не будут точно определены, потому что есть несколько записей, которые на самом деле равны 0. Однако в идеале каждый столбец должен иметь большую ( i, j ) запись всякий раз, когда w i и w j находятся в одном подпространстве, и маленькие (по абсолютной величине) записи всякий раз, когда w i и w j не являются.Эта ситуация имитирует то, что делается в спектральной кластеризации, в том, что матрица, полученная из первой части алгоритма спектральной кластеризации, не имеет строк, которые лежат точно на осях координат, заданных собственными векторами лапласиана графа; однако, будем надеяться, что это небольшие возмущения таких векторов, и базовый алгоритм кластеризации, такой как k , может дать правильные кластеры. Мы обсудим производительность нескольких различных базовых алгоритмов кластеризации, используемых на этом этапе в дальнейшем.
В оставшейся части этого раздела описанный выше протокол исследуется, сначала рассматривая его производительность на синтетических данных, после чего первоначальные результаты впоследствии проверяются с использованием набора данных сегментации движения, известного как Hopkins155 [67].
7.2. Моделирование с использованием синтетических данных
Набор моделирования разработан с использованием синтетических данных. Чтобы результаты были сопоставимы с результатами для случая сегментации движения, представленного в следующем разделе, данные строятся аналогичным образом.В частности, в синтетических экспериментах данные поступают из объединения независимых 4-х мерных подпространств ℝ 300 . Это соответствует функции, отслеживаемой в течение 5 секунд в видеопотоке со скоростью 30 кадров в секунду. Два случая, похожие на те, что в наборе данных Hopkins155, исследуются на предмет увеличения уровня шума. В первом случае случайным образом генерируются два подпространства размерности 4, а во втором – три подпространства. В обоих случаях данные выбираются случайным образом из единичного шара подпространств.В обоих случаях уровень шума на W постепенно увеличивается от начального бесшумного состояния до максимального уровня шума. Записи шума i.i.d. N (0, σ2) случайных величин (т.е. с нулевым средним и дисперсией σ 2 ), где дисперсия увеличивается как σ = [0,000, 0,001, 0,010, 0,030, 0,050, 0,075, 0,10].
В каждом случае для каждого уровня шума случайным образом генерируется 100 матриц данных, содержащих 50 векторов данных в каждом подпространстве. После того, как каждая матрица данных W сформирована, матрица подобия Ξ W генерируется с использованием прототипа алгоритма для кластеризации подпространств CUR.Используются следующие параметры: на шаге аппроксимации CUR (строка 2) мы выбираем все столбцы и ожидаемое ранговое количество строк. Следовательно, матрица Y теоремы 2 имеет вид R † R . Ожидаемое ранговое количество строк (то есть количество подпространств, умноженное на 4) выбирается равномерно случайным образом из W , и гарантируется, что R имеет ожидаемый ранг перед продолжением; шаг определения порога (строка 4) использует объемный порог, описанный в предыдущем подразделе, поэтому в случае 1 мы удаляем половину записей Y , а в случае 2 мы удаляем 2/3 записей; ставим k = 25, т.е.е. мы вычисляем 25 отдельных матриц подобия для каждой из 100 матриц данных и затем берём начальную медианную из 25 матриц подобия (строка 8) – обширное тестирование не показывает реального улучшения для больших значений k , поэтому это значение было установлено эмпирически. ; наконец, мы использовали три различных алгоритма кластеризации в строке 10: k – средство, спектральная кластеризация [24] и кластеризация главных координат (PCC) [68]. Чтобы избежать ненужного беспорядка, мы отображаем только результаты лучшего алгоритма кластеризации на рисунке 2, который оказывается PCC, и просто заявляем здесь, что использование алгоритма Matlab k означает очень низкую производительность даже при низких уровнях шума, в то время как Спектральная кластеризация дает хорошие характеристики при низких уровнях шума, но быстро ухудшается примерно после σ = 0.05. Более конкретно, k –средний имеет диапазон ошибок от 0 до 50% даже для σ = 0 в случае 2, в то время как среднее значение ошибки кластеризации составляет 36 и 48% в случаях 1 и 2, соответственно для максимальный уровень шума σ = 0,1. Между тем, спектральная кластеризация показала в среднем идеальную классификацию до уровня шума σ = 0,03 в обоих случаях, но быстро подскочила до среднего значения ошибки 12 и 40% в случаях 1 и 2, соответственно, для случая σ = 0,1. На рисунке 2 ниже показаны графики ошибок для обоих случаев при использовании PCC.Для полного описания PCC читателю предлагается обратиться к [68], но по существу он исключает использование лапласиана графа, как в спектральной кластеризации, и вместо этого использует главные координаты первых нескольких левых сингулярных векторов в разложении по сингулярным значениям Ξ Вт . А именно, если Ξ W имеет тощий SVD порядка M (количество подпространств) UMΣMVM *, то PCC кластеризует строки ΣMVM *, используя k –средний.
Результаты для случаев 1 и 2 с использованием PCC приведены на рисунке 1.Для иллюстрации на рисунке 2 показана производительность однократного разложения CUR для получения Ξ W . Как и ожидалось, случайность, связанная с нахождением разложения CUR, играет весьма нетривиальную роль в алгоритме кластеризации. Примечательно, однако, отметить колоссальное улучшение, которое дает процедура усреднения для более высоких уровней шума, что можно увидеть при сравнении двух цифр.
Рисунок 1 . Синтетические случаи 1 и 2 для Ξ W рассчитаны с использованием медианы 25 разложений CUR. (A) Случай 1, (B) Случай 2.
Рисунок 2 . Синтетические случаи 1 и 2 для Ξ W , рассчитанные с использованием одного разложения CUR. (A) Вариант 1, (B) Случай 2.
7.3. Набор данных сегментации движения: Hopkins155
Набор данных о движении Hopkins155 содержит 155 видеороликов, которые можно разбить на несколько категорий: последовательности шахматной доски, где движущиеся объекты накладываются на узор шахматной доски для получения множества характерных точек на каждом движущемся объекте, последовательности движения и шарнирное движение (например, ходьба людей) где движущееся тело содержит какие-то суставы, что делает неверным предположение о четырехмерном подпространстве траекторий.С каждым видео связана матрица данных, содержащая траектории всех функций движущихся объектов (эти функции заранее зафиксированы для удобства сравнения). Следовательно, матрица данных уникальна для каждого видео, и основная истина для кластеризации известна априори , что позволяет вычислить ошибку кластеризации, которая представляет собой просто процент неправильно сгруппированных точек характеристик. Пример неподвижного кадра из одного из видеороликов в Hopkins155 показан на рисунке 3. Здесь мы сосредоточены только на проблеме кластеризации данных движения; тем не менее, существует множество работ по классификации движений в видеопоследовательностях различного характера (например,г., [69–71]).
Рисунок 3 . Примеры кадров из последовательности автомобилей (слева) и шахматной доски (справа) из набора данных движения Hopkins155.
Как уже упоминалось, производительность кластеризации с использованием разложения CUR тестируется с использованием набора данных Hopkins155. В этом наборе экспериментов мы используем по существу те же параметры, что обсуждались в предыдущем подразделе при тестировании синтетических данных. То есть мы используем аппроксимацию CUR в виде W R † R , где точно ожидаемое количество строк выбирается равномерно случайным образом, используется объемный порог и мы берем медианное значение 50 подобия. матрицы для каждой из 155 матриц данных (здесь мы используем k = 50 вместо 25, чтобы добиться более надежной производительности на реальном наборе данных).Опять же, PCC предпочтительнее, чем k –means и Spectral Clustering из-за резкого увеличения производительности.
Оказывается, что для реальных данных движения CUR дает лучшие общие результаты, чем SIM, другой метод чистой матрицы сходства. Это разумно, учитывая гибкость разложения CUR. Нахождение нескольких матриц подобия и их усреднение приводит к усреднению некоторого внутреннего шума в данных. Ошибки классификации для нашего метода, а также многих тестов приведены в таблицах 1–3.Из-за изменчивости любого отдельного испытания по набору данных Hopkins155, данные CUR, представленные в таблицах, представляют собой среднее значение 20 прогонов алгоритма по всему набору данных. Целью этой работы не является точная настройка производительности CUR на наборе данных Hopkins155; тем не менее, результаты, полученные с использованием этого простого метода, уже лучше, чем многие из тех, что описаны в литературе.
Таблица 1 . % ошибок классификации для последовательностей с двумя движениями.
Таблица 2 .% ошибок классификации для последовательностей с тремя движениями.
Таблица 3 . % ошибок классификации для всех последовательностей.
Чтобы лучше сравнить производительность, мы синхронизировали метод на основе CUR, описанный выше, по сравнению с некоторыми из тестов времени, приведенных в Tron и Vidal [67]. Для прямого сравнения мы запустили все алгоритмы на одном компьютере – Macbook Pro середины 2012 года с процессором Intel Core i7 с тактовой частотой 2,6 ГГц и 8 ГБ оперативной памяти. Результаты представлены в таблице 4.Мы сообщаем время для различных значений k , как на шаге 1 прото-алгоритма, указывая, сколько аппроксимаций CUR усредняется для вычисления матрицы подобия.
Таблица 4 . Время выполнения (в секундах) для всего набора данных Hopkins155 для различных алгоритмов.
7,4. Обсуждение
Следует отметить, что после тщательного экспериментирования с зашумленными данными использование разложения CUR, которое берет все столбцы и точно ожидаемое ранговое число строк, дает лучшую производительность.То есть разложение формы W = W R † R в среднем работает лучше, чем форма W = CU † R . Тот факт, что выбор большего количества столбцов работает лучше, когда матрица W зашумлена, имеет смысл в том, что любое представление формы W = CX является представлением W в терминах векторов кадров C . Следовательно, выбор большего количества столбцов в матрице C означает, что мы добавляем избыточность к кадру, и хорошо известно, что одним из преимуществ представлений кадра является то, что избыточность обеспечивает большую устойчивость к шуму.Кроме того, мы экспериментально заметили, что выбор в разложении ровно r строк W R † R показывает лучшую производительность. Пока не ясно, почему это так.
Как видно из таблиц выше, предложенный алгоритм кластеризации на основе CUR работает значительно лучше, чем SIM, но не превосходит лучшие современные достижения, полученные первым и четвертым авторами в Aldroubi and Sekmen [72]. Необходимы дополнительные исследования, чтобы определить, есть ли способ лучше использовать разложение CUR для учета шума.Особый интерес может представлять метод выпуклой релаксации, недавно предложенный Li et al. [54].
Одно интересное замечание из результатов в приведенных выше таблицах заключается в том, что, хотя некоторые методы кластеризации движения лучше работают с клетчатыми последовательностями, а не с последовательностями трафика (например, NLS, SSC и SIM), CUR, похоже, не замечает эту разницу в тип данных. Было бы интересно исследовать это явление дальше, чтобы определить, одинаково ли работает предложенный метод для различных типов данных движения.Мы оставляем эту задачу на будущее.
В качестве последнего замечания отметим, что производительность CUR уменьшается, поскольку k , количество разложений CUR, усредненных для получения матрицы подобия, увеличивается. Ошибка начинает выравниваться за пределы примерно k = 50, тогда как время неуклонно увеличивается, как и k (см. Таблицу 4). Можно легко реализовать адаптивный способ выбора k для каждой матрицы данных вместо того, чтобы удерживать ее фиксированной. Чтобы проверить это, мы реализовали простой порог, взяв для каждого i в Прото-алгоритме временную матрицу подобия Ξ˜W (i): = abs (median (ΞW (1),… ΞW (i)) ).То есть ~ W (i) – это медиана всех матриц подобия CUR, созданных до сих пор в цикле for. Затем мы вычислили || Ξ ~ W (i) -Ξ ~ W (i-1) || 2 и сравнили его с порогом (в данном случае 0,01). Если норма была меньше порога, мы останавливали цикл for, а если нет, мы продолжали работать, устанавливая абсолютный предел 100 для количества используемых разложений CUR. Мы обнаружили, что в среднем использовалось 57 разложений CUR, минимум 37, максимум 100 (пороговое значение) и стандартное отклонение 13.Таким образом, кажется, что примерно оптимальная область для быстрой работы по времени и хорошей точности кластеризации составляет примерно от k = 50 до k = 60 разложений CUR.
7,5. Надежная матрица подобия CUR для подпространственной кластеризации
Теперь перейдем к модификации прото-алгоритма, рассмотренного выше. Одна из основных причин использования разложения CUR в отличие от матрицы взаимодействия форм (VrVr *) заключается в том, что последняя не устойчива к шуму. Однако Ji et al.[33] предложили роботизированную версию SIM, названную RSIM. Ключевая особенность их алгоритма заключается в том, что они заранее не устанавливают ранг кластеризации, но находят диапазон возможных рангов, составляют матрицу сходства для каждого ранга в этом диапазоне и выполняют спектральную кластеризацию на модификации SIM. Затем они сохраняют метки кластеризации из матрицы подобия для ранга r , что минимизирует ассоциированное количество minCut на графе, определенном матрицей подобия.
Напомним, что для взвешенного неориентированного графа G = ( V, E ) и разбиения его вершин, { A 1 ,…, A k }, значение Ncut перегородки
Ncutk (A1,…, Ak): = 12∑i = 1kW (Ai, AiC) vol (Ai),где W (A, AC): = ∑i∈A, j∈ACwi, j, где w i, j – вес кромки ( v i , v j ) (определяется как 0, если такой край не существует).Метод RSIM изменяет ранг r SIM (т. Е. Ранг взятого SVD) и минимизирует соответствующее количество Ncut по сравнению с r .
Дополнительная особенность алгоритма RSIM заключается в том, что вместо того, чтобы просто использовать VrVr * в качестве матрицы сходства, они сначала нормализуют строки V r , а затем получают поэлементную мощность результирующей матрицы. Это следует интуиции Лауэра и Шнорра [26] и должно рассматриваться как тип пороговой обработки, как на шаге 4 прото-алгоритма.Для полного алгоритма RSIM обратитесь к [33], но мы представляем аналог CUR, который поддерживает большинство шагов в нем.
Основное отличие алгоритма 1 от алгоритма Ji et al. [33] заключается в том, что в последнем шаги 2–8 в алгоритме 1 заменены вычислением тонкого SVD порядка r и нормализацией строк V r , а затем установкой ΞW = VrVr * . В Ji et al. [33] предпочтительным является алгоритм кластеризации Normalized Cuts, который также называется спектральной кластеризацией с лапласианом симметричного нормализованного графа [24].В нашем тестировании RCUR выяснилось, что этапы нормализации и поэлементного включения питания мешают основной системе координат в кластеризации ПК; поэтому мы использовали спектральную кластеризацию, как и в случае с RSIM. Результаты представлены в таблицах 5–7. Обратите внимание, что значения RSIM могут отличаться от тех, что указаны в Ji et al. [33]; там авторы представили ошибки только для всех последовательностей с двумя движениями, всех последовательностей с тремя движениями и в целом, а не рассматривали каждый подкласс (например, клетчатый или трафик).Мы использовали код из [33] для значений, заданных их алгоритмом, и сообщаем о его производительности в таблицах ниже (в общем, приведенные здесь значения лучше, чем в [33]).
Алгоритм 1 : Надежная матрица подобия CUR (RCUR)
Таблица 5 . % ошибок классификации для последовательностей с двумя движениями.
Таблица 6 . % ошибок классификации для последовательностей с тремя движениями.
Таблица 7 .% ошибок классификации для всех последовательностей.
Результаты, отображаемые в таблице, получены путем выбора k = 50 для фиксирования (на основе анализа в предыдущем разделе) и взятия факторизации CUR в виде W≈CiRi † Ri, где мы выбираем r строк. для формирования R i , где r задается на шаге 1 алгоритма. Это, согласно следствию 5, теоретический эквивалент принятия VrVr *, как в RSIM. Из-за случайности нахождения факторизаций CUR в алгоритме 1 алгоритм был запущен 20 раз, и средняя производительность была указана в таблицах 5–7.Мы также отмечаем, что стандартное отклонение производительности по 20 испытаниям было менее 0,5% для всех категорий, за исключением категории 3-х сочлененных движений, и в этом случае стандартное отклонение было большим (5,48%).
Как можно видеть, предложенный здесь алгоритм не дает наилучшей производительности по всем аспектам набора данных Hopkins155; тем не менее, он дает лучший общий результат классификации на сегодняшний день со средней ошибкой классификации всего 0,36%. В качестве дополнительного примечания, выполнение алгоритма 1 только с k = 10 факторизациями CUR, используемыми для каждой матрицы данных, по-прежнему дает относительно хорошие результаты (общая ошибка 2-движения равна 0.41%, общая ошибка трех движений 1,21% и общая ошибка для всех Хопкинса155 0,59%), что позволяет сократить время вычислений. Предварительные тесты также показывают, что использование меньшего количества строк на этапе факторизации CUR в алгоритме 1 работает намного лучше, чем в версии протоалгоритма, использованной в предыдущих разделах (например, если взять половину доступных столбцов и r строк по-прежнему дает <0,5% общей погрешности). Однако цель текущей работы не состоит в том, чтобы оптимизировать все аспекты алгоритма 1, поскольку необходимо провести гораздо больше экспериментов, чтобы определить правильные параметры для алгоритма, и его необходимо протестировать на большом количестве наборов данных, которые приблизительно удовлетворяют рассмотренное здесь предположение об объединении подпространств.Эту задачу мы оставляем на будущее.
8. Заключительные замечания
Мотивом этой работы было действительно осознание того, что точное CUR-разложение теоремы 1 может быть использовано для задачи кластеризации подпространств. Мы продемонстрировали, что, помимо своей полезности в рандомизированной линейной алгебре, CUR занимает видное место среди решений проблемы кластеризации подпространств. CUR предоставляет теоретический зонтик, под которым находится известная матрица взаимодействия форм, но он также обеспечивает мост к другим методам решения, основанным на сжатых измерениях, т.е.е., связанные с решением задачи минимизации ℓ 1 . Более того, мы полагаем, что полезность CUR для кластеризации и других приложений будет только возрастать в будущем. Ниже мы приводим некоторые причины практической полезности декомпозиции CUR, особенно связанные с анализом данных и кластеризацией, а также некоторые будущие направления.
Преимущества CUR:
• С теоретической точки зрения, CUR-разложение матрицы использует структуру кадра, а не базовую структуру для факторизации матрицы, и, следовательно, обладает уровнем гибкости, превосходящим что-то вроде SVD.Этот факт должен предоставить полезность для приложений.
• Кроме того, разложение CUR остается верным структуре данных. Например, если данные являются разреженными, то и C , и R будут разреженными, даже если U † в целом не является. Напротив, взятие SVD разреженной матрицы дает полные матрицы U и V в целом.
• Часто при получении реальных данных многие записи могут отсутствовать или сильно повреждены.Например, при отслеживании движения некоторые функции могут быть скрыты из поля зрения на несколько кадров. Следовательно, может потребоваться некоторая форма завершения матрицы. С другой стороны, взгляд на разложение CUR показывает, что целые строки матрицы данных могут отсутствовать, если мы все еще можем выбрать достаточно строк, чтобы результирующая матрица R имела тот же ранг, что и W .
Будущие направления
• Алгоритм 1 и другие итерации представленного здесь Прото-алгоритма нуждаются в дальнейшем тестировании, чтобы определить наилучший способ использования разложения CUR для данных подпространства кластера.В настоящее время алгоритм 1 является в некоторой степени эвристическим, поэтому необходима более понятная теория, касающаяся его производительности. Отметим, что некоторое обоснование идей RSIM дано в Ji et al. [33]; однако изложенные там идеи не полностью объясняют выдающуюся производительность алгоритма. Как отмечалось выше, одним из преимуществ обсуждаемого здесь прото-алгоритма является его гибкость, которая обеспечивает явное преимущество перед методами на основе SVD.
• Другое направление – комбинировать метод CUR с разреженными методами для построения алгоритмов, которые сильно устойчивы к шуму и позволяют кластеризацию, когда точки данных не извлекаются из объединения независимых подпространств.
Авторские взносы
Все перечисленные авторы внесли существенный, прямой и интеллектуальный вклад в работу и одобрили ее к публикации.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Исследование AS и AK поддержано грантом Министерства обороны США W911NF-15-1-0495.Исследование AA поддержано NSF Grant NSF / DMS 1322099. Исследование AK также поддерживается TUBITAK-2219-1059B1150. Большая часть работы над этой статьей была сделана, когда К. Х. был доцентом Университета Вандербильта. На заключительном этапе проекта исследование KH было частично поддержано проектом NSF TRIPODS в рамках гранта CCF-1423411.
Авторы также благодарят рецензентов за конструктивные комментарии, которые помогли улучшить качество рукописи.
Список литературы
3.Дринес П., Каннан Р., Махони М.В. Быстрые алгоритмы Монте-Карло для матриц I: аппроксимирующее умножение матриц. SIAM J. Comput. (2006) 36 : 132–57. DOI: 10.1137 / S0097539704442684
CrossRef Полный текст | Google Scholar
4. Дринес П., Каннан Р., Махони М.В. Быстрые алгоритмы Монте-Карло для матриц II: вычисление приближения низкого ранга к матрице. SIAM J. Comput. (2006) 36 : 158–83. DOI: 10.1137 / S0097539704442696
CrossRef Полный текст | Google Scholar
5.Дринес П., Каннан Р., Махони М.В. Быстрые алгоритмы Монте-Карло для матриц III: вычисление сжатого приближенного разложения матриц. SIAM J. Comput. (2006) 36 : 184–206. DOI: 10.1137 / S0097539704442702
CrossRef Полный текст | Google Scholar
6. Georghiades AS, Belhumeur PN, Kriegman DJ. От немногих к многим: модели световых конусов для распознавания лиц при переменном освещении и позы. IEEE Trans Pattern Anal Mach Intell. (2001) 23 : 643–60.DOI: 10.1109 / 34.4
CrossRef Полный текст | Google Scholar
7. Басри Р., Джейкобс Д. В.. Ламбертовское отражение и линейные подпространства. IEEE Trans Pattern Anal Mach Intell. (2003) 25 : 218–33. DOI: 10.1109 / TPAMI.2003.1177153
CrossRef Полный текст | Google Scholar
8. Канатани К., Сугая Ю. Многоступенчатая оптимизация для сегментации движения нескольких тел. В: IEICE Transactions on Information and Systems (2003). п. 335–49.
Google Scholar
9. Альдроуби А., Зарингалам К. Нелинейные методы наименьших квадратов в ℝ n . Acta Appl Math. (2009) 107 : 325–37. DOI: 10.1007 / s10440-008-9398-9
CrossRef Полный текст | Google Scholar
10. Альдроуби А., Кабрелли С., Молтер У. Оптимальные нелинейные модели для разреженности и отбора проб. J Four Anal Appl. (2009) 14 : 793–812. DOI: 10.1007 / s00041-008-9040-2
CrossRef Полный текст | Google Scholar
12.Фишлер М., Боллес Р. Консенсус по случайной выборке: парадигма для подгонки модели с приложениями для анализа изображений и автоматизированной картографии. Commun ACM (1981) 24 : 381–95. DOI: 10.1145 / 358669.358692
CrossRef Полный текст | Google Scholar
13. Сильва Н., Костейра Дж. Сегментация подпространств с выбросами: грассманов подход к максимальному консенсусному подпространству. В: Конференция компьютерного общества IEEE по компьютерному зрению и распознаванию образов .Анкоридж, AK (2008).
Google Scholar
14. Zhang T, Szlam A, Wang Y, Lerman G. Рандомизированное гибридное линейное моделирование с помощью локальных оптимальных плоскостей. В: Конференция IEEE по компьютерному зрению и распознаванию образов . Сан-Франциско, Калифорния (2010). п. 1927–34.
Google Scholar
15. Чжан Ю.В., Шлам А., Лерман Г. Гибридное линейное моделирование с помощью локальных оптимальных плоскостей. Int J Comput Vis. (2012) 100 : 217–40. DOI: 10.1007 / s11263-012-0535-6
CrossRef Полный текст | Google Scholar
17.Ма Й, Ян А.Ю., Дерксен Х., Фоссум Р. Оценка расположения подпространств с приложениями в моделировании и сегментировании смешанных данных. SIAM Ред. (2008) 50 : 1–46. DOI: 10.1137 / 060655523
CrossRef Полный текст | Google Scholar
18. Цакирис М.К., Видаль Р. Фильтрованная спектрально-алгебраическая кластеризация подпространств. SIAM J Imaging Sci . (2017) 10 : 372–415. DOI: 10.1137 / 16M1083451
CrossRef Полный текст | Google Scholar
19.Эльдар Ю.К., Мишали М. Устойчивое восстановление сигналов из структурированного объединения подпространств. IEEE Trans Inform Theory (2009) 55 : 5302–16. DOI: 10.1109 / TIT.2009.2030471
CrossRef Полный текст | Google Scholar
20. Эльхамифар Э., Видаль Р. Кластеризация разреженных подпространств. В: Конференция IEEE по компьютерному зрению и распознаванию образов . Майами, Флорида (2009). п. 2790–97.
PubMed Аннотация | Google Scholar
21. Эльхамифар Э., Видаль Р.Кластеризация непересекающихся подпространств с помощью разреженного представления. В: Международная конференция IEEE по акустике, речи и обработке сигналов (2010).
Google Scholar
22. Лю Г., Линь З., Ю. Ю. Робастная сегментация подпространств с помощью представления низкого ранга. В: Международная конференция по машинному обучению. Хайфа (2010). п. 663–70.
Google Scholar
23. Лю Г., Линь З., Янь С., Сун Дж, Ю. Ю., Ма Ю. Робастное восстановление структур подпространств с помощью представления низкого ранга. IEEE Trans Pattern Anal Mach Intell. (2013) 35 : 171–84. DOI: 10.1109 / TPAMI.2012.88
PubMed Аннотация | CrossRef Полный текст | Google Scholar
25. Чен Г., Лерман Г. Кластеризация спектральной кривизны (SCC). Int J Comput Vis . (2009) 81 : 317–30. DOI: 10.1007 / s11263-008-0178-9
CrossRef Полный текст | Google Scholar
26. Лауэр Ф., Шнорр С. Спектральная кластеризация линейных подпространств для сегментации движения.В: Международная конференция IEEE по компьютерному зрению . Киото (2009).
Google Scholar
27. Ян Дж., Поллефейс М. Общая основа для сегментации движения: независимая, сочлененная, жесткая, нежесткая, вырожденная и невырожденная. В: 9-я Европейская конференция по компьютерному зрению. Грац (2006). п. 94–106.
Google Scholar
28. Го А., Видаль Р. Сегментирование движений различных типов с помощью неконтролируемой кластеризации многообразий. В: Конференция IEEE по компьютерному зрению и распознаванию образов, 2007.CVPR ’07. Миннеаполис, Миннесота (2007). п. 1–6.
Google Scholar
29. Чен Г., Лерман Г. Основы многофакторной спектральной кластерной структуры для гибридного линейного моделирования. Found Comput Math. (2009) 9 : 517–58. DOI: 10.1007 / s10208-009-904
CrossRef Полный текст | Google Scholar
31. Альдроуби А., Секмен А., Коку А.Б., Чакмак А.Ф. Структура матрицы подобия для данных из объединения подпространств. Appl Comput Harmon Anal. (2018) 45 : 425–35.DOI: 10.1016 / j.acha.2017.08.006
CrossRef Полный текст | Google Scholar
32. Костейра Дж., Канаде Т. Многотельный метод факторизации для независимо движущихся объектов. Int J Comput Vis. (1998) 29 : 159–79. DOI: 10.1023 / A: 1008000628999
CrossRef Полный текст | Google Scholar
33. Джи П., Зальцманн М., Ли Х. Матрица взаимодействия форм пересмотрена и робастирована: эффективная кластеризация подпространств с поврежденными и неполными данными. В: Труды Международной конференции IEEE по компьютерному зрению. Сантьяго (2015). п. 4687–95.
Google Scholar
34. Голуб Г.Х., Van Loan CF. Матричные вычисления , Vol. 3 . JHU Press (2012).
Google Scholar
35. Алексеев Б., Кэхилл Дж., Миксон Д.Г. Полные искровые рамы. J Fourier Anal Appl. (2012) 18 : 1167–94. DOI: 10.1007 / s00041-012-9235-4
CrossRef Полный текст | Google Scholar
36. Донохо Д.Л., Элад М. Оптимально разреженное представление в общих (неортогональных) словарях через 1 минимизацию. Proc Natl Acad Sci USA . (2003) 100 : 2197–202. DOI: 10.1073 / pnas.0437847100
CrossRef Полный текст | Google Scholar
37. Горейнов С.А., Замарашкин Н.Л., Тыртышников Э.Е. Псевдоскелетные аппроксимации матрицами максимального объема. Math Notes (1997) 62 : 515–9. DOI: 10.1007 / BF02358985
CrossRef Полный текст | Google Scholar
38. Чиу Дж., Деманет Л. Сублинейные рандомизированные алгоритмы для разложения скелета. SIAM J Matrix Anal Appl. (2013) 34 : 1361–83. DOI: 10.1137 / 110852310
CrossRef Полный текст | Google Scholar
39. Горейнов С.А., Тыртышников Э.Е., Замарашкин Н.Л. Теория приближений псевдоскелета. Linear Algebra Appl. (1997) 261 : 1–21. DOI: 10.1016 / S0024-3795 (96) 00301-1
CrossRef Полный текст | Google Scholar
40. Caiafa CF, Cichocki A. Обобщение разложения матрицы столбец-строка на многосторонние массивы. Linear Algebra Appl. (2010) 433 : 557–73. DOI: 10.1016 / j.laa.2010.03.020
CrossRef Полный текст | Google Scholar
41. Гантмахер FR. Теория матриц. 2В. Chelsea Publishing Company (1960).
Google Scholar
42. Пенроуз Р. О наилучших приближенных решениях линейных матричных уравнений. Math Proc Cambridge Philos Soc . (1956) 52 : 17–9. DOI: 10.1017 / S0305004100030929
CrossRef Полный текст | Google Scholar
43.Стюарт Г. Четыре алгоритма для эффективного вычисления аппроксимаций усеченных сводных QR-кодов для разреженной матрицы. Numer Math. (1999) 83 : 313–23. DOI: 10.1007 / s002110050451
CrossRef Полный текст | Google Scholar
44. Берри М.В., Пулатова С.А., Стюарт Г. Алгоритм 844: вычисление разреженных приближений пониженного ранга к разреженным матрицам. ACM Trans Math Soft . (2005) 31 : 252–69. DOI: 10.1145 / 1067967.1067972
CrossRef Полный текст | Google Scholar
46.Дринес П., Махони М.В., Мутукришнан С. Разложение матрицы CUR относительной ошибки. SIAM J Matrix Anal Appl. (2008) 30 : 844–81. DOI: 10.1137 / 07070471X
CrossRef Полный текст | Google Scholar
47. Воронин С., Мартинссон П.Г. Эффективные алгоритмы текущего и интерполяционного разложения матриц. Расширенные вычисления . (2017) 43 : 495–516. DOI: 10.1007 / s10444-016-9494-8
CrossRef Полный текст | Google Scholar
49.Освал Ю., Джайн С., Сюй К.С., Эрикссон Б. Блок CUR: разложение больших распределенных матриц. arXiv [Препринт]. arXiv: 170306065 . (2017).
Google Scholar
50. Li X, Pang Y. Детерминированное разложение матриц на основе столбцов. IEEE Trans Knowl Data Eng. (2010) 22 : 145–9. DOI: 10.1109 / TKDE.2009.64
CrossRef Полный текст | Google Scholar
51. Ип К.В., Махони М.В., Салай А.С., Чабай И., Будавари Т., Вайс РФ и др. Объективная идентификация информативных областей длин волн в спектрах галактик. Astron J. (2014) 147 : 110. DOI: 10.1088 / 0004-6256 / 147/5/110
CrossRef Полный текст | Google Scholar
52. Ян Дж., Рубель О., Махони М. В., Боуэн Б. П.. Идентификация важных ионов и позиций в данных масс-спектрометрии с использованием разложения матрицы CUR. Anal Chem. (2015) 87 : 4658–66. DOI: 10.1021 / ac5040264
PubMed Аннотация | CrossRef Полный текст | Google Scholar
53. Сюй М., Цзинь Р., Чжоу Чж. Алгоритм CUR для частично наблюдаемых матриц.В: Международная конференция по машинному обучению . Лилль (2015). п. 1412–21.
Google Scholar
54. Li C, Wang X, Dong W, Yan J, Liu Q, Zha H. Совместное активное обучение с выбором характеристик посредством разложения матрицы CUR. В: IEEE Transactions on Pattern Analysis and Machine Intelligence. (2018). DOI: 10.1109 / TPAMI.2018.2840980
PubMed Аннотация | CrossRef Полный текст | Google Scholar
55. Халко Н., Мартинссон П.Г., Тропп Дж.А.Нахождение структуры со случайностью: вероятностные алгоритмы построения приближенных разложений матриц. SIAM Ред. (2011) 53 : 217–88. DOI: 10.1137 / 0806
CrossRef Полный текст | Google Scholar
56. Мухаммад Н., Биби Н. Нанесение водяных знаков на цифровые изображения с использованием частичного поворотного нижнего и верхнего треугольного разложения в вейвлет-область. IET Image Process. (2015) 9 : 795–803. DOI: 10.1049 / iet-ipr.2014.0395
CrossRef Полный текст | Google Scholar
57.Мухаммад Н., Биби Н., Касим И., Джахангир А., Махмуд З. Цифровые водяные знаки с использованием метода разложения изображения свойств Холла. Pattern Anal Appl. (2018) 21 : 997–1012. DOI: 10.1007 / s10044-017-0613-z
CrossRef Полный текст | Google Scholar
58. Otazo R, Candès E, Sodickson DK. Низкоранговая и разреженная матричная декомпозиция для ускоренной динамической МРТ с разделением фоновой и динамической составляющих. Магн Резон Мед . (2015) 73 : 1125–36.DOI: 10.1002 / mrm.25240
PubMed Аннотация | CrossRef Полный текст | Google Scholar
60. Вэй С., Линь З. Анализ и улучшение представления низкого ранга для сегментации подпространств. arXiv [Препринт]. arXiv: 1107.1561 [cs.CV] (2011).
Google Scholar
61. Мека Р., Джайн П., Караманис К., Диллон И.С. Минимизация ранга через онлайн-обучение. В: Материалы 25-й Международной конференции по машинному обучению . Хельсинки (2008).п. 656–63.
Google Scholar
62. Recht B, Xu W, Hassibi B. Необходимые и достаточные условия успеха эвристики ядерной нормы для минимизации ранга. В: 47-я конференция IEEE по решениям и контролю, 2008. CDC 2008. Канкун (2008). п. 3065–70.
Google Scholar
63. Рехт Б., Сюй В., Хассиби Б. Условия нулевого пространства и пороговые значения для минимизации ранга. Математическая программа. (2011) 127 : 175–202. DOI: 10.1007 / с10107-010-0422-2
CrossRef Полный текст | Google Scholar
64. Канатани К., Мацунага С. Оценка количества независимых движений для сегментации движения нескольких тел. В: 5-я Азиатская конференция по компьютерному зрению . Мельбурн, Виктория (2002). п. 7–9.
Google Scholar
65. Секмен А., Альдроуби А., Коку А.Б., Хамм К. Реконструкция матрицы: разложение скелета в сравнении с разложением по сингулярным значениям. В: 2017 Международный симпозиум по оценке производительности компьютерных и телекоммуникационных систем (SPECTS). Сиэтл, Вашингтон (2017). п. 1–8.
Google Scholar
66. Мухаммад Н., Биби Н., Джахангир А., Махмуд З. Шумоподавление изображения с помощью оценок слияния, взвешенных по норме. Pattern Anal Appl. (2018) 21 : 1013–22. DOI: 10.1007 / s10044-017-0617-8
CrossRef Полный текст | Google Scholar
67. Трон Р., Видаль Р. Тест для сравнения алгоритмов сегментации трехмерного движения. В: Конференция IEEE по компьютерному зрению и распознаванию образов. Миннеаполис, Миннесота (2007). п. 1–8.
Google Scholar
68. Секмен А., Альдроуби А., Коку А.Б., Хамм К. Кластеризация основных координат. В: 2017 Международная конференция IEEE по большим данным (Big Data). Бостон, Массачусетс (2017). п. 2095–101.
Google Scholar
69. Чо К., Чен Х. Классификация и визуализация последовательностей захвата движения с использованием глубоких нейронных сетей. В: 2014 Международная конференция по теории и приложениям компьютерного зрения (VISAPP) , Vol.2 . Лиссабон (2014). п. 122–30.
Google Scholar
70. Хан М.А., Акрам Т., Шариф М., Джавед М.Ю., Мухаммад Н., Ясмин М. Реализация оптимизированной структуры для классификации действий с использованием многослойной нейронной сети на выбранных слитых объектах. Pattern Anal Appl. (2018) 1–21. DOI: 10.1007 / s10044-018-0688-1
CrossRef Полный текст
71. Арн Р., Нараяна П., Дрейпер Б., Эмерсон Т., Кирби М., Петерсон К. Сегментация движения с помощью обобщенных кривизн.В: IEEE Transactions on Pattern Analysis and Machine Intelligence (2018).
PubMed Аннотация | Google Scholar
72. Алдроуби А., Секмен А. Алгоритм близости к локальному подпространству для сегментации подпространства и движения. IEEE Signal Process Lett. (2012) 19 : 704–7. DOI: 10.1109 / LSP.2012.2214211
CrossRef Полный текст | Google Scholar
Систем линейных уравнений: Матрицы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Матрица– Энциклопедия математики
Математика 2010 Классификация предметов: Начальная школа: 15Axx [MSN] [ZBL]
Матрица представляет собой прямоугольный массив $$ \ begin {pmatrix} a_ {11} & \ dots & a_ {1n} \\ \ точки и \ точки и \ точки \\ а_ {m1} & \ точки & a_ {mn} \\ \ конец {pmatrix} \ label {x} $$ состоящий из $ m $ строк и $ n $ столбцов, записи $ a_ {ij} $ из которых принадлежат некоторому набору $ K $.(1) называется также $ (m \ times n) $ – размерная матрица над $ K $, или матрица размерностей $ m \ times n $ над $ K $. Пусть $ \ def \ M {\ mathrm {M}} \ M_ {m, n} (K) $ обозначает множество всех $ (m \ times n) $ -мерных матриц над $ K $. Если $ m = n $, то матрица (1) называется квадратной матрицей порядка $ n $. Набор всех квадратных матриц порядка $ n $ над $ K $ обозначается $ \ M_n (K) $.
Альтернативные обозначения матриц: $$ \ begin {bmatrix} a_ {11} & \ dots & a_ {1n} \\ \ точки и \ точки и \ точки \\ а_ {m1} & \ dots & a_ {mn} \ end {bmatrix}, \ quad \ begin {Vmatrix} a_ {11} & \ dots & a_ {1n} \\ \ точки и \ точки и \ точки \\ а_ {m1} & \ dots & a_ {mn} \ end {Vmatrix}, {\ rm \ \ и \} \ quad (a_ {ij}).$$ В самом главном случаях роль $ K $ играет поле действительных чисел, поле комплексных чисел, произвольное поле, кольцо многочленов, кольцо целых чисел, кольцо функций или произвольная ассоциативная звенеть. Операции сложения и умножения, определенные на $ K $, следующие: естественным образом переносится на матрицы над $ K $, и таким образом привело к матричному исчислению – предмету теории матрицы.
Понятие матрицы возникло впервые в середине 19 века. в исследованиях В.Гамильтон и А. Кэли. Фундаментальный результаты по теории матриц принадлежат К. Вейерштрассу, К. Йордану. и Г. Фробениус. Я. Лаппо-Данилевский разработал теорию аналитических функций нескольких матричных переменных и применил его к исследование систем линейных дифференциальных уравнений.
Операции с матрицами.
Пусть $ K $ – ассоциативное кольцо и пусть $ A = (a_ {ij}), \; B = (b_ {ij}) \ in \ M_ {m, n} (K) $. Тогда сумма матриц $ A $ и $ B $ по определению равна $$ A + B = (a_ {ij} + b_ {ij}).k a _ {\ mu j} b_ {j \ nu}. $$ Произведение двух элементов $ \ M_n (K) $ всегда определено и принадлежит $ \ M_n (K) $. Умножение матриц ассоциативно: если $ A \ in \ M_ {m, k} (K) $, $ B \ in \ M_ {k, n} (K) $ и $ C \ in \ M_ {n, p} (К) $, тогда $$ (AB) C = A (BC) $$ и $ ABC \ in \ M_ {m, p} (K) $. Также выполняется правило дистрибутивности: для $ A \ in \ M_ {m, n} (K) $ и $ B, C \ in \ M_ {n, m} (K) $, $$ A (B + C) = AB + AC, \ quad (B + C) A = BA + CA. \ Label {y} $$ В частности, (2) выполняется также для $ A, B, C \ in \ M_ {n} (K) $. Следовательно, $ \ M_ {n} (K) $ является ассоциативное кольцо. Если $ K $ – кольцо с единицей, то матрица $$ \ def \ E {\ mathrm {E}} \ E_n = \ begin {pmatrix} 1 & \ dots & 0 \\ \ vdots & \ ddots & \ vdots \\ 0 & \ dots & 1 \ end {pmatrix} $$ тождество кольца $ \ M_ {n} (K) $: $$ \ E_n A = A \ E_n = A $$ для всех $ A \ in \ M_ {n} (K) $.Умножение матриц не коммутативно: если $ n \ ge 2 $, для каждого ассоциативное кольцо $ K $ с единицей существуют матрицы $ A, B \ in \ M_ {n} (K) $ такие, что $ AB \ ne BA $.
Пусть $ \ alpha \ in K $, $ A = (a_ {ij}) \ in \ M_ {m, n} (K) $; произведение матрицы $ A $ на элемент (число, скаляр) $ \ alpha $ по определению является матрицей $ \ alpha A = (\ alpha a_ {ij}) $. потом $$ (\ alpha + \ beta) A = \ alpha A + \ beta A, \ quad \ alpha (\ beta A) = (\ alpha \ beta) A, \ quad \ alpha (A + B) = \ alpha A + \ beta B. $$ Пусть $ K $ – кольцо с удостоверением личности.n a_ {ij} e_ {ij}. $$ Если $ K $ – поле, то $ \ M_ {m, n} (K) $ – $ nm $ -мерный векторное пространство над $ K $, а матрицы $ e_ {ij} $ образуют основу в этом пространстве.
Блочные матрицы.
Пусть $ m = m_1 + \ dots + m_k $, $ n = n_1 + \ dots + n_l $, где $ m_ \ mu $ и $ n_ \ nu $ положительны целые числа. Тогда матрицу $ A \ in \ M_ {m, n} (K) $ можно записать в виде $$ A = \ begin {pmatrix} A_ {11} & \ dots & A_ {1l} \\ \ точки и \ точки и \ точки \\ A_ {k1} & \ dots & A_ {kl} \\ \ end {pmatrix} \ label {z} $$ куда $ A _ {\ mu \ nu} \ in \ M_ {m_ \ mu, n_ \ nu} (K) $, $ \ mu = 1, \ dots, k $, $ \ nu = 1, \ dots, l $.l A _ {\ mu i} B_ {ij}. $$ Например, если $ n = kl $, тогда $ \ M_n (K) $ можно рассматривать как $ \ M_k (\ Sigma) $, где $ \ Sigma = M_l (K) $.
Матрица $ A \ in \ M_n (K) $ вида $$ \ begin {pmatrix} A_ {1} & 0_ {12} & \ dots & 0_ {1k} \\ 0_ {21} & A_ {2} & \ dots & 0_ {2k} \\ \ точки и \ точки и \ точки и \ точки \\ 0_ {k1} & 0_ {k2} & \ dots & A_ {k} \\ \ end {pmatrix}, $$ где $ A_i \ in \ M_ {n_i} (K) $ и $ 0_ {ij} \ in \ M_ {n_i n_j} (K) $ – нулевая матрица, обозначается $ \ def \ diag {\ mathrm {diag}} \ diag [A_1, \ dots, A_k] $ и называется блочной диагональю.Имеет место следующее:
$$ \ diag [A_1, \ dots, A_k] + \ diag [B_1, \ dots, B_k] = \ diag [A_1 + B_1, \ dots, A_k + B_k], $$
$$ \ diag [A_1, \ dots, A_k] \ diag [B_1, \ dots, B_k] = \ diag [A_1 B_1, \ dots, A_k B_k], $$
при условии совпадения порядков $ A_i $ и $ B_i $ при $ i = 1, \ dots, k $.
Квадратные матрицы над полем.
Пусть $ K $ – поле, пусть $ A \ in \ M_n (K) $ и пусть $ \ det A $ – определитель матрицы $ A $. $ A $ называется невырожденным (или невырожденным), если $ \ det A \ ne 0 $.т $$ определено.
Каждая матрица из $ \ M_n (K) $ приводит к линейному преобразованию $ n $ -мерное векторное пространство $ V $ над $ K $. Пусть $ v_1, \ dots v_n $ – базис в $ V $ и пусть $ \ sigma: V \ to V $ – линейное преобразование $ V $. потом $ \ sigma $ однозначно определяется набором векторов $$ u_1 = \ sigma (v_1), \ dots, u_n = \ sigma (v_n). $$ Кроме того, $$ \ displaylines {\ sigma (v_1) = v_1 a_ {11} + \ cdots + v_n a_ {n1}, \ cr \ cdots \ cdots \ cr \ sigma (v_n) = v_1 a_ {1n} + \ cdots + v_n a_ {nn},} \ label {zz} $$ где $ a_ {ij} \ in K $. {- 1} AT $ – матрица преобразования $ \ sigma $ в базисе $ [w_1, \ точки, w_n] $.{-1} AT $ и ранги матриц $ A $ и $ B $ совпадают. Линейное преобразование $ \ sigma $ называется невырожденным, или неособые, если $ \ sigma (V) = V $; $ \ sigma $ невырождена тогда и только тогда, когда ее матрица невырожден. Если $ V $ рассматривать как пространство столбцов $ \ M_ {n, 1} (K) $, то каждое линейное преобразование в $ V $ задается левым умножение столбцов $ \ nu \ in V $ на некоторый $ A \ in \ M_n (K) $: $ \ sigma (v) = Av $, а матрица $ \ sigma $ в базисе $$ v_1 = \ begin {pmatrix} 1 \\ 0 \\ \ vdots \\ 0 \ end {pmatrix}, \ dots, v_n = \ begin {pmatrix} 0 \\ \ vdots \\ 0 \\ 1 \ end {pmatrix} $$ совпадает с $ A $.T $ – стохастические
Полиномиальные матрицы.
Пусть $ K $ – поле и пусть $ K [x] $ – кольцо все многочлены от переменной $ x $ с коэффициентами из $ K $. А матрица над $ K [x] $ называется полиномиальной матрицей. Для элементов ring $ M_n (K [x]) $ one вводит следующие элементарные операции: 1) умножение строки или столбца матрицы на ненулевой элемент поле $ K $; и 2) прибавление к строке (столбцу) другой строки (соответственно столбец) данной матрицы, умноженный на полином из $ K [x] $.Две матрицы $ A, B \ in \ M_n (K [x]) $ называются эквивалентными $ (A \ sim B) $, если $ B $ может быть получается из $ A $ конечным числом элементарных операций.
Пусть $$ N = \ diag [f_1 (x), \ dots, f_r (x), 0, \ dots, 0] \ in M_n (K [x]), $$ где а) $ f_i (x) \ ne 0 $; б) $ f_j (x) $ делится на $ f_i (x) $ при $ j> i $; и в) коэффициент перед старшим членом в $ f_i (x) $ равен 1. Тогда $ N $ равен называется канонической полиномиальной матрицей. Каждый класс эквивалентности элементов кольца $ \ M_n (K [x]) $ содержит единственную каноническую матрицу.Если $ A \ sim N $, куда $$ N = \ diag [f_1 (x), \ dots, f_r (x), 0, \ dots, 0] $$ – каноническая матрица, то многочлены $$ f_1 (x), \ точки, f_r (x) $$ находятся называется инвариантными факторами $ A $; число $ r $ совпадает с в ранг $ A $. Матрица $ A \ in \ M_n (K [x]) $ имеет обратную матрицу в $ \ M_n (K [x]) $ тогда и только тогда, когда если $ A \ sim E_n $. Последнее условие, в свою очередь, эквивалентно $ \ det A \ in K \ setminus 0 $. Две матрицы $ A, B \ in \ M_n (K [x]) $ эквивалентны тогда и только тогда, когда $$ B = PAQ, $$ где $ P, Q \ in \ M_n (K [x]) $, $ P \ sim Q \ sim E_n $.n \ in K [x] $$ существует $ F \ in \ M_n (K [x]) $ такое, что $$ \ det (xE_n-A) = f (x) $$ Такова, например, матрица $$ F = \ begin {pmatrix} 0 & 0 & \ точки & 0 & – \ alpha_0 \\ 1 & 0 & \ точки & 0 & – \ alpha_1 \\ 0 & 1 & \ точки & 0 & – \ alpha_2 \\ \ ddots & \ ddots & \ ddots & \ vdots & \ vdots \\ 0 & 0 & \ точки & 1 & – \ alpha_0 \\ \ end {pmatrix} $$ Характеристические многочлены двух аналогичные матрицы совпадают. Однако тот факт, что две матрицы имеют одинаковые характеристические полиномы не обязательно влекут за собой Дело в том, что матрицы похожи.Критерий сходства: два матрицы $ A, B \ in \ M_n (K [x]) $ подобны тогда и только тогда, когда полиномиальные матрицы $ xE_n-A $ и $ xE_n-B $ эквивалентны. Множество всех матриц из $ \ M_n (K [x]) $, имеющих заданный характеристический многочлен $ f (x) $ разбивается на конечный количество классов одинаковых матриц; этот набор сводится к единственному class тогда и только тогда, когда $ f (x) $ не имеет множественных факторов в $ K [x] $.
Пусть $ A \ in \ M_n (K) $, $ v \ in \ M_ {n, 1} (K) $, $ v \ ne 0 $, и предположим, что $ Av = \ lambda v $, где $ \ lambda \ в K $.Тогда $ v $ вызывается собственный вектор $ A $ и $ \ lambda $ называется собственным значением $ A $. An элемент $ \ lambda \ in K $ является собственным значением матрицы $ A $ тогда и только тогда, когда он является корень характеристического многочлена $ A $. Набор всех столбцов $ u \ in \ M_ {n, 1} (K) $ такое, что $ Au = \ lambda u $ для фиксированного собственного значения $ \ lambda $ $ A $ является подпространством $ \ M_ {n, 1} (K) $. Размерность этого подпространства равна дефекту (или недостатку) $ d $ матрицы $ \ lambda \ E_n – A \ $ ($ d = n-r $, где $ r $ – ранг матрицы $ \ lambda \ E_n – A $).{n_t}, \ quad \ lambda_j \ in K $$ и корни $ \ lambda_j $ различны, то имеет место подобна диагональной матрице тогда и только тогда, когда для каждого $ \ lambda_j $, $ j = 1, \ dots, t $, дефект $ \ lambda_j \ E_n – A $ совпадает с $ n_j $. В частности, каждая матрица с $ n $ различные собственные значения похожи на диагональную матрицу. Более алгебраически замкнутое поле любая матрица из $ \ M_n (K) $ похожа на некоторую треугольная матрица из $ \ M_n (K) $. Теорема Гамильтона – Кэли: если $ f (x) $ – характеристический многочлен матрицы $ A $, то $ f (A) $ – нуль матрица.
По определению минимальным многочленом матрицы $ A \ in \ M_ {n} (K) $ является многочлен $ m (x) \ in K [x] $ со свойствами:
$ \ alpha) $) $ m (A) = 0 $;
$ \ beta $) коэффициент старший член равен 1; а также
$ \ gamma $) если $ 0 \ ne \ psi (x) \ in K [x] $ и степень $ \ psi (x) $ меньше степени $ m (x) $, то $ \ фунт / кв. дюйм (A) \ ne 0 $.
Каждая матрица имеет уникальный минимальный многочлен. Если $ g (x) \ in K [x] $ и $ g (A) = 0 $, то минимальный многочлен $ m (x) $ $ A $ делит $ g (x) $.Минимальный многочлен и характеристика полином от $ A $ совпадает с последним инвариантным множителем, и, соответственно произведение всех инвариантных множителей матрицы $ x \ E_n -A $. Минимальный многочлен от $ A $ равен $$ \ frac {\ det (x \ E_n -A)} {d_ {n-1} (x)} $$ где $ d_ {n-1} (x) $ – это наибольший общий делитель несовершеннолетних (ср. Minor) порядка $ n-1 $ матрицы $ x \ E_n-A $. Матрица $ A \ in \ M_n (K) $ есть подобна диагональной матрице над полем $ K $ тогда и только тогда, когда ее минимальный многочлен – это произведение различных линейных множителей в кольце $ K [x] $.п $. Каждая нильпотентная матрица из $ M_n (K) $ похожа на некоторую треугольную матрицу с нулями на диагонали.
Список литературы
| [Be] | Р. Беллман, «Введение в матричный анализ», McGraw-Hill (1970) MR0258847 Zbl 0216.06101 |
| [Bo] | Н. Бурбаки, «Элементы математики. Алгебра: алгебраические структуры. Линейная алгебра», 1 , Addison-Wesley (1974), стр. 1; 2 (перевод с французского) MR0354207 |
| [Ga] | Ф.Р. [F.R. Гантмахер] Гантмахер, “Теория матриц”, 1 , Челси, перепечатка (1977). |
| [Ko] | А.И. Кострикин, “Введение в алгебру”, Springer (1982) MR0661256 Zbl 0482.00001 |
| [Ku] | А.Г. Курош, «Высшая алгебра», МИР (1972) Zbl 0237.13001 |
| [La] | П. Ланкастер, “Теория матриц”, Акад.Пресс (1969) MR0245579 Zbl 0186.05301 |
| [млн лет] | А.И. Мальцев, “Основы линейной алгебры”, Фримен (1963). |
| [MaMi] | М. Маркус, Х. Минк, “Обзор теории матриц и матричных неравенств”, Allyn & Bacon (1964) MR0162808 Zbl 0126.02404 |
| [Pr] | И. Б. Проскуряков, “Высшая алгебра. Линейная алгебра, многочлены, общая алгебра”, Пергамон (1965) MR0184948 Zbl 0132.25004 |
| [Ty] | A.R.I. Тышкевич, «Линейная алгебра и аналитическая геометрия», Минск (1976). |
| [Vo] | В.В. Воеводин, “Algèbre linéare”, МИР (1976) (пер. С рус.) |
Результат о канонических полиномиальных матрицах, цитируемых выше имеет естественное обобщение на матрицы над главным идеалом домены. $ (M \ times n) $ – матрица $ A $ над областью главных идеалов $ R $ форма $$ \ diag [d_1, \ dots, d_r, 0, \ dots, 0] $$ с $ d_i $, делящимся на $ d_ {i + 1} $, $ i = 1, \ dots, r-1 $, считается принадлежащим Смиту каноническая форма.Каждая матрица $ A $ над областью главных идеалов $ R $ имеет вид эквивалентно одному в канонической форме Смита в том смысле, что есть $ (m \ times m) $ – матрица $ P $ и $ (n \ times n) $ – матрица $ Q $ такие, что $ P $ и $ Q $ равны обратима в $ \ M_m (R) $ и $ \ M_n (R) $ соответственно, и такая, что $ PAQ $ принадлежит Смиту каноническая форма.

 Числа матрицы называются элементами матрицы.
Числа матрицы называются элементами матрицы.

 Матрица заполняется значениями, представляющими счет конкретного игрока в конкретный ход. Например, на третьем повороте у Даниэля было 4 очка.
Матрица заполняется значениями, представляющими счет конкретного игрока в конкретный ход. Например, на третьем повороте у Даниэля было 4 очка.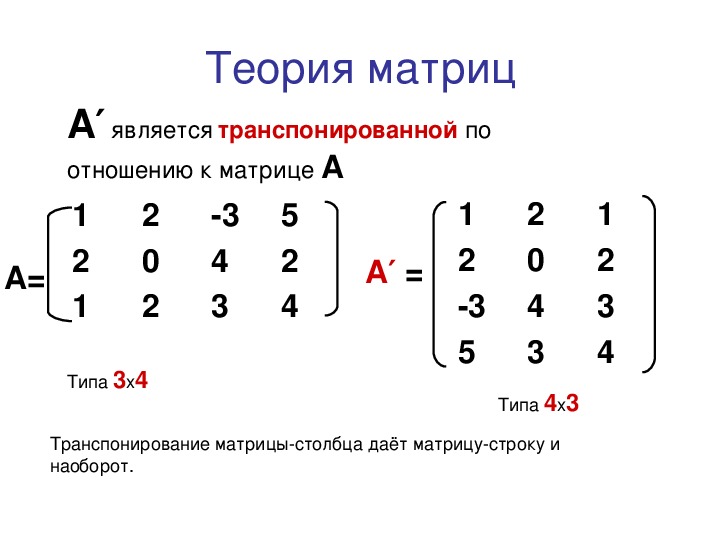 1: Собственные значения и собственные векторы
1: Собственные значения и собственные векторы