Почему магнитные силы: Что такое магнитная сила? (статья) - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Магнитные силы – Технарь

«Первые опыты по вопросу, рассматриваемому в настоящем труде, связаны с лекциями об электричестве, гальванизме и магнетизме, читанными мною прошедшей зимой».

В ту зиму 1819—1820 гг. электричеством называли силы, действующие между неподвижными зарядами (закон Кулона). К гальванизму же относились те явления, которые наблюдались при движении зарядов, т. е. при наличии тока, а к магнетизму — явления, связанные с такими загадочными предметами, как магниты и стрелки компасов, находящиеся в магнитном поле Земли. Все три вида явлений считались самостоятельными; хотя многие чувствовали, что между ними должна существовать некая связь, обнаружить ее никому не удавалось. В ту зиму Эрстед занимался тем, что пропускал гальванический ток по проводу, расположенному параллельно небольшой магнитной стрелке, в результате чего он обнаружил (фиг. 299), что:

«В данном случае стрелка изменит свое положение, и полюс, находящийся под той частью соединительной проволоки, которая ближе к отрицательному концу гальванического аппарата¹⁾, отклонится к западу».

Мы видели, что силы, действующие между заряженными частицами, являются чисто ньютоновскими. Кулоновская сила не только подчиняется третьему закону, но и совпадает по форме с гравитационной.

1) Устройство, создающее разность потенциалов с помощью химических реакций, например, батарея.

Если бы на кулоновской силе наука кончалась, то в процессе изучения гравитационных сил можно было бы ограничиться небольшой ссылкой на то, что в некоторых случаях сходные силы действуют и между так называемыми заряженными частицами. Величины этих сил различаются: помимо притяжения возможно отталкивание частиц, но в остальном эти силы неразличимы. Однако наука не кончается на силах Кулона. При дальнейшем изучении электрических сил обнаруживается столько разнообразных и тонких эффектов, что мы вынуждены не только расширять пределы применимости ньютоновской системы, но в конце концов выйти за ее рамки.

Открытие Эрстеда возвестило о начале активных исследований в этой области; в течение последующих десяти лет Ампер и Фарадей разработали теорию магнитных взаимодействий токов. Эрстеду удалось не только установить эффект воздействия движущегося заряда, или тока, на магнитную стрелку, но и обнаружить удивительное свойство этого эффекта: магнитная стрелка устанавливалась перпендикулярно направлению движения тока (фиг. 300). Более того, оказалось, что в плоскости, перпендикулярной проводу, направления стрелки образуют замкнутые окружности. Это можно проиллюстрировать с помощью простенького опыта, которым любят забавляться дети в дождливые дни. Если насыпать на бумагу мелкие металлические стружки (каждая из которых ведет себя, как маленькая магнитная стрелка), они наглядно передадут конфигурацию поля для различных систем токов.

Наиболее удивительная особенность этого открытия, которая отчасти объясняет, почему оно не было сделано ранее, связана с тем, что неподвижный заряд не оказывает никакого воздействия на магнитную стрелку. Чтобы вызвать эффект, который обнаружил Эрстед, необходимо, чтобы заряд пришел в движение. Таким образом, мы впервые встречаемся с силой, которая оказывается зависящей от движения тел, порождающих ее.

Менее чем через год (2 октября 1820 г.) Ампер опубликовал в журнале «Annals of Chemistry and Physics» работу, в которой он установил, что два токонесущих провода взаимодействуют друг с другом. Он обнаружил, что два провода, по которым текут токи в одном направлении, притягиваются, а два провода, по которым токи текут в противоположные стороны, отталкиваются. Казалось, что эти новые силы существенно отличались от электрических, так как они не зависели от величины не скомпенсированного заряда в проводах. Если имеется очень длинный токонесущий провод и параллельно ему расположен второй провод, как показано на фиг. 301, то первый провод будет притягивать второй, если ток в последнем течет в том же направлении, что и в первом, и будет отталкивать, если направление тока противоположное. Величина силы зависит от расстояния между проводами, от токов в проводах и от длины второго провода; в системе СГС выражение для силы имеет вид:

Здесь I₁ — ток в первом проводе, I₂ — ток во втором проводе, l — длина второго провода и r — расстояние между проводами. Буква с, стоящая в знаменателе (20.9), обозначает постоянную:

Она имеет размерность скорости, и сейчас мы знаем, что ее величина совпадает со скоростью света²⁾.

Чтобы дать представление о величине силы, которая действует между проводами, положим, что длина второго провода 1 см, отстоит ом от первого на расстоянии тоже 1 см, а токи в проводах равны 10 А.

2) Ответ на вопрос: «Почему собственно в знаменателе стоит значение скорости света?» (это не единственное выражение, куда входит скорость света; мы увидим позже, что она появляется во многих уравнениях, описывающих электрические и магнитные явления) будет указан при изучении электромагнитной теория света. Когда впервые было получено это соотношение, в него не входила скорость света. Просто в результате измерений токов в двух проводах и расстояния между ними было найдено, что величина силы удовлетворяет соотношению:
Значение постоянной зависит от используемой системы единиц. В системе СГС (которая, кстати, не использовалась при выводе этого соотношения) ее значение равно примерно:
Значительно позже (как мы увидим) ее отождествили с величиной 2/(скорость света)².

(Для перевода амперов в единицы СГС обратимся к табл. 10: 10 А— с единиц СГС, т. е. с статампер.) Подставляя эти величины в (20.9), получаем:

Сила 2 дин не очень велика (порядка двух, тысячных грамма), однако измерить ее легко. Для сравнения укажем, например, что если в проводе диаметром 0,1 см нескомпенсирован всего лишь один электрон на каждые 10⁶ атомов, то возникает сила 10⁸ дин (порядка 0,1 т) на каждый сантиметр провода.

Мы могли бы ожидать, что ток окажет силовое воздействие на движущийся заряд. Именно так и происходит. Сила, действующая на провод, фактически приложена к движущимся зарядам, создающим ток. Она проявляется как сила, приложенная к проводу. С помощью электронной пушки можно наглядно продемонстрировать силу, с которой провод с током действует на пучок заряженных частиц (электронов) (фиг. 302). Невооруженным глазом видно, что пучок электронов отклоняется под действием силы, вызванной током, текущим по проводу.

Качественные свойства этой силы оказываются сложными и весьма необычными. Рассмотрим провод, по которому течет ток (фиг, 303). Если электрон движется в направлении тока (а), сила отклоняет его от провода; если же он движется против тока (б), сила приближает его в проводе. Если направление движения электрона произвольно относительно провода, действующая сила все равно изменяет это направление; однако в любом случае действующая сила будет перпендикулярна скорости электрона (фиг.304), а ее величина будет прямо пропорциональна этой скорости и обратно пропорциональна расстоянию между проводом и электроном.

Таким образом, мы обнаружили силу, которая зависит не только от положения электрона, но и от его скорости и направления движения. Свойства этой силы гораздо сложнее, чем свойства сил, рассмотренных ранее. Для дальнейшего ее изучения удобно ввести понятие магнитного поля.

Метки: АмпергальванизмЗакон кулоназаряженные частицыкулоновская силакулоновские силымагнетизмМагнитные силыФарадейЭрстед

Магнитное поле и магнитная сила — одно и то же: разные аспекты и факты?

Магнитное поле и магнитная сила идут рука об руку. В этой статье мы обсудим увлекательные отношения между этими двумя.

A магнитное поле представляет собой реальную сущность, заполняющую пространство вокруг проводника с током, движущегося заряда или магнита. В дополнение к этому сила, действующая магнитным полем на движущуюся заряженную частицу, равна магнитная сила.

Как магнитное поле связано с магнитной силой

Чтобы понять точнее, если поставить статический зарядe в магнитное поле, заряд не испытывает силы, поэтому для определения магнитного поля мы берем заряд q, который движется с vэлокитy v в таком поле [рис. 1 (а)]

Если [latex]F_{m}[/latex] — сила, действующая со стороны поля на движущийся заряд, то экспериментально установлено, что;

[латекс]F_{м}\propto v[/латекс]
[латекс]F_{м}\propto q[/латекс]
[латекс]F_{m}\propto v\sin\Theta[/латекс]

Если [латекс]F_{m}[/латекс] — сила, действующая со стороны поля на движущийся заряд, то экспериментально установлено, что;

Комбинируя указанные выше три точки, получаем

[латекс]F_{m}= Bqvsin\Theta[/латекс] …………(1)

Ссылка на B пропорциональная постоянная, и она дает величина магнитного поля, Он также известен как плотность магнитного потока или магнитное поле индукция или просто магнитное поле. {\circ}= vB[ /латекс]

В этом случае [латекс]F_{m}= qvB[/латекс]

Так как [латекс]F_{m}= qvB[/латекс]

[латекс]B= \frac{F_{m}}{qv}[/latex]

If [латекс]F_{м}[/латекс] = 1N, q=1C и v = 1 м/с

Тогда [латекс]1T= \frac{N}{C(м/с)}[/latex]

[латекс]1T= \frac{N}{Ампер}[/latex]

Игровой автомат SI единица B называется тесла (Т)

Таким образом, магнитное поле в точке считается равным одному тесла, если заряд в 1 кулон при движении перпендикулярно направлению магнитного поля со скоростью 1 метр / секунду испытывает силу в 1 ньютон.

Направление магнитного поля и магнитной силы

Магнитное поле не течет в направлении своего источника, то есть тока; вместо этого он течет нормально к направлению тока. Кроме того, магнитная сила действуют перпендикулярно магнитному полю.

Направление магнитного поля можно определить с помощью правила для большого пальца правой руки. Согласно правилу большого пальца правой руки; Если держать в руке токопроводящий провод, то направление большого пальца указывает направление тока, а направление пальцев указывает направление потока магнитного поля.

Пример

Если мы возьмем стержневой магнит и поднесите его к железному гвоздю, в какой-то момент гвоздь движется в сторону магнита и прилипает к нему. Более того, он остается там, пока мы вручную не отделим его от магнита. Так почему же к магниту прилипает железный гвоздь?

Причина в том, что сила притяжения который соединяет гвоздь и магнит вместе. Эта сила прилагается магнитом к ногтю, поэтому она называется магнитной силой.

Вот один интересный вопрос, на который я хочу, чтобы вы ответили; Магнитная сила контактная силаили, другими словами, необходим ли контакт между магнитом и гвоздем, чтобы магнит притягивал гвоздь?

Когда мы медленно перемещаем магнит к железному гвоздю, и в этот момент гвоздь также начинает двигаться к магниту, это означает, что сила вступила в действие, даже когда не было контакта между магнитом и гвоздем. Следовательно, мы можем сказать, что магнитная сила не является контактная сила.

При чем здесь бесконтактный характер магнитной силы скажите нам

Он говорит нам, что в пространстве вокруг него есть невидимое поле, создаваемое магнитом, и если вы принесете какое-то ферромагнитный материал в этом поле, то он испытывает эту силу притяжения. Мы не можем видеть это поле, но оно существует.

А теперь еще один интересный вопрос: как вы думаете, сила этого поля постоянна во всей области вокруг магнита?

Позвольте мне объяснить это проще, предположим, что в каком-то месте есть работающий беспроводной маршрутизатор. Он дает нам сигнал о направлениях на некотором расстоянии. в настоящее время, чтобы подключить мобильный телефон к сети, мы хотели бы использовать его только в течение этого времени. Этот сигнал тем сильнее, чем ближе к маршрутизатору.

«Чем ближе вы подносите свой сотовый телефон к роутеру, тем сильнее сигнал».

Можно понять магнит с таким же подходом. Магнит содержит вокруг себя силовое поле. Сила этого поля больше ближе к магниту и уменьшается по мере того, как мы склонны удаляться от него.

Когда вы подносите любой ферромагнитный объект в это поле, он испытывает силу притяжения. Чем ближе мы стремимся поднести этот объект к магниту, тем большую силу он будет испытывать до тех пор, пока в какой-то момент сила не станет достаточно большой, чтобы предмет подпрыгнул к магниту.

Проблемы магнитного поля и магнитной силы

Давайте поймем взаимосвязь магнитного поля и магнитной силы, решив некоторые основные проблемы.

Проблема 1

Найти магнитное поле, приложенное к заряду 20 кулонов, движется перпендикулярно направлению магнитного поля со скоростью 2 м / с и испытывает силу 5 ньютонов.

Решение:

Учитывая магнитную силу, [латекс]F_{м}[/латекс]

Скорость заряженной частицы, [latex]v[/latex]

Магнитное поле,

Сила магнитного поля составляет 0. 125 тесла.

Проблема 2

Найти магнитную силу, испытываемую заряженной частицей с 50-кулоновским зарядом, движущейся с единичной скоростью под прямым углом к магнитному полю силой 2 тесла.

Решение:

We знать, что уравнение магнитной силы а магнитное поле

Итак, сила, которую испытывает частица, составляет 100 ньютонов.

Часто задаваемые вопросы | FAQs

Q.

Как магнитное поле и магнитная сила меняются друг с другом?

Ответ: «Магнитная сила F прямо пропорциональна сила магнитного поля. » По мере того, как магнитное поле становится сильнее, магнитная сила также увеличивается, и наоборот.

В. В какой точке магнитного поля заряженная частица испытывает наибольшее воздействие магнитной силы?

Ответ: силовые линии магнитного поля проходят через Южный полюс магнита и листьев от северного полюса. Из-за этого магнитная сила может быть наиболее сильной на любом из полюсов по сравнению с противоположным полюсом.

Q.

Влияет ли магнитное поле на магнитную силу?

Ответ: Сила, испытываемая движущимся зарядом, различна в разных точках магнитного поля.

Магнитные силы притяжения или отталкивания, вызванные движением электрически заряженных частиц, ответственны за электродвигатель и притяжение железа к магнитоподобным эффектам. Статические заряды испытывают электрическое поле, тогда как электрическое поле и магнитное поле могут испытывать движущиеся заряды. Эту магнитную силу между двумя движущимися зарядами можно понять как воздействие на один заряд магнитным полем другого.

Q.

Почему магнитная сила перпендикулярна магнитному полю?

Ответ: Если два объекта или сущности расположены под прямым углом друг к другу, это означает, что они перпендикулярны друг другу.

Так как магнитное (лоренцево) поле прямо пропорциональна [латекс]v\times B[/латекс], где v — скорость движущегося заряда, а B — напряженность магнитного поля. Как известно, векторное векторное произведение всегда находится под прямым углом друг к другу векторных множителей, сила перпендикулярна v.

Q.

Магнитная сила работает?

Ответ: Магнитные силы не действуют.

Поскольку, если Q перемещает количество [latex]dl= vdt[/latex], выполненная работа равна

Это происходит потому, что [латекс](B\times v)[/латекс] перпендикулярен v, поэтому [латекс](B\times v).v= 0[/латекс]

«Магнитные силы могут изменить направление движения заряженной частицы, но не могут ускорить или замедлить ее».

Магнитная сила – EWT

Фон

Магнетизм – это вторая часть электромагнитной силы. В предыдущем разделе была описана электрическая сила. Магнит является примером магнитной силы. Два магнита, помещенные вместе, могут притягиваться друг к другу или раздвигаться в зависимости от выравнивания положительных и отрицательных зарядов и вращения (также называемых полюсами: северный и южный). Это происходит даже тогда, когда магниты не находятся в движении.

Авторы и права: Geek3 (commons.wikimedia.org)

Магнитная сила – постоянные магниты

Магнетизм также может быть вызван электрическим током, или ток может быть вызван магнетизмом. Это связывает электрическую силу и магнитную силу, известную как закон силы Лоренца, где B — магнитное поле, а частица движется со скоростью v. Когда ток течет по проводу, он создает магнитное поле. Чем сильнее ток (больше скорость частиц), тем сильнее магнитная сила.

Магнитная сила – Электромагнетизм

Пояснение

Магнитная сила является результатом вращения частицы, создающей поперечную выходную волну. Продольная внутриволновая энергия заставляет движение одного или нескольких центров волн перемещаться к узлам стоячей волны, вводя вращение частицы в одном из двух направлений (например, по часовой стрелке, против часовой стрелки) и поперечную волну, которая движется вдоль оси вращения (перпендикулярно движению центра волны). Энергия, необходимая для движения центра волны, немного уменьшает амплитуду продольной внешней волны, поскольку энергия передается новой поперечной волне от спина. Подобно электрической силе, сила притяжения или отталкивания из-за магнетизма основана на интерференции волн, но теперь основана на интерференции поперечных волн, а не продольных волн.

Конструктивная интерференция поперечных волн – частицы одного спина увеличивают амплитуду между частицами, раздвигая частицы.

Деструктивная интерференция поперечных волн – частицы противоположного спина уменьшают амплитуду между частицами, притягивая частицы.*

Отталкивающая магнитная сила – Два электрона с одинаковым спином увеличивают поперечную амплитуду между частицами

Магнитная сила притяжения – Два электрона с противоположным спином уменьшают поперечную амплитуду между частицами*

* При отсутствии какой-либо другой силы. Два электрона имеют конструктивную интерференцию продольных волн, которая заставляет два электрона отталкиваться.

Линии магнитного поля

Когда частица вращается, создаются две поперечные волны, движущиеся вдоль оси вращения. Однако частица постоянно вращается, что влияет на направление вращения и генерируемые волны. Центры волн в частице постоянно располагаются в узле волны (минимизируя амплитуду). Это вызывает странное вращение частицы для электрона и протона (известное как вращение 1/2), а также является причиной того, что для поддержания вращения частицы постоянно требуется энергия — когда один волновой центр расположен в узле, он вытесняет другой из узла. , поэтому постоянно крутится.

Вращение частицы вызывает магнитные линии, как показано выше. Когда спин частицы конструктивный, линии сильнее в осевых направлениях (внизу слева на рисунке). Когда эти силовые линии встречаются с линиями частиц с противоположным спином, волны разрушаются и образуют новый узор (внизу справа на рисунке).

Магнитная сила – в состоянии покоя

В состоянии покоя отдельный электрон обладает магнитным моментом из-за постоянного вращения, поскольку центры волн перемещаются внутри электрона. Магнитный момент известен как магнетон Бора, который является фундаментальной физической константой. Кроме того, показано, что небольшая потеря энергии продольной волны также является силой тяжести. Магнитный момент электрона и небольшая потеря продольной энергии могут быть получены с использованием полной формы продольной внутренней и внешней энергии частиц.

Магнетизм также наблюдается в постоянных магнитах (дипольных магнитах), где сила магнетизма велика на коротких расстояниях, но быстро уменьшается с кубом расстояния. Эта сила проявляется в орбитальной силе, удерживающей электрон на орбите, которая также уменьшается в кубе расстояния. Неуравновешенные частицы, которые не компенсируют эту поперечную волну, будут испытывать силу.

Магнитная сила – в движении

Электрическое поле вызывает магнитное поле и наоборот. Когда частица движется за счет конструктивных или деструктивных продольных волн (электрическая сила), она теперь имеет скорость и направление (скорость). Скорость частицы заставляет ее вращаться быстрее – отдельные волновые центры быстрее достигают входящих продольных волн, вызывая более быстрое вращение. Теперь электроны, которые могли нейтрализовать магнитные спиновые волны в состоянии покоя, больше не компенсируются, поскольку одна или несколько частиц могут вращаться быстрее. Дополнительная энергия – это магнитная энергия в результате движения.

Магнитная сила – электромагнетизм

Уравнение

В простых терминах сила Электромагнитизм для индуцированного тока (движущийся электроны) с использованием двух групп (Q) секунды на расстоянии. (r), а также свойства массы и радиуса электрона (m _e и r _e ) показаны ниже. Это магнитная сила электрона, движущегося со скоростью (v). Это электрическая сила с v ² заменяет c ², так как это кинетическая энергия движущегося электрона.

Магнитная сила

Доказательство

Доказательство Объяснения энергетической волны для магнитной силы, а отношение к гравитации – это производные и расчеты:

Bohr Magneton
Константы гравитационного взаимодействия
Расчеты магнитных сил – см. пример расчета ниже

Два электрона на радиусе Бора (

разность скоростей 2,5E-4 м/с ) – Расчет

Расчет показан с уравнением магнитной силы в двух форматах (классические константы и волновые постоянные). Оба приводят к одному и тому же решению.

Переменные:

Q ₁ = – 1 ( электрон )
Q ₂ = – 1 ( электрон )
r = a ₀ = 5,2918E-11 м ( радиус Бора )
v = 2,5E-4 м/с

Уравнение № 1: Уравнение магнитной силы-Классический формат
Результат: 5,729E-32 Newtons (кг м/с ²)

9000 9000 #09

9000 9000 Уравнение – формат волны
Результат: 5,729E-32 ньютона (кг м/с ² )

Комментарии:
Нет никакой разницы (0,000%) с новым магнетизмом Distinti для точечных частиц, использующих любой из форматов уравнения.

Примечание: На этом сайте можно найти сводку различных расчетов магнитной силы; более подробные расчеты с инструкциями по воспроизведению этих расчетов можно найти в статье Forces .

Обзор видео 9(Maywood) Авторская рукопись; доступно в PMC 2012 Feb 1.
Опубликовано в окончательной редакции как:
Exp Biol Med (Maywood). 2011 февраль; 236(2): 132–137.
doi: 10.1258/ebm.2010.010236
PMCID: PMC3079438
NIHMSID: NIHMS262122
PMID: 21321309
Информация об авторе Информация об авторских правах и лицензии Отказ от ответственности
Сила Лоренца (сила, действующая на токи в магнитном поле) играет все более важную роль в методах отображения тока и проводимости. В этом обзоре будут обобщены несколько приложений, связанных с силой Лоренца, включая 1) магнитоакустическое изображение тока, 2) изображение с эффектом Холла, 3) изображение проводимости с помощью силы Лоренца, индуцированной ультразвуком, 4) магнитоакустическая томография с магнитной индукцией, и 5) визуализация силы Лоренца токов действия с использованием магнитно-резонансной томографии.
Ключевые слова: сила Лоренца, магнитное поле, ультразвук, магнитно-резонансная томография, проводимость, магнитоакустическая визуализация
За последние двадцать лет несколько исследовательских групп разработали методы визуализации, в которых используется сила, действующая на биотоки, когда магнитное поле присутствует. Лежащий в основе механизм знаком каждому, кто прошел вводный курс физики ¹ : провод, по которому течет ток I , имеющий длину L , и лежащий перпендикулярно магнитному полю B испытывает магнитную силу F=ILB , часто называемую «силой Лоренца». Направление силы находится под прямым углом как к проволоке, так и к магнитному полю, и может быть определено с помощью «правила правой руки». Это та самая сила, которая заставляет работать электродвигатели.
Поскольку сила Лоренца возникает в результате действия магнитного поля и вызывает механическое движение, возникающие в результате этого явления часто называют «магнитоакустикой». В биологической ткани, где проводов нет, удобнее говорить о силе Лоренца на единицу объема, F , возникающие из плотности тока Дж и магнитного поля В: F = Дж × B , где «×» обозначает векторное произведение (). В целом магнитоакустические эффекты невелики, но небольшие эффекты лежат в основе многих важных методов визуализации.
Открыть в отдельном окне
Сила Лоренца. Плотность тока Дж течет вправо, а магнитное поле B направлен из бумаги (обозначен символом ), в результате чего сила F направлена вниз.
В этом мини-обзоре я расскажу о биологических и медицинских применениях магнитоакустики. Эти методы могут быть полезны для картирования электрической активности мозга и сердца, а также для обнаружения аномальных тканей, таких как опухоли, по изменениям электрических свойств. Я сосредоточусь на магнитных силах, которые действуют на электрический ток, с акцентом на то, как эти силы можно использовать для отображения тока или проводимости. Темы, которые я не буду затрагивать, включают: вопросы безопасности, связанные с сильными магнитными полями ² ^– ⁴ , эффекты, возникающие из-за присутствия железа, которые приводят к особенно большим магнитным силам (например, частицы магнетита в магнитоактивных бактериях ⁵ ), и явления, связанные с электронным или ядерным спином (такие как ядерный магнитный резонанс).
В 1988 году Брюс Тоу и его коллеги ⁶ ^, ⁷ разработали «новый метод неинвазивного измерения низкоуровневых ионно проводимых электрических токов, протекающих в электролитах и тканях». Они пропускают переменный ток (3 кГц) силой в несколько микроампер через хомяка, помещенного в магнитное поле 0,2 Тл (). Акустический сигнал, возникающий от силы Лоренца, регистрируется с помощью микрофона и синхронного усилителя. Они заключают ⁶ «Эти эксперименты показывают, что можно неинвазивно обнаруживать наличие ионных токов, протекающих внутри проводящей среды, путем приложения магнитных полей и наблюдения за результирующими акустическими откликами. Этот принцип представляет интерес как возможная основа для нового метода неинвазивного измерения биоэлектрических токов в живых организмах». Позже компания Towe ⁸ разработала прибор, который «по сути представляет собой очень чувствительный силовой баланс, который может измерять силы Лоренца, испытываемые ионными токами, протекающими в небольших объектах при воздействии сильных осциллирующих магнитных полей». Хотя этот метод еще не получил широкого распространения для отображения тока, он демонстрирует возможность измерения магнитоакустических эффектов и иллюстрирует действующие физические принципы.
Открыть в отдельном окне
Эксперимент по магнитоакустическому обнаружению тока в хомяке. От Towe and Islamic ⁶. (© IEEE, 1988 г.)
Техника Тоу может обнаруживать приложенные переменные токи известной частоты, но можно ли ее использовать для обнаружения эндогенных токов действия в нервах и мышцах? Чтобы ответить на этот вопрос, Рот, Бассер и Виксво ⁹ провели теоретический анализ магнитоакустических явлений. Рассчитывают давление р и водоизмещение U , полученная с помощью плотности тока J в эластичной проводящей ткани, имеющей модуль сдвига G и подвергаемое воздействию магнитного поля B , начиная с уравнения Navier,
G. , начиная с уравнения Navier,
G. . ² U -∇ P + J × B = 0.
(1)
¹⁰ , в котором давление создается жидкостью (считается несжимаемой, ∇ · u = 0), а модуль сдвига возникает из-за упругих свойств коллагеновых волокон. Уравнение 1 связывает силы, возникающие при упругом сдвиге, градиентах давления и силе Лоренца. Расхождение уравнения 1 видно, что источником давления является вихрь плотности тока
∇ ² p = (∇ × Дж ) · B .
(2)
Этот результат показывает аналогию между магнитоакустической токовой визуализацией и биомагнитной токовой визуализацией ⁹ . Скручивание закона Ampere, ∇ × B = μ _O J, Управление биомагнитным полем B , продуцируемых с помощью Action Currents B , Yields
∇ ² B. = − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − g = hields

∇ 2 . _o ∇ × J ,

(3)

где μ _o — проницаемость свободного пространства. Записи магнитоакустического давления (уравнение 2) и биомагнитные измерения (уравнение 3) отображают токи действия эквивалентным образом: они оба имеют ∇ × Дж в качестве источника.

Рот и др. ⁹ получить аналитические решения для смещения, произведенного диполем тока силой q в центре проводящей сферы радиусом a . Величина смещения на поверхности сферы порядка кБ/( 4π млрд лет) . Для диполя силой q = 1 мкА·м, модулем сдвига G = 10 ⁴ Н/м ² , магнитным полем B = 1 Тл и радиусом a = 1 см, смещение поверхности очень мало, порядка 1 нм. Их анализ показывает, что «магнитоакустическая визуализация эндогенных биоэлектрических токов может быть значительно более сложной для достижения, чем можно было бы предположить из экспериментов, о которых сообщалось на сегодняшний день».

Аммари и др. ¹¹ математически изучили методы локализации магнитоакустических токовых изображений. Их подход заключается в усреднении измерений давления, взвешенных по конкретным решениям волнового уравнения, что позволяет им определять местонахождение дипольных источников. Этот метод может быть распространен на случай, когда давление измеряется только над частью границы ткани.

Han Wen ¹² ^– ¹⁴ и его коллеги разработали метод визуализации электрических свойств образца, используя то, что они называют «классическим эффектом Холла» (). Их сигнал производится ¹² «явление разделения зарядов в проводящем объекте, движущемся в магнитном поле. Это разделение зарядов является результатом действия противоположных сил Лоренца на положительные и отрицательные заряды и приводит к внешнему обнаружению напряжения …. Амплитуда напряжения определяется силой Лоренца, плотностью и подвижностью заряда». Они проверяют свой метод, применяя ультразвуковой сигнал (1 МГц) к камере с солевым раствором, содержащей образец (поликарбонатный блок), помещенный в постоянное магнитное поле силой 4 Тл. Движение образца вызывается ультразвуковой волной. Они измеряют наведенное напряжение электродами и могут получать четкие сигналы, соответствующие верхней и нижней поверхностям образца. Рот и Виксво ¹⁵ задались вопросом, является ли «эффект Холла» правильным названием физического механизма, лежащего в основе этого явления, но в любом случае этот метод представляет собой новое и важное применение сил Лоренца в биомедицинской визуализации.

Открыть в отдельном окне

Напряжение, вызванное движением. Ткань движется со скоростью v вправо в присутствии магнитного поля B , направленного из бумаги. Отрицательные ионы испытывают восходящую силу Лоренца, а положительные ионы испытывают направленную вниз силу Лоренца. Результирующее разделение зарядов создает отрицательное напряжение в верхней части ткани и положительное напряжение в нижней части.

Возможен метод визуализации с обратным эффектом Холла, когда ток возбуждается источником напряжения, а движение создается силой Лоренца (как в магнитоакустической визуализации). Вен и др. ¹² пишут, что «в обратном режиме, или в режиме обнаружения ультразвука, генератор импульсов, который использовался для привода датчика ультразвука, теперь подключен к паре электродов, которые использовались для обнаружения … напряжения в прямом режиме, и сигнал -сенсорная электроника подключена к датчику. Когда импульсный генератор генерирует импульс напряжения на электродах, [он производит] плотность тока, пропорциональную местной кажущейся проводимости. На границах раздела с изменяющейся проводимостью плотность тока становится прерывистой, как и силы Лоренца, воздействующие на токи… [что приводит к] ультразвуковым импульсам, исходящим от этих границ». Они используют этот метод для получения изображений слоев жира и мышц в беконе (). Рот и Виксво ¹⁵ проанализируйте этот обратный метод и выведите волновое уравнение для ультразвукового сигнала давления, аналогичное уравнению. 2 выше

Открыть в отдельном окне

Фотография поперечного сечения блока бекона, изображение бекона, полученное с помощью метода визуализации на эффекте Холла в обратном режиме, и эхо-ультразвуковое изображение того же поперечного сечения. Из Wen et al. ¹² . (© 1998 IEEE)

∇2p−1c2∂2p∂t2=(∇+J)·B,

(4)

, где c — скорость звука в ткани. Они пришли к выводу, что ¹⁵ «многое из того, что мы узнали из квазистатического анализа магнитоакустической визуализации, может быть применено [ко] второму [обратному] методу визуализации, предложенному Wen et al».

Вдохновленные методом Вена и др., Амальрик Монталибет и его коллеги ¹⁶ ^, ¹⁷ продолжили разработку методов измерения электропроводности с помощью силы Лоренца, индуцированной ультразвуком (). Суть их методики такая же, как описана Веном и др.: «Ионы растворов, подвергающиеся воздействию ультразвука в присутствии магнитного поля, испытывают силу Лоренца. Их движение вызывает локальную плотность электрического тока, которая пропорциональна электропроводности среды… Величина измеренного тока составляет 50 нА в солевом растворе с проводимостью 0,5 См/м. Методика позволила определить электропроводность образца свиной крови по отношению к гематокриту» ¹⁷ .

Открыть в отдельном окне

Схема экспериментальной установки для обнаружения токов, вызванных ультразвуковой силой Лоренца. Ось Oz является осью распространения ультразвука, Ox имеет ту же ориентацию, что и магнитное поле, а вдоль Oy ток взаимодействия положителен. Начало координат O расположено в фокусе преобразователя. Из Montalibet et al. ¹⁶ .

Принимая во внимание, что Montalibet et al. ¹⁶ ^, ¹⁷ применяют импульсный ультразвук в своих экспериментах, Roth и Schalte ¹⁸ разработали томографический метод для определения проводимости ткани с использованием непрерывного ультразвука. Сила и время электрического диполя, вызванного ультразвуковой силой Лоренца, определяют амплитуду и фазу преобразования Фурье изображения проводимости. Таким образом, электрические измерения на различных длинах волн и в различных направлениях эквивалентны отображению преобразования Фурье распределения проводимости в пространственно-частотном пространстве. Изображение самой проводимости затем находится с помощью обратного преобразования Фурье. В альтернативном подходе Haider et al. ¹⁹ изучили эту проблему с точки зрения свинцовых полей. Интересно, что Олаффсон и соавт. ²⁰ показали, что ультразвуковая волна сама по себе может изменять проводимость, и этот эффект, возможно, необходимо учитывать при визуализации проводимости.

Ценг и Рот ²¹ описали новую особенность силы Лоренца, индуцированной ультразвуком, в анизотропной ткани: колеблющийся электрический потенциал распространяется вместе с ультразвуковой волной. Этот потенциал аналогичен потенциалам ультразвуковых колебаний, возникающим из-за различий в инерции между положительными и отрицательными носителями заряда в коллоидных суспензиях или ионных растворах 9.0119 22 , но это вызвано другим механизмом. показаны три полуволны ультразвуковой волны, распространяющейся вправо в магнитном поле, исходящем из бумаги. Плотность тока из-за силы Лоренца отклоняется от направления z из-за анизотропии (диагональные линии указывают направление волокна). Это вызывает накопление положительного заряда там, где сходятся векторы тока, и отрицательного заряда там, где они расходятся. Заряд производит свой собственный электрический ток и потенциал, который колеблется вместе с ультразвуковой волной.

Открыть в отдельном окне

Три полудлины ультразвуковой волны, распространяющейся вправо. Магнитное поле B выходит из бумаги, а смещение u происходит вдоль оси x . Плотность тока, вызванная силой Лоренца, Дж _{Лоренца} , вращается за счет анизотропии ткани (ось волокон показана диагональными линиями), создавая плотность тока и электрический потенциал, вызванный зарядом, J _{зарядка} . От Ценга и Рота31.

Недавно Бинь Хе и его коллеги разработали магнитоакустические методы измерения импеданса ²³ ^– ³¹ . Новая особенность их метода заключается в том, что они индуцируют вихревые токи в образце с помощью магнитной индукции (закон Фарадея: изменяющееся магнитное поле индуцирует электрическое поле). «Образец находится в постоянном магнитном поле и переменном во времени магнитном поле. Изменяющееся во времени магнитное поле индуцирует в образце вихревой ток. Следовательно, образец будет излучать ультразвуковые волны силой Лоренца. Ультразвуковые сигналы собираются вокруг объекта для восстановления изображений, связанных с распределением электрического импеданса в образце» ²³ . Ли и др. ²⁵ получили изображения границ проводимости с высоким пространственным разрешением из солевых и гелевых фантомов (), что указывает на осуществимость их метода, который они называют магнитоакустической томографией с магнитной индукцией (MAT-MI). Brinker и Roth ³² проанализировали MAT-MI и обнаружили, что при визуализации нерва или мышцы электрическая анизотропия может оказывать значительное влияние на акустический сигнал и должна учитываться для получения точных изображений. Аммари и др. ¹¹ изучили методы реконструкции MAT-MI математически.

Открыть в отдельном окне

Аллен Сонг и его коллеги ³³ ^– ³⁵ предложили метод МРТ-обнаружения биотоков, называемый «визуализация эффекта Лоренца».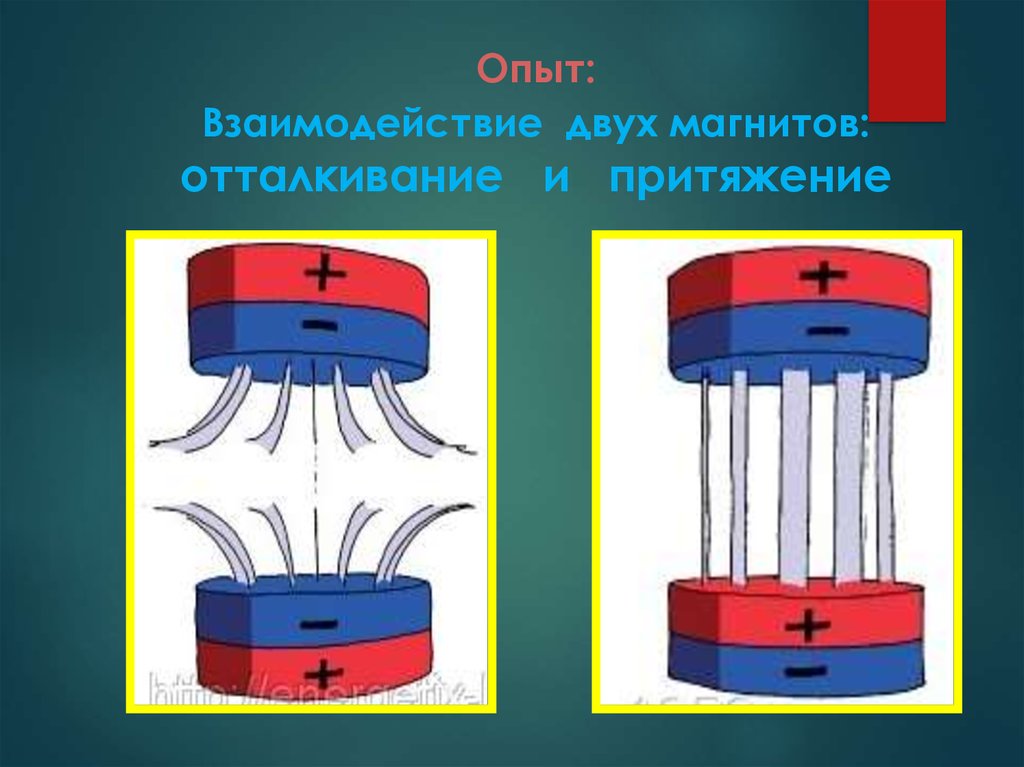 При воздействии магнитного поля на ток в организме действует сила Лоренца (). Эта сила деформирует ткань, вызывая движение нервных волокон, несущих ток. Когда присутствует градиент магнитного поля, это движение смещает нерв в область с другой напряженностью магнитного поля. Если изменение магнитного поля достаточно велико, оно вызывает артефакт в сигнале магнитного резонанса, который можно использовать для обнаружения активных нейронов. Песня и Такахаши ³³ продемонстрируйте этот метод, визуализируя движение медной проволоки в гелевом фантоме с помощью МРТ. Совсем недавно Труонг и Сонг ³⁵ применили «серию осциллирующих градиентов (с положительными и отрицательными лепестками одинаковой амплитуды и продолжительности) синхронно с нервной стимуляцией, так что нейроэлектрическая активность возникает только во время отрицательных лепестков». Они пришли к выводу, что «успешное обнаружение нейроэлектрической активности in vivo с использованием нашей техники демонстрирует, что активацию нейронов можно визуализировать неинвазивно с помощью МРТ с высоким пространственным и временным разрешением». Басфорд и др. ³⁶ также исследовали движение, вызванное силой Лоренца, во время магнитно-резонансной томографии.

Рот и Бассер ³⁷ анализируют силу Лоренца МРТ и предсказывают, что пиковое смещение u нерва радиуса a в плече радиуса b составляет

u=BJ4Ga2ln(ba),

4 (5)

, где В — магнитное поле, Дж — плотность тока и Г — модуль сдвига. Используя реалистичные параметры для человеческого срединного нерва в поле 4 Тл, они рассчитали максимальное смещение 13 нм или меньше и нашли распределение смещения, которое не локализовано вокруг нерва (4). Они предполагают, что это смещение слишком мало и диффузно, чтобы его можно было обнаружить методами МРТ. На самом деле, биомагнитные поля, создаваемые токами действия, должны приводить к большему артефакту на МРТ, чем вызванный эффектом Лоренца 9.0119 38

, и могут ли такие биомагнитные поля использоваться с МРТ для визуализации токов действия, остается открытым вопросом ³⁹ . Анализ эффекта Лоренца на ионы в растворе также вызывает споры ⁴⁰ ^, ⁴¹ , и в этом случае могут быть важны магнитогидродинамические эффекты ⁴² .
Открыть в отдельном окне
Вверху: Нерв радиусом a , лежащий в плече радиусом b . Магнитное поле находится в x направление. Ток внутри нерва течет в положительном направлении z (вне страницы), а ток в окружающих тканях течет в отрицательном направлении z . Внизу: смещение, вызванное силой Лоренца. (а) Вся рука и (б) подробный вид смещения вокруг нерва. Длина стрелок смещения увеличена для удобства просмотра. От Roth and Basser ³⁷.
Сила Лоренца — новый инструмент для получения изображений тока и проводимости в тканях. В общем случае эти силы и возникающие при этом перемещения малы. Наиболее многообещающие результаты на сегодняшний день получены при работе на высоких частотах, когда колебательная сила порождает ультразвуковые волны, которые можно обнаружить, даже если глубинное смещение очень мало.

Визуализация проводимости может быть выполнена двумя способами: с использованием осциллирующей силы Лоренца для создания ультразвуковых изображений () или с применением ультразвука и обнаружением результирующего электрического сигнала (). Пока неясно, какой из этих методов будет наиболее полезен в биомедицинской визуализации. Методы силы Лоренца для измерения тока имеют интересные аналогии с биомагнитными методами и имеют много общих сильных и слабых сторон. Эти методы обычно требуют сильных магнитных полей, которые могут быть сложными и дорогими в производстве. Тем не менее, они используют и сочетают в себе многие сильные стороны как биоэлектрических, так и биомагнитных методов с хорошо зарекомендовавшими себя методами ультразвуковой визуализации. Магнитоакустические методы измерения силы тока будут конкурировать с общепризнанными методами, такими как электрокардиограмма, магнитокардиограмма, электроэнцефалограмма и магнитоэнцефалограмма. Методы измерения электропроводности дадут ту же информацию, что и электроимпедансная визуализация.
Таким образом, все большее число методов визуализации основано на силе Лоренца, и эти методы открывают большие перспективы для получения изображений тока и проводимости.
Я благодарю Steffan Puwal и Katherine Roth за комментарии к этой рукописи. Я также благодарю Брюса Тоу, Хана Вена, Амальрика Монталибета и Сюй Ли за разрешение воспроизвести их рисунки в этом обзоре. Эта работа была поддержана грантом Национального института здравоохранения R01EB008421.
1. Хобби Р.К., Рот Б.Дж. Промежуточная физика для медицины и биологии. 4. Нью-Йорк: Спрингер; 2007. [Google Академия]

2. Шенк Дж.Ф. Безопасность сильных статических магнитных полей. J Mag Reson Imag. 2000; 12: 2–19. [PubMed] [Google Scholar]
3. Wikswo JP, Jr, Barach JP. Оценка постоянной напряженности магнитного поля, необходимой для воздействия на нервную проводимость. IEEE Trans Biomed Eng. 1980; 27: 722–723. [PubMed] [Google Scholar]
4. Sekino M, Tatsuoka H, Yamaguchi S, Eguchi Y, Ueno S. Влияние сильных статических магнитных полей на нервное возбуждение. IEEE Trans Mag. 2006;42:3584–3586. [Академия Google]
5. Франкель Р.Б., Блейкмор Р.П., Вулф Р.С. Магнетит в пресноводных магнитотактических бактериях. Наука. 1979; 203: 1355–1356. [PubMed] [Google Scholar]

6. Towe BC, Islamic MR. Магнитоакустический метод неинвазивного измерения биоэлектрических токов. IEEE Trans Biomed Eng. 1988; 35: 892–894. [PubMed] [Google Scholar]
7. Ислам М.Р., Towe BC. Реконструкция изображения биоэлектрического тока на основе магнитоакустических измерений. IEEE Trans Med Imag. 1988; 7: 386–391. [PubMed] [Академия Google]
8. БЛ Тауэр. Исследование биомагнитометра с силой Лоренца. IEEE Trans Biomed Eng. 1997; 44: 455–461. [PubMed] [Google Scholar]
9. Roth BJ, Basser PJ, Wikswo JP., Jr Теоретическая модель магнитоакустической визуализации биоэлектрических токов. IEEE Trans Biomed Eng. 1994; 41: 723–728. [PubMed] [Google Scholar]

10. Охаян Дж., Чедвик Р. С. Влияние микроструктуры коллагена на механику левого желудочка. Биофиз Дж. 1988; 54: 1077–1088. [Бесплатная статья PMC] [PubMed] [Google Scholar]
11. Аммари Х., Капдебоск Ю., Канг Х., Кожемяк А. Математические модели и методы реконструкции в магнитоакустической визуализации. Евро J Appl Math. 2009; 20:303–317. [Google Scholar]
12. Вен Х., Шах Дж., Балабан Р.С. Изображение с эффектом Холла. IEEE Trans Biomed Eng. 1998;45:119–124. [Бесплатная статья PMC] [PubMed] [Google Scholar]

13. Вэнь Х. Объемная томография на эффекте Холла — технико-экономическое обоснование. Ультразвуковая визуализация. 1999; 21: 186–200. [Бесплатная статья PMC] [PubMed] [Google Scholar]
14. Вэнь Х. Возможности биомедицинских приложений визуализации на основе эффекта Холла. Ультразвуковая визуализация. 2000; 22: 123–136. [PubMed] [Google Scholar]
15. Roth BJ, Wikswo JP., Jr Комментарии к «Визуализации эффекта Холла» IEEE Trans Biomed Eng. 1998; 45: 1294–1295. [PubMed] [Google Scholar]
16. Montalibet A, Jossinet J, Matias A. Сканирование градиентов электропроводности с помощью ультразвуковой силы Лоренца. Ультразвуковая визуализация. 2001; 23:117–132. [PubMed] [Академия Google]
17. Монталибет А., Жоссине Дж., Матиас А., Катиньол Д. Электрический ток, генерируемый ультразвуковой силой Лоренца в биологических средах. Med Biol Eng Comput. 2001; 39:15–20. [PubMed] [Google Scholar]
18. Roth BJ, Schalte K. Ультразвуковая силовая томография Лоренца. Med Biol Eng Comput. 2009; 47: 573–577. [Бесплатная статья PMC] [PubMed] [Google Scholar]
19. Haider S, Hrbek A, Xu Y. Магнито-акустоэлектрическая томография: потенциальный метод визуализации плотности тока и электрического импеданса. Физиол Изм. 2008;29: С41–С50. [PubMed] [Google Scholar]
20. Olafsson R, Witte RS, Huang S-W, O’Donnell M. Ультразвуковая визуализация плотности источника тока. IEEE Trans Biomed Eng. 2008; 55: 1840–1848. [Бесплатная статья PMC] [PubMed] [Google Scholar]
21. Tseng N, Roth BJ. Потенциал, индуцированный в анизотропной ткани силой Лоренца, индуцированной ультразвуком. Med Biol Eng Comput. 2008; 46: 195–197. [PubMed] [Google Scholar]
22. Беверидж А.С., Ван С., Диболд Г.Дж. Визуализация на основе потенциала ультразвуковых колебаний. Appl Phys Lett. 2004; 85: 5466–5468. [Академия Google]
23. Xu Y, He B. Магнитоакустическая томография с магнитной индукцией (MAT-MI) Phys Med Biol. 2005; 50: 5175–5187. [Бесплатная статья PMC] [PubMed] [Google Scholar]
24. Li X, Xu Y, He B. Магнитоакустическая томография с магнитной индукцией для визуализации электрического импеданса биологической ткани. J Appl Phys. 2006;99:066112. [PMC free article] [PubMed] [Google Scholar]
25. Li X, Xu Y, He B. Визуализация электрического импеданса на основе акустических измерений с помощью магнитоакустической томографии с магнитной индукцией (MAT-MI) IEEE Trans Biomed Eng. 2007; 54: 323–330. [PubMed] [Академия Google]
26. Xia R, Li X, He B. Магнитоакустическая томографическая визуализация электрического импеданса с магнитной индукцией. Appl Phys Lett. 2007;91:083903. [Бесплатная статья PMC] [PubMed] [Google Scholar]
27. Ma Q, He B. Исследование генерации магнитоакустического сигнала с помощью магнитной индукции и его применение для реконструкции электропроводности. физ.-мед. биол. 2007; 52: 5085–5099. [PubMed] [Google Scholar]
28. Ma QY, He B. Магнитоакустическая томография с магнитной индукцией: Строгая теория. IEEE Trans Biomed Eng. 2008; 55: 813–816. [Бесплатная статья PMC] [PubMed] [Google Scholar]
29. Li X, Li X, Zhu SN, He B. Решение прямой задачи магнитоакустической томографии с магнитной индукцией с помощью метода конечных элементов. физ.-мед. биол. 2009; 54: 2667–2682. [Бесплатная статья PMC] [PubMed] [Google Scholar]
30. Xia RM, Li X, He B. Реконструкция векторных акустических источников в томографии во временной области. IEEE Trans Med Imag. 2009; 28: 669–675. [Бесплатная статья PMC] [PubMed] [Google Scholar]
31. Xia RM, Li X, He B. Сравнительное исследование трех различных алгоритмов реконструкции изображений для MAT-MI. IEEE Trans Biomed Eng. 2010;57:708–713. [Бесплатная статья PMC] [PubMed] [Google Scholar]
32. Бринкер К., Рот Б.Дж. Эффект электрической анизотропии при магнитоакустической томографии с магнитной индукцией. IEEE Trans Biomed Eng. 2008; 55:1637–1639. [PubMed] [Google Scholar]
33. Song AW, Takahashi AM. Изображение эффекта Лоренца. Magn Res Imag. 2001; 19: 763–767. [PubMed] [Google Scholar]
34. Truong T-K, Wilbur JL, Song AW. Синхронизированное обнаружение мельчайших электрических токов с помощью МРТ с использованием визуализации эффекта Лоренца. Дж Магн Рез. 2006; 179: 85–91. [Бесплатная статья PMC] [PubMed] [Google Scholar]
35. Чыонг Т-К, Сонг А.В. Обнаружение нейроэлектрической активности при колебаниях магнитного поля (НАМО) с помощью магнитно-резонансной томографии in vivo. ПНАС. 2006; 103:12598–12601. [Бесплатная статья PMC] [PubMed] [Google Scholar]
36. Basford AT, Basford JR, Kugel J, Ehman RL. Движение в проводящих средах под действием силы Лоренца.