Некоторые сведения о векторах.
Элементы векторной алгебры. Скаляр. Вектор.
Правила сложения векторов. Скалярное и векторное произведение.
Векторами называются величины, характеризующиеся численным значением и направлением. Численное значение вектора называется модулем (модуль дает длину вектора). Модуль вектора – скаляр, причем всегда положительный.
Сложение векторов достигается, если начало второго вектора совместить с концом первого, а затем провести из начала первого в конец второго результирующий вектор.
Разностью двух векторов а и b называется такой вектор с , который в сумме с вектором b дает вектор а.
Умножение
вектора на скаляр.
В результате умножения вектора а на
скаляр α получается новый вектор b=
αа. Из определения операции умножения
вектора на скаляр следует, что всякий
вектор а можно представить в виде а=,
где- модуль вектора а,- вектор с модулем, равным единице,
имеющий такое же направление, как и а.
Проекция вектора. Рассмотрим некоторое направление в пространстве, которое мы зададим осью l. Пусть вектор а образует с осью l угол . Величина
(а – модуль вектора) называется проекцией вектора а на ось l.
Проекция вектора есть величина алгебраическая. Если вектор образует с данным направлением острый угол, то cos>0, так что проекция положительна. Если угол тупой, то cos<0, и проекция отрицательна. Когда вектор перпендикулярен к данной оси, проекция равна нулю.
Радиус-вектор
.
Радиус-вектор можно представить в виде
где
i,
j,
k
– орты осей.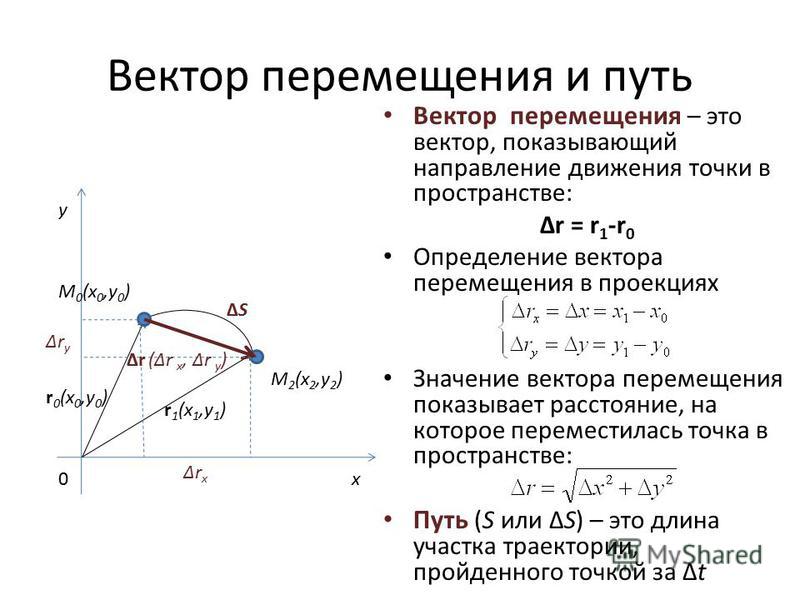
Тогда
Скалярное произведение векторов. Скалярным произведением векторов а и b называется скаляр, равный произведению модулей этих векторов на косинус угла α между ними: . Когда α острыйаb>0, при α тупом аb<0. Скалярное произведение взаимно перпендикулярных векторов равно нулю.
Векторное произведение. Векторным произведением векторов а и b называется вектор с:
а и b – модули перемножаемых векторов, α – угол между векторами, n – единичный вектор нормали
1. Кинематика
1.1. Системы отсчета. Прямолинейное движение
Механика – наука о
движении тел. Простейшей формой движения
материи является механическое движение. Механическое
движение –
это процесс изменения взаимного
расположения тел. Совокупность тел,
выделенная для рассмотрения, называется механической
системой. Какие тела следует включить в систему,
зависит от характера решаемой задачи.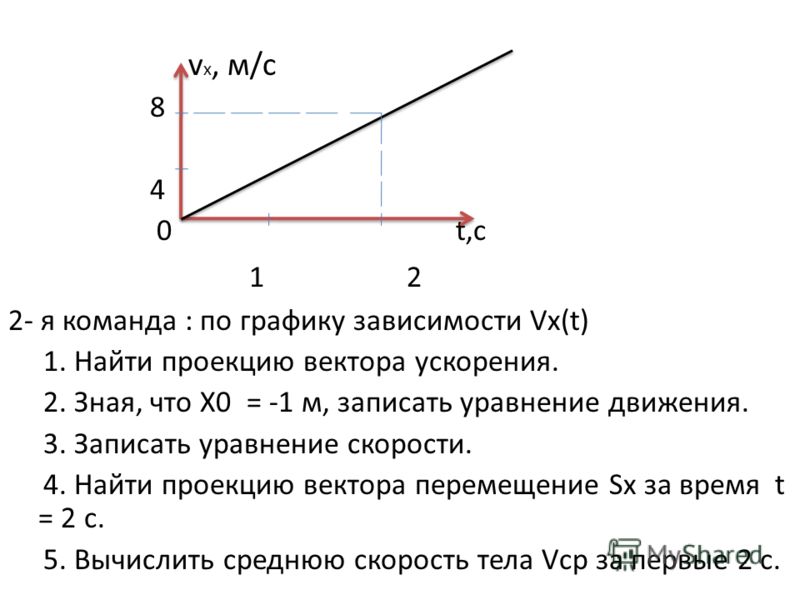
Вообще при движении тела в пространстве нужно учитывать его размеры и расположения его в пространстве. Это иногда осложняет решение задачи. Поэтому к рассмотрению вводят материальную точку. Но любое тело можно рассматривать, как систему материальных точек, то есть, иначе говоря, движение этого тела есть суперпозиция движений отдельных материальных точек, из которых состоит предоставленное тело.
Линия, вдоль которой перемещается тело, называется траекторией. По виду траектории движения разделяются на два типа: прямолинейное и криволинейное.
Материальная
точка – это тело, размерами которого
можно пренебречь в данных условиях
задачи. (При
рассмотрении движения Земли вокруг
Солнца вполне можно пренебречь размерами
Земли.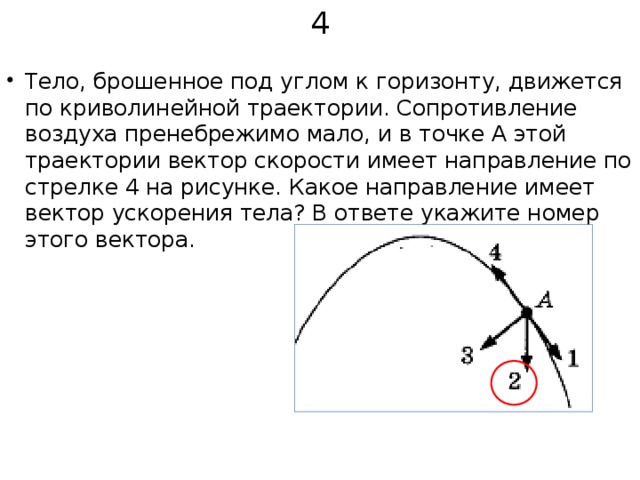 При этом описание движения
значительно упрощается – положение
Земли в пространстве можно определить
одной точкой.)
При этом описание движения
значительно упрощается – положение
Земли в пространстве можно определить
одной точкой.)
Кинематика – раздел механики, изучающий движение, безотносительно к причинам его породившим. Все системы отсчета в кинематике равноправны. В зависимости от свойств объекта кинематика распределяется на кинематику материальной точки и кинематику твердого тела. В кинематике различают прямую и обратную задачи. Прямая задача кинематики – по заданному положению тела в пространстве в любой момент времени определить скорость и ускорение также в любой момент времени.
Обратная задача – по заданному ускорению, как функции времени найти скорость и координаты или радиус-вектор частицы в любой момент времени.
Описать движение – это значит знать в любой момент времени: где находится тело; с какой скоростью оно движется; какое у него ускорение.
В зависимости от
того, каким образом задают положение
тела в пространстве, выделяют различные
способы описания движения.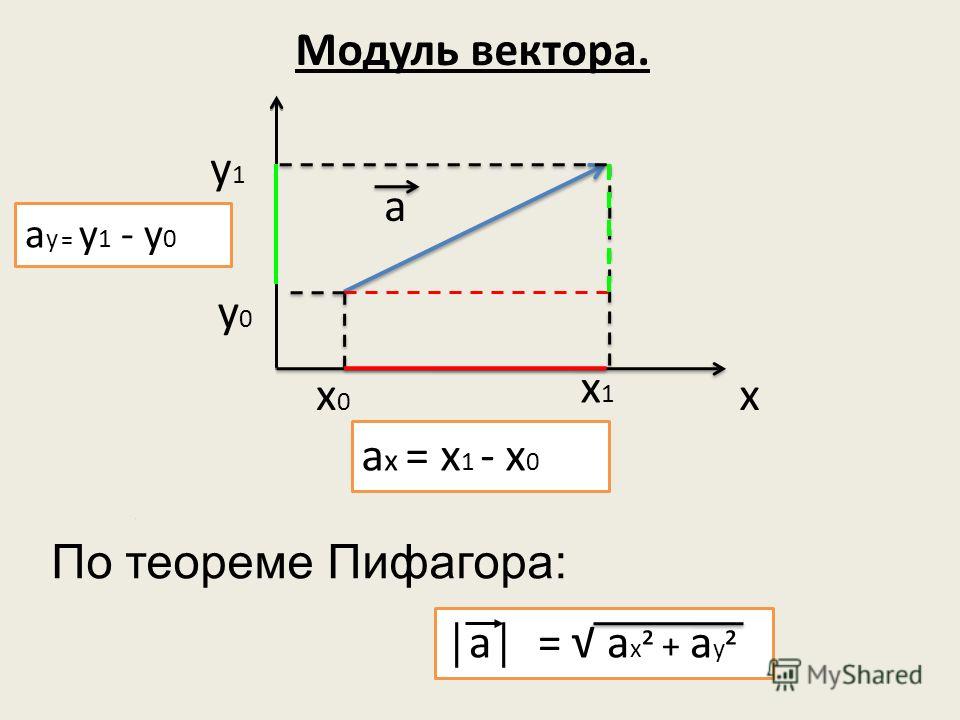
а) векторный способ. Рассмотрим прямую задачу кинематики.
В векторном способе положение точки в пространстве определяется при помощи радиус-вектора. Радиус-вектором точки А относительно, например точки О, называют вектор, начало которого находится в точке О, а конец в точке А.
Пусть за времятело переместилось вдоль некоторой траектории из точки 1 в точку 2. Вектор, соединяющий начальное и конечное положение тела называют перемещением. Из рис. видно, что перемещение тела равно приращению радиус-вектора за время:.
Любое перемещение происходит в пространстве по времени, поэтому для характеристики движения вводят понятие вектор скорости движения, которое определяется изменением перемещения по времени. Различают мгновенную и среднюю скорости.
Мгновенная
скорость –
это предел отношения перемещения тела
ко времени за которое оно совершено при
стремлении
к нулю.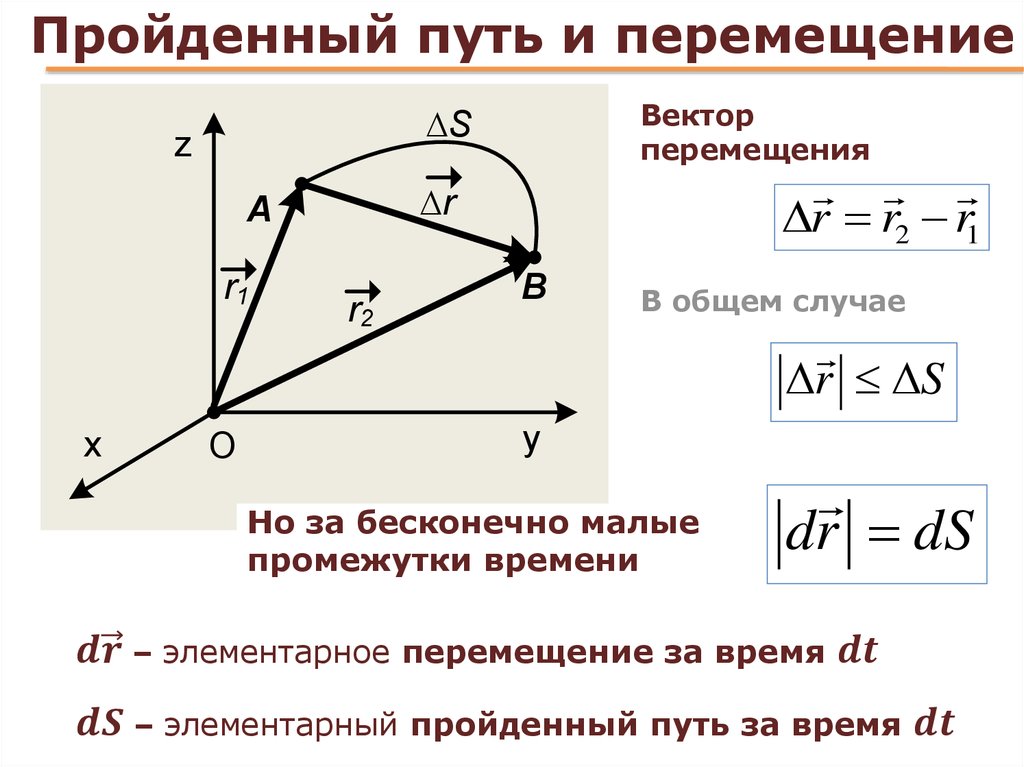 (это скорость в предоставленный
момент времени, то есть это производная
радиуса-векторапо времени):
(это скорость в предоставленный
момент времени, то есть это производная
радиуса-векторапо времени):
(1.1)
Средним вектором скорости называют отношение перемещения тела ко времени, за которое оно совершено:
(1.2)
Скорость изменения скорости называют ускорением тела.
(1.3)
Таким образом, для того чтобы задать движение тела векторным способом достаточно знать зависимость от времени радиус-вектора. При этом, местоположение тела определяется радиус-вектором, скорость тела – первой производной от радиус-вектора по времени, а ускорение – второй производной от радиус-вектора по времени.
Обратная
задача кинематики. Задано
ускорение как функция времени. Найти
скорость и радиус-вектор. Для однозначного
решения обратной задачи необходимо
задать начальные условия, то есть
начальное положение тела и его скорость
в начальный момент. Даны начальные
условия
и
Даны начальные
условия
и
Рассмотрим движение тела с постоянным ускорением .
По определению ускорение . Тогда приращение скорости, соответствующее бесконечно малому времениdt
(1.4)
Проинтегрируем обе части уравнения (1.4), с учетом начальных условий.
После интегрирования получим
Получаем, что в момент времени t
(1.5)
Так как скорость по определению , то отсюда приращение радиус вектора. Интегрируем обе части
Находим зависимость радиус-вектора от времени:
(1.6)
Соотношения (1.5) и (1.6) дают хорошо известные из школьного курса соотношения для равноускоренного движения.
Путь пройденный телом есть:
В
случае замедленного движения может
наступить момент времени
,
при котором скорость тела становится
равной нулю.
б) координатный способ.
В этом способе положение тела в пространстве в момент времени t задается при помощи его координат, например, декартовых, которые можно рассматривать как проекции радиус-вектора на соответствующие оси (см.рис. 1.2)
Первые производные от координат по времени определяют проекции вектора скорости на соответствующие координатные оси:
Тогда вектор скорости определяется как векторная сумма его компонент:
где единичные векторы (орты) вдоль осей
Модуль вектора скорости:
Аналогично находим проекции вектора ускорения:
Тогда вектор ускорения определяется как векторная сумма его компонент
Модуль вектора ускорения:
Таким образом, для
того чтобы задать движение тела
координатным способом достаточно знать
зависимость от времени его координат.
Обратная задача: заданы проекции ускорения, необходимо найти проекции вектора скорости и координаты. Начальные условия имеют вид
и
Решается аналогично векторному способу.
Например, для проекций на ось х:
.
Аналогично для у, z и , .
Средней скоростью тела называют скалярную величину, равную отношению пути S(t) ко времени t, за которое этот путь пройден.
1.2. Вращательное движение.
Основными кинематическими величинами, что характеризуют вращательное движение точки, имеется ее угловая скорость и угловое ускорение.
Угловая скорость точки в определенный момент времени определяется отношением вектора углового смещения к соответствующему промежутку времени
. (1.10)
Вектор
совпадает за направлением с вектором
и также является аксиальным вектором. За единицу угловой скорости в системе
отсчета СИ принят радиан за секунду
(рад/с).
За единицу угловой скорости в системе
отсчета СИ принят радиан за секунду
(рад/с).
Изменение вектору со временем характеризуют вектором углового ускорения,который определяют как
. (1.11)
Направление вектора углового ускорения совпадает с направлением прироста вектора . Вектор, как и, является аксиальным. За единицу углового ускорения в СИ принят радиан за секунду в квадрате (рад/с2).
Решение всех задач на вращение твердого тела вокруг неподвижной вехе аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величине на соответствующие угловые, получим соотношение для вращательного движения тела (см.табл. 1.1). const
Таблица 1.1
Основные величины и равнения | ||||||||
поступательного движения | вращательного движения | |||||||
Перемещение | Угол поворота радиус-вектора | |||||||
Пройденный путь | ||||||||
Линейная скорость | Угловая скорость | |||||||
Линейное ускорение | Угловое ускорение | |||||||
Равномерное прямолинейное движение | Равномерное вращательное движение | |||||||
Равнопеременное прямолинейное движение | Равнопеременное вращательное движение | |||||||
9.
 3. Понятие о производной вектора по скалярному аргументу
3. Понятие о производной вектора по скалярному аргументуПри рассмотрении задач кинематики и динамики мы встретимся с необходимостью вычисления производных векторов, имеющих различный физический смысл и являющихся функциями различных скалярных аргументов (времени, дуги и пр.). Поэтому в начале этого параграфа мы определим понятие производной вектора по скалярному аргументу в общем виде, не придавая конкретного физического значения вектору и аргументу.
Пусть вектор задан в какой-либо системе координат как непрерывная функция скалярного аргумента
.
П ри изменении аргумента будет меняться как модуль вектора , так и его направление. Конец вектора при изменении аргумента описывает кривую – годограф вектора . Пусть – некоторое фиксированное значение аргумента, а – его приращение. Тогда при значении аргумента вектор будет иметь другой модуль и другое направление, чем при значении аргумента, равном .
Разность
называется
приращением вектора
.
Предел отношения
при , если он существует, называется производной вектора по скалярному аргументу и обозначается через , т.е.
.
Заметим, что вектор всегда направлен по секущей годографа вектора , а значит, и вектор направлен также по секущей. При секущая займет предельное положение, совпадающее с касательной к годографу вектора . Следовательно, производная вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.
Приведем без доказательства свойства производной вектора по скалярному аргументу:
Производная постоянного по величине и направлению вектора равна
нулю.
Производная суммы векторов равна сумме производных, т.е.
.
Производные скалярного и векторного произведений векторов
соответственно определяются выражениями:
,
.
Пусть вектор задан в неподвижной прямоугольной системе координат, тогда
,
где , , – проекции вектора
на оси . Так как векторы постоянные, то
Так как векторы постоянные, то
.
С другой стороны, вектор можно записать через его проекции следующим образом:
.
Сравнивая оба выражения, найдем проекции производной вектора на координатные оси
, , .
Эти равенства можно прочитать следующим образом: проекции производной вектора на неподвижные оси равны производным от соответствующих проекций вектора.
Модуль производной определяется из равенства
.
Если модуль вектора остается постоянным при изменении аргумента , то годографом вектора будет кривая, расположенная на сфере радиуса . Следовательно, производная , направленная по касательной к годографу вектора , будет в этом случае перпендикулярна вектору .
Перейдем теперь к определению понятия скорости точки и методам ее нахождения.
Пусть в момент времени положение точки определяется радиусом-вектором , а в момент – радиусом-вектором . Вектор
будем называть
вектором перемещения за время .
Отношение вектора к промежутку времени называется средней скоростью точки за промежуток времени
.
С коростью в данный момент времени называется предел отношения сектора перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, т.е.
.
Размерность скорости будет
.
Единицами измерения могут быть , , .
Из этого определения видно, что скорость точки равна произведению радиуса-вектора точки по времени. На рис. показаны средняя скорость и скорость точки . Как следует из общей теории, скорость точки – это вектор, направленный по касательной к траектории в сторону движения точки.
Скорость точки при координатном способе задания движения. Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т.е. пусть заданы координаты точки как функции времени
,
,
.
Согласно выражению (9.8) имеем
.
Так как единичные векторы выбранной системы координат постоянны, то на основании формулы (9.11) получаем
.
На рис. показано разложение скорости на составляющие по осям координатной системы .
Таким образом, проекции скорости , , на координатные оси будут
, , ,
т.е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.
Т ак как производную по времени мы условились обозначать точкой сверху, то полученные формулы можно переписать в виде
, , . (9.12)
Модуль скорости определяется формулой
, (9.13) а направление скорости – направляющими косинусами
(9. 14)
14)
Если модуль скорости не изменяется с течением времени, то движение называется равномерным.
Задача 9.4. Движение точки задано уравнениями
, , .
Найти скорость точки.
Решение. В соответствии с выражениями (9.12) получим проекции скорости
, , .
Модуль скорости определяется формулой (9.13)
.
Направление скорости найдем, используя формулы (9.14)
Из этих соотношений видно, что точка движется равномерно , но направление скорости изменяется с течением времени.
Исследуем траекторию точки. Из первых двух уравнений движения найдем
.
Это – уравнение цилиндра радиуса , ось которого совпадает с осью .
О пустим теперь из точки на плоскость перпендикуляр и обозначим угол между осью и прямой через . Координаты точки будут
, .
Сравнивая эти соотношения с уравнениями движения, найдем
.
Таким образом, угол
изменяется пропорционально времени. Из этого следует, что прямая
равномерно вращается, а точка
в это время равномерно перемещается по
образующей .
Следовательно, точка движется по винтовой
линии. Уравнения линии в параметрической
форме совпадают с уравнениями движения,
а в координатной форме имеют вид
Из этого следует, что прямая
равномерно вращается, а точка
в это время равномерно перемещается по
образующей .
Следовательно, точка движется по винтовой
линии. Уравнения линии в параметрической
форме совпадают с уравнениями движения,
а в координатной форме имеют вид
, .
Рассмотрим теперь движение, заданное в полярных координатах, т.е пусть даны как функции времени полярный радиус и угол , определяющие положение точки.
Введем в рассмотрение единичные векторы: , направленный по радиусу-вектору в сторону возрастания , и , повернутый относительно на угол в сторону возрастания угла . Единичные векторы и могут быть представлены через единичные векторы координатных осей:
,
.
В дальнейшем нам будут нужны выражения для производных по времени от единичных векторов , .
Дифференцируя по времени, получим
. (9.15) Аналогично
.
(9. 16)
16)
Радиус вектор , определяющий положение точки, может быть представлен в виде . При движении точки меняются как модуль, так и направление радиуса-вектора , следовательно, и , и являются функциями времени. На основании равенства (9.11) имеем
.
Используя соотношение (9.15), будем иметь
.
Полученная формула дает разложение вектора скорости на две взаимно перпендикулярные составляющие: радиальную и поперечную .
Проекция скорости на радиальное и поперечное направления
и (9.17) называются соответственно радиальной и поперечной скоростями.
Модуль скорости находится по формуле
. (9.18)
Формулу (9.18) можно получить, используя связь между декартовыми и полярными координатами,
, .
Продифференцировав эти соотношения по
времени , и используя равенство (9.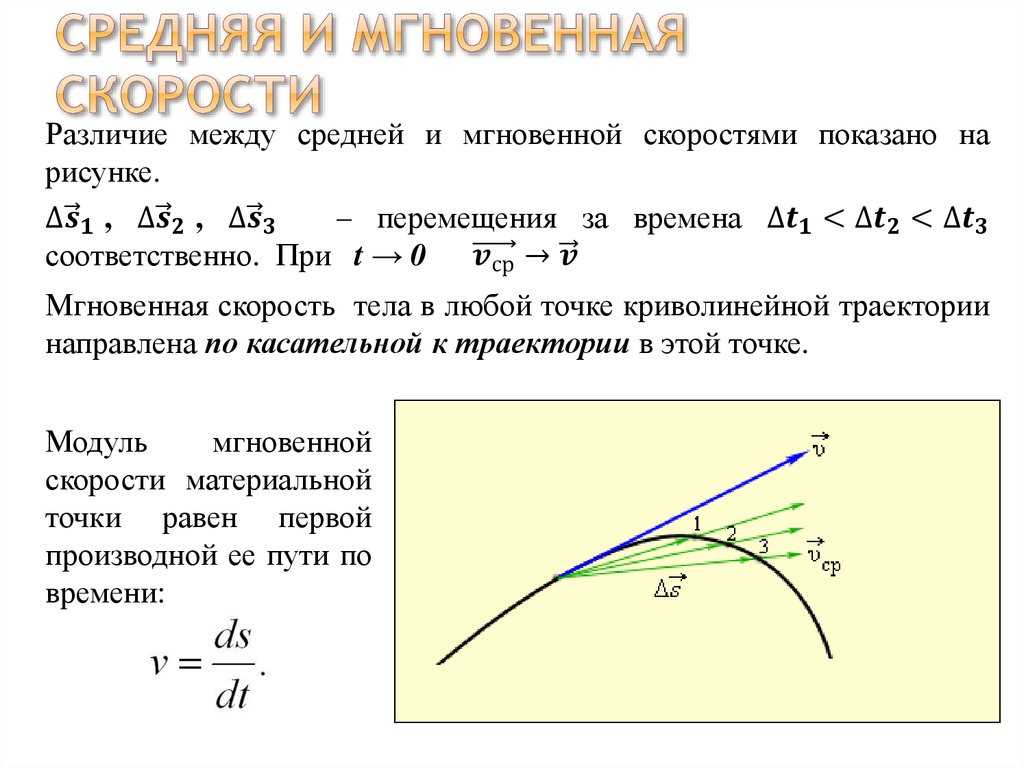 13), получим
13), получим
.
Нахождение скорости при естественном способе задания движения. Пусть точка движется по какой-либо кривой. За промежуток времени точка переместится из положения в положение . Дуга , если движение точки происходит в сторону положительного отсчета дуги, и если, если движение происходит в противоположную сторону. На основании (9.11) имеем
.
Перепишем это равенство в виде
.
Т ак как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей совпадает с направлением касательной к кривой в точке ,то
,
где – единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.
Действительно,
если ,
то вектор направлен в сторону
,
а при
вектор
направлен в сторону, противоположную
.
В обоих случаях этот вектор, а следовательно,
и его предел ,
направлены в сторону возрастания дуги
(на рис. положительное направление
отсчета дуги
выбрано вправо от начала отсчета
).
Принимая во внимание, что
,
имеем
. (9.19)
Обозначая , получим
. (9.20) Из формулы (9.20) следует, что . Очевидно, что , если движение происходит в сторону положительного отсчета дуги, и , если движение происходит в противоположную сторону.
Так как проходимый точкой путь всегда положителен, то элемент пути
и, следовательно, модуль скорости можно определить по формуле
.
презентация 🎓
1
Первый слайд презентации
Изображение слайда
2
Слайд 2: Повторение: 1.
 Какое движение называется прямолинейным равноускоренным? 2. Что называется ускорением? 3. Что характеризует ускорение? 4. Что является единицей ускорения? 5. Что понимают под мгновенной скоростью неравномерного движения?
Какое движение называется прямолинейным равноускоренным? 2. Что называется ускорением? 3. Что характеризует ускорение? 4. Что является единицей ускорения? 5. Что понимают под мгновенной скоростью неравномерного движения?
Изображение слайда
3
Слайд 3: Отвечаем на вопросы:
1 Чему равна мгновенная скорость камня, брошенного вертикально вверх, в верхней точке траектории? 2 О какой скорости – средней или мгновенной – идет речь в следующих случаях: А) пуля вылетает из винтовки со скоростью 800 м/с. Б) самолет летит из Киева в Москву со скоростью 800 км/ч В) скоростемер на тепловозе показывает 75 км/ч?
Изображение слайда
4
Слайд 4: Выведем формулу скорости
Изображение слайда
5
Слайд 5
Если в начальный момент тело покоилось, т. 2 в течение 40 c
2 в течение 40 c
t Vx Мы знаем известны по условию 0 0 20 30 40 60 график движения 10 20 30 40 50 60 50 40 30 20 10
Изображение слайда
8
Слайд 8
Построим график зависимости от времени проекции вектора скорости для случая, когда начальная скорость на равна 0.
Изображение слайда
9
Слайд 9
t
Vx
Мы знаем
известны по условию
0
10
2
12,8
график движения
10 20 30 40 50
По дороге едет автомобиль со скоростью 10 м / с.Водитель
автомобиля, увидев дорожный знак, снимающий ограничение скорости, нажал на педаль газа, в результате чего автомобиль стал двигаться с постоянным ускорением 1, 4 м / с 2. 1 2 3 4 5
13
11
9
7
5
3
1
1 2 3 4 5
13
11
9
7
5
3
1
Изображение слайда
10
Слайд 10
t Vx Мы знаем известны по условию 0 20 5 10 график движения По дороге едет автомобиль со скоростью 20 м / с.Водитель автомобиля начинает тормозить. В результате автомобиль движется с ускорением 2 м / с 2 и через 10 с останавливается. 30 25 20 15 10 5 9 10
Изображение слайда
11
Слайд 11: Графики зависимости скорости от времени
Изображение слайда
12
Слайд 12
График проекции вектора скорости может находиться под осью Ot, поскольку знак зависит проекции вектора скорости от выбора системы координат. С 5 секунды тело движется в отрицательном направлении оси X
тело движется в положительном направлении оси X
Первые 5 с тело движется в положительном направлении оси X
С 5 секунды тело движется в отрицательном направлении оси X
тело движется в положительном направлении оси X
Первые 5 с тело движется в положительном направлении оси X
Изображение слайда
13
Слайд 13: С каким по модулю ускорением движется тело?
График модуля вектора скорости не может находиться под осью Ot, поскольку модуль вектора скорости всегда положителен.
Изображение слайда
14
Слайд 14: Записать уравнение скорости от времени v х (t) для каждого участка графика
Изображение слайда
15
Слайд 15: Записать уравнение скорости от времени v х ( t ) для каждого участка графика
Изображение слайда
16
Слайд 16: Какой вид движения изображён на графике? Записать уравнение скорости от времени
Изображение слайда
17
Последний слайд презентации: презентация: Домашнее задание: § 6, упр6(1-4)
Изображение слайда
Проекции вектора на направление.
 Проекция вектора на ось
Проекция вектора на осьАлгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b – скалярное произведение векторов , |a| – модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Заданы :две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.

Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Yandex.RTB R-A-339285-1
Если имеем ось L и ненулевой вектор A B → , то можем построить вектор A 1 B 1 ⇀ , обозначив проекции его точек A 1 и B 1 .
A 1 B → 1 будет являться проекцией вектора A B → на L .
Определение 1
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. n p L A B → → принято обозначать проекцию A B → на L . Для построения проекции на L опускают перпендикуляры на L .
Пример 1
Пример проекции вектора на ось.
На координатной плоскости О х у задается точка M 1 (x 1 , y 1) . Необходимо построить проекции на О х и О у для изображения радиус-вектора точки M 1 . Получим координаты векторов (x 1 , 0) и (0 , y 1) .
Получим координаты векторов (x 1 , 0) и (0 , y 1) .
Если идет речь о проекции a → на ненулевой b → или проекции a → на направление b → , то имеется в виду проекция a → на ось, с которой совпадает направление b → . Проекция a → на прямую, определяемая b → , имеет обозначение n p b → a → → . Известно, что когда угол между a → и b → , можно считать n p b → a → → и b → сонаправленными. В случае, когда угол тупой, n p b → a → → и b → противоположно направлены. В ситуации перпендикулярности a → и b → , причем a → – нулевой, проекция a → по направлению b → является нулевым вектором.
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.
Определение 2
Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.
Числовая проекция A B → на L имеет обозначение n p L A B → , а a → на b → – n p b → a → . , мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
, мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
Определение 3
Числовой проекцией вектора a → на ось, совпадающей по направлению с b → , называют отношение скалярного произведения векторов a → и b → к длине b → . Формула n p b → a → = a → , b → b → применима для нахождения числовой проекции a → на прямую, совпадающую по направлению с b → , при известных a → и b → координатах.
Пример 3
Задан b → = (- 3 , 4) . Найти числовую проекцию a → = (1 , 7) на L .
Решение
На координатной плоскости n p b → a → = a → , b → b → имеет вид n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 , при a → = (a x , a y) и b → = b x , b y . Чтобы найти числовую проекцию вектора a → на ось L , нужно: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5 .
Ответ: 5.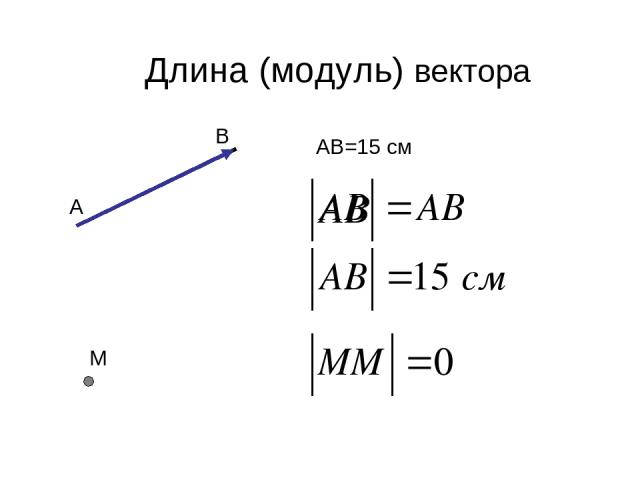
Пример 4
Найти проекцию a → на L , совпадающей с направлением b → , где имеются a → = – 2 , 3 , 1 и b → = (3 , – 2 , 6) . Задано трехмерное пространство.
Решение
По заданным a → = a x , a y , a z и b → = b x , b y , b z вычислим скалярное произведение: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Длину b → найдем по формуле b → = b x 2 + b y 2 + b z 2 . Отсюда следует, что формула определения числовой проекции a → будет: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .
Подставляем числовые значения: n p L a → = n p b → a → = (- 2) · 3 + 3 · (- 2) + 1 · 6 3 2 + (- 2) 2 + 6 2 = – 6 49 = – 6 7 .
Ответ: – 6 7 .
Просмотрим связь между a → на L и длиной проекции a → на L . Начертим ось L , добавив a → и b → из точки на L , после чего проведем перпендикулярную прямую с конца a → на L и проведем проекцию на L . Существуют 5 вариаций изображения:
Первый случай при a → = n p b → a → → означает a → = n p b → a → → , отсюда следует n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .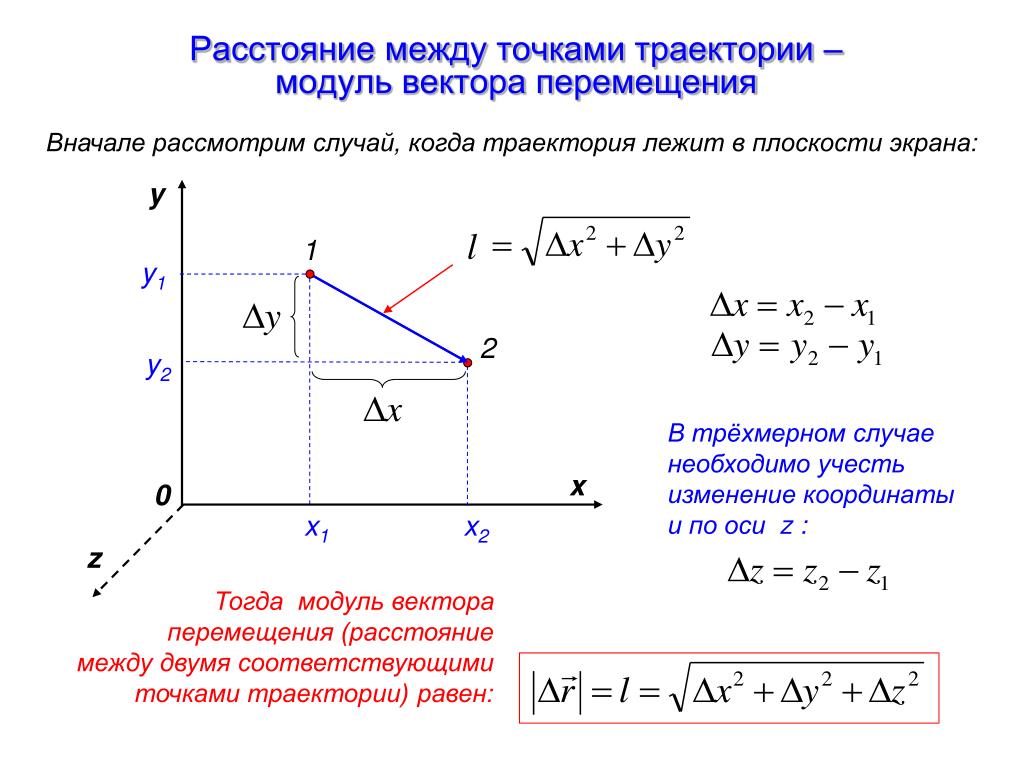 = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
= 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
По условию угол острый, тогда числовая проекция a → = длине проекции вектора a → : n p L a → = n p L a → → = 9 . Данный случай показывает, что векторы n p L a → → и b → сонаправлены, значит имеется число t , при котором верно равенство: n p L a → → = t · b → . Отсюда видим, что n p L a → → = t · b → , значит можем найти значение параметра t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .
Тогда n p L a → → = 3 · b → с координатами проекции вектора a → на ось L равны b → = (- 2 , 1 , 2) , где необходимо умножить значения на 3. Имеем n p L a → → = (- 6 , 3 , 6) . Ответ: (- 6 , 3 , 6) .
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Рис. 3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 – вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» – в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О – начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
Таким образом, в обоих случаях справедливо утверждение теоремы.
ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L – угол , кроме того сами векторные проекции образуют между собой угол , то
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.

- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A”$ – начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B”$ – конец искомого вектора. Вектор $\overline{A”B”}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A”$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B”$ (рис. 7).
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот.
Возьмем следующее координатное уравнение: x = x(t), y = y(t), z = z(t). В данном случае функция скорости будет спроецирована на три оси и будет иметь следующий вид: V(x) = dx / dt = x”(t), V(y) = dy / dt = y”(t), V(z) = dz / dt = z”(t). Отсюда следует, что для нахождения скорости необходимо брать производные. Сам же вектор скорости выражается уравнением такого вида: V = V(x) i + V(y) j + V(z) k. Здесь i, j, k являются единичными векторами координатных осей x, y, z соответственно. 2).
2).
Скорость прямолинейного равномерного движения | Физика
Представим себе, что мы имеем дело с равномерно движущимся по прямой велосипедистом, который проезжает за каждую секунду не 5 м (как в предыдущем параграфе), а, например, 10 м. При этом выбрана та же система отсчета. Тогда зависимость координаты фары от времени будет выглядеть несколько иначе, так как в правой части полученного нами выражения на месте числа 5 будет стоять число 10:
x = x0 + 10 * t.
Если при этом включить секундомер в момент времени, когда координата фары будет, например, x0 = 15 м, то мы получим следующее выражение:
x = 15 + 10 * t.
Как вы понимаете, в этом случае график движения фары будет отличаться от показанного на рис. 14. Построим новый график. Для этого, используя выражение x = 15 + 10 * t, найдем координаты фары велосипедиста в моменты времени t0 = 0, t1 = 1 с, t2 = 2 с и т. д. Полученные точки соединим прямой линией (рис. 16).
16).
Из этого графика видно, что начальная координата фары за каждую секунду увеличивается на 10 м. Значит, велосипедист движется в положительном направлении оси X. Если бы он ехал в отрицательном направлении оси X, то координата фары уменьшалась бы с течением времени. В этом случае изменение координаты было бы отрицательными и зависимость координаты фары от времени имела бы вид:
x = x0 – 10 * t.
Таким образом, в зависимости от направления движения изменение координаты тела (разность между значениями его координаты в последующий и предыдущий моменты времени) может быть как положительной, так и отрицательной величиной. Если же конечная и начальная координаты тела совпадают, то изменение координаты этого тела равно нулю.
В зависимости от направления движения изменение координаты тела может быть как положительной, так и отрицательной величиной.
В общем случае зависимость координаты тела от времени для прямолинейного равномерного движения имеет вид:
x = x0 + v * t.
Закон прямолинейного равномерного движения содержит постоянную величину v. Как вы понимаете, она численно равна изменению координаты тела за единицу времени.
Если тело движется равномерно прямолинейно, то физическую величину v, численно равную изменению его координаты за единицу времени, называют значением скорости равномерного прямолинейного движения.
В СИ единица скорости — метр в секунду (сокращенное обозначение — м/с).
Значение скорости показывает, насколько быстро изменяет свою координату равномерно движущееся тело, т. е. какое расстояние проходит оно за каждую секунду. В рассмотренных примерах о движении велосипедиста скорость v имела значения 5 и 10 м/с. Ясно, что для других тел она может принимать другие значения.
Ранее мы рассматривали примеры, в которых скорость муравья составляла 2 см/с. Кроме того, вы знаете, что скорость, например, автомобилей, поездов, самолетов измеряют в километрах в час (100 км/ч, 60 км/ч, 900 км/ч). Так как СИ устанавливает единицу этой физической величины метр в секунду (м/с), другие единицы могут быть приведены к общепринятой единице через коэффициенты. Например, 1 м/с = 3,6 км/ч (если автомобиль движется по дороге со скоростью 30 м/с, то его скорость составляет 30 * 3,6 = 108 км/ч).
Например, 1 м/с = 3,6 км/ч (если автомобиль движется по дороге со скоростью 30 м/с, то его скорость составляет 30 * 3,6 = 108 км/ч).
Из определения значения скорости равномерного прямолинейного движения можно сделать важные выводы.
- Если тело движется в положительном направлении оси X, то с течением времени его координата увеличивается. Значит, изменение координаты x положительно. В этом случае значение скорости v > 0.
- Если тело движется в отрицательном направлении оси X, то с течением времени его координата уменьшается. Значит, изменение координаты x отрицательно. В этом случае значение скорости v < 0.
- Если тело покоится, т. е. его координата остается постоянной, то значение скорости v = 0.
Получается, что скорость — это величина, которая не только характеризует быстроту изменения координаты тела, но и показывает направление движения тела в выбранной системе отсчета. Поэтому скорость принято изображать в виде отрезка со стрелкой в конце. Направление стрелки совпадает с направлением движения тела. При этом чем больше значение скорости, тем больше длина отрезка, изображающего скорость.
Направление стрелки совпадает с направлением движения тела. При этом чем больше значение скорости, тем больше длина отрезка, изображающего скорость.
Величины, которые характеризуются не только числовым значением, но и направлением, называют векторными. Таким образом, скорость — вектор. Векторы обозначаются буквой со стрелкой над ней. Например, скорость обозначают символом .
Для изображения вектора скорости тела поступают следующим образом. Вначале выбирают отрезок, длина которого соответствует модулю единичной скорости 1 м/с, – единичный отрезок (рис. 17). Теперь, чтобы изобразить скорость, равную, например, 5 м/с, нужно нарисовать отрезок, длина которого в 5 раз больше единичного. Чтобы изобразить скорость, равную 1/3 м/с, нужно начертить отрезок, длина которого в 3 раза меньше единичного.
Число, выраженное в единицах скорости и равное отношению длины отрезка, изображающего данную скорость, к длине отрезка, изображающего единичную скорость, называют модулем скорости.
Модуль скорости принято записывать в виде ||. В приведенном примере .
Модуль скорости, в отличие от ее значения, всегда положителен или равен нулю.
Например, модуль скорости, имеющей значение -5 м/с, равен 5 м/с.
Подведем итоги.
Если значение скорости положительно, то скорость направлена в положительном направлении оси X. В этом случае ее изображают отрезком со стрелкой. Направленной в положительном направлении оси X. Так направлен вектор скорости велосипедиста на рис. 18. Наоборот, если значение скорости отрицательно, то она направлена в отрицательном направлении оси X. Тогда ее изображают отрезком со стрелкой, направленной в отрицательном направлении оси X (вектор скорости бегуна на рис. 18).
Длины векторов изображаются на рисунке в масштабе. Так, на рис. 18 длина вектора скорости велосипедиста в два раза больше длины вектора скорости бегуна. Поскольку скорость измеряют в метрах в секунду (м/с), длина отрезка со стрелкой (вектор скорости) не имеет отношения к расстояниям между телами, которые измеряют в метрах.
Отметим особо, что если тело покоится, то его координата в выбранной системе отсчета не изменяется. В этом случае говорят, что скорость движения тела равна нулю.
Представив закон движения тела в аналитическом виде x = x0 + v * t, в котором известны начальная координата x0 и значение скорости v, мы полностью описали прямолинейное равномерное движение тела.
Теперь можно сформулировать приведенное ранее определение равномерного прямолинейного движения иначе.
Если координата тела изменяется с течением времени по закону x = x0 + vt, при этом x0 и v не зависят от времени, то тело движется вдоль оси X равномерно.
Постоянная величина v в этом выражении равна значению скорости равномерного прямолинейного движения вдоль оси X.
Эта формулировка определения равномерного прямолинейного движения является более удобной при решении конкретных задач.
Итоги
Зависимость координаты тела от времени при равномерном прямолинейном движении имеет вид: x = x0 + vt, где x0 — начальная координата тела, v — значение скорости равномерного прямолинейного движения, t — рассматриваемый момент времени, x — координата тела в момент времени t.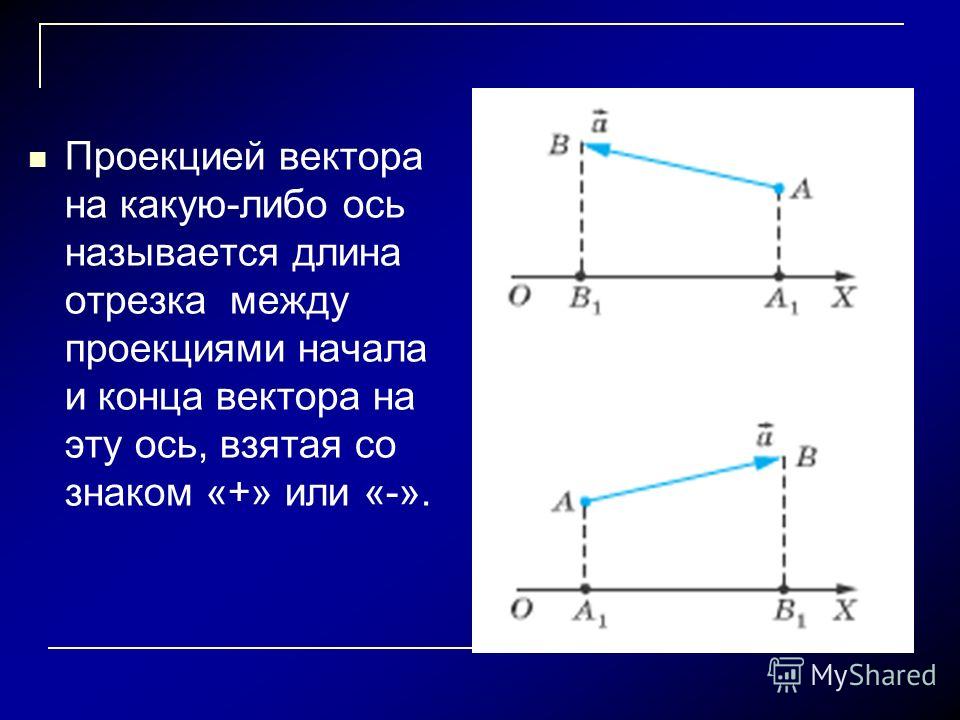
Если тело движется равномерно прямолинейно, то физическую величину v, численно равную изменению его координаты за единицу времени, называют значением скорости равномерного прямолинейного движения.
В СИ единица скорости — метр в секунду (м/с).
Скорость — векторная величина, которая характеризуется не только своим модулем, но и направлением.
Если значение скорости положительно, то скорость направлена в положительном направлении оси X. Если же значение скорости отрицательно, то скорость направлена в отрицательном направлении оси X.
Вопросы
- В чем заключается аналитический способ описания движения? Запишите закон прямолинейного равномерного движения в аналитической форме.
- Что такое значение скорости равномерного прямолинейного движения? Что оно характеризует?
- Что означает утверждение, что движение тела описано полностью? Приведите пример.
- Можно ли однозначно утверждать, что тело покоилось в течение промежутка времени от момента времени t = 0 с до момента времени t = 10 с, если изменение его координаты за этот промежуток времени равно нулю? Приведите примеры возможных ситуаций.

Упражнения
- Найдите зависимости координаты тел от времени, используя для этого графики движения тел на рис. 19. Объясните, в каком направлении двигалось тело в выбранной системе отсчета в этих случаях. Движется ли тело в случае в?
- Постройте графики движения тел, используя следующие законы движения: а) x = 3 +2t; б) x = 30 – 5t; в) x = 7. В этих законах время выражено в секундах, а расстояние – в метрах.
- Объясните, в какую сторону двигались тела (если двигались) в выбранной системе отсчета и на сколько изменялись их координаты за каждую секунду в упражнениях 1 и 2.
- Чему равны значения скоростей тел, зависимости координат которых от времени даны в упражнениях 1 и 2.
- Выразите в метрах в секунду значения скоростей: 3,6; 36; 72 км/ч.
- Выразите в километрах в час значения скоростей: 10; 20; 25 м/с.
- Запланируйте и проведите эксперимент по определению скорости течения ручья на его прямолинейном участке длиной 10 метров, используя закон прямолинейного равномерного движения.

Нормальное, тангенциальное и полное ускорения – Справочник
Виды ускорения в биомеханике нормальное полное тангенциальное
Движение тела характеризуется скоростью и ускорением, которые могут изменяться во времени. Пусть материальная точка движется по плоской криволинейной траектории с переменной по величине и направлению скоростью (рис. 4). Для характеристики степени криволинейности вводится понятие радиуса кривизны в данной точке траектории.
Радиусом кривизны R траектории называют радиус окружности, которая сливается с криволинейной траекторией на бесконечно малом ее участке.
В данной точке траектории касательная всегда перпендикулярна радиусу кривизны.
Пусть и скорость, и ускорение меняются по величине и направлению.
Мы знаем, что ускорение тела при движении есть.
Вектор скорости можно представить как произведение модуля скорости и некоторого единичного вектора, сонаправленного с вектором линейной скорости, направленного по касательной к траектории.
Таким образом, полное ускорение материальной точки при криволинейном движении можно представить в виде суммы двух слагаемых. Первое слагаемое.
Вектор направлен по касательной к траектории и называется тангенциальным или касательным ускорением. Его модуль равен, поэтому характеризует быстроту изменения скорости криволинейного движения только по величине, так как вектор не изменяется.
Следовательно, можно заключить, что — тангенциальное ускорение, характеризует изменение скорости по величине и направлено по касательной к траектории.
Второе слагаемое называется нормальным ускорением.
Так как вектор сонаправлен с вектором, который определяет изменение направления вектора линейной скорости, то он характеризует изменение скорости криволинейного движения по направлению.
Перпендикулярно скорости, направлено вдоль радиуса кривизны траектории к центру окружности.
Полное ускорение материальной точки при криволинейном движении характеризует быстроту изменения скорости как по величине, так и по направлению (рис. 6).
6).
Вектор направлен по касательной к траектории и называется тангенциальным или касательным ускорением.
Studopedia. ru
07.08.2019 5:29:41
2019-08-07 05:29:41
Источники:
Https://studopedia. ru/1_95015_normalnoe-tangentsialnoe-i-polnoe-uskoreniya. html
Тангенциальное, нормальное и полное ускорение » /> » /> .keyword { color: red; }
Виды ускорения в биомеханике нормальное полное тангенциальное
Криволинейное движение всегда происходит с ускорением, поскольку если даже величина скорости не изменяется, происходит изменение ее направления.
Вектор ускорения Направлен параллельно вектору изменения скорости в сторону вогнутости траектории (рисунок 1.4).
Рисунок 1.4 – Направление вектора ускорения.
В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.
Вектор полного ускорения тела при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости – Тангенциальное ускорение и перпендикулярно скорости – Нормальное ускорение.
Рисунок 1.5 – Касательное и нормальное ускорения.
Тангенциальное ускорение характеризует быстроту изменения величины скорости при криволинейном движении по величине, а нормальное ускорение – быстроту изменения направления вектора скорости.
Как видно из рисунка 1.5, Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:
Тангенциальное уско рение характеризует быстроту изменения величины скорости при криволинейном движении по величине, а нормальное ускорение быстроту изменения направления вектора скоро сти.
Poznayka. org
24.01.2017 15:01:09
2017-01-24 15:01:09
Источники:
Https://poznayka. org/s80023t1.html
Ускорение. Тангенциальное, нормальное и полное ускорение » /> » /> .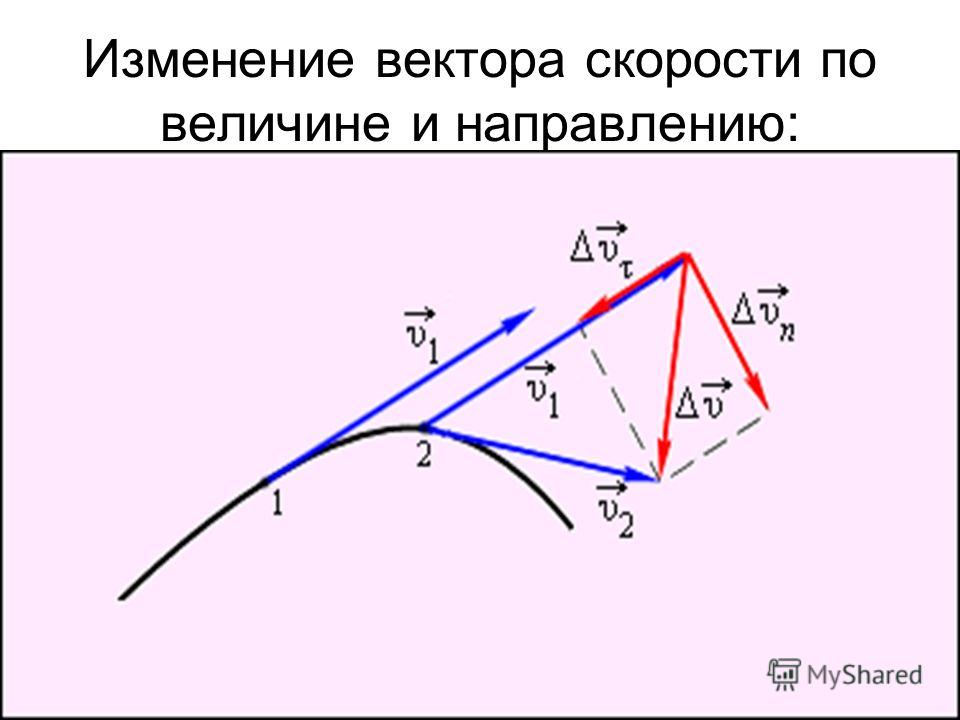 keyword { color: red; }
keyword { color: red; }
Виды ускорения в биомеханике нормальное полное тангенциальное
В общем случае, при движении материальной точки по криволинейной траектории вектор скорости может меняться по Величине и направлению. Пусть за малый промежуток времени точка переместилась из положения А в положение В и при этом скорость ее изменилась от до. Перенесем вектор скорости в точку В методом параллельного переноса, тогда – изменение вектора скорости за время движения тела из А в В.
Векторная величина, равная пределу, к которому стремится отношение при неограниченном уменьшении промежутка времени называется Ускорением. Вектор ускорения равен первой производной вектора скорости по времени:
Как всякий вектор, ускорение можно представить в виде суммы проекций на оси (x, y, z):
Модуль вектора ускорения
Единица измерения ускорения – [м/c 2 ]. Вектор ускорения сонаправлен с вектором изменения скорости. Пусть за время скорость материальной точки изменилась по величине и по направлению. Тогда вектор изменения скорости можно представить в виде суммы двух векторов, один из которых характеризует изменение скорости по направлению, другой – изменение скорости по величине.
Вектор ускорения сонаправлен с вектором изменения скорости. Пусть за время скорость материальной точки изменилась по величине и по направлению. Тогда вектор изменения скорости можно представить в виде суммы двух векторов, один из которых характеризует изменение скорости по направлению, другой – изменение скорости по величине.
В этом случае вектор ускорения также можно представить в виде суммы двух векторов ( и ) где – Нормальное ускорение, характеризующее быстроту изменения скорости по Направлению, а – Тангенциальное ускорение, характеризующее быстроту изменения скорости по Величине.
| Тангенциальное ускорение удобно рассмотреть на примере неравномерного прямолинейного движения. При этом скорость изменяется только по величине , поэтому : Т. е. |
В векторной форме, где – единичный вектор, сонаправленный с вектором скорости.
Нормальное ускорение удобно рассмотреть на примере равномерного движения по окружности.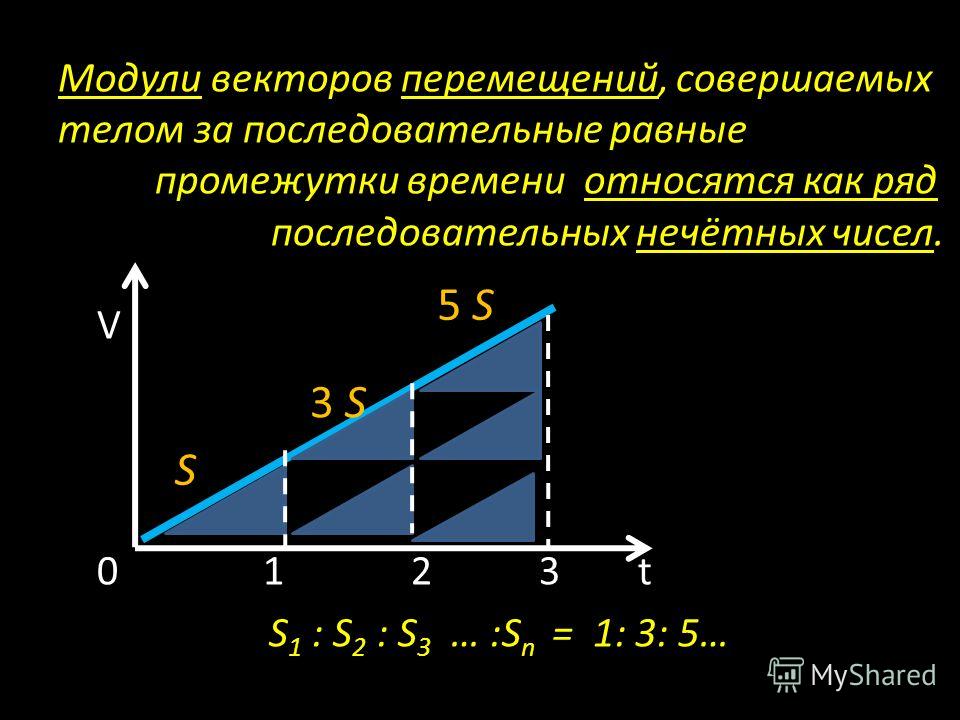 При этом.
При этом.
Перенесем вектор скорости из точки А в точку В методом параллельного переноса
Если время перемещения точки из А в В мало, то малый угол поворота радиуса-вектора точки может быть записан следующим образом: ,где АВ – длина дуги окружности радиуса R, – угол в радианах. Тогда,
| . |
В векторной форме: где – единичный вектор, направленный по радиусу к центру кривизны траектории в данной точке, т. е. перпендикулярно вектору скорости (рис. 1.8).
Таким образом, вектор полного ускорения материальной точки равен
А модуль вектора полного ускорения :
На рис. показано направление векторов при ускоренном и замедленном движении. Модуль вектора Тангенциального ускорения положителен при ускоренном движении (рис. 1.9, А) и отрицателен при замедленном движении (рис. 1. 9, Б). Модуль вектора Нормального ускорения всегда положителен.
9, Б). Модуль вектора Нормального ускорения всегда положителен.
Ньютон дал более общую формулировку закону инерции как первому закону движения: всякое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на него силы не изменят это состояние.
В жизни этот закон описывает случай когда, если перестать тянуть или толкать движущееся тело, то оно останавливается, а не продолжает двигаться с постоянной скоростью. Так автомобиль с выключенным двигателем останавливается. По закону Ньютона на катящийся по инерции автомобиль должна действовать тормозящая сила, которой на практике является сопротивление воздуха и трение автомобильных шин о поверхность шоссе. Они-то и сообщают автомобилю отрицательное ускорение до тех пор, пока он не остановиться.
Недостатком данной формулировки закона является то, что в ней не содержалось указания на необходимость отнесения движения к инерциальной системе координат. Дело в том, что Ньютон не пользовался понятием инерциальной системы координат, – вместо этого он вводил понятие абсолютного пространства – однородного и неподвижного, – с которым и связывал некую абсолютную систему координат, относительно которой и определялась скорость тела. Когда бессодержательность абсолютного пространства как абсолютной системы отсчета была выявлена, закон инерции стал формулироваться иначе: относительно инерциальной системы координат свободное тело сохраняет состояние покоя или равномерного прямолинейного движения.
Когда бессодержательность абсолютного пространства как абсолютной системы отсчета была выявлена, закон инерции стал формулироваться иначе: относительно инерциальной системы координат свободное тело сохраняет состояние покоя или равномерного прямолинейного движения.
studopedia. org — Студопедия. Орг — 2014-2022 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.014 с) .
Нормальное ускорение удобно рассмотреть на примере равномерного движения по окружности. При этом.
Модуль вектора ускорения
Таким образом, вектор полного ускорения материальной точки равен.
Studopedia. org
02.11.2017 1:58:21
2017-11-02 01:58:21
Источники:
Https://studopedia. org/8-64648.html
ньютоновская механика – Может ли величина быть отрицательной?
Задавать вопрос
спросил
Изменено 3 года, 7 месяцев назад
Просмотрено 6к раз
$\begingroup$
Мой учитель сказал, что величина — это положительное значение этой величины или модуль этой величины.
он также сказал, что векторные величины имеют как величину, так и направление, а скалярные величины имеют только величину и, следовательно, всегда положительны.
Однако гравитационная потенциальная энергия всегда отрицательна, за исключением того, что она равна 0 (на бесконечности).
Но гравитационная потенциальная энергия также является скалярной величиной.
Значит, величина отрицательная?
Я подумал об этом, так это о том, что его величина отрицательна.
Возьмем в качестве примера любую векторную величину, скажем, скорость.
Если тело движется со скоростью -5 м/с, это означает, что оно движется со скоростью 5 м/с в направлении, противоположном положительному. А здесь тело каждую секунду проходит 5 метров, хотя его скорость -5 м/с.
Но если тело имеет потенциальную энергию -40 Дж, это не означает, что оно имеет реальную потенциальную энергию 40 Дж, но имеет противоположное направление, поэтому величина должна быть отрицательной
Скажите, пожалуйста, магнитуда будет положительной или отрицательной?
- ньютоновская механика
- энергия
- терминология
- потенциальная энергия
- определение
$\endgroup$
2
$\begingroup$
Скалярные величины могут быть отрицательными. Вместо того, чтобы говорить, что «скалярные величины имеют только величины», лучше было бы описать, что скалярную величину можно описать, используя только одно число для каждой точки пространства. Это число может быть положительным или отрицательным.
Вместо того, чтобы говорить, что «скалярные величины имеют только величины», лучше было бы описать, что скалярную величину можно описать, используя только одно число для каждой точки пространства. Это число может быть положительным или отрицательным.
Напротив, векторную величину нельзя описать, используя только одно число для каждой точки пространства. В трехмерном пространстве нам нужно 3 числа на точку пространства, чтобы описать векторную величину.
Слово «величина», независимо от того, применяется ли оно к скаляру, вектору или чему-то еще, обычно относится к неотрицательному числу . Иногда он используется для обозначения абсолютного значения скаляра, а иногда используется для обозначения нормы (например, длины) вектора.
Подводя итог, вот как обычно используются слова:
Скаляр обычно относится к одиночному элементу числового поля (или к одному элементу на точку в пространстве), такому как действительное число (которое может быть положительным или отрицательным) или даже комплексное число (это обычное дело в контексте квантовой физики).

Величина обычно относится к неотрицательному действительному числу.
Настоящим виновником здесь являются утверждения вроде «у вектора есть и величина, и направление, а у скаляра есть только величина». Последняя часть этого утверждения либо (1) налагает нетрадиционное ограничение на использование слова «скаляр», либо (2) проявляет нетрадиционную свободу в использовании слова «величина».
$\endgroup$
$\begingroup$
Это очень распространенное заблуждение среди студентов-физиков, поэтому позвольте мне посмотреть, смогу ли я привести несколько примеров, которые сделают различие более ясным.
ВЕКТОРЫ – это величины, имеющие величину и направление. Величина скорости равна скорости, которая всегда положительна.
- Примеры : Как вы указали, одним из простейших примеров векторной величины является скорость.
 Другими хорошими примерами являются силы и импульсы.
Другими хорошими примерами являются силы и импульсы. - Для вектора $\vec{v}$ величина вектора, $|\vec{v}|$ – это длина вектора. Эта величина всегда положительна! Величина скорости, например, есть скорость, которая всегда положительна. (Если автомобиль движется со скоростью 95 миль в час, радар зарегистрирует скорость автомобиля как 95 миль в час независимо от того, движется ли автомобиль назад, вперед или боком). Точно так же величина силы всегда является положительным числом, даже если сила направлена вниз. Если у вас есть $7$ N сил, направленных вверх, вниз, влево и вправо, величина всех этих сил составляет всего $7$ N. Еще раз, Величина вектора — это его длина, которая всегда положительна.
SCALARS , с другой стороны, работают совершенно иначе. Скалярные величины имеют числовое значение и знак.
Примеры : Температура — хороший простой пример. Другие включают время, энергию, возраст и рост.

Для скаляра $s$ абсолютное значение скаляра $|s|$ представляет собой просто то же числовое значение, что и раньше, с обрезанным отрицательным знаком (если он существовал). Мы не говорим (или, по крайней мере, не должны!) говорить о “величине” скаляра! Концептуально я рекомендую думать об абсолютном значении скаляра и величине вектора как о совершенно разных вещах. Если на улице $-3°F$, то говорить о величине температуры не имеет смысла. Однако вы можете вычислить абсолютное значение температуры как $3°F$.
Обратите внимание, что некоторые скалярные величины не имеют смысла как отрицательные числа: возраст человека является скалярной величиной, и на самом деле мы не говорим об отрицательном возрасте. Другим примером является температура, измеряемая по шкале Кельвина.
Итак, чтобы ответить на ваш вопрос, энергия является скаляром, поэтому у нее нет величины. Если тело имеет потенциальную энергию -40 Дж, то оно просто на 40 Дж меньше, чем ваша произвольная нулевая точка.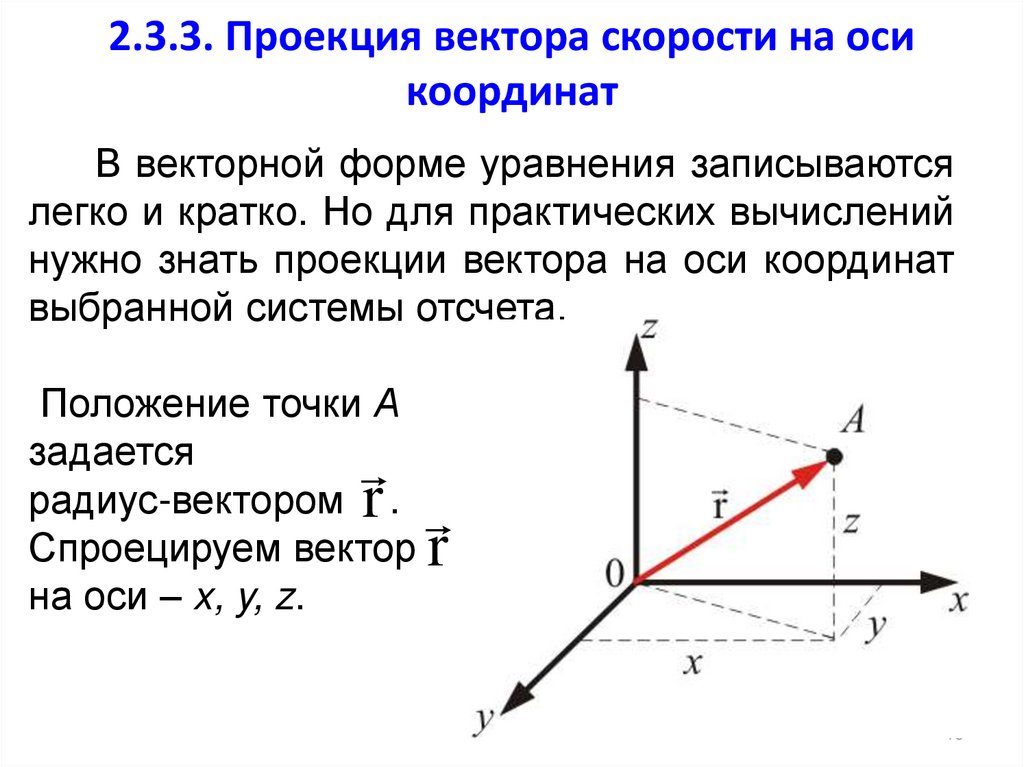 Говорить о величине этой скалярной величины не имеет смысла. Пожалуйста, дайте мне знать, если это помогло или навредило вашему пониманию!
Говорить о величине этой скалярной величины не имеет смысла. Пожалуйста, дайте мне знать, если это помогло или навредило вашему пониманию!
$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Терминология
Терминология– Почему и как существует отрицательная скорость?
спросил
Изменено 7 месяцев назад
Просмотрено 85 тысяч раз
$\begingroup$
Почему и как существует отрицательная скорость? Я читал в Интернете об отрицательной скорости, но до сих пор не понимаю, как она вообще может существовать, ведь время положительно, как и длина. Проведя некоторые математические расчеты, я пришел к выводу, что этого не может и не должно существовать, и все же есть так много статей и видео, пытающихся объяснить это.
- терминология
- скорость
- скорость
$\endgroup$
1
$\begingroup$
- Скорость — это вектор.
 Скорость это ее величина.
Скорость это ее величина. - Позиция является вектором. Длина (или расстояние ) — это его величина.
Вектор указывает направление в пространстве. Отрицательный вектор (или, точнее, «отрицательный вектор») просто указывает в противоположную сторону.
Если я веду из домой в работу (определяя мое положительное направление ), то моя скорость будет положительной, если я иду на работу , но отрицательной, когда я иду домой с работы. Все дело в направлении, которое видно из того, как я определил свою положительную ось .
Рассмотрим пример, в котором я оказался дальше, чем начал. У меня должно быть отрицательных чистых скоростей, чтобы в конечном итоге двигаться назад (я заканчиваю на отрицательная позиция ). Но только потому, что назад и вперед четко определены как отрицательное и положительное направления соответственно, прежде чем я начну.
Итак, существует ли отрицательная скорость? Ну, так как это всего лишь слова, описывающие событие, то да . Отрицательная скорость просто означает скорость в направлении, противоположном положительному.
$\endgroup$
20
$\begingroup$
С математической точки зрения у вас не может быть «отрицательной скорости» самой по себе, только «отрицательная скорость в заданном направлении».
Скорость является трехмерным вектором, не существует положительного или отрицательного трехмерного вектора.
Однако, если вы рассматриваете скорость в направлении $\mathrm{x}$ , где $\hat{\mathbf{e}}_{\mathrm{x}}$ – некоторый единичный вектор, задающий опорное направление ( скажем, «запад»), то скорость «в направлении $\mathrm{x}$» — это просто скалярное произведение скорости и $\hat{\mathbf{e}}_{\mathrm{x}}$. Эта величина является действительным числом и может быть отрицательным. Если оно отрицательное, оно равно $-1 \times \text{(скорость в направлении -x)}$: вычислите скорость в противоположном направлении и поменяйте знак.
Эта величина является действительным числом и может быть отрицательным. Если оно отрицательное, оно равно $-1 \times \text{(скорость в направлении -x)}$: вычислите скорость в противоположном направлении и поменяйте знак.
$\endgroup$
1
$\begingroup$
Я думаю, что одна из основных причин, по которой у вас есть скорость, заключается в том, чтобы изолировать конкретное направление движения от вашей скорости движения вперед.
Если вы движетесь на северо-северо-восток, вы можете определить скорость, с которой вы движетесь на восток, рассчитав свою скорость на восток (возможно, 1/3 вашей скорости движения на северо-северо-восток).
Отрицательные скорости, вероятно, появились как следствие того, что при измерении скорости нужно определять направление.
$\endgroup$
$\begingroup$
Отрицательное и положительное значения произвольны. Если бы я определил север как положительный, юг был бы отрицательным. Если бы я определил юг как положительный, север был бы отрицательным. Обозначения просто служат для указания направления вектора скорости относительно некоторого определенного положительного направления. Все направления произвольны, и вы можете создать любую систему координат для своих мероприятий, главное, чтобы все согласовывалось друг с другом.
Если бы я определил север как положительный, юг был бы отрицательным. Если бы я определил юг как положительный, север был бы отрицательным. Обозначения просто служат для указания направления вектора скорости относительно некоторого определенного положительного направления. Все направления произвольны, и вы можете создать любую систему координат для своих мероприятий, главное, чтобы все согласовывалось друг с другом.
Это соглашение необходимо нам, например, для объяснения позиции как функции времени. Если бы скорость была зафиксирована положительной или, аналогично, если бы она была скалярной, у механики были бы некоторые проблемы, поскольку это означало бы, что объект никогда не мог бы замедляться, не говоря уже о том, чтобы двигаться назад.
$\endgroup$
$\begingroup$
Я буду рассматривать только одномерное движение (движение вдоль одной оси). Основная цель таких терминов, как положение и скорость, состоит в том, чтобы легко описать движение объекта.
Мы определяем скорость как скорость изменения положения. По соглашению мы выбираем фиксированную точку (вдоль оси движения), называем ее началом и определяем положение объекта на этой линии на основе расстояния от этой точки. Опять же, общее соглашение заключается в том, что расстояния, измеренные вправо, являются положительными, а расстояния, измеренные влево, отрицательными (вы можете использовать их в обратном порядке, если хотите). Вы можете легко увидеть, что при определении измерения положения таким образом мы покрыли все точки на оси. .В этих соглашениях позиция 2 м означает 2 м вправо от исходной точки, а позиция -6 м означает 6 м влево от исходной точки.
Вы бы слышали, что знак скорости дает направление, но, прежде всего, направления – это опять же просто сделанные нами ссылки. Методом проб и ошибок мы можем разобрать физический смысл знака + или -.
(По соглашению вы называете направление, в котором увеличиваются отрицательные числа, отрицательным направлением (т. е. влево в этом случае), а направление, в котором положительное число увеличивается, положительным направлением (т.е. вправо в этом случае)).
е. влево в этом случае), а направление, в котором положительное число увеличивается, положительным направлением (т.е. вправо в этом случае)).
Пример:-
Вы видите объект сначала на расстоянии 2 м, а затем на -3 м через 5 с. Вы говорите, что он сдвинулся влево или в отрицательном направлении. Теперь по определению скорости вы вычисляете изменение положения (-3-2)m = -5m (анализируя вы можете видеть, что “-” получилось автоматически в результате нашего соглашения) и изменение во времени = 5с. Разделив, вы получите скорость как (-1 м/с), или вы можете сказать, что объект двигался влево со скоростью 1 м/с. Таким образом, вы можете понять, что означает отрицательный знак. Это просто означает, что движение происходит в отрицательном направлении или влево. (Как видите, наши определения и соглашения помогают нам полностью описать движение объекта, как скорость, с которой он движется, так и куда он движется)
$\endgroup$
$\begingroup$
На языке программирования FORTH черепаха может перемещаться в любом месте плоскости, всегда двигаясь «впереди» на X единиц и поворачивая влево или вправо на угол Y единиц. Черепаха игнорирует понятие негатива, и все же она движется, т.е. в любом референтном пространстве координаты меняются во времени, и у нее есть скорость.
Черепаха игнорирует понятие негатива, и все же она движется, т.е. в любом референтном пространстве координаты меняются во времени, и у нее есть скорость.
Вопрос и несколько ответов не знают разницы между положительным характером любого количества физической величины и представлением в референциале, построенном по соглашению и простоте использования. Сравните полярный референт, в котором нет отрицаний, и обычный декартовский.
Например, : длина чего-то, расстояние отсюда до туда всегда положительна.
Вектор представляет собой пару величины и направления, его длина положительна по определению.
Когда мы представляем, что объект перемещается из положения 0 в -X и затем обратно в 0, мы не можем сказать, что он переместился на 0 единиц (-4+4=0) длины. На самом деле он переместился вдвое на длину 4, т. е. на 8 единиц длины.
Если это движение заняло 2 секунды (см. понятие скорости относительно скорости), то мы не можем сложить два вектора и сказать, что .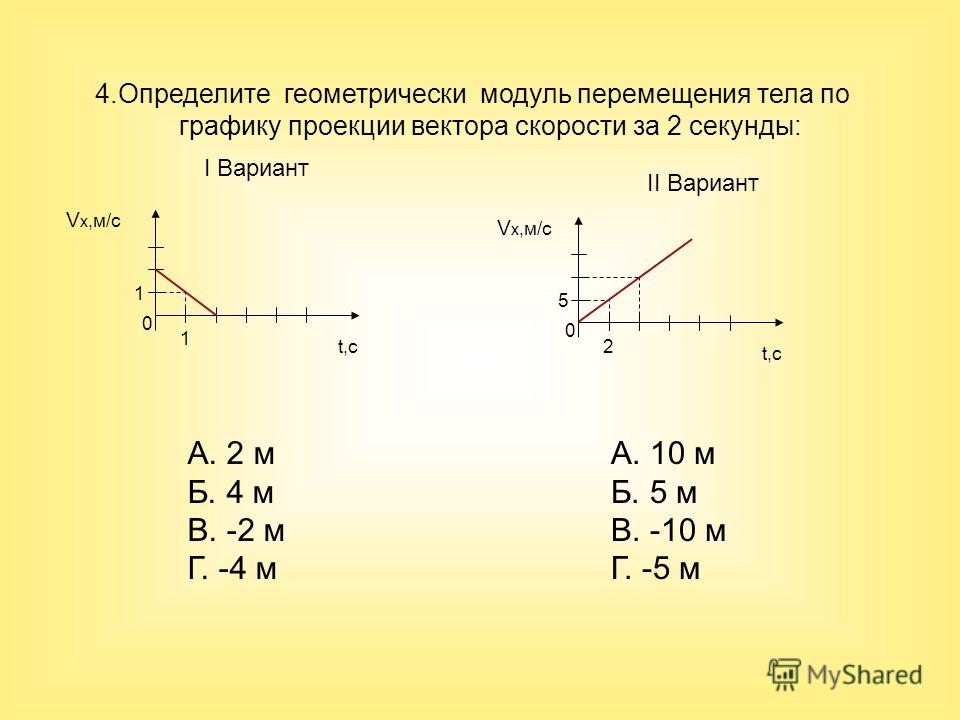 . равно 0,
. равно 0,
Эта ссылка обеспечивает различие между двумя разными понятиями скорости в учебниках и понятием скорости.
def 1 : $s=\frac{distance}{\Delta\ t}$ (зависит от пути)
def 2 : $s=\left|\frac{\vec{v}}{\Delta\ т}\право|$
$\endgroup$
домашнее задание и упражнения – Что означает отрицательное с точки зрения векторов и направления (физика 10 класс)?
$\begingroup$
Автомобиль массой 1370 кг буксует по горизонтальной поверхности. Автомобиль замедляется со скорости 27,6 м/с до состояния покоя за 3,15 секунды. Считая сопротивление воздуха пренебрежимо малым, определить коэффициент трения между шинами автомобиля и дорожным покрытием.
источник: https://www.physicsclassroom.com/calcpad/newtlaws/prob30.cfm
У меня есть этот вопрос здесь, но я немного застрял, когда я получил, что сила трения равна приложенной силе, которая равна $F=ma$. Ускорение кажется отрицательным, и в результате приложенная сила имеет отрицательное значение. Что это значит? Я знаю, что отрицание включает в себя направление, но я до сих пор не совсем понимаю, как использовать отрицательный знак. Итак, всегда ли мы предполагаем, что объект движется вправо или по оси x? Если это так, f=negative не имеет смысла. Означает ли это также, что трение положительное и идет правильно?
Ускорение кажется отрицательным, и в результате приложенная сила имеет отрицательное значение. Что это значит? Я знаю, что отрицание включает в себя направление, но я до сих пор не совсем понимаю, как использовать отрицательный знак. Итак, всегда ли мы предполагаем, что объект движется вправо или по оси x? Если это так, f=negative не имеет смысла. Означает ли это также, что трение положительное и идет правильно?
- домашние задания и упражнения
- ньютоновская механика
- силы
- системы отсчета
- системы координат
$\endgroup$
1
$\begingroup$
Положительное и отрицательное зависит от выбранной вами системы координат. Когда вы выбираете направление как «положительное», вы выбираете систему координат. Ускорение есть производная скорости по времени и равна вектор . В одномерной задаче его направление однозначно определяется его знаком (возможны только 2 направления: положительное и отрицательное). В данном случае это может выглядеть как скаляр, но на самом деле это вектор. Когда ускорение положительное, это говорит нам о том, что скорость движется вправо по числовой прямой.
В одномерной задаче его направление однозначно определяется его знаком (возможны только 2 направления: положительное и отрицательное). В данном случае это может выглядеть как скаляр, но на самом деле это вектор. Когда ускорение положительное, это говорит нам о том, что скорость движется вправо по числовой прямой.
Отрицательное ускорение, с другой стороны, означает, что скорость объекта уменьшается (либо замедляется в положительном направлении, либо ускоряется в отрицательном направлении), т. е. движется влево по числовой прямой. Это не говорит нам, насколько близка к нулю на числовой прямой скорость . Это работа термина «скорость», который сообщает нам величину скорости, как далеко она от нуля . Как положительное, так и отрицательное ускорение может вызвать ускорение объекта (в соответствующих направлениях). Объект, движущийся влево и ускоряющийся, будет иметь совершенно другое движение по сравнению с объектом, движущимся вправо и замедляющимся, но оба они будут иметь отрицательное ускорение, поскольку их скорости движутся влево по числовой прямой. Будьте осторожны, различая «уменьшение скорости» с «замедлением»; первый говорит о скорости, а второй говорит о скорости.
Будьте осторожны, различая «уменьшение скорости» с «замедлением»; первый говорит о скорости, а второй говорит о скорости.
Таким образом, само по себе ускорение ничего не говорит нам о скорости, с которой уже движется объект, оно только сообщает нам, как быстро и в каком направлении изменяется его скорость. Отсюда постоянный член, когда ускорение интегрируется по времени.
$\endgroup$
10
$\begingroup$
Я мог бы представить силу $\vec G$ в виде вектора $\vec G = G\,\hat g$, где $\hat g$ — единичный вектор в направлении силы, а $G$ — величина силы.
В этом уравнении $G$ всегда положительно, потому что это величина силы.
Теперь предположим, что сила $\vec F$ действует параллельно оси x и единичный вектор в направлении увеличения $x$ равен $\hat x$.
Силу в этом случае можно записать в виде $\vec F = F \,\hat x$, где $F$ называется составляющей силы в направлении $\hat x$.
Важным отличием от прежних обозначений силы $\vec G$ является то, что теперь компонента $F$ может быть как положительной, так и отрицательной величиной.
Сила $3\, \hat x$ имеет составляющую $3$ в направлении $\hat x$, т.е. это вектор длины (величины) $3$ в положительном направлении x.
Сила $-5\, \hat x=5(-\hat x)$ имеет составляющую $-5$ в направлении $\hat x$, т.е. это вектор длины (величины) $5$ в отрицательной x-направление.
—-
Ваше уравнение второго закона Ньютона представляет собой векторное уравнение $\vec F = m\, \vec a$, которое можно записать как $F \hat x = m\, a \hat x$, где $F$ и $a$ — компоненты силы и ускорения в направлении $\hat x$ (положительном направлении x).
Удаление единичных векторов, встречающихся на обеих сторонах туалета $F=ma$.
Теперь предположим, что скорость равна $7\hat x$.
Замедление (уменьшение величины скорости) означает, что ускорение направлено в сторону, противоположную скорости, и может быть равно $-2\hat x$.
Используя $F=ma$, помните, что это происходит из $F\hat x = m \hat x$, вы получаете $F = m (-2) = -2 m$, что говорит вам, что сила действует в отрицательном x -направление (-\hat x), т.е. противоположное направлению скорости, которое находится в положительном направлении x.
Если бы начальная скорость была $-7\hat x$ (в отрицательном направлении x), то замедление могло бы быть $2\hat x$ (в положительном направлении x).
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Всегда ли величина вектора положительна? – Краткий факт
по Консультация
Admin
Содержание
- 1 Всегда ли величина вектора положительна?
- 2 Всегда ли величина положительна в физике?
- 3 Может ли модуль вектора быть отрицательным?
- 4 Вектор положительный или отрицательный?
- 5 Является ли вектор положительным?
- 6 Всегда ли скаляр положителен?
- 7 Как узнать, является ли вектор отрицательным?
- 8 Скаляр положительный или отрицательный?
- 9 Может ли вектор иметь положительные и отрицательные компоненты?
- 10 Может ли вектор быть положительным или отрицательным?
Всегда ли величина вектора положительна?
Нет: Величина всегда положительна, даже если направление отрицательное. Чтобы сумма двух векторов равнялась нулю, сумма их соответствующих компонентов должна равняться нулю.
Всегда ли в физике величина положительна?
Точно так же величина силы всегда является положительным числом, даже если сила направлена вниз.
Может ли величина скаляра быть отрицательной объяснить?
Полный ответ: диапазоном скалярной величины является вся числовая строка, но эта скалярная величина принимает только одно значение из целой числовой строки, т. е. категорию вещественных чисел. Теперь, поскольку действительные числа включают как положительные, так и отрицательные числа, скаляр может быть отрицательным.
Может ли модуль вектора быть отрицательным?
Ответ: Величина любой физической величины всегда положительна, потому что ее модуль всегда положителен, т.е. |M|>0. Поэтому вектор может быть положительным или отрицательным, но если вас спросят о величине, то он всегда будет положительным.
Вектор положительный или отрицательный?
Векторы отрицательны только по отношению к другому вектору. Величина или длина вектора не может быть отрицательной; он может быть нулевым или положительным. Знак минус используется здесь, чтобы указать, что вектор имеет направление, противоположное опорному вектору.
Может ли величина быть отрицательной?
Ответ: Величина не может быть отрицательной. Это длина вектора, который не имеет направления (положительного или отрицательного). Нулевой вектор (вектор, все значения которого равны 0) имеет величину 0, но все остальные векторы имеют положительную величину.
Является ли вектор положительным?
Два вектора равны, если они имеют одинаковую величину и одинаковое направление. Точно так же, как скаляры, которые могут иметь положительные или отрицательные значения, векторы также могут быть положительными или отрицательными. Отрицательный вектор — это вектор, который имеет направление, противоположное эталонному положительному направлению.
Всегда ли скаляр положителен?
Они имеют как величину, так и направление. Они имеют только величину. Сумма векторов может быть нулевой, положительной и отрицательной. Сумма скаляров — положительное число… Скорость.
| Скорость | Скорость |
|---|---|
Это скалярная величина. | Это векторная величина. |
| Всегда положительный. | Может быть положительным, отрицательным или нулевым. |
Является ли нулевой вектор линейно независимым?
В теории векторных пространств набор векторов называется линейно зависимым, если существует нетривиальная линейная комбинация векторов, равная нулевому вектору. Если такой линейной комбинации не существует, то говорят, что векторы линейно независимы.
Как узнать, является ли вектор отрицательным?
Нахождение отрицательного вектора заданного вектора можно выполнить, поставив перед ним знак минус. Например, пусть X — вектор. Чтобы получить отрицательный вектор X, мы умножаем X на -1, что делает его -X. Помните, что величина вектора –X такая же, как у вектора X.
Скаляр положительный или отрицательный?
Скаляр — это просто число, которое может быть как положительным, так и отрицательным. Возможно, вы путаете это с «длиной» вектора, которая никогда не бывает отрицательной.
Какой вектор должен быть отрицательным?
Любой вектор, величина которого больше 1, никогда не будет отрицательным вектором. Скорость падающего объекта направлена вниз, то есть в сторону отрицательной оси Y. Значит, этот вектор отрицательный.
Может ли вектор иметь положительные и отрицательные компоненты?
Векторы в первом квадранте (I) имеют обе скалярные компоненты положительные, а векторы в третьем квадранте имеют обе скалярные компоненты отрицательные. Для векторов в квадрантах II и III угол направления вектора равен
Может ли вектор быть положительным или отрицательным?
Два вектора равны, если они имеют одинаковую величину и одинаковое направление. Точно так же, как скаляры, которые могут иметь положительные или отрицательные значения, векторы также могут быть положительными или отрицательными. Отрицательный вектор — это вектор, указывающий в направлении, противоположном эталонному положительному направлению.
Может ли вектор иметь отрицательное значение?
Да, вектор может быть отрицательным, по крайней мере, согласно аксиоме векторного пространства 5. Если u, v и w являются объектами в векторном пространстве V, они называются векторами. Это отрицательное значение другого вектора или, как я уже говорил ранее, отрицательное значение относительно другого вектора.
Обзор векторов и снарядов — с ответами №1
Перейдите к:
Главная страница обзорной сессии — листинг 9 темы0003
Векторы и снаряды – Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || #1-9 || #10-45 || # 46-55 || # 56-72
[#1 | #2 | №3 | №4 | №5 | #6 | #7 | #8 | #9]
Часть A: Множественный выбор
1. Какие из следующих утверждений верны для скаляров и векторов? Перечислите все, что ВЕРНО.
Какие из следующих утверждений верны для скаляров и векторов? Перечислите все, что ВЕРНО.
- С векторной величиной всегда связано направление.
- Скалярная величина может иметь связанное с ней направление.
- Векторы могут быть сложены вместе; скалярные величины не могут.
- Векторы могут быть представлены стрелкой на масштабной диаграмме; длина стрелки представляет величину вектора, а направление, на которое она указывает, представляет направление вектора.
Ответ: AD
а. ИСТИНА . Векторы определяются как величины, полностью описываемые как по величине, так и по направлению. По определению, вектор имеет связанное с ним направление. Если бы это было не так, то это НЕ был бы вектор.
б. ЛОЖЬ – Скаляры определяются как величины, которые полностью описываются только их величиной. Скаляры не обращают внимания на направление, и бессмысленно связывать направление с такой величиной. Если бы с величиной было связано направление, то эта величина не была бы вектором.
Если бы с величиной было связано направление, то эта величина не была бы вектором.
в. FALSE – Можно складывать как векторы, так и скаляры. Правила сложения векторов уникальны для векторов и не могут использоваться при сложении скаляров. При сложении двух векторов необходимо учитывать направление вектора. Направление не имеет значения при добавлении скаляров.
д. TRUE – Именно так и сделано во всем блоке.
2. Какие из следующих величин являются векторами? Включите все, что применимо.
- пройденное расстояние
- рабочий объем
- средняя скорость
- средняя скорость
- мгновенная скорость
- ускорение
Ответ: BDEF
Из пяти перечисленных здесь кинематических величин (расстояние, перемещение, скорость, скорость и ускорение) три являются векторами. Перемещение, скорость (как средняя, так и мгновенная) и ускорение требуют упоминания направления, чтобы полностью описать величину.
3. Для различных величин указаны числовые значения и направления. Какие из этих утверждений представляют векторное описание? Включите все, что применимо.
- 20 метров, запад
- 9,8 м/с/с
- 35 миль/ч, юг
- 16 лет
- 60 минут
- 3,5 м/с/с, юг
- -3,5 м/с/с
- +20 градусов С
Ответ: ACFG
Выражения векторных величин будут включать величину (число, значение и т. д.) и направление. Направление можно описать как север, юг, восток, запад или влево, вправо, вверх, вниз. Иногда для описания направления используется «+» или «-». Так как математические вычисления на калькуляторах плохо справляются с вводом «юг», для заданного направления часто заменяется знак -. В случае g , единицы указывают величину ускорения. Знак «-» указывает направление. Следует быть осторожным, предполагая, что знак «+» или «-» является верным признаком величины, являющейся направлением, поскольку другие не векторные величины также могут использовать такие знаки (как в случае h ).
4. Какие из следующих утверждений верны для диаграмм сложения векторов, вычитания векторов и диаграмм сложения векторов? Перечислите все, что применимо.
- Векторы A, B и C складываются вместе как A + B + C. Если порядок, в котором они складываются, изменить на C + B + A, то результат будет другим.
- Векторы A, B и C складываются вместе как A + B + C. Если порядок их сложения изменить на C + B + A, то результатом будет вектор с той же величиной, но в противоположном направлении. .
- При построении векторной диаграммы для A + B + C нет абсолютной необходимости, чтобы векторы B и C использовали тот же масштаб, что и вектор A.
- Результирующая в диаграмме сложения векторов всегда простирается от начала последнего вектора до хвоста первого вектора.
- Если векторы A и B складываются под прямым углом друг к другу, то можно быть уверенным, что результирующий будет иметь величину, превышающую величины любого из отдельных векторов A и B.

- Если векторы А и В сложить под прямым углом друг к другу, то можно быть уверенным, что результирующая будет иметь величину, меньшую арифметической суммы величин А и В.
- Диаграммы сложения векторов нельзя использовать для определения результата при выполнении операции вычитания векторов.
Ответ: EF
а. FALSE – Изменение порядка добавления трех векторов не влияет на результат процесса добавления. A + B + C = C + B + A. Каждый порядок операций дает результирующую с той же величиной и направлением.
б. FALSE – Как упоминалось выше в a, изменение порядка добавления трех векторов не влияет на результат процесса добавления. Обратный порядок дает результирующую с той же величиной и тем же направлением.
в. ЛОЖЬ – При построении векторной диаграммы сложения необходимо выбрать масштаб и придерживаться его. Масштаб, использованный для рисования вектора А, должен быть использован и для векторов В и С. Нельзя менять лошадей посреди потока .
Нельзя менять лошадей посреди потока .
д. FALSE – Результирующее значение на диаграмме сложения векторов рисуется от конца первого вектора (начальная точка ) до начала последнего вектора (конечная точка ).
е. ИСТИНА – Предположим, что A = 3 единицы и B = 4 единицы и что два вектора направлены под прямым углом друг к другу. Сумма векторов или результат A + B составляет 5 единиц, что явно больше, чем любой из добавляемых векторов. В общем случае равнодействующая в таком случае будет представлена на диаграмме сложения векторов как гипотенуза прямоугольного треугольника. Гипотенуза всегда больше двух других катетов треугольника. Так что это утверждение всегда верно.
ф. ИСТИНА – Предположим, что A = 3 единицы и B = 4 единицы и что два вектора направлены под прямым углом друг к другу. Векторная сумма или результат A + B составляет 5 единиц, тогда как арифметическая сумма составляет 7 единиц. В этом случае и во всех случаях векторная сумма двух прямоугольных векторов всегда будет меньше арифметической суммы. То есть Sqrt(a 2 + b 2 ) всегда будет меньше, чем a + b.
То есть Sqrt(a 2 + b 2 ) всегда будет меньше, чем a + b.
г. FALSE – Когда выполняется операция вычитания вектора, обычно рекомендуется просто преобразовать ее в операцию сложения векторов. Это достигается добавлением отрицательного значения вектора, который вычитается. Таким образом, A – B будет эквивалентно A + (-B). Таким образом, диаграмма сложения векторов может быть использована для определения результата.
5. Какие из следующих описаний движущихся объектов точно изображают снаряд? Перечислите все, что применимо.
- объект, движущийся по воздуху и не касающийся какой-либо поверхности
- падающий парашютист с раскрытым парашютом
- любой предмет, сопротивление воздуха которому можно пренебречь
- свободно падающий объект
- объект, на который действует только сила тяжести
- падающее перо
- падающее перо в вакуумной камере
- Падающее перо в падающей вакуумной камере.

Ответ: DEGH
Снаряд — это объект, на который действует только сила тяжести. Сопротивление воздуха должно быть незначительным или отсутствовать. Другие силы, возникающие в результате того, что люди или предметы тянут или толкают, прикрепленных веревок или контакта с поверхностями, не должны присутствовать.
а. НЕТ – Самолет движется по воздуху и не касается какой-либо поверхности. Но самолет явно не снаряд.
б. NO – Падающий парашютист обычно испытывает значительное сопротивление воздуха. Популярно описывать таких парашютистов как находящихся в свободном падении . Это ошибочное использование термина.
в. НЕТ – Когда вы сидите в кресле, сопротивление воздуха незначительно. Вы точно не снаряд (по крайней мере, мы на это надеемся).
д. YES – Снаряд – это объект в свободном падении.
эл. ДА – Объект, на который единственной значимой силой является гравитация, соответствует определению снаряда (при условии, что значимость означает “имеющий влияние”).
ф. NO – Падающие перья сталкиваются с сопротивлением воздуха, которое препятствует нисходящему ускорению и заставляет перо падать почти с постоянной скоростью.
г. ДА – Когда перо падает в вакууме, сопротивление воздуха устраняется, и перо может свободно падать.
ч. ДА – Когда перо падает в вакууме, а вакуум также свободно падает, сопротивление воздуха устраняется, и наблюдатель заметит, что и вакуумная камера, и перо находятся в свободном падении.
6. Какие из следующих утверждений верны для снарядов? Перечислите все, что применимо.
- Снаряд — свободно падающий объект.
- Снаряд испытывает незначительное сопротивление воздуха или не испытывает его вообще.
- Снаряд должен двигаться вниз.
- Снаряд должен двигаться с ускорением в направлении вниз.
- Снаряд не обязан двигаться горизонтально.

- Снаряд может начать движение с нисходящей скоростью.
- Снаряд не обязательно должен “падать”.
Ответ: ABDEF и, возможно, G
a. ВЕРНО – Свободно падающие объекты, такие как снаряды, являются объектами, на которые действует только гравитация.
б. ВЕРНО – Единственная сила, действующая на снаряд, – это гравитация; сопротивления воздуха не должно быть или оно не должно влиять на движение снаряда.
в. ЛОЖЬ – Снаряды могут двигаться либо вверх, либо вниз, либо под углом к вертикали. Однако они должны двигаться вниз с ускорением в соответствии с действием гравитации на объект.
д. ВЕРНО – Сила тяжести действует прямо вниз на объект, вызывая нисходящее ускорение. Любой снаряд должен ускоряться вниз независимо от других особенностей его движения.
эл. TRUE – Снаряд мог двигаться строго в вертикальном направлении без горизонтального движения. Мяч, брошенный прямо в воздух, был бы таким случаем.
ф. TRUE – Нет правила, определяющего, в каком направлении должен двигаться снаряд в момент его выброса. Он мог бы начать свое движение с начальной нисходящей скоростью.
г. ПРАВДА – Слово “падение” может означать разные вещи для разных людей. Если «падение» предполагает движение вниз во все моменты времени, то снаряду не обязательно «падать». Для многих «падение» означает падение под действием силы тяжести. При этом снаряд должен «падать».
7. Какие из следующих утверждений верны для горизонтального движения снарядов? Перечислите все, что применимо.
- Снаряд не имеет горизонтальной скорости.
- Снаряд с направленной вправо составляющей движения будет иметь правонаправленную составляющую ускорения.
- Горизонтальная скорость снаряда изменяется на 9,8 м/с каждую секунду.
- Снаряд с горизонтальной составляющей движения будет иметь постоянную горизонтальную скорость.

- Горизонтальная скорость снаряда равна 0 м/с на пике его траектории.
- Горизонтальная скорость снаряда не зависит от вертикальной скорости; эти две составляющие движения независимы друг от друга.
- Горизонтальное смещение снаряда зависит от времени полета и начальной горизонтальной скорости.
- Конечная горизонтальная скорость снаряда всегда равна начальной горизонтальной скорости.
- Когда снаряд поднимается к пику своей траектории, горизонтальная скорость уменьшается; когда он падает с пика своей траектории, его горизонтальная скорость будет уменьшаться.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированной скоростью пуска и переменным углом и приземлившийся на уровне земли. Горизонтальное смещение (т.е. диапазон ) снаряда всегда будет увеличиваться при увеличении угла пуска от 0 до 90 градусов.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированным углом запуска и переменной скоростью запуска, и приземлившийся на уровне земли.
 Горизонтальное смещение (т. е. дальность ) снаряда всегда будет увеличиваться по мере увеличения скорости пуска.
Горизонтальное смещение (т. е. дальность ) снаряда всегда будет увеличиваться по мере увеличения скорости пуска.
Ответ: DFGHK
а. ЛОЖЬ — Многие снаряды движутся слева направо и справа налево, так как они одновременно свободно падают. Такие снаряды имеют горизонтальное движение. Хотя снаряд может совершать горизонтальное движение, он не может иметь горизонтальное ускорение. Какое бы движение оно ни совершало в горизонтальном измерении, оно должно быть движением с постоянной скоростью.
б. ЛОЖЬ – Снаряд с движением вправо (в дополнение к вертикальному движению) будет иметь постоянную скорость в направлении вправо. Это означает, что он не имеет горизонтального ускорения.
в. ЛОЖЬ – Снаряд имеет постоянную горизонтальную скорость. Каждую секунду вертикальная скорость будет изменяться на 9,8 м/с.
д. ПРАВДА – Совершенно верно! Снаряды – это объекты, на которые действует только сила тяжести. Таким образом, есть вертикальное ускорение, но нет горизонтального ускорения. Горизонтальная скорость снаряда либо равна нулю, либо является постоянной величиной, отличной от нуля.
Таким образом, есть вертикальное ускорение, но нет горизонтального ускорения. Горизонтальная скорость снаряда либо равна нулю, либо является постоянной величиной, отличной от нуля.
эл. ЛОЖЬ – Вертикальная скорость снаряда равна 0 м/с на пике его траектории; но горизонтальная составляющая скорости на пике равна тому значению, которое было, когда впервые запустил .
ф. ВЕРНО – Для любого двумерного движения (будь то движение снаряда или проблемы с речным судном или …), перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикальной составляющей не повлияет на горизонтальные составляющие движения.
г. ИСТИНА – Горизонтальное смещение (x) можно рассчитать по формуле x = v ox • t, где v ox — начальная горизонтальная скорость, а t — время. Это две переменные, влияющие на горизонтальное смещение снаряда.
ч. TRUE – Поскольку у снаряда нет горизонтального ускорения, начальная горизонтальная скорость равна конечной горизонтальной скорости.
я. FALSE – Это верное описание вертикальной составляющей скорости. Горизонтальная скорость не меняется на протяжении всей траектории снаряда.
л. FALSE – Диапазон (или горизонтальное смещение) будет увеличиваться при увеличении угла с 0 до 45 градусов. Максимальная дальность приходится на 45 градусов. При дальнейшем увеличении угла до значений, превышающих 45 градусов, горизонтальное смещение уменьшается.
к. TRUE – При увеличении скорости запуска компоненты начальной скорости (как горизонтальной, так и вертикальной) также увеличиваются. Это заставляет снаряд оставаться в воздухе в течение более длительного периода времени и двигаться быстрее в горизонтальном направлении. В результате увеличение скорости пуска всегда приводит к увеличению горизонтального смещения.
8. Какие из следующих утверждений верны для вертикального движения снарядов? Перечислите все, что применимо.
- Вертикальная составляющая скорости снаряда является постоянной величиной 9,8 м/с.
- Вертикальная составляющая скорости снаряда постоянна.
- Изменяется вертикальная составляющая скорости снаряда.
- Вертикальная составляющая скорости снаряда изменяется с постоянной скоростью.
- Снаряд с направленной вверх составляющей движения будет иметь направленную вверх составляющую ускорения.
- Снаряд с нисходящей составляющей движения будет иметь нисходящую составляющую ускорения.
- Величина вертикальной скорости снаряда изменяется на 9,8 м/с каждую секунду.
- Вертикальная скорость снаряда равна 0 м/с на пике его траектории.
- Горизонтальная скорость не влияет на вертикальную скорость снаряда; эти две составляющие движения независимы друг от друга.
- Конечная вертикальная скорость снаряда всегда равна начальной вертикальной скорости.
- Вертикальное ускорение снаряда равно 0 м/с/с, когда он находится на пике своей траектории.

- Когда снаряд поднимается к пику своей траектории, вертикальное ускорение уменьшается; когда он падает с пика своей траектории, его вертикальное ускорение будет уменьшаться.
- Когда снаряд поднимается к пику своей траектории, вертикальное ускорение направлено вверх; когда он падает с пика своей траектории, его вертикальное ускорение направлено вниз.
- Пиковая высота, на которую снаряд поднимается над местом запуска, зависит от начальной вертикальной скорости.
- Когда снаряд поднимается к пику своей траектории, вертикальная скорость уменьшается; когда он падает с пика своей траектории, его вертикальная скорость будет уменьшаться.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированной скоростью пуска и переменным углом и приземлившийся на уровне земли. Вертикальное смещение снаряда в течение первой половины его траектории (т. е. пиковая высота ) всегда будет увеличиваться по мере увеличения угла запуска от 0 до 90 градусов.

- Рассмотрим снаряд, запущенный с уровня земли с фиксированным углом запуска и переменной скоростью запуска, и приземлившийся на уровне земли. Вертикальное смещение снаряда на первой половине его траектории (т. е. пиковая высота ) всегда будет увеличиваться по мере увеличения скорости пуска.
Ответ: CDFGHINPQ
а. ЛОЖЬ – Вертикальная составляющая скорости снаряда постоянно меняется. Это ускорение, которое имеет значение 9,8 м/с/с.
б. ЛОЖЬ — Снаряды — это объекты, на которые действует только сила тяжести. Таким образом, существует вертикальное ускорение; вертикальная скорость не постоянна, а изменяется.
в. ИСТИНА – См. часть b выше.
д. ВЕРНО – Снаряд имеет вертикальное ускорение 9,8 м/с/с на протяжении всей траектории. Это значение ускорения является постоянным. Это означает, что вертикальная скорость изменяется на ту же величину – 9.8 м/с – в течение каждой секунды его движения. Вертикальная скорость изменяется на постоянную величину.
Вертикальная скорость изменяется на постоянную величину.
эл. ЛОЖЬ – Все снаряды испытывают нисходящее ускорение независимо от того, движутся ли они вверх или вниз. Снаряды, движущиеся вверх, имеют восходящую скорость, но реальные значения скорости становятся меньше; то есть снаряд замедляется на пути к своей вершине.
ф. ИСТИНА – Это верное утверждение. Можно также сказать, что снаряд с восходящей составляющей движения также имеет нисходящее ускорение. Все снаряды ускоряются в направлении вниз. Период.
г. ПРАВДА – Это абсолютно верно.
ч. ИСТИНА – На пике своей траектории снаряд находится в процессе смены направления. Вертикальная скорость должна измениться с положительного значения (+ вверх) на отрицательное значение (- вниз). Этот переход означает, что значение вертикальной скорости должно когда-то находиться между + и – числом. Промежуточное число равно 0 м/с, и это происходит на пике.
я. ИСТИНА . Для любого двумерного движения (будь то движение снаряда, речное судно или…) перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикальной составляющей не повлияет на горизонтальные составляющие движения.
Для любого двумерного движения (будь то движение снаряда, речное судно или…) перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикальной составляющей не повлияет на горизонтальные составляющие движения.
л. ЛОЖЬ – Снаряд, запущенный под углом, формирует параболическую траекторию. Предположим, что нужно проследить движение снаряда вперед во времени от пика и назад во времени от пика. Если бы это было сделано, можно было бы обнаружить, что значение вертикальной скорости имеет одинаковую величину для равного количества раз, прослеживаемых вперед и назад от пика. Таким образом, за одно и то же время до и после пика снаряд имеет одинаковую скорость. Однако некоторые снаряды запускаются не с той высоты, на которой они приземляются. Конечная высота не совпадает с начальной высотой, и поэтому время подъема на пик не равно времени падения с пика. В таких случаях начальная вертикальная скорость не равна конечной вертикальной скорости.
к. ЛОЖЬ – Нет! Нет! Нет! Вертикальная скорость равна 0 м/с в пике, а вертикальное ускорение равно -9,8 м/с/с на протяжении всей траектории.
ЛОЖЬ – Нет! Нет! Нет! Вертикальная скорость равна 0 м/с в пике, а вертикальное ускорение равно -9,8 м/с/с на протяжении всей траектории.
л. ЛОЖЬ – Это верное описание вертикальной скорости. Но вертикальное ускорение является постоянной величиной 9,8 м/с/с на протяжении всей траектории.
м. ЛОЖЬ – Мало того, что величина вертикального ускорения является постоянной величиной на протяжении всей траектории снаряда, направление также является постоянным. Снаряд все время, независимо от любой другой переменной, будет ускоряться вниз на 90,8 м/с/с. Это, пожалуй, самая важная истина о снарядах, которую нужно усвоить.
н. ИСТИНА — Начальная вертикальная скорость влияет на время, необходимое снаряду, чтобы подняться к своей вершине. Это также влияет на среднюю скорость снаряда, когда он поднимается к своему пику. В результате любое изменение вертикальной скорости изменит пиковую высоту снаряда.
о. FALSE – Взлетающие вверх снаряды имеют нисходящее ускорение; это означает, что они замедляются по мере роста. Величина их скорости уменьшается. Снаряды, движущиеся вниз, также имеют нисходящее ускорение; это означает, что они ускоряются. Величина их скорости увеличивается.
Величина их скорости уменьшается. Снаряды, движущиеся вниз, также имеют нисходящее ускорение; это означает, что они ускоряются. Величина их скорости увеличивается.
стр. TRUE – Увеличение угла запуска (от 0 до 90 градусов) всегда будет увеличивать вертикальную составляющую начальной скорости (v iy ). Это увеличение v iy приведет к увеличению времени подъема снаряда к своей вершине. А увеличенный угол заставляет снаряд двигаться с большей средней скоростью на пути к своей вершине. Оба этих эффекта приводят к тому, что пиковая высота снаряда будет увеличиваться по мере увеличения угла пуска от 0 до 9°.0 градусов.
кв. TRUE – При увеличении скорости запуска компоненты начальной скорости (как горизонтальной, так и вертикальной) также увеличиваются. Это заставляет снаряд оставаться в воздухе в течение более длительного периода времени и двигаться быстрее в вертикальном направлении. В результате увеличение скорости пуска всегда приводит к увеличению высоты полета снарядов.
9. Какие из следующих утверждений о времени полета снаряда верны? Перечислите все, что применимо.
- Время, в течение которого снаряд находится в воздухе, зависит от горизонтальной составляющей начальной скорости.
- Время нахождения снаряда в воздухе зависит от вертикальной составляющей начальной скорости.
- Для снаряда, приземлившегося на той же высоте, с которой он был выброшен, время подъема до пика равно времени падения с пика до первоначальной высоты.
- При одинаковых углах пуска вверх снаряды будут оставаться в воздухе дольше, если увеличить начальную скорость.
- Предположим, что удар по мячу в футболе является снарядом. Если мячу требуется 3 секунды, чтобы подняться до вершины своей траектории, то ему потребуется 6 секунд, чтобы упасть с вершины своей траектории на землю.
Ответ: BCD
а. ЛОЖЬ – Время вертикального подъема снаряда до пика (и последующего падения на землю) зависит от начальной вертикальной скорости. Изменение горизонтальной скорости вызовет только большее горизонтальное смещение снаряда (x).
ЛОЖЬ – Время вертикального подъема снаряда до пика (и последующего падения на землю) зависит от начальной вертикальной скорости. Изменение горизонтальной скорости вызовет только большее горизонтальное смещение снаряда (x).
б. ПРАВДА – Совершенно верно. Снаряды с большей вертикальной составляющей начальной скорости будут находиться в воздухе большее количество раз (при условии, что направление v iy вверх). Изменение значения v iy изменит время полета снаряда независимо от направления v iy .
в. TRUE — Для снарядов, запущенных под углом вверх и приземлившихся на исходной высоте, время до подъема на пик равно времени падения с пика. Если требуется 3 секунды, чтобы подняться вверх, потребуется 3 секунды, чтобы упасть.
д. TRUE – Для постоянного угла запуска увеличение начальной скорости (v i ) увеличит вертикальную скорость (v iy ). Это приводит к увеличению времени замедления снаряда до 0 м/с по мере его подъема к своему пику. Таким образом, снаряду требуется больше времени, чтобы добраться до вершины, больше времени, чтобы упасть с вершины, и в целом более длительное время находится в воздухе.
Таким образом, снаряду требуется больше времени, чтобы добраться до вершины, больше времени, чтобы упасть с вершины, и в целом более длительное время находится в воздухе.
эл. ЛОЖЬ – Близко, но очень ложно. Если подъем на вершину занимает 3 секунды, то и падение с вершины занимает 3 секунды; 6 секунд – это общее время полета снаряда.
Перейдите к:
Обзорная сессия Главная – Список тем
Векторы и снаряды – Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || #1-9 || #10-45 || # 46-55 || # 56-72
Вам также может понравиться…
Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, включая встроенную обратную связь и инструкции. Если это то, что вы ищете, вам также может понравиться следующее:
Если это то, что вы ищете, вам также может понравиться следующее:
- Блокнот-калькулятор
Блокнот-калькулятор содержит текстовые задачи по физике, организованные по темам. Каждая проблема сопровождается всплывающим ответом и звуковым файлом, в котором подробно объясняется, как подходить и решать проблему. Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.
Посещение: Калькулятор Главная | Блокнот калькулятора — векторы и снаряды
- Серия приложений Minds On Physics
Приложение Minds On Physics («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно относятся к улучшению своего концептуального понимания физики. Каждый модуль серии охватывает отдельную тему и далее разбит на подтемы. «Опыт MOP» предоставит учащемуся сложные вопросы, обратную связь и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, компьютеров Chromebook и Macintosh.
 Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает Векторы и Снаряды.
Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает Векторы и Снаряды.Посещение: MOP Главная страница приложения || Швабра в приложении – часть 1
Введение в векторы — Math Insight
Определение вектора
Вектор — это объект, который имеет как величину, так и направление. Геометрически мы можем изобразить вектор как направленный отрезок линии, длина которого равна величине вектора и со стрелкой, указывающей направление. Направление вектора от хвоста к голове.
Два вектора одинаковы, если они имеют одинаковую величину и направление. Это означает, что если мы возьмем вектор и переместим его в новое положение (не поворачивая его), то вектор, который мы получим в конце этого процесса, будет тем же вектором, который у нас был в начале.
Два примера векторов представляют силу и скорость.
И сила, и скорость имеют определенное направление. Величина
вектор будет указывать силу силы или скорость, связанную со скоростью.
Величина
вектор будет указывать силу силы или скорость, связанную со скоростью.
Мы обозначаем векторы жирным шрифтом, как в $\vc{a}$ или $\vc{b}$. Особенно при письме от руки, где нельзя легко писать полужирным шрифтом, люди иногда обозначают векторы стрелками, как в $\vec{a}$ или $\vec{b}$ или используют другие обозначения. Здесь нам не нужно будет использовать стрелки. Обозначим величину вектора $\vc{a}$ через $\|\vc{a}\|$. Когда мы хотим сослаться на число и подчеркнуть, что это не вектор, мы можем назвать это число скаляром. Мы будем обозначать скаляры с курсивом, как в $a$ или $b$.
Вы можете изучить понятие величины и направления вектора, используя приведенный ниже апплет. Обратите внимание, что перемещение вектора не меняет вектор, так как положение вектора не влияет на величину или направление.
Но если вы растянете или повернете вектор, перемещая только его голову или хвост, величина или направление изменятся. (Этот апплет также показывает координаты вектора, о которых вы можете прочитать на другой странице. )
)
Величина и направление вектора. Синяя стрелка обозначает вектор $\vc{a}$. Два определяющих свойства вектора, величина и направление, показаны красной полосой и зеленой стрелкой соответственно. Длина красной полосы — это величина $\|\vc{a}\|$ вектора $\vc{a}$. Зеленая стрелка всегда имеет длину единицу, но ее направление совпадает с направлением вектора $\vc{a}$. Единственным исключением является случай, когда $\vc{a}$ является нулевым вектором (единственным вектором с нулевой величиной), для которого направление не определено. Вы можете изменить любой конец $\vc{a}$, перетащив его мышью. Вы также можете переместить $\vc{a}$, перетащив середину вектора; однако изменение положения $\vc{a}$ таким образом не меняет вектор, так как его величина и направление остаются неизменными.
Дополнительная информация об апплете.
Существует одно важное исключение для векторов, имеющих направление. ноль
вектор, обозначенный полужирным шрифтом $\vc{0}$, является вектором нулевой длины. Поскольку у него нет длины, он не указывает ни в каком конкретном направлении.
Существует только один вектор нулевой длины, поэтому мы можем говорить о нулевом векторе .
Поскольку у него нет длины, он не указывает ни в каком конкретном направлении.
Существует только один вектор нулевой длины, поэтому мы можем говорить о нулевом векторе .
Операции над векторами
Ряд операций над векторами можно определить геометрически без ссылка на любую систему координат. Здесь мы определяем сложение, вычитание и умножение скаляром. На отдельных страницах мы обсуждаем два разных способа умножения двух векторов: скалярное произведение и перекрестное произведение.
Сложение векторов
По двум векторам $\vc{a}$ и $\vc{b}$ образуем их сумму $\vc{a}+\vc{b}$ следующим образом. Сдвигаем вектор $\vc{b}$ до тех пор, пока его хвост не совпадет с головой вектора $\vc{a}$. (Напомним, что такой перевод не меняет вектор.) Тогда направленный отрезок из хвоста $\vc{a}$ в начало $\vc{b}$ представляет собой вектор $\vc{a}+\vc{b}$.
Сложение векторов — это способ объединения сил и скоростей. Например,
если машина едет строго на север со скоростью 20 миль в час, а ребенок сзади
Сиденье позади водителя бросает предмет со скоростью 20 миль в час в его сторону. 2}=20\sqrt{2}$
миль в час относительно земли.
2}=20\sqrt{2}$
миль в час относительно земли.
Добавление векторов удовлетворяет двум важным свойствам.
Коммутативный закон, который гласит, что порядок сложения не имеет значения: $$\vc{a}+\vc{b}=\vc{b}+\vc{a}.$$ Этот закон также называется законом параллелограмма, как показано на рисунке ниже. изображение. Два ребра параллелограмма определяют $\vc{a}+\vc{b}$, а другая пара ребер определяет $\vc{b}+\vc{a}$. Но обе суммы равны равна той же диагонали параллелограмма.
Ассоциативный закон, утверждающий, что сумма трех векторов не зависит от того, какая пара векторов добавляется первой: $$(\vc{a}+\vc{b})+\vc{c} = \vc{a} + (\vc{b}+\vc{c}).$$
Вы можете изучить свойства сложения векторов с помощью следующего апплета. (Этот апплет также показывает координаты векторов, о которых вы можете прочитать на другой странице.)
Сумма двух векторов. Сумма $\vc{a}+\vc{b}$ вектора $\vc{a}$ (синяя стрелка) и вектора $\vc{b}$ (красная стрелка) показана зеленой стрелкой . Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$. То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$. То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
Дополнительная информация об апплете.
Вычитание вектора
Перед определением вычитания мы определяем вектор $-\vc{a}$, который является противоположностью $\vc{a}$. Вектор $-\vc{a}$ — это вектор с той же величиной, что и $\vc{a}$, но направленной в противоположном направлении.
Мы определяем вычитание как сложение с противоположным вектором:
$$\vc{b}-\vc{a} = \vc{b} + (-\vc{a}). $$
Это эквивалентно переворачиванию вектора $\vc{a}$ при применении
вышеуказанные правила добавления. Вы видите, как вектор $\vc{x}$ в
ниже рисунок равен $\vc{b}-\vc{a}$? Обратите внимание, как это то же самое
как утверждается, что $\vc{a}+\vc{x}=\vc{b}$, как и при вычитании
скалярные числа.
$$
Это эквивалентно переворачиванию вектора $\vc{a}$ при применении
вышеуказанные правила добавления. Вы видите, как вектор $\vc{x}$ в
ниже рисунок равен $\vc{b}-\vc{a}$? Обратите внимание, как это то же самое
как утверждается, что $\vc{a}+\vc{x}=\vc{b}$, как и при вычитании
скалярные числа.
Скалярное умножение
Имея вектор $\vc{a}$ и действительное число (скаляр) $\lambda$, мы можем сформировать вектор $\lambda\vc{a}$ следующим образом. Если $\lambda$ положительна, то $\lambda\vc{a}$ — это вектор, направление которого совпадает с направлением $\vc{a}$, а длина равна $\lambda$, умноженной на длину $ \vc{а}$. В этом случае умножение на $\lambda$ просто растягивает (если $\lambda>1$) или сжимает (если $0
Если, с другой стороны, $\lambda$ отрицательно, то мы должны взять
напротив $\vc{a}$ перед его растяжением или сжатием. Другими словами,
вектор $\lambda\vc{a}$ указывает направление, противоположное вектору $\vc{a}$,
а длина $\lambda\vc{a}$ равна $|\lambda|$, умноженной на длину $\vc{a}$. Независимо от знака $\lambda$, мы наблюдаем, что величина $\lambda\vc{a}$ в $|\lambda|$ умножается на величину $\vc{a}$: $\| \лямбда \vc{а}\| = |\лямбда| \|\vc{a}\|$.
Независимо от знака $\lambda$, мы наблюдаем, что величина $\lambda\vc{a}$ в $|\lambda|$ умножается на величину $\vc{a}$: $\| \лямбда \vc{а}\| = |\лямбда| \|\vc{a}\|$.
Скалярные умножения удовлетворяют многим из тех же свойств, что и обычное умножение.
- $s(\vc{a}+\vc{b}) = s\vc{a} + s\vc{b}$ (распределительный закон, форма 1)
- $(s+t)\vc{a} = s\vc{a}+t\vc{a}$ (распределительный закон, форма 2)
- $1\vc{a} = \vc{a}$
- $(-1)\vc{a} = -\vc{a}$
- $0\vc{a} = \vc{0}$
В последней формуле ноль слева — это число 0, а ноль справа — это вектор $\vc{0}$, уникальный вектор, длина которого равна нулю.
Если $\vc{a} = \lambda\vc{b}$ для некоторого скаляра $\lambda$, то мы говорим что векторы $\vc{a}$ и $\vc{b}$ параллельны. Если $\lambda$ отрицательно, некоторые люди говорят, что $\vc{a}$ и $\vc{b}$ антипараллельны, но мы не использовать этот язык.
Мы смогли описать векторы, сложение векторов, вычитание векторов и
скалярное умножение без привязки к какой-либо системе координат.




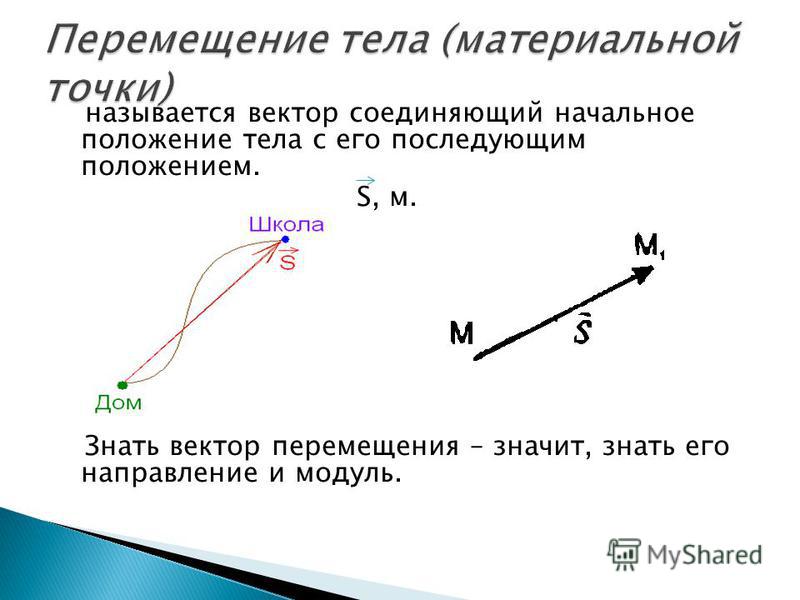

 Другими хорошими примерами являются силы и импульсы.
Другими хорошими примерами являются силы и импульсы.
 Скорость это ее величина.
Скорость это ее величина.