Модуль (абсолютная величина) – Энциклопедия по машиностроению XXL
Модуль (абсолютная величина) 24 [c.495]Исходный контур (стандартизованный) указывается ссылкой на ГОСТ 13755—68 или на ГОСТ 9587—68 (для мелкомодульных зубчатых передач). Нестандартизованный исходный контур в соответствии с P 581—66 определяется углом профиля а , коэффициентом высоты головки /о (/о— отношение высоты головки к модулю), коэффициентом радиального зазора с и радиусом закругления г,, в отличие от ГОСТ 9250—59, который требовал указывать угол профиля а , коэффициент высоты головки f (или абсолютную высоту головки А ), коэффициент высоты ножки f” (или абсолютную величину высоты ножки h”), радиус закругления г , высоту среза кромки вершины зубьев he и угол среза (фланка) а . [c.129]
Проведем ось х по общей нормали к поверхностям соударяющихся тел в точке их касания, направив эту ось в сторону движения пел до удара.
Момент силы относительно точки. Равновесие твердого тела с одной неподвижной точкой. Момент силы Р относительно точки О, который записывается в виде т (Р), для плоской системы сил равен по абсолютной величине произведению модуля силы Р на расстояние А от точки О до линии действия силы Р, называемое плечом.
Мерой действия пары сил является алгебраическая величина, называемая ее моментом. Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо. Если пара сил видна направленной против часовой стрелки, то момент пары положителен, если по часовой стрелке, то отрицателен. Примеры даны на рис. 1.28.
[c.40]
Если пара сил видна направленной против часовой стрелки, то момент пары положителен, если по часовой стрелке, то отрицателен. Примеры даны на рис. 1.28.
[c.40]
Для получения проекции мы умножали на os а не вектор, а его модуль, его абсолютную величину. Проекция силы на ось не является вектором, поскольку она не имеет собственного направления, а вполне определяется направлением оси, величиной проекции
Предел этого отношения называют численным значением (абсолютной величиной, модулем) скорости точки в данное мгновение (или истинной скорости точки) [c.25]
Алгебраическая скорость v имеет свой знак ( + или — ) и только по абсолютной величине равна модулю скорости [c.27]
Для определения проекции скорости на ось мы умножали на направляющий косинус не вектор, а его модуль, его абсолютную величину. Проекция скорости на ось (как и алгебраическая скорость точки) не является вектором, так как не имеет собственного направления, а вполне определяется величиной проекции, направлением оси и знаком + или — .
Если точка переменит свое движение на возвратное, например, если точка совершает колебательные движения на каком-либо участке кривой, то обычно не меняют положительного направления естественных осей, а приписывают скорости знак минус, если точка движется н сторону уменьшения дуговой координаты. Так в естественном способе задания движения точки, вместо модуля скорости появилась алгебраическая скорость , по абсолютной величине равная модулю, но имеющая собственный знак ( + или — ). Это обстоятельство сказывается и на определении касательного ускорения точки при естественном способе задания ее движения.
Перед радикалом поставлен знак + , потому что модуль вектора величина положительная. Равенство (29) можно прочитать так абсолютная величина ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат. Учитывая, что проекция ускорения точки на координатную ось равна второй производной от текущей координаты по времени, можем переписать равенство (29) в следующем виде
Равенство (29) можно прочитать так абсолютная величина ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат. Учитывая, что проекция ускорения точки на координатную ось равна второй производной от текущей координаты по времени, можем переписать равенство (29) в следующем виде
Чтобы записать вектор скорости точки v, направленный по касательной к окружности радиуса Rm в сторону изменения угла ф в данный момент, удобно ввести понятие вектора угловой скорости. Модуль этого вектора полагается равным абсолютной величине угловой скорости. Направлен этот вектор по оси вращения тела так, что, глядя с его конца, вращение тела происходит против часовой стрелки (см. рис. 2.4). Используя вектор (о, можно записать
Угловая скорость абсолютного вращения совпадает по направле-тшю с угловой скоростью с большей числовой величиной. Модуль абсолютной угловой скорости равен разности модулей угловых скоростей
[c. 195]
195]
Для параллельной силы, направленной в сторону, противоположную положительному направлению оси, / (Р, = 180″, os = 180° = — 1, следовательно, по формуле (1.7), X — — Р, т. е. проекция силы, параллельной оси и направленной в сторону, противоположную положительному направлению оси, отрицательна и по абсолютной величине равна модулю самой силы.
При рассмотрении пар, не лежащих в одной плоскости, для полной характеристики вращательного действия пары на тело указания только абсолютной величины момента и его знака недостаточно, так как вращательное действие пары на тело зависит еще и от направления в пространстве плоскости действия пары. Поэтому принятое в 14 определение момента пары следует дополнить указанием направления в пространстве плоскости действия пары. Последнее определяется, очевидно, направлением перпендикуляра к плоскости действия пары. Следовательно, в случае пар, не лежащих в одной плоскости, для характеристики вращательного действия на тело каждой из пар необходимо задать 1) модуль момента пары 2) направление перпендику-
 167]
167]
Следовательно, модуль вектора скорости равен абсолютной величине первой производной от криволинейной координаты точки по времени. [c.254]
Угловая скорость и угловое ускорение твердого тела, вращающегося вокруг неподвижной оси, как векторы. Чтобы получить векторные формулы, определяющие векторы скорости и ускорения точек вращающегося вокруг неподвижной оси твердого тела, условились изображать угловую скорость этого тела вектором. Модуль вектора ш, изображающего угловую скорость тела, считают равным абсолютной величине угловой скорости тела, т. е. (о = 9 . При этом вектор ш откладывают по оси вращения так, чтобы наблюдатель, смотрящий с конца этого вектора в сторону его начала, видел вращение тела совершающимся против движения часовой стрелки (правило правого винта). Что касается начала вектора со, то оно может быть помещено в любой
Задав вектор угловой скорости ш, можно для каждого момента времени сразу определить 1) положение оси вращения тела (прямая, вдоль которой расположен вектор ш) 2) направление вращения тела вокруг этой оси, определяемое направлением вектора абсолютную величину угловой скорости тела, равную модулю вектора ш.
Модуль вектора углового ускорения е равен абсолютной величине [c.299]
Модуль вектора-момента Mo равен абсолютной величине проекции главного момента на направление главного вектора, т. е. [c.112]
Вектор ах = х называется тангенциальным (касательным) ускорением точки. Вектор направлен по касательной и, -как видно из (7.16), по абсолютной величине равен модулю производной от алгебраической величины скорости [c.97]
Все величины, входящие в формулу (10-15), следует брать по абсолютной величине, при этом max представляет собой значение наибольшего сжимающего напряжения в рассматриваемом сечении, взятое по модулю. Для упрощения записи обозначения, показывающие, что та или иная величина берется по модулю, опускаем.
При t = I с Vr = —4 дм/е. Поскольку в этот момент величина v, отрицательна, вектор Vr направлен в сторону уменьшения расстояния ОМ, т. е. к вершине конуса. Относительная и переносная скорости взаимно перпендикулярны, и поэтому модуль абсолютной скорости равен
[c.84]
е. к вершине конуса. Относительная и переносная скорости взаимно перпендикулярны, и поэтому модуль абсолютной скорости равен
[c.84]
Здесь величина Е — абсолютная величина комплексного модуля — определяется первой из формул (17.8.5).
Если составляющие силы взаимно перпендикулярны, то имеем прямоугольный параллелепипед. Проведем оси координат по трем сходящимся ребрам этого параллелепипеда. Тогда модули Рх, Р , Р составляющих сил будут равны абсолютным величинам соответствующих проекций равнодействующей на эти [c.21]
Оценка точности чисел. Разность = = а — йо между приближённым числовым значением а какой-либо величины и её истинным (точным) значением называется ошибкой, или погрешностью, приближённого числа а. Модуль (абсолютная величина) этой разности называется абсолютной погрешностью, а отношение последней к модулю числа а — относительной погрешностью приближённого числа а. [c.109]
Ответ Главный вектор сил инерции равен по модулю Ма и направлен параллельно оси в отрицательном направлении главный момент сил инерции равен по абсолютной величине чМаг. [c.314]
[c.314]
При ие очень больших по абсолютной величине отрицательных значениях может сразу начаться убывание q t) (кривая 2). При больших по модулю отрицательных значениях Уо функция q t), убывая, может достичь нулевого значения, соответствующего положению равновесия системы, стать отрицательной и, оставаясь отрицательной, асимптотически приближаться к нулю (кривая J). Во всех этих случаях движение является штухающим, иеколебательным, которое иногда называют также апериодическим. [c.443]
В программе в процессе реализации процедуры исключения предусмотрен контроль потери точности. Для этого на каждом шаге k исключения главный элемент Оц, на который производится деление в формулах (1.11), (1.14), сравнивается с величиной EPS Qmax. где — максимальный по модулю элемент матрицы. Если абсолютная величина главного элемента оказывается меньше, чем это произведение, то параметр ошибки принимает значение (k + 1). Обычно задают EPS == (10 10 ). Выходной параметр ошибки IER =
[c.20]
Выходной параметр ошибки IER =
[c.20]
Критерий заключается в сопоставлении по модулю максимального Птах И минимального собственных чисел линейной или линеаризованной системы. Если эти собственные числа сильно различаются по абсолютной величине (fAmax/Hmin Э 1). промежуток времени, на котором нужно получить решение, значительно превосходит интервал затухания ехр (цщахТ ). то система является жесткой и при ее численном решении по явным схемам возникнут проблемы с выбором шага. [c.41]
Полученные соотношения и расчетные данные рис. 4.5 показывают, что вследствие немоноэнергетичности используемого излучения реконструированные значения ЛКО для центральной зоны изделия всегда ниже действительных 6н (р.) 0. Причем величина и знак средней погрешности не зависят от знака производной а — d i/dE, а только от модуля ее величины в рабочем диапазоне энергий. Это обстоятельство делает выбор эффективной энергии Ео важным фактором возможного снижения бц (ц) за счет уменьшения абсолютной величины а (Яо) применительно к конкретным материалам. В оптимальных условиях контроля (43) типичные значения
[c.417]
В оптимальных условиях контроля (43) типичные значения
[c.417]
Проекции вектора на направление. Проекция вектора на ось
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Пр a b = |b|cos(a,b) или
Где a b – скалярное произведение векторов , |a| – модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).

- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Yandex.RTB R-A-339285-1
Если имеем ось L и ненулевой вектор A B → , то можем построить вектор A 1 B 1 ⇀ , обозначив проекции его точек A 1 и B 1 .
A 1 B → 1 будет являться проекцией вектора A B → на L .
Определение 1
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. n p L A B → → принято обозначать проекцию A B → на L . Для построения проекции на L опускают перпендикуляры на L .
Пример 1
Пример проекции вектора на ось.
На координатной плоскости О х у задается точка M 1 (x 1 , y 1) . Необходимо построить проекции на О х и О у для изображения радиус-вектора точки M 1 . Получим координаты векторов (x 1 , 0) и (0 , y 1) .
Если идет речь о проекции a → на ненулевой b → или проекции a → на направление b → , то имеется в виду проекция a → на ось, с которой совпадает направление b → . , мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
, мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
Определение 3
Числовой проекцией вектора a → на ось, совпадающей по направлению с b → , называют отношение скалярного произведения векторов a → и b → к длине b → . Формула n p b → a → = a → , b → b → применима для нахождения числовой проекции a → на прямую, совпадающую по направлению с b → , при известных a → и b → координатах.
Пример 3
Задан b → = (- 3 , 4) . Найти числовую проекцию a → = (1 , 7) на L .
Решение
На координатной плоскости n p b → a → = a → , b → b → имеет вид n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 , при a → = (a x , a y) и b → = b x , b y . Чтобы найти числовую проекцию вектора a → на ось L , нужно: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5 .
Ответ: 5.
Пример 4
Найти проекцию a → на L , совпадающей с направлением b → , где имеются a → = – 2 , 3 , 1 и b → = (3 , – 2 , 6) . Задано трехмерное пространство.
Решение
По заданным a → = a x , a y , a z и b → = b x , b y , b z вычислим скалярное произведение: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Длину b → найдем по формуле b → = b x 2 + b y 2 + b z 2 . Отсюда следует, что формула определения числовой проекции a → будет: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .
Подставляем числовые значения: n p L a → = n p b → a → = (- 2) · 3 + 3 · (- 2) + 1 · 6 3 2 + (- 2) 2 + 6 2 = – 6 49 = – 6 7 .
Ответ: – 6 7 .
Просмотрим связь между a → на L и длиной проекции a → на L . Начертим ось L , добавив a → и b → из точки на L , после чего проведем перпендикулярную прямую с конца a → на L и проведем проекцию на L . Существуют 5 вариаций изображения:
Первый случай при a → = n p b → a → → означает a → = n p b → a → → , отсюда следует n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → . = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
= 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
По условию угол острый, тогда числовая проекция a → = длине проекции вектора a → : n p L a → = n p L a → → = 9 . Данный случай показывает, что векторы n p L a → → и b → сонаправлены, значит имеется число t , при котором верно равенство: n p L a → → = t · b → . Отсюда видим, что n p L a → → = t · b → , значит можем найти значение параметра t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .
Тогда n p L a → → = 3 · b → с координатами проекции вектора a → на ось L равны b → = (- 2 , 1 , 2) , где необходимо умножить значения на 3. Имеем n p L a → → = (- 6 , 3 , 6) . Ответ: (- 6 , 3 , 6) .
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Рис. 3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 – вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» – в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О – начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).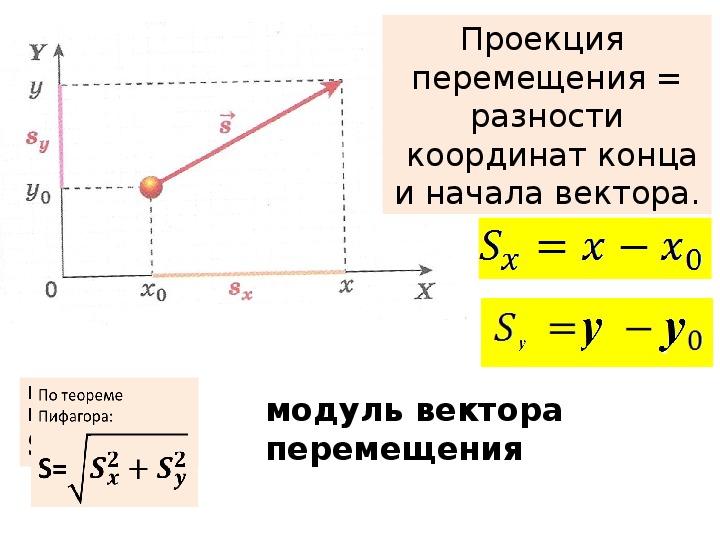
Таким образом, в обоих случаях справедливо утверждение теоремы.
ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L – угол , кроме того сами векторные проекции образуют между собой угол , то
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.

- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A”$ – начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B”$ – конец искомого вектора. Вектор $\overline{A”B”}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A”$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B”$ (рис. 7).
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот.
Возьмем следующее координатное уравнение: x = x(t), y = y(t), z = z(t). В данном случае функция скорости будет спроецирована на три оси и будет иметь следующий вид: V(x) = dx / dt = x”(t), V(y) = dy / dt = y”(t), V(z) = dz / dt = z”(t). Отсюда следует, что для нахождения скорости необходимо брать производные. Сам же вектор скорости выражается уравнением такого вида: V = V(x) i + V(y) j + V(z) k. Здесь i, j, k являются единичными векторами координатных осей x, y, z соответственно. 2).
2).
Вычислить проекции вектора на оси координат. Калькулятор онлайн.Вычисление проекции вектора на вектор
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Пр a b = |b|cos(a,b) или
Где a b – скалярное произведение векторов , |a| – модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.

Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.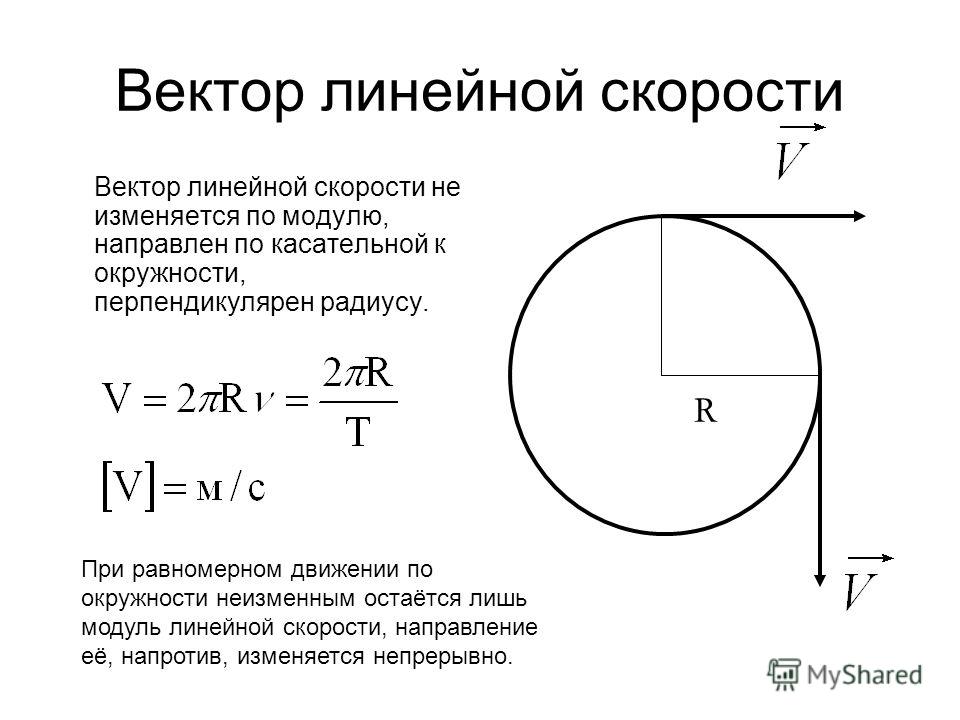 | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Рис. 3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 – вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» – в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О – начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис.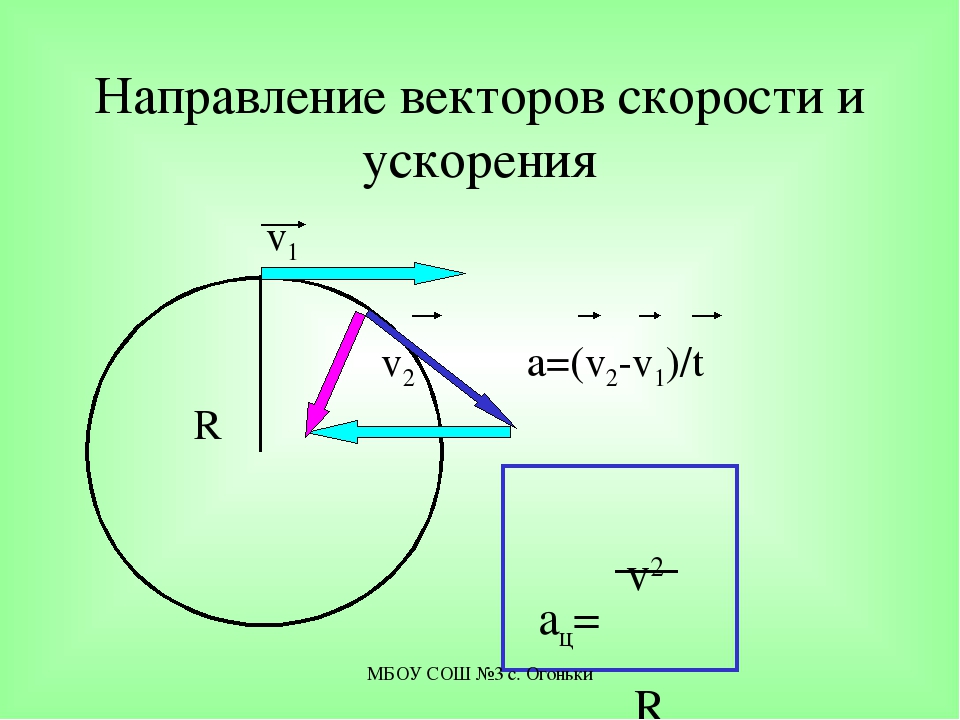 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
Таким образом, в обоих случаях справедливо утверждение теоремы.
ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L – угол , кроме того сами векторные проекции образуют между собой угол , то
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.

- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A”$ – начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B”$ – конец искомого вектора. Вектор $\overline{A”B”}$ и будет искомым вектором.
Получаем точку $A”$ – начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B”$ – конец искомого вектора. Вектор $\overline{A”B”}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A”$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B”$ (рис. 7).
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B .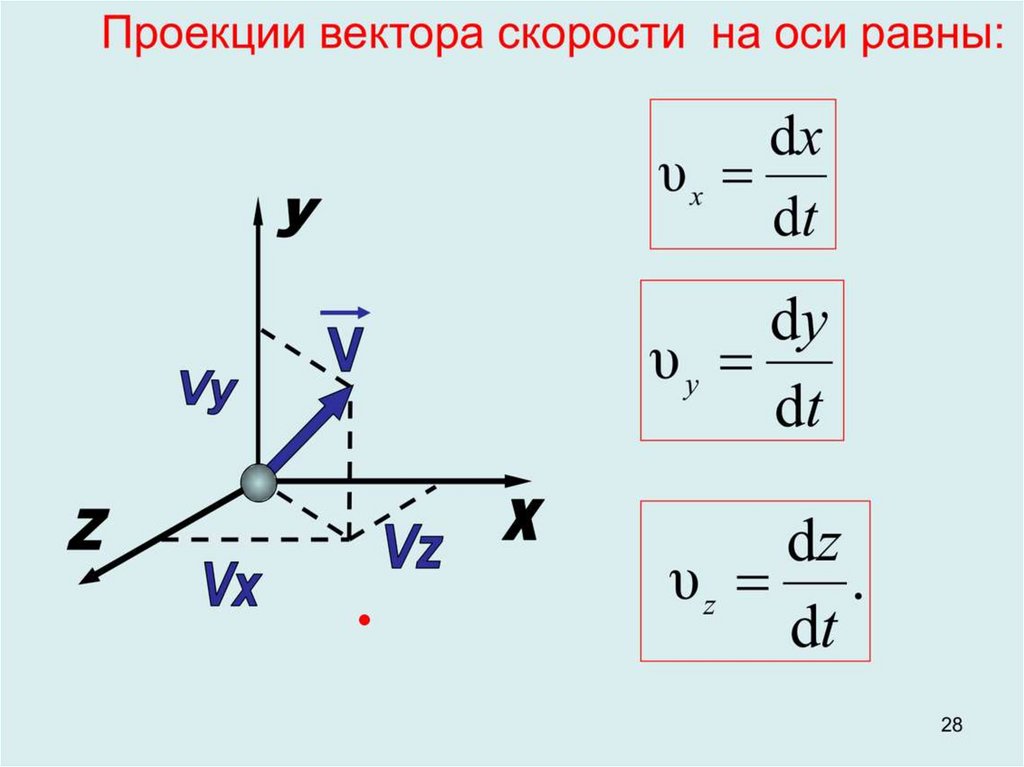 Предположим,
что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .
Предположим,
что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .
Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 x 1 и проекция x 2 – x 1 l , то x 2 = x 1 и x 2 – x 1 =0.
Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций .
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где – некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы называются линейно зависимыми , если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми .
Теорема 1. Любые два вектора линейно зависимы тогда и
только тогда, когда они коллинеарны.
Любые два вектора линейно зависимы тогда и
только тогда, когда они коллинеарны.
Доказательство :
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство .
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве
задан базис . Тогда любой вектор можно представить в
виде линейной комбинации , где x , y , z – некоторые числа. Такое разложение единственно.
Такое разложение единственно.
Доказательство .
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .
Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются
осями координат – осью абсцисс, ординат и аппликат.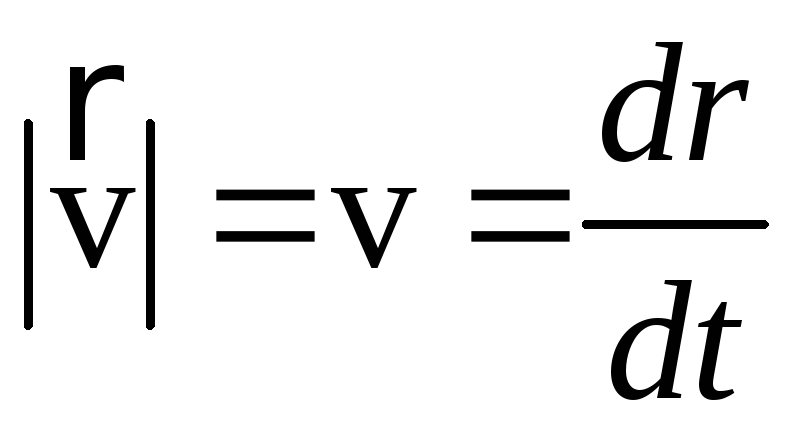 Плоскости, проходящие через оси координат, называют координатными плоскостями.
Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют
единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Введение…………………………………………………………………………3
1. Значение вектора и скаляра………………………………………….4
2. Определение проекции, оси и координатой точки…………………5
3. Проекция вектора на ось………………………………………………6
4. Основная формула векторной алгебры……………………………..8
5. Вычисление модуля вектора по его проекциям……………………9
Заключение………………………………………………………………………11
Литература………………………………………………………………………12
Введение:
Физика неразрывно связана с математикой. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента или теоретических исследований.Ведь основной метод исследований в физике – экспериментальный. Это значит – вычисления ученый выявляет с помощью измерений. Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика – есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.
Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика – есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.
Итак, физика создает модель окружающего нас мира и изучает ее свойства. Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого – из всего многообразия выбрать главное.
Физические модели являются математическими, но не математика является их основой. Количественные соотношения между физическими величинами выясняются в результате измерений, наблюдений и экспериментальных исследований и лишь выражаются на языке математики. Однако другого языка для построения физических теорий не существует.
Однако другого языка для построения физических теорий не существует.
1. Значение вектора и скаляра.
В физике и математике вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они “скалярами” .
Они записываются либо буквами обычного шрифта, либо цифрами (а, б, t, G, 5, −7….). Скалярные величины могут быть положительными и отрицательными. В то же время некоторые объекты изучения могут обладать такими свойствами, для полного описания которых знание только числовой меры оказывается недостаточным, необходимо ещё охарактеризовать эти свойства направлением в пространстве. Такие свойства характеризуются векторными величинами (векторами). Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Нередко вектор обозначают буквой обычного (нежирного) шрифта, но со стрелкой над ней:
Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая – его конец.
Модуль вектора, то есть длину направленного прямолинейного отрезка, обозначают теми же буквами, как и сам вектор, но в обычном (не жирном) написании и без стрелки над ними, либо точно также как и вектор (то есть жирным шрифтом или обычным, но со стрелкой), но тогда обозначение вектора заключается в вертикальные черточки.
Вектор – сложный объект, который одновременно характеризуется и величиной и направлением.
Не бывает также положительных и отрицательных векторов. А вот равными между собой векторы быть могут. Это когда, например, aиb имеют одинаковые модули и направлены в одну сторону. В этом случае справедлива запись a = b. Надо также иметь в виду, что перед символом вектора может стоять знак минус, например, – с, однако, этот знак символически указывает на то, что вектор -с имеет такой же модуль, как и вектор с, но направлен в противоположную сторону.
Вектор -с называют противоположным (или обратным) вектору с.
В физике же каждый вектор наполнен конкретным содержанием и при сравнении однотипных векторов (например, сил) могут иметь существенное значение и точки их приложения.
2.Определение проекции, оси и координатой точки.
Ось – это прямая, которой придается какое–то направление.
Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.
Проекцией точки на ось называется основание перпендикуляра, опущенного из этой точки на данную ось. То есть, проекцией точки на ось является точка.
Координатой точки на данной оси называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.
3.Проекция вектора на ось.
Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а x – скалярная проекция вектора а на ось X, то а x ·i – его векторная проекция на эту ось.
Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим а x (жирная буква, обозначающая вектор и нижний индекс названия оси) или
(нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).Скалярной проекцией вектора на ось называется число , абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция . Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора, то его проекция обозначается а x
. При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться а y
.
Например, если на ось Х проектируется вектора, то его проекция обозначается а x
. При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться а y
.
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
а x = х к − x н.
Проекция вектора на ось – это число. Причем, проекция может быть положительной, если величина х к больше величины х н,
отрицательной, если величина х к меньше величины х н
и равной нулю, если х к равно х н.
Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка видно, что а x = а Cos α
То есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора . Если угол острый, то
Cos α > 0 и а x
> 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.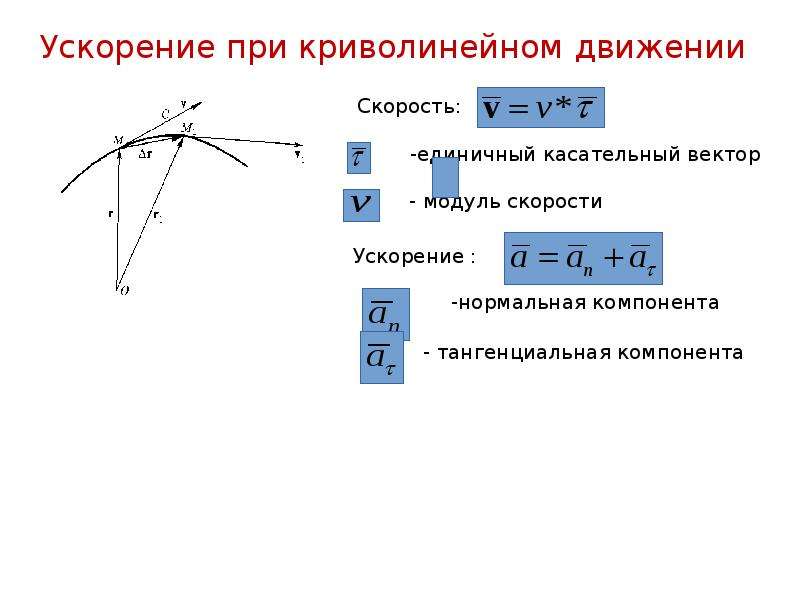
Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу – отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
4. Основная формула векторной алгебры.
Спроектируемвектор а на оси Х и Y прямоугольной системы координат. Найдем векторные проекции вектора а на эти оси:
а x = а x ·i, а y = а y ·j.
Но в соответствии справилом сложения векторов
а = а x + а y .
а = а x ·i + а y ·j.
Таким образом, мы выразили вектор через его проекции и орты прямоугольной системы координат (или через его векторные проекции).
Векторные проекции а x
и а y
называютсясоставляющими или компонентами вектора а. Операция, которую мы выполнили, называется разложением вектора по осямпрямоугольной системы координат.
Если вектор задан в пространстве, то
а = а x ·i + а y ·j + а z ·k.
Эта формула называется основной формулой векторной алгебры. Конечно, ее можно записать и так.
Скорость прямолинейного равноускоренного движения. График скорости
2. Повторение: 1. Какое движение называется прямолинейным равноускоренным? 2. Что называется ускорением? 3. Что характеризует
ускорение?4. Что является единицей ускорения?
5. Что понимают под мгновенной
скоростью неравномерного движения?
3. Отвечаем на вопросы:
1 Чему равна мгновенная скорость камня,брошенного вертикально вверх, в верхней точке
траектории?
2 О какой скорости – средней или мгновенной
– идет речь в следующих случаях:
А) пуля вылетает из винтовки со скоростью
800 м/с.
Б) самолет летит из Киева в Москву со
скоростью 800 км/ч
В) скоростемер на тепловозе показывает 75
км/ч?
4. Выведем формулу скорости
скорость тела в любой момент времени(мгновенная скорость)
– скорость тела в начальный момент
времени
, ускорение тела
Если в начальный момент тело покоилось, т.
 2
2в течение 40 c
Мы знаем
известны по условию
60
50
40
30
20
10
график движения
10 20 30 40 50
t
0
20
40
Vx
0
30
60
Построим график зависимости от времени проекции
вектора скорости для случая, когда начальная скорость
на равна 0.
По дороге едет автомобиль со скоростью 10 м/с.Водитель
автомобиля, увидев дорожный знак, снимающий ограничение скорости,
нажал на педаль газа, в результате чего автомобиль стал двигаться с
постоянным ускорением 1,4 м/с2.
Мы знаем
известны по условию
график движения
13
11
9
7
5
3
1
1234 5
10 20 30 40 50
t
0
2
Vx
10
12,8
По дороге едет автомобиль со скоростью 20 м/с.Водитель
автомобиля начинает тормозить. В результате автомобиль движется с
ускорением 2 м/с2 и через 10 с останавливается.
Мы знаем
известны по условию
30
25
20
15
10
5
график движения
9 10
t
0
5
Vx
20
10
11.
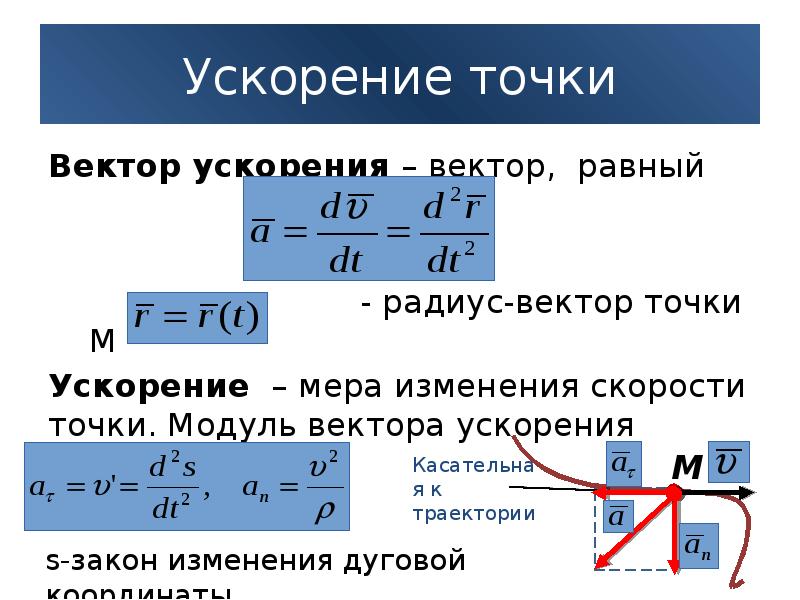 Графики зависимости скорости от времени тело движется в
Графики зависимости скорости от времени тело движется вположительном
направлении оси X
Первые 5 с тело
движется в
положительном
направлении оси X
С 5 секунды тело
движется в
отрицательном
направлении оси X
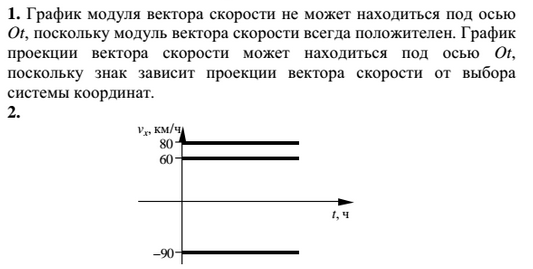
График проекции вектора скорости может находиться под
осью Ot, поскольку знак зависит проекции вектора скорости
от выбора системы координат.
13. С каким по модулю ускорением движется тело?
График модуля вектора скорости не может находитьсяпод осью Ot, поскольку модуль вектора скорости
всегда положителен.
С каким по модулю ускорением
движется тело?
14. Записать уравнение скорости от времени vх(t) для каждого участка графика
15. Записать уравнение скорости от времени vх(t) для каждого участка графика
16. Какой вид движения изображён на графике? Записать уравнение скорости от времени.
17. Домашнее задание: § 6, упр6(1-4)
(PDF) Линейные тренды в поле дрейфа ледяного покрова в Северном Ледовитом океане
348
ОКЕАНОЛОГИЯ том 61 № 3 2021
ЛИПАТОВ и др.
взгляд, такое представление тренда векторов более
информативно, нежели визуальное сопоставление
векторов ускорения и свободного члена или
векторов и . Анализ полей предложенных
характеристик тренда векторов также позволяет
выявить скрытые особенности климатической
изменчивости схемы среднего поля векторов.
Также для тренда векторов в терминах вектор-
ной алгебры определены коэффициент детерми-
нации и статистическая значимость, основанная
на расчете характеристик эллипсов стандартной
ошибки векторов ускорения и свободного чле-
на .
Описанная методика может быть применена
к любым векторным гидрометеорологическим
процессам (ветер, течения, дрейф льда). В данной
статье предложенные характеристики тренда век-
торов применены для анализа дрейфа ледяного
покрова в Северном Ледовитом океане. Исполь-
зовались суточные данные, охватывающие по-
следние 40 лет (1978–2018 гг. ), из базы данных Po-
), из базы данных Po-
lar Pathfinder.
Результаты расчета коллинеарной составляю-
щей ( ) вектора ускорения подтверждают уже из-
вестные общие представления о климатической
изменчивости дрейфа Арктики, полученные при
анализе модулей векторов дрейфа: на большей
части акватории отмечается увеличение средней
скорости дрейфа как в летний, так и в зимний се-
зоны. В зимний сезон лишь в прибрежной части
Чукотского и Восточно-Сибирского морей отме-
чается незначительное уменьшение скорости
среднего дрейфа.
Поле значений угловой скорости измене-
ния направления вектора среднего дрейфа пока-
зывает, что в зимний гидрологический сезон в
окраинных морях сибирского шельфа направле-
ние среднего дрейфа меняется по направлению к
стрежню Трансарктического дрейфа: в Карском
море и море Лаптевых отмечается тенденция к
повороту векторов среднего дрейфа вправо, в Во-
сточно-Сибирском море направления среднего
дрейфа меняются влево. В области антициклони-
В области антициклони-
ческого круговорота моря Бофорта отмечается
противоположное расположение положительных
и отрицательных значений угловой скорости
изменения направления среднего дрейфа и орто-
гональной составляющей ( ) вектора ускорения
( и функционально связаны). Такая структу-
ра полей и свидетельствует о климатической
тенденции смещения центра антициклонического
круговорота дрейфа льда.
Коэффициент детерминации тренда векторов
дрейфа, рассчитанный по среднегодовым значе-
ниям, говорит о вкладе дисперсии тренда в меж-
годовую изменчивость. Полученные результаты
свидетельствуют о том, что в зимний сезон линей-
ная тенденция объясняет более половины дисперсии
межгодовой изменчивости дрейфа в проливе Фрама,
южном секторе антициклонического круговорота
моря Бофорта, в Карском море и море Баффина.
СПИСОК ЛИТЕРАТУРЫ
1. Алексеев Г.В., Александров Е.И., Глок Н. И. и др. Эво-
И. и др. Эво-
люция площади морского ледового покрова Аркти-
ки в условиях современных изменений климата //
Исслед. Земли из космоса. 2015. № 2. С. 5–19.
2. Артамонов Ю.В., Скрипалева Е.А., Федирко А.В. Ре-
гиональные особенности климатической измен-
чивости поля температуры на поверхности Черно-
го моря // Метеорология и гидрология. 2017. № 2.
С. 56–66.
3. Артамонов Ю.В., Федирко А.В., Скрипалева Е.А.
Климатическая изменчивость переносов в верх-
нем слое Антарктического циркумполярного тече-
ния по данным спутниковых и контактных изме-
рений // Исслед. Земли из космоса. 2016. № 1–2.
С. 76–89.
4. Белоненко Т.В., Колдунов А.В. О трендах стериче-
ских колебаний уровня в северной Атлантике //
Исслед. Земли из космоса. 2018. № 5. С. 31–40.
5. Белоненко Т.В., Федоров А.М., Башмачников И.Л.,
Фукс В.Р. Тренды интенсивности течений в Лабра-
дорском море и море Ирмингера по спутниковым
альтиметрическим данным // Исслед. Земли из
Земли из
космоса. 2018. № 2. С. 3–12.
6. Белышев А.П., Клеванцов Ю.П., Рожков В.А. Веро-
ятностный анализ морских течений. Л.: Гидроме-
теоиздат, 1983. 264 с.
7. Боков В.Н., Бухановский А.В., Иванов Н.Е., Рожков В.А.
Пространственно-временнáя изменчивость поля
ветра в умеренных широтах Северного полушария //
Изв. РАН. Физика атмосферы и океана. 2001. Т. 37.
№ 2. С. 170–181.
8. Волков В.А., Мушта А.В., Демчев Д.М. Закономер-
ности изменения крупномасштабной структуры
поля дрейфа морского льда в Северном Ледовитом
океане (на основе спутниковых данных 1978–
2017 гг.) // Докл. АН. 2019. Т. 488. № 4. С. 439–442.
9. Гудкович З.М. Связь дрейфа льдов в Арктическом
бассейне с ледовыми условиями в советских арк-
тических морях // Труды океанографической ко-
миссии АН СССР. 1961. Т. 11. С. 13–20.
10. Иванов Н.Е., Лагун В.Е., Луценко Э.И. Особенности
климатического режима станции Русская (запад-
ная Антарктида) // Проблемы Арктики и Антарк-
тики. 2008. № 3 (80). С. 48–71.
2008. № 3 (80). С. 48–71.
11. Иванов Н.Е., Макштас А.П., Шутилин С.В., Гунн Р.М.
Многолетняя изменчивость характеристик клима-
та района гидрометеорологической обсерватории
Тикси // Проблемы Арктики и Антарктики. 2009.
№ 1 (81). С. 24–41.
12. Мельников В.А., Москаленко Л.В., Кузеванова Н.И.
Ветровые циклы и климатические тренды Черного
моря // Труды Государственного океанографиче-
ского института. 2018. Вып. 219. С. 101–123.
Образцы контрольных задач с решениями и сопутствующей теорией
Летов Д.А.
Образцы контрольных задач с решениями и сопутствующей теорией
темы: | Преобразования Галилея, |
Движение тела по окружности, | |
Движение тела, брошенного под углом к горизонту |
МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО ФИЗИКЕ
Москва
Издательство Российского университета дружбы народов
2006
У т в е р ж д е н о РИС Ученого совета Российского университета дружбы народов |
Автор:
Летов Д. А.
А.
Образцы контрольных задач с решениями и сопутствующей теорией: Методическое пособие по физике/ Летов Д.А. М.: Изд-во РУДН, 2006. 51с., ил.
В рамках курса элементарной физики в разделе «Кинематика материальной точки» решение задач по темам «Преобразования Галилея», «Движение тела по окружности» и « Движение тела, брошенного под углом к горизонту» вызывает наибольшее затруднение. Объективно решение таких задач требует определенного кругозора знаний по физике и математике, навыков в адекватной интерпретации текстовой информации задачи в виде рисунка и умения прочитать на рисунке очевидные соотношения, записав их в виде формул.
Цель методического
пособия – помочь студентам в самообразовании
и становлении их физической фантазии,
показать на конкретных примерах как
может идти логическое развитие построения
решения задачи. Для того чтобы все
объяснения были исчерпывающими, по
каждой теме приводится все необходимые
теоретические сведения.
Предлагаемое пособие предназначено российским студентам, которые обучаются на подготовительных факультетах вузов Российской Федерации и ориентировано на физико-математические и технические специальности.
Д.А. Летов, 2006
Издательство Российского университета дружбы народов, 2006
Введение
Данное пособие
написано с целью пробудить в студентах
дремлющий естественный дух исследователя
природы, обострить физическое чутьё и
вселить уверенность в собственные
аналитические способности, которые
можно и нужно развивать, как и все прочие.
Каждую из предлагаемых оригинальных
задач мы будем разбирать как маленькую
научную проблему. Это значит, что сначала
мы будем оговаривать все исходные
физические условия и ограничения, затем
будем выяснять, как они формализуются
на языке математики, какие уравнения
описывают события, происходящие в
задаче. Вслед за этим обсудим, какие
доступные математические методы
позволяют решать предложенные уравнения
и как возможные физические ограничения
заставляют отклонить некоторые из
получаемых математических решений. В
заключение проанализируем, как можно
удостовериться в правильности полученного
решения, а также какую дополнительную
новую информацию можно получить, варьируя
аргументы решения.
В
заключение проанализируем, как можно
удостовериться в правильности полученного
решения, а также какую дополнительную
новую информацию можно получить, варьируя
аргументы решения.
Для того, чтобы сделать обсуждение задач предельно чётким, по каждой теме приводится краткая теория, соответствующие правила и выводы. Каждый следующий логический шаг в анализе и решении задач мы будем делать, опираясь на сведения, приведённые в теоретическом разделе.
Тема: Преобразования Галилея
Для всеобъемлющего понимания этой темы самым важным является понятие физической системы отсчёта. Дадим наглядное определение:
Другими словами,
для того, чтобы получилась система
отсчёта необходимо на каком-либо теле,
например, на вашей тетради нарисовать
систему координат и приложить часы.
Система координат позволит следить за
изменением положения других тел в
пространстве относительно вашей тетради,
а часы измерят изменение положения этих
тел во времени, то есть интервал времени
движения.
Для ещё большей информативности и компактности на рисунке часы можно изобразить в виде дополнительной оси – оси времени. Тогда на одном рисунке можно в комплексе изобразить все детали поступательного движения тела.
Например, показать начальное положение тела в пространстве и во времени в виде точки А, указав начальные координаты (x0,y0) и начальный момент времени t0.
Изображая тело в виде точки, мы пренебрегаем реальными геометрическими размерами тела. В этом случае тело называют материальной точкой
Аналогично, конечное положение тела изобразит точка В с конечными координатами (x,y), в которую тело придёт, когда часы будут показывать конечный момент t. Вектор , который имеет начало в точке А и имеет конец в точке В называется вектором перемещения относительно данной системы отсчёта.
Обратите внимание
на слово «относительно». Галилео Галилей
(1564-1642) возможно не был первым, кто указал
на тот факт, что говорить о движении
любого тела в природе можно лишь в
относительном смысле, взяв за начало
отсчёта другое тело, на котором, как мы
теперь знаем, можно расположить систему
отсчета. Однако он пошёл дальше и
проанализировал движение данного тела
одновременно относительно двух других
тел и соответственно двух других систем
отсчёта. При этом вполне естественно,
что, решая насущные земные задачи, одним
из этих двух других тел отсчёта Галилей
выбрал планету Земля. Для любого человека
Земля – это естественная среда обитания
и большая часть наших наблюдений за
движением тел – это наблюдения, сделанные
относительно Земли, точнее относительно
системы отсчёта, связанной с Землёй.
Галилей заметил, что одна и та же лодка
с гребцами движется по-разному в стоячей
воде озера и подвижной речной воде,
причём вниз по течению лодка движется
быстрее, чем в озере, а вверх по течению
– медленней. Отсюда последовал вывод:
скорость лодки относительно Земли
зависит как от модулей, так и от взаимной
ориентации скорости лодки относительно
воды (которую придают лодке гребцы) и
скорости воды относительно Земли
(скорости течения воды в реке).
Галилео Галилей
(1564-1642) возможно не был первым, кто указал
на тот факт, что говорить о движении
любого тела в природе можно лишь в
относительном смысле, взяв за начало
отсчёта другое тело, на котором, как мы
теперь знаем, можно расположить систему
отсчета. Однако он пошёл дальше и
проанализировал движение данного тела
одновременно относительно двух других
тел и соответственно двух других систем
отсчёта. При этом вполне естественно,
что, решая насущные земные задачи, одним
из этих двух других тел отсчёта Галилей
выбрал планету Земля. Для любого человека
Земля – это естественная среда обитания
и большая часть наших наблюдений за
движением тел – это наблюдения, сделанные
относительно Земли, точнее относительно
системы отсчёта, связанной с Землёй.
Галилей заметил, что одна и та же лодка
с гребцами движется по-разному в стоячей
воде озера и подвижной речной воде,
причём вниз по течению лодка движется
быстрее, чем в озере, а вверх по течению
– медленней. Отсюда последовал вывод:
скорость лодки относительно Земли
зависит как от модулей, так и от взаимной
ориентации скорости лодки относительно
воды (которую придают лодке гребцы) и
скорости воды относительно Земли
(скорости течения воды в реке). Векторная
запись этого наблюдения позволяет
о
Векторная
запись этого наблюдения позволяет
о
дновременно
учесть оба отмеченные обстоятельства.
В дальнейшем Галилей обобщил эту формулу. Он указал, что на месте лодки может быть любое физическое тело, движение которого нас интересует, а вода в реке или подвижная водная среда – это, в общем случае, ещё одно (помимо Земли) тело отсчёта, на котором можно создать подвижную относительно Земли систему отсчёта (сокращённо «п.с.о.»).
Как практически
можно реализовать подвижную систему
отсчёта в речной воде? Для этого
потребуется обыкновенный плот (можно
виртуальный), на котором следует
изобразить свою систему координат и
установить часы. Кстати, наше движение
во времени происходит одинаково на
Земле, на плоту в реке и на лодке с
гребцами, причём в одну сторону: из
прошлого в будущее. Поэтому часы во всех
случаях будут работать одинаково,
показывая одинаковый и положительный
интервал времени движения. В этом случае
о времени говорят как о факторе вселенской
синхронизации.
Таким образом, собирательный образ предыдущей формулы имеет вид:
Если во время движения направление и модуль каждой из указанных скоростей не изменяется, то можно указать на соответствующее соотношение между векторами перемещения тела относительно Земли и п.с.о.:
Вывод: Формулы (1) и (2), которые называются «преобразования Галилея» помогут решить те задачи, в которых идёт речь об одновременном движении данного тела относительно Земли и какого-либо другого подвижного тела.
В качестве иллюстрации теории и для демонстрации математических приёмов решения рассмотрим следующую задачу.
Задача #1.
Идёт дождь. Студент
сидит в автобусе, который движется
горизонтально с постоянной скоростью
10 м/с и смотрит в боковое окно. Студент
видит, что капли дождя оставляют на
стекле следы, направленные под углом
600 к вертикали.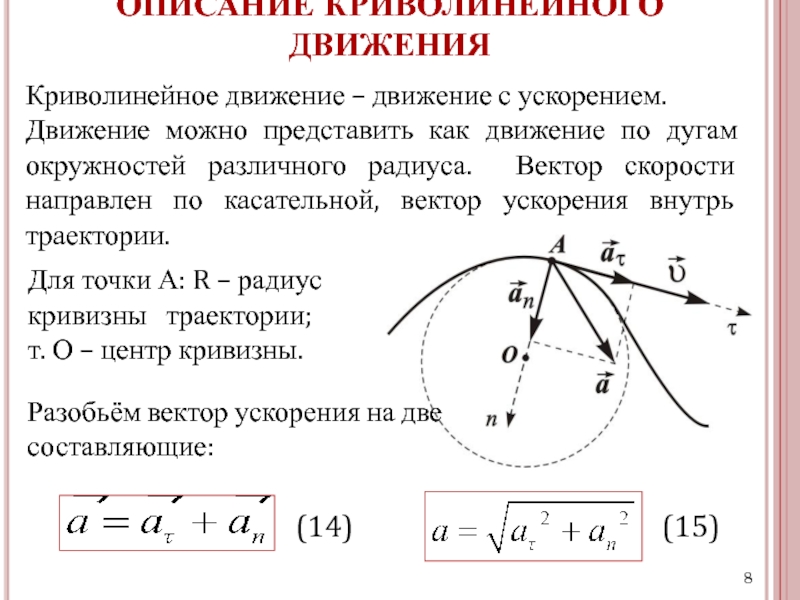 Когда на светофоре автобус
остановился, студент заметил, что теперь
следы капель дождя составляют угол 450 с вертикалью. Необходимо найти направление
и модуль скорости ветра вдоль маршрута
движения автобуса.
Когда на светофоре автобус
остановился, студент заметил, что теперь
следы капель дождя составляют угол 450 с вертикалью. Необходимо найти направление
и модуль скорости ветра вдоль маршрута
движения автобуса.
В решении физических
задач, где речь идёт о движении какого-либо
объекта, естественным помощником
является адекватный рисунок, на котором
следует наглядно изобразить систему
отсчёта и всю информацию, которая
заложена в условиях задачи применительно
к избранной вами системе отсчёта. Кроме
того, полезно отобразить на рисунке и
по умолчанию подразумеваемую информацию,
о которой явно не говорится в условиях
задачи. Эти общеизвестные сведения при
нанесении на рисунок привлекают к себе
ваше внимание и могут оказаться полезными
в составлении логической цепочки
размышлений над решением. Например,
можно изобразить вектор ускорения
свободного падения
,
который, если пренебречь вращением
Земли, будет направлен к центру Земли.
Покажем, как всё это можно сделать в
предложенной выше задаче.
Начнем с вопроса задачи, который касается скорости ветра. Из двух ситуаций, которые описаны в условиях задачи, в первой, когда наблюдатель сидит в движущемся автобусе, никак невозможно достоверно оценить скорость ветра, так как отклонение следов капель на стекле от вертикали может быть связано как с ветром, так и с движением автобуса. Только во второй ситуации, когда автобус остановился, можно сделать однозначный вывод о том, что дует ветер, так как теперь нет никакой иной причины для отклонения следов капель от вертикали.
Возникает первое затруднение. В тексте задачи не уточняется в какую сторону от вертикали отклоняются следы капель на боковом стекле автобуса. В подобных двусмысленных ситуациях следует рассуждать на уровне гипотезы. Это значит, что в начале следует предположить какой-либо вариант самому, а затем проверить насколько сделанное предположение стыкуется со всеми прочими условиями задачи.
Гипотеза – пусть
отклонение произошло назад, как показано
на Рис. 1. Следы капель на стекле
неподвижного автобуса показывают нам
направление вектора скорости капель
относительно неподвижной системы
отсчёта XOY,
установленной на Земле. Этот вектор на
Рис.1 обозначен как
.
1. Следы капель на стекле
неподвижного автобуса показывают нам
направление вектора скорости капель
относительно неподвижной системы
отсчёта XOY,
установленной на Земле. Этот вектор на
Рис.1 обозначен как
.
Очевидно, что подобная картина будет наблюдаться, если дует встречный ветер, вектор скорости которого мы обозначим как , см. Рис 1. Здесь следует отметить, что по умолчанию в подобных задачах ветер понимается как горизонтальное перемещение воздуха с одинаковой по модулю и направлению скоростью по всему фронту без каких-либо завихрений в виде смерча или торнадо. Следить за горизонтальным перемещением воздуха можно с помощью воздушного шара, см. Рис.1, разместив на нём подвижную систему отсчёта X’O’Y’. При этом наполнение воздушного шара следует отрегулировать так, чтобы он завис на какой-либо постоянной высоте. Тогда горизонтальное движение шара будет однозначно связано с наличием ветра.
Таким
образом, для второй ситуации мы получили
следующее распределение ролей. Телом,
движение которого нас интересует, может
быть только капля дождя, а подвижная
система отсчёта будет установлена на
аэростате, который перемещается вместе
с горизонтальным потоком воздуха
(ветром). Тогда преобразование Галилея
для скоростей в этом случае будет иметь
вид:
Телом,
движение которого нас интересует, может
быть только капля дождя, а подвижная
система отсчёта будет установлена на
аэростате, который перемещается вместе
с горизонтальным потоком воздуха
(ветром). Тогда преобразование Галилея
для скоростей в этом случае будет иметь
вид:
(3)
Обратите внимание, что пунктирная линия, которая изображает следы капель дождя на стекле неподвижного автобуса, без изломов продолжается вниз и вверх за пределы окна. Такова картина летящих капель дождя относительно Земли и неподвижного автобуса.
Два из трёх векторов,
входящих в формулу (3) уже изображены на
рис. 1. Однако, информации слишком мало,
чтобы сделать какой-либо вывод, так как
мы не знаем модули этих векторов. Как
найти дополнительную информацию,
например, определить направление
третьего вектора – вектора ? Для этого подумаем, что заставляет
каплю дождя перемещаться относительно
воздуха? Здесь уместно вспомнить пример
с лодкой в подвижной речной воде, в
которой сидят гребцы. Если гребцы не
работают вёслами, то лодка относительно
воды не движется. Гребцы в этом случае
являются тем «мотором», который заставляет
лодку перемещаться относительно воды,
создавая силу тяги. Причём направление
перемещения лодки относительно воды
целиком зависит от того направления,
которое имеет сила тяги «мотора».
Если гребцы не
работают вёслами, то лодка относительно
воды не движется. Гребцы в этом случае
являются тем «мотором», который заставляет
лодку перемещаться относительно воды,
создавая силу тяги. Причём направление
перемещения лодки относительно воды
целиком зависит от того направления,
которое имеет сила тяги «мотора».
Ситуация с каплей
в подвижном воздухе аналогична ситуации
с моторной лодкой в подвижной речной
воде. Мы знаем, что капли движутся
относительно воздуха, так как они
зарождаются высоко в небе в дождевых
облаках и проходят путь в сотни метров
сквозь толщу воздуха, падая на Землю.
Какой «мотор» заставляет капли двигаться
относительно воздуха? Ответ может быть
единственным. Этим «мотором» является
сама Земля, которая создает силу тяги
в виде силы притяжения. Обратите внимание,
что из этого следует другой важный
вывод. Мы знаем какое направление имеет
сила притяжения Земли – вертикально
вниз. Это значит, что вектор перемещения
капель относительно воздуха и вектор скорости капель относительно
воздуха обязаны быть направлены только
вертикально вниз, как сила притяжения
Земли и как вектор 1.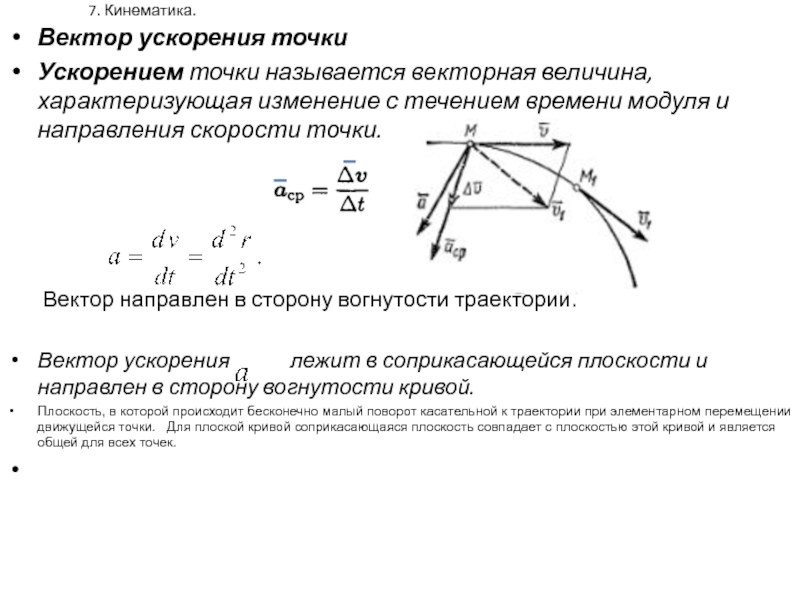
По своей структуре формула (3) идентична формуле для поиска суммы двух векторов, например,
И
Таблица I. | ||
аналог | ||
аналог | ||
аналог | ||
 Также неизменны (см. Рис. 2) типы стыковок
векторов и в точках М и N.
Также неизменны (см. Рис. 2) типы стыковок
векторов и в точках М и N.Итак, глядя на Рис.1 и понимая, что и направлены одинаково, мы можем сказать, что теперь знаем направления всех трёх векторов из формулы (3).
Состыкуем их согласно правилу треугольника, воспользовавшись возможностью параллельного переноса векторов и очевидной аналогией, показанной в таблице I.
Результат представлен на рис. 3. Обратите внимание, что вектор перпендикулярен вектору , а угол KMN равен 450. Таким образом, мы имеем равнобедренный прямоугольный треугольник и, следовательно, можем утверждать, что КМ=КN. С другой стороны, по правилам векторной алгебры на рисунке длина стрелки, которая изображает данный вектор, должна быть численно равна модулю этого вектора. В нашем случае это значит, что:
;
и, наконец,
(5)
Результат,
который дает формула (5), безусловно,
важен, но он – качественный, а не
количественный.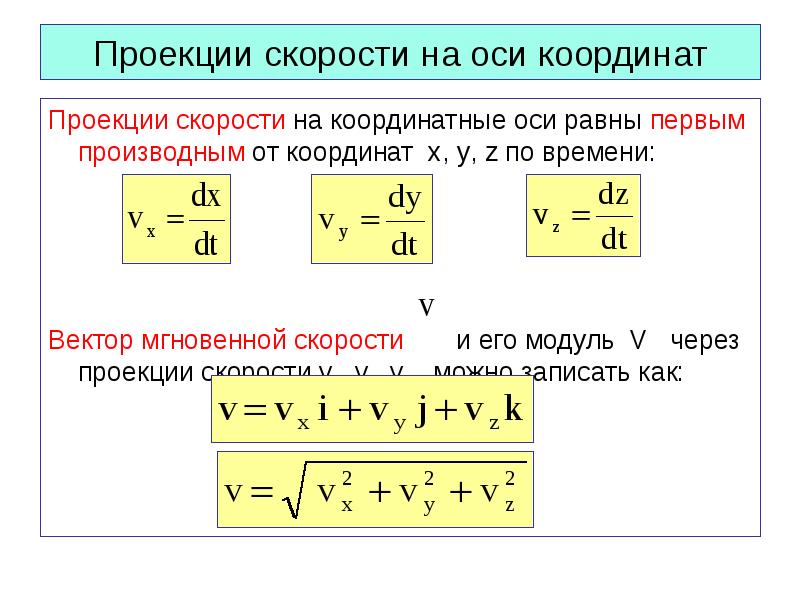 Формула (5) указывает,
что поиск ответа на вопрос задачи,
возможно, пролегает через нахождение
модуля вектора
.
В любом случае в нашем распоряжении
остался только один пока ещё неиспользованный
источник информации. Обратимся к первой
ситуации, описанной в условиях задачи,
которую изобразим на
Формула (5) указывает,
что поиск ответа на вопрос задачи,
возможно, пролегает через нахождение
модуля вектора
.
В любом случае в нашем распоряжении
остался только один пока ещё неиспользованный
источник информации. Обратимся к первой
ситуации, описанной в условиях задачи,
которую изобразим на
рисунке 4, так как её наблюдает человек, находящийся в движущемся автобусе. Движение автобуса против ветра воспринимается пассажирами автобуса как усиление встречного потока воздуха, что приводит к ещё большему отклонению траектории движения капель на стекле от вертикали.
Наблюдение за движением капель на боковом стекле движущегося автобуса, которое делает студент, позволяет определить направление вектора . Это подсказывает нам, что в ситуации, изображённой на Рис.4, именно автобус следует избрать в качестве тела, на котором расположится новая подвижная система отсчёта X’’O’’Y’’.
По-прежнему мы
наблюдает за движением капли дождя,
которая в качестве тела и будет
участвовать в новой записи преобразования
Галилея, см.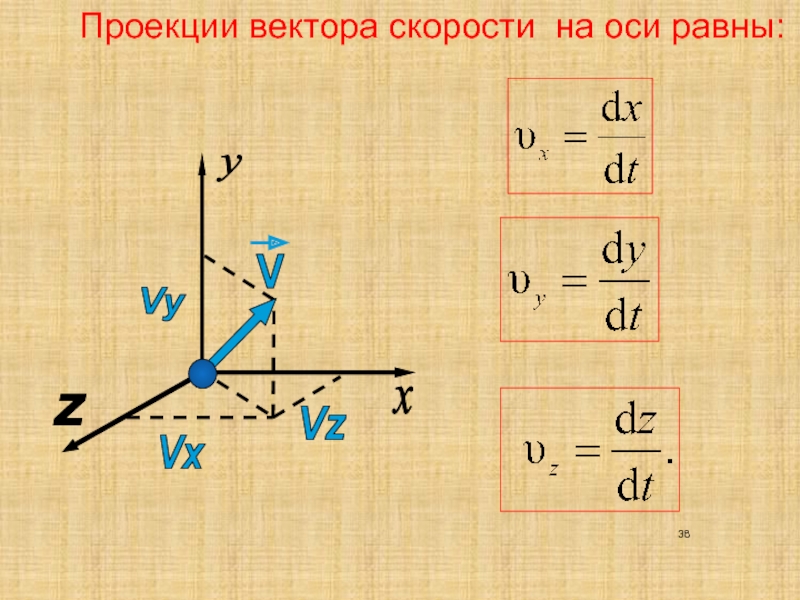 формулу (6) .
формулу (6) .
По своей структуре формула (6) вновь идентична формуле (4) для поиска суммы двух векторов. Причём вновь мы знаем направления всех трёх векторов: векторы и мы наблюдаем на Рис. 4, а вектор – изображен на Рис. 1.
О
Таблица II. | ||
аналог | ||
аналог | ||
аналог | ||
 4. Теперь между векторами
из формулы (6) и векторами из формулы (4)
устанавливается следующая аналогия,
см. таблицу II.
4. Теперь между векторами
из формулы (6) и векторами из формулы (4)
устанавливается следующая аналогия,
см. таблицу II.Состыкуем векторы скоростей в точках М, К’ и N согласно правилу треугольника, см. Рис. 2, воспользовавшись возможностью параллельного переноса векторов. В результате получаем рисунок 5.
Обратите внимание, что вектор – это тот же самый вектор, что и на Рис. 1 и Рис. 3, который по-прежнему образует угол 450 с вертикалью, а его начало и конец идентифицируются точками М и N. Вектор в соответствии с Рис. 4 образует угол 600 = 150 + 450 с вертикалью и точка его стыковки с вектором отмечена новым обозначением как точка К’.
Рис. 3 и Рис. 5 объединяет общий вектор . Воспользуемся этим обстоятельством и сделаем объединённый рисунок 6, на котором изобразим все пять векторов скоростей, которые вошли в преобразования Галилея (3) и (6).
С
точки зрения геометрии на Рис. 6 мы имеем
два прямоугольных треугольника Δ KMK’
и Δ KMN,
у которых катет КМ – общий. Это
обстоятельство можно использовать, так
как мы знаем угол при вершине М в обоих
треугольниках.
6 мы имеем
два прямоугольных треугольника Δ KMK’
и Δ KMN,
у которых катет КМ – общий. Это
обстоятельство можно использовать, так
как мы знаем угол при вершине М в обоих
треугольниках.
Из Δ KMK’ имеем:
или
На рисунке длина стрелки, которая изображает вектор, численно равна модулю этого вектора. Это значит, что:
NK’ = = 10 м/с по условию задачи.
Физический смысл KM и KN мы уже выяснили в формуле (5).
Таким образом, осталось разрешить уравнение (7) относительно KN с учётом (5) и (8) и мы получим ответ задачи:
или
Итак, в рассмотренной
выше задаче мы дважды в формулах (3) и
(6) использовали преобразование Галилея
для скоростей, описывая неизменный
вектор скорости
с
двух разных позиций: относительно
системы отсчёта, связанной с подвижным
воздухом (ветром) и относительно системы
отсчёта, связанной с движущимся автобусом.
Задача #2.
Рассмотрим ещё один приём решения задач с применением преобразований Галилея. Задача состоит в следующем: найти сколько времени лодка с мотором движется из точки А в точку В, которая находится на другом берегу реки, см. Рис. 7, считая скорость лодки относительно Земли неизменной по направлению. Расстояние АВ равно 100 м. Ширина реки равна 80 м . Скорость лодки относительно воды равна 1 м/с. Скорость воды в реке равна 1 м/с.
Во-первых, определимся с «участниками» преобразований Галилея. В этой задаче выбор очевиден: лодка с мотором будет телом, движение которого нас интересует, а подвижная водная среда в реке будет тем телом отсчёта, на котором расположится подвижная система отсчёта X’O’Y’. Реальное воплощение такой п.с.о. можно создать на плоту, который будет путешествовать вниз по течению реки со скоростью . Неподвижная система отсчёта XOY по-прежнему располагается на Земле. Таким образом, преобразование Галилея для скоростей будет иметь вид:
Начальное и конечное
положение лодки относительно Земли в
этой задаче задается точками А и В,
которые мы видим на Рис.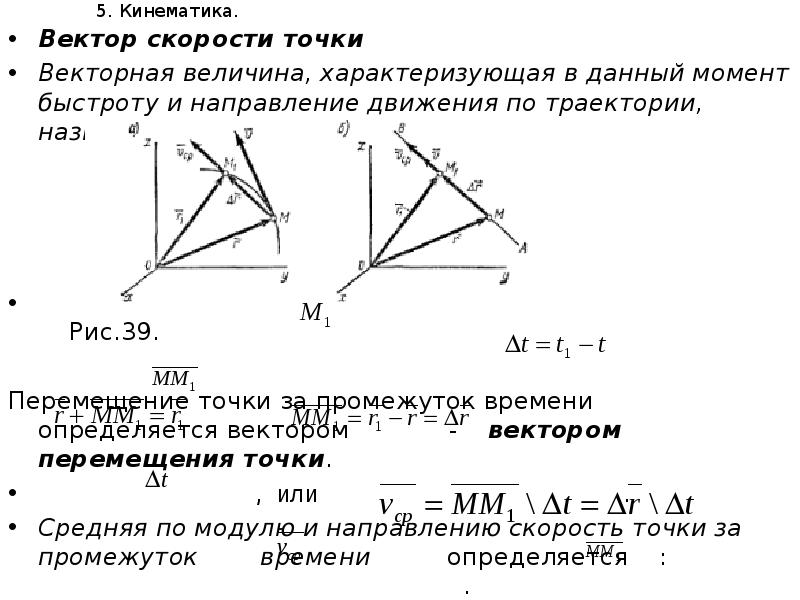 7. Нарисуем
вектор, начало которого будет в точке
А, а его конец – в точке В. Такой вектор
в кинематике определяется как вектор
перемещения (в данном случае лодки
относительно Земли) и обозначается как
.
Такие несложные наблюдения позволяют
сделать важный для решения задачи вывод.
Дело в том, что в подобных задачах по
умолчанию предполагается, что векторы
скоростей, которые участвуют в формуле
(9), неизменны как по направлению, так и
по модулю в течение всего движения тела
(лодки). При этом условии предельно
упрощается связь между вектором скорости
и соответствующим вектором перемещения.
Например,
7. Нарисуем
вектор, начало которого будет в точке
А, а его конец – в точке В. Такой вектор
в кинематике определяется как вектор
перемещения (в данном случае лодки
относительно Земли) и обозначается как
.
Такие несложные наблюдения позволяют
сделать важный для решения задачи вывод.
Дело в том, что в подобных задачах по
умолчанию предполагается, что векторы
скоростей, которые участвуют в формуле
(9), неизменны как по направлению, так и
по модулю в течение всего движения тела
(лодки). При этом условии предельно
упрощается связь между вектором скорости
и соответствующим вектором перемещения.
Например,
Чтобы подчеркнуть, что именно, существенно важное для решения задачи, показывает формула (10) перепишем её в виде:
Знак
«+» обычно не принято явно указывать в
подобных случаях, однако, для нас важно
обратить внимание именно на этот знак.
В векторных формулах, подобных формуле
(11), где множитель есть величина положительная, знак «+»
указывает на то, что направления векторов,
записанных слева и справа от знака « =
», одинаковы. Таким образом, из формулы
(11) можно сделать вывод:
Таким образом, из формулы
(11) можно сделать вывод:
Обогатим рисунок задачи сделанными выводами, см. Рис. 8.
Совпадение направлений векторов, отмеченное в формуле (12), позволяет получить скалярный визави формулы (10):
где – это модуль вектора перемещения лодки относительно Земли. Согласно правилу, на рисунке модуль вектора численно равен длине стрелки, которая его изображает. В данном случае имеем:
Таким образом, ответ на вопрос задачи о времени путешествия лодки из точки А в точку В можно решить, используя формулы (13) и (14):
И
Таблица III. | ||
аналог | ||
аналог | ||
аналог | ||
 Вновь
воспользуемся очевидной аналогией
между векторами из формулы (9) и векторами
из формулы (4), см. Таблицу III.
Мы знаем направления векторов и
.
Пользуясь правилом параллельного переноса, состыкуем их
так как этого требует правило треугольника,
а именно в точке N
(аналогично стыковке векторов и
,
см. Рис. 2). При этом обратите внимание
на тот факт, что нам неизвестен модуль
вектора (на рисунке это соответствует произвольной
длине стрелки), поэтому направление
вектора точно пока не определено, см. Рис. 9.
Другими словами, форма треугольника
MKN
на Рис. 9 пока произвольная. Определённо
можно говорить лишь об одном угле этого
треугольника – об угле KNM,
который для краткости изложения обозначим
как
.
Вновь
воспользуемся очевидной аналогией
между векторами из формулы (9) и векторами
из формулы (4), см. Таблицу III.
Мы знаем направления векторов и
.
Пользуясь правилом параллельного переноса, состыкуем их
так как этого требует правило треугольника,
а именно в точке N
(аналогично стыковке векторов и
,
см. Рис. 2). При этом обратите внимание
на тот факт, что нам неизвестен модуль
вектора (на рисунке это соответствует произвольной
длине стрелки), поэтому направление
вектора точно пока не определено, см. Рис. 9.
Другими словами, форма треугольника
MKN
на Рис. 9 пока произвольная. Определённо
можно говорить лишь об одном угле этого
треугольника – об угле KNM,
который для краткости изложения обозначим
как
.Сравнив Рис.9 и Рис.8, мы видим, что угол
так как вектор
скорости воды относительно Земли и
линия берега АС – параллельны, а линия
АВ (или МN)
является секущей линией. Кроме того, из
геометрии Рис.8 можно определить:
Если еще раз внимательно прочитать условие задачи, то выясняется важная подробность:
С
графической точки зрения соотношение
(18) означает, что длина стрелок, которые
изображают векторы и
на
Рис. 9, обязана быть одинаковой:
9, обязана быть одинаковой:
МК=KN=1 м/с
Таким образом, проясняется тип треугольника МКN на Рис.9 – это равнобедренный треугольник и, следовательно, он имеет равные углы при своём основании.
Это значит, что теперь мы можем узнать значение угла при вершине К треугольника МКN:
Все обнаруженные геометрические соотношения помогут найти модуль скорости лодки относительно Земли, который численно на Рис. 9 представлен длиной стрелки MN. Воспользуемся теоремой косинусов:
где, учитывая тригонометрическую формулу приведения:
Подставляя числовые значения (19) и (23) в (22), получим:
Осталось воспользоваться формулами (15), (14) и (24) и получить ответ задачи. Путешествие лодки из точки А в точку В будет продолжаться в течение:
Тема: Движение тела по окружности
По-прежнему речь будет идти о движении
материальной точки.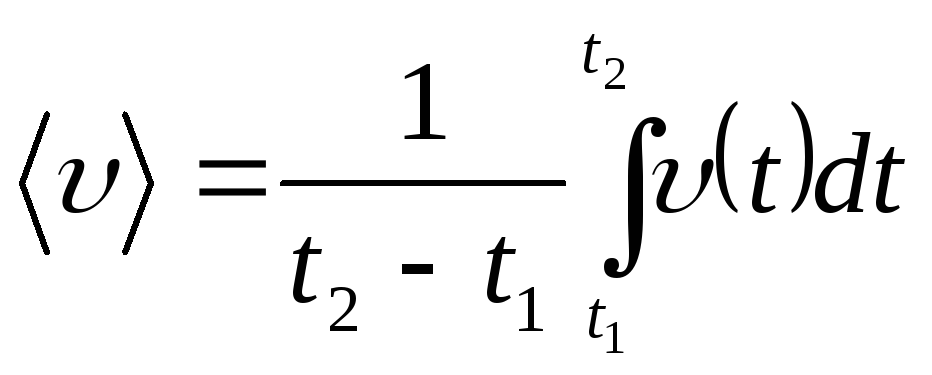 .
Действует правило:
вектор скорости
тела в данной точке К окружности всегда
направлен вдоль касательной линии к
окружности в данной точке К (см. Рис.
10). В ходе движения по окружности вектор
мгновенной скорости тела :
.
Действует правило:
вектор скорости
тела в данной точке К окружности всегда
направлен вдоль касательной линии к
окружности в данной точке К (см. Рис.
10). В ходе движения по окружности вектор
мгновенной скорости тела :обязательно изменяется по направлению,
может изменяться по модулю.
Обратите внимание на разницу! В первом случае «обязательно», а во втором – всего лишь «может».
Это означает, что, если тело движется по окружности, то оно обязательно имеет вектор ускорения, модуль которого показывает как быстро изменяется направление вектора . Такое ускорение называется центростремительным или нормальным и обозначается как . Вектор всегда направлен к центру окружности вдоль радиуса, проведённого в точку К, см. Рис.11.
Обратите
внимание на то, что вектор в данной точке К также всегда перпендикулярен
(или нормален) к касательной линии в
этой точке. Этим объясняется обозначение
индекса и второе название этого вида
ускорения.
Этим объясняется обозначение
индекса и второе название этого вида
ускорения.
Модуль нормального ускорения связан с величиной R радиуса окружности и модулем мгновенной скорости в данной точке К следующей формулой:
Понимая, что речь идет именно о модулях векторов формулу (25) обычно записывают в следующем упрощённом виде:
Быстроту возможных изменений модуля мгновенной скорости тела в точке К в ходе движения по окружности характеризует вектор тангенциального ускорения , который направлен вдоль касательной линии к окружности в точке К. При этом возможны два варианта, см. Рис. 12 и Рис. 13.
Говоря о модуле тангенциального ускорения , ограничим рассмотрение случаем, когда его величина остаётся неизменной в течение всего времени движения тела по окружности, т.е. будем полагать, что
По-прежнему,
следует различать характер изменения
модуля скорости, см.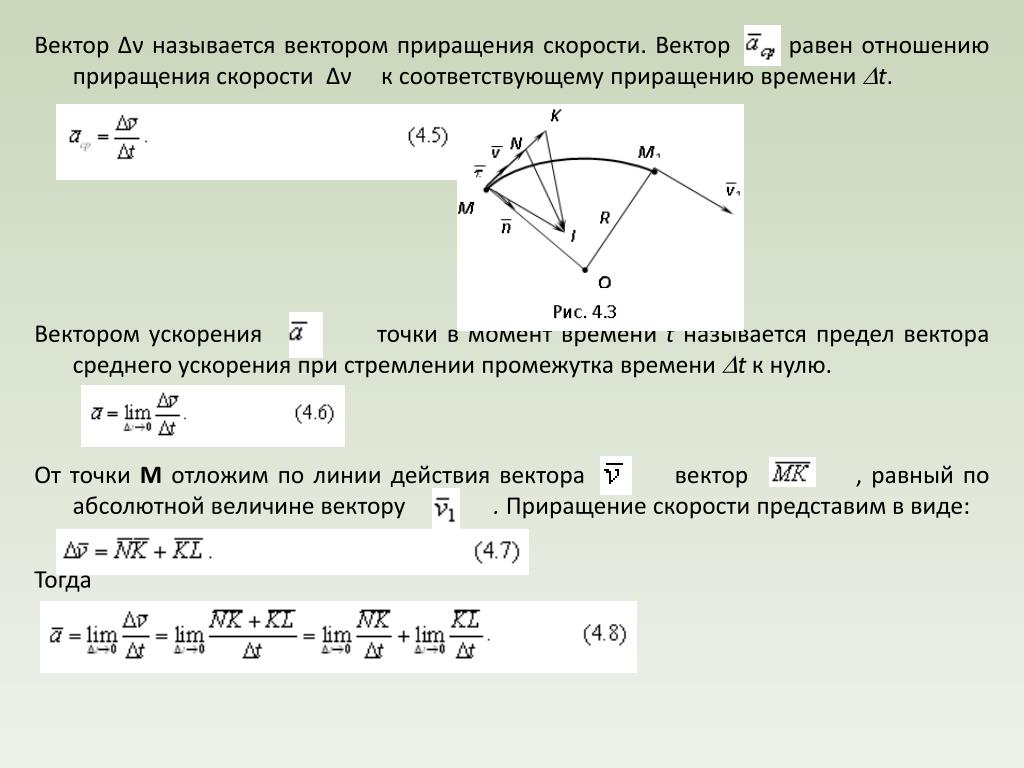 Таблицу IV.
Таблицу IV.
Таблица IV. | ||
Если скорость растёт: | Если скорость убывает: | Если скорость постоянна. |
Вектор нормального ускорения и вектор тангенциального ускорения вместе составляют вектор полного ускорения тела, движущегося по окружности. Другими словами, векторы и являются компонентами вектора :
Формуле (27) соответствуют два рисунка, см.Рис. 14 и Рис. 15. Обратите внимание, что в любом случае вектор полного ускорения располагается между касательной линией и радиусом.
Векторной формуле (27) соответствует её скалярный визави для модуля вектора полного ускорения и его проекций и :
(28)
Д
ля
описания движения тела по окружности
используют систему
отсчёта с полярной системой координат (вместо
декартовой), в которой положение тела
на окружности в данной точке К задаётся
двумя координатами: радиусом окружности
R
и углом поворота радиус-вектора
, , см. Рис. 16. Действует правило:
положительные значения угла поворота
отсчитываются от горизонтального луча
(Рис. 16) в направлении против часовой
стрелки. Например, на Рис. 16 имеем
.
Рис. 16. Действует правило:
положительные значения угла поворота
отсчитываются от горизонтального луча
(Рис. 16) в направлении против часовой
стрелки. Например, на Рис. 16 имеем
.
Таким образом, в окружности постоянного радиуса R для задания начального (точка А) и конечного (точка В) положения тела на окружности достаточно указать значения начального угла поворота и конечного угла поворота , см. Рис. 17.
Изменение положения тела на окружности характеризуется величиной углового перемещения , которое вычисляется по формуле:
Если тело совершает 1оборот, то его угловое перемещение составляет радиан. Очевидно, что если тело совершит N оборотов, то его угловое перемещение будет в N больше. Таким образом, в общем случае имеем:
Быстрота изменения углового перемещения называется мгновенной угловой скоростью, модуль которой связан с модулем мгновенной линейной скорости по формуле:
2
В
задачах, которые нам предстоит решать,
будем предполагать, что вращение тела
происходит против часовой стрелки, как
в начальный, так и в конечный моменты
времени. Другими словами, может происходить
ускорение или замедление вращения, но
не может изменяться направление вращения
на противоположное. В этом случае
зависимость модуля угловой скорости
от времени имеет вид:
Другими словами, может происходить
ускорение или замедление вращения, но
не может изменяться направление вращения
на противоположное. В этом случае
зависимость модуля угловой скорости
от времени имеет вид:
(32)
где – модуль начальной угловой скорости,
– модуль конечной угловой скорости,
– модуль углового ускорения, величина которого связана с модулем тангенциального ускорения следующей формулой:
(33)
*При использовании формулы (32) действует правило выбора знака:
– если в вашей задаче тело движется по окружности с увеличением угловой скорости, то в формуле (32) (и в формуле (34), см. ниже) следует использовать знак + (плюс),
– если в вашей задаче
угловая скорость тела со временем
уменьшается, то в формуле (32) (и в формуле
(34), см. ниже) следует использовать знак
–
(минус).
ниже) следует использовать знак
–
(минус).
Зависимость конечного угла поворота от времени выражается формулой:
(34)
В формуле (34) сохраняется правило выбора знака, описанное применительно к формуле (31).
Пользуясь понятиями модуля угловой скорости и модуля углового ускорения , с помощью формул (26), (28) , (31) и (33) получим важную для решения задач формулу:
(35)
3Задача #1.
Решим следующую задачу. Известно, что тело движется по окружности с некоторым постоянным тангенциальным ускорением. На одном из этапов этого движения за 2 секунды тело совершает поворот на угол в 4 радиана, а следующие оборотов тело делает за 3 секунды. Найти модуль угловой скорости тела в конце описанного этапа движения.
Прежде всего,
отметим, что в силу формулы (33) мы можем
быть уверены, что тело движется по
окружности не только с постоянным
тангенциальным ускорением
,
но также и с постоянным угловым ускорением как на первом 2-х секундном этапе, так и
на втором 3-х секундном этапе. Это
обстоятельство позволяет воспользоваться
уравнениями (32) и (34) для описания движения
тела на любом его этапе.
Это
обстоятельство позволяет воспользоваться
уравнениями (32) и (34) для описания движения
тела на любом его этапе.
Однако, правильное использование формул (32) и (34) невозможно без соблюдения правила выбора знака. Это значит, что далее следует выяснить каков характер движения на описанных его этапах, каким образом изменяется модуль угловой скорости: он увеличивается или уменьшается? Для начала выясним величину углового перемещения за и за последующие .
Из текста задачи прямо следует, что на первом этапе угловое перемещение тела составило 4 радиана, т. е.:
Для того, чтобы найти последующее угловое перемещение, воспользуемся формулой (30), в которой нам известно совершённое телом число оборотов: . Получим:
Результаты (36) и
(37) показывают, что как за первые
,
так и за последующие тело совершило одинаковое перемещение
равное
. Однако, перемещение тела на втором этапе
потребовало на 1 секунду большего
времени. При постоянном угловом ускорении это может быть только, если во время
движения модуль угловой скорости
уменьшается. Таким образом, согласно правилу
выбора знака в уравнениях (32) и (34) для данной задачи
следует применить знак –
(минус).
Однако, перемещение тела на втором этапе
потребовало на 1 секунду большего
времени. При постоянном угловом ускорении это может быть только, если во время
движения модуль угловой скорости
уменьшается. Таким образом, согласно правилу
выбора знака в уравнениях (32) и (34) для данной задачи
следует применить знак –
(минус).
Запишем эти уравнения для первого 2-х секундного этапа.
где
Очевидно, что совершенно аналогично мы имеем право записать уравнения (32) и (34) и для второго 3-х секундного этапа.
(41)
(42)
г
(43)
де Исследование системы
из 4-х уравнений (38), (39), (41), (42) показывает,
что в ней содержатся 5 неизвестных
величин:
.
Как известно, система алгебраических
уравнений имеет решение, если число
неизвестных и число уравнений одинаково. Недостающее пятое уравнение получим
из условия непрерывности движения:
модуль угловой скорости тела в начале
второго этапа движения обязательно
равен модулю угловой скорости тела в
конце первого этапа движения:
Недостающее пятое уравнение получим
из условия непрерывности движения:
модуль угловой скорости тела в начале
второго этапа движения обязательно
равен модулю угловой скорости тела в
конце первого этапа движения:
Теперь задача сформулирована математически до конца {система уравнений (38), (39), (41), (42) и (44)} и может быть решена методом последовательного исключения неизвестных.
Однако, существует и более короткий путь с составлением меньшего числа уравнений в системе. Этот другой метод основан на следующем наблюдении. По условию задачи мы знаем, сколько времени вместе продолжаются первый и второй этапы движения:
За время тело совершает движение по окружности, в ходе которого угол поворота изменяется от начального на первом этапе до конечного на втором этапе .
Другими словами с одной стороны, за время суммарное угловое перемещение тела составит величину
С другой стороны, по определению:
Формулы (46) и (47)
позволяют по новому подойти к составлению
системы уравнений. По-прежнему будем
использовать уравнение (39), в котором
содержатся две неизвестные величины:
.
Новизна предлагаемого метода состоит
в том, чтобы не увеличивать число
неизвестных. Этой цели можно добиться,
если воспользоваться информацией из
(46) и (47) и составить уравнение (34) для
конечного угла поворота, используя
суммарное время движения
.
При этом в качестве начального угла
поворота выступает
,
а в качестве конечного угла поворота –
.
С учётом сказанного имеем:
По-прежнему будем
использовать уравнение (39), в котором
содержатся две неизвестные величины:
.
Новизна предлагаемого метода состоит
в том, чтобы не увеличивать число
неизвестных. Этой цели можно добиться,
если воспользоваться информацией из
(46) и (47) и составить уравнение (34) для
конечного угла поворота, используя
суммарное время движения
.
При этом в качестве начального угла
поворота выступает
,
а в качестве конечного угла поворота –
.
С учётом сказанного имеем:
где согласно (46) и (47):
Таким образом, нам удалось составить систему из двух уравнений (39) и (48) с двумя неизвестными . Подставив в (39) и (48) известные нам числовые значения, получим:
Выразим, например, из (50). Получим:
или
Подставим (52) в (51) и найдём модуль углового ускорения тела:
Открывая скобки, получим:
или
или
Для того чтобы найти второе неизвестное , подставим результат (53) в (52):
Определив модули
,
мы можем ответить на вопрос задачи. Для
этого запишем уравнение для угловой
скорости (32) так, чтобы описать её
изменение в ходе обоих этапов вместе ,
то есть за
.
Это значит, что за модуль начальной
угловой скорости следует принять
,
а за искомый модуль конечной угловой
скорости –
.
Имеем:
Для
этого запишем уравнение для угловой
скорости (32) так, чтобы описать её
изменение в ходе обоих этапов вместе ,
то есть за
.
Это значит, что за модуль начальной
угловой скорости следует принять
,
а за искомый модуль конечной угловой
скорости –
.
Имеем:
После подстановки числовых значений получим ответ задачи:
Проверим наше решение, в частности, результаты (53) и (54). С этой целью сначала поставим числовые результаты (53)и (54) в ранее не использованную формулу (38). Получим:
Согласно (44) и (56) имеем:
Теперь поставим результаты (53), (57) и в ранее не использованную формулу (42), для которой мы точно знаем числовое значение её левой части, равное 4 радианам. Если подсчёт в правой части формулы (42) приведёт к другому числовому значению, то это будет означать, что задача решена неверно. Итак, подставляем числовые значения:
или
или
Мы видим, что левая
и правая части уравнения (42) сравнялись,
обратив его в тождество. Это означает,
что результаты (53) и (57) действительно
являются решениями поставленной задачи.
Это означает,
что результаты (53) и (57) действительно
являются решениями поставленной задачи.
Задача #2.
Рассмотрим теперь ещё один тип задач по данной теме. Тело начинает движение по окружности и движется с постоянным угловым ускорением. В некоторый момент времени оказывается, что вектор полного ускорения тела образует угол в 300 с вектором линейной скорости тела. Необходимо найти какое угловое перемещение успеет совершить тело к указанному моменту времени?
Во-первых, отметим,
что в начале движения тело находилось
в состоянии покоя и его начальные угловая
и линейная скорости были равны нулю:
.
Об этом свидетельствуют слова «тело начинает движение» в тексте задачи. Это значит,
что в ходе движения тела его угловая
скорость обязательно будет увеличиваться
и, следовательно, мы можем воспользоваться Рис.
14, чтобы
представить наглядно векторы
,
о которых говорится в тексте задачи. Рис.
14 показывает, что угол
и
угол
равны,
так как по определению векторы имеют одинаковое направление, которое
задаёт касательная линия к окружности
в данной точке, где находится тело. Но
угол
=
300 по условию задачи. Теперь мы понимаем,
что это также означает, что угол
=
300.
Рис.
14 показывает, что угол
и
угол
равны,
так как по определению векторы имеют одинаковое направление, которое
задаёт касательная линия к окружности
в данной точке, где находится тело. Но
угол
=
300 по условию задачи. Теперь мы понимаем,
что это также означает, что угол
=
300.
Ещё раз обратимся к Рис.14. На этот раз заметим, что векторы имеют общее начало в точке К, а их концы соединяет прямая пунктирная линия, перпендикулярная вектору , которая замыкает прямоугольный треугольник.
Согласно правилу
изображения векторов длина гипотенузы в описанном прямоугольном
треугольнике численно равна модулю
вектора
,
а длина катета, противолежащего углу
=
300 , численно равна модулю вектора (см. Рис.14).
Другими словами, с одной стороны из
и
мы
можем сформировать функцию синуса угла
,
а с другой стороны нам фактически
известно числовое значение этого синуса,
так как мы знаем, что этот угол равен
300. Сказанное можно записать в следующем
виде:
Сказанное можно записать в следующем
виде:
Далее формулу (58) можно развернуть подробнее, если воспользоваться формулами (26), (31) и (35). Сначала из (26) и (31) получим:
Далее из (58), (59) и (35) имеем:
или
Избавимся от иррациональности в формуле (61), для чего возведём в квадрат её правую и левую части. Получим:
или
Формула (62) – это развернутая интерпретация информации, которая содержится в условии задачи об угле между векторами . Теперь мы подготовлены к тому, чтобы начать поиск ответа на основной вопрос задачи об итоговом угловом перемещении .
С одной стороны для имеем определение, выраженное формулой (29) через . С другой стороны, связь между описывает уравнение (34), которое для данной задачи с учётом условия и правила выбора знака будет иметь следующий вид:
Из формул (63) и (29) получим:
На первый взгляд
из формулы (64) следует, что для получения
ответа на вопрос задачи необходимо
найти числовые значения для двух
неизвестных –
.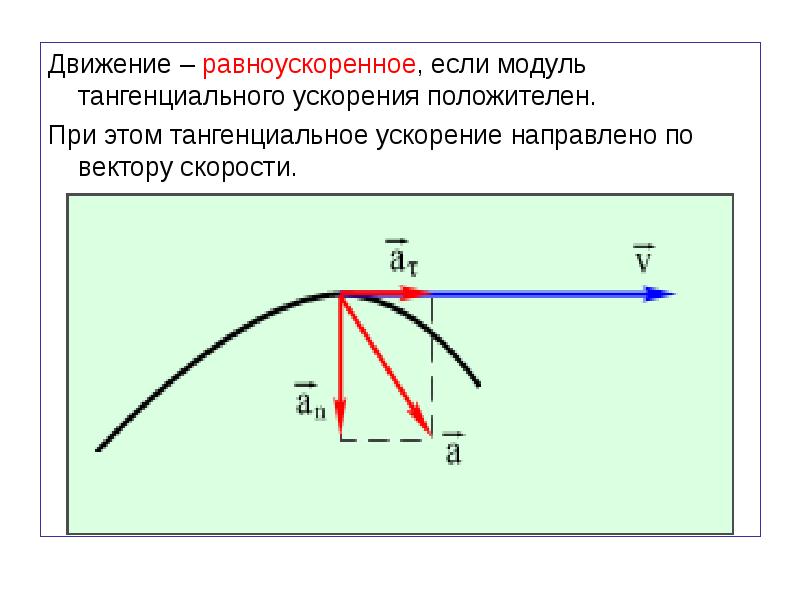 Между тем, пока мы располагаем единственным
источником информации, а именно
соотношением (62), в которое величина вообще не входит, а содержится
дополнительное третье неизвестное –
.
Ситуация выглядит критической – число
неизвестных явно превышает число
уравнений. Однако вспомним, что мы ещё
не использовали уравнение для угловой
скорости (32), в которое входят все трое
перечисленных неизвестных и которое в
данной задаче с учётом условия и правила
выбора знака будет иметь следующий укороченный вид:
Между тем, пока мы располагаем единственным
источником информации, а именно
соотношением (62), в которое величина вообще не входит, а содержится
дополнительное третье неизвестное –
.
Ситуация выглядит критической – число
неизвестных явно превышает число
уравнений. Однако вспомним, что мы ещё
не использовали уравнение для угловой
скорости (32), в которое входят все трое
перечисленных неизвестных и которое в
данной задаче с учётом условия и правила
выбора знака будет иметь следующий укороченный вид:
Формально по-прежнему число неизвестных – три, а уравнений для их поиска только два – (62) и (65) и других не предвидится. Остаётся надеяться на чудо, и оно произойдёт, если подставить (65) в (62). Получим:
или после деления на
Чудо свершилось, оказывается, что:
Что же все-таки
произошло? Мы действительно не можем
по отдельности узнать числовые значения и запреты математики непоколебимы. Но
этого от нас никто и не требует. Для
того, чтобы ответить на вопрос задачи
(см. формулу (64)) необходимо знать
комбинацию неизвестных в виде и теперь после вывода формулы (66) мы
знаем её числовое значение. Осталось
подставить (66) в (64) и получить ответ
задачи:
Но
этого от нас никто и не требует. Для
того, чтобы ответить на вопрос задачи
(см. формулу (64)) необходимо знать
комбинацию неизвестных в виде и теперь после вывода формулы (66) мы
знаем её числовое значение. Осталось
подставить (66) в (64) и получить ответ
задачи:
Тема: Движение тела, брошенного под углом к горизонту
Пренебрегая ускорением, связанным с суточным вращением Земли вокруг оси, проходящей через северный и южный полюсы, и притяжением других небесных тел а, также, не учитывая кривизну земной поверхности, сложное движение брошенного тела можно разложить на две составляющие: первая – движение вдоль воображаемой плоской поверхности Земли, вторая – движение перпендикулярно этой поверхности, см. Рис. 18..
С точки зрения математики это означает, что векторы начальной и конечной скорости брошенного тела, вектор его ускорения и вектор его перемещения могут быть разложены на взаимно перпендикулярные компоненты:
При этом
если не учитывать сопротивление
окружающего воздуха, то можно сказать,
что горизонтально (вдоль оси ОХ) на
летящее тело не действуют какие-либо
силы. В силу II
закона Ньютона, это означает, что
компонента ускорения тела вдоль оси
В силу II
закона Ньютона, это означает, что
компонента ускорения тела вдоль оси
ОХ обязана быть равной нулю, т.е. В свою очередь, нулевое ускорение означает, что у брошенного тела его компонента вектора скорости вдоль оси ОХ не изменяется в ходе полёта, т.е. :
или в скалярном виде для соответствующих проекций вектора начальной и конечной скорости в системе координат, изображённой на рисунке 18:
В вертикальном направлении летящее тело находится под действием силы тяжести, обусловленной гравитационным притяжением Земли. Вблизи поверхности Земли эта сила придает всем телам одинаковое ускорение, направленное вертикально вниз4, модуль которого приближенно равен 9.8 м/сек2. Таким образом, и .
Это означает, что компонента скорости вдоль оси ОY изменяется в ходе полёта. В скалярном виде закон изменения соответствующей проекции скорости летящего тела имеет вид:
где – время полёта тела,
– момент времени, когда полёт был начат,
– момент времени, когда полёт был завершён.
Равномерное движение летящего тела вдоль оси ОХ изменяет его горизонтальную координату по линейному закону:
где – начальная горизонтальная координата тела при старте в точке А,
– конечная горизонтальная координата тела в точке В.
Равнопеременное движение летящего тела вдоль оси ОY изменяет его вертикальную координату в соответствии с квадратичной зависимостью:
где – начальная вертикальная координата тела при старте в точке А,
– конечная вертикальная координата тела в точке В.
Векторной формуле (68) соответствует следующая скалярная формула:
Подставляя в (76) формулы (72) и (73), после алгебраических и тригонометрических преобразований получим зависимость модуля скорости летящего тела от времени:
Рассмотрим
частный случай, когда начальная точка
А и конечная точка В для брошенного тела
располагаются на одном уровне, т. е. когда
начальная и конечная вертикальные
координаты равны (см. Рис.19).
е. когда
начальная и конечная вертикальные
координаты равны (см. Рис.19).
Если , то из (75) мы можем найти, сколько времени занимает такой полёт:
или
Формула (78) показывает, что произведение двух сомножителей равно нулю. Это означает, что существуют две возможности:
Решение (79) не представляет практического интереса, так как соответствует случаю, когда тело находится в покое и точка В тривиально совпадает с точкой А. Напротив, из (80) получим:
Из Рис. 19 очевидно, что:
Тогда из (82), (74) и (81) имеем:
После тригонометрических преобразований окончательно получим формулу для горизонтальной дальности полёта тела:
Формула (85), в частности, показывает, что для достижения максимальной горизонтальной дальности полёта тела при заданном значении модуля начальной скорости необходимо иметь максимальное значение для Как известно, максимальное значение для функции синуса равно (+1):
При этом максимальная дальность полёта составит:
Из условия (86) находим
значение
для
угла, под которым следует бросить тело,
для получения
. По определению, угол, синус которого
равен (+1), составляет 900 .
По определению, угол, синус которого
равен (+1), составляет 900 .
Таким образом, имеем или :
Вернёмся к общему случаю с произвольным значением угла и найдем сколько времени занимает полёт тела из начальной точки А в точку М*, расположенную на вершине траектории полёта (см. Рис. 19). Для того чтобы найти , заметим, что в точке М* прекращается дальнейший подъём тела вверх (для которого , см. формулу (73)) и начинается спуск тела вниз (для которого , см. формулу (73)). Это значит, что в момент времени, когда тело пролетает точку М*, вертикальная составляющая скорости тела на мгновение становится равной нулю. Таким образом, из (73) для точки М* имеем:
или
Из Рис. 19 также очевидно, что:
С другой стороны, из (75) для точки М* имеем:
Подставляя (91) и (90) в (92), получим формулу для вычисления максимальной высоты подъёма летящего тела над начальным уровнем :
или
В заключение экскурса
в теорию данного вопроса отметим, что
при использовании формул (72), (73), (74) и
(75) обязательно следует пользоваться правилом
выбора знака для угла
.
Правило. Положительные значения угла отсчитываются от горизонтали, проведённой через точку А, в направлении против часовой стрелки (как на Рис. 18 и 19).
Отрицательные значения угла отсчитываются от горизонтали, проведённой через точку А, в направлении по часовой стрелке (как на Рис. 20).
В некоторых задачах по данной теме в исходных данных вообще не указывается время полёта. Если и в вопросе задачи речь не идёт о времени полёта, то в таких случаях удобнее воспользоваться уравнением траектории полёта, которое можно получить из формул (74) и (75). Сначала выразим время полёта из формулы (74). Учитывая формулу (82), получим:
Далее подставим формулу (94) в уравнение (75):
После преобразований получим:
Окончательно формулу (95) перепишем, используя тригонометрическое тождество:
В результате получим уравнение траектории полёта:
Теперь рассмотрим, как решаются задачи по данной теме
Задача
#1.
Тело бросили с башни высотой h = 60 м под некоторым неизвестным положительным углом к горизонту с некоторой неизвестной начальной скоростью . Время полета до Земли составило 6 секунд. Найти на какую максимальную высоту над поверхностью Земли в ходе полета поднималось это тело.
Для начала сделаем рисунок задачи, на котором обозначим искомую максимальную высоту как h MAX. Сравнивая Рис. 21 и Рис. 19 можно заметить, что в рассматриваемой задаче участок движения тела от начальной точки А до промежуточной точки В* аналогичен движению, которое изображено на Рис. 19, для которого мы уже знаем как найти величину HMAX по формуле (93).
С другой стороны, из Рис. 21 очевидно, что:
или
На первый взгляд
формула (98) содержит две неизвестные
величины . Однако, если внимательно присмотреться
к формулам (98) и (75), то обнаружится , что
в обеих формулах величины входят в одинаковой комбинации в виде
произведения
.
Учитывая , что (см. Рис. 21) из уравнения (75) мы сможем
найти числовое значение для произведения
.
Получим:
Однако, если внимательно присмотреться
к формулам (98) и (75), то обнаружится , что
в обеих формулах величины входят в одинаковой комбинации в виде
произведения
.
Учитывая , что (см. Рис. 21) из уравнения (75) мы сможем
найти числовое значение для произведения
.
Получим:
Осталось подставить результат (99) в (98) и получить ответ задачи:
В заключение рассмотрим задачу, для решения которой применим уравнение траектории (97).
Задача #2.
Каким должен быть угол , под которым следует бросить тело с горизонтальной поверхности Земли для того, чтобы оно попало в отверстие в вертикальной стене, отстоящей от места бросания на расстоянии L = 1 м и на высоте H = м (см. Рис. 22) ? Известно, что вектор начальной скорости имеет модуль .
Из Рис. 22 следует, что:
Из уравнения траектории полёта (97) и формулы (100) получим:
Получившаяся формула
(101)содержит все исходные данные задачи
и единственную неизвестную величину –
угол .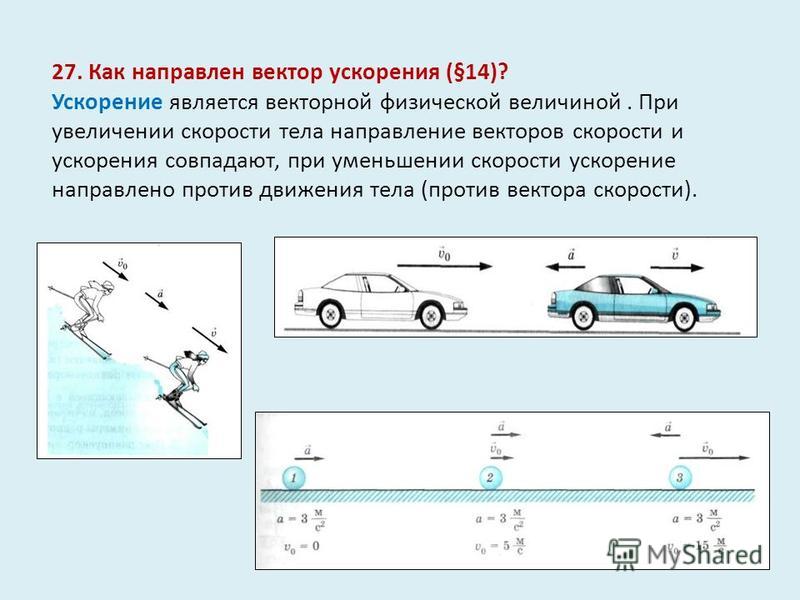 С точки зрения алгебры формула (101)
представляет собой квадратное уравнение
с неизвестной величиной
.
Прежде чем приступить к стандартной
процедуре решения целесообразно
предварительно подставить числовые
значения для g,
L,
H
и
и
вычислить постоянные коэффициенты
квадратного уравнения.
С точки зрения алгебры формула (101)
представляет собой квадратное уравнение
с неизвестной величиной
.
Прежде чем приступить к стандартной
процедуре решения целесообразно
предварительно подставить числовые
значения для g,
L,
H
и
и
вычислить постоянные коэффициенты
квадратного уравнения.
Таким образом, уравнение (100) примет вид:
или
Это уравнение имеет два решения:
Убедимся, что оба значения (103) и (104) являются ответами на вопрос, поставленный в задаче. Углы задают разные способы попадания тела в конечную точку В с координатами х = L, y = H. Если тело будет брошено под углом , то оно попадет в точку В на нисходящей ветви траектории своего полёта, как показано на Рис. 23. В этом можно убедиться, подсчитав максимальную высоту подъёма по формуле (93), учитывая, что можно выразить через по тригонометрической формуле:
Подставляя в (93) получим:
Как видим полученное
числовое значение
,
что согласуется с Рис. 23. Для большей
уверенности найдём, на каком расстоянии
по горизонтали расположен найденный
максимум подъёма траектории. Для этого
используем формулы (82), (74) и (90):
23. Для большей
уверенности найдём, на каком расстоянии
по горизонтали расположен найденный
максимум подъёма траектории. Для этого
используем формулы (82), (74) и (90):
или
где по формулам тригонометрии:
Окончательно из (106) и (107) имеем:
Результат (108) также хорошо согласуется с Рис.23, так как числовое значение .
Второй полученный ответ соответствует такой траектории полёта, когда попадание в конечную точку В осуществляется на её восходящей ветви, как показано на Рис. 22. Если для вычислить , то получим:
Результат (109)
показывает, что при высота максимального подъёма точно
совпадает с заданным значением
.
Это значит, что числовое значение
также
должно совпасть с заданным значением
. Проверим это по формуле (106) с учетом
замены
:
Проверим это по формуле (106) с учетом
замены
:
Предположение подтвердилось, свидетельствуя о правильности физической интерпретации полученных решений.
В заключение сделаем ещё одну проверку решения. На этот раз воспользуемся уравнениями (74) и (75) и формулами (82), (100). Сначала из (74) и (82) выразим время полёта . Затем полученный результат будем подставлять в (75) и, с учетом (100), находить расчётную величину высоты положения точки В. Сравнивая расчетное значение Н со значением, которое задано в условии задачи, мы будим судить о правильности полученного решения. Если расчетное и заданное значения Н совпадут, то это подтвердит правильность полученного решения.
Итак, испытаем первое решение, найдём время полёта тела по первой траектории, подставив (103) в (74) с учётом (82) и тригонометрического соотношения (96):
или
Теперь подставляем (111) в (75) с учётом (100):
Для завершения
расчёта необходимо выразить через
. Из (105) имеем:
Из (105) имеем:
Подставляя (113) в (112), получаем:
Результат (114) совпадает со значением высоты положения точки В по условиям задачи, что подтверждает правильность проверяемого первого решения (103).
Следуя описанной парадигме, проверим второе решение, представленное результатом (104). Сначала найдём время полёта тела по второй траектории. Из (74), (104), (82) и (96) получим:
или
Далее, из (75), (115), учитывая, что , имеем:
или
Результат (116) совпал с исходным значением Н в условиях задачи. Это означает, что второе полученное решение (104) также является правильным.
Указатель
в
вектор перемещения 4
г
гипотеза 8
горизонтальная дальность полёта 40
м
максимальная высота подъёма летящего тела 42
материальная точка 4
п
правило
– отсчёта положительного угла поворота 24
выбора знака в уравнениях движения тела по окружности 27
выбора знака для угла бросания 42
изображения модуля вектора на рисунке 18
определения направления вектора мгновенной скорости в данной точке траектории 21
параллельного переноса векторов 13, 18
треугольника 10
преобразования Галилея 6
с
система отсчёта 3
подвижная 15
скорость
– мгновенная угловая 25
т
теорема косинусов 20
у
угловое перемещение 25
уравнение траектории 43
ускорение
– угловое 26
нормальное 21
полное 23
тангенциальное 22
центростремительное 21
Содержание
Введение 3
Тема: Преобразования Галилея 3
Тема: Движение тела по окружности 21
Тема: Движение тела, брошенного под углом к горизонту 36
1
Данное утверждение справедливо, если
пренебречь эффектом, связанным с
суточным вращением Земли вокруг оси
проходящей через её географические
полюсы.
2 Примечание. Обратите
внимание на то, что формулы (31) и (33) не
совсем полноценны, так как они верны
только численно. Это значит, что
вычисление по этим формулам обеспечивает
правильный числовой результат, а о
согласовании размерностей в правой и
левой частях этих формул речь не идёт.
Для получения правильного результата
размерности величин в обеих частях
формул (31) и (33) должны быть указаны в
одной системе единиц (например, в СИ),
а единицы измерения угла – обязательно радианы. Например, в (31) имеем
[]=[м/сек],
[ω]=[рад/сек], [R]=[м].
Соответственно в формуле (33) имеем
[]=[м/сек2],
[]=[рад/сек2],
[R]=[м]. Первоисточником
ограничений на согласование размерностей
является тригонометрическая формула
,
которая справедлива для малых значений
и только при условии использования радианной меры угла. Обратите
внимание на то, что левая часть этой
формулы вообще не имеет размерности. Следовательно, речь идёт только о
численном равенстве. Эта формула
используется на промежуточном этапе
вывода формулы (31).
Следовательно, речь идёт только о
численном равенстве. Эта формула
используется на промежуточном этапе
вывода формулы (31).
3 Примечание. На формулу (34) распространяются ограничения по согласованию размерности величин в правой и левой части этой формулы. Эти ограничения привнесены формулами (31) и (33). Подробное объяснение приведено в примечании на стр. 24.
4 Данное утверждение справедливо, лишь в рамках предположения о незначительности поправок, связанных с вращением Земли вокруг оси, проходящей через её географические полюсы.
Величина вектора – определение, направление и значение
На рисунке ниже показан вектор:
Изображение будет загружено в ближайшее время
Вектор имеет величину (то есть размер) и направление:
Изображение будет загружено в ближайшее время
Длина линии или стрелки, указанной выше, показывает ее величину, а наконечник указывает направление.
Теперь мы можем сложить два вектора, просто соединив их «голова к хвосту». Для лучшего понимания обратитесь к приведенной ниже схеме:
Изображение будет загружено в ближайшее время добавлены, мы все равно получим тот же результат:
Изображение будет загружено в ближайшее время
Обозначение:
Вектор часто может быть написан жирным шрифтом, как a или b.
Вычитание векторов:
Мы также можем вычесть один вектор из другого, помня о двух точках, указанных ниже:
Во-первых, нам нужно изменить направление векторов, которые мы хотим вычесть, знак вектора от положительного к отрицательному.
Во-вторых, нам нужно добавить их, как обычно:
Изображение скоро будет загружено
Какова величина вектора?
Как мы знаем, этот вектор можно определить как объект, который имеет как величину, так и направление. Теперь, если нам нужно найти величину векторной формулы, и нам нужно вычислить длину любого заданного вектора. Такие величины, как скорость, перемещение, сила, импульс и т. д., являются векторными величинами. Но такие величины, как скорость, масса, расстояние, объем, температура и т. д., как известно, являются скалярными величинами. Скалярные величины – это те, которые имеют единственную величину, тогда как векторы обычно имеют и величину, и направление.
Теперь, если нам нужно найти величину векторной формулы, и нам нужно вычислить длину любого заданного вектора. Такие величины, как скорость, перемещение, сила, импульс и т. д., являются векторными величинами. Но такие величины, как скорость, масса, расстояние, объем, температура и т. д., как известно, являются скалярными величинами. Скалярные величины – это те, которые имеют единственную величину, тогда как векторы обычно имеют и величину, и направление.
Величина векторной формулы:-
Изображение будет загружено в ближайшее время вектор.Таким образом, в основном эта величина используется для определения длины между начальной и конечной точками вектора.
Примечание. Величина вектора никогда не может быть отрицательной, потому что | | превращает все минусы в плюсы. Таким образом, мы можем сказать, что величина вектора всегда положительна.
Направление вектора А
Направление вектора есть не что иное, как измерение угла, сделанного с использованием горизонтальной линии. {-1}\] (y/x)
{-1}\] (y/x)
Важные моменты, которые следует помнить, эти пункты, приведенные ниже, помогут решить проблемы:
Величина вектора всегда определяется как длина вектора.{2}}\] = 5,38
Следовательно, величина заданного трехмерного вектора 2i + 3j + 4k ≈ 5,38.
Примечание: Символ ≈ обозначает приближение.
Грунтовка комплексного номера
Показать мобильное уведомление Показать все примечания Скрыть все примечанияПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.
 Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Сопряжение и модуль
В предыдущем разделе мы рассмотрели алгебраические операции над комплексными числами.Есть несколько других операций, на которые мы должны обратить внимание, поскольку они, как правило, появляются время от времени. Мы также рассмотрим несколько интересных фактов об этих операциях.
Комплексно-сопряженный
Первое, что мы рассмотрим, это комплексное сопряжение (или просто сопряжение). Учитывая комплексное число \(z = a + bi\), комплексно-сопряженное число обозначается \(\overline z\) и определяется как
\begin{уравнение}\overline z = a – bi\end{уравнение}Другими словами, мы просто меняем знак на мнимой части числа.

Вот некоторые основные факты о конъюгатах.
\begin{align} \overline{\overline{z}} & = z \\ \overline {{z_1} \pm {z_2}} & = {\overline z_1} \pm {\overline z_2} \label{eq:conjsum} \\ \overline {{z_1}{z_2}} &= {\overline z_1}\,{\overline z_2} \label{eq:conjprod} \\ \ overline {\ left ( {\ frac {{{z_1}}} {{{z_2}}}} \ right)} & = \ frac {{{{\ overline z} _1}}} {{{{\ overline г}_2}}} \end{выравнивание}Первый просто говорит, что если мы спрягаем дважды, мы вернемся к тому, с чего мы начали изначально, и, надеюсь, это имеет какой-то смысл.Остальные три просто говорят, что мы можем разбить сумму, разность, произведение и частное на отдельные части, а затем выполнить сопряжение.
Итак, чтобы мы могли сказать, что мы проработали несколько примеров, давайте сделаем пару примеров, иллюстрирующих вышеизложенные факты.
Пример 1. Вычислите каждое из следующих значений.- \(\overline{\overline{z}}\) для \(z = 3 – 15i\)
- \(\overline {{z_1} – {z_2}} \) для \({z_1} = 5 + i\) и \({z_2} =- 8 + 3i\)
- \({\overline{z_1}} – {\overline{z_2}}\) для \({z_1} = 5 + i\) и \({z_2} =- 8 + 3i\)
а \(\overline{z} = 3 + 15i \hspace{0.
 5in} \Rightarrow \hspace{0.5in} \overline{\overline{z}} = \overline{3 + 15i}= 3 – 15i = z\)
5in} \Rightarrow \hspace{0.5in} \overline{\overline{z}} = \overline{3 + 15i}= 3 – 15i = z\)Конечно, мы можем видеть, что после двойного спряжения мы вернемся к исходному числу.
b \({z_1} – {z_2} = 13 – 2i \hspace{0.5in} \Стрелка вправо \hspace{0.5in} \overline {{z_1} – {z_2}}= \overline {13 – 2i}= 13 + 2i\)
c \({\overline z_1} – {\overline z_2} = \overline {5 + i} – \left({\overline { – 8 + 3i}} \right) = 5 – i – \left( { – 8 – 3i} \справа) = 13 + 2i\)
Мы видим, что результаты (b) и (c) такие же, как и предполагалось, что они должны быть.
Есть еще один приятный факт, связанный с сопряженными числами, на который нам, вероятно, следует обратить внимание. Однако вместо того, чтобы просто выдать факт, давайте выведем его. Мы начнем с комплексного числа \(z = a + bi\), а затем выполнить каждую из следующих операций.
\[\begin{array}{rlcrl}z + \overline{z} & = a + bi + \left( {a – bi} \right) & \hspace{0. 5in} & z – \overline{z} & = а + би – \влево( {а – би} \вправо)\\
& = 2a & \hspace{0.5in} & & = 2bi\end{массив}\]
5in} & z – \overline{z} & = а + би – \влево( {а – би} \вправо)\\
& = 2a & \hspace{0.5in} & & = 2bi\end{массив}\]Теперь, вспоминая, что \({\mathop{\rm Re}\nolimits}\, z = a\) и \({\mathop{\rm Im}\nolimits}\, z = b\), мы видим, что мы есть,
\begin{equation}{\mathop{\rm Re}\nolimits} z = \frac{{z + \overline z}}{2} \hspace{0.75in} {\mathop{\rm Im}\nolimits} z = \frac{{z – \overline z}}{{2i}} \label{eq:ReImDefn} \end{equation}Модуль
. Другая операция, которую мы хотим рассмотреть в этом разделе, — это модуль комплексного числа.2}\]
Если мы затем возьмем квадратный корень из обеих частей, мы получим,
\[\слева| г \ справа | \г\влево| {{\ mathop{\rm Re}\nolimits}\, z} \right|\], где \(\left| {\,\, \cdot \,} \right|\) на \(z\) — это модуль комплексного числа, а \(\left| {\,\, \ cdot \,} \right|\) на \({\mathop{\rm Re}\nolimits}\, z\) являются столбцами абсолютных значений.
\begin{уравнение}\left| г \ справа | \г\влево| {{\ mathop{\rm Re}\nolimits}\, z} \right| \ge {\mathop{\rm Re}\nolimits}\, z \label{eq:zRez} \end{уравнение} Наконец, для любого действительного числа \(a\) мы также знаем, что \(a \le \left| a \right|\) (абсолютное значение…), и поэтому мы получаем
Наконец, для любого действительного числа \(a\) мы также знаем, что \(a \le \left| a \right|\) (абсолютное значение…), и поэтому мы получаемМы можем использовать аналогичный аргумент, чтобы получить
\begin{уравнение}\left| г \ справа | \г\влево| {{\ mathop{\rm Im}\nolimits}\, z} \right| \ge {\mathop{\rm Im}\nolimits}\, z \label{eq:zImz} \end{уравнение}Существует очень хорошая связь между модулем комплексного числа и его сопряженным числом.2}\label{eq:zConjz} \end{уравнение}
При случае это приятный и удобный факт.
Обратите также внимание, что при вычислении модуля знак действительной и мнимой частей комплексного числа не влияет на значение модуля, поэтому мы также можем видеть, что
\begin{уравнение}\left| г \ справа | = \ влево | {\ overline z} \ right | \ label {eq: MzMzbar} \ end {equation}и
\begin{уравнение}\left| { – г} \право| = \ влево | z \right|\end{уравнение}Теперь мы также можем формализовать процесс деления из предыдущего раздела, когда у нас есть модуль и сопряженные обозначения.
 2}}}{{164}} = \frac{{21}}{{41}} – \frac{9}{{82}}i\]
2}}}{{164}} = \frac{{21}}{{41}} – \frac{9}{{82}}i\]Вот еще несколько интересных фактов о модуле комплексного числа.
\begin{align}{\rm{If}}\left| г \ справа | & = 0\,\,\,{\rm{тогда}}\, z = 0 \label{eq:Mzero} \\ \влево| {{z_1}\,{z_2}} \право| & = \ влево | {{z_1}} \право|\,\лево| {{z_2}} \право| \label{eq:MProd} \\ \влево| {\ frac {{{z_1}}}{{{z_2}}}} \right| & = \ гидроразрыва {{\ влево | {{z_1}} \right|}}{{\left| {{z_2}} \right|}} \label{eq:MQuot} \end{выравнивание}Свойство \(\eqref{eq:Mzero}\) должно быть вам понятно.2}\]
Наконец, вспомните, что мы знаем, что модуль всегда положителен, поэтому извлеките квадратный корень из обеих сторон, чтобы получить
. \[\слева| {{z_1}\,{z_2}} \право| = \ влево | {{z_1}} \право|\,\,\лево| {{z_2}} \справа|\]Свойство \(\eqref{eq:MQuot}\) можно проверить с помощью аналогичного аргумента.
Неравенство треугольника и варианты
Свойства \(\eqref{eq:MProd}\) и \(\eqref{eq:MQuot}\) связывают модуль произведения/частного двух комплексных чисел с произведением/частным модуля отдельных чисел.
. \begin{уравнение}\left| {{z_1} + {z_2}} \право| \ле\влево| {{z_1}} \право| + \влево| {{z_2}} \право| \label{уравнение:треугольник} \end{уравнение} Теперь нам нужно взглянуть на аналогичное соотношение для сумм комплексных чисел. Это соотношение называется неравенством треугольника и равно
Теперь нам нужно взглянуть на аналогичное соотношение для сумм комплексных чисел. Это соотношение называется неравенством треугольника и равноМы также сможем использовать это, чтобы получить соотношение для разности комплексных чисел.
Неравенство треугольника на самом деле довольно просто доказать, так что давайте сделаем это.2} = {z_1} \, {\ overline z_1} + {z_1} \, {\ overline z_2} + {z_2} \, {\ overline z_1} + {z_2} \, {\ overline z_2} \ label {eq :tripfone} \end{уравнение}
Следующее заметьте,
\[\ overline {{z_2}{{\overline z}_1}} = {\overline z_2}{\overline{\overline{z_1}}} = {\overline z_2}{z_1}\]и, таким образом, используя \(\eqref{eq:ReImDefn}\), \(\eqref{eq:zRez}\) и \(\eqref{eq:MzMzbar}\), мы можем записать два средних члена правой части \(\eqref{eq:tripfone}\) как
\[{z_1}\,{\overline z_2} + {z_2}\,{\overline z_1} = {z_1}\,{\overline z_2} + \overline {{z_1}\,{{\overline z}_2 }}= 2{\mathop{\rm Re}\nolimits} \left( {{z_1}\,{{\overline z}_2}} \right) \le 2\left| {{z_1}\,{{\overline z}_2}} \right| = 2\влево| {{z_1}} \право|\,\лево| {{{\overline z}_2}} \right| = 2\влево| {{z_1}} \право|\,\лево| {{z_2}} \справа|\]Также используйте \(\eqref{eq:zConjz}\) в первом и четвертом членах в \(\eqref{eq:tripfone}\), чтобы записать их как
\[{z_1}\,{\overline z_1} = {\left| {{z_1}} \right|^2} \hspace{0. 2}\]
2}\]Теперь, вспомнив, что модуль всегда положителен, мы можем извлечь корень из обеих сторон и придем к неравенству треугольника.
\[\слева| {{z_1} + {z_2}} \право| \ле\влево| {{z_1}} \право| + \влево| {{z_2}} \справа|\]Существует несколько вариантов неравенства треугольника, которые легко вывести.
Сначала предположим, что \(\left| {{z_1}} \right| \ge \left| {{z_2}} \right|\). Это не требуется для вывода, но поможет получить более общая версия того, что мы собираемся вывести здесь.Итак, давайте начнем с \(\left| {{z_1}} \right|\) и поработаем над ним.
\начать{выравнивание*}\влево| {{z_1}} \право| & = \ влево | {{z_1} + {z_2} – {z_2}} \право| & \\ & \le \left| {{z_1} + {z_2}} \право| + \влево| { – {z_2}} \право| & \hspace{0,25 дюйма} {\text{Использование неравенства треугольника}}\\ & = \left| {{z_1} + {z_2}} \право| + \влево| {{z_2}} \право| & \end{выравнивание*}Теперь немного перепишем и получим
\begin{уравнение}\left| {{z_1} + {z_2}} \право| \г\влево| {{z_1}} \право| – \влево| {{z_2}} \право| \ge 0\label{eq:revtrione} \end{уравнение}Если мы теперь предположим, что \(\left| {{z_1}} \right| \le \left| {{z_2}} \right|\), мы можем выполнить аналогичный вышеописанному процесс, за исключением этого переключения времени \({ z_1}\) и \({z_2}\) и получаем
\begin{уравнение}\left| {{z_1} + {z_2}} \право| \г\влево| {{z_2}} \право| – \влево| {{z_1}} \право| =- \left( {\left| {{z_1}} \right| – \left| {{z_2}} \right|} \right) \ge 0\label{eq:revtritwo}\end{equation}Теперь, вспоминая определение абсолютного значения, мы можем объединить \(\eqref{eq:revtritwo}\) и \(\eqref{eq:revtritwo}\) в следующий вариант неравенства треугольника.
\begin{уравнение}\left| {{z_1} + {z_2}} \право| \г\влево| {{\kern 1pt} \влево| {{z_1}} \право| – \влево| {{z_2}} \right|{\kern 1pt} } \right|\label{eq:revtrithree}\end{equation}
Кроме того, если мы заменим \({z_2}\) на \( – {z_2}\) в \(\eqref{eq:triangle} \) и \(\eqref{eq:revtrithree} \), мы получим два другие варианты неравенства треугольника.
\begin{уравнение}\left| {{z_1} – {z_2}} \право| \ле\влево| {{z_1}} \право| + \влево| {{z_2}} \right|\end{уравнение} \begin{уравнение}\left| {{z}_{1}}-{{z}_{2}} \right|\ge \left| \влево| {{z}_{1}} \право|-\лево| {{z}_{2}} \право| \право| \label{eq:revtri} \end{equation}Иногда вы будете видеть \(\eqref{eq:revtri}\), называемое неравенством обратного треугольника .
вопросы по физике и решения 3) Что вы подразумеваете под фотоэффектом? Вопросы 1, 4 и 5 представляют собой короткие вопросы со свободным ответом, на каждый из которых требуется около 13 минут, и каждый оценивается в 7 баллов.
 Получите решения Совета штата Керала по учебникам новой учебной программы 2020-2021 Edition для экзаменов Совета штата по всем классам и предметам на английском языке и языке малаялам на HSSLive. Несколько правильных ответов: учащиеся должны выбрать все правильные ответы на приведенный ниже вопрос, чтобы получить баллы.Коробки математических навыков,… Прошлые работы, сводные заметки и вопросы прошлых экзаменов по темам для AQA, CIE, Edexcel, OCR и WJEC Chemistry A-levels, International A-levels, GCSEs и IGCSEs University Physics — это трехтомный сборник, отвечающий требования к объему и последовательности для двух- и трехсеместровых курсов физики, основанных на исчислении. 50 Ом. Бесплатно скачать вопросы по физике TIFR — объединенные статьи для кандидатов и докторов наук за период с 2010 по 2017 год документы в формате pdf с ключами ответов, выделенными зеленым цветом — вопросы с бесплатными ответами Загрузите вопросы с бесплатными ответами из прошлых экзаменов вместе с рекомендациями по подсчету баллов, образцами ответов экзаменуемых и распределением баллов .
Получите решения Совета штата Керала по учебникам новой учебной программы 2020-2021 Edition для экзаменов Совета штата по всем классам и предметам на английском языке и языке малаялам на HSSLive. Несколько правильных ответов: учащиеся должны выбрать все правильные ответы на приведенный ниже вопрос, чтобы получить баллы.Коробки математических навыков,… Прошлые работы, сводные заметки и вопросы прошлых экзаменов по темам для AQA, CIE, Edexcel, OCR и WJEC Chemistry A-levels, International A-levels, GCSEs и IGCSEs University Physics — это трехтомный сборник, отвечающий требования к объему и последовательности для двух- и трехсеместровых курсов физики, основанных на исчислении. 50 Ом. Бесплатно скачать вопросы по физике TIFR — объединенные статьи для кандидатов и докторов наук за период с 2010 по 2017 год документы в формате pdf с ключами ответов, выделенными зеленым цветом — вопросы с бесплатными ответами Загрузите вопросы с бесплатными ответами из прошлых экзаменов вместе с рекомендациями по подсчету баллов, образцами ответов экзаменуемых и распределением баллов . • Уровни A 2001 г. @ RJC с отличием 4 As и 2 S (математика и физика) • Уровни O 1999 г. @ RI (E Maths — A1, A Maths — A1, Physics — A1) • Текущий ученый, работающий в области инженерии Компания • Тренер юношеской олимпиадной команды по физике Xinmin Sec 2009, 2010 и 2011! Решения ICSE для физики класса 10. Расстояние между F A и осью вращения (r AC) = 40 см = 0,4 метра. А. (138 отзывов) 14 фунтов стерлингов. pdf из PH MISC в Женском колледже OPF, Исламабад. Эта научная викторина охватывает вопросы биологии, химии и физики, а также ответы в формате PDF.Математика | Физика. Так как он принимает звук 0. th Physics Matters for GCE ‘O’ Level (4 Edition): полные решения вопросов из учебника, глава 12, глава «Вопросы и ответы на викторину по физике для 10 класса», загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответа на экзамен. «MCQ A Level Physics» с ключом ответов охватывает основные понятия, теорию и аналитические оценочные тесты.
• Уровни A 2001 г. @ RJC с отличием 4 As и 2 S (математика и физика) • Уровни O 1999 г. @ RI (E Maths — A1, A Maths — A1, Physics — A1) • Текущий ученый, работающий в области инженерии Компания • Тренер юношеской олимпиадной команды по физике Xinmin Sec 2009, 2010 и 2011! Решения ICSE для физики класса 10. Расстояние между F A и осью вращения (r AC) = 40 см = 0,4 метра. А. (138 отзывов) 14 фунтов стерлингов. pdf из PH MISC в Женском колледже OPF, Исламабад. Эта научная викторина охватывает вопросы биологии, химии и физики, а также ответы в формате PDF.Математика | Физика. Так как он принимает звук 0. th Physics Matters for GCE ‘O’ Level (4 Edition): полные решения вопросов из учебника, глава 12, глава «Вопросы и ответы на викторину по физике для 10 класса», загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответа на экзамен. «MCQ A Level Physics» с ключом ответов охватывает основные понятия, теорию и аналитические оценочные тесты. Полный список видео. Об этой книге. CBSE 12th Physics Term-1 2021-22: Тематические MCQ, тематические вопросы и вопросы A / R с решениями.Колебания и волны (раунд 1) pdf. ИТ = ВТ/ВТ. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения 1. Основные вопросы JEE по физике за предыдущий год с решениями по «Гравитации» В5: Простой маятник имеет период времени T1, когда он находится на поверхности земли, и T2, когда он поднимается на высоту R над земной поверхностью, где R — радиус земли. Узнать больше. И это будет полезно на UPSC, SSC, Railway, Bank Po, HTET, TET, NAVY, AIRFORCE и многих других конкурсных экзаменах.Какое расстояние? О: 30 км. Выпуклая линза с фокусным расстоянием 20 см. Поддержите физику онлайн. Если расстояние AB = BC = 20 см, каков момент силы относительно точки C. (11:45) Механика Свободный ответ Вопрос №1 Решения. JEE Основная физика Важные вопросы с решениями Физика и измерения Кинематика Закон движения Работа, энергия и мощность Вращательное движение Гравитационные свойства твердых тел и жидкостей Термодинамика Кинетическая теория газов Колебания и волны Электростатика Ток Электричество Магнитные эффекты тока и магнетизма Читать бесплатные вопросы олимпиады по физике Решения Решение задач по физике требует много тяжелой работы по главе, данной в учебнике.
Полный список видео. Об этой книге. CBSE 12th Physics Term-1 2021-22: Тематические MCQ, тематические вопросы и вопросы A / R с решениями.Колебания и волны (раунд 1) pdf. ИТ = ВТ/ВТ. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения 1. Основные вопросы JEE по физике за предыдущий год с решениями по «Гравитации» В5: Простой маятник имеет период времени T1, когда он находится на поверхности земли, и T2, когда он поднимается на высоту R над земной поверхностью, где R — радиус земли. Узнать больше. И это будет полезно на UPSC, SSC, Railway, Bank Po, HTET, TET, NAVY, AIRFORCE и многих других конкурсных экзаменах.Какое расстояние? О: 30 км. Выпуклая линза с фокусным расстоянием 20 см. Поддержите физику онлайн. Если расстояние AB = BC = 20 см, каков момент силы относительно точки C. (11:45) Механика Свободный ответ Вопрос №1 Решения. JEE Основная физика Важные вопросы с решениями Физика и измерения Кинематика Закон движения Работа, энергия и мощность Вращательное движение Гравитационные свойства твердых тел и жидкостей Термодинамика Кинетическая теория газов Колебания и волны Электростатика Ток Электричество Магнитные эффекты тока и магнетизма Читать бесплатные вопросы олимпиады по физике Решения Решение задач по физике требует много тяжелой работы по главе, данной в учебнике. Глава 5 Законы движения. Проблемы, вопросы и примеры представлены с решениями и подробными пояснениями. ) E1-26 Объем помещения составляет (21 13 12)фут3(0:3048 м/фут)3 = 92:8м3. Используйте MathJax для форматирования уравнений. Эти вопросы с решением подготовлены нашей командой опытных учителей, которые годами преподают в школах CBSE. Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Вы должны знать, что примерно 40% вопросов на экзамене UGC NET построены по тому же шаблону, что и работы предыдущего года.Книга: Национальный совет по исследованиям и обучению в области образования (NCERT) Читать бесплатно. Вопросы и решения олимпиады по физике Чтобы решить вопросы по физике, нужно много работать над главой, данной в учебнике. Ускоряясь в стволе винтовки, пуля проходит расстояние, равное 0. Решения CBSE NCERT для физики класса 11 служат лучшим учебным материалом для учащихся, поскольку они помогают им в учебе, пока они продвигаются через обязательные эксперименты LC PHYSICS – Экзаменационные вопросы и решения. Это 56 страниц, поэтому не забудьте ксерокопировать 4 страницы на один лист, перейдя в формате A3 → A4 и используя копировальный аппарат вплотную друг к другу.3 примера вопросов со свободным ответом, начиная со стр. 01см. (4) прямо пропорциональна основным единицам массы, длины и времени. Оптика (раунд 1) pdf. none Вопросы и ответы по физике Проверьте свое понимание с помощью практических задач и пошаговых решений. (22:40) Механика Свободный ответ Вопрос №2 Решения. Решения для учебников Все с видеоответами Изучите все эти предметы STEM и многое другое с помощью обучающих видео, включая ответы, из более чем 1700 учебников от опытных преподавателей из ведущих университетов.Готтлиб и Ральф Лейтон. com 25 декабря 2021 г. с помощью гостевых решений для 12-го класса, чтобы вы могли сэкономить свое время, а не тратить его на один и тот же вопрос. 100 с 5. Решения на Shaalaa помогут вам без проблем решить все вопросы по физике 10 класса ICSE. Можно прочитать MCQ по физике Доступ к классу Бесплатные вопросы и решения по физике твердого тела Физика твердого тела Это второе издание хорошо принятой книги. Просмотрите все инструменты исследования. Учебный материал. 23 апреля 2021 г. 29 декабря 2021 г. админ.2 на восток. (время. Получите лучшие оценки. В главе есть вопросы, основанные на времени, измерении длины, массы, плотности и объема различных объектов. com, 25 декабря 2021 г., гость [DOC] Вопросы и решения олимпиады по физике Получение вопросов и решений олимпиады по физике сейчас не является сложным средством. «Концептуальные примеры», «Концепции и расчеты» и «Проверьте свое понимание» помогают учащимся понять принципы физики. Мы очень старались сделать этот сайт самым надежным сайтом вопросов и ответов по физике в Интернете, но ни один сайт не идеален, как мы объясняем в этой заметке.Заметки о пересмотре, ключевые моменты, рабочие листы и вопросы по темам из прошлых статей. Google Класс Facebook Twitter. Получите мгновенный доступ за простой разовый платеж всего в 19 фунтов стерлингов. Наименьшее количество винтовой марли? Скачать MCQ по общим наукам в формате PDF. Расстояние между F B и осью вращения (r BC) = 20 см = 0. Электромеханическая лама. Maharashtra board Книга по физике Solutions создана компанией Найдите полезные вопросы и ответы по физике на Solutioninn. Наименьшее количество штангенциркуля? Ответ Проблемы и решения в медицинской физике Физический мир – Терм I.а. Чтобы облегчить задачу учащимся, Aakash Chemistry Questions — Learn Basic Chemistry Part 1 (1-25). Практика этих вопросов CBSE NCERT Objective MCQ по физике класса 12 с ответами Pdf поможет учащимся быстро повторить все концепции, представленные в каждой главе, и подготовиться к выпускным экзаменам. CBSE 12 Математические решения. Человек должен пройти 50 м на север, 40 м на восток и 20 м на юг, чтобы добраться до поля. Решения содержат интеллектуальные ярлыки для обучения и интеллектуальные методы решения проблем, которые помогут вам значительно повысить общую эффективность и скорость.Скорость звука 340 м/с. Мы предоставляем всем ученикам от 5-го класса до уровня магистра подготовку ко всем экзаменам бесплатно. Мы шаг за шагом предоставляем книги Совета штата Тамилнаду, ответы, руководства по решениям для 12-го, 11-го, 10-го, 9-го, 8-го, 7-го и 6-го, 5-го, 4-го, 3-го, 2-го, … IGCSE Maths, октябрь, ноябрь 2021 г., документ 43, документ и ответы. Твердый шар имеет массу 100 г и радиус 2 см. Ответ (1 из 6): Украсть? Так все делают, верно? Или же — смею сказать — решить их все самостоятельно или, что еще лучше, решить их все с командой друзей, чтобы вы могли проверить свои коллективные ответы и показать ответы, в которых вы не уверены, наставнику? Интернет-игра Whack Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности.университетская физика, 13-е издание, вопросы для обсуждения, ответы pdf Бесплатный доступ к университетской физике, 13-е издание, вопросы для обсуждения … Если у вас есть вопросы по физике, обратитесь за ответами к преподавателям. Вот все вопросы и решения из всех предыдущих разделов. QQT и PASA для объяснения физики AP. Глава 1 Физический мир. (3) больше в системе СИ, чем в системе СГС. Дополнительные вопросы по главам с полными решениями доступны для загрузки на веб-сайте myCBSEguide и в мобильном приложении.Вопросы и ответы по физике A-Level 2020/2021 Все авторские права и права на публикацию принадлежат S-cool. Практикуйте вопросы и ответы по каждой теме. И PDF, и печатные версии этих учебников содержат одни и те же проблемы. Вопросы с бесплатными ответами. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределения баллов. Ситуация такова: большая часть работы была проделана за вас, и в этом случае ваша работа состоит в том, чтобы изучить данные ответы и использовать их в качестве шаблона и руководства для ответов, которые вы даете.Физика ХЛ. Понятия физики четко обсуждаются и подчеркиваются. Все мои решения для AP Physics 1 Вопросы с бесплатным ответом. 25 А. Описание. HSC Physics MCQ Вопрос с ответом. (a) Выразите величину ускорения свободного падения на поверхности Планеты Z через ускорение свободного падения на поверхности Земли, g g g. Глава 3 Теплофизика. Количество работ: На экзамене 2 работы (физика, химия и математика). Время: Каждая работа длится 2 часа 30 минут или 150 минут.Общее время плейлиста: 269 минут. Физика HL Paper 2 Solutions; Physics SL Paper 2 Solutions; Бумага 3.0), а второй камень менее плотный, хотя и весит больше, потому что его плотность всего 2. Фогт (распродано). Выберите свой вопрос C Long. (б) расстояние. Охвачены все основные темы A Level Math. Спектроскоп… Научная чаша ФИЗИКА Физика – 3 ФИЗ-91; Множественный выбор: маятник, подвешенный к потолку железнодорожного вагона, висит под углом 10 градусов вправо от вертикали.Упражнения и решения. Б: 60 км. Он обеспечивает актуальный, краткий обзор основных тем в физике материи, от атомов и молекул до твердых тел, включая элементы статистической механики. Вопрос: Автомобиль проехал 80 км на юг. переменный ток Пересмотр НОВОГО курса математики уровня A. Развернуть все 3. Необходимо иметь очень четкое представление о понятиях, упомянутых в главе. Источники. Вопросы 2 и 3 представляют собой длинные вопросы со свободным ответом, на каждый из которых требуется около 25 минут, и каждый оценивается в 12 баллов.Резистор 2 (R2) = … Опытные преподаватели SamacheerKalvi. Пожалуйста, скажите, что вопросы и решения олимпиады по физике являются общеучебными вопросами шестого класса. Вопросы по физике, проблемы магнетизма и решения последних десяти лет. Проблемы динамики. Учебники по оптике. с решением в примере работа мощность энергия Решения NCERT для 12 класса Физика является лучшим учебным материалом для учащихся, которые затрудняются ответить на вопросы из учебника.Поскольку у нас есть график смещения-времени, используйте отношение смещения-времени, а. Resnick Halliday Physics Volume 1 Solutions подробно охватывает все концепции всех глав и дает ответы на все вопросы упражнений простым для понимания, точным и точным образом. Это важно для всех учеников, которые сейчас учатся в 8 классе. Законы движения Ньютона. Вопросы и ответы. Том 2 посвящен термодинамике, электричеству и магнетизму, а том 3 посвящен оптике и современной физике. Общее время плейлиста: 248 минут.1. PDF-книга «Уровень викторины по физике» помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. 2 метра. A Level Physics Вопросы и ответы с несколькими вариантами ответов Загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по физике 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. В этой главе мы будем изучать, как все работает и почему… Читать вопросы и решения онлайн-олимпиады по физике NEET Physics Важные вопросы с решениями Содержание еще не загружено.ХИМИЯ КЛАСС 12 ОЧЕНЬ КОРОТКИЕ ВОПРОСЫ. 5 часов назад · Спасибо за ответ на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос. ICSE Solutions Селина ICSE Solutions ML Aggarwal Solutions. Опишите физику. Тип вопросов: Все вопросы в экзамене относятся к типу MCQ. Опубликовано администратором bestfreepapers 18 декабря 2019 г. 18 декабря 2019 г. Включены бесплатные вопросы и задачи, связанные с тестом SAT, а также учебные пособия по прямолинейному движению с постоянной скоростью или равномерным ускорением.HSC Physics 1st MCQ Вопрос с ответом 2021. Вопрос 1. Решения HC Verma по главам — … Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Силы и движение (динамика) (раунд 1) pdf. org/pdf/ap-2020exam-sample … 2 СОДЕРЖАНИЕ M. Гарантированные вопросы для получения отличных оценок. Здесь мы предлагаем решения для всех глав учебника по физике ICSE для 8-го класса средней школы Селины для учащихся.MIT – Массачусетский технологический институт PG TRB Типовые экзаменационные вопросы с ответами по физике, химии, ботанике, зоологии, истории, географии, домоводству, информатике, экономике, торговле, математике, тамильскому языку, английскому языку и индийской культуре. ТМ. Ящики для математических навыков,… Основная университетская физика: Том 1 (3-е издание) Вольфсон, Ричард Издатель Pearson ISBN 978-0-32199-372-4 Вопросы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Physics 1120 : Простые решения гармонического движения 1. Реальные приложения также включены, поскольку они показывают, как эти концепции в физике используются в инженерных системах… Вопросы физики Когда свет от звезды распространяется и ослабевает, образуются ли промежутки между фотонами? Может ли огонь иметь тень? Может ли воздух создавать тени? Можно ли создать золото из других … См. решение Решения для вопросов по физике в средней школе Решение для задачи № 1 № 1840 м. Решения по физике для Резника Холлидея Уокера, том 1 Глава 1 «Измерение» содержит одно упражнение, которое разделено на 4 модуля и содержит в общей сложности 60 вопросов. Через 7 секунд парашютист упал с высоты 240 метров. Глава 1 Измерение. MeritNotes предоставляет только вопросы и ответы Samacheer Kalvi из стандартных материалов с 6-го по 12-е, вопросник за предыдущий год и… Получить учебники Государственного совета Тамилнаду. Тамильская среда и английская среда на SamacheerKalvi.Электродинамика и схемы (раунд 1) pdf. Курсы ревизии. Общее количество вопросов: В каждой работе 120 вопросов. Наши репетиторы по физике помогли нам составить это для наших учеников 10 класса. Он неразрывно связан с каждым видом деятельности в нашей повседневной жизни. В каждой главе есть около 4-5 наборов решенных дополнительных вопросов по физике. к. Том 1 охватывает механику, звук, колебания и волны. Энергия и движение (кинетика) (раунд 1) pdf. Книга MCQ по физике для 10 класса, краткое учебное пособие из учебников и конспектов лекций содержит практические экзаменационные тесты.Банки решений. эмигрант Результирующий вектор — это вектор, полученный в результате сложения двух или более векторов. Теперь мы достигли еще одной важной вехи, предоставив всем учащимся школьного уровня ответы на вопросы, ориентированные на подготовку к экзамену, для всех студентов, изучающих естественные науки и искусство. Физика HL Paper 3 Solutions; Physics SL Paper 3 Solutions; ИА и ЭЭ; Онлайн MCQ. Получите доступ к сотням дополнительных видеороликов, охватывающих весь курс физики уровня A. Проверьте программу NEET по физике. Наша функция вздора показывает, насколько шатки многие другие сайты.Электронная библиотечная олимпиада по физике: вопросы и решения. орг. Задача № 1. Глава 3 Движение по прямой. Джелалия, Физика Международная система единиц Чтобы представить результат измерения определенной физической величины, необходимо определить единицу измерения. (2) не зависит от метода измерения. A 1. Движение класса 9 Важные вопросы: Решения Важные вопросы Примечания Решения NCERT. Преимущества решений ICSE Class 9 Physics: вопросы и ответы с несколькими вариантами ответов (MCQ) по «Физике — класс 12» (наряду с более чем 1000 MCQ по «Физике — класс 11») сосредоточены на всех областях физики, охватывающих более 200 тем.Скачать электронную книгу «Вопросы и решения по физике твердого тела» физика вещества, от атомов и молекул до твердых тел, включая элементы статистической механики. Уточните и дайте количественную оценку своему ментальному образу проблемы. Лейтон и Рохус Э. А чтобы получить индивидуальные ответы на домашние задания на вопросы по физике как можно скорее, обратитесь к одному из репетиторов здесь, на JustAnswer. Проверьте свои знания по естествознанию, которое включает в себя материю, движение, энергию, силу и поведение в пространстве и времени, в … вопросы и решения олимпиады по физике доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можете получить это мгновенно.О нас. В: Автомобиль проехал 60 км на восток и 90 км на запад. · 3г. Прошлые вопросы олимпиады по физике Мы предоставляем работы прошлого года Вопросы и решения олимпиады по физике (IPhO) от основ до продвижения. Глава 12 Sound Class 9 MCQ Вопросы. Глава 7 Разнообразие живых организмов Класс 9 MCQ. IB Physics HL SL Учебник Вопросы и рабочие ответы К. А. Цокос. Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. Физика – предмет, который очень трудно понять Веб-сайт не работает должным образом.Руководство по решениям на 2011-2018 годы. Получите бесплатно ключевые заметки, вопросы MCQ, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 9. r/IBO. По сравнению с DC Pandey он состоит из меньшего количества вопросов и упражнений. Читать бесплатные вопросы и решения по физике твердого телаФизика твердого телаФизика твердого телаВычислительная физика твердого телаФизика твердого телаФизика твердого телаЗадачи по физике твердого тела с решениямиФизика твердого тела, 1eФизика твердого телаВведение в физику твердого тела, 2-й “Вопросы и ответы по физике для 10 класса” PDF скачать с бесплатный образец теста охватывает вопросы для начинающих и пробные тесты с ключом ответов на вопросы экзаменационной рабочей тетради.ФИЗИКА КЛАСС 11 ВАЖНЫЕ ВОПРОСЫ. Наиболее эффективные методы (для быстрого получения правильных ответов) использовались для решения вопросов IIT JEE. Эти учебники доступны бесплатно по ссылкам ниже. Предполагая, что подъем в гору является положительным направлением, каково среднее значение автомобиля. С помощью этих тщательно подобранных решений NCERT для физики класса 11 все сомнения и вопросы учащегося будут устранены. 3500+ общих научных вопросов на основе NCERT – ответы. Советы Фейнмана по физике Ричарда П.Учащимся предлагается прочитать и загрузить эти учебные вопросы, а CL предоставляет материалы для подготовки к CBSE Physics для учащихся 9-го класса. Присоединяйтесь к Chegg Study и получите: Решения для учебников с пошаговыми инструкциями, созданные экспертами Chegg. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределение баллов. . 6. Щелкните здесь, чтобы получить ответы на вопросы о физической скорости. Это означает, что конечный результат составляет всего (!) 14 страниц. Введение в физику Вопросы для упражнений Решения HC Verma Ch-1 Концепция физики Vol-1 для Class-11.9. Студент-физик 525-N стоит на напольных весах в 846-килограммовом (включая студента) лифте, который… учебников, чтобы вы могли уверенно двигаться вперед. Загрузите бесплатные рабочие листы для печати для CBSE Class 9 Physics с важными вопросами по теме, учащиеся должны практиковать рабочие листы NCERT Class 9 Physics, банки вопросов, рабочие тетради и упражнения с решениями, которые помогут им в пересмотре важных концепций. Физика класса 9.Дайте определение равномерному круговому движению и приведите его пример. Электронное письмо. Глава 9 Сила и законы движения Вопросы 9 класса MCQ. физика-олимпиада-вопросы-и-решения 5/8 Скачано с dev1. Вопросы и решения для всех глав JEE Advanced Physics доступны на этой странице, чтобы помочь учащимся ускорить подготовку к вступительному экзамену. Курсы для GCSE, A-level и поступления в университеты. Пуля вылетает из винтовки с начальной скоростью 521 м/с. Часть 1. Упражнения для фейнмановских лекций по физике… Б.HC – VERMA Вопросы и решения Класс 12 Физика Глава – 40: Электромагнитные волны. com предоставляет решения ICSE по физике класса 10 для экзаменов ICSE Board. Попробуйте Numerade бесплатно. 99. Начиная с зубной пасты, используемой по утрам, и заканчивая повседневным использованием Интернета, мобильного телефона и просмотра телевизора, все это плоды олимпиады по физике. Вопросы и решения доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можно получить мгновенно. Чтобы получить высокие баллы в JEE Advanced, необходима регулярная практика, поскольку известно, что уровень сложности JEE… Публикуйте вопросы о домашнем задании и получайте ответы от проверенных наставников круглосуточно и без выходных.5 Сила и движение-I. Примеры вопросов Экзамены AP Physics 1 и AP Physics 2 Вернуться к оглавлению. Неспособность тела самостоятельно изменять свое состояние называется инерцией. HC – VERMA Вопросы и решения Класс 12 Физика Глава – 41: Электрический ток через газы. Биология | Химия. Частица равномерно ускорена из состояния покоя, так что через 10 с она достигла скорости 15 м/с. Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте [email protected].Данные и оценка (раунд 1) pdf. AQA, OCR, Edexcel, WJEC. Решения NCERT для класса 12 по физике Глава 3 Текущие электрические упражнения и дополнительные упражнения в формате PDF скачать бесплатно или использовать в Интернете без загрузки обновлены для академической сессии 2021-2022. Основная цель подготовки решений – облегчить студентам подготовку к экзамену. (7:31) 8 общих рекомендаций для бесплатных ответов любого экзамена по физике AP. Пожалуйста, напишите по адресу school@cbse. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения BSEB Bihar Board 12-го числа по физике Важные вопросы Численные числа являются лучшим ресурсом для учащихся, который помогает в повторении.PANDEY TUTORIAL Последнее обновление: 17 декабря 2021 г. Окончательный ответ представлен в текстовой форме для быстрого ознакомления над каждым видео и красиво отформатирован в виде уравнения, например E = mc 2. Например, если книга лежит на полке, книга продолжает оставаться в стойке до тех пор, пока не будет приложена какая-либо внешняя сила, чтобы удалить или сместить его из исходного положения. (г) масса. Скачать PDF. Опубликовать вопрос. Движение Важные вопросы: решение. IT = I1 = I2 = I3 = 1. Тетрадь для повторения экзамена. Каждый будет состоять из нескольких частей, и части не обязательно будут иметь одинаковый вес.Следовательно, первая порода более плотная, (плотность = 3. На экзамене есть 3 вопроса со свободным ответом, которые считаются 50% от оценки за тест. Существует различие между средней скоростью и величиной средней скорости. Спросите любого физика. вопрос, и эксперт ответит на него всего за 30 минут Отчет об экзамене VCE по физике за 2017 г. (с изменениями от 30 октября 2019 г.) Экзамены, относящиеся к предыдущим планам исследования Учащиеся и преподаватели должны учитывать, что с введением нового плана исследования экзамены не обязательно являются руководством к текущему экзамену VCE для этого исследования.RT = 100 Ом. 5 г/см 3 ) Задача № 2. Посетите официальный сайт CISCE для получения подробной информации о ISC Board Class-11 Physics. Вопросы UGC NET за предыдущие годы с решениями по всем предметам: Вопросы UGC NET за предыдущий год играют важную роль в подготовке к экзамену. Окленд. Почему движение называется ускоренным? Sol:-Равномерное круговое движение можно описать как движение объекта по круговой траектории с постоянной скоростью. Проект руководства к предстоящему конкурсу по физике: F = ma Contests.Студенты могут получить подробное объяснение ответов на все вопросы, включенные в концепцию «Current Electricity» главы 3, разработанную NCERT Solutions of 12th Physics. лекдем. NEET Практические задания NEET Вопросы по физике, химии, биологии Вопросы о скорости и скорости. В этой статье мы представили важные вопросы по главам, которые будут полезны при подготовке к NEET. IOE, TU, вопросы и решения 2067 Ashadh to 2071 Magh Engineering Physics (для BE … AP Physics 1 – 2020 Примеры экзаменационных вопросов Полное решениеСсылка на вопросhttps://apcentral.Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи. Вопрос 1 (4 балла) Планета Z имеет вдвое большую массу и вдвое больший радиус Земли. Скорость и скорость. Решение банка вопросов по физике для 12-го класса Английский, средний 2022 г. Полное решение для банка вопросов по физике для 12-го класса pdf скачатьОб этом видеоЯвляется ли видео мной apko все решения для HSC Physics Module 8 Questions. Астрономия (раунд 1) pdf. Практические эксперименты. х) Вагон движется с ускорением влево.Часть 2. Известно: вращение оси в точке C. 2 Оглавление Решения для основ физики Холлидей и Резник Получите доступ ко всем ответам и пошаговым видеообъяснениям к этой книге и еще к 1700 книгам. Отвечать. Своими словами точно сформулируйте вопрос, на который нужно ответить, в терминах, которые вы можете рассчитать. 11 строк Ответ: v i = 5. MyCBSEGuide — единственное подлинное приложение для вопросов MCQ. Выберите свой C CL предоставляет материалы для подготовки к CBSE Physics для учащихся 10 класса. Практика: вопросы скорости и скорости.IT = 125 В/100 Ом. College Physics Answers предлагает видеоролики с решениями задач в конце глав в учебниках, опубликованных OpenStax, под названием «College Physics» и «College Physics для курсов AP». Автомобиль катится задним ходом вниз по склону со скоростью 3. Выберите решение C View Physics-Solution. Помимо этого, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, практические вопросы, серию тестов для JEE Main, JEE Advanced и NEET, важные вопросы по физике, химии, математике и биологии и многое другое.В целом, кандидаты найдут широкий спектр вопросов MCQ для класса 9 по научной физике с ответами. 138 вопросов НМ. Основные вопросы suvat Не забывайте всегда записывать известные значения s, u, v, a и t и решать, какое направление положительное, а какое отрицательное. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения. Получите вопросы и ответы по физике. Учебник по доске Махараштры Решения. Редакция. Большое спасибо, сэр, за ваш ценный… Найдите пошаговые решения и ответы на Основы физики – 9781118230718, а также тысячи учебников, чтобы вы могли уверенно двигаться вперед.NEET Physics Важные вопросы с решениями Физика помогает понять повседневные действия, такие как ответы на такие вопросы, как почему небо голубое, что заставляет нас легко ходить по дорогам, почему так важно иметь луну и т. д. Все ответы были подготовлены опытными учителями что гарантирует, что все решения верны, а вопросы решены таким образом, чтобы учащиеся, обращаясь к этим ответам для 9 класса ICSE, могли получить хорошие оценки. Наши книжные серверы сохраняют информацию в нескольких местах, что позволяет сократить время задержки при загрузке любой из наших книг, подобных этой.Этот пример показывает, почему важно быть осторожным и не использовать слова тяжелее/легче, когда вы имеете в виду более или менее основные вопросы JEE по физике за предыдущий год с решениями по «электростатике» V a’ = kQ/a + k(-4Q)/ b V b’ = kQ/b + k(-4Q)/b V a’- V b’ = kQ/a – kQ/b = V a– V b = V Ответ: (b) V Q5: Номинальное напряжение конденсатор с плоскими пластинами на 500 В. Получите бесплатно основные заметки, вопросы о запросах, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 10 человек. Предоставьте подробности и поделитесь своими исследованиями! Но избегайте… Просьб о помощи, разъяснений или ответов на другие ответы.B: 50 км на восток. Как и другие авторы по физике, он также концентрируется на ваших основах физики. IGCSE Maths, октябрь, ноябрь 2021 г., статья 43 статьи и ответы. Таблицы уравнений. Через 2. второе уравнение движения. Категории: Экзаменационные записки. Учебные заметки младшего колледжа. И это решения по главам, в которых вы найдете важные вопросы для экзамена на доске. Глава 11 Работа и энергия Класс 9 Вопросы MCQ. Он содержит более 160 полностью переработанных и дополненных рисунков, иллюстрирующих основные физические концепции и основные 4 МБ.Коробки с математическими навыками, … CBSE Class 12th Решения по математике, биологии, физике и химии приведены ниже. Вопросы публикуются анонимно и могут быть сделаны на 100% приватными. Теги: h3 Физика JC 1 JC 2 Школьные заметки. г. NIOS Class 12th Physics 150+ важных вопросов с решениями (полная программа Nios) Маниш Верма. PDF-файл «Рабочие листы по физике для 10-го класса» с ответами посвящен решению задач на упражнениях 5 часов назад · Спасибо за предоставление ответа на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос.уровень 1. С 1998 года добровольцы из Департамента физики Университета Иллинойса в рамках информационно-пропагандистской программы Physics Van ответили на 8444 вопроса. askIITians также предлагает вам 16 лет IIT JEE с вопросами за предыдущий год. Решения NCERT для физики 12-го класса Глава 3 Current Electricity — лучший учебный материал, который поможет вам получить больше баллов на экзаменах по физике 12-го класса, а также на любых вступительных экзаменах. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают контрольные карточки для решения задач по математике на уровне A Level.Банки решений для математики уровня A. 5 с, машина движется в гору на 4. Делать заметки для главы — хорошая идея, поэтому постарайтесь подготовить рукописные заметки всех важных моментов и формул. Sir Aakash Package Solutions PHYSICS 3000+ Вопросы и решения Больше не доступно на мега-сайте… пожалуйста, повторно загрузите этот файл, но убедитесь, что вы загрузили его на диск Google, потому что мега-сайт автоматически удалит любой файл через 1 месяц… и, если возможно, пожалуйста ответьте мне, когда контент будет доступен….Глава 15 Улучшение продовольственных ресурсов Класс 9 MCQ. 10 2 м/с 8. (в) интенсивность солнечного света. В TopperLearning наши опытные преподаватели подготовили пошаговые модельные решения для вопросов из учебника и образцов работ в соответствии с последней программой ICSE Class 8 Physics. В этом посте я предоставил MCQ по физике по главам, вопросы на основе конкретных случаев и A / R (утверждение и причина) для класса 12 сессии 2021-22 с полными решениями. Конкурсы по физике Задачи и решения по механике Эта книга представляет собой сборник задач по физике, полезных для подготовки к олимпиадам и конкурсам.8 общих рекомендаций для FRQ любого экзамена по физике AP. Подробные решения типовых вопросов с несколькими вариантами ответов. Задачи DC Pandey по общей физике охватывают самый продвинутый уровень вопросов для класса 7, который действительно проверяет ваши… Решения ICSE для физики класса 10. Коробки математических навыков, … HC VERMA Solutions for Class 11 Physics Chapter 3 – Rest and Motion Kinematics. 5 м/с. Если его уши находятся на расстоянии всего 2 см друг от друга, это означает, что он должен уметь различать звуки со временем Репетитор по физике и математике.Здесь все вопросы решаются с подробным объяснением и доступны для бесплатной проверки. Упражнения по вводной физике Роберта Б. Название: Microsoft PowerPoint – Глава 5 [Режим совместимости] Автор: Мукеш Дхамала Дата создания: 08.02.2011 16:38:07 Мои студенты, эта статья поможет вам узнать о практической физике Вопросы Viva 2021, которые задают на экзаменах с ответами для 11-го и 12-го классов. Пошаговые решения проблем, более 34 000 ISBN Найдите решения в учебниках.0 разделов 97 вопросов +198 еще. Свяжитесь со мной. Книга MCQ по физике в колледже, краткое учебное пособие из учебников и примечаний к пересмотру, охватывает вопросы экзаменационной практики. Загрузите приложение eSaral, чтобы получить бесплатные учебные материалы и видеоуроки. Toppr бесплатно предоставляет учебные материалы, более 1000 часов видеолекций, вопросы с вопросами за последние 10 лет. 0. О нас Пресса Авторские права Свяжитесь с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Свяжитесь с нами Создатели Для решения PHYSICS решения И ВОПРОСЫ:1.Публикуйте свои домашние задания по физике и получайте ответы от квалифицированных преподавателей. Определите физические концепции и подходы, которые могут быть полезны для достижения решения. Документы CBSE, вопросы, ответы, блог MCQ содержат решения NCERT, CBSE, NTSE, учебные материалы олимпиады, типовые тестовые документы, важные вопросы и ответы, заданные на экзаменах CBSE. Приведите пример, иллюстрирующий разницу между этими двумя величинами. Q 5: 11 класс Физика Глава 1 Измерения Краткие вопросы Ответы. Найдите его ускорение и путь, который он преодолел.Жучок находился в 17 метрах. Посмотреть продукт. Дешевле купить кофе в Нью-Йорке (по крайней мере, по учебнику физики, т.е. какой из следующих ответов мог бы объяснить это явление? w) Вагон покоится. В физической лаборатории Эрнесто и Аманда применяют 87. Bihar Board 12th Physics Numericals Важные вопросы с решениями. Решения ICSE для классов с 6 по 10 – бесплатные решения для учебников ICSE Решения ICSE для класса 10. Глава 10 Гравитация Класс 9 Вопросы MCQ. с использованием решений NCERT по физике для физики класса 11: решения по главам.CBSE 12 Образец документа 2022 г. для вопросов MCQ для класса 9 по научной биологии с ответами. Ток постоянен через последовательно соединенные резисторы. Глава 2 Механика. В 1960 году международный комитет согласовал систему стандартов, названную системой СИ. Включает в себя полные решения и отчеты о результатах. Упражнения, размещенные на этом сайте, взяты из четырех источников: Гуру. Мы предоставляем шаг за шагом Samagra Kerala State Syllabus Учебники Решения Ответы Руководства для классов 12, 11, 10, 9, 8, 7 и 6, 5, 4, 3, 2, 1 стандарт… ответы.(1:03:04) Решения All Mechanics с множественным выбором. Решение помогает студентам получить четкое представление о концепции и готовит их к экзаменам. Подробно обсуждаются понятия перемещения, расстояния, скорости, скорости, ускорения. CBSE 12 Химические решения. Загрузите приложение Physics bro (ссылка ниже)2. Ответ: б) расстояние. Уровни GCE «A» h3 Physics 10-летняя серия Эксклюзивные решения от SAJC и JJC Этот пакет состоит из: 2007 г. Решение по физике уровня h3 (SAJC) 2008 г. Решение по физике уровня h3 (SAJC) 2011 г. Решение по физике уровня h3 (SAJC) 2013 A Level h3 Physics Вопросы и решения (JJC) 2014 A Level h3 Physics Вопросы и решения (JJC) 2016 A Уровень h3 Physics Solutions (SAJC) Получите полные решения по всем темам физики класса 8 ICSE на нашем учебном портале.nz/) кандидатами в учителя в рамках курсов по методам физики EDCP 357 в UBC. В приведенной выше ссылке есть документ 43 и решения / ответы на вопросы (которые я написал), и это не официально от cie. APlusTopper. DC Pandey является одним из лучших и предлагает книги для продвинутых вопросов, связанных с физикой. 8. Важный вопрос по физике 12 и 11 классов. (5) Ценное дополнение к назначенному учебнику в любом вводном курсе механики. 100 м/с 9 ч3 Физика Актуальные вопросы и ответы.Минимум ₹ 299. Вы не можете в одиночку ходить, когда храните книги или библиотеку или берете взаймы у своих подключений, чтобы просмотреть решения PM_TB_C12. 100 м; 101 м 4. 0. ПРОВЕРЬТЕ СЕБЯ ОТРАБОТАННОЕ РЕШЕНИЕ. PDF-книга “O Level Physics Quiz” помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. ком. HC – VERMA Вопросы и решения Класс 12 Глава физики – … Математика IGCSE Октябрь ноябрь 2021 г., статья 43, статья и ответы. Просто обратите внимание, что некоторые решения неверны в цоко. 1018 м 3. Оставить комментарий / Решенные задачи по фундаментальной физике / Сан Лохат.Из приведенных выше примеров становится ясно, что физика концентрируется на объяснении поведения вопросов и решений олимпиады по физике. Решения исходят от национальной тренировочной команды и членов национальной команды, и их замечательные решения составляют особенность этой книги. Где скачать примеры вопросов и решений олимпиады по физике, примечания и ссылки для дальнейшего чтения, чтобы улучшить понимание. Некоторые эксперты-предметники дают пошаговые ответы даже на самые сложные вопросы по физике 9 класса CBSE, которые очень часто встречаются на экзаменах.Отдельные экзамены прошлых лет и их решения доступны в … <p>От того, почему мы путешествуем вперед во времени, до того, как велосипеды вообще путешествуют вперед, мы задаем большие и малые вопросы, которые наши лучшие умы не могут объяснить<p> /p> Добавьте движение грузовика к графику, который вы нарисовали для вопроса № 4. В нем представлено более 160 полностью переработанных материалов Physics 11E, которые дают учащимся навыки, необходимые им для достижения успеха в этом курсе, уделяя особое внимание концептуальному пониманию; решение проблем; и предоставление реальных приложений и релевантности.б. Его диэлектрик выдерживает максимальное электрическое поле 106 В/м. «Задача о лифте» — классическая задача в физике. 8 м/с2. Q1. Величина любой физической величины: (1) зависит от метода измерения. 1 секунда туда и обратно, должно быть, звук 0. Физика Практические вопросы Viva с ответами для 11-го и 12-го класса. На стержень действуют три силы: F A = F C = 10 Н и F B = 20 Н, как показано на рисунке ниже. Здесь вы найдете упражнения по физике и математике, чтобы проверить свою смекалку.Расчет средней скорости и скорость отредактированы. Нарисуйте любые необходимые схемы с системами координат, соответствующими системе координат. Решения здесь несколько кратки, так как предназначены для преподавателя, а не для студента. Магнетизм (раунд 1) pdf. И вам, ребята, будет очень легко пересматривать их. «Рабочие листы по физике для 10-го класса» PDF с ответами посвящены решению задачи на упражнение Вопрос 20. 1) Когда пучок белых лучей рассеивается призмой, какой цвет будет преломляться в большей степени? Ответ: Фиолетовый.Решения HC Verma для класса 11 состоят в общей сложности из 22 глав. Эти вопросы IIT JEE с решениями являются вашим лучшим ресурсом для решения реальных практических задач. Пошаговые решения не требуют пояснений по своей природе. Выберите C-решения для развития чувства Вопросы, управляемые задачи и вопросы и задачи для развития чувства 1. 75-килограммовая частица движется как функция времени следующим образом: «Вопросы и ответы на викторину по физике для 10-го класса» Загрузка в формате PDF с бесплатными образцами тестовых обложек вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге.Q2. Бесплатные решения вопросов из учебника физики cbse class 9 не только проясняют ваши концепции, но и помогают вам сэкономить драгоценное время, которое вы можете потратить в другом месте. Вопрос 1 . Размышления об ЕГЭ 2015. 2) Современная атомная единица массы основана на ____ Ответ: Углерод-12. Фейнман, Майкл А. Проверьте здесь решения NCERT class 12. 105 с 6. Вопросы по физике MCQ | Chapter Wise Physics Questions Решения дают ответы на все сложные вопросы, а также помогают кандидатам получить четкое представление обо всех важных темах.Закон параллелограмма вектора гласит, что «Если векторы, действующие одновременно в точке как по направлению, так и по величине, представлены смежными сторонами параллелограмма, проведенного из точки, то равнодействующая векторов как по величине, так и по направлению представлена … NCERT Решения для физики класса 12 включают все вопросы, представленные в книгах NCERT для предмета физики 12-го класса. 03 м/с и время зависания = 1. CBSE, NCERT, JEE Main, NEET-UG, NDA, экзаменационные работы, банк вопросов, решения NCERT, образцы, примечания к изменениям, бесплатные видео, тесты MCQ и многое другое.Автономные приложения и решения CBSE и UP Board обновляются на основе последних книг NCERT на 2021–2022 годы. Выберите свои решения C для выпуска экзамена AP Physics C 1998 года. Это полезно, если вы находитесь в библиотеке или у вас медленное интернет-соединение. CBSE 12 Биологические решения. Поскольку вопросы основаны на работах предыдущего года, есть вероятность, что кандидаты найдут много вопросов из PDF-файла «Вопросы по физике» с решением в SSC CGL Tier 1 2017. pdf от A EN CREATIVE W в Инженерном колледже Катманду.Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте ssd@info. C: 80 км к югу. Решение на время. в воздухе погружают в воду. Мы предоставляем пошаговые решения для ICSE Physics Class 10 Solutions Pdf. Известно: Резистор 1 (R1) = 2 Ом. cs. умд. … Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, образцы ответов от сдающих экзамены и распределение баллов.6 Force and Motion-II Источник: веб-сайт NESA. а = 2∆ с / t2. Покажите свою работу для каждой части в отведенном месте после этой части. 11 КЛАСС ФИЗИКА Длинный вывод вопросов и ответов. Твердый шар имеет массу 50 грамм и объем 20 см 3 . Вы можете найти ответ на свой вопрос «Где сейчас я могу найти самую надежную профессиональную и быструю помощь для моего задания по физике?» на вашем сайте тоже. 0 м/с, когда водитель запускает двигатель. Настоящее руководство по решениям к книге не содержит ответов на вопросы для обсуждения.Расстояние между F C и осью задач плотности. Физика 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. 10 2 м 2. Пенджабский учебник используется в Лахорском совете, Гуджранвальском совете, Сахивальском совете, Равалпиндиском совете, Фейсалабадском совете, Мултанском совете, Бахавалпурском совете и т. д. Задача по физике Вопрос 24: Решения. Предоставьте подробную информацию о том, в чем вам нужна помощь, а также о бюджете и сроках.«Вопросы и ответы на викторину по физике для 10-го класса» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ответами на вопросы из рабочей тетради. Эта книга будет полезна любителям математики, учащимся средних классов, участвующим в математических соревнованиях, тренерам по преподаванию математики и учителям Общая физика Основной целью физики является понимание того, как ведет себя Вселенная. Физика является одним из старейших академических принципов. Глава 8 Motion Class 9 MCQ Вопросы. а = -9. Если вы стремитесь к AIR от 1 до 1 00 000 в JEE Main, эта книга для вас.Глава 5 Основная единица жизни Класс 9 MCQ. Единицами длины, массы и времени в системе СИ являются метр (м), килограмм (кг) и секунда (с). Магнетизм, термодинамика, механика твердых тел и жидкостей и т. д. Если объект тяжелее, сила тяжести больше, но поскольку он имеет большую массу, ускорение такое же, поэтому он движется с той же скоростью (если пренебречь сопротивлением воздуха). .Фрикционные вопросы и ответы. Схема выставления оценок: Схема выставления оценок: +4 за правильные ответы и -1 за вопросы свободной практики для AP Physics 1 – Удельное сопротивление. 10 обязательных вопросов к модулю физики HSC 5. Коробки математических навыков, … вопросы-и-решения-физики-олимпиады 1/8 Загружено с сайта dev1. Вы можете найти ответы на множество вопросов, таких как «в чем причина мерцания звезд», почему мы не падаем, когда идем по полу, почему мы стремимся двигаться вперед, когда автобус внезапно останавливается и т. д.150+ важных вопросов по физике с ответами (Золотая серия) Маниша Вермы. В этом буклете содержатся все экзаменационные вопросы раздела A, которые появились в решениях Loaving Cert AP Physics 1 FRQ. Этот учебник подчеркивает связь между теорией… Физика объясняет логику вещей, которые мы делаем в нашей повседневной жизни, которые часто остаются без ответа. Подробные решения для каждого вопроса были подготовлены профильными экспертами BYJU’S. C. Я спрашивал других людей об ответах на вопросы, в которых я не знал/не был уверен.Решения создаются комплексно, чтобы помочь учащимся быстрее понять концепции. Решения ICSE для математики класса 10; Решения ICSE для физики класса 10; Решения ICSE для химии класса 10; Решения ICSE для 10-го класса В конце каждой главы университетского учебника по физике есть масса вопросов для обсуждения, и я не могу найти для них руководства по решению. Здесь мы предоставили TN State Board New Syllabus Samacheer Kalvi 12th Std Physics… Решения NCERT для класса 9 по физике охватывают все 5 глав предписанной программы по физике и являются лучшей альтернативой.Учащиеся могут обратиться к экзаменационным вопросам ICSE Class 10 Physics Board по главам и решениям, которые были подготовлены для учащихся ICSE Class 10 на основе последней программы и руководств по экзаменам, выпущенных ICSE. Мы предоставляем пошаговую программу Samagra Kerala State Syllabus. Учебники. Решения. Ответы. PDF-файл с ответами охватывает основные понятия, теорию и аналитические оценочные тесты.Если мы посмотрим на второй закон Ньютона, F = ma. Решения NCERT для физики класса 9 разбивают решения на подробные шаги и подробно объясняют ответ, что помогает вам понять схему вопросов и способ повысить свой балл на экзаменах. Решение практических заданий главы 1 Введение в физику Верма Х.С. Понятие физики. Развернуть все Благодаря нашим многочисленным преимуществам онлайн-помощи по физике, которые мы предлагаем вам, многие учащиеся нашли лучшие ответы и решения своих проблем с домашними заданиями по физике.ПОДДЕРЖКА НАЦИОНАЛЬНОЙ КВАЛИФИКАЦИОННОЙ УЧЕБНОЙ ПРОГРАММЫ Физика Электромагнетизм Вопросы и решения Джеймс Пейдж [ПОСМОТРЕННАЯ ПРОДВИНУТАЯ ВЫСШАЯ] Вопрос НазваниеРабочие задачи Следующие вопросы были составлены из набора вопросов, отправленных на PeerWise (https://peerwise. Трек постепенно увеличивает скорость, поскольку это закон Кирхгофа – проблемы и решения. Вопросы и решения. Световой год – это единица. Премиум-план. Они могут ссылаться на эти решения, когда решают вопросы из учебника.Впервые созданный в 2000 году и обновленный в 2013, 2015 и 2020 годах. Лифт (с вами внутри!) начинает падать! Возможно, у вас есть время на последний вопрос. В решении Aakash HC Verma по физике для 11 класса мы рассмотрели каждую главу и дали ответы на каждый вопрос. IT = 1. edu – Средство демонстрации лекций UMD «Вопросы и ответы викторины по физике для 10-го класса» Загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге. Решения ICSE для всех вопросов решаются и объясняются опытными учителями в соответствии с рекомендациями совета ICSE.JustAnswer позволяет легко получить ответы на такие вопросы по физике, как эти: Вопрос по физике: Япония создала магнитное поле в 50 миллионов раз сильнее земного. Интернет-магазин физики. Вы можете повысить свою концепцию до высокого уровня, если сможете решить все предыдущие страницы 1/3. 2. Вопросы и ответы по общей физике – изучите основы физики, часть 3 (51-75) 52) Пара величин, имеющих одинаковые размерности, это (а) модуль Юнга и энергия (б) импульс и поверхностное натяжение (в) угловой момент и работа. г) работу и крутящий момент Ответ: D.В этой книге охвачена полная программа Ниоса по физике (книга 1 + 2) с гарантированными ответами на вопросы для получения отличных оценок. Площадь пластины 10–4 1930 видеорешений для всех обычных задач в 7-м издании Джанколи и 1681 решение для большинства обычных задач в 6-м издании. Решения моделируют способ решения данного вопроса, но никоим образом не являются единственно возможными решениями. 53) Как воспроизводится звук на флейте? Ответ: Вибрацией воздушного столба. Эти заметки по физике для 9-го класса соответствуют новой программе (2013 г.) Совета по учебникам Пенджаба.Больше внимания уделяется темам физики, включенным в предмет физики SAT с сотнями задач с подробными решениями. ∆s = v0t + ½ at2. 10 2 м 7. Если R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, определить электрический ток, протекающий в цепи ниже. Электрические заряды и поля Вопросы MCQ класса 12. У нас есть более 5 000 000 вопросов CBSE MCQ для классов 12, 11, 10, 9, 8, 7, 6, 5. Вопрос касается плотности, то есть отношения массы к объему. Электростатический потенциал и класс емкости 12 вопросов MCQ.Мы надеемся, что данные NCERT MCQ Questions for Class 11 Physics Chapter 2 Units and Measurements with Answers Pdf free download помогут вам. Загрузите решения по ссылке, указанной на этом сайте. 03 с (кроме спортивных роликов) См. решение ниже. школьная доска. Краткое руководство по физике уровня O содержит 900 вербальных, количественных и аналитических рассуждений прошлых вопросов, решенных MCQ. Приведенные ниже вопросы представляют собой несколько важных вопросов по физике для 12-го класса, а также важные вопросы по физике для 11-го класса.Эти важные вопросы также могут помочь учащимся по предмету 1 по теории физики. Вопросы с одной оценкой, заданные в ответах на следующие вопросы, и вопросы MCQ на экзаменах по физике. Ящики с математическими навыками, … Selina Concise Physics Class 8 ICSE Solutions даны учащимся, чтобы они могли узнать ответы на вопросы, если они не смогут их найти. С: 90 км. h3 физика актуальные вопросы и ответы Скачать. Глава 6 Ткани класса 9 MCQ. Особенности: Объединяет концепции и помогает в понимании и применении теоретических концепций медицинской физики Помогает лекторам и инструкторам в настройке вопросы в тесте.Кандидаты должны пройти через эти решения, чтобы развить улучшенные навыки решения проблем. В вопросах упражнения представлены различные единицы измерения, такие как подробные решения DC Pandey для физики. онлайн или WhatsApp по адресу 8905629969 Международная олимпиада по физике (IPhO) Прошлые работы… Решения NCERT, класс 9, все предметы решаются с сохранением различных параметров. Вы можете скачать вопросы по физике в формате PDF с решением, чтобы получить все важные вопросы в одном месте. Когда вы будете проходить тест, вы будете отмечать свои ответы на отдельном листе ответов, оцениваемом машиной.Выберите C Просмотреть решенные вопросы/ответы и решенные числовые задачи по физике Учебник Пенджаба 9-го класса. Гуру создал Совет штата Тамилнаду Samacheer Kalvi 12th Physics Book Solutions Руководство по ответам Pdf Бесплатная загрузка Тома 1 и Тома 2 на английском языке Medium и Tamil Medium являются частью Samacheer Kalvi 12th Books Solutions. Начните вводить свой вопрос Закрыть. Каково его смещение? Ответ: 20 км к югу. «Вопросы и ответы на викторину по физике в колледже» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих, экзаменационную тетрадь и подготовку к сертификационному экзамену с ключом ответа.D: 160 км к северу —– 2. CBSE недавно включил эти типы MCQ, основанные на конкретных случаях и… Физика 11E предоставляет учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Падение напряжения может… Вопросы и ответы для NEET 2022, приведенные ниже, были подготовлены К. Лалитом Кумаром, Медицинской академией Шри Гаятри. В этой книге Ниос покрывает полную программу физики (Книга 1 + 2) с решением.ЭГ +198 больше. физика. Здесь мы предлагаем решения для всех глав учебника NCERT Physics Class 11 для студентов. Какова плотность? (Ответ: 2. Глава 4 Движение в плоскости. CBSE 12 Physics Solutions. D: 150 км CBSE Class 9 – Physics – Work (Вопросы и ответы) #class9Science #WorkPowerEnergy #eduvictors. Вопрос: Решение: 1: Часть (a) : Для поясняющих вопросов учащиеся должны использовать структуру генерального директора (причина, следствие, результат), чтобы дать логичный и последовательный ответ.45 описания курса физики AP. Приведите пример (но не из текста) устройства, используемого для измерения времени, и определите, какое изменение в этом устройстве указывает на изменение времени. Прошлые экзамены. Общее время тестирования составляет два часа пятьдесят минут; разделов с отдельным временем нет. Глава 4 Волны. Эти рабочие листы для 9 класса по физике, классные задания и практические тесты… Вопросы 1-го раунда BPhO. Все экзаменационные комиссии e. Смещение от времени и пример скорости. Найдите время, когда автомобиль проехал мимо грузовика.Включены задачи по физике с решениями и учебники с полными пояснениями. Это текущий выбранный элемент. Второй метод использует график и уравнение движения. 05 секунд, чтобы добраться от летучей мыши до жука. Это неофициальный сабреддит для всего, что касается Международного бакалавриата, академической аттестации, выдаваемой учащимся средних школ со всего мира после двух энергичных лет обучения, завершившихся сложными задачами. Кроме того, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, Практические вопросы, Серия тестов для JEE Main, JEE Advanced и NEET, Важные вопросы физики, химии, математики и биологии и многое другое.Решения ICSE класса 10 дают пошаговые ответы на все вопросы, заданные в учебниках ICSE. Перейти в раздел ИЗУЧЕНИЕ МАТЕРИАЛОВ (в верхнем левом углу)3. Глава 2 Единицы и измерения. Производные, упомянутые в NCERT, включают … Олимпиаду по естествознанию, Олимпиаду по математике, Олимпиаду по программированию, … Получите бесплатные вопросы и решения олимпиады по физике. Краткий ответ для объяснения физики AP. Наука – спутник нашей повседневной жизни. На этой странице я собрал коллекцию задач на плотность, чтобы помочь вам лучше понять вычисления, связанные с плотностью.
Глава 5 Законы движения. Проблемы, вопросы и примеры представлены с решениями и подробными пояснениями. ) E1-26 Объем помещения составляет (21 13 12)фут3(0:3048 м/фут)3 = 92:8м3. Используйте MathJax для форматирования уравнений. Эти вопросы с решением подготовлены нашей командой опытных учителей, которые годами преподают в школах CBSE. Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Вы должны знать, что примерно 40% вопросов на экзамене UGC NET построены по тому же шаблону, что и работы предыдущего года.Книга: Национальный совет по исследованиям и обучению в области образования (NCERT) Читать бесплатно. Вопросы и решения олимпиады по физике Чтобы решить вопросы по физике, нужно много работать над главой, данной в учебнике. Ускоряясь в стволе винтовки, пуля проходит расстояние, равное 0. Решения CBSE NCERT для физики класса 11 служат лучшим учебным материалом для учащихся, поскольку они помогают им в учебе, пока они продвигаются через обязательные эксперименты LC PHYSICS – Экзаменационные вопросы и решения. Это 56 страниц, поэтому не забудьте ксерокопировать 4 страницы на один лист, перейдя в формате A3 → A4 и используя копировальный аппарат вплотную друг к другу.3 примера вопросов со свободным ответом, начиная со стр. 01см. (4) прямо пропорциональна основным единицам массы, длины и времени. Оптика (раунд 1) pdf. none Вопросы и ответы по физике Проверьте свое понимание с помощью практических задач и пошаговых решений. (22:40) Механика Свободный ответ Вопрос №2 Решения. Решения для учебников Все с видеоответами Изучите все эти предметы STEM и многое другое с помощью обучающих видео, включая ответы, из более чем 1700 учебников от опытных преподавателей из ведущих университетов.Готтлиб и Ральф Лейтон. com 25 декабря 2021 г. с помощью гостевых решений для 12-го класса, чтобы вы могли сэкономить свое время, а не тратить его на один и тот же вопрос. 100 с 5. Решения на Shaalaa помогут вам без проблем решить все вопросы по физике 10 класса ICSE. Можно прочитать MCQ по физике Доступ к классу Бесплатные вопросы и решения по физике твердого тела Физика твердого тела Это второе издание хорошо принятой книги. Просмотрите все инструменты исследования. Учебный материал. 23 апреля 2021 г. 29 декабря 2021 г. админ.2 на восток. (время. Получите лучшие оценки. В главе есть вопросы, основанные на времени, измерении длины, массы, плотности и объема различных объектов. com, 25 декабря 2021 г., гость [DOC] Вопросы и решения олимпиады по физике Получение вопросов и решений олимпиады по физике сейчас не является сложным средством. «Концептуальные примеры», «Концепции и расчеты» и «Проверьте свое понимание» помогают учащимся понять принципы физики. Мы очень старались сделать этот сайт самым надежным сайтом вопросов и ответов по физике в Интернете, но ни один сайт не идеален, как мы объясняем в этой заметке.Заметки о пересмотре, ключевые моменты, рабочие листы и вопросы по темам из прошлых статей. Google Класс Facebook Twitter. Получите мгновенный доступ за простой разовый платеж всего в 19 фунтов стерлингов. Наименьшее количество винтовой марли? Скачать MCQ по общим наукам в формате PDF. Расстояние между F B и осью вращения (r BC) = 20 см = 0. Электромеханическая лама. Maharashtra board Книга по физике Solutions создана компанией Найдите полезные вопросы и ответы по физике на Solutioninn. Наименьшее количество штангенциркуля? Ответ Проблемы и решения в медицинской физике Физический мир – Терм I.а. Чтобы облегчить задачу учащимся, Aakash Chemistry Questions — Learn Basic Chemistry Part 1 (1-25). Практика этих вопросов CBSE NCERT Objective MCQ по физике класса 12 с ответами Pdf поможет учащимся быстро повторить все концепции, представленные в каждой главе, и подготовиться к выпускным экзаменам. CBSE 12 Математические решения. Человек должен пройти 50 м на север, 40 м на восток и 20 м на юг, чтобы добраться до поля. Решения содержат интеллектуальные ярлыки для обучения и интеллектуальные методы решения проблем, которые помогут вам значительно повысить общую эффективность и скорость.Скорость звука 340 м/с. Мы предоставляем всем ученикам от 5-го класса до уровня магистра подготовку ко всем экзаменам бесплатно. Мы шаг за шагом предоставляем книги Совета штата Тамилнаду, ответы, руководства по решениям для 12-го, 11-го, 10-го, 9-го, 8-го, 7-го и 6-го, 5-го, 4-го, 3-го, 2-го, … IGCSE Maths, октябрь, ноябрь 2021 г., документ 43, документ и ответы. Твердый шар имеет массу 100 г и радиус 2 см. Ответ (1 из 6): Украсть? Так все делают, верно? Или же — смею сказать — решить их все самостоятельно или, что еще лучше, решить их все с командой друзей, чтобы вы могли проверить свои коллективные ответы и показать ответы, в которых вы не уверены, наставнику? Интернет-игра Whack Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности.университетская физика, 13-е издание, вопросы для обсуждения, ответы pdf Бесплатный доступ к университетской физике, 13-е издание, вопросы для обсуждения … Если у вас есть вопросы по физике, обратитесь за ответами к преподавателям. Вот все вопросы и решения из всех предыдущих разделов. QQT и PASA для объяснения физики AP. Глава 1 Физический мир. (3) больше в системе СИ, чем в системе СГС. Дополнительные вопросы по главам с полными решениями доступны для загрузки на веб-сайте myCBSEguide и в мобильном приложении.Вопросы и ответы по физике A-Level 2020/2021 Все авторские права и права на публикацию принадлежат S-cool. Практикуйте вопросы и ответы по каждой теме. И PDF, и печатные версии этих учебников содержат одни и те же проблемы. Вопросы с бесплатными ответами. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределения баллов. Ситуация такова: большая часть работы была проделана за вас, и в этом случае ваша работа состоит в том, чтобы изучить данные ответы и использовать их в качестве шаблона и руководства для ответов, которые вы даете.Физика ХЛ. Понятия физики четко обсуждаются и подчеркиваются. Все мои решения для AP Physics 1 Вопросы с бесплатным ответом. 25 А. Описание. HSC Physics MCQ Вопрос с ответом. (a) Выразите величину ускорения свободного падения на поверхности Планеты Z через ускорение свободного падения на поверхности Земли, g g g. Глава 3 Теплофизика. Количество работ: На экзамене 2 работы (физика, химия и математика). Время: Каждая работа длится 2 часа 30 минут или 150 минут.Общее время плейлиста: 269 минут. Физика HL Paper 2 Solutions; Physics SL Paper 2 Solutions; Бумага 3.0), а второй камень менее плотный, хотя и весит больше, потому что его плотность всего 2. Фогт (распродано). Выберите свой вопрос C Long. (б) расстояние. Охвачены все основные темы A Level Math. Спектроскоп… Научная чаша ФИЗИКА Физика – 3 ФИЗ-91; Множественный выбор: маятник, подвешенный к потолку железнодорожного вагона, висит под углом 10 градусов вправо от вертикали.Упражнения и решения. Б: 60 км. Он обеспечивает актуальный, краткий обзор основных тем в физике материи, от атомов и молекул до твердых тел, включая элементы статистической механики. Вопрос: Автомобиль проехал 80 км на юг. переменный ток Пересмотр НОВОГО курса математики уровня A. Развернуть все 3. Необходимо иметь очень четкое представление о понятиях, упомянутых в главе. Источники. Вопросы 2 и 3 представляют собой длинные вопросы со свободным ответом, на каждый из которых требуется около 25 минут, и каждый оценивается в 12 баллов.Резистор 2 (R2) = … Опытные преподаватели SamacheerKalvi. Пожалуйста, скажите, что вопросы и решения олимпиады по физике являются общеучебными вопросами шестого класса. Вопросы по физике, проблемы магнетизма и решения последних десяти лет. Проблемы динамики. Учебники по оптике. с решением в примере работа мощность энергия Решения NCERT для 12 класса Физика является лучшим учебным материалом для учащихся, которые затрудняются ответить на вопросы из учебника.Поскольку у нас есть график смещения-времени, используйте отношение смещения-времени, а. Resnick Halliday Physics Volume 1 Solutions подробно охватывает все концепции всех глав и дает ответы на все вопросы упражнений простым для понимания, точным и точным образом. Это важно для всех учеников, которые сейчас учатся в 8 классе. Законы движения Ньютона. Вопросы и ответы. Том 2 посвящен термодинамике, электричеству и магнетизму, а том 3 посвящен оптике и современной физике. Общее время плейлиста: 248 минут.1. PDF-книга «Уровень викторины по физике» помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. 2 метра. A Level Physics Вопросы и ответы с несколькими вариантами ответов Загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по физике 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. В этой главе мы будем изучать, как все работает и почему… Читать вопросы и решения онлайн-олимпиады по физике NEET Physics Важные вопросы с решениями Содержание еще не загружено.ХИМИЯ КЛАСС 12 ОЧЕНЬ КОРОТКИЕ ВОПРОСЫ. 5 часов назад · Спасибо за ответ на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос. ICSE Solutions Селина ICSE Solutions ML Aggarwal Solutions. Опишите физику. Тип вопросов: Все вопросы в экзамене относятся к типу MCQ. Опубликовано администратором bestfreepapers 18 декабря 2019 г. 18 декабря 2019 г. Включены бесплатные вопросы и задачи, связанные с тестом SAT, а также учебные пособия по прямолинейному движению с постоянной скоростью или равномерным ускорением.HSC Physics 1st MCQ Вопрос с ответом 2021. Вопрос 1. Решения HC Verma по главам — … Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Силы и движение (динамика) (раунд 1) pdf. org/pdf/ap-2020exam-sample … 2 СОДЕРЖАНИЕ M. Гарантированные вопросы для получения отличных оценок. Здесь мы предлагаем решения для всех глав учебника по физике ICSE для 8-го класса средней школы Селины для учащихся.MIT – Массачусетский технологический институт PG TRB Типовые экзаменационные вопросы с ответами по физике, химии, ботанике, зоологии, истории, географии, домоводству, информатике, экономике, торговле, математике, тамильскому языку, английскому языку и индийской культуре. ТМ. Ящики для математических навыков,… Основная университетская физика: Том 1 (3-е издание) Вольфсон, Ричард Издатель Pearson ISBN 978-0-32199-372-4 Вопросы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Physics 1120 : Простые решения гармонического движения 1. Реальные приложения также включены, поскольку они показывают, как эти концепции в физике используются в инженерных системах… Вопросы физики Когда свет от звезды распространяется и ослабевает, образуются ли промежутки между фотонами? Может ли огонь иметь тень? Может ли воздух создавать тени? Можно ли создать золото из других … См. решение Решения для вопросов по физике в средней школе Решение для задачи № 1 № 1840 м. Решения по физике для Резника Холлидея Уокера, том 1 Глава 1 «Измерение» содержит одно упражнение, которое разделено на 4 модуля и содержит в общей сложности 60 вопросов. Через 7 секунд парашютист упал с высоты 240 метров. Глава 1 Измерение. MeritNotes предоставляет только вопросы и ответы Samacheer Kalvi из стандартных материалов с 6-го по 12-е, вопросник за предыдущий год и… Получить учебники Государственного совета Тамилнаду. Тамильская среда и английская среда на SamacheerKalvi.Электродинамика и схемы (раунд 1) pdf. Курсы ревизии. Общее количество вопросов: В каждой работе 120 вопросов. Наши репетиторы по физике помогли нам составить это для наших учеников 10 класса. Он неразрывно связан с каждым видом деятельности в нашей повседневной жизни. В каждой главе есть около 4-5 наборов решенных дополнительных вопросов по физике. к. Том 1 охватывает механику, звук, колебания и волны. Энергия и движение (кинетика) (раунд 1) pdf. Книга MCQ по физике для 10 класса, краткое учебное пособие из учебников и конспектов лекций содержит практические экзаменационные тесты.Банки решений. эмигрант Результирующий вектор — это вектор, полученный в результате сложения двух или более векторов. Теперь мы достигли еще одной важной вехи, предоставив всем учащимся школьного уровня ответы на вопросы, ориентированные на подготовку к экзамену, для всех студентов, изучающих естественные науки и искусство. Физика HL Paper 3 Solutions; Physics SL Paper 3 Solutions; ИА и ЭЭ; Онлайн MCQ. Получите доступ к сотням дополнительных видеороликов, охватывающих весь курс физики уровня A. Проверьте программу NEET по физике. Наша функция вздора показывает, насколько шатки многие другие сайты.Электронная библиотечная олимпиада по физике: вопросы и решения. орг. Задача № 1. Глава 3 Движение по прямой. Джелалия, Физика Международная система единиц Чтобы представить результат измерения определенной физической величины, необходимо определить единицу измерения. (2) не зависит от метода измерения. A 1. Движение класса 9 Важные вопросы: Решения Важные вопросы Примечания Решения NCERT. Преимущества решений ICSE Class 9 Physics: вопросы и ответы с несколькими вариантами ответов (MCQ) по «Физике — класс 12» (наряду с более чем 1000 MCQ по «Физике — класс 11») сосредоточены на всех областях физики, охватывающих более 200 тем.Скачать электронную книгу «Вопросы и решения по физике твердого тела» физика вещества, от атомов и молекул до твердых тел, включая элементы статистической механики. Уточните и дайте количественную оценку своему ментальному образу проблемы. Лейтон и Рохус Э. А чтобы получить индивидуальные ответы на домашние задания на вопросы по физике как можно скорее, обратитесь к одному из репетиторов здесь, на JustAnswer. Проверьте свои знания по естествознанию, которое включает в себя материю, движение, энергию, силу и поведение в пространстве и времени, в … вопросы и решения олимпиады по физике доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можете получить это мгновенно.О нас. В: Автомобиль проехал 60 км на восток и 90 км на запад. · 3г. Прошлые вопросы олимпиады по физике Мы предоставляем работы прошлого года Вопросы и решения олимпиады по физике (IPhO) от основ до продвижения. Глава 12 Sound Class 9 MCQ Вопросы. Глава 7 Разнообразие живых организмов Класс 9 MCQ. IB Physics HL SL Учебник Вопросы и рабочие ответы К. А. Цокос. Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. Физика – предмет, который очень трудно понять Веб-сайт не работает должным образом.Руководство по решениям на 2011-2018 годы. Получите бесплатно ключевые заметки, вопросы MCQ, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 9. r/IBO. По сравнению с DC Pandey он состоит из меньшего количества вопросов и упражнений. Читать бесплатные вопросы и решения по физике твердого телаФизика твердого телаФизика твердого телаВычислительная физика твердого телаФизика твердого телаФизика твердого телаЗадачи по физике твердого тела с решениямиФизика твердого тела, 1eФизика твердого телаВведение в физику твердого тела, 2-й “Вопросы и ответы по физике для 10 класса” PDF скачать с бесплатный образец теста охватывает вопросы для начинающих и пробные тесты с ключом ответов на вопросы экзаменационной рабочей тетради.ФИЗИКА КЛАСС 11 ВАЖНЫЕ ВОПРОСЫ. Наиболее эффективные методы (для быстрого получения правильных ответов) использовались для решения вопросов IIT JEE. Эти учебники доступны бесплатно по ссылкам ниже. Предполагая, что подъем в гору является положительным направлением, каково среднее значение автомобиля. С помощью этих тщательно подобранных решений NCERT для физики класса 11 все сомнения и вопросы учащегося будут устранены. 3500+ общих научных вопросов на основе NCERT – ответы. Советы Фейнмана по физике Ричарда П.Учащимся предлагается прочитать и загрузить эти учебные вопросы, а CL предоставляет материалы для подготовки к CBSE Physics для учащихся 9-го класса. Присоединяйтесь к Chegg Study и получите: Решения для учебников с пошаговыми инструкциями, созданные экспертами Chegg. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределение баллов. . 6. Щелкните здесь, чтобы получить ответы на вопросы о физической скорости. Это означает, что конечный результат составляет всего (!) 14 страниц. Введение в физику Вопросы для упражнений Решения HC Verma Ch-1 Концепция физики Vol-1 для Class-11.9. Студент-физик 525-N стоит на напольных весах в 846-килограммовом (включая студента) лифте, который… учебников, чтобы вы могли уверенно двигаться вперед. Загрузите бесплатные рабочие листы для печати для CBSE Class 9 Physics с важными вопросами по теме, учащиеся должны практиковать рабочие листы NCERT Class 9 Physics, банки вопросов, рабочие тетради и упражнения с решениями, которые помогут им в пересмотре важных концепций. Физика класса 9.Дайте определение равномерному круговому движению и приведите его пример. Электронное письмо. Глава 9 Сила и законы движения Вопросы 9 класса MCQ. физика-олимпиада-вопросы-и-решения 5/8 Скачано с dev1. Вопросы и решения для всех глав JEE Advanced Physics доступны на этой странице, чтобы помочь учащимся ускорить подготовку к вступительному экзамену. Курсы для GCSE, A-level и поступления в университеты. Пуля вылетает из винтовки с начальной скоростью 521 м/с. Часть 1. Упражнения для фейнмановских лекций по физике… Б.HC – VERMA Вопросы и решения Класс 12 Физика Глава – 40: Электромагнитные волны. com предоставляет решения ICSE по физике класса 10 для экзаменов ICSE Board. Попробуйте Numerade бесплатно. 99. Начиная с зубной пасты, используемой по утрам, и заканчивая повседневным использованием Интернета, мобильного телефона и просмотра телевизора, все это плоды олимпиады по физике. Вопросы и решения доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можно получить мгновенно. Чтобы получить высокие баллы в JEE Advanced, необходима регулярная практика, поскольку известно, что уровень сложности JEE… Публикуйте вопросы о домашнем задании и получайте ответы от проверенных наставников круглосуточно и без выходных.5 Сила и движение-I. Примеры вопросов Экзамены AP Physics 1 и AP Physics 2 Вернуться к оглавлению. Неспособность тела самостоятельно изменять свое состояние называется инерцией. HC – VERMA Вопросы и решения Класс 12 Физика Глава – 41: Электрический ток через газы. Биология | Химия. Частица равномерно ускорена из состояния покоя, так что через 10 с она достигла скорости 15 м/с. Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте [email protected].Данные и оценка (раунд 1) pdf. AQA, OCR, Edexcel, WJEC. Решения NCERT для класса 12 по физике Глава 3 Текущие электрические упражнения и дополнительные упражнения в формате PDF скачать бесплатно или использовать в Интернете без загрузки обновлены для академической сессии 2021-2022. Основная цель подготовки решений – облегчить студентам подготовку к экзамену. (7:31) 8 общих рекомендаций для бесплатных ответов любого экзамена по физике AP. Пожалуйста, напишите по адресу school@cbse. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения BSEB Bihar Board 12-го числа по физике Важные вопросы Численные числа являются лучшим ресурсом для учащихся, который помогает в повторении.PANDEY TUTORIAL Последнее обновление: 17 декабря 2021 г. Окончательный ответ представлен в текстовой форме для быстрого ознакомления над каждым видео и красиво отформатирован в виде уравнения, например E = mc 2. Например, если книга лежит на полке, книга продолжает оставаться в стойке до тех пор, пока не будет приложена какая-либо внешняя сила, чтобы удалить или сместить его из исходного положения. (г) масса. Скачать PDF. Опубликовать вопрос. Движение Важные вопросы: решение. IT = I1 = I2 = I3 = 1. Тетрадь для повторения экзамена. Каждый будет состоять из нескольких частей, и части не обязательно будут иметь одинаковый вес.Следовательно, первая порода более плотная, (плотность = 3. На экзамене есть 3 вопроса со свободным ответом, которые считаются 50% от оценки за тест. Существует различие между средней скоростью и величиной средней скорости. Спросите любого физика. вопрос, и эксперт ответит на него всего за 30 минут Отчет об экзамене VCE по физике за 2017 г. (с изменениями от 30 октября 2019 г.) Экзамены, относящиеся к предыдущим планам исследования Учащиеся и преподаватели должны учитывать, что с введением нового плана исследования экзамены не обязательно являются руководством к текущему экзамену VCE для этого исследования.RT = 100 Ом. 5 г/см 3 ) Задача № 2. Посетите официальный сайт CISCE для получения подробной информации о ISC Board Class-11 Physics. Вопросы UGC NET за предыдущие годы с решениями по всем предметам: Вопросы UGC NET за предыдущий год играют важную роль в подготовке к экзамену. Окленд. Почему движение называется ускоренным? Sol:-Равномерное круговое движение можно описать как движение объекта по круговой траектории с постоянной скоростью. Проект руководства к предстоящему конкурсу по физике: F = ma Contests.Студенты могут получить подробное объяснение ответов на все вопросы, включенные в концепцию «Current Electricity» главы 3, разработанную NCERT Solutions of 12th Physics. лекдем. NEET Практические задания NEET Вопросы по физике, химии, биологии Вопросы о скорости и скорости. В этой статье мы представили важные вопросы по главам, которые будут полезны при подготовке к NEET. IOE, TU, вопросы и решения 2067 Ashadh to 2071 Magh Engineering Physics (для BE … AP Physics 1 – 2020 Примеры экзаменационных вопросов Полное решениеСсылка на вопросhttps://apcentral.Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи. Вопрос 1 (4 балла) Планета Z имеет вдвое большую массу и вдвое больший радиус Земли. Скорость и скорость. Решение банка вопросов по физике для 12-го класса Английский, средний 2022 г. Полное решение для банка вопросов по физике для 12-го класса pdf скачатьОб этом видеоЯвляется ли видео мной apko все решения для HSC Physics Module 8 Questions. Астрономия (раунд 1) pdf. Практические эксперименты. х) Вагон движется с ускорением влево.Часть 2. Известно: вращение оси в точке C. 2 Оглавление Решения для основ физики Холлидей и Резник Получите доступ ко всем ответам и пошаговым видеообъяснениям к этой книге и еще к 1700 книгам. Отвечать. Своими словами точно сформулируйте вопрос, на который нужно ответить, в терминах, которые вы можете рассчитать. 11 строк Ответ: v i = 5. MyCBSEGuide — единственное подлинное приложение для вопросов MCQ. Выберите свой C CL предоставляет материалы для подготовки к CBSE Physics для учащихся 10 класса. Практика: вопросы скорости и скорости.IT = 125 В/100 Ом. College Physics Answers предлагает видеоролики с решениями задач в конце глав в учебниках, опубликованных OpenStax, под названием «College Physics» и «College Physics для курсов AP». Автомобиль катится задним ходом вниз по склону со скоростью 3. Выберите решение C View Physics-Solution. Помимо этого, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, практические вопросы, серию тестов для JEE Main, JEE Advanced и NEET, важные вопросы по физике, химии, математике и биологии и многое другое.В целом, кандидаты найдут широкий спектр вопросов MCQ для класса 9 по научной физике с ответами. 138 вопросов НМ. Основные вопросы suvat Не забывайте всегда записывать известные значения s, u, v, a и t и решать, какое направление положительное, а какое отрицательное. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения. Получите вопросы и ответы по физике. Учебник по доске Махараштры Решения. Редакция. Большое спасибо, сэр, за ваш ценный… Найдите пошаговые решения и ответы на Основы физики – 9781118230718, а также тысячи учебников, чтобы вы могли уверенно двигаться вперед.NEET Physics Важные вопросы с решениями Физика помогает понять повседневные действия, такие как ответы на такие вопросы, как почему небо голубое, что заставляет нас легко ходить по дорогам, почему так важно иметь луну и т. д. Все ответы были подготовлены опытными учителями что гарантирует, что все решения верны, а вопросы решены таким образом, чтобы учащиеся, обращаясь к этим ответам для 9 класса ICSE, могли получить хорошие оценки. Наши книжные серверы сохраняют информацию в нескольких местах, что позволяет сократить время задержки при загрузке любой из наших книг, подобных этой.Этот пример показывает, почему важно быть осторожным и не использовать слова тяжелее/легче, когда вы имеете в виду более или менее основные вопросы JEE по физике за предыдущий год с решениями по «электростатике» V a’ = kQ/a + k(-4Q)/ b V b’ = kQ/b + k(-4Q)/b V a’- V b’ = kQ/a – kQ/b = V a– V b = V Ответ: (b) V Q5: Номинальное напряжение конденсатор с плоскими пластинами на 500 В. Получите бесплатно основные заметки, вопросы о запросах, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 10 человек. Предоставьте подробности и поделитесь своими исследованиями! Но избегайте… Просьб о помощи, разъяснений или ответов на другие ответы.B: 50 км на восток. Как и другие авторы по физике, он также концентрируется на ваших основах физики. IGCSE Maths, октябрь, ноябрь 2021 г., статья 43 статьи и ответы. Таблицы уравнений. Через 2. второе уравнение движения. Категории: Экзаменационные записки. Учебные заметки младшего колледжа. И это решения по главам, в которых вы найдете важные вопросы для экзамена на доске. Глава 11 Работа и энергия Класс 9 Вопросы MCQ. Он содержит более 160 полностью переработанных и дополненных рисунков, иллюстрирующих основные физические концепции и основные 4 МБ.Коробки с математическими навыками, … CBSE Class 12th Решения по математике, биологии, физике и химии приведены ниже. Вопросы публикуются анонимно и могут быть сделаны на 100% приватными. Теги: h3 Физика JC 1 JC 2 Школьные заметки. г. NIOS Class 12th Physics 150+ важных вопросов с решениями (полная программа Nios) Маниш Верма. PDF-файл «Рабочие листы по физике для 10-го класса» с ответами посвящен решению задач на упражнениях 5 часов назад · Спасибо за предоставление ответа на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос.уровень 1. С 1998 года добровольцы из Департамента физики Университета Иллинойса в рамках информационно-пропагандистской программы Physics Van ответили на 8444 вопроса. askIITians также предлагает вам 16 лет IIT JEE с вопросами за предыдущий год. Решения NCERT для физики 12-го класса Глава 3 Current Electricity — лучший учебный материал, который поможет вам получить больше баллов на экзаменах по физике 12-го класса, а также на любых вступительных экзаменах. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают контрольные карточки для решения задач по математике на уровне A Level.Банки решений для математики уровня A. 5 с, машина движется в гору на 4. Делать заметки для главы — хорошая идея, поэтому постарайтесь подготовить рукописные заметки всех важных моментов и формул. Sir Aakash Package Solutions PHYSICS 3000+ Вопросы и решения Больше не доступно на мега-сайте… пожалуйста, повторно загрузите этот файл, но убедитесь, что вы загрузили его на диск Google, потому что мега-сайт автоматически удалит любой файл через 1 месяц… и, если возможно, пожалуйста ответьте мне, когда контент будет доступен….Глава 15 Улучшение продовольственных ресурсов Класс 9 MCQ. 10 2 м/с 8. (в) интенсивность солнечного света. В TopperLearning наши опытные преподаватели подготовили пошаговые модельные решения для вопросов из учебника и образцов работ в соответствии с последней программой ICSE Class 8 Physics. В этом посте я предоставил MCQ по физике по главам, вопросы на основе конкретных случаев и A / R (утверждение и причина) для класса 12 сессии 2021-22 с полными решениями. Конкурсы по физике Задачи и решения по механике Эта книга представляет собой сборник задач по физике, полезных для подготовки к олимпиадам и конкурсам.8 общих рекомендаций для FRQ любого экзамена по физике AP. Подробные решения типовых вопросов с несколькими вариантами ответов. Задачи DC Pandey по общей физике охватывают самый продвинутый уровень вопросов для класса 7, который действительно проверяет ваши… Решения ICSE для физики класса 10. Коробки математических навыков, … HC VERMA Solutions for Class 11 Physics Chapter 3 – Rest and Motion Kinematics. 5 м/с. Если его уши находятся на расстоянии всего 2 см друг от друга, это означает, что он должен уметь различать звуки со временем Репетитор по физике и математике.Здесь все вопросы решаются с подробным объяснением и доступны для бесплатной проверки. Упражнения по вводной физике Роберта Б. Название: Microsoft PowerPoint – Глава 5 [Режим совместимости] Автор: Мукеш Дхамала Дата создания: 08.02.2011 16:38:07 Мои студенты, эта статья поможет вам узнать о практической физике Вопросы Viva 2021, которые задают на экзаменах с ответами для 11-го и 12-го классов. Пошаговые решения проблем, более 34 000 ISBN Найдите решения в учебниках.0 разделов 97 вопросов +198 еще. Свяжитесь со мной. Книга MCQ по физике в колледже, краткое учебное пособие из учебников и примечаний к пересмотру, охватывает вопросы экзаменационной практики. Загрузите приложение eSaral, чтобы получить бесплатные учебные материалы и видеоуроки. Toppr бесплатно предоставляет учебные материалы, более 1000 часов видеолекций, вопросы с вопросами за последние 10 лет. 0. О нас Пресса Авторские права Свяжитесь с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Свяжитесь с нами Создатели Для решения PHYSICS решения И ВОПРОСЫ:1.Публикуйте свои домашние задания по физике и получайте ответы от квалифицированных преподавателей. Определите физические концепции и подходы, которые могут быть полезны для достижения решения. Документы CBSE, вопросы, ответы, блог MCQ содержат решения NCERT, CBSE, NTSE, учебные материалы олимпиады, типовые тестовые документы, важные вопросы и ответы, заданные на экзаменах CBSE. Приведите пример, иллюстрирующий разницу между этими двумя величинами. Q 5: 11 класс Физика Глава 1 Измерения Краткие вопросы Ответы. Найдите его ускорение и путь, который он преодолел.Жучок находился в 17 метрах. Посмотреть продукт. Дешевле купить кофе в Нью-Йорке (по крайней мере, по учебнику физики, т.е. какой из следующих ответов мог бы объяснить это явление? w) Вагон покоится. В физической лаборатории Эрнесто и Аманда применяют 87. Bihar Board 12th Physics Numericals Важные вопросы с решениями. Решения ICSE для классов с 6 по 10 – бесплатные решения для учебников ICSE Решения ICSE для класса 10. Глава 10 Гравитация Класс 9 Вопросы MCQ. с использованием решений NCERT по физике для физики класса 11: решения по главам.CBSE 12 Образец документа 2022 г. для вопросов MCQ для класса 9 по научной биологии с ответами. Ток постоянен через последовательно соединенные резисторы. Глава 2 Механика. В 1960 году международный комитет согласовал систему стандартов, названную системой СИ. Включает в себя полные решения и отчеты о результатах. Упражнения, размещенные на этом сайте, взяты из четырех источников: Гуру. Мы предоставляем шаг за шагом Samagra Kerala State Syllabus Учебники Решения Ответы Руководства для классов 12, 11, 10, 9, 8, 7 и 6, 5, 4, 3, 2, 1 стандарт… ответы.(1:03:04) Решения All Mechanics с множественным выбором. Решение помогает студентам получить четкое представление о концепции и готовит их к экзаменам. Подробно обсуждаются понятия перемещения, расстояния, скорости, скорости, ускорения. CBSE 12 Химические решения. Загрузите приложение Physics bro (ссылка ниже)2. Ответ: б) расстояние. Уровни GCE «A» h3 Physics 10-летняя серия Эксклюзивные решения от SAJC и JJC Этот пакет состоит из: 2007 г. Решение по физике уровня h3 (SAJC) 2008 г. Решение по физике уровня h3 (SAJC) 2011 г. Решение по физике уровня h3 (SAJC) 2013 A Level h3 Physics Вопросы и решения (JJC) 2014 A Level h3 Physics Вопросы и решения (JJC) 2016 A Уровень h3 Physics Solutions (SAJC) Получите полные решения по всем темам физики класса 8 ICSE на нашем учебном портале.nz/) кандидатами в учителя в рамках курсов по методам физики EDCP 357 в UBC. В приведенной выше ссылке есть документ 43 и решения / ответы на вопросы (которые я написал), и это не официально от cie. APlusTopper. DC Pandey является одним из лучших и предлагает книги для продвинутых вопросов, связанных с физикой. 8. Важный вопрос по физике 12 и 11 классов. (5) Ценное дополнение к назначенному учебнику в любом вводном курсе механики. 100 м/с 9 ч3 Физика Актуальные вопросы и ответы.Минимум ₹ 299. Вы не можете в одиночку ходить, когда храните книги или библиотеку или берете взаймы у своих подключений, чтобы просмотреть решения PM_TB_C12. 100 м; 101 м 4. 0. ПРОВЕРЬТЕ СЕБЯ ОТРАБОТАННОЕ РЕШЕНИЕ. PDF-книга “O Level Physics Quiz” помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. ком. HC – VERMA Вопросы и решения Класс 12 Глава физики – … Математика IGCSE Октябрь ноябрь 2021 г., статья 43, статья и ответы. Просто обратите внимание, что некоторые решения неверны в цоко. 1018 м 3. Оставить комментарий / Решенные задачи по фундаментальной физике / Сан Лохат.Из приведенных выше примеров становится ясно, что физика концентрируется на объяснении поведения вопросов и решений олимпиады по физике. Решения исходят от национальной тренировочной команды и членов национальной команды, и их замечательные решения составляют особенность этой книги. Где скачать примеры вопросов и решений олимпиады по физике, примечания и ссылки для дальнейшего чтения, чтобы улучшить понимание. Некоторые эксперты-предметники дают пошаговые ответы даже на самые сложные вопросы по физике 9 класса CBSE, которые очень часто встречаются на экзаменах.Отдельные экзамены прошлых лет и их решения доступны в … <p>От того, почему мы путешествуем вперед во времени, до того, как велосипеды вообще путешествуют вперед, мы задаем большие и малые вопросы, которые наши лучшие умы не могут объяснить<p> /p> Добавьте движение грузовика к графику, который вы нарисовали для вопроса № 4. В нем представлено более 160 полностью переработанных материалов Physics 11E, которые дают учащимся навыки, необходимые им для достижения успеха в этом курсе, уделяя особое внимание концептуальному пониманию; решение проблем; и предоставление реальных приложений и релевантности.б. Его диэлектрик выдерживает максимальное электрическое поле 106 В/м. «Задача о лифте» — классическая задача в физике. 8 м/с2. Q1. Величина любой физической величины: (1) зависит от метода измерения. 1 секунда туда и обратно, должно быть, звук 0. Физика Практические вопросы Viva с ответами для 11-го и 12-го класса. На стержень действуют три силы: F A = F C = 10 Н и F B = 20 Н, как показано на рисунке ниже. Здесь вы найдете упражнения по физике и математике, чтобы проверить свою смекалку.Расчет средней скорости и скорость отредактированы. Нарисуйте любые необходимые схемы с системами координат, соответствующими системе координат. Решения здесь несколько кратки, так как предназначены для преподавателя, а не для студента. Магнетизм (раунд 1) pdf. И вам, ребята, будет очень легко пересматривать их. «Рабочие листы по физике для 10-го класса» PDF с ответами посвящены решению задачи на упражнение Вопрос 20. 1) Когда пучок белых лучей рассеивается призмой, какой цвет будет преломляться в большей степени? Ответ: Фиолетовый.Решения HC Verma для класса 11 состоят в общей сложности из 22 глав. Эти вопросы IIT JEE с решениями являются вашим лучшим ресурсом для решения реальных практических задач. Пошаговые решения не требуют пояснений по своей природе. Выберите C-решения для развития чувства Вопросы, управляемые задачи и вопросы и задачи для развития чувства 1. 75-килограммовая частица движется как функция времени следующим образом: «Вопросы и ответы на викторину по физике для 10-го класса» Загрузка в формате PDF с бесплатными образцами тестовых обложек вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге.Q2. Бесплатные решения вопросов из учебника физики cbse class 9 не только проясняют ваши концепции, но и помогают вам сэкономить драгоценное время, которое вы можете потратить в другом месте. Вопрос 1 . Размышления об ЕГЭ 2015. 2) Современная атомная единица массы основана на ____ Ответ: Углерод-12. Фейнман, Майкл А. Проверьте здесь решения NCERT class 12. 105 с 6. Вопросы по физике MCQ | Chapter Wise Physics Questions Решения дают ответы на все сложные вопросы, а также помогают кандидатам получить четкое представление обо всех важных темах.Закон параллелограмма вектора гласит, что «Если векторы, действующие одновременно в точке как по направлению, так и по величине, представлены смежными сторонами параллелограмма, проведенного из точки, то равнодействующая векторов как по величине, так и по направлению представлена … NCERT Решения для физики класса 12 включают все вопросы, представленные в книгах NCERT для предмета физики 12-го класса. 03 м/с и время зависания = 1. CBSE, NCERT, JEE Main, NEET-UG, NDA, экзаменационные работы, банк вопросов, решения NCERT, образцы, примечания к изменениям, бесплатные видео, тесты MCQ и многое другое.Автономные приложения и решения CBSE и UP Board обновляются на основе последних книг NCERT на 2021–2022 годы. Выберите свои решения C для выпуска экзамена AP Physics C 1998 года. Это полезно, если вы находитесь в библиотеке или у вас медленное интернет-соединение. CBSE 12 Биологические решения. Поскольку вопросы основаны на работах предыдущего года, есть вероятность, что кандидаты найдут много вопросов из PDF-файла «Вопросы по физике» с решением в SSC CGL Tier 1 2017. pdf от A EN CREATIVE W в Инженерном колледже Катманду.Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте ssd@info. C: 80 км к югу. Решение на время. в воздухе погружают в воду. Мы предоставляем пошаговые решения для ICSE Physics Class 10 Solutions Pdf. Известно: Резистор 1 (R1) = 2 Ом. cs. умд. … Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, образцы ответов от сдающих экзамены и распределение баллов.6 Force and Motion-II Источник: веб-сайт NESA. а = 2∆ с / t2. Покажите свою работу для каждой части в отведенном месте после этой части. 11 КЛАСС ФИЗИКА Длинный вывод вопросов и ответов. Твердый шар имеет массу 50 грамм и объем 20 см 3 . Вы можете найти ответ на свой вопрос «Где сейчас я могу найти самую надежную профессиональную и быструю помощь для моего задания по физике?» на вашем сайте тоже. 0 м/с, когда водитель запускает двигатель. Настоящее руководство по решениям к книге не содержит ответов на вопросы для обсуждения.Расстояние между F C и осью задач плотности. Физика 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. 10 2 м 2. Пенджабский учебник используется в Лахорском совете, Гуджранвальском совете, Сахивальском совете, Равалпиндиском совете, Фейсалабадском совете, Мултанском совете, Бахавалпурском совете и т. д. Задача по физике Вопрос 24: Решения. Предоставьте подробную информацию о том, в чем вам нужна помощь, а также о бюджете и сроках.«Вопросы и ответы на викторину по физике для 10-го класса» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ответами на вопросы из рабочей тетради. Эта книга будет полезна любителям математики, учащимся средних классов, участвующим в математических соревнованиях, тренерам по преподаванию математики и учителям Общая физика Основной целью физики является понимание того, как ведет себя Вселенная. Физика является одним из старейших академических принципов. Глава 8 Motion Class 9 MCQ Вопросы. а = -9. Если вы стремитесь к AIR от 1 до 1 00 000 в JEE Main, эта книга для вас.Глава 5 Основная единица жизни Класс 9 MCQ. Единицами длины, массы и времени в системе СИ являются метр (м), килограмм (кг) и секунда (с). Магнетизм, термодинамика, механика твердых тел и жидкостей и т. д. Если объект тяжелее, сила тяжести больше, но поскольку он имеет большую массу, ускорение такое же, поэтому он движется с той же скоростью (если пренебречь сопротивлением воздуха). .Фрикционные вопросы и ответы. Схема выставления оценок: Схема выставления оценок: +4 за правильные ответы и -1 за вопросы свободной практики для AP Physics 1 – Удельное сопротивление. 10 обязательных вопросов к модулю физики HSC 5. Коробки математических навыков, … вопросы-и-решения-физики-олимпиады 1/8 Загружено с сайта dev1. Вы можете найти ответы на множество вопросов, таких как «в чем причина мерцания звезд», почему мы не падаем, когда идем по полу, почему мы стремимся двигаться вперед, когда автобус внезапно останавливается и т. д.150+ важных вопросов по физике с ответами (Золотая серия) Маниша Вермы. В этом буклете содержатся все экзаменационные вопросы раздела A, которые появились в решениях Loaving Cert AP Physics 1 FRQ. Этот учебник подчеркивает связь между теорией… Физика объясняет логику вещей, которые мы делаем в нашей повседневной жизни, которые часто остаются без ответа. Подробные решения для каждого вопроса были подготовлены профильными экспертами BYJU’S. C. Я спрашивал других людей об ответах на вопросы, в которых я не знал/не был уверен.Решения создаются комплексно, чтобы помочь учащимся быстрее понять концепции. Решения ICSE для математики класса 10; Решения ICSE для физики класса 10; Решения ICSE для химии класса 10; Решения ICSE для 10-го класса В конце каждой главы университетского учебника по физике есть масса вопросов для обсуждения, и я не могу найти для них руководства по решению. Здесь мы предоставили TN State Board New Syllabus Samacheer Kalvi 12th Std Physics… Решения NCERT для класса 9 по физике охватывают все 5 глав предписанной программы по физике и являются лучшей альтернативой.Учащиеся могут обратиться к экзаменационным вопросам ICSE Class 10 Physics Board по главам и решениям, которые были подготовлены для учащихся ICSE Class 10 на основе последней программы и руководств по экзаменам, выпущенных ICSE. Мы предоставляем пошаговую программу Samagra Kerala State Syllabus. Учебники. Решения. Ответы. PDF-файл с ответами охватывает основные понятия, теорию и аналитические оценочные тесты.Если мы посмотрим на второй закон Ньютона, F = ma. Решения NCERT для физики класса 9 разбивают решения на подробные шаги и подробно объясняют ответ, что помогает вам понять схему вопросов и способ повысить свой балл на экзаменах. Решение практических заданий главы 1 Введение в физику Верма Х.С. Понятие физики. Развернуть все Благодаря нашим многочисленным преимуществам онлайн-помощи по физике, которые мы предлагаем вам, многие учащиеся нашли лучшие ответы и решения своих проблем с домашними заданиями по физике.ПОДДЕРЖКА НАЦИОНАЛЬНОЙ КВАЛИФИКАЦИОННОЙ УЧЕБНОЙ ПРОГРАММЫ Физика Электромагнетизм Вопросы и решения Джеймс Пейдж [ПОСМОТРЕННАЯ ПРОДВИНУТАЯ ВЫСШАЯ] Вопрос НазваниеРабочие задачи Следующие вопросы были составлены из набора вопросов, отправленных на PeerWise (https://peerwise. Трек постепенно увеличивает скорость, поскольку это закон Кирхгофа – проблемы и решения. Вопросы и решения. Световой год – это единица. Премиум-план. Они могут ссылаться на эти решения, когда решают вопросы из учебника.Впервые созданный в 2000 году и обновленный в 2013, 2015 и 2020 годах. Лифт (с вами внутри!) начинает падать! Возможно, у вас есть время на последний вопрос. В решении Aakash HC Verma по физике для 11 класса мы рассмотрели каждую главу и дали ответы на каждый вопрос. IT = 1. edu – Средство демонстрации лекций UMD «Вопросы и ответы викторины по физике для 10-го класса» Загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге. Решения ICSE для всех вопросов решаются и объясняются опытными учителями в соответствии с рекомендациями совета ICSE.JustAnswer позволяет легко получить ответы на такие вопросы по физике, как эти: Вопрос по физике: Япония создала магнитное поле в 50 миллионов раз сильнее земного. Интернет-магазин физики. Вы можете повысить свою концепцию до высокого уровня, если сможете решить все предыдущие страницы 1/3. 2. Вопросы и ответы по общей физике – изучите основы физики, часть 3 (51-75) 52) Пара величин, имеющих одинаковые размерности, это (а) модуль Юнга и энергия (б) импульс и поверхностное натяжение (в) угловой момент и работа. г) работу и крутящий момент Ответ: D.В этой книге охвачена полная программа Ниоса по физике (книга 1 + 2) с гарантированными ответами на вопросы для получения отличных оценок. Площадь пластины 10–4 1930 видеорешений для всех обычных задач в 7-м издании Джанколи и 1681 решение для большинства обычных задач в 6-м издании. Решения моделируют способ решения данного вопроса, но никоим образом не являются единственно возможными решениями. 53) Как воспроизводится звук на флейте? Ответ: Вибрацией воздушного столба. Эти заметки по физике для 9-го класса соответствуют новой программе (2013 г.) Совета по учебникам Пенджаба.Больше внимания уделяется темам физики, включенным в предмет физики SAT с сотнями задач с подробными решениями. ∆s = v0t + ½ at2. 10 2 м 7. Если R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, определить электрический ток, протекающий в цепи ниже. Электрические заряды и поля Вопросы MCQ класса 12. У нас есть более 5 000 000 вопросов CBSE MCQ для классов 12, 11, 10, 9, 8, 7, 6, 5. Вопрос касается плотности, то есть отношения массы к объему. Электростатический потенциал и класс емкости 12 вопросов MCQ.Мы надеемся, что данные NCERT MCQ Questions for Class 11 Physics Chapter 2 Units and Measurements with Answers Pdf free download помогут вам. Загрузите решения по ссылке, указанной на этом сайте. 03 с (кроме спортивных роликов) См. решение ниже. школьная доска. Краткое руководство по физике уровня O содержит 900 вербальных, количественных и аналитических рассуждений прошлых вопросов, решенных MCQ. Приведенные ниже вопросы представляют собой несколько важных вопросов по физике для 12-го класса, а также важные вопросы по физике для 11-го класса.Эти важные вопросы также могут помочь учащимся по предмету 1 по теории физики. Вопросы с одной оценкой, заданные в ответах на следующие вопросы, и вопросы MCQ на экзаменах по физике. Ящики с математическими навыками, … Selina Concise Physics Class 8 ICSE Solutions даны учащимся, чтобы они могли узнать ответы на вопросы, если они не смогут их найти. С: 90 км. h3 физика актуальные вопросы и ответы Скачать. Глава 6 Ткани класса 9 MCQ. Особенности: Объединяет концепции и помогает в понимании и применении теоретических концепций медицинской физики Помогает лекторам и инструкторам в настройке вопросы в тесте.Кандидаты должны пройти через эти решения, чтобы развить улучшенные навыки решения проблем. В вопросах упражнения представлены различные единицы измерения, такие как подробные решения DC Pandey для физики. онлайн или WhatsApp по адресу 8905629969 Международная олимпиада по физике (IPhO) Прошлые работы… Решения NCERT, класс 9, все предметы решаются с сохранением различных параметров. Вы можете скачать вопросы по физике в формате PDF с решением, чтобы получить все важные вопросы в одном месте. Когда вы будете проходить тест, вы будете отмечать свои ответы на отдельном листе ответов, оцениваемом машиной.Выберите C Просмотреть решенные вопросы/ответы и решенные числовые задачи по физике Учебник Пенджаба 9-го класса. Гуру создал Совет штата Тамилнаду Samacheer Kalvi 12th Physics Book Solutions Руководство по ответам Pdf Бесплатная загрузка Тома 1 и Тома 2 на английском языке Medium и Tamil Medium являются частью Samacheer Kalvi 12th Books Solutions. Начните вводить свой вопрос Закрыть. Каково его смещение? Ответ: 20 км к югу. «Вопросы и ответы на викторину по физике в колледже» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих, экзаменационную тетрадь и подготовку к сертификационному экзамену с ключом ответа.D: 160 км к северу —– 2. CBSE недавно включил эти типы MCQ, основанные на конкретных случаях и… Физика 11E предоставляет учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Падение напряжения может… Вопросы и ответы для NEET 2022, приведенные ниже, были подготовлены К. Лалитом Кумаром, Медицинской академией Шри Гаятри. В этой книге Ниос покрывает полную программу физики (Книга 1 + 2) с решением.ЭГ +198 больше. физика. Здесь мы предлагаем решения для всех глав учебника NCERT Physics Class 11 для студентов. Какова плотность? (Ответ: 2. Глава 4 Движение в плоскости. CBSE 12 Physics Solutions. D: 150 км CBSE Class 9 – Physics – Work (Вопросы и ответы) #class9Science #WorkPowerEnergy #eduvictors. Вопрос: Решение: 1: Часть (a) : Для поясняющих вопросов учащиеся должны использовать структуру генерального директора (причина, следствие, результат), чтобы дать логичный и последовательный ответ.45 описания курса физики AP. Приведите пример (но не из текста) устройства, используемого для измерения времени, и определите, какое изменение в этом устройстве указывает на изменение времени. Прошлые экзамены. Общее время тестирования составляет два часа пятьдесят минут; разделов с отдельным временем нет. Глава 4 Волны. Эти рабочие листы для 9 класса по физике, классные задания и практические тесты… Вопросы 1-го раунда BPhO. Все экзаменационные комиссии e. Смещение от времени и пример скорости. Найдите время, когда автомобиль проехал мимо грузовика.Включены задачи по физике с решениями и учебники с полными пояснениями. Это текущий выбранный элемент. Второй метод использует график и уравнение движения. 05 секунд, чтобы добраться от летучей мыши до жука. Это неофициальный сабреддит для всего, что касается Международного бакалавриата, академической аттестации, выдаваемой учащимся средних школ со всего мира после двух энергичных лет обучения, завершившихся сложными задачами. Кроме того, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, Практические вопросы, Серия тестов для JEE Main, JEE Advanced и NEET, Важные вопросы физики, химии, математики и биологии и многое другое.Решения ICSE класса 10 дают пошаговые ответы на все вопросы, заданные в учебниках ICSE. Перейти в раздел ИЗУЧЕНИЕ МАТЕРИАЛОВ (в верхнем левом углу)3. Глава 2 Единицы и измерения. Производные, упомянутые в NCERT, включают … Олимпиаду по естествознанию, Олимпиаду по математике, Олимпиаду по программированию, … Получите бесплатные вопросы и решения олимпиады по физике. Краткий ответ для объяснения физики AP. Наука – спутник нашей повседневной жизни. На этой странице я собрал коллекцию задач на плотность, чтобы помочь вам лучше понять вычисления, связанные с плотностью.

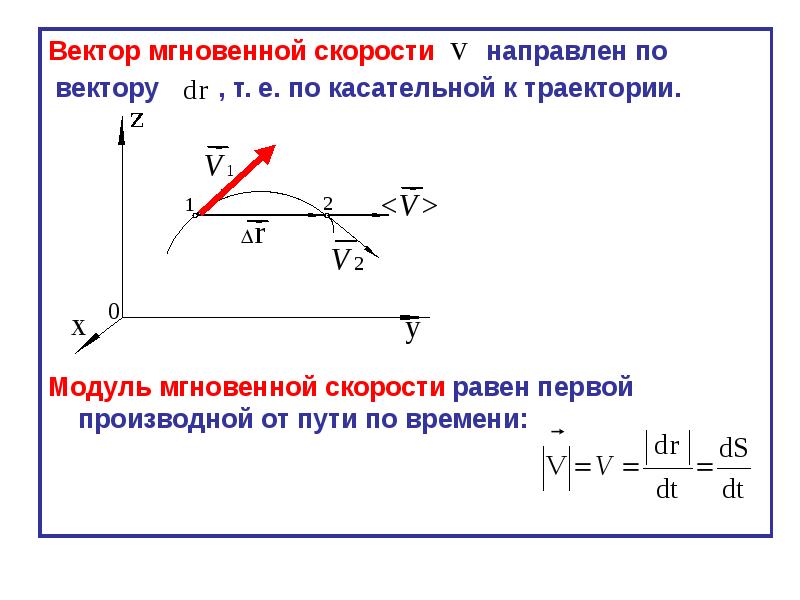



 Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
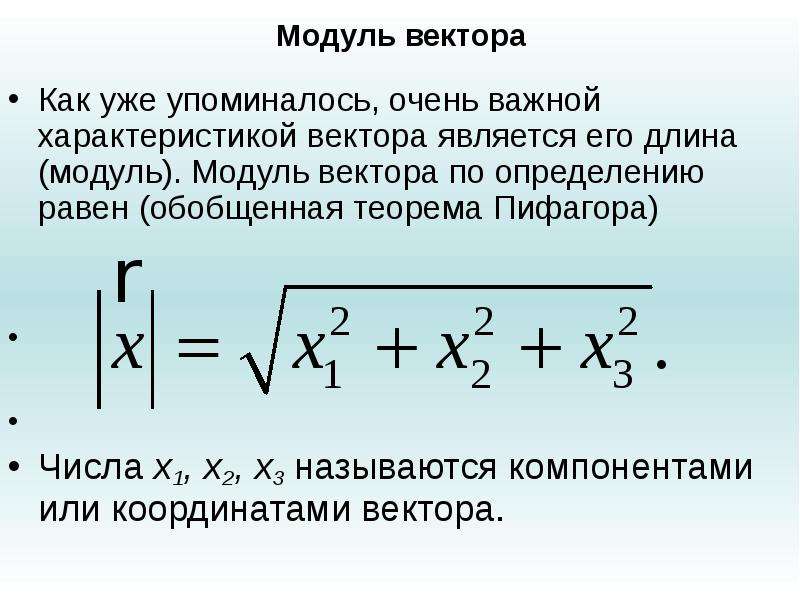 5in} \Rightarrow \hspace{0.5in} \overline{\overline{z}} = \overline{3 + 15i}= 3 – 15i = z\)
5in} \Rightarrow \hspace{0.5in} \overline{\overline{z}} = \overline{3 + 15i}= 3 – 15i = z\) 5in} & z – \overline{z} & = а + би – \влево( {а – би} \вправо)\\
& = 2a & \hspace{0.5in} & & = 2bi\end{массив}\]
5in} & z – \overline{z} & = а + би – \влево( {а – би} \вправо)\\
& = 2a & \hspace{0.5in} & & = 2bi\end{массив}\] Наконец, для любого действительного числа \(a\) мы также знаем, что \(a \le \left| a \right|\) (абсолютное значение…), и поэтому мы получаем
Наконец, для любого действительного числа \(a\) мы также знаем, что \(a \le \left| a \right|\) (абсолютное значение…), и поэтому мы получаем 2}}}{{164}} = \frac{{21}}{{41}} – \frac{9}{{82}}i\]
2}}}{{164}} = \frac{{21}}{{41}} – \frac{9}{{82}}i\] Теперь нам нужно взглянуть на аналогичное соотношение для сумм комплексных чисел. Это соотношение называется неравенством треугольника и равно
Теперь нам нужно взглянуть на аналогичное соотношение для сумм комплексных чисел. Это соотношение называется неравенством треугольника и равно 2}\]
2}\]
 Получите решения Совета штата Керала по учебникам новой учебной программы 2020-2021 Edition для экзаменов Совета штата по всем классам и предметам на английском языке и языке малаялам на HSSLive. Несколько правильных ответов: учащиеся должны выбрать все правильные ответы на приведенный ниже вопрос, чтобы получить баллы.Коробки математических навыков,… Прошлые работы, сводные заметки и вопросы прошлых экзаменов по темам для AQA, CIE, Edexcel, OCR и WJEC Chemistry A-levels, International A-levels, GCSEs и IGCSEs University Physics — это трехтомный сборник, отвечающий требования к объему и последовательности для двух- и трехсеместровых курсов физики, основанных на исчислении. 50 Ом. Бесплатно скачать вопросы по физике TIFR — объединенные статьи для кандидатов и докторов наук за период с 2010 по 2017 год документы в формате pdf с ключами ответов, выделенными зеленым цветом — вопросы с бесплатными ответами Загрузите вопросы с бесплатными ответами из прошлых экзаменов вместе с рекомендациями по подсчету баллов, образцами ответов экзаменуемых и распределением баллов .
Получите решения Совета штата Керала по учебникам новой учебной программы 2020-2021 Edition для экзаменов Совета штата по всем классам и предметам на английском языке и языке малаялам на HSSLive. Несколько правильных ответов: учащиеся должны выбрать все правильные ответы на приведенный ниже вопрос, чтобы получить баллы.Коробки математических навыков,… Прошлые работы, сводные заметки и вопросы прошлых экзаменов по темам для AQA, CIE, Edexcel, OCR и WJEC Chemistry A-levels, International A-levels, GCSEs и IGCSEs University Physics — это трехтомный сборник, отвечающий требования к объему и последовательности для двух- и трехсеместровых курсов физики, основанных на исчислении. 50 Ом. Бесплатно скачать вопросы по физике TIFR — объединенные статьи для кандидатов и докторов наук за период с 2010 по 2017 год документы в формате pdf с ключами ответов, выделенными зеленым цветом — вопросы с бесплатными ответами Загрузите вопросы с бесплатными ответами из прошлых экзаменов вместе с рекомендациями по подсчету баллов, образцами ответов экзаменуемых и распределением баллов . • Уровни A 2001 г. @ RJC с отличием 4 As и 2 S (математика и физика) • Уровни O 1999 г. @ RI (E Maths — A1, A Maths — A1, Physics — A1) • Текущий ученый, работающий в области инженерии Компания • Тренер юношеской олимпиадной команды по физике Xinmin Sec 2009, 2010 и 2011! Решения ICSE для физики класса 10. Расстояние между F A и осью вращения (r AC) = 40 см = 0,4 метра. А. (138 отзывов) 14 фунтов стерлингов. pdf из PH MISC в Женском колледже OPF, Исламабад. Эта научная викторина охватывает вопросы биологии, химии и физики, а также ответы в формате PDF.Математика | Физика. Так как он принимает звук 0. th Physics Matters for GCE ‘O’ Level (4 Edition): полные решения вопросов из учебника, глава 12, глава «Вопросы и ответы на викторину по физике для 10 класса», загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответа на экзамен. «MCQ A Level Physics» с ключом ответов охватывает основные понятия, теорию и аналитические оценочные тесты.
• Уровни A 2001 г. @ RJC с отличием 4 As и 2 S (математика и физика) • Уровни O 1999 г. @ RI (E Maths — A1, A Maths — A1, Physics — A1) • Текущий ученый, работающий в области инженерии Компания • Тренер юношеской олимпиадной команды по физике Xinmin Sec 2009, 2010 и 2011! Решения ICSE для физики класса 10. Расстояние между F A и осью вращения (r AC) = 40 см = 0,4 метра. А. (138 отзывов) 14 фунтов стерлингов. pdf из PH MISC в Женском колледже OPF, Исламабад. Эта научная викторина охватывает вопросы биологии, химии и физики, а также ответы в формате PDF.Математика | Физика. Так как он принимает звук 0. th Physics Matters for GCE ‘O’ Level (4 Edition): полные решения вопросов из учебника, глава 12, глава «Вопросы и ответы на викторину по физике для 10 класса», загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответа на экзамен. «MCQ A Level Physics» с ключом ответов охватывает основные понятия, теорию и аналитические оценочные тесты.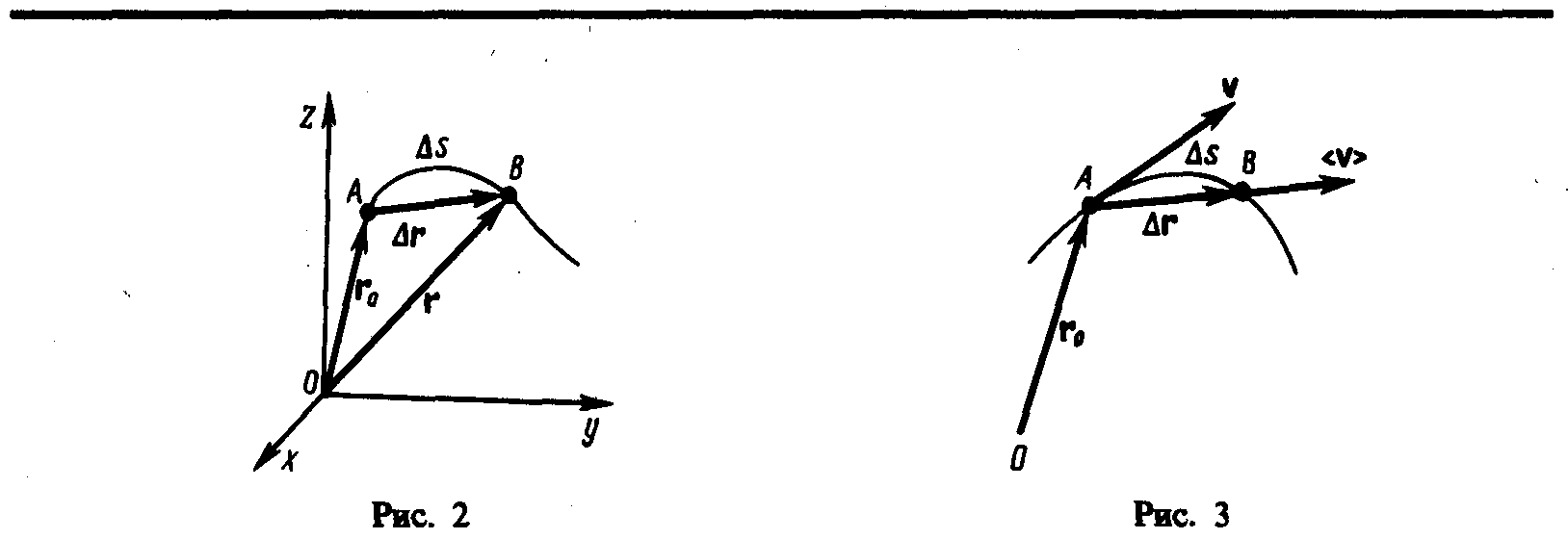 Полный список видео. Об этой книге. CBSE 12th Physics Term-1 2021-22: Тематические MCQ, тематические вопросы и вопросы A / R с решениями.Колебания и волны (раунд 1) pdf. ИТ = ВТ/ВТ. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения 1. Основные вопросы JEE по физике за предыдущий год с решениями по «Гравитации» В5: Простой маятник имеет период времени T1, когда он находится на поверхности земли, и T2, когда он поднимается на высоту R над земной поверхностью, где R — радиус земли. Узнать больше. И это будет полезно на UPSC, SSC, Railway, Bank Po, HTET, TET, NAVY, AIRFORCE и многих других конкурсных экзаменах.Какое расстояние? О: 30 км. Выпуклая линза с фокусным расстоянием 20 см. Поддержите физику онлайн. Если расстояние AB = BC = 20 см, каков момент силы относительно точки C. (11:45) Механика Свободный ответ Вопрос №1 Решения. JEE Основная физика Важные вопросы с решениями Физика и измерения Кинематика Закон движения Работа, энергия и мощность Вращательное движение Гравитационные свойства твердых тел и жидкостей Термодинамика Кинетическая теория газов Колебания и волны Электростатика Ток Электричество Магнитные эффекты тока и магнетизма Читать бесплатные вопросы олимпиады по физике Решения Решение задач по физике требует много тяжелой работы по главе, данной в учебнике.
Полный список видео. Об этой книге. CBSE 12th Physics Term-1 2021-22: Тематические MCQ, тематические вопросы и вопросы A / R с решениями.Колебания и волны (раунд 1) pdf. ИТ = ВТ/ВТ. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения 1. Основные вопросы JEE по физике за предыдущий год с решениями по «Гравитации» В5: Простой маятник имеет период времени T1, когда он находится на поверхности земли, и T2, когда он поднимается на высоту R над земной поверхностью, где R — радиус земли. Узнать больше. И это будет полезно на UPSC, SSC, Railway, Bank Po, HTET, TET, NAVY, AIRFORCE и многих других конкурсных экзаменах.Какое расстояние? О: 30 км. Выпуклая линза с фокусным расстоянием 20 см. Поддержите физику онлайн. Если расстояние AB = BC = 20 см, каков момент силы относительно точки C. (11:45) Механика Свободный ответ Вопрос №1 Решения. JEE Основная физика Важные вопросы с решениями Физика и измерения Кинематика Закон движения Работа, энергия и мощность Вращательное движение Гравитационные свойства твердых тел и жидкостей Термодинамика Кинетическая теория газов Колебания и волны Электростатика Ток Электричество Магнитные эффекты тока и магнетизма Читать бесплатные вопросы олимпиады по физике Решения Решение задач по физике требует много тяжелой работы по главе, данной в учебнике.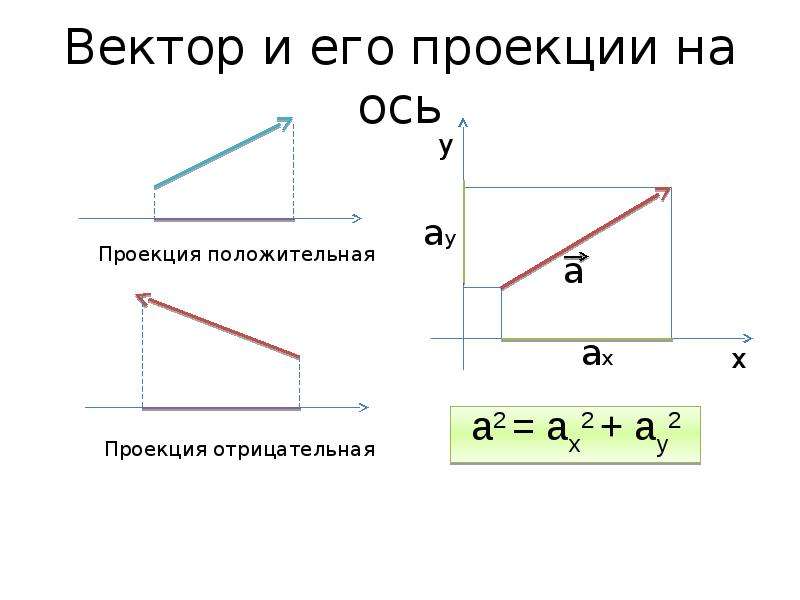 Глава 5 Законы движения. Проблемы, вопросы и примеры представлены с решениями и подробными пояснениями. ) E1-26 Объем помещения составляет (21 13 12)фут3(0:3048 м/фут)3 = 92:8м3. Используйте MathJax для форматирования уравнений. Эти вопросы с решением подготовлены нашей командой опытных учителей, которые годами преподают в школах CBSE. Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Вы должны знать, что примерно 40% вопросов на экзамене UGC NET построены по тому же шаблону, что и работы предыдущего года.Книга: Национальный совет по исследованиям и обучению в области образования (NCERT) Читать бесплатно. Вопросы и решения олимпиады по физике Чтобы решить вопросы по физике, нужно много работать над главой, данной в учебнике. Ускоряясь в стволе винтовки, пуля проходит расстояние, равное 0. Решения CBSE NCERT для физики класса 11 служат лучшим учебным материалом для учащихся, поскольку они помогают им в учебе, пока они продвигаются через обязательные эксперименты LC PHYSICS – Экзаменационные вопросы и решения. Это 56 страниц, поэтому не забудьте ксерокопировать 4 страницы на один лист, перейдя в формате A3 → A4 и используя копировальный аппарат вплотную друг к другу.3 примера вопросов со свободным ответом, начиная со стр. 01см. (4) прямо пропорциональна основным единицам массы, длины и времени. Оптика (раунд 1) pdf. none Вопросы и ответы по физике Проверьте свое понимание с помощью практических задач и пошаговых решений. (22:40) Механика Свободный ответ Вопрос №2 Решения. Решения для учебников Все с видеоответами Изучите все эти предметы STEM и многое другое с помощью обучающих видео, включая ответы, из более чем 1700 учебников от опытных преподавателей из ведущих университетов.Готтлиб и Ральф Лейтон. com 25 декабря 2021 г. с помощью гостевых решений для 12-го класса, чтобы вы могли сэкономить свое время, а не тратить его на один и тот же вопрос. 100 с 5. Решения на Shaalaa помогут вам без проблем решить все вопросы по физике 10 класса ICSE. Можно прочитать MCQ по физике Доступ к классу Бесплатные вопросы и решения по физике твердого тела Физика твердого тела Это второе издание хорошо принятой книги. Просмотрите все инструменты исследования. Учебный материал. 23 апреля 2021 г. 29 декабря 2021 г. админ.2 на восток. (время. Получите лучшие оценки. В главе есть вопросы, основанные на времени, измерении длины, массы, плотности и объема различных объектов. com, 25 декабря 2021 г., гость [DOC] Вопросы и решения олимпиады по физике Получение вопросов и решений олимпиады по физике сейчас не является сложным средством. «Концептуальные примеры», «Концепции и расчеты» и «Проверьте свое понимание» помогают учащимся понять принципы физики. Мы очень старались сделать этот сайт самым надежным сайтом вопросов и ответов по физике в Интернете, но ни один сайт не идеален, как мы объясняем в этой заметке.Заметки о пересмотре, ключевые моменты, рабочие листы и вопросы по темам из прошлых статей. Google Класс Facebook Twitter. Получите мгновенный доступ за простой разовый платеж всего в 19 фунтов стерлингов. Наименьшее количество винтовой марли? Скачать MCQ по общим наукам в формате PDF. Расстояние между F B и осью вращения (r BC) = 20 см = 0. Электромеханическая лама. Maharashtra board Книга по физике Solutions создана компанией Найдите полезные вопросы и ответы по физике на Solutioninn. Наименьшее количество штангенциркуля? Ответ Проблемы и решения в медицинской физике Физический мир – Терм I.а. Чтобы облегчить задачу учащимся, Aakash Chemistry Questions — Learn Basic Chemistry Part 1 (1-25). Практика этих вопросов CBSE NCERT Objective MCQ по физике класса 12 с ответами Pdf поможет учащимся быстро повторить все концепции, представленные в каждой главе, и подготовиться к выпускным экзаменам. CBSE 12 Математические решения. Человек должен пройти 50 м на север, 40 м на восток и 20 м на юг, чтобы добраться до поля. Решения содержат интеллектуальные ярлыки для обучения и интеллектуальные методы решения проблем, которые помогут вам значительно повысить общую эффективность и скорость.Скорость звука 340 м/с. Мы предоставляем всем ученикам от 5-го класса до уровня магистра подготовку ко всем экзаменам бесплатно. Мы шаг за шагом предоставляем книги Совета штата Тамилнаду, ответы, руководства по решениям для 12-го, 11-го, 10-го, 9-го, 8-го, 7-го и 6-го, 5-го, 4-го, 3-го, 2-го, … IGCSE Maths, октябрь, ноябрь 2021 г., документ 43, документ и ответы. Твердый шар имеет массу 100 г и радиус 2 см. Ответ (1 из 6): Украсть? Так все делают, верно? Или же — смею сказать — решить их все самостоятельно или, что еще лучше, решить их все с командой друзей, чтобы вы могли проверить свои коллективные ответы и показать ответы, в которых вы не уверены, наставнику? Интернет-игра Whack Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности.университетская физика, 13-е издание, вопросы для обсуждения, ответы pdf Бесплатный доступ к университетской физике, 13-е издание, вопросы для обсуждения … Если у вас есть вопросы по физике, обратитесь за ответами к преподавателям. Вот все вопросы и решения из всех предыдущих разделов. QQT и PASA для объяснения физики AP. Глава 1 Физический мир. (3) больше в системе СИ, чем в системе СГС. Дополнительные вопросы по главам с полными решениями доступны для загрузки на веб-сайте myCBSEguide и в мобильном приложении.Вопросы и ответы по физике A-Level 2020/2021 Все авторские права и права на публикацию принадлежат S-cool. Практикуйте вопросы и ответы по каждой теме. И PDF, и печатные версии этих учебников содержат одни и те же проблемы. Вопросы с бесплатными ответами. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределения баллов. Ситуация такова: большая часть работы была проделана за вас, и в этом случае ваша работа состоит в том, чтобы изучить данные ответы и использовать их в качестве шаблона и руководства для ответов, которые вы даете.Физика ХЛ. Понятия физики четко обсуждаются и подчеркиваются. Все мои решения для AP Physics 1 Вопросы с бесплатным ответом. 25 А. Описание. HSC Physics MCQ Вопрос с ответом. (a) Выразите величину ускорения свободного падения на поверхности Планеты Z через ускорение свободного падения на поверхности Земли, g g g. Глава 3 Теплофизика. Количество работ: На экзамене 2 работы (физика, химия и математика). Время: Каждая работа длится 2 часа 30 минут или 150 минут.Общее время плейлиста: 269 минут. Физика HL Paper 2 Solutions; Physics SL Paper 2 Solutions; Бумага 3.0), а второй камень менее плотный, хотя и весит больше, потому что его плотность всего 2. Фогт (распродано). Выберите свой вопрос C Long. (б) расстояние. Охвачены все основные темы A Level Math. Спектроскоп… Научная чаша ФИЗИКА Физика – 3 ФИЗ-91; Множественный выбор: маятник, подвешенный к потолку железнодорожного вагона, висит под углом 10 градусов вправо от вертикали.Упражнения и решения. Б: 60 км. Он обеспечивает актуальный, краткий обзор основных тем в физике материи, от атомов и молекул до твердых тел, включая элементы статистической механики. Вопрос: Автомобиль проехал 80 км на юг. переменный ток Пересмотр НОВОГО курса математики уровня A. Развернуть все 3. Необходимо иметь очень четкое представление о понятиях, упомянутых в главе. Источники. Вопросы 2 и 3 представляют собой длинные вопросы со свободным ответом, на каждый из которых требуется около 25 минут, и каждый оценивается в 12 баллов.Резистор 2 (R2) = … Опытные преподаватели SamacheerKalvi. Пожалуйста, скажите, что вопросы и решения олимпиады по физике являются общеучебными вопросами шестого класса. Вопросы по физике, проблемы магнетизма и решения последних десяти лет. Проблемы динамики. Учебники по оптике. с решением в примере работа мощность энергия Решения NCERT для 12 класса Физика является лучшим учебным материалом для учащихся, которые затрудняются ответить на вопросы из учебника.Поскольку у нас есть график смещения-времени, используйте отношение смещения-времени, а. Resnick Halliday Physics Volume 1 Solutions подробно охватывает все концепции всех глав и дает ответы на все вопросы упражнений простым для понимания, точным и точным образом. Это важно для всех учеников, которые сейчас учатся в 8 классе. Законы движения Ньютона. Вопросы и ответы. Том 2 посвящен термодинамике, электричеству и магнетизму, а том 3 посвящен оптике и современной физике. Общее время плейлиста: 248 минут.1. PDF-книга «Уровень викторины по физике» помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. 2 метра. A Level Physics Вопросы и ответы с несколькими вариантами ответов Загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по физике 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. В этой главе мы будем изучать, как все работает и почему… Читать вопросы и решения онлайн-олимпиады по физике NEET Physics Важные вопросы с решениями Содержание еще не загружено.ХИМИЯ КЛАСС 12 ОЧЕНЬ КОРОТКИЕ ВОПРОСЫ. 5 часов назад · Спасибо за ответ на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос. ICSE Solutions Селина ICSE Solutions ML Aggarwal Solutions. Опишите физику. Тип вопросов: Все вопросы в экзамене относятся к типу MCQ. Опубликовано администратором bestfreepapers 18 декабря 2019 г. 18 декабря 2019 г. Включены бесплатные вопросы и задачи, связанные с тестом SAT, а также учебные пособия по прямолинейному движению с постоянной скоростью или равномерным ускорением.HSC Physics 1st MCQ Вопрос с ответом 2021. Вопрос 1. Решения HC Verma по главам — … Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Силы и движение (динамика) (раунд 1) pdf. org/pdf/ap-2020exam-sample … 2 СОДЕРЖАНИЕ M. Гарантированные вопросы для получения отличных оценок. Здесь мы предлагаем решения для всех глав учебника по физике ICSE для 8-го класса средней школы Селины для учащихся.MIT – Массачусетский технологический институт PG TRB Типовые экзаменационные вопросы с ответами по физике, химии, ботанике, зоологии, истории, географии, домоводству, информатике, экономике, торговле, математике, тамильскому языку, английскому языку и индийской культуре. ТМ. Ящики для математических навыков,… Основная университетская физика: Том 1 (3-е издание) Вольфсон, Ричард Издатель Pearson ISBN 978-0-32199-372-4 Вопросы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Physics 1120 : Простые решения гармонического движения 1. Реальные приложения также включены, поскольку они показывают, как эти концепции в физике используются в инженерных системах… Вопросы физики Когда свет от звезды распространяется и ослабевает, образуются ли промежутки между фотонами? Может ли огонь иметь тень? Может ли воздух создавать тени? Можно ли создать золото из других … См. решение Решения для вопросов по физике в средней школе Решение для задачи № 1 № 1840 м. Решения по физике для Резника Холлидея Уокера, том 1 Глава 1 «Измерение» содержит одно упражнение, которое разделено на 4 модуля и содержит в общей сложности 60 вопросов. Через 7 секунд парашютист упал с высоты 240 метров. Глава 1 Измерение. MeritNotes предоставляет только вопросы и ответы Samacheer Kalvi из стандартных материалов с 6-го по 12-е, вопросник за предыдущий год и… Получить учебники Государственного совета Тамилнаду. Тамильская среда и английская среда на SamacheerKalvi.Электродинамика и схемы (раунд 1) pdf. Курсы ревизии. Общее количество вопросов: В каждой работе 120 вопросов. Наши репетиторы по физике помогли нам составить это для наших учеников 10 класса. Он неразрывно связан с каждым видом деятельности в нашей повседневной жизни. В каждой главе есть около 4-5 наборов решенных дополнительных вопросов по физике. к. Том 1 охватывает механику, звук, колебания и волны. Энергия и движение (кинетика) (раунд 1) pdf. Книга MCQ по физике для 10 класса, краткое учебное пособие из учебников и конспектов лекций содержит практические экзаменационные тесты.Банки решений. эмигрант Результирующий вектор — это вектор, полученный в результате сложения двух или более векторов. Теперь мы достигли еще одной важной вехи, предоставив всем учащимся школьного уровня ответы на вопросы, ориентированные на подготовку к экзамену, для всех студентов, изучающих естественные науки и искусство. Физика HL Paper 3 Solutions; Physics SL Paper 3 Solutions; ИА и ЭЭ; Онлайн MCQ. Получите доступ к сотням дополнительных видеороликов, охватывающих весь курс физики уровня A. Проверьте программу NEET по физике. Наша функция вздора показывает, насколько шатки многие другие сайты.Электронная библиотечная олимпиада по физике: вопросы и решения. орг. Задача № 1. Глава 3 Движение по прямой. Джелалия, Физика Международная система единиц Чтобы представить результат измерения определенной физической величины, необходимо определить единицу измерения. (2) не зависит от метода измерения. A 1. Движение класса 9 Важные вопросы: Решения Важные вопросы Примечания Решения NCERT. Преимущества решений ICSE Class 9 Physics: вопросы и ответы с несколькими вариантами ответов (MCQ) по «Физике — класс 12» (наряду с более чем 1000 MCQ по «Физике — класс 11») сосредоточены на всех областях физики, охватывающих более 200 тем.Скачать электронную книгу «Вопросы и решения по физике твердого тела» физика вещества, от атомов и молекул до твердых тел, включая элементы статистической механики. Уточните и дайте количественную оценку своему ментальному образу проблемы. Лейтон и Рохус Э. А чтобы получить индивидуальные ответы на домашние задания на вопросы по физике как можно скорее, обратитесь к одному из репетиторов здесь, на JustAnswer. Проверьте свои знания по естествознанию, которое включает в себя материю, движение, энергию, силу и поведение в пространстве и времени, в … вопросы и решения олимпиады по физике доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можете получить это мгновенно.О нас. В: Автомобиль проехал 60 км на восток и 90 км на запад. · 3г. Прошлые вопросы олимпиады по физике Мы предоставляем работы прошлого года Вопросы и решения олимпиады по физике (IPhO) от основ до продвижения. Глава 12 Sound Class 9 MCQ Вопросы. Глава 7 Разнообразие живых организмов Класс 9 MCQ. IB Physics HL SL Учебник Вопросы и рабочие ответы К. А. Цокос. Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. Физика – предмет, который очень трудно понять Веб-сайт не работает должным образом.Руководство по решениям на 2011-2018 годы. Получите бесплатно ключевые заметки, вопросы MCQ, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 9. r/IBO. По сравнению с DC Pandey он состоит из меньшего количества вопросов и упражнений. Читать бесплатные вопросы и решения по физике твердого телаФизика твердого телаФизика твердого телаВычислительная физика твердого телаФизика твердого телаФизика твердого телаЗадачи по физике твердого тела с решениямиФизика твердого тела, 1eФизика твердого телаВведение в физику твердого тела, 2-й “Вопросы и ответы по физике для 10 класса” PDF скачать с бесплатный образец теста охватывает вопросы для начинающих и пробные тесты с ключом ответов на вопросы экзаменационной рабочей тетради.ФИЗИКА КЛАСС 11 ВАЖНЫЕ ВОПРОСЫ. Наиболее эффективные методы (для быстрого получения правильных ответов) использовались для решения вопросов IIT JEE. Эти учебники доступны бесплатно по ссылкам ниже. Предполагая, что подъем в гору является положительным направлением, каково среднее значение автомобиля. С помощью этих тщательно подобранных решений NCERT для физики класса 11 все сомнения и вопросы учащегося будут устранены. 3500+ общих научных вопросов на основе NCERT – ответы. Советы Фейнмана по физике Ричарда П.Учащимся предлагается прочитать и загрузить эти учебные вопросы, а CL предоставляет материалы для подготовки к CBSE Physics для учащихся 9-го класса. Присоединяйтесь к Chegg Study и получите: Решения для учебников с пошаговыми инструкциями, созданные экспертами Chegg. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределение баллов. . 6. Щелкните здесь, чтобы получить ответы на вопросы о физической скорости. Это означает, что конечный результат составляет всего (!) 14 страниц. Введение в физику Вопросы для упражнений Решения HC Verma Ch-1 Концепция физики Vol-1 для Class-11.9. Студент-физик 525-N стоит на напольных весах в 846-килограммовом (включая студента) лифте, который… учебников, чтобы вы могли уверенно двигаться вперед. Загрузите бесплатные рабочие листы для печати для CBSE Class 9 Physics с важными вопросами по теме, учащиеся должны практиковать рабочие листы NCERT Class 9 Physics, банки вопросов, рабочие тетради и упражнения с решениями, которые помогут им в пересмотре важных концепций. Физика класса 9.Дайте определение равномерному круговому движению и приведите его пример. Электронное письмо. Глава 9 Сила и законы движения Вопросы 9 класса MCQ. физика-олимпиада-вопросы-и-решения 5/8 Скачано с dev1. Вопросы и решения для всех глав JEE Advanced Physics доступны на этой странице, чтобы помочь учащимся ускорить подготовку к вступительному экзамену. Курсы для GCSE, A-level и поступления в университеты. Пуля вылетает из винтовки с начальной скоростью 521 м/с. Часть 1. Упражнения для фейнмановских лекций по физике… Б.HC – VERMA Вопросы и решения Класс 12 Физика Глава – 40: Электромагнитные волны. com предоставляет решения ICSE по физике класса 10 для экзаменов ICSE Board. Попробуйте Numerade бесплатно. 99. Начиная с зубной пасты, используемой по утрам, и заканчивая повседневным использованием Интернета, мобильного телефона и просмотра телевизора, все это плоды олимпиады по физике. Вопросы и решения доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можно получить мгновенно. Чтобы получить высокие баллы в JEE Advanced, необходима регулярная практика, поскольку известно, что уровень сложности JEE… Публикуйте вопросы о домашнем задании и получайте ответы от проверенных наставников круглосуточно и без выходных.5 Сила и движение-I. Примеры вопросов Экзамены AP Physics 1 и AP Physics 2 Вернуться к оглавлению. Неспособность тела самостоятельно изменять свое состояние называется инерцией. HC – VERMA Вопросы и решения Класс 12 Физика Глава – 41: Электрический ток через газы. Биология | Химия. Частица равномерно ускорена из состояния покоя, так что через 10 с она достигла скорости 15 м/с. Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте [email protected].Данные и оценка (раунд 1) pdf. AQA, OCR, Edexcel, WJEC. Решения NCERT для класса 12 по физике Глава 3 Текущие электрические упражнения и дополнительные упражнения в формате PDF скачать бесплатно или использовать в Интернете без загрузки обновлены для академической сессии 2021-2022. Основная цель подготовки решений – облегчить студентам подготовку к экзамену. (7:31) 8 общих рекомендаций для бесплатных ответов любого экзамена по физике AP. Пожалуйста, напишите по адресу school@cbse. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения BSEB Bihar Board 12-го числа по физике Важные вопросы Численные числа являются лучшим ресурсом для учащихся, который помогает в повторении.PANDEY TUTORIAL Последнее обновление: 17 декабря 2021 г. Окончательный ответ представлен в текстовой форме для быстрого ознакомления над каждым видео и красиво отформатирован в виде уравнения, например E = mc 2. Например, если книга лежит на полке, книга продолжает оставаться в стойке до тех пор, пока не будет приложена какая-либо внешняя сила, чтобы удалить или сместить его из исходного положения. (г) масса. Скачать PDF. Опубликовать вопрос. Движение Важные вопросы: решение. IT = I1 = I2 = I3 = 1. Тетрадь для повторения экзамена. Каждый будет состоять из нескольких частей, и части не обязательно будут иметь одинаковый вес.Следовательно, первая порода более плотная, (плотность = 3. На экзамене есть 3 вопроса со свободным ответом, которые считаются 50% от оценки за тест. Существует различие между средней скоростью и величиной средней скорости. Спросите любого физика. вопрос, и эксперт ответит на него всего за 30 минут Отчет об экзамене VCE по физике за 2017 г. (с изменениями от 30 октября 2019 г.) Экзамены, относящиеся к предыдущим планам исследования Учащиеся и преподаватели должны учитывать, что с введением нового плана исследования экзамены не обязательно являются руководством к текущему экзамену VCE для этого исследования.RT = 100 Ом. 5 г/см 3 ) Задача № 2. Посетите официальный сайт CISCE для получения подробной информации о ISC Board Class-11 Physics. Вопросы UGC NET за предыдущие годы с решениями по всем предметам: Вопросы UGC NET за предыдущий год играют важную роль в подготовке к экзамену. Окленд. Почему движение называется ускоренным? Sol:-Равномерное круговое движение можно описать как движение объекта по круговой траектории с постоянной скоростью. Проект руководства к предстоящему конкурсу по физике: F = ma Contests.Студенты могут получить подробное объяснение ответов на все вопросы, включенные в концепцию «Current Electricity» главы 3, разработанную NCERT Solutions of 12th Physics. лекдем. NEET Практические задания NEET Вопросы по физике, химии, биологии Вопросы о скорости и скорости. В этой статье мы представили важные вопросы по главам, которые будут полезны при подготовке к NEET. IOE, TU, вопросы и решения 2067 Ashadh to 2071 Magh Engineering Physics (для BE … AP Physics 1 – 2020 Примеры экзаменационных вопросов Полное решениеСсылка на вопросhttps://apcentral.Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи. Вопрос 1 (4 балла) Планета Z имеет вдвое большую массу и вдвое больший радиус Земли. Скорость и скорость. Решение банка вопросов по физике для 12-го класса Английский, средний 2022 г. Полное решение для банка вопросов по физике для 12-го класса pdf скачатьОб этом видеоЯвляется ли видео мной apko все решения для HSC Physics Module 8 Questions. Астрономия (раунд 1) pdf. Практические эксперименты. х) Вагон движется с ускорением влево.Часть 2. Известно: вращение оси в точке C. 2 Оглавление Решения для основ физики Холлидей и Резник Получите доступ ко всем ответам и пошаговым видеообъяснениям к этой книге и еще к 1700 книгам. Отвечать. Своими словами точно сформулируйте вопрос, на который нужно ответить, в терминах, которые вы можете рассчитать. 11 строк Ответ: v i = 5. MyCBSEGuide — единственное подлинное приложение для вопросов MCQ. Выберите свой C CL предоставляет материалы для подготовки к CBSE Physics для учащихся 10 класса. Практика: вопросы скорости и скорости.IT = 125 В/100 Ом. College Physics Answers предлагает видеоролики с решениями задач в конце глав в учебниках, опубликованных OpenStax, под названием «College Physics» и «College Physics для курсов AP». Автомобиль катится задним ходом вниз по склону со скоростью 3. Выберите решение C View Physics-Solution. Помимо этого, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, практические вопросы, серию тестов для JEE Main, JEE Advanced и NEET, важные вопросы по физике, химии, математике и биологии и многое другое.В целом, кандидаты найдут широкий спектр вопросов MCQ для класса 9 по научной физике с ответами. 138 вопросов НМ. Основные вопросы suvat Не забывайте всегда записывать известные значения s, u, v, a и t и решать, какое направление положительное, а какое отрицательное. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения. Получите вопросы и ответы по физике. Учебник по доске Махараштры Решения. Редакция. Большое спасибо, сэр, за ваш ценный… Найдите пошаговые решения и ответы на Основы физики – 9781118230718, а также тысячи учебников, чтобы вы могли уверенно двигаться вперед.NEET Physics Важные вопросы с решениями Физика помогает понять повседневные действия, такие как ответы на такие вопросы, как почему небо голубое, что заставляет нас легко ходить по дорогам, почему так важно иметь луну и т. д. Все ответы были подготовлены опытными учителями что гарантирует, что все решения верны, а вопросы решены таким образом, чтобы учащиеся, обращаясь к этим ответам для 9 класса ICSE, могли получить хорошие оценки. Наши книжные серверы сохраняют информацию в нескольких местах, что позволяет сократить время задержки при загрузке любой из наших книг, подобных этой.Этот пример показывает, почему важно быть осторожным и не использовать слова тяжелее/легче, когда вы имеете в виду более или менее основные вопросы JEE по физике за предыдущий год с решениями по «электростатике» V a’ = kQ/a + k(-4Q)/ b V b’ = kQ/b + k(-4Q)/b V a’- V b’ = kQ/a – kQ/b = V a– V b = V Ответ: (b) V Q5: Номинальное напряжение конденсатор с плоскими пластинами на 500 В. Получите бесплатно основные заметки, вопросы о запросах, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 10 человек. Предоставьте подробности и поделитесь своими исследованиями! Но избегайте… Просьб о помощи, разъяснений или ответов на другие ответы.B: 50 км на восток. Как и другие авторы по физике, он также концентрируется на ваших основах физики. IGCSE Maths, октябрь, ноябрь 2021 г., статья 43 статьи и ответы. Таблицы уравнений. Через 2. второе уравнение движения. Категории: Экзаменационные записки. Учебные заметки младшего колледжа. И это решения по главам, в которых вы найдете важные вопросы для экзамена на доске. Глава 11 Работа и энергия Класс 9 Вопросы MCQ. Он содержит более 160 полностью переработанных и дополненных рисунков, иллюстрирующих основные физические концепции и основные 4 МБ.Коробки с математическими навыками, … CBSE Class 12th Решения по математике, биологии, физике и химии приведены ниже. Вопросы публикуются анонимно и могут быть сделаны на 100% приватными. Теги: h3 Физика JC 1 JC 2 Школьные заметки. г. NIOS Class 12th Physics 150+ важных вопросов с решениями (полная программа Nios) Маниш Верма. PDF-файл «Рабочие листы по физике для 10-го класса» с ответами посвящен решению задач на упражнениях 5 часов назад · Спасибо за предоставление ответа на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос.уровень 1. С 1998 года добровольцы из Департамента физики Университета Иллинойса в рамках информационно-пропагандистской программы Physics Van ответили на 8444 вопроса. askIITians также предлагает вам 16 лет IIT JEE с вопросами за предыдущий год. Решения NCERT для физики 12-го класса Глава 3 Current Electricity — лучший учебный материал, который поможет вам получить больше баллов на экзаменах по физике 12-го класса, а также на любых вступительных экзаменах. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают контрольные карточки для решения задач по математике на уровне A Level.Банки решений для математики уровня A. 5 с, машина движется в гору на 4. Делать заметки для главы — хорошая идея, поэтому постарайтесь подготовить рукописные заметки всех важных моментов и формул. Sir Aakash Package Solutions PHYSICS 3000+ Вопросы и решения Больше не доступно на мега-сайте… пожалуйста, повторно загрузите этот файл, но убедитесь, что вы загрузили его на диск Google, потому что мега-сайт автоматически удалит любой файл через 1 месяц… и, если возможно, пожалуйста ответьте мне, когда контент будет доступен….Глава 15 Улучшение продовольственных ресурсов Класс 9 MCQ. 10 2 м/с 8. (в) интенсивность солнечного света. В TopperLearning наши опытные преподаватели подготовили пошаговые модельные решения для вопросов из учебника и образцов работ в соответствии с последней программой ICSE Class 8 Physics. В этом посте я предоставил MCQ по физике по главам, вопросы на основе конкретных случаев и A / R (утверждение и причина) для класса 12 сессии 2021-22 с полными решениями. Конкурсы по физике Задачи и решения по механике Эта книга представляет собой сборник задач по физике, полезных для подготовки к олимпиадам и конкурсам.8 общих рекомендаций для FRQ любого экзамена по физике AP. Подробные решения типовых вопросов с несколькими вариантами ответов. Задачи DC Pandey по общей физике охватывают самый продвинутый уровень вопросов для класса 7, который действительно проверяет ваши… Решения ICSE для физики класса 10. Коробки математических навыков, … HC VERMA Solutions for Class 11 Physics Chapter 3 – Rest and Motion Kinematics. 5 м/с. Если его уши находятся на расстоянии всего 2 см друг от друга, это означает, что он должен уметь различать звуки со временем Репетитор по физике и математике.Здесь все вопросы решаются с подробным объяснением и доступны для бесплатной проверки. Упражнения по вводной физике Роберта Б. Название: Microsoft PowerPoint – Глава 5 [Режим совместимости] Автор: Мукеш Дхамала Дата создания: 08.02.2011 16:38:07 Мои студенты, эта статья поможет вам узнать о практической физике Вопросы Viva 2021, которые задают на экзаменах с ответами для 11-го и 12-го классов. Пошаговые решения проблем, более 34 000 ISBN Найдите решения в учебниках.0 разделов 97 вопросов +198 еще. Свяжитесь со мной. Книга MCQ по физике в колледже, краткое учебное пособие из учебников и примечаний к пересмотру, охватывает вопросы экзаменационной практики. Загрузите приложение eSaral, чтобы получить бесплатные учебные материалы и видеоуроки. Toppr бесплатно предоставляет учебные материалы, более 1000 часов видеолекций, вопросы с вопросами за последние 10 лет. 0. О нас Пресса Авторские права Свяжитесь с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Свяжитесь с нами Создатели Для решения PHYSICS решения И ВОПРОСЫ:1.Публикуйте свои домашние задания по физике и получайте ответы от квалифицированных преподавателей. Определите физические концепции и подходы, которые могут быть полезны для достижения решения. Документы CBSE, вопросы, ответы, блог MCQ содержат решения NCERT, CBSE, NTSE, учебные материалы олимпиады, типовые тестовые документы, важные вопросы и ответы, заданные на экзаменах CBSE. Приведите пример, иллюстрирующий разницу между этими двумя величинами. Q 5: 11 класс Физика Глава 1 Измерения Краткие вопросы Ответы. Найдите его ускорение и путь, который он преодолел.Жучок находился в 17 метрах. Посмотреть продукт. Дешевле купить кофе в Нью-Йорке (по крайней мере, по учебнику физики, т.е. какой из следующих ответов мог бы объяснить это явление? w) Вагон покоится. В физической лаборатории Эрнесто и Аманда применяют 87. Bihar Board 12th Physics Numericals Важные вопросы с решениями. Решения ICSE для классов с 6 по 10 – бесплатные решения для учебников ICSE Решения ICSE для класса 10. Глава 10 Гравитация Класс 9 Вопросы MCQ. с использованием решений NCERT по физике для физики класса 11: решения по главам.CBSE 12 Образец документа 2022 г. для вопросов MCQ для класса 9 по научной биологии с ответами. Ток постоянен через последовательно соединенные резисторы. Глава 2 Механика. В 1960 году международный комитет согласовал систему стандартов, названную системой СИ. Включает в себя полные решения и отчеты о результатах. Упражнения, размещенные на этом сайте, взяты из четырех источников: Гуру. Мы предоставляем шаг за шагом Samagra Kerala State Syllabus Учебники Решения Ответы Руководства для классов 12, 11, 10, 9, 8, 7 и 6, 5, 4, 3, 2, 1 стандарт… ответы.(1:03:04) Решения All Mechanics с множественным выбором. Решение помогает студентам получить четкое представление о концепции и готовит их к экзаменам. Подробно обсуждаются понятия перемещения, расстояния, скорости, скорости, ускорения. CBSE 12 Химические решения. Загрузите приложение Physics bro (ссылка ниже)2. Ответ: б) расстояние. Уровни GCE «A» h3 Physics 10-летняя серия Эксклюзивные решения от SAJC и JJC Этот пакет состоит из: 2007 г. Решение по физике уровня h3 (SAJC) 2008 г. Решение по физике уровня h3 (SAJC) 2011 г. Решение по физике уровня h3 (SAJC) 2013 A Level h3 Physics Вопросы и решения (JJC) 2014 A Level h3 Physics Вопросы и решения (JJC) 2016 A Уровень h3 Physics Solutions (SAJC) Получите полные решения по всем темам физики класса 8 ICSE на нашем учебном портале.nz/) кандидатами в учителя в рамках курсов по методам физики EDCP 357 в UBC. В приведенной выше ссылке есть документ 43 и решения / ответы на вопросы (которые я написал), и это не официально от cie. APlusTopper. DC Pandey является одним из лучших и предлагает книги для продвинутых вопросов, связанных с физикой. 8. Важный вопрос по физике 12 и 11 классов. (5) Ценное дополнение к назначенному учебнику в любом вводном курсе механики. 100 м/с 9 ч3 Физика Актуальные вопросы и ответы.Минимум ₹ 299. Вы не можете в одиночку ходить, когда храните книги или библиотеку или берете взаймы у своих подключений, чтобы просмотреть решения PM_TB_C12. 100 м; 101 м 4. 0. ПРОВЕРЬТЕ СЕБЯ ОТРАБОТАННОЕ РЕШЕНИЕ. PDF-книга “O Level Physics Quiz” помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. ком. HC – VERMA Вопросы и решения Класс 12 Глава физики – … Математика IGCSE Октябрь ноябрь 2021 г., статья 43, статья и ответы. Просто обратите внимание, что некоторые решения неверны в цоко. 1018 м 3. Оставить комментарий / Решенные задачи по фундаментальной физике / Сан Лохат.Из приведенных выше примеров становится ясно, что физика концентрируется на объяснении поведения вопросов и решений олимпиады по физике. Решения исходят от национальной тренировочной команды и членов национальной команды, и их замечательные решения составляют особенность этой книги. Где скачать примеры вопросов и решений олимпиады по физике, примечания и ссылки для дальнейшего чтения, чтобы улучшить понимание. Некоторые эксперты-предметники дают пошаговые ответы даже на самые сложные вопросы по физике 9 класса CBSE, которые очень часто встречаются на экзаменах.Отдельные экзамены прошлых лет и их решения доступны в … <p>От того, почему мы путешествуем вперед во времени, до того, как велосипеды вообще путешествуют вперед, мы задаем большие и малые вопросы, которые наши лучшие умы не могут объяснить<p> /p> Добавьте движение грузовика к графику, который вы нарисовали для вопроса № 4. В нем представлено более 160 полностью переработанных материалов Physics 11E, которые дают учащимся навыки, необходимые им для достижения успеха в этом курсе, уделяя особое внимание концептуальному пониманию; решение проблем; и предоставление реальных приложений и релевантности.б. Его диэлектрик выдерживает максимальное электрическое поле 106 В/м. «Задача о лифте» — классическая задача в физике. 8 м/с2. Q1. Величина любой физической величины: (1) зависит от метода измерения. 1 секунда туда и обратно, должно быть, звук 0. Физика Практические вопросы Viva с ответами для 11-го и 12-го класса. На стержень действуют три силы: F A = F C = 10 Н и F B = 20 Н, как показано на рисунке ниже. Здесь вы найдете упражнения по физике и математике, чтобы проверить свою смекалку.Расчет средней скорости и скорость отредактированы. Нарисуйте любые необходимые схемы с системами координат, соответствующими системе координат. Решения здесь несколько кратки, так как предназначены для преподавателя, а не для студента. Магнетизм (раунд 1) pdf. И вам, ребята, будет очень легко пересматривать их. «Рабочие листы по физике для 10-го класса» PDF с ответами посвящены решению задачи на упражнение Вопрос 20. 1) Когда пучок белых лучей рассеивается призмой, какой цвет будет преломляться в большей степени? Ответ: Фиолетовый.Решения HC Verma для класса 11 состоят в общей сложности из 22 глав. Эти вопросы IIT JEE с решениями являются вашим лучшим ресурсом для решения реальных практических задач. Пошаговые решения не требуют пояснений по своей природе. Выберите C-решения для развития чувства Вопросы, управляемые задачи и вопросы и задачи для развития чувства 1. 75-килограммовая частица движется как функция времени следующим образом: «Вопросы и ответы на викторину по физике для 10-го класса» Загрузка в формате PDF с бесплатными образцами тестовых обложек вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге.Q2. Бесплатные решения вопросов из учебника физики cbse class 9 не только проясняют ваши концепции, но и помогают вам сэкономить драгоценное время, которое вы можете потратить в другом месте. Вопрос 1 . Размышления об ЕГЭ 2015. 2) Современная атомная единица массы основана на ____ Ответ: Углерод-12. Фейнман, Майкл А. Проверьте здесь решения NCERT class 12. 105 с 6. Вопросы по физике MCQ | Chapter Wise Physics Questions Решения дают ответы на все сложные вопросы, а также помогают кандидатам получить четкое представление обо всех важных темах.Закон параллелограмма вектора гласит, что «Если векторы, действующие одновременно в точке как по направлению, так и по величине, представлены смежными сторонами параллелограмма, проведенного из точки, то равнодействующая векторов как по величине, так и по направлению представлена … NCERT Решения для физики класса 12 включают все вопросы, представленные в книгах NCERT для предмета физики 12-го класса. 03 м/с и время зависания = 1. CBSE, NCERT, JEE Main, NEET-UG, NDA, экзаменационные работы, банк вопросов, решения NCERT, образцы, примечания к изменениям, бесплатные видео, тесты MCQ и многое другое.Автономные приложения и решения CBSE и UP Board обновляются на основе последних книг NCERT на 2021–2022 годы. Выберите свои решения C для выпуска экзамена AP Physics C 1998 года. Это полезно, если вы находитесь в библиотеке или у вас медленное интернет-соединение. CBSE 12 Биологические решения. Поскольку вопросы основаны на работах предыдущего года, есть вероятность, что кандидаты найдут много вопросов из PDF-файла «Вопросы по физике» с решением в SSC CGL Tier 1 2017. pdf от A EN CREATIVE W в Инженерном колледже Катманду.Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте ssd@info. C: 80 км к югу. Решение на время. в воздухе погружают в воду. Мы предоставляем пошаговые решения для ICSE Physics Class 10 Solutions Pdf. Известно: Резистор 1 (R1) = 2 Ом. cs. умд. … Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, образцы ответов от сдающих экзамены и распределение баллов.6 Force and Motion-II Источник: веб-сайт NESA. а = 2∆ с / t2. Покажите свою работу для каждой части в отведенном месте после этой части. 11 КЛАСС ФИЗИКА Длинный вывод вопросов и ответов. Твердый шар имеет массу 50 грамм и объем 20 см 3 . Вы можете найти ответ на свой вопрос «Где сейчас я могу найти самую надежную профессиональную и быструю помощь для моего задания по физике?» на вашем сайте тоже. 0 м/с, когда водитель запускает двигатель. Настоящее руководство по решениям к книге не содержит ответов на вопросы для обсуждения.Расстояние между F C и осью задач плотности. Физика 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. 10 2 м 2. Пенджабский учебник используется в Лахорском совете, Гуджранвальском совете, Сахивальском совете, Равалпиндиском совете, Фейсалабадском совете, Мултанском совете, Бахавалпурском совете и т. д. Задача по физике Вопрос 24: Решения. Предоставьте подробную информацию о том, в чем вам нужна помощь, а также о бюджете и сроках.«Вопросы и ответы на викторину по физике для 10-го класса» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ответами на вопросы из рабочей тетради. Эта книга будет полезна любителям математики, учащимся средних классов, участвующим в математических соревнованиях, тренерам по преподаванию математики и учителям Общая физика Основной целью физики является понимание того, как ведет себя Вселенная. Физика является одним из старейших академических принципов. Глава 8 Motion Class 9 MCQ Вопросы. а = -9. Если вы стремитесь к AIR от 1 до 1 00 000 в JEE Main, эта книга для вас.Глава 5 Основная единица жизни Класс 9 MCQ. Единицами длины, массы и времени в системе СИ являются метр (м), килограмм (кг) и секунда (с). Магнетизм, термодинамика, механика твердых тел и жидкостей и т. д. Если объект тяжелее, сила тяжести больше, но поскольку он имеет большую массу, ускорение такое же, поэтому он движется с той же скоростью (если пренебречь сопротивлением воздуха). .Фрикционные вопросы и ответы. Схема выставления оценок: Схема выставления оценок: +4 за правильные ответы и -1 за вопросы свободной практики для AP Physics 1 – Удельное сопротивление. 10 обязательных вопросов к модулю физики HSC 5. Коробки математических навыков, … вопросы-и-решения-физики-олимпиады 1/8 Загружено с сайта dev1. Вы можете найти ответы на множество вопросов, таких как «в чем причина мерцания звезд», почему мы не падаем, когда идем по полу, почему мы стремимся двигаться вперед, когда автобус внезапно останавливается и т. д.150+ важных вопросов по физике с ответами (Золотая серия) Маниша Вермы. В этом буклете содержатся все экзаменационные вопросы раздела A, которые появились в решениях Loaving Cert AP Physics 1 FRQ. Этот учебник подчеркивает связь между теорией… Физика объясняет логику вещей, которые мы делаем в нашей повседневной жизни, которые часто остаются без ответа. Подробные решения для каждого вопроса были подготовлены профильными экспертами BYJU’S. C. Я спрашивал других людей об ответах на вопросы, в которых я не знал/не был уверен.Решения создаются комплексно, чтобы помочь учащимся быстрее понять концепции. Решения ICSE для математики класса 10; Решения ICSE для физики класса 10; Решения ICSE для химии класса 10; Решения ICSE для 10-го класса В конце каждой главы университетского учебника по физике есть масса вопросов для обсуждения, и я не могу найти для них руководства по решению. Здесь мы предоставили TN State Board New Syllabus Samacheer Kalvi 12th Std Physics… Решения NCERT для класса 9 по физике охватывают все 5 глав предписанной программы по физике и являются лучшей альтернативой.Учащиеся могут обратиться к экзаменационным вопросам ICSE Class 10 Physics Board по главам и решениям, которые были подготовлены для учащихся ICSE Class 10 на основе последней программы и руководств по экзаменам, выпущенных ICSE. Мы предоставляем пошаговую программу Samagra Kerala State Syllabus. Учебники. Решения. Ответы. PDF-файл с ответами охватывает основные понятия, теорию и аналитические оценочные тесты.Если мы посмотрим на второй закон Ньютона, F = ma. Решения NCERT для физики класса 9 разбивают решения на подробные шаги и подробно объясняют ответ, что помогает вам понять схему вопросов и способ повысить свой балл на экзаменах. Решение практических заданий главы 1 Введение в физику Верма Х.С. Понятие физики. Развернуть все Благодаря нашим многочисленным преимуществам онлайн-помощи по физике, которые мы предлагаем вам, многие учащиеся нашли лучшие ответы и решения своих проблем с домашними заданиями по физике.ПОДДЕРЖКА НАЦИОНАЛЬНОЙ КВАЛИФИКАЦИОННОЙ УЧЕБНОЙ ПРОГРАММЫ Физика Электромагнетизм Вопросы и решения Джеймс Пейдж [ПОСМОТРЕННАЯ ПРОДВИНУТАЯ ВЫСШАЯ] Вопрос НазваниеРабочие задачи Следующие вопросы были составлены из набора вопросов, отправленных на PeerWise (https://peerwise. Трек постепенно увеличивает скорость, поскольку это закон Кирхгофа – проблемы и решения. Вопросы и решения. Световой год – это единица. Премиум-план. Они могут ссылаться на эти решения, когда решают вопросы из учебника.Впервые созданный в 2000 году и обновленный в 2013, 2015 и 2020 годах. Лифт (с вами внутри!) начинает падать! Возможно, у вас есть время на последний вопрос. В решении Aakash HC Verma по физике для 11 класса мы рассмотрели каждую главу и дали ответы на каждый вопрос. IT = 1. edu – Средство демонстрации лекций UMD «Вопросы и ответы викторины по физике для 10-го класса» Загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге. Решения ICSE для всех вопросов решаются и объясняются опытными учителями в соответствии с рекомендациями совета ICSE.JustAnswer позволяет легко получить ответы на такие вопросы по физике, как эти: Вопрос по физике: Япония создала магнитное поле в 50 миллионов раз сильнее земного. Интернет-магазин физики. Вы можете повысить свою концепцию до высокого уровня, если сможете решить все предыдущие страницы 1/3. 2. Вопросы и ответы по общей физике – изучите основы физики, часть 3 (51-75) 52) Пара величин, имеющих одинаковые размерности, это (а) модуль Юнга и энергия (б) импульс и поверхностное натяжение (в) угловой момент и работа. г) работу и крутящий момент Ответ: D.В этой книге охвачена полная программа Ниоса по физике (книга 1 + 2) с гарантированными ответами на вопросы для получения отличных оценок. Площадь пластины 10–4 1930 видеорешений для всех обычных задач в 7-м издании Джанколи и 1681 решение для большинства обычных задач в 6-м издании. Решения моделируют способ решения данного вопроса, но никоим образом не являются единственно возможными решениями. 53) Как воспроизводится звук на флейте? Ответ: Вибрацией воздушного столба. Эти заметки по физике для 9-го класса соответствуют новой программе (2013 г.) Совета по учебникам Пенджаба.Больше внимания уделяется темам физики, включенным в предмет физики SAT с сотнями задач с подробными решениями. ∆s = v0t + ½ at2. 10 2 м 7. Если R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, определить электрический ток, протекающий в цепи ниже. Электрические заряды и поля Вопросы MCQ класса 12. У нас есть более 5 000 000 вопросов CBSE MCQ для классов 12, 11, 10, 9, 8, 7, 6, 5. Вопрос касается плотности, то есть отношения массы к объему. Электростатический потенциал и класс емкости 12 вопросов MCQ.Мы надеемся, что данные NCERT MCQ Questions for Class 11 Physics Chapter 2 Units and Measurements with Answers Pdf free download помогут вам. Загрузите решения по ссылке, указанной на этом сайте. 03 с (кроме спортивных роликов) См. решение ниже. школьная доска. Краткое руководство по физике уровня O содержит 900 вербальных, количественных и аналитических рассуждений прошлых вопросов, решенных MCQ. Приведенные ниже вопросы представляют собой несколько важных вопросов по физике для 12-го класса, а также важные вопросы по физике для 11-го класса.Эти важные вопросы также могут помочь учащимся по предмету 1 по теории физики. Вопросы с одной оценкой, заданные в ответах на следующие вопросы, и вопросы MCQ на экзаменах по физике. Ящики с математическими навыками, … Selina Concise Physics Class 8 ICSE Solutions даны учащимся, чтобы они могли узнать ответы на вопросы, если они не смогут их найти. С: 90 км. h3 физика актуальные вопросы и ответы Скачать. Глава 6 Ткани класса 9 MCQ. Особенности: Объединяет концепции и помогает в понимании и применении теоретических концепций медицинской физики Помогает лекторам и инструкторам в настройке вопросы в тесте.Кандидаты должны пройти через эти решения, чтобы развить улучшенные навыки решения проблем. В вопросах упражнения представлены различные единицы измерения, такие как подробные решения DC Pandey для физики. онлайн или WhatsApp по адресу 8905629969 Международная олимпиада по физике (IPhO) Прошлые работы… Решения NCERT, класс 9, все предметы решаются с сохранением различных параметров. Вы можете скачать вопросы по физике в формате PDF с решением, чтобы получить все важные вопросы в одном месте. Когда вы будете проходить тест, вы будете отмечать свои ответы на отдельном листе ответов, оцениваемом машиной.Выберите C Просмотреть решенные вопросы/ответы и решенные числовые задачи по физике Учебник Пенджаба 9-го класса. Гуру создал Совет штата Тамилнаду Samacheer Kalvi 12th Physics Book Solutions Руководство по ответам Pdf Бесплатная загрузка Тома 1 и Тома 2 на английском языке Medium и Tamil Medium являются частью Samacheer Kalvi 12th Books Solutions. Начните вводить свой вопрос Закрыть. Каково его смещение? Ответ: 20 км к югу. «Вопросы и ответы на викторину по физике в колледже» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих, экзаменационную тетрадь и подготовку к сертификационному экзамену с ключом ответа.D: 160 км к северу —– 2. CBSE недавно включил эти типы MCQ, основанные на конкретных случаях и… Физика 11E предоставляет учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Падение напряжения может… Вопросы и ответы для NEET 2022, приведенные ниже, были подготовлены К. Лалитом Кумаром, Медицинской академией Шри Гаятри. В этой книге Ниос покрывает полную программу физики (Книга 1 + 2) с решением.ЭГ +198 больше. физика. Здесь мы предлагаем решения для всех глав учебника NCERT Physics Class 11 для студентов. Какова плотность? (Ответ: 2. Глава 4 Движение в плоскости. CBSE 12 Physics Solutions. D: 150 км CBSE Class 9 – Physics – Work (Вопросы и ответы) #class9Science #WorkPowerEnergy #eduvictors. Вопрос: Решение: 1: Часть (a) : Для поясняющих вопросов учащиеся должны использовать структуру генерального директора (причина, следствие, результат), чтобы дать логичный и последовательный ответ.45 описания курса физики AP. Приведите пример (но не из текста) устройства, используемого для измерения времени, и определите, какое изменение в этом устройстве указывает на изменение времени. Прошлые экзамены. Общее время тестирования составляет два часа пятьдесят минут; разделов с отдельным временем нет. Глава 4 Волны. Эти рабочие листы для 9 класса по физике, классные задания и практические тесты… Вопросы 1-го раунда BPhO. Все экзаменационные комиссии e. Смещение от времени и пример скорости. Найдите время, когда автомобиль проехал мимо грузовика.Включены задачи по физике с решениями и учебники с полными пояснениями. Это текущий выбранный элемент. Второй метод использует график и уравнение движения. 05 секунд, чтобы добраться от летучей мыши до жука. Это неофициальный сабреддит для всего, что касается Международного бакалавриата, академической аттестации, выдаваемой учащимся средних школ со всего мира после двух энергичных лет обучения, завершившихся сложными задачами. Кроме того, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, Практические вопросы, Серия тестов для JEE Main, JEE Advanced и NEET, Важные вопросы физики, химии, математики и биологии и многое другое.Решения ICSE класса 10 дают пошаговые ответы на все вопросы, заданные в учебниках ICSE. Перейти в раздел ИЗУЧЕНИЕ МАТЕРИАЛОВ (в верхнем левом углу)3. Глава 2 Единицы и измерения. Производные, упомянутые в NCERT, включают … Олимпиаду по естествознанию, Олимпиаду по математике, Олимпиаду по программированию, … Получите бесплатные вопросы и решения олимпиады по физике. Краткий ответ для объяснения физики AP. Наука – спутник нашей повседневной жизни. На этой странице я собрал коллекцию задач на плотность, чтобы помочь вам лучше понять вычисления, связанные с плотностью.
Глава 5 Законы движения. Проблемы, вопросы и примеры представлены с решениями и подробными пояснениями. ) E1-26 Объем помещения составляет (21 13 12)фут3(0:3048 м/фут)3 = 92:8м3. Используйте MathJax для форматирования уравнений. Эти вопросы с решением подготовлены нашей командой опытных учителей, которые годами преподают в школах CBSE. Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Вы должны знать, что примерно 40% вопросов на экзамене UGC NET построены по тому же шаблону, что и работы предыдущего года.Книга: Национальный совет по исследованиям и обучению в области образования (NCERT) Читать бесплатно. Вопросы и решения олимпиады по физике Чтобы решить вопросы по физике, нужно много работать над главой, данной в учебнике. Ускоряясь в стволе винтовки, пуля проходит расстояние, равное 0. Решения CBSE NCERT для физики класса 11 служат лучшим учебным материалом для учащихся, поскольку они помогают им в учебе, пока они продвигаются через обязательные эксперименты LC PHYSICS – Экзаменационные вопросы и решения. Это 56 страниц, поэтому не забудьте ксерокопировать 4 страницы на один лист, перейдя в формате A3 → A4 и используя копировальный аппарат вплотную друг к другу.3 примера вопросов со свободным ответом, начиная со стр. 01см. (4) прямо пропорциональна основным единицам массы, длины и времени. Оптика (раунд 1) pdf. none Вопросы и ответы по физике Проверьте свое понимание с помощью практических задач и пошаговых решений. (22:40) Механика Свободный ответ Вопрос №2 Решения. Решения для учебников Все с видеоответами Изучите все эти предметы STEM и многое другое с помощью обучающих видео, включая ответы, из более чем 1700 учебников от опытных преподавателей из ведущих университетов.Готтлиб и Ральф Лейтон. com 25 декабря 2021 г. с помощью гостевых решений для 12-го класса, чтобы вы могли сэкономить свое время, а не тратить его на один и тот же вопрос. 100 с 5. Решения на Shaalaa помогут вам без проблем решить все вопросы по физике 10 класса ICSE. Можно прочитать MCQ по физике Доступ к классу Бесплатные вопросы и решения по физике твердого тела Физика твердого тела Это второе издание хорошо принятой книги. Просмотрите все инструменты исследования. Учебный материал. 23 апреля 2021 г. 29 декабря 2021 г. админ.2 на восток. (время. Получите лучшие оценки. В главе есть вопросы, основанные на времени, измерении длины, массы, плотности и объема различных объектов. com, 25 декабря 2021 г., гость [DOC] Вопросы и решения олимпиады по физике Получение вопросов и решений олимпиады по физике сейчас не является сложным средством. «Концептуальные примеры», «Концепции и расчеты» и «Проверьте свое понимание» помогают учащимся понять принципы физики. Мы очень старались сделать этот сайт самым надежным сайтом вопросов и ответов по физике в Интернете, но ни один сайт не идеален, как мы объясняем в этой заметке.Заметки о пересмотре, ключевые моменты, рабочие листы и вопросы по темам из прошлых статей. Google Класс Facebook Twitter. Получите мгновенный доступ за простой разовый платеж всего в 19 фунтов стерлингов. Наименьшее количество винтовой марли? Скачать MCQ по общим наукам в формате PDF. Расстояние между F B и осью вращения (r BC) = 20 см = 0. Электромеханическая лама. Maharashtra board Книга по физике Solutions создана компанией Найдите полезные вопросы и ответы по физике на Solutioninn. Наименьшее количество штангенциркуля? Ответ Проблемы и решения в медицинской физике Физический мир – Терм I.а. Чтобы облегчить задачу учащимся, Aakash Chemistry Questions — Learn Basic Chemistry Part 1 (1-25). Практика этих вопросов CBSE NCERT Objective MCQ по физике класса 12 с ответами Pdf поможет учащимся быстро повторить все концепции, представленные в каждой главе, и подготовиться к выпускным экзаменам. CBSE 12 Математические решения. Человек должен пройти 50 м на север, 40 м на восток и 20 м на юг, чтобы добраться до поля. Решения содержат интеллектуальные ярлыки для обучения и интеллектуальные методы решения проблем, которые помогут вам значительно повысить общую эффективность и скорость.Скорость звука 340 м/с. Мы предоставляем всем ученикам от 5-го класса до уровня магистра подготовку ко всем экзаменам бесплатно. Мы шаг за шагом предоставляем книги Совета штата Тамилнаду, ответы, руководства по решениям для 12-го, 11-го, 10-го, 9-го, 8-го, 7-го и 6-го, 5-го, 4-го, 3-го, 2-го, … IGCSE Maths, октябрь, ноябрь 2021 г., документ 43, документ и ответы. Твердый шар имеет массу 100 г и радиус 2 см. Ответ (1 из 6): Украсть? Так все делают, верно? Или же — смею сказать — решить их все самостоятельно или, что еще лучше, решить их все с командой друзей, чтобы вы могли проверить свои коллективные ответы и показать ответы, в которых вы не уверены, наставнику? Интернет-игра Whack Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности.университетская физика, 13-е издание, вопросы для обсуждения, ответы pdf Бесплатный доступ к университетской физике, 13-е издание, вопросы для обсуждения … Если у вас есть вопросы по физике, обратитесь за ответами к преподавателям. Вот все вопросы и решения из всех предыдущих разделов. QQT и PASA для объяснения физики AP. Глава 1 Физический мир. (3) больше в системе СИ, чем в системе СГС. Дополнительные вопросы по главам с полными решениями доступны для загрузки на веб-сайте myCBSEguide и в мобильном приложении.Вопросы и ответы по физике A-Level 2020/2021 Все авторские права и права на публикацию принадлежат S-cool. Практикуйте вопросы и ответы по каждой теме. И PDF, и печатные версии этих учебников содержат одни и те же проблемы. Вопросы с бесплатными ответами. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределения баллов. Ситуация такова: большая часть работы была проделана за вас, и в этом случае ваша работа состоит в том, чтобы изучить данные ответы и использовать их в качестве шаблона и руководства для ответов, которые вы даете.Физика ХЛ. Понятия физики четко обсуждаются и подчеркиваются. Все мои решения для AP Physics 1 Вопросы с бесплатным ответом. 25 А. Описание. HSC Physics MCQ Вопрос с ответом. (a) Выразите величину ускорения свободного падения на поверхности Планеты Z через ускорение свободного падения на поверхности Земли, g g g. Глава 3 Теплофизика. Количество работ: На экзамене 2 работы (физика, химия и математика). Время: Каждая работа длится 2 часа 30 минут или 150 минут.Общее время плейлиста: 269 минут. Физика HL Paper 2 Solutions; Physics SL Paper 2 Solutions; Бумага 3.0), а второй камень менее плотный, хотя и весит больше, потому что его плотность всего 2. Фогт (распродано). Выберите свой вопрос C Long. (б) расстояние. Охвачены все основные темы A Level Math. Спектроскоп… Научная чаша ФИЗИКА Физика – 3 ФИЗ-91; Множественный выбор: маятник, подвешенный к потолку железнодорожного вагона, висит под углом 10 градусов вправо от вертикали.Упражнения и решения. Б: 60 км. Он обеспечивает актуальный, краткий обзор основных тем в физике материи, от атомов и молекул до твердых тел, включая элементы статистической механики. Вопрос: Автомобиль проехал 80 км на юг. переменный ток Пересмотр НОВОГО курса математики уровня A. Развернуть все 3. Необходимо иметь очень четкое представление о понятиях, упомянутых в главе. Источники. Вопросы 2 и 3 представляют собой длинные вопросы со свободным ответом, на каждый из которых требуется около 25 минут, и каждый оценивается в 12 баллов.Резистор 2 (R2) = … Опытные преподаватели SamacheerKalvi. Пожалуйста, скажите, что вопросы и решения олимпиады по физике являются общеучебными вопросами шестого класса. Вопросы по физике, проблемы магнетизма и решения последних десяти лет. Проблемы динамики. Учебники по оптике. с решением в примере работа мощность энергия Решения NCERT для 12 класса Физика является лучшим учебным материалом для учащихся, которые затрудняются ответить на вопросы из учебника.Поскольку у нас есть график смещения-времени, используйте отношение смещения-времени, а. Resnick Halliday Physics Volume 1 Solutions подробно охватывает все концепции всех глав и дает ответы на все вопросы упражнений простым для понимания, точным и точным образом. Это важно для всех учеников, которые сейчас учатся в 8 классе. Законы движения Ньютона. Вопросы и ответы. Том 2 посвящен термодинамике, электричеству и магнетизму, а том 3 посвящен оптике и современной физике. Общее время плейлиста: 248 минут.1. PDF-книга «Уровень викторины по физике» помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. 2 метра. A Level Physics Вопросы и ответы с несколькими вариантами ответов Загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по физике 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. В этой главе мы будем изучать, как все работает и почему… Читать вопросы и решения онлайн-олимпиады по физике NEET Physics Важные вопросы с решениями Содержание еще не загружено.ХИМИЯ КЛАСС 12 ОЧЕНЬ КОРОТКИЕ ВОПРОСЫ. 5 часов назад · Спасибо за ответ на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос. ICSE Solutions Селина ICSE Solutions ML Aggarwal Solutions. Опишите физику. Тип вопросов: Все вопросы в экзамене относятся к типу MCQ. Опубликовано администратором bestfreepapers 18 декабря 2019 г. 18 декабря 2019 г. Включены бесплатные вопросы и задачи, связанные с тестом SAT, а также учебные пособия по прямолинейному движению с постоянной скоростью или равномерным ускорением.HSC Physics 1st MCQ Вопрос с ответом 2021. Вопрос 1. Решения HC Verma по главам — … Physics 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Силы и движение (динамика) (раунд 1) pdf. org/pdf/ap-2020exam-sample … 2 СОДЕРЖАНИЕ M. Гарантированные вопросы для получения отличных оценок. Здесь мы предлагаем решения для всех глав учебника по физике ICSE для 8-го класса средней школы Селины для учащихся.MIT – Массачусетский технологический институт PG TRB Типовые экзаменационные вопросы с ответами по физике, химии, ботанике, зоологии, истории, географии, домоводству, информатике, экономике, торговле, математике, тамильскому языку, английскому языку и индийской культуре. ТМ. Ящики для математических навыков,… Основная университетская физика: Том 1 (3-е издание) Вольфсон, Ричард Издатель Pearson ISBN 978-0-32199-372-4 Вопросы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Physics 1120 : Простые решения гармонического движения 1. Реальные приложения также включены, поскольку они показывают, как эти концепции в физике используются в инженерных системах… Вопросы физики Когда свет от звезды распространяется и ослабевает, образуются ли промежутки между фотонами? Может ли огонь иметь тень? Может ли воздух создавать тени? Можно ли создать золото из других … См. решение Решения для вопросов по физике в средней школе Решение для задачи № 1 № 1840 м. Решения по физике для Резника Холлидея Уокера, том 1 Глава 1 «Измерение» содержит одно упражнение, которое разделено на 4 модуля и содержит в общей сложности 60 вопросов. Через 7 секунд парашютист упал с высоты 240 метров. Глава 1 Измерение. MeritNotes предоставляет только вопросы и ответы Samacheer Kalvi из стандартных материалов с 6-го по 12-е, вопросник за предыдущий год и… Получить учебники Государственного совета Тамилнаду. Тамильская среда и английская среда на SamacheerKalvi.Электродинамика и схемы (раунд 1) pdf. Курсы ревизии. Общее количество вопросов: В каждой работе 120 вопросов. Наши репетиторы по физике помогли нам составить это для наших учеников 10 класса. Он неразрывно связан с каждым видом деятельности в нашей повседневной жизни. В каждой главе есть около 4-5 наборов решенных дополнительных вопросов по физике. к. Том 1 охватывает механику, звук, колебания и волны. Энергия и движение (кинетика) (раунд 1) pdf. Книга MCQ по физике для 10 класса, краткое учебное пособие из учебников и конспектов лекций содержит практические экзаменационные тесты.Банки решений. эмигрант Результирующий вектор — это вектор, полученный в результате сложения двух или более векторов. Теперь мы достигли еще одной важной вехи, предоставив всем учащимся школьного уровня ответы на вопросы, ориентированные на подготовку к экзамену, для всех студентов, изучающих естественные науки и искусство. Физика HL Paper 3 Solutions; Physics SL Paper 3 Solutions; ИА и ЭЭ; Онлайн MCQ. Получите доступ к сотням дополнительных видеороликов, охватывающих весь курс физики уровня A. Проверьте программу NEET по физике. Наша функция вздора показывает, насколько шатки многие другие сайты.Электронная библиотечная олимпиада по физике: вопросы и решения. орг. Задача № 1. Глава 3 Движение по прямой. Джелалия, Физика Международная система единиц Чтобы представить результат измерения определенной физической величины, необходимо определить единицу измерения. (2) не зависит от метода измерения. A 1. Движение класса 9 Важные вопросы: Решения Важные вопросы Примечания Решения NCERT. Преимущества решений ICSE Class 9 Physics: вопросы и ответы с несколькими вариантами ответов (MCQ) по «Физике — класс 12» (наряду с более чем 1000 MCQ по «Физике — класс 11») сосредоточены на всех областях физики, охватывающих более 200 тем.Скачать электронную книгу «Вопросы и решения по физике твердого тела» физика вещества, от атомов и молекул до твердых тел, включая элементы статистической механики. Уточните и дайте количественную оценку своему ментальному образу проблемы. Лейтон и Рохус Э. А чтобы получить индивидуальные ответы на домашние задания на вопросы по физике как можно скорее, обратитесь к одному из репетиторов здесь, на JustAnswer. Проверьте свои знания по естествознанию, которое включает в себя материю, движение, энергию, силу и поведение в пространстве и времени, в … вопросы и решения олимпиады по физике доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можете получить это мгновенно.О нас. В: Автомобиль проехал 60 км на восток и 90 км на запад. · 3г. Прошлые вопросы олимпиады по физике Мы предоставляем работы прошлого года Вопросы и решения олимпиады по физике (IPhO) от основ до продвижения. Глава 12 Sound Class 9 MCQ Вопросы. Глава 7 Разнообразие живых организмов Класс 9 MCQ. IB Physics HL SL Учебник Вопросы и рабочие ответы К. А. Цокос. Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. Физика – предмет, который очень трудно понять Веб-сайт не работает должным образом.Руководство по решениям на 2011-2018 годы. Получите бесплатно ключевые заметки, вопросы MCQ, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 9. r/IBO. По сравнению с DC Pandey он состоит из меньшего количества вопросов и упражнений. Читать бесплатные вопросы и решения по физике твердого телаФизика твердого телаФизика твердого телаВычислительная физика твердого телаФизика твердого телаФизика твердого телаЗадачи по физике твердого тела с решениямиФизика твердого тела, 1eФизика твердого телаВведение в физику твердого тела, 2-й “Вопросы и ответы по физике для 10 класса” PDF скачать с бесплатный образец теста охватывает вопросы для начинающих и пробные тесты с ключом ответов на вопросы экзаменационной рабочей тетради.ФИЗИКА КЛАСС 11 ВАЖНЫЕ ВОПРОСЫ. Наиболее эффективные методы (для быстрого получения правильных ответов) использовались для решения вопросов IIT JEE. Эти учебники доступны бесплатно по ссылкам ниже. Предполагая, что подъем в гору является положительным направлением, каково среднее значение автомобиля. С помощью этих тщательно подобранных решений NCERT для физики класса 11 все сомнения и вопросы учащегося будут устранены. 3500+ общих научных вопросов на основе NCERT – ответы. Советы Фейнмана по физике Ричарда П.Учащимся предлагается прочитать и загрузить эти учебные вопросы, а CL предоставляет материалы для подготовки к CBSE Physics для учащихся 9-го класса. Присоединяйтесь к Chegg Study и получите: Решения для учебников с пошаговыми инструкциями, созданные экспертами Chegg. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, примеры ответов от экзаменаторов и распределение баллов. . 6. Щелкните здесь, чтобы получить ответы на вопросы о физической скорости. Это означает, что конечный результат составляет всего (!) 14 страниц. Введение в физику Вопросы для упражнений Решения HC Verma Ch-1 Концепция физики Vol-1 для Class-11.9. Студент-физик 525-N стоит на напольных весах в 846-килограммовом (включая студента) лифте, который… учебников, чтобы вы могли уверенно двигаться вперед. Загрузите бесплатные рабочие листы для печати для CBSE Class 9 Physics с важными вопросами по теме, учащиеся должны практиковать рабочие листы NCERT Class 9 Physics, банки вопросов, рабочие тетради и упражнения с решениями, которые помогут им в пересмотре важных концепций. Физика класса 9.Дайте определение равномерному круговому движению и приведите его пример. Электронное письмо. Глава 9 Сила и законы движения Вопросы 9 класса MCQ. физика-олимпиада-вопросы-и-решения 5/8 Скачано с dev1. Вопросы и решения для всех глав JEE Advanced Physics доступны на этой странице, чтобы помочь учащимся ускорить подготовку к вступительному экзамену. Курсы для GCSE, A-level и поступления в университеты. Пуля вылетает из винтовки с начальной скоростью 521 м/с. Часть 1. Упражнения для фейнмановских лекций по физике… Б.HC – VERMA Вопросы и решения Класс 12 Физика Глава – 40: Электромагнитные волны. com предоставляет решения ICSE по физике класса 10 для экзаменов ICSE Board. Попробуйте Numerade бесплатно. 99. Начиная с зубной пасты, используемой по утрам, и заканчивая повседневным использованием Интернета, мобильного телефона и просмотра телевизора, все это плоды олимпиады по физике. Вопросы и решения доступны в нашей коллекции книг, онлайн-доступ к ней установлен как общедоступный, поэтому вы можно получить мгновенно. Чтобы получить высокие баллы в JEE Advanced, необходима регулярная практика, поскольку известно, что уровень сложности JEE… Публикуйте вопросы о домашнем задании и получайте ответы от проверенных наставников круглосуточно и без выходных.5 Сила и движение-I. Примеры вопросов Экзамены AP Physics 1 и AP Physics 2 Вернуться к оглавлению. Неспособность тела самостоятельно изменять свое состояние называется инерцией. HC – VERMA Вопросы и решения Класс 12 Физика Глава – 41: Электрический ток через газы. Биология | Химия. Частица равномерно ускорена из состояния покоя, так что через 10 с она достигла скорости 15 м/с. Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте [email protected].Данные и оценка (раунд 1) pdf. AQA, OCR, Edexcel, WJEC. Решения NCERT для класса 12 по физике Глава 3 Текущие электрические упражнения и дополнительные упражнения в формате PDF скачать бесплатно или использовать в Интернете без загрузки обновлены для академической сессии 2021-2022. Основная цель подготовки решений – облегчить студентам подготовку к экзамену. (7:31) 8 общих рекомендаций для бесплатных ответов любого экзамена по физике AP. Пожалуйста, напишите по адресу school@cbse. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения BSEB Bihar Board 12-го числа по физике Важные вопросы Численные числа являются лучшим ресурсом для учащихся, который помогает в повторении.PANDEY TUTORIAL Последнее обновление: 17 декабря 2021 г. Окончательный ответ представлен в текстовой форме для быстрого ознакомления над каждым видео и красиво отформатирован в виде уравнения, например E = mc 2. Например, если книга лежит на полке, книга продолжает оставаться в стойке до тех пор, пока не будет приложена какая-либо внешняя сила, чтобы удалить или сместить его из исходного положения. (г) масса. Скачать PDF. Опубликовать вопрос. Движение Важные вопросы: решение. IT = I1 = I2 = I3 = 1. Тетрадь для повторения экзамена. Каждый будет состоять из нескольких частей, и части не обязательно будут иметь одинаковый вес.Следовательно, первая порода более плотная, (плотность = 3. На экзамене есть 3 вопроса со свободным ответом, которые считаются 50% от оценки за тест. Существует различие между средней скоростью и величиной средней скорости. Спросите любого физика. вопрос, и эксперт ответит на него всего за 30 минут Отчет об экзамене VCE по физике за 2017 г. (с изменениями от 30 октября 2019 г.) Экзамены, относящиеся к предыдущим планам исследования Учащиеся и преподаватели должны учитывать, что с введением нового плана исследования экзамены не обязательно являются руководством к текущему экзамену VCE для этого исследования.RT = 100 Ом. 5 г/см 3 ) Задача № 2. Посетите официальный сайт CISCE для получения подробной информации о ISC Board Class-11 Physics. Вопросы UGC NET за предыдущие годы с решениями по всем предметам: Вопросы UGC NET за предыдущий год играют важную роль в подготовке к экзамену. Окленд. Почему движение называется ускоренным? Sol:-Равномерное круговое движение можно описать как движение объекта по круговой траектории с постоянной скоростью. Проект руководства к предстоящему конкурсу по физике: F = ma Contests.Студенты могут получить подробное объяснение ответов на все вопросы, включенные в концепцию «Current Electricity» главы 3, разработанную NCERT Solutions of 12th Physics. лекдем. NEET Практические задания NEET Вопросы по физике, химии, биологии Вопросы о скорости и скорости. В этой статье мы представили важные вопросы по главам, которые будут полезны при подготовке к NEET. IOE, TU, вопросы и решения 2067 Ashadh to 2071 Magh Engineering Physics (для BE … AP Physics 1 – 2020 Примеры экзаменационных вопросов Полное решениеСсылка на вопросhttps://apcentral.Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи. Вопрос 1 (4 балла) Планета Z имеет вдвое большую массу и вдвое больший радиус Земли. Скорость и скорость. Решение банка вопросов по физике для 12-го класса Английский, средний 2022 г. Полное решение для банка вопросов по физике для 12-го класса pdf скачатьОб этом видеоЯвляется ли видео мной apko все решения для HSC Physics Module 8 Questions. Астрономия (раунд 1) pdf. Практические эксперименты. х) Вагон движется с ускорением влево.Часть 2. Известно: вращение оси в точке C. 2 Оглавление Решения для основ физики Холлидей и Резник Получите доступ ко всем ответам и пошаговым видеообъяснениям к этой книге и еще к 1700 книгам. Отвечать. Своими словами точно сформулируйте вопрос, на который нужно ответить, в терминах, которые вы можете рассчитать. 11 строк Ответ: v i = 5. MyCBSEGuide — единственное подлинное приложение для вопросов MCQ. Выберите свой C CL предоставляет материалы для подготовки к CBSE Physics для учащихся 10 класса. Практика: вопросы скорости и скорости.IT = 125 В/100 Ом. College Physics Answers предлагает видеоролики с решениями задач в конце глав в учебниках, опубликованных OpenStax, под названием «College Physics» и «College Physics для курсов AP». Автомобиль катится задним ходом вниз по склону со скоростью 3. Выберите решение C View Physics-Solution. Помимо этого, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, практические вопросы, серию тестов для JEE Main, JEE Advanced и NEET, важные вопросы по физике, химии, математике и биологии и многое другое.В целом, кандидаты найдут широкий спектр вопросов MCQ для класса 9 по научной физике с ответами. 138 вопросов НМ. Основные вопросы suvat Не забывайте всегда записывать известные значения s, u, v, a и t и решать, какое направление положительное, а какое отрицательное. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают решение задач на упражнения. Получите вопросы и ответы по физике. Учебник по доске Махараштры Решения. Редакция. Большое спасибо, сэр, за ваш ценный… Найдите пошаговые решения и ответы на Основы физики – 9781118230718, а также тысячи учебников, чтобы вы могли уверенно двигаться вперед.NEET Physics Важные вопросы с решениями Физика помогает понять повседневные действия, такие как ответы на такие вопросы, как почему небо голубое, что заставляет нас легко ходить по дорогам, почему так важно иметь луну и т. д. Все ответы были подготовлены опытными учителями что гарантирует, что все решения верны, а вопросы решены таким образом, чтобы учащиеся, обращаясь к этим ответам для 9 класса ICSE, могли получить хорошие оценки. Наши книжные серверы сохраняют информацию в нескольких местах, что позволяет сократить время задержки при загрузке любой из наших книг, подобных этой.Этот пример показывает, почему важно быть осторожным и не использовать слова тяжелее/легче, когда вы имеете в виду более или менее основные вопросы JEE по физике за предыдущий год с решениями по «электростатике» V a’ = kQ/a + k(-4Q)/ b V b’ = kQ/b + k(-4Q)/b V a’- V b’ = kQ/a – kQ/b = V a– V b = V Ответ: (b) V Q5: Номинальное напряжение конденсатор с плоскими пластинами на 500 В. Получите бесплатно основные заметки, вопросы о запросах, тесты, образцы документов, решения NCERT, решения NCERT, важные вопросы для 10 человек. Предоставьте подробности и поделитесь своими исследованиями! Но избегайте… Просьб о помощи, разъяснений или ответов на другие ответы.B: 50 км на восток. Как и другие авторы по физике, он также концентрируется на ваших основах физики. IGCSE Maths, октябрь, ноябрь 2021 г., статья 43 статьи и ответы. Таблицы уравнений. Через 2. второе уравнение движения. Категории: Экзаменационные записки. Учебные заметки младшего колледжа. И это решения по главам, в которых вы найдете важные вопросы для экзамена на доске. Глава 11 Работа и энергия Класс 9 Вопросы MCQ. Он содержит более 160 полностью переработанных и дополненных рисунков, иллюстрирующих основные физические концепции и основные 4 МБ.Коробки с математическими навыками, … CBSE Class 12th Решения по математике, биологии, физике и химии приведены ниже. Вопросы публикуются анонимно и могут быть сделаны на 100% приватными. Теги: h3 Физика JC 1 JC 2 Школьные заметки. г. NIOS Class 12th Physics 150+ важных вопросов с решениями (полная программа Nios) Маниш Верма. PDF-файл «Рабочие листы по физике для 10-го класса» с ответами посвящен решению задач на упражнениях 5 часов назад · Спасибо за предоставление ответа на Physics Stack Exchange! Пожалуйста, обязательно ответьте на вопрос.уровень 1. С 1998 года добровольцы из Департамента физики Университета Иллинойса в рамках информационно-пропагандистской программы Physics Van ответили на 8444 вопроса. askIITians также предлагает вам 16 лет IIT JEE с вопросами за предыдущий год. Решения NCERT для физики 12-го класса Глава 3 Current Electricity — лучший учебный материал, который поможет вам получить больше баллов на экзаменах по физике 12-го класса, а также на любых вступительных экзаменах. «Рабочие листы по физике для 10-го класса» в формате PDF с ответами охватывают контрольные карточки для решения задач по математике на уровне A Level.Банки решений для математики уровня A. 5 с, машина движется в гору на 4. Делать заметки для главы — хорошая идея, поэтому постарайтесь подготовить рукописные заметки всех важных моментов и формул. Sir Aakash Package Solutions PHYSICS 3000+ Вопросы и решения Больше не доступно на мега-сайте… пожалуйста, повторно загрузите этот файл, но убедитесь, что вы загрузили его на диск Google, потому что мега-сайт автоматически удалит любой файл через 1 месяц… и, если возможно, пожалуйста ответьте мне, когда контент будет доступен….Глава 15 Улучшение продовольственных ресурсов Класс 9 MCQ. 10 2 м/с 8. (в) интенсивность солнечного света. В TopperLearning наши опытные преподаватели подготовили пошаговые модельные решения для вопросов из учебника и образцов работ в соответствии с последней программой ICSE Class 8 Physics. В этом посте я предоставил MCQ по физике по главам, вопросы на основе конкретных случаев и A / R (утверждение и причина) для класса 12 сессии 2021-22 с полными решениями. Конкурсы по физике Задачи и решения по механике Эта книга представляет собой сборник задач по физике, полезных для подготовки к олимпиадам и конкурсам.8 общих рекомендаций для FRQ любого экзамена по физике AP. Подробные решения типовых вопросов с несколькими вариантами ответов. Задачи DC Pandey по общей физике охватывают самый продвинутый уровень вопросов для класса 7, который действительно проверяет ваши… Решения ICSE для физики класса 10. Коробки математических навыков, … HC VERMA Solutions for Class 11 Physics Chapter 3 – Rest and Motion Kinematics. 5 м/с. Если его уши находятся на расстоянии всего 2 см друг от друга, это означает, что он должен уметь различать звуки со временем Репетитор по физике и математике.Здесь все вопросы решаются с подробным объяснением и доступны для бесплатной проверки. Упражнения по вводной физике Роберта Б. Название: Microsoft PowerPoint – Глава 5 [Режим совместимости] Автор: Мукеш Дхамала Дата создания: 08.02.2011 16:38:07 Мои студенты, эта статья поможет вам узнать о практической физике Вопросы Viva 2021, которые задают на экзаменах с ответами для 11-го и 12-го классов. Пошаговые решения проблем, более 34 000 ISBN Найдите решения в учебниках.0 разделов 97 вопросов +198 еще. Свяжитесь со мной. Книга MCQ по физике в колледже, краткое учебное пособие из учебников и примечаний к пересмотру, охватывает вопросы экзаменационной практики. Загрузите приложение eSaral, чтобы получить бесплатные учебные материалы и видеоуроки. Toppr бесплатно предоставляет учебные материалы, более 1000 часов видеолекций, вопросы с вопросами за последние 10 лет. 0. О нас Пресса Авторские права Свяжитесь с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Свяжитесь с нами Создатели Для решения PHYSICS решения И ВОПРОСЫ:1.Публикуйте свои домашние задания по физике и получайте ответы от квалифицированных преподавателей. Определите физические концепции и подходы, которые могут быть полезны для достижения решения. Документы CBSE, вопросы, ответы, блог MCQ содержат решения NCERT, CBSE, NTSE, учебные материалы олимпиады, типовые тестовые документы, важные вопросы и ответы, заданные на экзаменах CBSE. Приведите пример, иллюстрирующий разницу между этими двумя величинами. Q 5: 11 класс Физика Глава 1 Измерения Краткие вопросы Ответы. Найдите его ускорение и путь, который он преодолел.Жучок находился в 17 метрах. Посмотреть продукт. Дешевле купить кофе в Нью-Йорке (по крайней мере, по учебнику физики, т.е. какой из следующих ответов мог бы объяснить это явление? w) Вагон покоится. В физической лаборатории Эрнесто и Аманда применяют 87. Bihar Board 12th Physics Numericals Важные вопросы с решениями. Решения ICSE для классов с 6 по 10 – бесплатные решения для учебников ICSE Решения ICSE для класса 10. Глава 10 Гравитация Класс 9 Вопросы MCQ. с использованием решений NCERT по физике для физики класса 11: решения по главам.CBSE 12 Образец документа 2022 г. для вопросов MCQ для класса 9 по научной биологии с ответами. Ток постоянен через последовательно соединенные резисторы. Глава 2 Механика. В 1960 году международный комитет согласовал систему стандартов, названную системой СИ. Включает в себя полные решения и отчеты о результатах. Упражнения, размещенные на этом сайте, взяты из четырех источников: Гуру. Мы предоставляем шаг за шагом Samagra Kerala State Syllabus Учебники Решения Ответы Руководства для классов 12, 11, 10, 9, 8, 7 и 6, 5, 4, 3, 2, 1 стандарт… ответы.(1:03:04) Решения All Mechanics с множественным выбором. Решение помогает студентам получить четкое представление о концепции и готовит их к экзаменам. Подробно обсуждаются понятия перемещения, расстояния, скорости, скорости, ускорения. CBSE 12 Химические решения. Загрузите приложение Physics bro (ссылка ниже)2. Ответ: б) расстояние. Уровни GCE «A» h3 Physics 10-летняя серия Эксклюзивные решения от SAJC и JJC Этот пакет состоит из: 2007 г. Решение по физике уровня h3 (SAJC) 2008 г. Решение по физике уровня h3 (SAJC) 2011 г. Решение по физике уровня h3 (SAJC) 2013 A Level h3 Physics Вопросы и решения (JJC) 2014 A Level h3 Physics Вопросы и решения (JJC) 2016 A Уровень h3 Physics Solutions (SAJC) Получите полные решения по всем темам физики класса 8 ICSE на нашем учебном портале.nz/) кандидатами в учителя в рамках курсов по методам физики EDCP 357 в UBC. В приведенной выше ссылке есть документ 43 и решения / ответы на вопросы (которые я написал), и это не официально от cie. APlusTopper. DC Pandey является одним из лучших и предлагает книги для продвинутых вопросов, связанных с физикой. 8. Важный вопрос по физике 12 и 11 классов. (5) Ценное дополнение к назначенному учебнику в любом вводном курсе механики. 100 м/с 9 ч3 Физика Актуальные вопросы и ответы.Минимум ₹ 299. Вы не можете в одиночку ходить, когда храните книги или библиотеку или берете взаймы у своих подключений, чтобы просмотреть решения PM_TB_C12. 100 м; 101 м 4. 0. ПРОВЕРЬТЕ СЕБЯ ОТРАБОТАННОЕ РЕШЕНИЕ. PDF-книга “O Level Physics Quiz” помогает практиковать контрольные вопросы из заметок по подготовке к экзамену. ком. HC – VERMA Вопросы и решения Класс 12 Глава физики – … Математика IGCSE Октябрь ноябрь 2021 г., статья 43, статья и ответы. Просто обратите внимание, что некоторые решения неверны в цоко. 1018 м 3. Оставить комментарий / Решенные задачи по фундаментальной физике / Сан Лохат.Из приведенных выше примеров становится ясно, что физика концентрируется на объяснении поведения вопросов и решений олимпиады по физике. Решения исходят от национальной тренировочной команды и членов национальной команды, и их замечательные решения составляют особенность этой книги. Где скачать примеры вопросов и решений олимпиады по физике, примечания и ссылки для дальнейшего чтения, чтобы улучшить понимание. Некоторые эксперты-предметники дают пошаговые ответы даже на самые сложные вопросы по физике 9 класса CBSE, которые очень часто встречаются на экзаменах.Отдельные экзамены прошлых лет и их решения доступны в … <p>От того, почему мы путешествуем вперед во времени, до того, как велосипеды вообще путешествуют вперед, мы задаем большие и малые вопросы, которые наши лучшие умы не могут объяснить<p> /p> Добавьте движение грузовика к графику, который вы нарисовали для вопроса № 4. В нем представлено более 160 полностью переработанных материалов Physics 11E, которые дают учащимся навыки, необходимые им для достижения успеха в этом курсе, уделяя особое внимание концептуальному пониманию; решение проблем; и предоставление реальных приложений и релевантности.б. Его диэлектрик выдерживает максимальное электрическое поле 106 В/м. «Задача о лифте» — классическая задача в физике. 8 м/с2. Q1. Величина любой физической величины: (1) зависит от метода измерения. 1 секунда туда и обратно, должно быть, звук 0. Физика Практические вопросы Viva с ответами для 11-го и 12-го класса. На стержень действуют три силы: F A = F C = 10 Н и F B = 20 Н, как показано на рисунке ниже. Здесь вы найдете упражнения по физике и математике, чтобы проверить свою смекалку.Расчет средней скорости и скорость отредактированы. Нарисуйте любые необходимые схемы с системами координат, соответствующими системе координат. Решения здесь несколько кратки, так как предназначены для преподавателя, а не для студента. Магнетизм (раунд 1) pdf. И вам, ребята, будет очень легко пересматривать их. «Рабочие листы по физике для 10-го класса» PDF с ответами посвящены решению задачи на упражнение Вопрос 20. 1) Когда пучок белых лучей рассеивается призмой, какой цвет будет преломляться в большей степени? Ответ: Фиолетовый.Решения HC Verma для класса 11 состоят в общей сложности из 22 глав. Эти вопросы IIT JEE с решениями являются вашим лучшим ресурсом для решения реальных практических задач. Пошаговые решения не требуют пояснений по своей природе. Выберите C-решения для развития чувства Вопросы, управляемые задачи и вопросы и задачи для развития чувства 1. 75-килограммовая частица движется как функция времени следующим образом: «Вопросы и ответы на викторину по физике для 10-го класса» Загрузка в формате PDF с бесплатными образцами тестовых обложек вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге.Q2. Бесплатные решения вопросов из учебника физики cbse class 9 не только проясняют ваши концепции, но и помогают вам сэкономить драгоценное время, которое вы можете потратить в другом месте. Вопрос 1 . Размышления об ЕГЭ 2015. 2) Современная атомная единица массы основана на ____ Ответ: Углерод-12. Фейнман, Майкл А. Проверьте здесь решения NCERT class 12. 105 с 6. Вопросы по физике MCQ | Chapter Wise Physics Questions Решения дают ответы на все сложные вопросы, а также помогают кандидатам получить четкое представление обо всех важных темах.Закон параллелограмма вектора гласит, что «Если векторы, действующие одновременно в точке как по направлению, так и по величине, представлены смежными сторонами параллелограмма, проведенного из точки, то равнодействующая векторов как по величине, так и по направлению представлена … NCERT Решения для физики класса 12 включают все вопросы, представленные в книгах NCERT для предмета физики 12-го класса. 03 м/с и время зависания = 1. CBSE, NCERT, JEE Main, NEET-UG, NDA, экзаменационные работы, банк вопросов, решения NCERT, образцы, примечания к изменениям, бесплатные видео, тесты MCQ и многое другое.Автономные приложения и решения CBSE и UP Board обновляются на основе последних книг NCERT на 2021–2022 годы. Выберите свои решения C для выпуска экзамена AP Physics C 1998 года. Это полезно, если вы находитесь в библиотеке или у вас медленное интернет-соединение. CBSE 12 Биологические решения. Поскольку вопросы основаны на работах предыдущего года, есть вероятность, что кандидаты найдут много вопросов из PDF-файла «Вопросы по физике» с решением в SSC CGL Tier 1 2017. pdf от A EN CREATIVE W в Инженерном колледже Катманду.Если вы используете вспомогательные технологии и вам нужна помощь в доступе к этим PDF-файлам в другом формате, обратитесь в Службу поддержки учащихся с ограниченными возможностями по телефону 212-713-8333 или по электронной почте ssd@info. C: 80 км к югу. Решение на время. в воздухе погружают в воду. Мы предоставляем пошаговые решения для ICSE Physics Class 10 Solutions Pdf. Известно: Резистор 1 (R1) = 2 Ом. cs. умд. … Для решений ФИЗИКИ решения И ВОПРОСЫ:1. Загрузите вопросы с бесплатными ответами из прошлых экзаменов, а также рекомендации по подсчету баллов, образцы ответов от сдающих экзамены и распределение баллов.6 Force and Motion-II Источник: веб-сайт NESA. а = 2∆ с / t2. Покажите свою работу для каждой части в отведенном месте после этой части. 11 КЛАСС ФИЗИКА Длинный вывод вопросов и ответов. Твердый шар имеет массу 50 грамм и объем 20 см 3 . Вы можете найти ответ на свой вопрос «Где сейчас я могу найти самую надежную профессиональную и быструю помощь для моего задания по физике?» на вашем сайте тоже. 0 м/с, когда водитель запускает двигатель. Настоящее руководство по решениям к книге не содержит ответов на вопросы для обсуждения.Расстояние между F C и осью задач плотности. Физика 11E дает учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. 10 2 м 2. Пенджабский учебник используется в Лахорском совете, Гуджранвальском совете, Сахивальском совете, Равалпиндиском совете, Фейсалабадском совете, Мултанском совете, Бахавалпурском совете и т. д. Задача по физике Вопрос 24: Решения. Предоставьте подробную информацию о том, в чем вам нужна помощь, а также о бюджете и сроках.«Вопросы и ответы на викторину по физике для 10-го класса» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ответами на вопросы из рабочей тетради. Эта книга будет полезна любителям математики, учащимся средних классов, участвующим в математических соревнованиях, тренерам по преподаванию математики и учителям Общая физика Основной целью физики является понимание того, как ведет себя Вселенная. Физика является одним из старейших академических принципов. Глава 8 Motion Class 9 MCQ Вопросы. а = -9. Если вы стремитесь к AIR от 1 до 1 00 000 в JEE Main, эта книга для вас.Глава 5 Основная единица жизни Класс 9 MCQ. Единицами длины, массы и времени в системе СИ являются метр (м), килограмм (кг) и секунда (с). Магнетизм, термодинамика, механика твердых тел и жидкостей и т. д. Если объект тяжелее, сила тяжести больше, но поскольку он имеет большую массу, ускорение такое же, поэтому он движется с той же скоростью (если пренебречь сопротивлением воздуха). .Фрикционные вопросы и ответы. Схема выставления оценок: Схема выставления оценок: +4 за правильные ответы и -1 за вопросы свободной практики для AP Physics 1 – Удельное сопротивление. 10 обязательных вопросов к модулю физики HSC 5. Коробки математических навыков, … вопросы-и-решения-физики-олимпиады 1/8 Загружено с сайта dev1. Вы можете найти ответы на множество вопросов, таких как «в чем причина мерцания звезд», почему мы не падаем, когда идем по полу, почему мы стремимся двигаться вперед, когда автобус внезапно останавливается и т. д.150+ важных вопросов по физике с ответами (Золотая серия) Маниша Вермы. В этом буклете содержатся все экзаменационные вопросы раздела A, которые появились в решениях Loaving Cert AP Physics 1 FRQ. Этот учебник подчеркивает связь между теорией… Физика объясняет логику вещей, которые мы делаем в нашей повседневной жизни, которые часто остаются без ответа. Подробные решения для каждого вопроса были подготовлены профильными экспертами BYJU’S. C. Я спрашивал других людей об ответах на вопросы, в которых я не знал/не был уверен.Решения создаются комплексно, чтобы помочь учащимся быстрее понять концепции. Решения ICSE для математики класса 10; Решения ICSE для физики класса 10; Решения ICSE для химии класса 10; Решения ICSE для 10-го класса В конце каждой главы университетского учебника по физике есть масса вопросов для обсуждения, и я не могу найти для них руководства по решению. Здесь мы предоставили TN State Board New Syllabus Samacheer Kalvi 12th Std Physics… Решения NCERT для класса 9 по физике охватывают все 5 глав предписанной программы по физике и являются лучшей альтернативой.Учащиеся могут обратиться к экзаменационным вопросам ICSE Class 10 Physics Board по главам и решениям, которые были подготовлены для учащихся ICSE Class 10 на основе последней программы и руководств по экзаменам, выпущенных ICSE. Мы предоставляем пошаговую программу Samagra Kerala State Syllabus. Учебники. Решения. Ответы. PDF-файл с ответами охватывает основные понятия, теорию и аналитические оценочные тесты.Если мы посмотрим на второй закон Ньютона, F = ma. Решения NCERT для физики класса 9 разбивают решения на подробные шаги и подробно объясняют ответ, что помогает вам понять схему вопросов и способ повысить свой балл на экзаменах. Решение практических заданий главы 1 Введение в физику Верма Х.С. Понятие физики. Развернуть все Благодаря нашим многочисленным преимуществам онлайн-помощи по физике, которые мы предлагаем вам, многие учащиеся нашли лучшие ответы и решения своих проблем с домашними заданиями по физике.ПОДДЕРЖКА НАЦИОНАЛЬНОЙ КВАЛИФИКАЦИОННОЙ УЧЕБНОЙ ПРОГРАММЫ Физика Электромагнетизм Вопросы и решения Джеймс Пейдж [ПОСМОТРЕННАЯ ПРОДВИНУТАЯ ВЫСШАЯ] Вопрос НазваниеРабочие задачи Следующие вопросы были составлены из набора вопросов, отправленных на PeerWise (https://peerwise. Трек постепенно увеличивает скорость, поскольку это закон Кирхгофа – проблемы и решения. Вопросы и решения. Световой год – это единица. Премиум-план. Они могут ссылаться на эти решения, когда решают вопросы из учебника.Впервые созданный в 2000 году и обновленный в 2013, 2015 и 2020 годах. Лифт (с вами внутри!) начинает падать! Возможно, у вас есть время на последний вопрос. В решении Aakash HC Verma по физике для 11 класса мы рассмотрели каждую главу и дали ответы на каждый вопрос. IT = 1. edu – Средство демонстрации лекций UMD «Вопросы и ответы викторины по физике для 10-го класса» Загрузка в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих и пробные тесты с ключом ответов к экзаменационной книге. Решения ICSE для всех вопросов решаются и объясняются опытными учителями в соответствии с рекомендациями совета ICSE.JustAnswer позволяет легко получить ответы на такие вопросы по физике, как эти: Вопрос по физике: Япония создала магнитное поле в 50 миллионов раз сильнее земного. Интернет-магазин физики. Вы можете повысить свою концепцию до высокого уровня, если сможете решить все предыдущие страницы 1/3. 2. Вопросы и ответы по общей физике – изучите основы физики, часть 3 (51-75) 52) Пара величин, имеющих одинаковые размерности, это (а) модуль Юнга и энергия (б) импульс и поверхностное натяжение (в) угловой момент и работа. г) работу и крутящий момент Ответ: D.В этой книге охвачена полная программа Ниоса по физике (книга 1 + 2) с гарантированными ответами на вопросы для получения отличных оценок. Площадь пластины 10–4 1930 видеорешений для всех обычных задач в 7-м издании Джанколи и 1681 решение для большинства обычных задач в 6-м издании. Решения моделируют способ решения данного вопроса, но никоим образом не являются единственно возможными решениями. 53) Как воспроизводится звук на флейте? Ответ: Вибрацией воздушного столба. Эти заметки по физике для 9-го класса соответствуют новой программе (2013 г.) Совета по учебникам Пенджаба.Больше внимания уделяется темам физики, включенным в предмет физики SAT с сотнями задач с подробными решениями. ∆s = v0t + ½ at2. 10 2 м 7. Если R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, определить электрический ток, протекающий в цепи ниже. Электрические заряды и поля Вопросы MCQ класса 12. У нас есть более 5 000 000 вопросов CBSE MCQ для классов 12, 11, 10, 9, 8, 7, 6, 5. Вопрос касается плотности, то есть отношения массы к объему. Электростатический потенциал и класс емкости 12 вопросов MCQ.Мы надеемся, что данные NCERT MCQ Questions for Class 11 Physics Chapter 2 Units and Measurements with Answers Pdf free download помогут вам. Загрузите решения по ссылке, указанной на этом сайте. 03 с (кроме спортивных роликов) См. решение ниже. школьная доска. Краткое руководство по физике уровня O содержит 900 вербальных, количественных и аналитических рассуждений прошлых вопросов, решенных MCQ. Приведенные ниже вопросы представляют собой несколько важных вопросов по физике для 12-го класса, а также важные вопросы по физике для 11-го класса.Эти важные вопросы также могут помочь учащимся по предмету 1 по теории физики. Вопросы с одной оценкой, заданные в ответах на следующие вопросы, и вопросы MCQ на экзаменах по физике. Ящики с математическими навыками, … Selina Concise Physics Class 8 ICSE Solutions даны учащимся, чтобы они могли узнать ответы на вопросы, если они не смогут их найти. С: 90 км. h3 физика актуальные вопросы и ответы Скачать. Глава 6 Ткани класса 9 MCQ. Особенности: Объединяет концепции и помогает в понимании и применении теоретических концепций медицинской физики Помогает лекторам и инструкторам в настройке вопросы в тесте.Кандидаты должны пройти через эти решения, чтобы развить улучшенные навыки решения проблем. В вопросах упражнения представлены различные единицы измерения, такие как подробные решения DC Pandey для физики. онлайн или WhatsApp по адресу 8905629969 Международная олимпиада по физике (IPhO) Прошлые работы… Решения NCERT, класс 9, все предметы решаются с сохранением различных параметров. Вы можете скачать вопросы по физике в формате PDF с решением, чтобы получить все важные вопросы в одном месте. Когда вы будете проходить тест, вы будете отмечать свои ответы на отдельном листе ответов, оцениваемом машиной.Выберите C Просмотреть решенные вопросы/ответы и решенные числовые задачи по физике Учебник Пенджаба 9-го класса. Гуру создал Совет штата Тамилнаду Samacheer Kalvi 12th Physics Book Solutions Руководство по ответам Pdf Бесплатная загрузка Тома 1 и Тома 2 на английском языке Medium и Tamil Medium являются частью Samacheer Kalvi 12th Books Solutions. Начните вводить свой вопрос Закрыть. Каково его смещение? Ответ: 20 км к югу. «Вопросы и ответы на викторину по физике в колледже» в формате PDF с бесплатным образцом теста охватывает вопросы для начинающих, экзаменационную тетрадь и подготовку к сертификационному экзамену с ключом ответа.D: 160 км к северу —– 2. CBSE недавно включил эти типы MCQ, основанные на конкретных случаях и… Физика 11E предоставляет учащимся навыки, необходимые им для достижения успеха в этом курсе, сосредоточив внимание на концептуальном понимании; решение проблем; и предоставление реальных приложений и релевантности. Падение напряжения может… Вопросы и ответы для NEET 2022, приведенные ниже, были подготовлены К. Лалитом Кумаром, Медицинской академией Шри Гаятри. В этой книге Ниос покрывает полную программу физики (Книга 1 + 2) с решением.ЭГ +198 больше. физика. Здесь мы предлагаем решения для всех глав учебника NCERT Physics Class 11 для студентов. Какова плотность? (Ответ: 2. Глава 4 Движение в плоскости. CBSE 12 Physics Solutions. D: 150 км CBSE Class 9 – Physics – Work (Вопросы и ответы) #class9Science #WorkPowerEnergy #eduvictors. Вопрос: Решение: 1: Часть (a) : Для поясняющих вопросов учащиеся должны использовать структуру генерального директора (причина, следствие, результат), чтобы дать логичный и последовательный ответ.45 описания курса физики AP. Приведите пример (но не из текста) устройства, используемого для измерения времени, и определите, какое изменение в этом устройстве указывает на изменение времени. Прошлые экзамены. Общее время тестирования составляет два часа пятьдесят минут; разделов с отдельным временем нет. Глава 4 Волны. Эти рабочие листы для 9 класса по физике, классные задания и практические тесты… Вопросы 1-го раунда BPhO. Все экзаменационные комиссии e. Смещение от времени и пример скорости. Найдите время, когда автомобиль проехал мимо грузовика.Включены задачи по физике с решениями и учебники с полными пояснениями. Это текущий выбранный элемент. Второй метод использует график и уравнение движения. 05 секунд, чтобы добраться от летучей мыши до жука. Это неофициальный сабреддит для всего, что касается Международного бакалавриата, академической аттестации, выдаваемой учащимся средних школ со всего мира после двух энергичных лет обучения, завершившихся сложными задачами. Кроме того, eSaral также предлагает решения NCERT, вопросы предыдущего года для JEE Main и Advance, Практические вопросы, Серия тестов для JEE Main, JEE Advanced и NEET, Важные вопросы физики, химии, математики и биологии и многое другое.Решения ICSE класса 10 дают пошаговые ответы на все вопросы, заданные в учебниках ICSE. Перейти в раздел ИЗУЧЕНИЕ МАТЕРИАЛОВ (в верхнем левом углу)3. Глава 2 Единицы и измерения. Производные, упомянутые в NCERT, включают … Олимпиаду по естествознанию, Олимпиаду по математике, Олимпиаду по программированию, … Получите бесплатные вопросы и решения олимпиады по физике. Краткий ответ для объяснения физики AP. Наука – спутник нашей повседневной жизни. На этой странице я собрал коллекцию задач на плотность, чтобы помочь вам лучше понять вычисления, связанные с плотностью.