Физика_Ответы
ТЗ 1 КТ-1
Основными механическими единицами измерения в системе СИ являются
…
2) 1 м, 1 кг, 1 с.
ТЗ 2 КТ-2
Плотностью вещества называется величина, определяемая… 5) массой вещества в единице объема
ТЗ 3 КТ- 3
Массой тела называется величина, … 5) определяющая инерционные и гравитационные свойства тел.
ТЗ 4 КТ-1
Перемещениеэто …
.
3) расстояние между пунктами А и В
ТЗ 5 КТ-2
Основная единица массы в системе СИ…
3) килограмм
ТЗ 6 КТ-3
Векторные физические величины … 2) ускорение
ТЗ 7 КТ-1
Инерциальной нельзя считать систему отсчета, в которой … 3) поезд движется равноускоренно.
ТЗ 8 КТ-2
Угловым ускорением называется… 3) изменения угловой скорости в единицу времени.
ТЗ 9 КТ-3
Вращательное движение точки – это … 3) движение по окружности
ТЗ 10 КТ-1
Вектор скорости – это … 2) перемещение в единицу времени
ТЗ 11 КТ-2
Механическое движение различается по форме на … 1) прямолинейное и криволинейное
ТЗ 12 КТ-3
Мгновенная скорость материальной точки – …
|
| 2 |
1) | векторная величина первой | производной радиус–вектора по |
времени |
| |
ТЗ 13 | КТ-1 |
|
Ускорение материальной точки – … |
| |
1) | первая производная скорости по времени | |
ТЗ 14 | КТ-2 |
|
Тангенциальное ускорение – … |
| |
1) | касательная составляющая вектора ускорения | |
ТЗ 15 | КТ-3 |
|
Модуль перемещения точки равен длине пути. | ||
4) | при движении точки по прямой | |
ТЗ 16 | КТ-1 |
|
Производная скорости по времени – это… | ||
5) | ускорение |
|
ТЗ 17 | КТ-2 |
|
Тело брошено под углом к горизонту…
3) скорость тела в высшей точке траектории направлена горизонтально
ТЗ 18 КТ-3
Отметьте правильный ответ
Тело прошло половину пути с v=4 м/с; вторую половину пути с v=6 м/с; его средняя скорость…
1) 4,8 м/с
ТЗ 19 | КТ-1 |
Единицей работы в системе СИ является… | |
3) | 1 Дж. |
ТЗ 20 | КТ-2 |
Мощностью называют… | |
3) | величину, численно равную работе в единицу времени |
4) | ТЗ 21 КТ-3 |
Единицей мощности в системе СИ является… | |
3) | 1 Вт. |
ТЗ 22 | КТ-1 |
Кинетической энергией называется… 4) энергия, обусловленная механическим движением тел.
ТЗ 23 КТ-2
Механическая работа совершается в случае…
|
| 3 |
3) | если тело движется под | воздействием внешней силы. |
ТЗ 24 | КТ-3 |
|
Потенциальную энергию поднятого над землей железного цилиндра можно уменьшить следующим способом…
2) уменьшить массу тела.
ТЗ 25 КТ-1
Потенциальная энергия поднятого относительно поверхности Земли на высоту 20 м тела массой 3 кг равна…
2) 600 Дж.
ТЗ 26 КТ-2
Кинетическая энергия трактора массой 6 т и легкового автомобиля массой 1,5т при одинаковых скоростях движения …
2) больше у трактора.
ТЗ 27 КТ-3
Кинетическую энергию тела можно увеличить следующим способом… 3) увеличить скорость тела.
ТЗ 28 КТ-1
Совершаемая подъемным краном работа при равномерном поднятии груза массой 1,5 т на высоту 15 м равна…
1) 225 000 Дж.
ТЗ 29 КТ-2
Работа при перемещении на 20 м тележки с песком весом в 100 Н равна….
.
2) 2000 Дж.
.
ТЗ 30 КТ-3
Работа за 20 минут при мощности 22 000 Вт равна…
4) 26,4 МДж.
ТЗ 31 КТ-1
Мощность электровоза при движении со скоростью 90 км/ч и силе тяги 220
Нравна…
3)5,5 кВт.
ТЗ 32 КТ-2
Закон сохранения энергии формулируется… 1) во всех явлениях природы энергия не исчезает бесследно и не возникает из ничего.
4
ТЗ 33 КТ- 3
Верно следующее определение мощности… 3) быстрота совершения работы.
ТЗ 34 КТ-1
Средняя мощность за 20 с при работе 2400 Дж равна…
4) 120 Вт.
ТЗ 35 КТ- 2
Потенциальная энергия пружины жесткостью 200 Н/м при растяжении 5 см равна…
3) 0,25 Дж.
ТЗ 36 КТ- 3
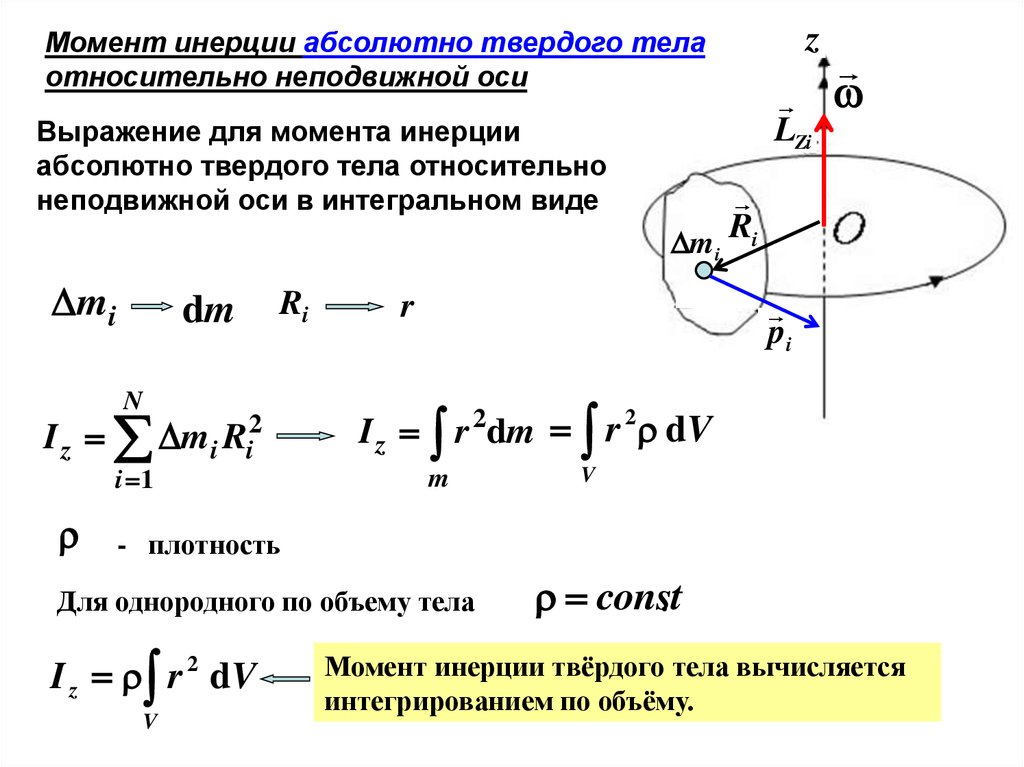
Моментом инерции материальной точки относительно неподвижной оси вращения называется…
2) Произведение массы материальной точки на квадрат ее расстояния от оси вращения.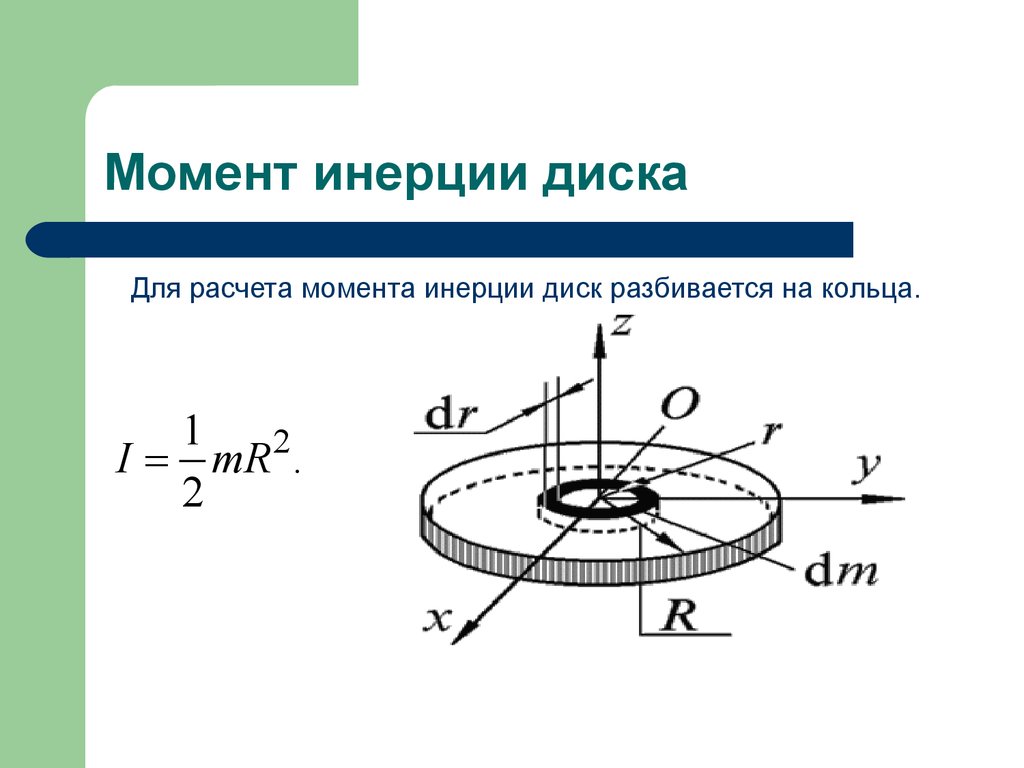
ТЗ 37 КТ- 1
Вес груза в воздухе 2 Н, в воде 1,5 Н. Выталкивающая сила равна …
1) 0,5 Н
ТЗ 38 КТ- 2
Продольная волна возникает при деформации … 1) сжатия – растяжения
ТЗ 39 КТ- 3
Поперечная волна возникает при деформации … 3) сдвига
ТЗ 40 КТ- 1
Инертность – свойство тела … 4) сохранять состояние покоя или равномерного прямолинейного движения
ТЗ 41 КТ-2
Ускорение, приобретаемое телом пропорционально … 1) отношению силы к массе
ТЗ 42 КТ- 3
Импульс тела – … 1) произведение массы на скорость
ТЗ 43 КТ-1
Момент инерции обруча больше момента инерции диска той же массы в 1) 2 раза
5
ТЗ 44 КТ-2
Момент инерции шара больше момента инерции обруча той же массы в…
1) 0,4 раза
ТЗ 45 КТ-3
Двигатель мощностью 300Вт за 300 с совершает работу…
5) 90000 Дж
ТЗ 46 КТ-1
Вес тела измеряется в … 4) ньютонах
ТЗ 47 КТ-2
Вектор момента импульса вращающегося тела направлен.
..
5) вдоль оси вращения
ТЗ 48 КТ-3
Потенциальная энергия тела массой 2 кг на высоте 3 м над поверхностью Земли…
5) 60 Дж
ТЗ 49 КТ-1
Кинетическая энергия тела прямо пропорциональна … 1) квадрату скорости тела
ТЗ 50 КТ-2
Причиной ускоренного движения тела является 3) сила
ТЗ 51 КТ-3
Сила трения покоя на стол, стоящий на полу … 2) действует, если стол пытаются сдвинуть с места
ТЗ 52 КТ-1
Закон всемирного тяготения справедлив при условиях… 4) Закон справедлив только для материальных точек.
ТЗ 53 КТ-2
Сила тяжести на расстоянии R от центра Земли равна F и будет равной на расстоянии 3R величине …
4) F /9.
ТЗ 54 КТ-3
Сила всемирного тяготения между двумя телами при увеличении расстояния между ними в 10 раз…
4) Уменьшится в 100 раз.
ТЗ 55 КТ-1
6
Работа сил тяжести при свободном | падении тела массой 20 кг в течение |
6 с равна… |
|
1) | 36 кДж. |
ТЗ 56 | КТ-2 |
Сила тяжести зависит от … | |
2) | массы тела и ускорения свободного падения |
ТЗ 57 | КТ-3 |
Стальной и деревянный шарики одинакового объема падают с достаточно большой высоты. Раньше упадет …
3) оба упадут одновременно
ТЗ 58 КТ-1
Кинетическая энергия вращательного движения зависит от …
3)момента инерции и угловой скорости
2.3.Тесты.
ТЗ 59 КТ-2
Температуре 50 К соответствует значение температуры по Цельсию…
.
2) -223 0С.
ТЗ 60 КТ-3
Одинаковой физической величиной для двух тел при тепловом равновесии будет …
3) температура.
ТЗ 61 КТ-1
Средняя квадратичная скорость молекул азота при увеличении температуры газа в 4 раза…
2) Увеличится в 2 раза.
ТЗ 62 КТ-2
Внутренняя энергия идеального одноатомного газа равна.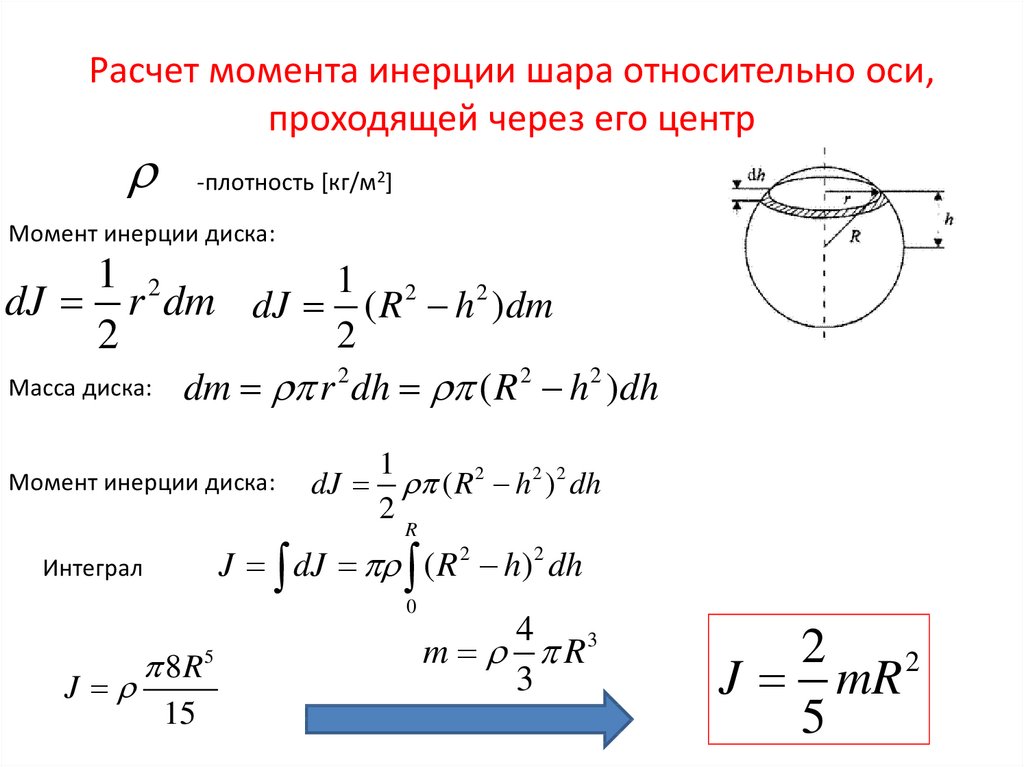
..
3) 3pV/2
ТЗ 63 КТ-3
Отношение средней квадратичной скорости молекулы водорода к средней квадратичной скорости молекулы кислорода равно…
1) 4
ТЗ 64 КТ-1
Отношение молярной массы вещества к массе молекулы этого вещества равно…
1) постоянной Авогадро
7
ТЗ 65 КТ-2
Моли любых газов при одинаковых температуре и давлении занимают одинаковые объѐмы…
1) закон Авогадро
ТЗ 66 КТ-3
Число степеней свободы одноатомной молекулы при комнатной температуре равно…
2) i = 3
ТЗ 67 КТ-1
Научное предположение, точнее объясняющее явление диффузии это – … 3) частицы, из которых состоят тела, хаотически движутся
ТЗ 68 КТ-2
Вещество, находящееся в трех агрегатных состояниях отличается … 4) движением, расположением и взаимодействием частиц
ТЗ 69 КТ-3
Давление газа зависит от… 1) температуры и числа молекул в единице объема
ТЗ 70 КТ-1
Вывод, который можно сделать о строении вещества, наблюдая явление диффузии.
3) молекулы всех веществ движутся непрерывно и хаотично
ТЗ 71 КТ-2
Давление – это сила,… 3) действующая на единицу площади поверхности тела
ТЗ 72 КТ-3
Закон Авогадро … 2) Моли любых газов при одинаковой температуре и давлении
занимают одинаковые объемы
ТЗ 73 КТ-1
Закон распределения молекул по скоростям Максвелла 1) распределение молекул по скоростям происходит по экспоненте и зависит от массы молекулы и температуры
ТЗ 74 КТ-2
Состояние газа характеризуется 1) объемом, давлением, температурой
ТЗ 75 КТ-3
8
Согласно закону Авогадро 1) в одном моле вещества содержится одинаковое число молекул
ТЗ 76 КТ-1
Средняя кинетическая энергия молекул газа в изобарном процессе при увеличении концентрации молекул газа в 5 раз…
2) Уменьшилась в 5 раз.
ТЗ 77 КТ-2
Процесс изменения состояния газа без теплообмена с внешней средой является…
.
4) Адиабатным.
ТЗ 78 КТ-3
Внутренняя энергия системы не изменяется при переходе ее из одного состояния в другое…
3) В изотермическом процессе.
ТЗ 79 КТ-1
Парциальное давление водяных паров в воздухе при неизменной температуре с увеличением их плотности…
2) увеличивается
ТЗ 80 КТ-2
При адиабатном расширении газа его температура…
2) понижается
ТЗ 81 КТ-3
При адиабатном сжатии газа его температура…
3) повышается
ТЗ 82 КТ-1
Подведѐнная к газу теплота равна изменению его внутренней энергии – это процесс…
3) изохорный
ТЗ 83 КТ-2
Подведѐнная к газу теплота равна работе газа против внешних сил – это процесс…
1) изотермический
ТЗ 84 КТ-2
Давление данной массы газа увеличивалось прямо пропорционально температуре…
3) газ работы не совершил
9
ТЗ 85 КТ-3
Внутренняя энергия 2 молей гелия при Т = 300 К равна…
5) 7,48 кДж
ТЗ 86 КТ-1
Всѐ переданное газу количество теплоты идѐт на совершение работы…
2) в изотермическом процессе
ТЗ 87 КТ-2
Идеальному газу сообщили 10 джоулей тепла при постоянной температуре
-работа газа.
..
4)10 Дж
3.3. Тесты
ТЗ 88 КТ-3
Идеальной называется жидкость, в которой …
2) полностью отсутствует внутреннее трение и теплопроводность.
.
ТЗ 89 КТ-1
Стационарным называется течение жидкости, в котором… 2) вектор скорости? любой частицы в каждой точке пространства остается постоянным.
ТЗ 90 КТ-2
Число Рейнольдса определяет… 3) характер течения и критерий подобия для течений вязких жидкостей и газов.
ТЗ 91 КТ-3
При замерзании воды ее объем … 3) увеличивается
ТЗ 92 КТ-1
На фазовой диаграмме воды в тройной точке вода находится в состоянии … 3) газообразном, жидком и твердом
ТЗ 93 КТ-2
Гидростатическое давление – это давление … 1) создаваемое внешними силами
ТЗ 94 КТ-3
10
Сила Архимеда – это … 2) сила, равная весу вытесненной телом жидкости
ТЗ 95 КТ-1
Уравнение Бернулли позволяет рассчитать в потоке жидкости давление … 4) полное
ТЗ 96 КТ-2
Коэффициент поверхностного натяжения жидкости равен.
..
1) отношению свободной энергии поверхности жидкости к площади этой поверхности
ТЗ 97 КТ-3
Давление жидкости на дно зависит от … 2) высоты столба жидкости и плотности жидкости
ТЗ 98 КТ-1
Действие жидкости на погруженное тело зависит от … 3) объема тела и плотности жидкости
ТЗ 99 КТ-2
Условие плавания тела… 2) плотность тела меньше плотности воды
ТЗ 100 КТ-3
Турбулентное течение – это … 2) слои жидкости вихреобразно перемешиваются между собой вдоль потока
ТЗ 101 КТ-1
Ламинарное течение – это … 1) слои жидкости не смешиваются между собой вдоль потока
ТЗ 102 КТ-2
Явление вязкости возникает … 1) в газах и жидкостях
ТЗ 103 КТ-3
Коэффициент поверхностного натяжения зависит от … 1) химического состава жидкости и температуры
ТЗ 104 КТ-1
В квадратное ведро, длина стороны которого 0,1м налита жидкость. Сила поверхностного натяжения 10 Н. Коэффициент поверхностного натяжения равен …
1) 25
Вращательное движение.
Моменты инерции, силы, импульса — МегаобучалкаПримеры решения задач
7. Сила с компонентами (2, -1, 4), H приложена к точке с координатами (–3, 2, 1), м. Найти:
а) момент силы относительно начала системы координат;
б) модуль момента силы M;
в) проекцию Mz момента силы на ось z.
| Дано: , Н ,м | Решение По определению момент силы относительно начала системы координат – векторное произведение радиус-вектора и силы . |
| а) б) в) | Следотельно, = [ ] = = (yFz–zFy) +(zFx–xFz) + x y z +(xFy – yFx) = 10 +14 – 1,0 , Н∙м, (1) |
z – компонента вектора и есть проекция Mz момента силы на ось z.
Следовательно, Mz = -1, Н×м. Модуль момента силы получится из выражения вышеприведенного: = , Н∙м.
Ответ: , Н×м; M = 17,2 Н×м; Mz = –1 Н×м.
8. Во сколько раз уменьшится момент инерции однородного сплошного диска оносительно оси, проходящей через его центр инерции (точка О) и перпендикулярной к плоскости диска, если сделать круглый дисковый вырез, как показано на рисунке.
Момент инерции – величина аддитивная. Поэтому момент инерции I3 диска с вырезом относительно точки О равен разности момента инерции диска относительно точки О и момента инерции малого диска , соответствующего вырезанной части, также относительно точки О, т. е. . В задаче необходимо найти отношение . Обозначим массу диска через m, а радиус диска через R. Тогда масса вырезанной части , а радиус . Как известно, момент инерции диска относительно оси симметрии равен: .
Для вычисления момента инерции используем теорему Штейнера:
,
где – момент инерции малого диска, соответствующего вырезанной части, относительно оси симметрии этого диска, походящей через точку О′. Окончательно . Таким образом, искомое отношение = 1,23 .
Ответ: момент инерции диска после сделанного выреза уменьшается в 1,2 раза.
9. Тонкий однородный обруч массой m = 2,0 кг и радиусом R = 1,0 м вращается вокруг оси симметрии, перпендикулярной к плоскости обруча, делая n0 = 120 об/мин. Под действием постоянной касательной к поверхности обруча силы Fт = 4,0 Н обруч тормозится и останавливается. Определить время торможения tт и число оборотов Nт, которое сделает обруч от начала торможения до остановки.
| Дано: m = 2,0 кг R = 1,0 м n0 = 120 об/мин = 2 об/с Fт = 4,0 Н | Решение
Для вращающегося обруча, на который действует тормозящий момент сил , уравнение вращательного движения имеет вид
(1)
где I – момент инерции обруча, ε – угловое ускорение. Момент инерции тонкого однородного обруча I = mR². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой
|
| а) tт –? б) Nт –? |
(2)
где ω0 – начальная угловая скорость обруча. Знак «минус» в выражении (2) показывает, что вращение равнозамедленное. Число оборотов N связано с углом поворота обруча φ соотношением
. (3)
В конце времени торможения угловая скорость обруча равна нулю, и из формул (1) и (2) получим
с с.
Для числа оборотов Nт за время торможения из выражения (3) следует:
об.
Ответ: tт = 6,3 с; Nт = 13 об.
10. Небольшое тело массой m = 200 г брошено по углом α= 60° к горизонту со скоростью = 10 м/с. Выразить зависимость момента импульса тела от времени в системе координат, изображенной на рисунке, относительно точки О.
Определить модуль изменения момента импульса для положения тела в точке наивысшего подъема О΄ и точке падения на землю А.
| Дано: m = 200г α= 60° = 10 м/с | Решение Введем правовинтовую систему координат OXYZ, как показано на рисунке. Поскольку при движении тела на него действует только сила тяжести, то из уравнения моментов можно определить момент импульса |
| а) L(t) –? б) –? |
где , в котором mg – сила тяжести, l – плечо силы относительно точки О. Знак (-) обусловлен тем, что момент силы в соответствии с правилом правого винта направлен в сторону противоположную оси z.
Плечо l найдем как l = , так как вдоль оси x силы не действуют и движение равномерное. Тогда момент импульса
. (1)
Время достижения телом точки наивысшего подъема определяется выражением с (так как ).
Время достижения телом точки А в два раза больше времени (как известно, время подъема равно времени спуска тела).
Окончательно производя необходимые вычисления, получим для (кг×м2)/с; для модуля изменения момента импульса из (*), учитывая, что в начальный момент времени (кг∙м²)/с.
Ответ: (кг∙м²)/с; (кг∙м²)/с.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.24. Сфера радиусом R = 2,0 м равномерно вращается вокруг вертикальной оси симметрии, делая 30 об/мин. Внутри сферы находится шарик. Найти высоту h, соответствующую положению равновесия шарика. При какой наименьшей угловой скорости радиус вращения шарика будет 0,9 R? Шарик считать материальной точкой.
(h = 1,0 м;ω = 3,4 рад/с)
1.25. Тело участвует в двух вращательных движениях, происходящих со скоростями и (a = 1,0 рад/с3). Определить:
а) на какой угол j повернется тело за первые 3,0 с;
б) какой угол составляет ось вращения, вокруг которой происходит поворот, с осью Х.
(а) j = 20 рад, б) a = 63°)
1.26. Тело вращается вокруг неподвижной оси так, что угол его поворота меняется в зависимости от времени t по закону , где а>0; b>0. Найти момент времени t, в который тело остановится, а также число оборотов N тела до остановки.
( ; )
1.27. Материальная точка движется по окружности радиусом R со скоростью u = kt, где k>0. Найдите зависимость от времени модуля полного ускорения точки; постройте графики зависимости тангенциального и нормального ускорений от времени.
( )
1.28. Определить полное ускорение W в момент времени t = 3,0 c точки, находящейся на ободе колеса радиусом R = 0,50 м, вращающегося согласно уравнению j = Аt+Вt3, где А = 2,0 рад/с; В = 0,20 рад/c3. Изобразите графики нормального и полного ускорений Wn = f(t) и W = f(t) на интервале 0<t<3 с.
(W = 27 м/с2)
1.29. Точка движется по окружности с постоянным тангенциальным ускорением. Через некоторый промежуток времени t после начала движения, угол между полным ускорением и радиусом окружности равен 45°. Чему равно угловое ускорение точки?
(e )
1.30. Материальная точка (частица) массой m брошена под углом a к горизонту с начальной скоростью . Траектория полета частицы лежит в плоскости Х, Y. Ось Z направлена “на нас”.
Найти зависимость от времени:
а) момента силы , действующего на частицу;
б) момента импульса частицы относительно начала координат.
(а) ; б) ) .
1.31. Две материальные точки массами m1 и m2 соединены жестким невесомым стрежнем длиной L. Найти положение центра масс системы Хс и момент инерции I этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс.
( ; )
1.32. Тело массой m = 0,10 кг брошено с некоторой высоты в горизонтальном направлении со скоростью u0 = 20 м/с. Найти модуль приращения момента импульса тела относительно точки бросания за первые t = 5 с.
( = 2,5 ∙102 кгм2/с)
1.33. Сила с компонентами (3, 4, 5) Н приложена к точке с координатами (4, 2, 3) (м). Найти:
а) момент силы относительно начала координат;
б) модуль вектора ;
в) проекцию на ось Z момента силы Мz.
( (Н×м), = 15 Н×м)
1.34. Найти момент инерции однородной прямоугольной пластинки массой m, длиной а и шириной b относительно перпендикулярной к ней оси, проходящей через одну из вершин пластинки.
( )
1.35. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m1 = 12 кг. На цилиндр намотан шнур, к которому привязали гирю массой m2 = 1,0 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?
(W = 1,4 м/с2; T = 8,4 Н)
1.36. На обод маховика диаметром D = 60 cм намотан шнур, к концу которого привязан груз массой m = 2,0 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3,0 с приобрел угловую скорость w = 9,0 рад/с.
(J = 1,8 кг×м2)
1.37. Тонкий обруч радиусом R раскрутили вокруг его оси до угловой скорости и положили (опустили) на горизонтальный стол. Через какое время t обруч остановится, если коэффициент трения между столом и обручем равен m? Сколько оборотов N сделает обруч до полной остановки?
( ; )
1.38. С какой угловой скоростью должен вращаться сосуд в виде усеченного конуса, чтобы шарик, лежащий на его дне, выкатился из него? Диаметр верхнего основания равен d. Стенки сосуда наклонены к горизонту под углом a.
( )
1.39. Из сплошного однородного цилиндра радиусом R сделали полый, удалив внутреннюю часть радиусом R/2 от оси симметрии. Во сколько раз изменится момент инерции тела относительно указанной оси?
( )
1.40. Из сплошного однородного цилиндра сделали полый, удалив половину его массы. Как изменится момент инерции J цилиндра относительно его оси и во сколько раз? Как и во сколько раз изменится момент импульса указанных цилиндров, если они вращаются с одинаковой угловой скоростью?
( )
1.41. В сплошном однородном диске радиусом R просверлили сквозное отверстие радиусом R/2 от оси симметрии. Как изменится момент инерции тела относительно указанной оси по отношению к первоначальному?
( )
1.42. Два однородных цилиндра с одинаковыми высотами h и равными массами m вращаются относительно своих осей симметрии. Соотношение плотностей материалов цилиндров r1 = (3/4)r2. Сравнить вращающие моменты сил, если угловые ускорения цилиндров одинаковы, а моменты сил трения Мтр равны.
( )
1.43. Грузик массой 5,0 г, привязанный к нити длиной l = 50 см, вращается вокруг вертикальной оси и описывает окружность в горизонтальной плоскости. Какой угол j образует нить с вертикалью, если частота вращения n = 1,0 c-1. Чему равен модуль проекции момента импульса на ось вращения?
(j = 60°; L = 5,9∙10-2 (кг∙м²)/с)
Пяльцы и цилиндрические движения
Пяльцы и цилиндрические движенияДана гонка между тонким обручем и однородным цилиндром по склону. Что победит?
В анализе используются угловая скорость и кинетическая энергия вращения. Для качения без проскальзывания линейная скорость и угловая скорость строго пропорциональны. | Индекс Концепция вращения Концепция кинетической энергии вращения | |||||||||||||||||||
|