Курс общей физики, Т.2
Курс общей физики, Т.2
ОглавлениеПРЕДИСЛОВИЕМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. Электрический заряд § 2. Закон Кулона § 3. Системы единиц § 4. Рационализованная запись формул § 5. Электрическое поле. Напряженность поля § 6. Потенциал § 7. Энергия взаимодействия системы зарядов § 8. Связь между напряженностью электрического поля и потенциалом § 9. Диполь § 10. Поле системы зарядов на больших расстояниях § 11. Описание свойств векторных полей Дивергенция. Циркуляция. Теорема Стокса. § 12. Циркуляция и ротор электростатического поля § 13. Теорема Гаусса Поле двух разноименно заряженных плоскостей. Поле заряженной сферической поверхности. Поле объемно-заряженного шара. ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ § 15. Полярные и неполярные молекулы § 16. Поляризация диэлектриков § 17.  Поле внутри диэлектрика§ 18. Объемные и поверхностные связанные заряды § 19. Вектор электрического смешения § 20. Примеры на вычисление поля в диэлектриках § 21. Условия на границе двух диэлектриков § 22. Силы, действующие на заряд в диэлектрике § 23. Сегнетоэлектрики § 24. Равновесие зарядов на проводнике § 25. Проводник во внешнем электрическом поле § 26. Электроемкость § 27. Конденсаторы ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 28. Энергия заряженного проводника § 29. Энергия заряженного конденсатора § 30. Энергия электрического поля ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 31. Электрический ток § 32. Уравнение непрерывности § 33. Электродвижущая сила § 34. Закон Ома. Сопротивление проводников § 35. Закон Ома для неоднородного участка цепи § 36. Разветвленные цепи. Правила Кирхгофа § 37. Мощность тока § 38. Закон Джоуля — Ленца § 39. 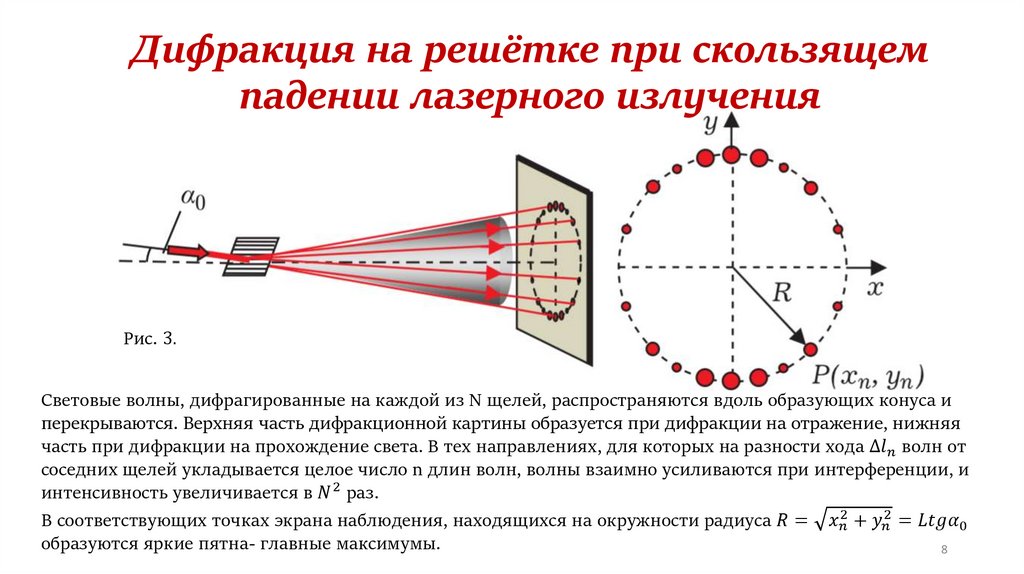 Взаимодействие токов§ 40. Магнитное поле § 41. Поле движущегося заряда § 42. Закон Био — Савара § 43. Сила Лоренца § 44. Закон Ампера § 45. Магнитное взаимодействие как релятивистский эффект § 46. Контур с током в магнитном поле § 47. Магнитное поле контура с током § 48. Работа, совершаемая при перемещении тока в магнитном § 49. Дивергенция и ротор магнитного поля § 50. Поле соленоида и тороида ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ § 51. Намагничение магнетика § 52. Напряженность магнитного поля § 54. Условия на границе двух магнетиков § 55. Виды магнетиков § 56. Магнитомеханические явления § 57. Диамагнетизм § 58. Парамагнетизм § 59. Ферромагнетизм ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 60. Явление электромагнитной индукции § 61. Электродвижущая сила индукции § 62. Методы измерения магнитной индукции § 63. Токи Фуко § 64. Явление самоиндукции § 65.  Ток при замыкании и размыкании цепи§ 66. Взаимная индукция § 67. Энергия магнитного поля § 68. Работа перемагничивания ферромагнетика § 69. Вихревое электрическое поле § 70. Ток смещения § 71. Уравнения Максвелла ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ § 72. Движение заряженной частицы в однородном магнитном поле § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями § 74. Определение заряда и массы электрона § 75. Определение удельного заряда ионов. Масс-спектрографы § 76. Ускорители заряженных частиц ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ § 77. Природа носителей тока в металлах § 78. Элементарная классическая теория металлов § 79. Эффект Холла ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ § 80. Несамостоятельная и самостоятельная проводимость § 82. Ионизационные камеры и счетчики § 83. 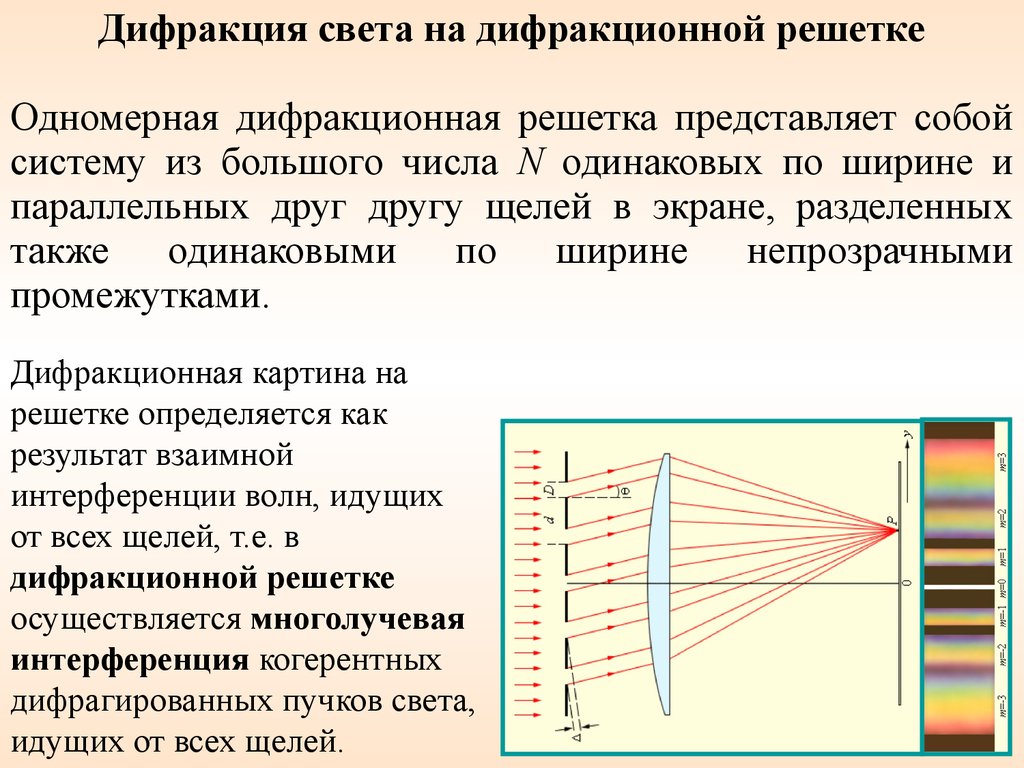 Процессы, приводящие к появлению носителей тока при самостоятельном разряде§ 84. Газоразрядная плазма § 85. Тлеющий разряд § 86. Дуговой разряд § 87. Искровой и коронный разряды ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ § 88. Квазистационарные токи § 89. Свободные колебания в контуре без активного сопротивления § 90. Свободные затухающие колебания § 91. Вынужденные электрические колебания § 92. Переменный ток § 93. Распространение волн в упругой среде § 94. Уравнения плоской и сферической волн § 95. Уравнение плоской волны, распространяющейся в произвольном направлении § 96. Волновое уравнение § 97. Скорость упругих волн в твердой среде § 98. Энергия упругой волны § 99. Стоячие волны § 100. Колебания струны § 101. Звук § 102. Скорость звука в газах § 103. Эффект Доплера для звуковых волн ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 104. Волновое уравнение для электромагнитного поля § 105.  Плоская электромагнитная волна§ 106. Экспериментальное исследование электромагнитных волн § 108. Импульс электромагнитного поля § 109. Излучение диполя ЧАСТЬ 3. ОПТИКА § 110. Световая волна § 111. Представление гармонических функций с помощью экспонент § 112. Отражение и преломление плоской волны на границе двух диэлектриков § 113. Световой поток § 114. Фотометрические величины и единицы § 115. Геометрическая оптика § 116. Центрированная оптическая система § 117. Тонкая линза § 118. Принцип Гюйгенса ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА § 119. Интерференция световых волн § 120. Когерентность § 121. Способы наблюдения интерференции света § 122. Интерференция света при отражении от тонких пластинок § 124. Многолучевая интерференция ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА § 126. Принцип Гюйгенса—Френеля § 127. Зоны Френеля § 128. Дифракция Френеля от простейших преград § 129. 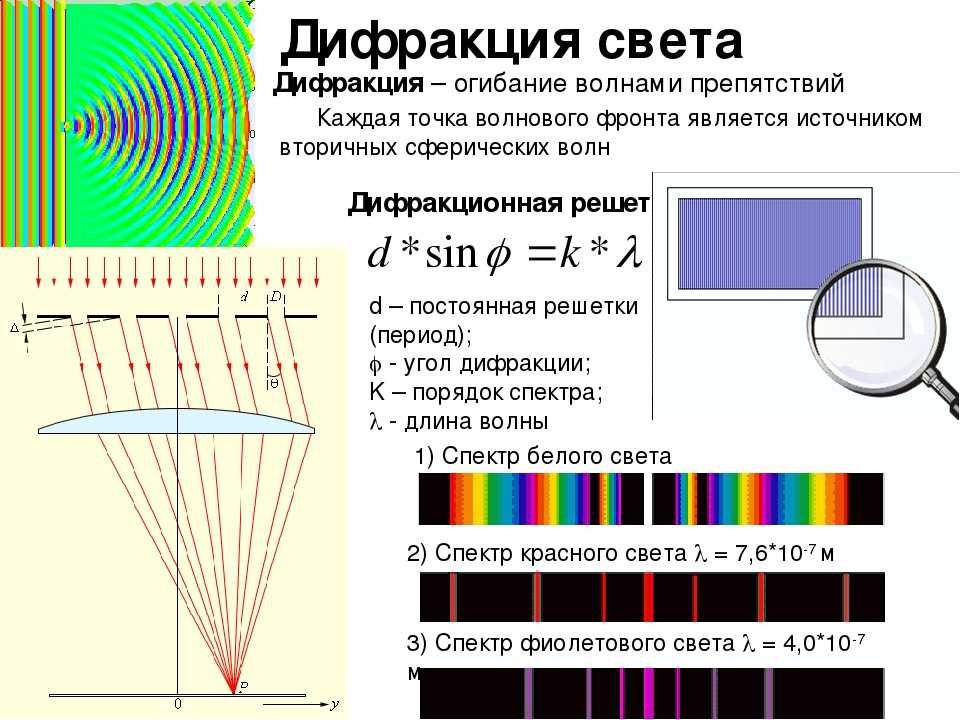 Дифракция Фраунгофера от щели§ 130. Дифракционная решетка § 131. Дифракция рентгеновских лучей § 132. Разрешающая сила объектива § 133. Голография ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА § 134. Естественный и поляризованный свет § 135. Поляризация при отражении и преломлении § 136. Поляризация при двойном лучепреломлении § 138. Прохождение плоскополяризованного света через кристаллическую пластинку § 139. Кристаллическая пластинка между двумя поляризаторами § 140. Искусственное двойное лучепреломление § 141. Вращение плоскости поляризации ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ § 142. Дисперсия света § 143. Групповая скорость § 144. Элементарная теория дисперсии § 145. Поглощение света § 146. Рассеяние света § 147. Эффект Вавилова — Черенкова ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД § 148. Скорость света § 149. Опыт Физо § 150. Опыт Майкельсона § 151.  ПРИЛОЖЕНИЯ I. Единицы электрических и магнитных величин в СИ и в гауссовой системе Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе Приложение III. Векторный потенциал |
Вопрос 4. Дифракция рентгеновских лучей на кристаллической решетке.
В 1895 г. Рентген обнаружил, что при электрическом разряде в вакуумной трубке возникает излучение, невидимое для глаз. Дальнейшие исследования показали, что это излучение, названное в дальнейшем рентгеновским, возникает при бомбардировке вещества быстрыми электронами. В современных рентгеновских трубках мишенью, обстреливаемой электронами, является металлическая пластинка – катод, расположенный под углом 45° к потоку электронов. Скорость электронов определяется величиной разности потенциалов между анодом и катодом.
Рентгеновское
излучение – жесткое электромагнитное
излучение, и оно обладает
волновыми свойствами.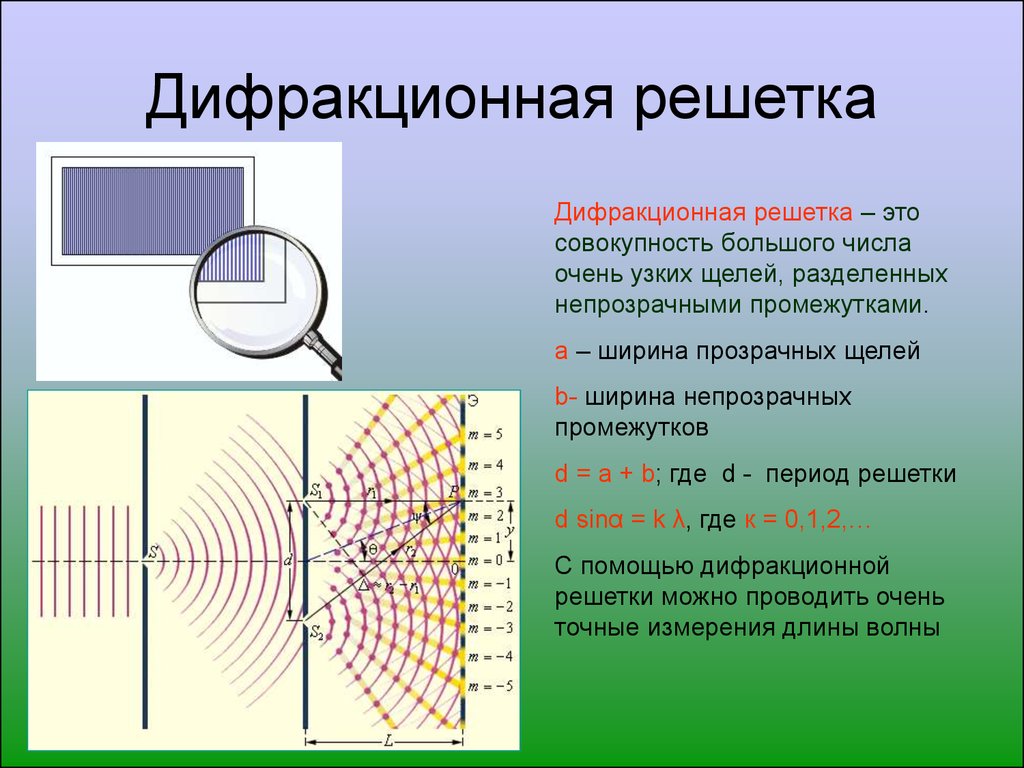
Для
того чтобы обнаружить дифракцию его,
необходимо чтобы размеры щелей
и преград, образующих правильную решетку
на пути волн, были сравнимы
с длиной волны. Рентгеновское
излучение обладает столь малой длиной
волны, что для него на обычных дифракционных
решетках дифракция не наблюдается.
Дифракция электромагнитного излучения наблюдается не только на одномерной дифракционной решетке, но и на двух- и трехмерных периодических структурах. Проделаем мысленно следующее. Поставим две дифракционные решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка даст, например, в горизонтальном направлении ряд максимумов, положения которых определяются условием
l1 sin1 = m1 (m1 = 0, 1,2,3,..,). (10.15)
Вторая решетка разобьет каждый из образовавшихся таким образом пучков излучения на расположенные по вертикали максимумы, положения которых определяются условием:
l2 sin2 = m2 (m2 =0, 1,2,.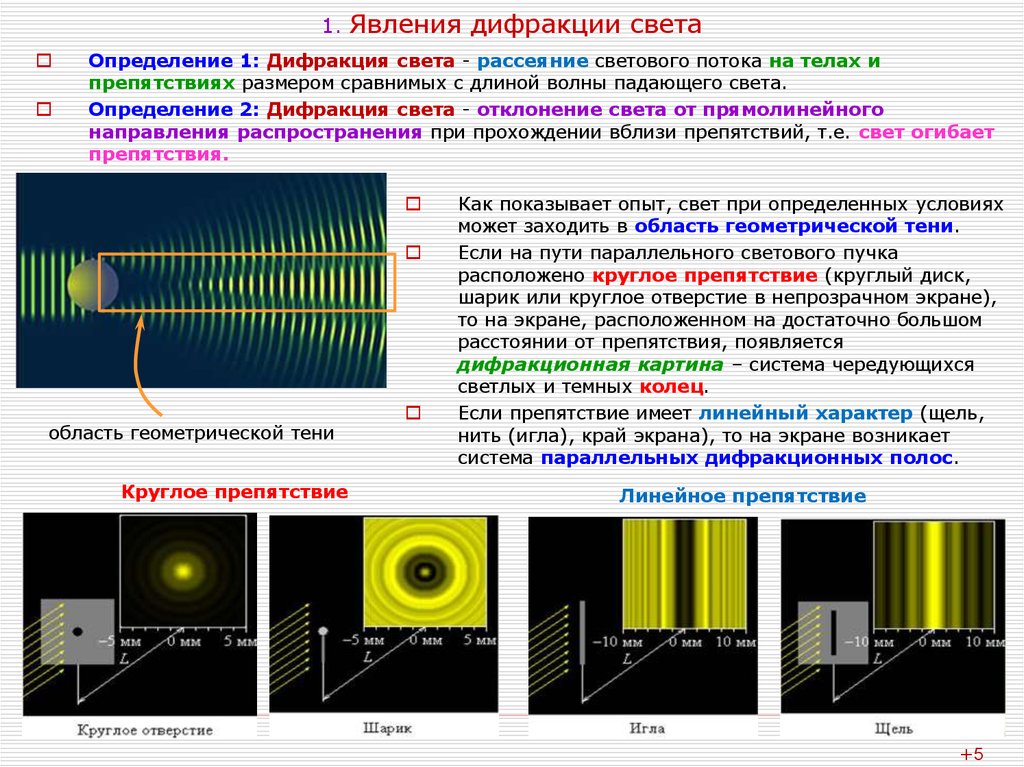
..). (10.16)
В итоге дифракционная картина будет иметь вид правильно расположенных светлых пятен.
Такая же дифракционная картина получится, если вместо двух решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Подобная пластинка представляет собой двумерную периодическую структуру.
Дифракция наблюдается также на трехмерных структурах, т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами являются все кристаллические тела. Однако их период ( 10-10 м) слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие l выполняется только для рентгеновского излучения.
Впервые
дифракция на кристаллах
с
использованием очень узких пучков
рентгеновского излучения наблюдалась
в 1913 г.
в опыте Лауэ, Фридриха и Книппинга.
Первые
методы расчета дифракции от объемной
решетки дал Лауэ. Совершенно
эквивалентные формулам Лауэ, но гораздо
более удобные для анализа,
формулы были даны независимо русским
ученым Вульфом и английскими физиками
У. Г. и У. Л. Брэггами. Метод, предложенный
ими, состоит в следующем.
Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости (рис.10.9), называемые атомными слоями.
Если падающая на кристалл волна плоская, то огибающая вторичных
волн, порождаемых атомами, лежащими в таком слое, также будет представлять собой плоскость. Таким образом, суммарное действие
атомов, лежащих в одном слое, можно представить в виде плоской
волны,отразившейся от усеянной атомами поверхности по обычному
Рис.10.9.
закону отражения.
Плоские
вторичные волны, отразившиеся от разных
атомных слоев, когерентны
и будут интерферировать между собой
подобно волнам, посылаемым в данном
направлении различными щелями
дифракционной решетки.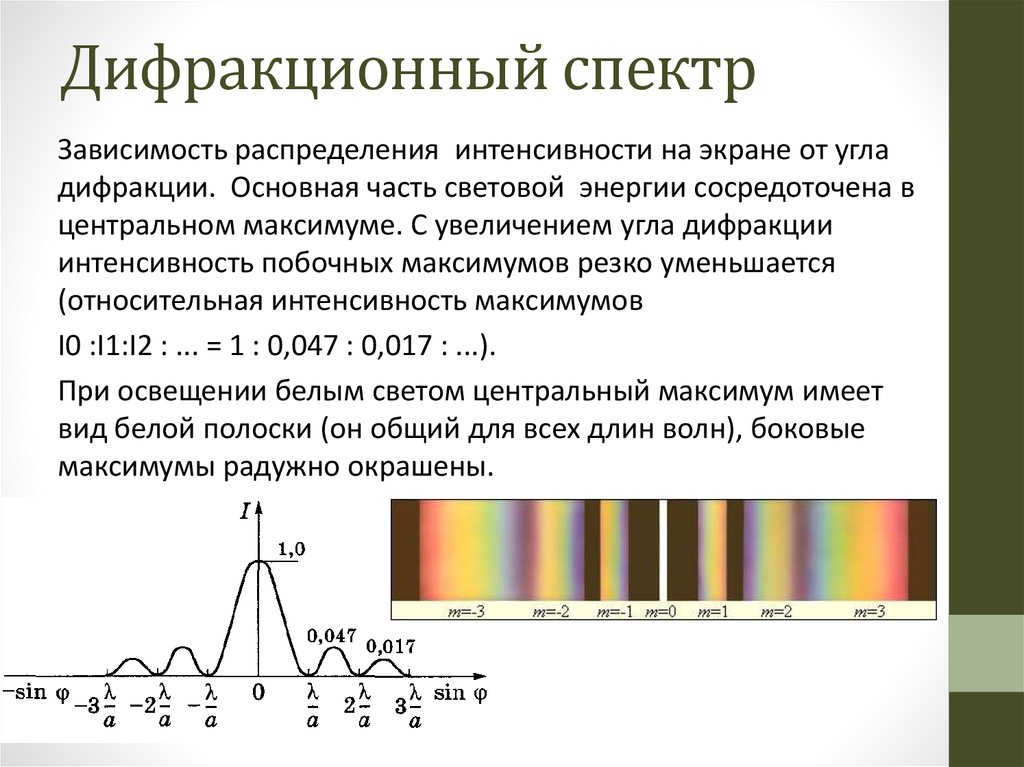
Вторичные
волны будут практически гасить друг
друга во всех направлениях, кроме
тех, для которых разность хода между
соседними волнами является кратной .
Из рис.10.9 видно, что разность хода двух
волн, отразившихся от двух соседних
атомных слоев,
равна 2lsinθ,
где l – период идентичности кристалла в
направлении, перпендикулярном к
рассматриваемым слоям, θ – угол скольжения падающих
лучей. Следовательно, направления, в
которых получаются дифракционные
максимумы
рентгеновского излучения, определяется
условием
2 l sinθ = ± m (m =1,2,…). (10.17)
Это соотношение называется формулой Вульфа – Брэггов.
Атомные
слои в кристалле можно провести множеством
способов. Каждая система
слоев может дать дифракционный максимум,
если для нее окажется выполнимым (10.17).
Однако
заметную интенсивность имеют лишь те
максимумы интенсивности, которые
получаются за
счет отражений от слоев, достаточно
густо усеянных атомами.
При произвольном
направлении падения монохроматического
рентгеновского излучения на кристалл
дифракция не возникает. Чтобы ее
наблюдать, надо, поворачивая кристалл,
найти определенный угол скольжения.
Дифракционная картина может быть
получена и при произвольном положении
кристалла, для чего нужно пользоваться
рентгеновским излучением с непрерывным
спектром. Тогда для таких условий опыта
всегда найдутся длины волн ,
удовлетворяющие условию (10.17).
Дифракция рентгеновских лучей от кристаллов находит два основных применения. Она используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия) и для изучения структуры кристаллов (рентгеноструктурный анализ). Определяя направления максимумов, получающихся при дифракции рентгеновского излучения с неизвестной длиной волны от кристаллов с известной структурой, можно определить длину волны.
В
методе структурного анализа узкий пучок
рентгеновского излучения направляется
на кристалл.
Для каждой системы слоев, достаточно
густо усеянных атомами, находится в
излучении длина волны, при которой
выполняется условие (10.17). Поэтому на
помещенной за кристаллом фотопластинке
регистрируется (после проявления)
совокупность
черных пятнышек, взаимное расположение
которых отражает
симметрию кристалла. Расшифровывая
рентгенограммы, по расстоянию между
пятнышками и по их интенсивности,
удается найти размещение атомов в
кристалле и расстояния между ними.
Контрольные вопросы:
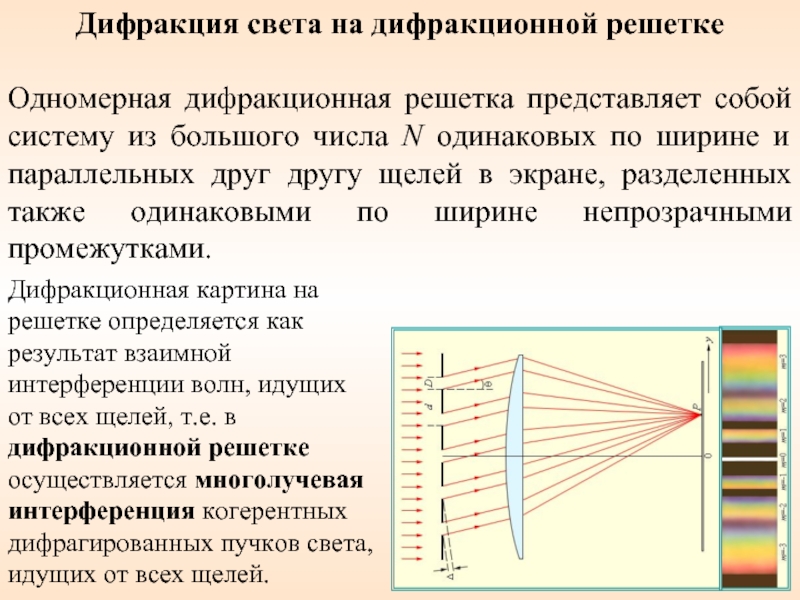
1 . Почему дифракционная решетка разлагает белый свет в спектр?
2. Определите наибольшие порядки спектров дифракционных решеток, имеющих 100 и 1800 штрихов на 1 мм длины.
3. Как изменится дифракционная картина при удалении экрана от решетки?
4. Почему при использовании белого света только центральный
максимум белый, а боковые максимумы радужно окрашены?
5.
Почему штрихи на дифракционной решетке
должны быть тесно расположены друг к
другу? Почему их должно быть большое
число?
6. Запишите условия дифракционных минимумов для одной щели и главных максимумов для решетки. Каков характер этих дифракционных картин?
7. Как объяснить голубой цвет неба? Почему при закате и восходе солнце кажется красным?
8. Когда два одинаковых точечных источника разрешимы по Рэлею?
9. От чего зависит разрешающая способность дифракционной решетки?
10. Почему на кристаллах наблюдается дифракция рентгеновского излучения, но не наблюдается дифракция видимого света?
лазер – Использование видимого света для получения (слабой) дифракционной информации о кристаллах?
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 143 раза
$\begingroup$ Если кристалл имеет диаметр примерно 0,25 мм и содержит элементарные ячейки (скажем, кубы) со стороной около 1 ангстрема, то диаметр кристалла составляет около 2,5 миллионов элементарных ячеек.
Применяется закон Брэгга (n$\lambda = 2d\sin\theta)$, который говорит нам, что мы хотели бы использовать длину волны порядка 1 ангстрема для исследования кристалла.
Но если $\lambda = 5000$ ангстрем (лазер), кажется, мы все еще можем получить преломление параллельных волн, разделенных примерно 2500 ангстрем, или около $0,25$мм/$2500$ ангстрем $= 1000$ усиливая преломления в приведенном выше кристалле , учитывая только одно измерение. Отсюда мой вопрос:
Возможно ли, что хотя мы не можем различать структуры меньше нескольких ангстрем без использования рентгеновских лучей, мы можем получить информацию (хотя и ослабленную) об идентичных повторяющихся структурах (кристаллах), используя более длинные волны?
Редактировать:
Изображения ниже могут помочь прояснить ситуацию. Вверху показана средняя радиальная интенсивность, рассчитанная в Python для лазерной дифракции изображения циркона (внизу центральный луч удален). С одной стороны, я бы не стал пытаться сопоставить расчет с расчетами XRD, с другой стороны, на изображении, похоже, есть некоторая неслучайная информация.
По крайней мере, это может прояснить мои заблуждения.
Редактировать 2
Добавляя
ZrO2.
неотредактированное фото ZrO2.
- лазер
- рентгеновская кристаллография
- закон Брэггса
Нижеследующее на самом деле не ответ, а своего рода опровержение.
Использование видимого света для получения (слабой) дифракционной информации о кристаллы
, конечно, было бы очень интересно сделать, поэтому я как химик обратил на это внимание. Но я боюсь, что в соответствии с общепринятым восприятием это на самом деле невозможно и то, что выставлено напоказ в вопросе, является чем-то другим.
Сначала я провел быстрый тест с монокристаллическим кристаллом кальцита размером с мой большой палец. Я посветил через него зеленым указателем стоимостью $532\mathrm{нм}$ ($8000\mathrm{мВт}$) и получил два ослабленных центральных луча и совершенно случайный “ореол” рассеянного света.
Никакой дифракционной картины.
Затем я измельчил в ступке пестиком немного кухонной соли (химически $\text{NaCl}$) и насыпал ее в стеклянную капиллярную трубку.
Но пытаться направить на него лазерный луч — пустая трата времени: как и большинство сыпучих прозрачных материалов (стекло, кристаллы сахарозы, кристаллы соли и т. д.), их измельченные версии просто не прозрачны для видимого света.
Они были бы для рентгеновских лучей, но это дало бы круговых дифракционных картин . Только монокристаллические материалы могут показать такую дифракционную картину, которую показывает ОП в своем вопросе.
Итак, я не знаю, чем вызвана эта интересная картина, но я не думаю, что это связано с дифракцией. Но я хотел бы узнать больше об экспериментальной установке ОП, чтобы понять, что может вызывать наблюдаемый эффект.
$\endgroup$ 3Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гость
Электронная почтаТребуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Рентгеновская кристаллография
Рентгеновская кристаллографияО модульной ячейке
Кристаллы представляют собой трехмерные упорядоченные структуры, которые невозможно описать как повторение одинаковых элементарных ячеек. Элементарная ячейка состоит из наименьший возможный объем, который при повторении репрезентативен для цельный кристалл. Размеры элементарной ячейки можно описать с помощью 3 длина ребра (a,b,c) и 3 угла (альфа, бета, гамма). 3D-локация атомов в элементарной ячейке могут быть перечислены как их декартовы x, y, z Координаты. Пространственные группы описывают симметрию элементарной ячейки, из которых есть 230 вариаций. В программе молекулярного оригами, нажав на Использовать кристаллографическую информацию СЕЙЧАС вы можете поэкспериментируйте со всеми различными типами пространственных групп.
Для чего используются рентгеновские лучи?
Используя видимый свет, невозможно увидеть атомы даже под
самый мощный из микроскопов.
Чтобы объект был виден,
его размер должен быть не менее половины длины волны используемого света.
чтобы увидеть это. Так как видимый свет имеет длину волны намного больше длины волны
расстояние между атомами бесполезно видеть молекулы. Для того, чтобы см. молекул необходимо использовать форму электромагнитного
излучение с длиной волны порядка длины связи, например
рентген.
Почему рентген
дифракция ?К сожалению, в отличие от видимого света, не существует известного способа фокусировки. рентген с линзой. Это приводит к тому, что рентгеновский микроскоп невозможно, если кто-то не найдет способ сфокусировать рентгеновские лучи. До тех пор это необходимо использовать кристаллы для дифракции рентгеновских лучей и создания дифракционных шаблон, который может быть математически интерпретирован компьютером. Этот превращает компьютер в виртуальный объектив, поэтому на мониторе мы можем посмотрите на структуру молекулы.
Кристаллы важны
потому что по определению они имеют повторяющуюся элементарную ячейку внутри себя.
дифракция рентгеновских лучей от одной элементарной ячейки не будет существенной.
К счастью, повторение элементарных ячеек внутри кристалла усиливает
дифракции достаточно, чтобы дать результаты, которые компьютеры могут превратить в изображение.Выращивание кристаллов
Для проведения рентгеноструктурного анализа необходимо выращивать кристаллы с края вокруг 0,1-0,3 мм. Кристаллы образуются в условиях пересыщенный раствор медленно меняют. Есть три степени насыщения в растворе, и кристаллографы пользуются этим при выращивании кристаллов:
Одна из теорий выращивания кристаллов состоит в том, чтобы начать с получения нескольких кристаллов для растут в сильно пересыщенном растворе.
Тогда кристаллы
подвергаются воздействию менее насыщенного раствора, чтобы они могли расти. Готово
либо перемещением кристаллов, либо изменением насыщенности раствора. Для небольших молекул относительно просто вырастить достаточно большие кристаллы. Взяв перенасыщенный раствор раствора и постепенно меняя условия, кристаллы начнут расти. Если оставить в покое на несколько дней в идеале вырастет несколько крупных кристаллов.
Белки трудно кристаллизовать из-за их сложности и тот факт, что ученые-белки обычно работают с небольшим количеством белок.
Существуют различные методы выращивания кристаллов белка:
- Диффузия паров (метод висячей капли)
- Это, пожалуй, самый распространенный способ выращивания кристаллов. Капля белковый раствор подвешивают над резервуаром, содержащим буфер и осаждающий. Вода диффундирует из капли в раствор, оставляя капли с оптимальными условиями роста кристаллов.
- Периодическая кристаллизация
- Насыщенный белковый раствор, оставленный в герметичном контейнере, чтобы
кристаллы растут.
- Микроциклическая кристаллизация
- Каплю белкового раствора помещают в инертное масло и оставляют для роста. Здесь, вероятно, происходит некоторая диффузия белков в масло, снижающая насыщение во времени.
- Макропосев
- Кристалл выращивают в сильно насыщенном растворе и помещают в менее насыщенный, где будет происходить только рост кристалла.
- Микропосев
- Несколько кристаллов выращивают, затем измельчают и помещают в окончательный раствор который объединяет их в несколько хороших кристаллов. Это включает совсем немного экспериментировать с концентрацией растворов, чтобы получить желаемую количество кристаллов.
- Свободное распространение интерфейса
- Контейнер имеет разную степень насыщения. Форма кристаллов
первоначально в высоконасыщенной части, но по мере перемешивания раствора
в конечном итоге только поддерживает рост кристаллов.
- Диализ
- Аналогичен предыдущему, но с разделительной полупроницаемой мембраной
слои.
Белки кристаллизуются в таких малых масштабах, что их трудно воспроизвести концентрации. Это делает кристаллизующиеся белки почти более искусства, чем науки, и иногда перед тем, как выращиваются кристаллы нужного размера.
Рентгеновская дифракция
Когда рентгеновские лучи направляются на кристалл, электроны преломляют рентгеновские лучи. что вызывает дифракционную картину. Используя математический Фурье преобразовать эти узоры могут быть преобразованы в электрон карты плотности. На этих картах показаны изолинии электронной плотности. Поскольку электроны более или менее равномерно окружают атомы, можно определить, где расположены атомы. К сожалению, поскольку водород имеет только один электрон, его трудно карта водородов. Чтобы получить трехмерное изображение, кристалл вращают при компьютеризированный детектор создает двумерные карты электронной плотности для каждый угол поворота. Третье измерение происходит от сравнения вращение кристалла с серией изображений.