Почему второй закон ньютона называют основным законом движения: Почему второй закон ньютона называют основным законом движения?

Второй закон Ньютона

Определение 1

Второй закон Ньютона представляет собой основной закон динамики. Данный закон может выполняться только в инерциальных системах отсчета.

Формулируя второй закон, стоит обратить внимание на то, что в динамике вводятся масса тела m и сила F→, а также способы их измерения. Масса является количественной характеристикой инертных свойств тела и показывает реакцию тела на внешнее воздействие. Сила же F→ представляет из себя количественную меру действия одного объекта на другой.

2-ой закон Ньютона, определение и формула

Второй закон Ньютона – фундаментальный закон природы, являющийся обобщением опытных фактов, подразделяющихся на две категории:

1. Если на обладающие разной массой тела подействовать одной и той же силой, то приобретаемые телами ускорения окажутся обратно пропорциональны их массам:

a~1m, при F=const.

2. Если силами различной величины подействовать на одно тело, то ускорения тела окажутся прямо пропорциональными приложенным силам:

a→~F→, при m=const.

Основной закон динамики был сформулирован Ньютоном путем обобщения данных фактов:

Определение 2

Сила, которая оказывает воздействие на тело, эквивалентна произведению массы тела на сообщаемое данной силой ускорение:

F→=ma→.

Приведенное выражение и представляет собой второй закон Ньютона.

С помощью него стало возможным вычисление ускорение тела в случае, если известна его масса m и действующая на него сила F→: 

a→=F’m.

Определение 3

В Международной системе единиц (СИ) в качестве единицы силы считают такую силу, которая сообщающая телу массой 1 кг ускорение 1 м/с2. Данная единица называется ньютоном (Н). В (СИ) ее принимают за эталон силы.

1 Н=1кг·мс2.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Равнодействующая сила

В том случае, если на тело одновременно воздействуют несколько сил, как например, F1→, F2→ и F3→, то силой F→ в формуле второго закона Ньютона считается равнодействующая всех сил это величина, выражающаяся в виде формулы: 

F→=F1→+F2→+F3→.

Рисунок 1.8.1. Сила F→ – равнодействующая силы тяжести F→Т и силы нормального давления FN→, действующих на лыжницу на гладкой горе. Сила F→ вызывает ускорение лыжника.

В случае же, когда равнодействующая сила F→=0, тело будет пребывать в состоянии покоя или равномерного прямолинейного движения. Выходит, что формально второй закон Ньютона включает в себя в качестве частного случая первый закон Ньютона. Но первый закон Ньютона обладает более глубоким физическим значением. Он обуславливает существование инерциальных систем отсчета.

Рисунок 1.8.1. Модель движения тел на легком блоке.

Второй закон Ньютона

| на главную | доп. материалы | физика как наука и предмет | физические основы механики |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Второй закон Ньютона — основной закон динамики поступательного движения — от­вечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:

а ~ F (т = const).                                                                    (6.1)

При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно

а ~ 1/т (F = const).                                                (6.2)

Используя выражения (6.1) и (6.2) и учитывая, что сила и ускорение—величины векторные, можем записать

а = kF/m.                                                                (6.3)

Соотношение (6.

3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

В СИ коэффициент пропорциональности k= 1. Тогда

или

                                                       (6.4)

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:

                                                   (6.5)

Векторная величина

                                                                        (6.6)

численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материаль­ной точки.

Подставляя (6.6) в (6.5), получим

                                                        (6. 7)

Это выражение — более общая формулировка второго закона Ньютона: скорость изме­нения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки

.

Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе 1 кг сообщает ускорение 1 м/с² в направлении действия силы:

1 Н = 1 кг×м/с².

Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенст­ва нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (6.3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (6.7).

В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач. Например, на рис. 10 действующая сила F=ma разложена на два компонен­та: тангенциальную силу F_t, (направлена по касательной к траектории) и нормальную силу F

_n (направлена по нормали к центру кривизны). Используя выражения  и , а также , можно записать:

  

Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под F во втором законе Ньютона понимают результирующую силу.

---

Второй закон динамики Ньютона – Энциклопедия по машиностроению XXL

Второй закон динамики Ньютона ускорение, приобретаемое телом, пропорционально действующей на него силе и обратно пропорционально массе тела. Первая производная от импульса математической точки по времени равна действующей на нее силе  [c. 198]

Так, второй закон динамики Ньютона для тела с постоянной массой имеет вид  [c.199]

ВТОРОЙ ЗАКОН ДИНАМИКИ НЬЮТОНА 61  [c.61]

Второй закон динамики Ньютона  [c.61]

При установлении основных физических закономерностей процесса теплопроводности рассматривались закон сохранения тепловой энергии и закон Фурье. Основные физические закономерности конвективного теплообмена могут быть установлены на основании предыдущих законов, а также законов, описывающих движение жидкости. К последним относится основной закон динамики (второй закон динамики Ньютона) и закон сохранения массы (принцип неразрывности жидкости). Два этих закона позволяют найти поле скорости жидкости.  

[c.215]

Чтобы получить дифференциальные уравнения движения системы материальных точек, нужно выразить составляющие ускорения через координаты движущихся точек, применяя второй закон динамики Ньютона, согласно которому составляющая ускорения точки по любой координатной оси равна сумме составляющих по той же оси всех сил, действующих иа эту точку, поделенной на ее массу. Но это правило справедливо только для неподвижной системы координат и поэтому в нашем случае, где система координат движется вместе с точкой Мо, непосредственно неприменимо.   [c.355]

Второй закон динамики (Ньютон). Ускорение материальной точки относительно инерциальной системы координат прямо пропорционально силе, приложенной к точке, и обратно пропорционально ее массе, т.е.  [c.41]

Классическая динамика свободной материальной точки вытекает из законов И. Ньютона ( 124—131 т. I). Формулировка основного — второго закона И. Ньютона основывается на понятии о количестве движения материальной точки ( 126 т. I).  [c.521]

Эта формула математически выражает второй закон динамики, установленный Ньютоном на основе обобщения опытов, подобных рассмотренным выше. Он утверждает  [c.33]

Зависимость между силой и сообщаемым ею ускорением устанавливает второй закон динамики, или второй закон Ньютона, который формулируется так ускорение, сообщаемое материальной точке силой, имеет направление силы и пропорционально ее модулю.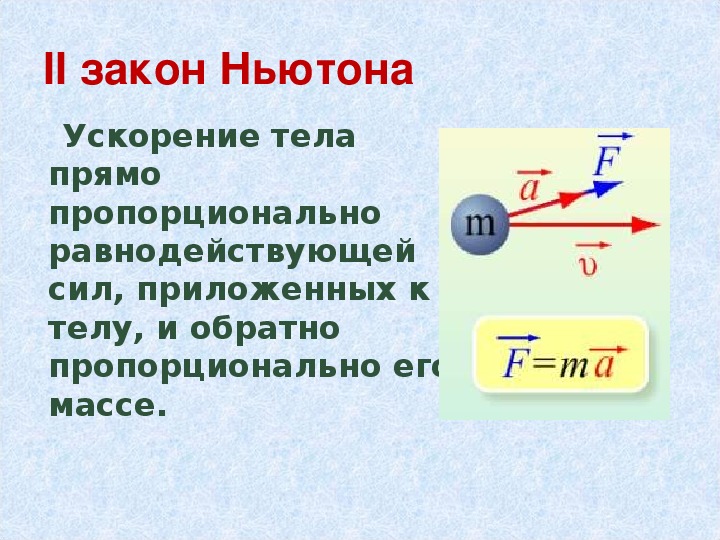  [c.124]

Ньютон сформулировал второй закон динамики так Изменение количества движения пропорционально движущей силе и происходит по направлению той прямой, по которой эта сила действует ).  [c.66]

Зависимость между силой и сообщаемым ею ускорением устанавливает второй закон динамики, или второй закон Ньютона, который формулируется так  [c.141]

Основным законом динамики является второй закон Ньютона производная по времена от количества движения материальной точки равна действующей на нее силе, т. е.  [c.319]

Галилей открыл (1589 г.) законы падения тел на Землю. Ньютон пришел к общему понятию движения с переменной скоростью. К этому он присоединил очень трудное и важное для динамики понятие массы. Соотношение между изменением движения и силой сформулировано им во втором законе.  [c.256]

Обратимся к прямой задаче динамики и рассмотрим уравнение, выражающее второй закон Ньютона  [c. 170]

Вторая аксиома динамики (второй закон Ньютона)  [c.205]

Вторая аксиома, или основной закон динамики, принадлежащий Ньютону, устанавливает зависимость ускорения точки относительно инерциальной системы отсчета 01 действующей на нее силы и массы точки ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе (рис, 1). Если Р есть приложенная к точке сила и а — ее ускорение относительно инерциальной системы отсчета Охуг, то основной закон можно выразить в форме  [c.225]

Основное уравнение динамики материальной точки представляет собой не что иное, как математическое выражение второго закона Ньютона  [c.45]

Второй закон Ньютона положен в основу составления систем дифференциальных уравнений движения материальной точки. В связи с этим второй закон Ньютона иногда называют основным законом динамики.  [c.318]

Это название обусловлено также и тем, что основные теоремы динамики, как будет показано далее, являются следствиями, главным образом, второго закона Ньютона.  [c.318]

Основой динамики абсолютного движения материальной точки является второй закон Ньютона, который формально охватывает и первый закон Ньютона — закон инерции. Действительно, если предполагать, что масса точки не зависит от времени, то из соотношения (П1.5Ь) вытекает, что при равенстве нулю равнодействующей Е сил, приложенных к точке, равно нулю и ускорение т. е. материальная точка движется по инерции равномерно и прямолинейно.  [c.441]

Как и в классической динамике, эти уравнения вытекают из второго закона Ньютона ( 128 т. I). При рассмотрении второго закона Ньютона отмечалось, что в теории относительности следует исходить из равенства (III. 5а), указанного в т. I. Это равенство на основании соотношений (IV. 138) — (IV. 139) имеет следующий вид  [c. 523]

Открытие Галилеем законов свободного падения тел сыграло основополагающую роль в деле создания ньютоновской динамики и, в частности, второго закона Ньютона.  [c.13]

Если к материальной точке приложены две или несколько сил, то ускорение, приобретаемое ею под действием равнодействующей этих сил, построенной по правилу параллелограмма, определится как векторная сумма ускорений точки под действием каждой слагаемой силы по отдельности. Это заключение является простым следствием второго закона Ньютона в принятой векторной формулировке (2). При этом используется допущение, что в динамических условиях, так же как и в статических, приложенные к материальной точке силы действуют на нее независимо друг от друга, т. е. наличие одних сил не вызывает изменений в действии других. Это положение составляет содержание принципа независимости действия сил, позволяющего применять в динамике правило параллелограмма сил и все те операции над системами сил, которые были установлены в статике.  [c.16]

Из постановки этих двух основных задач динамики непосредственно следует, что из трех переменных, входящих в формулу (2) второго закона (масса, кинематика движения, сила), задаются только две масса и кинематические уравнения движения— в первой задаче динамики, масса и сила —во второй. Это говорит о том, что второй закон Ньютона, выраженный векторной формулой (2) или аналитически системой (7), не является тождеством (определением понятия силы), а представляет собой уравнение с неизвестным вектором силы F (первая задача динамики) или вектор-радиусом r t) (вторая задача динамики).  [c.20]

Масса. Второй закон Ньютона (основная аксиома динамики). Наблюдение и опыт показывают, что материальные тела обладают рожденным свойством, из-за которого тело с трудом выводится из состояния покоя или изменяет свое движение. Способность материальной точки сопротивляться изменению ее скорости называется инертностью.  [c.71]

В такой форме второй закон Ньютона носит название основного уравнения динамики материальной точки и читается так  [c. 238]

Выражение (5.5), которое может быть также получено с помощью строгого анализа [4, 5], показывает, что величина Йк лри рассмотрении вопросов динамики электронов играет роль классического импульса. Тем не менее, хотя формула (5.5) выглядит как второй закон Ньютона, она ему не эквивалентна, поскольку в выражение для силы F не включена сила, связанная с периодическим полем кристалла, а Як определено неоднозначно и представляет собой не импульс, а квазиимпульс.  [c.89]

Дифференциальное уравнение движения выражает собой основной закон динамики (второй закон Ньютона) применительно к движущейся сплошной среде. Идею вывода уравнения движения рассмотрим на элементарном примере движения жидкости между двумя параллельными плоскостями (рис. 12.2). Как и в случае уравнения энергии, ограничимся случаем несжимаемой жидкости (капельная жидкость или газ при умеренной скорости движения).  [c.272]

Первый и второй законы динамики Ньютона справедливы в инерциальной системе отсчета. С достаточной для практики точностью такой системой можно считать гелиоцентрическую с началом в центре Солнца и с осями, направленными на неподвижные звезды. Любая система, покоящаяся или движущаяся равномерно и прямолинейно относительно инерциальной, тоже инерциальна. Так как Земля вращается вокруг своей оси и вокруг Солнца, то главным образом по первой причине система отсчета, связанная с ее поверхностью, не является инерциальной. Однако ошибка при допущении об инерциальности геоцентрической системы в большинстве практических расчетов пренебрежимо мала.  [c.199]

Правило параллелограмма сил установлено в результате работ ряда ученых, из которых следует упомянуть С. Стевина (умер в 1633 г.) И. Ньютона и П. Вариньона (1654—1722). Симон Стевин доказал правило параллелограмма сил, исходя из невозможности существования вечного двигателя (perpetuum mobile).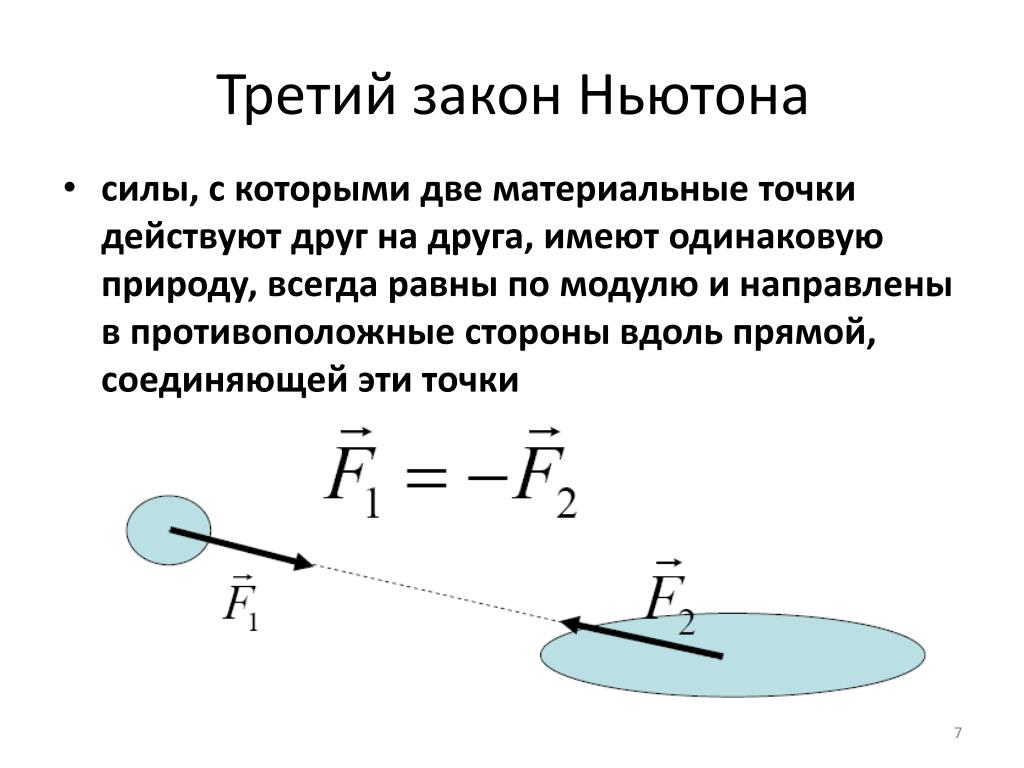 И. Ньютон и П. Вариньон доказывали правило параллелограмма сил, основываясь на принципах динамики. Собственно И. Ньютон рассматривал правило параллелограмма как добавление ко второму закону динамики, подтверждающее с современной нам точки зрения векторные свойства силы. Вариньон, не ограничиваясь дедуктивными соображениями, проверил правило параллелограмма экспериментально на построенном им приборе.  [c.251]

Ньютоном второй закон динамики был дан в более общей форме, иначе, чем это было сделано в предыдущих параграфах Для характеристики механического состояния при двнжеиии тела вводится еще одна величина — количество движения тела (или импульс). Количество движения тела — векторная физическая величина, численно равная произведению массы на скорость и имеющая направление, совпадающее с направлением скорости тела. Если количество движения тела с массой т обозначим К, то при скорости V  [c.66]

Сделаем предварительно следующее замечание об использовании уравнений Лагранжа для описания относительного движения в неинерциальной системе отсчета. В гл. И было установлено, что второй закон Ньютона (а значит, и основные теоремы динамики) может быть использован и в неинерциальной системе отсчета, если к /-Й точке системы (/=],. .., N) помимо действующих сил приложить силы инерции — переносную, Ji ep = = — miWi ер. и кориолисову, Ji кор = — 2т,- (ш х / o, )-  [c.160]

Теорема 5.1.1. (Приыщш Даламбера-Лагранжа). Для того чтобы ускорения Ги материальных точек (ш,у,г ), I/ = удовлетворяли второму закону Ньютона в инерциальной системе отсчета под действием активных сил и идеальных двусторонних связей (см. 3.8), необходимо и достаточно выполнение общего уравнения динамики  [c.378]

В этой главе будет рассмотрен ряд основных положений динамики, дающих возможность находить первые интегралы дифференциальных уравнений двилгения материальной точки. Эти положения динамики будем называть теоремами, так как они являются непосредственными следствиями из основных законов и аксиом механики. Заметим, что иногда эти теоремы называют также законами, но, конечно, при этом их надо четко отличать от основных законов механики — законов Ньютона.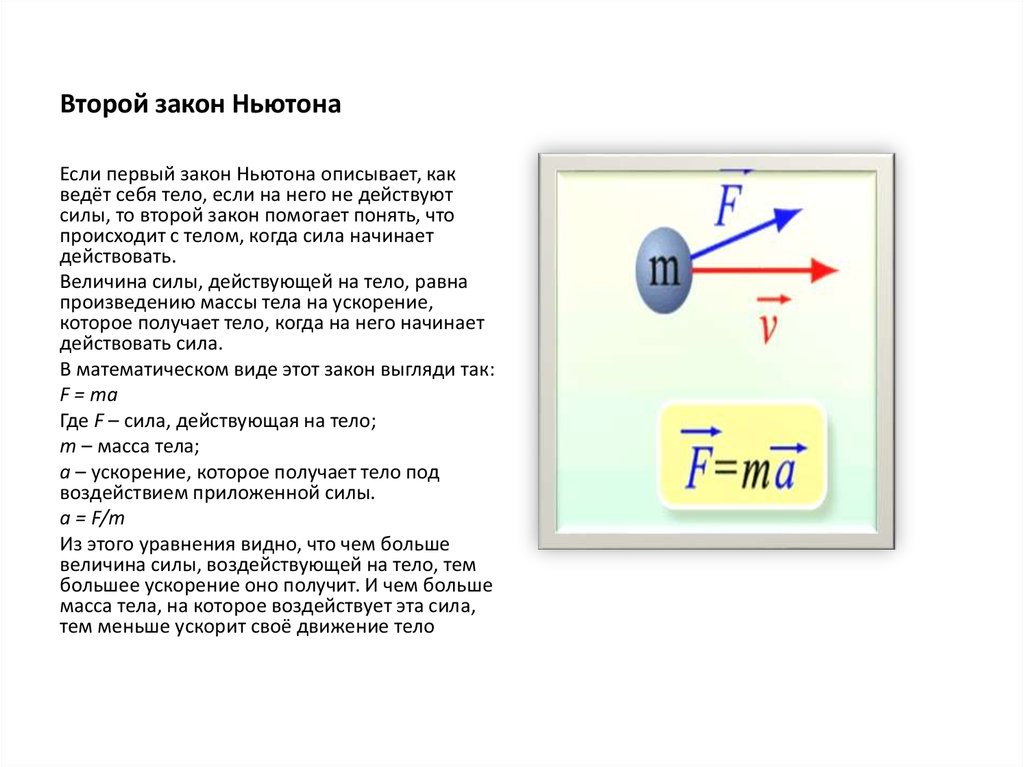 Основные теоремы динамики — это выводы в первую очередь из второго закона Ньютона, который поэтому называется основным законом механики.  [c.359]

Теорему об изменении кинетического момента системы в ее движении относительно центра инерции можно было доказать иначе, не используя формулу (1.51), а исходя из основного закона динамики относительного движения ( 230 т. I). Как известно, всякую задачу при изучении относительного движения материальной точки можно решать как задачу об абсолЕОТ-ном движении, но вместо второго закона Ньютона для абсолютного движения нужно пользоваться основным законом динамики относительного движения  [c.66]

Почти все выводы, получеппые в предыдущих главах, о двииа–иии механических систем опирались на второй закон Ньютона, устанавливающий зависимость ме кду ускорением точки и действующей на нее силой. Одпако второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем неремеи пого состава требует особого рассмотрения.  [c.214]

Второй закон Ньютона (основной закон динамики). Произведение массы точки на ускорение, получаемое точкой относительно инерциалъной системы координат под действием приложенной к ней силы, равно этой силе, т. е.  [c.94]

---

Второй закон Ньютона

«Второй закон Ньютона»

Цель: вывести формулы второго закона Ньютона, ознакомить учащихся с формулировкой основного закона динамки.

Задачи урока:

Образовательная: Обеспечить проверку и оценку знаний учащихся по теме «первый закон Ньютона», ускорение. Выяснить причину появления у тела ускорения, вывести формулу второго закона Ньютона. Формировать умения применять второй  Ньютона при решении задач.

Воспитательная: стимулировать учащихся к работе на занятиях, продолжить формирование познавательного интереса к предмету «Физика», продолжать развивать навыки грамотной, монологической и диалогической  речи  учащихся с использованием физических терминов. Содействовать развитию у учащихся умения общаться, приучать к доброжелательному общению, взаимопомощи, формировать навыки  коллективной  работы, продолжить работу по развитию внимания учащихся, самостоятельности и целеустремлённости в достижении поставленных целей.

Развивать физическое мировоззрение, воспитывать у учащихся уважение к учёным в области физики.

Развивающая:  Продолжать развивать умение учащихся проводить анализ и оценку работы одногруппников, продолжать работу по развитию умения наблюдать, сопоставлять, сравнивать и обобщать результаты.

 

Ход урока

 

I.                  Организационный момент (2 мин.)

Сегодня на уроке мы изучим второй закон Ньютона, а также познакомимся с личностью гениального ученного И. Ньютона и ознакомимся с интересные факты из его жизни.

II.               Актуализация знаний. (8 мин.)

·        Дайте определение ускорению.

·        В каких единицах в СИ оно измеряется?

·        Чему равно ускорение в случае равномерного прямолинейного движения ?

·        Что такое сила?

·        Сформулируйте первый закон Ньютона.

·        Как называются системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела или равнодействующая всех сил равна нулю?

·        Как называется система отсчета, относительно которой тело движется с ускорением?

III.           Изучение нового материала. (30 мин.)

Ньютон – это великий человек-светило, который издавна известен мировой науке. Интересные факты из жизни Ньютона говорят о том, что знаменитый физик и математик смог сформировать теорию движения, исчисления и гравитации, и это все не считая решения других вопросов, которые ему пришлось изучить за годы жизни. Факты из жизни Ньютона заинтересуют каждого человека, потому что о великих людях хочется знать все.

 

Предлагает вашему вниманию пять интересных фактов из жизни гениального учёного.

1. Исаак Ньютон, как известно, был членом палаты лордов, и заседания палаты посещал самым регулярным образом. Однако на протяжении многих лет он не проронил ни слова на заседаниях. Все замерли, когда, наконец, великий ученый вдруг попросил слова. Все ожидали услышать грандиозную речь, но Ньютон в гробовой тишине провозгласил: ”Господа, я прошу закрыть окно, иначе я могу простудиться!”

2. В последние годы своей жизни Исаак Ньютон серьёзно взялся за богословие и под большим секретом писал собственную книгу, о которой высказывался, как о самом великом и важном своем труде. Он считал, что этот труд сможет решительным образом изменить жизнь людей. Кто знает, какой бы была эта книга, но по вине любимой собаки Ньютона, которая опрокинула лампу, случился пожар. В результате кроме самого дома и всего имущества сгорела и рукопись.

3. Во времена Ньютона ценность монет была эквивалентна содержащемуся в них количеству металла. В связи с этим существовала проблема – мошенники срезали небольшие кусочки металла с краёв, чтобы делать из них новые монеты. Решение проблемы предложил Исаак Ньютон. Его идея была очень простой – прорезать на краях монеты маленькие линии, из-за которых стёсанные края были бы сразу заметны. Эта часть на монетах оформляется таким образом и по сей день и носит название гурт.

4. Исаак Ньютон интересовался многими аспектами не только физики, но и других наук, и не боялся проводить некоторые эксперименты на себе. Свою догадку о том, что мы видим окружающий мир из-за давления света на сетчатку глаза, он проверял так: вырезал из слоновой кости тонкий изогнутый зонд, запустил его себе в глаз и надавил им на заднюю сторону глазного яблока. Возникшие цветные вспышки и круги подтвердили его гипотезу.

5. Хотя многоцветный спектр радуги непрерывен, по традиции в нём выделяют семь цветов. Считается, что первым выбрал число семь Исаак Ньютон. Причём первоначально, он различал только пять цветов – красный, жёлтый, зелёный, голубой и фиолетовый, о чём и написал в своей ”Оптике”.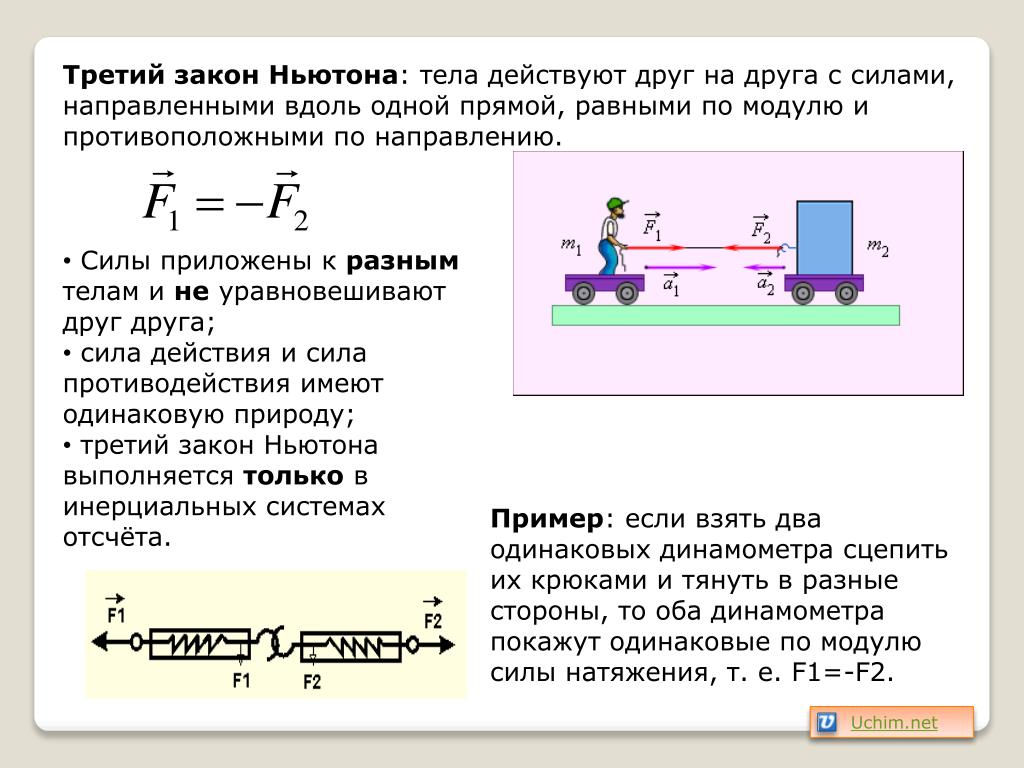 Но впоследствии, стремясь создать соответствие между числом цветов спектра и числом основных тонов музыкальной гаммы, он добавил ещё два цвета.

А теперь перейдём к изучению второго закона Ньютона.

Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.

Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила  а также способы их измерения. Первая из этих величин – масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила  – является количественной мерой действия одного тела на другое.

Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:

Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам: 

при F = const.

Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам: 

при m = const.

Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:

Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила : 

В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с².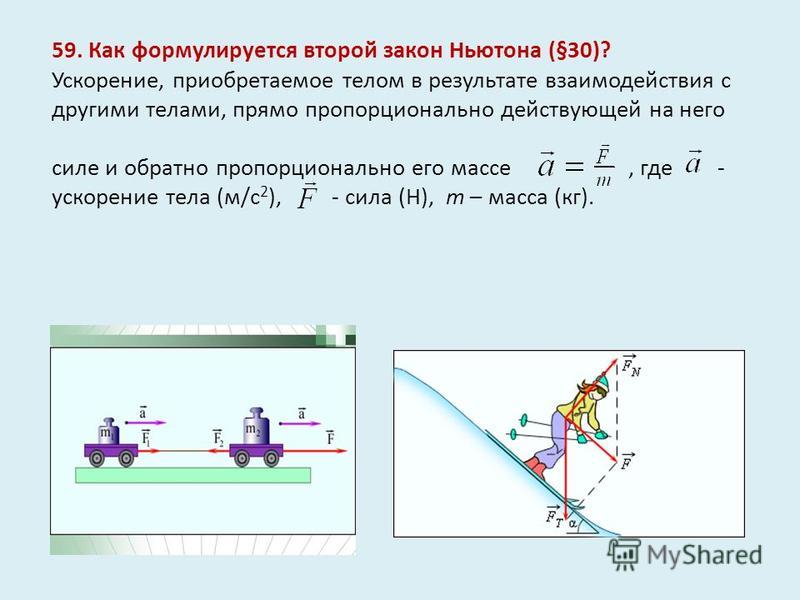 Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы: 

Если на тело одновременно действуют несколько сил (например, F₁, F₂ и F₃, то под силой  в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил: 

 

 

 

 

 

Если равнодействующая сила  , то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

Оценивая значение второго закона Ньютона, А. Эйнштейн писал:

«Дифференциальный закон является той единственной формой причинного объяснения, которая может полностью удовлетворять современного физика. Ясное понимание дифференциального закона есть одно из величайших духовных достижений Ньютона… Только переход к рассмотрению явления за бесконечно малое время (т. е. к дифференциальному закону) позволил Ньютону дать формулировку, пригодную для описания любого движения… Так Ньютон пришёл… к установлению знаменитого закона движения. Это — фундамент всей механики и, пожалуй, всей теоретической физики».

 

 

 

 

 

Решение задачи на применение второго закона Ньютона:

 

Решение количественных задач:

·        Определите силу, под действием которой велосипедист скатывается с горки с ускорением, равным 0,8 м/с2, если масса велосипедиста вместе с велосипедом равна 50 кг.

·        Герой одного из рассказов О’ Генри дал пинок поросенку с такой силой, что тот полетел, «опережая звук собственного визга». С какой силой должен был ударить поросенка герой рассказа, чтобы описанный случай произошел в действительности? Массу поросенка примем равной 5 кг, а продолжительность удара 0,01 с.

IV. Рефлексия учебной деятельности (2 мин.) 

Подведение итогов.

Взаимная оценка работы на уроке.

V. Домашнее задание (3 мин.) 

 

Урок по теме “I и II законы Ньютона” с использованием модульной технологии

М. Законы динамики. I и II законы Ньютона.

№ УЭ

Содержание учебного материала.

Цели и задачи.

Комментарии для учащегося

УЭ 0

Необходимо знать:

– понятие инерциальной системы отсчёта

– формулировку I закона Ньютона

– формулировку и математическое выражение II закона Ньютона

– границы применимости законов.

Запишите тему урока в рабочую тетрадь.

УЭ 1

Изучение вопроса «I закон Ньютона»

1. 1. Продолжите запись:

1. Закон инерции Галилео Галилея:

«Тела находятся в покое или ___________________».

2. В изложении Ньютона закон инерции читается так:

«Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока ___________________________________________»

1.2 Стремление тел сохранить состояние покоя или равномерного прямолинейного движения называется инертностью.

1.3 Основные факты

– Системы отсчета, в которых выполняется I закон Ньютона называются инерциальными системами отсчета.

– Сам закон называют иногда законом инерции.

– Системы отсчета, в которых I закон Ньютона не выполняется, называются неинерциальными.

– Свойство тела противиться попыткам изменить его состояние движения называется инертностью. В качестве количественной характеристики инертности используется величина, называемая массой тела.

1.4 С точки зрения современных представлений первый закон Ньютона формулируется так: «Существуют такие системы отсчёта______________________________».

К инерциальным системам отсчёта можно отнести с высокой степенью точности гелиоцентрическую систему и любую другую систему отсчёта, которая движется равномерно и прямолинейно относительно неё.

Записываете в рабочих тетрадях. Информацию для записи нового материала найдите в § 10

УЭ 2

Изучение вопроса «II закон Ньютона»

1. 1. Из курса физики 7 класса нам известно:

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. Масса измеряется в килограммах [кг]. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10-12 их значения).
Сила — векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Сила измеряется в Ньютонах [Н].
Материальная точка — объект, размерами которого в условиях данной задачи можно пренебречь, считая его массу сосредоточенной в одной точке пространства.

1.2 Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:

1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам: 

   при F = const.

2. Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам: 

  при m = const.

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Обычно этот закон записывается в виде формулы:

где  — ускорение тела,  — сила, приложенная к телу, а  — масса материальной точки.

Или, в ином виде:

Особенности применимости закона: Второй закон Ньютона в виде  приближённо справедлив только для скоростей, много меньших скорости света, и в инерциальных системах отсчёта.

В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с².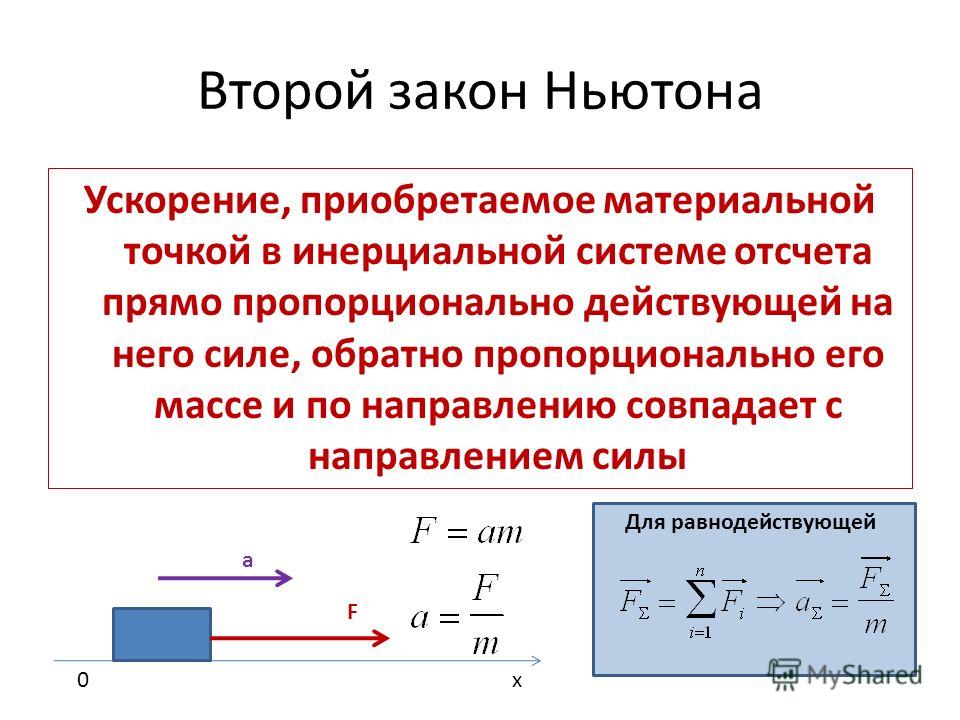 Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы: 

Если на тело одновременно действуют несколько сил то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил: 

Второй закон Ньютона в общем случае имеет вид:

Если равнодействующая сила равна нулю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

Для изучения материала воспользуйтесь § 11.

Рассмотрите рисунок 20 учебника и запишите основные выводы.

УЭ 3

Закрепление изученного материала.

Выполните задания упр. 11 № 1,2 на стр. 47

Работаете в тетрадях

УЭ 4

Запись домашнего задания.

1.§ 10,11 – читать, основные понятия выучить.

2. решить задачи упр. 10 – устно, упр. 11 № 4 в тетради.

На следующем уроке сдать тетради на проверку.

УЭ 5

Подведение итогов. Рефлексия.

Проанализируйте соответствие изученного материала с необходимыми знаниями, отмеченными в УЭ0. При необходимости приготовьте вопросы учителю

Рис. 1. Взаимодействие двух тел

Третий закон Ньютона. Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны.

Основные законы динамики в теоретической механике

Основные законы динамики

Свои основные положения динамика берет из опыта и наблюдений и с их помощью, а также с помощью кинематики и геометрии выводит законы движения.

Древние ученые имели смутное представление о законах движения. Аристотель (384—322 гг. до и. э.) не знал еще закона инерции, считая, что с прекращением действия силы тела прекращают двигаться. Только после долгих наблюдений над происходящими в природе движениями Галилеем был раскрыт один из основных законов движения, устанавливающий, что всякое тело пребывает в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока внешние силы не выведут его из этого состояния. Этот закон не был сформулирован Галилеем в его универсальной форме, хотя Галилей и пользовался им в явном виде для объяснения различных явлений.

Закон инерции Галилея

Закон инерции Галилея является обобщением опытных фактов, накопленных человечеством. Опираясь на него, Ньютон сформулировал свои основные законы движения.

Первый закон Ньютона. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние.

Под телом здесь подразумевается материальная точка, а сила определяется как причина, изменяющая равномерное и прямолинейное движение материальной точки. За меру силы Ньютон принял то ускорение, которое эта сила вызывает, в связи с чем сила в механике Ньютона называется ускоряющей.

Первый закон Ньютона

Первый Закон Ньютона называют еще законом инерции. Под инерцией понимают способность тела сохранять свое движение или состояние покоя при отсутствии сил или изменять это состояние под действием сил.

Связь между силой и ускорением устанавливает второй закон Ньютона.

Второй закон Ньютона

Второй закон Ньютона. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.

Математически этот закон можно представить в виде уравнения

где v —скорость движущейся точки; m — ее масса; mv — количество движения. Считая массу материальной точки величиной постоянной, второму закону Ньютона можно придать и другую математическую формулировку:

т. е. ускорение, которое получает материальная точка, пропорционально действующей на точку силе. Это уравнение является основным законом движения материальной точки. Масса m входит в него как коэффициент пропорциональности между силой и ускорением. Из этого определения видно, что масса является характеристикой инертного свойства материальной точки, т. е. способности ее под действием заданной силы получать определенное ускорение. Так же, как и первый закон Ньютона, второй закон является результатом обобщения многовекового опыта всего человечества и принимается как одна из основных аксиом механики.

Третий закон Ньютона

Третий закон Ньютона. Действию всегда есть равное и противоположное противодействие, другими словами — действия двух тел друг на друга всегда равны и направлены в противоположные стороны.

Этот закон рассматривался нами при изучении аксиом статики.

Можно заметить, что второй закон Ньютона содержит в себе и закон инерции Галилея. В самом деле, если положить то из второго закона следует или т. e. если сила

не действует на материальную точку, то последняя движется равномерно и прямолинейно. Тем не менее закон инерции Галилея устанавливает само понятие ускоряющих сил в механике.

Из второго закона Ньютона следует, что так же, как и ускорение, понятие силы в механике связано с определенной системой отсчета. Поскольку сила измеряется ускорением, которое она сообщает материальной точке, а ускорение имеет смысл только по отношению к той или иной системе отсчета, то и понятие силы должно быть относительным понятием и связано с выбором системы отсчета.

В различных системах отсчета математическая форма законов природы различна, однако существуют такие, так называемые инерцнальные системы отсчета, в которых эти законы имеют наиболее простой вид. Такими инерциальными системами называются системы отсчета, в которых материальная точка при отсутствии действующих на нес сил взаимодействия (по третьему закону Ньютона) движется равномерно и прямолинейно, т. е. системы, для которых справедлив закон инерции Галилея (силы можно считать отсутствующими в том случае, когда все тела, от которых эти силы могут исходить, достаточно удалены, так что можно пренебрегать их влиянием). С достаточной точностью такой инерциальной системой можно считать гелиоцентрическую систему координат. В первом приближении (для малых движений) система отсчета, связанная с Землей, так же может рассматриваться как инерциальная система координат.

Уравнение справедливо только по отношению к инерциальной системе координат, в которой определена сила, действующая на материальную точку. Для всякой другой системы отсчета, движущейся относительно данной инерциальной системы поступательно и с постоянной скоростью, законы Ньютона остаются справедливыми, так как основной характеристикой в этих законах является ускорение, а не скорость.

В большинстве технических задач, в которых движения точек ограничены, основная система отсчета может быть связана с Землей. Для астрономических задач принятие такой системы невозможно, и приходится учитывать вращение Земли, а за основную систему отсчета выбирать систему, связанную со звездами. Подробнее’ эти вопросы будут рассмотрены в разделе, посвященном относительному движению материальной точки.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Второй закон Ньютона, или основной закон динамики

Второй закон Ньютона – дифференциальный закон механического движения, который описывает зависимость ускорения (если ускорение отрицательно, то его называют замедлением) тела от равнодействующей всех приложенных к телу сил F1 и массы тела m в виде

Или ускорение, приобретаемое телом, прямо пропорционально вызывающей его силе F и совпадает с ней по направлению и обратно пропорционально массе m тела. Уравнения, соответствующие данному закону, называются дифференциальными уравнениями движения.

Рис. 2.1. Ускоренное движение автомобиля.

Так, например, если суммарная сила тяги на ведущих колесах переднеприводного автомобиля при его прямолинейном движении, как показано на рис. 2.1, постоянна и равна F, то этот автомобиль в данный момент времени t ускоряется в направлении действия этой силы с ускорением а:

Тогда при неизменном ускорении скорость автомобиля в некоторый момент времени t равна интегралу от выражения для ускорения плюс постоянная интегрирования – начальная скорость автомобиля в момент времени t=0:

Путь, пройденный автомобилем за время t, равен интегралу от его скорости плюс постоянная интегрирования – начальный путь автомобиля в момент времени t=0:

Выражения (2.2) и (2.3) можно записать как производные по времени, где первая производная по времени обозначается символом с точкой наверху, а вторая производная по времени – с двумя точками наверху: скорость есть первая производная от функции пути от времени, ускорение есть первая производная от функции скорости от времени и, соответственно, вторая производная от функции пути от времени:

В общем случае сила, ускорение и скорость – векторные величины. Тогда уравнения (2.2) – (2.5) записываются либо в векторном виде, либо в виде проекций на оси неподвижной системы координат.

Чтобы получить связь скорости и пути ускорения (замедления) автомобиля, выражение для ускорения a из (2.5) можно записать в виде

После упрощения выражение (2.6) принимает вид

Тогда левую и правую части выражения (2.7) можно проинтегрировать, записав постоянную интегрирования в виде половины квадрата начальной скорости автомобиля:

После интегрирования получаем

Откуда после преобразования выражение для квадрата скорости принимает вид

Или, извлекая квадратный корень из левой и правой части равенства (2.10), получаем выражение для скорости автомобиля v в м/с в зависимости от пути x, на котором автомобиль ускорялся или замедлялся:

Выражение (2.11) может быть преобразовано для более привычной единицы измерения скорости транспортных средств в км/ч с учетом, что 1 м/с = 3.6 км/ч:

В выражении (2. 12) использовано, что 2х3.6²=25.92, или с округлением до целого равно 26.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Закон силы и ускорения – Второй закон движения Ньютона

Согласно второму закону движения Ньютона , также известному как Закон силы и ускорения , сила, действующая на объект, заставляет его ускоряться в соответствии с формулой чистая сила = масса x ускорение . Таким образом, ускорение объекта прямо пропорционально силе и обратно пропорционально массе.

Закон силы и ускорения. Это также известно как второй закон движения Ньютона.Второй закон Ньютона состоит из трех компонентов. Первый заключается в том, что сила, действующая на объект, заставляет другой ускоряться, второй – это ускорение прямо пропорционально силе, поэтому чем сильнее я толкаю, тем сильнее он ускоряется. В-третьих, это ускорение обратно пропорционально массе объекта, поэтому, если я толкаю пустую тележку для покупок, я смогу заставить ее двигаться намного быстрее, чем если бы я толкал полную тележку для покупок. продуктов.

Хорошо, это имеет смысл, и мы можем показать это соотношение по формуле Ньютона здесь, сила равна массе, умноженной на ускорение, хорошо.Итак, давайте займемся практической задачей, чтобы вы могли убедиться, что это хорошее применение второго закона движения Ньютона. Допустим, у нас есть ракета в космосе, поэтому нет сопротивления воздуха или чего-то еще, она ускоряется со скоростью 40 метров в секунду, но при ускорении теряет массу, потому что сжигает топливо. Топливо фактически превращается в тягу, которая заставляет его ускоряться, поэтому в точке, где оно сжигает половину своей массы из-за потери топлива, и тяга увеличивается втрое, какое ускорение будет в этот момент, хорошо?

Хорошо, если мы скажем, что сила равна массе, умноженной на ускорение, и мы скажем, что сила тяги утроится за это время, но масса уменьшится вдвое, тогда то, что происходит с ускорением, хорошо, поэтому мы собираемся сказать, что x равно изменение ускорения в порядке. Что ж, если я скажу, что это увеличение в 3 раза, а это уменьшение вдвое, тогда наше ускорение должно увеличиться в 6 раз. Итак, 6 умноженных на 40 метров в секунду – это 240 метров в секунду в квадрате, что является ускорением в данный момент и время. И это одна из причин, по которой ракеты действительно ускоряются в космосе, потому что они теряют массу, а потеря массы, наоборот, увеличивает их ускорение, понятно? Это хорошая практическая задача, демонстрирующая второй закон движения Ньютона.

Ньютонов Второй Закон – Сила

Второй закон Ньютона гласит, что когда на объект действует чистая сила, изменение состояния движения объекта будет обратно пропорционально массе объекта и прямо пропорционально чистой силе, действующей на объект.

Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с силой . В нем говорится, что когда на объект действует чистая сила, изменение состояния движения объекта будет обратно пропорционально массе ( м, ) объекта и прямо пропорционально чистой силе ( F, _{, чистая} ). ) воздействуя на объект.Это может быть записано как:

F _чистая = ma

Уравнение показывает, что ускорение системы прямо пропорционально чистой внешней силе , действующей на систему, и в том же направлении, что и чистая внешняя сила , и обратно пропорционально ее массе. Эффект силы, ускорение , представляет собой изменение скорости объекта (по величине, направлению или и того, и другого). Чем меньше масса испытывает заданную силу, тем больше ее ускорение.Чем больше масса испытывает данную силу, тем меньше результирующее ускорение или действие этой силы. Прямая пропорциональность между F и a демонстрирует, что для данной массы, чем больше сила, тем больше ускорение.

F _net = м используется для определения единиц силы в терминах трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с ² .То есть, поскольку F _net = м a , 1 N = 1 кг м / с ² .

В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.

Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, – это сила тяжести, обычно называемая его весом , Вт. Вес можно обозначить как вектор w, потому что он имеет направление; вниз , по определению, является направлением силы тяжести, и, следовательно, вес – это сила, направленная вниз. Величина веса обозначается как w . При отсутствии сопротивления воздуха все предметы падают с одинаковым ускорением g .

Уравнение для веса – сила тяжести, действующая на массу m:

w = мг
g = 9,80 м / с ² (на Земле)

Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что оно находится в пределах свободного падения .То есть единственной силой, действующей на объект, является сила тяжести . В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.

Помните, важно знать, что вес и масса очень разные физические величины. Масса – это скалярное измерение, количество материи (сколько «вещества») и не изменяется в классической физике.Между тем, вес является векторным измерением силы тяжести и изменяется в зависимости от силы тяжести.

Практические вопросы

Академия Хана

Механика стоячих весов

Напряжение в мышцах

Пациенты в инвалидной коляске

Испытание нового шовного материала

Силы по камню в почках

Травмы колена у спортсменов

Сотрясения мозга у профессиональных спортсменов

Сила натяжения

Силы трения ходунков

Лифт в больнице

Пандус в административном кабинете

Холмы, ненастная погода и автомобили

Весы под водой

Ишемическая болезнь сердца и артериальное давление

Гидротерапия и полное погружение в тело

Официальная подготовка MCAT (AAMC)

Пакет вопросов по физике Вопрос 57

Physics Question Pack Отрывок 15 Вопрос 89

Практический экзамен 4 Раздел C / P Отрывок 10 Вопрос 55

Ключевые точки

• Ускорение ( a ) определяется как изменение скорости, означающее изменение ее величины или направления, или и того, и другого.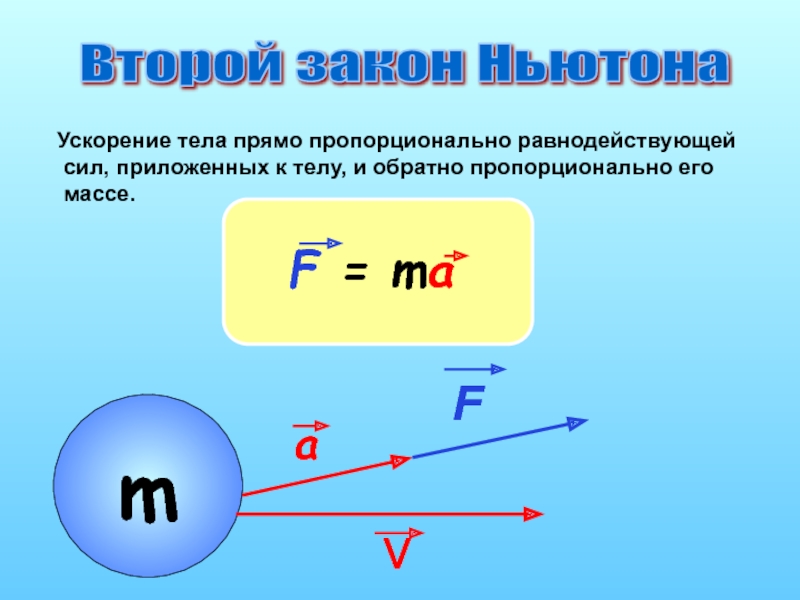

• Внешняя сила – это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.

• Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.

• В форме уравнения второй закон движения Ньютона: a = Fnet / m

• Часто это записывается в более привычной форме: F _net = m a .

• Вес объекта w определяется как сила тяжести, действующая на объект массой м . Объект испытывает ускорение свободного падения g : w = m g .

• Если единственная сила, действующая на объект, вызвана силой тяжести, объект находится в свободном падении.

• Трение – это сила, которая препятствует движению соприкасающихся объектов друг за другом.

Ключевые термины

Второй закон движения Ньютона : Когда на объект действует чистая сила, изменение состояния движения этого объекта будет обратно пропорционально массе ( м ) объекта и прямо пропорционально чистой силе ( F ), воздействующие на объект.Его можно записать как F = ma .

Сила : Сила – это любое взаимодействие, которое без сопротивления изменяет движение объекта. Сила может заставить объект с массой изменить свою скорость (в том числе начать движение из состояния покоя), то есть ускориться.

Система : Часть физической вселенной, выбранная для анализа. Все, что находится вне системы, называется окружающей средой. Окружающая среда игнорируется, за исключением ее воздействия на систему.2

Свободное падение : Ситуация, в которой единственная сила, действующая на объект, – это сила гравитационного трения: сила, действующая друг на друга соприкасающихся объектов; примеры включают шероховатую поверхность и сопротивление воздуха.

Гравитация: Естественная сила, заставляющая предметы падать на землю; в уравнениях записывается как g (g = 9,8 м / с ² ).

Масса: Мера количества вещества в веществе или объекте.

Вес: Вес объекта связан с силой, действующей на объект, либо из-за силы тяжести, либо из-за силы реакции, удерживающей его на месте.

10 примеров второго закона движения Ньютона в повседневной жизни – StudiousGuy

Второй закон движения Ньютона, также известный как закон ускорения, гласит, что величина силы, действующей на объект, равна произведению массы этого конкретного объекта и ускорения, с которым он движется.Это означает, что ускорение, производимое телом, прямо пропорционально приложенной к нему силе и обратно пропорционально массе объекта. Законы движения были открыты в 1687 году английским математиком, физиком, астрономом, теологом и писателем сэром Иссаком Ньютоном. Законы движения упоминаются в одной из написанных им книг под названием Philosophiae Naturalis Principia Mathematica, широко известной как Principia. Короче говоря, согласно второму закону движения, объект с большей массой ускоряется больше, чем объект с меньшей массой.Также в нем говорится, что с увеличением силы ускорение увеличивается и наоборот.

Указатель статей (Нажмите, чтобы перейти)

Примеры второго закона движения Ньютона

1. Толкание автомобиля и грузовика

Второй закон движения Ньютона можно наблюдать, сравнивая ускорение автомобиля и грузовика после приложения одинаковой силы к обоим. Легко заметить, что, толкнув автомобиль и грузовик с одинаковой интенсивностью, автомобиль разгоняется сильнее, чем грузовик.Это потому, что масса автомобиля меньше массы грузовика.

2. Тележка для покупок

Толкать пустую тележку для покупок легче, чем толкать загруженную тележку. Это связано с соотношением массы объекта, приложенной к нему силы и создаваемого ускорения. Поскольку масса имеет обратную зависимость от ускорения, загруженная тележка имеет тенденцию двигаться медленнее, чем пустая тележка.

3.Два человека идут вместе

Представьте себе двух людей разной массы, идущих вместе. Из-за обратной зависимости между массой и ускорением человек с большей массой имеет тенденцию двигаться медленнее, а человек с меньшей массой имеет тенденцию двигаться быстрее. Этот сценарий оправдывает второй закон движения Ньютона в реальной жизни, устанавливая связь между массой, ускорением и силой.

4. Удар по мячу

После удара мяч развивает определенное ускорение.Ускорение, с которым движется мяч, прямо пропорционально приложенной к нему силе. Это означает, что чем сильнее вы ударяете по мячу, тем быстрее он будет двигаться, демонстрируя тем самым второй закон движения Ньютона в повседневной жизни.

5. Запуск ракеты

Чтобы ракета покинула околоземную орбиту и вошла в космическое пространство, требуется сила, называемая тягой. Согласно второму закону движения, данному сэром Иссаком Ньютоном, сила пропорциональна ускорению; поэтому для запуска ракеты величина тяги увеличивается, что, в свою очередь, увеличивает ускорение.Скорость, достигаемая ракетой, наконец, помогает ей покинуть гравитационное поле Земли и выйти в космос.

6. Автокатастрофа

Во время автомобильной аварии существует сила между препятствием и автомобилем, известная как сила удара. Величина силы удара зависит от массы объектов, участвующих в столкновении, и скорости, с которой эти объекты движутся. Это означает, что чем больше масса объектов, участвующих в столкновении, тем больше будет сила удара.Точно так же, чем больше будет ускорение, с которым движется автомобиль, тем больше будет величина силы удара.

7. Объект, брошенный с высоты

Когда объект бросают с определенной высоты, гравитационное притяжение земли помогает ему развивать ускорение. Ускорение увеличивается по мере того, как объект приближается к земле. Согласно второму закону движения Ньютона, ускорение, развиваемое телом, прямо пропорционально силе.Когда объект ударяется о землю, в действие вступает сила удара. Это причина того, что хрупкий предмет, брошенный из высокого здания, страдает большей деформацией, чем ситуация, когда тот же предмет брошен из сравнительно более короткого здания.

8. Каратэ разбивает кирпичную плиту

Каратэист использует второй закон движения, чтобы разбить кирпичную плиту. Поскольку согласно закону сила пропорциональна ускорению, игрок имеет тенденцию быстро перемещать руки по плите из кирпичей.Это помогает ему / ей набрать ускорение и создать пропорциональную силу. Силы достаточно, чтобы сломать кирпичи.

9. Вождение автомобиля

Проще говоря, второй закон движения Ньютона гласит, что если сила приложена к любому объекту, имеющему массу, это приведет к возникновению эквивалентной величины ускорения в объекте. Например, когда мы включаем систему зажигания автомобиля, двигатель автомобиля создает достаточную силу, которая позволяет автомобилю двигаться с пропорциональным ускорением.

10. Гоночный автомобиль

Конструируя гоночный автомобиль, инженеры стремятся уменьшить массу автомобиля. Это потому, что, согласно второму закону движения Ньютона, масса объекта обратно пропорциональна ускорению. Уменьшая массу гоночного автомобиля, можно значительно увеличить ускорение, тем самым увеличивая шанс выиграть гонку.

Нарушение законов Ньютона.

Студенты-физики изучают законы Ньютона, но немногие полностью понимают то, что они говорят нам о природе. Конечно, мы можем проверить эти законы в лаборатории, и в каждом случае законы выполняются настолько точно, насколько мы можем измерить. Но универсальны ли они?

Время от времени кто-то предлагает эксперимент, который, кажется, нарушает третий закон Ньютона. Это привлекательная идея, поскольку тогда вы могли бы создать устройство, которое двигалось бы само без внешнего воздействия силы, импульса или энергии.Некоторые называют такое устройство «безреакционным двигателем». Представьте себе ракету, которая не требует топлива!

Корреспондент высказывает такую ​​возможность.

Рассмотрим возможность существования двух необычных частиц с замечательным свойством: частица A притягивается к частице B, а частица B отталкивается частицей A. Вместе они образуют систему, которая непрерывно ускоряется в одном направлении, а частица A всегда преследует частицу. Б.

Сила B на A и сила A на B показаны ниже.Это только силы, которые действуют на каждую частицу.

 
       о ---> F 0 ---> F
       А Б
  

Ясно, что эта ситуация предполагает , что эти две частицы не подчиняются третьему закону Ньютона. Сторонник этой идеи, по-видимому, предполагает, что второй закон Ньютона (или что-то очень похожее на него) применим к каждой частице, поскольку он говорит, что система (обе частицы) ускоряются из-за этих сил.Возможен ли вообще этот процесс и эти частицы?

Единственная известная сила отталкивания в классической физике – это сила двух одинаковых зарядов, отталкивающих друг друга. В отличие от обвинений притягиваются друг к другу. Эти силы неукоснительно подчиняются третьему закону Ньютона. Итак, эта гипотетическая проблема не является системой обычных обвинений. Это должны быть очень необычные частицы. Здесь что-то не так.

Когда два тела с массой сталкиваются, во время столкновения происходит пара контактных сил действие-реакция, которая является отталкивающей.Но эти силы симметричны, равны по размеру и противоположно направлены, подчиняясь третьему закону Ньютона. Здесь нет ничего удивительного, поскольку источником этих сил являются электрические силы, возникающие из-за атомов и молекул во время деформации тел, и все они подчиняются третьему закону Ньютона.

Это не относится к этому воображаемому взаимодействию частиц. В природе нет известных частиц, которые ведут себя подобным образом. Если бы оно было, это было бы совершенно другое место.

Но давайте вспомним нашу физику первокурсника.Законы Ньютона применимы к системам, а также ко всем без исключения частям систем. Представим себе границу, определяющую нашу воображаемую систему, включающую обе частицы. Какая внешняя сила действует на эту систему? Нуль. В условии задачи мы заявили, что никакие другие силы не действуют на какую-либо часть системы. Следовательно, второй закон Ньютона, примененный ко всей системе, говорит нам, что центр масс системы не может ускоряться. Ой!

Здесь мы понимаем, что у нас серьезные проблемы.В реальном мире законы Ньютона применимы к системам, а также ко всем отдельным частям систем во всех возможных ситуациях. Студенты часто «знают» об этом, но могут не осознавать его далеко идущие последствия. Изобретатель этой гипотетической системы говорит, что обе частицы ускоряются из-за действия их предполагаемых взаимных сил. Таким образом, он также предполагает, что второй закон Ньютона применим к каждому из них. Но применительно к системе второй закон Ньютона говорит нам, что центр масс системы не ускоряется.Как бы вы ни пытались, вы не сможете удовлетворить законы Ньютона для частиц и системы с помощью любого воображаемого движения двух тел. Геометрия этому препятствует.

Мы начинаем понимать, что нельзя нарушить третий закон Ньютона, не нарушив также второй закон Ньютона. Они логически связаны, и одно без другого невозможно. Это понимание, которое вы не получите, просто изучив два уравнения F = m a и F ₁₂ = -F ₂₁ по отдельности.Это почти как если бы эти два уравнения (вместе с евклидовой геометрией), взятые вместе, «знали», что вы можете попробовать сделать что-то невозможное, и сорвали вашу попытку.

Так что, черт возьми. Давайте с радостью предположим, что мы нарушили оба закона Ньютона. Какие серьезные последствия это могло иметь? На ум приходят несколько. Мы нарушили бы

• закон сохранения энергии,
• сохранение количества движения,
• сохранение углового момента,
,
• и законы термодинамики.

Предположительно наша самоускоряющаяся система не нуждается во внешней силе для ускорения, поэтому не нуждается во внешней работе. Тем не менее, он постоянно получает кинетическую энергию. Это явно нарушает закон сохранения энергии.

Точно так же эта система постоянно набирает обороты без воздействия на нее какой-либо внешней силы. Таким образом, эта система нарушает закон сохранения количества движения.

Мы могли заставить частицы двигаться только по круговой траектории и, следовательно, нарушить закон углового момента.

Поскольку законы термодинамики для систем частиц логически выводятся из законов Ньютона, а эти гипотетические частицы нарушают законы Ньютона, то мы просто разрушили термодинамику.

Учитывая первоначальные предположения, эти два тела будут постоянно ускоряться, пока не превысят скорость света. Ой ой! Теория относительности идет насмарку.

Мы показали силы равного размера, но предыдущие аргументы зависят только от направления сил, а не от их размера.

Эти результаты не должны удивлять любого, кто действительно понимает логические связи между законами физики. Законы сохранения математически выводятся из законов Ньютона. Таковы законы термодинамики. Законы сохранения также являются логическим следствием геометрии Вселенной и симметрии физических процессов при различных геометрических преобразованиях. Все это связано воедино, и изменение или уничтожение одной его части приводит к краху всей логической структуры.Более серьезно, это разрушило бы те части физики, которые были тщательно проверены и признаны действительными.

Этот хитрый лис, Исаак Ньютон, вероятно, знал, что его второй закон F = m a был просто неадекватным и бесполезным без третьего закона. [Первый закон Ньютона можно рассматривать как частный случай второго закона, когда тело m находится в состоянии покоя (его ускорение равно нулю).] Ньютон не размышлял, почему третий закон должен выполняться по природе.Его знаменитый комментарий «Я не притворяюсь гипотезой» мог быть его способом сказать: «Не трать мое время на вопросы, на которые нет ответа».

Редко кто-то предлагает что-либо, что, по их мнению, нарушает второй закон Ньютона. Ясно, что они не видят связи.

Но универсальны ли эти законы?

Серьезный студент должен задаться вопросом, может ли третий закон Ньютона быть верным, если речь идет о больших расстояниях. Если тело A воздействует на очень удаленное тело B, этой силе требуется время, чтобы преодолеть расстояние между ними.Теперь мы понимаем, что ничто материальное и никакие силы не могут распространяться быстрее конечной скорости света. Итак, если тело A движется, скажем, ближе к B, пройдет некоторое время, прежде чем B «узнает», что это произошло. Таким образом, во время движения сила A, оказываемая на B, может отличаться по величине от силы, которую B прикладывает к A.

Законы механики Ньютона неявно «предполагали», что такие силовые воздействия распространяются мгновенно, и никто в его время даже не осознавал, что скорость света конечна. Тогда еще не были изобретены электрические и магнитные поля.Теперь мы знаем об этом, но у нас есть теория относительности, чтобы иметь дело с такими высокоскоростными явлениями. Я не эксперт в этом, но я принимаю вердикт тех, кто таковыми: эти факты не бросают вызов законам Ньютона, если их правильно интерпретировать.

А как насчет закона всемирного тяготения Ньютона? Часто утверждают, что гравитация – это фундаментальная сила природы, о которой мы меньше всего знаем, даже если она доминирует в нашей повседневной жизни. Подлежит ли гравитационная сила универсальному ограничению скорости? Почему это закон обратных квадратов, а не обратный куб или что-то еще?

Давайте посмотрим на последний вопрос.Все силы, электрические, магнитные и гравитационные, подчиняются закону обратных квадратов. Электрическая сила была изучена в лаборатории, и цифра 2 в знаменателе известна примерно с 10 десятичными знаками. Это загадочно? Это удивительно? Или мы должны были этого ожидать?

Рассмотрим этот классический анализ. Возьмем, к примеру, свет. Интенсивность света от изотрипного точечного источника пропорциональна закону обратных квадратов. Это вполне ожидаемо, так как это следует из закона сохранения энергии.Энергия распространяется по постоянно увеличивающемуся объему пространства. Мы измеряем его на заданном расстоянии и обнаруживаем, что, проинтегрированная по сфере радиуса r, полная энергия, достигающая поверхности этой сферы, такая же, как и для любой сферы меньшего радиуса, и будет такой же для любого большего радиуса, предполагая нет поглощения света или производства в космосе. В конце концов, площадь сферы пропорциональна квадрату ее радиуса в евклидовом пространстве. [И наше локальное окружение во Вселенной оказалось евклидовым настолько, насколько мы можем измерить.] Таким образом, распространение световой энергии в обратном квадрате – это только то, что можно было бы ожидать от евклидовой геометрии и закона сохранения энергии.)

Тот же геометрический аргумент применим к электрическим полям и, насколько мы можем измерить, гравитационным полям. И снова природа говорит нам, что сохранение энергии – это просто неизбежное следствие геометрии Вселенной. Мы снова сталкиваемся с наблюдаемым фактом, что в природе многие вещи «связаны друг с другом».”Спекулятивное вмешательство в любую его часть влияет на многие другие ее части. [1]

Проницательный студент может заметить еще одну «проблему» с законами Ньютона. Закон обратных квадратов гравитации предсказывает, что две очень близкие друг к другу частицы будут оказывать друг на друга огромную силу, так как 1 / R ² стремится к бесконечности, как R стремится к нулю. Каков предел малых масштабов, при котором закон «нарушается»? Эта интересная проблема носит более технический характер, чем я собираюсь здесь рассматривать, но она не имеет никакого эффекта, о котором я могу думать, на любой эксперимент, который вы могли бы провести в университетской лаборатории физики.Он также не может служить основой сверхединичного вечного двигателя.

Исторические прецеденты.

Принцип «бутстрапа» барона Мюнхгаузена в действии.

Читатель, вероятно, уже понял, что эта двухчастичная система могла быть вдохновлена ​​фантастической историей барона Мюнхгаузена, который однажды спас себя из опасной ситуации, когда увяз в болоте, поднявшись и подняв себя и свою лошадь за волосы. (косичка).См .: барон Мюнхгаузен. В более поздних вариантах этой сказки он поднимался за собственные ремни. Это может быть первый литературный пример нарушения законов Ньютона. Это смешно, потому что читатели сразу понимают, что природа так не работает.

Примечания.

[1] Говорить о физике одними словами сложно. Слова имеют разные значения, включая разговорные, технические и философские. И слишком часто есть тонкие понятия, в которых нет четко определенных слов.

Физика включает в себя широкий спектр законов, теорий и принципов, и они могут быть выражены уравнениями, сопровождаемыми пояснительными словами. Многие из этих уравнений логически (математически связаны) с другими. Это «костяк» предмета, и я назвал их «фундаментальными» или «основными» уравнениями. [Я не знаю общепринятого названия этой концепции.] Другие уравнения представляют собой законы, обычно более узкие, которые описывают какой-то конкретный процесс, но имеют лишь слабые (а иногда и не полностью известные) связи с другими законами.Эти законы, скорее всего, будут изменены научными достижениями.

Фундаментальные уравнения – это те уравнения, которые выдержали самые обширные испытания в самом широком диапазоне явлений. Например, законы Ньютона прошли экспериментальную проверку гравитационных взаимодействий планет, промышленного оборудования, электрического оборудования и естественных процессов в геологии, метеорологии и почти во всех других областях физической науки.

Суть в том, что фундаментальное ядро ​​законов настолько логически и физически взаимосвязано и настолько тщательно проверено, что изменение любого из них повлияет почти на все остальное.Поэтому маловероятно, что новые открытия сделают один из этих законов недействительным. А если один из них будет признан недействительным, потребуется изменить всю структуру основных законов. Это непростая задача для любого потенциального кандидата на Нобелевскую премию. Фактически, всякий раз, когда кажется, что эксперимент опровергает один из фундаментальных законов, наиболее вероятная причина заключается в том, что эксперимент был ошибочным или какое-то незамеченное влияние повлияло на результат. Нередко причина кроется в простой математической ошибке.

– Дональд Э. Симанек, февраль 2010 г., исправлено в июне 2011 г.

---

Вернитесь в Музей неработающих устройств.
Вернуться в главное меню.

Второй закон движения Ньютона

Второй закон движения Ньютона
Далее: Третий закон Ньютона Up: Законы движения Ньютона Предыдущая: Первый закон Ньютона Второй закон движения Ньютона по существу гласит, что если точечный объект подвергается внешней силе, то его уравнение движения дан кем-то

(13)

где импульс, – произведение инерциальной масса“ и его скорость“.Если не является функцией времени, то приведенное выше выражение сводится к знакомое уравнение

(14)

Обратите внимание, что это уравнение действительно только в инерциальной системе координат . Ясно, что инерционная масса объекта измеряет его сопротивление отклонению. из своего предпочтительного состояния равномерного движения по прямой (в инерциальный каркас). Конечно, указанное выше уравнение движения может быть решено только в том случае, если у нас есть независимое выражение для силы ( i.е. , закон силы). Предположим, что это так.

Важным следствием второго закона Ньютона является то, что сила – это вектор К-во . Это должно быть так, поскольку закон приравнивает силу к произведение скаляра (массы) и вектора (ускорение). Обратите внимание, что ускорение, очевидно, является вектором, потому что оно напрямую связано со смещением, которое является прототипом всех векторов – см. Приложение A. Одним из следствий того, что сила является вектором, является что две силы, и обе действуют при заданном точка, имеет тот же эффект, что и единичная сила, , действуя в той же точке, где суммирование производится по законы сложения векторов – см. Приложение А.Аналогично, единственная сила, действующая на заданная точка имеет то же действие, что и две силы, и, действуя в том же месте, при условии, что . Этот метод объединения и разделения сил известен как разрешение сил и лежит в основе многих расчетов в ньютоновской динамике.

Взяв скалярное произведение уравнения (14) на скорость,, мы получаем

(15)

Это можно написать

(16)

куда

(17)

Правая часть уравнения (16) представляет скорость при какая сила действует на объект: i.е. , г. скорость, с которой сила передает энергию объекту. Количество представляет энергию, которой объект обладает в силу своего движения. Этот тип энергии обычно известен как кинетическая энергия , . Таким образом, уравнение (16) утверждает, что любая работа, выполняемая над точечным объектом внешней силой идет на увеличение кинетической энергии объекта.

Предположим, что под действием силы наш объект движется от момента к моменту времени. В чистое изменение кинетической энергии объекта получается путем интегрирования Уравнение (16):

(18)

поскольку .Вот элемент пути объекта между точками и, а интеграл в представляет собой чистую работу, выполненную силы, когда объекты движутся по пути от до.

Как описано в Разделе A.15, в основном есть два типа сил в природе. Во-первых, те, для которых линейные интегралы типа зависят от конечных точек, но не на пути, пройденном между этими точками. Во-вторых, те, для которых линейные интегралы типа зависеть как на конечных точках, так и на пути, пройденном между этими точками.Первый тип силы называется консервативной , тогда как второй вид называется неконсервативным . Это также в разделе A.15 показано, что если линейный интеграл не зависит от пути , тогда сила всегда может можно записать как градиент скалярного поля. Другими словами, все консервативные силы удовлетворяют

(19)

для некоторого скалярного поля. Обратите внимание, что

(20)

независимо от пути между и.Следовательно, из уравнения (18) следует что

(21)

для консервативных сил. Другой способ написать это

(22)

Конечно, мы распознаем это как уравнение сохранения энергии : – полная энергия объекта, которая сохраняется; энергия объект имеет в силу своего движения, иначе известный как его кинетическая энергия ; и энергия, которую объект имеет благодаря своему положению, иначе известному как потенциал энергия .Обратите внимание, однако, что мы можем записать только такое сохранение энергии уравнения для консервативных сил. Гравитация – хороший пример консервативной силы. С другой стороны, неконсервативные силы не экономят энергию. В общем, это происходит из-за какой-то потери энергии на трение, которая истощает энергию от динамической системы, пока она остается в движении. Обратите внимание, что потенциальная энергия не определяется произвольной аддитивной постоянной. Фактически, это всего лишь разность потенциальной энергии между различные точки в пространстве, что четко определено.

---

Далее: Третий закон Ньютона Up: Законы движения Ньютона Предыдущая: Первый закон Ньютона

Ричард Фицпатрик 2011-03-31

Второй закон Ньютона и равномерное круговое движение – Видео и стенограмма урока

Формула

Обычно, когда мы используем Второй закон Ньютона, довольно легко определить и для ускорения. Чаще всего это выражается в метрах в секунду в квадрате в заданном направлении или в какой-либо другой подобной единице.Однако, поскольку мы движемся по кругу, нам нужен другой способ определения ускорения. В противном случае мы бы застряли, определяя новое направление каждую миллисекунду. Чтобы преодолеть это, мы утверждаем, что ускорение равно квадрату скорости, деленному на радиус. Это также можно найти, возведя в квадрат угловую скорость и умножив ее на радиус, в зависимости от того, какая информация у вас есть. Мы просто подставляем это новое число в наше обычное уравнение, что означает, что теперь F равно m для массы, умноженное на s для скорости, в квадрате, деленное на r для радиуса.

Объяснение простым языком

Некоторые люди могут взглянуть на эту математику, пожать плечами и мгновенно усвоить, что она означает. К сожалению, я не такой человек, поэтому позвольте мне объяснить это по-английски. Чем круче ваша кривая, тем сильнее вы изменяете ускорение. В конце концов, это имеет смысл. Если вы хотите обойти купол диаметром десять метров, вы увидите, что ваше направление и, следовательно, ваше ускорение постоянно меняются. Между тем, вы действительно не чувствуете, как меняется ваше направление, когда идете по поверхности Земли, потому что это далеко не такой крутой поворот.Говоря о крутых поворотах, вы когда-нибудь чувствовали себя так, как будто вас выбросило из-за поворота и в итоге вы приземлились на боку? Несмотря на то, что вам говорят, это не так называемое центробежное движение. Вместо этого это просто инерция . В каждый момент ваше тело толкает вас в этом направлении. Между тем, существует сила, которая тянет вас назад, так называемое центростремительное движение . Это равное и противоположное действие всех остальных сил, выталкивающих вас. Это то, что удерживает вас от вылета из круга.Представим, что вы на карусели. Тебе лучше держаться, потому что, если ты этого не сделаешь, тебя сбросят, верно? Ощущение того, что вас отбрасывают, если вы не держитесь, – это не центробежное движение, а скорее инерция . Как вы помните, инерция – это желание объекта продолжать двигаться в том же направлении, в котором он движется в этот самый момент. Это причина того, что когда вы бросаете мяч, он летит прямо, а не по круговой схеме вашей подачи. Между тем, есть еще сила, которая продолжает тянуть вас к центру.А именно это центростремительное движение . В нашем примере с каруселью это сила, которую вы должны приложить, чтобы удержаться. Когда карусель крутится медленно, держаться так сильно не нужно. Это потому, что центростремительная сила может быть меньше. Между тем, если он вращается быстрее, вам придется держаться с гораздо большей силой.

Примеры

Давайте рассмотрим пару примеров, чтобы убедиться, что мы все поняли. Мы сделаем один с математикой, а другой – с концепцией.Во-первых, концептуальный пример. Допустим, вы гонщик, едущий в поворот. Какие силы действуют на вашу машину? Во-первых, у вас есть инерция, ведущая вашу машину в прямом направлении, где бы вы ни находились в данный момент. Во-вторых, вас тянет назад центростремительная сила. Итак, как вы думаете, что центростремительная сила может противодействовать вашей мчащейся машине? Если повезет, кривые будут в наклоне. Это означает, что на вашу машину может действовать меньшая сила инерции, потому что теперь она действует против нормальной силы, прилагаемой поверхностью к находящемуся на ней предмету.2 / р. Пять в квадрате – 25, деление на 1 – все равно 25. Умножьте это на 5, и вы обнаружите, что на нашу бедную кошку действует 125 ньютонов силы.

Краткое содержание урока

В этом уроке мы рассмотрим Второй закон Ньютона и равномерное круговое движение. Помните, что второй закон движения Ньютона гласит, что сила равна массе, умноженной на ускорение, и равномерное круговое движение относится к идеально круговому движению вокруг центральной точки. Мы вычисляем это, заменяя ускорение квадратом скорости, деленной на радиус, хотя общая идея о том, что чем меньше радиус, тем больше силы прилагается, остается верной.

Каковы применения закона движения Ньютона? – MVOrganizing

Каковы применения закона движения Ньютона?

Законы движения Ньютона можно применять во многих ситуациях для решения задач движения. Нормальная сила, действующая на объект, не всегда по величине равна весу объекта. Если объект ускоряется, нормальная сила будет меньше или больше веса объекта.

Каково применение первого закона движения Ньютона?

Человек в движении остается в движении с той же скоростью и в том же направлении, если только на него не действует неуравновешенная сила ремня безопасности.Да! Ремни безопасности используются для обеспечения безопасности пассажиров, движение которых регулируется законами Ньютона.

Как законы Ньютона применимы к повседневной жизни?

Закон Ньютона очень важен, потому что он связан практически со всем, что мы видим в повседневной жизни. Эти законы точно говорят нам, как вещи движутся или сидят на месте, например, почему вы не выскакиваете из кровати или не падаете через пол в доме. Так что благодарите закон действия и реакции Ньютона каждый раз, когда вы куда-то едете!

Каков пример второго закона движения Ньютона в повседневной жизни?

Ниже приведены примеры второго закона Ньютона из повседневной жизни: толкать автомобиль легче, чем толкать грузовик с такой же силой, поскольку масса автомобиля меньше массы грузовика.В игре в гольф ускорение мяча для гольфа прямо пропорционально силе удара клюшки.

Каков пример третьего закона движения Ньютона в повседневной жизни?

Примеры третьего закона движения Ньютона повсеместно встречаются в повседневной жизни. Например, когда вы прыгаете, ваши ноги прикладывают силу к земле, а земля прикладывает равную и противоположную силу реакции, которая толкает вас в воздух. Инженеры применяют третий закон Ньютона при разработке ракет и других снарядов.

Какие три примера второго закона Ньютона?

Второй закон движения Ньютона гласит, что ускорение (увеличение скорости) происходит, когда сила действует на массу (объект). Езда на велосипеде – хороший пример того, как действует этот закон движения. Ваш велосипед – это масса. Мышцы ваших ног, толкающие педали велосипеда, – это сила.

Каковы 3 примера третьего закона Ньютона?

Во время гребли на лодке, когда вы хотите двигаться вперед на лодке, вы гребете, толкая воду назад, заставляя вас двигаться вперед.Во время ходьбы вы толкаете пальцами ног пол или поверхность, по которой идете, и поверхность подталкивает ваши ноги вверх, помогая вам поднять ноги.

Каково определение третьего закона движения Ньютона?

Его третий закон гласит, что на каждое действие (силу) в природе существует равное и противоположное противодействие. Другими словами, если объект A воздействует на объект B, то объект B также оказывает равное и противоположное воздействие на объект A.

Какой пример действия и противодействия?

Силы действия и противодействия на объект взаимны (противоположны).Примеры могут включать: Пловец, плывущий вперед: пловец отталкивается от воды (сила действия), вода отталкивает пловца (сила реакции) и толкает его вперед.

Как называется второй закон Ньютона?

Второй закон движения Ньютона – F = ma, или сила равна массе, умноженной на ускорение. Узнайте, как использовать формулу для расчета ускорения. Создал Сал Хан.

Что такое второй класс закона Ньютона 9?

Второй закон движения Ньютона гласит, что скорость изменения количества движения объекта пропорциональна приложенной неуравновешенной силе в направлении силы.т.е. F = ma. Где F – приложенная сила, m – масса тела, а a – создаваемое ускорение.

Почему второй закон Ньютона – действительный закон?

Ответ: Второй закон движения Ньютона называется реальным законом движения, потому что все законы могут быть выведены и содержатся в этом законе. Доказательство: мы знаем, что F = m. Это означает, что покоящийся объект всегда будет неподвижен, а объект, движущийся с равномерным движением по прямой линии, будет продолжать это делать, что является первым законом.

Сколько существует законов движения?

три закона

Как еще называют первый закон движения Ньютона?

закон инерции

Каков первый закон движения примеров?

Движение шара, падающего через атмосферу, или запуск модели ракеты в атмосферу – оба примера первого закона Ньютона.Движение воздушного змея при смене ветра также можно описать первым законом.

Сколько видов законов существует в физике?

Важные законы физики

Законы физики
Закон косинуса Ламбертса	Заявление Кельвина Планка
Закон сохранения энергии	Принцип Архимеда
Закон Био-Савара	Закон Фарадея
Закон Ампера	Законы электролиза Фарадея

Каковы 4 закона природы?

Согласно нынешнему пониманию, существует четыре фундаментальных взаимодействия или силы: гравитация, электромагнетизм, слабое взаимодействие и сильное взаимодействие.

Каковы принципы природы?

Итак, есть три принципа природы, а именно материя, форма и отсутствие; из которых одно – это то, к чему происходит порождение, а именно форма, а два других – те, из которых происходит порождение. Следовательно, материя и лишение одинаковы по своему предмету, но различаются по своим понятиям.

Каков первый закон природы?

1. Пословица Все живые существа ставят собственное выживание выше всего остального и будут делать все необходимое, чтобы остаться в живых.Самосохранение – это первый закон природы, и они могут причинить вам серьезный вред, пытаясь сбежать. …

Каков основной закон природы?

Первый и основной закон природы гласит: «Каждый человек должен стремиться к Миру, насколько он надеется обрести его; а когда он не может получить его, он может искать и использовать любую помощь и все преимущества Варра ». Это подчеркивает общее правило «Ищи мир и следуй ему».

Каковы три основных закона природы?

Наука включает в себя множество принципов, которые, по крайней мере, когда-то считались законами природы: закон тяготения Ньютона, его три закона движения, законы идеального газа, законы Менделя, законы спроса и предложения и так далее.