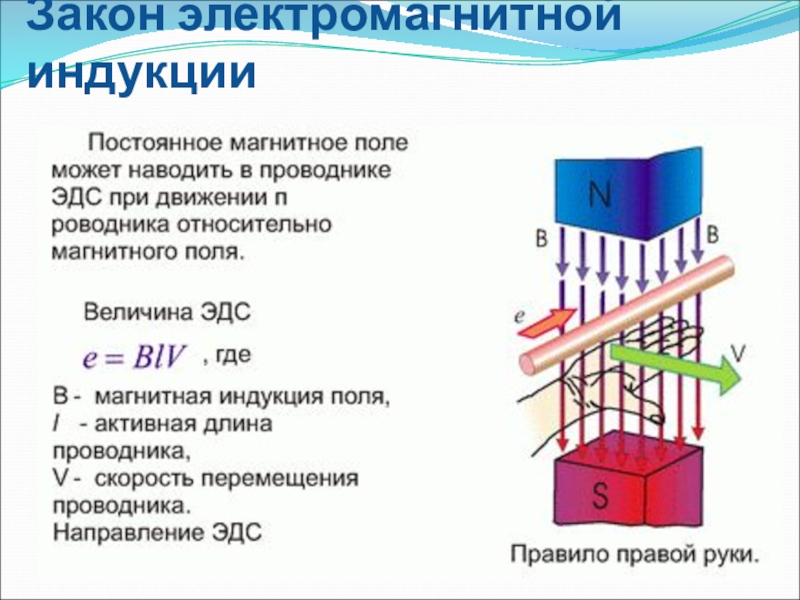
«Закон электромагнитной индукции – Электромагнитная индукция
Закон электромагнитной индукции – Электромагнитная индукция – Основы электродинамики
Цель: сформулировать закон электромагнитной индукции.
Ход урока
I. Организационный момент
II. Повторение
– Опишите опыты, в которых можно наблюдать индукцию тока.
– Каким должно быть магнитное поле, чтобы в неподвижном проводнике появился индукционный ток?
– От чего зависит число силовых линий магнитного ноля, пронизывающих данный контур?
– Как определяют направление нормали к контуру?
– Что такое «магнитный поток»?
– В каких единицах измеряется магнитный поток?
– В чем заключается правило Ленца?
 Проведение лабораторной работы
Проведение лабораторной работыЛабораторная работа по теме «Исследование зависимости силы индукционного тока от скорости изменения магнитного потока»
Оборудование: источник питания, миллиамперметр, катушка- моток, катушка с железным сердечником от разборного электромагнита, магнит дугообразный, реостат ползунковый, ключ замыкания тока, комплект проводов.
Ход работы
1. Подключите катушку-моток к зажимам миллиамперметра.
2. Вставляйте и вынимайте дугообразный магнит из катушки с различной скоростью и для каждого случая замечайте максимальную силу индукционного тока.
3. Катушку соедините с миллиамперметром, наденьте на катушку с железным сердечником и подключите последнюю через реостат и ключ замыкания тока к источнику питания.
4. Изменяйте силу тока в катушке электромагнита при помощи реостата с различной скоростью и для каждого случая замечайте максимальную силу индукционного тока.
5. Ответьте на вопросы:
а) В каком случае скорость изменения магнитного потока через катушку, соединенную с миллиамперметром, была больше: при медленном или быстром движении магнита? При медленном или быстром изменении силы тока в катушке электромагнита?
Ads by optAd360
б) Что можно сказать о зависимости силы индукционного тока и ЭДС-индукции от скорости изменения магнитного потока через катушку?
6. Ответы запишите в тетрадь.
IV. Изучение нового материала
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S.
Если за малое время Δt магнитный поток меняется на ΔФ, то скорость изменения потока
Известно, что в цепи появляется электрический ток в том случае, если на свободные заряды проводника действуют сторонние силы.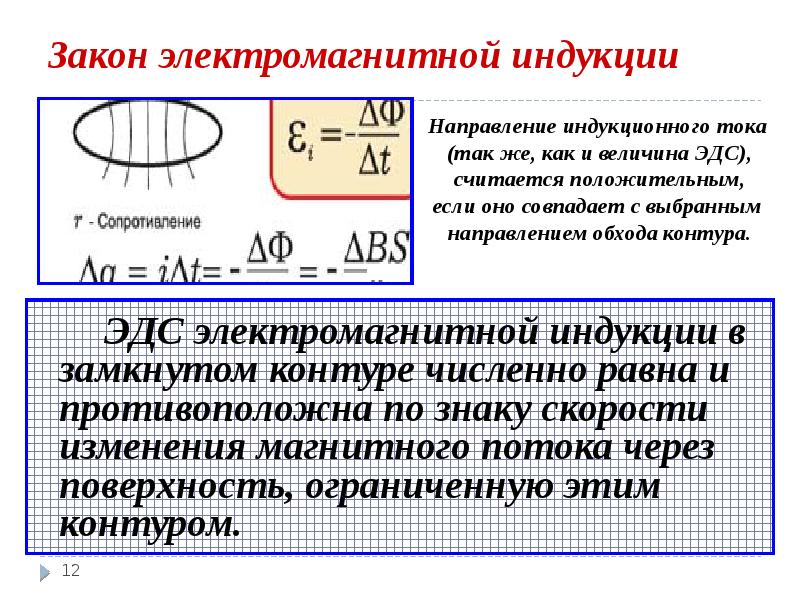
Сопротивление зависит от изменения магнитного потока. Закон электромагнитной индукции формулируется для ЭДС.
Законом в таком виде можно пользоваться при равномерном изменении магнитного потока. В противном случае:
Ads by optAd360
V. Закрепление изученного
– Почему закон электромагнитной индукции формулируется для ЭДС, а не для силы тока?
– Как формулируется закон электромагнитной индукции?
– Почему в законе электромагнитной индукции стоит знак «минус»?
– Что можно сказать о зависимости силы индукционного тока и ЭДС-индукции от скорости изменения магнитного потока через катушку?
VI. Решение задач
1. За какой промежуток времени магнитный поток изменяется на 0,004 Вб, если в контуре возбуждается ЭДС индукции 16 В? (Ответ: Δt = 2,5 мс. )
)
2. Соленоид содержит 100 витков проволоки. Найти ЭДС индукции, если в этом соленоиде за 5 мс магнитный поток равномерно изменяется от 3 мВб до 1,5 мВб. (Ответ: 0,3 В.)
3. В обмотке на стальном сердечнике с площадью поперечного сечения 100 см2 в течение 0,01 с возбуждается ЭДС индукции 150 В при изменении магнитной индукции от 0,3 Тл до 1,3 Тл. Сколько витков в обмотке? (Ответ: 150.)
4. Проволочная прямоугольная рамка со сторонами 18 см и 5 см расположена в однородном магнитном поле перпендикулярно к силовым линиям. Определите индукцию этого поля, если при его исчезновении за 0,015 с в рамке возникает ЭДС = 4,5 · 10-3 В. (Ответ: ΔВ = 7,5 · 10
5. Магнитный поток через контур проводника сопротивлением 3 · 10-2 Ом за 2 с изменился на 1,2 · 10-2 Вб. Какова сила тока, протекающего по проводнику, если изменения происходят равномерно? (Ответ: I = 0,2 А. )
)
6. Соленоид, состоящий из 80 витков и имеющий диаметр 8 см, находится в однородном магнитном поле, индукция которого равна 60,3 Тл. Соленоид поворачивается на 180° в течение 0,2 с. Найти среднее значение ЭДС, возникающее в соленоиде, если его ось до и после поворота направлена вдоль поля. (Ответ: ε = 0,24 В.)
VII. Подведение итогов урока
Домашнее задание
п. 4;
Р – 911; Р – 912.
План-конспект урока по физике. Тема: Закон электромагнитной индукции ❤️
Цель урока: сформулировать количественный закон электромагнитной индукции; учащиеся должны усвоить, что такое ЭДС магнитной индукции и что такое магнитный поток.
Ход урока
Проверка домашнего задания методом фронтального опроса
1. Как взаимодействует магнит с индукционным током?
2. Почему необходимо совершить работу при сближении катушки и магнита?
Почему необходимо совершить работу при сближении катушки и магнита?
3. Что бы произошло, если бы магнит сам устремлялся к катушке?
4. Пояснить различие в двух опытах: удаление магнита от катушки и его приближение.
5.
Сформулировать правило Ленца.6. Для определения направления индукционного тока применяют правило Ленца. Каким образом?
7. 7. На рисунках показано направление индукционного тока в 4 случаях.
loading=”lazy” src=”/fizika3/image672.gif”/>Стрелкой показано движение проводников. Решите задачи для Ii— индукционного тока.N N N N
Изучение нового материала
Если за время Δt магнитный поток ΔФ меняется, то отношение ΔФ/Δt – называется скоростью изменения магнитного потока. Из опыта вытекает вывод: скорость изменения магнитного потока, проходящего через поверхность, охваченную контуром пропорциональна силе индукционного тока. Ii ~ ΔФ/Δt.
Электродвижущая сила индукции.
Электрический ток появляется в цепи, когда на свободные заряды действуют сторонние силы.
Работа этих сил создает ЭДС. При изменении магнитного потока через поверхность, ограниченную контуром, в контуре возникают сторонние силы, которые в свою очередь создают ЭДС индукции. ξi – ЭДС индукции. Ii = ξi/R — закон Ома для замкнутой цепи справедлив для индукционного тока.
Закон электромагнитной индукции.
Закон электромагнитной индукции формулируется для ЭДС, но не для силы тока, так как ЭДС не зависит от свойств проводников.
Закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока ,проходящего через поверхность, ограниченную контуром.
ξ I = |ΔФ/Δt|- математическая форма записи закона электромагнитной индукции
Чтобы в законе электромагнитной индукции учесть направление индукционного тока рассмотрим рисунок. Нормаль n̄ образует правый винт с направлением обхода. Магнитная индукция направлена вдоль нормали и с течением времени растет. Значит, Ф >0 и ΔФ/Δt >0. Магнитный поток Фʹ<0 образует индукционный ток. Применяя правило буравчика ,найдем, что индукционный ток направлен по часовой стрелке, значит ЭДС индукции отрицательна.
Нормаль n̄ образует правый винт с направлением обхода. Магнитная индукция направлена вдоль нормали и с течением времени растет. Значит, Ф >0 и ΔФ/Δt >0. Магнитный поток Фʹ<0 образует индукционный ток. Применяя правило буравчика ,найдем, что индукционный ток направлен по часовой стрелке, значит ЭДС индукции отрицательна.
ξi= — ΔФ/Δt — закон электромагнитной индукции. Знак минус (-) показывает, что ξi и ΔФ/Δt имеют разные знаки.
Закрепление изученного материала
— Как возникает магнитный поток?
— Как появляется ЭДС индукции? Какие сторонние силы ее создают?
— Почему сформулировали закон электромагнитной индукции не для силы тока, а для ЭДС?
— Записать закон электромагнитной индукции.
— В законе электромагнитной индукции стоит знак «минус». Почему?
Подведем итоги урока
Домашнее задание: § 11, повт. § 11, упр. 2, № 3,4.
Конспект урока по теме “Закон электромагнитной индукции.
 Правило Ленца”
Правило Ленца”Поурочный план
Урок № 7 | Дата проведения: 23.09 | Предмет: физика | |
Класс: 11-А, 11-Б | Учитель: Лешкевич Е.В. | ||
Тема урока: Закон электромагнитной индукции. Правило Ленца | |||
Цель урока: | – Создать условия для формирования у учащихся умения определять направление индукционного тока на основе правила Ленца. | ||
Планируемые результаты, УУД |
Предметные:
Личностные: убежденность в познании природы, использование достижений науки для дальнейшего развития, мотивация к учению. | ||
Тип урока | урок «открытия» нового знания | ||
Оборудование, информационное обеспечение: |
| ||
Ход урока
1.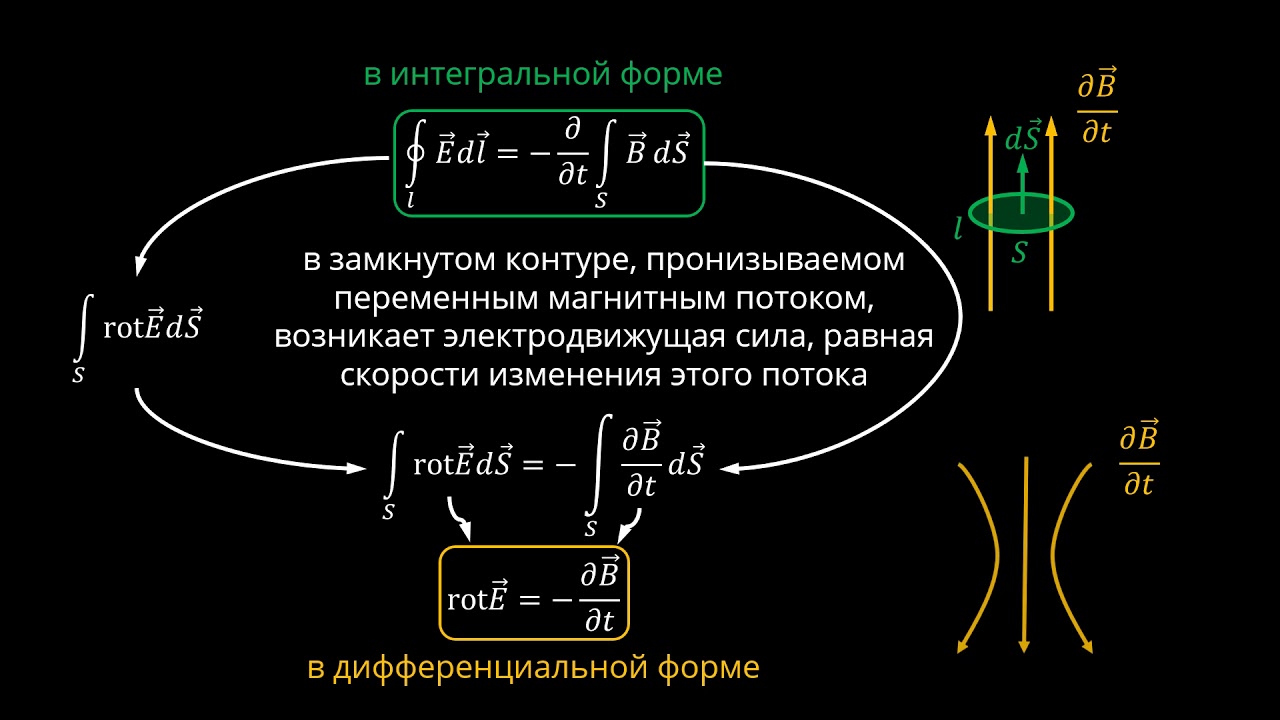 Орг.момент
Орг.момент
2. Проверка домашнего задания
3.
Сформулируем закон электромагнитной
индукции количественно. Опыты Фарадея показали, что сила индукционного тока I
Магнитный поток можно графически представить как число линий магнитной индукции, пронизывающих поверхность площадью S. Чем больше индукция магнитного поля, тем большее число линий магнитной индукции пронизывает эту поверхность. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.
Если за малое время Аt магнитный поток меняется на АФ, то скорость изменения магнитного потока равна . Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:
 3)
3)ЭДС индукции. Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Величину, численно равную работе этих сил при перемещении единичного положительного заряда вдоль замкнутого контура, называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляются сторонние силы, действие которых характеризует ЭДС, называемая ЭДС индукции.
Согласно закону Ома для замкнутой цепи. Сопротивление проводника R
не зависит от изменения магнитного потока. Следовательно, соотношение (2.3) справедливо только потому, что ЭДС индукции пропорциональна .
Закон электромагнитной индукции. Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы индукционного тока, т. к. сила тока зависит и от свойств проводника, а ЭДС определяется только изменением магнитного потока. Согласно закону электромагнитной индукции ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
Как в законе электромагнитной индукции учесть направление индукционного тока (или знак ЭДС индукции) в соответствии с правилом Ленца?
На рисунке изображен замкнутый
контур.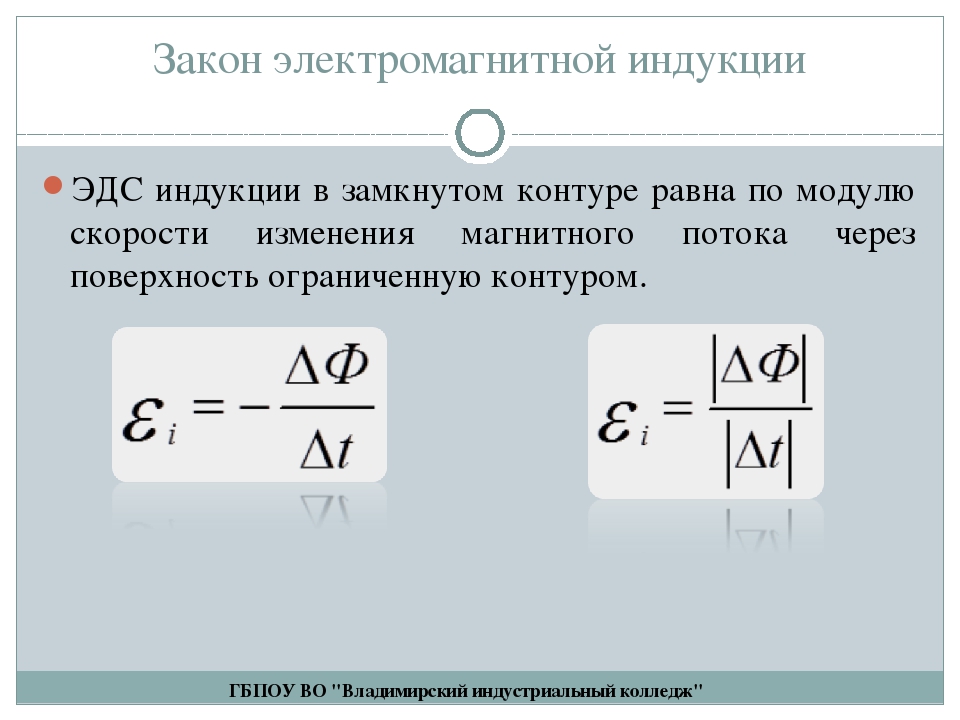 Будем считать положительным направление обхода контура против часовой
стрелки. Нормаль п к контуру образует правый винт с направлением обхода.
Будем считать положительным направление обхода контура против часовой
стрелки. Нормаль п к контуру образует правый винт с направлением обхода.
Пусть магнитная индукция В внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Ф 0 и 0. Согласно правилу Ленца индукционный ток создает магнитный поток Ф’
Если контур (например, катушка) состоит из нескольких витков, то
1. 3. Выявление места и причины затруднения |
| |||||||||||||||||||||||||||
Магнитный поток, пронизывающий катушку, изменяется со временем, так как показано на графике. Что вы можете сказать об ЭДС индукции в промежутки времени 0-t1, t1-t2, t2-t3? Можете ли вы сравнить индукционные токи, возникающие в катушке в промежутки времени 0-t1, t2-t3? | ЭДС
индукции в промежуток времени 0-t1 имеет отрицательное значение; в промежуток времени t1-t2 – равна нулю, в промежуток времени t2-t3 принимает
положительное значение. Модуль ЭДС индукции принимает наибольшее значение в промежуток времени t2-t3. Согласно закону Ома для замкнутой цепи, сила тока пропорциональна ЭДС. Значит, ток максимален в промежуток времени t2-t3. | |||||||||||||||||||||||||||
Можете ли вы сравнить направления токов в контурах. | Да. Токи имеют противоположное направление. | |||||||||||||||||||||||||||
Что повлияло на направление индукционного тока? | Характер изменения магнитной индукции: в первой задаче индукция уменьшалась, во второй увеличивалась. | |||||||||||||||||||||||||||
Как менялся магнитный поток? | В первом случае уменьшался, во втором увеличивался. | |||||||||||||||||||||||||||
Еще раз обратимся к опыту Фарадея. Что происходит с магнитным потоком при внесении и вынесении магнита из катушки? Обратим
внимание на отклонение стрелки гальванометра при внесении магнита в катушку и
при вынесении. О чем это свидетельствует?
Какой вывод вы можете сделать?
Можете ли вы определить направление индукционного тока? |
При внесении – увеличивается, при вынесении – уменьшается.
В одном случае стрелка отклонялась влево, в другом – вправо.
Об изменении направления индукционного тока в контуре. Направление индукционного тока в контуре зависит от характера изменения магнитного потока через поверхность, ограниченную контуром. Нет. | |||||||||||||||||||||||||||
2. 4. Построение проекта выхода из затруднения |
| |||||||||||||||||||||||||||
Какую цель вы поставите себе на сегодняшнем уроке?
| Научиться определять направление индукционного тока в конкретной учебной задаче. | |||||||||||||||||||||||||||
Тема урока
«Правило Ленца». Именно российскому ученому Э.Х. Ленцу в 1833 году удалось сформулировать закон, который определил направление индуцируемого тока, и сегодня этот закон известен как Правило Ленца. В 1834 году его открытия хватило на избрание академиком по физике. |
| |||||||||||||||||||||||||||
3. 5. Реализация построенного проекта |
| |||||||||||||||||||||||||||
Я предлагаю вам приступить к исследованиям, поработать в парах. | Приложение 1 | |||||||||||||||||||||||||||
Отчет групп о проделанной работе по схеме: 1. Что делали? 2. Какой получился результат? | Учащиеся заполняют таблицу на доске и поясняет результаты.
| |||||||||||||||||||||||||||
В результате на доске появляется таблица:
Третью строку предлагается заполнить
самостоятельно. | ||||||||||||||||||||||||||||
Постараемся найти общую закономерность, проявляющуюся в рассмотренных опытах.
| Индукционный ток в кольце имеет такое направление, что созданное им магнитное поле будет направлено противоположно магнитному полю магнита, если магнитное поле магнита увеличивается. Индукционный ток в кольце имеет такое направление, что созданное им магнитное поле будет сонаправлено с магнитным полем магнита, если магнитное поле магнита уменьшается.
| |||||||||||||||||||||||||||
Учащиеся читают правило Ленца в учебнике и сравнивают свои выводы с правилом | ПРАВИЛО ЛЕНЦА Индукционный ток всегда имеет такое направление, что созданное им магнитное поле стремится скомпенсировать изменение магнитного потока, которое вызвало данный ток. | |||||||||||||||||||||||||||
Создадим алгоритм применения правила Ленца:
| 1. 1. Установить направление линий магнитной индукции внешнего магнитного поля . 2. 2. Выяснить, как изменяется поток магнитной индукции этого поля. 3. 3. Установить направление линий магнитного поля этого поля: , если >0 и , если <0 (по правилу Ленца). 4. 4. Зная направление линий магнитной индукции , найти направление индукционного тока , пользуясь правилом правой руки.
| |||||||||||||||||||||||||||
Проблемный вопрос: Что было бы, если бы индуцированный ток не компенсировал, а наоборот усиливал внешний магнитный поток? (Рассуждения учащихся
проиллюстрировать рисунком на доске). | Если бы индукционный ток не компенсировал, а наоборот усиливал внешний магнитный поток (т.е. имел бы другое направление), то это привело бы к новому увеличению магнитного потока, а вместе с ним к еще большему возрастанию силы тока. Но такое «беспричинное» возрастание индукционного тока и магнитного поля явно противоречило бы закону сохранения энергии. Таким образом, закон сохранения энергии помогает найти ответ и на вопрос: как направлена магнитная индукция возникшего тока? Итак, мы приходим к выводу, что магнитное поле индукционного тока ослабляет изменение магнитного поля магнита. | |||||||||||||||||||||||||||
Вернемся к результатам задач, решенных в начале урока, а соответственно к закону электромагнитной индукции. Поясним знак минус. | Знак «минус» в этой формуле как раз и
свидетельствует о «противодействии», оказываемом индукционным током его
изменению. | |||||||||||||||||||||||||||
4. 6. Первичное закрепление |
| |||||||||||||||||||||||||||
Решение задачи: Проводящее кольцо с разрезом поднимают вверх из начального положения к полосовому магниту, а сплошное проводящее кольцо из начального положения смещают вправо. В каком кольце при этом возникнет индукционный ток? Определите его направление. № 6.33 1.За 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает с 7 мВб до 3 мВб. Найдите величину ЭДС индукции в соленоиде. 2. В катушке, содержащей 500 витков провода, магнитный поток равномерно убывает от 20 до 5 мВб за 5 мс. Какова величина ЭДС индукции в катушке? Постройте график зависимости ЭДС индукции от времени в интервале от 0 до 5 мс.
| ||||||||||||||||||||||||||||
5. 7. Самостоятельная работа с самопроверкой по эталону | Выполнение теста
| |||||||||||||||||||||||||||
6. | § | |||||||||||||||||||||||||||
9.Рефлексия учебной деятельности |
| |||||||||||||||||||||||||||
Закон электромагнитной индукции – Электромагнитное поле – ЭЛЕКТРОДИНАМИКА – ВСЕ УРОКИ ФИЗИКИ 11 КЛАСС АКАДЕМИЧЕСКИЙ УРОВЕНЬ – конспекты уроков – План урока – Конспект урока – Планы уроков – разработки уроков по физике
1-й семестр
ЭЛЕКТРОДИНАМИКА
3. Электромагнитное поле
УРОК 7/34
Тема. Закон электромагнитной индукции
Цель урока: ознакомить учащихся с законом электромагнитной индукции.
Тип урока: урок изучения нового материала.
ПЛАН УРОКА
Контроль знаний |
4 мин. |
1. Поток магнитной индукции. 2. Явление электромагнитной индукции. 3. Правило Ленца. |
Демонстрации |
5 мин. |
1. Зависимость ЭДС индукции от скорости изменения магнитного потока. 2. Фрагменты видеофильма «Явление электромагнитной индукции». |
Изучение нового материала |
24 мин. |
1. Закон электромагнитной индукции. 2. Вихревое электрическое поле. 3. ЭДС индукции в движущихся проводниках. |
Закрепление изученного материала |
12 мин. |
1. Качественные вопросы. 2. Учимся решать задачи. |
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
1. Закон электромагнитной индукции
Как известно, электрический ток существует в замкнутом контуре, если выполняются два условия: наличие свободных заряженных частиц и наличие электрического поля. Но в опытах Фарадея в кругу катушки, замкнутой на гальванометр, нет электрического поля, созданного электрическими зарядами (но ток есть!). Это может означать только одно: в случае изменения магнитного потока, пронизывающего проводящий контур, в контуре возникают посторонние (не кулоновские) силы, которые перемещают электрические заряды вдоль контура, выполняя при этом работу.
Работу сторонних сил (ACT) по перемещению единичного положительного заряда называют ЭДС индукции
Эту величину можно измерить, используя закон Ома для полного круга, согласно которому где Iинд – сила индукционного тока, R – сопротивление контура. Опытным путем было установлено закон электромагнитной индукции:
Опытным путем было установлено закон электромагнитной индукции:
Ø ЭДС индукции в замкнутом контуре равна модулю скорости изменения магнитного потока, пронизывающего этот контур:
Для возникновения индукционного тока проводник должен быть замкнутым, при этом сила тока зависит не только от скорости изменения магнитного потока, но и от сопротивления проводника:
Для катушки, состоящей из N витков, помещенной в переменное магнитное поле, ЭДС индукции будет в N раз больше:
С учетом правила Ленца закон электромагнитной индукции записывается в виде
Таким образом, ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока через этот контур, взятый с противоположным знаком.
2. Вихревое электрическое поле
Откуда же берутся посторонние силы, которые действуют на заряды в контуре? В случае неподвижного относительно наблюдателя проводника причина появления посторонних сил – переменное магнитное поле. Дело в том, что переменное магнитное поле порождает в окружающем пространстве электрическое поле – именно оно действует на свободные заряженные частицы в проводнике. Но порождение электрического поля магнитным полем происходит даже там, где нет ведущего контура и не возникает электрический ток. Как видим, магнитное поле может не только передавать магнитные взаимодействия, но и быть причиной появления другой формы материи – электрического поля.
Дело в том, что переменное магнитное поле порождает в окружающем пространстве электрическое поле – именно оно действует на свободные заряженные частицы в проводнике. Но порождение электрического поля магнитным полем происходит даже там, где нет ведущего контура и не возникает электрический ток. Как видим, магнитное поле может не только передавать магнитные взаимодействия, но и быть причиной появления другой формы материи – электрического поля.
Однако электрическое поле, порождаемое переменным магнитным полем, имеет существенное отличие от поля, созданного заряженными частицами.
Электрическое поле, создаваемое переменным магнитным полем, является вихревым, то есть его силовые линии являются замкнутыми.
Вихревое электрическое поле имеет некоторые особенности:
1) поле проявляет себя через силовое воздействие на заряженные частицы, поэтому основной характеристикой вихревого электрического поля является напряженность ;
2) в отличие от электростатического поля, линии напряженности вихревого электрического поля являются замкнутыми. Направление этих линий можно определить с помощью, например, левой руки, как показано на рисунке:
Направление этих линий можно определить с помощью, например, левой руки, как показано на рисунке:
3) в отличие от электростатического поля, работа вихревого электрического поля по замкнутой траектории не равна нулю (вихревое электрическое поле является непотенціальним).
3. ЭДС индукции в движущихся проводниках
Рассмотрим проводник длиной l, движущегося поступательно в однородном магнитном поле с индукцией со скоростью , напрямленою под углом к линиям магнитной индукции поля.
На электроны, движущиеся вместе с проводником в магнитном поле, действует сила Лоренца, направленная вдоль проводника. Ее модуль
где q0 – заряд свободной заряженной частицы. Под действием этой силы происходит разделение зарядов – свободные заряженные частицы сместятся к одному концу проводника, а на другом конце возникнет их нехватка, то есть будет превышать заряд противоположного знака. Следовательно, в этом случае сторонняя сила – это сила Лоренца. Разделение зарядов приведет к появлению электрического поля, что будет препятствовать дальнейшему разделению зарядов. Этот процесс прекратится, когда сила Лоренца и сила = q0 уравновесят друг друга. Следовательно, внутри проводника напряженность электрического поля E = Bsin, а разность потенциалов на концах проводника U = El = Blsin. Поскольку мы рассматриваем разомкнутое круг, разность потенциалов на концах проводника равна ЭДС индукции в этом проводнике. Таким образом,
Следовательно, в этом случае сторонняя сила – это сила Лоренца. Разделение зарядов приведет к появлению электрического поля, что будет препятствовать дальнейшему разделению зарядов. Этот процесс прекратится, когда сила Лоренца и сила = q0 уравновесят друг друга. Следовательно, внутри проводника напряженность электрического поля E = Bsin, а разность потенциалов на концах проводника U = El = Blsin. Поскольку мы рассматриваем разомкнутое круг, разность потенциалов на концах проводника равна ЭДС индукции в этом проводнике. Таким образом,
Если такой проводник замкнуть, то по кругу пройдет электрический ток. Таким образом, движущийся в магнитном поле проводник можно рассматривать как своеобразный источник тока характеризуется ЭДС индукции.
ВОПРОС К УЧАЩИМСЯ В ХОДЕ ИЗЛОЖЕНИЯ НОВОГО МАТЕРИАЛА
Первый уровень
1. Почему в неподвижных проводниках, находящихся в переменном магнитном поле, возникает индукционный ток?
2. Какова причина возникновения индукционного тока при движении проводника в постоянном магнитном поле?
Какова причина возникновения индукционного тока при движении проводника в постоянном магнитном поле?
3. Какие особенности вихревого электрического поля?
Второй уровень
1. Какова природа сторонних сил, которые обусловливают появление индукционного тока в неподвижном проводнике?
2. Почему закон электромагнитной индукции формулируют для ЭДС, а не для силы тока?
3. Какова природа ЭДС индукции в проводнике, движущемся в магнитном поле?
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
1). Качественные вопросы
1. Почему от удара молнии иногда перегорают предохранители даже выключенного из розетки прибора?
2. Почему для обнаружения индукционного тока замкнутый проводник лучше брать в виде катушки, а не в виде прямолинейного провода?
2). Учимся решать задачи
1. С помощью гибких проводов прямолинейный проводник длиной 60 см присоединен к источнику постоянного тока с ЭДС 12 В и внутренним сопротивлением 0,5 Ом. Проводник движется в однородном магнитном поле индукцией 1,6 Тл со скоростью 12,5 м/с перпендикулярно к линиям магнитной индукции. Определите силу тока в проводнике, если сопротивление внешней цепи равно 2,5 Ом.
Проводник движется в однородном магнитном поле индукцией 1,6 Тл со скоростью 12,5 м/с перпендикулярно к линиям магнитной индукции. Определите силу тока в проводнике, если сопротивление внешней цепи равно 2,5 Ом.
Решения. На заряды в проводнике действуют две силы: сила Лоренца и сила со стороны электрического поля источника тока. С учетом этого можно записать: Воспользовавшись законом Ома, можно найти силу тока в цепи:
В подвижном проводнике ЭДС индукции
Окончательно имеем:
Выясняем значение искомой величины:
Ответ: сила тока в проводнике 8 А.
2. Линии магнитной индукции однородного магнитного поля образуют угол 30° с вертикалью. Модуль вектора магнитной индукции равен 0,2 Тл. Какой магнитный поток пронизывает горизонтальное проволочное кольцо радиусом 10 см?
3. Проводник длиной 20 см движется в однородном магнитном поле индукцией 25 мТл перпендикулярно к линиям магнитной индукции. Найдите ЭДС индукции в проводнике, если скорость его движения 2 м/с.
Найдите ЭДС индукции в проводнике, если скорость его движения 2 м/с.
4. Магнитный поток, пронизывающий проводящий контур сопротивлением 0,24 Ом, равномерно изменился на 0,6 Вб так, что ЭДС индукции оказалась равной 1,2 В. Определите время изменения магнитного потока и силу тока в проводнике.
ЧТО МЫ УЗНАЛИ НА УРОКЕ
• Закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока через этот контур, взятый с противоположным знаком.
• Электрическое поле, создаваемое переменным магнитным полем, является вихревым, то есть его силовые линии являются замкнутыми.
• ЭДС индукции в движущихся проводниках:
Домашнее задание
1. Подр-1: § 22; подр-2: § 12 (п. 3).
2. Сб.:
Рів1 № 8.14; 8.15; 8.16; 8.17.
Рів2 № 8.34; 8.35; 8.42; 8.43.
Рів3 № 8. 55, 8.56; 8.57; 8.58.
55, 8.56; 8.57; 8.58.
Урок на тему “Явление электромагнитной индукции. Правило Ленца. Закон электромагнитной индукции”
Цели урока:
- обучающие: изучить явление электромагнитной индукции и условия его возникновения; показать причинно-следственные связи при наблюдении явления электромагнитной индукции; раскрыть сущность явления при постановке опытов, изучить правило Ленца (правила для определения направления индукционного тока), разъяснить закон электромагнитной индукции.
- развивающие: развивать логическое мышление и внимание, умение анализировать, сопоставлять полученные результаты, делать соответствующие выводы, представлять результаты проделанной работы, развивать общую культуру речи, навыки групповой работы.
- воспитательные: вызвать заинтересованность
к изучаемой теме с точки зрения получаемой
профессии, способствовать самостоятельному
получению знаний.

Тип урока: изучение нового материала
Методы обучения: Метод проблемного изложения, частично-поисковый.
Формы организации познавательной деятельности:
- Групповая
- Фронтальная
Оборудование: электронная доска, презентация, мультимедийный курс Физика: полный курс.7-11 классы (под ред. В. Акопяна), полосовой магнит, соединительные провода, гальванометр, миллиамперметр, катушки, источник тока, ключ, проволочные мотки, магнит дугообразный, прибор для демонстрации правила Ленца.
План урока
| Этапы урока | Время, мин | Приемы и методы |
| Создание проблемной ситуации, исторические сведения | 8 мин | Создание проблемной ситуации
преподавателем. Демонстрации, подводящие к цели
урока. Демонстрации, подводящие к цели
урока.Беседа. |
| Изучение нового материала в ходе экспериментальной работы в группах (явление ЭМИ, правило Ленца) | 2 мин | Эксперимент. Наблюдение. Выделение главного. Формулировка выводов. |
| Изучение нового материала (правила определения направления индукционного тока, закон электромагнитной индукции). | 20 мин | Беседа. Ответы на вопросы. |
| Подведение итогов. Домашнее задание. | 5 мин | Выделение главного. Оценивание (взаимооценивание) “Цепочка”. |
Ход урока
1. Создание проблемной ситуации (дальняя перспектива)
Здравствуйте, ребята! На слайде (Слайд 1)
презентации изображены опоры ЛЭП в разных
странах: в Финляндии, например в виде оленей. Но
опоры не меняют содержание: все ЛЭП
предназначены для передачи электрического тока
на большие расстояния, и все ЛЭПы –
высоковольтные.
Но
опоры не меняют содержание: все ЛЭП
предназначены для передачи электрического тока
на большие расстояния, и все ЛЭПы –
высоковольтные.
Почему все линии электропередачи высоковольтные?
(Ответы обучающихся, как правило – “Течет ток высокого напряжения”).
Зачем повышают напряжение? (Слайд 2). Посмотрите на схему передачи электроэнергии: трансформатор повышает и без того высокое напряжение, а в быту, в осветительной сети необходимо всего 220В! Так зачем повышают напряжение? (Ответы обучающихся)
Пока мы вели с вами беседу через проволочный моток протекал электрический ток.
Демонстрация 1: Проволочный моток закреплен в лапке штатива, по нему пропускают электрический ток.
Какое действие электрического тока можно заметить?
(Ответы обучающихся, как правило – “Проводник, по которому течет ток нагревается. Это тепловое действие тока”).
Молодцы, верно! Ток, текущий по ЛЭП, нагревает
линию (провод) происходит потеря энергии: часть
электрической энергии превращается в тепловую. Потери тепловой энергии необходимо
минимизировать. (Слайд 3) Давайте вспомним закон
Джоуля-Ленца: уменьшить тепловые потери можно
уменьшив, например, силу тока. Прибор, который
уменьшает силу тока и одновременно с этим
повышает напряжение во столько же раз (и
наоборот), практически без потери мощности был
изобретен в 1878 году русским ученым П.Н.
Яблочковым и был назван трансформатором.
Потери тепловой энергии необходимо
минимизировать. (Слайд 3) Давайте вспомним закон
Джоуля-Ленца: уменьшить тепловые потери можно
уменьшив, например, силу тока. Прибор, который
уменьшает силу тока и одновременно с этим
повышает напряжение во столько же раз (и
наоборот), практически без потери мощности был
изобретен в 1878 году русским ученым П.Н.
Яблочковым и был назван трансформатором.
Давайте подведем небольшой итог: чтобы уменьшить тепловые потери при передаче электроэнергии на большие расстояния необходимо понизить силу тока, а эту роль выполнит повышающий трансформатор, но одновременно с этим он во столько же раз повысит напряжение. Вот почему все линии электропередач высоковольтные.
2. Создание проблемной ситуации (ближняя перспектива)
Но на каком принципе построена работа трансформатора?
(Обучающиеся затрудняются с ответом)
Его работа основана на явлении
электромагнитной индукции, которое было открыто
Майклом Фарадеем в 1831 году и является величайшим
открытием ХIХ века. (Слайд 4)
(Слайд 4)
На этом явлении построен принцип работы индукционных печей (ОМД, сталеплавильное производство) и лагов, индукционных варочных панелей (Технолог), металлодетекторов, трансформаторов(Сварщик) и генераторов переменного тока(Техническое обслуживание электрического и электромеханического оборудования). Ваша будущая профессия (специальность) неразрывно связана с этим явлением: без электрического тока вырабатываемого генераторами на ЭС невозможна работа станков (Станочник), электромагнитов (Машинист крана), электрических печей и плит (Технолог) и т.д.
Демонстрация 2. Моток закреплен в лапке штатива, по нему пропускают электрический ток, подносят магнит.
Какое действие электрического тока можно заметить?
(Ответы обучающихся, как правило – “Магнитное. Если по проводнику течет ток, то вокруг проводника возникает магнитное поле”). Молодцы!
Верно. Если электрический ток порождает собой магнитное поле, то не может ли в свою очередь, магнитное поле породить электрический ток?
В 1821 году этим вопросом был озадачен Майкл
Фарадей. “Превратить магнетизм в
электричество” было написано у него в дневнике.
Через 10 лет, 29 августа 1831 года эта задача была
решена.
“Превратить магнетизм в
электричество” было написано у него в дневнике.
Через 10 лет, 29 августа 1831 года эта задача была
решена.
Запишите тему урока. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. ПРАВИЛО ЛЕНЦА. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
Давайте экспериментально установим, при каких условиях магнитное поле может породить электрический ток в проводнике (контуре).
(Обучающиеся выполняют экспериментальные задания по группам).
- 1 группа: Приложение 1
- 2 группа: Приложение 2
- 3 группа: Приложение 3
Подведем итоги работы наших групп:
1 группа (Ответы обучающихся). (Слайд 5) (ответы обучающихся 1 группы дополняются ответами обучающихся из других групп)
Вывод: В проводящем замкнутом контуре
возникает электрический ток, если контур
находится в переменном магнитном поле или
движется в постоянном во времени поле так, что число
линий магнитной индукции, пронизывающих контур,
меняется.
Из истории вопроса: Почти одновременно с Фарадеем получить электрический ток в катушке с помощью магнита пытался швейцарский физик Колладон. При работе он пользовался гальванометром, легкая магнитная стрелка которого помещалась внутри катушки прибора. Чтобы магнит не оказывал непосредственного влияния на стрелку, концы катушки, куда вводили магнит, были выведены в соседнюю комнату и там присоединены к гальванометру. Вставив магнит в катушку, Колладон шел в соседнюю комнату и с огорчением убеждался, что гальванометр не показывал тока. Стоило бы ему все время находится рядом с гальванометром, а кого-нибудь попросить заняться магнитом, замечательное открытие было бы сделано. Но этого не случилось. Покоящийся относительно катушки магнит не вызывает в ней тока.
Введем понятие магнитного потока. (Слайд 6)
Магнитный поток — физическая величина, равная произведению модуля вектора магнитной индукции B на площадь S косинус угла ? между векторами и
Ф = В S cos
1 Вб = 1 Тл*1м2
Магнитный поток в 1 Вебер создается магнитным
полем с индукцией 1 Тл через поверхность площадью
1 м2, расположенную перпендикулярно вектору
магнитной индукции.
Ток, возникающий в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называют индукционным током.
2 группа (Ответы обучающихся).
Вывод: Величина индукционного тока зависит (Слайд 7)
- сила индукционного тока зависит не от скорости изменения магнитной индукции, а от скорости изменения потока магнитной индукции (от скорости изменения магнитного потока)
- от числа витков в контуре
Общий вывод работы 1 и 2 группы:
Явление возникновения индукционного тока в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называют явлением электромагнитной индукции.
3 группа (Ответы обучающихся). (Слайд 8). Правило Ленца.
Исследуя явление электромагнитной индукции, Э. X. Ленц в 1833 г. установил общее правило для определения направления индукционного тока:
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым был вызван.

Направление индукционного тока.
Правило правой руки
Если правую руку расположить так, чтобы вектор B входил в ладонь, а отогнутый на 90о большой палец был направлен по движению проводника, то четыре пальца руки укажут направление индукционного тока проводнике.
При объяснении материала можно использовать мультимедийный курс Физика: полный курс.7-11 классы (под ред. В.Акопяна) (урок “Явление электромагнитной индукции”)
- Определить направление линий индукции внешнего поля.
- Определить, увеличивается или уменьшается магнитный поток через контур (если магнит вдвигается в кольцо, то Ф>0, если выдвигается, то Ф<0).
- Определить направление линий индукции магнитного поля В’, созданного индукционным током (если Ф>0, то линии В и В’ направлены в противоположные стороны; если Ф<0, то линии В и В’ сонаправлены).
- Пользуясь правилом буравчика (правой руки),
определить направление индукционного тока.

Закон электромагнитной индукции
Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сторонних сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока, через поверхность, ограниченную контуром, в последнем появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции.
Так как
~ и =, то= – для 1 витка= * N- для N витков
В соответствии с правилом Ленца:
= – *N – для N витков
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
Ребята, сегодня мы познакомились с явлением
электромагнитной индукции (ЭМИ). Работа многих
приборов основана на этом явлении, особенную
роль следует отвести генераторам переменного
тока, в которых механическая энергия
превращается в электрическую. Без
электрического тока жизнь современного человека
представить практически невозможно, так же как и
Вашу будущую работу: индукционные варочные
панели – Технолог, индукционные печи – ОМД,
трансформатор – Сварщик и т.д.
Без
электрического тока жизнь современного человека
представить практически невозможно, так же как и
Вашу будущую работу: индукционные варочные
панели – Технолог, индукционные печи – ОМД,
трансформатор – Сварщик и т.д.
Подведем итог урока, ответим на вопросы:
Вопросы:
1. В чем заключается явление электромагнитной индукции?
2. Что называют магнитным потоком?
3. Как связана работа станочника (машиниста крана, машиниста локомотива и т. д.) с явлением ЭМИ?
4. Почему закон электромагнитной индукции формулируется для ЭДС, а не для силы тока? Сформулируйте закон ЭМИ.
5. Почему в законе электромагнитной индукции стоит знак “минус”?
6. Как определить направление индукционного тока?
Сегодня мы плодотворно работали, проводили опыты, ребята оцените работу каждой группы: работу своей группы и работу студентов в других группах.
(Обсуждение, диалог обучающихся)
3. Домашнее задание:
8-11,
конспект, стр. 27 (привести примеры возникновения
индукционного тока, используя две катушки на
общем сердечнике), подготовить сообщения
(Металлодетекторы, поезд на магнитной подушке,
индукционные печи, индукционные варочные
панели).
27 (привести примеры возникновения
индукционного тока, используя две катушки на
общем сердечнике), подготовить сообщения
(Металлодетекторы, поезд на магнитной подушке,
индукционные печи, индукционные варочные
панели).
Цепочка:
Как обычно, выходим из класса по “цепочке” (необходимо назвать физическую величину и единицы измерения физической величины).
Приложение 1
| Опыт | Вывод |
| Внесите постоянный магнит в катушку,
оставьте его в состоянии покоя. Наблюдается ли возникновение тока? | |
| Осуществляйте движение постоянного
магнита относительно катушки. Наблюдается ли возникновение тока? | |
| При внесении и вынесении постоянного магнита из катушки изменялось ли направление возникающего тока? | |
Осуществляйте движение катушки
относительно лежащего неподвижно постоянного
магнита, лежащего неподвижно. Наблюдается ли возникновение тока? |
Приложение 2
| Опыт | Вывод |
| Осуществляйте движение постоянного
магнита внутри катушки: а) медленно б) быстро Наблюдается ли возникновение тока? Что можно сказать о величине тока? | |
| Подключите катушку с бльшим числом витков. Изменилась ли сила возникающего тока? | |
| Осуществите движение проволочного
мотка между полюсами подковообразного магнита: а) перпендикулярно силовым линиям магнитного поля б) вдоль силовых линий магнитного поля В каком случае сила возникающего тока больше? |
Приложение 3
| Опыт | Вывод |
Внесите постоянный магнит северным
полюсом в разомкнутое кольцо. Что удается
пронаблюдать? Что удается
пронаблюдать? | |
| Внесите постоянный магнит южным полюсом в разомкнутое кольцо. Что удается пронаблюдать? | |
| Поднести постоянный магнит к замкнутому кольцу. Что удается пронаблюдать? Медленно удаляйте магнит от кольца. Что удается пронаблюдать? |
Закон электромагнитной индукции. Кто открыл явление электромагнитной индукции
Явление электромагнитной индукции было открыто Майлом Фарадеем в 1831 году. Еще за 10 лет до этого Фарадей думал о способе превратить магнетизм в электричество. Он считал, что магнитное поле и электрическое поле должны быть как-то связаны.
Открытие электромагнитной индукции
Например, с помощью электрического поля можно намагнитить железный предмет. Наверное, должна существовать возможность с помощью магнита получить электрический ток.
Сначала Фарадей открыл явление электромагнитной индукции в неподвижных относительно друг друга проводниках. При возникновении в одной из них тока в другой катушке тоже индуцировался ток. Причем в дальнейшем он пропадал, и появлялся снова лишь при выключении питания одной катушки.
При возникновении в одной из них тока в другой катушке тоже индуцировался ток. Причем в дальнейшем он пропадал, и появлялся снова лишь при выключении питания одной катушки.
Через некоторое время Фарадей на опытах доказал, что при перемещении катушки без тока в цепи относительно другой, на концы которой подается напряжение, в первой катушке тоже будет возникать электрический ток.
Следующим опытом было введение в катушку магнита, и при этом тоже в ней появлялся ток. Данные опыты показаны на следующих рисунках.
Фарадеем была сформулирована основная причина появления тока в замкнутом контуре. В замкнутом проводящем контуре ток возникает при изменении числа линий магнитной индукции, которые пронизывают этот контур.
Чем больше будет это изменение, тем сильнее получится индукционный ток. Неважно, каким образом мы добьемся изменения числа линий магнитной индукции. Например, это можно сделать движением контура в неоднородном магнитном поле, как это происходило в опыте с магнитом или движением катушки. А можем, например, изменять силу тока в соседней с контуром катушке, при этом будет изменяться магнитное поле, создаваемое этой катушкой.
А можем, например, изменять силу тока в соседней с контуром катушке, при этом будет изменяться магнитное поле, создаваемое этой катушкой.
Формулировка закона
Подведем краткий итог. Явление электромагнитной индукции – это явление возникновения тока в замкнутом контуре, при изменении магнитного поля в котором находится этот контур.
Для более точной формулировки закона электромагнитной индукции необходимо ввести величину, которая бы характеризовала магнитное поле – поток вектора магнитной индукции.
Магнитный поток
Вектор магнитной индукции обозначается буквой B. Он будет характеризовать магнитное поле в любой точке пространства. Теперь рассмотрим замкнутый контур, ограничивающий поверхность площадью S. Поместим его в однородное магнитное поле.
Между вектором нормали к поверхности и вектором магнитной индукции будет некоторый угол а. Магнитный поток Ф через поверхность площадью S называется физическая величина, равная произведению модуля вектора магнитной индукции на площадь поверхности и косинус угла между вектором магнитной индукции и нормалью к контуру. 2, которая расположена перпендикулярно вектору магнитной индукции.
2, которая расположена перпендикулярно вектору магнитной индукции.
После открытий Эрстеда и Ампера стало ясно, что электричество обладает магнитной силой. Теперь необходимо было подтвердить влияние магнитных явлений на электрические. Эту задачу блистательно решил Фарадей.
Майкл Фарадей (1791-1867) родился в Лондоне, в одной из беднейших его частей. Его отец был кузнецом, а мать – дочерью земледельца-арендатора. Когда Фарадей достиг школьного возраста, его отдали в начальную школу. Курс, пройденный Фарадеем здесь, был очень узок и ограничивался только обучением чтению, письму и началам счета.
В нескольких шагах от дома, в котором жила семья Фарадеев, находилась книжная лавка, бывшая вместе с тем и переплетным заведением. Сюда-то и попал Фарадей, закончив курс начальной школы, когда возник вопрос о выборе профессии для него. Майклу в это время минуло только 13 лет. Уже в юношеском возрасте, когда Фарадей только что начинал свое самообразование, он стремился опираться исключительно только на факты и проверять сообщения других собственными опытами.
Эти стремления доминировали в нем всю жизнь как основные черты его научной деятельности Физические и химические опыты Фарадей стал проделывать еще мальчиком при первом же знакомстве с физикой и химией. Однажды Майкл посетил одну из лекций Гэмфри Дэви, великого английского физика.
Фарадей сделал подробную запись лекции, переплел ее и отослал Дэви. Тот был настолько поражен, что предложил Фарадею работать с ним в качестве секретаря. Вскоре Дэви отправился в путешествие по Европе и взял с собой Фарадея. За два года они посетили крупнейшие европейские университеты.
Вернувшись в Лондон в 1815 году, Фарадей начал работать ассистентом в одной из лабораторий Королевского института в Лондоне. В то время это была одна из лучших физических лабораторий мира С 1816 по 1818 год Фарадей напечатал ряд мелких заметок и небольших мемуаров по химии. К 1818 году относится первая работа Фарадея по физике.
Опираясь на опыты своих предшественников и скомбинировав несколько собственных опытов, к сентябрю 1821 года Майкл напечатал «Историю успехов электромагнетизма». Уже в это время он составил вполне правильное понятие о сущности явления отклонения магнитной стрелки под действием тока.
Уже в это время он составил вполне правильное понятие о сущности явления отклонения магнитной стрелки под действием тока.
Добившись этого успеха, Фарадей на целых десять лет оставляет занятия в области электричества, посвятив себя исследованию целого ряда предметов иного рода. В 1823 году Фарадеем было произведено одно из важнейших открытий в области физики – он впервые добился сжижения газа, и вместе с тем установил простой, но действительный метод обращения газов в жидкость. В 1824 году Фарадей сделал несколько открытий в области физики.
Среди прочего он установил тот факт, что свет влияет на цвет стекла, изменяя его. В следующем году Фарадей снова обращается от физики к химии, и результатом его работ в этой области является открытие бензина и серно-нафталиновой кислоты.
В 1831 году Фарадей опубликовал трактат «Об особого рода оптическом обмане», послуживший основанием прекрасного и любопытного оптического снаряда, именуемого «хромотропом». В том же году вышел еще один трактат ученого «О вибрирующих пластинках». Многие из этих работ могли сами- по себе обессмертить имя их автора. Но наиболее важными из научных работ Фарадея являются его исследования в области электромагнетизма и электрической индукции.
Строго говоря, важный отдел физики, трактующий явления электромагнетизма и индукционного электричества, и имеющий в настоящее время такое громадное значение для техники, был создан Фарадеем из ничего.
К тому времени, когда Фарадей окончательно посвятил себя исследованиям в области электричества, было установлено, что при обыкновенных условиях достаточно присутствия наэлектризованного тела, чтобы влияние его возбудило электричество во всяком другом теле. Вместе с тем было известно, что проволока, по которой проходит ток и которая также представляет собою наэлектризованное тело, не оказывает никакого влияния на помещенные рядом другие проволоки.
Отчего зависело это исключение? Вот вопрос, который заинтересовал Фарадея и решение которого привело его к важнейшим открытиям в области индукционного электричества. По своему обыкновению Фарадей начал ряд опытов, долженствовавших выяснить суть дела.
На одну и ту же деревянную скалку Фарадей намотал параллельно друг другу две изолированные проволоки. Концы одной проволоки он соединил с батареей из десяти элементов, а концы другой – с чувствительным гальванометром. Когда был пропущен ток через первую проволоку,
Фарадей обратил все свое внимание на гальванометр, ожидая заметить по колебаниям его появление тока и во второй проволоке. Однако ничего подобного не было: гальванометр оставался спокойным. Фарадей решил увеличить силу тока и ввел в цепь 120 гальванических элементов. Результат получился тот же. Фарадей повторил этот опыт десятки раз и все с тем же успехом.
Всякий другой на его месте оставил бы опыты, убежденный, что ток, проходящий через проволоку, не оказывает никакого действия на соседнюю проволоку. Но фарадей старался всегда извлечь из своих опытов и наблюдений все, что они могут дать, и потому, не получив прямого действия на проволоку, соединенную с гальванометром, стал искать побочные явления.
Сразу же он заметил, что гальванометр, оставаясь совершенно спокойным во все время прохождения тока, приходит в колебание при самом замыкании цепи и при размыкании ее Оказалось, что в тот момент, когда в первую проволоку пропускается ток, а также когда это пропускание прекращается, во второй проволоке также возбуждается ток, имеющий в первом случае противоположное направление с первым током и одинаковое с ним во втором случае и продолжающийся всего одно мгновение.
Эти вторичные мгновенные токи, вызываемые влиянием первичных, названы были Фарадеем индуктивными, и это название сохранилось за ними доселе. Будучи мгновенными, моментально исчезая вслед за своим появлением, индуктивные токи не имели бы никакого практического значения, если бы Фарадей не нашел способ при помощи остроумного приспособления (коммутатора) беспрестанно прерывать и снова проводить первичный ток, идущий от батареи по первой проволоке, благодаря чему во второй проволоке беспрерывно возбуждаются все новые и новые индуктивные токи, становящиеся, таким образом, постоянными. Так был найден новый источник электрической энергии, помимо ранее известных (трения и химических процессов), – индукция, и новый вид этой энергии – индукционное электричество.
Продолжая свои опыты, Фарадей открыл далее, что достаточно простого приближения проволоки, закрученной в замкнутую кривую, к другой, по которой идет гальванический ток, чтобы в нейтральной проволоке возбудить индуктивный ток направления, обратного гальваническому току, что удаление нейтральной проволоки снова возбуждает в ней индуктивный ток уже одинакового направления с гальваническим, идущим по неподвижной проволоке, и что, наконец, эти индуктивные токи возбуждаются только во время приближения и удаления проволоки к проводнику гальванического тока, а без этого движения токи не возбуждаются, как бы близко друг к другу проволоки ни находились.
Таким образом, было открыто новое явление, аналогичное вышеописанному явлению индукции при замыкании и прекращении гальванического тока. Эти открытия вызвали в свою очередь новые. Если можно вызвать индуктивный ток замыканием и прекращением гальванического тока, то не получится ли тот же результат от намагничивания и размагничивания железа?
Работы Эрстеда и Ампера установили уже родство магнетизма и электричества. Было известно, что железо делается магнитом, когда вокруг него обмотана изолированная проволока и по последней проходит гальванический ток, и что магнитные свойства этого железа прекращаются, как только прекращается ток.
Исходя из этого, Фарадей придумал такого рода опыт: вокруг железного кольца были обмотаны две изолированные проволоки; причем одна проволока была обмотана вокруг одной половины кольца, а другая – вокруг другой. Через одну проволоку пропускался ток от гальванической батареи, а концы другой были соединены с гальванометром. И вот, когда ток замыкался или прекращался и когда, следовательно, железное кольцо намагничивалось или размагничивалось, стрелка гальванометра быстро колебалась и затем быстро останавливалась, то есть в нейтральной проволоке возбуждались все те же мгновенные индуктивные токи – на этот раз: уже под влиянием магнетизма.
Таким образом, здесь впервые магнетизмбыл превращен в электричество. Получив эти результаты, Фарадей решил разнообразить свои опыты. Вместо железного кольца он стал употреблять железную полосу. Вместо возбуждения в железе магнетизма гальваническим током он намагничивал железо прикосновением его к постоянному стальному магниту. Результат получался тот же: в проволоке, обматывавшей железо, всегда! возбуждался ток в момент намагничивания и размагничивания железа.
Затем Фарадей вносил в проволочную спираль стальной магнит – приближение и удаление последнего вызывало в проволоке индукционные токи. Словом, магнетизм, в смысле возбуждения индукционных, токов, действовал совершенно так же, как и гальванический ток.
В то время физиков усиленно занимало одно загадочное явление, открытое в 1824 году Араго и не находившее объяснения, несмотря на; то, что этого объяснения усиленно искали такие выдающиеся ученые того времени, как сам Араго, Ампер, Пуассон, Бабэдж и Гершель.
Дело состояло в следующем. Магнитная стрелка, свободно висящая, быстро приходит в состояние покоя, если под нее подвести круг из немагнитного металла; если затем круг привести во вращательное движение, магнитная стрелка начинает двигаться за ним.
В спокойном состоянии нельзя было открыть ни малейшего притяжения или отталкивания между кругом и стрелкой, между тем как тот же круг, находившийся в движении, тянул за собою не только легкую стрелку, но и тяжелый магнит. Это поистине чудесное явление казалось ученым того времени таинственной загадкой, чем-то выходящим за пределы естественного.
Фарадей, исходя из своих вышеизложенных данных, сделал предположение, что кружок немагнитного металла, под влиянием магнита, во время вращения обегается индуктивными токами, которые оказывают воздействие на магнитную стрелку и влекут ее за магнитом.
И действительно, введя край кружка между полюсами большого подковообразного магнита и соединив проволокою центр и край кружка с гальванометром, Фарадей получил при вращении кружка постоянный электрический ток.
Вслед за тем Фарадей остановился на другом вызывавшем тогда общее любопытство явлении. Как известно, если посыпать на магнит железных опилок, они группируются по определенным линиям, называемым магнитными кривыми. Фарадей, обратив внимание на это явление, дал основы в 1831 году магнитным кривым название «линий магнитной силы», вошедшее затем во всеобщее употребление.
Изучение этих «линий» привело Фарадея к новому открытию, оказалось, что для возбуждения индуктивных токов приближение и удаление источника от магнитного полюса необязательны. Для возбуждения токов достаточно пересечь известным образом линии магнитной силы.
Дальнейшие работы Фарадея в упомянутом направлении приобретали, с современной ему точки зрения, характер чего-то совершенно чудесного. В начале 1832 года он демонстрировал прибор, в котором возбуждались индуктивные токи без помощи магнита или гальванического тока.
Прибор состоял из железной полосы, помещенной в проволочной катушке. Прибор этот при обыкновенных условиях не давал ни малейшего признака появления в нем токов; но лишь только ему давалось направление, соответствующее направлению магнитной стрелки, в проволоке возбуждался ток.
Затем Фарадей давал положение магнитной стрелки одной катушке и потом вводил в нее железную полосу: ток снова возбуждался. Причиною, вызывавшею в этих случаях ток, был земной магнетизм, вызывавший индуктивные токи подобно обыкновенному магниту или гальваническому току. Чтобы нагляднее показать и доказать это, Фарадей предпринял еще один опыт, вполне подтвердивший его соображения.
Он рассуждал, что если круг из немагнитного металла, например, из меди, вращаясь в положении, при котором он пересекает линии магнитной силы соседнего магнита, дает индуктивный ток, то тот же круг, вращаясь в отсутствие магнита, но в положении, при котором круг будет пересекать линии земного магнетизма, тоже должен дать индуктивный ток.
И действительно, медный круг, вращаемый в горизонтальной плоскости, дал индуктивный ток, производивший заметное отклонение стрелки гальванометра. Ряд исследований в области электрической индукции Фарадей закончил открытием, сделанным в 1835 году, «индуктирующего влияния тока на самого себя».
Он выяснил, что при замыкании или размыкании гальванического тока в самой проволоке, служащей проводником для этого тока, возбуждаются моментальные индуктивные токи.
Русский физик Эмиль Христофорович Ленц (1804-1861) дал правило для определения направления индукционного тока. «Индукционный ток всегда направлен так, что создаваемое им магнитное поле затрудняет или тормозит вызывающее индукцию движение, – отмечает А.А. Коробко-Стефанов в своей статье об электромагнитной индукции. – Например, при приближении катушки к магниту возникающий индукционный ток имеет такое направление, что созданное им магнитное поле будет противоположно магнитному полю магнита. В результате между катушкой и магнитом возникают силы отталкивания.
Правило Ленца вытекает из закона сохранения и превращения энергии. Если бы индукционные токи ускоряли вызывающее их движение, то создавалась бы работа из ничего. Катушка сама собой после небольшого толчка устремлялась бы навстречу магниту, и одновременно индукционный ток выделял бы в ней теплоту. В действительности же индукционный ток создается за счет работы по сближению магнита и катушки.
Почему возникает индукционный ток? Глубокое объяснение явления электромагнитной индукции даланглийский физик Джемс Клерк Максвелл – творец законченной математической теории электромагнитного поля.
Чтобы лучше понять суть дела, рассмотрим очень простой опыт. Пусть катушка состоит из одного витка проволоки и пронизывается переменным магнитным полем, перпендикулярным к плоскости витка. В катушке, естественно, возникает индукционный ток. Исключительно смело и неожиданно истолковал этот эксперимент Максвелл.
При изменении магнитного поля в пространстве, по мысли Максвелла, возникает процесс, для которого присутствие проволочного витка не имеет никакого значения. Главное здесь – возникновение замкнутых кольцевых линий электрического поля, охватывающих изменяющееся магнитное поле. Под действием возникающего электрического поля приходят в движение электроны, и в витке возникает электрический ток. Виток – это просто прибор, позволяющий обнаружить электрическое поле.
Сущность же явления электромагнитной индукции в том, что переменное магнитное поле всегда порождает в окружающем пространстве электрическое поле с замкнутыми силовыми линиями. Такое поле называется вихревым».
Изыскания в области индукции, производимой земным магнетизмом, дали Фарадею возможность высказать еще в 1832 году идею телеграфа, которая затем и легла в основу этого изобретения. А вообще открытие электромагнитной индукции недаром относят к наиболее выдающимся открытиям XIX века – на этом явлении основана работа миллионов электродвигателей и генераторов электрического тока во всем мире…
Источник информации: Самин Д. К. «Сто великих научных открытий»., М.:«Вече», 2002 г.
Ответ:
Следующим важным шагом в развитии электродинамики после опытов Ампера было открытие явления электромагнитной индукции. Открыл явление электромагнитной индукции английский физик Майкл Фарадей (1791 – 1867).
Фарадей, будучи еще моло дым ученым, так же как и Эрстед, думал, что все силы природы связаны между собой и, более того, что они способны превращаться друг в друга. Интересно, что эту мысль Фарадей высказывал еще до установления закона сохранения и превращения энергии. Фарадей знал об открытии Ампера, о том, что он, говоря образным языком, превратил злектричество в магнетизм. Раздумывая над этим открытием, Фарадей пришел к мысли, что если “электричество создает магнетизм” , то и наоборот, “магнетизм должен создавать электричество”. И вот еще в 1823 г. он записал в своем дневнике: “Обратить магнетизм в электричество”. В течение восьми лет Фарадей работал над решением поставленной задачи. Долгое время его преследовали неудачи, и, наконец, в 1831 г. он решил ее – открыл явление электромагнитной индукции.
во-первых, Фарадей обнаружил явление электромагнитной индукции для случая, когда катушки намотаны на один и тот же барабан. Если в одной катушке возникает или пропадает электрический ток в результате подключения к ней или отключения от нее гальванической батареи, то в другой катушке в этот момент возникает кратковременный ток. Этот ток обнаруживается гальванометром, который присоединен ко второй катушке.
Затем Фарадей установил также наличие индукционного тока в катушке, когда к ней приближали или удаляли от нее катушку, в которой протекал электрический ток.
наконец, третий случай электромагнитной индукции, который обнаружил Фарадей, заключался в том, что в катушке появлялся ток, когда в нее вносили или же удаляли из нее магнит.
Открытие Фарадея привлекло внимание многих физиков, которые также стали изучать особенности явления электромагнитной индукции. На очереди стояла задача установить общий закон электромагнитной индукции. Нужно было выяснить, как и от чего зависит сила индукционного тока в проводнике или от чего зависит значение электродвижущей силы индукции в проводнике, в котором индуцируется электрический ток.
Эта задача оказалась трудной. Она была полностью решена Фарадеем и Максвеллом позже в рамках развитого ими учения об электромагнитном поле. Но ее пытались решить и физики, которые придерживались обычной для того времени теории дальнодействия в учении об электрических и магнитных явлениях.
Кое-что этим ученым удалось сделать. При этом им по могло открытое петербургским академиком Эмилием Христиановичем Ленцем (1804 – 1865) правило для нахождения направления индукционного тока в разных случаях электромагнитной индукции. Ленц сформулировал его так: “Если металлический проводник движется поблизости от гальванического тока или магнита, то в нем возбуждается гальванический ток такого направления, что если бы данный проводник был неподвижным, то ток мог бы обусловить его перемещение в противоположную сторону; при этом предполагается, что покоящийся проводник может перемещаться только в направлении движения или в противоположном направлении”.
Это правило очень удобно для определения направления ицдукционного тока. Им мы пользуемся и сейчас, только оно сейчас формулируется несколько иначе, с упогребпением понятия электромагнитной индукции, которое Ленц не использовал.
Но исторически главное значение правила Ленца заключалось в том, что оно натолкнуло на мысль, каким путем подойти к нахождению закона электромагнитной индукции. Дело в том, что в атом правиле устанавливается связь между электромагнитной индукцией и явлением взаимодействии токов. Вопрос же о взаимодействии токов был уже решен Ампером. Поэтому установление этой связи на первых порах дало возможность определить выражение электродвижущей силы индукции в проводнике для ряда частных случаев.
В общем виде закон электромагнитной индукции, как мы об этом сказали, был установлен Фарадеем и Максвеллом.
Электромагнитная индукция – явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока – изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Самоиндукция – возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру.
При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока – убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.
Созданию первого реле предшествовало изобретение в 1824 г. англичанином Стардженом электромагнита – устройства, преобразующего входной электрический ток проволочной катушки, намотанной на железный сердечник, в магнитное поле, образующееся внутри и вне этого сердечника. Магнитное поле фиксировалось (обнаруживалось) своим воздействием на ферромагнитный материал, расположенный вблизи сердечника. Этот материал притягивался к сердечнику электромагнита.
Впоследствии эффект преобразования энергии электрического тока в механическую энергию осмысленного перемещения внешнего ферромагнитного материала (якоря) лег в основу различных электромеханических устройств электросвязи (телеграфии и телефонии), электротехники, электроэнергетики. Одним из первых таких устройств было электромагнитное реле, изобретенное американцем Дж. Генри в 1831 г.
До сих пор мы рассматривали электрические и магнитные поля, не изменяющиеся с течением времени. Было выяснено, что электрическое поле создается электрическими зарядами, а магнитное поле – движущимися зарядами, т. е. электрическим током. Перейдем к знакомству с электрическим и магнитным полями, которые меняются со временем.
Самый важный факт, который удалось обнаружить, – это теснейшая взаимосвязь между электрическим и магнитным полями. Изменяющееся во времени магнитное поле порождает электрическое поле, а изменяющееся электрическое поле порождает магнитное. Без этой связи между полями разнообразие проявлений электромагнитных сил не было бы столь обширным, каким оно является на самом деле. Не существовало бы ни радиоволн, ни света.
Не случайно первый, решающий шаг в открытии новых свойств электромагнитных взаимодействий был сделан основоположником представлений об электромагнитном поле – Фарадеем. Фарадей был уверен в единой природе электрических и магнитных явлений. Благодаря этому он сделал открытие, которое впоследствии легло в основу устройства генераторов всех электростанций мира, превращающих механическую энергию в энергию электрического тока. (Другие источники: гальванические элементы, аккумуляторы и др. – дают ничтожную долю вырабатываемой энергии.)
Электрический ток, рассуждал Фарадей, способен намагнитить кусок железа. Не может ли магнит, в свою очередь, вызвать появление электрического тока?
Долгое время эту связь обнаружить не удавалось. Трудно было додуматься до главного, а именно: только движущийся магнит или меняющееся во времени магнитное поле может возбудить электрический ток в катушке.
Какого рода случайности могли помешать открытию, показывает следующий факт. Почти одновременно с Фарадеем швейцарский физик Колладон пытался получить электрический ток в катушке с помощью магнита. При работе он пользовался гальванометром, легкая магнитная стрелка которого помещалась внутри катушки прибора. Чтобы магнит не оказывал непосредственного влияния на стрелку, концы катушки, в которую Колладон вдвигал магнит, надеясь получить в ней ток, были выведены в соседнюю комнату и там присоединены к гальванометру. Вставив магнит в катушку, Колладон шел в соседнюю комнату и с огорчением
убеждался, что гальванометр не показывает тока. Стоило бы ему все время наблюдать за гальванометром и попросить кого-нибудь заняться магнитом, замечательное открытие было бы сделано. Но этого не случилось. Покоящийся относительно катушки магнит не вызывает в ней тока.
Явление электромагнитной индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется. Оно было открыто 29 августа 1831 г. Редкий случай, когда дата нового замечательного открытия известна так точно. Вот описание первого опыта, данное самим Фарадеем:
«На широкую деревянную катушку была намотана медная проволока длиной в 203 фута и между витками ее намотана проволока такой же длины, но изолированная от первой хлопчатобумажной нитью. Одна из этих спиралей была соединена с гальванометром, а другая – с сильной батареей, состоящей из 100 пар пластин… При замыкании цепи удавалось заметить внезапное, но чрезвычайно слабое действие на гальванометре, и то же самое замечалось при прекращении тока. При непрерывном же прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого-либо индукционного действия на другую спираль, несмотря на то что нагревание всей спирали, соединенной с батареей, и яркость искры, проскакивающей между углями, свидетельствовали о мощности батареи» (Фарадей М. «Экспериментальные исследования по электричеству», 1-я серия).
Итак, первоначально была открыта индукция в неподвижных друг относительно друга проводниках при замыкании и размыкании цепи. Затем, ясно понимая, что сближение или удаление проводников с током должно приводить к тому же результату, что и замыкание и размыкание цепи, Фарадей с помощью опытов доказал, что ток возникает при перемещении катушек друг
относительно друга. Знакомый с трудами Ампера, Фарадей понимал, что магнит – это совокупность маленьких токов, циркулирующих в молекулах. 17 октября, как зарегистрировано в его лабораторном журнале, был обнаружен индукционный ток в катушке во время вдвигания (или выдвигания) магнита. В течение одного месяца Фарадей опытным путем открыл все существенные особенности явления электромагнитной индукции.
В настоящее время опыты Фарадея может повторить каждый. Для этого надо иметь две катушки, магнит, батарею элементов и достаточно чувствительный гальванометр.
В установке, изображенной на рисунке 238, индукционный ток возникает в одной из катушек при замыкании или размыкании электрической цепи другой катушки, неподвижной относительно первой. В установке на рисунке 239 с помощью реостата меняется сила тока в одной из катушек. На рисунке 240, а индукционный ток появляется при движении катушек друг относительно друга, а на рисунке 240, б – при движении постоянного магнита относительно катушки.
Уже сам Фарадей уловил то общее, от чего зависит появление индукционного тока в опытах, которые внешне выглядят по-разному.
В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих площадь, ограниченную этим контуром. И чем быстрее меняется число линий магнитной индукции, тем больше возникающий индукционный ток. При этом причина изменения числа линий магнитной индукции совершенно безразлична. Это может быть и изменение числа линий магнитной индукции, пронизывающих площадь неподвижного проводящего контура вследствие изменения силы тока в соседней катушке (рис. 238), и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве (рис. 241).
Вектор магнитной индукции \(~\vec B\) характеризует магнитное поле в каждой точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величину называют потоком вектора магнитной индукции, или магнитным потоком .
Выделим в магнитном поле настолько малый элемент поверхности площадью ΔS , чтобы магнитную индукцию во всех его точках можно было считать одинаковой. Пусть \(~\vec n\) – нормаль к элементу, образующая угол α с направлением вектора магнитной индукции (рис. 1).
Потоком вектора магнитной индукции через поверхность площадью ΔS называют величину, равную произведению модуля вектора магнитной индукции \(~\vec B\) на площадь ΔS и косинус угла α между векторами \(~\vec B\) и \(~\vec n\) (нормалью к поверхности):
\(~\Delta \Phi = B \cdot \Delta S \cdot \cos \alpha\) .
Произведение B ∙cos α = В n представляет собой проекцию вектора магнитной индукции на нормаль к элементу. Поэтому
\(~\Delta \Phi = B_n \cdot \Delta S\) .
Поток может быть как положительным, так и отрицательным в зависимости от значения угла α .
Если магнитное поле однородно, то поток через плоскую поверхность площадью S равен:
\(~\Phi = B \cdot S \cdot \cos \alpha\) .
Поток магнитной индукции наглядно может быть истолкован как величина, пропорциональная числу линий вектора \(~\vec B\) , пронизывающих данную площадку поверхности.
Вообще говоря, поверхность может быть замкнутой. В этом случае число линий индукции, входящих внутрь поверхности, равно числу линий, выходящих из нее (рис. 2). Если поверхность замкнута, то положительной нормалью к поверхности принято считать внешнюю нормаль.
Линии магнитной индукции замкнуты, что означает равенство нулю потока магнитной индукции через замкнутую поверхность. (Выходящие из поверхности линии дают положительный поток, а входящие – отрицательный.) Это фундаментальное свойство магнитного поля связано с отсутствием магнитных зарядов. Если бы не было электрических зарядов, то и электрический поток через замкнутую поверхность был бы равен нулю.
Электромагнитная индукция
Открытие электромагнитной индукции
В 1821 г. Майкл Фарадей записал в своем дневнике: «Превратить магнетизм в электричество». Через 10 лет эта задача была им решена.
М. Фарадей был уверен в единой природе электрических и магнитных явлений, но долгое время взаимосвязь этих явлений обнаружить не удавалось. Трудно было додуматься до главного: только меняющееся во времени магнитное поле может возбудить электрический ток в неподвижной катушке или же сама катушка должна двигаться в магнитном поле.
Открытие электромагнитной индукции, как назвал Фарадей это явление, было сделано 29 августа 1831 г. Вот краткое описание первого опыта, данное самим Фарадеем. «На широкую деревянную катушку была намотана медная проволока длиной в 203 фута (фут равен 304,8 мм), и между витками ее намотана проволока такой же длины, но изолированная от первой хлопчатобумажной нитью. Одна из этих спиралей была соединена с гальванометром, а другая – с сильной батареей, состоящей из 100 пар пластин… При замыкании цепи удалось заметить внезапное, но чрезвычайно слабое действие на гальванометр, и то же самое замечалось при прекращении тока. При непрерывном же прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого-либо индукционного действия на другую спираль, не смотря на то что нагревание всей спирали, соединенной с батареей, и яркость искры, проскакивающей между углями, свидетельствовали о мощности батареи».
Итак, первоначально была открыта индукция в неподвижных друг относительно друга проводниках при замыкании и размыкании цепи. Затем, ясно понимая, что сближение или удаление проводников с током должно приводить к тому же результату, что и замыкание и размыкание цепи, Фарадей с помощью опытов доказал, что ток возникает при перемещении катушек относительно друг друга (рис. 3).
Знакомый с трудами Ампера, Фарадей понимал, что магнит – это совокупность маленьких токов, циркулирующих в молекулах. 17 октября, как зарегистрировано в его лабораторном журнале, был обнаружен индукционный ток в катушке во время вдвигания (или выдвигания) магнита (рис. 4).
В течение одного месяца Фарадей опытным путем открыл все существенные особенности явления электромагнитной индукции. Оставалось только придать закону строгую количественную форму и полностью вскрыть физическую природу явления. Уже сам Фарадей уловил то общее, от чего зависит появление индукционного тока в опытах, которые внешне выглядят по-разному.
В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. Это явление называется электромагнитной индукцией.
И чем быстрее меняется число линий магнитной индукции, тем больше возникающий ток. При этом причина изменения числа линий магнитной индукции совершенно безразлична. Это может быть и изменение числа линий магнитной индукции, пронизывающих неподвижный проводник вследствие изменения силы тока в соседней катушке, и изменение числа линий вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве (рис. 5).
Правило Ленца
Индукционный ток, возникший в проводнике, немедленно начинает взаимодействовать с породившим его током или магнитом. Если магнит (или катушку с током) приближать к замкнутому проводнику, то появляющийся индукционный ток своим магнитным полем обязательно отталкивает магнит (катушку). Для сближения магнита и катушки нужно совершить работу. При удалении магнита возникает притяжение. Это правило выполняется неукоснительно. Представьте себе, что дело обстояло бы иначе: вы подтолкнули магнит к катушке, и он сам собой устремился бы внутрь нее. При этом нарушился бы закон сохранения энергии. Ведь механическая энергия магнита увеличилась бы и одновременно возникал бы ток, что само по себе требует затраты энергии, ибо ток тоже может совершать работу. Индуцированный в якоре генератора электрический ток, взаимодействуя с магнитным полем статора, тормозит вращение якоря. Только поэтому для вращения якоря нужно совершать работу, тем большую, чем больше сила тока. За счет этой работы и возникает ин-дукционный ток. Интересно отметить, что если бы магнитное поле нашей планеты было очень большим и сильно неоднородным, то быстрые движения проводящих тел на ее поверхности и в атмосфере были бы невозможны из-за интенсивного взаимодействия индуцированного в теле тока с этим полем. Тела двигались бы как в плотной вязкой среде и при этом сильно разогревались бы. Ни самолеты, ни ракеты не могли бы летать. Человек не мог бы быстро двигать ни руками, ни ногами, так как человеческое тело – неплохой проводник.
Если катушка, в которой наводится ток, неподвижна относительно соседней катушки с переменным током, как, например, у трансформатора, то и в этом случае направление индукционного тока диктуется законом сохранения энергии. Этот ток всегда направлен так, что созданное им магнитное поле стремится уменьшить изменения тока в первичной обмотке.
Отталкивание или притяжение магнита катушкой зависит от направления индукционного тока в ней. Поэтому закон сохранения энергии позволяет сформулировать правило, определяющее направление индукционного тока. В чем состоит различие двух опытов: приближение магнита к катушке и его удаление? В первом случае магнитный поток (или число линий магнитной индукции, пронизывающих витки катушки) увеличивается (рис. 6, а), а во втором случае – уменьшается (рис. 6, б). Причем в первом случае линии индукции В ’ магнитного поля, созданного возникшим в катушке индукционным током, выходят из верхнего конца катушки, так как катушка отталкивает магнит, а во втором случае, наоборот, входят в этот конец. Эти линии магнитной индукции на рисунке 6 изображены штрихом.
Рис. 6Теперь мы подошли к главному: при увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки. Ведь вектор индукции \(~\vec B”\) этого поля направлен против вектора индукции \(~\vec B\) поля, изменение которого порождает электрический ток. Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с индукцией \(~\vec B”\) , увеличивающее магнитный поток через витки катушки.
В этом состоит сущность общего правила определения направления индукционного тока, которое применимо во всех случаях. Это правило было установлено русским физиком Э. X. Ленцем (1804-1865).
Согласно правилу Ленца
возникающий в замкнутом контуре индукционный ток имеет такое на-правление, что созданный им магнитный поток через поверхность, ограниченную контуром, стремится препятствовать тому изменению потока, которое порождает данный ток.
индукционный ток имеет такое направление, что препятствует причине его вызывающей.
В случае сверхпроводников компенсация изменения внешнего магнитного потока будет полной. Поток магнитной индукции через поверхность, ограниченную сверхпроводящим контуром, вообще не меняется со временем ни при каких условиях.
Закон электромагнитной индукции
Опыты Фарадея показали, что сила индукционного тока I i в проводящем контуре пропорциональна скорости изменения числа линий магнитной индукции \(~\vec B\) , пронизывающих поверхность, ограниченную этим контуром. Более точно это утверждение можно сформулировать, используя понятие магнитного потока.
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S . Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока. Если за малое время Δt магнитный поток меняется на ΔФ , то скорость изменения магнитного потока равна \(~\frac{\Delta \Phi}{\Delta t}\) .
Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:
сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
\(~I_i \sim \frac{\Delta \Phi}{\Delta t}\) .
Известно, что в цепи возникает электрический ток в том случае, когда на свободные заряды действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции. Обозначим ее буквой E i .
Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.
Согласно закону электромагнитной индукции (ЭМИ)
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
\(~|E_i| = |\frac{\Delta \Phi}{\Delta t}|\) .
Как в законе электромагнитной индукции учесть направление индукционного тока (или знак ЭДС индукции) в соответствии с правилом Ленца?
На рисунке 7 изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль к контуру \(~\vec n\) образует правый винт с направлением обхода. Знак ЭДС, т. е. удельной работы, зависит от направления сторонних сил по отношению к направлению обхода контура. Если эти направления совпадают, то E i > 0 и соответственно I i > 0. В противном случае ЭДС и сила тока отрицательны.
Пусть магнитная индукция \(~\vec B\) внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Ф > 0 и \(~\frac{\Delta \Phi}{\Delta t}\) > 0. Согласно правилу Ленца индукционный ток создает магнитный поток Ф ’ B ’ магнитного поля индукционного тока изображены на рисунке 7 штрихом. Следовательно, индукционный ток I i направлен по часовой стрелке (против положительного направления обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак минус:
\(~E_i = – \frac{\Delta \Phi}{\Delta t}\) .
В Международной системе единиц закон электромагнитной индукции используют для установления единицы магнитного потока. Эту единицу называют вебером (Вб).
Так как ЭДС индукции E i выражают в вольтах, а время в секундах, то из закона ЭМИ вебер можно определить следующим образом:
магнитный поток через поверхность, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции равная 1 В:
1 Вб = 1 В ∙ 1 с.
Вихревое поле
Изменяясь во времени, магнитное поле порождает электрическое поле . К этому выводу впервые пришел Дж. Максвелл.
Теперь явление электромагнитной индукции предстает перед нами в новом свете. Главное в нем – это процесс порождения магнитным полем поля электрического. При этом наличие проводящего контура, например катушки, не меняет существа дела. Проводник с запасом свободных электронов (или других частиц) лишь помогает обнаружить возникающее электрическое поле. Поле приводит в движение электроны в проводнике и тем самым обнаруживает себя. Сущность явления электромагнитной индукции в неподвижном проводнике состоит не столько в появлении индукционного тока, сколько в возникновении электрического поля, которое приводит в движение электрические заряды.
Электрическое поле, возникающее при изменении магнитного поля, имеет совсем другую структуру, чем электростатическое. Оно не связано непосредственно с электрическими зарядами, и его линии напряженности не могут на них начинаться и кончаться. Они вообще нигде не начинаются и не кончаются, а представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Это так называемое вихревое электрическое поле . Может возникнуть вопрос: а почему, собственно, это поле называется электрическим? Ведь оно имеет другое происхождение и другую конфигурацию, чем статическое электрическое поле. Ответ прост: вихревое поле действует на заряд q точно так же, как и электростатическое, а это мы считали и считаем главным свойством поля. Сила, действующая на заряд, по-прежнему равна \(~\vec F = q \vec E\) , где \(~\vec E\) – напряженность вихревого поля. Если магнитный поток создается однородным магнитным полем, сконцентрированным в длинной узкой цилиндрической трубке радиусом r 0 (рис. 8), то из соображений симметрии очевидно, что линии напряженности электрического поля лежат в плоскостях, перпендикулярных линиям \(~\vec B\) , и представляют собой окружности. В соответствии с правилом Ленца при возрастании магнитной индукции \(~\left (\frac{\Delta B}{\Delta t} > 0 \right)\) линии напряженности \(~\vec E\) образуют левый винт с направлением магнитной индукции \(~\vec B\) .
В отличие от статического или стационарного электрического поля работа вихревого поля на замкнутом пути не равна нулю. Ведь при перемещении заряда вдоль замкнутой линии напряженности электрического поля работа на всех участках пути имеет один и тот же знак, так как сила и перемещение совпадают по направлению. Вихревое электрическое поле, так же как и магнитное поле, не потенциальное.
Работа вихревого электрического поля по перемещению единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике.
Итак, переменное магнитное поле порождает вихревое электрическое поле. Но не кажется ли вам, что одного утверждения здесь недостаточно? Хочется знать, каков же механизм данного процесса. Нельзя ли разъяснить, как эта связь полей осуществляется в природе? И вот тут-то ваша естественная любознательность не может быть удовлетворена. Никакого механизма здесь просто нет. Закон электромагнитной индукции – это фундаментальный закон природы, значит, основной, первичный. Действием его можно объяснить многие явления, но сам он остается необъяснимым просто по той причине, что нет более глубоких законов, из которых бы он вытекал в виде следствия. Во всяком случае сейчас такие законы неизвестны. Таковыми являются все основные законы: закон тяготения, закон Кулона и т.д.
Мы, конечно, вольны ставить перед природой любые вопросы, но не все они имеют смысл. Так, например, можно и нужно исследовать причины различных явлений, но пытаться выяснить, почему вообще существует причинность, – бесполезно. Такова природа вещей, таков мир, в котором мы живем.
Литература
- Жилко В.В. Физика: Учеб. пособие для 10-го кл. общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, А.В. Лавриненко, Л.Г. Маркович. – Мн.: Нар. асвета, 2001. – 319 с.
- Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. – М.: Дрофа, 2005. – 476 с.
Рекомендуем также
Лестницы. Входная группа. Материалы. Двери. Замки. Дизайн
Урок правило ленца. Урок на тему “Явление электромагнитной индукции. Правило Ленца. Закон электромагнитной индукции”
Цели урока:
- обучающие: изучить явление электромагнитной индукции и условия его возникновения; показать причинно-следственные связи при наблюдении явления электромагнитной индукции; раскрыть сущность явления при постановке опытов, изучить правило Ленца (правила для определения направления индукционного тока), разъяснить закон электромагнитной индукции.
- развивающие: развивать логическое мышление и внимание, умение анализировать, сопоставлять полученные результаты, делать соответствующие выводы, представлять результаты проделанной работы, развивать общую культуру речи, навыки групповой работы.
- воспитательные: вызвать заинтересованность к изучаемой теме с точки зрения получаемой профессии, способствовать самостоятельному получению знаний.
Тип урока: изучение нового материала
Методы обучения: Метод проблемного изложения, частично-поисковый.
Формы организации познавательной деятельности:
- Групповая
- Фронтальная
Оборудование: электронная доска, презентация, мультимедийный курс Физика: полный курс.7-11 классы (под ред. В. Акопяна), полосовой магнит, соединительные провода, гальванометр, миллиамперметр, катушки, источник тока, ключ, проволочные мотки, магнит дугообразный, прибор для демонстрации правила Ленца.
План урока
| Этапы урока | Время, мин | Приемы и методы |
| Создание проблемной ситуации, исторические сведения | 8 мин | Создание проблемной ситуации преподавателем. Демонстрации, подводящие к цели урока. |
| Изучение нового материала в ходе экспериментальной работы в группах (явление ЭМИ, правило Ленца) | 2 мин | Эксперимент. Наблюдение. Выделение главного. Формулировка выводов. |
| Изучение нового материала (правила определения направления индукционного тока, закон электромагнитной индукции). | 20 мин | Беседа. Ответы на вопросы. |
| Подведение итогов. Домашнее задание. | 5 мин | Выделение главного. Оценивание (взаимооценивание) “Цепочка”. |
Ход урока
1. Создание проблемной ситуации (дальняя перспектива)
Здравствуйте, ребята! На слайде (Слайд 1) презентации изображены опоры ЛЭП в разных странах: в Финляндии, например в виде оленей. Но опоры не меняют содержание: все ЛЭП предназначены для передачи электрического тока на большие расстояния, и все ЛЭПы – высоковольтные.
Почему все линии электропередачи высоковольтные?
(Ответы обучающихся, как правило – “Течет ток высокого напряжения” ).
Зачем повышают напряжение? (Слайд 2). Посмотрите на схему передачи электроэнергии: трансформатор повышает и без того высокое напряжение, а в быту, в осветительной сети необходимо всего 220В! Так зачем повышают напряжение? (Ответы обучающихся)
Пока мы вели с вами беседу через проволочный моток протекал электрический ток.
Демонстрация 1: Проволочный моток закреплен в лапке штатива, по нему пропускают электрический ток.
(Ответы обучающихся, как правило – “Проводник, по которому течет ток нагревается. Это тепловое действие тока” ).
Молодцы, верно! Ток, текущий по ЛЭП, нагревает линию (провод) происходит потеря энергии: часть электрической энергии превращается в тепловую. Потери тепловой энергии необходимо минимизировать. (Слайд 3) Давайте вспомним закон Джоуля-Ленца: уменьшить тепловые потери можно уменьшив, например, силу тока. Прибор, который уменьшает силу тока и одновременно с этим повышает напряжение во столько же раз (и наоборот), практически без потери мощности был изобретен в 1878 году русским ученым П.Н. Яблочковым и был назван трансформатором.
Давайте подведем небольшой итог: чтобы уменьшить тепловые потери при передаче электроэнергии на большие расстояния необходимо понизить силу тока, а эту роль выполнит повышающий трансформатор, но одновременно с этим он во столько же раз повысит напряжение. Вот почему все линии электропередач высоковольтные.
2. Создание проблемной ситуации (ближняя перспектива)
Но на каком принципе построена работа трансформатора?
(Обучающиеся затрудняются с ответом)
Его работа основана на явлении электромагнитной индукции, которое было открыто Майклом Фарадеем в 1831 году и является величайшим открытием ХIХ века. (Слайд 4)
На этом явлении построен принцип работы индукционных печей (ОМД, сталеплавильное производство) и лагов, индукционных варочных панелей (Технолог), металлодетекторов, трансформаторов(Сварщик) и генераторов переменного тока(Техническое обслуживание электрического и электромеханического оборудования). Ваша будущая профессия (специальность) неразрывно связана с этим явлением: без электрического тока вырабатываемого генераторами на ЭС невозможна работа станков (Станочник), электромагнитов (Машинист крана), электрических печей и плит (Технолог) и т.д.
Демонстрация 2. Моток закреплен в лапке штатива, по нему пропускают электрический ток, подносят магнит.
Какое действие электрического тока можно заметить?
(Ответы обучающихся, как правило – “Магнитное. Если по проводнику течет ток, то вокруг проводника возникает магнитное поле” ). Молодцы!
Верно. Если электрический ток порождает собой магнитное поле, то не может ли в свою очередь, магнитное поле породить электрический ток?
В 1821 году этим вопросом был озадачен Майкл Фарадей. “Превратить магнетизм в электричество” было написано у него в дневнике. Через 10 лет, 29 августа 1831 года эта задача была решена.
Запишите тему урока. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. ПРАВИЛО ЛЕНЦА. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
Давайте экспериментально установим, при каких условиях магнитное поле может породить электрический ток в проводнике (контуре).
(Обучающиеся выполняют экспериментальные задания по группам).
- 1 группа: Приложение 1
- 2 группа: Приложение 2
- 3 группа: Приложение 3
Подведем итоги работы наших групп:
1 группа (Ответы обучающихся). (Слайд 5) (ответы обучающихся 1 группы дополняются ответами обучающихся из других групп)
Вывод: В проводящем замкнутом контуре возникает электрический ток , если контур находится в переменном магнитном поле или движется в постоянном во времени поле так, что число линий магнитной индукции, пронизывающих контур, меняется.
Из истории вопроса: Почти одновременно с Фарадеем получить электрический ток в катушке с помощью магнита пытался швейцарский физик Колладон. При работе он пользовался гальванометром, легкая магнитная стрелка которого помещалась внутри катушки прибора. Чтобы магнит не оказывал непосредственного влияния на стрелку, концы катушки, куда вводили магнит, были выведены в соседнюю комнату и там присоединены к гальванометру. Вставив магнит в катушку, Колладон шел в соседнюю комнату и с огорчением убеждался, что гальванометр не показывал тока. Стоило бы ему все время находится рядом с гальванометром, а кого-нибудь попросить заняться магнитом, замечательное открытие было бы сделано. Но этого не случилось. Покоящийся относительно катушки магнит не вызывает в ней тока.
Введем понятие магнитного потока. (Слайд 6)
Магнитный поток – физическая величина, равная произведению модуля вектора магнитной индукции B на площадь S косинус угла? между векторами и
1 Вб = 1 Тл*1м 2
Магнитный поток в 1 Вебер создается магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции.
Ток, возникающий в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называют индукционным током.
2 группа (Ответы обучающихся).
Вывод: Величина индукционного тока зависит (Слайд 7)
- сила индукционного тока зависит не от скорости изменения магнитной индукции, а от скорости изменения потока магнитной индукции (от скорости изменения магнитного потока)
- от числа витков в контуре
Общий вывод работы 1 и 2 группы:
Явление возникновения индукционного тока в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называют явлением электромагнитной индукции.
3 группа (Ответы обучающихся). (Слайд 8). Правило Ленца.
Исследуя явление электромагнитной индукции, Э. X. Ленц в 1833 г. установил общее правило для определения направления индукционного тока:
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым был вызван.
Направление индукционного тока.
Правило правой руки
Если правую руку расположить так, чтобы вектор B входил в ладонь, а отогнутый на 90 о большой палец был направлен по движению проводника, то четыре пальца руки укажут направление индукционного тока проводнике.
При объяснении материала можно использовать мультимедийный курс Физика: полный курс.7-11 классы (под ред. В.Акопяна) (урок “Явление электромагнитной индукции”)
Закон электромагнитной индукции
Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сторонних сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока, через поверхность, ограниченную контуром, в последнем появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции.
~ и =, то = – для 1 витка = * N- для N витков
В соответствии с правилом Ленца:
= – *N – для N витков
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
Ребята, сегодня мы познакомились с явлением электромагнитной индукции (ЭМИ). Работа многих приборов основана на этом явлении, особенную роль следует отвести генераторам переменного тока, в которых механическая энергия превращается в электрическую. Без электрического тока жизнь современного человека представить практически невозможно, так же как и Вашу будущую работу: индукционные варочные панели – Технолог, индукционные печи – ОМД, трансформатор – Сварщик и т.д.
Подведем итог урока, ответим на вопросы:
Вопросы:
1. В чем заключается явление электромагнитной индукции?
2. Что называют магнитным потоком?
3. Как связана работа станочника (машиниста крана, машиниста локомотива и т. д.) с явлением ЭМИ?
4. Почему закон электромагнитной индукции формулируется для ЭДС, а не для силы тока? Сформулируйте закон ЭМИ.
5. Почему в законе электромагнитной индукции стоит знак “минус”?
6. Как определить направление индукционного тока?
Сегодня мы плодотворно работали, проводили опыты, ребята оцените работу каждой группы: работу своей группы и работу студентов в других группах.
(Обсуждение, диалог обучающихся)
3. Домашнее задание:
8-11, конспект, стр. 27 (привести примеры возникновения индукционного тока, используя две катушки на общем сердечнике), подготовить сообщения (Металлодетекторы, поезд на магнитной подушке, индукционные печи, индукционные варочные панели).
Цепочка:
Как обычно, выходим из класса по “цепочке” (необходимо назвать физическую величину и единицы измерения физической величины).
Приложение 1
Приложение 2
Приложение 3
Конспект урока по физике в 8 классе.
Тема. Правило Ленца.
Цели:
образовательные:
Сформулировать правило Ленца для определения направления индукционного тока;
Сформировать навыки применения правила Ленца;
развивающие:
Развивать умения наблюдать, сопоставлять, сравнивать и обобщать результаты экспериментов;
Развивать умение находить решение проблемы;
воспитательные:
– воспитывать познавательную потребность и интерес к предмету;
Расширять кругозор учащихся.
Оборудование: прибор для демонстрации правила Ленца, полосовой и дугообразный магниты, гальванометр, катушка, экран, ноутбук, проектор, раздаточный материал (карточки-задания), презентация.
Ход урока.
I. Организационный момент.
Английский философ Герберт Спенсер когда-то сказал: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы!»
Эти слова будут эпиграфом к уроку, на котором нам предстоит поработать «мозговыми мышцами».
II. Проверка домашнего задания.
Экспресс-тест.
Явление электромагнитной индукции.
1. При вдвигании магнита северным полюсом в катушку…
2. При выдвигании магнита северным полюсом из катушки…
В. в катушке в некоторых случаях возникает индукционный ток
3. При выдвигании магнита южным полюсом из катушки…
А. в катушке не возникает индукционный ток
Б. в катушке возникает индукционный ток
В. в катушке в некоторых случаях возникает индукционный ток
4. При вдвигании магнита южным полюсом в катушку…
А. в катушке возникает индукционный ток
Б. в катушке не возникает индукционный ток
В. в катушке в некоторых случаях возникает индукционный ток
5. Если магнит неподвижен относительно катушки…
А. в катушке не возникает индукционный ток
Б. в катушке возникает индукционный ток
В. в катушке в некоторых случаях возникает индукционный ток
6. Если двигать катушку относительно недвижного магнита…
А. в катушке возникает индукционный ток
Б. в катушке не возникает индукционный ток
В. в катушке иногда возникает индукционный ток
7. Сила индукционного тока больше…
А. медленно вдвигать магнит в катушку
Б. быстро выдвигать магнит из катушки
В. медленно выдвигать магнит из катушки
А. направления движения магнита относительно катушки (вносят магнит или удаляют)
Б. от того, каким полюсом вносят или удаляют магнит
В. направления движения магнита относительно катушки (вносят магнит или удаляют) и от того, каким полюсом вносят или удаляют магнит
9. Явление электромагнитной индукции…
А. это явление возникновения электрического тока в замкнутом контуре при изменении внешнего магнитного поля внутри катушки
Б. это явление возникновения электрического тока в замкнутом контуре
В. это явление возникновения магнитного поля в замкнутом контуре
10. Явление электромагнитной индукции обнаружил…
А. Эрстед
В. Фарадей
Работа в парах: взаимопроверка.
(каждый учащийся ответы дает в двух экземплярах: один – для взаимопроверки, второй сдают для проверки учителем).
10 верных ответов – «5», 8-9 – «4», 7 – «3», 6 – «3-», 5 и меньше – «2».
Психологическая разрядка – здоровьесбережение.
«Пятерки» – похлопали в ладоши.
«Четверки» – похлопали в ладоши.
«Тройки» – вздохнули.
«Двойки» – глубоко вздохнули.
III . Мотивация учебной деятельности.
Герман Людвиг Фердинанд Гельмгольц – немецкий физик об открытии Майкла Фарадея сказал: «До тех пор, пока люди пользуются благами электричества, они всегда будут с благодарностью вспоминать имя Фарадея».
Фарадей указал причину возникновения индукционного тока – это изменяющееся магнитное поле. Кроме того, для каждого конкретного случая (для каждого опыта) указывал направление индукционного тока.
Как вы думаете, если причина возникновения тока одна, то существует общий подход к определению направления индукционного тока, а не каждого случая?
Возможный ответ. Существует.
Действительно, есть правило, определяющее направление индукционного тока.
IV . Целеполагание.
Какую цель мы ставим перед собой на уроке?
Возможный ответ. Изучить правило, которое позволит определять направление индукционного тока.
V. Сообщение темы урока.
(записали в тетрадь)
VI . Изучение нового материала.
После открытия Фарадеем явления электромагнитной индукции ряд ученых предложили довольно сложные «правила», позволяющие в частных случаях определять направление индукционного тока.
Внимательно изучив все работы в этой области, российский физик, один из основоположников электротехники, Эмилий Христианович Ленц в 1832 г. поставил ряд оригинальных опытов, а в ноябре 1833-го выступил в Академии наук с докладом «Об определении направления гальванических токов, возбуждаемых электродинамической индукцией».
Мы с вами тоже можем установить это правило при помощи несложного опыта.
Прибор представляет собой два алюминиевых кольца соединены алюминиевой перекладиной. Одно из этих колец имеет разрез (не замкнутое), второе кольцо сплошное. Перекладина установлена на острие иглы, которая закреплена на подставке.
Опыт 1. Внести магнит в кольцо с разрезом.
Что наблюдаете?
Ответ. Никаких изменений не наблюдается.
Опыт 2. Внести магнит северным полюсом в сплошное кольцо.
Что наблюдаете?
Ответ. Кольцо уходит от магнита.
Опыт 3. Вытянуть магнит из сплошного кольца.
Что наблюдаете?
Ответ. Кольцо следует за магнитом.
Опыты 4-5. Повторить опыт вдвигая и выдвигая магнит из сплошного кольца южным полюсом.
Что наблюдаете?
При внесении магнита южным полюсом в сплошное кольцо удаляется от магнита. При вынесении магнита из кольца кольцо следует за ним.
Таким образом, при внесении в сплошное кольцо любого полюса магнита кольцо удаляется от него, а при выдвигании магнита из кольца любым полюсом кольцо следует за магнитом.
Объясним наблюдаемые явления.
Эвристическая беседа.
Демонстрация. Что происходит, если в катушку вдвигать магнит?
Ответ. В катушке возникает индукционный ток.
Что происходит, если в кольцо вдвигать магнит?
Ответ. В кольце возникает индукционный ток.
К чему приводит возникновение индукционного тока?
Ответ. Вокруг кольца с током возникает магнитное поле.
Итак, кольцо приобретает свойства магнита, и мы наблюдали взаимодействие магнита с кольцом-магнитом.
Как взаимодействуют полюсы магнитов?
Ответ. Разноименные полюсы притягиваются, одноименные – отталкиваются.
Поскольку, кольцо отталкивается от магнита, то следует, что кольцо и магнит обращены друг к другу одноимёнными полюсами.
Демонстрация. Что скажем о направлении индукционного тока при вдвигании и выдвигании магнита из катушки?
Ответ. Возникающий ток при вдвигании магнита имеет одно направление, а при выдвигании – противоположное.
При выдвигании магнита из кольца кольцо следует за магнитом. Направление тока изменилось на противоположное, и кольцо теперь обращено противоположным с магнитом полюсом.
Физкультминутка.
На уроке дадим поработать и мышцам глаз, и мышцам пальцев, и мышцам рук.
Продолжим. Изобразим механизм происходящего.
Что собой представляют магнитные линии магнитного поля полосового магнита?
Ответ. Магнитные линии полосового магнита – замкнутые линии, выходят из северного полюса входят в южный.
Применим правило правой руки для кольца: если направить большой палец правой руки по направлению магнитных линий, то четыре согнутых пальца укажут направление тока в кольце.
Теперь рассмотрим, что происходит, если выдвигать магнит из кольца.
В кольце с разрезом индукционный ток не возникает, кольцо с магнитом не взаимодействует.
Отодвигаясь от приближающегося магнита, кольцо противодействует увеличению проходящего сквозь него внешнего магнитного поля. Следуя за удаляющимся магнитом, кольцо противодействует уменьшению проходящего сквозь него внешнего магнитного поля.
Таким образом, мы пришли к тому же выводу, что и в 1833 году Эмилий Христианович Ленц:
возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению внешнего магнитного поля, которое вызвало этот ток.
Правило Ленца является следствием закона сохранения энергии.
V . Закрепление изученного материала.
Повторим этапы применения правила Ленца для определения направления индукционного тока:
1. Выясняем, приближаем или удаляем магнит от замкнутого контура. То есть, выясняем, как изменяется магнитное поле через замкнутый контур.
2. Показываем магнитные линии этого (внешнего) магнитного поля.
3. Показываем магнитные линии магнитного поля индукционного тока:
Если внешнее магнитное поле увеличивается, то магнитные линии магнитного поля индукционного тока направляем противоположно магнитным линиям внешнего магнитного поля;
Если внешнее магнитное поле уменьшается, то магнитные линии магнитного поля индукционного тока направляем как направлены магнитные линии внешнего магнитного поля.
4. Применяя правило правой руки, определяем направление индукционного тока.
VI . Домашнее задание.
§22 (учить).
Задание. Как направлен индукционный ток в кольце:
а) магнит вдвигать в кольцо южным полюсом;
б) магнит выдвигать из кольца южным полюсом.
VII . Рефлексия.
Как поработали мозговыми мышцами?
«Отлично!» – похлопали;
Почувствовали «красоту» правила Ленца?
«Все получилось!» – похлопали;
«Не очень…» – глубоко вздохнули.
от класса до кухни – Наука в школе
Автор (ы): Пауло Андре, Ана Рита Бастос и Руте Феррейра
Изучите электромагнитную индукцию и одно из ее широко известных приложений – индукционную плиту – с помощью этих практических занятий.
Многие современные устройства основаны на электромагнитной индукции.Закон индукции Фарадея, сформулированный в 1831 году, описывает, как переменное магнитное поле индуцирует электродвижущую силу (ЭДС). Применения этого закона включают:
- генераторы, которые производят большую часть электроэнергии, потребляемой во всем мире
- Поезда на магнитной подушке
- индукционные плиты на кухне
- звукосниматели для электрогитары Коврики для беспроводной передачи энергии
- , используемые для зарядки мобильных устройств.
Преподавание закона индукции Фарадея в средней школе является сложной задачей.Учащиеся в возрасте 16–19 лет должны применять как математические вычисления, так и концептуальное понимание, чтобы исследовать науку, лежащую в основе электромагнитной индукции, и исследовать ее применение в повседневной жизни.
В этом упражнении студенты получают непосредственный опыт работы с электромагнитной индукцией. Эти задания подходят для студентов-физиков в возрасте 16–19 лет, и вместе они занимают около часа, хотя для подготовки к заданию 2 перед уроком требуется дополнительное время.
Индукционная плитаPxHere – CC0
По окончании занятия студенты должны уметь:
- понять, с экспериментальной точки зрения, закон индукции Фарадея
- идентифицируют параметры, которые влияют на применение закона индукции Фарадея.
- исследовать взаимосвязь между изменениями магнитного потока и наведенной электродвижущей силой
- построить электрический генератор, используя катушку и индукционную плиту для питания светодиода.
Закон индукции Фарадея гласит, что изменение магнитной среды катушки с проволокой вызывает электродвижущую силу (ЭДС), представленную соотношением ε :
, где Н, – количество витков катушки, а Φ – магнитный поток через катушку.
Если масштаб времени небольшой, производная d Φ / d t может быть аппроксимирована Δ Φ / Δ t . Это приближение особенно полезно, если студенты недостаточно знакомы с дифференциальным исчислением.
Магнитный поток зависит от площади катушки A , напряженности магнитного поля B и угла θ , образованного между силовыми линиями магнитного поля и вектором, нормальным (под углом 90 °) к плоскости катушки:
Любое изменение напряженности магнитного поля, площади катушки или угла приводит к наведенной ЭДС, которую можно измерить с помощью гальванометра и использовать для демонстрации принципов индукции.Эта установка показана на рисунке 1.
Рисунок 1: Электрическая цепь с гальванометром и квадратной катушкой в магнитном поле с напряженностью B и направлением.Изображение любезно предоставлено Пауло Андре
Действие 1: свободно падающий магнит
В этом эксперименте, проводимом учениками, магнитный диполь пропускается через катушку, вызывая ЭДС, вызывая кратковременное изменение интенсивности магнитного поля. Для наблюдения за изменением ЭДС катушку можно подключить к гальванометру или светодиоду (LED).Использование светодиода (рис. 2) имеет то преимущество, что дает видимый выходной сигнал (вспышку света), когда наведенная ЭДС превышает пороговое значение (~ 1,5 В).
Рис. 2. Эксперимент со свободно падающим магнитом с использованием светодиодаИзображение любезно предоставлено Пауло Андре.
Материалы
- Катушка с N> 10 000 витков
- Маленький стержневой магнит
- светодиод
- Линейка
- Смартфон (для съемок свободного падения)
Процедура
- Подсоедините клеммы катушки к контактным площадкам светодиода.Если требуется пайка, этот шаг должен быть выполнен учителем заранее.
- С помощью линейки поместите магнит на 20 см выше центра катушки (и выровняйте с центром катушки).
- Настройте камеру смартфона для записи события, желательно в замедленной съемке.
- Отпустите магнит и посмотрите на светодиод (рис. 3).
- Поэкспериментируйте с освобождением катушки с разной высоты над катушкой. Какие различия, если они есть, вы замечаете?
- Теперь поверните катушку на 180º и повторите эксперимент.Наблюдаются ли какие-либо изменения?
, когда магнит находится внутри катушки, а светодиод горит (красный).
Изображение любезно предоставлено Пауло Андре
Обсуждение
Учителя могут обсудить со студентами следующие вопросы, чтобы изучить ключевые концепции:
- Как интенсивность излучения светодиода зависит от расстояния, на котором выпущен магнит?
- При одинаковом расстоянии падения поворот катушки на 180 ° приводит к разной интенсивности излучения светодиода?
Учащиеся могут посмотреть свои видеозаписи эксперимента, чтобы найти доказательства своих ответов, или просмотреть предоставленное видео.В реальной жизни процесс происходит очень быстро, поэтому для прояснения деталей необходимо замедленное видео.
Пояснение
Эксперимент должен показать четкую разницу в интенсивности излучения светодиода при увеличении начального расстояния между магнитом и катушкой, что приведет к увеличению скорости магнита и большей скорости изменения магнитного потока.
Светодиод является поляризованным устройством, что означает, что он излучает свет только в том случае, если приложенная ЭДС положительна (когда электрический ток может течь).Положительная или отрицательная ЭДС зависит от направления движения магнита (какой полюс магнита в данный момент движется через катушку) и от того, в каком направлении катушка подключена к контактным площадкам светодиода.
Мы можем увидеть это более подробно в моделировании, показанном на рисунке 4e. Здесь ЭДС положительна только приблизительно в течение половины периода времени, в течение которого магнит находится внутри катушки, и что положительная ЭДС имеет более высокое максимальное значение, чем отрицательная ЭДС, из-за ускорения магнита при прохождении через катушку.
Расширение деятельности 1: математическое моделирование
Хотя мигающий светодиод указывает на наведенную ЭДС в результате изменения магнитного потока, он не дает количественных значений. Мы можем более точно определить изменяющиеся значения магнитного потока при прохождении магнита через катушку, используя следующее уравнение:
, где y представляет координату магнита, y 0 – координату центра катушки, B max – максимальное значение напряженности магнитного поля, а σ – параметр, описывающий спад напряженности магнитного поля.
Здесь мы делаем следующие предположения или приближения:
- Длина магнита мала по сравнению с катушкой
- его вектор магнитного поля совмещен с его продольной осью
- Φ (магнитный поток через катушку) является максимальным, когда геометрические центры катушки и магнита совпадают.
Параметр σ (расстояние для B ~ 37% от B max ) можно принять как находящийся в диапазоне 5–10 мм, полную процедуру экспериментального определения можно найти в работе.[1].
Для магнита в свободном падении смещение y магнита в момент времени t связано с ускорением свободного падения g посредством уравнения 4:
В таблице 1 приведен пример используемых параметров.
| Параметры | Символ | Значение | Блок |
|---|---|---|---|
| Площадь змеевика | А | 250 | мм 2 |
| Число витков катушки | N | 12000 | |
| Максимальная напряженность магнитного поля | B макс. | 3 | мТ |
| Распад магнитного поля | σ | 10 | мм |
| Координата центра катушки | y 0 | 200 | мм |
Используя значения в таблице 1, уравнениях 3 и 4 и прилагаемой электронной таблице, мы можем создать математическую модель, которая графически отображает эти изменения, как показано в результатах и графиках на рисунке 4. [2] Здесь магнитный поток через катушку и наведенная ЭДС показаны как функция положения и времени. Магнит отпускается при y = 0 и t = 0, и он падает в положительном направлении оси. Катушка центрируется в позиции y 0 .
Рис. 4: а) Схема эксперимента. b – e) Смоделированные значения для магнита в свободном падении: магнитный поток как функция положения (b) и времени (d), и ЭДС как функция положения (c) и времени (e)Изображение любезно предоставлено Пауло Андре
Обсуждение
Используя рисунок 4 и таблицу, учителя могут обсудить со студентами следующие вопросы:
- Как изменяется магнитный поток по мере приближения магнита к центру катушки? (Увеличивается, затем уменьшается после прохождения центра – см. Рис.4б.)
- На рисунке 4c, что происходит с ЭДС, когда магнит проходит через центр катушки? (Знак меняется с отрицательного на положительный.)
- На рисунке 4e форма кривой ЭДС симметрична до и после прохождения магнита через центр катушки? (Нет, он асимметричный, потому что магнит находится в свободном падении, поэтому его скорость увеличивается со временем, а скорость изменения магнитного потока и наведенной ЭДС также увеличивается со временем.)
Мероприятие 2: индукционная плита
Реальное применение закона Фарадея – приготовление пищи с использованием индукционной плиты, где сковорода нагревается за счет электрической индукции, а не за счет теплопроводности от пламени или электрической плиты.Индукционные плиты генерируют тепло внутри самой посуды, что делает этот метод приготовления более эффективным. Однако все сковороды должны быть изготовлены из ферромагнитного металла (обычно из чугуна или нержавеющей стали).
Индукционная плита имеет катушку, питаемую переменным электрическим током, под керамической пластиной. Переменный ток создает колеблющееся магнитное поле, которое индуцирует колеблющийся магнитный поток в основании кастрюли, установленной на плиту. Это создает электрический ток (называемый вихревым током) в дне посуды, нагревая его.
В индукционных плитах напряженность магнитного поля обычно мала (~ 100 мТл), но колеблется с высокой частотой (27 кГц). Это означает, что скорость изменения напряженности магнитного поля очень высока, что приводит к высоким значениям наведенной ЭДС и, следовательно, для произведенного нагрева.
В этом упражнении студенты исследуют наведенные ЭДС вокруг индукционной плиты, снова используя светодиод, подключенный к катушке.
Материалы
- Кухонная индукционная плита
- Светодиоды (разные цвета свечения)
- 0.Медный провод диаметром 2 мм для изготовления катушки
- Карандаш
- Бумага
- Клейкая лента
Указание по безопасности
Хотя индукционная плита не нагревается, сковорода и вода нагреваются, поэтому учеников следует предупредить, чтобы они не прикасались к ней, и следует позаботиться о том, чтобы ручка сковороды не мешала и ее нельзя было легко ударить при переноске. вне эксперимента. Следует проявлять особую осторожность, если ученики должны выполнять этап пайки самостоятельно, и это должно выполняться только под пристальным наблюдением учителя.
Процедура
- Возьмите карандаш, накройте его листом бумаги (это будет внутренняя часть катушки) и намотайте на него 300–400 витков проволоки.
- Наклейте ленту, чтобы закрыть провод, и удерживайте ее на месте; затем удалите карандаш.
- Удалите эмаль с медных проводов на каждом конце катушки.
- Припаяйте два светодиода к медным проводам встречно-параллельно (параллельно, но с обратной полярностью относительно друг друга). Учитель может выполнить этот шаг или ученики могут сделать это под присмотром учителя.
- Поставьте кастрюлю с водой в центр индукционной плиты.
- Поместите змеевик рядом с поддоном.
- Включите варочную панель, начиная с низкой интенсивности (рис. 5).
- Переместите змеевик по окружающим участкам варочной панели. Попробуйте выяснить, какие изменения приводят к тому, что светодиод становится ярче или тусклее.
Изображение любезно предоставлено Пауло Андре
Обсуждение
Учителя могут обсудить со студентами следующие вопросы, чтобы изучить ключевые концепции.
- Как яркость светодиода зависит от расстояния до варочной панели?
- Поворот катушки в том же положении приведет к изменению яркости светодиода?
Ученики должны обнаружить, что магнитное поле в основном ограничено областью кастрюли, а интенсивность поля быстро уменьшается по мере удаления от плиты. Вращение катушки приводит к изменению ЭДС в соответствии с уравнением (2) из-за изменения угла между катушкой и силовой линией магнитного поля.
Майкл Фарадей (1791–1867)
Портрет Майкла Фарадея. АвторТомас Филлипс (1842)
Общественное достояние
Майкл Фарадей был британским ученым, который изложил принципы, лежащие в основе электромагнитной индукции. Хотя Фарадей не получил формального образования, он стал одним из величайших ученых-первооткрывателей в истории. Единица электрической емкости, фарад (F), названа в его честь, и во многом благодаря усилиям Фарадея электричество стало практичным для широкого использования.Некоторые концепции, которые он извлек из экспериментов, например, силовые линии магнитного поля, стали важными теоретическими идеями в физике, положив начало современной теории электромагнетизма.
Фарадей работал в лаборатории Королевского института в Лондоне. В 1831 году он продемонстрировал принцип индукции: это позволило разработать динамо-машину (или генератор), вырабатывающую электричество механическими средствами. В 1845 году Фарадей также установил, что сильное магнитное поле может вращать плоскость поляризации света (теперь известную как эффект Фарадея), показывая лежащую в основе взаимосвязь между магнетизмом и светом.
Фарадей прекратил исследовательскую работу в 1855 году, но продолжал работать лектором до 1861 года.
Благодарности
Эта работа была разработана в рамках проекта CICECO-Aveiro Institute of Materials (UIDB / 50011/2020 & UIDP / 50011/2020), Instituto de Telecomunicações (UIDB / 50008/2020-UIDP / 50008/2020) и WinLEDs (POCI-01-0145-FEDER-030351) финансируется из национальных фондов через FCT / MEC и, при необходимости, софинансируется FEDER в рамках Партнерства PT2020 через Европейский фонд регионального развития (ERDF) в рамках Программы повышения операционной конкурентоспособности и интернационализации ( POCI).
Скачать
Загрузить эту статью в формате PDF
Ссылки
[1] Enrique A et al. (2015) Измерение магнитного поля малых магнитов с помощью смартфона: очень экономичная лабораторная практика для вводных курсов физики. Европейский журнал физики 36 : 1–11. DOI: 10.1088 / 0143-0807 / 36/6/065002
[2] Амрани Д. (2005) Электродвижущая сила: закон индукции Фарадея рассматривается как свободно падающий магнит. Физическое образование 40 : 313–314. DOI: 10.1088 / 0031-9120 / 40/4 / F02
Ресурсы
Автор (ы)
Пауло Андре является профессором телекоммуникационной инженерии в Высшем техническом институте Лиссабонского университета, Португалия. Он имеет докторскую степень в области инженерной физики, и его исследовательские интересы включают устройства и системы фотоники.
Ана Бастос – младший научный сотрудник Департамента физики и Института материалов CICECO Университета Авейру, Португалия.В ее специальные исследовательские интересы входят системы оптоэлектроники, интегрированная оптика и оптическая связь.
Руте Феррейра – доцент кафедры физики Университета Авейру, Португалия. Она координирует исследования в области информационных и коммуникационных технологий в Институте материалов CICECO Университета Авейру. В настоящее время ее научные интересы сосредоточены на органических / неорганических гибридах с перспективными приложениями в областях оптоэлектроники / зеленой фотоники (твердотельное освещение и интегрированная оптика) и фотовольтаики (люминесцентные солнечные концентраторы).
Лицензия
Фарадей и электромагнитная теория света
Майкл Фарадей (22 сентября 1791 – 25 августа 1867), вероятно, наиболее известен своим открытием электромагнитной индукции, его вкладом в электротехнику и электрохимию или тем, что он отвечал за введение концепции поля в физике. описать электромагнитное взаимодействие. Но, возможно, не так хорошо известно, что он также внес фундаментальный вклад в электромагнитную теорию света .
В 1845 году, всего 170 лет назад, Фарадей обнаружил, что магнитное поле влияет на поляризованный свет – явление, известное как магнитооптический эффект или эффект Фарадея. Чтобы быть точным, он обнаружил, что плоскость колебаний луча линейно поляризованного света, падающего на кусок стекла, вращалась, когда магнитное поле было приложено в направлении распространения луча. Это было одно из первых указаний на связь электромагнетизма и света. В следующем году, в мае 1846 года, Фарадей опубликовал статью Мысли о вибрациях лучей , пророческую публикацию , в которой он предположил , что свет может быть вибрацией электрических и магнитных силовых линий.
Майкл Фарадей (1791-1867) / Источники: WikipediaСлучай Фарадея нечасто встречается в истории физики: хотя его обучение было очень простым, законы электричества и магнетизма в гораздо большей степени связаны с экспериментальными открытиями Фарадея, чем с любыми другими учеными. Он открыл электромагнитной индукции , что привело к изобретению динамо-машины, предшественницы электрического генератора. Он объяснил электролиз с точки зрения электрических сил, а также представил такие концепции, как поле , и силовых линий, , которые не только были фундаментальными для понимания электрических и магнитных взаимодействий, но и легли в основу дальнейших достижений в физике.
Майкл Фарадей родился в Южном Лондоне в скромной семье. Единственное базовое формальное образование, которое он получил в детстве, – это чтение, письмо и арифметика. Он бросил школу, когда ему было тринадцать, и начал работать в переплетном магазине. Его страсть к науке была пробуждена описанием электричества , которое он прочитал в копии Британской энциклопедии , которую он подписывал, после чего он начал экспериментировать в импровизированной лаборатории. 1 марта 1813 года Фарадей был нанят в качестве лаборанта Хэмфри Дэви в Королевском институте в Лондоне, членом которого он был избран в 1824 году и где он проработал до своей смерти в 1867 году, сначала помощником Дэви, затем его сотрудником и, наконец, , после смерти Дэви, как его преемник.Фарадей произвел на Дэви такое впечатление, что когда последнего спросили о его величайшем открытии, Дэви ответил: «Моим величайшим открытием был Майкл Фарадей». В 1833 году он стал первым фуллеровским профессором химии в Королевском институте. Фарадей также признан великим популяризатором науки. В 1826 году Фарадей основал в Королевском институте «Пятничные вечерние лекции», которые являются каналом связи между учеными и непрофессионалами. В следующем году он запустил Рождественские лекции для молодежи, которые ежегодно транслируются по национальному телевидению, серию, цель которой – представить науку широкой публике.Многие из этих лекций читал сам Фарадей. Оба они продолжаются по сей день.
Майкл Фарадей читал рождественскую лекцию в Королевском институте в 1856 г. / Источники: ВикипедияФарадей сделал свое первое открытие электромагнетизма в 1821 г. Он повторил эксперимент Эрстеда , поместив небольшой магнит вокруг токоведущего провода и убедившись, что сила, прилагаемая ток на магните был круговым. Как он объяснил много лет спустя, провод был окружен бесконечной серией круговых концентрических силовых линий , которые он назвал магнитным полем тока. Он взял за отправную точку работы Эрстеда и Ампера по магнитным свойствам электрических токов и в 1831 году получил электрический ток из изменяющегося магнитного поля, явление, известное как электромагнитная индукция . Он обнаружил, что, когда через катушку пропускают электрический ток, в соседней катушке генерируется еще один очень короткий ток. Это открытие ознаменовало решающую веху в прогрессе не только науки, но и общества , и сегодня оно используется для производства электроэнергии в больших масштабах на электростанциях.Это явление открывает кое-что новое об электрических и магнитных полях. В отличие от электростатических полей, создаваемых электрическими зарядами в состоянии покоя, циркуляция которых по замкнутому пути равна нулю (консервативное поле), циркуляция электрических полей, создаваемых магнитными полями, происходит по замкнутому пути, отличному от нуля. Эта циркуляция, которая соответствует индуцированной электродвижущей силе, равна скорости изменения магнитного потока, проходящего через поверхность, граница которой представляет собой проволочную петлю ( закон индукции Фарадея ).Фарадей изобрел первый электродвигатель, первый электрический трансформатор, первый электрический генератор и первую динамо-машину, поэтому Фарадея можно без всяких сомнений назвать отцом электротехники .
Фарадей отказался от теории жидкости для объяснения электричества и магнетизма и ввел концепции поля и силовых линий , отойдя от механистического объяснения природных явлений, таких как действия Ньютона на расстоянии. Введение Фарадеем концепции поля в физику, возможно, является его наиболее важным вкладом, и он был описан Эйнштейном как великое изменение в физике , потому что оно предоставило электричеству, магнетизму и оптике общую основу физических теорий.Однако силовые линии Фарадея не были приняты до тех пор, пока несколько лет спустя не появился Джеймс Клерк Максвелл.
Как отмечалось в начале этой статьи, другим и, возможно, менее известным эффектом, обнаруженным Фарадеем, было влияние магнитного поля на поляризованный свет, явление, известное как эффект Фарадея или магнитооптический эффект . Пытливый ум Фарадея не удовлетворился простым открытием взаимосвязи между электричеством и магнетизмом. Он также хотел определить, влияют ли магнитные поля на оптические явления. Он верил в единство всех сил природы, в особенности света, электричества и магнетизма. 13 сентября 1845 г. г. он обнаружил, что плоскость поляризации линейно поляризованного света поворачивается, когда этот свет проходит через материал, к которому приложено сильное магнитное поле в направлении распространения света. Фарадей написал в абзаце № 7504 своего документа Dairy :
.«Сегодня работал с магнитными силовыми линиями, проводя их через разные тела (прозрачные в разных направлениях) и в то же время пропуская через них поляризованный луч света (…) на поляризованном луче производился эффект, и, таким образом, магнитный доказано, что сила и свет связаны друг с другом ».
Это, безусловно, было первым четким указанием того, что магнитная сила и свет связаны друг с другом, а также показало, что свет связан с электричеством и магнетизмом. В связи с этим явлением Фарадей также писал в том же абзаце:
.«Этот факт, скорее всего, окажется чрезвычайно плодотворным и очень ценным при исследовании обоих условий естественной силы».
Он не ошибся. Этот эффект является одним из краеугольных камней электромагнитной теории света.
Вращение поляризации из-за эффекта Фарадея / Источники: адаптировано из ВикипедииВ выступлении королевского института в пятницу вечером, проведенном в апреле 1846 года , Фарадей предположил, что свет может быть некоторой формой возмущения, распространяющегося вдоль силовых линий . На самом деле именно в эту пятницу Чарльз Уитстон должен был выступить с докладом о своем хроноскопе. Однако в последнюю минуту Уитстона охватил приступ страха перед сценой, и Фарадей выступил с речью Уитстона.Так как он закончил раньше времени, он заполнил оставшиеся минуты, раскрывая свои мысли о природе света . Речь Фарадея была опубликована в том же году в журнале Philosophical Magazine под заголовком Мысли о лучевых вибрациях . Фарадей даже осмелился поставить под сомнение существование светоносного эфира – научная ересь того времени – который должен был быть средой для распространения света, как так элегантно Френель описал в своей волновой теории света.Он предположил, что свет может быть не результатом вибраций эфира, а вибрацией физических силовых линий. Фарадей попытался исключить эфир, но он сохранил вибрации. Почти извиняющимся тоном Фарадей заканчивает свой доклад, в котором говорится:
.«Я думаю, что вполне вероятно, что я сделал много ошибок на предыдущих страницах, потому что даже для меня мои идеи по этому поводу кажутся только тенью спекуляции ».
Однако эта идея Фарадея была воспринята со значительным скепсисом и отвергалась всеми до тех пор, пока в 1865 году не была опубликована статья Максвелла под названием Динамическая теория электромагнитного поля .В этой статье Максвелл не только описывает свою основополагающую электромагнитную теорию света – одну из вех, отмеченных в этом Международном году света 2015 – но также приписывает идеи, которые в конечном итоге легли в основу его теории, мыслям Фарадея о лучевых вибрациях . На странице 466 своей статьи со скромностью, всегда свойственной Максвеллу, он ссылается на статью Фарадея 1846 года следующим образом:
«Концепция распространения поперечных магнитных возмущений за исключением нормальных четко изложена профессором Фарадеем в его« Мыслях о лучевых колебаниях ».Электромагнитная теория света, предложенная им [Фарадеем], по сути та же, что и та, которую я начал развивать в этой статье, за исключением того, что в 1846 году не было данных для расчета скорости распространения ».
И на странице 461 своей статьи 1865 года Максвелл также упоминает о магнитооптическом эффекте, заявляя:
«Фарадей обнаружил, что когда плоско поляризованный луч пересекает прозрачную диамагнитную среду в направлении силовых линий магнитного поля, создаваемых соседними магнитами или токами, плоскость поляризации вращается».
Всего Майкл Фарадей цитируется шесть раз и трижды упоминается в статье Максвелла 1865 года. Однако это неудивительно, учитывая, что большая часть работ Максвелла основана на работах Фарадея, и Максвелл математически смоделировал большинство открытий Фарадея по электромагнетизму в теорию, которую мы знаем сегодня.
Электромагнитные волны, о существовании которых Фарадей размышлял в 1846 году в своих мыслях о лучевых колебаниях , и которые были математически предсказаны Максвеллом в 1865 году, наконец, были получены в лаборатории Герца в 1888 году.Остальное уже история. Ясно, что Максвелл открыл дверь в физику двадцатого века, но не менее ясно, что Фарадей дал Максвеллу некоторые из ключей, которые он использовал.
В 1676 году Ньютон послал своему сопернику Гуку письмо, в котором написал: «Если я видел дальше, то это было то, что он стоял на плечах гигантов» (*). Двести пятьдесят лет спустя, во время одного из визитов Эйнштейна в Кембридж, Великобритания, кто-то заметил: «Вы сделали великие дела, но стоите на плечах Ньютона». Эйнштейн ответил: «Нет, я стою на плечах Максвелла».Если бы кто-то сказал то же самое Максвеллу, он, вероятно, сказал бы, что он стоял на плечах Фарадея .
(*) Хотя это предложение интерпретируется некоторыми авторами как саркастическое замечание, направленное на горбатую внешность Гука, в настоящее время эта фраза обычно используется в положительном ключе. Комментарий Ньютона – это заявление о том, что наука представляет собой серию постепенных достижений, в основе которых лежат уже достигнутые ранее (см., Например, книгу Стивена Хокинга под названием На плечах гигантов ).
Аугусто БелендесПрофессор прикладной физики Университета Аликанте (Испания) и член Королевского физического общества Испании
Библиография
- A. Díaz-Hellín, Faraday: El gran cambio en la Física (Nívola. Madrid, 2001).
- Ордоньес, В. Наварро и Х. М. Санчес Рон, Historia de la ciencia (Espasa Calpe. Madrid, 2013).
- Форбс и Б. Махон, Фарадей, Максвелл и электромагнитное поле: как два человека революционизировали физику (Prometheus Books.Нью-Йорк, 2014).
- Зайонц, Улавливая свет: переплетенная история света и разума (Oxford University Press, Нью-Йорк, 1995).
- Хокинг, На плечах гигантов: великие труды по физике и астрономии (Running Press. Philadelphia, 2002)
- Мансурипур, Классическая оптика и ее приложения (Издательство Кембриджского университета. Кембридж, 2002)
Почему закон Фарадея и сила Лоренца создают одинаковую электродвижущую силу? – ScienceDaily
Формула индукции (правило потока) электромагнетизма Фарадея гласит, что электродвижущая сила (ЭДС), создаваемая в проводящей цепи, равна скорости, с которой изменяется магнитный поток через проводящую цепь, как это написано на высоком школьный текст по физике.Эту ЭДС можно рассчитать двумя способами: либо используя формулу силы Лоренца, либо вычисляя силу, действующую на электроны в движущемся проводнике цепи; или с помощью одного из уравнений Максвелла (закона Фарадея) и вычисления изменения магнитного потока, проникающего через цепь. Формула силы Лоренца и уравнения Максвелла – это два разных физических закона, но оба метода дают одинаковые результаты.
Почему два результата совпадают, неизвестно. Другими словами, правило потока состоит из двух физически различных законов в классических теориях.Интересно, что эта проблема была также мотивацией разработки теории относительности Альбертом Эйнштейном. В 1905 году Эйнштейн написал в первом абзаце своей первой статьи по теории относительности: «Известно, что электродинамика Максвелла – как обычно понимается в настоящее время – в применении к движущимся телам приводит к асимметриям, которые, по-видимому, не проявляются. присущие явлениям “. Но аргумент Эйнштейна отошел от этой проблемы и сформулировал специальную теорию относительности, поэтому проблема не была решена.
Ричард Фейнман однажды описал эту ситуацию в своей знаменитой лекции (The Feynman Lectures on Physics, Vol. II, 1964): «Мы не знаем другого места в физике, где такой простой и точный общий принцип требует для своего реального понимания анализа в термины двух разных явлений. Обычно оказывается, что такое красивое обобщение проистекает из единственного глубоко лежащего в основе принципа. ・ ・ ・ ・ ・ Мы должны понимать «правило» как комбинированные эффекты двух совершенно разных явлений ».
Доктор.Исследование Хироясу Коидзуми, недавно опубликованное в «Журнале сверхпроводимости и нового магнетизма», показало, что является «единым глубоким основополагающим принципом» в «правиле потока», предусмотренном Фейнманом. Это двойственность фазового фактора U (1), добавленного к волновой функции; он описывает поступательное движение электронов, а также дает зависящий от времени калибровочный потенциал, который индуцирует эффективное электрическое поле на электронах. Первая точка зрения соответствует результату, полученному по формуле силы Лоренца, а вторая – результату с использованием уравнения Максвелла для закона Фарадея.
За этим открытием стоят два больших достижения в физике 20 века. Один из них – рождение квантовой механики, а другой – установление физической реальности электромагнитного поля как калибровочного поля U (1). В приведенном выше исследовании электроны в проводнике описываются волновыми функциями квантовой механики, а магнитное поле выражается как калибровочное поле U (1). Калибровочное поле имеет произвол, называемый калибровочной степенью свободы. Этот произвол может быть применен к фазовому коэффициенту U (1) волновой функции и может быть зафиксирован требованием минимума энергии.Затем двойственность, заключающаяся в том, что фазовый фактор U (1) может быть добавлена к волновой функции, поскольку поступательное движение электронов позволяет проявиться «зависящему от времени калибровочному потенциалу». Такая же фиксация калибровки использовалась в исследовании д-ра Коидзуми по сверхпроводимости, где фиксация калибровки достигается требованием минимума энергии при ограничении, что волновая функция является однозначной функцией координат электрона.
Работа доктора Коидзуми также открывает новые перспективы в области сверхпроводимости и, возможно, теории струн.Поскольку сейчас наиболее многообещающими кубитами для квантовых компьютеров являются кубиты, использующие сверхпроводники, ожидается, что настоящее открытие внесет вклад в разработку квантовых компьютеров, которые могут вытеснить классические компьютеры.
История Источник:
Материалы предоставлены Университетом Цукуба . Примечание. Содержимое можно редактировать по стилю и длине.
Поляризация: ключевое различие между антропогенными и естественными электромагнитными полями в отношении биологической активности
Все критические биомолекулы либо электрически заряжены, либо полярны 11 .В то время как естественные неполяризованные ЭДС / ЭМИ любой интенсивности не могут вызвать какие-либо специфические / когерентные колебания на этих молекулах, поляризованные искусственные ЭМП / ЭМИ будут вызывать когерентные вынужденные колебания на каждой заряженной / полярной молекуле в биологической ткани. Это фундаментально для нашего понимания биологических явлений. Эти колебания будут наиболее очевидны для свободных (подвижных) ионов, которые несут чистый электрический заряд и существуют в больших концентрациях во всех типах клеток или внеклеточной ткани, определяя практически все клеточные / биологические функции 11 .Хотя все молекулы колеблются случайным образом с гораздо более высокими скоростями из-за теплового движения, это не имеет никакого биологического эффекта, кроме повышения температуры ткани. Но когерентные поляризованные колебания даже с энергией в миллионы раз меньшей, чем средняя тепловая молекулярная энергия 26 , могут вызвать биологические эффекты.
Вынужденные колебания подвижных ионов, вызванные внешней поляризованной ЭДС, могут приводить к нерегулярному закрытию каналов электроприводных ионов на клеточных мембранах.Это подробно описано в Panagopoulos et al . 19,20 . Согласно этой теории – правдоподобие которой в реальных биологических условиях было подтверждено численным тестом 27 – вынужденные колебания ионов вблизи датчиков напряжения управляемых по напряжению ионных каналов могут оказывать на эти датчики силы, равные или больше, чем известные физиологически силы, закрывающие эти каналы. Нерегулярное закрытие этих каналов может потенциально нарушить электрохимический баланс и функцию любой клетки 11 , что приведет к множеству биологических / медицинских последствий, включая самые пагубные, такие как повреждение ДНК, гибель клеток или рак 28 .
Большинство катионных каналов (Ca +2 , K + , Na + и т. Д.) На мембранах всех клеток животных имеют потенциал-стробирование 11 . Они взаимно преобразуются между открытым и закрытым состояниями, когда электростатическая сила, действующая на электрические заряды их датчиков напряжения из-за изменений трансмембранного напряжения, превышает некоторое критическое значение. Датчики напряжения этих каналов представляют собой четыре симметрично расположенных трансмембранных положительно заряженных спиральных домена, каждый из которых обозначен как S4.Изменения трансмембранного потенциала порядка 30 мВ обычно требуются для затвора электропроводных каналов 29,30 . Несколько ионов могут одновременно взаимодействовать с доменом S4 на расстоянии порядка 1 нм, поскольку – за исключением одного иона, который может проходить через поры канала, когда канал открыт – еще несколько ионов связаны близко к поры канала в определенных сайтах связывания иона (например, три в калиевых каналах) 31 . Подробную информацию о структуре и функции катионных электросенсорных каналов можно найти в 11,29,31 .
Рассмотрим, например, четыре иона калия на расстоянии порядка 1 нм от каналов-датчиков (S4) и приложенная извне осциллирующая ЭДС / ЭМИ. Электрическая (и магнитная) сила, действующая на каждый ион из-за любого неполяризованного поля, равна нулю (уравнение 8). Напротив, сила, обусловленная поляризованным полем с электрическим компонентом E , составляет F = Ezq e . Для синусоидального переменного поля Ε = Ε 0 sin ωt уравнение движения свободного иона с массой m i , составляет 19,20 :
, где r – ион смещения из-за вынужденных колебаний, z – валентность иона ( z = 1 для ионов калия), q e = 1.6 × 10 −19 C – элементарный заряд, λ – коэффициент затухания для смещения иона (рассчитанный, чтобы иметь значение внутри канала), ω 0 = 2πν 0 (ν 0 – собственное колебание иона). частота принята равной зарегистрированной частоте спонтанных внутриклеточных колебаний иона порядка 0,1 Гц), ω = 2πν (ν частота поля / излучения) и E 0 амплитуда поля 19,20 .
Общее решение уравнения.22, это 19,20 :
Член в решении представляет постоянное смещение, но не влияет на колеблющийся член. Это постоянное смещение удваивает амплитуду вынужденных колебаний в тот момент, когда поле прикладывается или прерывается, или в течение его первого и последнего периодов, и смещение иона будет в два раза больше амплитуды вынужденных колебаний. Для импульсных полей (таких как большинство областей современной цифровой связи) это будет происходить постоянно с каждым повторяющимся импульсом.Таким образом, импульсные поля – теоретически – вдвое более сильные, чем непрерывные / непрерывные поля с теми же другими параметрами, что согласуется с несколькими экспериментальными данными 1,32 .
Амплитуда вынужденных колебаний (без учета постоянного члена в уравнении 23) составляет:
Сила, действующая на эффективный заряд q домена S4 через колеблющийся одновалентный свободный катион, составляет: , ( r – расстояние свободного иона от эффективного заряда S4).Каждый колеблющийся катион, смещенный на dr , вызывает силу на каждый датчик S4:
В то время как в случае неполяризованного приложенного поля и, в случае поляризованного приложенного поля, суммарная сила на датчик канала от всех четыре катиона:
Это даже более важное различие между поляризованными и неполяризованными ЭМП в отношении биологической активности, чем способность интерференции.
Эффективная плата за каждый домен S4 составляет: q = 1.7 q e 30 . Минимальная сила, действующая на этот заряд, обычно необходимая для закрытия канала, равная силе, создаваемой изменением на 30 мВ мембранного потенциала 30 , вычисляется 19 и составляет:
Смещение одного одновалентного катиона внутри канала, необходимое для приложения этой минимальной силы рассчитывается по формуле. 25 должно быть:
Для 4 катионов, колеблющихся в фазе и в параллельных плоскостях из-за внешнего поляризованного поля / излучения, минимальное смещение уменьшается до: dr = 10 −12 м.
Следовательно, любая внешняя поляризованная осциллирующая ЭДС, способная заставить свободные ионы колебаться с амплитудой, способна нерегулярно закрывать катионные каналы на клеточных мембранах. Для z = 1 (ионы калия) и подставляя значения для q e , λ в последнем условии, получаем:
(ν в Гц, 0 в В / м)
Для двухвалентных катионов ( z = 2) (например, Ca +2 ) условие принимает следующий вид:
(ν в Гц, Ε 0 в В / м)
[Подробное описание Кратко представленный механизм можно найти в 19,20 .]
Для электрических полей (ν = 50 Гц) Условие 27 становится,
Таким образом, ЭДС промышленной частоты с интенсивностью, превышающей 5 мВ / м, потенциально способны нарушить функцию клетки. Для количества источников ЭМП N одинаковой поляризации (например, N количество параллельных линий электропередачи) последнее значение делится на N (согласно уравнению 19) в местах конструктивных помех и, следовательно, даже больше. уменьшилось. Такие минимальные значения напряженности поля промышленной частоты распространены в повседневной городской среде и даже ближе к высоковольтным линиям электропередачи 7 .
Для импульсных полей вторая часть условия 27 делится на 2 и становится:
(ν в Гц, Ε 0 в В / м).
Для полей / излучения цифровой мобильной телефонной связи, излучающих КНЧ-импульсы с частотой повторения импульсов ν = 217 Гц (среди других частот КНЧ они передают) 33 , Условие 29 становится:
Для частоты повторения импульсов ν = 8,34 Гц ( также включается в сигналы мобильной телефонии) 33,34 , Условие 29 становится:
Как видно из описанного механизма, поле не закрывает канал силами, действующими непосредственно на датчики канала.Для этого потребуется поле порядка трансмембранного поля (10 6 –10 7 В / м). Именно посредничество колеблющихся свободных ионов в непосредственной близости от датчиков канала S4 позволяет таким слабым полям создавать необходимые силы для закрытия канала.
Таким образом, электрические поля СНЧ, излучаемые мобильными телефонами и базовыми станциями сильнее 0,0004 В / м, также потенциально способны нарушить работу любой живой клетки. Это значение интенсивности ELF излучается обычными сотовыми телефонами на расстоянии до нескольких метров и базовыми станциями на расстоянии до нескольких сотен метров 6,34,35 .Для числа вертикально ориентированных антенн мобильной телефонной связи N последнее значение делится на N (согласно уравнению 19) в местах возникновения конструктивных помех.
Мы не делаем различий между ЭМП, прикладываемой извне, и ЭМП, индуцированной внутри живой ткани, особенно в случае СНЧ по следующим причинам: 1. Живая ткань не является металлом для защиты от электрических полей и, конечно же, не является ферромагнитным металлом (Fe, Co, Ni) для защиты от магнитных полей.Более того, известно, что особенно поля КНЧ не могут быть легко экранированы даже клетками Фарадея, и для того, чтобы значительно их минимизировать, рекомендуется полностью заключать их в закрытые металлические коробки 6 . Таким образом, электрические поля СНЧ проникают в живую ткань с определенной степенью затухания, а магнитные поля проникают с нулевым затуханием. 2. Даже в том случае, если поля СНЧ значительно ослаблены во внутренних тканях живого тела, глаза, мозг, клетки кожи или мириады окончаний нервных волокон, которые оказываются на внешнем эпидермисе, подвергаются прямому воздействию интенсивности поля, измеренные снаружи на поверхности живой ткани.
Было показано, что тканевые препараты (такие как фибробласты крупного рогатого скота или куриные сухожилия) реагируют на приложенные извне импульсные или синусоидальные электрические поля СНЧ (изменениями в скорости синтеза ДНК или белка, скорости пролиферации, выравнивании по направлению поля и т. Д. ), при очень низких порогах ~ 10 −3 В / м 1,36,37,38 . Эти пороговые значения очень близки к прогнозируемым в настоящем исследовании.
За исключением прямого воздействия электрического поля внешним полем, внутри тканей может быть электрическое поле, индуцированное приложенным извне осциллирующим магнитным полем, которое, как объяснялось, проникает в живую ткань с нулевым затуханием.Туор и др. . 34 измерили магнитные поля СНЧ от сотовых телефонов порядка 1 Гс (= 10 −4 Тл) при 217 Гц. Это может индуцировать электрические поля порядка ~ 0,1 В / м в человеческом теле, что можно показать, применяя закон электромагнитной индукции Максвелла:
(,, напряженности магнитного и индуцированного электрического поля соответственно, приращение длины по замкнутому пути l циркуляции индуцированного электрического поля, охватывающего поверхность S.- единичный вектор, вертикальный к поверхности S ).
Допустим, параллельна и независима от l , вертикальна и не зависит от S и l круговой путь с радиусом α, включая поверхность S , уравнение. 32 становится:
, что дает:
( E ind в В / м, B в T, α в м).
Заменяя в последнем уравнении α = 0,20 м (достаточно большой радиус для окружности тела взрослого человека) и [согласно Туору и др. . 34 ], получаем E ind ~ 0,1 В / м. Это напряженность электрического поля, наведенного внутри человеческого тела импульсами мобильной телефонной связи с частотой 217 Гц, и она примерно в десять раз больше минимального расчетного значения, способного вызвать биологические эффекты на этой частоте в соответствии с Условием 30.
Физическая модель для низкочастотная электромагнитная индукция в ближнем поле на основе прямого взаимодействия электронов передатчика и приемника
Proc Math Phys Eng Sci.2016 июл; 472 (2191): 20160338.
Рэй Т. Смит
1 Факультет электротехники и электроники Ливерпульского университета, Ливерпуль L69 3GJ, Великобритания
Фред П.М. Чжунджу
1 Факультет электротехники и электроники , Ливерпульский университет, Ливерпуль L69 3GJ, Великобритания
Иэн С. Янг
2 Институт интегративной биологии Ливерпульского университета, Ливерпуль L69 3BX, Великобритания
Стивен Тейлор
1 Департамент электротехники и электроники , Ливерпульский университет, Ливерпуль L69 3GJ, Великобритания
Саймон Махер
1 Факультет электротехники и электроники Ливерпульского университета, Ливерпуль L69 3GJ, Великобритания
1 Факультет электротехники и электроники Ливерпульского университета , Ливерпуль L69 3GJ, Великобритания
2 Институт интегративной биологии Ливерпульского университета, Liverpool L69 3BX, UK
Получено 13 мая 2016 г .; Принята в печать 21 июня 2016 г.
Опубликовано Королевским обществом в соответствии с условиями лицензии Creative Commons Attribution License http://creativecommons.org/licenses/by/4.0/, которая разрешает неограниченное использование при условии указания автора и источника. другие статьи в PMC.Abstract
Разработана физическая модель электромагнитной индукции, которая напрямую связывает силы между электронами в передающей и приемной обмотках концентрических коаксиальных конечных катушек в ближней зоне.Применяя принцип суперпозиции, вклады ускоряющихся электронов в последовательных токовых петлях суммируются, что позволяет точно предсказать пиковое индуцированное напряжение в приемнике. Результаты показывают хорошее согласие между теорией и экспериментом для различных приемников с разным радиусом, до пяти раз превышающим радиус передатчика. Обсуждаются ограничения линейной теории электромагнитной индукции с точки зрения неравномерного распределения тока, вызванного скин-эффектом.В частности, объяснение в терминах электромагнитной энергии и теоремы Пойнтинга противопоставляется более прямому объяснению, основанному на переменной индукции нити в поперечном сечении проводника. Поскольку разработанная здесь прямая физическая модель имеет дело только с силами между дискретными токовыми элементами, ее можно легко адаптировать к различным геометриям катушек и широко применять в различных областях исследований, таких как связь ближнего поля, конструкция антенны, беспроводная передача энергии, датчик приложений и не только.
Ключевые слова: катушки, электромагнитная индукция, распространение, беспроводная передача энергии, соленоиды, трансформаторы
1. Введение
Электромагнитные (ЭМ) взаимодействия ближнего поля используются в различных областях применения, таких как связь с магнитной индукцией (МИ) [ 1], MI томография [2,3] и беспроводная передача энергии [4]. Они все чаще используются в беспроводных подземных сенсорных сетях [5,6] для таких приложений, как мониторинг окружающей среды (в почве [7] и воде [8]), обследование оползней [9] и наблюдение за подземными трубопроводами [10].Традиционные подходы к беспроводным датчикам тормозятся сложными встречающимися средами распространения (например, почвой, камнями, водой). Однако при использовании ближнего поля и низкочастотных магнитных полей трудности, связанные с задержкой распространения, замиранием и многолучевым распространением, становятся менее заметными. Термин ближнее поле относится к безызлучательному распространению на короткие расстояния магнитных или электрических полей из-за индуктивной или емкостной связи соответственно. Напротив, дальнее поле относится к радиационным электромагнитным полям на больших расстояниях от источника, которые получили широкое освещение [11–14].
Было проведено несколько ценных исследовательских инициатив по моделированию электромагнитных полей в ближней зоне, которые обычно включают точные представления и / или вычислительно-интенсивные процедуры [15–23], которые, согласно Mikki & Antar [24], «не могут привести к значительным результатам. понимание общих вопросов, таких как природа электромагнитного излучения или внутренняя структура антенны в ближнем поле ». Тем не менее, моделирование магнитного поля в ближней зоне является важной задачей, например, при проектировании сложных схем для определения соответствия стандартам ЭМС [25].
В этой статье мы разрабатываем метод для случая многооборотной пары катушек конечного передатчика и приемника круговой геометрии, расположенных концентрически. Основой этого метода, адаптированного для расчета наведенной ЭДС в приемнике на некотором расстоянии от источника, является формула силы Вебера, которую можно рассматривать как модификацию закона Кулона для зарядов при относительном движении [26–32]. . Эта сила напрямую связана с силой между движущимися зарядами с точки зрения их смещения, относительной радиальной скорости и относительного радиального ускорения в дискретной системе.
Определение границ ближней зоны является неоднозначной задачей, поскольку зависит от геометрии и возбуждения рассматриваемого передатчика. Микки и Антар справедливо подчеркивают в своем подробном и всестороннем обзоре теории антенн в ближнем поле “ необходимость постоянного, всестороннего и строгого подхода к теме ближнего поля, подхода, учитывающего особую природу поля зрения ”. электромагнитное поведение в этой зоне [24] ». Принято считать, что «ближнее поле» включает, по крайней мере, окружающее пространство на расстоянии до одной длины волны и может распространяться дальше.Мы также представляем предварительные результаты того, как наведенное напряжение изменяется как с расстоянием, так и с частотой, на основе взаимодействий между частицами в этой зоне.
Во-первых, мы исследуем теоретические основы низкочастотной электромагнитной индукции. При этом мы разрабатываем модель прямого действия, которая напрямую связана с распределением тока в конечных катушках передатчика и приемника. Модель подтверждается экспериментальными измерениями путем расчета отклика приемника на увеличивающихся расстояниях от источника.Наконец, мы обсуждаем преимущества и ограничения модели и даем предложения по дальнейшим исследованиям.
2. Теория
Рассматриваемый случай электромагнитной индукции иногда называют индукцией трансформатора. Устройство состоит из коаксиальных катушек, расположенных концентрично с передатчиком (T), заданным внутренней катушкой, и приемником (R), заданным внешней, как показано на.
Конфигурация коаксиальных конечных катушек с воздушным сердечником. Передатчик (T) длины L T , радиус r T с N T близко намотанных витков расположен внутри приемника (R) длины L R , радиус, r R и N R закрученных витков.(Онлайн-версия в цвете.)
(a) Закон индукции Фарадея
Закон Фарадея связывает наведенную ЭДС, e , в замкнутой цепи со скоростью изменения магнитного потока в этой цепи. Обычно это дается
где ∅ – магнитный поток (уравнение (2.1) действительно только для провода бесконечно малого сечения). Для компоновки на катушку передатчика подается переменный ток, I = I 0 sin ω t , где I 0 – пиковый ток, а ω – это пиковый ток. радиальная частота равна, ω = 2 πf .Магнитный поток через приемник следует за током, так что = 0 sin 2 πft , а наведенная ЭДС в приемнике определяется выражением
eR = −d∅dt = −∅02πf cos (2πft).
2,2
Для случая бесконечной многовитковой катушки плотность магнитного потока в центральной области определяется как B = μ 0 nI 0 , где μ 0 – проницаемость свободного пространства, а n – плотность намотки (= N / L ).Пиковый магнитный поток на виток, соединяющий передатчик и приемник, определяется как произведение плотности потока и площади поперечного сечения одного витка ( Bπr 2 T ). Предполагая, что приемник намотан близко к передатчику, так что r R – r T ≅0, тогда пиковая ЭДС, индуцированная в приемнике, определяется выражением
(eR) 0 = −2π2rT2nTNRI0fε0c2,
2.3
, где ε 0 = диэлектрическая проницаемость свободного пространства, c = скорость света и n T – плотность поворота передатчика.
(b) Формула взаимной индуктивности Неймана
Более общий метод расчета наведенной ЭДС между замкнутыми цепями может быть получен из формулы Неймана. Предполагая, что плотность магнитного потока пропорциональна току (закон Био – Савара) и выражая поток через векторный потенциал ( A ), тогда для замкнутых контуров T и R с элементами d l T , d l R на расстоянии r друг от друга
∅ R = ∮ A T ⋅ d l R ,
где
Так что
∅R = μ0IT4π∮∮dlTr⋅dlR
Потому что ∅ R = M RT I T , где M RT = M TR , что является взаимным индуктивности двух контуров, то формула Неймана имеет вид
MRT = μ04π∮∮1rdlT⋅dlR.
2,4
Взаимная индуктивность между двумя замкнутыми контурами – это геометрическая величина, относящаяся к размеру, форме и относительному положению двух контуров, и не зависит от того, какая цепь действует как передатчик или приемник. Переписав закон Фарадея с учетом взаимной индуктивности ( M ), переменного тока передатчика I и соответствующего изменяющегося магнитного потока, наведенная ЭДС в приемнике определяется выражением
Предположим, как и раньше, что приемник намотан близко к передатчику, так что r R – r T ≅0.Затем, отмечая, что M = μ 0 πr 2 T ( N T / l T ) и I = I 0 sin ω t , с числом витков приемника, действующим как множитель, пиковая ЭДС в приемнике определяется как
(eR) 0 = −2π2rT2nTNRI0fε0c2
, что совпадает с (2.3).
(c) Решение Гровера, когда
r T ≠ r RКонкретное решение для концентрических коаксиальных катушек разного радиуса дается в ссылке [33]:
М = 0.004π2rT2nTNR (B1r1 − B2r2),
, где r1 = rR2 + (1/4) (lT + lR) 2 и r2 = rR2 + (1/4) (lT − lR) 2
Функции B 1 и B 2 зависит от параметров, p12 = rR2 / r12, p22 = rR2 / r22, α = r T / r R и может быть получено из таблиц в [33 ]. Например, используя конкретные данные катушки в настоящем эксперименте, значения для M были рассчитаны как 9,22 мГн ( r T / r R = 1) и 8.66 мГн ( r T / r R = 0,78), что дает увеличение примерно на 6%, если предполагается, что приемник тесно намотан.
(d) Векторный потенциал
Векторный потенциал вне длинного соленоида получается как: A = / 2 πr , где ∅ – полный магнитный поток внутри катушки передатчика. Электрическое поле вне передатчика тогда составляет E = −∂ A / ∂ t = – (1/2 πr ) (d∅ / dt ).Приравнивая ∅ = LI = μ 0 nIπr 2 T , где L – индуктивность на единицу длины бесконечной многооборотной катушки, а n – количество витков на единичной длины, то для одиночного контура радиуса r R , охватывающего передатчик
E = −½ ( μ 0 n r T 2 π f ) I 0 cos ω t .
Интегрирование по одному контуру и включение коэффициента умножения для учета Н R оборотов приемника
(eR) 0 = ∮E.dl = 2πrTE = −2π2rT2nTNRI0fε0c2
, что, опять же, является (2.3).
3. Подход прямого действия
Рассмотрим два одинарных кольцевых контура передатчика (T) и приемника (R). Контур передатчика имеет радиус r T и возбуждается переменным током заданной частоты f , тогда как окружающий контур приемника имеет радиус r R , на котором индуцируется ЭДС ( r R > r T ), как показано на.
Геометрия одиночных кольцевых петель, составляющих часть катушек передатчика и приемника. На вставке показана геометрия, спроецированная на двумерную плоскость ( x – y ).
Используя декартову систему координат, мы определяем центр контура приемника как начало координат. При применении закона силы Вебера к этому случаю сила определяется между линейным элементом заряда (= r T δθ ) в передатчике, расположенном в точке M , и единичным зарядом, расположенным в приемнике в точке N , где расстояние между этими точками задается как MN = r .- единичный вектор вдоль r , u r – относительная скорость вдоль r и u – относительная скорость между M и N . В этом случае, когда в приемнике нет чистого тока, относительная скорость между M и N задается скоростью дрейфа электронов, v , при M в контуре передатчика. Следовательно, в (3.1) u 2 = v 2 .Относительная скорость вдоль r задается как u r = d r / d t = v cos β = v b sin θ / р . Оба члена u 2 и ur2, которые появляются в (3.1), включают члены v 2 , которые можно игнорировать для малых токов, оставляя только член ускорения, r (d 2 r / d t ) = r (d u r / d t ) и r определяется тригонометрическим методом, r2 = rT2 + rR2−2rTrR cosθ + z2.Различая u r и отмечая, что v = r T (d θ / d t ), игнорируя термины v 2 , получаем r d u r / d t = r R sin θ (d v / d t ). Поскольку I = n ′ Ave , тогда v˙ = I˙ / n′Ae и, следовательно,
Fr = rTrR sinθ4πε0c2r2I˙.
3,2
Разрешение по касательной к приемной петле дает силу на единицу заряда как, E T = F r cos γ , где cos γ = – r T sin θ / r и, следовательно,
ET = −rT2rRI˙4πε0c2sin2θr3δθ.
3,3
Индуцированная ЭДС в приемнике задается интегрированием по замкнутому контуру, так что
er = ∮E.dl = 2πrRET = −2πrT2rR2I˙4πε0c2sin2θr3δθ.
3,4
Путем дифференцирования тока передатчика мы получаем индуцированную пиком ЭДС в одном контуре приемника как
(eR) 0 = πrT2rR2I0ε0c2f∫02πsin2θr3dθ.
3,5
Чтобы вычислить наведенную ЭДС в конечной многооборотной катушке, принцип суперпозиции применяется к токовым вкладам от каждого отдельного витка катушки. Подынтегральное выражение из (3.5) вычисляется для диапазона значений z от каждого поворота. Значения z относятся к вертикальному расстоянию между витками, выраженному в диаметре проволоки, d .Затем с помощью стандартного численного интегрирования (правило трапеции с интервалами 5 ° ) дает
(eR) 0 = 2 × πrT2rR2I0fε0c2∑e (−314d) ⋯ e (335d) ⋮ ⋱ ⋮ e (−333d) ⋯ e (316d),
3,6
где r2 = rT2 + rR2−2rTrRcos + z2. Коэффициент 2 учитывает вклады от обоих слоев передатчика (т. Е. Катушка передатчика имеет двойную намотку). Матрица имеет 20 ( N R ) строк по 650 ( N T /2) столбцов, представляющих все вклады отдельных поворотов, где значение z равно нулю для случая, когда отдельные витки катушки передатчика и приемника совмещены напрямую.Суммирование в (3.6) производится для всех отдельных членов матрицы. Например, суммирование первой строки матрицы дает индуцированное напряжение в первом витке приемника от всех 650 отдельных витков передатчика (см. Приложение A).
4. Экспериментальная
Чтобы проверить вышеупомянутый подход, были проведены следующие экспериментальные измерения. Экспериментальная установка состоит из конечной коаксиальной внутренней катушки передатчика и внешней катушки приемника, как показано на.Катушка передатчика (внутренняя) длиной L T = 0,5 м состоит из 1300 витков, двояко намотанных одножильным эмалированным медным проводом диаметром 0,7 мм и плотностью обмотки = 2600 витков на метр на каркасе из радиус, r T примерно 0,0292 м. Были использованы три приемные катушки, каждая с одинаковой плотностью витков и числом витков ( N R = 20), но с разными радиусами: r R 0,0375, 0,075 и 0.15 мес.
Катушка передатчика была подключена к генератору цифровых сигналов (Lascells, Великобритания), обеспечивающему синусоидальный ток передатчика 3 мА (среднеквадратичное значение), измеренный 5,5-разрядным мультиметром Keithley в диапазоне частот 0–14 кГц. Напряжение, индуцированное приемником, одновременно измерялось цифровым осциллографом (Tektronix, США). Принципиальная электрическая схема показана на рис. Для улучшения отношения сигнал / шум приемная катушка была экранирована от внешних помех по окружности с помощью мю-металлического экрана (полностью термообработанный, 0.Толщиной 35 мм, ASTM A753 Alloy 4, Магнитные экраны, Великобритания). Все расчеты выполнены с использованием Matlab 2014a (MathWorks, США).
Принципиальная схема экспериментальной установки для измерения наведенной ЭДС в приемной катушке.
5. Результаты
Результаты экспериментов сведены в -. показывает наведенную ЭДС приемника (размах) в зависимости от частоты для двух различных радиусов приемной катушки 3,75 и 15 см. Меньшая катушка приемника находится менее чем примерно в 1 см от внешней поверхности катушки передатчика, тогда как большая катушка приемника находится примерно в 12 см от катушки передатчика с диаметром примерно в пять раз больше, чем катушка передатчика.Обе катушки следуют одной и той же тенденции с наведенной ЭДС, большей для катушки с меньшим радиусом (то есть ближе к передатчику), чем для большей для каждого измерения. Первоначально тенденция зависимости наведенной ЭДС от частоты следует линейному отклику. Это ясно видно в том, что также включает смоделированные данные, рассчитанные с использованием (3.6) с эквивалентными параметрами модели. В, рассчитанная модельная тенденция в зависимости от радиусов приемника сравнивается с результатами измерений для трех различных экспериментальных радиусов катушки приемника ( r R = 0.0375, 0,075, 0,15 м) на разных частотах.
Отклик на индуцированную ЭДС ( pk – pk , мВ) в зависимости от частоты для радиусов приемника 3,75 и 15 см. (Онлайн-версия в цвете.)
Отклик на индуцированную ЭДС ( pk – pk , мВ) в зависимости от частоты в диапазоне 1–8 кГц по сравнению с расчетными данными для радиусов приемника 3,75 и 15 см. (Онлайн-версия в цвете.)
Расчетный отклик наведенной ЭДС ( pk – pk , мВ) в зависимости от радиуса приемника для диапазона частот, дополненный измерениями для радиусов приемника 3.75, 7 и 15 см для f ≤5 кГц. (Онлайн-версия в цвете.)
6. Обсуждение
Преимущество формулировки, основанной на Вебере, состоит в том, что она может легко приспособиться к различным радиусам приемника и передатчика. Сравнение между экспериментом и теорией показано там, где смоделированные данные находятся в пределах экспериментальной ошибки, в линейном режиме ( f < около ,5 кГц). Согласно модели, ЭДС уменьшается с увеличением радиуса приемника из-за уменьшения межэлектронных сил, поскольку связь между катушками уменьшается с расстоянием.
Нелинейность, связанная с наведенной ЭДС на более высоких частотах, очевидна в. Примерно выше 5 кГц характеристика отклоняется от линейного поведения. Из (3.5) видно, что модель прямого действия линейно зависит от частоты, как в случае с законом Фарадея, приведенным в (2.3). Согласно закону Фарадея, наведенная ЭДС зависит от скорости изменения тока, отсюда линейная зависимость от f . Аналогично, для подхода прямого действия относительные ускорения электронов также линейно зависят от частоты.Насколько известно авторам, не существует какой-либо удовлетворительной теории, которая могла бы иметь дело со случаем электромагнитной индукции переменной частоты. Фейнман [34] обсуждает попытки модифицировать уравнения Максвелла, все из которых сталкиваются с трудностями, связанными с предположением о точечных зарядах, самовоздействием заряда на себя (реакция излучения) и ролью, которую играет масса ЭМ в отличие от механической массы.
Для модели прямого действия предполагается, что ток равномерно распределен по поперечному сечению провода и что принцип суперпозиции применяется к последовательным участкам катушки.С увеличением частоты любая линейная индукционная модель будет разрушаться, поскольку распределение тока станет неравномерным, что приведет к хорошо известным скин-эффектам и эффектам близости. Явление, получившее название скин-эффекта, было обнаружено Максвеллом, который выдвинул гипотезу о неравномерном распределении тока [35]. Высокочастотное сопротивление может быть задано как сопротивление постоянному току эквивалентной «кожи» с определенной глубиной проникновения. Эффект близости относится к токовым помехам между отдельными соседними контурами, потому что геометрическая форма поля не постоянна, а изменяется с частотой.Это представляет собой серьезную проблему для любой модели электромагнитной индукции. Однако подход прямого действия имеет существенное преимущество, заключающееся в том, что он может учитывать условия ускорения более высокого порядка. На более высоких частотах теория может быть адаптирована для моделирования тонких трубок тока, а не делать предположение об однородной плотности тока.
Были разработаны различные концепции и решения для определения скин-эффекта для ряда состояний [36–42]. Более прямое и физическое объяснение скин-эффекта заключается в большей индуктивности (электронной инерции) нитей вблизи центра проводника по сравнению с нитями на поверхности.То есть реверсирование тока в центральных нитях вызывает более высокое сопротивление / реактивное сопротивление по сравнению с нитями на поверхности. Следовательно, по мере увеличения частоты ток становится более ограниченным до внешних областей проводника. Возможная физическая основа скин-эффекта была предложена в терминах электромагнитной массы ( M e ). Калвик [43] предположил, что эффективный заряд электронов проводимости не является зарядом всех имеющихся электронов проводимости и что ток переносится небольшим количеством электронов, движущихся с высокой скоростью.Следуя этим рассуждениям, индуктивность можно рассматривать как аналог электромагнитной массы. Гровер [33], напротив, описывает скин-эффект следующим образом: «Электромагнитная энергия проникает на поверхность провода и по мере приближения к центру все более и более ослабляется и замедляется по фазе. На очень высоких частотах затухание настолько велико, что амплитуда тока становится незаметной после того, как волна проникает в провод всего на долю миллиметра. По сути, это объяснение, основанное на теореме Пойнтинга, согласно которой энергия, подводимая к проводнику, по которому проходит ток, проходит не через провод, а через окружающее электромагнитное поле [44].
Поскольку в настоящее время не существует удовлетворительной общей нелинейной теории электромагнитной индукции, полезно подогнать данные наведенной частоты ЭДС с помощью некоторой формы эмпирического закона. Существует линейное изменение примерно до 5 кГц в соответствии с законом Вебера. Выше приблизительно 5 кГц, когда скин-эффект становится все более значительным, задействуются частотные члены более высокого порядка. Используя инструмент подбора кривой Matlab, следующие выражения получены для значений выше 5 кГц (),
( e R ) p k – p k ⟨ r R = 0.0375⟩ = 2,3 f 2 – 22,4 f + 127,5
6,1
и
( e R ) p k – p k ⟨ r R = 0,15 = 2,2 f 2 – 23,1 f + 124 ,
6.2
, где наведенная ЭДС – размах напряжения в мВ, а частота – в кГц. Квадратичный ответ получается с коэффициентом детерминации ( R 2 ), рассчитанным как 0.9983 и 0,9986 для уравнений (6.1) и (6.2) соответственно. Такие эмпирические соответствия для данной геометрии могут оказаться полезными в качестве основы для сравнения взаимной индуктивности в диапазоне частот.
Наконец, стоит прокомментировать, почему любая нелинейная теория индукции оказывается сложной. Электрон проводимости, на который действует переменная сила, приводится в принудительную вибрацию, в которой он подвергается как восстанавливающим, так и демпфирующим силам. По мере того, как частота воздействия увеличивается и поток электронов ограничивается внешними областями проводника, тот же самый ток через уменьшенную площадь вызовет повышенную скорость дрейфа электронов и, следовательно, увеличенную амплитуду колебаний.Затем это приводит к возникновению нелинейной восстанавливающей силы (т.е. не слишком отличной от пружины, которая может стать «жестче» или «мягче» в механической системе). Следствием этого является то, что гармоническое движение при малых амплитудах может стать гармоническим при больших амплитудах и, таким образом, привести к появлению частотных членов более высокого порядка, которые затем требуются для описания изменения напряжения вторичной катушки.
7. Выводы
Для изученной схемы коаксиальной катушки подход прямого действия показывает хорошее согласие с экспериментальными измерениями для прогнозирования наведенной ЭДС в катушке приемника на различных расстояниях от передатчика в ближнем поле (до пяти диаметров катушка передатчика).Модель представляет интерес помимо рассмотренной здесь компоновки, так как ее вполне можно адаптировать для других геометрий катушки. Модель учитывает радиус каждой катушки, приложенную частоту, амплитуду тока возбуждения и вклады от отдельных витков катушки, как указано в (3.6).
Показано, что линейность между наведенной ЭДС и частотой сохраняется до частот приблизительно 5 кГц. Выше этого, постепенное ограничение тока внешними областями проводника (скин-эффект) приводит к нелинейной зависимости наведенного напряжения от частоты.Было обнаружено, что данные соответствуют квадратичной зависимости от частоты, как указано в (6.1) и (6.2). Что касается скин-эффекта, стандартное объяснение, основанное на центрах поля, заключает, что в соответствии с теоремой Пойнтинга он включает боковой поток электромагнитной энергии в проводник. Модель, разработанная в этом исследовании, предполагает, что альтернативное объяснение связано с изменением инерции / индуктивности электронов в проводнике. В последнее время возобновился интерес к гидродинамическим аналогиям электронного потока в конкретных материалах, и появились некоторые свидетельства того, что электронная вязкость играет важную роль в определении электрического сопротивления [45].В связи с этим интересно отметить, что существует также гидродинамическая аналогия электрической глубины скин-слоя, связанная с акустическим течением в заполненной воздухом трубке, в которой низкочастотный пульсирующий поток накладывается на существующий установившийся поток [46]. Показано, что скорость частицы достигает максимального значения на расстоянии от стенки трубы, определяемом как dw≈υ / πf, где υ – кинематическая вязкость. Это контрастирует с глубиной электрического скин-слоя, δ = 1 / πfμ0σ. Поскольку μ 0 постоянно и ρ = 1/ σ , то δ≈ρ / πf, следовательно, обеспечивает аналогию с электронной вязкостью и электрическим сопротивлением.
Дальнейшая работа будет включать в себя разработку этой модели для других случаев, включая конкретные приложения, представляющие интерес, такие как получение изображений MI, а также изучение возможности расширения модели за счет включения частотных членов более высокого порядка. Этот подход представляет интерес помимо того, что изучается здесь, поскольку он обеспечивает альтернативные и, возможно, более эффективные средства моделирования электромагнитной индукции в ближнем поле, которые могут быть полезны в смежных областях, таких как связь ближнего поля, радиочастотная идентификация и совместимость с электромагнитными помехами.Точность прогнозирования модели на значительном расстоянии от передатчика означает, что устройство может быть адаптировано в качестве эталона для калибровки измерителей напряженности поля для приемных рамочных антенн. Кроме того, этот метод может иметь значение для изучения влияния электромагнитных взаимодействий ближнего поля с биологическими телами. Поскольку формулировка силы Вебера описывает движущиеся заряды, и это не обязательно должны быть электроны в медной проволоке, теорию можно было бы распространить на движущиеся заряженные частицы [47–51] или ионные частицы в биомедицинских системах [52–54], в частности, дает представление о влиянии электромагнитной индукции на конкретные биологические процессы.
Благодарности
Авторы признают положения Департамента электротехники и электроники Ливерпульского университета.
Приложение A
показывает отдельные повороты передатчика-приемника, используемые при суммировании уравнения (3.6).
Рис. 7.
( a ) На эскизе показаны положения отдельных витков в расположении катушки передатчика-приемника. ( b ) Разложение матрицы из уравнения (3.6) для иллюстрации процедуры суммирования. (Онлайн-версия в цвете.)
Авторские работы
R.T.S. и С. разработал и инициировал проект. Эксперименты проводились R.T.S при поддержке S.M., F.P.M.J. и I.S.Y. Рукопись и рисунки подготовлены R.T.S. и С. Все авторы рецензировали рукопись.
Конкурирующие интересы
Авторы не заявляют о конфликте интересов.
Финансирование
Это исследование не получало специального грантового финансирования.
Ссылки
7. Ма Дж, Чжан Х, Хуанг Q, Ченг Л., Лу М. Экспериментальное исследование влияния проводимости почвы на подземный магнитоиндуктивный канал. Антенны IEEE и беспроводное распространение. Lett. 14, 1782–1785. (DOI: 10.1109 / LAWP.2015.2423687) 10. Сунь З., Ван П., Вуран М.С., Аль-Родхаан М.А., Аль-Делаан А.М., Акылдиз И.Ф. 2011 г. MISE-PIPE: беспроводные сенсорные сети на основе магнитной индукции для мониторинга подземных трубопроводов. Ad Hoc Netw. 9, 218–227. (DOI: 10.1016 / j.adhoc.2010.10.006) [Google Scholar] 11. Хуан И, Бойл К. 2008 г. Антенны: от теории к практике . Чичестер, Великобритания: John Wiley & Sons. [Google Scholar] 15. Вернер Д.Х. 1998 г. Метод моментов для эффективного и точного моделирования цилиндрических проволочных антенн средней толщины. IEEE Trans. Антенны Propag. 46, 373–382. (DOI: 10.1109 / 8.662656) [Google Scholar] 16. Оверфельт П. 1996 г. Вблизи полей постоянного тока тонкая круглая рамочная антенна произвольного радиуса. IEEE Trans. Антенны Propag. 44, 166–171. (DOI: 10.1109 / 8.481643) [Google Scholar] 18. Вернер DH, Колгроув TW. 1999 г. О новом цилиндрическом гармоническом представлении сферических волн. IEEE Trans. Антенны Propag. 47, 97–100. (DOI: 10.1109 / 8.752999) [Google Scholar] 19. Фикиорис Г., Папаканеллос П.Дж., Анастассиу Х.Т. 2008 г. Об использовании невырожденных ядер в некоторых интегральных уравнениях для тонкопроволочных антенн с круговой рамкой. IEEE Trans. Антенны Propag. 56, 151–157.(DOI: 10.1109 / TAP.2007.6) [Google Scholar]22. Микки С.М., Антар Ю.М. 2011 г. О пространственной структуре антенны электромагнитного ближнего поля . На Генеральной ассамблее и научном симпозиуме , 2011 г., XXXI URSI, Стамбул, Турция, 13–20 августа г. С. 1–4.
23. Микки С.М., Антар Ю.М. 2015 г. Анализ типичных взаимодействий в ближней зоне с использованием функции Грина антенны. Прог. Электромагнит. Res. C 59, 1–9. (DOI: 10.2528 / PIERC15060304) [Google Scholar]25.Эме Дж., Руде Дж., Клавель Э, Ауин О, Лабарр С., Коста Ф, Экраби Дж. 2007 г. Прогнозирование и измерение ближнего магнитного поля статического преобразователя . В Industrial Electronics, 2007. ISIE 2007. IEEE Int. Symp ., Виго, Испания, 4–7 июня , стр. 2550–2555. Пискатауэй, Нью-Джерси: IEEE.
32. Smith RT, Jjunju FP, Maher S. 2015 г. Оценка отклонения электронного пучка через соленоид с использованием электродинамики Вебера – Ритца и Максвелла – Лоренца. Прог. Электромагнит.Res. 151, 83–93. (DOI: 10.2528 / PIER15021106) [Google Scholar] 33. Grover FW. 2004 г. Расчет индуктивности . Минеола, Нью-Йорк: Dover Publications. [Google Scholar] 34. Фейнман Р.П., Лейтон Р.Б., Сэндс М. 1963 г. Лекции Фейнмана по физике, в основном по электромагнетизму и материи. , vol. II Редвуд-Сити: Эддисон Уэсли. [Google Scholar] 35. Максвелл Дж. 1954 г. Трактат об электричестве и магнетизме , т. 2 Нью-Йорк, штат Нью-Йорк: Дувр. [Google Scholar] 38. О, KS. 2000 г. Точная имитация переходных процессов в ЛЭП со скин-эффектом. IEEE Trans. Компьютерный Des. Интегр. Circ. Syst. 19, 389–396. (DOI: 10.1109 / 43.833207) [Google Scholar] 39. Бир О, Бом П., Прейс К., Вачутка Г. 2000 г. Краевой конечно-элементный анализ проблем переходного скин-эффекта. IEEE Trans. Magn. 36, 835–839. (DOI: 10.1109 / 20.877574) [Google Scholar] 41. Айелло Дж., Альфонцетти С., Борзи Дж., Салерно Н. 2001 г. Усовершенствованная схема решения задач скин-эффекта с открытыми границами. IEEE Trans. Magn. 37, 3474–3477. (DOI: 10.1109 / 20.952640) [Google Scholar] 42. Джафари-Шапурабади Р., Конрад А., Синклер А. 2002 г. Сравнение трех составов для решения проблем с вихревыми токами и скин-эффектом. IEEE Trans. Magn. 38, 617–620. (DOI: 10.1109 / 20.996161) [Google Scholar]43. Cullwick EG. 1949 г. Основы электромагнетизма . Кембридж, Великобритания: Издательство Кембриджского университета.
44. Чубыкало А, Еспиноза А, Цончев Р. 2004 г. Экспериментальная проверка совместимости определений плотности электромагнитной энергии и вектора Пойнтинга. Eur. Phys. J. D 31, 113–120. (DOI: 10.1140 / epjd / e2004-00135-x) [Google Scholar] 46. Ричардсон EG. 1961 г. Динамика реальных жидкостей . Лондон, Великобритания: Эдвард Арнольд. [Google Scholar] 49. Сайед С.У., Махер С., Эйкель Г.Б., Эллис С.Р., Чжунджу Ф., Тейлор С., Херен Р.М. 2015 г. Метод прямой ионной визуализации для исследования динамики ионов в многополюсных ионопроводах. Анал. Chem. 87, 3714–3720. (DOI: 10.1021 / ac5041764) [PubMed] [Google Scholar] 50. Махер С., Сайед С.У., Хьюз Д.М., Гибсон Дж. Р., Тейлор С.2013. Построение диаграммы устойчивости квадрупольного масс-спектрометра с приложенным статическим поперечным магнитным полем. J. Am. Soc. Масс-спектрометрия. 24, 1307–1314. (DOI: 10.1007 / s13361-013-0654-5) [PubMed] [Google Scholar] 51. Срикумар Дж., Хоган Т.Дж., Тейлор С. 2012 г. Моделирование QMS, включая эффекты давления в ионном источнике электронного удара. IEEE Trans. Instrum. Измер. 61, 3024–3030. (DOI: 10.1109 / TIM.2012.2202166) [Google Scholar] 53. Лю Ц., Дуань В., Сюй С., Чен Ц., Хэ М, Чжан Л., Ю З., Чжоу З.2013. Воздействие радиочастотного электромагнитного излучения с частотой 1800 МГц вызывает окислительное повреждение оснований ДНК в линии клеток, полученных из сперматоцитов мыши. Toxicol. Lett. 218, 2–9. (doi: 10.1016 / j.toxlet.2013.01.003) [PubMed] [Google Scholar]электрических и магнитных полей от линий электропередач
Факты о радиации
- Научные исследования четко не показали, увеличивает ли воздействие ЭМП риск рака.
Электрические и магнитные поля, также известные как электромагнитные поля (ЭМП), состоят из волн электрической и магнитной энергии, движущихся вместе.Эти энергетические поля окружают нас все время. Научные исследования четко не показали, увеличивает ли воздействие ЭМП риск рака. Несколько исследований связали ЭМП и воздействие на здоровье, но повторить их не удалось. Это означает, что они неубедительны. Ученые продолжают исследования по этому поводу.
На этой странице:
Об электрических и магнитных полях от линий электропередач
Электромагнитное излучение (ЭМИ)
Это изображение травяного поля с окружающими деревьями; в центре изображения – линии электропередач и их опоры.Электромагнитное излучение (ЭМИ) состоит из волн электрической и магнитной энергии, движущихся вместе в пространстве. Примером электромагнитного излучения является видимый свет. Электромагнитное излучение может находиться в диапазоне от низкой до высокой частоты, которая измеряется в герцах, и может варьироваться от низкой до высокой энергии, которая измеряется в электрон-вольтах. Длина волны, еще один термин, связанный с электромагнитным излучением, – это расстояние от пика одной волны до другой.
Существует два основных вида электромагнитного излучения: ионизирующее излучение и неионизирующее излучение.Ионизирующее излучение достаточно мощно, чтобы сбить электроны с орбиты вокруг атома. Этот процесс называется ионизацией и может повредить клетки организма. Неионизирующее излучение обладает достаточной энергией, чтобы перемещать атомы в молекуле и заставлять их вибрировать, что приводит к нагреванию атома, но недостаточно для удаления электронов из атомов.
Электромагнитные поля (ЭМП)
Электромагнитные поля, связанные с электричеством, представляют собой тип низкочастотного неионизирующего излучения, и они могут исходить как от естественных, так и от искусственных источников.Например, молния во время грозы создает электромагнитное излучение, потому что она создает ток между небом и землей. Этот ток окружает электромагнитное поле. Одним из примеров является магнитное поле Земли. Мы всегда находимся в магнитном поле Земли, которое генерируется ядром Земли. Это магнитное поле заставляет работать компасы, а также используется голубями и рыбами для навигации. На изображении ниже показан диапазон частот для различных форм электромагнитного излучения, присутствующих в электромагнитном спектре.
Волны от линий электропередач и электрических устройств имеют гораздо более низкую частоту, чем другие типы ЭМИ, такие как микроволны, радиоволны или гамма-лучи. Однако низкочастотная волна не обязательно означает ее низкую энергию; зарядный кабель для телефона создает низкочастотное электромагнитное поле с низкой энергией, в то время как линия электропередачи высокого напряжения может создавать электромагнитное поле с гораздо большей энергией, которое по-прежнему имеет низкую частоту.
ЭМИ, связанное с линиями электропередач, представляет собой тип низкочастотного неионизирующего излучения.Электрические поля создаются электрическими зарядами, а магнитные поля создаются потоком электрического тока через провода или электрические устройства. Из-за этого низкочастотное ЭМИ обнаруживается в непосредственной близости от источников электричества, таких как линии электропередач. Когда ток проходит по линии электропередачи, он создает магнитное поле, называемое электромагнитным полем. Сила ЭДС пропорциональна количеству электрического тока, проходящего через линию электропередачи, и уменьшается по мере удаления от вас.Из-за этого свойства воздействие электромагнитного поля, которое вы получаете от линии электропередачи, уменьшается с расстоянием.
Что вы можете сделать
Если вас беспокоит возможный риск для здоровья от электрических и магнитных полей, вы можете:
- Увеличьте расстояние между собой и источником. Чем больше расстояние между вами и источником ЭДС, тем меньше ваша экспозиция.
- Ограничьте время, проводимое рядом с источником. Чем меньше времени вы проводите рядом с ЭМП, тем меньше ваша экспозиция.
Электромагнитная индукция – MagLab
В 1831 году Майкл Фарадей провел множество экспериментов, чтобы доказать, что электричество может быть произведено из магнетизма. Он не только продемонстрировал электромагнитную индукцию, но и разработал хорошее представление о происходящих в ней процессах.
В 1831 году Майкл Фарадей провел многочисленные эксперименты, пытаясь доказать, что электричество может быть произведено из магнетизма.В течение нескольких недель великий экспериментатор не только ясно продемонстрировал это явление, известное теперь как электромагнитная индукция , но и разработал хорошее представление о происходящих в нем процессах. В одном из экспериментов, проведенных Фарадеем в тот важный год, использовались постоянный магнит и гальванометр, подключенные к катушке с проволокой, намотанной вокруг бумажного цилиндра, аналогично тем, что показаны в этом руководстве.
Чтобы смоделировать эксперимент Фарадея, щелкните и перетащите стержневой магнит назад и вперед внутри катушки.Обратите внимание на то, что вольтметр , подключенный к катушке, показывает наличие тока только тогда, когда магнит действительно находится в движении, и что его стрелка отклоняется в одном направлении, когда магнит перемещается в катушку, и в противоположном направлении, когда его перетаскивают. из катушки. Также обратите внимание на линий магнитного поля , изображенных синим цветом, исходящих от магнита, и то, как направление тока (указано черными стрелками) изменяется в зависимости от того, в каком направлении движется магнит.Как вы можете заметить, когда северный конец магнита входит в катушку, индуцируется ток, который распространяется вокруг катушки против часовой стрелки; когда магнит затем вытаскивается из катушки, направление меняется на по часовой стрелке.
Также обратите внимание, что возникающий ток сильнее, когда магнит перемещается быстро, а не постепенно. Отрегулируйте ползунок числа витков и снова переместите магнит внутрь и из катушки, чтобы определить соотношение между витками провода в катушке и током, индуцируемым в этой катушке.Как показывает вольтметр, большее напряжение может быть наведено в катушках, сделанных из большего числа витков провода.
Используйте синюю кнопку перекидного магнита , чтобы увидеть, как все меняется, когда южный конец магнита, демонстрирующий различные силовые линии, взаимодействует с катушками провода.







 Найти направление индукционного тока (пользуясь
правилом правой руки)
Найти направление индукционного тока (пользуясь
правилом правой руки)

 8. Домашнее задание
8. Домашнее задание