Подготовка по контрольной по математике: Контрольная работа по математике. Вне табличное умножение и деление - Пройти онлайн тест - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Контрольные работы по математике – 8 класс

В этом разделе представлены контрольные работы по математике для 8 класса.

Векторы

Виды квадратных уравнений и способы их решений

Входная контрольная работа по алгебре для 8 класса

Годовая контрольная работа по геометрии

Диагностическая работа по математике для 8 класса в форме ОГЭ

Задания к переводному экзамену для 8 класса

Знатоки геометрии

Итоговая аттестация по алгебре за 8 класс

Итоговая контрольная работа для 8 класса

Итоговая контрольная работа по алгебре за 1 полугодие для 8 класса

Итоговая контрольная работа по геометрии

Итоговая контрольная работа по математике

Итоговая контрольная работа по математике в 8 классе

Итоговая контрольная работа по математике для 8 класса

Итоговая контрольная работа по математике за 1-й триместр 8 класс

Итоговый тест по геометрии

Квадрат теңдеулердің шешу

Квадратичная функция

Квадратные уравнения

Квадратный корень

Квадраттық теңдеу

Контрольная по алгебре 8 класс по теме дроби

Контрольная работа за 1 полугодие для 8 класса

Контрольная работа за 1 полугодие по алгебре, 8 кл. (текст, ключ, схема анализа)

Контрольная работа за 8 класс

Контрольная работа за первое полугодие по алгебре и геометрии 8 класс

Контрольная работа по геометрии по теме “Площади четырехугольников” для 8 класса

Контрольная работа по математике 8 класс 1 четверть

Контрольная работа по математике за 1 полугодие для 8 класса

Контрольная работа по математике за курс 8 класса в форме ГИА

Контрольная работа по теме “ГИА 8” для 8 класса

Контрольная работа по теме: “Решение квадратных уравнений”

Контрольные работы по алгебре для 8 класса

Контрольные работы по алгебре за І полугодие

Материалы для проведения переводного экзамена по математике за курс 8 класса. Вариант 2

Многоугольники

Неравенства и их свойства

Параллелограмм и трапеция

переводная экзаменационная работа по математике в 8 классе

Площадь и подобие

Подкоренные выражения

Практическая работа по теме “Алгебраический квадратный корень”

Презентация урока информатики в 10 классе по теме: “НОД”

Преобразование графиков функций

Признаки подобия треугольников

Применение подобия к решению задач. Соотношения между сторонами и углами прямоугольного треугольника

Проверочная работа по алгебре в VIII классе по темам “Квадратные корни”, “Квадратные уравнения”

Разместить материал

4829 на сайте контрольных

Сертификат о публикации

Ресурсы сайта

Анекдот

Теперь в школах, перед сочинением на тему “Кем я хочу стать”, учителя обязательно предупреждают, что работы про профессию уборщицы в Газпроме приниматься не будут.

Тематические тесты и контрольные работы по математике. Пособие для систематизации знаний и подготовки к ЕГЭ. Часть 2. Учебное пособие (Александр Иванов)

649 ₽

+ до 97 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Купить

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Последний экземпляр

Цель издания книги – помочь школьникам в систематизации знаний по математике. Приведены тесты пяти уровней сложности по темам: логарифмическая и показательная функции, тригонометрия, последовательности, геометрия, производная и ее приложения, а также 10-вариантные письменные тематические контрольные работы. Предназначены учащимся общеобразовательных учреждений для самотестирования и выполнения письменных контрольных работ при подготовке к единому государственному экзамену по профильной математике и вступительным экзаменам в вузы; студентам математических специальностей и школьным учителям для проверки знаний учащихся по указанным темам.

Описание

Характеристики

Физматкнига

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Тематические тесты и контрольные работы по математике. Пособие для систематизации знаний и подготовки к ЕГЭ. Часть 2. Учебное пособие» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Александр Иванов «Тематические тесты и контрольные работы по математике.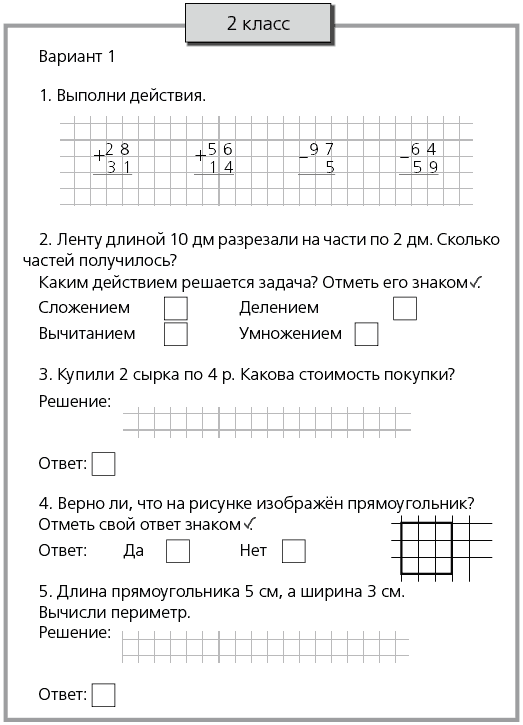 Пособие для систематизации знаний и подготовки к ЕГЭ. Часть 2. Учебное пособие» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Mathematics Practice Questions 1

1. В магазине инструментов всем учащимся предоставляется скидка 10% от первоначальной стоимости инструмента. Во время распродажи «Снова в школу» скидка составляет 15% от цены со скидкой. Джули, ученица местной средней школы, покупает флейту за 306 долларов. Сколько он стоил изначально?

2. Если y (x-1) = z, то x =

Y-Z
z/y + 1
y(z-1)
z(y-1)
1-zy

3. Какое из следующих значений НЕ равно 34(58+9)?

34 * 67
58 (34 + 9)
34 * 58 + 34 * 9
1 972 + 306
(9 + 58) 34

4.

85°. Чему равен третий угол?

50°
55°
60°
80°
90°

5. Если 5 унций равны 140 граммам молотого мяса, то сколько граммов мяса составляет 2 фунта?

6. В каком году больше всего детей занималось плаванием?

1990
1991
1992
1994
1995

7. Между каким годом произошло наибольшее сокращение детей, занимающихся плаванием?

1990-1991
1991-1992
1992-1993
1993-1994
1994-1995

8. Сколько в среднем детей посещало уроки плавания с 1990 по 1995 год?

250
308
385
450
1850

9. Какое из следующих чисел равно 5,93 * 10-2?

0,0593
0,00593
593
5930
59300

10.

На карте 201 миля. Расстояние между двумя городами равно 6 1/5 дюйма. Сколько миль на самом деле между двумя городами?

65 миль
84 мили
124 мили
138 миль
145 миль

11. Какой из следующих графиков является правильным графиком x>1, x

<4?

Строка A
Строка B
Строка C
Строка D
Строка E

глубина на 12 дюймов в ширину и 9 дюймов в высоту, при этом крышка все еще может быть закрыта?

13. Сара вдвое старше своего младшего брата. Если разница между их возрастами составляет 15 лет. Сколько лет ее младшему брату?

Какая из следующих дробей равна 6

/ 8 ?

²⁰ / ₃₀
¹⁵ /₂₄
²⁵ /₃₀
⁴⁰ /₅₄
² /
² /

9015

² /

шириной на 20 футов в длину, если плитка стоит 8,91 доллара за квадратный ярд?

224,51
237,6
246,55
271,38
282,32

Второй занявший второе место получает ¼ того, что выиграл победитель.

Какова общая сумма призовых, если победитель получит 6000 долларов?

6000$
8500$
12000$
15000$
18500$

17. Вы находитесь в футах от дерева 120 Вы смотрите на вершину дерева. Приблизительно на каком расстоянии от вершины дерева по прямой находится ваш слух?

50 футов
75 футов
120 футов
130 футов
150 футов

Какова средняя скорость велосипедиста за поездку туда и обратно в милях в час?

19. Если бывание стоила 2,32 долл. США за 12-дюймовый камень, и вы хотите двойной слой края вокруг вашего цветочного кровати, который составляет 6 ярдов 1 ярды. . Сколько будет стоить окантовка вашей клумбы?

$32.48
$64.96
$97.44
$129.92
$194.88

20. If 3x=6x-15 then x + 8=

21.

Количество миллилитрах в 1 литр составляет

10 000
1000
0,1
0,01
0,001

22. и водитель с дополнительной стоимостью 50 центов за пассажира. Если плата за посадку на паром составляет 6,50 долларов, сколько человек было в машине?

23. Что такое

¹ / ₉ из 9?

¹ /₉
0
1
2
3

24. В своем кармане мальчик имеет 3 красных шарика, 4 синих шарика и 4 зеленого храря. Сколько ему придется вынуть из кармана, чтобы убедиться, что он вынул хотя бы по одной фишке каждого цвета?

25. Какая дробь равна 0,20%?

¹ / ₂₀
_{¹ /40}
¹ / ₅₀
¹ / ₄₀₀
¹ / ₅₀₀

26 Найдите пропущенный член в следующей последовательности: 4, 9, 19, __, 79

апрель 2001?

$ 617,80
$ 620,92
$ 622,50
$ 626,38
$ 633,20

28.

Какова средняя сумма денег, которую бюджет Джессики позволила для одежды первых шести месяцев 2001 года?

$ 249,90
$ 250,40
$ 251,32
$ 253,33
$ 255,75

29. Если Джессика потратила только 20% вместо 25% запланированного на питание в мае 2001 года, как она сэкономила?

131,10 $
144,30 $
$ 148,32
$ 152,22
$ 153,33

Работая вместе, сколько времени им потребуется, чтобы напечатать один и тот же документ?

5 минут
10 минут
15 минут
18 минут
20 минут

31. Из следующих дробей, которая меньше

² / ₃ ?

⁷ / ₈
⁵ / ₆
³ / ₄
³ / ₅
⁵ / ₇

32 Хоккейная команда выиграла 6 игр и проиграла 8.

Каково отношение побед к количеству игр?

⁶ / ₈
⁸ / ₆
³ / ₇
⁸ / ₁₄
⁶ / ₇

33. Получает еженедельную комиссию от всех продаж плюс 1 $

. На этой неделе у Сью было 3000 долларов продаж. Сколько всего она заработала?

$ 375
$ 450
$ 480
$ 510
$ 525

34. Если периметр прямоугольного дома составляет 25

¹ /₃ Yards, и длина. Какова ширина?

16 футов
35 футов
37 футов
40 футов
42 фута

. Лодка продана за сколько?

$ 17 250,00
$ 16 540,44
$ 16 230,34
$ 15,980,55
$ 15 870,88

36. Недавнее исследование показало, что увеличение веса тела на 10 KILOGRAMS.

Какая дробь равна 0,15%?

³ / ₂₀₀₀
² / ₇₅₀
⁷ / ₄₀₀₀
⁵ / ₃₄₆₂
¹ / ₅₀₀

37 . 6.334 * 10

⁴ =

0,0006334
0,06334
6334
63340
633400

38. Если 3x + 5x = -8, тогда x + 10005.4000

.9000 9000.9000 9000.9000

. 1

39. Два угла в треугольнике равны 120°. Чему равен третий угол?

60°
70°
80°
90°
120°

40. Какая из следующих единиц будет подходящей единицей измерения сахара для рецепта печенья?

литров
чашек
кварт
килограммов
фунтов

1. C: Уравнение x -0,10 x -0,15( x -0,10 x )=306 можно использовать для решения задачи. Решение для x дает 0,90 x – 0,15 x + 0,015 x = 306, где x = 400. Таким образом, исходная цена составляла 400 долларов.

2. B: Уравнение можно решить, сначала распределив y по выражению x – 1 в левой части уравнения. Это дает: x y – y = Z . Добавление y к обеим частям уравнения дает: x y = Z + y . Наконец, деление обеих частей уравнения на y дает: x = ( Z + y )/ y или x = Z / 906,95.

3. B: Эта задача иллюстрирует распределительное свойство умножения над сложением. Распределяемый фактор может не измениться.

4. D: Величина третьего угла треугольника равна 180°-(15° + 85°) или 80°.

5. C: Поскольку в 2 фунтах содержится 32 унции (16 унций = 1 фунт), можно записать следующую пропорцию: 5/140=32/ x . Решение для x дает x = 896. Таким образом, в 2 фунтах мяса содержится 896 граммов.

6. E: Наибольшее количество детей, занимающихся плаванием в течение одного года, составляло 500 человек в 1995 году.

7. C: Единственное уменьшение числа детей, посещающих уроки плавания, произошло с 1992 по 1993 год, на 200 детей.

8. B: Среднее значение может быть записано как (200+250+400+200+300+500)/6, что примерно равно 308.

9. A: Перемещение запятой на два знака слева дает 0,0593.

10. C: Для решения задачи можно использовать следующую пропорцию: 1/20=6,2/ x . Решение для x дает x = 124, поэтому на самом деле между двумя городами 124 мили.

11. A: Правильный график должен показывать отрезок между 1 и 4, включая точки 1 и 4.

12. D: Объем жестяной банки составляет 972 дюйма”. Объем каждого кусочка помадки составляет 27 дюймов». 972 ÷ 27 = 36.

13. B: Для решения задачи можно использовать следующую систему уравнений: ( s =2 b @ s – б =15). Подстановка 2 b вместо s во втором уравнении дает: 2 b – b = 15, где b = 15. Младшему брату 15 лет.

14. C: Умножение числителя и знаменателя данной дроби на 5 дает дробь 25/30, которая эквивалентна.

15. B: Преобразуя футы в ярды, размеры можно переписать как 4 ярда на 6 2/3 ярда. Таким образом, площадь пола равна 26 2/3 ярда». Умножение этой площади на стоимость квадратного ярда дает выражение 26 2/3×8,9.1, что равно 237,6. Таким образом, стоимость составляет $237,60.

16. C: Следующее уравнение может быть решено для x : 6000 = 1/2 x . Решение для x дает x = 12 000. Таким образом, сумма розыгрыша призовых составила 12 000 долларов.

17. D: Расстояние можно определить, написав и решив следующее уравнение для c : 50 ² +120 ² = c ² . с = 130, таким образом, расстояние равно 130 футам.

18. D: Средняя стоимость поездки туда и обратно равна общему пройденному расстоянию, деленному на общее время в пути. Пройденное расстояние = 2x. Время в пути = х/10+х/8=4х/40+5х/40=9х/40. Средняя скорость = 2xx9x/40=(2xx40)/9x=80/9 = приблизительно 8,9 миль в час.

19. E: Длина равна 216 дюймам. Ширина равна 36 дюймам. Таким образом, длину можно покрыть 18 камнями по 12 дюймов, а ширину — 3 камнями по 12 дюймов. Всего на один слой нужно 42 камня, а на два слоя нужно 84 камня. Умножение 84 на 2,32 доллара дает 19.4.88. Таким образом, общая стоимость составляет $194,88.

20. E: Уравнение можно решить для x , сначала вычитая 6 x из обеих частей уравнения. Это дает -3 x = -15, где x = 5. Подстановка 5 вместо x во второе выражение дает 5 + 8, что равно 13.

21. B: 0 в 1 л.

22. D: Задачу можно смоделировать с помощью уравнения 6,50 = 5,00 + 0,50 x , где x – количество пассажиров. Решение для x дает x = 3. Таким образом, в машине было 3 пассажира плюс 1 водитель, всего 4 человека.

23. C: Эта задача может быть представлена как 1/9 ^. 9, что равняется 1.

24. D: Извлечение по 3 каждого цвета гарантирует, что у него будет по 1 каждому цвету. Таким образом, всего ему нужно вынуть 9 шариков.

25. E: 0,20% = 0,002, а 1/500 = 0,002.

26. D: Увеличение от семестра к семестру вдвое больше, чем за два предыдущих семестра. Таким образом, увеличение от 19 до недостающего члена будет 20, или удвоенное увеличение 10. Таким образом, недостающий член равен 19 + 20, или 39.

27. C: Решение может быть смоделировано с помощью выражение, 0,25(2490). Таким образом, в ее бюджете на апрель 2001 г. было выделено 622,50 доллара на жилье.0)+0,10(2622)+0,10(2555))/6, что упрощается как (257,80+243,20+266,80+249,00+262,20+255,50)/6 или 255,75. Средняя сумма бюджета на одежду за первые шесть месяцев 2001 года составила 255,75 долларов.

29. A: Сумма, которую она сэкономила, может быть представлена выражением 0,25(2622) – 0,20(2622), что равно 131,10. Таким образом, она сэкономила 131,10 доллара.

30. B: Задачу можно смоделировать с помощью уравнения 1/40+1/30+1/24=1/ t . Решение для t дает t = 10. Таким образом, работая вместе, они могут напечатать один и тот же документ за 10 минут.

31. D: Дробь 3/5 равна 0,6, что меньше 2/3.

32. C: Отношение может быть записано как 6/14, что сокращается до 3/7.

33. B: Сумма заработанных ею денег может быть представлена выражением 90 + 0,12 x , где x представляет собой объем продаж. Если заменить x на 3000, получится 90 + 0,12(3000), что равно 450. Итак, на этой неделе она заработала 450 долларов.

34. A: Во-первых, измерение периметра может быть преобразовано в футы. Умножение 25 1/3 ярда на 3 дает эквивалентное измерение 76 футов. Таким образом, можно написать следующее уравнение: 76 = 2(22) + 2 w 90 695 , что упрощается до 76 = 44 + 2 90 694 w 90 695 , где 90 694 w 90 695 = 16. Ширина дома составляет 16 футов 90 689.

35. A: Задачу можно смоделировать с помощью выражения 15 000 + 0,15 (15 000), что равно 17 250. Таким образом, он продал лодку за 17 250 долларов.

36. А: 3/2000=0,0015, что эквивалентно 0,15%.

37. D: Перемещение десятичной точки на 4 знака вправо дает 63 340.

38. C: Решение данного уравнения для x дает x = -1. Подстановка -1 вместо x во втором уравнении дает -1 + 1 = 0,

39, A: Внутренний угол треугольника в сумме равен 180°. Таким образом, мера третьего угла равна разности 180° и 120°, или 60°.

40. B: Чашки – это подходящая мера вместимости сахара.

TEAS 7 Практический тест по математике (обновлено в 2023 г.)

Математический раздел TEAS требует, чтобы вы использовали алгебру, числа, измерения и данные для успешного решения задач. Чтобы помочь вам подготовиться к этому разделу TEAS, эта страница содержит все, что вам нужно знать, в том числе какие темы рассматриваются, сколько вопросов есть и как вы можете учиться эффективно.

Нажмите «Начать тест» ниже, чтобы пройти бесплатный практический тест по математике TEAS 7!

Начало теста

Онлайн-курс TEAS
Учебное пособие TEAS
Карточки TEAS

Что находится в математическом разделе TEAS?

Контрольный список TEAS

Онлайн-курс TEAS

Если вы хотите полностью подготовиться, Mometrix предлагает онлайн-курс подготовки к TEAS. Курс предназначен для предоставления вам любых ресурсов, которые могут вам понадобиться во время обучения. Курс TEAS включает:

106 уроков по каждой теме
Более 2000 практических вопросов TEAS
Более 190 видеоуроков
311 электронных карточек
Гарантия возврата денег
Легкий мобильный доступ
и многое другое!

Подготовительный курс TEAS разработан, чтобы помочь любому учащемуся получить все необходимое для подготовки к экзамену TEAS; нажмите ниже, чтобы проверить это.

Онлайн-курс TEAS

Часто задаваемые вопросы

Кто сдает TEAS?

Программа TEAS предназначена для 90 335 студентов, желающих поступить на программы ухода за больными или смежные медицинские программы . Многие учебные заведения требуют, чтобы студенты сдавали TEAS. Учащимся предлагается узнать больше о требованиях к баллам в своей школе.

Сколько вопросов на экзамене TEAS по математике?

Математический раздел TEAS содержит 38 вопросов . Этот раздел включает четыре «предварительных» вопроса, которые не учитываются при подсчете окончательной оценки.

Сколько длится экзамен TEAS по математике?

У учащихся есть 57 минут , чтобы выполнить математический раздел, состоящий из 38 вопросов.

Можете ли вы использовать калькулятор для TEAS?

Да . В день теста администратор теста предоставит вам четырехфункциональный калькулятор (в зависимости от локации). Калькуляторы со встроенными или специализированными функциями не допускаются.

Что такое проходной балл TEAS по математике?

Выбранная вами программа ухода определяет требования к баллам для TEAS. В конце экзамена учащиеся получают «основной» или общий балл, который суммирует все четыре раздела (естественные науки, математика, чтение и английский язык и использование языка). Студенты также получают отдельные баллы по каждому разделу. Многие программы медсестер требуют, чтобы студенты набрали в общей сложности 9 баллов. 0335 не менее 60% – 70% . Студентам предлагается набрать больше баллов, чем минимальное требование программы, чтобы увеличить их шансы на поступление.

Исследование для теста TEAS, нажав ниже:
Руководство по изучению теста TEAS
Примеры задач TEAS по математике
Вот три примера вопросов из экзамена TEAS по математике, каждый с простым объяснением, показывающим, как решается задача решается.
1. Найдите $x$:
$2x+4=x–6$
Чтобы решить уравнение с переменной по обе стороны от знака равенства, необходимо переставить члены. В частности, используйте обратные операции сложения или умножения, чтобы собрать переменные члены в одну сторону, а константы в другую:
Шаг 1 : Переместите $x$-член из правой части уравнения влево, вычитая $х$ из обеих частей уравнения.
Шаг 2 : Переместите постоянный член 4 из левой части вправо, вычитая 4 из обеих частей уравнения.
Следовательно, решение $x=-10$ .
2. Сколько кубических дюймов воды мог бы вместить этот аквариум, если бы он был заполнен полностью?
Этот вопрос касается объема прямоугольного аквариума с заданными размерами длины, ширины и высоты. Формула для определения объема: $V = l \cdot w \cdot h$
Подставьте эти размеры в формулу:
$V=(20)(12)(15)$ $V=3600$
В контексте это означает, что показанный аквариум вмещает 3600 кубических дюймов воды, если он будет полностью заполнен.
3. Решите задачу:
Лаборант взял у пациента 400 миллилитров крови. Для дальнейшего исследования использовали 1/7 часть крови. Сколько миллилитров крови было использовано для дальнейших анализов? Округлите ответ до сотых.

В реальных приложениях часто есть ключевые слова, которые напрямую преобразуются в математическую операцию.