Подсчет производной онлайн: Производные. Пошаговый калькулятор

Мы выяснили, что есть два основных способа вычислить градиент: аналитический и числовой. Числовой метод достаточно прост, но работает очень медленно и выдаёт приблизительные значения. Аналитический градиент более точный и быстрый, но в при его подсчёте можно легко допустить ошибки. Чтобы избежать этого и легко вычислять градиент даже для сложных функций, лучше всего использовать вычислительные графы.

Вычислительный граф — это иллюстрированная запись какой-либо функции, состоящая из вершин и рёбер. Вершины (иногда их ещё называют узлы) — вычислительные операции, которые необходимо выполнить, а рёбра связывают их в определённую последовательность. 

На рисунке выше изображён пример графа с нашим классификатором. Узел с операцией (*) означает умножение матриц параметров W и данных x, результатом которого является вектор весов s. Следующая вершина зависимых потерь (hinge loss) определяет потери данных L. Узел R вычисляет регуляризацию. И, наконец, в самом конце мы получаем общие потери, суммируя регуляризацию и потери данных.

Преимущество графов в том, что они позволяют использовать так называемый метод обратного распространения ошибки (backpropagation). Этот алгоритм рекурсивно использует правило дифференцирования сложной функции для вычисления градиента каждой переменной в графе. Метод становится очень полезным для действительно сложных функций, которые применяются в свёрточных нейросетях. Рассмотрим, как он работает.

Начнём с простого примера:

У нас есть функция f(x,y,z) = (x+y)z и мы хотим найти её градиенты по отношению к каждой из переменных. На вычислительном графе отражены операции x+y и (x+y)z в виде вершин сложения (+) и умножения (*). Для примера взяты значения x = -2, y = 5, z = -4, поэтому: -2 + 5 = 3 (промежуточный результат после узла сложения), а 3 * (-4) = -12 (результат умножения).

Обозначим какими-нибудь буквами наши промежуточные значения. Пусть переменная после (+) называется q (q = x+y), тогда функция f будет равна qz. Выпишем градиенты (частные производные): градиент q зависит от переменных x и y, а градиент f — от q и z. Поскольку мы ищем градиент исходной функции f, которая зависит от всех трёх переменных x, y и z, то нам хотелось бы найти dfdx, dfdyи dfdz.

Частные производные dqdx и dqdy равны единице — это означает, что при любом изменении x или y q изменится точно так же.

Попробуем рекурсивно воспользоваться правилом дифференцирования сложной функции. Начнём с конца вычислительного графа и будем двигаться к началу, по пути считая все градиенты. Самое последнее полученное нами значение — функция f и её промежуточный результат -12, частная производная по которому равна единице. Далее идёт переменная z, и мы знаем, что dfdz= q = 3. Переходим к вершине (+) и переменной q: производная dfdq равна z, то есть -4. 

Получилось довольно интересно: в двух рёбрах, входящих в вершину умножения, градиент каждого из входов равен значению другого входа, умноженному на предыдущий градиент. И это не совпадение — можете взять правило на заметку.

Теперь мы приблизились к производной dfdy. Правило дифференцирования сложной функции говорит, что она может быть записана как dfdqdqdy. Значения dfdq и dqdyнам известны: они равны -4 и 1 соответственно, поэтому производная dfdy равна -4. Точно так же это работает и для dfdx:

Здесь мы нашли ещё одну закономерность: в вершине сложения оказались равными все три градиента: и самой вершины, и входящие в неё. Обратите внимание: значение производной для узла, который следует за текущим, называется восходящий градиент, а для предыдущего узла — локальный градиент. Например, для (+) восходящим градиентом является производная dfdf, а локальным — производные dfdx и dfdy.

Мы справились с задачей и нашли градиенты каждой переменной. Метод обратного распространения ошибки может сильно упрощать вычисление градиентов для громоздких функций. Убедимся в этом на более сложном примере.

Возьмём функцию f, вычислительный граф которой выглядит следующим образом:

Здесь сходу посчитать производные уже не так просто, как в предыдущем случае. Нам нужно найти градиенты dfdw0, dfdw1, dfdw2, dfdx0 и dfdx1. Для вычислений возьмём тестовые значения w0=2, w1=-3, w2=-3, x0=-1 и x1=-2. Если подставить их в функцию, то на выходе получим f=0.73.

Снова начнём с конца и посчитаем производную функции df/df, которая, очевидно, равна единице. Движемся дальше — первая вершина содержит сложную функцию 1/x. Можно воспользоваться таблицей производных и вспомнить, что 1/x=x^-1. В следующем узле находится константа +1, производная которой, как вы помните, равна нулю. Третья вершина — это экспонента в степени x, а четвёртая — умножение на -1. 

На рисунке выше расписаны вычисления градиентов для первых четырёх узлов. Заметьте, что на каждом шаге мы умножаем локальный градиент на восходящий, чтобы выполнялось правило дифференцирования. Локальные градиенты считаются по формулам в нижней части рисунка.

Мы подошли к узлу сложения с двумя входящими в него рёбрами, для которого известен восходящий градиент 0.2. В предыдущем простом примере мы выяснили, что в вершине сложения градиент по отношению к каждому из входов будет равен 1. Поэтому мы просто берём единицу (локальный градиент) и умножаем её на восходящий градиент для обоих рёбер:

Точно так же выполняем и со следующим узлом сложения. 

Продвинемся к первым двум переменным: w0 и x0. Перед ними находится вершина умножения. Ранее мы обнаружили, что в этом случае градиент по отношению к одному из входов просто является значением другого входа, умноженным на восходящий градиент. Поэтому dfdw0= 2 x 0.2 = 0.4, а dfdw0= (-1) x 0.2 = -0.2. Таким же образом разбираемся со второй вершиной напротив w1 и x1:

Вот и всё! Было непросто, но мы справились.

Во всех предыдущих случаях мы разбивали граф на множество простейших вершин. Но на самом деле это не всегда необходимо: вершины можно группировать друг с другом, если они образуют какую-нибудь легко дифференцируемую функцию. Это может существенно сократить и упростить вычисления.

Возьмём, например, сигмоиду. Если присмотреться, то она похожа на функцию из предыдущего примера. У сигмоиды есть очень полезное свойство: её производная легко выражается через саму функцию.

Переменные степени экспоненты w0, w1, w2, x0 и x1 складываются в вершине сложения, которая следует сразу за w2. Поэтому мы можем взять ту часть графа, которая полностью совпадает с сигмоидой, и объединить несколько узлов в один. Проверим, что локальные градиенты в этом случае окажутся одинаковыми: просто подставим значение функции f в выражение производной сигмоиды:

Видим, что градиенты совпадают. Теперь наш граф выглядит следующим образом:

Всегда ли необходимо группировать вершины? Это зависит от того, что вам нужно больше: короткий граф со сложными вычислениями, или объёмный с более простыми.

Мы рассмотрели пример со скалярными величинами, но точно так же можно работать с векторами и матрицами: в этом случае на каждом шаге придётся считать матрицу производных, которая также называется матрица Якоби.

Все наши предыдущие действия над вычислительными графами делятся на два больших этапа:

1. Проходим по графу в прямом направлении, подставляя исходные значения переменных и считая все промежуточные результаты;
2. Идём в обратном направлении, вычисляя градиенты и пользуясь правилом дифференцирования.

В коде их можно описать функциями forward и backward, которые будут выглядеть примерно так:

При этом мы можем установить механику forward и backward для каждой вершины. Вот пример функции, которая обрабатывает узел умножения по установленным правилам:

Рассмотрим популярный фреймворк для глубокого обучения Caffe. Зайдём в его репозиторий и откроем папку Layers:

По сути, все эти слои представляют собой те же самые вершины вычислительного графа. Они могут быть более сложными, чем в наших примерах, но часто встречаются и стандартные функции. Вот, например, слой с сигмоидой:

Таким образом, почти любую нейросеть можно представить в виде графа. Теперь мы плавно приблизились к тому, как устроены архитектуры настоящих нейронных сетей.

Очень часто люди сравнивают искусственные сети с настоящими нейронами в мозге. Мы обсудим это сравнение чуть позже и сначала посмотрим на нейросети, не погружаясь в биологические аналогии.

Вспомним функцию линейного классификатора, о которой мы так много говорили: f = Wx. Если мы захотим «превратить» её в нейросеть, то нам надо будет разделить параметры W на две части: W1 и W2 и применить одно линейное преобразование поверх другого:

Мы получили простую двухслойную нейросеть с двумя линейными слоями. На рисунке выше x — входные данные, h — промежуточная нелинейность (мы поговорим о ней чуть позже) и s — выходной вектор оценок. В более широком смысле, нейронные сети — это сложные функции, состоящие из простых. 

В одной из предыдущих лекций мы упоминали, что каждая строка весовой матрицы W является шаблоном одного из классов. Эти шаблоны выглядели, как некий усреднённый объект:

Также мы говорили о том, что с такими единичными шаблонами возникает проблема: например, в классе “car” машина окрашена в красный цвет, в то время как в реальных данных могут встречаться автомобили и других цветов. Многослойные сети решают этот вопрос: W1 содержит те же единичные шаблоны, но теперь оценки для них хранятся в промежуточной нелинейной переменной h. И следующий слой W2 объединит шаблоны с помощью взвешенной суммы, что позволит дать более точные оценки для машин других цветов и прочих разнообразных объектов.

Кстати, ничто не мешает нам добавить ещё один слой, чтобы повысить точность распознавания:

Именно так появляются глубокие нейросети.

Для наглядности посмотрим на код простой двухслойной сети, которую можно реализовать всего в 20 строк:

На самом деле искусственные и биологические нейронные сети имеют мало общего. Тем не менее, именно изучение человеческого мышления вдохновило учёных на создание AI. 

В нашем мозге присутствует огромное число нейронов, которые соединены друг с другом специальными «ветвями» — аксонами. Когда происходит какая-либо мыслительная деятельность, по нейронам проходят электрические импульсы, передающиеся от одних клеток к другим. У нейронов есть дендриты — это отростки, к которым приходят импульсы. Тело клетки объединяет в себе все поступающие сигналы и посылает их в следующие нейроны через свой аксон. Место, где происходит контакт двух нейронов, называется синапс.

Если мы посмотрим на вершины вычислительных графов, то сможем провести параллели: например, данные x_i — это исходные импульсы, поступающие в узел через дендрит, а веса w_i — синапсы. Тело клетки обрабатывает сигналы и отправляет их к следующим вершинам через выходной аксон с помощью функции активации.

Функция активации вычисляет выходное значение текущего нейрона в зависимости от результата взвешенной суммы. Сигмоида, кстати, — одна из её разновидностей. Это и есть та самая нелинейность, которая вводится между линейными слоями нейросети. В биологическом смысле она служит для приведения нейронов в активное состояние.

Хотя искусственные и настоящие нейроны кажутся очень похожими, всё-таки нужно учесть несколько важных моментов:

— биологические нейроны делятся на множество разновидностей;

— реальные дендриты могут выполнять сложные нелинейные вычисления;

— синапсы — это не просто веса, а сложная нелинейная динамическая система;

— обычной функции активации на практике может быть недостаточно.

Поэтому будьте осторожны с биологическими аналогиями.

⌘⌘⌘

В следующий раз мы поговорим о свёрточных нейросетях, обсудим их историю, особенности архитектуры и области применения. Не забывайте задавать вопросы в комментариях, если что-то кажется вам сложным или непонятным — мы всегда поможем разобраться.

Следующие лекции (список будет дополняться по мере появления материалов):

Лекция 5. Свёрточные нейронные сети
Лекция 6. Обучение нейросетей, часть 1
Лекция 7. Обучение нейросетей, часть 2
Лекция 8. ПО для глубокого обучения
Лекция 9. Архитектуры CNN
Лекция 10. Рекуррентные нейронные сети

С оригинальной лекцией можно ознакомиться на YouTube.

что это такое и как рассчитать

Дюрация — это эффективный срок до погашения облигации. Эффективный срок учитывает все купонные платежи, выплаченные в разное время, и различные особенности облигации, такие как амортизация или оферта. Если купонных платежей, амортизации и оферты нет, то дюрация совпадает со сроком до погашения облигации.

Юлия Семенюк

частный инвестор

Для чего нужна и где используется

С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций. Дюрация показывает зависимость облигаций от изменения процентных ставок, и это полезно при выборе облигаций.

Также дюрация позволяет оценить другие финансовые активы с фиксированными выплатами. Например, банки могут рассчитывать дюрацию кредитов и кредитных портфелей.

Как узнать дюрацию

Необязательно считать самостоятельно: значение можно посмотреть на справочных сайтах, например в облигационном разделе «Смарт-лаба», на cbonds.ru или rusbonds.ru.

Но мы все же рассмотрим несколько методик расчета.

Дюрация Маколея: формула расчета

Первый и наиболее известный способ расчета дюрации — формула Маколея. Дюрация Маколея показывает эффективный срок до погашения облигации.

Чтобы рассчитать дюрацию, надо сложить все будущие платежи с учетом срока их поступления и поделить результат на рыночную цену облигации с учетом накопленного купонного дохода. Будущие платежи по облигации — это купоны и погашение номинала частями или в конце срока.

Пример расчета дюрации. Допустим, номинал и текущая цена облигации с учетом НКД равны 1000 Р, купон в 10% выплачивается раз в год. До погашения облигации осталось 4 года, доходность до погашения — 10%.

В числителе мы складываем все денежные потоки: четыре купонных платежа и погашение номинала облигации. Так как это будущие платежи разного времени, нужно каким-то образом привести их к сегодняшнему дню. С точки зрения математики эти платежи надо освободить от 10% доходности, то есть дисконтировать. Дисконтирование — это процесс, обратный начислению процентов. В нашем случае ставка дисконтирования — это годовая доходность, то есть 10%.

Далее надо поделить это на цену облигации с НКД — и мы получим дюрацию.

Если купоны выплачиваются чаще раза в год, то расчет усложнится. Квартальных или полугодовых платежей больше, и их надо дисконтировать по квартальной или полугодовой ставке.

Как вложиться и не облажаться

Расскажем в еженедельной рассылке для инвесторов. Подпишитесь и получайте письма каждый понедельник

Модифицированная дюрация

Модифицированная дюрация — это второй способ измерения дюрации. С ее помощью инвестор определяет, на сколько процентов изменится цена облигации, если изменятся процентные ставки.

MD = Дюрация Маколея / (1 + процентная ставка)

Для небольших изменений работает следующая формула:

Изменение цены / Рыночная цена с НКД = −MD × Изменение ставок

Например, MD равна 3, цена облигации с учетом НКД — 95%, доходность к погашению — 8% годовых. Мы можем определить, как изменится цена, если доходность вырастет на 0,5 процентного пункта и станет равна 8,5%.

Х / 0,95 = −3 × 0,005

Х = −3 × 0,005 × 0,95 = −0,01425

Если доходность вырастет на 0,5%, цена облигации снизится на 1,4%.

Эффективная дюрация и оферта

Эффективная дюрация — третий способ измерить дюрацию. Подходит для облигаций, которые содержат встроенные условия — то есть эмитент может их выкупить раньше срока погашения по оферте. Вероятность того, что облигация будет выкуплена, сокращает ее дюрацию.

Дюрацию облигаций с офертой рассчитывают по формуле эффективной дюрации:

В числителе стоит разница между ценой облигации в условиях падения ставок и ее ценой при росте ставок. В знаменателе — первоначальная цена, умноженная на разницу ставок.

Например, у облигации Тинькофф 001Р-02R дюрация на 23 октября 2019 года составляет 674 дня, хотя срок обращения облигации — 3640 дней. Дюрация существенно меньше срока обращения, потому что по облигации предусмотрена оферта 4 апреля 2022 года и дюрация рассчитывается на момент оферты.

Дюрация портфеля облигаций

Дюрация портфеля облигаций — это средневзвешенная дюрация отдельных облигаций.

Например, в портфеле инвестора два вида облигаций — РЖД 001P-12R с дюрацией 1308 дней и ПИК БО-П03 с дюрацией 866 дней. Доли в портфеле — 70 и 30% соответственно.

ДПорт = 1308 × 0,7 + 866 × 0,3 = 915,6 + 259,8 = 1175,4 дня

Дюрация проекта

По экономическому смыслу дюрация проекта близка к показателю срока окупаемости проекта, но она учитывает только дисконтированные денежные потоки и не учитывает размер инвестиций.

Формула дюрации проекта:

Например, есть проект, который принесет по 500 Р в четвертый и пятый годы существования. Ставка дисконтирования зависит от многих факторов, например от риска инвестиций. В данном случае она составляет, допустим, 20%. Скорее всего, проект рискованный, поэтому по нему предлагают доходность выше, чем по надежным банковским депозитам. Рассчитаем дюрацию этого проекта.

Таким образом, без учета первоначальных вложений проект окупится через четыре года и пять с половиной месяцев.

Свойства дюрации

Дюрация купонных облигаций меньше времени до погашения, потому что инвестор регулярно получает купонные платежи.

Дюрация дисконтных облигаций равна времени до погашения, потому что по дисконтным облигациям инвесторы не получают купоны. Если купон один и выплачивается при погашении, дюрация также будет равна сроку до погашения.

При прочих равных чем меньше купон по облигации, чем реже его выплачивают или чем больше времени до погашения, тем больше дюрация: инвестор будет дольше возвращать свои деньги. И наоборот: если купонные платежи большие и более частые, а времени до погашения немного, то дюрация будет меньше, потому что инвестор быстрее вернет свои деньги.

Если рыночная цена облигации падает, то ее доходность растет и дюрация уменьшается, потому что инвестор покупает облигацию дешевле и возвращает вложения быстрее. И наоборот: если рыночная цена облигации растет, то ее доходность падает, а дюрация увеличивается, потому что инвестор больше платит за покупку и медленнее возвращает вложенные деньги.

Как посчитать доходность облигаций?

Зависимость от процентных ставок

Если купонные платежи по облигациям зафиксированы, то риск для инвесторов заключается в колебаниях цены облигации. Цена облигации и процентные ставки связаны обратной зависимостью: если процентные ставки в экономике растут, то цена ранее выпущенных облигаций падает, и наоборот.

Чем меньше дюрация, тем меньше цена облигации изменится при изменении процентных ставок. Например, по облигациям Тинькофф БО-07 на 23 октября 2019 года дюрация всего 64 дня, потому что 30 декабря банк погасит облигации по номиналу. Скорее всего, за оставшиеся несколько месяцев цена облигации практически не поменяется.

И наоборот: чем выше дюрация, тем больше вероятность того, что цена облигаций существенно изменится при изменении процентных ставок. Например, по облигациям РЖД 001P-12R на 23 октября дюрация составляет 1308 дней, или 3,6 года. За несколько лет ставки могут измениться, а значит, и цена облигации изменится.

Что такое выпуклость облигаций и как она связана с дюрацией

Зависимость цены облигации от ее доходности не линейная, а выпуклая. Выпуклость облигаций бывает позитивной и негативной, а точное значение выпуклости для конкретных облигаций можно посмотреть на rusbonds. ru. В некоторых источниках выпуклость называют конвекцией.

На графике цена облигации C с негативной выпуклостью — желтая линия — при росте ставки меняется, а при падении ставки остается стабильной. Оценка таких облигаций с помощью дюрации дает очень большую погрешность из-за асимметрии между ценой и доходностью облигации. На графике асимметрия — это расстояние между пунктирной и сплошными линиями, которое увеличивается из-за выпуклости. Поэтому при больших изменениях процентной ставки используют выпуклость.

Профессиональные управляющие используют выпуклость для оценки инвестиционных портфелей. Частным инвесторам выпуклость может быть полезна, если дюрация облигаций одинаковая.

На рисунке дюрация двух облигаций с позитивной выпуклостью — красная и зеленая линии — одинаковая, но выпуклость облигации А больше, чем у облигации В. При падении ключевой ставки ЦБ цена облигации А вырастет больше, чем цена облигации В. При росте ключевой ставки ЦБ цена облигации А упадет меньше, чем цена облигации В. Таким образом, более выпуклая облигация А выгоднее для инвестора.

Как ставка ЦБ влияет на доходность облигаций?

Как применять дюрацию на практике

На практике с помощью модифицированной дюрации вычисляют, как изменится цена облигации при изменении рыночных процентных ставок.

Например, доходность облигации к погашению — 12%, а модифицированная дюрация — 3,469. Мы можем определить, как изменится цена облигации при росте рыночных ставок на 1%:

−3,469 × 0,01 / 1,12 = −0,031 = −3,1%

При росте ставок на 1% цена этой облигации снизится на 3,1%.

С помощью обычной дюрации инвесторы сравнивают похожие облигации и выбирают ту, у которой дюрация меньше. Так можно уменьшить процентный риск.

Например, у облигаций Мегафон БО-001Р-03 и МТС 001P-01 по 10 купонных периодов и одинаковый срок обращения — 1820 дней. Но у облигаций МТС купон равен 44,88 Р, а у облигаций «Мегафона» — 39,14 Р. Соответственно, дюрация у облигаций МТС — 836 дней, а у бумаг «Мегафона» — 1016. При других похожих параметрах инвестору безопаснее купить облигации с меньшей дюрацией.

Если инвестор полагает, что процентные ставки в экономике будут снижаться, разумно купить облигации с большим сроком погашения и, соответственно, большей дюрацией. Цена таких облигаций вырастет, а кроме того, по ним по-прежнему будут выплачиваться более высокие купоны, чем по новым облигациям.

Напротив, если ожидается повышение процентных ставок, облигации с меньшей дюрацией могут оказаться более подходящими, так как их цена снизится в меньшей степени.

Использование дюрации для оценки риска облигаций. Чтобы уменьшить процентный риск, инвестор выбирает облигации с низкой дюрацией или формирует портфель с заданной дюрацией.

Например, инвестор хочет составить портфель из двух видов облигаций — с дюрациями 3,4 и 5,6 года — и застраховаться от риска изменения процентных ставок на 5 лет. Инвестор не может повлиять на изменение рыночных процентных ставок, но на время дюрации он получает гарантированный купонный доход. Если рыночные ставки растут, то цена облигаций падает. Инвестор реинвестирует купоны под более высокий процент и этим компенсирует падение цены облигации. Таким образом, для страхования риска инвестор должен составить портфель с дюрацией 5 лет и определить доли облигаций.

Доля облигаций А + Доля облигаций В = 100%

Дюрация портфеля = Доля А × 3,4 + Доля В × 5,6 = 5 лет

Доля облигаций А = 27%

Доля облигаций В = 73%

Эта техника называется иммунизацией портфеля, и она работает для небольших изменений процентных ставок.

– Онлайн-калькулятор процентного изменения

Percent Change Calculator – это онлайн-инструмент, который помогает рассчитать процент увеличения или уменьшения в процентах от одного числа к другому.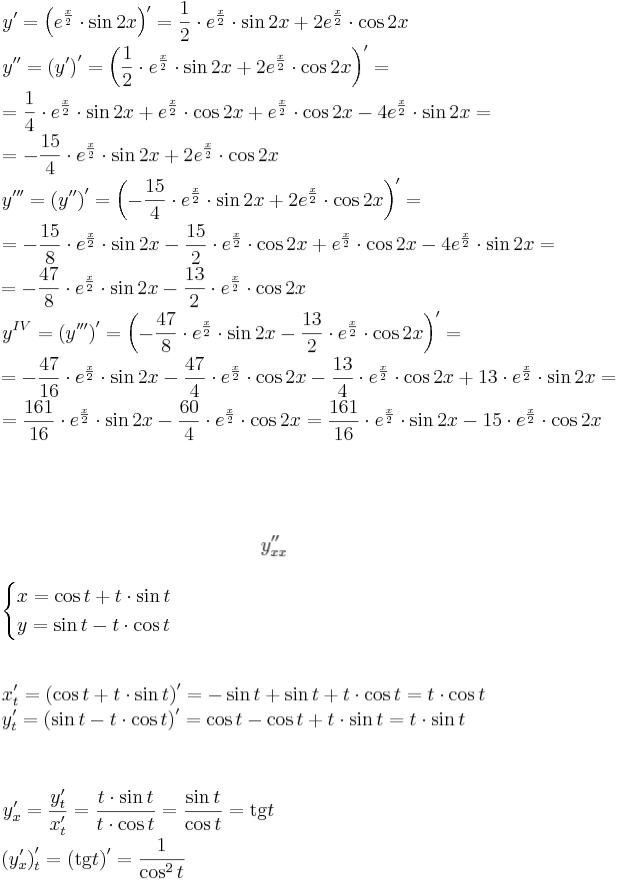 Процентное изменение используется для обозначения степени изменения, проявляемого величиной за период времени.

Что такое калькулятор процентного изменения?

помогает вычислить процентное изменение одного числа на другое. Он используется для расчета степени увеличения или уменьшения количества за определенный период времени.Для использования калькулятора процентного изменения введите значения в указанные поля ввода.

Калькулятор процентного изменения

Как пользоваться калькулятором процентного изменения?

Следуйте инструкциям ниже, чтобы найти процентное изменение с помощью калькулятора процентного изменения:

• Шаг 1 : Зайдите в онлайн-калькулятор процентного изменения Cuemath.
• Шаг 2: Введите начальное и конечное значения в поля ввода.
• Шаг 3 : Щелкните « Calculate », чтобы найти процентное изменение.
• Шаг 4 : Щелкните « Reset », чтобы очистить поля и ввести новые значения.

Как работает калькулятор процентного изменения?

Процентное изменение можно применить к любому количеству. Процентное изменение может быть как положительным, так и отрицательным значением. Положительное значение указывает на то, что количество увеличилось с течением времени.Точно так же отрицательное значение показывает, что количество уменьшилось за данный период времени. Концепция процентного изменения широко используется в сфере финансов. Банки используют процентное изменение для отслеживания цены ценной бумаги. Кроме того, процентное изменение также используется для сравнения цен различных валют. Шаги для расчета процентного изменения между старым значением и новым значением следующие:

1. Вычтите начальное значение количества из его окончательного значения.
2. Разделите значение, полученное на шаге 1, на начальное значение.
3. Умножьте результат на 100, чтобы получить процентное изменение.

Процентное изменение рассчитывается по формуле:

Процентное изменение = ((Конечное значение – Начальное значение) / начальное значение) × 100

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенных примеров по процентному изменению

Пример 1: Найдите процентное изменение, если 70 увеличится до 150, и проверьте его с помощью калькулятора процентов.

Решение:

Дано: начальное значение = 70, конечное значение = 150

Процентное изменение = ((Конечное значение – Начальное значение) / начальное значение) × 100

= ((150 – 70) / 70) × 100

= (80/70) × 100

= 1,142 × 100%

= 114,28%

Поскольку ответ положительный, это процентное увеличение.

Пример 2: Найдите процентное изменение, если количество идет от 90 до 20, и проверьте его с помощью калькулятора процентов.

Решение:

Дано: начальное значение = 90, конечное значение = 20

Процентное изменение = ((Конечное значение – Начальное значение) / начальное значение) × 100

= ((20 – 90) / 90) × 100

= (-70 / 90) × 100

= -0,7778 × 100

= -77,78%

Поскольку ответ отрицательный, это процентное уменьшение.

Точно так же вы можете попробовать калькулятор процентного изменения, чтобы найти процентное изменение для следующих значений.

• Начальное значение = 180, Конечное значение = 250
• Начальное значение = 120, Конечное значение = 100

☛ Математические калькуляторы:

в App Store

дает пошаговую помощь по поиску производных. Калькулятор производной функции для решения ваших производных уравнений.

Используйте это приложение калькулятора предельной производной для точного вычисления производной функции.

Дифференциация включает в себя скорость изменения функции по отношению к определенной переменной. С учетом простого в использовании калькулятора дифференцирования для правильного дифференцирования функции.

Пример:

Предположим, что машина движется с определенной скоростью относительно времени и внезапно меняет ее. Это изменение является ускорением и действует как производная функции скорости по времени. Наш онлайн-инструмент для поиска производных немедленно обнаруживает такие мгновенные изменения и отображает результаты на вашем экране.

Геометрическая интерпретация производной:

В геометрии дифференциация относится к наклону линии. Эта конкретная прямая лежит на касательной к кривой. Вы можете легко ввести функцию линии в этом калькуляторе производных.

Как вычислить производную сложных функций:

Этот калькулятор d / dx дает вам возможность мгновенно определять вариации сложных функций. Фактически, вы также можете рассчитать производную шаг за шагом в любой определенный момент с помощью онлайн-калькулятора производных финансовых инструментов.

Как работает калькулятор производной исчисления?

Введите функцию в строке меню
Выберите переменную4, по которой вы хотите определить производную данной функции
Выберите количество повторений до уровня 5
Нажмите кнопку «Рассчитать»

Особенности онлайн-калькулятора дифференциала:

Удобный интерфейс
Расширенная клавиатура для ввода тригонометрических и логарифмических функций
Доступна как в режиме онлайн, так и в автономном режиме
100% абсолютные результаты
Бесплатно загружаемый PDF-файл окончательных результатов с подробными пошаговыми инструкциями
Пошаговые вычисления
Простота использования

Так что возьмите этот бесплатный калькулятор производных и сразу же определите отклонения более простых или даже сложных функций.

, онлайн-калькулятор и формула

Онлайн калькулятор для вычисления производной сигмовидной функции

Вычислить производную сигмовидной функции

На этой странице рассчитывается производная сигмовидной функции. Эта производная сигмовидной функции является первой производной сигмовидной функции. который описан в формуле ниже.

Кривая производной сигмовидной функции

Формулы производной сигмоидной функции

Эта производная сигмовидной функции является первой производной сигмовидной функции, который описывается следующими уравнениями. Производная сигмовидная функция используется как функция активации в нейронных сетях.

Расчет числовой производной с помощью научного калькулятора TI-36X Pro

Управление настройками файлов cookie

Вы можете управлять своими предпочтениями в отношении того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.

Категория	Описание	Разрешить
Аналитические и рабочие файлы cookie	Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте).
Рекламные и маркетинговые файлы cookie	Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей.Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы.
Функциональные файлы cookie	Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, в том числе более персонализированный и релевантный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.
Файлы cookie социальных сетей	Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей.
Строго необходимо	Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на сайте TI. com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie).	Всегда на связи

Калькулятор производных – (Обновлено для 2021-2022) | CoolGyan.Org

Калькулятор производной – это бесплатный онлайн-инструмент, который отображает производную заданной функции. Онлайн-калькулятор производных от CoolGyan ускоряет вычисления и показывает производные функции первого, второго и третьего порядка за доли секунды.

Как пользоваться калькулятором производной?

Процедура использования калькулятора производной выглядит следующим образом:

Шаг 1: Введите функцию в соответствующее поле ввода и выберите порядок производной

Шаг 2: Теперь нажмите кнопку «Рассчитать», чтобы получить производная

Шаг 3: Производная данной функции будет отображаться в новом окне

Что такое производная функции?

В исчислении одним из основных понятий является производная функции. Он занимает центральное место в математическом анализе. Мы знаем, что дифференциация и интеграция – два важных понятия. Дифференциация – это процесс нахождения производной функции, тогда как интегрирование – это процесс нахождения первообразной функции. Производная функции описывает скорость изменения. Это означает, что он показывает величину, на которую функция изменяется в данной точке.

Стандартная форма

Стандартная форма для представления производной функции приведена ниже:

Бесконечно малое изменение переменной «x» обозначается dx.Таким образом, производная переменной «y» по отношению к переменной «x» равна dy / dx .

Часто задаваемые вопросы о калькуляторе производной

Что такое производная от нуля?

В исчислении дифференцирование – это процесс нахождения производной функции. Мы знаем, что дифференциация любого постоянного значения равна нулю. Таким образом, производная 0 равна 0.

Какие существуют различные методы нахождения производных?

Существуют следующие различные методы поиска производной функции:

• Расчет производной по определению
• Правило продукта
• Правило цепочки
• Неявная дифференциация
• Правило частного

Определите первый и второй порядок производная.