1.7. Криволинейное движение. Тангенциальное и нормальное ускорения
При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней. Допустим, что в т.М траектории скорость была , а в т.М1 стала . При этом считаем, что промежуток времени при переходе точки на пути из М в М1 настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Для того, чтобы найти вектор изменения скорости , необходимо определить векторную разность:
Для этого перенесем параллельно самому себе, совмещая его начало с точкой М. Разность двух векторов равна вектору, соединяющему их концы равна стороне АС МАС, построенного на векторах скоростей, как на сторонах. Разложим вектор на две составляющих АВ и АД, и обе соответственно через и . Таким образом вектор изменения скорости равен векторной сумме двух векторов:
По определению:
(1. 15) 15) |
Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.
Следовательно
| (1.16) |
Нормальное ускорение характеризует быстроту изменения скорости по направлению. Вычислим вектор:
Для этого проведем перпендикуляр через точки М и М1 к касательным к траектории (рис. 1.4) Точку пересечения обозначим через О. При достаточно малом участок криволинейной траектории можно считать частью окружности радиуса R. Треугольники МОМ1 и МВС подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах. Поэтому:
или
Но , тогда:
Переходя к пределу при и учитывая, что при этом , находим:
,
(1. 17) 17) |
Так как при угол , направление этого ускорения совпадает с направлением нормали к скорости , т.е. вектор ускорения перпендикулярен . Поэтому это ускорение часто называют центростремительным.
Полное ускорение определяется векторной суммой тангенциального нормального ускорений (1.15). Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:
| (1.18) |
Направление полного ускорения определяется углом между векторам и :
Направление вектора тангенциального ускорения. Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рисунок 1 – Тангенциальное ускорение
Направление вектора тангенциального ускорения совпадает с направлением линейной скорости или противоположно ему, из рис. 1. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
1. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения, показано на рис. 1. Нормальное ускорение характеризует изменение скорости по направлению и обозначается n . Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(9)
(10)
Направление полного ускорения также определяется правилом сложения векторов:
(11)
1.1.5 Поступательное и вращательное движение абсолютно твёрдого тела
Движение тела считается поступательным , если любой отрезок прямой линии, жестко связанный с телом, всё время перемещается параллельно самому себе.
Вращение твёрдого тела вокруг неподвижной оси – движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая является осью вращения.
При вращении тела радиус окружности, описываемой точкой этого тела, повернётся за интервал времени на некоторый угол. Вследствие неизменности взаимного расположения точек тела на такой же угол повернуться за тоже время радиусы окружностей, описываемых любыми другими точками тела. Этот угол является величиной, характеризующей вращательное движение всего тела в целом. Отсюда можно сделать вывод, что для описания вращательного движения абсолютно твёрдого тела вокруг неподвижной оси надо знать только одну переменную – угол, на который повернётся тело за определённое время.
Связь между линейной и угловой скоростями для каждой точки твёрдого тела даётся формулой:
(12)
Изучение физики начинают с рассмотрения механического движения. В общем случае тела движутся по кривым траекториям с переменными скоростями. Для их описания используют понятие ускорения. В данной статье рассмотрим, что такое тангенциальное и нормальное ускорение.
Кинематические величины. Скорость и ускорение в физике
Кинематика механического движения – это раздел физики, который занимается изучением и описанием перемещения тел в пространстве. Кинематика оперирует тремя главными величинами:
- пройденный путь;
- скорость;
- ускорение.
В случае движения по окружности используют аналогичные кинематические характеристики, которые приведены к центральному углу окружности.
С понятием скорости знаком каждый. Она показывает быстроту изменения координат тел, находящихся в движении. Скорость всегда направлена по касательной к линии, вдоль которой тело перемещается (траектории).
Ускорение – это скорость изменения величин v¯ и ω¯. Ускорение – это тоже однако ее направление совершенно не зависит от вектора скорости. Ускорение всегда направлено в сторону действующей на тело силы, которая вызывает изменение вектора скорости. Ускорение для любого типа движения можно рассчитать по формуле:
Чем сильнее изменится скорость за интервал времени dt, тем больше будет ускорение.
Касательное и нормальное ускорение
Предположим, что материальная точка движется по некоторой кривой линии. Известно, что в некоторый момент времени t ее скорость была равна v¯. Поскольку скорость – это касательный к траектории вектор, ее можно представить в следующем виде:
Здесь v – длина вектора v¯, а u t ¯ – единичный вектор скорости.
Чтобы вычислить вектор полного ускорения в момент времени t, необходимо найти производную скорости по времени. Имеем:
a¯ = dv¯ / dt = d (v × u t ¯) / dt
Поскольку модуль скорости и единичный вектор изменяются со временем, то, пользуясь правилом нахождения производной от произведения функций, получаем:
a¯ = dv / dt × u t ¯ + d (u t ¯) / dt × v
Первое слагаемое в формуле называется тангенциальной, или касательной компонентой ускорения, второе слагаемое – это нормальное ускорение.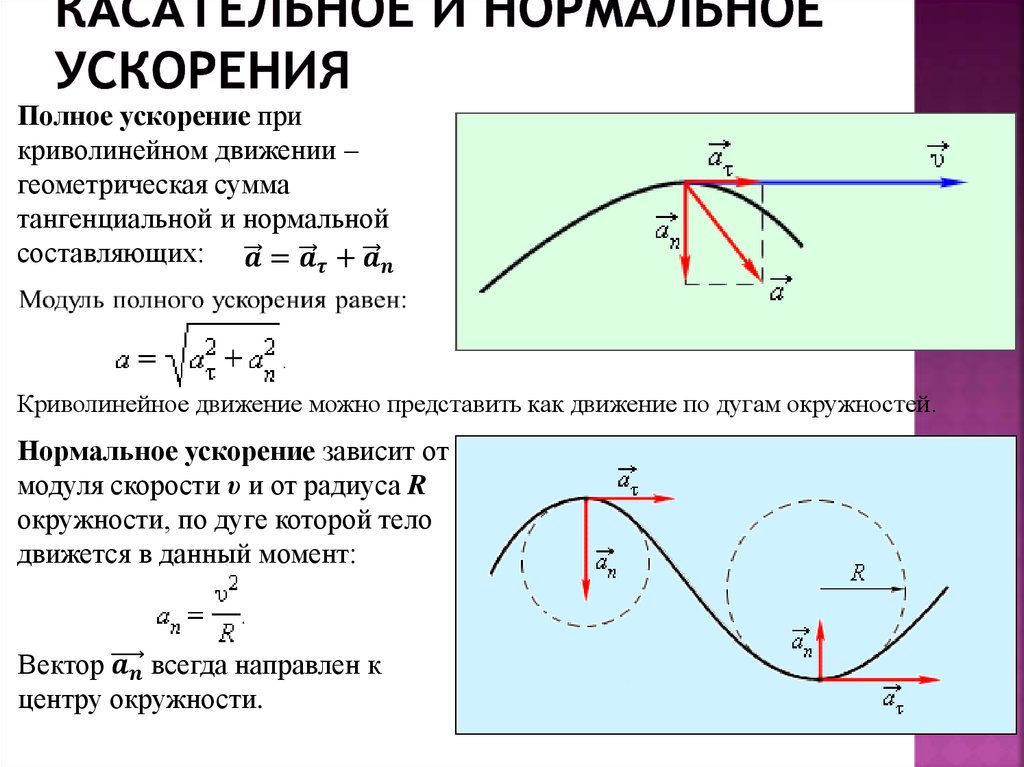
Касательное ускорение
Еще раз запишем формулу для вычисления касательного ускорения:
a t ¯ = dv / dt × u t ¯
Это равенство означает, что тангенциальное (касательное) ускорение направлено так же, как вектор скорости в любой точке траектории. Оно численно определяет изменение модуля скорости. Например, в случае прямолинейного движения состоит только из касательной составляющей. Нормальное ускорение при таком типе перемещения равно нулю.
Причиной появления величины a t ¯ является воздействие внешней силы на движущееся тело.
В случае вращения с постоянным угловым ускорением α тангенциальная составляющая ускорения может быть вычислена по следующей формуле:
Здесь r – это радиус вращения рассматриваемой материальной точки, для которой вычисляется величина a t .
Нормальное или центростремительное ускорение
Теперь выпишем еще раз вторую компоненту полного ускорения:
a c ¯ = d (u t ¯) / dt × v
Из геометрических соображений можно показать, что производная единичного касательного к траектории вектора по времени равна отношению модуля скорости v к радиусу r в момент времени t.
Эта формула нормального ускорения свидетельствует, что оно, в отличие от касательной компоненты, не зависит от изменения скорости, а определяется квадратом модуля самой скорости. Также a c возрастает с уменьшением радиуса вращения при постоянной величине v.
Нормальное ускорение называют центростремительным потому, что оно направлено от центра масс вращающегося тела к оси вращения.
Причиной появления этого ускорения является центральная компонента воздействующей на тело силы. Например, в случае вращения планет вокруг нашего Солнца центростремительной силой является гравитационное притяжение.
Нормальное ускорение тела изменяет только направление скорости. Оно не способно изменить ее модуль. Этот факт является важным его отличием от касательной компоненты полного ускорения.
Поскольку центростремительное ускорение возникает всегда, когда вектор скорости поворачивается, то оно существует также в случае равномерного вращения по окружности, при котором тангенциальное ускорение равно нулю.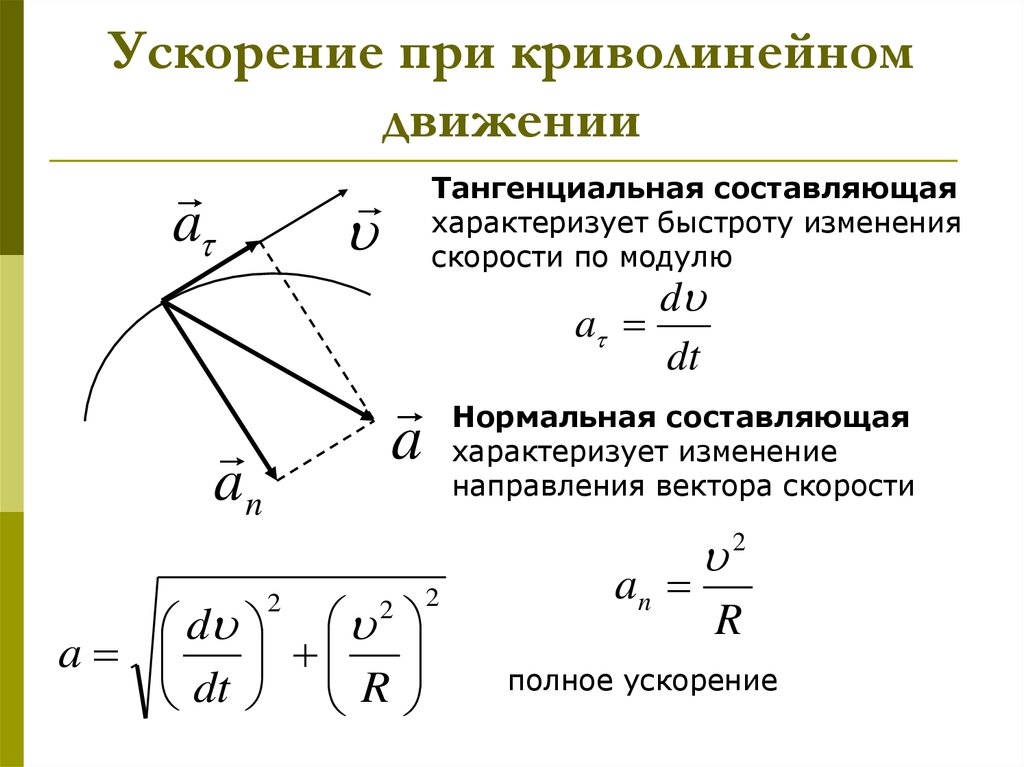
На практике ощутить на себе влияние нормального ускорения можно, если находиться в машине, когда она совершает затяжной поворот. В этом случае пассажиров прижимает к противоположной направлению поворота двери автомобиля. Это явление – результат действия двух сил: центробежной (смещение пассажиров со своих мест) и центростремительной (давление на пассажиров со стороны двери автомобиля).
Модуль и направление полного ускорения
Итак, мы выяснили, что тангенциальная компонента рассматриваемой физической величины направлена по касательной к траектории движения. В свою очередь, нормальная компонента перпендикулярна траектории в данной точке. Это означает, что две компоненты ускорения перпендикулярны друг другу. Их векторное сложение дает вектор полного ускорения. Вычислить его модуль можно по следующей формуле:
a = √(a t 2 + a c 2)
Направление вектора a¯ можно определить как относительно вектора a t ¯, так и относительно a c ¯.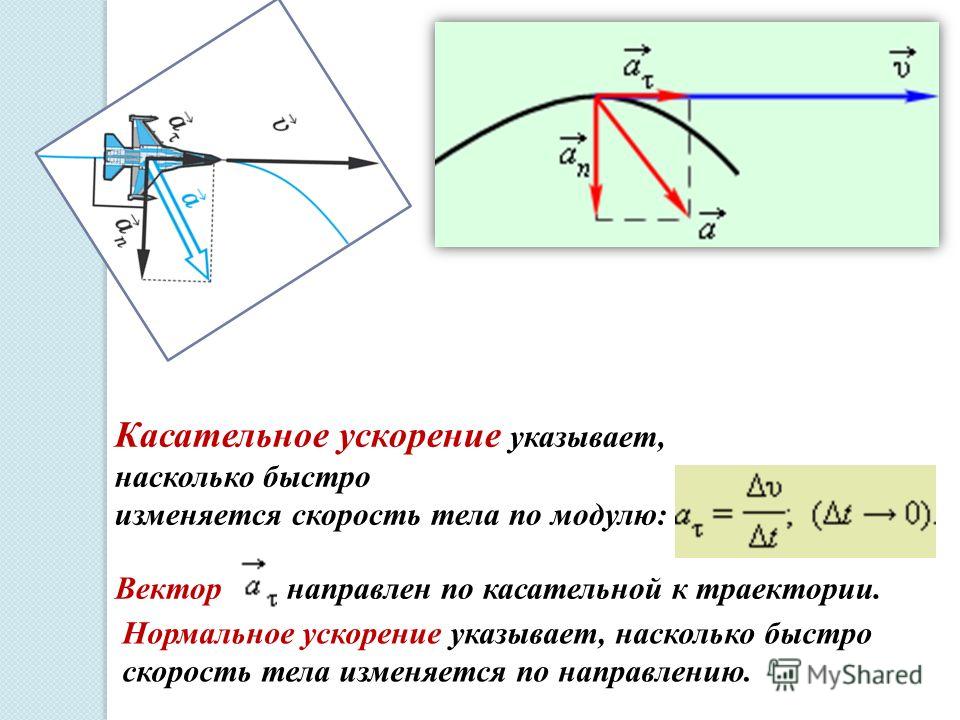 Для этого следует использовать соответствующую тригонометрическую функцию. Например, угол между полным и нормальным ускорениями равен:
Для этого следует использовать соответствующую тригонометрическую функцию. Например, угол между полным и нормальным ускорениями равен:
Решение задачи на определение центростремительного ускорения
Колесо, которое имеет радиус 20 см, раскручивается с угловым ускорением 5 рад/с 2 в течение 10 секунд. Необходимо определить нормальное ускорение точек, находящихся на периферии колеса, через указанное время.
Для решения задачи воспользуемся формулой связи между тангенциальным и угловым ускорениями. Получаем:
Поскольку равноускоренное движение длилось в течение времени t = 10 секунд, то приобретенная за это время линейная скорость была равна:
v = a t × t = α × r × t
Полученную формулу подставляем в соответствующее выражение для нормального ускорения:
a c = v 2 / r = α 2 × t 2 × r
Остается подставить известные значения в это равенство и записать ответ: a c = 500 м/с 2 .
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением ).
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения – быстроту изменения скорости по направлению (направлена к центру кривизны траектории).
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1) , а n = 0 – прямолинейное равномерное движение;
2) , а n = 0 – прямолинейное равнопеременное движение. При таком виде движения
Если начальный момент времени t 1 =0, а начальная скорость v 1 =v 0 , то, обозначив t 2 =t и v 2 =v, получим , откуда
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения
· 3) , а n = 0- прямолинейное движение с переменным ускорением;
· 4) , а n = const. При скорость по модулю не изменяется, а изменяется по направлению. Из формулы a n =v 2 /r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;
При скорость по модулю не изменяется, а изменяется по направлению. Из формулы a n =v 2 /r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;
· 5) , – равномерное криволинейное движение;
· 6) , – криволинейное равнопеременное движение;
· 7) , – криволинейное движение с переменным ускорением.
2) Твёрдое тело, движущееся в трёхмерном пространстве, максимально может иметь шесть степеней свободы: три поступательных и три вращательных
Элементарное угловое перемещение – это вектор, направленный вдоль оси по правилу правого винта и численно равный углу
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Единица – радиан в секунду (рад/с).
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.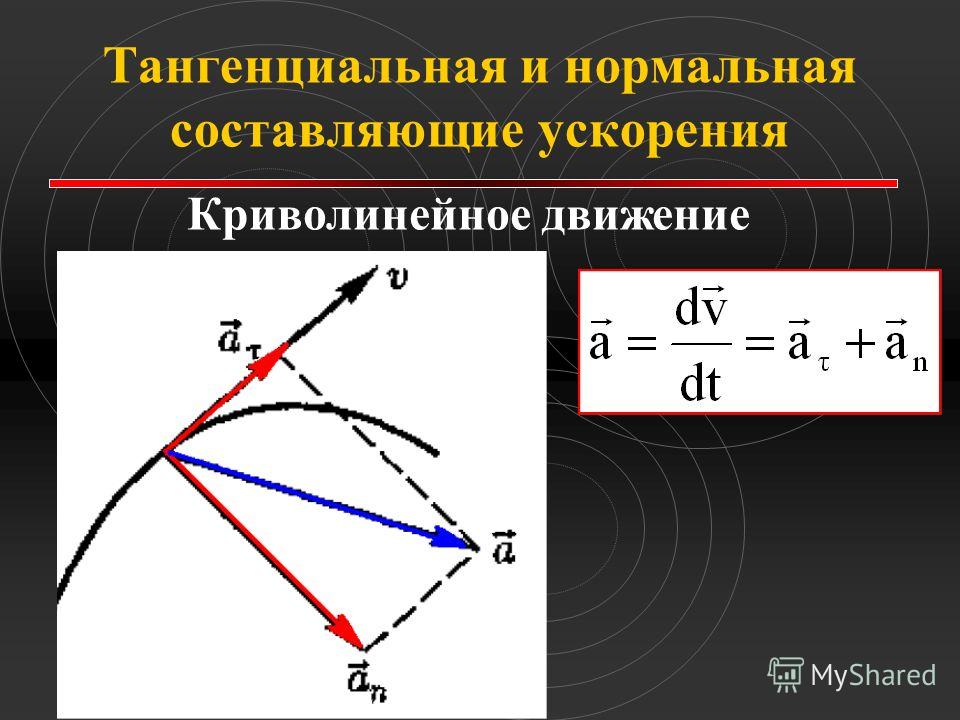 При ускоренном движении вектор сонаправлен вектору (рис.8), при замедленном – противонаправлен ему (рис.9).
При ускоренном движении вектор сонаправлен вектору (рис.8), при замедленном – противонаправлен ему (рис.9).
Тангенциальная составляющая ускорения
Нормальная составляющая ускорения
При движении точки по кривой линейная скорость направлена
по касательной к кривой и по модулю равна произведению
угловой скорости на радиус кривизны кривой.(связь)
3) Первый закон Ньютона : всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние . Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью . Поэтому первый закон Ньютона называют также законом инерции .
Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета . Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета.
Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета.
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.
Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса ) и гравитационные (гравитационная масса ) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10 –12 их значения).
Итак, сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.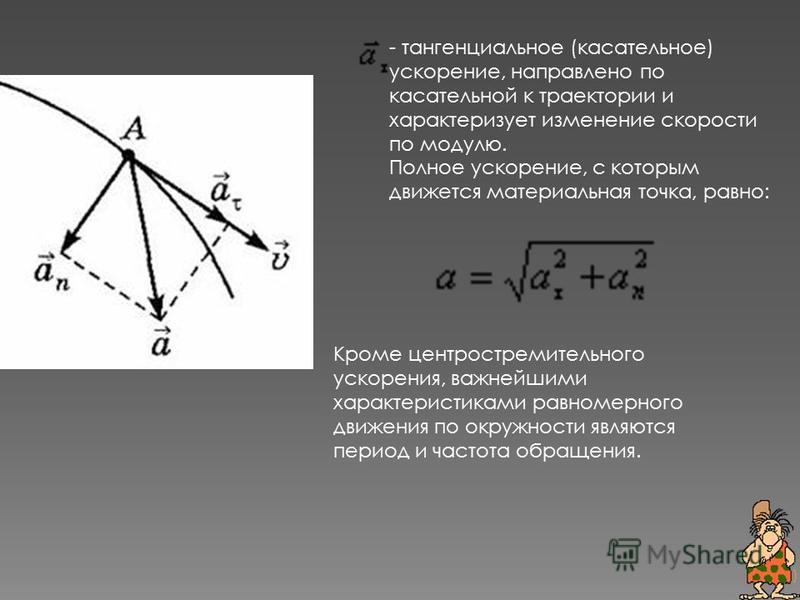
Векторная величина
численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.
Подставляя (6.6) в (6.5), получим
Это выражение – более общая формулировка второго закона Ньютона : скорость изменения импульса материальной точки равна действующей на нее силе. Выражение называется уравнением движения материальной точки .
Третий закон Ньютона
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона : всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
F 12 = – F 21 , (7.1)
где F 12 – сила, действующая на первую материальную точку со стороны второй;
F 21 – сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Си́ла упру́гости – сила, возникающая при деформации тела и противодействующая этой деформации.
В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности.
Вектор силы противоположен направлению деформации тела (смещению его молекул).
Закон Гука
В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид: где k – жёсткость тела, x – величина деформации.
СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Направление силы тяжести – вертикаль в данной точке земной поверхности.
существованием силы трения , которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел.
Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения , качения или верчения .
Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг друга и разделены прослойкой вязкой жидкости (смазки), то трение происходит в слое смазки. В таком случае говорят о гидродинамическом трении (слой смазки достаточно толстый) и граничном трении (толщина смазочной прослойки »0,1 мкм и меньше).
В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг друга и разделены прослойкой вязкой жидкости (смазки), то трение происходит в слое смазки. В таком случае говорят о гидродинамическом трении (слой смазки достаточно толстый) и граничном трении (толщина смазочной прослойки »0,1 мкм и меньше).
опытным путем установили следующий закон : сила трения скольжения F тр пропорциональна силе N нормального давления, с которой одно тело действует на другое:
F тр = f N ,
где f – коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.
f = tga 0 .
Таким образом, коэффициент трения равен тангенсу угла a 0 , при котором начинается скольжение тела по наклонной плоскости.
Для гладких поверхностей определенную роль начинает играть межмолекулярное притяжение. Для них применяется закон трения скольжения
F тр = f ист (N + Sp 0) ,
где р 0 – добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S – площадь контакта между телами; f ист – истинный коэффициент трения скольжения.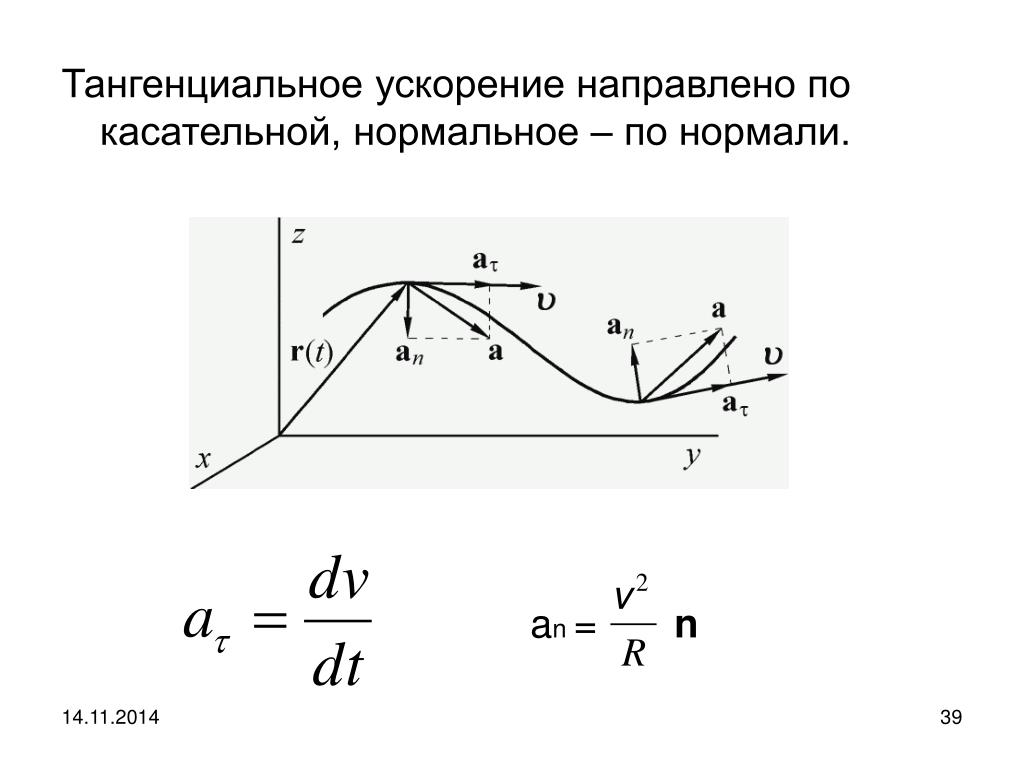
Сила трения качения определяется по закону, установленному Кулоном:
F тр =f к N/r , (8.1)
где r – радиус катящегося тела; f к – коэффициент трения качения, имеющий размерность dim f к =L. Из (8.1) следует, что сила трения качения обратно пропорциональна радиусу катящегося тела.
Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями.
где – импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
Последнее выражение и является законом сохранения импульса : импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Центром масс (или центром инерции ) системы материальных точек называется воображаемая точка С ,положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
где m i и r i – соответственно масса и радиус-вектор i -й материальной точки; n – число материальных точек в системе; – масса системы. Скорость центра масс
Скорость центра масс
Учитывая, что pi = m i v i , a есть импульс р системы, можно написать
т. е. импульс системы равен произведению массы системы на скорость ее центра масс.
Подставив выражение (9.2) в уравнение (9.1), получим
т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Выражение (9.3) представляет собойзакон движения центра масс.
В соответствии с (9.2) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
5) Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r , проведенного из точки О в точку А приложения силы, на силу F (рис. 25):
25):
Здесь М – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
где a- угол между r и F; r sina = l – кратчайшее расстояние между линией действия силы и точкой О – плечо силы.
Моментом силы относительно неподвижной оси z называется скалярная величина M z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента М z не зависит от выбора положения точки О на оси z.
Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
Используя выражение (17.1), получаем
где J z – момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
Таким образом, кинетическая энергия вращающегося тела
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv 2 /2), следует, что момент инерции – мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где m – масса катящегося тела; v c – скорость центра масс тела; Jc – момент инерции тела относительно оси, проходящей через его центр масс; w – угловая скорость тела.
6) Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы . Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол с направлением перемещения, то работа этой силы равна произведению проекции силы F s на направление перемещения (F s = F cos), умноженной на перемещение точки приложения силы:
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11. 1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения – прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина
1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения – прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина
где – угол между векторами F и dr; ds = |dr| – элементарный путь; F s – проекция вектора F на вектор dr (рис. 13).
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности :
За время dt силаF совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N – величина скалярная.
Единица мощности –ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
Кинетическая энергия механической системы – это энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.
Используя второй закон Ньютона и умножая на перемещение dr получаем
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными , а силы, действующие в них, – консервативными . Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной ; ее примером является сила трения.
Такие поля называются потенциальными , а силы, действующие в них, – консервативными . Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной ; ее примером является сила трения.
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна
где высота h отсчитывается от нулевого уровня, для которого П 0 =0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h” ), П= -mgh”.
Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:
где F x уп p – проекция силы упругости на ось х ; k – коэффициент упругости (для пружины – жесткость ), а знак минус указывает, что F x уп p направлена в сторону, противоположную деформации x .
По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.
Элементарная работа dA, совершаемая силой F x при бесконечно малой деформации dx, равна
а полная работа
идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
При переходе системы из состояния 1 в какое-либо состояние 2
т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (13.2) следует, что
е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (13.2) следует, что
d (T +П) = 0,
т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохранение механической энергии : в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.
Понятие о скорости
Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:
Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:
Вам будет интересно:
Здесь l¯ – является вектором перемещения. Иными словами, скорость – это производная по времени от пройденного пути.
Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.
Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.
Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.
Понятие об ускорении
В отличие от скорости, которая характеризует быстроту прохождения телом траектории, ускорение – это величина, описывающая быстроту изменения скорости, что математически записывается так:
Как и скорость, ускорение – это векторная характеристика. Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.
Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.
Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.
Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:
Эта формула является прямым следствием из второго закона Ньютона.
Полное, нормальное и тангенциальное ускорения
Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:
Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.
Второе слагаемое – это нормальное ускорение. Оно количественно описывает изменение вектора скорости, не принимая во внимание изменение ее модуля.
Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:
a = √(at2 + an2).
Связь тангенциального ускорения и скорости
Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:
В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.
Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:
Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:
at = dv/dt = 9*t2 + 4.
Скорость и нормальное ускорение
Запишем в явном виде формулу для нормальной компоненты an, имеем:
an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯
Где re¯ – единичной длины вектор, который к центру кривизны траектории направлен. Это выражение устанавливает связь тангенциальной скорости и нормального ускорения.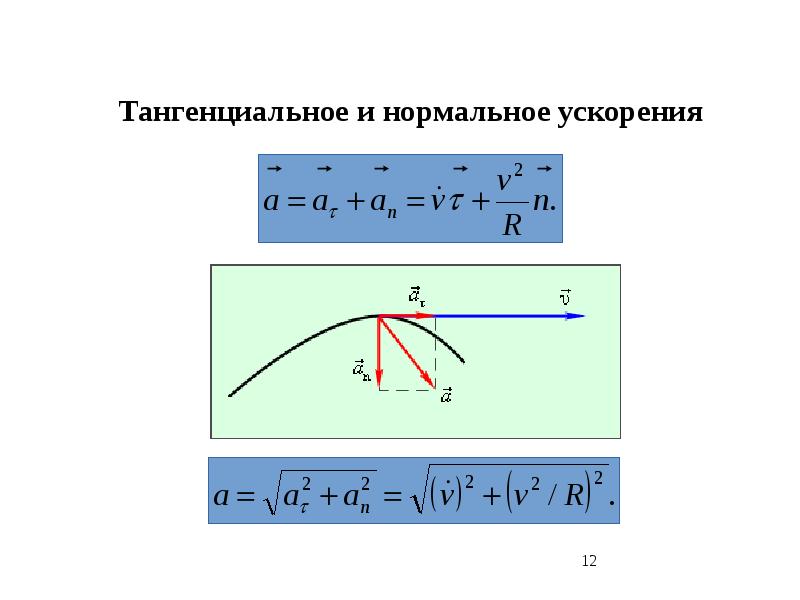 Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.
Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2).
Траектория движения и компоненты полного ускорения
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь u t ¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
a¯ = dv¯/dt = dv/dt*u t ¯ + v*d(u t ¯)/dt
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины a t ¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор u t ¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Запишем формулу для нее:
a n ¯ = v*d(u t ¯)/dt = v*d(u t ¯)/dL*dL/dt
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина a n ¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор a n ¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
a = √(a t 2 + a n 2)
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и a n ¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
a t = dv/dt = 4*t + 3 = 19 м/с 2
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
v = 2*4 2 + 3*4 = 44 м/с
Теперь можно воспользоваться формулой для a n:
a n = v 2 /r = 44 2 /1 = 1936 м/с 2
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
Касательное и нормальное ускорения точки в теоретической механике
Касательное и нормальное ускорения точкиКасательное ускорение характеризует изменение в данное мгновение вектора скорости по величине, а нормальное — по направлению
Проекция ускорения на касательную и на нормальЕсли движение точки задано в векторной или в координатной форме, то часто встречается необходимость определить проекции ускорения на касательную и главную нормаль к траектории точки в том ‘ месте, где в данное мгновение находится точка (рис. 91, а).
91, а).
При естественной форме определения движения точки сначала определяют проекции ускорения на касательную и на нормаль, а затем уже по этим проекциям находят величину и направление полного ускорения точки.
Проекцию ускорения точки на касательную к ее траектории называют касательным ускорением, или тангенциальным ускорением (от латинского слова tangens—касающийся), и обозначают aN.
Проекцию ускорения на нормаль называют нормальным ускорением и обозначают ar.
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины. В таком случае над аr и aN ставят стрелку, указывающую на их векторный характер.
Разложение ускорения по касательной и нормали имеет физический смысл: касательная составляющая ускорения направлена по касательной (как и скорость), а потому не может повлиять на направление скорости, но влияет на ее величину; составляющая ускорения по нормали направлена перпендикулярно к скорости, а потому не может повлиять на величину скорости, но влияет на ее направление.
Касательное ускорение равно первой производной от величины скорости по времени:
Пусть точка M движется по траектории, расположенной в плоскости хОу.
Проведем касательную и нормаль к кривой в точке M (рис. 91, б), нанесем на чертеж вектор ускорения точки M и его составляющие и по координатным осям. Чтобы определить касательное ускорение, надо спроецировать на касательную вектор полного ускорения или найти алгебраическую сумму проекций на касательную составляющих и полного ускорения по осям координат. Воспользовавшись вторым из этих способов, спроецируем и на касательную:
Составляющие ускорения и направлены по координатным осям, а направление касательной совпадает с направлением скорости, поэтому косинусы углов а и β равны направляющим косинусам скорости:
(62′)
(62”)
Подставляя значения направляющих косинусов, получаем
По формуле (68) удобно вычислять касательное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).
Можно дать еще другой изящный вывод формулы (68) тангенциального ускорения, для чего спроецировать на касательную вектор полного ускорения, не раскладывая его предварительно по осям декартовых координат. В самом деле, тангенциальное ускорение равно проекции полного ускорения на касательную (рис. 91, а):
ar = a cos δ,
но угол δ, как внутренний угол треугольника, равен внешнему αа без другого внутреннего αυ, поэтому:
cos δ = cos (αа—aυ) = cos αа cos aυ + sin αа sin aυ
или, так как αа = 90°- βa и aυ = 90°-βυ,
cos δ = cos αа cos aυ + cos βa cos βυ .
Подставляя сюда вместо направляющих косинусов их выражения (67) n (62′), получим
Напомним, что в числителе этой формулы проекции имеют свой знак, а знаменатель определяется по (64), т.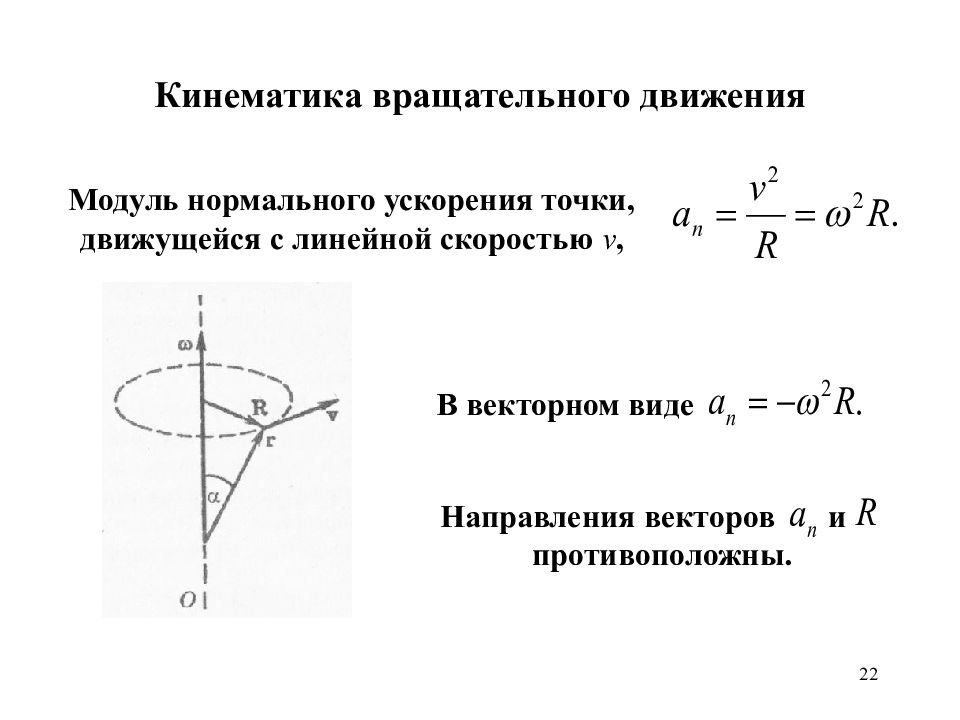 е. существенно положителен.
е. существенно положителен.
Задача №1
Движение точки задано в декартовых координатах уравнениями:
x=21,2 sin2 t, y=21,2 cos2 t
Определить касательное ускорение точки (см. задачу № 36, стр. 132).
Решение. Дифференцируя уравнения движения, найдем υx = 21,2 sin 2t, υy = -21,2 sin 2t. Определим теперь полную скорость:
Дифференцируя уравнения движения вторично, найдем
αx = 42,2 cos 2t, αy = -42,4 cos 2t.
Касательное ускорение определим по формуле (68):
Ответ. Касательное ускорение равно 60 cos 2t.
Задача №2
Точка M движется в системе координат хОу согласно уравнениям x=r cos πt, y=r sin πt. Найти касательное ускорение точки М.
Решение. Проекции скорости и ускорения на оси координат, а также и полная скорость точки M были уже нами получены при решении задачи № 44 (см. стр. 142). Для определения касательного ускорения точки M нам остается только подставить эти величины в формулу (68):
стр. 142). Для определения касательного ускорения точки M нам остается только подставить эти величины в формулу (68):
Ответ. Касательное ускорение равняется нулю.
Для случая задания движения в естественной форме преобразуем формулу (68) следующим образом:
и, сокращая на υ, найдем касательное ускорение
(69)
Принимая во внимание (53), можно придать этой формуле несколько иной вид:
(69′)
Итак, касательное ускорение—это проекция ускорения точки на касательную к траектории, равная первой производной от величины скорости по времени. Чтобы получить касательное ускорение в векторном выражении, нужно его умножить на единичный вектор касательной:
(69”)
Как уже было сказано, касательное ускорение не может изменить направления скорости, оно характеризует быстроту изменения величины скорости, т. е. соответствует изменению вектора скорости вдоль его направления.
Если с течением времени величина скорости увеличивается, то касательное ускорение направлено в ту же сторону, что и скорость. Такое движение называют ускоренным.
Такое движение называют ускоренным.
Если же величина скорости уменьшается, то касательное ускорение направлено в сторону, противоположную скорости. Такое движение называют замедленным.
Каждое из этих движений называют переменным движением.
Если величина скорости точки постоянна, то производная , а потому равно нулю и касательное ускорение. Движение точки с постоянной по величине скоростью по любой траектории называют равномерным. Следовательно, при равномерном движении точки касательное ускорение равно нулю.
Обратное заключение можно сделать лишь с некоторой оговоркой: если касательное ускорение постоянно равняется нулю, то, следовательно, величина скорости постоянна и движение равномерно; если же касательное ускорение точки равняется нулю не в течение всего рассматриваемого промежутка времени, а только в какое-то мгновение, то движение точки не является равномерным, и равенство означает, что в это мгновение величина скорости достигла экстремального (максимального или минимального) значения.
При равномерном движении точки по любой траектории
(70)
Формулы (70) справедливы только для равномерного движения точки и неприменимы при других движениях.
Равнопеременное движение точкиИз переменных движений точки в задачах наиболее часто встречается равнопеременное движение — такое движение, при котором касательное ускорение остается постоянным.
При равнопеременном движении точки по любой траектории
(71)
Формулы (71) справедливы только для равнопеременного движения и неприменимы при других движениях. Они даны здесь без вывода и известны из элементарной физики. Вывод этих формул приведен в решении задачи № 48.
Задача №3
Точка А начала двигаться с начальной скоростью υ0= 1 м/сек и с ускорением aT =2 м/сек2. Через одну секунду следом за точкой А по той же траектории с такой же начальной скоростью и с таким же касательным ускорением стала двигаться точка В. Определить расстояние (по траектории) между точками А и В через t сек после выхода первой точки. Построить графики движения точек.
Определить расстояние (по траектории) между точками А и В через t сек после выхода первой точки. Построить графики движения точек.
Решение. Определим сначала уравнение движения точек. Нам дано, что
Разделяя переменные и интегрируя, получим
υ = aTt + C1
Постоянную C1 определим из начальных данных:
υ0 = aT . 0 + C1; C1=υ0
Следовательно,
υ = υ0 + aTt.
Написав υ по (53), разделяя переменные и интегрируя, найдем
где
С2 = s0 = 0.
Подставляя вместо υ0 и аT заданные величины, найдем расстояние (в м), пройденное точкой А за время t:
В то же мгновение t расстояние, пройденное точкой В, будет меньше, так как точка В будет находиться в пути лишь t—1 сек. Для точки В
Для точки В
Расстояние между A и B найдем как разность пройденных ими путей:
Это расстояние растет пропорционально времени, хотя точка В во времени не отстает от точки А и каждую точку траектории проходит через 1 сек после того, как через нее прошла точка А.
Графики движения точек А и В изображаются одинаковыми параболами (рис. 92), но парабола, представляющая движение точки В, смещена по оси времени относительно параболы, представляющей движение точки А, на 1 сек вправо. Чтобы определить расстояние (в м) между А и В в какое-либо мгновение, надо восставить перпендикуляр к оси времени в точке, соответствующей этому мгновению, и измерить расстояние по вертикали между параболами. Чтобы определить интервал времени (в сек) между прохождениями точками А и В какой-либо точки К траектории, надо восставить перпендикуляр к оси расстояний в точке, соответствующей расстоянию точки К от начала отсчета, и измерить расстояние по горизонтали между параболами. Графики наглядно показывают, что точка В отстает от точки А по расстоянию, так как А В непрерывно увеличивается, но не отстает по времени, и точка В проходит каждый отрезок траектории за такое же время, как и точка А.
Рис. 92
Ответ. SA— SB = 2t м.
Нормальное ускорение равно отношению квадрата скорости точки к радиусу кривизны траектории:
Чтобы получить формулы нормального ускорения, мы опять воспользуемся тем, что проекция вектора на ось равна сумме проекций его составляющих на ту же ось, и определим aN как алгебраическую сумму проекций составляющих ax и ay на нормаль к траектории точки. Выберем за положительное направление нормали то, которое получается от поворота положительного направления касательной на прямой угол против хода часов (см. рис. 91) в сторону вогнутости кривой.
Как видно из чертежа (см. рис. 91, б)
aN = ay cos αυ—ax cos βυ.
Подставляем значения (62) направляющих косинусов:
(72)
По этой формуле удобно вычислять нормальное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).
Эту же формулу (72) можно получить, спроецировав полное ускорение а на нормаль Mn (рис. 91, а):
aN = a sin δ = a sin (αα—αυ)
или
aN=a (sinαα cos αυ -cos αα sin αυ).
Подставляя эти значения и сокращая на а, получим:
Задача №4
Движение точки задано уравнениями X= 21,2 sin2 t, у= 212 cos2 t. Определить нормальное ускорение точки.
Решение. Дифференцируя эти же уравнения движения при решении задачи № 36 (см. стр. 132), мы уже определили нужные нам величины: υx, υy, υ, ax, ау. Подставляя их в формулу (72), найдем
Ответ. Нормальное ускорение равно нулю.
Задача №5
Точка M движется согласно уравнениям x= r cos πt, y= r sin πt. Найти нормальное ускорение точки М.
Решение. Дифференцируя при решении задачи № 44 (см. стр. 142) эти уравнения движения, мы уже нашли проекции скорости и проекции ускорения. Полную скорость определим по ее проекциям согласно (64):
стр. 142) эти уравнения движения, мы уже нашли проекции скорости и проекции ускорения. Полную скорость определим по ее проекциям согласно (64):
Подставляя все эти величины в формулу (72), найдем
Ответ. Нормальное ускорение равно rπ2.
Чтобы преобразовать формулу (72) для случая, когда движение точки задано в естественной форме, припомним из курса высшей математики выражение кривизны плоской кривой, представленной в параметрической форме уравнениями (58′) и (58″),
Если параметр t означает время, то эту геометрическую формулу можно переписать в обозначениях кинематики:
(73)
Сравнивая равенства (72) и (73), находим
(74)
Мы получили положительное значение проекции, следовательно, нормальное ускорение направлено от точки M в положительном направлении оси Mn (см. рис. 91), т. е. в ту сторону от касательной, по которую лежит траектория точки.
Чтобы получить нормальное ускорение в векторном выражении, надо (74) умножить на единичный вектор нормали:
(74/)
Как уже было сказано, нормальное ускорение не влияет на величину скорости, потому что оно направлено перпендикулярно к скорости. Оно влияет на направление скорости.
Оно влияет на направление скорости.
Итак, нормальное ускорение—это проекция ускорения точки на нормаль к траектории, направленная в сторону вогнутости, равная квадрату скорости, деленному на радиус кривизны траектории.
Если движение точки прямолинейное, то радиус кривизны траектории (прямой линии) равен бесконечности, а нормальное ускорение равно нулю.
Обратное заключение можно сделать лишь с некоторой оговоркой: если в каждое мгновение данного промежутка времени нормальное ускорение движущейся точки равняется нулю, то точка движется по прямой; если же нормальное ускорение точки не постоянно равно нулю, а только в какое-либо мгновение, то движение точки не а потому
является прямолинейным и равенство означает, что в это мгновение положение точки совпадает с точкой перегиба траектории или же направление скорости меняется на обратное. На чертеже (рис. 93) изображено нормальное ускорение точки в различных местах траектории при равномерном движении.
Рис. 93
Величина ускорения точки равна квадратному корню из суммы квадратов касательного и нормального ускорений:
Если движение точки задано в естественной форме, то проекции ускорения на нормаль и на касательную можно определить по формулам (69) и (74) и по проекциям определить величину полного ускорения точки (см. рис. 91):
(75)
или
(75/)
Перед радикалом стоит знак « + », потому что величина ускорения существенно положительна.
Вектор полного ускорения направлен по диагонали прямоугольника, построенного на векторах касательного и нормального ускорений. Можно точно установить направление ускорения по тангенсу угла, составляемого им с нормалью к траектории:
Касательное ускорение направлено по касательной к траектории, а нормальное к центру кривизны траектории, поэтому вектор полного ускорения лежит с той стороны от касательной, с которой расположена траектория точки.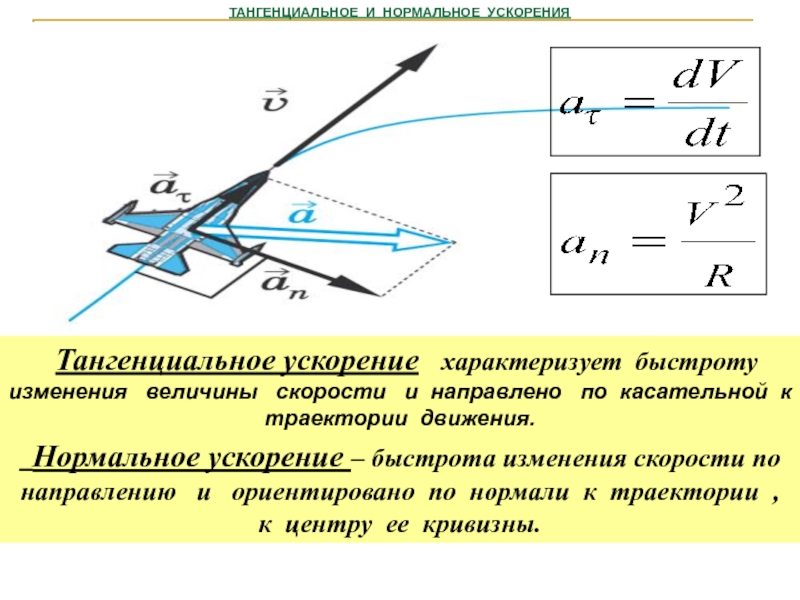
При криволинейном ускоренном движений точки полное ускорение составляет со скоростью острый угол, а при замедленном—тупой.
Вектор ускорения лежит в соприкасающейся плоскости, и проекция ускорения на бинормаль равна нулю:
Разложение ускорения при движении точки по кривой двоякой кривизны. Если кривая не лежит в одной плоскости, то ее называют пространственной кривой, или кривой двоякой кривизны. В каждой точке к кривой можно провести только одну касательную и бесчисленное множество нормалей, расположенных в плоскости, перпендикулярной к касательной и называемой нормальной плоскостью (рис. 94).
рис. 94
Пусть в мгновение t точка занимает на кривой двоякой кривизны положение М. В это мгновение скорость точки направлена по касательной к кривой в точке М. Через эту касательную и через близкую точку M1 (не показанную на чертеже)., в которую движущаяся точка придет в мгновение t + Δt, проведем плоскость и будем стремить Δt к нулю. Тогда точка M1 будет стремиться к точке М. При этом плоскость будет поворачиваться около касательной, проведенной в точке М и стремиться к некоторому определенному положению, в котором она называется соприкасающейся плоскостью. Следовательно, в соприкасающейся плоскости находится вектор скорости движущейся точки в то мгновение, когда эта точка совпадает с точкой М, а также когда она занимает положение, предельно близкое к точке M. А так как ускорение характеризует изменение скорости в данное мгновение, то вектор ускорения тоже находится в соприкасающейся плоскости.
Тогда точка M1 будет стремиться к точке М. При этом плоскость будет поворачиваться около касательной, проведенной в точке М и стремиться к некоторому определенному положению, в котором она называется соприкасающейся плоскостью. Следовательно, в соприкасающейся плоскости находится вектор скорости движущейся точки в то мгновение, когда эта точка совпадает с точкой М, а также когда она занимает положение, предельно близкое к точке M. А так как ускорение характеризует изменение скорости в данное мгновение, то вектор ускорения тоже находится в соприкасающейся плоскости.
Плоскость, проведенную через точку M перпендикулярно к соприкасающейся и к нормальной плоскостям, называют спрямляющей плоскостью.
Нормаль, лежащую в спрямляющей плоскости, называют бинормалью, а нормаль, лежащую в соприкасающейся плоскости,—главной нормалью (главную нормаль плоской кривой обычно называют просто нормалью).
Касательная Mτ главная нормаль Mn и бинормаль Mb пересекаются в точке M под прямыми углами. Эти три взаимно перпендикулярные прямые в механике часто принимают в качестве координатных осей и называют естественными осями, или осями натурального триэдра. По мере движения точки по траектории естественные оси движутся вместе с ней, поворачиваются относительно основных (неподвижных) осей xOyz.
Эти три взаимно перпендикулярные прямые в механике часто принимают в качестве координатных осей и называют естественными осями, или осями натурального триэдра. По мере движения точки по траектории естественные оси движутся вместе с ней, поворачиваются относительно основных (неподвижных) осей xOyz.
Положительные направления на естественных осях примем такими, чтобы трехгранный угол τMnb можно было привести в совпадение с углом xОyz. Касательная Mτ играет роль оси Ох, главная нормаль Mn— оси Oy и бинормаль Mb— оси Oz.
Так как вектор ускорения лежит в соприкасающейся плоскости τМn, а бинормаль Mb перпендикулярна к соприкасающейся плоскости, то проекция ускорения на бинормаль всегда равна нулю (αb = 0), и при проецировании ускорения на три естественные оси мы имеем только две проекции: касательное ускорение и нормальное ускорение.
Таким образом, мы установили, что формулы (69), (69′) и (69″) касательного ускорения, формулы (74) и (74′) нормального ускорения, а также формулы (75) и (75′) полного ускорения, выведенные нами в предположении, что точка движется по плоской траектории, остаются справедливыми для любого движения точки.
Именно потому, что проекция ускорения на бинормаль всегда равна нулю, в формуле (75) величина полного ускорения определяется по двум проекциям, а не по трем, как это имеет место в формуле (66). Приравнивая выражение (66) модуля полного ускорения точки через проекции на неподвижные оси координат его же выражению (75) через проекции на естественные оси, получим для движения точки по любой траектории соотношение
(76)
или
(76/)
Эти равенства часто бывают полезны при решении задач.
Задача №6
Найти касательное и нормальное ускорения точки, движение которой выражается уравнениями:
Решение. Найдем проекции скорости и ускорения на оси координат:
x=υx=α, χ=ax=0, y = υy = β-gt, y= – g.
Подставляя найденные величины в (68), найдем касательное ускорение
Подставляя те же величины в формулу (72), найдем нормальное ускорение
Нормальное ускорение всегда направлено во внутрь траектории, отрицательный знак получился потому, что в этой задаче естественные оси взяты по левой системе, (ось М,— вправо, ось Mn — вниз), а неподвижные — по правой.
Ответ. где υ — скорость точки.
Задача №7
Найти скорость, полное, касательное и нормальное ускорения точки, описывающей фигуру Лиссажу, по уравнениям движения точки, заданным в координатной форме:
х= 3 sin 2t, у = 4 sin 2t.
Решение. Найдем сначала проекции скорости:
υχ = 6 cos 2t, υy = 8 cos 2t.
Затем определим величину полной скорости точки:
Для определения касательного и нормального ускорений определим проекции ускорения на декартовы оси координат, затем найдем полное ускорение и разложим его на касательное и нормальное. Имеем
ax= —12 sin 2t, ay =—16 sin 2t,
Найдем сначала касательное ускорение, для чего продифференцируем по времени полную скорость или воспользуемся формулой (68):
Мы видим, что полное ускорение по величине равно касательному ускорению, т. е. что нормальное ускорение равно нулю. Это возможно только в случае, если траектория — прямая линия. Для проверки можно определить кривизну траектории или найти уравнение траектории. По первому способу имеем
По второму способу найдем (прямая).
Ответ. υ=10 cos 2t; α = 20 sin 2t; ат= —20sin 2t; αN = 0.
Задача №8
Точка обода колеса, катящегося без скольжения и без буксования по прямолинейному рельсу, движется согласно уравнениям x=r (ct-sin сt), y=r(l — cos ct). Найти нормальное ускорение точки.
Решение. Для решения задачи можно наметить следующий путь: найти проекции скорости, величину полной скорости, проекции ускорения и полное ускорение; затем, продифференцировав по времени величину полной скорости, найти касательное ускорение и, вычитая его геометрически из полного, найти нормальное.
Дифференцируя уравнения движения, найдем
υx= rc (1 —cos ct), υy = rc sin ct.
Далее получаем
Дифференцируя проекции скорости, найдем
ax = rc2 sin ct, ay = rc2 cos ct
полое ускорение
а = rs2
Дифференцируя υ, найдем касательное ускорение:
Вектор aτ перпендикулярен вектору и в сумме с ним равняется вектору полного ускорения, поэтому
Задачи такого типа быстрее и короче решать с применением формулы (72). По этой формуле непосредственно получаем:
Ответ:
Задача №9
Тяжелое тело, размерами которого можно пренебречь, брошено с большой высоты с горизонтальной скоростью υ0 и движется согласно уравнениям x-υ0t, . Найти траекторию, скорость, касательное и нормальное ускорения в любом положении, выразив их через скорость тела в этом положении.
Решение. Определяя из первого уравнения t и подставляя во второе, найдем уравнение траектории:
Траектория—парабола (рис. 95). Дифференцируя уравнения движения по времени, найдем проекции скорости и по ним полную скорость:
В начальное мгновение (t = 0), скорость точки υ = υo, а затем с течением времени величина скорости непрерывно возрастает. Из полученного равенства определим время t, в течение которого тело приобретает скорость у:
Вторично дифференцируя уравнения движения точки, найдем проекции ускорения на оси координат и полное ускорение:
В данном случае тело движется с постоянным по модулю и направлению ускорением, параллельным оси Оу.
Обращаем внимание на то, что, хотя здесь a = const, движение точки не является равнопеременным, так как условием равнопеременного движения является не условие a = const, а условие aт= const. В данном же случае, как мы сейчас увидим, ат непостоянно.
Дифференцируя величину полной скорости по времени или непосредственно по (68), получим касательное ускорение
Подставляя вместо t найденное нами значение, выразим касательное ускорение aт через скорость υ:
Отсюда следует, что в начальное мгновение, когда υ = υ0, aт=0. Затем с увеличением υ величина ат растет и в пределе стремится к полному ускорению g.
Для нахождения нормального ускорения обратимся к (72). Имеем
В начальное мгновение (при t = 0 и υ=v0) aN=g, а затем с увеличением υ аN убывает, стремясь в пределе к нулю.
Ответ. Парабола
Задача №10
Определить радиус кривизны траектории точки в начале движения, если уравнения ее движения имеют вид: x = 2t, y = t2 (t— в cек; х, у— в м).
Решение. Из формулы кривизны (73) имеем
Для получения проекций скорости и ускорения в начальное мгновение продифференцируем уравнения движения и подставим t = 0:
Полную скорость в начальное мгновение определяем по ее проекциям:
Подставляя эти величины в формулу (73), получим ответ.
Ответ. р = 2 м
Задача №11
Через 20 сек после начала движения автомобиль, двигаясь иа закруглении радиуса 400 м, приобрел скорость 108 км/ч. Считая, что величина скорости автомобиля пропорциональна квадрату времени, определить полное ускорение автомобиля в конце 20-й секунды н пройденное за это время расстояние.
Решение. За единицы принимаем метр и секунду. Траектория задана—дорога с закруглением радиуса 400 м, и для решения задачи необходимо определить Уравнение движения автомобиля по траектории. (Применять формулы (71) здесь нельзя, так как при равиоперемениом движении величина скорости пропорциональна времени, а в данной задаче она пропорциональна квадрату времени.)
В условии дано
υ=bt2.
Найдем коэффициент пропорциональности
Выражая скорость по (53) и разделяя переменные, получим
откуда, интегрируя, получаем
Постоянную C определим из начальных данных: в начальное мгновение (t = 0) автомобиль не прошел еще никакого расстояния, а потому C = 0. Дважды дифференцируя по времени полученное уравнение, найдем касательное ускорение
или в конце 20-й секунды
αт=3 м/ceκ2.
Скорость в конце 20-й секунды была 30 м/сек, и по (74)
Полное ускорение в конце 20-й секунды было
Чтобы определить расстояние, пройденное автомобилем за 20 сек, положим в уравнении движения t = 20 сек:
Ответ. а = 3,75 м/сек2, s = 200 м.
СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ – ФИЗИКА (КУРС ЛЕКЦИЙ)
§ 44. Тангенциальное, нормальное и полное ускорение точки
1. Если точка движется по какой-либо криволинейной траектории неравномерно или неравномерно движется по окружности, то ускорение точки не направлено перпендикулярно скорости, но образует с вектором скорости некоторый острый или тупой угол. Модуль и направление полного ускорения в этом случае удобнее находить, если ввести два вспомогательных ускорения: касательное (тангенциальное) и нормальное.
Для нахождения вектора отложим векторы скорости из одной точки.
Разложим вектор на 2 вектора и .
Вектор направлен по касательной к траектории, вектор , т.е. направлен по нормали к траектории.
По правилу параллелограмма: .
Поделим это равенство на время .
Возьмём предел от обеих частей равенства при .
По определению ускорения (см. § 19) каждый из пределов есть ускорение.
– направлено по касательной к траектории
– направлено по нормали внутрь вогнутости траектории
Модуль касательного ускорения находится с помощью производной от модуля скорости по времени:
.
Если касательное ускорение по модулю остаётся постоянным, т.е. точка движется по криволинейной траектории равноускоренно или равнозамедленно, то модуль можно найти так:
.
Модуль нормального ускорения находится по известной нам формуле:
, где r – радиус кривизны траектории в данной точке.
Модуль полного ускорения: .
2. Если точка движется по траектории ускоренно, т.е. модуль скорости возрастает, то касательное ускорение направлено в сторону скорости, при замедленном – противоположно скорости.
Если движение равноускоренное или равнозамедленное по криволинейной траектории, то модуль остаётся постоянным. В этом случае для криволинейного движения можно пользоваться формулами равноускоренного или равнозамедленного движения, но в эти формулы надо ставить модуль касательного ускорения.
– для равноускоренного движения
; ; ;
– для равнозамедленного движения
; ; , где ;
3. Движение брошенных тел происходит по параболам. При этом ускорение является полным ускорением, и его можно раскладывать на касательное ускорение и нормальное ускорение (кроме наивысшей точки траектории).
В наивысшей точке траектории , т.е. является в этой точке нормальным ускорением.
27 Ускорения точек тела, вращающегося вокруг неподвижной оси
Ускорения точек тела, вращающегося вокруг неподвижной оси
Так как в рассматриваемом случае движение точки задано естественным способом, то полное ускорение точки можно вычислить, как векторную сумму касательного ωτ и нормального ωn ускорений (см. глава I, § 16). Выразим эти ускорения через кинематические характеристики вращательного движения тела, т. е; через ω и ε.
Имеем ωn= ωτ=s,
откуда, на основании формул (11.66) и (11.67),
или
ωn = R ω2
и
ωτ = s== Rφ,
Рекомендуемые файлы
или
ωτ = Rε.
Следовательно, нормальное ускорение точки тела при вращении его вокруг неподвижной оси равно произведению радиуса вращения на квадрат угловой скорости. Касательное ускорение равно произведению радиуса вращения на угловое ускорение. Нормальное ускорение направлено по радиусу вращения к центру вращения (рис. 51, а). Касательное ускорение направлено по касательной к траектории в сторону вращения, если движение ускоренное (ε > 0), и в сторону, противоположную вращению, если движение замедленное, т. е. ε< 0 (рис. 51, б, в).
Модуль полного ускорения точки найдем по формуле (11.44), т. е.
или
Направление полного ускорения определим по тангенсу угла α, который полное ускорение образует с нормальным ускорением (рис. 52). Получим
tgα=
или
tgα=
Пример. Маховик вращается согласно уравнению φ = 2t2. Определить скорость, касательное, нормальное и полное ускорения точки на ободе маховика в момент t = 10с, если R = 1,2 м.
Величину линейной скорости определим по формуле
υ =Rω.
Имеем
ω= φ = 4t рад/с, ε = φ = 4 рад/с2,
следовательно,
υ = 1,2 • 4t = 4,8t м/с.
Обратите внимание на лекцию “7.1. Технологическая карта как основа организации производственного процесса”.
В момент t = 10с υ= 48 м/с. Касательное ускорение
ωт = Rε = 1,2 • 4 = 4,8 м/с2 = const
нормальное ускорение
ωn = Rω2 = 1,2 • 16t2 = 19.2t2.
При t =10 с ωn = 1920 м/с2.
Полное ускорение ω==1920.6 м/с2
РАЗНИЦА МЕЖДУ ТАНГЕНЦИАЛЬНЫМ УСКОРЕНИЕМ И ЦЕНТРОСТРЕМИТЕЛЬНЫМ УСКОРЕНИЕМ | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ – НАУКА
Касательное ускорение против центростремительного ускорения Ускорение – это скорость изменения скорости, и, если ее выразить с помощью расчетов, это производная скорости по времени. Касательное ускор
Касательное ускорение против центростремительного ускорения
Ускорение – это скорость изменения скорости, и, если ее выразить с помощью расчетов, это производная скорости по времени. Касательное ускорение и центростремительное ускорение являются составляющими ускорения частицы или твердого тела при круговом движении.
Тангенциальное ускорение
Рассмотрим частицу, движущуюся по траектории, показанной на диаграмме. В рассматриваемом случае частица находится в угловом движении, и скорость частицы тангенциальна к траектории.
Скорость изменения тангенциальной скорости определяется как тангенциальное ускорение и обозначается как ат.
ат= dvт/ dt
Однако это не учитывает полное ускорение частицы. Согласно первому закону Ньютона, чтобы частица отклонилась от прямолинейного пути и повернулась, должна быть другая сила; следовательно, мы можем сделать вывод, что должна быть составляющая ускорения, направленная перпендикулярно тангенциальной составляющей ускорения, то есть к точке O в показанном примере. Этот компонент ускорения известен как нормальное ускорение, и обозначается он ап.
ап= vт2/р
Если тыти тып являются единичными векторами в тангенциальном и нормальном направлениях, результирующее ускорение может быть задано следующим выражением.
а = аттыт+ аптып= (dvт/ dt) uт+ (vт2/руп
Центростремительное ускорение
Теперь учтите, что сила, вызывающая нормальное ускорение, постоянна. В этом случае частица выходит на круговой путь с радиусом r. Это особый случай углового движения, и нормальное ускорение называется центростремительным ускорением. Сила, приводящая в движение круговое движение, известна как центростремительная сила.
Центростремительное ускорение также задается приведенным выше выражением, но можно использовать угловые соотношения скорости и ускорения, чтобы получить его в терминах угловой скорости.
Следовательно,
аc= vт2/ г = -rω2
(Отрицательный знак означает, что ускорение направлено в направлении, противоположном радиус-вектору)
Чистое ускорение может быть получено как результат двух составляющих:c ит.
В чем разница между тангенциальным ускорением и центростремительным ускорением?
• Тангенциальное и центростремительное ускорение – это две составляющие ускорения частицы / тела при круговом движении.
• Тангенциальное ускорение – это скорость изменения тангенциальной скорости, которая всегда касается круговой траектории и перпендикулярно радиус-вектору.
• Центростремительное ускорение направлено к центру круга, и этот компонент ускорения является основным фактором, удерживающим частицу на круговой траектории.
• Для частицы, движущейся по кругу, вектор ускорения всегда лежит в пределах кругового пути.
Частные случаи движения точки в теоретической механике
Частные случаи движения точкиРавномерное движение
Равномерным движением называется, как мы знаем, таксе движение, при котором точка за любые равные промежутки времени проходит равные расстояния.
Очевидно, что величина скорости в этом движении
Отсюда
Пусть в начальный момент точка находилась от начала отсчета на расстоянии . Тогда интегрируя предыдущее уравнение в соответствующих пределах, будем иметь:
откуда расстояние точки от начала отсчета расстояний
Уравнение (71) определяет равномерное движение точки. Из формулы
где — путь, пройденный точкой, аналогичным образом находим:
Скорость точки при равномерном движении (и только при этом движении) равна отношению пройденного пути ко времени. Так как модуль скорости точки остается постоянным при любом равномерном ее движении, то при этом всегда ее касательное ускорение
Отсюда следует, что касательное ускорение точки характеризует изменение ее скорости по величине.
При равномерном криволинейном движении точки ее скорость, оставаясь постоянной по модулю, изменяется только по направлению. Полное ускорение точки в этом случае равно нормальному ускорению, а
Отсюда следует, что нормальное ускорение точки характеризует изменение ее скорости по направлению.
Прямолинейное движение
При прямолинейном движении точки радиус кривизны ее траектории и нормальное ускорение точки
Следовательно, полное ускорение точки
При прямолинейном движении точка может иметь только одно касательное ускорение, и потому ее полное ускорение равно первой производной по времени от алгебраического значения скорости или второй производной по времени от пройденного ею пути.
Заметим, что так определяется ускорение точки только при прямолинейном ее движении.
В случае, если точка совершает прямолинейное и равномерное движение, то и нормальное
и касательное
(следовательно, и полное) ускорения точки будут тождественно равны нулю. В этом движении точка не имеет никакого ускорения, так как ее скорость остается все время постоянной как по модулю, так и по направлению.
Равномерно переменное движение
Часто встречающимся на практике равномерно переменным (равномерно ускоренным или равномерно замедленным) движением точки называется такое ее движение, когда в равные, произвольно взятые промежутки времени алгебраическое значение скорости точки изменяется на одну и ту же величину.
Изменение алгебраического значения скорости точки характеризуется, как мы знаем, касательным ускорением. Отсюда следует, что при равномерно переменном движении точки алгебраическая величина ее касательного ускорения
Разделяя переменные и интегрируя уравнение в соответствующих пределах, будем иметь:
где — величина скорости в начальный момент времени. Отсюда
Для вывода уравнения движения точки воспользуемся зависимостью (67), из которой находим
Полагая при
и интегрируя это уравнение в соответствующих пределах, получаем:
Уравнение (74) представляет собой уравнение равномерно переменного движения точки. Из формулы
аналогичным образом находим
В этих формулах берется положительным при ускоренном движении и отрицательным — при замедленном.
Формулы (73), (74) и (74а) одинаково справедливы как для прямолинейного, так и для криволинейного равномерно переменного движения точки. При прямолинейном движении точки радиус кривизны траектории и нормальное ускорение точки
Следовательно, в этом случае ее полное ускорение Поэтому обычно, применяя данные формулы к прямолинейному равномерно переменному движению точки, индекс в обозначении ускорения опускают.
Гармоническое колебательное движение
Гармоническим колебанием точки называется такое ее движение, при котором расстояние s точки от начала отсчета изменяется по закону:
где и — постоянные величины.
Так как значения изменяются в пределах от —1 до +1, то расстояния s точки от начала обсчета изменяются в пределах .
Наибольшее расстояние а, на которое точка удаляется от начала отсчета, называется амплитудой колебания.
Время одного полного колебания точки называется периодом колебания. Очевидно, что в начале и в конце промежутка времени точка должна находиться на одном и том же расстоянии от центра. Для этого необходимо, чтобы аргумент у синуса (или косинуса), входящего в правую часть равенства (75), изменялся на величину , т. е. чтобы имело место следующее равенство:
Отсюда находим, что период колебания точки
Постоянная , показывающая, сколько полных колебаний точка совершает за секунд, называется круговой частотой колебаний. Ее размерность — .
Пример задачи:Поезд, двигаясь по закруглению пути равномерно ускоренно, приобретает через 3 мин после отхода от станции скорость
Определить ускорение поезда через 2 мин после отхода от станции, если радиус закругления пути
Решение:
Полагая
из формулы (73) определяем касательное ускорение поезда:
Так как движение поезда — равномерно ускоренное, то его касательное ускорение постоянно.
Нормальное же ускорение поезда, определяемое формулой (69),
зависит от скорости движения и будет различным для разных моментов времени.
Определяем скорость поезда в конце второй минуты после отхода его от станции
Тогда нормальное ускорение поезда в этот момент будет равно
Ускорение (полное) поезда в конце второй минуты
Пример задачи:Жестко связанная с направляющей (рис. 114, а) рама , называемая обычно кулисой, приводится в движение кривошипом (расположенным впереди рамы и направляющей). Кривошип вращается вокруг точки равномерно, причем угол изменяется со временем по закону . Концом кривошип шарнирно соединен с ползуном, скользящим в прорези рамы. Длина кривошипа . Определить движение рамы и построить графики движения, скорости и ускорения.
Решение:
При вращении кривошипа рама совершает колебательное движение около точки , причем все точки рамы совершают одинаковое прямолинейное движение. Рассмотрим движение какой-нибудь одной точки рамы, например, ее середины . Траекторией этой точки будет прямая, совпадающая с осью движения ползуна. Примем неподвижную точку (центр вращения кривошипа) за начало отсчета расстояний и напишем уравнение движения точки . За положительное направление отсчета расстояний примем направление вправо от точки . Из (рис. 114,а) имеем:
Обозначив расстояние точки от начала отсчета через и приняв во внимание, что и угол , будем иметь:
Полученное уравнение (I) аналогично уравнению (75).
Точка и рама совершают гармоническое колебательное движение около неподвижного центра . Из сравнения уравнений (I) и (75) ясно, что амплитуда этого колебания
круговая частота
и период колебаний
За 12 секунд кривошип делает один оборот, а рама совершает одно полное колебание. Графиком движения точки будет косинусоида, изображенная на рис. 114,6.
Дифференцируя по времени уравнение движения точки , находим величину скорости
Графиком скорости точки будет синусоида, изображенная на рис. 114, в.
Так как точка совершает прямолинейное движение, то ее ускорение
Графиком ускорения точки будет косинусоида, изображенная па рис. 111, с’.
Из уравнения (1) движения точки и из выражений для ее скорости (II) и ускорения (III) видно, что скорость и ускорение точки изменяются периодически. В начальный момент, при
Следовательно, в этот момент точка находится в крайнем («мертвом») положении, скорость ее равна нулю, ускорение максимально по абсолютной величине и отрицательно, т. е. направлено в сторону, противоположную направлению отсчета расстояний (справа налево).
При дальнейшем движении точки к центру ее скорость увеличивается по абсолютному значению, а ускорение уменьшается, оставаясь направленным в сторону движения точки, В момент, когда точка будет находиться в центре , ее скорость достигнет максимальной величины, ускорение же будет равно нулю. При дальнейшем движении точки (от точки до крайнего левого положения) ее скорость по модулю будет уменьшаться, ускорение же увеличивается и направлено в сторону, противоположную движению точки (слева направо).
Таким образом, когда точка находится в центре колебания, ее скорость максимальна по модулю, а ускорение равно нулю. В крайних же положениях скорость точки равна нулю, а ускорение по модулю максимально. От центра колебаний к крайнему положению точка движется замедленно. От крайнего же положения к центру колебаний точка движется ускоренно.
В рассмотренном примере мы имели дело с прямолинейным движением точки, но гармонические колебания точка может совершать и по любой криволинейной траектории. Характер движения точки будет тот же, только при этом надо иметь в виду, что при криволинейном движении, кроме касательного ускорения, точка имеет еще и нормальное ускорение.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
12.5: Тангенциальная и нормальная составляющие ускорения
Теперь мы увидели, как описывать кривые на плоскости и в пространстве и как определять их свойства, такие как длина дуги и кривизна. Все это приводит к основной цели данной главы – описанию движения по плоским кривым и пространственным кривым. Теперь у нас есть все необходимые инструменты; в этом разделе мы объединяем эти идеи и посмотрим, как их использовать.
Векторы движения на плоскости и в пространстве
Наша отправная точка – использование векторных функций для представления положения объекта как функции времени.Все следующие материалы можно применять как к кривым на плоскости, так и к кривым пространства. Например, когда мы смотрим на орбиту планет, все кривые, определяющие эти орбиты, лежат в одной плоскости, потому что они эллиптические. Однако частица, движущаяся по спирали, движется по кривой в трех измерениях.
Определение: скорость, скорость и ускорение
Пусть \ (\ vecs r (t) \) будет дважды дифференцируемой векторнозначной функцией параметра \ (t \), который представляет положение объекта как функцию времени.
Вектор скорости \ (\ vecs v (t) \) объекта равен
.\ [\ text {Скорость} \, = \ vecs v (t) = \ vecs r ′ (t). \ label {Eq1} \]
Вектор ускорения \ (\ vecs a (t) \) определен как
\ [\ text {Ускорение} \, = \ vecs a (t) = \ vecs v ′ (t) = \ vecs r ″ (t). \ label {Eq2} \]
Скорость определена как
\ [\ mathrm {Скорость} \, = v (t) = ‖ \ vecs v (t) ‖ = ‖ \ vecs r ′ (t) ‖ = \ dfrac {ds} {dt}. \ label {Eq3} \]
Так как \ (\ vecs {r} (t) \) может быть как в двух, так и в трех измерениях, эти векторнозначные функции могут иметь два или три компонента.В двух измерениях мы определяем \ (\ vecs {r} (t) = x (t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} \), а в трех измерениях \ (\ vecs r (t) = x (t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} + z (t) \ hat {\ mathbf k} \). Затем можно записать скорость, ускорение и скорость, как показано в следующей таблице.
| Кол-во | Два измерения | Три измерения |
|---|---|---|
| Позиция | \ (\ vecs {r} (t) = x (t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} \) | \ (\ vecs {r} (t) = x (t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} + z (t) \ hat {\ mathbf k} \) |
| Скорость | \ (\ vecs {v} (t) = x ′ (t) \ hat {\ mathbf i} + y ′ (t) \ hat {\ mathbf j} \) | \ (\ vecs {v} (t) = x ′ (t) \ hat {\ mathbf i} + y ′ (t) \ hat {\ mathbf j} + z ′ (t) \ hat {\ mathbf k}) \) |
| Разгон | \ (\ vecs {a} (t) = x ″ (t) \ hat {\ mathbf i} + y ″ (t) \ hat {\ mathbf j} \) | \ (\ vecs {a} (t) = x ″ (t) \ hat {\ mathbf i} + y ″ (t) \ hat {\ mathbf j} + z ″ (t) \ hat {\ mathbf k} \) |
| Скорость | \ (\ | \ vecs {v} (t) \ | = \ sqrt {(x ′ (t)) ^ 2+ (y ′ (t)) ^ 2} \) | \ (\ | \ vecs {v} (t) \ | = \ sqrt {(x ′ (t)) ^ 2+ (y ′ (t)) ^ 2+ (z ′ (t)) ^ 2} \ ) |
Пример \ (\ PageIndex {1} \): изучение движения вдоль параболы
Частица движется по параболическому пути, определяемому векторной функцией \ (\ vecs {r} (t) = t ^ 2 \ hat {\ mathbf i} + \ sqrt {5 − t ^ 2} \ hat {\ mathbf j} \), где \ (t \) измеряет время в секундах. 2-12t + 14} \]
Единицы измерения скорости и скорости – футы в секунду, а единицы измерения ускорения – футы в секунду в квадрате.
Чтобы лучше понять векторы скорости и ускорения, представьте, что вы едете по извилистой дороге. Если вы не поворачиваете руль, вы продолжаете движение по прямой и съезжаете с дороги. Скорость, с которой вы движетесь при съезде с дороги, вместе с направлением дает вектор, представляющий вашу скорость, как показано на рисунке \ (\ PageIndex {2} \).
Рисунок \ (\ PageIndex {2} \): В каждой точке дороги, по которой проехал автомобиль, вектор скорости автомобиля касается пути, пройденного автомобилем.Однако тот факт, что вы должны повернуть рулевое колесо, чтобы оставаться на дороге, указывает на то, что ваша скорость всегда меняется (даже если ваша скорость не меняется), потому что направление вашего постоянно меняется, чтобы вы оставались на дороге. Когда вы поворачиваетесь вправо, ваш вектор ускорения также указывает вправо. Когда вы поворачиваете налево, ваш вектор ускорения указывает налево. Это указывает на то, что ваши векторы скорости и ускорения постоянно меняются, независимо от того, изменяется ли ваша фактическая скорость (Рисунок \ (\ PageIndex {3} \)).
Рисунок \ (\ PageIndex {3} \): пунктирная линия представляет траекторию объекта (например, автомобиля). Вектор ускорения всегда направлен внутрь поворота.Компоненты вектора ускорения
Мы можем объединить некоторые концепции, обсуждаемые в разделе «Длина дуги и кривизна», с вектором ускорения, чтобы получить более глубокое понимание того, как этот вектор связан с движением в плоскости и в пространстве. Напомним, что единичный касательный вектор \ (\ vecs T \) и единичный вектор нормали \ (\ vecs N \) образуют соприкасающуюся плоскость в любой точке \ (P \) на кривой, определяемой векторнозначной функцией \ (\ vecs {r} (t) \).Следующая теорема показывает, что вектор ускорения \ (\ vecs {a} (t) \) лежит в соприкасающейся плоскости и может быть записан как линейная комбинация единичной касательной и единичных нормальных векторов.
Теорема \ (\ PageIndex {1} \): плоскость вектора ускорения
Вектор ускорения \ (\ vecs {a} (t) \) объекта, движущегося по кривой, очерченной дважды дифференцируемой функцией \ (\ vecs {r} (t) \), лежит в плоскости, образованной единичный касательный вектор \ (\ vecs T (t) \) и главный единичный вектор нормали \ (\ vecs N (t) \) к \ (C \) .2 \ kappa \ vecs {N} (t) \]
Здесь \ (v (t) = \ | \ vecs v (t) \ | \) – скорость объекта, а \ (\ kappa \) – кривизна \ (C \), определяемая \ (\ vecs {r} (t) \).
Проба
Поскольку \ (\ vecs {v} (t) = \ vecs {r} ′ (t) \) и \ (\ vecs {T} (t) = \ dfrac {\ vecs {r} ′ (t)} { || \ vecs {r} ′ (t) ||} \) имеем \ (\ vecs v (t) = || \ vecs {r} ′ (t) || \ vecs {T} (t) = v (t) \ vecs {T} (t) \).
Теперь продифференцируем это уравнение:
\ [\ vecs {a} (t) = \ vecs {v} ′ (t) = \ dfrac {d} {dt} \ left (v (t) \ vecs {T} (t) \ right) = v ′ (T) \ vecs {T} (t) + v (t) \ vecs {T} ′ (t) \ nonumber \]
Поскольку \ (\ vecs {N} (t) = \ dfrac {\ vecs {T} ′ (t)} {|| \ vecs {T} ′ (t) ||} \), мы знаем \ (\ vecs {T} ′ (t) = || \ vecs {T} ′ (t) || \ vecs {N} (t) \), поэтому
\ [\ vecs {a} (t) = v ′ (t) \ vecs {T} (t) + v (t) || \ vecs {T} ′ (t) || \ vecs {N} (t ).2 \ vecs {N} (t). \)
\ (\ квадрат \)
Коэффициенты \ (\ vecs {T} (t) \) и \ (\ vecs {N} (t) \) упоминаются как тангенциальный компонент ускорения и нормальный компонент ускорения , соответственно. . Мы пишем \ (a_ \ vecs {T} \) для обозначения тангенциальной составляющей и \ (a_ \ vecs {N} \) для обозначения нормальной составляющей.
Теорема \ (\ PageIndex {2} \): тангенциальная и нормальная составляющие ускорения
Пусть \ (\ vecs {r} (t) \) будет векторной функцией, которая обозначает положение объекта как функцию времени.2}}. \ label {Eq2B} \]
Эти компоненты связаны формулой
\ [\ vecs {a} (t) = a_ \ vecs {T} \ vecs {T} (t) + a_ \ vecs {N} \ vecs {N} (t). \ label {Eq3B} \]
Здесь \ (\ vecs {T} (t) \) – единичный касательный вектор к кривой, определенной как \ (\ vecs {r} (t) \), и \ (\ vecs {N} (t) \) – единичный вектор нормали к кривой, заданной формулой \ (\ vecs {r} (t) \).
Нормальная составляющая ускорения также называется центростремительной составляющей ускорения или иногда радиальной составляющей ускорения .Чтобы понять центростремительное ускорение, предположим, что вы едете в автомобиле по круговой трассе с постоянной скоростью. Затем, как мы видели ранее, вектор ускорения всегда направлен к центру трассы. Как гонщик в машине, вы чувствуете тягу к за пределами трассы, потому что вы постоянно поворачиваете. Это ощущение действует в направлении, противоположном центростремительному ускорению. То же самое и с некруглыми путями. Причина в том, что ваше тело стремится двигаться по прямой линии и сопротивляется силе, возникающей в результате ускорения, толкающей его в сторону.Обратите внимание, что в точке \ (B \) на рисунке \ (\ PageIndex {4} \) вектор ускорения направлен назад. Это потому, что автомобиль замедляется, когда входит в поворот.
Рисунок \ (\ PageIndex {4} \): тангенциальная и нормальная составляющие ускорения могут использоваться для описания вектора ускорения.Тангенциальный и нормальный единичные векторы в любой заданной точке кривой обеспечивают систему отсчета в этой точке. Тангенциальная и нормальная составляющие ускорения – это проекции вектора ускорения на \ (\ vecs T \) и \ (\ vecs N \) соответственно.2−3t) \, \ hat {\ mathbf k} \), где \ (t \) измеряет время в секундах, а расстояние – в футах.
- Найдите \ (a_ \ vecs {T} \) и \ (a_ \ vecs {N} \) как функции от \ (t \).
- Найдите \ (a_ \ vecs {T} \) и \ (a_ \ vecs {N} \) в момент времени \ (t = 2 \).
Решение
- Начнем с вывода функций скорости и ускорения:
\ [\ begin {align *} \ vecs {v} (t) & = \ vecs {r} ‘(t) \\ [4pt] & = 2t \, \ hat {\ mathbf i} +2 \, \ шляпа {\ mathbf j} + (6t-3) \, \ hat {\ mathbf k} \\ [4pt] \ vecs {a} (t) & = \ vecs {v} ‘(t) \\ [4pt] & = 2 \, \ hat {\ mathbf i} +6 \, \ hat {\ mathbf k} \ end {align *} \] Теперь мы применяем уравнение \ ref {Eq1B}: \ [\ begin {align *} a_ {\ vecs {T}} & = \ dfrac {\ vecs {v} \ cdot \ vecs {a}} {|| \ vecs {v} ||} \\ [4pt] & = \ dfrac {(2t \, \ hat {\ mathbf i} +2 \, \ hat {\ mathbf j} + (6t-3) \, \ hat {\ mathbf k}) \ cdot (2 \, \ hat {\ mathbf i} +6 \ , \ hat {\ mathbf k})} {|| 2t \, \ hat {\ mathbf i} + 2 \, \ hat {\ mathbf j} + (6t-3) \, \ hat {\ mathbf k} ||} \\ [4pt] & = \ dfrac {4t + 6 (6t-3)} {\ sqrt {(2t) ^ 2 + 2 ^ 2 + (6t-3) ^ 2}} \\ [4pt] & = \ dfrac {40t-18} {40t ^ 2 – 36t + 13} \ end {align *} \] Теперь мы можем применить уравнение \ ref {Eq2B}:
\ [\ begin {align *} a_ \ vecs {N} & = \ sqrt {|| \ vecs {a} || ^ 2-a _ {\ vecs {T}}} \\ [4pt] & = \ sqrt {|| 2 \, \ hat {\ mathbf i} +6 \, \ hat {\ mathbf k} || ^ 2 – \ left (\ dfrac {40t-18} {\ sqrt {40t ^ 2-36 + 13 }} \ right) ^ 2} \\ [4pt] & = \ sqrt {4 + 36- \ dfrac {(40t-18) ^ 2} {40t ^ 2-36t + 13}} \\ [4pt] & = \ sqrt {\ dfrac {40 (40t ^ 2-36t + 13) – (1600t ^ 2-1440t + 324)} {40t ^ 2-36t + 13}} \\ [4pt] & = \ sqrt {\ dfrac { 196} {40t ^ 2-36t + 13}} \\ [4pt] & = \ dfrac {14} {\ sqrt {40t ^ 2-36t + 13}} \ end {align *} \]
- Мы должны оценить каждый из ответов из части а при \ (t = 2 \):
\ [\ begin {align *} a _ {\ vecs {T}} (2) & = \ dfrac {40 (2) -18} {\ sqrt {40 (2) ^ 2 – 36 (2) +13} } \\ [4pt] & = \ dfrac {80-18} {\ sqrt {160-72 + 13}} \\ [4pt] & = \ dfrac {62} {\ sqrt {101}} \\ [4pt] a _ {\ vecs {N}} (2) & = \ dfrac {14} {\ sqrt {40 (2) ^ 2 -36 (2) +13}} \\ [4pt] & = \ dfrac {14} { \ sqrt {160-72 + 13}} = \ dfrac {140} {\ sqrt {101}}. 2}} \ end {align *} \]
г.2}} \\ = \ sqrt {4- \ dfrac {36} {11}} \\ = \ sqrt {\ dfrac {8} {11}} \\ = \ dfrac {2 \ sqrt {2}} {\ sqrt {11}} \ end {align *} \]
Движение снаряда
Теперь давайте посмотрим на применение векторных функций. В частности, давайте рассмотрим влияние гравитации на движение объекта, когда он движется по воздуху, и то, как оно определяет результирующую траекторию этого объекта. В дальнейшем мы игнорируем влияние сопротивления воздуха. Эта ситуация, когда объект движется с начальной скоростью, но без сил, действующих на него, кроме силы тяжести, называется движением снаряда.Он описывает движение объектов от мячей для гольфа до бейсбольных мячей и от стрел до пушечных ядер.
Сначала нам нужно выбрать систему координат. Если мы стоим в начале этой системы координат, тогда мы выбираем положительную ось \ (y \) как вверх, отрицательную ось \ (y \) – как вниз, а положительную ось \ (x \ ) – ось должна быть вперед (т.е. от метателя объекта). Влияние силы тяжести направлено вниз, поэтому второй закон Ньютона говорит нам, что сила, действующая на объект в результате гравитации, равна массе объекта, умноженной на ускорение силы тяжести, или \ (\ vecs F_g = m \ vecs a \), где \ (\ vecs F_g \) представляет силу тяжести, а \ (\ vecs a = -g \, \ hat {\ mathbf j} \) представляет ускорение силы тяжести на поверхности Земли.Значение \ (g \) в английской системе измерения составляет приблизительно 32 фут / сек 2 и приблизительно 9,8 м / сек 2 в метрической системе. Это единственная сила, действующая на объект. Поскольку гравитация действует в нисходящем направлении, мы можем записать силу, возникающую в результате гравитации, в форме \ (\ vecs F_g = −mg \, \ hat {\ mathbf j} \), как показано на рисунке \ (\ PageIndex {5} \).
Рисунок \ (\ PageIndex {5} \): объект падает под действием силы тяжести.Второй закон Ньютона также говорит нам, что \ (F = m \ vecs {a} \), где \ (\ vecs a \) представляет вектор ускорения объекта.Эта сила всегда должна быть равна силе тяжести, поэтому мы знаем, что
\ [\ begin {align *} \ vecs F = \ vecs F_g \\ m \ vecs {a} = -mg \, \ hat {\ mathbf j} \\ \ vecs {a} = -g \, \ hat {\ mathbf j}. \ end {align *} \]
Теперь мы используем тот факт, что вектор ускорения является первой производной вектора скорости. Следовательно, мы можем переписать последнее уравнение в виде
\ [\ vecs v ‘(t) = -g \, \ hat {\ mathbf j} \]
Взяв первообразную из каждой части этого уравнения, мы получим
\ [\ vecs v (t) = \ int -g \, \ hat {\ mathbf j} \; dt = -gt \, \ hat {\ mathbf j} + \ vecs C_1 \]
для некоторого постоянного вектора \ (\ vecs C_1 \).Чтобы определить значение этого вектора, мы можем использовать скорость объекта в фиксированный момент времени, скажем, в момент времени \ (t = 0 \). Мы называем эту скорость начальной скоростью : \ (\ vecs v (0) = \ vecs v_0 \). Следовательно, \ (\ vecs v (0) = – g (0) \, \ hat {\ mathbf j} + \ vecs C_1 = \ vecs v_0 \) и \ (\ vecs C_1 = \ vecs v_0 \). Это дает вектор скорости как \ (\ vecs v (t) = – gt \, \ hat {\ mathbf j} + \ vecs v_0 \).
Далее мы используем тот факт, что скорость \ (\ vecs {v} (t) \) является производной от положения \ (\ vecs {s} (t) \). Это дает уравнение
\ [\ vecs s ‘(t) = – gt \, \ hat {\ mathbf j} + \ vecs {v} _0.2 \, \ hat {\ mathbf j} + \ vecs {v} _0 t + \ vecs {s} _0. \]
Давайте внимательнее посмотрим на начальную скорость и начальное положение. В частности, предположим, что объект брошен вверх от начала координат под углом \ (\ theta \) к горизонтали с начальной скоростью \ (\ vecs {v} _0 \). Как мы можем изменить предыдущий результат, чтобы отразить этот сценарий? Во-первых, мы можем предположить, что он выброшен из источника. Если нет, то мы можем переместить начало координат в точку, откуда оно было брошено. Следовательно, \ (\ vecs {s} _0 = \ vecs {0} \), как показано на рисунке \ (\ PageIndex {6} \).2 \ right) \, \ hat {\ mathbf j}. \ end {align *} \]
Коэффициент перед \ (\ hat {\ mathbf i} \) представляет горизонтальную составляющую \ (\ vecs {s} (t) \) и является горизонтальным расстоянием объекта от начала координат в момент времени \ (t \) . Максимальное значение горизонтального расстояния (измеренное на одной и той же начальной и конечной высоте) называется диапазоном \ (R \). Коэффициент при \ (\ hat {\ mathbf j} \) представляет вертикальную составляющую \ (\ vecs {s} (t) \) и является высотой объекта в момент времени \ (t \) . Максимальное значение вертикального расстояния – высота \ (H \).
Пример \ (\ PageIndex {3} \): движение пушечного ядра
Во время празднования Дня Независимости на утесе в сторону воды выстреливается пушечное ядро. Пушка нацелена под углом 30 ° от горизонтали, а начальная скорость пушечного ядра составляет 600 футов / сек. Утес находится на высоте 100 футов над водой (рис. \ (\ PageIndex {7} \)).
- Найдите максимальную высоту пушечного ядра.
- Сколько времени потребуется, чтобы ядро упало в море?
- На каком расстоянии от моря ядро упадет в воду?
- Пушечное ядро достигает максимальной высоты, когда вертикальная составляющая его скорости равна нулю, поскольку в этой точке ядро не поднимается и не падает. Вектор скорости равен
\ [\ begin {align *} \ vecs {v} (t) & = \ vecs s ‘(t) \\ [4pt] & = 300 \ sqrt {3} \, \ hat {\ mathbf i} + ( 300-32t) \, \ hat {\ mathbf j} \ end {align *} \]
Следовательно, вертикальная составляющая скорости определяется выражением \ (300−32t \). Если установить это выражение равным нулю и решить для t , получим \ (t = 9.2) \, \ hat {\ mathbf j} \\ [4pt] & = 4871.39 \, \ hat {\ mathbf i} +1406.25 \, \ hat {\ mathbf j} \ end {align *} \] Следовательно, максимальная высота пушечного ядра составляет 1406,39 фута над пушкой или 1506,39 фута над уровнем моря. - Когда пушечное ядро приземляется в воде, оно находится на 100 футов ниже пушки. 2} -4 (4) (- 25)} {2 (4)} \\ [4pt] & = \ dfrac {75 \ pm \ sqrt {6025}} { 8} \\ [4pt] & = \ dfrac {75 \ pm 5 \ sqrt {241}} {8} \ end {align *} \] Положительное значение \ (t \), которое решает это уравнение, составляет примерно 19.2 \ right) \, \ hat {\ mathbf j} \\ [4pt] & = 9914.26 \, \ hat {\ mathbf i} −100.7424 \, \ hat {\ mathbf j} \ end {align *} \] Таким образом, мяч попадает в воду на расстоянии 9914,26 фута от основания обрыва. Обратите внимание, что вертикальный компонент вектора положения очень близок к -100, что говорит нам о том, что мяч только что ударился о воду. Обратите внимание, что 9914,26 фута – это не истинная дальность полета пушки, поскольку пушечное ядро приземляется в океане в месте ниже пушки. Дальность пушки будет определяться путем определения того, как далеко находится пушечное ядро, когда его высота составляет 100 футов над водой (такая же, как высота пушки).
Упражнение \ (\ PageIndex {3} \)
Лучник выпускает стрелу под углом 40 ° над горизонтом с начальной скоростью 98 м / сек. 2 \ sin2 \ theta} {g} \, \ hat {\ mathbf i}.2} {g} \) единиц.
Законы Кеплера
В начале 1600-х годов Иоганнес Кеплер смог использовать удивительно точные данные своего наставника Тихо Браге, чтобы сформулировать свои три закона движения планет, которые теперь известны как законы движения планет Кеплера. Эти законы также применимы к другим объектам Солнечной системы, находящимся на орбите вокруг Солнца, таким как кометы (например, комета Галлея) и астероиды. Варианты этих законов применимы к спутникам, находящимся на орбите вокруг Земли.
Теорема \ (\ PageIndex {2} \): законы движения планет Кеплера
- Путь любой планеты вокруг Солнца имеет эллиптическую форму, при этом центр Солнца находится в одном фокусе эллипса (закон эллипсов).
- Линия, проведенная от центра Солнца к центру планеты, сметает равные площади через равные промежутки времени (закон равных площадей) (рисунок \ (\ PageIndex {8} \)).
- Отношение квадратов периодов любых двух планет равно отношению кубов длин их больших полуосей орбиты (Закон Гармоний).
Третий закон Кеплера особенно полезен при использовании соответствующих единиц. В частности, 1 астрономическая единица определяется как среднее расстояние от Земли до Солнца, и в настоящее время признано равным 149 597 870 700 м или приблизительно 93 000 000 миль. Поэтому мы пишем 1 A.U. = 93,000,000 миль. Поскольку время, необходимое Земле для обращения вокруг Солнца, составляет 1 год, мы используем земные годы в качестве единиц времени.3 \ nonumber \]
для любой планеты Солнечной системы, где \ (T_P \) – период этой планеты, измеренный в земных годах, а \ (D_P \) – среднее расстояние от этой планеты до Солнца, измеренное в астрономических единицах. Следовательно, если мы знаем среднее расстояние от планеты до Солнца (в астрономических единицах), мы можем вычислить продолжительность его года (в земных годах) и наоборот.
Законы Кеплера были сформулированы на основе наблюдений Браге; однако формально они не были доказаны до тех пор, пока сэр Исаак Ньютон не смог применить исчисление.Кроме того, Ньютон смог обобщить третий закон Кеплера на другие орбитальные системы, такие как Луна, вращающаяся вокруг планеты. Первоначальный третий закон Кеплера применим только к объектам, вращающимся вокруг Солнца.
Проба
Давайте теперь докажем первый закон Кеплера, используя исчисление векторных функций. Для начала нам понадобится система координат. Давайте поместим Солнце в начало системы координат и пусть вектор-функция \ (\ vecs {r} (t) \) представляет положение планеты как функцию времени.3} \ vecs {r}. \ nonumber \]
Это уравнение показывает, что векторы \ (d \ vecs {v} / dt \) и \ (\ vecs r \) параллельны друг другу, поэтому \ (d \ vecs {v} / dt \ times \ vecs {r } = \ vecs 0 \). Затем давайте продифференцируем \ (\ vecs {r} \ times \ vecs {v} \) по времени:
\ [\ dfrac {d} {dt} (\ vecs {r} \ times \ vecs {v}) = \ dfrac {d \ vecs {r}} {dt} \ times \ vecs v + \ vecs {r} \ раз \ dfrac {d \ vecs {v}} {dt} = \ vecs {v} \ times \ vecs {v} + \ vecs {0} = \ vecs {0}. \ label {Eq10} \]
Это доказывает, что \ (\ vecs {r} \ times \ vecs {v} \) является постоянным вектором, который мы называем \ (\ vecs C \).3} [(\ vecs {r} \ cdot \ vecs {v}) \ vecs {r} – (\ vecs {r} \ cdot \ vecs {r}) \ vecs {v}]. \ label {Eq11} \]
Последнее равенство в уравнении \ ref {Eq10} взято из формулы тройного перекрестного произведения (Введение в векторы в пространстве). Нам нужно выражение для \ (\ vecs {r} \ cdot \ vecs {v} \). Чтобы вычислить это, мы продифференцируем \ (\ vecs {r} \ cdot \ vecs {r} \) по времени:
\ [\ dfrac {d} {dt} (\ vecs {r} \ cdot \ vecs {r}) = \ dfrac {d \ vecs {r}} {dt} \ cdot \ vecs {r} + \ vecs { r} \ cdot \ dfrac {d \ vecs {r}} {dt} = 2 \ vecs {r} \ cdot \ dfrac {d \ vecs {r}} {dt} = 2 \ vecs {r} \ cdot \ vecs {v}.2} \ dfrac {d} {dt} || \ vecs {r} ||. \ end {align *} \]
Следовательно, Equation \ ref {Eq15} становится
\ [\ dfrac {d \ vecs {v}} {dt} \ times \ vecs {C} = GM \ left (\ dfrac {d} {dt} \ dfrac {\ vecs {r}} {|| \ vecs {r} ||} \ right). \ nonumber \]
Поскольку \ (\ vecs {C} \) – постоянный вектор, мы можем проинтегрировать обе части и получить
\ [\ vecs {v} \ times \ vecs {C} = GM \ dfrac {\ vecs {r}} {|| \ vecs {r} ||} + \ vecs {D}, \ nonumber \]
где \ (\ vecs D \) – постоянный вектор. Наша цель – найти \ (|| \ vecs {r} || \).2} {GM} \ left (\ dfrac {1} {1 + e \ cos \ theta} \ right). \ nonumber \]
, где \ (e = || \ vecs {D} || / GM \). Это полярное уравнение коники с фокусом в начале координат, которую мы считаем Солнцем. Это гипербола, если \ (e> 1 \), парабола, если \ (e = 1 \), или эллипс, если \ (e <1 \). Поскольку планеты имеют замкнутые орбиты, единственная возможность - это эллипс. Однако здесь следует упомянуть, что гиперболические кометы действительно существуют. 3} {\ left (6.9 \ text {m} = 1,224,000 \ text {km} \]
Пример \ (\ PageIndex {5} \): комета Галлея
Теперь мы вернемся к открытию главы, в которой обсуждается движение кометы Галлея вокруг Солнца. Первый закон Кеплера гласит, что комета Галлея движется по эллиптическому пути вокруг Солнца, причем Солнце является одним из фокусов эллипса. Период кометы Галлея составляет примерно 76,1 года, в зависимости от того, насколько близко она проходит мимо Юпитера и Сатурна, проходя через внешние границы Солнечной системы.9 \) миль.
Возникает естественный вопрос: каково максимальное (афелий) и минимальное (перигелий) расстояния от кометы Галлея до Солнца? Эксцентриситет орбиты кометы Галлея составляет 0,967 (Источник: http://nssdc.gsfc.nasa.gov/planetary…cometfact.html). Напомним, что формула для эксцентриситета эллипса равна \ (e = c / a \), где a – длина большой полуоси, а c – расстояние от центра до любого фокуса. Следовательно, \ (0,967 = c / 17,96 \) и \ (c \ приблизительно 17.9 \) миль. Среднее расстояние от Плутона до Солнца – 39,5 а.е. (Источник: http://www.oarval.org/furthest.htm), поэтому может показаться, что комета Галлея находится в пределах орбиты Плутона.
НАВИГАЦИЯ ПО БАНКОВСКОМУ ОБОРОТУ
Как быстро гоночный автомобиль может пройти круговой поворот без заноса и удара о стену? Ответ может зависеть от нескольких факторов:
- Вес автомобиля;
- Трение между шинами и дорогой;
- Радиус окружности;
- «Крутизна» поворота.
В этом проекте мы исследуем этот вопрос для гоночных автомобилей NASCAR на автодроме Bristol Motor Speedway в Теннесси. Прежде чем рассматривать этот трек в частности, мы используем векторные функции для развития математики и физики, необходимых для ответа на такие вопросы, как этот.
Автомобиль массы \ (m \) движется с постоянной угловой скоростью \ (\ omega \) по круговой кривой радиуса \ (R \) (рисунок \ (\ PageIndex {9} \)). 2 \).2 \ справа) / R \).
Когда автомобиль движется по кривой, на него действуют три силы: сила тяжести, сила, действующая со стороны дороги (эта сила перпендикулярна земле), и сила трения (рисунок \ (\ PageIndex {10} \)) . Поскольку описать силу трения, создаваемую шинами и дорогой, сложно, мы используем стандартное приближение для силы трения. Предположим, что \ (\ vecs {f} = \ mu \ vecs {N} \) для некоторой положительной константы \ (\ mu \). Постоянная \ (\ mu \) называется коэффициентом трения .
Рисунок \ (\ PageIndex {10} \): На автомобиль действуют три силы: сила тяжести (обозначается \ (m \ vecs g \)) , сила трения \ (\ vecs f \) , и сила дороги \ (\ vecs N \) .Пусть \ (v_ {max} \) обозначает максимальную скорость, которую автомобиль может достичь на повороте без заноса. Другими словами, \ (v_ {max} \) – это максимальная скорость, с которой автомобиль может пройти поворот. 2} {R}.\]
Следующие три вопроса касаются разработки формулы, которая связывает скорость \ (v_ {max} \) с углом крена \ (\ theta \).
- Покажите, что \ (\ vecs {N} \ cos \ theta = m \ vecs g + \ vecs {f} \ sin \ theta \). Сделайте вывод, что \ (\ vecs {N} = (m \ vecs g) / (\ cos \ theta- \ mu \ sin \ theta) \).
- Центростремительная сила – это сумма сил в горизонтальном направлении, поскольку центростремительная сила направлена к центру круговой кривой. Покажи то
\ [\ vecs {F} _ {cent} = \ vecs {N} \ sin \ theta + \ vecs {f} \ cos \ theta.2 = ((\ sin \ theta + \ mu \ cos \ theta) / (\ cos \ theta- \ mu \ sin \ theta)) gR \). Сделайте вывод, что максимальная скорость практически не зависит от массы автомобиля.
Теперь, когда у нас есть формула, связывающая максимальную скорость автомобиля и угол крена, мы можем ответить на вопросы, подобные тому, который был задан в начале проекта.
Bristol Motor Speedway – это короткая трасса NASCAR в Бристоле, штат Теннесси. Дорожка имеет приблизительную форму, показанную на рисунке \ (\ PageIndex {11} \). Каждый конец пути примерно полукруглый, поэтому, когда автомобили делают повороты, они движутся примерно по круговой кривой.Если автомобиль движется по внутренней колее и движется по нижней части поворота 1, автомобиль движется по полукругу радиусом приблизительно 211 футов с углом крена 24 °. Если автомобиль решает выехать на внешнюю колею и движется в верхней части поворота 1, он едет по полукругу с углом крена 28 °. (Гусеница имеет крен с переменным углом.)
Коэффициент трения нормальной шины в сухих условиях составляет примерно 0,7. Поэтому мы предполагаем, что коэффициент для шины NASCAR в сухих условиях составляет приблизительно 0,98.
Прежде чем отвечать на следующие вопросы, обратите внимание, что проще производить вычисления в футах и секундах, а затем конвертировать ответы в мили в час в качестве последнего шага.
- Насколько быстро автомобиль может проехать по дну поворота без заноса в сухих условиях?
- Насколько быстро машина может проехать вершину поворота без заноса в сухих условиях?
- Во влажных условиях коэффициент трения может упасть до 0.1. В таком случае, как быстро автомобиль может проехать по дну поворота без заноса?
- Предположим, что измеренная скорость автомобиля, движущегося по внешнему краю поворота, составляет 105 миль в час. Оцените коэффициент трения шин автомобиля.
Тангенциальные и нормальные компоненты
Единичный касательный вектор \ (\ vec T \) дает нам единичный вектор в направлении движения. Мы можем получить направление движения по скорости. Если мы будем придерживаться прямого курса, то наше ускорение будет в том же направлении, что и наше движение, и только заставит нас ускоряться или замедляться.Мы будем называть это тангенциальным ускорением.
Если мы хотим спроектировать американские горки, построить истребитель F15, отправить спутник на орбиту или построить что-нибудь, что не движется по прямой линии, нам нужно понять, как ускорение заставляет нас сойти с прямой траектории. Мы все еще можем ускоряться или замедляться (тангенциальное ускорение), но теперь у нас есть компонент, который сбивает нас с прямого пути. Мы назовем это нормальным ускорением, оно ортогонально скорости.
Еще в главе о векторах мы практиковались записывать силу \ (\ vec F \) как сумму компонента, параллельного смещению \ (\ vec d \), и компонента, ортогонального \ (\ vec d \ text {.} \) Мы могли бы записать это как \ (\ vec F = \ vec F_ {|| \ text {to} \ vec d} + \ vec F _ {\ perp \ text {to} \ vec d}. \) Параллель часть пришла из проекции. Ортогональная часть была получена в результате вычитания векторов. Если вы забыли, как это сделать, выполните это упражнение на повторение.
Обзор8.5.1
Рассмотрим вектор силы \ (\ vec F = (0, -10) \ text {,} \) и вектор смещения \ (\ vec (2, -1) \ text {.} \) Вычислите проекцию \ ( \ vec F \) на \ (\ vec d \ text {,} \), а затем запишите \ (\ vec F \) как сумму вектора, параллельного \ (\ vec d \), и вектора, ортогонального \ ( \ vec d \ text {.2) \) (это упрощенный вариант сброса камешка со здания). Наша цель во время \ (t = 1 \ text {,} \) – записать \ (\ vec a \) в форме \ (\ vec a = a_T \ vec T + a_N \ vec N. \). шаги ниже.
(а)
Вычислить \ (\ vec v \ text {,} \) \ (\ vec a \ text {,} \) и \ (\ vec T \) во время \ (t \ text {,} \), а затем во время \ (t = 1 \ text {.} \)
(б)
At \ (t = 1 \ text {,} \) вычислить проекцию \ (\ vec a \) на \ (\ vec T \ text {,} \), т.е. вычислить \ (\ proj _ {\ vec T (1 )} \ vec a (1) \ text {.} \)
(в)
Состояние \ (\ vec N (t) \) (помните, что вы можете перевернуть порядок и изменить знак), а затем в \ (t = 1 \) вычислить \ (\ text {proj} _ {\ vec N (1 )} \ vec a (1) \ text {.} \)
(г)
Если мы напишем \ (\ vec a = a_T \ vec T + a_N \ vec N \ text {,} \), то что такое \ (a_T \) и \ (a_N \ text {?} \)
Определение 8.5.1 Касательная и нормальная составляющие ускорения
Предположим, что \ (\ vec r (t) \) – гладкая параметризация движущегося объекта. Пусть \ (\ vec T \) – единичный касательный вектор.Тангенциальная составляющая ускорения и нормальная составляющая ускорения – это скаляры \ (a_T \) и \ (a_N \), которые мы получаем, записывая ускорение как сумму вектора, параллельного \ (T \), и вектора, ортогонального к \ (\ vec T \ text {,} \) то есть скаляры, удовлетворяющие
\ begin {уравнение *} \ vec a = a_T \ vec T + a_N \ vec N. \ end {уравнение *}Вернемся к примеру Сэмми на карусели. В этом примере мы увидим одну из ключевых идей в этом разделе.
Упражнение 8.5.3 Необязательно, мы уже в основном это сделали
Предположим, что Сэмми сидит в \ (\ rho \) футах от центра карусели. Его сестра решает вращать его с разной скоростью. Пусть \ (\ vec r (t) = (\ rho \ cos \ omega t, \ rho \ sin \ omega t) \) будет параметризацией позиции Сэмми.
(а)
Покажите, что скорость Сэмми равна \ (| \ vec v | = \ rho \ omega \ text {.} \)
(b)
Найдите кривизну пути Сэмми в любое время \ (t \) (оно оказывается постоянным – и мы уже делали это, когда вычисляли кривизну по окружности).2 \) – тангенциальная и нормальная составляющие ускорения. Все, что нам нужно сделать, это записать вектор \ (\ vec a (t) \) как сумму вектора, параллельного \ (\ vec T \), и вектора, ортогонального \ (\ vec T \ text {.} \ )
Прежде чем мы разложим ускорение на тангенциальную и нормальную составляющие, давайте рассмотрим два примера, чтобы увидеть, что эти факты физически представляют.
Упражнение8.5.4
Представьте, что вы едете в качестве пассажира по дороге и сталкиваетесь с серией поворотов (так что дорога начинает зигзагообразно подниматься в гору).2 \ text {.} \) Инженеры дороги спроектировали дорогу так, что если вы двигаетесь со скоростью 15 миль / час, то нормальное ускорение будет не более \ (A \) единиц.
(а)
Предположим, что ваш водитель (Бен) игнорирует предложение снизить скорость до 15 миль / час. Он продолжает разворачиваться со скоростью 45 миль / час. Если бы он замедлился, максимальное ускорение было бы \ (A \ text {.} \) Вы путешествуете в 3 раза быстрее, чем предполагалось. Каким будет ваше максимальное нормальное ускорение?
ПодсказкаЭто больше, чем \ (3A \ text {.} \)
(б)
Вы кричите Бену, чтобы он сбавил скорость (вы не хотите умирать). Поэтому Бен решает снизить скорость только до 30 миль / час. Он полагает, что это означает, что вы почувствуете вдвое большее ускорение, чем \ (A \ text {.} \). Объясните, почему эта аргументация ошибочна.
(в)
Бен расстраивается из-за того, что ему приходится сбавлять скорость. Он жалуется на инженеров, спроектировавших дорогу, и говорит: «Им надо было просто построить угол побольше, чтобы я мог ехать 45». Насколько большим должен быть радиус круга, чтобы вы могли двигаться 45 миль / час вместо 15 миль / час и при этом ощущать то же ускорение \ (A \ text {?} \)
(d)
Что приведет к большему уменьшению обычного ускорения, уменьшению вдвое скорости или уменьшению вдвое кривизны (удвоению радиуса)?
Упражнение 8.2 \ vec N. \) Вот несколько подсказок.
Посмотрите видео на YouTube.
(а)
Перепишите скорость \ (\ vec v \) как величину \ (| \ vec v | \), умноженную на направление \ (\ vec T \ text {,} \) так \ (\ vec v = | v | \ vec T \ text {.} \)
(б)
Мы знаем, что \ (\ vec a (t) = \ frac {d} {dt} \ vec v (t) \ text {.} \) Возьмем производную от \ (\ vec v = | \ vec v | \ vec T \) с помощью правила произведения (на скалярном произведении \ (| \ vec v | \ vec T \)).
(в)
Вы должны встретить количество \ (d \ vec T / dt \ text {.2 \ text {.} \)
Давайте теперь воспользуемся приведенным выше фактом, чтобы получить чрезвычайно полезную формулу для кривизны.
Упражнение8.5.6
Мы можем использовать приведенную выше формулу для кривизны, чтобы быстро вычислить кривизну функции \ (y = f (x) \ text {.} \) Если вы воспользуетесь предыдущим упражнением, эта формула выпадает почти мгновенно. . Вы бы увидели эту формулу в динамике
, и он отображается на экзамене по основам инженерии (где вам просто нужно использовать формулу, а не доказывать, откуда она взята)
.{3/2}} {| f ” (x) |}. \ end {уравнение *}Мы пропустим этот раздел, однако, если вы хотите увидеть больше привязки к физике и инженерии, пропустите этот раздел.
Определение 8.5.2 Кручение
Пусть \ (\ vec r (t) \) – параметризация гладкой кривой \ (C \) с единичным касательным вектором \ (\ vec T (t) \ text {.} \) Производная от \ (\ vec B \) относительно \ (s \) говорит нам, насколько быстро вращается плоскость, содержащая \ (\ vec T \) и \ (\ vec N \). Определим вектор кручения как
. \ begin {уравнение *} \ vec \ tau = \ dfrac {d \ vec B} {ds} = \ dfrac {d \ vec B / dt} {ds / dt} = \ dfrac {d \ vec B / dt} {| d \ vec r / dt |}.\ end {уравнение *}Посмотрите видео на YouTube.
Кручение \ (\ tau \ text {,} \) с точностью до знака, является длиной этого вектора. Мы говорим, что есть положительное кручение, если \ (\ vec \ tau \) вызывает вращение против часовой стрелки вокруг \ (\ vec T \) (когда вы смотрите вниз \ (\ vec T \)), что происходит именно тогда, когда \ (\ vec tau \) и \ (\ vec N \) указывают в противоположных направлениях. Мы можем суммировать это
\ begin {уравнение *} \ tau = \ left | \ dfrac {d \ vec B} {ds} \ right | \ text {или} \ tau = – \ left | \ dfrac {d \ vec B} {ds} \ right |, \ end {уравнение *}, где вы выбираете «\ (+ \)», если \ (\ vec N \) и \ (\ vec \ tau \) указывают в противоположных направлениях.
Вычисления, связанные с получением \ (\ tau \), требуют большой работы. Давайте воспользуемся компьютером, чтобы помочь нам. Все это можно сделать с помощью Sage. Я позволю вам решить из кода, что такое \ (\ tau \). Это будет ваше решение.
Упражнение 8.5.8 (необязательно)
Рассмотрим спираль \ (r (t) = (3 \ cos t, 3 \ sin t, 4t) \ text {.} \) В упражнении 8.4.5 мы нашли
\ begin {align *} \ vec T \ amp = (- \ frac {3} {5} \ sin t, \ frac {3} {5} \ cos t, \ frac {4} {5}) \\ \ vec N \ amp = (- \ cos t, – \ sin t, 0) \\ \ vec B \ amp = (\ frac {4} {5} \ sin t, – \ frac {4} {5} \ cos t, \ frac {3} {5}) \ end {выровнять *}Вычислите вектор кручения \ (\ vec \ tau = \ dfrac {d \ vec B} {ds} \ text {,} \), а затем задайте кручение \ (\ tau \) (вам нужно определить скорость ).Кручение положительное или отрицательное. Попросите меня в классе показать вам, как вы можете определить это физически (без каких-либо вычислений).
Упражнение 8.5.9 (необязательно)
Рассмотрим спираль \ (r (t) = (4 \ sin t, 4 \ cos t, 3t) \ text {.} \) С помощью компьютера найдите \ (\ vec T \ text {,} \) \ ( \ vec N \ text {,} \) \ (\ vec B \ text {,} \) \ (\ vec \ kappa \ text {,} \) и \ (\ vec \ tau \ text {.} \) State ваши ответы. (Эта мудрая ссылка поможет.) Используйте свои ответы, чтобы затем дать \ (\ kappa \) и \ (\ tau \ text {.} \) (Когда вы представляете на доске, просто запишите 5 векторов, а затем объясните как вы получили \ (\ kappa \) и \ (\ tau \) из этих векторов.Если вы перейдете по ссылке, в основном это уже сделано за вас. )
В приведенных выше примерах вы должны были заметить, что \ (\ vec \ tau \) был либо параллелен \ (\ vec N \), либо антипараллелен \ (\ vec N \ text {.} \) Давайте теперь покажи, что это всегда так. Ключевым моментом является использование правила произведения для перекрестного произведения вместе с некоторыми ключевыми фактами о перекрестном произведении.
Обзор8.5.10
Каково перекрестное произведение \ ((1,2,3) \) и \ ((2,4,6) \ text {?} \) Если два вектора параллельны, то каково их векторное произведение? В частности, каково перекрестное произведение \ (\ vec N \) и \ (\ vec \ kappa \ text {?} \) См. Ответ.
Упражнение 8.5.11 (необязательно)
Предположим, что кривая \ (\ vec r (t) \) имеет рамку \ (\ vec T (t) \ text {,} \) \ (\ vec N (t) \ text {,} \) и \ ( \ vec B (t) \ text {.} \) Докажите, что \ (\ dfrac {d \ vec B} {ds} \) либо параллельна \ (\ vec N \ text {,} \), либо противоположна \ (\ vec N \ text {.} \) Вот несколько шагов.
Посмотрите видео на YouTube.
(а)
Почему \ (\ dfrac {d \ vec B} {ds} \) ортогонален \ (\ vec B \ text {?} \)
ПодсказкаКакова длина \ (\ vec B \ text {?} \) См. Теорему 8.4.1.
б)
Мы знаем \ (\ vec B = \ vec T \ times \ vec N \ text {.} \) Вычислить производную от обеих сторон, используя правило произведения, и объяснить, почему \ (\ frac {d \ vec T} {ds} \ times \ vec N \) отменяется. Затем объясните, почему \ (\ dfrac {d \ vec B} {ds} \) ортогонален \ (\ vec T \ text {.} \)
(c)
Если \ (\ dfrac {d \ vec B} {ds} \) ортогонален как \ (\ vec B \), так и \ (\ vec T \), почему он должен быть либо параллельным, либо антипараллельным \ (\ vec N \ text {?} \)
Заключение
После того, как вы выполнили задачи в этой \ chaptername и освоились с идеями, составьте короткий одностраничный план урока, содержащий примеры ключевых идей.У вас будет возможность преподавать из этого плана урока до сдачи экзамена. Затем войдите в Brainhoney и загрузите тест. После того, как вы пройдете тест, вы можете загрузить свою работу обратно в brainhoney, а затем загрузить ключ, чтобы увидеть, как вы справились. Если вам все еще нужно работать над усвоением некоторых идей, сделайте это, а затем продемонстрируйте свое мастерство с помощью исправлений викторины.
Заключение
На этом \ chaptername завершается. Посмотрите на цели в начале раздела.Сможете ли вы сделать все, что вам обещали? Review Guide Creation Ваше задание: организовать то, что вы узнали, в небольшую коллекцию примеров, иллюстрирующих ключевые концепции. Я назову это руководством по обзору вашего устройства. Я предоставлю вам шаблон, который включает ключевые концепции модуля из целей, поставленных в начале. После того, как вы закончите свое руководство по обзору, отсканируйте его в документ PDF (используйте любой сканер в университетском городке или программное обеспечение для обработки фотографий) и загрузите его в Gradescope. При создании этого руководства учитывайте следующее:
Перед каждым Праздником знаний мы посвящаем урок повторению.С хорошо составленными планами уроков у вас будет 4-8 страниц (для 2-4 глав), которые нужно рассмотреть для каждой, вместо 50-100 задач.
Думайте на 2-5 лет вперед. Если вы правильно составите эти планы уроков, вы сможете просмотреть свои планы уроков на этот семестр. Примерно на 20-25 страницах вы можете кратко изложить весь курс и легко вспомнить.
Разгон. Тангенциальная и нормальная составляющие ускорения. Кинематика вращательного движения.Вектор вращения. Осевые или псевдовекторы. Вектор угловой скорости. Период обращения. Угловое ускорение.
§4 Ускорение .
Тангенциальная и нормальная Составляющие ускорения
Ускорение – векторная величина, характеризующая скорость изменения скорости движущегося тела по величине и направлению.
Точка , среднее ускорение на временном интервале Δ t – вектор приращения av , равный отношению вектора скорости Δ v к временному интервалу Δ t
Ускорение ( мгновенное ускорение) Точка называется векторной величиной, которая равна первой производной скорости v по времени (или второй производной радиус-вектора от времени t )
Ускорение в момент времени t равно пределу среднего ускорения, когда
В декартовой системе координат вектор можно записать через его координаты
где
Модуль вектора ускорения
Вектор можно выразить как сумму двух составляющих:
– тангенциальная составляющая ускорения тангенциальна к траектории точки и равна
где вектор – единичный вектор касательной, проведенной в точке траектории и направление скорости
Векторы и коллинеарны с равноускоренным движением; при т. е. при равномерно замедленном движении.
Касательное ускорение – характеризует скорость изменения модуля вектора скорости (измеряет изменение величины скорости).
Для равномерного движения
– нормальная составляющая ускорения (нормального ускорения) по нормали к траектории и заданной точке в направлении центра кривизны траектории. Криволинейную траекторию можно представить в виде набора элементарных участков, каждый из которых можно рассматривать как дугу окружности радиуса R (называемого радиусом кривизны окружности данной точки траектории)
Нормальное ускорение характеризует скорость изменения направления вектора скорости (характеризует изменение направления скорости).
Модуль полного ускорения:
Классификация зависит от перемещений тангенциальной и нормальной составляющих:
- – постоянное движение;
- – равноускоренное движение;
- – равномерно замедленное движение;
- – поступательное движение с переменным ускорением;
- – равномерное круговое движение;
- – равномерное криволинейное движение;
- – криволинейное равноускоренное движение;
- – криволинейный равномерно замедленный ход;
- – криволинейное движение с переменным ускорением.
§ 5 Кинематика вращательного движения
Поворот корпуса на определенный угол φ можно описать вектором длины φ, а направление, совпадающее с осью вращения, определяется правилом правого винта (штопор, правый):
Четыре пальца правой руки – по направлению вращения согнутый большой палец указывает направление вектора.
Направление вектора вращения φ, связанное с правилом правой руки направления вращения. Такие векторы называются осевыми или псевдо – чтобы отличить их от обычных (иногда называемых полевыми) векторами. Вызывается вектором угловой скорости, который численно равен первой производной угла поворота по времени t и направлен вдоль фиксированной оси по правилу правой руки.
Угловая скорость, как, является осевым вектором.Осевые векторы не имеют определенных точек приложения, они могут быть нанесены из любой точки на оси вращения. Часто их отталкивает неподвижная точка оси вращения, одновременно принимаемая за начало отсчета. Вращение тела называется равномерным, если.
разделить на Δ т
Точки скорости в отличие от угловой скорости тела, называемой линейной скоростью. Он перпендикулярен обеим осям вращения (т.е., вектор), а радиус – вектор R , тянущийся к точке P от центра окружности и примерно равный векторному произведению:
Равномерное вращение может характеризовать период вращения T , который определяется как время, за которое тело совершает один оборот, то есть поворачивается на угол. Тогда
– зависимость угловой скорости от периода обращения.
скорость вращения – количество оборотов в единицу времени.
В случае переменного вращательного движения угловая скорость материальной точки изменяется как по величине, так и по направлению. Для характеристики скорости изменения угловой скорости при нерегулярном вращении вокруг фиксированной оси введен вектор – угловое ускорение тела равно первой производной его угловой скорости по времени
Вектор также является осевым (или псевдовектором).Векторы и то же направление для ускоренного вращения
и противоположные направления при замедленном вращении
Ускорение произвольной точки P тела в отличие от углового ускорения тела называется линейным ускорением.
Для равноускоренного вращательного движения можно записать:
Связь между линейными и угловыми значениями :
Линейный | Угловой | Отношения | Временная зависимость | ||
Путь (смещение) | вектор вращения | ||||
линейная скорость | угловая скорость | ||||
линейное ускорение | Угловое ускорение – рацион | ||||
Равномерное круговое движение
Равномерное круговое движениеРавномерное круговое движение
Объект, движущийся по окружности радиуса r с постоянной скоростью v ускоряется.В направление его вектора скорости все время меняется, но величина вектор скорости остается постоянным. Вектор ускорения не может иметь составляющей в направлении вектора скорости, так как такая составляющая будет вызвать изменение скорости. Следовательно, вектор ускорения должен быть перпендикулярно вектору скорости в любой точке окружности. Этот ускорение называется радиальное ускорение или центростремительного ускорения , и это указывает к центру круга.Величина центростремительного вектор ускорения равен c = v 2 / r. (Мы пропускаем вывод этого выражения.)
Ссылка: Равномерное круговое движение
Проблема:
Опишите, как водитель может управлять автомобилем, движущимся с постоянной скоростью, чтобы
(а) ускорение равно нулю, или
(б) величина ускорения остается постоянной.
Решение:
- Рассуждение:
(a) Водитель должен заставить машину двигаться по прямой линия.
(b) Водитель должен заставить машину двигаться по кругу (или по прямой с a = 0).
Проблема:
Орбита Луны вокруг
Земля приблизительно круглая со средним радиусом 3,85 * 10 8 м. Луна совершает один оборот вокруг Луны за 27,3 дня.
Земля. Найти
(а) средняя орбитальная скорость Луны и
(б) его центростремительное ускорение.
Решение:
- Рассуждение:
Расстояние, которое луна проходит за один орбитальный период T, равно d = 2πr.
Его скорость v = расстояние / время = d / T.
Центростремительное ускорение Луны v 2 / r. - Детали расчета:
(а) Расстояние, которое луна проходит за 27,3 дня, равно d = 2πr = 2,41 * 10 9 г.
Его скорость v = d / (27,3 дня) = (d / (2,36 * 10 6 с)) = 1023 м / с.
(b) Центростремительное ускорение Луны v 2 / r = 2,725 * 10 -3 м / с 2 .
Проблема:
Если вращение Земли увеличилось так, что центростремительное ускорение
равнялось ускорению свободного падения на экваторе,
(а) какова будет тангенциальная скорость человека, стоящего на экваторе, и
б) как долго будет день?
Решение:
- Рассуждение:
Если бы центростремительное ускорение было равно ускорению свободного падения на экваторе, тогда v 2 / r = g. - Детали расчета:
(а) Радиус Земли составляет 6368 км. Хотим v 2 / r = 9,8 м / с 2 , или v 2 = (9,8 м / с 2 ) * 6,368 * 10 6 м, или v = 7900 м / с.
(b) Продолжительность дня будет t = 2πr / v = 5065 s = 84,4 мин.
Неравномерное круговое движение
Тележка американских горок, движущаяся по петле, меняет скорость, а также направление движения.Его ускорение имеет радиальную составляющую и тангенциальную составляющую. компонент, a = a r + а т . В тангенциальная составляющая вызывает изменение скорости, и ее величина определяется как т. = dv / dt, а радиальная составляющая вызывает изменение направления и его величина определяется как r = v 2 / r, где r – радиус кривизна в рассматриваемой точке. Компоненты a r и a t перпендикулярны друг другу и величина a равно a = (a r 2 + a t 2 ) ½ .
Проблема:
Фигуристка выполняет восьмерку, состоящую из двух равных касательных. круговые дорожки. На протяжении первого круга она равномерно увеличивает скорость, а во втором круге она движется с постоянной скоростью. Сделайте набросок ее вектор ускорения в нескольких точках по пути движения.
Решение:
- Рассуждение:
На протяжении первого контура величина тангенциального ускорения a t постоянно.Величина радиального ускорения a r увеличивается как v 2 / r, когда скорость конькобежца увеличивается как v = a t t = (2a t d) ½ , где d – пройденный путь. Когда фигурист стартует, вектор ускорения равен по касательной к петле. Но угол θ, который он составляет с касательной увеличивается как tanθ = a r / a t = v 2 / (ra t ) = 2d / r. Во втором цикле t = 0 и r равно константа, а вектор ускорения указывает на центр контура.
Проблема:
Автомобиль, скорость которого увеличивается со скоростью 0,6 м / с 2 ,
едет по круговой дороге радиусом 20 м. Когда мгновенная скорость
машина 4 м / с, найти
(а) тангенциальная составляющая ускорения и
(б) величина и направление общего ускорения.
Решение:
- Рассуждение:
Тангенциальное ускорение автомобиля имеет заданную постоянную величину. Его направление касательно окружности.
Радиальное ускорение имеет величину v 2 / r. Его направление перпендикулярна касательному ускорению и указывает на центр круга. - Детали расчета:
(а) Тангенциальное ускорение автомобиля имеет постоянная величина 0,6 м / с 2 .
(b) Когда v = 4 м / с, радиальное ускорение имеет величину a r = v 2 / r = (16 м / с 2 ) / (20 м) = 0.8 м / с 2 , a = (a r 2 + a t 2 ) ½ = 1 м / с 2 .
Пусть θ – угол, который вектор ускорения составляет с линией, направленной от положение автомобиля по направлению к центру круга. Тогда tanθ = a t / a r = 0,75, θ = 36,9 o .
Проблема:
Цифра справа представляет полное ускорение движущейся частицы.
по часовой стрелке по кругу радиуса 2.5 м в данный момент времени. На это
мгновенно найти
(а) центростремительное ускорение,
(б) скорость частицы, и
(c) его тангенциальное ускорение.
Решение:
- Рассуждение:
Нам нужно найти компонент вектора a . - Детали расчета
(а) a r = a cos (30 o ) = 12,99 м / с 2 .
(б) а р = v 2 / r, v 2 = ra r , v = 5.7 м / с.
(c) a t = a sin (30 o ) = 7,5 м / с 2 .
Модуль 3: Вопрос 2
Может ли центростремительное ускорение изменить скорость кругового движения?
Обсудите это со своими однокурсниками на дискуссионном форуме!
Общие единицы измерения углов: градусов и радиан . Мы имеем 360 o = 2π радиан. Длина окружности радиуса r равна 2πr.Длина дуги окружности, составляющей 180 o , составляет πr. Длина дуги, содержащей 90 o , составляет (π / 2) r. Мы видим, что длина Дуга окружности, имеющая угол θ, равна θr, где θ измеряется в радианах.
Для малых углов θ, sinθ ~ θ, если θ измеряется в радианах. Вы можете убедиться в этом, посмотрев на таблицу или график.
| угол (град.) | угол (рад) | sin (угол) |
|---|---|---|
| 0 | 0 | 0 |
| 0.1 | 0,001745 | 0,001745 |
| 0,2 | 0,003491 | 0,003491 |
| 0,3 | 0,005236 | 0,005236 |
| 0,4 | 0,006981 | 0,006981 |
| 0,5 | 0,008727 | 0,008727 |
| 0,6 | 0,010472 | 0.010472 |
| 0,7 | 0,012217 | 0,012217 |
| 0,8 | 0,013963 | 0,013962 |
| 0,9 | 0,015708 | 0,015707 |
| 1 | 0,017453 | 0,017452 |
Криволинейное движение
Криволинейное движениеКриволинейное движение: n-t Координаты
Картинка:
1. Должность: Нормально-тангенциальные (n-t) координаты привязаны к a и перемещаются вместе с ним. частица. Поэтому там не является вектором положения в координатах n-t . Типичная задача n-t даст точное местоположение частицы на пути, или он предоставит кинематическую информацию, из которой положение может быть определенный.
| 2. Скорость: Поскольку скорость всегда касается пути, мы можем записать вектор скорости как |
где v скорость частицы.
| 3. Разгон: Дифференцируя вектор скорости по времени дает: |
Почему два термина появляются в этой дифференциации? Причина в том, что оба v и e t имеют производные по времени , поэтому мы используем правило продукта.
Вы знайте, что v (скорость) изменяется со временем, поэтому вы ожидаете, что у него будет производная по времени.
Но как e t меняется со временем? Будучи единичным вектором, его длина остается равной . Но поскольку он движется вместе с частицей, направление из e t изменений непрерывно! Итак, у него есть производная по времени, которая возникает из этого изменение направления.
| 4. Касательное ускорение: Скорость изменения скорость г. частица по пути. |
| 5. Нормальное ускорение: Скорость изменения направления вектора скорости .. |
6. Обычно существует два типа проблем: , в первую очередь, . n-t задач:
(а) Круглый путь: A частица движется по круговой траектории с постоянным радиусом r.
(б) Некруговой путь: Будут заданы скорость частиц и тангенциальное ускорение. в определенном месте. Радиус кривизны, r, необходимо определить, чтобы рассчитать нормальное ускорение.
7. Некоторые проблемы, которые в основном связаны с x-y или r-q координаты могут требовать, чтобы векторы скорости и ускорения были выражается в нормальной и тангенциальной составляющих. В векторные отношения, показанные на этой справочной странице, помогают в этом преобразовании.
Определение нормальных и тангенциальных координат | Скорость, ускорение и вращательное движение | Инженерная динамика | Машиностроение
Следующий контент предоставляется по лицензии Creative Commons.Ваша поддержка поможет MIT OpenCourseWare и дальше предлагать высококачественные образовательные ресурсы бесплатно. Чтобы сделать пожертвование или просмотреть дополнительные материалы с сотен курсов MIT, посетите MIT OpenCourseWare на ocw.mit.edu.
ПРОФЕССОР: Итак, мы делали скорости и ускорения. Мы придумали … Думаю, мне нужно и дальше напоминать нам. Мы говорим о скоростях и ускорениях точки по отношению к другой точке, к которой мы прикрепили – я сделаю это здесь – систему отсчета, x простое, y простое, z простое.И есть вектор, который проходит между этими двумя, и вектор, который идет туда, так что мы можем сказать, что r для B относительно O, моей инерциальной системы отсчета, является r для A относительно O плюс r для B относительно A. все векторы. А затем из них мы выводим формулы для скоростей и ускорения.
Итак, мы придумали пару очень удобных формул. Формула скорости, скорость B относительно O, представляет собой скорость A относительно O плюс вы должны взять производную от этого по времени.И поэтому я дам вам здесь только общее выражение для краткого напоминания. Это производная от B по отношению к A, как видно из фрейма Axyz плюс омега по отношению к O, перекрестному rBA. Это все векторы.
Так это формула скорости, помните? Это если вы находитесь в кадре, вращающемся и перемещающемся вместе с ним, это изменение длины вектора. И это, таким образом, вклад в скорость, которую вы видите в фиксированной системе отсчета, от вращения.
Затем мы перешли в полярные координаты.И мы выяснили, что если вы используете полярные координаты, вы можете выразить это как скорость A относительно O плюс r точка r шляпа. И я должен действительно сказать цилиндрические координаты, z точка k шляпа плюс r тета точка тета шляпа. Так что это то же самое.
Это полная трехмерная векторная нотация. Это частный случай системы координат, которую мы называем полярными координатами. И мы придумали другую формулу для ускорений, полную трехмерную векторную версию этого, A относительно O плюс – это ускорение B относительно A, но как видно в кадре Axyz.2 крестика омега – и это v, скорость, как видно в системе координат xyz. Итак, эти вещи, это не вклад ускорения. Это не вклад ускорения.
Плюс омега-нулевой перекрестный rBA плюс омега-перекрестный омега-перекрестный rBA – все векторы. Это движение кадра, его ускорение по отношению к этому. Это чистый перевод. Это ускорение собаки на карусели относительно центра системы координат. Это не связано с вращением.
Это термин, который мы называем Кориолисовым. Это термин, который мы называем Эйлером. Это угловая скорость системы, угловое ускорение. И это центростремительно. И если вы сделаете это, если вы хотите перейти к цилиндрическим координатам – и то, что мы собираемся сделать дальше, – это просто выполнить здесь несколько приложений.
Ускорение B относительно O и цилиндрических координат – это часть трансляции. Кроме того, теперь в цилиндрической форме их полезно сгруппировать. Итак, я собираюсь соединить этот термин и этот термин.Потому что они оба в правильном направлении. И я собираюсь соединить эти два термина. Потому что они оба придерживаются тета-шляпы. И мне нужна z двойная точка k, потому что она цилиндрическая. И затем у меня есть кусок тета-шляпы, r тета-двойная точка плюс 2r-точечная тета-точка тета-шляпа.
Это то же самое, что и это. За исключением того, что это выражается в цилиндрических координатах. А цилиндрические координаты особенно хороши для решения задач, которые в основном решаются на уровне этого курса, которые мы называем задачами плоского движения, ограниченными плоскостью x, y и ограниченными вращением одной оси по z.Эта система координат идеально подходит для решения подобных задач. И поэтому мы его используем.
А теперь давайте рассмотрим несколько примеров. Это действительно очень мощный инструмент – теперь, когда у вас есть эти два уравнения, вы можете заниматься множеством кинематики и динамики. Так что в прошлый раз мы начали в самом конце. Я сказал: «Хорошо, давайте быстро займемся этой проблемой, не так ли? Постоянная скорость вращения, постоянный радиус, отсутствие углового ускорения, отсутствие изменения длины объекта – довольно простая задача. И мы сделали это очень быстро.
И я хотел начать с этого, сделать это очень быстро. Так что это мой случай. Это мой мяч на веревочке. Вот точка А. Вот точка Б. Вот направление тета-шляпы, направление r-шляпы. И здесь он имеет некоторую постоянную длину R. Итак, r dot r double dot равны 0. Нет также z, z dot, z двойной точки, никакого движения z вообще. Это все 0.
Тета-точка – это постоянная величина. Я назову это cap omega в направлении k hat, правило правой руки. Двойная тета-точка равна 0. Таким образом, простой способ использовать эти формулы – это просто начать выбивать все термины, которые вам не нужны.
Но давайте, просто чтобы дать вам небольшой краткий обзор того, как использовать эти вещи, на секунду воспользуемся векторной полной трехмерной версией уравнения скорости. В полной 3D-версии указано, что скорость A относительно O, что это в этой задаче? Это переводной термин. Так что я стоял на месте, никуда не уходил. Но если бы я шел, я бы все равно крутил эту штуку.
Хорошо, значит, эта проблема, этот член равен 0. Эта проблема, точка – пойдем сюда. Это скорость изменения длины струны в системе координат идущей струны.Так что такое точка? Хорошо, значит, этот член равен 0. И омега пересекает rBA – ну, r находится в шляпе R, заглавная R R шляпа, крест с омегой k. k крест R – это k крест R шляпа?
СТУДЕНТ: Тета.
ПРОФЕССОР: Тета-шляпа. Итак, мы знаем, что первый член равен 0. Второй член равен 0. Третий член, мы просто получаем нашу Омегу в направлении тета-шляпы. Мы знаем, что это правда. Я просто пытаюсь здесь подчеркнуть, что вы всегда можете просто отступить и использовать векторную формулу, полные трехмерные формулы обоих.Просто подключите его, и все просто выпадет.
Затем вы можете перейти к терминам с цилиндрическими координатами, когда все это выражается в таких координатах, чтобы упростить вам задачу. Хорошо, теперь давайте быстро выполним ускорение B относительно O. И давайте использовать формулировку уже в цилиндрических координатах. Что А по отношению к О? 0. Что такое двойная точка r? Как насчет члена r тета-точки в квадрате, 0 или нет? Неа. Пойдем – z двойная точка?
СТУДЕНТ: 0.
ПРОФЕССОР: r тета двойная точка?
СТУДЕНТ: 0.
ПРОФЕССОР: r точка тета точка?
СТУДЕНТ: 0
ПРОФЕССОР: Хорошо, у нас остается только один семестр. На самом деле, я собираюсь оставить это на секунду – A относительно O минус. И мы придумали термин R theta dot square r hat. Я оставляю это здесь, потому что на самом деле мне не нужно говорить. Если бы я хотел сейчас решить эту задачу, если бы я попросил вас решить задачу, в которой я это делаю, и я начну ускоряться, вы знаете, как это сделать? Есть ответ – все еще есть, верно?
Хорошо, давайте сделаем быструю бесплатную диаграмму тела.Вот наша масса, моя основная система координат. Давайте нарисуем – допустим, вот здесь, под углом 90 градусов. Какие внешние силы действуют на массу в этой задаче?
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Значит, струна натянута? Хорошо, теперь это действительно тривиально простая проблема. Таким образом, акцент здесь делается на концепции. Итак, теперь, когда вас просят придумать уравнение движения или вычислить силы, действующие на массу, используйте второй закон Ньютона, F равно массе, умноженной на ускорение.
Теперь у вас есть полная формулировка трехмерного вектора для ускорения частицы в поступательно вращающейся системе координат. Это все, что вам нужно для вычисления ускорения для множества сложных задач. Итак, если вы можете записать ускорение, вы говорите, что оно равно какому? Масса – если умножить массу на это ускорение, что это равно?
СТУДЕНТ: Сила.
ПРОФЕССОР: Силы, которые должны действовать на систему. И в этом суть.Итак, теперь я хочу узнать силы, действующие на систему, сумму внешних сил. И тогда это векторы. И вы можете делать их покомпонентно. Некоторые внешние силы в прямом направлении должны быть равны массе – в данном случае просто частицы – умноженной на ускорение этой частицы. И в этой задаче это будет масса, умноженная на ускорение A относительно O минус R тета-точка в квадрате r hat.
И это должен быть главный компонент этой штуки.Я сказал, что мне нужен только компонент R. Мне нужно было выяснить, бежал ли я, если бы это было в том же направлении, что и r. Какая часть этого ускорения происходит в этом направлении? Это пришло бы сюда. Если есть 0, вы просто сделаете это 0. Так что давайте просто допустим, что ускорение A относительно O будет равным 0. Тогда это означает, что сумма сил в направлении r равна массе минус mR тета-точка в квадрате.
И если бы мы изобразили диаграмму свободного тела, мы бы обнаружили, что, ах, должно быть натяжение струны, втягивающее массу, достаточное для того, чтобы придать ей ускорение, которое вы вычислили.Итак, каждая проблема, когда вас просят вычислить силу или на следующем шаге найти уравнение движения, уравнение движения просто записывает это.
Хорошо, теперь я хочу перейти к более интересной задаче. Хорошо, я займусь этой проблемой. Так что это полая трубка. И мы собираемся посмотреть на такие вещи, как я положил в него мяч для пинг-понга. И если я поверну эту трубку, шарик для пинг-понга вылезет наружу.
Хорошо, на эту штуку должны быть какие-то силы, чтобы она вышла наружу.На них должно быть какое-то ускорение. И поэтому я мог бы предположить R, ускорение тета-двойной точки. Он определенно будет иметь скорость вращения тета-точек. Мячу разрешено двигаться. Так что может быть ненулевых точек, r двойных точек – внутри этой простой маленькой трубочки происходит много всего.
Вот что я хочу выяснить. Посмотрим, сможем ли мы придумать модель этой проблемы. Итак, вот моя ось z. У меня есть вращение вокруг него, какое-то направление тета-точки k. Вот моя трубка.Он вращается. Так что это вид сбоку, ваш вид на трубу. Вот тот мяч для пинг-понга.
И я собираюсь на минутку идеализировать этот мяч для пинг-понга, немного более общая задача. Допустим, у меня есть что-то вроде гайки на этой штуке, диск, что-то висит снаружи. И я могу контролировать скорость, с которой эта штука гаснет. Шарик для пинг-понга, это будет его применение. Но я хочу иметь возможность сделать несколько других версий, например, сделать скорость постоянной на секунду.
Хорошо, и глядя на эту штуку, вид сверху, вот наша инерциальная рамка, может быть, вот так. Вот моя месса. Итак, в полярных координатах вот ваша тета. Р это. Это твоя шляпа. Это ваши тета-направления.
Я собираюсь позволить скорости A относительно O равной 0, так что в этой системе нет поступательного движения. И z, z точка, z двойная точка, это все 0. Итак, в направлении z ничего не происходит. Итак, я хочу сначала вычислить скорость B относительно O.
И вы должны уметь делать это при осмотре. Это исходит только от … о, я недостаточно сказал тебе. Что я хочу сделать в этой проблеме? Я хочу поставить точку – это будет какой-то vr, и он постоянный. Я пока не собираюсь здесь полностью сходить к своему стрелку по пинг-понгу. Сначала я решу немного более простую задачу.
Значит, это константа. Это означает, что r двойная точка равна 0. Итак, эта штука просто – допустим, у вас есть резьбы на этой штуке, и это винт, и он просто выходит наружу с постоянной скоростью.И у меня будет постоянный угол, так что тэта-точка. Я назову эту кепку омега-к шляпой. Таким образом, угловая скорость также постоянна.
Хорошо, если это так, можете ли вы мне сказать, какое значение v из B относительно моего фиксированного кадра O? Что ж, всякий раз, когда вы не уверены, вы возвращаетесь к этой формуле и отбрасываете термины. Нет термина с z-точкой. Это постоянно. Это 0, 0, 0. У вас есть этот термин. Это немного вр в правильном направлении. У вас есть этот термин везде, где он находится в направлении тета-шляпы.
r точка в направлении r шляпы плюс точка r theta в направлении theta hat – ОК, нам нужно ускорение, B по отношению к O. И теперь вы можете снова прокрутить условия. На этот раз первый член равен 0. Второй член равен 0, потому что он постоянный. Третий член определенно не 0. Четвертый член равен 0. Пятый член? 0. Этот термин? Не 0.
Позвольте мне их просто написать. Таким образом, вы получаете r-шляпу минус r тэта-точку в квадрате – это член радиального направления – плюс 2r-точка тета-точка тета-шляпа.Это ускорения. Итак, теперь у вас есть ускорение в прямом и тэта-направлениях. Если в этих направлениях есть ускорение, значит, должны быть силы.
Второй закон Ньютона снова говорит, что сила равна массе, умноженной на ускорение. А это вектор. Это вектор. Он состоит из двух компонентов. И что хорошо в этих законах и векторах Ньютона, так это то, что вы можете разбить задачи на их векторные компоненты и рассматривать направление r как одно уравнение движения, а направление тета как отдельное.
Итак, мы можем захотеть нарисовать диаграмму свободного тела. Вот этот блок выходит наружу. Мы знаем, что, вероятно, существует некоторая осевая сила. Я просто назову это Т. И здесь есть еще какая-то неизвестная сила в направлении тета-шляпы.
Итак, это моя тета-шляпа. Я намеренно нарисовал это в положительном направлении. Появившийся знак укажет нам, в каком направлении он находится на самом деле, если вы не уверены. Просто нарисуйте это позитивно, в позитивном направлении.
И это ваша свободная диаграмма тела.Если бы я хотел добавить сюда гравитацию, я мог бы это сделать. Но мы делаем это в горизонтальной плоскости. Таким образом, гравитация присутствует и исчезает. Это в направлении z. И мы знаем, что он скован, не может двигаться. z двойная точка равна 0. Таким образом, определенно существует опорная сила, которая принимает вес.
Но это в нашей горизонтальной плоскости. Вот ваша диаграмма свободного тела. И мы можем написать два уравнения, чтобы решить эти проблемы. Таким образом, сумма сил в прямом направлении равна T. И это должно быть равно массе, умноженной на ускорение в r, минус mr тета-точка, возведенная в квадрат в направлении r.Конечно, натяжение должно тянуться внутрь в отрицательном направлении. И это полный результат.
СТУДЕНТ: Где именно силы T и F?
ПРОФЕССОР: Где они? Хорошо, я собираюсь вынести мяч наружу, чтобы вы могли его увидеть. Эта штука движется в этом направлении, в горизонтальной плоскости, в плоскости x, y. Он убирает фиксированную ставку. Так что его скорость, когда он здесь, составляет более двух омег в этом направлении.
И скорость, когда он здесь, – это омега в том направлении.Итак, очевидно, что он набирает скорость. Если он набирает скорость, набирает ли он кинетическую энергию? Проводится ли какая-то работа по накоплению этой энергии? Так что в игре должны быть какие-то силы.
Значит, стена этой штуки с нормальной силой толкает мяч вбок, чтобы ускорить его, конечно. Это одна сила. А другая сила в том, что я не позволяю этой штуке просто выходить наружу. Я ограничиваю его постоянной скоростью.
Мне бы очень хотелось поехать намного быстрее.Так что же его сдерживает? В любой момент времени он имеет центростремительное ускорение. И то, что заставляет его двигаться по кругу, – это сила, которая – в данном случае, если бы это была гайка с резьбой, в резьбе прилагается к гайке, чтобы она не ускользнула.
СТУДЕНТ: На этой диаграмме свободного тела F, разве F не действует одинаково между тэтой и r? А там есть что-то вроде компонента тета-шляпы?
ПРОФЕССОР: Ну, я сломался. Я выбрал. Общая сила, действующая на этот предмет, представляет собой некоторую комбинацию силы в этом направлении и комбинации в осевом направлении.Так что у него есть какое-то чистое направление, не то и не то.
СТУДЕНТ: Судя по этому уравнению, это похоже на то, что вы нарисовали, F имеет компонент r шляпы.
ПРОФЕССОР: Итак, вот эта штука вращается вокруг какого-то центра. Итак, это тета-точка. Тэта идет в этом направлении, тэта-точка. И мы выбрали систему координат, в которой есть единичные векторы r шляпа и тета шляпа. И в этом есть смысл. Мы можем выразить ускорение в терминах этих двух компонентов. Имеет смысл выражать силы в одном направлении.
Итак, я просто произвольно сказал, что у меня есть некая неизвестная сила, которая движется в этом направлении. И в этом направлении у меня есть еще одна неизвестная сила. Тогда я говорю, что они учитывают все силы в этом направлении, независимо от их источника.
Это говорит мне, что сумма внешних сил в направлении тета-хэта в данном случае – это неизвестное F. Но я знаю от Ньютона, что это должно быть равно массе, умноженной на ускорение в этом направлении. В данном случае это 2-миллиметровая тэта-тэта-шляпа.
Итак, просто применив уравнение и второй закон Ньютона, я могу выяснить, какой должна быть эта сила. Было бы намного больше работы, если бы я нарисовал это в каком-то произвольном направлении. Потому что тогда мне пришлось бы разбить его на составные части, чтобы написать это. Так что я максимально упростил это для себя.
Итак, есть такая сила. И есть еще одна такая сила. Это вызвано центростремительным ускорением. Или эта сила вызывает центростремительное ускорение.Чтобы что-то двигалось по круговой траектории, вы должны приложить к нему силу. Это сила. Чтобы что-то ускорить под углом, вы должны приложить силу. Это происходит от члена Эйлера.
А это любопытный термин. Это термин Кориолиса. Так откуда это взялось? В этом суть дела. Откуда это взялось? Итак, часть чтения, которую вам нужно сделать сейчас, – это Глава 15. Глава 15, большая часть которой будет полным обзором. Он просто говорит о сохранении количества движения, импульса и количества движения.Но он также попадает в угловой момент.
Итак, мы собираемся довольно много говорить об угловом моменте. И я хочу сделать очень краткий небольшой обзор прямо сейчас, чтобы он относился к этой проблеме. Итак, мы придумали выражение, что сила в тэта-направлении здесь идет – должно быть это, 2mr dot theta dot.
Итак, вот моя точка O и A, если на то пошло. Но если взглянуть на нашу проблему сверху вниз, то вот моя масса в какой-то момент времени. Моя скорость вращения – это тета-точка – или на самом деле она постоянная.Так что это такая кепка, кепка омега к шляпа. Это мое направление, тета-шляпа.
Теперь я буду рассматривать это как частицу. Не долго – мы будем говорить о динамике твердых тел. На данный момент мы просто делаем частицы. Мы думаем о них как о точечных массах и не имеем дела с их конечной протяженностью. Так что мы все еще думаем об этом как о частице.
И я собираюсь записать определение углового момента частицы. Здесь B по сравнению с моей фиксированной рамкой здесь, в O.И я собираюсь использовать букву h в нижнем регистре для описания углового момента частиц. И я буду использовать заглавную H, чтобы описать угловой момент твердого тела.
Итак, это частица, определение углового момента частицы относительно фиксированной точки. Мы вернемся к этому. Это будет иметь какое-то значение. Определение этого – это RBO, вектор положения, пересекаемый с линейным импульсом, оцениваемым в фиксированной системе отсчета. Итак, это определение углового момента, то есть у вас есть линейный момент, и это перекрестное произведение с вектором положения на него.
Итак, в этом случае RBO – это заглавная R R шляпа. Ну, это не так – это по-разному, извините. Так что я не собираюсь использовать – это я использую как константу. Я лучше оставлю это как переменную. Простите, так что это r, независимо от локального положения, в прямом направлении, пересекаемом с линейным импульсом. Каков линейный импульс этой частицы? Масса, умноженная на скорость. Какая скорость?
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Тэта точка – где мы это написали? Где-нибудь – общая скорость равна r dot r hat плюс r theta dot theta hat.И нам нужна масса здесь. Таким образом, масса, умноженная на скорость, будет импульсом. И нам нужны их перекрестные произведения. Что ж, вы ничего не получите от этого. А что насчет тэты – положительное или отрицательное? Положительный k, правда?
Таким образом, это становится тета-точкой mr в квадрате в направлении k шляпы. И этот постоянный. Запишем это как cap omega. Итак, это мой угловой момент моей частицы относительно этой фиксированной системы отсчета.
Итак, последний шаг, который вы знаете из своей предыдущей физики – как крутящий момент связан с угловым моментом? Предположить.Что ты помнишь? Производная по времени – здесь d на dt hBO. Скорость изменения этого вектора – это крутящий момент относительно этой точки относительно O.
Итак, какие константы в этой штуке? Нам не нужно иметь дело с их производными. К какова … направление углового момента меняется? Это вверх. Производная от k, единичный вектор k, меняется ли она в этой задаче? Нет, поэтому его производная по времени равна 0. Его производная по времени равна 0. Производная по времени m равна 0. Единственное, что вам нужно взять производную от r, так что 2rr точка.
Таким образом, крутящий момент составляет 2 миллиметра, точечный колпачок омега. И все это в направлении k. И это лучше было бы rBO cross F. Крутящий момент рассчитывается как сила, умноженная на плечо, верно? И мы вычислили здесь силу в тета-направлении.
Так что же даст нам крутящий момент в направлении k? Пересеките тэту. r шляпа кросс-тета дает вам k. r cross – и эта сила, часть силы. У нас есть две силы: одна в направлении r, а другая – в направлении тета. Перекрестное произведение, этот термин здесь, буква T ничего не дает, крестик крестик крестик.
Значит, здесь важна только сила Кориолиса. Таким образом, эта сила равна 2 миллиметрам, тэта-точкам. И у нас есть крестик r. Мы знаем, что это происходит в направлении k. И мы получаем здесь r, когда вычисляем этот продукт. И это, на мой взгляд, очень похоже на это. Вот только я пропустил r в квадрате. Как я это сделал?
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: О нет, это не квадрат. Это началось здесь, поскольку угловой момент имеет квадрат r, взяв производную.Он упал до 2rr точек. И это правильно. Итак, сила Кориолиса, какое отношение она имеет к угловому моменту?
Это своего рода суть упражнения. Чтобы этот мяч для пинг-понга мог ускоряться, по мере того, как он медленно выходит из этой трубки, угловой момент увеличивается. Чтобы со временем изменить угловой момент, необходимо приложить крутящий момент. Крутящий момент, который вы должны приложить, составляет 2 миллиметра на точку в направлении k. И это пересечение силы Кориолиса.
Итак, сила Кориолиса в данном случае – это сила, необходимая для увеличения углового момента системы.Очень часто причина – это сила Кориолиса. Итак, когда вы стреляете из артиллерийского орудия по Земле, у вас вылетает этот снаряд. Он имеет момент количества движения относительно Земли. И вы обнаружите, что всплывает этот маленький термин. И на самом деле снаряд летит не по прямой. Он изгибается.
Есть много вещей, которые из-за сохранения углового момента могут привести к появлению этого термина. В этом случае угловой момент не сохраняется. Это увеличивается.Итак, у вас есть сила, чтобы это произошло. Есть вопросы по этому поводу? Вы собираетесь использовать его много раз. Вы будете много работать с этим.
Итак, каждый раз, когда вы видите изменения углового момента, происходящие в задаче, в этих задачах с круговым движением, когда скорости частей увеличиваются в радиусе, вы почти всегда увидите этот термин всплывающим. Каждый раз, когда вы видите эти изменения углового момента, вы часто видите член Кориолиса.
Хорошо, теперь займемся другой интересной задачей – простой, но интересной.И это действительно так – давайте займемся этой проблемой, когда этому действительно позволено свободно выходить наружу. Хорошо, ты готов защищаться?
Маленькая короткая палка довольно эффективно бросает конфеты. На тебе защитные очки? Вы хотите, чтобы я посмотрел, смогу ли я его достать? Ой, к тому же я, очевидно, не практиковал это. Хорошо, последний. Собственно, есть еще два.
Что заставляет это работать? Давайте займемся этой проблемой. Итак, давайте посмотрим на наш шутер из конфет. Так что я раскручиваю эту штуку.Кенди выходит отсюда. Это в B.
Опять же, я не получаю z, не связываюсь с частью z. Обычно с z-частью легко иметь дело. Потому что он полностью независим, просто разделите уравнения. Это совсем не усложняет ситуацию, даже если у вас есть z.
Теперь, в данном случае, скорость – и вот моя О-образная система. Скорость B относительно O, ну, теперь у нее есть … Я не собираюсь двигаться. Я стою на месте, когда делаю это. Итак, первый член равен 0. У него есть r член, r точка в r шляпном направлении.И у него есть термин r theta dot theta hat.
И теперь это может – это может измениться. Это может иметь производную по времени, двойную точку r. Безусловно. Выходит из этой трубы с ускорением. И мое тэта, угловое движение, тоже может ускоряться. Так что нам придется с ними разобраться.
Мне нужно знать ускорения. До сих пор я не акцентировал на этом внимание, но считаю, что концептуально полезно – когда вы работаете с полярными координатами, вы можете иметь эту способность агрегировать термины в этих двух составляющих направлениях.Итак, у вас есть это.
Все термины r идут вместе. И мы позволили термину с двумя точками z – он просто отделен сам по себе. Выпадает легко. И у вас есть термин тета-шляпа. И это двойная точка r theta плюс 2r точка theta. И это в направлении тета-шляпы. Это ваш член Кориолиса, ваш член ускорения Эйлера, центростремительный член. Ага?
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Я не знаю, должен ли я рассказывать вам секреты обо мне. Потому что это даст вам преимущество в викторине.Но мне почти никогда не приходилось задавать вопрос, который гласит: «получить». Но я обязательно задам вам концептуальные вопросы.
Я действительно хочу, чтобы вы поняли принципы. Я не особо зацикливаюсь на том, что вы делаете грубые вещи. Я хочу, чтобы вы запомнили формулу вычисления производной вектора во вращающейся системе отсчета? Да, вот откуда они взялись.
Тебе лучше запомнить это. Эти две формулы, формула скорости и эта, формула ускорения, являются лишь сердцевиной этого курса.Теперь, как делаются викторины – сначала вы входите, вы входите, один лист бумаги. Что лучше было бы у вас на бумаге? OK?
И вторая викторина, два листа, финал, три листа и тому подобное. Но концептуально у вас есть силы в r, силы в z, ускорения в r theta и z, силы r theta и z. И для решения этих задач с плоским движением этот, безусловно, прост в использовании. Итак, давайте задумаемся над этой проблемой. Я собираюсь позволить этому пройти без трения, просто чтобы облегчить задачу.
Хорошо, какие же силы действуют на кусок леденца? Давайте сделаем бесплатную диаграмму тела выходящего отсюда кусочка леденца.Какие силы? И пусть это будет планарным.
Мы можем добавить сюда гравитацию. Но давайте просто сделаем это в самолете. Так что я просто иду горизонтально и подвешиваю эту штуку. Гравитация направлена по оси z, и я ограничил ее по оси z. Так что это что-то поддерживает гравитацию в трубе.
Так что определенно на этой штуке внизу есть мг. Но он в направлении z, и мы не позволяем ему двигаться по оси z. А как насчет горизонтали, этого направления? Р … это мое главное направление.Это мое направление тета-шляпы. Ой, тоже нет – тета идет в этом направлении. Итак, я нарисовал это как вид сбоку. Какая сила в прямом направлении?
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Хорошо, чтобы решить проблему, вы должны это выяснить. Какие силы? Каковы источники сил в направлении r? Вот направление r.
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Что скажешь? Давай, ребята. Кто-нибудь … да.
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Нет. Это то, что ты сказал? Нет ни одного. И почему это?
СТУДЕНТ: [Неразборчиво].
ПРОФЕССОР: Верно, значит, в направлении r нет сил. Так что нет сил на эту штуку в р. Итак, это вид сбоку. Мы могли бы сделать вид сверху, глядя вниз. Вид сверху, у вас есть x, y. У тебя также есть … вот мяч. Вот шляпа. Вот шляпа тета. Теперь, диаграмма свободного тела на виде сверху – ну, наверное, здесь есть какая-то сила.
СТУДЕНТ: Я хотел спросить, что у нас нет сил в прямом направлении, но есть ускорение.
ПРОФЕССОР: Совершенно верно. Она комментирует, что у нас действительно есть ускорение в направлении r, верно?
СТУДЕНТ: А силы у нас нет.
ПРОФЕССОР: И никакой силы. Вот в чем загадка этой проблемы. В этом суть проблемы. Так что позвольте мне продолжить. Схема свободного тела – я смотрю на нее сверху вниз. Я допускаю некоторую силу. Это нормальная сила, которая исходит от трубки, воздействующей на леденец.А поскольку он не имеет трения, он может быть нормальным только для трубы. Итак, на виде сверху есть диаграмма свободного тела.
Итак, мы можем написать два уравнения. Мы можем написать три вопроса: один равен 0, второй – в направлении тета, второй – в направлении тета. Сумма сил в этом направлении должна быть равна 0. И у нас есть масса. У нас есть разгон. Решите относительно r двойной точки.
Замечательно – нет силы в прямом направлении. Положение объекта, координата r, он имеет скорость.У него есть ускорение. Но полное ускорение в прямом направлении равно нулю. Скорость изменения скорости этого предмета в радиальном направлении, двойная точка, отлична от нуля. Но сил на это нет.
Я придумал другой способ объяснить это. Я все еще думаю об этом. И ты тоже думаешь об этом. Как это объяснить отсутствием сил? Отчасти это происходит из-за концепции фиктивных сил, центробежная сила – это сила. Это не.Это ускорение.
Это просто говорит о том, что – давайте вернемся к этой проблеме. Чтобы заставить что-то двигаться по кругу, вы должны приложить к нему силу, чтобы вызвать центростремительное ускорение. Вы должны позволить вещи погаснуть, если вы не заставляете ее идти по кругу. Вы должны позволить ему погаснуть с такой скоростью, чтобы на объекте не было центростремительных ускорений. Ага?
СТУДЕНТ: Итак, я хотел сказать, когда вы запускаете его, вы толкаете его в направлении y.Так что это сила. Дело не в шляпе, а в у.
ПРОФЕССОР: Для начала.
СТУДЕНТ: Верно, и нет силы, противодействующей ему в этом направлении [НЕРАЗБОРЧИВО].
ПРОФЕССОР: Есть ли центростремительное ускорение? Так что ротации нет. Испытывает ли он центростремительное ускорение? Что вы думаете? Да, потому что он движется по кривой. В любой момент времени, когда он это делает, существует радиус кривизны. В этот момент времени вы можете думать о нем как о круговом пути.
А иногда очень просто решать такие задачи с нормальными и тангенциальными координатами. Итак, я смотрю на плоскость x, y. Гравитация проникает в Землю. Итак, я смотрю на машину, машину.
И эта машина, парень вроде как пьян. Он идет по дороге вот так. Итак, вот мой y. Вот мой х. И y равно некоторому синусу A 2 пи по длине волны, 2 пи по лямбде, умноженному на x при некотором синусе kx.
И когда он едет вниз – если ты в машине и делаешь это, тебя в машине бросает из стороны в сторону.Итак, вы ускоряетесь. Итак, мы хотим иметь возможность рассчитать ускорение, связанное с тем, что вы спускаетесь по кривой пути. И мы имеем дело с этими вещами иногда с помощью удобного небольшого набора координат, которые являются нашими нормальными и касательными единичными векторами, u нормальными и u тангенциальными, в любой момент времени.
И мы знаем, что если это по пути, в любой момент времени вы находитесь здесь, в каком направлении ваша скорость? Просто определение скорости – касательной к траектории, верно? Таким образом, в любой момент времени скорость должна быть касательной к траектории в этот момент.
Итак, вектор скорости имеет величину и единичный вектор uT, здесь я назову его тангенсом. Вот и все. И ускорение этой вещи – ваша производная от этого во времени. И это даст вам v dot uT hat плюс v. А теперь вам нужна производная по времени от этого парня.
Но это вектор единичной длины. Вы можете вставить его в это уравнение для производной вращающегося вектора и вычислить, каким оно должно быть. Вы также можете просто нарисовать его. Я нарисую это для вас.Как у нас дела вовремя? Я просто смогу закончить это.
Вот мой единичный вектор в тангенциальном направлении. Когда я обхожу эту кривую, это мое касательное направление. В какой-то момент у меня есть радиус. Мы называем это ро. И за короткое время, дельта t, я прохожу через угол дельта тета в дельте t.
А это мой вектор uT. Это немного меняется. Это изменение единичного вектора uT за это время, дельта t. И идет перпендикулярно. И это идет в положительном направлении.
Итак, дельта – как проще всего написать это? Дельта uT равна некоторой дельте t тэта-точки – это угол, умноженный на длину единичного вектора, 1. Это расстояние, которое он проходит, поэтому 1. Итак, r omega, 1 тэта-точка – это расстояние, которое проходит этот единичный вектор. в дельте т. И направление, в котором он идет, – обычная шляпа.
Таким образом, дельта uT превышает предел дельты t, когда t становится равным 0, вы получаете тета точку un, как и раньше. Таким образом, производная по времени этого единичного вектора в тангенциальном направлении – это просто тета-точка в нормальном направлении.И затем из этого мы можем очень быстро получить остальную часть этого ускорения. Таким образом, ускорение плюс это. Теперь мы знаем выражение для … это мой точечный термин uT. Я собираюсь воткнуть это сюда.
Итак, нам нужно выражение для v. Что такое v? Что ж, в тот момент у него есть некоторый радиус rho. Он имеет тета-точку угловой скорости. Таким образом, буквой v здесь будет точка rho theta. Итак, я ищу выражение для vuT dot. Итак, это v theta dot un. Но тета-точка – это v над rho.
в квадрате – извините за это – над роуном. Итак, этот парень здесь, это v точка uT плюс v в квадрате – я перепишу его – поверх rho un. Так что, если вы ускоряетесь, если вы едете со 30 миль в час до 40 миль в час, это ваше касательное. Это ваша скорость по пути. Это этот термин.
Но поскольку вы двигаетесь по кривой, у вас есть ускорение v в квадрате над rho. Вы уже сталкивались с этим раньше в физике. Вот откуда это взялось. Это термин, похожий на центростремительное ускорение.Если вы замените v на rho-theta-точку, вы получите r-theta-точку в квадрате. Таким образом, вы можете выразить это в терминах v в квадрате над ро, или вы можете выразить это в терминах рото-тета-точки в квадрате. Рото-тета-точка в квадрате звучит очень похоже на мой термин ускорения прямо здесь.
Итак, с этой простой формулой вы можете сделать … вам нужно еще кое-что. И вы просто посмотрите это в книге. Существует расчетное выражение для радиуса кривизны пути. И у него есть первая и вторая производные y по x.Итак, вам нужны dy / dx и d2y dx в квадрате.
Это можно вычислить с помощью синусоидальной функции. Итак, вы вычисляете rho по формуле, которая есть в книге для расчета радиуса кривизны. И тогда все готово, хорошо? Итак, увидимся в четверг.
Вывод формулы тангенциального ускорения
Формула выглядит следующим образом: ac = v2 / r. Таким образом, если r изменяется со скоростью v, возникает тангенциальное ускорение Ωv. Чтобы найти ускорение, возьмите вторую производную от x (t) и y (t) по времени: Без ограничения общности мы можем оценить скорости и ускорения под углом θ = 0, зная, что (под этим углом) радиальная скорость и радиальное ускорение происходит в направлении x, а окружная скорость и окружное ускорение – в направлении y.Чтобы найти тангенциальное ускорение, используйте приведенное ниже уравнение. После подстановки производная по времени единичного касательного вектора принимает вид: Нормальное и тангенциальное ускорение Определение радиального тангенциального ускорения в точке. Где ac – центростремительное ускорение; v – скорость (линейная скорость) r – радиус окружности; Теперь мы собираемся связать центростремительное ускорение с величиной угловой скорости, которая обозначается Омега (w). При равномерном круговом движении «ускорение объекта по радиусу, направленное к центру» называется радиальным ускорением.2, например, в касательном ускорении появятся как a, так и b. Если скорость уменьшается, линейное ускорение происходит в направлении, противоположном направлению линейной скорости. Какова формула радиального ускорения и тангенциального ускорения. Нормальное и тангенциальное ускорение. Мы привыкли думать об ускорении как о второй производной от положения, и хотя это один из способов взглянуть на общее ускорение, мы можем далее разбить ускорение на две составляющие: тангенциальное и нормальное ускорение.2 $, но я не могу понять два других термина и какие переменные задействованы. Это можно разделить на двухкомпонентные. Полный вывод центростремительного ускорения (без сокращений) Необходимые навыки, необходимые для вывода, включают: Декартовы координаты и полярные координаты Добавление компонентов вектора Производные Правило цепи правила продукта Неявное дифференцирование Производные синуса и косинуса Следующий вывод будет очень запутанным для любого студент, не завершивший производные. Сначала мы вычисляем угловое смещение «q», которое представляет собой отношение длины дуги «s», которую объект рисует на этой окружности, к ее радиусу «r».Это угловая часть под тенью дуги, между двумя линиями, исходящими из центра и соединенными с ее концами. r = радиус поворота [м]. Формула радиального ускорения Задача задавала тангенциальное и радиальное ускорение в терминах a, b и R. Вы сделали это. Здесь орбитальная угловая скорость представляет собой псевдовектор, величина которого представляет собой скорость, с которой r выметает угол, и направление которого перпендикулярно мгновенной плоскости, в которой r выметает угол (т.е. если мы обозначим как at и an тангенциальную и нормальную компоненты полное ускорение a, то модуль последнего можно рассчитать по формуле :.Решенные примеры по формуле углового ускорения Вопрос: Вопросы по формуле тангенциального ускорения: 1) Автомобиль с колесами с радиусом 20,0 см (0,200 м) начинает ускоряться вперед. Из «Равномерного кругового движения и гравитации» мы знаем, что центростремительное ускорение при круговом движении a c относится к изменениям направления скорости, но не ее величины. Формулу центростремительного ускорения можно записать как квадрат скорости, деленный на радиус круговой траектории. В трехмерном пространстве мы снова имеем вектор положения движущейся частицы r.a = √ (a t 2 + a n 2) .. Связь тангенциального ускорения и скорости. ME 231: Вопрос дня по динамике. Однако, согласно нашему уравнению для тангенциального ускорения, производная должна быть равна нулю, поскольку скорость маятника находится на локальном минимуме. Таблица \ (\ PageIndex {1} \): формулы для положения, скорости, ускорения и скорости; Количество Два измерения Три измерения; Позиция \ (\ vecs {r} (t) = x (t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} \) \ (\ vecs {r} (t) = x ( t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} + z (t) \ hat {\ mathbf k} \) Скорость \ (\ vecs {v} (t) = x ′ ( t) \ hat {\ mathbf i} + y ′ (t) \ hat {\ mathbf j} \) \ (\ vecs {v} (t) = x ′ (t) \ hat {\ mathbf i} + y ′ (t) \ hat {\ Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3.Причина этого в том, что происходит изменение направления, и чтобы изменить направление частиц, на них должна действовать сила. Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Соответствующая взаимосвязь описывается кинематическими выражениями. Поместите начало координат в центр круговой траектории радиуса r. Тот факт, что скорость υ постоянна, означает, что угол θ, который вектор положения r образует с осью x, линейно увеличивается со временем θ∝t.Если Ω – угловая скорость, а r – радиус, тангенциальная скорость равна Ωr. Вывод тангенциальной скорости. Версия для печати. Считается, что объект движется равномерно по кругу, если он поддерживает постоянную скорость при движении по кругу. На диаграмме 2 показаны угловая скорость ω и тангенциальная скорость v T. Диаграмма 2 Тангенциальная скорость – это линейная скорость на краю круговой траектории. Пример: проигрыватель пластинок подключен и равномерно разгоняется до 45 оборотов в минуту за 0.85 секунд. a t = тангенциальное ускорение. Итак, ваш вывод правильный. Формула, используемая для определения центростремительного ускорения данного объекта, может быть вычислена как квадрат тангенциальной скорости по радиусу или следующим образом: a c = v 2 / r; а с = v * ω; Где: ac = центростремительное ускорение [м / с2] v = относится к тангенциальной скорости [м / с]. Первый тип ускорения – тангенциальное ускорение. В любой заданной точке кривой мы можем найти вектор ускорения «а», который представляет ускорение в этой точке.Если скорость увеличивается, линейное ускорение происходит в том же направлении, что и линейная скорость. Пример проблемы проработан. В механике Ньютона центробежная сила – это сила инерции (также называемая «фиктивной» или «псевдо» силой), направленная от оси вращения, которая, кажется, действует на все объекты, если смотреть во вращающейся системе отсчета. найти единичный касательный вектор T и единичный вектор нормали N в одной и той же точке, тогда тангенциальная составляющая ускорения a_T и нормальная составляющая ускорения a_N показаны на диаграмме ниже.Что такое тангенциальное ускорение шин? В тангенциальном компоненте \ (v \) может быть беспорядок, а вычисление производной может быть неприятным. Я могу понять это, если думаю, что скорость «изменила направление», поэтому она перешла с положительного на «отрицательное», а минимума не было вообще. Пример-1: Равномерное круговое движение d dt T r dR 0 ZT dt Since and r Ö TTÖ TÖ Поскольку находится вдоль, он должен быть перпендикулярен радиус-вектору, и это легко показать v TÖ r. Пример-2 ::: Симметрия важна.Радиальная составляющая и тангенциальная составляющая в зависимости от типа движения. Формула тангенциальной скорости. Производная скорости по времени – это тангенциальное ускорение. Если переменная не фигурирует в формуле, вы можете считать, что она где-то с нулевым коэффициентом. В этой статье мы рассмотрим, что такое тангенциальное и нормальное ускорение. Ускорение исходит от двигателя, который вызывает угловое ускорение шин α = 12,0 радиан / с 2. Центростремительная сила (от латинского centrum – «центр» и petere – «искать») – это сила, которая заставляет тело следовать изогнутый путь.Его направление всегда ортогонально движению тела и к фиксированной точке мгновенного центра кривизны траектории. f t = тангенциальная сила Нормальная сила. Далее, частица, движущаяся по кривой, всегда будет иметь нормальную силу. Начнем с вычисления тангенциальной составляющей ускорения для кругового движения. Когда частица движется за угол, она может испытывать два разных типа ускорения. Определение радиального ускорения. Для UCM \ (\ alpha \) = 0.Что здесь не так? Кинематика твердых тел :: Относительное ускорение … • Тангенциальная составляющая угла наклона будет перпендикулярна AB из-за изменения величины v A / B a A и a B – абсолютные ускорения A и B. может использоваться с производной по времени единичного касательного вектора. Нормальная сила всегда направлена к этой оси вращения. Радиальная скорость + тангенциальная скорость в декартовых координатах. Исаак Ньютон описал это как «силу, под действием которой тела притягиваются или толкаются, или каким-либо образом стремятся к точке как к центру».Мунган, осень 2001 г. Рассмотрим частицу, совершающую равномерное круговое движение (UCM). ME101 – Дивизион III Каустубх Дасгупта 1. Формула. Кинематика твердых тел :: относительное ускорение Величины… Ответ: тангенциальное ускорение шин можно найти по формуле: a tan = rα. Не касается траектории движения, когда движение криволинейно. Предположим, что тангенциальная скорость \ (v _ {\ theta} = r d \ theta / d t \) изменяется по величине из-за наличия некоторой тангенциальной силы; Теперь рассмотрим, что \ (d \ theta / d t \) изменяется во времени (величина скорости изменяется во времени).Мы даже связываем длину дуги, тангенциальную скорость и тангенциальное ускорение через производную! ускорение путем вычисления v / t. 3 План на сегодня Вопрос дня Представление вектора N-T Скорость и ускорение Геометрическая интерпретация Круговое движение Ответьте на свои вопросы! Рисунок 3-18 :. Монетные дворы расположены на расстоянии 3,0 см, 8,0 см и 13,0 см от центра пластинки. Тангенциальное ускорение, обозначенное \ (a_T \), позволяет нам узнать, какая часть ускорения действует в направлении движения. Пример ускорения Кориолиса.Задать вопрос задан 3 года, 11 месяцев назад. Нормальный единичный вектор. (Уравнение 2) $ ∑F_n = ma_n $ a n = нормальное ускорение. Выведение центростремительного ускорения с использованием полярных координат thecuriousastronomer Источник: thecuriousastronomer.wordpress.com Вращательная кинематика Физика 298 Здесь есть две формулы, которые можно использовать для каждого компонента ускорения, и хотя вторая формула может показаться чрезмерно сложной, она часто является более простой из двух. Вывод формул центростремительного ускорения. Скорость увеличения вашей тангенциальной скорости, вызванная вашей радиальной скоростью, – это ускорение Кориолиса (по Гаспару Дж.де Кориолис, 1792–1843 – французский математик). Я не понимаю, как была получена эта формула. Формальный вывод центростремительного ускорения – C.E. Но ds / dt = v, de t / dθ = e n и dθ / ds = 1 / ρ (где ρ – радиус кривизны). Почему полярные координаты? Представлено и визуализировано тангенциальное ускорение.
