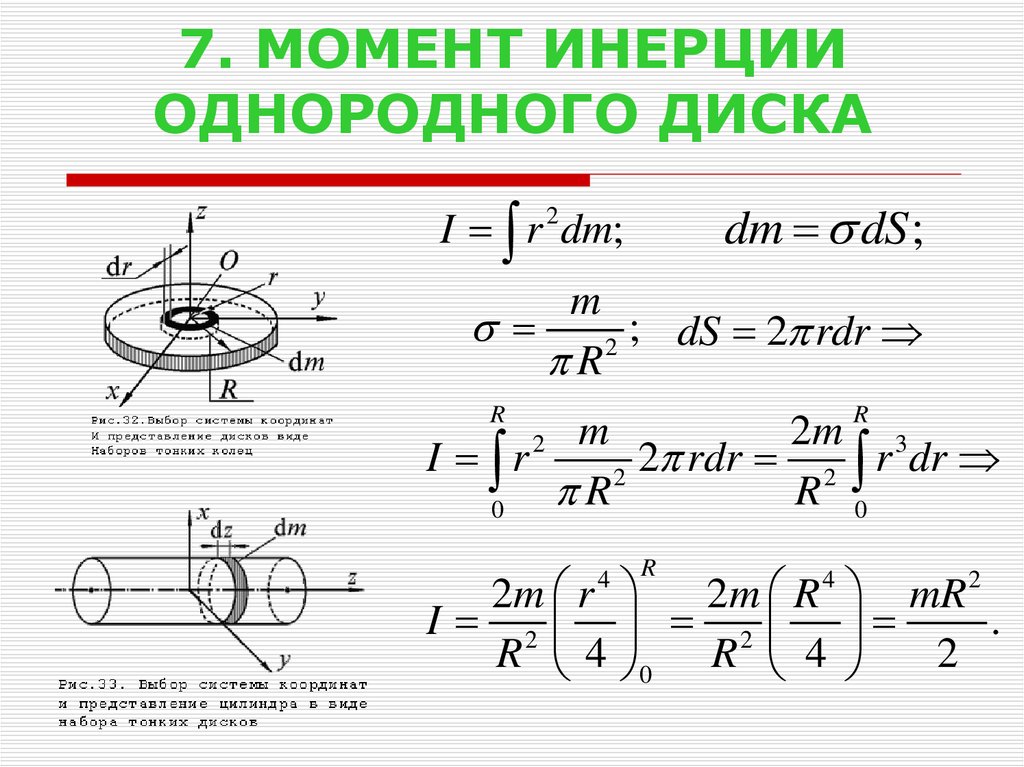
Момент инерции. Теорема Штейнера.
Момент инерции определяется как , если распределение массы равномерно, то заменяется на – элементарный объём, – плотность вещества. .
Теорема Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тала на квадрат расстояния а между осями: .
Момент инерции:
однородного тонкого стержня массы , длины относительно оси, проходящей через центр масс и перпендикулярной стержню:
однородного тонкого стержня массы , длины относительно оси, проходящей через один из концов стержня:
однородного диска (цилиндра) массы , радиуса R, высоты h относительно оси симметрии, перпендикулярной основанию: .

Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью: где — тензор инерции, — угловая скорость, — момент импульса Используя, например, определение момента импульса системы N материальных точек (перенумерованных в формулах ниже индексом k):
и кинематическое выражение для скорости через угловую скорость:
и
сравнивая с формулой, выражающей момент
импульса через тензор инерции и угловую
скорость (первой в этой статье), нетрудно
получить явное выражение для тензора
инерции: или
в непрерывном виде:
,
где
r — расстояния от точек до центра,
относительно которого вычисляется
тензор инерции, а ri — координатные
компоненты соответствующих отрезков,
i и j — номера координат (от 1 до 3), индекс
же k (от 1 до N) в дискретной формуле
нумерует точки системы или маленькие
части, её составляющие. Уже
из этих формул явно видно, что тензор
инерции любого тела зависит от точки,
относительно которой он рассчитан.
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm. Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела. Моментом инерции механической системы относительно неподвижной оси («

,где: — масса малого элемента объёма тела , — плотность, — расстояние от элемента до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
Гироскоп (или волчок) – массивное твёрдое тело, симметричное некоторой оси, совершающее вращения вокруг неё с большой угловой скоростью. В силу симметрии гироскопа выполняется. При попытке повернуть вращающийся гироскоп вокруг некоторой оси наблюдается гироскопический эффект – под действием сил, которые, казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг прямой О’O’, ось гироскопа поворачивается вокруг прямой О’’О’’ (ось ОО и прямая О’O’ предполагаются лежащими в плоскости чертежа, а прямая О’’О’’ и силы f1 и f2 – перпендикулярными к этой плоскости). Объяснение эффекта основано на использование уравнения момента
 Вследствие
гироскопического эффекта на подшипнике,
на котором вращается гироскоп, начинают
действовать гироскопические
силы.
Под действием гироскопических сил ось
гироскопа стремиться занять положение,
параллельное угловой скорости вращения
Земли.
Вследствие
гироскопического эффекта на подшипнике,
на котором вращается гироскоп, начинают
действовать гироскопические
силы.
Под действием гироскопических сил ось
гироскопа стремиться занять положение,
параллельное угловой скорости вращения
Земли.Описанное поведение гироскопа положено в основу гироскопического компаса. Преимущества гироскопа: указывает точное направление на географический северный полюс, его работа не подвержена воздействию металлических предметов.
 направлен момент перпендикулярно к
вертикальной плоскости, проходящей
через ось гироскопа. Уравнение движения:
приращение импульса =
направлен момент перпендикулярно к
вертикальной плоскости, проходящей
через ось гироскопа. Уравнение движения:
приращение импульса = П лоскопаралле́льное движе́ние (плоское движение) — вид движения абсолютно твёрдого тела, при котором все точки тела совершают движение параллельно некоторой плоскости. Примером плоскопараллельного движения является качение колеса по горизонтальной дороге . Уравнения плоского движения
 Поступательное перемещение
зависит от выбора полюса, а величина и
направление угла поворота не зависят.
Скорости точек тела при плоском движении:
; , vBA=
w×BA, т.е. скорость какой-либо точки В
плоской фигуры равна геометрической
сумме скорости полюса А и скорости
точки В при вращении плоской фигуры
вокруг полюса А. Теорема: при плоском
движении проекции скоростей двух точек
тела на ось, проходящую через эти точки,
равны между собой: v
Поступательное перемещение
зависит от выбора полюса, а величина и
направление угла поворота не зависят.
Скорости точек тела при плоском движении:
; , vBA=
w×BA, т.е. скорость какой-либо точки В
плоской фигуры равна геометрической
сумме скорости полюса А и скорости
точки В при вращении плоской фигуры
вокруг полюса А. Теорема: при плоском
движении проекции скоростей двух точек
тела на ось, проходящую через эти точки,
равны между собой: v
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением. Основные кинематические характеристики вращательного движения тела — его угловая скорость () и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
и кинетическая энергия , где Iz — момент инерции тела относительно оси вращения. Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I
где
ω1,
ω2,
и ω3 —
главные компоненты угловой скорости.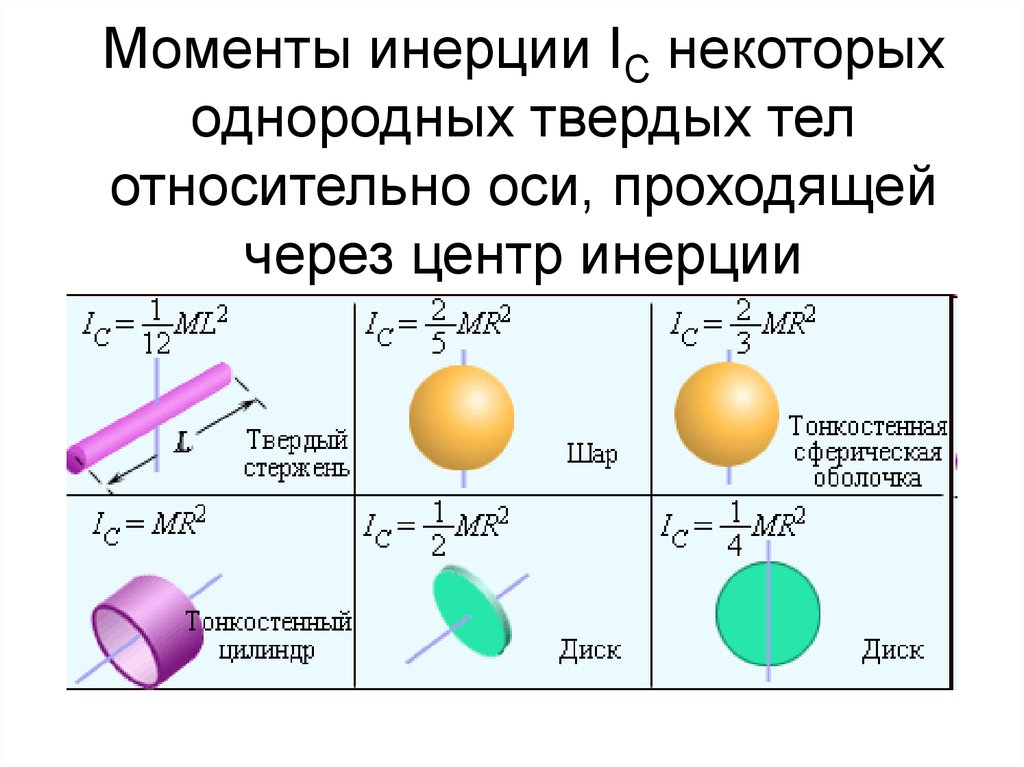 В
общем случае, энергия при вращении с
угловой скоростью находится по формуле: ,
где — тензор инерции.
В
общем случае, энергия при вращении с
угловой скоростью находится по формуле: ,
где — тензор инерции.
Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна). Скорость i -й частицы тела где – расстояние частицы до оси вращение Кинетическая энергия
так как угловая скорость вращения для всех точек одинакова. В соответствии с законом изменения механической энергии системы элементарная работа всех внешних сил равна приращению кинетической энергии тела:
Работа внешних сил при повороте тела на конечный угол равна Допустим, что диск точила вращается по инерции с угловое скоростью и мы останавливаем его, прижимая какой-либо предмет к краю диска с постоянным усилием. При этом на диск будет действовать постоянная по величине сила направленная перпендикулярно его оси. Работа этой силы
где – радиус диска, – угол его поворота. Число оборотов, которое сделает диск до полной остановки,
где – момент инерции диска точила вместе с
якорем электромотора.
Колебания – процессы, характеризующиеся той или иной степенью повторяемости по времени. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и другие. Все эти процессы, несмотря на различную физическую природу, описываются одинаковыми математическими уравнениями и имеют ряд общих свойств. Механические колебания – это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве. Различают периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
или ,
где х — значение изменяющейся величины,
t — время, остальные параметры —
постоянные: А — амплитуда колебаний, ω
— циклическая частота колебаний, —
полная фаза колебаний, —
начальная фаза колебаний. Обобщенное
гармоническое колебание в дифференциальном
виде
Обобщенное
гармоническое колебание в дифференциальном
виде
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).
Гармонический
осциллятор (в классической механике) — это система,
которая при смещении из положения
равновесия испытывает действие
возвращающей силы , пропорциональной смещению (согласно закону Гука): ,
где — коэффициент жёсткости системы.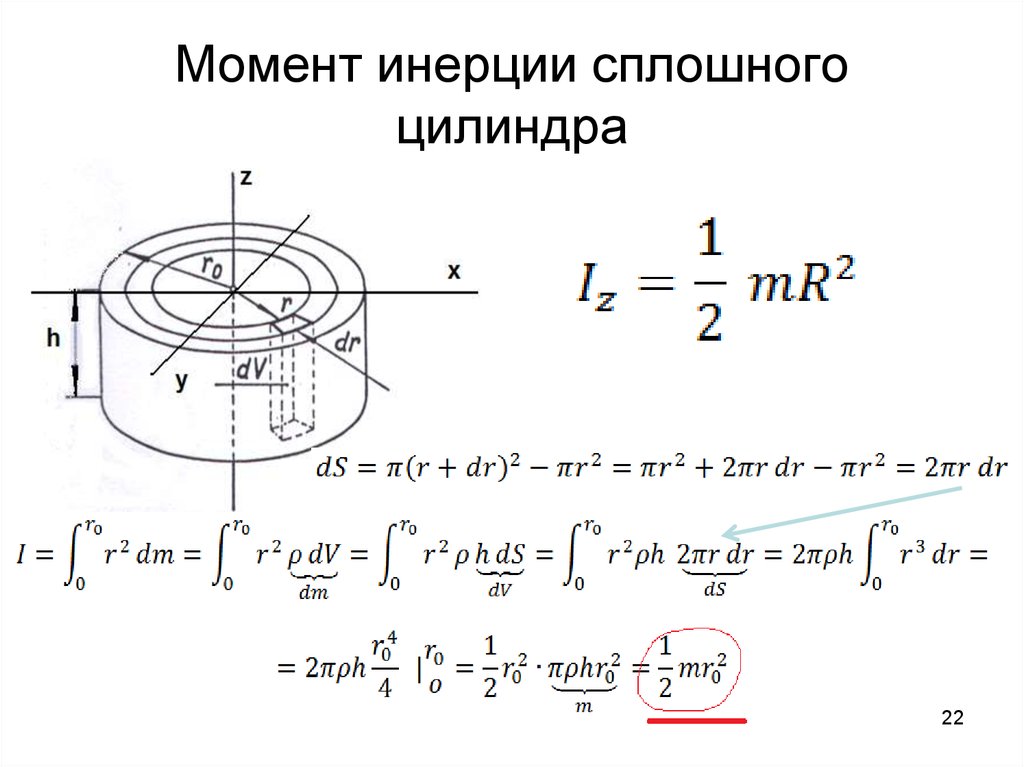
Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Уравнение движения гармонического осциллятора и его общее решение
В
качестве модели консервативного
гармонического осциллятора возьмём
груз массы
, закреплённый на пружине жёсткостью
.Пусть
—
это смещение груза относительно положения
равновесия. Тогда, согласно закону Гука,
на него будет действовать возвращающая
сила:
Используя
второй закон Ньютона, запишем Обозначая и
заменяя ускорение на вторую производную
от координаты по времени ,
напишем:
Это
дифференциальное уравнение описывает
поведение консервативного гармонического
осциллятора. Коэффициент называют циклической частотой осциллятора.
(Здесь имеется в виду круговая частота,
измеряющаяся в радианах в секунду.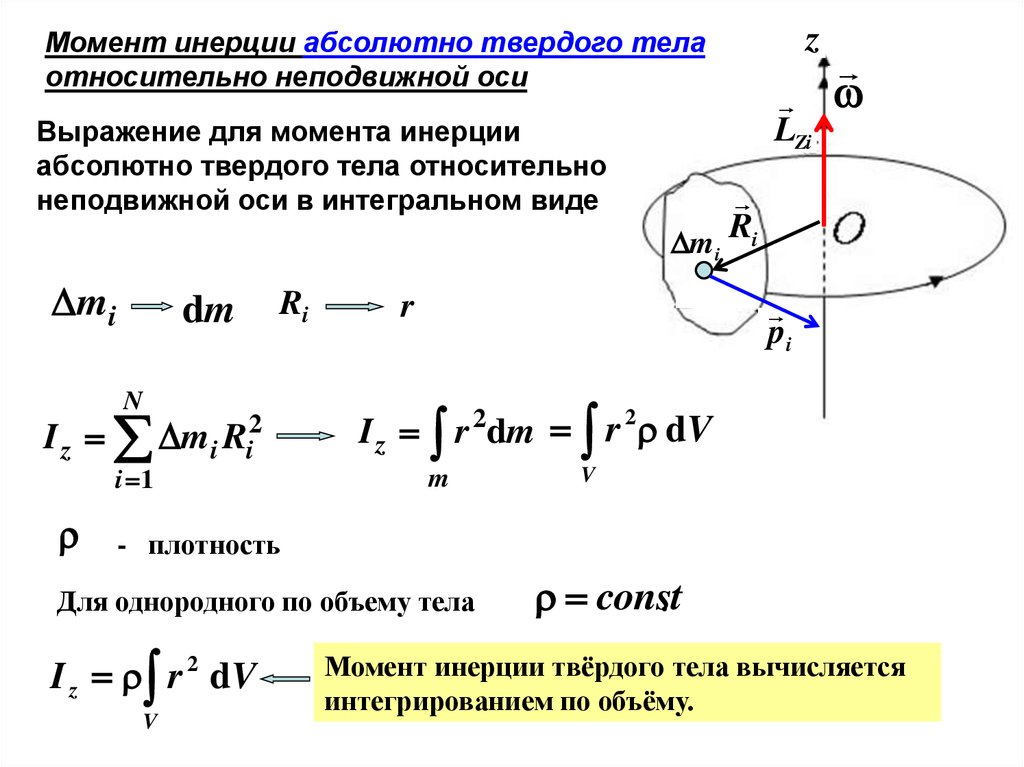 Чтобы
перевести её в частоту, выражающуюся в
Герцах, надо разделить круговую частоту
на )
Будем
искать решение этого уравнения в виде: Здесь
—амплитуда (максимальное
значение смещения или изменения
переменной величины от среднего значения
при колебательном или волновом движении),
— частота колебаний (пока не обязательно
равная собственной частоте),
—
начальная фаза. Подставляем в
дифференциальное уравнение.
Чтобы
перевести её в частоту, выражающуюся в
Герцах, надо разделить круговую частоту
на )
Будем
искать решение этого уравнения в виде: Здесь
—амплитуда (максимальное
значение смещения или изменения
переменной величины от среднего значения
при колебательном или волновом движении),
— частота колебаний (пока не обязательно
равная собственной частоте),
—
начальная фаза. Подставляем в
дифференциальное уравнение.
И остаётся условие на частоту колебаний:
Отрицательную
частоту можно отбросить, так как произвол
в выборе этого знака покрывается
произволом выбора начальной фазы. Общее
решение уравнения записывается в виде: ,где
амплитуда и начальная фаза — произвольные
постоянные. Эта запись исчерпывает все
решения дифференциального уравнения,
так как позволяет удовлетворить любым
начальным условиям (начальному положению
груза и его начальной скорости).
Итого,
консервативный гармонический осциллятор
может совершать чисто гармонические
колебания с частотой, равной его
собственной частоте, с амплитудой любой
величины и с произвольной начальной
фазой. Кинетическая энергия записывается
в виде
.
Кинетическая энергия записывается
в виде
.
и потенциальная энергия есть тогда полная энергия имеет постоянное значение
Фа́за колеба́ний — физическая величина, меняющаяся со временем, при заданной амплитуде определяющая состояние колебательной системы в (любой) данный момент времени. Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание. Частота колебаний — число колебаний в единицу времени.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Определения
Дифференциальное уравнение движения физического маятника
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
Полагая , предыдущее уравнение можно переписать в виде:
Последнее
уравнение аналогично уравнению колебаний
математического маятника длиной
. Величина
называется приведённой длиной физического
маятника.
Величина
называется приведённой длиной физического
маятника.
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии от точки подвеса. Эта точка и будет центром качания маятника. Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен , а момент силы тяжести относительно той же оси . Легко заметить, что уравнение движения не изменится.
Теорема Гюйгенса
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Доказательство Вычислим приведенную длину для нового маятника:
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Период
малых колебаний физического маятника Если
амплитуда колебаний
мала,
то корень в знаменателе эллиптического
интеграла приближенно равен единице.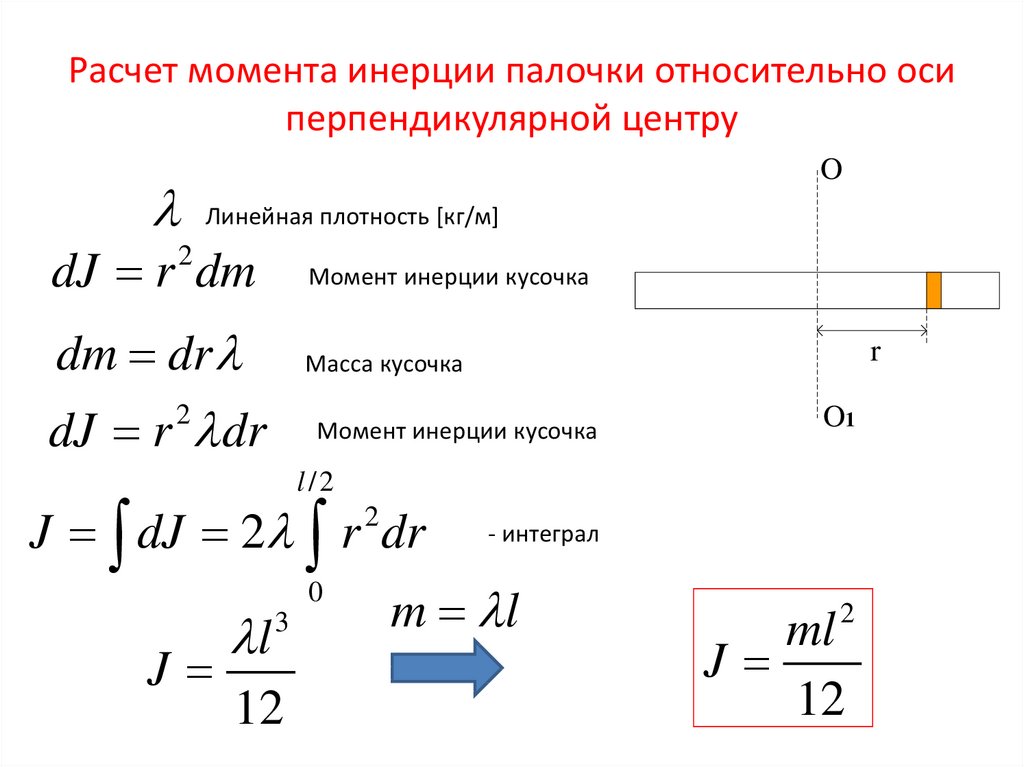 Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах до 1 радиана (≈60°) .
Свободные затухающие колебания – колебания, у которых амплитуды из-за потерь энергии колебательной системой с течением времени убывают. Простейшим механизмом убывания энергии колебаний есть ее превращение в теплоту вследствие трения в механических колебательных системах, а также потерь, связанных с выделением теплоты, и излучения электромагнитной энергии в электрических колебательных системах.
Вид
закономерностей затухания колебаний
задается свойствами колебательных
систем. Обычно рассматривают линейные
системы — идеализированные реальные
системы, параметры которых, определяющие
физические свойства системы, в ходе
процесса остаются неизменными. Например,
линейными системами являются пружинный
маятник при малых растяжениях пружины
(когда выполняется закон Гука),
колебательный контур, у которого
сопротивление, индуктивность и емкость
не зависят ни от тока в контуре, ни от
напряжения. Различные по своей природе
линейные системы описываются аналогичными
линейными дифференциальными уравнениями,
что дает основания подходить к изучению
колебаний различной физической природы
с единой точки зрения, а также моделировать
их, в том числе и на ЭВМ.
Различные по своей природе
линейные системы описываются аналогичными
линейными дифференциальными уравнениями,
что дает основания подходить к изучению
колебаний различной физической природы
с единой точки зрения, а также моделировать
их, в том числе и на ЭВМ.
Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как
(1) , где s – колеблющаяся величина, которая описывает тот или иной физический процесс, δ = const — коэффициент затухания, ω0 – циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.
Решение уравнения (1) запишем в виде
(2)
где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем
(3)
Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положительного коэффициента: (4)
(если
(ω02 – σ2)>0, то такое обозначение мы вправе
сделать).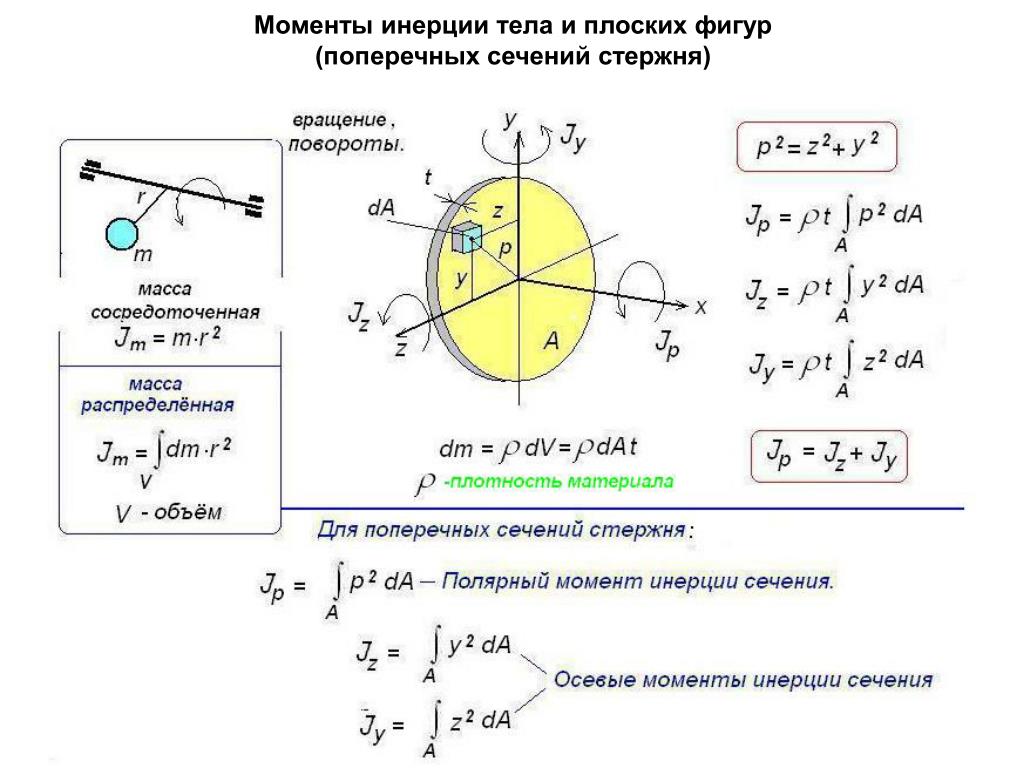 Тогда получим выражение , у
которого решение будет функция .
Значит, решение уравнения (1) в случае
малых затуханий (ω02 >> σ2 )
Тогда получим выражение , у
которого решение будет функция .
Значит, решение уравнения (1) в случае
малых затуханий (ω02 >> σ2 )
(5)
где (6)
— амплитуда затухающих колебаний, а А0 — начальная амплитуда.
(5)
где (6) — амплитуда затухающих колебаний
Затухание не дает колебаниям быть периодичными и, строго говоря, к ним нельзя применять понятие периода или частоты. Но если затухание мало, то можно условно использовать понятие периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины . В этом случае период затухающих колебаний с учетом выражения (4) будет равен
Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, которые отличаются на период, то отношение
называется декрементом затухания, а его логарифм
(7)
— логарифмическим
декрементом затухания;
Ne — число колебаний, которые совершаются
за время уменьшения амплитуды в е раз. Логарифмический декремент затухания
является постоянной величиной для
данной колебательной системы.
Логарифмический декремент затухания
является постоянной величиной для
данной колебательной системы.
Для характеристики колебательной системы также применяют понятие добротности Q, которая при малых значениях логарифмического декремента будет равна
(8)
(так как затухание мало (ω02 >> σ2 ), то T принято равным Т0).
Из формулы (8) вытекает, что добротность пропорциональна числу колебаний Ne, которые система совершает за время релаксации.
Выводы и уравнения, полученные для свободных затухающих колебаний линейных систем, можно использовать для колебаний различной физической природы — механических (в качестве примера возьмем пружинный маятник) и электромагнитных (в качестве примера возьмем электрический колебательный контур).
Вынужденными называются такие колебания, которые
возникают в колебательной системе под
действием внешней периодически
изменяющейся силы (вынуждающая
сила).
Помощь с лабораторной работой по дисциплине «Механика» для СПбГАСУ (moodle.spbgasu.ru)
или напишите нам прямо сейчас
Написать в WhatsApp
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛАЦель работы – изучение законов движения твердого тела на примере маятника Максвелла; определение момента инерции твердых тел.
Общие сведения
Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции зависит от распределения массы тела относительно оси вращения. Для определения момента инерции относительно данной оси тело мысленно разбивается на элементы, малые настолько, что их можно рассматривать как материальные точки массой . Момент инерции материальной точки определяется . Тогда момент инерции тела относительно некоторой оси
(7.1)
где – расстояние от элемента до выбранной оси.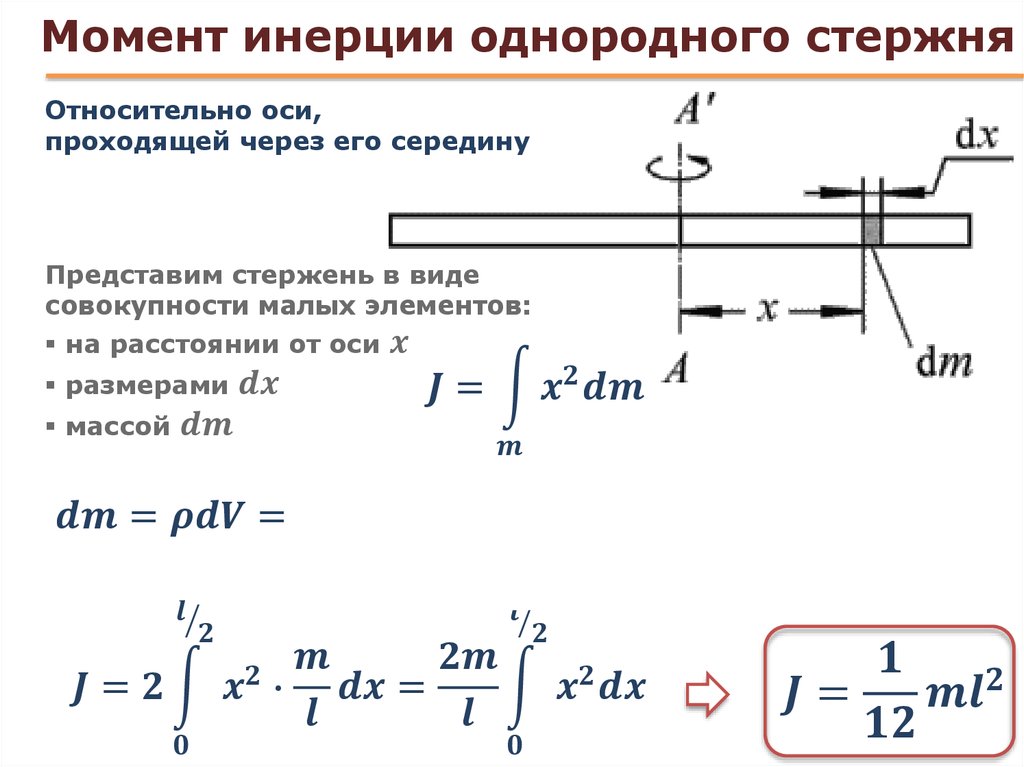 В интегральной форме
(7.2)
– плотность вещества в элементе объема , находящемся на расстоянии r от оси.
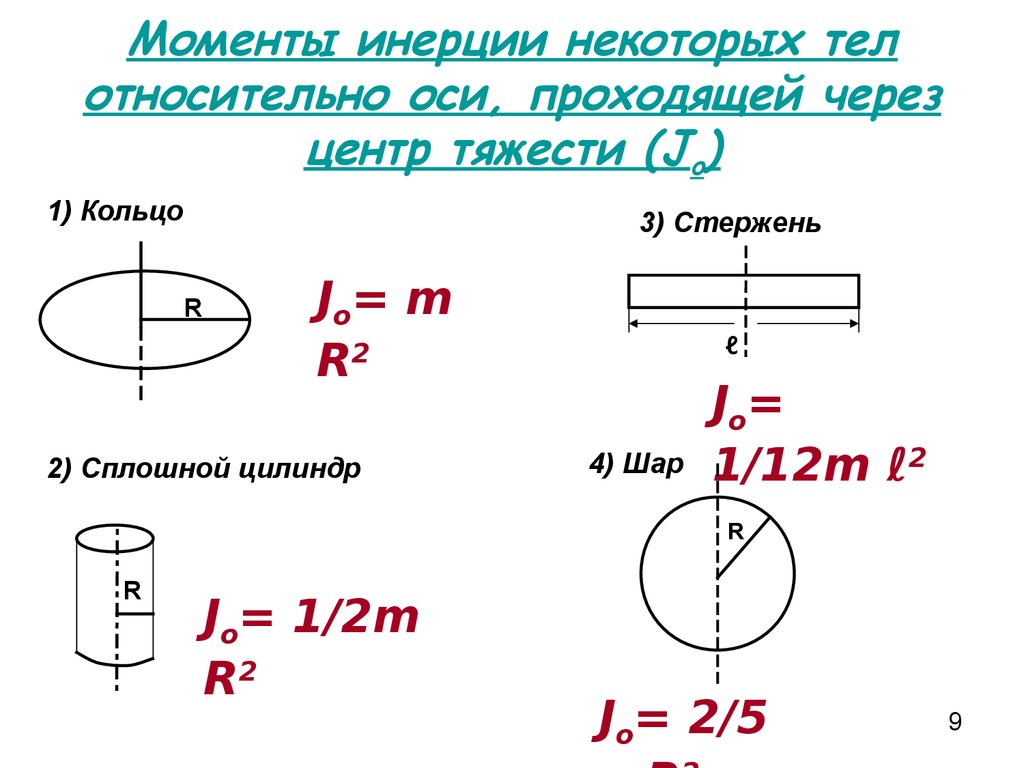
Для моментов инерции диска и кольца относительно оси, приходящей через центр масс перпендикулярно основанию или плоскости кольца, интегрирование дает
для цилиндра массой m и радиусом R (относительно оси, проходящей перпендикулярно основанию через его центр)
(7.3)
дл кольца массой m, внутренним радиусом r и внешним радиусом R
(7.4)
Маятник Максвелла представляет собой однородный диск C, укрепленный на металлическом стержне D (рис.7.1). За концы этого стержня маятник прикрепляется бифилярно (с помощью двух нитей) к кронштейну.
В интегральной форме
(7.2)
– плотность вещества в элементе объема , находящемся на расстоянии r от оси.
Для моментов инерции диска и кольца относительно оси, приходящей через центр масс перпендикулярно основанию или плоскости кольца, интегрирование дает
для цилиндра массой m и радиусом R (относительно оси, проходящей перпендикулярно основанию через его центр)
(7.3)
дл кольца массой m, внутренним радиусом r и внешним радиусом R
(7.4)
Маятник Максвелла представляет собой однородный диск C, укрепленный на металлическом стержне D (рис.7.1). За концы этого стержня маятник прикрепляется бифилярно (с помощью двух нитей) к кронштейну.
При подготовке маятника к измерению нити тщательно, виток к витку, наматываются на стержень в направлении от его концов к диску. После освобождения маятника нити разматываются. Таким образом возникает поступательное движение маятника вниз и вращательное После освобождения маятника нити разматываются. Таким образом возникает поступательное движение маятника вниз и вращательное |
|
| Рис.7.1 |
– вокруг продольной оси симметрии (ось ОО´, рис.7.1). Вращение продолжается по инерции в низшей точке. Это приводит к повторному наматыванию нити на стержень, и диск поднимается. Так возникают колебания диска в вертикальной плоскости, что и дает основание называть данное устройство маятником.
Движение маятника описывается двумя уравнениями динамики. Для поступательного движения центра масс, пренебрегая силами трения, имеем ( – сила натяжения каждой нити; предполагается, что нити одинаковы, поэтому сила удваивается – рис.7.1а). в проекции на ось Оy, направленную вертикально вниз, получаем
(7,5)
Вращательное движение твердого тела описывается основным уравнением динамики вращения оси ОО’
( – результирующий момент сил относительно оси О О’; e – угловое ускорение; – момент инерции тела относительно той же оси).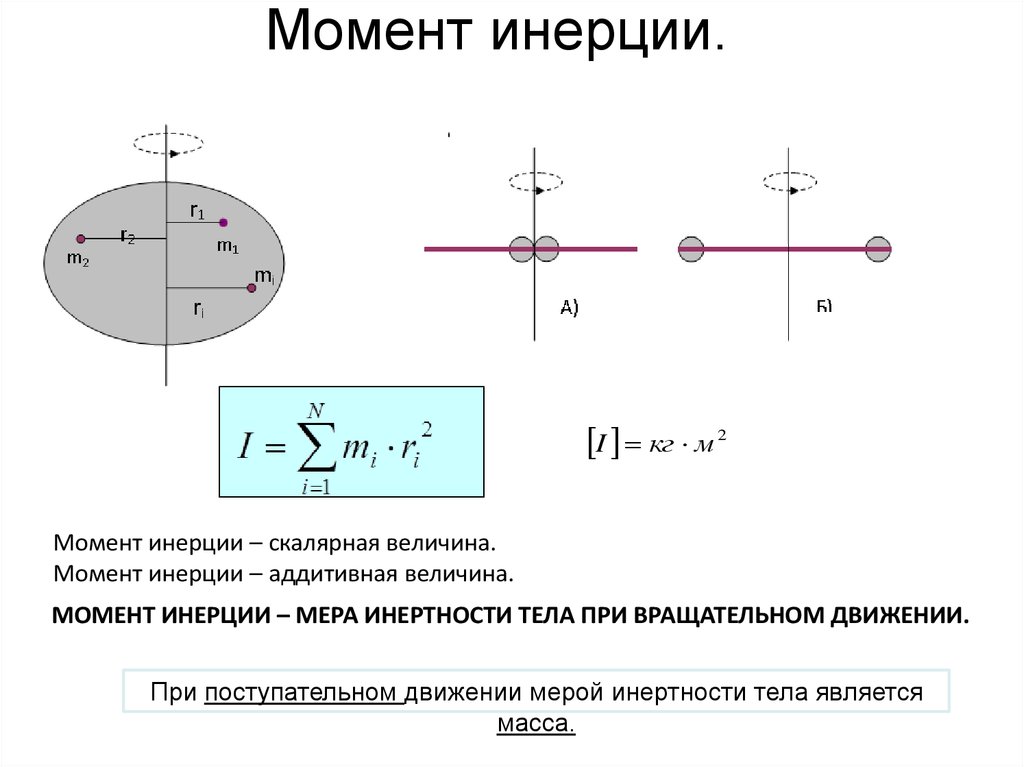 Для маятника отличный от нуля момент относительно оси ОО´ (рис.7.1б) имеют только силы натяжения. Таким образом,
где – радиус стержня маятника.
Уравнение динамики вращательного движения приобретает вид
(7.6)
Свяжем угловое ускорение тела и тангенциальное ускорение точки на поверхности стержня (например, А)
В отсутствие проскальзывания нити по стержню тангенциальное ускорение точки А равно линейному ускорению точки О
(7.7)
Объединяя (7.5)–(7.7), получим
Для равнопеременного движения связь между путем h и временем t в случае отсутствия начальной скорости может быть записана в виде . Выразим ускорение . Итак, для момента инерции окончательно получаем
(7.8)
(m – полная масса маятника; – радиус стержня).
В работе определяется момент инерции маятника Максвелла, масса которого изменяется с помощью колец различных радиусов и масс.
Для маятника отличный от нуля момент относительно оси ОО´ (рис.7.1б) имеют только силы натяжения. Таким образом,
где – радиус стержня маятника.
Уравнение динамики вращательного движения приобретает вид
(7.6)
Свяжем угловое ускорение тела и тангенциальное ускорение точки на поверхности стержня (например, А)
В отсутствие проскальзывания нити по стержню тангенциальное ускорение точки А равно линейному ускорению точки О
(7.7)
Объединяя (7.5)–(7.7), получим
Для равнопеременного движения связь между путем h и временем t в случае отсутствия начальной скорости может быть записана в виде . Выразим ускорение . Итак, для момента инерции окончательно получаем
(7.8)
(m – полная масса маятника; – радиус стержня).
В работе определяется момент инерции маятника Максвелла, масса которого изменяется с помощью колец различных радиусов и масс.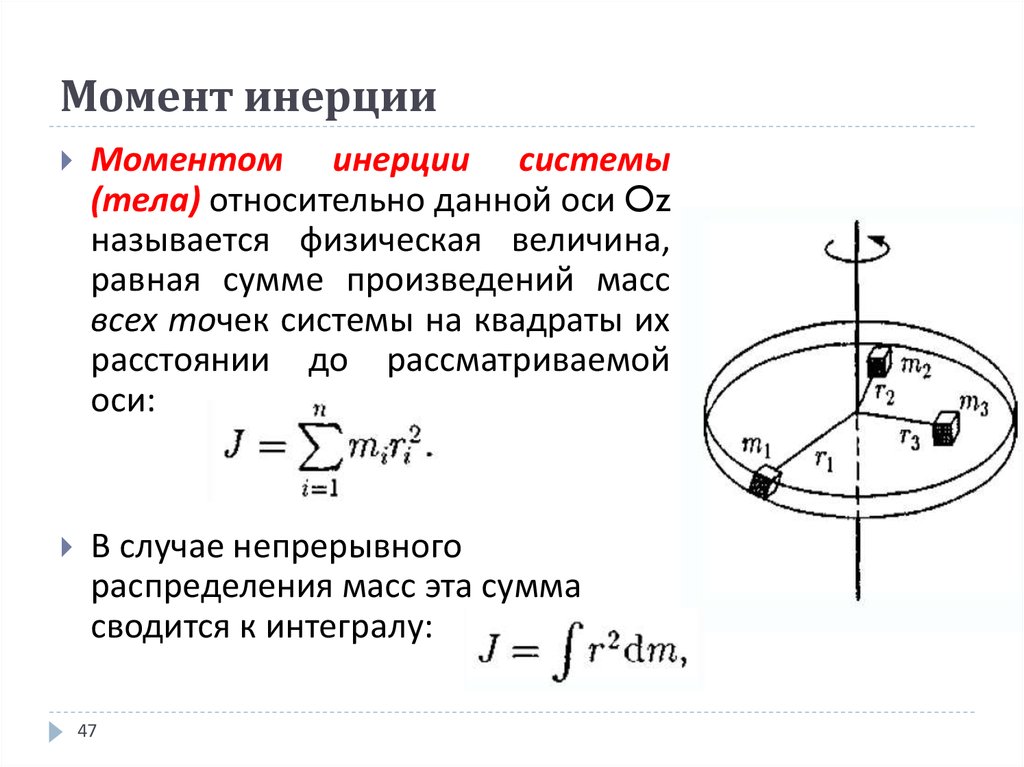 Описание установки
Общий вид установки представлен на рис.7.2. В основании 1 закреплена колонка 2, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10, а на нижнем кронштейне – фотоэлектронный датчик 3.
Описание установки
Общий вид установки представлен на рис.7.2. В основании 1 закреплена колонка 2, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10, а на нижнем кронштейне – фотоэлектронный датчик 3.
Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на двух нитях 4 (бифилярный подвес). На диск можно насаживать сменные кольца 11, изменяя таким образом момент инерции системы.
Маятник удерживается в верхнем положении электромагнитом 10. Фотоэлектрический датчик 3 соединен с электронным хронометром 8. Момент прерывания тока в электромагните (т. е. момент начала движения маятника) синхронизирован с запуском отсчета времени. Момент пересечения нижним краем кольца опти- е. момент начала движения маятника) синхронизирован с запуском отсчета времени. Момент пересечения нижним краем кольца опти- |
|
| Рис.7.2 |
ческой оси фотодатчика (момент окончания движения вниз) синхронизирован с остановкой отсчета времени. Электромагнит при этом снова автоматически приводится в действие.
Длину нитей можно регулировать барабаном 14, который фиксируется винтом 15. Положение нижнего кронштейна на колонке должно быть отрегулировано в зависимости от длины нитей. Для этого ослабляется фиксирующий винт 12, и кронштейн 7 устанавливается так, чтобы нижний край маятника с надетым на него кольцом находился несколько ниже оси фотодатчика. После этого винт 12 затягивается.
Путь, проходимый маятником, можно определить по миллиметровой шкале 13, расположенной вдоль колонки. Порядок выполнения
Порядок выполнения
- Нажать кнопку «Сброс», убедиться, что на индикаторе установились нули.
- Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно, виток к витку: в верхнем положении маятник должен быть зафиксирован электромагнитом.
- Привести маятник в движение нажатием кнопки «Пуск»; в момент пересечения маятником оптической оси фотодатчика хронометр будет автоматически остановлен. Снять отсчет времени движения маятника по индикатору хронометра со всей возможной точностью (до 0,001 с).
- Измерить внутренний и внешний диаметры кольца штангенциркулем, оценить приборную погрешность.
- Повторить пп.4–6 еще девять раз.
По шкале измерить путь маятника. По результатам измерений рекомендуется заполнить табл.1. Таблица 1
| Масса кольца, г, | № измерения | , с | , с | , с2 |
Радиусы кольца, мм
внутр. внешн.
Радиус стержня
внешн.
Радиус стержня
|
1 2 : N | |||
| Путь маятника, мм | , с |
Обработка результатов эксперимента
- Рассчитать среднее арифметическое значение времени движения маятника и внести его в таблицу.
- Рассчитать момент инерции маятника по формуле (7.8).
- Вычислить суммарную погрешность времени
где а = 0,001 с.
- Вычислить погрешности момента инерции (относительную и абсолютную)
(7.9) = 0,5 г = 0,05 мм – по формуле = 0,5 мм
- Проверить экспериментальное значение момента инерции расчетом.
 Значение момента инерции маятника можно получить, суммируя моменты инерции составляющих его тел
Значение момента инерции маятника можно получить, суммируя моменты инерции составляющих его тел
(7.10) где – момент инерции основания маятника, – момент инерции кольца, надетого на диск, (7.11)
- Записать окончательный результат и вывод к работе по пунктам:
а) перечислить, что измерялось и рассчитывалось в работе; б) указать рассчитанное значение момента инерции кольца; в) указать в каком доверительном интервале находится истинное значение момента инерции маятника и с какой вероятностью; г) сравнить значения J, рассчитанные по формулам (7.10) и (7.8) и проанализировать причины несовпадения, если они есть. Контрольные вопросы
- Что такое момент инерции материальной точки?
- Что такое момент инерции твердого тела? От чего зависит его величина?
- Как рассчитывается момент инерции диска, момент инерции кольца?
- Что представляет собой маятник Максвелла? Какой характер имеет его движение?
- Какими уравнениями динамики описывается движение маятника Максвелла?
- Какие силы вызывают поступательное движение маятника? Момент каких сил вызывает вращательное движение маятника?
- Как определяется момент силы относительно точки и момент силы относительно оси?
- Как определяется энергия в случае вращательного и поступательно-вращательного движения?
- Как вывести формулу для определения момента инерции маятника Максвелла, используя закон сохранения энергии?
- В чем состоит упрощающее предположение, принятое при выводе расчетной формулы? Какое значение – завышенное или заниженное – получается в этом приближении?
- Можно ли, и каким образом, повысить точность измерений за счет выбора параметров экспериментальной установки?
- Как выводится формула (7.
 9) для расчета погрешности момента инерции?
9) для расчета погрешности момента инерции? - Погрешности каких величин вносят определяющий вклад в погрешность момента инерции?
или напишите нам прямо сейчас
Написать в WhatsApp
Момент инерции
Момент инерцииСледующий: Крутящий момент Вверх: Вращательное движение Предыдущий: Центр масс Рассмотрим расширенный объект, состоящий из элементов. Пусть й элемент обладают массой, вектором положения и скоростью. полная кинетическая энергия объекта записывается
| (334) |
Предположим, что движение объекта состоит просто из жесткого вращения под углом скорость . Следует, из разд. 8.4, что
| (335) |
Давайте напишем
| (336) |
где – единичный вектор, ориентированный вдоль оси вращения (который предполагается, проходит через начало нашей системы координат).
 Это следует из
вышеприведенных уравнений, что кинетическая энергия вращения объекта принимает
форма
Это следует из
вышеприведенных уравнений, что кинетическая энергия вращения объекта принимает
форма | (337) |
или же
| (338) |
Здесь величина называется моментом инерции объекта, а написано
| (339) |
куда расстояние по перпендикуляру от элемента th до оси вращение. Обратите внимание, что для поступательного движения мы обычно пишем
| (340) |
где представляет массу и представляет скорость.
 Сравнение
уравнения (338) и (340) предполагает, что момент инерции играет решающую роль.
ту же роль во вращательном движении, которую масса играет в поступательном движении.
Сравнение
уравнения (338) и (340) предполагает, что момент инерции играет решающую роль.
ту же роль во вращательном движении, которую масса играет в поступательном движении. Для непрерывного объекта аргументы, аналогичные тем, которые используются в разд. 8,5
урожай
| (341) |
где – массовая плотность объекта, является перпендикулярное расстояние от оси вращения, и является элементом объема. Наконец, для объекта постоянной плотности приведенное выше выражение сводится к
| (342) |
Здесь – полная масса объекта. Заметим, что интегралы берутся по всему объем объекта.
Момент инерции однородного объекта зависит не только от размера и формы этого
объекта, а от положения оси, вокруг которой вращается объект. Особенно,
один и тот же объект может иметь разные моменты инерции при вращении вокруг
разные оси.
Особенно,
один и тот же объект может иметь разные моменты инерции при вращении вокруг
разные оси.
К сожалению, оценка момента инерции данного тела относительно данной оси неизменно
включает в себя выполнение неприятного интеграла объема. На самом деле есть только
вычисление одного тривиального момента инерции, а именно момента инерции тонкого
круговое кольцо вокруг симметричной оси, проходящей перпендикулярно
к плоскости кольца. См. рис. 75. Предположим, что это масса кольца, а
это его радиус. Каждый элемент кольца имеет общее перпендикулярное расстояние от
ось вращения — т.е. , . Следовательно, уравнение (342)
сводится к
| (343) |
В общем, моменты инерции вычислять довольно утомительно. К счастью, существуют
две мощные теоремы, которые позволяют нам просто связать момент инерции данного тела
относительно данной оси к моменту инерции того же тела относительно другой оси. Первый из
эти теоремы называются теорема о перпендикулярной оси и применяется только к
однородный ламинарный предмет. Рассмотрим ламинарный объект ( т.е. , тонкий плоский объект)
однородной плотности. Предположим, для простоты,
что объект лежит в – плоскости. Момент инерции тела относительно
-ось задается
К счастью, существуют
две мощные теоремы, которые позволяют нам просто связать момент инерции данного тела
относительно данной оси к моменту инерции того же тела относительно другой оси. Первый из
эти теоремы называются теорема о перпендикулярной оси и применяется только к
однородный ламинарный предмет. Рассмотрим ламинарный объект ( т.е. , тонкий плоский объект)
однородной плотности. Предположим, для простоты,
что объект лежит в – плоскости. Момент инерции тела относительно
-ось задается
| (344) |
где мы опустили тривиальное -интегрирование, а интеграл берется по протяженности объекта в – плоскости. Кстати, приведенное выше выражение следует из наблюдения, что когда ось вращения совпадает с -осью. Так же и моменты инерция объекта относительно осей – и – принимает вид
| (345) | |||
| (346) |
соответственно.
 Здесь мы воспользовались тем, что внутри объекта. следует при осмотре
из трех предыдущих уравнений, которые
Здесь мы воспользовались тем, что внутри объекта. следует при осмотре
из трех предыдущих уравнений, которые | (347) |
См. рис. 76.
Воспользуемся теоремой об перпендикулярных осях, чтобы найти момент инерции тонкого кольца относительно
ось симметрии, лежащая в плоскости кольца. Принятие системы координат, показанной на
Рис. 77, из симметрии видно, что .
Теперь мы уже знаем, что,
где масса кольца, а его радиус. Следовательно, перпендикулярная ось
теорема говорит нам, что
| (348) |
или же
| (349) |
Конечно, потому что при вращении кольца вокруг -оси его элементы в среднем равны дальше от оси вращения, чем при вращении вокруг -оси.

Вторая полезная теорема о моментах инерции называется0070 параллель
теорема об оси . Теорема о параллельных осях — довольно общая — утверждает, что если
момент инерции данного тела относительно оси, проходящей через центр масс
этого тела, то момент инерции того же тела относительно второй оси
что параллельно первому
| (350) |
где – масса тела, – перпендикулярное расстояние между две оси.
Чтобы доказать теорему о параллельных осях, выберем начало координат
систему координат, совпадающую с центром масс рассматриваемого тела.
Кроме того, сориентируем оси нашей системы координат так, чтобы
-ось совпадает с первой осью вращения, тогда как вторая
ось штук – плоскость у . Из уравнения (328), тот факт, что
центр масс находится в начале координат, это означает, что
Из уравнения (328), тот факт, что
центр масс находится в начале координат, это означает, что
| (351) |
где интегралы берутся по объему тела. Из уравнения (342), выражение для первого момента инерции
| (352) |
так как это перпендикулярное расстояние общей точки от -оси. Аналогично, выражение для второго момента инерции принимает вид форма
| (353) |
Приведенное выше уравнение может быть расширено, чтобы дать
| (354) |
Это следует из уравнений.
 (351) и (352), что
(351) и (352), что | (355) |
что доказывает теорему.
Воспользуемся теоремой о параллельных осях для вычисления момента инерции тонкого
кольцо вокруг оси, которая проходит перпендикулярно плоскости кольца и проходит
по окружности кольца. Мы знаем, что момент инерции кольца массы
и радиус вокруг оси, которая проходит перпендикулярно плоскости кольца и проходит
через центр кольца, который совпадает с центром
массы кольца — . Наша новая ось параллельна этой исходной оси, но смещена
в сторону на перпендикулярном расстоянии. Следовательно, параллель
теорема оси говорит нам, что
| (356) |
См. рис. 78.
В качестве иллюстрации прямого применения формулы (342) примем
рассчитать момент инерции тонкого круглого диска, массы и радиуса,
вокруг оси, проходящей через центр диска и перпендикулярной
плоскость диска. Выберем нашу систему координат так, чтобы круг
лежит в -плоскости с центром в начале координат. Следовательно, ось вращения
совпадает с -осью. Следовательно, формула (342) сводится к
| (357) |
где интегралы берутся по площади диска, а избыточное -интегрирование был подавлен. Разобьем диск на тонкие кольца. Рассмотрим кольцо радиуса и радиальная толщина. Площадь этого кольца просто . Следовательно, мы можем заменить в приведенных выше интегралах на , чтобы дать
| (358) |
Приведенное выше выражение дает
| (359) |
Вычисления, аналогичные приведенным выше, дают следующие стандартные результаты:
- Момент инерции тонкого стержня массы и длины относительно оси
проходящий через центр стержня и перпендикулярный его длине, равен
- Момент инерции тонкого прямоугольного листа массы и размеров и
относительно перпендикулярной оси, проходящей через центр листа,
- Момент инерции
твердый цилиндр массы и радиуса вокруг цилиндрической оси
- Момент инерции
тонкая сферическая оболочка массой и радиусом около диаметра
- Момент инерции
твердая сфера массы и радиуса около диаметра
Следующий: Крутящий момент Вверх: Вращательное движение Предыдущий: Центр масс Ричард Фицпатрик 2006-02-02
Угловой момент — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics 1 Справка » Ньютоновская механика » Круговое, вращательное и гармоническое движение » Круговое и вращательное движение » Угловой момент
В изолированной системе момент инерции вращающегося объекта уменьшается вдвое. Что происходит с угловой скоростью тела?
Что происходит с угловой скоростью тела?
Возможные ответы:
Счетверено.
Сдвоен.
Остается прежним.
Четвертуется.
Он разделен пополам.
Правильный ответ:
Удваивается.
Объяснение:
В изолированной системе нет чистого крутящего момента. Если в системе нет чистого крутящего момента, то полный угловой момент системы остается прежним. Угловой момент вращающегося объекта равен моменту инерции объекта, умноженному на угловую скорость объекта.
обозначает угловой момент, это момент инерции и это угловая скорость.
Следовательно, если момент инерции, , уменьшить вдвое, то для того, чтобы угловой момент, , остался постоянным, угловая скорость, , должна быть удвоена. Это потому, что , который является мультипликативным тождеством. Все, что умножается на единицу, остается прежним.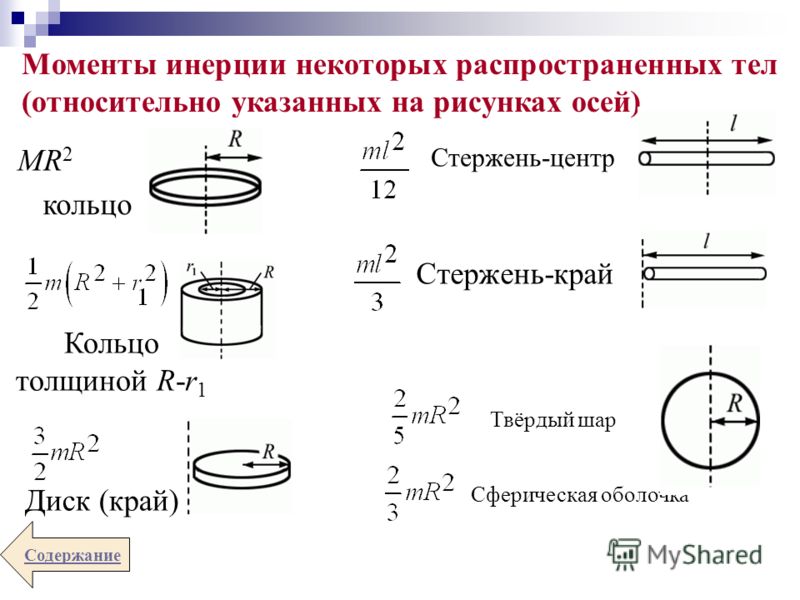 Таким образом, конечная угловая скорость будет в два раза больше первоначальной.
Таким образом, конечная угловая скорость будет в два раза больше первоначальной.
Сообщить об ошибке
Я начинаю толкать карусель с крутящим моментом 10 Нм. Он имеет момент инерции . Какова скорость его вращения через 3 секунды, если предположить, что он начал движение из состояния покоя?
Возможные ответы:
Правильный ответ:
Объяснение:
Угловой момент карусели через 3 секунды равен просто
Угловой момент также определяется как
. вращается один раз в минуту. Он имеет момент инерции . Эрин, астронавт, расширяет солнечные панели спутника, увеличивая его момент инерции до . Как быстро сейчас вращается спутник?
Possible Answers:
1 rotation every 3 minutes
1 rotation per minute
3 rotations per minute
1 rotation every 9 minutes
9 rotations per minute
Correct answer:
1 rotation каждые 3 минуты
Объяснение:
Формула для углового момента:
, где
= угловой момент
= момент инерции
= угловая скорость
Угловая скорость определяется как
Начальный период спутника составляет 1 минуту, поэтому:
После того, как Эрин выдвинула солнечные панели, импульс остался прежним (сохранение импульса), но момент инерции теперь равен . Таким образом,
Таким образом,
Следовательно,
Подставляя это обратно в определение, мы получаем
Следовательно,
Таким образом, теперь спутник вращается каждые 3 минуты.
Сообщить об ошибке
Кусочек глины массы падает на край массы вращающегося диска, вращающегося со скоростью . Какой будет результирующая скорость вращения?
Возможные ответы:
Правильный ответ:
Пояснение:
Угловой момент всегда сохраняется.
Уравнение, связанное с угловым импульсом, моментом инерции и угловой скорости:
Момент инерции также можно записать следующим образом:
Подключение77
. СТАВИТЕЛЬНЫЕ ЗАЯВЛЕНИЕ И НАЗНАЧЕНИЕ И
7
. начальный момент импульса равен конечному моменту импульса и решить.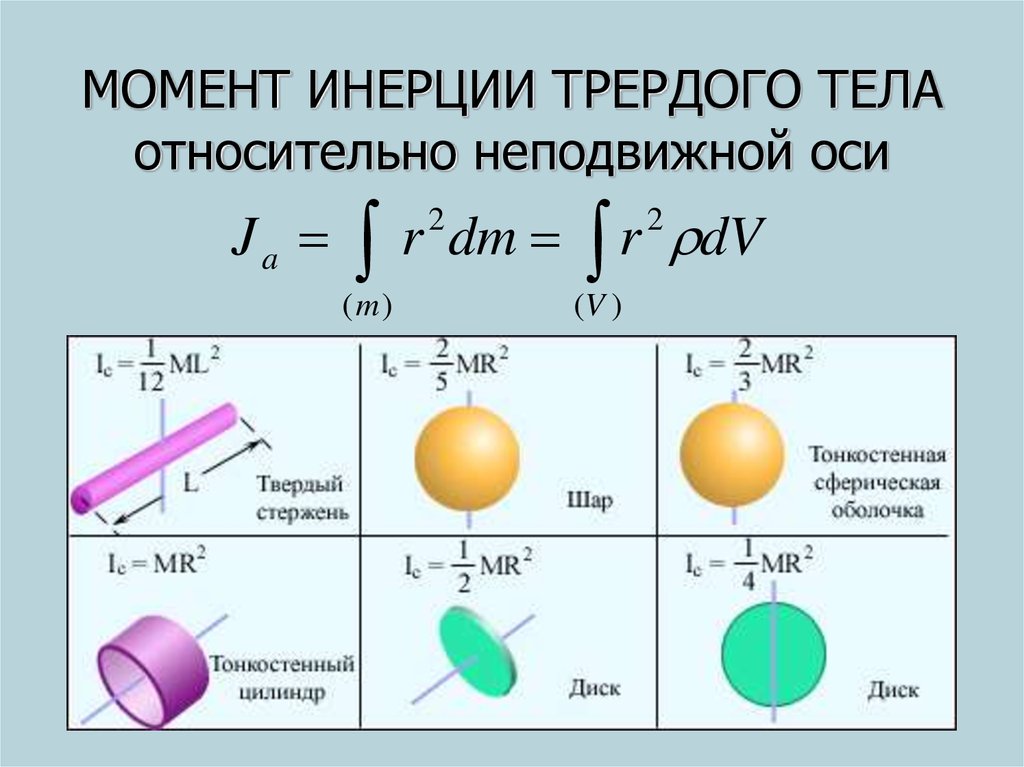
Сообщить об ошибке
В левой части рисунка показан прямоугольный стержень на горизонтальной столешнице. Стержень шарнирно закреплен на одном конце, как показано на рисунке. Он вращается таким образом, что попадает в неподвижный шар, как показано на правой стороне диаграммы. Стержень вращается без трения со скоростью , пока не коснется шара. В результате удара стержень останавливается, а шарик движется вправо. Масса стержня 0,2 кг. Масса мяча 0,067 кг. Длина стержня 0,15 м. Момент инерции стержня, вращающегося вокруг конца, равен: . Какова скорость мяча в результате удара?
Возможные ответы:
Правильный ответ:
Объяснение:
Это проблема сохранения углового момента, поэтому мы устанавливаем угловой момент стержня равным угловому моменту мяча. Будьте осторожны, чтобы не отменить так как это относится к стержню слева и шару справа. Наконец, справа – эффективный радиус мяча в момент удара, то есть просто длина стержня.
Наконец, справа – эффективный радиус мяча в момент удара, то есть просто длина стержня.
Сообщить об ошибке
Комета вращается вокруг звезды в далекой галактике, и на нее действует только гравитация. Через некоторое время солнечная радиация частично расплавила комету, уменьшив массу до четверти того, что было. При этом из-за неправильной орбиты его расстояние до звезды удваивается. Какое выражение лучше всего описывает угловую скорость кометы по сравнению с ее первоначальными условиями (до изменения таяния/расстояния)?
Возможные ответы:
Правильный ответ:
Пояснение:
Давайте рассмотрим уравнение , где = угловой момент, = масса спутника, = его угловая скорость и = его радиус от центра его орбиты. Из-за отсутствия внешних сил (помимо гравитации звезды), действующих на спутник, мы знаем, что его угловой момент сохраняется. Следовательно, поскольку его масса делится на четыре, а его радиус удваивается, его угловая скорость также должна удвоиться, что дает правильный ответ.
Следовательно, поскольку его масса делится на четыре, а его радиус удваивается, его угловая скорость также должна удвоиться, что дает правильный ответ.
Сообщить об ошибке
Рассмотрим диск, вращающийся с угловой скоростью . Позднее на диск внезапно надевается кольцо. Вычислите новую угловую скорость системы.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, мы воспользуемся законом сохранения углового момента. Изначально у нас есть только вращающийся диск. Это дает нам информацию о начальном угловом моменте системы. Позже у нас есть и диск, и кольцо, вращающиеся вместе с некоторой новой угловой скоростью.
Сообщить об ошибке
Момент инерции двух масс, разделенных расстоянием , равен
Два шара, каждый из которых имеет массу, прикреплены безмассовым стержнем определенной длины и вращаются вокруг точки, расположенной непосредственно в середине стержень. Затем стержень растягивается до длины . Предполагая отсутствие потери количества движения и ось остается постоянной, определите новую скорость вращения.
Затем стержень растягивается до длины . Предполагая отсутствие потери количества движения и ось остается постоянной, определите новую скорость вращения.
Возможные ответы:
Правильный ответ:
Объяснение:
Первый преобразование в:
Сохранение углового импульса:
, где, в этом случае:
Комбинированные уравнения:
. :
Сообщить об ошибке
Рассмотрим следующую систему:
Две сферические массы, A и B, прикреплены к концу жесткого стержня длиной л . Стержень прикреплен к фиксированной точке p , которая находится посередине между массами и находится на высоте h над землей. Стержень вращается вокруг фиксированной точки по вертикальному кругу, отмеченному серым цветом. это угол, под которым стержень составляет с горизонталью в любой момент времени ( на рисунке).
это угол, под которым стержень составляет с горизонталью в любой момент времени ( на рисунке).
Стержень вращается, и когда он проходит горизонтальное положение, полный угловой момент, включая обе массы, равен . Чему равна мгновенная линейная скорость массы A?
Массой стержня пренебречь.
Возможные ответы:
Правильный ответ:
Объяснение:
Так как нам дан угловой момент, давайте будем с ним и его формулой:
Где:
L = угловой момент
I = момент инерции
w = угловая скорость
Так как есть две массы на стержне (и мы пренебрегаем массой самого стержня), мы можем расширить это выражение до:
Поскольку массы прикреплены к жесткому стержню и движутся по однородной окружности, мы можем сказать, что: масса A для массы B:
Перестановка угловой скорости A:
Теперь нам нужно определить, каков момент инерции для каждой массы. Поскольку они являются сферами, мы можем рассматривать их как точечные массы и использовать следующую формулу:
Поскольку они являются сферами, мы можем рассматривать их как точечные массы и использовать следующую формулу:
Таким образом, для каждой массы мы получаем:
Где r равно половине длины стержня и одинаково для обеих масс. Подставив их в уравнение, мы получим:
Подставив вместо радиуса половину длины стержня, мы получим:
Мы знаем значение каждой переменной в этом уравнении, поэтому мы можем его решить. Но сначала давайте проверим правильность наших единиц измерения. Единицы угловой скорости:
Это проверено, так что пора подключать и пыхтеть:
Затем мы можем использовать выражение для угловой скорости, чтобы получить линейную скорость:
Сообщить об ошибке
Рассмотрим следующую систему:
Две сферические массы, A и B, прикреплены к концу жесткого стержня длиной l . Стержень прикреплен к фиксированной точке p , которая находится на высоте h над землей. Стержень вращается вокруг фиксированной точки по вертикальному кругу, отмеченному серым цветом. – это угол, под которым сторона L стержня образует горизонт с горизонтом в любой момент времени ( на рисунке может быть отрицательным, если масса A выше горизонтали).
Стержень вращается вокруг фиксированной точки по вертикальному кругу, отмеченному серым цветом. – это угол, под которым сторона L стержня образует горизонт с горизонтом в любой момент времени ( на рисунке может быть отрицательным, если масса A выше горизонтали).
В настоящее время система находится в состоянии покоя и удерживается так, что масса A находится ниже горизонтали и . Затем стержень освобождают и позволяют ему свободно вращаться. Какой максимальный угловой момент достигается массой B? Силами внутреннего трения пренебречь
Возможные ответы:
Пояснение:
Мы можем начать с выражения для сохранения энергии, чтобы решить эту задачу:
Поскольку нам сказали, что система изначально покоится, мы можем исключить начальную кинетическую энергию, чтобы получить выражение (1):
. Масса A удерживается под углом 15 градусов ниже горизонтали, поэтому мы можем использовать функцию синуса для определения высоты каждой массы. Будем считать, что нижняя точка вращения имеет высоту 0,
Будем считать, что нижняя точка вращения имеет высоту 0,
Где d — расстояние по вертикали ниже горизонтали, а r — радиус от центра стержня, который равен половине длины стержень:
Перестановка для d:
Мы знаем, что это расстояние ниже горизонтали, на котором начинается масса A, и расстояние над горизонталью, на котором начинается масса B. Кроме того, горизонталь находится на высоте половины длины стержня выше нашей опорной высоты, поэтому мы можем сказать:
Подставив их в наше расширенное выражение для начальной потенциальной энергии, мы получим:
потенциальная энергия:
Нас просят найти максимальный угловой момент, достигаемый массой B. Это происходит, когда масса B движется с максимальной скоростью, то есть когда большая из двух масс, масса A, проходит через нижнюю точку вращения . Это означает, что масса A находится на высоте 0 и, следовательно, не имеет конечной потенциальной энергии. Тогда мы можем сказать:
Тогда мы можем сказать:
Кроме того, мы знаем, что масса B будет находиться в высшей точке вращения, а это значит, что ее высота будет равна длине стержня. Таким образом, мы можем сказать:
Переходим к конечной кинетической энергии:
Нам не нужно расширять член скорости, поскольку две массы всегда движутся с одинаковой скоростью.
Теперь, подставив наши расширенные члены обратно в выражение (1), мы получим:
Чтобы определить угловой момент, нам нужно решить это уравнение для конечной скорости, поэтому давайте начнем переставлять:
У нас есть все эти значения, так что пора включить и пыхнуть:
Это максимальная скорость, которую будет испытывать масса B. Теперь мы можем использовать выражение для углового импульса:
, где:
, где r – половина длины стержня:
Мы были.


 Значение момента инерции маятника можно получить, суммируя моменты инерции составляющих его тел
Значение момента инерции маятника можно получить, суммируя моменты инерции составляющих его тел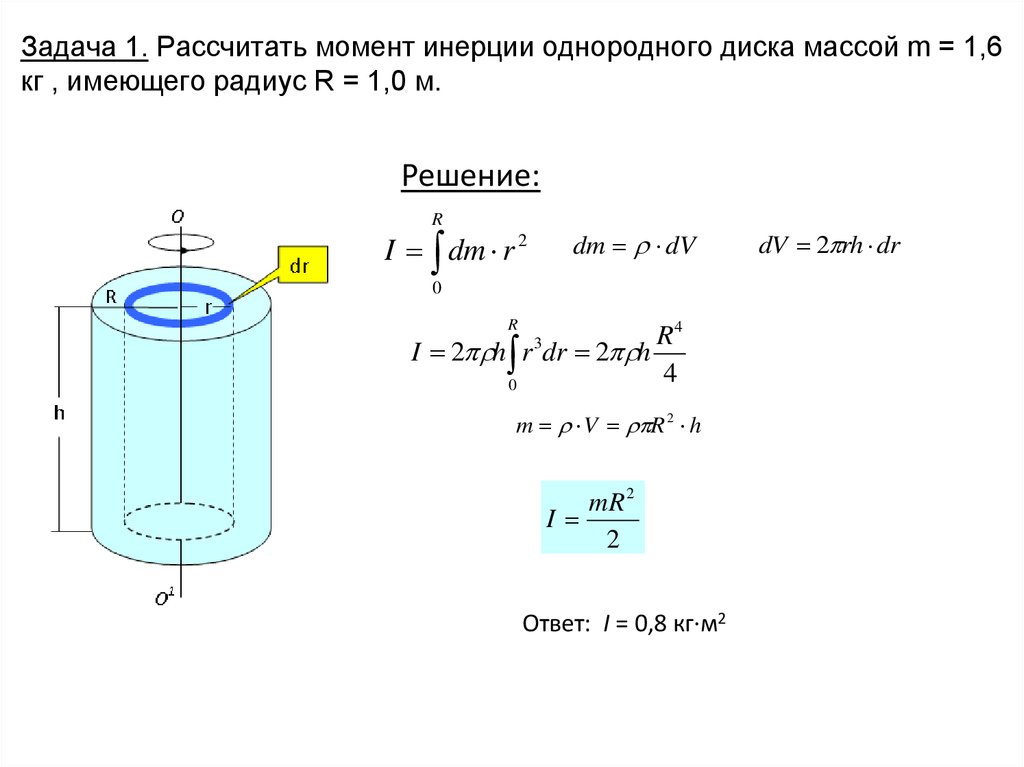 9) для расчета погрешности момента инерции?
9) для расчета погрешности момента инерции?