группа Matrix. — Клёвый код
Условие вида «дана матрица размера $$M \times N$$» означает, что вначале дается фактический размер двумерного массива-матрицы (количество строк $$M$$ и количество столбцов $$N$$), а затем приводятся элементы этого массива (количество элементов равно $$M*N$$). Если в задании явно не указывается, какие значения могут принимать размеры исходной матрицы, то предполагается, что и число строк, и число столбцов может меняться в пределах от $$2$$ до $$10$$. Порядковые номера начальной строки и начального столбца матрицы считаются равными $$1$$. Ввод и вывод элементов матрицы осуществляются по строкам. Квадратной матрицей порядка $$M$$ называется двумерный массив-матрица размера $$M \times M$$.
Если в задании, связанном с созданием (преобразованием) матрицы, не описан результирующий набор данных, то предполагается, что этим набором является созданная (преобразованная) матрица, и необходимо вывести все ее элементы.
Формирование матрицы и вывод ее элементов
В заданиях на формирование матрицы предполагается, что размер результирующей матрицы не превосходит $$10 \times 10$$.
Matrix1. Даны целые положительные числа $$M$$ и $$N$$. Сформировать целочисленную матрицу размера $$M \times N$$, у которой все элементы $$I$$-й строки имеют значение $$10*I$$ $$(I = 1, …, M)$$.
Решение задачи, на языке: Паскаль
Matrix2. Даны целые положительные числа $$M$$ и $$N$$. Сформировать целочисленную матрицу размера $$M \times N$$, у которой все элементы J-го столбца имеют значение $$5*J$$ $$(J = 1, …, $$N$$)$$.
Решение задачи, на языке: Паскаль, C++
Matrix3. Даны целые положительные числа $$M$$, $$N$$ и набор из $$M$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой в каждом столбце содержатся все числа из исходного набора (в том же порядке).
Решение задачи, на языке: Паскаль
Matrix4. Даны целые положительные числа $$M$$, $$N$$ и набор из $$N$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой в каждой строке содержатся все числа из исходного набора (в том же порядке).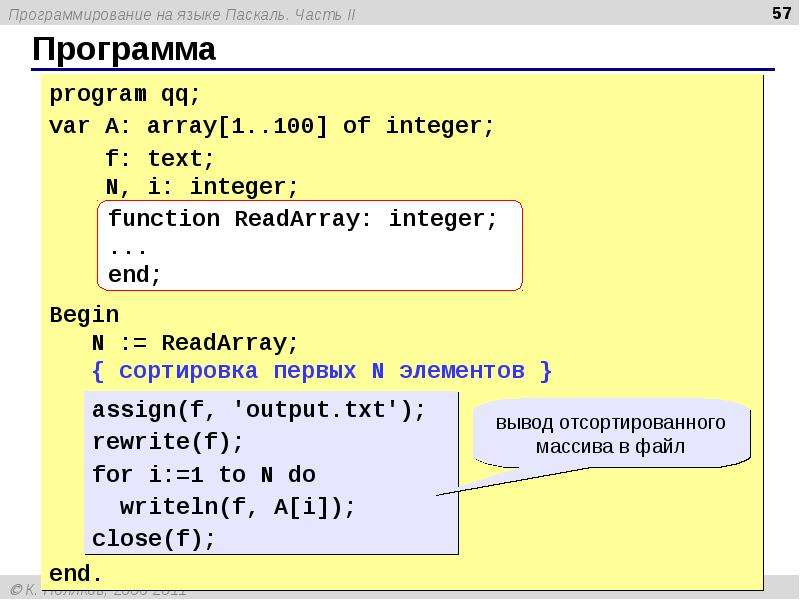
Решение задачи, на языке: Паскаль
Matrix5. Даны целые положительные числа $$M$$, $$N$$, число $$D$$ и набор из $$M$$ чисел.Сформировать матрицу размера $$M \times N$$, у которой первый столбец совпадает с исходным набором чисел, а элементы каждого следующего столбца равны сумме соответствующего элемента предыдущего столбца и числа $$D$$ (в результате каждая строка матрицы будет содержать элементы арифметической прогрессии).
Решение задачи, на языке: Паскаль
Matrix6. Даны целые положительные числа $$M$$, $$N$$, число $$Q$$ и набор из $$N$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой первая строка совпадает с исходным набором чисел, а элементы каждой следующей строки равны соответствующему элементу предыдущей строки, умноженному на $$Q$$ (в результате каждый столбец матрицы будет содержать элементы геометрической прогрессии).
Решение задачи, на языке: Паскаль
Matrix7. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Вывести элементы $$K$$-й строки данной матрицы.
Вывести элементы $$K$$-й строки данной матрицы.
Решение задачи, на языке: Паскаль
Matrix8. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Вывести элементы $$K$$-го столбца данной матрицы.
Решение задачи, на языке: Паскаль
Matrix9. Дана матрица размера $$M \times N$$. Вывести ее элементы, расположенные в строках с четными номерами $$(2, 4, …)$$. Вывод элементов производить по строкам, условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix10. Дана матрица размера $$M \times N$$. Вывести ее элементы, расположенные в столбцах с нечетными номерами $$(1, 3, …)$$. Вывод элементов производить по столбцам, условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix11. Дана матрица размера $$M \times N$$. Вывести ее элементы в следующем порядке: первая строка слева направо, вторая строка справа налево, третья строка слева направо, четвертая строка справа налево и т.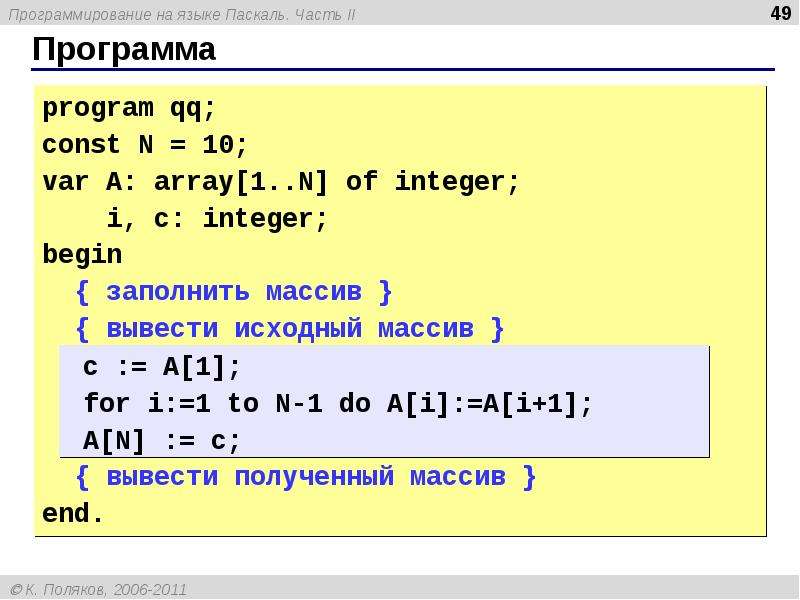 д.
д.
Matrix12. Дана матрица размера $$M \times N$$. Вывести ее элементы в следующем порядке: первый столбец сверху вниз, второй столбец снизу вверх, третий столбец сверху вниз, четвертый столбец снизу вверх и т. д.
Решение задачи, на языке: Паскаль
Matrix13. Дана квадратная матрица $$A$$ порядка $$M$$. Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первой строки; элементы последнего столбца, кроме первого (уже выведенного) элемента; оставшиеся элементы второй строки; оставшиеся элементы предпоследнего столбца и т. д.; последним выводится элемент $$A_{M,1}$$.
Решение задачи, на языке: Паскаль
Matrix14. Дана квадратная матрица $$A$$ порядка $$M$$. Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первого столбца; элементы последней строки, кроме первого (уже выведенного) элемента; оставшиеся элементы второго столбца; оставшиеся элементы предпоследней строки и т. д.; последним выводится элемент $$A_{1,M}$$.
д.; последним выводится элемент $$A_{1,M}$$.
Решение задачи, на языке: Паскаль
Matrix15. Дана квадратная матрица $$A$$ порядка $$M$$ ($$M$$ — нечетное число). Начиная с элемента $$A_{1,1}$$ и перемещаясь по часовой стрелке, вывести все ее элементы по спирали: первая строка, последний столбец, последняя строка в обратном порядке, первый столбец в обратном порядке, оставшиеся элементы второй строки и т. д.; последним выводится центральный элемент матрицы.
Решение задачи, на языке: Паскаль
Matrix16. Дана квадратная матрица $$A$$ порядка $$M$$ ($$M$$ — нечетное число). Начиная с элемента $$A_{1,1}$$ и перемещаясь против часовой стрелки, вывести все ее элементы по спирали: первый столбец, последняя строка, последний столбец в обратном порядке, первая строка в обратном порядке, оставшиеся элементы второго столбца и т. д.; последним выводится центральный элемент матрицы.
Решение задачи, на языке: Паскаль
Анализ элементов матрицы
Matrix17. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Найти сумму и произведение элементов $$K$$-й строки данной матрицы.
Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Найти сумму и произведение элементов $$K$$-й строки данной матрицы.
Решение задачи, на языке: Паскаль
Matrix18. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Найти сумму и произведение элементов $$K$$-го столбца данной матрицы.
Решение задачи, на языке: Паскаль
Matrix19. Дана матрица размера $$M \times N$$. Для каждой строки матрицы найти сумму ее элементов.
Решение задачи, на языке: Паскаль
Matrix20. Дана матрица размера $$M \times N$$. Для каждого столбца матрицы найти произведение его элементов.
Решение задачи, на языке: Паскаль
Matrix21. Дана матрица размера $$M \times N$$. Для каждой строки матрицы с нечетным номером $$(1, 3, …)$$ найти среднее арифметическое ее элементов. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix22. Дана матрица размера $$M \times N$$. Для каждого столбца матрицы с четным номером $$(2, 4, …)$$ найти сумму его элементов. Условный оператор не использовать.
Дана матрица размера $$M \times N$$. Для каждого столбца матрицы с четным номером $$(2, 4, …)$$ найти сумму его элементов. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix23. Дана матрица размера $$M \times N$$. В каждой строке матрицы найти минимальный элемент.
Решение задачи, на языке: Паскаль
Matrix24. Дана матрица размера $$M \times N$$. В каждом столбце матрицы найти максимальный элемент.
Решение задачи, на языке: Паскаль, C++
Matrix25. Дана матрица размера $$M \times N$$. Найти номер ее строки с наибольшей суммой элементов и вывести данный номер, а также значение наибольшей суммы.
Решение задачи, на языке: Паскаль
Matrix26. Дана матрица размера $$M \times N$$. Найти номер ее столбца с наименьшим произведением элементов и вывести данный номер, а также значение наименьшего произведения.
Решение задачи, на языке: Паскаль
Matrix27. Дана матрица размера $$M \times N$$. Найти максимальный среди минимальных элементов ее строк.
Дана матрица размера $$M \times N$$. Найти максимальный среди минимальных элементов ее строк.
Решение задачи, на языке: Паскаль
Matrix28. Дана матрица размера $$M \times N$$. Найти минимальный среди максимальных элементов ее столбцов.
Решение задачи, на языке: Паскаль
Matrix29. Дана матрица размера $$M \times N$$. В каждой ее строке найти количество элементов, меньших среднего арифметического всех элементов этой строки.
Решение задачи, на языке: Паскаль
Matrix30.
Решение задачи, на языке: Паскаль
Matrix31. Дана матрица размера $$M \times N$$. Найти номера строки и столбца для элемента матрицы, наиболее близкого к среднему значению всех ее элементов.
Решение задачи, на языке: Паскаль
Matrix32. Дана целочисленная матрица размера $$M \times N$$. Найти номер первой из ее строк, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких строк нет, то вывести $$0$$.
Найти номер первой из ее строк, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких строк нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix33. Дана целочисленная матрица размера $$M \times N$$. Найти номер последнего из ее столбцов, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких столбцов нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix34. Дана целочисленная матрица размера $$M \times N$$. Найти номер последней из ее строк, содержащих только четные числа. Если таких строк нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix35. Дана целочисленная матрица размера $$M \times N$$. Найти номер первого из ее столбцов, содержащих только нечетные числа. Если таких столбцов нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль, C++
Matrix36. Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные строки матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество строк, похожих на первую строку данной матрицы.
Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные строки матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество строк, похожих на первую строку данной матрицы.
Решение задачи, на языке: Паскаль
Matrix37. Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец данной матрицы.
Решение задачи, на языке: Паскаль
Matrix38. Дана целочисленная матрица размера $$M \times N$$. Найти количество ее строк, все элементы которых различны.
Решение задачи, на языке: Паскаль
Matrix39. Дана целочисленная матрица размера $$M \times N$$. Найти количество ее столбцов, все элементы которых различны.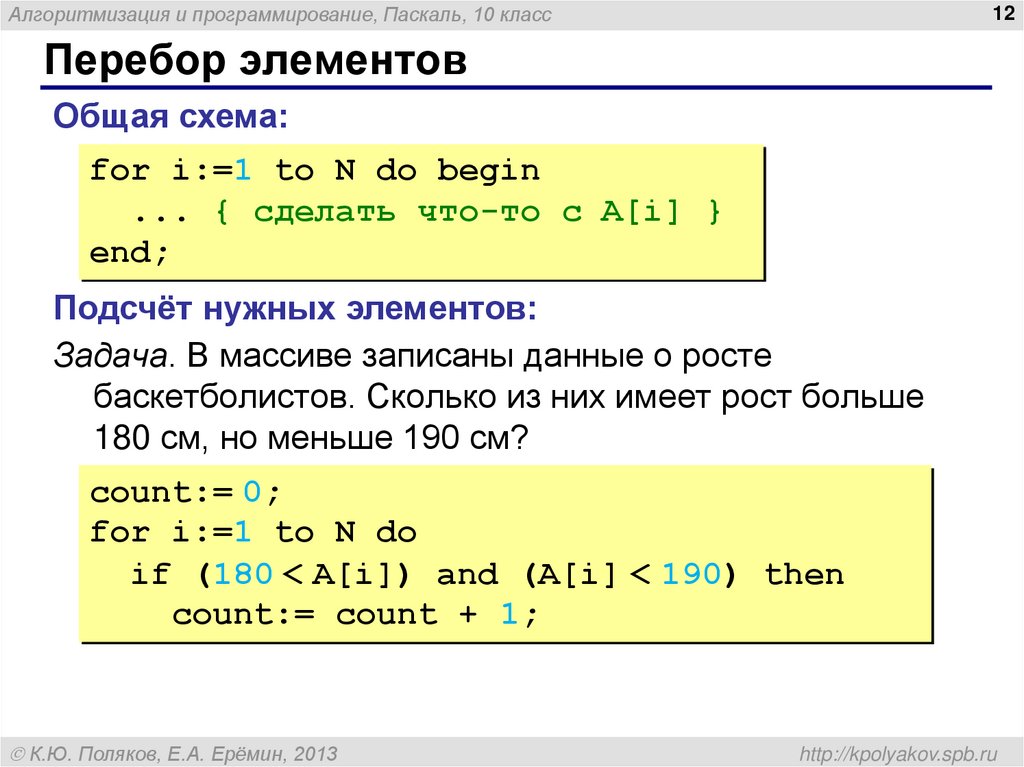
Решение задачи, на языке: Паскаль
Matrix40. Дана целочисленная матрица размера $$M \times N$$. Найти номер последней из ее строк, содержащих максимальное количество одинаковых элементов.
Решение задачи, на языке: Паскаль
Matrix41. Дана целочисленная матрица размера $$M \times N$$. Найти номер первого из ее столбцов, содержащих максимальное количество одинаковых элементов.
Решение задачи, на языке: Паскаль
Matrix42. Дана матрица размера $$M \times N$$. Найти количество ее строк, элементы которых упорядочены по возрастанию.
Решение задачи, на языке: Паскаль
Matrix43. Дана матрица размера $$M \times N$$. Найти количество ее столбцов, элементы которых упорядочены по убыванию.
Решение задачи, на языке: Паскаль, C++
Matrix44. Дана матрица размера $$M \times N$$. Найти минимальный среди элементов тех строк, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные строки в матрице отсутствуют, то вывести $$0$$.
Если упорядоченные строки в матрице отсутствуют, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix45. Дана матрица размера $$M \times N$$. Найти максимальный среди элементов тех столбцов, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные столбцы в матрице отсутствуют, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix46. Дана целочисленная матрица размера $$M \times N$$. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце. Если такой элемент отсутствует, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Преобразование матрицы
При выполнении заданий из данного пункта (за исключением заданий Matrix74 и Matrix75) не следует использовать вспомогательные двумерные массивы-матрицы.
Matrix47. Дана матрица размера $$M \times N$$ и целые числа $$K_1$$ и $$K_2$$ $$(1 \le K_1 < K_2 \le M)$$. Поменять местами строки матрицы с номерами $$K_1$$ и $$K_2$$ .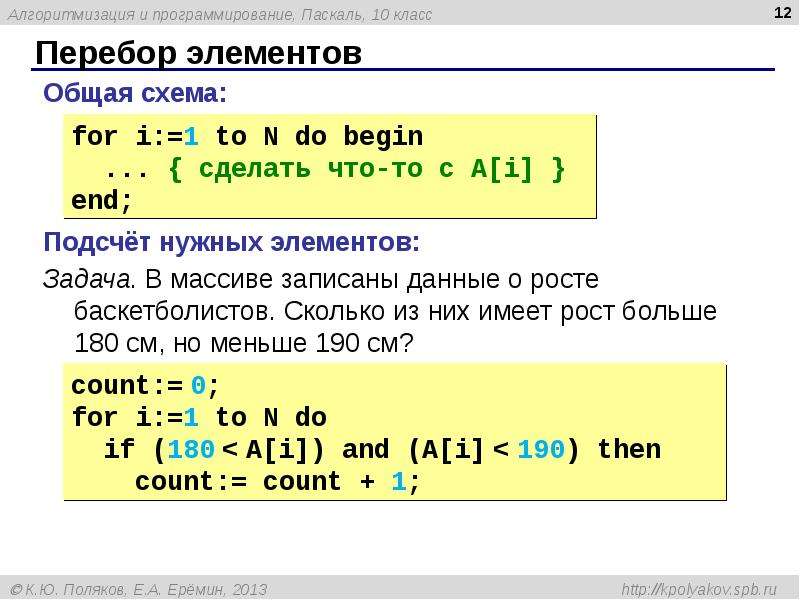
Решение задачи, на языке: Паскаль
Matrix48. Дана матрица размера $$M \times N$$ и целые числа $$K_1$$ и $$K_2$$ $$(1 \le K_1 < K_2 \le N)$$. Поменять местами столбцы матрицы с номерами $$K_1$$ и $$K_2$$ .
Решение задачи, на языке: Паскаль
Matrix49. Дана матрица размера $$M \times N$$. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждой строке.
Решение задачи, на языке: Паскаль
Matrix50. Дана матрица размера $$M \times N$$. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждом столбце.
Решение задачи, на языке: Паскаль
Matrix51. Дана матрица размера $$M \times N$$. Поменять местами строки, содержащие минимальный и максимальный элементы матрицы.
Решение задачи, на языке: Паскаль
Matrix52. Дана матрица размера $$M \times N$$. Поменять местами столбцы, содержащие минимальный и максимальный элементы матрицы.
Решение задачи, на языке: Паскаль
Matrix53. Дана матрица размера $$M \times N$$. Поменять местами столбец с номером $$1$$ и последний из столбцов, содержащих только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix54. Дана матрица размера $$M \times N$$. Поменять местами столбец с номером $$N$$ и первый из столбцов, содержащих только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix55. Дана матрица размера $$M \times N$$ ($$M$$ — четное число). Поменять местами верхнюю и нижнюю половины матрицы.
Решение задачи, на языке: Паскаль, C++
Matrix56. Дана матрица размера $$M \times N$$ ($$N$$ — четное число). Поменять местами левую и правую половины матрицы.
Решение задачи, на языке: Паскаль
Matrix57. Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую верхнюю и правую нижнюю четверти матрицы.
Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую верхнюю и правую нижнюю четверти матрицы.
Решение задачи, на языке: Паскаль
Matrix58. Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую нижнюю и правую верхнюю четверти матрицы.
Решение задачи, на языке: Паскаль
Matrix59. Дана матрица размера $$M \times N$$. Зеркально отразить ее элементы относительно горизонтальной оси симметрии матрицы (при этом поменяются местами строки с номерами $$1$$ и $$M$$, $$2$$ и $$M-1$$ и т. д.).
Решение задачи, на языке: Паскаль
Matrix60. Дана матрица размера $$M \times N$$. Зеркально отразить ее элементы относительно вертикальной оси симметрии матрицы (при этом поменяются местами столбцы с номерами $$1$$ и $$N$$, $$2$$ и $$N-1$$ и т. д.).
Решение задачи, на языке: Паскаль
Matrix61. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$.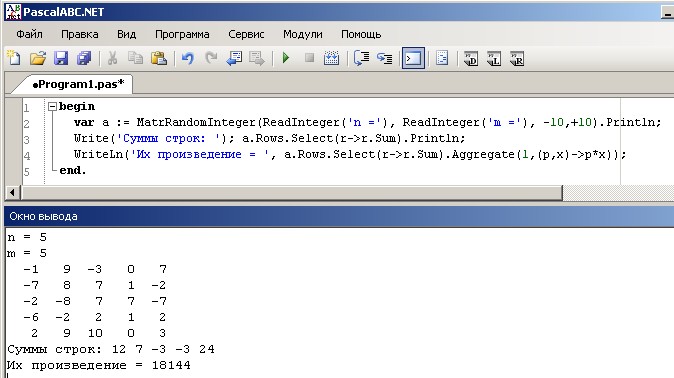 Удалить строку матрицы с номером $$K$$.
Удалить строку матрицы с номером $$K$$.
Решение задачи, на языке: Паскаль
Matrix62. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Удалить столбец матрицы с номером $$K$$.
Решение задачи, на языке: Паскаль, C++
Matrix63. Дана матрица размера $$M \times N$$. Удалить строку, содержащую минимальный элемент матрицы.
Решение задачи, на языке: Паскаль
Matrix64. Дана матрица размера $$M \times N$$. Удалить столбец, содержащий максимальный элемент матрицы.
Решение задачи, на языке: Паскаль
Matrix65. Дана матрица размера $$M \times N$$. Удалить ее первый столбец, содержащий только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix66. Дана матрица размера $$M \times N$$. Удалить ее последний столбец, содержащий только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix67. Дана матрица размера $$M \times N$$, содержащая как положительные, так и отрицательные элементы. Удалить все ее столбцы, содержащие только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix68. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Перед строкой матрицы с номером $$K$$ вставить строку из нулей.
Решение задачи, на языке: Паскаль
Matrix69. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. После столбца матрицы с номером $$K$$ вставить столбец из единиц.
Решение задачи, на языке: Паскаль
Matrix70. Дана матрица размера $$M \times N$$. Продублировать строку матрицы, содержащую ее максимальный элемент.
Решение задачи, на языке: Паскаль
Matrix71. Дана матрица размера $$M \times N$$. Продублировать столбец матрицы, содержащий ее минимальный элемент.
Дана матрица размера $$M \times N$$. Продублировать столбец матрицы, содержащий ее минимальный элемент.
Решение задачи, на языке: Паскаль
Matrix72. Дана матрица размера $$M \times N$$. Перед первым столбцом, содержащим только положительные элементы, вставить столбец из единиц. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix73. Дана матрица размера $$M \times N$$. После последнего столбца, содержащего только отрицательные элементы, вставить столбец из нулей. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix74. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на нули. При решении допускается использовать вспомогательную матрицу.
Решение задачи, на языке: Паскаль
Matrix75. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным максимумом, если он больше всех окружающих его элементов. Поменять знак всех локальных максимумов данной матрицы на противоположный. При решении допускается использовать вспомогательную матрицу.
Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным максимумом, если он больше всех окружающих его элементов. Поменять знак всех локальных максимумов данной матрицы на противоположный. При решении допускается использовать вспомогательную матрицу.
Решение задачи, на языке: Паскаль, C++
Matrix76. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их первые элементы образовывали возрастающую последовательность.
Решение задачи, на языке: Паскаль, С++
Matrix77. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их последние элементы образовывали убывающую последовательность.
Решение задачи, на языке: Паскаль
Matrix78. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их минимальные элементы образовывали убывающую последовательность.
Решение задачи, на языке: Паскаль
Matrix79. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их максимальные элементы образовывали возрастающую последовательность.
Упорядочить ее столбцы так, чтобы их максимальные элементы образовывали возрастающую последовательность.
Решение задачи, на языке: Паскаль
Диагонали квадратной матрицы
Matrix80. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов ее главной диагонали, то есть диагонали, содержащей следующие элементы:
$$A_{1,1}, A_{2,2}, A_{3,3}, …, A_{M,M}$$.
Решение задачи, на языке: Паскаль
Matrix81. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов ее побочной диагонали, то есть диагонали, содержащей следующие элементы:
$$A_{1,M}, A_{2,M-1}, A_{3,M-2}, …, A_{M,1}$$.
Решение задачи, на языке: Паскаль
Matrix82. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль
Matrix83. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Найти сумму элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль, C++
Matrix84. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль
Matrix85. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль
Matrix86. Дана квадратная матрица $$A$$ порядка $$M$$. Найти минимальный элемент для каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль
Matrix87. Дана квадратная матрица $$A$$ порядка $$M$$. Найти максимальный элемент для каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль
Matrix88. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие ниже главной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix89. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие выше побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль, C++
Matrix90. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на побочной диагонали и ниже нее. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix91. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на главной диагонали и выше нее. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix92. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно выше главной диагонали и выше побочной диагонали.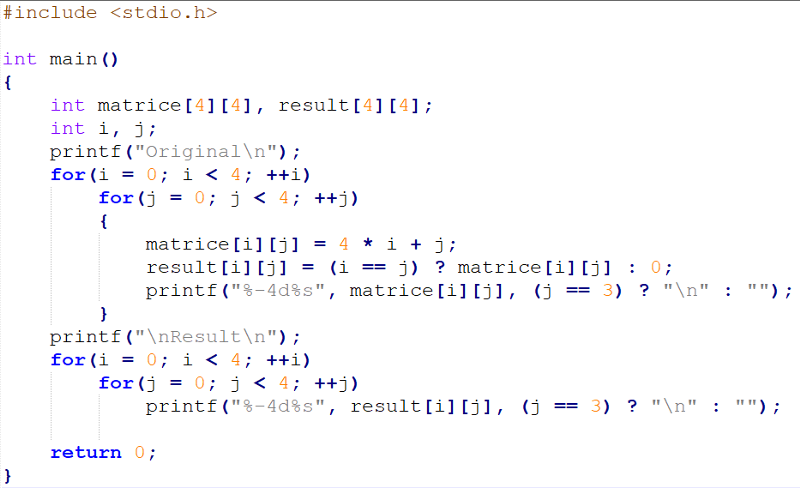 Условный оператор не использовать.
Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix93. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно выше главной диагонали и ниже побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix94. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и выше побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix95. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и ниже побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix96. Дана квадратная матрица $$A$$ порядка $$M$$. Зеркально отразить ее элементы относительно главной диагонали (при этом элементы главной диагонали останутся на прежнем месте, элемент $$A_{1,2}$$ поменяется местами с $$A_{2,1}$$, элемент $$A_{1,3}$$ — с $$A_{3,1}$$ и т.\circ$$ в отрицательном направлении, то есть по часовой стрелке (при этом элемент $$A_{1,1}$$ перейдет в $$A_{1,M}$$, элемент $$A_{1,M}$$ — в $$A_{M,M}$$ и т. д.). Вспомогательную матрицу не использовать.
Решение задачи, на языке: Паскаль
Если вы хотите выложить решение для задач, но нет решения на нужном языке, или вообще к задаче нет решений. Можете разместить его в виде комментария к данной статье.
Другие задачи по программированию, для проверки своих знаний.
Перестановка строк и столбцов в матрице
1. Перестановка строк и столбцов в матрице
Практическая работа1.Составить любые 2 программы по теме.
2. Пройти тест:
https://onlinetestpad.com/ru/test/211366dvumernye-massivy
Все элементы двумерного массива A размером10х10
элементов первоначально были равны 0. Затем
значения элементов меняются с помощью вложенного
оператора цикла в представленном фрагменте
программы:
for n:=1 to 4 do
for k:=n to 4 do begin
A[n,k] := A[n,k] + 1;
A[k,n] := A[k,n] + 1;
end;
Сколько элементов массива в результате будут равны 1?
1) 0
2) 16
3) 12 4) 4
таким образом, правильный ответ – 3.
В программе используется одномерный целочисленный массив A с
индексами от 0 до 9. Ниже представлен фрагмент программы,
записанный на разных языках программирования, в котором
значения элементов сначала задаются, а затем меняются.
for i:=0 to 9 do
A[i]:=9-i;
for i:=0 to 4 do begin
k:=A[i];
A[i]:=A[9-i];
A[9-i]:=k;
end;
Чему будут равны элементы этого массива после выполнения
фрагмента программы?
1) 9 8 7 6 5 4 3 2 1 0
2) 0 1 2 3 4 5 6 7 8 9
3) 9 8 7 6 5 5 6 7 8 9
4) 0 1 2 3 4 4 3 2 1 0
Ответ: 2.
Дан фрагмент программы, обрабатывающей двухмерный массив A
размера n×n.
k := 1;
for i:=1 to n do begin
c := A[i,i];
A[i,i] := A[k,i];
A[k,i] := c;
end
Представим массив в виде квадратной таблицы, в которой для
элемента массива A[i,j] величина i является номером строки, а
величина j – номером столбца, в котором расположен элемент. Тогда
данный алгоритм меняет местами
1) два столбца в таблице
2) две строки в таблице
3) элементы диагонали и k-ой строки таблицы
4) элементы диагонали и k-го столбца таблицы
таким образом, правильный ответ – 3
5. Операции с матрицами
Программирование на языке Паскаль. Часть II5
Операции с матрицами
Задача 4. Перестановка строк или столбцов. В матрице из N
строк и M столбцов переставить 2-ую и 4-ую строки.
j
A[2,j]
2
1
2
5
2
1
4
7
3
1
3
7
A[4,j]
for j:=1 to M do begin
c := A[2,j];
A[2,j] := A[4,j];
A[4,j] := c;
end;
Задача 5. К третьему столбцу добавить шестой.
for i:=1 to N do
A[i,3] := A[i,3] + A[i,6];
К. Поляков, 2006-2011
http://kpolyakov.narod.ru
6. Перестановка строк и столбцов
Алгоритмизация и программирование, язык Python, 10 класс6
Перестановка строк и столбцов
2-я и 4-я строки:
A[2], A[4] = A[4], A[2]
0
1
2
3
4
2-й и 4-й столбцы:
for i in range(N):
A[i][2], A[i][4] = A[i][4], A[i][2]
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru
5
67
8
43
23
63
89
89
76
5
67
93
2
34
38
91
40
55
78
92
12
11
18
88
9
58
39
7
55
68
91
34
67
20
87
59
81
35
61
22
39
96
43
45
94
74
53
47
23
Для перестановки двух
элементов в массиве
необходимо
воспользоваться
вспомогательной
переменной:
T:=A[2,5]
A[2,5]:=A[5,2];
A[5,2]:=T;
Особое значение при работе с
квадратными массивами занимает
задача «транспонирования», т.е
переворачивания массива
относительно главной диагонали.
Для выполнения этой задачи нужно
поменять местами элементы
A[i,j] и A[j,i]
5
89
38
11
55
59
43
67
76
91
18
68
81
45
8
5
40
88
91
35
94
43
67
55
9
34
61
74
23
93
78
58
67
22
53
63
2
92
39
20
39
47
89
34
12
7
87
96
23
Для переворачивания всего массива используется двойной цикл.
8. транспонирование
Программирование на языке Паскаль. Часть IIтранспонирование
Переворот массива относительно главной
диагонали
for i:=1 to n do
for j:=i to n do
begin
t:=a[i,j];
a[i,j]:=a[j,i];
a[j,i]:=t;
end;
К. Поляков, 2006-2011
5
67
89
8
38
43
11
23
55
63
59
89
43
89
67
76
5
91
67
18
93
68
2
81
34
45
38
8
91
5
40
55
88
78
91
92
35
12
94
11
43
18
67
88
55
9
58
34
39
61
7
74
55
23
68
93
91
78
34
58
67
67
20
22
87
53
59
63
81
2
35
92
61
39
22
20
39
39
96
47
43
89
45
34
94
12
74
7
53
87
47
96
23
23
http://kpolyakov.narod.ru
9. Задание:
Программирование на языке Паскаль. Часть IIЗадание:
1. В матрице из N строк и M столбцов переставить 3-ий и 4ый столбцы.
2. К третьей строке добавить пятую.
3.ст. 211, уп11.
Пиксели рисунка закодированы числами (обозначающими
цвет) в виде матрицы, содержащей N строк и M столбцов.
Выполните отражение рисунка сверху вниз:
4. ст. 211,12.
Выполните поворот матрицы
на 900 как показано на
рисунке:
К. Поляков, 2006-2011
http://kpolyakov.narod.ru
10. Задание:
Программирование на языке Паскаль. Часть IIЗадание:
5. Составить программу, которая создает и выводит
на экран массив такого вида:
К. Поляков, 2006-2011
0
1
1
1
1
1
0
1
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
0
1
1
1
1
1
0
1
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
0
http://kpolyakov.narod.ru
Двумерный массив в python и обработка элементов массива
На уроке рассматриваются алгоритмы работы с двумерными массивами в Python: создание матрицы, инициализация элементов, вывод, обработка элементов матрицы
Создание, вывод и ввод матрицы в Питоне
- Таким образом, получается структура из вложенных списков, количество которых определяет количество строк матрицы, а число элементов внутри каждого вложенного списка указывает на количество столбцов в исходной матрице.
- Вывод матрицы можно осуществить одним оператором, но такой простой способ не позволяет выполнять какой-то предварительной обработки элементов:
Для работы с матрицами в Python также используются списки. Каждый элемент списка-матрицы содержит вложенный список.
Рассмотрим пример матрицы размера 4 х 3:
matrix = [[-1, 0, 1],
[-1, 0, 1],
[0, 1, -1],
[1, 1, -1]] |
matrix = [[-1, 0, 1], [-1, 0, 1], [0, 1, -1], [1, 1, -1]]
Данный оператор можно записать в одну строку:
matrix = [[-1, 0, 1], [-1, 0, 1], [0, 1, -1], [1, 1, -1]] |
matrix = [[-1, 0, 1], [-1, 0, 1], [0, 1, -1], [1, 1, -1]]
Результат:
- способ:
- способ:
1 2 3 4 5 | def printMatrix ( matrix ):
for i in range ( len(matrix) ):
for j in range ( len(matrix[i]) ):
print ( "{:4d}".format(matrix[i][j]), end = "" )
print () |
def printMatrix ( matrix ): for i in range ( len(matrix) ): for j in range ( len(matrix[i]) ): print ( “{:4d}”.format(matrix[i][j]), end = “” ) print ()
В примере i – это номер строки, а j – номер столбца;
len(matrix) – число строк в матрице.
1 2 3 4 5 | def printMatrix ( matrix ):
for row in matrix:
for x in row:
print ( "{:4d}".format(x), end = "" )
print () |
def printMatrix ( matrix ): for row in matrix: for x in row: print ( “{:4d}”.format(x), end = “” ) print ()
Внешний цикл проходит по строкам матрицы (row), а внутренний цикл проходит по элементам каждой строки (x).
1 2 3 4 | from random import randint n, m = 3, 3 a = [[randint(1, 10) for j in range(m)] for i in range(n)] print(a) |
from random import randint n, m = 3, 3 a = [[randint(1, 10) for j in range(m)] for i in range(n)] print(a)
Обработка элементов двумерного массива
Нумерация элементов двумерного массива, как и элементов одномерного массива, начинается с нуля.
Т.е. matrix[2][3] — это элемент третьей строки четвертого столбца.
Пример обработки элементов матрицы:
Найти произведение элементов двумерного массива.
✍ Решение:
1 2 3 4 5 | p = 1
for i in range(N):
for j in range(M):
p *= matrix[i][j]
print (p) |
p = 1 for i in range(N): for j in range(M): p *= matrix[i][j] print (p)
Пример:
Найти сумму элементов двумерного массива.
✍ Решение:
Более подходящий вариант для Python:1 2 3 4 | s = 0 for row in matrix: s += sum(row) print (s) |
s = 0 for row in matrix: s += sum(row) print (s)
Для поиска суммы существует стандартная функция sum.
Задание Python 8_0:Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:
| Номер станции | 1-й день | 2-й день | 3-й день | 4-й день |
|---|---|---|---|---|
| 1 | -8 | -14 | -19 | -18 |
| 2 | 25 | 28 | 26 | 20 |
| 3 | 11 | 18 | 20 | 25 |
Т.е. запись показаний в двумерном массиве выглядела бы так:
| t[0][0]=-8 | t[0][1]=-14 | t[0][2]=-19 | t[0][3]=-18 |
| t[1][0]=25 | t[1][1]=28 | t[1][2]=26 | t[1][3]=20 |
| t[2][0]=11 | t[2][1]=18 | t[2][2]=20 | t[2][3]=25 |
- Распечатать температуру на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день.
- Распечатать показания термометров всех метеостанций за 2-й день.
- Определить среднюю температуру на 3-й метеостанции.
- Распечатать, в какие дни и на каких метеостанциях температура была в диапазоне 24-26 градусов тепла.
Задание Python 8_1:
Написать программу поиска минимального и максимального элементов матрицы и их индексов.
Задание Python 8_2:
Написать программу, выводящую на экран строку матрицы, сумма элементов которой максимальна.
for i in range(N): # работаем с matrix[i][i] |
for i in range(N): # работаем с matrix[i][i]
for i in range(N): # работаем с matrix[i][N-1-i] |
for i in range(N): # работаем с matrix[i][N-1-i]
Пример:Переставить 2-й и 4-й столбцы матрицы. Использовать два способа.
✍ Решение:
for i in range(N): c = A[i][2] A[i][2] = A[i][4] A[i][4] = c |
for i in range(N): c = A[i][2] A[i][2] = A[i][4] A[i][4] = c
for i in range(N): A[i][2], A[i][4] = A[i][4], A[i][2] |
for i in range(N): A[i][2], A[i][4] = A[i][4], A[i][2]
Задание Python 8_3:
Составить программу, позволяющую с помощью датчика случайных чисел сформировать матрицу размерностью N. Определить:
Матрица Паскаля
Матрица смежности – один из способов представления графа в виде матрицы Матрица смежности графа G с конечным числом вершин n пронумерованных числами
Матрица Кирхгофа матрица Лапласа Матрица смежности Зейделя Матрица Татта Матрицы Кабибо – Кобаяши – Москавы Гамма матрицы Дирака Матрицы Паули Матрицы Гелл – Манна
Пари Паскаля – предложенный математиком и философом Блезом Паскалем аргумент для демонстрации рациональности религиозной веры. Текст аргументации является
шифрования с открытым ключом, таких как RSA. Матрица может также быть факторизована на произведение матриц специального вида для приложений, в которых
квадратную матрицу отсчитав N элементов по катетам треугольника Паскаля и повернув матрицу на любой из четырёх углов, то детерминант этих четырёх матриц равен
Массив в некоторых языках программирования также таблица, ряд, матрица – структура данных, хранящая набор значений элементов массива идентифицируемых
так же, как и в Паскале В Турбо Паскале объявления указывают также в модулях собственное расширение Турбо Паскаля по отношению к Паскалю в разделе interface
Цилиндр заполняется водой, маслом или другой подходящей жидкостью. По закону Паскаля давление в любом месте неподвижной жидкости одинаково по всем направлениям
переменных. Новая таблица TN 1 компонуется как матрица 2 2 таблиц TN, причём правый верхний блок матрицы очищается. Алгебра Жегалкина Капитонова Ю. В
Меррифилд – За предложенную методологию химического синтеза на твёрдых матрицах Физиология и медицина – Нильс Ерне, Георг Кёлер, Сезар Мильштейн – За
можно получить разрешение 128 129 матрица знакоместа 2 3, 43 строки высотой 6 линий или 192 102 матрица 3 2, 51 строки высотой 4 линии К
Суть метода заключается в наличии всего одной штамп – матрицы вместо особо точной пары матрица – пуансон давление на лист металла оказывает жидкая среда
аренизавра была построена матрица с использованием 57 признаков для 22 таксонов. Для этого использовался набор данных из исследования Паскаля Годфруа и коллег
жизни, а его место в философии заступает бог философов по выражению Паскаля и бог – перводвигатель Ньютон, Бэкон Зло, как понятие, теряет своё единое
поспешными: Также по мнению российских учёных, при написании статьи командой Паскаля Годфруа были использованы более ранние труды самих российских учёных. К
легко штампуются на термопласт – автоматах из пластика. Для особых случаев матрица может быть изготовлена из тугоплавкой керамики, отлита из чугуна или другого
PascalABC.NET – язык программирования Паскаль нового поколения, включающий классический Паскаль большинство возможностей языка Delphi, а также ряд собственных
сделали прошлым летом – Бен Уиллис 1999 – Быть Джоном Малковичем 1999 – Матрица 2000 – Гладиатор 2000 – Идеальный шторм – Боб Браун 2000 – Дракула 2000
унистохастических unistochastic матриц третьего порядка образует дельтоиду. Поперечное сечение множества унистохастических unistochastic матриц третьего порядка образует
принимают ЛСД и открывают истину. Пародия на кинофильм Матрица В реальности фильм Матрица вышел в 1999 году, спустя год после событий игры. Pastmaster
пронумерованы с 1, как в Паскале Построим такую матрицу n H: если i – префикс needle совпадает с haystack в позициях j i 1 j, ставим в матрице 1 в позиции i, j
элементов массива DOT PRODUCT скалярное произведение MATMUL умножение матриц Добавились справочные функции, а также функции переформирования и свёртки
образования биномиальных коэффициентов, ныне известный как треугольник Паскаля В Европе он был открыт лишь 250 лет спустя. Термин алгебра взят из
единственный вид Wulagasaurus dongi назван и описан бельгийским палеонтологом Паскалем Годфруа и коллегами в 2008 году. Родовое имя образовано от названия города
выдающимися учёными своего времени. Помимо Ферма, он переписывался с Мерсенном, Паскалем Декартом и Джоном Валлисом. Современники отмечали его талант вычислителя
знакогенератор из двух наборов по 256 символов расположен в специальном ПЗУ матрица символа – 8 16 точек графический с собственной независимой видеопамятью
заданной частоте как правило, 1000 Гц выраженное в милливольтах на паскаль мВ Па Чем больше это значение, тем выше чувствительность микрофона.
распределения, в связи с тем, что математическое ожидание и ковариационная матрица полностью характеризуют нормальное распределение. Формулировки и решения
простая внешняя платка контроллера цвета дающая 4 или 8 цветов Клавиатура: матрица контактов в 72 1 клавиши в оригинале – плёночная обслуживаемая процессором
всегда удобной часто критикуются бесконечные begin – end в программах на Паскале который унаследовал эту особенность именно от Алгола но на момент появления
Дата публикации:
04-19-2021
Дата последнего обновления:
04-19-2021Excel поменять строки местами
Excel поменять строки местами
Добрый день, уважаемые читатели! Наболевший вопрос, который откладывал долгое время. Сразу оговорюсь – о транспортировании (замены столбца на строку и наоборот) мы поговорим в следующих статьях.
Сегодня речь пойдёт о замене значений двух строк/столбцов, то есть нам нужно просто поменять местами столбцы или строки в таблице Excel. Что мы для этого обычно делаем:
- Выделяем строку/столбец, которые будем переносить;
- Даём команду “Вырезать”;
- Выделяем место где должны быть строки/столбцы;
- Даём команду “Вставить”.
Также можно просто перетаскивать за рамку выделения нужные нам диапазоны.
Но бывают случаи, когда в наличии имеется большая таблица, в которой нужно поменять местами значения, но места под новые столбцы/строки взять негде. Не будем рассматривать вариант вставки новой строки/столбца, он может нарушить выверенную структуру и формулы. Что же тогда делать? Попробуем решить данную проблему с помощью макроса.
Для замены необходимо соблюдение двух условий:
1) диапазон ячеек ОБЯЗАТЕЛЬНО должен быть одинаковой величины;
2) ОБЯЗАТЕЛЬНО должны быть выделены два диапазона ячеек.
Текст:
Sub ChangePlaces()
Dim ra As Range: Set ra = Selection
msg1 = “Нужно выделить ДВА диапазона ячеек одинакового размера!”
msg2 = “Нужно выделить диапазоны ОДИНАКОВОГО размера!”
If ra.Areas.Count <> 2 Then MsgBox msg1, vbCritical, “Ошибка”: Exit Sub
If ra.Areas(1).Count <> ra.Areas(2).Count Then MsgBox msg2, vbCritical, “Ошибка”: Exit Sub
Application.ScreenUpdating = False
arr2 = ra.Areas(2).Value
ra.Areas(2).Value = ra.Areas(1).Value
ra.Areas(1).Value = arr2
End Sub
Немного пояснений:
- ra – это область выделения;
- msg1 и msg2 – сообщение о соответствующих ошибках;
- If ra.Areas.Count <> 2 – условие выделения двух диапазонов;
- If ra.Areas(1).Count <> ra – условие выделения одинаковых по длине диапазонов ячеек;
- Application.ScreenUpdating – экране не обновится если не выполнены два условия;
- остальное показывает, что диапазоны будут заменены друг на друга.
Добавим новый модуль к нашей книге. Вкладка “Разработчик”, кнопка “Visual basic”, далее “Insert” и “Module”.
Теперь проверим правильность работы макроса. Выделим с помощью клавиши Ctrl два одинаковых диапазона ячеек (это может быть строка, столбец, просто ячейка). Воспользуемся сочетанием клавиш Alt+F8, чтобы вызвать диалоговое окно “Макросы” или перейдём на вкладку “Разработчик” и нажмём одноимённую кнопку. Появится список макросов, нажимаем кнопку “Выполнить” и наблюдаем результат.
Видим, макрос работает!
Если остались вопросы – посмотрите наше новое видео!
Вас может заинтересовать на урок – Удаление пустых ячеек.
100 NumPy задач | Python 3 для начинающих и чайников
100 (на самом деле, пока меньше) задач для NumPy, перевод английского варианта https://github.com/rougier/numpy-100
Импортировать NumPy под именем np
Напечатать версию и конфигурацию
print(np.__version__) np.show_config()
Создать вектор (одномерный массив) размера 10, заполненный нулями
Z = np.zeros(10) print(Z)
Создать вектор размера 10, заполненный единицами
Создать вектор размера 10, заполненный числом 2.5
Z = np.full(10, 2.5) print(Z)
Как получить документацию о функции numpy.add из командной строки?
python3 -c "import numpy; numpy.info(numpy.add)"
Создать вектор размера 10, заполненный нулями, но пятый элемент равен 1
Z = np.zeros(10) Z[4] = 1 print(Z)
Создать вектор со значениями от 10 до 49
Z = np.arange(10,50) print(Z)
Развернуть вектор (первый становится последним)
Z = np.arange(50) Z = Z[::-1]
Создать матрицу (двумерный массив) 3×3 со значениями от 0 до 8
Z = np.arange(9).reshape(3,3) print(Z)
Найти индексы ненулевых элементов в [1,2,0,0,4,0]
nz = np.nonzero([1,2,0,0,4,0]) print(nz)
Создать 3×3 единичную матрицу
Создать массив 3x3x3 со случайными значениями
Z = np.random.random((3,3,3)) print(Z)
Создать массив 10×10 со случайными значениями, найти минимум и максимум
Z = np.random.random((10,10)) Zmin, Zmax = Z.min(), Z.max() print(Zmin, Zmax)
Создать случайный вектор размера 30 и найти среднее значение всех элементов
Z = np.random.random(30) m = Z.mean() print(m)
Создать матрицу с 0 внутри, и 1 на границах
Z = np.ones((10,10)) Z[1:-1,1:-1] = 0
Выяснить результат следующих выражений
0 * np.nan np.nan == np.nan np.inf > np.nan np.nan - np.nan 0.3 == 3 * 0.1
Создать 5×5 матрицу с 1,2,3,4 под диагональю
Z = np.diag(np.arange(1, 5), k=-1) print(Z)
Создать 8×8 матрицу и заполнить её в шахматном порядке
Z = np.zeros((8,8), dtype=int) Z[1::2,::2] = 1 Z[::2,1::2] = 1 print(Z)
Дан массив размерности (6,7,8). Каков индекс (x,y,z) сотого элемента?
print(np.unravel_index(100, (6,7,8)))
Создать 8×8 матрицу и заполнить её в шахматном порядке, используя функцию tile
Z = np.tile(np.array([[0,1],[1,0]]), (4,4)) print(Z)
Перемножить матрицы 5×3 и 3×2
Z = np.dot(np.ones((5,3)), np.ones((3,2))) print(Z)
Дан массив, поменять знак у элементов, значения которых между 3 и 8
Z = np.arange(11) Z[(3 < Z) & (Z <= 8)] *= -1
Создать 5×5 матрицу со значениями в строках от 0 до 4
Z = np.zeros((5,5)) Z += np.arange(5) print(Z)
Есть генератор, сделать с его помощью массив
def generate():
for x in xrange(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)Создать вектор размера 10 со значениями от 0 до 1, не включая ни то, ни другое
Z = np.linspace(0,1,12)[1:-1] print(Z)
Отсортировать вектор
Z = np.random.random(10) Z.sort() print(Z)
Проверить, одинаковы ли 2 numpy массива
A = np.random.randint(0,2,5) B = np.random.randint(0,2,5) equal = np.allclose(A,B) print(equal)
Сделать массив неизменяемым
Z = np.zeros(10) Z.flags.writeable = False Z[0] = 1
Дан массив 10×2 (точки в декартовой системе координат), преобразовать в полярную
Z = np.random.random((10,2)) X,Y = Z[:,0], Z[:,1] R = np.hypot(X, Y) T = np.arctan2(Y,X) print(R) print(T)
Заменить максимальный элемент на ноль
Z = np.random.random(10) Z[Z.argmax()] = 0 print(Z)
Создать структурированный массив с координатами x, y на сетке в квадрате [0,1]x[0,1]
Z = np.zeros((10,10), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,10),
np.linspace(0,1,10))
print(Z)Из двух массивов сделать матрицу Коши C (Cij = 1/(xi – yj))
X = np.arange(8) Y = X + 0.5 C = 1.0 / np.subtract.outer(X, Y) print(np.linalg.det(C))
Найти минимальное и максимальное значение, принимаемое каждым числовым типом numpy
for dtype in [np.int8, np.int32, np.int64]: print(np.iinfo(dtype).min) print(np.iinfo(dtype).max) for dtype in [np.float32, np.float64]: print(np.finfo(dtype).min) print(np.finfo(dtype).max) print(np.finfo(dtype).eps)
Напечатать все значения в массиве
np.set_printoptions(threshold=np.nan) Z = np.zeros((25,25)) print(Z)
Найти ближайшее к заданному значению число в заданном массиве
Z = np.arange(100) v = np.random.uniform(0,100) index = (np.abs(Z-v)).argmin() print(Z[index])
Создать структурированный массив, представляющий координату (x,y) и цвет (r,g,b)
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)Дан массив (100,2) координат, найти расстояние от каждой точки до каждой
import scipy.spatial Z = np.random.random((10,2)) D = scipy.spatial.distance.cdist(Z,Z) print(D)
Преобразовать массив из float в int
Z = np.arange(10, dtype=np.int32) Z = Z.astype(np.float32, copy=False)
Дан файл:
1,2,3,4,5 6,,,7,8 ,,9,10,11
Как прочитать его?
Z = np.genfromtxt("missing.dat", delimiter=",")Каков эквивалент функции enumerate для numpy массивов?
Z = np.arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])Сформировать 2D массив с распределением Гаусса
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10)) D = np.hypot(X, Y) sigma, mu = 1.0, 0.0 G = np.exp(-((D - mu) ** 2 / (2.0 * sigma ** 2))) print(G)
Случайно расположить p элементов в 2D массив
n = 10 p = 3 Z = np.zeros((n,n)) np.put(Z, np.random.choice(range(n*n), p, replace=False), 1)
Отнять среднее из каждой строки в матрице
X = np.random.rand(5, 10) Y = X - X.mean(axis=1, keepdims=True)
Отсортировать матрицу по n-ому столбцу
Z = np.random.randint(0,10,(3,3)) n = 1 # Нумерация с нуля print(Z) print(Z[Z[:,n].argsort()])
Определить, есть ли в 2D массиве нулевые столбцы
Z = np.random.randint(0,3,(3,10)) print((~Z.any(axis=0)).any())
Дан массив, добавить 1 к каждому элементу с индексом, заданным в другом массиве (осторожно с повторами)
Z = np.ones(10) I = np.random.randint(0,len(Z),20) Z += np.bincount(I, minlength=len(Z)) print(Z)
Дан массив (w,h,3) (картинка) dtype=ubyte, посчитать количество различных цветов
w,h = 16,16 I = np.random.randint(0, 2, (h,w,3)).astype(np.ubyte) F = I[...,0] * 256 * 256 + I[...,1] * 256 + I[...,2] n = len(np.unique(F)) print(np.unique(I))
Дан четырехмерный массив, посчитать сумму по последним двум осям
A = np.random.randint(0,10, (3,4,3,4)) sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1) print(sum)
Найти диагональные элементы произведения матриц
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B).Дан вектор [1, 2, 3, 4, 5], построить новый вектор с тремя нулями между каждым значением
Z = np.array([1,2,3,4,5]) nz = 3 Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz)) Z0[::nz+1] = Z print(Z0)
Поменять 2 строки в матрице
A = np.arange(25).reshape(5,5) A[[0,1]] = A[[1,0]] print(A)
Рассмотрим набор из 10 троек, описывающих 10 треугольников (с общими вершинами), найти множество уникальных отрезков, составляющих все треугольники
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)Дан массив C; создать массив A, что np.bincount(A) == C
C = np.bincount([1,1,2,3,4,4,6]) A = np.repeat(np.arange(len(C)), C) print(A)
Посчитать среднее, используя плавающее окно
def moving_average(a, n=3):
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
print(moving_average(np.arange(20), 3))Дан вектор Z, построить матрицу, первая строка которой (Z[0],Z[1],Z[2]), каждая последующая сдвинута на 1 (последняя (Z[-3],Z[-2],Z[-1]))
from numpy.lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)Инвертировать булево значение, или поменять знак у числового массива без создания нового
Z = np.random.randint(0,2,100) np.logical_not(arr, out=arr) Z = np.random.uniform(-1.0,1.0,100) np.negative(arr, out=arr)
Рассмотрим 2 набора точек P0, P1 описания линии (2D) и точку р, как вычислить расстояние от р до каждой линии i (P0[i],P1[i])
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0] - p[...,0]) * T[:,0] + (P0[:,1] - p[...,1]) * T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U * T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))Дан массив. Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Z = np.random.randint(0,10, (10,10)) shape = (5,5) fill = 0 position = (1,1) R = np.ones(shape, dtype=Z.dtype)*fill P = np.array(list(position)).astype(int) Rs = np.array(list(R.shape)).astype(int) Zs = np.array(list(Z.shape)).astype(int) R_start = np.zeros((len(shape),)).astype(int) R_stop = np.array(list(shape)).astype(int) Z_start = (P - Rs//2) Z_stop = (P + Rs//2)+Rs%2 R_start = (R_start - np.minimum(Z_start, 0)).tolist() Z_start = (np.maximum(Z_start, 0)).tolist() R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist() Z_stop = (np.minimum(Z_stop,Zs)).tolist() r = [slice(start,stop) for start,stop in zip(R_start,R_stop)] z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)] R[r] = Z[z] print(Z) print(R)
Посчитать ранг матрицы
Z = np.random.uniform(0,1,(10,10)) rank = np.linalg.matrix_rank(Z)
Найти наиболее частое значение в массиве
Z = np.random.randint(0,10,50) print(np.bincount(Z).argmax())
Извлечь все смежные 3×3 блоки из 10×10 матрицы
Z = np.random.randint(0,5,(10,10)) n = 3 i = 1 + (Z.shape[0] - n) j = 1 + (Z.shape[1] - n) C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides) print(C)
Создать подкласс симметричных 2D массивов (Z[i,j] == Z[j,i])
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, (i,j), value):
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)Рассмотрим множество матриц (n,n) и множество из p векторов (n,1). Посчитать сумму p произведений матриц (результат имеет размерность (n,1))
p, n = 10, 20 M = np.ones((p,n,n)) V = np.ones((p,n,1)) S = np.tensordot(M, V, axes=[[0, 2], [0, 1]]) print(S) # It works, because: # M is (p,n,n) # V is (p,n,1) # Thus, summing over the paired axes 0 and 0 (of M and V independently), # and 2 and 1, to remain with a (n,1) vector.
Дан массив 16×16, посчитать сумму по блокам 4×4
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)Написать игру “жизнь”
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N == 3) & (Z[1:-1,1:-1]==0)
survive = ((N == 2) | (N == 3)) & (Z[1:-1,1:-1] == 1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100):
print(Z)
Z = iterate(Z)Найти n наибольших значений в массиве
Z = np.arange(10000) np.random.shuffle(Z) n = 5 print (Z[np.argpartition(-Z,n)[:n]])
Построить прямое произведение массивов (все комбинации с каждым элементом)
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = map(len, arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print(cartesian(([1, 2, 3], [4, 5], [6, 7])))Даны 2 массива A (8×3) и B (2×2). Найти строки в A, которые содержат элементы из каждой строки в B, независимо от порядка элементов в B
A = np.random.randint(0,5,(8,3)) B = np.random.randint(0,5,(2,2)) C = (A[..., np.newaxis, np.newaxis] == B) rows = (C.sum(axis=(1,2,3)) >= B.shape[1]).nonzero()[0] print(rows)
Дана 10×3 матрица, найти строки из неравных значений (например [2,2,3])
Z = np.random.randint(0,5,(10,3)) E = np.logical_and.reduce(Z[:,1:] == Z[:,:-1], axis=1) U = Z[~E] print(Z) print(U)
Преобразовать вектор чисел в матрицу бинарных представлений
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8) print(np.unpackbits(I[:, np.newaxis], axis=1))
Дан двумерный массив. Найти все различные строки
Z = np.random.randint(0, 2, (6,3)) T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1]))) _, idx = np.unique(T, return_index=True) uZ = Z[idx] print(uZ)
Даны векторы A и B, написать einsum эквиваленты функций inner, outer, sum и mul
# Make sure to read: http://ajcr.net/Basic-guide-to-einsum/
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j', A, B) # np.outer(A, B)Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовательская работа
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
биномиальных коэффициентов – значения для начала частичной строки треугольника Паскаля
Мы пытаемся найти число в $ n_1 + n_2 $ -й строке и $ k_1 + k_2 $ -м столбце модифицированного треугольника Паскаля.Назовем это число $ F \ left (n_1, k_1, n_2, k_2 \ right) $. Я сделаю это, взяв число в исходном треугольнике Паскаля и вычтя $ f \ left (n_1, k_1, n_2, k_2 \ right ) $ из него. Наша задача – найти $ f $. Тогда $$ F \ left (n_1, k_1, n_2, k_2 \ right) = {{n_1 + n_2} \ choose {k_2}} – f \ left (n_1, k_1, n_2, k_2 \ right) $$
Начнем с рассмотрения примера. Вот отображение значений $ f $, то есть разницы между исходным треугольником Паскаля и нашей модифицированной версией.
0
0 0
0 0 0
0 0 0 0
0 0 0 4 1
0 0 0 4 5 1
0 0 0 4 9 6 1
0 0 0 4 13 15 7 1
Исправляя $ n_1 $ и $ k_1 $, мы видим, что $ f $ действует как треугольник Паскаля в этом $$ f \ left (n_2, k_2 \ right) + f \ left (n_2, k_2 + 1 \ right) = f \ left (n_2 + 1, k_2 + 2 \ right) $$ Интересный.Интуитивно это имеет смысл. Ячейка $ (4, 3) $ на 4 меньше, чем обычно, а $ (4, 4) $ на 1 меньше, чем обычно. Отсюда следует, что ячейка $ (5, 4) $ должна быть на 5 меньше, чем обычно, просто потому, что так работает треугольник Паскаля.
Давайте сделаем еще один шаг и «рассечем» этот искореженный треугольник Паскаля на $ f $. Что произойдет, если только $ (4, 3) $ заменить на 0? А как насчет того, чтобы заменить только $ (4, 4) $ на 0?
4 0 0 1
4 4 0 0 1 1
4 8 4 0 0 1 2 1
4 12 12 4 0 0 1 3 3 1
Только замена (4, 3) Только замена (4, 4)
Ну да черт возьми! Похоже, что каждое число в строке $ n_1 $ справа от $ k_1 $ создает свой собственный миниатюрный увеличенный треугольник Паскаля, и каждое из них складывается вместе, образуя треугольник $ f $.
А теперь обобщим. Посмотрим, что произойдет, если мы заменим $ t_ {n_1, k_1 + i} $ нулем. Затем, еще одна строка $ n_2 $ вниз и строка $ k_2 $, число уменьшается на $$ {{n_1} \ choose {k_1 + 1}} {{n_2} \ choose {k_2-k_1-1}} $$ Вообще говоря, замена ряда $ i $ строк справа от $ \ left (n_1, k_1 \ right) $ приводит к разнице в $$ {{n_1} \ choose {k_1 + i + 1}} {{n_2} \ choose {k_2-k_1-i-1}} $$ Итак, мы можем построить нашу финальную функцию следующим образом: $$ F \ left (n_1, k_1, n_2, k_2 \ right) = {{n_1 + n_2} \ choose {k_2}} – \ sum \ limits_ {i = 0} ^ {n_1-k_1} {{n_1} \ выбрать {k_1 + i + 1}} {{n_2} \ выбрать {k_2-k_1-i-1}} $$ Я не уверен, есть ли способ еще больше уменьшить это.Похоже, что это работает с предоставленным примером, хотя я еще не тестировал его на других случаях.
linear algebra – Перестановка строк меняет знак определителя
Это проблема с курицей и яйцом, если вы так думаете. Все следующие идеи связаны друг с другом;
1- Переставляя любые 2 строки матрицы, меняет знак ее определителя.
2- Определитель произведения двух матриц равен произведению определителей тех же двух матриц.
3- Определитель матрицы инвариантен к элементарным операциям со строками.
4- Умножение всей строки (или столбца) матрицы на константу, увеличивает детерминант на эту константу.
Если вы предположите какое-либо подмножество из них, остальные останутся довольными.
Я использовал элементарные операции со строками и умножил всю строку на константу, чтобы показать, что доказательство довольно простое.
Если поменять местами 2 строки, знак определителя меняется на противоположный.{n \ times n} $, как показано ниже;
$$ \ mathrm {A} = \ begin {bmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {bmatrix} $
Тогда определитель $ \ mathrm {A} $ имеет вид;
$$ \ det {\ mathrm {A}} знак равно \ begin {vmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} $
Рассмотрите две отдельные строки, которые вы хотите поменять местами, и добавьте одну из них в другую.W.L.O.G здесь предполагает, что первая строка добавляется ко второй строке. Обычно это справедливо для любых двух строк (или столбцов).
$ Строка 2: = Строка 2 + Строка 1 $
$$ \ det {\ mathrm {(A)}} знак равно \ begin {vmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} + a_ {11} & a_ {22} + a_ {12} & \ cdots & a_ {2n} + a_ {1n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} $
Затем вычтите получившуюся строку 2 из строки 1.
$ Строка1: = Строка1 – Строка2 $
$$ \ det {\ mathrm {(A)}} знак равно \ begin {vmatrix} -a_ {21} & -a_ {22} & \ cdots & -a_ {2n} \\ a_ {21} + a_ {11} & a_ {22} + a_ {12} & \ cdots & a_ {2n} + a_ {1n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} $
Добавьте получившуюся строку 1 к строке 2.
$ Строка2: = Строка2 + Строка1 $
$$ \ det {\ mathrm {(A)}} знак равно \ begin {vmatrix} -a_ {21} & -a_ {22} & \ cdots & -a_ {2n} \\ a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} $
Возьмите $ -1 $ обыкновенный из первой строки, это выпадает из определителя.
$$ \ det {\ mathrm {A}} знак равно (-1) \ begin {vmatrix} a_ {21} & a_ {22} & \ cdots & a_ {2n} \\ a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} $
Наконец-то у нас есть;
$$ \ begin {vmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} знак равно (-1) \ begin {vmatrix} a_ {21} & a_ {22} & \ cdots & a_ {2n} \\ a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ cdots & a_ {nn} \\ \ end {vmatrix} \ quad \ blacksquare $
Тот же аргумент справедлив для замены любых двух строк (или столбцов).
NumPy: транспонировать ndarray (поменять местами строки и столбцы, переставить оси)
Чтобы транспонировать массив NumPy ndarray (поменять местами строки и столбцы), используйте атрибут T ( .T ), метод ndarray транспонирование () и функция numpy.transpose () .
С помощью ndarray.transpose () и numpy.transpose () вы можете не только транспонировать 2D-массив (матрицу), но и переставлять оси многомерного массива в любом порядке.
В этой статье описывается следующее содержимое.
- Транспонировать двумерный массив (матрицу)
-
Tатрибут -
ndarray.transpose () -
np.transpose ()
-
- Одномерный массив и вектор-строка, вектор-столбец
- Поменять местами оси многомерного массива (3D или выше)
- Результат по умолчанию
- Укажите порядок осей с помощью
транспонирования () - Пример: транспонировать несколько матриц одновременно
Если вы хотите поменять местами строки и столбцы панд.DataFrame или двумерный список (список списков) см. В следующей статье.
Транспонировать двумерный массив (матрицу)
Атрибут T
Вы можете получить транспонированную матрицу исходного двумерного массива (матрицы) с атрибутом T .
импортировать numpy как np
a_2d = np.arange (6) .reshape (2, 3)
печать (a_2d)
# [[0 1 2]
# [3 4 5]]
a_2d_T = a_2d.T
печать (a_2d_T)
# [[0 3]
# [1 4]
# [2 5]]
Атрибут T возвращает представление исходного массива, и изменение одного приводит к изменению другого.
Вы можете проверить, ссылается ли ndarray на данные в той же памяти с помощью np.shares_memory () .
печать (np.shares_memory (a_2d, a_2d_T))
# Истинный
a_2d_T [0, 1] = 100
печать (a_2d_T)
# [[0 100]
# [1 4]
# [2 5]]
печать (a_2d)
# [[0 1 2]
# [100 4 5]]
a_2d [1, 0] = 3
печать (a_2d)
# [[0 1 2]
# [3 4 5]]
печать (a_2d_T)
# [[0 3]
# [1 4]
# [2 5]]
Если вы хотите обрабатывать его как отдельные данные, сделайте копию с помощью copy () .
a_2d_T_copy = a_2d.T.copy ()
печать (a_2d_T_copy)
# [[0 3]
# [1 4]
# [2 5]]
print (np.shares_memory (a_2d, a_2d_T_copy))
# Ложь
a_2d_T_copy [0, 1] = 100
печать (a_2d_T_copy)
# [[0 100]
# [1 4]
# [2 5]]
печать (a_2d)
# [[0 1 2]
# [3 4 5]]
ndarray.transpose ()
transpose () предоставляется как метод ndarray . Как и T , вид возвращается.
печать (a_2d.transpose ())
# [[0 3]
# [1 4]
# [2 5]]
печать (нп.share_memory (a_2d, a_2d.transpose ()))
# Истинный
нп. Транспонирование ()
numpy.transpose () также предоставляется функция. В качестве первого аргумента укажите исходный массив. Это также возвращает представление.
печать (np.transpose (a_2d))
# [[0 3]
# [1 4]
# [2 5]]
print (np.shares_memory (a_2d, np.transpose (a_2d)))
# Истинный
1D-массив и вектор-строка, вектор-столбец
Применение T или transpose () к одномерному массиву возвращает только массив, эквивалентный исходному массиву.
a_1d = np.arange (3)
печать (a_1d)
# [0 1 2]
печать (a_1d.T)
# [0 1 2]
печать (a_1d.transpose ())
# [0 1 2]
печать (np.transpose (a_1d))
# [0 1 2]
Матрица только с одной строкой называется вектором-строкой, а матрица с одним столбцом называется вектором-столбцом, но нет различия между строками и столбцами в одномерном массиве ndarray .
Двумерный массив используется, чтобы четко указать, что присутствуют только строки или столбцы.
Здесь преобразуйте форму с помощью reshape () .
a_row = a_1d.reshape (1, -1)
печать (a_row)
# [[0 1 2]]
печать (a_row.shape)
# (1, 3)
печать (a_row.ndim)
# 2
a_col = a_1d.reshape (-1, 1)
печать (a_col)
# [[0]
# [1]
# [2]]
печать (a_col.shape)
# (3, 1)
печать (a_col.ndim)
# 2
Как упоминалось выше, двумерные массивы можно транспонировать.
печать (a_row.T)
# [[0]
# [1]
# [2]]
печать (a_col.Т)
# [[0 1 2]]
Поменять местами оси многомерного массива (3D или выше)
Результат по умолчанию
T , transpose () может применяться к многомерным массивам в формате 3D или выше.
Результат по умолчанию следующий. np.transpose () имеет тот же результат.
a_3d = np.arange (24) .reshape (2, 3, 4)
печать (a_3d)
# [[[0 1 2 3]
# [4 5 6 7]
# [8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
печать (a_3d.Т)
# [[[0 12]
# [4 16]
# [8 20]]
#
# [[1 13]
# [5 17]
# [9 21]]
#
# [[2 14]
# [6 18]
# [10 22]]
#
# [[3 15]
# [7 19]
# [11 23]]]
печать (a_3d.T.shape)
# (4, 3, 2)
печать (a_3d.transpose ())
# [[[0 12]
# [4 16]
# [8 20]]
#
# [[1 13]
# [5 17]
# [9 21]]
#
# [[2 14]
# [6 18]
# [10 22]]
#
# [[3 15]
# [7 19]
# [11 23]]]
печать (a_3d.transpose (). shape)
# (4, 3, 2)
Трудно понять, просто взглянув на результат вывода, но порядок оси (размера) (0-я ось, 1-я ось, 2-я ось) обратный, как (2-я ось, 1-я ось, 0-я ось) .
В 2D-массиве порядок (0-я ось, 1-я ось) = (строка, столбец) изменяется на порядок (1-я ось, 0-я ось) = (столбец, строка) .
Укажите порядок осей с помощью transpose ()
Использование T всегда меняет порядок, но используя transpose () , вы можете указать любой порядок.
В следующем примере укажите тот же обратный порядок, что и по умолчанию, и убедитесь, что результат не изменится.
В методе ndarray transpose () укажите порядок оси с аргументами переменной длины или кортежем.
печать (a_3d.transpose (2, 1, 0))
# [[[0 12]
# [4 16]
# [8 20]]
#
# [[1 13]
# [5 17]
# [9 21]]
#
# [[2 14]
# [6 18]
# [10 22]]
#
# [[3 15]
# [7 19]
# [11 23]]]
print (a_3d.transpose (2, 1, 0) .shape)
# (4, 3, 2)
print (a_3d.transpose ((2, 1, 0)). shape)
# (4, 3, 2)
В np.transpose () укажите порядок в качестве второго аргумента кортежа. Его нельзя указать с аргументами переменной длины.
принт (нп.транспонировать (a_3d, (2, 1, 0)))
# [[[0 12]
# [4 16]
# [8 20]]
#
# [[1 13]
# [5 17]
# [9 21]]
#
# [[2 14]
# [6 18]
# [10 22]]
#
# [[3 15]
# [7 19]
# [11 23]]]
print (np.transpose (a_3d, (2, 1, 0)). shape)
# (4, 3, 2)
# print (np.transpose (a_3d, 2, 1, 0))
# TypeError: transpose () принимает от 1 до 2 позиционных аргументов, но было дано 4
Ошибка возникает, если количество указанных осей не соответствует количеству измерений исходного массива или если указано несуществующее измерение.
# print (a_3d.transpose (0, 1))
# ValueError: оси не соответствуют массиву
# print (a_3d.transpose (0, 1, 2, 3))
# ValueError: оси не соответствуют массиву
# print (a_3d.transpose (0, 1, 3))
# AxisError: ось 3 находится за пределами массива размерности 3
Пример: транспонировать сразу несколько матриц
transpose () полезно, например, когда трехмерный массив представляет собой группу двумерных массивов.
Если данные матриц хранятся как трехмерный массив формы (n, строка, столбец) , все матрицы можно транспонировать следующим образом.
печать (a_3d)
# [[[0 1 2 3]
# [4 5 6 7]
# [8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
печать (a_3d.shape)
# (2, 3, 4)
печать (a_3d.transpose (0, 2, 1))
# [[[0 4 8]
# [1 5 9]
# [2 6 10]
# [3 7 11]]
#
# [[12 16 20]
# [13 17 21]
# [14 18 22]
# [15 19 23]]]
print (a_3d.transpose (0, 2, 1) .shape)
# (2, 4, 3)
Если фигура (строка, столбец, n) , вы можете сделать следующее.
печать (a_3d.транспонировать (1, 0, 2))
# [[[0 1 2 3]
# [12 13 14 15]]
#
# [[4 5 6 7]
# [16 17 18 19]]
#
# [[8 9 10 11]
# [20 21 22 23]]]
print (a_3d.transpose (1, 0, 2) .shape)
# (3, 2, 4)
print (a_3d [:,:, 0])
# [[0 4 8]
# [12 16 20]]
print (a_3d.transpose (1, 0, 2) [:,:, 0])
# [[0 12]
# [4 16]
# [8 20]]
Matrix Market: форматы файлов
Matrix Market: форматы файловКратко опишем форматы файлов ASCII для матриц, распространяемых Матричный рынок:
Обратите внимание, что большинство файлов данных, которые мы распространяем, сжаты с использованием gzip , а некоторые представляют собой многофайловые архивы на основе Unix tar .Обратитесь к нашему документу о сжатии, если вам нужно помогите в расшифровке этих файлов.
Форматы обмена Matrix Market
Это собственный формат обмена для Matrix Market. Мы предоставляем только краткий обзор этого формата на этой странице; полный описание приведено в статье Форматы матричного рынка: первоначальный дизайн [Gziped PostScript, 51 Кбайт] [PostScript, 189 Кбайт].
Форматы обмена Matrix Market (MM) предоставляют простой механизм для облегчить обмен матричными данными.В частности, цель была для определения минимального базового формата файла ASCII, который можно очень легко объяснить и разбирается, но может легко адаптироваться к приложениям с более жесткой структурой, или расширен на связанные объекты данных. Формат обмена MM для матриц: действительно набор дочерних форматов, которые разделяют элементы дизайна. В нашем В исходной спецификации определены два формата матриц.
- Формат координат
Формат файла, подходящий для представления общих разреженных матриц.Предоставляются только ненулевые записи, и координаты каждого ненулевая запись указывается явно. Это проиллюстрировано в примере ниже. - Формат массива
Формат файла, подходящий для представления общих плотных матриц. Все записи представлены в заранее определенном (ориентированном на столбцы) порядке.
Формат координат MM подходит для представления разреженных матриц. Необходимо кодировать только ненулевые записи, и координаты каждой дано явно. Это проиллюстрировано на следующем примере реального Общая разреженная матрица 5×5.
1 0 0 6 0
0 10,5 0 0 0
0 0 .015 0 0
0 250,5 0 -280 33,32
0 0 0 0 12
В формате координат MM это можно представить следующим образом.%% матрица MatrixMarket координата вещественная общая % ================================================= ================================ % % Этот файл ASCII представляет собой разреженную матрицу MxN с L % ненулевые в следующем формате Matrix Market: % % + ---------------------------------------------- + % | %% MatrixMarket матричная координата вещественная общая |
Первая строка содержит код типа.В этом примере это означает, что представляемый объект представляет собой матрицу в формате координат, и что числовой следующие данные являются действительными и представлены в общем виде. (Под общими мы подразумеваем что формат матрицы не использует никаких свойств симметрии.)
Варианты формата координат определены для матриц со сложными и целочисленные записи, а также для тех, в которых только позиция ненулевого записей (шаблонных матриц).(Это будет обозначено изменение вещественного числа на комплексное, целое или узор соответственно в строке заголовка). Дополнительные варианты определены для случаев, когда симметрии могут быть использованы для значительного уменьшения размер данных: симметричный, кососимметричный и эрмитовский . В этих случаях только входы в нижнюю треугольную часть необходимо поставить . В кососимметричном В этом случае диагональные элементы равны нулю, поэтому они также опускаются.(Эти будет обозначено изменением общего на симметричный, кососимметричный или эрмитовый соответственно по заголовку линия).
Следующие пакеты программного обеспечения доступны для помощи в чтении и записи. матрицы в формате Matrix Market.
Harwell-Boeing Exchange Format
Формат Harwell-Boeing – самый популярный механизм для текстовых файлов. обмен разреженными матричными данными. Следующая информация, взято из Руководство пользователя коллекции разреженных матриц Harwell-Boeing предоставляет спецификацию для этого формата.Данные матрицы хранятся в 80-столбцах фиксированной длины. формат для переносимости. Каждая матрица начинается с кратного блок заголовка строки, за которым следуют два, три или четыре данных блоки. Блок заголовка содержит сводку информация о форматах хранения и требованиях к пространству. Из только блок заголовка, пользователь может определить, сколько потребуется место для хранения матрицы. Информация о размер изображения в строках приведен для удобства в пропуск ненужных данных.
Если нет правых векторов, матрица имеет блок заголовка из четырех строк, за которым следуют два или три блока данных содержащий, по порядку, начало столбца (или элемента) указатели, индексы строк (или переменных) и числовые значения. Если правые части присутствуют, есть пятая строка в блоке заголовка и четвертый блок данных содержащую правую (ые) часть (и). Блоки, содержащие числовые значения и правая часть (и) необязательны.Правая часть (и) может присутствовать только тогда, когда числовые значения присутствуют. Если правые части присутствуют, то векторы для начальных догадок и раствор также может присутствовать; если так, они отображаются как отдельные полные массивы в правом блоке после правого боковой вектор (ы).
Первая строка содержит заголовок из 72 символов и 8-значный идентификатор, по которому ссылается матрица в нашей документации. Вторая строка содержит количество строк для каждого из следующие блоки данных, а также общее количество строк, за исключением блока заголовка.Третья линия содержит трехсимвольную строку, обозначающую тип матрицы а также количество строк, столбцов (или элементов), элементов, а в случае несобранных матриц – всего количество записей в элементарных матрицах. В четвертая строка содержит переменные форматы Fortran для следующие блоки данных. Пятая строка присутствует, только если есть правые части. Он содержит один символьная строка, обозначающая формат хранения для правые части, а также количество правых частей, и количество записей указателя строк (для собранного корпуса).Точный формат дается следующим, где имена Переменные Fortran в последующих программах указаны в скобках:
Линия 1 (A72, A8)
| Колонка 1 – 72 | Титул ( TITLE ) |
| Кол.73 – 80 | Ключ ( KEY ) |
Строка 2 (5I14)
| Полковник1–14 | Общее количество строк без заголовка ( TOTCRD ) |
| Кол. 15 – 28 | Количество строк для указателей ( PTRCRD ) |
| Кол. 29 – 42 | Количество строк для индексов строк (или переменных) ( INDCRD ) |
| Кол.43 – 56 | Количество строк для числовых значений ( VALCRD ) |
| Полковник57 – 70 | Кол-во строк для правых сторон ( RHSCRD ) |
| (включая исходные предположения и векторы решений, если они есть) | |
| (ноль означает отсутствие данных с правой стороны) |
Строка 3 (A3, 11X, 4I14)
| Кол. 1 – 3 | Тип матрицы (см. Ниже) ( MXTYPE ) |
| Полковник15 – 28 | Количество строк (или переменных) ( NROW ) |
| Кол. 29 – 42 | Количество столбцов (или элементов) ( NCOL ) |
| Кол.43 – 56 | Количество индексов строк (или переменных) ( NNZERO ) |
| (равно количеству записей для собранных матриц) | |
| Полковник57 – 70 | Количество элементов элементарной матрицы ( NELTVL ) |
| (ноль в случае собранных матриц) |
Строка 4 (2A16, 2A20)
| Столбец 1 – 16 | Формат для указателей ( PTRFMT ) |
| Кол. 17 – 32 | Формат для индексов строк (или переменных) ( INDFMT ) |
| Полковник33–52 | Формат числовых значений матрицы коэффициентов ( VALFMT ) |
| Кол. 53 – 72 | Формат числовых значений правых частей ( RHSFMT ) |
Строка 5 (A3, 11X, 2I14) Присутствует только при наличии правых сторон
| Кол. 1 | Тип правой стороны: |
| F для полного хранения или | |
| M для того же формата, что и матрица | |
| Полковник2 | G , если задан начальный вектор (предположения). ( RHSTYP ) |
| Кол. 3 | X , если предоставлен точный вектор (ы) решения. |
| Кол. 15 – 28 | Количество правых сторон ( NRHS ) |
| Кол. 29 – 42 | Количество индексов строк ( NRHSIX ) |
| (игнорируется в случае несобранных матриц) |
Примечание: Для матриц элементарной формы два ведущих измерения в в заголовке указано количество переменных в конечном элементе приложение и количество элементов.Часто не все переменные в приложении появляются в линейной алгебре подзадача; следовательно, представленная матрица может быть более низкого порядка, чем первый параметр, описываемый как «количество переменных ( NROW ) “. Переменные конечных элементов пронумерованы от 1 до . NROW , , но только подмножество переменных, которые фактически появляются в списке переменные для элементов определяют строки и столбцы матрица.Фактический порядок квадратной матрицы не может быть определен пока не будут прочитаны все индексы.
Поле трехсимвольного типа в строке 3 описывает тип матрицы. В следующей таблице перечислены допустимые значения для каждого из трех персонажи. В качестве примера поля типа RSA означает, что матрица реальная, симметричная, сборная.
Первый символ:
| R Реальная матрица |
| C Комплексная матрица |
| P Только шаблон (числовые значения не предоставляются) |
Второй символ:
| S Симметричный |
| U Несимметричный |
| H Эрмитский |
| Z Наклон симметричный |
| R прямоугольный |
Третий символ:
| A В собранном виде |
| E Элементные матрицы (в разобранном виде) |
Пример кода Fortran для чтения файлов Harwell-Boeing
Чтобы формализовать логическую блочную структуру данных, мы включены два образца кода FORTRAN для чтения матрица в формате набора тестов разреженных матриц.Оба кода Предположим, что данные поступают от блока ввода LUNIT. Нет и полного кода. Настоящий код должен содержать ошибку проверка того, что целевые массивы, в которые данные читаются достаточно большие. Конструкция позволяет массивы для чтения отдельной подпрограммой, которая может избежать использование возможно неэффективных неявных DO-циклов.Приведенный выше код описывает структуру данных. В интерпретация массивов индексов строк (или переменных) потребует знания матрицы и правой части типы, как читается в этом коде.
Процедуры Matlab для чтения / записи файлов Harwell-Boeing
Разработчики коллекции матриц NEP предоставили m-файл Matlab для написать разреженную матрицу Matlab в формате Harwell-Boeing. Также доступна версия для сложных матриц.
Группа тестирования и оптимизации Беркли (BeBOP) разработала библиотека и отдельная утилита для конвертации между Harwell-Boeing, Matrix Market, и форматы разреженных матриц MATLAB.
Текстовый файл с координатами
Примечание: Этот формат постепенно сокращается.
Текстовый формат координат обеспечивает простой и переносимый способ обмена разреженные матрицы. Любой язык или компьютерная система, которая понимает текст ASCII. можно прочитать этот формат файла с помощью простого цикла чтения. Это делает эти данные доступны не только пользователям в сообществе Fortran, но и разработчикам с использованием сред C, C ++, Pascal или Basic.
В формате текстового файла координат в первой строке перечислены три целых числа: число строк m , столбцов n и ненулевых nz в матрице. В затем перечисляются ненулевые матричные элементы, по одному в строке, путем указания индекса строки i , индекс столбца j и значение a (i, j) в указанном порядке. Например,
м м нз
i1 j1 val1
i2 j2 val2
i3 j3 val3
.. .
. . .
. . .
inz jnz valnz
Пробелы не имеют значения (т.е. фиксированный столбец не используется). Ненулевой значения могут быть в виде с фиксированной или с плавающей запятой, для любого точность (хотя Fortran и C обычно разбирают менее 20 значащих цифр). Например, допустимы следующие значения: 3, 3.141, + 3.1415626536E000, 3.1e0.
Эксперименты показывают, что эти файлы координат примерно на 30% больше, чем соответствующие файлы Harwell-Boeing.Версии, сжатые с помощью Unix compress или gzip обычно демонстрирует аналогичные соотношения.
Чтобы представить только структурную информацию разреженной матрицы, один ноль может быть помещенным в позицию значения , например
M N nz
i1 j1 0
i2 j2 0
i3 j3 0
. . .
. . .
. . .
inz jnz 0
Хотя доступны более эффективные схемы, это позволяет той же процедуре
читать оба типа файлов.Добавление одного байта к каждой строке
файл обычно не имеет большого значения.Обратите внимание, что нет никакого подразумеваемого порядка для элементов матрицы. Это позволяет написать простые процедуры печати, которые пересекают разреженную матрицу в любом естественный порядок, заданный конкретной схемой хранения.
Также обратите внимание, что аннотации не используются для хранения матриц со специальными структура. (Это упрощает процедуру синтаксического анализа.) Симметричные матрицы могут быть представлены только их верхней или нижней треугольной частью, но файл формат показывает только это — программа чтения видит только треугольник матрица. (Приложение отвечает за переосмысление этого.)
Доступна функция MATLAB (M-файл), которая считывает матрицу в координатах формат текстового файла и создает разреженную матрицу.
Матричный рынок – это услуга Отделение математических и вычислительных наук / Лаборатория информационных технологий / Национальный институт стандартов и технологий
[ Дом ] [ Поиск ] [Обзор] [ Ресурсы ]
Последнее изменение на этой странице: 14 августа 2013 г. .[
[email protected] ].Программирование на Lua: 11.2
Программирование на Lua: 11.2 Это первое издание было написано для Lua 5.0. Хотя все еще актуально для более поздних версий, есть некоторые отличия.
Четвертое издание предназначено для Lua 5.3 и доступно в Amazon и других книжных магазинах.
Покупая книгу, вы также помогаете поддерживать проект Lua.
11.2 – Матрицы и многомерные массивы
Есть два основных способа представления матриц в Lua.Первый – использовать массив массивов,
то есть таблица, в которой каждый элемент является другой таблицей.
Например, вы можете создать матрицу нулей с помощью
размеры N на M со следующим кодом:
mt = {} - создать матрицу
для i = 1, N do
mt [i] = {} - создать новую строку
для j = 1 M do
mt [i] [j] = 0
конец
конец
Поскольку таблицы являются объектами в Lua,
вы должны создать каждую строку явно, чтобы создать матрицу.
С одной стороны, это определенно более многословно, чем просто
объявление матрицы, как в C или Pascal.С другой стороны, это дает вам больше гибкости.
Например, вы можете создать треугольную матрицу, изменяя
линия
для j = 1 M do
в предыдущем примере, чтобы
для j = 1 я делаю
С этим кодом треугольная матрица использует только половину памяти.
оригинального. Второй способ представить матрицу в Lua – это составить
два индекса в один.
Если два индекса являются целыми числами,
вы можете умножить первый на константу, а затем добавить
второй индекс.При таком подходе
следующий код создаст
наша матрица нулей размером N на M :
mt = {} - создать матрицу
для i = 1, N do
для j = 1 M do
mt [i * M + j] = 0
конец
конец
Если индексы являются строками,
вы можете создать единый индекс, объединяющий оба индекса
с символом между ними, чтобы разделить их.
Например, вы можете проиндексировать матрицу m со строковыми индексами с и т с кодом м [с.. ':' .. t] ,
при условии, что и s , и t не содержат двоеточия
(в противном случае пары вроде ( "a:" , "b" ) и ( "a" , ": b" )
свернется в единый индекс "a :: b" ).
В случае сомнений,
вы можете использовать управляющий символ, например ` \ 0 ´
разделить индексы.
Довольно часто в приложениях используется разреженная матрица ,
матрица, в которой большинство элементов равно 0 или нулю.
Например, вы можете представить граф его матрицей смежности,
который имеет значение x в позиции м, n только тогда, когда
узлы м и n соединены стоимостью x ;
когда эти узлы не подключены,
значение в позиции м, n составляет ноль .Чтобы представить граф с десятью тысячами узлов,
где у каждого узла около пяти соседей,
вам понадобится матрица со ста миллионами записей
(квадратная матрица с 10 000 столбцов и 10 000 строк),
но примерно пятьдесят тысяч из них не будут ноль (пять ненулевых столбцов для каждой строки,
соответствующие пяти соседям каждого узла).
Многие книги по структурам данных подробно обсуждают
как реализовать такие разреженные матрицы, не тратя 400 МБ памяти,
но вам не нужны эти методы при программировании на Lua.Поскольку массивы представлены таблицами,
они от природы редки.
С нашим первым представлением
(таблицы таблиц) вам понадобится десять тысяч таблиц,
в каждом из них около пяти элементов,
всего пятьдесят тысяч записей.
При втором представлении
у вас будет одна таблица,
с пятьюдесятью тысячами записей в нем.
Каким бы ни было представление,
вам нужно только место для элементов, отличных от nil.
| Copyright © 2003–2004 Роберто Иерусалимши. Все права защищены. |
Matlab смежности
Вернуть матрицу смежности G. Параметры Если вам нужно представление матрицы смежности на чистом Python, попробуйте networkx.convert.to_dict_of_dicts, который вернет словарь-словари …
Определение матрицы смежности. Матрица смежности определяется следующим образом: Пусть G – граф с «n» вершинами, которые, как предполагается, упорядочены от v 1 до v n. Матрица A размера n x n, в которой a ij = 1, если существует путь от v i к v j, a ij = 0 в противном случае, называется матрицей смежности.Вычисление пути между вершинами
В Matlab массивы хранятся в виде строк и столбцов. Существуют различные типы функций. В Matlab массивы ячеек могут быть представлены с помощью функции ячеек. Мы также можем просто объявить тип …
Если у вас есть сопутствующий m-файл adjacency.m, доступный для рабочего пути MATLAB, вы можете ввести M для этой матрицы. Если вершины графа Кейп-Эйр соответствуют соответственно Бостону, Хайеннису, Мартас-Винъярд, Нантакету, Нью-Бедфорду, Провиденсу и Провинстауну, то матрица смежности для Кейп-Эйр равна 0 1 1 1 001 1 011 00 0 1 1 0…
05 июля 2011 г. · У меня есть матрица расстояний в Matlab, представляющая расстояние между кучей случайных узлов. Мне нужно создать функцию, которая проанализирует всю матрицу и создаст матрицу смежности из этих чисел.
