1. Числовая последовательность и ее предел
Определение 1. Если каждому натуральному числу по определённому правилу ставится в соответствие число , то множество чисел называется числовой последовательностью.
Определение 2. Числа, из которых составлена последовательность, называют её членами.
Задать числовую последовательность – значит, задать правило, с помощью которого по номеру члена можно найти этот член, т. е. задать функцию , где – правило соответствия между и , а .
Определение 3. Общим членом последовательности называется её –й член , записанный в виде функции от , т. е. .
Если задано, то последовательность имеет вид . Последовательность нельзя задать указанием нескольких её первых членов.
Определение 4. Числовая последовательность, у которой все члены равны между собой, называется постоянной последовательностью или просто постоянной.
Пример 1. , т. е. .
Пример 2. , т. е. .
Числовая последовательность – частный случай дискретной переменной величины , принимающей значение .
Определение 5. Постоянное число называется пределом числовой последовательности , если для всякого можно указать такой номер , начиная с которого все последующие члены последовательности удовлетворяют неравенству
. (1)
Записывается это так: при или (читают: « стремится к при , стремящемся к бесконечности, или предел при , стремящемся к бесконечности, равен »).
Неравенство (1) можно переписать в виде
Или . (2)
Рисунок 1
Определение 6. Интервал (промежуток) называется – окрестностью точки . (рис.1)
Пользуясь понятием – окрестности, определение предела числовой последовательности можно сформулировать следующим образом: число есть предел последовательности , если можно указать такой номер , что все члены последовательности с номерами большими , находятся в – окрестности точки , где – любое как угодно малое положительное число . Иначе говоря, все члены последовательности с номерами, большими , на оси (см.
Определение 7. Последовательность, имеющая предел, называется сходящейся.
Определение 8. Последовательность, не имеющая предела, называется расходящейся.
Пример 3. Доказать, что предел последовательности с общим членом равен , т. е. .
Решение. По определению предела последовательности число 2 будет пределом данной последовательности, если для любого укажем такой номер , что для всех членов последовательности с номерами будет выполняться неравенство
, или .
Пусть задано положительное число , тогда из последнего неравенства находим , или . Если теперь в качестве взять любое натуральное число, не меньше , то при всех для любого будет выполняться неравенство
, или ;
Значит, по определению .
Пусть, например, , тогда и . Возьмем любой член данной последовательности с номером, большим 19, например , и найдём значение .
Если , то и .
Возьмём член последовательности с номером, большим , например
,
И найдём значение
.
Для любого , пользуясь выражением , можно подобрать натуральное число такое, что все члены последовательности с номерами, большими , будут, находится в –окрестности числа 2, а это значит (по определению), что .
Ответ: .
Пример 4. Доказать, что последовательность
С общим членом
Предела не имеет.
Решение. Легко установить, что точки с нечетными номерами «стягиваются» к точке 0, а точки с четными номерами – к точке 1. Следовательно, любая окрестность точки 0, а также любая окрестность точки 1 содержит бесконечное множество точек . Пусть есть произвольное действительное число. Всегда можно выбрать настолько малое , чтобы –окрестность точки не содержала по крайней мере некоторую окрестность одной из точек 0 или 1, тогда вне этой окрестности будет находиться бесконечное множество чисел и поэтому нельзя утверждать, что все числа , начиная с некоторого, попадут в –окрестность точки .
| Следующая > |
|---|
Предел числовой последовательности, сходящиеся и расходящиеся последовательности
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Сходящиеся и расходящиеся последовательности
- Последовательность на бесконечности
Определение
Последовательность $\left\{x_{n}\right\}$ называется сходящейся, если существует такое число $a \in R$ такое, что последовательность $\left\{x_{n}-a\right\}$ является бесконечно малой последовательностью.
Определение
Число $a$ называется пределом последовательности
Число $a$ называется пределом последовательности $\left\{x_{n}\right\}$ , если для любого $\epsilon>0$ существует номер $n_{0}=n_{0}(\epsilon)$ такой, что для любого $n>n_{0}$ выполняется неравенство $\left|x_{n}-a\right| \lt \epsilon$ :
$\lim _{n \rightarrow \infty} x_{n}=a \Leftrightarrow \forall \epsilon>0, \exists n_{0}=n_{0}(\epsilon) : \forall n>n_{0},\left|x_{n}-a\right| \lt \epsilon$
Определение
Целой частью $[x]$ некоторого числа $x$ называется наибольшее целое число, не превосходящее $x$
Пример
Задание.
Найти целую часть чисел – 2,36; 2,36; 2.
Решение. $[-2,36]=-3,[2,36]=2,[2]=2$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Доказать равенство: $\lim _{n \rightarrow \infty} \frac{1}{n}=0$
Доказательство. Исходя из определения, 0 будет пределом последовательности $\frac{1}{n}$ , если для любого $\epsilon>0$ найдется такой номер $n_{0}=n_{0}(\epsilon)$, что для любого $n>n_{0}$ выполняется неравенство $\left|x_{n}-0\right| \lt \epsilon$:
$\left|x_{n}-a\right|=\left|\frac{1}{n}-0\right|=\left|\frac{1}{n}\right|=\frac{|1|}{|n|}=\frac{1}{n} \lt \epsilon \Rightarrow n>\frac{1}{\epsilon}$
В качестве $n_{0}$ возьмем $n_{0}=\left[\frac{1}{\epsilon}\right]+1$
Итак, для любого $n>n_{0}$ указано соответствующее
значение $n_{0}$ , а тогда равенство $\lim _{n \rightarrow \infty} \frac{1}{n}=0$ доказано.
Доказательство. Пусть $a$ – предел рассматриваемой последовательности, то есть $\lim _{n \rightarrow \infty} x_{n}=a$. Рассмотрим $\epsilon=\frac{1}{10} \Rightarrow \exists n_{0}=n_{0}(\epsilon) \in N : n>n_{0} :\left|x_{n}-a\right| \lt \epsilon$
Пусть $n=2 k$ :
$\left|x_{2 k}-a\right| \lt \frac{1}{10} \Rightarrow|-1-a| \lt \frac{1}{10} \Rightarrow|1+a| \lt \frac{1}{10}$
Пусть $n=2 k+1$ :
$\left|x_{2 k+1}-a\right| \lt \frac{1}{10} \Rightarrow|1-a| \lt \frac{1}{10}$
Так как полученные выражения не равны, то данная последовательность предела не имеет.
Постоянная последовательность $\left\{x_{n}\right\}=\{c\}$ имеет предел, равный числу $c$ : $\lim _{n \rightarrow \infty} x_{n}=\lim _{n \rightarrow \infty} c=c$
Теорема
Сходящаяся последовательность имеет только один предел.
Теорема
(Необходимый признак сходимости последовательности).
Сходящаяся последовательность ограничена.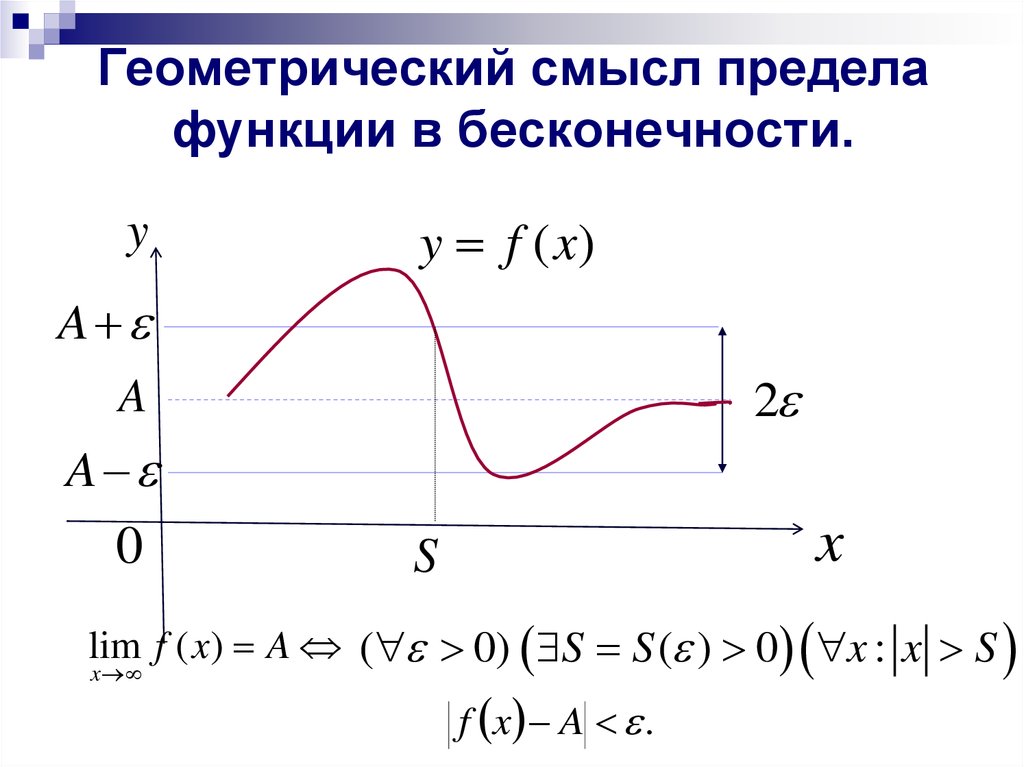
Последовательность на бесконечности
Последовательность $\left\{x_{n}\right\}$ имеет бесконечный предел, если для любого $\epsilon>0, \exists n_{0} \in N : n>n_{0} :$ $x_{n}>\epsilon : \lim _{n \rightarrow \infty} x_{n}=\infty$
Последовательность $\left\{x_{n}\right\}$ называется бесконечно малой, если $\lim _{n \rightarrow \infty} x_{n}=0$
Последовательность $\left\{x_{n}\right\}$ называется бесконечно большой, если для любого $\epsilon>0$ существует номер $n_{0}$ такое, что для любого $n>n_{0} :\left|x_{n}\right|>\epsilon$
Теорема
Пусть $\lim _{n \rightarrow \infty} x_{n}=a, \lim _{n \rightarrow \infty} y_{n}=b$ , тогда
а) $\lim _{n \rightarrow \infty}\left(x_{n}+y_{n}\right)=\lim _{n \rightarrow \infty} x_{n}+\lim _{n \rightarrow \infty} y_{n}=a+b$ ;
в) если $b \neq 0$ , то начиная с некоторого номера заданная последовательность $\lim _{n \rightarrow \infty} \frac{x_{n}}{y_{n}}=\frac{a}{b}$
Читать дальше: предельный переход в неравенствах.
реальный анализ – Как вы определяете последовательности, которые сходятся к бесконечности?
спросил
Изменено 2 месяца назад
Просмотрено 13 тысяч раз
$\begingroup$
Например, рассмотрим последовательность $\{1,0,2,0,3,0,4,0,..\}$ Интуитивно мы знаем, что последовательность сходится к $\infty$, но как мы можем проверить это строго . Если я воспроизведу формальное определение конвергенции, то я полагаю, что в лучшем случае мы можем прийти к чему-то вроде этого: 92.$ Однако это определение не показывает, что вышеупомянутая последовательность $\{1,0,2,0,3,0,4,0,..\}$ сходится к $\infty$. Таким образом, я предполагаю, что «существует» лучшее определение.
Поэтому, пожалуйста, предложите мне несколько ссылок или, может быть, дайте мне определение, способное позаботиться о сходимости к $\infty$ в целом.
- реальный анализ
$\endgroup$
8
$\begingroup$
Общая идея пределов, сходящихся к $\infty$, такова:
- Существует топологическое понятие предела в терминах открытых множеств или открытых окрестностей, а не в терминах расстояния
- $+\infty$ и $-\infty$ лучше всего понимать как точки в расширенных действительных числах
Приведенное вами определение фактически эквивалентно тому, что означает сходимость последовательности вещественных чисел к $+\infty$ в расширенных действительных числах.
Проблема в том, что рассматриваемая вами последовательность не сходится . В расширенных действительных числах это расходящаяся последовательность с двумя предельными точками: $0$ и $+\infty$.
В этом отношении она сравнима с последовательностью $0,1,0,1,0,1,\ldots$.
Без дополнительных примеров или попыток разработки, я не уверен, что вы думаете о том, что вы неправильно дали имя “сходящееся к $\infty$”. Одна возможность состоит в том, что вы просто имеете в виду идею последовательности , неограниченной выше . Это последовательность, имеющая $+\infty$ в качестве предельной точки или, альтернативно, нечто, удовлетворяющее свойству
Для всех действительных $M$ существует некоторое $n$ такое, что $x_n > M$
$\endgroup$
$\begingroup$
Обычное определение состоит в том, что для каждого действительного числа $x$ существует натуральное число $N$ такое, что $a_m>x$ для всех $m\geq N$.
Это очень похоже на обычное определение сходимости, вместо этого мы требуем, чтобы все числа были достаточно «большими» после точки.
(вместо того, чтобы просить, чтобы все числа были достаточно «близки» к пределу после точки). 9n\right)$, который расходится, но не до бесконечности.
Формальное определение, которое вы даете расходимости на бесконечность, по существу правильно.
$\endgroup$
2
$\begingroup$
Ваше определение прекрасно (даже если «сходиться к бесконечности» — неоптимальный выбор слов, поскольку сходимость к конечному пределу подразумевает множество полезных свойств, которых нет при стремлении к бесконечности), это последовательность, которая не сходится. Если последовательность сходится (или стремится к бесконечности), то каждая подпоследовательность должна сходиться к одному и тому же пределу (или стремиться к бесконечности). Это неверно для подпоследовательности $\{0,0,0,…\}$ (которая не стремится к бесконечности).
Верхний предел $\left(\limsup_{n \rightarrow \infty} x_n = \lim_{n \rightarrow \infty} \sup_{m \ge n} x_n\right)$ бесконечен, но этого недостаточно для утверждения «стремится к бесконечности».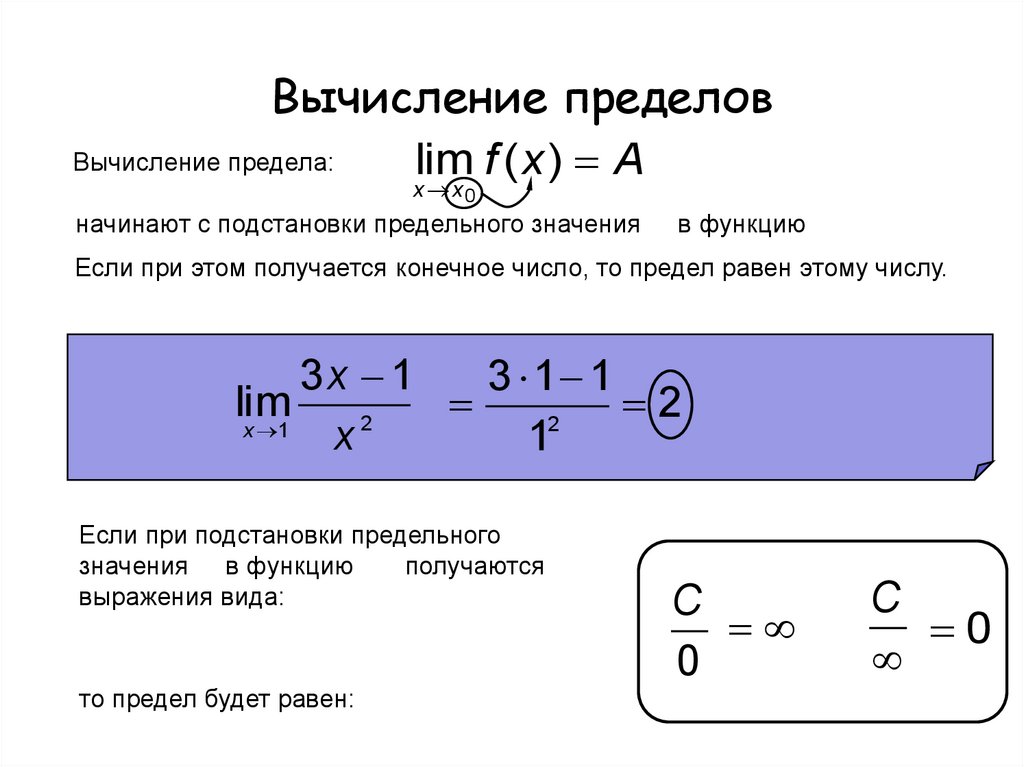
Как указал Уилл Р в комментарии, последовательность $\{1,1,1,{1\более 2},1,{1\более 3},1,{1\более 4},…\} $ не сходится к нулю, несмотря на то, что его нижний предел равен нулю. Другое (необходимое, но недостаточное для утверждения о «стремлении к бесконечности») свойство последовательности состоит в том, что она не ограничена сверху $\left( \forall M \ \exists n \mid x_n \gt M \right)$ (как упоминается Хуркилом)
Возможно полезный (хотя и не идеальный) способ осмысления определения стремления к бесконечности $\left( \lim_{n \rightarrow \infty} x_n = \infty \Leftrightarrow \forall k \ \exists N \mid n \ gt N \Rightarrow x_n \gt k\right)$ означает, что «каждая подпоследовательность превосходит все границы».
Источники: в настоящее время изучает информатику
$\endgroup$
Докажите, что последовательность расходится до бесконечности.
спросил
92-104$. Ясно, что $g(x)$ возрастает при $x>2$.