Постоянная r в термодинамике: Справка по универсальной газовой постоянной. Единицы измерения универсальной газовой постоянной. Конвектор величин универсальной газовой постоянной..

Молярная газовая постоянная r – численно равна работе, совершаемой одним молем идеального газа, расширяющимся при постоянном давлении при нагревании его на один Кельвин.

Внутреннею энергию одного моля идеального газа можно вычислить по формуле

(21)

Следовательно,

(22)

(23)

(24)

Примеры приведены в таблице 1.

Примеры для различных газов

Таблица 1

Газ	:i
Гелий	3	12,5	20,9	1,67
Кислород	5	20,9	28,9	1,40
Окись углерода	5	21,0	29,3	1,40
Пары воды	6	27,8	36,2	1,31

4.

Адиабатический процесс. Уравнение пуассона

Адиабатическим называется процесс, протекающий без теплообмена с внешней средой.

Практически адиабатический процесс может быть осуществлен в системе, окруженной теплоизолирующей оболочкой.

Так как процесс теплообмена требует некоторого времени, то адиабатическими можно считать также процессы, происходящие достаточно быстро, т.е. такие, при которых система не успевает вступить в теплообмен с окружающей средой.

При адиабатическом процессе Тогда I закон термодинамики

(25)

т.е. работа, совершаемая системой при адиабатическом процессе, происходит за счет ее внутренней энергии:

а то

Произведем интегрирование

Учитывая, что и

(26)

Это уравнение показывает, как адиабатическое изменение объема идеального газа влияет на изменение его температуры.

(27)

(27) – уравнение Пуассона.

Определим работу, совершаемую массой m газа, адиабатически расширяющегося от состояния 1 (P₁,V₁,T₁) До состояния 2 ((P₂,V₂,T₂). При адиабатическом процессе работа целиком совершается за счет внутренней энергии газа:

(28)

ЗАКЛЮЧЕНИЕ

Первый закон термодинамики является по существу одним из общих законов природы – законом сохранения и превращения энергии. Установленные первого закона термодинамики коренным образом изменило развитие классической физики во второй половине 19 в. и привело в конечном счете к крушению механических представлений в физике.

Закон сохранения и превращения энергии, по словам М.Планка, стал незыблемой основной всего естествознания и исходным пунктом дальнейшего исследования.

В настоящее время закон сохранения и превращения энергии служит безошибочным критерием для проверки физических теорий и гипотез в любой области физики.

Вместе с тем, успехи применения закона сохранения и превращения энергии привели в конце 80-х годов XIX века к возникновению реакционного идеалистического учения – энергетизма.

В современной физике энергия, так же как и масса, рассматривается как неотъемлемое свойство материи. При этом масса характеризует инерционные и гравитационные свойства материи, энергия связана с движением материи и является мерой превращения одной формы движения в другую.

11

Постоянная Больцмана

Материал из свободной русской энциклопедии «Традиция»

Для постоянной, связанной с энергией излучения чёрного тела, смотри Постоянная Стефана-Больцмана

Значение постоянной k [1]	Размерность
1,380 6504(24) • 10−23	Дж•К−1
8,617 343(15) • 10−5	эВ•К−1
1,3807• 10−16	эрг•К−1
Смотри также Значения в различных единицах ниже.

Постоянная Больцмана (k или k_B) — физическая постоянная, определяющая связь между температурой вещества и энергией теплового движения частиц этого вещества. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её экспериментальное значение в системе СИ равно

Дж/К.

В таблице последние цифры в круглых скобках указывают стандартную погрешность значения постоянной. В принципе, постоянная Больцмана может быть получена из определения абсолютной температуры и других физических постоянных. Однако точное вычисление постоянной Больцмана с помощью основных принципов слишком сложно и невыполнимо при современном уровне знаний.

Экспериментально постоянную Больцмана можно определить с помощью закона теплового излучения Планка, описывающего распределение энергии в спектре равновесного излучения при определённой температуре излучающего тела, а также другими методами.

Существует связь между универсальной газовой постоянной и числом Авогадро , из которой следует значение постоянной Больцмана:

Размерность постоянной Больцмана такая же, как и у энтропии.

Содержание 1 История 2 Уравнение состояния идеального газа 3 Связь между температурой и энергией 3.1 Соотношения газовой термодинамики 4 Множитель Больцмана 5 Роль в статистическом определении энтропии 6 Роль в физике полупроводников: тепловое напряжение 7 Применения в других областях 8 Постоянная Больцмана в планковских единицах 9 Постоянная Больцмана в теории бесконечной вложенности материи 10 Значения в различных единицах 11 Ссылки 12 См. также

История

В 1877 г. Больцман впервые связал между собой энтропию и вероятность, однако достаточно точное значение постоянной k как коэффициента связи в формуле для энтропии появилось лишь в трудах М. Планка. При выводе закона излучения чёрного тела Планк в 1900–1901 гг. для постоянной Больцмана нашёл значение 1,346 • 10

−23 Дж/K, почти на 2,5% меньше принятого в настоящее время.^[2]

До 1900 г. соотношения, которые сейчас записываются с постоянной Больцмана, писались с помощью газовой постоянной R, а вместо средней энергии на одну молекулу использовалась общая энергия вещества. Лаконичная формула вида S = k log W на бюсте Больцмана стала таковой благодаря Планку. В своей нобелевской лекции в 1920 г. Планк писал: ^[3]

Эта константа часто называется постоянной Больцмана, хотя, насколько я знаю, сам Больцман никогда не вводил её — странное состояние дел, при том, что в высказываниях Больцмана не было речи о точном измерении этой константы.

Такая ситуация может быть объяснена проведением в то время научных дебатов по выяснению сущности атомного строения вещества. Во второй половине 19 века существовали значительные разногласия в отношении того, являются ли атомы и молекулы реальными, либо они лишь удобный способ описания явлений. Не было единства и в том, являются ли “химические молекулы”, различаемые по их атомной массе, теми же самыми молекулами, что и в кинетической теории. Далее в нобелевской лекции Планка можно найти следующее:^[3]

«Ничто не может лучше продемонстрировать положительную и ускоряющуюся скорость прогресса, чем искусство эксперимента за последние двадцать лет, когда было открыто сразу множество методов измерения массы молекул практически с той же точностью, что и измерение массы какой-нибудь планеты».

Уравнение состояния идеального газа

Для идеального газа справедлив объединённый газовый закон, связывающий давление P, объём V, количество вещества n в молях, газовую постоянную R и абсолютную температуру T:

В данном равенстве можно сделать замену . Тогда газовый закон будет выражаться через постоянную Больцмана и количество молекул N в объёме газа V:

Связь между температурой и энергией

В однородном идеальном газе, находящемся при абсолютной температуре T, энергия, приходящаяся на каждую поступательную степень свободы, равна, как следует из распределения Максвелла, kT / 2. При комнатной температуре (≈ 300 K) эта энергия составляет Дж, или 0,013 эВ.

Соотношения газовой термодинамики

В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия 3kT / 2. Это хорошо согласуется с экспериментальными данными. Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню из атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона.

Кинетическая теория даёт формулу для среднего давления P идеального газа:

Учитывая, что средняя кинетическая энергия прямолинейного движения равна:

находим уравнение состояния идеального газа:

Это соотношение неплохо выполняется и для молекулярных газов; однако зависимость теплоёмкости изменяется, так как молекулы могут иметь дополнительные внутренние степени свободы по отношению к тем степеням свободы, которые связаны с движением молекул в пространстве. Например, двухатомный газ имеет уже приблизительно пять степеней свободы.

Множитель Больцмана

В общем случае система в равновесии с тепловым резервуаром при температуре T имеет вероятность p занять состояние с энергией E, что может быть записано с помощью соответствующего экспоненциального множителя Больцмана:

В данном выражении фигурирует величина kT с размерностью энергии.

Вычисление вероятности используется не только для расчётов в кинетической теории идеальных газов, но и в других областях, например в химической кинетике в уравнении Аррениуса.

Роль в статистическом определении энтропии

Основная статья: Термодинамическая энтропия

 

Вена, Zentralfriedhof, изображение Больцмана и формулы для энтропии на бюсте.

Энтропия S изолированной термодинамической системы в термодинамическом равновесии определяется через натуральный логарифм от числа различных микросостояний W, соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией E):

Коэффициент пропорциональности k является постоянной Больцмана. Это выражение, определяющее связь между микроскопическими и макроскопическими состояниями (через W  и энтропию S соответственно), выражает центральную идею статистической механики и является главным открытием Больцмана.

В классической термодинамике используется выражение Клаузиуса для энтропии:

Таким образом, появление постоянной Больцмана  k  можно рассматривать как следствие связи между термодинамическим и статистическим определениями энтропии.

Энтропию можно выразить в единицах k , что даёт следующее:

В таких единицах энтропия точно соответствует информационной энтропии.

Характерная энергия kT равна количеству теплоты, необходимому для увеличения энтропии S^‘ на один нат.

Роль в физике полупроводников: тепловое напряжение

В отличие от других веществ, в полупроводниках существует сильная зависимость электропроводности от температуры:

где множитель σ₀ достаточно слабо зависит от температуры по сравнению с экспонентой, E_A – энергия активации проводимости. Плотность электронов проводимости также экспоненциально зависит от температуры. Для тока через полупроводниковый p-n-переход вместо энергии активации рассматривают характерную энергию данного p-n перехода при температуре T  как характерную энергию электрона в электрическом поле:

где q – элементарный электрический заряд, а V_T  есть тепловое напряжение, зависящее от температуры.

Данное соотношение является основой для выражения постоянной Больцмана в единицах эВ∙К⁻¹. При комнатной температуре (≈ 300 K) значение теплового напряжения порядка 25,85 милливольт ≈ 26 мВ.

В классической теории часто используют формулу, согласно которой эффективная скорость носителей заряда в веществе равна произведению подвижности носителей μ на напряженность электрического поля. В другой формуле плотность потока носителей связывается с коэффициентом диффузии D и с градиентом концентрации носителей n:

Согласно соотношению Эйнштейна-Смолуховского, коэффициент диффузии связан с подвижностью:

Постоянная Больцмана k  входит также в закон Видемана-Франца, по которому отношение коэффициента теплопроводности к коэффициенту электропроводности в металлах пропорционально температуре и квадрату отношения постоянной Больцмана к электрическому заряду.

Применения в других областях

Для разграничения температурных областей, в которых поведение вещества описывается квантовыми или классическими методами, служит температура Дебая:

где – постоянная Дирака, есть предельная частота упругих колебаний кристаллической решётки, u – скорость звука в твёрдом теле, n – концентрация атомов.

При температурах ниже Q_D требуется использовать квантовую статистику. Если же температуры выше Q_D, то тепловая энергия (порядка kT) превышает характерную энергию колебаний решётки и система может быть описана формулами классической статистической механики.

Постоянная Больцмана входит в формулу Найквиста, определяющую средний квадрат шумового напряжения в электрической цепи с сопротивлением R в полосе частот Δν при температуре T. В классическом приближении формула для теплового шума имеет вид:

Постоянная Больцмана в планковских единицах

В планковской системе естественных единиц постоянная Больцмана равна 1. Это даёт

как среднюю кинетическую энергию газовой молекулы на одну степень свободы; при этом определение термодинамической энтропии совпадает с определением информационной энтропии:

Планковская единица температуры равна 1,416 785(71) • 10³² К, соответствуя энергии покоя планковской массы.

Постоянная Больцмана в теории бесконечной вложенности материи

С точки зрения теории бесконечной вложенности материи, постоянная Больцмана является характеристикой лишь одного, а именно атомного уровня материи. Как показывает анализ естественных единиц измерения физических величин, при использовании вместо температурной шкалы шкалы тепловой энергии, содержащейся в единице количества вещества, постоянная Больцмана становится излишней. Отсюда следует, что при использовании температуры как физической величины на некотором масштабном уровне материи необходимо пересчитывать значение постоянной Больцмана для этого уровня материи с помощью соответствующих коэффициентов подобия. Теоретической основой для этой процедуры является SPФ-симметрия.

Для уровня звёзд аналогично звёздной постоянной Планка, задающей характерный момент импульса типичных звёздных объектов, появляется звёздная постоянная Больцмана. Eё значение равно K_ps = k ∙ Ф = 9,187∙10³² Дж/К, где Ф – коэффициент подобия по массе. ^[4] Звёздная постоянная Больцмана определяет связь между эффективной температурой совокупности типичных звёздных объектов как меры тепловой энергии, и средней кинетической энергией движения в расчёте на один звёздный объект. Кроме этого, она связывает внутреннюю температуру звёздных объектов с внутренней энергий вещества этих объектов. Аналогичные постоянные могут быть вычислены для каждого масштабного уровня материи. Следовательно, обычная постоянная Больцмана не только позволяет оценить кинетическую температуру частиц вещества по известной энергии этого вещества, но и даёт возможность найти температуру вещества внутри самих частиц, например, внутри нуклона.

Значения в различных единицах

Значение k	Размерность	Примечание
1,380 6504(24) • 10−23	Дж / К	единицы СИ, значение CODATA 2006[1]
8,617 343(15) • 10−5	эВ/K	1  эВ = 1,602 176 53(14) • 10−19 Дж 1/k = 11 604,51(2)  K/эВ
2,303 6644(36) • 1010	Гц/K	1 Гц = 6,626 068 96(33) • 10−34 Дж
3,166 815(36) • 10−6	EH/K	EH = 2R∞hc = 4,359 743 94(22) • 10−18 Дж
1,380 6504(24) • 10−16	эрг/K	1  эрг = 1• 10−7 Дж
3,297 6268(56) • 10−24	кал/K	1 калория = 4,1868 Дж
1,832 0149(31) • 10−24	кал/R	1 градус Ранкина = 4/9 K
1,039 9503(18) • 10−23	Фут фунт/R	1 Фут-фунт сила = 1,355 817 948 331 4004 Дж
0,695 0356(12)	см−1/K	1 см−1 = 1,986 445 501(99) • 10−23 Дж

Поскольку k есть константа пропорциональности между температурой и энергией, численное значение k зависит от выбора единиц изменения температуры и энергии. Шкала температур Кельвина выбиралась из того условия, чтобы интервал температур, в котором существует жидкая вода, равнялся 100 градусов. Малое численное значение k является отражением малости энергии в джоулях, необходимой для увеличения энергии частицы на 1 К. Как правило, в физических выражениях используется произведение kT как характерная энергия при температуре T. Если измерять температуру в энергетических единицах, подобно планковским единицам, тогда постоянная Больцмана будет не нужна вообще, равняясь точно 1. ^[5]

Ссылки

1. ^абCODATA, 2006
2. Max Planck «Ueber das Gesetz der Energieverteilung im Normalspectrum» // Annalen der Physik. — 1901. — Т. 309. — № 3. — С. 553–63.. English translation: “On the Law of Distribution of Energy in the Normal Spectrum”.
3. ^аб Max Planck «The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture)».  — 2 June 1920.
4. Федосин С. Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
5. Kalinin, M; Kononogov, S «Boltzmann’s Constant, the Energy Meaning of Temperature, and Thermodynamic Irreversibility» // Measurement Techniques. — 2005. — Т. 48. — № 7. — С. 632–36.

См. также

• Число Авогадро
• Универсальная газовая постоянная
• Уравнение состояния идеального газа
• Планковские единицы
• Бесконечная вложенность материи
• Звёздные постоянные
• Звёздная постоянная Больцмана

Постоянная Больцмана • Джеймс Трефил, энциклопедия «Двести законов мироздания»

200 законов мироздания > Физика

Постоянная Больцмана перекидывает мост из макромира в микромир, связывая температуру с кинетической энергией молекул.

Людвиг Больцман — один из создателей молекулярно-кинетической теории газов, на которой зиждется современная картина взаимосвязи между движением атомов и молекул с одной стороны и макроскопическими свойствами материи, такими как температура и давление, с другой. В рамках такой картины давление газа обусловлено упругими ударами молекул газа о стенки сосуда, а температура — скоростью движения молекул (а точнее, их кинетической энергией).Чем быстрее движутся молекулы, тем выше температура.

Постоянная Больцмана дает возможность напрямую связать характеристики микромира с характеристиками макромира — в частности, с показаниями термометра. Вот ключевая формула, устанавливающая это соотношение:

    1/2 mv² = kT

где m и v — соответственно масса и средняя скорость движения молекул газа, Т — температура газа (по абсолютной шкале Кельвина), а k — постоянная Больцмана. Это уравнение прокладывает мостик между двумя мирами, связывая характеристики атомного уровня (в левой части) с объемными свойствами (в правой части), которые можно измерить при помощи человеческих приборов, в данном случае термометров. Эту связь обеспечивает постоянная Больцмана k, равная 1,38 x 10^–23 Дж/К.

Раздел физики, изучающий связи между явлениями микромира и макромира, называется статистическая механика. В этом разделе едва ли найдется уравнение или формула, в которых не фигурировала бы постоянная Больцмана. Одно из таких соотношений было выведено самим австрийцем, и называется оно просто уравнение Больцмана:

    S = k log p + b

где S — энтропия системы (см. Второе начало термодинамики), p — так называемый статистический вес (очень важный элемент статистического подхода), а b — еще одна константа.

Всю жизнь Людвиг Больцман в буквальном смысле опережал свое время, разрабатывая основы современной атомной теории строения материи, вступая в яростные споры с подавляющим консервативным большинством современного ему научного сообщества, считавшего атомы лишь условностью, удобной для расчетов, но не объектами реального мира. Когда его статистический подход не встретил ни малейшего понимания даже после появления специальной теории относительности, Больцман в минуту глубокой депрессии покончил с собой. Уравнение Больцмана высечено на его надгробном памятнике.

Людвиг Эдвард БОЛЬЦМАН
Boltzmann, 1844–1906

Австрийский физик. Родился в Вене в семье госслужащего. Учился в Венском университете на одном курсе с Йозефом Стефаном (см. Закон Стефана—Больцмана). Защитившись в 1866 году, продолжил научную карьеру, занимая в разное время профессорские должности на кафедрах физики и математики университетов Граца, Вены, Мюнхена и Лейпцига. Будучи одним из главных сторонников реальности существования атомов, сделал ряд выдающихся теоретических открытий, проливающих свет на то, каким образом явления на атомном уровне сказываются на физических свойствах и поведении материи.

---

5

Показать комментарии (5)

Свернуть комментарии (5)

---

NikolaevSemen  18. 05.2008  19:05 Ответить

Молекулярно-кинетическая теория не кинетическая.
Внутренняя энергия вещества складывается из двух видов энергии.
Первое. Энергии подвижности атомов и молекул вещества (эффект Броуновского движения в жидкости и газах), средняя кинетическая энергия которой величина постоянная и ни от чего не зависит, в том числе и от температуры. Этот вид энергии связан с непрерывной нейтринной бомбардировкой атомов и молекул вещества. Только благодаря этому виду энергии газ объёмный, существует диффузия и теплопроводность.
Второе. Тепловой энергии, которая переносится инфракрасными фотонами и которая не постоянная.
Слово кинетическая не отображает процессов изменения внутренней энергии вещества.
Поэтому лучше подходит слово молекулярно-фотонная теория.
Формула Больцмана о связи средней кинетической энергии атомов и молекул вещества с температурой – ошибочная. Нельзя, не зная природы подвижности атомов и молекул вещества, выводить какие-либо формулы. Соответственно, ошибочна и постоянная Больцмана.
Более подробно об этом написано в третьем и четвёртом изданиях книги Николаева С.А. “Эволюционный круговорот материи во Вселенной”.
С Уважением, Николаев Семен, Санкт-Петербург.

Ответить

• 005 NikolaevSemen 01.08.2009  21:58 Ответить

  Кинетическая это означает Движение
  Мы знаем значения 0с ?1 и ?2 100с вода тв и жид состояний Т1 0с и Т2 100с
  ?100-?0=К(Т1-Т2)=?100-?0=к*100К=(5,14-3,76)*10-21
  к=5,14-3,76/100*-21=1,38*10-23дж/К

  Ответить

• sasakosh NikolaevSemen 22.11.2009  20:17 Ответить

  Вообще, на википедии например, принято перед такими заявлениями указывать, что излагаемая теория носит неакадемический характер. Ну а постоянная Больцмана найдена экспериментальным путем с достаточной точностью. Причем и прямыми измерениями в том числе.

  Ответить

Написать комментарий

---

около 420 г. до н.э.	Атомная теория строения вещества
1798	Механическая теория теплоты
1849	Молекулярно-кинетическая теория
1877	Постоянная Больцмана

---

1900

Постоянная Планка

0000

Подобное растворяется в подобном

Новостная рассылка  

«Элементы» в соцсетях: 

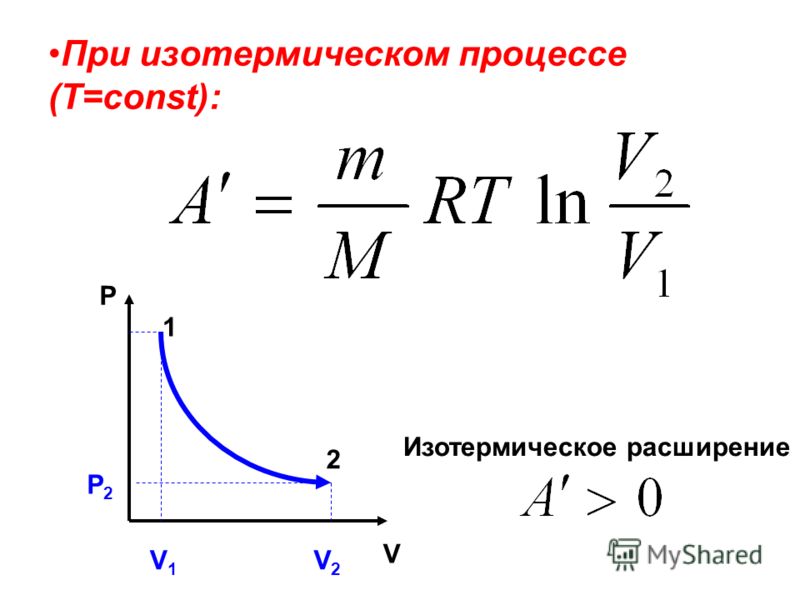
Универсальные и индивидуальные газовые постоянные

Универсальные и индивидуальные газовые постоянные известны из закона идеального газа.

Индивидуальная газовая постоянная –

R

Индивидуальная газовая постоянная зависит от конкретного газа и связана с молекулярной массой газа. Значение не зависит от температуры. Индивидуальная газовая постоянная R для газа может быть рассчитана по универсальной газовой постоянной R _u (данной в нескольких единицах ниже) и молекулярной массе газа M _GAS :

R = R _U /M _GAS [1]

В Имперской системе Наиболее распространенные единицы для отдельной константы газа составляют футов фунтов /80022 O R . В системе СИ наиболее распространенными единицами являются Дж/кг K .

Преобразование единиц измерения: 1 Дж/кг K = 5,97994 фут-фунт/слаг °R, и 1 фут-фунт/слаг °R = 0,167226 Дж/кг K.

Индивидуальная газовая постоянная для газов:

Для полной таблицы – повернуть экран!

3 0.0261

8 2 0,0563

Gas		Molecular Weight	Individual Gas Constant – R
Name	Formula	[g/mol], [кг/кмоль]	[Дж/кг·К]	[кДж/кг·К]	[Втч/(кг·К)]	[ккал] , [БТЕ(ИТ)/фунт °F]	[kcal/(lb °F)]	[ft lb f /lb °R]	[ft lb f /slug °R]
Acetylene	C 2 H 2	26. 038	319.32	0.3193	0.08870	0.07627	0.0623	59.350	1910
Air	A mixture	28.9647	287.05	0.2871	0.07974	0.06856	0.0560	53.353	1717
Ammonia	NH 3	17.031	488.21	0.4882	0.13561	0.11661	0.0952	90.740	2919
Argon	Ar	39.948	208.13	0.2081	0.05781	0.04971	0.0406	38.684	1245
Butane	C 4 H 10	58. 122	143.05	0.1431	0.03974	0.03417	0.0279	26.588	855
Butene	C 4 H 8	56.106	148.19	0.1482	0.04116	0.03539	0.0289	27.543	886
Carbon Dioxide	CO 2	44.010	188,92	0,1889	0,05248	0,04512	0,0368	3514	0,0368	3514	0,0368	3514	.0043 1130
Carbon Monoxide	CO	28.010	296.84	0.2968	0.08246	0.07090	0.0579	55. 171	1775
Carbonic acid	H 2 CO 3	62,025	134,05	0,1341	0,03724	24.915	802
Chlorine	Cl 2	70.906	117.26	0.1173	0.03257	0.02801	0.0229	21.794	701
Хлорметан	Ch4Cl	50,488	164,68	0,1647	0,04575 7533	0.0321	30.608	985
Dichlorofluorumethane	CHCl2F	102.923	80.78	0.0808	0.02244	0.01929	0.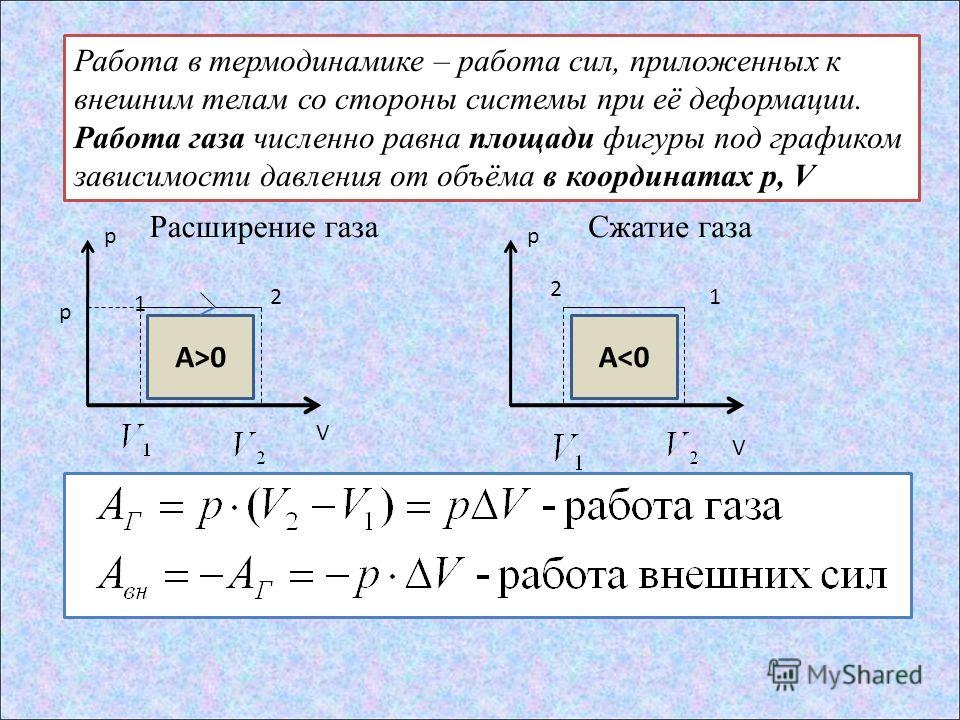 0158	15.015	483
Этан	C 2 H 6	30,069	276,51	0,27650042	0.07681	0.06604	0.0539	51.393	1654
Ethene	C 2 H 4	28.053	296.38	0.2964	0.08233	0.07079	0,0578	55,086	1772
Фтор	F 2	3 37042	0033 218.82	0.2188	0.06078	0.05226	0.0427	40.670	1309
Helium	He	4.003	2077.1	2.0771	0.57696	0. 49610	0,4050	386,047	12421
Водород	H 2 0	43	43 2,0410430043 4124.2	4.1242	1.14563	0.98506	0.8043	766.541	24663
Hydrogen bromide	HBr	80.912	102.76	0.1028	0.02854	0.02454	0,0200	19,099	614
Хлористый водород	HCl		90,4610042	228.04	0.2280	0.06334	0.05447	0.0445	42.384	1364
Hydrogen sulfide	h3S	34.081	243.96	0.2440	0. 06777	0.05827	0.0476	45.344	1459
Криптон	Кр	8.0042	99.22	0.0992	0.02756	0.02370	0.0193	18.441	593
Methane (natural gas)	CH 4	16.042	518.28	0.5183	0.14397	0.12379	0.1011	96.329	3099
Neon	Ne	20.180	412.02	0.4120	0.11445	0.09841	0.0803	76.579	2464
Nitrogen	N 2	28.013	296.80	0. 2968 Двуокись азота0042	NO 2	46.006	180.73	0.1807	0.05020	0.04317	0.0352	33.590	1081
Nitrogen trifluoride	NF 3	71.002	117,10	0,1171	0,03253	0,02797	0,0228	21,765	700 9.765	9	0042
Nitrous oxide	N 2 O	44.012	188.91	0.1889	0.05248	0.04512	0.0368	35.112	1130
Oxygen	O 2	31.999	259.84	0.2598	0.07218	0. 06206	0.0507	48.294	1554
Propane	C 3 H 8	44.096	188.56	0.1886	0.05238	0.04504	0.0368	35.045	1128
Propene	C 3 H 6	42.080	197,59	0,1976	0,05489	0,0471	0,05489	0,1971919	0.0385	36.724	1182
Sulfur dioxide	SO 2	64.064	129.78	0.1298	0.03605	0.03100	0.0253	24.122	776
Гексафторид серы	SF 6	146,055	56,93		0. 01581	0.01360	0.0111	10.581	340
Sulfur trioxide	SO 3	80.063	103.85	0.1038	0.02885	0.02480	0.0203	19.302	621
Водяной пар	H 2 O	18.015 9004 4 9.00333 30034	0.4615	0.12820	0.11023	0.0900	85.780	2760
Xenon	Xe	131.293	63.33	0.0633	0.01759	0.01513	0.0123	11.770	379

Универсальная газовая постоянная –

R _u

Универсальная газовая постоянная – R _u – появляется в законе идеального газа и может быть выражено как произведение между Индивидуальной газовой постоянной – R – для конкретного газа – и Молекулярным весом – M _GAS – для газа, и то же самое для всех идеальных или идеальных газов :

R _U = M _GAS R [2]

Универсальная константа определяется в терминах.

постоянная Больцмана

Универсальная константа газа может быть определена в терминах постоянной K k AS:

R _U = K N _A [3]

, где
K = константа Boltzmann = 1,381 x 10 ^{-23 -23 -23 -23 -2} [Дж/К]
N _A = Число Авогадро = 6,022 x 10 ²³ [1/моль]

Молекулярная масса газовой смеси

Средняя молекулярная масса газовой смеси равна сумма мольных долей каждого газа, умноженная на молекулярную массу этого конкретного газа:

M _Смесь = σx _I *M _I = (x ₁ *M ₁ + …… + x _N *M _N ) [4]

, где

x _I = мольские фракции каждого газа
M _I = молярная масса каждого газа

Универсальная константа газа –

R _U – в альтернативных единицах

• Amt. см ³ /(моль. К) : 82,057338
• ATM.FT ³ /(LBMOL.K): 1,31443
• ATM.FT ³ /(LBMOL. ^O R): 0,73024
• 55. K) : 0.0820 57338
• bar.cm ³ /(mol.K) : 83.144598
• bar.l/(mol.K) : 0.083144 598
• Btu/( фунт моль ^o R) : 1,9872036
• кал/(моль.К) : 1,9859
• ERG/(MOL.K): 83144 598
• HP.H/(LBMOL. ^O R): 0,0007805
• inhg.ft ³ /(LBMOL. ^{2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222232222232322222н. :  21.85}
• J/(mol.K) :  8.3144598 
  
• kJ/(kmol.K) :  8.3144598
  
• J/(kmol.K) : 8314.472
• (кгс/см ² ).л/(моль.К) : 0,084784
• кПа. см ³ /(mol.K) : 8314.4 598
• kWh/(lbmol. ^o R) : 0.000582
• lbf.ft/(lbmol. ^o R) : 1545.349
• мм рт. Ст. моль.К) : 62,363577
• Па·м ³ /(моль.К) : 8,3144 598
• psf.ft ³ /(lbmol. ^o R) : 1545.3465
• psi.ft ³ /(lbmol. ^o R) : 10.73
• Torr.cm ³ /(mol.K) : 62364

См. также:
– Дополнительные свойства материалов
– Закон идеального газа – Газы обладают высокой сжимаемостью, при этом изменения плотности напрямую связаны с изменениями температуры и давления.
– Смесь газов – Свойства смесей газов.
– Подробнее о температуре

В PV=nRT Что такое константа R?

В химии формула PV=nRT представляет собой уравнение состояния гипотетического идеального газа. Закон идеального газа описывает поведение идеального образца газа и то, как это поведение связано с давлением (P), температурой (T), объемом (V) и молярностью (n) образца газа. В уравнении PV=nRT термин «R» обозначает универсальную газовую постоянную .

Универсальная газовая постоянная — это константа пропорциональности, которая связывает энергию образца газа с температурой и молярностью газа. Иногда его называют идеальная газовая постоянная, молярная газовая постоянная . Ее также иногда называют константой Рено , в честь французского химика Анри Реньо, чьи количественные данные впервые были использованы для точного расчета значения константы. В настоящее время принятое значение универсальной газовой постоянной R:

R Постоянная = 8,3144598 Дж/моль·К

Единицей газовой постоянной является джоуль на моль-кельвин. Это можно прочитать как «работа на моль на градус». По сути, газовая постоянная связывает молярное количество газа и температуру газа с количеством кинетической энергии газа. Универсальную газовую постоянную можно рассчитать, разделив произведение давления и объема газа на молярность и температуру газа:

R = PV/ n T

Вывод закона об идеальном газе

благодаря большому действию тепла на их расширение, а также единообразию и простоте законов, управляющих этими изменениями». — Джеймс Клерк Максвелл

Закон идеального газа — одно из самых фундаментальных уравнений в физической химии, которое было независимо выведено путем экспериментального анализа и теоретической экстраполяции. Первоначально закон идеального газа появился как комбинация 4 других различных математических выражений, которые связывают различные свойства газа друг с другом. Четыре отдельных закона: закон Шарля, закон Бойля, закон Гей-Люссака и закон Авагадро.

Закон Шарля

Закон Шарля — это эмпирический закон, который утверждает, что объем газа прямо пропорционален температуре газа. Другими словами, сохраняя равными все остальные факторы, если увеличить температуру газа, они будут наблюдать соответствующее увеличение объема газа. Точно так же, если понизить температуру газа, они увидят соответствующее уменьшение объема. Математически закон Шарля можно записать так:

• V ∝ T

, где «∝» означает «прямо пропорционально», или

• V/T = константа  

Дело в том, что газы имеют свойство расширяться при нагревании.

Закон Бойля

Закон Бойля — это газовый закон, который описывает, как давление образца газа имеет тенденцию к увеличению по мере уменьшения объема этого образца. Закон Бойля можно сформулировать как «давление газа в замкнутой системе при постоянном количестве и температуре обратно пропорционально объему газа». Математически это можно записать как:

• V ∝ 1/P

или

• PV = константа

Закон Бойля в основном говорит нам, что если мы сжимаем газ тяжелее и занимаем меньше места, то он стены на его контейнере.

Закон Гей-Люссака

Закон Гей-Люссака представляет собой эмпирическое обобщение, которое отмечает связь между температурой образца газа и его давлением. Закон Гей-Люссака гласит: «При постоянном объеме и количестве давление газа прямо пропорционально температуре газа. Этот закон может быть записан математически как:

• P ∝ T

или,

• P/T = константа

В принципе, закон Гей-Люссака говорит нам, что если мы нагреем соответствующий образец газа, в его давлении. Температура — это всего лишь мера молекулярного движения, поэтому нагревание газа заставляет составляющие его частицы двигаться быстрее. Чем быстрее движутся составляющие молекулы, тем большую силу они будут оказывать на стенки сосуда — газ будет оказывать большее давление. Закон Гей-Люссака предлагает объяснение того, почему нагревание запечатанного контейнера с газом может взорвать этот контейнер; давление, оказываемое газом, становится слишком большим, чтобы материал мог с ним справиться, и он разрывается.

Закон Авагадро

Последней из 4 частей уравнения идеального газа является закон Авагадро. Закон Авагадро гласит, что объем газа при постоянном давлении и температуре прямо пропорционален количеству частиц, составляющих газ. Другой способ сформулировать закон состоит в том, что если 2 образца газа имеют одинаковый объем при постоянной температуре и давлении, то 2 образца газа содержат одинаковое количество частиц. Уравнение для закона Авагадро:

• V ∝ n

, где n — количество отдельных частиц. Закон Авагадро также можно записать так:

• V/ n = константа

Закон Авагадро очень интуитивен. Здравый смысл подсказывает, что при прочих равных условиях чем больше газа, тем больше места он займет. В качестве альтернативы, если два газа имеют одинаковый объем, они должны иметь одинаковое количество частиц.

Вывод закона идеального газа

Теперь, когда у нас есть 4 фундаментальных уравнения состояния газа, мы можем объединить их в одно выражение, чтобы получить закон идеального газа. Мы можем комбинировать законы следующим образом:

• V ∝ T (закон Шарля)
• V ∝ 1/P (закон Бойля)
• P ∝ T (закон Гей-Люссака)
• V ∝ 5 (закон )

Объединение этих выражений дает нам:

• В ∝ n T/P

Поскольку «∝» представляет прямую пропорциональность, мы можем заменить «∝» на «=», добавив константу пропорциональности к правая сторона. Экспериментально мы проверили, что эта константа равна значению R, поэтому добавление R к уравнению дает::

• V = N RT/P

Перестраница Это уравнение дает нам:

• PV = N RT

. красота звезд — всего лишь сгустки газовых атомов. Я тоже могу видеть звезды ночью в пустыне и чувствовать их. Но вижу ли я меньше или больше?» — Ричард П. Фейнман

Так что же такое — универсальная газовая постоянная? Все остальные параметры в уравнении идеального газа, по-видимому, соответствуют некоторой физически значимой переменной; давление (P), объем (V), количество вещества ( n ) , и температура (T). Однако R, похоже, этого не делает. Как и в случае со многими математическими константами, термин R явно не отображается на какую-либо физическую величину, сущность или процесс. Вместо этого параметр R представляет отношение , которое выполняется между некоторыми физическими величинами, в частности, давлением и объемом газа, а также температурой и количеством газа. В частности, R равно отношению PV/ n T.

Точное численное значение газовой постоянной зависит от выбранных единиц измерения. Числовое значение R как 8,3144598 является результатом использования определенных единиц измерения. Это значение R является результатом измерения физических величин газов в стандартных единицах СИ. Стандартные единицы СИ и их символ для каждого параметра в уравнении идеального газа:

• Давление (P) – Ньютоны (кг·м/с²)
• Объем (V) – Метры (м³)
• Температура (T) – Кельвин (К)
• Количество вещества ( n ) – моль (моль)

Если мы изменили наши единицы измерения, то изменится и численное значение газовой постоянной. Например, допустим, мы решили измерять объем газа в литрах (л) вместо метров, а давление газа в стандартных атмосферах (атм) вместо ньютонов. В этих единицах универсальная газовая постоянная принимает числовое значение R = 0,082057 л·атм/моль·К. Аналогичным образом, скажем, мы решили измерить давление в миллиметрах ртутного столба (мм рт. ст.). Тогда газовая постоянная принимает числовое значение R = 62,3636711 м³·мм рт.ст./моль·К

Важно понимать, что изменение единиц измерения не означает, что изменяется сама газовая постоянная. Газовая постоянная — это всего лишь константа , поэтому она не меняется. Изменение единиц измерения просто изменяет числовое значение , используемое для выражения константы. Теоретически можно было бы выбрать систему единиц, которая изменяет численное значение газовой постоянной на 1. В такой системе единиц уравнение идеального газа можно было бы просто записать как PV = n T. Имейте в виду, однако, что в этом уравнении универсальная газовая постоянная не исчезла . Газовая постоянная все еще присутствует, просто она имеет численное значение R = 1. Сама постоянная по-прежнему требуется для соответствующего размерного анализа используемых единиц измерения.

По сути, параметр R представляет собой отношение, которое существует между физическими параметрами газа и единицами измерения, которые мы выбираем для измерения этих физических параметров. Следовательно, газовую постоянную можно использовать для преобразования физических измерений газа в различные системы единиц.

Ограничения закона идеального газа

Есть причина, по которой его называют законом «идеального» газа, а не законом «фактического» газа. Справедливость уравнения идеального газа зависит от нескольких идеализированных предположений о характере и поведении газов. Во-первых, закон идеального газа предполагает, что частицы в газе подчиняются законам механики Ньютона. Это означает, что предполагается, что частицы газа подчиняются законам силы и гравитации, описанным Исааком Ньютоном, а эффекты электростатического межмолекулярного притяжения не учитываются.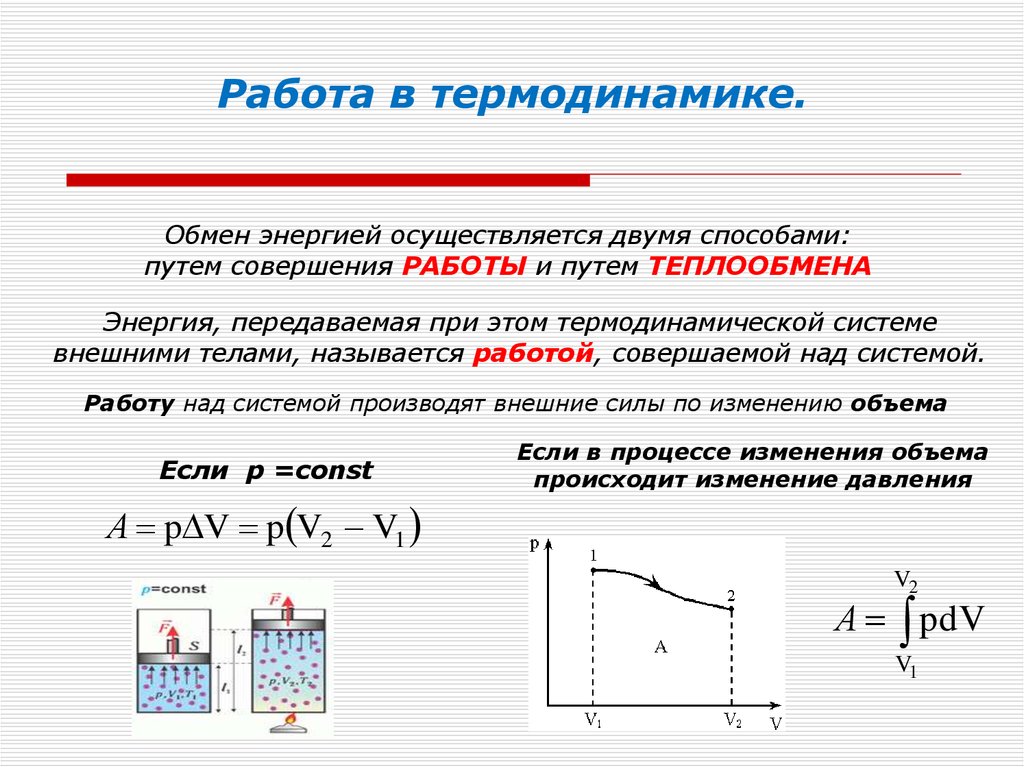

«Сегодняшняя научная фантастика — это завтрашний научный факт». — Исаак Азимов

Во-вторых, предполагается, что молекулы газа пренебрежимо малы по сравнению со всем объемом газа. Это предположение позволяет ученым упростить расчеты объема, исключая ненулевой объем, которым на самом деле обладают молекулы.

В-третьих, столкновения между молекулами и стенками сосуда считаются абсолютно упругими, то есть при столкновениях не теряется кинетическая энергия. На самом деле небольшое количество кинетической энергии поглощается стенками контейнера и рассеивается в виде тепла. Обычно это крошечное количество энергии незначительно, и им можно пренебречь.

Из-за этих предположений «универсальный» газовый закон технически не является универсальным и точен только в определенных пределах. В частности, в очень холодной пробе газа межмолекулярные взаимодействия превышают кинетическую энергию частиц, что делает поведение газа отклоняющимся от идеального. Более сложные уравнения состояния, такие как уравнения Ван-дер-Ваальса, используются для учета влияния на поведение частиц межмолекулярных сил.

Константы, используемые в PrepChem1

Константы, используемые в PrepChem1 Константы, используемые в этой книге (экспериментальные значения, , т. е. с учетом ошибки измерения)

Константа	Значение	Единиц	Использование
п Ав	6,0221×10 23	частицы	Номер Авогадро
Р	0,08206	л·атм/К·моль	постоянная идеального газа
Р	8.3145	Дж/К·моль	постоянная идеального газа
Р	1,9872	кал/к·моль	постоянная идеального газа
В м	22. 414	л/моль	закон идеального газа при 0°C
В м	24.465	л/моль	Закон идеального газа при 25°C
с	2,9979×10 8	м/с	скорость света
г	9.80665	м/с 2	стандартная плотность
ч	6,6261×10 -34	кг·м 2 /с	постоянная Планка
и 0	5,2918×10 -11	м	Боровский радиус
к	1,3807×10 -23	Дж/К	постоянная Больцмана
С	6,2415×10 18	и	Закон Кулона
Ф	96485	Кл/моль	Постоянная Фарадея
Р	1,097×10 7	м -1	постоянная Ридберга
Р Н	2,18×10 -18	Дж	Постоянная Ридберга водорода
а. е.м.	1,6605×10 -27	кг	атомная единица массы
масса е – , е +	9,1094×10 -31	кг	элементарная частица
масса р +	1,6726×10 -27	кг	элементарная частица
масса № 0	1,6749×10 -27	кг	элементарная частица
зарядка е	1,6022×10 -19	С	элементарная частица
энергия E n	931,5	МэВ	элементарная частица
Фактор Нернста	0,0592	—	Уравнение Нернста
К ш	1,0×10 -14	—	константа автоионизации воды
К а, Н 2 О	1,8×10 -16	—	константа кислотности воды

Коэффициенты пересчета единиц измерения (по определению, т. е. не зависит от погрешности измерения)

0	°С	=	273,15	К
1	фут	=	12	дюйма
1	мили	=	5280	футов
1	дюймов	=	2,54	см
1	мили	=	1,609	км
1	Å	=	1×10 -10	м
1	кал	=	4.184	Дж
1	Калибр	=	1000	кал
1	эВ	=	1,602×10 -19	Дж
1	эВ	=	96. 485	кДж/моль
1	л·атм	=	101,3	Дж
1	фунтов	=	453,6	г
1	кг	=	2,205	фунтов
1	галлона	=	3,785	л
1	Н	=	1	кг·м/с 2
1	Дж	=	1	Н·м
1	Па	=	1	Н/м 2
1	атм	=	14,7	фунтов на кв. дюйм
1	атм	=	760	мм рт. ст.
1	атм	=	760	торр
1	атм	=	1.01325	бар
1	атм	=	1,01325×10 5	Па
1	Д	=	3,34×10 -30	см
1	Ci	=	3,7×10 10	с -1
1	Гр	=	1	Дж/кг
1	Гр	=	100	рад
1	Р	=	2,58×10 -4	Кл/кг
1	г. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: