Электричество и магнетизм
|
Потоком вектора магнитной индукции В (магнитным потоком) через малую поверхность площадью dS называется скалярная физическая величина, равная
|
Здесь , — единичный вектор нормали к площадке площадью dS, Вn — проекция вектора В на направление нормали, — угол между векторами В и n (рис. 6.28).
Рис. 6.28. Поток вектора магнитной индукции через площадку
Магнитный поток ФB через произвольную замкнутую поверхность
|
|
(6. |
27)Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поэтому поток вектора В через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S выполняется условие
|
|
(6.28) |
Формула (6.28) выражает теорему Остроградского — Гаусса для вектора :
|
Поток вектора магнитной индукции через произвольную замкнутую поверхность тождественно равен нулю. |
Подчеркнем еще раз: эта теорема является математическим выражением того факта, что в природе отсутствуют магнитные заряды, на которых начинались бы и заканчивались линии магнитной индукции, как это имело место в случае напряженности электрического поля 
Это свойство существенным образом отличает магнитное поле от электрического. Линии магнитной индукции замкнуты, поэтому число линий, входящих в некоторый объем пространства, равно числу линий, выходящих из этого объема. Если входящие потоки брать с одним знаком, а выходящие — с другим, то суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю.
|
В системе СИ единицей измерения магнитного потока является
|
Рис. 6.29. В. Вебер (1804–1891) — немецкий физик
Отличие магнитного поля от электростатического проявляется также в значении величины, которую мы называем циркуляцией — интеграла от векторного поля по замкнутому пути. В электростатике равен нулю интеграл
взятый по произвольному замкнутому контуру.
Это связано с потенциальностью электростатического поля, то есть с тем фактом, что работа по перемещению заряда в электростатическом поле не зависит от пути, но лишь от положения начальной и конечной точек.
Посмотрим, как обстоит дело с аналогичной величиной для магнитного поля. Возьмем замкнутый контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В, то есть
Как было получено выше, магнитная индукция, создаваемая прямолинейным проводником с током на расстоянии R от проводника, равна
Рассмотрим случай, когда контур, охватывающий прямой ток, лежит в плоскости, перпендикулярной току, и представляет собой окружность радиусом R с центром на проводнике. В этом случае циркуляция вектора
| (6. |
29)откуда
| (6.30) |
Можно показать, что результат для циркуляции вектора магнитной индукции не меняется при непрерывной деформации контура, если при этой деформации контур не пересекает линий тока. Тогда в силу принципа суперпозиции циркуляция вектора магнитной индукции по пути, охватывающем несколько токов, пропорциональна их алгебраической сумме (рис. 6.30)
| (6.31) |
Рис. 6.30. Замкнутый контур (L) с заданным направлением обхода.
Изображены токи I1, I2 и I3, создающие магнитное поле.
Вклад в циркуляцию магнитного поля вдоль контура (L) дают только токи I
Если выбранный контур не охватывает токов, то циркуляция по нему равна нулю.
При вычислении алгебраической суммы токов следует учитывать знак тока: положительным будем считать ток, направление которого связано с направлением обхода по контуру правилом правого винта. Например, вклад тока I2 в циркуляцию — отрицательный, а вклад тока I3 — положительный (рис. 6.18). Воспользовавшись соотношением
между силой тока
| (6.32) |
где S — любая замкнутая поверхность, опирающаяся на данный контур L.
Итак,
Циркуляция магнитной индукции отлична от нуля, если контур, по которому она берется, охватывает ток. |
Такие поля называются вихревыми. Поэтому для магнитного поля нельзя ввести потенциал, как это было сделано для электрического поля точечных зарядов. Наиболее наглядно разницу потенциального и вихревого полей можно представить по картине силовых линий. Силовые линии электростатического поля похожи на ежей: они начинаются и кончаются на зарядах (либо уходят в бесконечность). Силовые линии магнитного поля никогда не напоминают «ежей»: они всегда замкнуты и охватывают текущие токи.
Для иллюстрации применения теоремы о циркуляции найдем другим методом уже известное нам магнитное поле бесконечного соленоида. Возьмем прямоугольный контур 1-2-3-4 (рис. 6.31) и вычислим циркуляцию вектора
(6.33) |
Рис.
6.31. Применение теоремы о циркуляции В к определению магнитного поля соленоида
Второй и четвертый интегралы равны нулю в силу перпендикулярности векторов и . Третий интеграл можно положить равным нулю, ввиду малости магнитного поля вне соленоида. Поэтому
| (6.34) |
Рассмотренный контур охватывает суммарный ток nlI, где n — число витков соленоида, приходящееся на единицу длины, I — сила тока в соленоиде. Следовательно,
или
| (6.35) |
Мы воспроизвели результат (6.20) без интегрирования магнитных полей от отдельных витков.
Полученный результат (6.35) можно использовать для нахождения магнитного поля тонкого тороидального соленоида (рис.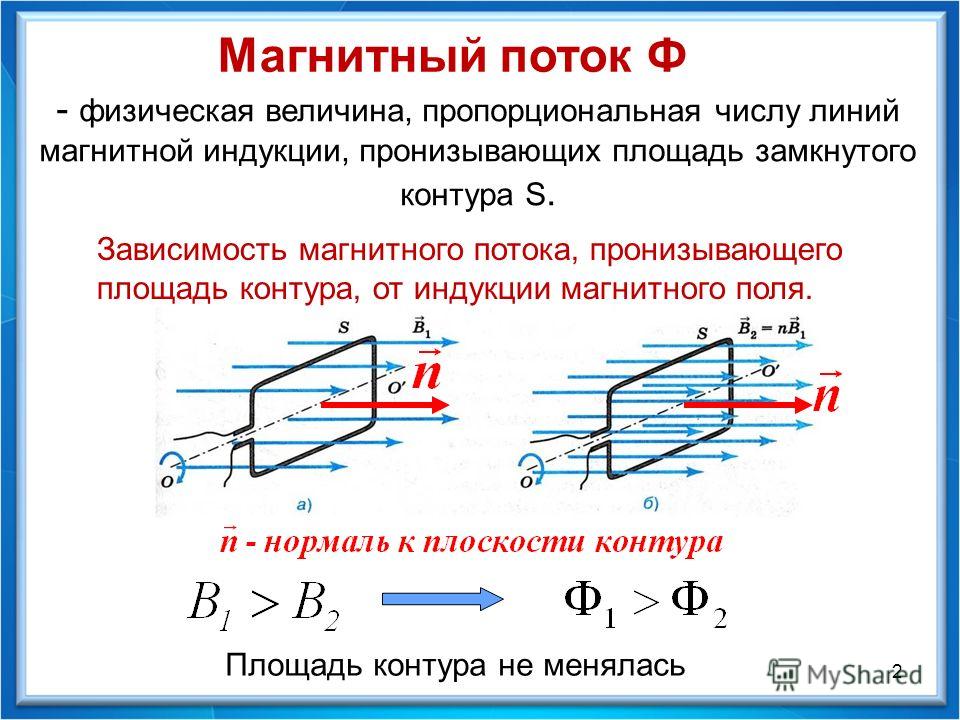
Рис. 6.32. Тороидальная катушка: линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рисунке
Дополнительная информация
http://www.magnet.fsu.edu/education/tutorials/pioneers/weber.html — Вильгельм Вебер (1804–1891).
Однородное магнитное поле. Магнитный поток
Конспект по физике для 9 класса «Однородное магнитное поле. Магнитный поток». ВЫ УЗНАЕТЕ: Что такое однородное магнитное поле. Что такое магнитный поток. В каких единицах измеряется магнитный поток.
Конспекты по физике Учебник физики Тесты по физике
На прошлом уроке вы познакомились с силовой характеристикой магнитного поля, которую называют магнитной индукцией.
Однако это не единственная количественная характеристика магнитного поля. Но прежде чем перейти к рассмотрению другой не менее важной характеристики магнитного поля, остановимся на вопросе о том, что такое однородное и неоднородное магнитное поле.
ОДНОРОДНОЕ И НЕОДНОРОДНОЕ МАГНИТНОЕ ПОЛЕ
Рассмотрим магнитное поле между полюсами кольцевого магнита. Магнитные линии здесь расположены параллельно друг другу. Так как во всех точках поля вектор магнитной индукции B не только одинаково направлен, но и имеет одно и то же значение, значит, и густота линий магнитной индукции в любой области поля между полюсами будет одна и та же.
Магнитное поле называют однородным, если во всех его точках магнитная индукция B одинакова как по направлению, так и по значению. В противном случае магнитное поле называют неоднородным. Примерами неоднородного магнитного поля могут служить: поле тока, протекающего по прямолинейному участку проводника; магнитное поле вокруг катушки с током; магнитное поле полосового магнита.
В этом не трудно убедиться с помощью магнитных стрелок, установленных вблизи источника магнитного поля. По характеру ориентации стрелок можно качественно судить о степени неоднородности поля в конкретном случае.
ПОТОК МАГНИТНОЙ ИНДУКЦИИ
Ещё одной характеристикой магнитного поля является физическая величина, зависящая от числа линий магнитной индукции, пронизывающих некоторую поверхность. Эту величину называют потоком вектора магнитной индукции или магнитным потоком и обозначают буквой Ф.
Понятие магнитного потока можно рассмотреть на примере однородного магнитного поля, в каждой точке которого индукция одинакова, а линии индукции параллельны друг другу.
Наглядно поток магнитной индукции можно рассматривать как величину, пропорциональную числу магнитных линий, проходящих через площадь S, ограничивающую некоторую поверхность.
Поскольку число магнитных линий зависит от их густоты, то, очевидно, магнитный поток пропорционален модулю вектора индукции магнитного поля: Ф ~ В.
Чем больше индукция, тем больший магнитный поток Ф1 пронизывает контур площадью S. Вместе с тем магнитный поток зависит и от площади контура: при том же значении магнитной индукции магнитный поток Ф2, пронизывающий контур большей площади, будет больше. Следовательно, магнитный поток пропорционален также площади контура.
Очевидно, что в случаях, когда линии магнитной индукции перпендикулярны плоскости контура, магнитный поток принимает наибольшее значение. Однако при изменении ориентации контура в магнитном поле, например при вращении вокруг оси ОО’, магнитный поток будет уменьшаться. В том случае, когда плоскость контура окажется параллельной линиям магнитной индукции, магнитный поток станет равным нулю.
ЕДИНИЦЫ МАГНИТНОГО ПОТОКА
В Международной системе единиц (СИ) за единицу магнитного потока принят вебер (Вб).
1 Вб — это магнитный поток через поверхность площадью 1 м2, расположенную в однородном магнитном поле индукцией 1 Тл, перпендикулярной линиям индукции: 1 Вб = 1 Тл * 1 м2 = 1 Тл м2.
На практике часто используется и меньшая единица магнитного потока — милливебер: 1 мВб = 0,001 Вб.
Вы смотрели Конспект по физике для 9 класса «Однородное магнитное поле. Магнитный поток».
Вернуться к Списку конспектов по физике (Оглавление).
2.5: Плотность магнитного потока — Инженерные тексты
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3906
- Стивен В.
Эллингсон - Политехнический институт Вирджинии и Государственный университет через Инициативу открытого образования Технологических библиотек Вирджинии
ЭллингсонПлотность магнитного потока — это векторное поле, которое мы идентифицируем с помощью символа \({\bf B}\) и которое имеет единицы СИ тесла (T). Прежде чем предложить формальное определение, полезно рассмотреть более широкое понятие магнитного поля .
Магнитные поля являются неотъемлемым свойством некоторых материалов, в первую очередь постоянных магнитов. Основное явление, вероятно, знакомо и показано на рисунке \(\PageIndex{1}\). Стержневой магнит имеет «полюса», обозначенные как «N» («север») и «S» («юг»). N-конец одного магнита притягивает S-конец другого магнита, но отталкивает N-конец другого магнита и так далее. Существование векторного поля очевидно, поскольку наблюдаемая сила действует на расстоянии и утверждается в определенном направлении. В случае постоянного магнита магнитное поле возникает из-за механизмов, происходящих в масштабе атомов и электронов, составляющих материал.
Эти механизмы требуют некоторых дополнительных пояснений, которые мы пока отложим.
Магнитные поля также появляются при наличии тока. Например, обнаружено, что катушка проволоки, по которой течет ток, влияет на постоянные магниты (и наоборот) так же, как постоянные магниты влияют друг на друга. Это показано на рисунке \(\PageIndex{2}\). Из этого мы делаем вывод, что лежащий в основе механизм такой же, то есть векторное поле, создаваемое катушкой с током, представляет собой то же явление, что и векторное поле, связанное с постоянным магнитом. Каким бы ни был источник, нас теперь интересует количественная оценка его поведения.
Рисунок \(\PageIndex{2}\): Доказательство того, что ток также может создавать магнитное поле. (CC BY 4.0; Ю. Цинь). Для начала рассмотрим действие магнитного поля на электрически заряженную частицу.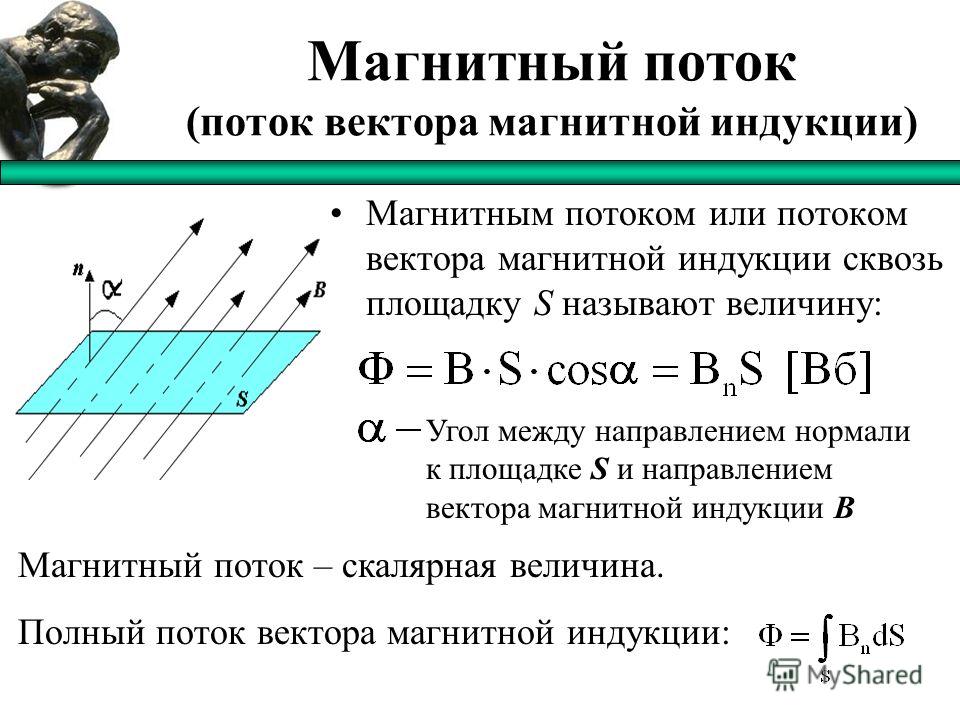
Во-первых, представьте себе область свободного пространства без электрических или магнитных полей. Далее представьте, что появилась заряженная частица. Эта частица не будет испытывать никакой силы. Далее появляется магнитное поле; возможно, это связано с постоянным магнитом или током поблизости. Эта ситуация показана на рисунке \(\PageIndex{2}\) (вверху). Тем не менее, никакая сила не приложена к частице. На самом деле ничего не происходит, пока частица не придет в движение. На рисунке \(\PageIndex{3}\) (внизу) показан пример. Внезапно частица воспринимает силу. Через мгновение мы перейдем к деталям о направлении и величине, но основная идея уже ясна. Магнитное поле — это то, что прикладывает к движущейся заряженной частице силу, отличную от (фактически, в дополнение к) силы, связанной с электрическим полем.
0; Y. Qing).Теперь стоит отметить, что одиночная заряженная частица в движении — это простейшая форма тока. Помните также, что движение необходимо для того, чтобы магнитное поле воздействовало на частицу. Следовательно, не только ток является источником магнитного поля, магнитное поле также воздействует на ток. Итого:
Магнитное поле описывает силу, действующую на постоянные магниты и токи в присутствии других постоянных магнитов и токов.
Итак, как мы можем количественно определить магнитное поле? Ответ из классической физики включает другое экспериментально полученное уравнение, которое предсказывает силу как функцию заряда, скорости и векторного поля \({\bf B}\), представляющего магнитное поле. Вот оно: Сила, приложенная к частице, несущей заряд \(q\), равна
.\[\mathbf {F} = q \mathbf {v} \times \mathbf {B} \label{m0005_eFqvB} \]
, где \({\bf v}\) — скорость частицы, а «\(\times\)» обозначает векторное произведение. Перекрестное произведение двух векторов находится в направлении, перпендикулярном каждому из двух векторов, поэтому сила, действующая со стороны магнитного поля, перпендикулярна как направлению движения, так и направлению, в котором указывает магнитное поле.
Читатель имеет полное право задаться вопросом, почему сила, создаваемая магнитным полем, должна быть перпендикулярной к \({\bf B}\). Если на то пошло, почему сила должна зависеть от \(\bf v\)? Это вопросы, на которые классическая физика не дает очевидных ответов. Эффективные ответы на эти вопросы требуют концепций квантовой механики, где мы обнаруживаем, что магнитное поле является проявлением фундаментального и точно названного электромагнитная сила . Электромагнитная сила также порождает электрическое поле, и лишь ограниченная интуиция, основанная на классической физике, приводит нас к восприятию электрического и магнитного полей как отдельных явлений. Для наших нынешних целей — и для наиболее часто встречающихся инженерных приложений — нам не нужны эти понятия. Достаточно принять эту кажущуюся странность как факт и действовать соответственно.
Анализ размерностей \ref{m0005_eFqvB} показывает, что \({\bf B}\) имеет единицы (N\(\cdot\)s)/(C\(\cdot\)m).
2\) \(=\) 1 T. 92\)) — это описание магнитного поля, которое можно определить как решение уравнения \ref{m0005_eFqvB}.
При описании магнитных полей мы иногда ссылаемся на концепцию линии поля , определяемой следующим образом:
Линия магнитного поля — это кривая в пространстве, описываемая в направлении, в котором указывает вектор магнитного поля.
Эта концепция проиллюстрирована на рисунке \(\PageIndex{4}\) для постоянного стержневого магнита и на рисунке \(\PageIndex{5}\) для катушки с током.
Рисунок \(\PageIndex{5}\): Магнитное поле катушки с током, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).Линии магнитного поля примечательны по следующей причине:
Линия магнитного поля всегда образует замкнутый контур.
В некотором смысле это верно даже для силовых линий, которые, кажется, образуют прямые линии (например, те, которые проходят вдоль оси стержневого магнита и катушки на рисунках \(\PageIndex{4}\) и \(\PageIndex{5 }\), так как силовая линия, уходящая в бесконечность в одном направлении, выходит из бесконечности в противоположном направлении.
0036
Эта страница под названием 2.5: Плотность магнитного потока распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Стивеном В. Эллингсоном (Инициатива открытого образования технических библиотек Вирджинии) посредством исходного контента, который был отредактирован к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Стивен В. Эллингсон
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- Инициатива открытого образования технических библиотек Вирджинии
- Показать оглавление
- нет
- Теги
- Плотность магнитного потока
- источник@https://doi. org/10.21061/electromagnetics-vol-1
org/10.21061/electromagnetics-vol-1Магнитный поток: что это такое, уравнение, единицы измерения, плотность
Обновлено 28 декабря 2020 г.
Кевин Бек
Электричество и магнетизм неразрывно связаны, что привело к принятию термина электромагнетизм для описания связанных явлений. На самом деле, степень, в которой это верно, в значительной степени ускользала от ученых до второй половины 1800-х годов, когда Джеймс Клерк Максвелл, опираясь на работы уважаемых физиков до него, создал свой знаменитый набор из четырех дифференциальных (исчислений) уравнений, связывающих воедино различные свойства магнитных полей и электрических полей.
Понимание магнитного потока или силовых линий магнитного поля, проходящих через определенную геометрическую плоскость, называемую векторной областью , приводит к нескольким важным физическим явлениям, включая электромагнитную индукцию , или генерацию электродвижущей силы.
сила (ЭДС).
Что такое магнитный поток?
Общий магнитный поток, по сути, является мерой того, сколько силовых линий магнитного поля проходит через данную площадь поверхности A – то есть мера силы магнитного поля. Более формально он определяется как:
\Phi_B=B\cdot A=BA\cos{\theta}
, где θ — угол между магнитным полем B и перпендикуляром к A в определенной области.
- Магнитное поле B, или плотность магнитного потока на единицу площади , измеряется в теслах (Тл) в единицах СИ, а A – это площадь, через которую проходит поле, в м 2 . Единицей магнитного потока в СИ является вебер (Вб), где Вб = Т⋅м 2 .
Если B не является однородным по всей поверхности A, определение исчисления состоит в том, что Φ = ∫B⋅dA. Эта интегральная функция поверхности означает, что значения потока через почти бесконечно малые участки A определяются независимо и суммируются для получения составного значения.
Какое значение имеет магнитный поток?
Закон Гаусса: Чистый магнитный поток через замкнутую поверхность равен 0 . Это второе уравнение Максвелла, и оно согласуется с идеей об отсутствии магнитных монополей.
Независимо от того, насколько маленький объем вы выберете, магнитное поле всегда можно описать как включающее в себя диполь или крошечный невидимый стержневой магнит. Это контрастирует с электрическими полями, которые генерируются точечными зарядами (или массивами изолированных точечных зарядов).
Закон электромагнетизма Фарадея: Наведенная электродвижущая сила (ЭДС) в катушке провода с N витками равна N, умноженному на изменение потока во времени:
ЭДС=N\frac{\ Дельта \Phi}{\Delta t}
Поток можно изменить во времени, изменяя B, изменяя площадь поперечного сечения A или изменяя угол между B и A, вращая катушку или источник поля.
- ЭДС имеет единицы измерения напряжения (разности потенциалов), а не силы. Это называют «силой», потому что напряжение — это то, что заставляет заряды двигаться, производя ток, в первую очередь.
Закон Ленца: Наведенный электрический ток течет в направлении, противоположном вызвавшему его изменению. Например, скажем, у вас есть катушка провода, не подключенная к какому-либо источнику питания.
Представьте себе, что стержневой магнит перемещается вдоль его оси в середину катушки, как если бы вы вставили стержень прямо в середину длинной трубки, не касаясь стенок трубки. Это усиленное поле в катушке заставляет ток течь в таком направлении, что он создает магнитное поле, противодействующее увеличению.
Если вы повторите эту процедуру после того, как поменяете местами южный и северный полюсы магнита, произведенное изменение будет равным по величине и противоположным по направлению по сравнению с первым случаем, и в результате ток будет течь в противоположном направлении.