Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования.
Пример
Задание. Найти интеграл $\int \frac{d x}{3-5 x}$
Решение. Заменим знаменатель на переменную $t$ и приведем исходный интеграл к табличному.
$$\int \frac{d x}{3-5 x}\left\|\begin{array}{l} 3-5 x=t \\ -5 d x=d t \\ d x=-\frac{d t}{5} \end{array}\right\|=\int \frac{-\frac{d t}{5}}{t}=-\frac{1}{5} \int \frac{d t}{t}=$$$=-\frac{1}{5} \ln |t|+C=-\frac{1}{5} \ln |3-5 x|+C$
Ответ. $\int \frac{d x}{3-5 x}=-\frac{1}{5} \ln |3-5 x|+C$
Подробнее о данном методе решении интегралов по ссылке →
4. Интегрирование по частям
Интегрированием по частям называют интегрирование по формуле
$\int u d v=u v-\int v d u$
При нахождении функции $v$ по ее дифференциалу
$d v$ можно брать любое значение постоянной интегрирования
$C$, так как она в конечный результат не входит.
Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой.
Пример
Задание. Найти интеграл $\int x \cos x d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.
$$\int x \cos x d x\left\|\begin{array}{ll} u=x & v=\sin x \\ d u=d x & d v=\cos x d x \end{array}\right\|=x \sin x-\int \sin x d x=$$Ответ. $\int x \cos x d x=x \sin x+\cos x+C$
Подробнее о данном методе решении интегралов по ссылке →
Читать дальше: метод непосредственного интегрирования.
Некоторые методы интегрирования
Если функция задана в виде формулы, включающей в себя степени, корни, показательные функции, логарифмы, тригонометрические функции и арифметические операции между ними, её производная может быть найдена алгоритмически — последовательным применением теорем о производных сумм-произвденений-частных и производной сложной функции.
Есть функции, выглядящие довольно невинно, у которых первообразная вообще не выражается через другие функции, которые мы обсуждали до сих пор. Например, такой функцией является ex2. Даже если первообразную какой-то функции можно записать в виде формулы, найти эту формулу часто бывает сложно. Теоретически, существует относительно универсальный алгоритма Риша, но его описание занимает сотню страниц, и уж конечно при подсчёте интегралов вручную люди используют не его, а некоторый набор известных приёмов, которые, при некотором везении, иногда позволяют интеграл отыскать.
В общем, не будет большим преувеличением сказать, что дифференцирование — это ремесло, а интегрирование — искусство.
Изучение этого искусства долгое время было существенной частью образования
любого человека, использующего математику в своей профессиональной деятельности. Однако, со временем развитие систем компьютерной алгебры сделало знание десятков
разных методов и приёмов интегрирования не столь важным.
Однако, со временем развитие систем компьютерной алгебры сделало знание десятков
разных методов и приёмов интегрирования не столь важным.
Тем не менее, некоторые сравнительно простые приёмы знать полезно — в первую очередь, поскольку они позволяют лучше понять природу интегрирования. Именно им будет посвящена сегодняшняя лекция.
26.1Преобразования неопределённых интегралов
26.1.1Кто такие неопределённые интегралы
До сих пор мы обсуждали определённые интегралы, то есть выражения вроде∫51(x2+3x)dx.
Определенный интеграл — это число. При нахождении определённого интеграла с помощью формулы Ньютона — Лейбница нам нужно находить первообразную подынтегральной функции, и хочется иметь какое-то обозначение для этой операции. В качестве этого обозначения используется интеграл, у которого не указаны пределы интегрирования. Определение 1. Неопределённым интегралом∫f(x)dx.
∫x2dx=x33+C.
Тот факт, что справа мы пишем +C, показывает, что первообразной является не только одна конкретная функция x3/3, а целое семейство функций, отличающихся разными константами. Преподаватели матанализа обычно расстраиваются, когда студенты забывают эту «плюс константу», решая задачи на нахождение неопределённых интегралов. Если вы будете использовать получившуюся функцию в формуле Ньютона — Лейбница, от константы ничего не зависит, однако в некоторых других приложениях (например, в дифференциальных уравнениях) если забыть константу, можно сделать ошибку — найти не все решения.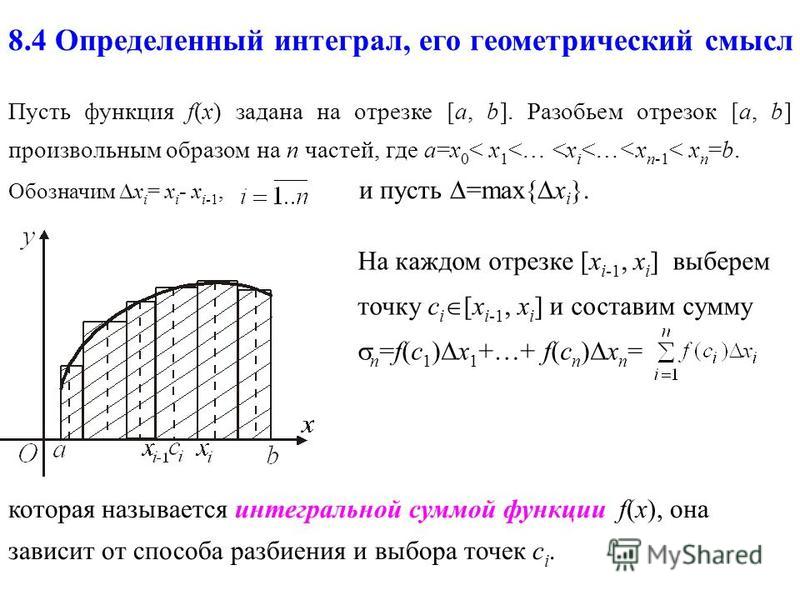 В правой части (26.2) записана сумма двух
семейств функций — это новое семейство функций, которое состоит из
сумм всевозможных первообразных f и g.
Доказательство. Это мгновенное следствие из соответствующих свойств производных. Например,
если F — первообразная f и G — первообразная g, значит
В правой части (26.2) записана сумма двух
семейств функций — это новое семейство функций, которое состоит из
сумм всевозможных первообразных f и g.
Доказательство. Это мгновенное следствие из соответствующих свойств производных. Например,
если F — первообразная f и G — первообразная g, значит26.1.2Интегрирование по частям
Пусть f и g — некоторые дифференцируемые функции. Справедливо равенство:(f(x)g(x))′=f′(x)g(x)+f(x)g′(x).(26.4)
Можно его проинтегировать: множество всех первообразных левой части должно совпадать со множеством всех первообразных правой части: В правой части записан интеграл суммы, а он равен сумме интегралов. Значит,
можно записать это равенство так:
В правой части записан интеграл суммы, а он равен сумме интегралов. Значит,
можно записать это равенство так:∫(f(x)g(x))′dx=∫f′(x)g(x)dx+∫f(x)g′(x)dx,
после чего перенести одно из слагаемых из левой части в правую и перевернуть равенство. Получится такая штука:∫f(x)g′(x)dx=∫(f(x)g(x))′dx−∫f′(x)g(x)dx.
Теперь заметим, что мы знаем по крайней мере одну первообразную для функции (f(x)g(x))′ — это f(x)g(x). Можно записать:Равенство (26.5) и называется правилом интегрирования по частям.
Пример 2. Найдём следующий интеграл:∫xsinxdx.
Мы хотим применить равенство (26.5). Для этого нужно представить подынтегральную функцию в виде f(x)g′(x) для некоторых функций f и g. Наша подынтегральная функция xsinx состоит из двух сомножителей. Как выбрать, какой из них обозначит за f, а какой за g′? Ну, во-первых, обозначать за g′ можно тот сомножитель, для которого мы можем найти g.
∫xsinxdx=∫(x22)′sinxdx=x22sinx−∫x22(sinx)′dx=x22sinx−∫x22cosxdx.
С помощью интегрирования по частям можно «перебросить» производную с одного сомножителя на другой. Однако, помогло ли это нам в достижении нашей цели? Кажется, не очень: новое выражение проинтегрировать не проще, чем старое. Давайте попробуем иначе: пусть теперь f(x)=x и g′(x)=sinx. Интегрируя
синус, положим g(x)=−cosx. Тогда
∫xsinxdx=∫x(−cosx)′dx=−xcosx−∫(−cosx)x′dx==−xcosx+∫cosxdx=−xcosx+sinx+C.
Теперь получилось! В результате перебрасывания производных мы
продифференцировали сомножитель x, он превратился в единцу и перестал нам
мешаться.
Можно проверить ответ дифференцированием:
(−xcosx+sinx)′=xsinx−cosx+cosx=xsinx.
Ура, получилась подынтегральная функция — значит, интегрирование по частям работает! Пример 3. Иногда интегрирование по частям удаётся применить в довольно неожиданных ситуациях. Например, найдём первообразную логарифма: Интегрирование по частям возникает из правила дифференцирования произведения и
применяется в основном в ситуациях, когда подынтегральное выражение является
произведением двух функций. Однако, увы, в отличие от своего «прародителя»,
интегрирование по частям далеко не так универсально — не всегда удаётся
проинтегрировать хотя бы один из сомножителей, а если удаётся, не всегда
«перебрасывание производной» делает интеграл проще. Впрочем, попробовать обычно
стоит.
Впрочем, попробовать обычно
стоит.
26.1.3Замена переменных
Второе правило интегрирования, которое мы сегодня обсудим, происходит из теоремы о производной сложной функции.Пусть функция F(t) является первообразной некоторой функции f(t), то есть
F′(t)=f(t).
Пусть t=h(x) — некоторая дифференцируемая функция. Первообразной какой функции является функция G(x):=F(h(x))? Ответить на этот вопрос легко: достаточно продифференцировать G с помощью правила дифференцирования сложной функции.G′(x)=F′(h(x))h′(x)=f(h(x))h′(x)
Итак, мы выяснили, что функция F(h(x)) является первообразной функции f(h(x))h′(x). Используя неопредёленные интегралы это можно записать так:∫f(h(x))h′(x)dx=(∫f(t)dt)∣∣∣t=h(x)(26.6)
где выражение в правой части означает, что нужно взять соответствующий неопределённый интеграл, получить выражение вида F(t)+C, а затем в этом выражении подставить вместо t значение h(x), то есть получить F(h(x))+C. Мы знаем, что эта штука является первообразной для функции f(h(x))h′(x), то есть действительно принадлежит неопределённому интегралу, записанному слева.
Равенство (26.6) называется формулой замены переменных в неопределённом интеграле.
Пример 4. Найдём интеграл∫xsinx2dx.
Заметим, что подынтегральную функцию можно записать в виде f(h(x))h′(x) если взять h(x)=x2 и f(t)=12sint. Коэффициент 1/2 возникает из-за того, что при дифференцировании h получается 2x, и нам нужно избавиться от этой двойки. Согласно формуле (26.6), наш интеграл равен интегралу от f(t), в который подставили (после интегрирования) t=h(x), то есть∫xsinx2dx=(∫12sintdt)∣∣∣t=x2
поскольку константу можно выносить за знак интеграла,∫12sintdt=12∫sintdt=−12cost+C.
Подставляя в это выражение t=x2, получаем:∫xsinx2dx=−12cosx2+C.
Действительно, можно проверить дифференцированием:(−12cosx2+C)′=−12(−sinx2)2x=xsinx2.
Всё работает!26.2Преобразование определённых интегралов
26.2.1Интегрирование по частям
Правило интегрирования по частям в определённом интеграле выводится так же, как в неопределённом. Пусть равенство (26. 4) верно для всех x∈[a,b].
Проинтегрируем его по этому отрезку (слева написана какая-то функция, справа
такая же функция, их интегралы по одному и тому же отрезку должны быть, конечно,
равны):
4) верно для всех x∈[a,b].
Проинтегрируем его по этому отрезку (слева написана какая-то функция, справа
такая же функция, их интегралы по одному и тому же отрезку должны быть, конечно,
равны):∫ba(f(x)g(x))′dx=∫ba(f′(x)g(x)+f(x)g′(x))dx.(26.7)
Интеграл в левой части легко посчитать: одной из первообразных (f(x)g(x))′ является функция f(x)g(x), и значит по формуле Ньютона — Лейбница этот интеграл равенf(x)g(x)|ba=f(b)g(b)−f(a)g(a).
Представим интеграл в правой части (26.7) в виде суммы интегралов, перенесём одно из слагаемых в левую часть и перевернём равенство. Получим:∫baf(x)g′(x)dx=f(x)g(x)|ba−∫baf′(x)g(x)dx.
Это и есть правило интегрирования по частям в определённом интеграле. Его также можно было бы вывести, применяя интегрирование по частям в неопределённом интеграле, а затем формулу Ньютона — Лейбница. Тут ничего особо интересного не происходит.26.2.2Замена переменных в определённом интеграле
Формулу замены переменных в определённом интеграле также можно выводить из аналогичной формулы для неопределённых интегралов с последующим применением формулы Ньютона — Лейбница. Однако, мне больше нравится непосредственный подход,
использующий определение интеграла Римана. Он позволяет довольно наглядно
увидеть, что именно происходит при замене переменных. Впрочем, главный эффект
можно увидеть на следующем простом примере.
Пример 5. Рассмотрим два интеграла:
Однако, мне больше нравится непосредственный подход,
использующий определение интеграла Римана. Он позволяет довольно наглядно
увидеть, что именно происходит при замене переменных. Впрочем, главный эффект
можно увидеть на следующем простом примере.
Пример 5. Рассмотрим два интеграла:I1=∫π0sintdt
иI2=∫π/20sin(2x)dx.
Значения, которые функция sint принимает, когда t меняется от 0 до π, в точности совпадают со значениями, которые принимает функция sin2x, когда x меняется от 0 до π/2. Однако, интегралы I1 и I2 не равны.Действительно, графики функций y=sint и y=sin2x связаны друг с другом: второй получается из первого сжатием в два раза в горизонтальном направлении. Область, площадь которой соответствует интегралу I2, получается из области, которая соответствует интегралу I1, также путём сжатия в два раза, см. рис. 26.1. Поэтому второй интеграл вдвое меньше первого:
∫π/20sin2xdx=12∫π0sintdt.
Мораль этого примера такая: если мы возьмём подынтегральную функцию и просто подставим в неё вместо t какую-то функцию от x, область, площадь которой равна интегралу, будет растягиваться или сжиматься в горизонтальном направлении. Это сжатие или растяжение может быть разным в разных точках и
задаётся производной функции, которая осуществляет замену. (В нашем примере
эта функция была линейной и её производная во всех точках равнялась
константе, но это пример такой простой.) Корректная формула замены
переменных в интеграле должна учитывать этот эффект.
Это сжатие или растяжение может быть разным в разных точках и
задаётся производной функции, которая осуществляет замену. (В нашем примере
эта функция была линейной и её производная во всех точках равнялась
константе, но это пример такой простой.) Корректная формула замены
переменных в интеграле должна учитывать этот эффект.import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(6, 6))
t = np.linspace(-0.5, 3.6, 200)
t_clip = np.linspace(0, np.pi)
ax1.plot(t, np.sin(t), label='$y=sin(t)$')
ax1.fill_between(t_clip, np.sin(t_clip), alpha=0.5)
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-0.5, xmax=3.6, ymin=-1.2, ymax=1.2,
xlabel="t", ylabel="y", ax=ax1)
ax1.legend()
ax1.set_xticks([np.pi])
ax1.set_xticklabels([r'$\pi$'])
ax1.set_yticks([])
x = np.linspace(-0.5, 3.6, 200)
x_clip = np.linspace(0, np. pi / 2)
ax2.plot(x, np.sin(2 * x), label='$y=sin(2x)$')
ax2.fill_between(x_clip, np.sin(2 * x_clip), alpha=0.5)
ax2.legend()
ob.center_spines(grid=False, minor_ticks=False, ax=ax2)
ob.settle_axes(xmin=-0.5, xmax=3.6, ymin=-1.2, ymax=1.2,
xlabel="x", ylabel="y", ax=ax2)
ax2.set_xticks([np.pi/2, np.pi])
ax2.set_xticklabels([r'$\frac{\pi}{2}$', r'$\pi$'])
ax2.set_yticks([])
pi / 2)
ax2.plot(x, np.sin(2 * x), label='$y=sin(2x)$')
ax2.fill_between(x_clip, np.sin(2 * x_clip), alpha=0.5)
ax2.legend()
ob.center_spines(grid=False, minor_ticks=False, ax=ax2)
ob.settle_axes(xmin=-0.5, xmax=3.6, ymin=-1.2, ymax=1.2,
xlabel="x", ylabel="y", ax=ax2)
ax2.set_xticks([np.pi/2, np.pi])
ax2.set_xticklabels([r'$\frac{\pi}{2}$', r'$\pi$'])
ax2.set_yticks([])∫h(b)h(a)f(t)dt=∫baf(h(x))h′(x)dx.(26.8)
Доказательство. По-хорошему, нам следовало бы доказать, что интеграл в правой части (26.8) в принципе существует. Но я этого делать не буду — это не очень сложно, но отвлекает от главного. Поэтому я предлагаю в существование поверить.Разбиения. Будем использовать определение интеграла Римана. Возьмём произвольное неразмеченное разбиение P отрезка [a,b]:
Возьмём произвольное неразмеченное разбиение P отрезка [a,b]:
a=x0<x1<…<xn−1<xn=b.
Рассмотрим набор точек (t0,…,tn), где tk=h(xk), k=0,…,n. Это разбиение отрезка [h(a),h(b)]. Действительно, в силу монотонности h,h(a)=h(x0)<h(x1)<…<h(xn−1)<h(xn)=h(b).
Обозначим это разбиение через h(P). Пусть как обычноΔxk=xk−xk−1(26.9)
иΔtk=tk−tk−1=h(xk)−h(tx−1).(26.10)
Преобразование длин отрезков. Как связаны между собой Δtk и Δxk, то есть длины отрезков разбиения P и длины их образов под действием отображения f, являющихся отрезками разбиения h(P)? Ранее мы обсуждали (см. раздел про производную сложной функции в лекции 16), что производная показывает, во сколько раз растягиваются маленькие отрезки под действием отображения. Так что логично ожидать, что Δtk получается из Δxk умножением на производную функции h, взятую в подходящей точке. Докажем это.
Применим теорему Лагранжа о конечных приращениях к функции h и отрезку [xk−1,xk]. Найдётся такая точка c∈(xk−1,xk), что
h(xk)−h(xk−1)xk−xk−1=h′(c). (26.11)
(26.11)
ΔtkΔxk=h′(x∗k),
то естьΔtk=h′(x∗k)Δxk.(26.12)
Это то, что мы хотели!Разметки разбиений. Поскольку x∗k лежит в [xk−1,xk], то есть в k-м отрезке разбиения P, точки (x∗1,…,x∗n) образуют разметку для этого разбиения.
Пусть t∗k:=h(x∗k), k=1,…,n. В силу монотонности функции h,
t∗k=h(x∗k)∈[h(xk−1),h(xk)]=[tk−1,tk].
Таким образом, набор точек (t∗k) образует разметку разбиения h(P).Интегральные суммы. Запишем интегральную сумму для функции f(t) и разметки h(P) с разметкой (t∗k):
S(h(P),f)=n∑k=1f(t∗k)Δtk.
Подставляя в эту формулу t∗k=h(x∗k) (по определению t∗k) и Δtk=h′(x∗k)Δxk (см. (26.12)), получаем:S(h(P),f)=n∑k=1f(h(x∗k))h′(x∗k)Δxk.
Но ведь это интегральная сумма для функции f(h(x))h′(x) по разбиению P с разметкой (x∗k)! Остаётся перейти к пределу при d(P)→0 — и дело в шляпе! Интегральная
сумма S(h(P),f) должна стремиться к интегралу от функции f(t) по отрезку
[h(a),h(b)], и она же должна стремиться к интегралу от функции
f(h(x))h′(x) по отрезку [a,b]. Значит, эти интегралы равны. Что и
требовалось доказать.∎
Значит, эти интегралы равны. Что и
требовалось доказать.∎
26.2.3Немного о дифференциалах
При замене переменных в интеграле часто используют такой приём. Напомним обозначения Лейбница для производной:f′(x0)=dfdx(x0).
Пусть t=h(x). Тогда производную h′(x) можно обозначить какdhdx,
а можно и какdtdx.
Ну действительно, мы ведь знаем, что t — это примерно то же самое, что h, так что можно поменять в обозначениях одну букву на другую. Итак,dtdx=h′(x).
Когда мы обсуждали обозначения Лейбница, мы говорили, что дробь в левой части — это не совсем настоящая дробь, потому что не совсем понятно, что означают по отдельности её числитель и знаменатель. Однако, забудем об этом, и умножим наше равенство на dx. Получится такая штука:dt=h′(x)dx.(26.13)
Заметим, что это равенство очень похоже на равенство (26.12). Мы также говорили, что все эти dx и dt в интегралах — это наши воспоминания о том, что в интегральных суммах есть сомножители типа Δxk или Δtk. Таким образом, равенство (26.12) является дополнительным
аргументом в пользу того, чтобы поверить в равенство (26.13) — по
крайней мере, в контексте интегрирования.
Таким образом, равенство (26.12) является дополнительным
аргументом в пользу того, чтобы поверить в равенство (26.13) — по
крайней мере, в контексте интегрирования.Оказывается, это равенство — по большому счёту, единственное, что вам нужно знать, чтобы делать корректную замену переменных. Надо просто помнить, что вместе с заменой в подынтегральной функции и преобразованием пределов интегрирования, нужно ещё преобразовать вот эти вот dx или dt, пользуясь равенством (26.13).
Давайте посмотрим, как это работает.
Пример 6. Рассмотрим интеграл∫√π0xsinx2dx.
Сделаем замену переменных t=x2. Когда x пробегает значения от 0 до √π, t пробегает значения от 0 до π. Таким образом мы видим, как меняются пределы интегрирования.Теперь заметим, что согласно (26.13),
dt=(x2)′dx=2xdx.
В подынтегральном выражении у нас есть сомножитель xdx, который с точностью до умножения на 2 совпадает с правой частью этого равенства. Запишем:xdx=12dt.
Теперь сделаем следующие преобразования в исходном интеграле:- Пределы интегрирования [0,√π] нужно заменить на [0,π].

- В подынтегральном выражении x2 нужно заменить на t.
- В подынтегральном выражении сомножитель xdx нужно заменить на 12dt.
∫√π0xsinx2dx=∫π0(sint)12dt=12∫π0sintdt=12(−cost)|t=πt=0=12⋅2=1.
При вычислении неопределенных интегралов эту запись часто сокращают до такой:∫xsinx2dx=12∫sinx2d(x2)=12(−cosx2)+C,
в этом контексте x2 становится одновременно обозначением замены и как бы новой переменной, полученной после замены. Теперь, наверное, вы мне поверите, что от этих dx в интегралах есть польза
— они «помнят», как устроены переменные, по которым мы интегрируем, а их
преобразования при заменах координат показывают, как меняются длины отрезочков,
участвующих в интегральных суммах, и, следовательно, как искажаются площади.
Поначалу работа с формулой (26.13) может показаться какой-то магией (в
конце концов, мы до сих пор не понимаем, кто такие эти dt и dx!), но после
накопления некоторого опыта вы будете чувствовать себя вполне уверенно.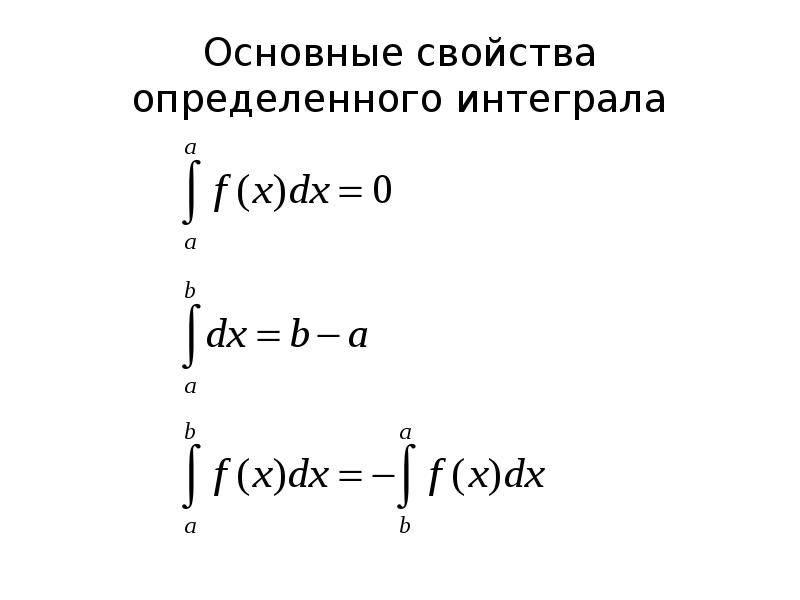
Однако, если вы опасаетесь применять магию вне Хогвартса, всегда можно использовать формулу (26.8) — просто расписывать, что является функцией f, что функцией h, и как устроена ваша замена. Общее правило математики: не уверен — распиши всё явно и используй железобетонные формулы.
Кстати, выражение h(x)dx называется дифференциалом функции h. Но что это такое я всё равно не скажу.
26.3Заключение
Мы обсудили интегрирование по частям и замену переменных — два самых простых, но уже довольно нетривиальных способа преобразовывать интегралы. При должной тренировке вы научитесь видеть, какое правило когда разумно применять — это расширит пространство функций, которые вы умеете интегрировать. Дополнительно, обсуждение правила замены переменных в определенном интеграле позволило глубже понять механизмы интегрирования. И наконец мы получили какую-то пользу от того, что в интегралах приходится каждый раз писать непонятный dx.← Предыдущая глава Следующая глава →
Федеральные государственные образовательные стандарты высшего образования
– Последние новости
21. 07.2021
07.2021
На сайте www.fgosvo.ru в разделе «Координационные Советы и федеральные УМО» в подразделе «Координационные советы по областям образования: Науки об обществе» на странице ФУМО в системе высшего образования по УГСН «41.00.00 Политические науки и регионоведение» добавлена информация о новом составе ФУМО
16.07.2021
На сайте www.fgosvo.ru размещен проект документа «О внесении изменений в Порядок приема на обучение по образовательным программам высшего образования – программам бакалавриата, программам специалитета, программам магистратуры, утвержденный приказом Министерства науки и высшего образования Российской Федерации от 21 августа 2020 г. № 1076»
14.07.2021
На сайте fgosvo.ru размещено Постановление Правительства Российской Федерации от 11 июля 2021 года № 1038 «О внесении изменений в Правила размещения на официальном сайте образовательной организации в информационно-телекоммуникационной сети “Интернет” и обновления информации об образовательной организации»
13. 07.2021
07.2021
На сайте www.fgosvo.ru размещено письмо Директора Департамента государственной политики в сфере высшего образования Минобрнауки России Рябко Т.В. от 05 июля 2021 г. № МН-5/2865 «О направлении разъяснений» (разъяснения по некоторым вопросам применения Порядка приема на обучение по образовательным программам высшего образования – программам бакалавриата, программам специалитета, программам магистратуры)
11.07.2021
На сайте www.fgosvo.ru размещено Письмо Директора Департамента государственной политики в сфере высшего образования Минобрнауки России Рябко Т.В от 02 июля 2021 г. № МН-5/2657 «О направлении информации» (о направлении модуля «Системы искусственного интеллекта» для включения в образовательные программы)
Основные правила интегрирования
1. Неопределённый интеграл от алгебраической суммы (или разности) конечного числа непрерывных функций равен алгебраической сумме (или разности) интегралов от этих функций:
.
2. Постоянный множитель можно выносить за знак интеграла:
, .
3. (Инвариантность формулы интегрирования)
Если , то и , где – произвольная функция, имеющая непрерывную производную.
Таблица основных интегралов
1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
10. .
11. .
12. .
13. .
14. .
В таблице переменная интегрирования может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
Непосредственное интегрирование
Непосредственным интегрированием называется метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (выражения) и применения свойств неопределенного интеграла сводится к табличному интегралу.
Примеры.
1. .
2. .
3. .
4. .
5. .
6. .
Интегрирование путем подведения под знак дифференциала и методом подстановки
При сведении интеграла к табличному часто используют метод интегрирования путем подведения под знак дифференциала. В данном случае используют следующую формулу:
,
где – функция, имеющая непрерывную производную на рассматриваемом промежутке.
Применяют также интегрирование методом подстановки.
Обозначим , тогда получим . Тогда
.
Подведение под знак дифференциала есть одна из реализаций метода замены переменной.
Удачная замена переменной позволяет упростить исходный интеграл, а иногда свести его даже к табличному.
Примеры.Вычислить следующие интегралы:
1. .
1 способ.
.
2 способ.
.
2. .
1 способ.
.
2 способ.
.
3. .
1 способ.
.
2. способ.
.
4. .
1 способ.
.
2 способ.
.
Метод интегрирования по частям
Пусть функции и имеют непрерывные производные на заданном интервале, тогда справедлива формула интегрирования по частям:
.
Метод интегрирования по частям целесообразно применять в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен, при этом за берется та функция, которая при дифференцировании упрощается, а за берется та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Выделяют следующие типы интегралов, которые удобно вычислять методом интегрирования по частям:
1. , , , где – многочлен степени , – число.
При вычислении данных интегралов формулу применяют n раз, обозначив за .
2. , , , , .
При вычислении интегралов второго типа удобно обозначить за .
3. , , – числа.
В данном случае обозначают .
Примеры.
1.
2.
.
Иногда формулу интегрирования по частям приходится применять более одного раза.
Пример.
.
Интегрирование простейших рациональных дробей
1. Интегралы вида сводят к табличным заменой .
2. Интегралы вида разбиваются на сумму двух интегралов и . Первый решается заменой . А второй представляет собой табличный интеграл.
3. Интегралы вида решаются с помощью выделения полного квадрата в знаменателе
.
Аналогично решаются интегралы вида .
Определенный интеграл
Пусть функция определена и ограничена на и произвольное разбиение этого отрезка на элементарных отрезков. На каждом отрезке выберем точку . Тогда сумма называется интегральной суммой для функции на отрезке .
На каждом отрезке выберем точку . Тогда сумма называется интегральной суммой для функции на отрезке .
Если предел интегральной суммы при стремлении к нулю существует и конечен, то он называется определенным интегралом от функции в пределах от до и обозначается:
.
Определенный интеграл не должен зависеть от способа выбора точек и точек
Для вычисления определенного интеграла используется формула Ньютона-Лейбница:
,
где любая первообразная функции на отрезке .
Таким образом, при вычислении определенного интеграла с использованием формулы Ньютона-Лейбница сначала, используя технику нахождения неопределенного интеграла, находят первообразную для подынтегральной функции , а затем вычисляют приращение первообразной на данном отрезке.
Примеры.
1.
2.
Таблица основных неопределенных интегралов. Правила интегрирования.
 Интегралы от степенной, показательной, тригонометрических функцийГлавные интегралы, которые должен знать каждый студент
Интегралы от степенной, показательной, тригонометрических функцийГлавные интегралы, которые должен знать каждый студентПеречисленные интегралы – это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!
Интеграл от константы
∫Adx=Ax+C (1)Интегрирование степенной функции
В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.
∫xdx=x22+C (2)∫x2dx=x33+C (3)
∫1xdx=2x+C (4)
∫1xdx=ln|x|+C (5)
∫1x2dx=−1x+C (6)
∫xndx=xn+1n+1+C(n≠−1) (7)
Интегралы от показательной функции и от гиперболических функций
Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.
Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.
∫axdx=axlna+C(a>0,a≠1) (9)
∫shxdx=chx+C (10)
∫chxdx=shx+C (11)
Базовые интегралы от тригонометрических функций
Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен “минус косинусу”, а вот интеграл от cosx равен “просто синусу”:
∫sinxdx=−cosx+C (12)∫cosxdx=sinx+C (13)
∫1cos2xdx=tgx+C (14)
∫1sin2xdx=−ctgx+C (15)
Интегралы, сводящиеся к обратным тригонометрическим функциям
Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) – частный случай (19).
∫11+x2dx=arctgx+C=−arcctgx+C (16)∫1×2+a2=1aarctgxa+C(a≠0) (17)
∫11−x2dx=arcsinx+C=−arccosx+C (18)
∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0) (19)
Более сложные интегралы
Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.
Они также используются достаточно часто, а их вывод довольно утомителен.
∫1×2−a2dx=ln|x+x2−a2|+C (21)
∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) (22)
∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) (23)
∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) (24)Общие правила интегрирования
1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx (25)
2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫(f(x)−g(x))dx=∫f(x)dx−∫g(x)dx (26)
3) Константу можно выносить за знак интеграла: ∫Cf(x)dx=C∫f(x)dx (27)
Легко заметить, что свойство (26) – это просто комбинация свойств (25) и (27).
4) Интеграл от сложной функции, если внутренняя функция является линейной: ∫f(Ax+B)dx=1AF(Ax+B)+C(A≠0) (28)
Здесь F(x) – первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.
Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:
∫f(x)g(x)dx=?∫f(x)g(x)dx=? (30)Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ “борьбы” с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже “школьные” формулы алгебры или тригонометрии.
Простой пример на вычисление неопределенного интеграла
Пример 1. Найти интеграл: ∫(3×2+2sinx−7ex+12)dxВоспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем: ∫3x2dx+∫2sinxdx−∫7exdx+∫12dx
Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду
3∫x2dx+2∫sinxdx−7∫exdx+12∫1dxА теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:
Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:
После элементарных преобразований получаем окончательный ответ:
x3−2cosx−7ex+12x+CПроверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.
Сводная таблица интегралов
| ∫Adx=Ax+C |
| ∫xdx=x22+C |
| ∫x2dx=x33+C |
| ∫1xdx=2x+C |
| ∫1xdx=ln|x|+C |
| ∫1x2dx=−1x+C |
| ∫xndx=xn+1n+1+C(n≠−1) |
| ∫exdx=ex+C |
| ∫axdx=axlna+C(a>0,a≠1) |
| ∫shxdx=chx+C |
| ∫chxdx=shx+C |
| ∫sinxdx=−cosx+C |
| ∫cosxdx=sinx+C |
| ∫1cos2xdx=tgx+C |
| ∫1sin2xdx=−ctgx+C |
| ∫11+x2dx=arctgx+C=−arcctgx+C |
| ∫1×2+a2=1aarctgxa+C(a≠0) |
| ∫11−x2dx=arcsinx+C=−arccosx+C |
| ∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0) |
| ∫1×2+a2dx=ln|x+x2+a2|+C |
| ∫1×2−a2dx=ln|x+x2−a2|+C |
| ∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) |
| ∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) |
| ∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) |
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике. Будем решать Ваши проблемы вместе!
Будем решать Ваши проблемы вместе!
07.4.1. Основные правила интегрирования. Замена переменной в определенн
ТЕОРЕМА 5. Пусть: 1) F(X) — непрерывная функция на отрезке [А, b]; 2) Функция φ(T) дифференцируема на [α, β], Причем φ‘(T) непрерывна на [α, β] и множеством значений функции φ(T) является отрезок [А, b], 3) φ(α) = А, φ(β) = b. Тогда справедлива формула
Формула (7.12) называется Формулой замены переменной Или Подстановки в определенном интеграле.
Заметим, что при вычислении определенного интеграла с помощью замены переменной нет нужды возвращаться к прежней переменной, как это делалось при вычислении неопределенного интеграла, так как определенный интеграл представляет собой число, которое согласно формуле (7. 12) равно значению каждого из рассматриваемых интегралов. Теперь при подстановке следует сначала найти новые пределы интегрирования и затем выполнить необходимые преобразования подынтегральной функции.
12) равно значению каждого из рассматриваемых интегралов. Теперь при подстановке следует сначала найти новые пределы интегрирования и затем выполнить необходимые преобразования подынтегральной функции.
Заметим также, что при замене переменной в определенном интеграле необходимо соблюдать условия теоремы 7.5, иначе можно получить неверный результат (особое внимание следует уделять выполнению условия 2 теоремы).
Вычислить определенные интегралы методом подстановки.
Решение. Выполним подстановку T = 1 + Х2. Тогда Dt = 2Х Dx, t = 1 при Х = 0 и T = 2 при Х = 1. Поскольку функция Х = Непрерывна на [1, 2], то и новая подынтегральная функция также непрерывна, и, значит, для нее в силу теоремы 7.5 существует первообразная на этом отрезке. Получаем
Решение. Применим здесь подстановку Х = A Sin T. Тогда Dx = A cos T Dt, = A cos T, T = arcsin , T = 0 при X = 0, T = при X = А. Подставляя все это в исходный интеграл, получим
Тогда Dx = A cos T Dt, = A cos T, T = arcsin , T = 0 при X = 0, T = при X = А. Подставляя все это в исходный интеграл, получим
Решение. По формуле Ньютона-Лейбница имеем
Вычислим этот интеграл при помощи замены переменной T = tg Х. Тогда T = 0 при Х = 0 и T = 0 при Х = π, Х = arctg T, Т. е. Dx = Dt / (l + T2). Подстановка в исходный интеграл дает
Полученное противоречие объясняется тем, что функция замены переменной T = Tg X имеет разрыв при Х = π/2 и не удовлетворяет условию 2 теоремы 7.5.
| < Предыдущая | Следующая > |
|---|
Свойства определенных интегралов
Интегрирует: \ (f \), \ (g \), \ (u \), \ (v \)
Первообразные: \ (F \), \ (G \)
Независимые переменные: \ (x \), \ (t \)
Пределы интегрирования: \ (a \), \ (b \), \ (c \), \ (d \)
Подынтервалы интегрирования: \ (\ Delta {x_i} \)
Произвольная точка подынтервала: \ ({\ xi_i} \)
Натуральные числа: \ (n \), \ (i \)
Площадь криволинейной трапеции: \ (S \)
- Пусть вещественная функция \ (f \ left (x \ right) \) определена и ограничена на интервале \ (\ left [{a, b} \ right] \).
 {\, \ prime} \ left (x \ right) = g \ left (x \ right). \)
{\, \ prime} \ left (x \ right) = g \ left (x \ right). \)
Исчисление – свойства определенных интегралов
Это устройство не может отображать анимацию Java. Вышеупомянутое статическое изображение заменяет1. Правило нуля и обратные пределы
Аплет показывает график экспоненциальной функции с площадью под кривой от a до b зеленым цветом. Перетащите ползунок a или b , чтобы сделать a = b . Какой район? Это иллюстрирует правило нуля : Теперь перетащите ползунки так, чтобы b < a .Что происходит с районом? Как видите, меняет на противоположные пределы определенного интеграла, меняя знак, или: .
2. Постоянное множественное правило
Выберите второй пример из раскрывающегося меню. Это показывает линию и область под кривой от a до b в зеленом. Также показана вторая функция (красным цветом), которая является постоянным кратным c первой функции. (т.е. h ( x ) = c f ( x )).Изначально c = 2. Что вы заметили в областях (значения областей показаны в верхнем левом углу графика)? Перетащите ползунок c или введите другие значения для c в поле ввода c . Что ты заметил? Попробуйте сделать c равным -1. Это иллюстрирует правило множественного числа констант : Другими словами, если подынтегральное выражение в определенном интеграле умножить на константу, вы можете «вытащить константу за пределы» интеграла.
(т.е. h ( x ) = c f ( x )).Изначально c = 2. Что вы заметили в областях (значения областей показаны в верхнем левом углу графика)? Перетащите ползунок c или введите другие значения для c в поле ввода c . Что ты заметил? Попробуйте сделать c равным -1. Это иллюстрирует правило множественного числа констант : Другими словами, если подынтегральное выражение в определенном интеграле умножить на константу, вы можете «вытащить константу за пределы» интеграла.
3. Дополнительное правило
Выберите третий пример. Зеленая кривая – это линия f ( x ) = x , синяя кривая – это экспоненциальная функция g ( x ) = e x а красная функция – их сумма, h ( x ) = f ( x ) + g ( x ). Что вы замечаете в областях? Переместите ползунки a и b и посмотрите, сохраняется ли эта связь. Вы должны заметить, что площадь под красной кривой представляет собой сумму площадей под синей и зеленой кривыми. Это имеет смысл, поскольку суммы Римана состоят только из высоких тонких прямоугольников, а высота красных прямоугольников – это просто сумма высот зеленого и синего прямоугольников.
Итак, правило добавления гласит: Это говорит о том, что интеграл от суммы двух функций – это сумма интегралов каждой функции.
Показывает плюс / минус, так как это правило работает для разницы двух функций.
(попробуйте, отредактировав определение h ( x ) на f ( x ) – g ( x )).
Вы должны заметить, что площадь под красной кривой представляет собой сумму площадей под синей и зеленой кривыми. Это имеет смысл, поскольку суммы Римана состоят только из высоких тонких прямоугольников, а высота красных прямоугольников – это просто сумма высот зеленого и синего прямоугольников.
Итак, правило добавления гласит: Это говорит о том, что интеграл от суммы двух функций – это сумма интегралов каждой функции.
Показывает плюс / минус, так как это правило работает для разницы двух функций.
(попробуйте, отредактировав определение h ( x ) на f ( x ) – g ( x )).
4. Дополнение внутреннее
Выберите четвертый пример. Здесь показана одна функция: f ( x ) = e x . Зеленая область – от a до c , а синяя область – от c до b . Значения этих двух областей плюс значение области от a до b отображаются в верхнем левом углу. Что вы заметили во взаимосвязи между этими тремя областями? Попробуйте перетащить ползунок c , чтобы проверить, сохраняется ли эта связь, в то время как c находится между a и b .Теперь попробуйте перетащить c за a или b ; отношения все еще сохраняются? Это называется внутренним добавлением : Другими словами, вы можете разделить определенный интеграл на два интеграла с одним и тем же подынтегральным выражением, но с разными пределами, если соблюдается шаблон, показанный в правиле.
Что вы заметили во взаимосвязи между этими тремя областями? Попробуйте перетащить ползунок c , чтобы проверить, сохраняется ли эта связь, в то время как c находится между a и b .Теперь попробуйте перетащить c за a или b ; отношения все еще сохраняются? Это называется внутренним добавлением : Другими словами, вы можете разделить определенный интеграл на два интеграла с одним и тем же подынтегральным выражением, но с разными пределами, если соблюдается шаблон, показанный в правиле.
5. Доминирование
Выберите пятый пример. Зеленая кривая представляет собой экспоненту, f ( x ) = ½ e x , а синяя кривая также является экспоненциальной, g ( x ) = e x .В интервале от a до b , g ( x ) всегда больше, чем f ( x ). Это означает, что прямоугольники в сумме Римана для г ( x ) всегда будут выше, чем прямоугольники для f ( x ). Следовательно, площадь под г будет больше, чем площадь под f , как вы можете видеть, в данном случае верно.
Следовательно, площадь под г будет больше, чем площадь под f , как вы можете видеть, в данном случае верно.
Если g ( x ) ≥ f ( x ) на закрытом интервале [ a , b ], то В качестве особого случая установите f ( x ) = 0, введя в поле определения f и нажав Enter.Это говорит о том, что если g положителен всюду на некотором интервале, то определенный интеграл также положителен на этом интервале.
6. Мин. – Макс. Неравенство
Выберите шестой пример. Функция: f ( x ) = e x , показано зеленым цветом. Высота меньшего зеленовато-серого прямоугольника соответствует минимальному значению f на интервале [ a , b ], а высота темно-серого прямоугольника является максимальным значением f на том же интервале. интервал.Ясно, что область под f находится где-то между площадью этих двух прямоугольников. Формально мы говорим, что где min f – минимальное значение f на [ a , b ], а max f – максимальное значение f на этом интервале. ( b – a ) – ширина интервала (и показанных прямоугольников).
Формально мы говорим, что где min f – минимальное значение f на [ a , b ], а max f – максимальное значение f на этом интервале. ( b – a ) – ширина интервала (и показанных прямоугольников).
7. Площадь между кривыми
Выберите седьмой пример. Это показывает область между двумя линейными функциями: f ( x ) как верхняя функция зеленым цветом и g ( x ) как нижняя функция синим цветом.Вы можете думать о площади между двумя кривыми двумя разными способами. Вы можете найти площадь верхней функции и вычесть из нее площадь нижней функции, или Вы также можете подумать о сумме Римана, в которой вершины прямоугольников находятся в верхней функции, а нижняя часть прямоугольников – в нижней функции. Тогда высота прямоугольников составляет f ( x ) – g ( x ), поэтому площадь равна
Попробуйте отредактировать определение g ( x ), поставив знак минус впереди (т. е.е., сделайте – 0,5 x ) и нажмите Enter. Есть ли смысл в увеличении площади между кривыми? Удалите только что добавленный минус (т. Е. Сделайте g ( x ) = 0,5 x ) и составит f ( x ) = – x (т.е. поставьте знак минус перед определением для f и нажмите Enter). Что происходит с районом? Почему он отрицательный, если «верхняя» функция фактически находится ниже «нижней» функции?
е.е., сделайте – 0,5 x ) и нажмите Enter. Есть ли смысл в увеличении площади между кривыми? Удалите только что добавленный минус (т. Е. Сделайте g ( x ) = 0,5 x ) и составит f ( x ) = – x (т.е. поставьте знак минус перед определением для f и нажмите Enter). Что происходит с районом? Почему он отрицательный, если «верхняя» функция фактически находится ниже «нижней» функции?
8.Пересечение кривых
Выберите восемь примеров. Это показывает более сложную ситуацию, когда две функции пересекаются. Площадь слева от точки пересечения будет считаться отрицательно, потому что g ( x ) больше в этой области, а площадь справа от точки пересечения будет считаться положительно, потому что f ( x ) больше.
Исследуйте
Вы можете поэкспериментировать с собственными примерами, выбрав свойство в поле выбора; это настроит поля ввода, ползунки и график соответствующим образом. Затем вы можете ввести определения функций, значения для a , b и c (в соответствии с примером) и масштабировать / панорамировать график.
Затем вы можете ввести определения функций, значения для a , b и c (в соответствии с примером) и масштабировать / панорамировать график.
Другие темы «Определенный интеграл»
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
– исчисление, как
В исчислении «правило сумм» на самом деле представляет собой набор из трех различных правил, в зависимости от того, для чего вы его используете.Щелкните раздел, чтобы перейти к нужному вам правилу:
- Пределы
- Производные инструменты
- Интеграция
Правило суммы (также называемое правилом суммы функций) для пределов
Лимит суммы равен сумме лимитов. Другими словами, определите предел для каждой части, а затем сложите их вместе.
Пример : Найдите предел при x → 2 для x 2 + 5
- Предел x 2 при x → 2 (с использованием прямой подстановки) равен x 2 = 2 2 = 4
- Предел постоянной 5 (правило 1 выше) равен 5
- Складываем (1) и (2) вместе: 4 + 5 = 9
Обратите внимание, что в исчислении есть еще одно правило сумм, связанное с интегрированием. Не путайте эти два понятия (если вы имеете дело с ограничениями, придерживайтесь этой страницы, а для интегралов см .: Правило суммы: определение и примеры).
Не путайте эти два понятия (если вы имеете дело с ограничениями, придерживайтесь этой страницы, а для интегралов см .: Правило суммы: определение и примеры).
Правило расширенной суммы:
Все это говорит о том, что вы можете продолжать добавлять пределы к правилу сумм.
Пример : Найдите предел при x → 2 для x 2 + 5 + 10x
- Предел x 2 при x → 2 (с использованием прямой подстановки) равен x 2 = 2 2 = 4
- Предел постоянной 5 (правило 1 выше) равен 5
- Предел 10x (снова используя прямую замену) = 10 (2) = 20
- Складываем (1), (2) и (3) вместе: 4 + 5 + 20 = 29
Правило сумм для производных гласит, что если у вас есть две функции f + g, то производная – это просто сумма двух производных: f ’+ g’.
Пример вопроса: Какая производная y = x + x 2 ?
Шаг 1: Найдите отдельные производные (игнорируя символ +). В этом примере у вас есть две производные: x и x 2 :
В этом примере у вас есть две производные: x и x 2 :
- Производная y = x равна y ’= 1
- Производная y = x 2 равна y ’= 2x
Шаг 2: Добавьте производные из шага 1. На самом деле вы не суммируете их (как в 1 + 2 = 3), а просто помещаете между ними символ «+» (как в 1 + 2):
Складывая их вместе, получаем y = 1 + 2x
Правило сумм гласит, что если у вас есть две функции, сумма (сложение) их интегралов всегда равна интегралу их суммы.Другими словами, если у вас есть набор аддитивных функций, вы можете интегрировать их по очереди.
Это правило применяется как к определенным интегралам, так и к неопределенным интегралам.
Правило суммы для неопределенных интегралов
Для неопределенных интегралов правило сумм:
Правило сумм для неопределенных интегралов.
Где:
- f (x) – интегрируемая функция (подынтегральное выражение ),
- dx – переменная, по которой мы интегрируем.
Пример
Интегрируйте следующее выражение, используя правило сумм:
Шаг 1: Перепишите уравнение в два интеграла:
∫ (4x 2 + 1) / dx становится:
Шаг 2: Используйте обычные правила интеграции для интеграции каждой части.
∫4x 2 dx
∫ 1 шт.
- Здесь интеграл постоянной – это та константа, умноженная на x:
∫ x dx = 1 * x = x.
Шаг 3: Суммируйте все части и добавьте константу:
Правило суммы для определенных интегралов
Для определенных интегралов правило сумм другое (но не намного). Основное отличие состоит в том, что после выполнения описанных выше шагов для нахождения неопределенного интеграла вам необходимо вычислить значения в пределах интегрирования.
В качестве примера добавим границу от 0 до 4 к указанной выше задаче:
Шаг 1. Найдите неопределенный интеграл.Для этого конкретного примера мы уже вычислили неопределенный интеграл выше, который был:
Расчет границ
В следующей части, которая отличается от шагов, описанных выше для неопределенного интеграла, вы ищите конкретную область. В этом примере это область между 0 и 4 на графике (т.е. границы интегрирования, указанные в задаче):
Шаг 1: Вычислите интеграл по верхней границе (которая равна 4):
Шаг 2 : Вычислить интеграл по нижней границе (которая равна 0):
Шаг 3: Вычислить окончательный ответ путем вычитания частей (верхняя граница – нижняя граница):
Вот и все!
————————————————– —————————-Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Wolfram | Примеры альфа: интегралы
Неопределенные интегралы
Найдите первообразные математических выражений.
Вычислить неопределенный интеграл:
Вычислите неопределенный интеграл, который нельзя выразить элементарными терминами:
Сгенерируйте таблицу интегралов, содержащих заданную функцию:
Другие примеры
Определенные интегралы
Найдите интегралы с нижним и верхним пределами, также известные как интегралы Римана.
Вычислить определенный интеграл:
Вычислить неправильный интеграл:
Составьте таблицу определенных интегральных формул:
Другие примеры
Кратные интегралы
Вычисляет определенные вложенные интегралы от нескольких переменных.
Вычислить кратный интеграл:
Вычислить интеграл по неограниченной области:
Другие примеры
Другие примеры
Численное интегрированиеИнтегрируйте выражения, используя численное приближение.
Численно интегрируйте функции, которые не могут быть объединены символически:
Приближаем интеграл с помощью указанного численного метода:
Другие примеры
Интегральные представления
Изучите интегральные представления различных математических функций.
Найдите интегральные представления для функции:
Другие примеры
Интегралы, относящиеся к специальным функциям
Найдите определенные или неопределенные интегралы, связанные с определенной специальной функцией.
Изучите интересные неопределенные интегралы, содержащие специальные функции:
Изучите интересные определенные интегралы, содержащие специальные функции:
Другие примеры
Неопределенные интегралы – Задача 1
Одним из полезных свойств неопределенных интегралов является правило постоянного кратного числа.Это правило означает, что вы можете извлечь константы из интеграла, что может упростить задачу. Например, интеграл от 2x + 4 такой же, как 2, умноженный на интеграл от x + 2. Однако важно, чтобы из интеграла извлекались только константы, а не переменные.
Еще одно свойство – это правило мощности первообразных (помните, что принять интеграл чего-либо – значит антидифференцировать). Правило мощности утверждает, что первообразная x n равна x n + 1 / n + c, где c – некоторая константа.
Решим несколько неопределенных интегралов. Сначала нам понадобятся два свойства. Это свойство; постоянное множественное правило.
Если вы интегрируете постоянную, умноженную на некоторую функцию, вы можете извлечь константу из интегралов, это действительно полезно. Мы используем это в этих примерах. Второй – это властное правило антипроизводных. Когда вы интегрируете x в n, антипроизводные равны 1 по n плюс 1, x по n плюс 1 плюс c.Итак, мы используем и то, и другое.
Давайте рассмотрим эту проблему. Он говорит: выполните антидифференцировку. Это хорошо, потому что напоминает нам, что решение неопределенных интегралов означает антидифференцирование; придумав первообразные этой функции. Проверьте, дифференцируя свой ответ. Студенты этого недостаточно делают. Вы всегда должны проверять свой ответ, если не уверены в том, что придумали. Поэтому я хочу попытаться приучить вас к этому, сделав это сам.
Итак, прежде всего, давайте воспользуемся возможностью использовать правило кратных постоянных для этого интеграла.3 – константа, так что могу вытащить. Это делает интеграл таким: x до 4-го dx. Таким образом, это 3-кратный интеграл от x до 4-го dx. Этот интеграл можно решить с помощью этой формулы. Итак, n равно 4, поэтому у меня будет 1 больше 4 плюс 1; 1 на 5. Итак, это 3 умножения на 1 на 5 x к 5, плюс, назовем это c1.
Теперь я собираюсь распределить 3 по этим условиям. Я получаю 3 / 5x к 5-му плюс 3 раза c1. Обычно в конце вы просто конвертируете это в новую константу и называете ее c.3 раза c1 – это просто произвольная константа, поэтому вы можете просто назвать ее c. Думайте об этом как о переименовании константы. 3 раза переименование c1, просто c. Итак, это мой набор первообразных. 3 / 5x к 5-му плюс c.
Теперь я хочу проверить, дифференцируя. Так что я собираюсь выделить это и, надеюсь, снова получу это. Так что позвольте мне сделать это здесь. Производная по x от 3/5 x до пятой плюс c. Итак, я получаю 3/5 раза, а производная x до 5-го равна 5x для четвертого. Производная части плюс c равна нулю.Теперь 3/5 умножить на 5 равно 3. Итак, я получаю 3х до 4-го. Я начал с этой функции. Так что это правильно. Это проверяет.
Давайте посмотрим на другой пример. При интеграле 12 по x до 5-го. Теперь я хочу переписать это в форме, которая позволит мне использовать правило мощности. Когда у вас в знаменателе степень x, вы все равно можете использовать правило мощности. Это то же самое, что 12 умножить на x до -5 dx. К этой функции будет применяться правило мощности.
Во-первых, я хочу убрать 12, используя постоянное правило.Итак, 12-кратный интеграл от x до -5 dx. Правило мощности гласит, что это будет x до -5. Я всегда добавляю 1. Может, мне стоит это написать. X до -5 плюс 1 больше -5 плюс 1 плюс, я назову это c1.
Теперь -5 плюс 1 равно -4. Таким образом, это 12 умноженных на x: -4 больше -14 плюс c1. Тогда я могу распределить 12. Итак, 12, разделенное на -4, даст мне -3x к -4 плюс 12c1. Тогда я могу переименовать это просто c. Я мог бы также записать это как -3 вместо x до 4-го. Итак, это мой набор первообразных; -3 больше x до 4-го плюс c.
Теперь я должен проверить это дифференцированием. Я собираюсь начать с этой формы, поскольку, когда я дифференцирую, я также использую правило мощности для деривативов. Таким образом, производная от -3x до -4 плюс c в -3 раза больше производной от x до -4. Это -4x к, помните, что правило мощности уменьшилось, поэтому от -4 до -5. Тогда производная плюс c, 0, -3, умноженная на -4, будет 12. Таким образом, я получаю 12x до -5. Давай просто проверим. Это то, с чего я начал, от 12x до -5. Так что это правильно. Значит, это мой правильный ответ.Это мои первообразные от 12 по х до 5-го.
Определенные интегралы | Блестящая вики по математике и науке
Являясь одним из основных инструментов исчисления, интегралы обладают большим количеством свойств, вытекающих из геометрии координатной плоскости, определения функционала и взаимосвязи между интегралами и производными. Интегралы также имеют алгебраическую интерпретацию, которая позволяет использовать очень полезные методы, такие как uuu-подстановка, которые необходимы для многих типов интегральных вычислений (и в доказательствах многих свойств ниже!).{g (b)} \ frac {f \ big (h (u) \ big)} {g ‘(u)} \, du. Ab f (x) dx = ∫g (a) g (b) g ′ (u) f (h (u)) du.
Обратите внимание, что, например, одно из свойств в предыдущем подразделе следует из uuu-подстановки u = a + b − xu = a + b – xu = a + b − x.
Наконец, в некоторых свойствах сравниваются значения различных интегралов. Многие из них расширяют интуицию мышления об интеграле как о типе суммирования.
Если f (x) abf (x) dx <∫abg (x) dx.{1 / p}. (Ab ∣∣ f (x) + g (x) ∣∣ pdx) 1 / p≤ (∫ab ∣∣ f (x) ∣∣ pdx) 1 / p + (∫ab ∣∣ G (x) ∣∣ pdx) 1 / стр. Исчисление – это фундаментальная часть любого типа статистических упражнений. Хотя вы, возможно, не используете производные и интеграл в своей повседневной работе в качестве аналитика, исчисление лежит в основе многих используемых нами концепций: максимизации, ожидания и кумулятивной вероятности. Среднее значение величины – это тип взвешенного среднего, где потенциальные значения, грубо говоря, взвешиваются по их вероятности.\ infty_ {j = 1} x_j P (X = x_j) \] даже более конкретно, если потенциальные значения \ (X \) конечны, то мы можем записать ожидаемое значение как взвешенное среднее, где веса – это вероятность того, что значение произойдет. \ [E (X) = \ large \ sum_ {x} \ quad \ left (\ underbrace {x} _ {\ text {value}} \ cdot \ underbrace {P (X = x)} _ {\ text { вес, или PMF}} \ right) \] Производная \ (f \) в \ (x \) – это скорость его изменения в \ (x \): насколько \ (f (x) \) изменяется при изменении \ (x \).Скорость изменения является дробной – рост за пробег – но поскольку не все линии прямые и формула нарастания за пробег даст нам разные значения в зависимости от исследуемого диапазона, нам нужно взять предел (Раздел 2 ). Определение 3.1 (производная) Пусть \ (f \) будет функцией, область определения которой включает открытый интервал, содержащий точку \ (x \). Производная от \ (f \) в точке \ (x \) равна \ [\ frac {d} {dx} f (x) = \ lim \ limits_ {h \ to 0} \ frac {f (x + h) -f (x)} {(x + h) -x} = \ lim \ limits_ {h \ to 0} \ frac {f (x + h) -f (x)} {h}
\] Есть два основных способа обозначить производное: Если \ (f (x) \) – прямая линия, производная – это наклон.Для кривой наклон изменяется на значения \ (x \), поэтому производная – это наклон линии, касательной к кривой в точке \ (x \). См., Например, рисунок 3.1. Рисунок 3.1: Производная как наклон Если \ (f ‘(x) \) существует в точке \ (x_0 \), то \ (f \) называется дифференцируемой в точке \ (x_0 \). Это также означает, что \ (f (x) \) непрерывно в \ (x_0 \). Предположим, что \ (f \) и \ (g \) дифференцируемы в \ (x \) и что \ (\ alpha \) – константа.Тогда функции \ (f \ pm g \), \ (\ alpha f \), \ (fg \) и \ (f / g \) (при условии \ (g (x) \ ne 0 \)) также являются дифференцируема в точке \ (x \). Дополнительно Постоянное правило: \ [\ left [k f (x) \ right] ‘= k f’ (x) \] Правило суммы: \ [\ left [f (x) \ pm g (x) \ right] ‘= f’ (x) \ pm g ‘(x) \] Имея немного больше алгебры, мы можем применить определение производных, чтобы получить формулу для производной продукта и производной частного. 2}, ~ g (x) \ neq 0 \] Наконец, один из способов представить себе мощность производных состоит в том, что они упрощают функцию на ступеньку ниже по сложности.{(m + 1) – 1}
\ конец {выравнивание *} \] Следовательно, правило выполняется для случая \ (k = m + 1 \), если мы предположили, что оно выполняется для \ (k = m \). В сочетании с первым случаем это завершает доказательство по индукции – теперь мы доказали, что утверждение верно для всех целых чисел \ (k = 1, 2, 3, \ cdots \). Чтобы показать, что это верно и для действительных дробей, мы можем доказать, что этот показатель выражается дробью двух целых чисел. Эти «правила» становятся очевидными при применении приведенного выше определения производной к каждому из «производных», но они возникают так часто, что лучше повторять, пока это не станет мышечной памятью.2-1} \) Первая производная применяет определение производных к функции, и ее можно выразить как \ [f ‘(x), ~~ y’, ~~ \ frac {d} {dx} f (x), ~~ \ frac {dy} {dx} \] Мы можем продолжать применять процесс дифференцирования к функциям, которые сами являются производными. 2} \ ] Аналогично, производная от \ (f ” (x) \) будет называться третьей производной и обозначается \ (f ” ‘(x) \).{\ прайм \ прайм \ прайм \ прайм} (х) & = 0 \\
\ конец {выравнивание *} \] Ранее, в разделе 3.1, мы говорили, что если функция дифференцируема в данной точке, то она должна быть непрерывной. Далее, если \ (f ‘(x) \) само непрерывно, то \ (f (x) \) называется непрерывно дифференцируемым. Все это имеет значение, потому что многие из наших выводов об оптимизации (раздел 4) основаны на дифференциации, и поэтому мы хотим, чтобы наша функция была дифференцируемой на как можно большем количестве уровней. Функция, которая непрерывно дифференцируема бесконечно, называется «гладкой».2 \) может показаться тривиальным, но правило сумм может быть легко применено к первому, в то время как на самом деле не очевидно, что делать со вторым. Составные функции формируются путем подстановки одной функции в другую и обозначаются как \ [(f \ circ g) (x) = f [g (x)]. \] Чтобы сформировать \ (f [g (x)] \), диапазон \ (g \) должен содержаться (по крайней мере частично) в области \ (f \). Область определения \ (f \ circ g \) состоит из всех точек в области определения \ (g \), для которых \ (g (x) \) находится в области определения \ (f \).2, 0 <х <\ infty \] Имея обозначение составных функций, теперь мы можем ввести полезное дополнительное правило, которое будет иметь дело с производной составных функций как цепочкой концентрических производных. Правило цепочки : Пусть \ (y = (f \ circ g) (x) = f [g (x)] \). Производная \ (y \) по \ (x \) равна \ [\ frac {d} {dx} \ {f [g (x)] \} = f ‘[g (x)] g’ ( x) \] Мы можем читать это как: «производная сложной функции \ (y \) – это производная от \ (f \), вычисленная в \ (g (x) \), умноженная на производную от \ (g \).« Цепное правило можно рассматривать как производную от «внешней», умноженную на производную «внутренней», помня, что производная внешней функции оценивается по значению внутренней функции. Глава 3 Исчисление | Предварительная подготовка по математике для политологов
Пример: среднее – это тип интеграла
Производные
Свойства производных инструментов
Производные финансовые инструменты высшего порядка (производные от производных финансовых инструментов)
Частные производные
Что происходит, когда изменяется не только переменная?
Если вы можете делать обычные производные, вы можете делать частные производные: просто сохраняйте все остальные входные переменные постоянными, кроме той, по которой вы дифференцируете. (Математические заметки Джо Блицштейна)
Предположим, теперь у нас есть функция \ (f \) двух (или более) переменных, и мы хотим определить скорость изменения относительно одной из переменных.Для этого мы должны найти его частную производную, которая определяется аналогично производной функции одной переменной.
Частичная производная : Пусть \ (f \) будет функцией переменных \ ((x_1, \ ldots, x_n) \). Частная производная от \ (f \) по \ (x_i \) равна
\ [\ frac {\ partial f} {\ partial x_i} (x_1, \ ldots, x_n) = \ lim \ limits_ {h \ to 0} \ frac {f (x_1, \ ldots, x_i + h, \ ldots , x_n) -f (x_1, \ ldots, x_i, \ ldots, x_n)} {h} \]
Изменяется только \ (i \) -я переменная – остальные считаются константами.2 f} {\ partial x \ partial y} (x, y) & = \ конец {выравнивание *} \]
Приближение серии Тейлора
Обычная форма аппроксимации, используемая в статистике, включает производные. Ряд Тейлора – это способ представления общих функций в виде бесконечного ряда (суммы бесконечных элементов) производных функции в некоторой точке \ (a \).
Например, ряды Тейлора очень полезны для представления нелинейных (читай: сложных) функций как линейных (читай: управляемых) функций. Таким образом, можно аппроксимировать функции , используя конечный ряд более низкого порядка, известный как полиномы Тейлора .2 \]
Чем больше добавляется производных, тем меньше остаток \ (R \) и тем точнее приближение. Доказательства, включающие пределы, гарантируют, что остаток сходится к 0 при увеличении порядка вывода.
Неопределенная интеграция
До сих пор мы интересовались поиском производной \ (f = F ‘\) функции \ (F \). Однако иногда нас интересует обратное: найти функцию \ (F \), для которой \ (f \) является ее производной. Мы называем \ (F \) первообразной \ (f \).{3x} \)
Из производных мы знаем, как манипулировать \ (F \), чтобы получить \ (f \). Но как вы выразите процедуру манипулирования \ (f \), чтобы получить \ (F \)? Для этого нам понадобится новый символ, который мы назовем неопределенным интегрированием.
Определение 3.3 (неопределенный интеграл) Записывается неопределенный интеграл от \ (f (x) \)
\ [\ int f (x) dx \]
и совпадает с первообразной \ (f \).
Пример 3.7 Нарисуйте функцию \ (f (x) \) и ее неопределенный интеграл \ (\ int \ limits f (x) dx \)
\ [f (x) = (x ^ 2-4) \]
Решение.3 – 4x + 1 \), потому что константа 1 исчезает при взятии производной.
Некоторые из этих функций показаны в нижней части рисунка 3.4 пунктирными линиями.
Рисунок 3.4: Множество неопределенных интегралов функции
Обратите внимание на эти примеры, что, хотя существует только одна производная для любой функции, существует несколько первообразных: одна для любой произвольной константы \ (c \). \ (c \) просто сдвигает кривую вверх или вниз по оси \ (y \). Если имеется дополнительная информация о первообразной — e.x} dx \)
Определенный интеграл: площадь под кривой
Если есть неопределенный интеграл, то должен быть определенным интегралом. В самом деле, есть, но понятие определенных интегралов исходит из другой цели: найти a под функцией. Мы обнаружим, возможно, примечательно, что формула, которую мы находим для получения суммы, оказывается выражаемой с помощью антипроизводной.
Предположим, мы хотим определить площадь \ (A (R) \) области \ (R \), определяемую кривой \ (f (x) \) и некоторым интервалом \ (a \ le x \ le b \) . nf (x_i ) \ Delta x \] и называется суммой Римана .3 + 50. \) Мы хотим приблизить площадь под кривой между значениями \ (x \) от 0 до 10. Мы можем сделать это в блоках произвольной ширины, где сумма прямоугольников (площадь которой равна ширине, умноженной на \ (f (x) \) вычисляется в середине полосы) показывает сумму Римана. Чем меньше ширина полос \ (\ Delta x \), тем точнее оценка \ (A (R) \).
Вот как мы определяем «Определенный» интеграл:
Определение 3.4 (Определенный интеграл (Риман)) Если для данной функции \ (f \) сумма Римана приближается к пределу как \ (\ Delta x \ to 0 \), то этот предел называется интегралом Римана от \ (f \) от \ (a \) до \ (b \).bf (x) dx \] как определенный интеграл \ (f \) от \ (a \) до \ (b \), и мы определили как площадь под «кривой» \ (f (x) \) от точки \ (x = a \) к \ (x = b \).
Основная теорема исчисления показывает нам, что эта сумма фактически является первообразной.
Теорема 3. \ prime (x) = f (x) \) на \ ((a, b) \) .х} dx = \) Из второй фундаментальной теоремы исчисления мы теперь знаем, что быстрый способ получить определенный интеграл – это сначала найти неопределенный интеграл, а затем просто подставить границы. Иногда подынтегральное выражение (то, что мы пытаемся взять интегралом) не представляется интегрируемым с использованием общих правил и первообразных. Метод, который можно попробовать, – это интеграция путем замены , которая связана с правилом цепочки. Предположим, мы хотим найти неопределенный интеграл \ [\ int g (x) dx \], но \ (g (x) \) сложный, и ни одна из формул, которые мы видели до сих пор, похоже, не применима немедленно. Уловка состоит в том, чтобы придумать новую функцию \ (u (x) \), такую, что \ [g (x) = f [u (x)] u ‘(x). \] Почему введение еще одной функции в конец упрощает вещи? Назовем первообразную \ (f \) \ (F \). Тогда цепное правило говорит нам, что \ [\ frac {d} {dx} F [u (x)] = f [u (x)] u ‘(x) \]. Итак, \ (F [u (x)] \) – первообразная \ (g \).Затем мы можем написать \ [\ int g (x) dx = \ int f [u (x)] u ‘(x) dx = \ int \ frac {d} {dx} F [u (x)] dx = F [u (x)] + c \] Подводя итог, процедура определения неопределенного интеграла \ (\ int g (x) dx \) методом подстановки: Интеграция путем замены
Интеграция по частям
Другой полезный метод интеграции – это интеграция по частям , которая связана с правилом дифференциации продукта. Правило продукта гласит, что \ [\ frac {d} {dx} (uv) = u \ frac {dv} {dx} + v \ frac {du} {dx} \] Интегрируя это и переставляя, мы получаем \ [\ int u \ frac {dv} {dx} dx = uv – \ int v \ frac {du} {dx} dx \] или \ [\ int u (x) v ‘(x) dx = u (x) v ( х) – \ int v (x) u ‘(x) dx \]
Более легко запомнить с помощью мнемоники «Ультрафиолетовое вуду»: \ [\ int u dv = uv – \ int v du \], где \ (du = u ‘(x) dx \) и \ (dv = v’ (x) dx \).

 pi / 2)
ax2.plot(x, np.sin(2 * x), label='$y=sin(2x)$')
ax2.fill_between(x_clip, np.sin(2 * x_clip), alpha=0.5)
ax2.legend()
ob.center_spines(grid=False, minor_ticks=False, ax=ax2)
ob.settle_axes(xmin=-0.5, xmax=3.6, ymin=-1.2, ymax=1.2,
xlabel="x", ylabel="y", ax=ax2)
ax2.set_xticks([np.pi/2, np.pi])
ax2.set_xticklabels([r'$\frac{\pi}{2}$', r'$\pi$'])
ax2.set_yticks([])
pi / 2)
ax2.plot(x, np.sin(2 * x), label='$y=sin(2x)$')
ax2.fill_between(x_clip, np.sin(2 * x_clip), alpha=0.5)
ax2.legend()
ob.center_spines(grid=False, minor_ticks=False, ax=ax2)
ob.settle_axes(xmin=-0.5, xmax=3.6, ymin=-1.2, ymax=1.2,
xlabel="x", ylabel="y", ax=ax2)
ax2.set_xticks([np.pi/2, np.pi])
ax2.set_xticklabels([r'$\frac{\pi}{2}$', r'$\pi$'])
ax2.set_yticks([])
 {\, \ prime} \ left (x \ right) = g \ left (x \ right). \)
{\, \ prime} \ left (x \ right) = g \ left (x \ right). \)