Правила производных функций: Правила вычисления производных - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Темы школьной программы — математика 5-11 класс. Таблица производных и правила дифференцирования функций

Таблица производных в алгебре нужна для решения целого ряда различных прикладных задач. Поскольку смысл производной иначе интерпретируется как «скорость изменения», то, каждый раз, беря производную, мы находим величину на ступеньку более «быструю», чем та, от которой мы берем производную. Например, беря производную от y(x) по x, мы фактически находим скорость изменения координаты y в зависимости от изменения координаты x, а беря производную от скорости изменения координаты y в зависимости от координаты x, мы находим ускорение.

Содержание

Что такое производная функции

Например, при использовании производной в физике, мы знаем, что производная расстояния s по времени — это скорость. Потому что скорость — это величина, характеризующая быстроту изменения расстояния в зависимости от времени. А производная скорости — ничто иное как ускорение, так как ускорение — это величина, характеризующая быстроту изменения скорости.
Поскольку производная находится по формуле: , то бесконечное количество различных функций усложняют задачу дифференцирования, так как удобно функцию, которую можно представить из различных элементарных функций, дифференцировать основываясь на уже выведенных выражениях для производных этих элементарных функций.

Характеристика производной и ее смысл

Производная характеризует быстроту изменения функции в зависимости от изменения аргумента.

Таблица производных

Таким образом, чтобы работать с производными, необходима таблица производных элементарных функций. Руководствуясь этой таблицей, можно взять производную от какой угодно функции. Но прежде чем работать с таблицей — нужно знать как брать производную функции, есть определенные правила дифференцирования, которые представим в таблице.

Правила дифференцирования

№ правила	Название правила	Правило дифференцирования
1	Производная постоянной величины	, С-постоянная
2	Производная суммы	.
3	Производная произведения постоянной на функцию	, С — постоянная
4	Производная переменной x
5	Производная произведения двух функций
6	Производная деления двух функций
7	Производная сложной функции

Таблица производных простых и сложных функций

Теперь таблица производных для элементарных и для сложных функций.

Номер формулы	Название производной	Основные элементарные функции	Сложные функции
1	Производная натурального логарифма по x
2	Производная логарифмической функции по основанию a
3	Производная по x в степени n
4	Производная квадратного корня
5	Производная a в степени x
6	Производная e в степени x
7	Производная синуса
8	Производная косинуса
9	Производная тангенса
10	Производная котангенса
11	Производная арксинуса
12	Производная арккосинуса
13	Производная арктангенса
14	Производная арккотангенса

Примеры нахождения производных

Пример 1

Пользуясь формулами и правилами дифференцирования, найти производную функции: .

Решение:

Мы использовали правило 2 дифференцирования суммы. Теперь найдем производную каждого слагаемого:

По формуле 3 «производная по x в степени n» (у нас в степени 2).

По правилам дифференцирования 3 и 4.

По первому правилу дифференцирования «производная постоянной равна нулю»

Итак, получим: .

Пример 2

Найти производную функции

Решение:

Находим производную, пользуясь правилам дифференцирования 6.

Ответ:

Пример 3

Найти производную функции

Решение: здесь все просто, мы возьмем производную из таблицы производных.

Ответ:

Пример 4

Найдите производную функции

Решение: Здесь мы уже имеем не простую функцию, а сложную функцию и брать производную мы будем по формуле 8 таблицы производных для сложных функций.

Ответ:

Пример 5

Пользуясь правилами дифференцирования и таблицей производных, найдите производную функции

Решение: У нас сложная функция, так как под корнем стоит не просто , а квадратная функция.

То есть мы имеем функцию вида .

Возьмем производную этой функции:

Ответ:

Пример 6

Найдите скорость тела, если траектория его движения задана уравнением м

Решение: скорость тела — это первая производная траектории по времени: . м/с.

Находим скорость тела:

Ответ: 3 м/с.

Итак, таблица производных и правила дифференцирования дают возможность легко брать производные и простых, и сложных функций.

Правила дифференцирования: формулы, производная функций, примеры

Формулы дифференцирования
Производная суммы двух функций
Производная функции с постоянным множителем
Производная произведения двух функций
Производная частного двух функций
Производная степенной функции
Примеры

п.

2)\ ‘=2x\). Поэтому $f'(1)=2\cdot 1=2$

п.2. Производная суммы двух функций

Рассмотрим функцию $h(x)$, которую можно представить в виде суммы двух других функций: $h(x)=f(x)+g(x)$. Найдем её производную из общего алгоритма.
Пусть $\triangle x$ – некоторое приращение аргумента. Тогда приращение функции $h(x)$: \begin{gather*} \triangle h=h(x+\triangle x)-h(x)=(f(x+\triangle x)+g(x+\triangle x))-(f(x)+g(x))=\\ =(f(x+\triangle x)-f(x))+(g(x+\triangle x)-g(x))=\triangle f+\triangle g \end{gather*} где $\triangle f$ и $\triangle g$ – приращения каждой из функций-слагаемых.
Ищем производную: \begin{gather*} h'(x)=\lim_{\triangle x\rightarrow 0}\frac{\triangle h}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle f+\triangle g}{\triangle x}= \lim_{\triangle x\rightarrow 0}\frac{\triangle f}{\triangle x}+\lim_{\triangle x\rightarrow 0}\frac{\triangle g}{\triangle x}=f'(x)+g'(x) \end{gather*} Или: $\left(f(x)+g(x)\right)’=f'(x)+g'(x)$

Производная суммы двух функций равна сумме производных: $$ \left(f(x)+g(x)\right)’=f'(x)+g'(x) $$

Например:
$\left(x^2+\frac1x\right)’=(x^2)’+\left(\frac1x\right)’=2x-\frac{1}{x^2}$

п.

2\)

п.4. Производная произведения двух функций

Рассмотрим функцию $h(x)$, которую можно представить в виде произведения двух других функций: $h(x)=f(x)\cdot g(x)$. Найдем её производную из общего алгоритма.
Пусть $\triangle x$ – некоторое приращение аргумента. Тогда приращение функции $h(x)$: \begin{gather*} \triangle h=h(x+\triangle x)-h(x)=(f(x+\triangle x)\cdot g(x+\triangle x))-(f(x)\cdot g(x)) \end{gather*} Приращения каждого из множителей: \begin{gather*} \triangle f=f(x+\triangle x)-f(x)\Rightarrow f(x+\triangle x)=\triangle f+f(x)\\ \triangle g=g(x+\triangle x)-g(x)\Rightarrow g(x+\triangle x)=\triangle g+g(x) \end{gather*} Подставим: \begin{gather*} \triangle h=(\triangle f+f(x))\cdot (\triangle g+g(x))-f(x)\cdot g(x)=\\ =\triangle f\cdot \triangle g+\triangle f\cdot g(x)+f(x)\cdot \triangle g+f(x)\cdot g(x)-f(x)\cdot g(x)=\\ =\triangle f\cdot \triangle g+\triangle f\cdot g(x)+f(x)\cdot \triangle g \end{gather*} Ищем производную: \begin{gather*} h'(x)=\lim_{\triangle x\rightarrow 0}\frac{\triangle h}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle f\cdot \triangle g+\triangle f\cdot g(x)+f(x)\cdot\triangle g}{\triangle x}=\\ =\lim_{\triangle x\rightarrow 0}\left(\frac{\triangle f}{\triangle x}\cdot\frac{\triangle g}{\triangle x}\right)+\lim_{\triangle x\rightarrow 0}\frac{\triangle f}{\triangle x}\cdot g(x)+f(x)\cdot\lim_{\triangle x\rightarrow 0}\frac{\triangle g}{\triangle x}=\\ =f'(x)\cdot g'(x)\cdot 0+f'(x)\cdot g(x)+f(x)\cdot g'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{gather*} Или: $\left(f(x)\cdot g(x)\right)’=f'(x)\cdot g(x)+f(x)\cdot g'(x)$

Производная произведения двух функций равна сумме двух слагаемых:
производная первой функции на вторую плюс первая функция на производную второй: $$ \left(f(x)\cdot g(x)\right)’=f'(x)\cdot g(x)+f(x)\cdot g'(x) $$

Например:
$ (x^2\sqrt{x})’=(x^2)’\cdot\sqrt{x}+x^2\cdot (\sqrt{x})’=2x\sqrt{x}+\frac{x^2}{2\sqrt{x}}=x\sqrt{x}\left(2+\frac12\right)=\frac52x\sqrt{x} $

п.

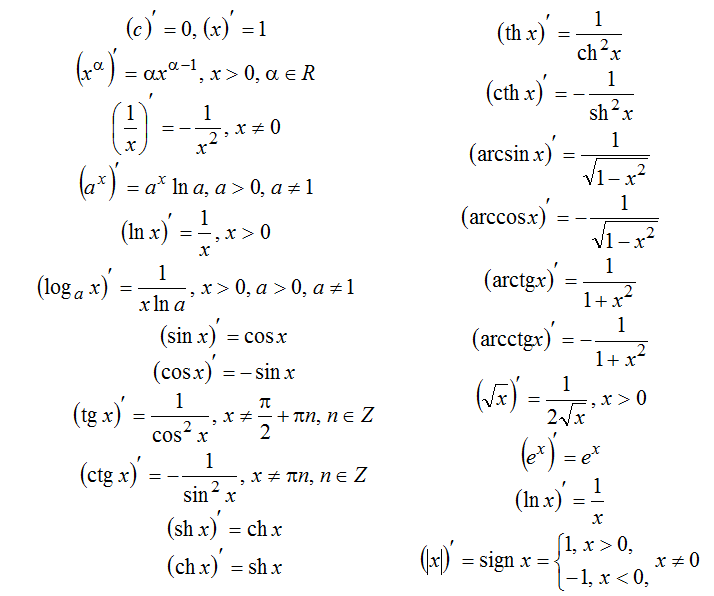5. Производная частного двух функций

Рассмотрим функцию $h(x)$, которую можно представить в виде частного двух других функций: $h(x)=\frac{f(x)}{g(x)}$. Найдем её производную из общего алгоритма.
Пусть $\triangle x$ – некоторое приращение аргумента. Тогда приращение функции $h(x)$: \begin{gather*} \triangle h=h(x+\triangle x)-h(x)=\frac{f(x+\triangle x)}{g(x+\triangle x)}-\frac{f(x)}{g(x)} \end{gather*} Приращения каждого из множителей: \begin{gather*} \triangle f=f(x+\triangle x)-f(x)\Rightarrow f(x+\triangle x)=\triangle f+f(x)\\ \triangle g=g(x+\triangle x)-g(x)\Rightarrow g(x+\triangle x)=\triangle g+g(x) \end{gather*} Подставим: \begin{gather*} \triangle h=\frac{\triangle f+f(x)}{\triangle g+g(x)}-\frac{f(x)}{g(x)}=\frac{\triangle f\cdot g(x)+f(x)\cdot g(x)-f(x)\cdot \triangle g-f(x)\cdot g(x)}{\left(\triangle g+g(x)\right)\cdot g(x)}=\\ =\frac{\triangle f\cdot g(x)-f(x)\cdot \triangle g}{\left(\triangle g+g(x)\right)\cdot g(x)}=\frac{\triangle f\cdot g(x)-f(x)\cdot \triangle g}{g(x+\triangle x)\cdot g(x)} \end{gather*} Ищем производную: \begin{gather*} h'(x)=\lim_{\triangle x\rightarrow 0}\frac{\triangle h}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle f\cdot g(x)-f(x)\cdot \triangle g}{\triangle x\cdot g(x+\triangle x)\cdot g(x)}=\\ =\frac{\lim_{\triangle x\rightarrow 0}\left(\frac{\triangle f}{\triangle x}\cdot g(x)\right)-\lim_{\triangle x\rightarrow 0}\left(f(x)\cdot\frac{\triangle g}{\triangle x}\right)}{g(x+0)\cdot g(x)}=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{g^2(x)} \end{gather*} Или: $ \left(\frac{f(x)}{g(x)}\right)’=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{g^2(x)} $

Производная частного двух функций равна дроби:
в числителе производная первой функции на вторую минус первая функция на производную второй, в знаменателе – квадрат второй функции: $$ \left(\frac{f(x)}{g(x)}\right)’=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{g^2(x)} $$

Например:
\begin{gather*} \left(\frac{3x+2}{x^2}\right)’=\frac{(3x+2)’\cdot x^2-(3x+2)\cdot (x^2)’}{(x^2)^2}=\frac{3x^2-(3x+2)\cdot 2x}{x^4}=\\ =\frac{3x^2-6x^2-4x}{x^4}=\frac{-3x^2-4x}{x^4}=-\frac{x(3x+4)}{x^4}=-\frac{3x+4}{x^3} \end{gather*}

п.

2=\frac12 \end{array} \right. \Rightarrow \left[ \begin{array}{l} x=0\\ x=\pm\frac{1}{\sqrt{2}} \end{array} \right. \end{gather*} Ответ: $\left\{0;\pm\frac{1}{\sqrt{2}}\right\}$

Производная функции в точке (в картинках)

Приводятся определения, теоремы, свойства и методы вычислений производной функции в точке в сжатом виде – в виде изображений. Каждая картинка снабжена ссылкой на страницу с подробным изложением материала.

Далее приводятся главные картинки раздела «Производная функции в точке». На них изображены основные понятия и формулы дифференцирования. Каждое изображение снабжено заголовком, описанием и ссылкой на страницу с подробным изложением материала. Пройдя по этой ссылке можно посмотреть доказательство выбранного правила и примеры его применения. Также, просматривая картинки, можно освежить в памяти основные понятия, связанные с вычислением производных.

Определение производной и основные понятия

Производная функции в точке – определения, теоремы и свойства

Приводятся формулировки определений, теорем и свойств производной функции одной переменной в точке. Даны методы вычислений производных и формулы производных элементарных функций. Рассмотрены производные и дифференциалы высших порядков.

Примеры решений производных

Страница содержит ссылки на 51 пример решений производных.

Физический смысл производной

На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени.

Определение производной функции в точке

Определение производной функции в точке. Примеры вычисления производных, используя определение. Односторонние производные справа и слева. Лемма об односторонних производных.

Дифференцируемые функции в точке – определение и свойства

Определение дифференцируемой функции одной переменной в точке. Важность понятия дифференцируемости для функций, зависящих от многих переменных. Доказательство теорем: об эквивалентности дифференцируемости и существованием производной; о непрерывности дифференцируемой функции.

Геометрический смысл производной

Проведен анализ геометрического смысла производной. Выявлено, что производная функции в точке связана с углом наклона касательной, проведенной к графику функции в рассматриваемой точке. Дано определение касательной, и получено ее уравнение. Рассмотрены случаи, когда производная равна бесконечности.

Касательная и нормаль к графику функции

Уравнения касательной и нормали к графику функции в точке. Определения, подкасательной и поднормали. Угол между двумя кривыми. Полезные формулы аналитической геометрии. Примеры решения задач на составления уравнений касательной и нормали, и на вычисление угла между кривыми.

Первый дифференциал функции в точке

Определение первого дифференциала функции, его суть и геометрический смысл. Доказательство арифметических свойств и инвариантности формы первого дифференциала.

Таблица производных элементарных функций

Представлена таблица производных элементарных функций для обучающихся студентов. Приводится таблица производных сложных функций. Даны основные правила дифференцирования.

Методы вычисления производных

Правила дифференцирования – основные формулы вычисления производных

В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила.

Производная постоянной функции (константы)

Производная постоянной (константы). Вынесение постоянной за знак производной. Примеры вычисления производных. Пример вычисления производной от функции, составленной из корней.

Производная суммы и разности функций

Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы.

Производная произведения двух функций

Формула производной произведения двух функций. Доказательство и подробно разобранные примеры применения этой формулы.

Формула Лейбница для n-й производной произведения двух функций

Приводится формула Лейбница для вычисления n-й производной произведения двух функций. Дано ее доказательство двумя способами. Рассмотрен пример вычисления производной n-го порядка.

Производная дроби из двух функций

Формула производной дроби из двух функций. Доказательство двумя способами. Подробно разобранные примеры дифференцирования частного.

Доказательство формулы производной сложной функции

Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных.

Примеры применения формулы производной сложной функции

Приводятся примеры вычисления производных с применением формулы производной сложной функции.

Теорема о производной обратной функции

Приводится доказательство теоремы о производной обратной функции. Приводятся примеры применения этой теоремы.

Вычисление производных с помощью логарифмической производной

Приводятся примеры вычисления производных с помощью логарифмической производной.

Вычисление производных степенно-показательных функций

Определение степенно-показательной функции. Вывод формулы для вычисления ее производной. Подробно разобраны примеры вычисления производных степенно-показательных функций.

Примеры вычисления производных высших порядков явных функций

Рассмотрены примеры вычисления производных высших порядков явных функций. Даны полезные формулы для вычисления производных n-го порядка.

Производная функции, заданной параметрическим способом

Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.

Производная функции, заданной неявно

Формула производной функции, заданной неявно. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.

Производные элементарных функций (вывод формул)

Производные основных элементарных функций и их вывод

Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков.

Производные элементарных функций. Доказательство теоремы

Доказательство теоремы о производных элементарных функций. Доказательство основывается на методах вычисления пределов функций и правилах дифференцирования.

Производная натурального логарифма и логарифма по основанию a

Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции.

Производная e в степени x и показательной функции

Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). Примеры вычисления производных от e^2x, e^3x и e^nx. Формулы производных высших порядков.

Производная степенной функции (степени и корни)

Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных.

Производные тригонометрических функций

Представлены производные тригонометрических функций. Доказательство и вывод формул. Производные высшего порядка для синуса и косинуса.

Производная синуса: (sin x)′

Представлено доказательство и вывод формулы для производной синуса – sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.

Производная косинуса: (cos x)′

Представлено доказательство и вывод формулы для производной косинуса – cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка.

Производная тангенса: (tg x)′

Представлен вывод формулы для производной тангенса – tg(x). Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x).

Производная котангенса: (ctg x)′

Представлен вывод формулы для производной котангенса – ctg(x). Дана формула производной котангенса n-го порядка в виде многочлена по степеням ctg(x). Коэффициенты этого многочлена связаны рекуррентным соотношением.

Вывод производных обратных тригонометрических функций

Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул.

Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′

Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами.

Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)

Представлен вывод производных высших порядков арксинуса (arcsin x). Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса.

Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′

Представлен вывод производных первого порядка арктангенса (arctg x)′ и арккотангенса (arcctg x)′. Для каждой из функций, вывод дан двумя способами.

Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)

Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах – выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка.

Производная функции y 4. Правила вычисления производных

Дата: 10.05.2015

Правила дифференцирования.

Чтобы найти производную от любой функции, надо освоить всего три понятия:

2. Правила дифференцирования.

3. Производная сложной функции.

Именно в таком порядке. Это намёк.)

Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных – доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.

Дифференцирование – это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения “найти производную функции” и “продифференцировать функцию” – это одно и то же.

Выражение “правила дифференцирования” относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.

Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:

В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 – это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.

Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).

Рассмотрим несколько примеров. Сначала – самые простые.

Найти производную функции y=sinx – x 2

Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx – это функция U , а x 2 – функция V. Имеем полное право написать:

y” = (sinx – x 2)” = (sinx)”- (x 2)”

Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и

x 2 ), смотрим, какие у них производные и записываем ответ:

y” = (sinx)” – (x 2)” = cosx – 2x

Вот и все дела. Правило 1 дифференцирования суммы работает точно так же. nx. Формулы производных высших порядков.

Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′ = e x .

Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a :
(2) .

Вывод формулы производной экспоненты, e в степени x

Экспонента – это показательная функция, у которой основание степени равно числу e , которое является следующим пределом:

.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.

Вывод формулы производной экспоненты

Рассмотрим экспоненту, e в степени x :
y = e x .
Эта функция определена для всех . Найдем ее производную по переменной x . По определению, производная является следующим пределом:
(3) .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
А)

Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь – некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .

Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.

Сделаем подстановку . Тогда ; .
В силу непрерывности экспоненты,
.
Поэтому при , . В результате получаем:
.

Сделаем подстановку . Тогда . При , . И мы имеем:
.

Применим свойство логарифма (5):
. Тогда
.

Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:

.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.

Тем самым мы получили формулу (1) производной экспоненты.

Вывод формулы производной показательной функции

Теперь выведем формулу (2) производной показательной функции с основанием степени a . Мы считаем, что и . Тогда показательная функция
(8)
Определена для всех .

Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма .
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.

Производные высших порядков от e в степени x

Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:

(14) .
(1) .

Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.

Отсюда видно, что производная n-го порядка также равна исходной функции:
.

Производные высших порядков показательной функции

Теперь рассмотрим показательную функцию с основанием степени a :
.
Мы нашли ее производную первого порядка:
(15) .

Дифференцируя (15), получаем производные второго и третьего порядка:
;
.

Мы видим, что каждое дифференцирование приводит к умножению исходной функции на . Поэтому производная n-го порядка имеет следующий вид:
.

Производная по переменной x от синуса x равна косинусу x:
(sin x)′ = cos x .

Доказательство

Для вывода формулы производной синуса, мы воспользуемся определением производной:
.

Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.

1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы .

Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и , то
(4) .

Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3) .
В нашем случае
; . Тогда
;
;
;
.

Теперь сделаем подстановку . При , . Применим первый замечательный предел (1):

Сделаем такую же подстановку и используем свойство непрерывности (2):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

Формула производной синуса доказана.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2 x и y = sin 3 x .

Пример 1

Найти производную от sin 2x .

Решение

Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.

Применяем .
.
Здесь .

Ответ

(sin 2x)′ = 2 cos 2x.

Пример 2

Найти производную от синуса в квадрате:
y = sin 2 x .

Решение

Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.

.
Здесь .

Можно применить одну из формул тригонометрии. Тогда
.

Ответ

Пример 3

Найти производную от синуса в кубе:
y = sin 3 x .

Производные высших порядков

Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции :

.
Здесь .

Теперь мы можем заметить, что дифференцирование

sin x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5) .

Докажем это, применяя метод математической индукции.

Мы уже проверили, что при , формула (5) справедлива.

Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .

Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:

.
Здесь .
Итак, мы нашли:
.

Если подставить , то эта формула примет вид (5).

Формула доказана.

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.

Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.

Пошаговые примеры – как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Поиск производной математической функции называется дифференцированием. Найти производную от математической функции – частая задача, встречающаяся в высшей математике. Говорить можно по-разному: найти производную, вычислить производную, продифференцировать функцию, взять производную, но все это одни и те же понятия. Бывают, конечно, и сложные задания, в которых нахождение производной всего лишь один из компонентов задачи. На нашем сервисе сайт у вас есть возможность вычислить производную онлайн как от элементарных, так и от сложных функций, не имеющих аналитического решения. Производная онлайн на нашем сервисе может быть найдена практически от любой математической функции, даже самой сложной, которую вам не смогли решить другие сервисы. А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение». Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис сайт призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также сайт отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса. Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, – сервис абсолютно бесплатный. От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе. Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение. Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле. Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн. Уже давно созданы и можно легко встретить таблицы производных для элементарных функций, поэтому вычислить производную элементарной (простой) математической функции – довольно простое дело. Однако когда требуется найти производную сложной математической функции, то это уже не тривиальная задача и она потребует немало усилий и затрат времени. 2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Практика: решай 7 задание и тренировочные варианты ЕГЭ по математике (профильной)

Производная онлайн

Примеры решенийЭкстремумы функцииНайти интеграл Точки перегиба Точки разрыва функцииИнтервалы возрастания функции Асимптоты функции Диф уравнения онлайнПредел функции Правило Лопиталя

Производной функции y=f(x) в точке x₀ называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.

Решение онлайн
Видеоинструкция
Также решают

Функция задана в явном виде

f(x) =

Функция задана в неявном виде Примеры

F(x,y) =

Функция задана в параметрическом виде Примеры

x =

y =

Упрощать выражение
Находить вторую производную

Правила ввода функции, заданной в явном виде

Примеры
≡ x^2/(x+2)
cos²(2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

Правила ввода функции, заданной в неявном виде

Примеры
≡ x^2/(1+y)
cos²(2x+y) ≡ (cos(2*x+y))^2
≡ 1+(x-y)^(2/3)

Если функция задана в виде y²-x=cos(y), то ее необходимо записать так: y^2-x-cos(y). (2/3)

Вместе с этим калькулятором также используют следующие:
Точки разрыва функции

Решение пределов

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление интегралов

Таблица производных

(x^α)’ = α x^α^-1
= ¹/₂x^1/2 =
(a^x)’ = a^x·lna
(e^x)’ = e^x
(sinx)’ = cosx
(cosx)’ = -sinx
(shx)’ = chx
(chx)’ = shx

Примечание:
– гиперболический синус
– гиперболический косинус
– гиперболический тангенс
– гиперболический котангенс

Как найти производную, исходяя из ее определения?

Правила нахождения производных

Пример 1.

Найти производную функции y=cos⁴x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos⁴x)′_{cos x} = 4cos^4-1x = 4cos³x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′_x = (cos⁴x)′_{cos x}·(cosx)′_x = 4·cos³x·(-sin x) = -4·cos³x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.

Пример 2. Найти производную функции
.

.
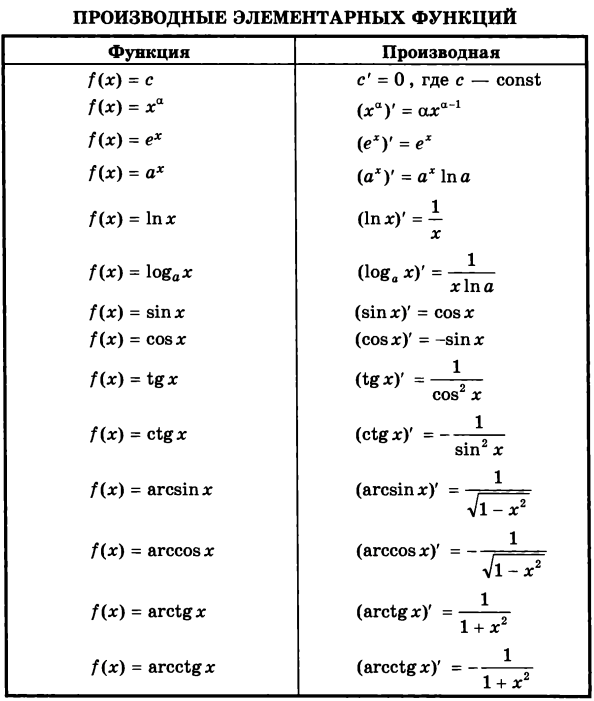
В некоторых случаях, если, например, нужно найти производную функции y = (u(x))^v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.

Пример 3. Найти производную функции
.
Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию

Учитывая, что , будем иметь Но , откуда
.

Пример 4. Найти производную функции y=x^{e^x}
Решение.
;
.

Прикладное использование производной

Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.

Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной: f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления.
Значение производной в точке x₀ позволяет находить уравнение касательной к графику функции.
Отношение производных позволяет вычислять пределы по правилу Лопиталя.
В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

3.3 Правила дифференциации. Расчет, том 1

Цели обучения

3.3.1 Сформулируйте постоянные, постоянные кратные и степенные правила.
3.3.2 Примените правила суммы и разности, чтобы объединить производные.
3.3.3 Используйте правило произведения для нахождения производной произведения функций.
3.3.4 Используйте правило отношения для нахождения производной частного функции.
3.3.5 Распространите правило степени на функции с отрицательными показателями.
3.3.6 Объедините правила дифференцирования, чтобы найти производную полиномиальной или рациональной функции.

Нахождение производных функций с помощью определения производной может быть длительным и, для некоторых функций, довольно сложным процессом. Например, ранее мы обнаружили, что ddx(x)=12xddx(x)=12x, используя процесс, включающий умножение выражения на сопряженное перед вычислением предела. Процесс, который мы могли бы использовать для оценки ddx(x3)ddx(x3) с помощью определения, хотя и похож, но более сложен. В этом разделе мы разрабатываем правила нахождения производных, позволяющие обойти этот процесс. Начнем с основ.

Основные правила

Функции f(x)=cf(x)=c и g(x)=xng(x)=xn, где nn — натуральное число, являются строительными блоками, из которых строятся все многочлены и рациональные функции. Чтобы эффективно находить производные полиномов и рациональных функций, не прибегая к предельному определению производной, мы должны сначала разработать формулы для дифференцирования этих основных функций.

Постоянное правило

Сначала мы применяем предельное определение производной, чтобы найти производную постоянной функции, f(x)=c.f(x)=c. Для этой функции как f(x)=cf(x)=c, так и f(x+h)=c,f(x+h)=c, поэтому мы получаем следующий результат:

f′(x)=limh→0f(x+h)−f(x)h=limh→0c−ch=limh→00h=limh→00=0.f′(x)=limh→0f(x+ h)−f(x)h=limh→0c−ch=limh→00h=limh→00=0.

Правило дифференцирования постоянных функций называется постоянным правилом. В нем говорится, что производная постоянной функции равна нулю; то есть, поскольку постоянная функция представляет собой горизонтальную линию, наклон или скорость изменения постоянной функции равен 0,0. Мы повторяем это правило в следующей теореме.

Теорема 3.2

Постоянное правило

Пусть cc — константа.

Если f(x)=c,f(x)=c, то f′(x)=0.f′(x)=0.

В качестве альтернативы мы можем выразить это правило как

ddx(c)=0.ddx(c)=0.

Пример 3.17

Применение постоянного правила

Найдите производную f(x)=8.f(x)=8.

Решение

Это одношаговое применение правила:

f′(x)=0.f′(x)=0.

Контрольно-пропускной пункт 3.11

Найдите производную g(x)=−3.g(x)=−3.

Правило силы

Мы показали, что

ddx(x2)=2xandddx(x1/2)=12x−1/2.ddx(x2)=2xandddx(x1/2)=12x−1/2.

В этот момент вы можете увидеть начало развития шаблона для производных формы ddx(xn).ddx(xn). Мы продолжаем изучение формул производных путем дифференцирования степенных функций вида f(x)=xnf(x)=xn, где nn — натуральное число. Мы разрабатываем формулы для производных этого типа функций поэтапно, начиная с натуральных степеней. Прежде чем сформулировать и доказать общее правило для производных функций этого вида, рассмотрим частный случай ddx(x3).ddx(x3). Когда мы пройдем этот вывод, обратите внимание, что техника, используемая в этом случае, по существу такая же, как и техника, используемая для доказательства общего случая.

Пример 3.18

Дифференцирование x3x3

Найти ddx(x3).ddx(x3).

Решение

ddx(x3)=limh→0(x+h)3−x3h=limh→0x3+3x2h+3xh3+h4−x3hОбратите внимание, что первый член в разложении (x+h)3 равен x3, а второй член равен 3x2h. Все остальные члены содержат степени h, которые в два раза больше.=limh→03x2h+3xh3+h4hНа этом шаге x3члены были отменены, остались только члены, содержащие h.=limh→0h(3×2+3xh+h3)hВынесите из общего множителя h.=limh→0( 3×2+3xh+h3) После сокращения общего множителя h единственный член, не содержащий его3×2. =3×2, переходит к 0.ddx(x3)=limh→0(x+h)3−x3h=limh→0x3+3x2h+3xh3+h4− x3hОбратите внимание, что первый член в разложении (x+h)3 равен x3, а второй член равен 3x2h. Все остальные члены содержат степени h, которые в два раза больше.=limh→03x2h+3xh3+h4h limh→0h(3×2+3xh+h3)hВынесите за скобки общий множитель h.=limh→0(3×2+3xh+h3)0019

Контрольно-пропускной пункт 3.12

Найти ddx(x4).ddx(x4).

Как мы увидим, процедура нахождения производной общего вида f(x)=xnf(x)=xn очень похожа. Хотя часто неразумно делать общие выводы из конкретных примеров, заметим, что при дифференцировании f(x)=x3,f(x)=x3 степень при xx становится коэффициентом при x2x2 в производной, а степень при xx в производной уменьшается на 1. Следующая теорема утверждает, что правило степени выполняется для всех положительных целых степеней x.x. Со временем мы распространим этот результат на отрицательные целые степени. Позже мы увидим, что это правило также может быть распространено сначала на рациональные степени xx, а затем на произвольные степени x. x. Имейте в виду, однако, что это правило не применяется к функциям, в которых константа возводится в переменную степень, например, f(x)=3x.f(x)=3x.

Теорема 3.3

Правило силы

Пусть nn — целое положительное число. Если f(x)=xn,f(x)=xn, то

f′(x)=nxn−1.f′(x)=nxn−1.

В качестве альтернативы мы можем выразить это правило как

ddxxn=nxn−1.ddxxn=nxn−1.

Доказательство

Для f(x)=xnf(x)=xn, где nn — натуральное число, мы имеем

f′(x)=limh→0(x+h)n−xnh.f′(x)=limh→0(x+h)n−xnh.

Поскольку (x+h)n=xn+nxn−1h+(n2)xn−2h3+(n3)xn−3h4+…+nxhn−1+hn, Поскольку (x+h)n=xn+nxn−1h+(n2) xn−2h3+(n3)xn−3h4+…+nxhn−1+hn,

мы видим, что

(x+h)n−xn=nxn−1h+(n2)xn−2h3+(n3)xn−3h4+…+nxhn−1+hn.(x+h)n−xn=nxn−1h+(n2)xn− 2h3+(n3)xn−3h4+…+nxhn−1+hn.

Затем разделите обе части на ч :

(x+h)n−xnh=nxn−1h+(n2)xn−2h3+(n3)xn−3h4+…+nxhn−1+hnh. (x+h)n−xnh=nxn−1h+(n2)xn− 2h3+(n3)xn−3h4+…+nxhn−1+hnh.

Итак,

(x+h)n−xnh=nxn−1+(n2)xn−2h+(n3)xn−3h3+…+nxhn−2+hn−1.(x+h)n−xnh=nxn−1+( n2)xn−2h+(n3)xn−3h3+…+nxhn−2+hn−1.

Наконец,

f′(x)=limh→0(nxn−1+(n2)xn−2h+(n3)xn−3h3+…+nxhn−1+hn)=nxn−1.f′(x)=limh→0( nxn−1+(n2)xn−2h+(n3)xn−3h3+…+nxhn−1+hn)=nxn−1.

□

Пример 3.19

Применение степенного правила

Найдите производную функции f(x)=x10f(x)=x10, применив степенное правило.

Решение

Используя степенное правило с n=10,n=10, получаем

f′(x)=10×10−1=10×9.f′(x)=10×10−1=10×9.

Контрольно-пропускной пункт 3.13

Найдите производную f(x)=x7.f(x)=x7.

Сумма, разность и постоянные множественные правила

Мы находим наши следующие правила дифференцирования, рассматривая производные сумм, разностей и постоянных кратных функций. Так же, как и при работе с функциями, существуют правила, облегчающие нахождение производных функций, которые мы складываем, вычитаем или умножаем на константу. Эти правила резюмируются в следующей теореме.

Теорема 3.4

Сумма, разность и постоянные множественные правила

Пусть f(x)f(x) и g(x)g(x) — дифференцируемые функции, kk — константа. Тогда выполняется каждое из следующих уравнений.

Правило суммы. Производная суммы функции ff и функции gg равна сумме производной функции ff и производной g.g.

ddx(f(x)+g(x))=ddx(f(x))+ddx(g(x));ddx(f(x)+g(x))=ddx(f(x) )+ddx(g(x));

то есть

для j(x)=f(x)+g(x),j′(x)=f′(x)+g′(x).forj(x)=f(x)+g(x),j ′(х)=f′(х)+g′(х).

Правило разности. Производная разности функции f и функции g такая же, как разность производной f и производной g:g:

ddx(f(x)−g(x ))=ddx(f(x))−ddx(g(x));ddx(f(x)−g(x))=ddx(f(x))−ddx(g(x));

, то есть

для j(x)=f(x)−g(x),j′(x)=f′(x)−g′(x).forj(x)=f(x)− g(x),j′(x)=f′(x)−g′(x).

Постоянное множественное правило. Производная константы k , умноженное на функцию f , равно константе, умноженной на производную:

ddx(kf(x))=kddx(f(x));ddx(kf(x))=kddx(f (Икс));

, то есть

forj(x)=kf(x),j′(x)=kf′(x).forj(x)=kf(x),j′(x)=kf′(x) .

Доказательство

Здесь мы приводим только доказательство правила сумм. Остальные следуют аналогичным образом.

Для дифференцируемых функций f(x)f(x) и g(x),g(x) положим j(x)=f(x)+g(x).j(x)=f(x)+ г(х). Используя предельное определение производной, имеем

j′(x)=limh→0j(x+h)−j(x)h.j′(x)=limh→0j(x+h)−j(x)h.

Путем замены j(x+h)=f(x+h)+g(x+h)j(x+h)=f(x+h)+g(x+h) и j(x)=f (x)+g(x),j(x)=f(x)+g(x), получаем

j′(x)=limh→0(f(x+h)+g(x+h))−(f(x)+g(x))h.j′(x)=limh→0(f(x +h)+g(x+h))−(f(x)+g(x))h.

Переставляя и перегруппировывая члены, мы имеем

j′(x)=limh→0(f(x+h)−f(x)h+g(x+h)−g(x)h).j′(x)=limh→0(f( х+h)−f(x)h+g(x+h)−g(x)h).

Применим теперь закон сумм для пределов и определение производной, чтобы получить

j′(x)=limh→0(f(x+h)−f(x)h)+limh→0(g(x+h)−g(x)h)=f′(x)+g ′(x).j′(x)=limh→0(f(x+h)−f(x)h)+limh→0(g(x+h)−g(x)h)=f′( х)+g'(х).

□

Пример 3.20

Применение правила постоянного множителя

Найдите производную g(x)=3x2g(x)=3×2 и сравните ее с производной f(x)=x2.f(x)=x2.

Решение

Мы используем правило степени напрямую: (2x)=6x.

Поскольку f(x)=x2f(x)=x2 имеет производную f′(x)=2x,f′(x)=2x, мы видим, что производная g(x)g(x) в 3 раза больше производной функции f(x).f(x). Эта взаимосвязь показана на рис. 3.18.

Рисунок 3.18 Производная g(x)g(x) в 3 раза больше производной f(x).f(x).

Пример 3.21

Применение основных правил производных

Найдите производную f(x)=2×5+7.f(x)=2×5+7.

Решение

Начнем с применения правила дифференцирования суммы двух функций, за которым следуют правила дифференцирования постоянных кратных функций и правило дифференцирования степеней.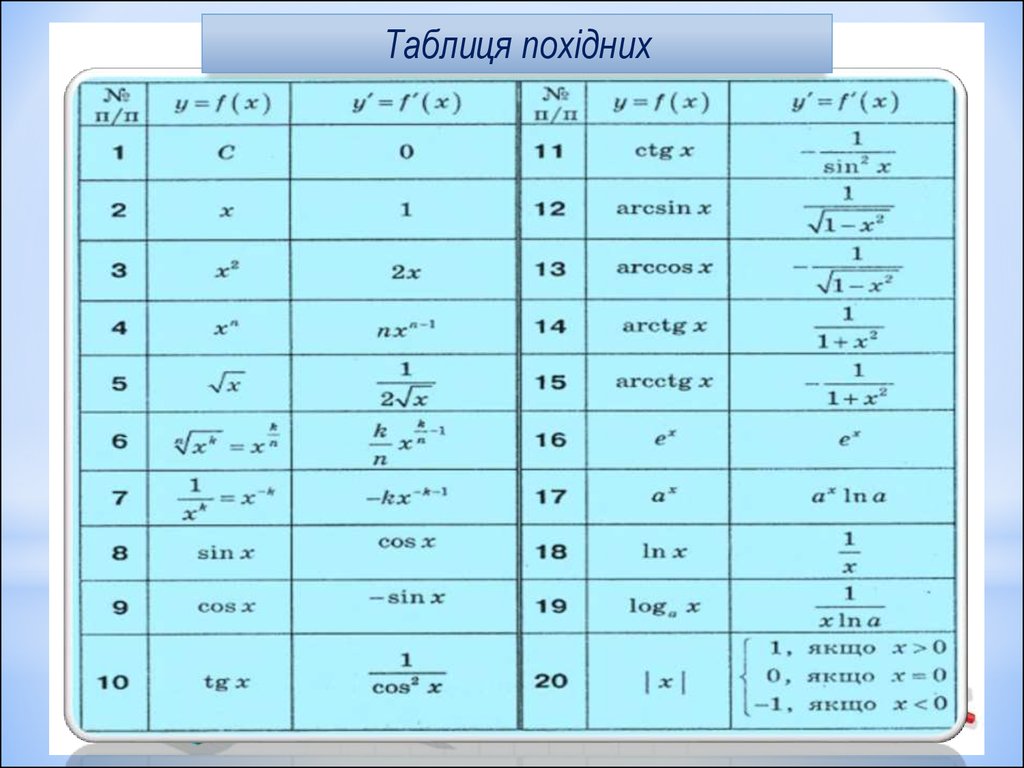 Чтобы лучше понять последовательность, в которой применяются правила дифференцирования, мы используем обозначения Лейбница во всем решении:

f′(x)=ddx(2×5+7)=ddx(2×5)+ddx(7)Применить правило сумм.=2ddx(x5)+ddx(7)Применить постоянное кратное правило.=2(5×4) +0Применить правило степени и правило констант.=10×4.Simplify.f′(x)=ddx(2×5+7)=ddx(2×5)+ddx(7)Применить правило суммы.=2ddx(x5)+ddx( 7) Применить постоянное кратное правило. = 2 (5×4) + 0 Применить правило степени и постоянное правило. = 10×4. Упростить.

Контрольно-пропускной пункт 3.14

Найдите производную f(x)=2×3−6×2+3.f(x)=2×3−6×2+3.

Пример 3,22

Нахождение уравнения касательной

Найдите уравнение касательной к графику f(x)=x2−4x+6f(x)=x2−4x+6 при x=1.x=1.

Решение

Чтобы найти уравнение касательной, нам нужны точка и наклон. Чтобы найти точку, вычислите

f(1)=12−4(1)+6=3.f(1)=12−4(1)+6=3.

Это дает нам точку (1,3).(1,3). Поскольку наклон касательной в точке 1 равен f′(1),f′(1), мы должны сначала найти f′(x).f′(x). Используя определение производной, имеем

f′(x)=2x−4f′(x)=2x−4

, поэтому наклон касательной равен f′(1)=−2.f′(1)=−2. Используя формулу точки-наклона, мы видим, что уравнение касательной линии имеет вид

y−3=−2(x−1).y−3=−2(x−1).

Преобразуя уравнение прямой в виде точки пересечения, получаем

y=−2x+5.y=−2x+5.

Контрольно-пропускной пункт 3.15

Найдите уравнение касательной к графику f(x)=3×2−11f(x)=3×2−11 при x=2.x=2. Используйте форму точка-наклон.

Правило продукта

Теперь, когда мы изучили основные правила, мы можем приступить к изучению некоторых более сложных правил. Первый исследует производную произведения двух функций. Хотя может показаться заманчивым предположить, что производная произведения является произведением производных, аналогично правилам суммы и разности, правило произведения не следует этому образцу. Чтобы понять, почему мы не можем использовать этот шаблон, рассмотрим функцию f(x)=x2,f(x)=x2, производная которой равна f′(x)=2xf′(x)=2x, а не ddx(x) · ddx (х)=1·1=1.ddx(x)·ddx(x)=1·1=1.

Теорема 3,5

Правило продукта

Пусть f(x)f(x) и g(x)g(x) — дифференцируемые функции. Тогда

ddx(f(x)g(x))=ddx(f(x))·g(x)+ddx(g(x))·f(x).ddx(f(x)g(x ))=ddx(f(x))·g(x)+ddx(g(x))·f(x).

То есть

, если j(x)=f(x)g(x), то j′(x)=f′(x)g(x)+g′(x)f(x).ifj(x )=f(x)g(x), тогда j′(x)=f′(x)g(x)+g′(x)f(x).

Это означает, что производная произведения двух функций равна произведению первой функции на вторую плюс производная второй функции на первую функцию.

Доказательство

Начнем с предположения, что f(x)f(x) и g(x)g(x) — дифференцируемые функции. В ключевом моменте этого доказательства нам нужно использовать тот факт, что, поскольку g(x)g(x) дифференцируема, она также непрерывна. В частности, мы используем тот факт, что, поскольку g(x)g(x) непрерывна, limh→0g(x+h)=g(x). limh→0g(x+h)=g(x).

Применяя предельное определение производной к j(x)=f(x)g(x),j(x)=f(x)g(x), мы получаем

j′(x)=limh→0f(x+h)g(x+h)−f(x)g(x)h.j′(x)=limh→0f(x+h)g(x+h) −f(x)g(x)h.

Добавляя и вычитая f(x)g(x+h)f(x)g(x+h) в числителе, мы получаем

j′(x)=limh→0f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g( x)h.j′(x)=limh→0f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g (х)ч.

После разделения этого частного и применения закона сумм для пределов производная становится равной

j′(x)=limh→0(f(x+h)g(x+h)−f(x)g(x+h)h)+limh→0(f(x)g(x+h) )−f(x)g(x)h).j′(x)=limh→0(f(x+h)g(x+h)−f(x)g(x+h)h)+limh →0(f(x)g(x+h)−f(x)g(x)h).

Переставляя, получаем

j′(x)=limh→0(f(x+h)−f(x)h·g(x+h))+limh→0(g(x+h)−g(x)h·f (x)).j′(x)=limh→0(f(x+h)−f(x)h·g(x+h))+limh→0(g(x+h)−g(x )h·f(x)).

Используя непрерывность g(x),g(x), определение производных от f(x)f(x) и g(x),g(x) и применяя предельные законы, мы приходим к правило продукта,

j′(x)=f′(x)g(x)+g′(x)f(x). j′(x)=f′(x)g(x)+g′(x)f( Икс).

□

Пример 3,23

Применение правила произведения к функциям в точке

Для j(x)=f(x)g(x),j(x)=f(x)g(x) используйте правило произведения, чтобы найти j′ (2)j′(2) если f(2)=3,f′(2)=−4,g(2)=1,f(2)=3,f′(2)=−4,g( 2)=1 и g′(2)=6.g′(2)=6.

Решение

Поскольку j(x)=f(x)g(x),j′(x)=f′(x)g(x)+g′(x)f(x),j(x)=f(x )g(x),j′(x)=f′(x)g(x)+g′(x)f(x), и, следовательно,

j′(2)=f′(2)g(2 )+g′(2)f(2)=(−4)(1)+(6)(3)=14.j′(2)=f′(2)g(2)+g′(2) f(2)=(−4)(1)+(6)(3)=14.

Пример 3,24

Применение правила произведения к биномам

Для j(x)=(x2+2)(3×3−5x),j(x)=(x2+2)(3×3−5x) найти j′(x)j ′(x), применяя правило произведения. Проверьте результат, сначала найдя произведение, а затем дифференцируя его.

Решение

Если мы установим f(x)=x2+2f(x)=x2+2 и g(x)=3×3−5x,g(x)=3×3−5x, то f′(x)=2xf′(x) =2x и g′(x)=9×2−5. g′(x)=9×2−5. Таким образом,

j′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3×3−5x)+(9×2−5)(x2+2). j′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3×3−5x)+(9×2−5)(x2+2).

Упрощая, имеем

j′(x)=15×4+3×2−10.j′(x)=15×4+3×2−10.

Для проверки видим, что j(x)=3×5+x3−10xj(x)=3×5+x3−10x и, следовательно, j′(x)=15×4+3×2−10.j′(x)=15×4 +3×2−10.

Контрольно-пропускной пункт 3.16

Используйте правило произведения для получения производной от j(x)=2×5(4×2+x).j(x)=2×5(4×2+x).

Частное правило

Разработав и применив правило произведения, мы теперь рассмотрим дифференцирование частных функций. Как мы видим из следующей теоремы, производная частного не есть частное производных; скорее, это производная функции в числителе, умноженная на функцию в знаменателе, минус производная функции в знаменателе, умноженная на функцию в числителе, и все это делится на квадрат функции в знаменателе. Чтобы лучше понять, почему мы не можем просто взять частное производных, имейте в виду, что

ddx(x2)=2x,notddx(x3)ddx(x)=3×21=3×2. ddx(x2)=2x,notddx(x3)ddx(x)=3×21=3×2.

Теорема 3,6

Частное правило

Пусть f(x)f(x) и g(x)g(x) — дифференцируемые функции. Тогда

ddx(f(x)g(x))=ddx(f(x))·g(x)−ddx(g(x))·f(x)(g(x))2.ddx( f(x)g(x))=ddx(f(x))·g(x)−ddx(g(x))·f(x)(g(x))2.

То есть

, если j(x)=f(x)g(x), то j′(x)=f′(x)g(x)−g′(x)f(x)(g(x ))2.если j(x)=f(x)g(x), то j′(x)=f′(x)g(x)−g′(x)f(x)(g(x))2 .

Доказательство правила отношения очень похоже на доказательство правила произведения, поэтому здесь оно опущено. Вместо этого мы применяем это новое правило для нахождения производных в следующем примере.

Пример 3,25

Применение правила отношения

Используйте правило отношения, чтобы найти производную k(x)=5x24x+3.k(x)=5x24x+3.

Решение

Пусть f(x)=5x2f(x)=5×2 и g(x)=4x+3.g(x)=4x+3. Таким образом, f′(x)=10xf′(x)=10x и g′(x)=4.g′(x)=4. Подставляя в факторное правило, мы имеем

k′(x)=f′(x)g(x)−g′(x)f(x)(g(x))2=10x(4x+3)− 4(5×2)(4x+3)2.k′(x)=f′(x)g(x)−g′(x)f(x)(g(x))2=10x(4x+3) −4(5×2)(4x+3)2.

Упрощая, получаем

k′(x)=20×2+30x(4x+3)2.k′(x)=20×2+30x(4x+3)2.

Контрольно-пропускной пункт 3.17

Найдите производную h(x)=3x+14x−3.h(x)=3x+14x−3.

Теперь можно использовать правило отношения для расширения правила степени для нахождения производных функций вида xkxk, где kk — отрицательное целое число.

Теорема 3,7

Расширенное правило мощности

Если kk — отрицательное целое число, то

ddx(xk)=kxk−1.ddx(xk)=kxk−1.

Доказательство

Если kk — отрицательное целое число, мы можем установить n=−k,n=−k, так что n будет положительным целым числом с k=−n.k=−n. Поскольку для каждого положительного целого числа n,x−n=1xn,n,x−n=1xn, теперь мы можем применить правило отношения, установив f(x)=1f(x)=1 и g(x)=xn. g (х)=хп. В этом случае f′(x)=0f′(x)=0 и g′(x)=nxn−1.g′(x)=nxn−1. Таким образом,

ddx(x−n)=0(xn)−1(nxn−1)(xn)2.ddx(x−n)=0(xn)−1(nxn−1)(xn)2.

Упрощая, мы видим, что

ddx(x−n)=−nxn−1x2n=−nx(n−1)−2n=−nx−n−1.ddx(x−n)=−nxn−1x2n=−nx(n−1)− 2n=-nx-n-1.

Наконец, обратите внимание, что, поскольку k=−n,k=−n, подстановкой мы имеем

ddx(xk)=kxk−1.ddx(xk)=kxk−1.

□

Пример 3,26

Использование расширенного правила мощности

Найдите ddx(x−4).ddx(x−4).

Решение

Применяя расширенное правило степени с k=−4,k=−4, мы получаем

ddx(x−4)=−4x−4−1=−4x−5.ddx(x−4)=−4x −4−1=−4x−5.

Пример 3,27

Использование правила расширенной мощности и правила постоянного множителя

Используйте правило расширенной степени и правило постоянного множителя, чтобы найти производную от f(x)=6×2.f(x)=6×2.

Решение

Может показаться заманчивым использовать правило отношения для нахождения этой производной, и это, конечно, не будет неправильным. Однако гораздо проще дифференцировать эту функцию, сначала переписав ее как f(x)=6x−2.f(x)=6x−2.

f′(x)=ddx(6×2)=ddx(6x−2)Переписать6x2as6x−2.=6ddx(x−2)Применить постоянное кратное правило.=6(−2x−3)Использовать расширенное правило мощности для дифференцироватьx-2.=-12x-3Упростить.f'(x)=ddx(6×2)=ddx(6x-2)Переписать6×2как6x-2.=6ddx(x-2)Применить постоянное кратное правило.=6(-2x- 3) Используйте расширенное правило мощности, чтобы дифференцировать x-2.=-12x-3Упростить.

Контрольно-пропускной пункт 3.18

Найдите производную от g(x)=1x7g(x)=1×7, используя правило расширенной степени.

Объединение правил дифференциации

Как мы видели из примеров в этом разделе, редко случается, что нам приходится применять только одно правило дифференцирования, чтобы найти производную заданной функции. На этом этапе, комбинируя правила дифференцирования, мы можем найти производные любой полиномиальной или рациональной функции. Позже мы встретимся с более сложными комбинациями правил дифференцирования. Хорошее эмпирическое правило, которое можно использовать при применении нескольких правил, состоит в том, чтобы применять правила в порядке, обратном порядку, в котором мы оцениваем функцию.

Пример 3,28

Объединение правил дифференцирования

Для k(x)=3h(x)+x2g(x),k(x)=3h(x)+x2g(x) найти k′(x).k′(x) .

Решение

Для нахождения этой производной требуется правило сумм, правило постоянного кратного и правило произведения.

k′(x)=ddx(3h(x)+x2g(x))=ddx(3h(x))+ddx(x2g(x)) Применить правило сумм.=3ddx(h(x))+ (ddx(x2)g(x)+ddx(g(x))x2) Применить правило множителя констант к дифференцированию3h(x) и правило произведения к дифференцированиюx2g(x).=3h′(x)+2xg(x)+g ′(x)x2k′(x)=ddx(3h(x)+x2g(x))=ddx(3h(x))+ddx(x2g(x)) Применить правило сумм.=3ddx(h(x) )+(ddx(x2)g(x)+ddx(g(x))x2) Применить правило множителя констант для дифференцирования3h(x) и правило произведения для дифференцированияx2g(x). =3h′(x)+2xg(x) +g′(x)x2

Пример 3,29

Расширение правила продукта

Для k(x)=f(x)g(x)h(x),k(x)=f(x)g(x)h(x) выразить k′(x )k′(x) через f(x),g(x),h(x),f(x),g(x),h(x) и их производные.

Решение

Мы можем думать о функции k(x)k(x) как о произведении функции f(x)g(x)f(x)g(x) и функции h(x).h(x). То есть k(x)=(f(x)g(x))·h(x).k(x)=(f(x)g(x))·h(x). Таким образом,

k′(x)=ddx(f(x)g(x))·h(x)+ddx(h(x))·(f(x)g(x)) Примените правило произведения к произведение off(x)g(x)andh(x).=(f′(x)g(x)+g′(x)f(x))h(x)+h′(x)f(x) g(x)Применить правило произведения tof(x)g(x).=f′(x)g(x)h(x)+f(x)g′(x)h(x)+f(x) g(x)h′(x).Simplify.k′(x)=ddx(f(x)g(x))·h(x)+ddx(h(x))·(f(x)g( x)) Примените правило произведения к произведению off(x)g(x)andh(x).=(f′(x)g(x)+g′(x)f(x))h(x)+h ′(x)f(x)g(x)Применить правило произведения tof(x)g(x).=f′(x)g(x)h(x)+f(x)g′(x)h (x)+f(x)g(x)h′(x). Упростить.

Пример 3.30

Сочетание правила частного и правила произведения

Для h(x)=2x3k(x)3x+2,h(x)=2x3k(x)3x+2 найдите ).

Решение

Эта процедура типична для нахождения производной рациональной функции.

h′(x)=ddx(2x3k(x))·(3x+2)−ddx(3x+2)·(2x3k(x))(3x+2)2Применить правило отношения.=(6x2k(x )+k′(x)·2×3)(3x+2)−3(2x3k(x))(3x+2)2Применить правило произведения, чтобы найтиddx(2x3k(x)).Useddx(3x+2)=3. =−6x3k(x)+18x3k(x)+12x2k(x)+6x4k′(x)+4x3k′(x)(3x+2)2Simplify.h′(x)=ddx(2x3k(x))·( 3x+2)−ddx(3x+2)·(2x3k(x))(3x+2)2Применить правило частных.=(6x2k(x)+k′(x)·2×3)(3x+2)−3 (2x3k(x))(3x+2)2Применить правило произведения к findddx(2x3k(x)).Useddx(3x+2)=3.=−6x3k(x)+18x3k(x)+12x2k(x)+ 6x4k′(x)+4x3k′(x)(3x+2)2Упростить.

Контрольно-пропускной пункт 3.19

Найти ddx(3f(x)−2g(x)).ddx(3f(x)−2g(x)).

Пример 3.31

Определение, где функция имеет горизонтальную касательную

Определите значения xx, для которых f(x)=x3−7×2+8x+1f(x)=x3−7×2+8x+1 имеет горизонтальную касательную.

Решение

Чтобы найти значения xx, для которых f(x)f(x) имеет горизонтальную касательную, мы должны решить f′(x)=0. f′(x)=0. Поскольку

f′(x)=3×2−14x+8=(3x−2)(x−4),f′(x)=3×2−14x+8=(3x−2)(x−4),

мы должны решить (3x−2)(x−4)=0.(3x−2)(x−4)=0. Таким образом, мы видим, что функция имеет горизонтальные касательные в точках x=23x=23 и x=4x=4, как показано на следующем графике.

Рисунок 3.19 Эта функция имеет горизонтальные касательные на x = 2/3 и x = 4.

Пример 3,32

Определение скорости

Положение объекта на оси координат в момент времени tt определяется как s(t)=tt2+1.s(t)=tt2+1. Какова начальная скорость тела?

Решение

Поскольку начальная скорость v(0)=s′(0),v(0)=s′(0), начнем с нахождения s′(t)s′(t), применяя правило частных:

с ′(t)=1(t2+1)−2t(t)(t2+1)2=1−t2(t2+1)2.s′(t)=1(t2+1)−2t(t) (t2+1)2=1−t2(t2+1)2.

После вычисления мы видим, что v(0)=1.v(0)=1.

Контрольно-пропускной пункт 3.

Найдите значения xx, для которых график f(x)=4×2−3x+2f(x)=4×2−3x+2 имеет касательную, параллельную прямой y=2x+3.y=2x+3 .

Студенческий проект

Трибуны Формулы-1

Автомобильные гонки Формулы-1 могут быть очень увлекательными и привлекать множество зрителей. Дизайнеры трасс Формулы-1 должны обеспечить достаточное пространство на трибунах вокруг трассы для размещения этих зрителей. Однако автомобильные гонки могут быть опасными, и соображения безопасности имеют первостепенное значение. Трибуны должны располагаться так, чтобы зрители не подвергались опасности в случае потери водителем управления автомобилем (рис. 3.20).

Рисунок 3.20 Трибуна рядом с прямой трассой Circuit de Barcelona-Catalunya, расположенная там, где зрителям ничего не угрожает.

**********

Безопасность особенно важна на поворотах. Если водитель недостаточно замедлится перед входом в поворот, автомобиль может соскользнуть с гоночной трассы. Обычно это просто приводит к более широкому повороту, который замедляет водителя. Но если водитель полностью потеряет управление, машина может полностью вылететь с трассы по касательной к кривой гоночной трассы.

Предположим, вы проектируете новую трассу Формулы-1. Один участок пути можно смоделировать функцией f(x)=x3+3×2+xf(x)=x3+3×2+x (рис. 3.21). Текущий план предусматривает строительство трибун вдоль первой прямой и вокруг части первого поворота. Планируется, что передний угол трибуны будет располагаться в точке (−1,9,2.8).(−1.9,2.8). Мы хотим определить, представляет ли эта локация опасность для зрителей, если водитель потеряет контроль над автомобилем.

Рисунок 3.21 (a) Один участок беговой дорожки можно смоделировать функцией f(x)=x3+3×2+x.f(x)=x3+3×2+x. (b) Передний угол трибуны расположен в точках (−1.9, 2.8).(−1.9, 2.8).

Физики определили, что водители, скорее всего, потеряют контроль над своими автомобилями при входе в поворот в точке, где наклон касательной равен 1. Найдите (x,y)(x,y) координаты этой точки возле поворота.
Найдите уравнение касательной к кривой в этой точке.
Чтобы определить, угрожают ли зрители в этом сценарии, найдите x -координату точки, где касательная пересекает линию y=2.8.y=2.8. Безопасно ли находится эта точка справа от трибуны? Или зрители в опасности?
Что, если водитель потеряет управление раньше, чем запланируют физики? Предположим, что водитель теряет управление в точке (−2,5,0,625).(−2,5,0,625). Каков наклон касательной в этой точке?
Если водитель теряет управление, как описано в части 4, зрители в безопасности?
Сохранить текущий дизайн трибун или трибуны нужно переместить?

Раздел 3.3 Упражнения

Для следующих упражнений найдите f′(x)f′(x) для каждой функции.

106.

f(x)=x7+10f(x)=x7+10

107.

f(x)=5×3−x+1f(x)=5×3−x+1

108.

f(x)=4×2−7xf(x)=4×2−7x

109.

f(x)=8×4+9×2−1f(x)=8×4+9×2−1

110.

f(x)=x4+2xf(x)=x4+2x

111.

f(x)=3x(18×4+13x+1)f(x)=3x(18×4+13x+1)

112.

f(x)=(x+2)(2×2−3)f(x)=(x+2)(2×2−3)

113.

f(x)=x2(2×2+5×3)f(x)=x2(2×2+5×3)

114.

f(x)=x3+2×2−43f(x)=x3+2×2−43

115.

f(x)=4×3−2x+1x2f(x)=4×3−2x+1×2

116.

f(x)=x2+4×2−4f(x)=x2+4×2−4

117.

f(x)=x+9×2−7x+1f(x)=x+9×2−7x+1

Для следующих упражнений найдите уравнение касательной T(x)T(x) к графику заданной функции в указанной точке. Используйте графический калькулятор, чтобы построить график функции и касательной.

118.

[T] y=3×2+4x+1y=3×2+4x+1 в (0,1)(0,1)

119.

[T] y=2×2+1y=2×2+1 в (1,3)(1,3)

120.

[T] y=2xx−1y=2xx−1 в точке (−1,1)(−1,1)

121.

[T] y=2x−3x2y=2x−3×2 в точке (1,−1)(1,−1)

Для следующих упражнений предположим, что функции f(x)f(x) и g(x)g(x) являются дифференцируемыми функциями для всех x.x. Найдите производную каждой из функций h(x).h(x).

122.

h(x)=4f(x)+g(x)7h(x)=4f(x)+g(x)7

123.

ч(х)=x3f(х)ч(х)=x3f(х)

124.

h(x)=f(x)g(x)2h(x)=f(x)g(x)2

125.

h(x)=3f(x)g(x)+2h(x)=3f(x)g(x)+2

Для следующих упражнений предположим, что f(x)f(x) и g(x)g(x) являются дифференцируемыми функциями со значениями, указанными в следующей таблице. Используйте следующую таблицу для расчета следующих производных.

хх	11	22	33	44
ф(х)ф(х)	33	55	−2−2	00
г(х)г(х)	22	33	−4−4	66
f'(x)f'(x)	−1−1	77	88	−3−3
г'(х)г'(х)	44	11	22	99

126.

Найдите h′(1)h′(1), если h(x)=xf(x)+4g(x).h(x)=xf(x)+4g(x).

127.

Найдите h′(2)h′(2), если h(x)=f(x)g(x).h(x)=f(x)g(x).

128.

Найдите h′(3)h′(3), если h(x)=2x+f(x)g(x).h(x)=2x+f(x)g(x).

129.

Найдите h′(4)h′(4), если h(x)=1x+g(x)f(x).h(x)=1x+g(x)f(x).

В следующих упражнениях используйте следующий рисунок, чтобы найти указанные производные, если они существуют.

130.

Пусть h(x)=f(x)+g(x).h(x)=f(x)+g(x). Найти

ч'(1),ч'(1),
ч'(3),ч'(3) и
ч'(4).ч'(4).

131.

Пусть h(x)=f(x)g(x).h(x)=f(x)g(x). Найти

ч'(1),ч'(1),
ч'(3),ч'(3) и
ч'(4).ч'(4).

132.

Пусть h(x)=f(x)g(x). h(x)=f(x)g(x). Найти

ч'(1),ч'(1),
ч'(3),ч'(3) и
ч'(4).ч'(4).

Для следующих упражнений

оценить f'(a),f'(a) и
начертите график функции f(x)f(x) и касательной в точке x=a.x=a.

133.

[Т] f(x)=2×3+3x−x2,a=2f(x)=2×3+3x−x2,a=2

134.

[Т] f(x)=1x−x2,a=1f(x)=1x−x2,a=1

135.

[Т] f(x)=x2−x12+3x+2,a=0f(x)=x2−x12+3x+2,a=0

136.

[Т] f(x)=1x−x2,a=−1f(x)=1x−x2,a=−1

137.

Найдите уравнение касательной к графику f(x)=2×3+4×2−5x−3f(x)=2×3+4×2−5x−3 в точке x=−1.x=−1.

138.

Найдите уравнение касательной к графику f(x)=x2+4x−10f(x)=x2+4x−10 при x=8. x=8.

139.

Найдите уравнение касательной к графику f(x)=(3x−x2)(3−x−x2)f(x)=(3x−x2)(3−x−x2) при x= 1.х=1.

140.

Найдите точку на графике f(x)=x3f(x)=x3 такую, что касательная в этой точке имеет точку пересечения xx, равную 6.

141.

Найдите уравнение прямой, проходящей через точку P(3,3)P(3,3) и касательной к графику f(x)=6x−1.f(x)=6x−1.

142.

Определить все точки на графике f(x)=x3+x2−x−1f(x)=x3+x2−x−1, для которых

касательная горизонтальна
касательная имеет наклон −1,−1.

143.

Найдите квадратичный многочлен такой, что f(1)=5,f′(1)=3f(1)=5,f′(1)=3 и f″(1)=−6.f″(1) =-6.

144.

Автомобиль, движущийся по автостраде с движением, проехал s(t)=t3−6t2+9ts(t)=t3−6t2+9t метров за tt секунд.

Определить время в секундах, когда скорость автомобиля равна 0.
Определить ускорение автомобиля, когда скорость равна 0.

145.

[T] Сельдь, плывущая по прямой, прошла s(t)=t2t2+2s(t)=t2t2+2 футов за tt секунд.

Определите скорость селедки, когда она пройдет 3 секунды.

146.

Популяция в миллионах полярных камбал в Атлантическом океане моделируется функцией P(t)=8t+30,2t2+1, P(t)=8t+30,2t2+1, где tt измеряется в годах.

Определите начальную популяцию камбал.
Определите P'(10)P'(10) и кратко интерпретируйте результат.

147.

[T] Концентрация антибиотика в кровотоке tt часов после введения определяется функцией C(t)=2t2+tt3+50,C(t)=2t2+tt3+50, где измеряется КК в миллиграммах на литр крови.

Найдите скорость изменения C(t). C(t).
Определите скорость изменения для t=8,12,24,t=8,12,24 и 36,36.
Кратко опишите, что происходит по мере увеличения количества часов.

148.

Функция затрат книжного издательства определяется формулой C(x)=x3+2x+3×2, C(x)=x3+2x+3×2, где x — количество экземпляров книги в тысячах, а C — стоимость книги в долларах. Оцените C′(2)C′(2) и объясните его значение.

149.

[T] Согласно закону всемирного тяготения Ньютона сила FF между двумя телами постоянной массы m1m1 и m2m2 определяется формулой F=Gm1m2d2,F=Gm1m2d2, где GG — гравитационная постоянная, а dd — расстояние между телами.

Предположим, что G, m1 и m2 G, m1 и m2 являются константами. Найти скорость изменения силы FF на расстоянии d.d.
Найти скорость изменения силы FF с гравитационной постоянной G=6,67×10-11G=6,67×10-11 Нм2/кг2, Нм2/кг2 на двух телах массой 1000 кг каждое на расстоянии 10 м друг от друга.

6.3 Правила дифференцирования | Дифференциальное исчисление

6.2 Отличие от первых принципов

6.4 Уравнение касательной к кривой

6.3 Правила дифференцирования (EMCH7)

Определение производной функции из первых принципов требует длительных вычислений и легко ошибиться. Однако мы можем использовать этот метод нахождения производной от первого принципы для получения правил, которые значительно упрощают нахождение производной функции.

Правила дифференцирования

Отличие от первых принципов в следующем:
1. $е\влево(х\вправо)=х$
2. 9{3}\)
3. $е\влево(х\вправо)=\фракция{1}{х}$
4. $е\влево(х\вправо)=-\фракция{2}{х}$
Заполните таблицу:
$е\влево(х\вправо)$ ${f}’\влево(х\вправо)$
$х$ 9{3}\)
$\frac{1}{x}$
$-\frac{2}{x}$
Можете ли вы определить закономерность определения производной? 9{n-1}, \text{ где } n \in \mathbb{R} \text{ и } n \ne 0. \]
Производная константы равна нулю.
\[\frac{d}{dx}\left[k\right]= 0\]
Производная константы, умноженная на функцию, равна постоянная, умноженная на производную функции.
\[\frac{d}{dx}\left[k \cdot f\left(x\right) \right]=k \frac{d}{dx}\left[ е\влево(х\вправо) \вправо]\]
Производная суммы равна сумме производных.
\[\frac{d}{dx}\left[f\left(x\right)+g\left(x\right)\right]=\frac{d}{dx}\left[f\left(x \Правильно) \right] + \frac{d}{dx}\left[g\left(x\right)\right]\]

Производная разности равна разнице производных.

\[\frac{d}{dx}\left[f\left(x\right) – g\left(x\right)\right]=\frac{d}{dx}\left[f\left(x\right) \right] – \frac{d}{dx}\left[g\left(x\right)\right]\] 9{\ гидроразрыва {3} {2}}} \конец{выравнивание*}

Когда использовать правила дифференцирования:

Если в вопросе не указано, как мы должны определить производную, то используем правила для дифференциации.

Когда проводить различие с использованием первых принципов:

Если в вопросе конкретно указано использование первых принципов. 9{2}-5x+6}{x-2}\\ & = \ гидроразрыв {(х-3)(х-2)}{х-2}\\ & = х-3\\ f'(x) & = \text{1} \end{align*}

Найти ${f}’\left(y\right)$, если $f\left(y\right)=\sqrt{y}$. {-\frac{1}{2}}\\ & = \frac{1}{2\sqrt{y}} \end{выравнивание*} 9{2}} \end{align*}

Найти $\frac{dy}{dx}$, если $x=2y+3$.

Сделать $y$ предметом формулы, чтобы дифференцировать $y$ относительно $х$.

\начать{выравнивать*} y & = \frac{1}{2}x – \frac{3}{2} \\ \поэтому \frac{dy}{dx}& = \frac{1}{2} \конец{выравнивание*} 9{\ гидроразрыва {3} {2}}} \конец{выравнивание*}

6. 2 Отличие от первых принципов

Оглавление

6.4 Уравнение касательной к кривой

2.1: Элементарные правила производных — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы
4299

Мэтью Болкинс, Дэвид Остин и Стивен Шликер
Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли

Цели обучения

В этом разделе мы стремимся понять идеи, порожденные следующими важными вопросами:

Какие существуют альтернативные обозначения производной?
Как мы можем иногда использовать алгебраическую структуру функции $f (x)$, чтобы легко вычислить формулу для $f'(x)$? 9Икс\)?
Если мы знаем производную $y = f (x)$, как вычисляется производная $y = k f (x)$, где $k$ – константа?
Если мы знаем производные $y = f (x)$ и $y = g(x)$, как вычисляется производная $y = f (x) + g(x)$ ?

В главе 1 мы разработали понятие производной функции. Теперь мы знаем, что производная $f’$ функции $f$ измеряет мгновенную скорость изменения $f$ по отношению к $x$, а также наклон касательной к $y = f (x)$ при любом заданном значении $x$. На сегодняшний день мы сосредоточились главным образом на интерпретации производной графически или, в контексте функций в физической среде, как значимой скорости изменения. Чтобы фактически вычислить значение производной в определенной точке, мы обычно полагались на предельное определение производной.

В этой главе мы исследуем, как предельное определение производной

\[f'(x) = \lim_{h→0} f (x + h) − f (x) h ,\]

приводит к интересным шаблонам и правилам, которые позволяют нам быстро найти формулу для $f'(x)$ на основе формулы для $f (x)$ без непосредственного использования определения предела. Например, мы уже знаем, что если $f (x) = x$, то отсюда следует $f'(x) = 1$. Хотя мы могли бы использовать предельное определение производной, чтобы подтвердить это, мы знаем, что это верно, потому что $f (x)$ является линейной функцией с наклоном 1 при каждом значении $x$. Одна из наших целей — иметь возможность использовать стандартные функции, скажем, такие, как 9.2\), что мы можем обозначить его производную через $f'(x)$, и мы пишем $f'(x) = 2x$. Эквивалентно, если мы больше думаем об отношении между $y$ и $x$, мы иногда обозначаем производную $y$ по $x$ символом

\[\ frac { d y } { d x }\]

, которое мы читаем как «dee-y dee-x». Это обозначение исходит из того факта, что производная связана с наклоном линии, а наклон измеряется как $\frac {\Delta y} {\Delta x}$. Обратите внимание, что хотя мы читаем $\frac {\Delta y} {\Delta x}$ как «изменение $y$ по сравнению с изменением $x$», для производного символа $\frac { d y } { d x }$, мы видим, что это один символ, а не частное двух величин 92\), напишем, что производная равна $\frac { d y } { d x }=2x$.

Кроме того, мы используем вариант нотации $\frac { d y } { d x }$ для передачи инструкции взять производную от определенной величины по заданной переменной. { 2 } \right] = 2 x \). 9{ 2 } }.\]

В дальнейшем мы будем работать над расширением нашего набора функций, для которых мы можем быстро вычислить соответствующую формулу производной

Постоянные, степенные и экспоненциальные функции

Пока что мы знать формулы производных для двух важных классов функций: постоянных функций и степенных функций. Для первого вида заметим, что если $f (x) = c$ — постоянная функция, то ее график представляет собой горизонтальную линию с нулевым наклоном в каждой точке. Таким образом, $\frac {d} {d x} [c] = 0$. Подытожим это следующим правилом. 9{n−1}\).

Когда мы в следующий раз обратимся к размышлениям о производных комбинаций основных функций, будет полезно иметь еще один тип основной функции, формула производной которой нам известна. Пока мы просто формулируем это правило без объяснения и обоснования; мы рассмотрим, почему это правило верно, в одном из упражнений в конце этого раздела, а также мы встретимся с графическим объяснением того, почему правило правдоподобно, в предварительном упражнении 2. 2.

Экспоненциальные функции

Икс\). Как видно из правил, это сильно меняет форму производной.
Следующее упражнение проверит ваше понимание производных трех основных типов функций, упомянутых выше.
Activity $\PageIndex{1}$
Используйте три приведенных выше правила для определения производной каждой из следующих функций. Для каждого укажите свой ответ, используя полные и правильные обозначения, пометив производную ее названием. Например, если вам дана функция $h(z)$, вы должны написать «$h ‘(z) =$» или «$\frac { d h } { d z } = $ » как часть вашего ответа. 9{ 3 } }\)

Постоянные кратные и суммы функций

Конечно, большинство функций, с которыми мы сталкиваемся в математике, более сложны, чем просто константы, степень переменной или основание, возведенное в переменную степень. В этом и нескольких последующих разделах мы научимся быстро вычислять производную функции, построенной как алгебраическая комбинация основных функций. Например, мы хотели бы понять, как взять производную полиномиальной функции, такой как 92 − 9,\]

, которая представляет собой функцию, состоящую из постоянных кратных и сумм степеней $t$. С этой целью мы разрабатываем два новых правила: постоянное множественное правило и правило суммы .

Допустим, у нас есть функция $y = f (x)$, формула производной которой известна. Как производная $y = k f (x)$ связана с производной исходной функции? Напомним, что когда мы умножаем функцию на константу $k$, мы вертикально растягиваем график в $|k|$ раз (и отражаем график через $y = 0$, если $k < 0$). Это вертикальное растяжение влияет на наклон графика, делая наклон функции $y = k f (x)$ в $k$ раз более крутым, чем наклон $y = f (x)$. С точки зрения производной это, по сути, означает, что когда мы умножаем функцию на коэффициент $k$, мы также меняем значение ее производной на коэффициент $k$. Таким образом 9{−3 }).\]

Далее мы исследуем, что происходит, когда мы берем сумму двух функций. Если у нас есть $y = f (x)$ и $y = g(x)$, мы можем вычислить новую функцию $y = (f + g)(x)$, добавив выходные данные две функции: $( f + g)(x) = f (x) + g(x)$. Это приводит не только к тому, что значение новой функции является суммой значений двух известных функций, но и наклон новой функции является суммой наклонов известных функций. Таким образом, ³ , мы приходим к следующему правилу сумм для производных: 9{ \ простое число } ( х ) \) .

Другими словами, Правило сумм говорит нам, что «производная суммы есть сумма производных». Это также говорит нам, что каждый раз, когда мы берем сумму двух дифференцируемых функций, результат также должен быть дифференцируемым. Кроме того, поскольку мы можем рассматривать разностную функцию

\[y = ( f −g)(x) = f (x)−g(x) \textit{ как y} = f (x)+(−1 · g (x)),\]

Правило сумм и Правила постоянного кратного вместе говорят нам, что

\[\dfrac{d}{dx} [ f (x) + (−1 · g(x))] = f ‘(х) – g ‘(х),\] 9{ – 4 }.\]

Activity $\PageIndex{2}$

Используйте только правила для постоянных, степенных и экспоненциальных функций вместе с правилами постоянного множителя и суммы для вычисления производной каждой функции ниже по данной независимой переменной. Обратите внимание, что мы еще не знаем никаких правил дифференцирования произведения или частного функций. Это означает, что вам, возможно, придется сначала выполнить некоторые алгебраические вычисления с приведенными ниже функциями, прежде чем вы сможете использовать существующие правила для вычисления желаемой формулы производной. В каждом случае помечайте производную, которую вы вычисляете, ее именем, используя соответствующие обозначения, такие как $f'(x)$, $h ‘(z)$, $d r / d t$ и т. д. 9{ 2 } – а + 12 \)

Точно так же, как у нас есть правила быстрого доступа, помогающие нам находить производные, мы вводим более простой и короткий язык. Часто вместо того, чтобы сказать «взять производную $f$», мы говорим просто «дифференцировать $f$». Эта формулировка связана с идеей наличия производной для начала: если производная существует в точке, мы говорим, что $f$ дифференцируема, что связано с тем фактом, что $f$ можно дифференцировать .

По мере того, как мы все больше и больше работаем с алгебраической структурой функций, важно стремиться к созданию общей картины того, что мы делаем. Здесь мы можем отметить несколько общих наблюдений, основанных на правилах, которые у нас есть до сих пор. Во-первых, производная любой полиномиальной функции будет другой полиномиальной функцией, и что степень производной на единицу меньше степени исходной функции. Например, если 9{ z } \ln ( 2 ) \), которая также является экспоненциальной.

Кроме того, хотя в настоящее время мы делаем акцент на изучении быстрых правил для нахождения производных без непосредственного использования определения предела, мы должны быть уверены, что не упускаем из виду тот факт, что сохраняется все значение производной, которое мы разработали в главе 1. То есть каждый раз, когда мы вычисляем производную, эта производная измеряет мгновенную скорость изменения исходной функции, а также наклон касательной в любой выбранной точке кривой. В следующем упражнении вам предлагается объединить только что разработанные производные правила с некоторыми ключевыми перспективами, которые мы изучали в главе 1.

Activity $\PageIndex{3}$

В каждом из следующих вопросов предлагается использовать производные для ответа на ключевые вопросы о функциях. {t} + 32\), где $t$ измеряется в днях. 9{ 2 } – a + 12 \) в точке, где $a = −1$.

В чем разница между заданием найти наклон касательной (задается в (a)) и уравнением касательной (задается в (c))?

Резюме

В этом разделе мы столкнулись со следующими важными идеями:

Для заданной дифференцируемой функции $y = f (x)$ мы можем выразить производную от f в нескольких различных обозначениях: $f ‘(x)$, $\ frac {d f } {d x } $ , $\ frac {d y } {d x } $ и $\ frac {d } {d x } [ f ( x ) ] $. 9{ \ простое число } ( х ) \].

________

¹ То есть мы не говорим «ди-и вместо ди-икс».

² Правило постоянного кратного можно формально доказать как следствие свойств пределов, используя предельное определение производной.

³ Подобно правилу постоянного кратного, правило сумм может быть формально доказано как следствие свойств пределов с использованием предельного определения производной.

Эта страница под названием 2.1: Elementary Derivative Rules распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Мэтью Болкинсом, Дэвидом Остином и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Активное исчисление
Лицензия
CC BY-SA
Версия лицензии
4,0
Показать страницу TOC
нет
Теги
1. постоянное множественное правило
2. силовое правило
3. источник@https://activecalculus. org/single
4. Правило суммы

Производные правила – Что такое правила дифференциации? Примеры

Производные правила используются для различения различных типов функций. Все эти правила в основном выведены из «производной с использованием первого принципа» (предельное определение производной). Поскольку использование определения предела затруднено, производные правила, выведенные из определения предела, очень полезны для упрощения процесса дифференциации.

Давайте посмотрим производные правила вместе с их доказательствами и многими другими примерами.

1.	Что такое производные правила?
2.	Правила дифференциации различных функций
3.	Важные производные правила
4.	Таблица правил деривативов
5.	Часто задаваемые вопросы о производных правилах

Что такое производные правила?

Производные правила в исчислении используются для нахождения производных различных операций и различных типов функций, таких как степенные функции, логарифмические функции, экспоненциальные функции и т. д. Некоторые важные производные правила:

Степенное правило
Правило суммы/разности
Правило продукта
Частное правило
Цепное правило

Все эти правила получаются из предельного определения производной, согласно которому производная функции f(x) (обозначаемой через f'(x)) задается пределом: f'(x) = limₕ→₀ [ f(x + h) – f(x)] / h. Производная функции y = f(x) записывается как f'(x) (или) dy/dx (или) d/dx (f(x)) и дает наклон кривой в фиксированной точке. Он также дает скорость изменения функции по отношению к переменной. Давайте подробно изучим каждое из правил дифференцирования в следующих разделах.

Правила дифференциации различных функций

Давайте посмотрим правил дифференцирования различных типов функций. Если вы хотите увидеть доказательство каждого производного правила, нажмите на соответствующую ссылку.

Производные правила экспоненциальных функций

Показательная функция — это функция, основание которой является константой, а показатель степени — переменной. В основном есть два типа экспоненциальных функций: e ^x и a ^x , где «e» — число Эйлера, а «a» — любая константа. Мы увидим правила для производных экспоненциальных функций.

Производная от e ^x равна d/dx (e ^x ) = e ^x .
Производная от ^x равна d/dx (a ^x ) = a ^x ln a.

Производные правила логарифмических функций

Логарифмическая функция включает логарифм (рядовой или натуральный логарифм). т. е. имеет вид log _a x (или) ln x. Правила нахождения производных этих двух логарифмических функций следующие:

Производная log _a x is, d/dx (log _a x) = 1 / (x ln a)
Производная от ln x равна d/dx (ln x) = 1/x.

Производные правила тригонометрических функций

У нас есть шесть тригонометрических функций: sin, cos, tan, csc, sec и cot. Вот правила нахождения производных тригонометрических функций.

Производная от sin x равна d/dx (sin x) = cos x
Производная от cos x равна d/dx (cos x) = – sin x
Производная tan x is, d/dx (tan x) = sec ² x
Производная csc x is, d/dx (csc x) = – csc x cot x
Производная sec x равна d/dx (sec x) = sec x tan x
Производная cot x is, d/dx (cot x) = – csc ² x

Производные правила обратных тригонометрических функций

Существует 6 обратных тригонометрических функций, соответствующих вышеуказанным тригонометрическим функциям. Помните, что производные обратных тригонометрических функций НЕ включают никаких тригонометрических/обратных тригонометрических функций. Вот правила:

Производная обратного синуса d/dx (sin ^-1 x) = 1/√(1-x ² )
Производная арккосинуса равна d/dx (cos ^-1 x) = -1/√(1-x ² )
Производная обратного тангенса, d/dx (тангенс ^-1 х) = 1/(1 + х ² )
Производная обратного коэффицента, d/dx (csc ^-1 x) = -1/ [x √(x ² – 1) ], x ≠ 1, -1, 0
Производная обратной сек, d/dx (сек ^-1 x) = 1/[x √(x ² – 1) ], x ≠ 1, -1, 0
Производная обратной кроватки, d/dx (кроватка ^-1 х) = -1/(1 + х ² )

Правила производных гиперболических функций

Существует 6 гиперболических функций, соответствующих 6 тригонометрическим функциям. Каждая тригонометрическая функция, за которой следует буква «h», является соответствующей гиперболической функцией. Вот производные гиперболических функций.

Производная от sh x равна d/dx (sinh x) = ch x
Производная ch x is, d/dx (ch x) = sh x
Производная тангенса x is, d/dx (tanh x) = sech ² x
Производная csch x is, d/dx (csch x) = – csch x coth x
Производная от sech x is, d/dx (sech x) = – sech x tanh x
Производная coth x is, d/dx (coth x) = – csch ² x

Производные правила обратных гиперболических функций

Имеются снова 6 обратных гиперболических функций, которые соответствуют 6 гиперболическим функциям. Вот правила нахождения их производных.

Производная sin ^-1 x is, d/dx (sinh ^-1 x) = 1/√(1+x ² )
Производная ch ^-1 x is, d/dx (ch ^-1 x) = 1/√(x ² -1), x>1
Производное tanh ^-1 x is, d/dx (tanh ^-1 x) = 1/(1-x ² ), |x|<1
Производная csch ^-1 x is, d/dx (csch ^-1 x) = -1/ [ |x| √(1-x ² ) ], x ≠ 0
Производная от sech ^-1 x is, d/dx (sech ^-1 x) = -1/[x√(1-x ² ) ], 0 < x < 1
Производная coth ^-1 x is, d/dx (coth ^-1 x) = 1/(1-x ² ), |x|>1

Важные производные правила

Здесь очень важные правила дифференцирования, такие как правило произведения, правило частных, правило сумм, правило разности и т. д., и эти правила используются для различных комбинаций вышеупомянутых функций. Давайте также посмотрим на некоторые примеры каждого правила.

Степенное правило производных

Степенное правило производных говорит d/dx (x ⁿ ) = n · x ^{n – 1} . Вот несколько примеров применения этого правила.

d/dx (x ² ) = 2x ^{2 – 1} = 2x
д/д (г ⁵ ) = 5г ^{5 – 1} = 5г ⁴

Используя это правило, мы получаем две вещи:

Производная x относительно самого себя равна 1, т. е. d/dx (x) = 1,
Это потому, что
d/dx (x) = d/dx (x ¹) = 1 x ^1-1 = 1x ⁰ = 1,
Производная постоянной функции равна 0, т. е. d/dx (c) = 0, , где ‘c’ — константа (это правило называется постоянным правилом ).
Это потому, что
d/dx (c) = d/dx (c x ⁰) = c d/dx (x ⁰) = c (0 x ^0-1) = 0

Почему мы написали здесь «с» вне различия? Это происходит из-за следующего правила.

Постоянное кратное правило производных

Постоянное кратное правило производных говорит, что d/dx (c f(x)) = c d/dx (f(x)) . Это означает, что если константа умножается на функцию, то эта константа не участвует в процессе дифференцирования и выходит. Например:

d/dx (2x ³) = 2 d/dx(x ³) = 2(3x ²) = 6x ²
d/dx (4x) = 4 d/dx (x) = 4 d/dx (x) = 4(1) = 4.

Вот два примера, чтобы избежать путаницы, когда константа участвует в дифференцировании.

d/dx (4 + x) = d/dx (4) + d/dx (x) = 0 + 1 = 0
д/дх (4х) = 4 д/дх (х) = 4(1) = 4

Почему мы разделили d/dx на 4 и x на d/dx (4 + x) здесь? Давайте посмотрим на правило, стоящее за этим.

Правило суммы/разности производных

Это правило гласит, что процесс дифференцирования может быть распределен по функциям в случае суммы/разности. т. е. d/dx (f(x) ± g(x)) = d/dx (f(x)) ± d/dx (g(x)). Вот несколько примеров применения этого правила.

д/дх (х ³ + х ² ) = d/dx (x ³ ) + d/dx (x ² ) = 3x ² + 2x
d/dx (x ³ – x ²) = d/dx (x ³) – d/dx (x ²) = 3x ² – 2x

Правило произведения производных

Правило произведения используется для нахождения производной произведения двух функций. Там написано d/dx (f(x)) · g(x)) = f(x) d/dx (g(x)) + g(x) d/dx (f(x)). Другими словами, это можно записать как (uv)’ = u v’ + v u’. Мы можем понять это правило на следующих примерах.

d/dx (x sin x) = x d/dx (sin x) + sin x d/dx (x) = x cos x + sin x (1) = x cos x + sin x
d/dx (x ² ln x) = x ² d/dx (ln x) + ln x d/dx (x ² ) = x ² (1/x) + ln x (2x ) = х + 2х ln х

Частное правило производных

Частное правило производных состоит в том, чтобы найти производную дроби, где и числитель, и знаменатель включают переменную. {2}}\). Другими словами, правило частных говорит d/dx (u/v) = (v u’ – u v’) / v ² . Вот несколько примеров.

d/dx (x / sin x) = [sin x d/dx (x) – x d/dx (sin x)] / (sin x) ² = (sin x – x cos x) / sin ² х.
d/dx (x / ln x) = [ln x d/dx (x) – x d/dx (ln x)] / (ln x) ² = (ln x – x(1/x)) / ( ln x) ² = (ln x – 1) / (ln x) ² .

Цепное правило производных

Цепное правило производных используется для дифференцирования сложной функции, или, другими словами, цепное правило используется для нахождения производной функции, которая находится внутри другой функции. Например, его можно использовать для дифференциации таких функций, как sin (x ²), ln (2x + 1), tan (ln x) и т. д. Цепное правило гласит: d/dx (f(g(x)) = f ‘(g(x)) · g'(x Это правило просто означает, что мы находим производную, найденную с помощью производных правил, по производной внутренней функции Например:

d/dx (sin (x ² )) = cos (x ² ) · d/dx (x ² ) = 2x cos (x ² )
d/dx (tan (ln x)) = sec ² (ln x) · d/dx (ln x) = sec ² (ln x)/x

9{-1}(1)\right]}\) . .. (1)
Чтобы найти f ^-1 (1), предположим, что f ^-1 (1) = x ⇒ 1 = f(x ) ⇒ 1 = x ³ – 7 ⇒ x ³ = 8 ⇒ x = 2.
Итак, f ^-1 (1) = 2 … (2)
Теперь f ‘(x) = 3x ² – 0 = 3x ² .
Тогда f'(f ^-1(1)) = f'(2) (из (2))
= 3(2) ²
= 12
Подставляя это в (1):
(f ^-1 )(1) = 1/12.
Производные правила касательной и нормали
Касательная линия кривой y = f(x) — это линия, которая касается кривой в одной точке. Нормаль касательной – это прямая, перпендикулярная касательной. Наклоны касательной и нормали можно найти с помощью производной.
Наклон касательной равен f ‘(x)
Наклон нормальной линии – 1/f ‘(x)
Таблица правил для деривативов
В следующей таблице приведены важные правила для деривативов.
Функция в x Производная
с (постоянная) 0
х 1
x ^нет х ^н-1
е ^х е ^х
а ^х в ^x в
бревно _а x 1/(х вп)
длина х 1/х
sin x cos х
соз х – грех х
желтовато-коричневый x сек ² x
csc x – csc x детская кроватка x
сек x сек x тангенс x
Детская кроватка x – csc ² х
грех ^-1 x 1/√(1-x ² )
потому что ^-1 х -1/√(1-x ² )
рыжевато-коричневый ^-1 x 1/(1 + х ² )
csc ^-1 x -1/ [х √(х ² – 1) ]
сек ^-1 x 1/ [х √(х ² – 1) ]
детская кроватка ^-1 x -1/(1 + х ² )
Вот таблица с важными правилами дифференцирования, которые помогают находить производные сложных функций.
9{-1}(а)\справа]}\)
Название правила Правило дифференциации
☛Ссылки по теме:
Калькулятор производных
Калькулятор второй производной
Производные формулы
Неявное дифференцирование
Часто задаваемые вопросы о производных правилах
Что такое четыре основных правила производных?
Четыре основных производных правила :
Производное правило суммы: (u + v) ‘= u’ + v’
Производное правило разности: (u – v) ‘= u’ – v’
Производная по правилу произведения: (uv)’ = u v’ + v u’
Производная правила частного: (u/v)’ = (vu’ – uv’)/v ²
Как использовать производные правила для нахождения производной квадратного корня?
Мы знаем, что квадратный корень можно заменить показателем степени 1/2. т. е. √x можно записать как x ^1/2, и, следовательно, мы можем применить правило степени, чтобы дифференцировать это. Используя это, d/dx (√x) = d/dx (x ^1/2 ) = (1/2) x ^-1/2 = 1/(2√x).
Что такое правила дифференциации?
Правила дифференцирования (также известные как правила производных) в исчислении — это правила, которые используются для нахождения производных. Существуют различные правила дифференцирования, такие как правило произведения, правило отношения, правило степени и т. д. Кроме того, у нас есть различные правила дифференцирования для нахождения производных логарифмических функций, экспоненциальных функций, тригонометрических функций и т. д.
Что такое правила производных e?
Производные правила, включающие «e», следующие:
d/dx (e ^x ) = e ^x
d/dx (e ^x ) = a e ^x
Что такое триггер правил дифференциации?
Правила дифференцирования в тригонометрии — это формулы для нахождения производных от sin x, cos x, tan x, csc x, sec x и cot x. Они таковы:
(sin x)’ = cos x
(cos x)’ = – sin x
(тангенс х)’ = 9 сек.1337 2 х
(csc x)’ = – csc x детская кроватка x
(сек х)’ = сек х тангенс х
(кроватка x)’ = – csc ² x
Каковы применения производных правил?
Вот применение правил дифференцирования.
Нахождение максимумов и минимумов.
Поиск критических точек.
Нахождение точек перегиба.
Нахождение мгновенной скорости изменения.
Нахождение интервалов возрастания/убывания функции.
Что такое производные правила?
Производные правила, включающие логарифмы:
d/dx (log x) = 1 / (x ln 10)
d/dx (ln x) = 1/x
Правило произведения для трех и более функций — Krista King Math
Как расширить правило продукта с двух до трех функций
Правило произведения — это правило производной, которое позволяет нам взять производную функции, которая сама является произведением двух других функций. Правило произведения говорит нам, что производная уравнения типа
???y=f(x)g(x)???
будет выглядеть так:
???\frac{dy}{dx}=f\prime(x)g(x)+f(x)g\prime(x)???
Но что делать, если наша функция является произведением более чем двух функций? В этой ситуации, если наша функция
???y=f(x)g(x)h(x)???
, то производная выглядит так:
???\frac{dy}{dx}=f\prime(x)g(x)h(x)+f(x)g\prime(x)h( х)+f(x)g(x)h\prime(x)???
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Мы видим, что исходная функция была произведением трех функций, а ее производная была суммой трех произведений. Если бы наша функция была произведением четырех функций, производная была бы суммой четырех произведений.
Как видите, когда мы берем производную по правилу произведения, мы берем производную одной функции за раз, умножая на две другие исходные функции. Чтобы быть более конкретным, мы берем производную от ???f(x)??? и умножаем ее на ???g(x)??? и ???h(x)???, оставив эти два как есть. Затем мы добавляем к этому производную от ???g(x)???, умноженную на ???f(x)??? и ???ч(х)??? оставили как есть. Мы можем продолжить эту схему, взяв производную только от одной из функций и оставив остальные в покое, для такого количества функций, сколько было перемножено в нашей исходной задаче.
Глядя на уравнение, которое является произведением четырех функций, например
???y=f(x)g(x)h(x)j(x)???
производная равна
???\frac{dy}{dx}=f\prime(x)g(x)h(x)j(x)+f(x)g\prime(x)h( х)j(x)+f(x)g(x)h\prime(x)j(x)+f(x)g(x)h(x)j\prime(x)???
Видеопример применения правила произведения для производных к произведению трех функций
9{13}\справа)\cdot\Big[12\sin{4x}\cos{5x}???
???+2\sin{4x}\cos{5x}???
???+x\sin{4x}\cos{5x}???
???-5x\sin{4x}\sin{5x}???
???+4x\cos{4x}\cos{5x}\Big]???
Получите доступ к полному курсу исчисления 1
Начать
Изучайте математикуКриста Кинг 21 января 2019 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, правило произведения, правило произведения для производных, производные, правила производных, три функции, много функций, правило произведения для трех функций
0 лайков
Экспоненциальное правило для производной: теория и приложения
Когда дело доходит до расчета производных, существует эмпирическое правило, которое звучит примерно так: либо функция является базовой , и в этом случае мы можем обратиться к таблица производных , или функция составная , и в этом случае мы можем дифференцировать ее рекурсивно — разбив ее на производные ее составляющие через ряд производных правил .
В самом деле, те из нас, кто когда-либо читал учебник по математическому анализу или посещал курс математического анализа, возможно, уже знакомы с большинством, если не со всеми, из этих производных правил:
Постоянное правило
Если функция $cf$ определена на отрезке $I$ и $f$ дифференцируема на $I$, то $\displaystyle (cf)’=cf’$ на $I$. {r-1}$ для всех $x \in \mathbb{R}$ . В случае, когда $r$ меньше $1$ (и 9{r-1}$ для всех $x \ne 0$.
Правило сумм
Если функция $f+g$ корректно определена на интервале $I$, причем $f$ и $g$ дифференцируемы по на $I$, то $\displaystyle (f+ g)’ = f’ + g’$ на $I$.
Правило разности
Если функция $f-g$ корректно определена на интервале $I$, причем $f$ и $g$ являются -дифференцируемыми на $I$, то $\displaystyle (f-g)’ = f’ – g’$ на $I$.
Правило произведения
Если функция $fg$ корректно определена на интервале $I$, где $f$ и $g$ равны 9{-1}(x)]} \qquad (x \in I) \end{align*}
(подробности см. в руководстве по теореме об обратной функции )
По большей части эти правила более чем достаточно для обработки подавляющего большинства функций, с которыми можно столкнуться. Однако, когда мы смотрим на наш репертуар функций , мы видим, что чего-то еще не хватает, а именно:
А как насчет функций, построенных с помощью возведения в степень ?
Здесь, подсказка необычное чувство безотлагательности, мы продолжаем играть с идеей производной степени , впоследствии заканчивая тем, что разрабатываем правило именно для этой цели. g (A+B)$, где:
$A$ получается путем взятия производной степени , умноженной на логарифм основания .
$B$ получается путем взятия производной от по основанию , умноженной на отношение с показателем степени в верхней части.
На самом деле, немного потренировавшись, можно освоить Экспонентное правило так же хорошо, как мы делаем это с Частным правилом — и это не говоря уже о том, какой новый мир он открывает для наших фанатиков ментального исчисления !
Традиционно, чтобы вычислить производную степенной функции , нужно было бы либо прибегнуть к логарифмическому дифференцированию , либо стандартизации base-e перед дифференцированием. С появлением правила экспоненты оба эти подхода в основном устарели — не потому, что они неуместны сами по себе, а потому, что они уже применялись во время вывода правила экспоненты. x$ и его производной здесь: 9{\, \ln x}$, из которого видно, что:
$\ln x$ определяется только тогда, когда $x>0$.
$\cos x>0$ только тогда, когда $\displaystyle -\frac{\pi}{2} < x < \frac{\pi}{2} \pmod{2\pi}$.
Таким образом, если мы обозначим через $I$ множество, удовлетворяющее обоим ограничениям. То есть
\begin{align*}I \stackrel{df}{=} \left\{ x \in \mathbb{R_+} \mathrel{\Big|} -\frac{\pi}{2} < x < \frac{\pi}{2} \,\, (\mathrm{mod \ } 2\pi ) \right\} \end{align*}
{\, \ln x}}$ и его производная. Довольно круто. Верно?
Да. Это было немного перебором символов, но, надеюсь, это иллюстрирует, почему правило экспоненты может быть ценным активом в нашем арсенале производных правил . В то время как для простой степенной функции этот подход может показаться излишним , для неоднократно возводимых в степень степенных функций с одной вложенной внутри другой становится очевидным, что правило экспоненты является абсолютно правильным.

Функция в x	Производная
с (постоянная)	0
х	1
x ^нет	х ^н-1
е ^х	е ^х
а ^х	в ^x в
бревно _а x	1/(х вп)
длина х	1/х
sin x	cos х
соз х	– грех х
желтовато-коричневый x	сек ² x
csc x	– csc x детская кроватка x
сек x	сек x тангенс x
Детская кроватка x	– csc ² х
грех ^-1 x	1/√(1-x ² )
потому что ^-1 х	-1/√(1-x ² )
рыжевато-коричневый ^-1 x	1/(1 + х ² )
csc ^-1 x	-1/ [х √(х ² – 1) ]
сек ^-1 x	1/ [х √(х ² – 1) ]
детская кроватка ^-1 x	-1/(1 + х ² )

Помимо автоматизации процесса дифференцирования степенных функций, правило экспоненты — особенно когда комбинирует с другими традиционными производными правилами — может действительно творить чудеса с точки зрения использования функций, которые ранее были слишком пугающими / утомительные для решения — например, те, которые нам трудно найти в типичном учебнике по математическому анализу. 🙂
В любом случае, давайте остановимся на этом и пока закончим. Для полноты картины вот Интерактивная таблица Суммирование того, что мы обнаружили до сих пор:
Стандартные правила производных
Правило показания (Теория)
Правило показания (примеры)
2 9{\, \ln x} )} \right]’ = $ вы знаете ~~что~~ как
1111111111111111111111111111111111111111111111. НЕПРАВИЛЬНЫЙ ПРАВИЛЬНЫЙ
Правило суммы
Правило разности
Правило произведения
Короче говоря, несмотря на то, что правило экспоненты относительно неизвестно, оно может быть мощным инструментом дифференцирования в нашем распоряжении.

\(е\влево(х\вправо)\)	\({f}’\влево(х\вправо)\)
\(х\)	9{3}\)
\(\frac{1}{x}\)
\(-\frac{2}{x}\)