Правила производных: Таблица производных и правила дифференцирования

Таблица производных. Таблица производных полная для студентов и правила дифференцирования. Таблица производных функций. Табличные производные. Формулы производных.

Если x – независимая переменная, то:
Производная степенной функции	Производная степенной функции
–
Производная экспоненциальной функции	Производная экспоненты
Производная сложной экспоненциальной функции	Производная экспоненциальной функции
–
Производная логарифмической функции	Производная натурального логарифма
	Производная натурального логарифма функции
–
Производная синуса	Производная косинуса
Производная косеканса	Производная секанса
Производная арксинуса	Производная арккосинуса
Производная арксинуса	Производная арккосинуса
Производная тангенса	Производная котангенса
Производная арктангенса	Производная арккотангенса
Производная арктангенса	Производная арккотангенса
Производная арксеканса	Производная арккосеканса
Производная арксеканса	Производная арккосеканса
–
Производная гиперболического синуса	Производная гиперболического косинуса
Производная гиперболического синуса в английской версии	Производная гиперболического косинуса в английской версии
Производная гиперболического тангенса	Производная гиперболического котангенса
Производная гиперболического секанса	Производная гиперболического косеканса

Производная функции.

Понятие производной. Геометрический смысл производной. Физический смысл производной. Правила дифференцирования. Производная сложной функции. Достаточное условие монотонности функции. Необходимое и достаточное условия экстремума.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Производная функции. Понятие производной. Геометрический смысл производной. Физический смысл производной. Правила дифференцирования. Производная сложной функции. Достаточное условие монотонности функции. Необходимое и достаточное условия экстремума. Поделиться:    Производная функции. Понятие производной. Геометрический смысл производной. Физический смысл производной. Правила дифференцирования. Производная сложной функции. Достаточное условие монотонности функции. Необходимое условие экстремума. Достаточное условие экстремума. Производная функции. Понятие производной, определение производной: Производной (первой производной)  f ‘ (x) функции f  (x) в точке xo называется предел отношения приращения функции Δ f (x) = f (x0 + Δx) – f (x0) к приращению аргумента Δx при Δx→0, если этот предел существует: Второй производной  f ” (x) функции f  (x) в точке xo называется производная от производной f ‘ (x) в точке xo Дифференцирование – это операция нахождения производной f ‘ (x) Производная функции. Геометрический смысл производной: Производная функции f  (x) в точке xo равна угловому коэффициенту (тангенсу угла наклона) касательной прямой  к графику функции y = f  (x)  в точке M0(x0 ,y0), то есть: f ‘ (x0) = k, где k = tg α Уравнение касательной к кривой y = f (x) в точке x0 имеет вид: y = f ‘ (x)(x-x0) + f(x0) Производная функции. Физический смысл производной: Если точка движется вдоль оси x и ее координата изменяется по закону x (t), то мгновенная скорость точки: а укорение (мгновенное ускорение): Производная функции. Правила дифференцирования: Производная функции. Производная сложной функции: Если у функции y= f (g (x))  существуют производные f’gи g’x, то : где индексы g и x указывают, по какому аргументу вычисляются производные функции. Производная функции. Достаточное условие монотонности функции: Если для функции f (x) в каждой точке  интервала (a;b) то функция f (x) возрастает на этом интервале Если для функции f (x) в каждой точке  интервала (a;b) то функция f (x) убывает на этом интервале Производная функции. Необходимое условие экстремума: Если  x0– точка экстремума некоторой функции f (x) , то эта точка является критической точкой данной функции, т.е. в данной точке производная либо  равна нулю, любо не существет. Производная функции. Достаточное условие экстремума: Если функция y = f (x)  непрерывна в точке x0  и производная f ‘ (x) меняет знак в этой точке, то x0 – точка экстремума функции y = f (x) ! В самой точке  x0  производной у функции  y = f (x) может не существовать. Если f ‘ (x) > 0 при x < x0, f ‘ (x) < 0 при x > x0, то x0 – точка максимума Если f ‘ (x) < 0 при x < x0, f ‘ (x) > 0 при x > x0, то x0 – точка минимума Производные элементарных функций: Справочно: Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции. Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Математика онлайн

Решение математики онлайн

Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.

Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.

Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.

О калькуляторах

По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.

Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]

Преимущества

1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.

2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.

3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.

4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.

5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.

Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.

Правила дифференцирования – это… Что такое Правила дифференцирования?

• Правила де Моргана
• Правила китайско-русской практической транскрипции

Смотреть что такое “Правила дифференцирования” в других словарях:

• Лейбниц, Готфрид Вильгельм — Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz …   Википедия

• Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная …   Википедия

• Дифференцирование функции — [ derivation  ] — операция определения производной рассматриваемой функции. Например, производная линейной функции (bx + a )’ = b, то есть является константой; производная  степенной функции ( xn)’ =  axn 1  ( х>0), то есть… …   Экономико-математический словарь

• дифференцирование функции — Операция определения производной рассматриваемой функции. Например, производная линейной функции (bx+a)?=b, то есть является константой; производная степенной функции (xn)?=axn 1 (х>0), то есть дифференцирование степенной функции уменьшает ее… …   Справочник технического переводчика

• Лейбниц Готфрид Вильгельм — Лейбниц (Leibniz) Готфрид Вильгельм (1.7.1646, Лейпциг, 14.11.1716, Ганновер), немецкий философ идеалист, математик, физик и изобретатель, юрист, историк, языковед. Изучал юриспруденцию и философию в Лейпцигском и Йенском университетах. В 1668… …   Большая советская энциклопедия

• Производная функция — Производная основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел… …   Википедия

• ТЕНЗОРНЫЙ АНАЛИЗ — матем. теория, изучающая объекты спец. рода тензорные поля (см. Тензор). Необходимость применения Т. а. возникает, когда для изучения того или иного физ. явления (относительно к рого имеется полная система непротиворечивых данных для создания… …   Физическая энциклопедия

• Лейбниц Готфрид Вильгельм — (Leibniz) (1646 1716), немецкий философ, математик, физик, языковед. С 1676 на службе у ганноверских герцогов. Основатель и президент (с 1700) Бранденбургского научного общества (позднее  Берлинская АН). По просьбе Петра I разработал проекты… …   Энциклопедический словарь

• Таблица производных — Вычисление производной  важнейшая операция в дифференциальном исчислении. Эта статья содержит список формул для нахождения производных от некоторых функций. В этих формулах f и g  произвольные дифференцируемые функции вещественной… …   Википедия

• Производные основных элементарных функций — Вычисление производной  важнейшая операция в дифференциальном исчислении. Эта статья содержит список формул для нахождения производных от некоторых функций. В этих формулах f и g произвольные дифференцируемые функции вещественной переменной, а c  …   Википедия

5.1.1.4. Правила дифференцирования

Производная произведения функций Если функции  и  дифференцируемы в точке , то функция  тоже дифференцируема в точке  и ее производная вычисляется по правилу: .   Доказательство Составим приращение  для функции . . Прибавим и вычтем выражение  и сгруппируем слагаемые попарно. . Из первой скобки можно вынести общий множитель , а из второй – . . Выражения в скобках представляют собой приращения функций  и , поэтому . Тогда, используя определение производной, можно записать: , или . Используя теоремы о пределе суммы и произведения функций, получим: . Из дифференцируемости функции  следует, что существует конечный предел. Из дифференцируемости функции  следует, что существует конечный предел . Так как дифференцируемая в точке  функция  непрерывна в этой точке, то по определению непрерывной функции . Следовательно,   Следствие Если функция  дифференцируема в точке , а  – конечное число, то функция  тоже дифференцируема в точке  и при этом .   Доказательство .   Производная частного Если функции  и  дифференцируемы в точке  и , то функция  тоже дифференцируема в точке  и ее производная вычисляется по правилу: .   Доказательство Составим приращение  для функции . . Прибавим и вычтем в числителе выражение  и сгруппируем слагаемые попарно. Получим . Из первой скобки можно вынести общий множитель , а из второй –  . Тогда приращение  запишется в виде: , или . Используя определение, запишем выражение для производной в виде , затем, проведя под знаком предела тождественные преобразования и учитывая, что  не зависит от переменной , преобразуем его . Так как  и  не зависят от переменной , то по теоремам о пределах получим . Из дифференцируемости  следует, что существует конечный предел . Из дифференцируемости (и непрерывности)  следует, что существуют конечные пределы  и . Поэтому , или  .   Теорема о производной обратной функции Если функция  монотонна на промежутке  и дифференцируема в точке , то существует обратная функция , которая дифференцируема в точке  и ее производная определяется из соотношения  .   Доказательство Функция  дифференцируема в точке , если существует конечный предел . Докажем это. Поскольку по условию существует конечный предел , причем в силу монотонности , то по теореме о пределе частного существует и конечен предел . Из дифференцируемости функции  в точке  следует ее непрерывность в этой точке, а это означает, что при  приращение функции . Учитывая это, можно от предела при  перейти к пределу при . Тогда . Следовательно, существует конечная производная , которая вычисляется по правилу: .   Производная сложной функции Если функция  дифференцируема в точке  и функция  дифференцируема в точке , то суперпозиция функций (сложная функция)  дифференцируема в точке  и ее производная по переменной  вычисляется по правилу: . при этом нижние индексы показывают, по какой переменной берется производная.   Доказательство . Умножим числитель и знаменатель дроби под знаком предела на приращение , получим . Так как функция  дифференцируема точке , следовательно, она в этой точке непрерывна. Поэтому приращение функции  при . Переходя в первом сомножителе от предела при  к пределу при , получим . Из дифференцируемости функций  и  следует, что оба предела существуют, конечны и равны производным по переменным  и  соответственно, то есть . Замечание Правило дифференцирования суперпозиции функций (сложной функции) следует понимать так, что если требуется вычислить производную от функции , то следует иметь в виду, что вычисляется производная суперпозиции функций , где . Тогда следует вычислить производную  и производную . Далее по правилу дифференцирования сложной функции .

формулы и правила дифференцирования

Просмотр содержимого документа
«формулы и правила дифференцирования»

Алгебра и начала математического анализа

10 класс

Глава 5. Производная.

Формулы и правила дифференцирования.

Составитель:

учитель математики МОУ СОШ №203 ХЭЦ

г. Новосибирск

Видутова Т. В.

Формулы дифференцирования

Основные правила дифференцирования.

Теорема 1.

Если функции u и v имеют производную в точке х, то и их сумма имеет производную в точке х , причем производная суммы равна сумме производных:

( ПРОИЗВОДНАЯ СУММЫ РАВНА СУММЕ ПРОИЗВОДНЫХ )

Пример:

Основные правила дифференцирования.

Теорема 2.

Если функция u имеет производную в точке х, то и функция ku имеет производную в точке х , причем :

( ПОСТОЯННЫЙ МНОЖИТЕЛЬ МОЖНО ВЫНЕСТИ ЗА ЗНАК ПРОИЗВОДНОЙ )

Пример:

Основные правила дифференцирования.

Теорема 3.

Если функции u и v имеют производную в точке х, то и их произведение имеет производную в точке х , причем:

Пример:

Основные правила дифференцирования.

Если функции u и v имеют производную в точке х, и в этой точке v ≠0 , то функция имеет производную в точке х , причем:

Теорема 4.

Пример:

Основные правила дифференцирования.

1 вариант

2 вариант

Формулы дифференциров ания

Правила дифференцирования

Правила нахождения производных. Таблицы производных

Выше, используя определение, была вычислена производная только функции . Точно таким же образом, исходя из определения производной, можно вычислить производные и от других известных функций. Результаты сведены в следующую простую таблицу производных :

1)2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12)

Первая формула в таблице говорит о том, что если функция равна постоянному числу (или, как говорят, функция является константой), то ее производная в любой точке равна 0. В формуле (под номером 3 в таблице производных) показатель степени может быть любым: целым положительным, целым отрицательным, дробным положительным, дробным отрицательным. Рассмотрим примеры применения этой формулы при различных типах показателя степени . Первый пример – показатель степени является целым и положительным.

Пример 1. { − целое положительное} .

В следующем примере показатель степени − целое отрицательное число. Сначала напомним определение отрицательного показателя степени: . Нам понадобится это равенство справа налево: .

Пример 2. { − целое отрицательное} .

Дальше показатель степени − дробное положительное число. Напомним определение степени с дробным показателем: . Нам снова понадобится это равенство в обратном порядке: .

Пример 3. { − дробное положительное} = .

Последний случай : показатель степени − дробное и отрицательное число.

Пример 4. { − дробное отрицательное} = .

Итак, пока мы умеем вычислять производные только от функций, перечисленных в таблице. А если формула, задающая функцию, содержит суммы, разности, произведения и частные от функций, содержащихся в этой таблице? Или содержит суперпозиции перечисленных функций (т. е. функции от функций, например, ) ? Для вычисления производных в этом случае используются правила, которые дает следующая

Теорема. 1. Пусть функции и дифференцируемы в точке (т.е. имеют производную в этой точке) , а а − некоторое число. Тогда в этой точке дифференцируемы и функции (если ), а их производные вычисляются по правилам:

а) постоянный множитель можно выносить за знак производной :

(1)

б) производная суммы-разности равна сумме-разности производных:

(2)

в) для производной от произведения аналогия не проходит :

(3)

г) наиболее громоздкая формула − для производной от частного (т.е. дроби):

(4) 2. Пусть функция дифференцируема на некотором интервале , а функция дифференцируема на области значений функции . Тогда сложная функция (или суперпозиция функций) дифференцируема на интервале , а ее производная вычисляется по формуле: . Кратко эта формула записывается в виде:

(5)

Для того чтобы было удобнее пользоваться формулой для дифференцирования (т.е. взятия производной) сложной функции, эта формула сразу применена ко всем функциям, составляющим выписанную выше таблицу производных. В применении к таблице производных эта формула говорит о том, что если в таблице производных в левой части вместо стоит любое более сложное выражение (функция ), то в правой части равенств нужно тоже поставить выражение вместо , а потом еще домножить эту правую часть на производную от , т.е. . Результаты такого применения выписаны следующей таблице, которая называется обобщенной таблицей производных (сравните с простой таблицей производных) :

3) 4) 5) 6) 7) 8) 9) 10) 11) 12)

Теперь при вычислении производных от различных функций можно практически забыть о формуле для производной сложной функции, а пользоваться только простой или обобщенной таблицей производных, руководствуясь следующим правилом: если под знаком функции (синуса, косинуса, логарифма и т. д.) стоит сам аргумент , то для вычисления производной надо использовать простую таблицу производных, а если же под знаком функции стоит более сложное выражение (представляющее собой некоторую формулу от ), то это выражение надо принимать за функцию и пользоваться обобщенной таблицей производных до тех пор, пока аргументы не упростятся, после чего опять будет окончательно использоваться простая таблица. Если в обобщенной таблице производных положить , то она перейдет в простую таблицу производных. Простая и обобщенная таблицы производных, а также правила вычисления производных от суммы, разности, произведения и частного (сформулированные в теореме) позволяют вычислять производную от функции, заданной сколь угодно сложной формулой. Надо только набраться опыта в их практическом применении. А опыт появляется только после решения примеров и задач.

Пример 5 . {формула 7 обобщенной таблицы производных} {формула 9 простой таблицы производных}= .

Пример 6 . {формула 8 обобщенной таблицы производных} {формула 5 обобщенной таблицы производных} {формула 9 простой таблицы производных} .

Пример 7 . . Найти производную . Решение. {правило (2) для производной от суммы-разности} {правило (1) − вынесение числового множителя за знак производной}{формулы 2 и 3 простой таблицы производных}=.

Пример 8 . . Найти производную . Решение. {правило (4) для производной от частного}= {формулы 5 и 7 простой таблицы производных}= .

Пример 9 . . Найти производную . Решение. {определение дробной и отрицательной степени}= {правило (3) для производной произведения}= {формула (3) из простой и (5) из обобщенной таблицы производных}= .

Пример 10 . {определение тангенса} {правило (4) для производной от частного} .

AC Правила элементарной производной

В главе 1 мы разработали концепцию производной функции. Теперь мы знаем, что производная \ (f ‘\) функции \ (f \) измеряет мгновенную скорость изменения \ (f \) относительно \ (x \ text {.} \). Производная также сообщает нам наклон касательной к \ (y = f (x) \) при любом заданном значении \ (x \ text {.} \). До сих пор мы сосредоточились на интерпретации производной графически или, в контексте физическая обстановка, как значимая скорость изменения.Чтобы вычислить значение производной в определенной точке, мы полагались на определение предела производной,

\ begin {уравнение *} f ‘(x) = \ lim_ {h \ to 0} \ frac {f (x + h) -f (x)} {h} \ text {.} \ end {уравнение *}

В этой главе мы исследуем, как определение предела производной приводит к интересным паттернам и правилам, которые позволяют нам быстро найти формулу для \ (f ‘(x) \), без , используя определение предела напрямую. Например, мы хотели бы применить ярлыки, чтобы различать функцию, такую ​​как \ (g (x) = 4x ^ 7 – \ sin (x) + 3e ^ x \)

Предварительный просмотр задания 2.

n \) где \ (n \) – положительное целое число, как вы думаете, какая формула для \ (f ‘(x) \ text {?} \)

Подраздел 2.1.1 Некоторые ключевые обозначения

В дополнение к нашему обычному обозначению \ (f ‘\), есть другие способы обозначения производной функции, а также инструкция взять производную. Если мы думаем о соотношении между \ (y \) и \ (x \ text {,} \), мы иногда обозначаем производную от \ (y \) по отношению к \ (x \) символом

.

\ begin {уравнение *} \ frac {dy} {dx} \ end {уравнение *}

, которое мы читаем как «ди-у ди-х.2 \ text {,} \) напишем, что производная равна \ (\ frac {dy} {dx} = 2x \ text {.} \) Это обозначение происходит из того факта, что производная связана с наклоном линия, а наклон измеряется как \ (\ frac {\ Delta y} {\ Delta x} \ text {.} \) Обратите внимание, что пока мы читаем \ (\ frac {\ Delta y} {\ Delta x} \) как «изменение \ (y \) по сравнению с изменением \ (x \ text {,} \)» мы рассматриваем \ (\ frac {dy} {dx} \) как один символ, а не как частное двух величин.

Мы используем вариант этого обозначения как указание на получение производной.2} \ text {.} \)

Далее мы создадим набор функций, для которых мы сможем быстро вычислить производную.

Подраздел 2.1.2 Постоянные, степенные и экспоненциальные функции

На данный момент мы знаем формулу производной для двух важных классов функций: постоянных функций и степенных функций. Если \ (f (x) = c \) – постоянная функция, ее график представляет собой горизонтальную линию с нулевым наклоном в каждой точке. Таким образом, \ (\ frac {d} {dx} [c] = 0 \ text {.} \) Мы резюмируем это следующим правилом.x \ text {.} \) Как видно из правил, это имеет большое значение в форме производной.

Мероприятие 2.1.2.

Используйте три приведенных выше правила для определения производной каждой из следующих функций. Для каждого из них сформулируйте свой ответ, используя полную и правильную нотацию, помечая производную ее именем. Например, если вам дана функция \ (h (z) \ text {,} \), вы должны написать «\ (h ‘(z) = \)» или «\ (\ frac {dh} {dz} = \) »Как часть вашего ответа. 3} \)

Подраздел 2.2–9 \ text {,} \ end {уравнение *}

, который представляет собой сумму постоянных кратных степеней \ (t \ text {.} \). С этой целью мы разрабатываем два новых правила: правило постоянного кратного и правило суммы.

Как производная от \ (y = kf (x) \) связана с производной от \ (y = f (x) \ text {?} \) Вспомните, что когда мы умножаем функцию на константу \ (k \ text {,} \) мы растягиваем график по вертикали с коэффициентом \ (| k | \) (и отражаем график через \ (y = 0 \), если \ (k \ lt 0 \)). Это вертикальное растяжение влияет на наклон графика, поэтому наклон функции \ (y = kf (x) \) в \ (k \) раз круче, чем наклон функции \ (y = f (x) \ text { .} \) Таким образом, когда мы умножаем функцию на коэффициент \ (k \ text {,} \), мы также меняем значение ее производной на коэффициент \ (k \). ¹ ,

Правило постоянной множественности может быть формально доказано как следствие свойств пределов, используя определение предела производной.

Постоянное множественное правило.

Для любого действительного числа \ (k \ text {,} \), если \ (f (x) \) – дифференцируемая функция с производной \ (f ‘(x) \ text {,} \), то \ (\ frac { d} {dx} [kf (x)] = k f ‘(x) \ текст {.{-3}) \ text {.} \)

Затем мы исследуем сумму двух функций. Если у нас есть \ (y = f (x) \) и \ (y = g (x) \ text {,} \), мы можем вычислить новую функцию \ (y = (f + g) (x) \) по сложение выходов двух функций: \ ((f + g) (x) = f (x) + g (x) \ text {.} \) Не только значение новой функции является суммой значений две известные функции, но наклон новой функции представляет собой сумму наклонов известных функций. Следовательно, ² , мы приходим к следующему правилу суммы для деривативов:

Как и правило постоянной множественности, правило суммы можно формально доказать как следствие свойств пределов, используя определение предела производной.

Правило суммы.

Если \ (f (x) \) и \ (g (x) \) – дифференцируемые функции с производными \ (f ‘(x) \) и \ (g’ (x) \) соответственно, то \ (\ frac {d} {dx} [f (x) + g (x)] = f ‘(x) + g’ (x) \ text {. } \)

На словах правило суммы говорит нам, что «производная суммы – это сумма производных ». Это также говорит нам, что сумма двух дифференцируемых функций также дифференцируема. Кроме того, поскольку мы можем рассматривать функцию разности \ (y = (fg) (x) = f (x) – g (x) \) как \ (y = f (x) + (-1 \ cdot g (x) ) \ text {,} \) Правило суммы и Постоянное множественное правило вместе говорят нам, что \ (\ frac {d} {dx} [f (x) + (-1 \ cdot g (x))] = f ‘( x) – g ‘(x) \ text {,} \) или что «производная разности есть разность производных.{-4} \ text {.} \)

Мероприятие 2.1.3.

Используйте только правила для постоянных, степенных и экспоненциальных функций, а также правила для постоянных кратных и сумм, чтобы вычислить производную каждой функции ниже по заданной независимой переменной. Обратите внимание: мы еще не знаем правил, как различать произведение или частное функций. Это означает, что вам, возможно, придется сначала выполнить некоторую алгебру над функциями, указанными ниже, прежде чем вы сможете фактически использовать существующие правила для вычисления желаемой производной формулы. 2 – а + 12 \)

Точно так же, как у нас есть правила быстрого доступа, которые помогают нам находить производные, мы вводим некоторый язык, который проще и короче. Часто вместо того, чтобы сказать «возьмите производную от \ (f \ text {,} \)», мы вместо этого просто скажем «дифференцировать \ (f \ text {.} \)». Аналогично, если производная существует в точке, мы говорим: «\ (f \) дифференцируем в этой точке» или что \ (f \) можно дифференцировать.

Когда мы работаем с алгебраической структурой функций, важно получить общее представление о том, что мы делаем.z \ ln (2) \ text {,} \), который также является экспоненциальным.

Мы не должны упускать из виду тот факт, что все значение производной, которое мы разработали в главе 1, остается в силе. Производная измеряет мгновенную скорость изменения исходной функции, а также наклон касательной в любой выбранной точке кривой.

Мероприятие 2.1.4.

В каждом из следующих вопросов предлагается использовать производные инструменты для ответа на ключевые вопросы о функциях. Обязательно тщательно обдумывайте каждый вопрос и используйте правильные обозначения в своих ответах.2 – a + 12 \) в точке, где \ (a = -1 \ text {.} \)

В чем разница между запросом наклона касательной (задано в (а)) и уравнением касательной линии (задано в (в))?

Mathwords: производные правила

индекс: нажмите на письмо индекс: предметные области
	эта страница обновлена 19-июл-17 Mathwords: Термины и формулы от алгебры I до исчисления написаны, проиллюстрированы и веб-мастером Брюса Симмонса Авторские права © 2000 Брюс Симмонс Все права защищены

Обзор исчисления: правила производных – Magoosh Blog

Производная – основа для большей части того, что мы узнаем в исчислении AP. В этой статье будут рассмотрены все общие шаги для определения производных, а также список общих правил производных, которые важно знать для экзамена AP Calculus.

Понимание определения деривативов

Прежде чем мы запоминаем правила производной, при подготовке к экзамену AP Calculus сначала убедитесь, что вы понимаете определение производной с самого начала. На экзамене обязательно возникнут вопросы, в которых вас немного спросят о том, чего ожидать от наклона между двумя точками, когда эти точки сближаются на кривой.Определение производной:

Вы должны уметь четко объяснить, что происходит в этом уравнении, почему оно важно и как его использовать.

Здесь есть разница между нашим определением и тем, как мы часто определяем производные. К тому времени, когда вы попадете на экзамен AP, вам нужно будет очень удобно находить производные с помощью правила мощности, правила произведения, правила частного и правила цепочки. Кроме того, вы должны знать несколько наиболее распространенных производных (6 триггерных функций, экспоненциальных функций и логарифмических функций).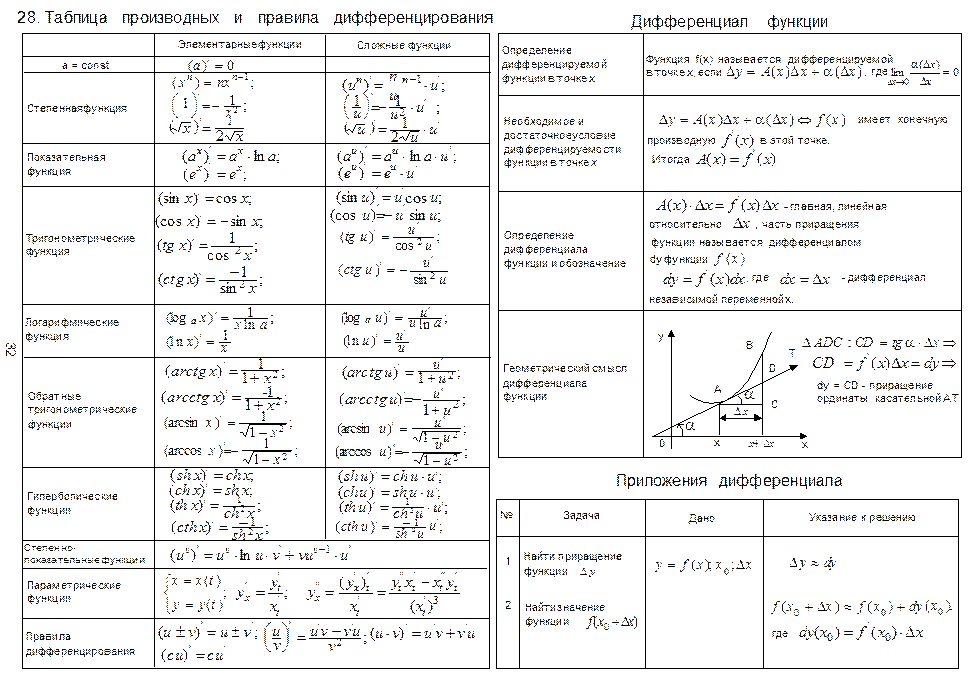 Вам не нужно знать, как эти формулы создаются из определения производной, данного выше, но это, безусловно, хорошее упражнение для вашего класса исчисления.

На экзамене AP производная используется для решения множества различных типов задач.

Некоторые из наиболее распространенных производных вопросов включают:

1. Определение уравнения прямой, касательной к кривой в точке.
2. Определение того, увеличивается или уменьшается функция в заданной точке.
3. Определите критические точки графика.
4. Определение скорости изменения физических систем. Это включает в себя понимание того, как скорость
   и ускорение частицы связаны с изменением положения частицы со временем.
5. Определение минимума и максимума функции.
6. Использование правила Л’Опиталя для определения пределов функций (например: найти предел, когда x стремится к 0 из sin (x) / x)

Правила производных инструментов

Постоянное правило:

Правило сумм:

Правило различий:

Правило продукта:

Правило частного:

Это также можно рассматривать как правило произведения с 1 / г (x)

Правило мощности:

Правило цепочки:

Примеры использования производных правил:

Это две функции, умноженные друг на друга, поэтому мы используем правило произведения:

Это функция функции, поэтому мы используем цепное правило:

Это разделение на две функции, поэтому мы смотрим на правило частного:

Обратите внимание, это то же самое, что сказать

, которое мы можем решить с помощью правила продукта.

Общие производные инструменты

Общие триггерные производные

Гарантированно повысьте свой результат по SAT или ACT. Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!

Между прочим, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!

О Захари

Закари – бывший инженер-механик, а в настоящее время учитель физики, математики и информатики в средней школе.Он окончил Университет Макгилла в 2011 году и работал в автомобильной промышленности в Детройте, прежде чем перейти к образованию. Он преподает и занимается репетиторством в течение последних пяти лет, но вы также можете найти его в приключениях, чтении, скалолазании и путешествиях, когда появляется такая возможность.

Правила продуктов, питания и цепочки – лучше объяснение

Беспорядок правил получения деривативов никогда меня не устраивал. Правило сложения, правило продукта, правило частного – как они сочетаются друг с другом? Что мы вообще пытаемся сделать сделать ?

Вот мой взгляд на деривативы:

• У нас есть система для анализа, наша функция f
• Производная f ‘(также известная как df / dx) – это поведение от момента к моменту
• Оказывается, f является частью более крупной системы (h = f + g)
• Используя поведение частей, можем ли мы выяснить поведение целого?

Да. У каждой части есть «точка зрения» на то, сколько изменений она внесла. Комбинируйте все точки зрения, чтобы получить общее поведение. Каждое производное правило является примером объединения различных точек зрения.

А почему бы нам не проанализировать сразу всю систему? По той же причине не съешь гамбургер за один раз: мелкими кусочками легче обернуть голову.

Вместо того, чтобы запоминать отдельные правила, давайте посмотрим, как они сочетаются друг с другом:

Цель состоит в том, чтобы по-настоящему понять понятие «комбинирование перспектив». 2 “и пихает вам в лицо график. Неужели это помогает нашей интуиции?

Не для меня. Отображает входные и выходные данные в виде единой кривой и скрывает механизмы, которые превращают одно в другое. Но производные правила: около машин, так что давайте посмотрим!

Я представляю функцию как процесс «input (x) => f => output (y)».

Это не только я. Взгляните на этот невероятный компьютер с механическим прицелом (начало серии YouTube).

Машина вычисляет такие функции, как сложение и умножение с шестеренками – вы можете видеть , как разворачивается механика !

Думайте о функции f как о машине с входным рычагом «x» и выходным рычагом «y». Когда мы регулируем x, f устанавливает высоту для y. Другая аналогия: x – это входной сигнал, f принимает его, творит чудеса и выдает сигнал y. Используйте любую аналогию, которая помогает щелкнуть мышью.

Wiggle Wiggle Wiggle

Покачивание, покачивание, покачивание

Производная – это “момент за моментом” поведение функции.Что это обозначает? (И не бормочите бездумно: «Производная – это наклон». Видите графики вокруг этих частей, парень? )

Производная – это то, насколько мы покачиваемся. Рычаг находится в точке x, мы «покачиваем» его и смотрим, как изменяется y. «О, мы переместили входной рычаг на 1 мм, а выходной – на 5 мм. Интересно».

Результат может быть записан как «выходное покачивание на входное покачивание» или «dy / dx» (в нашем случае 5 мм / 1 мм = 5). Обычно это формула, а не статическое значение, потому что оно может зависеть от ваших текущих настроек ввода.2 производная равна 2x. Да, вы это запомнили. Что это значит?

Если наш рычаг ввода находится в положении x = 10 и мы слегка его покачиваем (перемещая его на dx = 0,1–10,1), выход должен измениться на dy. Сколько именно?

• Мы знаем, что f ‘(x) = dy / dx = 2 * x
• При x = 10 «покачивание выходного сигнала на входное движение» равно = 2 * 10 = 20. 2 и (10.2 составляет около 2. Производная оценивает, как далеко может переместиться выходной рычаг (идеальное бесконечно маленькое покачивание переместило бы 2 единицы; мы переместились на 2,01).

  Ключ к пониманию производных правил:

  • Настройте вашу систему
  • Покачивайте каждую часть системы отдельно, смотрите, как далеко перемещается вывод
  • Объединить результаты

  Общее покачивание – это сумма покачиваний каждой части.

  Сложение и вычитание

  Время для нашей первой системы:

  Что происходит при изменении входа (x)?

  В голове я думаю: «Функция h принимает один вход.Он подает один и тот же вход на f и g и добавляет рычаги вывода. f и g двигаются независимо и даже не знают друг о друге! »

  Функция f знает, что она будет способствовать некоторому покачиванию (df), g знает, что она будет способствовать некоторому покачиванию (dg), и мы, бродячие надзиратели, которыми мы являемся, знаем, что их индивидуальное покачивающееся поведение добавляется:

  Опять опишем каждую «точку зрения»:

  • Общая система имеет поведение dh
  • С точки зрения f, он вносит вклад в df в целом [он не знает о g]
  • С точки зрения g, он способствует dg в целом [он не знает о f]

  Каждое изменение в системе происходит из-за изменения некоторых частей (f и g). Если мы добавим вклады от каждой возможной переменной, мы описали всю систему.

  df против df / dx

  Иногда мы используем df, иногда df / dx – что дает? (Это меня на время смутило)

  • df – это общее понятие «сколько бы f ни изменилось»
  • df / dx – это конкретное понятие «сколько бы f не изменилось, с точки зрения того, насколько изменилось x»

  Общий “df” помогает нам увидеть общее поведение.

  Аналогия: представьте, что вы едете по пересеченной местности и хотите измерить топливную экономичность вашего автомобиля.Вы измеряете пройденное расстояние, проверяете свой баллон, чтобы узнать, сколько бензина вы использовали, и, наконец, выполняете деление, чтобы вычислить «миль на галлон». Вы измеряли расстояние и бензин отдельно – вы не прыгали в бензобак, чтобы получить скорость на ходу!

  В расчетах иногда мы хотим думать о фактических изменениях, а не о соотношении. Работа на уровне «df» дает нам возможность подумать о том, как функция в целом колеблется. Мы можем в конечном итоге уменьшить его с точки зрения конкретного ввода.

  И мы сделаем это сейчас. Приведенное выше правило сложения может быть записано на основе “на dx” как:

  Умножение (правило произведения)

  Следующая загадка: предположим, наша система умножает части «f» и «g». Как она себя ведет?

  Хм, хитрость – детали более тесно взаимодействуют. Но стратегия та же: посмотрите, как каждая часть вносит свой вклад со своей точки зрения, и объедините их:

  • общее изменение h = вклад f (с точки зрения f) + вклад g (с точки зрения g)

  Посмотрите на диаграмму:

  Что происходит?

  • У нас есть система: f и g умножаются, давая h (площадь прямоугольника)
  • Ввод “x” изменяется на dx на расстоянии.f изменяется на некоторую величину df (подумайте об абсолютном изменении, а не о скорости!). Точно так же g изменяется на свою собственную величину dg. Поскольку f и g изменились, изменится и площадь прямоугольника.
  • Какое изменение площади с точки зрения f? Что ж, f знает, что он изменился с помощью df, но не знает , что случилось с g. С точки зрения f, он единственный, кто переместился и добавит кусок площади = df * g
  • Точно так же g не знает, как изменилось f, но знает, что добавит как часть области “dg * f”

  Общее изменение в системе (dh) – это два среза площади:

  Теперь, как и в нашем примере миль на галлон, мы «делим на dx», чтобы записать это в терминах изменения x:

  (В сторону: Делить на dx? Инженеры кивают, математики нахмурились.Технически df / dx – это не дробь: это вся операция взятия производной (с ограничением и всем остальным). Но с точки зрения бесконечно малых, интуитивно мы «масштабируемся на dx». Я улыбаюсь.)

  Ключ к правилу продукта: добавьте два «кусочка площади», по одному с каждой точки обзора.

  Попался: Но разве нет какого-то эффекта от одновременного изменения f и g (df * dg)?

  Ага. Однако эта область бесконечно малая * бесконечно малая («бесконечно малая 2-го порядка») и невидима на текущем уровне.Это сложная концепция, но (df * dg) / dx исчезает по сравнению с обычными производными, такими как df / dx. Мы изменяем f и g независимо и объединяем результаты и игнорируем результаты их совместного движения.

  Цепное правило: это не так уж и плохо

  Допустим, g зависит от f, которое зависит от x:

  Цепное правило позволяет нам «приблизить» функцию и увидеть, как начальное изменение (x) может повлиять на конечный результат по строке (g).

  Интерпретация 1: преобразование ставок

  Распространенное толкование – умножение ставок:

  x покачивание f.Это создает скорость изменения df / dx, которая изменяет g на dg / df. Тогда весь покачивание будет:

  Аналогичен методу «фактор-метка» в классе химии:

  Если ваша скорость «миль в секунду» изменится, умножьте на коэффициент преобразования, чтобы получить новое «миль в час». Второй не знает о часе напрямую – он проходит через преобразование секунда => минута.

  Точно так же g не знает напрямую о x, только f. Функция g знает, что ей следует масштабировать свой ввод на dg / df, чтобы получить результат.Начальная скорость (df / dx) изменяется по мере продвижения вверх по цепочке.

  Интерпретация 2: преобразование покачивания

  Я предпочитаю видеть цепное правило на основе “покачивания”:

  • x покачивается на dx, поэтому
  • f покачивается на df, поэтому
  • г покачивается от dg

  Cool. Но как они на самом деле связаны? Ах да, производная! (Это выходное покачивание за входное покачивание):

  Помните, производная f (df / dx) – это то, насколько масштабировать начальное покачивание.То же самое и с g:

  Он будет масштабировать любое покачивание, происходящее вдоль его входного рычага (f), на dg / df. Если мы запишем df wiggle в терминах dx:

  У нас есть другая версия правила цепочки: dx запускает цепочку, что приводит к некоторому окончательному результату dg. Если мы хотим окончательное покачивание с точки зрения dx, разделите обе стороны на dx:

  Цепное правило – это не просто отмена единицы фактор-метка – это распространение покачивания, которое корректируется на каждом шаге.2). На входе было f, и он рассматривает f как одно значение. Позже мы спешим и перепишем f в терминах x. Но g не имеет к этому никакого отношения – его не волнует, что f можно переписать в терминах меньших частей.

  Во многих примерах переменная «x» является «концом строки».

  Вопросы касаются df / dx, т.е. «Дайте мне изменения с точки зрения x». Теперь x может зависеть от чего-то более глубокого, но этого не просят. Это как сказать: «Я хочу миль в час.Меня не волнуют мили в минуту или мили в секунду. Просто дайте мне мили в час ». Df / dx означает« перестаньте смотреть на входные данные, как только дойдете до x ».

  Почему мы умножаем производные по цепному правилу, но складываем их для остальных?

  Обычные правила – это около совмещающих точек зрения для получения общей картины. Какие изменения он видит? Какое изменение видит? Сложите их и получите общее количество.

  Цепное правило заключается в том, чтобы углубиться в одну часть (например, f) и посмотреть, контролируется ли она другой переменной.4 действительно x * x * x * x. Это умножение 4 «независимых» переменных. Каждый x не знает о других, с таким же успехом это может быть x * u * v * w.

  Теперь подумайте о точке зрения первого x:

  • Изменяется с x на x + dx
  • Изменение общей функции: [(x + dx) – x] [u * v * w] = dx [u * v * w]
  • Изменение на основе “на dx” составляет [u * v * w]

  Аналогично

  • С точки зрения u, меняется на du.4 объединены четыре идентичные «точки зрения». Буйа!

    Возьми передышку

    Надеюсь, вы видите производную в новом свете: у нас есть система частей, мы качаем наши входные данные и смотрим, как движется все это. Речь идет об объединении перспектив: что каждая часть добавляет к целому?

    В следующей статье мы рассмотрим еще более мощные правила (показатели, частные и другие). Счастливая математика.

    Другие сообщения в этой серии

    1. Нежное введение в изучение исчисления
    2. Понимание исчислений с помощью метафоры банковского счета
    3. Доисторическое исчисление: открытие числа Пи
    4. Аналогия с исчислением: интегралы как умножение
    5. Исчисление: построение интуиции для производных
    6. Как понять деривативы: правила продукта, власти и цепочки
    7. Как понимать производные: правило частного, экспоненты и логарифмы
    8. Интуитивное знакомство с ограничениями
    9. Интуиция к серии Тейлора (аналогия с ДНК)
    10. Зачем нужны пределы и бесконечно малые?
    11. Обучение исчислению: преодоление нашей искусственной потребности в точности
    12. Дружеский чат о том, 0.999 … = 1
    13. Аналогия: камера исчисления
    14. Практика абстракции: графы исчисления
    15. Quick Insight: более простая арифметика с исчислением
    16. Как сложить от 1 до 100 с помощью исчисления
    17. Интеграл греха (x): геометрическая интуиция

    Чтение: Правила для деривативов | Бизнес-расчет

    В этом разделе мы получим правила для производных, которые позволят нам находить формулы для производных, когда наша функция приходит к нам в виде формулы. {n-1} [/ latex], кроме случая n = 0.x \ cdot \ text {ln} (a) [/ latex]

  • Натуральный логарифм: [латекс] \ frac {d} {dx} (\ text {ln} x) = \ frac {1} {x} [/ latex]

  Правило суммы, разности и постоянного кратного в сочетании с правилом мощности позволяет нам легко найти производную любого многочлена.

  В этом видео показан пример поиска производной функции, содержащей радикалы:

  Правила продуктов и коэффициентов

  Основные правила позволят нам взяться за простые функции.Но что произойдет, если нам понадобится производная от комбинации этих функций?

  Правила нахождения производных от произведений и частных немного сложны, но они избавляют нас от гораздо более сложной алгебры, с которой мы могли бы столкнуться, если бы попытались перемножить вещи. Они также позволяют нам иметь дело с продуктами, в которых множители не являются полиномами. Мы можем использовать эти правила вместе с основными, чтобы находить производные от многих сложных на вид функций.

  Далее a и b являются дифференцируемыми функциями x .2} [/ латекс]

  Правило цепочки

  Есть еще один тип сложных функций, которые мы захотим различать: композиция. Правило цепочки позволит нам найти производную от композиции.

  Далее a и b являются дифференцируемыми функциями x.

  Правило цепочки: Если [латекс] f (x) = a (b (x)) [/ latex], то [latex] f ‘(x) = a’ (b (x)) \ cdot b ‘(x ) [/ латекс]

  Может быть полезно вспомнить поговорку: «Производное от композиции – это производное от внешнего ВРЕМЕНИ, производное от внутреннего».”

  Текст:

  http://www.opentextbookstore.com/appcalc/Chapter2-3.pdf
  http://www.opentextbookstore.com/appcalc/Chapter2-4.pdf
  http://www.opentextbookstore.com/appcalc/Chapter2 -5.pdf

  Правила производных финансовых инструментов – Правило силы

  Силовое правило исчисления выглядит следующим образом:

  Производная x ⁿ равна n * x ^(n-1)

  Примечание: производная константы равна нулю.

  Этот метод дифференцирования используется для простых многочленов или рациональных выражений, которые могут быть упрощены до одного многочлена.

  Также важно помнить правила экспонент:

  https://www.onlinemathlearning.com/exponent-rules.html

  Пример 1 – найти производную от f (x) = 2x ² + 3x + 4

  Давайте применим правило мощности к каждому члену полинома:

  x ² , n = 2: (2) * 2x ^2-1 = 4x ¹ = 4x
  3x, n = 1: (3) * x ^1-1 = 3x ⁰ = 3 * 1 = 3
  4: 0 (4 – константа, поэтому ее производная равна нулю)

  Производная f (x) равна f ’(x) = 4x + 3 + 0 = 4x + 3

  Пример 2 – найти производную f (x) =

  Давайте упростим этот член до одного полинома.

  Давайте применим правило мощности к каждому члену полинома:

  2x ² , n = 2: (2) * 2x ^2-1 = 4x ¹ = 4x
  3x ¹ , n = 1: (1) * 3x ^1-1 = 3x ⁰ = 3 * 1 = 3
  4x ^-2 , n = -2: (- 2) * 4x ^-2-1 = -8x ^-3

  Производная f (x) равна f ’(x) = 4x + 3-8x ^-3

  Пример 3 – найти производную f (x) = при x = 3

  Давайте упростим этот член до одного полинома.

  Давайте применим правило мощности к каждому члену полинома:

  x, n = 1: 1 * x ^1-1 = 1x ⁰ = 1 * 1 = 1
  -3: 0 (поскольку 3 – константа, производная равна нулю)

  Производная f (x) равна 1 +0 = 1 = f ’(x)

  Поскольку производная является константой (1), производная при любом значении x равна 1.

  График исходной функции доказывает это:

  Пример 4 – найти производную от f (x) = 2x ^-3 + 4x ^-2 + x ^-1

  Давайте применим правило мощности к каждому члену полинома:

  Объединяя результаты, производная f (x) равна f ’(x) =

  .

  Производные правила – A Plus Topper

  Производные правила

  Скорость изменения одной величины по отношению к другой величине имеет большое значение.
  Скорость изменения величины «y» по отношению к другой величине «x» называется производной или дифференциальным коэффициентом y по отношению к x.

  Производная означает наклон функции в любой точке.

  Некоторые стандартные формулы дифференциации

  (1) Дифференциация некоторых общих функций:
  
  (2) Дифференциация алгебраических функций:
  В частности
  
  (3) Дифференциация тригонометрических функций:
  
  (4) Дифференциация логарифмической и экспоненциальной функции:
  
  (5) Дифференциация обратных тригонометрических функций:
  
  (6) Дифференциация гиперболических функций:
  
  (7) Подходящие замены
  

  Правила дифференциации

  Пусть f (x), g (x) и u (x) – дифференцируемые функции

  1. Если во всех точках определенного интервала f ‘(x) = o, то функция f (x) имеет постоянное значение внутри этого интервала.
  2. Правило цепочки
     (i) Случай I: , если y является функцией u, а u является функцией x, тогда производная y по x равна
     
     (ii) Случай II: Если y и x выражаются через t, y и x дифференцируемы по t, тогда
     
  3. Правило суммы и разности: использование линейного свойства
     
  4. Правило продукта
     
  5. Скалярное правило множественного числа:
     
  6. Правило частного:
     
     При условии g 0.
  .