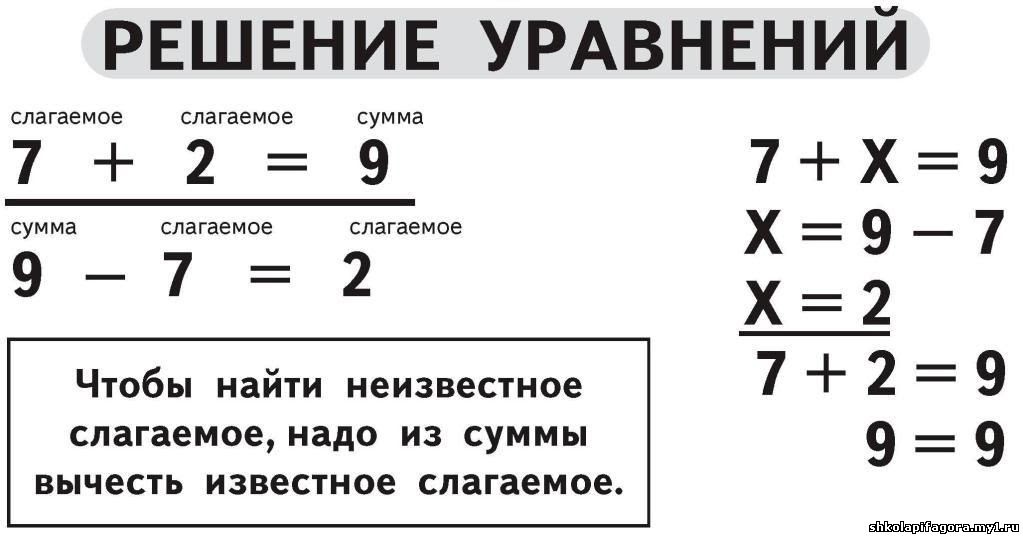
§ Как решать линейные уравнения 7 класс
Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби
Для решения линейных уравнений используют два основных правила (свойства).
Свойство № 1
или
правило переноса
Запомните!
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный.
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую.
Так как в левой части уравнения у числа «3» был знак «+», значит в правую часть уравнения «3» перенесется со знаком «−».
Полученное числовое значение «x = 2» называют корнем уравнения.
Важно!
Не забывайте после решения любого уравнения записывать ответ.
Рассмотрим другое уравнение.
По правилу переноса перенесем «4x» из правой части уравнения в левую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака, мы понимаем, что перед «4x» стоит знак «+».
5x = 4x + 9
5x = +4x + 9
5x − 4x = 9
Теперь приведем подобные и решим уравнение до конца.
5x − 4x = 9
x = 9
Ответ: x = 9
Свойство № 2
или
правило деления
Запомните!
В любом уравнении можно разделить левую и правую часть на одно и то же число.
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.
Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент
«1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы
получить
«1»?».
Ответ очевиден, нужно разделить на «4».
Используем правило деления и разделим левую и правую части уравнения на «4». Не забудьте, что делить нужно и левую, и правую части.
Используем сокращение дробей и решим линейное уравнение до конца.
Как решить уравнение, если «x» отрицательное
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент. Как, например, в уравнении ниже.
−2x = 10
Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить «−2», чтобы получить «1»?». Нужно разделить на «−2».
−2x = 10 |:(−2)
=
x = −5
Ответ: x = −5
Важно!
При делении на отрицательное число помните про правило знаков.
Примеры решения линейных уравнений
Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно
применять оба свойства (правило переноса и правило деления).
Обычно для решения уравнений нужно
применять оба свойства (правило переноса и правило деления).
Также требуется вспомнить правило раскрытия скобок и правило приведения подобных.
- 25x − 1 = 9
25x = 9 + 1
25x = 10 |: 25
=
x =
Ответ: x = - 11(y − 4) + 10(5 − 3y) − 3(4 − 3y) = −6
11y − 44 + 50 − 30y − 12 + 9y = −6
11y − 30y + 9y − 44 + 50 − 12 = −6
20y − 30y + 6 − 12 = −6
−10y − 6 = −6
−10y = −6 + 6
−10y = 0 |:(−10)
=−10y −10
y = 0
Ответ: y = 0
Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
§ Как решать уравнения с пропорцией
Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Запомните!
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции, то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−», обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции для дальнейшего решения.
Теперь раскроем скобки с помощью правила раскрытия скобок.
Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
- =
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число - =
0,21 6,8 3x · 6,8 = 0,21 · 1,7
20,4 x=
·20
x =21 · 17 100 · 10
=204 · x 10 21 · 17 100 · 10 204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
21 · 17 · 10 204 · 1000 x =
21 · 17 204 · 100 x =
7 · 17 68 · 100 x =
119 : 17 6800 : 17 x =
Ответ: x =
Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби
Ваши комментарии
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
показателей – определение, примеры | Свойства показателей степени
Показатель степени числа показывает, сколько раз число умножается само на себя. Например, 3 4 означает, что 3 умножается на себя четыре раза, то есть 3 × 3 × 3 × 3 = 3
| 1. | Что такое экспоненты? |
2. | Законы (свойства или правила) экспонентов |
| 3. | Отрицательные показатели |
| 4. | Экспоненты с дробями |
| 5. | Десятичные степени |
| 6. | Научное обозначение с показателями |
| 7. | Часто задаваемые вопросы по экспонентам |
Что такое экспоненты?
Показатель степени числа показывает, сколько раз число умножается само на себя. Например, 2 × 2 × 2 × 2 можно записать как 2 4 , так как 2 умножается на себя 4 раза. Здесь 2 называется «основание», а 4 — «показатель степени» или «степень».
Значение показателей степени
Степень степени — это способ выражения больших чисел в степени. Например, 4, умноженное 3 раза само на себя, может быть выражено как 4 × 4 × 4 = 4 3 , где 3 — показатель степени числа 4. Посмотрите на следующий рисунок, чтобы увидеть, как мы выражаем показатель степени числа. Он показывает, что x n означает, что x умножается сам на себя n раз.
Посмотрите на следующий рисунок, чтобы увидеть, как мы выражаем показатель степени числа. Он показывает, что x n означает, что x умножается сам на себя n раз.
Здесь в члене x n ,
- x называется «базой»
- n называется «показатель степени»
- x n читается как «x в степени n» (или) «x в степени n».
Вот несколько примеров показателей степени:
- 3 × 3 × 3 × 3 × 3 = 3 5
- -2 × -2 × -2 = (-2) 3
- а × а × а × а × а × а = а 6
Показатель степени важен, потому что, когда число многократно умножается само на себя, его легко выразить в виде показателей степени. Например, проще написать 5 7 вместо того, чтобы писать как 5 × 5 × 5 × 5 × 5 × 5 × 5.
Свойства показателей степени
свойства показателей степени , которые также известны как законы показателей степени, используются для решения задач, связанных с показателями степени. Эти свойства также рассматриваются как правила основных показателей. Основные свойства показателей приведены ниже.
Эти свойства также рассматриваются как правила основных показателей. Основные свойства показателей приведены ниже.
- Закон произведения: a m × a n = a m+n
- Закон частного: а м /а н = а м-н
- Закон нулевой степени: a 0 = 1
- Закон отрицательного показателя степени: a -m = 1/a m
- Закон Силы Силы: (a m ) n = a mn
- Закон силы продукта: (ab) m = a m b m
- Закон степени частного: (a/b) m = a m /b m
Отрицательные показатели степени
Отрицательный показатель степени говорит нам, сколько раз нам нужно умножить обратное основание. Например, если известно, что a -n , его можно разложить как 1/a n . Это означает, что мы должны умножить обратную величину a, то есть 1/a ‘n’ раз. Отрицательные показатели степени используются при записи дробей с показателями степени. Некоторые примеры отрицательных показателей: 2 × 3 -9 , 7 -3 , 67 -5 и т. д. Мы можем преобразовать их в положительные показатели следующим образом:
Отрицательные показатели степени используются при записи дробей с показателями степени. Некоторые примеры отрицательных показателей: 2 × 3 -9 , 7 -3 , 67 -5 и т. д. Мы можем преобразовать их в положительные показатели следующим образом:
- 2 × 3 -9 = 2 × (1/3 9 ) = 2/3 9
- 7 -3 = 1/7 3
- 67 -5 = 1/67 5
Экспоненты с дробями
Если показатель степени числа представляет собой дробь, он называется дробным показателем. Квадратные корни, кубические корни, корень n th являются частями дробных показателей. Число со степенью 1/2 называется квадратным корнем из основания. Точно так же число со степенью 1/3 называется кубическим корнем из основания. Некоторые примеры показателей степени с дробями: 5 2/3 , -8 1/3 , 10 5/6 и т. д. Мы можем записать их следующим образом:
- 5 2/3 = (5 2 ) 19300 = 25 1/3 = ∛25
- -8 1/3 = ((-2) 3 ) 1/3 = -2
- 10 5/6 = (10 5 ) 6 = 6 √10 5 = 6 √100000
Десятичные экспоненты
Если показатель степени числа задан в десятичной форме, он известен как десятичный показатель степени. Немного сложно оценить правильный ответ любого десятичного показателя степени, поэтому мы находим приблизительный ответ для таких случаев. Десятичные показатели степени можно решить, сначала преобразовав десятичную дробь в дробную форму. Например, 4 1,5 можно записать как 4 3/2 , что можно еще упростить, чтобы получить окончательный ответ 8, то есть 4 3/2 = (2 2 ) 3/2 = 2 3 = 8.
Немного сложно оценить правильный ответ любого десятичного показателя степени, поэтому мы находим приблизительный ответ для таких случаев. Десятичные показатели степени можно решить, сначала преобразовав десятичную дробь в дробную форму. Например, 4 1,5 можно записать как 4 3/2 , что можно еще упростить, чтобы получить окончательный ответ 8, то есть 4 3/2 = (2 2 ) 3/2 = 2 3 = 8.
Научное обозначение с показателями
Научная нотация — это стандартная форма записи очень больших или очень маленьких чисел. При этом числа записываются с помощью десятичных знаков и степеней 10. Говорят, что число записывается в экспоненциальном представлении, когда число от 0 до 10 умножается на степень 10. В случае числа больше, чем 1 , степень 10 будет положительным показателем, а в случае чисел меньше 1 , степень 10 будет отрицательной. Давайте разберемся с этапами записи чисел в экспоненте с экспонентами:
- Шаг 1: Поставьте десятичную точку после первой цифры числа слева.
 Если в числе только одна цифра без нулей, то десятичную ставить не нужно.
Если в числе только одна цифра без нулей, то десятичную ставить не нужно. - Шаг 2: Умножьте это число на степень 10 так, чтобы степень была равна количеству сдвигов десятичной точки.
Следуя этим двум простым шагам, мы можем записать любое число в стандартной форме с показателями, например, 560000 = 5,6 × 10 5 , 0,00736567 = 7,36567 × 10 -3 .
Чтобы узнать больше об использовании показателей степени при написании экспоненциального представления чисел, посетите следующие статьи:
- Как записать 2,5 миллиона в экспоненциальном представлении?
- Как записать 12 миллионов в экспоненциальном представлении?
- Как записать 0,0001 в экспоненциальном представлении?
- Какое научное обозначение для 8 миллионов?
- Как записать 13 миллионов в экспоненциальном представлении?
- Какое из следующих выражений записано в экспоненциальной записи
Советы и подсказки:
- Если дробь имеет отрицательный показатель степени, то мы берем обратную дробь, чтобы показатель степени был положительным, т.
 е. (a/b) -m = (b/a) м .
е. (a/b) -m = (b/a) м . - Десятичные показатели степени можно решить, сначала преобразовав десятичную дробь в форму дроби, т. е. 2 0,5 можно записать как 2 1/2
☛ Связанные темы по показателям степени
Посмотрите еще несколько интересных статей, основанных на показателях степени в математике.
- Умножение показателей степени
- Экспоненциальные функции
- Экспоненциальные уравнения
- Иррациональные Показатели
Показатели Примеры
Пример 1: Найдите произведение следующих выражений: a 5 × b 3 × a 8
Решение:
. м × a n = a (m+n)
Это будет a 5 × b 3 × a 8 = a 5+8 × b 90 90 3 3 0006 × b 3 = a 13 b 3
Пример 2: Найдите произведение числа 5 7 × 5 3 , используя свойства показателей степени.

Решение:
5 3 × 5 7 = 5 10 (используя формулу показателей степени = a m × a n
= 5
m x a n= 5
n6)
Пример 3: Упростите следующее выражение: p 12 ÷ p 4 q.
Решение:
Данное выражение равно p 12 ÷ p 4 q. Чтобы упростить это выражение, мы используем закон отношения показателей степени, который гласит:
⇒ p 12 /p 4 q
⇒ p 12-4 /q
⇒ p 8 /q
9 Следовательно ÷ p 4 q = p 8 /q
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Exponents
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по экспонентам
Что такое экспоненты в математике?
Показатель степени — это число, которое помещается над числом в виде надстрочного индекса. Другими словами, это указывает на то, что основание возведено в определенную степень. Показатель степени также называют другими именами, такими как индекс и мощность. Если m — положительное число, а n — его показатель степени, то m n означает, что m умножается само на себя n раз. Здесь m n читается как «m в степени n», и в этом случае «m» — это основание, а «n» — показатель степени.
Каковы свойства экспонент?
Свойства показателей степени — это некоторые правила, которые мы используем при решении выражений, включающих показатели степени. Эти правила помогают нам легко и быстро упрощать выражения. Несколько важных свойств экспонент перечислены ниже:
Несколько важных свойств экспонент перечислены ниже:
- a m × a n = a m+n
- a м /a n = a m-n
- а 0 = 1
- а -м = 1/а м
- ( м ) n = мн
- (ab) м = a м b м
- (a/b) м = a м /b м
Каковы примеры показателей степени?
Ниже приведены некоторые примеры показателей степени:
- 7 × 7 × 6 × 6 × 6 = 7 2 × 6 3 . Здесь 2 и 3 — показатели степени.
- -4 × -4 × -4 × -4 = (-4) 4 . Здесь 4 – показатель степени.
- п × п × п × п × п = п 5 . Здесь 5 – показатель степени.
Как экспоненты относятся к реальной жизни?
В реальной жизни мы используем понятие экспоненты для упрощенного и краткого написания чисел. Повторное умножение можно легко записать с помощью показателей степени. Кроме того, мы используем показатель степени для записи больших чисел, например, расстояния Луны от Земли, количества бактерий, присутствующих на поверхности, и т. д.
Повторное умножение можно легко записать с помощью показателей степени. Кроме того, мы используем показатель степени для записи больших чисел, например, расстояния Луны от Земли, количества бактерий, присутствующих на поверхности, и т. д.
Как добавить экспоненты?
Экспоненты не могут быть добавлены. Мы можем добавлять только одинаковые термины (термы, имеющие один и тот же показатель степени и одну и ту же переменную). Но, в случае умножения членов с одинаковыми переменными, мы прибавляем показатели степени переменной к умножению. Например, х 2 × х 4 = х (2+4) = х 6 . Попробуйте калькулятор сложения показателей степени от Cuemath и получите ответы быстро и легко.
Почему показатели степени важны?
Экспоненты важны для записи значений чисел в упрощенной форме. Мы знаем, что многократное сложение можно записать как умножение. Точно так же многократное умножение можно записать просто с помощью показателей степени. Показатель степени также важен, потому что, когда число многократно умножается само на себя, его легко выразить в виде показателей степени. Например, проще написать 13 6 , чем записать это как 13 × 13 × 13 × 13 × 13 × 13.
Показатель степени также важен, потому что, когда число многократно умножается само на себя, его легко выразить в виде показателей степени. Например, проще написать 13 6 , чем записать это как 13 × 13 × 13 × 13 × 13 × 13.
Как вычислить показатели степени с помощью калькулятора степени?
«Калькулятор степени» — это онлайн-инструмент, который находит значение экспоненциального выражения. Проверьте теперь калькулятор экспоненты Cuemath и найдите значение экспоненциального выражения для заданного значения основания и экспоненты в течение нескольких секунд.
☛ Также проверьте:
- Калькулятор отрицательных показателей
- Калькулятор степени деления
- Калькулятор умножения показателей степени
- Калькулятор правил экспоненты
- Калькулятор дробей с показателями степени
Как умножать показатели степени?
Когда необходимо умножить показатели степени, мы сначала решаем числа в скобках, степень вне скобок умножается на каждую степень внутри скобок. Например, (3x 2 y 3 ) 2 = 3 2 x x 2 x 2 x y 3 x 2 = 9 x 4 6
Например, (3x 2 y 3 ) 2 = 3 2 x x 2 x 2 x y 3 x 2 = 9 x 4 6 y
Какая польза от свойств показателей?
Свойства показателей степени широко используются в математике, особенно в алгебре. С помощью свойств показателей мы можем легко упростить выражения. Давайте разберемся в этом на примере. С помощью свойств экспоненты 2 4 × 2 6 можно упростить в два быстрых шага как 2 4 × 2 6 = 2 (4 + 6) = 2 10 .
Каково реальное применение экспонентов?
Экспоненты имеют различные применения. Ниже перечислены несколько приложений экспонентов:
- Экспоненты широко используются в компьютерных играх, измерительных весах и т. д.
- Научные шкалы, такие как шкала рН или шкала Рихтера, основаны на показателях степени.
- Они используются при вычислении площади, объема и задач, связанных с измерением.

- Чаще всего они используются в соответствующих областях науки, техники, экономики, бухгалтерского учета и финансов.
- Они часто используются для представления памяти компьютера или ноутбука.
Как законы экспоненты используются в алгебре?
Законы экспоненты очень полезны в алгебре. Например, алгебраическую формулу (a – b) 2 = a 2 + b 2 – 2ab можно легко записать и вычислить, применяя правила возведения в степень. Многие такие алгебраические формулы зависят только от законов показателей.
Как отрицательные показатели используются в реальной жизни?
Отрицательные показатели степени используются для записи очень маленьких чисел в реальной жизни, что означает числа со значениями от 0 до 1.
Что такое нулевой показатель?
Нулевой показатель степени означает числа, у которых показатель степени равен 0. Значения этих чисел всегда равны 1. Любое число с 0 в качестве его степени равно 1. Например, 5 0 = 1, 34 0 = 1, a 0 = 1
Например, 5 0 = 1, 34 0 = 1, a 0 = 1
Полномочия?
Показатели и степени означают одно и то же. Давайте разберемся в этом на примерах. В выражении 10 4 10 — это основание, а 4 — показатель степени, и мы читаем его как 10, возведенное в степень 4. Аналогично, в 6 3 , 6 – это основание, а 3 – показатель степени, и мы читаем это как 6, возведенное в степень 3.
Скачать БЕСПЛАТНО учебные материалы
Рабочие листы по экспонентам [PDF]
Математика – Правила для уравнений
Здесь представляют собой набор правил, которые можно применять к частям уравнения, которые не повлияют на истинность уравнения.
| правило | имя | описание |
|---|---|---|
| х + у = у + х | коммутативный – аддитивный | Операция является коммутативной, если порядок ее операндов может быть изменен без влияние на результат |
| х * у = у * х | коммутативное – мультипликативное | |
| х + (у + г) = (х + у) + г | ассоциативный – добавка | Операция является ассоциативной, если порядок выполнения нескольких операций не важно |
| х * (у * г) = (х * у) * г | ассоциативный – мультипликатив | |
| х * (у + г) = (х * у) + (х * г) | дистрибутив | Когда в этой алгебре есть две операции, скажем, + и *, тогда * говорят быть распределительным свыше + |
| х + 0 = х | тождественный оператор – аддитивный (справа) | добавление 0 не меняет результат |
| 0 + х = х | тождественный оператор – аддитивный (слева) | |
| х * 1 = х | тождественный оператор – мультипликативный (правый) | умножение на 1 не меняет результат |
| 1 * х = х | тождественный оператор – мультипликативный (левый) | |
, если z = x + y тогда х = г – у | Вычитаниеявляется обратным сложением | .

 Если в числе только одна цифра без нулей, то десятичную ставить не нужно.
Если в числе только одна цифра без нулей, то десятичную ставить не нужно. е. (a/b) -m = (b/a) м .
е. (a/b) -m = (b/a) м .