Правило ампера левой руки: Правило левой руки для силы Ампера – примеры и формулировка определения кратко

Правило левой руки

Проводник с током в магнитном поле. Магнитная индукция.

Если проводник, по которому проходит электрический ток, внести в магнитное поле, то в результате взаимодействия магнитного поля и проводника с током проводник будет перемещаться в ту или иную сторону.
Направление перемещения проводника зависит от направления тока в нем и от направления магнитных линий поля.

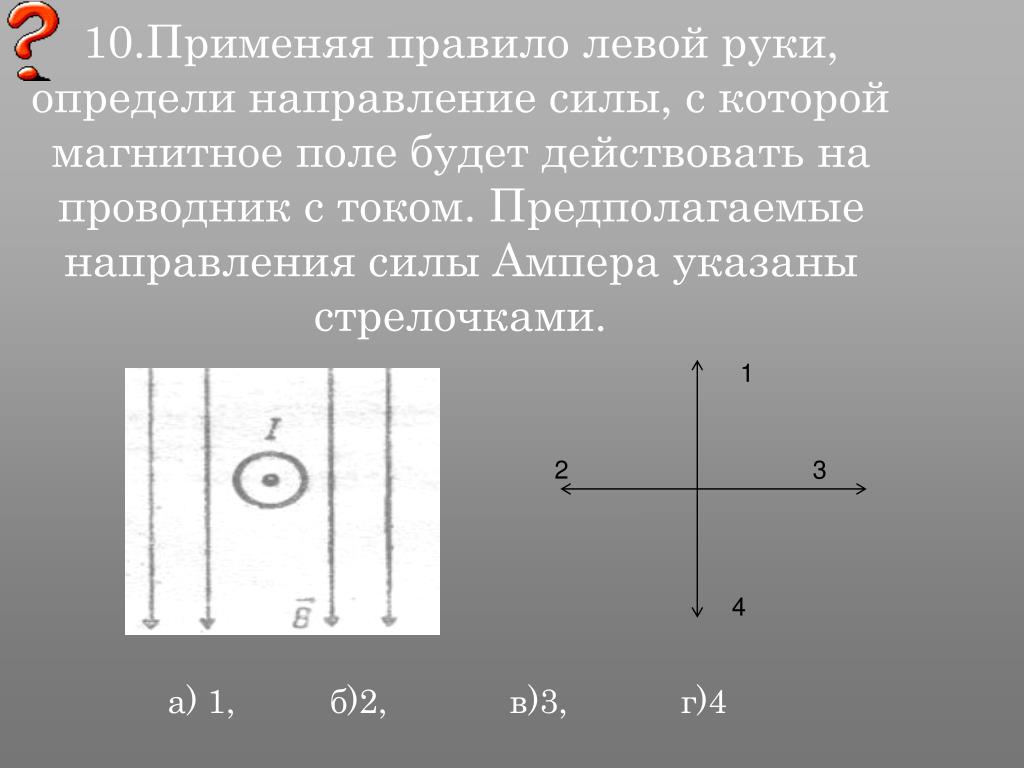
Допустим, что в магнитном поле магнита NS находится проводник, расположенный перпендикулярно плоскости рисунка; по проводнику протекает ток в направлении от нас за плоскость рисунка.

Ток, идущий от плоскости рисунка к наблюдателю, обозначается условно точкой, а ток, направляющийся за плоскость рисунка от наблюдателя,— крестом.

Движение проводника с током в магнитном поле
1 — магнитное поле полюсов и тока проводника,

2 — результирующее магнитное поле.

Всегда всё уходящее на изображениях обозначается крестом,
а направленное на смотрящего – точкой.

Под действием тока вокруг проводника образуется свое магнитное поле рис.1.
Применяя правило буравчика, легко убедиться, что в рассматриваемом нами случае направление магнитных линий этого поля совпадает с направлением движения часовой стрелки.

При взаимодействии магнитного поля магнита и поля, созданного током, образуется результирующее магнитное поле, изображенное на рис.2.
Густота магнитных линий результирующего поля с обеих сторон проводника различна. Справа от проводника магнитные поля, имея одинаковое направление, складываются, а слева, будучи направленными встречно, частично взаимно уничтожаются.

Следовательно, на проводник будет действовать сила, большая справа и меньшая слева. Под действием большей силы проводник будет перемещаться по направлению силы F.

Перемена направления тока в проводнике изменит направление магнитных линий вокруг него, вследствие чего изменится и направление перемещения проводника.

Для определения направления движения проводника в магнитном поле можно пользоваться правилом левой руки, которое формулируется следующим образом:

Если расположить левую руку так, чтобы магнитные линии пронизывали ладонь, а вытянутые четыре пальца указывали направление тока в проводнике, то отогнутый большой палец укажет направление движения проводника.

Сила, действующая на проводник с током в магнитном поле, зависит как от тока в проводнике, так и от интенсивности магнитного поля.

Основной величиной, характеризующей интенсивность магнитного поля, является магнитная индукция В. Единицей измерения магнитной индукции является тесла (Тл=Вс/м2).

О магнитной индукции можно судить по силе действия магнитного поля на проводник с током, помещенный в это поле. Если на проводник длиной 1 м и с током 1 А, расположенный перпендикулярно магнитным линиям в равномерном магнитном поле, действует сила в 1 Н (ньютон), то магнитная индукция такого поля равна 1 Тл (тесла).

Магнитная индукция является векторной величиной, ее направление совпадает с направлением магнитных линий, причем в каждой точке поля вектор магнитной индукции направлен по касательной к магнитной линии.

Сила F, действующая на проводник с током в магнитном поле, пропорциональна магнитной индукции В, току в проводнике I и длине проводника l, т. е.
F=BIl.

Эта формула верна лишь в том случае, когда проводник с током расположен перпендикулярно магнитным линиям равномерного магнитного поля.
Если проводник с током находится в магнитном поле под каким-либо углом а по отношению к магнитным линиям, то сила равна:
F=BIl sin a.
Если проводник расположить вдоль магнитных линий, то сила F станет равной нулю, так как

а=0.
(Подробно и доходчиво в видеокурсе “В мир электричества – как в первый раз!”)

Как обнаружить магнитное поле.

Правило левой руки

1.	Проводник в магнитном поле	1 вид – рецептивный	лёгкое	1 Б.	Определение направления действия силы на проводник с током.
2.	Правило левой руки	1 вид – рецептивный	лёгкое	1 Б.	Анализ информации правила левой руки.
3.	Технические устройства	1 вид – рецептивный	среднее	2 Б.	Применение силы Ампера и силы Лоренца в технических устройствах.
4.	Полюса магнитов	2 вид – интерпретация	среднее	2 Б.	Определение полюсов магнитов.
5.	Направление силы Ампера и силы Лоренца	2 вид – интерпретация	среднее	2 Б.	Определение направления силы, действующей на движущуюся, заряженную частицу в магнитном поле.
6.	Заряд частицы	2 вид – интерпретация	среднее	2 Б.	Определение заряда частицы, влетевшей в магнитное поле.
7.	Обнаружение магнитного поля	2 вид – интерпретация	среднее	2 Б.	Анализ содержания правила левой руки.
8.	Равновесие весов	3 вид – анализ	сложное	3 Б.	Определение по рисунку направления движения стрелки весов.
9.	Траектория движения частицы в магнитном поле	3 вид – анализ	сложное	3 Б.	Определение траектории движения заряженной частицы в магнитном поле.

Обнаружение магнитного поля по его действию на проводник с током :: Класс!ная физика

ОБНАРУЖЕНИЕ МАГНИТНОГО ПОЛЯ ПО ЕГО ДЕЙСТВИЮ НА ПРОВОДНИК С ТОКОМ

На проводник с током, помещенный в магнитное поле, действует сила Ампера.

Вспомни прошлый учебный год:

действие магнитного поля на проводник с током;

постоянные магниты.

ПРАВИЛО ЛЕВОЙ РУКИ
для проводника с током

служит для определения направления силы Ампера, действующей на проводник с током
в магнитном поле.

Если ЛЕВУЮ РУКУ расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по току, то отставленный на 90 градусов большой палец покажет направление действующей на проводник силы.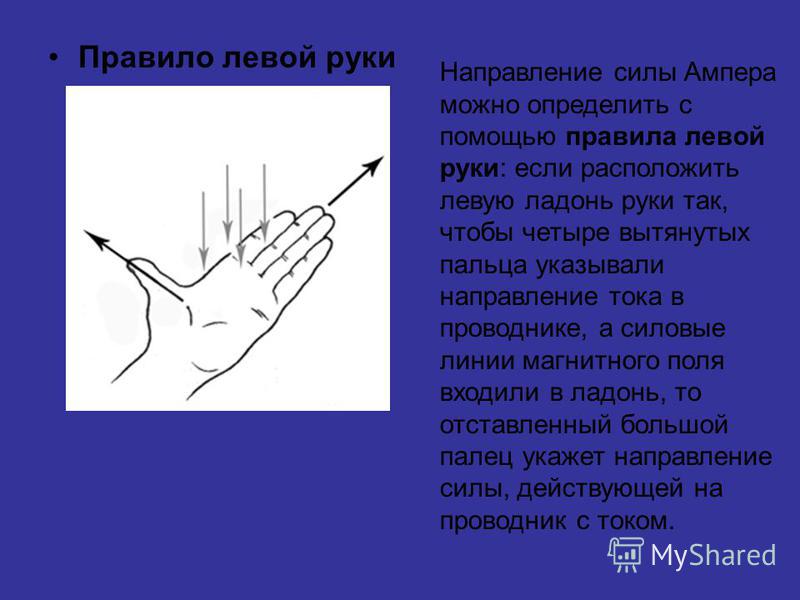

ПРАВИЛО ЛЕВОЙ РУКИ
для заряженной частицы

служит также для определения направления силы, действующей на отдельную заряженную частицу, движущуюся в магнитном поле.

Если ЛЕВУЮ РУКУ расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной частицы) , то отставленный на 90 градусов большой палец покажет направление действующей на частицу силы.

КНИЖНАЯ ПОЛКА

Тайны магнита.

ПОПРОБУЙ СДЕЛАТЬ, ВДРУГ ПРИГОДИТСЯ !

1.Определите направление силы, действующей на проводник с током со стороны магнитного поля.

2 .В какую сторону отклонится электрон под действием магнитного поля?

3. Укажите направление силы, с которой магнитное поле действует на частицу.

4.Укажите направление магнитных линий магнитного поля.

5. Укажите направление тока в проводнике.

ЗНАЕШЬ ЛИ ТЫ ?

Учеными из США разработан светочувствительный пластиковый магнит, работающий при температуре – 75 К. Магнитные свойства нового магнита увеличиваются в 1,5 раза при облучении лучами синего цвета. Зеленый цвет производит обратный эффект.

Устали? – Отдыхаем!

39 — сила Ампера • 31415.ru

Сила Ампера - сила воздействия магнитного поля на проводник с током.

I — ток в проводнике, А (Ампер)
B — индукция магнитного поля, Тл (Тесла)
L — длина проводника, м (метр)
На провод с током со стороны магнита действует сила 1 Ньютон, если по проводу протекает ток 1 Ампер, длина провода 1 метр и магнитная индукция магнита 1 Тесла.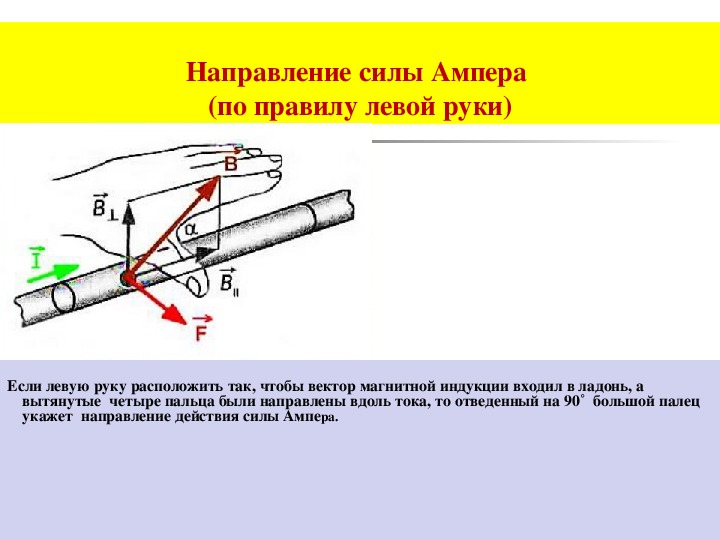


Возникновение магнитного поля вокруг проводника с током — это одно из самых удивительных явлений в физике. Первым открыл это явление датский физик Ханс Кристиан Эрстед в 1820 году. Проводя эксперименты с электричеством, он заметил что стрелка компаса реагирует на протекание тока по проводнику.

Электромагнит — является примером использования силы Ампера. Сила электромагнита прямо пропорциональна длине проводника L и силе тока I, протекающего через проводник.

Сила Ампера направлена перпендикулярна току и линиям магнитной индукции B. Для определения направления силы Ампера, используют правило левой руки.

Правило левой руки гласит: «Если линии магнитной индукции входят в ладонь, а четыре пальца направлены вдоль тока, то большой палец покажет направление силы Ампера».

Для использования этого правила нужно запомнить, что линии магнитной индукции (обозначаются буквой B) направлены от северного полюса к южному, то есть СТРОГО НА ЮГ. Это легко запомнить, потому что «Строго на юг» — так называется известный детективный сериал о приключениях канадского полицейского с волком.

Электрический ток принято считать направленным от плюса к минусу. При использовании правила левой руки нужно использовать именно такое направление тока.

Сила Ампера определяется только перпендикулярной составляющей магнитной индукции к току. Если линии индукции магнитного поля B направлены к току I под углом больше или меньше 90 градусов, то в формуле для силы Ампера, нужно вычислять проекцию вектора индукции B на перпендикуляр к проводнику.

Лекция о магнитном поле.

 

Эксперимент с проводником в магнитном поле

 

Эксперимент с рамкой в магнитном поле

 

Задача 39.
На проводник с током, расположенный в однородном магнитном поле под углом 30⁰ к магнитным линиям, действует сила 10 Н. Какая сила будет действовать на проводник, если в три раза увеличить угол между проводником и магнитными линиями.
Показать ответОтвет: F=20 Н
 

 

 

7 “Б”

Урок
1/1		Что изучает физика. Физические термины. Наблюдения и опыты.	§ 1 – 3, Л № 5, 12
2/2		Физические величины. Измерение физических величин. Погрешность и точность измерений	§ 4, 5, упр.1
3/3		Определение цены деления измерительного прибора	§ 4, 5
4/4		Физика и техника	§ 6,
		Первоначальные сведения о строении вещества
5/1		Строение вещества. Молекулы	§ 7, 8
6/2		Определение размеров малых тел	§ 7, 8
7/3		Движение молекул. Диффузия в газах, жидкостях и твердых телах	§ 9,
8/4		Взаимодействие молекул
9/5		Три состояния вещества	§ 11, 12
10/6		Повторение. Контрольная работа №1 “Первоначальные сведения о строении вещества”	§ 12

Презентация направление тока правило левой руки.

Правило правой руки. Использование силы Ампера в технике

«Магнитное поле» – 14. Т о к направлен к нам. 24. 5. Гальванический элемент. За направление магнитного поля в данной точке принимается положительное направление нормали. Степанова Екатерина Николаевна доцент кафедры ОФ ФТИ ТПУ. Электромагнетизм. 8. Правило буравчика.

«Магнитное поле физика» – Можно ли увидеть магнитное поле. Точнее, магнитные поля являются необходимым следствием существования электрических полей. Фотографирование невозможных объектов. Происходить отклонение электронного пучка магнитным полем. На экране телевизора произойдет изменение цвета в месте, где приближен магнит. Можно также рассматривать магнитное поле, как составляющую электрического поля.

«Направление линий магнитного поля» – Выполнила: Кадичева Анна. Правило правой руки. Что можно определить,используя правило буравчика? Известно, что вокруг электрического тока всегда существует магнитное поле. Что называется линиями магнитной индукции? Электрический ток и магнитное поле неотделимы друг от друга.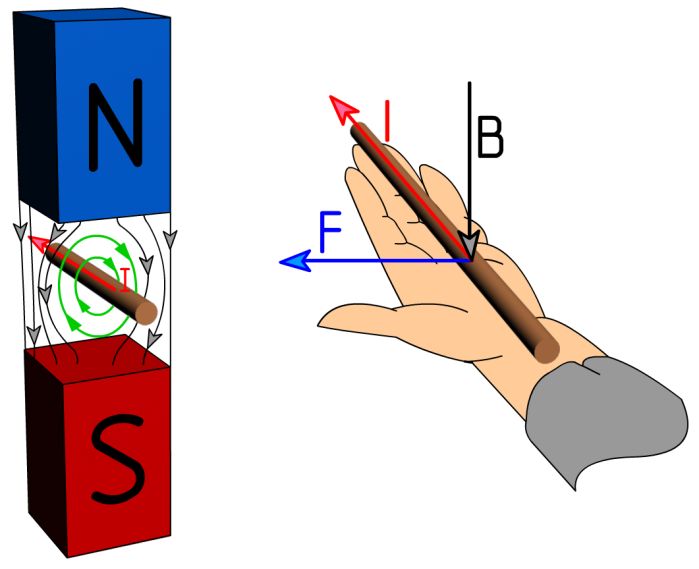 На всякий проводник с током.

«Магнитное поле урок физики» – О б о р у д о в а н и е. Продолжить формирование базиса понимания современной научной картины мира. З а д а ч и. S. Урок физики по теме «магнитное поле тока». Ганс христиан эрстед (1777 – 1851). b). Ваш вывод Что может изменить величину угла отклонения стрелки? Поменять полярность. Задания на повторение.

«Физика Сила Лоренца» – Переход от покоящегося источника к движущемуся приводит к возникновению динамических добавок к статической силе: В полевой силе Лоренца: В согласии с указанной логикой Полевая физика приводит к следующему выражению для силы Лоренца: Сила электростатического взаимодействия двух заряженных объектов (закон Кулона):

«Сила Лоренца» – Направление силы Лоренца. Правило левой руки. Магнитное поле. Радиус кривизны. Согласно второму закону Ньютона: Отсюда радиус: В каком случае частица движется в магнитном поле прямолинейно? Закон Ампера? Сила Ампера: Уравнение для силы тока в проводнике: Сила Лоренца Модуль силы Лоренца.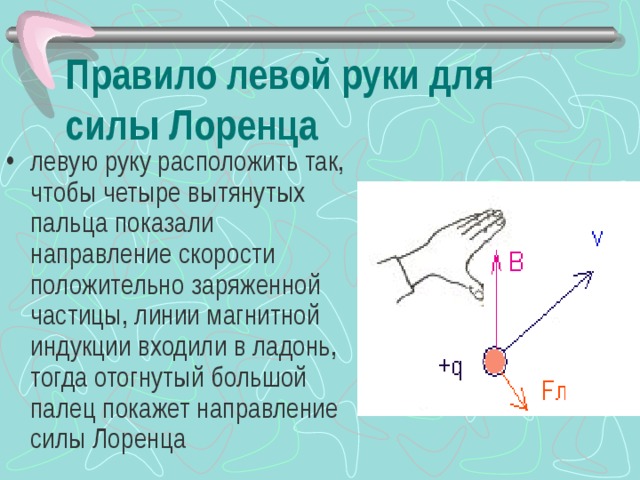 Дайте определение силе Лоренца.

Всего в теме 20 презентаций

Учитель физики Коваль В.С. 2010 г. сайт

Слайд 2

Тестовая работа

1. Когда электрические заряды находятся в покое, то вокруг них обнаруживается… А. Электрическое поле. Б. Магнитное поле. В. электрическое и магнитное поля. 2. Как располагаются железные опилки в магнитном поле прямого тока? А. Беспорядочно. Б. По прямым линиям вдоль проводника. В. По замкнутым кривым, охватывающим проводник. 3. Когда к магнитной стрелке поднесли один из полюсов постоянного магнита, то южный полюс стрелки оттолкнулся. Какой полюс поднесли? А.Северный. Б. Южный.

Слайд 3

Тестовая работа

4. Каким способом можно усилить магнитное поле катушки? А. Сделать катушку большего диаметра. Б. Внутрь катушки вставить железный сердечник. В. Увеличить силу тока в катушке. 5. Какие вещества из указанных ниже совсем не притягиваются магнитом? А. Стекло. В. Никель. Б. Сталь. Г. Чугун 6. Середина магнита не притягивает к себе железных опилок Магнит ломают на две части. . Будут ли концы на месте излома магнита притягивать железные опилки? А. Будут, но очень слабо. Б. Не будут.

Слайд 4

Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки.

Слайд 5

На проводник с током, помещенный в магнитное поле, действует сила со стороны магнитного поля.

Слайд 6

ПРАВИЛО ЛЕВОЙ РУКИ для проводника с током служит для определения направления силы, действующей на проводник с током в магнитном поле

Если ЛЕВУЮ РУКУ расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по току, то отставленный на 90 градусов большой палец покажет направление действующей на проводник силы.

Слайд 7

ПРАВИЛО ЛЕВОЙ РУКИ для заряженной частицы с целью определения направления силы, действующей на отдельную заряженную частицу, движущуюся в магнитном поле.

Если ЛЕВУЮ РУКУ расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной частицы), то отставленный на 90 градусов большой палец покажет направление действующей на частицу силы.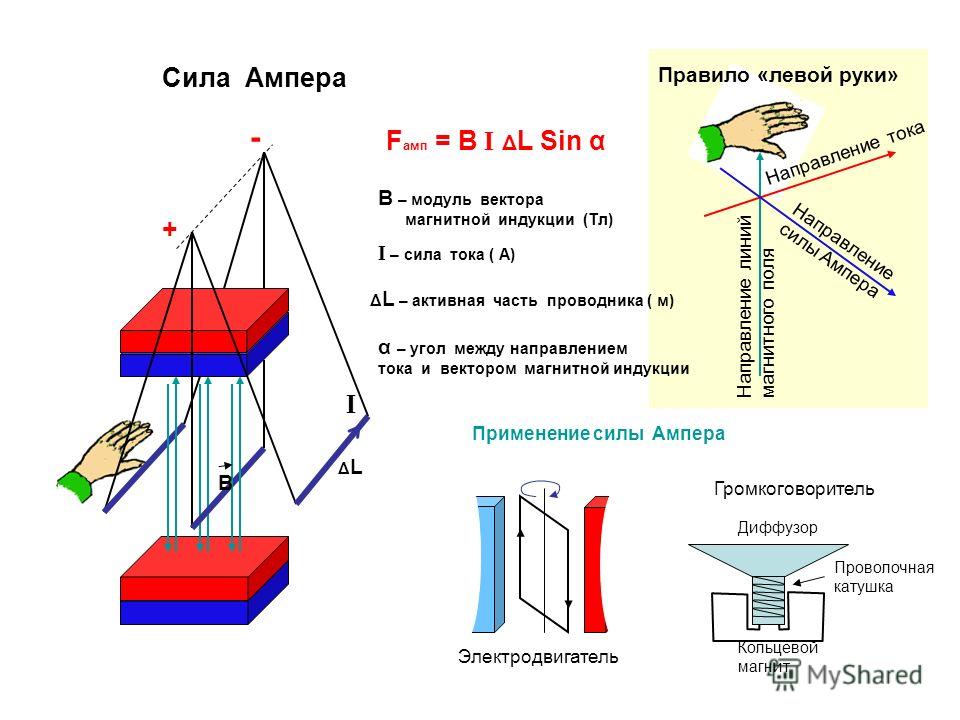

Слайд 8

Закрепление

Определите направление силы, действующей на проводник с током со стороны магнитного поля

Слайд 9

В какую сторону отклонится электрон под действием магнитного поля?

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Физический диктант. Причиной возникновения магнитного поля в проводнике является… Однородное магнитное поле-это… В какой точке действие магнитного поля наибольшее? Причиной возникновения магнитного поля в постоянной магните является… Неоднородное магнитное поле-это… В какой точке действие магнитного поля наименьшее? А В С I А В С

Физический диктант 4. Сформулировать правило буравчика. 5. Определить направление магнитных линий в т. О. 4. Сформулировать правило правой руки. 5. Определить направление магнитных линий в т. О. О I О I

03.05.17 Обнаружение магнитного поля по его действию на электрический ток.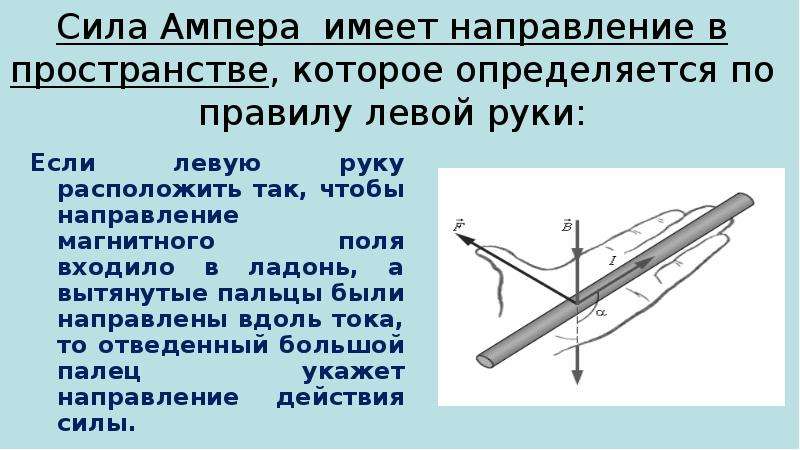 Правило левой руки.

Силу, действующую на проводник с током со стороны магнитного поля, называют силой Ампера. Ампер Андре Мари (1775-1836 г.г.)

Правило левой руки для тока:

Силу, действующую на движущиеся заряженные частицы со стороны магнитного поля, называют силой Лоренца Хе́ндрик А́нтон Ло́ренц (1853-1928 г.г.)

Правило левой руки для частиц:

Домашнее задание: § 45, Упр. 36 (3,4,5).

Задание 1: определить направление действия силы Ампера. N S I

Задание 2: определить направление тока в проводнике. N S I

Задание 3: определить направление действия силы Лоренца. +

Задание 4: определить направление движения частицы. –

По теме: методические разработки, презентации и конспекты

Урок физики 9 класс. «Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки»

Урок физики 9 класс.«Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки»Учитель физики Даузе М. Г. МБОУ «Краснохолмская сош №2 им.С.Забавина»Цели урока:Образоват…

Данная разработка полностью охватывает повторение темы магнитное поле и его графическое изображение, а также знакомит ребят с новыми понятиями, как силы Ампера и Лоренца. В данном уроке отрабаты…

презентация на тему: “Правило левой руки. Сила Ампера”

Просмотр содержимого документа

Урок в 9 классе по теме: «Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки. Сила Ампера ».

Цели урока:

Образовательные:

изучить как обнаруживается магнитное поле по его действию на электрический ток, изучить правило левой руки, повторить ранее пройденные определения электрического поля, магнитного поля, условия их возникновения, свойства; закрепить правила правой и левой руки с помощью упражнений;

закрепить знания по предыдущим темам;

научить применять знания, полученные на уроке;

показать связь с жизнью;

расширить межпредметные связи.

Воспитательные:

формировать интерес к предмету, к учебе, воспитывать инициативу, творческое отношение, воспитывать добросовестное отношение к учебе, прививать навыки, как самостоятельной работы, так и работы в коллективе, воспитывать познавательную потребность и интерес к предмету.

Развивающие :

развивать физическое мышление учащихся, их творческие способности, умение самостоятельно формулировать выводы, расширять познавательный интерес путем привлечения дополнительного материала, а также потребности к углублению и расширению знаний;

развивать речевые навыки;

формировать умения выделять главное, делать выводы, развивать способность быстро воспринимать информацию и выполнять необходимые задания; развивать логическое мышление и внимание, умение анализировать, сопоставлять полученные результаты, делать соответствующие выводы.

Этапы урока:

1. Организационный момент – 2 мин.
2. Проверка домашнего задания, знаний и умений – 6 мин.
3. Объяснение нового материала – 18 мин.
4. Закрепление. Решение задач – 15 мин.
5. Итоги. Выводы. Домашнее задание – 4 мин.

ХОД УРОКА

I . Проверка домашнего задания, знаний и умений – 6 мин

Слайд 2.

1. Магнитное поле порождается______________ (электрическим током).

2. Магнитное поле создается ______________заряженными частицами (движущимися).

3. За направление магнитной линии в какой-либо ее точке условно принимают направление, которое указывает _________полюс магнитной стрелки, помещенной в эту точку (северный).
4.Магнитные линии выходят из _________ полюса магнита и входят в ________. (Северного, южный).

Поменялись листочками и проверили друг друга. На экране высвечиваются правильные ответы.

Слайд 3.

Правильных ответов: 4 ответов– 5 баллов, 3 ответа – 4 балла, 2 ответа – 3 балла, 0-1 ответа – 2 балла.

II . Объяснение нового материала – 15 мин

Слайд 4.

Учитель: Как можно обнаружить магнитное поле? Оно не действует на наши органы чувств – не имеет запаха, цвета, вкуса. Мы не можем, правда, с уверенностью утверждать, что в животном мире нет существ, чувствующих магнитное поле. В США и Канаде для отгона осьминог с места скопления мальков на реках, впадающих в Великие озера, установлены электромагнитные барьеры. Ученые объясняют способность рыб ориентироваться в просторах океана их реакцией на магнитные поля…

Сегодня на уроке мы изучим, как обнаружить магнитное поле по его действию на электрический ток и изучим правило левой руки.

На всякий проводник с током, помещенный в магнитное поле и не совпадающий с его магнитными линиями, это поле действует с некоторой силой, наличие такой силы можно посмотреть с помощью такого опыта: проводник подвешен на гибких проводах, который через ключ присоединен к аккумуляторам. Проводник помещен между полюсами подковообразного магнита, т. е. находится в магнитном поле. При замыкании ключа в цепи возникает электрический ток, и проводник приходит в движение. Если убрать магнит, то при замыкании цепи проводник с током двигаться не будет. (Демонстрация опыта)

Слайд 5.

Если ученики смогут сами ответить : Значит, со стороны магнитного поля на проводник с током действует некоторая сила, отклоняющая его от первоначального положения. Эта сила получила название силы Ампера.

Выясним, от чего зависит направление силы Ампера, действующей на проводник с током в магнитном поле. Опыт показывает, что при изменении направления тока изменяется и направление движения проводника, а значит, и направление действующей на него силы.

Направление силы изменится и в том случае, если, не меняя направления тока, поменять местами полюсы магнита (т. е. изменить направление линий магнитного поля).
Следовательно, направление тока в проводнике, направление линий магнитного поля и направление силы, действующей на проводник, связаны между собой.

Слайд 6.

Направление силы, действующей на проводник с током в магнитном поле, можно определить, пользуясь правилом левой руки. В наиболее простом случае, когда проводник расположен в плоскости, перпендикулярной линиям магнитного поля, это правило заключается в следующем: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по току, то отставленный на 90 ° большой палец покажет направление действующей на проводник силы.

Ученики: за направление тока во внешней части электрической цепи (т.е. вне источника тока) принимается направление от положительного полюса источника тока к отрицательному.

Пользуясь правилом левой руки, можно определить не только направление силы, действующей в магнитном поле на проводник с током. По этому правилу мы можем определить направление тока (если знаем, как направлены линии магнитного поля и действующая на проводник сила), направление магнитных линий (если известны направления тока и силы), знак.
Сила действия магнитного поля на проводник с током равна нулю, если направление тока в проводнике совпадает с линиями магнитного поля или параллельны им.

Слайд 7.

Использование силы Ампера в технике:

Электродвигатели;

Электроизмерительные приборы;

Громкоговорители, динамики.

IV . Закрепление материала. Решение задач – 15 мин.

Слайд 8.

Слайд 9.

Слайд 10.

Учитель: Упр. 36 (1). В какую сторону покатится легкая алюминиевая трубочка при замыкании цепи?

Ученики дают ответы: по правилу левой руки линии магнитного поля входят в ладонь, электрический ток течет по трубочке, значит, трубочка покатится к источнику тока.

Итоги

Сегодня на уроке мы изучили, как обнаружить магнитное поле по его действию на электрический ток. Изучили силу Ампера и ее применение в технике. Рассмотрели правило левой руки для определения направления силы Ампера.

Слайд 11.

V . § 46, упр. 36 (2, 3, 4, 5).

Просмотр содержимого презентации

«9 класс _Правило левой руки_»

Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки. Сила Ампера.

Вставьте пропущенные слова.

• 1.Магнитное поле порождается ___________ .
• 2 . Магнитное поле создается ______________ заряженными частицами.
• 3. За направление магнитной линии в какой-либо ее точке условно принимают направление, которое указывает _________ полюс магнитной стрелки, помещенной в эту точку.
• 4.Магнитные линии выходят из _________ полюса магнита и входят в ________.

• 1. Магнитное поле порождается электрическим током .
• 2 . Магнитное поле создается движущимися заряженными частицами.
• 3. За направление магнитной линии в какой-либо ее точке условно принимают направление, которое указывает северный полюс магнитной стрелки, помещенной в эту точку.
• 4. Магнитные линии выходят из северного полюса магнита и входят в южный .

• Со стороны магнитного поля на проводник с током действует некоторая сила, отклоняющая его от первоначального положения.
• Направление тока в проводнике, направление линий магнитного поля и направление силы, действующей на проводник, связаны между собой.
• Эта сила получила название силы Ампера (F A).

• Правило левой руки : если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по току, то отставленный на 90° большой палец покажет направление действующей на проводник силы Ампера.

• Как будет двигаться проводник, изображенный на рисунке. Направление тока показано стрелками.

• Между полюсами магнитов расположены проводники с током. Как движется каждый из них?

• Упражнение 36. Задание № 1.

• Упражнение 36 (2,3,4,5) письменно в тетрадке

Сила Ампера

Самые простые задачи на определение силы, индукции поля, длины проводника или угла, под которым этот проводник расположен. Направление силы определяем по правилу ЛЕВОЙ руки: если расположить руку так, чтобы магнитные линии втыкались в ладонь, а четыре пальца направить по току, то отведенный большой палец укажет направление действия силы.

Задача 1. Прямолинейный проводник длиной м находится в однородном магнитном поле с индукцией Тл. Сила тока в проводнике А. Проводник перпендикулярен магнитной индукции (рис.). Найти модуль и направление силы, действующей на проводник.

К задаче 1

Со стороны поля на проводник с током действует сила Ампера:

   

У нас проводник перпендикулярен линиям индукции, поэтому

   

Определяем направление. Левую руку расположим так, чтобы линии индукции втыкались в ладонь, то есть ладошкой вниз. Четыре вытянутых пальца направим вдоль тока – то есть влево. Тогда большой палец укажет направление действия силы – за плоскость рисунка, от нас.

Ответ: Н, от нас за плоскость рисунка.

Задача 2. Прямолинейный проводник длиной м находится в однородном магнитном поле (рис.). На проводник со стороны поля действует сила Н. Сила тока в проводнике А. Найти модуль и направление индукции магнитного поля, если она перпендикулярна проводнику.

К задаче 2

Со стороны поля на проводник с током действует сила Ампера:

   

У нас проводник перпендикулярен линиям индукции, поэтому

   

Для определения направления левую руку расположим пальцами вниз – они указывают направление тока, большим пальцем вправо – он указывает направление действия силы. Тогда ладонь окажется развернутой к нам – в раскрытую ладонь должны втыкаться линии магнитной индукции, следовательно, они направлены от нас за плоскость чертежа.

Ответ: Тл, от нас за плоскость чертежа.
Задача 3. На прямой проводник длиной м, расположенный под углом к силовым линиям поля с индукцией Тл, действует сила Н. Найти силу тока в проводнике.

Со стороны поля на проводник с током действует сила Ампера:

   

   

Ответ: 30 А.

Задача 4. Прямой провод длиной см находится в однородном магнитном поле с индукцией Тл. Сила тока в проводнике А. Найти угол  между направлением магнитной индукции и направлением тока, если на провод действует сила Н.

Со стороны поля на проводник с током действует сила Ампера:

   

   

Синус, равный , имеет угол в .
Ответ: .

 

Задача 5. Проводник находится в равновесии в горизонтальном магнитном поле с индукцией мТл. Сила тока в проводнике А. Угол между направлением тока и вектором магнитной индукции  . Определить длину проводника, если его масса  кг.

Так как поле горизонтально, а проводник в нем «висит», то очевидно, что сила Ампера уравновесила силу тяжести:

   

   

Откуда

   

Ответ: 25,8 см.

Задача 6. Проводник длиной м расположен перпендикулярно силовым линиям горизонтального магнитного поля с индукцией мТл. Какой должна быть сила тока в проводнике, чтобы он находился в равновесии в магнитном поле? Масса проводника кг.

Аналогично предыдущей задаче,

   

   

Откуда

   

Ответ: 10 А.

Левые правила | Школы онлайн

В нашем исследовании магнитных полей и правил левой руки имейте в виду, что правила правой руки в учебнике применимы только к обычному (положительному) току. Во многих случаях электричество часто имеет нетрадиционный (неположительный) ток. Нетрадиционный ток подчиняется правилам левой руки. В этом объяснении мы будем использовать только три левых правила. Кроме того, следующие определения помогут понять, как и почему работают правила левой руки.

Постоянный магнит имеет два полюса: полюс, направленный на север, и полюс, направленный на юг. Северный полюс притягивается к южному полюсу любого магнита и отталкивает северный полюс любого магнита. То же самое и с Южным полюсом. Северный полюс любого магнита всегда будет выровнен с ch как компас, если его подвешивать на нитке и оставлять в покое.

Соленоид – это модное слово для обозначения длинной струны проволоки, обернутой вокруг другого цилиндрического объекта. Когда обычный ток протекает через провод, как показано, магнитное поле равномерно проходит через центральный цилиндр. Ниже приведено изображение соленоида (синие линии – это силовые линии магнитного поля). На схеме показано, что внутри соленоида в левой части схемы будет отображаться северный магнитный полюс.

Применяется только к третьему правилу левой руки:

Где:

• = Сила (Н)

• = Ток (А)

• = Тесла (Н / (А x м))

• = Длина провода (м)

Одна из самых запутанных частей магнитных полей заключается в том, что, в отличие от электрических полей, магнитные поля требуют трехмерного анализа, потому что поле вращается вокруг тока в проводе. Вверх, вниз, влево и вправо больше недостаточно для описания направления поля. Теперь магнитные поля могут перемещаться по странице и выходить за ее пределы.

Графика и правило, описанные ниже, неверны – это должно быть правило захвата правой руки Ампера (также известное как правило штопора), тот же принцип, но правая рука не левая …

Представьте, что вы обхватываете пальцами тонкий стержень (другими словами, сожмите кулак), и направьте большой палец в направлении тока (I).Магнитное поле будет вращаться вокруг вашего кулака, как показано на следующей диаграмме. Кроме того, магнитное поле всегда будет указывать в том направлении, в котором сгибаются ваши пальцы. Используйте следующую диаграмму для ссылки как на новые векторы, так и на первое правило левой руки.

Оберните пальцы вокруг соленоида так, чтобы пальцы двигались в том же направлении, что и ток (I). Вытяните большой палец вдоль цилиндрического объекта. Пока ток продолжает течь в том направлении, в котором согнуты ваши пальцы, ваш большой палец всегда будет указывать на северный полюс. Посмотрите на диаграмму выше, чтобы понять это, за исключением того, что стержень будет соленоидом, а направление, указывающее большой палец, – на северный полюс.

Это правило используется для описания силы, когда ток или электроны проходят через магнитное поле. Чтобы найти величину силы, просто используйте F = BIL. Чтобы найти направление, вы открываете ладонь и помещаете большой палец перпендикулярно пальцам. Ваш большой палец показывает направление тока или скорость электрического заряда (I).Остальные четыре пальца представляют направление магнитного поля (B). Наконец, направление вашей ладони – это направление вектора силы. Помните, что когда вы применяете эти правила, у вас есть шесть основных векторов для работы (вверх, вниз, влево, вправо, внутрь, из).

Лекция 19

км
По проводу идет электрический ток на север. В каком направлении указывает B прямо над проводом?
А.Северный
Б. Юг
С. Восток
Д. Вест
E. Вверх
F. Ответ вниз

Рыцарь2 33.stt.4
Ток в этой петле течет _____, если смотреть сверху, и северный магнитный полюс его поле находится на _____ стороне цикла.
A. по часовой стрелке … вверху
Б. по часовой стрелке … снизу
C. против часовой стрелки … сверху
D. против часовой стрелки … снизу
Ответ

POP5 22.35
Каково магнитное поле при P на рисунке, если радиус кривой равен 0,60 м и ток 3,00 А?
A. 5,75 µ T
Б. 572 нТл
С. 262 нТл
D. 108 нТл
Ответ

gc6 20,26
Кабель-перемычка, используемый для запуска заглохшего автомобиля, пропускает ток 65 А. Насколько сильна магнитная поле на расстоянии 6.0 см от него?
А. 2.17 × 10 ⁻⁴ T
Б. 6,90 × 10 ⁻⁵ Т
С.3,45 × 10 ⁻⁵ T
D. 1,38 × 10 ⁻⁶ T
Ответ

Walker5e рис 22-32
Два токоведущих провода пересекаются под прямым углом, как показано на рисунке.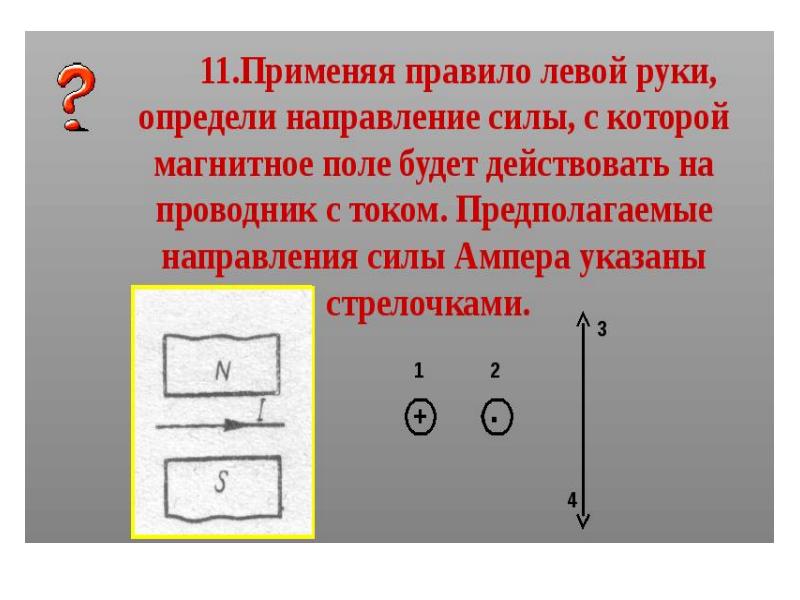 В каких точках магнитный поле быть сильнейшим?
A. Пункт 3
B. Пункты 1 и 2
С. Пункты 1 и 3
D. Пункты 2 и 4
Ответ

Walker5e CnEx 22-12
Показанное ниже магнитное поле возникает из-за горизонтального токоведущего провода.Какой путь делает ток в проводе течет?

A. слева
Б. вправо
C. в любом направлении создается одинаковое магнитное поле.
Ответ

К. Восток
Используя правило правой руки, направьте большой палец на север, в том же направлении, что и течение. Завитые пальцы вашей правой руки будут указывать на восток прямо над проводом.

Б.по часовой стрелке … снизу

Второе правило правой руки гласит, что если пальцы вашего правая рука согните в направлении тока, большой палец указывает в направлении магнитного поле в центре токовой петли. Если вы направите большой палец правой руки вниз с изображением поле, пальцы сгибаются по часовой стрелке . Поскольку силовые линии магнитного поля выходят из северного полюса в юг, мы заключаем, что северный полюс находится на дне петли.

К. 262 нТл

A. 2,17 × 10 ⁻⁴ T

Это эквивалентно 217 µ Тл, что примерно в четыре раза сильнее магнитного поля Земли.

D. Пункты 2 и 4
Используя правило правой руки, вы можете найти, что магнитные поля из-за токов каждый из страниц с правой стороны вертикальной проволоки и над горизонтальной проволокой. Это означает, что два поля имеют тенденцию добавлять в точках 2 (каждый вне страницы) и 4 (каждый в страницу) и имеют тенденцию отменять в точках 1 и 3.

А. слева
Используя правило правой руки, ваши пальцы указывают на страницу над проводом и за страницу под проводом, когда большой палец указывает влево. Это направление электрического тока в проводе.

22.3: Закон Ампера – Physics LibreTexts

Закон Ампера похож на закон Гаусса, поскольку он позволяет нам (аналитически) определять магнитное поле, создаваемое электрическим током в конфигурациях с высокой степенью симметрии. {enc} \) – это чистый ток, который пересекает поверхность, определяемую замкнутым путем, часто называемый «током, заключенным в пути». Это отличается от закона Гаусса, где интеграл ведется по замкнутой поверхности (а не по замкнутому пути, как здесь). В контексте закона Гаусса мы имеем в виду «вычисление потока электрического поля через замкнутой поверхности»; в контексте закона Ампера мы имеем в виду «вычисление циркуляции магнитного поля вдоль замкнутого пути».

Мы применяем закон Ампера во многом так же, как мы применяем закон Гаусса.

СООТВЕТСТВУЮЩИЙ ЗАКОНУ Ампера

1. Составьте хорошую схему, определите симметрии.
2. Выберите замкнутый путь для расчета циркуляции магнитного поля (см. Ниже, как выбрать путь). Путь часто называют «петлей амперова» (подумайте о «гауссовой поверхности»).
3. Вычислить интеграл циркуляции.
4. Определите, какой ток «заключен» в амперовскую петлю.
5. Применить закон Ампера.

Аналогично закону Гаусса, нам нужно выбрать путь (вместо поверхности), по которому мы будем вычислять интеграл. Интеграл будет легко вычислить, если:

1. Угол между \ (\ vec B \) и \ (d \ vec l \) постоянен вдоль пути , так что:

\ [\ begin {align} \ oint \ vec B \ cdot d \ vec l = \ oint Bdl \ cos \ theta = \ cos \ theta \ oint Bdl \ end {align} \]

, где \ (\ theta \) – угол между \ (\ vec B \) и \ (d \ vec l \).

2. Величина \ (\ vec B \) постоянна на пути , так что:

\ [\ begin {align} \ cos \ theta \ oint Bdl = B \ cos \ theta \ oint dl \ end {align} \]

Выбор пути, удовлетворяющего этим двум условиям, возможен только при наличии высокой степени симметрии.

Рассмотрим бесконечно длинный прямой провод, по которому проходит ток \ (I \) за пределы страницы, как показано на рисунке \ (\ PageIndex {1} \). Магнитное поле от провода должно выглядеть одинаково независимо от угла, под которым мы рассматриваем провод («азимутальная симметрия»).Таким образом, магнитное поле должно либо образовывать концентрические круги вокруг провода (что, как мы знаем, имеет место из закона Био-Савара), либо оно должно быть в радиальном направлении (направленным к проводу или от него). Эти две возможности проиллюстрированы на рисунке \ (\ PageIndex {1} \), и пока мы будем делать вид, что не знаем, какой из них правильный.

Рис. \ (\ PageIndex {1} \): По симметрии магнитное поле от бесконечного провода с током (показано током, исходящим из страницы) должно образовывать концентрические круги (левая панель) или находиться в радиальном направлении. направление (правая панель).Мы знаем, что первое (кружки, левая панель) – правильный выбор. Пунктирными линиями показаны «петли Ампера», которые можно использовать для вычисления интеграла в законе Ампера.

Чтобы применить закон Ампера, мы выбираем петлю Ампера (вместо «гауссовой поверхности»).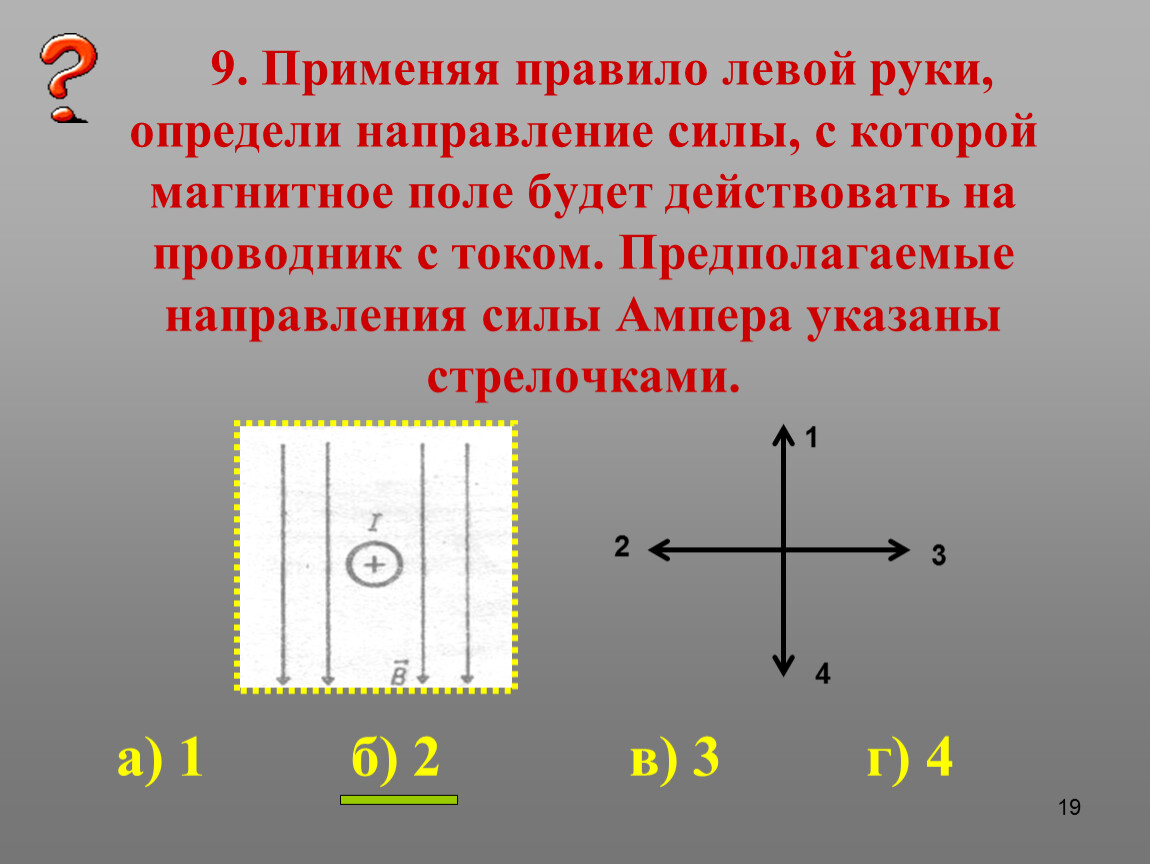 В случае бесконечного провода с током, окружность, которая концентрична с проводом, будет соответствовать свойствам, указанным выше, независимо от двух возможных конфигураций магнитного поля: с круговой петлей амперова угол между магнитным полем и элемент \ (d \ vec l \) постоянен вдоль всей петли, а величина магнитного поля постоянна вдоль петли.Наш выбор петли проиллюстрирован на рисунке \ (\ PageIndex {2} \), где мы проиллюстрировали магнитное поле для случая, когда оно образует концентрические круги.

Рисунок \ (\ PageIndex {2} \): Петля Ампера, представляющая собой круг радиуса \ (h \), позволит нам определять магнитное поле на расстоянии \ (h \) из бесконечно длинного токоведущий провод.

Циркуляция магнитного поля по круговой траектории с радиусом \ (h \) определяется выражением:

\ [\ begin {выровнено} \ oint \ vec B \ cdot d \ vec l = \ oint Bdl \ cos \ theta = \ cos \ theta \ oint Bdl = B \ cos \ theta \ oint dl = B \ cos \ theta (2 \ пи ч) \ конец {выровнено} \]

, где \ (\ cos θ \) равно \ (1 \), если поле образует круги (правильно), или \ (0 \), если поле радиальное (неверно). {enc} \\ B \ cos \ theta (2 \ pi h) & = \ mu_ {0} I \ end {align} \]

Здесь ясно, что cos θ не может быть нулевым, поскольку правая часть уравнения не равна нулю. Таким образом, мы можем заключить, что магнитное поле действительно должно образовывать концентрические круги, как мы определили ранее. Величина магнитного поля определяется выражением:

.

\ [\ begin {align} B = \ frac {\ mu_ {0} I} {2 \ pi h} \ end {align} \]

, как мы обнаружили ранее с законом Био-Савара. Опять же, по аналогии с законом Гаусса, нужно применить некоторые знания о симметрии и спорить, в каком направлении должно указывать магнитное поле, чтобы эффективно использовать закон Ампера.

Упражнение \ (\ PageIndex {1} \)

Закон Ампера доказывает, что магнитное поле в центре токоведущей петли равно нулю, потому что нет приложенного тока:

1. Верно.
2. Ложь

Ответ

Пример \ (\ PageIndex {1} \)

По длинному сплошному однородному кабелю радиуса \ (R \) проходит ток \ (I \) с плотностью тока, равномерной по всему поперечному сечению кабеля.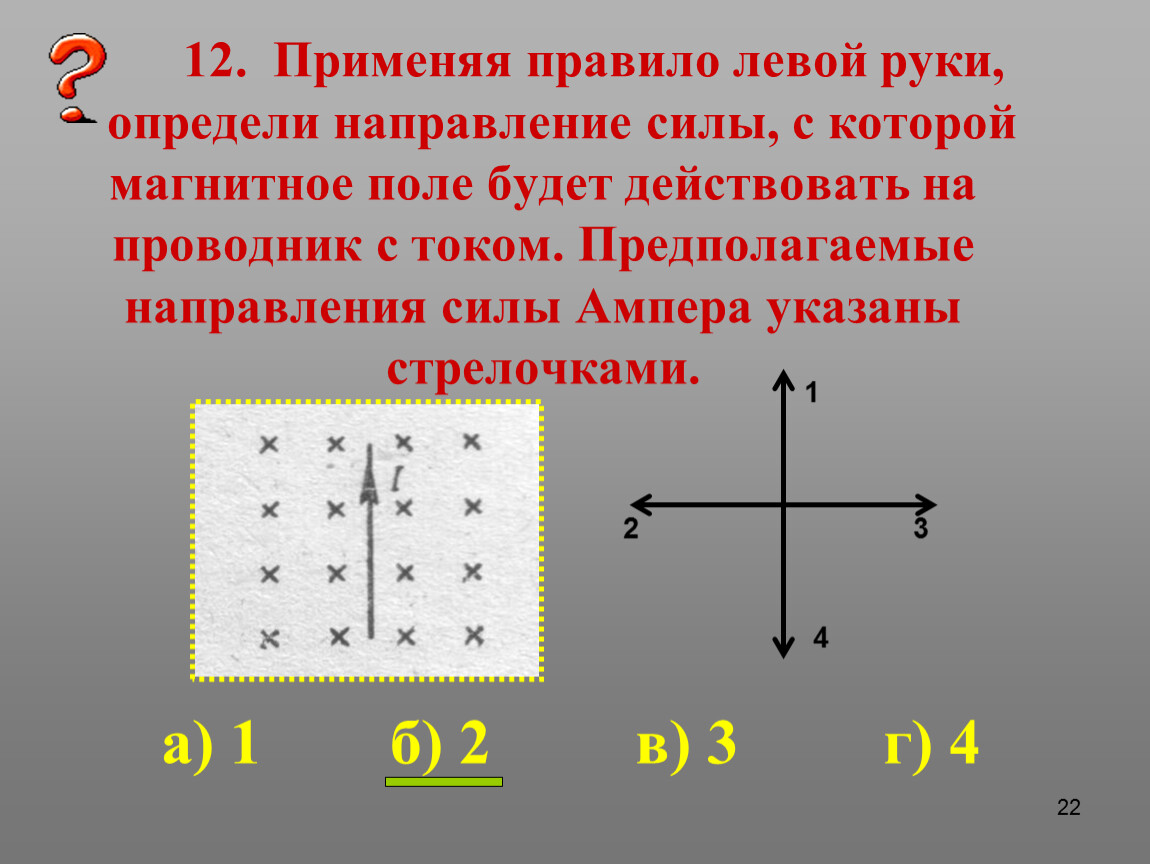 Определите силу магнитного поля как функцию \ (r \), расстояния от центра кабеля внутри и снаружи кабеля.

Решение :

В этом случае нам нужно определить магнитное поле как внутри, так и снаружи кабеля. На рисунке \ (\ PageIndex {3} \) показаны две круговые петли Ампера, которые мы можем использовать, чтобы применить закон Ампера для определения магнитного поля внутри и снаружи кабеля.

Рисунок \ (\ PageIndex {3} \): две круговые петли амперова для определения величины магнитного поля внутри и снаружи токоведущего кабеля с радиусом \ (R \) (с равномерным током, выходящим из страницы) .

Благодаря симметрии и следуя обсуждению в этой главе, мы знаем, что магнитное поле должно образовывать концентрические круги как внутри, так и снаружи кабеля. За пределами кабеля действуем так же, как указано выше, выбирая амперовскую петлю с радиусом \ (r> R \), так что циркуляция задается выражением:

\ [\ begin {align} \ oint \ vec B \ cdot d \ vec l = B2 \ pi r \ end {align} \]

Весь кабель заключен в петлю, так что заключенный ток равен \ (I \). {enc} \\ B (2 \ pi r) & = \ mu_ {0} I \\ \ поэтому B & = \ frac {\ mu_ {0} I} {2 \ pi r} \ quad (r \ geq R) \ end {align} \]

Внутри кабеля интеграл циркуляции по круговой траектории с радиусом \ (r

\ [\ begin {align} \ oint \ vec B \ cdot d \ vec l = B2 \ pi r \ end {align} \]

Однако в этом случае меньшая петля Ампера не охватывает весь ток, протекающий по кабелю.{2}} г \ конец {выровнено} \]

, и мы обнаруживаем, что магнитное поле равно нулю в центре кабеля (r = 0) и линейно увеличивается до края кабеля \ ((r = R) \).

Обсуждение :

В этом примере мы использовали закон Ампера для моделирования силы магнитного поля внутри и снаружи токоведущего кабеля. Чтобы применить закон Ампера внутри кабеля, мы приняли во внимание, что только часть тока проходит через петлю Ампера.Эта проблема аналогична применению закона Гаусса для определения электрического поля внутри и снаружи однородно заряженной сферы.

Интерпретация закона Ампера и векторное исчисление

В этом разделе мы обсуждаем закон Ампера в контексте векторного исчисления и предлагаем другую перспективу, в основном в информационных целях. Интеграл, фигурирующий в законе Ампера, называется «циркуляцией» векторного поля, \ (\ vec B \):

\ [\ begin {выравнивается} \ oint \ vec B \ cdot d \ vec l \ end {выравнивается} \]

Тираж, как следует из названия, является мерой того, «сколько вращения есть в поле».Чтобы визуализировать это, представьте, что векторное поле – это поле скоростей для точек в жидкости. Области жидкости, где есть маленькие водовороты (так называемые «водовороты»), соответствуют областям поля с ненулевой циркуляцией (знак интеграла указывает нам направление вращения, используя правило правой руки для осевых векторов. ). Примеры полей с циркуляцией и без нее показаны на рисунке \ (\ PageIndex {4} \). Вы узнаете, что статические электрические заряды создают электрические поля без циркуляции (правая панель), тогда как статические токи создают магнитные поля с циркуляцией.

Рисунок \ (\ PageIndex {4} \): Примеры полей с циркуляцией (левая панель) и без (правая панель), оцененные по замкнутому циклу, показанному пунктирной линией. Таким образом, закон

Ампера является утверждением, что электрический ток вызовет поле с величиной, пропорциональной току, которое имеет некоторую степень вращения. Направление вращения этого поля соответствует правилу правой руки для осевых векторов применительно к току (ваш большой палец указывает в направлении тока, так что ваши пальцы сгибаются в направлении вращения связанного поля).

Циркуляция, определяемая интегралом по замкнутому контуру, не является локальным свойством поля, так как оно зависит от того, что поле делает в целом на пути контура. Подобно тому, как можно получить «локальную» версию закона Гаусса, можно также получить локальную версию закона Ампера, используя методы продвинутого векторного исчисления (которые выходят за рамки этого учебника).

Теорема Стокса позволяет преобразовать интеграл циркуляции (интеграл по путям в замкнутом контуре) в интеграл по (открытой) поверхности, которая определяется контуром:

\ [\ begin {align} \ oint_ {C} \ vec Bd \ vec l = \ int_ {S} (\ nabla \ times \ vec B) \ cdot d \ vec A \ end {align} \]

, где нижний индекс \ (C \) указывает, что интеграл выполняется по одномерному пути, тогда как нижний индекс \ (S \) указывает, что интеграл выполняется по двумерной поверхности.{enc} = \ int_ {S} \ vec j \ cdot d \ vec A \ end {align} \]

Таким образом, мы можем записать закон Ампера с интегралами по одной и той же поверхности по обе стороны уравнения, подразумевая, что подынтегральные выражения должны быть одинаковыми:

\ [\ начало {выровнено} \ int_ {S} (\ nabla \ times \ vec B) \ cdot d \ vec A = \ mu_ {0} \ int_ {S} \ vec j \ cdot d \ vec A \ end {выровнено} \]

\ [\ поэтому \ nabla \ times \ vec B = \ mu_ {0} \ vec j \]

Это последнее уравнение теперь связывает локальное свойство (плотность тока) с магнитным полем в этой точке и является обычной формой, в которой представлен закон Ампера (так называемая «дифференциальная форма», а не «интегральная форма»). .

Ротор магнитного поля, \ (∇ × \ vec B \), представляет собой вектор, который задается следующим образом:

\ [\ begin {align} \ nabla \ times \ vec B = \ left (\ frac {\ partial B_ {z}} {\ partial y} – \ frac {\ partial B_ {y}} {\ partial z}} ” \ right) \ hat x + \ left (\ frac {\ partial B_ {x}} {\ partial z} – \ frac {\ partial B_ {z}} {\ partial x} \ right) \ hat y + \ left ( \ frac {\ partial B_ {y}} {\ partial x} – \ frac {\ partial B_ {x}} {\ partial y} \ right) \ hat z \ end {align} \]

, и название «curl» выбрано, потому что это мера степени вращения (curl) в поле.В дифференциальной форме закон Ампера можно читать так: «плотность тока создает (магнитное) поле с ненулевым ротором».

Поскольку закон Ампера в дифференциальной форме является векторным уравнением (обе стороны являются векторами), он действительно соответствует трем уравнениям в декартовых координатах, по одному на компонент. Например, компонент \ (x \) уравнения является «уравнением в частных производных» для компонент магнитного поля \ (y \) и \ (z \):

\ [\ begin {align} \ left (\ frac {\ partial B_ {z}} {\ partial y} – \ frac {\ partial B_ {y}} {\ partial z} \ right “) = \ mu_ {0 } j_ {x} \ end {align} \]

, который, как правило, трудно решить без компьютера (и требуются все три уравнения, поскольку они «связаны», поскольку заданная составляющая магнитного поля появляется в двух из трех уравнений).

5.8 Магнитные поля, создаваемые токами: закон Ампера

Магнитное поле, создаваемое токопроводящим соленоидом

Соленоид – это длинная катушка с проводом (с множеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть как очень однородным, так и очень сильным. Поле сразу за катушками почти равно нулю. На рис. 5.33 показано, как поле выглядит и как его направление задает RHR-2.

Рисунок 5.33 (a) Из-за своей формы поле внутри соленоида длиной 11 размера 12 {l} {} удивительно однородно по величине и направлению, на что указывают прямые и равномерно разнесенные силовые линии. Поле вне катушек почти равно нулю. (b) Этот разрез показывает магнитное поле, создаваемое током в соленоиде.

Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Только ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет те же сложности, что и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто равна

. 5.27 B = μ0nI (внутри соленоида), B = μ0nI (внутри соленоида), размер 12 {B = μ rSub {size 8 {0}} ital “nI” `\ (” внутри соленоида “\),} { }

, где nn размер 12 {n} {} – количество петель на единицу длины соленоида (n = N / l, (n = N / l, размер 12 {\ (n = N / l} {} с NN размер 12 {N} {} – количество петель, а размер 12 {l} {} длина). Обратите внимание, что BB размер 12 {B} {} – это напряженность поля в любом месте однородной области интерьера, а не только в центре. Большие однородные поля, распределенные по большому объему, возможны с соленоидами, как в Примере 5.7 подразумевает.

Пример 5.7 Расчет напряженности поля внутри соленоида

Что такое поле внутри соленоида длиной 2,00 м, имеющего 2000 петель и пропускающего ток 1600 А?

Стратегия

Чтобы найти напряженность поля внутри соленоида, мы используем B = μ0nI.B = μ0nI.size 12 {B = μ rSub {size 8 {0}} ital “nI”} {} Сначала отметим количество витков на длина агрегата

5,28 n = Nl = 2,0002,00 м = 1000 м-1 = 10 см-1, n = Nl = 2,0002,00 м = 1,000 м-1 = 10 см-1.размер 12 {n rSup {размер 8 {- 1}} = {{N} больше {l}} = {{“2000”} больше {2 “.” “00” m}} = “1000” “m” rSup {size 8 {- 1}} = “10” “cm” rSup {size 8 {- 1}} “.” } {}

Решение

Подстановка известных значений дает

5.29 B = μ0nI = 4π × 10−7T⋅m / A1,000m − 11600 A = 2,01 T.B = μ0nI = 4π × 10−7T⋅m / A1000m − 11600 A = 2,01 T.

Обсуждение

Это большая напряженность поля, которая может быть установлена ​​над соленоидом большого диаметра, например, при использовании в медицине магнитно-резонансной томографии (МРТ).Однако очень большой ток указывает на то, что поля такой силы нелегко получить. Такой большой ток через 1000 петель, сжатых до метра, приведет к значительному нагреву. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, потому что сверхпроводящее состояние нарушается очень сильными магнитными полями.

Применение научных практик: заряженная частица в магнитном поле

Зайдите сюда и запустите апплет моделирования «Частица в магнитном поле (2D)», чтобы изучить магнитную силу, которая действует на заряженную частицу в магнитном поле.Поэкспериментируйте с симуляцией, чтобы увидеть, как она работает и какие параметры вы можете изменить; затем составьте план методического исследования того, как магнитные поля влияют на заряженные частицы. Вот некоторые вопросы, на которые вы, возможно, захотите ответить в ходе эксперимента:

• Всегда ли пути заряженных частиц в магнитных полях одинаковы в двух измерениях? Почему или почему нет?
• Как можно сравнить путь нейтральной частицы в магнитном поле с путем заряженной частицы?
• Чем путь положительной частицы отличался бы от пути отрицательной частицы в магнитном поле?
• Какие величины определяют свойства пути частицы?
• Если бы вы пытались измерить массу заряженной частицы, движущейся в магнитном поле, что бы вам нужно было измерить относительно ее пути? Вам нужно было бы увидеть, как он движется с разными скоростями или через разную напряженность поля, или было бы достаточно одной попытки, если бы ваши измерения были правильными?
• Изменит ли удвоение заряда путь через поле? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.
• Изменит ли удвоение скорости путь через поле? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.
• Изменит ли удвоение напряженности магнитного поля путь через поле? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.
• Может ли увеличение массы изменить путь? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.

Есть интересные варианты плоской катушки и соленоида.Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, изогнутый в круг. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя силовым линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов создает большую напряженность поля и может существенно повлиять на форму поля.Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля за его пределами) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.

Закон, связывающий напряженность магнитного поля H с его источник, плотность тока Дж , составляет

Отметим, что в отличие от интегральной формулировки закона Гаусса, (1.3.1), символы поверхностных интегралов справа не имеют кружков. Это означает, что интеграции производятся на открытых поверхностях с краями. Обозначается контуром C . Такая поверхность S , ограниченная контуром C , является показано на рис. 1.4.1. На словах интегральный закон Ампера в формуле (1) требует, чтобы строка интеграл (циркуляция) магнитного поля интенсивность H по замкнутому контуру равна чистому току проходящей через поверхность, охватывающую контур плюс скорость изменение чистой плотности потока смещения _o E через поверхность (ток смещения ).

Направление положительного d a определяется правилом правой руки, как также показано на рис. 1.4.1. Пальцами правой руки в направлении d s большой палец имеет направление d a . Как вариант, большим пальцем правой руки в направлении d s , пальцы будут в положительном направлении: d a .

В законе Ампера H появляется без _o .Этот закон поэтому устанавливает основные единицы H как кулон / (метр-секунда). В гл. 1.1, единицы плотности потока _o H определяются силой Лоренца, поэтому второй эмпирический константа, проницаемость свободного пространства , составляет _o = 4 x 10 ^-7 генри / м (генри = вольт-сек / ампер).

Постоянный ток в направлении z внутри кругового цилиндрическая область радиусом R , показанная на рис.1.4.2, простирается от до бесконечность до + бесконечность вдоль оси z и представлена плотность

где J _o и R – заданные постоянные. Связанное магнитное поле Интенсивность имеет только азимутальную составляющую.

Рисунок 1.4.2. Осесимметричный ток распределение и связанное с ним радиальное распределение азимутального магнитного напряженность поля. Контур C используется для определения азимутального H , в то время как C ‘ используется, чтобы показать, что поле, направленное z , должно быть униформа.

Чтобы увидеть, что в этом поле не может быть r составляющей, заметим, что вращение источника вокруг радиальной оси, как показано на рис. 1.4.2, меняет местами источник (тогда ток идет в направлении -z ) и следовательно, необходимо перевернуть поле. Но компонент поля r делает не реверсировать при таком повороте и, следовательно, должен быть равен нулю. В Этот аргумент не исключает компонентов H и H _z . Однако если они существуют, они не должны зависеть от координат и z , потому что вращение источника вокруг оси z и перемещение источника вдоль оси z не изменяет источник и, следовательно, не меняет поле.

Ток не зависит от времени, поэтому мы предполагаем, что поля тоже. Следовательно, последнее слагаемое в (1), смещение ток равен нулю. Затем закон используется с S , поверхность, имеющая охватывающий контур C на произвольном радиусе r , как показано на рис. 1.4.2. Тогда элементы площади и линии

и правая часть (1) принимает вид

Интегрирование в левой части сводится к умножению независимый H по длине C .

Эти последние два выражения используются для оценки (1) и получения

Таким образом, азимутальная напряженность магнитного поля имеет радиальную Распределение показано на рис. 1.4.2.

Компонент z для H в лучшем случае является однородным. Это видно по применение интегрального закона к контуру C ^‘ , также показано на Рис. 1.4.2. Интеграция на верхних и нижних ножках дает ноль потому что H _r = 0 .Таким образом, внести вклады из-за H _z на вертикальных опорах отменить, это Необходимо, чтобы H _z не зависело от радиуса. Такое однородное поле должно быть вызвано источниками на бесконечности и поэтому устанавливается равным нулю если такие источники не постулируются в постановке задачи.

Закон Ампера: определение и примеры – видео и стенограмма урока

Уравнение

Поле, создаваемое длинным прямым проводом с током, имеет форму концентрических кругов.И по мере того, как вы удаляетесь от проволоки, эти круги отдаляются друг от друга – или, другими словами, поле становится слабее. Мы могли бы создать уравнение для этого, используя закон Ампера и выполнив некоторые вычисления. Но на самом деле мы можем вывести это уравнение вообще без каких-либо исчислений.

Вместо интеграла воспользуемся суммой. Сумма всех элементов магнитного поля, которые составляют концентрическую окружность: магнитное поле B, , умноженное на длину элемента, delta-L, , равно mu-zero (проницаемость свободного пространства), умноженное на ток в провод I .Это закон Ампера.

Затем поймите, что, суммируя все эти элементы, ваша delta-L становится окружностью концентрической окружности, 2pi r . Переставьте это так, чтобы магнитное поле стало объектом, и вы получите ЭТО окончательное уравнение для поля, созданного токоведущим проводом.

Здесь B – магнитное поле в определенной точке пространства, измеренное в теслах.-6. I – ток, протекающий по проводу, измеряется в амперах. А r – это радиальное расстояние от провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии – от токоведущего провода.

Благодаря уравнению можно рассчитать напряженность поля. Но как насчет направления? Для этого мне нужно, чтобы ты показал мне большой палец правой руки. Нет, серьезно, сделай это прямо сейчас.

Используя эту схему токоведущего провода, укажите большим пальцем в направлении, в котором движется ток, в направлении стрелки, обозначенной I . А теперь представьте, что вы обвиваете пальцами проволоку, хватая ее. Направление, указываемое вашими пальцами, соответствует направлению, в котором указывают линии поля – куда идут стрелки на концентрических кругах. Это называется правилом правой руки, и жизненно важно, чтобы вы случайно не использовали левую руку, потому что вы получите совершенно неправильный ответ.

Примеры

Хорошо, давайте рассмотрим пример. Допустим, у вас есть токоведущий провод, направленный на север. Если по проводу течет ток 0,1 А, каковы величина и направление магнитного поля на расстоянии 0,01 метра над проводом?

Прежде всего, давайте запишем то, что мы знаем. Сила тока I равна 0,1, расстояние от провода r равно 0.-6 тесла. И это наша величина.

В качестве направления вы можете провести ток на листе бумаги, направив его вверх к верхней части страницы, которую вы можете отметить на севере. Теперь поднимите вверх большой палец правой руки, направьте большой палец к верхней части страницы и представьте, как вы сгибаете пальцы вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проводом и направо над проводом. Если вверх по странице север, то вправо будет восток.-6 тесла к востоку.

Краткое содержание урока

Полная версия закона Ампера является одним из уравнений Максвелла, описывающих электромагнитную силу. Закон Ампера , в частности, гласит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока с константой пропорциональности, равной проницаемости свободного пространства. Стационарные заряды создают электрические поля, пропорциональные величине заряда. Но движущиеся заряды создают магнитные поля, пропорциональные току (заряд и движение).

Единственная проблема с законом Ампера заключается в том, что это дифференциальное уравнение – другими словами, вам нужно провести некоторое исчисление, чтобы использовать его. Но мы можем избежать этого, посмотрев на результат всех этих вычислений для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.

Здесь B – магнитное поле в определенной точке пространства, измеренное в теслах.-6. I – ток, протекающий по проводу, измеряется в амперах. А r – это радиальное расстояние от провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии – от токоведущего провода. Чтобы получить направление этого поля, мы должны использовать правило правой руки и указывать большими пальцами в направлении тока.

Результаты обучения

После завершения этого урока вы должны уметь:

• Закон штата Ампера
• Рассчитайте магнитное поле токоведущего провода, используя закон Ампера.
• Вспомните правило правой руки при вычислении текущего направления

Уравнения Максвелла: Закон Ампера

Четвертое уравнение Максвелла

На этой странице мы объясним значение последнего из уравнений Максвелла, Закон Ампера , который дан в уравнении [1]:

		[Уравнение 1]

Ампер был ученым, экспериментировавшим с силами на проводах, по которым проходит электрический ток.Он проводил эти эксперименты еще в 1820-х годах, примерно в то же время, что и Фардей работал над законом Фарадея. Ампер и Фарде не знали, что там работа будет объединена самим Максвеллом, примерно 4 десятилетия спустя.

Силы на проводах мне не особо интересны, потому что у меня никогда не было иногда использовать очень сложные уравнения в ходе моей работы (который включает докторскую степень, некоторые работы в национальной лаборатории, а также занятость в обеих сторонах защиты и промышленность бытовой электроники).Итак, я начну с представляя закон Ампера, который связывает электрический ток, протекающий и магнитное поле вокруг него:

		[Уравнение 2]

Уравнение [2] можно объяснить: Предположим, у вас есть проводник, несущий ток, I . Тогда этот ток производит Магнитное поле который обводит проволоку.

Левая часть уравнения [2] означает: Если вы возьмете любое воображаемое путь, опоясывающий проволоку, и вы складываете магнитное поле в каждой точке на этом пути, а затем будет численно равняться количеству тока, окруженного этот путь (поэтому мы пишем для замкнутого или замкнутого тока).

Давайте сделаем пример для развлечения. Предположим, у нас есть длинный провод, по которому постоянный электрический ток, I [Ампер]. Что такое магнитное поле вокруг провод, на любое расстояние r [метров] от провода?

Давайте посмотрим на схему на рисунке 1. У нас есть длинный провод, по которому течет ток. I Ампер. Мы хотим знать, что такое магнитное поле на расстоянии r из проволоки. Итак, мы проводим воображаемый путь вокруг провода, который синяя пунктирная линия справа на рисунке 1:

Фигура 1.Расчет магнитного поля по закону Ампера.

Закон Ампера [Уравнение 2] гласит, что если мы сложим (интегрируем) Магнитные Поле вдоль этого синего пути, тогда численно это должно быть равно вложенный ток I .

Теперь в силу симметрии магнитное поле будет однородным (не меняющимся) при расстояние р от провода. Длина пути синего пути на рисунке 1 длина окружности равна радиусу r : .

Если мы складываем постоянное значение магнитного поля (назовем его H ), то левая часть уравнения [2] становится простой:

		[Уравнение 3]

Таким образом, мы выяснили, какова величина поля H . А поскольку r было произвольным, мы знаем, что такое H-поле везде. Уравнение [3] утверждает, что магнитное поле уменьшается по величине при движении. дальше от провода (из-за члена 1 / r).

Итак, мы использовали закон Ампера (Уравнение [2]), чтобы найти величину Магнитное поле вокруг провода. Однако поле H является Векторное поле, Это означает, что в каждом месте есть как величина, так и направление. Направление H-поля всюду касательно мнимых петель, как показано на рисунке 2. Правило правой руки определяет направление магнитного поля:

Рис. 2. Величина и направление магнитного поля вокруг провода.

Манипулирование математикой закона Ампера

Мы собираемся проделать тот же трюк с теоремой Стокса, который мы сделали. когда смотришь на Закон Фарадея. Мы можем переписать закон Ампера в уравнении [2]:

		[Уравнение 4]

В правой части равенства в уравнении [4] мы использовали теорему Стокса изменить линейный интеграл вокруг замкнутого контура на завиток того же поля через поверхность, заключенную в петлю ( S ).

Мы также можем переписать общий ток () как поверхностный интеграл Плотность тока ( Дж, ):

		[Уравнение 5]

Итак, теперь у нас есть исходный закон Ампера (уравнение [2]), переписанный в терминах поверхностные интегралы (уравнения [4] и [5]). Следовательно, мы можем заменить их вместе и получите новую форму закона Ампера:

		[Уравнение 6]

Теперь у нас есть новая форма закона Ампера: ротор магнитного поля равен к Плотность электрического тока.Если вы проницательный ученик, вы можете заметить, что уравнение [6] не окончательная форма, которая записана в уравнении [1]. Существует проблема с уравнением [6], но только в 1860-х годах Джеймс Клерк Максвелл разобрались в проблеме и объединили электромагнетизм с уравнениями Максвелла.

Плотность тока смещения

Закон Ампера был записан как в Уравнении [6] до Максвелла. Итак, начнем посмотрите, что с этим не так. Сначала я должен выбросить еще один векторная идентичность – расхождение завиток любого векторного поля всегда равно нулю:

		[Уравнение 7]

Итак, давайте рассмотрим расхождение закона Ампера, записанное в уравнении [6]:

		[Уравнение 8]

Таким образом, уравнение [8] следует из уравнений [6] и [7].Но там сказано, что расхождение плотности тока Дж всегда равно нулю. Это правда?

Если расхождение Дж всегда равно нулю, это означает, что электрическая ток, текущий в любую область, всегда равен электрическому току, текущему вне региона (без расхождения). Это кажется несколько разумным, поскольку электрический ток в цепях течет по петле. Но давайте посмотрим, что будет, если мы поставить в цепь конденсатор:

Рисунок 3. Напряжение, приложенное к конденсатору.

Теперь мы знаем из теории электрических цепей, что если напряжение непостоянно (например, любая периодическая волна, такая как напряжение 60 Гц, выходящее из вашего розетки), то через конденсатор будет протекать ток. То есть у нас есть I не равно нулю на рисунке 3.

Однако конденсатор в основном представляет собой две параллельные проводящие пластины, разделенные воздуха. Следовательно, нет токопроводящего пути для протекания тока. Это означает, что электрический ток не может проходить через воздух конденсатора.Это проблема, если мы подумаем об уравнении [8]. Чтобы показать это более наглядно, возьмем объем, который проходит через конденсатор, и посмотрим, дивергенция Дж равна нулю:

Рис. 4. Дивергенция J не равна нулю.

На рисунке 4 мы нарисовали воображаемый объем красным цветом и хотим проверить если расходимость плотности тока равна нулю. Выбранный нами объем, имеет один конец (обозначенный стороной 1), где ток поступает в объем через черный провод.Другой конец нашего объема (обозначенный стороной 2) делит конденсатор пополам.

Мы знаем, что ток течет в петле. Итак, ток поступает через сторону 1 нашего красного тома. Однако на стороне 2 отсутствует электрический ток. В воздухе конденсатора ток не течет. Это означает, что текущий входит в объем, но из него ничего не выходит – поэтому расхождение Дж составляет не ноль. Мы только что нарушили наше уравнение [8], что означает, что теория не верна.И так было до тех пор, пока пришел наш друг Максвелл.

Максвелл знал, что электрическое поле (и Плотность электрического потока ( D ) внутри конденсатора менялся. И он знал, что изменяющееся во времени магнитное поле возникло соленоидальное электрическое поле (т.е. это закон Фарде – curl E равен производной по времени B ). Итак, почему это не так изменяющееся во времени поле D вызовет соленоидальное поле H (я.е. рождает завиток H ). Вселенная любит симметрию, так почему бы не ввести этот термин? И другие Максвелл так и сделал, и он назвал этот термин плотностью тока смещения :

		[Уравнение 9]

Этот термин «исправит» проблему схемы, показанную на рисунке 4, и сделает Закон Фарде и Закон Ампера более симметричны. Это был большой вклад Максвелла. И можно подумать, что это слабый вклад.Но существование этого термина объединил уравнения и привел к пониманию распространения электромагнитных волны и доказательство того, что все волны движутся с одинаковой скоростью (скоростью света)! И именно это объединение уравнений, которое представил Максвелл, привело к коллективное множество, известное как уравнения Максвелла. Итак, если мы добавим ток смещения согласно закону Ампера, как записано в уравнении [6], тогда мы имеют окончательную форму закона Ампера:

		[Уравнение 10]

Так появился Закон Ампера!

Интерпретация закона Ампера

Итак, что означает уравнение [10]? Следующие последствия этого закона:

Протекающий электрический ток ( Дж ) вызывает магнитное поле, которое вращает ток

Изменяющаяся во времени плотность электрического потока ( D ) вызывает магнитное поле, которое окружает поле D

Закон Ампера с участием Максвелла заложил основу для Электромагнетизм, как мы это понимаем сейчас.