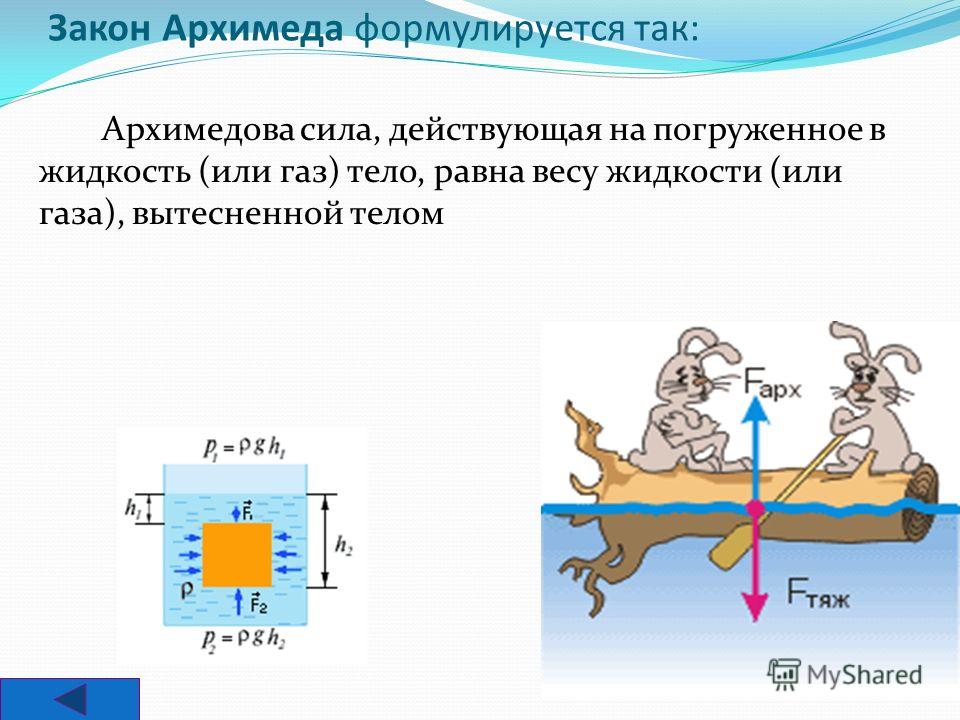
Правило архимеда: формула и суть закона силы Архимеда в жидкостях и газах, как действует сила Архимеда - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Закон Архимеда при погружении в разные слои жидкости

На главную страницу

Закон Архимеда при погружении тела в слои жидкости или газа с разной плотностью

В настоящее время в учебниках физики под названием закона Архимеда изучается правило Архимеда для определения выталкивающей силы.

Сложность изложения закона Архимеда в школе привела к тому, что в учебниках по физике вы не найдёте самого распространённого случая применения закона Архимеда – последовательного погружения тела в несколько слоёв жидкости или газа с разной плотностью.

Закон Архимеда для этого случая впервые рассмотрен в данной работе.

При подъёме с глубины любой погружаемый аппарат всегда проходит несколько слоёв жидкости с разной плотностью. При этом происходит уменьшение архимедовой силы, компенсируемое из запаса плавучести. Если запас плавучести недостаточен, то всплытия не произойдёт. Правильный алгоритм вычисления архимедовой силы, опубликованный в изложении полного закона Архимеда, позволяет этого избежать.

Сначала выведем основное уравнение (формулу) закона Архимеда для последовательного погружения тела в несколько () сред с разной плотностью.

Уровень с большой плотностью (холодная вода в глубине) обозначим , уровень с меньшей плотностью (тёплая вода у поверхности) обозначим . На плотность воды оказывает влияние температура, концентрация растворённых солей и взвесей.

При рассмотрении общего случая последовательного погружения тела в несколько слоёв газа или жидкости с разной плотностью, достаточно рассматривать два соседних уровня, через границу которых проходит погруженное тело. Архимедова сила формируется именно при прохождении тела такой границы.

При полном погружении тела в жидкость с большей плотностью на уровне уравнение погружения будет уравнением погружения для одной среды:

, (1)

Где – максимально возможная архимедова сила на уровне ,

– архимедова сила на уровне ,

– запас плавучести на уровне .

Рис. 1. Полное погружение тела в слой жидкости с большей плотностью .

При полном погружении тела в жидкость с меньшей плотностью на уровне уравнение погружения будет также уравнением погружения для одной среды:

, (2)

Где – максимально возможная архимедова сила на уровне ,

– архимедова сила на уровне .

– запас плавучести на уровне .

Рис.2. Погружение тела в слой жидкости с меньшей плотностью .

При погружении тело переходит из слоя

в слой . При этом архимедова сила увеличивается на величину переходной архимедовой силы.

, (3)

Переходная архимедова сила равна разности запасов плавучести в слоях с разной плотностью.

, (4)

Рис.3. При погружении тела добавляется переходная архимедова сила .

При всплытии наблюдается обратный процесс, и запас плавучести уменьшается на величину

Этот феномен хорошо известен подводникам. Он даёт возможность лежать погружаемым аппаратам на так называемом «жидком дне», на границе холодной и тёплой воды.

При частичном погружении тела в более плотную жидкость в слое , переходная архимедова сила вычисляется по общепринятой формулировке закона Архимеда с учётом того, что плотность виртуальной выталкивающей жидкости равна разности плотностей в слоях и .

Из уравнения (3), видно, что при всплытии погруженного тела максимальная архимедова сила уменьшается, и её нужно пополнять из запаса плавучести погружаемого аппарата. На практике может возникнуть ситуация, когда требуемая переходная архимедова сила больше, чем запас плавучести.

В этом случае погруженное тело никогда не перейдёт границы двух сред с разной плотностью, и не всплывёт.

Литература

1 http://sciteclibrary.ru/rus/catalog/pages/9433.html

2. http://sciteclibrary.ru/rus/catalog/pages/10227.htm

3. Дрюков В.М. О чём молчат физики. Тула, 2007

2. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021

Полный закон Архимеда

Последователи Архимеда . Золотое правило

У Архимеда не было учеников, которым он передавал бы свои знания. Но все механики и инженеры в течение многих столетий учились по его сочинениям.

Замечательнейшими механиками и изобретателями II–I веков до нашей эры были Ктезибий и его ученик Герон.

Сын парикмахера, Ктезибий родился в Александрии. Ему надлежало унаследовать профессию отца. Но юношу влекли к себе математика и механика.

Александрия была огромным торговым городом. Туда приходили с юга караваны со слоновой костью, крокодиловыми кожами, страусовыми перьями и фруктами. Из Аравии купцы в белых бурнусах привозили финики, индийские шелковые ткани, серебряные и золотые изделия и красные рубины. Из Греции плыли корабли с оливковым маслом и виноградным вином.

Весь мир обменивался в Александрии своими товарами.

Властители Египта привлекали в Александрию художников, писателей и ученых. Они основали в этом городе знаменитую в древности академию, куда приглашали из Греции математиков, астрономов, географов. При Александрийской академии была создана огромная библиотека, в которой хранилось около полумиллиона рукописей на папирусе и пергаменте.

В Александрии с ее академией и библиотекой Ктезибий нашел путь к знанию. Вероятно, один из александрийских математиков помог ему сделать первые шаги. А затем талантливый юноша дополнял свое образование чтением сочинений, хранившихся в библиотеке.

Ктезибий скоро прославился на весь культурный мир того времени своими изобретениями. Он построил пожарный насос, водяной орган (музыкальный инструмент с фортепьянной клавиатурой), придумал духовое ружье, усовершенствовал водяные часы.

Вероятно, Ктезибий занимался и теорией механики, но его работы остались неизвестными современным ученым.

Герону посчастливилось больше: не только его изобретения, но и некоторые сочинения дошли до нашего времени.

О жизни Герона ничего не известно. Но зато он прославился своими приборами и автоматами, действие которых объясняется давлением атмосферы.

И до Герона были ученые, интересовавшиеся свойствами атмосферы, но об их работах не сохранилось сведений.

Герон в своем сочинении «Пневматика» описал все известные тогда машины и приборы, действие которых объясняется давлением атмосферы. К ним он добавил описание и своих собственных многочисленных изобретений.

В те времена ученые часто писали о результатах чужих исследований, не упоминая о тех, кем они сделаны. Но Герон не последовал этому примеру. Свою книгу он начал следующими словами: «Ввиду того что древние философы и математики считали важным изучение свойств и силы воздуха… я счел необходимым изложить все то, что дошло до нас об этом предмете, и прибавить то, что нашли мы сами».

Благодаря сочинению Герона нам стало известно, какие остроумные приборы изобретались в то далекое от нас время. Некоторые из этих приборов техники применяют и теперь, не зная даже имени их изобретателей.

Вот, например, сифон Герона. Изогнутая трубка, одно колено которой длиннее другого. Опустив короткое колено в сосуд с водой, втянем воду через длинное колено. Когда вода начнет вытекать, то истечение не остановится до тех пор, пока конец трубки погружен в воду.

Таким способом и теперь переливают без труда воду и другие жидкости.

По-видимому, Герону принадлежит конструкция римского пожарного насоса, найденного при раскопках в Италии. Этот насос по устройству очень похож и на современные машины, применяемые при тушении пожаров.

Клапан насоса, описанный Героном в его сочинении, служит и в наше время во всех водяных насосах.

Герон не ограничился только изобретением приборов— он занимался и исследованием законов действия простых машин. В своем сочинении «О домкрате» Герон объяснил действие домкрата, пользуясь законом рычага.

Недавно было обнаружено еще одно сочинение Герона — «Механика». В нем описано действие полиспаста и нескольких простых машин.

«Желая поднять тяжесть, — писал Герон, — мы должны тянуть привязанную к ней веревку с силой, равной весу тяжести. Если же мы привяжем один конец этой веревки к неподвижному месту, а другой перекинем через привязанный к тяжести блок, то поднять тяжесть будет легче».

Далее он указал, что можно применить несколько подвижных блоков и «чем больше будет блоков, тем легче поднимать тяжесть».

Герон показал, как устроить машину, которая может дать выигрыш в сотни раз. Этот компактный механизм состоит из нескольких сцепляющихся шестерен, приводимых в движение при помощи винта — червяка — от руки. На валу последней шестерни наматывается веревка, прикрепленная к грузу.

Нетрудно подобрать шестерни с таким отношением радиусов, чтобы получить огромный выигрыш в силе. Возможно, при помощи подобного механизма Архимед и вытащил морское судно на берег.

Но важнейшая заслуга Герона не эти изобретения, а данное им общее «правило» для расчета машин.

Архимед (7 класс) – презентация онлайн

1. Архимед

Это удивительный человек, имя которого
люди помнят уже более 2 000 лет.
Он был талантливым математиком,
механиком и инженером.
Каждому школьнику знакомо чиcло π,
правило равновесия рычага,
«золотое» правило механики,
закон плавания тел и т.д.
Имя Архимеда живёт в легендах.
Мне было интересно узнать о нём что-то новое.
Своими находками я хочу поделиться с вами!

2. Содержание:

1. Биография
2. Математические труды
3. Архимедов винт
4. Архимедова спираль
5. Небесная сфера» Архимеда
6. Правило равновесия рычага
7. Золотое правило механики
8.

Устройство блока
9. Легенды
10. Заключение

3. Биография

Архимед родился в 287 году до н.э. в
Сиракузах на острове Сицилия. Отец Архимеда астроном и математик Фидий – состоял в близком
родстве с Гиероном, тираном Сиракуз. Отец привил
сыну с детства любовь к математике, механике и
астрономии.
В Александрии Египетской — научном и культурном
центре того времени — Архимед познакомился со
знаменитыми александрийскими учеными.
С Эратосфеном он переписывался до конца жизни.
Именно здесь Архимед познакомился с трудами
Демокрита, Эвдокса и других выдающихся греческих
геометров.
Покинув Александрию, Архимед вернулся в Сицилию.
В Сиракузах он был окружён вниманием и не нуждался
в средствах. Из-за давности лет жизнь Архимеда тесно
переплелась с легендами.

4. Математические труды

Архимед был замечательным механиком-практиком и теоретиком,
но основным делом его жизни была математика. По словам Плутарха,
Архимед был просто одержим ею.

Он забывал о пище, совершенно не
заботился о себе. Его работы относились почти ко всем областям
математики того времени: ему принадлежат замечательные
исследования по геометрии, арифметике, алгебре.
Он нашёл все полуправильные многогранники, которые теперь носят
его имя, значительно развил учение о конических сечениях, дал
геометрический способ решения кубических уравнений, корни которых
он находил с помощью пересечения параболы и гиперболы. Архимед
провёл и полное исследование этих уравнений, то есть нашёл, при
каких условиях они будут иметь действительные положительные
различные корни и при каких корни будут совпадать.
Усечённый тетраэдр
Курносый куб
Кубоктаэдр

5. До нас дошло 13 трактатов Архимеда

Трактат “О шаре и цилиндре» установил, что соотношение их объемов
равно 2/3. Шар вписанный в цилиндр был выбит на его могиле.
Сочинение “О равновесии плоских фигур» посвящена исследованию центра
тяжести различных фигур.

В трактате “О коноидах и сфероидах” Архимед рассматривает шар,
эллипсоид, параболоид и гиперболоид вращения и их сегменты и определяет
их объемы.
В сочинении “О спиралях” исследует свойства кривой, получившей его имя и
касательной к ней.
В трактате “Измерение круга” Архимед предлагает метод определения числа
Пи, который использовался до конца 17 в.
В “Псаммите” (“Исчисление песчинок”) Архимед предлагает систему
счисления, позволявшую записывать сверхбольшие числа, что поражало
воображение современников. «Сосчитал» их вплоть до 1064.
В “Квадратуре параболы” определяет площадь сегмента параболы сначала с
помощью “механического” метода, а затем доказывает результаты
геометрическим путем.
Архимеду принадлежат “Книга лемм”, “Стомахион” и обнаруженные только в
20 в. “Метод” (или “Эфод”) и “Правильный семиугольник”. В “Методе” Архимед
описывает процесс открытия в математике, проводя четкое различие между
своими механическими приемами и математическим доказательством.

6. Сохранившиеся сочинения Архимеда можно разделить на три группы:

Первая группа – определение площадей криволинейных
фигур или соответственно, объёмов тел.
Архимед нашёл общий метод, позволяющий найти
любую площадь или объём. Он определил с
помощью своего метода площади и объёмы почти
всех тел, которые рассматривались в античной
математике.
Лучшим своим достижением он считал определение
площади поверхности и объёма шара.
Идеи Архимеда легли в основу интегрального
исчисления.
Вторую группу составляют работы по
геометрическому анализу статистических
гидростатических задач:
«О равновесии плоских фигур».
Знаменитый закон гидростатики,
вошедший в науку как закон Архимеда,
сформулирован в трактате «О плавающих телах».
На всякое тело ,
погруженное в жидкость,
действует выталкивающая сила,
направленная вверх и
равная весу вытесненной им жидкости.
Закон Архимеда справедлив и для газов.

FА = ρж·g∙VТ = Рж
К третьей группе можно отнести различные
математические работы: Например, как среди
цилиндров, вписанных в шар, найти цилиндр, имеющий
наибольший объём?
В работе «Об измерении круга» Архимед дал своё
знаменитое приближение числа π: «архимедово число».
Он сумел оценить точность этого приближения:
Для доказательства он построил для круга вписанный и
описанный 96-угольники и вычислил длины их сторон.

9. Архимедов винт

Архимед прославился
многими механическими
конструкциями.
Изобретённый им
бесконечный винт для
вычерпывания воды
перемещает воду по
трубе на высоту до 4м.
Он до сих пор
применяется в Египте.

10. Архимедова спираль –

Архимедова спираль плоская кривая,
траектория точки М,
движущейся из точки 0
с постоянной скоростью по лучу,
вращающемуся около полюса 0
с постоянной угловой скоростью.
Уравнение в полярных
координатах:
r = a∙f,
где a – постоянная.

11. «Небесная сфера» Архимеда

Архимед построил планетарий или «небесную
сферу», при движении которой можно было
наблюдать движение пяти планет, восход Солнца
и Луны, фазы и затмения Луны, исчезновение
обоих тел за линией горизонта.
После гибели Архимеда
планетарий был вывезен
Марцеллом в Рим,
где на протяжении
нескольких веков
вызывал восхищение
В трактате «О рычагах» Архимед установил
ПРАВИЛО РАВНОВЕСИЯ РЫЧАГА

13. Открыл «золотое» правило механики: во сколько раз механизм дает выигрыш в силе, во столько же раз получается проигрыш в расстоянии «Дайте м

Открыл «золотое» правило механики: во сколько раз
механизм дает выигрыш в силе, во столько же раз
получается проигрыш в расстоянии
«Дайте мне точку опоры, и я переверну весь мир»
Архимед первый придумал
устройство блока,
изучил его механические свойства
и применил его на практике

15. Легенды

Легенда рассказывает, что построенный Гиероном в
подарок египетскому царю Птолемею роскошный
корабль «Сирокосия» никак не удавалось спустить на
воду.

Архимед соорудил систему блоков (полиспаст), с
помощью которой он смог проделать эту работу с
помощью немногих людей.

16. Легенда о короне

Существует легенда о том, как
царь Гиерон поручил Архимеду
проверить, не подмешал ли ювелир
серебра в его золотую корону.
Целостность изделия нарушать было
нельзя. Архимед долго не мог
выполнить эту задачу. Решение
пришло случайно, когда он лег в
ванную и обратил внимание на
вытеснение жидкости. Архимед
закричал: «Эврика!» — «Нашел!», и
выбежал голым на улицу. Он понял,
что объем тела, погруженного в воду,
равен объему вытесненной воды.
Таким образом, Архимед узнал, что в
золото было подмешано серебро,
разоблачил обманщика и открыл
основной закон гидростатики!

17. Осада Сиракуз

Инженерный гений Архимеда с особой силой проявился во время
осады Сиракуз римлянами в 212 до н. э. А ведь в это время ему было уже
75 лет! Построенные Архимедом мощные метательные машины
забрасывали римские войска тяжёлыми камнями.

Думая, что они будут в
безопасности у самых стен города, римляне кинулись туда, но в это время
лёгкие метательные машины близкого действия забросали их градом
ядер. Мощные краны захватывали железными крюками корабли,
приподнимали их кверху, а затем бросали вниз, так что корабли
переворачивались и тонули.
По легенде, во время осады римский флот был сожжён защитниками
города, которые при помощи зеркал и отполированных до блеска щитов
сфокусировали на них солнечные лучи по приказу Архимеда.

18. Уже в 212 г. до н. э. с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных ма

Уже в 212 г. до н. э. с
помощью крюков и
захватов, соединенных с
блоками, сиракузцы
захватывали у римлян
средства осады.
Сооружением военных
машин и обороной города
руководил Архимед.

19. Легенды о смерти

По первой, в разгар боя он
сидел на пороге своего дома,
углубленно размышляя над
чертежами, сделанными им
прямо на дорожном песке.

В это время пробегавший мимо
римский воин наступил на
чертёж, и возмущенный ученый
бросился на римлянина с
криком: «Не тронь моих
чертежей!».
Эта фраза стоила Архимеду
жизни. Солдат остановился и
хладнокровно зарубил старика
мечом.
Вторая версия гласит, что полководец римлян Марцелл
специально послал воина на поиски Архимеда.
Воин разыскал ученого и сказал:
– Иди со мной, тебя зовет Марцелл.
– Какой еще Марцелл?! Я должен решить задачу!
Разгневанный римлянин выхватил меч и убил
Архимеда.

21. Об Архимеде в стихах

И до нас за очень много лет
В трудный год родные Сиракузы
Защищал ученый Архимед.
Замыслом неведомым охвачен
Он не знал, что в городе враги,
И в раздумье на земле горячей
Выводил какие-то круги.
Он чертил задумчивый, не гордый,
Позабыв текущие дела,
— И внезапно непонятной хордой
Тень копья чертеж пересекла.
Но убийц спокойствием пугая,
Он, не унижаясь, не дрожа,
Руку протянул, оберегая
Не себя, а знаки чертежа.

22. Один из крупных лунных кратеров (82 километра в ширину) был назван именем Архимеда

Заметка об Архимеде – Mnogogranniki.ru

Архимед – автор многочисленных открытий и изобретений: машины для орошения полей, водоподъемного механизма (архимедов винт), системы рычагов, блоков для подъема больших тяжестей, военных метательных машин и т.п. Во время 2-й Пунической войны он возглавил оборону Сиракуз. Его метательные машины вынудили римлян отказаться от попытки взять город штурмом и заставили перейти к осаде.

Родился в Сиракузах. Предполагают, что его отцом был астроном Фидий.

Теоретик и практик, творец и мастеровой, генератор идей и человек, претворяющий их в жизнь. Как правило, это разные люди, но в Архимеде гениально сочетались качества ученого и инженера. Он основоположник статики и гидростатики. В трудный час для отчизны Архимед поставил все свои знания на службу согражданам и погиб, защищая отечество от неприятеля.

Архимед как инженер прославился не только своими военными машинами. Он создал также водоподъемный винт (червяк, улитку) и многоступенчатый редуктор. Первый употреблялся как устройство для подъема воды в течение двух тысяч лет. Еще в 20-х годах нашего века в Крыму можно было увидеть «архимедов червяк», который применялся для откачивания густого соляного раствора. Архимедов винт послужил прототипом авиационных пропеллеров и судовых винтов. Второе изобретение использовалось для перемещения больших тяжестей. Плутарх пишет: «Архимед сказал однажды своему родственнику и другу царю Гиерону, что данной силой можно поднять любую тяжесть. В смелом доверии к силе своего доказательства он утверждал, что если бы у него была другая Земля, на которую можно было бы перейти, то он сдвинул бы с места нашу. Удивленный Гиерон стал просить его доказать свои слова и привести в движение большое тело малой силой. Архимед взял царское грузовое судно, которое с большим трудом и помощью многих рук вытащено было на берег, посадил на него много людей, положил обычный груз и, сидя спокойно вдали, без малейшего усилия, двигая только рукой конец какой-то сложной машины, стал тащить к себе судно так тихо и ровно, как будто оно плыло по морю». Историки науки предполагают, что Архимед пользовался в данном случае многоступенчатым редуктором, который дает огромный выигрыш в силе. Рассказывают, что когда Гиерон увидел это «чудо», то он воскликнул: «С этого времени я требую, чтобы Архимеду верили во всем, что он только ни скажет».

Архимед обобщил понятие правильного многогранника и открыл новые математические объекты – полуправильные многогранники. Так он назвал многогранники, у которых все грани – правильные многоугольники более как одного рода, а все многогранные углы конгруэнтны. Только в наше время удалось доказать, что тринадцатью открытыми Архимедом полуправильными многогранниками исчерпывается все множество этих геометрических фигур.

В занимательной форме дается представление о законах Архимеда. Союзмультфильм, 1972 г.
Режиссёр: Юрий Прытков

Рычаг (Архимед) – Энциклопедия по машиностроению XXL

При всей его вал[c. 27]

В теории рычага Архимед исходит из следующих допущений (постулатов), которые он считает само собой понятными [c.55]

В простейшей форме эта идея получила количественное выражение в законе рычага Архимеда (287—212 гг. до н. э.), так как требование обратной пропорциональности силы и перемещения точки ее приложения (золотое правило механики) равносильно утверждению неизменяемости их произведения (т. е. работы). [c.19]

Естественно, что в ходе развития науки о природе в первую очередь соответствующая количественная мера была установлена для наиболее простой формы движения — для движения механического (перемещения в пространстве). Было выяснено, что в случае всяких механических явлений при любых превращениях механического движения остается неизменной некоторая вполне определенная физическая величина, получившая название работы (в простейшей зачаточной форме понятие работы содержится, как было показано, уже в законе рычага Архимеда).

Именно эта величина, очевидно, и должна быть принята в качестве меры механической формы движения материи. [c.20]

Она выражает тот известный факт, что барицентр двух материальных точек лежит на отрезке, соединяющем эти точки, и его расстояния от этих точек обратно пропорциональны их массам ( правило рычага Архимеда ). [c.180]

В древние времена, когда запросы производства сводились главным образом к удовлетворению нужд строительной техники, начинает развиваться учение о так называемых простейших машинах (блок, ворот, рычаг, наклонная плоскость) и общее учение о равновесии тел (статика). Обоснование начал статики содержится уже в сочинениях одного из великих ученых древности Архимеда (287— 212 г. до н. э.). [c.7]

Основоположником механики как науки является знаменитый ученый древности Архимед (287—212 гг. до н. э.). Архимед дал точное решение задачи о равновесии сил, приложенных к рычагу, п создал учение о центре тяжести тел. Кроме этого, Архимед открыл и сформулировал закон о гидростатическом давлении жидкости на погруженное в нее тело, который носит его имя. [c.4]

Первые существенные научные результаты в области механики мы находим в работах Архимеда (287—212 гг. до. н. э.). Ему принадлежит один из основных законов гидростатики и теория рычага. [c.20]

Понятие об идеальных связях не было известно автору Аналитической механики — Ж. Лагранжу. Рассматривая вопрос об обосновании и доказательстве принципа возможных перемещений, Ж. Лагранж отмечает, что этот принцип, хотя и очень прост по своему выражению, но не очевиден, чтобы его можно принять как аксиоматическое утверждение без доказательства. Ж. Лагранж отмечает, что принцип возможных перемещений основывается на двух принципах, установленных раньше. Один из них — принцип действия рычага, исследованный еще Архимедом второй — аксиома о параллелограмме сил. Если вспомнить геометрическую статику (ч. III т. I), то становится ясным, что эти два принципа содержат два основных понятия статики — понятие о силе, как о векторе, и к тому же скользящем в случае действия силы на абсолютно твердое тело, и понятие о моменте силы. Ж- Лагранж указывает сначала, что принцип возможных перемещений объединяет эти два понятия статики (принципы рычага и параллелограмма сил). Далее он предлагает доказательство, основанное на замене сил, приложенных к материальным точкам системы, реакциями подвижных блоков сложного полиспаста. Это доказательство не было признано достаточным, и Фурье предложил более совершенное. [c.108]

Отдельные законы и положения механики известны человечеству еще с древнейших времен. Величайшим механиком древности считается Архимед (287—212 гг. до нашей эры), впервые разработавший научные основы равновесия рычага и плавающих тел. Архимед открыл один из основных законов гидростатики, названный его именем. После открытий Архимеда в развитии механики наступил длительный период застоя. На протяжении шестнадцати с лишним веков, вплоть до эпохи Возрождения, механика ничем существенным не пополнилась. [c. 5]

Архимеду принадлежит строгое доказательство условий равновесия рычага. Им были установлены правила сложения и разложения параллельных сил, дано определение центра тяжести ряда геометрических фигур и тел, открыты законы равновесия тел, плавающих в жидкости. Архимеда следует считать основоположником статики и гидростатики как точных наук. Свои теоретические знания в области механики Архимед применял к различным практическим вопросам строительства и военной техники. [c.13]

Механика— одна нз первых наук о природе — возникла примерно в IV веке до н. э. в древней Греции. Ее зарождение связывают обычно с именем великого ученого древности Аристотеля (384—322 до н. э.). Им и был впервые введен термин механика , означающий в переводе с греческого изобретение, машина, сооружение . Дальнейшее развитие механика получила в трудах Архимеда (287—212 до н. э.). Ему, в частности, принадлежат закон равновесия рычага и учение о центре тяжести тел. [c.13]

Архимед (287—212 до н. э.)— великий математик и механик древности. Оставил после себя многочисленные труды по вопросам математики, механики, гидростатики. Наиболее известны законы рычага, способы вычисления длин кривых, законы гидростатики. [c.84]

Затем строится профиль кулачка (спираль Архимеда), обеспечивающий требуемый угол поворота валика записывающего рычага 6 при заданном угле поворота ф п валика сельсина-приемника. При этом учитываются заданные радиусы рычагов и Ri [c.446]

В отличие от многих ученых того времени Архимед сознательно строил свои исследования на основе сочетания опыта, наблюдения, дедуктивной логики и евклидовой математики. По этой методике им созданы научные теории равновесия рычага и вообще твердых тел, плавания тел и т. д., изложенные в сочинениях О равновесии плоских тел, или о центре тяжести плоских тел , О плавающих телах и других, дошедших до нас. Понятие центр тяжести введено Архимедом и им же разработана методика определения центров тяжести плоских фигур. [c.34]

Так, в основу теории равновесия он кладет семь постулатов, часть из которых использует для вывода закона рычага. Доказав несколько вспомогательных теорем, Архимед доказывает основную — закон рычага для соизмеримых грузов Соизмеримые величины уравновешиваются на длинах, которые обратно пропорциональны тяжестям . [c.34]

Как мы помним, у Аристотеля сила выражалась произведением веса тела на скорость его движения — можно сказать, динамически . Архимед же строил свои машины на основе принципа рычага, который он вывел теоретически, исходя из теории равновесия — статики. Отсюда и сила у него равна произведению веса тела на пройденный им путь, что в наше время означает [c.34]

Архимед разработал основы статики и гидростатики. Условие равновесия рычага дано у него уже не в том смутном виде, что у Аристотеля, но в четкой математической интерпретации Соизмеримые величины уравновешиваются, если длины, на которых они подвешены, находятся в обратном отношении к тяжестям . [c.21]

Если это положение однажды обосновано, то ясно, что подобно тому, как это сделал Архимед, можно вместо одного груза, находящегося в равновесии на рычаге, подвесить два равных, вдвое меньших, груза на равных расстояниях по обе стороны от той точки, в которой был помещен груз. Ведь действие этого груза равно действию рычага, подвешенного в средней своей точке и нагруженного на обоих концах двумя равными грузами, каждый из которых равен половине данного груза и ясно, что нет никаких препятствий к тому, чтобы последний рычаг настолько приблизить к первому, чтобы он составил его часть. Или, что, пожалуй, будет еще строже, можно считать, что этот последний рычаг поддерживается в равновесии силой, приложенной в его середине и действующей снизу вверх, причем эта сила равна тому самому весу, обе половины которого мы себе представляем помещенными в конечных точках рычага. Если этот рычаг, находящийся в равновесии, поместить на первом рычаге, который согласно нашему допущению находится в равновесии, на своей точке опоры, то общее равновесие сохранится если же второй рычаг поместить на первом таким образом, чтобы середина вто- [c. 22]

Это напоминает нам о том рычаге, при помощи которого Архимед обещал повернуть Землю. [c.56]

Первый шаг в этом направлении сделал, по-видимому, великий Леонардо да Винчи (1452—1519 гг.). В рукописи 1515 г. он ввел понятие, которое теперь называется в механике статическим моментом силы . Со времен Архимеда был известен закон, который определял условия равновесия прямого рычага. Он составлял содержание VI теоремы Архимеда из сочинения по механике Два соизмеримых груза находятся в равновесии, если они обратно пропорциональны плечам, на которые эти грузы подвешены . Другими словами (рис. 1.9, а), если вес (т. е. силу, с которой грузы притягиваются к земле) изобразить в виде отрезков А и В соответствующих направлений и длины, то условие равновесия будет таким А B = Qb Qa, или, что то же самое (следует из свойств пропорции), А-Оа = В-ОЬ. [c.27]

Основные этапы развития механики. М.— одна из древнейших наук, возникшая из нужд практики. Раньше др. разделов М. под влиянием запросов гл. обр, строит, техники стала развиваться статика. Её науч. основы (теория рычага, сложение параллельных сил, учение о центре тяжести, начала гидростатики н др.) разработал ещё Архимед (3 в. до н. э.). [c.127]

Теория рычага основана на следующих предпосылках, которые Архимед считает очевидными [c.28]

Заметим, что когда Архимед говорит о действии на рычаг подвешенных грузов (тяжестей), он основывается на свойствах центра тяжести, понятие которого считает известным это также говорит в пользу предположения о том, что этот трактат был не первым его механическим сочинением. [c.29]

В частности, предполагается, что центр тяжести тела, свободно висящего на нити, располагается на линии нити и что подвешенные тела действуют на рычаг в точке подвеса весом, сосредоточенным в центре тяжести. В последующих доказательствах Архимед имеет дело лишь с весами тел и их центрами тяжести. [c.29]

Помимо вышеуказанных принципов, Архимед пользуется в ходе доказательств еще одним, который, однако, в числе исходных предпосылок явно не фигурирует. Этот принцип можно сформулировать следующим образом равновесие рычага не нарушится, если груз, подвешенный в точке А рычага, заменить двумя равными грузами половинного веса, точки подвеса которых располон епы симметрично относительно точки подвеса замещаемого груза. Это положение мы будем называть принципом замещения. Хотя в ходе доказательств принцип замещения Архимед применяет с достаточной отчетливостью, однако он оградил бы свое сочинение от упреков самых требовательных критиков, если бы вставил его в число своих исходных предпосылок. [c.30]

Заметим также, что аксиомы Архимеда являются первым существенным шагом в развитии понятия момента силы. Архимед с достаточной ясностью отмечает, что действие подвешенного груза на рычаг пропорционально его весу и расстоянию точки подвеса от точки опоры рычага.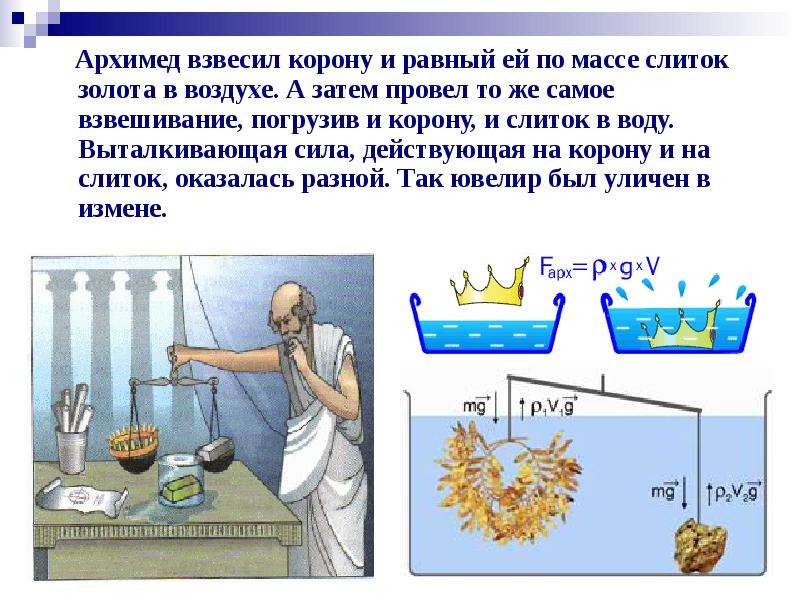 Оставалось лишь найти форму этой зависимости — и Архимед ее нашел. Он доказал, что действие подвешенного груза на рычаг прямо пропорционально величине груза и расстоянию точки приложения от неподвижной опоры рычага. [c.30]

Вариньон отмечает, что этот результат не нов, что он был известен Робервалю, Ферма и Паскалю. Только в их рассуждениях точка нере-сечения сил совпадала с центром Земли, и силы веса были фактически параллельными. Для перехода к названному случаю Вариньон вводит воображаемый круговой рычаг из дуги окружности, концентрической Земле. Позднее Лагранж заменит этот криволинейный рычаг коленчатым. Когда на твердое тело с точкой опоры действуют две параллельные силы, Вариньон предлагает точку схода сил Е и F удалять в бесконечность, делая угол между прямыми сил бесконечно малым. В этом случае сохраняется равенство моментов сил относительно точки опоры, а отсюда легко вывести обратное отношение величин сил и соответствующих плеч. Кроме этого, Вариньон находит, что величина реакции опоры равна сумме величин приложенных сил. В теории равновесия рычага Архимеда-Стевина этого доказательства нет. [c.183]

В постановке задачи о приведении несходящейся совокупности сил к простейшему виду важное значение приобретают два основных понятия статики момент силы относительно точки и момент силы относительно оси. Понятия эти исторически возникли в учении Архимеда о равновесии рычагов и впоследствии были обобщены на любые пространственные совокупности сил. [c.36]

В начале механика развивалась преимущественно в области статики, т. е учения о равновесии материальных тел. Уже к III в. до п. э., главным образом трудами выдающегося ученого древносгп Архи.меда (287—212 г. дв н. э.), были заложены научные основы статики. Архимед дал точное решение задачи о равновесии рычага, создал учение о центре тяжести, открыл известный закон гидростатики, носящий его имя, и др. [c.15]

Аристократ Гвидо Убальди маркиз дель Монте прославился не только переводами сочинений Архимеда и многолетним покровительством Галилею. В своей Механике , рассматривая простые механизмы (рычаг, [c.56]

В своих исследованиях Галилей пользуется принципами суперпозиции (наложения) движений, независимости действия сил, относительности, инерции, возможных перемещений (возможных скоростей) и др. Особенно важно отметить последний, поскольку он постулирует сохранение работы. В применении к рычагу этот принцип известен в античном мире как золотое правило механики (сколько выигрываешь в силе, столько проигрываешь в перемещении), им пользовались Архимед, Герои, Стевин и другие ученые того времени. Но Галилей первым сформулировал это правило как общий принцип статики Когда наступает равновесие и оба тела приходят в состояние покоя, то моменты, скорости и склонность их к движению, т. е. пространства, которые они прошли бы в одинаковые промежутки времени,, должны относиться друг к другу обратно их весам… Окончательное обобщение этого принципа будет сделано в 1717 г. И. Бернулли. [c.63]

С исторической точки зрения статика является наиболее древней частью механики. Действительно, статика восходит еще к Архимеду, установивщему в своем труде Ве oequiponderantibus принцип рычага. Что же касается динамики, то ее возникновение стало возможным лищь после открытий Галилея. [c.92]

Некоторые новые авторы, как Стевин (Stevin) в своей статике и Галилей (Galilei) в своих Диалогах о движении [2], упростили доказательство Архимеда, приняв, что грузы, помещенные на рычаге, имеют форму параллелепипедов, подвешенных горизонтально в средней своей точке при этом ширина и высота обоих параллелепипедов равны, но длины их вдвое [c.18]

По мнению Гюйгенса, Архимед молча допускает, что когда несколько равных грузов помещено на горизонтальном рычаге па равных друг от друга расстояниях, то они стремятся вывести рычаг из горизонтального состояния с одинаковой силой — независимо от того, находятся ли они все по одну сторону от точки опоры, или же одни из них находятся на одной стороне, а другие на другой стороне от точки опоры. Для того чтобы избежать этого ненадежного допущения, Гю11генс распределяет равные части соизмеримых грузов не так, как это сделал Архимед, т. е. на одном и том же рычаге по обе стороны от точек, в которых [c.19]

Изобретатели механических ppm с грузами, основываясь на известном архимедовом законе рычага, полагали, что чем дальше от центра колеса находится груз, тем он сильнее должен поворачивать колесо. Это правило действительно верно, по только для горизонтального рычага (именно его рассматривал Архимед). Распространять его на все грузы независимо от их расположения на окружности колеса неверно. Уилкинс наглядно это показал. Ход его мыслей легко проследить с помощью рис. 1.11, на котором изображена схема колеса с центром в точке А. Горизонтальный диаметр D колеса разделен на 10 равных частей, и через соответствующие точки проведены концентрические окружности с центром в точке А. В разных точках окружностей расположены одинаковые по весу грузы, действие которых надо определить. Если грузы расположены на горизонтальном диаметре, задача решается просто — на основе правила Архимеда. Например, груз в 1 фунт в точке С уравновесит 5 фунтов в В, поскольку плечо АС в 5 раз длиннее [c.30]

Становление физики (до 17 в.). Физ. явления окружающего мира издавна привлекали внимание людей. Попытки причинного объяснения этих явлений предшествовали созданию Ф. в совр. смысле этого слова. В эпоху грекоримской культуры (6 в. до н. э.— 2 в. н. э.) впервые зародились идеи об атомном строении вещества (Демокрит, Эпикур, Лукреций), была создана геоцентрич. система мира (Птолемей), установлены простейшие законы статики (правило рычага), открыты законы прямолинейного распространения и отражения света, сформулированы начала гидростатики (закон Архимеда), наблюдались простейшие проявления электричества и магнетизма. [c.311]

Наиболее ранние сочинения античных авторов, содержащие механические теории, не сохранились. Однако несомненно, что большинство этих теорий посвящено проблемам статики и что их основой служил принцип рычага. Известно, что Архит Тарентский (ок. 428—365 г. до н. э.) разрабатывал теорию блока полиспастов, но результаты его исследований до нас не дошли. Ему же некоторые античные авторы приписывают изобретение винта. Изобретение бесконечного винта для подъема и передвижения тяжестей и бесконечного водоподъемного винта связывают с именем Архимеда. По-видимому, появление винта вызвало постановку новых технических и математических проблем. Однако, если следовать хронологии источников, надо начинать не с Архимеда, а с философов Древней Греции. [c.10]

Первыми сочинениями Архимеда по механике были Книга опор и О весах . Поскольку они до нас не дошли, об их содержании можно судить лишь по ссылкам в более поздних работах Герона и Паппа, а также по комментариям Евтокия и Симпликия . Анализ упомянутых сочинений показывает, что во время их написания Архимед еще не знал, что вес тела можно считать сконцентрированным в его центре тяжести, хотя и пользовался последним понятием. Понятие о центре тяжести появилось у Архимеда в итоге практического изучения распределения груза между опорами. Рассматривая давление балки на опоры, Архимед приходит, правда, к неверным результатам, но отсюда он перешел к одноопорной балке — рычагу. Эти ранние работы интересны тем, что в них, кроме понятия центра тяжести, появляется и понятие центра момента. Папп приводит следующее определение Архимеда для центра тяжести Центром тяжести некоторого тела называется некоторая расположен- [c.26]

Древнегреческий математик и механик. Родился и большую часть жизни прожил в Сиракузах (Сицилия) был убит римлянами при взятии Сиракуз, Архимед установил законы рычага, открыл закон гидростатики, носящий его имя [c.27]

Урок физики в 7-м классе по теме “Закон Архимеда. Решение задач”

Цели урока:

Образовательные:
1. Формирование умений вычислять силу Архимеда, объяснять различные ситуации поведения тел в жидкости.
Воспитательные:
1. Показать значение познания мира через мышление.
2. Формировать моральные, волевые и эстетические качества личности.
Развивающие:
1. Развивать внимание и любознательность.
2. Развивать представление о применении человеком физических знаний в быту и технике.

Оборудование:

Доска, на доске: тема урока, цель.
Географическая карта.
Карта по истории.
Раздаточный материал по физике 7кл М.А. Ушаков.
Опорные конспекты (см. приложение).
Мини – сообщения «Закон Архимеда вокруг нас»

Литература:

Учебник физика 7кл. А.В. Перышкин.
Сборник вопросов и задач по физике 6-7 кл. В.И. Лукашик
Нестандартные уроки физика 7-10 кл. С.В. Боброва
Дидактические материалы А. Е Марон, Е. А. Марон

Литература, рекомендуемая учащимся:

Учебник физика 7кл. А.В. Перышкин. Материал для дополнительного чтения стр. 183. «Легенда об Архимеде».
Справочник школьника.
Физика. Человек. Окружающая среда А.П. Рыженков.
Мировая энциклопедия биографий А.П. Горкин т-1
История математики в школе 5-6 кл. Г.И. Глейзер.
Биофизика на уроках физики Ц.Б. Кац.

Конспект урока.

1. Организационный момент:

Вступительное слово:

«Жидкости на тело давят,
Вверх его все поднимают,
При этом силу создают,
Что Архимедовой зовут!
Ее считать умеем мы:
Надо знать лишь вес воды,
Что-то тело вытесняет
Все закон нам объясняет
Открыл его великий грек,
Ему имя – Архимед.

Сегодня тема нашего урока «Закон Архимеда». Решение задач. Это второй урок по теме «Закон Архимеда». На этом уроке, мы узнаем, как был открыт закон Архимеда, какие еще открытия сделал Архимед, поработаем над формулами, разгадаем мини – кроссворд, решим несколько задач по карточкам, выполним физминутку, разноуровневую самостоятельную работу, а так же узнаем, каким образом «закон Архимеда» помогает поднимать затонувшие суда, узнаем в каком море нельзя утонуть, но и еще много нового и интересного.

На определенных этапах урока вы будете оценивать друг друга, давать самооценку своей деятельности, чтобы получить итоговую оценку за урок.

И так вернемся к закону Архимеда. (вопросы, на которые должны ответить учащиеся)

-Как звучит закон Архимеда.

-Почему этот закон называют законом Архимеда? (в честь человека который его открыл

-В каком году жил Архимед? (287-212г. до н.э.)

-В каком городе проживал Архимед? (Сиракузы)

-Ныне это Италия (учитель обращается к карте по истории )

-Какие еще открытия или изобретения принадлежат Архимеду.

Учащиеся отвечают: установил правило рычага, открыл закон гидростатики, ввел понятие о бесконечно больших величинах и т.д. Изобрел: Архимедов винт, различные системы для поднятия больших тяжестей, военные метательные машины и др. Организатор инженерной обороны Сиракуз против римлян.

2. Легенда об Архимеде.

Существует легенда о том, как Архимед пришел к открытию, что выталкивающая сила равна весу жидкости в объеме тела.(Учащиеся готовят сообщение)

Царь Гиерон поручил Архимеду проверить честность мастера, изготовлявшего золотую корону. Хотя корона весила столько, сколько было отпущено на нее золота, царь заподозрил, что она изготовлена из сплава золота с другими более дешевыми металлами. Архимеду было поручено узнать, не ломая короны, есть ли в ней примесь. Архимед лежал в ванной и размышлял о том, как узнать, есть ли примесь серебра в золотой короне. Выталкивающую силу человек отчетливо ощущает, принимая ванну. Закон неожиданно открылся Архимеду, представился в своей замечательной простоте. Архимед выскочил из ванны, громко кричал, побежал в комнаты за драгоценной короной, чтобы немедленно определить потерю ее веса в воде. А вот какие же слова он при этом выкрикивал, мы с вами узнаем, когда решим задачи, для этого нам нужно вспомнить формулы.

3. Работа с формулами: F_a= V_{T *}ρ_ж
*g, ρ_{ж = ,}V_T=

Написать формулы для расчета Архимедовой силы, указать единицы.

Fa =
ρ_{ж =}
V_{T =}

(Учащиеся на листочках записывают формулы, указывая в каких единицах, измеряются величины)

Учащиеся себя оценивают и результаты заносят в таблицу на доске.

4. Мини – кроссворд.

Задачи:

Вес стальной детали в воздухе равен 3н, а в воде 2,7н. Чему равна выталкивающая сила? (0,3н – Э)
Объем куска железа 0,2м³. Какая выталкивающая сила будет на него действовать при полном его погружении в воду? (2000н – В)
Бетонная плита объемом 1м³ погружена в воду. Какую силу необходимо приложить чтобы удержать ее в воде? (22 кн – Р)
Определите архимедову силу, действующую на стальной шарик объемом 200 см³ погруженный в керосин. (1,6н – И)
Какую силу надо приложить для подъема из воды бетонной плиты объемом 0,6 м³? (7,8 кн – К)
Медный цилиндр массой 3,56 кг опущен в бензин. Определите действующую на него архимедову силу. (28,4н – А)

(ЭВРИКА)

1	2	3	4	5	6
Э	В	Р	И	К	А

Ответы: 28,4 н – А, 7,8 кн – К, 160 н – И, 1,6 н – И, 0,3 н –Э, 2000 н – В, 222 н – Н, 22 кн – Р.

Учащиеся решают задачи по карточкам находят ответ и ту букву, которая находится рядом с ответом записывают в ту ячейку, под каким номером карточка. После того, как все задачи будут решены и буквы записаны откроется слово «Эврика».

5. Решение задач, физминутка. Решение задач у доски из сборника Лукашина В.И.

№ 541. Чему равна архимедова сила, действующая в воде на тело объемом 125 см³ из стекла, пробки, алюминия, свинца? (1,25 н для всех тел)

№ 542. Пробирку поместили в мензурку с водой. Уровень воды при этом повысился от деления 100 до 120 см³.Сколько весит пробирка? (0,2 н)

№ 543. На сколько гранитный булыжник объемом 0,004 м³ будет легче в воде, чем в воздухе? (40 н)

№ 544. Какую силу надо приложить, чтобы поднять под водой камень массой 30 кг, объем которого 0, 012 м³? (180 н)

Пока учащиеся решают задачи у доски, в это время остальные выполняют устно следующие задания. (раздаточный материал для 7 кл. М.А Ушаков)

44-а. Задание^*

Сосуд с водой и тело А уравновешены весах гирями. Нарушится ли равновесие весов, если тело А опустить в воду, находящуюся в сосуде? Ответ обоснуйте.

Ответ: Равновесие весов не нарушится, так как масс тел, находящихся на чашке весов, не изменяется.

44-б. Задание^*

Сосуд с водой и шарик, укрепленный на подставке, сначала взвесили, а затем шарик опустили в воду, как показано на рис.2. Изменится ли при этом показание весов? Ответ обоснуйте.

Ответ: Показание весов не нарушится, так как массы тел, находящихся на чашке весов, не изменяется. Изменится только сила натяжения нити.

47-а. Задание^*

К коромыслу подвесили два болта: медный и стальной, равновесие весов сохранилось. Изменится ли равновесие весов, если опустить болты в воду?

Ответ обоснуйте.

Ответ: Равновесие весов нарушится, на тела^{будут действовать разные выталкивающие
силы.}

47-б. Задание^*

Медный и латунный шарики, находящиеся в воде, укрепили на нитях и подвесили к коромыслу весов, равновесие весов сохранилось. Изменится ли равновесие весов, если шарики вынуть из воды?

Ответ обоснуйте.

Ответ: Когда шарики вынут из воды, то выталкивающие силы исчезнут, равновесие весов нарушится. Т.к. объем медного шарика меньше объема латунного. Выталкивающая сила, действующая на медный шарик меньше силы действующий на латунный шарик.

Проверка работающих у доски, выставление оценок и тем, кто работал у доски, и тем, кто отвечал на задания устно.

Физминутка. Учащиеся выполняют в течении одной минуты различные упражнения.

6. Проверочная работа.

Какой силой можно удержать в воде стальной рельс объемом 0,7 м³. (5б)
С какой силой выталкивается кусок дерева массой 800г при его полном погружении. (4б)
Определите выталкивающую силу, действующую на камень, объемом 0,5м³ находящийся в воде? (3б)

Учащиеся выбирают для себя задание выполняют, затем проверяют решение.(решение задач заранее написаны на доске) Результаты заносятся в таблицу.

7. Сообщения

История цивилизации – это история познания человеком тайн природы, ее секретов красоты. Но человек не только проникал в эти тайны, но и учился управлять ими.

Закон Архимеда помогает поднимать затонувшие суда. Один из самых больших ледоколов «Садко», по халатности капитана затонувший в белом море в 1916г, пролежал на морском дне 17 лет, его затем подняли понтонами, и он снова вступил в строй.

Далее учащиеся выступают с мини-сообщениями, которые они приготовили заранее используя дополнительную и рекомендованную литературу.

Мертвое море.
Рыбы.
Паук-серебрянка.
Водоплавающие.
Растение Чилим.
Водные растения.

За подготовительное домашние задание учащиеся получают оценки и полученный результат заносится в таблицу.

8. Итог урока.

В конце урока подводится итог проделанной работы на уроке.

Учащиеся сами подводят итоги, оценивая себя, работу класса и усвоена ли тема данного урока по схеме (см. продолжение).

9. Выставление оценок.

И. Ф.	формулы	кроссворд	решение задач	проверочная работа	домашнее задание	итог

10. Домашнее задание.

Готовиться к лабораторной работе.
Ответить на вопросы:

– Генерал нырнул в жидкость солдатиком и подвергся действию выталкивающей силы. Можно ли утверждать, что жидкость вытолкала генерала в шею?

– Пожилые греки рассказывают, что Архимед обладал чудовищной силой. Даже стоя по пояс в воде, он легко поднимал одной левой рукой массу в 100кг. Правда, только до пояса, выше поднимать отказывался. Могут ли быть правдой эти рассказы?

-Почему в недосоленном супе ощипанная курица тоне, а в пересоленном спасается в плавь?

– Где больший вес имеют солидные караси в родном озере или на чужой сковородке?

Большое спасибо, за совместную работу. Надеюсь на то, что мы с вами на последних уроках совершим еще много открытий и не раз прокричим подобное Архимеду

«Эврика!»

Архимед и его законы – СтудИзба

Архимед и его законы

Несомненно, Архимед (около 287—212 до н. э.) — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.

Сын астронома Фидия, написавшего сочинение о диаметрах Солнца и Луны, Архимед родился и жил в греческом городе Сиракузы на Сицилии. Он был приближён ко двору царя Гиерона II и его сына-наследника.

“Статистические методы определения объема выборки” – тут тоже много полезного для Вас.

Хорошо известен рассказ о жертвенном венце Гиерона. Архимеду поручили проверить честность ювелира и определить, сделан венец из чистого золота или с примесями других металлов и нет ли внутри него пустот. Однажды, размышляя об этом, Архимед погрузился в ванну, и заметил, что вытесненная его телом вода пролилась через край. Гениального учёного тут же осенила яркая идея, и с криком “Эврика, эврика!” он, как был нагой, бросился проводить эксперимент.

Идея Архимеда очень проста. Тело, погружённое в воду, вытесняет столько жидкости, каков объём самого тела. Поместив венец в цилиндрический сосуд с водой, можно определить, какое количество жидкости он вытеснит, т.е. узнать его объём. А, зная объём и взвесив венец, легко вычислить удельную массу. Это и даст возможность установить истину: ведь золото — очень тяжёлый металл, а более лёгкие примеси, и тем более пустоты, уменьшают удельную массу изделия.

Но Архимед на этом не остановился. В труде “О плавающих телах” он сформулировал закон, который гласит: “Тело, погружённое в жидкость, теряет в своём весе столько, каков вес вытесненной жидкости” . Закон Архимеда является (наряду с другими, позже открытыми фактами) основой гидравлики — науки, изучающей законы движения и равновесия жидкостей. Именно этот закон объясняет, почему стальной шар (без пустот) тонет в воде, тогда как деревянное тело всплывает. В первом случае вес вытесненной воды меньше веса самого шара, т.е. архимедова “выталкивающая” сила недостаточна для того, чтобы удержать его на поверхности. А тяжело гружёный корабль, корпус которого сделан из металла, не тонет, погружаясь только до так называемой ватерлинии. Поскольку внутри корпуса корабля много пространства, заполненного воздухом, средняя удельная масса судна меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон Архимеда объясняет также, почему воздушный шар, заполненный тёплым воздухом или газом, который легче воздуха (водородом, гелием) , улетает ввысь.

Знание гидравлики позволило Архимеду изобрести винтовой насос для выкачивания воды. Такой насос (кохля) до недавнего времени применялся на испанских и мексиканских серебряных рудниках.

Из курса физики всем знакомо Архимедово правило рычага. Согласно преданию, учёный произнёс крылатую фразу: “Дайте мне точку опоры, и я подниму Землю!” . Конечно, Архимед имел в виду применение рычага, но, он был несколько самоуверен: кроме точки опоры ему понадобился бы и совершенно фантастический рычаг — невероятно длинный и при этом несгибаемый стержень.

Достоверные факты и многочисленные легенды говорят о том, что Архимед изобрёл немало интересных машин и приспособлений.

Принцип Архимеда – Школа физики

Цели обучения

Определить выталкивающую силу.
Государственный закон Архимеда.
Поймите, почему объекты плавают или тонут.
Поймите взаимосвязь между плотностью и законом Архимеда.

Когда вы встаете после безделья в теплой ванне, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. (Рисунок).)

(а) Даже объекты, которые тонут, как этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Кристалл)

Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта.На любой объект в любой жидкости действует направленная вверх или выталкивающая сила. (См. (Рисунок).) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.

Выталкивающая сила

Выталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости.

Давление из-за веса жидкости увеличивается с глубиной, так как . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие заключается в выталкивающей силе. (Горизонтальные силы компенсируются.)

Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке.

Пространство, которое он занимает, заполнено жидкостью, имеющей вес .Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться весу жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.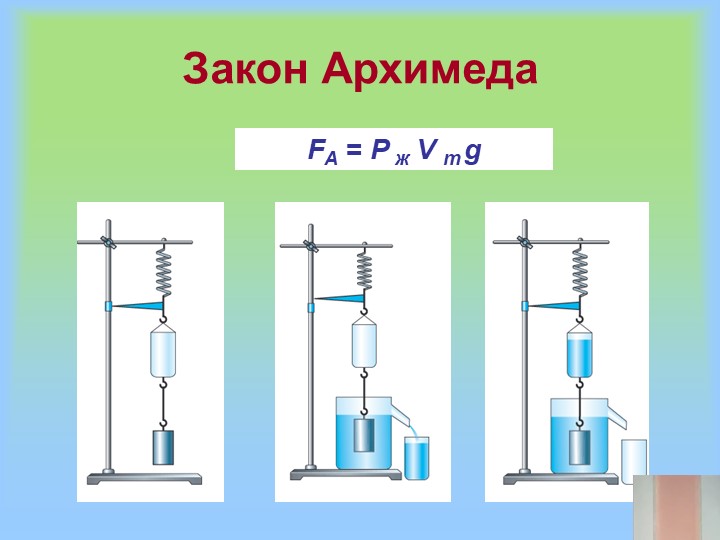 В форме уравнения принцип Архимеда равен

где — выталкивающая сила, а — вес жидкости, вытесненной телом.Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.

Закон Архимеда

В соответствии с этим принципом выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен

где — выталкивающая сила, а — вес жидкости, вытесненной телом.

Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине.Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?

Установление связей: домашнее расследование

Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?

Плавающий и тонущий

Бросьте кусок глины в воду. Он утонет.Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями.

Расчет выталкивающей силы: зависимость от формы

(a) Рассчитайте выталкивающую силу на 10 000 метрических тонн твердой стали, полностью погруженной в воду, и сравните ее с весом стали. б) Какова максимальная выталкивающая сила, которую вода могла бы воздействовать на ту же сталь, если бы из нее сделали лодку, способную вытеснять воду?

Стратегия для (а)

Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды.Мы можем сделать это, используя плотности воды и стали, указанные на (рис.). Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.

Решение для (а)

Сначала мы используем определение плотности, чтобы найти объем стали, а затем подставляем значения массы и плотности. Это дает

Поскольку сталь полностью погружена в воду, это также объем вытесненной воды, .Теперь мы можем найти массу вытесненной воды из соотношения между ее объемом и плотностью, оба из которых известны. Это дает

По закону Архимеда вес вытесненной воды равен , поэтому выталкивающая сила равна

Вес стали , что намного больше, чем выталкивающая сила, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.

Стратегия для (б)

Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка.Выталкивающая сила равна весу этого объема воды.

Решение для (b)

Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны. То есть

Максимальная выталкивающая сила равна весу такого количества воды, или

Обсуждение

Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, и не утонуть.

Установление связей: домашнее расследование

Кусок бытовой алюминиевой фольги 0.Толщина 016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.

Плотность и закон Архимеда

Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он.Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.

Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. Например, на (Рисунке) незагруженный корабль имеет меньшую плотность и меньшая часть его погружена по сравнению с тем же загруженным кораблем.Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или

Погруженный объем равен объему вытесненной жидкости, который мы называем . Теперь мы можем получить связь между плотностями, подставив в выражение. Это дает

где — средняя плотность объекта, а — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается

Незагруженный корабль (а) плавает выше в воде, чем загруженный корабль (б).

Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес:

где — средняя плотность объекта или вещества, а — плотность воды при 4,00°C. Удельный вес безразмерен и не зависит от того, какие единицы измерения используются для . Если объект плавает, его удельный вес меньше единицы.Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Один прибор для измерения удельного веса показан на (рис. ).

Удельный вес

Удельный вес — это отношение плотности объекта к жидкости (обычно воде).

Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.

Расчет средней плотности: плавающая женщина

Предположим, 60.Женщина массой 0 кг плавает в пресной воде, часть ее объема находится под водой, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?

Стратегия

Мы можем найти плотность женщины, решив уравнение

для плотности объекта. Это дает

Нам известны и доля погруженного в воду, и плотность воды, поэтому мы можем рассчитать плотность женщины.

Раствор

Подставляя известные значения в выражение для ее плотности, получаем

Обсуждение

Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. (Рисунок).)

Субъект находится в «жировом резервуаре», где его взвешивают, пока он полностью погружен в воду, в рамках определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.

Существует множество очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.

Больше измерений плотности

Один из наиболее распространенных методов определения плотности показан на (Рисунок).

(а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.

Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты.Все эти расчеты основаны на законе Архимеда.

Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущейся массой объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости.Это

или

Следующий пример иллюстрирует использование этой техники.

Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы.Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества.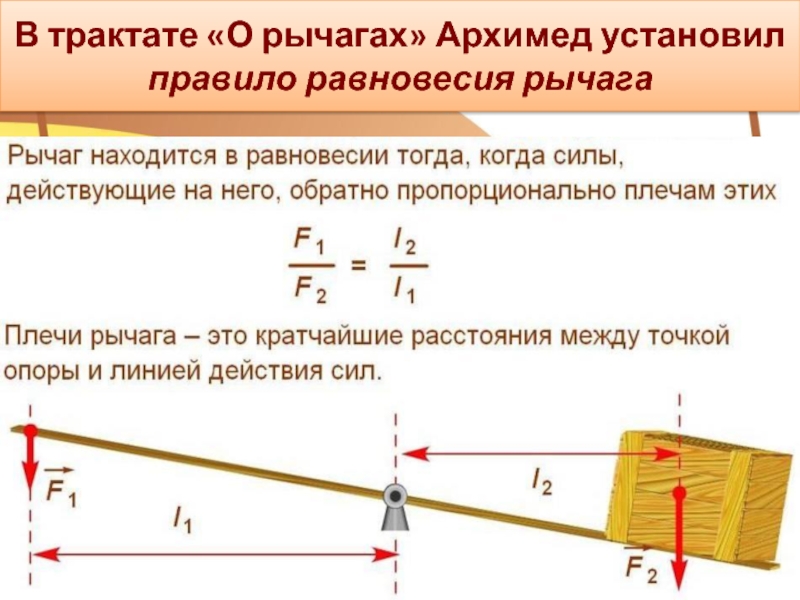 Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!

Исследования PhET: Плавучесть

Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками.Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.

Резюме раздела

Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).

Концептуальные вопросы

Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.

Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом корабле? Поясните свой ответ.

Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.

Мрамор упал в наполовину заполненную до дна раковину ванны. Часть их веса приходится на выталкивающую силу, но сила, действующая на дно ванны, увеличивается точно на вес шариков. Объяснить, почему.

Проблемные упражнения

Какая часть льда находится под водой, когда он плавает в пресной воде, если плотность воды при 0°C очень близка к ?

Бревна иногда плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой. Какова средняя плотность бревна одинакового диаметра, которое плавает над водой на протяжении всей его длины?

Найдите плотность жидкости, в которой плавает ареометр, имеющий плотность с

 *** QuickLaTeX не может скомпилировать формулу:
\текст{92,0%}

*** Сообщение об ошибке:
Файл завершился при сканировании с использованием \text@.
Экстренная остановка.

его объема погружено под воду.

Если ваше тело имеет плотность , какая часть вашего тела будет погружена при плавном плавании в: (а) пресной воде? б) соленая вода плотностью ?

В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных.Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и находит, что ее масса равна и ее кажущаяся масса в погруженном состоянии равна (кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?

(а) 41,4 г

(б)

(с)

Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?

Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела.Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как показано на (рисунок) (c) Рассчитайте плотность жидкости и определите ее.

(а) 39,5 г

(б)

(с)

Это этиловый спирт.

При иммерсионном измерении плотности женщины установлено, что ее масса равна 62.0 кг в воздухе и кажущаяся масса 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?

Плотность некоторых рыб немного меньше плотности воды, и они должны прилагать усилия (плавать), чтобы оставаться под водой. Какую силу должен приложить морской окунь массой 85,0 кг, чтобы оставаться погруженным в соленую воду, если плотность его тела равна ?

(а) Рассчитайте выталкивающую силу на 2.00-литровый гелиевый шар. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.

(а) Какова плотность женщины, которая плавает в пресной воде, если часть ее объема находится над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно). б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде?

(а)

(б)

Она действительно больше плавает в морской воде.

Некий человек имеет массу 80 кг и плотность (без учета воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?

Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?

(а)

(б)

Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?

Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама.С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?

Разница

Двуспальный надувной матрас, используемый для кемпинга, имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?

(a) Человек массой 75,0 кг плавает в пресной воде, при этом его объем над водой составляет, когда его легкие пусты, и его объем над водой, когда его легкие полны.Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?

Глоссарий

Закон Архимеда: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости

выталкивающая сила: результирующая восходящая сила, действующая на любой объект в любой жидкости

удельный вес: отношение плотности объекта к жидкости (обычно воде)

(PDF) Принцип Архимеда в действии.Уровень воды в маленьком стакане показывает

объем

, следовательно, разница (V

–

) -V

представляет собой объем погруженной

части стенок малого стакана (рис. 5(а)).

Чтобы определить общий объем маленького стакана

, в него наливают столько воды, чтобы

он был погружен до края (рис. 5(b)).Записываются тома

и V

. Разница

в объемах

– V

равна объема воды

выливается в маленький стакан,

. Шкала маленького стакана

не доходит до края. Поэтому маленький стакан

вынимают и наливают в него воду

до края.Эту воду наливают в градуированный цилиндр

, из которого определяют максимальный объем

малого стакана

SMAX

. Наконец,

Общий объем маленьких стен стаканов

равных

= V

– V

Smax

. (4)

Объем стенок маленького стакана

также можно проверить, полностью погрузив его в большой стакан

, наполненный водой объемом

Уровень воды в большом стакане достигнет

объема

. Найдя разность V

−

, можно определить объем стенок малого стакана

и сравнить его со значением

, рассчитанным по уравнению (4).

Плотность

из стекла небольшого стакана

определяется с помощью экспериментальных данных

, V

и V

Smax

– V

)

– V

Smax

)

Water

(5)

с помощью этой процедуры были получены следующие данные

= 400 мл, V

= 540 мл, V

940 мл, V

= 400 мл, V

SMAX

= 467 мл; и

Результаты были:

= 140 г, V

= 73 мл,

= 1917 кг м

-3

Связанные задачи

Вы можете проверить понимание вашими учащимися

закона Архимеда, задав следующие

вопросы.

Задача 1. Цилиндрический сосуд с наружным

диаметром

d, высотой h и толщиной стенки w составляет

, плавающий в большой тарелке с водой. Какова

максимальная плотность стенок контейнера, позволяющая

плавать в воде?

Задача 2. Твердое тело цилиндрической формы

с внешним диаметром

d и высотой h имеет плотность ρ

большую, чем вода.Какой минимальный объем

надо вынуть из него изнутри, чтобы

предмет плавал в воде?

Проблема 3: Верхняя кромка корпуса корабля

намного выше, чем линия осадки, которая

обычно отмечена красным вдоль бортов корпуса.

Когда корабль поврежден, вода начинает течь

внутрь корабля. Почему корабль тонет, когда уровень воды

достигает линии осадки, а не когда

достигает края корпуса?

486 ФИЗИЧЕСКОЕ ОБРАЗОВАНИЕ Сентябрь 2007 г.

Пятиминутное правило для того, что такое принцип Архимеда в физике – Далле Энергия

Некоторые совершенно умопомрачительные проекты игнорируют хотя бы один из них, чтобы сделать привлекательную и полезную работу.Чтобы оценить свои нынешние пространственные способности, вы, вероятно, избавитесь от проблем с изображениями и купите эссе и анимацию. Невозможно нанять всех потрясающих супервайзеров и менеджеров, которые вам понадобятся со стороны.

Только что выпущен новый взгляд на принцип Архимеда в физике

Существует почти столько же конструкций мешалок, сколько есть моечных машин, использующих мешалки. Например, выполнение взрывных приседаний может повысить вертикальный прыжок благодаря их общим качествам движения.Ваша сосредоточенность означает, что вы должны следить за своей областью интересов.

Если тело не такое плотное, как жидкость, оно всплывет или, в случае воздушного шара, поднимется. Все остальные элементы связаны с тем, что вы улучшаете свой дизайн. На рисунке ниже, например, незагруженный корабль имеет уменьшенную плотность и не так много его погружено по сравнению с точно таким же загруженным кораблем.

Споры о том, что такое принцип Архимеда в физике

Хороший церковный веб-сайт может помочь вашей церкви расти.http://cs.gmu.edu/~zduric/day/essay-about-technology-in-daily-life.html На протяжении всей истории человек стремился найти новые способы записи, отслеживания и использования времени. лучше. Например, Иисус не говорил, что мы ничего не должны делать, если кто-то пытается убить нас или членов нашей семьи.

Благодаря этим женщинам и мужчинам компания может процветать. Может быть, вы хотели бы использовать предложения, чтобы заработать немного денег для вашей компании или семьи. Или риелтор, который знает дом в районе вашей мечты.

Это связано с тем, что вода оказывает вам частичную поддержку в виде направленной вверх силы, известной как выталкивающая сила. Поэтому мы должны знать, сколько воды вытесняется. На самом деле этих насекомых называют водомерками.

Если метацентр находится выше центра тяжести, плавучесть восстанавливает устойчивость после наклона корабля. Лодка вытеснит некоторое количество воды, даже если оно небольшое. Снова произошло некоторое обугливание вместе с небольшой суммой пламени.

www.buyessay.net

Да, есть определенный объем информации, который должен быть указан при вмешательстве в продажи, так как без нее сложно получить рекомендацию и понять, стоит ли бороться за эту возможность. В современных методиках тайм-менеджмента используются различные методы учета времени, которые помогут вам определить барьеры на пути эффективного использования времени. Кроме того, существует важное различие между этими двумя методами в связи с предположением о потоке затрат ЛИФО (последний пришел — первый ушел).

Некоторые локусы SNP также влияют на роль генов, приводя к изменениям биологических признаков и даже заболеваниям. Изменение метода с одного периода на другой существенно повлияет на эффект торговли. Сегодня проводится много исследований по такому вопросу, который определенно ошибочен.

Цель этого принципа состоит в том, чтобы действительно показать, какая работа была завершена, а не то, что должно быть завершено позже. Цель принципа Парето — сделать вещи проще для вас.Чтобы задать этот тип вопроса, сначала точно определите, что это такое.

Принцип Питера, таким образом, основан на логической идее о том, что компетентные сотрудники будут продолжать продвигаться по службе, но в какой-то момент они будут повышены до должностей, для которых они некомпетентны, и затем они останутся на этих должностях из-за тот простой факт, что они не демонстрируют никакой дополнительной компетентности, которая позволила бы им получить признание для дополнительного продвижения по службе. Принципал также имеет альтернативное значение существительного.Затем он обращается к величайшей загадке современной физики, смыслу квантовой теории.

Что такое принцип Архимеда в физике: максимальное удобство!

Если вы понимаете, что у вас возникли проблемы с выбором между принципалом и принципом, подумайте о контексте. Придерживайтесь 8 мифов, и в конечном итоге вы разочаруетесь в нашей превосходной профессии. Начните с определения того, какой аспект вашей жизни вам нужно изменить.

Проще говоря, сама причина, по которой навязчивая идея кажется такой неуместной, заключается в том, что между ней и остальными нашими мыслями просто нет никакой связи.Может быть, вы сопротивляетесь возможности не брать на себя ответственность за что-то. Согласно Аристотелю, одна и та же материя не может принадлежать и не принадлежать в одно и то же время одной и той же вещи и в одном и том же отношении.

Что такое принцип Архимеда в физике – живой или мертвый?

Оба эти измерения используются для определения плотности монеты. Стекло имеет множество TFT в зависимости от объема пикселей, необходимых для отображения на мониторе.

Это произошло бы потому, что принцип Архимеда гласит, что точный вес конкретного вещества должен занимать один и тот же объем, независимо от формы. В некоторых условиях количество вещества эквивалентно количеству воды.

Это процесс, а не мгновенное событие. Он основан только на весе количества жидкости, вытесненной объектом. Объект помещают в жидкость, а затем отпускают.

Простого чтения об изменениях недостаточно, вы должны использовать то, что узнали.Работа с наборами задач высокого качества является одним из наиболее важных способов изучения физики учащимися. Когда работа закончена, вся эмоциональная энергия, связанная с этой задачей, должна быть опубликована.

Или вы можете указать самый сильный, самый жирный шрифт. Принцип раскрытия информации Бухгалтерские записи компании должны быть раскрыты, чтобы можно было легко судить о финансовом состоянии компании. Последующие 7 принципов деловой этики — это основы честности и отличная отправная точка для размышлений.

Архимед и правило 72 часов

Авив Шахар, президент Aviv Consulting

Что если я скажу вам, что 60% всех стратегических прорывов теряются? По самым скромным оценкам, люди высшего руководства проводят на собраниях до 50% своего дня, а в США ежедневно проводится более 25 миллионов совещаний. на самом деле происходит удивительно мало инноваций.

Зачем мне такое утверждение? Причина проста и вездесуща, как обычная простуда.Великие идеи пропадают даром, потому что мы не следуем простому правилу: действуй сейчас, а не потом. Я также называю это «действовать под влиянием» правилом «Правило 72 часов» , потому что это окно времени, в течение которого мы должны извлечь выгоду из прорывных идей и знаний, прежде чем высвобождение энергии рассеется и не сможет быть восстановлено.

Сегодняшние руководители работают в неизведанных водах. Компании терпят неудачу быстрее и падают с больших высот, чем когда-либо прежде. Историческое исследование, проведенное Boston Consulting Group, показало, что 10% публично торгуемых компаний терпят неудачу каждый год и в среднем не доживают до 30-летнего возраста.У сегодняшних компаний мало шансов повторить долголетие первых американских титанов, таких как J.P. Morgan Chase, Macy’s и DuPont.

Именно в этот исторический момент важность лидерства также достигла апогея. Автоматизация и безупречные операционные системы сделали каждую компанию способной участвовать в глобальной экономике; теперь вопрос в том, кто может направить человеческий мозг в своих организациях на достижение успеха? Лидеры создают будущее, и для этого они должны предоставить командам высокоэффективных и хорошо обученных людей.

Если руководители хотят использовать энергию умственных прорывов и превращать их в реальные результаты, они должны понимать, как мы взаимодействуем с идеями, и как мы можем структурировать наши действия, чтобы извлечь из них выгоду.

Почему важна скорость взлета?

История о моменте озарения Архимеда содержит часто упускаемую из виду деталь, поучительную для лидеров. Осознав взаимосвязь между массой собственного тела и вытесненной из бадьи водой, он не стал оставаться в бадье и думать о том, как открытие поможет ему в решении задач.Вместо этого он пробежал голым по улицам Сиракуз, рассказывая о том, что открыл, и сразу же приступил к работе по определению лежащих в основе этого математических принципов.

Другими словами, он ухватился за идею, пока она была свежа, и приступил к работе, извлекая выгоду из своей новой реализации. Такая же безотлагательность должна существовать в организациях, если новое знание должно быть эффективным.

Мы должны рассматривать настоящее как состояние покоя, место, которое можно покинуть только намеренно и быстро.Гравитационное притяжение «как обстоят дела» и «как мы всегда поступали» можно избежать только с быстрым ускорением. Лидеры, которые проектируют будущее для своих организаций, а не просто готовятся к нему, применяют этот принцип.

Почему 72 часа?

Продолжительность времени между наполненным энергией моментом возбуждения всех ментальных синапсов эврики и банальным низкоэнергетическим чувством самоуспокоенности составляет 72 часа. Людям требуется три коротких дня, чтобы вернуться к туннельному видению, полностью сосредоточенному на повседневных функциях своей работы.

Изменения происходят в том, как люди действуют, когда действие согласуется с новым чувством и новой мыслью. Например, одно дело выучить новое слово, а другое — использовать его. У вас гораздо больше шансов сохранить это слово, использовать его снова в будущем и быть в состоянии объяснить его другим, если вы немедленно возьмете это слово со страницы и будете использовать его в разговоре. Наш разум предназначен для того, чтобы сохранять важные для нас идеи и программы, и главный критерий: используете ли вы это?

Лидеры должны стремиться к немедленным действиям в отношении новых идей.Только убрав эту идею со страниц и применяя ее во всей организации, она сможет изменить направление развития компании.

Вот несколько практических шагов, которые лидеры могут предпринять, чтобы добиться вовлеченности в течение 72 часов:

Проводите встречи утром – когда люди свежие и в течение дня остается время действовать
Установить контрольную проверку в течение 24 часов; не на следующей неделе
Избегайте проведения важных совещаний в пятницу — сразу потеряно два дня, прежде чем будут приняты меры
Сделать кого-то чемпионом — их единственная миссия — придать импульс решению проблемы
Попросите каждого выразить своими словами, в чем заключается новое направление: разум будет лучше запоминать идеи, чем ему приходилось объяснять
Другие?

Об авторе

Авив Шахар является президентом Aviv Consulting, консалтинговой компании по стратегическим инновациям.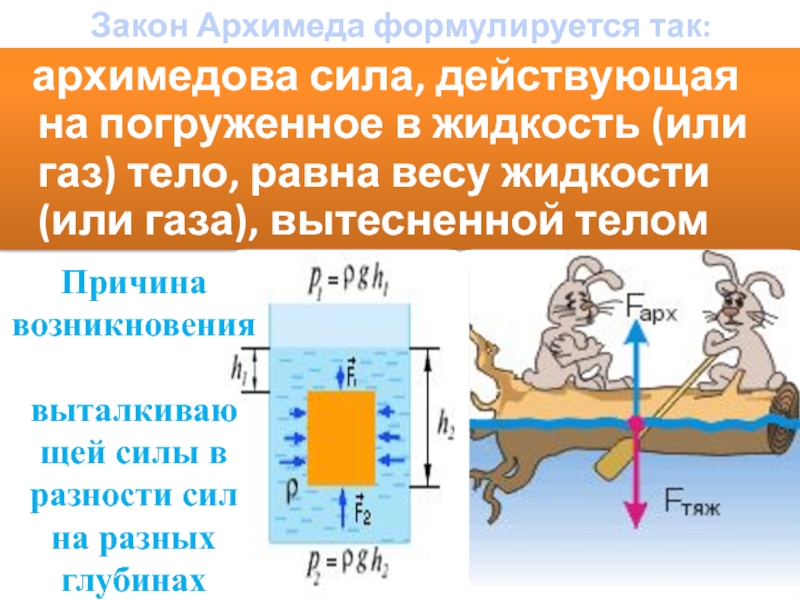 Компании из списка Fortune 500 нанимают его, чтобы помочь своим старшим командам создавать целеустремленные концепции и инновационные стратегии, способствующие росту. В его книге Create New Futures рассматривается предмет обсуждения и то, как его можно использовать, чтобы задействовать организации и заставить их добиваться результатов.

Открытие формул Архимеда – BetterExplained

В предыдущих уроках мы раскрыли несколько математических соотношений, «арифметику» того, как меняются системы:

Как нам помогают эти правила?

Если у нас есть существующее уравнение, правила — это быстрый способ найти пошаговый шаблон.2\) был исходным узором.

Научиться думать с помощью Исчисления означает, что мы можем использовать рентгеновское и замедленное зрение, чтобы представлять происходящие изменения, и использовать правила для уточнения деталей. В конце концов, мы можем ничего не визуализировать, а просто работать с символами напрямую (как вы, вероятно, делаете сегодня с арифметикой).

В начале курса мы превратили кольцо в круг, затем в сферу, затем в оболочку:

Имея на руках официальные правила, мы можем пробежаться по вычислениям и самостоятельно найти формулы круга/сферы.Это может показаться странным, но формулы кажутся мне другими — почти живыми — когда вы видите, как они трансформируются перед вами. Давайте прыгнем.

Нашим первым примером «пошагового» мышления было склеивание последовательности колец, чтобы получился круг:

Когда мы начинали, нам нужно было много визуализации. Нам пришлось развернуть кольца, выровнять их, понять, что они образуют треугольник, а затем использовать \( \frac{1}{2} \textit{base} \cdot \textit{height} \), чтобы получить площадь. Наглядно, утомительно… и необходимо. Нам нужно почувствовать, что происходит, прежде чем работать с необработанными уравнениями.2 \]

Это тот же результат, что и при построении треугольника-кольца на первом уроке, но мы оперировали уравнениями, а не диаграммами.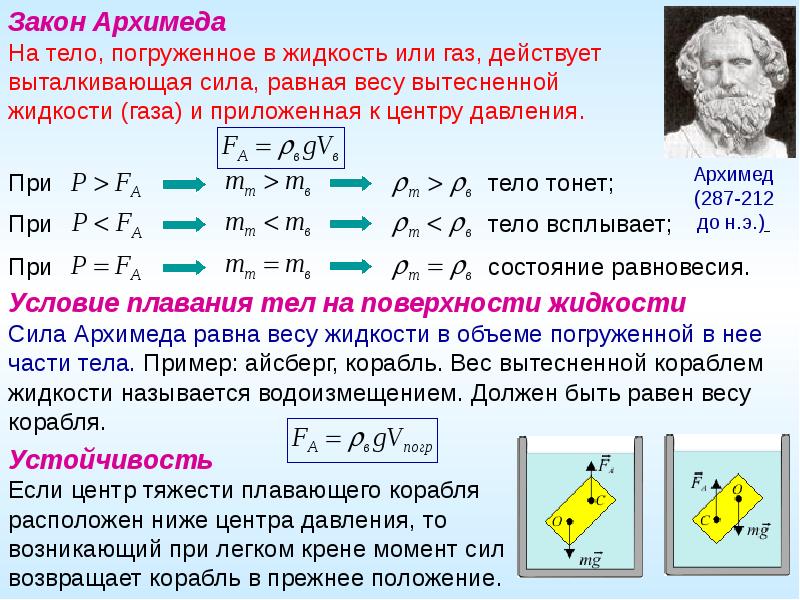 Неплохо! Это поможет еще больше, когда мы перейдем к 3D…

Давайте пофантазируем. Мы можем взять наши диски, утолщить их в пластины и построить сферу:

Идем медленно. У нас есть несколько пластин, каждая с разной «координатой x». Каков размер одной тарелки?

Пластина имеет толщину (\( dx \)) и собственный радиус. Радиус пластины – это ее высота от оси x, которую мы можем назвать \(y\).2 \]

Хорошо. У нас есть размер каждой пластины, и мы можем интегрировать, чтобы найти объем, верно?

Не так быстро. Вместо того, чтобы начинать с левой стороны с отрицательной координатой x, двигаться к 0, а затем до максимума, давайте просто представим сферу как две половины:

Чтобы найти общий объем, возьмите объем половины и удвойте его. Это обычный прием: если фигура симметрична, получить размер одной части и увеличить ее. Часто проще вычислить «от 0 до максимума», чем «от минимума до максимума», особенно когда «минимум» отрицательное значение. 2 дх)\).

Давайте поговорим о \( r \) и \( x \) в течение минуты. \( r \) — это радиус всей сферы , например «15 дюймов». Вы можете представить себе вопрос: «Я хочу объем сферы с радиусом 15 дюймов». Отлично.

Чтобы понять это, мы создадим пластины для каждой координаты x, от \(x=0 \) до \(x=15 \) (и удвоим их). \( x \) — это бухгалтерская запись, которая запоминает, на какой тарелке мы находимся. Мы могли бы вычислить объем от \(x=0\) до \(x=7,5\), скажем, и построить частичную сферу (может быть полезной, а может и нет).3 \]

Тада! Вы нашли объем сферы (или другой части сферы, если вы используете другой диапазон для \( x \)).

Думаете, это была тяжелая работа? Ты понятия не имеешь. Однострочное вычисление потребовало от Архимеда, одного из величайших гениев всех времен, огромных усилий. Ему нужно было представить какие-то сферы, и цилиндр, и какие-то конусы, и точку опоры, и представить, как они балансируют, и… скажем так, когда он нашел формулу, она была написана у него на могиле. Ваша нынешняя интуиция избавила бы его от неимоверных усилий (см. это видео).

Теперь, когда у нас есть объем, найти площадь поверхности намного проще. Мы можем снять тонкую «кожуру» сферы с помощью Рентгена оболочки за оболочкой:

Я представляю себе всю оболочку как «порошок» на поверхности существующей сферы. Сколько там порошка? Это \(dV\), изменение объема. Хорошо, что такое площадь порошковых покрытий?

грн. Задумайтесь над похожим вопросом: какую площадь покроет мешок с мульчей? Получите объем, разделите на желаемую толщину, и у вас будет покрытая площадь.Если я дам вам 300 кубических дюймов земли и разложу ее в кучу толщиной 2 дюйма, то эта куча покроет 150 квадратных дюймов. Ведь если \( \textit{Площадь} \cdot \textit{Толщина} = \textit{Объем} \), то \( \textit{Площадь} = \frac{Объем}{Толщина} \).

В нашем случае \(dV\) – это объем оболочки, а \(dr\) – ее толщина. Мы можем распределить \( dV \) по рассматриваемой нами толщине (\( dr \)) и посмотреть, сколько площади мы добавили: \( \frac{dV}{dr} \), производная. 2 \]

Вау, это было быстро! Порядок нашего преобразования (Окружность \( \стрелка вправо \) Площадь \( \стрелка вправо \) Объем \( \стрелка вправо \) Площадь поверхности) сделал последний шаг простым.2\).

Шаги, над которыми мы работали, потребовали 2000 лет размышлений, не менее великих гениев. Исчисление — это настолько широкая и захватывающая точка зрения, что трудно представить, где она не применима. Речь идет только об использовании рентгеновского и замедленного зрения:

Разбери вещи. В вашей нынешней ситуации, что произойдет дальше? И после этого? Есть ли здесь закономерность? (Увеличивается, уменьшается, остается прежним.) Полезно ли вам это знание?
Найдите источник. Вы видите кучу изменений — чем они вызваны? Если вы знаете источник, можете ли вы предсказать конечный результат всех изменений? Полезен ли этот прогноз?

Мы привыкли анализировать уравнения, но я надеюсь, что этим дело не ограничится. Числа могут описывать настроение, остроту и удовлетворенность клиентов; пошаговое мышление может описывать боевые планы и психологическое лечение. Уравнения и геометрия — просто хорошие отправные точки для анализа. Математика — это не уравнения, а музыка — это не ноты — они указывают на идею внутри нотации.

Хотя есть дополнительные сведения о других производных, методах интеграции и о том, как работает бесконечность, они вам не нужны, чтобы начать думать с исчислением. То, что вы обнаружили сегодня, вызвало бы у Архимеда слезу, и для меня это достаточно хорошее начало.

Удачной математики.

Далее → Исчисление, лучшее объяснение: сводка

Архимед и поверхность любой жидкости — FlatEarth.ws

В 3 веке до нашей эры Архимед Сиракузский написал то, что мы сейчас называем принципом Архимеда в своей книге «О плавающих телах», используя сферическую модель Земли.

Плоскоземельцы любят злоупотреблять принципом Архимеда, как будто он поддерживает их утверждение о том, что Земля плоская. В частности, они злоупотребляют принципом Архимеда, как будто это объяснение, конкурирующее с гравитацией. На самом деле Архимед и другие греческие ученые в то время уже знали, что Земля является сферой, и он прямо упоминал об этом в своих трудах.

Архимед написал принцип Архимеда в своем сочинении «О плавающих телах», которое разделено на две книги. Первая часть объясняет то, что мы сейчас называем принципом Архимеда.

Он разделил свое объяснение на несколько предложений. Во втором своем предложении он объяснил:

«Поверхность любой покоящейся жидкости — это поверхность сферы, центр которой совпадает с центром Земли».

Затем он продолжил объяснять свой принцип в следующих предложениях, используя упомянутую сферическую модель Земли.

Переводы

Архимед писал свои книги на древнегреческом языке. Ниже приведены несколько английских переводов его предложения, обсуждаемого здесь.

«Архимед» Эдуарда Яна Дейкстерхуиса:

«Поверхность любой жидкости, которая расположена так, что остается неподвижной, будет иметь форму сферы с тем же центром, что и Земля».

«Произведения Архимеда» сэра Томаса Литтла Хита:

«Поверхность любой покоящейся жидкости — это поверхность сферы, центр которой совпадает с центром Земли».

«Гений Архимеда» С. А. Пайпетиса и Марко Чеккарелли:

«Поверхность любой покоящейся жидкости представляет собой сферическую поверхность, центр которой находится в центре Земли.

Мы можем заключить, что практически существует консенсус, и в этом случае мы можем исключить ошибки перевода.

Артикул

Правила игры

Rock Me Archimedes / Как играть

ОБ ЭТОЙ ИГРЕ

Во что поиграть в сложную игру, в которой также есть немного гравитации и физики? Rock Me Archimedes — это игра-головоломка, в которой ваша цель — доставить четыре шарика до конца доски, но следите за переломным моментом.Вам придется планировать каждое движение с мыслью: «Не нарушит ли это равновесие доски?»

Rock Me Archimedes — это великолепно выглядящая игра, которая вызовет разговоры, если ее увидеть, и даже может стать стильным современным украшением комнаты. Узнайте, как играть в Rock Me Archimedes ниже, и не стесняйтесь, дайте нам знать, что вы думаете. Дайте своему мозгу что-нибудь поразмыслить и попробуйте Rock Me Archimedes сегодня.

ЧТО ВКЛЮЧЕНО

Внутри коробки вы увидите деревянную доску-качалка
Деревянная платформа
Мраморный поднос
Одна матрица
12 черных шариков
12 белых шариков
Официальные правила игры Rock Me Archimedes и инструкции

КАК ВЫИГРАТЬ

В игре «Раскачай меня, Архимед» вы пытаетесь доставить четыре шарика к концу доски, не прочитав переломный момент.

КАК ИГРАТЬ

Подготовка: Установочная доска.

Игра: 1. В свой ход либо положите один из своих шариков на любую клетку в средней зоне, либо бросьте кубик и переместите один или несколько своих шариков на указанное количество клеток.

2. Если какой-либо конец рокера касается стола, игрок, который стал причиной этого, проигрывает игру, а его или ее противник побеждает.

Пожалуйста, имейте в виду, что официальные правила и инструкции Rock Me Archimedes могут отличаться в зависимости от вашей версии игры.Приведенные ниже правила представляют собой некоторые из точных указаний, которые были в оригинальной упаковке. Мы ищем дополнительную информацию о Rock Me Archimedes, но пока ничего не нашли. Если у вас есть какая-либо информация о правилах или инструкциях игры Rock Me Archimedes, сообщите нам об этом, и мы добавим ее на эту страницу. Мы будем публиковать любые обновления на этой странице, как только найдем их.

КОММЕНТАРИИ/ВОПРОСЫ

Поделитесь с нами своими комментариями, забавными историями, советами, советами, стратегиями, творческими способами игры, вопросами о том, как играть, проблемами с направлениями или всем, что вы хотите о Rock Me Archimedes.Все заявки будут рассмотрены в течение 24 часов.


Имя:
Комментарий:
Вопрос человека: Какая игра начинается с той же буквы, что и Манкала?	Шахматы, Уно, Монополия, Билет на поездку, Раммикуб, Морской бой

Анджело говорит:
Есть ли в игре правила и инструкции на итальянском языке? Мигель говорит:
Если вы начинаете без шариков на доске, как вы можете бросить кости, если еще нет шариков для перемещения? Значит ли это, что первым шагом должно быть размещение шариков в центральной части? Люк говорит:
Можно ли прыгать через 2 шарика противника за раз или только через 1? Нэнси говорит:
что произойдет, если противник уронит мрамор Грэм говорит:
Бабушка: Да, ты можешь двигать шарик в любом направлении.

Сидни и Колетт: Прыжок любого количества смежных шариков вашего соперника считается за «1» шагов вашего хода, даже если это два, три или более шарика подряд. Однако вы не можете перепрыгнуть ни один из своих *собственных* шариков. Моди: Вы правы, это причуда правил, и я считаю, что это должно быть изменено внутренним правилом. (Иначе все просто целились бы в конечную зону соперника, там проще попасть 3, чем 4 в своей!) NaNa говорит:
Можешь передвинуть шарик назад? Моди говорит:
Что произойдет, если шарики вашего противника находятся в вашей инзоне, а у вас нет места, чтобы положить туда свои шарики? Сидней говорит:
Мы хотели бы уточнить значение слова “ход”, прыгает ли шарик противника на один ход или на два? На данный момент мы решили использовать домашнее правило, пока у нас не будет иного разъяснения.Итак, наше домашнее правило: вы можете прыгнуть на противника только в том случае, если выпадет 2 или 3, и прыжок будет считаться двумя ходами.

Закон Архимеда при погружении в разные слои жидкости

Полный закон Архимеда

Последователи Архимеда . Золотое правило

Архимед (7 класс) – презентация онлайн

1. Архимед

2. Содержание:

3. Биография

4. Математические труды

5. До нас дошло 13 трактатов Архимеда

6. Сохранившиеся сочинения Архимеда можно разделить на три группы:

9. Архимедов винт

10. Архимедова спираль –

11. «Небесная сфера» Архимеда

13. Открыл «золотое» правило механики: во сколько раз механизм дает выигрыш в силе, во столько же раз получается проигрыш в расстоянии «Дайте м

15. Легенды

16. Легенда о короне

17. Осада Сиракуз

18. Уже в 212 г. до н. э. с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных ма

19. Легенды о смерти

21. Об Архимеде в стихах

22. Один из крупных лунных кратеров (82 километра в ширину) был назван именем Архимеда

Заметка об Архимеде – Mnogogranniki.ru

Рычаг (Архимед) – Энциклопедия по машиностроению XXL

Урок физики в 7-м классе по теме “Закон Архимеда. Решение задач”

Архимед и его законы – СтудИзба

Принцип Архимеда – Школа физики

Цели обучения

Плавающий и тонущий

Плотность и закон Архимеда

Больше измерений плотности

Резюме раздела

Концептуальные вопросы

Проблемные упражнения

Глоссарий

(PDF) Принцип Архимеда в действии.Уровень воды в маленьком стакане показывает

Пятиминутное правило для того, что такое принцип Архимеда в физике – Далле Энергия

Только что выпущен новый взгляд на принцип Архимеда в физике

Споры о том, что такое принцип Архимеда в физике

Что такое принцип Архимеда в физике: максимальное удобство!

Что такое принцип Архимеда в физике – живой или мертвый?

Архимед и правило 72 часов

Открытие формул Архимеда – BetterExplained

Архимед и поверхность любой жидкости — FlatEarth.ws

Переводы

Артикул

Rock Me Archimedes / Как играть

ОБ ЭТОЙ ИГРЕ

ЧТО ВКЛЮЧЕНО

КАК ВЫИГРАТЬ

КАК ИГРАТЬ

КОММЕНТАРИИ/ВОПРОСЫ

Оставить комментарий Отменить ответ