Правило левой руки для силы ампера и лоренца: Силы Ампера и Лоренца 10 класс онлайн-подготовка на Ростелеком Лицей

Силы Ампера и Лоренца 10 класс онлайн-подготовка на Ростелеком Лицей

Силы Ампера и Лоренца

Магнитное поле действует не только на магниты, но и на движущиеся заряды. Здесь может быть два случая:

1. Действие на движение отдельных зарядов в свободном пространстве.
2. Действие на движение зарядов в проводнике.

1. Действие магнитного поля на отдельный заряд

Магнитное поле не действует на неподвижные заряды – только на движущиеся. Магнитное поле действует действует на заряды не прямолинейно, а всегда вбок.

Рассмотрим заряд, движущийся с некоторой скоростью. Если магнитное поле направленно вдоль этой скорости, то никакая сила со стороны магнитного поля не действует.

Сила появляется, если магнитное поле направленно перпендикулярно скорости частицы. Эта сила перпендикулярна и вектору индукции магнитного поля B ⃗, и скорости.

Сила, действующая на отдельный заряд со стороны магнитного поля:

Когда магнитное поле перпендикулярно скорости, сила тем больше, чем сильнее магнитное поле, больше заряд и больше его скорость:

F=qυB

Если магнитное поле направленно под углом, то разложим магнитное поле на перпендикулярную и продольную составляющие. И вспомним, что продольная составляющая не действует на частицу; действует только перпендикулярная составляющая. Т.е. в выражении для силы надо вместо B написать B_⊥. Если угол между магнитным полем и скоростью alpha, то можно это выражение переписать в виде:

F_L=qυBsinα

Эта сила называется силой Лоренца.

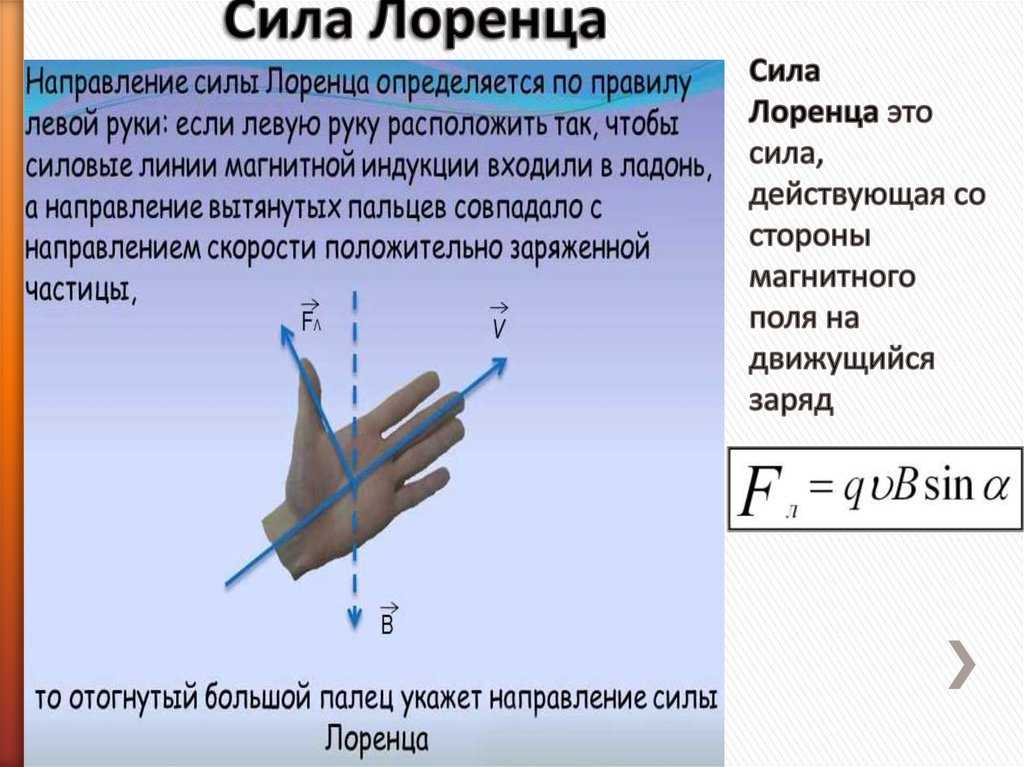
Направление этой силы можно определить с помощью правила левой руки:

1. Приложить левую руку так, чтобы скорость была направленна вдоль четырех пальцев. 

2. Повернуть руку так, чтобы магнитное поле входило в ладонь.

 3. Оттопыренный под прямым углом большой палец укажет направление силы.

 

Это работает для положительного заряда. Если заряд отрицательный, то направление силы будет противоположным.

2. Действие магнитного поля на проводник с током

Предположим, что магнитное поле перпендикулярно проводнику. Ток – это движение заряженных частиц, поэтому их скорости в среднем направленны вдоль проводника.

И на каждую из них действует магнитное поле. Поэтому на проводник будет действовать некоторая суммарная сила, называемая силой Ампера.

В общем случае выражение для силы:

F_A = IBlsinα

По сути, сила Ампера – это макроскопическое проявление силы Лоренца. Поэтому полезно сравнить размерности выражений для этих сил. Если все записано правильно, они должны совпадать. Действительно, для обоих выражений мы получаем Кл⋅м/c⋅Тл.

 

Направление силы Ампера также определяется правилом левой руки. Четыре пальца направляются на этот раз по току, магнитное поле входит в ладонь, большой палец указывает направление силы.

В таблице с формулами описывающими создание поля зарядами и действие поля на заряды добавились две формулы.

Задача

Рейка с сопротивлением R, массы m и длины l может без трения скользить по двум направляющим, оставаясь при этом всегда перпендикулярным им. К направляющим подключен источник, создающий напряжение U. Система помещена в однородное магнитное поле с индукцией B, перпендикулярное плоскости рисунка. Рейку отпускают без начальной скорости. До какой скорости она разгонится, пройдя расстояние L? Сопротивлением направляющих пренебречь.

Решение

Перед нами система, которая может ускорять металлические объекты

Вспомним урок «закон сохранения энергии»

Такая система называется рельсотрон. В мирных целях, она может двигать транспорт, разгонять объекты до огромных скоростей и даже имитировать падение космических микрометеоритов.

Сила Ампера и сила Лоренца – формулы и определение правила правой руки кратко (9 класс)

4.6

Средняя оценка: 4.6

Всего получено оценок: 326.

Обновлено 15 Января, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 326.

Обновлено 15 Января, 2021

Из курса физики 9 класса известно, что электрический ток — это движение заряженных частиц.

Опыты показывают, что при движении заряженные частицы взаимодействуют с магнитным полем. Рассмотрим особенности этого взаимодействия.

Сила Ампера и сила Лоренца

Если рассмотреть устройство любого электрического двигателя, то в нём всегда можно найти два элемента:

• статор, создающий магнитное поле;
• ротор, двигающийся под действием статора и состоящий из рамок, проводящих электрический ток.

Рис. 1. Устройство электродвигателя.

Магнитное поле, создаваемое статором, порождает силу, которая действует на рамку с электрическим током и поворачивает ее. Сила, которая при этом возникает, называется силой Ампера — именем физика, открывшего ее.

Если ток в рамке исчезнет, то и сила Ампера также уменьшится до нуля. А поскольку ток — это движение заряженных частиц, то можно предположить, что сила Ампера возникает при действии магнитного поля на заряженные частицы, и проводник здесь не обязателен.

Опыт полностью подтверждает это предположение. Если в вакууме создать поток заряженных частиц (как правило, электронов) и направить их через магнитное поле, то траектории движения перестанут быть прямыми. А при определенных соотношениях скоростей и силы магнитного поля траектории могут даже стать окружностями или спиралями.

Рис. 2. Движение зарядов в магнитном поле.

Сила Ампера, действующая на проводник с током, возникает потому, что магнитное поле действует на заряды, движущиеся в проводнике. Этот механизм возникновения силы Ампера был открыт физиком Х. Лоренцем, и поэтому сила, действующая на движущийся заряд в магнитном поле, была названа его именем.

Можно спросить: определяет ли сила Лоренца закон Ампера? Ответ утвердителен: да, определяет.

Формулы силы Ампера и силы Лоренца

Поскольку сила Ампера — это результат действия силы Лоренца, то и формулы, описывающие эти силы, близки, единицы измерения одинаковы. Сила Ампера и сила Лоренца пропорциональны величине перпендикулярной составляющей индукции $B_\perp=Bsin\alpha$, следовательно, эта часть в обеих формулах будет общей.

Кроме того, обе этих силы пропорциональны величине заряда и его скорости движения. То есть формула силы Лоренца примет вид:

$$F_L = qBv sin \alpha$$

Формула силы Ампера будет аналогичной, место заряда займет величина тока $I$ (поскольку ток равен отношению заряда, проходящего по проводнику, ко времени прохождения), место скорости займет длина проводника $Δl$ (поскольку скорость равна отношению длины, которую прошел заряд, ко времени этого прохождения). В результате формула силы Ампера примет вид:

$$F_A = I B Δl sin \alpha$$

Направление силы Ампера и силы Лоренца

В отличие от многих других сил, направление силы Лоренца (а значит, и силы Ампера) не совпадает с направлением движения носителя и не совпадает с направлением на источник магнитного поля. Для определения направления этих сил используется мнемоническое правило левой руки.

Если расположить левую руку так, чтобы четыре вытянутых пальца указывали на направление движения положительных зарядов (направление тока), а магнитные линии входили в ладонь, «прокалывая» ее, то отставленный большой палец укажет направление действия силы Лоренца (или Ампера).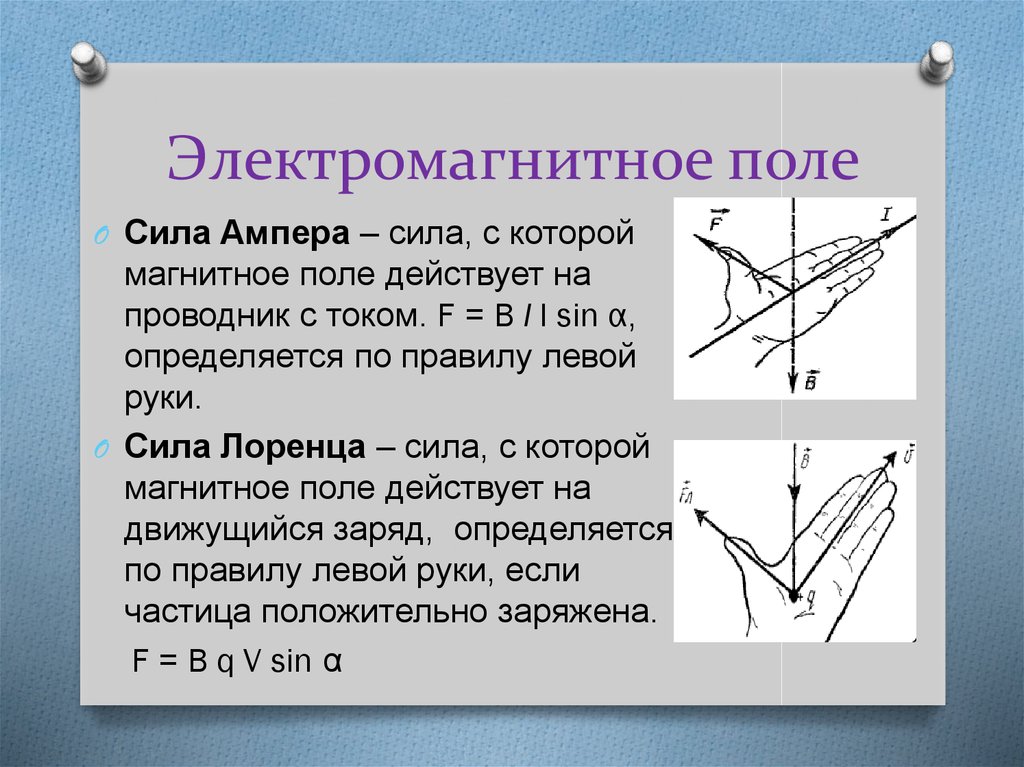

Например, если линии магнитного поля направлены сверху вниз, то руку надо располагать ладонью вверх. Теперь, если проводник с током направлен вперед и мы расположим четыре вытянутых пальца вперед, то отставленный большой палец укажет направление справа налево. Это и будет направление силы Ампера, действующей на данный проводник, или силы Лоренца, если двигаются заряды.

Рис. 3. Правило левой руки.

Что мы узнали?

На заряд, движущийся в магнитном поле, действует сила Лоренца. Поскольку электрический ток — это упорядоченное движение зарядов, то на проводник с током в магнитном поле действует сила Ампера, которая представляет собой сумму сил Лоренца, действующих на движущиеся в проводнике заряды.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 326.

---

А какая ваша оценка?

Как определить направление силы Лоренца

Уровень 2 (без высшей математики)

Уровень 2 требует школьной математики. Подходит для школьников.

Обновлено Александром Фуфаевым 04.09.2022

Содержание

1. Ингредиент №1: Движущиеся заряды Краткое пояснение, что такое электрический ток и что важно при движении зарядов.
2. Ингредиент № 2: Магнитное поле Здесь вы узнаете, как представляется направление магнитного поля и почему магнитное поле важно для правила правой руки.
3. Компонент №3: Магнитная сила (сила Лоренца) Краткое введение в магнитную силу и то, как ее направление зависит от типа заряда.
4. Как применить правило левой/правой руки? Здесь вы узнаете, как использовать свои три пальца, чтобы вычислить неизвестную величину (ток, силу или магнитное поле).
5. Пример №1: Отклонение токоведущего провода
6. Пример №2: Отклонение качания проводника

Видео — Сила Лоренца просто объясняется за 6 минут!

Воспроизвести видео: Keynote (Google I/O ’18)

Используя правило правой руки, вы можете легко ответить на следующие вопросы:

• В каком направлении действует сила Лоренца \( \class{green }{\boldsymbol{F}} \) действуют на электрический заряд, движущийся в магнитном поле?

• В каком направлении течет электрический ток \( \class{red}{\boldsymbol{I}} \)?

• В каком направлении магнитное поле \( \class{violet}{\boldsymbol{B}} \) направлен?

• Отклонялась ли положительно или отрицательно заряженная частица в магнитном поле? Таким образом, вы также можете узнать тип заряда с помощью правила правой руки!

Правило правой руки весьма полезно при работе с магнитными полями и электрическими токами. Давайте сначала проясним несколько основ, чтобы достичь того же уровня знаний.

Ингредиент №1: Движущиеся заряды

Чтобы вообще применить правило правой руки, вам нужно движущихся электрических зарядов . Акцент сделан на слова « перемещение » и « заряд ». У вас нет никаких транспортных расходов? Никуда не движутся положительно заряженные протоны? Нет отрицательно заряженных электронов? Нет других положительно или отрицательно заряженных частиц? Тогда правило правой руки бесполезно.

Обычно движение заряда, изображенное на рисунке, отмечается вектором (“стрелка”). Этот вектор говорит вам, в каких направление частица движется. Обычно рядом с вектором находится его метка, а именно буква \( \class{red}{\boldsymbol{v}} \). Буква представляет собой аббревиатуру английского слова «\(\class{red}{\boldsymbol{v}}elocity\)». Очевидно, движущийся заряд должен иметь некоторую скорость. ..

движущийся заряд имеет скорость \( \class{red}{\boldsymbol{v}} \) в каком-то направлении представлен вектором.

Движущийся положительный заряд в направлении \( \class{red}{\boldsymbol{v}} \). Движущийся отрицательный заряд в направлении \(\class{blue}{\boldsymbol{v}} \).

Иногда у вас не один движущийся заряд, а много ! Эти заряды обычно движутся в одном направлении. Это коллективное движение электрических зарядов в определенном направлении мы называем электрическим током .

Движущийся электрический заряд генерирует электрический ток.

На предыдущих уроках вы уже узнали, что такое электрический ток. Электрический ток обозначается буквой \(\class{red}{\boldsymbol{I}}\) и показывает, сколько электрических зарядов в секунду проходит, например, по кабелю. Таким образом, электрический ток описывает движение многих заряженных частиц.

Текущее направление, то есть направление движения всех зарядов, также представлено вектором (то есть стрелкой). На векторе мы пишем букву \(\class{red}{\boldsymbol{I}}\), чтобы сказать: «Здесь и в этом направлении течет электрический ток».

Что такое электрический ток?

Электрический ток \(\class{red}{\boldsymbol{I}}\), представленный вектором, представляет собой движение многих зарядов в конкретном направление .

Правило правой руки можно применить к одному движущемуся заряду, а также к нескольким движущимся зарядам, т. е. к электрическому току. Так что не имеет значения, сколько зарядов движется, гораздо важнее вопрос:

Есть ли у меня вообще ДВИЖУЩИЙСЯ электрический ЗАРЯД или ТОК ?

Если вы можете ответить на этот вопрос ДА, то необходимое условие для применения правила правой руки уже выполнено.

Компонент №2: Магнитное поле

Направление магнитного поля внутри подковообразного магнита.

Однако одного движущегося заряда недостаточно. Он просто продолжал бы двигаться прямо вперед. Чего вам все еще не хватает, так это магнитного поля . Сокращено буквой \(\class{violet}{\boldsymbol{B}} \). Магнитное поле подобно скорости и току направленной величине. Таким образом, мы можем спросить себя не только в каком направлении движется заряд или в каком направлении течет ток, но и в каком направлении указывает магнитное поле \( \class{violet}{\boldsymbol{B}} \). Магнитному полю также можно присвоить вектор («стрелку»), указывающий направление магнитного поля.

Направление магнитного поля определяется точкой от северного полюса к южному полюсу . Так что, если вы возьмете, например, подковообразный магнит, вам сначала нужно выяснить, где находятся его северный и южный полюса. Если вы этого не знаете, то правило правой руки поможет вам разобраться. Вы узнаете, как сделать это в мгновение ока!

Иногда встречаются двухмерные изображения, на которых магнитное поле указывает на или на изображение.

• Если вы видите крестик ⨂ (обычно с кружком вокруг него), это означает, что магнитное поле направлено на изображение (на экран). Магнитное поле направлено от вас.

• Когда вы видите точку ⨀ с кружком вокруг нее, это означает, что магнитное поле направлено за пределы изображения (за пределы экрана). Магнитное поле направлено на вас.

Магнитное поле указывает на изображение. Он указывает в сторону от вас. Магнитное поле направлено за пределы изображения. Оно направлено на вас.

Как применить правило левой/правой руки?

Важно! Вам предстоит иметь дело с тремя направлениями:

• С направлением движущегося заряда или тока \(\class{blue}{\boldsymbol{I}}\).

• С направлением магнитного поля \(\class{violet}{\boldsymbol{B}}\).

• С направлением отклонения силой Лоренца \(\class{green}{\boldsymbol{F}}\).

Необходимо указать ДВА направления из трех! Вы также должны знать, имеете ли вы дело с положительными или отрицательными зарядами .

Например, вы знаете направление \(\class{blue}{\boldsymbol{I}}\) и \(\class{violet}{\boldsymbol{B}}\) и знаете, что мы имеем дело с отрицательно заряженными электронами. Затем вы можете узнать третье направление, а именно направление силы Лоренца \(\class{green}{\boldsymbol{F}}\), с помощью правила левой/правой руки. Пока ясно?

Итак, у вас есть один или несколько движущихся зарядов в магнитном поле. Хороший. Далее вы должны ответить на следующий вопрос:

Мне нужно использовать правую или левую руку?

Этот вопрос разъясняет, с каким типом оплаты (+ или -) вы имеете дело. После того, как вы ответили на этот вопрос, вам нужно ответить только на самый последний вопрос:

Какое направление величин \(\class{blue}{\boldsymbol{I}}\), \(\class{violet}{\ boldsymbol{B}}\), \(\class{green}{\boldsymbol{F}}\) неизвестен?

Правило левой руки для отрицательных зарядов: вот как должны быть выровнены ваши пальцы. Правило правой руки для положительных зарядов: вот как должны быть выровнены ваши пальцы.

Используйте пальцы выбранной руки следующим образом:

• Большой палец – вытяните большой палец в направлении движущегося заряда или в направлении тока \(I\).

• Указательный палец – вытяните указательный палец перпендикулярно большому пальцу в направлении магнитного поля \( \class{violet}{\boldsymbol{B} } \). Итак, в направлении магнитного южного полюса.

• Средний палец – вытяните средний палец как можно перпендикулярнее к двум другим пальцам, тогда средний палец покажет вам направление силы Лоренца \( \class{green}{\boldsymbol{F} } \). .

Почему бы вам не попробовать правило левой/правой руки на следующих двух иллюстрациях…

• Квест #1 : \(\class{blue}{\boldsymbol{ v}}\) и \( \class{violet}{\boldsymbol{B} } \) направления известны. В каком направлении отклоняются положительный и отрицательный заряд?

• Квест #2 : На этот раз направления \(\class{blue}{\boldsymbol{v}}\) и \( \class{green}{\boldsymbol{F} } \) известны. Где находится южный полюс магнита?

• Квест #3: Теперь представьте, что вы не знаете, слева или справа вошел заряд в магнитное поле. Вы знаете только, в каком направлении был отклонен заряд, направление \( \class{violet}{\boldsymbol{B} } \), а также тип заряда. С какого направления должен был прийти заряд?

• Квест #4: Теперь все три направления \(\class{blue}{\boldsymbol{v}}\), \( \class{violet}{\boldsymbol{B} } \) и \( \class{green}{\boldsymbol{F} } \) известны, а тип заряда – нет. Отклонялась ли в магнитном поле положительно или отрицательно заряженная частица?

Положительный заряд в магнитном поле отклоняется вверх. Отрицательный заряд в магнитном поле отклоняется вниз.

Пример №1: Прогиб токоведущего провода

Проводник с током в магнитном поле.

У вас есть провод, по которому течет ток с электронами. Провод находится в магнитном поле, которое направлено на экран.

Сила Лоренца действует на провод слева или справа?

У вас есть электронных потоков . Это означает: вам нужна левая рука.

1. Большой палец – указывает в направлении потока электронов.

2. Указательный палец – указывает на экран.

3. Средний палец – затем указывает вправо.

Таким образом, на провод справа действует сила Лоренца.

Пример #2: Отклонение качания проводника

Отклонение качания проводника наружу.

Возьмите подковообразный магнит. Согласно определению, линии магнитного поля внутри подковообразного магнита указывают от северного до южного полюса 9.0056 . Затем вы берете проволоку, формируете из нее подобие круга или прямоугольника и вставляете одну сторону подковообразного магнита (на иллюстрации 14 это сторона южного полюса) в образовавшийся круг/прямоугольник. Провод должен отклоняться внутри подковообразного магнита, чтобы эксперимент вообще работал. Назовем такой провод проводник свинг .

Проводник будет отклоняться внутрь или наружу?

Прежде всего, здесь мы имеем дело с положительным зарядным током . Это означает: вам нужна ваша правая рука.

1. Большой палец – указывает в сторону положительного тока.

2. Указательный палец – указывает в сторону южного полюса подковообразного магнита.

3. Средний палец – затем указывает на внешнюю сторону подковообразного магнита.

Таким образом, на качели проводника действует сила Лоренца наружу.

В следующем уроке вы узнаете, как именно движущаяся заряженная частица отклоняется силой Лоренца в магнитном поле и почему это заставляет частицу двигаться по круговой или спиральной траектории.

Правило правой руки [Encyclopedia Magnetica]

Содержание

• Правило правой руки

  • Основания для «правила руки»

  • Направление магнитного поля

  • Направление магнитной силы

    • Магнитная сила в двигателях и генераторах

  • Множественность правил в литературе

  • См. также

  • Ссылки

Стэн Зурек, Правило правой руки, Encyclopedia Magnetica, E-Magnetica. pl

Правило правой руки – правило, которое используется для определения направления или «направленности» магнитного поля или магнитной силы по отношению к направлению условного электрического тока или движения положительных электрических зарядов. ^{Для отрицательных зарядов, таких как электроны, направление магнитной силы меняется на противоположное.}

. Существуют две основные версии «правила рук»: одна для направления магнитного поля , а другая для направления магнитной силы . Обычно они представляются как два отдельных правила, но в конечном итоге вытекают из одного и того же основного принципа.

В литературе есть много различных описаний этих правил с использованием: согнутых пальцев, вытянутых пальцев, открытой ладони и т. д., с несколькими мнемоническими приемами, которым обучают учеников и студентов, чтобы помочь запомнить, какие направления должны быть назначены данному пальцу, большому пальцу, или ладонь. Кроме того, обычно направление магнитной силы в двигателе и генераторе показано левой или правой рукой. Следовательно, у этих правил много названий: правило правой руки Флеминга , правило левой руки Флеминга , правило правой руки Ампера , правило большого пальца , правило штопора , конечное правило , правило часов или правило удара .

Все эти правила эквивалентны, поскольку направление физической магнитной силы (силы Лоренца) всегда одинаково.

«Ручные правила» для направления магнитной силы были предложены в 1890 году Джоном Амброузом Флемингом.

→ → → Полезная страница? Поддержите нас! → → →

PayPal

← ← ← Помогите нам с всего за $0,10 в месяц? Давай… ← ← ←

Причины «правила руки»

Определение левой и правой системы координат с векторным векторным произведением $\vec{c}=\vec{a} × \vec {b}$ выражается пальцами, вытянутыми под прямым углом

На фундаментальном уровне невозможно вычислить абсолютным образом значение бинарных величин, таких как положительное/отрицательное (электрический заряд), по часовой/против часовой стрелки (направление вращения), вверх/вниз (сторона поверхности), и т. д. Они могут быть определены только по отношению друг к другу или к какому-то близкому направлению в одной и той же системе координат.

Для трехмерной системы координат также ортогональность трех осей может быть определена как «левосторонняя» или «правосторонняя». Общепринято (по соглашению), что, если не указано иное, для некоторых расчетов, опубликованных в литературе, предполагается правосторонняя система. Это связано с тем, что некоторые математические функции (например, векторное перекрестное произведение) возвращали бы отрицательное значение, если бы расчет был выполнен в противоположной системе.

Правостороннюю систему можно определить двумя пальцами и большим пальцем, расположенными под прямым углом друг к другу:

• указательный палец указывает в положительном направлении как первая ось ( x )

• средний палец указывает в положительном направлении второй оси ( y )

• большой палец указывает в положительном направлении третьей оси ( z )

Положительное направление движения вектора по траектории C также определяется правой рукой

Векторное произведение двух векторов $\vec{a}$ и $\vec{b}$ представляет собой вектор $\vec{c}$, указывающий в третьем ортогональном направлении, поэтому то же самое правило правой руки можно использовать для определить направление результирующего вектора.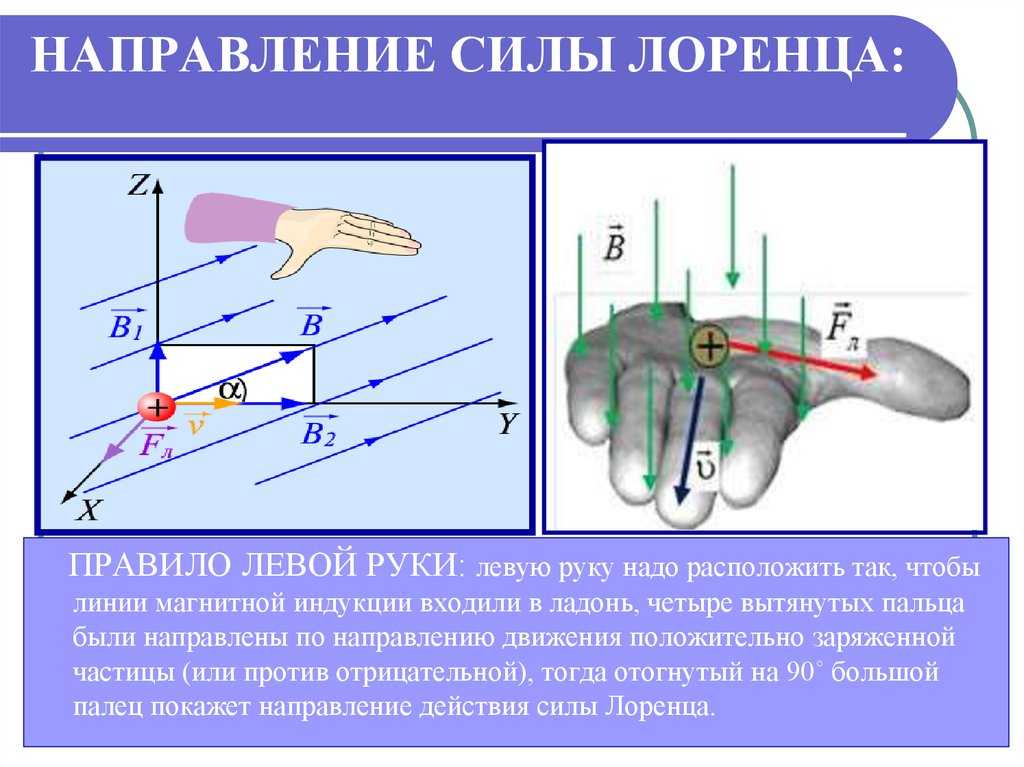

«Круговорот» вектора в правой системе также определяется правилом правой руки. Положительное направление единичного вектора $\hat{n}$, нормальное к поверхности $a$, указано большим пальцем, а согнутые пальцы указывают, в каком направлении следует брать интеграл по пути $C$.

Расчеты магнитных сил в трехмерном пространстве включают векторное исчисление, которое по соглашению работает в правосторонней системе, поэтому следует использовать правила правой руки (как указано выше).

Направление магнитного поля

Циркуляция вектора магнитного поля по отношению к току $I$ следует правилу правой руки циркулирует по прямому проводу с током, или магнитное поле создается вдоль оси петли с током или соленоида

Для направления магнитного поля правило аналогично правилу обращения вектора.

Правая рука изображена с большим пальцем, следующим за направлением тока в прямом проводе, а согнутые пальцы показывают направление, в котором магнитное поле (плотность потока B или напряженность магнитного поля H ) циркулирует вокруг провода.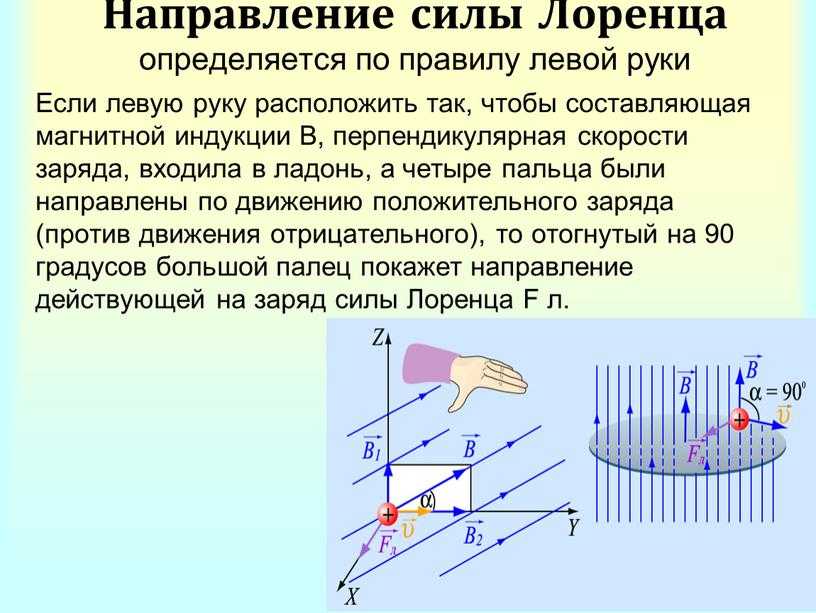

Правило в равной степени применимо и к альтернативной ситуации, когда ток течет по контуру (или соленоиду) и магнитное поле создается вдоль направления оси такого контура.

Тогда правило применяется даже в том случае, если большой палец указывает в направлении поля, а согнутые пальцы показывают направление тока в петле.

Для такой петли магнитные полюса N и S появляются на каждом конце, и их можно отличить по стилизованным буквам со стрелками на концах, которые показывают видимое направление «вращения» тока в петле. Как показано на рисунке, если смотреть с конца, отмеченного буквой «N», кажется, что ток течет в направлении против часовой стрелки. В то же время, если смотреть с конца, отмеченного буквой «S», кажется, что ток течет по часовой стрелке.

На некоторых иллюстрациях показана рука, сжимающая соленоид или провод, отсюда и название правила захвата .

Большой палец указывает в том же направлении, что и северный магнитный полюс при применении правила правой руки к соленоиду; магнитные полюса обозначаются N и S

Магнитные полюса N и S созданы для любого контура электрического тока

Compass needles follow the direction of magnetic field ( B or H ) around the wire with current I

Направление магнитной силы

Другое применение правила правой руки связано с аналогией направления магнитной силы, действующей на движущуюся заряженную частицу или провод с током, помещенный в магнитное поле. В некоторой литературе это правило обсуждается так, как если бы оно было отдельным правилом от правила, описанного в разделе выше, но оно вытекает из тех же принципов.

Сила Лоренца F , действующая на электрический заряд q , движущийся со скоростью v , обусловлена ​​электрическим полем E и магнитным полем B магнитным потоком:

$$\vec{F} = q·\vec{E} + q·\vec{v} × \vec{B}$$

(N)

В отсутствие электрического поля (Е=0) или если его влияние пренебрежимо мало, уравнение сводится к приведенному ниже, и поле, удовлетворяющее действию B вектор считается, что определение магнитного поля :

Силы магнитной. Следуют Правило правого холма:

1111111111111111111111111111111111111111111110 ГОДА. движение (текущее $I$) по пути $l$

• средний палец показывает направление магнитного поля $B$

• Большой палец показывает направление магнитной силы $F$

$$\vec{F} = q·\vec{v} × \vec{B}$$

(N)

Это уравнение включает векторное перекрестное произведение, которое вычисляется в правосторонней системе координат, и, следовательно, магнитная сила следует тому же правостороннему принципу, что и для определения самой правосторонней системы – с помощью двух пальцев и большого пальца, помещенных под прямым углом друг к другу.

Указательный палец показывает направление первого вектора, который в данном случае является направлением первоначального движения положительного заряда $q$, составляющего условных единиц электрического тока $I$. В обычном проводнике, если к нему приложить некоторое напряжение, электроны будут течь в противоположном направлении, но здесь учитывается обычный ток (текущий от плюса к минусу).

Средний палец показывает направление второго вектора, который является направлением магнитное поле $B$.

Большой палец указывает в третьем ортогональном направлении, а именно в направлении магнитной силы $F$, действующей на заряд, движущийся в магнитном поле.

Если электрический заряд имеет отрицательное значение (например, электрон), то сила действует в противоположном направлении.

Если и направление движения, и полярность заряда меняются местами, то сила действует в том же направлении. Например, на иллюстрации справа показана ситуация для гипотетического положительного заряда, движущегося от плюса к минусу за счет тока в проводе, и сила действует вверх. В том же проводе электроны будут течь от минуса к плюсу в направлении, противоположном обычному току. А поскольку две переменные были изменены (полярность заряда и направление его движения), то на такие электроны сила все равно будет действовать вверх. В самом деле, в реальном проводе движутся только отрицательно заряженные электроны, а положительно заряженные протоны остаются связанными с атомами, неподвижными по отношению к телу провода.

Сила магнитного поля в двигателях и генераторах

Здесь следует отметить, что магнитная сила для положительного заряда всегда следует этому правилу, независимо от каких-либо других условий. Следовательно, одно и то же правило правой руки применимо как к двигателям, так и к генераторам.

В двигателях обычное движение зарядов вызывается обычным током, протекающим по рассматриваемому проводнику. Магнитная сила толкает проводник в третьем ортогональном направлении, вызывая физическое перемещение проводника и создавая полезный выходной крутящий момент.

Однако в генераторах заряды изначально перемещаются, потому что провод толкается некоторым входным крутящим моментом. Заряды движутся вместе с проводом, а магнитная сила толкает их вдоль провода, создавая таким образом электродвижущую силу (ЭДС).

Поэтому правило правой руки легко запомнить, так как указательный палец всегда показывает исходное направление движения заряда (как если бы указательный палец толкал заряд), средний палец всегда показывает направление магнитного поля, а указательный палец всегда показывает направление движения заряда. большой палец всегда показывает направление магнитной силы. Эта логика согласуется с применением векторного векторного произведения, как объяснялось выше для правосторонней системы координат.

Магнитная сила в двигателе подчиняется правилу правой руки:

• указательный палец – направление тока $I$ (который перемещает заряд $q$)

• средний палец – направление магнитного поля $B$

• большой палец показывает направление магнитной силы $F$

• сила пропорциональна длине провода $l$

Магнитная сила в генераторе также подчиняется правилу правой руки: движение

средний палец – направление магнитного поля $B$

большой палец – направление магнитной силы $F$, действующей на заряд и индуцирующей электродвижущую силу ЭДС

Множественность правил в литературе

. правой руки, в таком положении, чтобы они были как можно ближе друг к другу под прямым углом (см. рис. 45). Затем сделайте следующие ассоциации. Пусть направление указательного пальца представляет направление магнитного потока ( F руда и F люкс). Пусть направление большого пальца представляет направление движения проводника (чт M b и M otion). Наконец, пусть направление среднего пальца представляет собой направление индуцируемой электродвижущей силы (M I ddle и I индуцируемая).

^{Э. и Ф. Н. Спон, общественное достояние}

Первоначальное «правило руки», введенное Флемингом, определяло направление индуцированной электродвижущей силы. В книге «Магниты и электрические токи», изданной в 1902, Флеминг дал следующее описание и мнемонику, связывающую буквы с названиями пальцев и переменных. В этой публикации было определено только правило правой руки, как показано на рисунке.

Однако в настоящее время есть публикации, в которых упоминается правило левой руки Флеминга для магнитной силы в двигателях и правило правой руки для генераторов.

Одна версия с левой рукой иногда в просторечии упоминается мнемоническим словом «ФБР», что облегчает запоминание, потому что в этой конкретной версии:

• M движение в направлении чт M б (для силы F )

• F люкс или F поле действует в направлении F первого пальца (для магнитного поля B )

• С ток в направлении се С на палец (для тока я )

Таким образом, в последовательности «большой палец — первый — второй» создается мнемоника F-B-I.

Имя правило штопора сравнивает направления вращения штопора или правого винта

Однако следует подчеркнуть, что все эти различные изображения правильны только в отношении направлений и числовых значений. Упрощенные скалярные уравнения, такие как: $F = B·l·I$ и $EMF = B·l·v$, работают только при неявном предположении, что все значения представлены ортогональными векторами, что неверно для общего случая ( если заряд движется вдоль магнитного поля, то магнитной силы нет). Следовательно, должна быть включена дополнительная информация, такая как косинус угла между величинами. ^{Принимая во внимание, что с векторной записью правило правой руки эффективно иллюстрирует векторное перекрестное произведение, которое верно при любых условиях, если векторное умножение учитывается правильно.}

Иногда правило правой руки также сравнивают с направлением вращения, которое делается при закручивании штопора или правого винта (то есть любого обычного винта или резьбы, например, крышки на банке или бутылке), чтобы затянуть его. или как если бы сверление происходило по часовой стрелке (если смотреть сверху).

Одно и то же правило, представленное левой или правой рукой, требует, чтобы разные пальцы были присвоены разным переменным

Эта множественность создает ненужные сложности и путаницу, что затрудняет понимание всего предмета.

Скорее всего, это связано с тем, что один и тот же тип ортогональности может быть представлен различными конфигурациями пальцев на любой руке. Пальцы могут быть вытянуты ортогонально, а ладонь может быть плоской (отсюда правило пощечины ).

Как объяснялось выше, все эти различные версии (правая или левая рука, открытая ладонь или вытянутые пальцы) абсолютно эквивалентны в том, что касается направлений, потому что магнитная сила всегда действует одним и тем же образом.

См. также

• Магнитная сила

Ссылки

---

¹⁾ Lexico.com / Правило правой руки, {дата обращения: 02.06.2021}

²⁾ Правило Флеминга правой и левой руки, Энциклопедия электротехники, www.RealInfo.com, {дата обращения: 02.06.2021}

³⁾ Йоахим Штер; Ганс Кристоф Зигманн, Магнетизм, от основ до нанодинамики, Springer Nature, 2007, ISBN 3540302832

^{4) , 4) , 4) , 4) , 4) , 4) , 4)} Э. М. Перселл, Д.Дж. Морин, Электричество и магнетизм, 3-е издание, Cambridge University Press, 2013, ISBN 9781107014022

^{5) , 5)} Правило захвата правой руки/большого пальца, правило штопора и правило конца/часа, Electrical Technology, www.electricaltechnology.org, {дата обращения: 02.06.2021}

⁶⁾ Charles H. Holbrow, Джеймс Н. Ллойд, Джозеф К. Амато, Энрике Гальвез, М. Элизабет Паркс, Современная вводная физика, 2-е изд., Спрингер, Нью-Йорк, ISBN 97803877

^{7) , 7) , 7) , 7) , 7)} Ричард Фейнман, Роберт Лейтон, Мэтью Сэндс, Ферромагнетизм, Фейнмановские лекции по физике, Vol. II, Basic Books, ISBN: 9780465079988

^{8) , 8) , 8)} Дэвид Дж. Гриффитс, Введение в электродинамику, 4-е изд., Пирсон, Бостон, 2013, ISBN 0321856562

^{9) , 9) , 9)} Дж.А. Флеминг, Магниты и электрические токи, Элементарный трактат для использования мастерами-электриками и учителями естественных наук, 2-е издание, E. & FN. Спон Лимитед, Нью-Йорк, 19 лет.02

¹⁰⁾ Правила правой и левой руки, Magnet Academy, https://nationalmaglab.org, {дата обращения: 02.06.2021}

¹¹⁾ Б.Д. Каллити, К.Д. Грэм, Введение в магнитные материалы, 2-е издание, Wiley, IEEE Press, 2009, ISBN 9780471477419

¹²⁾ AE Fitzgerald, Charles Kingsley Jr., Stephen D. Umans, Electric Machinery, 6-е издание, Бостон, 2003 г., ISBN 0-07-112193-5

¹³⁾ Славомир Туманьски, Справочник по магнитным измерениям, CRC Press / Taylor & Francis, Boca Raton, FL, 2011, ISBN 9780367864958

¹⁴⁾ Д.П. Котари, И.Дж. Награт, Электрические машины, 4-е издание, Tata McGraw Hill Education, Лондон, ISBN 9780070699670

^{15) , 15)} Махеш Шеной, правление левой руки Флеминга, Академия Хана, {дата обращения: 14.06.2021}

¹⁶⁾ Валерий Руднев; Дон Лавлесс; Раймонд Л.