Математический анализ. Дифференциальное исчисление
Математический анализ. Дифференциальное исчисление
ОглавлениеПРЕДИСЛОВИЕГЛАВА 1. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ 2.  Определение непрерывности функции в точке «на языке приращений».2. Связь между непрерывностью и дифференцируемостью функции в точке. 3. Производная и дифференциал. 4. Односторонние и бесконечные производные. § 3. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧ 2. Геометрические приложения производной. 3. Применения производной в физических задачах. Механический смысл производной. § 4. ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАЦИЙ 2. Дифференцирование произведения. 3. Дифференцирование частного. § 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ 2. Инвариантность формы записи дифференциала. § 6. ДИФФЕРЕНЦИРОВАНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Дифференцирование обратной функции. 4. Дифференцирование показательной и логарифмической функций. 5. Дифференцирование гиперболических функций. 6. Сводка правил и формул дифференцирования.  7. Логарифмическое дифференцирование. § 7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. Механический смысл второй производной. 3. Натуральная степень бинома (формула Ньютона). 4. Свойства производной n-го порядка. 5. Дифференциалы высшего порядка. ГЛАВА 2. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 1. СВЯЗЬ МЕЖДУ ХОДОМ ИЗМЕНЕНИЯ ФУНКЦИИ И ЕЕ ПРОИЗВОДНОЙ § 2. ТЕОРЕМА ЛАГРАНЖА И ЕЕ СЛЕДСТВИЯ 2. Теорема 2 (теорема Ролля). 3. Теорема Лагранжа. 4. Условие постоянства функции. § 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ 2. Исследование функций на экстремум с помощью первой производной. 3. Использование второй производной для исследования функций на экстремум. 4. Нахождение наибольшего и наименьшего значений функции на данном отрезке. § 4. ВЫПУКЛЫЕ ФУНКЦИИ 2. Достаточные условия выпуклости. 3. Точки перегиба. § 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ И РЕШЕНИЮ УРАВНЕНИЙ 2.  § 6. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ФУНКЦИЙ 2. Правило Лопиталя. § 7. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ § 8. КРИВЫЕ НА ПЛОСКОСТИ 2. Жордановы кривые. 3. Связь между различными видами уравнений линий. 4. Дифференцирование параметрически заданных функций. 5. Полярное уравнение кривой. 6. Производная второго порядка для параметрически заданной функции. 7. Построение кривых, заданных параметрическими уравнениями. 8. Построение кривых, заданных полярными уравнениями. ОТВЕТЫ |
44.Правило Лопиталя. Следствие о раскрытии неопределенностей разных видов.
Если функции f
Поэтому можно поставить задачу вычисления
предела этого отношения при x→a. Вычисление таких пределов называют
обычно «раскрытием неопределенностей
вида {0/0}».Теорема 20.3 (правило Лопиталя). Пусть функции f(x) и g
Доказательство.
Выберем Из теоремы Коши следует, что такое, что . По условию теоремы f(a)=g(a)=0, поэтому . При . При этом, если существует , то существует и . Поэтому Теорема доказана.
Пример. при a>0.
Замечание 1. Если f(x) или g(x) не определены при х=а, можно доопределить их в этой точке значениями
Тогда обе функции будут непрерывными
в точке а,
и к этому случаю можно применить теорему
20.3.Замечание 2. Если f′(a)=g′(a)=0 и f′(x) и g′(x) удовлетворяют условиям, наложенным в теореме 20.3 на f(x) и g(x), к отношению можно еще раз применить правило Лопиталя: и так далее.
Пример.
Правило Лопиталя можно применять и для раскрытия неопределенностей вида , то есть для вычисления предела отношения двух функций, стремящихся к бесконечности при
Теорема 20.4. Пусть функции f(x) и g(x) непрерывны и дифференцируемы при в окрестности точки а, причем в этой окрестности. Тогда, если и существует , то существует и , причем
.
Доказательство.
Выберем
в рассматриваемой окрестности точки а точки α и х так, чтобы α < x < a (или a < x < α).
, откуда . (20.3) Так как , можно для любого малого ε выбрать α настолько близким к а, что для любого с будет выполняться неравенство ,
или . (20.4) Для этого же значения ε из условия теоремы следует, что (так как ), поэтому
, или . (20.5)
Перемножив неравенства (20.4) и (20.5), получим
, или, после использования равенства (20.3):
. Поскольку ε – произвольно малое число, отсюда следует, что А= , что и требовалось доказать.
Замечание 1. Теорема 20.4 верна и при А= . В этом случае . Тогда и
, следовательно, .
Замечание
2. Теоремы 20.3 и 20.4 можно доказать и для
случая, когда .
Пример.
Рассмотрим функцию y=f(x), имеющую в окрестности точки х=а все производные до порядка (n+1) включительно, и поставим задачу: найти многочлен y=Pn(x) степени не выше
(21.1)
Пусть искомый многочлен имеет вид:
Pn(x)=C0+C1(x-a)+C2(x-a)²+…+Cn(x-a)n. (21.2)
При этом
Тогда
(21.3)
Из формул (21.3) можно выразить коэффициенты Сi через значения производных данной функции в точке
Замечание. Произведение последовательных натуральных чисел 1∙2∙3∙…∙(n-1)n называется факториалом числа n и обозначается
n! = 1∙2∙3∙…∙(n-1)n . (21.4)
Дополнительно вводится 0!=1.
Используя это обозначение, получим:
(21.5)
Таким образом, искомый многочлен имеет вид:
(21.6)
Обозначим через Rn(x) разность значений данной функции f(x) и построенного многочлена Pn(x): Rn(x) = f(x) – Pn(x), откуда f(x) = Pn(x) + Rn(x) или
(21.
7)
Полученное представление функции называется формулой Тейлора, а Rn(x) называется остаточным членом формулы Тейлора. Для тех значений х, для которых Rn(x) мало, многочлен Pn(x) дает приближенное представление функции f(x). Следовательно, формула (21.7) дает возможность заменить функцию y = f(x) многочленом y = Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn(x).
Исчисление– Доказательство правила L’Hospitals
Это ответ на запрос Долдрамса, но слишком длинный для комментария.
Теорема:
Если производная функции $\hspace{.04 in}f$ всюду неотрицательна, то $\hspace{.04 in}f$ не убывает.
$\implies$
Если $\hspace{.04 in}f$ дифференцируемо и $\:\hspace{.04 in}f'(x) = 0\:$ для всех $\;\; x\: \in \: (a,b) \;\;$, $\;\;$, то $\hspace{.04 in}f$ является константой.
Доказательство:
Предположим, что $\hspace{.04 in}f$ дифференцируемо и $\:\hspace{.04 in}f'(x) = 0\:$ для всех $\:\: x\: \in \: ( а, б) \;\;$.
Пусть $\;\; g \: : \: (a,b) \to \mathbb{R} \;\;$ определяется выражением $\: g(x) = -(\hspace{0,05 in}f(x)) \; $.
Для всех $\:\: x\: \in \: (a,b) \:\:$,
$g'(x) \: = \: (g(x))’ \: = \: (-(\hspace{.05 in}f(x)))’ \: = \: -((\ hspace{0,05 дюйма}f(x))’) \: = \: -(\hspace{0,05 дюйма}f'(x)) = -0 = 0 \;\;\;$.
Для всех элементов $x$ и $y$ из $(a,b)$, $\;\;$[$\;\; \hspace{.04 in}f(x) \leq \hspace{.04 in}f(y) \: \text{ и } \: g(x) \leq g(y)$
$\ подразумевает \;\;\hspace{0,04 дюйма}f(x) \leq \hspace{0,04 дюйма}f(y) \: \text{ и } \: -\hspace{-0,04 дюйма}( \hspace{0,05 дюйма}f(x)) = g(x) \leq g(\hspace{0,03 дюйма}y) = -(\hspace{0,05 дюйма}f(\hspace{0,03 дюйма}y ))$
$\подразумевает \;\; \hspace{0,04 дюйма}f(x) \leq \hspace{0,04 дюйма}f(\hspace{0,03 дюйма}y) \: \text{ и } \: \hspace{0,04 дюйма}f(\ hspace{.
03 in}y) \leq \hspace{.04 in}f(x) \;\; \подразумевает\;\; \hspace{0,04 дюйма}f(x) = \hspace{0,04 дюйма}f(\hspace{0,03 дюйма}y) \;\;$]$\;\;$.
Если $\hspace{0,04 in}f$ и $g$ неубывают, то $\hspace{0,04 in}f$ является константой.
Если выполнено первое предложение (основного) следствия теоремы,
, то верно второе предложение этой теоремы. $\:$ Следовательно, теорема верна.
Теорема: $\;\;\;$ Если $\:\operatorname{Dom}(\hspace{.05 in}f\hspace{.02 in})\:$ интервал, то
Если производная функции $\hspace{.04 in}f$ всюду неотрицательна, то $\hspace{.04 in}f$ не убывает.
$\implies$
Если производная функции $\hspace{.04 in}f$ везде строго положительна,
, то $\hspace{.04 in}f$ — строго возрастающая функция.
.
Доказательство:
Предположим, что верно первое предложение стрелки теоремы, а затем предположим, что производная от $\hspace{.04 in}f$ везде строго положительна, и что входы $x$ и $y$ такой, что $\: x< y\:$ и $\: \hspace{.
04 in}f(x) \leq \hspace{.04 in}f(\hspace{.03 in}y) \ ;$. $\;\;\;$ Для всех элементов $z$ из $[x,y]$, $\: \hspace{.04 in}f(x) \leq \hspace{.04 in}f(z) \leq \hspace{0,04 дюйма}f(\hspace{0,03 дюйма}y) = \hspace{0,04 дюйма}f(x) \;$.
$\hspace{0,04 in}f$ постоянно на $[x,y]$. $\;\;\;$ Для $\: w = \frac{x+z}2 \:$ и $h$ такие, что $\: 0 < |h| < \frac{y-x}2 \:$, $\:$ $\;\; w+h \: \in \: [x,y] \;\;\;$.
Для $\: w = \frac{x+z}2 \:$ и $h$ таких, что $\: 0 < |h| < \frac{y-x}2 \:$, $\:$ $\: \frac{\hspace{0,04 дюйма}f(w+h)-\hspace{0,04 дюйма}f(w)}h = \ frac{\hspace{0,04 дюйма}f(w+0)-\hspace{0,04 дюйма}f(w+0)}h = \frac{0-0}h = \frac0h = 0 \;\;$ .
Поскольку $\: x< y\:$, $\: 0 < \frac{y-x}2 \:$, $\:$, поэтому $\;\; \hspace{04 дюйма}f'(w) \; "=" \displaystyle\lim_{h\to 0} \frac{\hspace{0,04 дюйма}f(w+h)-\hspace{0,04 дюйма}f(w)}h \; "=" \displaystyle\lim_{h\to 0} \: 0 \; "=" 0 \;\;$,
, что противоречит предположению второго предложения стрелки теоремы.
Это противоречие показывает, что второе предложение стрелки теоремы следует
из предположения в начале этого доказательства.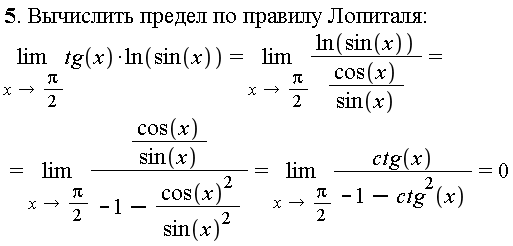
$\:$ Следовательно, теорема верна.
Теорема:
Если $x$ находится внутри $\operatorname{Dom}(\hspace{.05 in}f\hspace{.02 in})$ и $x$ является локальным слабым
существует экстремум $\hspace{.04 in}f$ и $\hspace{.04 in}f'(x)$, тогда $\: \hspace{.04 in}f'(x) = 0 \; $.
Доказательство:
Предположим, $\epsilon$ таков, что $\:0<\epsilon \:$ и $\: (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\ hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon) \subseteq \operatorname{Dom}(\hspace{0,05 дюйма}f\hspace{0,02 дюйма}) \:$ и $x$ слабо
максимизирует $\hspace{0,04 дюйма}f$ на интервале $\:(x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{ -0,04 дюйма}\эпсилон)\;$. $\;\;\;$ Для всех $h$, $\: \big|\hspace{-0,04 дюйма}\pm\hspace{-0,04 дюйма}|h|\big| = |ч| \;$.
Для всех $h$, если $\: 0<|\hspace{.02 in}h\hspace{.01 in}|<\epsilon \:$, то $\:h\neq 0\:$ и $\ ;\; x\hspace{-0,02 дюйма}\pm\hspace{-0,01 дюйма}|h| \: \in \: (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon) \subseteq \operatorname{ Дом}(\hspace{0,05 дюйма}f\hspace{0,02 дюйма}) \;\;$.
Для всех $h$, если $\: 0<|\hspace{.02 in}h\hspace{.01 in}|<\epsilon \:$, то $\:\: \frac{\hspace{.04 in}f(x+|h|)-f(x)}{|h|} \leq \frac{\hspace{0,04 дюйма}f(x)-\hspace{0,04 дюйма}f(x)}{ |h|} = \frac{0-0}{|h|} = \frac0{|h|} = 0 \;\;$.
Для всех $h$, если $\: 0<-|\hspace{.02 in}h\hspace{.01 in}|<\epsilon \:$, то $0 = \frac0{|h|} = \frac {0-0}{|h|} = \frac{\hspace{0,04 дюйма}f(x)-\hspace{0,04 дюйма}f(x)}{|h|} = \frac{\hspace{ 0,04 дюйма}f(x)-\hspace{0,04 дюйма}f(x+(-|h|))}{|h|} \leq \frac{-(\hspace{0,04 дюйма}f(x+( -|h|))-f(x))}{|h|} = \frac{--(\hspace{.04 in}f(x+(-|h|))-f(x))}{ -|h|} = \frac{\hspace{0,04 дюйма}f(x+(-|h|))-f(x)}{-|h|} \;\;$.
Для всех $h$, если $\: 0 < |h| < \epsilon \:$, тогда $\: \frac{\hspace{0,04 дюйма}f(x+|h|)-f(x)}{|h|} \leq 0\leq \frac{\hspace{. 04 in}f(x+(-|h|))-f(x)}{-|h|} \;$.
Если $\; \displaystyle\lim_{h\to 0} \frac{\hspace{0,04 in}f(x+h)-f(x)}h \;$ существует, тогда $\;\; \displaystyle\lim_{h\to 0} \frac{\hspace{0,04 дюйма}f(x+h)-f(x)}h \; “=” 0 \;\;\;$.
Если $\hspace{.04 in}f'(x)$ существует, то $\: \hspace{.04 in}f'(x) = 0 \;$.
Теперь предположим, что $\epsilon$ таков, что $\:0<\epsilon \:$ и $x$ слабо минимизирует $\hspace{0,04 in}f$ на интервале $\:(x\hspace{-0,04 in }-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon)\;$.
Пусть $g$ задается как $\:g(y) = -(\hspace{.05 in}f(y))\;$. $\;\;\;$ Для всех $\: y\in (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 in}\эпсилон) \:$,
$-(г(х)) \; “=” –(\hspace{0,05 дюйма}f(x)) \; “=” \hпробел{0,04 дюйма}f(x) \; \leq\; \hspace{04 дюйма}f(y) \; “=” –(\hspace{0,05 дюйма}f(y)) \; “=” -(г(у)) \;\;\;$.
Для всех $\: y\in (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon) \: $, $\:$ $\: g(y) \leq g(x) \;$. $\;\;\;$ $x$ слабо максимизирует $g$ на $\:(x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\ hspace{-0,04 дюйма}\эпсилон)\;$.
Согласно предыдущей части этого доказательства, если $g'(x)$ существует, то $\:g'(x) = 0 \;$. $\;\;\;$ Если $\hspace{.04 in}f'(x)$ существует, то
$\hspace{0,04 дюйма}f'(x) \: = \: (\hspace{0,05 дюйма}f(x))’ \: = \: -\hspace{-0,04 дюйма}-\hspace{ -0,04 дюйма}((\hspace{0,05 дюйма}f(x))’) \: = \: -((-(\hspace{0,05 дюйма}f(x)))’) \: = \: -((g(x))’) \: = \: -(g'(x)) \: = \: -0 \: = \: 0 \;\;\;$.
В обоих случаях получено, что “если $\hspace{.04 in}f'(x)$ существует, то $\:\hspace{.04 in}f'(x) = 0\:$”. $\;\;$ Следовательно, теорема верна.
анализ – Почему правило Лопиталя требует существования предела? О доказательстве.
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 602 раза
$\begingroup$
Доказательство правила Лопиталя (на этот раз только частный случай):
Предположим, что $$ f(a)=g(a)=0 .
$$
Используя МВТ, получаем $$ \frac {f (x)} {g (x)} = \ frac {f (x) -f (a)} {g (x) -g (a)} = \ frac {f ‘(\ zeta)} {g ‘(\zeta)}, \ \mathrm{где} \ \zeta \in (a, x) \ \mathrm{or} \ \zeta \in (x, a) $$ и поэтому $$ \lim_{x \rightarrow a} \frac{f(x)}{g(x)}=\lim_{x \rightarrow a} \frac{f'(\zeta)}{g'(\zeta)}= \lim_{\zeta \rightarrow a} \frac{f'(\zeta)}{g'(\zeta)}=\lim_{x \rightarrow a} \frac{f'(x)}{g'(x )}. $$
В литературе всегда предполагается, что предел $$ \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)} $$ существует. Почему так и как это показано в доказательстве? Согласно приведенному выше доказательству, не должен ли предел f/g всегда совпадать с пределом f’/g’? Если lim f’/g’ не определено, то и lim f/g не следует определять.
Очевидно, это не так, потому что есть примеры функций f и g s.t. lim f/g существует, хотя lim f’/g’ не существует.
- пределы
- анализ
- решение-проверка
$\endgroup$
7
$\begingroup$
Правило Лопиталя — это утверждение «если», а не «если и только если».
Это говорит нам, что если
$\displaystyle \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}$
существует, то
$\displaystyle \lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}$
, но ничего не говорит о случае, когда $\displaystyle \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}$ не существует. В этом случае $\displaystyle \lim_{x \rightarrow a} \frac{f(x)}{g(x)}$ может существовать или не существовать – как вы говорите, есть примеры каждой возможности.
Если $\displaystyle \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}$ не существует, то, хотя мы можем знать, что
$\displaystyle \frac {f (x)}{g(x)} = \frac {f'(\zeta_1)}{g'(\zeta_2)}$
для некоторых $\zeta_1, \zeta_2 \in (x,a)$, правая часть не стремится к определенному значению как $x \rightarrow a$, поэтому мы не можем ничего сказать о поведении левой части.
$\endgroup$
2
$\begingroup$
Правило L’Hospital «требует» наличия предела, потому что если его нет, вы застряли, и правило бесполезно.
В частности, функции $f,g$ могут быть недифференцируемыми.
$\endgroup$
$\begingroup$
Я думаю, что путаница происходит из-за конкретной версии L’Hosital используется. Вот версия Лопиталя, которая явно требует существования предельного отношения производных. Я также приведу пример, когда это не удается. Надеюсь, это поможет.
Теорема: Предположим, что $f,g$ — дифференцируемые функции в интервале $(a,b)$. Если
- $\lim_{x\rightarrow a+}f(x)=0=\lim_{x\rightarrow a+}g(x)$,
- $g'(x)\neq0$ в $(a,b)$ и
- $\lim_{x\rightarrow a+}\frac{f'(x)}{g'(x)}$ существует и имеет значение $L$ (здесь $L$ — либо вещественное число, $\infty$, либо $-\infty$)
, то $\lim_{x\rightarrow a+}\frac{f(x)}{g(x)}$ существует и равен $L$.
Примечания:
- Аналогичный результат справедлив для $x\rightarrow b-$.
- Аналогичные версии существуют, когда в (1) $0$ заменяется на $\pm\infty$.
Вот краткое доказательство того, что $a$ и $L$ конечны . По условию (1) мы можем расширить $f$ и $g$ до $[a,b)$, положив $f(a)=0=g(a)$. Для $\varepsilon>0$ существует $x_\varepsilon\in (a,b)$ такое, что
$$
\Big|\frac{f'(x)}{g'(x)}-L\Big|<\varepsilon, \qquad\text{для всех}\quad a Случай, когда $L$ не конечен, обрабатывается аналогично. Когда $a=-\infty$ ($b=\infty$), работает небольшая модификация приведенного выше доказательства. Наблюдения: Из всех предположений, сделанных в формулировке теоремы Лопиталя, предположение (3) является источником многих неправильных представлений среди студентов. важно понять, что на самом деле говорит Лопиталь: при условии (1) и (2) существование $\lim_{x\rightarrow a+}\frac{f'(x)}{g ‘(x)}$ подразумевает существование $\lim_{x\rightarrow a+}\frac{f(x)}{g(x)}$, , но не наоборот (см. примеры 1, 3) . При условиях (1) и (2) существование $\lim_{x\rightarrow a+}\frac{f(x)}{g(x)}$ не влечет существование $\lim_ {x \ rightarrow a+} \ frac {f'(x)}{g'(x)}$. Конечно, при рассмотрении изложенного выше доказательства существование первого подразумевает существование второго на подмножестве значений ($c_x$), приближающемся к $a+$, но это не то же самое, что сказать, что предел $\lim_ {x\rightarrow a+}f'(x)/g'(x)$ (неограниченный подход к $a+$) существует (см. пример 3). Отсутствие априорной информации об условии (3) означает, что при применении процедуры замены оценки предела $f/g$ на оценку предела отношения $f’/g’$, результат может быть неопределенным и неубедительным (обходить петли).
Это связано с тем, что хотя (1) и (2) легко проверить, (3) обычно не поддается априорной проверке. Предположение (3) является разновидностью условия clarivoyant .