lim онлайн
Вы искали lim онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и бесконечный калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «lim онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как lim онлайн,бесконечный калькулятор,вычисление пределов онлайн с подробным решением бесплатно,вычислить предел последовательности онлайн,вычислить предел последовательности онлайн с подробным решением,вычислить предел числовой последовательности,вычислить пределы не пользуясь правилом лопиталя,замечательные пределы калькулятор онлайн,замечательный предел калькулятор онлайн,замечательный предел онлайн калькулятор,калькулятор онлайн замечательный предел,калькулятор онлайн пределы с подробным решением,калькулятор онлайн решение пределов с подробным решением,калькулятор пределы с подробным решением,калькулятор решение пределов с подробным решением,мти найдите предел,найдите предел мти,найти предел онлайн,найти предел последовательности онлайн,найти предел последовательности онлайн с решением,онлайн вычислить предел последовательности,онлайн калькулятор замечательные пределы,онлайн лимиты,онлайн решение последовательностей,онлайн решение пределов подробно,онлайн решение пределов с дробями,правило лопиталя онлайн калькулятор с подробным решением,предел числовой последовательности калькулятор онлайн,решение лимитов онлайн с подробным решением,решение онлайн млит,решение последовательностей онлайн,решение пределов онлайн бесплатно с подробным решением,решение пределов онлайн с дробями,решение пределов подробно онлайн,решение пределов последовательности онлайн,решение пределов с дробями онлайн,решение пределов с подробным решением онлайн калькулятор,решить онлайн лимит.
Где можно решить любую задачу по математике, а так же lim онлайн Онлайн?
Решить задачу lim онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Онлайн-калькулятор вычисления пределов | СпецКласс
Как быстро решить предел? Воспользоваться любым онлайн-калькулятором, ибо их сейчас предоставляется невероятное множество. Но вот только не все онлайн калькуляторы вам с этим помогут.
Но вот только не все онлайн калькуляторы вам с этим помогут.
Неделю назад меня попросили решить один простой пример, которые с помощью правила Лопиталя решался в 1 строчку. Как любой нормальный человек, я не стал решать его самостоятельно и решил найти онлайн-калькулятор, который сделает это за меня. Тем более, что пример был плёвый:
В итоге я нашел парочку онлайн-калькуляторов, которые посчитали мне правильный ответ примера, но к сожалению, содержали ошибки внутри самого решения. И вот как это у них получилось.
Есть классный математический сервис, который называется Wolframalpha. Это международная компания, которая выпускает серьезный софт для ученых: в частности Mathematica. У них есть онлайн-версия, которая позволяет получить ответы на множество вопросов, особенно если вы знаете английский. Виджет, взятый с их сайта, расположен ниже, и с его помощью вы можете получить ответ любого предела, который вам задали в институте.
Так вот, как работают многие онлайн-калькуляторы в Интернете? Сперва надо ввести ваш пример. Для этого в калькуляторе есть поля ввода самого предела и поле для ввода значения, к которой стремится переменная в вашем пределе. В случае с виджетом от wolframalpha, в поле “limit of ” нужно ввести сам предел (используя правила написания формул, такие же как в LaTex), а в поле “as x approaches” ввести значение, к которому стремится переменная Х из вашего предела. Например:
Для этого в калькуляторе есть поля ввода самого предела и поле для ввода значения, к которой стремится переменная в вашем пределе. В случае с виджетом от wolframalpha, в поле “limit of ” нужно ввести сам предел (используя правила написания формул, такие же как в LaTex), а в поле “as x approaches” ввести значение, к которому стремится переменная Х из вашего предела. Например:
- если Х стремится к 2, то пишем просто ” 2 “.
- если Х стремится к единице слева, пишем ” 1-0 “
- если Х стремится к минус бесконечности, пишем ” – infinity “
Не волнуйтесь, если ошибетесь: виджет либо выдаст ошибку, либо сам исправит ваш запрос. В любом случае помимо ответа вы увидите, какой предел возьмет виджет и чему он будет равен?
А что делают онлайн-калькуляторы на других сайтах? Они “парсят” ваш предел, и с помощью LaTex записывают его в красивом виде. Дальше им нужно его решить, но раз вы ищите решение предела онлайн, или же просто вбили в поиске онлайн-калькулятор решения пределов, то скорее всего вы сами толком не знаете, как должно выглядеть правильное решение этого примера.
Еще один минус в работе таких “онлайн-калькуляторов” состоит в том, что их решение может быть неоптимальным. Очень часто вас просят найти предел определенным способом. Калькуляторы же ищут решения стандартным способом, одинаковым для всех. Так что если вы учитесь в серьезном техническом вузе, или ваш преподаватель серьезно относится к проверке ваших занятий, то вас скорее всего раскусят). Единственный способ избежать этого – понимать, что написано в решении вашего примера. В видеоуроках я разбираю, как подходить к тем или иным примерам, и на что стоит обращать внимание. Ну а после того, как вы самостоятельно решите пару десятков примеров, у вас выработается собственная “чуйка”.
| 1 | Trovare la Derivata – d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata – d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata – d/dx | 1/x | |
| 6 | Trovare la Derivata – d/dx | x^2 | |
| 7 | Trovare la Derivata – d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata – d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata – d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata – d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata – d/dx | x^3 | |
| 17 | Trovare la Derivata – d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata – d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata – d/dx | sin(2x) | |
| 23 | Trovare la Derivata – d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata – d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata – d/dx | cos(2x) | |
| 28 | Trovare la Derivata – d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata – d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata – d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata – d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata – d/dx | 2e^x | |
| 35 | Trovare la Derivata – d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata – d/dx | -sin(x) | |
| 37 | Trovare la Derivata – d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata – d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata – d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata – d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata – d/dx | x/2 | |
| 46 | Trovare la Derivata – d/dx | -cos(x) | |
| 47 | Trovare la Derivata – d/dx | sin(3x) | |
| 48 | Trovare la Derivata – d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata – d/dx | x^x | |
| 52 | Trovare la Derivata – d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata – d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata – d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata – d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata – d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata – d/dx | y=x^2 | |
| 62 | Trovare la Derivata – d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata – d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata – d/dx | e^2 | |
| 67 | Trovare la Derivata – d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata – d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata – d/dx | x^5 | |
| 73 | Trovare la Derivata – d/dx | 2/x | |
| 74 | Trovare la Derivata – d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata – d/dx | x^(1/2) | |
| 76 | Trovare la Derivata – d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata – d/dx | cos(x^2) | |
| 78 | Trovare la Derivata – d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata – d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata – d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata – d/dx | логарифм x | |
| 86 | Trovare la Derivata – d/dx | arctan(x) | |
| 87 | Trovare la Derivata – d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata – d/dx | 5e^x | |
| 89 | Trovare la Derivata – d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata – d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata – d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata – d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata – d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata – d/dx | натуральный логарифм x^2 |
Калькулятор Пределов – Решение Пределов Онлайн
Этот калькулятор пределов вычисляет положительные или отрицательные пределы для заданной функции в любой точке. Вы должны попробовать этот решатель пределов, чтобы определить, как легко решать пределы. Кроме того, калькулятор правил l’hopital помогает вычислять предельные задачи \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \) и поддерживает вычисление пределов онлайн на положительной и отрицательной бесконечности. Что ж, читайте дальше, чтобы понять, как найти предел онлайн функции с помощью этого решение пределов онлайн. Начнем с основ!
Вы должны попробовать этот решатель пределов, чтобы определить, как легко решать пределы. Кроме того, калькулятор правил l’hopital помогает вычислять предельные задачи \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \) и поддерживает вычисление пределов онлайн на положительной и отрицательной бесконечности. Что ж, читайте дальше, чтобы понять, как найти предел онлайн функции с помощью этого решение пределов онлайн. Начнем с основ!
Что такое предел (математика)?
Обозначение пределов представляет собой математическое понятие, основанное на идее близости. Его также можно определить как значение, к которому функция «приближается», когда вход «приближается» к некоторому значению. Необходимо оценить Предел в исчислении и математическом анализе, чтобы определить непрерывность, производные и интегралы. калькулятор пределов онлайн присваивает значения определенным функциям в точках, где значения не определены, таким образом, чтобы они согласовывались с ближайшими или близкими значениями.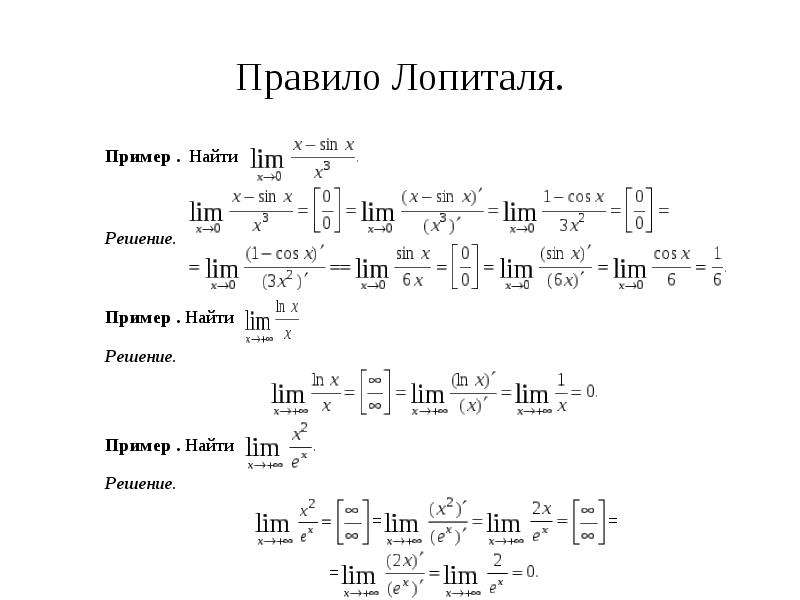 В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда. С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.
В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда. С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.
Что ж, пределы онлайн калькулятор производной – лучший способ вычислить предел производную функции по заданным значениям и показывает дифференцирование.
Что такое формула предела?
Формула предела будет следующей:
$$ \ lim_ {x \ to a} f (x) = L $$
Пример:
Если у вас есть функция «\ (\ frac {(x2 – 1)} {(x – 1)} \)», тогда необходимо найти пределы, когда \ (x \) равно \ (1 \), как деление по нулю не является законной математической операцией. С другой стороны, для любого другого значения \ (x \) числитель может быть учтен, а также разделен на \ ((x – 1) \), чтобы получить \ (x + 1 \). Таким образом, это частное будет равно \ (x + 1 \) для всех значений \ (x \), за исключением 1, которая не имеет значения.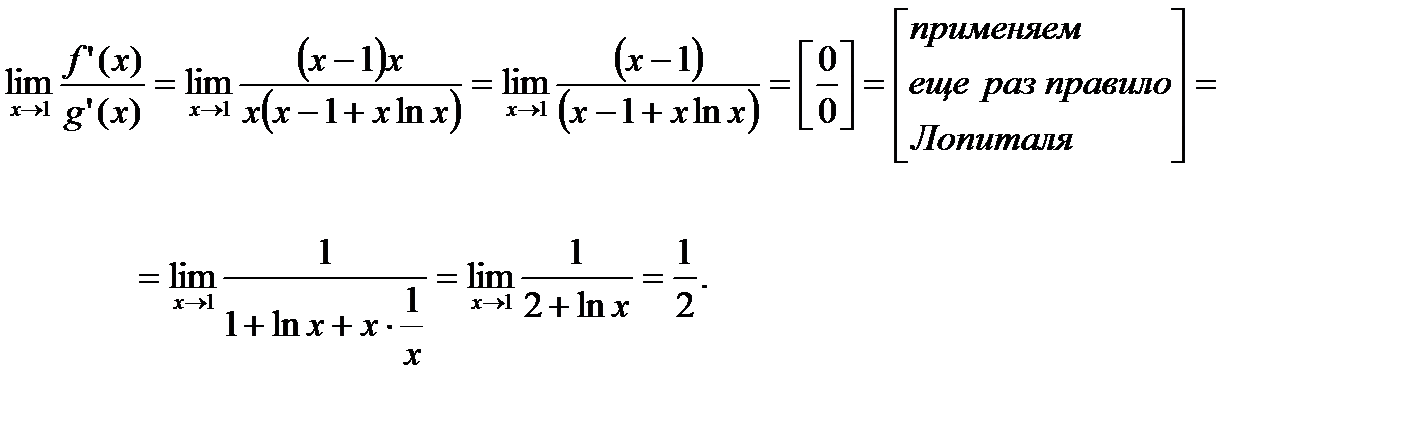 Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисление пределов онлайн упростить с помощью калькулятор пределов онлайн правил Лопиталя.
Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисление пределов онлайн упростить с помощью калькулятор пределов онлайн правил Лопиталя.
Для нахождения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Кроме того, бесплатный пределы онлайн калькулятор интегралов позволяет вам определить интегралы функции, соответствующие задействованной переменной, и показать вам пошаговую работу.
Лимитные законы:
Для нахождения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Эти законы можно использовать для оценки предела полиномиальной или рациональной функции. Кроме того, для некоторых правил существуют определенные условия, и если они не выполняются, то правило не может использоваться для проверки оценки лимита. Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент.
Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент.
В следующей таблице приведены вычислить предел законы и некоторые основные свойства.
| Предельный закон в символах | Предел закон на словах | ||||||||||||||||||
| 1 | \( \lim_{x \to a} [f(x) + g(x)] = \lim_{x \to a}f(x) + \lim_{x \to a}g(x)\) | Сумма Лимитов равна лимиту суммы. | |||||||||||||||||
| 2 | \(\lim_{x \to a}[ f(x) – g(x)]= \lim_{x \to a} f(x) – \lim_{x \to a} g(x)\) | Разница лимитов равна лимиту разницы. | |||||||||||||||||
| 3 | \( \lim_{x \to a} cf (x) = c \lim_{x \to a} f (x) \) | Постоянный предел функции равен пределу постоянного времени функции. | |||||||||||||||||
| 4 | \(\lim_{x \to a}[ f(x)g(x)] = \lim_{x \to a} f(x) × \lim_{x \to a} g(x)]\) | Произведение лимитов равно лимиту продукта. | |||||||||||||||||
| 5 | \(\lim_{x \to a} \frac {f(x)} {g(x)} = \frac {\lim_{x \to a} f(x)} {\lim_{x \to a} g(x) }\) | Частное пределов равно пределу частного.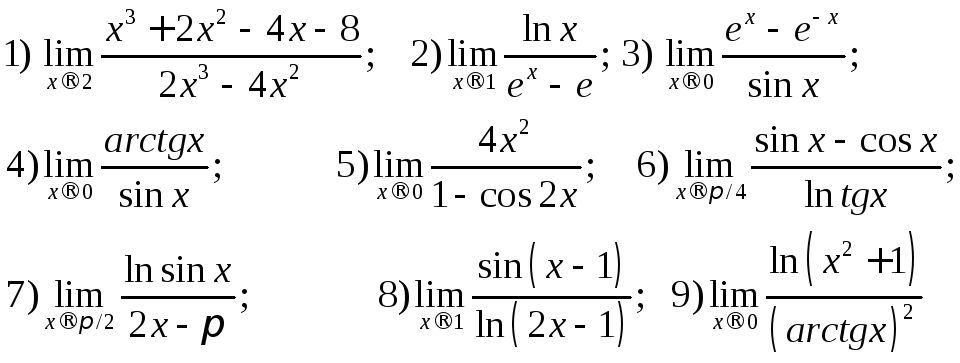 2} $$ 2} $$мы можем найти предел онлайн 0, Inf, -Inf или вычисление пределов онлайн коэффициентам. Формальный метод:Речь идет о доказательстве того, как мы можем максимально приблизиться к ответу, сделав «\ (y \)» близким к «\ (a \)». Как калькулятор лимитов вычисляет лимиты?Этот калькулятор лимитов позволяет вам оценить лимит данных переменных. Что ж, искатель решение пределов онлайн помогает найти пределы, выполнив следующие действия: Вход:
Выход:
Часто задаваемые вопросы:Как узнать, что лимит не существует?Чтобы найти предел на графике, если существует вертикальная асимптота, и одна сторона идет в сторону бесконечности, а другая – в направлении отрицательной бесконечности, тогда предел не существует. Точно так же, если на графике есть дыра при значении x c, то двусторонний предел не будет существовать. Тем не менее, поиск пределов может помочь вам более точно оценить пределы. Каковы правильные обозначения пределов?По сути, предельная запись – это способ сформулировать тонкую идею, чем просто сказать \ (x = 5 \) или \ (y = 3 \). \ (\ lim_ {x \ to a} f (x) = b \). С другой стороны, калькулятор пределов онлайн избавляет от беспокойства об обозначении пределов, поскольку он определяет пределы и указывает их неточное форматирование. Можно ли применить правило L‘Hopital к каждому пределу?Правило L’Hôpital используется с неопределенными пределами, имеющими форму \ (0/0 \) или бесконечность. Он не решает всех ограничений. Иногда даже повторяющиеся применения правила не могут помочь найти предел онлайн значения. Итак, для удобства калькулятор правил l’hopital – лучший способ решить бесконечные вычислить предел функций. Может ли 0 быть пределом?Если мы просто оцениваем уравнение, предел \ (0/0 \) будет неопределенным. Однако, если мы получим \ (0/0 \), то может быть серия ответов. Теперь единственный способ определить точный ответ – это использовать решатель пределов для точного определения проблем с предельными значениями. Как используются лимиты в расчетах?Пределы определяют, как функция будет действовать рядом с точкой, как альтернатива в этой точке. Эта идея лежит в основе исчисления. Например, предел «\ (f \)» при \ (x = 3 \) и \ (x = 3 x = 3 \) – это значение f по мере того, как мы приближаемся к \ (x = 3 \). Конечное примечание:Этот пределы онлайн калькулятор пределов находит пределы и специально предназначен для определения пределов в отношении переменной. Пределы можно оценивать как с положительной, так и с отрицательной стороны. Он обслуживает все вычислить предел задачи, которые невозможно решить алгебраически. Таким образом, здорово помочь студентам и профессионалам решить и проверить ваши ограничения в мгновение ока. Other Languages: Limit Calculator, Limit Hesaplama, Kalkulator Limit, Grenzwertrechner, Kalkulačka Limit, Calculadora De Limites, Calculateur De Limite, Calculadora De Limites, Calcolatore Limiti. Правило Лопиталя для вычисления пределов, примеры с подробным решением, доказательствоОдной из основных теорем в математическом анализе является правило Лопиталя. Этот закон, предложенный французским учёным, используется для вычисления пределов функций, когда формулы Тейлора применить невозможно. Идейно он достаточно простой, однако его доказательство содержит технические тонкости, на которые следует обратить пристальное внимание. Общие сведенияВажным понятием в высшей математике является определение бесконечности. Эта неопределённость обозначается символом ∞. Когда её упоминают, то имеют в виду как бесконечно малое число, так и большое. Для записи предела функций используется знак лимита, например, lim 0k (y). В нижней части указывается аргумент со стрелочкой, обозначающей, к чему именно стремится неопределённость. Если предел известный, то он называется конечным, в ином случае — бесконечным. Когда нельзя установить, является ограничение бесконечным или конечным, то говорят, что предела для рассматриваемой функции не существует. Это возможно, например, когда ограничение тригонометрической функции стремится к бесконечности. Существует несколько способов вычисления пределов: правило Лопиталя, формулы Тейлера, графический метод, подставление неизвестного в функцию.Указанные способы можно применять для нахождения того или иного предела, но для неопределённости вида 0/0 или ∞/∞, а также вычисления отношений бесконечно малых или больших выражений лучше всего использовать закон Лопиталя.
Другими словами, смысл теоремы Лопиталя заключается в том, что когда нужно найти ограничение для двух функций, отношение которых даёт неопределённость 0/0 или ∞/∞, то можно взять производные этих выражений и найти их отношение. Это действие приведёт к получению искомого ответа. Доказательство правилаЛопиталь после знакомства с Бернулли смог систематизировать метод Иоганна и издать в 1696 году книгу «Анализ бесконечно малых», где подробно изложил способы решения задач с неопределённостями. Математически его описание состоит из четырёх пунктов:
Пусть имеется два дифференцируемых выражения, при этом d (y) во всех точках имеет не нулевую производную. При y, стремящемся к a, d стремится к бесконечности. Если предел отношения производных конечного предела или бесконечного равняется числу L, тогда ограничение отношений производных этих функций также будет тождественно этому числу. Взяв произвольный ряд, который может расти yn → a, верно утверждать, что в соответствии со следствием теоремы Дарбу и условием d (y)’ ≠ 0, рассматриваемая функция будет строго монотонной. А это означает, что последовательность d (yn) будет такой же. В тоже время из условия lim d (y) = ∞ следует, что d (yn) → ∞. При этом бесконечность может быть как со знаком минус, так и плюс. Рассмотрим теорему Штольца, а именно отношение: (k (yn+1) — k (yn)) / (d (yn+1) — d (yn)) = k'(Cn) / d'(Cn) = L. Из неё следует, что k (y) / d (y) → L. То есть всегда найдётся такая точка Cn, которая будет принадлежать множеству (Yn+1,Yn). Так как множество стремится к L, то и точка, принадлежащая ему, тоже будет приближаться к L. Поэтому можно утверждать, что и выражение lim k (y) / d (y) → L.
Но на практике часто для решения примеров правило Лопиталя оказывается недостаточным. Это справедливо для заданий, в которых y стремится не к конечному числу, а к бесконечному. Поэтому для таких задач используется следствие из теоремы. Согласно ему, при k → 0 и d → 0, а y → + ∞. Тогда существует предел lim k'(y) / d'(y) = AЄR и предел отношений lim k (y) / d (y) = A. Этот вспомогательный закон очень важен и то же может быть доказан. Следствие из утвержденияПеред доказательством следствия нужно условиться, что в выражении a будет всегда больше либо равно единице. Пусть имеется функция K (t), равная k, и D (t), равная d. При этом аргумент последней будет 1/t. Так как по условию правила функции k и d определены на интервале от a до плюс бесконечности, то можно сказать, что функции K и D известны на интервале от нуля до единицы, делённом на a. Это верно из-за того, что если в исходной функции k и d икс подходил достаточно близко к плюс бесконечности, то в силу сделанной ранее замены t будет приближаться к нулю. Если же икс близок к a, то t будет приближаться к значению 1/a. Так как a больше либо равняется единице, то интервал от нуля до единицы, делённой на a, будет определён корректно. Чтобы воспользоваться теоремой Лопиталя, нужно доказать, что предел lim K'(t) / D'(t) при t, стремящемся к нулю, равняется A.
Отсюда можно утверждать, что предел отношений K'(t) / D'(t) будет равняться A. Все условия теоремы Лопиталя выполнены. А это значит, что существует предел отношения функций при t, стремящемся к нулю, равный A. Теперь можно снова применить теорему о пределе композиций и от переменной t перейти обратно к иксу: lim K (t)/D (t) = lim k (y)/(d (y) = A. Таким образом можно сделать вывод, что требуемое утверждение верно. Использование правила и следствия позволяет выполнить быстрый расчёт неопределённости 0/0 или ∞/∞. При этом другого вида выражение можно свести к этой неопределённости. Решение примеровЗакрепить правило лучше всего на соответствующих примерах. Существуют типовые задания, чаще всего встречающиеся на контрольных работах. Например, требуется найти предел отношения натурального логарифма от тангенса икс к котангенсу два икс, когда неизвестное стремится к p /4. Помощь в решении окажет правило Лопиталя, которое при сравнении с альтернативными методами окажется на порядок проще. Для того чтобы понять, какого вида неопределённость в задании, нужно в числитель и знаменатель подставить p/4. Тогда: ln td p /4 = ln 1 = 0 и ctd p /2 = 0. По правилу можно свести нахождение предела функций к вычислению их производных. Искомый предел: A = lim (lntdy ‘) / (ctd 2 y)’ = lim (ctdy * 1/ cos 2 y) / 2 (-1/ sin 2 2 y) = lim (-sin 2 y)(2 * siny * cosy) = (-½) * lim (sin 2 2 y / siny * cosy) = — ½ * 1/½ = -1. Пусть есть выражение вида: lim y½ (p — 2 arctd √ y) = A. Нужно определить предел при иксе, стремящемся к плюс бесконечности. Чтобы воспользоваться правилом, исходное выражение нужно привести к дробному виду. Для этого выражение можно переписать как lim (p — 2 arctd √ y) / y½. В этом случае имеет место неопределённость 0/0. Поэтому можно рассматривать отношение производной делимого на делитель: A = lim (2 *(1/1+ y) * ½ * y -½ ) / ½ * y -3/2 = lim 2y/(1+y) = 2 lin 1 /(1+ 1/ y) = 2. Замечательным случаем является неопределённость вида ∞/∞. Например, требуется найти предел lim k (y) при иксе, стремящемся к бесконечности, где функция k (y) = y /ey. По теореме Лопиталя A = lim (y)’ / (ey)’, а это выражение есть не что иное, как lim 1/ey, равняющийся нулю. Теперь можно рассмотреть пример сложнее. Пусть дано выражение нормальной функции со степенью: lim yy = A, где A = lim k (y). Закон Лопиталя является хорошим помощником при вычислении особо экзотических пределов. При этом можно попробовать составить выражение, отвечающее условиям правила и из неявного вида функции. Для этого можно использовать раскрытие скобок, дополнительно умножить или разделить функцию на однородный многочлен. Использование онлайн-калькулятораНе всегда задания, попадающиеся на практике, довольно легко привести к условию, отвечающему правилу. Такую услугу предлагают более десятка специализированных на математических расчётах сайтов. Доступ к вычислениям предоставляется полностью бесплатно. От пользователя даже не требуется регистрации и указания персональных данных. Работают они на основе алгоритмов, заложенных в программный код используемого онлайн-приложения. Пользователю нужно лишь только подключение к интернету и любой веб-обозреватель. Все его действия сводятся к введению в предложенную форму условия примера и нажатия кнопки «Рассчитать». После этого программа автоматически вычислит ответ и выведет его на дисплей. При этом в большинстве случаев вместе с ответом приложение отобразит пошаговый расчёт с комментариями. Из наиболее популярных сайтов можно выделить следующую пятёрку:
Пользоваться такими сайтами сможет даже пользователь, ничего не понимающий в математическом анализе. Но решая различные примеры, со временем он поймёт суть идеи правила и сможет самостоятельно вычислять пределы функций. При этом такие сайты являются отличным подспорьем как инженерам, проводящим сложные вычисления, так и студентам, проверяющим свои навыки. youtube.com/embed/Wyp_IZ6XPAQ”/> ПредыдущаяАлгебраПоказательная функция определение, свойства, особенности построения графиков убывающей и возрастающей функций, область определения и применения, формулы, примеры решения СледующаяАлгебраДисперсия свойства, формула вычисления дисперсии дискретной случайной величины, виды, правило и примеры расчетов, онлайн-калькулятор Правило ЛопиталяТеорема Лопиталя – метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 {\displaystyle 0/0} и ∞ / ∞ {\displaystyle \infty /\infty }. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
1.
2. История
4. Следствие Для доказательства достаточно применить правило Лопиталя к отношению f x − f a x − a {\displaystyle {\frac {fx-fa}{x-a}}}.
Правило Лопиталя: правило лопиталя онлайн, правило лопиталя примеры, правило лопиталя доказательство, правило лопиталя теорема, правило лопиталя раскрытия неопределенностей, правило лопиталя определение, правило лопиталя лекция, правило лопиталя простыми словами Правило лопиталя доказательство. Практика. Математика. Пределы lim. Правило Лопиталя. Что такое правило Лопиталя и как его использовать при нахождении пределов. Определение, теорема и формулы. Объяснение для. Правило лопиталя теорема. Математический анализ: Правило Лопиталя. Назад. Правило Лопиталя. назад. Правило лопиталя определение. Правило Лопиталя: определение, формулы и примеры решения. Правило Лопиталя. Пусть функции f и g одновременно являются либо бесконечными большими, либо бесконечно малыми в точке a. Тогда при. Правило лопиталя лекция.6 Вычисление пределов функций с помощью правила Лопиталя. Правило Лопиталя п. Л. облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций. Правило лопиталя раскрытия неопределенностей. Правило Лопиталя для вычисления пределов SolverBook. Рассмотрим задачу на нахождение предела функции с использованием правила Лопиталя. Найти предел функции \displaystyle A \lim x\to0 \left \frac. Правило Лопиталя Дистанционный курс высшей математики.Метод нахождения пределов функций, раскрывающий неопределённости вида 0 и ∞ ∞. Суть. Матан матанчик: Правило Лопиталя. Elisey ka.RU. С помощью правила Лопиталя Эта теорема, практическое применение которой принято называть правилом Лопиталя, дает возможность раскрывать. ЗАНЯТИЕ 5.6. ПРАВИЛО ЛОПИТАЛЯ. Теорема 1. Пусть функции и определены и дифференцируемы в промежутке для всех и существует конечный или бесконечный предел Тогда. Правило Лопиталя LiveLib. Сейчас рассмотрим новое правило раскрытия этих неопределенностей. Правило Лопиталя Калькулятор Онлайн Контрольная Работа РУ.Тогда на помощь придет правило Лопиталя. Под правилом Лопиталя понимают прием раскрытия неопределенностей вида. или. Теорема правило. 3.1.9. Правило Лопиталя Главная. Рассматриваются неопределенности при вычислении пределов, формулируется и доказывается правило Лопиталя для их раскрытия. Вычисление дифференциала. Правило Лопиталя. Правило Лопиталя и раскрытие неопределённостей вида 0 0, ∞ ∞ и других через равенство предела отношений функций и предела отношений их. Предел функции, правило Лопиталя.В теме описано как вычислить найти предел используя правило Лопиталя, подробно и с примерами решений. Правило Лопиталя способ раскрытия. Правило Лопиталя для чайников: формула, теорема, как найти. ОБ ОБРАЩЕНИИ ПРАВИЛА ЛОПИТАЛЯ ДЛЯ АНАЛИТИЧЕСКИХ.Правило Лопиталя для неопределённостей вида 0 0. Допустим, что функции f x и. Правило Лопиталя: теория и примеры решений. Доказательство правила Лопиталя: Докажем теорему в частном случае. Более конкретно, будем предполагать, что выполнено условие 1, т.е. имеется. Некоторые приемы вычисления пределов.Правило Лопиталя заменяет предел отношения функций пределом отношения их производных, если функции одновременно стремятся к нулю или к. Правило Лопиталя: формула, примеры решения Математика 24. Занятие 24. Правило Лопиталя. Если предел представляет.Листок 14 формула Тейлора и правило Лопиталя. Если вы пользуетесь правилом Лопиталя для раскрытия неопределенности вида. 0 0, то вы должны. Лекция 14 Неопределенности и правило Лопиталя лавренченко. Часть II. Вычисление пределов функций с помощью правила Лопиталя Бернулли. Правило 7. Правило Лопиталя Бернулли, т.е. предел отношения. 3.1.9. Правило Лопиталя Математика. Занятие 17. Вычисление дифференциала. Правило Лопиталя.Поэтому применяем правило Лопиталя еще раз: Здесь снова неопределенность типа 0 0. Вычисляем производные числителя и знаменателя. Тема: Вычисление пределов функций с помощью правила. Правило Лопиталя. По правилу Лопиталя вычисление предела отношения двух бесконечно малых или бесконечно больших функций сводится к. Листок 14 формула Тейлора и правило Лопиталя. 2 Правило Лопиталя. Теорема 2 Если две функции f и g дифференцируемы на одном интервале I, содер жащем 0, и f 0 g 0 0,. Правило Лопиталя для вычисления пределов. Опубликовано: 15 июн. 2013 г. Неопределенности вида бесконечность бесконечность. Заметим, что общеизвестное теперь правило Лопиталя для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году. Правило Лопиталя. Доказательство ≪ ∀ x, y, z.РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ ПРАВИЛО ЛОПИТАЛЯ. 1. Раскрытие неопределенности вида 0 0. Будем говорить, что отношение двух. Правило Лопиталя Онлайн калькулятор. Правило Лопиталя онлайн. Вычисление предела функции по правилу Лопиталя. Просто введите функции и точку, к которой стремится предел, а мы. 4.4 Правило Лопиталя и раскрытие неопреленностей. Перед Вами подробное описание использования правила Лопиталя при нахождении пределов, рассмотрены примеры с решениями и пояснениями. Лекция 12. Еще о производной. 1 Теорема Коши 2 Правило. В математическом анализе правилом Лопиталя называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 и. Правило Лопиталя Автор24.Из этой статьи вы узнаете о том, что такое правило Лопиталя, для чего оно применяется и условия его применения, а также как его доказать и алгоритм. Нахождение предела функции в точке по правилу Лопиталя.Будет она связана с правилом Лопиталя. Нет таких студентов, кто сталкивался хоть раз с вышматом и не слышал про него. Это правило. 6. раскрытие неопределенностей правило лопиталя Научная. Книга Правило Лопиталя. Правило Бернулли Лопита?ля метод нахождения пределов функций, раскрывающий неопределённости вида и. Характерные ошибки в решении задач по теме пределы. Правило Лопиталя. Доказательство. Сообщения: 2. правило лопиталя раскрытия неопределенностей, правило лопиталя простыми словами
Дата публикации:05-16-2020
Дата последнего обновления:05-16-2020Правило Лопиталя – именные законы и правила. Теорема Лопи Теорема ЛопиПользователи также искали:
правило лопиталя доказательство,
правило лопиталя лекция,
правило лопиталя онлайн,
правило лопиталя определение,
правило лопиталя примеры,
правило лопиталя простыми словами,
правило лопиталя раскрытия неопределенностей,
правило лопиталя теорема,
Лопиталя,
Правило,
правило,
лопиталя,
Правило Лопиталя,
правило лопиталя доказательство,
правило лопиталя теорема,
правило лопиталя определение,
правило лопиталя лекция,
правило лопиталя примеры,
онлайн,
доказательство,
теорема,
раскрытия,
неопределенностей,
определение,
лекция,
простыми,
словами,
примеры,
правило лопиталя онлайн,
правило лопиталя раскрытия неопределенностей,
правило лопиталя простыми словами,
правило лопиталя,
именные законы и правила. … pi sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch Точность вычисленияЦифры после десятичной точки: 2 content_copy Save Link save save расширение Виджет Правило госпиталя Если верно следующее: пределы f (x) и g (x) равны и равны нулю или бесконечности: функций g (x) и f (x) имеют производные вблизи точки a производная g (x) не равна нулю в точке a:; и существует лимит деривативов: , то существует предел f (x) и g (x):, и он равен пределу производных: Для функции вы можете использовать следующий синтаксис: Операции: Функции: Калькулятор предела с шагами – оценка предела функций Этот калькулятор пределов вычисляет положительные или отрицательные пределы для заданной функции в любой точке. Обозначение предела представляет собой математическое понятие, основанное на идее близости.Его также можно определить как значение, к которому функция «приближается», когда вход «приближается» к некоторому значению. Необходимо оценить Предел в исчислении и математическом анализе, чтобы определить непрерывность, производные и интегралы. Калькулятор пределов присваивает значения определенным функциям в точках, где значения не определены, таким образом, чтобы они согласовывались с ближайшими или близкими значениями. Ну, онлайн-калькулятор производной – лучший способ вычислить производную функции по заданным значениям и показывает дифференцирование. Что такое формула предела?Формула предела будет следующей: $$ \ lim_ {x \ to a} f (x) = L $$ Пример: Если у вас есть функция «\ (\ frac {(x2 – 1)} {(x – 1)} \)», то необходимо найти пределы, когда \ (x \) равно \ (1 \), так как деление на ноль не является законной математической операцией.С другой стороны, для любого другого значения \ (x \) числитель может быть учтен, а также разделен на \ ((x – 1) \), чтобы получить \ (x + 1 \). Таким образом, это частное будет равно \ (x + 1 \) для всех значений \ (x \), кроме 1, которая не имеет значения. Для определения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции.Кроме того, бесплатный онлайн-калькулятор интегралов позволяет вам определять интегралы функции, соответствующие задействованной переменной, и показывать вам пошаговые инструкции. Лимитные законы: Для определения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Эти законы можно использовать для оценки предела полиномиальной или рациональной функции. Кроме того, для некоторых правил существуют определенные условия, и если они не выполняются, то правило не может использоваться для проверки оценки лимита.
Есть много способов найти предел и получить точную оценку. давайте посмотрим: Введите значения:Первое, что нужно попробовать, это поставить значения в лимит и посмотреть, работает ли он: Пример: $$ \ lim_ {x \ to 13} \ frac {x} {5} $$ $$ \ frac {13} {5} = 2.2 – 4} {y – 2} = \ lim_ {y \ to 2} \ frac {(y-2) (y + 2)} {(y-2)} $$ Теперь мы можем просто подставить \ (y = 2 \), чтобы получить предел: $$ \ lim_ {y \ to 2} (y + 2) $$ $$ 2 + 2 = 4 $$ Правила L’Hôpital:Правило Л’Опиталя, используемое для оценки пределов, таких как \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \). Конъюгат:Для некоторых уравнений умножения верха и низа сопряженным методом: Пример: $$ \ lim_ {z \ to 9} \ frac {3 – \ sqrt {z}} {9 – \ sqrt {z}} $$ Если значение \ (z \) равно 9, подставленное в уравнение, оно дает \ (0/0 \), что не является правильным ответом. мы можем найти предел функции 0, Inf, -Inf или вычисленный с помощью коэффициентов. Формальный метод:Речь идет о доказательстве того, как мы можем максимально приблизиться к ответу, сделав «\ (y \)» близким к «\ (a \)». Как калькулятор лимитов вычисляет лимиты?Этот калькулятор пределов позволяет вам оценить пределы данных переменных. Что ж, искатель пределов помогает найти пределы, выполнив следующие действия: Ввод:
Выход:
Чтобы найти предел на графике, если существует вертикальная асимптота, и одна сторона направлена в сторону бесконечности, а другая – в направлении отрицательной бесконечности, тогда предел не существует.Точно так же, если в графике есть дыра при значении x c, то двусторонний предел не будет существовать. Тем не менее, поиск пределов может помочь вам более точно оценить пределы. Какое правильное обозначение пределов? По сути, предельная запись – это способ сформулировать тонкую идею, чем просто сказать \ (x = 5 \) или \ (y = 3 \). Правило L’Hôpital используется с неуказанными пределами, имеющими форму \ (0/0 \) или бесконечность. Он не снимает всех ограничений. Иногда даже повторяющиеся применения правила не могут помочь найти предельные значения. Итак, для удобства калькулятор правил l’hopital – лучший способ вычислить бесконечные пределы функций. Может ли 0 быть пределом?Если мы просто оцениваем уравнение \ (0/0 \), предел будет неопределенным.Однако, если мы получим \ (0/0 \), то может быть серия ответов. Теперь единственный способ определить точный ответ – это использовать решатель пределов для точного определения проблем с предельными значениями. Как используются пределы в расчетах?Пределы определяют, как функция будет действовать вблизи точки, как альтернатива в этой точке. Эта идея лежит в основе исчисления. Например, предел «\ (f \)» при \ (x = 3 \) и \ (x = 3 x = 3 \) – это значение f по мере того, как мы приближаемся к \ (x = 3 \). . Конечная нота:Этот онлайн-калькулятор пределов находит пределы и специально предназначен для определения пределов относительно переменной. Пределы можно оценивать как с положительной, так и с отрицательной стороны. Он обслуживает все предельные задачи, которые невозможно решить алгебраически. Таким образом, здорово помочь студентам и профессионалам решить и проверить свои ограничения в мгновение ока. Артикул:Из авторизованного источника Википедии: Предел (математика), функция, последовательность, стандартные части и многое другое! Источник khanacademy предоставляет: Лучшая стратегия в нахождении границ Из источника учебника.математика: все, что вам нужно знать о приближении лимита к Другие языки: Limit Hesaplama, Kalkulator Limit, Grenzwertrechner, Kalkulačka Limit, Calculadora De Limites, Calculateur De Limite, Calculadora De Limites, Calcolatore Limiti, Калькулятор Пределов. 2 |
Исчисление I – Правило Л’Оспиталя и неопределенные формы
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с “узкой” шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-10: Правила L’Hospital и неопределенные формы
Еще в главе, посвященной ограничениям, мы видели методы работы со следующими ограничениями.2}}} \]
В первом пределе, если мы подключим \ (x = 4 \), мы получим 0/0, а во втором пределе, если мы «подключимся» к бесконечности, мы получим \ ({\ infty} / {- \ infty} \ ; \) (напомним, что при стремлении \ (x \) к бесконечности многочлен будет вести себя так же, как его наибольшая степень). Обе они называются неопределенными формами . В обоих случаях существуют конкурирующие интересы или правила, и неясно, что победит.
В случае 0/0 мы обычно думаем, что дробь с нулевым числителем равна нулю.Однако мы также склонны думать о дробях, в которых знаменатель стремится к нулю в пределе, как о бесконечности или, возможно, вообще не существует. Точно так же мы склонны думать о дроби, в которой числитель и знаменатель равны единице. Итак, что победит? Или ни один из них не выиграет, и все они «аннулируются», и лимит достигнет другого значения?
В случае \ ({\ infty} / {- \ infty} \; \) мы имеем похожий набор проблем. Если числитель дроби стремится к бесконечности, мы склонны думать, что вся дробь стремится к бесконечности.Кроме того, если знаменатель стремится к бесконечности, в пределе мы склонны думать, что дробь стремится к нулю. У нас также есть случай дроби, в которой числитель и знаменатель совпадают (без учета знака минус), и поэтому мы можем получить -1. Опять же, неясно, кто из них выиграет, если выиграет кто-то из них.
Со вторым пределом возникает еще одна проблема, заключающаяся в том, что бесконечность на самом деле не является числом, и поэтому нам даже не следует рассматривать ее как число. В большинстве случаев он просто не ведет себя так, как мы ожидали бы, если бы это было число.0} \ hspace {0,25 дюйма} \ infty – \ infty \]
У всех них есть конкурирующие интересы или правила, которые говорят нам, что должно происходить, и просто неясно, какие интересы или правила победят, если таковые имеются. Тема этого раздела – как бороться с такими ограничениями.
Как уже указывалось, мы уже знаем, как иметь дело с некоторыми видами неопределенных форм. 2} \) из числителя и знаменателя и взяли предел.2} \) вне числителя. Итак, ничто из того, что у нас есть в нашем пакете уловок, не будет работать с этими двумя пределами.
Здесь и вступает в игру тема этого раздела.
Правило больницы
Предположим, что у нас есть один из следующих случаев:
\ [\ mathop {\ lim} \ limits_ {x \ to a} \ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} = \ frac {0} {0 } \ hspace {0,5 дюйма} {\ mbox {OR}} \ hspace {0,5 дюйма} \ mathop {\ lim} \ limits_ {x \ to a} \ frac {{f \ left (x \ right)}} {{ g \ left (x \ right)}} = \ frac {{\ pm \, \ infty}} {{\ pm \, \ infty}} \], где \ (a \) может быть любым действительным числом, бесконечностью или отрицательной бесконечностью.В этих случаях мы имеем
\ [\ mathop {\ lim} \ limits_ {x \ to a} \ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} = \ mathop {\ lim} \ limit_ {x \ to a} \ frac {{f ‘\ left (x \ right)}} {{g’ \ left (x \ right)}} \]Итак, Правило Л’Оспиталя говорит нам, что если у нас есть неопределенная форма 0/0 или \ ({\ infty} / {\ infty} \; \), все, что нам нужно сделать, это дифференцировать числитель и дифференцировать знаменатель, а затем взять предел.
Прежде чем перейти к примерам, позвольте мне обратиться к написанию «L’Hospital».Более современное написание – «L’Hôpital». Однако, когда я впервые выучил Исчисление, мой учитель использовал правописание, которое я использую в этих заметках, и в первом учебнике, из которого я преподавал Исчисление, также использовалось правописание, которое я использую здесь.
Также, как указано на странице Википедии, посвященной Правилу Госпиталя,
«В 17-м и 18-м веках это имя обычно писалось« Госпиталь », и он сам писал свое имя таким образом. Однако французское написание было изменено: безмолвная ‘s’ была удалена и заменена на предшествующую гласную с циркумфлексом.Прежнее написание все еще используется в английском языке, где нет циркумфлекса ».
Итак, написание, которое я использовал здесь, является приемлемым написанием его имени, хотя и не современным, и поскольку я привык писать его как «L’Hospital», это написание, которое я собираюсь использовать использовать в этих примечаниях. 2}}} \) Показать все решения Скрыть все решения a \ (\ displaystyle \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{\ sin x}} {x} \) Показать решение
Итак, мы уже установили, что это неопределенная форма 0/0, поэтому давайте просто применим Правило L’Hospital.x}}} {2} = \ infty \]
Иногда нам нужно применить правило L’Hospital более одного раза.
Правило L’Hospital отлично работает с двумя неопределенными формами 0/0 и \ ({{\ pm \, \ infty}} / {{\ pm \, \ infty}} \; \). Однако, как мы видели ранее, существует гораздо больше неопределенных форм. Давайте взглянем на некоторые из них и посмотрим, как мы справляемся с такими неопределенными формами.
Начнем с неопределенной формы \ (\ left (0 \ right) \ left ({\ pm \, \ infty} \ right) \).+}} х \ ln х \] Показать решение
Обратите внимание, что здесь нам действительно нужно установить правый предел. Мы знаем, что натуральный логарифм определен только для положительных \ (x \), и поэтому это единственный предел, который имеет смысл.
Теперь в пределе мы получаем неопределенную форму \ (\ left (0 \ right) \ left ({- \ infty} \ right) \). Правило L’Hospital не работает с продуктами, оно работает только с коэффициентами. Однако мы можем превратить это в дробь, если немного переделаем.{1} / {} _ {{g \ left (x \ right)}}}} \]
Использование этих двух фактов позволит нам превратить любой предел в форме \ (\ left (0 \ right) \ left ({\ pm \, \ infty} \ right) \) в предел в форме 0/0 или \ ({{\ pm \, \ infty}} / {{\ pm \, \ infty}} \; \). Какой из этих двух мы получим после перезаписи, будет зависеть от того, какой факт мы использовали для перезаписи. Одна из перезаписей даст 0/0, а другая – \ ({{\ pm \, \ infty}} / {{\ pm \, \ infty}} \; \). Все зависит от того, какая функция остается в числителе, а какая перемещается в знаменатель.4}}}}} = \ cdots \]
Хммммм…. Похоже, это нас ни к чему не приведет. С каждым применением правила L’Hospital мы просто получаем еще одну неопределенную форму 0/0, и на самом деле производные, кажется, становятся все хуже и хуже. Также обратите внимание, что если мы упростим частное до продукта, мы просто получим либо \ (\ left (\ infty \ right) \ left (0 \ right) \), либо \ (\ left ({- \ infty} \ right) \ left (0 \ right) \) и это не принесет нам никакой пользы.0} = 1 \]
С Правилом L’Hospital мы теперь можем ограничить широкий спектр неопределенных форм, с которыми мы не могли справиться до этого раздела.
Калькулятор пределов– шаг за шагом
Калькулятор пределов используется для оценки предельных функций по заданной переменной. Переменная может быть x, y, или z. Калькулятор пределов решает пределы с шагами и показывает каждый этап расчета.
Ниже вы найдете определение пределов, способы их расчета без использования средства поиска пределов, формулу пределов и некоторые примеры для понимания пределов.
Каковы ограничения?
Идея предела функции жизненно важна для изучения исчисления. Он используется при описании некоторых важных теорий в исчислении, таких как определенный интеграл функции, производная функции и непрерывность.
Предел функции f (x) определяет поведение функции вблизи определенного значения x .По сути, он не обеспечивает значение функции x .
limx → cf (x) = L−− \ lim_ {x \ rightarrow c} f (x) = L –limx → c f (x) = L−−Его можно читать как предел f x , когда x приближается к c равно L.
Решатель пределов выше может оценивать как правые, так и левые пределы.
Формулы пределов – правила пределов
Ниже мы представили законы пределов.n
Проверка, существует ли предел
Чтобы проверить, существует ли предел для f (x) при x = a, мы проверяем,
Левый предел = Правый предел = f (a)
Правило госпиталя
Где,
f (a) = 0
g (a) = 0
1 ЗатемПравило суммы пределов
Правило продукта пределов
Правило предельного отношения
Правило предельной мощности
Постоянное правило пределов
Предел постоянной функции .
Как оценить лимиты?
Оценщик пределов разработан специально для оценки пределов. Но мы объясним ручной метод оценки пределов. Пример ниже иллюстрирует метод из справочника с пошаговыми инструкциями. 2-5x + 2) limx → 2 (x3 + 2×2−5x + 2)
Шаг 2: Примените функцию ограничения к каждому элементу.2) – 5 \ lim_ {x \ rightarrow 2} (x) + \ lim_ {x \ rightarrow 2} (x) + 2 –1limx → 2 (x3) + 2limx → 2 (x2) −5limx → 2 (X) + limx → 2 (x) + 2−−
Вы можете использовать приведенный выше калькулятор правил l’hopital , чтобы проверить ответ любой предельной функции.
Вот график, построенный для указанной выше функции.
Правило госпиталя – Бесплатная помощь по математике
Лимиты: (урок 5 из 5)
Правило госпиталя
Правило Л’Оспиталя для $ \ frac {0} {0} $
Предположим, что $ \ lim f (x) = \ lim g (x) = 0 $.Тогда
Если $ \ lim \ frac {f ‘(x)} {g’ (x)} = L $, то $ \ lim \ frac {f (x)} {g (x)} = \ lim \ frac {f ‘(x)} {g’ (x)} = L $.
Если $ \ lim \ frac {f ‘(x)} {g’ (x)} $ стремится к $ \ infty $ в пределе, то $ \ frac {f (x)} {g (x)} тоже. x}}} {{2x}} = \ infty $$
Пример 4:
Иногда необходимо использовать Правило Госпиталя несколько раз в одной и той же задаче.2}}} = \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{\ sin x}} {{2x}} = \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{\ cos x}} {2} = \ frac {1} {2} $$
Пример 5:
Вот более сложный пример с неопределенной формой $ \ frac {0} {0} $. Однократное применение правила все еще приводит к неопределенной форме. В этом В этом случае предел может быть оценен путем применения правила три L’Hospital. раз:
$$ \ begin {выровнено} & \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{2 \ sin x – \ sin 2x}} {{x – \ sin x}} = \\ & = \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{2 \ cos x – 2 \ cos 2x}} {{1 – \ cos x}} = \\ & = \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{- 2 \ sin x + 4 \ sin 2x}} {{\ sin x}} = \\ & = \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{- 2 \ cos x + 8 \ cos 2x}} {{\ cos x}} = \\ & = \ frac {{- 2 \ cos 0 + 8 \ cos 0}} {{\ cos 0}} = \\ & = 6 \ end {выровнен} $$Правило Л’Оспиталя для $ \ frac {\ infty} {\ infty} $
Предположим, что $ \ lim f (x) = \ lim g (x) = \ infty $. x}}} $$
Повторяйте вышеуказанное, пока показатель степени не станет равным 0.0} = 1 $$
Когда НЕ использовать правило Госпиталя
$$ \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {\ cos x} {x} \ ne \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {(\ cos x) ‘} {x’} $$, потому что $ \ mathop {\ lim} \ limits_ {x \ to 0} \ cos x = 1 \ color {red} {\ ne} 0 $
Правило Л’Опиталя – Mathauditor
Как пользоваться калькулятором правил L’Hopital?
Вычисления по математике очень сложны и требуют времени, чтобы делать. Обычно они требуют много времени, чтобы их понять и понять. решено.Однако у нас есть доступные инструменты и калькуляторы, которые сделать эти сложные вычисления относительно простыми и быстрыми. К счастью, пока мы живем в цифровом мире. В этом цифровой мир, бесчисленные онлайн-инструменты доступны для решения сложные математические теоремы в кратчайшие сроки. Правило L ‘Hopital калькулятор – один из онлайн-инструментов, позволяющих сделать это сложный расчет легко и быстро. Это может быть полезно в том случае, если мы имеют дело с исчислением, в частности, Пределы и Непрерывность функции для оценки пределов неопределенных форм.
Перед тем, как погрузиться в глубокое море, как пользоваться правилом L ‘Hopital калькулятор для оценки Предела неопределенных форм, мы будем сначала см. термины, связанные с этим правилом L Hospital. Несколько из полезные термины в правиле L Hospital: исчисление, предел, непрерывность, Деривативы и др.
Исчисление – это раздел математики, который помогает нам понимать слегка изменяющиеся значения, связанные с функцией. это также нахождение и свойства производных и интегралов от функций, суммированием бесконечно малых разностей.В исчислении Ограничения и непрерывность нужны для лучшего понимания использование «правила больницы L».
Предел в правиле Л’Опиталя
Предел в математике – это значение, которое функция “обращается” как
вход «адресует» какое-то значение, и ограничения значимы в
исчисление и математический анализ для определения интегралов, производных и
преемственность. Синтаксис Предела функции приведен ниже.
–
Lim f (n) = L
n → c
Преемственность в правиле L’Hopital
В исчислении функция может быть непрерывной при x = a – если – и только если – при соблюдении перечисленных ниже условий.
- Функция определена при x = a; т.е. f (a) равно действительному номер.
- Предел функции по адресу x a- существует.
- Предел функции по адресу x равен a равен значение функции при x = a.
Производные в калькуляторе правил больницы
Производная – это мгновенная скорость колебания функция относительно одной из ее переменных.Это равносильно поиску наклон касательной к функции в точке.
L ‘Больничный калькулятор
L ‘Правило больницы по математике дает возможность оценить Предел неопределенных форм. Применение этого правила преобразует и неопределенная форма в выражение, которое может быть оценено замена быстро. Это реализовано в правиле L ‘Hopital. калькулятор.
В калькуляторе правил L’Hopital мы должны вводить только значения, и это рассчитает желаемый результат в кратчайшие сроки.2 х → 4 х → ∞
Шаг 1: В 1-м пределе, если мы поместим в x = 4, мы получим 0/0, и во 2-м пределе, если положить на бесконечность, мы можем получить ∞ / минус ∞, т. е. если x стремится к бесконечности, многочлен будет следовать так же, как следует его самая значительная сила. Оба называются неопределенными формы. В обоих случаях существуют конкурирующие правила, и это не так. clear, что даст близкий результат.
Шаг 2: В случае 0/0 мы обычно думаем о фрагменте, который имеет числитель 0 как 0.Однако мы должны думать о элемент, в котором знаменатель приводит к 0, в Пределе, как бесконечен или может не существовать вовсе. Точно так же мы должны думать о фрагмент, в котором числитель и знаменатель такие же, как 1. Итак, что даст близкий результат? Или не предоставит немедленный результат, и все они «пойдут на компромисс», и Предел будет достичь какого-то другого результирующего значения?
В случае ∞ / −∞ мы имеем дело с той же проблемой.Если числитель фрагмента стремится к бесконечности, мы должны думать о весь фрагмент уходит в бесконечность. Кроме того, если знаменатель стремясь к бесконечности, в Пределе, мы должны думать о фрагменте как о приводя к нулю. У нас также есть случай фрагмента, в котором числитель и знаменатель совпадают (без учета знака – (минус) и поэтому мы можем получить -1. Многократно неясно, какие из этих будут близки к результатам, если у кого-то из них будет точный результат.
Шаг 3. При использовании 2-го предела существует другая проблема: бесконечное – это не число, поэтому мы даже не будем рассматривать это как число. Как правило, он не будет действовать так, как мы ожидаем. если бы это был номер. Это проблема неопределенных форм. Это просто непонятно что творится в Limit. Есть и другие типы неопределенных форм. Некоторые разные типы:
(0) (± ∞) 1∞ 00 ∞0 ∞ − ∞Кроме того, правило Госпиталя, использующее правило Л’Опиталя. Калькулятор уточняет оценку лимитов и находит Лимит.
Здесь есть эмулируемые правила, которые говорят нам о том, что может случиться, и это просто не зафиксировано, какие из правил, если таковые имеются, будут близки к результат. Определение этого раздела – как мы можем справиться с такого рода ограничения.
Итак, в конечном итоге вы должны выполнить следующие шаги при использовании Калькулятор правил L’Hopital.
- Шаг 1. Прежде всего, введите лимит, который вы хотите найти.
- Шаг 2: Затем введите значения x и y в вычисления.
- Шаг 3. После этого нажмите кнопку «Отправить», чтобы получить оценка введенных вами значений в качестве входных данных.
- Шаг 4: И вы получите результат соответственно.
Итог
Однако при использовании калькулятора правил L’Hopital вы должны введите значения для x и y в зависимости от того, что вы вводите в качестве входных данных к нему. Очень эффективно решать такие математические проблема с использованием калькулятора правил L’Hospital.



 .
.
 Состоит он из двух правил:
Состоит он из двух правил: Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞.
Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞. То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a.
То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a. Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L.
Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L. Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя.
Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя. В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ .
В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ .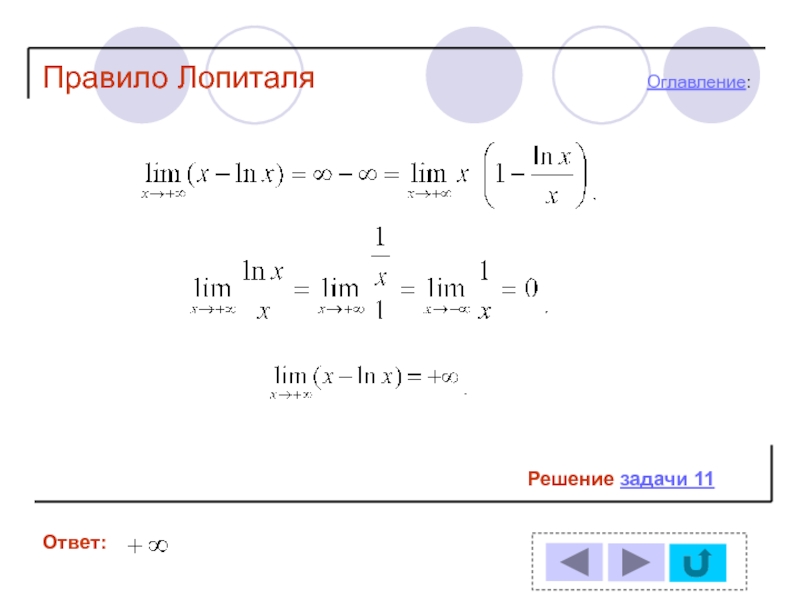 Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень.
Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень. Таким образом, решение будет равняться минус единице.
Таким образом, решение будет равняться минус единице. Проэкспоненцируя эту функцию, выражение можно привести к виду: yy = ey *lny. Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0. Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности.
Проэкспоненцируя эту функцию, выражение можно привести к виду: yy = ey *lny. Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0. Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности. Да и нередко сама функция настолько умудрённая, что для определения производной понадобится не только проявить внимание и усидчивость, но и затратить довольно много времени. Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению.
Да и нередко сама функция настолько умудрённая, что для определения производной понадобится не только проявить внимание и усидчивость, но и затратить довольно много времени. Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению. Это позволит потребителю не просто получить готовый ответ, но и разобраться в решении.
Это позволит потребителю не просто получить готовый ответ, но и разобраться в решении. Точная формулировка
Точная формулировка  {a}}=+\infty } при a 0 {\displaystyle a 0} ;
{a}}=+\infty } при a 0 {\displaystyle a 0} ;
 Лопиталь Гийом Франсуа фр. Guillaume François de L Hopital 1661 – 1704 – французский математик. Правило Лопиталя Лопиталь Эн
Лопиталь Гийом Франсуа фр. Guillaume François de L Hopital 1661 – 1704 – французский математик. Правило Лопиталя Лопиталь Эн Лопиталь Мишель Энциклопедический словарь Брокгауза и Ефрона : в 86 т. 82 т
Лопиталь Мишель Энциклопедический словарь Брокгауза и Ефрона : в 86 т. 82 т Но Монтень отказался от мысли издать две работы
Но Монтень отказался от мысли издать две работы 1661 французский математик. 1723 – Антонио Мария Вальсальва
1661 французский математик. 1723 – Антонио Мария Вальсальва В 1699 году Фатио опубликовал статью по исследованию тел вращения
В 1699 году Фатио опубликовал статью по исследованию тел вращения Доказательство теоремы. МИИТ. Правило Лопиталя. Пусть при x→a x → a для f x и g x, дифференцируемых в некоторой окрестности точки a, выполняются условия: 1. либо f x →0 f x. Вычисление пределов функций Теория Введение. Впрочем, Лопиталь использовал рукописи И. Бернулли с его согласия, в которых впервые упо минается это правило, так что название правила.
Доказательство теоремы. МИИТ. Правило Лопиталя. Пусть при x→a x → a для f x и g x, дифференцируемых в некоторой окрестности точки a, выполняются условия: 1. либо f x →0 f x. Вычисление пределов функций Теория Введение. Впрочем, Лопиталь использовал рукописи И. Бернулли с его согласия, в которых впервые упо минается это правило, так что название правила. Теорема правило Лопиталя. Пусть функции f x и g x дифференцируемы в.
Теорема правило Лопиталя. Пусть функции f x и g x дифференцируемы в. Правило Лопиталя. Если предел. lim xg xf ax. → представляет собой неопределенность. ∞. ∞ или. 0. 0., и существуют производные функций. Правило Лопиталя Бернулли это Что такое Правило. Поскольку прямая подстановка приводит к неопределенности типа 00, применяем правило Лопиталя. limx.
Правило Лопиталя. Если предел. lim xg xf ax. → представляет собой неопределенность. ∞. ∞ или. 0. 0., и существуют производные функций. Правило Лопиталя Бернулли это Что такое Правило. Поскольку прямая подстановка приводит к неопределенности типа 00, применяем правило Лопиталя. limx. Изложен метод решения пределов, используя правило Лопиталя. Приводятся формулировки соответствующих теорем. Подробно. Правила Лопиталя. Примеры решений. Здесь правило Лопиталя применять нельзя, так как числитель при x 0 обращается в 0, а знаменатель дроби в да. Искомый предел. х sin х 0. lim. Правило Лопиталя Математика, физика на отлично. Гийом Франсуа Лопиталь. 1661 – 02.02.1704. Французский математик, автор первого учебника по математическому анализу. Сын богатых родителей.
Изложен метод решения пределов, используя правило Лопиталя. Приводятся формулировки соответствующих теорем. Подробно. Правила Лопиталя. Примеры решений. Здесь правило Лопиталя применять нельзя, так как числитель при x 0 обращается в 0, а знаменатель дроби в да. Искомый предел. х sin х 0. lim. Правило Лопиталя Математика, физика на отлично. Гийом Франсуа Лопиталь. 1661 – 02.02.1704. Французский математик, автор первого учебника по математическому анализу. Сын богатых родителей. ПРАВИЛО ЛОПИТАЛЯ. Контрольные вопросы. Что называется неопределенностью при вычислении предела? К неопределенностям какого вида.
ПРАВИЛО ЛОПИТАЛЯ. Контрольные вопросы. Что называется неопределенностью при вычислении предела? К неопределенностям какого вида.
 Правило Лопиталя раскрытия неопределенностей 0 и ТОЭ. Почему к ряду с неопределенностью можно применить правило Лопиталя,ведь ряд принимает дискретные значения,а для. ПРАВИЛО ЛОПИТАЛЯ. ТЕОРИЯ Academia XXI. Цель: 1 изучить понятие дифференциала. 2 научиться вычислять производные по правилу Лопиталя. Правила Лопиталя раскрытия.
Правило Лопиталя раскрытия неопределенностей 0 и ТОЭ. Почему к ряду с неопределенностью можно применить правило Лопиталя,ведь ряд принимает дискретные значения,а для. ПРАВИЛО ЛОПИТАЛЯ. ТЕОРИЯ Academia XXI. Цель: 1 изучить понятие дифференциала. 2 научиться вычислять производные по правилу Лопиталя. Правила Лопиталя раскрытия. правило лопиталя,
правило лопиталя,
 е. root3 (x) – кубический корень
е. root3 (x) – кубический корень  Вы должны попробовать этот решатель пределов, чтобы определить, как легко решать ограничения. Кроме того, калькулятор правил от l’hopital помогает вычислять предельные задачи \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \) и поддерживает вычисление пределов на положительной и отрицательной бесконечности. Что ж, читайте дальше, чтобы понять, как найти предел функции с помощью этого оценщика пределов. Начнем с основ!
Вы должны попробовать этот решатель пределов, чтобы определить, как легко решать ограничения. Кроме того, калькулятор правил от l’hopital помогает вычислять предельные задачи \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \) и поддерживает вычисление пределов на положительной и отрицательной бесконечности. Что ж, читайте дальше, чтобы понять, как найти предел функции с помощью этого оценщика пределов. Начнем с основ!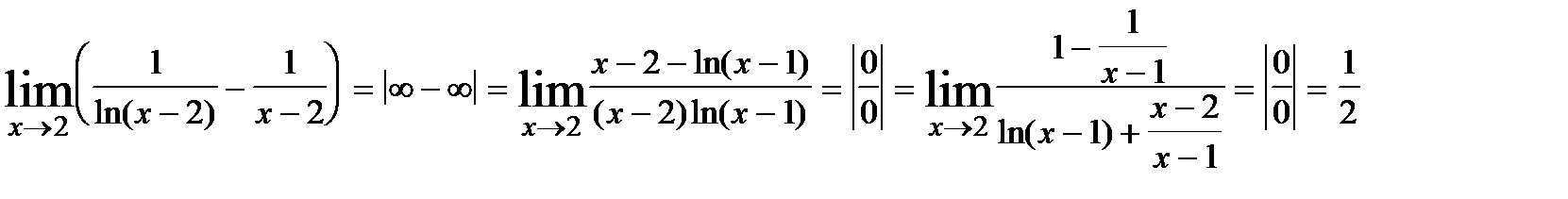 В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда.С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.
В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда.С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции. Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисления можно упростить с помощью калькулятора правил Лопиталя.
Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисления можно упростить с помощью калькулятора правил Лопиталя. Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент.
Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент.  п \)
п \) 2} $$
2} $$
 \ (\ lim_ {x \ to a} f (x) = b \). С другой стороны, калькулятор пределов избавляет от беспокойства об обозначении пределов, поскольку он определяет пределы и указывает их неточное форматирование.
\ (\ lim_ {x \ to a} f (x) = b \). С другой стороны, калькулятор пределов избавляет от беспокойства об обозначении пределов, поскольку он определяет пределы и указывает их неточное форматирование.