правило лопиталя
Правило Лопиталя | |||
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или . Пусть a является некоторым конечным действительным числом или равно бесконечности.
Правило
Лопиталя можно также применять к
неопределенностям типа .
Первые две неопределенности можно
свести к типу или с
помощью алгебраических преобразований. Правило Лопиталя справедливо также и для односторонних пределов. | |||
Пример 1 | |||
Вычислить предел . Решение. Дифференцируя числитель и знаменатель, находим значение предела:
| |||
Пример 2 | |||
Вычислить предел . Решение. Поскольку прямая подстановка приводит к неопределенности типа , применяем правило Лопиталя.
| |||
Пример 3 | |||
Вычислить
предел . Решение. Здесь мы имеем дело с неопределенностью типа . После простых преобразований, получаем
| |||
Пример 4 | |||
Найти предел . Решение. Используя правило Лопиталя, можно записать
| |||
Пример 5 | |||
Найти предел . Решение. Здесь мы встречаемся с неопределенностью типа . Обозначим . После логарифмирования получаем
Далее, по правилу Лопиталя, находим
Соответственно,
| |||
Пример 6 |
15.
Правила Лопиталя*
Швейцарский
математик Иоганн
I Бернулли (1667-1748)
после успешного окончания Базельского
университета, путешествуя по Европе, в
1690 году приезжает в Париж. В литературном
салоне философа Никола Мальбранша
(1638-1715) Иоганн знакомится с французским
математиком маркизом Гийомом Франсуа
Антуаном де Лопиталем (1661-1704). В ходе
оживленной беседы Лопиталь удивился,
как легко, “как бы играя”, юнец Бернулли
решал трудные задачи по новому исчислению.
Поэтому Лопиталь попросил прочитать
ему несколько лекций. Устные беседы
понравились Лопиталю, и он за приличный
гонорар стал получать материалы в
письменном виде. Заметим, что общеизвестное
теперь “правило Лопиталя” для раскрытия
неопределенностей также было передано
ему Иоганном. Уже в 1696 году появился
знаменитый трактат Лопиталя “Введение
в анализ бесконечно малых для понимания
кривых линий”. Вторая часть курса,
изложенного Иоганном I Бернулли, была
опубликована лишь в 1742 году и называлась
“Математические лекции о методе
интегралов и другие; написаны для
знаменитого маркиза Госпиталия; годы
1691-1692”.
Теорема (Коши). Пусть функции и непрерывны на , дифференцируемы на и . Тогда :
Доказательство. Рассмотрим функцию
выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .
По теореме Ролля существует :
Первое правило Лопиталя
Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Пусть конечно.
По выберем :
в интервале выполняется
неравенство
Применим теорему Коши к отрезку , где . Существует :
и, значит,
Это и означает, что .
В случае, когда бесконечно, неравенство (1) заменяется на
или
в зависимости от знака . В остальном доказательство не меняется.
Второе правило Лопиталя
Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема.
то и
Доказательство. Пусть конечно. По выберем : в интервале выполняется неравенство
Определим функцию из условия
Имеем
при .
Применим к отрезку теорему
Коши. Получим, что существует :
Для тех , для которых
Так как произвольно мало, то
В случае, когда , неравенство (2) заменяется на
а неравенство (4) – на неравенство
имеющим место при , достаточно близких к a в силу (3).
Аналогично рассматривается случай .
Правило Лопиталя с примерами решения
Содержание:
- Примеры с решением
- СПРАВОЧНЫЕ СВЕДЕНИЯ
Теорема 6.8 (правило Лопиталя). Пусть функции одновременно стремятся к нулю или к бесконечности при ( — заданное число) или при Если при этом отношение производных имеет предел, то отношение функций также имеет предел, равный пределу отношения производных, т.е
Доказательство.
Докажем теорему для случая, когда при обе функции имеют пределы, равные нулю, и непрерывны в точке т.
Возьмем интервал считая, что — некоторое фиксированное значение, достаточно близкое к Тогда в этом интервале, включая всюду существуют производные Следовательно, в интервале функции и являются непрерывными, поскольку они дифференцируемы. Кроме того, функции непрерывны и в точке Таким образом, функции и непрерывны в замкнутом интервале и дифференцируемы всюду внутри него.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Дополнительно предположим, чтонигде в этом интервале не обращается в нуль (это предположение является естественным, так как в формуле (6.7) стоит в знаменателе).
Таким образом, эти две функции удовлетворяют всем условиям теоремы Коши. Поэтому для них и интервала справедлива указанная теорема, когда в ней и Итак,
Но и Следовательно, эта формула примет вид
Согласно условию теоремы существует предел отношения производных Отсюда согласно определению предела заключаем что существует и предел
Этот предел будет равен предыдущему, и получим
В соотношении (6.8) перейдем к пределу, когда и учитывая, что предел правой части существует. Тогда будет существовать и предел левой части, равный первому:
Сравнив формулы (6.9) и (6.10), придем к формуле (6.7). Теорема для указанного случая доказана. Случай, когда приводится к рассмотренному заменой при этом Доказательство для случая, когда опускаем.
Возможно вам будут полезны данные страницы:
Вычислить площадь фигуры ограниченной линиями |
Площадь фигуры ограниченной линиями |
Признак Лейбница |
Как решать пределы: пример решения |
Замечание.
Может оказаться, что функции и одновременно стремятся к нулю или к бесконечности при или
Тогда к пределу отношения производных вновь можем применить правило Лопиталя, т. е
Примеры с решением
Пример 1:
Требуется найти предел Поскольку при то согласно правилу Лопиталя если существует последний предел. Здесь снова и числитель, и знаменатель стремятся к нулю при поэтому для нахождения последнего предела снова можем воспользоваться правилом Лопиталя. Поэтому окончательно
и
Замечание к теореме. Если предел отношения производных не существует, то правило Лопиталя неприменимо. Сказанное покажем на примере. Рассмотрим предел отношения функций
Возьмем предел отношения производных этих функций
но этот предел не существует, так как при неограниченном изменении угла измеренного в радианах, функция принимает значения, заключенные между и следовательно, ни к какому пределу не стремится.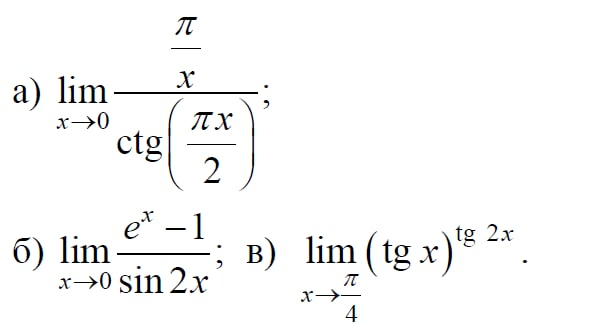
Однако предел (6.11) отношения функций существует. Убедимся в этом.
Предел (6.11) запишем так: Согласно теореме о пределе суммы он равняется сумме пределов, а предел постоянной равен ей самой. Следовательно, Здесь второй предел равен нулю, так как т.е. является
бесконечно малой функцией при а является ограниченной функцией при так как Но произведение бесконечно малой функции и ограниченной функции есть снова бесконечно малая функция. Итак, предел в правой части последней формулы равен нулю, и мы получили
СПРАВОЧНЫЕ СВЕДЕНИЯТаким образом, предел (6.11) отношения функций существует и равен в то время как предел отношения их производных не существует.
Теорема (правило Лопиталя раскрытия неопределенности вида или ). Пусть функции и
а) дифференцируемы в окрестности точки за исключением, быть может, самой точки причем в этой окрестности;
б) функции и являются одновременно либо бесконечно малыми, либо бесконечно большими при
в) существует конечный
Тогда существует
Если функции и дифференцируемы в точке то
Пример 2:
Найти
Применяя формулу (2), получаем
Теорема остается в силе при а также в случае одностороннего предела при выполнении условий соответственно на интервалах
Если выполнены условия а), б), равен или то также равен соответственно или
Пример 3:
Найти
Раскрывая неопределенность вида по правилу Лопиталя, получаем
Пример 4:
Найти
Раскрывая неопределенность вида по правилу Лопиталя, получаем
Применяя правило Лопиталя, часто бывает выгодно предварительно использовать асимптотические равенства вида
Пример 5:
Найти
Замечая, что при по правилу Лопиталя находим
Пример 6:
Найти
Замечая, что при и применяя правило Лопиталя, получаем
Иногда при вычислении пределов правило Лопиталя приходится применять несколько раз.
Пример 7:
Найти
Применяя правило Лопиталя, снова получаем неопределенность
Пользуясь еще раз правилом Лопиталя, находим
Следовательно, искомый предел равен 9/2
Пример 8:
Найти где
Пусть тогда Применяя правило Лопиталя раз, получаем
Пример 8. Найти
Пусть тогда и (пример 7).
Неопределенности вида и часто удается свести к виду или с помощью алгебраических преобразований, а затем применить правило Лопиталя.
Пример 9:
Найти
Преобразуя неопределенность вида к виду и применяя правило Лопиталя, получаем
Пример 10:
Найти
Полагая получаем
Пример 11:
Найти
Преобразуя неопределенность вида к виду и используя асимптотическую формулу при получаем
Так как
(пример 4), то искомый предел равен 2/3.
При вычислении пределов функций вида часто приходится раскрывать неопределенности вида Представляя функцию в виде можно свести вычисление предела функции к раскрытию неопределенности вида
Пример 12:
Найти
А Так как (пример 9), то
Пример 13:
Найти
Так как то, применяя правило Лопиталя, получаем
а, следовательно,
Пример 14:
Найти
По правилу Лопиталя находим
и поэтому
Введение в правило Лопиталя ‹ OpenCurriculum
Правило Лопиталя – это мощный инструмент, который можно использовать, когда вы застряли на определенных типах производных.
Многие производные, которые в противном случае кажутся неопределенными, могут быть взломаны с помощью правила Лопиталя. В этой статье мы рассмотрим две части этого правила и поможем учащимся, изучающим математику, стать более способными и уверенными в вычислении пределов. Приведенные здесь примеры также могут быть использованы учителем для всестороннего ознакомления с предметом.
0 Деление на 0 Неопределенные формы
Один сценарий, в котором применимо правило Лопиталя, — это когда числитель и знаменатель предела стремятся к нулю. Если \(f(x)\) и \(g(x)\) – числитель и знаменатель предела \(x \rightarrow a\), и \(\lim_{x \rightarrow a}f(x) = 0\) и \(\lim_{x \rightarrow a}g(x) = 0\), то имеем
$$\lim_{x \rightarrow a}\frac{f(x)}{g( x)} = \lim_{x \rightarrow a}\frac{f'(x)}{g'(x)}$$
Это первая часть правила Лопиталя. Также предполагается, что и числитель, и знаменатель являются дифференцируемыми функциями. \(a\) может быть любым вещественным числом, положительным или отрицательным.
Чтобы увидеть, применима ли эта форма правила Лопиталя, используйте прямую замену как в числителе, так и в знаменателе с заданным пределом. Если вы получаете \(\frac{0}{0}\), вы можете использовать эту форму правила Лопиталя. Дифференцируйте и числитель, и знаменатель, и повторяйте процесс снова, пока не получите либо определенное значение предела, либо приведите его к другой неопределенной форме. То, что вы делаете с другой неопределенной формой, варьируется, и мы не будем сейчас вдаваться в это.
Пример 1: Вычислить предел \(\lim_{x \rightarrow 0}\frac{\sin x}{x}\). Это классический пример!
Решение: Предел числителя и знаменателя равен \(0\). Следовательно, это неопределенная форма \(\frac{0}{0}\), и мы можем использовать правило Лопиталя. Производная числителя равна \(\cos x\), а производная деонимнатора равна \(1\), поэтому по правилу Лопиталя:
$$\lim_{x \rightarrow 0}\frac{\ sin x}{x} = \lim_{x \rightarrow 0}\frac{\cos x}{1} = \cos(0) = 1$$ 92 + 4(2) – 1} = \frac{4 + 1}{3(4) + 8 – 1} = \frac{5}{12 + 7} = \frac{5}{19}$$
Бесконечность, разделенная на бесконечность Неопределенные формы
Существует еще одна форма правила Лопиталя, которая называется формой \(\frac{\infty}{\infty}\).
В этом случае и числитель, и знаменатель дроби стремятся к бесконечности с заданным пределом. Обычно значение, к которому приближается переменная, равно положительной или отрицательной бесконечности, но иногда это может быть что-то другое. Если числитель и знаменатель являются дифференцируемыми функциями и стремятся к бесконечности с заданным пределом:
$$\lim_{x \rightarrow a}\frac{f(x)}{g(x)} = \lim_{x \rightarrow a}\frac{f'(x)}{g'(x) }$$
Это точно такая же операция, которая выполняется, когда и числитель, и знаменатель приближаются к нулю! Таким образом, единственное различие между двумя частями правила Лопиталя — это сценарий, в котором это правило применимо. Имейте в виду, однако, что правило Лопиталя нельзя использовать, когда числитель приближается к бесконечности, а знаменатель приближается к нулю.
Пример 4: Вычислите предел \(\lim_{x \rightarrow \infty}\frac{x – 1}{x}\).
Решение 1: И числитель, и знаменатель предела стремятся к бесконечности, поэтому мы можем дифференцировать числитель и знаменатель:
$$\lim_{x \rightarrow \infty}\frac{x – 1}{x} = \lim_{x \rightarrow \infty}\frac{1}{1} = 1$$
Решение 2: Если вы не знаете правило Лопиталя, вы можете просто переписать дробь следующим образом:
$$\lim_{x \стрелка вправо \infty}\frac{x – 1}{x} = \lim_{x \стрелка вправо \infty}\left(\frac{x}{x} – \frac{1}{ x}\right) = \lim_{x \rightarrow \infty}\left(1 – \frac{1}{x}\right)$$ 92 + x}$$
Итак, этот предел снова имеет неопределенную форму \(\frac{\infty}{\infty}\), поэтому мы снова используем правило Лопиталя (подсказка: вы можете использовать его столько раз, сколько нужно в одной задаче, лишь бы каждый раз выполнялись условия использования правила):
$$\lim_{x \rightarrow \infty}\frac{4x}{4x + 1}$ $
Используйте его еще раз, так как это все еще та же неопределенная форма:
$$\lim_{x \rightarrow \infty}\frac{4}{4} = 1$$
Пример 6: 94 – 1}{\cos x}\).
Решение: Функция косинуса постоянно колеблется; оно не приближается к определенному значению, когда \(х\) стремится к бесконечности. Другими словами, \(\lim_{x \rightarrow \infty}\cos x\) не определено. Таким образом, это не может быть неопределенная форма \(\frac{0}{0}\) или \(\frac{\infty}{\infty}\). В результате правило Лопиталя не может быть использовано.
Правило Лопиталя | Brilliant Math & Science Wiki
Чунгсу Хонг, Пи Хан Го, Тадеуш Абий, а также
способствовал
Содержимое
- Правило Лопиталя
- Основные примеры
- Промежуточные примеры
- Повторное применение правила Лопиталя — основное
- Повторное применение правила Лопиталя — средний уровень
- Решение проблем
- Сходимость последовательностей
- Сходимость несобственных интегралов
Правило Лопиталя
Предположим, что fff и ggg — такие дифференцируемые функции, что
- g′(x)≠0g'(x) \neq 0g′(x)=0 на открытом интервале III, содержащем a;a;a;
- limx→af(x)=0 и limx→ag(x)=0,\displaystyle \lim_{x\to a} f(x) = 0 \text{и } \displaystyle \lim_{x \to a} g(x) = 0,x→alimf(x)=0 и x→alimg(x)=0, или limx→af(x)=±∞ и limx→ аг(х)=±∞; \displaystyle \lim_{x\to a} f(x) = \pm \infty \text{ и }\displaystyle \lim_{x\to a} g(x) = \pm \infty; x→alimf(x)=±∞ и x→alimg(x)=±∞;
- limx→af′(x)g′(x){\displaystyle \lim_{x\to a}} \frac{f'(x)}{g'(x)} x→alimg′( x)f′(x) существует.
Затем
limx→af(x)g(x)=limx→af′(x)g′(x).\lim_{x\to a} \frac{f(x)}{g(x) } = \lim_{x\to a} \frac{f'(x)}{g'(x)}. х→алимg(x)f(x)=x→алимg′(x)f′(x).
У нас есть
f′(a)g′(a)=limx→af(x)−f(a)x−alimx→ag(x)−g(a)x−a=limx→af( х)−f(a)x−ag(x)−g(a)x−a=limx→af(x)−f(a)g(x)−g(a)=limx→af (x)−0g(x)−0=limx→af(x)g(x). □\begin{выровнено} \ гидроразрыв {е ‘(а)} {г’ (а)} &= \frac{\lim_{x \to a}{\frac{f(x) – f(a)}{x – a}}}{\lim_{x \to a}{\frac{g(x ) – г(а)}{х – а}}} \\\\ & = \ lim_ {x \ to a} {\ frac {\ hspace {4 мм} \ frac {f (x) -f (a)} {xa} \ hspace {4 мм}} {\ frac {g (x) – г(а)}{х-а}}} \\\\ &= \lim_{x \to a}{\frac{f(x)-f(a)}{g(x)-g(a)}} \\\\ &= \lim_{x \to a}{\frac{f(x) – 0}{g(x) – 0}} \\\\ &= \lim_{x \to a}{\frac{f(x)}{g(x)}}. \ _\площадь \end{выровнено}g′(a)f′(a)=limx→ax−ag(x)−g(a)limx→ax-af(x)−f(a) =x→alimx−ag(x)−g(a)x−af(x)−f(a)=x→alimg(x)−g(a)f(x)− f(a)=x→alimg(x)−0f(x)−0=x→alimg(x)f(x). □
Оценить
limx→0sinxx.
\lim_{x \to 0}{\frac{\sin{x}}{x}}.x→0limxsinx.
Непосредственное применение x=0x=0x=0 приводит предел к неопределенной форме. Поскольку и член в числителе, и член в знаменателе равны нулю при x=0x = 0x=0 и поскольку sinx\sin{x}sinx и xxx оба дифференцируемы при x=0x=0x=0, мы можем используйте правило Лопиталя:
limx→0sinxx=cosx1∣x=0=11=1. □\lim_{x \to 0}{\frac{\sin{x}}{x}} = \left. \frac{\cos{x}}{1}\right|_{x = 0} = \frac{1}{1} = 1 .\ _\squarex→0limxsinx=1cosx∣∣∣x =0=11=1. □
\lim_{x \to 0}{\frac{\sin{x}}{x}}.x→0limxsinx.Оценить
limx→0x+9−3x.\lim_{x \to 0}{\frac{\sqrt{x+9}-3}{x}}.x→0limxx+9−3.
Опять же, прямое применение x=0x=0x=0 приводит к неопределенной форме. Пусть выражение в числителе будет f(x),f(x),f(x), а выражение в знаменателе g(x)g(x)g(x). Поскольку f(0)f(0)f(0) и g(0)g(0)g(0) равны нулю, а f(x)f(x)f(x) и g(x)g(x )g(x) оба дифференцируемы при x=0x=0x=0, мы можем использовать правило Лопиталя:
limx→0x+9−3x=12x+92 +1 \большой).
До сих пор мы рассматривали оценку пределов, сводящихся к неопределенной форме
00 или ∞∞.\frac{0}{0}\quad \text{ или }\quad \frac{\infty}{\infty} .00 или ∞∞.
Но как бы мы оценили пределы, которые сводятся к 0×∞?0\times\infty?0×∞? Мы можем иметь дело с такими формами, записывая их как частные или переставляя их. Полезно следующее тождество:
f×g=f1g.f \times g = \frac{f}{\hspace{2mm} \frac{1}{g}\hspace{2mm} } .f×g=g1 ф. 9{-2}} = 0. \ _\квадрат x→0+limxln(x)=x→0+limx1ln(x)=x→0+lim−x−2x−1 =0. □
лн(к2+1).Оценить
limx→∞xsin1x.\lim_{x \to \infty}{x \sin{\frac{1}{x}}}.x→∞limxsinx1.
Прямое применение x=0x=0x=0 дает неопределенную форму ∞⋅0\infty \cdot 0∞⋅0. Эта форма предела не может быть оценена так же, как случай 00\frac0000. Эту, казалось бы, серьезную проблему можно решить, введя замену переменной x=1yx = \frac{1}{y}x=y1. Используя замену, предельное выражение меняется на 9{ 2 } } } \right) } =0x→0lim(x3sin2x+a+x2b)=0
верно для констант aaa и bbb, тогда каково значение 3a+b?3a+b?3a +б?
В случае, когда применение правила Лопиталя приводит к неопределенной форме, если полученное предельное выражение удовлетворяет условиям, необходимым для использования правила Лопиталя, его можно использовать снова.
Примечание: Мы также можем решить этот предел, используя аппроксимацию tanx≈x \tan x \ приблизительно x tanx≈x для относительно небольших xxx.
2 Ax dxdtanAx=Asec2Ax для некоторой константы AAA. Таким образом, предел становится 92(0)} = \frac{41}{152}. \ _\квадрат x→0lim456сек2(456x)123сек2(123x)=456сек2(0)123сек2(0)=15241. □Оценить лимит
limx→0sinxtanx. \lim_{x\to0} \frac{\sin x}{\tan x}.x→0limtanxsinx.
Обратите внимание, что предел действительно имеет форму 00. \frac00.00. Однако мы можем упростить данное выражение, заметив, что tanx=sinxcosx \tan x = \frac{\sin x}{\cos x} tanx=cosxsinx. Таким образом, взяв их отношение, мы остаемся с cosx,\cos x, cosx, и его предел, когда xxx приближается к 000, равен просто 1. □1. \ _\квадрат1. □ 92} \\ &=\lim_{x\to0} \frac{\sin x}{120x} \\ &=\lim_{x\to0} \frac{\cos x}{120} \\ &= \frac1{120}. \end{align} x→0limx5sinx+Ax+Bx3=x→0lim60×2-cosx+1=x→0lim120xsinx=x→0lim120cosx=1201.
