Урок 4. Частные методики умножения двузначных чисел до 30
Преимуществом трех способов умножения двузначных для устного счета, описанных в прошлом уроке, состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако, эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.
Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.
Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10.
Умножать на 11 таким способом можно любые двузначные числа. Для наглядности приведены примеры:
81 * 11 = 8 (8+1) 1 = 891
68 * 11 = 6 (6+8) 8 = 748
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа – об этом читайте в данной статье, а также в книге “Система быстрого счета по Трахтенбергу”.
Квадрат суммы, квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
232
692 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
152 = (1*(1+1)) 25 = 225
252 = (2*(2+1)) 25 = 625
852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Умножение чисел до 20
1 шаг. Для примера возьмём два числа – 16 и 18. К одному из чисел прибавляем кол-во единиц второго – 16+8=24
2 шаг. Полученное число умножаем на 10 – 24*10=240
3 шаг. Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
Методика умножения чисел до 20 очень проста:
Если записать короче, то:
16*18 = (16+8)*10+6*8 = 288
Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8.
По сути, этот метод является частным способом использования опорных чисел (о которых будет сказано в следующем уроке). В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100… Подробнее о методе использования опорного числа читайте в следующем уроке.
Опорное число
Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8. Для того, чтобы узнать их произведение, нужно совершить следующие операции:
- К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
- Затем 23 умножаем на опорное число, то есть на 10.
 Ответ: 230
Ответ: 230 - К 230 прибавляем произведение 5*8. Ответ: 270.
Подробнее о методике использования опорного числа для счета в уме читайте в следующем уроке.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Евгений БуяновУмножение в столбик — как умножать в столбик в 3 и 4 класс
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
- Однозначное — состоит из одного знака
- Двузначное — из двух
- Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
- В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения1. От перестановки множителей местами произведение не меняется. 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. |
Важно помнить правило: умножение в столбик с нулями дает в результате ноль
- а * 0 = 0, где а — любое натуральное число.
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
5. Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 * 2:
1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
3. Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 * 8063:
- Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
- Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
- Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.
- По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
- Далее складываем два произведения в столбик.
- Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Повтори тему – деление в столбик, она очень полезная!
Алгоритм перемножения двузначных чисел | Обучонок
2.8 Алгоритм перемножения двузначных чисел, близких к 100
Например: 98 х 97 = 9506
Здесь я пользуюсь таким алгоритмом: если хочешь перемножить два
двузначных числа, близких к 100, то поступай так:
1) найди недостатки сомножителей до сотни;
2) вычти из одного сомножителя недостаток второго до сотни;
3) к результату припиши двумя цифрами произведение недостатков
сомножителей до сотни.
2.9 Умножение трёхзначного числа на 999
Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9. Например:
385 * 999 = 384615
573 * 999 = 572427 943 * 999 = 942057
2.10 Умножение на шесть ( по Трахтенбергу)
Нужно прибавить к каждой цифре половину «соседа».
Пример: 0622084 * 6
0622084 * 6 4 является правой цифрой этого числа и, так 4 как «соседа» у неё нет, прибавлять нечего.
06222084 * 6 Вторая цифра 8, е «сосед» – 4. Мы берём 8 04 прибавляем половину 4 (2) и получаем 10, ноль пишем, 1 в перенос.
06222084 * 6 Следующая цифра ноль. Мы прибавляем к ней
504 половину «соседа» 8 (4), то есть 0 + 4 = 4 плюс
перенос (1).
Остальные цифры аналогичны.
Ответ: 06222084 * 6
3732504
Правило умножения на 6: является «сосед» чётным или не чётным – никакой роли не играет. Мы смотрим только на саму цифру: если она чётная, прибавляем к ней её целую часть половины «соседа», если нечётная, то кроме половины «соседа» прибавляем еще 5.
Пример: 0443052 * 6
0443052 * 6 2 – чётная и не имеет «соседа», напишем её снизу
2
0443052 * 6 5 – нечётная: 5+5 и плюс половина «соседа» 2 (1)
12 будет 11. Запишем 1 и в перенос 1
0443052 * 6 половина от 5 будет 2, и прибавим перенос 1, то будет 3
312
0443052 * 6 3 – нечетная, 3 + 5 = 8
8312
0443052 * 6 4 + половина от 3 (1) будет 5
58312
0443052 * 6 4 + половина от 4 (2) будет 6
658312
0443052 * 6 ноль + половина от 4 (2) будет 2
2658312 Ответ: 2658312.
Выводы
Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.

В школьных учебниках практически нет приемов быстрого счета, поэтому результат данной работы – памятка для быстрого счета будет очень полезной для учащихся 5-6 классов.
Как мы видим, быстрый счёт это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит, её можно изучать, ей можно следовать, ею можно овладевать.
Все рассмотренные мною методы устного умножения говорят о многолетнем интересе ученых, и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.
Заключение
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
Изучение старинных способов вычислений показало, что эти арифметические действия были трудными и сложными из-за многообразия способов и их громоздкости выполнения.
Современные способы вычислений просты и доступны всем.
При знакомстве с научной литературой обнаружил более быстрые и надежные способы вычислений.
Результаты своей работы я оформил в памятку (Приложение 2), которую предложу всем своим одноклассникам. Возможно, что с первого раза не у всех получится быстро, с ходу выполнять вычисления с применением этих приемов, даже если сначала не получится использовать прием, показанный в памятке, ничего страшного, просто нужна постоянная вычислительная тренировка. Она и поможет приобрести полезные навыки.
Список использованной литературы
1. Ванцян А.Г. Математика: Учебник для 5 класса. – Самара: Издательский дом «Фёдоров», 1999г.
2. Зайкин М.Н. Математический тренинг. – Москва, 1996.
3. Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. //Начальная школа. – 1990, №6.
4. Иванова Т. Устный счёт. // Начальная школа. – 1999, №7.
5. Кордемский Б.А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
6. Минских Е.М. «От игры к знаниям», М., «Просвещение», 1982г.
7. Перельман Я.И. Живая математика. – Екатеринбург, Тезис, 1994.
8. Свечников А.А. Числа, фигуры, задачи. М., Просвещение, 1977г.
Интернет-источники
1. school.edu.ru
2. ik.net/~stepanov/
3. junior.ru
Приложение 1
Приложение 2
Перейти к содержанию
Исследовательской работы “Приемы устного счета и их применение
Умножение чисел, в записи которых есть нули
Привет, ребята!
Сегодня мы продолжим разговор об умножении многозначных чисел. И особое внимание уделим тем случаям, когда в записи первого множителя есть нули.
Некоторые случаи умножения
трёхзначных чисел с нулями мы уже разбирали. Помните, как мы умножали семьсот
пятьдесят два на триста девять?
Помните, как мы умножали семьсот
пятьдесят два на триста девять?
752 · 309 = 232 368
А ещё шестьсот сорок три умножали на четыреста тридцать.
643 · 430
А сейчас давайте разберём вот такой пример. Умножим четыре тысячи восемьсот на семьдесят шесть 4 800 · 76. Как записать это столбиком?
А вот как! Вы уже знаете, что, если многозначное число
оканчивается нулями, при записи умножения столбиком эти нули как бы остаются
справа. В данном примере мы сорок восемь сотен будем умножать на семьдесят
шесть и выполнять действие так, как оно выполняется при умножении двузначных
чисел. Восемью шесть – сорок восемь. Восемь пишем, четыре запоминаем. Четырежды
шесть – двадцать четыре. Да ещё четыре – двадцать восемь. Первое неполное
произведение записано. Умножаем первый множитель на семь десятков. Восемью
семь – пятьдесят шесть. Шесть пишем, пять запоминаем. Четырежды семь – двадцать
восемь. Да ещё пять – тридцать три. Теперь есть и второе неполное
произведение. Складываем их. Переносим нули из первого множителя вниз
и пишем справа от получившейся суммы. Ответ: триста шестьдесят четыре
тысячи восемьсот.
Да ещё пять – тридцать три. Теперь есть и второе неполное
произведение. Складываем их. Переносим нули из первого множителя вниз
и пишем справа от получившейся суммы. Ответ: триста шестьдесят четыре
тысячи восемьсот.
Ну а если нули стоят не в конце, а в середине первого множителя, как вот в этом числовом выражении?
3 009 · 54
В данном случае все записываем как обычно – единицы под единицами, десятки под десятками. Умножаем на единицы. Девятью четыре – тридцать шесть. Шесть пишем, три запоминаем. Нуль умножаем на четыре – нуль. Да ещё три – получается три. И снова нуль умножаем на четыре – нуль. Трижды четыре – двенадцать. Записано первое неполное произведение.
Умножаем на пять десятков. Девятью пять – сорок пять. Пять
пишем, четыре запоминаем. Нуль умножаем на пять – нуль. Пишем четвёрку, которую
запомнили. Ведь мы её прибавляем к нулю. Вновь умножаем нуль и получаем нуль. Трижды пять – пятнадцать. Вот и второе неполное произведение.
Складываем. Ответ: сто шестьдесят две тысячи четыреста восемьдесят шесть.
Трижды пять – пятнадцать. Вот и второе неполное произведение.
Складываем. Ответ: сто шестьдесят две тысячи четыреста восемьдесят шесть.
Ну а теперь попробуем перемножить два трёхзначных числа с нулями в разряде десятков – шестьсот девять и двести семь.
Записываем числа одно под другим. Умножаем шестьсот девять на семь единиц. Девятью семь – шестьдесят три. Три пишем под единицами, а шесть. Вы сейчас подумали: она скажет «запоминаем»! А вот и нет! Так как дальше умножать нужно нуль, и результат, конечно, тоже нуль, шестёрку можно не запоминать, а сразу писать в разряде десятков. А теперь шесть умножаем на семь и пишем сорок два. Первое неполное произведение готово.
На нуль умножать не будем.
Теперь шестьсот девять умножим на две сотни. И не забудьте!!!
Писать начнём под сотнями. Девятью два – восемнадцать. Пишем восемь и. один –
ведь впереди опять умножение нуля. Шестью два – двенадцать. Складываем неполные
произведения. Ответ: сто двадцать шесть тысяч шестьдесят три.
Складываем неполные
произведения. Ответ: сто двадцать шесть тысяч шестьдесят три.
Ну и последний пример. Умножаем два трёхзначных числа с нулями в разряде единиц.
Например, пятьсот восемьдесят и триста шестьдесят.
580 · 360
Так как нулей в обоих числах одинаковое количество, записываем их точно одно под другим. А умножать будем так, как будто нам даны не трёхзначные, а двузначные числа.
Умножаем на шесть десятков. Восемью шесть – сорок восемь. Восемь пишем, четыре запоминаем. Пятью шесть – тридцать. Да ещё четыре – тридцать четыре.
Умножаем на три сотни. Восемью три – двадцать четыре. Четыре пишем, два запоминаем. Пятью три – пятнадцать, да ещё два – семнадцать.
Складываем неполные произведения. А теперь оба нуля переносим вниз и пишем справа от получившейся суммы. Ответ: двести восемь тысяч восемьсот.
Ну вот и подходит к концу наша встреча. Но я думаю, что вы
тоже хотите попробовать свои силы и решить примеры подобные тем, о которых я
рассказала.
Но я думаю, что вы
тоже хотите попробовать свои силы и решить примеры подобные тем, о которых я
рассказала.
Решайте, а потом вы сможете проверить свою работу.
2670 · 36; 4190 · 27; 709 · 340; 902 · 506
Ребята, проверьте своё решение.
Я надеюсь, вы справились с заданием. Если, конечно, были внимательны и аккуратны.
А теперь я прощаюсь с вами! До новой встречи, друзья!
Способы умножения трехзначных чисел. Четыре способа умножения без калькулятора. Актуальность использования приемов быстрого счета
Кандидат педагогических наук Наталья Карпушина.
Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа. В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
Умножение способом решётки. Иллюстрация из первой печатной книги по арифметике. 1487 год.
Палочки Непера. Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год.
Джон Непер (1550-1617).
Модель счётной машины Шиккарда. Это не дошедшее до нас вычислительное устройство изготовлено изобретателем в 1623 году и описано им годом позже в письме Иоганну Кеплеру.
Вильгельм Шиккард (1592-1635).
Наследие индусов — способ решётки
Индусы, с давних времён знавшие десятичную систему счисления, предпочитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, – умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения – в Европе. Способ решётки именовали также индийским, мусульманским или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского – «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.
Суть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, – по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально – число 73.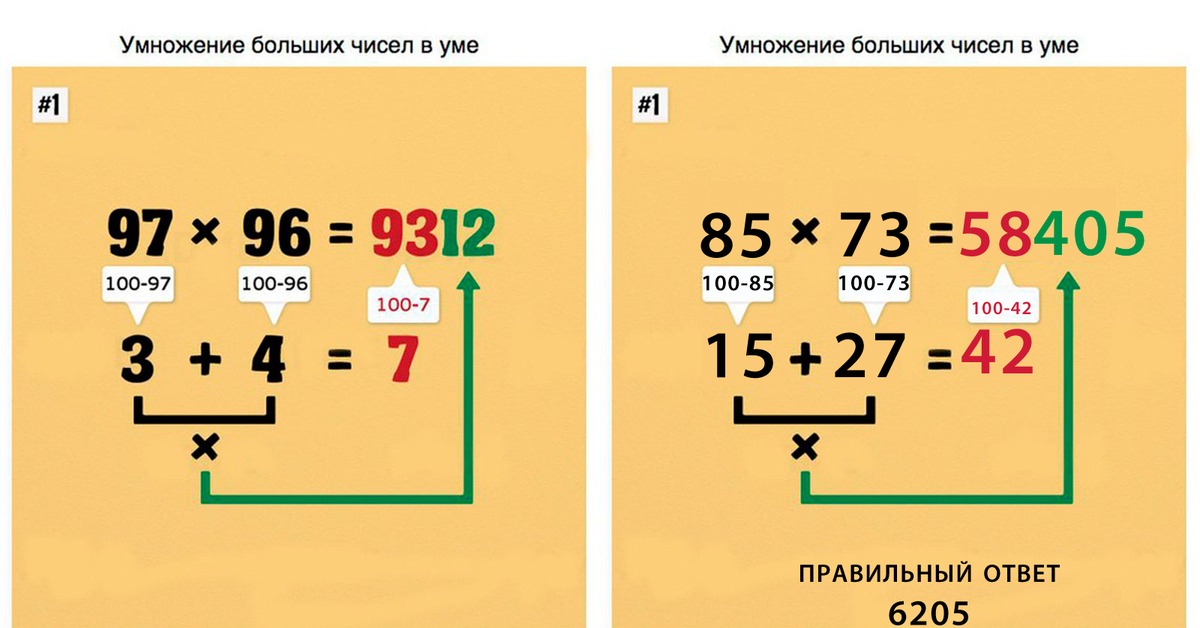 Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Почему способ решётки приводит к правильному ответу? В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 + 90 + 6 и 70 + 3.
Как видим, в первой косой полосе стоят единицы, во второй – десятки, в третьей – сотни и т.д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:
Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:
296 x 73 = (200 + 90 + 6) x (70 + 3) = 14 000 + 6300 + 420 + 600 + 270 + 18 = 10 000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70 + 20 + 10) + 8 = 21 608.
Палочки Непера
Умножение способом решётки лежит в основе простого и оригинального счётного прибора – палочек Непера. Его изобретатель Джон Непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.
В истории науки он известен, прежде всего, как один из создателей логарифмов.
Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней – число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.
Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие – с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.
Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
Таким образом,
296 x 73 = 20 720 + 888 = 21 608.
Палочки Непера применялись и для более сложных операций – деления и извлечения квадратного корня. Этот счётный прибор не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения чисел, например с повторяющимися цифрами, нужны были несколько комплектов палочек. Но такая проблема решалась заменой линеек вращающимися цилиндрами с нанесённой на поверхность каждого из них таблицей умножения в том же виде, как её представил Непер. Вместо одного набора палочек получалось сразу девять.
Подобные ухищрения в самом деле ускоряли и облегчали расчёты, однако не затрагивали главный принцип работы прибора Непера. Так способ решётки обрел вторую жизнь, продлившуюся ещё несколько столетий.
Машина Шиккарда
Учёные давно задумывались над тем, как переложить непростую вычислительную работу на механические устройства. Первые успешные шаги в создании счётных машин удалось осуществить только в XVII столетии. Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
По сути, машина Шиккарда представляет собой шестиразрядный механический калькулятор, выполняющий сложение, вычитание, умножение и деление чисел. В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.
В работе счётная машина Шиккарда очень проста. Чтобы узнать, чему равно произведение 296 x 73, нужно установить цилиндры в положение, при котором в верхнем ряду окошек появится первый множитель: 000296. Произведение 296 x 3 получим, открыв окошки третьего ряда и просуммировав увиденные цифры, как в способе решётки. Точно так же, открыв окошки седьмого ряда, получим произведение 296 x 7, к которому припишем справа 0. Остаётся только сложить найденные числа на суммирующем устройстве.
Придуманный некогда индусами быстрый и надёжный способ умножения многозначных чисел, много веков применявшийся при расчётах, ныне, увы, забыт. А ведь он мог бы выручить нас и сегодня, если бы под рукой не оказалось столь привычного всем калькулятора.
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких-нибудь разрядов, определяется нулями, приписываемыми к цифрам.
Занимаемое место, в случае отсутствия каких-нибудь разрядов, определяется нулями, приписываемыми к цифрам.
Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:
Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.
За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494 г. ) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.
Некоторые способы быстрого устного умножения мы уже с Вами разобрали, теперь давайте подробнее разберемся, как быстро умножать числа в уме, используя различные вспомогательные способы. Вы, возможно, уже знаете, а некоторые из них довольно экзотические, например, древний китайский способ умножения чисел.
Раскладка по разрядам
Является самым простым приемом быстрого умножения двухзначных чисел. Оба множителя нужно разбить на десятки и единицы, а затем все эти новые числа перемножить друг на друга.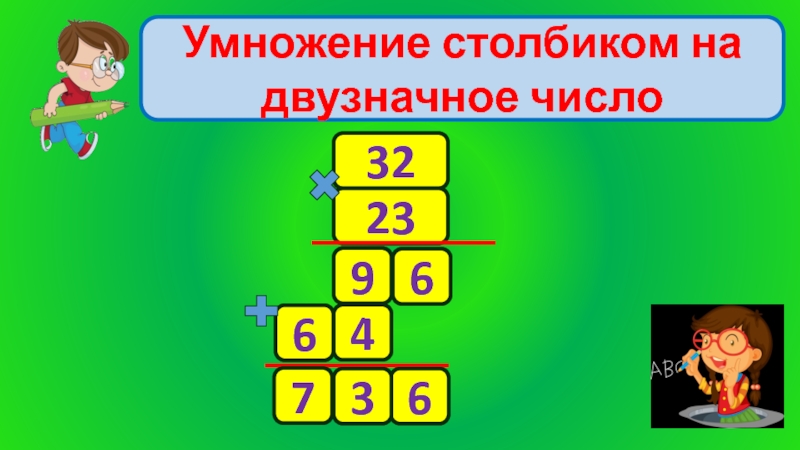
Данный способ требует умения удерживать в памяти одновременно до четырех чисел, и делать с этими числами вычисления.
К примеру, нужно перемножить числа 38 и 56 . Делаем это следующим образом:
38 * 56 = (30 + 8) * (50 + 6) = 30 * 50 + 8 * 50 + 30 * 6 + 8 * 6 = 1500 + 400 + 180 + 48 = 2128 Еще проще будет делать устное умножение двухзначных чисел в три действия. Сначала нужно перемножить десятки, затем прибавить два произведения единиц на десятки, и затем прибавить произведение единиц на единицы. Выглядит это так: 38 * 56 = (30 + 8) * (50 + 6) = 30 * 50 + (8 * 50 + 30 * 6) + 8 * 6 = 1500 + 580 + 48 = 2128 Для того, чтобы успешно пользоваться этим способом, нужно хорошо знать таблицу умножения, уметь быстро складывать двухзначные и трехзначные числа, и переключаться между математическими действиями, не забывая промежуточные результаты. Последнее умение достигается с помощью и визуализации.
Данный способ не самый быстрый и эффективный, потому стоит изучить еще и другие способы устного умножения.
Подгонка чисел
Можно попробовать привести арифметическое вычисление к более удобному виду. Например, произведение чисел 35 и 49 можно себе представить таким образом: 35 * 49 = (35 * 100) / 2 — 35 = 1715
Этот способ может оказаться более эффективным, чем предыдущий, но он не универсальный, и подходит не ко всем случаям. Не всегда можно найти подходящий алгоритм для упрощения задачи.
На эту тему вспомнился анекдот про то, как математик проплывал по реке мимо фермы, и заявил собеседникам, что ему удалось быстро подсчитать количество овец в загоне, 1358 овец. Когда его спросили, как ему это удалось, он сказал, что все просто — нужно подсчитать количество ног, и разделить на 4.
Визуализация умножения в столбик
Этот один из самых универсальных способов устного умножения чисел, развивающий пространственное воображение и память. Для начала следует научиться умножать в столбик в уме двухзначные числа на однозначные. После этого Вы легко сможете умножать двухзначные числа в три действия. Сначала двухзначное число нужно умножить на десятки другого числа, затем умножить на единицы другого числа, и после этого просуммировать полученные числа.
Сначала двухзначное число нужно умножить на десятки другого числа, затем умножить на единицы другого числа, и после этого просуммировать полученные числа.
Выглядит это таким образом: 38 * 56 = (38 * 5) * 10 + 38 * 6 = 1900 + 228 = 2128
Визуализация с расстановкой чисел
Очень интересный способ перемножения двухзначных чисел следующий. Нужно последовательно перемножить цифры в числах, чтобы получились сотни, единицы и десятки.
Допустим, Вам нужно умножить 35 на 49 .
Сначала перемножаете 3 на 4 , получаете 12 , затем 5 и 9 , получаете 45 . Записываете 12 и 5 , с пробелом между ними, а 4 запоминаете.
Получаете: 12 __ 5 (запоминаете 4 ).
Теперь умножаете 3 на 9 , и 5 на 4 , и суммируете: 3 * 9 + 5 * 4 = 27 + 20 = 47 .
Теперь нужно к 47 прибавить 4 , которое мы запомнили. Получаем 51 .
Получаем 51 .
Пишем 1 в середине, а 5 прибавляем к 12 , получаем 17 .
Итого, число, которое мы искали, 1715 , оно является ответом:
35 * 49 = 1715
Попробуйте таким же образом перемножить в уме: 18 * 34, 45 * 91, 31 * 52 .
Китайское, или японское, умножение
В азиатских странах принято умножать числа не в столбик, а рисуя линии. Для восточных культур важно стремление к созерцанию, и визуализации, поэтому, наверное, они и придумали такой красивый метод, позволяющий перемножать любые числа. Сложен этот способ только на первый взгляд. На самом деле, большая наглядность позволяет использовать этот способ гораздо эффективнее, чем умножение в столбик.
Кроме того, знание этого древнего восточного етода повышает Вашу эрудицию. Согласитесь, не каждый может похвастаться тем, что знает древнюю систему умножения, которой китайцы пользовались еще 3000 лет назад.
Видео о том, как китайцы перемножают числа
Более подробные сведения Вы можете получить в разделах “Все курсы” и “Полезности”, в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.
В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.
Также Вы можете подписаться на блог, и узнавать о всех новых статьях.
Это не займет много времени. Просто нажмите на ссылку ниже:
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Оригинальные способы умножения многозначных чисел и возможности их применения на уроках математики
Руководитель:
Шашкова Екатерина Олеговна
Вступление
1. Немного истории
2. Умножение на пальцах
3. Умножение на 9
4. Индийский способ умножения
5. Умножение способом «Маленький замок»
6.Умножение способом «Ревность»
7. Крестьянский способ умножения
8. Новый способ умножения
Новый способ умножения
Заключение
Литература
Вступление
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
Однажды мне случайно попалась книга С.Н. Олехника, Ю.В. Нестеренко и М.К. Потапова «Старинные занимательные задачи». Листая эту книгу, мое внимание привлекла страничка под названием «Умножение на пальцах». Оказалось, что можно умножать не только так как предлагают нам в учебниках математики. Мне стало интересно, а есть ли еще какие-нибудь способы вычислений. Ведь способность быстро производить вычисления вызывает откровенное удивление.
Постоянное применение современной вычислительной техники приводит к тому, что учащиеся затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или счетной машины. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического цикла.
Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического цикла.
Цель работы:
Показать необычные способы умножения.
Задачи:
Ш Найти как можно больше необычных способов вычислений.
Ш Научиться их применять.
Ш Выбрать для себя самые интересные или более легкие, чем те которые предлагаются в школе, и использовать их при счете.
1. Немного истории
Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления – приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках».
И все эти приемы умножения – «шахматный или органчиком», «загибанием», «крестиком», «решеткой», «задом наперед», «алмазом» и прочие соперничали друг с другом и усваивались с большим трудом.
Давайте рассмотрим наиболее интересные и простые способы умножения.
2. Умножение на пальцах
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев(2+3=5) и перемножить количества не загнутых(2*3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
Если сложить количества загнутых пальцев(2+3=5) и перемножить количества не загнутых(2*3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
3. Умножение на 9
Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится “на пальцах”. Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 5 пальцев не загнуто, справа – 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип “вычисления”.
Слева у нас 5 пальцев не загнуто, справа – 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип “вычисления”.
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве “счетной машинки” не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа – 2 клеточки. Значит 9·8=72. Все очень просто. способ умножение упрощенный интересный
4. Индийский способ умножения
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких-нибудь разрядов, определяется нулями, приписываемыми к цифрам.
Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:
Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:
5. Умножен ие способом «МАЛЕНЬКИЙ ЗАМОК»
Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.
За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.
6. Умно жение чисел методом « Ревность »
Второй способ носит романтическое название «ревность», или «решётчатое умножение».
Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, – пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.
В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063.
7 . К рестьянский способ умножения
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
Последнее удвоенное число и дает искомый результат.
В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением
Произведение всех пар соответственных чисел одинаковое, поэтому
37 32 = 1184 1 = 1184
В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:
24 17 = 24 (16+1)=24 16 + 24 = 384 + 24 = 408
8 . Новый способ умножения
Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35
Левую цифру (в нашем примере – ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.
В итоге получаем: 078235. Число 78235 и есть результат умножения.
Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.
Из всех найденных мною необычных способов счета более интересным показался способ «решетчатого умножения или ревность». Я показал его своим одноклассникам, и он им тоже очень понравился.
Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.
Я думаю, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы.
Литература
1. Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954. – 140 с.
2. Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/
3. ОлехникС. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.
4. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.
5. Перельман Я.И. Занимательная арифметика. М.Русанова,1994–205с.
6. Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004.
7. Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с.
«Математика». – М.: Аванта +, 2003. – 688 с.
Размещено на Allbest.ru
…Подобные документы
Как люди научились считать, возникновение цифр, чисел и систем счисления. Таблица умножения на “пальцах”: методика умножения для чисел 9 и 8. Примеры быстрого счета. Способы умножения двузначного числа на 11, 111, 1111 и т.д. и трехзначного числа на 999.
курсовая работа , добавлен 22.10.2011
Применение способа решета Эратосфена для поиска из заданного ряда простых чисел до некоторого целого значения. Рассмотрение проблемы простых чисел-близнецов. Доказательство бесконечности простых чисел-близнецов в исходном многочлене первой степени.
контрольная работа , добавлен 05.10.2010
Ознакомление с действиями умножения и деления. Рассмотрение случаев замены суммы произведением. Решения примеров с одинаковыми и разными слагаемыми. Вычислительный прием деления, деление на равные части. Преподавание таблицы умножения в игровой форме.
презентация , добавлен 15. 04.2015
04.2015
Характеристика истории изучения значения простых чисел в математике путем описания способов их нахождения. Вклад Пьетро Катальди в развитие теории простых чисел. Способ Эратосфена составления таблиц простых чисел. Дружественность натуральных чисел.
контрольная работа , добавлен 24.12.2010
Назначение, состав и структура арифметическо-логических устройств, их классификация, средства представления. Принципы построения и функционирования АЛУ ЭВМ. Создание блок-схемы алгоритма умножения, определение набора управляющих сигналов, схемное решение.
курсовая работа , добавлен 25.10.2014
Понятие “матрица” в математике. Операция умножения (деления) матрицы любого размера на произвольное число. Операция и свойства умножения двух матриц. Транспонированная матрица – матрица, полученная из исходной матрицы с заменой строк на столбцы.
контрольная работа , добавлен 21.07.2010
Исторические факты исследования простых чисел в древности, настоящее состояние проблемы. Распределение простых чисел в натуральном ряде чисел, характер и причина их поведения. Анализ распределения простых чисел-близнецов на основе закона обратной связи.
Распределение простых чисел в натуральном ряде чисел, характер и причина их поведения. Анализ распределения простых чисел-близнецов на основе закона обратной связи.
статья , добавлен 28.03.2012
Основные понятия и определения кубических уравнений, способы их решения. Формула Кардано и тригонометрическая формула Виета, сущность метода перебора. Применение формулы сокращенного умножения разности кубов. Определение корня квадратного трехчлена.
курсовая работа , добавлен 21.10.2013
Рассмотрение различных примеров комбинаторных задач в математике. Описание способов перебора возможных вариантов. Использование комбинаторного правила умножения. Составление дерева вариантов. Перестановки, сочетания, размещения как простейшие комбинации.
презентация , добавлен 17.10.2015
Определение собственного вектора матрицы как результата применения линейного преобразования, задаваемого матрицей (умножения вектора на собственное число). Перечень основных действий и описание структурной схемы алгоритма метода Леверрье-Фаддеева.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
“Счёт и вычисления – основа порядка в голове”.
Песталоцци
Цель:
- Познакомиться со старинными приемами умножения.
- Расширить знания по различным приемам умножения.
- Научиться выполнять действия с натуральными числами, используя старинные способы умножения.
- Старинный способ умножение на 9 на пальцах
- Умножение методом Ферроля.
- Японский способ умножения.
- Итальянский способ умножения (“Сеткой”)
- Русский способ умножения.
- Индийский способ умножения.

Ход занятия
Актуальность использования приемов быстрого счета.
В современной жизни каждому человеку часто
приходится выполнять огромное количество
расчётов и вычислений. Поэтому цель моей работы
– показать лёгкие, быстрые и точные методы счёта,
которые не только помогут вам во время каких-либо
расчётах, но вызовут немалое удивление у
знакомых и товарищей, ведь свободное выполнение
счётных операций в значительной степени может
свидетельствовать о незаурядности вашего
интеллекта. Основополагающим элементом
вычислительной культуры являются сознательные и
прочные вычислительные навыки. Проблема
формирования вычислительной культуры актуальна
для всего школьного курса математики, начиная с
начальных классов, и требует не простого
овладения вычислительными навыками, а
использования их в различных ситуациях. Владение
вычислительными умениями и навыками имеет
большое значение для усвоения изучаемого
материала, позволяет воспитывать ценные
трудовые качества: ответственное отношение к
своей работе, умение обнаруживать и исправлять
допущенные в работе ошибки, аккуратное
исполнение задания, творческое отношение к
труду.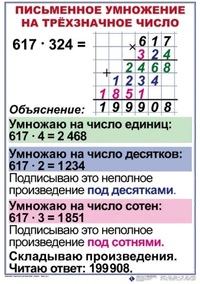 Однако, в последнее время уровень
вычислительных навыков, преобразований
выражений имеет ярко выраженную тенденцию к
снижению, учащиеся допускают массу ошибок при
подсчетах, все чаще используют калькулятор, не
мыслят рационально, что отрицательно
сказывается на качестве обучения и уровне
математических знаний учащихся в целом. Одной из
составляющих вычислительной культуры
является устный
счёт , который имеет большое значение. Умение
быстро и правильно произвести несложные
вычисления “в уме” необходимо для каждого
человека.
Однако, в последнее время уровень
вычислительных навыков, преобразований
выражений имеет ярко выраженную тенденцию к
снижению, учащиеся допускают массу ошибок при
подсчетах, все чаще используют калькулятор, не
мыслят рационально, что отрицательно
сказывается на качестве обучения и уровне
математических знаний учащихся в целом. Одной из
составляющих вычислительной культуры
является устный
счёт , который имеет большое значение. Умение
быстро и правильно произвести несложные
вычисления “в уме” необходимо для каждого
человека.
Старинные способы умножения чисел.
1. Старинный способ умножение на 9 на пальцах
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
2. Умножение методом Ферроля.
Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.
Например: 12х14=168
а) 2х4=8, пишем 8
б) 1х4+2х1=6, пишем 6
в) 1х1=1, пишем 1.
3. Японский способ умножения
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:
Этот рисунок состоит из 10 линий (количество может быть любым)
- Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
- А эти линии обозначают число 13 (1 линия, отступ, 3 линии)
(пересечения на рисунке указаны точками)
Количество пересечений:
- Верхний левый край: 2
- Нижний левый край: 6
- Верхний правый: 4
- Нижний правый: 12
1) Пересечения в верхнем левом крае (2) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа
3) Пересечения в нижнем правом крае (12) – третье
число ответа.
Получается: 2; 10; 12.
Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.
4. Итальянский способ умножения (“Сеткой”)
В Италии, а также во многих странах Востока, этот способ приобрел большую известность.
Использование приема:
Например, умножим 6827 на 345.
1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
2. Умножаем число каждого ряда последовательно на числа каждой колонки.
- 6*3 = 18. Записываем 1 и 8
- 8*3 = 24. Записываем 2 и 4
Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.
(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)
3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
Ответ: 2355315.
5. Русский способ умножения.
Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:
- 32 * 13 (32 делим на 2, а 13 умножаем на 2)
- 16 * 26 (16 делим на 2, а 26 умножаем на 2)
- 8 * 52 (и т.д.)
- 4 * 104
- 2 * 208
- 1 * 416 =416
Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение
Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, – гласит правило, – в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):
- 19*17
- 4 *68*
- 2 *136*
- 1 *272
Сложив незачеркнутые числа, получаем вполне правильный результат:
Ответ: 323.
6. Индийский способ умножения.
Такой способ умножения использовали в Древней Индии.
Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.
Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила:
- Правило 1. Единицы первого произведения следует писать в той же колонке, что и множитель, то есть в данном случае под 9.
- Правило 2. Последующее произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.
Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).
Затем складываем цифры в колонках и получаем ответ: 72956.
Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат.
Заключение
Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, “экономическую – ситуацию” в стране, погоду на “завтра”, описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора – “Всё есть число!”.
Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)
Литература.
- Энциклопедия для детей. “T.23”. Универсальный энциклопедический словарь \ ред. коллегия: М. Аксёнова, Е.Журавлёва, Д.Люри и др. – М.: Мир энциклопедий Аванта +, Астрель, 2008. – 688 с.
- Ожегов С. И. Словарь русского языка: ок. 57000 слов/ Под ред. чл. – корр. АНСИР Н.Ю. Шведовой. – 20 – е изд.– М. : Просвещение, 2000. – 1012 с.
- Xочу всё знать! Большая иллюстрированная энциклопедия интеллекта / Пер. с англ. А. Зыковой, К. Малькова, О.Озёровой. – М.: Изд-во ЭКМО, 2006. – 440 с.
- Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка 5-6 кл./ О.С.Шейнина, Г.М. Соловьева – М.: Изд-во НЦЭНАС, 2007. – 208 с.
- Кордемский Б. А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.
- Минских Е. М. “От игры к знаниям”, М., “Просвещение” 1982г.
- Свечников А. А. Числа, фигуры, задачи М., Просвещение, 1977г.
- http://matsievsky. newmail. ru/sys-schi/file15.htm
- http://sch69.narod. ru/mod/1/6506/hystory. html
| Русский язык | Тема урока: Предложения распространенные и нераспространенные. Правило стр. 238, упр. 375, 376-списать, выполнить задания к упражнениям. Д.з. правило учить наизусть, стр. 240, упр. 380-списать, выполнить задания к нему. | Тема урока: Однородные члены предложения. Правило стр. 241, упр.381, 382-списать, выполнить задания к упражнениям. Д.з. — правило учить наизусть стр. 241, упр. 382, стр.241-242, списать, выполнить задания к упражнению. | Тема урока: Однородные сказуемые. Стр. 242, упр. 384-списать, выполнить задания к упражнению. Д.з. – Составить 5 предложений с однородными членами, подчеркнуть главные члены предложений. | Тема урока: Однородные второстепенные члены предложения. Стр. 243, упр.385 – списать, выполнить задания к упражнениям. Д.з стр.243, упр.387 — списать, выполнить задания к упражнениям, повторять правила. | Чтение (литературное чтение) | Классная работа Весенние ручьи. А.Толстой. стр.152-154, читать, отвечать на вопросы. А. Пушкин. «Гонимы вешними лучами…» стр.154, читать 3 раза, отвечать на вопросы. Весна. И. Соколов-Микитов стр.156-157, читать, отвечать на вопросы. Д.з. Нарисовать в тетради рисунки к произведениям, которые читали в классной работе. | Классная работа И. Бунин. «Крупный дождь в лесу зеленом…» стр.158, читать 3 раза, отвечать на вопросы. Черемуха. С. Есенин. Выразительное чтение, стр. 159, читать, отвечать на вопросы. Д.з. Черемуха. С. Стр.159. Есенин., выучить наизусть. | Классная работа Я. Аким. Весна, весною, о весне, стр.159-160. На поле Куликовом. По О. Тихомирову. Москва собирает войско, стр 195-196, читать, отвечать на вопросы. Д.з.- Стр. 195-196, читать, отвечать на вопросы. | Классная работа Куликовская битва, стр.197-199, читать,отвечать на вопросы. Слава героям, стр.200-201, читать, отвечать на вопросы. Д.з.- Стр. 197-201 читать, нарисовать рисунок в тетради. Гагаринский урок. | Математика | Классная работа. Тема урока: Умножение двузначных чисел на однозначное число с переходом через разряд. Стр. 165, № 770, 1) Рассмотрите решение примера. Образец запишите в тетрадь. № 771, (1 ст.) Напишите примеры столбиком и решите их. Стр. 167, № 782 (1-2 ст.) Решите примеры. Домашнее задание: 1 группа: стр. 166, № 779 (3 ст.) 2 группа: стр. 166, № 774 (1 ст.) | Классная работа. Тема урока: Умножение трёхзначных чисел на однозначное число с переходом через разряд. Стр. 167, № 789, 1) Рассмотрите решение примера. Образец запишите в тетрадь. № 789, 3) (1 ст.) Напишите примеры в столбик и решите их. № 793, 1) Образец запишите в тетрадь. (1 ст.) Решите примеры по образцу 2) Образец запишите в тетрадь. (1 ст.) Решите примеры по образцу Стр. 169, № 801 (1-2 ст.) Решите примеры. Домашнее задание: 1 группа: стр. 169 № 798 (1 ст.) 2 группа: стр. 169 № 797 (1 ст.) | Классная работа. Тема урока: Умножение двузначных и трёхзначных чисел на однозначное число с переходом через разряд. Решение задач. Стр. 167, № 784 (2 ст.) Стр. 169, № 797 (2 ст.) № 796. Задача. Домашнее задание: 1 группа: стр. 170 № 809 (2-3 ст.) 2 группа: стр. 170 № 809 (2 ст.) | Классная работа. Тема урока: Умножение двузначных и трёхзначных чисел на однозначное число с переходом через разряд. Закрепление. Решите примеры. стр. 171, № 822 (2-3 ст.) № 818, 2) Домашнее задание: 1 группа: стр. 171 № 820 (1 ст.) 2 группа: стр. 171 № 822 (3-4 ст.) |
Секреты быстрого счета (или математические трюки). Секреты математики – Оценок.нет
Умножение двузначного числа на 11.
При умножении двузначного числа на 11 цифры этого числа раздвигают и в середину ставят сумму этих цифр.
Например:
а) 35 ⋅ 11 = 385, т. к. 3 + 5 = 8
б) 68 ⋅ 11 = 748, т.к. 6 + 8 = 14 то число десятков будет равно 4, а цифра сотен увеличится на единицу и будет равна 7.
Умножение десятичной дроби на 11.
Умножаем, не обращая внимания на запятую, а затем в полученном результате отделяем справа запятой столько цифр, сколько их стояло после запятых в обоих множителях вместе.
Например:
а) 4, 7 ⋅ 0,11 = 0,517, т. к. 47 ⋅ 11 = 517 и отделяем запятой справа 3 цифры (1 + 2)
б) −0,32 ⋅ 1,1 = −0,352. Произведение чисел с разными знаками – число отрицательное. 32 ⋅ 11 = 352 и отделили запятой 3 цифры справа
в) 0,062 ⋅ 1100 = 68,2. Умножили 62 на 11, получили 682, приписали 2 нуля, получилось 68200 и отделили справа запятой 3 цифры. Получилось 68,200 = 68,2
г) −730 ⋅ (−0,011) = 8,03. Произведение двух отрицательных чисел – число положительное. 73 умножаем на 11, получаем 803, приписываем справа ноль и отделяем запятой справа 3 цифры.
Деление трехзначных чисел, состоящих из одинаковых цифр, на число 37.
Результат равен сумме этих одинаковых цифр трехзначного числа.
Например:
а) 222 : 37 = 6, т. к. 2 + 2 + 2 = 6.
б) 333 : 37 = 9, т. к. 3 + 3 + 3 = 9.
в) 777 : 37 = 21, т. к 7 + 7 + 7 = 21.
г) 888 : 37 = 24, т. к. 8 + 8 + 8 = 24.
Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножаем первую цифру саму на себя +1, а в конце дописываем 25. Вот и все!
252 = (2 ⋅ (2 + 1)) и 25
2 ⋅ 3 = 6
625
Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.
Возьмем любое число, разделим на 2 (другими словами, поделим пополам). Если в результате получилось целое число, приписываем 0 в конце. Если нет, не обращаем внимание на запятую и в конце добавляем 5. Это срабатывает всегда:
2682 ⋅ 5 = (2682 : 2) и приписать 5 или 0
2682 : 2 = 1341 (целое число, поэтому добавьте 0)
13410
Попробуем другой пример:
5887 ⋅ 5
2943,5 (дробное число, пропускаем запятую, добавляем 5)
29435
Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрим на руки. Загнем палец, который соответствует умножаемому числу (например 9 ⋅ 3 – загибаем третий палец), посчитаем пальцы до загнутого пальца (в случае 9 ⋅ 3 – это 2), затем посчитаем после загнутого пальца (в нашем случае –7). Ответ –27.
Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58 • 4 = (58 • 2) + (58 • 2) = (116) + (116) = 232
Сложное умножение
Если нужно умножать большие числа, причем одно из них — четное, ты можешь просто перегруппировать их, чтобы получить ответ:
32 ⋅ 125 все равно, что:
16 ⋅ 250 все равно, что:
8 ⋅ 500 все равно, что:
4 ⋅ 1000 = 4,000
Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, – просто умножить на 2 и перенести запятую: 195 : 5
Шаг 1. 195 ⋅ 2 = 390
Шаг 2. Переносим запятую: 39,0 или просто 39.
2978 : 5
Шаг 1. 2978 ⋅ 2 = 5956
Шаг 2. 595,6
Вычитание из 1000
Чтобы выполнить вычитание из 1000, можно пользоваться этим простым правилом: Отнимаем от 9 все цифры, кроме последней. А последнюю цифру отнимаем от 10:
1000 − 648
Шаг 1: от 9 отними 6 = 3
Шаг 2: от 9 отними 4 = 5
Шаг 3: от 10 отними 8 = 2
Ответ: 352
Если нужно оставить 15% чаевых, есть простой способ сделать это. Высчитываем 10% (делим число на 10), а потом добавляем получившееся число к его половине и получаем ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
Быстрый счет: задачи и решения
4-значное умножение на 2-значное
Метод
Прежде чем мы начнем, давайте рассмотрим правила умножения многозначных чисел. Сначала напишите числа вертикально, так чтобы большее число было поверх меньшего. Во-вторых, числа должны быть выровнены по разрядам. Единицы в меньшем числе должны быть непосредственно под единицами в большем числе. Размер 1000 x 15 будет выглядеть так:
Теперь, когда у нас есть правила, давайте займемся проблемой дохода.Допустим, вы выгуливаете всех собак в своем районе и зарабатываете в общей сложности 1350 долларов каждый месяц в течение 12 месяцев. Ваша задача будет размером 1350 долларов на 12. Взгляните на изображение.
Умножение – 1 раунд
Поскольку вы умножаете на двузначное число, вы умножаете на два раза. Но давайте пока просто посмотрим на первый раунд.
В первом раунде мы будем использовать 2 из 12 (пока забудьте про 1 из 12).Двойка умножается на все четырехзначное число, начиная с единицы, затем переходя к десяткам, сотням и заканчивая тысячами.
Начните с 2 умножить на 0, что равно 0, и поместите его на разряды единиц. Далее следует 2 умножить на 5, что равно 10, поставить 0 вниз и перенести 1, 2 умножить на 3, что равно 6 плюс перенесенная 1. И последнее – 2 умножить на 1 в разряде тысяч, что равно 2.
Умножение – второй раунд
Теперь мы будем использовать число 1 из числа 12, НО, поскольку число, которое вы сейчас используете для умножения, находится в разряде десятков, единиц не будет; Итак, вы ДОЛЖНЫ поставить 0 вместо единиц ответа (показано желтым 0).Если вы не поставите этот 0, вы будете каждый раз получать неправильный ответ. Теперь 1 будет умножаться на каждую из четырех цифр 1350 долларов.
Завершить добавлением
Теперь, когда мы умножили все цифры в нашем нижнем числе, мы сложим два ответа вместе, чтобы сформировать окончательный ответ, который составляет 16 200 долларов.
Задача со словом
В одной миле 5280 футов. Чтобы добраться до дома друга, нужно проехать 25 миль. Сколько это футов? Мы берем количество футов в одной миле и умножаем его на 25.
5280 x 25 =? футов
После написания нашей задачи по вертикали, выровняв цифры в единицах, мы можем начать умножение.
Во-первых, мы используем 5 из 25, чтобы умножить на 5280, начиная с 0. Посмотрите на изображение.
Во-вторых, мы используем 2 из 25, НО перед тем, как умножить, мы должны поставить этот 0 на разряды единиц ниже первой строки. После того, как 0 окажется на месте единиц, мы можем начать умножать 5280 на 2.
Наконец, мы складываем два ответа, чтобы получить окончательный ответ! До дома вашего друга 132 000 футов. Это слишком много обуви!
Краткое содержание урока
При умножении четырехзначного числа на двузначное число, каждая из цифр двузначного числа, начиная с цифры в разряде единиц, получит свою очередь умножаться. Затем вы складываете два ответа, чтобы получить окончательный ответ.
Что такое длинное умножение? – Определение, факты и примеры
Длинное умножениеДлинное умножение – это метод умножения двух чисел, которые сложно перемножить.
Например, мы можем легко найти произведение 55 × 20, умножив 55 на 2, а затем добавив 0 в самом правом месте ответа.
55 × 2 = 110 и 55 × 20 = 1100.
Но зачастую найти продукт не так просто. В такие моменты мы используем длинный метод умножения.
Шаги для умножения с использованием длинного умноженияУмножение 2-значных чисел на 2-значные числа
Умножим 47 на 63, используя метод длинного умножения.
1. Напишите два числа одно под другим в соответствии с местами их цифр. Напишите большее число сверху и знак умножения слева. Нарисуйте линию под числами.
2. Умножьте единичную цифру верхнего числа на единичную цифру нижнего числа.
Напишите продукт, как показано.
3. Умножьте цифру десятков верхнего числа на цифру единиц нижнего числа.
Это наш первый частичный продукт, который мы получили, умножив верхнее число на единичную цифру нижнего числа.
4. Напишите 0 под цифрой единиц, как показано. Это потому, что теперь мы будем умножать цифры верхнего числа на цифру десятков нижнего числа. Следовательно, мы пишем 0 вместо единиц.
5. Умножьте цифру единиц верхнего числа на цифру десятков нижнего числа.
6. Умножьте цифру десятков верхнего числа на цифру десятков нижнего числа.
Это второй частичный продукт, полученный при умножении верхнего числа на разряд десятков нижнего числа.
7. Добавьте два неполных продукта.
В методе длинного умножения число наверху называется множимым. Число, на которое оно умножается, то есть нижнее число, называется множителем.
Итак, в задаче с длинным делением будет:
Мы используем тот же метод для умножения чисел, превышающих 2-значные.
На рисунке ниже показан метод длинного деления для умножения 357 на 23
.Интересный факт:
|
МНОГИЕ ТАЙНЫ ЧИСЛА 9
Хотя наша современная числовая система повсеместно признана языком математики и науки, она была практически неизвестна за пределами Индии, где она возникла, примерно до 8-го века.До этого европейцы обходились более неуклюжими системами, включая римские цифры. А просто попробуйте заняться арифметикой римскими цифрами. «Индийская система счета была самым успешным интеллектуальным нововведением, когда-либо созданным на нашей планете», – пишет английский математик Джон Барроу в своей недавней книге «Пи в небе». Что делает эту систему счисления настолько удобной, так это то, что она является десятично-циклической. Другими словами, каждое «место» в числе имеет абсолютное значение в диапазоне от нуля до девяти и «разрядное значение», которое увеличивается справа налево, кратно десяти – один, 10, 100, 1000 и так далее.Таким образом, например, четырехзначное число может быть представлено как dcba с пониманием того, что цифра в позиции, помеченной d, может быть любой от 0 до 9, но понимается как d x 1000. Точно так же цифра в c может быть любой цифрой, но подразумевается, что это c 100. Таким образом, наибольшее возможное четырехзначное число – 9 999. Хотя сейчас мы принимаем такой способ представления чисел как должное, его общие значения и многие из его, казалось бы, странных характеристик редко оцениваются. Например, тот факт, что 9 – это самая большая возможная цифра в любом заданном «месте», порождает некоторые поразительные свойства чисел в целом, называемые «Правилами девяти».Некоторые из этих важных правил проиллюстрированы ниже. Правило 1. Когда любое число умножается на девять, если складывать отдельные цифры в полученном продукте, они всегда будут в сумме девять, пока вы продолжаете суммировать цифры, полученные на каждом этапе, пока вы получите однозначное число. Это всегда будет девять. Вы можете проверить это для произведения девяти, умноженного на любое другое однозначное число, с помощью этой таблицы умножения: 2 9 = 18; 1 + 8 = 9 3 9 = 27; 2 + 7 = 9 4 9 = 36; 3 + 6 = 9 5 9 = 45; 4 + 5 = 9 6 9 = 54; 5 + 4 = 9 7 9 = 63; 6 + 3 = 9 8 9 = 72; 7 + 2 = 9 9 9 = 81; 8 + 1 = 9 Если вы думаете, что однозначные числа – это особый случай, попробуйте его с любым числом.Умножьте это число на девять, а затем начните суммировать цифры. Вот один пример: начните с числа 54 321. Умножьте на девять, чтобы получить 488 889. Сложите эти цифры, и у вас будет 45. Если, как здесь, сумма больше одной цифры, сложите их. Четыре плюс пять – девять. Правило 2. Обратное Правилу 1 также верно, то есть, если всего цифр числа составляет девять или кратно девяти, то само число должно быть кратным девяти. Справедливость этого правила можно увидеть, например, если рассмотреть общую форму 10 b + a для двузначного числа.Если a + b равно девяти, то число можно записать как 10 b + 9 – b = 9 (b + 1). Аналогичное доказательство можно построить для чисел с большим количеством цифр. Рассмотрим число 1233, цифры которого складываются в девять. Ясно, что оно кратно девяти и равно 137 9. Цифры числа 17 982 всего 27, что кратно девяти. Следовательно, само число также должно быть кратным девяти. Действительно, 17 982 равно 1 998 умноженным на 9. Правило 3. Правило 2 ведет непосредственно к другому, более поразительному правилу. Если многозначное число кратно девяти, все остальные числа, образованные перестановкой его цифр, также будут кратны девяти.Таким образом, помимо 1233, все другие комбинации цифр 1, 2, 3 и 3, такие как 3 321, 3 123, 2313 и 3231, также кратны девяти. Точно так же, чтобы выбрать большее число, поскольку 17 982 кратно девяти, другие числа с такими же цифрами, например 97 821, 89 172 и 71 928, также кратны девяти. Правило 4. Если после любого места числа, кратного девяти, добавить один или несколько нулей, полученное число останется кратным девяти. Это правило следует непосредственно из правила 2.Рассмотрим 189, кратное девяти. Нетрудно проверить, что 1089, 1809, 10809 и так далее кратны девяти. Также из правила 3 следует, что 9,801, 90,801, 9,081 и т. Д. Также будут кратны девяти. Правило 5. Если одна или несколько девяток или кратных девяти вводятся в любом месте числа, кратного девяти, результирующее число также будет кратным девяти. Это также следует из правила 2. Таким образом, если мы снова рассмотрим 189, мы можем отбросить девять или кратные девяти в любом месте или вокруг него, и результат всегда будет кратным девяти.Например: 1899, 9 189, 1989, 18 279 кратны девяти. Правило 6. Здесь немного меняем темп. Суммируйте цифры любого многозначного числа. На этот раз вы не всегда получите девять. Но если вы затем вычтите эту сумму из исходного числа, цифр полученного числа всегда составит девять. Это правило следует непосредственно из правила 1 и из общей формы чисел в системе счисления. Таким образом, например, используя общую форму 1000 d + 100 c + 10 b + a для четырехзначного числа и вычитая сумму цифр (d + c + b + a), мы получаем 999 d + 99 c + 9 б = 9 (111 д + 11 в + б).Поскольку число всегда кратно девяти, сумма его цифр должна составлять девять. Опять же, это правило лучше всего понять на реальных примерах. Рассмотрим двузначное число 35. Сумма цифр равна восьми. Вычтите это из исходного числа: 35 – 8 = 27. Очевидно, результат кратен девяти, а его цифры прибавятся к девяти. Попробуйте с гораздо большим числом – 429 517. Сумма его цифр составляет 28 и 429 517 – 28 = 429 489, кратное девяти равно 9 47 721. Правило 7. Если любое число перевернуть и меньшее из двух чисел вычесть из большего, то полученное число всегда будет кратным девяти.Возьмем, к примеру, 657. Переверните его, чтобы получить 756. Вычтите 657 из 756, и вы получите 99, что очевидно кратно девяти. Справедливость этого правила можно увидеть, снова рассмотрев общую форму двузначного числа, а именно 10 b + a, и вычтя из него обратное, 10 a + b. Результат – 10 (b – a) + (a – b) или 9 (b – a), и правило легко следует. Как и другие правила, это будет применяться независимо от того, насколько велико число. Возьмем 98 723 456 человек. Вычитание обратной цифры этого числа из самого себя дает 98 723 456 – 65 432 789 = 33 290 667.Сумма цифр последнего числа равна 36, а 3 + 6 = 9, поэтому само число кратно девяти. Правило 8. Это расширение правила 7. Если трехзначное число поменять местами, и меньшее число вычтено из большего, и если результат обратный и добавлен к самому себе, то полученное число всегда будет 1089. Возьмем 783. Если вычесть из него обратную сторону, получится 396, а 396 + 693 = 1089. Или рассмотрите 423. Вычитая его обратную сторону, 324, остается 99. Чтобы это сработало, вам нужно принять результат как 099.В обратном порядке, чтобы получить 990, прибавьте его к 099, и результат будет 1089. Правило 9. Если любые две цифры многозначного числа поменять местами и меньшее из двух чисел вычесть из большего, результат всегда будет кратен девяти. Доказательство может быть сделано с использованием общей формы многозначного числа, но числовой пример более нагляден. Возьмем 142897 человек. Если мы поменяем местами четыре и девять, у нас будет 192 847. Вычитание меньшего исходного числа дает 4 995, что в 555 раз больше девяти.Деление на девять В приведенных выше примерах использовалось умножение на девять. Однако столь же поразительные результаты дает разделение других цифр на девять, как показано ниже. 1 9 = 0,111111111. . . . 2 9 = 0,222222222. . . . 3 9 = 0,333333333. . . . Другими словами, деление любой цифры на девять дает повторяющееся десятичное представление, в котором цифра повторяется бесконечно. Таким образом, наша современная система числовых значений содержит множество загадок. Часто мы пользуемся системой, даже не подозревая о них.Обратите внимание, что все вышеперечисленные свойства уникальны для индийской системы счисления. Их не существует, например, в римской системе счисления. В самом деле, поскольку девятка в римской системе представлена как IX, два символа I и X в ней фактически составляют 11. Это совсем не весело. ЗАГОЛОВОК: Культурные девятки: корм для кошек Nine Lives, Сонни Юргенсен в роли Redskin No. 9, песня Beatles под названием «Revolution 9» и Девять муз из мифологии.
Последние две цифры большого числа
Здесь мы увидим, как найти две последние цифры большого числа.y $
Видео:
Видео содержит объяснение того, как найти две последние цифры числа, возведенного в степень, на основе разряда единиц этого числа.
Понимание основ – последние две цифры продукта
Последние две цифры числа в основном представляют собой разряды десятков и разрядов единиц этого числа. Итак, для числа, скажем, 1439, последние две цифры этого числа – 3 и 9, что довольно просто.Теперь, как нам найти две последние цифры в произведении 1439 x 2786? Один из возможных подходов – использование вертикального и перекрестного умножения.
Процесс вычисления последних двух цифр продукта:
В произведении двух чисел скажем A и B (в нашем случае A – 1439, а B – 2786). Если a и b, соответственно, представляют собой цифры в разряде десятков и одно место в A, и аналогично c и d соответственно представляют цифры в разряде десятков и одно место в B, то
- цифра единиц A x B определяется как цифра единиц в произведении b и d.Если произведение b и d дает более одной цифры, лишняя цифра будет перенесена влево. то есть в 1439 x 2786, умножьте 9 и 6, что даст 54. Здесь 4 образует цифру единиц 1439 x 2786, а 5 идет как перенос на шаг 2.
- На этом шаге мы перемножаем a и d, c и b, а затем добавить получившиеся продукты. т.е. в 1439 x 2786 => 3 × 6 + 9 × 8 = 90
- Если перенос создается на этапе 1, добавьте его к результату, полученному на этапе 2. т.е. 5 + 90 = 95
- Цифра единиц в Результат, полученный на шаге 3, образует цифру десятков в произведении A и B.{6}} $
Здесь 2, увеличенное до 10, оканчивается на 24, а 24, повышенное до 105, что является нечетным числом, заканчивается на 24. Также 2, повышенное до 6, заканчивается на 64. Использование техники вертикального и крестообразного умножения в последнюю очередь две цифры произведения чисел, оканчивающихся на 24 и 64, равны 3 и 6.
Случай 4: Цифра единиц в x – 5- Цифра в разряде десятков – , нечетное и показатель степени y – нечетное , тогда число заканчивается на 75. {243}} $ равны 2 и 5.{243}} $ заканчивается на 75.
Викторина: проверьте свое понимание
Начните викторину!
Поделитесь викториной, чтобы показать свои результаты!
Последние две цифры большого числа Я получил %% score %% of %% total %% rightЧто дальше?
Можете ли вы вычислить наибольшую степень 15 из 24! или количество нулей в конце 1000 !? Нажмите на сообщение ниже, чтобы узнать больше о наибольшей степени чисел в факториале.
Математический трюк для возведения двухзначных чисел в квадрат
(последнее обновление: 1 июня 2018 г.)
Если вы когда-либо сталкивались с возведением чисел в квадрат, вы знаете, что как только вы выйдете за пределы однозначных чисел, результат будет таким: продукт довольно большой.И, видя ответ, вы, вероятно, вздрагиваете, когда думаете: «Как я мог сделать это без калькулятора?»Ну вот в чем дело – вы действительно можете! Все, что вам нужно сделать, это запомнить эти 4 шага ниже. Вам может потребоваться небольшая практика, чтобы привыкнуть к процессу и узнать, какое число какое есть в уравнении, но как только вы разберетесь со всем, вы станете мастером квадратуры.
Готовы попробовать? Вот математический трюк для возведения двузначных чисел в квадрат:
Этапы возведения двузначных чисел в квадратДопустим, вы пытаетесь возвести в квадрат 32.Выполните следующие действия (см. Значения ниже):
Шаг 1 : Добавьте последнюю цифру числа, которое вы пытаетесь возвести в квадрат, к самому числу, получая сумму.
Шаг 2: Умножьте сумму (шаг 1) на первую цифру основного числа.
Шаг 3: Возвести в квадрат последнюю цифру основного числа.
Шаг 4: Добавьте квадратное число (шаг 3) к произведению, вычисленному выше (шаг 2).Например, : 32²
Базовый номер: 32 Первая цифра: 3 Последняя цифра: 2Шаг 1: 2 + 32 = 34
Шаг 2: 34 x 3 = 102
Шаг 3: 2² = 4
Шаг 4: 1024Давайте попробуем еще один пример.Как насчет 21²?
Базовый номер: 21 Первая цифра: 2 Последняя цифра: 1Шаг 1: 1 + 21 = 22
Отказ от двузначных чисел
Шаг 2: 22 x 2 = 44
Шаг 3: 1² = 1
Шаг 4: 441Но что, если квадратное число двузначное? Если вы вычислили квадрат значения на шаге 3, а результат – двузначное число, не волнуйтесь. Точно так же, как когда вы были в начальной школе, вы должны носить его и добавлять его!
Вот еще один пример: 69²
Базовый номер: 69 Первая цифра: 6 Последняя цифра: 9Шаг 1: 9 + 69 = 78
Шаг 2: 78 x 6 = 468
Шаг 3: 9² = 81
Шаг 4: 4761 (где 8 и 8 добавлены вместе, а 1 переносится на предыдущую цифру.По сути, проблема становится 4680 + 81 )Как насчет 17²?
Базовый номер: 17 Первая цифра: 1 Последняя цифра: 7Шаг 1: 7 + 17 = 24
Шаг 2: 24 x 1 = 24
Шаг 3: 7² = 49
Шаг 4: 289 (240 + 49)Возьмите лист бумаги и карандаш и потренируйтесь в них, чтобы научиться ходить. По общему признанию, на то, чтобы по-настоящему освоиться, может потребоваться некоторое время.В конце концов, надеюсь, вы сможете отказаться от бумаги и применить свои умственные математические навыки. Вскоре вы можете стать экспертом в возведении двузначных чисел в квадрат в своей голове!
Думаете, у вас все получилось? Если да, проверьте свои знания о возведении двузначных чисел в квадрат в приведенной ниже викторине. И обязательно ознакомьтесь с другими сообщениями в нашем блоге о математических трюках.
Комментарии
комментария
Практика высокого кредитного плеча
Реагируйте на распространенные модели мышления
если учащиеся неправильно умножают два числа, кратных 10,
тогда продемонстрировать разбиение на части, кратные 10 или 100.
40 – это то же самое, что 4 × 10, а 60 – то же самое, что 6 × 10. Итак, 40 × 60 то же самое, что 4 × 6 × 10 × 10 или 24 × 100.
Выявить студенческое мышление
Задавайте вопросы, чтобы помочь студентам расширить свое мышление.
Не могли бы вы использовать стратегию разделения прямоугольников, чтобы умножить двузначный множитель на трехзначный?
Как бы выглядел этот прямоугольник?
Изменить задачи
если учащиеся испытывают трудности с добавлением частичных продуктов,
тогда добавление модели по разряду, начиная с тысяч.
Выберите примеры, в которых суммы определенных разрядов больше 10.
Запишите прибавление вертикально.
Двоичное умножение – правила, метод умножения двоичных чисел, примеры.
Двоичное умножение – это процесс умножения двоичных чисел. Процесс умножения двоичных чисел такой же, как и процесс арифметического умножения на десятичные числа. Единственное отличие состоит в том, что в двоичном умножении используются числа, состоящие из нулей и единиц, тогда как при десятичном умножении используются числа, состоящие из цифр от 0 до 9. Давайте изучим процесс двоичного умножения шаг за шагом.
Правила двоичного умножения
Двоичное умножение аналогично умножению десятичных чисел.У нас есть множитель и множимое. В результате умножения получается продукт. Поскольку в двоичном умножении участвуют только двоичные цифры, мы можем умножать только нули и единицы. Правила двоичного умножения следующие.
Множимое Множитель Продукт 0 0 0 × 0 = 0 0 1 0 × 1 = 0 1 0 1 × 0 = 0 1 1 1 × 1 = 1 Как умножать двоичные числа?
Процесс умножения двоичных чисел аналогичен процессу десятичного умножения и его проще выполнить, поскольку двоичные числа состоят только из двух цифр: 0 и 1.Ниже приводится метод умножения двоичных чисел. Тот же набор правил также применяется к двоичным числам с десятичной точкой. Давайте возьмем пример умножения (\ (11101) _ {2} \) и (\ (1001) _ {2} \). Десятичный эквивалент (\ (11101) _ {2} \) равен 29, а десятичный эквивалент (\ (1001) _ {2} \) – 9. Теперь давайте перемножим эти числа.
Шаг 1: Запишите множимое (\ (11101) _ {2} \) и множитель (\ (1001) _ {2} \) один под другим в нужных местах.
Шаг 2: Умножьте крайнюю правую цифру или младший бит (LSB) умножителя (1) на все цифры множимого (\ (11101) _ {2} \).
Шаг 3: Добавьте заполнитель «0» или «X» перед умножением следующей более высокой цифры множителя & на множимое.
Шаг 4: Повторите тот же процесс для всех следующих старших цифр, пока мы не дойдем до самого старшего бита (MSB), который является самой левой цифрой множимого с множителем.
Шаг 5: Продукт, полученный в каждой строке, называется частичным продуктом. Наконец, добавьте все неполные продукты. Чтобы сложить все двоичные числа, используйте правила двоичного сложения.(Правила двоичного сложения перечислены ниже: 0 + 0 = 0, 0 + 1 = 1 и 1 + 1 = 0 с переносом 1. Итак, 1 + 1 = 10 и 1 + 1 + 1 = 11 в двоичной системе счисления)
Давайте посмотрим на следующий процесс двоичного умножения, как описано выше.
Следовательно, произведение (\ (11101) _ {2} \) и (\ (1001) _ {2} \) равно (\ (100000101) _ {2} \). Проверим наш ответ. Десятичный эквивалент (\ (100000101) _ {2} \) – 261. Чтобы узнать, как преобразовать двоичное число в десятичное, щелкните здесь.Десятичный эквивалент & (\ (11101) _ {2} \) равен 29, а десятичный эквивалент (\ (1001) _ {2} \) – 9. Когда мы умножаем 29 и 9, произведение равно 261. Десятичный эквивалент of (\ (100000101) _ {2} \) равно 261. Следовательно, продукт правильный.
Темы, связанные с двоичным умножением
Ознакомьтесь с некоторыми интересными темами, связанными с двоичным умножением.
Часто задаваемые вопросы о двоичном умножении
Что такое двоичное умножение?
Двоичное умножение – это процесс умножения двоичных чисел.Двоичные числа образуют систему счисления с основанием 2. Данные хранятся в компьютере в виде нулей и единиц. Процесс умножения двоичных чисел такой же, как и арифметическая операция умножения, которая выполняется над десятичными числами или числами с основанием 10. Единственная разница в том, что двоичные числа состоят из нулей и единиц.
Каковы правила двоичного умножения?
Двоичное умножение также аналогично умножению десятичных чисел (от 0 до 9). Двоичные числа состоят только из нулей и единиц.Следовательно, нам нужно знать произведение, когда 0 умножается на 0 и 1, а 1 умножается на 0 и 1. Правила двоичного умножения следующие.
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
Каков результат двоичного умножения (\ (111) _ {2} \) и (\ (111) _ {2} \)?
Произведение (\ (111) _ {2} \) и (\ (111) _ {2} \) равно (\ (110001) _ {2} \).
Что нужно делать для двоичного умножения?
Двоичное умножение двух чисел можно выполнить, выполнив действия, указанные ниже.
Шаг 1: Установите множитель и множимое в правильные позиции. Например, мы можем умножить трехзначное число на двухзначное. В этом случае двузначное число должно быть правильно размещено под трехзначным числом, например,
. 110
× 10
——–
_____Шаг 2: Следующим шагом является умножение каждой цифры множимого на каждую цифру множителя, начиная с самой правой цифры или младшего разряда (LSB).Произведение, полученное после умножения каждой цифры множимого на множитель, называется частичным произведением. Наконец, мы складываем частичные продукты, полученные на каждом этапе, используя правило двоичного сложения.
Каково произведение (\ (1111) _ {2} \) и (\ (1111) _ {2} \) с использованием двоичного умножения?
Произведение (\ (1111) _ {2} \) и (\ (1111) _ {2} \) с использованием двоичного умножения равно (\ (11100001) _ {2} \). В этом двоичном умножении множитель и множимое являются одними и теми же двоичными числами.Мы используем правила двоичного умножения: «0 × 0 = 0, 1 × 0 = 0, 0 × 1 = 0 & и 1 × 1 = 1» и умножаем числа в соответствии с обычным методом арифметического умножения.
Что такое двоичное умножение отрицательных чисел?
В десятичной системе счисления или системе счисления с основанием 10 существуют отрицательные числа, такие как -1, -2, -3 и т. Д. Также можно умножить отрицательное число на положительное или отрицательное число на отрицательное число в двоичном формате.Для этого мы представляем каждое число с помощью 8 бит. В этом случае мы используем 4 бита для представления числа в дополнительном двоичном коде и 4 бита для представления знака. Если знак числа положительный, мы используем четыре нуля, а если число отрицательное, мы используем четыре нуля. Дополнение до 2 двоичного числа получается добавлением 1 к дополнению двоичного числа до единицы. Дополнение до единицы означает изменение местами каждого 0 на 1 и каждой единицы на 0.
- Цифра в разряде десятков – , нечетное и показатель степени y – нечетное , тогда число заканчивается на 75. {243}} $ равны 2 и 5.{243}} $ заканчивается на 75.

 Ответ: 230
Ответ: 230
 Это сделает подсчет упорядоченным и быстрым.
Это сделает подсчет упорядоченным и быстрым.
