Прд физика формулы: Прямолинейное равноускоренное движение. Ускорение — урок. Физика, 9 класс.

Уравнение координаты при равноускоренном прямолинейном движении

Определение и формулы

Уравнение координаты — зависимость координаты тела от времени:

x = x(t)

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x

0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с². Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с

2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).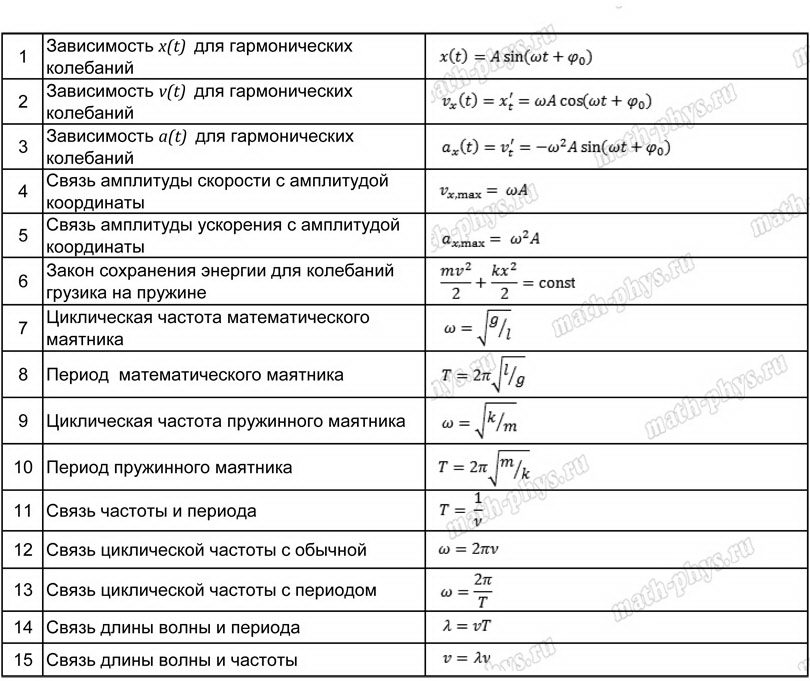

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с² и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с², достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Задание EF18609

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

---

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17682 Мимо остановки по прямой улице с постоянной  скоростью проезжает грузовик. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с ², и догоняет грузовик на расстоянии 150 м от остановки. Чему равна скорость грузовика?

---

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

Исходные данные:

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с².

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет вид:

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 13. 7k

Равномерное прямолинейное движение, равноускоренное прямолинейное движение и решение заданий ЕГЭ по физике

Автор Марина Андреева На чтение 8 мин Просмотров 2.9к. Опубликовано 20 ноября, 2019

Движением тела называется изменение его положения в пространстве относительно других. Рассмотрим равномерное прямолинейное движение тела, для этого введем следующие понятия.

Содержание

1. Определение равномерного прямолинейного движения тела
2. Равноускоренное прямолинейное движение
3. Применение производной в кинематике
4. Примеры выполнения заданий ЕГЭ по физике
5. Задание 1.
6. Задание 2.
7. Задание 3.
8. Задание 4.
9. Задание 5.
10. Задание 6
11. Задание 7
12. Задание 8
13. Задание 9
14. Задание 10
15. Задание 11.
16. Задание 12.

Определение равномерного прямолинейного движения тела

Равномерное прямолинейное движение тела — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Координата— величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.

Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.

Траектория — это линия, вдоль которой движется тело.

Путь — это длина траектории, вдоль которой движется тело.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения  тела к времени t, за которое это перемещение произошло .

Скорость ― это векторная величина!

В заданиях, где дана зависимость скорости тела от времени,

пройденный путь можно вычислить как площадь под графиком:

Следующие три переменные включены в равномерное прямолинейное движение:

Координаты: координата, с которой тело начинает двигаться (начальная позиция) и координата, куда он прибывает через некоторое время (конечная позиция) и координата, куда он прибывает через некоторое время (конечная позиция) .
Скорость: скорость всегда будет постоянной .
Время: момент, в который объект начинает двигаться (начальное время) и время, необходимое для прохождения определенного расстояния (конечное время) и время, необходимое для прохождения определенного расстояния (конечное время) .
Эти три переменные связаны этой формулой:

,

где .

Равноускоренное прямолинейное движение

Равноускоренное прямолинейное движение тела — движение, при котором его ускорение не меняется, ни по величине, ни по направлению.

Уравнение равноускоренного движения в проекции на ось Ox  имеет вид:

, где:

— начальная координата тела;

— проекция начальная скорость на ось x;

— проекция ускорения на ось x;

— время движения

Ускорением тела называется векторная величина, равная отношению изменения скорости за любой промежуток времени к величине этого промежутка:

Зависимость скорости от времени при наличии ускорения определяется выражением:

, где:

— скорость тела в момент времени t; t — время;

— начальная скорость тела;
— ускорение тела.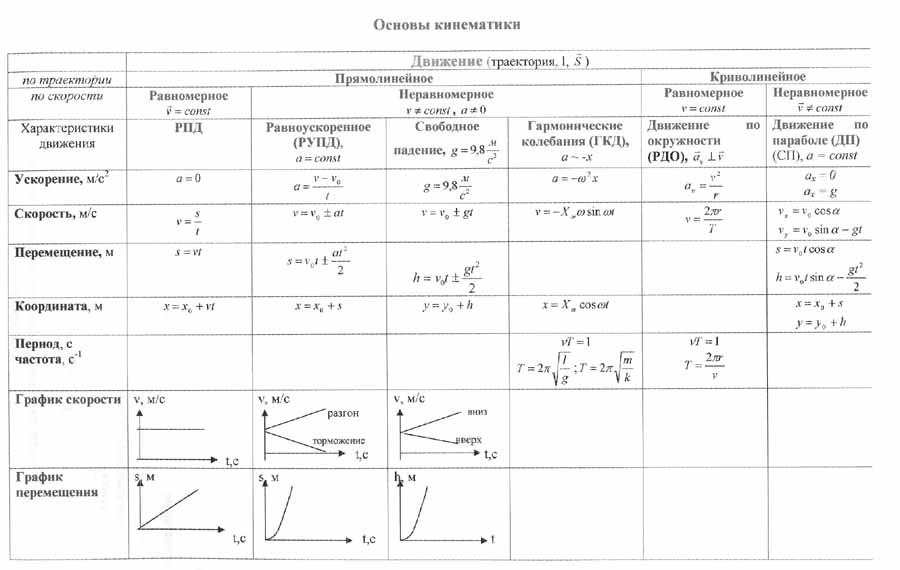

Применение производной в кинематике

Если существует зависимость координаты от времени  x(t), то зависимость скорости от времени можно получить, взяв производную по времени от этой зависимости.

Скорость ― это производная координаты тела по времени:

Например, если зависимость координаты тела при равноускоренном движении имеет вид , то взяв первую производную от координаты, мы получим зависимость скорости тела от времени:

Точно также, ускорение ― это производная от скорости тела:

.

Примеры выполнения заданий ЕГЭ по физике

Задание 1.

На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите, сколько секунд, после начала движения, когда точка стала двигаться со скоростью 10 м/с.

Ответ:1

Решение: Чтобы определить скорость движения точки на интервале, разделим путь, пройденный точкой, на все время движения на каждом отрезке графика. На интервале с начала движения и до 1 с точка прошла 10 м, следовательно, ее скорость была 10 м/с. Скорость точки на следующих интервалах пути ― 2,5 м/с, 0 м/с и 5 м/с соответственно.

Задание 2.

На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х= 0, а пункт Б ― в точке х= 30 км. Чему равна скорость автобуса на пути из А в Б? Ответ выразить в км/ч.

Ответ: 60 км/ч

Решение:

Согласно графику, зависимость пути автобуса от времени линейна, следовательно, скорость автобуса на всех участках пути постоянна.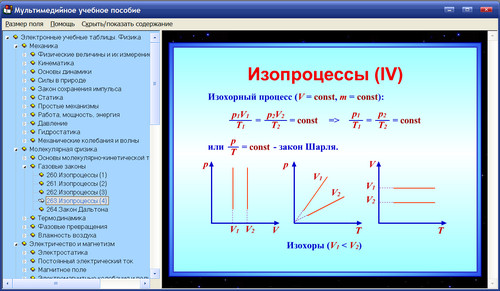 Из пункта А в пункт Б, находящиеся друг от друга на расстоянии S = 30 км автобус идет

t = 0,5 ч.

Уравнение движения автобуса: S = vt, откуда v = S/t = 30 км/ 0,5 ч = 60 км/ч.

Задание 3.

На рисунке изображены графики зависимости модуля скорости движения четырех автомобилей от времени. Какой из автомобилей — 1, 2, 3 или 4 — прошел наибольший путь за первые 10 с движения?

Ответ: 3

Решение:

Путь, пройденный каждым из автомобилей, равен площади под соответствующим графиком зависимости модуля скорости автомобиля от времени движения.

Как видно из следующих рисунков, наименьшая площадь под графиком скорости автомобиля 4, наибольшая ― под графиком скорости автомобиля 3.

Автомобиль 1 прошел путь:

Автомобиль 2 прошел путь:

Автомобиль 3:

Путь, который проехал автомобиль 4:

Задание 4.

На рисунке представлен график зависимости скорости v автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 3 с.

Ответ: 25 м

Решение: Путь, пройденный автомобилем, равен площади под соответствующим графиком зависимости модуля скорости автомобиля от времени движения.

Площадь образовавшейся трапеции равна: м.

Задание 5.

Тело движется по оси x. По графику зависимости проекции скорости тела υ_x от времени t установите, какой путь прошло тело за время от t₁= 0 до t₂= 4 c.

Ответ: 20.

Решение:

Путь, пройденный телом равен площади под соответствующим графиком зависимости модуля скорости тела от времени движения. Так как тело движется по оси х, других составляющих скорости, кроме υ_x у тела нет.

Площадь образовавшегося под графиком треугольника равна:

Задание 6

На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите ускорение тела.

Ответ: 6 м/с²

Решение: Модуль ускорения автомобиля равен м/с².

Задание 7

По графику зависимости скорости от времени (см. рисунок) определите ускорение прямолинейно движущегося тела в момент времени 2 с.

Ответ: 2 м/с².

Решение: Так как движение равноускоренное, то ускорение постоянная величина и в момент времени 2 с ускорение такое же как и в момент времени 3 с. Определяем ускорение по формуле: м/с².

Задание 8

Зависимость пути от времени прямолинейно движущегося тела имеет вид: x(t) = –4t + 10t², где все величины выражены в СИ. Чему равно ускорение тела?

Ответ: 20 м/с².

Ускорение есть вторая производная координаты по времени. Имеем м/с².

Задание 9

Тело начинает падать из состояния покоя и перед ударом о Землю имеет скорость 80 м/с. Каково время падения? Сопротивлением воздуха пренебречь.

Ответ: 8с.

Решение: Все тела, падающие на Землю из состояния покоя, движутся с ускорением свободного падения g = 10 м/с². Скорость падающего тела равна v(t) = v₀ + gt, так как начальной скорости у тела нет (v₀ =0), то время падения тела равно:

отсюда отсюда с.

Задание 10

Автомобиль трогается с места и движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с?

Ответ: 22,5 м.

Решение: Пройденный автомобилем путь равен , где a ― ускорение автомобиля, равное a = 5 м/с², t ― время его движения. Скорость автомобиля равна v(t) = at. Согласно условию, начальной скорости движения автомобиля нет.

Определим время, которое понадобилось автомобилю, чтобы развить конечную скорость v = 15 м/с:

Автомобиль прошел путь: м.

Задание 11.

При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему равно ускорение автомобиля?

Ответ: 1,5 м/с2.

Решение: Уравнение движения автомобиля , где v₀ ― начальная скорость автомобиля v₀ = 5 м/с, а ―постоянное ускорение автомобиля, t ― время движения автомобиля, S = 25 м.

Скорость автомобиля равна v = v₀ + at, конечная скорость равна v = 10 м/с. Выразим из этого уравнения время движения автомобиля:

И определим ускорение из уравнения движения:

м/с².

Задание 12.

Скорость пули при вылете из ствола пистолета равна 250 м/с. Длина ствола 0,1 м. Каково ускорение пули в конце ствола, если считать ее движение равноускоренным? Ответ выразить в км/с².

Ответ: 312,5 км/с².

Решение: Уравнение движения пули , где v₀ ― начальная скорость пули v₀ = 0 м/с, а ―постоянное ускорение пули, t ― время движения пули в стволе, S = 0,1 м ― путь, который проходит пуля в стволе.

Скорость пули при вылете из ствола считается по формуле v = v₀ + at и равна по условию v = 250 м/с. Отсюда, время движения пули равно , а пройденный пулей путь:

Отсюда, ускорение пули равно:

м/с² или 312,5 км/с².

Таким образом, теперь вы сможете решать задания ЕГЭ по физике на темы равномерное прямолинейное движение и равноускоренное прямолинейное движение.

Physics Formulas.pdf – PHYSIGSFORMULAS PHYSIGSFORMULAS SCIENTIFICOTATION множители nd/or Префиксы nd символы o

Предварительный просмотр неформатированного текста: PHYSIGSFORMULAS ФИЗИЧЕСКИЕ ФОРМУЛЫ НАУЧНОСТЬ кратные й/или Префиксы и символы формы формадесятичная й/или дольные. дольные. десятичные кратные Власть эн 1012 10е 106 103 102 Э Обозначение Э + 12 Е + 09 Е + 06 Е+03 E+02 Десятичный Эквивалент 1 000 000 000000 000000 000000 1 000 000000 000 000 1 000 000 000000 1000 100 Префикс тера гига мега килограмм гектофонический символ Т тер’а джига г мега М килограмм к хек’то ч 10′ 102 103 10 6 10 е 10’12 10 минут 1 с 10’18 Э+ – 0011 01.

01 0 0,01 Е-02 Е-03 0,001 Э – 06 0,000001 0,000 001 Э – 090,000000 001 0.000000 Э – 12 0.000000000 0.000000 000 001 Э – 15 000000 000 000001 000 001 0.000000 0,000 Е – 18 0,000000 000000 000000 000 001 0.000000000 дек ок я центи Милли микро нано пико фемто атто дека дези сенли мили микро нано пеко фемто в’то да г с м п н п т КИНЕМАТИКОРМУЛА КИНЕМАТИЧЕСКИЙ ОРМУЛАС г= Трение: г Коэффициент Коэффициент трения: r = коэффициент f трения F = сила сила скорости трения: “”, = Масса и Энергияi E = m.c2 отношения между Рефейшншип между массой ru = ИТИССС c = скорость полета света E = Энергия ОПТИЧЕСКИЕ СООТНОШЕНИЯ ОПТИЧЕСКИЕ ОТНОШЕНИЯ Волна eФормула: = f L v = wdV€ peed /= частота E= T освещеннаяПоверхность: Поверхность: E= Равномерно освещенный Е = освещение освещенный А = равномерно ре а l m = световой поток неуклюжий ты х Равномерно освещенные зеркала и линзы: ndLenses: & = + Do= объект расстояние расстояние до объекта Д, = изображение изображениерасстояние расстояние 111 Фокусное расстояние зеркал и линз: ,f = фокусное расстояние изображениерасстояние расстояние Делать = объект расстояние до объекта расстояние D, = изображение с Закон Снеффа: n, sin 0, = nrsin 0, размер Итак = объект объектный размер S i= изображение i z e T= q-E ni= рефракливендекс рефракливендексоф i-го материала 0, = €lrtgle между ау и нормалью к поверхности r'” = средняя скорость d = расстояние r = прошедшее время Ускорение: eav ‘t,’ t a_ = dV€f€lge dV€f€lgускорение ускорение г ‘= окончательный конечная скорость скорость v; = начальная скорость r = прошедшее время / = время F=kQ,’Q’ Электростатика: F=k Закон электростатики Кулона: Т “=” F сила между двумя зарядами пропорциональностьпостоянная 2 = пропорциональность постоянный ” “=” из обвинения эфез Продукт d = расстояние epdrating harges 4 = количество заряда \ Емкость конденсатора: C = + Емкость C = емкость f конденсатора V = разность потенциалов между пластинами обвинение на пластине 4 = заряд 2-й закон движения Ньютона: F = m. ‘Д’ Закон всемирного тяготения: Универсальная гравитация: F = G F = сила сила притяжения 5; = гравитационная постоянная tI ElectricCurrent: =+ 1 = вырезка I ql = ЭЛЕКТРИЧЕСТВОN D МАГНИТИЗМ # силанормальная нормальная поверхность N = сила l, = w€lV€ w€lV€длина длина lm tr ffifffi2 = масса продукта f центры d = расстояние между наследниками центры E = I. R Сопротивление Закон сопротивления Ома 1= CUIfe[t n схема E = €rTrf f источник R = сопротивление цепи – закон Джоуля. К-П. Р . т тепловая энергия энергия 1= куфлео R = сопротивление I = время Q = котел: = ry Centripetalorce: o rce F = центральная деталь rn=n’t€rsS ,=v:. 99рай я Маятник: T=2n l r = радиус радиус пути Закон электролиза Фарадеяi 7n 7olo1 q эквивалент z = электрохимический эквивалент 1=манжета r=время 1=период g = lускорение f гравитационное поле: E = – N Магнитное поле: вырабатываемая ЭДС: ЭДС: катушка в магните N = более тупые мехи E = индуцированная mf ls /=длина Работа: W = F. d t l’= 1y 9f l1 F= f c e д = расстояние ( лглухие механическиепреимущества: Механическое преимущество: IMA = do/d, который применяется орк6F F действует д. = расстояние черезкоторое прикладной орк6 расстояниесквозь W без трения д, = расстояние груз движется против движется против силы orceW дальняя дорога Фактическое механическое преимущество: M echanicalAdvantage:MA МА = ВФ Механический эквивалент Механический Эквивалент тепла: Вт = Дж. Q l1’= работа l1’= работа / = механический эквивалент f тепло Q = лечение ЭНЕРГИЯ ОТНОШЕНИЯ Кинетическая энергия: K – 112m.v2 ln= ITr€tsS K = кинетическая энергия v = скорость PotentiafEnergy: V = m.9.час Потенциальная энергия: tr’=потенциал tr’= потенциальная энергия g= ускорение f силы тяжести нт = fll8SS h = высота по вертикали) t?z= ITI€ISS # do = изменение потока n за заданный интервал f времени время 3 E = фр.л.в Магнитное поле: Поле:E Индуцированная ЭДС: Гондуктор и Магнитный поле магнитное поле В = поток плотность потока E = индуцированная мс плотность f магнитного длина я = длина дирижера поле кроссмагнеиполь v = скорость f поперечно-магнитного проводника fnstantaneousVoltagei e = {* sin 0 fnмгновенное напряжение мгновенная перегрузка старость е = мгновенный E*= максимальное напряжение дирижирует и он 0 = угол между плоскостью проводки угол между (перемещение) перпендикулярно магнитному люксу (смещение англ) Мгновенный ток: Мгновенный Текущий: i = l. * sin 0 я = мгновенный мгновенный ток срочный ITlaximumurrent л.- = ITслабый срочный 0 = смещение угол offsetngle Если вы хотите использовать математику и физику физиказнание знание высокотехнологичной среды, возьмем он ВМФ. Вы найдете много возможностей и и часто повторные шансы шансы или повышение производительности.n получить ментальный мент ипроизводительность. на флоте вы получите хорошая зарплата основанный на ваших способностях и и возможность освоить передовые технологические навыки, которые подготовят вас к яркий. прочное будущее. ИнтернетИнтернет Для получения более подробной информации звоните подробности, звоните по бесплатному номеру: 1-800-USA-NAVY, по бесплатному номеру: 1-800-USA-NAVY или посетите веб-сайт военно-морского флота. . сайт.http:// сайт. . В Пуэрто-Рико, Пуэрто-Рико, звоните по бесплатному номеру l-800-872-6289.cSCo= = nyporenuse o= тано загар sec0= = nyporenuse 1 СБСЕ 1 море sin0 грех 0 потому что потому что = потому что 0 Первая напротив гипотенузы sin (-0) = -sin 0 соз (-е) = соз 0 загар (-0) = -загар 0 детская кроватка (-e) = -кроватка 0 (-е) = сек (-0) = -csc сек 00 csc ПРОДУКТ: sin 0 sin 0 = ‘/r[cos(0 – O) cos (e + Q)] cos e cos Q = 1 / r [cos e – 0) + cos (e + 0 )] sin 0 cos 0 = ‘/'[sin(e + 0) + sin (e – Q)] ( 0 + 0) – грех ( е – $ )] cos e sin Q = 1/z[sin ЗАКОН СИНУСОВ 1 смежный грех sinA COS€ -hvpotenuse –:- напротив РЕДУКЦИОННОЙ ОРМУЛЫ: = 1 грех sin0 0 ПИФАГОРИЧЕСКИЕ СУЩЕСТВА: ПИФАГОРИЧЕСКИЕ СУЩЕСТВА: sin20+cos20=1 загар20+1=сек20 cot20+1=csc20 aDc = t = sinB грех Б грех С ЗАКОН КОСИНУСОВ a2=tf+C-2bccosA ff=e2+C-2accosB C=a2+ff-2abcosC СУММА ИЛИ РАЗНОСТЬ F ДВУХ УГЛОВ: sin (0+Q) sirl 0 cos Q+ cos 0 sin q sin (e-Q) = sin 0 cos Q cos 0 sin Q cos (0+Q) Гос Гос0 0 cos Q sin 0 sin Q cos (0-Q) = cos 0 cos S + sin 0 sin q загар (0+Q) загар (e-Q)= загар0+tand 1-tan0tanq ttne-tan0 1+tan0tand D O U BL EAN G L E: sin20=2sin0cos0 cos20 2cos2 -1 = 1-2sin20 2tan0 r?n zH = 1-: tenz e ПОЛОВИННЫЙ УГОЛ: sin20 1lz(1-cos20) c о s 2 = 1 l z ( 1 c о s2 с2 0 ) t a n -e = 1- =- c- o s 0 2 грех0 грех0 1+cos0 ГРЕЧЕСКИЙ АЛФАВИТ ГРЕЧЕСКИЙ АЛФАВИТ Буква A Б ф А Е Z ЧАС @ я К А М нет II п Т Г о Х Г О кл Б 6 e r q e t К л. тр в о Э п о t 1J а х ву Имя альфа бета гамма дельта эпсилон дзета и др. тета йота каппа лямбда мю ню xi омикрон Пи р хо сигма та ты ипсилон фи Чи PS я омега…
Просмотр Полный документ

Physics Formulas 1586636634, 9781586636630 – DOKUMEN.PUB

Citation preview

---

PhysicsForm 8.0 4/15/03 12:16 PM Page 1

PHYSICAL CONSTANTS Acceleration due to gravity

Avogadro’s number

ELECTROMAGNETIC CONSTANTS WAVELENGTHS СВЕТА В ВАКУУМЕ (м)

г

9,8 м/с

NA

6.022 × 10

2

23

K

9 × 109 N · M2 /C2

Гравитационная постоянная

G

6.67 × 10–11 н.

Constant Planck

H

6.63 × 10

Blue

Идеальная константа газа

R

Проницаемость свободного пространства

ε0

8,8541 × 10-12 C/(V · M)

PRIMAILIBLIBLIBLIBLIBLIBLIBLIBLIBLIBLO пробел

µ0

4π × 10–7 WB/(A · M)

J · S

331 м/с

3,00 × 108 м/с

Электронный заряд

E

1,60 × 10

Electron Volt

EV

1,6022 × 10

Блок атомной массы

U

1,6606 × 10 кг = 931,5 МэВ/C2

Масса отдыха электрона

ME

9,11 × 10-31 K = 0,000549 U = 0,511 ME

9,11 × 10-31 K = 0,00049 U = 0,511111111119,11.

мп

1,6726 × 10–27 кг = 1,00728 u = 938,3 МэВ/с2

… Proton

−19

J

−27

Масса Земли

5,976 × 1024 кг

Радиус Земли

6,378 × 10 М

4.9 – 5.7 × 10 000 70007

9000 2, 1011

1012

Микроволны

1 10-1 10-2 = Длина волны (в M)

4,2-4,9 × 10–7

10-3

1013

1014

1015

10-4-4-4-4-4-4-4-4-4-4-4-4-4-4-4-4-4-4-4

1016

1017

1018

ультрафиолет

Инфракрасный 10-5

10-6

10-7

10-8

10-9

1020

1019

Гамма

x Rays 10-10

R y y g B-

100002 100002 x Rays 10-10

R y y g B-

1000019 100002 100002 x Rays 10-10

r y y g ba

x Rays 10-10

r y y g Ba

. 11

10-12

V

= 780 нм видимый свет

4,0-4,2 × 10–7

Вайонный

360 нм

Инценсы преломления для общих веществ (L = 5,9 x 10–7 М) Воздух

1,00

Спирт

1,36

кукурузное масло

1,47 1,47

Diamond

2,42 1,33

Глицерил

Вода

Падающий Ray

θ θ θ -gropted c n = (v является скоростью света в среде) V

2 Закон о C -n = (V является скоростью света в среде) v

22 2 Закон о отравлении.

Индекс преломления

Угол падения

01 0 ‘

Угол отражения

N1 sin θ1 = n2 sin θ2 � � θc = sin -1 nn21

Закон Снелла

.0002 02

Нормальный угол рефракции

Преломленный луча отраженного луча

Линзы и изогнутые зеркала

1,6750 × 10–27 кг = 1,008665 U = 939,6 МэВ/C2

… Neutron

91077

70007 70007 и регрессия

70007 70007 70007 70007 70007 70007 70007

70007

.

C

−19

109

Радиоволсы

Оптика

C

Скорость света в вакууме

108

5,7 – 5,9 × 10-7

Желтый

8,314.7 – 5,9 × 10-7

Желтый

8,31414 J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/J/7 – 5,9 × 100007

. К) = 0,082 атм·л/(моль·К)

Скорость звука при STP

ƒ = частота (в Гц)

Оранж 5,9 – 6,5 × 10–7

Постоянная кулонина

−34

6,5 – 7,0 × 10-7

Red

Моликулы / 7,0 × 10-7

Red

/ mol

q размер изображения =− p размер объекта

1 1 1 + = f q p

Оптический инструмент Линза: Вогнутая Выпуклая

Фокусное расстояние f

Расстояние до изображения q

Тип изображения q

Негатив 7 90 негатив 90 позитив

7 90 та же сторона) отрицательная (та же сторона) положительная (противоположная сторона)

виртуальный, прямой 1 виртуальный, прямой 2 реальный, перевернутый 3

отрицательный (обратная сторона)

виртуальный, прямой

отрицательный (обратная сторона) положительный (та же сторона)

виртуальный, прямой 5 реальный, перевернутый 6

PF

P

H

CONGEX

Отрицательный

CONGAVE

Положительный

PF

V

F

Mirror:

6

4

Q

Q

Q

Q

Q

Q

Q

0007

6

ЗАКОНЫ НЬЮТОНА 1. Первый закон: Объект остается в состоянии покоя или движения с постоянной скоростью, если на него не действует результирующая внешняя сила. dp F = 2. Второй закон: Fnet = ma dt 3. Третий закон: На ​​каждое действие есть равное и противоположное противодействие. Вес

FW = MG

Нормальная сила

FN = Mg COS θ (θ – угол горизонтального)

H

H

F P

1

V

P

Q

1

V

P

Q

0007

Кинетическое трение fk = µk FN

µs – коэффициент статического трения. µk – коэффициент кинетического трения. Для пары материалов µk

W = F · s = F s cos θ � W = F · ds

$5,95 CAN $3,95

mv 2 Центростремительная сила Fc = r

ˆ a = axˆi + ayˆi + az k

Величина

а = |а| =

Скалярный продукт

a · b = ax bx + ay by + az yz = ab cos θ

�

a2x + a2y + a2z

Перекрестное произведение

a × b = (ay bz � � ax � = �� ax � ˆi

axb

Гравитационная потенциальная энергия

Ug = mgh

Полная механическая энергия

907 02 Среднее значение Power

PAVG =

Мгновенная мощность

Momentum и Impulse Linear Momentum

P = MV

Impulse

J = �ft = ∆P J = F DT = ∆P

A

Collsies B

ˆP

A

B

ˆP

A

B

ˆ ˆ − az by ) ˆi + (az bx − ax bz) ˆj + (ax by − ay bx ) k � ay az �� ay bz �� ˆj ˆ � k

Авторские права на этот загружаемый файл PDF © 2004 SparkNotes LLC.

∆W ∆t

P =F·v

a b

p2 1 mv 2 = 2m 2

∆U = −W

Потенциальная энергия

| = ab sin θ a × b точки в направлении, заданном правилом правой руки:

KE =

Кинетическая энергия

Все столкновения

m1 v1 + m2 v2 = m1 v1� + m2 v2�

Упругие столкновения

1 1 1 1 2 2 m1 v12 + m2 v22 = m1 (v1� ) + m2 (v2� ) 2 2 2 2

V1 – V2 =

– (V1�

–

V2�)

Q

V

H

F

V

F

P

H

P

H

V

V

P

V

P

V

.

Q

4

3

Работа, Энергия, Работа по питанию

F P

(для консервативных сил)

Векторные формулы

(θ – угла между a и b)

F

-Энергетическая теорема W = ∆KE

однородное круговое движение V2 Центрипетальное ускорение AC = R

Q

2

Статическое трение трения FS, MAX = µS FN

H

В

P

Q

5

Kinematics Avarmation Velocity Avarmity Velocity Velocity Velocity Velocity Velocity Velocity Armitics. =

∆S ∆T

Расстояние S (M)

Мгновенный DS V = скорость DT

Смещение ∆S =

Среднее ускорение

�

AAVG =

В DT

�

0002 ∆v ∆t

Мгновенное dv a= ускорение dt

Изменение скорости

vf = v0 + at 1 vavg = (v0 + vf ) 2

s = s0 + v0 t +7 10 at = S0 – VF T +

1 в 2

= S0 + Vavg T

=

V02

Velocity V (M/S)

+

T (S)

∆V =

�.

ПОСТОЯННОЕ УСКОРЕНИЕ

vf2

t (с)

a dt

– УСКОРЕНИЕ a (м/с2)

+

t (s)

–

+ 2a(sf − s0 ) ПРОДОЛЖЕНИЕ НА ДРУГОЙ СТОРОНЕ

Waves

Электричество

T

Волна на натяжении строки в струне FT

Массовая плотность µ =

Длина L

Длина массы

F = K

Электрическое поле

E =

Потенциальные разница

E =

.

Вт ∆V = q

FON Q Q

F = EQ

ЦЕПИ ∆Q ∆T

Ток

I =

Сопротивление

R = ρ

.

P = V I = I 2R

Частота биений

Тепловая энергия, рассеиваемая резистором

Вт = P t = I 2 Rt

Скорость стоячей волны

v=

Длина волны стоячей волны

7

0002 FT µ

2L n

fbeat = |f1 − f2 |

Движение эффекта допплера стационарного источника

Движение Observer

Стационарный

V λ

F

VE ff = V + Vo λe ff = λ � � o Fe ff = F v + V

по отношению к источнику AT

По направлению к наблюдателю в точке vs

Вдали от наблюдателя в точке vs

� v feff = f v+v s

veff = v ± vo � s λefff = λ v±v v � o feff = f v±v v±vs

вдали от источника в vo vo ff = v – Vo

λe ff = λ � � o fe ff = f v – v v

Положение по вращенному движению

Агмальная скорость

ωavg =

∆θ

ωavg =

∆θ

ω =

=

∆T

ω =

ωavg =

∆T

ω =

ωavg =

∆T

ωavg =

∆T

ωavg.

V R Dθ DT при r Dω DT

ω =

α =

Агловое ускорение

αAVG =

S R

∆ω ∆T

α =

A

Констант ωF = ωF + α +0707

ωf = ωF + α + α +

T = 2π

�

v=0 U = max KE = 0

Система массового стрижки

R

R

Сфера

R

MR 2 Кольцо

Диск

Эластичная потенциальная энергия

ПЕРИОД 2 MR 5

L

ROD

TOURT и ANGULAR MOVERUM. Крутящий момент

τ =

dL dt

F = −k(∆)x ∆x — расстояние, на которое пружина растягивается или сжимается от положения равновесия, а k — постоянная пружины.

1 МЛ2 12

Р

R2 R3

Магнитная сила на движущийся заряд

F = qvB sin θ

F = q (v × B)

Магнитная сила на проводе с током

F = BI� sin θ

F = I ( � × B)

МАГНИТНОЕ ПОЛЕ, ОБРАЗОВАННОЕ… Магнитным полем, создаваемым движущимся зарядом

B=

µ0 qv × ˆr 4π r2

Магнитное поле, создаваемое проводником с током

µ

π I=

7 90 r

Магнитное поле, создаваемое соленоидом

B = µ0 Ni

Закон Biort-Savart

DB =

Закон Ленца и Закон Фарадея

ε =-

Уравнения Максвелла.

Возвращающая сила

МОМЕНТЫ ИНЕРЦИИ (I ) � I= r 2 дм Момент инерции 1 MR 2 2

мг cos 0

v=0 U = max KE = 0

положение равновесия

= ωθg t

MR 2

v = макс U = мин KE = макс

τ = F r sin θ τ =r×F τ = Iα

Угловой момент

L = pr sin θ

L=r×p

L = Iω

Вращательная энергия KE rot = 22

Законы о газе Универсальный закон газа

P V = NRT

Комбинированный закон газа

P2 V2 P1 V1 = T2 T1

2π T

=

�

1 K (∆x) 2 2 � M T = T = T = T = T = T = T = T = T =

2π k Ue =

x = A sin(ωt)

Уравнение движения

где ω =

км

— угловая частота

, а A = (∆x)max — амплитуда.

ТЕРМОДИНАМИКА 1. Первый закон ∆ (внутренняя энергия) = ∆Q + ∆W 2. Второй закон: Все системы спонтанно стремятся к максимальной энтропии. ∆Qout Альтернативно, эффективность e = 1 − ∆Qin любой тепловой машины всегда удовлетворяет условию 0 ≤ e

P1 V1 = P2 V2

Закону Чарльза

P2 P1 = T2 T1

Авторские права на этот загружаемый PDF-файл © 2004 by SparkNotes LLC .

R3

R1

mg sin 0

1 = (ω0 + ωf ) 2

ωf2 = ω02 + 2α(θf − θ0 )

R2

Параллельные цепи Ieq = = V1 + I2 + Iq2 + · · = V3 = . . . 1 1 1 1 + ··· + + = r2 R2 R1 REQ

T

� G

1 αT 2

Частица

0

ПЕРИОД

мг

ωAVG

θ = θ0 + ω 00007

ωAVG

θ = θ + 00007

ωAVG

t +

2g� (1 − cos θmax )

R1

МАГНИТИЗМ

Скорость в положении равновесия

�

Последовательные цепи Ieq = I1 = I2 = I3 = . . . Veq = V1 + V2 + V3 + · · · Req = R1 + R2 + R3 + · · ·

Правило цикла: Сумма всех (со знаком) разностей потенциалов вокруг любого замкнутого контура равна нулю. Правило узла: общий ток, входящий в соединение, должен равняться общему току, выходящему из соединения.

МАЯТНИК

v=

V R

ПРАВИЛА КИРХГОФА

ПРОСТОЕ ГАРМОНИЧЕСКОЕ ДВИЖЕНИЕ

θ=

L A 90’0027

7

C

�

Закон Ampere’s

�C

Ampere-Maxwell Law

C

E · DA =

R) µ0 I (D� × ˆ r2 4π

DφB DT

QENCESCESCOSES ε ˆ 4π

DφB DT

QENCESOSES q ˆ 4π

Dφ DT

QENCESOSED QUCESOSED QCESCOSED QCESSOSES ε ˆ 4π

QENCESOSED QUNCESSISSISIS.

B · DA = 0 E · DS = –

4

�

SparkCharts

�� T

1 Q2 Q2 Q2 = 4πε0 R 2 R2

Закон Кулона

$ 5,95 CAN

WAW SPEED COULOMP’S

$ 5.95 CAN

WAW SPEED COULOMP’S

$ 5,95

WAW SPEED COULOMB

$ 5,957

WAW SPEED. v = f λ Волновое уравнение � � y(x, t) = A sin(kx − ωt) = A sin 2π λx −

ELECTROSTATICS

$3.95

2π T

∂ ∂ΦB =− ∂t ∂t

�

s

B · dA

B · ds = µ0 Ienclosed B · ds = µ0 Ienclosed + µ0 ε0

∂ ∂t

�

s

E · dA

GRAVITY m1 m2 r2

Newton’s Law of Universal Gravitation

F =G

Acceleration due to gravity

a=

Gravitational potential

U (r) = −

Скорость убегания

VESCAP E

20593 36340

ω = 2πf =

7

1 2π = F ω

Англуна Частота ω

TM

ПЕРИОД T

Совместные: Bernell K.