Предел 1 бесконечность: Недопустимое название | Научные парадоксы Wiki

Раскрытие неопределенностей при вычислении пределов

С данной статьи начинаем цепочку публикаций, которые научат Вас находить особенности в границах, классифицировать неопределенности и применять правильную методику раскрытия. Дело заключается в том, что разработано много правил и приемов, которые позволяют по виду заданной функции или последовательности быстро сориентироваться как находить предел. Однако при изучении теоретического материала или на практических занятиях Вам или на этом не отмечают, или Ваши мысли гуляют за пределами аудитории.
Для охвата всего материала мы собрали много примеров из студенческой практики, модулей, контрольных, заказов и попытаемся здесь разъяснить, как и в каких случаях применять приведенные алгоритмы.

 

Пример 1. Вычислить предел последовательности:

Решение: При подстановке бесконечности получим неопределенность вида бесконечность разделить на бесконечность (∞/∞). Разделим числитель и знаменатель на переменную в наибольшей степени и сократим на нее.

В результате избавимся от неопределенности, а слагаемые что останутся, будут стремиться к нулю при больших номерах последовательности

Все числа, что останутся и укажут куда стремится предел.

 

Пример 2. Вычислить предел последовательности:

Решение: При прямой подстановке бесконечно большого номера получим неопределенность бесконечность минус бесконечность (∞-∞).
Правило раскрытия такого типа неопределенности хорошо расписано в литературе и заключается в умножении и разделении неопределенности на множитель, сопряженный к ней.
Как правило, такие примеры содержат корни и чтобы их лишиться используем умножение на сопряженный множитель, что приводит к разности квадратов или кубов, в то время в знаменателе (или числителе) получим выражение с корнем, которое не содержит неопределенности.

Далее из числителя и знаменателя выделяем доминирующий множитель и упрощаем на него.
Все числа, что останутся и составят предел последовательности.
На языке формул этому отвечает запись

 

 

Пример 3. Найти предел функции:

Решение: При подстановке x=3 получим неопределенность 0/0.
Это означает, что и числитель и знаменатель содержат особенность.
Для раскрытия неопределенности выделим в числителе (x-3), а знаменатель умножим и разделим на сопряженное выражение .

В результате получим множитель (x-3), на который упрощаем дробь. Далее предел вычисляется методом подстановки переменной

 

Пример 4. Найти предел функции:

Решение: Задание для большинства студентов чрезвычайно сложное, а все потому что необходимо свести неопределенность типа 0/0 до известных случаев.
В результате преобразования функций получим выражения вида ln(1+x)/x, tan(x)/x, sin(x)/x при переменной стремящейся к нулю.
Далее выделяем первую замечательный предел и ее следствие, затем расписываем через произведение известных пределов.
Все остальное сводится к произведению единиц и отдельного множителя, который и является пределом заданной функции.

Внимательно разберите приведенный пример, он Вас многому научит. x = e qquad (1) $$

Из выражения, стоящего под знаком предела вычитаем единицу, чтобы его подстроить под формулу (1).

Перепишем предел из условия задачи в новом виде и подставим в него $x o infty$.

Пользуясь формулой (1) проведем вычисление лимита. В скобках перевернем дробь.

По условиями формулы второго замечательного предела (1) в скобках знаменатель дроби должен быть равен степени за скобкой. Выполним преобразование степени. Для этого умножим и разделим на $frac<3x+2><-6>$.

Остаётся сократить степень экспоненты и найти её предел.

Предел дроби равен отношению коэффициентов при старшей степени $x$.

Правило Лопиталя и раскрытие неопределённостей

Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):

.

Как показывает формула выше, при вычислении предела отношений двух бесконечно малых или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Перейдём к более точным формулировкам правил Лопиталя.

Правило Лопиталя для случая предела двух бесконечно малых величин. Пусть функции f(x) и g(x) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a. А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g(x) не равна нулю (

g‘(x)≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю:

.

Тогда предел отношения этих функций равен пределу отношения их производных:

.

Правило Лопиталя для случая предела двух бесконечно больших величин. Пусть функции f(x) и g(x) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a. А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g(x) не равна нулю (

g‘(x)≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:

.

Тогда предел отношения этих функций равен пределу отношения их производных:

.

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому числу, или бесконечный, то есть равный бесконечности).

Замечания.

1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x =

a.

2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”

Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе – производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.

Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

.

Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

.

Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить

.

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

.

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.

Пример 6. Вычислить

.

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.

Пример 7. Вычислить

.

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида – ∞/∞, а затем неопределённость вида 0/0.

Пример 8. Вычислить

.

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.

Применить правило Лопиталя самостоятельно, а затем посмотреть решение

Пример 9. Вычислить

.

Подсказка. Здесь придётся попыхтеть несколько больше обычного над преобразованием выражений под знаком предела.

Пример 10. Вычислить

.

Подсказка. Здесь правило Лопиталя придётся применять трижды.

Раскрытие неопределённостей вида “ноль умножить на бесконечность”

Пример 11. Вычислить

.

(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как

а затем применили правила Лопиталя).

Пример 12. Вычислить

.

В этом примере использовано тригонометрическое тождество .

Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”

Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .

Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.

Пример 13. Вычислить, пользуясь правилом Лопиталя

.

Вычисляем предел выражения в показателе степени

.

.

Пример 14. Вычислить, пользуясь правилом Лопиталя

.

Вычисляем предел выражения в показателе степени

.

.

Пример 15. Вычислить, пользуясь правилом Лопиталя

.

Вычисляем предел выражения в показателе степени

.

Раскрытие неопределённостей вида “бесконечность минус бесконечность”

Это случаи, когда вычисление предела разности функций приводит к неопределённости “бесконечность минус бесконечность”: .

Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:

В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т. д.

Пример 16. Вычислить, пользуясь правилом Лопиталя

.

Решение. Пользуясь вышеперечисленными рекомендациями, получаем

Пример 17. Вычислить, пользуясь правилом Лопиталя

.

Решение. Пользуясь вышеперечисленными рекомендациями, получаем

Предел функции на бесконечности, урок и презентация

Дата публикации: 09 апреля 2017.

Что будем изучать:

1. Что такое Бесконечность?
2. Предел функции на бесконечности
3. Предел функции на плюс бесконечности.
4. Предел функции на минус бесконечности.
5. Свойства. 6. Примеры.

Предел функции на бесконечности

Ребята, давайте посмотрим, что такое предел функции на бесконечности?
А, что такое бесконечность?
Бесконечность — используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в нашем случае характеристика чисел.

Бесконечность –сколь угодно большое(малое), безграничное число.
Если рассмотреть координатную плоскость то ось абсцисс(ординат) уходит на бесконечность, если ее безгранично продолжать влево или вправо(вниз или вверх).

Предел функции на плюс бесконечности

Теперь давайте перейдем к пределу функции на бесконечности:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:

Будем читать наше выражение как:
предел функции y=f(x) при x стремящимся к плюс бесконечности равен b

Предел функции на плюс бесконечности.

Теперь давайте перейдем к пределу функции на бесконечности:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:

Будем читать наше выражение как: предел функции y=f(x) при x стремящимся к плюс бесконечности равен b

Предел функции на минус бесконечности

Посмотрим немного другой случай:

Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a], и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:

Будем читать наше выражение как: предел функции y=f(x) при x стремящимся к минус бесконечности равен b

Предел функции на бесконечности

Так же наши соотношения могут выполняться одновременно:

Тогда принято записывать как:

предел функции y=f(x) при x стремящимся к бесконечности равен b

Примеры

Построить график функции y=f(x), такой что:
1) Область определения – множество действительных чисел.
2) f(x)- непрерывная функция
3) 4) Решение: Нам надо построить непрерывную функцию на (-∞; +∞). Покажем пару примеров нашей функции.

Основные свойства

Для вычисления предела на бесконечности пользуются несколькими

1) Для любого натурально числа m справедливо следующее соотношение:

2) Если то:
а) Предел суммы равен сумме пределов:

б) Предел произведения равен произведению пределов:

в) Предел частного равен частному пределов:

г) Постоянный множитель можно вынести за знак предела:

Пример 1.

Найти: Решение: Разделим числитель и знаменатель дроби на x. Воспользуемся свойством предел частного равен частному пределов:

Ребята, вспомните предел числовой последовательности.

Получим:

Пример 2.

Найти предел функции y=f(x), при x стремящимся к бесконечности.
Решение.

Разделим числитель и знаменатель дроби на x в третьей степени.

Воспользуемся свойствами предела на бесконечности

Предел числителя равен: 5-0=5; Предел знаменателя равен: 10+0=10

Пример 3.

Найти предел функции y=f(x), при x стремящимся к бесконечности.

Разделим числитель и знаменатель дроби на x в третьей степени.

Воспользуемся свойствами предела на бесконечности

Предел числителя равен: 0; Предел знаменателя равен: 8

Задачи для самостоятельного решения

1) Построить график непрерывной функции y=f(x). Такой что предел при x стремящимся к плюс бесконечности равен 7, а при x стремящимся к минус бесконечности 3.

2) Построить график непрерывной функции y=f(x). Такой что предел при x стремящимся к плюс бесконечности равен 5 и функция возрастает.

3) Найти пределы:

4) Найти пределы:

Бесконечность не предел: как торговые роботы обогнали трейдеров :: Новости :: РБК Инвестиции

Торговые роботы почти достигли скорости света. Значит ли это, что их развитие зашло в тупик? Технический директор корпоративного и инвестиционного бизнеса Райффайзенбанка Сергей Мельников уверен в обратном

«Ручной труд» теряет свою эффективность во многих сферах. Инвестиции  не исключение. Людей заменила алгоритмическая торговля — сделки в считаные доли секунды проводит компьютерный софт. Такие роботы справляются с задачей быстрее, чем человек. А за их создание отвечают выпускники лучших вузов.

От людей к «железкам»

Если представить процесс принятия торгового решения в виде системы координат, то по оси X расположится показатель времени, а по оси Y — сложность. Решения, которые принимают трейдеры, довольно сложны, поэтому требуют времени: минимум нескольких секунд.

Подобный «ручной труд» во многом неэффективен. Чтобы его оптимизировать, трейдеры, которые умели программировать, начали писать собственные программы — алгоритмические стратегии.

Типичный алгоритм первого поколения фактически представлял из себя сравнение двух чисел: цены покупки и цены продажи. Если можно купить дешевле и продать дороже, сделка совершается. Но нет более любимого инженерами занятия, чем оптимизация формальной метрики — например, скорости работы простого алгоритма.

В погоне за скоростью

Специально для электронной торговли начали строить выделенные линии связи. И это даже не оптоволокно, а микроволновые вышки. Между вышками сигнал распространяется по воздуху, что позволяет добиться ощутимо большей скорости распространения сигнала, чем в оптоволокне.

Однако для совершения торговых операций мало просто передать сигнал из точки А в точку Б по суперскоростному каналу, нужно еще максимально быстро его обработать. За это отвечают даже не процессоры, а специальные чипы программируемой логики, расположенные прямо в сетевой карте. В чипах и «прошита» торговая стратегия — то самое сравнение двух чисел.

Но невозможно передать информацию быстрее, чем скорость, с которой сигнал распространяется в среде. Так эпоха гонки за скорость в алгоритмической торговле закончилась непреодолимым препятствием — скоростью света. Она одинакова для всех, а значит, преимущества нет ни у кого.

Значит ли это, что эпоха алгоритмической торговли прошла? Каким будет алгоритмический трейдинг завтра?

Два пути эволюции

На мой взгляд, эволюция алгоритмической торговли проходит такие же этапы, что и биологическая. Первые живые организмы действовали в рамках простой логики, рефлекторно. Увидели — съели. Но с развитием головного мозга поведение организмов усложнялось, порождая все более сложные реакции и решения. Так и в алготрейдинге.

Первые алгоритмы совершали «рефлекторные» действия на уровне «купи-продай», сравнивая два числа. Желание заработать стимулировало дальнейшую эволюцию и вело их к ускорению реакций. И когда они и здесь достигли своего предела, остался единственный способ продолжать развиваться: алгоритмы должны становиться сложнее.

В будущем они научатся анализировать все большее количество входных данных и принимать более сложные, комплексные решения за меньший промежуток времени. Скорость принятия таких решений будет, вероятно, ниже, чем у самых простых «рефлекторных» алгоритмов, но все еще значительно выше, чем у человека. Так что назовем такие алгоритмы и стиль торговли вообще среднечастотными. Именно в среднечастотных торговых стратегиях, быстро анализирующих огромное количество вводных данных, мы видим будущее алгоритмического трейдинга.

В какую сторону будет проходить дальнейшая эволюция среднечастотной торговли? С одной стороны, определенно придется увеличивать сложность принимаемого решения и количество анализируемых данных при заданной скорости, с другой стороны — сокращать время работы алгоритмов. На этом и сосредоточена работа всей команды, разрабатывающей среднечастотную алгоритмическую стратегию.

Кто создает алгоритмы

Кто же будет создавать следующее поколение торговых алгоритмов? Эти люди должны обладать широкой экспертизой в разных областях знаний, от математики и computer science до экономики и знания неформальных законов рынка, хорошо работать как с кодом, так и с трейдерами.

Алгоритмическая торговля стремительно эволюционирует. Это та область финансового сектора, в которой необходимо всегда применять новейшие технологии и самые прогрессивные подходы к программированию. Не потому, что это модно или круто, а потому, что приносит деньги. Я считаю, что именно эта область в какой-то момент стала драйвером технологической трансформации всех направлений банковского бизнеса и примером того, как IT и «бизнес» не противостоят друг другу, а совместно работают на достижение общих целей.

Инвестиции — это вложение денежных средств для получения дохода или сохранения капитала. Различают финансовые инвестиции (покупка ценных бумаг) и реальные (инвестиции в промышленность, строительство и так далее). В широком смысле инвестиции делятся на множество подвидов: частные или государственные, спекулятивные или венчурные и прочие. Подробнее

Автор

Сергей Мельников

МИДИС

Образование с трудоустройством

Скачай средний уровень заработных плат по специальностям МИДИС

Высшее образование 14 специальностей Колледж 11 специальностей

Ещё 5 специальностей Скрыть Ещё 2 специальности Скрыть

Об институте

Об институте

год основания

3

в ТОП 100 образовательных организаций РФ движения WorldSkills

60

медалей чемпионатов профессий WorldSkills

9

стран — география стажировок

Наши

партнеры Ресурсы

Бассейн

Ресурсы

Актовый зал

Ресурсы

Спортзал

Ресурсы

Столовая

Ресурсы

Мастерская интерьера

Ресурсы

Швейная мастерская

Ресурсы

Мастерская живописи

Ресурсы

Кабинет витринистински

Ресурсы

Учебный ресторан

Ресурсы

Учебная кухня

Ресурсы

Турофис

Ресурсы

Учебный банк

Больше историй

презентация к уроку “Предел функции на бесконечности”

библиотека
материалов

Содержание слайдов

Номер слайда 1

Предел функции на бесконечности

Номер слайда 2

Понятие «бесконечность»  используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в нашем случае характеристика чисел. Бесконечность – сколь угодно большое(малое), безграничное число.

Номер слайда 3

Предел функции на плюс бесконечности. Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:

Номер слайда 4

Предел функции на минус бесконечности. Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a], и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:

Номер слайда 5

Предел функции на бесконечности. Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (−∞,+∞) и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке: 

Номер слайда 6

Основные свойства: Для любого натурально числа m справедливо следующее соотношение: lim𝑥→∞1𝑥𝑚=0 2. Если  lim𝑥→∞𝑓(𝑥)=b  и  lim𝑥→∞𝑔(𝑥)=c, тоа) Предел суммы равен сумме пределов: lim𝑥→∞(𝑓𝑥+ 𝑔(𝑥))=lim𝑥→∞𝑓(𝑥)+lim𝑥→∞𝑔(𝑥)= b+ cб) Предел произведения равен произведению пределов: lim𝑥→∞(𝑓𝑥∙ 𝑔(𝑥))=lim𝑥→∞𝑓(𝑥)∙lim𝑥→∞𝑔(𝑥)= b ∙ cв) Предел частного равен частному пределов lim𝑥→∞𝑓𝑥𝑔(𝑥)=lim𝑥→∞𝑓(𝑥)lim𝑥→∞𝑔(𝑥)=bcг) Постоянный множитель можно вынести за знак предела:lim𝑥→∞𝑘∙𝑓(𝑥)=𝑘∙lim𝑥→∞𝑓(𝑥)=𝑘∙𝑏 

Номер слайда 7

ПРИМЕР:

Номер слайда 8

Дробно-рациональная функция – это такая алгебраическая дробь, у которой числитель и знаменатель представляют собой многочлены некоторой степени. ПРИМЕР: Дробно-линейная функция (частный случай дробно-рациональной функции) – это такая алгебраическая дробь    , у которой числитель и знаменатель представляют собой линейные функции. ПРИМЕР:

Номер слайда 9

Построим график функции Преобразуем функцию, выделив целую частьфункция имеет две асимптоты: горизонтальную y=2  и вертикальную x=1. Точки пересечения графика с осями координат:при x=0 y=3 , точка (0; 3)при y=0 x=1,5 , точка (1,5; 0)

Номер слайда 10

Домашняя работа: построить график функции (см. образец слайд 9) и указать предел

Номер слайда 11

Домашняя работа: Найти предел

Номер слайда 12

пределов – бесконечность над бесконечностью и умноженная на ноль бесконечность в вычислении, которое дает (правильно) 1

Надеюсь, вы не дублируете мой вопрос, поскольку он предназначен для конкретного случая, который я вам сейчас покажу, а именно о расчетах.

Я читал о теме бесконечности над бесконечностью, которая считается неопределенной, и я также прочитал эту ветку. Бесконечность – это число? что интересно, хотя в большей степени историческое и философское, поэтому менее актуально для вопроса, который я задаю.2-1) $, я бы поступил следующим образом (просто для согласованности, потому что в предыдущем упражнении с той же функцией, но с пределом, приближающимся к 1, я проделал те же алгебраические шаги):

lim x, который приближается к бесконечности, $ (x-2) (x + 1) / (x-1) (x + 1) $, применяя свойства пределов и алгебраическое свойство: lim x, которое приближается к бесконечности $ (x- 2) $ * lim x, который приближается к бесконечности $ (1 / x-1) $, засорение: (бесконечность – 2 = бесконечность) * (1 / бесконечность – 1 = бесконечность; 1 / бесконечность = 0).

Таким образом: бесконечность * 0 = undef .

Первый вопрос: это соглашение, что бесконечность * ноль и ноль * бесконечность не определены? Можно ли применить в этом случае свойство коммутативности? Не можем ли мы каким-либо образом интерпретировать эту операцию с 1 в результате? .

Также, если я сделаю такое же вычисление другим способом (хотя, возможно, неверным с алгебраической точки зрения … Я не уверен, на самом деле, насчет этого … поскольку я не разрешаю процесс ограничения внутри скобка) Я получаю бесконечность * (1 / бесконечность) = бесконечность / бесконечность , и результат следует интерпретировать как неопределенный.То же самое с ограничением на минус бесконечность, я получаю -infinity * (1 / – inifnity) = -infinity / – infinity = undefined .

Однако Я знаю из графика, что бесконечно удаленный предел этой функции дает ровно 1! Означает ли это, что заявление о том, что операции не определены, является произвольным фактом или я делаю ошибки в своих алгебраических шагах? .

Если я поместил функцию в калькулятор, он выбрал бы разные алгебраические шаги – применяя более одного алгебраического свойства – чтобы избежать ситуации, которую я показал, а именно: бесконечность над бесконечностью, минус бесконечность над минус бесконечностью, 0 * бесконечность , как и в калькуляторе, мы окончательно вычисляем: $ (1-2 / x) / (1-1 / x) $, что дает $ 1-0 / 1-0 = 1 $.

Однако, поскольку я не вижу явных алгебраических ошибок в своих отрывках, я задаю вам этот вопрос. Из прочтения, которое у меня есть, я понимаю, что есть споры о бесконечности над бесконечностью, и это не так очевидно, учитывая операции, показанные выше как неопределенные, и, возможно, выбор зависит от отрасли математики и операции, которую мы выполняем или я совершенно не прав?

С практической точки зрения, вы предлагаете мне использовать отрывки из калькулятора для моих упражнений?

PS.Infinity

Шаг 1: Перепишите задачу как

e в натуральный логарифм вашей функции. Затем вы возьмете предел показателей функции e .

Переписав вашу проблему как e в натуральный журнал вашей функциональной задачи и взяв предел экспоненты, вы получите это.

Поскольку вы используете натуральный логарифм, вы можете перенести экспоненту вашей функции, x , перед естественным логарифмом. Это еще одна причина, по которой вы переписываете свою проблему как e в естественный журнал вашей функциональной проблемы. Возможность перемещать показатель степени позволяет намного легче найти предел. После того, как вы переместили показатель своей функции, вы можете переписать задачу еще раз, на этот раз переместив показатель вашей функции, x , в знаменатель. Как видите, теперь написано:

Это определенно становится немного сложнее.Infinity

Шаг 2: Примените правило L’Hopital, чтобы найти свой предел.

Правило Л’Опиталя гласит, что если ваш предел равен 0/0, вы можете взять производную как от числителя, так и от знаменателя, а затем найти предел этого.

Итак, применяя правило Л’Опиталя, вы берете производную своего числителя и знаменателя. Чтобы взять производную вашего числителя, вы применяете правила вывода для натурального логарифма вместе с правилом цепочки и правилом для нахождения производной двух разделенных функций. Infinity

Найдя ответ, возведя функцию e в степень 0, вы получите 1.Таким образом, предел вашей функции 2 x /3 ​​ x до степени x при переходе к бесконечности равен 1.

Но только потому, что эта задача дает вам ответ 1, это не означает, что ваша ситуация от 1 до бесконечности всегда будет равна 1. Есть и другие задачи, на которые вы получите другой ответ.

Пример «Не всегда» 1

Взгляните на эту проблему.

Вы обнаружите, что ваш ответ на самом деле не 1.Во-первых, попытка найти здесь свой предел дает неопределенную форму от 1 до бесконечности. Теперь вы идете и следуйте инструкциям.

Переписав эту задачу с использованием e в натуральный логарифм вашей техники функции, вы получите эту проблему, когда показатель вашей функции, x /10, был перемещен.

Если вы возьмете предел экспоненты функции e , вы обнаружите, что снова получите неопределенную форму. infinity – это неопределенная форма , что означает, что предел не может быть вычислен, только глядя на пределы функций самостоятельно. Однако есть два шага, которые мы можем выполнить и выполнили в этом уроке, чтобы ответить на этот вопрос.

Шаг 1: Перепишите задачу как e в натуральный логарифм вашей функции. Затем вы возьмете предел показателей функции e . И Шаг 2. Примените правило L’Hopital, чтобы найти свой предел.{\ pm \ infty} $$$ и снова неопределенная форма.

Основная проблема этой неопределенной формы состоит в том, чтобы узнать, откуда $$ f (x) $$ стремится к единице (вправо или влево) и какая функция быстрее достигает своего предела.

Для решения этого предела мы будем использовать следующие две формулы, в зависимости от того, какая из них более удобна. Они преобразуют неопределенную форму в ту, которую мы можем решить.

Две формулы следующие: Если $$ \ displaystyle \ lim_ {x \ to {+} \ infty} {f (x)} = 1 $$ и $$ \ displaystyle \ lim_ {x \ to {+} \ infty} {g (x)} = \ pm \ infty $$, тогда

1. $$ \ displaystyle \ lim_ {x \ to {+} \ infty} {f (x) ^ {g (x)}} = e ^ {\ Big (\ displaystyle \ lim_ {x \ to {+} \ infty} {(f (x) -1) \ cdot g (X)} \ Big)} $$
2. $$ \ displaystyle \ lim_ {x \ to {+} \ infty} {f (x) ^ {g (x)}} = e ^ {\ Big (\ displaystyle \ lim_ {x \ to {+} \ infty } {g (x) \ cdot \ ln f (x)} \ Big)} $$

Давайте посмотрим на несколько примеров:

1) $$$ \ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (\ frac {1} {1 + x ^ 2} \ Big) ^ 2x} = e ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (\ frac {1} {1 + x ^ 2} -1 \ Big) \ cdot 2x}} = $$$

$$$ = е ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (\ frac {1} {1 + x ^ 2} – \ frac {1 + x ^ 2} {1 + x ^ 2} \ Big) \ cdot 2x}} = e ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {\ frac {-x ^ 2} {1 + x ^ 2} \ cdot 2x }} = $$$

$$$ = e ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {\ frac {-2x ^ 3} {1 + x ^ 2}}} = e ^ {- \ infty} = 0 $$$

2) $$$ \ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (\ frac {1} {1 + x ^ 2} \ Big) ^ 2x} = e ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {2x \ cdot \ Big (\ frac {1} {1 + x ^ 2} \ Big)}} = $$$

$$$ = е ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {- 2 \ cdot \ ln (1 + x ^ 2)}} = e ^ {- \ infty} = 0 $$ $

3) $$$ \ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (1 – \ frac {2} {x ^ 2} \ Big) ^ {x ^ 2}} = e ^ { \ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (1 – \ frac {2} {x ^ 2} – 1 \ Big) \ cdot x ^ 2}} = $$$

$$$ = e ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (- \ frac {2x ^ 2} {x ^ 2} \ Big)}} = e ^ {- 2 } = \ frac {1} {e ^ 2} $$$

4) $$$ \ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (1+ \ frac {1} {2 ^ x} \ Big) ^ x} = e ^ {\ displaystyle \ lim_ {x \ to {+} \ infty} {\ Big (1+ \ frac {1} {2 ^ x} -1 \ Big) \ cdot x}} = e ^ {\ displaystyle \ lim_ {x \ to {+ } \ infty} {\ frac {x} {2 ^ x}}} = e ^ 0 = 1 $$$

Бесконечность и DNE в пределах

Лучший способ понять, почему мы используем бесконечность вместо несуществующей (сокращенно DNE), даже если они технически одно и то же, – это сначала определить, что означает бесконечность. 2) будет продолжать расти все выше и выше.Вы можете представить, как он уходит со страницы и продолжает движение вверх. Другими словами, предел, когда x приближается к нулю для g (x), равен бесконечности, потому что он продолжает расти без остановки.

Итак, хотя бесконечность технически бессмысленна / просто математическая конструкция, ее можно использовать для описания результатов ограничений, когда функция продолжает работать вечно (что обычно происходит, когда у вас есть вертикальная асимптота).

Для ясности, ограничения на самом деле не существует, поскольку мы не можем присвоить ему номер (он продолжается вечно), поэтому вы можете сказать:

И это было бы технически правильно, но это более полезно ( и интуитивно понятно, если вы посмотрите на график), чтобы сказать, что он уходит в бесконечность.Точно так же, если у вас есть:

Предел, когда x приближается к нулю, будет отрицательной бесконечностью, поскольку график постоянно уменьшается при приближении к нулю с любой стороны:

Как правило, , когда вы берете предел и знаменатель равно нулю, предел будет идти на бесконечность или отрицательную бесконечность (в зависимости от знака функции).

Так когда бы вы сказали, что ограничения не существует?

Когда односторонние пределы не равны друг другу.

Во-первых, односторонний предел – это когда вы приближаетесь к значению с одной стороны. Вы указываете, с какой стороны вы идете, с плюсом или минусом по отношению к приближающемуся x. Если вы подходите справа, вы используете +, слева вы используете -.

Например:

Когда вы приближаетесь к x = 5 справа (обозначено пунктирной линией), f (x) = 2. Это односторонний предел, идущий с правой стороны.

По мере приближения к x = 5 слева f (x) = 2 снова. Это односторонний предел слева.

Так как пределы справа и слева одинаковы. Предел существует и равен тому, чему равны оба односторонних предела.

Итак:

Но что, если бы у вас было:

Односторонние пределы не равны, поэтому предел, когда x приближается к 1, не существует.

В качестве примечания, положительная и отрицательная бесконечность может быть тем, к чему приближается x. 2

Пределы бесконечности — Концепция.Как решить на примерах

Ошибка: Нажмите «Не робот», затем повторите попытку.

Краткий обзор

• «Пределы в бесконечности» исследуют, что происходит со значением функции, когда $$ x $$ становится бесконечно большим.
• Для существования предела на бесконечности функция должна приближаться к конкретному конечному значению.
• Горизонтальные асимптоты определяются как пределы на бесконечности.

Горизонтальные асимптоты

Напомним, что асимптота – это значение, которому функция становится действительно, очень близким, поскольку $$ x $$ становится все больше и больше, как на графике ниже.

Это в точности идея предела на бесконечности!

Определение

Предположим, что $$ f (x) $$ становится сколь угодно близким к определенному конечному значению $$ L $$, когда $$ x $$ становится бесконечно большим.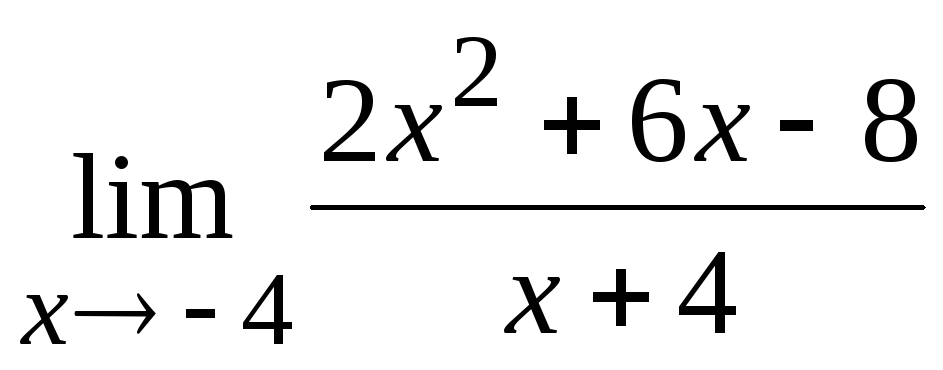 Тогда $$ L $$ является пределом $$ f (x) $$, поскольку $$ x $$ стремится к бесконечности, и мы пишем

$$ \ Displaystyle \ lim_ {х \ к \ infty} е (х) = L. $$

Обозначение Объяснение

Пределы отрицательной бесконечности

Аналогично, $$ \ displaystyle \ lim_ {x \ to- \ infty} f (x) = L $$ означает, что функция приближается к $$ L $$, поскольку $$ x $$ становится бесконечно большим в отрицательном направлении.

Оценка пределов на бесконечности с помощью графиков и таблиц

Пример 1

Используйте график ниже, чтобы оценить $$ \ lim \ limits_ {x \ to \ infty} f (x) $$.

График, кажется, показывает, что значение функции приближается к 4 по мере увеличения $$ x $$.

Отвечать

$$ \ lim \ limits_ {x \ to \ infty} f (x) \ приблизительно 4 $$

Пример 2

Используйте график ниже, чтобы оценить стоимость

1. $$ \ displaystyle \ lim_ {x \ to \ infty} f (x) $$
2. $$ \ Displaystyle \ lim_ {х \ to- \ infty} е (х) $$

Ответ

1. $$ \ Displaystyle \ lim_ {x \ to \ infty} f (x) \ приблизительно 3 $$
2. $$ \ displaystyle \ lim_ {x \ to- \ infty} f (x) \ приблизительно 0 $$

Пример 3

Используйте приведенную ниже таблицу, чтобы оценить $$ \ lim \ limits_ {x \ to- \ infty} f (x) $$.

$$ \ begin {array} {c | c} {x} & {f (x)} \\ \ hline -10 и 8,5 \\ -50 & 8,1 \\ -100 и 8,013 \\ -1000 и 8,0014 \\ -10000 и 8.00013 \\ -100000 и 8.000014 \ end {массив} $$

Чем больше $$ x $$ становится в отрицательном направлении, тем ближе функция к 8.

Отвечать

$$ \ lim \ limits_ {x \ to- \ infty} f (x) \ приблизительно 8 $$

Когда пределов в бесконечности не существует

Чтобы существовал предел на бесконечности, функция должна приближаться к определенному конечному значению. Рассмотрим следующий пример.

Пример 4

Изучите $$ \ lim \ limits_ {x \ to \ infty} \ sin x $$.

Решение

Синусоидальная функция всегда колеблется от 1 до $$ – 1 $$. Независимо от того, насколько большим станет значение $$ x $$ -, это поведение не изменится (см. Ниже).

Отвечать

$$ \ lim \ limits_ {x \ to \ infty} \ sin x $$ не существует.2 = \ infty $$

Важно! Как и раньше, утверждение о том, что предел бесконечен, также означает, что предел не существует.

Пример 6

Используйте график $$ f (x) = x + \ frac 1 3 x \ sin 2x $$, чтобы понять $$ \ displaystyle \ lim_ {x \ to \ infty} f (x) $$. 2 (2x) $$.2 (2x) $$ не существует.

Ошибка: Нажмите «Не робот», затем повторите попытку.

бесконечных лимитов; Вертикальные асимптоты – концепция

Когда предел исчисления неограниченно уменьшается или увеличивается вблизи определенных значений независимых переменных, мы называем эти бесконечные пределы .В общем, дробная функция будет иметь бесконечный предел, если предел знаменателя равен нулю, а предел числителя не равен нулю. Бесконечный предел может быть положительным или отрицательным и определяется знаком частного числителя и знаменателя.

Давайте еще раз посмотрим на односторонние пределы, рассмотрим функцию g от x = 10x над x-2. И я хочу конкретно посмотреть на предел, когда x приближается к 2 слева от g x. Теперь вы знаете, что произойдет что-то интересное, потому что, если x = 2, это не определено. Так что мы собираемся прокрасться по нему слева.
Давайте начнем с числа 1, так что у нас g of x равно 10×1 или 10 больше 1-2, -1 это будет -10. Теперь давайте немного приблизимся к 2, 1,9 10×1,9 это 19. 1,9-2 это -0,1 это будет, это как 19x-10 -190.
И позвольте мне ускорить это, остальные значения 1.99, 1.999 Я бы получил -1990, -19990. Что происходит с g значений x, когда x становится все ближе и ближе к 2. Кажется, что они уменьшаются все быстрее и быстрее, и мы говорим, что они стремятся к отрицательной бесконечности. Таким образом, мы бы сказали, что этот предел – отрицательная бесконечность. Предел, когда x приближается к 2 слева от g x, равен отрицательной бесконечности. Ценности неограниченно уменьшаются.
Теперь посмотрим, что происходит, когда x приближается к двум справа. Так что выберите число справа от 2, например 3, 10×3 – это 30, а не 3-2, 1 – 30. Давайте попробуем немного приблизиться к 2 2.1, 10×2.1 – это 21, а не 2.1-2 из 0.1, которое будет 210, а затем, чтобы просто заполнить остальные значения, все ближе и ближе к 2, у нас есть 2.01, 2.001 и мы получаем 2010, 20010. Вы можете видеть, что по мере того, как эти значения становятся все ближе и ближе к 2, значения y становятся все ближе и ближе или они неограниченно увеличиваются, они приближаются к бесконечности.
Итак, мы говорим, что этот предел равен бесконечности, теперь вы видели такие функции, прежде чем это g of x равно 10x по x-2. Когда x приближается к 2 слева, функция стремится к отрицательной бесконечности.И когда x приближается к 2 справа, он стремится к положительной бесконечности. Эти пределы сигнализируют о наличии вертикальной асимптоты.
И это приводит нас к этому определению: линия вертикальная линия x = a – это вертикальная асимптота графика функции y = f от x, если одна из этих четырех вещей истинна. Либо предел, когда x приближается к a слева от f от x, равен плюс бесконечности, либо минус бесконечности.