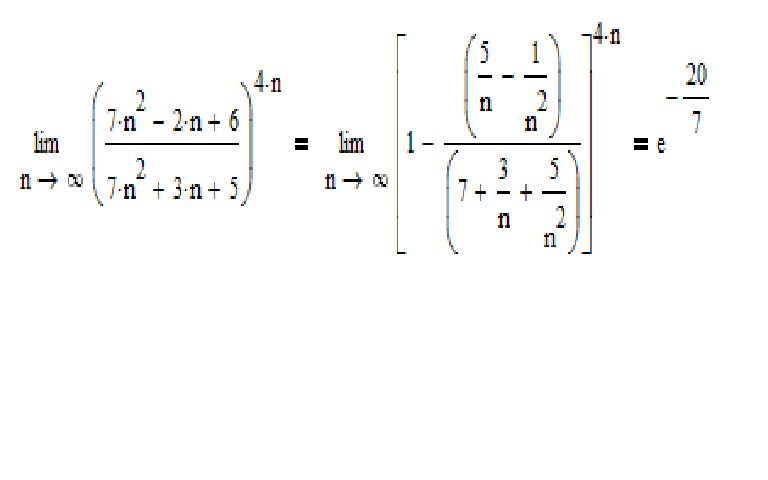Способы определения
Число e может быть определено несколькими способами.
Через предел:
(второй замечательный предел).
Как сумма ряда:
или .
Свойства
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения является функция , где c — произвольная константа.
Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
Число e является вычислимым (а значит, и арифметическим) числом.
, см. формула Эйлера, в частности
Ещё одна формула, связывающая числа е и π, т.
Второй замечательный предел
Второй замечательный предел имеет вид: или в другой записи В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность . Разберем несколько примеров нахождения предела по второму замечательному пределу с подробным оприсанием решения. Пример. Вычислить предел Решение. Подставляем бесконечность: Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела. Сделаем замену переменных. Пусть Если , то Исходный предел после замены примет вид:
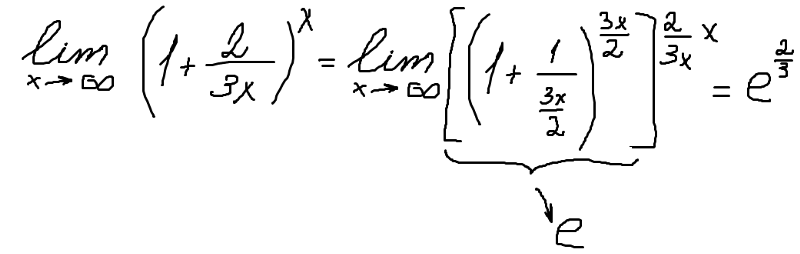Выделим целую часть в основании
показательно степенной функции: Тогда
предел запишется в виде: Сделаем
замену переменных. Пусть Если
,
то
Исходный
предел после замены примет вид:
В
преобразованиях были использованы
свойства степени и свойства
пределов. Ответ: 10)
Предел функции по Коши
Окрестностное определение по Коши
Значение
называется пределом (предельным
значением)
функции
в
точке
,
если для любой окрестности
точки
существует
выколотая окрестность
точки
такая,
что образ этой окрестности
лежит
в
.
Фундаментальное обоснование данного
определения предела можно найти в
статье Предел
вдоль фильтра.
Геометрическая интерпретация предела функции.
Обратимся к рисунку 1, на котором представлен фрагмент графика функции .
Рис. 1. Секущая AB образует угол β с положительным направлением оси 0x. Касательная к графику функции проведена в точке A.
Угловой коэффициент секущей AB равен средней скорости изменения функции на промежутке [x, x + ∆x]:
| (5) |
|
Предельным положением секущей AB при перемещении точки B к точке A по дуге кривой является касательная к графику в точке A. Поэтому угловой коэффициент касательной равен пределу углового коэффициента секущей при ∆x → 0:
| (6) |
|
Рис.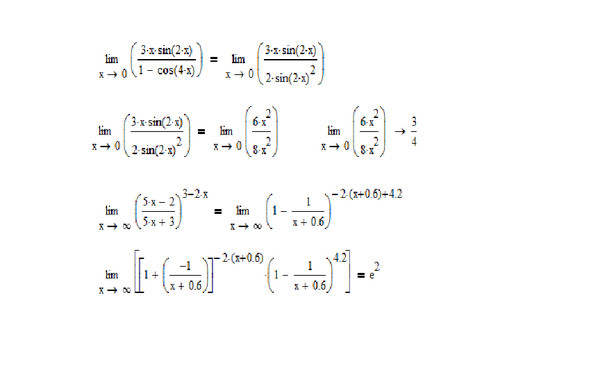
2.
Касательная является предельным
положением секущей
Таким образом, производная в точке x равна тангенсу угла, образованного касательной к графику функции в этой точке с положительным направлением оси 0x.
11)
Пусть переменная x стремится к a, оставаясь больше a, и при этом . Тогда число A называют правосторонним пределом (или пределом справа Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае при x → a со стороны меньших значений: Для существования обычного (двустороннего) предела функции в точке a необходимо и достаточно равенство между собой односторонних пределов:
Например, в точке x = 3 односторонние пределы функции отличаются друг от друга:
Поэтому
в рассматриваемой точке предел функции
не существует. |
12) Первым замечательным пределом именуют . Известны также и следствия из первого замечательного предела:
Все приведенные выше формулы получаются из основной: . Примечательность последней формулы состоит в том, что вместо х можно подставлять любое выражение, лишь бы это выражение стремилось к нулю. Например, так как при , то . Собственно говоря, на этом и основаны примеры на первый замечательный предел. Суть решения таких заданий проста: формально подогнать условие под вид первого замечательного предела, после чего использовать формулу . Допустим, нужно найти . Простой подстановкой проблему не решить, потому как , т.е. тут мы имеем дело с неопределенностью вида . Если такая неопределенность встречается вкупе с тригонометрическими выражениями, то для стандартных типовых расчетов это почти стопроцентная гарантия первого замечательного предела. Подгоним данную задачу под вид упомянутого предела, учитывая :
Осуществим
следующее преобразование: в числителе
домножим на 7х и разделим на 7х.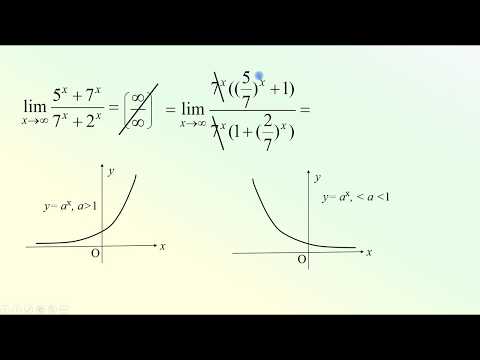
Что нам это даст? Так как при имеем , то можно применить первый замечательный предел: . Учитывая это, получим:
Сокращая х и вспомнив, что , получим: . Приведем ещё несколько примеров решения задач на первый замечательный предел:
13) Классификация бесконечно малых функций
Во многих случаях представляет интерес сравнение бесконечно малых между собой по характеру их приближения к нулю. Рассмотрим две бесконечно малые (x) и (x) при xx0 и предположим, что (x) не обращается в ноль в некоторой проколотой окрестности точки x0. Будем сравнивать эти бесконечно малые, изучая поведение их отношения при xx0.
Дадим следующие определения.
Если
,
то говорят, что (x)
и (x)
бесконечно малые одного порядка при
xx0.
Если , то говорят, что (x) бесконечно малая более высокого порядка по сравнению с (x) при xx0, и пишут , xx0.
Если (x) и k(x) – бесконечно малые одного порядка (k>0), то говорят, что (x) величина k-го порядка относительно бесконечно малой (x) при xx0 и пишут , xx0.
Если , то говорят, что (x) и (x) эквивалентные бесконечно малые при xx0 и пишут , xx0.
Замечание. Та же терминология применяется и при сравнении функций, не являющихся бесконечно малыми при xx0. В этом случае добавляется ещё одно определение.
Если существует число C > 0 такое, что в некоторой проколотой окрестности точки x0 справедливо неравенство , то говорят, что функция (x) ограничена относительно функции (x) при xx0, и пишут , xx0.
Примеры. 1. Привести примеры на каждое из определений.
2. Доказать, что при x0.
3. Вычислить: .
4. Доказать, что при x0.
Логарифм
по основанию e (e – трансцендентное число,
приближенно равное 2,718281828.
14) Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения. График непрерывной функции можно начертить «не отрывая карандаш от бумаги».
Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.
Рефераты по математике.Второй замечательный предел.
?Previous Entry | Next Entry
Реферат по математикестудента 1 курса факультета управления:”Менеджмент”
Кулагина Максима.
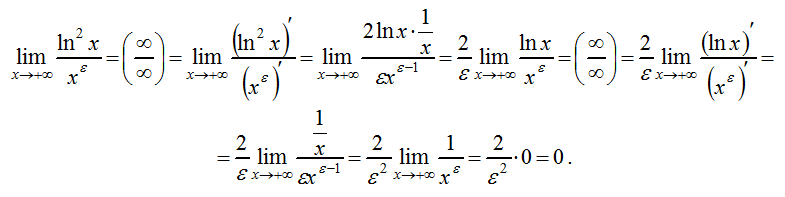
Второй замечательный предел.
Доказательство второго замечательного предела:
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:
1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.
- Отсюда следует: , поэтому
- .
- Если , то . Поэтому, согласно пределу , имеем:
- .
- По признаку (о пределе промежуточной функции) существования пределов .
2. Пусть . Сделаем подстановку , тогда
- .
Из двух этих случаев вытекает, что для вещественного Х.
Следствия
- для ,
Разберем несколько примеров нахождения предела по второму замечательному пределу способным описанием решения.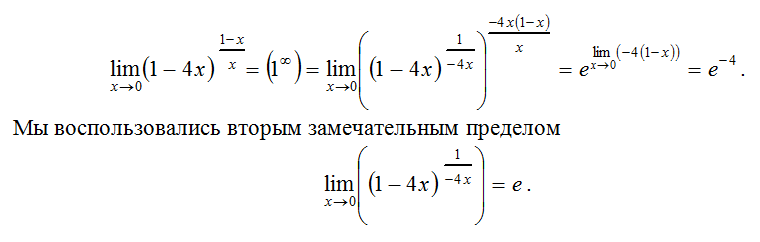
Примеры:
Вычислить предел
Решение.
Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность.Сделаем замену переменных. ПустьЕсли , то Исходный предел после замены примет вид:
Ответ:
Пример.
Вычислить предел
Решение.
Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
Тогда предел запишется в виде:
Сделаем замену переменных. Пусть
Если , то
Исходный предел после замены примет вид:
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:
Пример.
Вычислить предел
Решение.
Преобразуем функцию, чтобы применить второй замечательный предел:
Сейчас домножим показатель на и разделим на это же выражение, затем используем свойства степени:
Так как показатели степени числителя и знаменателя дроби одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях :
Если произвести замену , то получим второй замечательный предел в чистом виде, следовательно,
Ответ:
Ссылки:http://ru.
wikipedia.org/wiki/%C7%E0%EC%E5%F7%E0%F2%E5%EB%FC%ED%FB%E5_%EF%F0%E5%E4%E5%EB%FB
http://www.mathprofi.ru/zamechatelnye_predely.html
http://www.cleverstudents.ru/the_second_remarkable_limit.html
| November 2013 | ||||||
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- Андрей Чуприна : (no subject) [+0]
Powered by LiveJournal.com
Единица в степени бесконечности
Единица в степени бесконечности
Единица в степени бесконечности может быть одним из следующих.
| -NFINITY | Отрицательная бесконечность |
| +Infinity | Положительная бесконечность |
Когда мы столкнемся с такой ситуацией? Допустим, вы хотите найти предел следующей функции по мере приближения к бесконечности:
Когда мы подставляем бесконечность в эту функцию, мы видим, что она принимает неопределенную форму единицы в степени бесконечности. Чтобы решить эту проблему, давайте рассмотрим пример.
Лучшие репетиторы по математике
Поехали
Пример
Возьмем следующее уравнение .
Возьмем предел следующей функции, когда он приближается к нулю.
Чтобы взять предел , мы сначала заменим все значения x нашим нулевым значением a.
Результат дает единицу в степени 1 на 0 .
1 больше нуля не определено. Когда мы берем предел, приближаясь к нулю от справа и слева сбоку, посмотрим что получится.
| x | y |
| 0.1 | 10 |
| 0.001 | 1000 |
| 0.00001 | 100000 |
| … | … |
| -0,0001 | -10000 |
| -0,001 | -1000 |
| -0.1 | -10 |
| A | +infinity |
| B | -infinity |
This gives us an indeterminate form, just как в предыдущем разделе.
Чтобы решить эту проблему, мы должны просмотреть ограничения.
Сводка пределов
Когда вы берете предел функции, вы хотите знать, к какому значению он приближается, когда x достигает конкретное значение. Давайте рассмотрим обозначения.
| LIM | Символ для предела |
| X -> | AS x приближается функции мы находим предел для |
Когда вы берете предел функции, вы можете приблизиться к значению справа или слева.
| A | B | ||
| Определение | Подход от правого | . значение a справа | Приближение к значению a слева |
Неопределенные формы
Существует три общих метода нахождения предела функции.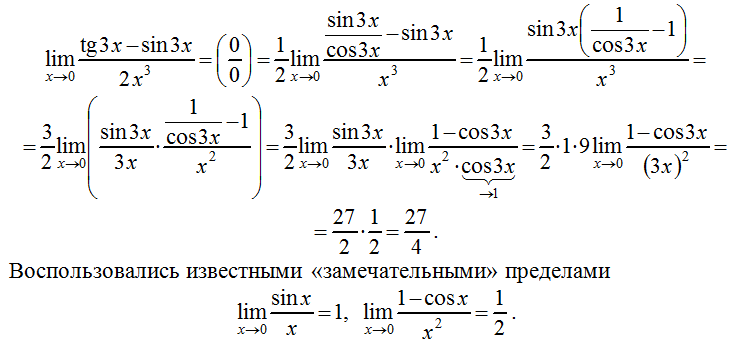
Возьмите это, например:
| Метод 1 | Подключите значение A в для x | Заместитель 4 в для X |
| Метод 2 | ПЛИГИКИ. in a for x | Умножьте верхнюю функцию, чтобы получить , затем подставьте 4 в |
| Метод 3 | Правило Лопиталя | При наличии неопределенной формы взять производную функций |
Неопределенная форма – это когда значение неизвестно или неопределенно. Взгляните на обычные, неопределенные формы.
| Фракция | , |
| Стандарт | , |
| Power | |
| 7000 | |
| 7 | |
| 9000 | 0015 , ,
Правило Лопиталя
Правило Лопиталя используется, когда у нас есть неопределенная форма, такая как 1 в степени бесконечности, и утверждает следующее:
предел любой рациональной функции равен пределу деления производной каждой функции друг на друга.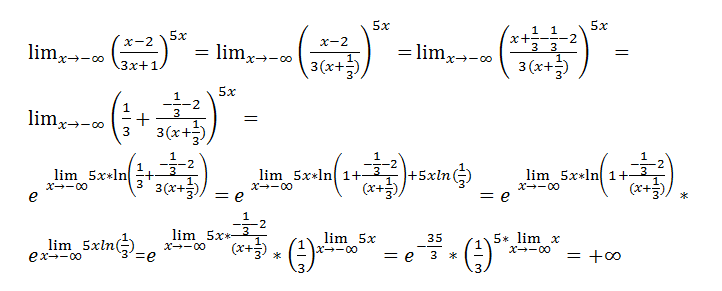
Решение единицы для увеличения бесконечности
Возьмем , следующий за примером :
Как мы увидим, это ограничение приведёт к неопределенной форме. Здесь мы можем использовать правило Лопиталя для решения предела .
Шаг 1
Первым шагом в нахождении предела является попытка подставить значение a в функцию .
Как видите, мы получаем 1 в степени 1 больше нуля. Единица над нулем на самом деле является неопределенной формой сама по себе. Взгляните на таблицу ниже, чтобы узнать почему.
| x | y |
| 0.5 | 2 |
| 0.1 | 10 |
| 0.001 | 1000 |
| 0.0001 | 10000 |
| 0,00001 | 100000 |
Один больше нуля неизвестен, поскольку по мере того, как знаменатель приближается к 0, значение y приближается к бесконечности.
Поскольку единица над нулем равна бесконечности, результат нашей функции, когда мы подставляем ноль, равен единице до бесконечности:
Шаг 2
Поскольку подстановка предела в функцию приводит к неопределенной форме, нам нужно использовать правило Лопиталя. Второй шаг в этом процессе — положить предел равным y.
Теперь, чтобы получить более упрощенную версию предела, возьмем натуральный логарифм с обеих сторон.
Напомним, логарифмические правила позволяют нам переместить показатель перед журналом.
На данный момент у нас есть функция perfect для использования правила Лопиталя. Если в этот момент мы подставим ноль, мы все равно получим неопределенную форму: ноль над нулем. Однако правило Лопиталя гласит, что мы можем взять производную любой рациональной функции.
Шаг 2
Возьмем производную от числителя и знаменателя независимо друг от друга.
Мы можем делать каждую из них независимо благодаря правилу Лопиталя.
Мы получили этот результат, используя производные правила для натурального логарифма. Теперь попробуем подставить ноль в функцию.
Теперь вы можете видеть, что мы получаем натуральный логарифм y равным , равным 3.
Шаг 4
быть у. Это означает, что нам нужно получить y само по себе. Для этого мы можем привести e к ln(y). Это заставит e и ln отмениться.
Теперь у нас есть предел нашей исходной функции , которая равна e в степени 3.
вычисление – 1 в степени бесконечности формула
спросил
Изменено 6 месяцев назад
Просмотрено 76 тысяч раз 9{\ lim_ {х \ к} г (е-1)} \end{align}
Где первый предел является формой определения предела $e$.
Я поставил пометку (*) рядом с одним шагом, который меня беспокоит. Я не уверен, почему мы можем отдельно оценивать пределы здесь. Возможно, кто-то еще может прокомментировать это.
$\endgroup$
1
$\begingroup$
Помните, что $f$ и $g$ являются функциями от $x$, поэтому, чтобы быть более точным, мы должны писать $f(x)$ и $g(x)$ вместо $f$ и $g$. Это относится к ответу ниже и к другим ответам, которые также приняли стенографию, используемую в вопросе $f$ для $f(x)$ и $g$ для $g(x)$. 9п &= \infty \\ \end{align}
Ограничения полностью связаны с тем, как осуществляется подход. Я мог бы призвать сюда Роберта Фроста (две тропы расходятся в лесу…), достаточно сказать, взять любое число (хоть на $\varepsilon$) больше 1, возвести его до сколь угодно большого числа, и путешествие завершится до $\infty$.
$\endgroup$
$\begingroup$
Вообще неправильно.