Первый замечательный предел
Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.
Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:
Приведённое выше равенство основано на эквивалентности бесконечно малых . Следовательно, верно равенство и следующего отношения:
.
Это разновидность первого замечательного предела.
Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.
Пример 1. Найти предел .
Решение. Подстановка вместо x нуля приводит к неопределённости:
.
В знаменателе – синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:
.
В знаменателе – синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .
И приходим к разновидности первого замечательного предела:
,
потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.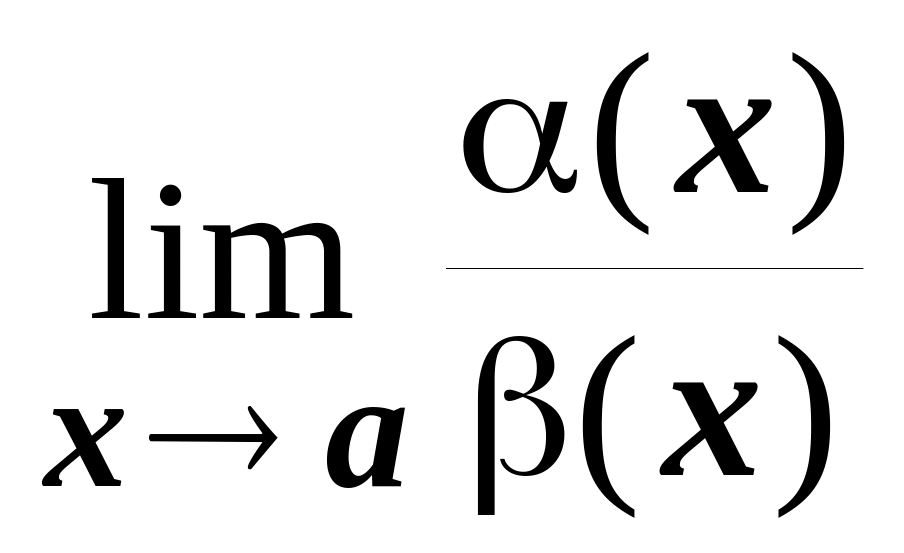
Умножаем икс на три и тут же делим:
.
.
Теперь можем окончательно решить данный предел:
.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 2. Найти предел .
Решение. Непосредственная подстановка вновь приводит к неопределённости “нуль делить на нуль”:
.
Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:
.
Пример 3. Найти предел .
Решение. При подстановке вновь получаем неопределённость “нуль делить на нуль”:
.
Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:
.
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 4. Найти предел .
Решение. Вновь получаем неопределённость “нуль делить на нуль”:
.
Можем получить отношение двух первых замечательных пределов.
Делим и числитель, и знаменатель на икс.
Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс
умножаем на 3 и тут же делим на 3. Получаем:
Пример 5. Найти предел .
Решение. И вновь неопределённость “нуль делить на нуль”:
.
Помним из тригонометрии, что тангенс – это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:
.
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела.
Представляем его как отношение синуса к косинусу.
.
Так как , то и
Пример 7. Найти предел .
Решение. И вновь неопределённость “ноль делить на ноль” и синус под знаком предела. Значит надо приводить к первому замечательному пределу. Умножим числитель и знаменатель на выражение сопряжённое числителю и получим
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 8. Найти предел .
Решение. Бороться с неопределённостью “ноль делить на ноль” будем приведением к первому замечательному пределу. Вспоминаем
формулу тригонометрической единицы и подставляем её. Потом вспоминаем, что косинус в квадрате нуля и просто косинус нуля равны единице, а они у нас с противоположными знаками,
значит взаимно уничтожаются. Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю.
Начало темы “Предел”
Продолжение темы “Предел”
определение, свойства и примеры решения
Содержание:
Определение
Функция $\alpha(x)$ называется бесконечно малой функцией (б.м.ф.) при $x \rightarrow a$ (или в точке $x=a$ ), если $\lim _{x \rightarrow a} \alpha(x)=0$
Пример
Функция $y=x$ является бесконечно малой (б.м) функцией при $x \rightarrow 0$.
Основные свойства бесконечно малых функций
1 Сумма конечного числа б.м функций является функцией б.м.
2 Произведение б.м функции на ограниченную есть функция б.м.
3 Произведение двух б.м функций есть функция б.м.
4 Произведение б.м функции на константу является б.м функцией.
5 Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
6 Функция $\frac{1}{\alpha(x)}$, обратная к б.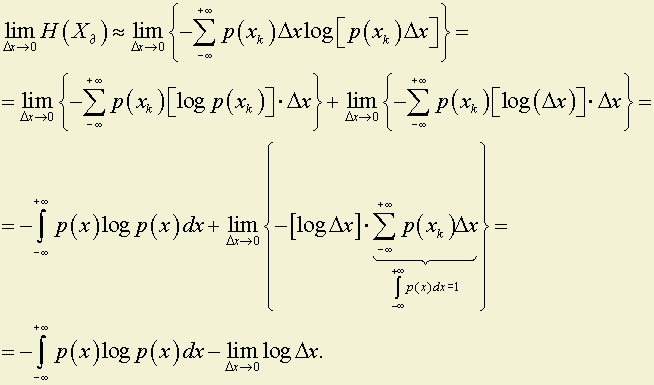
м функции
$\alpha(x) \neq 0$, есть функция бесконечно большая. Верно и обратное.
Слишком сложно?
Бесконечно малые функции не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Доказать, что функция $\alpha(x)=(x+1) \cdot \operatorname{arctg}(x)$ является бесконечно малой в точке $x=-1$.
Доказательство. Из того, что $\lim _{x \rightarrow-1}(x+1)=-1+1=0$ делаем вывод, что функция $f(x)=x+1$ является б.м при $x \rightarrow-1$. Функция $g(x)=\operatorname{arctg}(x)$ является ограниченной: $-\frac{\pi}{2} \lt g(x) \lt \frac{\pi}{2}$. А тогда их произведение $\alpha(x)=f(x) g(x)$, согласно свойству №3, является функцией б.м.
Теорема
Пусть $b$ –
предел функции
$y=f(x)$ в точке
$a$:
$\lim _{x \rightarrow a} f(x)=b$ . Тогда заданную функцию можно представить в
виде $f(x)=b+\alpha(x)$, где
$\alpha(x)$ – б.м функция. Верно и обратное утверждение.
Пример
Задание. Доказать, что $\lim _{x \rightarrow 1}(2 x+3)=5$.
Доказательство. Рассматриваемую функцию $f(x)=2 x+3$ представим в виде суммы предела этой функции – числа 5 и бесконечно малой функции $\alpha(x)=2(x-1)$ :
$f(x)=2 x+3=5+2 x+3-5=5+2 x-2=5+2(x-1)$
А тогда, по выше приведенной теореме, делаем вывод, что $\lim _{x \rightarrow 1}(2 x+3)=5$.
Читать дальше: сравнение бесконечно малых функций.
ПРЕДЕЛЫ ФУНКЦИИ В ТОЧКЕ И НА БЕСКОНЕЧНОСТИ
ПРЕДЕЛЫ ФУНКЦИИ В ТОЧКЕ И НА БЕСКОНЕЧНОСТИ
Введем понятие предела функции в точке и на бесконечности.
Пусть на множестве D задана функция у = f(х). Рассмотрим поведение функции при стремлении аргумента к числу х0, т. е. х→х0.
Выберем произвольную последовательность значений аргумента {x 1, x 2, …xn, …}={xn}, общий член которой xn неограниченно близко приближается к числу х0, т.
е. стремится xn→х0.
При этом соответствующие значения функции образуют числовую последовательность {f(x 1), f(x 2), …f(xn), …} = {f(xn)}.
у А 0 х0 х
Число А называется пределом функции у = f(х) в точке х = х0, если для любой последовательности значений аргумента {xn}, стремящейся к х0, т. е. xn→х0, соответствующая последовательность значений функции {f(xn)} стремится к числу А, т. е. f(xn)→A
Предел в точке обозначается:
Существуют также односторонние пределы в точке – пределы слева и справа, когда значения аргумента приближаются к точке х=х0 со стороны больших или меньших значений:
Теорема. Для того чтобы функция у = f(х) имела предел в точке х=х0, необходимо и достаточно, чтобы в этой точке существовали равные между собой правый и левый пределы, которые и определяют предел функции в точке:
Введём понятие предела функции на бесконечности.
В этом случае значение аргумента неограниченно возрастает до бесконечности. Дадим определение.
Число А называется пределом функции у = f(х) на бесконечности при х→∞, если для любой последовательности значений аргумента, стремящейся к бесконечности, т. е. xn→∞, соответствующая последовательность значений функции стремится к числу А, т. е. f(xn)→A.
Предел на бесконечности обозначается:
Отметим, что функция может иметь пределы как на +∞, так и на -∞:
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ И ИХ СЛЕДСТВИЯ
где u=u(x)→ 0 при x→ 0
Следствия из первого замечательного предела:
Второй замечательный предел:
где е 2. 73…-натуральное число, а logex = lnx называется натуральным логарифмом.
Следствия из второго замечательного предела:
БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
Функция называется бесконечно малой в точке х=х0 или на бесконечности при х , если её пределы равны нулю:
Функция называется бесконечно большой в точке х=х0 или на бесконечности при х , если её пределы равны бесконечности:
Следует отметить, что одна и та же функция может быть одновременно бесконечно малой или бесконечно большой в разных точках.
На рисунке функция является бесконечно малой в точке х=1 и при , а в точке х=0 эта функция является бесконечно большой.
у 0 1 х
Теорема о связи бесконечно малых или бесконечно больших функций: Если функция является бесконечно малой в точке х=х0 или на бесконечности при х , то функция
– является бесконечно большой и наоборот, если бесконечно большая функция, то бесконечно малая функция.
Пример. Функция является бесконечно малой в точке х=2, т. к
а функция является бесконечно является большой в точке х=2, т. к.
Две бесконечно малые функции в точке х=х0 или на бесконечности при х называются эквивалентными, если предел их отношения равен единице, т. е.
При нахождении пределов бесконечно малые функции можно заменять на эквивалентные.
ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
1)sinu~ u; tgu~ u; arcsinu~ u; arctgu~u, 2) еu-1~u; 3) au-1~u lna; 4) ln(1+u) ~u; 5) (u+1) ~ u; 6) (1 -cosu)~ , где u=u(x)→ 0 –бесконечно малая функция;
Теорема об арифметических операциях над пределами: Если функции f(x) и φ(х) имеют конечные пределы в точке х=х0 или на бесконечности при х , то
при условии
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
При вычислении пределов необходимо выделить случаи, когда функция определена или неопределенна в предельной точке.
Если функция определена в предельной точке х=х0, то вычисление предела сводится к вычислению частного значения функции в этой точке путем подстановки в неё значения аргумента, т. е.
Пример.
Если функция неопределенна в предельной точке х=х0, то для характерных неопределенностей типа:
имеется ряд практических приемов вычисления пределов для раскрытия этих неопределенностей.
Неопределенность типа:
Если эта неопределенность возникла для тригонометрических функций, то можно использовать первый замечательный предел и его следствия, а также можно провести замену эквивалентных бесконечно малых функций.
Пример. sin 2 x=(sinx)2~x 2; arctg 3 x~3 x; (e 6 x-1) ~6 x =
Если эта неопределенность возникла при делении многочленов, то нужно в числителе и знаменателе выделить и сократить сомножитель, стремящийся к 0.
Пример.
Неопределенность типа
раскрывается путем деления числителя и знаменателя дроби на наибольшую степень переменной х и замены бесконечно большой переменной х→ на новую бесконечно малую переменную
Пример.
Неопределенности типа:
путем преобразования приводятся к неопределенностям вида:
Примеры.
Неопределенность типа:
раскрывается с помощью второго замечательного предела.
Пример.
Предел и производная: Замечательные пределы
lim (1 + х)х =е , при х стремящемся к бесконечности -первый замечательный предел.
lim sinx/x=1 при х стремящемся к бесконечности – второй замечательный предел .
Замечательные пределы- пределы стремящиеся к бесконечности.
Второй замечательный предел замечателен не только тем. что он суще-ствует, но и тем. что его величина
— это знаменитое неперово числое = 2.71828… .
Что касается первого замечательного предела, то. как известно, он равен единице,
но при условии, что угол х измеряется в радианах. А это значит, что и он связан с другим не ме-нее
замечательным числом — архимедовым числом тг (тг — отношениедлины любой окружности к ее диаметру,
одно и то же для всех окруж-ностей по соображениям подобия).
илона варкки 11с
http://www.finmath.ru/vocabulary/90/
http://ru.wikipedia.org/
http://209.85.135.132/search?q=cache:vqzHC-3nLJAJ:files.school-collection.edu.ru/dlrstore/d62fa4b8-a780-11dc-945c-d34917fee0be/i5145153.pdf
Второй замечательный предел
Второй замечательный предел — это формула
,
где e = 2,718281828.
m-1/x}=m
Они замечательны тем, что помогают вычислению многих других пределов.
Так, с помощью первого замечательного предела можно установить важную для приложений эквивалентность при стремлении х к нулю следующих бесконечно малых величин: ax, sinax, tgax, arcsinax, arctgax(эквивалентность означает, что их отношение стремится к 1 при стремлении х к нулю). Отметим, что аргументы тригонометрических и обратных тригонометрических функций здесь измеряются в радианах, как это обычно бывает при рассмотрении подобных функций.
http://www.math.com.ua/mathdir/lim_great.html
http://school149.avers-telecom.ru/dlrstore/631e3ba7-726e-4dbe-ab83-f11858b1f1d7/Zamechatelnye_predely.html
darja sahhova
Так называют следующие равенства:
lim sin x/x=1 -первый замечательный предел;
lim(1+x)1/x=lim(1+1/x)x=e=2,718281…
-второй замечательный предел.
Они замечательны тем, что помогают вычислению многих других пределов.
x = exp
Они замечательны тем, что помогают вычислению многих других пределов.
Так, с помощью первого замечательного предела можно установить важную для приложений эквивалентность при стремлении х к нулю следующих бесконечно малых величин: ax, sinax, tgax, arcsinax, arctgax
Второй замечательный предел служит для раскрытия неопределенности
http://school-collection.edu.ru/catalog/res/631e3ba7-726e-4dbe-ab83-f11858b1f1d7/view/
http://www.tstu.tver.ru/faculties/civil/vm/math_on_line/topic/funczija/lect_1/lect_1_8.html
Анна Фадеева 11b
Уважаемые блоггеры! Кто ни будь знает кто дал название замечательным пределам? Если есть информация по этому вопросу, поделитесь пожалуйста…
Как найти предел arctan left ex right в математике класса 11 CBSE
Подсказка: Эта проблема связана с нахождением предела заданной функции, поскольку переменная функции стремится к бесконечности.
В исчислении, если что-то бесконечно, мы просто подразумеваем, что его значениям нет предела. Мы говорим, что когда $ x $ приближается к 0, предел $ f (x) $ бесконечен. Теперь предел – это число или граница. Поэтому, когда мы говорим, что предел – бесконечность, мы имеем в виду, что не существует числа, которое мы могли бы назвать.x}} \ right) $ по мере приближения $ x $ к $ \ infty $ составляет $ \ dfrac {\ pi} {2} $. Примечание: Обратите внимание, что пределы арктангенса существуют в $ – \ infty $ (минус бесконечность) и $ + \ infty $ (плюс бесконечность). Функция арктангенса имеет предел в $ – \ infty $, который равен $ – \ dfrac {\ pi} {2} $. Функция арктангенса имеет предел в $ \ infty $, равный $ \ dfrac {\ pi} {2} $.
| 1 | Найдите производную – d / dx | натуральное бревно х | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную – d / dx | e ^ x | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную – d / dx | 1 / х | |
| 6 | Найдите производную – d / dx | х ^ 2 | |
| 7 | Найдите производную – d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную – d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную – d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную – d / dx | cos (x) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x относительно x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную – d / dx | х ^ 3 | |
| 17 | Найдите производную – d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную – d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную – d / dx | грех (2x) | |
| 23 | Найдите производную – d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл от 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную – d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную – d / dx | cos (2x) | |
| 28 | Найдите производную – d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл 2x по отношению к x | |
| 30 | Найдите производную – d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную – d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную – d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную – d / dx | 2e ^ x | |
| 35 | Найдите производную – d / dx | натуральное бревно 2х | |
| 36 | Найдите производную – d / dx | -sin (х) | |
| 37 | Найдите производную – d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную – d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную – d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл от cos (2x) относительно x | |
| 42 | Найдите производную – d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную – d / dx | х / 2 | |
| 46 | Найдите производную – d / dx | -cos (x) | |
| 47 | Найдите производную – d / dx | грех (3x) | |
| 48 | Найдите производную – d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную – d / dx | х ^ х | |
| 52 | Найдите производную – d / dx | х натуральное бревно х | |
| 53 | Найдите производную – d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл от x ^ 2 натурального логарифма x относительно x | |
| 56 | Найдите производную – d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную – d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную – d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную – d / dx | у = х ^ 2 | |
| 62 | Найдите производную – d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную – d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную – d / dx | e ^ 2 | |
| 67 | Найдите производную – d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную – d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную – d / dx | х ^ 5 | |
| 73 | Найдите производную – d / dx | 2 / х | |
| 74 | Найдите производную – d / dx | натуральное бревно 3х | |
| 75 | Найдите производную – d / dx | х ^ (1/2) | |
| 76 | Найдите производную – d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную – d / dx | cos (x ^ 2) | |
| 78 | Найдите производную – d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную – d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную – d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 относительно x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную – d / dx | бревно х | |
| 86 | Найдите производную – d / dx | арктан (х) | |
| 87 | Найдите производную – d / dx | натуральное бревно 5х | |
| 88 | Найдите производную – d / dx | 5e ^ x | |
| 89 | Найдите производную – d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную – d / dx | 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 93 | Найдите производную – d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную – d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную – d / dx | 2sin (x) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную – d / dx | натуральный логарифм x ^ 2 |
Докажите, что предел \ arctan (x), когда x стремится к бесконечности, равен \ frac {\ pi} {2}.
Найдите объем V описываемого твердого тела S. Основание S – круговой диск с радиусом 5r. Параллельные сечения перпендикулярны основанию квадратов.
Найдите объем V описываемого твердого тела S.
Основание S представляет собой круглый диск радиусом 5r. Параллельные сечения, перпендикулярные основанию, представляют собой квадраты.
Можно получить полный объем твердого объекта с помощью исчисления, если дано его поперечное сечение.б {Adx} {/ экв}. Где, {eq} A {/ eq} – это площадь одного поперечного сечения, а {eq} dx {/ eq} – его ширина.
Ответ и объяснение:
Дано:
- Основание {eq} S {/ eq} – круговой диск с радиусом {eq} 5r {/ экв}.
- Параллельные поперечные сечения, перпендикулярные основанию, представляют собой квадраты.
Цель состоит в том, чтобы найти объем описываемого твердого вещества.
Предположим, что круговой диск с центром в начале координат с радиусом {eq} 5r {/ экв}.
3}}} {3} {/ eq} куб.
Пределы на бесконечности | Открытые учебники для Гонконга
Определение предела в терминах бесконечно малых значений немедленно распространяется на предельные процессы, в которых x становится все больше и больше, а не все ближе и ближе к некоторому конечному значению. Например,
функция явно становится все ближе и ближе к 3 по мере того, как становится все больше и больше. Если – бесконечное число, то определение говорит, что вычисление этого выражения в, где бесконечно мало, дает результат, стандартная часть которого равна 3.Не имеет значения, что оказывается бесконечным, определение все равно работает. Также отметим, что в этом примере это
не имеет значения, что такое бесконечное число; предел равен 3 для любого бесконечного. Мы можем записать этот факт как
где символ следует интерпретировать как «нет, нет, я не
даже неважно, какое бесконечное число вы здесь поместите, я утверждаю, что оно сработает до 3, несмотря ни на что ».
Символ не
интерпретироваться как обозначение любого конкретного бесконечного числа.Это была бы ошибка, лежащая в основе ложного доказательства в Безопасном использовании бесконечно малых величин, что 1 = 1/2, которое предполагало, что все бесконечности должны быть одинаковыми.
размер.
Несколько иной пример – функция арктангенса. Арктангенс 1000 равен примерно 1,5698, и ввод все больших и больших чисел дает ответы, которые кажутся более близкими и близкими. ближе к. Но арктангенс -1000 равен примерно -1,5698, т.е. очень близко к. Из этих числовых наблюдения, мы предполагаем, что
равно для положительной бесконечности, но для
отрицательная бесконечность.Было бы неправильно писать
потому что не имеет значения, какое бесконечное число мы выберем. Вместо этого мы пишем
Некоторые выражения вообще не имеют такого ограничения. Например, если вы возьмете синусы больших чисел, таких как тысяча, миллион и т.
Д., На своем калькуляторе, результаты будут по существу случайными.
числа, лежащие между 1 и 1. Они не устанавливаются на какое-либо конкретное значение, потому что функция синуса постоянно колеблется взад и вперед.Чтобы формально доказать, что это не определено, предположим, что функция синуса, определенная на действительных числах, имеет
свойство, что вы всегда можете изменить его результат как минимум на 0,1, если вы добавите 1,5 или 1,5 к его входным данным. Например, и. Применяя принцип переноса к этому утверждению, мы обнаруживаем, что то же самое верно и для
гиперреалы. Следовательно, не может быть никакого значения l, которое бесконечно мало отличается от всех положительных бесконечных значений.
Часто мы заинтересованы в поиске предела по мере приближения к бесконечности выражение, записанное как неопределенная форма, например, где оба и бесконечны.
Пример
Оцените предел
Интуитивно понятно, что если он станет достаточно большим, постоянные члены будут
незначительно, а сверху и снизу будут преобладать и
термины, соответственно, давая ответ, приближающийся к 2.
Один из способов проверить это – разделить верх и низ на, давая
Если x бесконечно, то стандартная часть вершины равна 2, стандартная часть нижней части равна 1, и поэтому стандартная часть всего этого равна 2.
Другой подход – использовать правило Л’Опиталя. Производная верхней части равна 2, а производная нижней части равна 1, поэтому предел равен.
Что такое загар, обратный бесконечности? – Реабилитацияrobotics.net
Что такое загар, обратный бесконечности?
Диапазон инверсии загара составляет от минус π на 2 до π на 2 открытая скобка, следовательно, возможное значение инверсии загара на бесконечность равно π на 2. π ÷ 2. Диапазон инверсии загара составляет от (-π ÷ 2, π ÷ 2).Следовательно, tan inverse (бесконечность) = π / 2.
Приближается ли Тан к бесконечности?
tan x стремится к бесконечности, когда x приближается к пи / 2, потому что tan x = sin x / cos x, а cos x приближается к нулю, когда x приближается к пи / 2.
В прямоугольном треугольнике Tan противоположен смежному. Таким образом, если касательная большая, то противоположная сторона намного больше, чем соседняя сторона, то есть угол близок к 90 градусам.
Что такое арктангенс бесконечности?
Главное значение arctan (бесконечности) – пи / 2.Арктангенс определяется как функция арктангенса в диапазоне (-pi / 2, pi / 2). Это означает, что x = arctan (y) является решением уравнения y = tan (x), где x определяется как находящееся между -pi / 2 и pi / 2.
Какова тангенс отрицательной бесконечности?
Tan 90 – бесконечность, угол измеряется по часовой стрелке в первом квадранте. Следовательно, загар, обратная бесконечность, составляет 90 градусов и находится в первом квадранте. Точно так же загар, обратный минус бесконечность, составляет -90 градусов, то есть в четвертом квадранте и измеряется относительно начала координат по часовой стрелке от оси x.
Что такое Ln бесконечность?
1 Ответ. Амори В.
Ответ – ∞. Функция натурального логарифма строго возрастает, поэтому она всегда растет, хотя и медленно.
Чему равен арктангенс?
По соглашению диапазон arctan ограничен от -90 ° до + 90 ° *. Итак, если вы используете калькулятор для решения, скажем, арктангенса 0,55, из бесконечного числа возможностей он вернет 28,81 °, значение в диапазоне функции…. Для y = arctan x:
| Диапазон | – π 2 |
|---|---|
| Домен | Все вещественные числа |
Что такое Arctan 2 с точки зрения пи?
Арктангенс 2 равен функции арктангенса 2, которая равна 1.107 радиан или 63,435 градуса: arctan 2 = tan-1 2 = 1,107 рад = 63,435º
Чему равен тангенс, обратный 1?
Тут не нужно много решений. Выражение arctan (1) означает все углы, тангенсы которых равны 1. Касательные – это наклоны, то есть все углы, лучи которых имеют наклон 1. Это один из двух наших треугольников, 45∘ и 180∘ + 45∘ = 225∘ плюс их концевых собратьев.
Что такое загар, обратный 0?
арктан
Где загар равен 1?
Важные углы: 30 °, 45 ° и 60 °
| Уголок | Тан = Sin / Cos |
|---|---|
| 30 ° | 1 √3 = √3 3 |
| 45 ° | 1 |
| 60 ° | √3 |
Как называется загар 1?
арктангенс
Для чего используется tan 1?
Обратные тригонометрические функции sin − 1 (x), cos − 1 (x) и tan − 1 (x) используются для нахождения неизвестной меры угла прямоугольного треугольника, когда известны две длины сторон.
Какова формула тангенса?
Тангенс x определяется как его синус, деленный на его косинус: tan x = sin x / cos x. Котангенс x можно определить как косинус x, деленный на синус x: cot x = cos x / sin x. 2.
Что такое касательная к окружности?
Касательная к окружности – это прямая линия, которая касается окружности только в одной точке.
Эта точка называется точкой касания. Касательная к окружности перпендикулярна радиусу в точке касания.
Что такое общая касательная?
Определение общей касательной Касательной к окружности называется линия, которая проходит ровно через одну точку на окружности и перпендикулярна линии, проходящей через центр окружности. Линия, касающаяся более чем одной окружности, называется общей касательной обеих окружностей.
Может ли линия иметь касательную?
Касательная, в геометрии, прямая линия (или плавная кривая), которая касается заданной кривой в одной точке; в этой точке наклон кривой равен наклону касательной.Касательная линия может считаться ограничивающим положением секущей линии, поскольку две точки, в которых она пересекает кривую, приближаются друг к другу.
Что такое касательная к функции?
Касательная линия к функции f (x) в точке x = a – это линия, которая только касается графика функции в рассматриваемой точке и является «параллельной» (некоторым образом) графику в этой точке.
Во второй показанной точке (точка, где линия не является касательной) мы иногда будем называть ее секущей линией.
Сколько касательных у кривой?
2 касательные
Как найти касательную к кривой?
1) Найдите первую производную f (x). 2) Подставьте значение x указанной точки в f ‘(x), чтобы найти наклон в x. 3) Подставьте значение x в f (x), чтобы найти координату y точки касания. 4) Объедините наклон из шага 2 и точку из шага 3, используя формулу угла наклона точки, чтобы найти уравнение для касательной.
Каков наклон касательной к кривой?
Наклон кривой y = f (x) в точке P означает наклон касательной в точке P.Нам нужно найти этот наклон для решения многих приложений, поскольку он сообщает нам скорость изменения в конкретный момент. [Мы пишем y = f (x) на кривой, поскольку y является функцией от x. То есть, когда изменяется x, изменяется и y.]
Как найти нормаль кривой?
Найдите уравнение касательной к кривой y = x3 в точке (2, 8).
Градиент касательной при x = 2 равен 3 × 22 = 12. Вас также могут попросить найти градиент нормали к кривой. Нормаль к кривой – это линия, перпендикулярная (под прямым углом) к касательной к кривой в этой точке.
Каковы 3 характеристики нормальной кривой?
Свойства нормального распределения Среднее значение, мода и медиана равны. Кривая симметрична в центре (т.е. около среднего μ). Ровно половина значений находится слева от центра, а ровно половина значений – справа. Общая площадь под кривой 1.
Почему важна нормальная кривая?
Колоколообразная кривая – общая черта природы и психологии. Нормальное распределение является наиболее важным распределением вероятностей в статистике, потому что многие непрерывные данные в природе и психологии отображают эту колоколообразную кривую при составлении и построении графика.
Что нормально кривой?
Касательная к кривой – это линия, которая касается кривой в одной точке и имеет тот же наклон, что и кривая в этой точке.
Нормаль к кривой – это линия, перпендикулярная касательной к кривой.
1.8: Пределы и непрерывность обратных тригонометрических функций
Обратные функции
Напомним, что функция \ (f \) взаимно однозначно (часто записывается как \ (1-1 \)), если она присваивает различные значения \ (y \) различным значениям \ (x \) .Другими словами, если \ (x_1 \ ne x_2 \), то \ (f (x_1) \ ne f (x_2) \). Эквивалентно \ (f \) взаимно однозначно, если \ (f (x_1) = f (x_2) \) влечет \ (x_1 = x_2 \). Существует простое горизонтальное правило для определения, является ли функция \ (y = f (x) \) взаимно однозначной: \ (f \) взаимно однозначно тогда и только тогда, когда каждая горизонтальная линия пересекает график функции \ (y = f (x) \) в \ (xy \) – координатной плоскости не более одного раза (см. рисунок 5.3.3).
Рисунок 5.3.3 Горизонтальная линейка для однозначных функций
Если функция \ (f \) взаимно однозначна в своей области определения, то \ (f \) имеет обратную функцию , обозначенную \ (f ^ {- 1} \), такую, что \ (y = f (x) \) тогда и только тогда, когда \ (f ^ {- 1} (y) = x \).
{- 1} x \) (иногда называемую арксинусом и обозначаемую \ (y = \ arcsin \; (x \)), область определения которой интервал \ ([- 1,1] \), а диапазон – интервал \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \).{-1} x) ~ & = ~ x \ quad && \ text {for \ (- 1 \ le x \ le 1 \)} \ label {eqn: arcsin2}
\ end {alignat} \]
Сводка обратных тригонометрических функций
Проиллюстрируем сводку тригонометрических функций и обратных тригонометрических функций в следующей таблице:
| Тригонометрическая функция | график тригонометрической функции | Ограниченный домен и ассортимент | Обратная тригонометрическая функция | график обратной тригонометрической функции | Недвижимость |
| \ (е (х) = \ грех (х) \) | \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \) и \ ([- 1,1] \) | \ (f ^ {- 1} (x) = \ sin ^ {- 1} x \) | |||
| \ (f (x) = \ cos (x) \) | \ ([0, \ pi] \) и \ ([- 1,1] \) | \ (f ^ {- 1} (x) = \ cos ^ {- 1} x \) | \ [\ begin {alignat} {3} \ cos ^ {- 1} (\ cos \; y) ~ & = ~ y \ quad && \ text {для \ (0 \ le y \ le \ pi \)} \ label {eqn: arccos1} \\ \ cos \; (\ cos ^ {- 1} x) ~ & = ~ x \ quad && \ text {для \ (- 1 \ le x \ le 1 \)} \ label {eqn: arccos2} \ end {alignat} \] | ||
\ (е (х) = \ загар (х) \) | \ (\ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) \) и \ (\ mathbb {R} \) | \ (f ^ {- 1} (x) = \ tan ^ {- 1} x \) | \ [\ begin {alignat} {3} \ tan ^ {- 1} (\ tan \; y) ~ & = ~ y \ quad && \ text {для \ (- \ tfrac {\ pi} {2} < y < \ tfrac {\ pi} {2} \)} \ label {eqn: arctan1} \\ \ tan \; (\ tan ^ {- 1} x) ~ & = ~ x \ quad && \ text {для все реальные \ (x \)} \ label {eqn: arctan2} \ end {alignat} \] | ||
\ (f (x) = \ детская кроватка (x) \) | \ [\ begin {alignat} {3} \ cot ^ {- 1} (\ cot \; y) ~ & = ~ y \ quad && \ text {for \ (0 \ конец {alignat} \] | ||||
| \ (f (x) = \ sec (x) \) | \ ([0, \ pi] \), с \ (x \ ne \ frac {\ pi} {2} \) и \ (\ mathbb {R} \) | \ [\ begin {alignat} {3} \ [\ begin {alignat} {3} |
Ниже приведены примеры:
Пример \ (\ PageIndex {1} \):
Найдите \ (\ sin ^ {- 1} \ left (\ sin \; \ frac {\ pi} {4} \ right) \).
{-1} x \), что доказывает тождество.
В чем основная ценность Arctan? – Цвета-NewYork.com
В чем основная ценность Arctan?
Основные ценности
| Имя | Обычное обозначение | Диапазон обычного главного значения (градусы) |
|---|---|---|
| арктангенс | y = arctan (x) | −90 ° <у <90 ° |
| арккотангенс | y = arccot (x) | 0 ° <у <180 ° |
| угол дуги | y = arcsec (x) | 0 ° ≤ y <90 ° или 90 ° |
| дуга | y = arccsc (x) | −90 ° ≤ y <0 ° или 0 ° |
Как найти основную стоимость?
Поскольку cos x положителен, главное значение находится в первом квадранте.Мы должны подумать об угле cos, для которого мы получаем значение √3 / 2. Следовательно, главное значение x равно π / 6. Всякий раз, когда у нас есть cos θ, главное значение θ должно быть в [0, π].
Что такое формула Arctan?
Определение арктангенса Арктангенс x определяется как функция арктангенса x, когда x является вещественным (x∈ℝ). Когда тангенс y равен x: tan y = x. Тогда арктангенс x равен функции арктангенса x, которая равна y: arctan x = tan-1 x = y.
Как вы относитесь к ценностям Arctan?
Это означает, что arctan (tan (x)) = x и tan (arctan (x)) = x. Мы можем рассматривать тангенс и арктангенс как «уничтожающие» друг друга. Другой способ увидеть arctan (x) – это как tan (x) в обратном порядке.
Что такое Арктан 0 в Пи?
Таблица арктангенса
| y | x = arctan (y) | |
|---|---|---|
| градуса | радиан | |
| 0 | 0 ° | 0 |
| 0./ td> | 30 ° | π / 6 |
| 1 | 45 ° | π / 4 |
Что такое Арктан 1 в Пи?
Единственные значения θ, которые делают уравнение tanθ = 1 истинным, – это π4 и 5π4.
Однако мы должны учитывать диапазон функции arctg, которая равна (−π2, π2). В этот интервал попадает только π4. Таким образом, arctan1 = π4.
Чему равен арктангенс?
arctan (x) cot (x) = 1 / tan (x), поэтому котангенс в основном является обратной величиной тангенса или, другими словами, мультипликативной обратной величиной.arctan (x) – угол, тангенс которого равен x.
Что такое Арктан бесконечности?
Арктангенс – это функция арктангенса. Предел арктангенса x, когда x приближается к бесконечности, равен пи / 2 радиан или 90 градусов: Предел арктангенса x, когда x приближается к минус бесконечности, равен -pi / 2 радиан или -90 градусов: Arctan ►
Чему равен тангенс, обратный 1?
Таблица касательных
| x | коричневый (x) | |
|---|---|---|
| градуса | радиан | |
| 0 ° | 0 | 0 |
| 30 ° | π / 6 | 0. / td> |
| 45 ° | π / 4 | 1 |
Какое значение tan инверсия 0?
В тригонометрии значение tan 0 равно 0.
Что такое обратный загар корня 3?
Точное значение arctan (√3) равно π3. Касательная функция положительна в первом и третьем квадрантах.
Является Tan 0 undefined?
Правильный ответ: Котангенс является обратной величиной тангенса, поэтому котангенс любого угла x, для которого tan x = 0, должен быть неопределенным, поскольку его знаменатель будет равен 0.Значение tan (0) равно 0, поэтому котангенс (0) не должен быть определен.
Почему tan 90 не определяется?
Почему Tan 90 не определен? Поскольку мы получили результат как бесконечность, и мы не можем определить бесконечность, значение tan 90 не определено.
Почему загар 90 не существует?
tan90∘ не определено, потому что вы не можете разделить 1 ни на что. Ничто, умноженное на 0, не даст ответ 1, поэтому ответ не определен.
Арктан когда-либо был неопределенным?
Арктангенс неопределенного выражения, естественно, не определен.Однако предел атана (C / x), где C – любая константа, имеет действительное значение. Если x приближается к 0 снизу, предел равен -pi / 2, а если приближается сверху, предел равен pi / 2.
Может ли Арктан быть отрицательным?
Арктангенс нуля равен нулю, tan-1 (0) равен 0. Арктангенс отрицательного числа представляет собой отрицательный угол первого квадранта, sin-1 (-) находится в квадранте -I, угол по часовой стрелке меньше – /2….Когда вы упрощаете выражение, обязательно используйте арксинус.
| Упростить. | Ответов. |
|---|---|
| 3. arcsin (sin (x)) | x, одна функция отменяет другую |
Является ли Arctan равным Arcsin Arccos?
Точно, поскольку arccos (x) = 0⟺x = 1, область определения g равна [−1,1). Функция arctan нечетная, а g – нет. Действительно, поскольку arcsin нечетно, f = g означало бы, что arccos (x) = arcsin (x) arctan (x) четно, что, как известно, неверно.
Чему равен Arcsin?
Функция arcsin является обратной функцией синуса.Он возвращает угол, синус которого является заданным числом. Значит: угол, грех которого равен 0,5, равен 30 градусам. Используйте arcsin, если вы знаете синус угла и хотите узнать фактический угол.
Почему arcsin (- 2 не определен?
Как вещественная функция arcsin2 не определена, поскольку sin (x) ∈ [−1,1] для всех x∈R.
Как рассчитать Арксин?
arcsin определяется как величина, обратная sin, но ограниченная определенным диапазоном. Следовательно, arcsin (sin (x)) = x, если x находится в этом диапазоне (обычно от 0 до 2π или от −π до π), или значение y такое, что sin (y) = sin (x) i.е. y = x + 2πn или y = π − x + 2πm для некоторого n∈Z или m∈Z и y находится в этом диапазоне.
Исключает ли Arcsin грех?
Нет, sin (arcsin (3x)) = 3x. Спасибо за ответ.
Что такое Arcsin на калькуляторе?
Функция арксинуса является обратной функцией y = sin (x).
arcsin (y) = sin-1 (y) = x + 2kπ
Что такое Асин на калькуляторе?
Описание. Функция арксинуса. ASIN (x) возвращает арксинус x. Функция арксинуса является обратной функцией функции синуса и вычисляет угол для заданного синуса.
Асин – это то же самое, что грех 1?
Пояснение. График ASIN визуализирует вывод функции от -1 до 1. ASIN является обратным SIN. Однако, поскольку SIN является периодической функцией, вывод ASIN ограничен диапазоном от -π / 2 до π / 2.
Arcsin – это то же самое, что CSC?
Арксин – это тригонометрическая функция, обратная синусу, а косеканс – величина, обратная синусу. Поскольку синус противоположен гипотенузе, косеканс может быть выражен как гипотенуза относительно противоположной точки или как 1 / синус.Косеканс – это отдельная тригонометрическая функция, а не обратная функция, как arcsin.
Что такое Асин в математике?
Математика. asin () возвращает арксинус числа. Примечание. Параметр, переданный в math.