Свойства пределов функции, основные свойства пределов
Содержание:
Предел функции
Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к L.
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).
Предел функции обозначается как
$$f(x) \rightarrow L \quad$ при $\quad x \rightarrow a$$или через символ предела функции:
$$\lim _{x \rightarrow 0} f(x)=L$$Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике, геометрии, химии, теории вероятности и многим другим предметам.
Свойства пределов функции
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
$$\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)$$Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:
$$\lim _{x \rightarrow a}\left[f_{1}(x)+\ldots+f_{n}(x)\right]=\lim _{x \rightarrow a} f_{1}(x)+\ldots+\lim _{x \rightarrow 0} f_{n}(x)$$Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
$$\lim _{x \rightarrow a} k f(x)=k \lim _{x \rightarrow a} f(x)$$4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
$$\lim _{x \rightarrow 0}[f(x) g(x)]=\lim _{x \rightarrow 0} f(x) \cdot \lim _{x \rightarrow 2} g(x)$$Расширенное свойство предела произведения
Предел произведения нескольких функций равен произведению пределов этих функций:
$$\lim _{x \rightarrow a}\left[f_{1}(x) f_{2}(x) \ldots f_{n}(x)\right]=\lim _{x \rightarrow a} f_{1}(x) \cdot \lim _{x \rightarrow 0} f_{2}(x) \cdot \ldots \cdot \lim _{x \rightarrow 2} f_{n}(x)$$Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
$$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow \infty} f(x)}{\lim _{x \rightarrow 0} g(x)}, \quad$ ecл $\lim _{x \rightarrow a} g(x) \neq 0$$Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Решение высшей математики онлайн
Заметим, что во всех определениях предыдущего пункта ключевым оказывалось определение набора тех множеств, в которые последовательно, при своём изменении в соответствии с рассматриваемым условием, попадает переменное ( или ), от которого зависит изменяющаяся величина ( или ).
В случае условия эти множества имеют вид ; в случае — вид ; в случае — вид . Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний — базой предела. Базу предела будем обозначать так же, как само условие, а именно, , , и т. п. Таким образом,
Нетрудно видеть, что в рассмотренных выше трёх примерах баз, действительно, все окончания — непустые множества и пересечение двух окончаний совпадает с одним из них (с меньшим) и, тем самым, можно взять равным этому меньшему окончанию.
Произвольную базу будем обозначать , а её окончания — буквой , быть может, снабжённой индексами. Если , причём , то окончание будем называть более далёким, чем окончание . Например, для базы окончание более далёкое, чем , если ; для базы окончание является тем более далёким, чем меньше число .
Теперь дадим определение предела по заданной базе .
Нетрудно заметить, что в случае баз , и это общее определение предела, при соответствующей подстановке вида окончаний этих баз, означает ровно то же самое, что приведённые выше, в предыдущем разделе, частные определения пределов.
Геометрический смысл данного определения предела таков: на плоскости , на которой нарисован график функции , проведём горизонтальную полосу ширины вокруг горизонтальной прямой .
Рис.2.8.График функции, имеющей предел, умещается в любую узкую полосу на достаточно далёком окончании
Пример 2.4 Постоянная величина, то есть функция, значения которой не зависят от аргумента , имеет предел, равный этой постоянной, при любой (допустимой для данного множества аргументов ) базе .(Неудивительно: ведь график постоянной — это горизонтальная прямая линия; тем самым, этот график целиком умещается в горизонтальную полосу любой, сколь угодно малой ширины.
)
Выгода от введения общего определения предела по базе заключается в том, что теперь, чтобы дать определение предела при некотором новом условии, нам достаточно лишь указать ту базу (набор окончаний), которая этому условию соответствует. Кроме того, весьма многие свойства пределов окажутся общими для пределов по любой базе, и устанавливать эти свойства можно будет исходя из общего определения; было бы слишком расточительно доказывать каждое из общих свойств для каждой новой базы отдельно.
Приведём несколько примеров широко используемых в математическом анализе баз.
Определение 2.5 Правосторонний предел функции. Рассмотрим базу , окончаниями которой служат интервалы, примыкающие справа к точке , то есть интервалы вида , где . Легко видеть, что все такие интервалы действительно образуют базу. Предел функции по этой базе называется пределом функции при , стремящемся к справа. База обозначается также или , а предел по этой базе обозначается так: .
Рис.2.9.Предел справа
Оказываясь во все более далёких окончаниях базы, то есть в интервалах с уменьшающимися значениями , точка приближается к точке , оставаясь справа от неё. Это объясняет название предела, вычисляемого по данной базе.
Упражнение 2.2 Запишите с помощью неравенств, содержащих и , данное выше определение в развёрнутом виде.Левосторонний и правосторонний пределы функции называются односторонними пределами этой функции при . Чтобы подчеркнуть отличие от односторонних пределов, предел называют двусторонним пределом.
Рис.2.11.Пределы справа и слева совпадают с двусторонним пределом
Доказательство. Пусть фиксировано некоторое число .
Так как , то существует такое окончание базы , при из которого выполняется неравенство . Так как , то существует такое окончание базы , при из которого также выполняется неравенство . Рассмотрим теперь меньшее из чисел и и обозначим его . Тогда при и при , то есть на объединении этих двух интервалов , выполняется неравенство . Однако такое объединение интервалов — это окончание базы . Тем самым при любом мы предъявили окончание базы двустороннего предела, такое что при всех из этого окончания верно неравенство . По определению это и означает, что .
Обратно, если существует , то при всех из некоторого двустороннего окончания базы и, следовательно, из каждой из двух половинок (окончания базы ) и (окончания базы ) выполнено неравенство .
Это и означает, что и .
Введённый этим определением двусторонний (при ) предел уже не имеет такого “наглядного смысла”, как, например, пределы при , . Действительно, как представить себе, что переменная “уходит бесконечно далеко” сразу и направо, в , и налево, в ? Тем не менее, понятие базы позволяет вычислять такой предел с не большими усилиями, чем пределы при условиях, имеющих “наглядное представление”.
Упражнение 2.3 Покажите, пользуясь последним определением, что предел функции, рассмотренной в примере 2.3, при равен 3. Найдите окончание базы , на котором при данном выполняется неравенство .В дальнейшем при изучении высшей математики нам понадобятся и гораздо более экзотические базы пределов, в которых представить себе, что именно и к чему стремится, совсем нелегко. Например, при введении определённых интегралов они будут получаться как пределы некоторых величин (интегральных сумм), зависящих от сложного параметра, называемого размеченным разбиением, при некоторой базе, называемой измельчением размеченного разбиения.
Тем не менее, и случай таких сложных пределов будет отлично укладываться в общую схему предела по базе, и нам не понадобится доказывать каких-то дополнительных теорем о свойствах таких пределов.
Для того, чтобы нагляднее представлять себе обсуждаемые общие результаты, читатель должен выбрать какую-либо конкретную базу (рекомендуем или какой-либо из односторонних пределов) и наглядно представлять себе, что означает общий результат применительно к выбранной конкретной базе.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Почему “критерий Коши” для предела функции дополнительно доказывается, хотя до этого доказывается “критерий Коши” для предела последовательности?
Предел функции обобщает предел последовательности.
Если предел последовательности есть число а для всех пронумерованных натуральными числами х, то предел функции – число L для всех f(x), которое существует при условии существования числа а для всех х. Эти числа являются точками накопления (точками сгущения) для почти всех (за исключением конечного) числа элементов последовательности (или функции). Т.е. почти все члены содержатся в некоторой произвольной ипсилон или дельта окрестностях.
Получается, что в рамках понятия предела функции акцент перемещается на область значений функции. Т.е. если х – прообраз, у – образ, то предел функции определяется для образов, а предел последовательности – для прообразов. Можно утверждать, что f(a) = L.
Иными словами, постулируется, что если существует предел, к которому стремится прообраз функции, то должен существовать предел, к которому стремится образ функции. Поэтому Коши вводится так называемый “испилон-дельта формализм”.
При этом определение предела функции можно представить и как предел последовательности образов, это уже будет определением по Гейне. По сути, определения по Коши и по Гейне эквивалентны (на самом деле не всегда. Если в рамках теории множеств отрицается аксиома выбора, то данные определения уже не являются эквивалентными).
Это надо истолковывать аккуратно: это не означает, что оба предела совпадают, или что они конечны. х может расходиться в бесконечность, в то время как у будет стремиться к 0 или конечному числу.
Вот как пример: x -> oo lim n-1/n = 1. у(x) стремится к 1, а х стремится к бесконечности. Но тем не менее, конечный предел существует и равен f(x).
Поэтому существует отдельно критерий Коши сходимости последовательности и отдельно критерий Коши существования предела функции. Надо ведь убедиться, что это свойство аргумента функции переходит и к зависимой переменной.
Как определить границы функций — видео и расшифровка урока
Разбивка функции
Если мы вернемся к нашей функции, f( x ) = ( x – 3)sin( x ) + 10, и мы хотим найти предел, поскольку x идет до 3.
7 этой функции, мы рассмотрим эти части по отдельности. Мы будем использовать правило произведения, чтобы отделить x – 3 от sin( x ), мы будем использовать правило сложения, чтобы посмотреть на это + 10, и мы будем использовать правило вычитания , что похоже на правило сложения, чтобы разделить x – 3 на x и 3.Теперь я почти уверен, что если я выведу на график x и 3, я могу показать, что если x переходит в 3,7, то x также переходит в 3,7. Поскольку x переходит в 3,7, 3 превращается в 3. Я также вполне уверен, что когда x превращается в 3,7, 10 останется на 10. Так что я могу подставить все эти числа, кроме этого греха ( x ). Так что же нам с этим делать?
Оказывается, есть еще одно полезное правило для нахождения пределов. Для всех многочленов и рациональных функций (и даже тригонометрических функций и квадратных корней), если функция определена на пределе, значение функции на этом пределе равно самому пределу.
Итак, что это значит? Это означает, что предел x подходит к некоторому числу (например, 3,7) некоторой функции, равному значению этой функции в этом числе, если функция является полиномиальной, рациональной функцией, тригонометрической функцией или квадратным корнем. где это определено. Если я вернусь и спрошу, каков предел, поскольку x соответствует 3,7 от sin( x ), я знаю, что sin( x ) определен везде, поэтому я могу просто найти sin(3,7), который около -0,5 (не забудьте использовать радианы).Итак, если я включу все эти вещи в свою исходную функцию, то я знаю, что предел x достигает 3,7 моей функции f( x ), которую можно разделить, используя все известные нам правила, и вычислить примерно 9,63. Почему это так?
Непрерывные функции
Почему иногда вы можете записать предел, поскольку x переходит в какое-то число, например C f( x ) равно f( C )? И что еще более важно, когда вы не можете использовать это правило? Ну, фишка в преемственности .
Все эти функции (определенные тригонометрические функции, квадратные корни, когда они определены, многочлены, рациональные функции) являются непрерывными функциями. Когда у вас есть непрерывная функция, предел этой функции, когда вы приближаетесь к некоторому числу, например C , равняется значению этой функции в C . Итак, это как раз то, что мы говорили ранее: предел x переходит в C от f( x ) равно f( C ). Тут не до прыжков. Если вы рисуете это, ваш палец всегда остается на бумаге.Так что имеет смысл, что когда вы приближаетесь к какому-то числу, вы достигнете этого числа; нет разрыва.
Если я посмотрю на такую функцию, как f( x ) = x 3 * (cos( x +3))2, я знаю, что это непрерывная функция. Я могу сделать это графически. Я также знаю, что везде эта функция определена.
Итак, я знаю, что если я хочу, чтобы предел f( x ), поскольку x , равнялся 9.1 этой функции, я могу просто подключить 9.1 для x (не забудьте переключить ваш калькулятор на радианы). Когда я это делаю, я подсчитываю, что предел f( x ) при переходе x к 9,1 составляет примерно 601,2.
Пределы в бесконечности
Давайте теперь посмотрим на непрерывные функции, когда x становится больше и больше или меньше и меньше. Это называется нахождением предела при приближении x к бесконечности или нахождением предела при приближении x к отрицательной бесконечности соответственно.Для многих непрерывных функций, таких как f( x ) = x 3 , когда x приближается к бесконечности, f( x ) может увеличиваться или уменьшаться. В этих случаях мы говорим, что предел либо равен + ∞ (положительная бесконечность), либо равен – ∞ (отрицательная бесконечность).
Для других функций, таких как f( x ) = 1/ x , когда x приближается к бесконечности (или отрицательной бесконечности), функция f( x ) приближается к 0.
Затем мы имеем горизонтальную асимптоту при г = 0.
Фактически, для любого натурального числа n предел f( x ) = 1 / ( x n ‘) при приближении x к бесконечности (или отрицательной бесконечности) равен 0. Оставим этот факт на потом.
Еще одним важным примером является функция f( x ) = arctan x . График арктангенса (он же арктангенс) имеет две горизонтальные асимптоты, а именно y = π/2 и y = – π/2.Это означает, что предел f( x ) = arctan x при приближении к x + ∞ не равен пределу при приближении к x – ∞.
В будущем мы будем использовать эти факты вместе с различными свойствами пределов для изучения более сложных функций.
Резюме урока
Напомним, простой способ найти пределы: Для непрерывных функций используйте подстановку для нахождения пределов. Под этим я подразумеваю, что если f( x ) является непрерывным, то предел x переходит в C для f( x ), равно f , оцениваемого как C .
Что такое предел в исчислении? Лимит – это просто…
Вспомнить
Обе части расчета основаны на пределах!
Предел функции — это значение, к которому $$f(x)$$ приближается по мере того, как $$x$$ приближается к некоторому числу.
Примеры
Пример 1
Давайте посмотрим на график $$f(x) = \frac 4 3 x -4$$ и исследуем точки, в которых $$x$$ “близок” к $$x = 6$$.Мы начнем с точек, где $$x$$ меньше 6.
Обратите внимание, что по мере того, как значения $$x$$ приближаются к 6, значения функции приближаются к $$y = 4$$. Теперь давайте посмотрим на точки функции, где $$x$$ больше 6.
Таблица нанесенных точек
$$
\начать{массив}{л|с}
х & f(x)\\\hline
\hline
7 и 5.
33333\\\hline
6,5 и 4,66667\\\hлиния
6,25 и 4,33333\\\hлиния
6.1 и 4.13333\\\hлиния
6.01 и 4.01333\\\hлиния
\конец{массив}
$$
Как и раньше, чем ближе мы подходили к $$x = 6$$, тем ближе подходила функция к $$y = 4$$.
Конечно, поскольку $$f(6) = 4$$, это может показаться неудивительным. Тем не менее, это идея предела, и ее можно резюмировать следующим образом:
Когда $$x$$ приближается к определенному числу, к чему приближается функция?
Предельное обозначение
У математиков есть специальные обозначения, указывающие на то, что они работают с предельными значениями.Например, ответ на Пример 1 будет записан так:
Пример 2
Предположим, что $$f(x) = \frac{\sin x}{x }$$.
Что такое $$\displaystyle \lim_{x\to0} f(x)=$$?
Заманчиво просто подставить $$x$$ = 0, чтобы попытаться получить ответ, но если мы попробуем
$$f(0) = \frac{\sin 0} {\color{red}{0}} \mbox{не определено! (Деление на ноль)}$$
Несмотря на то, что функция не определена, когда $$x$$ = 0, мы все равно можем ответить на вопрос. вопрос с использованием лимита.
Следующие две таблицы помогут нам понять, что происходит вблизи $$x$$ = 0.
При приближении $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline -1 & 0,84143\\\hлиния -0.5 и 0,9588\\\hлиния -0,1 и 0,99808\\\hлиния -0,01 и 0,99945\\\hлиния -0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
ИЛИ
По мере приближения $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline 1 & 0,84143\\\hлиния 0,5 и 0,9588\\\hлиния 0,1 и 0,99808\\\hлиния 0,01 и 0,99945\\\hлиния 0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
В обеих таблицах чем ближе x приближается к 0, тем ближе функция приближается к 1. Теперь давайте взглянем на график функции, просто для визуальной проверки.
Как и в таблицах, график показывает, что по мере приближения к $$x$$ = 0, Значение $$y$$ приближается к 1 !
Или, если использовать математические обозначения:
$$\displaystyle\lim_{x\to0}\frac{\sin x} x = 1$$.
Важно
$$\displaystyle \lim_{x\to0} \frac{\sin x} x = 1$$ НЕ говорит $$f(x) = 1$$, когда $$x=0$$ $$\displaystyle \lim_{x\to0} \frac{\sin x} x = 1$$ говорит, что $$f(x)$$ получает $$\textit{close}$$ до 1, если $$x$ $ приближается к 0 .Проблема с нашей точностью
Давайте еще раз взглянем на эти таблицы из второго примера.
По мере приближения $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline -1 & 0,84143\\\hлиния -0,5 и 0,9588\\\hлиния -0,1 и 0,99808\\\hлиния -0,01 и 0,99945\\\hлиния -0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
ИЛИ
При приближении $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline 1 & 0,84143\\\hлиния 0.5 и 0,9588\\\hлиния 0,1 и 0,99808\\\hлиния 0,01 и 0,99945\\\hлиния 0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
Во втором примере мы сказали, что $$f(x)$$ приближается к 1.Но разве они не приближаются к 0,9999999? Так что же верно?
$$ \displaystyle\lim_{x\to0} \frac{\sin x} x = 1? $$
ИЛИ
$$
\displaystyle\lim_{x\to0}\frac{\sin x} x = 0.
9999999?
$$
Это проблема с использованием таблиц значений (такая же проблема с графиками). Они недостаточно точны, чтобы получить точный ответ!
Существуют способы точного определения предельных значений, но эти методы рассматриваются в последующих уроках. На данный момент важно помнить, что при использовании таблиц или графиков лучшее, что мы можем сделать, — это оценить.
Следовательно, по таблицам и графики, ответы на два примера выше должны быть
Пример 1: $$\displaystyle \lim_{x\to6} \left(\frac 4 3 x – 4\right) \приблизительно 4$$и
Пример 2: $$\displaystyle \lim_{x\to0} \frac{\sin x} x \приблизительно 1$$ Ошибка: Нажмите «Не робот», затем повторите попытку загрузки.
Лимит | Encyclopedia.com
История
Предел последовательности
Предел функции
Приложения
Ресурсы
В математике понятие предела формально выражает понятие произвольной близости. То есть предел — это значение, к которому переменная величина приближается сколь угодно близко. Операции дифференцирования и интегрирования из исчисления основаны на теории пределов.
Теория пределов основана на особом свойстве действительных чисел; а именно, что между любыми двумя действительными числами, независимо от того, насколько они близки друг к другу, всегда есть другое. Между любыми двумя действительными числами всегда есть бесконечно много других.
Близость является ключом к пониманию пределов: только после определения близости предел обретает точное значение. Соответственно, окрестность точек вблизи любой заданной точки составляет окрестность. Окрестности – это определяющие компоненты бесконечных пределов последовательности.
Древнегреческий математик Архимед Сиракузский (287–212 гг. до н. э.) впервые разработал идею пределов измерения изогнутых фигур и объема сферы в третьем веке до нашей эры. Разделив эти фигуры на маленькие части, которые можно аппроксимировать, затем увеличив количество частей, предел суммы частей может дать желаемое количество. Тезис Архимеда Метод был утерян до 1906 года, когда математики обнаружили, что Архимед был близок к открытию исчисления бесконечно малых.
Поскольку работы Архимеда были неизвестны до двадцатого века, другие разработали современную математическую концепцию пределов. Английский физик и математик сэр Исаак Ньютон (1642–1727) и немецкий математик Готфрид Вильгельм Лейбниц (1646–1716) независимо разработали общие принципы исчисления (важной частью которого является теория пределов) в семнадцатом веке.
Древнегреческий философ (из южной Италии) Зенон Элейский (ок. 490–430 до н. э.), возможно, был одним из первых математиков, задумавшихся о пределе последовательности и задавшихся вопросом, как он связан с окружающим миром.
Зенон утверждал, что всякое движение невозможно, потому что для того, чтобы переместиться на расстояние (l), сначала необходимо пройти половину расстояния, затем половину оставшегося пути, затем половину этого оставшегося пути и так далее. Таким образом, утверждал он, расстояние (l) никогда нельзя пройти полностью.
Рассмотрим последовательность 1, 1/2, 1/4, 1/8,. . .(1/2) n , когда n становится очень большим. Поскольку (1/2) n равно 1/2, умноженной на себя n раз, (1/2) n становится очень маленьким, когда n позволяет стать бесконечно большим.Говорят, что последовательность сходится, что означает, что числа, которые находятся очень далеко в последовательности (соответствует большому «N»), очень близко друг к другу и очень близко к одному значению, называемому пределом.
Последовательность чисел сходится к заданному числу, если разность между членами последовательности и данным числом образует бесконечно малую последовательность. Для этой последовательности (1/2) n сколь угодно близко к 0, поэтому 0 является пределом последовательности.
Числа в последовательности никогда не достигают предела, но и не превышают его.
Если бесконечная последовательность расходится, промежуточная сумма членов в конечном итоге отклоняется от любого конкретного значения, поэтому у расходящейся последовательности нет предельной суммы.
Рассмотрим произвольную функцию y = f (x). (Функция — это множество упорядоченных пар, для которых первый и второй элементы каждой пары связаны друг с другом фиксированным образом. Когда элементами упорядоченных пар являются действительные числа, отношение обычно выражается в виде уравнение.) Предположим, что последовательные значения x выбраны так, чтобы соответствовать значениям сходящейся последовательности, такой как последовательность S из предыдущего примера.Возникает вопрос, что делают значения функции, то есть что происходит с последовательными значениями у. Фактически всякий раз, когда значения x образуют последовательность, значения f (x) также образуют последовательность.
Если эта последовательность является сходящейся последовательностью, то предел этой последовательности называется пределом функции. В более общем смысле, когда значение функции f (x) приближается к определенному значению L, поскольку независимая переменная x приближается к действительному числу p, тогда L называется пределом функции.Формально это записывается так:
lim f(x) = l
x → p
и читается как «Предел f от x, когда x приближается к p, равен L». Это не зависит от того, какая конкретная последовательность чисел выбрана для представления x; необходимо только, чтобы последовательность сходилась к пределу. Предел может зависеть от того, является ли последовательность возрастающей или убывающей. То есть предел, когда x приближается к p сверху, может отличаться от предела, когда x приближается к p снизу. В некоторых случаях тот или иной из этих пределов может даже не существовать.В любом случае, поскольку значение x приближается к конечному значению p, разность (p x) приближается к нулю.
Именно это определение предела обеспечивает основу для развития производной и интеграла в исчислении.
Существует второй тип функционального предела: предел, когда значение независимой переменной приближается к бесконечности. Хотя говорят, что последовательность, стремящаяся к бесконечности, расходится, существуют случаи, когда применение определяющего правила функции к расходящейся последовательности приводит к созданию сходящейся последовательности.Такой функцией является функция, определяемая уравнением y = 1/x. Если для функции существует конечный предел, когда
КЛЮЧЕВЫЕ ТЕРМИНЫ
Схождение —Схождение означает приближение к пределу, имеющему конечное значение.
Интервал — Интервал — это подмножество действительных чисел, соответствующее отрезку линии конечной длины и включающее все действительные числа между его конечными точками. Интервал является закрытым, если конечные точки включены, и открытым, если они не включены.
Вещественное число —Набор чисел, содержащий целые числа и все десятичные дроби, включая повторяющиеся и неповторяющиеся десятичные дроби.
Последовательность —Последовательность представляет собой ряд терминов, в котором каждый последующий термин связан с предыдущим фиксированной формулой.
независимая переменная стремится к бесконечности, формально это записывается как:
lim f (x) = L
x → ∞
и читается как «Предел f x, когда x приближается к бесконечности, равен L.Интересно отметить, что функция, определяемая y = 1/x, не имеет предела, когда x приближается к 0, но имеет предел L = 0, когда x приближается к ∞.
Понятие предела необходимо для понимания системы действительных чисел и ее отличительных характеристик. В определенном смысле действительные числа можно определить как числа, являющиеся пределами сходящихся последовательностей рациональных чисел. Одно из применений концепции пределов относится к производной. Производная представляет собой скорость потока или изменения и может быть вычислена на основе некоторых концепций ограничений.Пределы также являются ключом к вычислению интегралов (выражений площадей).
Интеграл вычисляет всю площадь области путем суммирования бесконечного числа ее маленьких кусочков. Пределы также являются частью итеративного процесса. Итерация многократно выполняет подпрограмму, используя выходные данные одного шага в качестве входных данных для следующего шага. Каждый вывод представляет собой итерацию. Некоторые успешные итерации могут максимально приблизиться к теоретически точному значению.
КНИГИ
Эббот, Персиваль. Научите себя: исчисление. Лондон, Великобритания: Hodder and Stoughton Education, и Чикаго, Иллинойс: Contemporary Books, 2003.
Бертон, Дэвид М. История математики: введение. Нью-Йорк: McGraw-Hill, 2007.
Ларсон, Рон. Исчисление: прикладной подход. Бостон, Массачусетс: Houghton Mifflin, 2003.
Ларсон, Рон. Исчисление с аналитической геометрией. Бостон: Houghton Mifflin College, 2002.
Люблинскава, Ирина Е. Связь математики с наукой: эксперименты для предварительного исчисления.
Emeryville, CA: Key Curriculum Press, 2003.
Сетек, Уильям М. Основы математики. Upper Saddle River, NJ: Pearson Prentice Hall, 2005.
J. R. Maddocks
Limits — High School Math
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Ограничения
— IB Math Stuff
Знакомство с ограничениями
Пределы являются основой для большей части расчетов.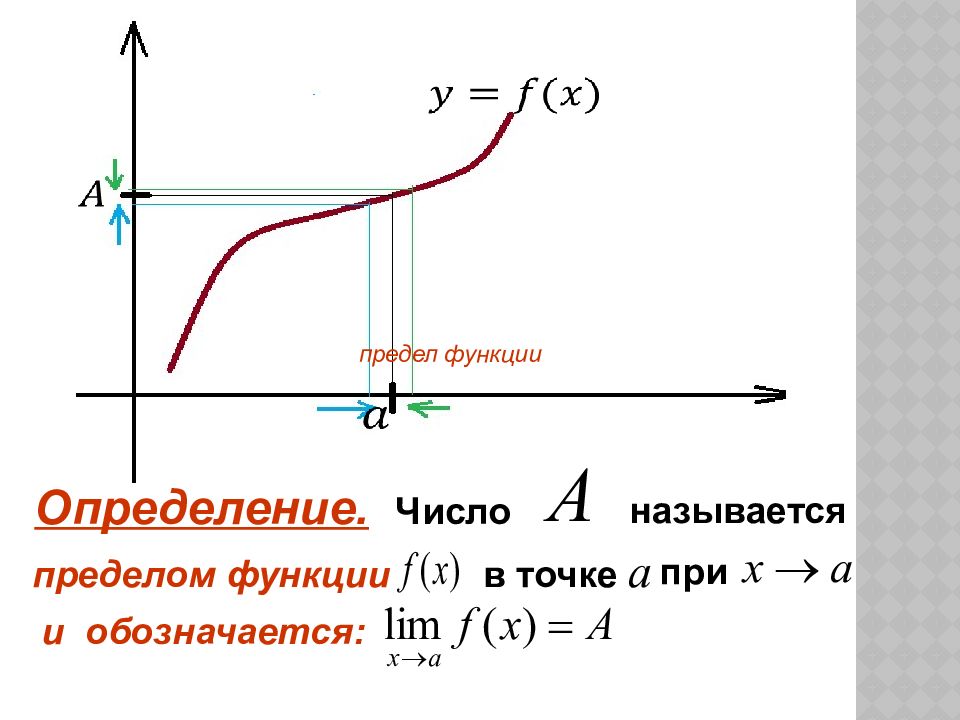
Они также очень абстрактны. Развитие исчисления застопорилось отчасти из-за неспособности математиков иметь дело с пределами.Пределы тесно связаны с идеей бесконечности (как бесконечно большой, так и малой).
Пределы, неформально, — это концепция исследования того, что происходит с функцией по мере того, как ее аргумент все ближе и ближе приближается к определенному значению. Большинство функций, которые вы видели, ведут себя хорошо (и поэтому довольно скучны), но некоторые ведут себя по-другому… Но прежде чем мы перейдем к функциям, давайте посмотрим на последовательности чисел. Ниже приведена последовательность чисел, которая приближается к значению по мере увеличения «числа термина»:
.| Номер термина | $n=1$ | $n=2$ | $n=3$ | $n=4$ | $n=5$ |
| Стоимость срока | 0.3 | 0,33 | 0,333 | 0,3333 | 0,33333 |
По мере продвижения последовательности значение члена становится больше, но значение каждого последующего члена приближается к значению.
Подумайте об этом… Число становится все больше и больше, но существует ограничение в – 90 453 на то, насколько большим может быть это число (если следовать шаблону). Независимо от того, сколько терминов вы выберете, значение термина становится все ближе и ближе к $\frac{1}{3}$!
Ограничения функции очень похожи.{-х}$. Давайте начнем со старого доброго «подключи и пыхни», сначала взглянем на большие положительные значения x и посмотрим, что произойдет с функцией:
| Значение x | 2 | 5 | 10 | 15 |
| Значение функции | 0,25 | 0,03125 | 0,000977 | 0,0000305 |
Так что же происходит с функцией, когда x становится все больше и больше? Ясно, что функция стремится к нулю.Это можно легко (и быстрее) увидеть, просто построив график функции на калькуляторе. На самом деле многие (но не все) вопросы об ограничениях можно решить, просто построив график функции и наблюдая, что происходит.
Также можно использовать метод plug-and-chug, который в разы точнее…
Предельное обозначение
Опять же, в пределах мы задаем вопрос, что происходит с функцией, поскольку переменная что-то делает. Обозначение пределов выглядит примерно так:
.Полное обозначение является пределом, а не только часть “ lim “.2 = ? \конец{выравнивание}
Это можно сделать графически или численно, но в этом случае численно может быть проще (ограничения по мере приближения аргумента к положительной или отрицательной бесконечности часто проще всего выполнить графически).
| Значение x | 1 | 1,5 | 1,9 | 1,99 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Значение функции | 1 | 2,82 | 3,732 | 3.2}{х} = ? \конец{выравнивание} Этот пример не простой, так как предыдущая функция не определена для $x=0$. Решение этого графически может не пролить весь свет, который необходимо пролить. Немного алгебры, и проблема стала гораздо более осязаемой. Совершенно ясно видно, что по мере того, как x становится все ближе и ближе к 0, функция будет все ближе и ближе приближаться к 5. Эту проблему можно было бы решить численно с помощью небольшого количества проб и ошибок с самого начала, но алгебра немного элегантнее и, откровенно говоря, проще и быстрее. Правила ограничений Я предоставляю их для справки. \begin{align} \lim_{x \rightarrow 0} \: c = c \end{align} (6)\begin{align} \lim_{x \rightarrow a} \: c \: f(x)= c \: \lim_{x \rightarrow a} f(x) \end{align} (7)\begin{align} \lim_{x \rightarrow a} [f(x) \pm g(x)] = \lim_{x \rightarrow a} f(x) \pm \lim_{x \rightarrow a} g (х) \end{align} (8)\begin{align} \lim_{x \rightarrow a} [f(x) \times g(x)] = \lim_{x \rightarrow a} f(x) \times \lim_{x \rightarrow a} g (х) \end{align} (9)\begin{align} \lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \frac{ \lim_{x \rightarrow a} f(x)} { \lim_{x \rightarrow a} g(x)} \end{align} Хотите добавить или прокомментировать эти заметки? Сделайте это ниже.лимитов: бесконечные лимитыЧтобы обсудить бесконечные пределы, давайте исследуем функцию f(x)=5x−1. Глядя на график этой функции, показанный здесь, вы можете видеть, что при x→1− значение f(x) неограниченно уменьшается, а при x→1+ значение f(x) неограниченно увеличивается. Таблица значений покажет такое же поведение.
Предел, в котором f(x) неограниченно увеличивается или уменьшается по мере приближения значения x к произвольному числу c, называется бесконечным пределом . Это не означает, что предел существует или что ∞ является числом. На самом деле предела не существует. Значения ±∞ просто говорят о том, что предел не существует, потому что значения, когда x приближается к c, неограниченно увеличиваются/уменьшаются. Бесконечные пределы обозначаются: limx→af(x)=∞ и читается как «предел f (x), когда x приближается к a, равен бесконечности». ОПРЕДЕЛЕНИЕ БЕСКОНЕЧНОГО ПРЕДЕЛА Пусть f(x) — функция, которая может быть определена по обе стороны от точки a и может быть определена или не определена в точке a: limx→af(x)= +∞ или limx→af(x)=−∞ означает, что когда x приближается к a, но не равно a, значение f(x) неограниченно увеличивается/уменьшается. Линия, на которой предел функции неограниченно возрастает или убывает, называется вертикальной асимптотой . ОПРЕДЕЛЕНИЕ ВЕРТИКАЛЬНОЙ АСИМПТОТЫ Линия x = a является вертикальной асимптотой f(x), если верно одно из следующих утверждений: limx→af(x)=∞ limx→a−f(x )=∞ limx→a+f(x)=∞ limx→af(x)=−∞ limx→a−f(x)=−∞ limx→a+f(x)=−∞ Давайте найдем бесконечные пределы в паре примеров. Пример 1: Найти limx→4+xx−4 и limx→4−xx−4, построить график и определить вертикальную асимптоту.
Пример 2: Найдите limx→−5x−1x+5, если он существует. Если его нет объясните почему.
Образы предела функции, сформированные в ходе математических занятий в университетеБруссо, Г.: 1997, Теория дидактических ситуаций в математике , Kluwer Academic Publishers, Дордрехт. Google Scholar Корню, Б.: 1983, Apprentissage de la notion de limite: концепции и препятствия , докторская диссертация, Научно-медицинский университет, Гренобль. Google Scholar Дэвис, Р. Б. и Виннер С.: 1986, «Понятие предела; некоторые, казалось бы, неизбежные этапы заблуждения», The Journal of Mathematical Behavior 5, 281–303. Google Scholar Дубинский Е.: 1991, «Рефлексивная абстракция в продвинутом математическом мышлении», в Д. Талле (ред.), Advanced Mathematical Thinking , Kluwer Academic Publishers, Дордрехт, стр. 95–126. Google Scholar Дубинский, Э.: 1992, «Подход теории обучения к исчислению», в З.А. Кариан (редактор), Символьные вычисления в математической теории бакалавриата , MAA Notes 24, Вашингтон, стр. 43-55. Эрвинк, Г.: 1981, «Концептуальные трудности для студентов первого курса университета в приобретении понятия предела функции», Труды Пятой конференции Международной группы по психологии математического образования , Беркли, стр. 330-333. Феррини-Манди, Дж. и Грэм, К.: 1994, «Исследования в области обучения исчислению: понимание пределов, производных и интегралов», в Дж. Капут и Э. Дубинский (ред.), Вопросы исследований в Обучение математике бакалавриата , MAA Notes 33, Вашингтон, стр. Фишбейн, Э., Тирош, Д. и Гесс, П.: 1979, «Интуиция бесконечности», Образовательные исследования по математике 10, 3–40. Фишбейн, Э.: 1987, Интуиция в науке и математике. Образовательный подход , издательство D. Reidel Publishing Company, Дордрехт. Google Scholar Голдин, Г.А.: 1990, «Эпистемология, конструктивизм и изучение открытий в математике», Журнал исследований в области математического образования, Монография № 4 – Конструктивистские взгляды на преподавание и изучение математики , стр.31-47. Харел, Г. и Тргалова, Дж.: 1996, «Высшее математическое образование», в журнале А.Дж. Бишоп, К. Клементс, К. Кейтель, Дж. Килпатрик и К. Лаборд (ред.), International Handbook of Mathematics Education , Kluwer Academic Publishers, Дордрехт, стр. 675–700. Google Scholar Юнг, К. Google Scholar Митрофф И.И. и Килманн, Р.Х.: 1975, «Об оценке научных исследований: вклад психологии науки», Технологическое прогнозирование и социальные изменения 8, с. 163–174. Артикул Google Scholar Ноддингс, Н.: 1990, «Конструктивизм в математическом образовании», Журнал исследований в области математического образования, Монография № 4 -Конструктивистские взгляды на преподавание и изучение математики , стр.7-18. Nosal, C.S.: 1992, Diagnoza typow umyslu , PWN, Варшава. Google Scholar Piaget, J.: 1977, Развитие мысли: уравновешивание когнитивных структур , The Viking Press, Нью-Йорк. Google Scholar Prochnicka, M.: 1991, Informacja a umysl , Universitas, Krakow. Google Scholar Прцениосло, М.: 2000, Rozumienie granicy funkcji wyniesione ze zkoly sredniej , Takt, Kielce. Google Scholar przenioslo, м.: 2001, “Трудносский zwiazane z procesem procesem proznawania pojec pojec analizy mateMatycznej ‘, annales societatis mathematicae polonae , серии v -dydaktyka matematyki 23, с. 95-124. Google Scholar Прцениосло, М.: 2002, Образец гранитных функций uksztaltowany w czasie studiow matematycznych , Wydawnictwo Akademii Swietokrzyskiej, Kielce. Google Scholar Роберт, А. и Боше, Ф.: 1981, «Приобретение концепции конвергенции числовых наборов в превосходном строении», Бюллетень APMEP 330, стр. Google Scholar Роберт А.: 1982, «Приобретение понятия конвергенции числовых наборов в высшем знании», Recherches en Didactique des Mathématiques 3, 307–341. Google Scholar Шварценбергер Р.Л. и Талл Д.: 1978, «Конфликт при изучении действительных чисел и пределов», Преподавание математики 82, 44–49. Google Scholar Серпинская А.: 1985, «Относительные эпистемологические препятствия к понятию предела», Recherches en Didactique des Mathématiques 6, 5–68. Google Scholar Серпинска, А.: 1987, «Студенты-гуманитарии и эпистемологические препятствия, связанные с пределами», Образовательные исследования в области математики 18, 371–397. Артикул Google Scholar Серпинская А. Google Scholar Серпинска, А.: 1994, Понимание математики , The Falmer Press, Лондон. Google Scholar Серпинская, А.: 1998, «Три эпистемологии, три взгляда на общение в классе: конструктивизм, социокультурные подходы, интеракционизм», в книге Х.Стейнбринг, М.Г. Бартолини Бусси и А. Серпинска (редакторы), Язык и общение в классе математики , Национальный совет учителей математики, Рестон, стр. 30–62. Google Scholar Стеффе, Л. П. и Гейл, Дж. (редакторы): 1995, Конструктивизм в образовании , Издательство Ассоциации Лоуренса Эрлбаума, Хиллсдейл, Нью-Джерси. Google Scholar Высокий, Д.и Виннер, С.: 1981, «Образ понятия и определение понятия в математике с особым упором на предел и непрерывность», Образовательные исследования по математике 12, 151–169. Артикул Google Scholar Талл, Д.: 1991, «Психология продвинутого математического мышления», в Д. Талле (ред.), Advanced Mathematical Thinking , Kluwer Academic Publishers, Дордрехт, стр. 3–23. Google Scholar Высокий, Д.: 1996, «Функция и исчисление», в А.Дж. Бишоп, К. Клементс, К. Кейтель, Дж. Килпатрик и К. Лаборд (ред.), International Handbook of Mathematics Education , Kluwer Academic Publishers, Дордрехт, стр. 289–325. Google Scholar Виннер, С.: 1991, «Роль определений в преподавании и изучении математики», в Д. Талле (ред.), Advanced Mathematical Thinking , Kluwer Academic Publishers, Дордрехт, стр.65–81. Google Scholar Выготский Л.С.: 1962, Мысль и язык , Массачусетский технологический институт им. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если бы вы могли увеличить масштаб или ваш калькулятор умен, вы бы увидели, что на графике есть пробел в точке $x=0$. Итак, еще раз, , мы исследуем то, что происходит с функцией, когда она приближается к 0, а не то, что происходит при 0! В этом случае нам потребуется немного алгебры. Оба слагаемых в числителе имеют общий член x , так что давайте разложим его (это наиболее полезно, так как в данном случае только один член является фактором x ).2}{x} = \lim_{x \rightarrow 0} \frac{x(5+x)}{x} = \lim_{x \rightarrow 0} \: (5+x) = 5 \end{align}
Если найду время, могу привести несколько доказательств на примере…
00001
001
1
1
0001
9
999
1
0001
31-45.
Г.: 1971, Психологические типы , Издательство Принстонского университета, Принстон. Словарь современного английского языка Longman: 1987, Longman Group UK, Лондон.
649–674.
: 1990, «Некоторые замечания о понимании математики», Для изучения математики 10, 24–36.
