Предел функции: основные понятия и определения
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
В математике принципиально важным является понятие бесконечности, обозначаемое символом ∞. Его следует понимать как бесконечно большое +∞ или бесконечно малое -∞ число. Когда мы говорим о бесконечности, часто мы имеем в виду сразу оба этих ее смысла, однако запись вида +∞ или -∞ не стоит заменять просто на ∞.
Запись предела функции имеет вид limx→x0f(x). В нижней части мы пишем основной аргумент x, а с помощью стрелочки указываем, к какому именно значению x0 он будет стремиться. Если значение x0 является конкретным действительным числом, то мы имеем дело с пределом функции в точке. Если же значение x0 стремится к бесконечности (не важно, ∞, +∞ или -∞), то следует говорить о пределе функции на бесконечности.
Предел бывает конечным и бесконечным. Если он равен конкретному действительному числу, т.е. limx→x0f(x)=A, то его называют конечным пределом, если же limx→x0f(x)=∞, limx→x0f(x)=+∞ или limx→x0f(x)=-∞, то бесконечным.
Если он равен конкретному действительному числу, т.е. limx→x0f(x)=A, то его называют конечным пределом, если же limx→x0f(x)=∞, limx→x0f(x)=+∞ или limx→x0f(x)=-∞, то бесконечным.
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
Определение 1Число A является пределом функции f(x) при x→∞, если последовательность ее значений будет сходиться к A для любой бесконечно большой последовательности аргументов (отрицательной или положительной).
Запись предела функции выглядит так: limx→∞f(x)=A.
Определение 2При x→∞ предел функции f(x) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Запись выглядит как limx→∞f(x)=∞.
Пример 1Докажите равенство limx→∞1×2=0 с помощью основного определения предела для x→∞.
Решение
Начнем с записи последовательности значений функции 1×2 для бесконечно большой положительной последовательности значений аргумента x=1, 2, 3,…, n,….
11>14>19>116>…>1n2>…
Мы видим, что значения будут постепенно уменьшаться, стремясь к 0. См. на картинке:
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
x=-1, -2, -3,…, -n,…
11>14>19>116>…>1-n2>…
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
Ответ: Верность данного в условии равенства подтверждена.
Пример 2Вычислите предел limx→∞e110x.
Решение
Начнем, как и раньше, с записи последовательностей значений f(x)=e110x для бесконечно большой положительной последовательности аргументов. Например, x=1, 4, 9, 16, 25,…, 102,…→+∞.
Например, x=1, 4, 9, 16, 25,…, 102,…→+∞.
e110; e410; e910; e1610; e2510;…; e10010;…==1,10; 1,49; 2,45; 4,95; 12,18;…;22026,46;…
Мы видим, что данная последовательность бесконечно положительна, значит, f(x)=limx→+∞e110x=+∞
Переходим к записи значений бесконечно большой отрицательной последовательности, например, x=-1, -4, -9, -16,-25,…, -102,…→-∞.
e-110; e-410; e-910; e-1610; e-2510;…;e-10010;…==0,90; 0,67; 0,40; 0,20; 0,08;…;0,000045;…x=1, 4, 9, 16, 25,…,102 ,…→∞
Поскольку она тоже стремится к нулю, то f(x)=limx→∞1e10x=0.
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
Ответ: limx→∞e110x=+∞, при x→+∞0, при x→-∞.
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Число B является пределом функции f(x) слева при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются меньше a (xn<a).
Такой предел на письме обозначается как limx→a-0f(x)=B.
Теперь сформулируем, что такое предел функции справа.
Определение 4Число B является пределом функции f(x) справа при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются больше a (xn>a).
Этот предел мы записываем как limx→a+0f(x)=B.
Мы можем найти предел функции f(x) в некоторой точке тогда, когда для нее существуют равные пределы с левой и правой стороны, т.е. limx→af(x)=limx→a-0f(x)=limx→a+0f(x)=B. В случае бесконечности обоих пределов предел функции в исходной точке также будет бесконечен.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
Докажите, что существует конечный предел функции f(x)=16(x-8)2-8 в точке x0=2 и вычислите его значение.
Решение
Для того чтобы решить задачу, нам потребуется вспомнить определение предела функции в точке. Для начала докажем, что у исходной функции имеется предел слева. Запишем последовательность значений фукнции, которая будет сходиться к x0=2, если xn<2:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8,667; 2,667; 0,167; -0,958; -1,489; -1,747; -1,874;…; -1,998;…→-2
Поскольку приведенная последовательность сводится к -2, мы можем записать, что limx→2-016x-82-8=-2.
Далее докажем наличие предела справа: запишем аргументы в последовательности, которая будет сходиться к x0=2, если xn>2:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Значения функции в этой последовательности будут выглядеть так:
f(6); f(4); f(3); f212; f234; f278; f21516;…; f210231024;…==-7,333; -5,333; -3,833; -2,958; -2,489; -2,247;-2,124;.
Данная последовательность также сходится к -2, значит, limx→2+016(x-8)2-8=-2.
Мы получили, что пределы с правой и левой стороны у данной функции будут равными, значит, предел функции f(x)=16(x-8)2-8 в точке x0=2 существует, и limx→216(x-8)2-8=-2.
Вы можете увидеть ход решения на иллюстрации (зеленые точки– последовательность значений, сходящаяся к xn<2, синие – к xn>2).
Ответ:
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Предыдущая статья
Метод трапеций
Следующая статья
Интегрирование тригонометрических функций
- Второй замечательный предел
- Основные неопределенности пределов и их раскрытие
- Первый замечательный предел
- Предел показательно степенной функции, примеры нахождения
- Все темы по математике
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
Приложение для планирование графикаДолжно всплывать уведомление то есть к примеру я внес в эту программу данные что завтра должна быть какаято важная встреча к примеру в и автоматически должно всплывать уведомление
Вид работы:
Отчёт по практике
Выполнена:
4 июня 2022 г.

Стоимость:
4 800 руб
Заказать такую же работу
Способы материального представления и записи визуальной информации
Вид работы:
Реферат
Выполнена:
13 апреля 2022 г.

Стоимость:
800 руб
Заказать такую же работу
Контрольная работа
Вид работы:
Контрольная работа
Выполнена:
13 апреля 2022 г.

Стоимость:
3 900 руб
Заказать такую же работу
разработка дизайнпроекта ресторана в датском стиле с элементами экостиля
Вид работы:
Курсовая работа
Выполнена:
20 марта 2022 г.

Стоимость:
2 200 руб
Заказать такую же работу
Статистическая обработка результатов многократных измерений
Вид работы:
Контрольная работа
Выполнена:
28 января 2022 г.

Стоимость:
3 800 руб
Заказать такую же работу
Построение модели парной линейной регрессии
Вид работы:
Контрольная работа
Выполнена:
14 декабря 2021 г.

Стоимость:
1 700 руб
Заказать такую же работу
Смотреть все работы по c#
Урок по теме “Предел функции”
- Сморода Александр Александрович, учитель математики
Разделы: Математика
Цели урока:
- Образовательные:
- ввести понятие предела числа, предела функции;
- дать понятия о видах неопределенности;
- научиться вычислять пределы функции;
- систематизировать полученные знания,
активизировать самоконтроль, взаимоконтроль.

- Развивающие:
- уметь применять полученные знания для вычисления пределов.
- развивать математическое мышление.
- Воспитательная: воспитать интерес к математике и к дисциплинам умственного труда.
Тип урока: первый урок
Формы работы учащихся: фронтальная, индивидуальная
Необходимое оборудование: интерактивная доска, мультимедиа проектор, карточки с устными и подготовительными упражнениями.
План урока
1. Организационный момент (3 мин.)
2. Ознакомление с теорией предела функции.
Подготовительные упражнения. (12 мин.)
3. Вычисление пределов функции (10 мин.)
4. Самостоятельные упражнения (15 мин.)
5. Подведение итогов урока (2 мин.)
6. Домашнее задание (3 мин.)
ХОД УРОКА
1. Организационный момент
Организационный момент
Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.
2. Ознакомление с теорией предела функции. Подготовительные упражнения.
Предел функции (предельное
значение функции) в заданной точке, предельной для
области определения функции, — такая величина, к
которой стремится рассматриваемая функция при
стремлении её аргумента к данной точке.
Записывается предел следующим образом .
Вычислим предел:
Подставляем вместо х – 3.
Заметим, что предел числа равен самому числу.
Примеры: вычислите пределы
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).
Вычислим значение функции в точке x0 = 3 и
значение его предела в этой точке.
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.
Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
Основные виды неопределенностей:
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
- упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
- если предел при раскрытии неопределенностей
существует, то говорят, что функция сходится к
указанному значению, если такого предела не
существует, то говорят, что функция расходится.

Пример: вычислим предел.
Разложим числитель на множители
3. Вычисление пределов функции
Пример 1. Вычислите предел функции:
При прямой подстановке, получается неопределенность:
Разложим на множители числитель и знаменатель и вычислим предел.
Пример 2. Вычислите предел функции:
При прямой подстановке, получается неопределенность.
Помножим и числитель, и знаменатель на .
Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел Аналогично
Пример 3. Вычислите предел функции:
При прямой подстановке, получается неопределенность.
Помножим и числитель, и знаменатель на .
Мы учли, что
4. Самостоятельные упражнения
Вычислите пределы:
5. Подведение итогов урока
Подведение итогов урока
Данный урок первый по теме: «Предел функции». На уроке рассмотрены способы нахождения пределов. Разобрано что такое неопределенность, как раскрывать неопределенности. Надо заметить, что есть пределы, для которых невозможно найти числовое значение.
6. Домашнее задание
Домашнее задание раздается на карточках каждому ученику.
Предел. Непрерывность функции (Лекция №1)
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ
В результате измерения
физических величин (время, площадь, объем, масса, скорость и т.д.) определяются
их числовые значения. Математика занимается величинами, отвлекаясь от их
конкретного содержания. В дальнейшем, говоря о величинах, мы будем иметь в виду
их числовые значения. В различных явлениях некоторые величины изменяются, а
другие сохраняют свое числовое значение. Например, при равномерном движении
точки время и расстояние меняются, а скорость остается постоянной.
В различных явлениях некоторые величины изменяются, а
другие сохраняют свое числовое значение. Например, при равномерном движении
точки время и расстояние меняются, а скорость остается постоянной.
Переменной величиной называется величина, которая принимает различные числовые значения. Величина, числовые значения которой не меняются, называется постоянной. Переменные величины будем обозначать буквами x, y, z,…, постоянные – a, b, c,…
Заметим, что в математике постоянная величина часто рассматривается как частный случай переменной, у которой все числовые значения одинаковы.
Областью изменения переменной величины называется совокупность всех принимаемых ею числовых значений. Область изменения может состоять как из одного или нескольких промежутков, так и из одной точки.
УПОРЯДОЧЕННАЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Будем говорить,
что переменная x есть упорядоченная переменная величина, если известна область ее
изменения, и про каждые из двух любых ее значений можно сказать, какое из них
предыдущее и какое последующее.
Частным случаем упорядоченной переменной величины является переменная величина, значения которой образуют числовую последовательность x1,x2,…,xn,… Для таких величин при i < j, i, j Î N, значение xi считается предшествующим, а xj – последующим независимо от того, какое из этих значений больше. Таким образом, числовая последовательность – это переменная величина, последовательные значения которой могут быть перенумерованы. Числовую последовательность будем обозначать . Отдельные числа последовательности называются ее элементами.
Например, числовую последовательность образуют следующие величины:
- ,
- ,
- , где а, d – постоянные числа.
ФУНКЦИЯ
При изучении
различных явлений природы и решении технических задач, а, следовательно, и в
математике приходится рассматривать изменение одной величины в зависимости от
изменения другой. Так, например, известно, что площадь круга выражается через
радиус формулой S = πr2. Если радиус r принимает различные
числовые значения, то площадь S также
принимает различные числовые значения, т.е. изменение одной переменной влечет
изменение другой.
Так, например, известно, что площадь круга выражается через
радиус формулой S = πr2. Если радиус r принимает различные
числовые значения, то площадь S также
принимает различные числовые значения, т.е. изменение одной переменной влечет
изменение другой.
Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y называется функцией переменной х. Символически будем записывать y=f(x). При этом переменная x называется независимой переменной или аргументом.
Запись y=C, где C – постоянная, обозначает функцию, значение которой при любом значении x одно и то же и равно C.
Множество
значений x, для которых можно
определить значения функции y по
правилу f(x), называется
областью определения функции.
Заметим, что числовая последовательность также является функцией, область определения которой совпадает с множеством натуральных чисел.
К основным элементарным функциям относятся все функции, изучаемые в школьном курсе математики:
Элементарной функцией называется функция, которая может быть задана основными элементарными функциями и постоянными при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
ПОНЯТИЕ ПРЕДЕЛА ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
В дальнейшем курсе математики понятие предела будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа – производная, интеграл и др.
Начнем с понятия предела числовой последовательности.
Число a называется пределом последовательности x = {xn},
если для произвольного заранее заданного сколь угодно малого положительного
числа ε найдется такое натуральное число N, что при всех n>N
выполняется неравенство |xn – a| < ε.
Если число a есть предел последовательности x = {xn}, то говорят, что xn стремится к a, и пишут .
Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.
Окрестностью точки x0 называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x0, для которой x0 является серединой, тогда x0 называется центром окрестности, а величина (b–a)/2 – радиусом окрестности.
Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде
Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).
Следовательно, постоянное число a есть предел числовой
последовательности {xn}, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности
точки a) найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности.
Примеры.
- Пусть переменная величина x последовательно принимает значения
Докажем, что предел этой числовой последовательности равен 1. Возьмем произвольное положительное число ε. Нам нужно найти такое натуральное число N, что при всех n>N выполняется неравенство |xn – 1| < ε. Действительно, т.к.
,
то для выполнения соотношения |xn – a| < ε достаточно, чтобы или . Поэтому, взяв в качестве N любое натуральное число, удовлетворяющее неравенству , получим что нужно. Так если взять, например, , то, положив N=6, для всех n>6 будем иметь .
- Используя определение предела числовой последовательности, доказать что .
Возьмем произвольное ε > 0. Рассмотрим
.
Тогда , если или , т.е. . Поэтому выберем любое натуральное число, удовлетворяющее неравенству .
Сделаем несколько замечаний.
Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение xn = c, то предел этой последовательности будет равен самой постоянной. Действительно, при любом ε всегда выполняется неравенство |xn – c| = |c – c| = 0 < ε.
Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что xn → a и одновременно xn → b. Возьмем любое и отметим окрестности точек a и b радиуса ε (см. рис.). Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а, так и в окрестности точки b, что невозможно.
Замечание 3. Не следует думать, что
каждая числовая последовательность имеет предел. Пусть, например, переменная
величина принимает значения . Несложно заметить, что эта последовательность не стремится
ни к какому пределу.
Несложно заметить, что эта последовательность не стремится
ни к какому пределу.
ПРЕДЕЛ ФУНКЦИИ
Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b.Тогда говорят, что число b есть предел функции f(x) при x → a.
Введем строгое определение предела функции.
Функция y=f(x) стремится к пределу b при x → a, если для
каждого положительного числа ε, как бы мало оно
не было, можно указать такое положительное число δ,
что при всех x ≠ a
из области определения функции, удовлетворяющих неравенству |x – a| < δ, имеет место неравенство |f(x) – b| < ε. Если b есть предел функции f(x) при x → a, то пишут или f(x) → b при x → a.
Если b есть предел функции f(x) при x → a, то пишут или f(x) → b при x → a.
Проиллюстрируем это определение на графике функции. Т.к. из неравенства |x – a| < δ должно следовать неравенство |f(x) – b| < ε, т.е. при x Î (a – δ, a + δ) соответствующие значения функции f(x) Î (b – ε, b + ε), то, взяв произвольное ε > 0, мы можем подобрать такое число δ, что для всех точек x, лежащих в δ – окрестности точки a, соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε.
Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно и если при x → a функция имеет предел, то он единственный.
Примеры.
- Найти предел функции y=2x+1 при x → 1.
 Используя
график функции, можно увидеть, что если x → 1 с любой
стороны, то соответствующие точки M(x, y) графика стремятся
к точке M(1, 3), т.е. можно предположить, что . Докажем это. Зададим произвольное число ε
> 0. Нам нужно, чтобы выполнялось неравенство |(2x+1) – 3|<ε или |2x–2| < ε,
откуда |x– 1| < ε.
Таким образом, если положить δ = ε/2, то при всех x, удовлетворяющих
неравенству |x– 1|<δ, будет выполняться неравенство |y – 3| < ε. По определению предела это
и означает, что 3 есть предел функции y=2x+1 при x → 1.
Используя
график функции, можно увидеть, что если x → 1 с любой
стороны, то соответствующие точки M(x, y) графика стремятся
к точке M(1, 3), т.е. можно предположить, что . Докажем это. Зададим произвольное число ε
> 0. Нам нужно, чтобы выполнялось неравенство |(2x+1) – 3|<ε или |2x–2| < ε,
откуда |x– 1| < ε.
Таким образом, если положить δ = ε/2, то при всех x, удовлетворяющих
неравенству |x– 1|<δ, будет выполняться неравенство |y – 3| < ε. По определению предела это
и означает, что 3 есть предел функции y=2x+1 при x → 1.
- Найти предел функции y=ex+1
при x → 0.
Используя график заданной функции, несложно заметить, .
ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ
До сих пор мы рассматривали пределы для случая, когда переменная величина
x стремилась к определенному постоянному числу.
Будем говорить, что переменная x стремится к бесконечности, если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х=х0, начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M.
Например, пусть переменная х принимает значения x1= –1, x2=2, x3= –3, …, xn=(–1)nn, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M.
Переменная величина x → +∞, если при произвольном M > 0 все последующие значения переменной, начиная с некоторого, удовлетворяют неравенству x > M.
Аналогично, x → – ∞, если при любом M > 0 x < -M.
Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x|>M, выполняется неравенство |f(x) – b| < ε.
Обозначают .
Примеры.
- Используя определение, доказать, что .
Нужно доказать, что при произвольном ε будет выполняться неравенство , как только |x|>M, причем число М должно определяться выбором ε. Записанное неравенство эквивалентно следующему , которое будет выполняться, если |x|>1/ε=M. Это и значит, что (см. рис.).
- Несложно заметить, что .
- не существует.
БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
Ранее мы рассмотрели случаи, когда функция f(x)
стремилась к некоторому конечному пределу b при x → a
или x → ∞.
Рассмотрим теперь случай, когда функция y=f(x) стремится к бесконечности при некотором способе изменения аргумента.
Функция f(x) стремится к бесконечности при x → a, т.е. является бесконечно большой величиной, если для любого числа М, как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х≠a, удовлетворяющих условию |x-a| < δ, имеет место неравенство |f(x)| > M.
Если f(x) стремится к бесконечности при x→a, то пишут или f(x)→∞ при x→a.
Сформулируйте аналогичное определение для случая, когда x→∞.
Если f(x) стремится к бесконечности при x→a и при этом принимает только положительные или только отрицательные значения, соответственно пишут или .
Примеры.
- .
- (см. рис.).
- .
- Функция при x→0 не стремится ни к какому пределу (см.
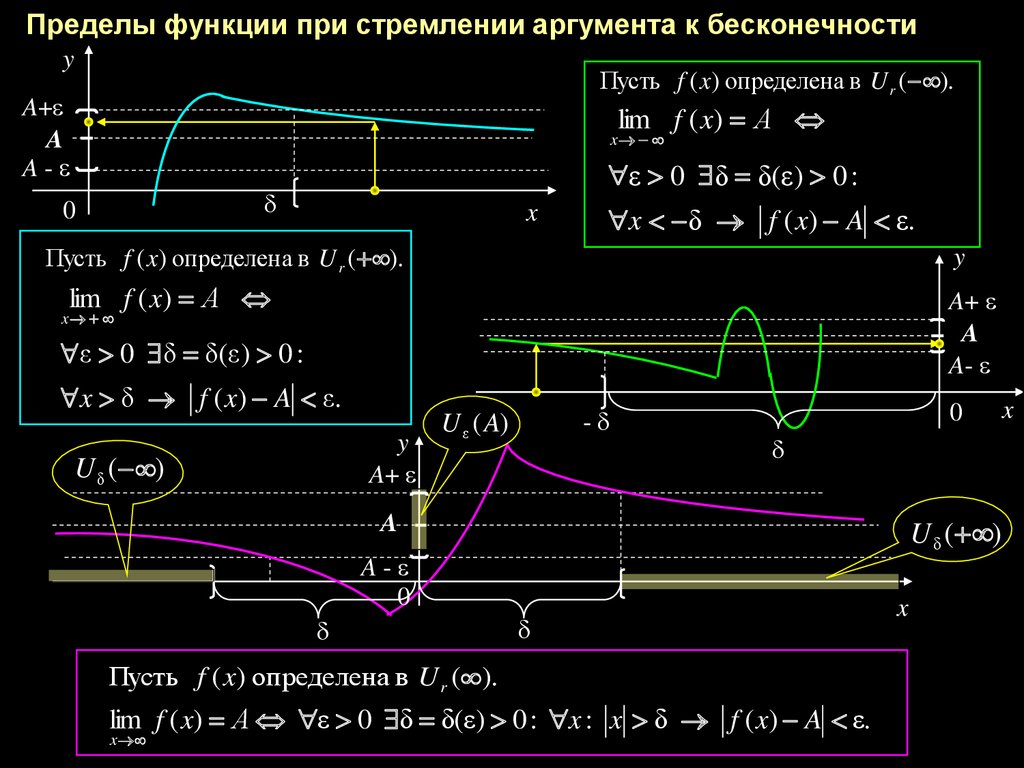 рис.).
рис.).
ОГРАНИЧЕННЫЕ ФУНКЦИИ
Пусть задана функция y=f(x), определенная на некотором множестве D значений аргумента.
Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D.
Примеры.
- Функция y=sin x, определенная при -∞<x<+∞, является ограниченной, так как при всех значениях x |sin x|≤1 = M.
- Функция y=x2+2 ограничена, например, на отрезке [0, 3], так как при всех x из этого отрезка |f(x)| ≤f(3) = 11.
- Рассмотрим функцию y=ln x при x Î (0; 1).
 Эта функция
неограниченна на указанном отрезке, так как при x→0 ln x→-∞.
Эта функция
неограниченна на указанном отрезке, так как при x→0 ln x→-∞.
Функция y=f(x) называется ограниченной при x → a, если существует окрестность с центром в точке а, в которой функция ограничена.
Функция y=f(x) называется ограниченной при x→∞, если найдется такое число N>0, что при всех значениях х, удовлетворяющих неравенству |x|>N, функция f(x) ограничена.
Установим связь между ограниченной функцией и функцией, имеющей предел.
Теорема 1. Если и b – конечное число, то функция f(x) ограничена при x→a.
Доказательство. Т.к. , то при любом ε>0 найдется
такое число δ>0, что при вех значениях х,
удовлетворяющих неравенству |x-a|<δ, выполняется неравенство |f(x) –b|<ε. Воспользовавшись свойством модуля |f(x) – b|≥|f(x)| – |b|, последнее неравенство
запишем в виде |f(x)|<|b|+ ε. Таким образом, если
положить M=|b|+ ε, то при x→a |f(x)|<M.
Таким образом, если
положить M=|b|+ ε, то при x→a |f(x)|<M.
Замечание. Из определения ограниченной функции следует, что если , то она является неограниченной. Однако обратное неверно: неограниченная функция может не быть бесконечно большой. Приведите пример.
Теорема 2. Если , то функция y=1/f(x) ограничена при x→a.
Доказательство. Из условия теоремы следует, что при произвольном ε>0 в некоторой окрестности точки a имеем |f(x) – b|<ε. Т.к. |f(x) – b|=|b – f(x)| ≥|b| – |f(x)|, то |b| – |f(x)|< ε. Следовательно, |f(x)|>|b| – ε >0. Поэтому и
Решение высшей математики онлайн
‹– Назад
Заметим, что во всех определениях предыдущего пункта ключевым оказывалось определение набора тех множеств, в которые последовательно, при своём изменении в соответствии с рассматриваемым условием, попадает переменное ( или ), от которого зависит изменяющаяся величина ( или ). В случае условия эти множества имеют вид ; в случае — вид ; в случае — вид . Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний — базой предела. Базу предела будем обозначать так же, как само условие, а именно, , , и т. п. Таким образом,
В случае условия эти множества имеют вид ; в случае — вид ; в случае — вид . Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний — базой предела. Базу предела будем обозначать так же, как само условие, а именно, , , и т. п. Таким образом,
Итак, база предела — это набор окончаний, которые должны удовлетворять таким свойствам: все они непусты и если и — два разных окончания (одной и той же базы), то база должна содержать третье окончание , которое содержится в каждом из первых двух: .
Нетрудно видеть, что в рассмотренных выше трёх примерах баз, действительно, все окончания — непустые множества и пересечение двух окончаний совпадает с одним из них (с меньшим) и, тем самым, можно взять равным этому меньшему окончанию. Получили, что рассмотренные наборы множеств действительно являются базами.
Получили, что рассмотренные наборы множеств действительно являются базами.
Произвольную базу будем обозначать , а её окончания — буквой , быть может, снабжённой индексами. Если , причём , то окончание будем называть более далёким, чем окончание . Например, для базы окончание более далёкое, чем , если ; для базы окончание является тем более далёким, чем меньше число .
Теперь дадим определение предела по заданной базе .
Определение 2.4 Пусть — некоторая база и функция определена во всех точках некоторого окончания базы (и, значит, определена во всех точках более далёких окончаний ). Число называется пределом функции по базе (или при базе ) и обозначается
если
для любого (сколь угодно малого) числа найдётся такое окончание базы , что при всех выполняется неравенство
Тот факт, что , записывают ещё в виде
Нетрудно заметить, что в случае баз , и это общее определение предела, при соответствующей подстановке вида окончаний этих баз, означает ровно то же самое, что приведённые выше, в предыдущем разделе, частные определения пределов.
Геометрический смысл данного определения предела таков: на плоскости , на которой нарисован график функции , проведём горизонтальную полосу ширины вокруг горизонтальной прямой . Тот факт, что , означает, что найдётся достаточно далёкое окончание базы , на котором график функции целиком лежит в этой полосе. При уменьшении ширины полосы окончание, возможно, придётся брать более далёким, но, всё равно, и в любую более узкую полосу умещается график на достаточно далёком окончании.
Рис.2.8.График функции, имеющей предел, умещается в любую узкую полосу на достаточно далёком окончании
Пример 2.4 Постоянная величина, то есть функция, значения которой не зависят от аргумента , имеет предел, равный этой постоянной, при любой (допустимой для данного множества аргументов ) базе .
Действительно, пусть при всех из некоторого окончания базы . Тогда при любом, сколь угодно малом и любом
Тогда при любом, сколь угодно малом и любом
Это и означает, что .
(Неудивительно: ведь график постоянной — это горизонтальная прямая линия; тем самым, этот график целиком умещается в горизонтальную полосу любой, сколь угодно малой ширины.)
Выгода от введения общего определения предела по базе заключается в том, что теперь, чтобы дать определение предела при некотором новом условии, нам достаточно лишь указать ту базу (набор окончаний), которая этому условию соответствует. Кроме того, весьма многие свойства пределов окажутся общими для пределов по любой базе, и устанавливать эти свойства можно будет исходя из общего определения; было бы слишком расточительно доказывать каждое из общих свойств для каждой новой базы отдельно.
Приведём несколько примеров широко используемых в математическом анализе баз.
Определение 2.5 Правосторонний предел функции. Рассмотрим базу , окончаниями которой служат интервалы, примыкающие справа к точке , то есть интервалы вида , где . Легко видеть, что все такие интервалы действительно образуют базу. Предел функции по этой базе называется пределом функции при , стремящемся к справа. База обозначается также или , а предел по этой базе обозначается так: .
Рассмотрим базу , окончаниями которой служат интервалы, примыкающие справа к точке , то есть интервалы вида , где . Легко видеть, что все такие интервалы действительно образуют базу. Предел функции по этой базе называется пределом функции при , стремящемся к справа. База обозначается также или , а предел по этой базе обозначается так: .
Рис.2.9.Предел справа
Оказываясь во все более далёких окончаниях базы, то есть в интервалах с уменьшающимися значениями , точка приближается к точке , оставаясь справа от неё. Это объясняет название предела, вычисляемого по данной базе.
Упражнение 2.2 Запишите с помощью неравенств, содержащих и , данное выше определение в развёрнутом виде.
Аналогично определяется предел функции при , стремящемся к слева. Для этого достаточно указать, какие множества являются окончаниями базы этого предела.
Для этого достаточно указать, какие множества являются окончаниями базы этого предела.
Определение 2.6 Левосторонний предел. База состоит из интервалов , , примыкающих к точке слева.
Рис.2.10.Предел слева
База обозначается также . Предел по этой базе называется пределом функции при , стремящемся к слева и обозначается так: .
Левосторонний и правосторонний пределы функции называются односторонними пределами этой функции при . Чтобы подчеркнуть отличие от односторонних пределов, предел называют двусторонним пределом.
Теорема 2.1 Если функция имеет оба односторонних предела при и эти пределы равны одному и тому же числу , то существует двусторонний предел , который также равен ; ноаборот, если существует двусторонний предел , то существуют оба односторонних предела и оба они равны числу .
Рис.2.11.Пределы справа и слева совпадают с двусторонним пределом
Доказательство. Пусть фиксировано некоторое число . Так как , то существует такое окончание базы , при из которого выполняется неравенство . Так как , то существует такое окончание базы , при из которого также выполняется неравенство . Рассмотрим теперь меньшее из чисел и и обозначим его . Тогда при и при , то есть на объединении этих двух интервалов , выполняется неравенство . Однако такое объединение интервалов — это окончание базы . Тем самым при любом мы предъявили окончание базы двустороннего предела, такое что при всех из этого окончания верно неравенство . По определению это и означает, что .
По определению это и означает, что .
Обратно, если существует , то при всех из некоторого двустороннего окончания базы и, следовательно, из каждой из двух половинок (окончания базы ) и (окончания базы ) выполнено неравенство . Это и означает, что и .
Определение 2.7 Через (или ) обозначим базу, окончаниями которой служат объединения двух лучей , где . При увеличении получаем всё более далёкие окончания, уходящие в бесконечность в обе стороны. Предел по такой базе обозначается или .
Введённый этим определением двусторонний (при ) предел уже не имеет такого “наглядного смысла”, как, например, пределы при , . Действительно, как представить себе, что переменная “уходит бесконечно далеко” сразу и направо, в , и налево, в ? Тем не менее, понятие базы позволяет вычислять такой предел с не большими усилиями, чем пределы при условиях, имеющих “наглядное представление”.
Действительно, как представить себе, что переменная “уходит бесконечно далеко” сразу и направо, в , и налево, в ? Тем не менее, понятие базы позволяет вычислять такой предел с не большими усилиями, чем пределы при условиях, имеющих “наглядное представление”.
Упражнение 2.3 Покажите, пользуясь последним определением, что предел функции, рассмотренной в примере 2.3, при равен 3. Найдите окончание базы , на котором при данном выполняется неравенство .
Упражнение 2.4 Сформулируйте и докажите теорему о связи односторонних (при и ) и двустороннего (при ) пределов, аналогичную теореме 2.1.
В дальнейшем при изучении высшей математики нам понадобятся и гораздо более экзотические базы пределов, в которых представить себе, что именно и к чему стремится, совсем нелегко. Например, при введении определённых интегралов они будут получаться как пределы некоторых величин (интегральных сумм), зависящих от сложного параметра, называемого размеченным разбиением, при некоторой базе, называемой измельчением размеченного разбиения. Тем не менее, и случай таких сложных пределов будет отлично укладываться в общую схему предела по базе, и нам не понадобится доказывать каких-то дополнительных теорем о свойствах таких пределов.
Например, при введении определённых интегралов они будут получаться как пределы некоторых величин (интегральных сумм), зависящих от сложного параметра, называемого размеченным разбиением, при некоторой базе, называемой измельчением размеченного разбиения. Тем не менее, и случай таких сложных пределов будет отлично укладываться в общую схему предела по базе, и нам не понадобится доказывать каких-то дополнительных теорем о свойствах таких пределов.
Для того, чтобы нагляднее представлять себе обсуждаемые общие результаты, читатель должен выбрать какую-либо конкретную базу (рекомендуем или какой-либо из односторонних пределов) и наглядно представлять себе, что означает общий результат применительно к выбранной конкретной базе.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Статьи по математике на Gee Test
02. 12.2016 | автор: Денис Борисов
12.2016 | автор: Денис Борисов
*и немного немецкого автопрома
Скажу сразу, что в этой статье нет ни грамотного определения предела функции, ни достаточного количества разнообразных примеров, ни правил и основных приёмов определения предела. Всё это можно и нужно читать в учебниках и задачниках. Цель этой статьи – помочь понять смысл, суть, скрывающуюся за цифрами, правилами и терминами.
Предел функции f(x) в какой-либо точке х0 – это значение, к которому она стремится при стремлении x к значению х0
В это грубое, неверное с точки зрения математики, определение криво,но вписывается сама суть предела функции. Если разобраться с ним, то потом можно и разбираться во всех тонкостях, которые вполне подробно описаны в учебниках.
Важно разобраться буквально с каждым словом в определении, в этом есть ключ к осознанию определения. Стремление – вот один из основных терминов в определении. Стремление – это максимально возможное приближение. То есть стремление х к какому-либо конкретному значению (обозначаемому как х0, если кто не понял) – это максимальное приближение х к данному значению. В простом случае, если функция имеет значение в точке х0 , то максимально возможное приближение, и есть х0 .
То есть стремление х к какому-либо конкретному значению (обозначаемому как х0, если кто не понял) – это максимальное приближение х к данному значению. В простом случае, если функция имеет значение в точке х0 , то максимально возможное приближение, и есть х0 .
А если при х0 функция не существует? Придётся говорить несколько иначе. А иначе говоря, стремление – это минимальное отличие. Что такое минимальное отличие? Минимальное отличие, это отличие на минимальную величину, на минимальное число. Какое число будет являться минимальным? 0 сразу отбросим, так как отличия на 0 не бывает, если два числа отличаются на 0, то они совпадают, этот случай мы уже описали. Тогда какое это число? 0.1, 0.0001, 0.000000000000000000000000000000001? Но мы всегда можем добавить пару-тройку нолей после запятой и тем самым уменьшить число на несколько порядков, и уменьшать мы можем бесконечно, ну или пока не умрём. Вот тут мы подошли к важному моменту. Товарищи математики в этом случае придумали такую штуку как «Бесконечно Малая Величина» (далее БМВ (= ). БМВ – это величина, которая по модулю меньше любого наперёд заданного числа. Это значит, что для числа 10000 мы можем считать бесконечно малой 0.1, но как только мы озвучили «0.1» БМВ стала 0.0000001 и снова мы озвучили значение БМВ и она стала ещё меньше, например 0.000000000000001, и мы снова это сделали, мы озвучили её значение и она стала… не буду повторять, вы поняли. Она всегда меньше любого озвученного числа, в этом и есть вся магия. Возвращаясь к нашей функции и х0 , в котором она не имеет значения, отметим, что при всех других, хоть сколько-нибудь отличающихся от х0 значениях, она существует, даже если это отличие на БМВ. То есть, если функция при х0 не существует, то стремление х к х0 есть отличие значения х от х0 на БМВ. Подводя черту скажем, что стремление х к х0 – это либо само х0 (если f(x) существует в х0), либо значение, отличающееся от х0 на БМВ (х0±БМВ) (если f(x) не существует в х0 ).
БМВ – это величина, которая по модулю меньше любого наперёд заданного числа. Это значит, что для числа 10000 мы можем считать бесконечно малой 0.1, но как только мы озвучили «0.1» БМВ стала 0.0000001 и снова мы озвучили значение БМВ и она стала ещё меньше, например 0.000000000000001, и мы снова это сделали, мы озвучили её значение и она стала… не буду повторять, вы поняли. Она всегда меньше любого озвученного числа, в этом и есть вся магия. Возвращаясь к нашей функции и х0 , в котором она не имеет значения, отметим, что при всех других, хоть сколько-нибудь отличающихся от х0 значениях, она существует, даже если это отличие на БМВ. То есть, если функция при х0 не существует, то стремление х к х0 есть отличие значения х от х0 на БМВ. Подводя черту скажем, что стремление х к х0 – это либо само х0 (если f(x) существует в х0), либо значение, отличающееся от х0 на БМВ (х0±БМВ) (если f(x) не существует в х0 ).
Разберём теперь это на конкретных примерах.
Допустим, есть у нас функция f(x)=3x-1, данная функция определена на всём промежутке по оси х (выражение 3х-1 можно вычислить для любого значения х), следовательно, никаких проблемных мест нет и мы всегда можем вычислить предел данной функции, просто подставив вместо х интересующее нас значение. Если нас интересует предел функции при стремлении х к конечному значению, то всё просто (см. выше):
Если нас интересует предел функции при стремлении х к конечному значению, то всё просто (см. выше):
Если нас интересует стремление х в бесконечность, то нам всегда поможет простое рассуждение: [Логично, что если умножить любое конечное число на бесконечно большую величину, оно станет бесконечно большим; а если отнять от бесконечно большого числа конечное число, то оно останется бесконечно большим:]
Допустим, функция f(x) выглядит, как представленно ниже:Данная функция определена не на всём промежутке по оси х (при х=2 знаменатель дроби обращается в 0, а деление на ноль обращает всё сущее в прах и никто на ноль поэтому не делит), поэтому наиболее интересен предел функции при стремлении х к 2.
[Отметим, что 0 здесь это не «ноль» а БМВ, так как на самом деле мы вместо х подставляем не «два», а число, отличающееся от двух на БМВ; кроме того, логично, что если поделить конечное число на бесконечно малое, то оно возрастёт в бесконечное число раз и станет бесконечно большим (попробуйте поделить 2 на 0,0000000000000001)]
Если быть более строгим (что правильно), то стремление х к конкретному значению может быть как с большей, так и с меньшей стороны, в описанном выше примере это приводит к двум случаям (обозначим «2+БМВ» как «2+» (стремление с большей стороны), а «2-БМВ» как «2-»(стремление с меньшей стороны)): 2-2+=-0; 2-2-= 0 – (снова, 0 здесь, это БМВ), следовательно и конечный результат для каждого случая будет иметь значения + бесконечность и – бесконечность. Этот случай иллюстрирует пример предела справа и предела слева, используемые для таких ситуёвин:
Этот случай иллюстрирует пример предела справа и предела слева, используемые для таких ситуёвин:
Кроме того, отличаются пределы и при стремлении х к любой из бесконечностей. Всё это легко проследить на графике:
На этом статья себя уже исчерпала, всё остальное (включая правильное определение предела функции) ищите в учебниках по высшей математике.
Презентация по математике по теме “Понятие предела функции в точке”
Урюпинский филиал ГБОУ СПО «Волгоградский медицинский колледж»
Понятие предела функции в точке
Преподаватель математики Багрова Г.Г.
Основные вопросы:
- Определение предела функции в точке, бесконечно малой и бесконечно большой функции в точке. Связь между б/малыми и б/большими функциями в точке.
- Основные теоремы о пределах функций (суммы, произведения и частного).

12/20/16
Предел функции
Предел – одно из основных понятий математического анализа. Понятие предела использовалось еще Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.
Различают – предел функции в точке и предел функции на бесконечности .
Рассмотрим функции, графики которых изображены на следующих рисунках:
Во всех трех случаях изображена одна и та же кривая, но все же изображают они три разные функции, отличающиеся друг от друга своим поведением в точке
.
Рассмотрим каждый из этих графиков подробнее:
Для функции
,
график которой изображен на
этом рисунке, значение
не существует, функция
в указанной точке не
определена.
Для функции
график которой изображен на
этом рисунке, значение
,
существует, но оно
отличное от, казалось бы,
естественного значения
точка
как бы
выколота.
Для функции
,
график которой изображен на
этом рисунке, значение
существует и оно вполне
естественное.
Для всех трех случаев используется одна и та же запись:
при
которую читают: «предел функции
стремлении
к равен ».
Содержательный смысл этой фразы следующий: если значения аргумента выбирать все ближе и ближе к значению
, то значения функции все меньше и меньше
отличаются от предельного значения
Или можно сказать так: в достаточно малой окрестности точки
справедливо приближенное равенство:
исключается из рассмотрения.
При этом сама точка
Прежде чем перейти к разбору решений
примеров заметим, что если предел функции
при стремлении
к
равен значению
функции в точке
, то в таком случае
функцию называют непрерывной .
График такой функции представляет собой
сплошную линию, без «проколов» и «скачков» .
Функцию
называют непрерывной
на промежутке
, если она непрерывна в
каждой точке этого промежутка.
Примерами непрерывных функций на всей числовой
прямой являются:
а
Функция
непрерывна на луче
непрерывна на промежутках
функция
Предел функции в точке
Число В называется пределом функции в точке а , если для всех значений х , достаточно близких к а и отличных от а , значение функции f (x) сколь угодно мало отличается
от В .
Теорема.
Если функция f ( x ) имеет предел в точке х 0 , то этот предел единственный .
Бесконечно малая функция и бесконечно большая функция.
- Функция α ( x ) называется бесконечно малой при x → a (здесь a – конечное число или ∞), если
- Функция f(x) называется бесконечно большой функцией (или бесконечно большой величиной) при х→а, если
Графическая иллюстрация
- х →0
Таким образом, величина, обратная бесконечно малой, есть бесконечно большая, и наоборот.
Теорема 1.
Предел суммы (разности) 2-х функций равен сумме (разности) их пределов, если последние существуют:
Теорема 2.
Предел константы равен самой этой константе.
Теорема 3.
Предел произведения 2-х функций равен произведению их пределов, если последние существуют:
Теорема 4.
Предел отношения 2-х функций равен отношению их пределов, если последние существуют и предел знаменателя отличен от 0 :
Теорема 5.
Постоянный множитель можно выносить за знак предела
Теорема 6.
Предел степени переменного равен той же степени предела основания:
Вычисление пределов
Вычисление предела :
начинают с подстановки предельного значения x 0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
Если при подстановки предельного значения x 0 в функцию f(x) получаются выражения вида:
то предел будет равен:
Вычислить пределы:
Примеры
Вычисление пределов
Часто при подстановке предельного значения x 0 в функцию f(x) получаются выражения следующих видов:
Эти выражения называются неопределенности , а вычисление пределов в этом случае называется раскрытие неопределенности .
Методы вычисления пределов на неопределенность
Раскрыть соответствующую неопределенность – это значит найти предел (если он существует) соответствующего выражения, что, однако не всегда просто.
Правило № 1
- В большинстве случаев, чтобы раскрыть неопределенность вида , достаточно
числитель и знаменатель дроби разделить на множители, и затем сократить на множитель, приводящий к неопределенности.
Пример №1:
Разложим числитель и знаменатель на множители:
Пример № 2:
Правило № 2
- Чтобы раскрыть неопределенность данного вида, зависящую от иррациональности, достаточно перевести иррациональность (или иррациональности) из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности.
Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель дроби
Если f(x) – иррациональная дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.
Упражнения:
Домашнее задание:
2.2: Предел функции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 43626
- OpenStax
- OpenStax
Цели обучения
- Используя правильные обозначения, опишите предел функции.
- Используйте таблицу значений, чтобы оценить предел функции или определить, когда предел не существует.
- Используйте график, чтобы оценить предел функции или определить, когда предел не существует.
- Дайте определение односторонним ограничениям и приведите примеры.

- Объясните взаимосвязь между односторонними и двусторонними пределами.
Концепция предела или ограничивающего процесса, необходимая для понимания исчисления, существует уже тысячи лет. На самом деле ранние математики использовали ограничивающий процесс для получения все более и более точных приближений площадей кругов. Однако формальное определение предела — в том виде, в каком мы его знаем и понимаем сегодня — появилось только в конце XIX в.2}\),
, которые показаны на рисунке \(\PageIndex{1}\). В частности, давайте сосредоточим наше внимание на поведении каждого графа при \(x=2\) и около него.
Рисунок \(\PageIndex{1}\): На этих графиках показано поведение трех различных функций вокруг \(x=2\). Каждая из трех функций не определена в точке \(x=2\), но если мы делаем это утверждение и никакое другое, мы даем очень неполную картину того, как каждая функция ведет себя вблизи точки \(x=2\). Чтобы более полно выразить поведение каждого графа в окрестности \(2\), нам нужно ввести понятие предела. 92−4)/(x−2)\) ведет себя примерно так, как \(x=2\) на рисунке \(\PageIndex{1}\). Поскольку значения \(x\) приближаются к \(2\) по обе стороны от \(2\), значения \(y=f(x)\) приближаются к \(4\). Математически мы говорим, что предел \(f(x)\) при приближении \(x\) к \(2\) равен \(4\). Символически мы выражаем этот предел как
92−4)/(x−2)\) ведет себя примерно так, как \(x=2\) на рисунке \(\PageIndex{1}\). Поскольку значения \(x\) приближаются к \(2\) по обе стороны от \(2\), значения \(y=f(x)\) приближаются к \(4\). Математически мы говорим, что предел \(f(x)\) при приближении \(x\) к \(2\) равен \(4\). Символически мы выражаем этот предел как
\(\displaystyle \lim_{x \to 2} f(x)=4\).
Из этого очень краткого неформального взгляда на один предел давайте начнем разрабатывать интуитивное определение предела . Мы можем думать о пределе функции при числе \(a\) как об одном действительном числе \(L\), к которому функциональные значения приближаются по мере того, как \(x\)-значения приближаются к \(a\), при условии, что такое вещественное число \(L\) существует. Сформулировав более тщательно, мы имеем следующее определение:
Определение (интуитивное): Предел
Пусть \(f(x)\) – функция, определенная для всех значений в открытом интервале, содержащем \(a\), за возможным исключением самого \(a\), и пусть \(L\) — действительное число. Если все значения функции \(f(x)\) приближаются к действительному числу \(L\), а значения \(x(≠a)\) приближаются к числу \(a\), то мы говорим, что предел \(f(x)\) при приближении \(x\) к \(a\) равен \(L\). (Более кратко, поскольку \(x\) приближается к \(a\), \(f(x)\) приближается и остается близким к \(L\).) Символически мы выражаем эту идею как
Если все значения функции \(f(x)\) приближаются к действительному числу \(L\), а значения \(x(≠a)\) приближаются к числу \(a\), то мы говорим, что предел \(f(x)\) при приближении \(x\) к \(a\) равен \(L\). (Более кратко, поскольку \(x\) приближается к \(a\), \(f(x)\) приближается и остается близким к \(L\).) Символически мы выражаем эту идею как
\[\lim_{x \to a} f(x)=L. \label{limit} \]
Мы можем оценить пределы, составив таблицы функциональных значений и просмотрев их графики. Этот процесс описан в следующей стратегии решения проблем.
Стратегия решения проблем: оценка предела с использованием таблицы функциональных значений
1. Чтобы оценить \(\displaystyle \lim_{x \to a} f(x)\), мы начнем с заполнения таблицы функциональных значений . Мы должны выбрать два набора \(x\)-значений: один набор значений приближается к \(a\) и меньше \(a\), а другой набор значений приближается к \(a\) и больше \(a\) \). В таблице \(\PageIndex{1}\) показано, как могут выглядеть ваши таблицы.
| \(х\) | \(f(x)\) | \(х\) | \(f(x)\) |
|---|---|---|---|
| \(а-0,1\) | \(ф(а-0,1)\) | \(а+0,1\) | \(f(а+0,1)\) |
| \(а-0,01\) | \(f(a-0,01)\) | \(а+0,01\) | \(f(а+0,01)\) |
| \(а-0,001\) | \(ф(а-0,001)\) | \(а+0,001\) | \(f(а+0,001)\) |
| \(а-0,0001\) | \(ф(а-0,0001)\) | \(а+0,0001\) | \(ф(а+0,0001)\) |
При необходимости используйте дополнительные значения. | При необходимости используйте дополнительные значения. | ||
2. Далее давайте посмотрим на значения в каждом из столбцов \(f(x)\) и определим, приближаются ли значения к одному значению по мере продвижения вниз по каждому столбцу. В наших столбцах мы смотрим на последовательность \(f(a-0,1)\), \(f(a-0,01)\), \(f(a-0,001)\), \(f(a-0,0001) \) и так далее, и \(f(a+0,1), \;f(a+0,01), \;f(a+0,001), \;f(a+0,0001)\) и так далее. (Примечание. Хотя мы выбрали \(x)-значения \(a±0,1, \;a±0,01, \;a±0,001, \;a±0,0001\) и т. д., и эти значения, вероятно, работают почти каждый раз, в очень редких случаях нам может потребоваться изменить наш выбор.)
3. Если оба столбца приближаются к общему \(y\)-значению \(L\), мы указываем \(\displaystyle \lim_{x \to a}f(x)=L\). Мы можем использовать следующую стратегию для подтверждения результата, полученного из таблицы, или в качестве альтернативного метода оценки предела.
4. С помощью графического калькулятора или компьютерной программы, которая позволяет нам графически отображать функции, мы можем построить график функции \(f(x)\), убедившись, что функциональные значения \(f(x)\) для \(x\ )-значения рядом с \(a\) находятся в нашем окне. Мы можем использовать функцию трассировки, чтобы перемещаться по графику функции и наблюдать за показаниями \(y\)-значения по мере того, как \(x\)-значения приближаются к \(a\). Если \(y\)-значения приближаются к \(L\), когда наши \(x\)-значения приближаются к \(a\) с обоих направлений, то \(\displaystyle \lim_{x \to a}f(x )=L\). Возможно, нам придется увеличить наш график и повторить этот процесс несколько раз.
Мы применяем эту стратегию решения проблем для вычисления лимита в примерах \(\PageIndex{1A}\) и \(\PageIndex{1B}\).
Пример \(\PageIndex{1A}\): оценка предела с помощью таблицы функциональных значений
Оценка \(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) с использованием таблица функциональных значений.
Решение
Мы рассчитали значения \(f(x)=\dfrac{\sin x}{x}\) для значений \(x\), перечисленных в таблице \(\PageIndex{2 }\).
| \(х\) | \(\frac{\sin x}{x}\) | \(х\) | \(\frac{\sin x}{x}\) |
|---|---|---|---|
| -0,1 | 0,998334166468 | 0,1 | 0,998334166468 |
| -0,01 | 0,999983333417 | 0,01 | 0,999983333417 |
| -0,001 | 0,999999833333 | 0,001 | 0,999999833333 |
| -0,0001 | 0,999999998333 | 0,0001 | 0,999999998333 |
Примечание. Значения в этой таблице были получены с помощью калькулятора и с использованием всех мест, указанных в выходных данных калькулятора.
Значения в этой таблице были получены с помощью калькулятора и с использованием всех мест, указанных в выходных данных калькулятора.
Читая каждый столбец \(\dfrac{\sin x}{x}\), мы видим, что значения в каждом столбце приближаются к единице. Таким образом, вполне разумно заключить, что \(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). График \(f(x)=\dfrac{\sin x}{x}\), построенный калькулятором или компьютером, будет аналогичен графику, показанному на рисунке \(\PageIndex{2}\), и подтверждает наши оценивать.
Рисунок \(\PageIndex{2}\): график \(f(x)=(\sin x)/x\) подтверждает оценку из таблицы \(\PageIndex{2}\).Пример \(\PageIndex{1B}\): оценка предела с помощью таблицы функциональных значений
Оценка \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4 }\) с помощью таблицы функциональных значений.
Решение
Как и прежде, мы используем таблицу — в данном случае Table \(\PageIndex{3}\) — для перечисления значений функции для заданных значений \(x\).
| \(х\) | \(\frac{\sqrt{x}−2}{x−4}\) | \(х\) | \(\ гидроразрыва {\ sqrt {х}-2} {х-4} \) |
|---|---|---|---|
| 3,9 | 0,251582341869 | 4.1 | 0,248456731317 |
| 3,99 | 0,25015644562 | 4.01 | 0,24984394501 |
| 3,999 | 0,250015627 | 4. 001 001 | 0,249984377 |
| 3,9999 | 0,250001563 | 4.0001 | 0,249998438 |
| 3,99999 | 0,25000016 | 4.00001 | 0,24999984 |
Изучив эту таблицу, мы видим, что функциональные значения меньше 4 уменьшаются до 0,25, тогда как функциональные значения больше 4 увеличиваются до 0,25. Мы заключаем, что \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0,25\). Мы подтверждаем эту оценку, используя график \(f(x)=\dfrac{\sqrt{x}−2}{x−4}\), показанный на рисунке \(\PageIndex{3}\).
Упражнение \(\PageIndex{1}\)
Оценка \(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\) с использованием таблицы функциональных ценностей. Используйте график, чтобы подтвердить свою оценку.
- Подсказка
Используйте 0,9, 0,99, 0,999, 0,9999, 0,99999 и 1,1, 1,01, 1,001, 1,0001, 1,00001 в качестве табличных значений.
- Ответить
\[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber \]
На данный момент мы видим из примеров \(\PageIndex{1A}\) и \(\PageIndex{1b}\), что может быть так же просто, если не проще, оценить предел функции, исследуя его график, как он есть, для оценки предела с помощью таблицы функциональных значений. В примере \(\PageIndex{2}\) мы оцениваем ограничение исключительно по графику, а не по таблице функциональных значений.
Пример \(\PageIndex{2}\): оценка предела с помощью графика {х\к-1}г(х)\).
Рисунок \(\PageIndex{4}\): График \(g(x)\) включает одно значение не на гладкой кривой.Решение :
Несмотря на то, что \(g(-1)=4\), при приближении \(x\)-значений к \(-1\) с любой стороны, \(g(x) \) значения приближаются к \(3\). Следовательно, \(\displaystyle \lim_{x\to-1}g(x)=3\). Заметим, что мы можем определить этот предел, даже не зная алгебраического выражения функции.
На основе примера \(\PageIndex{2}\) мы делаем следующее наблюдение: возможно, что предел функции существует в точке, и функция может быть определена в этой точке, но предел функции и значение функции в точке могут быть разными.
Упражнение \(\PageIndex{2}\)
Используйте график \(h(x)\) на рисунке \(\PageIndex{5}\) для оценки \(\displaystyle \lim_{x \to 2 }h(x)\), если это возможно.
Рисунок \(\PageIndex{5}\):- Подсказка
К какому \(y\)-значению приближается функция, когда \(x\)-значение приближается к \(2\)?
- Решение
\(\displaystyle \lim_{x \to 2}h(x)=−1.
 \)
\)
Глядя на таблицу функциональных значений или глядя на график функции, мы получаем полезную информацию о значении предела функции в данной точке. Однако эти методы слишком полагаются на догадки. Со временем нам потребуется разработать альтернативные методы оценки пределов. Эти новые методы носят более алгебраический характер, и мы рассмотрим их в следующем разделе; однако на этом этапе мы вводим два специальных ограничения, которые лежат в основе будущих методов.
Два важных ограничения
Пусть \(a\) — действительное число, а \(c\) — константа.
- \(\displaystyle \lim_{x \to a}x=a\)
- \(\displaystyle \lim_{x \to a}c=c\)
Мы можем сделать следующие замечания относительно этих двух пределов.
- Для первого предела заметим, что по мере того, как \(x\) приближается к \(a\), приближается и \(f(x)\), потому что \(f(x)=x\). Следовательно, \(\displaystyle \lim_{x \to a}x=a\).
- Для второго ограничения рассмотрим таблицу \(\PageIndex{4}\).

| \(х\) | \(f(x)=c\) | \(х\) | \(f(x)=c\) |
|---|---|---|---|
| \(а-0,1\) | \(с\) | \(а+0,1\) | \(с\) |
| \(а-0,01\) | \(с\) | \(а+0,01\) | \(с\) |
| \(а-0,001\) | \(с\) | \(а+0,001\) | \(с\) |
| \(а-0,0001\) | \(с\) | \(а+0,0001\) | \(с\) |
Обратите внимание, что для всех значений \(x\) (независимо от того, приближаются ли они к \(a\)), значения \(f(x)\) остаются постоянными при \(c\). У нас нет другого выбора, кроме как заключить \(\displaystyle \lim_{x \to a}c=c\).
У нас нет другого выбора, кроме как заключить \(\displaystyle \lim_{x \to a}c=c\).
Существование предела
Когда мы рассматриваем предел в следующем примере, имейте в виду, что для того, чтобы предел функции существовал в точке, функциональные значения должны приближаться к единственному вещественному значению в этой точке. Если функциональные значения не приближаются к единому значению, то предела не существует.
Пример \(\PageIndex{3}\): оценка несуществующего предела
Вычислить \(\displaystyle\lim_{x \to 0}\sin(1/x)\) с помощью таблицы значений.
Решение
В таблице \(\PageIndex{5}\) перечислены значения функции \(\sin(1/x)\) для заданных значений \(x\).
| \(х\) | \(\sin(1/x)\) | \(х\) | \(\sin(1/x)\) |
|---|---|---|---|
| -0,1 | 0,544021110889 | 0,1 | −0,544021110889 |
| -0,01 | 0,50636564111 | 0,01 | −0,50636564111 |
| -0,001 | −0,8268795405312 | 0,001 | 0,8268795405312 |
| -0,0001 | 0,305614388888 | 0,0001 | −0,305614388888 |
| -0,00001 | −0,035748797987 | 0,00001 | 0,035748797987 |
| -0,000001 | 0,3499187 | 0,000001 | −0,3499187 |
Изучив таблицу функциональных значений, мы видим, что \(y\)-значения не приближаются ни к одному единственному значению. Получается, что предела не существует. Прежде чем сделать такой вывод, давайте подойдем более системно. Возьмем следующую последовательность \(x\)-значений, приближающихся к \(0\):
Получается, что предела не существует. Прежде чем сделать такой вывод, давайте подойдем более системно. Возьмем следующую последовательность \(x\)-значений, приближающихся к \(0\):
\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac {2}{9π},\;\frac{2}{11π},\;….\nonumber \]
Соответствующие \(y\)-значения равны
\[1,\;-1,\ ;1,\;-1,\;1,\;-1,\;….\nonumber \]
На данный момент мы действительно можем заключить, что \(\displaystyle \lim_{x \to 0} \ sin(1/x)\) не существует. (Математики часто сокращают «не существует» до DNE. Таким образом, мы будем писать \(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) График \(f(x) =\sin(1/x)\) показан на рисунке \(\PageIndex{6}\) и дает более четкое представление о поведении \(\sin(1/x)\) при \(x\) приближается к \(0\). Вы можете видеть, что \(\sin(1/x)\) все более сильно колеблется между \(-1\) и \(1\) по мере того, как \(x\) приближается к \(0\). 92−4∣}{x−2}\) не существует.
Односторонние пределы
Иногда указание на то, что предел функции не существует в какой-то точке, не дает нам достаточно информации о поведении функции в этой конкретной точке. Чтобы убедиться в этом, вернемся к функции \(g(x)=|x−2|/(x−2)\), представленной в начале раздела (см. рисунок \(\PageIndex{1}\)(b )). Поскольку мы выбираем значения \(x\), близкие к \(2\), \(g(x)\) не приближаются к одному значению, поэтому предел при приближении \(x\) к \(2\) не существуют, то есть \(\displaystyle \lim_{x \to 2}g(x)\) DNE. Однако одно это утверждение не дает нам полной картины поведения функции вокруг \(x\)-значения \(2\). Чтобы обеспечить более точное описание, мы вводим идею 9+}g(x)=1.\nonumber \]
Чтобы убедиться в этом, вернемся к функции \(g(x)=|x−2|/(x−2)\), представленной в начале раздела (см. рисунок \(\PageIndex{1}\)(b )). Поскольку мы выбираем значения \(x\), близкие к \(2\), \(g(x)\) не приближаются к одному значению, поэтому предел при приближении \(x\) к \(2\) не существуют, то есть \(\displaystyle \lim_{x \to 2}g(x)\) DNE. Однако одно это утверждение не дает нам полной картины поведения функции вокруг \(x\)-значения \(2\). Чтобы обеспечить более точное описание, мы вводим идею 9+}g(x)=1.\nonumber \]
Теперь мы можем дать неформальное определение односторонних пределов.
Определение: односторонние пределы
Мы определяем два типа односторонних пределов.
Предел слева:
Пусть \(f(x)\) – функция, определенная при всех значениях в открытом интервале вида \((z,a)\), и пусть \(L\ ) — действительное число. Если значения функции \(f(x)\) приближаются к действительному числу \(L\), как значения \(x\) (где \(x Рассмотрим теперь связь между пределом функции в точке и пределами справа и слева в этой точке. Кажется очевидным, что если предел справа и предел слева имеют общее значение, то это общее значение является пределом функции в этой точке. Точно так же, если предел слева и предел справа принимают разные значения, предел функции не существует. Эти выводы обобщены в примечании. 9+} f(x)=L\). Упражнение \(\PageIndex{5}\) Вычисление \(\displaystyle\lim_{x \to 1}f(x)\) для \(f(x)\), показанное здесь: Сравните ограничение справа с ограничением слева. \(\displaystyle\lim_{x \to 1}f(x)\) не существует Эта страница под названием 2.2: Ограничение функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. –> Звоните прямо сейчас, чтобы записаться на обучение: (888) 888-0446 8 Диагностические тесты
613 практических тестов
Вопрос дня
Карточки
Learn by Concept Справка по математике для старших классов »
Предварительный расчет »
Пределы Возможные ответы: Правильный ответ: Объяснение: Предел описывает, к какому значению приближается функция при приближении к определенному значению (в данном случае ). Замена на дает нам неопределенное значение (это НЕ то же самое, что 0). Это означает, что функция не определена в этой точке. Однако то, что функция не определена в какой-то точке, не означает, что она не имеет предела. Предел — это просто любое значение, которое получает функция закрыть к. Один из способов найти предел — максимально упростить уравнение: Как видите, между числителем и знаменателем есть общие множители, которые можно сократить. (Помните, когда вы вычеркиваете множитель из рационального уравнения, это означает, что функция имеет дырку — неопределенную точку — где этот множитель равен нулю.) После вычеркивания общих множителей мы осталось: Несмотря на то, что область определения исходной функции ограничена (не может равняться), мы все же можем подставить в это упрощенное уравнение, чтобы найти предел в Сообщить об ошибке Пусть . Найти . Возможные ответы: Предел не существует. Правильный ответ: Объяснение: Это график . Мы знаем, что это не определено; следовательно, нет значения для . Но если мы посмотрим на график, то увидим, что по мере приближения к 0 слева значение приближается к отрицательной бесконечности. Это можно проиллюстрировать, представив маленькие отрицательные числа. ПРИМЕЧАНИЕ: Обратите внимание на односторонние ограничения, так как легко выбрать неправильный ответ, если вы не будете осторожны. на самом деле бесконечность, а не отрицательная бесконечность. Сообщить об ошибке Оцените предел ниже: Возможные ответы: Правильный ответ: будет приближаться при приближении, поэтому будет иметь тип, как показано ниже: Итак, мы можем применить правило больницы L0032 отсюда: Сообщить об ошибке Возможные ответы: Правильный ответ: 2
Объяснение: Сообщить об ошибке Рассчитать . Возможные ответы: Предел не существует. Правильный ответ: Объяснение: Это можно переписать следующим образом: Мы можем заменить , отметив, что as , : , что является правильным выбором. Сообщить об ошибке Скорость автомобиля, движущегося по шоссе, определяется следующей функцией времени: Что вы можете сказать о скорости автомобиля по прошествии длительного времени (то есть по мере приближения к бесконечности)? Возможные ответы: Скорость автомобиля зависит от стартовой скорости. Скорость автомобиля приближается к бесконечности. Скорость автомобиля приближается к нулю. Скорость автомобиля приближается к постоянному числу. Из данной функции ничего нельзя сделать. Правильный ответ: Скорость автомобиля стремится к бесконечности. Объяснение: Указанная функция является многочленом с таким членом, который больше 1. Всякий раз, когда это так, мы можем сказать, что вся функция расходится (стремится к бесконечности) в пределе по мере приближения к бесконечности. Это говорит нам о том, что данная функция не очень реалистично описывает скорость автомобиля для больших ! Сообщить об ошибке Уведомление об авторских правах Посмотреть репетиторов Дженнифер Университет Маккендри, бакалавр делового администрирования, бухгалтерского учета и управления бизнесом. Линденвудский университет, магистр… Посмотреть репетиторов Филип Университет Джорджа Мейсона, бакалавр наук, правоохранительные органы. Просмотр репетиторов Джон Университет Камерон, бакалавр делового администрирования, делового администрирования и менеджмента. Университет штата Мичиган, штат Д… 8 диагностических тестов
613 практических тестов
Вопрос дня
Карточки
Учитесь по концепции GALE Просмотры Обновлено мая 18 2018 г. ИСТОРИЯ Предел последовательности Ограничение функции Применение Ресурсы Применение Ресурсы . произвольная близость. То есть предел — это значение, к которому переменная величина приближается сколь угодно близко. Операции дифференцирования и интегрирования из исчисления основаны на теории пределов. Теория пределов основана на особом свойстве действительных чисел; а именно, что между любыми двумя действительными числами, независимо от того, насколько они близки друг к другу, всегда есть другое. Между любыми двумя действительными числами всегда есть бесконечно много других. Близость является ключом к пониманию пределов: только после определения близости предел обретает точное значение. Соответственно, окрестность точек вблизи любой заданной точки составляет окрестность. Окрестности – это определяющие компоненты бесконечных пределов последовательности. Древнегреческий математик Архимед Сиракузский (287–212 гг. до н. э.) впервые разработал идею пределов измерения изогнутых фигур и объема сферы в третьем веке до нашей эры. Разделив эти фигуры на маленькие части, которые можно аппроксимировать, затем увеличив количество частей, предел суммы частей может дать желаемое количество. Тезис Архимеда, Метод, был утерян до 1906 года, когда математики обнаружили, что Архимед был близок к открытию исчисления бесконечно малых. Поскольку работы Архимеда были неизвестны до двадцатого века, другие разработали современную математическую концепцию пределов. Английский физик и математик сэр Исаак Ньютон (1642–1727) и немецкий математик Готфрид Вильгельм Лейбниц (1646–1716) независимо разработали общие принципы исчисления (важной частью которого является теория пределов) в семнадцатом веке. Древнегреческий философ (из южной Италии) Зенон Элейский (ок. 490–430 до н. э.), возможно, был одним из первых математиков, задумавшихся о пределе последовательности и задавшихся вопросом, как он связан с окружающим миром. Зенон утверждал, что всякое движение невозможно, потому что для того, чтобы переместиться на расстояние (l), сначала необходимо пройти половину расстояния, затем половину оставшегося пути, затем половину этого оставшегося пути и так далее. Таким образом, утверждал он, расстояние (l) никогда нельзя пройти полностью. Рассмотрим последовательность 1, 1/2, 1/4, 1/8,. . .(1/2) n , когда n становится очень большим. Последовательность чисел сходится к заданному числу, если разность между членами последовательности и данным числом образует бесконечно малую последовательность. Для этой последовательности (1/2) n произвольно приближается к 0, поэтому 0 является пределом последовательности. Числа в последовательности никогда не достигают предела, но и не превышают его. Если бесконечная последовательность расходится, промежуточная сумма членов в конечном итоге отклоняется от любого конкретного значения, поэтому у расходящейся последовательности нет предельной суммы. Рассмотрим произвольную функцию y = f (x). lim f(x) = l x → p и читается как «Предел f от x, когда x приближается к p, равен L». Это не зависит от того, какая конкретная последовательность чисел выбрана для представления x; необходимо только, чтобы последовательность сходилась к пределу. Предел может зависеть от того, является ли последовательность возрастающей или убывающей. То есть предел, когда x приближается к p сверху, может отличаться от предела, когда x приближается к p снизу. В некоторых случаях тот или иной из этих пределов может даже не существовать. В любом случае, поскольку значение x приближается к конечному значению p, разность (p x) приближается к нулю. Именно это определение предела обеспечивает основу для развития производной и интеграла в исчислении. Существует второй тип функционального предела: предел, когда значение независимой переменной приближается к бесконечности. Хотя говорят, что последовательность, стремящаяся к бесконечности, расходится, существуют случаи, когда применение определяющего правила функции к расходящейся последовательности приводит к созданию сходящейся последовательности. Схождение —Схождение означает приближение к пределу, имеющему конечное значение. Интервал — Интервал — это подмножество действительных чисел, соответствующее отрезку линии конечной длины и включающее все действительные числа между его конечными точками. Интервал является закрытым, если конечные точки включены, и открытым, если они не включены. Вещественное число —Набор чисел, содержащий целые числа и все десятичные дроби, включая повторяющиеся и неповторяющиеся десятичные дроби. Последовательность —Последовательность представляет собой ряд терминов, в котором каждый последующий термин связан с предыдущим фиксированной формулой. независимая переменная стремится к бесконечности формально записывается как: lim f (x) = L x → ∞ и читается как «Предел f от x, когда x приближается к бесконечности, равен L». Понятие предела необходимо для понимания системы действительных чисел и ее отличительных характеристик. В определенном смысле действительные числа можно определить как числа, являющиеся пределами сходящихся последовательностей рациональных чисел. Одно из применений концепции пределов относится к производной. Производная представляет собой скорость потока или изменения и может быть вычислена на основе некоторых концепций ограничений. Пределы также являются ключом к вычислению интегралов (выражений площадей). Интеграл вычисляет всю площадь области путем суммирования бесконечного числа ее маленьких кусочков. Пределы также являются частью итеративного процесса. Итерация многократно выполняет подпрограмму, используя выходные данные одного шага в качестве входных данных для следующего шага. Каждый вывод представляет собой итерацию. Некоторые успешные итерации могут максимально приблизиться к теоретически точному значению. Эббот, Персиваль. Научись: исчисление. Лондон, Великобритания: Hodder and Stoughton Education, и Чикаго, Иллинойс: Contemporary Books, 2003. Бертон, Дэвид М. История математики: введение. Нью-Йорк: McGraw-Hill, 2007. Ларсон, Рон. Исчисление: прикладной подход. Бостон, Массачусетс: Houghton Mifflin, 2003. Ларсон, Рон. Исчисление с аналитической геометрией. Бостон: Колледж Хоутон-Миффлин, 2002. Люблинская Ирина Евгеньевна Связь математики с наукой: эксперименты для предварительного исчисления. Эмеривилл, Калифорния: Key Curriculum Press, 2003. Сетек, Уильям М. Основы математики. Верхняя Седл -Ривер, Нью -Джерси: Пирсон Прентис Холл, 2005. Дж. Р. Мэддоки Энциклопедия Гейла Науки Гейл Просмотры Обновлен мая 18 в Близость является ключом к пониманию пределов: только после определения близости предел обретает точное значение. Соответственно, окрестность точек вблизи любой заданной точки составляет окрестность. Окрестности – это определяющие компоненты бесконечных пределов последовательности. Архимед Сиракузский впервые разработал идею пределов для измерения изогнутых фигур и объема сферы в третьем веке до н.э. Разделив эти фигуры на маленькие части, которые можно аппроксимировать, затем увеличив количество частей, предел суммы частей может дать желаемое количество. Поскольку работы Архимеда были неизвестны до двадцатого века, другие разработали современную математическую концепцию пределов. Англичанин сэр Исаак Ньютон и немец Готфрид Вильгельм фон Лейбниц независимо друг от друга разработали общие принципы исчисления (важной частью которого является теория пределов) в семнадцатом веке. Древнегреческий философ Зенон, возможно, был одним из первых математиков, задумавшихся над пределом последовательности и задавшимся вопросом, как он связан с окружающим миром. Зенон утверждал, что все движение было невозможно, потому что для того, чтобы пройти расстояние л, нужно сначала пройти половину пути, затем половину оставшегося пути, затем половину этого оставшегося пути и так далее. Таким образом, утверждал он, расстояние l никогда нельзя пройти полностью. Рассмотрим последовательность 1, 1/2, 1/4, 1/8,…(1/2)n, когда n становится очень большим. Поскольку (1/2)n равно 1/2, умноженному само на себя n раз, (1/2)n становится очень маленьким, когда n позволяет стать бесконечно большим. Говорят, что последовательность сходится, что означает, что числа, находящиеся очень далеко в последовательности (соответствующие большому n), становятся очень близкими друг к другу и очень близкими к одному значению, называемому пределом. Последовательность чисел сходится к заданному числу, если разности между членами последовательности и данным числом образуют бесконечно малую последовательность. Для этой последовательности (1/2)n сколь угодно близко к 0, поэтому 0 является пределом последовательности. Числа в последовательности никогда не достигают предела, но и не превышают его. Если бесконечная последовательность расходится, промежуточная сумма членов в конечном итоге отклоняется от любого конкретного значения, поэтому у расходящейся последовательности нет предельной суммы. Рассмотрим произвольную функцию , y = f(x). (Функция — это множество упорядоченных пар, для которых первый и второй элементы каждой пары связаны друг с другом фиксированным образом. Когда элементами упорядоченных пар являются действительные числа, отношение обычно выражается в виде уравнение.) Предположим, что последовательные значения x выбраны так, чтобы соответствовать значениям сходящейся последовательности, такой как последовательность S из предыдущего примера. Возникает вопрос, что делают значения функции, то есть что происходит с последовательными значениями у. На самом деле всякий раз, когда значения x образуют последовательность, значения f(x) также образуют последовательность. Если эта последовательность является сходящейся последовательностью, то предел этой последовательности называется пределом функции. В более общем случае, когда значение функции f(x) приближается к определенному значению L, поскольку независимая переменная x приближается к действительному числу p, тогда L называется пределом функции. и гласит: «Предел f от x, когда x приближается к p, равен L». Это не зависит от того, какая конкретная последовательность чисел выбрана для представления x; необходимо только, чтобы последовательность сходилась к пределу. Предел может зависеть от того, является ли последовательность возрастающей или убывающей. То есть предел, когда x приближается к p сверху, может отличаться от предела, когда x приближается к p снизу. В некоторых случаях тот или иной из этих пределов может даже не существовать. В любом случае, поскольку значение x приближается к конечному значению p, разница (p-x) приближается к ноль . Именно это определение предела обеспечивает основу для развития производной и интеграла в исчислении. Существует второй тип функционального предела: предел, когда значение независимой переменной приближается к бесконечности . Хотя говорят, что последовательность, стремящаяся к бесконечности, расходится, существуют случаи, когда применение определяющего правила функции к расходящейся последовательности приводит к созданию сходящейся последовательности. и гласит: «Предел f от x, когда x приближается к бесконечности, равен L». Интересно отметить, что функция, определяемая y = 1/x, не имеет предела, когда x приближается к 0, но имеет предел L = 0, когда x приближается к ∞. Понятие предела необходимо для понимания системы действительных чисел и ее отличительных характеристик. В определенном смысле действительные числа можно определить как числа, являющиеся пределами сходящихся последовательностей рациональных чисел. Одно из применений концепции пределов относится к производной. Производная скорость потока или изменения, и может быть рассчитана на основе некоторых концепций пределов. Пределы также являются ключом к вычислению интегралов (выражений площадей). Интеграл вычисляет всю площадь области путем суммирования бесконечного числа ее маленьких кусочков. Эббот П. и М. Э. Уордл. Научись исчислению. Lincolnwood: NTC Publishing, 1992. Аллен Г.Д., К. Чуи и Б. Перри. Элементы исчисления. 2-е изд. Pacific Grove: Brooks/Cole Publishing Co., 1989. Говар, Норман. Приглашение к математике. Нью-Йорк: Издательство Оксфордского университета, 1979. Ларсон, Рон. Исчисление с аналитической геометрией. Бостон: Колледж Хоутон-Миффлин, 2002. Сильверман, Ричард А. Основное исчисление с приложениями. Нью-Йорк: Дувр, 1989. Маклафлин, Уильям И. «Разрешение парадоксов Зенона». Дж. Р. Мэддокс . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . —Схождение означает приближение к пределу, имеющему конечное значение. — Интервал — это подмножество действительных чисел, соответствующее отрезку линии конечной длины и включающее все действительные числа между его конечными точками. Интервал является закрытым, если конечные точки включены, и открытым, если они не включены. —Набор чисел, содержащий целые числа и все десятичные дроби, включая повторяющиеся и неповторяющиеся десятичные дроби. —Последовательность представляет собой ряд терминов, в котором каждый последующий термин связан с предыдущим фиксированной формулой. Научная энциклопедия Гейла gale просмотров обновлено 27 июня 2018 Понятие предела является важным компонентом Один из способов проверки пределов — использование последовательности чисел. В следующем примере показана последовательность чисел, в которой предел равен 0. Второе число в последовательности, ½, является результатом деления первого числа в последовательности, 1, на 2. Третье число в последовательности, ¼ — это результат деления второго числа в последовательности, ½, на 2. Этот процесс деления каждого числа на 2 для получения следующего числа в последовательности продолжается для получения каждого из оставшихся значений. Если последовательность продолжается бесконечно, значения в последовательности будут все ближе и ближе к 0. Однако числа в последовательности никогда не примут нулевое значение. Математическая концепция приближения к значению без достижения этого значения называется «концепцией предела». Значение, к которому приближаются, называется пределом последовательности. Предел последовательности … равен 0, В приведенном ниже примере показаны несколько последовательностей и их пределы. В каждом случае значения в последовательности приближаются к своему пределу. Пример 1: 0,9, 0,99, 0,999, 0,9999, 0,99999, 0,999999, 0,999999,… Предел: 1 Пример 2: 5,841, 5,8401, 5,84001, 5,840001, 5,8400001, 5,8401, 5,84001, 5,840001, 5,8400001, 5,8401, 5,84001, 5,840001, 5,8400001, 5,8401, 5,84001, 5,840001, 5,8400001, 5,8401, 5,84001, 5,840001, 5,84001, 5,8401: Ограничение: 0 Однако не все последовательности имеют ограничения. Пределы также можно проверять с помощью функций. Примером функции является . Один из способов проверить предел функции — составить список выборочных значений, составляющих функцию. Левую часть таблицы можно использовать для проверки предела функции при увеличении x . По мере увеличения значений в столбце x значения в столбце f ( x ) приближаются к 0. Предел функции равен значению, которое f ( x ) приближается столбец. Предел функции при приближении x к бесконечности равен 0. Функции также могут быть построены на декартовой плоскости . График функции показан на рисунке. Цветовая кривая представляет функцию. Важно учитывать, к какому значению приближается x при определении предела f ( x ). Если бы x приближались к 0 в предыдущем примере, f ( x ) не имели бы предела. Причину этого можно понять по средней и правой частям таблицы. Из таблицы следует, что значения для f ( x ) продолжают увеличиваться по мере приближения x к 0 от значений, превышающих 0. Из таблицы также следует, что значения для f ( x ) продолжают уменьшаться по мере приближения x к 0 от значений, меньших 0. Поскольку значения f ( x ) не приближаются к определенному значению, функция не имеет предела по мере приближения x к 0. Типичное применение понятия предела — определение площади. Если нужна точная площадь круга, количество треугольников, делящих круг, можно увеличить. Предел суммы площадей этих треугольников при стремлении числа треугольников к бесконечности равен стандартной формуле нахождения площади круга: A = πr 2 , где A — площадь круга. круг и r его радиус. Таким образом, предел относится к математическому понятию, в котором числовые значения становятся все ближе и ближе к заданному значению или приближаются к этому значению. Значение, к которому приближаются, называется «пределом». Ограничения можно использовать для понимания поведения числовых последовательностей и функций. см. также исчисление; Бесконечность. Барбара М. Москаль Джокуш, Элизабет А. и Патрик Дж. Маклафлин. «Внедрение стандартов: построение ключевых концепций исчисления в 7–12 классах». Учитель математики 83, нет. 7 (1990): 532–540. «Ограничения» Coolmath.com. Математика Москаль Варвара М. Оксфорд просмотров обновлено 29 мая 2018 lim·it / ˈlimit/ •
н. 1. точка или уровень, за который что-то не выходит или не может распространяться или пройти: пределы президентской власти 10-минутный лимит на речей не было предела его воображению. The Oxford Pocket Dictionary of Current English gale просмотров обновлено 11 июня 2018 как в случае с тварями, а не безгранично или бесконечно, как в случае с Богом. Основная проблема схоластической философии состоит в том, чтобы объяснить с точки зрения причин или принципов ограниченность одного существа по сравнению с другим (например, человека по сравнению с ангелами) и, в особенности, всех существ по сравнению с Богом. Томисты обычно называют двоякую причину качественной ограниченности данного существа. Во-первых, каждое ограниченное существо нуждается в некотором внешнем действующем действии или действующей причине, чтобы определить его способность или предел и сообщить соответствующую степень совершенства. Во-вторых, результатом или следствием в бытии определяющего действия его причины является некий внутренний принцип ограничения в самом бытии. Этот внутренний принцип ограничения фиксирует внутреннюю способность существа получать так много и не более данного атрибута или совершенства. Если взять аналогию из количественного порядка, если человек хочет наполнить кувшин водой, он должен налить столько-то воды; точно так же кувшин (получатель) сам должен иметь определенную форму или емкость, чтобы иметь возможность принимать воду. Эту внутреннюю причину или принцип ограничения св. Фома Аквинский назвал потенцией для получения совершенства или действием (см. потенция и действие). Оба эти термина он заимствовал у Аристотеля, первоначального сторонника потенции и действия, хотя сам Аристотель применял свою теорию только к проблеме изменения, а не к проблеме ограничения. Другие философы-схоласты, такие как John duns scotus и F. suÁrez, соглашаются со св. Фомой в отношении необходимости внешнего агента для определения ограничений существа, но отрицают, что какой-либо внутренний принцип потенции внутри ограниченного существа должен быть действительно отличное от совершенства, которое оно ограничивает. См. также: конечное существо; участие; совершенство, онтологическое. Библиография: w. н. Кларк, «Ограничение действия силой», Новая схоластика 26 (1952) 167–194. грамм. ginnini, Enciclopedia filosofica, 4 v. (Венеция – Рим, 1957) 3:54–58. [ш. н. clarke] Новая католическая энциклопедия CLARKE, W.N.
н. 1. (часто ограничения) ограничивающее правило или обстоятельство; ограничение: строгие ограничения на водопользование. ∎ состояние ограниченных возможностей; дефект или неисправность: она знала о своих ограничениях лучше, чем о себе. ∎ действие по ограничению чего-либо: ограничение полномочий органов местного самоуправления. 2. (также срок исковой давности) Закон установленный законом срок, по истечении которого иск может быть отклонен или право собственности не может продолжаться. См. также срок исковой давности. Оксфордский карманный словарь современного английского языка В имущественном праве ограничение в отношении имущества возникает, когда его продолжительность или качество каким-либо образом ограничиваются. Энциклопедия американского права Уэста Оксфорд просмотров обновлено 08 июня 2018 г. limit sb. XIV. липы 909 л.54 , предел — граница. Краткий Оксфордский словарь английской этимологии T. F. HOAD Задавать вопрос Спросил Изменено
5 лет, 3 месяца назад Просмотрено
4к раз $\begingroup$ В настоящее время я учусь на первом курсе факультета электротехники и информатики. Когда я пытаюсь выяснить, сходится или расходится бесконечный ряд (который никогда не заканчивается), почему я могу посмотреть на последовательность частичных сумм (бесконечных) этого ряда и на основе их сходимости или расхождения сказать, расходится или сходится весь ряд? Когда я прихожу к профессорам и задаю те или иные вопросы, они говорят мне, почему я задаюсь этим вопросом и что я должен принять это как должное. Тогда я просто хочу убить себя. Я имею в виду, разве я не пришел сюда, чтобы изучить, как и почему все работает? Я бы хотел, чтобы они просто сказали мне, что это какая-то «высшая» или более сложная часть математики, и что я узнаю об этом позже, или что это просто не знает, почему это работает так, как работает. Так должен ли я продолжать изучать эти вещи, так как я всегда буду сталкиваться с чем-то, что я не смогу понять (поскольку эти «базовые» ограничения меня смущают), и все эти профессора и академические круги будут говорить мне, что я не должен Я не беспокоюсь, почему это работает так, как работает, и что я должен принимать это как должное. Все теоремы, используемые для доказательства производной, интеграла, сходимости, расходимости и т.д., так или иначе используют ограничения. Но в определении предела говорится, что я могу сделать некоторое $f(x)$ как близкое к некоторому значению L, но не равное ему, если я готов сделать $x$ как можно ближе к некоторому значению $c$. Это определение должно быть математически строгим, но использование этих как близких к не кажется мне строгим. Пожалуйста, помогите мне, так как я не знаю, стоит ли мне продолжать учебу, потому что всегда есть какое-то математическое доказательство, которое я не могу понять и которое мешает мне идти вперед, и таким образом я всегда отстаю, и все ожидают, что все поймут первый раз слышу. Буду благодарен за все комментарии и предложения. $\endgroup$ 20 $\begingroup$ Функция $f:\>x\mapsto f(x)$, заданная некоторым выражением, имеет “естественную” область определения $D(f)$: множество всех $x$ в области дискурса ($ {\mathbb R}$ или, скажем, ${\mathbb C}$), для которых $f(x)$ можно вычислить, не задавая вопросов. В общем и целом понятие “лимит” – это инструмент для обработки таких “исключительных” или: “ограничивающих” случаев. Важнейшим примером является, конечно, следующий: когда $f$ определено в окрестности $x_0$, нас интересует функция
$$m:\quad x\mapsto{f(x)-f(x_0)\over x-x_0}$$
у которого есть “исключительная” точка $x_0$. Невозможно подставить $x:=x_0$ в определение $m$. Это подводит меня к вашему пункту 4. который касается сути дела. Я бы переписал центральное предложение следующим образом: В определении предела $f(x)$ для $x\to c$ говорится, что я могу сделать $f(x)$ как можно ближе к значению $L$, если я готов сделать $x$ достаточно близким к $c$. Идея такова: хотя в большинстве случаев невозможно поместить $x:=c$ в определение $f$, мы хотим описать, как ведет себя $f$, когда $x$ очень близко к $c$. Затем вы говорите, что «это определение должно быть математически строгим, но использование этих как близких к и достаточно близких к не выглядит строгим для меня». $\endgroup$ 2 $\begingroup$ Для определенности начнем с современного определения пределов. Если $f$ — функция с действительным знаком, определенная в некоторой удаленной окрестности действительного числа $c$, то мы говорим «$\lim(f, c) = L$», если: Для каждого $\varepsilon > 0$ существует $\delta > 0$ такое, что если $0 < |x - c| < \delta$, то $|f(x) - L| < \varepsilon$. Многие люди считают полезным рассматривать это определение как набор правил состязательной игры. Функция $f$, местоположение $c$ и предполагаемый предел $L$ заданы, как указано выше. Игрок $\varepsilon$ выдает “вызов” в виде положительного вещественного числа. Чтобы «выполнить» задачу, нужно убедиться, что $|f(x) – L| < \varepsilon$ для всех $x$, лежащих в некоторой удаленной окрестности $c$. Сказать “$\lim(f, c) = L$” значит сказать, что у игрока $\delta$ есть выигрышная стратегия против идеального противника ; то есть Player $\delta$ может ответить на произвольный вызов. Именно это имеется в виду, когда говорят: «Мы можем сделать $f(x)$ как можно более близким к $L$, взяв $x$ достаточно близко к $c$ (не равному $c$)». Пределы уникальны: если заданы $f$ и $c$, не более одного числа $L$ удовлетворяет предыдущему определению. В самом деле, если $L_1$ и $L_2$ оба удовлетворяют определению, то для каждого $\varepsilon > 0$ существует $\delta > 0$ такое, что если $0 < |x - c| < \delta$, то
$$
|f(x) - L_1| < \varepsilon/2\quad\text{and}\quad
|f(x) - L_2| < \varepsilon/2.
$$
(Это стандартная аналитическая идиома; выберите $\delta_1 > 0$, которая «работает» для $L_1$, выберите $\delta_2 > 0$, которая «работает» для $L_2$, и пусть $\delta = \min (\дельта_1, \дельта_2)$. Теперь выберите произвольный $x$ с $0 < |x - c| < \дельта$. По неравенству треугольника
$$
|Л_1 - Л_2|
= |L_1 - f(x) + f(x) - L_2|
\leq |f(x) - L_1| + |f(x) - L_2|
< \varepsilon/2 + \varepsilon/2 = \varepsilon.
$$
Но это неравенство является утверждением о двух (фиксированных) действительных числах, и если $|L_1 - L_2| < \varepsilon$ для каждые $\varepsilon > 0$, тогда $L_1 = L_2$. На практике, если мы покажем, что некоторый предел равен $2x$, то этот же предел не может быть $2x + \Delta x$, если только $\Delta x = 0$. 92$: зафиксировать действительное число $c$, определить
$$
f(h) = \frac{g(c + h) – g(c)}{h},\quad h \neq 0,
$$
и положим $L = 2c$. (Определение позволяет нам только «проверить» предполагаемый предел; чтобы использовать определение, мы должны угадать предел заранее . Здесь мы могли бы заметить, что $f(h) = 2c + h$ для $h \neq 0$ ; если мы произвольно установим $h = 0$, мы получим наше предположение для $L$. Пока мы ничего не доказали, насколько нам известно, это предположение неверно. (Условие “$n \geq N$” заменяет “$0 < |x - c| < \delta$"; очень грубо говоря, это условие утверждает, что “$n$ ближе к $\infty$, чем $N $ is”. Если эти замечания будут полезны: A Значение $f(x)$ может быть или не быть равным пределу $L$. Точно так же частичная сумма $s_n$ бесконечного ряда может быть или не быть равной сумме $s$. Вы не можете определить, сходится ряд или расходится, глядя на ограниченное число членов; вы должны посмотреть на произвольных конечных сумм. Это аналогично невозможности определить предел функции, исследуя только конечное число точек области. (Упражнения в исчислении, когда вы «оцениваете» предел, подставляя небольшие числа в калькулятор, интуитивно убедительны, но логически бессодержательны. Существование и вычисление $\lim(f, c)$ может 93}.
$$
Легко доказать, что $S$ непусто и ограничено сверху. Из “свойства полноты” действительной системы счисления следует, что $S$ имеет “верхнюю грань” или “наименьшую верхнюю границу” $s$, наименьшее действительное число, которое больше или равно каждому числу в $S$. Причина, по которой вы можете сказать, что его скорость равна $2x$, а не $2x+\Delta x$, заключается в определении слова скорость . В теоретической физике скорость определяется как предельное значение , только что описанное при $h\to0$ и , а не как любое значение отношения при любом положительном значении $h$. Немного парадоксально, что вы никогда не сможете по-настоящему измерьте эту скорость: даже если вы измерите положение в два очень близких момента и вычислите отношение, вы всегда будете получать это маленькое значение $\Delta x$ как возмущение в ваших вычислениях. Удивительно то, что если вы улучшите свои методы измерения и уменьшите интервал между измерениями, вы на самом деле каждый раз будете получать что-то ближе к $2x$. Тот факт, что вы уверены в том, что значения будут становиться все ближе и ближе к $2x$, когда вы приближаете отношение все меньшим и меньшим $\Delta x$ (это то, что вы математически доказываете с помощью $\epsilon- \delta$) — это то, что побуждает вас определять «реальную», «мгновенную» скорость равной $2x$. Эта скорость есть не отношение какого-либо действительно пройденного расстояния за какой-либо интервал времени, а предельное значение этих отношений. Почему это математическое, абстрактное определение работает на практике?
совершенно другой вопрос, и я боюсь, что ни у кого нет полного
ответь за это. Ведь это продукт разума, а не
наблюдение. Физик Юджин Вигнер написал известное эссе об этих
темы под названием «Необоснованная эффективность математики в
естественный
наук.
Некоторым религиозным людям нравится думать, что Бог действительно создал
физический мир с математическими правилами и законами, которые можно
обнаружены нами, другим нравится принимать, что это просто работает в большинстве
случаи (не квантовые или релятивистские сценарии) как показывает практика и
довольны этим, другие просто избегают вопроса. это”, это то, что вы цитируете, это 9\infty a_n$ не имеет смысла, пока мы не согласимся с тем, что мы под этим подразумеваем! Если вы думаете об этом символе как о предельном значении последовательности частичных сумм , когда он существует , вы можете присвоить ему значение: тогда у вас есть новая игрушка, с которой можно играть, и вы можете научиться играть с ней. . При определении чего-либо вам нужно, чтобы это определение отражало желаемые свойства: чтобы вы могли обращаться с бесконечными суммами и оперировать ими точно так же, как вы работаете с обычной суммой, и чтобы это работало. 3– Я думаю, что интеллектуальное любопытство очень важно. Вам не обязательно заканчивать поиск с вашими профессорами, вы, вероятно, обнаружите, что разные люди, которых вы встретите, смогут дать ответы на разные вопросы. В этом смысле хорошо, что вы спрашиваете об этом здесь. Никогда не помешает, если инженер хорошо знает свою математику, задает себе глубокие вопросы и старается серьезно на них ответить. Я думаю, что это, вероятно, сделает вас лучшим профессионалом (или лучшим человеком), если вы найдете свой собственный путь через обучение. 4– Этот четвертый вопрос был задан здесь несколькими людьми, у меня, возможно, нет лучшего ответа, чем у многих из них. $\endgroup$ $\begingroup$ Если я правильно понимаю, ваш вопрос состоит в следующем: как мы можем сказать, что предел равен $\textbf{равно}$ чему-то, если на самом деле он только когда-либо $\textbf{становится очень близким}$? Это связано с тем, как мы выбрали предел $\textbf{define}$. Можно сказать, это вопрос условности. Чтобы подчеркнуть это, обратите внимание на то, что говорит ваше определение дельта-эпсилон: “$\textbf{Мы говорим}$, что предел $f(x)$ при $x$ переходит в $a$ $\textbf{равно}$ $L$ тогда и только тогда, когда для всех $\varepsilon >0$ существует $\delta>0$, так что $|f(x)-L|<\varepsilon$ всякий раз, когда $|x-a|<\delta$. Теперь предположим, что у нас есть функция $f(x)=x$, и я задаю вам следующий вопрос: Какое уникальное число $L$ позволит мне сделать $|f(x)-L|$ сколь угодно маленьким, если я подберу $x$ очень близко к $0$ $\textit{ie.}$ если я возьму $|x-0|<\delta$? В этом случае работает число $L=0$. Так что же говорит наше определение об этом $L$? В нем говорится, что предел $f$, когда $x$ стремится к $0$, $\textbf{равно}$ $L$. Или запишите в более компактной форме $\lim\limits_{x \to 0}f(x)=L=0$. Когда мы говорим, что предел функции равен чему-то, мы имеем в виду, что он равен числу $L$ со свойствами, указанными в определении. $\endgroup$ 4 $\begingroup$ Интересные апплеты: Апплет Дельта-Эпсилон Определение предела Эпсилон-дельта $\endgroup$ $\begingroup$ Один из способов объяснить, как $2x+\Delta x$ «превращается» в $2x$, — это применить стандартную функцию части. Таким же образом можно объяснить и предел последовательности $(u_n)$. Здесь взятие предела включает два шага: (1) вычисление последовательности при бесконечном значении индекса $n=H$, скажем, и (2) взятие стандартной части. Например, пределом $(\frac{1}{n})$ является стандартная часть $\frac{1}{H}$. Поскольку $H$ бесконечно, $\frac{1}{H}$ бесконечно мала, а стандартная часть каждой бесконечно малости равна $0$. Таким образом, $$\lim _{n\to\infty}\frac{1}{n}=\text{st}\left(\frac{1}{H}\right)=0.$$ Редактировать 1. ОП написал: “После некоторых манипуляций я бы получил $\lim_{\Delta x \rightarrow 0} 2x + \Delta x$, а так как $\Delta x$ переходит в $0$, это будет равно $2x$. Объяснение в том, что вычисление предела с использованием действительных чисел составляет косвенная процедура. Сначала вам нужно угадать значение предела методом проб и ошибок или с помощью какой-либо эвристической процедуры, и только затем построить доказательство , обычно эпсилон-дельта, что это число работает. Здесь эпсилон-дельта — это окольный способ объяснить исчезновение остаточного члена $\Delta x$. С другой стороны, если рассматривать предел как двухэтапную процедуру, как описано выше (сначала оценить бесконечный индекс, а затем применить стандартную часть для отбрасывания оставшихся бесконечно малых), можно получить прямая процедура избавления от остаточного члена, позволяющая одновременно угадать ответ и доказать, что он правильный. $\endgroup$ $\begingroup$ Нам нужно опросить таких людей, как вы, в инженерии, математике и естественных науках. Шестьдесят лет назад и с тех пор у меня была точно такая же проблема. Вот идея предела, о котором вам не сказали. Некоторые функции имеют значение для определенного значения переменной, но его нельзя найти, подставив значение переменной, поскольку функция не определена для этого значения. Рассмотрим функцию x/x. Это не определено при x=0, потому что любое значение, умноженное на 0, равно 0. Но эта функция приближается к 1, когда x->0 с обеих сторон, поэтому мы придумали идею предела, который представляет собой более общий способ определения значения a. функционировать в точке. В этом суть. Это удивительно просто и гениально. Теперь рассмотрим функцию 1/x. Когда x приближается к 0 справа, функции приближаются к бесконечности, а слева – к отрицательной бесконечности; поэтому эта функция не имеет значения при x=0. Я надеюсь, что это поможет, и что вы продолжаете настаивать на том, что все имеет смысл. Нам нужны такие люди, как вы. $\endgroup$ 10 $\begingroup$ Во-первых, извините, это немного длинно… но, Я думаю, это может вам помочь. Это одна из вещей, которую мы изучили на курсе «Введение в анализ», когда мы работали с ограничениями. Лемма Если $x \in \mathbb{R}$ такое, что $\forall \delta \geq 0, \; 0\leq x < \delta$, то $x=0$. Доказательство: Предположим иначе, $x>0$. Тогда пусть $\delta=\frac{x}{2} \ подразумевает 0\leq \delta =\frac{x}{2} $ \поэтому x=0$. Как только это будет доказано, мы просто примем это, но это важно отметить. Это поможет вам немного объяснить 1. Во-первых, предел — это всего лишь предел. Это не функция $\Delta x$, хотя может быть удобно подставить значения, близкие к числу, к которому вы приближаетесь, чтобы почувствовать его. Идея заключалась бы в том, что предел не должен зависеть от переменной, используемой для определения предела ($\Delta x$), он должен «принимать» значение, к которому он стремится. В раннем определении непрерывности, без учета эпсилонов и дельт, вы говорите, что функция одной действительной переменной непрерывна в точке $c \in \mathbb{R}$, если: $\lim\limits_{x\rightarrow c} f(x)=f(c)$. В этом случае наш предел не имеет $x$, это просто число (надеюсь), если мы выберем функцию, непрерывную в c. Тогда вы можете говорить о функции, являющейся производной другой функции, если они совпадают в каждой точке некоторого набора/интервала. То же самое для нашей производной. $g(x)=\begin{cases} \frac{f(x)-f(c)}{x-c} \quad & \text{ if } x\neq c \\ f'(c) \quad & \text{ if } x=c \end{cases}$ Итак, если $f$ дифференцируема в $c, то f'(c)$ существует. Если бы мы не определяли второй случай $x=c$ отдельно в определении $g$ и предел существовал (и был конечен), то мы бы назвали $c$ устранимой особенностью $g$. По сути, мы знаем, что $g$ «имеет» там значение, но формула не позволяет нам напрямую подставляться. Вроде того, о чем вы говорили с проблемой $\frac{0}{0}$. Кажется, Апостол упоминает об этом в какой-то из своих книг по математике или, может быть, в книге по математическому анализу. Затем вы работаете над тем, чтобы сделать эти вещи строгими с эпсилонами и дельтами, как писали другие люди, поэтому я не буду повторяться (надеюсь, я уже этого не делал). Я думаю, что другие говорили что-то о сходимости сумм, так что я пока оставлю это. Так что в этом много всего, так что не расстраивайтесь, если вы застряли с частями этого, я тоже довольно часто застреваю. Надеюсь, это будет полезно и без опечаток/ошибок 🙂 $\endgroup$ $\begingroup$ Мне кажется, вы путаете понятие последовательности с понятием предела. Предположим, что $(x_n)_{n\in \mathbb{N}}$ — сходящаяся последовательность действительных чисел, а $x=\lim \limits_{n\to \infty} x_n$ — предел этой последовательности. Этот предел $x$ является действительным числом и представляет собой нечто совершенно иное, чем последовательность (формально последовательность $(x_n)$ — это отображение $f:\mathbb{N}\rightarrow \mathbb{R}$, где мы обозначаем $ f(n)$ на $x_n$). Тогда ваш вопрос сводится к следующему: почему производная $2x$, а не $2x +h_n$ для некоторого $n$? Ну, поскольку производная равна пределу последовательности, и этот предел равен $2x$. Неважно, что $h_n$ никогда не станет равным 0, достаточно, чтобы оно было сколь угодно близко к 0, потому что предел — это нечто отличное от последовательности и ее элементов. Итак, до сих пор я использовал такие понятия, как близость , которые вы критиковали в своем 4-м вопросе. Но, как указывает Кристиан Блаттер, существуют строгие определения, делающие эти понятия более точными, а именно определение предела и определение $\epsilon-\delta$. Поэтому, если вы доказываете свои теоремы, используя эти определения, проблем не возникает. 9{N}a_n$$ Термин бесконечная сумма может немного ввести в заблуждение, поскольку на самом деле это не сумма, а предел последовательности. $\endgroup$ 2 $\begingroup$ Прежде чем мы подумаем о пределах функций в исчислении, возможно, имеет смысл поговорить о пределах в топологическом смысле. A предельная точка , в топологическом смысле, — это точка $x$ в некотором топологическом пространстве $X$ ($\subset \mathbb{R}$, если угодно) такая, что каждая окрестность $x$ содержит точку в $X долларов, кроме $x$. Другими словами, какой бы маленький шар мы ни рисовали вокруг $x$, мы можем найти какую-то другую точку в этом шаре $y \in X$ такую, что $y \neq x$. Это определение не дает никакой информации о том, где может находиться точка $y$ по отношению к $x$, или любой другой подобной информации, которую можно извлечь из функции. Но что он делает, так это дает нам возможность построить последовательность . Помните, что определение предельной точки дает нам свободу выбора окрестности любого размера. Таким образом, для убывающей последовательности радиусов $\epsilon_1 > \epsilon_2 > \cdots$ мы можем найти точки $y_1, y_2, \ldots$, которые все ближе и ближе к $x$. Теперь поговорим о функциях. Предположим, что наше множество $X$ было образом функции $f(t)$. Далее предположим, что $t$ является предельной точкой $T$, и, следовательно, мы можем найти последовательность радиусов $\delta_1 > \delta_2 > \cdots$, которая индуцирует последовательность $t_1, t_2, \ldots$, приближающуюся к $ т$. Если наша функция обладает некоторыми хорошими свойствами (в частности, свойствами, которые мы определяем с помощью этих определений $\epsilon-\delta$!), то мы можем сказать, что последовательность $t_1, t_2, \ldots$ при преобразовании с помощью $f$ порождает последовательность $f(t_1), f(t_2), \ldots$, приближающуюся к $x$! Это топологическое определение удобно, потому что оно не заботится о символических причудах, которые приводят к ситуациям $\frac{0}{0}$ или $\frac{\infty}{\infty}$. Либо последовательности есть, либо их нет. Когда мы говорим что-то вроде $\lim_{t\to a} f(t) = a$, мы на самом деле утверждаем существование последовательности в области, которая индуцирует последовательность в диапазоне, удовлетворяющем определению предельной точки. Это же понятие может также объяснить, почему определение бесконечных рядов в виде частичной суммы имеет смысл. Каждая частичная сумма оценивается как число. Составим последовательность этих чисел. Если последовательность этих чисел образует путь к одной точке по мере того, как мы добавляем к последовательности все больше и больше чисел, то мы утверждаем, что бесконечный ряд сходится. Короче говоря, самый простой способ думать об ограничениях — это на мгновение отвлечься от функциональных обозначений и мышления и вместо этого подумать о пространстве. Поиск ограничений похож на поиск набора инструкций о том, как добраться до этой точки; или, что более уместно, доказательство того, что такой набор инструкций действительно существует. Это понятие также формализует нестрогое представление «числа, очень близкого к бла». $\endgroup$ $\begingroup$ Далее следует то, что я опубликовал в дискуссионной группе ap-calculus на форуме Math Forum 13 марта 2006 г., и это может быть полезно. Недавно я наткнулся на короткую заметку о том, как донести идею предела до учащихся, и я думал, что читатели этого списка сочтут ее полезной. Полный текст этой короткой заметки приведен ниже. Джеймс Клайд Брэдфорд, Анекдоты для пределов , Школьная естествознание и математика 92 – 1}{x-1}$ вычисляется, мы часто говорим, что нельзя позволить $x$ принимать значение $1$, так как функция в этой точке не определена. Я надеваю свои семиместные ботинки и отправляюсь в город. Эти сапоги таковы, что каждый последующий шаг уносит меня на половину оставшегося расстояния до города. Я никогда не добираюсь до города, но я подхожу достаточно близко, чтобы сделать покупки. Допустить, что $x$ равняется $1$, это все равно, что совершить грех. На самом деле мы не совершим греха, но подойдем достаточно близко, чтобы увидеть, на что это похоже. $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Обязательно, но не отображается Электронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie Дом Узнать Исчисление Предел — это математическое вычисление, которое сообщает нам значение, принимаемое математическим выражением/функцией, когда независимая переменная приближается к определенному значению.
определенное значение. Пусть функция `f(x`) определена на открытом интервале в окрестности числа “а”. Символически , `Lim_(x->a) f(x) = L ` И читается как “Предел `f(x)`, поскольку `x-> `a равно L” . В соответствии с этим определением предела функции мы можем разделить пределы на следующие три типа: Есть несколько фундаментальных теорем о пределах функций. Мы приводим их краткие заявления здесь. `Lim_(x->a) [u(x) – v(x)] `= `Lim_(x-> а) u(x)` – `Lim_(x->a) v(x) `= P – Q `Lim_( x->a) [Cu(x)]` = C `Lim_(x->a) [u(x)]` = CP `Lim_(x->a) [u(x) v(x)] `= `[Lim_(x->a) u(x)] [ Lim_(x->a) v(x)]` = P Q `Lim_(x->a) (( u(x))/( v(x)))` = ` ( Lim_(x->a) u(x))/(Lim_(x->a) v(x))`=` ( P )/( Q )(`При условии `Q ≠ 0)` 9n ` В исчислении много раз возникает ситуация, когда ввод значения `x` дает нам выражение формы `( 0 )/( 0 )` . Когда возникает такая ситуация,
мы используем метод упрощения, чтобы разложить на множители выражения числителя и знаменателя, чтобы увидеть, есть ли общий множитель для обоих. Если такой общий множитель все-таки встречается, мы их сокращаем и обычно получаем выражение, в котором введение предела не дает нам вида `( 0 )/( 0 ) `. Мы представили некоторые из примеров такого сценария здесь: При оценке пределов на бесконечности мы делим члены числителя и знаменателя на наибольшую степень переменной, которая появляется в знаменателе, и
затем поместите предел в новое сформированное выражение. Спираль Предлагаемые языки для вас: Америка Английский (США) StudySmarter — универсальное учебное приложение. 4.8 • Рейтинг +11k Более 3 миллионов загрузок Бесплатно Сохранять Распечатать Редактировать Ограничения Содержание : ОГЛАВЛЕНИЕ Вы когда-нибудь слышали поговорку « близко только в подковы и ручные гранаты »? Что ж, оказывается, это не совсем так. Близость, или , почти достигающая цели , также учитывается в исчислении — при работе с ограничивает , то есть! Основная концепция предела в математике необходима для вашего понимания исчисления. Эта концепция существует уже тысячи лет; ранние математики использовали эту концепцию, чтобы найти все более и более точные приближений из площадь круга , например. Однако формальное определение предела появилось только в 19 -м веке. Итак, чтобы начать свое путешествие к пониманию пределов, вам следует начать с интуитивного определения. Чтобы найти интуитивное определение предела, вы должны сначала иметь функцию (или несколько функций), о которой вы хотите узнать больше подробностей. Взгляните на графики следующих функций: 9{2}} \] Вы хотите обратить внимание на поведение этих графиков при приближении к значению \( x=2 \). Обратите внимание на график, где \( x = 2 \). Обратите внимание на график, где \( x = 2 \). Обратите внимание на график, где \( x = 2 \). Графики этих функций показывают их поведение при \( x=2 \) и около него. Чтобы сформулировать этот факт в математических терминах, вы бы сказали: «Предел \( f(x) \) при приближении \( x \) к \( 2 \) равен \( 4 \)». Это утверждение представлено в математической записи как: \[ \lim_{x \to 2} f(x) = 4. \] Отсюда вы можете начать развивать интуитивное определение предела – думая о пределе функции при числе \( a \) как о действительном числе \ ( L \ ), к которому функциональные значения приближаются по мере приближения его \ ( x \) -значения \ ( a \ ), при условии, что число \( L \) существует. Более формально это можно записать так: Пусть \( f(x) \) — функция, определенная при всех значениях открытого интервала, содержащего \( a \) (возможно, кроме \( a \)), и пусть \( L \) — вещественная количество. Или, проще говоря: По мере того как \( x \) все ближе и ближе к \( a \), \( f(x) \) становится все ближе и ближе и остается близким к \( L \). Идея предела представлена с помощью математической записи как: \[ \lim_{x \to a} f(x) = L \] Как видите, простое приближение к – или приближение – к Дело в том, как работают ограничения! Чтобы разработать и понять ключевые аспекты исчисления, вам сначала нужно освоиться с ограничениями и тем фактом, что приближения — или приближение к желаемому значению — являются основой исчисления. Итак, теперь вы можете изменить поговорку с: Прежде чем погрузиться в алгебраические методы, следующий шаг, который нужно сделать интуитивно, — разработать способ решения пределов путем их оценки. Решение ограничения с помощью таблицы функциональных значений Решение ограничения с помощью графика Чтобы решить предел с помощью таблицы функциональных значений, вы можете использовать эту стратегию решения проблем. Стратегия – Решение предела с помощью таблицы функциональных значений Можно расширить описанная выше стратегия решения проблем для решения предела с использованием графа. Стратегия – определение предела с помощью графика Обратите внимание, что вам может понадобиться увеличить график и повторить эти шаги несколько раз. Дополнительные сведения и примеры см. в статьях о нахождении пределов и нахождении пределов с помощью графика или таблицы. Хотя два описанных выше метода интуитивно понятны, они неэффективны и полагаются на слишком много догадок, чтобы выполнить работу. Но как вы можете пройти мимо этих методов? Ну, вам нужно изучить методы решения или оценки пределов, которые по своей природе более алгебраичны. И как вы можете это сделать? Во-первых, вы должны знать о двух специальных ограничениях; они обеспечивают основу алгебраических методов решения пределов. А что такого особенного в этих двух пределах? Эти два предела также известны как базовые пределы , поскольку они обеспечивают основу для законов пределов. Когда вы смотрите на графики ниже, что вы замечаете? Независимо от того, где на линии \( y = x \) находится точка \( (a, a) \), предел при приближении \(x\) к \(a\) всегда равен \(a\). Независимо от того, где на линии \( y = c \) находится точка \( (x, c) \), предел при приближении \(x\) к любому вещественному числу \(a\) всегда равен \(c \). Основываясь на этих графиках, вы можете алгебраически расписать предел этих функций. Их алгебраические интерпретации резюмируются в следующей теореме. Пусть \( a \) – действительное число. Пусть \(с\) — константа. Затем: \[ \begin{align}1. \; & \lim_{x \to a} x = a \\2. \; & \lim_{x \to a} c = c\end{align} \] Об этих двух пределах можно наблюдать следующее: Основываясь на этих первых двух основных правилах ограничения, правила ограничения (также называемые законами ограничения) перечислены ниже. Пусть \( f(x) \) и \(g(x) \) определены для всех \( x \neq a \) на открытом интервале, содержащем \( a \). Предположим, что \( L \) и \( M \) – действительные числа, такие, что: \[ \lim_{x \to a} f(x) = L \] и\[ \lim_{x \ к а} g(x) = M \] Пусть \( c \) — константа. Тогда верно следующее: Закон сумм для пределов : \[ \lim_{x \to a} (f(x) + g(x)) = \lim_{x \to a} f(x ) + \lim_{x \to a} g(x) = L + M \] Разностный закон для пределов : \[ \lim_{x \to a} (f(x) – g(x )) = \lim_{x \to a} f(x) – \lim_{x \to a} g(x) = L – M \] Постоянный кратный закон для пределов : \[ \lim_ {x \to a} (c \cdot f(x)) = c \cdot \lim_{x \to a} f(x) = cL \] 9{n} \mbox{ для каждого положительного целого числа } n \] Корневой закон для пределов : \[ \lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[ n]{\lim_{x \to a} f(x)} = \sqrt[n]{L} \mbox{ для всех } L \mbox{, если } n \mbox{ нечетно, и для } L \geq 0 \mbox{ если } n \mbox{ четно} \] Имейте в виду, что существуют и другие предельные законы – теорема сжатия и теорема о промежуточном значении. При работе со следующим примером помните, что для существования предела функциональные значения должны приближаться к одному вещественному значению; в противном случае предела не существует. Оценка несуществующего предела (DNE) Из-за колебаний Попытаться оценить \[ \lim_{x \to 0} sin \left( \frac{1}{x} \right ) \] с использованием таблицы функциональных значений. Решение : Предел : \( \lim_{x \to 0} sin \left( \frac{1}{x} \right) \) не существует потому что функция сильно колеблется как \( x \ ) приближается к пределу \( 0 \). Бывают случаи, когда утверждение, что предел функции не существует в какой-либо точке, не дает достаточной информации об этой точке. Чтобы убедиться в этом, еще раз взгляните на вторую функцию из начала этой статьи. \[ g(x) = \frac{|x-2|}{x-2} \] При выборе значений \( x \), которые все ближе и ближе к \( 2 \), \ ( g(x) \) приближается не к одному значению , а к двум значениям. \[ \lim_{x \to 0} g(x) \, DNE. \] Хотя это утверждение верно, не могли бы вы сказать, что оно не дает полной картины поведения \( g(x) \) при \( x = 2 \)? С односторонними пределами можно дать более точное описание поведения этой функции при \( x = 2 \). Для всех значений \( x \) до осталось от \( 2 \) – или отрицательная часть \( 2 \) – \( g(x) = -1 \). Итак, вы говорите, что , когда \( x \) приближается \( 2 \) слева, \( g(x) \) приближается \( -1 \) 9{+}} h(x) = +\infty \] Важно понимать, что когда вы говорите, что предел бесконечен, это не означает, что предел существует. Это просто более наглядный способ сказать, что предела не существует. \( \pm \infty \) не является действительным числом, поэтому любой бесконечный предел не является пределом, который существует. В общем, пределы на бесконечности определяются как: Три типа бесконечных пределов Используйте предельные законы для решения: \[ \lim_{x \to -3} (4x+2) \] Решение : Чтобы решить этот предел предельные законы по одному. Имейте в виду, что на каждом этапе вам нужно проверять, существует ли ограничение, прежде чем применять закон. В математике пределы — это значения, к которым приближаются функции, когда их входные данные приближаются к некоторому значению. Пределы — это инструмент, который можно использовать для определения поведения функции в непосредственной близости от ее неопределенных точек или диапазонов точек. Пределы являются основой исчисления и используются для определения непрерывности, производных и интегралов. В базовом исчислении предел — это значение, к которому приближается функция, когда ее вход приближается к некоторому значению. Чтобы найти предел функции, вы напрямую подставляете значение, к которому приближается независимая переменная (обычно x), и решаете. Если это невозможно, вы можете попробовать некоторые алгебраические манипуляции с функцией, например, Как только вы упростите предел с помощью этих методов, вы можете найти предел с помощью прямой подстановки. Проще говоря, предела не существует, если функциональные значения не приближаются к одному значению. Это происходит в следующих случаях: Вопрос Каково интуитивное определение предела? Показать ответ Ответ Думайте о пределе функции с числом а как о действительном числе L, к которому функциональные значения приближаются по мере того, как его значения x приближаются к а, при условии, что число L существует. Показать вопрос Вопрос Каково формальное определение предела? Показать ответ Ответ Пусть f(x) — функция, определенная для всех значений открытого интервала, содержащего a (возможно, кроме a), и пусть L — действительное число. Или, проще говоря: По мере того, как x становится все ближе и ближе к a, f(x) становится все ближе и ближе и остается близкой к L. Идея предела представлена с использованием математической записи как: Показать вопрос вопрос Каковы два способа интуитивного определения предела? Показать ответ Ответить Используя таблицу функциональных значений. Показать вопрос Вопрос Каковы два важных ограничения? Показать ответ Ответ Показать вопрос Вопрос Когда не существует предела? Показать ответ Ответ Предел не существует, если функциональные значения не приближаются к одному вещественному значению. Показать вопрос Вопрос В каких случаях предел не существует? Показать ответ Ответ Когда функция колеблется все более и более сильно по мере приближения к пределу. Показать вопрос Вопрос Какие существуют 3 типа бесконечных пределов? Показать ответ Ответить Показать вопрос Вопрос Каков закон сумм для пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всех на открытом интервале, содержащем a. Предположим, что L и M — действительные числа, такие, что: и Пусть c — константа. Тогда закон сумм для пределов: Показать вопрос Вопрос В чем отличие закона пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всего открытого интервала, содержащего a. и Пусть c — константа. Тогда разностный закон для пределов: Показать вопрос Вопрос Что такое постоянный кратный закон для пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всего открытого интервала, содержащего a. Предположим, что L и M — действительные числа, такие что: и Пусть c — константа. Тогда постоянный кратный закон для пределов: Показать вопрос Вопрос Каков закон произведения для пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всего открытого интервала, содержащего a. Предположим, что L и M — действительные числа, такие, что: и Пусть c — константа. Тогда закон произведения для пределов: Показать вопрос Вопрос Каков закон частных для пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всего открытого интервала, содержащего a. и Пусть c — константа. Тогда частное для пределов: Показать вопрос Вопрос Каков степенной закон для пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всего открытого интервала, содержащего a. Предположим, что L и M — действительные числа, такие, что: и Пусть c — константа. Тогда степенной закон для пределов: Показать вопрос Вопрос Каков основной закон для пределов? Показать ответ Ответ Пусть f(x) и g(x) определены для всего открытого интервала, содержащего a. Предположим, что L и M — действительные числа, такие что: и Пусть c — константа. Тогда основной закон для пределов: Показать вопрос Подробнее о лимитах Будьте идеально подготовлены вовремя с индивидуальным планом. 1,9999 2,92−4∣}{x−2}=4\) Ключевые понятия

Ключевые уравнения
Глоссарий
Авторы и авторство
 Платформа; подробная история редактирования доступна по запросу.
Платформа; подробная история редактирования доступна по запросу. org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 Ограничения – Математика средней школы
Ограничения – Математика средней школы СРЕДНЯЯ ШКОЛА
ВЫСШАЯ ШКОЛА
К-8
Поиск 50+ тестов
репетиторство по математике
репетиторство по естественным наукам
иностранные языки
начальное обучение
прочие
Поиск по 350+ темам
Все математические ресурсы средней школы
 Самый простой способ узнать, к какому -значению приближается функция, – это подставить -значение в уравнение.
Самый простой способ узнать, к какому -значению приближается функция, – это подставить -значение в уравнение.
2
Объяснение:
2 

Сертифицированный репетитор
Сертифицированный репетитор Онлайн-кампус Университета Феникса, магистр …
Онлайн-кампус Университета Феникса, магистр …
Сертифицированный репетитор Все ресурсы по математике для старших классов
Лимит | Encyclopedia.com


 Поскольку (1/2) n равно 1/2, умноженному само на себя n раз, (1/2) n становится очень маленьким, когда n позволяет стать бесконечно большим. Говорят, что последовательность сходится, что означает, что числа, которые находятся очень далеко в последовательности (соответствует большому «N»), очень близко друг к другу и очень близко к одному значению, называемому пределом.
Поскольку (1/2) n равно 1/2, умноженному само на себя n раз, (1/2) n становится очень маленьким, когда n позволяет стать бесконечно большим. Говорят, что последовательность сходится, что означает, что числа, которые находятся очень далеко в последовательности (соответствует большому «N»), очень близко друг к другу и очень близко к одному значению, называемому пределом. (Функция — это множество упорядоченных пар, для которых первый и второй элементы каждой пары связаны друг с другом фиксированным образом. Когда элементами упорядоченных пар являются действительные числа, отношение обычно выражается в виде уравнение.) Предположим, что последовательные значения x выбраны так, чтобы соответствовать значениям сходящейся последовательности, такой как последовательность S из предыдущего примера. Возникает вопрос, что делают значения функции, то есть что происходит с последовательными значениями у. Фактически всякий раз, когда значения x образуют последовательность, значения f (x) также образуют последовательность. Если эта последовательность является сходящейся последовательностью, то предел этой последовательности называется пределом функции. В более общем случае, когда значение функции f (x) приближается к определенному значению L, поскольку независимая переменная x приближается к действительному числу p, тогда L называется пределом функции.
(Функция — это множество упорядоченных пар, для которых первый и второй элементы каждой пары связаны друг с другом фиксированным образом. Когда элементами упорядоченных пар являются действительные числа, отношение обычно выражается в виде уравнение.) Предположим, что последовательные значения x выбраны так, чтобы соответствовать значениям сходящейся последовательности, такой как последовательность S из предыдущего примера. Возникает вопрос, что делают значения функции, то есть что происходит с последовательными значениями у. Фактически всякий раз, когда значения x образуют последовательность, значения f (x) также образуют последовательность. Если эта последовательность является сходящейся последовательностью, то предел этой последовательности называется пределом функции. В более общем случае, когда значение функции f (x) приближается к определенному значению L, поскольку независимая переменная x приближается к действительному числу p, тогда L называется пределом функции. Формально это записывается как:
Формально это записывается как: Такой функцией является функция, определяемая уравнением y = 1/x. Если для функции существует конечный предел, когда
Такой функцией является функция, определяемая уравнением y = 1/x. Если для функции существует конечный предел, когда КЛЮЧЕВЫЕ ТЕРМИНЫ
 Интересно отметить, что функция, определяемая y = 1/x, не имеет предела, когда x приближается к 0, но имеет предел L = 0, когда x приближается к ∞.
Интересно отметить, что функция, определяемая y = 1/x, не имеет предела, когда x приближается к 0, но имеет предел L = 0, когда x приближается к ∞.
КНИГИ
 То есть предел — это значение, которое переменная количество приближается настолько близко, насколько хочется. Операции дифференцирования и интегрирования из исчисления основаны на теории пределов. Теория пределов основана на особом свойстве действительных чисел ; а именно, что между любыми двумя действительными числами, независимо от того, насколько они близки друг к другу, всегда есть другое. Между любыми двумя действительными числами всегда есть бесконечно много других.
То есть предел — это значение, которое переменная количество приближается настолько близко, насколько хочется. Операции дифференцирования и интегрирования из исчисления основаны на теории пределов. Теория пределов основана на особом свойстве действительных чисел ; а именно, что между любыми двумя действительными числами, независимо от того, насколько они близки друг к другу, всегда есть другое. Между любыми двумя действительными числами всегда есть бесконечно много других. История
 Тезис Архимеда Метод был утерян до 1906 года, когда математики обнаружили, что Архимед был близок к открытию исчисления бесконечно малых.
Тезис Архимеда Метод был утерян до 1906 года, когда математики обнаружили, что Архимед был близок к открытию исчисления бесконечно малых. Предел последовательности


Предел функции
 Формально это записывается так:
Формально это записывается так: Такой функцией является функция, определяемая уравнением y = 1/x. Если для функции существует конечный предел, когда независимая переменная стремится к бесконечности, формально она записывается как:
Такой функцией является функция, определяемая уравнением y = 1/x. Если для функции существует конечный предел, когда независимая переменная стремится к бесконечности, формально она записывается как: Приложения
 Пределы также являются частью итеративного процесса. Итерация повторно выполняет подпрограмму, используя выходные данные одного шага в качестве входных данных для следующего шага. Каждый вывод представляет собой итерацию. Некоторые успешные итерации могут максимально приблизиться к теоретически точному значению.
Пределы также являются частью итеративного процесса. Итерация повторно выполняет подпрограмму, используя выходные данные одного шага в качестве входных данных для следующего шага. Каждый вывод представляет собой итерацию. Некоторые успешные итерации могут максимально приблизиться к теоретически точному значению. Ресурсы
книги
периодические издания
 Scientific American 271 (1994): 84-89.
Scientific American 271 (1994): 84-89. КЛЮЧЕВЫЕ ТЕРМИНЫ

Последовательности чисел
 Три точки означают, что последовательность не заканчивается последним числом в списке, а продолжается бесконечно.
Три точки означают, что последовательность не заканчивается последним числом в списке, а продолжается бесконечно. Последовательность 1, 2, 3, 4… увеличивается и не приближается ни к одному значению. Другой пример последовательности без ограничений: -1,1, 2,2, -3,3, 4,4, -5,5, 6,6, …. Поскольку нет определенного числа, к которому приближается эта последовательность, последовательность не имеет предела.
Последовательность 1, 2, 3, 4… увеличивается и не приближается ни к одному значению. Другой пример последовательности без ограничений: -1,1, 2,2, -3,3, 4,4, -5,5, 6,6, …. Поскольку нет определенного числа, к которому приближается эта последовательность, последовательность не имеет предела. Функции
 По мере увеличения значений x цветовая кривая или значения f ( x ) становятся все ближе и ближе к 0. И снова предел функции, когда x стремится к бесконечности, равен 0,9.0032
По мере увеличения значений x цветовая кривая или значения f ( x ) становятся все ближе и ближе к 0. И снова предел функции, когда x стремится к бесконечности, равен 0,9.0032 Геометрические фигуры
 Например, один из методов оценки площади круга состоит в том, чтобы разделить круг на маленькие треугольники, как показано ниже, и суммировать площади этих треугольников. Окружность в (а) разделена на шесть треугольников. Если требуется более точная оценка площади, круг можно разделить на меньшие треугольники, как показано на (b).
Например, один из методов оценки площади круга состоит в том, чтобы разделить круг на маленькие треугольники, как показано ниже, и суммировать площади этих треугольников. Окружность в (а) разделена на шесть треугольников. Если требуется более точная оценка площади, круг можно разделить на меньшие треугольники, как показано на (b).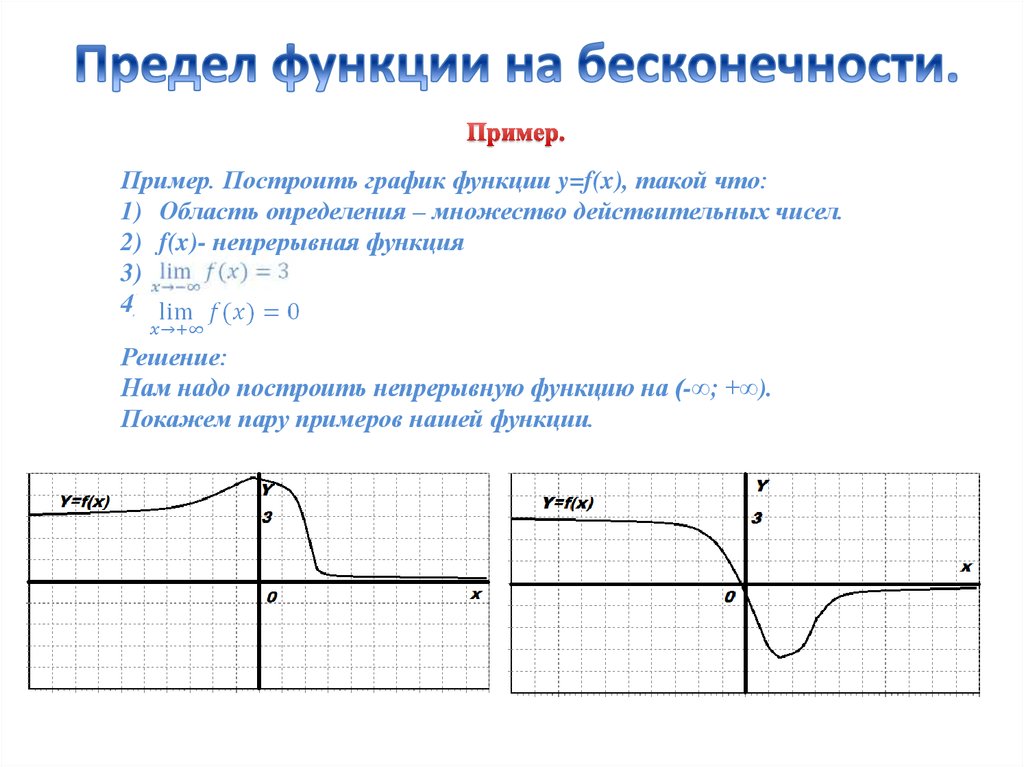 Их также можно использовать для определения площади геометрических фигур. Расширяя процесс, используемый для нахождения площади геометрической формы, можно также найти объем геометрических тел, используя концепцию предела.
Их также можно использовать для определения площади геометрических фигур. Расширяя процесс, используемый для нахождения площади геометрической формы, можно также найти объем геометрических тел, используя концепцию предела. Библиография
Интернет-ресурсы
 ∎ (часто ограничивает) конечная точка или граница области или движения: городские границы верхняя граница приливных участков. ∎ крайняя степень физической или умственной выносливости: Мэри Энн испытывала всеобщее терпение до предела другие лошади были на пределе. 2. ограничение размера или количества чего-либо допустимого или возможного: ограничение по возрасту ограничение по весу. ∎ ограничение скорости: ограничение 30 миль в час. ∎ (в карточных играх) согласованная максимальная ставка или ставка. ∎ (также установленный законом предел) максимальная концентрация алкоголя в крови, разрешенная законом у водителя транспортного средства: риск того, что пьющие непреднамеренно превысят лимит . 3. Матем. точка или значение, к которым можно постепенно приближать последовательность, функцию или сумму ряда, пока они не окажутся настолько близкими к точке или значению, насколько это необходимо.
∎ (часто ограничивает) конечная точка или граница области или движения: городские границы верхняя граница приливных участков. ∎ крайняя степень физической или умственной выносливости: Мэри Энн испытывала всеобщее терпение до предела другие лошади были на пределе. 2. ограничение размера или количества чего-либо допустимого или возможного: ограничение по возрасту ограничение по весу. ∎ ограничение скорости: ограничение 30 миль в час. ∎ (в карточных играх) согласованная максимальная ставка или ставка. ∎ (также установленный законом предел) максимальная концентрация алкоголя в крови, разрешенная законом у водителя транспортного средства: риск того, что пьющие непреднамеренно превысят лимит . 3. Матем. точка или значение, к которым можно постепенно приближать последовательность, функцию или сумму ряда, пока они не окажутся настолько близкими к точке или значению, насколько это необходимо. •
v. (limit·it·ed, lim·it·ing) [tr.] установить или служить ограничением для: попытаться ограничить количество выпитого размеры классов ограничены до максимум 10 [ как прил.] (ограничивающий) ограничивающий фактор. ФРАЗ: – предел инф. быть невыносимо беспокойным или раздражающим. не было темы, закрытой для обсуждения. в пределах умеренно; до определенного момента: без ограничений без ограничений. ПРОИЗВОДНЫЕ: lim·i·ta·tive / ˈliməˌtātiv/ прил.
•
v. (limit·it·ed, lim·it·ing) [tr.] установить или служить ограничением для: попытаться ограничить количество выпитого размеры классов ограничены до максимум 10 [ как прил.] (ограничивающий) ограничивающий фактор. ФРАЗ: – предел инф. быть невыносимо беспокойным или раздражающим. не было темы, закрытой для обсуждения. в пределах умеренно; до определенного момента: без ограничений без ограничений. ПРОИЗВОДНЫЕ: lim·i·ta·tive / ˈliməˌtātiv/ прил.
 Св. Фома утверждает, что никакое положительное качественное совершенство, такое как знание, добро, или сила, может быть тождественно своим предельным принципом, т. е. причиной, по которой данное существо обладает ею в ограниченной степени, а не в своей полноте. Следовательно, везде, где есть ограничение, должна быть внутренняя двойственность или реальное метафизическое различие элементов внутри ограниченного существа: один принцип заботиться о положительном совершенстве, которое получено или причастно; другой для ограничения возможностей субъекта, который получает или участвует. Это философское учение, именуемое ограничением действия потенцией, может быть резюмировано следующим образом: ни одно действие (или совершенство) не может быть найдено в ограниченном состоянии, если оно не воспринято в действительно отличной ограничивающей потенции.
Св. Фома утверждает, что никакое положительное качественное совершенство, такое как знание, добро, или сила, может быть тождественно своим предельным принципом, т. е. причиной, по которой данное существо обладает ею в ограниченной степени, а не в своей полноте. Следовательно, везде, где есть ограничение, должна быть внутренняя двойственность или реальное метафизическое различие элементов внутри ограниченного существа: один принцип заботиться о положительном совершенстве, которое получено или причастно; другой для ограничения возможностей субъекта, который получает или участвует. Это философское учение, именуемое ограничением действия потенцией, может быть резюмировано следующим образом: ни одно действие (или совершенство) не может быть найдено в ограниченном состоянии, если оно не воспринято в действительно отличной ограничивающей потенции.
 Например, в передаче «Владелец передает Blackacre A до тех пор, пока B не покинет страну», имущество A ограничено, поскольку A получает Blackacre только на определенный период времени.
Например, в передаче «Владелец передает Blackacre A до тех пор, пока B не покинет страну», имущество A ограничено, поскольку A получает Blackacre только на определенный период времени.
Так лимит вб. XIV. – (ИЗ. ограничитель или L. ограничитель . ограничение XIV. исчисление – Почему ограничивает работу
 Я умею вычислять пределы, производные, интегралы по одной переменной, т.е. вещи из исчисления одной переменной (математика 1). В математике 2 мы сейчас работаем над рядами (сходящиеся, расходящиеся, интегральные критерии, критерии Даламбера, критерии Коши, абсолютная сходимость…). Английский не мой родной язык, так что извините, я что-то неправильно написал или допустил грамматические ошибки. Я постараюсь объяснить свои вопросы как можно лучше. У меня несколько вопросов, но все они взаимосвязаны. Поскольку всем этим вещам «нужны» ограничения, они и вызывают у меня основную путаницу. 92$ это $2x$? В $\lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) – f(x)}{\Delta x}$ я не могу просто положить $0$, так как я получил бы $\frac {0}{0}$, что было бы “настоящей” производной, потому что я не знаю, что это такое. После некоторых манипуляций я бы получил $\lim_{\Delta x \rightarrow 0} 2x + \Delta x$, а поскольку $\Delta x$ переходит в $0$, это будет равно $2x$. Но этот $\Delta x$ никогда не будет равен $0$, по крайней мере, как я смотрю на это, и из определения предела можно сказать, что я могу сделать $\Delta x$ как близкое к $0$, но не равное, если я хочу сделать $x_1$ и $x_2$ как можно ближе друг к другу.
Я умею вычислять пределы, производные, интегралы по одной переменной, т.е. вещи из исчисления одной переменной (математика 1). В математике 2 мы сейчас работаем над рядами (сходящиеся, расходящиеся, интегральные критерии, критерии Даламбера, критерии Коши, абсолютная сходимость…). Английский не мой родной язык, так что извините, я что-то неправильно написал или допустил грамматические ошибки. Я постараюсь объяснить свои вопросы как можно лучше. У меня несколько вопросов, но все они взаимосвязаны. Поскольку всем этим вещам «нужны» ограничения, они и вызывают у меня основную путаницу. 92$ это $2x$? В $\lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) – f(x)}{\Delta x}$ я не могу просто положить $0$, так как я получил бы $\frac {0}{0}$, что было бы “настоящей” производной, потому что я не знаю, что это такое. После некоторых манипуляций я бы получил $\lim_{\Delta x \rightarrow 0} 2x + \Delta x$, а поскольку $\Delta x$ переходит в $0$, это будет равно $2x$. Но этот $\Delta x$ никогда не будет равен $0$, по крайней мере, как я смотрю на это, и из определения предела можно сказать, что я могу сделать $\Delta x$ как близкое к $0$, но не равное, если я хочу сделать $x_1$ и $x_2$ как можно ближе друг к другу. Почему теперь я могу взять это $2x$ и сказать, например, что производная чьего-то положения во времени равна $2x$, то есть его скорость равна $2x$, а не $2x +$ какой-то небольшой $\Delta x$?
Почему теперь я могу взять это $2x$ и сказать, например, что производная чьего-то положения во времени равна $2x$, то есть его скорость равна $2x$, а не $2x +$ какой-то небольшой $\Delta x$?
 {-x}$, когда $x\to\infty$ (здесь $\infty$ — «виртуальная» граничная точка $D(f)$).
{-x}$, когда $x\to\infty$ (здесь $\infty$ — «виртуальная» граничная точка $D(f)$). 2$ вместо ${\epsilon\over100}$.
2$ вместо ${\epsilon\over100}$. Противник, Игрок $\delta$, последовательно пытается выдать «ответ»: указать положительное действительное число $\delta$, такое, что каждое местоположение $x \neq c$ с $|x – c| < \delta$ удовлетворяет $|f(x) - L| < \varepsilon$.
Противник, Игрок $\delta$, последовательно пытается выдать «ответ»: указать положительное действительное число $\delta$, такое, что каждое местоположение $x \neq c$ с $|x – c| < \delta$ удовлетворяет $|f(x) - L| < \varepsilon$. )
) 2}{h}\right|
= |ч| < \varepsilon.
$$
Благодаря этой «наброске»/выработке стратегии Игрок $\delta$ обнаруживает, что может выиграть, ответив вызовом. То есть, если $\varepsilon > 0$ произвольно, существует $\delta > 0$ (в частности, $\delta = \varepsilon$ в этом примере), такое, что если $0 < |h| < \delta$, то
$$
|f(h) - L| = \cdots = |ч| < \varepsilon
$$
(потому что $\varepsilon = \delta$). 9н а_к.
$$
Сказать, что ряд имеет сумму $s$, значит сказать, что для любого $\varepsilon > 0$ существует натуральное число $N$ такое, что если $n \geq N$, то $|s – s_n| < \varepsilon$. Это определение представляет собой игру «вызов-ответ» того же типа, что и «настоящая» лимитная игра. «Значение функции» $f(x)$ становится $s_n$, предполагаемый «предел» равен $s$ (который, опять же, должен быть известен заранее), «вызов» равен $\varepsilon > 0$ и «ответ» — это $N$; ответ “выигрывает”, если $n \geq N$ подразумевает $|s – s_n| < \varepsilon$.
2}{h}\right|
= |ч| < \varepsilon.
$$
Благодаря этой «наброске»/выработке стратегии Игрок $\delta$ обнаруживает, что может выиграть, ответив вызовом. То есть, если $\varepsilon > 0$ произвольно, существует $\delta > 0$ (в частности, $\delta = \varepsilon$ в этом примере), такое, что если $0 < |h| < \delta$, то
$$
|f(h) - L| = \cdots = |ч| < \varepsilon
$$
(потому что $\varepsilon = \delta$). 9н а_к.
$$
Сказать, что ряд имеет сумму $s$, значит сказать, что для любого $\varepsilon > 0$ существует натуральное число $N$ такое, что если $n \geq N$, то $|s – s_n| < \varepsilon$. Это определение представляет собой игру «вызов-ответ» того же типа, что и «настоящая» лимитная игра. «Значение функции» $f(x)$ становится $s_n$, предполагаемый «предел» равен $s$ (который, опять же, должен быть известен заранее), «вызов» равен $\varepsilon > 0$ и «ответ» — это $N$; ответ “выигрывает”, если $n \geq N$ подразумевает $|s – s_n| < \varepsilon$. Условие $|s – s_n| < \varepsilon$ является прямым аналогом условия $|f(x) - L| < \varepsilon$.)
Условие $|s – s_n| < \varepsilon$ является прямым аналогом условия $|f(x) - L| < \varepsilon$.) Также просто доказать, что $s$ является суммой ряда. Когда мы говорим «$s$ неизвестно», мы просто имеем в виду, что не существует известной формулы для $s$ в терминах знакомых чисел (таких как $e$, $\pi$ или корни рациональных чисел).
Также просто доказать, что $s$ является суммой ряда. Когда мы говорим «$s$ неизвестно», мы просто имеем в виду, что не существует известной формулы для $s$ в терминах знакомых чисел (таких как $e$, $\pi$ или корни рациональных чисел).
 92$” столь же абстрактно? Даже если вы измеряете положение миллиард раз в секунду и игнорируете ошибки измерения, вы совершаете прыжок веры, полагая, что положение за бесконечное число секунд, которое вы не измеряли, подчиняется то же самое правило. В естественных науках обычно «наилучшее возможное» — это быть уверенным в вещах до определенного момента, а затем предполагать, что это всегда будет выполняться с помощью индуктивных рассуждений.
92$” столь же абстрактно? Даже если вы измеряете положение миллиард раз в секунду и игнорируете ошибки измерения, вы совершаете прыжок веры, полагая, что положение за бесконечное число секунд, которое вы не измеряли, подчиняется то же самое правило. В естественных науках обычно «наилучшее возможное» — это быть уверенным в вещах до определенного момента, а затем предполагать, что это всегда будет выполняться с помощью индуктивных рассуждений. Как инженер, вы, вероятно, также захотите, чтобы она была полезной, например, для решения таких задач, как дифференциальные уравнения. 9\infty b_n \,$ и так далее. Если вы изучите и поймете доказательства этих теорем, вы увидите, где и как используется это определение, и сможете оценить, почему оно было создано таким, каким оно было.
Как инженер, вы, вероятно, также захотите, чтобы она была полезной, например, для решения таких задач, как дифференциальные уравнения. 9\infty b_n \,$ и так далее. Если вы изучите и поймете доказательства этих теорем, вы увидите, где и как используется это определение, и сможете оценить, почему оно было создано таким, каким оно было. Я могу только настаивать на том, что строгость настолько близка к , насколько вы пожелаете, заключается в $\epsilon-\delta$ определении предела и в том факте, что вы можете доказать, что предел является уникальным, хорошо определенным объектом.
Я могу только настаивать на том, что строгость настолько близка к , насколько вы пожелаете, заключается в $\epsilon-\delta$ определении предела и в том факте, что вы можете доказать, что предел является уникальным, хорошо определенным объектом. ”
” Эта функция, обозначенная “st”, отбрасывает бесконечно малый член $\Delta x$, так что мы получаем $\text{st}(2x+\Delta x)= 2x$. С этой точки зрения производная равна не отношение $\frac{\Delta y}{\Delta x}$, а его стандартная часть, а именно $f'(x)=\text{st}\left(\frac{\Delta y}{ \Дельта х}\справа)$.
Эта функция, обозначенная “st”, отбрасывает бесконечно малый член $\Delta x$, так что мы получаем $\text{st}(2x+\Delta x)= 2x$. С этой точки зрения производная равна не отношение $\frac{\Delta y}{\Delta x}$, а его стандартная часть, а именно $f'(x)=\text{st}\left(\frac{\Delta y}{ \Дельта х}\справа)$. Но это $\Delta x$ никогда не будет равен $0$, по крайней мере, как я смотрю на это, и из определения предела можно сказать, что я могу сделать $\Delta x$ как близкое к $0$, но не равное [ему]” .
Но это $\Delta x$ никогда не будет равен $0$, по крайней мере, как я смотрю на это, и из определения предела можно сказать, что я могу сделать $\Delta x$ как близкое к $0$, но не равное [ему]” . Доказательство совпадает с эвристическим этапом.
Доказательство совпадает с эвристическим этапом. 2) приближается к бесконечности с обоих направлений, поэтому, хотя бесконечность не является числом, функция определена при x=0, так сказать. Бизнес с дельта-х — это просто аналитический способ добраться до него. Дельта x — это вымысел; мы действительно не обеспокоены его ценностью.
2) приближается к бесконечности с обоих направлений, поэтому, хотя бесконечность не является числом, функция определена при x=0, так сказать. Бизнес с дельта-х — это просто аналитический способ добраться до него. Дельта x — это вымысел; мы действительно не обеспокоены его ценностью. Один из хороших способов определить дифференцируемость функции состоит в том, чтобы сказать, что функция $f$ дифференцируема в $c$, если существует непрерывная функция $g$ в $c$ такая, что:
Один из хороших способов определить дифференцируемость функции состоит в том, чтобы сказать, что функция $f$ дифференцируема в $c$, если существует непрерывная функция $g$ в $c$ такая, что: Они работают так же, как и в лемме: вы связываете вещи и показываете, что можете сколь угодно близко подойти к некоторому пределу, и поэтому функция предполагает предел в «точке» (которая может быть бесконечностью, как в бесконечных суммах предел равен до бесконечности).
Они работают так же, как и в лемме: вы связываете вещи и показываете, что можете сколь угодно близко подойти к некоторому пределу, и поэтому функция предполагает предел в «точке» (которая может быть бесконечностью, как в бесконечных суммах предел равен до бесконечности). 2}{h_n} =\lim \limits_{n\to \infty}2x+h_n$$
2}{h_n} =\lim \limits_{n\to \infty}2x+h_n$$ Для простоты предположим, что в этом посте я говорю о реалах с обычной метрикой.
Для простоты предположим, что в этом посте я говорю о реалах с обычной метрикой.
 Другими словами, мы объявляем, что существует «путь» в диапазоне $f$, который ведет к точке $f(a)$. Этот путь может быть трудно или невозможно построить, но мы утверждаем, что он есть.
Другими словами, мы объявляем, что существует «путь» в диапазоне $f$, который ведет к точке $f(a)$. Этот путь может быть трудно или невозможно построить, но мы утверждаем, что он есть. Мы не просто выбираем число, которое почти «бла», мы выбираем вложенный набор проколотых окрестностей, которые гарантированно не пусты, и мы выбираем элементы из этих окрестностей. Просто мы большую часть времени не знаем, что это за районы, а только то, что они существуют.
Мы не просто выбираем число, которое почти «бла», мы выбираем вложенный набор проколотых окрестностей, которые гарантированно не пусты, и мы выбираем элементы из этих окрестностей. Просто мы большую часть времени не знаем, что это за районы, а только то, что они существуют. Далее, значение в одной точке не имеет ничего общего с пределом. Однако, поскольку функция определена для близких значений, мы можем подобрать $x$ достаточно близко к $1$, чтобы увидеть, что функция делает вблизи $1.$ Два анекдота иллюстрируют этот момент. Первое пришло от моего учителя математики профессора Амоса Барксдейла из штата Северный Техас, второе пришло от какого-то проповедника.
Далее, значение в одной точке не имеет ничего общего с пределом. Однако, поскольку функция определена для близких значений, мы можем подобрать $x$ достаточно близко к $1$, чтобы увидеть, что функция делает вблизи $1.$ Два анекдота иллюстрируют этот момент. Первое пришло от моего учителя математики профессора Амоса Барксдейла из штата Северный Техас, второе пришло от какого-то проповедника. Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость

Ограничение функции
дифференциальное исчисление Ссылки
в.ч. Ссылки

Если по мере того, как `x` приближается к “a” как с левой, так и с правой стороны от “a”, `f(x`) приближается к определенному числу “L”, тогда “L” называется пределом `f(x)` как ` x` приближается
а.
Лимит выражается следующим образом: 
1. Пусть у нас есть две функции `u` и `v`, для которых
`Lim_(x->a) u(x)= P` и `Lim_(x->a) v(x) = Q`, то
`Lim_(x->a) [u(x) + v(x)] `= `Lim_(x->a) u(x) `+ `Lim_(x->a) v(x) `= P + Q Пример 1:
2. Для двух функций u и v, рассмотренных выше,
Пример 2:
3. Пусть у нас есть действительное число c, тогда
Пример 3:
4. Предел Произведения двух функций равно произведению пределов двух функций.
Пример 4:
5. Предел частного двух функций равен частному пределов двух функций (при условии, что предел
знаменатель не равен нулю).

Пример 6:
Пример 7:

Пример 1:
Пример 2:
Пример 3:
Станьте участником сегодня!
Зарегистрируйтесь (бесплатно) Вы член? Войти!
Войдите в свою учетную запись Определение, типы, использование и примеры, математика
Ограничения: определение, типы, использование и примеры, математика Выберите язык

Основная концепция предела в математике

Интуитивное определение предела
 2-4}{x-2} \) ведет себя вблизи \( x = 2 \). Обратите внимание, что по мере того, как значения \( x \) приближаются к \ ( 2 \) с любой стороны \ ( 2 \), значения \ ( f (x) \) приближаются к \ ( 4 \).
2-4}{x-2} \) ведет себя вблизи \( x = 2 \). Обратите внимание, что по мере того, как значения \( x \) приближаются к \ ( 2 \) с любой стороны \ ( 2 \), значения \ ( f (x) \) приближаются к \ ( 4 \). Если , то все значений \( f(x) \) приближаются к действительному числу \( L \) так же, как значения \( x \) – за исключением \( x = a \) – приближаются к числу \( a \) , то можно сказать, что предел \( f(x) \) при приближении \( x \) к \( a \) равен \( L \) .
Если , то все значений \( f(x) \) приближаются к действительному числу \( L \) так же, как значения \( x \) – за исключением \( x = a \) – приближаются к числу \( a \) , то можно сказать, что предел \( f(x) \) при приближении \( x \) к \( a \) равен \( L \) . Нахождение пределов
 Это можно сделать одним из двух способов:
Это можно сделать одним из двух способов: Нахождение предела с помощью таблицы функциональных значений
Решение предела с помощью графика


Типы ограничений

Теорема: основные пределы
Значения, приближающиеся к \( a \), которые равны \( < a \) Значения, приближающиеся к \( a \), которые равны \( > a \) \( \bf{ f(x) = c } \) \( \bf{ x } \) \( \bf{ f(x) = c } \) \( а – 0,1 \) \( в \) \( а + 0,1 \) \( в \) 927 9.0 \(10 а – 9 \) \(с\) \(а + 0,01\) \(с\) \(а – 0,001\) \(с\) + 927.  0 )
0 ) \ (C \) \ (a – 0,0001 \) \ (C \) \ (A + 0,0001 \) \ (C \) \. что для всех значений \( x \) – приближаются ли они к \ ( a \) или нет – значения \ ( f ( x ) \) остаются постоянными при \ ( c \). Правила ограничения
Теорема: предельные законы
 Пожалуйста, обратитесь к этим статьям для получения дополнительной информации.
Пожалуйста, обратитесь к этим статьям для получения дополнительной информации. Наличие предела – когда предела не существует?
\(\bf{x}\) \(\bf{sin\left(\frac{1}{x}\right)}\) \(\bf{x}\) \(\bf{sin\left(\frac{1}{x}\right)}\) \(-0,1\) \(0,54402\) \(0,1\) \(-0.54402\) \(-0.01\) \(0.50636\) \(0.01\) \(-0.  50636\)
50636\) \(-0.001\ ) \(-0,82688\) \(0,001\) \ (0,82688 \) \ (-0,0001 \) \ (0,30561 \) \ (0,0001 \) \ (-0,30561 \) 7 \ (-0,30561 \) 9987 \. \(-0.03575\) \(0.00001\) \(0.03575\) \(-0.000001\) \(0.34999\) \(0.000001\) \ (-0,34999\)  Математический способ записать это так: \[ \lim_{x \to 0} sin \left( \frac{1}{x} \right) \, DNE \]Где DNE означает «не существует».
Математический способ записать это так: \[ \lim_{x \to 0} sin \left( \frac{1}{x} \right) \, DNE \]Где DNE означает «не существует». Односторонние ограничения
 Следовательно, предела не существует, т. е.
Следовательно, предела не существует, т. е. 9{+}} f(x) = -\infty. \]
9{+}} f(x) = -\infty. \] Примеры ограничений
 Для применения закона должен существовать новый предел.
Для применения закона должен существовать новый предел. Ограничения – основные выводы
Часто задаваемые вопросы о пределах
 То, как вы можете думать о пределе, состоит в том, что вход функции становится все ближе и ближе к некоторому значению, функция становится все ближе и ближе и остается близкой к пределу.
То, как вы можете думать о пределе, состоит в том, что вход функции становится все ближе и ближе к некоторому значению, функция становится все ближе и ближе и остается близкой к пределу.
Окончательный опрос о пределах
 Если все значений f(x) приближаются к действительному числу L, поскольку значения x – кроме x = a – приближаются к числу a, то можно сказать, что предел f(x) при x приближается это L .
Если все значений f(x) приближаются к действительному числу L, поскольку значения x – кроме x = a – приближаются к числу a, то можно сказать, что предел f(x) при x приближается это L .
 Предположим, что L и M — действительные числа, такие, что:
Предположим, что L и M — действительные числа, такие, что: Предположим, что L и M — действительные числа, такие, что:
Предположим, что L и M — действительные числа, такие, что: Откройте для себя подходящий контент для ваших тем
Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!
Учебный план

