Предел как найти: Как решать пределы для чайников, примеры решений

6.20 Найти предел последовательности . Непрерывность какой функции (и в какой точке) использовалась при вычислении предела?

Решение.

= .

Обозначим: . Тогда при (здесь мы воспользова­лись тем, что при , непрерывностью функции в нуле и определением непрерывности по Гейне).

Тогда =

Так как (мы использовали замечательный предел и определение предела по Гейне) и = = = = то = .

Последнее равенство требует обоснования. Перейдём от степенно-показательного выражения к показательному:

= = . Обозначим показатель через и найдём его предел. При предел равен . Поэтому предел равен (здесь мы воспользовались непрерывностью лога­рифма в точке ), то есть равен . Поэтому = = = = . Итак, = и поэтому = = (здесь мы воспользовались непре­рывностью экспоненты в точке ).

7.20. Найти область определения и исследовать на непрерывность функцию , заданную следующим образом:

Решение. Функция = определена при , то есть при . При этих имеем: и, следовательно, и, следовательно, функция = определена. Функция = определена при , то есть при . Обе функции, и определены при . Част­ное функций и определено только при (при и знаменатель равен нулю), однако, при функция специально доопределена: . Итак, областью определения функ­ции является полуинтервал .

Функция, заданная формулой , получена из обрат­ной тригонометрической функции и степенных функций примене­нием арифметических операций и композиций (конечное число раз), явля­ется элементарной и, следовательно, непрерывной в своей естественной области определения . Поскольку совпадает с на интер­вале , то и непрерывна во всех точках этого интервала.

Осталось исследовать на непрерывность в точке :

= = =

= = =

= =[замена: ]=

= =[замена: ]= = = .

Предел существует, но не равен заданному значению функции в точке и, следовательно, функция имеет в точке устранимый разрыв.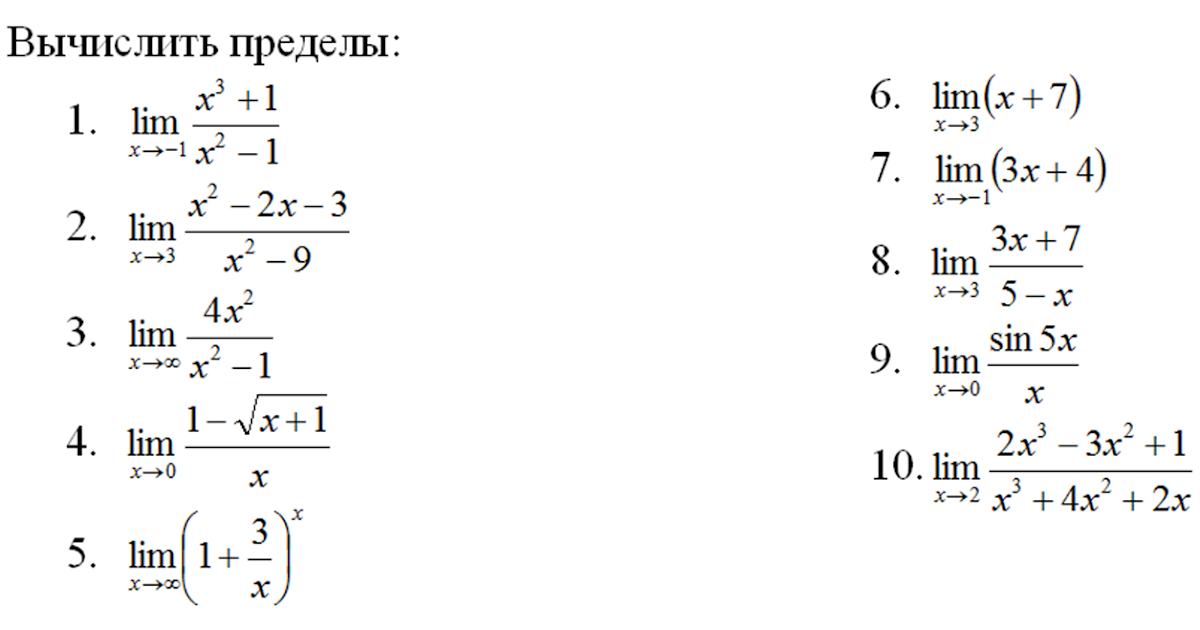

8.20. Исследовать на непрерывность функцию и оп­ределить характер точек разрыва.

Решение. Функция непрерывна во всех точках своей об­ласти определения. Так как функция непрерывна всюду, кроме точки , то композиция этих функций – функция непрерывна всюду, кроме, возможно, тех точек, в которых (и, конечно, кроме точки ). Решаем уравнение: . Учитывая непрерывность функции , делаем вывод о непрерывности данной функции во всех точках, кроме точки и, возможно, точек вида .

Заметим, что существует (и равен нулю) как предел произведения бесконечно малой при функции на ограничен­ную . Следовательно, в точке функция имеет устранимый разрыв.

Рассмотрим точку вида , где .

Справа от этой точки (точнее, в правосторонней окрестности ) имеем: и, следовательно, и, следовательно, и, следовательно, . Итак, в правосторонней окрестности точки имеем: и = = .

Отме­тим, что мы использовали непрерывность функции . Таким обра­зом, в рассматриваемой точке функция имеет конечный предел справа (и он равен ).

Аналогично, рассматривая левостороннюю окрестность точки , получим: в рассматриваемой точке функция имеет конечный предел справа (и он равен ).

Итак, в точках вида , где функция имеет разрывы пер­вого рода.

В точках вида , где можно было бы провести исследова­ние по аналогии с исследованием, проведённым в точках вида , где . Однако, проще учесть чётность данной функции и тот очевид­ный факт, что предел справа функции в точке равен пределу слева в точке , а предел слева в точке , соответственно, пре­делу справа в точке .

Лабораторная работа № 12

Производная и дифференциал функции: определения, геометрический смысл, физический смысл

Необходимые понятия и теоремы: дифференцируемость и дифферен­циал функции в точке, производная функции в точке, теорема о равно­сильности дифференцируемости и существования производной, теорема о дифференцируемости и непрерывности, касательная к графику функции, мгновенная скорость.

Литература: [1] с. 202 – 214, [2] с. – .

Левосторонний и правосторонний пределы функции в точке

Естественные науки / Математический анализ функции одной переменной / Левосторонний и правосторонний пределы функции в точке

Переходим к рассмотрению односторонних пределов функции в точке x₀, при которых переменная x «движется» к x₀ слева (левосторонний предел) или справа (правосторонний предел). Нам потребуется понятие полуокрестности.

Пусть d > 0. Интервал (a, x₀) называется левой полуокрестностью

точки x₀, интервал (x₀ – d, x₀) – левой d-полуокрестностью точки x₀. Интервалы (x₀, b), (x₀, x₀ + d) называются, соответственно, правой полуокрестностью и правой d-полуокрестностью точки x₀ (см. рис. 1.8, 1.9).

Пусть f(x₀) определена в левой полуокрестности точки

x₀.

Число b называется левосторонним пределом функции f(x) в точке x₀ (обозначение: f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих левой d-полуокрестности (x₀ – d, x₀), выполняется неравенство: |f(x) – b| < e.

Символическиf(x) = b означает: “e>0$d > 0 “x(x₀ – d < x < x₀ ® | f(x) – b | <

e) (см. рис. 1.8).

Аналогично, число b называется правосторонним пределом функции f(x) в точке x₀ (обозначение: f(x) = b), если для любого e > 0 найдется d > 0, такое, что для

всех значений x, принадлежащих правой d-полуокрестности (x₀, x₀ + d), выполняется неравенство: | f(x) – b | < e  (см. рис. 1.9).

Символическиf(x) =

b означает: “e >0 $d >0 “x(x₀ < x < x₀ + d ® |f(x) – b| < e).

Пример 3.

Функция f(x) задана равенством (рис. 1.10):

f(x) =   .

Найти f(x) и f(x).

Решение. Покажем, что f(x) = 1, а     f(x) = 3.

Рассмотрим значения x < 1, тогда f(x) = 2x – 1 и | f(x) – 1| = |2x – 1 – 1| = 2|x – 1|. Зафиксируем малое   e > 0. Подсчитаем: |

f(x) – 1| < e Û 2 |x – 1| < e Û  |x – 1| < . Так как x < 1, то  f(x) – 1| < e, если 1 –  < x < 1, следовательно, d = . Итак, если 1 –  < x < 1,   то | f(x) – 1| < e,    т.е.   f(x) = 1.

Рассмотрим значения x > 1,   тогда f(x) = 4 – x.   Зафиксируем e > 0,

| f(x) – 3| = |2 – x – 3| = |1 – x|.  Отсюда  | f(x) – 1| < e  Û  |1 –

x| < e, т.е. | f(x) – 1 | < e   для   x Î (1, 1 + e).   Значит,  f(x) = 3.

Очевидно, если f(x) = b,    то   f(x) = b   и    f(x) = b.

Верно и обратное, если f(x) = f(x) = b, то f(x) = b.

Если же правосторонний предел функции в точке x₀ не равен левостороннему пределу функции в точке x₀, то f(x) = b не существует.

Так, в примере 3 функция f(x) не имеет предела в точке x₀.

Как найти границы класса (с примерами)

---

В частотном распределении границы классов — это значения, разделяющие классы.

Мы используем следующие шаги для расчета границ класса в частотном распределении:

1.  Вычтите верхний предел класса для первого класса из нижнего предела класса для второго класса.

2. Разделить результат на два.

3.  Вычтите результат из нижнего предела класса и добавьте результат к верхнему пределу класса для каждого класса.

В следующих примерах показано, как использовать эти шаги на практике для расчета границ классов в частотном распределении.

Пример 1. Расчет границ классов

Предположим, у нас есть следующее распределение частот, которое представляет количество побед различных баскетбольных команд:

Для расчета границ классов выполните следующие шаги:

1.  

Вычтите верхний предел класса для первого класса из нижнего предела класса для второго класса.

Верхний предел класса для первого класса равен 30, а нижний предел класса для второго класса равен 31. Таким образом, мы получаем: 31 – 30 = 1 .

2. Разделите результат на два.

Далее делим результат на 2. Итак, получаем 1/2 = 0,5 .

3.  Вычтите результат из нижнего предела класса и добавьте результат к верхнему пределу класса для каждого класса.

Наконец, мы вычитаем 0,5 из нижнего предела класса и добавляем 0,5 к верхнему пределу класса для каждого класса:

Мы интерпретируем результаты следующим образом:

• Первый класс имеет нижнюю границу класса 25,5 и верхнюю границу класса 30,5.
• Второй класс имеет нижнюю границу класса 30,5 и верхнюю границу класса 35,5.
• Третий класс имеет нижнюю границу класса 35,5 и верхнюю границу класса 40,5.

И так далее.

Пример 2: Расчет границ классов

Предположим, у нас есть следующее распределение частот:

Используйте следующие шаги для расчета границ класса:

1.  Вычтите верхний предел класса для первого класса из нижнего предела класса для второго класса.

Верхний предел класса для первого класса равен 60,9, а нижний предел класса для второго класса равен 61. Таким образом, мы получаем: 61 – 60,9 = 0,1 .

2. Разделите результат на два.

Далее результат делим на 2. Итак, получаем 0,1/2 = 0,05 .

3.  Вычтите результат из нижнего предела класса и добавьте результат к верхнему пределу класса для каждого класса.

Наконец, мы вычитаем 0,05 из нижнего предела класса и добавляем 0,05 к верхнему пределу класса для каждого класса:

Мы интерпретируем результаты следующим образом: граница высшего класса 60,95.

Второй класс имеет нижнюю границу класса 60,95 и граница высшего класса 65,95.

Третий класс имеет нижнюю границу класса 65,95 и верхнюю границу класса 70,95.

И так далее.

Дополнительные ресурсы

Как найти средние точки классов
Как найти границы классов
Как найти интервалы классов
Калькулятор ширины класса
Как рассчитать ширину класса в Excel

Просмотреть все сообщения Zach

Найдите предел следующего уравнения

Исчисление Предварительное исчисление Пределы функции

Валеся С.

спросил 04.06.20

Когда x приближается к 2

(x ³ -8)/(x-2)

Подписаться І 1

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Уильям В. ответил 04.06.20

Репетитор

5,0 (838)

Top Pre-Calc Tutor

См. таких репетиторов

Смотрите таких репетиторов

x ³ – 8 = (x – 2)(x ² + 2x + 4)

Итак, когда мы разделим на (x – 2), “x – 2” отменит остаточный предел как x приближается к 2 из х ² + 2x + 4

Теперь мы можем подставить x = 2

2 ² + 2(2) + 4 = 3 + 4 + 4 = 12

Голосовать за 0 Понизить

Подробнее

Отчет

Марк Р. ответил 04.06.20

Репетитор

4.9 (59)

UT Аспирант по физике

Об этом репетиторе ›

Об этом репетиторе ›

Привет, Велесия,

Есть несколько различных способов сделать это, включая построение графика функции, вынесение на множители (x-2) и использование метода исчисления, известного как правило Лопиталя.

Поскольку в описании вы упомянули «исчисление», я загрузил короткое видео, которое проведет вас по этапам использования правила Лопиталя. Похоже, что Уильям У. уже объяснил, как разложить на множители, а затем подставить два, и это работает так же хорошо для этой задачи, но ваш учитель, вероятно, попросит вас использовать правило Лопиталя для вещей, которые нельзя также разложить на множители. .

Лучший,

Марк Р.

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.