Предел как решить: Как решать пределы для чайников, примеры решений

Содержание

Вычислить предел функции…решить только #9 срочно… -reshimne.ru

Новые вопросы

Ответы

Как жить с человеком, если у вас разное отношение к чистоте и порядку

4 октябряОтношения

Главное — найти приемлемый для всех предел беспорядка.

Дома мы отдыхаем и отключаемся от внешнего мира. Это единственное место, где мы по‑настоящему чувствуем себя расслабленно и комфортно. Именно поэтому совместная жизнь с кем‑то, кто по‑другому относится к порядку, а значит, и по‑другому понимает комфорт, порой становится невыносимой.

Неважно, насколько люди, которые делят одну жилплощадь, чистюли или неряхи. Главное, чтобы у них было одинаковое представление о пределе, которого может достигнуть беспорядок. Чем больше разница во взглядах, тем больше конфликтов будет в доме.

Обычно ситуация складывается следующим образом. Более аккуратный человек воспринимает беспорядок как посягательство на своё личное пространство. Он постоянно видит грязную посуду в раковине или пыль на полках и в конце концов берёт на себя обязанности по уборке и организации быта. Обида на партнёра или соседа по квартире нарастает, а затем переходит в полноценную ссору.

Кроме того, влияет и личный опыт. Люди, у которых допустимый предел беспорядка ниже, раздражаются при любом намёке на него и стараются сразу исправить ситуацию. Люди, у которых предел гораздо выше, часто просто не замечают, что пора делать уборку, потому что для них критическая отметка ещё не достигнута.

В результате более аккуратному человеку может показаться, что партнёр или сосед по квартире целенаправленно игнорирует проблему. «Мусор снова выношу я?! Видимо, меня совсем не уважают», — такие мысли только усугубляют конфликты и мешают договориться. Чтобы научиться жить мирно, необходимо понять свои различия и создать эффективную систему, которая будет их учитывать.

Как найти общий язык

Задавать вопросы

Обычно инициатором разговора становится более аккуратный человек. Так происходит, потому что его личный предел достигается гораздо раньше. Если это вы, у вас может возникнуть желание дать другому человеку совет, как поддерживать чистоту и порядок, или наброситься на него с критикой. Не стоит этого делать.

Психологи отмечают, что самая главная проблема, с которой сталкиваются люди во время беседы на эту тему, — чёрно‑белое видение ситуации. Хотя даже аккуратистам следует относиться к своей системе организации как к личному предпочтению, не более. Такой подход позволит начать разговор со своих чувств по поводу беспорядка, а значит, не заставит собеседника мгновенно переключиться в режим защиты.

Для старта обсуждения подойдут простые вопросы, которые покажут, что вы хотите найти решение, подходящее для всех. Например: «Когда вечером ты уходил из кухни, ты проверил, не забыл ли что‑то на столе?» Или: «После того, как ты убралась в ванной, ты обратила внимание, что зеркало осталось грязным?» Таким образом вы даёте возможность другому человеку признаться, что он действительно что‑то не заметил или случайно пропустил, и представить свою версию ситуации. В этот момент важно помнить, что у менее аккуратных людей порог толерантности к беспорядку гораздо выше.

После этого другой человек может расспросить вас о ваших предпочтениях в уборке и организации пространства. И тогда важно рассказать, какие чувства и почему вызывает у вас отношение вашего партнёра или соседа к беспорядку. На этом этапе собеседник, скорее всего, будет более внимателен к вашим желаниям. Когда мы начинаем разговор с целью узнать чужую точку зрения, а не доказать собственную правоту, пропадает элемент соперничества, который и приводит к ссорам.

Правильно объяснять ситуацию

Расскажите партнёру или соседу по квартире про концепцию предела беспорядка. Это позволит избежать обвинений и объяснить, что всё дело в разных его показателях, а не в том, что кто‑то неряха, а кто‑то чистюля и, значит, лучше. Просто ваш предел гораздо ниже, поэтому он достигается быстрее и вы выполняете больше работы по дому, но хотите, чтобы ситуация изменилась.

Такой подход также устранит вероятные негативные предубеждения, которые могут возникнуть у вас по отношению к другому человеку. Он не проявляет неуважение и не пытается превратить вашу жизнь в ад. Он просто не замечает проблемы и пока ещё находится в зоне своего комфорта. Возможно, он даже не осознаёт того, что вы убираете гораздо чаще. Объясните ситуацию и подчеркните, что вам хотелось бы, чтобы обязанности выполнялись по очереди.

Рассказывать о своих предпочтениях

Сформулируйте, что для вас абсолютно неприемлемо, когда дело касается порядка и организации пространства, а где вы готовы пойти на послабления. Возможно, вам важно, чтобы стол протирали после каждого приёма пищи, или вы терпеть не можете разбросанную у входной двери обувь. Дайте партнёру или соседу по квартире конкретные инструкции и объясните свои предпочтения и ожидания.

Распределять обязанности

Люди с более низким пределом беспорядка чаще становятся заложниками домашних обязанностей, которые ненавидят. Так происходит, потому что им практически всегда приходится ими заниматься.

Скажем, вы не любите, когда в раковине остаётся грязная посуда. И вы начинаете всякий раз мыть чашки и тарелки, которые оставляет ваш партнёр или сосед по квартире. Постепенно вы делаете это чаще, а значит, быстрее и лучше. А чем лучше вы справляетесь с определённой обязанностью, тем менее заметными становятся ваши усилия. В результате другой человек не понимает, сколько сил вы на это тратите. Более того, он может предположить, что вы любите мыть посуду, и сам будет делать это ещё реже.

Таким образом создаётся модель разделения труда, когда мы выполняем задачи, которые больше всего нас беспокоят и меньше всего нам нравятся. Поэтому не стоит делать всё самостоятельно. Лучше поговорите и решите, как ваш партнёр или сосед может выполнять свою часть домашних дел.

Возьмите на заметку 🙆‍♂️🙆‍♀️

Как поделить домашние обязанности, чтобы избежать ссор и не разрушить семью

Замечать вклад каждого в разных сферах

Да, возможно, ваш партнёр или сосед по квартире создаёт больше беспорядка. Но также возможно, что есть другие домашние или личные обязанности, которые он выполняет хорошо. Вспомните об этом, и вы почувствуете, что мир более справедлив.

Когда мы говорим о равенстве, дело не в том, чтобы кто‑то один убирал ванную на этой неделе, а кто‑то другой — на следующей. Дело в том, что вам дают эти отношения и стоят ли они тех усилий, которые вы прилагаете.

Если неряха — сосед, с которым вы снимаете квартиру, возможно, он чаще готовит, общается с надоедливыми соседями по подъезду или покупает забавные безделушки для дома. Если при этом он ваш друг, тогда, скорее всего, он даёт вам поддержку, приятное времяпрепровождение или что‑то другое, что может отчасти компенсировать его неаккуратность.

Если вы живёте с любимым человеком, плюсов может быть ещё больше. Помните, что вы влюбились в него не потому, что он прекрасно очищает раковину или шикарно пылесосит. Партнёр каждый день привносит в вашу совместную жизнь положительные эмоции, служит опорой и не только. Да, подобные вещи занимают меньше времени, чем уборка, но это не делает их менее значимыми.

Трезвая оценка ваших отношений с партнёром, другом или соседом позволит убедиться, что вы получаете столько, сколько отдаёте, только другими способами.

Как организовать уборку

Упростить процесс

В попытках контролировать хаос чистюли обычно придумывают запутанные системы организации и хранения, например используют разноцветные коробки для разных вещей или ящики с кучей отделений. Однако всё это работает только для таких же аккуратистов, но не для людей с высокой терпимостью к беспорядку. Поэтому гораздо лучше использовать системы из одного простого шага и, перед тем как добавить ещё один, убедиться, что он действительно необходим.

Возьмём корзину для белья. Она может быть с крышкой и без неё. Менее аккуратный человек может складывать вещи прямо на крышку, но если её нет, то одежда точно попадёт сразу в корзину. То же самое правило работает для контейнеров и отделений в холодильнике. Люди с высоким пределом беспорядка просто не заметят сложную систему организации или не будут вникать в неё так, как люди с более низким пределом. А значит, она окажется бесполезной.

Чем проще метод организации, тем легче ему следовать и тем меньше стресса для обеих сторон.

Разделить пространство на зоны

Общее пространство вряд ли всегда сможет выглядеть исключительно так, как вы хотите. А вот личное — вполне.

Выделите в квартире персональные зоны. Так у вас гарантированно будет своё место, где вы будете поддерживать всё в нужном порядке, а у вашего партнёра или соседа — своё, где его беспорядок не будет вас беспокоить.

Это позволит избежать конфликтов по поводу единой системы организации. Каждый получит свой уголок, где царит комфортная обстановка и не нужно следовать ничьим правилам.

Составить расписание

Люди с разным пределом беспорядка замечают грязь и бардак в разное время. Если вы договоритесь выполнять уборку «по мере необходимости», это будет делать только тот, у кого предел ниже. Именно поэтому важно составить чёткое и понятное расписание.

Подумайте, как часто вы хотели бы проводить уборку, и обсудите с партнёром или соседом по квартире, как он может участвовать в этом процессе. Спросите себя, с каким уровнем беспорядка вы готовы мириться, зная, что другой человек тоже будет проявлять инициативу. Например, если вы договорились, что он моет посуду минимум раз в день, вам будет гораздо легче оставить грязные тарелки в раковине и подождать, а не взять эту работу на себя.

Math Tutor – Функции – Обзор методов

Math Tutor – Функции – Обзор методов – Ограничения

Если вы хотите одновременно следовать другому тексту о пределах функций в отдельное окно, нажмите здесь, чтобы Теория и здесь для решения проблем.

Предел — один из важнейших инструментов исследования функций. Как и любой “хороший” вопрос, найти ответ не всегда легко и часто приходится преодолеть проблемы. Для многих из них у нас есть специальные методы и приемы. Если вы хотите быть опытным в оценке пределов, важно развивать (практикуя) ментальные «коробки» проблем, каждая коробка содержит предельные проблемы определенного типа. Когда вы сталкиваетесь с проблемой, вы находите соответствующую поле и вытащите соответствующий метод решения. Часто человек не получает ответ таким образом, просто предельная задача меняется на другую, поэтому приходится использовать несколько приемов один за другим. Есть также проблемы которые ни в какие рамки не влезают, то надежда только на опыт и интуиция.

Сначала мы кратко рассмотрим, какой ответ можно получить. заданная функция на данная точка может иметь предел, который является действительным числом (собственно

лимит ). В этом случае говорят, что функция сходится к (или сходится). сходится ) в этой точке. В противном случае функция расходящаяся там. Мы используем ту же классификацию для «задачи нахождения предела в точке», которую мы для краткости называем «пределом». Таким образом, мы бы сказали, что заданный предел (задача, которую нужно решить) сходится (существует собственный предел – результат) или расходится.
Среди расходящихся пределов (т. е. проблем) некоторые «красивее»: они склонны бесконечности или до минус бесконечности, то есть у них неправильный предел . Если существует некоторый предел — конечный для сходящихся пределов или бесконечный — мы говорим что предел существует , так как мы все равно получаем некоторую информацию. Последний случай, когда вообще нет предела, ни конечного, ни бесконечного. В этом случае мы говорят, что предела не существует, что часто сокращается как DNE.

Как найти пределы?

Начнем с определения самой важной ситуации:

Вопрос:
Пусть функция f определена в некоторой редуцированной окрестности точка a по некоторой алгебраической формуле.
Найдите его предел в a .
Альтернативные вопросы:
Пусть функция f определена на некотором редуцированном правом окрестности точки a по некоторой алгебраической формуле. Найдите его предел на справа.
Пусть функция f определена на некотором редуцированном левом окрестности точки a по некоторой алгебраической формуле. Найдите его предел на слева.

Эти вопросы решаются таким же образом, см. ниже.

Прежде чем показать, что делать, мы кратко рассмотрим другие ситуации. Что, если функция не задается одной общей формулой на некотором приведенном (одностороннем для односторонние пределы) окрестности

a ? Хороший случай, когда функция задается одной формулой справа и другой формулой слева из и , и нам нужен двусторонний лимит. Тогда можно перейти к одностороннему пределы, где мы находимся в ситуации, описанной в Вопросе, поэтому мы используем по алгоритму, изложенному ниже, находим ответы (если повезет) и сравниваем.

Если функция настолько странная, что ей даже не задается красивая формула на одностороннее соседство и , тогда мы должны решить проблему индивидуально опираясь на наше понимание пределов, алгоритма не существует.

Теперь вернемся к Вопросу.

Решение:
Шаг 1. “Подставить” точку a в данное выражение и попробовать найти результат с помощью предельная алгебра . В частности, нужно уметь подставлять бесконечность в элементарные функции. Может возникнуть необходимость работать с односторонними ограничениями и/или односторонние результаты лимитов, см. примечание 1 ниже, это чаще всего бывает когда вы встречаете выражение 1/0 (см. соответствующую рамку ниже).

Иногда помогает упростить выражение перед подстановкой и . Это особенно удобно при замене бесконечности степенями с отрицательным значением. степени, многим они больше нравятся в виде дробей.

Что может случиться?

а) Если предельная алгебра дала определенный ответ (число, бесконечность или минус бесконечность, или что предел ДНЭ см. примечание 2 ниже), то этот ответ тоже ответ на проблему предела, и все готово. Обратите внимание, что алгебра пределы, особенно с некоторыми бесконечностями, не является «настоящей алгеброй», так что, возможно, лучше не писать это как часть «официального решения».
Пример .

б) Другая возможность состоит в том, что предельная алгебра не привела к ответу потому что что-то пошло не так. В этом случае вы должны попробовать какой-то трюк, который то есть вы переходите к шагу 2.

Внимание! Иногда возникает соблазн заменить только “хорошие” детали выражения, а остальное оставьте на потом. Это не работает в Генеральная! Единственный способ сделать ограничения “по частям” – разбить их на дополнительные ограничения см. в этом примечании. За один предел, вы либо подставляете везде, либо не подставляете вообще.

Шаг 2. Если предельная алгебра не удалась, то должно быть какое-то проблема. Для многих видов задач существуют достаточно надежные методы, поэтому один должны также знать кое-что о более популярных проблемах (например, о неопределенных выражениях). «Замена» на на шаге 1, хотя и не удалась, все же должна сработать. очень ценная услуга, а именно она должна определить, какую проблему вы имеют. Это поможет вам поместить вашу проблему в соответствующую «коробку», затем вы просто применяете метод, рекомендованный в этом поле.

Неопределенные выражения являются распространенной причиной неудачи на шаге 1. и к счастью для каждого из них есть специальная коробочка с подходящей метод.
• поле “1/0”.
• поле “неопределенный соотношение” , ,
• поле “неопределенный продукт” ∞⋅0,
• коробка “неопределенный разница” ∞ − ∞,
• прямоугольник “неопределенный мощность” 1 ^∞ ,0 ⁰ ,∞ ⁰ .

Однако часто лучше пропустить эти общие поля и вместо этого использовать поле, которое специализируется на определенном выражении, появляющемся в пределе:
• поле “многочлены, суммы и отношения со степенями в бесконечности»,
• поле “полиномы в нужных точках» (отмена),
• поле “Разница корней».

Тогда есть поле, которое не узко ориентировано на определенный тип выражение или проблему, а скорее предлагает более общий метод решения с колебаниями и проблемами, с которыми трудно справиться:
• поле “Сравнение и колебание», которое обычно включает такие ограничения, как предел греха ( x ) на бесконечности.

Наконец, есть две коробки с методами, которые ничего не решают путем самих себя, но иногда они могут значительно приблизить нас к этому решению, значительно упрощая данный предел:
• коробка “красивая внешняя функция»,
• поле «замена».

В качестве бонуса добавляем
• коробка «эквивалентные бесконечно малые».

Иногда метод из соответствующего поля даст вам ответ. Но часто вы получаете еще один предел для оценки, а это значит, что вы должны пойти вернитесь к шагу 1 и начните снова и, возможно, снова, пока не получите ответ или пока не сдашься.

Важно следить за упрощениями. В частности, перед применяя приемы из какого-то ящика, следует проверить, нужно ли применять этот трюк ко всему заданному выражению. Иногда проблема вызвана просто часть выражения а остальное “красиво”, то обычно очень мудро разбить данный лимит на несколько частей и применить наиболее удобный метод к каждой части. Иногда бывает наоборот, вы вынуждены разделить лимит, так как нужный вам трюк применяется только к части заданного предел. Для более подробного обсуждения разделения лимитов и оценки его части см. это примечание.

Аналогичным образом, если вам нужно вернуться к шагу 1, настоятельно рекомендуется что вы посмотрите на то, что у вас получилось после применения трюков и по возможности упростите.

Обратите внимание, что существуют предельные задачи, которые не подходят ни к одному шаблону, который мы рассмотрели. здесь (то есть они точно не подходят ни к одному ящику ниже). Тогда чем больше опыт и понимание концепции предела у вас есть, тем лучше ваши шансы оценить предел.

Этот план должен иметь больше смысла, если вы посмотрите на некоторые Решенные проблемы – ограничения и сравните, как они решаются с общим описанием решения здесь.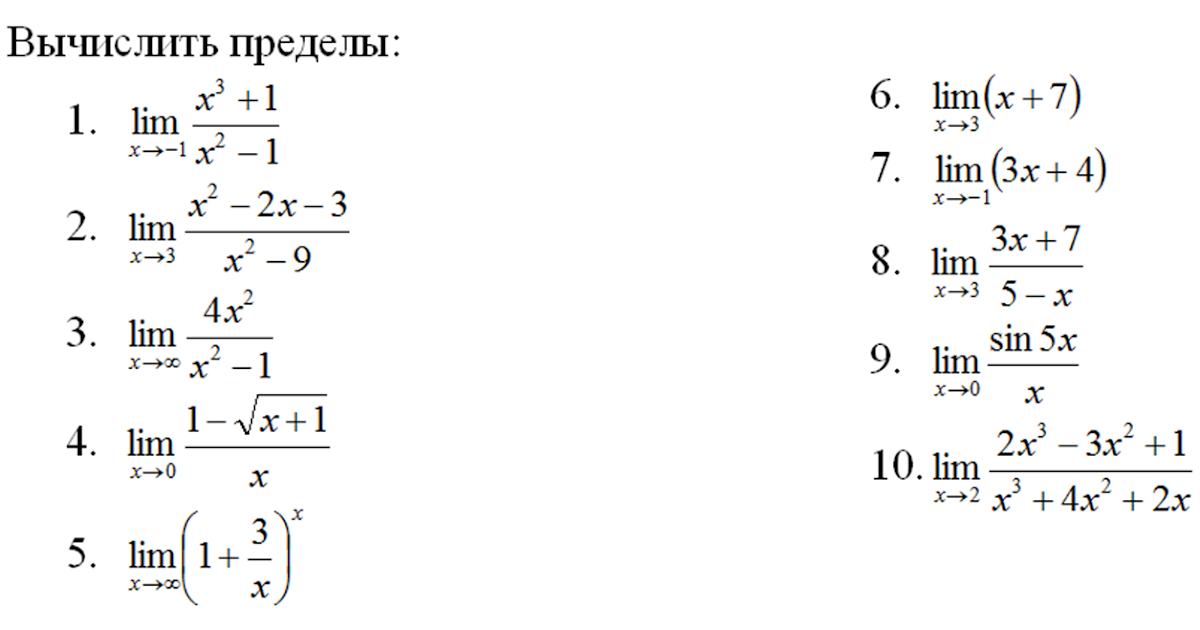 Там же вы найдете и другие полезные трюки.

У новичков иногда возникают проблемы с правильное обозначение своих расчетов и результатов.

Примечание 1.

Односторонние результаты пределов часто нужны при подстановке в функции. Эту информацию о результате обычно получают из сам данный предел (когда он дан односторонний), но иногда и следует из характера проблемы.

Пример: Предел e ^x − 1 для х → 0 ⁺ есть 0 ⁺ .
Действительно, подставив x = 0 в выражение мы получаем 0, теперь нам нужно выяснить, какой. Если x → 0 ⁺ , тогда x — это число, близкое к 0, что удовлетворяет x > 0. Тогда также e ^x > 1, следовательно e ^x − 1 > 0.

Пример: Предел 1 + 2 x − x ² для x →2 ^– 1 ⁺ .
Действительно, подставив x = 2 в выражение, мы получим 1, теперь нам нужно выяснить, какой. Если х → 2 ^–, тогда x — это число, близкое к 2, которое удовлетворяет x < 2. Однако неясно, что происходит с выражение. Есть два способа это узнать.

Математически правильно это: 1 + 2 x − x ² = 1 + x ⋅ (2 − x ). Если x < 2, то (2 − x ) > 0, а x – положительное значение при закрытии. до 2, поэтому x ⋅(2 − x ) > 0 и 1 + x ⋅ (2 − x ) > 1, что доказывает наше утверждение.

Этот метод был правильным, но специфичным для данного конкретного примера. В целом всегда можно попытаться исследовать монотонность данного выражения вокруг предельная точка, но на практике люди редко удосуживаются тратить время. Обычно используют другой метод, который гораздо удобнее, но имеет небольшой недостаток, заключающийся в том, что он не является математически правильным. Вот это приходит:

Если х → 2 ^–, тогда x – это что-то вроде 2 минус что-то очень-очень маленькое. Сказать, x = 1,9999. Когда мы подставляем это в выражение 1 + 2 x − x ² , получаем 0,99980001 < 1, что предполагает, что приближаемся к предельному результату 1 снизу. Конечно, это не доказывает ничего, для некоторых диких функций этот метод не работает. Однако большинство задачи имеют «разумные» функции, и, учитывая простоту этого метода, большинство людей (включая меня) используют его довольно часто, когда сталкиваются с более сложная проблема «односторонности».

Пример: Предел 1 + cos( x ) для x →0 2 ^– .
Действительно, подставив x = 0 в выражение, мы получим 2. При этом если х число близкое к 0 (неважно с какой стороны), то cos(x) < 1 (обратите внимание, что «близко к 0» не включает сам 0, поэтому точное неравенство верно). Следовательно 1 + cos(x)< 2, что доказывает утверждение.

Пример: Предел 1 + sin( x ) для x →0 это всего лишь 1.
Действительно, подставив x = 0 в выражение, мы получим 1. Однако мы не можем утверждать, что это будет 1 ⁺ или 1 ^–. В качестве x →0, это иногда отрицательное, а иногда положительное (это двусторонний предел), поэтому также sin( x ) иногда положительный, а иногда отрицательный. Независимо от того насколько малой редуцированной окрестностью 0 мы считаем функцию 1 + sin( x ) одновременно больше и меньше 1 на нем, поэтому односторонний вывод невозможен. возможный.

Еще один хороший пример с односторонностью находится в это примечание.

Примечание 2.

Мы достаточно хорошо знаем, как распознавать случаи, когда предел существует (предельная алгебра) и когда она беспокойный (неопределенный выражения). Менее изученной, но не менее важной является способность определить, каких пределов не существует. Это обычно игнорируется в расчетах курсы, так как в конце концов от нас ждут решения задач в школе.

Тем не менее, для полноты картины мы опустим пару слов об ограничениях, которые не существует. Для начала неплохо вспомнить некоторые «знаменитые» пределы, которые не существует. Наиболее частыми примерами являются пределы синуса и косинуса. при (минус) бесконечности и отношении 1/0, где 0 не является односторонним, следует отметить также пределы котангенса в 0 и его сдвиги и тангенса в π/2 и его сдвиги.

Затем полезно знать, как такие проблемные выражения взаимодействуют с другими. выражения. Возможных ситуаций много, мы постарались собрать как можно больше интересные в попытке алгебра N ( N для несуществующие), куда мы также включили неопределенные выражения.

Эта тема настолько игнорируется, что наш список, вероятно, единственный, в который вы собираетесь видеть где угодно, что говорит о том, что, возможно, это не так важно после все.

Концепции предельных значений — исчисление 2

Все ресурсы исчисления 2

9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 Следующая →

Исчисление 2 Помощь » Ограничения » Понятия предела

Оцените предел:

Возможные ответы:

Не существует

Правильный ответ:

Объяснение:

Прямая оценка предела даст неопределенный ответ .

Переписывая предел в терминах синуса и косинуса, мы можем попытаться манипулировать функцией, чтобы использовать свойство .

Умножая функцию на аргументы функции синуса, мы видим, что предел будет равен .

Сообщить об ошибке

Найти предел при приближении к бесконечности.

Возможные ответы:

Неубедительно

Правильный ответ:

3

Объяснение:

Выражение можно переписать как .

Вспомним, что теорему сжатия можно использовать для нахождения предела. Функция синуса имеет диапазон от , что означает, что диапазон должен находиться внутри этой границы.

Умножить член на.

Берем предел по мере приближения к бесконечности для всех членов.

Так как левый и правый концы этого интервала равны нулю, то можно сделать вывод, что он также должен стремиться к нулю.

Правильный ответ: 0.

Сообщить об ошибке

Определить предел.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы определить , постройте график функции и обратите внимание на направление слева и справа от кривой по мере ее приближения .

Как влево, так и вправо уходит в минус бесконечность.

Ответ:

Сообщить об ошибке

Что из следующего верно?

Возможные ответы:

Если и , то существует.

Если существует, то и оба существуют.

и существовать тогда и только тогда, когда существует.

Если ни , ни не существует, то также не существует.

Правильный ответ:

Если и , то существует.

Объяснение:

Если и , то существует.

Это можно строго доказать, используя определение предела, но, скорее всего, это выходит за рамки вашего класса.

Сообщить об ошибке

Определить лимит:

Возможные ответы:

Правильный ответ:

Объяснение:

Изолировать константу в пределе.

Свойство limit .

Следовательно:

Сообщить об ошибке

Оцените предел, если возможно:

Возможные ответы:

Правильный ответ: 9

3 Объяснение:

Чтобы оценить , обратите внимание, что внутренний член будет приближаться к бесконечности после подстановки. Арктангенс очень большого числа приближается к .

Ответ .

Сообщить об ошибке

Оцените следующий лимит:

Возможные ответы:

Правильный ответ:

Объяснение:

Первым шагом является вынесение члена высшей степени из полинома сверху и снизу (по сути, вытягивание 1):

, что становится

Оценивая предел, мы приближаемся .

Сообщить об ошибке

Оцените следующее ограничение:

Возможные ответы:

Правильный ответ:

3 Объяснение:
Чтобы оценить предел, сначала вытяните наибольший член степени сверху и снизу (по сути, мы удаляем 1):
, что становится
Подставляя бесконечность, мы находим, что числитель приближается к нулю, что приближает весь предел к 0,

Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
3
32 Объяснение:
Чтобы оценить предел, сначала вытащите член с наивысшей степенью из числителя и знаменателя (по сути, вы вытягиваете 1):
Как видите, члены и по мере приближения к бесконечности стремятся к нулю. . Осталось .

Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
3
32 Объяснение:
Чтобы легко вычислить этот предел, просто вытяните множитель члена высшей степени над членом высшей степени (1):
Как видите, после деления на 1 знаменатель становится равным 1 и числитель становится 0,
Следовательно, окончательный ответ .
Сообщить об ошибке
← Назад 1 2 3 4 5 Далее →
Уведомление об авторских правах
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
Как решить задачу с ограничениями
Здесь вы найдете все, что вам нужно знать о решении математических задач с ограничениями. Я подготовил список всех возможных случаев проблем. Если вы овладеете этими приемами, вы сможете решать любые задачи, связанные с ограничениями в исчислении.
Моя цель на этой странице — стать основным ресурсом для решения проблем. Вы найдете примеры решений и советы для каждого типа ограничений.
Если вы хотите получать больше таких уроков прямо на вашу электронную почту, охватывающих все, что касается исчисления, обязательно подпишитесь на
Здесь мы сосредоточимся на методах решения проблем. Если вы хотите интуитивно понять идею ограничений, посетите эти страницы:
Тип 1: Ограничения путем прямой замены
Это самые простые задачи. В этих задачах нужно только подставить значение, к которому приближается независимое значение.
Например:
Здесь мы просто заменяем x на a, чтобы получить
Я не думаю, что вам нужно много тренироваться, чтобы решить их. Они тоже не очень веселые. Однако здесь есть интересный вопрос читателя, который связывает технику, которую мы здесь используем, и концепцию непрерывности: Решение пределов с помощью непрерывности .
Тип 2: Пределы факторинга
Теперь это более интересно. В этих пределах, если попытаться подставить, как в предыдущем случае, получится неопределенность.
Например:
Если вы просто замените x на 1 в выражении, вы получите 0/0. Так что мы можем сделать? Мы используем наши алгебраические навыки, чтобы упростить выражение. В предыдущем примере мы можем разложить числитель на множители:
Проблемы такого типа легко заметить: всякий раз, когда вы видите частное двух многочленов, вы можете попробовать эту технику, если есть неопределенность.
Тип 3: Ограничения по рационализации
Они включают пределы с квадратным корнем.
В этих пределах мы применяем алгебраический метод, называемый рационализацией.
Например:
Если мы подставим, мы получим 0/0, и мы не можем это учесть. Хитрость заключается в умножении и делении дроби на удобное выражение. (Помните, что если вы умножаете и делите число на одно и то же, вы получаете одно и то же число). В этом случае мы используем следующее тождество:
(Просто выполните продукт слева, чтобы проверить его). Итак, всякий раз, когда вы видите разницу или сумму двух квадратных корней, вы можете применить предыдущее тождество. Два фактора слева называются сопряженными выражениями.
В приведенном выше примере сопряженным числителем является:
И это число, на которое мы будем умножать и делить нашу дробь:
Теперь в числителе мы используем только что упомянутое алгебраическое тождество:
Теперь (1-x) исчезает, и мы получаем желаемый результат:
В этих пределах вы всегда делаете то же самое. Вы узнаете разницу между двумя квадратными корнями и умножением и делением на сопряженное выражение. Другой пример:
Вы получите неопределенность, если замените h на ноль. Вы можете увидеть разницу между двумя квадратными корнями в числителе.
Все, что вам нужно сделать, это умножить и разделить на сопряженное число числителя и работать алгебраически.
Вот еще один проработанный пример: Ограничение рационализацией . Есть и другие примеры, которые сложнее, в том смысле, что вам нужно умножить на два выражения. Например:
(p и q — константы). В этом случае у вас есть квадратные корни как в числителе, так и в знаменателе.
В этом случае нужно умножить и разделить на два множителя: сопряженное числителя и затем сопряженное знаменателя.
Эта проблема является хорошей практикой, и я рекомендую вам попробовать ее. Если вы пытались и все еще не можете решить ее, вы можете задайте вопрос об этом вместе с вашей работой.
Тип 4: Пределы на бесконечности
В этих пределах независимая переменная стремится к бесконечности. Примером может служить предел:
Я уже написал очень популярную страницу об этой технике со многими примерами: Решение пределов в бесконечности . На следующей странице вы также можете найти пример предела на бесконечности с радикалами. В этом ограничении вам также необходимо применить методы рационализации, которые мы видели раньше: Предел с радикалами
Тип 5: Тригонометрические пределы
В большинстве пределов, включающих тригонометрические функции, вы должны применять фундаментальный предел: личности на выбор.
На следующей странице вы найдете все, что вам нужно знать о тригонометрических пределах, включая множество примеров: Теорема сжатия и пределы с тригонометрическими функциями .
Вот еще примеры тригонометрических пределов. Я думаю, вы найдете все методы, которые вам нужно знать, в этих:
Тригонометрический предел с касательной
Несколько иной тригонометрический предел
Тип 6: Ограничения, связанные с числом e
Число e определяется следующим пределом:
Существуют некоторые ограничения, которые можно решить с помощью этого фундаментального ограничения. Это похоже на то, что мы делаем с тригонометрическими пределами. Мы пытаемся приспособить функцию алгебраически, чтобы применить уже известный нам предел.
Здесь вы можете найти более сложный пример: Лимит на бесконечное число участников e .
Пределы по правилу Лопиталя
Если вы еще не знакомы с деривативами, можете пропустить этот раздел. С помощью правила Лопиталя мы можем решать ограничения, используя наши навыки поиска производных.
Это правило гласит, что для нахождения предела частного достаточно найти производные от числителя и знаменателя и снова применить предел.
Это работает, только если частное имеет неопределенную форму 0/0 или бесконечность на бесконечность. Например:
И числитель, и знаменатель стремятся к бесконечности. Таким образом, это неопределенность формы бесконечности над бесконечностью. Выводим числитель и знаменатель и снова применяем предел. То есть:
Это круто, не так ли? Вскоре я опубликую страницу, посвященную этому правилу.