Предел функции онлайн
Число A называется пределом функцииy=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
| lim
x→ |
1. Не знаю
2. Пределы вида (см. пример).
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6.
Вместе с этим калькулятором также используют следующие:
Точки разрыва функции
Производная функции:
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление интегралов
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.Примеры.
Вычислить указанные пределы:
1. = .
2. =
3. . Так как числитель и знаменатель обратились в нуль при.
4. .
5.
= =
6. – не существует, так как -1<cos(x)<1.
7. . Обозначим , причем заметим, что при x→16, y→2. Получим:
.
8. . (Ответ получается непосредственно подстановкой (-∞) вместо x.)
9. . Здесь следует рассмотреть односторонние пределы:
Следовательно, – не существует (так как у функции разные односторонние пределы).
Найти пределы функции, не применяя правило Лопиталя.
а) =
Ответ: 1/5
б)
=
Ответ: 1/6в) = e-2/2 = e-1
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет 
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
,
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д)
Ответ: 1/10определения, история развития, применение пределов на практике
Содержание:
- Основные определения
- История развития
- Применение пределов на практике
Понятие предела последовательности или функции является одним из фундаментальных понятий математического анализа.
Основные определения
Определение
Предел числовой последовательности, подробнее →
Число $a$ называется пределом последовательности $\left\{x_{n}\right\}$ , если для любого $\epsilon>0$ существует номер $n_{0}=n_{0}(\epsilon)$ такой, что для любого $n>n_{0}$ выполняется неравенство $\left|x_{n}-a\right| \lt \epsilon$ :
$\lim _{n \rightarrow \infty} x_{n}=a \Leftrightarrow \forall \epsilon>0, \exists n_{0}=n_{0}(\epsilon) : \forall n>n_{0},\left|x_{n}-a\right| \lt \epsilon$
Предел функции в точке, подробнее →
Число $b$ называется пределом функции
$f(x)$ в точке
$a$, если для
$\forall \epsilon>0 \exists \delta>0$
такое, что для
$\forall x \in(a-\delta ; a+\delta) \cap D[f]$ из того, что
$0 \lt |x-a| \lt \delta$ следует, что
$|f(x)-b| \lt \epsilon$ :
$\lim _{x \rightarrow a} f(x)=b$ или
$f(x) \rightarrow b$ при
$x \rightarrow a$ .
Предел функции на бесконечности, подробнее →
Число $b$ называется пределом функции $y=f(x)$ на бесконечности или при $x \rightarrow \infty$, если для любого $\forall \epsilon>0$ существует такое число $\delta=\delta(\epsilon)>0$ такое, что для всех $x \in D(f)$ из того, что $|x|>M$, выполняется неравенство $|f(x)-b| \lt \epsilon$.
История развития
Это понятие на интуитивном уровне использовалось ещё во второй половине 17 века английским физиком, математиком и
астрономом Исааком Ньютоном (1642 – 1727), а также математиками 18 века – швейцарским, немецким и русским математиком
Леонардом Эйлером (1707 – 1783) и французским математиком, астрономом и механиком Жозефом Луи Лагранжем (1736 – 1813).
Это было связано с тем, что ученые того времени не ставили перед собой задачу построения теории пределов. Первые
строгие определения
предела последовательности дали в 1816 году чешский математик, философ, теолог Бернард Больцано
(1781 – 1848) и французский математик Огустен Луи Коши (1789 – 1857) в 1821 году.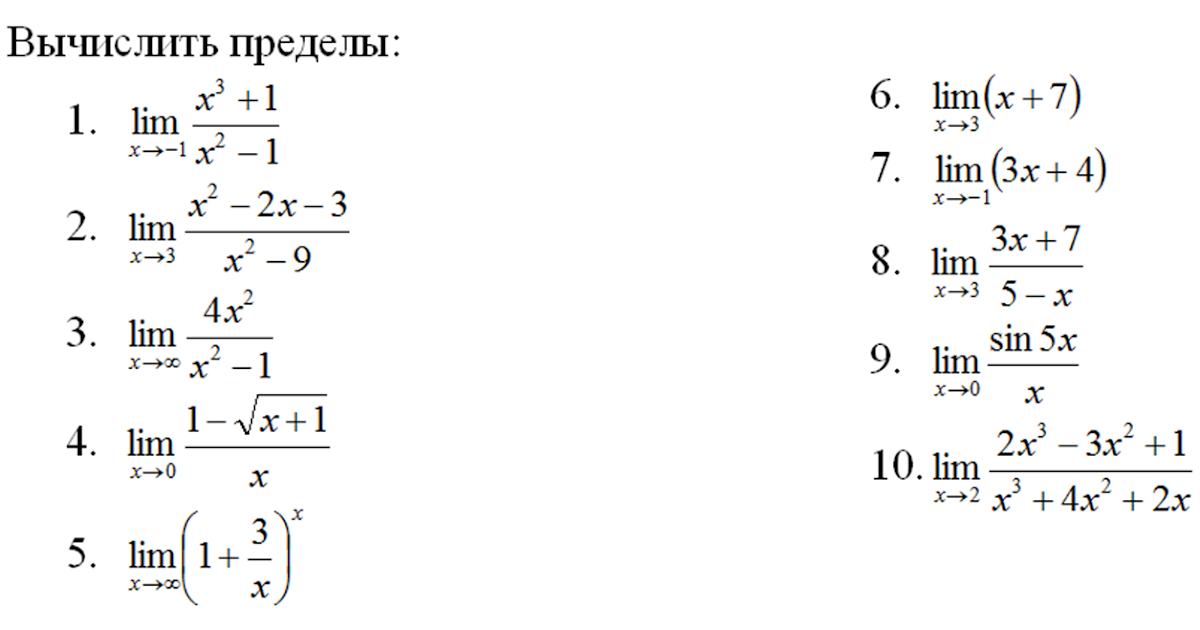
Применение пределов на практике
Теория пределов очень активно применяется в экономических расчетах, например, в доказательствах и расчетах, которые связаны с непрерывными процессами; в финансовых рентах. Пределы функции применяются для нахождения асимптот графика функции при ее исследовании.
Читать дальше: понятие числовой последовательности.
- Понятие числовой последовательности
- Односторонние пределы
- Предел функции на бесконечности. Бесконечно большая функция
- Свойства пределов функции
- Бесконечно малые функции
- Сравнение бесконечно малых функций
- Эквивалентные бесконечно малые функции. Таблица эквивалентных б.м. функций
- Признаки существования пределов
- Первый замечательный предел
- Второй замечательный предел
- Правило Лопиталя
- Ограниченные последовательности
- Основные неопределенности и способы их раскрытия
- Понятие непрерывности функции в точке
- Непрерывность функции на промежутке
- Точки разрыва функции и их классификация
- Основные теоремы о непрерывности функций.
Непрерывность элементарных функций - Бесконечно малые и бесконечно большие последовательности
- Монотонные последовательности
- Предел числовой последовательности
- Предельный переход в неравенствах
- Предел монотонной ограниченной последовательности. Число е
- Фундаментальные последовательности. Критерий Коши
- Предел функции в точке
Непрерывность элементарных функций1.1: Введение в понятие лимита
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 11015
Эта страница является черновиком и находится в активной разработке.
Цели обучения
- Используя правильные обозначения, опишите предел функции.
- Используйте таблицу значений, чтобы оценить предел функции или определить, когда предел не существует.
- Используйте график, чтобы оценить предел функции или определить, когда предел не существует.
- Дайте определение односторонним ограничениям и приведите примеры.
- Объясните взаимосвязь между односторонними и двусторонними пределами.
- Используя правильные обозначения, опишите бесконечный предел.
- Задайте вертикальную асимптоту.
Пределы
Две ключевые проблемы привели к первоначальной формулировке исчисления:
(1) проблема касательной, или как определить наклон линии, касательной к кривой в точке;
и (2) задача площади, или как определить площадь под кривой.
Концепция предела или ограничивающего процесса, необходимая для понимания исчисления, существует уже тысячи лет. На самом деле ранние математики использовали ограничивающий процесс для получения все более и более точных приближений площадей кругов. Однако формальное определение предела — в том виде, в каком мы его знаем и понимаем сегодня — появилось только в конце XIX в.
, которые показаны на рисунке \(\PageIndex{1}\). В частности, давайте сосредоточим наше внимание на поведении каждого графа при \(x=2\) и около него.
Рисунок \(\PageIndex{1}\): Эти графики показывают поведение трех различных функций вокруг \(x=2\).Каждая из трех функций не определена в точке \(x=2\), но если мы делаем это утверждение и никакое другое, мы даем очень неполную картину того, как каждая функция ведет себя вблизи точки \(x=2\). Чтобы более полно выразить поведение каждого графа в окрестности \(2\), нам нужно ввести понятие предела. 92−4)/(x−2)\) ведет себя примерно так, как \(x=2\) на рисунке \(\PageIndex{1}\). Поскольку значения \(x\) приближаются к \(2\) по обе стороны от \(2\), значения \(y=f(x)\) приближаются к \(4\). Математически мы говорим, что предел \(f(x)\) при приближении \(x\) к \(2\) равен \(4\). Символически мы выражаем этот предел как
\(\displaystyle \lim_{x \to 2} f(x)=4\).
Из этого очень краткого неформального взгляда на один предел давайте начнем разрабатывать интуитивное определение предела .
Мы можем думать о пределе функции при числе а как об одном действительном числе \(L\), к которому функциональные значения приближаются по мере того, как \(х\)-значения приближаются к а, при условии, что такое действительное число \(L\ ) существуют. Сформулировав более тщательно, мы имеем следующее определение:
Определение (интуитивное): Предел
Пусть \(f(x)\) — функция, определенная для всех значений в открытом интервале, содержащем \(a\), за возможным исключением самого a, и пусть \(L \) быть действительным числом. Если все значения функции \(f(x)\) приближаются к действительному числу \(L\), а значения \(x(≠a)\) приближаются к числу a, то мы говорим, что предел \( f(x)\) при приближении \(x\) к \(a\) есть \(L\). (Более кратко, поскольку \(x\) приближается к \(a\), \(f(x)\) приближается и остается близким к \(L\).) Символически мы выражаем эту идею как
\[\lim_{x \to a} f(x)=L.\]
Мы можем оценить пределы, составив таблицы функциональных значений и просмотрев их графики.
Этот процесс описан в следующей стратегии решения проблем.
Стратегия решения проблем: оценка предела с использованием таблицы функциональных значений
1. Чтобы оценить \(\displaystyle \lim_{x \to a} f(x)\), мы начнем с заполнения таблицы функциональных значений . Мы должны выбрать два набора \(x\)-значений: один набор значений приближается к \(a\) и меньше \(a\), а другой набор значений приближается к \(a\) и больше \(a\) \). В таблице \(\PageIndex{1}\) показано, как могут выглядеть ваши таблицы.
| \(х\) | \(f(x)\) | \(х\) | \(f(x)\) |
|---|---|---|---|
| \(а-0,1\) | \(ф(а-0,1)\) | \(а+0,1\) | \(f(а+0,1)\) |
| \(а-0,01\) | \(f(a-0,01)\) | \(а+0,001\) | \(f(а+0,001)\) |
| \(а-0,001\) | \(f(a-0,001)\) | \(а+0,0001\) | \(f(а+0,001)\) |
| \(а-0,0001\) | \(ф(а-0,0001)\) | \(а+0,00001\) | \(ф(а+0,0001)\) |
При необходимости используйте дополнительные значения. | При необходимости используйте дополнительные значения. | ||
2. Далее давайте посмотрим на значения в каждом из столбцов \(f(x)\) и определим, приближаются ли значения к одному значению по мере продвижения вниз по каждому столбцу. В наших столбцах мы смотрим на последовательность \(f(a-0,1)\), \(f(a-0,01)\), \(f(a-0,001)\), \(f(a-0,0001) \) и так далее, и \(f(a+0,1), \;f(a+0,01), \;f(a+0,001), \;f(a+0,0001)\) и так далее. (Примечание. Хотя мы выбрали \(x)-значения \(a±0,1, \;a±0,01, \;a±0,001, \;a±0,0001\) и т. д., и эти значения, вероятно, работают почти каждый раз, в очень редких случаях нам может потребоваться изменить наш выбор.)
3. Если оба столбца приближаются к общему \(y\)-значению \(L\), мы указываем \(\displaystyle \lim_{x \to a}f(x)=L\). Мы можем использовать следующую стратегию для подтверждения результата, полученного из таблицы, или в качестве альтернативного метода оценки предела.
4. С помощью графического калькулятора или компьютерной программы, которая позволяет нам графически отображать функции, мы можем построить график функции \(f(x)\), убедившись, что функциональные значения \(f(x)\) для \(x\ )-значения рядом с a находятся в нашем окне. Мы можем использовать функцию трассировки, чтобы перемещаться по графику функции и наблюдать за показаниями \(y\)-значения по мере того, как \(x\)-значения приближаются к a. Если \(y\)-значения приближаются к \(L\), когда наши \(x\)-значения приближаются к \(a\) с обоих направлений, то \(\displaystyle \lim_{x \to a}f(x )=L\). Возможно, нам придется увеличить наш график и повторить этот процесс несколько раз.
Мы применяем эту стратегию решения проблем для вычисления лимита в примерах \(\PageIndex{1A}\) и \(\PageIndex{1B}\).
Пример \(\PageIndex{1A}\): оценка предела с использованием таблицы функциональных значений
Оценка \(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) с таблица функциональных значений.
Решение
Мы рассчитали значения \(f(x)=\dfrac{\sin x}{x}\) для значений \(x\), перечисленных в таблице \(\PageIndex{2 }\).
| \(х\) | \(\frac{\sin x}{x}\) | \(х\) | \(\frac{\sin x}{x}\) |
|---|---|---|---|
| -0,1 | 0,998334166468 | 0,1 | 0,998334166468 |
| -0,01 | 0,999983333417 | 0,01 | 0,999983333417 |
| -0,001 | 0,999999833333 | 0,001 | 0,999999833333 |
| -0,0001 | 0,999999998333 | 0,0001 | 0,999999998333 |
Примечание.
Значения в этой таблице были получены с помощью калькулятора и с использованием всех мест, указанных в выходных данных калькулятора.
Читая каждый столбец \(\dfrac{\sin x}{x}\), мы видим, что значения в каждом столбце приближаются к единице. Таким образом, вполне разумно заключить, что \(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). График \(f(x)=\dfrac{\sin x}{x}\), построенный калькулятором или компьютером, будет похож на показанный на рисунке \(\PageIndex{2}\), и он подтверждает наши оценивать.
Рисунок \(\PageIndex{2}\): График \(f(x)=(\sin x)/x\) подтверждает оценку из табл.Пример \(\PageIndex{1B}\): оценка предела с помощью таблицы функциональных значений
Оценить \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) с помощью таблицы функциональных значений.
Решение
Как и прежде, мы используем таблицу — в данном случае Таблицу \(\PageIndex{3}\) — для перечисления значений функции для заданных значений \(x\).
| \(х\) | \(\frac{\sqrt{x}−2}{x−4}\) | \(х\) | \(\frac{\sqrt{x}−2}{x−4}\) |
|---|---|---|---|
| 3,9 | 0,251582341869 | 4. 1 | 0,248456731317 |
| 3,99 | 0,25015644562 | 4.01 | 0,24984394501 |
| 3,999 | 0,250015627 | 4.001 | 0,249984377 |
| 3,9999 | 0,250001563 | 4.0001 | 0,249998438 |
| 3,99999 | 0,25000016 | 4. 00001 | 0,24999984 |
Изучив эту таблицу, мы видим, что функциональные значения меньше 4 уменьшаются до 0,25, тогда как функциональные значения больше 4 увеличиваются до 0,25. Мы заключаем, что \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0,25\). Мы подтверждаем эту оценку, используя график \(f(x)=\dfrac{\sqrt{x}−2}{x−4}\), показанный на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\): График \(\frac{\sqrt{x}−2}{x−4}\) подтверждает оценку из таблицы. Упражнение \(\PageIndex{1}\ )
Оцените \(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\), используя таблицу функциональных значений. Используйте график, чтобы подтвердить свою оценку.
- Подсказка
Используйте 0,9, 0,99, 0,999, 0,9999, 0,99999 и 1,1, 1,01, 1,001, 1,0001, 1,00001 в качестве табличных значений.
- Ответ
\[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber\]
На данный момент из примеров \(\PageIndex{1A}\) и \(\PageIndex{1b}\) мы видим, что может быть так же просто, если не проще, оценить предел функции, исследуя его график, как он есть, для оценки предела с помощью таблицы функциональных значений.
В примере \(\PageIndex{2}\) мы оцениваем ограничение исключительно по графику, а не по таблице функциональных значений.
Пример \(\PageIndex{2}\): оценка предела с помощью графика
Для \(g(x)\), показанного на рис. {х\к-1}г(х)\).
Рисунок \(\PageIndex{4}\): График \(g(x)\) включает одно значение не на гладкой кривой.Решение :
Несмотря на то, что \(g(-1)=4\), при приближении \(x\)-значений к \(-1\) с любой стороны, \(g(x) \) значения приближаются к \(3\). Следовательно, \(\displaystyle \lim_{x\to-1}g(x)=3\). Заметим, что мы можем определить этот предел, даже не зная алгебраического выражения функции.
На основе примера \(\PageIndex{2}\) мы делаем следующее наблюдение: возможно, что предел функции существует в точке, и функция может быть определена в этой точке, но предел функции и значение функции в точке могут быть разными.
Упражнение \(\PageIndex{2}\)
Используйте график \(h(x)\) на рисунке \(\PageIndex{5}\) для оценки \(\displaystyle \lim_{x \to 2 }h(x)\), если это возможно.
- Подсказка
К какому \(y\)-значению приближается функция, когда \(x\)-значение приближается к \(2\)?
- Решение
\(\displaystyle \lim_{x \to 2}h(x)=−1.\)
Глядя на таблицу функциональных значений или глядя на график функции, мы получаем полезную информацию о значении предела функции в данной точке. Однако эти методы слишком полагаются на догадки. Со временем нам потребуется разработать альтернативные методы оценки пределов. Эти новые методы носят более алгебраический характер, и мы рассмотрим их в следующем разделе; однако на этом этапе мы вводим два специальных ограничения, которые лежат в основе будущих методов.
Два важных ограничения
Пусть \(a\) — действительное число, а \(c\) — константа.
- \(\displaystyle \lim_{x \to a}x=a\)
- \(\displaystyle \lim_{x \to a}c=c\)
Мы можем сделать следующие замечания относительно этих двух пределов.
- Для первого предела заметим, что по мере того, как \(x\) приближается к \(a\), приближается и \(f(x)\), потому что \(f(x)=x\). Следовательно, \(\displaystyle \lim_{x \to a}x=a\).
- Для второго ограничения рассмотрим таблицу \(\PageIndex{4}\).
| \(х\) | \(f(x)=c\) | \(х\) | \(f(x)=c\) |
|---|---|---|---|
| \(а-0,1\) | \(с\) | \(а+0,1\) | \(с\) |
| \(а-0,01\) | \(с\) | \(а+0,01\) | \(с\) |
| \(а-0,001\) | \(с\) | \(а+0,001\) | \(с\) |
| \(а-0,0001\) | \(с\) | \(а+0,0001\) | \(с\) |
Обратите внимание, что для всех значений \(x\) (независимо от того, приближаются ли они к \(a\)), значения \(f(x)\) остаются постоянными при \(c\). У нас нет другого выбора, кроме как заключить \(\displaystyle \lim_{x \to a}c=c\).
Существование предела
Когда мы рассматриваем предел в следующем примере, имейте в виду, что для того, чтобы предел функции существовал в точке, функциональные значения должны приближаться к единственному вещественному значению в этой точке. Если функциональные значения не приближаются к единому значению, то предела не существует.
Пример \(\PageIndex{3}\): оценка несуществующего предела
Вычислить \(\displaystyle\lim_{x \to 0}\sin(1/x)\) с помощью таблицы значений.
Решение
В таблице \(\PageIndex{5}\) перечислены значения функции \(\sin(1/x)\) для заданных значений \(x\).
| \(х\) | \(\sin(1/x)\) | \(х\) | \(\sin(1/x)\) |
|---|---|---|---|
| -0,1 | 0,544021110889 | 0,1 | −0,544021110889 |
| -0,01 | 0,50636564111 | 0,01 | −0,50636564111 |
| -0,001 | −0,8268795405312 | 0,001 | 0,8268795405312 |
| -0,0001 | 0,305614388888 | 0,0001 | −0,305614388888 |
| -0,00001 | −0,035748797987 | 0,00001 | 0,035748797987 |
| -0,000001 | 0,349993504187 | 0,000001 | −0,349993504187 |
Изучив таблицу функциональных значений, мы видим, что \(y\)-значения не приближаются ни к одному единственному значению. Получается, что предела не существует. Прежде чем сделать такой вывод, давайте подойдем более системно. Возьмем следующую последовательность \(x\)-значений, приближающихся к \(0\):
\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac {2}{9π},\;\frac{2}{11π},\;….\nonumber\]
Соответствующие \(y\)-значения равны
\[1,\;-1,\ ;1,\;-1,\;1,\;-1,\;….\nonumber\]
На данный момент мы действительно можем заключить, что \(\displaystyle \lim_{x \to 0} \ sin(1/x)\) не существует. (Математики часто сокращают «не существует» до DNE. Таким образом, мы будем писать \(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) График \(f(x) =\sin(1/x)\) показан на рисунке \(\PageIndex{6}\) и дает более четкое представление о поведении \(\sin(1/x)\) при \(x\) приближается к \(0\). Вы можете видеть, что \(\sin(1/x)\) все более сильно колеблется между \(-1\) и \(1\) по мере того, как \(x\) приближается к \(0\). 92−4∣}{x−2}\) не существует.
Авторы и ссылки
Гилберт Стрэнг (MIT) и Эдвин «Джед» Херман (Харви Мадд) со многими сотрудничающими авторами.
Этот контент от OpenStax лицензирован по лицензии CC-BY-SA-NC 4.0. Скачать бесплатно на http://cnx.org.Памини Тангараджа (Университет Маунт-Рояль, Калгари, Альберта, Канада)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- да
- Стадия
- Проект
- Теги
- расчет: да
- юпитер: питон
Репетитор по математике – Последовательности – Теория
Репетитор по математике – Последовательности – Теория – Пределы Мы начнем с рассмотрения нескольких основных свойств пределов. Затем мы смотрим на
теоремы об операциях, которые
приводит непосредственно к предельной алгебре, нашему основному инструменту для вычисления пределов.
Затем мы исследуем некоторые взаимодействия между конвергенцией
монотонность и ограниченность;
мы также смотрим на ограничения и
подпоследовательности. В конце мы кратко
познакомить с понятием
Последовательность Коши.
Несколько простых утверждений
Следующие утверждения должны быть понятны, если вы понимаете, что означает ограничение.
Факт.
Последовательность { a n } сходится к L если и только если { a n − L } сходится к 0.Факт.
Если последовательность { a n } переходит к L , затем {| a n |} идет к | л |.Факт.
Последовательность { a n } становится 0 тогда и только тогда, когда {| a n |} становится 0.Факт.
Предположим, что последовательности { a n } и { b n } сходятся. Предел { a n } равен предел { b n } тогда и только тогда, когда { a n − b n } переходит в 0.
Обратите внимание, что последнее утверждение больше не верно, если мы отбросим предположение о сходимости.
Факт.
Если последовательность { a n } имеет ненулевой предел, тогда существует N и константа m > 0 такое, что | a n | > м для k > N .
Ограничения и операции
При оценке предела отправной точкой является
элементарные пределы, которые мы
должен помнить; это основные строительные блоки. Более сложный
выражения создаются путем объединения таких элементарных выражений, поэтому мы
также нужно знать, как собрать их вместе в пределе.
Теорема (пределы и алгебраические операции).
Предположим, что последовательность { a n } имеет предел A и последовательность { b n } имеет ограничение B . Тогда верно следующее:
(i) Для любого действительного числа c последовательность { ca n } имеет ограничение cA , если это имеет смысл.
(ii) Последовательность { a n + b n } имеет предел A + B , если это имеет смысл.
(iii) Последовательность { a n − b n } имеет предел A – B , если это имеет смысл.
(iv) Последовательность { а н ⋅ б н } имеет предел A ⋅ B , если это имеет смысл.
(v) Последовательность { a n / b п } имеет предел A / B , если это имеет смысл.
(vi) Последовательность { а н б н } имеет предел A B , если это имеет смысл.
Теперь, что это насчет смысла? Если A и B реальны
чисел, то есть если две последовательности сходятся, то операции
(i) через (iv) всегда имеют смысл. Однако соотношение A/B имеет смысл только в том случае, если B не равно нулю. И это именно то, что
имеется в виду; мы можем применить эту теорему, если то, что мы получим в конце, имеет смысл.
На самом деле мы имеем здесь расширение обычной алгебры. Раньше, когда
мы написали “3 + 2 = 5″, мы имели в виду, что добавили три яблока
к двум яблокам дают пять яблок. Но теперь это может также означать, что «последовательность
сходится к 3 при добавлении к другой последовательности, которая сходится к 2
даст последовательность, которая сходится к 5”. Это “лимит
алгебра” и в отличие от обычной алгебры, в этой еще есть
бесконечности.
Теперь мы могли бы представить теорему со многими утверждениями, но это слишком легче начать с другого конца. Обратите внимание, что в приведенной выше теореме мы сделали не предполагайте, что A , B конечны, и некоторые операции могут быть определены также для случаев, когда они имеют бесконечность. Если мы используем эти операции в приведенной выше теореме и считаем, что они «имеют смысл», то все результаты мы получаем таким образом, являются правильными. Какие операции мы можем ввести?
Например, что мы получим, если сложим или умножим два безмерно огромных
числа? Еще одно безмерно огромное число. Мы просто утверждали, что
∞ + ∞ = ∞
а также
∞⋅∞ = ∞.
Можно также спросить, что происходит, когда бесконечности смешиваются с обычными
числа. Например, когда мы вычитаем 13 из действительно огромного числа, мы
по-прежнему остается с огромным числом (миллионер, потерявший доллар, по-прежнему
фактически миллионер). Действительно, для любого действительного числа L имеем
∞ − L = ∞.
Что же мы получим, если вычтем из другого безмерно огромное число безмерно огромное число? Ну, это зависит. Они могут быть равны, и мы получим ноль. Или один может быть больше, тогда результат зависит от того, какой и на сколько. Это показывает, что разность ∞ − ∞ может иметь много возможных результатов, в зависимости от ситуации. Действительно, это операция не определена, так как она не может быть выполнена разумно. такие выражения называются «неопределенными».
Полный список всех операций, а также примечания и многое другое см. подробности, нажмите здесь. В частности, вы найдете там важное замечание относительно некоторых ограничения этой алгебры. Другими словами, обязательно проверьте это. Для краткий список предельной алгебры, нажмите здесь.
Обратите внимание, что «смысл» работы с ограничениями несколько отличается от
имеет смысл для чисел. Причина в том, что теперь числа A , B представляют собой не реальные числа, то есть фиксированные количества, а результаты
пределы, другими словами, они представляют собой процессы, «почти числа». Это имеет
эффект, что некоторые операции, хотя и могут быть выполнены с реальными
числа, не работайте с лимитами. Лучшим примером является степень 0 0 .
Мы знаем, что как число оно имеет смысл, оно дает 1. Однако если эти нули
представляют пределы последовательностей, то мы находимся в ситуации, когда мы ищем
предел общей власти а н б н .
Когда n приближается к бесконечности, тогда оба и n и b n близки к 0, но небольшое число
поднятое до небольшого числа не обязательно должно быть близко к 1, оно может быть очень маленьким или
очень огромный, в зависимости от того, какой “почти ноль” ближе к нулю. Таким образом
исход предела (то есть выражения 0 0 в пределе
алгебра) зависит от того, как быстро идти и n и b n на 0 предел может даже не существовать. В пределе
алгебра, 0 0 — неопределенное выражение.
Неопределенные выражения так же важны, как и предельные. алгебра. При расчете лимита нужно знать, что работает, а что не. Полный список неопределенных выражений вместе с примечаниями и более подробную информацию, нажмите здесь. Чтобы просмотреть краткий список, щелкните здесь.
Наконец, здесь вы найдете несколько замечания об операциях с последовательностями, некоторые из которых не имеют предела. Это представляет меньший интерес, и мы включаем его только для полноты, или удовлетворить более любопытного читателя.
Таким образом, на практике мы следуем очень простому правилу.
Если мы хотим найти предел последовательности, заданной некоторым выражением, мы «подставить» в него бесконечность, и если задействованные операции имеют смысл, тогда результатом является правильный ответ на наш предел.
Однако обратите внимание, что это довольно неформально, и у некоторых профессионалов на это аллергия.
Поэтому безопаснее делать все
“бесконечность расчетов” сбоку. В наших расчетах мы положили их, наряду
с другими замечаниями, между большими двойными угловыми скобками ⟪ а также
&Звонок; чтобы указать, что они не
части “официального” решения. Вот очень простой пример, написанный на
долгий путь со всеми шагами; обычно вы бы сделали это быстрее.
Мы редко можем получить ответ так легко, в частности потому, что часто “кусочки” немного сложнее и мы их не знаем ограничения сразу же, нам нужно проработать их, прежде чем мы сможем попытаться поставить их вместе. Тогда сформулированная выше теорема немного неудобна; это больше удобно выразить в такой форме:
Важное замечание: каждое из этих равенств верно, только если выражение на
право имеет смысл. Следовательно, они «условны»: пока мы не узнаем, что
окончательный ответ в наших расчетах имеет смысл, все равенства в нем
не обязательно должно быть правдой. Иными словами, нет смысла разделять
выражение на части, если то, что мы получаем в конце, не имеет смысла. За
например, постоянная функция 1 имеет предел 1 на бесконечности. Однако, если мы
напиши это как
1 = (1 + n ) − н и
вычисляем предел каждого члена отдельно, получаем то, что не
иметь смысл:
∞ − ∞.
Теперь покажу простой пример:
Пример: Найти
Мы видим, что n всегда находится внутри некоторого простого терма, предел которого в
бесконечность мы уже знаем (см. элементарные пределы). А именно константы 13 и 5
сходятся к себе. Дальше:
(i) Мы знаем, что 1 делится на корень из n , что на самом деле
1/ n 1/2 , стремится к нулю ( n с положительной степенью находится в
знаменатель). Другой способ увидеть это: корень n уходит в бесконечность
и 1/∞ = 0,
(ii) По теореме сжатия (см. Предел и сравнение в Теории – Пределы) мы знаем, что
(−1) n / n →0.
(iii) Мы знаем, что n →∞.
(iv) Чтобы увидеть второй член в знаменателе, сначала перепишем
чтобы получить положительную мощность:
2 − № = 1/2 n . Теперь 2 n является
геометрическая прогрессия, основание которой
2 больше единицы, поэтому оно стремится к бесконечности. Следовательно,
1/2 n идет к
1/∞ = 0,
Также можно написать
2 − n = 1/2 n = (1/2) n .
Теперь это геометрическая прогрессия, у которой основание 1/2 (по модулю) меньше 1,
поэтому он сходится к 0.
Теперь воспользуемся приведенной выше теоремой, чтобы соединить эти основные факты и найти предел заданной последовательности. По теореме числитель сходится к 13 − 0 + 0 = 13, а знаменатель сходится к ∞ + 5⋅0 = ∞. Наконец, весь последовательность должна сходиться к 13/∞ = 0,
Сейчас мы покажем, как написать эту процедуру, используя предельную нотацию. Здесь мы напишем все шаги, чтобы показать, как мы разлагаем данное выражение шаг за шагом, обычно можно было бы написать это намного короче.
Это решение было правильным, но довольно долгим. Применяя предельную алгебру и
выполнение некоторых неофициальных расчетов сбоку (между двойными угловыми скобками)
мы можем сделать это намного быстрее:
И это мой любимый способ решения этой проблемы — правильный и короткий.
Некоторые советы и сведения о применении этой теоремы см. Методы обследования – Лимит.
Мы так и не рассмотрели одну важную операцию — композицию.
Теорема.
Пусть { a n } будет последовательностью с пределом A , предположим, что a n ≠ A для всех n . Пусть f будет функцией который имеет предел B , когда x → A . Затем последовательность { f ( a n )} имеет предел B .
Здесь A и/или B также могут быть бесконечными, если операторы
участие имеет смысл. Наиболее типичен случай, когда A — число и f продолжается на A , что для всех практических целей означает
что f задается некоторой формулой, которая не возражает против А подставил в него. В этом случае теорему можно выразить так:
Применение легко. Если мы ищем предел последовательности, которая имеет форму “какое-то выражение внутри красивой функции”, то мы можем игнорировать функцию, найти предел выражения внутри, а затем поставить этот предел в функцию. Простой пример здесь.
Обратите внимание, что это в некотором смысле согласуется с приведенным выше примером использования limit
алгебра. Там мы на мгновение проигнорировали операции и просто сосредоточились на
простые термины, основные строительные блоки, из которых данное выражение
построен. Мы поняли, что знаем, каковы их пределы, тогда мы поставили их
вместе, чтобы получить окончательный ответ. Эта теорема говорит нам, что мы также можем
сначала игнорируйте функции, оценивайте простые термины, а затем не просто составляйте
частичные ответы вместе с помощью предельной алгебры, но мы также можем
подставляем частичные ответы в функции и, если это имеет смысл, получаем
правильный ответ. Если вы посмотрите, например, на
этот пример, он должен быть
яснее.
Таким образом, практическое правило — подставить и посмотреть — применимо и к выражениям с композицией это общее правило для пределов, которые мы используем в качестве нашего первого подход. Конечно, многие, а может быть, и большинство ограничений не могут быть решены таким образом. Затем мы должны использовать приемы, которые заменяют данную последовательность на другую. это можно решить простым способом – собрав простые результаты, используя предельная алгебра.
Еще одно очень важное правило: если вы
знай что делаешь, всегда заканчивай все части . В частности, если
вы разделяете лимит продукта на продукт меньших лимитов и один из
оказывается равным нулю, вы не можете прекратить расчеты и утверждать, что все
вещь нулевая. Конечно, ноль, умноженный на число, снова равен нулю, но это только
работает в обычной алгебре. В предельной алгебре мы также можем иметь «нулевое время
бесконечность», который является неопределенным продуктом, который может быть чем угодно. Например, мы пробуем другое разложение 1:
lim(1) = lim((1/ n )⋅ n ) = lim(1/ n )⋅lim( n ) = 0⋅∞.
Очевидно, было бы ошибкой останавливаться, как только мы увидели, что первый предел исчерпан. ноль, но после заполнения другой части мы видим неопределенное произведение и знайте, что было плохой идеей разделить первоначальный лимит на два. Подробнее см. это примечание.
Предел и ограниченность, монотонность
Мы видели, что сходящаяся последовательность может странным образом приближаться к своему пределу, поэтому нельзя ожидать, что определенно сходящиеся последовательности будут монотонными вообще. Ограниченность не так безнадежна:
Теорема.
Каждая сходящаяся последовательность ограничена.
Можем ли мы, наоборот, получить некоторую информацию о сходимости из двух основных
характеристики? Противоположное утверждение выше говорит, что неограниченный
последовательность должна быть расходящейся, это одна часть информации. Можем ли мы получить
тоже что-то положительное? Нет. Пример
чередующаяся последовательность показывает, что
ограниченная последовательность не обязательно должна быть сходящейся, предела вообще нет (не
даже неприлично). Однако, если мы хотим потерять некоторые члены данного
последовательность, мы получаем что-то из ограниченности
(ср. Больцано-Вейерштрасс
теорема в функциях – теория – действительные числа – топологические понятия):
Теорема (теорема Больцано-Вейерштрасса).
Каждая ограниченная последовательность имеет сходящуюся подпоследовательность.
Еще одним полезным свойством является монотонность. Если вы попытаетесь представить все виды
увеличивая последовательности, у вас должно появиться (правильное) ощущение, что
такие последовательности либо растут к некоторой верхней границе, являющейся тогда их
предел и они сходятся, или они растут выше всех возможных пределов и они
поэтому стремятся к бесконечности; в любом случае у них есть предел. Действительно, это
верно, и, кроме того, ограниченность дает хороший способ избежать этой бесконечности.
Теорема.
У каждой монотонной последовательности есть предел.
Всякая ограниченная монотонная последовательность сходится.
Более подробно, каждая неубывающая последовательность (в частности, каждая возрастающая последовательность) либо сходится, либо уходит в бесконечность, а каждое невозрастающее последовательность (в частности, каждая убывающая последовательность) либо сходится, либо идет до минус бесконечности.
Предел и подпоследовательности
Начнем с одного теоретического результата.
Теорема.
Если последовательность сходится, то все ее подпоследовательности также сходятся и сходятся к пределу исходной последовательности.
Это не совсем полезно при исследовании сходимости, но следующее:
часто полезно более слабое утверждение в противоположном направлении.
Факт.
Если данная последовательность имеет две подпоследовательности, которые сходятся к разным пределы, то данная последовательность расходится.
Например, из чередующейся последовательности {1, −1, 1, −1, 1, −1, 1,…} мы может взять все нечетные члены, чтобы сформировать подпоследовательность {1, 1, 1, 1, 1,…} сходится к 1, и мы можем взять все четные членов для формирования подпоследовательности {−1, −1, −1, −1, −1,…} сходящейся к −1. По указанному выше факту знакопеременная последовательность расходится.
Последовательности Коши
Одно полезное замечание, которое можно сделать о последовательности, заключается в том, что по мере ее развития
вместе, он меняется все меньше и меньше. Чтобы определить его формально, мы снова воспользуемся идеей
игры. Кто-то дает нам терпимость, и мы хотим иметь возможность бросить
убрать какое-то начало данной последовательности так, чтобы ее оставшиеся члены никогда не
скачок больше, чем этот допуск.
Определение.
Рассмотрим последовательность { a n }. Мы говорим, что это последовательность Коши или что эта последовательность Коши , если для каждого ε > 0 существует некоторое натуральное число N такое, что для всех м , с ≥ с у нас есть | a n − − a m | < ε .
Если последовательность сходится, то она устанавливается на некоторое значение и делает не сильно измениться. Это кажется ясным и на самом деле это просто доказать. Менее легко доказать (например, с помощью теоремы Больцано-Вейерштрасса). выше) заключается в том, что если последовательность уляжется, то он должен сойтись (что опять же звучит как обычное смысл). Таким образом, мы получаем следующую теорему.
Теорема.
Последовательность действительных чисел сходится тогда и только тогда, когда она последовательности Коши.