Как найти предел последовательности?
А вот сейчас необходимо уметь решать пределы функций, как минимум, на уровне двух базовых уроков: Пределы. Примеры решений и Замечательные пределы. Потому что многие методы решения будут похожи. Но, прежде всего, проанализируем принципиальные отличия предела последовательности от предела функции:
В пределе последовательности «динамическая» переменная «эн» может стремитьсятолько к «плюс бесконечности» – в сторону увеличения натуральных номеров .
В пределе функции «икс» может быть направлен куда угодно – к «плюс/минус бесконечности» либо к произвольному действительному числу.
Последовательность дискретна (прерывна), то есть состоит из отдельных изолированных членов. Раз, два, три, четыре, пять, вышел зайчик погулять. Для аргумента же функции характерна непрерывность, то есть «икс» плавно, без приключений стремится к тому или иному значению. И, соответственно, значения функции будут так же непрерывно приближаться к своему пределу.
По причине дискретности в пределах последовательностей встречаются свои фирменные вещи, такие как факториалы, «мигалки», прогрессии и т.п. И сейчас я постараюсь разобрать пределы, которые свойственны именно для последовательностей.
Начнём с прогрессий:
Пример 1
Найти предел последовательности
Решение: нечто похожее на бесконечно убывающую геометрическую прогрессию, но она ли это? Для ясности распишем несколько первых членов:
Так как , то речь идёт о сумме членов бесконечно убывающей геометрической прогрессии, которая рассчитывается по формуле .
Оформляем решение:
Используем формулу суммы бесконечно убывающей геометрической прогрессии: . В данном случае: – первый член, – знаменатель прогрессии.
Главное, совладать с четырёхэтажностью дроби:
Есть.
Пример 2
Написать первые четыре члена последовательности и найти её предел
Это пример для самостоятельного решения. Для устранения неопределённости в числителе потребуется применить формулу суммы первых членов арифметической прогрессии:
Для устранения неопределённости в числителе потребуется применить формулу суммы первых членов арифметической прогрессии:
Поскольку в пределах последовательностей «эн» всегда стремится к «плюс бесконечности», то неудивительно, что неопределённость – одна из самых популярных.
И многие примеры решаются точно так же, как пределы функций!
Как вычислить эти пределы? Смотрите Примеры №№1-3 урока Пределы. Примеры решений.
А может быть что-нибудь посложнее наподобие ? Ознакомьтесь с Примером №3 статьи Методы решения пределов.
С формальной точки зрения разница будет лишь в одной букве – там «икс», а здесь «эн».
Приём тот же – числитель и знаменатель надо разделить на «эн» в старшей степени.
Также в пределах последовательностей достаточно распространена неопределённость . Как решать пределы вроде можно узнать из Примеров №11-13 той же статьи.
Чтобы разобраться с пределом , обратитесь к Примеру №7 урока Замечательные пределы (второй замечательный предел справедлив и для дискретного случая). Решение снова будет как под копирку с различием в единственной букве.
Следующие четыре примера (№№3-6) тоже «двулики», но на практике почему-то больше характерны для пределов последовательностей, чем для пределов функций:
Пример 3
Найти предел последовательности
Решение: сначала полное решение, потом пошаговые комментарии:
(1) В числителе дважды используем формулу .
(2) Приводим подобные слагаемые в числителе.
(3) Для устранения неопределённости делим числитель и знаменатель на («эн» в старшей степени).
Как видите, ничего сложного.
Пример 4
Найти предел последовательности
Это пример для самостоятельного решения, формулы сокращенного умножения в помощь.
В пределах с показательными последовательностями применяется похожий метод деления числителя и знаменателя:
Пример 5
Найти предел последовательности
Решение оформим по той же схеме:
(1) Используя свойства степеней, вынесем из показателей всё лишнее, оставив там только «эн».
(2) Смотрим, какие показательные последовательности есть в пределе: и выбираем последовательность с наибольшим основанием: . В целях устранения неопределённости делим числитель и знаменатель на .
(3) В числителе и знаменателе проводим почленное деление. Поскольку является бесконечно убывающей геометрической прогрессией , то она стремится к нулю. И тем более к нулю стремится константа, делённая на растущую прогрессию: . Делаем соответствующие пометки и записываем ответ.
Пример 6
Найти предел последовательности
Это пример для самостоятельного решения.
Как-то незаслуженно остался в забвении стильный почерк, присущий только пределу последовательности. Пора исправить ситуацию:
Пример 7
Найти предел последовательности
Последним множителем в произведении идёт шестёрка. Что нужно сделать, чтобы получить предыдущий множитель? Вычесть единицу: 6 – 1 = 5. Чтобы получить множитель, который располагается ещё дальше, нужно из пятёрки ещё раз вычесть единичку: 5 – 1 = 4. И так далее.
Не беспокойтесь, это не урок в первом классе коррекционной школы, на самом деле мы знакомимся с важным и универсальным алгоритмом под названием «как разложить любой факториал
Очевидно, что последним множителем в произведении будет .
Как получить предыдущий множитель? Вычесть единицу:
Как достать прадедушку? Ещё раз вычесть единицу: .
Ну и ещё на один шаг продвинемся вглубь:
Таким образом, наше чудовище распишется следующим образом:
С факториалами числителя всё проще, так, мелкие хулиганы.
Оформляем решение:
(1) Расписываем факториалы
(2) В числителе ДВА слагаемых. Выносим за скобки всё, что можно вынести, в данном случае это произведение . Квадратные скобки, как я где-то пару раз говорил, отличаются от круглых скобок только своей квадратностью.
(3) Сокращаем числитель и знаменатель на …. …хммм, флуда тут и впрямь много.
(4) Упрощаем числитель
(5) Сокращаем числитель и знаменатель на . Тут в известной степени повезло. В общем случае вверху и внизу получаются заурядные многочлены, после чего приходится выполнять стандартное действие – делить числитель и знаменатель на «эн» в старшей степени.
Более подготовленные студенты, которые легко раскладывают факториалы в уме, могут решить пример значительно быстрее. На первом шаге делим почленно числитель на знаменатель и мысленно выполняем сокращения:
Но способ с разложением всё-таки более основателен и надёжен.
Пример 8
Найти предел последовательности
Это пример для самостоятельного решения.
Желающие набить руку на рассмотренных типах пределов могут обратиться к сборнику Кузнецова. Около 150 прорешанных примеров можно найти здесь >>> (задачи №№2-6).
Как и в любом обществе, среди числовых последовательностей попадаются экстравагантные личности.
Теорема: произведение ограниченной последовательности на бесконечно малую последовательность – есть бесконечно малая последовательность.
Если вам не очень понятен термин «ограниченность», пожалуйста, изучите статью об элементарных функциях и графиках.
Аналогичная теорема справедлива, кстати, и для функций: произведение ограниченной функции на бесконечно малую функцию – есть бесконечно малая функция.
Пример 9
Найти предел последовательности
Решение: последовательность – ограничена: , а последовательность – бесконечно малА, значит, по соответствующей теореме:
Просто и со вкусом. Да-да, так и оформляем.
А почему бы и нет?
Пример 10
Найти предел последовательности
Это пример для самостоятельного решения.
Ещё две распространённые ограниченные функции – арктангенс и арккотангенс:
Аргументы перечисленных тригонометрических функций могут быть заполнены знатной абракадаброй, но это не должно приводить в панику – существенно то, что последовательности ограничены!
Иногда в ходе вычисления пределов последовательностей приходится использовать довольно неожиданные приёмы:
Пример 11
Найти предел последовательности
Решение: неопределённость можно раскрутить двумя способами. Первый путь – через первый замечательный предел, который справедлив, как ни странно, и для последовательностей:
Первый путь – через первый замечательный предел, который справедлив, как ни странно, и для последовательностей:
(1) Используем формулу .
(2) Избавляемся от косинуса, указывая, что он стремится к единице.
(3) Неопределённость не устранена, но теперь вместо тангенса у нас синус, и появляется возможность организовать 1-й замечательный предел. Проводим стандартный искусственный приём: делим всё выражение на и, чтобы ничего не изменилось, домножаем на .
(4) Используем первый замечательный предел , при этом, в качестве бесконечно малой величины выступает , которая, понятно, стремится к нулю при .
Дальнейшее просто.
Прокатывает и 2-й метод решения – через замечательные эквивалентности:
Заменим бесконечно малую последовательность эквивалентной:
при .
В данном случае
Готово.
Пример 12
Найти предел последовательности
Это пример для самостоятельного решения. Здесь аргумент арктангенса также бесконечно мал, поскольку его знаменатель более высокого порядка роста, чем числитель. Решать, разумеется, значительно выгоднее через замечательную эквивалентность.
Оба рассмотренных примера справедливы и для функций, похожие пределы также разобраны в Примерах 12-13 урока о бесконечно малых величинах.
В заключение урока рассмотрим ещё один важный вопрос:
Дата добавления: 2021-01-26; просмотров: 146; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Предел последовательности
4.1Примеры и мотивировка
В этой лекции мы введём, пожалуй, главное понятие математического анализа —
понятие предела. Это сложное понятие. Человеческий мозг не привык работать с
бесконечностями. Думая про какую-то последовательность, мы как правило
представляем себе лишь её первые несколько элементов. Сейчас же нам предстоит
вглядеться в бесконечный хвост последовательности и понять, как он устроен.
Сейчас же нам предстоит
вглядеться в бесконечный хвост последовательности и понять, как он устроен.
Пусть есть последовательность {an}. Можно думать про неё как про последовательность результатов измерения какого-то параметра (скажем, населения некоторой страны) в последовательные моменты времени (например, каждый год). Правда, в отличие от реальных результатов измерения, наша последовательность простирается бесконечно далеко в будущее, и именно это «бесконечное будущее» нас и интересует. Есть ли какое-то значение A, к которому члены последовательности будут становиться всё ближе и ближе — так, что, со временем их будет всё сложнее и сложнее отличить от A?
Давайте рассмотрим несколько примеров.
4.1.1Последовательность 1/2n
Пусть an=12n. Давайте выведем первые двадцать членов этой
последовательности. Я написал для этого короткий код на языке Python,
который приведён ниже вместе с результатом его выполнения. Код можно
скрывать и открывать, нажимая на кнопку-уголок. Если вы не знаете Python,
ничего страшного — для понимания он не понадобится. Но если знаете,
возможно, вам будет интересно самостоятельно проводить эксперименты, похожие
на приведенные.
Если вы не знаете Python,
ничего страшного — для понимания он не понадобится. Но если знаете,
возможно, вам будет интересно самостоятельно проводить эксперименты, похожие
на приведенные.
print("n a_n")
for n in range(1, 21):
a_n = 1 / 2 ** n
print(f"{n} {a_n:0.5f}")
# 0.5f означает, что будут выведены 5 знаков после десятичной точкиn a_n 1 0.50000 2 0.25000 3 0.12500 4 0.06250 5 0.03125 6 0.01562 7 0.00781 8 0.00391 9 0.00195 10 0.00098 11 0.00049 12 0.00024 13 0.00012 14 0.00006 15 0.00003 16 0.00002 17 0.00001 18 0.00000 19 0.00000 20 0.00000
Из результатов видно, что начиная с 18-го члена получаются нули. Конечно, мы
понимаем, что это не настоящие нули — ни один член этой последовательности
на самом деле не равен нулю. (Если вы делите положительное число на что
угодно, никак нельзя получить ноль — уравнение 1/x=0 не имеет решения,
потому что в противном случае 1 окажется равным 0⋅x, а этого не
может быть, потому что умножение чего угодно на 0 даёт 0. ) Однако, мы
вывели только 5 знаков после десятичной запятой (точки), поэтому все числа,
меньшие 0,00001, отображаются как нули.
) Однако, мы
вывели только 5 знаков после десятичной запятой (точки), поэтому все числа,
меньшие 0,00001, отображаются как нули.
Но ведь можно увеличить точность! Давайте отображать шесть цифр после запятой!
n a_n 1 0.500000 2 0.250000 3 0.125000 4 0.062500 5 0.031250 6 0.015625 7 0.007812 8 0.003906 9 0.001953 10 0.000977 11 0.000488 12 0.000244 13 0.000122 14 0.000061 15 0.000031 16 0.000015 17 0.000008 18 0.000004 19 0.000002 20 0.000001
Теперь первые 20 членов последовательности отчётливо ненулевые. Но последовательность на этом не заканчивается — давайте выведем ещё несколько членов.
n a_n 20 0.000001 21 0.000000 22 0.000000 23 0.000000 24 0.000000
Опять нули! Давайте ещё увеличим точность! Семь знаков после запятой!
n a_n 20 0.0000010 21 0.0000005 22 0.0000002 23 0.0000001 24 0.0000001
До 24-го члена значения ненулевые, а после?
n a_n 24 0.0000001 25 0.0000000 26 0.0000000 27 0.0000000 28 0.0000000 29 0.0000000
Похоже, дело безнадёжно. Какую бы точность отображения мы ни выбирали, начиная с некоторого момента последовательность будет выглядеть, как будто состоит из сплошных нулей!
Это и означает, что она стремится к нулю.
4.1.2Последовательность n+1n
Пусть теперь an=n+1n. Тоже можно вывести первые несколько значений.
n a_n 1 2.00000 2 1.50000 3 1.33333 4 1.25000 5 1.20000 6 1.16667 7 1.14286 8 1.12500 9 1.11111
Здесь эффект не столь очевиден. Давайте построим график. По горизонтальной оси будем откладывать n, по вертикальной — an. В отличие от обычного графика функции, он будет состоять из отдельных точек, соответствующих натуральным значениям n, см. рис. 4.1.
Рис. 4.1: График y=an.
По графику можно угадать, что точки, вероятно, приближаются к прямой y=1,
то есть элементы последовательности стремятся к 1. Для большей наглядности можно нарисовать эту
прямую (рис. 4.2).
Для большей наглядности можно нарисовать эту
прямую (рис. 4.2).
Рис. 4.2: График y=an и прямая y=1.
Хотя тенденция вроде бы налицо, нетрудно видеть, что между точками y=an и прямой y=1 есть некоторый зазор. Но что если взять побольше точек? См. рис. 4.3.
Рис. 4.3: График y=an: взяли побольше точек.
Видно, что зазор стал меньше и для больших значений n вообще непонятно, есть он или нет. Но если изменить масштаб вертикальной оси, станет видно, что он всё-таки есть (рис. 4.4).
Рис. 4.4: График y=an: увеличили масштаб вертикальной оси.
Но теперь можно добавить ещё больше точек (рис. 4.5)!
Рис. 4.5: График y=an: увеличили масштаб вертикальной оси, а потом взяли ещё больше точек
И снова зазор стал практически неразличим!
Так можно продолжать до бесконечности. Увеличивать масштаб вертикальной оси
(и следовательно нашу способность различать близкие точки) — находить зазор
— увеличивать количество точек — делать зазор неразличимым.
В общем, можно предположить, что наша последовательность стремится к числу 1. В принципе, это неудивительно. Можно преобразовать формулу для общего члена последовательности:
an=n+1n=1+1n
Когда n становится очень большим, 1n становится очень маленьким, поэтому вся сумма становится очень близкой к 1. Что мы и видим на графике.
4.1.4«Скачущая» последовательность
При рассмотрении предыдущих примеров, у вас могло возникнуть искушение дать такое определение: «последовательность {an} стремится к какому-то числу a, если её члены с ростом n становятся всё ближе и ближе к a: каждый следующий член ближе, чем предыдущий».
Более внимательный анализ показывает, что это определение неверно. Например,
последовательность n+1n, которую мы только что рассматривали,
«становится всё ближе и ближе» не только к 1, но и, например, к 0 — причём
каждый следующий член ближе, чем предыдущий. Тем не менее, нельзя сказать, что
она стремится к 0.
Более того, требование «каждый следующий член ближе, чем предыдущий», оказывается излишним.
Давайте рассмотрим такую последовательность:
an={n+1n,n — нечётное;n+3n,n — чётное.
Её первые члены выглядят следующим образом:
2, 52, 43, 74, 65,…
График этой последовательности изображен на рис. 4.6. Тут видно, что требование «каждый следующий элемент ближе к 1, чем предыдущий», нарушается: элементы с чётными номерами ближе к 1, чем элементы с нечётными номерами.
Рис. 4.6: Последовательность приближается и отдаляется от 1, но всё равно к ней стремится. Точки соединены пунктирной линией исключительно для наглядности: значения последовательности для нецелых n не определено.
Тем не менее, судя по графику на рис. 4.7, можно
предположить, что, несмотря на скачки, последовательность всё-таки стремится к
числу 1: с течением времени (то есть с ростом n) её элементы становятся
настолько близки к единице, что их трудно от неё отличить.
Рис. 4.7: Последовательность приближается и отдаляется от 1, но всё равно к ней стремится.
4.1.5Последовательности без предела
Последовательности, рассмотренные выше, стремились к какому-то числу. Приведём несколько примеров последовательностей, у которых предела нет.
Пример 1. Последовательность an=n2:
1, 4, 9, 16,…
Эта последовательность неограничена, и выглядит очевидным, что она не стремится ни к какому числу. У неё нет предела.
Пример 2. Последовательность
an=(−1)n+1n.(4.1)
В зависимости от чётности n, первое слагаемое оказывается равно 1 или −1. Посмотрим, как выглядит график этой последовательности (рис. 4.8).
Рис. 4.8: Последовательность скачет между двумя точками.
По графику видно, что нет одного числа, к которому члены последовательности
были бы очень близки при больших n: она скачет между двумя значениями, 1
и −1.
Пример 3. Наконец, рассмотрим такую последовательность:
an={12,∃k∈N:n=2k;n+1n,∀k∈N:n≠2k.(4.2)
Эта последовательность устроена так. Для тех n, которые являются степенями двойки (1, 2, 4, 8, 16 и т.д.), an равно 12. Для остальных n, an равно n+1n. Посмотрим на график на рис. 4.9.
Рис. 4.9: Последовательность всё реже и реже убегает от предельного значения
Понятно, что для тех номеров, которые не являются степенями двойки, элементы становятся сколь угодно близки к 1. Время от времени последовательность «убегает» в точку 12, однако эти моменты, будучи степенями двойки, встречаются всё реже и реже. Если бы мы стартовали с больших значений n, мы могли бы очень долго наблюдать последовательность, которая становится очень близка к 1.
Тем не менее, нельзя сказать, что её предел равен 1. Мы знаем, что с какого
бы начального момента времени мы ни стартовали, рано или
поздно n окажется степенью двойки, и в этот момент последовательность
«скакнёт» в число 1/2, уйдя от 1 на заметное расстояние.
4.2Определение предела
4.2.1Интуитивные соображения
Из обсуждения в предыдущем разделе должно быть понятно — по крайней мере, на интуитивном уровне — чего бы мы хотели потребовать от последовательности, чтобы сказать, что она стремится к некоторому числу A. Подведём промежуточный итог.
- Первые сколько-то членов могут быть достаточно далеки от A, это никак не мешает последовательности стремиться к A. Иными словами, «стремление» — это эффект, который зависит только от «хвоста» последовательности.
- Для достаточно больших значениий n члены последовательности должны становиться настолько близкими к A, чтобы их нельзя было отличить от A, скажем, на графике или на компьютерной распечатке, на которой числа выводятся с конечной точностью.
- Этот эффект должен сохраняться для всех достаточно больших n. Если
последовательность время от времени «убегает» от A на какое-то
заметное расстояние, и это происходит сколь угодно далеко в будущем,
последовательность не будет стремиться к A.

- Мы можем увеличить точность измерения — например, выводить больше цифр после запятой или увеличить масштаб на графике — и увидеть зазор между членами последовательности и числом A. Однако, мы можем взять ещё большие значения n, чтобы эффект «неразличимости» вернулся.
Теперь приступим к формализации понятия предела.
4.2.2Вспомогательные понятия
Нам потребуется несколько вспомогательных определений и обозначений.
Определение 1. Расстоянием между вещественными числами a и b называется модуль их разности: |a−b|. Это довольно естественное определение, если думать про числа как про точки на числовой прямой, см. рис. 4.10.
Рис. 4.10: Модуль разности — это расстояние между числами как точками числовой прямой.
Буквой ε (читается «эпсилон» — почему-то со слуха часто кажется, что там в
конце есть буква «т» — нет, её нет) мы будем обозначать положительные и как
правило маленькие вещественные числа.
Определение 2. Скажем, что два числа ε-близки («эпсилон-близки») друг к другу, если расстояние между ними меньше ε.
Вместо ε здесь можно подставлять другие буквы или конкретные числа — например, δ-близки («дельта-близки») или 0,1-близки. Скажем, утверждение «число π 0,1-близко к числу 3,14» является верным, поскольку расстояние между π и 3,14 (модуль разности) меньше, чем 0,1. Числа a и b будут ε-близки, если модуль их разности меньше ε: |a−b|<ε.
Определение 3. Рассмотрим последовательность {an}. Скажем, что её хвост ε-близок к числу A, если все её члены, начиная с некоторого, ε-близки к A. Иными словами, если все члены, начиная с некоторого, находятся на расстоянии меньше ε от A.
Формально это записывается так:
∃N∈N ∀n∈N:(n>N)⇒|an−A|<ε.(4.3)
∃N∈N ∀n∈N:(n>N)⇒⇒|an−A|<ε.(4.3)
Здесь сказано, что найдётся такой номер N, что все члены
последовательности с номерами от N+1 и больше находятся на расстоянии
меньше ε от A.
Импликация в этом определении говорит, что нас интересует выполнение условия |an−A|<ε не для всех n, а только для тех, для которых выполнено n>N, то есть «начиная с некоторого члена»; если оно нарушается для членов с меньшими номерами, это не будет нарушать утверждение, поскольку в этом случае посылка импликации n>N окажется ложной, и значит импликация будет истинной. Более кратко это определение можно записать так:
∃N∈N ∀n>N:|an−A|<ε.
На рис. 4.11 приведена иллюстрация к этому определению.
Множество точек, ε-близких к точке A — это интервал (A−ε,A+ε).
Если на графике последовательности нарисовать горизонтальные прямые y=A+ε и
y=A−ε, они образуют своего рода коридор вокруг A (его можно назвать ε-коридором). Утверждение, что хвост последовательности ε-близок к A,
означает, что начиная с некоторого номера n=N+1, все члены последовательности
находятся в интервале (A−ε,A+ε), а соответствующие им точки на графике
живут в нарисованном нами ε-коридоре. Точки с номерами меньше или равными
N, могут как принадлежать коридору, так и выходить из него.
Точки с номерами меньше или равными
N, могут как принадлежать коридору, так и выходить из него.
Рис. 4.11: Хвост последовательности ε-близок к числу A.
Заметим, что в этом определении не сказано, с какого именно члена начинается «хвост последовательности». Более того, для одной и той же последовательности «хвосты» могут быть разными, в зависимости от ε.
Пример 4. Рассмотрим последовательность an=1n. Её хвост 0,1-близок к 0. Действительно, возьмём N=10. Для всех n>N, an меньше 0,1 (поскольку n больше 10 обратная величина 1/n меньше 1/10).
Вопрос 1. Верно ли, что хвост последовательности an=1n является 0,01-близким к 0?
Нет, потому что существуют n>10, при которых расстояние между an и 0 больше, чем 0,01 — например, n=20, an=120=0,05, |an−0|=|an|=0,05>0,01.
Неверный ответ.
Это рассуждение неверно: совсем не обязательно в качестве N
брать именно 10, можно попробовать подобрать другое число,
так, чтобы требование выполнялось.
Неизвестно, зависит от N.
Неверный ответ. Нет, в формуле (4.3) переменная N является связанной (на неё «навешан» квантор) — мы не спрашиваем, при каких N верно или неверно то-то и то-то — мы спрашиваем, «найдётся ли такое N?»
Да, верно.
Верный ответ. Конечно! Чему равняется N?
10
Неверный ответ. Не-а.
20
Неверный ответ. Нет.
100
Верный ответ. Да, например, 100 подойдёт. (Или любое большее число.)
Пример 5. Последовательность из примера 2 (см. (4.1)) имеет хвост, 1,2-близкий к числу 0, однако неверно, что её хвост 0,9-близок к 0.
Вопрос 2. Для какого ε хвост этой последовательности ε-близок к числу 1?
ε=0,5
Неверный ответ. Нет, у последовательности есть члены со сколь угодно большими
номерами, лежащие на расстоянии больше 0,5 от 1 — например,
все члены с нечётными номерами.
Нет, у последовательности есть члены со сколь угодно большими
номерами, лежащие на расстоянии больше 0,5 от 1 — например,
все члены с нечётными номерами.
ε=1,5
Неверный ответ. Нет, у последовательности есть члены со сколь угодно большими номерами, лежащие на расстоянии больше 1,5 от 1 — например, все члены с нечётными номерами, большими 2 (хотя a1=0 находится на расстоянии 1 от числа 1).
ε=2
Верный ответ. Верно!
Ни для какого.
Неверный ответ. Нет, неверно.
Теперь мы готовы к Самому Главному Определению.
4.2.3Аккуратное определение предела
Мы хотим дать определение понятию, которое бы формализовало утверждение о том,
что члены последовательности an с ростом n становятся очень-очень близки к
некоторому фиксированному числу A — так, что, начиная с некоторого момента, мы
их практически не можем отличить от A.
Понятие ε-близости призвано формализовать идею о том, что два числа близки, если расстояние между ними маленькое. Можно думать, что ε — это точность или разрешающая способность наших измерительных приборов (чем меньше ε, тем точнее приборы). В этом случае если два числа отличаются меньше, чем на ε, у нас нет практической возможности их различить, для нас они совпадают. Например, если мы печатаем все числа лишь с двумя знаками после запятой, мы можем не различить два числа, расстояние между которыми меньше 0,001.
Но какой ε «достаточно маленький»? В отличие от других дисциплин, в
математике нет никакого естественного масштаба. С точки зрения географии,
расстояние в 1/10 метра — это очень маленькое расстояние — потому что мы
сравниваем его с типичными объектами, изучаемыми географией — странами,
городами, морями. А с точки зрения микробиологии — фантастически большое — по
сравнению с бактериями или ядром клетки. С точки зрения математики, невозможно
даже задать вопрос «является ли 1/10 маленьким числом?» — потому что непонятно,
с чем его сравнивать. Поэтому мы не можем выбрать какой-то конкретный ε и
сказать: «последовательность стремится к A, если её члены, начиная с
некоторого, ε-близки к A». Как же быть?
Поэтому мы не можем выбрать какой-то конкретный ε и
сказать: «последовательность стремится к A, если её члены, начиная с
некоторого, ε-близки к A». Как же быть?
Очень просто. Мы потребуем, чтобы утверждение «хвост последовательности ε-близок к A», выполнялось для любого положительного ε. Какой бы ни была разрешающая способность наших измерительных приборов, если подождать достаточно долго, мы перестанем отличать члены нашей последовательности от A.
Определение 4. Последовательность {an} имеет предел A, если для всякого ε>0 её хвост ε-близок к A.
Формально:
∀ε>0 ∃N∈N ∀n>N:|an−A|<ε.(4.4)
∀ε>0 ∃N∈N ∀n>N:|an−A|<ε.(4.4)
Если последовательность {an} имеет предел A, говорят также, что она стремится к A.
Коротко пишут так:
limn→∞an=A,
(читается «предел при n стремящемся к бесконечности от an равен A») или
an→A при n→∞,
(читается «an стремится к A при n стремящемся к бесконечности»).
Последовательность, имеющая предел, называется также сходящейся, а не имеющая предела — расходящейся.
Заметим, что в определении предела, число N (граница «хвоста
последовательности») выбирается в зависимости от ε — для разных ε
получаются разные N. Если последовательность {an} стремится к A,
гарантируется, что для любого ε найдётся «хорошее» N. Часто бывает удобно
это «хорошее» N, подходящее для какого-то ε, обозначать через N(ε).
(Вообще говоря, это N определяется не единственным образом — например, если
N подходит, то N+1 тоже подходит — но мы выберем какое-нибудь из подходящих
значений N и обозначим его через N(ε).) На рис. 4.12
приведена иллюстрация: для ε=ε1 мы могли выбрать N=3, то есть
положить N(ε1)=3. Но для ε=ε2 (см. нижний рисунок) это значение
N уже «не работает» (например, a4 выходит за границы нового коридора),
однако увеличив N до 8 (то есть положив N(ε2)=8) мы снова добились
соблюдения условия «все члены, начиная с n=N+1, находятся на расстоянии меньше
ε от A».
Мы могли бы ещё сильнее уменьшить ε — и снова должно было найтись своё N, которое бы обеспечивало выполнение этого условия. Это и значит, что последовательность стремится к A.
Рис. 4.12: Зависимость N от ε в определении предела.
4.3Пример доказательств утверждений о пределах
4.3.1Существование предела
Самый лучший способ понять определение — доказать какое-нибудь утверждение про него.
Утверждение 1. Предел последовательности an=n+1n равен 1:
limn→∞n+1n=1.
Доказательство. Нам нужно научиться по любому ε>0 строить такое N=N(ε), что для всех n>N,
∣∣∣n+1n−1∣∣∣<ε.(4.5)
Преобразуем это неравенство:
∣∣∣1+1n−1∣∣∣<ε;∣∣∣1n∣∣∣<ε.
Заметим, что n — натуральное число, значит положительное, значит
1n — тоже положительное, значит его модуль всегда равен ему
самому. Следовательно, знак модуля можно просто снять. Получим неравенство:
Получим неравенство:
1n<ε.
Можно умножить обе части этого неравенства на n и поделить на ε (благодаря тому, что n>0 и ε>0, эта операция является эквивалентным преобразованием и не приведёт к изменению знака неравенства). Получим такое неравенство:
1ε<n.
Наконец, можно переписать его справа налево:
n>1ε.(4.6)
Нам нужно найти такое N, что если n>N, то неравенство (4.5)
выполняется. Наши преобразования были эквивалентными, поэтому, в частности, если
выполняется неравенство (4.6), то выполняется и неравенство
(4.5). Значит, достаточно сделать так, чтобы выполнялось
неравенство (4.6). Очевидно, если выбрать какое-нибудь
N≥1ε, мы победим: в этом случае любое n, большее N, будет
также больше и 1ε, а значит неравенство (4.6)
выполнено. В принципе, можно было бы просто положить N=1ε, но
мы потребовали в определении 4, чтобы N было натуральным
числом. Значит, нужно выбрать какое-нибудь натуральное число, не меньшее
1ε. Это всегда можно сделать. Однако, для определенности,
давайте предложим конкретный механизм.
Значит, нужно выбрать какое-нибудь натуральное число, не меньшее
1ε. Это всегда можно сделать. Однако, для определенности,
давайте предложим конкретный механизм.
Определение 5. Пусть x — вещественное число. Его округлением вверх называется наименьшее целое число, не меньшее x. Например, 2,1 округляется вверх до 3. Число 17 округляется вверх до 17, потому что оно уже целое. Результат округления вверх числа x обозначается через ⌈x⌉. Функция y=⌈x⌉ также называется функцией «потолок» (англ. ceil).
Упражнение 1. Опишите, как действует функция ⌈x⌉, пользуясь представлением числа x в виде бесконечной десятичной дроби.
Итак, для всякого ε>0, положим N(ε):=⌈1ε⌉. По определению функции потолок, N(ε)≥1ε. Значит, для всех натуральных n, если n>N(ε), то n>1ε, а значит выполняется (4.6), а значит и (4.5). Ура!∎
Давайте рассмотрим ещё один пример.
Утверждение 2. Предел последовательности an=1n2+5n+12 равен нулю:
limn→∞1n2+5n+12=0.
Доказательство. По аналогии с предыдущим примером, запишем, что мы хотим получить. Мы хотим научиться для всякого ε>0 строить такое N=N(ε), что для всех n>N выполняется неравенство:
∣∣∣1n2+5n+12−0∣∣∣<ε.(4.7)
Можно попробовать преобразовать это неравенство. Во-первых, вычитание нуля ничего не меняет. Во-вторых, при натуральных n дробь положительна и знак модуля можно снять. Получаем такое неравенство:
1n2+5n+12<ε.(4.8)
Теоретически, дальше его можно мучительно решать относительно n, найдя
для каждого фиксированного ε все возможные значения n, которые ему
удовлетворяют. Делать это, однако, не нужно. Дело в том, что нам не нужны все без исключения значения n. Нам нужно добиться того, чтобы
неравенство (4.8) выполнялось, но нам не нужно находить
все значения n, при которых оно выполняется. Поэтому вместо эквивалентных
переходов, которые мы должны делать, когда решаем неравенство, нам
достаточно переходов к более сильным неравенствам — таким, из которых наше
следует. И это существенно упрощает жизнь! Смотрите.
И это существенно упрощает жизнь! Смотрите.
Заметим, что для натуральных n,
n2+5n+12>n2.
Действительно, 5n и 12 — положительные числа. Более того: для натуральных n, n2≥n (можно поделить это неравенство на n, поскольку n больше нуля, и получить неравенство n≥1, справедливое для всех натуральных n). Имеем цепочку неравенств:
n2+5n+12>n2≥n.
Значит
n2+5n+12>n
и следовательно
1n2+5n+12<1n.(4.9)
Оценивая знаменатель дроби снизу, мы оцениваем саму дробь сверху.
Пусть теперь мы подобрали какое-нибудь такое N, что при всех n>N выполняется неравенство 1n<ε. Тогда в силу неравнства (4.9), для тех же самых n, будет выполняться неравенство
1n2+5n+12<ε.
(Мы опять используем транзитивность неравенства: если A<B и B<C, то A<C.)
Таким образом, в качестве N(ε) можно взять то же выражение, что и в
предыдущем примере: N(ε):=⌈1ε⌉. И оно сработает! Это гораздо проще, чем решать
квадратное неравенство с параметром (можете попробовать — хотя вам вряд ли
понравится).
И оно сработает! Это гораздо проще, чем решать
квадратное неравенство с параметром (можете попробовать — хотя вам вряд ли
понравится).
Итак, если отбросить все мотивировки, полное доказательство выглядит так: для всякого ε>0, положим N(ε):=⌈1ε⌉. Тогда для всякого натурального n>N(ε) справедлива цепочка равенств и неравенств:
∣∣∣1n2+5n+12−0∣∣∣=∣∣∣1n2+5n+12∣∣∣==1n2+5n+12<1n<1⌈1/ε⌉≤11/ε=ε.
∣∣∣1n2+5n+12−0∣∣∣==∣∣∣1n2+5n+12∣∣∣==1n2+5n+12<<1n<1⌈1/ε⌉≤11/ε=ε.
Доказательство законечно. (Конечно, в аккуратном тексте нужно обосновать каждое из равенств и неравенств в цепочке, но мы это уже сделали выше.) ∎
4.3.2Предел не равен какому-то числу
Утверждение 3. Предел последовательности {an}, an=1n, не равен 1:
limn→∞1n≠1.
Доказательство. Нам нужно доказать, что неверно, что предел равен 1. Иными словами, опровергнуть следующее утверждение:
∀ε>0 ∃N∈N ∀n>N:∣∣∣1n−1∣∣∣<ε.
Опровергнуть утверждение — это всё равно, что доказать его отрицание. Запишем отрицание, пользуясь разделом 2.3.3 лекции 2:
∃ε>0 ∀N∈N ∃n>N:∣∣∣1n−1∣∣∣≥ε.(4.10)
∃ε>0 ∀N∈N ∃n>N:∣∣∣1n−1∣∣∣≥ε.(4.10)
Иными словами, нам нужно доказать, что существует такой ε>0, что какой бы номер N мы ни выбрали, найдётся номер n, больший, чем N, для которого элемент с номером n не является ε-близким к 1. Попросту нам нужно доказать, что для какого-то конкретного ε, время от времени — сколь угодно далеко в будущем — элементы последовательности будут на расстоянии как минимум ε от 1. В этом случае, конечно, ни о каком стремлении к 1 речи уже идти не будет.
Давайте посмотрим на картинку (рис. 4.13).
Рис. 4.13: График {1/n}.
Какое значение ε подойдёт? Например, подойдёт ли ε=1,5? Похоже, что
нет — на самом деле, все элементы последовательности находятся на расстоянии
не больше 1,5 от числа 1, см. рис. 4.14.
рис. 4.14.
Рис. 4.14: График {1/n} и коридор вокруг 1 с «размахом» ε=1,5.
Однако, уже значение ε=1/3 подходит. Действительно, лишь одна точка лежит внутри коридора с «размахом» 1/3 вокруг прямой y=1, см. рис. 4.15.
Рис. 4.15: График {1/n} и коридор вокруг 1 с «размахом» ε=1/3.
Итак, пусть мы взяли ε=1/3. Теперь в соответствии с формулой (4.10) для всякого натурального N нужно научиться строить такое n, что n>N и одновременно
∣∣∣1n−1∣∣∣≥1/3.(4.11)
По картинке видно, что нам подойдёт любое n, начиная с n=2. Поскольку минимальное значение для N равно 1, то любое n, удовлетворяющее условию n>N, удовлетворяет и условию n≥2, и значит, нам подходит. Осталось построить натуральное число n, которое гарантированно больше данного натурального числа N. Как это сделать? Можно просто прибавить единицу к N, и всё!
Итак, положим: n:=N+1. Осталось доказать, что выполняется неравенство
(4. 11). Действительно:
11). Действительно:
∣∣∣1N+1−1∣∣∣=1−1N+1≥1−12=12≥13=ε.(4.12)
∣∣∣1N+1−1∣∣∣=1−1N+1≥≥1−12==12≥13=ε.(4.12)
Первое равенство следует из того факта, что 1N+1 меньше единицы для натуральных N и модуль может быть раскрыт только так, первое неравенство следует из того факта, что 1N+1 ещё и меньше 1/2, т.к. N натуральное и не меньше 1.∎
4.3.3Несуществование предела
Не у всякой последовательности существует предел.
Утверждение 4. Последовательность an=(−1)n не имеет никакого предела.
Доказательство. Нас пожидает некоторая трудность в самом начале. Определение предела требует, чтобы мы назвали конкретное число A, которое является пределом. Здесь никакого A нет.
Формально, утверждение «последовательность {an} имеет предел» записывается так: найдётся какое-то число A, которое является пределом {an}. В кванторах:
∃A∈R ∀ε>0 ∃N∈N ∀n>N:|an−A|<ε.
Ух! Четыре квантора.
Давайте напишем отрицание к этому утверждению (это как раз то, что нам нужно доказать):
∀A∈R ∃ε>0 ∀N∈N ∃n>N:|an−A|≥ε.
Иными словами, для всякого вещественного числа A, справедливо утверждение: A не является пределом нашей последовательности.
Теперь будем его доказывать. Тут нужно разобрать два случая: A≠1 и A=1.
Случай A≠1. Как обычно, начнём с картинки, см. рис. 4.16. Мы отметили точку A между 0 и −1, но на самом деле она может быть какой угодно, кроме 1.
Рис. 4.16: График последовательности {(−1)n}.
Теперь нужно выбрать такое ε>0, что последовательность будет время от
времени выскакивать из ε-коридора сколько угодно далеко в будущем. Как
найти ε? Поскольку мы знаем, что A≠1, и также знаем, что сколь
угодно далеко в будущем последовательность посещает точку 1, логично
выбрать такой размах коридора, при котором он не будет содержать точки с
y=1. Это легко сделать: достаточно в качестве ε взять число, которое
было бы меньше, чем расстояние от A до 1. В этом случае, если элемент
последовательности равен 1, его расстояние до A будет гарантированно
больше, чем ε.
Это легко сделать: достаточно в качестве ε взять число, которое
было бы меньше, чем расстояние от A до 1. В этом случае, если элемент
последовательности равен 1, его расстояние до A будет гарантированно
больше, чем ε.
Положим
ε=|A−1|2.
Тут важно, что A≠1 и следовательно ε>0.
Тогда одна из границ коридора будет проходить в точности посередине между A и 1, см. рис. 4.17. Пусть теперь дано произвольное натуральное N. Из рисунка видно, что каким бы ни было это N, найдутся элементы последовательности, лежащие вне коридора между A+ε и A−ε после n=N (заштрихованная область на рисунке). Собственно, мы именно так и выбирали ε: для любого чётного n, an=1 и следовательно соответстующая точка лежит вне указанного коридора. Для любого N найдётся чётное натуральное число n>N — оно-то нам и нужно.
Рис. 4.17: График последовательности {(−1)n} и коридор для выбранного значения ε.
Чтобы сделать рассуждение совсем железобетонным, нужно привести явный способ
построения n по N. Тут можно действовать разными методами — например,
можно выбирать первое чётное, большее N, но можно проще: положить
Тут можно действовать разными методами — например,
можно выбирать первое чётное, большее N, но можно проще: положить
n=2N.
Действительно, 2N>N для всех натуральных N и число 2N гарантированно чётное.
Наконец, нужно доказать, что для выбранного таким образом n, будет выполняться неравенство |an−A|≥ε. Поскольку n чётно, an=1. Подставляя значение ε, имеем:
|1−A|≥|A−1|2.
Поскольку |1−A|=|A−1| и это положительное число, это неравенство заведомо верно.
Таким образом, для любого A≠1 мы предъявили такое значение ε=|A−1|2>0, что для всех натуральных N мы построили такое n=2N, что n>N и |an−A|≥ε. Значит, A не является пределом нашей последовательности.
Случай A=1. Он доказывается полностью аналогично, и даже проще, потому что теперь значение A известно. Хорошее упражнение — написать это доказательство явно и аккуратно, подобно тому, как выше разборан случай A≠1. Пожалуйста, сделайте это, прежде, чем идти дальше!∎
4.
 4Единственность предела
4Единственность пределаКогда мы записываем выражение типа
limn→∞an=A,(4.13)
мы подразумеваем, что левая часть равенства является каким-то однозначно определенным числом. Конечно, мы понимаем, что не всякое выражение обязано иметь числовое значение (например, арифметическое выражение 1/0 не имеет никакого числового значения), но если уж имеет, то мы предполагаем, что это значение определяется однозначно. Тем не менее, в определении предела никаких требований, связанных с единственностью предела, не накладывается. Как видно, это определение отвечает на вопрос «является ли A пределом последовательности {an}», но вдруг для одной и той же последовательности найдутся два разных числа, для которых ответ будет положительным? В этом случае запись вроде (4.13) потеряла бы всякую определенность.
К счастью, так не бывает. Давайте это докажем.
Теорема 1. Если предел последовательности существует, то он единственный. Иными
словами, пусть есть последовательность {an} и два числа, A1 и
A2, удовлетовряющие определению предела для этой последовательности.
Тогда обязательно A1=A2.
Иными
словами, пусть есть последовательность {an} и два числа, A1 и
A2, удовлетовряющие определению предела для этой последовательности.
Тогда обязательно A1=A2.
Доказательство. Будем доказывать от противного. Пусть A1 и A2 оба являются пределами последовательности {an}, но при этом A1≠A2. Запишем формально утверждения про пределы:
∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A1|<ε1;∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|an−A2|<ε2.(4.14)(4.15)
∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A1|<ε1;∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|an−A2|<ε2.(4.14)(4.15)
Мы обсуждали (см. раздел 3.2.3), что когда есть несколько
утверждений с кванторами, в которых участвуют одни и те же буквы, никакой
связи между этими буквами за пределами соответствующих утверждений нет.
Так что чтобы не путаться, мы добавили немножко индексов — например,
ε1 для утверждения про предел A1 и ε2 для утверждения про
предел A2. Мы также ввели очень полезное обозначение N1(ε1) и
N2(ε2) — таким образом мы сразу понимаем, N из какого определения
взято и для какого ε оно найдено.
Впрочем, давайте вернёмся с формального уровня на интуитивный. У нас есть два разных числа, A1 и A2, и два утверждения: одно говорит, что весь хвост последовательности, начиная с какого-то элемента, будет близок к A1, а другое утверждение говорит, что хвост той же самый последовательности (начинающийся, впрочем, с какого-нибудь другого элемента) целиком близок к A2. Могут ли эти два утверждения друг другу не противоречить? Зависит от того, что считать «близкими точками». Но это как раз регулируются нашими значениями ε1 и ε2. И они сейчас находятся в нашей власти — мы можем их выбирать какими хотим!
Действительно, до сих пор когда мы доказывали, что предел равен какому-то
числу, мы воспринимали ε как нечто данное, что от нас не зависит.
Потому что нам нужно было доказать утверждение, взятое из определения
предела, а оно начинается квантором «для всякого ε>0». В этот же раз мы
находимся в обратной ситуации. Нам дано (по предположению), что предел
последовательности равен A1. Значит, нам сказано, что для всякого
ε1>0 найдётся такое N1=N1(ε1), что какое-то там неравенство
выполняется. Если мы хотим найти N1 для ε1=1/10, мы можем это
сделать. И для ε1=1/100. И для любого другого положительного
ε1 можем найти. Аналогично и со вторым утверждением.
Значит, нам сказано, что для всякого
ε1>0 найдётся такое N1=N1(ε1), что какое-то там неравенство
выполняется. Если мы хотим найти N1 для ε1=1/10, мы можем это
сделать. И для ε1=1/100. И для любого другого положительного
ε1 можем найти. Аналогично и со вторым утверждением.
Как выбрать ε1 и ε2, чтобы имеющиеся у нас утверждения пришли к явному противоречию? Давайте посмотрим на картинку, рис. 4.18.
Рис. 4.18: Противоречие в доказательстве теоремы 1.
Известно, что, начиная с некоторого номера n=N1, все элементы последовательности лежат в ε1-коридоре вокруг точки A1. В то же время, начиная с некоторого n=N2, все элементы последовательности лежат в ε2-коридоре вокруг точки A2. Если выбрать эти коридоры непересекающимися, будет явное противоречие — точки не смогут жить в обоих одновременно!
Какими выбрать ε1 и ε2, чтобы коридоры не пересекались? Это
легко: давайте разделим расстояние между A1 и A2 на три. Тогда верхняя
граница нижнего (на картинке) коридора вокруг A2 будет проходить по
нижней трети отрезка [A2,A1], а нижняя граница верхнего коридора — по
верхней трети этого же отрезка. Конечно, пересечения не будет, и мы победим.
Конечно, пересечения не будет, и мы победим.
Давайте сделаем железобетонное рассуждение. Итак, пусть
ε1=ε2=|A1−A2|3.
Здесь мы воспользовались предположением, что A1≠A2, и значит наши ε1 и ε2 положительны.
Пусть также
N1:=N1(ε1)=N1(|A1−A2|3),N2:=N2(ε1)=N2(|A1−A2|3).(4.16)
N1:=N1(ε1)==N1(|A1−A2|3),N2:=N2(ε1)==N2(|A1−A2|3).(4.16)
Теперь нужно найти элемент (достаточно будет одного), который приведёт нас к противоречию. Его номер должен одновременно удовлетворять условию n>N1 (потому что утверждение про предел A1 (см. (4.14)) даёт нетривиальную оценку именно для таких n, а про меньшие n оно ничего не утверждает) и n>N2 (аналогично с утверждением про A2). Как найти такое n? Очень просто: можно взять максимум из N1 и N2 и прибавить 1. Положим:
n=max(N1,N2)+1.
Тогда n>N1 и согласно (4.14) в этом случае обязательно
|an−A1|<ε1=|A1−A2|3.
Одновременно n>N2 и согласно (4.15) в этом случае обязательно
|an−A2|<ε2=|A1−A2|3.
Чтобы не возиться с раскрытием модулей и рассмотрением разных случаев, применим известное неравенство треугольника: расстояние от A1 до A2 не превосходит сумму расстояний от A1 до an и от an до A2. Имеем:
|A1−A2|≤|A1−an|+|an−A2|<|A1−A2|3+|A1−A2|3=23|A1−A2|.(4.17)
|A1−A2|≤≤|A1−an|+|an−A2|<<|A1−A2|3+|A1−A2|3==23|A1−A2|.(4.17)
Но |A1−A2| — положительное число! Положительные числа уменьшаются, если их умножить на 2/3, а не увеличиваются, как следует из нашего неравенства. Противоречие! Теорема доказана.∎
4.5Заключение
Уфф, это была длинная лекция, но мы сделали самое главное: ввели аккуратное
определение предела последовательности и убедились, что оно корректно — то есть
для всякой последовательности, для которой предел существует, он задан
однозначно. Мы также рассмотрели несколько примеров доказательств утверждений о
существовании и не существовании пределов для конкретных последовательностей. На
следующей лекции мы докажем больше общих свойств о пределах, а на семинаре
потренируемся пользоваться определениями.
Мы также рассмотрели несколько примеров доказательств утверждений о
существовании и не существовании пределов для конкретных последовательностей. На
следующей лекции мы докажем больше общих свойств о пределах, а на семинаре
потренируемся пользоваться определениями.
← Предыдущая глава Следующая глава →
определение, теоремы, свойства, примеры с решением
Оглавление:
С понятием последовательности вы ознакомились ещё в основной школе, когда изучали арифметическую и геометрическую прогрессии. Несколько последовательностей:
1) бесконечная последовательность рациональных приближений числа с точностью до десятых, сотых, тысячных и т. д.:
1,4; 1,41; 1,414; 1,4142; 1,41421;… ; (*)
2) последовательность степеней с основанием 3, показателями которых являются рациональные приближения числа с точностью до десятых, сотых, тысячных и т. д.:
д.:
Числовой последовательностью называется функция , которая задана на множестве натуральных чисел. При таком задании , , — соответственно первый, второй, n-й,… члены числовой последовательности.
Обозначают числовые последовательности Числовые последовательности задают описательно, перечнем членов, либо с помощью формулы (n-го члена или рекуррентной).
Например:
В курсе геометрии, чтобы вывести формулы длины окружности и площади круга, рассматривают последовательности вписанных в круг и описанных вокруг круга многоугольников. При этом отмечают, что при неограниченном увеличении числа сторон многоугольника его периметр всё ближе и ближе приближается к длине окружности (рис. 41).
Так получают первое интуитивное понятие предела числовой последовательности. В курсе математического анализа — это одно из важнейших понятий. Рассмотрим его подробнее.
Пусть задано числовую последовательность . Вычислим её первые пять членов и изобразим их на координатной прямой (рис. 42). Имеем:
Как видим, с увеличением номера члена последовательности сами члены последовательности всё ближе и ближе приближаются к числу 1. Поскольку расстоянием между точками, которые соответствуют числам на координатной прямой, есть модуль разности этих чисел, то можно утверждать, что для данной последовательности
Очевидно, что при росте числа п члены заданной последовательности всё меньше и меньше будут отличаться от числа 1. Например: ,а
В данном случае для любого достаточно малого числа (эпсилон) можно найти такое число N (номер члена последовательности), что для всех последующих членов этой последовательности будет выполняться неравенство .
Например, в рассмотренной выше последовательности для таким членом будет , поскольку, а для таким членом будет (проверьте).
В этом случае говорят, что число 1 является пределом заданной числовой последовательности.
Число А называют пределом числовой последовательности , если для любого существует номер члена последовательности такой, что для всех выполяется неравенство
Обозначают: . Читают: предел числовой последовательности при n, стремящемся к бесконечности, равен А.
Пример №1Вычислите предел последовательности .
Решение:
Запишем несколько членов заданной последовательности: Как видим, ее члены стремятся к числу 1. Проверим наше предположение. По определению предела надо найти такое число N, что для всех будет выполняться неравенство . Имеем:
Следовательно, такое число существует. Например, при последнее неравенство будет иметь вид , или .
То есть, начиная с 100-го члена последовательности расстояние между любым членом последовательности и числом 1 будет меньше 0,01.
Следовательно, .
Докажите самостоятельно и запомните, что .
Если числовая последовательность имеет предел, то она называется сходящейся. Если числовая последовательность предела не имеет, то она называется расходящейся.
Рассмотрим свойства сходящихся последовательностей.
- Если последовательность имеет предел, то этот предел единственный.
- Предел постоянной последовательности равен значению любого члена этой последовательности, то есть
3. Предел суммы (разности) двух сходящихся последовательностей равен сумме (разности) пределов этих последовательностей , то есть:
4. Предел произведения двух сходящихся последовательностей равен произведению пределов этих последовательностей , т.е.
5.Если последовательности и — сходящиеся , . , то числовая последовательность тоже сходящаяся и выполняется равенство
, то числовая последовательность тоже сходящаяся и выполняется равенство
Найдите предел последовательности .
Решение:
Эту последовательность можно представить в виде суммы двух сходящихся последовательностей , (проверьте). На основании свойств 2 и 3 имеем:
Для вычисления предела последовательности, которая задается как отношение двух многочленов , используют следующее правило.
Для того чтобы вычислить предел числовой последователь кости, которая задаётся как отношение двух многочленов (одной переменной n, степеней m и k соответственно),каждый из которых имеет предел, равный бесконечности, необходимо каждый член заданных многочленов разделить на наивысшую степень п и выяснить, к чему стремится каждый из полученных членов заданного отношения.
Вычислите .
Решение:
Здесь , . Предел каждого многочлена равен бесконечности. Поскольку , , то делим каждый член многочленов на и выясняем, к чему стремится каждый из полученных членов.
Пример №4Вычислите:
a) ; б) .
Решение:
a)
б) .
Заметим, что здесь не происходит деление на ноль, поскольку знаменатель лишь стремится к нулю, но ему не равен.
Проанализируем полученные ответы. В примере 3 степень числителя меньше степени знаменателя. Это означает, что знаменатель стремится к бесконечности быстрее, чем числитель, а следовательно, предел их отношения будет равняться нулю. В примере 4, в задании а) степени числителя и знаменателя одинаковы и в результате получили отношение коэффициентов при старших степенях. В задании б) степень числителя больше степени знаменателя. Это означает, что числитель стремится к бесконечности быстрее, чем знаменатель, а потому предел их отношения равен бесконечности. Итак, имеем еще такое правило.
В задании б) степень числителя больше степени знаменателя. Это означает, что числитель стремится к бесконечности быстрее, чем знаменатель, а потому предел их отношения равен бесконечности. Итак, имеем еще такое правило.
Для того чтобы вычислить предел числовой последовательности при , которая задаётся как отношение двух многочленов (одной переменной n, степеней m и k соответственно)* каждый из которых имеет предел,равный бесконечности, необходимо сравнить эти степени. Если:
1 )m = k, то предел равен отношению коэффициентов при старших степенях заданных многочленов;
2) m < k , то предел равен нулю;
3) m> k, то предел равен бесконечности.
Пример №5Пользуясь определением предела числовой последовательности, докажите, что .
Решение:
Нужно доказать, что существует такое , что для всех выполняется неравенство . Преобразуем выражение , стоящее в левой части :
Пусть , тогда , а . Для любого можем найти соответствующее , например .
Итак, пределом заданной последовательности является число 2.
Пример №6Вычислите: а) ; б) .
Решение:
а) Умножим и разделим выражение, стоящее под знаком предела, на сопряжённое.
б) Разделим числитель и знаменатель дроби на n. Имеем:
Предел и непрерывность функцииЧасто говорят о значении функции в точке, пределе функции в точке, приращении функции в точке, непрерывности функции в точке. О каких точках идёт речь? О точках оси абсцисс — значениях аргумента.
Значение функции в точкеПусть задано, например, функцию . Если х = 1, то соответствующее значение функции равно 3. Говорят, что в точке х = 1 значение функции f(x) равно 3. В точке х = 0 её значение равно 1, в точке х = 10 значение функции f(x) равно 111. Пишут: , f(0) =1 , f(10)=111.
Если х = 1, то соответствующее значение функции равно 3. Говорят, что в точке х = 1 значение функции f(x) равно 3. В точке х = 0 её значение равно 1, в точке х = 10 значение функции f(x) равно 111. Пишут: , f(0) =1 , f(10)=111.
Рассмотрим ту же функцию . Если значения её аргумента х достаточно близко и с обеих сторон приближаются к 1, то соответствующие значения функции как угодно близко приближаются к числу 3 (рис. 43). Об этом свидетельствуют данные таблицы (рис. 44), в которой содержатся значения.
функции для 10 значений аргумента, близких к числу 1, и график, изображённый на рисунке 43.
Другими словами: разность может стать и оставаться сколь угодно малой, если разность будет достаточно малой. В этом случае говорят, что предел функции f(x) в точке х = 1 равен 3. Пишут: если х —> 1, то , или .
Существенная деталь: функция может иметь предел даже в такой точке, в которой она не определена, потому что знаменатель не может равняться нулю. Во всех остальных точках функция имеет такие же значения, как и функция f(x), ибо : , если . График функции изображён на (рис) 45.
Хотя значение функции в точке x= 1 не существует, а её предел в этой точке существует и равен 3.
Определение предела функции можно сформулировать так.
Число b называется пределом функции f(x)в точке ,если для любого положительного числа можно указать такое положительное число , что для всех значений х из промежутка кроме, возможно, самой точки , справедливо неравенство .
Пишут так:.
Определение предела функции имеет простое геометрическое толкование: какое бы ни было достаточно малое наперёд за-данное положительное число (), можно указать такое положительное число, что для всех точек х, которые удалены от точки не далее чем на , график функции лежит внутри полосы — шириной , ограниченной прямыми и (рис. 46).
Предел функции имеет интересные свойства. Например:
• функция не может иметь двух различных пределов в точке;
• если с — число, то ;
Несколько свойств сформулируем в виде теоремы.
Теорема. Если каждая из функций f(x) и g(x) имеет предел в точке , то в этой точке существуют пределы функций ,
справедливы равенства:
Другими словами можно сказать так.
Постоянный множитель можно выносить за знак предела. Предел суммы (разности, произведения) функций равен сумме (разности, произведению) пределов данных функций. Предел отношения двух функций равен отношению их пределов, если предел делителя не равен нулю.
Эти свойства используют для вычисления пределов функций в заданных точках.
Пример №7При условии, что вычислите предел функции f(x), если:
а)б)
Решение:
a) ;
б) .
Замечание. Решая такие упражнения, некоторые преобразования можно выполнять устно.
В предыдущих примерах для нахождения предела достаточно было подставить в данное выражение предельное значение аргумента. Но часто такая подстановка приводит к неопределённости вида , , ,, , , . В таких случаях и сначала необходимо преобразовать данное выражение, а уже потом вычислять предел. Нахождение предела таким образом называется раскрытием неопределённостей.
Нахождение предела таким образом называется раскрытием неопределённостей.
Найдите .
Решение:
Поскольку при предел знаменателя равен нулю, то использовать теорему о пределе частного нельзя. Непосредственная подстановка в данное выражение предельного значения аргумента х = 3 приводит к неопределенности вида — .
Чтобы её раскрыть, разложим числитель и знаменатель дроби на множители. Имеем:
Приращения аргумента и функцииПусть дано, например, функцию . В точке ее значение . Увеличим значение аргумента на 0,01, то есть, пусть . Соответствующее значение функции . По сравнению с предыдущим значением оно увеличилось на 0,0401. Здесь 0,01 — приращение аргумента, а 0,0401 — соответствующее приращение функции, а именно: приращение функции на промежутке [2; 2,01].
Приращением аргумента в точке называют разность , где х — произвольное число, которое мало отличается от и может быть положительным или отрицательным. Соответствующее приращение функции f(x) — разность .
Приращение аргумента х обозначают символом , а приращение функции , (читают: дельта икс, дельта эф, дельта игрек). Так, в рассматриваемом примере = 0,01, = 0,0401.
Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции — приращением ординаты этой точки (рис. 47),
Свойства этих понятий показано на рисунках 47 и 48. Если функция f(x) — возрастающая и , то — число положительное, а если f(х) — убывающая функция и , то — число отрицательное.
Непрерывность функцииКак связаны между собой приращения аргумента х и функции в точке = 2? Если , то = 0,0401; если = 0,001, то = 0,004001 и т. д. Вообще, если , то и , т. е. приращение функции стремится к нулю, когда стремится к нулю приращение аргумента (слева или справа). В таком случае говорят, что функция f(x) непрерывна в точке .
д. Вообще, если , то и , т. е. приращение функции стремится к нулю, когда стремится к нулю приращение аргумента (слева или справа). В таком случае говорят, что функция f(x) непрерывна в точке .
| Функция f(x) называется непрерывной в точке , если в этой точке достаточно малым приращениям аргумента соответствуют сколь угодно малые приращения функции.
Иначе:
Преобразуем последнее равенство:
Поскольку , когда то получим , отсюда
Функция у =f(x) называется непрерывной в точке , если существует предел функции в этой точке и он равен значению функции в точке .
Использование последней формулы существенно упрощает вычисление пределов для непрерывных функций.
Функция называется непрерывной на промежутке, если она непрерывна в каждой его точке. График такой функции — непрерывная кривая (её можно провести, не отрывая карандаш от бумаги).
На рисунке 49 изображены графики функций, имеющих разрывы в точке х = 1; они не являются непрерывными в этой точке.
Непрерывными в каждой точке своей области определения есть элементарные функции — рациональные, тригонометрические, , а также функции, образованные из них с помощью четырёх арифметических действий. Графики элементарных функций на каждом промежутке из области определения являются неразрывными линиями.
Теория пределов — большой и интересный раздел курса математического анализа, который изучается в университетах. В школе этот материал изучают обзорно, на основе наглядных представлений и интуиции. Представление о пределах и их свойствах желательно иметь для изучения производной и её применений — мощного аппарата для исследования многих реальных процессов.
Предлагаем вам ознакомиться с одним из интересных и важных фактов теории пределов. Рассмотрите таблицу, составленную с помощью Excel.
Как видим, при достаточно малых значениях , а .
В курсе математического анализа строго доказывается, что
Это равенство называется первым замечательным пределом. Его используют для нахождения пределов функций, связанных с тригонометрическими.
Пример №9Вычислите предел .
Решение:
Пример №10Вычислите:
а) б) в)
Решение:
а) В точке x = 3 предел каждой из дробей не существует, поэтому воспользоваться теоремами о пределах мы не можем. Упростим функцию, содержащуюся под знаком предела, выполнив действие вычитания. Имеем:
б) В тючке х = 1 данная функция не определена, но дробь можно сократить: .
Поскольку для вычисления предела при саму точку можно исключить и не рассматривать, то
в) Умножим числитель и знаменатель дроби на выражения, сопряжённые к данным.
Найдите приращение функции при переходе значения аргумента от 3 до 3,5.
Решение:
Способ 1. Имеем , a , тогда
До этой формуле можно вычислить значение для любых х и . В частности, в нашем примере х = 3,= 3,5 — 3 = 0,5, поэтому .
Способ 2. ,.
Пример №12Для функции найдите:
а) приращение функции при переходе от некоторой точки х к точке х + ;
б) предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
a) , .
б) , поскольку , а х — не зависит от .
Вычислить предел .
Решение:
Таблица производных основных элементарных функций
Правила дифференцирования
Вычислить производную функции у(х), заданной в неявной форме .
Решение:
В случае неявного задания функции F(x,y) = 0 для нахождения ее производной нужно:
1) вычислить производную по переменной х функции F(x, у(х)),
2) приравнять эту производную нулю,
3) решить полученное уравнение относительно у'(х). В нашем случае получаем ,
Отсюда получим, что при .
Пример №15Провести исследование функции
Решение:
1. Функция определена и непрерывна всюду, кроме точки х=1. Она равна нулю в точке х = 0.
Она равна нулю в точке х = 0.
2. Вычислим первую производную данной функции: .
3. Нахождение интервалов монотонности и точек экстремума функции.
Приравнивая первую производную функции нулю, находим ее критические точки (с учетом тех точек, где производная не существует): , , . Данные точки разбивают область определения функции на четыре промежутка монотонности:, , , . Так как у’ >0 при и у’ < 0 при ,то на промежутках и функция возрастает, а на промежутках (0; 1) и убывает. Точка х = 0 является точкой локального максимума .
4. Найдем промежутки выпуклости и точки перегиба графика функции. Для этого исследуем знак второй производной:
Так как у»>0 при ; и у»<0 при, то на промежутках и график функции является выпуклым вниз, а на промежутках и (0, 1) график функции является выпуклым вверх. При этом точка области определения функции, при переходе через которую вторая производная меняет знак, задает точку перегиба, .
При этом точка области определения функции, при переходе через которую вторая производная меняет знак, задает точку перегиба, .
Точка х = 1 не задает точку перегиба, поскольку она не входит в область определения функции.
5. Найдем асимптоты графика.
Вертикальной асимптотой является прямая х= 1, поскольку
Найдем наклонные асимптоты графика функции .
Уравнение наклонной асимптоты имеет вид . Для определения ее параметров последовательно вычислим два предела:
В результате получаем, что наклонной асимптотой является прямая у = х. Исследование функции закончено.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
{-n}+1\}\). Это в точности то же самое, что и функция выше, за исключением того, что доменом теперь являются натуральные числа, а не действительные числа. Если вы хотите узнать «предел, когда \(n\) стремится к бесконечности», вы будете искать очень большие значения \(n\), точно так же, как вы искали очень большие значения \(x\).
Если вы хотите узнать «предел, когда \(n\) стремится к бесконечности», вы будете искать очень большие значения \(n\), точно так же, как вы искали очень большие значения \(x\).Имея в виду, что процесс будет очень похож на просмотр пределов последовательностей и функций, давайте углубимся!
См. Ограничения функции для обзора функций и способов определения их пределов.
Определение предела последовательности
Во-первых, давайте взглянем на неформальное определение предела последовательности:
предел последовательности — это значение, к которому приближается последовательность, когда количество членов становится очень большой.
Более формально:
Пусть \( L \) будет действительным числом. Последовательность имеет предел \( L \) по мере того, как \( n \) приближается к \( \infty \), если задано \( \epsilon > 0 \) , существует число \( M > 0 \) такое, что \( n > M \) подразумевает \( \left| s_n – L \right| < \epsilon \). Мы пишем, что
Мы пишем, что
\[ \lim\limits_{n \to \infty} s_n = L, \]
и говорят, что последовательность сходится к \( L \) . Говорят, что последовательности, не имеющие предела, расходятся .
Взяв предел функции как \( x \to \infty\), вы взяли кандидата на предел (для удобства назовите его \( L \)), а затем проверили, сможете ли вы «поймать» функцию значения, близкие к \(L\), если \(x\) достаточно велики.
Прежде чем идти дальше, давайте посмотрим на картину происходящего. 9{-n} +1 \} \) . Кандидатом на предел является \( L = 1 \). Нарисуйте точки последовательности вместе с возможным пределом \( L = 1 \) и нарисуйте линии \( y = L + \epsilon = 1 + \epsilon \) и \( y = L – \epsilon = 1 – \эпсилон\) .
Перехват значений последовательности | StudySmarter Original
Как видите, каким бы маленьким ни было \( \epsilon \), вы всегда сможете уйти достаточно далеко (другими словами, выбрать достаточно большое \( M \) ), чтобы последовательность значения заключены между линиями \( y = 1 + \epsilon \) и \( y = 1 + \epsilon \). Это означает, что последовательность сходится к пределу \( L = 1 \).
Это означает, что последовательность сходится к пределу \( L = 1 \).
Как математически записать предел последовательности?
Существует два основных способа записи “предел последовательности при стремлении \(n\) к бесконечности равен \(L\)”, и вы можете использовать любой из них:
\[ \{ s_n \ } \к л; \] или
\[ \lim\limits_{n \to \infty} s_n = L . \]
Оба означают одно и то же. Вы также можете сказать, что последовательность \( \{s _n \} \) сходится к \( L \).
Естественно, вы не хотите выбирать кандидата для предела, а затем должны найти подходящее \( M \), которое достаточно велико каждый раз, когда вы хотите показать, сходится ли последовательность и к чему она сходится. К счастью, поскольку последовательности являются функциями, вы можете использовать те же правила ограничений для функций, что и для последовательностей.
Единственность предела сходящейся последовательности
Прежде чем говорить о единственности предела последовательности, давайте подумаем о решении линейного уравнения. Мы говорим, что линейное уравнение \[ ax+b=0, \], где \( a \) и \( b \) – действительные числа, имеет единственное решение. Это означает, что только одно значение \(x\) удовлетворяет любой заданной паре значений \(a\) и \(b\).
Мы говорим, что линейное уравнение \[ ax+b=0, \], где \( a \) и \( b \) – действительные числа, имеет единственное решение. Это означает, что только одно значение \(x\) удовлетворяет любой заданной паре значений \(a\) и \(b\).
То же самое можно сказать и о пределе последовательности. Если последовательность сходится к некоторому значению и, следовательно, имеет предел, мы говорим, что этот предел уникален для этой последовательности.
Пределы последовательности Формулы
Предположим, у вас есть две последовательности \( \{s _n \} \) и \( \{t _n \} \) , и вы знаете, что обе они сходятся. Другими словами, существуют числа \( L \) и \( P \) такие, что
\[ \lim\limits_{n \to \infty} s_n = L \mbox{ и } \lim\limits_{n \ в \infty} t_n = P . \]
Тогда выполняются следующие правила:
Правило суммы:
\[ \lim\limits_{n \to \infty} (s_n + t_n ) = \lim\limits_{n \to \infty} s_n + \lim\limits_{n \to \infty} t_n = L + P . \]
Правило разности:
\[ \lim\limits_{n \to \infty} (s_n – t_n ) = \lim\limits_{n \to \infty} s_n – \lim\limits_{n \to \ infty} t_n = L – P . \]
\]
Правило продукта:
\[ \lim\limits_{n \to \infty} (s_n \cdot t_n ) = \left( \lim\limits_{n \to \infty} s_n \right) \ cdot \left( \lim\limits_{n \to \infty} t_n \right) = L \cdot P . \]
Постоянное множественное правило: для любой константы \( C \),
\[ \lim\limits_{n \to \infty} (C \cdot s_n ) = C\cdot \lim\limits_{n \to \infty} s_n = C \cdot L. \]
Частное правило: Если \( P \not= 0 \) и \( t_n \not= 0 \) для всех \( n \in \mathbb{n} \), то
\[ \lim\ limit_{n \to \infty} \left( \frac{s_n}{t_n} \right) = \frac{\lim\limits_{n \to \infty} s_n}{\lim\limits_{n \to \infty } t_n }= \frac{L}{P} . \]
Необходимо знать, что оба предела, с которыми вы работаете, сойдутся, чтобы эти свойства оставались верными!
Итак, как свойства пределов последовательностей помогают понять, что если последовательность сходится, предел должен быть уникальным?
Предположим, у вас есть последовательность, которая сходится к двум разным вещам, скажем, \( \{ s_n \} \to L\) и \( \{ s_n \} \to P\) , где \( L \not= П \). {-n} +1 \} \) , используйте свойства пределов для последовательностей, чтобы найти предел как \( n \to \infty \ ). 9{-n} +\lim\limits_{n \to \infty} 1 \\ &= 0 + 1 \\ &= 1. \end{align} \]
{-n} +1 \} \) , используйте свойства пределов для последовательностей, чтобы найти предел как \( n \to \infty \ ). 9{-n} +\lim\limits_{n \to \infty} 1 \\ &= 0 + 1 \\ &= 1. \end{align} \]
Убедитесь, что условия для использования правил для последовательностей встретились очень важно. Помните, что вы должны знать, что обе последовательности сходятся и что, если вы используете правило отношения, у последовательности в знаменателе есть ненулевой предел. Если это не так, может случиться все что угодно!
Что произойдет, если одна из ваших последовательностей не сходится? Даже если предел произведения существует, вы не можете умножить то, чего не существует. Следующие три примера покажут вам, что может произойти, если оба предела не сходятся.
Пример 1: Возьмите последовательности \( \{ s_n \} = \{ n \} \) и
\[ \{ t_n \} = \left\{ \frac{1}{n} \right\} . \]
Тогда \( \{ s_n \} \) расходится, а \( \{ t_n \} \to \infty \). Но
\[ \begin{align} \lim\limits_{n \to \infty} (s_n \cdot t_n ) &= \lim\limits_{n \to \infty} n \cdot \frac{1}{n } \\ &= \lim\limits_{n \to \infty} 1 \\ &= 1 . \end{align} \]
\end{align} \]
Таким образом, здесь вы получаете 1 для лимита продукта.
Пример 2: Можно ли получить что-то еще за лимит продукта, если лимит одной из последовательностей не выходит? Если вместо этого вы возьмете последовательность 92 \cdot \frac{1}{n} \\ &= \lim\limits_{n \to \infty} n , \end{align} \]
и произведение расходится. Таким образом, вы можете получить лимит продукта, которого нет!
Таким образом, если у вас нет правильных условий для использования правила продукта, может случиться что угодно, и вы не можете заранее предсказать, что это может быть!
Примеры пределов последовательностей
Давайте посмотрим на другие примеры того, какие виды пределов может иметь функция и случаи, когда у нее нет предела.
Имеет ли последовательность
\[ \{ s_n \} = \left\{ 2 + \frac{4}{n} \right\} \]
предел? Если так, то, что это?
Ответ:
Другой способ сформулировать этот вопрос: “Приближается ли указанная выше последовательность к одному значению, когда \( n \) становится большим? Посмотрим!
В вопросе есть \( \frac{4 {n} \) term. Давайте посмотрим на функцию, эквивалентную этому. Для функции
Давайте посмотрим на функцию, эквивалентную этому. Для функции
\[ f(x) = \frac{1}{x} \]
вы знаете, что
\[ \begin {align} \lim\limits_{x \to \infty} f(x) &= \lim\limits_{x \to \infty} \frac{1}{x} \\ &= 0 \end{align} \ ]
, потому что функция имеет горизонтальную асимптоту \( y =0 \). Это означает, что последовательность
\[ \{ t_n \} = \left\{ \frac{1}{n} \right\} \]
также имеет
\[ \begin{align} \lim\limits_{ n \to \infty} t_n &= \lim\limits_{n \to \infty} \frac{1}{n} \\ &= 0 \end{align} \]
, так как последовательность такая же, как и функции, кроме домена. На самом деле, вы можете увидеть это и графически.
График последовательности {1/n} на положительной оси x | StudySmarter Оригинал
Теперь, когда мы вспомнили характеристики обратной функции, давайте вернемся к первоначальному вопросу. Теперь вы знаете, что можете применить правило суммы, чтобы получить
\[ \begin{align} \lim\limits_{n \to \infty} s_n &= \lim\limits_{n \to \infty} \left( 2 + \frac{4}{n} \right) \\ &= \lim\limits_{n \to \infty} 2 + \lim\limits_{n \to \infty} \frac{4}{n}, \end {align} \]
, а затем постоянное правило, чтобы получить:
\[ \begin{align} \lim\limits_{n \to \infty} 2 + \lim\limits_{n \to \infty} \frac {4}{n} &= 2 + 4 \lim\limits_{n \to \infty} \frac{1}{n} \\ &= 2 + 4 \cdot 0 \\ &= 2. \end{align } \]
\end{align } \]
Таким образом, последовательность имеет предел, и значение равно 2.
Сходится ли последовательность
\[ \left\{ \frac{1 + 4n}{5 + 6n} \right\} \]
? Если да, то к чему он сходится?
Ответ:
Иногда вам нужно попробовать разные вещи, чтобы найти ту, которая позволит вам правильно использовать правила. Вы хотели бы использовать правило отношения, чтобы решить эту проблему.
Сначала попробуйте настроить две последовательности: \( \{ s_n \} = \{ 1 + 4n \} \) и \( \{ t_n \} = \{ 5 + 6n \} \). К сожалению, есть проблема, поскольку правило отношения требует, чтобы обе эти последовательности имели предел, и ни одна из них не сходится к конечному числу!
Для второй попытки разбейте его на две части вместо одной. Вы знаете, что
\[ \frac{1+4n}{5+6n} = \frac{1}{5+6n} + 4 \cdot \frac{n}{5 + 6n}, \]
, которое определенно ближе к полезности, но все же не совсем из-за этого термина
\[ \frac{n}{5+6n} \]
.
Вторая попытка натолкнет вас на мысль, что сначала нужно вынести \( n \) из знаменателя. Тогда у вас есть
\[ \frac{1+4n}{5+6n} = \frac{1+4n}{n \left( \frac{5}{n}+6 \right) } . \]
Было бы очень хорошо сократить это \( n \) в знаменателе с единицей в числителе, но для этого вам нужно сначала разложить это на множители: \[ \begin{align} \frac{1 +4n}{5+6n} & =\frac{n \left(\frac{1}{n}+4 \right) }{n \left( \frac{5}{n}+6 \right) } \\ &= \frac{ \frac{1}{n} + 4}{ \frac{5}{n} + 6}. \end{align} \]
Алгебра на помощь! Теперь настройте две последовательности для использования частного правила:
\[ \{ s_n \} = \left\{\frac{1}{n}+4 \right\} \mbox{ и } \{ t_n \} = \left\{ \frac{5}{n} + 6 \right\}. \]
Оба из них имеют пределы, на самом деле
\[ \lim\limits_{n \to \infty} s_n = \lim\limits_{n \to \infty} \left( \frac{1}{n}+ 4 \right) = 4 \]
и
\[ \lim\limits_{n \to \infty} t_n = \lim\limits_{n \to \infty} \left( \frac{5}{n} +6 \right) = 6 \]
, где вы применили правило суммы и правило константы, как в предыдущем примере. Теперь вы знаете, что можете применить правило частного, чтобы получить
Теперь вы знаете, что можете применить правило частного, чтобы получить
\[ \begin{align} \lim\limits_{n \to \infty} \frac{1 + 4n}{5 + 6n} &= \lim\limits_{ n \to \infty} \frac{s_n}{t_n} \\ &= \frac{4}{6} \\ &= \frac{2}{3}. \end{выравнивание} \]
Следовательно, последовательность сходится, и предел равен \( \frac{2}{3} \).
Вы можете сделать эту задачу короче, если вспомните свойства рациональных функций. Если наибольшая степень в числителе совпадает с наибольшей степенью в знаменателе, вы можете «поделить» коэффициенты, чтобы получить предел. В этом случае наибольшая степень в числителе равна 4n , а наибольшая степень в знаменателе — 6n , поэтому деление дает 4/6 = 2/3, что одновременно является пределом и говорит вам, что 9n \право\} \) сходятся? Если да, то к чему он сходится?
Ответ:
Чтобы получить представление о том, как ведет себя эта последовательность, давайте выпишем некоторые члены этой последовательности.
\[ \{-1, 1, -1, 1, \dots \} \]
Если последовательность имеет предел, то предел должен быть либо \(-1 \), либо \(1 \) поскольку это единственные два значения в последовательности, и они вообще не меняются. Давайте посмотрим, что происходит графически, когда вы пытаетесь выбрать \( L = 1 \) в качестве предельного значения.
Давайте посмотрим, что происходит графически, когда вы пытаетесь выбрать \( L = 1 \) в качестве предельного значения.
Является ли L=1 пределом последовательности? | StudySmarter Original
Глядя на рисунок выше, вы можете видеть, что не имеет значения, насколько большое значение \( M \) вы выберете, невозможно получить все значения последовательности между двумя линиями \( y = 1 + \эпсилон\) и \(у = 1 – \эпсилон\). Это означает, что эта последовательность не сходится.
Можно также сказать, что последовательность расходится с .
Доказательство предела последовательности
Иногда вы столкнетесь с такой последовательностью, как
\[ \left\{ \frac{ \cos n }{n} \right\} \]
где невозможно применить свойства пределов для последовательностей. В таком случае может помочь Теорема сжатия. Поскольку последовательности — это всего лишь особый вид функций, теорему сжатия можно переформулировать для последовательностей.
Обзор теоремы о сжатии для функций см. в разделе Теорема о сжатии .
в разделе Теорема о сжатии .
Теорема сжатия: Предположим, что есть две последовательности \( \{ s_n \} \) и \( \{ t_n \} \), обе из которых сходятся к одному и тому же значению \( L \), и что существует существует \( N \ in \mathbb{N} \) такой, что \( s_n \ le w_n \le t_n \) для всех \( n \ge N \). Затем
\[ \lim\limits_{n \to \infty} w_n = L . \]
Давайте посмотрим, как применяется теорема сжатия. Возвращаясь к последовательности
\[ \left\{ \frac{ \cos n }{n} \right\}, \]
, идея состоит в том, чтобы «втиснуть» ее между двумя последовательностями, которые, как вы знаете, сходятся. Во-первых, давайте посмотрим на график некоторых значений этой последовательности.
График значений последовательности, сходящихся к 0 | StudySmarter Original
Конечно, похоже, что она сходится к нулю, но вам нужно найти две последовательности, которые, как вы знаете, сходятся к нулю, чтобы «втиснуть» ее между ними. Одна последовательность, с которой вы уже работали и которая сходится к нулю, — это последовательность 9. 0003
0003
\[ \{ s_n \} = \left\{ \frac{1}{n} \right\}. \]
Вы также знаете, что \( -1 \le \cos n \le 1 \) для любого \( n\), поэтому
\[ – \frac{1}{n} \le \frac{ \ cos n}{n} \le \frac{1}{n} \]
также для любого \( n \). Это означает, что вы можете взять вторую последовательность, которую вам нужно сжать, чтобы она была
\[ \{ t_n \} = \left\{ -\frac{1}{n} \right\}. \]
Взглянув на график для всех трех последовательностей,
Используя теорему о сжатии, найдя 2 последовательности, которые сходятся к 0, чтобы использовать их для «сжатия» исходной последовательности | StudySmarter Оригинал
Таким образом, использование теоремы сжатия для последовательностей доказывает, что последовательность
\[ \{ w_n \} = \left\{ \frac{ \cos n }{n} \right\} \]
сходится.
Теорема об абсолютном значении
Существует очень удобное следствие теоремы о сжатии для последовательностей, называемое теоремой об абсолютном значении.
Теорема абсолютного значения: Пусть \( \{ s_n \} \) будет последовательностью. Если
\[ \lim\limits_{n \to \infty} \left| с_н \право| = 0, \]
9п \право| \\ &= \lim\limits_{n \to \infty} 1 \\ &= 1. \end{align} \]Таким образом, хотя абсолютное значение последовательности сходится, сама последовательность не сходится. Поэтому проверка условия, что предел абсолютного значения последовательности равен нулю, с помощью применения теоремы об абсолютном значении очень важна!
Последовательности, расходящиеся до бесконечности
Иногда последовательность становится все больше и больше, как в случае с последовательностью. Это несколько более приятная ситуация, чем та, которая просто продолжает прыгать, но все равно не сходится. Вместо этого у него есть специальное имя. 9n = \infty , \]
последовательность \( \{ s_n \} \) расходится к бесконечности.
Ограничение последовательности – Ключевые выводы
- Пусть \(L\) будет действительным числом.
 Последовательность имеет предел \( L \) по мере того, как \( n \) приближается к \( \infty \), если задано \( \epsilon > 0 \) , существует число \( M > 0 \) такое, что \( n > M \) подразумевает \( \left| s_n – L \right| < \epsilon \). Мы пишем, что
Последовательность имеет предел \( L \) по мере того, как \( n \) приближается к \( \infty \), если задано \( \epsilon > 0 \) , существует число \( M > 0 \) такое, что \( n > M \) подразумевает \( \left| s_n – L \right| < \epsilon \). Мы пишем, что\[ \lim\limits_{n \to \infty} s_n = L, \]
и говорим, что последовательность сходится к \( L \) . Говорят, что последовательности, не имеющие предела, расходятся .
Если последовательность \( \{ s_n \} \) такова, что
\[ \lim\limits_{n \to \infty} s_n = \pm \infty , \]
, то мы говорим, что последовательность расходится до \(\pm\infty\).
Теорема сжатия: Предположим, что есть две последовательности \( \{ s_n \} \) и \( \{ t_n \} \), обе из которых сходятся к одному и тому же значению \( L \), и что существует \( N \ в \mathbb{N} \) такое, что \( s_n \ le w_n \le t_n \) для всех \( n \ge N \). Затем
\[ \lim\limits_{n \to \infty} w_n = L .
 \]
\]Абсолютное значение Теорема: Пусть \( \{ s_n \} \) будет последовательностью. Если
\[ \lim\limits_{n \to \infty} \left| с_н \право| = 0, \]
затем
\[ \lim\limits_{n \to \infty} s_n = 0. \]
Если последовательность сходится, то она имеет единственный предел.
Предположим, у вас есть две последовательности \( \{s _n \} \) и \( \{s _n \} \) , и существуют числа \( L \) и \( P \) такие, что
\[ \lim\limits_{n \to \infty} s_n = L \mbox{ и } \lim\limits_{n \to \infty} t_n = P . \]
Тогда выполняются следующие правила:
Правило суммы:
\[ \lim\limits_{n \to \infty} (s_n + t_n ) = \lim\limits_{n \to \infty} s_n + \lim\limits_{n \to \infty} t_n = L + P . \]
Правило разности:
\[ \lim\limits_{n \to \infty} (s_n – t_n ) = \lim\limits_{n \to \infty} s_n – \lim\limits_{n \ в \infty} t_n = L – P . \]
Правило продукта:
\[ \lim\limits_{n \to \infty} (s_n \cdot t_n ) = \left( \lim\limits_{n \to \infty} s_n \right) \cdot \ влево( \lim\limits_{n \to \infty} t_n \right) = L \cdot P .
 \]
\]Постоянное множественное правило: для любой константы \( C \),
\[ \lim\limits_{n \to \infty} (C \cdot s_n ) = C\cdot \lim\limits_{n \to \infty} s_n = C \cdot L. \]
Частное правило: Если \( P \not= 0 \) и \( t_n \not= 0 \) для всех \( n \in \mathbb {n} \), затем
\[ \lim\limits_{n \to \infty} \left( \frac{s_n}{t_n} \right) = \frac{\lim\limits_{n \to \infty} s_n} {\lim\ limit_{n \to \infty} t_n }= \frac{L}{P} . \]
Предел последовательности
Марко Табога, доктор философии
В этой лекции мы вводим понятие предела последовательность . Начнем с простого случая, когда является последовательностью действительных чисел, то мы имеем дело с общим случаем, когда может быть последовательностью объектов, которые не обязательно являются действительными числами.
Содержание
Предел последовательности действительных чисел
Неформальное определение предела последовательности действительных чисел
Формальное определение предела последовательности действительных чисел
Предел последовательности вообще
Неформальное определение предела – Общий случай
Метрики и определение расстояния
Формальное определение предела.
 Общий случай
Общий случайКритерий сходимости
Предел последовательности действительных чисел
Сначала мы даем неформальное определение, а затем более формальное определение предел последовательности действительных чисел.
Неформальное определение предела последовательности реальные числа
Позволять быть последовательностью действительных чисел. Позволять . Обозначим через последствие получается отбрасыванием первого условия , то есть, Ниже приводится интуитивное определение предела последовательности.
Определение (неофициальное)
Позволять
быть действительным числом. Мы говорим, что
является пределом последовательности действительных чисел, если, соответствующим образом выбрав
,
расстояние между
и любой член подпоследовательности
можно сделать сколь угодно близким к нулю. Если
является пределом последовательности
,
мы говорим, что последовательность
это сходящаяся последовательность и что она сходится к .
Укажем тот факт, что
является пределом
по
Если
является пределом последовательности
,
мы говорим, что последовательность
это сходящаяся последовательность и что она сходится к .
Укажем тот факт, что
является пределом
по
Таким образом, является пределом если, отбрасывая достаточно большое количество начальных членов , мы можем составить оставшиеся члены как можно ближе к как нам нравится. Интуитивно, является пределом если становится все ближе и ближе к позволив уйти в бесконечность.
Формальное определение предела последовательности реальные числа
Расстояние между двумя действительными числами есть абсолютное значение их
разница. Например, если
а также
является членом последовательности
,
расстояние между
а также
,
обозначается
,
это по
используя понятие расстояния, приведенное выше неформальное определение может быть сделано
тщательный.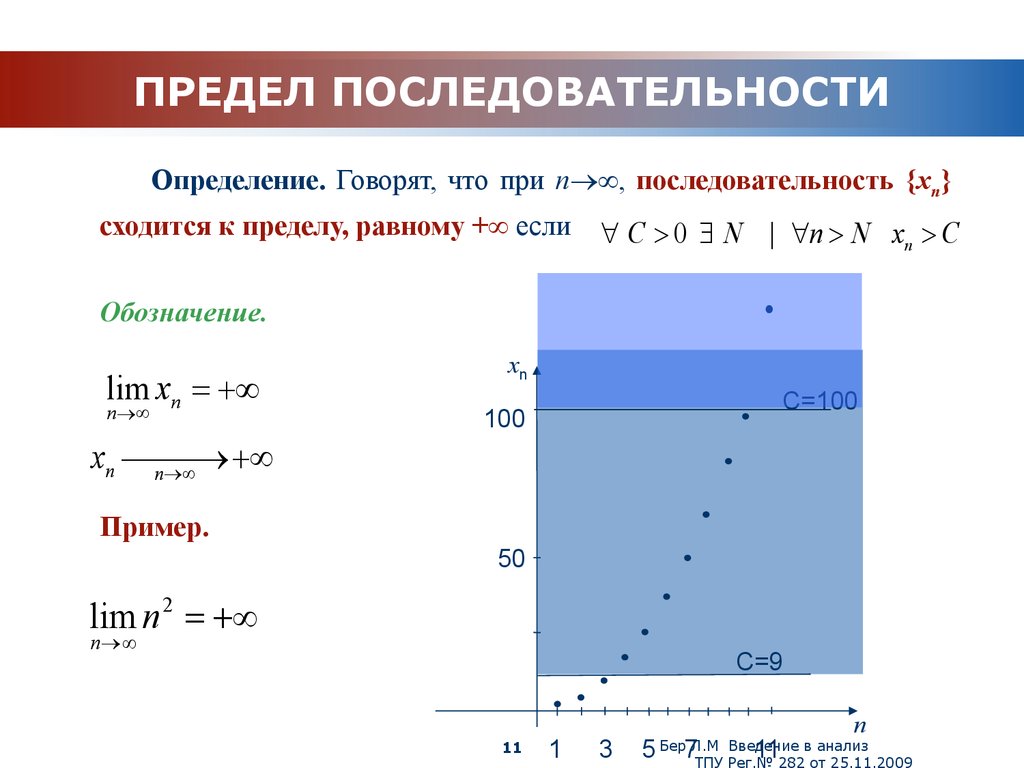
Определение (формальное) Позволять . Мы говорим, что это предел последовательности действительных чисел если если является пределом последовательности , мы говорим, что последовательность является сходящейся последовательностью и что она сходится к . Укажем тот факт, что является пределом по
Для тех, кто не знаком с универсальными кванторами
(любой) и
(существует), обозначение
читает
следующим образом: «Для любого сколь угодно малого числа
,
существует натуральное число
такое, что расстояние между
а также
меньше чем
на все условия
с
“,
который также можно переформулировать как «Для любого сколь угодно малого числа
,
можно найти подпоследовательность
такое, что расстояние между любым членом подпоследовательности и
меньше чем
”
или как «Отбрасывая достаточно большое количество начальных членов
,
вы можете сделать остальные условия как можно ближе к
как хочешь”.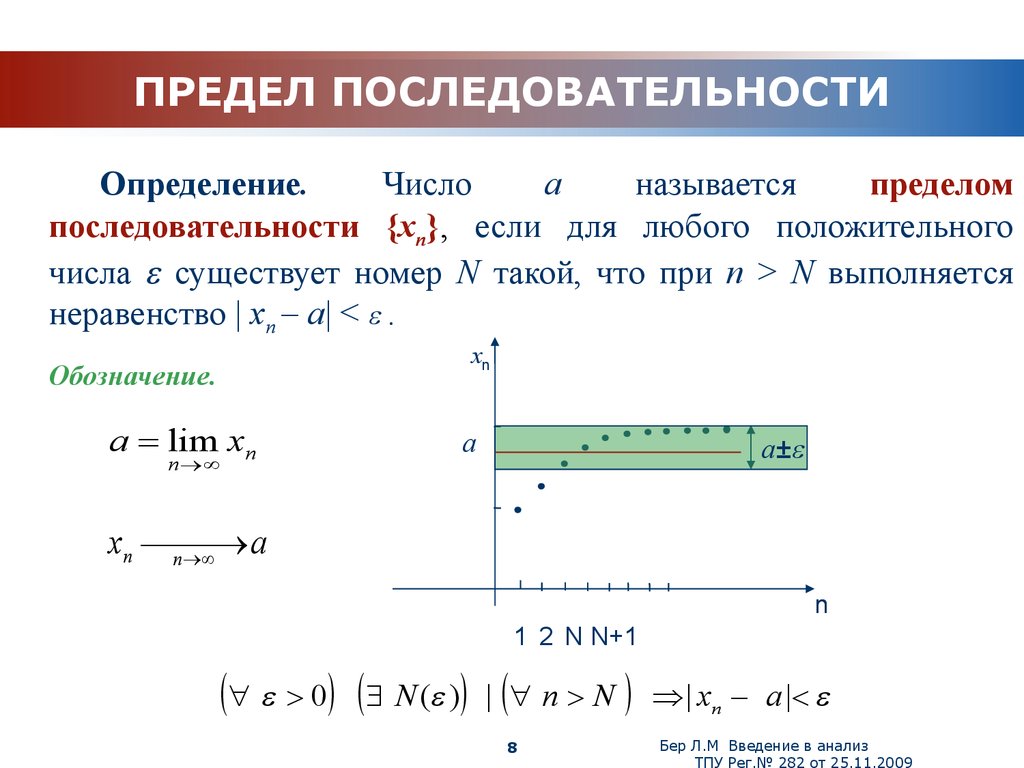
Также можно доказать, что сходящаяся последовательность имеет единственный предел, т. е. если имеет предел , тогда является уникальным пределом .
Пример
Определить последовательность
характеризуя его
-й
элемент
в качестве
следует:
элементы последовательности
,
,
,
и так далее. Выше
есть, чем меньше
есть и чем ближе
.
Поэтому интуитивно предел последовательности должен быть
:Это
просто доказать, что
действительно является пределом
с помощью приведенного выше определения. Выберите любой
.
Нам нужно найти
такое, что все члены подпоследовательности
иметь расстояние от нуля меньше, чем
:Примечание
во-первых, что расстояние между общим членом последовательности
а также
это здесь
последнее равенство получается из того, что все члены последовательности равны
положительные (следовательно, они равны своим абсолютным значениям). Поэтому нам нужно
найти
такое, что все члены подпоследовательности
удовлетворять
кондиционис
удовлетворен, если
,
что эквивалентно
.
Поэтому достаточно выбрать любой
такой, что
удовлетворить
состояниеВ
Подводя итог, мы только что показали, что для любого
,
мы можем найти
такое, что все члены подпоследовательности
иметь расстояние от нуля меньше, чем
.
Как следствие
является пределом последовательности
.
Поэтому нам нужно
найти
такое, что все члены подпоследовательности
удовлетворять
кондиционис
удовлетворен, если
,
что эквивалентно
.
Поэтому достаточно выбрать любой
такой, что
удовлетворить
состояниеВ
Подводя итог, мы только что показали, что для любого
,
мы можем найти
такое, что все члены подпоследовательности
иметь расстояние от нуля меньше, чем
.
Как следствие
является пределом последовательности
.
Ограничение последовательности вообще
Теперь рассмотрим более общий случай, когда члены последовательности не обязательно действительные числа. Как и прежде, мы сначала даем неформальную определение, а затем более формальное.
Неформальное определение предела – общий случай
Позволять
быть набором объектов (например, действительных чисел,
события, случайные
переменные) и пусть
быть последовательностью элементов
. Предел
определяется следующим образом.
Предел
определяется следующим образом.
Определение (неофициальное) Позволять . Мы говорим, что является пределом последовательности элементов , если при правильном выборе , расстояние между и любой член подпоследовательности можно сделать сколь угодно близким к нулю. Если является пределом последовательности , мы говорим, что последовательность это сходящаяся последовательность и что она сходится к . Укажем тот факт, что является пределом по
Определение то же, что мы дали выше, за исключением того факта, что теперь оба и условия последовательности относятся к общему набору объектов .
Метрики и определение расстояния
В приведенном выше определении мы неявно предполагали, что понятие
расстояние между элементами
хорошо определен. Таким образом, чтобы приведенное выше определение имело какой-либо смысл, нам необходимо
правильно определить расстояние.
Таким образом, чтобы приведенное выше определение имело какой-либо смысл, нам необходимо
правильно определить расстояние.
Нам нужна функция который ассоциируется с любой парой элементов действительное число, измеряющее расстояние между этими двумя элементами. Например, если а также являются двумя элементами , должно быть действительным числом, измеряющим расстояние между а также .
Функция считается допустимой функцией расстояния (и она называется метрикой на ) если оно удовлетворяет некоторым свойствам, перечисленным в следующем предложении.
Определение Позволять быть набором объектов. Позволять . считается действительной функцией расстояния (в этом случае она называется метрическая на ) если для любого , а также принадлежащий :
неотрицательность: ;
тождество неразличимых: если и только если ;
симметрия: ;
неравенство треугольника: .

Все четыре свойства очень интуитивно понятны: свойство 1) говорит, что расстояние между двумя точками не может быть отрицательного числа; свойство 2) говорит о том, что расстояние между двумя точками равно нулю тогда и только тогда, когда эти две точки совпадают; свойство 3) говорит о том, что расстояние от к такое же, как расстояние от к ; свойство 4) говорит (грубо говоря), что расстояние, которое вы преодолеваете, когда идете из к прямо меньше (или равно) расстоянию, которое вы преодолеваете, когда идете от к переход из третьей точки (если не на пути от к вы увеличиваете пройденное расстояние).
Пример (евклидово
расстояние)
Рассмотрим множество
-размерный
реальные векторы
.
Метрика, обычно используемая для измерения расстояния между элементами
так называемое евклидово расстояние. Если
а также
два вектора, принадлежащие
,
то их евклидово расстояние
это здесь
являются
компоненты
а также
являются
компоненты
.
Можно доказать, что евклидово расстояние удовлетворяет всем четырем
свойства, которым должна удовлетворять метрика. Кроме того, когда
,
Это
становится каким
совпадает с уже данным определением расстояния между действительными числами
выше.
Если
а также
два вектора, принадлежащие
,
то их евклидово расстояние
это здесь
являются
компоненты
а также
являются
компоненты
.
Можно доказать, что евклидово расстояние удовлетворяет всем четырем
свойства, которым должна удовлетворять метрика. Кроме того, когда
,
Это
становится каким
совпадает с уже данным определением расстояния между действительными числами
выше.
Всякий раз, когда мы сталкиваемся с последовательностью объектов и хотим оценить,
сходится, нам нужно сначала определить функцию расстояния на множестве
объекты, которым принадлежат члены последовательности, и убедиться, что предложенные
функция расстояния удовлетворяет всем свойствам правильной функции расстояния
(метрика). Например, в теории вероятностей и статистике мы часто имеем дело
с последовательностями случайных величин. Чтобы оценить, являются ли эти последовательности
сходящимся, нам нужно определить метрику для измерения расстояния между двумя
случайные переменные. Как мы увидим в лекции под названием
Последовательности случайных величин и их
конвергенции, существует несколько способов определения понятия расстояния
между двумя случайными величинами. Все эти способы законны и полезны в
разные ситуации.
Чтобы оценить, являются ли эти последовательности
сходящимся, нам нужно определить метрику для измерения расстояния между двумя
случайные переменные. Как мы увидим в лекции под названием
Последовательности случайных величин и их
конвергенции, существует несколько способов определения понятия расстояния
между двумя случайными величинами. Все эти способы законны и полезны в
разные ситуации.
Формальное определение предела — общий случай
Определив понятие метрики, мы теперь готовы сформулировать формальную определение предела последовательности.
Определение (формальное)
Позволять
быть набором объектов. Позволять
быть показателем
.
Мы говорим, что
является пределом последовательности объектов, принадлежащих
если если
является пределом последовательности
,
мы говорим, что последовательность
это сходящаяся последовательность и что она сходится к . Укажем тот факт, что
является пределом
по
Укажем тот факт, что
является пределом
по
Также и в этом случае можно доказать (см. ниже), что сходящаяся последовательность имеет единственный предел, т. е. если имеет предел , тогда является уникальным пределом .
Доказательство
Доказательство от противного. Предположим, что
а также
два предела последовательности
а также
.
Объединяя свойства 1) и 2) метрики (см. выше), она должна быть
то есть,
куда
строго положительная константа. Выберите любой термин
последовательности. По свойству 4) метрики (неравенству треугольника) имеем
иметьучитывая
что
,
предыдущее неравенство
становитсяСейчас,
возьми любой
.
С
является пределом последовательности, мы можем найти
такой, что
,
что значит
что и поэтому,
нельзя сделать меньше, чем
и как следствие
не может быть пределом последовательности.
Критерий сходимости
На практике обычно трудно оценить сходимость последовательности используя приведенное выше определение. Вместо этого конвергенцию можно оценить с помощью следующий критерий.
Лемма (критерий конвергенция) Позволять быть набором объектов. Позволять быть показателем . Позволять быть последовательностью объектов, принадлежащих а также . сходится к если и только если
Доказательство
Это легко доказать, определив последовательность действительных чисел чей общий термин остров отметив, что определение сходимости к , который искан быть написанным как который является определением сходимости к .
Итак, на практике задача оценки сходимости общего последовательность объектов упрощается следующим образом:
найти метрику измерить расстояние между членами последовательности и лимит кандидатов ;
определить новую последовательность , куда ;
изучить сходимость последовательности , это простая проблема, потому что представляет собой последовательность действительных чисел.

Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). “Предел последовательности”, Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/mathematical-tools/limit-of-a-sequence.
9.1: Последовательности — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2562
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Найти формулу для общего члена последовательности.
- Вычислить предел последовательности, если она существует.

- Определить сходимость или расхождение заданной последовательности.
В этом разделе мы вводим последовательности и определяем, что означает сходимость или расхождение последовательности. Мы покажем, как находить пределы сходящихся последовательностей, часто используя свойства пределов для функций, обсуждавшихся ранее. Мы завершаем этот раздел теоремой о монотонной сходимости — инструментом, который мы можем использовать для доказательства сходимости определенных типов последовательностей.
Терминология последовательностей
Для работы с этой новой темой нам понадобятся некоторые новые термины и определения. Во-первых, бесконечная последовательность — это упорядоченный список чисел вида 9∞_{n=1},\nonumber \]
или просто \(\{a_n\}\) для обозначения этой последовательности. Подобное обозначение используется для наборов, но последовательность — это упорядоченный список, тогда как набор не является упорядоченным. Поскольку для каждого положительного целого числа \(n\) существует определенное число \(a_n\), мы также можем определить последовательность как функцию, областью определения которой является множество положительных целых чисел.
Рассмотрим бесконечный упорядоченный список. a_1=2, a_2=4,\) и \(a_3=8.\) Возможно, вы видите, что термины в этой последовательности имеют следующий шаблон: 9{\text{th}}\) термин \(a_n\) через предыдущий термин \(a_{n−1}\). В частности, мы можем определить эту последовательность как последовательность \(\{a_n\}\), где \(a_1=2\) и для всех \(n≥2\) каждый член an определяется повторением отношение
\[a_n=2a_{n−1}. \nonumber \]
Определение: бесконечная последовательность
Бесконечная последовательность \(\{a_n\}\) представляет собой упорядоченный список чисел вида
\(a_1,\,a_2,\,…,\ ,a_n,\,….\)
Нижний индекс \(n\) называется переменная индекса последовательности. Каждое число \(a_n\) является членом последовательности. Иногда последовательности определяются явными формулами, в этом случае \(a_n=f(n)\) для некоторой функции \(f(n)\), определенной над положительными целыми числами. В других случаях последовательности определяются с помощью рекуррентного отношения . В рекуррентном отношении один член (или более) последовательности задается явно, а последующие члены определяются в терминах более ранних членов последовательности.
В других случаях последовательности определяются с помощью рекуррентного отношения . В рекуррентном отношении один член (или более) последовательности задается явно, а последующие члены определяются в терминах более ранних членов последовательности.
Обратите внимание, что индекс не обязательно должен начинаться с \(n=1\), но может начинаться с других целых чисел. Например, последовательность, заданная явной формулой \(a_n=f(n)\), может начинаться с \(n=0\), и в этом случае последовательность будет равна
\[a_0,\,a_1,\,a_2,….\nonumber \]
Аналогично, для последовательности, определяемой рекуррентным соотношением, термин \(a_0\) может быть задан явно, а термины \( a_n\) для \(n≥1\) может быть определено через \(a_{n−1}\). Поскольку последовательность \(\{a_n\}\) имеет ровно одно значение для каждого положительного целого числа \(n\), ее можно описать как функцию, областью определения которой является множество положительных целых чисел. В связи с этим имеет смысл обсудить граф последовательности. n}\). 9п\)}.
n}\). 9п\)}.
Часто встречаются два типа последовательностей, которым даются специальные названия: арифметические последовательности и геометрические последовательности. В арифметической последовательности разница между каждой парой последовательных членов одинакова. Например, рассмотрим последовательность
\[3,\,7,\,11,\,15,1\,9, \,\ldots\nonumber \]
Вы можете видеть, что разница между каждой последовательной парой условия равны \(4\). Предполагая, что этот шаблон продолжается, эта последовательность является арифметической последовательностью. Его можно описать с помощью рекуррентного соотношения
\[\begin{cases}a_1=3\\a_n=a_{n−1}+4, \text{ для }\ n≥2\end{case}.\nonumber \]
Обратите внимание, что
\[a_2=3+4\без числа \]
\[a_3=3+4+4=3+2⋅4\без числа \]
\[a_4=3+4+4+4=3+3⋅ 4.\nonumber \]
Таким образом, последовательность также может быть описана явной формулой любая последовательность вида \(a_n=cn+b.\)
В геометрической последовательности , отношение каждой пары последовательных членов одинаково. 3⋅2,\end{align*} \nonumber \] 9п}\).
3⋅2,\end{align*} \nonumber \] 9п}\).
Упражнение \(\PageIndex{2}\)
Найдите явную формулу для рекурсивно определенной последовательности, такой что \(a_1=−4\) и \(a_n=a_{n−1}+6\).
- Подсказка
Это арифметическая последовательность.
- Ответить
\(a_n=6n−10\)
Предел последовательности
Фундаментальный вопрос, возникающий в отношении бесконечных последовательностей, заключается в поведении членов при увеличении \(n\). Поскольку последовательность — это функция, определенная на целых положительных числах, имеет смысл обсудить предел терминов при \(n→∞\). Например, рассмотрим следующие четыре последовательности и их различное поведение как \(n→∞\) (рисунок \(\PageIndex{2}\)): 9n}{n}→0\) как \(n→∞.\) Рисунок \(\PageIndex{2}\): (a) Члены последовательности становятся сколь угодно большими при \(n→∞\). (b) Члены последовательности приближаются к \(1\) как \(n→∞\). (c) Члены последовательности чередуются между \(1\) и \(−1\) при \(n→∞\). (d) Члены последовательности чередуются с положительными и отрицательными значениями, но приближаются к \(0\) как \(n→∞\).
(b) Члены последовательности приближаются к \(1\) как \(n→∞\). (c) Члены последовательности чередуются между \(1\) и \(−1\) при \(n→∞\). (d) Члены последовательности чередуются с положительными и отрицательными значениями, но приближаются к \(0\) как \(n→∞\).
Из этих примеров мы видим несколько возможностей поведения членов последовательности при \(n→∞\). В двух последовательностях члены приближаются к конечному числу как \(n→∞.\). В двух других последовательностях члены не приближаются. Если члены последовательности приближаются к конечному числу \(L\) при \(n→∞\), мы говорим, что последовательность является сходящейся последовательностью, а действительное число L является пределом последовательности. Здесь мы можем дать неформальное определение.
Определение: сходящиеся и расходящиеся последовательности
Для данной последовательности \({a_n},\), если члены an становятся сколь угодно близкими к конечному числу \(L\), когда n становится достаточно большим, мы говорим \(\{a_n \}\) — это сходящаяся последовательность , а \(L\) — предел последовательности. n\right\}\) является сходящейся последовательностью и ее предел равен \(1\). Напротив, из рисунка видно, что члены последовательности \(1+3n\) не приближаются к конечному числу, когда \(n\) становится больше. Мы говорим, что \(\{1+3n\}\) — расходящаяся последовательность.
n\right\}\) является сходящейся последовательностью и ее предел равен \(1\). Напротив, из рисунка видно, что члены последовательности \(1+3n\) не приближаются к конечному числу, когда \(n\) становится больше. Мы говорим, что \(\{1+3n\}\) — расходящаяся последовательность.
В неформальном определении предела последовательности мы использовали термины «сколь угодно близкие» и «достаточно большие». Хотя эти фразы помогают проиллюстрировать значение сходящейся последовательности, они несколько расплывчаты. Чтобы быть более точным, мы теперь представляем более формальное определение предела для последовательности и показываем эти идеи графически на рисунке.
Определение: сходимость
Последовательность \(\{a_n\}\) сходится к действительному числу \(L\), если для всех \(ε>0\) существует целое число \(N\) такое, что для всех \(n ≥ N\) \(|a_n−L| < ε\). Число \(L\) является пределом последовательности, и мы пишем
\[\lim_{n→∞}a_n = L \text{ или } a_n→L. \nonumber \]
В этом случае мы говорим, что последовательность \(\{a_n\}\) является сходящейся последовательностью. Если последовательность не сходится, то это расходящаяся последовательность, и мы говорим, что предела не существует.
Если последовательность не сходится, то это расходящаяся последовательность, и мы говорим, что предела не существует.
Заметим, что сходимость или расходимость последовательности \(\{a_n\}\) зависит только от того, что происходит с членами \(a_n\) при \(n→∞\). Следовательно, если конечное число терминов \(b_1,b_2,…,b_N\) помещено перед \(a_1\) для создания новой последовательности
\[b_1,\,b_2,\,…,\,b_N,\,a_1,\,a_2,\,…,\nonumber \]
эта новая последовательность будет сходиться, если \(\{a_n\}\ ) сходится и расходится, если \(\{a_n\}\) расходится. Далее, если последовательность \(\{a_n\}\) сходится к \(L\), то эта новая последовательность также сходится к \(L\).
Рисунок \(\PageIndex{3}\): по мере увеличения \(n\) члены \(a_n\) становятся ближе к \(L\). Для значений \(n≥N\) расстояние между каждой точкой \((n,a_n)\) и линией \(y=L\) меньше, чем \(ε\). Как определено выше, если последовательность не сходится, она называется расходящейся последовательностью. n\right\}\) расходится, потому что члены чередуются между \(1\) и \(−1\), но не приближаются к одному значению, поскольку \(n→ ∞\). С другой стороны, последовательность \(\{1+3n\}\) расходится, потому что члены \(1+3n→∞\) при \(n→∞\). Мы говорим, что последовательность \(\{1+3n\}\) расходится к бесконечности, и пишем \(\displaystyle \lim_{n→∞}(1+3n)=∞\). Важно понимать, что это обозначение не означает, что предел последовательности \(\{1+3n\}\) существует. На самом деле последовательность расходится. Написание того, что предел равен бесконечности, предназначено только для предоставления дополнительной информации о том, почему последовательность расходится. Последовательность также может расходиться к отрицательной бесконечности. Например, последовательность \(\{−5n+2\}\) расходится к отрицательной бесконечности, потому что \(−5n+2→−∞\) при \(n→−∞\). Мы запишем это как \(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
n\right\}\) расходится, потому что члены чередуются между \(1\) и \(−1\), но не приближаются к одному значению, поскольку \(n→ ∞\). С другой стороны, последовательность \(\{1+3n\}\) расходится, потому что члены \(1+3n→∞\) при \(n→∞\). Мы говорим, что последовательность \(\{1+3n\}\) расходится к бесконечности, и пишем \(\displaystyle \lim_{n→∞}(1+3n)=∞\). Важно понимать, что это обозначение не означает, что предел последовательности \(\{1+3n\}\) существует. На самом деле последовательность расходится. Написание того, что предел равен бесконечности, предназначено только для предоставления дополнительной информации о том, почему последовательность расходится. Последовательность также может расходиться к отрицательной бесконечности. Например, последовательность \(\{−5n+2\}\) расходится к отрицательной бесконечности, потому что \(−5n+2→−∞\) при \(n→−∞\). Мы запишем это как \(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
Поскольку последовательность — это функция, областью определения которой является множество положительных целых чисел, мы можем использовать свойства пределов функций, чтобы определить, сходится ли последовательность.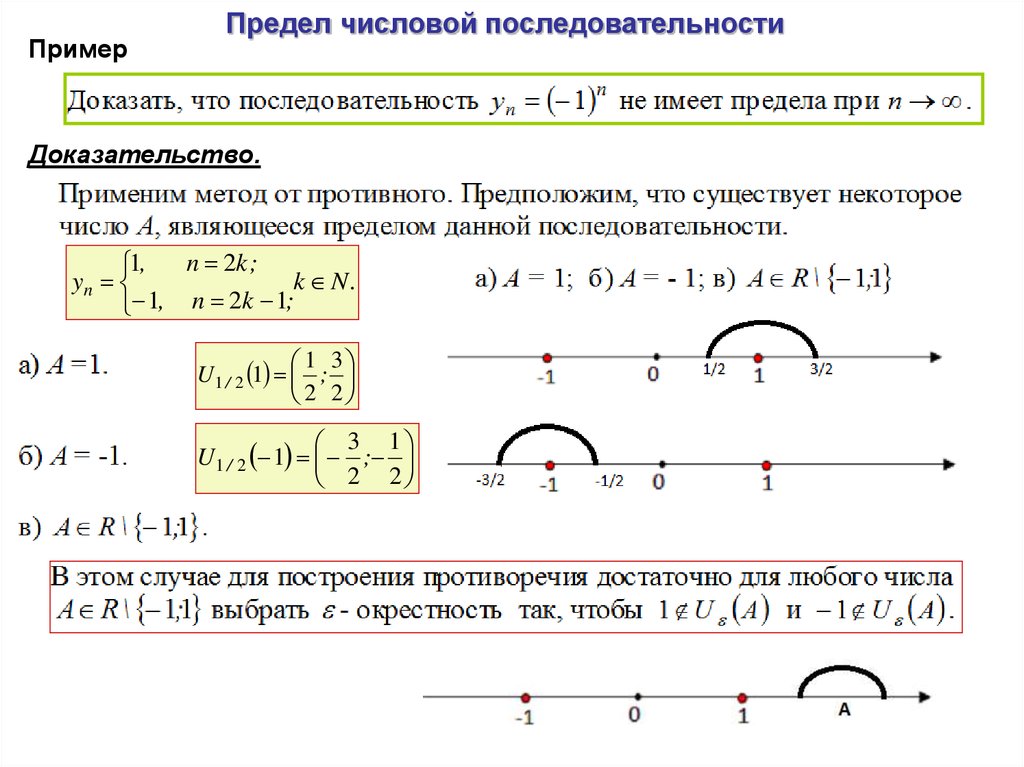 Например, рассмотрим последовательность \(\{a_n\}\) и связанную с ней функцию \(f\), определенную на всех положительных действительных числах, таких что \(f(n)=a_n\) для всех целых чисел \(n≥1 \). Поскольку область определения последовательности является подмножеством области определения \(f\), если \(\displaystyle \lim_{x→∞}f(x)\) существует, то последовательность сходится и имеет тот же предел. Например, рассмотрим последовательность \(\left\{\dfrac{1}{n}\right\}\) и связанную с ней функцию \(f(x)=\dfrac{1}{x}\). Поскольку функция \(f\), определенная на всех действительных числах \(x>0\), удовлетворяет условию \(f(x)=\dfrac{1}{x}→0\) при \(x→∞\), последовательность \(\left\{\dfrac{1}{n}\right\}\) должна удовлетворять \(\dfrac{1}{n}→0\) при \(n→∞.\) 9n\right\}\) сходится к \(0+0=0\). Точно так же, как мы смогли оценить предел, включающий алгебраическую комбинацию функций \(f\) и \(g\), взглянув на пределы \(f\) и \(g\) (см. Введение в пределы), мы можем оценить предел последовательности, члены которой являются алгебраическими комбинациями \(a_n\) и \(b_n\), оценивая пределы \(\{a_n\}\) и \(\{b_n\}\ ).
Например, рассмотрим последовательность \(\{a_n\}\) и связанную с ней функцию \(f\), определенную на всех положительных действительных числах, таких что \(f(n)=a_n\) для всех целых чисел \(n≥1 \). Поскольку область определения последовательности является подмножеством области определения \(f\), если \(\displaystyle \lim_{x→∞}f(x)\) существует, то последовательность сходится и имеет тот же предел. Например, рассмотрим последовательность \(\left\{\dfrac{1}{n}\right\}\) и связанную с ней функцию \(f(x)=\dfrac{1}{x}\). Поскольку функция \(f\), определенная на всех действительных числах \(x>0\), удовлетворяет условию \(f(x)=\dfrac{1}{x}→0\) при \(x→∞\), последовательность \(\left\{\dfrac{1}{n}\right\}\) должна удовлетворять \(\dfrac{1}{n}→0\) при \(n→∞.\) 9n\right\}\) сходится к \(0+0=0\). Точно так же, как мы смогли оценить предел, включающий алгебраическую комбинацию функций \(f\) и \(g\), взглянув на пределы \(f\) и \(g\) (см. Введение в пределы), мы можем оценить предел последовательности, члены которой являются алгебраическими комбинациями \(a_n\) и \(b_n\), оценивая пределы \(\{a_n\}\) и \(\{b_n\}\ ).
Законы алгебраического предела
Даны последовательности \(\{a_n\}\) и \(\{b_n\}\) и любое действительное число \(c\), если существуют константы \(A\) и \( B\) такие, что \(\displaystyle \lim_{n→∞}a_n=A\) и \(\displaystyle \lim_{n→∞}b_n=B\), то
- \(\displaystyle \lim_{n→∞}c=c\)
- \(\displaystyle \lim_{n→∞}ca_n=c\lim_{n→∞}a_n=cA\)
- \(\displaystyle \lim_{n→∞}(a_n±b_n)=\lim_{n→∞}a_n±\lim_{n→∞}b_n=A±B\)
- \(\displaystyle \lim_{n→∞}(a_n⋅b_n)=\big(\lim_{n→∞}a_n\big)⋅\big(\lim_{n→∞}b_n\big)=A⋅ Б\)
- \(\displaystyle \lim_{n→∞}\left(\dfrac{a_n}{b_n}\right)=\dfrac{\lim_{n→∞}a_n}{\lim_{n→∞}b_n}= \dfrac{A}{B}\), если \(B≠0\) и каждый \(b_n≠0.\)
Доказательство
Докажем часть III.
Пусть \(ϵ>0\). Поскольку \(\displaystyle \lim_{n→∞}a_n=A\), существует постоянное натуральное число \(N_1\), такое что для всех \(n≥N_1\). Поскольку \(\displaystyle \lim_{n→∞}b_n=B\), существует константа \(N_2\) такая, что \(|b_n−B|<ε/2\) для всех \(n≥N_2\ ). 2}}\). Как показано ранее, \(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Точно так же для любого положительного целого числа \(k\) мы можем заключить, что 9x\right]=\lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)\).
2}}\). Как показано ранее, \(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Точно так же для любого положительного целого числа \(k\) мы можем заключить, что 9x\right]=\lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)\).
Поскольку правая часть этого уравнения имеет неопределенный вид \(∞⋅0\), перепишем ее в виде дроби, чтобы применить правило Лопиталя. Напишите
\(\displaystyle \lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)=\lim_{x→∞}\dfrac{\ln\left(1 +4/х\вправо)}{1/х}\).
Поскольку правая часть теперь представлена в неопределенной форме 0/0, мы можем применить правило Лопиталя. Мы заключаем, что
\(\displaystyle \lim_{x→∞}\dfrac{\ln(1+4/x)}{1/x}=\lim_{x→∞}\dfrac{4}{1+ 4/х}=4.\) 9n\right\}.\) Определить, сходится ли последовательность. Если оно сходится, найти его предел.
- Подсказка
Используйте правило Лопиталя.
- Ответить
Последовательность сходится, и ее предел равен \(0\)
Напомним, что если \(f\) является непрерывной функцией при значении \(L\), то \(f(x)→f(L)\) при \(x→L\). 2}→5\). Поскольку \(\sqrt{x}\) является непрерывной функцией в точке \(x=5\), 92})}=\sqrt{5}.\nonumber \]
2}→5\). Поскольку \(\sqrt{x}\) является непрерывной функцией в точке \(x=5\), 92})}=\sqrt{5}.\nonumber \]
Непрерывные функции, определенные на сходящихся последовательностях
Рассмотрим последовательность \(\{a_n\}\) и предположим, что существует действительное число \(L\), такое что последовательность \(\{a_n\}\) сходится к \(L\). Предположим, что \(f\) — непрерывная функция в \(L\). Тогда существует целое число \(N\) такое, что \(f\) определено при всех значениях an для \(n≥N\), и последовательность \(\{f(a_n)\}\) сходится к \ (f(L)\) (Рисунок \(\PageIndex{4}\)).
Рисунок \(\PageIndex{4}\): Поскольку \(f\) является непрерывной функцией, поскольку входные данные \(a_1,\,a_2,\,a_3,\,…\) приближаются к \(L\), выходы \(f(a_1),\,f(a_2),\,f(a_3),\,…\) приближаются к \(f(L)\).Доказательство
Пусть \(ϵ>0.\) Поскольку \(f\) непрерывна в \(L\), существует \(δ>0\) такое, что \(|f(x)−f(L )|<ε\), если \(|x−L|<δ\). Поскольку последовательность \(\{a_n\}\) сходится к \(L\), существует \(N\) такое, что \(|a_n−L|<δ\) для всех \(n≥N\). Следовательно, для всех \(n≥N\) \(|a_n−L|<δ\), откуда следует \(|f(a_n)−f(L)|<ε\). Мы заключаем, что последовательность \(\{f(a_n)\}\) сходится к \(f(L)\).
Следовательно, для всех \(n≥N\) \(|a_n−L|<δ\), откуда следует \(|f(a_n)−f(L)|<ε\). Мы заключаем, что последовательность \(\{f(a_n)\}\) сходится к \(f(L)\).
□
Пример \(\PageIndex{4}\): ограничения, включающие непрерывные функции, определенные на сходящихся последовательностях 92}\right)=\cos 0=1.\)
Упражнение \(\PageIndex{4}\)
Определите, является ли последовательность \(\left\{\sqrt{\dfrac{2n+1}{3n +5}}\right\}\) сходится. Если оно сходится, найти его предел.
- Подсказка
Рассмотрим последовательность \(\left\{\dfrac{2n+1}{3n+5}\right\}.\)
- Ответить
Последовательность сходится, и ее предел равен \(\sqrt{2/3}\).
Другая теорема, касающаяся пределов последовательностей, является расширением теоремы о сжатии для пределов, обсуждавшейся во введении к пределам.
Теорема сжатия для последовательностей
Рассмотрим последовательности \(\{a_n\}, \, \{b_n\},\) и \(\{c_n\}\). Предположим, что существует целое число \(N\), такое что
Предположим, что существует целое число \(N\), такое что
\(a_n≤b_n≤c_n\) для всех \(n≥N.\)
Если существует действительное число \(L\), такое что
\[\lim_{n→∞}a_n=L=\lim_{n→∞}c_n, \nonumber \]
, тогда \(\{b_n\}\) сходится и \(\displaystyle \lim_{n→∞ }b_n=L\) (Рисунок \(\PageIndex{5}\)).
Рисунок \(\PageIndex{5}\): каждый терм bn удовлетворяет условию \(a_n≤b_n≤c_n\), а последовательности \(\{a_n\}\) и \(\{c_n\}\) сходятся к тот же предел, поэтому последовательность \(\{b_n\}\) также должна сходиться к тому же пределу.Доказательство
Пусть \(ε>0.\) Поскольку последовательность \(\{a_n\}\) сходится к \(L\), существует целое число \(N_1\), такое что \(|a_n−L |<ε\) для всех \(n≥N_1\). Точно так же, поскольку \(\{c_n\}\) сходится к \(L\), существует целое число \(N_2\) такое, что \(|c_n−L|<ε\) для всех \(n≥N_2\ ). По условию существует целое число \(N\) такое, что \(a_n≤b_n≤c_n\) для всех \(n≥N\). Пусть \(M\) будет наибольшим из \(N_1,\, N_2\) и \(N\). Мы должны показать, что \(|b_n−L|<ε\) для всех \(n≥M\). Для всех \(n≥M\), 9n\right\} \text{ расходится, если } r≤−1\)
Мы должны показать, что \(|b_n−L|<ε\) для всех \(n≥M\). Для всех \(n≥M\), 9n\right\} \text{ расходится, если } r≤−1\)
Ограниченные последовательности
Обратимся теперь к одной из наиболее важных теорем, касающихся последовательностей: теореме о монотонной сходимости. Прежде чем сформулировать теорему, нам необходимо ввести некоторую терминологию и мотивацию. Начнем с определения того, что означает ограниченность последовательности.
Определение: связанные последовательности
Последовательность \(\{a_n\}\) ограничена выше , если существует действительное число \(M\) такое, что
\(a_n≤M\)
для всех положительных целых чисел \(n\).
Последовательность \(\{a_n\}\) ограничена ниже , если существует действительное число \(m\) такое, что
\(m≤a_n\)
для всех натуральных чисел \(n\ ).
Последовательность \(\{a_n\}\) является ограниченной последовательностью , если она ограничена сверху и снизу. n\right\}\) — неограниченная последовательность.
n\right\}\) — неограниченная последовательность.
Теперь обсудим связь между ограниченностью и сходимостью. Предположим, что последовательность \(\{a_n\}\) неограничена. Тогда оно не ограничено сверху, или не ограничено снизу, или и то, и другое. В любом случае существуют члены an, величина которых сколь угодно велика по мере того, как \(n\) становится больше. В результате последовательность \(\{a_n\}\) не может сходиться. Следовательно, ограниченность является необходимым условием сходимости последовательности.
Сходящиеся последовательности ограничены
Если последовательность \(\{a_n\}\) сходится, то она ограничена. 9n\right\}\) ограничено, но последовательность расходится, потому что последовательность колеблется между \(1\) и \(−1\) и никогда не приближается к конечному числу. Обсудим теперь достаточное (но не необходимое) условие сходимости ограниченной последовательности.
Рассмотрим ограниченную последовательность \(\{a_n\}\). Предположим, что последовательность \(\{a_n\}\) возрастает. То есть \(a_1≤a_2≤a_3….\) Поскольку последовательность возрастает, члены не колеблются. Следовательно, есть две возможности. Последовательность может расходиться до бесконечности, а может и сходиться. Однако, поскольку последовательность ограничена, она ограничена сверху, и последовательность не может расходиться до бесконечности. Мы заключаем, что \(\{a_n\}\) сходится. Например, рассмотрим последовательность
То есть \(a_1≤a_2≤a_3….\) Поскольку последовательность возрастает, члены не колеблются. Следовательно, есть две возможности. Последовательность может расходиться до бесконечности, а может и сходиться. Однако, поскольку последовательность ограничена, она ограничена сверху, и последовательность не может расходиться до бесконечности. Мы заключаем, что \(\{a_n\}\) сходится. Например, рассмотрим последовательность
\[\left\{\dfrac{1}{2},\,\dfrac{2}{3},\,\dfrac{3}{4},\,\dfrac{4}{5}, \,…\Правильно\}. \nonumber \]
Поскольку эта последовательность возрастает и ограничена сверху, она сходится. Далее рассмотрим последовательность
\[\left\{2,\,0,\,3,\,0,\,4,\,0,\,1,\,−\dfrac{1}{2} ,\,−\dfrac{1}{3},\,−\dfrac{1}{4},\,…\right\}. \nonumber \]
Несмотря на то, что последовательность не возрастает для всех значений \(n\), мы видим, что \(−1/2<−1/3<−1/4<⋯\). Следовательно, начиная с восьмого члена, \(a_8=−1/2\), последовательность возрастает. В этом случае мы говорим, что последовательность в конечном счете возрастает. Поскольку последовательность ограничена сверху, она сходится. Также верно, что если последовательность убывает (или в конце концов убывает) и ограничена снизу, она также сходится.
Поскольку последовательность ограничена сверху, она сходится. Также верно, что если последовательность убывает (или в конце концов убывает) и ограничена снизу, она также сходится.
Определение
Последовательность \(\{a_n\}\) возрастает для всех \(n≥n_0\), если
\(a_n≤a_{n+1}\) для всех \(n≥n_0\) ).
Последовательность \(\{a_n\}\) убывает для всех \(n≥n_0\), если
\(a_n ≥ a_{n+1}\) для всех \(n≥n_0\).
Последовательность \(\{a_n\}\) является монотонной последовательностью для всех \(n≥n_0\), если она возрастает для всех \(n≥n_0\) или убывает для всех \ (n≥n_0\).
Теперь у нас есть необходимые определения, чтобы сформулировать теорему о монотонной сходимости, которая дает достаточное условие сходимости последовательности.
Определение: теорема о монотонной сходимости
Если \(\{a_n\}\) — ограниченная последовательность и существует натуральное число \(n_0\), такое что \(\{a_n\}\) монотонно для всех \ (n≥n_0\), то \(\{a_n\}\) сходится.
Доказательство этой теоремы выходит за рамки этого текста. Вместо этого мы приводим график, чтобы наглядно показать, почему эта теорема имеет смысл (рис. \(\PageIndex{6}\)).
Рисунок \(\PageIndex{6}\): Поскольку последовательность \(\{a_n\}\) возрастает и ограничена сверху, она должна сходиться. 9n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n\), если \(n≥3.\)Следовательно, последовательность убывает для всех \(n≥3\). Кроме того, последовательность ограничена снизу \(0\), потому что \(4n/n!≥0\) для всех натуральных чисел \(n\). Следовательно, по теореме о монотонной сходимости последовательность сходится.
Чтобы найти предел, мы используем тот факт, что последовательность сходится, и пусть \(\displaystyle L=\lim_{n→∞}a_n\). Теперь обратите внимание на это важное наблюдение. Рассмотрим \(\displaystyle \lim_{n→∞}a_{n+1}\). С
\(\{a_{n+1}\}=\{a_2,\,a_3,\,a_4,\,…\},\)
единственная разница между последовательностями \(\{a_{n+ 1}\}\) и \(\{a_n\}\) состоит в том, что \(\{a_{n+1}\}\) пропускает первый член. 2_n+1}{2a_n}\). 92_н\).
2_n+1}{2a_n}\). 92_н\).
Разделив обе части на \(2a_n\), получим
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n.\)
Используя определение \(a_{ n+1}\), заключаем, что
\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n\).
Поскольку \(\{a_n\}\) ограничено снизу и убывает, по теореме о монотонной сходимости оно сходится.
Чтобы найти предел, пусть \(\displaystyle L=\lim_{n→∞}a_n\). Затем, используя рекуррентное соотношение и тот факт, что \(\displaystyle \lim_{n→∞}a_n=\lim_{n→∞}a_{n+1}\), мы имеем 92=1\), откуда следует \(L=±1\). Поскольку все члены положительны, предел \(L=1\).
Упражнение \(\PageIndex{6}\)
Рассмотрим последовательность \(\{a_n\}\), определенную рекурсивно так, что \(a_1=1\), \(a_n=a_{n−1}/2 \). Используйте теорему о монотонной сходимости, чтобы показать, что эта последовательность сходится, и найти ее предел.
- Подсказка
Показать, что последовательность убывает и ограничена снизу.

- Ответить
\(0\).
Определение: Числа Фибоначчи
Числа Фибоначчи определяются рекурсивно последовательностью \(\left\{F_n\right\}\), где \(F_0=0, \, F_1=1\) и для \( n≥2,\)
\(F_n=F_{n−1}+F_{n−2}.\)
Здесь мы рассмотрим свойства чисел Фибоначчи.
1. Запишите первые двадцать чисел Фибоначчи.
2. Найдите замкнутую формулу для последовательности Фибоначчи, выполнив следующие действия. 9н\). Используя начальные условия \(F_0\) и \(F_1\), определите значения констант \(c_1\) и \(c_2\) и напишите замкнутую формулу \(F_n\).
3. Используйте ответ в 2 c. чтобы показать, что
\[\lim_{n→∞}\dfrac{F_{n+1}}{F_n}=\dfrac{1+\sqrt{5}}{2}.\nonumber \]
число \(ϕ=(1+\sqrt{5})/2\) известно как золотое сечение (рисунок и рисунок).
Рисунок \(\PageIndex{7}\): Семена подсолнуха имеют спиральные узоры, изгибающиеся влево и вправо. Количество спиралей в каждом направлении всегда является числом Фибоначчи — всегда. (кредит: модификация работы Эссдраса Кальдерана, Wikimedia Commons) Рисунок \(\PageIndex{8}\): пропорция золотого сечения встречается во многих известных образцах искусства и архитектуры Древнегреческий храм, известный как Парфенон, был спроектирован с учетом этих пропорций, и это соотношение снова проявляется во многих мелких деталях. (кредит: модификация работы TravelingOtter, Flickr).
Количество спиралей в каждом направлении всегда является числом Фибоначчи — всегда. (кредит: модификация работы Эссдраса Кальдерана, Wikimedia Commons) Рисунок \(\PageIndex{8}\): пропорция золотого сечения встречается во многих известных образцах искусства и архитектуры Древнегреческий храм, известный как Парфенон, был спроектирован с учетом этих пропорций, и это соотношение снова проявляется во многих мелких деталях. (кредит: модификация работы TravelingOtter, Flickr).Ключевые понятия
- Чтобы определить сходимость последовательности, заданной явной формулой \(a_n=f(n)\), мы используем свойства пределов для функций.
- Если \(\{a_n\}\) и \(\{b_n\}\) — сходящиеся последовательности, сходящиеся к \(A\) и \(B,\) соответственно, а \(c\) — любое вещественное число, то последовательность \(\{ca_n\} \) сходится к \(c\cdot A,\) последовательности \(\{a_n±b_n\}\) сходятся к \(A±B,\) последовательность \(\{a_n\cdot b_n\}\) сходится к \(A⋅B,\), а последовательность \(\{a_n/b_n\}\) сходится к \(A/B,\) при условии \(B ≠0.
 \) 9n\right\}\) сходится тогда и только тогда, когда \(|r|<1\) или \(r=1\).
\) 9n\right\}\) сходится тогда и только тогда, когда \(|r|<1\) или \(r=1\).
Глоссарий
- арифметическая последовательность
- последовательность, в которой разница между каждой парой последовательных членов одинакова, называется арифметической последовательностью
- ограниченный выше
- последовательность \(\{a_n\}\) ограничена сверху, если существует константа \(M\) такая, что \(a_n≤M\) для всех натуральных чисел \(n\)
- ограничено ниже
- последовательность \(\{a_n\}\) ограничена снизу, если существует константа \(M\) такая, что \(M≤a_n\) для всех натуральных чисел \(n\)
- ограниченная последовательность
- последовательность \(\{a_n\}\) является ограниченной, если существует константа \(M\) такая, что \(|a_n|≤M\) для всех натуральных чисел \(n\)
- сходящаяся последовательность
- сходящаяся последовательность — это последовательность \(\{a_n\}\), для которой существует действительное число \(L\) такое, что \(a_n\) сколь угодно близко к \(L\) до тех пор, пока \(n \) достаточно велик
- расходящаяся последовательность
- последовательность, которая не сходится, расходится
- явная формула
- последовательность может быть определена явной формулой так, что \(a_n=f(n)\)
- геометрическая последовательность
- последовательность \(\{a_n\}\), в которой отношение \(a_{n+1}/a_n\) одинаково для всех натуральных чисел \(n\), называется геометрической последовательностью
- индексная переменная
- нижний индекс, используемый для определения терминов в последовательности, называется индексом
- предел последовательности
- действительное число \(L\), к которому сходится последовательность, называется пределом последовательности
- монотонная последовательность
- возрастающая или убывающая последовательность
- рекуррентное соотношение
- рекуррентное отношение — это отношение, в котором термин \(a_n\) в последовательности определяется в терминах более ранних терминов в последовательности 9{\text{th}}\) член последовательности
- неограниченная последовательность
- неограниченная последовательность называется неограниченной
Эта страница под названием 9.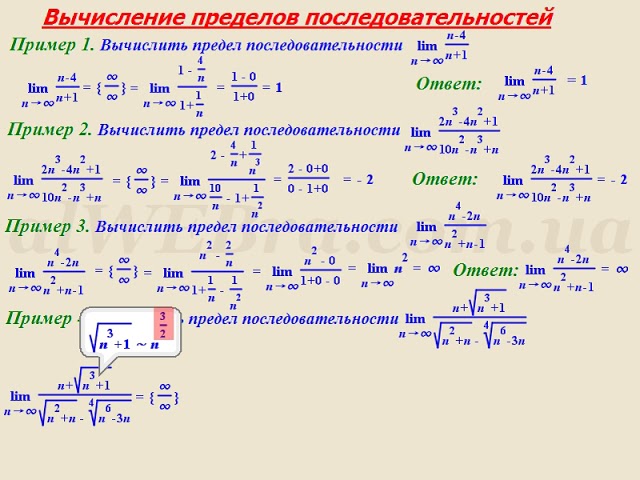

 0000001
25 0.0000000
26 0.0000000
27 0.0000000
28 0.0000000
29 0.0000000
0000001
25 0.0000000
26 0.0000000
27 0.0000000
28 0.0000000
29 0.0000000

 Последовательность имеет предел \( L \) по мере того, как \( n \) приближается к \( \infty \), если задано \( \epsilon > 0 \) , существует число \( M > 0 \) такое, что \( n > M \) подразумевает \( \left| s_n – L \right| < \epsilon \). Мы пишем, что
Последовательность имеет предел \( L \) по мере того, как \( n \) приближается к \( \infty \), если задано \( \epsilon > 0 \) , существует число \( M > 0 \) такое, что \( n > M \) подразумевает \( \left| s_n – L \right| < \epsilon \). Мы пишем, что \]
\] \]
\] Общий случай
Общий случай



 \) 9n\right\}\) сходится тогда и только тогда, когда \(|r|<1\) или \(r=1\).
\) 9n\right\}\) сходится тогда и только тогда, когда \(|r|<1\) или \(r=1\).