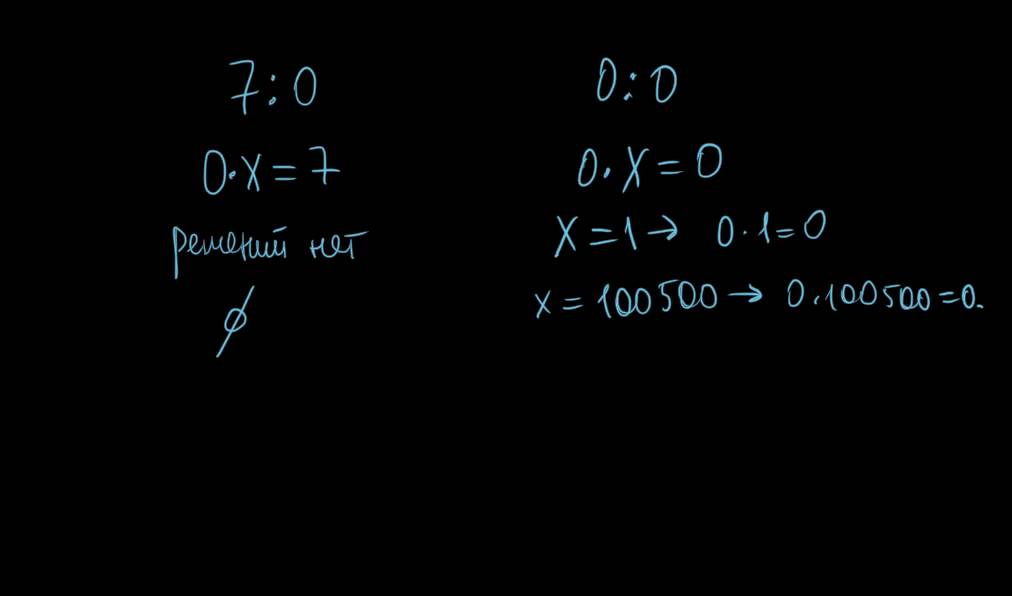ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23.  Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратовУпражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс Упражнения к главе XII |
Преобразователь давления ПДТВХ-1-02; с верхним пределом 40,0 МПа; выходной сигнал 4-20 мА; погрешность 1,0 % — X-Counter
Описание
Как правильно подобрать и купить преобразователь давления?
Работа любой автоматизированной системы контроля и управления, а также систем автоматического учета энергоресурсов основывается на полученной информации об измеряемых параметрах — температуре, давлении и других необходимых сведениях.
Информацию получают с помощью специальных датчиков, преобразующие полученные данные в сигналы, которые могут обрабатываться и учитываться устройствами сбора и передачи данных, входящими в систему. Для съема показаний о состоянии давления в системе и преобразования их в аналоговый сигнал применяются специальные датчики преобразователи давления. Устройства подходят для измерения давления в различных жидкостях и газообразных средах.
К основным сферам, где используются датчики ПДТВХ, относятся:
- системы учета водо- и теплоснабжения;
- оборудование систем автоматического учета;
- управляющие системы.
Датчик-преобразователь давления «Пульсар»
Датчики «Пульсар», используемые в системах тепло- и водоснабжения, автоматизированных системах учета, разработаны и производятся компанией НПП «Тепловодохран». Датчик преобразователь давления — измерительный прибор, позволяющий не только контролировать уровень давления, но и преобразовывать получаемые данные в сигнал, который затем передается в другие устройства системы для дальнейшей обработки.
Конструктивное исполнение датчика ПДТВХ представляет собой металлический цилиндр, оснащенный специальным присоединительным разъемом. В зависимости от сферы применения, выпускаются различные модификации датчиков с несколькими присоединительными размерами и различными пределами измерений.
Преимущества датчиков ПДТВХ «Пульсар»:
- неограниченная гарантия производителя, говорящая о высокой надежности и качестве преобразователей избыточного давления;
- обязательная техническая проверка прибора один раз в 4 года;
- высокая степень защиты датчиков, в том числе от гидроударов, пыли, влаги, механических повреждений.
- минимальная погрешность проводимых измерений.
| Измеряемая среда | газ, жидкость, пар |
| Верхние пределы измерений, МПа | 0,1; 0,25; 0,4; 0,6; 1,0; 1,6; 2,5; 4,0; 6,0; 10,0; 16,0; 25,0; 40,0; 60,0 |
| Пределы допускаемой основной погрешности, % | 0,25; 0,5 |
| Диапазон температур измеряемой среды, 0С | от минус 45 до плюс 125 (при превышении этой температуры следует использовать радиатор) |
| Диапазон изменения выходного сигнала | |
| постоянного тока, мА | 4. .20 |
| постоянного напряжения, В | 0..5; 0..10 |
| Электрическое питание преобразователей, В постоянного тока | 9…36 |
| Температура окружающей среды, 0С | от минус 40 до плюс 80 |
| Степень защиты | IP65, IP68 |
| Масса, г, не более | 200 |
| Габаритные размеры датчика давления | |
| диаметр, мм, не более, | 38 |
| длина, мм, не более | 150 |
| Подсоединение проводов | разъем по DIN 43650C, разъем PC4, специальный разъем для крепления металлорукава |
| Межповерочный интервал преобразователя давления | 4 года |
| Маркировка по взрывозащите | 0ExiallCT5 |
| Присоединение к системе | М20х1,5 |
Ноль над нулем | Superprof
Ноль над нулем
Давайте посмотрим, как выглядит ноль над нулем :
Эта форма известна как неопределенная, потому что она неизвестна.
На самом деле любое число, деленное на ноль, равно неизвестному. Взгляните на несколько примеров.
Когда мы столкнемся с такой ситуацией? Скажем, вы хотите найти предел следующей функции, когда он приближается к нулю: 0003 Когда мы подставляем ноль в эту функцию, мы видим, что она принимает неопределенный вид нуля над нулем. Чтобы решить эту проблему, давайте рассмотрим пример . Лучшие репетиторы по математике Поехали Возьмем следующее уравнение . Возьмем предел следующей функции по мере приближения к 2. Чтобы взять предел, мы сначала замените все значения x на наше значение a 2. Результат дает нам ноль над нулем . Как мы обсуждали в предыдущем разделе, ноль над нулем — это undefined. Когда мы берем предел, приближаясь к 2 справа и слева, мы видим, что происходит. We start to approach a limit, -0.5, as x approaches 2. However what’s another как мы можем сделать это, не подключая к во множестве различных значений x? Чтобы решить эту проблему, мы должны рассмотреть, что такое ограничения. Когда вы берете предел функции, вы хотите знать, к какому значению он приближается, когда x достигает определенного значения. Давайте рассмотрим 9Обозначение 0007. Пример
-0,40068 2.01 -0.49751 2.001 -0.49975 2.0001 -0.49998 Сводка пределов
| A | LIM | Символ для предела | LIM (5x+3) |
| 9007 B 9008 | |||
| C | F (x) | Функция Мы находим предел для |
, когда вы берете предел.
Стандартный метод 0007 заключается в том, чтобы просто вставить значение a в функцию. Возьмите этот пример.
| Шаг 1 | Идентификация значения A | A = 3 |
| Шаг 2 | Замените x значения A | 9999 9007 + 3 (3) 3 (3). + 3 |
| Шаг 3 | Нахождение предела | 18 |
Имейте в виду, что существует два способа приблизиться к пределу.
| Подход с правой стороны | Подход с левой стороны |
. Давайте рассмотрим наиболее распространенные примеры.
| A | Фракция |
| B | Стандарт |
| C | Power |
Часто вы будете сталкиваться с функциями, которые приводят к неопределенным формам. Взгляните на примеры ниже.
В этих случаях вы можете попытаться разложить функцию так, чтобы она не приводила к неопределенную форму или используйте правило Лопиталя.
Правило Лопиталя
Возьмем наш предыдущий пример , , который привел к неопределенной форме нуля над нулем.
Правило Лопиталя гласит, что когда у нас есть две функции, разделенные друг на друга, результат будет таким же, если мы возьмем производную каждой функции и разделим их на .
Это правило позволяет нам различать первую и вторую функции почти так же, как если бы мы различали две отдельные функции. Вот условия для использования этого правила:
| Предел должен существовать | Предел должен существовать в новой дифференцированной функции. |
| Дифференцируемый при | Функции должны быть дифференцируемыми, когда она приближается к правой или слева |
Решающий ноль более нулевой
в поле. неопределенной формы, возьмем следующий пример.
Когда мы подставляем ноль в функцию, мы получаем неопределенную форму нуля над нулем.
Здесь мы можем применить правило Лопиталя для нахождения предела.
Шаг 1
Первым шагом в использовании правила Лопиталя для нахождения предела функции является нахождение производной числителя и знаменателя независимо друг от друга.
Это означает, что вместо того, чтобы брать производную всей рациональной функции, мы можем начать с простого взятия производной числитель.
Вы можете найти производную функции, следуя правилам для производных .
Шаг 2
Следующим шагом является получение производной от знаменателя. Опять же, мы используем правила для деривативов, чтобы помочь нам.
Как видите, теперь у нас есть производная от функции верх и производная от функции низ .
Шаг 3
Теперь, когда мы взяли производную от числителя независимо от знаменателя, мы можем снова попробовать подставить наше значение a в уравнение, чтобы найти предел для функции.
Как видите, мы снова получаем неопределенную форму нуля над нулем. Давайте рассмотрим общий метод для использования правила Лопиталя, чтобы выяснить, что делать дальше.
| Шаг 1 | У вас есть неопределенная форма |
| Шаг 2 | Возьмите производную числителя и знаменателя независимо от одного еще |
| Шаг 3 | |
. функции. Если это приводит к другой неопределенной форме, перейдите к шагу 4. | |
| Шаг 4 | Повторите шаги 2 и 3. Если вы продолжаете получать неопределенную форму, вам, скорее всего, придется использовать метод факторинга, чтобы найти предел. |
Шаг 4
Теперь снова возьмем производную верхней и нижней функции .
Теперь мы найдем предел этой функции, снова подставив ноль в .
Результат 1 на 4. Это хорошая новость, мы нашли предел! Если бы это привело к другой неопределенной форме , такой как ноль над нулем снова, нам пришлось бы попытаться использовать другой метод, прежде чем использовать правило Лопиталя.
0 Разделить на 0: Решение предельных задач в исчислении, часть 1
Если вы похожи на многих студентов, изучающих математический анализ, вы понимаете идею пределов, но у вас могут возникнуть проблемы с решением предельных задач в домашнем задании, особенно когда вы сначала найдете «0 разделить на 0».
В этом посте мы покажем вам методы, которые вы должны знать для решения подобных проблем.
Обновление: По состоянию на сентябрь 2022 года у нас есть гораздо дополнительных интерактивных способов узнать об основополагающей концепции пределов, активно используя графические калькуляторы Desmos. Пожалуйста, посетите нашу Главу Ограничений до действительно запишите этот материал для себя. Все это бесплатно и ждет вас!
I. Идея ограничений и
Замена (очень просто, когда работает)Вам, наверное, уже говорили что-то вроде
, функция f приближается к L (даже если она никогда не равняется L ).
Вы уже на пути к пониманию пределов, если это утверждение имеет для вас смысл, и вы можете посмотреть на рисунок, подобный приведенному ниже, и сразу увидеть, что
$$\lim_{x \to 2}f(x) = 4 $$
потому что независимо от того, движемся ли мы к $x=2$ слева или справа, мы приближаемся к высоте $y = 4$.
В этом случае пределом является просто значение функции при x = 2: $\displaystyle{\lim_{x \to 2}f(x)} = f(2) = 4$.
А в некоторых домашних заданиях и тестовых вопросах (если ваш учитель чувствует себя хорошо), чтобы найти предел, вы просто подставляете значение x в функцию и находите значение в этом месте. Мы назовем этот подход Тактика №1: Замена .
Пример 1 .
Найдите $\displaystyle{\lim_{x \to 2}x+2}$.
Решение .
Давайте попробуем просто подставить $x=2$ в выражение:
$$\lim_{x \to 2}x+2 = 2 + 2 = 4 \quad \cmark$$
Это тот же предел, что показан на графике выше: на графике изображена функция $f(x) = x+2$, поэтому, приближаясь к $x =2$ слева или справа, мы приближаемся к фактическому значению функции по адресу $x=2$, то есть $y = f(2) = 4$.
В этом случае простая подстановка значения x = 2 в функцию работает: вы получаете число ($f(2) =4$), и все готово.
Достаточно было простой техники «Подстановки».
[Конец примера 1.]
Пример 2 .
Найдите $\displaystyle{\lim_{x \to \pi/2}\sin x}$.
Решение .
Давайте снова попробуем Подстановку и установим $x = \dfrac{\pi}{2}$:
$$\lim_{x \to \dfrac{\pi}{2}}\sin x = \sin \dfrac{ \pi}{2} = 1 \quad \cmark$$
График показывает $y = \sin x$. Когда вы приближаетесь к $x = \dfrac{\pi}{2}$ слева или справа, вы приближаетесь к высоте y = 1, которая является значением функции на $x = \dfrac {\pi}{2}$. Следовательно, предел как $x \to \dfrac{\pi}{2}$ sin x равен 1.
В этом случае снова работает подстановка: вы подставляете значение $x = \dfrac{\pi} {2}$, и вы получите число $\left(f\left(\dfrac{\pi}{2}\right) =1 \right)$. Вы закончили; легкий. 92-4}{x-2} = \frac{4-4}{2-2} = \frac{0}{0}$$
Это проблема. Давайте на мгновение остановим этот пример.
. .
Почти во всех ваших домашних заданиях и тестовых вопросах, когда вы пытаетесь заменить, вы получите 0, деленное на 0. Затем вам понадобится другая тактика, чтобы найти предел.
Морщина : Нам не понадобилось бы понятие предела, если бы вы всегда могли просто подставить число и найти там значение функции. Вместо этого, правда в том, что когда вы попробуете замену почти со всеми домашними заданиями и контрольными вопросами, вы получите $\dfrac{0}{0}$, «ноль, деленный на ноль». Этот результат известен как неопределенный предел , что является причудливым способом сказать «еще не известно». Он говорит вам, что на самом деле ответ может быть любым — вы просто еще не знаете — и поэтому у вас есть еще над чем поработать.
В частности, результат $\dfrac{0}{0}$ указывает на необходимость использования другого метода для нахождения предела. К счастью, три простые тактики позволят вам решить большинство проблем. Давайте посмотрим на каждый.
II. Когда вы получите 0, деленный на 0, сначала попробуйте
разложить на множители. Если вы попытаетесь заменить и получите $\dfrac{0}{0}$, вашим следующим шагом будет попытка 92-4}{x-2}} = \lim_{x \to 2}(x+2) = 4$.
[Конец примера 3.]
Если вы изучаете математический анализ, мы гарантируем, что вы столкнетесь со многими задачами, требующими факторизации функции для нахождения предела. Действительно, на каждом экзамене по математическому анализу, который мы видели, была по крайней мере одна проблема, когда вы изначально получаете $\dfrac{0}{0}$ и должны учитывать, чтобы получить окончательный ответ. Откройте следующее поле, чтобы увидеть больше примеров.
Откройте, чтобы увидеть больше примеров факторинга для нахождения предела. 92 -3x+2} &&= \lim_{x \to 1}\frac{(x+2)(x-1)}{(x-2)(x-1)} &&= \lim_{x \to 1}\frac{x+2}{x-2} &&= \frac{1+2}{1-2} = -3 \quad \cmark
\end{align*}
[collapse]
Эти Проблемы становятся простыми, как только вы научитесь их распознавать и умеете учитывать.
Если можешь, фактори.
Результат : Если подстановка дает результат в виде $\dfrac{0}{0}$, первое, что вы должны попробовать, – это факторинг. Если вы можете факторизовать числитель и/или знаменатель, проблемный член в знаменателе отменяется. Гарантировано.
ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ
- Наша глава о пределах (все, что вам нужно знать, с интерактивными компонентами, которые помогут вам почувствовать пределы)
- Оценка пределов: проблемы и полные решения 9 (устаревший материал 6038)
III. Тактика № 3. Используйте 90 457 сопряженных чисел
. Если функция содержит квадратный корень, а подстановка дает $\dfrac{0}{0}$, 0 делится на 0, умножьте числитель и знаменатель на 9.0481 $$1 = \frac{\text{сопряжение члена (числитель или знаменатель) с корнем}}{\text{сопряжение члена (числитель или знаменатель) с корнем}}$$
Как и факторинг, это подход, вероятно, приведет к возможности отмены термина.
Пример 4 иллюстрирует.
Пример 4 .
Найдите $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x}}$.
Раствор .
Сначала попробуем замену:
$$\lim_{x \to 0}\frac{\sqrt{x+5} – \sqrt{5}}{x} = \frac{\sqrt{0+5}-\ sqrt{5}}{0} = \frac{0}{0}$$
Поскольку предел представлен в виде $\dfrac{0}{0}$ , он не определен — мы еще не знаем, что это такое. Нам нужно проделать некоторую работу, чтобы привести его в форму, в которой мы сможем определить предел.
Итак, давайте избавимся от квадратных корней, используя сопряжение, как вы тренировались в алгебре: умножьте и числитель, и знаменатель на сопряжение числителя, $\sqrt{x+5} + \sqrt{5}$.
\begin{align*}
\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} &= \lim_{x \to 0}\dfrac{\ sqrt{x+5} – \sqrt{5}}{x} \cdot \dfrac{\sqrt{x+5} + \sqrt{5}}{\sqrt{x+5} + \sqrt{5}} \\\
&= \lim_{x \to 0}\dfrac{\sqrt{x+5}\sqrt{x+5} + \sqrt{x+5}\sqrt{5} – \sqrt{5}\sqrt{ x+5} -\sqrt{5}\sqrt{5}}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\ dfrac{(x+5) – 5}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{x}{x [\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{\cancel{x}}{\cancel{x}[\sqrt{ x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} \\ \ \
&=\dfrac{1}{\sqrt{0+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} \quad \cmark
\end{align*}
Функция, с которой мы начали, $\dfrac{\sqrt{x+5} – \sqrt{5}}{x}$, , и та, с которой мы закончили (после умножения на сопряженное ), $\dfrac{1}{\sqrt{x+5} + \sqrt{5}}$, одинаковы, за исключением того, что первая функция не определена при x = 0 (поскольку ее знаменатель там равен нулю) , а второго нет.
Мы показали это на параллельных графиках ниже. Следовательно, их пределы такие же, как $x \to 0$, и поэтому $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} = \ lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} }$.
[Конец примера 4.]
Как показано в примере 4, если подстановка дает вам $\dfrac{0}{0}$ и функция имеет квадратные корни, тактика умножения числителя и знаменателя на сопряженное части квадратного корня даст вам новую функцию, в которой работает подстановка. Всегда.
Откройте, чтобы увидеть еще один пример с квадратными корнями.
Пример 5 .
Найдите $\displaystyle{\lim_{x \to 9}\dfrac{9-x}{3-\sqrt{x}}}$.
Решение .
Сначала попробуем замену:
$$\lim_{x \to 9}\frac{9-x}{3-\sqrt{x}} = \frac{9-9}{3-\sqrt{9}} = \frac{0}{0} $$
Поскольку предел представлен в виде $\dfrac{0}{0}$ , он не определен – мы пока не знаем, что это такое.
Итак, давайте умножим числитель и знаменатель на сопряженное значение знаменателя, $3+\sqrt{x}$:
\begin{align*}
\lim_{x \to 9}\frac{9-x}{3-\ sqrt{x}} &= \lim_{x \to 9}\frac{9-x}{3-\sqrt{x}} \cdot \frac{3+\sqrt{x}}{3+\sqrt{ х}} \\[8px]
&= \lim_{х \до 9}\frac{(9-x)\left(3+\sqrt{x} \right)}{9 +3 \sqrt{x} -3 \sqrt{x} -x} \\[8px]
&= \lim_{x \to 9}\frac{(9-x)\left(3+\sqrt{x} \right)}{9 -x} \\[8px]
&= \lim_{x \to 9}\frac{\cancel{(9-x)}\left(3+\sqrt{x} \right)}{\cancel{9-x}} \\[8px]
&= \lim_{x \to 9}3+\sqrt{x} \\[8px]
&= 3+ \sqrt{9} = 3+3 = 6 \quad \cmark
\end{align*}
[свернуть]
Результат: Если у вас есть квадратные корни, умножьте числитель и знаменатель сопряженной частью квадратного корня.
Мы рассмотрим больше ключевых тактик для работы с 0, деленным на 0, в нашей следующей статье «Как решать задачи с ограничениями в исчислении — часть 2». Мы познакомим вас с некоторыми другими ограничениями, которые вы должны просто научиться распознавать.
Конечно тебе нужно потренироваться.
Конечно, недостаточно прочитать наше обсуждение. Вместо этого вам нужно попрактиковаться и сделать несколько ошибок для себя, чтобы все это стало для вас рутиной, когда вы будете сдавать экзамен. У нас есть много задач, которые вы можете попробовать, все с полными решениями одним щелчком мыши, чтобы вы могли быстро проверить свою работу или избавиться от зависаний без хлопот.
А пока посетите наш форум и сообщите нам:
- Какие у вас есть вопросы?
- Чем вам помог этот пост? Запутанно или менее полезно?
- Как у вас обстоят дела с исчислением?
Вы можете поддержать нашу работу чашечкой кофе
Мы — небольшая самофинансируемая команда, задача которой — предоставить высококачественные полезные материалы всем, кто хочет хорошо изучить исчисление. Мы предоставляем этот сайт без рекламы (!), и мы никому не продаем ваши данные .