Предел равен 1: Национальный исследовательский университет «Высшая школа экономики»

2

Урок 1. Предел функции | Уроки математики и физики для школьников и родителей

Найти предел:
РЕШЕНИЕ:
ОТВЕТ:  12

Найти предел:
РЕШЕНИЕ:

Предварительно убедимся, что предел делителя не равен нулю.
Таким образом, формула
применима и, значит,
ОТВЕТ:  ¹/₅

О пределе сложной функции.

– если существует конечный предел

а функция  f(u)  непрерывна в точке  u₀, то
Другими словами, для непрерывных функций символы предела и функции можно менять местами.
Непосредственное применение теоремы о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию.
Найти предел:
РЕШЕНИЕ:

Теорема о пределе частного здесь неприменима, так как

Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим.

2х² – 3х – 2 = 2(х – 2)(х + 0,5),
где  х₁ = 2, х₂ = –0,5 – корни квадратного трёхчлена. Теперь сократим дробь и вычислим предел данной функции:
ОТВЕТ:  ⁵

/₂

Примеры пределов с бесконечностью.
Найдите предел:
РЕШЕНИЕ:

Разберёмся, что такое
Это тот случай, когда  х  неограниченно возрастает, то есть сначала  

х = 10, потом  

х = 100, потом  

х = 1000, затем  

х = 1000000  и так далее до бесконечности.

А что в это время происходит с функцией  1 – х ?
Если
то функция  1 – х  стремится к минус бесконечности

Тут вместо <<икса>> подставляем в функцию  1 – х  бесконечность и получаем ответ.
Найдите предел:
РЕШЕНИЕ:

Начинаем увеличивать  х  до бесконечности, и смотрим на поведение функции:
Если  х = 10, то  10² – 2∙10 – 3 = 77, Если  х = 100, то  100² – 2∙100 – 3 = 9797, Если  х = 1000, то  1000² – 2∙1000 – 3 = 997997,
При
функция

неограниченно возрастает
ОТВЕТ:  ∞


Простейшие виды пределов.


Пределы с неопределённостью вида
и метод их решения.

Рассмотрим группу пределов, когда

а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены.

Вычислить предел:
РЕШЕНИЕ:

Подставим бесконечность в функцию. Что получается вверху ? Бесконечность. А внизу ? Тоже бесконечность. Таким образом получилась так называемая неопределённость вида

Можно было бы подумать, что
и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый приём решения, который и рассмотрим.
Сначала смотрим на числитель и находим  х  в старшей степени. Старшая степень в числителе равна двум. Затем смотрим на знаменатель. Старшая степень знаменателя равна двум. Метод решения следующий: Для того, чтобы раскрыть неопределённость
Необходимо разделить числитель и знаменатель на  х  в старшей степени.
Разделим числитель и знаменатель на  х².
ОТВЕТ:  ²/₃

Вычислить предел:
РЕШЕНИЕ:

Максимальная степень в числителе  3. Максимальная степень в знаменателе  4. Выбираем наибольшее значение, в данном случае четвёрку. Разделим числитель и знаменатель на  х⁴.
ОТВЕТ:  0

Вычислить предел:
РЕШЕНИЕ:

Максимальная степень <<икса>> в числителе:  2. Максимальная степень <<икса>> в знаменателе

:  1. Для раскрытия неопределённости
необходимо разделить числитель и знаменатель на  х².
Под записью
Подразумевается не деление на ноль (на ноль делить нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределённости вида
может получиться конечное число, ноль или бесконечность.  Пределы с неопределённостью вида
и метод их решения.

Рассмотрим группу пределов, когда  х  стремится к конечному числу, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены.
Вычислить предел:
РЕШЕНИЕ:  Сначала подставим  –1  в дробь:
В данном случае получилась неопределённость
Если в числителе и знаменателе находятся многочлены, и имеется неопределённость вида то для её раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращённого умножения. Решаем предел дальше. Разложим числитель и знаменатель на множители. Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
D = (–3)² – 4 ∙ 2 ∙ (–5) = 9 + 40 = 49.
И квадратный корень из него:
√͞͞͞͞͞D  = √͞͞͞͞͞49 = 7.
Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно, либо в задании опечатка. Далее находим корни:
Таким образом:

2х² – 3х – 5 = 2(х – (–1))(х – ⁵/₂) =  2(х + 1)(х – ⁵/₂) = (х + 1)(2х – 5).
ОТВЕТ:  –7

Вычислить предел:
РЕШЕНИЕ: 
Сначала подставляем  –2  в выражение под знаком предела. Это первое, что нужно выполнять для любого предела.
Разложим числитель на множители:
√͞͞͞͞͞ D = 3,
х² + х – 2 = (х + 2)(х – 1).  

Умножаем числитель и знаменатель на сопряжённое выражение:

= 4 ∙ (–3) = –12.  

ОТВЕТ:  –12

Задания к уроку 1

Внеклассный урок – Предел последовательности. Виды последовательности.

Предел последовательности

Предел последовательности – это число, в окрестности которой содержатся все члены последовательности.

Пример: Пределом последовательности чисел 1/2, 1/3, 1/4, 1/5, 1/6 и т.д. является 0.
Пояснение: ряд чисел стремится к нулю и ниже нуля не опустится.

Не любая последовательность имеет предел. К примеру, последовательность 1, 2, 3, 4, 5, 6 и т.д. бесконечна и не имеет предела.

Свойство последовательности иметь или не иметь предел называется сходимостью. Если у последовательности есть предел, то говорят, что она сходится. Если у последовательности нет предела, то говорят, что она расходится.

   Случай, когда последовательность не имеет предела.

Если |q| > 1, то последовательность y_n = qⁿ расходится и не имеет предела.

Пример: Пусть q = 3. Тогда мы можем создать следующую последовательность чисел:

3²; 3³; 3⁴; 3⁵; 3⁶; 3⁷ и т.д. Ряд стремится к бесконечности. Предела нет.

 

Виды последовательности.

Последовательность (yn) называется ограниченной снизу, если все ее члены не меньше некоторого числа. Для любого n выполняется неравенство yn ≥ m

Последовательность (yn) называется ограниченной сверху, если все ее члены не больше некоторого числа. Для любого n выполняется неравенство yn ≤ М

Если каждый член последовательности yn больше предыдущего, то это возрастающая последовательность. Если а > 1, то последовательность yn = an возрастает. Пример: y1 < y2 < y3 < y4 < y5…

Если каждый член последовательности меньше предыдущего, то это убывающая последовательность. Если 0 < a < 1, то последовательность убывает. Пример: 1/2, 1/3, 1/4, 1/5…

 

Теорема.

Если lim  xn = b,  lim  yn = c, то         n→∞          n→∞ 1) предел суммы равен сумме пределов:  lim  (xn + yn) = b + c n→∞ 2) предел произведения равен произведению пределов:  lim  (xn yn) = bc n→∞ 3) предел частного равен частному пределов:  lim  (xn/yn) = b/c, при c ≠ 0 n→∞ 4) постоянный множитель можно вынести за знак предела:  lim  (kxn) = kb n→∞

 

Пример 1: Найти предел последовательности

d_n = 6/n – 4/n² + 8.

Решение:

 lim  6/n – lim  4/n² + lim  8 = 0 – 0 + 8 = 8.
^{n→∞      n→∞         n→∞}

Пример решен.

 

Пример 2: Найти предел последовательности

           2n² + 3
  lim    ————
^n→∞    n² + 4

Решение.

Разделим числитель и знаменатель дроби на n², произведем сокращения и получим ответ:

           2n²/n²  +  3/n²                    2  +  3/n²           2  +  0
  lim   ———————   =   lim   —————  =  ————  = 2.
^n→∞   n²/n²  +  4/n^{2          n→∞}   1  +  4/n²          1  +  0

Пример решен.

Предел функции (1) – Документ

Предел функции

Пусть функция определена на множестве .

Определение. Точка – называется предельной точкой множества или точкой сгущения множества , если в любой окрестности существует точка из множества , отличная от ( и ), т. е

Например, для множества – все точки являются предельными, включая и .

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Пусть функция определена на множестве и – предельная точка для множества .

Определение 1 (на «языке последовательностей», или по Гейне). Число А называется пределом функции в точке (или при ), если для любой последовательности допустимых значений аргумента , , сходящейся к точке (т.е ), последовательность соответствующих значений функции , сходится к числу А (т.е. ).

В этом случае пишут или при . Геометрический смысл предела функции: означает, что для всех , достаточно близких к точке , соответствующие значения функции как угодно мало отличаются от А.

Это определение коротко можно записать так:

.

Определение 2 (на «языке», или по Коши). Число А называется пределом функции в точке (или при ), если для любого положительного найдется такое положительное число , что для всех , удовлетворяющих неравенству , выполняется неравенство .

Это определение коротко можно записать так:

.

Геометрический смысл предела функции , если для любой -окрестности точки найдется такая -окрестность точки , что для всех из этой -окрестности соответствующие значения функции лежат в -окрестности точки . Иными словами, точки графика функции лежат внутри полосы шириной , ограниченной прямыми , . Очевидно, что величина зависит от выбора , поэтому пишут .

Отрицание определения 1 (по Гейне).

что .

Отрицание определения 2 (по Коши).

.

Докажем эквивалентность определений 1 и 2. Доказательство проведем от противного: пусть имеет место определение по Гейне, но не имеет место определение по Коши, т.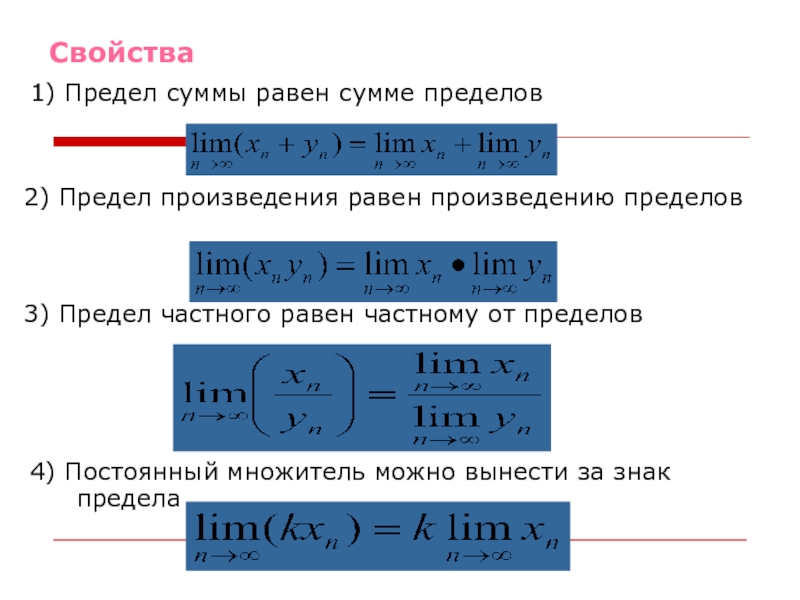 е. . Пусть , и как было уже отмечено что . Из условия , что , и . Из того, что . Мы построили последовательность , которая не равна , а , что противоречит определению Гейне.

Обратное. Пусть имеет место определение Коши, докажем, что имеет место определение по Гейне тоже. Возьмем любую последовательность и , тогда для по которому подберем некоторое число , что . Возьмем Так как , то для данного можно найти такой номер , что Если для , тогда по определению Коши . Итак, мы получили , что , что выполняется определение по Гейне.

Лемма. Пусть . Если , тогда окрестность , что и то .

Доказательство: Обозначим . Тогда для данного , что , , это значит что т.е. , т.к. .

Предел функции при .

Пусть функция определена в промежутке .

Определение. Число А называется пределом функции при , если для любого положительного числа найдется такое число , что при всех , удовлетворяющих неравенству , выполняется неравенство .

Это определение коротко можно записать так:

.

Если , то пишут , если , то – . Геометрический смысл этого определения таков: для , что при или при соответствующие значения функции попадут в -окрестность точки , т.е. точки графика лежат в полосе шириной , ограниченной прямыми и

Бесконечно большая функция (б.б.ф.)

Определение. Функция называется бесконечно большой при , если для любого числа существует , что для всех , удовлетворяющих неравенству , выполняется неравенство . Записывают или при .

Это определение коротко можно записать так:

.

Например, функция есть б.б.ф. при .

Если при и принимает лишь положительные значения, то пишут ; если лишь отрицательные значения, то .

Бесконечно большая функция при .

Определение. Функция , заданная на всей числовой прямой, называется бесконечно большой при , если для любого числа найдется такое число , что при всех , удовлетворяющих неравенству , выполняется неравенство .

Это определение коротко можно записать так:

.

Например, функция есть б.б.ф. при .

Бесконечно малые функции

Определение. Функция называется бесконечно малой при , если .

По определению предела функции равенство означает: для любого положительного найдется такое положительное число , что для всех , удовлетворяющих неравенству , выполняется неравенство .

Это определение коротко можно записать так:

.

Исчисление I – Предел

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с “узкой” шириной экрана (, т. е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-2: Предел

В предыдущем разделе мы рассмотрели несколько проблем, и в обеих задачах у нас была функция (наклон в случае касательной задачи и средняя скорость изменения в задаче скорости изменения), и мы хотели знать, как эта функция ведет себя в некоторая точка \ (x = a \).На этом этапе игры нас больше не волнует, откуда взялись функции, и нас больше не волнует, увидим мы их снова или нет. Все, что нам нужно знать или о чем беспокоиться, – это то, что у нас есть эти функции, и мы хотим что-то о них знать.

Чтобы ответить на вопросы в последнем разделе, мы выбираем значения \ (x \), которые все ближе и ближе к \ (x = a \), и вставляем их в функцию. Мы также убедились, что мы посмотрели на значения \ (x \), которые были как слева, так и справа от \ (x = a \).2} + 25}} {{t – 5}} = 15 \]

В этих обозначениях мы заметим, что мы всегда указываем функцию, с которой работаем, а также указываем значение \ (x \) (или \ (t \)), к которому мы движемся.

В этом разделе мы собираемся применить интуитивный подход к ограничениям и попытаться почувствовать, что они собой представляют и что они могут рассказать нам о функции. Помня об этой цели, мы пока не будем вдаваться в подробности того, как на самом деле вычислять пределы. Вместо этого мы будем полагаться на то, что мы сделали в предыдущем разделе, а также на другой подход, чтобы угадать значение пределов.

Оба подхода, которые мы собираемся использовать в этом разделе, призваны помочь нам понять, что такое ограничения. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления пределов, и во многих случаях их может быть очень сложно использовать даже для оценки значения предела и / или иногда мы даем неправильное значение. Мы рассмотрим фактически вычисляемые пределы в нескольких разделах.

Давайте сначала начнем со следующего «определения» лимита.

Определение

Мы говорим, что предел \ (f (x) \) равен \ (L \), когда \ (x \) приближается к \ (a \), и записываем это как

\ [\ mathop {\ lim} \ limits_ {x \ to a} f \ left (x \ right) = L \]

при условии, что мы можем сделать \ (f (x) \) настолько близким к \ (L \), насколько мы хотим, для всех \ (x \), достаточно близких к \ (a \), с обеих сторон, фактически не позволяя \ (x \) быть \ (а \).

Это не точное определение предела. Если вы хотите увидеть более точное и математическое определение лимита, вам следует ознакомиться с разделом «Определение лимита» в конце этой главы. Приведенное выше определение является скорее «рабочим» определением. Это определение помогает нам понять, что такое ограничения и что они могут сказать нам о функциях.

Так что же означает это определение? Что ж, предположим, что мы знаем, что предел действительно существует.Согласно нашему «рабочему» определению, мы можем решить, насколько близко к \ (L \) мы хотим сделать \ (f (x) \). В качестве аргумента предположим, что мы хотим сделать \ (f (x) \) не более чем на 0,001 от \ (L \). Это означает, что нам нужен один из следующих

\ [\ begin {array} {lcl} f \ left (x \ right) – L

Теперь, согласно «рабочему» определению, это означает, что если мы получим \ (x \) достаточно близко к \ (a \), мы можем сделайте одно из вышеперечисленных истинным. Однако на самом деле это говорит немного больше.Он говорит, что где-то в мире есть значение \ (x \), скажем \ (X \), так что для всех \ (x \), которые ближе к \ (a \), чем \ (X \), то одно из приведенных выше утверждений будет верным.

Это довольно важная идея. В мире есть много функций, которые мы можем сделать как можно ближе к \ (L \) для определенных значений \ (x \), которые близки к \ (a \), но будут и другие значения \ (x \) ближе к \ (a \), которые дают значения функций, далеко не близкие к \ (L \).Чтобы предел существовал, как только мы получим \ (f (x) \) настолько близко к \ (L \), насколько мы хотим для некоторого \ (x \), тогда ему нужно будет оставаться так близко к \ (L \ ) (или приблизиться) для всех значений \ (x \), которые ближе к \ (a \). Мы увидим пример этого позже в этом разделе.

В несколько более простых терминах определение говорит, что по мере того, как \ (x \) становится все ближе и ближе к \ (x = a \) (с обеих сторон, конечно …), то \ (f (x) \) должно быть приближаться и ближе к \ (L \). Или, когда мы приближаемся к \ (x = a \), тогда \ (f (x) \) должно двигаться к \ (L \).

Важно еще раз отметить, что мы должны смотреть на значения \ (x \), которые находятся по обе стороны от \ (x = a \). Мы также должны отметить, что нам не разрешено использовать \ (x = a \) в определении. Мы часто будем использовать информацию, которую дают нам ограничения, чтобы получить некоторую информацию о том, что происходит прямо в \ (x = a \), но само ограничение не связано с тем, что на самом деле происходит в \ (x = a \) . Предел касается только того, что происходит вокруг точки \ (x = a \). Это важное понятие об ограничениях, которое нам нужно иметь в виду.

Альтернативное обозначение, которое мы иногда будем использовать для обозначения пределов, –

. \ [f (x) \ to L \ hspace {0,25 дюйма} {\ rm {as}} \ hspace {0,25 дюйма} x \ to a \]

Как мы можем использовать это определение, чтобы помочь нам оценить пределы? Мы делаем именно то, что делали в предыдущем разделе. Мы берем \ (x \) с обеих сторон от \ (x = a \), которые перемещаются все ближе и ближе к \ (a \), и вставляем их в нашу функцию. Затем мы смотрим, можем ли мы определить, к какому числу движутся значения функции, и используем это в качестве нашей оценки. 2} – 2x}} \] Показать решение

Обратите внимание, что мы сказали «оценка значения лимита». Опять же, в этом разделе мы не собираемся напрямую вычислять пределы. Цель этого раздела – дать нам лучшее представление о том, как работают ограничения и что они могут рассказать нам о функции.

Итак, имея это в виду, мы будем работать с этим почти так же, как в предыдущем разделе. Мы выберем значения \ (x \), которые становятся все ближе и ближе к \ (x = 2 \), и подставим эти значения в функцию.Это дает следующую таблицу значений.

\ (х \)	\ (е (х) \)	\ (х \)	\ (е (х) \)
2,5	3,4	1,5	5,0
2,1	3.857142857	1. 9	4,157894737
2,01	3.985074627	1,99	4.015075377
2,001	3.998500750	1,999	4,001500750
2.0001	3.999850007	1,9999	4.000150008
2,00001	3.999985000	1,99999	4,000015000

Обратите внимание, что мы убедились и выбрали значения \ (x \), которые были по обе стороны от \ (x = 2 \), и что мы переместились очень близко к \ (x = 2 \), чтобы убедиться, что любые тенденции, которые мы можем наблюдать, на самом деле верны.2} – 2x}} = 4 \]

Давайте еще немного подумаем о том, что здесь происходит. Давайте изобразим график функции из последнего примера. График функции в интересующем диапазоне значений \ (x \) показан ниже.

Во-первых, обратите внимание на довольно большую открытую точку в точке \ (x = 2 \). Это нужно для того, чтобы напомнить нам, что функции (и, следовательно, графика) не существует в \ (x = 2 \).

Когда мы вставляли значения \ (x \) в функцию, мы фактически перемещаемся по графику в направлении точки как \ (x = 2 \).Это показано на графике двумя стрелками на графике, которые перемещаются к точке.

Когда мы вычисляем ограничения, мы действительно задаемся вопросом, к какому значению \ (y \) приближается наш график, когда мы приближаемся к \ (x = a \) на нашем графике. Мы НЕ спрашиваем, какое значение \ (y \) принимает график в рассматриваемой точке. Другими словами, мы спрашиваем, что делает график вокруг точки \ (x = a \). В нашем случае мы можем видеть, что по мере того, как \ (x \) приближается к 2 (с обеих сторон), функция приближается к \ (y = 4 \), хотя сама функция даже не существует в \ (x = 2 \ ). Таким образом, можно сказать, что лимит на самом деле равен 4.

Итак, что мы узнали об ограничениях? Пределы спрашивают, что делает функция вокруг \ (x = a \), и не связаны с тем, что функция на самом деле делает в \ (x = a \). Это хорошо, поскольку многие функции, которые мы рассмотрим, даже не будут существовать в \ (x = a \), как мы видели в нашем последнем примере.

Давайте рассмотрим еще один пример, чтобы доказать это.

Пример 2 Оцените значение следующего предела.2} – 2x}} & {\ mbox {if}} x \ ne 2 \\ 6 & {\ mbox {if}} x = 2 \ end {array} \ right. \] Показать решение

Прежде всего, следует отметить, что это точно такая же функция, как и в первом примере, за исключением того, что мы присвоили ей значение для \ (x = 2 \). Итак, сначала отметим, что

\ [g \ left (2 \ right) = 6 \]

Что касается оценки значения этого лимита, то по сравнению с первым примером ничего не изменилось. Мы могли бы составить таблицу значений, как в первом примере, или быстро взглянуть на график функции. Любой метод даст нам значение лимита.

Давайте сначала взглянем на таблицу значений и посмотрим, что она нам говорит. Обратите внимание, что наличие значения функции в \ (x = 2 \) не изменит наш выбор для \ (x \). Мы выбираем только значения \ (x \), которые приближаются к \ (x = 2 \), но никогда не берем \ (x = 2 \). Другими словами, таблица значений, которую мы использовали в первом примере, будет точно такой же, как и здесь.Итак, поскольку мы уже сделали это один раз, нет причин переделывать его здесь.

Из этой таблицы снова ясно, что предел равен

. \ [\ mathop {\ lim} \ limits_ {x \ to 2} g \ left (x \ right) = 4 \]

Предел НЕ 6! Помните из обсуждения после первого примера, что ограничения не заботятся о том, что функция на самом деле делает в рассматриваемой точке.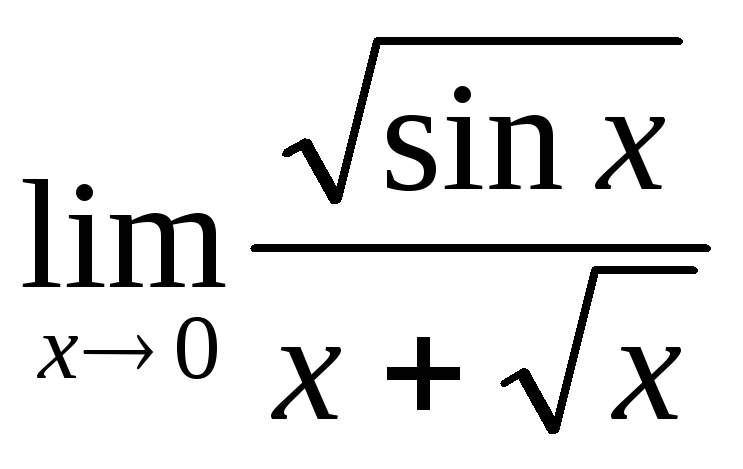 Пределы касаются только того, что происходит на около точки.Поскольку единственное, что мы изменили в функции, – это ее поведение при \ (x = 2 \), это не изменит предел.

Давайте также быстро взглянем на график этой функции, чтобы убедиться, что это то же самое.

Опять же, мы видим, что по мере того, как мы приближаемся к \ (x = 2 \) на нашем графике, функция все еще приближается к значению \ (y \), равному 4. Помните, что мы только спрашиваем, что функция делает вокруг \ (x = 2 \), и нам все равно, что функция на самом деле делает в \ (x = 2 \).График также подтверждает вывод о том, что предел составляет

\ [\ mathop {\ lim} \ limits_ {x \ to 2} g \ left (x \ right) = 4 \]

Давайте еще раз поговорим об этом, чтобы убедиться, что мы его поняли. Пределы , а не , связанные с тем, что происходит в \ (x = a \). Ограничения касаются только того, что происходит на около \ (x = a \). Мы постоянно говорим об этом, но это очень важная концепция ограничений, которую мы всегда должны помнить.Итак, мы воспользуемся любой возможностью, чтобы напомнить себе об этой идее.

Поскольку ограничения не связаны с тем, что на самом деле происходит в \ (x = a \), мы иногда будем видеть ситуации, подобные предыдущему примеру, где предел в точке и значение функции в точке различаются. Конечно, это не всегда будет происходить. Бывают случаи, когда значение функции и предел в одной точке совпадают, и в конечном итоге мы увидим несколько таких примеров. Однако важно не волноваться из-за того, что функция и предел не принимают одно и то же значение в одной точке.Иногда такое случается, поэтому нам нужно иметь возможность разбираться в тех случаях, когда они возникают.

Давайте взглянем на другой пример, чтобы попытаться опровергнуть эту идею.

Пример 3 Оцените значение следующего предела. \ [\ mathop {\ lim} \ limits _ {\ theta \ to 0} \, \ frac {{1 – \ cos \ left (\ theta \ right)}} {\ theta} \] Показать решение

Во-первых, не волнуйтесь о функции \ (\ theta \) in. Это просто буква, как \ (x \) буква! Это греческая буква, но это буква, и иногда вам будет предложено работать с греческими буквами, так что на этом этапе неплохо было бы начать к ним привыкать.

Теперь также обратите внимание, что если мы подключим \ (\ theta = 0 \), мы получим деление на ноль, и поэтому функция в данный момент не существует. Фактически, в этот момент мы получаем 0/0, но из-за деления на ноль этой функции не существует в \ (\ theta = 0 \).

Итак, как мы сделали в первом примере, давайте возьмем таблицу значений и посмотрим, что, если мы сможем угадать, к какому значению движется функция.

\ (\ theta \)	\ (е \ влево (\ тета \ вправо) \)	\ (\ theta \)	\ (е \ влево (\ тета \ вправо) \)
1	0. 45969769	-1	-0,45969769
0,1	0,04995835	-0,1	-0,04995835
0,01	0,00499996	-0,01	-0,00499996
0,001	0.00049999	-0,001	-0,00049999

Хорошо, похоже, что функция приближается к нулю, поскольку \ (\ theta \) приближается к 0, конечно с обеих сторон.

Следовательно, предположим, что предел имеет значение

\ [\ mathop {\ lim} \ limits _ {\ theta \ to 0} \, \ frac {{1 – \ cos \ left (\ theta \ right)}} {\ theta} = 0 \]

Итак, еще раз, предел имел значение, даже если функция не существовала в интересующей нас точке.

Пришло время поработать еще пару примеров, которые приведут нас к следующему представлению об ограничениях, которое мы собираемся обсудить.

Пример 4 Оцените значение следующего предела. \ [\ mathop {\ lim} \ limits_ {t \ to 0} \ cos \ left ({\ frac {\ pi} {t}} \ right) \] Показать решение

Давайте составим таблицу значений и посмотрим, что в этом случае происходит с нашей функцией.

\ (т \)	\ (f (t) \)	\ (т \)	\ (f (t) \)
1	-1	-1	-1
0.1	1	-0,1	1
0,01	1	-0,01	1
0,001	1	-0,001	1

Теперь, если бы мы угадали предел из этой таблицы, мы бы предположили, что предел равен 1. Однако, если бы мы сделали это предположение, мы ошиблись бы. Рассмотрим любую из следующих оценок функций.

\ [f \ left ({\ frac {1} {{2001}}} \ right) = – 1 \ hspace {0,55 дюйма} f \ left ({\ frac {2} {{2001}}} \ right) = 0 \ hspace {0,5 дюйма} f \ left ({\ frac {4} {{4001}}} \ right) = \ frac {{\ sqrt 2}} {2} \]

Во всех трех оценках функции мы оценили функцию с числом меньше 0,001 и получили три совершенно разных числа. Напомним, что определение предела, с которым мы работаем, требует, чтобы функция приближалась к единственному значению (наше предположение) по мере приближения \ (t \) к рассматриваемой точке.Это не говорит о том, что только некоторые значения функции должны приближаться к предположению. Он говорит, что все значения функций должны приближаться к нашему предположению.

Было бы удобно увидеть, что здесь происходит, на графике функции.

Из этого графика мы можем видеть, что по мере того, как мы приближаемся к \ (t = 0 \), функция начинает дико колебаться, и на самом деле колебания увеличиваются по скорости по мере приближения к \ (t = 0 \), которое мы получаем. Вспомните из нашего определения предела, что для существования предела функция должна устанавливаться в сторону одного значения по мере того, как мы приближаемся к рассматриваемой точке.

Эта функция явно не сводится к одному номеру, и поэтому этот предел не существует !

Этот последний пример указывает на недостаток простого выбора значений переменной и использования таблицы значений функций для оценки значения предела.Значения переменной, которые мы выбрали в предыдущем примере, были действительными и на самом деле, вероятно, были значениями, которые многие выбрали бы. Фактически, это были точно такие же значения, которые мы использовали в задаче до этой, и они работали в этой задаче!

При использовании таблицы значений всегда будет вероятность того, что мы не выберем правильные значения и что мы будем неправильно угадывать наш предел. Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение лимитов. Фактически, это такая проблема, что после этого раздела мы никогда не будем использовать таблицу значений, чтобы снова угадать значение лимита.

Этот последний пример также показал нам, что ограничения не должны существовать. До этого момента мы видели только существующие ограничения, но это не всегда так.

Давайте взглянем на еще один пример в этом разделе.

Пример 5 Оцените значение следующего предела. \ [\ mathop {\ lim} \ limits_ {t \ to 0} H \ left (t \ right) \ hspace {0.25 дюймов} {\ mbox {где,}} \ hspace {0,25 дюйма} H \ left (t \ right) = \ left \ {\ begin {array} {ll} 0 & {\ mbox {if}} t Показать решение

Эта функция часто называется функцией Heaviside или step . Мы могли бы использовать таблицу значений для оценки предела, но в этом случае, вероятно, так же быстро можно использовать график, так что давайте сделаем это. Ниже представлен график этой функции.

Из графика видно, что если мы приближаемся к \ (t = 0 \) с правой стороны, функция приближается к значению \ (y \), равному 1. На самом деле он просто остается на 1, но в терминологии, которую мы использовали в этом разделе, он приближается к 1…

.

Кроме того, если мы переместимся в сторону \ (t = 0 \) слева, функция будет двигаться в направлении значения \ (y \), равного 0.

Согласно нашему определению предела, функция должна приближаться к одному значению, когда мы приближаемся к \ (t = a \) (с обеих сторон). В данном случае этого не происходит, поэтому в этом примере мы также скажем, что ограничения не существует.

Обратите внимание, что ограничение в этом примере немного отличается от предыдущего. В предыдущем примере функция не сводилась к одному числу, когда мы приближались к \ (t = 0 \). Однако в этом примере функция сводится к одному числу как \ (t = 0 \) с обеих сторон. Проблема в том, что число разное с каждой стороны от \ (t = 0 \). Это идея, которую мы рассмотрим более подробно в следующем разделе.

Давайте подведем итог тому, что мы (надеюсь) узнали в этом разделе. В первых трех примерах мы видели, что ограничения не заботятся о том, что функция на самом деле делает в рассматриваемой точке. Их волнует только то, что происходит вокруг точки. Фактически, у нас могут быть пределы в \ (x = a \), даже если самой функции в этой точке не существует. Точно так же, даже если функция существует в какой-то точке, нет причин (на этом этапе) думать, что предел будет иметь то же значение, что и функция в этой точке. Иногда предел и функция будут иметь одно и то же значение в одной точке, а в других случаях – разные значения.

Далее, в третьем и четвертом примерах мы увидели основную причину отказа от использования таблицы значений для определения значения лимита. В этих примерах мы использовали точно такой же набор значений, однако они работали только в одном из примеров. Использование таблиц значений для угадывания значения лимитов – просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы это сделаем. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов.

Последние два примера показали нам, что на самом деле не все ограничения существуют.Мы не должны зацикливаться на идее, что ограничения будут существовать всегда. В большинстве курсов по математике мы работаем с ограничениями, которые существуют почти всегда, поэтому легко начать думать, что пределы существуют всегда. Ограничения существуют не всегда, поэтому не привыкайте предполагать, что они будут.

Наконец, в четвертом примере мы увидели, что единственный способ справиться с ограничением – это построить график функции. Иногда это единственный способ, однако этот пример также проиллюстрировал недостаток использования графиков.Чтобы использовать график, чтобы угадать значение предела, вам нужно иметь возможность на самом деле нарисовать график. Для многих функций это сделать не так просто.

Есть еще один недостаток в использовании графиков. Даже если у вас есть график, он будет полезен, только если значение \ (y \) приближается к целому числу. Если значение \ (y \) приближается, скажем, \ (\ frac {{- 15}} {{123}} \), вы никак не сможете угадать это значение по графику, а мы обычно требуются точные значения для наших пределов.

Итак, хотя графики функций могут иногда облегчить вам жизнь при угадывании значений пределов, они снова, вероятно, не лучший способ получить значения пределов. Они будут полезны только в том случае, если вы сможете их достать, а значение лимита – «хорошее» число.

Возникает естественный вопрос, почему мы вообще говорили об использовании таблиц и / или графиков для оценки пределов, если они не являются лучшим способом. На то было несколько причин.

Во-первых, они могут помочь нам лучше понять, что такое ограничения и что они могут нам сказать.Если мы не сделаем хотя бы пару ограничений таким образом, мы не сможем понять, что это за пределы.

Вторая причина использования ограничений таким образом – указать на их недостатки, чтобы у нас не возникало соблазна использовать их все время!

В конце концов мы поговорим о том, как мы действительно устанавливаем лимиты. 2

Нахождение предела (1-cos (x)) / x – Видео и стенограмма урока

Шаги для решения предела 1-Cos (

x ) / x

Когда дело доходит до определения предела функции, поскольку x приближается к некоторому значению a , существует множество различных методов, которые можно попробовать.В зависимости от функции некоторые из этих методов будут работать, а некоторые – нет. Мы ищем предел (1-cos ( x )) / x , как x → a .

Для этого мы используем два разных метода в зависимости от значения a . Один для случая, когда a = 0, а другой для случая, когда a ≠ 0. Во-первых, давайте посмотрим, когда a ≠ 0.

Когда a ≠ 0, найти предел (1 – cos ( x )) / x действительно довольно просто. Мы используем метод подключаемого модуля , который заключается в простом подключении и к (1 – cos ( x )) / x для x .

Мы видим, что когда a ≠ 0, мы получаем, что предел (1 – cos ( x )) / x , как x → a , равен (1 – cos ( a ) / a . Довольно просто и понятно, не так ли?

Теперь рассмотрим, когда a = 0.В таком случае найти этот предел немного сложнее. Причина этого в том, что если мы попытаемся использовать подключаемый метод, мы получим ноль в знаменателе, а одно из правил номер один в математике состоит в том, что мы не можем делить на ноль.

Поэтому, когда это так, мы используем хорошо известную теорему, которая утверждает, что предел греха ( x ) / x , как x → 0, равен 1.

Вам может быть интересно, какое отношение эта теорема имеет к нашей функции. Что ж, как оказалось, мы можем манипулировать функцией (1 – cos ( x )) / x , умножив числитель и знаменатель на 1 + cos ( x ) и используя тригонометрическое тождество sin2 ( x ) = 1 – cos2 ( x ), мы получаем функцию, включающую sin ( x ) / x . При этом мы превращаем задачу в следующее ограничение:

(sin ( x ) / x ) * (sin ( x ) / (1+ cos ( x ))

Теперь мы используем правило произведения для пределов , которое гласит, что предел произведения функций является произведением пределов функций.x} = e \]

Бесконечные пределы — Форма n / 0

Ошибка: Нажмите «Не робот», затем повторите попытку.

Краткий обзор

Предположим, что $$ \ red n \ neq 0 $$. 2} $$

Шаг 1

Определите форму лимита.2} % = \ frac {\ red 1} {0} \ qquad \ left (\ frac {\ red n} {0} \ mbox {form} \ right) $$

Поскольку ограничение имеет форму $$ \ frac {\ red n} {0} $$, мы знаем, что ограничение не существует. Однако это все еще может быть бесконечный предел.

Шаг 2

Изучите левый предел.2} = \ infty $$

Шаг 3

Изучите правый предел. 2 $$, он будет положительным.2} = \ infty $$

Шаг 4

Заключение

Оба односторонних предела говорят нам, что функция бесконечно растет в положительном направлении. Поскольку односторонние пределы указывают на одно и то же поведение, предел бесконечен.2} = \ infty $$

Пример 2

Вычислить: $$ \ displaystyle \ lim_ {x \ to 3} \, \ frac 1 {x-3} $$

Шаг 1

Определите форму лимита.

$$ \ displaystyle \ lim_ {x \ to 3} \, \ frac 1 {x-3} = \ frac 1 {3-3} = \ frac {\ red 1} {0} $$

Предел не существует, поскольку он имеет форму $$ \ frac {\ red n} {0} $$. Это также может быть бесконечный предел.

Шаг 2

Изучите левый предел.-} \, \ frac 1 {x-3} = – \ infty $$

Шаг 3

Изучите правый предел.

1. Числитель всегда положительный.
2. Знаменатель будет положительным, так как $$ x> 3 $$.+} \, \ frac 1 {x-3} = \ infty $$
   Шаг 4

   Заключение

   Поскольку односторонние ограничения разные, ограничения не существует.

   Ответ: $$ \ displaystyle \ lim_ {x \ to 3} \, \ frac 1 {x-3} $$ не существует.2-4 (2) +4} % = \ frac {\ red {-3}} {0} $$

   Предела не существует, но он может быть бесконечным. 2-4x + 4} = – \ infty $$

   Ошибка: Нажмите «Не робот», затем повторите попытку.

   Формальное определение лимита

   Формальное определение лимита

   К концу этой лекции вы должны быть в состоянии формально определить, что такое предел, используя точный математический язык, и использовать этот язык для объяснения расчетов пределов и графиков, которые мы выполнили в предыдущих разделах.

   До сих пор мы работали с неформальным определением лимита:

   Предел (неофициальное определение)

   Если f (x) в конечном итоге становится на все ближе и ближе к определенному значению L, поскольку x приближается к выбранному значению c из справа , то мы говорим, что предел f (x) как x подходит к c справа – это L .

   Если f (x) в конечном итоге становится на все ближе и ближе к определенному значению L, поскольку x приближается к выбранному значению c из слева , то мы говорим, что предел f (x) как x подходит к c слева – это L .

   Если предел f (x) при приближении x к c одинаков как справа, так и слева, то мы говорим, что предел f (x) при приближении x к c равен L .

   Если f (x) никогда не приближается к определенному конечному значению, поскольку x приближается к c , то мы говорим, что предел не существует .Если f (x) имеет разные правый и левый пределы, то двусторонний предел ( lim _{x → c} f (x) ) не существует .

   Обозначение:
   Конкретно пишем:

   • lim _{x → c-} f (x) = L , чтобы обозначить «предел f (x), когда x приближается к c слева, это L »

   • lim _{x → c +} f (x) = L для обозначения «предела » f (x) при приближении x к c слева составляет L “

   • lim _{x → c} f (x) = L для обозначения «предела » f (x) при приближении x c равно L »

   Однако это определение неформальное , потому что мы официально не определили, что мы подразумеваем под «подходами» или «в конечном итоге становится все ближе и ближе к».Чтобы придумать формальное определение, нам нужно будет уточнить, когда мы можем сказать, что x или f (x) приближаются к определенному значению. Мы делаем это сейчас, давая формальное математическое определение:

   Предел (формальное определение)

   Конечные ограничения:

   Если f (x) – это функция, которая определена на открытом интервале около x = c , а L – действительное число, то

   lim _{x → c} f (x) = L

   означает, что:

   Для любого числа ε> 0, которое мы выберем, можно найти другое число δ> 0, так что:

   для всех x между c-δ и c + δ (за исключением, возможно, c точно ), f (x) будет находиться между L-ε и L + ε.

   Другими словами, если мы выберем интервал на оси y вокруг L, мы всегда сможем найти интервал на оси x- вокруг c , который заставит f (x) оставаться с выбран диапазон y -значений (за исключением, пожалуй, f (c) ). Вероятно, лучше всего это понять, посмотрев на график:

   Если нам нужно формальное определение того, что означает неограниченное увеличение или уменьшение лимита, мы также можем адаптировать этот подход к этому случаю:

   Бесконечные лимиты:

   Если f (x) – функция, которая определена на открытом интервале около x = c , то

   lim _{x → c} f (x) = + ∞

   означает, что:

   Для любого числа M> 0, которое мы выберем, можно найти другое число δ> 0, так что:

   для всех x между c-δ и c + δ (за исключением, возможно, c точно ), f (x) будет больше, чем M.

   Другими словами, если мы выберем значение на оси y вокруг, мы всегда сможем найти интервал на оси x- вокруг c , который заставит f (x) оставаться выше этого значения. (за исключением, возможно, f (c) ). Вероятно, лучше всего это понять, посмотрев на график:

   Мы также можем использовать ту же идею для определения пределов на бесконечности:

   Пределы на бесконечности:

   Если f (x) – функция, а L – действительное число, то

   lim _{x → ∞} f (x) = L

   означает, что:

   Для любого числа ε> 0, которое мы выберем, можно найти другое число M> 0, так что:

   для всех x больше M, f (x) будет находиться между L-ε и L + ε.

   Другими словами, если мы выберем интервал на оси y вокруг L, мы всегда сможем найти значение отсечки на оси x- , которое заставит f (x) оставаться в выбранном диапазоне и -значения, когда он проходит через точку отсечки. Это также, вероятно, лучше всего понять, посмотрев на график:

   Итак, если существует ограничение, должна быть возможность ограничить область около c , что заставит f (x) оставаться в пределах любого выбранного конкретного расстояния L .Давайте посмотрим, как это определение можно применить к примерным расчетам пределов, которые мы сделали в предыдущих лекциях. В случаях, когда предел не существует, мы должны суметь понять, почему δ не существует для всех возможных ε: другими словами, мы должны быть в состоянии найти ε в этих случаях, для которых невозможно найти возможное δ. что заставит f (x) оставаться на расстоянии ε от L.

   Ограничения специальных функций

   Для каждого из следующих примеров мы рассмотрим, как формальное определение предела позволяет нам доказать, что предел существует или что он не существует.Мы делаем это как с помощью графиков, чтобы увидеть, можем ли мы аппроксимировать подходящие значения для δ или M, так и путем проверки, можем ли мы вычислить эти значения точно, подойдя к уравнению алгебраически.

   Простой пример, где

   lim _{x → c} f (x) = f (c) :

   Для этой функции нас интересует предел, поскольку x приближается к 1:

   .

   Мы уже вычислили этот предел графически и алгебраически и определили, что он равен 2.Но теперь мы хотели бы использовать формальное определение лимита, чтобы лучше понять, почему он существует. Для этого мы собираемся найти значение (я) δ, которое будет соответствовать требованиям определения предела для ε = 0,05.

   Чтобы сделать это графически, мы можем переместить ползунок ε на интерактивной анимации ниже, пока он не достигнет 0,05. Затем мы можем перемещать ползунок δ до тех пор, пока не появятся пунктирные зеленые линии, которые представляют часть графика, где все точки находятся в пределах δ-расстояния или меньше от x = 1.Как только эти зеленые пунктирные вертикальные линии будут достаточно близко друг к другу, чтобы гарантировать, что все f (x) между ними остаются внутри красной заштрихованной части графика, мы нашли δ, которое будет удерживать f (x) на расстоянии от ε предела 2. При приблизительно каком значении δ вертикальные зеленые пунктирные линии удерживают график f (x) внутри красной части графика?

   ε

   δ

   Взаимодействуя с анимацией, вы должны были обнаружить, что δ = 0.0248, или что-то близкое к нему, кажется достаточно малым, чтобы гарантировать, что f (x) останется на расстоянии 0,05 от предела 2.

   Теперь, чтобы сделать это алгебраически, мы начнем с ограничения f (x) с помощью L-ε слева и L + ε справа, а затем решим это неравенство для x . Это позволяет нам определить, какие значения x позволят нам удерживать f (x) на расстоянии ε от предела 2:

   .

   Итак, если x остается в пределах 0.025 расстояние c = 1, f (x) останется на расстоянии 0,05 от L = 2. (Конечно, любое значение δ меньше 0,025 также будет работать!)

   Пример с отверстием

   x = c:

   Нас снова интересует предел, поскольку x приближается к -2, и мы помним из последних нескольких лекций, что предел в этом случае равен -4. В этой задаче давайте поищем δ, которое будет работать при ε = 0,02.

   Для начала мы попытаемся найти δ графически, взаимодействуя с анимацией ниже, которая даст нам приблизительное значение:

   ε

   δ

   Взаимодействуя с анимацией, я получил значение около 0.0206 для δ. Что ты получил?

   Теперь решаем алгебраически относительно δ, чтобы получить точное значение:

   Пример с функцией, имеющей разрыв скачка при

   x = c , состоящий из одной точки :

   Нас снова интересует предел, поскольку x приближается к -2, и мы помним из последних нескольких лекций, что предел в этом случае равен -4. В этом примере мы снова ищем δ, которое работает при ε = 0.02.

   Сначала мы стремимся оценить δ графически, используя анимацию ниже:

   ε

   δ

   Мы замечаем, что эта проблема на самом деле ничем не отличается от предыдущей: единственная разница здесь заключается в том, что в то время как на предыдущем графике была дыра x = 2, тогда как на этом графике, помимо этой дыры, есть изолированная точка в (-2,1). Но это не влияет на лимит, потому что лимит не имеет отношения к тому, что происходит при x = c , а только к тому, что происходит около x = c .Таким образом, в этом случае наше предыдущее значение δ = 0,02 все еще будет работать, даже если точка (-2,1) находится не в пределах 0,02 от -4. Мы должны точно исключить этот момент, глядя на предел по определению.

   В следующем примере мы будем использовать формальное определение предела для оценки односторонних пределов, и прежде чем мы это сделаем, мы хотим кратко представить часть обозначений, которые мы будем использовать:

   Замечание: L _L и L _R

   Мы будем использовать обозначение L _R для обозначения предела, рассчитанного как x , приближается к c справа, и мы будем использовать обозначение L _L для обозначения предела, рассчитанного как x , приближается к c слева.

   Пример с функцией, которая имеет разрыв скачка при

   x = c и разные пределы справа и слева:

   Здесь нас интересует предел x → 1, и мы будем стремиться найти δ, удовлетворяющее формальному определению предела для ε = 0,1. Поскольку это кусочная функция с разрывом скачка при x = 1, сначала рассмотрим предел отдельно справа и слева:

   Сначала мы рассматриваем предел справа, который мы уже вычислили в предыдущей лекции, как 2.Сначала мы оценим его графически, используя интерактивную анимацию ниже, а затем вычислим его алгебраически.

   ε

   δ

   Используя ползунки для установки ε на 0,1, а затем перемещая ползунок для δ, пока зеленая пунктирная линия справа не удержит график f (x) слева от x = 1 в пределах красной заштрихованной области , Я получил аппроксимацию δ из графика, которая составила 0,0777. Что ты получил?

   Теперь, вычисляя алгебраически δ для правого предела:

   Теперь мы считаем предел слева, который мы уже вычислили в предыдущей лекции, как -2.Мы снова начнем с графической оценки, используя приведенную ниже анимацию, а затем вычислим ее алгебраически.

   ε

   δ

   Используя ползунки для установки ε на 0,1, а затем перемещая ползунок для δ, пока зеленая пунктирная линия слева не удержит график f (x) слева от x = 1 в пределах красной заштрихованной области , Я получил аппроксимацию δ из графика, которая составила 0,037. Что ты получил?

   Перейдем к алгебраическому вычислению значения δ для левого предела:

   Теперь рассмотрим двусторонний предел.Если мы попытаемся использовать формальное определение предела со значением ε = 0,1, мы столкнемся с проблемой: мы не можем выбрать любое δ, которое всегда будет удерживать f (x) на расстоянии ε от левого предела. -2 слева, потому что независимо от того, насколько маленьким мы сделаем наше δ, всегда будет кусок графика справа от x = 1, где f (x) выпадает далеко за пределы области, которая расстояние ε или меньше от левого предела. Точно так же мы не можем выбрать любое δ, которое всегда будет удерживать f (x) на расстоянии ε от правостороннего предела 2, потому что независимо от того, насколько маленьким мы сделаем наше δ, всегда будет немного графа, чтобы слева от x = 1, где f (x) находится далеко за пределами области, которая находится на расстоянии ε или меньше от правого предела.

   На самом деле, нам нужно иметь ε равное 4 или больше, чтобы заставить все значений f (x) в окрестности x = 1 находиться в пределах расстояния ε как слева, так и от правильные предельные значения. Но формальное определение гласит, что мы должны быть в состоянии найти δ для ВСЕХ возможных ненулевых вариантов для ε. Итак, если мы сможем найти хотя бы одно ненулевое значение для ε, для которого невозможно δ, мы показали, что предел не существует.

   Пример с функцией, которая имеет бесконечный разрыв (или вертикальную асимптоту) при

   x = c :

   Для этой функции нас интересует предел, поскольку x приближается к 0.Здесь мы видим, что мы не сможем найти δ для любого ε в этом случае, которое будет работать для конечного предела, потому что f (x) здесь неограниченно возрастает, поскольку x приближается к 0 с любой стороны. Итак, в этом случае мы будем использовать формальное определение бесконечных пределов, чтобы найти значение для δ, когда M = 100.

   Начнем с аппроксимации δ графически: с помощью ползунков на интерактивной анимации ниже.

   M

   δ

   Я получил приблизительное значение 0.095. Что ты получил?

   Теперь решаем относительно δ алгебраически:

   Пример с функцией, которая имеет бесконечный разрыв (или вертикальную асимптоту) при

   x = c, с различным поведением предела слева и справа:

   Для этой функции нас интересует предел, поскольку x приближается к 1. Давайте теперь посмотрим, сможем ли мы найти подходящее значение δ для M = 40 с правой стороны и соответствующее значение δ для M = -40 с левой стороны. , сначала используя график для аппроксимации значения:

   M

   δ

   M

   δ

   И для левого, и для правого я получил значение δ = 0.026, используя ползунки интерактивных анимаций выше. Что ты получил?

   Теперь вычислим δ точно алгебраически. Сначала мы начнем с определения того, какое значение δ сохранит f (x) выше M (в правой части).

   Теперь мы вычисляем, какое значение δ будет поддерживать f (x) ниже -40 (в левой части).

   Мы снова можем видеть, почему в этом случае не существует двустороннего предела, потому что не существует возможного δ, которое мы могли бы выбрать, которое удерживало бы все значения f (x) выше 40 (потому что всегда было бы какое-то значения слева от x = 1 включены, и все они отрицательны), независимо от того, насколько мало δ.Мы столкнулись бы с аналогичной проблемой с положительными значениями f (x) справа от 1, если бы попытались найти δ, которое работает для двустороннего предела, когда M = 40 (потому что всегда будут некоторые значения справа от x = 1 включено, и все они положительные).

   Пример с функцией, имеющей предел нуля на бесконечности:

   Для этой функции нас интересует предел, когда x приближается к -∞, и предел, когда x приближается к + ∞.Мы будем искать значения M, которые удовлетворяют формальному определению предела, когда ε равно 0,45. Из-за относительной сложности этого конкретного уравнения мы будем оценивать значения M только графически, а не проверять их алгебраически в этом случае. Используйте ползунки в интерактивной анимации ниже, чтобы найти M для ε = 0,45 для обоих пределов:

   ε

   M

   Рассматривая предел, когда x приближается к -∞, мы получаем значение M, равное примерно 4.4, и глядя на предел, когда x приближается к + ∞, мы получаем значение M, которое составляет приблизительно 4,35.

   Пример с функцией, предел которой не существует на бесконечности:

   Мы рассматриваем предел этой функции, когда x приближается к + ∞, и мы рассматриваем, можем ли мы найти M для ε = 0,5. Опять же, для этой проблемы, поскольку уравнение относительно сложное, мы используем анимацию для аппроксимации значений M, а не пытаемся найти M алгебраически.Попробуйте поэкспериментировать с ползунками ниже, чтобы увидеть, сможете ли вы найти значение M, которое сохранит значения f (x) в красной заштрихованной области для всех x > M.

   ε

   M

   Мы видим, что в этом примере никогда не удастся найти такое M, потому что по мере неограниченного увеличения x f (x) также неограниченно увеличивается. Независимо от того, какое значение мы выберем для M, мы никогда не сможем удержать график f (x) в пределах красной заштрихованной области.

   Пример функции с колеблющимся разрывом:

   Мы рассматриваем предел этой функции, поскольку x приближается к 1, и мы стремимся найти δ, которое удовлетворяет формальному определению предела для ε = 0,5. Это еще одна проблема, когда мы просто будем смотреть на график, чтобы попытаться найти δ, а не пытаться найти δ алгебраически. Глядя на анимацию ниже, потратьте некоторое время на эксперименты с ползунками, чтобы увидеть, сможете ли вы найти δ для ε = 0.5 для одностороннего или двустороннего ограничения при x = 1.

   ε

   δ

   ε

   M

   Вы, возможно, заметили, что невозможно найти такое δ, потому что независимо от того, насколько маленькое δ вы выберете, всегда будет какая-то часть графика внутри пунктирных зеленых линий, которая колеблется от 1 до -1. . Таким образом, не существует такого значения, которое удерживало бы график f (x) внутри красной заштрихованной области, и мы можем видеть, как формальное определение предела показывает нам, что этого предела не существует.

   В поисках предела – Бесплатная справка по математике

   Что такое лимит?

   Предел – это определенное значение, к которому приближается функция. Поиск предела обычно означает определение значения y, когда x приближается к определенному числу. Вы обычно можете сформулировать это как что-то вроде «предел функции f (x) равен 7, когда x приближается к бесконечности. Например, представьте себе такую ​​кривую, когда x приближается к бесконечности, эта кривая приближается к y = 0, в то время как никогда на самом деле добираюсь туда.Итак, как нам алгебраически найти этот предел? Один из способов найти предел – использовать метод замены .

   Например, предел следующего графика равен 0, когда x приближается к бесконечности, что ясно видно, когда график приближается к 0, вот так:

   Теперь давайте рассмотрим несколько примеров, где мы можем найти предел реальных функций:

   Пример A

   Найдите предел \ (f (x) = 4x \), когда x стремится к 3.

   Шагов:

   1) Заменить x на 3.
   2) Упростите.2-7x} {x} = \ frac {x (6x-7)} {x} = 6x-7 $$

   Мы отменили множитель x в числителе и знаменателе, оставив нам простой предел:

   $$ \ lim_ {x \ to0} (6x-7) $$

   Теперь мы можем заменить x на 0, чтобы найти предел -7:

   $$ \ lim_ {x \ to0} (6x-7) = -7 $$

   Примечание.