Числовой ряд — Википедия
Числовой ряд — одно из центральных понятий математического анализа. Ряд записывается как бесконечная сумма[1]:
- a1+a2+a3+…+an+…{\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{n}+\ldots }; краткая запись: ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Здесь a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.
Чтобы присвоить такому ряду числовое значение, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:
- S1=a1{\displaystyle S_{1}=a_{1}}
- S2=a1+a2{\displaystyle S_{2}=a_{1}+a_{2}}
- S3=a1+a2+a3{\displaystyle S_{3}=a_{1}+a_{2}+a_{3}}
- ⋯{\displaystyle \cdots }
- Sn=a1+a2+a3+⋯+an
ru.wikipedia.org
Как найти сумму ряда: примеры решений, определение
Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:
$$ \frac{1}{(2n+1)(2n+3)} = \frac{A}{2n+1} + \frac{B}{2n+3} = \frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$
Приравниваем числитель последней дроби к числителю первой дроби:
$$ A(2n+3)+B(2n+1) = 1 $$
Раскрываем скобки:
$$ 2An + 3A + 2Bn + B = 1 $$
Теперь определяем находим неизвестные коэффициенты:
$$ \begin{cases} n^0: &2A+2B=0 \\ n^1: &3A+B=1 \end{cases}\Rightarrow \begin{cases} A=\frac{1}{2} \\ B=-\frac{1}{2} \end{cases} $$
После разложения общий член ряда записывается следующим образом:
$$ a_n =\frac{1}{(2n+1)(2n+3)}=\frac{1}{2} \frac{1}{2n+1} – \frac{1}{2} \frac{1}{2n+3} $$
Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$
$$ a_1 = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}\bigg ) $$
$$ a_2 = \frac{1}{2} \bigg (\frac{1}{5}-\frac{1}{7}\bigg ) $$
$$ a_3 = \frac{1}{2} \bigg (\frac{1}{7}-\frac{1}{9}\bigg ) $$
$$ …………………………………. $$
$$ a_{n-1}=\frac{1}{2} \bigg (\frac{1}{2n-1}-\frac{1}{2n+1} \bigg ) $$
$$ a_n = \frac{1}{2} \bigg (\frac{1}{2n+1}-\frac{1}{2n+3} \bigg ) $$
| Замечание |
Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок. |
Итого, получаем:
$$ S_n = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}\bigg ) + \frac{1}{2} \bigg (\frac{1}{5}-\frac{1}{7}\bigg ) + \frac{1}{2} \bigg (\frac{1}{7}-\frac{1}{9}\bigg ) + … $$
$$ … + \frac{1}{2} \bigg (\frac{1}{2n-1}-\frac{1}{2n+1} \bigg ) + \frac{1}{2} \bigg (\frac{1}{2n+1}-\frac{1}{2n+3} \bigg ) = $$
Выносим дробь одну вторую $ \frac{1}{2} $ за скобки:
$$ = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9} … + $$
$$ + … \frac{1}{2n-1} – \frac{1}{2n+1} + \frac{1}{2n+1} – \frac{1}{2n+3} \bigg) = $$
Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:
$$ S_n = \frac{1}{2}\bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) $$
Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:
$$ S=\lim_{n\to\infty} S_n = \lim_{n\to\infty} \frac{1}{2}\bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) = $$
$$ = \frac{1}{2} \lim_{n\to\infty} \bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} $$
xn--24-6kcaa2awqnc8dd.xn--p1ai
∑ Сумма ряда онлайн
Введите данные для подчета суммы ряда
Найдем сумму ряда чисел. Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Сходимость ряда
Данный калькулятор умеет определять – сходится ли ряд, также показывает – какие признаки сходимости срабатывают, а какие – нет.
Также умеет определять сходимость степенных рядов.
Также строится график ряда, где можно увидеть скорость сходимости ряда (или расходимости).
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число – “Пи”, которое примерно равно 3.14
- sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- – умножение
- 3/x
- – деление
- x^3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
www.kontrolnaya-rabota.ru
Сумма ряда
Ряд
имеет общий членипоследовательность частичных суммРяд (1.2.1) называют сходящимся к числуS, если.
Следствие теоремы о пределе монотонной последовательности.Ряд с неотрицательными слагаемыми сходится тогда и только тогда, когда последовательность частичных сумм ограничена сверху.
Число е
Теорема 1.Предел последовательностисуществует и заключен между числами 2 и 3.
Доказательство. Обозначим . Если вычислять значения последовательности, то видим, что
Видим, что эта последовательность возрастает. Докажем этот факт. Используя бином Ньютона, получим:
При переходе к следующему члену последовательности каждый из сомножителей 1-k/n в правой части (1) увеличивается, а кроме того, добавляется еще одно (n+2)-е слагаемое. Итак, доказано, что, т.е. последовательностьмонотонно возрастает. Далее, если ограничить сверху каждый из сомножителей 1-k/n единицей, а 1/k! ограничить сверху, то
Итак, последовательность монотонно возрастает и ограничена сверху числом 3, следовательно, по аксиоме о пределе монотонно возрастающей и ограниченной сверху последовательности эта последовательность имеет предел, причем он меньше либо равен 3 по свойству ПР7.
Так как , то по свойству ПР7 следует, что это предел больше либо равен 2.□
Определение. Предел последовательностиобозначают e и называютоснованием натуральных логарифмов или числом е.
Приближенное значение e≈2.718281828 (1828 — год рождения Л.Н. Толстого). Чаще всего пользуются приближением e≈ 2.7.
Теорема 2.
Доказательство. Оценку (2) можно применить и к частичным суммам . Отсюда следует ограниченность сверху последовательности, значит она имеет предел, т.е. ряд в (3) имеет сумму. Из формулы (1) следует, что эта сумма больше либо равна. ???
Предел функции
В этом параграфе изучается важнейшее понятие анализа – предел функции.
Примеры
Составим таблицу значений функции при
1.9 | 1.95 | 1.98 | 1.99 | 1.999 | |
3.9 | 3.95 | 3.98 | 3.99 | 3.999 |
Заметим, что значение мы подставить не можем, так как получим неопределенность. Тем не менее, понятно, что значения функцииприближаются к числу 4 по мере того, как значения аргумента приближаются к 2. Это станет совершенно очевидно, после сокращения. Правая часть здесь уже определена прии имеет значение 4. Иными словами, простым алгебраическим преобразованием мы раскрыли неопределенностьи вычислили предел функциипри.
Рассмотрим еще один пример: вычислим предел . Преобразуем
При неограниченном увеличении аргумента знаменательстановиться больше чем любое наперед заданное число. Так как, то получаем нулевое значение предела.
Определение и свойства предела функции.
Интервал называют δ-окрестностью точки(здесь δ >0). Она задается неравенством. Множествоназываютпроколотой окрестностью точки. Она задается неравенством.
Пусть функция определена в некоторой проколотой окрестности точки. Число A называется пределом функциипристремящемся к, если чем ближе подходитктем меньше значение функцииотличается от своего предела. Мерой близостииможно считать. Однако мы не допускаем равенства, ибо функцияможет быть и неопределенной в точке.
Определение.Число A называетсяпределом функции при, если для любого положительного𝜺, найдется число, зависящее от() такое, чтодля всехпринадлежащих проколотой δ-окрестности точки, т.е. таких, что.
Предложение 1.Если предел функции существует, то он единственен.
Доказательство такое же как и для предела последовательности.
Предел функции призаписывают как. Формально,
Теперь приведем определение пределов на бесконечности. Число A называется пределом функции при, если для любого положительного𝜺найдется число C такое, чтодля всехтаких, чтоПредел функциипризаписывают как.
Аналогично, число называется пределом функциипри(), если для любого положительного𝜺найдется C такое, чтодля всех, таких, что.
Иногда приходится рассматривать предел при дополнительных условиях, ограничениях на переменную Например, совершенно ясно, что, ибопри ограничении. Аналогично,. Найденные пределы называются односторонними, первый – предел справа, второй – предел слева. Заметим, что «двустороннего» предела функцияприне имеет.
Число A называется пределом функции пристремящемся к справа, если для любого положительного𝜺найдется δ =δ (𝜺)>0 такое, чтодля всехтаких, что.
Предел функции присправа записывают как.
Число A называется пределом функции при стремящемся к слева(записываем как), если для любого положительного𝜺найдется δ =δ (𝜺)>0 такое, чтодля всехтаких что
Предложение 2.Предел функции существует тогда и только тогда, когда существуют оба односторонних предела, причем они совпадают.
Доказательство. Пусть . Тогда длянайдутсятакие, чтодля всехтаких чтои для всехтаких что. Взяв, получим, что неравенствовыполняется для всехиз проколотой-окрестности точки. В обратном направлении утверждение есть очевидная тавтология.
Предел функции и предел последовательности связаны между собой как показывает следующее утверждение.
Теорема 1.Пустьи– функция, определенная в проколотой окрестности точки. Тогда пределсуществует и равен A в том и только том случае, когда для любой последовательноститочек сходящихся ки отличных от, последовательность значенийсходится к A.
Доказательство. Пусть ) и– последовательность, сходящаяся к, причем для любогоnне равно. Возьмем какое-либо положительное𝜺и найдем для него δ >0 такое, чтокак только. Так как, то найдется номер N такой, что для всех n>N имеет место неравенство. Тогда. Это значит, что.
Наоборот, пусть равенство не имеет места. Тогда
Взяв здесь последовательность , сходящуюся к нулю и выбрав для нее соответствующие, получим последовательность, причем для любого n имеет место неравенство, поэтому пределне равенA.□
studfiles.net
Предел последовательности — Википедия
Материал из Википедии — свободной энциклопедии
| n | n sin(1/n) |
|---|---|
| 1 | 0.841471 |
| 2 | 0.958851 |
| … | |
| 10 | 0.998334 |
| … | |
| 100 | 0.999983 |
С ростом значения n значение функции n sin(1/n) приближается к 1. Говорят, что «предел последовательности n sin(1/n) равен 1».
У этого термина существуют и другие значения, см. Предел.В математике пределом последовательности элементов метрического пространства или топологического пространства называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементов топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. В метрическом пространстве окрестности определяются через функцию расстояния, поэтому понятие предела формулируется на языке расстояний. Исторически первым было понятие предела числовой последовательности, возникающее в математическом анализе, где оно служит основанием для системы приближений и широко используется при построении дифференциального и интегрального исчислений.
Обозначение: limn→∞xn=a{\displaystyle \lim _{n\to \infty }x_{n}=a}
(читается: предел последовательности икс энное при эн, стремящемся к бесконечности, равен a[1][2])
Свойство последовательности иметь предел называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательность сходится; в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. В хаусдорфовом пространстве и, в частности, метрическом пространстве[3], каждая подпоследовательность сходящейся последовательности сходится, и её предел совпадает с пределом исходной последовательности. Другими словами, у последовательности элементов хаусдорфово пространства не может быть двух различных пределов. Может, однако, оказаться, что у последовательности нет предела, но существует подпоследовательность (данной последовательности), которая предел имеет. Если из любой последовательности точек пространства можно выделить сходящуюся подпоследовательность, то, говорят, что данное пространство обладает свойством секвенциальной компактности (или просто компактности, если компактность определяется исключительно в терминах последовательностей).
В топологических пространствах, удовлетворяющих первой аксиоме счётности, понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке. Для произвольных топологических пространств такой последовательности может не существовать.
ru.wikipedia.org
Предел последовательности. Арифметические действия над пределами. Предел монотонной последовательности
Поиск ЛекцийЛекция 1. Последовательность и ее предел. Теоремы о пределах. Предел монотонной последовательности. Числовые ряды, их сходимость и расходимость. Действия со сходящимися рядами. Признак Коши сходимости рядов. Необходимый признак сходимости ряда. Знакоположительные ряды. Признаки сравнения, Даламбера и Коши
На предыдущих лекциях подробно изучались функции непрерывного аргумента, их пределы и свойства пределов. В теории рядов фундаментальную роль играют последовательности (т.е. функции дискретного аргумента) и их пределы. Перейдем к изучению соответствующего теоретического материала.
Предел последовательности. Арифметические действия над пределами. Предел монотонной последовательности
Последовательностью называется функция натурального аргумента. При этом называется общим членом, а множество областью определения последовательности
Например, последовательность, называе-
мая арифметической прогрессией ( постоянные, не зависяшие от ). Другой пример: Здесь областью определения является множество
Определение 1.Число называется пределом последовательности при если [1] При этом пишут и если этот предел существует и конечен, то говорят, что последовательность сходится; в противном случае она называется расходящейся последовательностью.
Перечислим основные свойства предела последовательности.
1. Если предел существует, то он единственный.
2. Если в последовательности отбросить любое конечное число членов или заменить их на любые другие числа, то новая последовательность и старая последовательность будут одновременно расходиться или сходиться (к одному и тому же пределу ).
Из этого свойства вытекает, что, не умоляя общности, можно считать, что последовательность определена при всех
3. Если предел существует и конечен, то последовательность ограничена, т.е.
4. Если пределы существуют и конечны, то сущес-
твуют и пределы
Если при этом то существует и предел частного
5(критерий Коши сходимости). Для того чтобы существовал конечный предел необходимо и достаточно, чтобы
6. При любом фиксированном последовательности и одновременно сходятся или одновременно расходятся, причем в случае сходимости они имеют один и тот же предел
7.Если последовательность не убывает (т.е. если )и ограничена сверху (т.е. ), то она имеет конечный предел Аналогичное утверждение верно и для невозрастающей и ограниченной снизу последовательности
Определение 2.Последовательность называется бесконечно малой, если При этом пишут Две бесконечно малые последовательности и называются эквивалентными, если . При этом пишут
8. Для того чтобы существовал (конечный) предел необходи-
мо и достаточно, чтобы имело место представление
9. Если то
При вычислении пределов последовательности часто используется следующая таблица эквивалентных бесконечно малых.
Таблица 1.
Если при то при верны следующие соотношения:
.
10)
Например, при вычислении предела 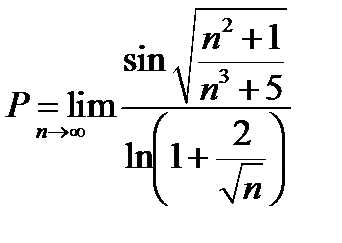 заменяем ,
заменяем ,
Будем иметь 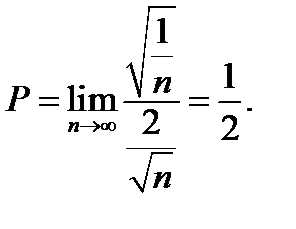
2.Числовые ряды, их сходимость и расходимость. Действия со сходящимися рядами. Признак Коши сходимости. Необходимое условие сходимости ряда. Признаки сходимости для знакоположительных рядов
Мы переходим к изучению бесконечных сумм, называемых рядами. Дадим их точное определение и придадим им здравый математический смысл.
Определение 3. Формальная сумма бесконечного числа слагаемых (чисел), называется числовым рядом. При этом конечная сумма называется й частичной суммой этого ряда, его общим членом, а сумма м остатком этого ряда.
Определение 4. Говорят, что ряд сходится к сумме если существует конечный предел последовательности его частичных сумм. При этом пишут Если указанный предел либо не существует, либо равен бесконечности, то говорят, что ряд расходится.
На языке “ ” это определение записывается так:
Ряд сходится к сумме
Важный пример.Рассмотрим ряд
(геометрическая прогрессия).
Здесь: знаменатель, первый член прогрессии. Вычислим частичную сумму
Отсюда видно, что если то Если или то Если же то Эта последовательность не имеет предела при Согласно определению 4 получаем, что при прогрессия (1) сходится к сумме а при она расходится.
Применяя свойство 2, сформулированное выше, к последовательности частичных сумм ряда , приходим к выводу, что на сходимость (расходимость) этого ряда не влияет его любое конечное число членов; их можно отбросить или заменить на другие числа. Вновь полученный ряд будет вести себя в смысле сходимости расходимости так же, как и исходный ряд.
Из свойства 4, примененного к частичным суммам сходящихся рядов
вытекает следующее утверждение.
Теорема 1.Если ряды (2) и (3)сходятся к суммам и соответственно, то при любых значениях постоянных и сходится и ряд причем
Эта теорема показывает, что сходящиеся ряды подчиняются тем же арифметическим законам, что и конечные суммы. Применяя свойство 5 к последовательности частичных сумм ряда (2), получим следующий критерий Коши сходимости для рядов:
10. Для того чтобы ряд (2) сходился, необходимо и достаточно, чтобы
Применим этот критерий для доказательства необходимого признака сходимости ряда.
Теорема 2.Если ряд сходится, то его общий член стремится к нулю, т.е.
Доказательство.Так как указанный ряд сходится, то для его частичных сумм справедлив признак Коши10, который при переходит в высказывание
Это высказывание означает, что а, следовательно Теорема доказана.
Замечание 1. Утверждение, обратное к теореме 1, вообще говоря, не верно. Например, ниже будет показано, что так называемый гармонический ряд расходится. Однако его общий член при Полезность необходимого признака заключается в том, что если общий член при то ряд заведомо расходится. Например, ряды расходятся, так как их общие члены не стремятся к нулю при
Используя критерий Коши сходимости 10, нетрудно доказать также следующее утверждение.
11. Если остаток при каком-нибудь сходится, то и сходится сам ряд Обратно: если сходится ряд то при любом сходится и любой его остаток причем
Кстати, из этой теоремы также вытекает, что на сходимость (расходимость) ряда не влияет любое конечное число его членов. Ниже будет использоваться следующее очевидное утверждение.
11. Какова бы ни была постоянная ряды сходятся или расходятся одновременно.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Предел последовательности – Энциклопедия по экономике
Вторая теорема о полноте. Анализ примера 5.1 показывают, что если конус К не является открытым множеством, то при небольшом изменении этого конуса соответствующее ему множество недоминируемых точек может изменяться значительно. Однако если ограничиться отношениями предпочтения с открытыми конусами, то множество недоминируемых точек относительно произвольного отношения, удовлетворяющего всем указанным в теореме 5.1 свойствам, может быть получено как предел последовательности множеств недоминируемых точек относительно некоторых конусных отношений, построенных на основе набора машинно реализуемой информации об относительной важности критериев. Точнее говоря, имеет место следующий результат. [c.141]Глава 3 Предел последовательности [c.43]
Таким образом, с течением времени цена на товар падает и приближается к единице. Единицу именуют пределом последовательности изменения цены товара. А [c.44]
В определении сходимости и предела последовательности нет ясного указания на то, как проверять сходимость и как находить предел. Поэтому для вычисления пределов используются специальные критерии. Этим критериям и посвящен следующий параграф. [c.47]
Для третьей последовательности из примера 1 показатель степени а = 1 > 0, поэтому предел последовательности равен нулю [c.49]
Таким образом, под суммой бесконечного геометрического ряда мы понимаем предел последовательности его частичных сумм. [c.53]
Определение. Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм — этот предел называется суммой ряда в противном случае ряд называется расходящимся. [c.54]
Таким образом, сумма бесконечного ряда получается не в результате суммирования всех членов, а как предел последовательности частичных сумм ряда. Понимание суммы ряда как суммирования всех его членов приводит к недоразумениям. Например, что считать суммой ряда [c.54]
Существует другое определение предела функции, в котором не используется понятие предела последовательности. [c.58]
Множество Ga по построению выпукло и замкнуто. Слабый предел последовательности, принадлежащей выпуклому замкнутому множеству, также принадлежит этому множеству. Следовательно, С .G”, a= I,. .. [c.326]
Принципиальная простота осуществленного в доказательстве теоремы из п. 10.1 третьего из этих этапов не должна вводить нас в заблуждение. Соответствующее доказательство является весьма неконструктивным (“неэффективным”), и взятое само по себе никаких методов нахождения оптимальных стратегий игроков, как пределов последовательностей их е-опти-мальных стратегий, не дает. [c.116]
Бесконечно большие и бесконечно малые числовые последовательности и их свойства. Арифметические операции с пределами последовательностей. Предельный переход в неравенстве. [c.13]
Значение сцепленного индекса, вообще говоря, зависит от разбиения интервала сопоставления и, в частности, от величины шага по времени. Шаг по времени является параметром метода, следовательно, результат измерения может зависеть от параметра метода измерения, подобно тому, как если бы результат измерения длины существенно зависел от выбора линейки. Это – плохо. Возникает естественный вопрос существует ли предел последовательности сцепленных индексов при уменьшении шага по времени до нуля, и если существует, то зависит ли он от выбора индексной формулы, используемой на шаге по времени сцепленного индекса Если окажется, что такой предел существует и не зависит от выбора индексной формулы (во всяком случае, среди формул некоторого множества), то именно его имело бы смысл считать результатом измерения, а сцепленные индексы – его аппроксимациями. [c.130]
Пределом последовательности Mk , Af R”, называется n-мерная точка М,0, если каждая е-окрестность точки М0 содержит все члены данной последовательности начиная с некоторого номера, т. е. для любого е>0 должен существовать номер /С (зависящий от е) такой, что Mk g Se (Mо) при всех Ik > /С. [c.79]
Если М0 является пределом последовательности Mk , то пишут Ма= lim Mt или Mk— М0 при k—>-e . [c.79]
При отыскании предела последовательности п-мерных точек (га 2) важную роль играет предел числовой последовательности, так как им е ют место следующие два утверждения [c.79]
ОСНОВНЫЕ ФАКТОРЫ, УЧИТЫВАЕМЫЕ В ПРОЦЕССЕ ПРИНЯТИЯ РЕШЕНИЯ О ЗАКУПКАХ. Наименьшее число решений приходится на долю покупателя, совершающего повторную закупку без изменений, наибольшее – в ситуациях закупок для решения новых задач. При совершении закупок для решения новых задач покупателю предстоит определить для себя 1 технические характеристики товара, 2) пределы цен, 3) время и условия поставки, 4) условия технического обслуживания, 5) условия платежа, 6) размер заказа, 7) приемлемых поставщиков и 8) избранного поставщика. На каждое решение оказывают влияние разные задействованные в этом процессе лица, а последовательность принятия решений меняется от случая к случаю. [c.228]
ЗАПРОГРАММИРОВАННЫЕ РЕШЕНИЯ. Нобелевский лауреат Герберт Саймон использовал термин запрограммированные, заимствованный из языка компьютерной технологии, для описания решений в высокой мере структурированных. ЗАПРОГРАММИРОВАННОЕ РЕШЕНИЕ есть результат реализации определенной последовательности шагов или действий, подобных тем, что предпринимаются при решении математического уравнения. Как правило, число возможных альтернатив ограничено и выбор должен быть сделан в пределах направлений, заданных организацией. [c.196]
Решения о месторасположении предприятий обычно идут от общего к частному. Предположим, что изготовитель бытовой электронной аппаратуры решает вопрос о размещении завода по производству проигрывателей компакт-дисков. При принятии решения будут последовательно рассмотрены следующие вопросы на каком континенте строить завод, в какой стране, в каком штате или в какой провинции, в каком городе, на какой площадке или в каком существующем здании. Конечно, не во всех случаях нужно рассматривать все эти уровни. Транспортной полиции шт. Джорджия, естественно, нет никакой необходимости рассматривать возможность расположения своего офиса за пределами своего штата. [c.611]
Метод контроля технологического процесса можно использовать как в сфере предоставления услуг, так и в сфере производства. Пример карты технологического контроля приведен на рис. 21.9. В течение дня в произвольные моменты из процесса отбирают три пробы. В данном случае считается, что процесс нарушен, если три из пяти последовательных образцов вышли за пределы допустимых отклонений. [c.639]
Далее последовательно по каждой операции, установке, агрегату указываются основные параметры обработки (в зависимости от используемого оборудования и вида процесса — прерывного или непрерывного) время, температура, давление, концентрация и др., соблюдение которых строго необходимо. Для ряда параметров указываются пределы их допустимых отклонений. [c.47]
Сложные производственные процессы состоят из нескольких простых, именуемых частичными, т. е. включают несколько последовательно протекающих основных технологических процессов, взаимосвязанно совершаемых в пределах одного производственного подразделения завода, например на одной комбинированной установке. [c.14]
В пределах ремонтного цикла имеют место техническое обслуживание и текущий ремонт, которые проводятся в определенном составе, объеме и последовательности через отрезки времени, регламентированные структурой ремонтного цикла. Время между двумя очередными текущими ремонтами или плановыми техническими обслуживаниями называют межремонтным периодом соответственно текущего ремонта или планового технического обслуживания. [c.86]
На основе анализа организационно-технических условий производства проектируется нормаль производственного процесса, которая должна содержать следующие основные данные структуру и содержание операций последовательность и методы исполнения операций режим работы оборудования схему элементов работ и рабочих мест с указанием расположения оборудования, приспособления, инструментов и материалов у рабочего места обоснование состава бригады и распределения труда между отдельными исполнителями требования по технике безопасности в пределах рабочего места. [c.170]
Несколько иной оттенок имеет понятие качества в технической практике. Здесь принято считать более качественной продукцию, отдельные свойства которой превосходят ранее достигнутые в отечественной или зарубежной промышленности. Показателем качества при этом становится мера совершенства конструкции, чистота обработки материала, мощность машины, производительность станка или какой-либо другой чисто технический параметр. Особенность такого понимания качества – его безотносительность к экономическим результатам потребления продукции. Конечно, такой голый техницизм в демонстративной форме в настоящее время почти изжит. К инженерам пришло осознание, что существенны не только сами по себе технические свойства продукта, но, главным образом, то, насколько они удовлетворяют определенную потребность. Поэтому техническое совершенство продукции признается потребителем лишь в той мере, в какой оно повышает степень его удовлетворения при заданном бюджетном ограничении. “Технически качество может быть очень высоким, а экономически – нет”. [З.С.14]. Например, промышленный робот с 10-ю степенями свободы рабочих органов может заменить несколько рабочих сборщиков и сварщиков, но ввиду большой стоимости управляющей системы его применение пока экономически нецелесообразно. Слово “пока” здесь оттеняет важное соображение о том, что экономически целесообразный предел совершенствования технических параметров изделия это всегда вопрос меры, выявляемой оптимизационным расчетом для конкретного этапа жизненного цикла данного изделия. Со временем оптимальное значение любого качественного параметра сдвигается на более высокий уровень в технологически освоенной области. Но такой сдвиг не произволен, а обусловлен взаимодействием комплекса технических, экономических, социальных, демографических, экологических факторов. Стратегия управления качеством во многом опирается на экономически обоснованный факторный прогноз оптимальных величин качественных параметров продукции. Таким образом, будучи принципиально непрерывным и бесконечным, процесс повышения качества представляет известную из диалектики узловую линию мер, т.е. последовательных оптимальных для своего времени ступеней восхождения к совершенству. Это имеет огромное значение. [c.7]
Последовательность уточнения потребности в них может быть показана на примере применения легких металлических конструкций для покрытий производственных зданий. На первом этапе должны быть определены области экономически целесообразного применения всех вариантов этих конструкций (см. табл. 10.3) в каждом территориальном районе строительства при различных расстояниях их перевозки. На втором этапе исходя из потребности в таких конструкциях в пределах каждого района на ближайшие пять лет, местонахождения заводов, их изготовляющих, и средних расстояний от ближайших к объектам железнодорожных станций до этих объектов, определяют экономически целесообразный объем производства легких конструкций сначала по всем районам, а затем суммарно по стране. Наконец, на третьем этапе выявляют в связи с увеличением потребности в новых конструкциях необходимость расширения или реконструкции действующих соответствующих заводов или строительства новых заводов, а также определяют капитальные вложения в эти заводы. [c.199]
С другой стороны, любая точка из N dom У заведомо принадлежит указанному пределу последовательности множеств, так как включения s с С5 + 1 с А влекут Ndom К с Ndom У при всех 5=1,2,… [c.143]
Таким образом, предел последовательности lim ,( ) = sign есть [c.89]
Подпоследовательность. Частичный предел последовательности. Верхний и нижний предел последовательности. Теорема Больцано-Вейерштрасса. Фундаментальные последовательности, критерий Коши. Число е. [c.13]
Точка М является пределом последовательности Mk , M4 R” тогда и только тогда, когда предел числовой последовательности p(Mk, M0) равен нулю (p(Mk, М0)—расстояние между точшамш Mk и М0). [c.79]
Не стоит поэтому удивляться, что, хотя о намерении стабилизировать цены говорили повсюду, но тз ответственность и последовательность, с которыми подошли к этому вопросу государственные органы Японии, не имели равных. Идеи эти прошли через все государственные программы тех лет. Но что наиболее характерно роль государства понималась далеко за пределами обычной для него сферы воздействия на цены, какой являются, скажем, импортные пошлины или косвенные налоги. Коль скоро речь зашла и об этом, надо подчеркнуть, что, несмотря на значительный дефицит госбюджета, правительство старалось не повышать косвенных налогов и но-выйЗ%-ный налог на продажу был введен (и то после большой [c.42]
Генеральный план представляет собой схему территории предприятия с указанием расположения технологических установок, производственных подразделений, транспортных, энергетических и прочих вспомогательных средств, баз снабжения. Основная цель генерального плана — обеспечение технологической последовательности и поточности производства. Технологические установки, связанные между собой, группируют и располагают вблизи друг друга. Установки по производству готовой продукции или полуфабрикатов, идущих на смешение, приближают к товарным паркам. Объекты водо- и энергоснабжения располагают в центральной части предприятия. Остальные объекты подсобно-вспомогательного хозяйства (лаборатории, ремонтную базу, цех КИПиА и др.) приближают к его границе. ТЭЦ, строительную базу, административное здание располагают за пределами предприятия. В генеральном плане четко определяют территорию производственной, складской, товарно-сырьевой и административно-хозяйственной зон. [c.24]
Определение трудоемкости нефтеперерабатывающей продукции сложный процесс и проводится в два этапа. На первом1 этапе определяют трудоемкость по отдельным технологическим установкам, т. е. все затраты труда по предприятию распределяют между установками, за исключением затрат, не связанных непосредственно с производством продукции (услуги на сторону и прочие работы промышленного характера). На втором этапе аналогично определению себестоимости рассчитывают трудоемкость отдельных продуктов. В пределах установки все затраты труда относят на целевую продукцию. Трудоемкость конечного продукта определяют последовательным расчетом трудоемкости производства полуфабрикатов, включая смешение, в соответствии с технологической схемой. [c.191]
Именно эти ловушки для нефти, которые могли образоваться в различных формах от простых куполообразных изгибов до сложных стратиграфических сдвигов, вызванных изменениями в признаках пород, и пытаются обнаружить нефтяные компании в ходе разведочных работ, предсказать же их наличие очень трудно. Бассейны осадочных отложений, которые обладают высокой пористостью и проницаемостью, позволяющей нефти мигрировать, очень широко распространены на земном шаре и занимают почти половину его поверхности суши. Нефть в малых количествах содержится в них повсеместно. Но требуемое сочетание нефтеносных пород, примыкающих коллекторских пород, конечных пластовых условий и прежде всего благоприятных структур для улавливания нефти и благоприятной последовательности осадконакопления во времени, в пределах которого все это происходит, встречается значительно реже. [c.423]
Общеобразовательные программы решают задачу формирования общей культуры личности, адаптации ее к жизни в обществе, создания основы для осознанного выбора и освоения профессиональных образовательных программ. К общеобразовательным относятся программы до-щкольного образования, начального общего образования, основного общего образования, среднего (полного) общего образования. Профессиональные образовательные программы направлены на решение задач последовательного повышения профессионального и общеобразовательного уровней, подготовку специалистов соответствующей квалификации. К профессиональным относятся программы начального профессионального образования, среднего профессионального образования, высшего профессионального образования, послевузовского профессионального образования. Обязательный минимум содержания каждой основной общеобразовательной или основной профессиональной образовательной программы по конкретной профессии, специальности устанавливается соответствующим гос. образовательным стандартом. С учетом потребностей и возможностей личности образовательные программы могут осваиваться в различных формах. В условиях образовательного учреждения это может быть очная, очно-заочная (вечерняя) и заочная формы. Кроме того, существуют семейное образование, самообразование, экстернат. Допускается сочетание различных форм получения обра- зования. Для всех форм получения образования в пределах конкретной основной общеобразовательной или основной профессиональной образовательной программы действует единый гос. образовательный стандарт. Образовательные учреждения по своим организационно-правовым формам могут быть гос., муниципальными и негос. Организационно-правовая форма образовательного учреждения зависит от того, кто является его учредителем. Учредителями образовательных учреждений могут быть органы гос. власти, органы местного самоуправления, отечественные и иностранные организации всех форм собственности, их объединения (ассоциации и союзы), отечественные и иностранные общественные и частные фонды, общественные и религиозные организации (объединения), зарегистрированные на территории РФ, граждане РФ и иностранные граждане. Закон не запре- [c.54]
Пределом комбинирования по последовательным стадиям переработки исходного оырья является [c.21]
economy-ru.info
