объяснение, теория, примеры решений. Как решать пределы для чайников
а 3 = – 1/8 и т. д.
Существует даже последовательность, состоящая из одного и того же числа. Так, а n =6 состоит из бесконечного множества шестёрок.
Определение предела последовательности
Пределы последовательностей давно существуют в математике. Конечно, они заслужили свое собственное грамотное оформление. Итак, время узнать определение пределов последовательностей. Для начала рассмотрим подробно предел для линейной функции:
- Все пределы обозначаются сокращённо lim.
- Запись предела состоит из сокращения lim, какой-либо переменной, стремящейся к определённому числу, нулю или бесконечности, а также из самой функции.
Легко понять, что определение предела последовательности может быть сформулировано следующим образом: это некоторое число, к которому бесконечно приближаются все члены последовательности. Простой пример: а x = 4x+1. Тогда сама последовательность будет выглядеть следующим образом.
5, 9, 13, 17, 21…x …
Таким образом, данная последовательность будет бесконечно увеличиваться, а, значит, её предел равен бесконечности при x→∞, и записывать это следует так:
Если же взять похожую последовательность, но х будет стремиться к 1, то получим:
А ряд чисел будет таким: 1.4, 1.8, 4.6, 4.944 и т. д. Каждый раз нужно подставлять число всё больше приближеннее к единице (0.1, 0.2, 0.9, 0.986). Из этого ряда видно, что предел функции — это пять.
Из этой части стоит запомнить, что такое предел числовой последовательности, определение и метод решения простых заданий.
Общее обозначение предела последовательностей
Разобрав предел числовой последовательности, определение его и примеры, можно приступить к более сложной теме. Абсолютно все пределы последовательностей можно сформулировать одной формулой, которую обычно разбирают в первом семестре.
Итак, что же обозначает этот набор букв, модулей и знаков неравенств?
∀ — квантор всеобщности, заменяющий фразы «для всех», «для всего» и т. п.
п.
∃ — квантор существования, в данном случае обозначает, что существует некоторое значение N, принадлежащее множеству натуральных чисел.
Длинная вертикальная палочка, следующая за N, значит, что данное множество N «такое, что». На практике она может означать «такая, что», «такие, что» и т. п.
Для закрепления материала прочитайте формулу вслух.
Неопределённость и определённость предела
Метод нахождения предела последовательностей, который рассматривался выше, пусть и прост в применении, но не так рационален на практике. Попробуйте найти предел для вот такой функции:
Если подставлять различные значения «икс» (с каждым разом увеличивающиеся: 10, 100, 1000 и т. д.), то в числителе получим ∞, но в знаменателе тоже ∞. Получается довольно странная дробь:
Но так ли это на самом деле? Вычислить предел числовой последовательности в данном случае кажется достаточно легко. Можно было бы оставить всё, как есть, ведь ответ готов, и получен он на разумных условиях, однако есть ещё один способ специально для таких случаев.
Для начала найдём старшую степень в числителе дроби — это 1, т. к. х можно представить как х 1 .
Теперь найдём старшую степень в знаменателе. Тоже 1.
Разделим и числитель, и знаменатель на переменную в высшей степени. В данном случае дробь делим на х 1 .
Далее найдём, к какому значению стремится каждое слагаемое, содержащее переменную. В данном случае рассматриваются дроби. При х→∞ значение каждой из дробей стремится к нулю. При оформлении работы в писменном виде стоит сделать такие сноски:
Получается следующее выражение:
Конечно же, дроби, содержащие х, не стали нулями! Но их значение настолько мало, что вполне разрешено не учитывать его при расчётах. На самом же деле х никогда не будет равен 0 в данном случае, ведь на ноль делить нельзя.
Что такое окрестность?
Предположим, в распоряжении профессора сложная последовательность, заданная, очевидно, не менее сложной формулой. Профессор нашёл ответ, но подходит ли он? Ведь все люди ошибаются.
Огюст Коши в своё время придумал отличный способ для доказательства пределов последовательностей. Его способ назвали оперированием окрестностями.
Предположим, что существует некоторая точка а, её окрестность в обе стороны на числовой прямой равна ε («эпсилон»). Поскольку последняя переменная — расстояние, то её значение всегда положительно.
Теперь зададим некоторую последовательность х n и положим, что десятый член последовательности (x 10) входит в окрестность а. Как записать этот факт на математическом языке?
Допустим, х 10 находится правее от точки а, тогда расстояние х 10 -а
Теперь пора разъяснить на практике ту формулу, о которой говорилось выше. Некоторое число а справедливо называть конечной точкой последовательности, если для любого её предела выполняется неравенство ε>0, причём вся окрестность имеет свой натуральный номер N, такой, что всё члены последовательности с более значительными номерами окажутся внутри последовательности |x n – a|
С такими знаниями легко осуществить решение пределов последовательности, доказать или опровергнуть готовый ответ.
Теоремы
Теоремы о пределах последовательностей — важная составляющая теории, без которой невозможна практика. Есть всего лишь четыре главных теоремы, запомнив которые, можно в разы облегчить ход решения или доказательства:
- Единственность предела последовательности. Предел у любой последовательности может быть только один или не быть вовсе. Тот же пример с очередью, у которой может быть только один конец.
- Если ряд чисел имеет предел, то последовательность этих чисел ограничена.
- Предел суммы (разности, произведения) последовательностей равен сумме (разности, произведению) их пределов.
- Предел частного от деления двух последовательностей равен частному пределов тогда и только тогда, когда знаменатель не обращается в ноль.
Доказательство последовательностей
Иногда требуется решить обратную задачу, доказать заданный предел числовой последовательности. Рассмотрим на примере.
Доказать, что предел последовательности, заданной формулой, равен нолю.
По рассмотренному выше правилу, для любой последовательности должно выполняться неравенство |x n – a|
Выразим n через «эпсилон», чтобы показать существование некоего номера и доказать наличие предела последовательности.
На этом этапе важно напомнить, что «эпсилон» и «эн» – числа положительные и не равны нулю. Теперь можно продолжать дальнейшие преобразования, используя знания о неравенствах, полученные в средней школе.
Откуда получается, что n > -3 + 1/ε. Поскольку стоит помнить, что речь идёт о натуральных числах, то результат можно округлить, занеся его в квадратные скобки. Таким образом, было доказано, что для любого значения окрестности «эпсилон» точки а=0 нашлось значение такое, что выполняется начальное неравенство. Отсюда можно смело утверждать, что число а есть предел заданной последовательности. Что и требовалось доказать.
Вот таким удобным методом можно доказать предел числовой последовательности, какой бы сложной она на первый взгляд ни была. Главное — не впадать в панику при виде задания.
Главное — не впадать в панику при виде задания.
А может, его нет?
Существование предела последовательности необязательно на практике. Легко можно встретить такие ряды чисел, которые действительно не имеют конца. К примеру, та же «мигалка» x n = (-1) n . очевидно, что последовательность, состоящая всего лишь из двух цифр, циклически повторяющихся, не может иметь предела.
Та же история повторяется с последовательностями, состоящими из одного числа, дробными, имеющими в ходе вычислений неопределённость любого порядка (0/0, ∞/∞, ∞/0 и т. д.). Однако следует помнить, что неверное вычисление тоже имеет место быть. Иногда предел последоватей найти поможет перепроверка собственного решения.
Монотонная последовательность
Выше рассматривались несколько примеров последовательностей, методы их решения, а теперь попробуем взять более определённый случай и назовём его «монотонной последовательностью».
Определение: любую последовательность справедливо называть монотонно возрастающей, если для нее выполняется строгое неравенство x n x n +1.
Наряду с этими двумя условиями существуют также подобные нестрогие неравенства. Соответственно, x n ≤ x n +1 (неубывающая последовательность) и x n ≥ x n +1 (невозрастающая последовательность).
Но легче понимать подобное на примерах.
Последовательность, заданная формулой х n = 2+n, образует следующий ряд чисел: 4, 5, 6 и т. д. Это монотонно возрастающая последовательность.
А если взять x n =1/n, то получим ряд: 1/3, ¼, 1/5 и т. д. Это монотонно убывающая последовательность.
Предел сходящейся и ограниченной последовательности
Ограниченная последовательность — последовательность, имеющая предел. Сходящаяся последовательность — ряд чисел, имеющий бесконечно малый предел.
Таким образом, предел ограниченной последовательности — это любое действительное или комплексное число. Помните, что предел может быть только один.
Предел сходящейся последовательности — это величина бесконечно малая (действительная или комплексная). Если начертить диаграмму последовательности, то в определённой точке она будет как бы сходиться, стремиться обратиться в определённую величину. Отсюда и название — сходящаяся последовательность.
Отсюда и название — сходящаяся последовательность.
Предел монотонной последовательности
Предел у такой последовательности может быть, а может и не быть. Сначала полезно понять, когда он есть, отсюда можно оттолкнуться при доказательстве отсутствия предела.
Среди монотонных последовательностей выделяют сходящуюся и расходящуюся. Сходящаяся — это такая последовательность, которая образована множеством х и имеет в данном множестве действительный или комплексный предел. Расходящаяся — последовательность, не имеющая предела в своём множестве (ни действительного, ни комплексного).
Причём последовательность сходится, если при геометрическом изображении её верхний и нижний пределы сходятся.
Предел сходящейся последовательности во многих случаях может быть равен нулю, так как любая бесконечно малая последовательность имеет известный предел (ноль).
Какую сходящуюся последовательность ни возьми, они все ограничены, однако далеко не все ограниченные последовательности сходятся.
Сумма, разность, произведение двух сходящихся последовательностей – также сходящаяся последовательность. Однако частное может быть также сходящейся, если оно определено!
Различные действия с пределами
Пределы последовательностей — это такая же существенная (в большинстве случаев) величина, как и цифры и числа: 1, 2, 15, 24, 362 и т. д. Получается, что с пределами можно проводить некоторые операции.
Во-первых, как и цифры и числа, пределы любых последовательностей можно складывать и вычитать. Исходя из третьей теоремы о пределах последовательностей, справедливо следующее равенство: предел суммы последовательностей равен сумме их пределов.
Во-вторых, исходя из четвёртой теоремы о пределах последовательностей, справедливо следующее равенство: предел произведения n-ого количества последовательностей равен произведению их пределов. То же справедливо и для деления: предел частного двух последовательностей равен частному их пределов, при условии что предел не равен нулю. Ведь если предел последовательностей будет равен нулю, то получится деление на ноль, что невозможно.
Ведь если предел последовательностей будет равен нулю, то получится деление на ноль, что невозможно.
Свойства величин последовательностей
Казалось бы, предел числовой последовательности уже разобран довольно подробно, однако не раз упоминаются такие фразы, как «бесконечно маленькие» и «бесконечно большие» числа. Очевидно, если есть последовательность 1/х, где x→∞, то такая дробь бесконечно малая, а если та же последовательность, но предел стремится к нулю (х→0), то дробь становится бесконечно большой величиной. А у таких величин есть свои особенности. Свойства предела последовательности, имеющей какие угодно малые или большие величины, состоят в следующем:
- Сумма любого количества сколько угодно малых величин будет также малой величиной.
- Сумма любого количества больших величин будет бесконечно большой величиной.
- Произведение сколь угодно малых величин бесконечно мало.
- Произведение сколько угодно больших чисел — величина бесконечно большая.

- Если исходная последовательность стремится к бесконечно большому числу, то величина, ей обратная, будет бесконечно малой и стремиться к нулю.
На самом деле вычислить предел последовательности – не такая сложная задача, если знать простой алгоритм. Но пределы последовательностей — тема, требующая максимума внимания и усидчивости. Конечно, достаточно просто уловить суть решения подобных выражений. Начиная с малого, со временем можно достигнуть больших вершин.
Сегодня на уроке мы разберём строгое определение последовательности и строгое определение предела функции , а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.
За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет!
Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!) о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.
Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа.
– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)
– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ноги руку помощи:
В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи

Какие значки помимо знаков неравенств и модуля вы знаете?
– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что» , в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;
– для всех «эн», бОльших чем ;
– знак модуля означает расстояние , т.е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.
Ну как, убийственно сложно? =)
После освоения практики жду вас в следующем параграфе:
И в самом деле, немного порассуждаем – как сформулировать строгое определение последовательности? …Первое, что приходит на ум в свете практического занятия : «предел последовательности – это число, к которому бесконечно близко приближаются члены последовательности».
Хорошо, распишем последовательность :
Нетрудно уловить, что подпоследовательность

А может быть предела два? Но тогда почему у какой-нибудь последовательности их не может быть десять или двадцать? Так можно далеко зайти. В этой связи логично считать, что если у последовательности существует предел, то он единственный .
Примечание : у последовательности нет предела, однако из неё можно выделить две подпоследовательности (см. выше), у каждой из которых существует свой предел.
Таким образом, высказанное выше определение оказывается несостоятельным. Да, оно работает для случаев вроде
Попытка вторая: «предел последовательности – это число, к которому приближаются ВСЕ члены последовательности, за исключением, разве что их конечного количества». Вот это уже ближе к истине, но всё равно не совсем точно. Так, например, у последовательности половина членов вовсе не приближается к нулю – они ему просто-напросто равны =) К слову, «мигалка» вообще принимает два фиксированных значения.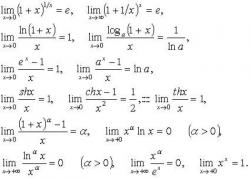
Формулировку нетрудно уточнить, но тогда возникает другой вопрос: как записать определение в математических знаках? Научный мир долго бился над этой проблемой, пока ситуацию не разрешил
Рассмотрим некоторую точку и её произвольную -окрестность:
Значение «эпсилон» всегда положительно, и, более того, мы вправе выбрать его самостоятельно . Предположим, что в данной окрестности находится множество членов (не обязательно все) некоторой последовательности . Как записать тот факт, что, например десятый член попал в окрестность? Пусть он находится в правой её части. Тогда расстояние между точками и должно быть меньше «эпсилон»: . Однако если «икс десятое» расположено левее точки «а», то разность будет отрицательна, и поэтому к ней нужно добавить знак

Определение : число называется пределом последовательности, если для любой его окрестности (заранее выбранной) существует натуральный номер – ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерами окажутся внутри окрестности:
Или короче: , если
Иными словами, какое бы малое значение «эпсилон» мы ни взяли, рано или поздно «бесконечный хвост» последовательности ПОЛНОСТЬЮ окажется в этой окрестности.
Так, например, «бесконечный хвост» последовательности ПОЛНОСТЬЮ зайдёт в любую сколь угодно малую -окрестность точки . Таким образом, это значение является пределом последовательности по определению. Напоминаю, что последовательность, предел которой равен нулю, называют бесконечно малой .
Следует отметить, что для последовательности уже нельзя сказать «бесконечный хвост зайдёт » – члены с нечётными номерами по факту равны нулю и «никуда не заходят» =) Именно поэтому в определении использован глагол «окажутся». И, разумеется, члены такой последовательности, как тоже «никуда не идут». Кстати, проверьте, будет ли число её пределом.
И, разумеется, члены такой последовательности, как тоже «никуда не идут». Кстати, проверьте, будет ли число её пределом.
Теперь покажем, что у последовательности не существует предела. Рассмотрим, например, окрестность точки . Совершенно понятно, что нет такого номера, после которого ВСЕ члены окажутся в данной окрестности – нечётные члены всегда будут «выскакивать» к «минус единице». По аналогичной причине не существует предела и в точке .
Закрепим материал практикой:
Пример 1
Доказать что предел последовательности равен нулю. Указать номер , после которого, все члены последовательности гарантированно окажутся внутри любой сколь угодно малой -окрестности точки .
Примечание : у многих последовательностей искомый натуральный номер зависит от значения – отсюда и обозначение .
Решение : рассмотрим произвольную найдётся ли номер – такой, что ВСЕ члены с бОльшими номерами окажутся внутри этой окрестности:
Чтобы показать существование искомого номера , выразим через .
Так как при любом значении «эн» , то знак модуля можно убрать:
Используем «школьные» действия с неравенствами, которые я повторял на уроках Линейные неравенства и Область определения функции . При этом важным обстоятельством является то, что «эпсилон» и «эн» положительны:
Поскольку слева речь идёт о натуральных номерах, а правая часть в общем случае дробна, то её нужно округлить:
Примечание : иногда для перестраховки справа добавляют единицу, но на самом деле это излишество. Условно говоря, если и мы ослабим результат округлением в меньшую сторону , то ближайший подходящий номер («тройка») всё равно будет удовлетворять первоначальному неравенству.
А теперь смотрим на неравенство и вспоминаем, что изначально мы рассматривали произвольную -окрестность, т.е. «эпсилон» может быть равно любому положительному числу.
Вывод : для любой сколько угодно малой -окрестности точки нашлось значение . Таким образом, число является пределом последовательности по определению. Что и требовалось доказать .
Таким образом, число является пределом последовательности по определению. Что и требовалось доказать .
К слову, из полученного результата хорошо просматривается естественная закономерность: чем меньше -окрестность – тем больше номер , после которого ВСЕ члены последовательности окажутся в данной окрестности. Но каким бы малым ни было «эпсилон» – внутри всегда будет «бесконечный хвост», а снаружи – пусть даже большое, однако конечное число членов.
Как впечатления? =) Согласен, что странновато. Но строго! Пожалуйста, перечитайте и осмыслите всё ещё раз.
Рассмотрим аналогичный пример и познакомимся с другими техническими приёмами:
Пример 2
Решение : по определению последовательности нужно доказать, что (проговариваем вслух!!!) .
Рассмотрим произвольную -окрестность точки и проверим, существует ли натуральный номер – такой, что для всех бОльших номеров выполнено неравенство:
Чтобы показать существование такого , нужно выразить «эн» через «эпсилон». Упрощаем выражение под знаком модуля:
Упрощаем выражение под знаком модуля:
Модуль уничтожает знак «минус»:
Знаменатель положителен при любом «эн», следовательно, палки можно убрать:
Перетасовка:
Теперь надо бы извлечь квадратный корень, но загвоздка состоит в том, что при некоторых «эпсилон» правая часть будет отрицательной. Чтобы избежать этой неприятности усилим неравенство модулем:
Почему так можно сделать? Если, условно говоря, окажется, что , то подавно будет выполнено и условие . Модуль может только увеличить разыскиваемый номер , и это нас тоже устроит! Грубо говоря, если подходит сотый, то подойдёт и двухсотый! В соответствии с определением, нужно показать сам факт существования номера (хоть какого-то), после которого все члены последовательности окажутся в -окрестности. Кстати, именно поэтому нам не страшнО финальное округление правой части в бОльшую сторону.
Извлекаем корень:
И округляем результат:
Вывод : т. к. значение «эпсилон» выбиралось произвольно, то для любой сколько угодно малой -окрестности точки нашлось значение , такое, что для всех бОльших номеров выполнено неравенство . Таким образом, по определению. Что и требовалось доказать .
к. значение «эпсилон» выбиралось произвольно, то для любой сколько угодно малой -окрестности точки нашлось значение , такое, что для всех бОльших номеров выполнено неравенство . Таким образом, по определению. Что и требовалось доказать .
Советую особо разобраться в усилении и ослаблении неравенств – это типичные и очень распространённые приёмы математического анализа. Единственное, нужно следить за корректностью того или иного действия. Так, например, неравенство ни в коем случае нельзя ослаблять , вычитая, скажем, единицу:
Опять же условно: если номер точно подойдёт, то предыдущий может уже и не подойти.
Следующий пример для самостоятельного решения:
Пример 3
Используя определение последовательности, доказать, что
Краткое решение и ответ в конце урока.
Если последовательность бесконечно велика , то определение предела формулируется похожим образом: точка называется пределом последовательности, если для любого, сколь угодно большого числа существует номер , такой, что для всех бОльших номеров , будет выполнено неравенство . Число называют окрестностью точки «плюс бесконечность» :
Иными словами, какое бы большое значение мы ни взяли, «бесконечный хвост» последовательности обязательно зайдёт в -окрестность точки , оставив слева лишь конечное число членов.
Дежурный пример:
И сокращённая запись: , если
Для случая запишите определение самостоятельно. Правильная версия в конце урока.
После того, как вы «набили» руку на практических примерах и разобрались с определением предела последовательности, можно обратиться к литературе по математическому анализу и/или своей тетрадке с лекциями. Рекомендую закачать 1-й том Бохана (попроще – для заочников) и Фихтенгольца (более подробно и обстоятельно) . Из других авторов советую Пискунова, курс которого ориентирован на технические ВУЗы.
Попытайтесь добросовестно изучить теоремы, которые касаются предела последовательности, их доказательства, следствия. Поначалу теория может казаться «мутной», но это нормально – просто нужно привыкнуть. И многие даже войдут во вкус!
Строгое определение предела функцииНачнём с того же самого – как сформулировать данное понятие? Словесное определение предела функции формулируется значительно проще: «число является пределом функции , если при «икс», стремящемся к (и слева, и справа) , соответствующие значения функции стремятся к » (см. чертёж) . Всё вроде бы нормально, но слова словами, смысл смыслом, значок значком, а строгих математических обозначений маловато. И во втором параграфе мы познакомимся с двумя подходами к решению данного вопроса.
Пусть функция определена на некотором промежутке за исключением, возможно, точки . В учебной литературе общепринято считают, что функция там не определена:
Такой выбор подчёркивает суть предела функции : «икс» бесконечно близко приближается к , и соответствующие значения функции – бесконечно близко к . Иными словами, понятие предела подразумевает не «точный заход» в точки, а именно бесконечно близкое приближение , при этом не важно – определена ли функция в точке или нет.
Первое определение предела функции, что неудивительно, формулируется с помощью двух последовательностей. Во-первых, понятия родственные, и, во-вторых, пределы функций обычно изучают после пределов последовательностей.
Рассмотрим последовательность точек (на чертеже отсутствуют) , принадлежащих промежутку и отличных от , которая сходится к . Тогда соответствующие значения функции тоже образуют числовую последовательность, члены которой располагаются на оси ординат.
Предел функции по Гейне для любой последовательности точек (принадлежащих и отличных от ) , которая сходится к точке , соответствующая последовательность значений функции сходится к .
Эдуард Гейне – это немецкий математик. …И не надо тут ничего такого думать, гей в Европе всего лишь один – это Гей-Люссак =)
Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность) . По мотивам предыдущего параграфа, запись означает, что некоторое значение функции находится внутри «эпсилон»-окрестности.
Теперь найдём -окрестность, которая соответствует заданной -окрестности (мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз) . Обратите внимание, что значение выбирается по длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определении важен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.
Предел функции по Коши : число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой) , существует -окрестность точки , ТАКАЯ , что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки) .
Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)
Короткая запись: , если
В чём суть определения? Образно говоря, бесконечно уменьшая -окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.
! Внимание : если вам потребуется сформулировать только определение по Гейне или только определение по Коши , пожалуйста, не забывайте о существенном предварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки » . Я обозначил это единожды в самом начале и каждый раз не повторял.
Согласно соответствующей теореме математического анализа, определения по Гейне и по Коши эквивалентны, однако наиболее известен второй вариант (ещё бы!) , который также называют «предел на языке »:
Пример 4
Используя определение предела, доказать, что
Решение : функция определена на всей числовой прямой кроме точки . Используя определение , докажем существование предела в данной точке.
Примечание : величина «дельта»-окрестности зависит от «эпсилон», отсюда и обозначение
Рассмотрим произвольную -окрестность. Задача состоит в том, чтобы по этому значению проверить, существует ли -окрестность, ТАКАЯ , что из неравенства следует неравенство .
Предполагая, что , преобразуем последнее неравенство:
(разложили квадратный трёхчлен )
Сходимость рядов. Признак Даламбера
Сходимость рядов. Признак Даламбера
Сходимость рядов. Признак Даламбера
Пусть задана бесконечная последовательность чисел . Выражение называется числовым рядом. При этом числа называются членами ряда.
Числовой ряд часто записывают в виде .
Теорема (необходимый признак сходимости ряда). Если ряд сходится,
то его -й
член стремится к нулю при неограниченном возрастании .
Следствие. Если -й
член ряда не стремится к нулю при ,
то ряд расходится.
Теорема (признак Даламбера). Если в ряде с положительными членами
отношение -го
члена ряда к -му
при
имеет конечный предел ,
т.е. ,
то:
– ряд сходится в случае ,
– ряд расходится в случае .
В случаях, когда предел не существует или он равен единице, ответа на вопрос
о сходимости или расходимости числового ряда теорема не дает. Необходимо провести
дополнительное исследование.
Примеры решения задач
Пример 1. Исследовать сходимость ряда .
Решение.
Применим признак сходимости
Даламбера. Сначала запишем формулы для -го
и -го
членов ряда:
Затем найдем предел отношения -го
члена ряда к -му
при :
И последнее, сделаем вывод о сходимости ряда, сравнив полученное значение предела
с 1. Поскольку ,
то данный ряд расходится.
Ответ: ряд
расходится.
Пример 2. Исследовать сходимость ряда .
Решение.
Применим признак сходимости Даламбера. Запишем формулы для -го и -го членов ряда:
Найдем предел отношения -го
члена ряда к -му
при :
Сравним полученное значение предела с 1. Поскольку ,
то данный ряд сходится.
Ответ: ряд сходится.
Пример 3. Исследовать сходимость ряда .
Решение.
Используем признак сходимости Даламбера, а также определение функции факториал. Поскольку для каждого целого положительного числа функция (читается «n факториал»), по определению, равна произведению всех целых чисел от 1 до , т.е. , то .
Теперь запишем формулы для -го
и -го
членов ряда:
С учетом вышесказанного найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд сходится.
Ответ: ряд сходится.
Пример 4. Исследовать сходимость ряда .
Решение.
Используем признак сходимости Даламбера. Запишем формулы для -го и -го членов ряда:
С учетом того, что ,
найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд расходится.
Ответ: ряд
расходится.
Пример 5. Исследовать сходимость ряда , пользуясь признаком сходимости Даламбера.
Решение.
Запишем формулы для -го и -го членов ряда:
.
Далее найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд расходится.
Ответ: ряд
расходится.
Пример 6. Исследовать сходимость ряда ,
пользуясь признаком сходимости Даламбера.
Решение.
Запишем формулы для -го и -го членов ряда:
Далее найдем предел отношения -го
члена ряда к -му
при :
И последнее, сделаем вывод о сходимости ряда, сравнив полученное значение предела
с 1. Поскольку ,
то данный ряд сходится.
Ответ: ряд
сходится.
Пример 7. Исследовать сходимость ряда , пользуясь признаком сходимости Даламбера.
Решение.
Сначала запишем формулы для -го и -го членов ряда:
Затем найдем предел отношения -го
члена ряда к -му
при :
Сравним полученное значение предела с 1. Поскольку ,
то данный ряд сходится.
Ответ: ряд сходится.
Пример 8. Исследовать сходимость ряда , пользуясь признаком сходимости Даламбера.
Решение.
Предварительно вспомним, что для каждого целого положительного числа функция , по определению, равна произведению всех целых чисел от 1 до , т.е. .
Тогда для
и
получим: ,
.
Теперь запишем формулы для -го
и -го
членов ряда:
Далее найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд сходится.
Ответ: ряд
сходится.
Задания для самостоятельной работы
Исследовать сходимость
ряда, пользуясь признаком сходимости Даламбера:
1. . Ответ: ,
ряд расходится.
2. . Ответ: , ряд сходится.
3. . Ответ: , ряд расходится.
4. . Ответ: , ряд сходится.
5. . Ответ: , ряд расходится.
6. . Ответ: , ряд расходится.
7. . Ответ: , ряд сходится.
8. . Ответ: , ряд сходится.
9. . Ответ: , ряд сходится.
10. . Ответ: , ряд сходится.
11. . Ответ: , ряд сходится.
12. . Ответ: , ряд сходится.
13. . Ответ: , ряд расходится.
14. . Ответ: , ряд сходится.
15. . Ответ: , ряд расходится.
16. . Ответ: , ряд сходится.
Цитаты про предел. Пределы в математике для чайников: объяснение, теория, примеры решений
Знай, у каждого разное «больно»,
Знай, у каждого разное «страшно».
Не суди со своей колокольни
Неизвестносколькоэтажной.
Не очерчивай взглядом границы,
Не придумывай мозгом пределы.
Что тебе в страшном сне не приснится,
Для кого-то – обычное дело.
Знай, у каждого разное «надо»,
Знай, у каждого разное «сложно».
Впрочем, и представление ада
Обобщить и сравнить невозможно.
Знай, что правда бывает другая,
А не та, что приносят на блюде.
Присмотрись к тем, чьи судьбы пугают,
Это – самые сильные люди.
Не говори, что я тебя не помню —
Я помню всё, и много раз на дню
Я повторяю номер телефонный,
Но никогда тебе не позвоню.
Вот-вот, казалось, сердце разорвется
И на пределе одиноких дней
За горизонт зашли в душе моей.
Была любовь, была любовь, была!
И к этой фразе нечего прибавить.
Сгорел волшебный замок наш дотла
И пепла не оставил нам на память.
Я помню всё, и сад цветущий помню,
И сквозь листву — лучи со всех сторон,
Как будто с белой-белой колокольни
В душе — ты слышишь — льётся тихий звон.
Любовь ушла и больше не вернётся,
И чтоб не вечно тосковать о ней,
Твои глаза, как два печальных солнца,
За горизонт зашли в душе моей.
За счастьем погоня опять неудачна…
И вечер дождливый, на улице мрачно…
А в детстве…намазала булку вареньем
И точно счастливая, до одуренья…
Гламур, этикет, бриллианты, джакузи…
Теперь, кроме счастья, в судьбе «All inclusive»,
А в детстве с подсолнуха семечки ела,
И счастью, казалось, не будет предела…
Мы стали похожи на клоунов очень…
У каждого грим, что снаружи хохочет…
А в детстве… лишь солнце с небес пробивалось
И сердце счастливое так улыбалось…
Людей отбираем, как в «Золушке» гречку…
Всех нужных – в контакты… Невыгодных в печку…
А в детстве в нас верило чистое небо…
Где радость от запаха свежего хлеба?
И дружба теперь покупается тоже…
Дожились… Живём в мире меха и кожи…
А в детстве дворнягу от ливня спасали…
И счастье давая, его получали.
Мы искренность, чуткость теряли с годами…
Границы и рамки придумали сами…
Есть булка и банка с вишнёвым вареньем?
Так будьте счастливыми, до одуренья!
Я смотрю на тебя и понимаю, что по-прежнему люблю тебя. Эта любовь – хроническая болезнь последних лет. Она приносит настолько нестерпимую боль, что я кидаюсь на совершенно посторонних людей, пытаясь обмануться ими, с ними вдруг в этих объятиях найду то самое обезболивающее, которое, по словам обладателей морщинистых сердец, вообще не существует. Я понимаю, что обманываюсь, но все равно продолжаю обниматься-убиваться не могу иначе, болит ведь, изводит, по ночам спать не дает, вот сижу на подоконнике и, еще минута, истошно закричу от пыток иллюзий. Обратиться к тебе за помощью? Бесполезно. Ты знаешь о моей любви, но тебе она ни к чему, «своих невысказанных чувств полный рот». Мы в одной паутине безответности, но не можем помочь друг другу. Ты обхватываешь руками тонкие белые нити-прутья и смотришь куда-то за пределы реальности, надеясь черт знает на чью помощь. И разница между нами одна: моя любовь к тебе почти сбила меня с ног, а твоя любовь к кому-то – подпитывает, оживляет тебя ожиданием, пусть и обманчивым. Я больше не хочу смотреть на тебя, я прогоняю возможность тебя из сердца, но от этого еще больнее. Вот и проходится шепотом страдать, тоже надеясь черт знает на чью помощь. Времени?..
Ваша жизнь – сплошное вранье, порнуха, бытовуха, интернет-зависимость и сотово-мобильное рабство. Ну разве я не прав? Вот скажите мне, вы когда-нибудь совершали что-нибудь по настоящему из ряда вон? Никогда. И не сможете. Знаете почему? Потому что все это находится за пределами вашей зоны комфорта. Вы упакованы в нее. Как в полипропиленовый мешок. Вы куски мяса, зажатые рамками быта и работы. Или я не прав? Может, я ошибаюсь? Поправьте меня.
Например, можете подарить свой мобильник первому встречному? А? Вопрос на засыпку. Можете прямо сейчас отформатировать винт на вашем компьютере? Стремно? Обосрались? А знаете, почему вы этого не сделаете? Потому что это равноценно самоубийству. Вы без этого не существуете.
Хранил в себе один секрет и был в семье примерный муж.
Всё было, вроде, как всегда: жена готовила обед…
Но приключилась вдруг беда: он взял и вспомнил про секрет.
Под шум и кислый запах щей, ворчанье суженой с утра,
Он вспомнил всё до мелочей, как будто было то вчера…
…Она сидела у окна, и мягкий чудный лунный свет
Окрасил в бледные тона её прекрасный силуэт…
Струились пряди по плечам, скользили змейками на грудь…
И он подумал сгоряча: «Женюсь на ней когда – нибудь!»
Он вспомнил всё до мелочей: изгибы линий, мягкость губ…
И жар её простых речей, и за окном огромный дуб.
Сплетенье рук… Слиянье тел… Каскад каштановых волос…
И то, как он её хотел до исступления, до слёз!
Признаний трепетных поток, как он на ушко их шептал!
Смешной над ухом завиток, что от дыханья трепетал…
Она смотрела на него глазами влажными, как ночь.
Слова пьянили, как вино: «Люблю тебя… Роди мне дочь…»
С утра он потерял покой: то суетился, то скучал…
Потом, закрыв лицо рукой, сидел на стуле и молчал.
Жена ворчала, как всегда. Ругала убежавший суп…
И он отметил, что года ей, постаревшей, не к лицу.
Как не идёт ей белый цвет и пряди крашеных волос.
И целых двадцать восемь лет всё как – то было не всерьёз…
Вдруг он вскочил, схватил пальто, забыл про шапку и носки.
Все двадцать восемь лет – не то… Все двадцать восемь зим – тоски.
Нашёл тот дом. У дома – дуб. Взбежал по лестнице стрелой…
Унять бы дрожь с холодных губ, и трусость гадкую – долой!
Наверное, она сейчас пьет чай и кутается в шаль…
И из её прекрасных глаз струится тихая печаль…
А может, принялась вязать? А может кружево плести?
Так много надо ей сказать! А главное сказать – прости…
Открыла дверь… В глазах – вопрос. Ей было снова двадцать лет…
Каскад каштановых волос… Знакомый сердцу силуэт…
Над ухом – лёгкий завиток… Как много лет назад – точь в точь…
” Вы не ошиблись?» – Нет, не мог… Вы Аня? ” Вера. Её дочь…»
” А Аня?”- ” Мамы больше нет… Кто Вы?» Он повернулся вспять:
«Я шёл к ней двадцать восемь лет…» – Она ждала Вас… Двадцать пять…
Как закружилась голова… Как сердце ухнуло в груди!
И вспомнил он её слова с мольбою: «Ты не уходи!»
Он сгорбился. Поплёлся прочь. Сплетенье рук… Слиянье тел…
Люблю тебя… Роди мне дочь… А он ведь вправду дочь хотел.
Как странно. Ани больше нет… Заплакал… Бросил в тишину:«Я буду много – много лет любить тебя… Тебя одну…»
P.S. БЕРЕГИТЕ ЛЮБОВЬ – она фундамент вашего счастья…
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
объяснение, теория, примеры решений. Понятие предела в математике
Рассмотрим функцию %%f(x)%%, определенную, по крайней мере, в некоторой проколотой окрестности %%\stackrel{\circ}{\text{U}}(a)%% точки %%a \in \overline{\mathbb{R}}%% расширенной числовой прямой.
Понятие предела по Коши
Число %%A \in \mathbb{R}%% называют пределом функции %%f(x)%% в точке %%a \in \mathbb{R}%% (или при %%x%%, стремящемся к %%a \in \mathbb{R}%%), если, каково бы ни было положительное число %%\varepsilon%%, найдется положительное число %%\delta%%, такое, что для всех точек проколотой %%\delta%%-окрестности точки %%a%% значения функции принадлежат %%\varepsilon%%-окрестности точки %%A%%, или
$$ A = \lim\limits_{x \to a}{f(x)} \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel{\circ}{\text{U}}_\delta(a) \Rightarrow f(x) \in \text{U}_\varepsilon (A) \big) $$
Это определение называется определением на языке %%\varepsilon%% и %%\delta%%, предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью.- (a)%% с окрестностями %%\text{U}_\varepsilon (A), \text{U}_\varepsilon (\infty), \text{U}_\varepsilon (+\infty), \text{U}_\varepsilon (-\infty)%%, получим 24 определения предела по Коши.
Геометрический смысл
Геометрический смысл предела функции
Выясним, в чем заключается геометрический смысл предела функции в точке. Построим график функции %%y = f(x)%% и отметим на нем точки %%x = a%% и %%y = A%%.
Предел функции %%y = f(x)%% в точке %%x \to a%% существует и равен A, если для любой %%\varepsilon%%-окрестности точки %%A%% можно указать такую %%\delta%%-окрестность точки %%a%%, что для любого %%x%% из этой %%\delta%%-окрестности значение %%f(x)%% будет находиться в %%\varepsilon%%-окрестности точки %%A%%.
Отметим, что по определению предела функции по Коши для существования предела при %%x \to a%% не важно, какое значение принимает функция в самой точке %%a%%. Можно привести примеры, когда функция не определена при %%x = a%% или принимает значение, отличное от %%A%%. Тем не менее предел может быть равен %%A%%.
Определение предела по Гейне
Элемент %%A \in \overline{\mathbb{R}}%% называется пределом функции %%f(x)%% при %% x \to a, a \in \overline{\mathbb{R}}%%, если для любой последовательности %%\{x_n\} \to a%% из области определения, последовательность соответствующих значений %%\big\{f(x_n)\big\}%% стремится к %%A%%.
Определение предела по Гейне удобно использовать, когда возникают сомнения в существовании предела функции в данной точке. Если можно построить хотя бы одну последовательность %%\{x_n\}%% с пределом в точке %%a%% такую, что последовательность %%\big\{f(x_n)\big\}%% не имеет предела, то можно сделать вывод о том, что функция %%f(x)%% не имеет предела в этой точке. Если для двух различных последовательностей %%\{x”_n\}%% и %%\{x””_n\}%%, имеющих одинаковый предел %%a%%, последовательности %%\big\{f(x”_n)\big\}%% и %%\big\{f(x””_n)\big\}%% имеют различные пределы, то в этом случае также не существует предел функции %%f(x)%%.n n\pi\right)} \equiv 0%% и %%\lim\big\{f(x_n)\big\} = 0%%.
Затем возьмем сходящуюся к той же точке последовательность $$ x”_n = \left\{ \frac{2}{(4n + 1)\pi} \right\}, $$
для которой %%\lim{x”_n} = +0%%, %%f(x”_n) = \sin{\big((4n + 1)\pi/2\big)} \equiv 1%% и %%\lim\big\{f(x”_n)\big\} = 1%%. Аналогично для последовательности $$ x””_n = \left\{-\frac{2}{(4n + 1)\pi} \right\}, $$
также сходящейся к точке %%x = 0%%, %%\lim\big\{f(x””_n)\big\} = -1%%.
Все три последовательности дали разные результаты, что противоречит условию определения по Гейне, т.е. данная функция не имеет предела в точке %%x = 0%%.
Теорема
Определение предела по Коши и по Гейне эквивалентны.
Доказывая свойства предела функции, мы убедились, что от проколотых окрестностей, в которых были определены наши функции и которые возникали в процессе доказательств, кроме свойств указанных во введении к предыдущему пункту 2, действительно ничего не потребовалось. Это обстоятельство служит оправданием для выделения следующего математического объекта.
а. База; определение и основные примеры
Определение 11. Совокупность В подмножеств множества X будем называть базой в множестве X, если выполнены два условия:
Иными словами, элементы совокупности В суть непустые множества и в пересечении любых двух из них содержится некоторый элемент из той же совокупности.
Укажем некоторые наиболее употребительные в анализе базы.
Если то вместо пишут и говорят, что х стремится к а справа или со стороны больших значений (соответственно, слева или со стороны меньших значений). При принята краткая запись вместо
Запись будет употребляться вместо Она означает, что а; стремится по множеству Е к а, оставаясь больше (меньше), чем а.
то вместо пишут и говорят, что х стремится к плюс бесконечности (соответственно, к минус бесконечности).
Запись будет употребляться вместо
При вместо мы (если это не ведет к недоразумению) будем, как это принято в теории предела последовательности, писать
Заметим, что все перечисленные базы обладают той особенностью, что пересечение любых двух элементов базы само является элементом этой базы, а не только содержит некоторый элемент базы. С другими базами мы встретимся при изучении функций, заданных не на числовой оси.
Отметим также, что используемый здесь термин «база» есть краткое обозначение того, что в математике называется «базисом фильтра», а введенный ниже предел по базе есть наиболее существенная для анализа часть созданного современным французским математиком А. Картаном понятия предела по фильтру
b. Предел функции по базе
Определение 12. Пусть – функция на множестве X; В – база в X. Число называется пределом функции по базе В, если для любой окрестности точки А найдется элемент базы, образ которого содержится в окрестности
Если А – предел функции по базе В, то пишут
Повторим определение предела по базе в логической символике:
Поскольку мы сейчас рассматриваем функции с числовыми значениями, полезно иметь в виду и следующую форму этого основного определения:
В этой формулировке вместо произвольной окрестности V (А) берется симметричная (относительно точки А) окрестность (е-окрестность). Эквивалентность этих определений для вещественнозначных функций вытекает из того, что, как уже говорилось, в любой окрестности точки содержится некоторая симметричная окрестность этой же точки (проведите доказательство полностью!).
Мы дали общее определение предела функции по базе. Выше были рассмотрены примеры наиболее употребительных в анализе баз. В конкретной задаче, где появляется та или иная из этих баз, необходимо уметь расшифровать общее определение и записать его для конкретной базы.
Рассматривая примеры баз, мы, в частности, ввели понятие окрестности бесконечности. Если использовать это понятие, то в соответствии с общим определением предела разумно принять следующие соглашения:
или, что то же самое,
Обычно под подразумевают малую величину. В приведенных определениях это, разумеется, не так. В соответствии с принятыми соглашениями, например, можем записать
Для того чтобы можно было считать доказанными и в общем случае предела по произвольной базе все те теоремы о пределах, которые мы доказали в пункте 2 для специальной базы , необходимо дать соответствующие определения: финально постоянной, финально ограниченной и бесконечно малой при данной базе функций.
Определение 13. Функция называется финально постоянной при базе В, если существуют число и такой элемент базы, в любой точке которого
Определение 14. Функция называется ограниченной при базе В или финально ограниченной при базе В, если существуют число с и такой элемент базы, в любой точке которого
Определение 15. Функция называется бесконечно малой при базе В, если
После этих определений и основного наблюдения о том, что для доказательства теорем о пределах нужны только свойства базы, можно считать, что все свойства предела, установленные в пункте 2, справедливы для пределов по любой базе.
В частности, мы можем теперь говорить о пределе функции при или при или при
Кроме того, мы обеспечили себе возможность применения теории пределов и в том случае, когда функции будут определены не на числовых множествах; в дальнейшем это окажется особенно ценным. К примеру, длина кривой есть числовая функция, определенная на некотором классе кривых. Если мы знаем эту функцию на ломаных, то потом предельным переходом определяем ее для более сложных кривых, например для окружности.
В данный же момент основная польза от сделанного наблюдения и введенного в связи с ним понятия базы состоит в том, что они избавляют нас от проверок и формальных доказательств теорем о пределах для каждого конкретного вида предельных переходов или, в нашей нынешней терминологии, для каждого конкретного вида баз.
Для того чтобы окончательно освоиться с понятием предела по произвольной базе, доказательства дальнейших свойств предела функции мы проведем в общем виде.
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что “скучная теория” должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $ |
| Решение |
а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$ б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ \text{a)} \lim \limits_{x \to 0} \frac{1}{x} = \infty \text{ б)}\lim \limits_{x \to \infty} \frac{1}{x} = 0 $$ |
Что делать с неопределенностью вида: $ \bigg [\frac{0}{0} \bigg ] $
| Пример 3 |
| Решить $ \lim \limits_{x \to -1} \frac{x^2-1}{x+1} $ |
| Решение |
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела.2-1}{x+1} = \infty $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: “ноль делить на ноль” или “бесконечность делить на бесконечность” и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность “ноль делить на ноль” нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность “бесконечность делить на бесконечность”, тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
Пусть функция у=ƒ (х) определена в некоторой окрестности точки х о, кроме, быть может, самой точки х о.
Сформулируем два, эквивалентных между собой, определения предела функции в точке.
Определение 1 (на «языке последовательностей», или по Гейне).
Число А называется пределом функции у=ƒ(х) в топке x 0 (или при х® х о), если для любой последовательности допустимых значений аргумента x n , n є N (x n ¹ x 0), сходящейся к х о последовательность соответствующих значений функции ƒ(х n), n є N, сходится к числу А
В этом случае пишут
или ƒ(х)->А при х→х о. Геометрический смысл предела функции:
означает,
что для всех точек х, достаточно близких к точке х о, соответствующие
значения функции как угодно мало отличаются от числа А.
Определение 2 (на «языке ε», или по Коши).
Число А называется пределом функции в точке х о (или при х→х о), если для любого положительного ε найдется такое положительное число δ, что для все х¹ х о, удовлетворяющих неравенству |х-х о |
Геометрический смысл предела функции:
если для любой ε-окрестности точки А найдется такая δ-окрестность точки х о, что для всех х¹ хо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
Доказать, что
Решение: Возьмем произвольное ε>0, найдем δ=δ(ε)>0 такое, что для всех х, удовлетворяющих неравенству |х-3|
Взяв δ=ε/2, видим, что для всех х, удовлетворяющих неравенству |х-3|3.
16.2. Односторонние пределы
В определении предела функции считается, что х стремится к x 0 любым способом: оставаясь меньшим, чем x 0 (слева от х 0), большим, чем х о (справа от х о), или колеблясь около точки x 0 .
Бывают случаи, когда способ приближения аргумента х к х о существенно влияет на значение придела функции. Поэтому вводят понятия односторонних пределов.
Число А 1 называется пределом функции у=ƒ(х) слева в точке х о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х 0 -δ;x o), выполняется неравенство |ƒ(х)-А|х 0 -0 или коротко: ƒ(х о- 0)=А 1 (обозначение Дирихле) (см. рис. 111).
Аналогично определяется предел функции справа, запишем его с помощью символов:
Коротко предел справа обозначают ƒ(х о +0)=А.
Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует , то существуют и оба односторонних предела, причем А=А 1 =А 2 .
Справедливо и обратное утверждение: если существуют оба предела ƒ(х 0 -0) и ƒ(х 0 +0) и они равны, то существует предел и А=ƒ(х 0 -0).
Если же А 1 ¹ А 2 , то етот придел не существует.
16.3. Предел функции при х ® ∞
Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→∞ , если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|
Геометрический смысл этого определения таков: для ” ε>0 $ М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).
16.4. Бесконечно большая функция (б.б.ф.)
Функция у=ƒ(х) называется бесконечно большой при х→х 0 , если для любого числа М>0 существует число δ=δ(М)>0, что для всех х, удовлетворяющих неравенству 0М.
Например, функция у=1/(х-2) есть б.б.ф. при х->2.
Если ƒ(х) стремится к бесконечности при х→х о и принимает лишь положительные значения, то пишут
если лишь отрицательные значения, то
Функция у=ƒ(х), заданная на всей числовой прямой, называется бесконечно большой при х→∞, если для любого числа М>0 найдется такое число N=N(M)>0, что при всех х, удовлетворяющих неравенству |х|>N, выполняется неравенство |ƒ(х)|>М. Коротко:
Например, у=2х есть б.б.ф. при х→∞.
Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. хєN, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность v n =n 2 +1, n є N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки х о является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у=хsinх.)
Однако, если limƒ(х)=А при х→x 0 , где А – конечное число, то функция ƒ(х) ограничена в окрестности точки х о.
Действительно, из определения предела функции следует, что при х→ х 0 выполняется условие |ƒ(х)-А|
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
объяснение, теория, примеры решений. Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
КОНСПЕКТ 20
20.1 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Пример 1
Решить предел Сначала попробуем подставить -1 в дробь:В данном случае получена так называемая неопределенность.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида, то для ее раскрытиянужно разложить числитель и знаменатель на множители .
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Разложим числитель на множители.
Пример 2
Вычислить предел
Разложим числитель и знаменатель на множители.
Числитель: Знаменатель:,
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 3
Найти предел
Умножим числитель и знаменатель на сопряженное выражение.
20.2 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример 4
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим
числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 5
Найти предел Снова в числителе и знаменателе находимв старшей степени:Максимальная степень в числителе: 3 Максимальная степень в знаменателе: 4 Выбираемнаибольшее значение, в данном случае четверку. Согласно нашему алгоритму, для раскрытия неопределенностиделим числитель и знаменатель на. Полное оформление задания может выглядеть так:
Пример 6
Найти предел Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1 (можно записать как) Для раскрытия неопределенностинеобходимо разделить числитель и знаменатель на. Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида у нас может получитьсяконечное число , ноль или бесконечность.
ПРАКТИКУМ 20
ЗАДАНИЕ N 1
Решение: Если вместо переменнойпоставить значение 7, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 2 Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение: Если вместо переменнойпоставить значение 0, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 3 Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение: Если вместо переменнойпоставить значение 6, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 4
Решение: Так каки
ЗАДАНИЕ N 5 Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Решение: Так какито
имеет место неопределенность видаДля
ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на.
Тогда, зная, чтополучим:
САМОСТОЯТЕЛЬНАЯ РАБОТА 20
ЗАДАНИЕ N 1 Тема: Раскрытие неопределенности вида “ноль на ноль”
ЗАДАНИЕ N 2 Тема: Раскрытие неопределенности вида “ноль на ноль”
ЗАДАНИЕ N 3 Тема: Раскрытие неопределенности вида “ноль на ноль”
ЗАДАНИЕ N 4 Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
ЗАДАНИЕ N 5 Тема: Раскрытие неопределенности вида “бесконечность на бесконечность” Предел функцииравен …
ЗАДАНИЕ N 6 Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Пример 4
Найти предел
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).
Если «икс» стремится к «минус бесконечности»Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел
Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
2) Вычислим предел
Здесь старшая степень опять чётная , поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:
3) Вычислим предел
Значение предела зависит только от . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна , значит:
4) Вычислим предел
Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.
Пример 5
Найти предел
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Решение тривиально:
Пример 6
Найти предел
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
Решаем:
Разделим числитель и знаменатель на
Пример 15
Найти предел
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
При подстановке единицы в предел получается неопределённость . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице . Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену:
Если , то
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .
Завершаем решение:
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .
Задание для самостоятельного решения:
Пример 17
Найти предел
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения , приходится использовать самые разные тригонометрические формулы , а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только о неопределённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.{3x}=1$.
Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёттолько об определённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы , преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции . На пример: .
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица , значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны . На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
и т.д.
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим .
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты : .
Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ .
! Примечание : не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще :
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
:
Пример 4
Разделим числитель и знаменатель на :
Примечание : самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание : слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя. .
Пример 22
Примечание : бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
Терпению есть предел. Пределы в математике для чайников: объяснение, теория, примеры решений
Знай, у каждого разное «больно»,
Знай, у каждого разное «страшно».
Не суди со своей колокольни
Неизвестносколькоэтажной.
Не очерчивай взглядом границы,
Не придумывай мозгом пределы.
Что тебе в страшном сне не приснится,
Для кого-то – обычное дело.
Знай, у каждого разное «надо»,
Знай, у каждого разное «сложно».
Впрочем, и представление ада
Обобщить и сравнить невозможно.
Знай, что правда бывает другая,
А не та, что приносят на блюде.
Присмотрись к тем, чьи судьбы пугают,
Это – самые сильные люди.
Не говори, что я тебя не помню —
Я помню всё, и много раз на дню
Я повторяю номер телефонный,
Но никогда тебе не позвоню.
Вот-вот, казалось, сердце разорвется
И на пределе одиноких дней
За горизонт зашли в душе моей.
Была любовь, была любовь, была!
И к этой фразе нечего прибавить.
Сгорел волшебный замок наш дотла
И пепла не оставил нам на память.
Я помню всё, и сад цветущий помню,
И сквозь листву — лучи со всех сторон,
Как будто с белой-белой колокольни
В душе — ты слышишь — льётся тихий звон.
Любовь ушла и больше не вернётся,
И чтоб не вечно тосковать о ней,
Твои глаза, как два печальных солнца,
За горизонт зашли в душе моей.
За счастьем погоня опять неудачна…
И вечер дождливый, на улице мрачно…
А в детстве…намазала булку вареньем
И точно счастливая, до одуренья…
Гламур, этикет, бриллианты, джакузи…
Теперь, кроме счастья, в судьбе «All inclusive»,
А в детстве с подсолнуха семечки ела,
И счастью, казалось, не будет предела…
Мы стали похожи на клоунов очень…
У каждого грим, что снаружи хохочет…
А в детстве… лишь солнце с небес пробивалось
И сердце счастливое так улыбалось…
Людей отбираем, как в «Золушке» гречку…
Всех нужных – в контакты… Невыгодных в печку…
А в детстве в нас верило чистое небо…
Где радость от запаха свежего хлеба?
И дружба теперь покупается тоже…
Дожились… Живём в мире меха и кожи…
А в детстве дворнягу от ливня спасали…
И счастье давая, его получали.
Мы искренность, чуткость теряли с годами…
Границы и рамки придумали сами…
Есть булка и банка с вишнёвым вареньем?
Так будьте счастливыми, до одуренья!
Я смотрю на тебя и понимаю, что по-прежнему люблю тебя. Эта любовь – хроническая болезнь последних лет. Она приносит настолько нестерпимую боль, что я кидаюсь на совершенно посторонних людей, пытаясь обмануться ими, с ними вдруг в этих объятиях найду то самое обезболивающее, которое, по словам обладателей морщинистых сердец, вообще не существует. Я понимаю, что обманываюсь, но все равно продолжаю обниматься-убиваться не могу иначе, болит ведь, изводит, по ночам спать не дает, вот сижу на подоконнике и, еще минута, истошно закричу от пыток иллюзий. Обратиться к тебе за помощью? Бесполезно. Ты знаешь о моей любви, но тебе она ни к чему, «своих невысказанных чувств полный рот». Мы в одной паутине безответности, но не можем помочь друг другу. Ты обхватываешь руками тонкие белые нити-прутья и смотришь куда-то за пределы реальности, надеясь черт знает на чью помощь. И разница между нами одна: моя любовь к тебе почти сбила меня с ног, а твоя любовь к кому-то – подпитывает, оживляет тебя ожиданием, пусть и обманчивым. Я больше не хочу смотреть на тебя, я прогоняю возможность тебя из сердца, но от этого еще больнее. Вот и проходится шепотом страдать, тоже надеясь черт знает на чью помощь. Времени?..
Ваша жизнь – сплошное вранье, порнуха, бытовуха, интернет-зависимость и сотово-мобильное рабство. Ну разве я не прав? Вот скажите мне, вы когда-нибудь совершали что-нибудь по настоящему из ряда вон? Никогда. И не сможете. Знаете почему? Потому что все это находится за пределами вашей зоны комфорта. Вы упакованы в нее. Как в полипропиленовый мешок. Вы куски мяса, зажатые рамками быта и работы. Или я не прав? Может, я ошибаюсь? Поправьте меня.
Например, можете подарить свой мобильник первому встречному? А? Вопрос на засыпку. Можете прямо сейчас отформатировать винт на вашем компьютере? Стремно? Обосрались? А знаете, почему вы этого не сделаете? Потому что это равноценно самоубийству. Вы без этого не существуете.
Хранил в себе один секрет и был в семье примерный муж.
Всё было, вроде, как всегда: жена готовила обед…
Но приключилась вдруг беда: он взял и вспомнил про секрет.
Под шум и кислый запах щей, ворчанье суженой с утра,
Он вспомнил всё до мелочей, как будто было то вчера…
…Она сидела у окна, и мягкий чудный лунный свет
Окрасил в бледные тона её прекрасный силуэт…
Струились пряди по плечам, скользили змейками на грудь…
И он подумал сгоряча: «Женюсь на ней когда – нибудь!»
Он вспомнил всё до мелочей: изгибы линий, мягкость губ…
И жар её простых речей, и за окном огромный дуб.
Сплетенье рук… Слиянье тел… Каскад каштановых волос…
И то, как он её хотел до исступления, до слёз!
Признаний трепетных поток, как он на ушко их шептал!
Смешной над ухом завиток, что от дыханья трепетал…
Она смотрела на него глазами влажными, как ночь.
Слова пьянили, как вино: «Люблю тебя… Роди мне дочь…»
С утра он потерял покой: то суетился, то скучал…
Потом, закрыв лицо рукой, сидел на стуле и молчал.
Жена ворчала, как всегда. Ругала убежавший суп…
И он отметил, что года ей, постаревшей, не к лицу.
Как не идёт ей белый цвет и пряди крашеных волос.
И целых двадцать восемь лет всё как – то было не всерьёз…
Вдруг он вскочил, схватил пальто, забыл про шапку и носки.
Все двадцать восемь лет – не то… Все двадцать восемь зим – тоски.
Нашёл тот дом. У дома – дуб. Взбежал по лестнице стрелой…
Унять бы дрожь с холодных губ, и трусость гадкую – долой!
Наверное, она сейчас пьет чай и кутается в шаль…
И из её прекрасных глаз струится тихая печаль…
А может, принялась вязать? А может кружево плести?
Так много надо ей сказать! А главное сказать – прости…
Открыла дверь… В глазах – вопрос. Ей было снова двадцать лет…
Каскад каштановых волос… Знакомый сердцу силуэт…
Над ухом – лёгкий завиток… Как много лет назад – точь в точь…
” Вы не ошиблись?» – Нет, не мог… Вы Аня? ” Вера. Её дочь…»
” А Аня?”- ” Мамы больше нет… Кто Вы?» Он повернулся вспять:
«Я шёл к ней двадцать восемь лет…» – Она ждала Вас… Двадцать пять…
Как закружилась голова… Как сердце ухнуло в груди!
И вспомнил он её слова с мольбою: «Ты не уходи!»
Он сгорбился. Поплёлся прочь. Сплетенье рук… Слиянье тел…
Люблю тебя… Роди мне дочь… А он ведь вправду дочь хотел.
Как странно. Ани больше нет… Заплакал… Бросил в тишину:«Я буду много – много лет любить тебя… Тебя одну…»
P.S. БЕРЕГИТЕ ЛЮБОВЬ – она фундамент вашего счастья…
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
NAT (Network Address Translation) для новичков и не только / Хабр
Приветствую всех читателей данной статьи!
Данная статья будет полезна как новичкам, так и опытным системным администраторам/ сетевым инженерам. Здесь затрагиваются понятия и принцип работы технологии NAT, ее значение в наше время, виды и создание с конфигурированием в программе-симуляторе Cisco Packet Tracer.
Введение
Интернет – всемирная система, состоящая из объединенных компьютерных сетей на базе протокола TCP/IP.
Сейчас интернет – это не просто сеть, а целая информационная вселенная, подчиняющаяся техническим, социальным и государственным законам в различных ее частях. В современном мире люди не обходятся без доступа во всемирную паутину. Интернет открывает множество возможностей получения информации из любой точки мира.
На данный момент в интернете больше всего распространены IP адреса версии – IPv4. Это позволяет создать 4.3 млрд. IP-адресов. Однако этого, казалось бы, большого количества критично не хватает. Чтобы решить эту проблему – был создан механизм преобразования сетевых адресов – NAT.
С задачей объединения устройств в единую сеть помогают различные компании, занимающиеся разработкой и внедрением сетевого оборудования.На сей момент на рынке сетевого оборудования доминируют компании Cisco Systems и Huawei. В данной статье будем вести работу с оборудованием Cisco.
Cisco Systems разработала собственную специальную межсетевую ОС для работы с оборудованием под названием IOS (Internet Operating System). IOS – многозадачная операционная система, выполняющая функции сетевой организации, маршрутизации, коммутации и передачи данных. ОС IOS представляет собой сложную операционную систему реального времени, состоящую из нескольких подсистем и имеющую множество возможных параметров конфигурирования.
В операционной системе IOS представлен специфичный интерфейс командой строки CLI (Command Line Interface). В этом интерфейсе возможно использовать некоторое количество команд. Количество зависит от выбранного режима и от уровня привилегий пользователя (пользовательский, привилегированный, глобальной конфигурации и специфической конфигурации).
Нехватка IP адресов. Технология NAT
В 80х годах ХХ века заложили основу IPv4, позволяющую создавать ~4.3 млрд. адресов, но никто не предполагал, что этот запас так быстро иссякнет. С каждым годом появлялось все больше и больше пользователей и с 25 ноября 2019г. в России и в Европе официально закончились IP адреса. Лимит исчерпан.
Для решения этой проблемы было придумано несколько способов:
Первый способ заключается в усилении контроля за IP адресами.
Пусть существует некоторый сайт N с IPv4 xxx.xxx.xxx.xxx, и его хост решил прекратить его поддержание данного сайта. Сайт заброшен, а IP продолжает числиться как занятый и таких случаев может быть очень много. То бишь необходимо провести “инвентаризацию” IP адресов и изъять неиспользуемые/заброшенные.
Второй способ – в массовом использовании системы IPv6.
Протокол IPv6 разработан как преемник протокола IPv4. Основные преимущества IPv6 над IPv4 заключаются в увеличенном адресном пространстве (IPv4 имел 32 бита, что ровнялось 232 адресам, а IPv6 имел 128 бит, что ровнялось 2128 адресам), 6 версия протокола стала безопаснее (т.к. в v4 не предусматривались многие аспекты безопасности, ибо расчет был на сторонние ПО, а в v6 появились контрольные суммы и шифрование пакетов), однако это далеко не все преимущества IPv6 над IPv4.
Проблема, казалось бы, решена, однако перейти с протокола IPv4 на IPv6 вызывает трудности, потому что эти протоколы несовместимы. И изюминкой причины тяжелого перехода на 6 версию протокола является денежная стоимость. Многие кампании не готовы вложить достаточное кол-во средств для перехода, хоть и стоит отметить, что процесс перехода с 4 на 6 версию постепенно идет.
И третий способ – использование технологии трансляции сетевых адресов – NAT.
Cогласно документу RFC 1918, IANA зарезервировала 3 блока адресов для частных IP (серых) (рис 1), остальные же IP адреса носят название публичных адресов (белых).
рис.1Network Address Translation – это механизм в сетях TCP/IP, позволяющий изменять IP адрес в заголовке пакета, проходящего через устройство маршрутизации трафика.
Принимая пакет от локального компьютера, маршрутизатор смотрит на IP-адрес назначения. Если это локальный адрес, то пакет пересылается другому локальному компьютеру. Если нет, то пакет надо переслать наружу в интернет.
Маршрутизатор подменяет обратный IP-адрес пакета на свой внешний (видимый из интернета) IP-адрес и меняет номер порта (чтобы различать ответные пакеты, адресованные разным локальным компьютерам). Комбинацию, нужную для обратной подстановки, маршрутизатор сохраняет у себя во временной таблице. Через некоторое время после того, как клиент и сервер закончат обмениваться пакетами, маршрутизатор сотрет у себя в таблице запись об n-ом порте за сроком давности.
Основная функция NAT – сохранение публичных адресов, однако дополнительной функцией является конфиденциальность сети, путем скрытия внутренних IPv4 адресов от внешней.
Существует множество типов технологии NAT, однако основными принято считать: Статический NAT (Static Network Address Translation), Динамический NAT (Dynamic Network Address Translation) и Перегруженный NAT (Network Address Translation Overload).
Статический NAT применяют для отображения незарегистрированного IP-адреса на зарегистрированный IP-адрес на основании один к одному. Особенно полезно, когда устройство должно быть доступным снаружи сети.
рис 2
Статический NAT используется чаще всего в корпоративных сетях, когда необходимо, чтобы какой-либо IP адрес всегда был доступен из глобальной сети. Зачастую статическим IP наделяют сервера и помещают их в DМZ (рис 2).
Динамический NAT отображает незарегистрированный IP-адрес на зарегистрированный адрес из группы зарегистрированных IP-адресов. Динамический NAT также устанавливает непосредственное отображение между незарегистрированными и зарегистрированными адресами, но отображение может меняться в зависимости от зарегистрированного адреса, доступного в пуле (pool – диапазон) адресов, во время коммуникации.
Перегруженный NAT. Этот тип NAT’a имеет множество названий:
NAT Overload, Many-to-One, PAT (Port Address Translation) и IP Masquerading, однако в большинстве источников указывается как NAT Overload. Перегруженный NAT – форма динамического NAT, который отображает несколько незарегистрированных адресов в единственный зарегистрированный IP-адрес, используя различные порты. При перегрузке каждый компьютер в частной сети транслируется в тот же самый адрес, но с различным номером порта.
Подготовка компьютерной сети
Логическая схема топологии сети будет выглядеть как показано на изображении (рис 3)
Отнесем PC – станции во VLAN 2, а сервер во VLAN 3. Для этого нужно настроить коммутатор S0 (рис 4). Для того, чтобы определить PC пользователей в отдельный VLAN, необходимо создать VLAN 2 и в 3 запихнуть сам сервер (удобства ради еще и обзовем VLAN’ы именами) (показано синим на рис 4), определить область портов коммутатора, которые будут входить во VLAN 2,3 и прописать соответствующие команды (показано красным на рис 4). Следующая задача – определить один порт типа trunk, для взаимодействия с маршрутизатором (показано зеленым рис 4). Таким образом, коммутатор выступает в роли “посредника” между оконечными устройствами и маршрутизатором.
рис 5Теперь нужно настроить непосредственно маршрутизатор. Технология sub-interface позволяет объединять несколько виртуальных интерфейсов в один и подключить их к физическому интерфейсу (на маршрутизаторе выбран физический интерфейс fa0/0). Необходимо дать для каждого VLAN’а свой под-интерфейс (показано красным на рис 5) и выдать им IP адрес (показано зеленым на рис 5).
Таким образом, в будущем мы будем NAT’ить трафик.
Дальше я бы посоветовал бы настроить протокол динамической выдачи IP адреса – DHCP, ибо прописывать каждому PC свой адрес – то еще “удовольствие”…
! Важно, чтобы сервер(а) всегда были со статичным IP адресом !
Дадим серверу статичный IP 192.168.3.2, а остальных оставим для динамического распределения адресов.
После настройки DHCP, нужно прописать на каждом саб-интерфейсе в R0 команду “ip helper-address 192.168.3.2”, тем самым указывая, куда стоит обращаться для получения IP адреса.
После данной команды, устройства получат запрашиваемые IP адреса.
Пингуем с рандомного ПК сам сервер (1 пинг) и шлюзы маршрутизатора (2- 3 пинг) (рис 6).
Дальше для удобства будем эмулировать подключение к провайдеру, путем создания в программе-симуляторе РС провайдера, сервера Serv2 с IP 213.234.60.2 (эмулирующий остальную сеть интернет) и роутера R3.
Настройка NAT
Ну и наконец-то мы дошли до самой настройки NAT…
Для внедрения NAT нужно определиться какие порты будут внешними(outside), а какие внутренними(inside).
Статичный NAT сопоставляет внутренний и внешний адреса один к одному, поэтому настроим Serv2 таким образом, чтобы любой компьютер мог подключиться к серверу, а сервер к компьютеру – нет. Для этого необходимо прописать следующие команды (рис 7):
По итогу, любой компьютер, находящийся во 2 VLAN’е может пинговать сервер провайдера, а обратно – нет (рис 8). Аналогично проделываем для Serv1, находящимся во VLAN 3.
рис 8рис 9А теперь, на финал, внедрим NAT Overload на R0.
Для этого создадим ACL и пропишем там сети, которые должны “натиться” (показано синим на рис 9) и, показав что нужно “натить”, активируем лист (показано красным на рис 9).
Таким образом, реализовав статическую и динамическую (типа PAT) настройку NAT, мы смогли защитить небольшую сеть от подключения извне.
Надеюсь вам понравилась данная статья.
Спасибо за ее чтение, всем хорошего настроения 🙂
P.S. Статью пишу впервые, не судите строго 🙂
Предельные законы объяснены на примерах с цветовой кодировкой
Ошибка: Нажмите «Не робот», затем повторите попытку.
Краткое описание
- Предельные законы – это простые формулы, которые помогают нам точно оценить пределы.
- Внизу страницы находится краткий список законов о лимитах.
Лимитные законы
Для следующих уравнений $$ a $$ и $$ k $$ являются константами, а $$ n $$ – целым числом. Также предположим, что существуют $$ \ displaystyle \ lim \ limits_ {x \ to a} f (x) $$ и $$ \ displaystyle \ lim \ limits_ {x \ to a} g (x) $$.
(1) Постоянный закон: $$ \ displaystyle \ lim \ limits_ {x \ to a} k = k $$Этот закон имеет дело с постоянными функциями (горизонтальными линиями). Поскольку $$ y $$ – это , всегда равно $$ k $$, то не имеет значения, к чему приближается $$ x $$.
Пример 1
$$ \ Displaystyle \ lim \ limits_ {х \ to6} 8 = 8 $$
(2) Закон идентичности: $$ \ displaystyle \ lim \ limits_ {x \ to a} x = a $$Этот закон имеет дело с функцией $$ y = x $$. Поскольку $$ y $$ и $$ x $$ равны, независимо от приближения к значению $$ x $$, $$ y $$ должен будет приблизиться к одному и тому же значению.
Пример 2
$$ \ displaystyle \ lim \ limits_ {x \ to 4} x = 4 $$
(3) большой закон сложения: $$ \ displaystyle \ lim \ limits_ {x \ to a} f (x) + g (x) = \ displaystyle \ lim \ limits_ {x \ to a} f (x) + \ displaystyle \ lim \ limits_ {x \ to a} g (x) $$Это просто означает, что когда мы берем предел добавления, мы можем просто взять предел каждого члена индивидуально, а затем сложить результаты.
Пример 3
$$ \ displaystyle \ lim \ limits_ {x \ to -7} (x + 5) $$
Решение:$$ \ begin {align *} \ displaystyle \ lim_ {x \ to -7} (\ blue {x} + \ red {5}) & = \ blue {\ lim_ {x \ to -7} x} + \ red {\ lim_ {x \ to -7} 5} && \ mbox {Закон сложения} \\ & = \ blue {-7} + \ red {5} && \ blue {Identity \ hspace {2mm} Law} \ hspace {2mm} и \ hspace {2mm} \ red {Constant \ hspace {2mm} Law} \\ & = -2 \ end {выровнять *} $$
(4) Закон вычитания: $$ \ displaystyle \ lim \ limits_ {x \ to a} f (x) – g (x) = \ displaystyle \ lim \ limits_ {x \ to a} f (x) – \ displaystyle \ lim \ limits_ {x \ to a} g (x) $$По сути то же, что и Закон сложения, но для вычитания.Работайте с каждым термином отдельно, а затем вычтите результаты.
Пример 4
$$ \ displaystyle \ lim \ limits_ {x \ to \ frac 1 2} (x-9) = $$
Решение:$$ \\ \ begin {align *} \ lim_ {x \ to \ frac 1 2} (\ blue {x} – \ red {9}) & = \ blue {\ lim_ {x \ to \ frac 1 2} x} – \ red {\ lim_ {x \ to \ frac 1 2} 9} && \ mbox {Закон вычитания} \\ % & = \ blue {\ frac 1 2} – \ red {9} && \ blue {Identity} \ hspace {2mm} и \ hspace {2mm} \ red {Constant} \ hspace {2mm} Законы \\ % & = \ frac 1 2 – \ frac {18} 2 \\ [6pt] % & = – \ frac {17} 2 \ end {выровнять *} \\ $$
(5) Закон постоянных коэффициентов: $$ \ displaystyle \ lim \ limits_ {x \ to a} k \ cdot f (x) = k \ displaystyle \ lim \ limits_ {x \ to a} f (x) $$Если ваша функция имеет коэффициент, вы можете сначала взять предел функции, а затем умножить на коэффициент.
Пример 5
$$ \ Displaystyle \ lim \ limits_ {x \ to 3} (8x) $$
Решение:$$ \ begin {align *} \ lim_ {x \ to 3} (8x) & = 8 \, \ lim_ {x \ to 3} x && \ mbox {Закон постоянных коэффициентов} \\ & = 8 (3) && \ mbox {Закон идентичности} \\ & = 24 \ end {выровнять *} $$
С помощью первых 5 предельных законов мы теперь можем найти пределы любой линейной функции, имеющей вид $$ y = mx + b $$.
Пример 6
$$ \ displaystyle \ lim \ limits_ {x \ to -2} (4x – 3) $$
Решение:$$ \ begin {align *} \ displaystyle \ lim_ {x \ to -2} (4 \ blue {x} – \ red {3}) & \ displaystyle \ lim_ {x \ to-2} (4 \ blue {x}) – \ lim_ {x \ to-2} \ red {3} && \ mbox {Закон вычитания} \\ & = 4 \, \ blue {\ lim_ {x \ to-2} x} – \ red {\ displaystyle \ lim_ {x \ to-2} 3} && \ mbox {закон постоянных коэффициентов} \\ & = 4 (\ blue {-2}) – \ red {3} && \ blue {Identity} \ hspace {2mm} и \ hspace {2mm} \ red {Constant} \ hspace {2mm} Законы \\ & = -8 – 3 \\ & = -11 \ end {выровнять *} $$
(6) Закон умножения: $$ \ lim \ limits_ {x \ to a} f (x) \ cdot g (x) = \ left (\ lim \ limits_ {x \ to a} f (x) \ right) \ слева (\ lim \ limits_ {x \ to a} g (x) \ right) $$Если функция включает произведение двух (или более) факторов, мы можем просто взять предел каждого фактора, а затем умножить результаты вместе.2 & = \ displaystyle \ lim_ {x \ to 5} (\ blue {x} \ cdot \ red {x}) \\ & = \ left (\ blue {\ lim_ {x \ to 5} x} \ right) \ left (\ red {\ lim_ {x \ to5} x} \ right) && \ mbox {Закон умножения} \\ & = (\ blue {5}) (\ red {5}) && \ mbox {Закон идентичности} \\ & = 25 \ end {выровнять *} $$
Первые 6 предельных законов позволяют нам находить пределы любой полиномиальной функции, хотя предельный закон 7 делает его немного более эффективным.3 + 5 (\ red {-2}) && \ mbox {Закон идентичности} \\ & = 4 (-8) – 10 \\ & = -32 – 10 \\ & = -42 \ end {выровнять *} $$
(8) Закон деления: $$ \ displaystyle \ lim \ limits_ {x \ to a} \ frac {f (x)} {g (x)} = \ frac {\ displaystyle \ lim \ limits_ {x \ to a} е (х)} {\ displaystyle \ lim \ limits_ {x \ to a} g (x)} $$ при условии $$ \ displaystyle \ lim \ limits_ {x \ to a} g (x) \ neq 0 $$Закон деления говорит нам, что мы можем просто найти предел числителя и знаменателя по отдельности, пока мы не получим ноль в знаменателе.
Пример 10
$$ \ displaystyle \ lim \ limits_ {x \ to 12} \ frac {2x} {x-4} $$
Решение:$$ \ begin {align *} \ displaystyle \ lim_ {x \ to 12} \ frac {2 \ blue x} {\ red x-4} & = \ frac {\ displaystyle \ lim \ limits_ {x \ to 12} (2 \ blue x)} { \ displaystyle \ lim \ limits_ {x \ to 12} (\ red x-4)} && \ mbox {закон деления} \\ [6pt] & = \ frac {2 \, \ displaystyle \ lim \ limits_ {x \ to12} \ blue x} {\ displaystyle \ lim \ limits_ {x \ to12} (\ red x- 4)} && \ mbox {закон постоянных коэффициентов } \\ [6pt] & = \ frac {2 \, \ blue {\ displaystyle \ lim \ limits_ {x \ to12} x}} {\ red {\ displaystyle \ lim \ limits_ {x \ to12} x} – \ displaystyle \ lim \ limits_ { x \ to12} 4} && \ mbox {Закон вычитания} \\ [6pt] & = \ frac {2 (\ blue {12})} {\ red {12} -4} && \ mbox {Законы идентичности и постоянные законы} \\ [6pt] & = \ frac {24} 8 \\ [6pt] & = 3 \ end {выровнять *} $$
С первыми 8 законами пределов теперь мы можем найти пределы любой рациональной функции.
(9) Корневой закон: $$ \ displaystyle \ lim \ limits_ {x \ to a} \ sqrt [n] {f (x)} = \ sqrt [n] L $$ при условии $$ L> 0 $$, когда $ $ n $$ – четное.Для корневых функций мы можем сначала найти предел внутренней функции, а затем применить корень. Мы должны быть осторожны, чтобы не извлечь квадратный корень из отрицательного числа!
Пример 11
$$ \ displaystyle \ lim \ limits_ {x \ to -2} \ sqrt {x + 18} $$
Решение:$$ \ begin {align *} \ displaystyle \ lim_ {x \ to -2} \ sqrt {\ blue x + \ red {18}} & = \ sqrt {\ displaystyle \ lim_ {x \ to -2} (\ blue x + \ red {18})} && \ mbox {Корневой закон} \\ & = \ sqrt {\ blue {\ displaystyle \ lim_ {x \ to -2} x} + \ red {\ displaystyle \ lim_ {x \ to -2} 18}} && \ mbox {Закон сложения} \\ & = \ sqrt {\ blue {-2} + \ red {18}} && \ mbox {Законы идентичности и постоянные законы} \\ & = \ sqrt {16} \\ & = 4 \ end {выровнять *} $$
(10) Закон о составеПредположим, что $$ \ lim \ limits_ {x \ to a} g (x) = M $$, где $$ M $$ – постоянная.Также предположим, что $$ f $$ непрерывен на $$ M $$. потом
$$ \ Displaystyle \ lim \ limits_ {х \ к а} е \ влево (г (х) \ вправо) = е \ влево (\ лим \ лимиты_ {х \ к а} г (х) \ вправо) = е ( M). $$
Пример 12
$$ \ Displaystyle \ lim \ limits_ {x \ to \ pi} \ sin (x) $$
Решение:$$ \ begin {align *} \ displaystyle \ lim_ {x \ to \ pi} \ sin (\ blue x) & = \ sin \ left (\ blue {\ displaystyle \ lim_ {x \ to \ pi} x} \ right) && \ mbox {закон композиции } \\ & = \ sin (\ blue \ pi) && \ mbox {Закон идентичности} \\ & = 0 \ end {выровнять *} $$
Пример 13
$$ \ Displaystyle \ lim_ {х \ к 3} е ^ {\ соз (\ пи х)} $$
Решение:$$ \ begin {align *} \ displaystyle \ lim_ {x \ to 3} e ^ {\ cos (\ pi \ blue x)} & = e ^ {\ displaystyle \ lim_ {x \ to 3} \ cos (\ pi \ blue x)} && \ mbox {Закон композиции} \\ & = е ^ {\ соз \ left (\ displaystyle \ lim_ {x \ to3} (\ pi \ blue x) \ right)} && \ mbox {закон композиции} \\ & = e ^ {\ cos \ left (\ pi \, \ blue {\ lim_ {x \ to 3} x} \ right)} && \ mbox {Закон постоянных коэффициентов} \\ & = e ^ {\ cos (\ pi (\ blue 3))} && \ mbox {Закон идентичности} \\ & = e ^ {\ cos (3 \ pi)} \\ & = e ^ {- 1} \\ & = \ frac 1 e \ end {выровнять *} $$
(11) Закон о неравенствеПредположим, что $$ f (x) \ geq g (x) $$ для всех $$ x $$ вблизи $$ x = a $$.Тогда $$ \ lim \ limits_ {x \ to a} f (x) \ geq \ lim \ limits_ {x \ to a} g (x) $$
Список предельных законов
Постоянный закон $$ \ lim \ limits_ {x \ to a} k = k $$
Закон идентичности $$ \ lim \ limits_ {x \ to a} x = a $$
Закон сложения $$ \ lim \ limits_ {x \ to a} f (x) + g (x) = \ lim \ limits_ {x \ to a} f (x) + \ lim \ limits_ {x \ to a } g (x) $$
Закон вычитания $$ \ lim \ limits_ {x \ to a} f (x) – g (x) = \ lim \ limits_ {x \ to a} f (x) – \ lim \ limits_ {x \ to a } g (x) $$
Закон постоянных коэффициентов $$ \ lim \ limits_ {x \ to a} k \ cdot f (x) = k \ lim \ limits_ {x \ to a} f (x) $$
Закон умножения $$ \ lim \ limits_ {x \ to a} f (x) \ cdot g (x) = \ left (\ lim \ limits_ {x \ to a} f (x) \ right) \ left ( \ lim \ limits_ {x \ to a} g (x) \ right) $$
Степенной закон $$ \ lim \ limits_ {x \ to a} \ left (f (x) \ right) ^ n = \ left (\ lim \ limits_ {x \ to a} f (x) \ right) ^ n $$ при условии $$ \ lim \ limits_ {x \ to a} f (x) \ neq 0 $$, если $$ n
Закон деления $$ \ lim \ limits_ {x \ to a} \ frac {f (x)} {g (x)} = \ frac {\ lim \ limits_ {x \ to a} f (x)} { \ lim \ limits_ {x \ to a} g (x)} $$ при условии $$ \ lim \ limits_ {x \ to a} g (x) \ neq 0 $$
Корневой закон $$ \ lim \ limits_ {x \ to a} \ sqrt [n] {f (x)} = \ sqrt [n] L $$ при условии $$ L> 0 $$ при $$ n $$ даже.
Закон композиции Предположим, что $$ \ lim \ limits_ {x \ to a} g (x) = M $$, где $$ M $$ – константа. Также предположим, что $$ f $$ непрерывен на $$ M $$. Тогда $$ \ lim \ limits_ {x \ to a} f \ left (g (x) \ right) = f \ left (\ lim \ limits_ {x \ to a} g (x) \ right) = f (M ) $$.
Закон о неравенстве Предположим, что $$ f (x) \ geq g (x) $$ для всех $$ x $$ вблизи $$ x = a $$.Тогда $$ \ displaystyle \ lim \ limits_ {x \ to a} f (x) \ geq \ lim \ limits_ {x \ to a} g (x) $$
Ошибка: Нажмите «Не робот», затем повторите попытку.
2.3. Предельные законы – Исчисление, том 1
Цели обучения
- Признать основные законы о лимитах.
- Используйте законы пределов, чтобы оценить предел функции.
- Вычислить предел функции факторингом.
- Используйте предельные законы, чтобы оценить предел полиномиальной или рациональной функции.
- Оцените предел функции путем факторизации или использования конъюгатов.
- Вычислите предел функции, используя теорему сжатия.
В предыдущем разделе мы оценивали пределы, глядя на графики или создавая таблицу значений.В этом разделе мы устанавливаем законы для расчета пределов и узнаем, как применять эти законы. В Студенческом проекте в конце этого раздела у вас есть возможность применить эти предельные законы, чтобы вывести формулу для площади круга, адаптировав метод, изобретенный греческим математиком Архимедом. Начнем с повторения двух полезных результатов о предельных значениях из предыдущего раздела. Эти два результата вместе с предельными законами служат основой для расчета многих пределов.
Первые два предельных закона были указаны на (Рисунок), и мы повторяем их здесь.Эти основные результаты вместе с другими предельными законами позволяют нам оценить пределы многих алгебраических функций.
Результаты базового лимита
Для любого действительного числа и любой константы
Оценка базового предела
Оцените каждый из следующих пределов, используя (Рисунок).
Теперь посмотрим на законы пределов, индивидуальные свойства пределов. Доказательства справедливости этих законов здесь не приводятся.
Сейчас мы практикуем применение этих законов о лимитах для оценки лимита.
Оценка лимита с использованием законов о лимитах
Используйте законы пределов для оценки.
Решение
Давайте применим законы предельных значений пошагово, чтобы убедиться, что мы понимаем, как они работают. Нам необходимо иметь в виду требование о том, что при каждом применении предельного закона должны существовать новые пределы для применения предельного закона.
Многократное использование предельных законов
Используйте законы пределов для оценки.
Решение
Чтобы найти этот предел, нам нужно применить законы пределов несколько раз. Опять же, нам нужно иметь в виду, что, когда мы переписываем предел с точки зрения других ограничений, каждый новый предел должен существовать для применения закона предела.
Используйте законы пределов для оценки. На каждом этапе указывайте применяемый предельный закон.
Решение
К настоящему времени вы, вероятно, заметили, что в каждом из предыдущих примеров именно так и было.Это не всегда верно, но это верно для всех многочленов при любом выборе и для всех рациональных функций при всех значениях, для которых рациональная функция определена.
Чтобы убедиться, что эта теорема верна, рассмотрим многочлен. Применяя законы суммы, постоянного кратного и степенного, мы получаем
Теперь из частного закона следует, что если и – многочлены, для которых, то
.(рисунок) применяет этот результат.
Оценка предела рациональной функции
Оцените.
Решение
Поскольку 3 находится в области определения рациональной функции, мы можем вычислить предел, подставив 3 вместо в функцию. Таким образом,
.Оценить.
Как мы видели, мы можем легко вычислить пределы многочленов и пределы некоторых (но не всех) рациональных функций с помощью прямой подстановки. Однако, как мы видели во вводном разделе, посвященном ограничениям, определенно возможно существование, когда не определено. Следующее наблюдение позволяет нам оценить многие ограничения этого типа:
Если на всем протяжении некоторого открытого интервала, содержащего, то.
Чтобы лучше понять эту идею, рассмотрим предел.
Функция
и функция идентичны для всех значений. Графики этих двух функций показаны на (Рисунок).
Рисунок 1. Графики и идентичны для всех. Их пределы на 1 равны.Мы видим, что
Предел имеет вид, где и. (В этом случае мы говорим, что имеет неопределенную форму 0/0.) Следующая стратегия решения проблем предоставляет общий план для оценки пределов этого типа.
Следующие примеры демонстрируют использование этой стратегии решения проблем. (Рисунок) иллюстрирует метод множителя и отмены; (Рисунок) показывает умножение на конъюгат. На (Рисунок) мы рассмотрим упрощение сложной дроби.
Оценка лимита путем факторинга и отмены
Оценить.
Оценить.
Решение
Вычисление предела умножением на конъюгат
Оценить.
Оценить.
Решение
Оценка предела путем упрощения сложной дроби
Оценить.
Оценить.
(рисунок) не соответствует ни одному из шаблонов, установленных в предыдущих примерах. Однако, проявив немного творчества, мы все же можем использовать те же самые техники.
Оценка лимита, когда законы о лимитах не применяются
Оценить.
Решение
Давайте вернемся к односторонним ограничениям.Простые модификации предельных законов позволяют применять их к односторонним пределам. Например, чтобы применить предельные законы к пределу формы, мы требуем, чтобы функция была определена на открытом интервале формы; для предела формы мы требуем, чтобы функция была определена на открытом интервале формы. (Рисунок) иллюстрирует этот момент.
Оценка одностороннего лимита с использованием предельных законов
По возможности оцените каждый из следующих пределов.
На (Рисунок) мы смотрим на односторонние пределы кусочно определенной функции и используем эти пределы, чтобы сделать вывод о двустороннем пределе той же функции.
Оценка двустороннего предела с использованием законов о предельных значениях
Для оценки каждого из следующих пределов:
Постройте график и оцените.
Решение
-1, который пересекал ось x и ось y в начале координат ».>
Теперь мы обратим наше внимание на оценку предела формы, где, где и. То есть имеет вид при.
Оценка предела формы с использованием предельных законов
Оценить.
Оценить.
Решение
Техника, которую мы разработали до сих пор, очень хорошо работает для алгебраических функций, но мы все еще не можем оценить пределы самых основных тригонометрических функций. Следующая теорема, называемая теоремой о сжатии , оказывается очень полезной для установления основных тригонометрических пределов. Эта теорема позволяет нам вычислять пределы, «сжимая» функцию с пределом в неизвестной точке между двумя функциями, имеющими общий известный предел в.(Рисунок) иллюстрирует эту идею.
Рисунок 4. Теорема сжатия применима, когда и.Применение теоремы о сжатии
Примените теорему сжатия для оценки.
Используйте теорему сжатия для оценки.
Теперь мы используем теорему сжатия, чтобы найти несколько очень важных ограничений. Хотя это обсуждение довольно продолжительное, эти ограничения оказываются неоценимыми для развития материала как в следующем разделе, так и в следующей главе. Первый из этих ограничений -.Рассмотрим единичный круг, показанный на (Рисунок). На рисунке мы видим, что это координата на единичной окружности, которая соответствует отрезку линии, показанному синим цветом. Радианная мера угла θ – это длина дуги, которую он проходит на единичной окружности. Таким образом, мы видим, что для.
Рис. 6. Синусоидальная функция показана в виде линии на единичном круге.Поскольку и, используя теорему сжатия, мы заключаем, что
.Чтобы увидеть это, обратите внимание на это для и, следовательно, для.Следовательно, Отсюда следует, что. Применение теоремы сжатия дает желаемый предел. Таким образом, поскольку и,
.Далее, используя идентификатор для, мы видим, что
.Теперь мы рассмотрим предел, который играет важную роль в следующих главах, а именно,. Чтобы оценить этот предел, мы используем единичный круг на (Рисунок). Обратите внимание, что этот рисунок добавляет еще один треугольник к (Рисунок). Мы видим, что длина стороны противоположного угла в этом новом треугольнике равна. Таким образом, мы видим, что для.
Рис. 7. Функции синуса и тангенса показаны линиями на единичной окружности.Разделив на все части неравенства, получим
.Эквивалентно
.Так как, заключаем, что. Применяя манипуляции, подобные тем, которые использовались при демонстрации этого, мы можем это показать. Таким образом,
.В (Рисунок) мы используем этот предел для установления. Этот предел также окажется полезным в следующих главах.
Оценка важного тригонометрического предела
Оценить.
Решение
На первом этапе мы умножаем на сопряжение, чтобы мы могли использовать тригонометрическую идентичность для преобразования косинуса в числителе в синус:
Следовательно,
.Оценить.
Ключевые понятия
- Законы пределов позволяют нам оценивать пределы функций без необходимости каждый раз проходить пошаговые процессы.
- Для многочленов и рациональных функций.
- Вы можете оценить предел функции, разложив на множители и отменив, умножив на конъюгат или упростив сложную дробь.
- Теорема сжатия позволяет вам найти предел функции, если функция всегда больше одной функции и меньше другой функции с известными пределами.
В следующих упражнениях используйте законы пределов для оценки каждого предела. Обоснуйте каждый шаг, указав соответствующий предельный закон (законы).
1.
Решение
Использовать постоянный множественный закон и разностный закон:
2.
3.
Решение
Использовать корневой закон:
4.
В следующих упражнениях используйте прямую замену для оценки каждого предела.
5.
6.
7.
8.
9.
Решение
10.
В следующих упражнениях используйте прямую замену, чтобы показать, что каждый предел приводит к неопределенной форме 0/0.Затем оцените предел.
12.
14.
16. , где – действительная константа
18.
20.
В следующих упражнениях используйте прямую подстановку, чтобы получить неопределенное выражение. Затем используйте метод (рисунок), чтобы упростить функцию и определить предел.
21.
Решение
22.
23.
Решение
24.
В следующих упражнениях предположим, что, и. Используйте эти три факта и законы пределов для оценки каждого предела.
25.
Решение
26.
27.
Решение
28.
29.
Решение
30.
31.
Решение
.
32.
В следующих упражнениях используйте калькулятор, чтобы построить график каждой кусочно определенной функции, и изучите график, чтобы оценить заданные пределы.
Решение
3. В точках (3, 7) есть открытый кружок, а наклон равен 1. ”>
a. 9; б. 7
Решение
= 2.Он имеет наклон -1 и точку пересечения по оси x в точке (3,0) ».>
a. 1; б. 1
В следующих упражнениях используйте следующие графики и законы пределов для оценки каждого предела.
-3. Другие ключевые точки: (0, 1), (-5,2), (1,2), (-7, 4) и (-9,6). Нижняя кусочная функция имеет линейный и криволинейный сегменты. Линейный сегмент существует для x <-3 и имеет убывающий наклон. Он переходит в (-3, -2) при x = -3. Изогнутый сегмент кажется правой половиной открывающейся вниз параболы.Он переходит в точку вершины (-3,2) при x = -3. Он пересекает ось y немного ниже y = -2. Другие ключевые точки: (0, -7/3), (-5,0), (1, -5), (-7, 2) и (-9, 4). ">
36.
37.
Решение
38.
39.
Решение
40.
41.
[show-answer q = ”957757 ″] Показать решение [/ show-answer][hidden-answer a = ”957757 ″]
42.
43.
Решение
Для следующих задач оцените предел с помощью теоремы сжатия. n}.3}. \]
См. Другие проблемы на странице 2.
методов оценки пределов | Каковы методы оценки пределов – примеры и решения
ОЦЕНКА ПРЕДЕЛОВ:Теперь мы обсудим различные методы, используемые для получения пределов. Каждый метод будет сопровождаться некоторыми примерами, иллюстрирующими этот метод.
(A) ПРЯМАЯ ЗАМЕНА
Это уже упоминается в начале текущего раздела, где мы видели, что для непрерывной функции предел может быть получен прямой заменой.5} – 4x + 3}} \ end {align} \)
Мы видим, что при замене x = 1 числитель и знаменатель становятся 0.
Следовательно, ( x – 1 ) является множителем как числителя, так и знаменателя (теорема о множителях)
Факторизация приводит к
(C) РАЦИОНАЛИЗАЦИЯ
В этом методе рационализация неопределенного выражения приводит к определенному. Следующие примеры подробно описывают этот метод.2} \,. \, \, \ Frac {1} {{\ cos \, h}} \ end {align} \]
Это выражение теперь содержит только пределы \ (\ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{\ sin x}} {x} = 1 \) и \ (\ mathop {\ lim} \ limit_ {x \ to 0} \ cos x = 1 \)
Следовательно, окончательный результат будет \ (\ frac {1} {{16}} \)
Теперь мы рассмотрим примеры, основанные на методах, описанных выше. Мы настоятельно рекомендуем вам сначала попробовать все эти примеры самостоятельно, прежде чем просматривать решения.
численное нахождение пределов | предварительное вычисление, исчисление
Численное нахождение пределов, что означает, что мы должны приблизительно рассмотреть некоторые значения x, которые ближе к заданному числу слева и справа.И проверьте, для какого значения x мы получаем функцию undefined. Мы также можем проверить это, построив графики.Шаги для построения эскиза графика
Шаг 1: Найдите точки пересечения по оси x данной функции.
Шаг 2: Найдите точку пересечения оси Y заданной функции.
Шаг 3: Отметьте, есть ли вертикальные или горизонтальные асимптоты, если таковые имеются.
Шаг 4: Получите некоторые значения x, вставьте эти значения в заданную функцию и найдите значения y.{3} -1} {x-1} $
Решение: Сначала мы построим график данной функции, используя технику построения кривых, описанную выше.
Поскольку знаменатель содержит x-1, мы не понимаем, что делать, когда x = 1. Итак, чтобы получить представление о поведении графика вблизи x = 1. Мы будем использовать два набора значений x, один набор значений с левой стороны приближается к 1, а другой набор значений с правой стороны приближается к 1.
График данной функции представляет собой параболу, но в точке (1,3) есть зазор, как показано на приведенном выше графике.{2} -3x-4} \ приблизительно 0,2 $
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
12-й класс по математикеОт численного определения пределов к дому
Wolfram | Alpha Примеры: пределы
Пределы
Вычислить пределы численно и символически.
Возьмем предел коэффициента разницы:
Вычислить предел с участием абстрактных функций:
Другие примеры
Односторонние ограничения
Вычисление односторонних пределов с заданного направления.
Вычислить односторонние ограничения в точке разрыва:
Укажите направление подхода:
Другие примеры
Предельные представления
Экспресс-функции в терминах лимитов.
Найдите предельные представления для функции:
Другие примеры
Как использовать теорему сжатия
До сих пор мы рассматривали, как находить и оценивать пределы для простых и более сложных функций.Однако, как и в большинстве тем математики, будут времена, когда оценка пределов станет невозможной без использования других методов. Вот где пригодится «Теорема сжатия».
Что такое теорема о сжатии
Прежде чем мы перейдем к математическому определению теоремы сжатия, давайте сначала подумаем об этом понятии в более привычных терминах. Представьте, что я бегун вместе с двумя моими друзьями, Джоном и Дэвидом. Вместо того, чтобы знать, как далеко я каждый раз пробегаю, я знаю свое расстояние по сравнению с Джоном и Дэвидом согласно следующему:
1) Я всегда бегаю наравне с Джоном или дальше его.
2) Я всегда бегаю меньше или равно Дэвиду.
Допустим, однажды я, Джон и Дэвид выбежали из дома. В этот день Джон и Дэвид оба пробегают по 3 км. Теперь вопрос в том, как далеко я убежал? Если мы ответим на этот вопрос в соответствии с двумя условиями, указанными выше, мы придем к единственно возможному ответу – 3 км. Теперь давайте разберем это алгебраически, чтобы вы могли ясно это увидеть:
– Пусть расстояние, которое я пробегаю, будет обозначено M (x)
– Пусть расстояние, которое пробегает Джон, будет представлено как J (x)
– Пусть расстояние, которое пробегает Дэвид, будет обозначено D (x)
Теперь, в соответствии с двумя вышеуказанными условиями:
J (x) ≤M (x) ≤D (x) J (x) \ leq M (x) \ leq D (x) J (x) ≤M (x) ≤D (x)
И если и Джон, и Дэвид пробежали по 3 км каждый:
3≤M (x) ≤33 \ leq M (x) \ leq 33≤M (x) ≤3
Это приводит нас к нашему ответу 3 км – это единственное значение, которое может удовлетворить это равенство, указанное выше.Именно функции, описывающие расстояние, пройденное Джоном и Дэвидом, «сжали» или «зажали» мою функцию расстояния и позволили нам найти ответ, ничего не зная о пройденном мной расстоянии. Это идея, лежащая в основе теоремы «сжатия» или «сэндвича» – она позволяет нам вычислить предел функции с помощью двух других, более простых функций, когда другие методы бесполезны. Для более алгебраического доказательства теоремы сжатия, если вам интересно, посмотрите здесь.
Как использовать теорему о сжатии
С математической точки зрения теорема сжатия определяется следующим образом:
г (х) ≤f (x) ≤h (x) g (x) \ leq f (x) \ leq h (x) g (x) ≤f (x) ≤h (x)
limn → A g (x) = lim_ {n \ to A} \; g \ left (x \ right) = limn → A g (x) = limn → A h (x) = Llim_ {n \ to A } \; h \ left (x \ right) = Llimn → A h (x) = L
Следовательно: limn → A f (x) = Llim_ {n \ to A} \; f \ left (x \ right) = Llimn → A f (x) = L
В принципе, для данного неравенства из трех членов, таких как одно выше – предел члена f (x) равен пределу g (x) и h (x), если эти пределы равны друг другу. 7}} limx → ∞ x716x3
Как видите, наш числитель имеет степень 3, а знаменатель – степень 7.7} = 0 = x70 = 0
Вот! Теперь, когда мы рассмотрели, как найти предел, давайте вернемся к тому, как использовать теорему сжатия.
Как выполнить теорему о сжатии
Хотя теорема сжатия теоретически может использоваться для любого набора функций, удовлетворяющих указанным выше условиям, она особенно полезна при работе с синусоидальными функциями. Как и в большинстве случаев в математике, лучший способ проиллюстрировать, как выполнять теорему сжатия, – это решать некоторые задачи по теореме сжатия.
Пример 1:
Найдите limx → ∞ cosxxlim_ {x \ to \ infty} \; \ frac {{{\ cos x}}} {{x}} limx → ∞ xcosx
Прежде чем мы перейдем к решению этой проблемы, давайте сначала рассмотрим, почему в этом случае необходимо использование теоремы сжатия.Простой ответ на этот вопрос состоит в том, что мы не можем вычислить cos бесконечности. Поскольку бесконечность на самом деле не является числом, мы ничем не можем заменить x, чтобы найти этот предел. По этой причине мы должны использовать теорему сжатия.
Шаг 1. Устранение неравенства
Из-за характера функции косинуса: −1≤cosx≤1-1 \ leq \ cos x \ leq 1−1≤cosx≤1
Шаг 2. Измените неравенство
Вы заметите, что нашего неравенства недостаточно для решения этой проблемы, поскольку нас просят найти предел cosx / x, а не только cosx.Поэтому нам нужно внести некоторые изменения. Разделив все неравенство на x, мы получаем то, что нас просят решить.
−1x≤cosxx≤1x- \ frac {1} {x} \ leq \ frac {\ cos x} {x} \ leq \ frac {1} {x} −x1 ≤xcosx ≤x1
Шаг 3. Оцените пределы для левой и правой руки
Помните – мы думали, что задача попросила нас решить предел cosx / x, когда x стремится к бесконечности, мы сделаем это, найдя предел для двух других функций, которые мы создали в неравенстве.
limx → ∞ −1x = lim_ {x \ to \ infty} \; – \ frac {1} {x} = limx → ∞ −x1 = limx → ∞ 1x = 0lim_ {x \ to \ infty} \; \ frac {1} {x} = 0limx → ∞ x1 = 0
ПРИМЕЧАНИЕ: Если левый и правый пределы не равны друг другу, мы не можем использовать теорему сжатия.

