Функции. Предел функции
10.1Понятие функции
10.1.1Функции и отображения
Мы, наконец, добрались до главного объекта математического анализа — до функций. Слова «функция» и «отображения» в принципе являются синонимами, они обозначают одно и то же математическое понятие, но в зависимости от контекста чаще используют одно или другое. Говоря «функция», мы будем как правило иметь в виду числовую функцию одной переменной, то есть отображение, которое числу ставит в соответствие число. Именно такие функции изучают в школе.
Определение 1. (Числовой) функцией (одной переменной) называется отображение
f:X→R,
где X⊂R — некоторое подмножество множества вещественных чисел. В этом случае X называется областью определения функции. Обозначают также X=:D(f).
Выбранный термин — функция или отображение — также влияет на выбор терминов для
обозначения некоторых связанных понятий.
Например, если x — некоторый элемент
области определения, а y=f(x), в терминах отображений x называется
10.1.2Функции и формулы
Функции можно задавать формулами.
Пример 1. Запись f(x)=x2 задаёт функцию, которая любому вещественному числу ставит в соответствие его квадрат, см. рис. 10.1.
Рис. 10.1: Функция y=x2 как отображение: точки с левой оси переходят в точки на правой оси. Стрелочек нужно было бы нарисовать бесконечно много, но тогда ничего нельзя было бы разобрать
Если функция задана формулой, и не сказано ничего специального про её область
определения, считается, что областью определения такой функции является
множество всех чисел, при которых значение формулы может быть вычислено (так
называемая естественная область определения).
Пример 2. Функция g(x)=1×2−1 определена во всех точках, кроме x=1 и x=−1. Её область опредеделения — R∖{−1,1}.
При необходимости можно задать функцию, определенную на каком-то более узком
подмножестве. Например, можно рассмотреть функцию g(x)=x2, x≥0.
Несмотря на то, что f из примера выше и только
что определенная g задаются одной и той же формулой, это разные функции,
поскольку у них разные области определения. Можно сказать, что функция g была
получена из функции f путём
g=f|[0,+∞),
то есть после имени функции ставят палочку, а внизу пишут множество, на которое функция ограничивается.
Иногда область определения функции ясна из контекста и смысла входящих в неё
переменных. Например, если x — это размер какой-нибудь популяции, вряд ли он
может быть отрицательным.
Пример 3. Функции можно задавать более сложными выражениями. Например:
f(x)={x2,x>0−x,x≤0
Это пример кусочного задания функции. В зависимости от того, какому условию удовлетворяет значение x, применяется либо одна формула, либо другая.
10.1.3График функции
Один из правильных способов думать про функции — это думать про их графики. По определению, график функции — это множество точек на декартовой плоскости, у которых x-координата равна какому-то значению из области определения функции, а y-координата равна f(x). Формально:
Gr(f):={(x,f(x))∣x∈D(f)}.
Функции можно задавать графиками. Eсли нарисовать произвольную кривую на декартовой плоскости, она будет графиком некоторой функции если и только если с любой вертикальной прямой x=x0 у неё будет не более одной точки пересечения, см. рис. 10.2.
Рис. 10.2: Кривые слева являются графиками функций.
Слева сверху функция принимает
значение 6 в точке 2 и значение 5 в точке 3,5. Слева снизу
функция не определена на интервале (4,7). Кривые справа не являются
графиками функций: для некоторых (в частности, отмеченных) вертикальных
прямых у них более одной точки пересечения.
Если точки пересечения нет, значит, функция не определена в точке x0. Если есть, y-координата точки пересечения задаёт значение функции в точке x0. Если бы нашлась вертикальная прямая с более чем одной точкой пересечения, было бы непонятно, какое значение принимает функция в соответствующей точке.
Как правило, думая о свойствах функции, правильнее всего представлять себе
именно графики, а не, скажем, формулы, которыми эти функции задаются. Однако,
нужно понимать, что любой физически нарисованный график — лишь приближение к
абстрактному математическому графику. Графики как правило сами по себе не могут
использоваться для доказательств утверждений, хотя придумать доказательства без
них часто может быть очень сложно.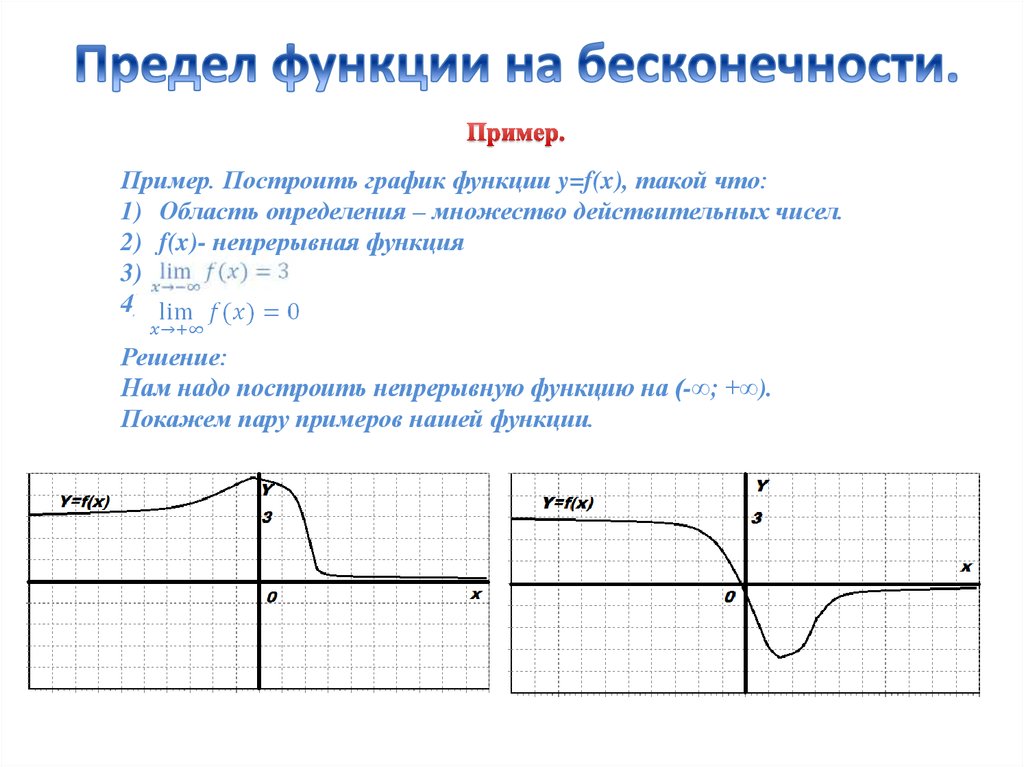
Впрочем, бывают функции, графики которых трудно себе представить.
Пример 4. Рассмотрим функцию Дирихле:
D(x)={1,x∈Q;0,x∉Q.
Она принимает значение 1 во всех рациональных точках и 0 во всех иррациональных. Представить себе её график довольно сложно — он не выглядит как привычная нам кривая. Поскольку и рациональные и иррациональные числа всюду плотны, на любом сколь угодно маленьком интервальчике будут как точки, в которых функция принимает значение 0, так и точки, в которых функция принимает значение 1. Получится два таких «дырявых» множества точек, одно лежит на прямой y=0, другое на y=1.
10.1.4Свойства функций
Часть свойств функций очень похожи на аналогичные свойства последовательностей.
Определение 2. Говорят, что функция f ограничена (ограничена сверху, ограничена снизу) на множестве A⊂D(f), если существует такое
C, что для всех x∈A выполняется неравенство |f(x)|<C
(соответственно, f(x)<C, f(x)>C).
В этом определении для краткости сформулированы сразу три определения: из скобок нужно выбирать соответствующие элементы. Если множество A не указано, считается, что A — вся область определения функции.
Пример 5. Функция f(x)=1x не является ограниченной, поскольку выражение 1x может принимать сколь угодно большие значения (для всякого C>0 можно выбрать x=1C+1 и получить |f(x)|=C+1>C). Однако, эта функция ограничена на отрезке [1,2].
Определение 3. Функция f называется
Пример 6. Рассмотрим функцию f(x)=sinx. Она возрастает на отрезке
[−π/2,π/2], убывает на отрезке [π/2,3π/2] и снова возрастает на
отрезке [3π/2,5π/2].
Вопрос 1. Верно ли, что функция f(x)=sinx возрастает на множестве [−π/2,π/2]∪[3π/2,5π/2]?
Неверный ответ. Не совсем, написано, что она возрастает на отрезке [−π/2,π/2] и на отрезке [3π/2,5π/2]. Возрастает ли она на их объединении? Проверьте с помощью определения.
Звучит странно, но нет, неверно.
Верный ответ. Именно так! Хотя функция возрастает на каждом из отрезков, она не возрастает на их объединении, поскольку требования определения не выполняются. Например, если x1=π2 и x2=3π/2, обе точки принадлежат объединению, x2>x1 и при этом f(x2)=−1<1=f(x1).
Ограниченностью и монотонностью дело не ограничивается, у функций ещё много разных свойств, которые не встречаются у последовательностей.
Определение 4. Пусть область определения функции f(x) симметрична относительно нуля, то
есть вместе с каждой точкой x содержит и точку (−x).
Функция f(x)
называется чётной, если для всех x∈D(f), f(−x)=f(x). Функция
f(x) называется нечётной, если для всех x∈D(f), f(−x)=−f(x).
График чётной функции симметричен относительно оси Oy: вместе с каждой точкой (x,f(x)) он содержит точку (−x,f(x)). График нечётной функции симметричен относительно начала координат: вместе с каждой точкой (x,f(x)) он содержит точку (−x,−f(x)).
Пример 7. Функция sin(x) является нечётной, а cos(x) — чётной. Функция f(x)=xn является чётной при чётных значениях n и нечётной при нечётных (отсюда и название).
10.1.5Экстремумы
Очень часто нам важно уметь отвечать на вопросы вроде «какое максимальное
значение может принимать данная функция» или «как бы так подобрать x, чтобы
f(x) было как можно меньше». Такого типа задачи называются задачами
оптимизации, и вся наша жизнь ими пронизана. Владелец компании хочет
максимизировать её прибыль, сотрудник — свою зарплату, программист — скорость
работы программы, собака — количество вкусняшек, кошка… Ладно, с кошками
непонятно, но они тоже наверняка что-нибудь оптимизируют.
Чтобы иметь возможность формулировать и решать задачи оптимизации нам нужно сформулировать ряд дополнительных понятий.
Определение 5. Говорят, что функция f достигает своего максимального значения в точке x0∈D(f), если для всех x∈D(f) выполняется неравенство f(x0)≥f(x). В этом случае точка x0 называется точкой глобального максимума функции f. Иногда слово «точка» опускается и говорят просто «глобальный максимум», имея в виду точку x0. Также под словами «глобальный максимум» может подразумеваться значение f(x0) или точка (x0,f(x0)) на графике функции. Как правило, из контекста ясно, что имеется в виду.
Определение 6. Ну и наоборот, f достигает своего минимального значения в точаке x0∈D(f), если для всех x∈D(f) выполняется неравенство f(x0)≤f(x). В этом случае точка x0 называется точкой глобального минимума функции f.
Совместно максимумы и минимумы называются экстремумами. То есть экстремум — это максимум или минимум.
Пример 8. У функции может не быть глобальных экстремумов. Например, функция f(x)=x, определенная на интервале (0,1), не имеет ни глобального максимума, ни глобального минимума.
Вопрос 2. А почему?
Узнать ответ
Верный ответ. Докажем от противного. Пусть x0∈(0,1) — точка глобального максимума. Возьмём точку x=(x0+1)/2 — это середина отрезка [x0,1]. Тогда f(x)=x=x0/2+1/2>x0/2+x0/2=x0=f(x0), поскольку 1>x0. Значит, x0 — не точка глобального максимума. Значит, никакого глобального максимума нет. Аналогично можно показать, что нет и глобального минимума.
Пример 9. У функции может быть много глобальных экстремумов. Например, у функции f(x)=cosx бесконечно много глобальных максимумов (все точки вида 2kπ, k — целое) и бесконечного много минимумов (каких?).
Вопрос 3. Может ли глобальный максимум совпадать с глобальным минимумом?
Нет.
Неверный ответ. А вот и нет.
Да.
Верный ответ. Действительно, у функции f(x)=42 бесконечно много глобальных максимумов и все они также являются глобальными минимумами.
Определение 7. Точка x0 называется точкой строгого глобального максимума (минимума) если для всех x∈D(f), не совпадающих с x0, выполняется неравенство f(x0)>f(x) (соответственно, f(x0)<f(x)). Иными словами, в определении экстремума мы заменили неравенство на строгое, и ещё добавили условие, что x не совпадает с x0 — если бы мы этого не сделали, никакая точка не могла бы удовлетворять определению.
Вопрос 4. Может ли у функции быть несколько строгих глобальных максимумов?
Нет.
Верный ответ. Действительно, не может: значение функции в каждом из них должно быть строго больше, чем в другом. Так не бывает.
Да.
Неверный ответ. Как же?
Вопрос 5. Может ли у функции быть строгий глобальный максимум, являющийся одновременно строгим глобальным минимумом?
Нет.
Верный ответ. Это почти правда: значение функции в строгом глобальном максимуме должно быть строго больше её значения в строгом глобальном минимуме, и значит это должно быть два разных значения, и значит две разные точки. Но есть одно исключение. Угадаете, какое?
Да.
Верный ответ. Технически, это верно: для любой функции, определённой лишь в одной точке, эта точка является одновременно глобальным максимумом и минимумом. Однако, такие функции не очень интересны — как говорят, это вырожденный пример.
Определение 8. Точка x0∈D(f) называется точкой локального максимума (минимума) функции
f, если существует такой интервал (a,b), содержащий точку x0, что
для всех x∈(a,b)∩D(f) выполняется неравенство f(x0)≥f(x)
(соответственно, f(x0)≤f(x)).
Как видно, определение локального экстремума отличается от определения глобального только требованиями на x. Например, в случае глобального максимума, мы хотим, чтобы f(x0) было не меньше, чем значение f в любой другой точке области определения, а в случае с локальным максимумом f(x0) должно быть не меньше, чем значения f в точках x, близких к x0. Любой глобальный максимум автоматически является локальным, но не всякий локальный максимум обязан быть глобальным.
Рис. 10.3: Точки локального и глобального максимума на графике функции y=f(x).
Перейдём теперь к ключевому понятию курса: пределу функции.
10.2Предел функции
10.2.1Примеры и мотивировка
Начнём как всегда с неформального описания и примеров.
Как бы определение 1. Говорят, что функция y=f(x) имеет предел в точке x=x0, равный b, если
значение этой функции становится сколь угодно близким к числу b если
значение x достаточно близко к x0, но при этом не равно x0.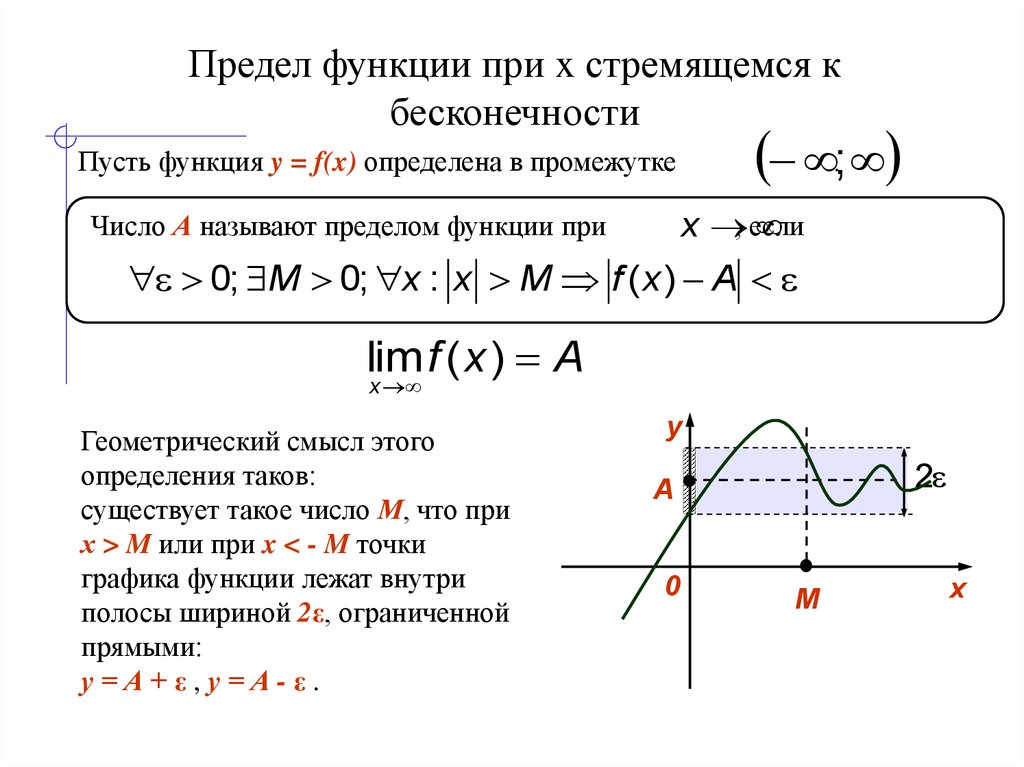
Обозначение:
limx→x0f(x)=b
или
f(x)→b при x→x0.
Рассмотрим несколько примеров.
Пример 10. Пусть f(x)=x2. К чему стремится f(x), если x стремится к 2? Можно посмотреть на график и увидеть, что если мы выибраем значения x, близкие к 2, то соответствующая точка на графике будет близка к точке (2,4).
Рис. 10.4: Предел функции y=x2 при x→2.
Значит, значение f(x) будет близким к 4. Таким образом, предел f при x стремящемся к двум равен четырём:
limx→2×2=4.
Казалось бы, зачем городить такой огород в предыдущем примере — понятно, что
достаточно просто подставить значение x в формулу для функции и получить
ответ. Однако, это не всегда работает. Во-первых, в квазиопределении
предела явно сказано, что мы не можем брать x, равное
x0. Во-вторых, функция может быть не определена в точке x0 — и это не
мешает ей иметь предел в этой точке.
Пример 11. Пусть
f(x)=x2−1x−1.
К чему приближается значение функции когда x приближается к 1? Если попытаться просто подставить значение x=1 в формулу, ничего не получится: знаменатель обнуляется и значение не определено. Однако, можно выбирать близкие значения x, подставлять их в формулу и посмотреть, что получается:
def f(x):
return (x ** 2 - 1) / (x - 1)
print("x\tf(x)")
for x in [1.01, 1.001, 1.0001, 1.00001,
0.99, 0.999, 0.9999, 0.99999]:
print(f"{x}\t{f(x)}")x f(x) 1.01 2.009999999999999 1.001 2.0009999999999177 1.0001 2.0000999999993923 1.00001 2.0000100000008274 0.99 1.990000000000001 0.999 1.9989999999999712 0.9999 1.9998999999994975 0.99999 1.9999899999991726
Из таблички, которую мы видим, можно сделать вывод, что значение f(x) приближается к 2. То же самое можно увидеть на графике.
Рис. 10.5: Функция не определена в точке, но предел у неё есть.
Как это можно было бы доказать?
Заметим, что выражение для f(x) можно упростить. Если разложить числитель на скобки, получится (x−1)(x+1):
f(x)=(x−1)(x+1)(x−1).
Если x≠1, дробь можно сократить на (x−1) и получится выражение (x+1). Если x=1, значение функции не определено. Таким образом, можно сказать, что функция f(x) определена при всех значениях x∈R∖{1}, и на этом множестве задаётся формулой
f(x)=x+1.(10.1)
Поскольку нас интересует, к чему приближается f(x), когда x приближается к 1, но не равен 1 (см. как бы определение 1), нас интересуют только значения функции при x≠1, и значит мы можем смело использовать формулу (10.1). Очевидно, если x приближается к 1, то (x+1) приближается к 2. Таким образом,
limx→1×2−1x−1=2.
Пример 12. Рассмотрим функцию
f(x)={1,x≠2;3,x=2.
Чему равняется её предел при x→2?
В этом примере функция определена в точке x=2 и может возникнуть искушение
подставить x=2 в формулу и сказать, что результат (число 3) и будет ответом.
Однако,
это неверно. На самом деле, значение функции в этой точке никак не влияет на
ответ: предел функции при x стремящемся к x0 зависит от значений
функции в точках, близких к x0, но не в самой точке x0.
Рис. 10.6: Предел функции в точке не равен её значению в этой точке.
Во всех точках, близких к 2, значение функции равно 1. Значит, предел этой функции при x→2 также равен 1:
limx→2f(x)=1.
Пример 13. Рассмотрим функцию
f(x)={x+1,x≤1;x−2,x>1.(10.2)
Что вы можете сказать про её предел при x→1?
Посмотрим на график.
Если x чуть меньше 1, действует верхняя строчка в определении функции и
значение оказывается чуть меньше 2. Однако, если x чуть больше 1,
действует уже нижняя строчка, и значение функции оказывается чуть больше
−1. Никакого одного числа, к которому бы приближалось значение функции,
когда x приближается к 1, нет.
Значит, нет и предела.
Итак, limx→1f(x) в этом случае не существует.
В этом примере несуществование предела было связано с тем фактом, что при приближении x с разных сторон значение функции приближалось к разным числам. Это не единственный механизм несуществования предела.
Пример 14. Рассмотрим функцию
f(x)=sinπx.
Что вы можете сказать про её предел при x→0? Просто подставить x=0 в формулу нельзя, да и как мы видели это не всегда работает. Попробуем использовать тот же приём, что и в примере 10: подставим в f какие-нибудь значения x, близкие к 0, и посмотрим, что получается.
import numpy as np
def f(x):
return np.sin(np.pi / x)
print(" x\t\t f(x)")
for x in [0.01, 0.001, 0.0001, 0.00001,
-0.01, -0.001, -0.0001, -0.00001]:
print(f"{x: .7f}\t{f(x): .7f}")x f(x) 0.0100000 0.0000000 0.0010000 -0.0000000 0.0001000 -0.0000000 0.0000100 -0.0000000 -0.0100000 -0.0000000 -0.0010000 0.0000000 -0.0001000 0.0000000 -0.0000100 0.0000000
0000000
-0.0010000 0.0000000
-0.0001000 0.0000000
-0.0000100 0.0000000
Чему же равен предел? Из таблички может сложиться ощущение, что нулю — во всех наших пробных точках значение функции нулевое. Однако, на самом деле это не так.
Рассмотрим последовательность точек xn=12n+1/2. Очевидно xn→0 при n→∞. Найдём f(xn):
f(xn)=sin⎛⎜⎝π12n+1/2⎞⎟⎠=sin(2nπ+π/2)=1.
Таким образом, существуют сколь угодно близкие к нулю числа, в которых значение функции принимает значение 1. Это значит, что предел никак не может быть равен нулю! На самом деле, предел в этом случае не существует: выбирая разные значения x, близкие к нулю, например, справа (то есть положительные числа), можно получать значения функции, близкие к 1, или к 0, или к −1, или ещё к чему-нибудь. Одного числа, к которому приближалось бы значение функции, не существует.
Упражнение 1. Крайне полезное упражнение — построить график функции y=sinπ/x.
Чтобы
понять, как он выглядит, полезно найти все значения x, при которых функция
принимает значения 0, 1 и −1 и отметить соответствуюие точки на графике.
10.2.2Строгое определение предела
Мы хотим формализовать квазиопределение 1. В нём есть слова «значение функции становится сколь угодно близким». Что это значит? Это значит, что мы можем сделать значения f(x) настолько близкими к числу b, насколько хотим. Но для этого нужно потребовать, чтобы x был достаточно близок к x0 (и при этом не равен x0). С чем-то подобным мы уже сталкивались, когда придумывали понятие предела последовательности. Определение предела функции очень похоже.
Нам понадобится пара вспомогательных определений.
Определение 9. Окрестностью точки x0 называется любой интервал (a,b),
содержащий точку x0, см. рис. 10.8. Проколотой
окрестностью точки x0 назвается окрестность, из которой выкинули
саму точку x0, то есть множество (a,x0)∪(x0,b), где
a<x0<b.
Эпсилон-окрестностью (ε-окрестностью)
точки x0 называется интервал (x0−ε,x0+ε). Проколотой
ε-окрестностью точки x0 называется множество
(x0−ε,x0)∪(x0,x0+ε)=(x0−ε,x0+ε)∖{x0}.
(x0−ε,x0)∪(x0,x0+ε)==(x0−ε,x0+ε)∖{x0}.
Обычно ε-окрестность точки x0 обозначается как Uε(x0), а проколотая ε-окрестность — как ˚Uε(x0).
Рис. 10.8: Различные типы окрестностей: обычная окрестность, проколотая окрестность, ε-окрестность и проколотая ε-окрестность.
Определение 10. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0,
то есть существует такая проколотая окрестность, в которой функция
определена; в самой точке x0 она может быть определена, а может и не
быть. Говорят, что предел функции f(x) в точке x=x0 равен числу b,
если для всякого ε>0 найдётся такое δ>0, что для всех x из
проколотой δ-окрестности точки x0 значения функции лежат в
ε-окрестности точки b, см.
рис. 10.9.
Формально: утверждение
limx→x0f(x)=b
по определению означает, что
∀ε>0 ∃δ>0 ∀x∈˚Uδ(x0):f(x)∈Uε(b),
или, с учётом замечания 3:
∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε.
∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε.
Рис. 10.9: Окрестности в определении предела. Заметим, что значение функции в самой точке x0 может не лежать в ε-окрестности точки b или быть вообще не определено, но может и лежать: про него мы ничего не говорим.
Пример. Вернёмся к примеру 10 и докажем, что limx→2×2=4, пользуясь только что сформулированным определением.
Пусть нам дано произвольное ε>0. Мы хотим подобрать такое δ>0, что для всех x из проколотой δ-окрестности точки 2, |x2−4|<ε. Заметим, что
|x2−4|=|(x−2)(x+2)|=|x−2|⋅|x+2|.
Если x лежит в проколотой дельта-окрестности точки 2, значит,
|x−2|<δ.
Таким образом мы получили оценку на первый сомножитель: его
можно сделать сколь угодно маленьким подходящим выбором δ. Осталось
оценить второй сомножитель. Поскольку δ мы выбираем сами, на неё можно
накладывать любые условия, какие мы хотим. Пусть δ≤1. (Почему именно
1? На самом деле, подойдёт любое фиксированное число, нужно взять какое-то
конкретное, почему бы и не 1?) Тогда
−1≤−δ<x−2<δ≤1
или (прибавим ко всем членам число 2):
1<x<3.
В этом случае выражение |x+2| обязательно меньше |3+2|=5: поскольку x>0, выражение под модулем гарантированно положительно и значит его нужно сделать как можно больше, чтобы модуль был как можно больше, и значит нужно брать как можно большее значение x, но x<3. Таким образом, если |x−x0|<δ≤1,
|x2−4|=|x−2|⋅|x+2|<δ⋅5.
Мы хотим, чтобы эта величина была меньше ε. Это будет выполняться, если
потребовать, чтобы δ≤ε/5.
Итак, у нас есть два условия на
δ: δ≤1 и δ≤ε/5. Чтобы они оба были
удовлетворены, достаточно взять
δ(ε):=min(ε/5,1).
Проверяем: для всех x∈˚Uδ(2) верно неравенство |x−2|<δ, и значит
|x2−4|<δ⋅5=5ε/5=ε.
Таким образом, выбранная нами δ удовлетворяет определению, и предел действительно равен 4, см. анимацию на рис. 10.10.
Рис. 10.10: Как работает определение предела: хотя значение ε уменьшается, нам каждый раз удаётся подобрать такое значение δ, чтобы все точки графика над проколотой δ-окрестностью точки x0=2 лежали в ε-окрестности точки b=4.
10.3Односторонние пределы
В мире последовательностей всё было просто: последовательность могла иметь
предел при n→∞, и больше никакого. В мире функций всё сложнее. Мало
того, что x может приближаться к различным точкам, и нужно уточнять, к чему
именно он приближается. Он ещё может это делать разными способами.
Рассмотрим функцию f(x), заданную формулой (10.2) (см. пример 13). У неё нет предела в точке x=1, поскольку при приближении по x к точке 1 справа или слева, значение функции f(x) приближается к разным числам (−1 и 2 соответственно). Чтобы сказать это формально, нужно дать определение односторонних пределов.
Определение 11. Пусть функция f(x) определена в правой полуокрестности точки x0, то есть на множестве (x0,x0+δ∗) для некоторого δ∗>0. Говорят, что предел функции f(x) при x стремящемся к x0 справа равен b, если для всякого ε>0 найдётся такая δ>0, что для всех x∈(x0,x0+δ) выполняется неравенство |f(x)−b|<ε.
Определение 12. Пусть функция f(x) определена в левой полуокрестности точки x0, то есть на множестве (x0−δ∗,x0) для некоторого δ∗>0. Говорят, что предел функции f(x) при x стремящемся к x0 слева равен b, если для всякого ε>0 найдётся такая δ>0, что для всех x∈(x0−δ,x0) выполняется неравенство |f(x)−b|<ε.
Записывают:
limx→x+0f(x)=b
для предела справа и
limx→x−0f(x)=b
для предела слева.
Упражнение 2. Докажите, что для функции f(x), заданной формулой (10.2), предел справа равен −1, а предел слева равен 2.
Упражнение 3. Докажите, что если у функции существует предел при x→x0, то пределы при x→x+0 и при x→x−0 также существуют, равны между собой и равны пределу при x→x0. Докажите, что верно и обратное: если оба односторонние пределы существуют и равны между собой, то предел при x→x0 также существует и его значение равно значению односторонних пределов.
10.4Заключение
Функции одной переменной нам всем знакомы со школы. Однако, объект этот не так прост, как может показаться. Чтобы приобрести хорошую интуицию о том, какими бывают функции и какими свойствами они могут обладать, придётся хорошо поработать. И для начала — освоить понятие предела функции в точке, которое мы будем постоянно использовать в будущем.
← Предыдущая глава Следующая глава →
Предел функции
Предел функции Math Task
1.
|
|||||||||||||||||||||||||||||
| 6 7 8 9 10 11 12 13 14 | |||||||||||||||||||||||||||||
Пусть задана некая функция f(x). Тогда число А будет называться пределом функции y = f(x) при х стремящимся к бесконечности, если при всех х больше определенного числа р, разность между значением функции и числом А по модулю будет меньше любого, сколь угодно малого положительного числа ɛ>0. | f(x)– А | < ɛ
Иными словами, при подставлении любого числа х>р данное неравенство всегда будет выполняться.
lim f(x) = А |
Рис.1 |
||||||||||||||||||||||||||||
Геометрический смысл предела функции y=f(x) в бесконечности заключается в том, что при стремлении х к бесконечности, значение функции f(x) стремится к числу А. Таким образом, неравенство | f(x) – А | < ɛ равносильно двойному неравенству: А – ɛ < f(x) < А + ɛ и функция принимает значения в диапазоне шириной 2ɛ (рис.1). |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Примеры. | |||||||||||||||||||||||||||||
| 6 7 8 9 10 11 12 13 14 | |||||||||||||||||||||||||||||
Предел функции.
Т.е. верно неравенство:
|
|
||
www. mathtask.ru |
||
Лимиты и ограничения | Vercel Docs
Чтобы предотвратить злоупотребление нашей платформой, мы применяем следующие ограничения ко всем учетным записям.
Hobby | Pro | Enterprise | |
|---|---|---|---|
Deployments Created per Day | 100 | 6000 | Custom |
бессерверных функций, созданных для каждого развертывания | 12* | ∞ | ∞ |
Serverless Function Execution Timeout (Seconds) | 10 | 60 | 900 |
Тайм-аут начального ответа пограничной функции (в секундах) | 30 | 30 | 30 |
3 | 30 | 30 | 30 |
Deployments Created from CLI per Week | 2000 | 2000 | Custom |
Team Members на команду | – | 10 | Пользовательский |
Vercel Projects Connected per Git Repository | 3 | 60 | Custom |
Routes created per Deployment | 1024 | 1024 | Custom |
Build Time per Deployment (Минуты) | 45 | 45 | 45 |
Параллельные сборки 30024 1 | 12 | Custom | |
Disk Size (GB) | 13 | 13 | 13 |
Cron Jobs (Beta) | 2* | 40 | 100 |
В случае «без серверных функций», созданных на развертывание », только учитаемые ламбдас считается одним без сервера.
С помощью Next.js Vercel будет автоматически объединять как можно больше бессерверных функций в одну лямбду, как указано в разделе об объединении бессерверных функций.
Ограничение «Маршруты, созданные для каждого развертывания» инкапсулирует несколько параметров, которые можно настроить в Vercel:
- Если вы используете файл конфигурации
vercel.json, каждое изменение, перенаправление или заголовок считается маршрутом - Если вы используете Build Output API, вы можете настроить маршруты для своих развертываний
Обратите внимание, что большинство фреймворков автоматически создают маршруты для вас. Например, Next.js создаст набор маршрутов, соответствующих вашему использованию динамических маршрутов, перенаправлений, перезаписи и пользовательских заголовков.
Задания Cron вызывают бессерверные или пограничные функции. Это означает одинаковое использование и будут применяться ценовые ограничения.
В плане хобби вы ограничены двумя ежедневными заданиями cron.
Это означает, что вы можете создать два задания cron, каждое из которых будет запускаться один раз в день.
В плане хобби мы не можем гарантировать своевременный вызов задания cron. Например, задание cron, настроенное как 0 1 \* \* \* (каждый день в 1:00), будет запускаться в любое время между 1:00 и 1:59. Для более точного и своевременного выполнения заданий cron обновите наш тарифный план Pro.
Hobby | Pro | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
. До 100 Гб-часов | До 1000 Гб-ч | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пограничные исполнительные блоки | 2 До 0 090,00027 | Up to 1,000,000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Edge Middleware Invocations | Up to 1,000,000 | Up to 1,000,000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Build Execution | Up to 100 Hrs | Up до 400 часов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Оптимизация изображения Исходные изображения | До 1000 изображений | До 5000 изображений | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Загрузки с удаленным кэшем | До 10 ГБ | До 10 ГБ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Удаленный кеш. Для Teams в плане Pro вы можете платить за дополнительное использование по мере использования. Примечание: Если ваш проект превысит эти ограничения и вам потребуются расширенные функции безопасности и конфиденциальности, обратитесь в отдел продаж Vercel, чтобы обсудить Enterprise. Для участников нашего плана Pro мы предлагаем модель оплаты по мере использования для дополнительного использования, что дает вам большую гибкость и контроль над вашим использованием. Типичные ежемесячные рекомендации по использованию, приведенные выше, все еще применяются, в то время как дополнительное использование будет автоматически взиматься по следующим ставкам:
Подробнее об ограничениях функции Analytics в Vercel см. в этом разделе. Максимальная продолжительность этапа сборки составляет 45 минут. Когда предел будет достигнут, этап сборки будет прерван, а развертывание завершится ошибкой. Каждой сборке предоставляются следующие ресурсы:
Это значение не может быть увеличено. Дополнительные сведения об устранении неполадок см. в разделе Создание ресурсов контейнера. Максимальный размер кэша сборки — 1 ГБ. Он сохраняется в течение одного месяца и применяется на уровне каждого ключа кэша сборки. Подробнее об ограничениях функции мониторинга в Vercel см. Существует два типа журналов: журналы построения и журналы выполнения. Оба имеют разное поведение при хранении журналов. Журналы сборки хранятся неограниченное время для каждого развертывания. Журналы выполнения хранятся в течение 1 часа для учетных записей Hobby и Pro и в течение 3 дней для учетных записей Enterprise. Чтобы узнать больше об этих ограничениях журналов, прочитайте здесь. Максимальное количество переменных среды для каждой среды на проект
это Общий размер ваших переменных среды, имен и значений ограничен 64 КБ для проектов, использующих среды выполнения Node.js, Python, Ruby, Go, Java и .NET. Это ограничение является общим, разрешенным для каждого развертывания, а также максимальным размером любой отдельной переменной среды. Дополнительные сведения см. в документации по переменным среды. Примечание: В то время как Vercel позволяет использовать переменные среды общим размером до 64 КБ, пограничные функции и промежуточное ПО Edge ограничены 5 КБ на переменную среды. Если вы используете системные переменные среды, то специфичные для платформы переменные (т. е. префикс имени платформы) отображаются только на этапе сборки, но не во время выполнения. Однако те, которые не относятся к фреймворку, отображаются во время выполнения. Только переменные среды, которые отображаются во время выполнения, учитываются при ограничении размера.
Максимальный размер бессерверной функции составляет 50 МБ, а максимальный размер в разархивированном виде — 250 МБ, включая слои, которые автоматически используются в зависимости от среды выполнения. Вы можете настроить функции с помощью Максимальный объем памяти для Бессерверной функции, развернутой в Личном кабинете (план Hobby), составляет 1024 МБ. Для Teams (план Pro) его можно увеличить до 3008 МБ. Примечание. Проекты, созданные до 8 ноября 2019 г., по умолчанию имеют размер 3008 МБ. Мы рекомендуем обновить эти функции проекта до нового значения по умолчанию 1024 МБ, чтобы уменьшить использование, где это применимо. С помощью свойства functions можно настроить размер памяти для каждой бессерверной функции. Количество времени (в секундах), в течение которого бессерверная функция может обрабатывать HTTP-запрос, прежде чем она должна ответить. Дополнительные сведения см. в разделе «Тайм-аут выполнения». По умолчанию максимальное количество одновременных запусков бессерверных функций составляет Ограничение скорости? Ознакомьтесь с нашим руководством по поддержке здесь. Если вам требуется ограничение выше Максимальный размер полезной нагрузки для тела запроса или тела ответа бессерверной функции составляет 4,5 МБ. Если бессерверная функция получает полезную нагрузку, превышающую лимит, она возвращает ошибку → 413: FUNCTION_PAYLOAD_TOO_LARGE. Бессерверные функции можно развернуть в нескольких регионах, однако эта функция ограничена планами Enterprise. См. также документацию для более подробной информации. При попытке развернуть бессерверные функции в нескольких регионах в рамках плана, отличного от Enterprise, произойдет сбой развертывания до перехода к этапу сборки. Максимальный размер функции Edge составляет 1 МБ (план Hobby). Для Teams максимальный размер составляет 2 МБ (план Pro) или 4 МБ (план Enterprise). Это общий сжатый размер вашей функции и ее зависимостей после объединения. Edge Middleware и Edge Functions выделяют 128 МБ памяти. Edge Middleware может в среднем использовать не более 50 мс процессорного времени. Это ограничение относится к фактическому чистому времени ЦП, то есть времени, затраченному на выполнение вычислений, а не к общему прошедшему выполнению или времени «настенных часов». Например, когда вы заблокированы, разговаривая с сетью, время, затраченное на ожидание ответа, составляет , а не учитываются при ограничении времени процессора. Edge Middleware и Edge Functions должны начать отправку ответа в течение 30 секунд. Вы можете продолжить трансляцию ответа после этого времени. Если вы хотите выполнить дополнительную работу, вы должны вернуть ответ как можно скорее и продолжить любые асинхронные рабочие нагрузки в фоновом режиме после возврата ответа. Vercel не поддерживает подключение проектов вашей Личной учетной записи к репозиториям Git, принадлежащим организациям Git. Вы можете либо переключиться на существующую команду, либо создать новую. То же ограничение применяется в потоке создания проекта при импорте существующего репозитория Git или при клонировании шаблона Vercel в новый репозиторий Git как часть вашей организации Git. Дополнительную информацию см. в документации по зарезервированным переменным среды. Ограничения скорости — это жесткие ограничения, которые применяются к платформе при выполнении действий, требующих ответа от нашего API. Таблица ограничений скорости состоит из следующих четырех столбцов:
Ниже приведены пять примеров, которые предоставляют дополнительную информацию о том, как работают ограничения скорости. Вы можете удалять до Вы можете удалять до Вы можете изменить свое имя пользователя до Вы можете создавать Примечание. Использование Next.js или любой аналогичной платформы для создания вашего развертывания классифицируется как сборка. Каждая бессерверная функция также классифицируется как сборка. Размещение статических файлов, таких как файл index.html, не классифицируется как сборка. Вы можете развертывать Масштабирование и размещение функций Azure
При создании приложения-функции в Azure необходимо выбрать план размещения для своего приложения. Для функций Azure доступно три базовых плана размещения: план потребления, план Premium и план Dedicated (служба приложений). Выбранный план хостинга определяет следующее поведение:
В этой статье представлено подробное сравнение различных планов хостинга, а также хостинга на основе Kubernetes. Примечание Если вы решите разместить свои функции в кластере Kubernetes, рассмотрите возможность использования кластера Kubernetes с поддержкой Azure Arc. Размещение в кластере Kubernetes с поддержкой Azure Arc в настоящее время находится в предварительной версии. Дополнительные сведения см. в разделе Служба приложений, функции и приложения логики в Azure Arc. Обзор плановНиже приводится сводка преимуществ трех основных планов хостинга для функций:
Сравнительные таблицы в этой статье также включают следующие варианты хостинга, которые обеспечивают максимальный уровень контроля и изоляции для запуска приложений-функций.
В остальных таблицах этой статьи сравниваются планы по различным функциям и поведению. Сравнение стоимости планов динамического хостинга (Потребление и Премиум) см. на странице цен на Функции Azure. Цены на различные варианты выделенного плана см. Операционная система/среда выполненияВ следующей таблице показана поддержка операционных систем и языков для тарифных планов хостинга.
1 Linux — единственная поддерживаемая операционная система для стека среды выполнения Python. Время ожидания приложения-функции Время ожидания для функций в приложении-функции определяется свойством В следующей таблице показаны значения по умолчанию и максимальные значения (в минутах) для определенных планов:
1 Независимо от настройки тайм-аута приложения-функции, 230 секунд — это максимальное время, в течение которого функция, запускаемая HTTP, может ответить на запрос. Масштаб В следующей таблице сравниваются характеристики масштабирования различных планов хостинга.
1 Во время масштабирования в настоящее время существует ограничение в 500 экземпляров на подписку в час для приложений Linux в плане потребления. Режим холодного пуска
Пределы обслуживания
1 По умолчанию время ожидания для среды выполнения Functions 1. Ограничения на создание новых приложений-функций в существующей группе ресурсовВ некоторых случаях при попытке создать новый план хостинга для приложения-функции в существующей группе ресурсов может появиться одна из следующих ошибок:
Это может произойти при соблюдении следующих условий:
Причина, по которой это происходит, связана с тем, как планы приложений-функций и веб-приложений сопоставляются с разными пулами ресурсов при создании. Для разных SKU требуется разный набор возможностей инфраструктуры. Когда вы создаете приложение в группе ресурсов, эта группа ресурсов сопоставляется и назначается определенному пулу ресурсов. Если вы попытаетесь создать другой план в этой группе ресурсов, а в сопоставленном пуле нет необходимых ресурсов, произойдет эта ошибка. При возникновении этой ошибки вместо этого создайте приложение-функцию и план размещения в новой группе ресурсов. Сетевые функции
Выставление счетов
|
в разделе «Ограничения и цены».
js, Go, Ruby, Python
Эти ограничения применяются AWS, чтобы гарантировать невозможность развертывания бессерверных функций, загрузка которых занимает много времени.
Максимальное время ожидания выполнения составляет 10 секунд при развертывании на Личном кабинете (план «Хобби»). Для Teams время ожидания выполнения составляет 60 секунд (план Pro) или 9 секунд.00 секунд (план Enterprise). Пограничные функции предоставляют альтернативу, которая не имеет максимального тайм-аута выполнения, а также позволяет продолжать потоковую передачу ответов.
В качестве альтернативы вы можете изучить пограничные функции, которые не имеют этих ограничений параллелизма.
Это значение не может быть изменено.
Все планы хостинга общедоступны (GA) на виртуальных машинах Linux и Windows.
на странице цен на службу приложений.
Это связано с тайм-аутом простоя Azure Load Balancer по умолчанию. Для более длительной обработки рассмотрите возможность использования асинхронного шаблона устойчивых функций или отложите фактическую работу и верните немедленный ответ. 
x в плане службы приложений не ограничено. 
Рабочие процессы доступны в трех фиксированных размерах: один виртуальный ЦП/3,5 ГБ ОЗУ; Два виртуальных ЦП/7 ГБ ОЗУ; Четыре виртуальных ЦП/14 ГБ ОЗУ. 
